El tripos matemático, el examen más duro que jamás existió
Hace unos años, escribiendo la biografía Cayley, el origen del algebra moderna (RBA, 2017) sobre el matemático británico Arthur Cayley (1821-1895), tuve la oportunidad de leer mucho sobre un curioso examen de matemáticas que se realizaba en la Universidad de Cambridge (Gran Bretaña), denominado tripos matemático (en inglés, Mathematical Tripos), un examen que, en los siglos XVIII y XIX, todos los estudiantes de esta universidad debían de aprobar si querían recibir el título de graduado. El objetivo de esta entrada del Cuaderno de Cultura Científica es mostrar algunas de las particularidades de este examen, que era capaz de causar crisis nerviosas a algunos estudiantes.
 Grabado del artista Robert W. Buss de la presentación del senior Wrangler (estudiante con mejor nota del examen tripos matemático) de 1842, que fue el estudiante, futuro matemático, Arthur Cayley, ante el rector de la Universidad de Cambridge. Imagen de la University of St Andrews Libraries and Museums
Grabado del artista Robert W. Buss de la presentación del senior Wrangler (estudiante con mejor nota del examen tripos matemático) de 1842, que fue el estudiante, futuro matemático, Arthur Cayley, ante el rector de la Universidad de Cambridge. Imagen de la University of St Andrews Libraries and MuseumsUn examen de matemáticas para todos
Los tripos son los exámenes para obtener el grado en la Universidad de Cambridge, una de las universidades más antiguas del mundo, fundada en 1209. Aunque en la actualidad cada grado tiene su propio examen, durante siglos todos los estudiantes de la Universidad de Cambridge debían de pasar una misma prueba, que durante mucho tiempo fue un examen de matemáticas.
En el siglo XV todos los candidatos tenían que realizar un debate oral en latín (de donde deriva el término wrangler, persona que toma parte en una discusión) con un representante de la universidad que se sentaba en un taburete de tres patas (en latín, trypus).
Hacia 1725 el debate oral fue sustituido por un examen escrito de matemáticas, el tripos matemático (inicialmente denominado “Examen de la Casa del Senado”, por el lugar en el que se desarrollaban los exámenes), aunque se mantuvo una parte de discusión oral en inglés. Se consideraba que las matemáticas eran un conocimiento básico importante para los jóvenes estudiantes, puesto que su estudio fortalecía y desarrollaba las facultades de la mente y los preparaba para su posterior desarrollo intelectual. El examen se realizaba en enero, tras los diez trimestres oficiales, más de tres cursos, en la universidad.
 Fotografía de la casa del Senado en la Universidad de Cambridge, junto al Gonville College y al Caius College, alrededor de 1870. Fotografía de la Cornell University Library. Imagen de la colección A. D. White Architectural Photographs, Cornell University Library Accession Number
Fotografía de la casa del Senado en la Universidad de Cambridge, junto al Gonville College y al Caius College, alrededor de 1870. Fotografía de la Cornell University Library. Imagen de la colección A. D. White Architectural Photographs, Cornell University Library Accession NumberGrado ordinario y grado con honores
La mayoría de estudiantes de la Universidad de Cambridge que aprobaban tenían un grado ordinario, sin honores, mientras que algunos ni siquiera pasaban el examen. Según el físico y matemático irlandés George G. Stokes (1819-1903), hacia 1850, el 38% de los que graduados obtenían puestos de honor, mientras que el resto obtenía un grado ordinario. Y sobre un sexto de los aspirantes suspendían el examen.
Desde 1753 hasta 1909 se publicaron las listas de honor del tripos matemático por orden de mérito en tres categorías, wranglers, senior optimes y junior optimes. El primer puesto de honor, senior wrangler, figura que sigue existiendo en el tripos matemático actual, era reconocido como un gran logro intelectual en todo Gran Bretaña y abría muchas puertas para una carrera exitosa. De hecho, en ese tiempo los cursos académicos en Cambridge se recordaban por la persona que había sido senior wrangler ese curso. Cada año la noticia sobre el examen aparecía en los periódicos. El último de los estudiantes de la lista de honor recibía el apodo de “cuchara de madera” y se hacía una celebración en la que se le entregaba una enorme cuchara de madera.
 El último estudiante que fue “cuchara de madera” fue Cuthbert Lempriere Holthouse, en 1909. Imagen de la Universidad de Cambridge
El último estudiante que fue “cuchara de madera” fue Cuthbert Lempriere Holthouse, en 1909. Imagen de la Universidad de CambridgeEscasez de matemáticos
El objetivo del tripos matemático no era enseñar una herramienta fundamental para la formación de los futuros científicos, ni la preparación de los nuevos matemáticos, sino que se consideraban un mero entrenamiento para la mente de los estudiantes, necesarias para su formación intelectual como graduados.
En más de 150 años, este sistema dio lugar a pocos matemáticos puros destacados, solo Arthur Cayley (1821-1895) –senior wrangler–, James J. Sylvester (1814-1897) –segundo wrangler–, William K. Clifford (1845-1879) –segundo wrangler–, Godfrey H. Hardy (1877-1947) –cuarto wrangler– y John E. Littlewood (1885-1977) –senior wrangler–, en contraste con la considerable cantidad de físicos o físicos matemáticos, entre ellos, James C. Maxwell (1831-1879) –segundo wrangler–, William Thomson, Lord Kelvin (1824-1907) –segundo wrangler–, George G. Stokes –senior wrangler–, John W. Strutt (1842-1919) –senior wrangler–, John C. Adams (1819-1892) –senior wrangler– o J. J. Thompson (1856-1940) –segundo wrangler–.
Además, entre los altos wranglers no solo se encontraban científicos, sino también ilustres personajes en ámbitos como la política, la iglesia, el derecho o la medicina.
 Retrato del naturalista Charles Darwin, realizado por el artista George Richmond (1809-1896) en 1840
Retrato del naturalista Charles Darwin, realizado por el artista George Richmond (1809-1896) en 1840
Por otra parte, no a todos los estudiantes se les daban bien las matemáticas, así el escritor y político Thomas Macaulay (1800-1854) las aborrecía y el naturalista Charles Darwin (1809-1882) no estaba interesado en ellas. Por ese motivo, ambos aspiraron solo a un grado ordinario.
El tripos matemático, el examenEl tripos matemático constaba de dos partes, el workbook, que consistía en memorizar teoremas y demostraciones, y la parte de resolución de problemas. El contenido y duración iría variando a lo largo del siglo XIX. En la década de los años 1840 cubría cuestiones de matemática pura y aplicada, y tenía una duración de 6 días, con jornadas de 6 horas, pero llegó a durar 8 días.
Por ejemplo, el año que se presentó Arthur Cayley al tripos matemático, el año 1842, el examen de la Casa del Senado empezó el miércoles 5 de enero y terminó el martes siguiente, con descanso el domingo. Entre todos los estudiantes que se presentaron, ciento veinte eran candidatos a la lista de honor. Soportando el duro frío que hacía en el interior del edificio, los candidatos se enfrentaron a ciento diecisiete problemas distribuidos en dos exámenes cada una de las seis jornadas. Cada college tenía su candidato favorito, aunque los dos estudiantes con más opciones para ser senior Wrangler ese año eran Arthur Cayley (Trinity College) y Charles Simpson (St. Johns College). La expectación era máxima y el ambiente de Cambridge festivo.
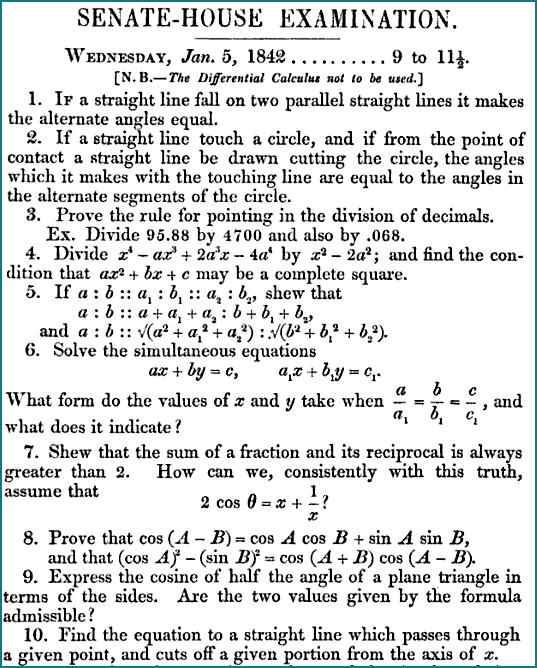 Hoja con problemas del tripos matemático de 1842
Hoja con problemas del tripos matemático de 1842
Aunque el mathematical tripos cambió de estructura y contenido a lo largo de todo este tiempo, en el artículo The Mathematical Tripos in the University of Cambridge / El tripos matemático en la Universidad de Cambridge, publicado en la revista Science, en 1883, se puede leer que constaba de tres partes. La primera era la básica y solía hacerse a principios del mes de junio. Su contenido era el siguiente: varios de los libros de Los Elementos de Euclides, aritmética, álgebra básica y las tres primeras secciones de los Principia (Philosophiæ naturalis principia mathematica / Principios matemáticos de la filosofía natural) de Isaac Newton, con partes elementales de trigonometría, secciones cónicas, mecánica, dinámica, hidroestática, óptica y astronomía.
Entre los aprobados de este examen, que ya tenían el grado ordinario, la universidad realizaba un listado de los estudiantes que podían presentarse a la segunda parte, para acceder a la lista de honor del tripos matemático, que se celebraba también en el mes de junio. Para este examen las materias eran: algebra, trigonometría (plana y esférica), teoría de ecuaciones, geometría analítica (plana y sólida, incluyendo curvatura de curvas y superficies), cálculo diferencial e integral, ecuaciones diferenciales, mecánica, hidroestática, dinámica de partículas, dinámica rígida, óptica y astronomía esférica.
Como consecuencia de los exámenes I y II, la universidad de Cambridge realizaba el listado de estudiantes por orden de méritos en las tres categorías mencionadas, wranglers, senior optimes y junior optimes. Y solamente los wranglers realizaban la última parte del examen, la más dura, que se realizaba en el mes de enero del siguiente año, como hemos mencionado en el caso de Arthur Cayley.
Entrenadores para preparar el examenEl matemático y lógico Augustus de Morgan (1806-1871) describe el tripos matemático como una «gran carrera de escritura», mientras que el matemático Godfrey H. Hardy (1877-1947), de quien recomiendo su libro Apología de un matemático (1940), se sintió como «un caballo de carreras para correr una carrera de ejercicios matemáticos». Era necesario un duro entrenamiento, memorizando teoremas, estudiando técnicas de resolución de problemas y trabajando los de cursos anteriores. Los estudiantes contrataban a «entrenadores» privados, no a profesores de la universidad, y dedicaban todo su tiempo a prepararse, por lo que no asistían a las clases regulares.
Consciente de su importancia, el estudiante y futuro matemático Arthur Cayley, como hacían también los demás estudiantes que aspiraban a la lista de honor, contrató a un «entrenador», William Hopkins (1793-1866), para preparar el «gran» examen. Hopkins era considerado el mejor entrenador y era conocido como «fabricante de wranglers»: en veintidós años obtuvo diecisiete senior wranglers y veintisiete segundos o terceros wranglers.
 Grabado de William Hopkins, de alrededor de 1850. Imagen del Peterhouse College de la Universidad de Cambridge
Grabado de William Hopkins, de alrededor de 1850. Imagen del Peterhouse College de la Universidad de Cambridge
El entrenamiento de Hopkins consistía en clases teóricas donde enseñaba las matemáticas puras y aplicadas que formaban parte del contenido del examen, desde Los Elementos, de Euclides, aritmética, álgebra, trigonometría, secciones cónicas o el binomio de Newton, hasta cálculo de variaciones, instrumentos astronómicos, hidrostática y dinámica, teoría lunar y planetaria, u óptica, sonido y luz. Así mismo, suministraba montones de hojas de problemas de años anteriores a sus estudiantes, que estos debían hacer sin descanso, trimestre tras trimestre, hasta el examen final.
Sin embargo, Hopkins no se limitaba al entrenamiento clásico, sino que inculcaba a sus pupilos el espíritu de la investigación matemática y les animaba a mantenerse al día leyendo las nuevas teorías, en particular, las provenientes del continente. Por ejemplo, el joven Cayley, tras la lectura de algunas obras del matemático y físico Joseph-Louis de Lagrange (1736-1813), demostró un nuevo teorema sobre integrales múltiples que publicó en dos artículos en la revista Cambridge Mathematical Journal (CMJ) en 1841.
La dureza del tripos matemáticoComo ya se ha comentado, el tripos matemático, era un examen muy difícil. El científico Francis Galton (1822-1911), en su libro Genio hereditario (1869), menciona que un año de la década de 1860 de los 17.000 puntos en juego en el examen, el senior wrangler obtuvo 7.634, el segundo wrangler 4.123 y el estudiante junior optime con la puntuación más baja, tan solo 237 (aunque este no realizó la tercera parte del examen). Y estos eran los mejores, los de la lista de honor. Si trasladamos estas puntuaciones a un examen actual, puntuado sobre 10, la mejor nota era un 4,49, ni siquiera llega al 5, al “aprobado”, y la peor de las notas, pero del grupo de honor, la de los mejores de la universidad ese año, era un 0,14, ¡¡un 0,14!!.
 Dos páginas del libro Genio hereditario (1869), del científico Francis Galton, una de ellas con un retrato del autor
Dos páginas del libro Genio hereditario (1869), del científico Francis Galton, una de ellas con un retrato del autorGalton sufrió una crisis nerviosa y acabó con un grado ordinario. El erudito estadounidense Charles A. Bristed (1820-1874) sufrió un colapso físico, quedando en los últimos lugares de la lista de junior optimes. El político y economista Henry Fawcett (1833-1884), favorito para senior wrangler, acabó siendo séptimo wrangler tras sufrir trastornos nerviosos e insomnio. El senior wrangler de 1859, James Wilson (1836-1931), sufrió una crisis nerviosa tras los exámenes y al recuperarse había olvidado todas las matemáticas estudiadas. O el también senior wrangler James Savage fue encontrado muerto en una zanja tres meses después del examen, el motivo de la muerte fue un derrame cerebral, posiblemente producido por el enorme esfuerzo realizado. Estos son solo algunos casos de la historia negra de este sistema.
Las mujeres en el tripos matemáticoHasta finales del siglo XIX las mujeres no podían asistir a la universidad en Gran Bretaña. Las universidades de Cambridge y Oxford empezaron a realizar exámenes de acceso a la universidad para mujeres en 1869, aunque estas solamente podían asistir a clase como oyentes y realizar exámenes con el permiso del profesor. Además, no se les concedía el título de graduadas.
A partir de 1880, las mujeres pudieron presentarse, con un permiso especial, al tripos matemático, aunque no recibían título o reconocimiento alguno. En 1880, la futura matemática Charlotte A. Scott (1858-1931) obtuvo una puntuación que se correspondía con el octavo wrangler. A partir de su logro, en 1882, se permitió a las mujeres participar oficialmente en el tripos y desde entonces se publicaban sus resultados en una lista complementaria a la de los hombres. Y en 1890, la futura matemática y educadora Philippa G. Fawcett (1868-1948) obtuvo la máxima distinción “por encima del senior wrangler”.
 La matemática y educadora Philippa G. Fawcett
La matemática y educadora Philippa G. FawcettHacia el final de la hegemonía matemática
En 1822 se crearía el tripos clásico, pero hasta el año 1850 solo se podían presentar aquellos que habían obtenido honores en el matemático. Los siguientes tripos en crearse, en la década de 1860, fueron los de ciencias morales y ciencias naturales. En la actualidad existen 28 tripos modernos, es decir, exámenes para obtener el título de graduado por la universidad de Cambridge.
 Camuflaje binario de la Casa del Senado, de la Universidad de Cambridge. Fotografía de Keith Edkins, en 2009
Camuflaje binario de la Casa del Senado, de la Universidad de Cambridge. Fotografía de Keith Edkins, en 2009
Bibliografía
1.- Raúl Ibáñez, Cayley, el origen del algebra moderna, RBA, 2017.
2.- Tony Crilly, Arthur Cayley, Mathematician Laureate of the Victorian Age, The Johns Hopkins University Press, 2006.
3.- R. Flood, A. Rice, R. Wilson, (editores), Mathematics in Victorian Britain, Oxford University Press, 2011.
4.- Revista Sciencia: The Mathematical Tripos in the University of Cambridge, Science, Vol. 1, No. 15, pp. 412-415, 1883.
5.- César Tomé López (2015) El Tripos y la profesionalización (serie Las matemáticas como herramienta) Cuaderno de Cultura Científica
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El tripos matemático, el examen más duro que jamás existió se ha escrito en Cuaderno de Cultura Científica.
El entrelazamiento perfecto no existe en el ruidoso mundo físico
Los físicos tienen una larga lista de problemas abiertos que consideran importantes para avanzar en el campo de la información cuántica. El problema 5 se planteó en 2001 y aborda la cuestión de si un sistema puede existir en su estado de máximo entrelazamiento en un escenario realista, en el que hay ruido.
Ahora Julio de Vicente, de la Universidad Carlos III de Madrid y el Instituto de Ciencias Matemáticas (ICMAT), ha respondido a esta pregunta cuántica fundamental con un rotundo “no”. De Vicente dice que espera que su trabajo “abra una nueva vía de investigación dentro de la teoría del entrelazamiento”.
 Ilustración: Laura Moreno-Iraola / ICMAT
Ilustración: Laura Moreno-Iraola / ICMATDe los sensores cuánticos a los ordenadores cuánticos muchas tecnologías requieren partículas entrelazadas mecanocuánticamente para funcionar. Las propiedades de estas partículas están correlacionadas de una manera que no sería posible en la física clásica.
Idealmente, para las aplicaciones tecnológicas estas partículas deberían estar en el llamado estado de máximo entrelazamiento, uno en el que se maximizan todas las posibles medidas de entrelazamiento. Los científicos predicen que las partículas pueden existir en este estado en ausencia de ruido experimental, ambiental y estadístico. Pero no estaba claro si las partículas también podrían existir en un estado de máximo entrelazamiento en situaciones del mundo real, donde el ruido es inevitable.
Para encontrar una respuesta de Vicente recurrió a las matemáticas. Ha demostrado que, si se introduce ruido en un sistema cuántico, es imposible maximizar simultáneamente todas las medidas de entrelazamiento del sistema, y, por tanto, el sistema no puede existir en un estado de máximo entrelazamiento.
Si bien el hallazgo de de Vicente resuelve un problema abierto, plantea muchos problemas más, incluyendo el problema tecnológico fundamental: qué condiciones se requieren para maximizar simultáneamente las múltiples medidas de entrelazamiento de un sistema.
Referencias:
Julio I. de Vicente (2024) Maximally Entangled Mixed States for a Fixed Spectrum Do Not Always Exist Phys. Rev. Lett. doi: 10.1103/PhysRevLett.133.050202
Ryan Wilkinson (2024) Long-Standing Quantum Problem Finally Solved Physics 17, s83
Ágata Timón García-Longoria (2024) Demuestran que el entrelazamiento perfecto no existe en el mundo real ICMAT
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El entrelazamiento perfecto no existe en el ruidoso mundo físico se ha escrito en Cuaderno de Cultura Científica.
El océano de Ariel
Los satélites que orbitan los gigantes de hielo de nuestro Sistema Solar son una verdadera caja de sorpresas a nivel geológico: en ellos encontramos una gran diversidad geológica, procesos activos e incluso ciclos “hidrológicos”. Pero todavía nos queda mucho por saber, especialmente de los de Urano y Neptuno, ya que han sido sistemas que todavía no hemos podido visitar de una manera más permanente como sí que hemos hecho en Júpiter y Saturno.
Pero mientras podamos volver allí -nada indica que será antes de la década de 2040- podemos hacer estudios gracias a los numerosos avances tecnológicos y a los telescopios, pero también con modelos físicos y geoquímicos que nos ayuden a conocer como puede ser el interior y si son capaces de albergar un océano por debajo de su superficie y cuáles podrían ser las fuentes de energía que todavía los mantengan en estado líquido a pesar del tiempo que ha pasado tras su formación.
 Ariel, observado por la Voyager 2 en Enero de 1986. Desde entonces no hemos vuelto a ver su superficie de cerca. Pero es que, además, solo hemos podido tomar imágenes de aproximadamente un tercio de su superficie. Cortesía de NASA/JPL.
Ariel, observado por la Voyager 2 en Enero de 1986. Desde entonces no hemos vuelto a ver su superficie de cerca. Pero es que, además, solo hemos podido tomar imágenes de aproximadamente un tercio de su superficie. Cortesía de NASA/JPL.Ariel, el satélite de Urano, es un firme candidato a albergar un océano subterráneo y, poco a poco, se empiezan a acumular pruebas a favor de esta teoría. Hay zonas de su superficie que exhiben chasmatas –chasmata es el plural de chasma, que en geología planetaria hacen referencia a depresiones alargadas y no muy anchas- así como otros detalles que sugieren la actividad criovolcánica. De hecho, algunos estudios sugieren que hay zonas de Ariel cuya edad sería inferior a los mil millones de años, lo que indicaría procesos de rejuvenecimiento de su superficie posteriores a su formación.
¿Qué hay de nuevo respecto a Ariel? Un equipo de científicos ha usado el telescopio espacial JWST para estudiar la composición de su superficie gracias al uso de uno de sus instrumentos, el espectrógrafo NIRSpec, que permite con mucha precisión detectar distintos compuestos -algunos de ellos de hielo- sobre la superficie del satélite.
El primer hallazgo destacado es la presencia de depósitos de hielo de dióxido de carbono más potentes -potentes en el sentido geológico, de espesor de la capa- de lo esperado y que podrían llegar a formar una capa superficial de 10 milímetros en determinadas zonas del satélite.
 En su superficie, además, podemos ver zonas más claras y oscuras… ¿Están relacionadas las zonas más claras con materiales que salen desde el interior del satélite hacia la superficie a través de impactos y de fenómenos criovolcánicos?. Imagen cortesía de NASA/JPL.
En su superficie, además, podemos ver zonas más claras y oscuras… ¿Están relacionadas las zonas más claras con materiales que salen desde el interior del satélite hacia la superficie a través de impactos y de fenómenos criovolcánicos?. Imagen cortesía de NASA/JPL.Pero además también se ha encontrado una capa de monóxido de carbono, algo que ha desconcertado un poco a los científicos. Y es que a las temperaturas que encontramos en la superficie de Ariel, aproximadamente entre -180 °C y -190 °C, el hielo compuesto de monóxido de carbono tendría que sublimarse -pasar del estado sólido al gaseoso sin pasar por el líquido- de una manera muy rápida. Esto podría indicar que hay mecanismos geológicos que van reponiendo el hielo de monóxido de carbono o que de alguna manera ocurren reacciones con el dióxido de carbono que lo estabilizan y lo hacen más resistente a la sublimación.
Otro de los detalles que nos aporta este estudio es que no aparecen determinadas especies químicas, como compuestos con amoniaco o el peróxido de hidrógeno, que a veces se forman por efecto de la radiación sobre el hielo de agua. Esta marcada ausencia podría significar dos cosas: O bien que la superficie está bien aislada por capas potentes de hielo de dióxido de carbono -y limitando las interacciones del hielo de agua con la radiación- o bien, la radiación del entorno que existe en la órbita de Ariel es menos intenso de lo que se piensa.
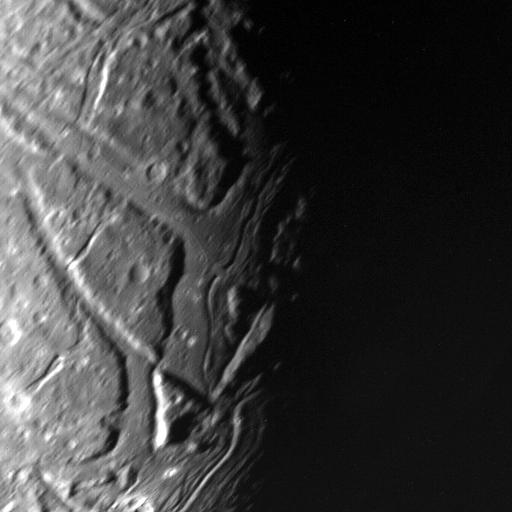 En esta imagen podemos apreciar perfectamente los chasmatas, formando depresiones alargadas que atraviesan la superficie de Ariel. Imagen cortesía de NASA/JPL.
En esta imagen podemos apreciar perfectamente los chasmatas, formando depresiones alargadas que atraviesan la superficie de Ariel. Imagen cortesía de NASA/JPL.Pero todavía queda un aspecto más a mencionar de este nuevo artículo: los científicos sugieren la presencia de carbonatos en la superficie de Ariel, una serie de minerales que se pueden formar por la interacción del agua líquida y las rocas, algo que de confirmarse, podría ocurrir en la interfaz entre el océano subterráneo y el núcleo rocoso del satélite, indicando unas condiciones de habitabilidad que podrían ser similares a las de océanos subterráneos como el que podría existir bajo Encélado o Europa.
¿Y qué nos quiere decir todo esto a nivel geológico? Pues que las capas de hielo de dióxido y de monóxido de carbono probablemente tengan un origen geológico, es decir, que estén formadas como consecuencia de procesos geológicos activos, como por ejemplo el criovulcanismo, que también sería el responsable de “subir” los carbonatos hasta la superficie. Y si es un mundo activo, ese mecanismo de “transmisión” del calor y de la materia desde el interior a la superficie podría ser un océano subterráneo algo que, de nuevo, aumenta las perspectivas astrobiológicas sobre este mundo.
Así que, aunque los satélites de los gigantes de hielo nos puedan parecer mundos algo anodinos lo cierto es que quizás lo que nos hace falta es poder visitarlos de nuevo y quizás descubrir así mundos fascinantes y con actividad geológica en el presente.
Referencias:
Cartwright, R. J., Holler, B. J., Grundy, W. M., Tegler, S. C., Neveu, M., Raut, U., Glein, C. R., Nordheim, T. A., Emery, J. P., Castillo-Rogez, J. C., Quirico, E., Protopapa, S., Beddingfield, C. B., Hedman, M. M., De Kleer, K., DeColibus, R. A., Morgan, A. N., Wochner, R., Hand, K. P., . . . Mueller, M. M. (2024). JWST Reveals CO Ice, Concentrated CO2 Deposits, and Evidence for Carbonates Potentially Sourced from Ariel’s Interior. The Astrophysical Journal Letters, 970(2), L29. doi: 10.3847/2041-8213/ad566a
El artículo El océano de Ariel se ha escrito en Cuaderno de Cultura Científica.
Un paso más hacia el robot aéreo autónomo: evitar colisiones
El Grupo de Inteligencia Computacional (GIC) de la UPV/EHU ha diseñado una nueva tecnología de bajo coste reproducible para todo tipo de robot aéreo.
 Fuente: Referencia
Fuente: ReferenciaUn estudio que ha realizado el Grupo de Inteligencia Computacional (GIC) de la UPV/EHU con un grupo de drones ha verificado que, “a pesar del reducido coste de la tecnología, la solución que hemos desarrollado ha sido validada con éxito en drones comerciales. Utilizando un equipo sencillo de bajo coste y un algoritmo basado en visión artificial, empleando la identificación de colores, hemos desarrollado una tecnología robusta para evitar satisfactoriamente la colisión entre drones que puede ser fácilmente extrapolable a la mayoría de los robots aéreos comerciales y de investigación; además, proporcionamos el código software completo de la solución”, señala Julián Estévez, investigador de la Universidad del País Vasco.
Hacia el robot aéreo autónomoLa mayoría de los drones que conocemos están tripulados, incluso aunque estén más allá de la vista del operador. Para que un dron sea totalmente autónomo tiene que ser capaz de tomar decisiones de vuelo por su propia cuenta y sin intervención humana, es decir, decidir por sí mismo cómo evitar las colisiones, cómo mantener rumbos frente a ráfagas de viento, controlar la velocidad de vuelo, esquivar edificios, árboles…
“Este trabajo es un pequeño paso hacia la navegación completamente autónoma —sin ninguna intervención humana—, y que los drones decidan qué maniobra realizar, qué dirección tomar y así evitar colisiones entre ellos o con otros obstáculos aéreos. Si asumimos que, en un futuro, nuestro espacio aéreo estará mucho más poblado por servicios comerciales realizados por estos drones, nuestro trabajo es una pequeña contribución en esta dirección”, indica Julián Estévez.
El autor del estudio explica que “nuestra propuesta de evitar colisiones no requiere que los drones intercambien información entre ellos; en su lugar, dependen únicamente de los sensores y cámaras de a bordo”. “Obtenemos la señal de la cámara que está a bordo de los drones y mediante el procesamiento de las imágenes ajustamos las reacciones de los robots para que vuelen con suavidad y precisión”, añade Estévez.
En los experimentos han tratado de imitar condiciones realistas de los drones, es decir, escenarios que pueden darse en un área urbana habitual en condiciones de iluminación no controladas, drones volando en diferentes direcciones, etc., por lo que sus aportaciones están enfocadas a aplicaciones en el mundo real, a pesar del trabajo inicial en laboratorio.
Algoritmos basados en el color“Hemos equipado cada dron con una tarjeta roja que permite al algoritmo software detectar la presencia de un dron que se aproxima y medir su proximidad”, explica Julián Estévez. “Nuestra propuesta —continúa el investigador— es muy sencilla: cada dron lleva equipada una cámara a bordo, cuya pantalla está dividida en dos mitades (izquierda y derecha). Esta cámara busca en todo momento el color rojo de las tarjetas que hemos indicado anteriormente. Mediante sencillos procesamientos de imágenes, podemos saber qué porcentaje de la cámara está ocupada por el color rojo, y si la mayor parte de esta región roja está a la izquierda o a la derecha de la pantalla. Si la mayor parte de la zona roja está en la parte izquierda de la pantalla, el dron volará hacia la derecha para evitar la colisión. Si la zona roja está en la derecha, lo hará hacia la izquierda. Y esto ocurre con todos los drones que se encuentran en el aire”.
Además, “cuando el porcentaje de color rojo en la pantalla vaya aumentando, esto significará que los drones se están aproximando de frente. De manera que cuando se supere un umbral, el robot sabrá que debe realizar la maniobra de evasión. Todo esto ocurre de manera autónoma, sin intervención del operador humano. Es una manera sencilla de evitar choques, capaz de realizarse mediante sensores y equipamiento low cost”, recalca Julián Estévez. Algo parecido a lo que ocurre cuando una persona va caminando por la calle y ve que alguien se le acerca por su izquierda, en ese caso la persona intenta retirarse hacia la derecha para no chocarse.
Referencia:
Julian Estevez, Endika Nuñez, Jose Manuel Lopez-Guede & Gorka Garate (2024) A low-cost vision system for online reciprocal collision avoidance with UAVs Aerospace Science and Technology doi: 10.1016/j.ast.2024.109190
El artículo Un paso más hacia el robot aéreo autónomo: evitar colisiones se ha escrito en Cuaderno de Cultura Científica.
La Geología, disciplina olímpica
Durante estas semanas, la mirada de todo el mundo se concentra en una misma ciudad europea: París. La capital de Francia se ha convertido en el centro de atención gracias a albergar el mayor evento deportivo mundial, ese que ocurre cada cuatro años (pandemia mediante) y que nos permite descubrir deportes que no sabíamos ni que existían y países que nunca habríamos podido posicionar en el mapamundi, los Juegos Olímpicos. Pero incluso entre largos en la piscina, triples saltos mortales en el pabellón de gimnasia o tiros libres en el pabellón de baloncesto, también podemos aprender algo de Geología. Para ello, no vamos a fijarnos en los metales con los que se forjan las medallas, sino en lo que se encuentra bajo los pies de las estrellas del deporte y de todas las sedes olímpicas del centro de Francia: la cuenca de París.
Geológicamente hablando, una cuenca es una zona deprimida del terreno en la que se acumulan sedimentos. Y eso es exactamente lo que sucede no solo en París, sino en toda la zona central de Francia, desde hace millones de años. Así que, para entenderlo, debemos viajar al pasado.
250 millones de años acumulando sedimentosTodo comenzó hace unos 250 millones de años, a finales del Periodo Pérmico y comienzos de Periodo Triásico, cuando el último gran supercontinente de la historia de nuestro planeta, Pangea, empezó a romperse. Desde entonces, debido a los movimientos tectónicos que han culminado con la actual disposición de los continentes en la superficie terrestre, toda la zona central de Francia ha sufrido un proceso de subsidencia más o menos continuo. Como ya os comenté en otra ocasión, la subsidencia es un término geológico que se refiere a un hundimiento continuado y relativamente lento del terreno, lo cual genera una zona deprimida que puede actuar como una excelente piscina olímpica que ha estado recibiendo el depósito de sedimentos durante estos últimos 250 millones de años prácticamente sin descanso.
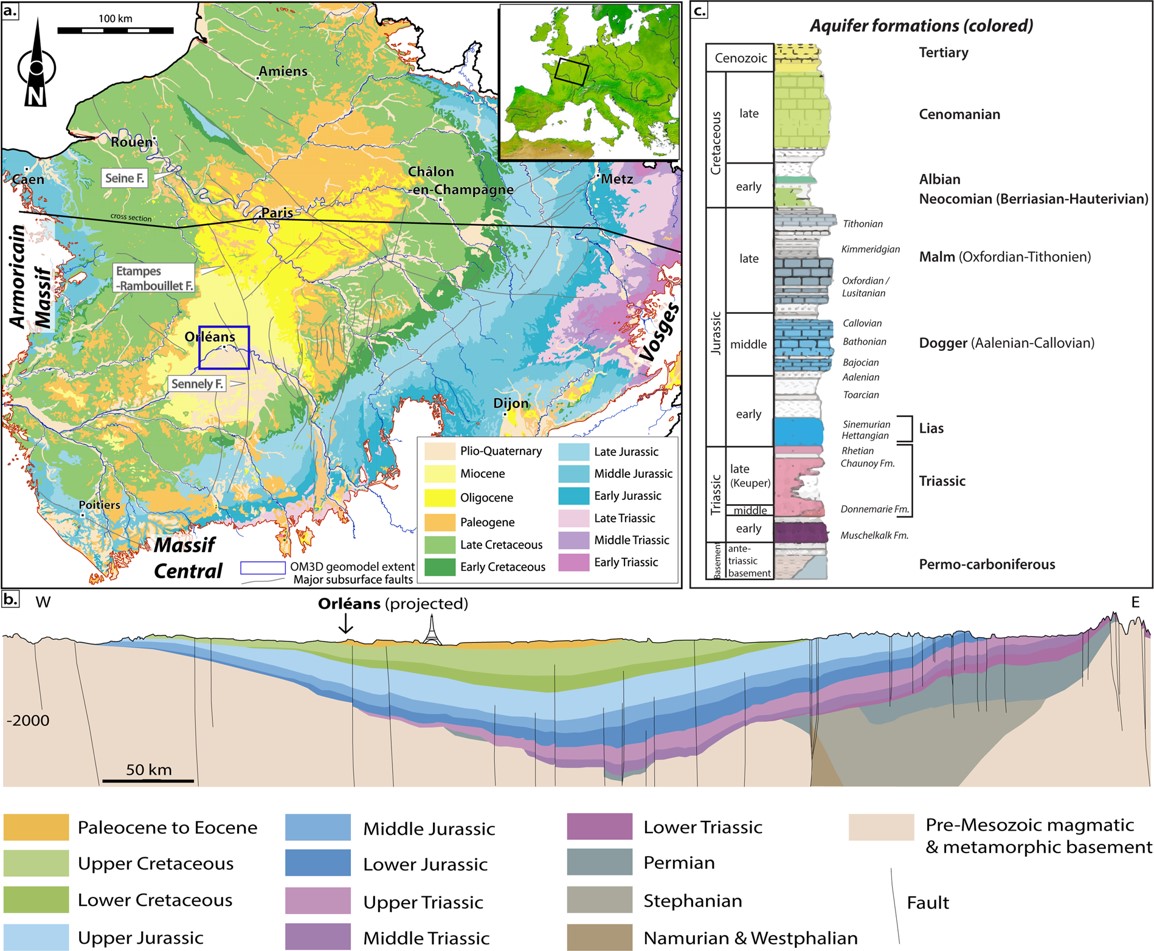 Mapa geológico de la cuenca de París y reconstrucción de una sección transversal de los materiales en profundidad con orientación oeste (W)-este (E). Imagen tomada de Mas, P., Calcagno, P., Caritg-Monnot, S., Beccaletto, L., Capar, L. y Hamm, V. (2022). A 3D geomodel of the deep aquifers in the Orléans area of the southern Paris Basin (France). Sci Data 9, 781.
Mapa geológico de la cuenca de París y reconstrucción de una sección transversal de los materiales en profundidad con orientación oeste (W)-este (E). Imagen tomada de Mas, P., Calcagno, P., Caritg-Monnot, S., Beccaletto, L., Capar, L. y Hamm, V. (2022). A 3D geomodel of the deep aquifers in the Orléans area of the southern Paris Basin (France). Sci Data 9, 781.Esto se observa claramente al mirar el mapa geológico de Francia, sobre todo si prestamos atención a la reconstrucción que se ha realizado de cómo se distribuyen esos materiales en profundidad, por debajo del suelo. Aquí se remarca con mucho detalle cómo la parte central del país vecino está hundida con respecto a sus márgenes, lo que ha permitido una gran acumulación de materiales geológicos desde comienzos del Triásico, situados en la parte inferior, hasta la actualidad, que recubren la superficie. Además, esta representación gráfica nos permite definir la morfología de la cuenca de París, que recuerda a los platos que sirven de objetivo al sobrevolar el foso de tiro o a los discos que lanzan sobre la pista de césped en el estadio de atletismo. Por ese motivo y gracias a que, como ya sabéis, en Geología no nos gusta comernos la cabeza a la hora de ponerle nombre a las cosas, a este tipo de cuencas sedimentarias se las conoce como “de tipo platillo”.
La de París, cuenca de referenciaLa cuenca de París, gracias a sus grandes dimensiones, la enorme acumulación casi continuada de sedimentos durante las Eras Mesozoica y Cenozoica y, sobre todo, al situarse en Francia una de las cunas de la Geología europea, se ha convertido en el modelo teórico de referencia para comprender cómo se comportan y evolucionan con el tiempo las cuencas sedimentarias de tipo platillo. Pero, además, tiene otra característica geológica que la convierte en un referente a nivel mundial y que se encuentra escondida entre los materiales de comienzos de la Era Cenozoica, pintados con esos colores anaranjados en el mapa.
 Lámina con ilustraciones de varios fósiles de gasterópodos del Luteciense de París, dibujada por las hermanas Lister en 1692. Imagen tomada de Merle, D. (2008). Les grands auteurs de la paléontologie du Lutétien. En: Stratotype Lutétien: Un peu d’histoire (Merle, D. ed.). Publications Scientifiques du Muséum, Paris; Biotope Mèze; BRGM La Source, pp. 35-46.
Lámina con ilustraciones de varios fósiles de gasterópodos del Luteciense de París, dibujada por las hermanas Lister en 1692. Imagen tomada de Merle, D. (2008). Les grands auteurs de la paléontologie du Lutétien. En: Stratotype Lutétien: Un peu d’histoire (Merle, D. ed.). Publications Scientifiques du Muséum, Paris; Biotope Mèze; BRGM La Source, pp. 35-46.Cuando a comienzos del siglo XIX Charles Lyell, uno de los padres de la Geología, estuvo trabajando en el sur de Francia, pudo estudiar los materiales más recientes de la cuenca de París. A partir de sus observaciones en los fantásticos afloramientos de toda esta zona, el geólogo se atrevió a subdividir la entonces llamada Era Terciaria (nombre ya obsoleto en el ámbito geológico) en tres periodos: Eoceno, Mioceno y Plioceno. Pero no fue el primero en analizar la Geología de esta zona. Otros pioneros franceses, desde finales del siglo XVIII, se habían centrado en recopilar miles de ejemplares fósiles de los numerosos yacimientos encontrados en las afueras de París, sobre todo de gasterópodos marinos del Periodo Eoceno. Con estos fósiles en la mano, el barón Georges Cuvier empezó a elucubrar sus ideas sobre la anatomía comparada, o Jean Baptiste Monet, caballero de Lamarck, le fue dando forma a su particular hipótesis sobre la evolución. Incluso, a finales del siglo XIX, Albert de Lapparent fue más allá que Lyell y propuso una subdivisión del Periodo Eoceno basado en estos yacimientos parisinos. Así nació el segundo Piso del Periodo Eoceno, cuyos límites temporales actualmente oscilan entre hace 47,8 y 41,3 millones de años y que ha sido nombrado en honor a la capital francesa. Pero no, no se llama Parisiense, Lapparent propuso emplear el nombre antiguo de la ciudad, ese que todo el mundo conocemos gracias a los cómics de Astérix: Lutecia. Había nacido el piso Luteciense.
Espero que, cuando sigáis los Juegos Olímpicos en la radio o la televisión, os acordéis de que los cimientos de las sedes olímpicas se sustentan sobre los materiales de una cuenca sedimentaria de record. Porque ahora el deporte es el protagonista en la capital francesa, pero la Geología ha sido y siempre será la principal estrella de París.
Agradecimientos:
Me gustaría dedicar este artículo a Daniel Ampuero y Gonzalo Da Cuña, dos de los periodistas de Radio Nacional de España que están dando cobertura a los Juegos Olímpicos de París, por compartir conmigo su amor por el deporte.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo La Geología, disciplina olímpica se ha escrito en Cuaderno de Cultura Científica.
Los números vistos como bosques
Todo el que tiene cuerpo
tiene un árbol.
Y dos que se juntan, bosque.
La suavidad sumaria de la hoja.
El rostro informe de la lluvia.
La tierra que se expande
como un pétalo
nocturno.
Un instante febril cuando el sol cae.
 Fuente: Freepik.
Fuente: Freepik.
En matemáticas, también existen bosques con árboles variados que viven en ellos…
Árboles y bosquesSe denomina bosque a un grafo acíclico, es decir, un grafo sin ciclos (un ciclo es un camino cerrado de aristas uniendo vértices, en los que no se repite ninguno salvo el primero y el último).
Los bosques matemáticos, como los naturales, están compuestos por árboles. Un árbol es un grafo en el que dos vértices cualesquiera están conectados por exactamente un camino. De otro modo, es un grafo conexo (es decir, “de una pieza”) acíclico. Observar que, en un árbol, la diferencia entre la cantidad de vértices y aristas es 1.
Así, los bosques son uniones disjuntas de árboles que pueden estar desconectados, es decir, un bosque puede ser un grafo disconexo. Los ejemplos más sencillos de bosques son precisamente los árboles, incluyendo el grafo vacío (sin vértices) y el grafo formado sólo por un vértice. De otro modo, los árboles son las componentes conexas (subgrafos conexos maximales) de los bosques.
¿Cuántos árboles tiene un bosque? Si denotamos por V el número de vértices de un bosque y por A su número de aristas, V − A es precisamente el número de árboles que forman un bosque. Esto se debe a que, como hemos comentado antes, en el caso de un árbol, V – A = 1.
Claramente, un bosque con K árboles y N vértices posee N – K aristas. En la página On-Line Encyclopedia of Integer Sequences (OEISA005195) se puede ver la cantidad de bosques diferentes que existen con una cantidad dada de vértices V; los primeros son:
Número de vértices V
Número de bosques
1
1
2
2
3
3
4
6
5
10
6
20
7
37
8
76
9
153
10
329
11
710
12
1601
13
3658
14
8599
14
20514
Por ejemplo, un bosque con 5 vértices tiene 10 configuraciones posibles, que se muestran en la imagen de debajo:
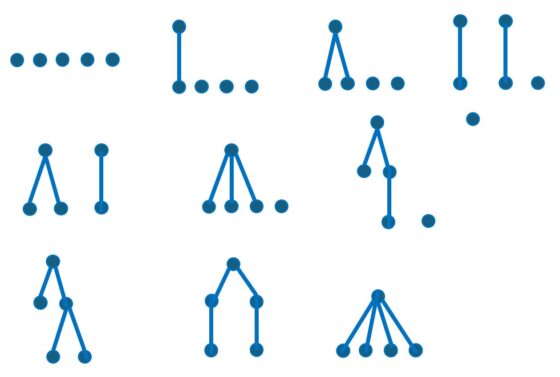 Los 10 posibles bosques formados por 5 vértices. En la primera fila aparecen los que tienen 5, 4 y 3 componentes conexas; en la segunda los posibles bosques con 2 árboles; en la tercera los bosques que poseen un único árbol (es decir, los árboles diferentes formados por 5 vértices).
Los 10 posibles bosques formados por 5 vértices. En la primera fila aparecen los que tienen 5, 4 y 3 componentes conexas; en la segunda los posibles bosques con 2 árboles; en la tercera los bosques que poseen un único árbol (es decir, los árboles diferentes formados por 5 vértices).Los números son bosques
En A Puzzle Forest se hace alusión a una bonita manera de representar la factorización de un número entero positivo mediante un bosque.
Cada primo es un árbol y cada entero positivo es un bosque cuyos árboles corresponden a los primos de su factorización. Explicamos este proceso a continuación:
- El número 2 es primo, que se representa como un árbol con un único vértice.
- El número 3 es primo, es el segundo número primo. Se representa como un árbol con dos vértices unidos por una arista.
- El número 4 se descompone como 22. Se representa como un bosque no conexo con dos vértices (la representación del primo 2 duplicada).
- El número 5 es el tercer número primo. Se representa mediante un árbol que se construye tomando un vértice raíz que se une al árbol que representa al 3.
- El número 6 se descompone como 2 x 3. Se representaría como un bosque formado por los árboles que representan al 2 y al 3.
- El número 7 es el cuarto número primo. Se representa entonces como un vértice raíz unido a la representación del número 4.
- El número 8 se descompone como 22 Se representa como un bosque no conexo con tres vértices.
- El número 9 se descompone como 32, así que se representa como un bosque con dos árboles iguales que corresponden al número 3.
Debajo se muestran varios ejemplos de representación de primos y algunos números enteros.
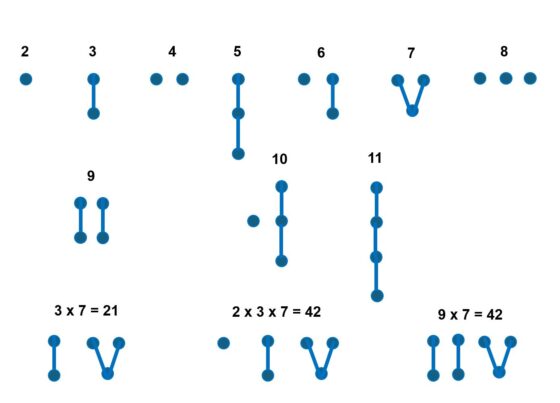 Representaciones de algunos números mediante bosques.
Representaciones de algunos números mediante bosques.
En general, un primo se representa a través de un vértice raíz que se conecta al bosque que representa su lugar en el conjunto de los números primos. Por ejemplo, 11 es el quinto número primo, así que se representa mediante un vértice raíz que se une a la representación del 5.
Es decir, la representación de cada número se obtiene recursivamente conociendo su factorización en primos y la cantidad de primos menores o iguales a un primo dado. Por supuesto, es preciso conocer la función contadora de números primos que calcula la cantidad de números primos menores o iguales a cualquier número entero positivo dado.
Robé a los bosques,
los confiados bosques.
Los árboles desprevenidos
mostraron sus frutos y sus musgos
para agradar a mis delirios.
Escudriñé, curiosa, sus adornos;
se los arrebaté, me atreví a robar.
¿Qué dirá el solemne abeto?
Y el roble, ¿qué dirá?
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
El artículo Los números vistos como bosques se ha escrito en Cuaderno de Cultura Científica.
El vacío del espacio se desintegrará antes de lo esperado (pero no pronto)
Uno de los campos cuánticos que permea el universo es especial porque su valor por defecto parece estar destinado a terminar cambiando, transformándolo todo.
Un artículo de Matt von Hippel. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Una burbuja de vacío de menor energía crecería a la velocidad de la luz, destruyendo todos los átomos en su camino. Ilustración: Nico Roper / Quanta Magazine
Una burbuja de vacío de menor energía crecería a la velocidad de la luz, destruyendo todos los átomos en su camino. Ilustración: Nico Roper / Quanta MagazineLa desintegración del vacío, un proceso que podría acabar con el universo tal como lo conocemos, podría ocurrir 10.000 veces antes de lo esperado. Afortunadamente, no ocurrirá hasta dentro de muchísimo tiempo.
Cuando los físicos hablan del “vacío”, el término suena como si se refiriera al espacio vacío, y en cierto sentido es así. Más específicamente, se refiere a un conjunto de valores predeterminados, como los ajustes de un tablero de control. Cuando los campos cuánticos que permean el espacio se encuentran en estos valores predeterminados, se considera que el espacio está vacío. Los pequeños ajustes en los valores predeterminados crean partículas: si se aumenta un poco el campo electromagnético, se obtiene un fotón. Los grandes ajustes, por otro lado, es mejor considerarlos como un conjunto de nuevos valores predeterminados. Crean una definición diferente de espacio vacío, con características diferentes.
Un campo cuántico en concreto es especial porque su valor por defecto puede cambiar. Se llama campo de Higgs y controla la masa de muchas partículas fundamentales, como los electrones y los cuarks. A diferencia de todos los demás campos cuánticos que ha descubierto la comunidad física, el campo de Higgs tiene un valor por defecto superior a cero. Si se aumenta o disminuye el valor del campo de Higgs, la masa de los electrones y otras partículas aumentaría o disminuiría. Si el valor del campo de Higgs fuera cero, esas partículas no tendrían masa.
Podríamos permanecer en el valor por defecto distinto de cero por toda la eternidad si no fuera por la mecánica cuántica. Un campo cuántico puede “hacer un túnel”, saltando a un nuevo valor de energía más bajo incluso si no tiene suficiente energía para pasar por los valores intermedios de energía más altos, un efecto similar al de atravesar una pared sólida.
Para que esto suceda, es necesario tener un estado de energía más bajo al que llegar mediante el túnel. Y antes de construir el Gran Colisionador de Hadrones, se pensaba que el estado actual del campo de Higgs podría ser el más bajo. Esta creencia ha cambiado ahora.
Siempre se ha sabido que la curva que representa la energía necesaria para diferentes configuraciones del campo de Higgs se parece a un sombrero con el ala hacia arriba. La configuración actual del campo de Higgs puede representarse como una bola que reposa en la parte inferior del ala.
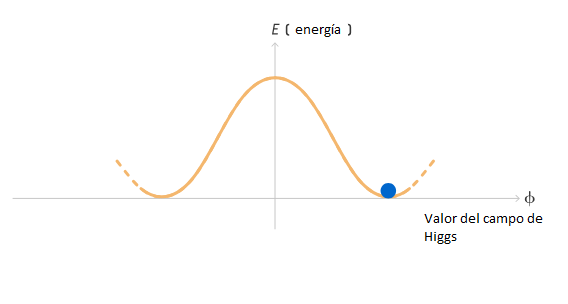 Ilustración: Mark Belan para Quanta Magazine
Ilustración: Mark Belan para Quanta MagazineSin embargo, correcciones cuánticas sutiles pueden cambiar la forma de la curva. Los campos cuánticos se retroalimentan energía entre sí. Las interacciones cuánticas entre los electrones y el campo electromagnético cambian los niveles de energía de los átomos, por ejemplo, un efecto descubierto en la década de 1940.
En el caso del campo de Higgs, la curvatura del ala del sombrero está determinada por la masa del bosón de Higgs, la partícula elemental que transmite los efectos del campo de Higgs, que se descubrió en el Gran Colisionador de Hadrones en 2012. Otras correcciones a la forma de la curva provienen de partículas que interactúan fuertemente con el bosón de Higgs: aquellas con masa alta, como el cuark cima, la partícula elemental más pesada conocida. Al comparar la masa del bosón de Higgs con la del cuark cima, los físicos ahora piensan que lo más probable es que el sombrero se hunda otra vez. En un valor por defecto mucho más alto del campo de Higgs, hay un estado de energía más bajo.
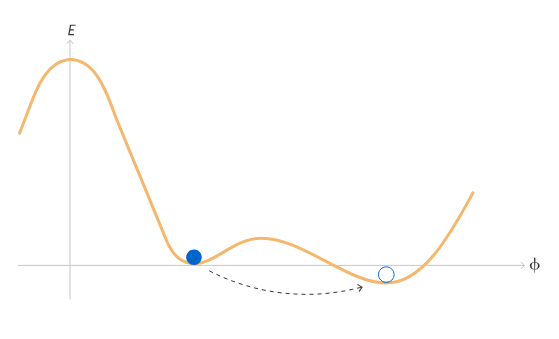 Ilustración: Mark Belan para Quanta Magazine
Ilustración: Mark Belan para Quanta MagazineEn ese caso, el campo de Higgs acabaría por atravesar ese túnel, o “se desintegraría”, hasta llegar a ese estado. Esta desintegración empezaría en un lugar y luego se extendería, formando una burbuja esférica que crecería a la velocidad de la luz transformando el universo. Las partículas fundamentales se volverían mucho más pesadas, de modo que la gravedad las atraería más que las otras fuerzas las mantienen separadas. Los átomos colapsarían.
Sin embargo, no llegaremos a ese valor por defecto del Higgs más alto en un futuro próximo. Los físicos calculan las probabilidades de desintegración del vacío de distintas maneras. En el método más directo, llevan un registro de las distintas transformaciones que serían necesarias para que el campo pasara de un valor a otro (transformaciones que violan la conservación de la energía, algo que la mecánica cuántica permite que ocurra brevemente), ponderando cada escenario según en qué medida viola reglas como la conservación de la energía. Según estas estimaciones, un gigapársec cúbico de espacio verá desintegrarse el vacío una vez cada 10794 años, o el dígito 1 seguido de 794 ceros, un lapso de tiempo inimaginable. Hasta ahora solo han pasado 1010 años desde el Big Bang.
Recientemente, un grupo de físicos de Eslovenia afirmó haber encontrado un pequeño error en el cálculo, que acelera el fin del universo tal como lo conocemos a 10790 años, en lugar de 10794. Si bien un cambio de un factor de 10.000 puede parecer enorme, es mucho menor que la incertidumbre de otras partes del cálculo. Lo más importante: ninguna de estas incertidumbres es lo suficientemente grande como para reducir los eones que se encuentran entre nosotros y los horrores de la desintegración del vacío.
El artículo original, Vacuum of Space to Decay Sooner Than Expected (but Still Not Soon), se publicó el 22 de julio de 2024 en Quanta Magazine.
Traducido por César Tomé López
El artículo El vacío del espacio se desintegrará antes de lo esperado (pero no pronto) se ha escrito en Cuaderno de Cultura Científica.
Las células cristal transportan oxígeno en Drosophila
Seguro que recuerdan alguna película en la que aparecen insectos gigantescos. Por ejemplo, la espléndida La humanidad en peligro (1954) nos muestra cómo las pruebas nucleares en el desierto han provocado mutaciones en las hormigas, que se convierten en descomunales amenazas.
Este escenario no es demasiado realista, ya que el tamaño de los insectos está constreñido por la forma en que respiran. En los libros de texto se nos explica que los insectos tienen respiración traqueal, mediante un sistema de finísimos tubos huecos que llevan el aire a todos los rincones de su cuerpo. Esto impone un tamaño limitado por los problemas de la difusión del aire dentro de las tráqueas. Curiosamente, el aire rico en oxígeno del periodo Carbonífero permitió que los insectos alcanzaran los mayores tamaños de su historia. La libélula Meganeura, por ejemplo, llegó a los 70 cm de envergadura.
Un reciente descubrimiento, publicado en la revista Nature por un equipo surcoreano, ha revelado que, además de las tráqueas, existen células sanguíneas en la larva de Drosophila capaces de transportar oxígeno mediante un mecanismo sorprendente. Se trata de las células cristal, así llamadas por contener estructuras cristalinas en su interior.
Las células cristal son uno de los tres tipos de hemocitos o células sanguíneas de Drosophila, y representan alrededor del 5% del total. Los más abundantes son los plasmatocitos (95%) una especie de células fagociticas, y el tercer tipo son los lamelocitos que sólo aparecen durante la activación del sistema inmune.
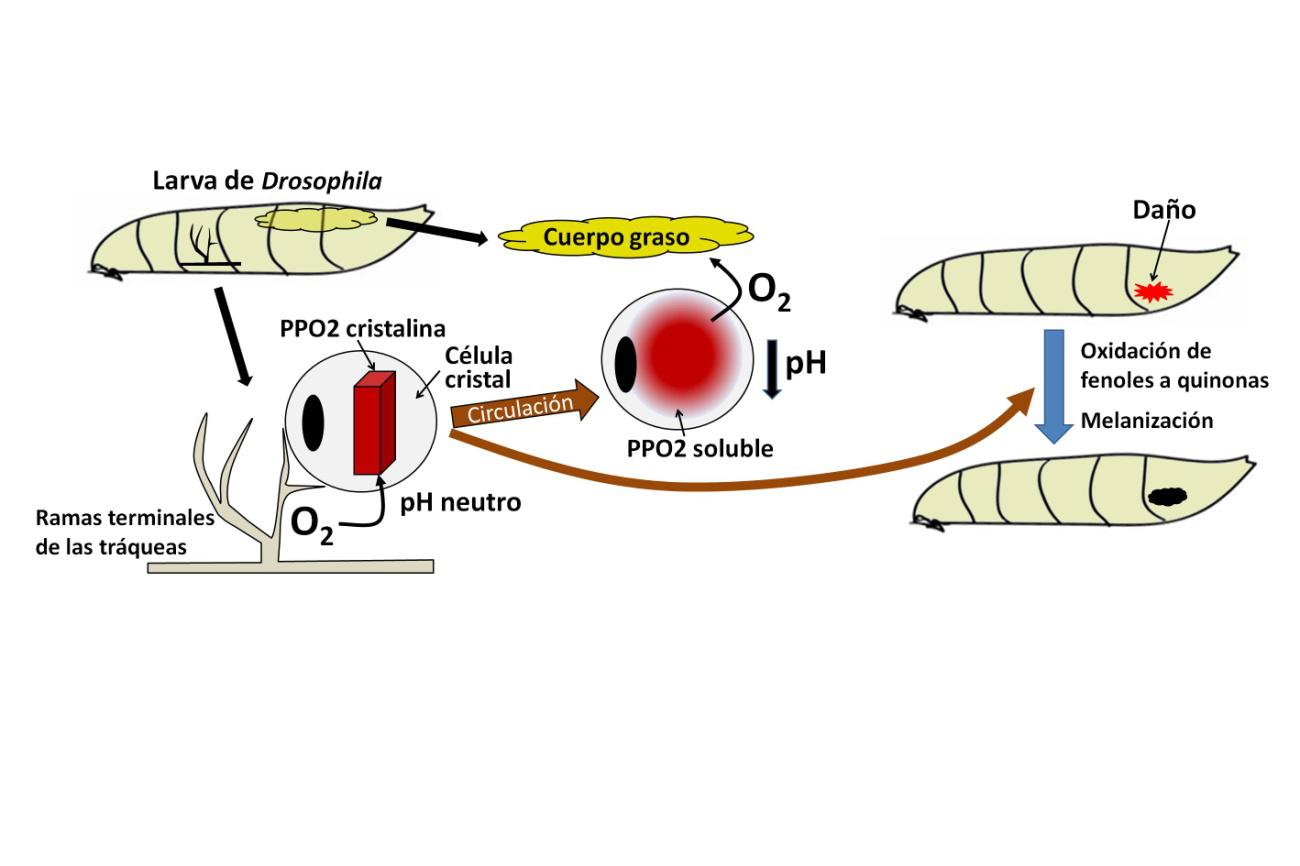 Figura 1. La función hasta ahora atribuida a las células cristal era la melanización, oxidación de fenoles para formar polímeros de melanina capaces de englobar patógenos y cicatrizar heridas (derecha). La nueva función descrita por Shin y cols. consiste en el transporte de oxígeno desde las tráqueas a tejidos como el cuerpo graso, alejados de ellas. El transporte implica un cambio de fase en la profenoloxidasa-2 (PPO2), que almacena oxígeno en estado cristalino y lo libera en la fase soluble, inducida por un descenso del pH.
Figura 1. La función hasta ahora atribuida a las células cristal era la melanización, oxidación de fenoles para formar polímeros de melanina capaces de englobar patógenos y cicatrizar heridas (derecha). La nueva función descrita por Shin y cols. consiste en el transporte de oxígeno desde las tráqueas a tejidos como el cuerpo graso, alejados de ellas. El transporte implica un cambio de fase en la profenoloxidasa-2 (PPO2), que almacena oxígeno en estado cristalino y lo libera en la fase soluble, inducida por un descenso del pH.Los cristales que dan nombre a las células cristal están formados por una proteína que contiene cobre, la profenoloxidasa-2 (PPO2). Esta enzima se encarga de oxidar fenoles y formar polímeros que engloban microorganismos patógenos y contribuyen a la cicatrización de heridas, la función principal que se atribuía a las células cristal hasta ahora (Figura 1). Como los polímeros tienen color oscuro, esta reacción defensiva se conoce como melanización. De hecho, nuestra síntesis de melanina responde a un mecanismo muy similar.
El grupo surcoreano utilizó tres cepas de larvas de moscas mutantes, carentes de células cristal, con ausencia de PPO2 o bien con una PPO2 incapaz de unirse al cobre en su sitio activo. Todas estas larvas muestran alta mortalidad en condiciones de laboratorio y un aumento en el número de ramas terminales de las tráqueas. Este incremento también se produce en larvas normales cultivadas en hipoxia, por lo que se considera una respuesta a la falta de oxígeno.
Estos defectos revierten si se aumenta la concentración de oxígeno en el aire hasta el 60%. De forma más sorprendente, también se rescatan los defectos de las larvas mutantes si se fuerza en las células cristal la expresión de la hemocianina del cangrejo de herradura. Recordemos que esta proteína transporta oxígeno en muchos crustáceos y algunos quelicerados, dando a su sangre color azul debido a su contenido en cobre. Todos estos resultados indican que la PPO2 contenida en las células cristal es indispensable para mantener los niveles de oxígeno en las larvas de las moscas.
Un transportador de oxígeno debe ser capaz de combinarse con esta molécula de forma reversible. En el caso de la hemoglobina o la hemocianina, la fijación se produce en el sitio activo que contiene hierro y cobre, respectivamente. Lo que reveló el estudio de los investigadores surcoreanos es que la combinación reversible de PPO2 con el oxígeno implicaba un cambio de fase en la organización de la proteína (Figura 1). Cuando la célula cristal está próxima a las ramas terminales de las tráqueas, su PPO2 en forma cristalina fija oxígeno. Para ello el pH del interior celular debe ser neutro. Luego, la célula cristal viaja por la cavidad circulatoria y alcanza tejidos alejados de las tráqueas. Allí, el pH citoplasmático disminuye por acción de la enzima anhidrasa carbónica, la proteína pasa de la forma cristalina a una variante soluble, y el oxígeno se libera. La célula cristal regresa a las ramas terminales de las tráqueas y el ciclo comienza de nuevo.
Este proceso ha explicado, por fin, cómo es posible el funcionamiento de un órgano larvario conocido como cuerpo graso, que tiene funciones detoxificadoras y de almacenamiento de lípidos. Su carencia de tráqueas planteaba la cuestión de cómo se satisfacía su demanda metabólica de oxígeno. Ahora sabemos que las células cristal se encargan de transportar el oxígeno desde las tráqueas hasta las proximidades del cuerpo graso.
El sorprendente descubrimiento de células transportadoras de oxígeno en la larva de Drosophila como complemento de la respiración traqueal plantea apasionantes preguntas. ¿Sucede esto en otros insectos, o en insectos adultos? ¿Interviene este tipo de mecanismo en el altísimo consumo de oxígeno que demanda el vuelo de los insectos?
Referencias:
Luschnig, S. (2024) Flies use blood cells to take a deep breath. Nature. doi: 10.1038/d41586-024-01649-6.
Shin, M., Chang, E., Lee, D., et al. (2024) Drosophila immune cells transport oxygen through PPO2 protein phase transition. Nature. doi: 10.1038/s41586-024-07583-x.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga
El artículo Las células cristal transportan oxígeno en Drosophila se ha escrito en Cuaderno de Cultura Científica.
Métodos matemáticos para armonizar la poesía
La Camerata Fiorentina fue un grupo de músicos, poetas y humanistas, bajo el patrocinio en Florencia del conde Giovanni Bardi y reunidos en su palacio entre los años 1572 y 1587 aproximadamente. Algunos de los más importantes miembros de la Camerata, como el músico Vincenzo Galilei, los cantantes Giulio Caccini y Jacopo Peri y el poeta Ottavio Rinuccini fueron quienes fundaron las bases intelectuales, teóricas y prácticas de lo que hoy llamamos la ópera.
 Patio del Palazzo Bardi en Florencia, atribuido a Bruneleschi, lugar de reunión de la Camerata Fiorentina. Foto: Francesco Bini / Wikimedia CommonsArmonizar la poesía: recitativos y tonemas
Patio del Palazzo Bardi en Florencia, atribuido a Bruneleschi, lugar de reunión de la Camerata Fiorentina. Foto: Francesco Bini / Wikimedia CommonsArmonizar la poesía: recitativos y tonemas
La Camerata heredó de la antigüedad importantes poemas o dramas clásicos que querían modernizar, musicalizar y representar en teatros. El recitativo de versos y diálogos fue un extraordinario invento musical de Giulio Caccini y Jacopo Peri, concebido para elevar la voz humana de actores y cantantes. Ello lo basaron en la entonación ordinaria de los lenguajes humanos, pero tratando -por medio de acertadas inflexiones de voz- de dotarles de mejor expresividad, comunicación, sentimiento y musicalidad.
En Fonética podemos sistematizar la entonación de una frase a través de los tonemas, que definen elevaciones o descensos del tono de la voz. La misma frase, entonada con diferentes tonemas, puede dar lugar a una expresión asertiva, o bien introducir una duda o una pregunta, o puede mostrar enfado, alegría, tristeza u otros sentimientos diferentes. Estas importantes inflexiones expresivas de la voz la formalizaron Caccini y Peri escribiendo notas musicales en un texto para recitar musicalmente los versos de un poema o la frase de una obra teatral. La técnica del Recitativo es por tanto el inicio de musicalizar la poesía y la literatura, esencial para desarrollar la ópera.
Matemáticas: melodía, entonación, eufonía y resoluciónSi queremos armonizar un poema, debemos introducir más de una voz, de forma que ambas a la vez suenen eufónicas. Vincenzo Galilei, en su obra Della musica antica et della moderna explicó matemáticamente la disonancia y la consonancia de dos notas sonando simultáneamente, basado en las ideas del teórico musical Gioseffo Zarlino. El discurso de dos frases musicales simultáneas fue descrito a través de unas sencillas reglas matemáticas de resolución de dichas frases. Ello consistía en una progresión ordenada de notas con mayor o menor eufonía que terminaba por medio de un salto tenso entre dos notas seguido por un regreso relajado a la nota final esperada por el lenguaje humano.
Así pues, mediante estas sencillas reglas matemáticas horizontales (melodía y entonación) y verticales (eufonía y resolución), se explica la más simple y conocida armonía entre dos personas cantando intuitivamente a dos voces, mediante intervalos de terceras, quintas, octavas o unísonos, que ya los Pitagóricos atesoraban por su pureza. Para más de dos voces simultáneas se siguen las mismas normas.
El ejemplo de HändelLas personas dedicadas a la música suelen considerarse “de letras”, quizás porque no les han explicado que las artes y especialmente la música beben de las matemáticas. Como ejemplo ilustrativo de cómo armonizar la poesía, mostraremos una sencilla práctica de uno de los pocos grandes compositores que adquirió en vida enorme éxito, reconocimiento y fortuna: Georg Friedrich Händel, que fue venerado en su país de adopción y fue enterrado en la Abadía de Westminster con honores de Estado.
Rinaldo fue la primera ópera que Händel estrenó en Londres el 24 de febrero de 1711 en el Queen’s Theatre de Haymarket. El estilo operístico italiano que el autor había aprendido, y el libreto en italiano del poeta Giacomo Rossi tuvo un éxito arrollador.
En la Figura 1 se muestra un fragmento del manuscrito original del Acto II de Rinaldo. Comienza un Recitativo de Argante: Oscura questo pianto il bel fuoco d’amor, ch’in me s’accese per te, mia cara. Responde Almirena: In questi lacci avvolta, non è il mio cor soggetto d’un amoroso affetto. En ambos recitativos, al puro estilo de la original invención musical de Giulio Caccini y Jacopo Peri, Händel coloca los tonemas mediante notas musicales para apropiada entonación de las frases.
 Figura 1: Manuscrito original de Rinaldo de G.F. Händel (Acto II, Escena IV): recitativos de Argante (Oscura questo pianto) y de Almirena (In questi lacci avvolta) y primeros compases de una de las arias más famosas de Almirena (Lascia ch’io pianga). Wikimedia Commons.
Figura 1: Manuscrito original de Rinaldo de G.F. Händel (Acto II, Escena IV): recitativos de Argante (Oscura questo pianto) y de Almirena (In questi lacci avvolta) y primeros compases de una de las arias más famosas de Almirena (Lascia ch’io pianga). Wikimedia Commons.La parte baja del manuscrito de la Figura 1 es la armonización completa de los primeros compases de una de las arias más famosas de esta ópera y de todo el repertorio operístico de Händel. La simplicísima armonización de los versos
Lascia ch’io pianga mia cruda sorte,
e che sospiri la libertà.
podemos pasarla a limpio para mostrar el ejemplo de ocho compases (cuatro para cada verso). Si no sabe usted leer música, no importa para entender lo escrito que explicaremos a continuación.
 Figura 2: Primer verso del aria a cuatro voces (el violín 1 equivale a la soprano)
Figura 2: Primer verso del aria a cuatro voces (el violín 1 equivale a la soprano)
 Figura 3: Segundo verso del aria a cuatro voces (el violín 1 equivale a la soprano)
Figura 3: Segundo verso del aria a cuatro voces (el violín 1 equivale a la soprano)
Diremos para empezar que el aria de Almirena está en tonalidad de Fa Mayor. La armonización está realizada a cuatro voces, que hemos colocado como si fuera un cuarteto de cuerda, o bien una pequeña orquesta de cuerda, donde la línea más aguda son los primeros violines o la soprano, que canta la letra.
Lectura horizontal y verticalEn las Figuras 2 y 3, leyendo horizontalmente la primera línea, la soprano canta la melodía. Además, sus dos versos cadenciosos están marcados por la combinación de sus importantes acentos de entonación en puntos expresivos clave (cru-da) y sus esenciales pausas rítmicas, que son los silencios.
Si ahora leemos verticalmente la Figura 2, vemos un primer compás con base en la primera nota de la tonalidad (Fa). Este acorde eufónico, muy Pitagórico, es Fa-La-Do, y lo rotulamos con un número romano (I). Las sencillas reglas matemáticas Galileanas -de progresión ordenada de acordes y la resolución de dichas frases- las podemos seguir mirando los números romanos en la parte del bajo de la partitura, que apenas se mueven, salvo algunas ligeras disonancias en el segundo y tercer compás. Ello nos deja el primer verso sin terminar, con carácter casi interrogativo, solicitando una respuesta.
Si ahora vamos a la Figura 3, continuamos leyendo verticalmente y si seguimos los números romanos, vemos que esta progresión del segundo verso cierra la frase con una tríada tensa (V) seguida por un regreso relajado a la nota final (I) esperada por el lenguaje humano, tal y como explicaba la Camerata Fiorentina. Este cierre V-I es lo que en música se llama cadencia (caída) auténtica, y que cierra frases en casi cualquier estilo musical.
Un poema armonizado no es solo “de letras”. Es también “de ciencias”: sus reglas matemáticas expresan sentimientos, y narran una conmovedora historia. Escuchemos el resultado de esta sencilla armonización que explica por qué Händel fue tan apreciado en vida:
Sobre el autor: Victor Etxebarria Ecenarro está diplomado como lutier por el Conservatorio Juan Crisóstomo de Arriaga (Bilbao) y es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (UPV/EHU)
El artículo Métodos matemáticos para armonizar la poesía se ha escrito en Cuaderno de Cultura Científica.
Día de pi 2024: Demostraciones visuales en dimensiones superiores

El número Pi, representado por la letra griega π, es una de las constantes matemáticas más famosas e importantes que existen en el mundo. Este número irracional, que determina la relación entre la longitud de una circunferencia y su diámetro, concierne a múltiples disciplinas científicas como la física, la ingeniería y la geología, y tiene aplicaciones prácticas sorprendentes en nuestro día a día.
La fascinación que ha suscitado durante siglos es tal, que se viene estudiando desde hace más de 4.000 años e, incluso, cuenta con su propio día en el calendario: el 14 de marzo. Este evento internacional vino de la mano del físico estadounidense Larry Shaw, quien en 1988 lanzó la propuesta de celebrar esta efeméride. La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática: 3-14 martxoaren 14 en euskara / 3-14 March, 14th en inglés. En los últimos años, la conmemoración del Día de Pi se ha ido extendiendo, hasta tal punto que el 26 de noviembre de 2019 la UNESCO proclamó el 14 de marzo Día Internacional de las Matemáticas.
Un año más, el Basque Center for applied Mathematics-BCAM y la Cátedra de Cultura Científica de la UPV/EHU nos sumamos a la celebración, organizando la quinta edición del evento BCAM NAUKAS, que se desarrolló a lo largo del 14 de marzo en el Bizkaia Aretoa de UPV/EHU.
Una demostración visual es una prueba matemática que no necesita de manipulación algebraica. En el Cuaderno de Cultura Científica hemos visto este tipo de demostraciones en la serie que hizo Raúl Ibáñez al respecto llamada Teoremas sin palabras. Pero, ¿pueden emplearse en dimensiones mayores que tres? Este es el fascinante (para las personas aficionadas a las matemáticas y matemáticas) tema de esta charla que nos trae Urtzi Bujis Martín.
Urtzi Bujis Martín es profesor de topología algebraica en la Universidad de Málaga y divulgador de las matemáticas en Archimedes Tub.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Día de pi 2024: Demostraciones visuales en dimensiones superiores se ha escrito en Cuaderno de Cultura Científica.
La capacidad de interpretar metáforas se desarrolla por completo a los 6 años
La investigadora de la Universidad del País Vasco Isabel Martín ha analizado con menores de 3 a 9 años la capacidad para interpretar las metáforas, y ha concluido que las comprenden completamente a los 6 años. En edades más tempranas muestran cierta intuición para captar el significado figurado, pero su capacidad no está totalmente desarrollada. La investigadora y sus colaboradoras han llegado a esta conclusión combinando las metodologías de selección de imágenes y de seguimiento de movimientos oculares.
 Fuente: ReferenciaMetáforas en neurotípicas y neurodivergentes
Fuente: ReferenciaMetáforas en neurotípicas y neurodivergentes
Un estudio que ha realizado el equipo de investigación Lindy Lab de la UPV/EHU con 80 niños y niñas de 3 a 9 años ha llegado a la conclusión de que la interpretación total de las metáforas se alcanza a partir de los 6 años. A pesar de ello, los resultados indican que la capacidad para intuir los significados no literales comienza a desarrollarse antes. “Se aprecia que en edades más tempranas captan en cierto modo el lenguaje figurado, pero no lo dominan y su capacidad es limitada. A los 6 identifican correctamente su significado y, es más adelante, hacia los 10, cuando parece que son capaces de explicar las metáforas”, aclara Isabel Martín. Los resultados de esta investigación se enmarcan dentro de la tesis que está realizando la doctoranda sobre la comprensión del lenguaje metafórico en personas tanto de desarrollo típico (neurotípicas) como con el llamado trastorno del espectro autista (neurodivergentes), con el objetivo de comparar lo que sucede en ambos grupos y poder comprender mejor la mente de personas con autismo.
La autora del estudio explica que para llegar a las citadas conclusiones se han servido de una investigación innovadora: “Hemos iniciado una nueva tendencia metodológica en psicología experimental y psicolingüística que nos ha permitido extraer conclusiones más matizadas que los trabajos ya existentes”. Y es que cabe recalcar, que hay diversos estudios que han analizado esta cuestión, pero sus resultados son dispares. El grupo de la Universidad del País Vasco ha logrado aportar información más completa al debate científico combinando dos metodologías diferentes de una manera que no se había hecho antes.
Selección de imágenes y desplazamiento de los ojosPor un lado, han empleado la metodología de la selección de imágenes. Han puesto en práctica un experimento en el que cada niño o niña escucha un audio en el que se dicta una metáfora (p. ej.: “Los saltamontes saltan mucho; ese niño es un saltamontes”), a la vez que visualizan cuatro imágenes (un niño saltando, un niño corriendo, un escarabajo y un saltamontes saltando). Entonces, los y las participantes deben elegir el dibujo que representa el mensaje que han oído (el niño saltando). “Esta metodología nos ha permitido saber que los participantes de 6 años comprenden los significados figurados, porque es en esa edad cuando se ve claramente que eligen la representación adecuada”, indica la investigadora.
Sin embargo, la selección de imágenes no ofrece información sobre cómo ha procesado cada participante los mensajes y en qué medida ha contemplado otras opciones. Para conocer esos detalles, el equipo de investigación de la Universidad del País Vasco ha aprovechado cada ejercicio planteado para analizar también sus movimientos oculares.
Mientras ven las imágenes, escuchan el estímulo auditivo y eligen el dibujo definitivo, una cámara de infrarrojos mide los desplazamientos de los ojos; tanto los sacádicos (movimientos rápidos del globo ocular e imperceptibles a simple vista) como las trayectorias y las fijaciones en cada imagen. Isabel Martín explica que estos datos permiten conocer cómo han procesado lo que han visto y oído: “La cámara capta cómo se han movido los ojos de una imagen a otra y nos da información sobre lo que está pasando dentro de sus cabezas antes de elegir el dibujo que consideran correcto: si han tenido dificultades, entre qué opciones han dudado… Dado que la imagen que finalmente seleccionan es el resultado de una decisión, que ha seguido todo un proceso”. El registro de los movimientos oculares les permite asomarse a ese proceso en sí y matizar los resultados obtenidos a través de la selección de imágenes.
Precisamente es gracias a la combinación de ambas metodologías que han podido saber que, aunque los niños y niñas menores de 6 años no interpretan con claridad las metáforas porque seleccionan con menos frecuencia la imagen correcta, sí que tienen cierta intuición para detectar los significados figurados. Y es que a través del seguimiento ocular han detectado que han dudado a la hora de elegir el dibujo. “Cuando tienen clarísimo qué significa la frase, no le dan más vueltas y fijan su mirada en la opción que consideran correcta. Pero cuando tienen dudas, miran a otros lugares. Y eso es lo que hemos podido percibir en menores de edades tempranas”, concreta la investigadora.
Referencia:
Isabel Martín-González, Camilo R. Ronderos, Elena Castroviejo, Kristen Schroeder, Ingrid Lossius-Falkum, Agustín Vicente (2024) That kid is a grasshopper! Metaphor development from 3 to 9 years of age Journal of Child Language doi: 10.1017/S0305000924000187
El artículo La capacidad de interpretar metáforas se desarrolla por completo a los 6 años se ha escrito en Cuaderno de Cultura Científica.
Un pequeño paso para Neil Armstrong, un gran salto para la ciencia ficción
El 20 de julio de 1969, Neil Armstrong y Buzz Aldrin se convertían en los primeros seres humanos en pisar la Luna, mientras un estoico Michael Collins permanecía, a la espera de la pena o la gloria de la misión, orbitando nuestro satélite. Todos conocemos esta historia, y algunos de los que estén leyendo este artículo, probablemente, también la vivieron en primera persona gracias a la colosal cobertura mediática que recibió el acontecimiento. Se estima que 600 millones personas lo vieron en directo en sus televisores, pero ¿y si no se hubiera retransmitido en vivo ni hubiera habido ese colosal despliegue mediático?, ¿hubiera impactado tan profundamente la llegada a la Luna en nosotros? Para muchos tal vez no, pero para algunos otros sí, y mucho. O, al menos, para los escritores de ciencia ficción que durante décadas habían estado imaginando y esperando ese momento.
 Buzz Aldrin fotografió su propia huella sobre el regolito lunar con fines científicos, pero esta imagen se ha convertido en un símbolo del logro de haber llegado a la luna. Fuente: NASA/Buzz Aldrin
Buzz Aldrin fotografió su propia huella sobre el regolito lunar con fines científicos, pero esta imagen se ha convertido en un símbolo del logro de haber llegado a la luna. Fuente: NASA/Buzz Aldrin
Hubo dos coberturas informativas de la misión Apolo 11 que tuvieron especial relevancia en ese sentido: la de la CBS (Columbia Broadcasting System) y la de la ABC (American Broadcasting Company). La programación especial de CBS News comenzó el 16 de julio de 1969, día del lanzamiento, a las seis de la mañana. Empezaban ocho días de retransmisiones en directo, casi sin descanso, bajo el título de: El hombre en la Luna: el viaje épico del Apolo 11.
La cara visible del despliegue informativo fue Walter Cronkite, uno de los periodistas más respetados del país. Corresponsal en Europa durante la Segunda Guerra Mundial, cubrió el Desembarco de Normandía y otras misiones de bombardeo sobre Alemania, así como los juicios de Núremberg durante los años posteriores. Y su carrera se extendería con éxito durante algunas décadas más. Era la elección lógica por parte de la cadena para cubrir el que sin duda se convertiría en uno de los mayores acontecimientos de la historia de la humanidad.
 El periodista de informativos Walter Cronkite fue el encargado de la cobertura de la misión Apollo 11 para CBS News. Fuente: CC BY-NC-SA 2.0/CBS News
El periodista de informativos Walter Cronkite fue el encargado de la cobertura de la misión Apollo 11 para CBS News. Fuente: CC BY-NC-SA 2.0/CBS News
Pero Walter Cronkite no estuvo solo, el desfile de corresponsales y expertos fue infinito. Y, entre esos expertos, ¿qué mejor que los escritores de ciencia ficción que habían estado especulando durante décadas con ese momento? Arthur C. Clarke apareció en antena hasta en doce ocasiones, pero la intervención más interesante se produjo el día del alunizaje. Aquel día, la CBS hizo una emisión de treinta horas ininterrumpidas, veintisiete de las cuales Cronkite estuvo en directo. En los momentos anteriores y posteriores al aterrizaje tuvo dos acompañantes de lujo: el propio Clarke, que lo acompañaba en el estudio de Nueva York, y Robert A. Heinlein, en conexión desde California, acompañado por Bill Stout.
La entrevista, que se puede ver completa en YouTube (abajo aparece un resumen de 10 minutos), es un documento maravilloso para los amantes de la carrera espacial y la ciencia ficción, sobre todo por el optimismo y la emoción que transmitían ambos escritores en aquel momento. Heinlein llega a decir en un momento de su intervención, visiblemente emocionado:
Este es el acontecimiento más grandioso de la historia de la humanidad hasta el momento. Esto es… hoy es el día de año nuevo del año uno.1 Si nosotros no modificamos el calendario, los historiadores lo harán […]. E iremos allá fuera, no solo a la Luna, sino a las estrellas: nos expandiremos […]. Nos vamos a expandir por todo el universo.
En aquello consistió la magia del momento: la ciencia ficción había soñado durante décadas con lo imposible y lo imposible sucedió el 20 de julio de 1969, ¿qué motivo habría para pensar que, una vez pisada la Luna, nos detendríamos ahí?
La cadena ABC recurrió, por otro lado, a Isaac Asimov, Frederik Pohl y John R. Pierce2 que participaron en una mesa redonda moderada por Rod Serling, guionista y productor televisivo conocido, sobre todo, por la serie The Twilight Zone. Tampoco ninguno de ellos mostró ninguna duda de que, desde que tenían uso de razón, la llegada del ser humano a la luna era una cuestión de tiempo. Parte de aquella intervención se puede ver también en YouTube.
La participación mediática de Isaac Asimov, Arthur C. Clarke, Robert A. Heinlein, Frederik Pohl y John R. Pierce, entre otros, en el que probablemente fue el logro tecnológico más importante del siglo XX fue, por un lado, el testimonio de que el sueño de la Edad de Oro de la ciencia ficción podía cumplirse. Por otro, un ejemplo del poder que la ciencia ficción puede ejercer en la manera en la que entendemos nuestra realidad e imaginamos nuestro futuro. Desde los tiempos de Julio Verne ―incluso antes―, sin las constricciones y formalismo de la ciencia, y con mucho sentido de la maravilla, aquellos escritores, y también divulgadores en muchos casos, inspiraron a varias generaciones de científicos, ingenieros y exploradores de lo desconocido, sembrando en ellos la idea de que un día sería posible pisar la Luna.
 Buzz Aldrin en la superficie de la Luna, fotografiado por Neil Armstrong. Fuente: NASA/Neil Armstrong
Buzz Aldrin en la superficie de la Luna, fotografiado por Neil Armstrong. Fuente: NASA/Neil Armstrong
Aunque es difícil calibrar el grado de influencia que la ciencia ficción de principios a mediados del siglo XX tuvo sobre el desarrollo de la carrera espacial, todo indica que la tuvo. Wernher von Braun y Arthur C. Clarke fueron grandes amigos. Tal vez eso signifique que, al fin y al cabo, la ciencia y la ciencia ficción ―science fact and science fiction― no se encuentren tan alejadas la una de la otra.
Bibliografía
Hsu, T. (15 de julio de 2019). The Apollo 11 mission was also a global media sensation. https://www.nytimes.com/2019/07/15/business/media/apollo-11-television-media.html
Knoll, S. (16 de julio de 1969). First man on the moon has TV network in orbit. Variety. https://variety.com/1969/biz/news/first-man-on-the-moon-has-tv-networks-in-orbit-1201342630/
Jeffrey, J. (11 de julio de 2019). Apollo 11: ‘The greatest single broadcast in television history’. BBC. https://www.bbc.com/news/world-us-canada-48857752
McAleer, N. (1992). Arthur C. Clarke. The authorized biography. Contemporary Books.
NASA (s. f.). Walter Cronkite. NASA. https://www.nasa.gov/people/walter-cronkite/
O’Donell, Norah (16 de julio de 2019). “Say something, I’m Speechless!”: Inside the CBS News coveragie of Apollo 11. CBS News. https://www.cbsnews.com/news/say-something-im-speechless-inside-the-cbs-news-coverage-of-apollo-11/
Patterson, W. H. (2014). Robert A. Heinlein. Vol. 2. The man who learned better. 1948-1988. Tor.
Notas:
1 No fue el único que lo pensó. Ray Bradbury comenzó a fechar su correspondencia de 1969 como «Apolo año 1». Lamentablemente, solo llegó hasta «Apolo año 3».
2 John R. Pierce, además de escritor de ciencia ficción, era ingeniero de los Bell Labs en Nueva York. Fue quien acuñó el término «transistor» para el dispositivo que John Bardeen, Walter Brattain y William Shockley habían desarrollado allí en 1947. Solía escribir bajo el seudónimo de J. J. Coupling.
 
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo Un pequeño paso para Neil Armstrong, un gran salto para la ciencia ficción se ha escrito en Cuaderno de Cultura Científica.
Teorema de los globos oculares
Como se decía en la entrada del Cuaderno de Cultura Científica titulada El teorema de Morley, la geometría euclidiana y, en particular, la geometría plana, está repleta de hermosos y sorprendentes teoremas, sobre algunos de los cuales ya hemos escrito con anterioridad, como el teorema de Pitágoras, el teorema de Napoleón o el teorema de Morley, por citar algunos. En esta entrada estival vamos a disfrutar de un nuevo resultado de la geometría del plano, el conocido teorema de los globos oculares.
 Fotografía de la escultura Ojo (2007), instalada en Dallas (Texas, EE.UU.), del artista estadounidense Tony Tasset. Fotografía realizada por la fotógrafa Carol M. Highsmith / Library of the Congress (USA)Lo que nos dice el teorema
Fotografía de la escultura Ojo (2007), instalada en Dallas (Texas, EE.UU.), del artista estadounidense Tony Tasset. Fotografía realizada por la fotógrafa Carol M. Highsmith / Library of the Congress (USA)Lo que nos dice el teorema
Este es un curioso resultado de geometría elemental sobre dos circunferencias disjuntas y las rectas tangentes a las mismas trazadas desde los centros de las circunferencias opuestas, que ha sido descubierto, o al menos publicado, hace unas décadas, aunque es posible que se conociese desde hace mucho tiempo.
Antes de nada, vayamos con su enunciado.
Teorema: Dadas dos circunferencias disjuntas de centros O y P, se consideran las dos rectas tangentes a la circunferencia de centro P que pasan por O, así como los dos puntos de intersección de estas con la circunferencia de centro O, denotados A y B, y las dos rectas tangentes a la circunferencia de centro O que pasan por P, así como los dos puntos de intersección de las mismas con la circunferencia de centro P, denotados X e Y, entonces los segmentos AB y XY tienen la misma longitud.
 Esquema del teorema de los globos oculares
Esquema del teorema de los globos oculares
Como podemos leer en el libro The Wonder Book of Geometry (El maravilloso libro de la geometría), de David Acheson, este resultado fue descubierto en 1960 por el matemático peruano Antonio Gutiérrez, creador de la página web GoGeometry, aunque es probable, ya que se trata de un resultado elemental, que ya fuese conocido desde la antigüedad. El propio Gutiérrez, en su artículo Eyeball theorems (publicado en el libro The Changing Shape of Geometry. Celebrating a Century of Geometry and Geometry Teaching / La forma cambiante de la geometría: celebrando un siglo de geometría y enseñanza de la geometría), dice “estoy convencido de que este resultado ha sido descubierto en casi todas las culturas”.
No conocemos si efectivamente era un resultado conocido en la antigüedad, aunque podamos sospecharlo. Lo que sí sabemos es que, en 1938 el matemático estadounidense George W. Evans publicó un artículo en la revista The Mathematics Teacher, titulado Ratio as multiplier, en el que se presenta un problema como “más fácil de resolver que de enunciar”, que encontró como problema propuesto en un examen (aunque no cita qué tipo de examen era, ni dónde se realizó) y que resulta ser el teorema de los globos oculares.
El nombre del teorema se debe a que el esquema del mismo nos recuerda a los típicos esquemas que describen la geometría de los rayos de luz en el ojo.
Una demostración simple del teoremaComo hemos comentado, el teorema de los globos oculares es un resultado geométrico elemental y sorprendente, pero además hermoso, motivo por el cual lo he elegido para esta entrada estival del Cuaderno de Cultura Científica. Al ser un resultado elemental, existen bastantes demostraciones relativamente sencillas. Una de ellas es la mostrada por el matemático George W. Evans en su artículo Ratio as multiplier y que explicamos a continuación.
 Esquema del teorema de los globos oculares
Esquema del teorema de los globos oculares
En el anterior esquema del teorema de los globos oculares se consideran las siguientes longitudes: a es la mitad de la longitud del segmento AB, x es la mitad de la longitud del segmento XY, d la distancia entre los centros, O y P, y r y s los radios de las dos circunferencias, en particular, r es igual a la longitud de los segmentos OA, OB y OS, y s es la longitud de los segmentos PX, PY y PT. Para demostrar que las longitudes de los segmentos AB y XY son iguales nos basta probar que a = x.
A continuación, consideramos dos triángulos rectángulos. Por una parte, el pequeño triángulo rectángulo formado por el segmento x y los vértices P e Y (coloreado de azul en la siguiente imagen) y el triángulo rectángulo O, S y P (con rayas azules). Como los ángulos de los dos triángulos rectángulos son los mismos, entonces los dos triángulos son semejantes, es decir, tienen la misma forma, pero distinto tamaño (uno es una ampliación/reducción del otro).
 Dos triángulos rectángulos semejantes, luego tienen la misma forma y distinto tamaño
Dos triángulos rectángulos semejantes, luego tienen la misma forma y distinto tamaño
Como los dos triángulos rectángulos seleccionados son semejantes, las longitudes de sus lados serán proporcionales, es decir, existe un factor de proporcionalidad f tal que las longitudes de los lados de uno de los triángulos son iguales a las longitudes de los lados del otro triángulo multiplicadas por ese factor f. En particular, se obtienen las dos igualdades siguientes
![]()
De forma análoga, si miramos a los otros dos triángulos rectángulos similares a los dos anteriores se obtiene que existe un factor de proporcionalidad g y se cumplen igualdades parecidas a las anteriores, en concreto, las siguientes igualdades
![]()
Utilizando las cuatro fórmulas anteriores, es fácil deducir que x = a, como se quería demostrar. Por lo tanto, las longitudes de los segmentos AB y XY son iguales, como afirma el teorema de los globos oculares.
Existen muchas otras demostraciones, desde la propuesta por el matemático peruano Antonio Gutiérrez, que podéis leer en su página GoGeometry, hasta una relacionada con un sangaku (puede leerse más sobre los sangakus en la entrada Sangakus, pasión por los desafíos matemáticos), que podéis leer en la página Cut the knot, del matemático Alexander Bogomolny.
 Portada del número 2, del volumen 53 (2022), de la revista The College Mathematics Journal, en el que se publica el artículo A Variant of the Eyeball Theorem, del ingeniero dominicano Emmanuel Antonio José García
Portada del número 2, del volumen 53 (2022), de la revista The College Mathematics Journal, en el que se publica el artículo A Variant of the Eyeball Theorem, del ingeniero dominicano Emmanuel Antonio José GarcíaBibliografía
1.- David Wells, The Penguin Dictionary of Curious and Interesting Geometry, Penguin, 1991.
2.- David Acheson, The Wonder Book of Geometry. Oxford University Press, 2020.
3.- Chris Pritchard (editor), The Changing Shape of Geometry. Celebrating a Century of Geometry and Geometry Teaching, Cambridge University Press, 2003.
4.- George W. Evans, Ratio as multiplier, The Mathematics Teacher, Vol. 31, No. 3, pp. 114-116, 1938.
5.- Claudi Alsina, Roger B. Nelsen, Icons of Mathematics: An Exploration of Twenty Key Images, MAA, 2011.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Teorema de los globos oculares se ha escrito en Cuaderno de Cultura Científica.
Los primeros homininos de Europa habrían llegado al sur de Iberia
Una de las controversias más importantes sobre la evolución y la expansión humana es cuándo y por qué camino llegaron los primeros homínidos a Europa desde el continente africano. Ahora, unas dataciones con técnicas geológicas de los yacimientos de Orce (cuenca de Baza, Granada) sitúan los restos humanos hallados en esta zona como los más antiguos de Europa, con aproximadamente 1,3 millones de años. Estos resultados refuerzan la hipótesis de la llegada de los seres humanos a Europa por el sur de la península Ibérica, a través del estrecho de Gibraltar, en lugar de dando la vuelta al Mediterráneo por la vía asiática. El trabajo, liderado por Lluís Gibert, investigador y profesor de la Facultad de Ciencias de la Tierra de la Universidad de Barcelona, ha contado con la participación de investigadores del Centro de Geocronología de Berkeley y de la Universidad Estatal de Murray (Estados Unidos).
 Principales yacimientos datados de homininos con más de 1 millón de años. Europa: 1. Orce, 2. Cueva Victoria, 3 Cueva Negra, 4. Atapuerca, 5. Barranc de la Boella, 6 Pirro Nord. Asia occidental: 7. Dmanisi, 8. Ubeidiya, 9. Gesher Benot. Asia Central: 10. Riwat, 11. Issanpur, 12 Attirampakkam. Asia Oriental: 13. Bose, 14. Yuanmou Basin, 15. Nihewan Basin, 16. Lounan Basin, 17 Sangiran, 18. Mojokerto, 19. Flores. África: 20. Ain Hanech, Ain Ain Boucherit 21. Thomas-1, 22. Gona, 23. Konso Kandula, 24. Omo, 25. Lokalalei, 26 Lomekwi, 27 Kokiselei 28, Kobi Fora, 29 Gaded, 30 M. Awash, 31 Hadar, 32 Ledi Geraru, 33 Olduvai, 34 Peninj, 35 Mwanganda, 36. Sterkfontein, 37 Swartkrans, 38 Vaal River. Fuente: Referencia.El paleomagnetismo de Orce
Principales yacimientos datados de homininos con más de 1 millón de años. Europa: 1. Orce, 2. Cueva Victoria, 3 Cueva Negra, 4. Atapuerca, 5. Barranc de la Boella, 6 Pirro Nord. Asia occidental: 7. Dmanisi, 8. Ubeidiya, 9. Gesher Benot. Asia Central: 10. Riwat, 11. Issanpur, 12 Attirampakkam. Asia Oriental: 13. Bose, 14. Yuanmou Basin, 15. Nihewan Basin, 16. Lounan Basin, 17 Sangiran, 18. Mojokerto, 19. Flores. África: 20. Ain Hanech, Ain Ain Boucherit 21. Thomas-1, 22. Gona, 23. Konso Kandula, 24. Omo, 25. Lokalalei, 26 Lomekwi, 27 Kokiselei 28, Kobi Fora, 29 Gaded, 30 M. Awash, 31 Hadar, 32 Ledi Geraru, 33 Olduvai, 34 Peninj, 35 Mwanganda, 36. Sterkfontein, 37 Swartkrans, 38 Vaal River. Fuente: Referencia.El paleomagnetismo de Orce
La nueva datación se ha basado en analizar el paleomagnetismo de un área de la región de Orce, donde nunca se había muestreado antes y que, ha sido protegida de la erosión que ha sufrido esta cuenca a lo largo de los años. Esta técnica es un método de datación relativo basado en estudiar la inversión de los polos magnéticos del planeta debido a la dinámica interna de la Tierra. Estos cambios no tienen una periodicidad concreta, pero quedan registrados en los minerales y permiten establecer períodos de tiempo a partir de los diferentes eventos magnéticos.
Estos nuevos datos son muy precisos gracias a la larga secuencia sedimentaria que aflora en Orce. «La singularidad de estos yacimientos es que están estratificados y dentro de una secuencia de sedimentaria muy larga, de más de ochenta metros. Normalmente, los yacimientos se encuentran en cuevas o dentro de secuencias estratigráficas muy cortas, que no te permiten desarrollar secuencias paleomagnéticas largas en las que puedas encontrar diferentes inversiones magnéticas», apunta Lluís Gibert.
Los investigadores han podido identificar una secuencia de polaridad magnética «con cinco eventos magnéticos que permiten situar a los tres yacimientos de Orce con presencia humana entre el subcrono Olduvai y Jaramillo, es decir, entre 1,77 y 1,07 millones de años (Ma)», explica el investigador. Posteriormente, han aplicado un modelo estadístico de edad para refinar con precisión la cronología de los distintos niveles estratigráficos con un margen de error de solo 70.000 años. El resultado de esta innovadora metodología es que el yacimiento más antiguo con presencia humana de Europa sería Venta Micena con una edad de 1,32 Ma, seguido de Barranco León, con una edad de 1,28 y finalmente Fuente Nueva 3, con una edad de 1,23 Ma. «Con estos datos, el otro gran yacimiento de la península, el de Sima del Elefante en Atapuerca, quedaría relegado a un segundo puesto, muy detrás de Orce, entre 0,2 y 0,4 Ma más moderno», añade el investigador.
La fauna apuntala la antigüedad del yacimiento Mapa que muestra la irradiación solar de la región mediterránea mostrando los principales yacimientos con restos de homininos. Fuente: Referencia
Mapa que muestra la irradiación solar de la región mediterránea mostrando los principales yacimientos con restos de homininos. Fuente: ReferenciaPara completar la datación, el estudio también ha analizado la fauna que se encuentra en los diferentes yacimientos de Orce, ya que esta es diferente según el período, y la ha comparado con la que se ha encontrado en otros yacimientos del Pleistoceno temprano situados en otros lugares de Europa.
En este sentido, en el trabajo se presenta un análisis detallado de los micromamíferos y grandes mamíferos de todos los yacimientos de Orce, realizado por el experto Robert Martin, a partir de las colecciones paleontológicas almacenadas en el Museo del Instituto Catalán de Paleontología Miguel Crusafont (IPS) de Sabadell. «Los resultados muestran que la fauna pequeña y grande de Orce es más primitiva que, por ejemplo, la de la Sima del Elefante, donde las evidencias muestran que el roedor Allophaiomys lavocati es más evolucionado que el Allophaiomys recuperado de los yacimientos de Orce», detalla Gibert.
Otro indicador relevante de la antigüedad de los yacimientos de Orce es la ausencia de los antepasados de los cerdos. «Son animales que se consideran inmigrantes asiáticos y que no se han encontrado en ningún yacimiento europeo con una antigüedad de entre 1 y 1,5 Ma, mientras que sí se han encontrado en la Sima del Elefante, apoyando que la fauna de Orce es más antigua», explica el investigador.
Evidencias que apuntan al paso por GibraltarEsta nueva datación se añadiría, según el investigador, a otras evidencias que decantarían, la balanza de la colonización de Europa por el estrecho de Gibraltar, en lugar de la vía alternativa: la vuelta al Mediterráneo por Asia, como por ejemplo «la existencia de una industria lítica con similitudes con la que se ha encontrado en el norte del continente africano y también por la presencia de restos de fauna africana en el sur de la península, como los de Hippopotamus, hallado en los yacimientos de Orce, y las de Theropithecus oswaldi, un primate africano similar a un papión, halladas en la cueva Victoria, un yacimiento cerca de Cartagena (Murcia), inexistentes en ningún otro lugar de Europa».
«También defendemos la hipótesis —añade el investigador— que llegaron desde Gibraltar porque no se han encontrado evidencias más antiguas en ningún otro yacimiento del recorrido alternativo».
Estos nuevos datos son muy precisos gracias a la larga secuencia sedimentaria que aflora en Orce.
Similitud con los homínidos de la isla de FloresCon estos resultados, los investigadores señalan un «diacronismo» entre la ocupación más antigua de Asia, mide 1,8 Ma y la más antigua de Europa, que sería de hace 1,3 Ma, de modo que los homínidos africanos habrían llegado en el suroeste de Europa más de 0,5 Ma después de salir por primera vez de África hace aproximadamente 2 Ma. «Estas diferencias en la expansión humana se explicarían porque Europa está aislada de Asia y de África por barreras biogeográficas difíciles de superar, tanto por el este: (estrecho del Bósforo, Dardanelos, mar de Mármara) como por el oeste (estrecho de Gibraltar). La humanidad llegó a Europa en el momento en que tuvo la tecnología necesaria para cruzar barreras marítimas, tal y como ocurrió antes del millón de años en la isla de Flores (Indonesia)», apunta Gibert. En este sentido, el investigador añade que la ruta de Gibraltar requiere actualmente atravesar hasta catorce kilómetros de vía marítima, pero «quizás en el pasado esta distancia era menor en algunos momentos debido a la alta actividad tectónica en esta región y las fluctuaciones del nivel del mar favoreciendo las migraciones».
«Tal y como se cita en el trabajo —añade—, hemos identificado otras migraciones de fauna africanas a través de Gibraltar en momentos anteriores, hace 6.2 y 5.5 Ma cuando el estrecho de Gibraltar era muy reducido».
Los vestigios humanos en OrceLos restos humanos encontrados en los yacimientos de Orce son un total de cinco, desde que se iniciaron las excavaciones en 1982 por el paleoantropólogo Josep Gibert. En primer lugar, se encontraron en Venta Micena dos fragmentos de húmero mordidos por las hienas y también partes de un fragmento craneal que consiste en dos parietales y un occipital, asociados a una abundante fauna del Pleistoceno temprano. La procedencia humana de estos restos generó una gran controversia durante años, aunque según estudios paleoproteómicos independientes realizados por las universidades de Granada y San Francisco identificaron proteínas humanas en los restos.
El descubrimiento posteriormente en los yacimientos cercanos de Barranco León y Fuente Nueva 3 de dos dientes molares humanos y miles de herramientas líticas olduvayanas —una de las primeras industrias líticas humanas— así como marcas de corte en huesos «sirvieron para consolidar la evidencia de la presencia de homínidos en el Pleistoceno temprano de Orce», concluye Lluís Gibert.
Referencia:
Luis Gibert, Gary Scott, Alan Deino, Robert Martin (2024) Magnetostratigraphic dating of earliest hominin sites in Europe Earth-Science Reviews doi: 10.1016/j.earscirev.2024.104855
Edición realizada por César Tomé López a partir de materiales suministrados por la Universidad de Barcelona
El artículo Los primeros homininos de Europa habrían llegado al sur de Iberia se ha escrito en Cuaderno de Cultura Científica.
Una nueva clase de martemotos
A estas alturas podemos decir sin duda alguna que la misión InSight de la NASA ha sido -y probablemente será en las próximas décadas con la reinterpretación de sus datos- una importante fuente de conocimiento sobre la estructura interna de Marte, pero también sobre procesos que ocurren mucho más próximos a su superficie, como lo fueron la detección de posibles terremotos de origen volcanotectónico o la caída e impacto de meteoroides y asteroides contra la superficie.
Precisamente, los impactos sobre las superficies planetarias nos han aportado una visión muy importante sobre como ha sido la historia y evolución de nuestro Sistema Solar en su conjunto, pero también son capaces de informarnos de manera individual como ha sido la evolución y el grado de actividad de cada uno de los cuerpos que podemos observar con detalle.
 Un impacto reciente sobre la superficie de Marte. Sabemos que es reciente porque todavía se ve la eyecta -el material que sale despedido por el impacto- de un color oscuro sobre la superficie y, en segundo lugar, por la forma todavía marcada del cráter. Conforme pase el tiempo la eyecta irá volviéndose anaranjada por el depósito de polvo y al cráter suavizar su forma. Imagen cortesía de NASA/JPL-Caltech/Universidad de Arizona.
Un impacto reciente sobre la superficie de Marte. Sabemos que es reciente porque todavía se ve la eyecta -el material que sale despedido por el impacto- de un color oscuro sobre la superficie y, en segundo lugar, por la forma todavía marcada del cráter. Conforme pase el tiempo la eyecta irá volviéndose anaranjada por el depósito de polvo y al cráter suavizar su forma. Imagen cortesía de NASA/JPL-Caltech/Universidad de Arizona.Y es que, en Marte, como en cualquier otro lugar, la frecuencia, tamaño y distribución de los cráteres de impacto nos sirven como una herramienta para calcular la edad de las superficies geológicas, permitiéndonos conocer el ritmo de los distintos procesos geológicos que están o estuvieron en funcionamiento y su grado de actividad. Y como hemos dicho más de una vez en esta sección, por norma general, cuanto más antigua es una superficie planetaria y menos ha cambiado, más cráteres acumulará por unidad de superficie, ya que ha estado más tiempo expuesta a la caída de cuerpos sobre esta.
De manera general, este método nos permite mediante el uso de las imágenes tomadas por los satélites en órbita -o que han pasado cerca- del planeta calcular la edad, pero tiene un importante problema relacionado con la formación de los cráteres más pequeños y numerosos, ya que desconocemos el ritmo aproximado de impactos por año capaces de generarlos.
Gracias a los datos sísmicos tomados durante la misión InSight parece que al menos para Marte podríamos tener una respuesta que nos permita una mejor calibración de estas escalas de edad basadas en los cráteres de impacto, ya que ha sido capaz de detectar con su sismógrafo algunos de los impactos ocurridos durante el desarrollo de su misión. Pero además de emplear la extraordinaria visión de la Mars Reconaissance Orbiter, su cámara HiRISE puede tomar imágenes con una resolución en el entorno de los 30 cm/pixel- para poder localizar el punto de impacto y el tamaño del cráter.
 Uno de los impactos detectados por la InSight y observado por la Mars Reconaissance Orbiter. En este caso el impacto ocurrió el 5 de septiembre de 2021. Imagen cortesía de NASA/JPL-Caltech/Universidad de Arizona.
Uno de los impactos detectados por la InSight y observado por la Mars Reconaissance Orbiter. En este caso el impacto ocurrió el 5 de septiembre de 2021. Imagen cortesía de NASA/JPL-Caltech/Universidad de Arizona.En un nuevo artículo publicado por Zenhäusern et al. (2024) los científicos han hecho una búsqueda y un análisis de un tipo de eventos sísmicos muy particulares, los martemotos de muy alta frecuencia o VHF. Este tipo de martemotos -discúlpenme si les disgusta este término- tienen unas características muy diferentes a los terremotos producidos por la actividad tectónica de Marte.
La primera es una liberación de energía muy fuerte en frecuencias que van de los 5 a los 30 Hz; La segunda, una frecuencia de corte o esquina que indica a los científicos que se trata de un evento de muy corta duración y, por último, una fuerte sacudida en la horizontal a frecuencias superiores a los 5 Hz. Estas tres características -que se pueden estudiar gracias a los datos obtenidos por el sismómetro de la InSight- son buenos marcadores de los impactos de meteoroides a hipervelocidad.
Los investigadores han confirmado que todos los impactos detectados durante la misión de la InSight muestran estas características en la señal, por lo que es plausible que todos los eventos de este tipo puedan atribuirse a los impactos contra la superficie de Marte. Y, además, la detección de algunos estos eventos concluyen con un tren de ondas que se interpretan como señales acústicas producidas por la perturbación que el impacto crea en la atmósfera.
 Otros tres impactos muy recientes captados por la InSight y la Mars Reconaissance Orbiter. En este caso, la fecha de los impactos fueron el 27 de mayo de 2020 y el 18 de febrero y 31 de agosto de 2021. Imagen cortesía de NASA/JPL-Caltech/Universidad de Arizona.
Otros tres impactos muy recientes captados por la InSight y la Mars Reconaissance Orbiter. En este caso, la fecha de los impactos fueron el 27 de mayo de 2020 y el 18 de febrero y 31 de agosto de 2021. Imagen cortesía de NASA/JPL-Caltech/Universidad de Arizona.Pero hay un dato más y que es muy importante detallar: la distribución espacial de este tipo de eventos muestra un patrón aleatorio, mientras que los eventos tectónicos detectados por la InSight, como es normal, tienden a agruparse en estructuras tectónicamente activas (como las fallas), al igual que ocurre en nuestro planeta.
El análisis de los datos sísmicos de la InSight ha permitido a los científicos estimar que cada año se forman sobre la superficie de Marte entre 280 y 360 cráteres mayores de 8 metros, coincidiendo este dato con los modelos cronológicos ya publicados, pero, y esto es importante, un ritmo mucho mayor que el que se aprecia a través de las imágenes de satélite… ¿Por qué de esta discrepancia?
Muy probablemente se deba a factores como la resolución de las cámaras, la cobertura en imágenes del planeta a alta resolución -ya que para ver nuevos cráteres las imágenes tienen que tomarse de manera repetida a lo largo del tiempo- y también, quizás, la cantidad de polvo que cubre algunas superficies, puesto que puede complicar la detección de cráteres más pequeños salvo que el ángulo de luz sea muy oblicuo.
¿Qué consecuencias puede tener este estudio? En primer lugar, a nivel científico, el ayudarnos a calibrar mejor las escalas temporales basadas en los cráteres de impacto, lo que a su vez nos permitiría “afinar” mejor las edades de las distintas capas de roca, de las coladas de lava o la duración de algunos eventos que podemos ver en el registro geológico del planeta rojo e, incluso, pone de manifiesto la utilidad de la toma de datos sísmicos en otros lugares de nuestro Sistema Solar para afinar las escalas temporales… ¿Veremos, por lo tanto, más sismómetros montados en sondas de superficie?
Y ya por último, nos puede ayudar a conocer mejor cuál es el riesgo que podrían sufrir las futuras misiones de exploración humana del planeta Marte y qué medidas de protección podrían ser útiles ante este tipo de colisiones que, por ahora, son inevitables.
Referencias:
Zenhäusern, Géraldine, Natalia Wójcicka, Simon C. Stähler, Gareth S. Collins, Ingrid J. Daubar, Martin Knapmeyer, Savas Ceylan, John F. Clinton, y Domenico Giardini (2024) An Estimate of the Impact Rate on Mars from Statistics of Very-High-Frequency Marsquakes Nature Astronomy doi: 10.1038/s41550-024-02301-z.
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Una nueva clase de martemotos se ha escrito en Cuaderno de Cultura Científica.
Alzhéimer, detección precoz con inteligencia artificial
La enfermedad de Alzheimer es la causa más común de demencia y afecta a millones de ancianos en todo el mundo. Solo en España se estima que existen más de 900 000 personas afectadas por esta enfermedad que se ha convertido en una prioridad de salud pública para el Ministerio de Sanidad.
 Imagen del encéfalo de un varón de 56 años generada por tomografía por emisión de positrones. Fuente: Jens Maus / Wikimedia Commons
Imagen del encéfalo de un varón de 56 años generada por tomografía por emisión de positrones. Fuente: Jens Maus / Wikimedia CommonsLa detección precoz es clave para mejorar la calidad de vida de los afectados y sus familias, pero identificarla en sus estadios iniciales no siempre es fácil. Para intentar mejorar en este campo y lograr mejores resultados, investigadores de la Universidad Politécnica de Madrid (UPM) han aplicado técnicas de inteligencia artificial (IA) de aprendizaje automático al análisis de diferentes modalidades de imágenes médicas utilizadas para el diagnóstico de enfermedades neurológicas.
«Desde un punto de vista clínico, la resonancia magnética (RM) y la tomografía por emisión de positrones (PET) son las dos modalidades de imágenes médicas utilizadas en el diagnóstico de este tipo de enfermedades, ya que aportan información complementaria de los aspectos anatómicos y metabólicos de la enfermedad», explica Consuelo Gonzalo, investigadora del Centro de Tecnología Biomédica de la UPM y una de las autoras de este trabajo.
“Pero lamentablemente estas pruebas no se realizan sincrónicamente lo que dificulta su integración y la interpretación adecuada de sus resultados por parte de los profesionales médicos”, continúa.
Abordar este problema es el objetivo que se marcaron los investigadores de la UPM y la propuesta para ello fue desarrollar una metodología que utiliza las redes neuronales convolucionales.
Esta herramienta se trata de una técnica de aprendizaje automático que potencia las tareas de análisis de imágenes y visión por ordenador, permitiendo obtener información significativa de imágenes digitales, vídeos y otras entradas visuales, así como tomar medidas basándose en esas entradas.
Diagnóstico de alzhéimer a partir de datos incompletosPara ello, los investigadores de la UPM realizaron un análisis sistemático de las imágenes de MRI y PET para la evaluación del estado de demencia, utilizando diferentes técnicas de fusión (fusiones temprana, tardía e intermedia).
 Fuente: Universidad Politécnica de Madrid
Fuente: Universidad Politécnica de MadridA continuación, diseñaron e implementaron una solución completamente basada en redes neuronales convolucionales 3D que extraía características de todo el volumen encefálicol en tres dimensiones. Una vez hecho esto, aplicaron una estrategia de entrenamiento capaz de manejar un conjunto de datos altamente desequilibrado e incompleto.
“Hasta donde sabemos, la metodología propuesta representa el primer trabajo que proporciona un análisis de diferentes técnicas de fusión basada en aprendizaje profundo multimodal para la evaluación de la severidad de la demencia”, explica la investigadora de la UPM.
“El tipo de soluciones que se desarrollan en este trabajo puede ser una herramienta de ayuda a la decisión de enorme interés práctico para los neurólogos”, añade.
En investigaciones futuras, los científicos pretenden seguir explorando la fusión de diferentes modalidades, analizando más a fondo las propiedades de la representación de características compartidas.
“Se deben investigar enfoques que pretendan mejorar la integración de datos heterogéneos, generalizándolos a casos de estudio con más de dos modalidades de imágenes. También se debe abordar la explicabilidad de los modelos implementados, evaluando las decisiones tomadas por las redes en comparación con el diagnóstico clínico», concluyen.
Referencia:
Michela Gravina, Ángel García-Pedrero, Consuelo Gonzalo-Martín, Carlo Sansone, Paolo Soda (2024) Multi input–Multi output 3D CNN for dementia severity assessment with incomplete multimodal data Artificial Intelligence in Medicine doi: 10.1016/j.artmed.2024.102774
Edición realizada por César Tomé López a partir de materiales suministrados por la Universidad Politécnica de Madrid
El artículo Alzhéimer, detección precoz con inteligencia artificial se ha escrito en Cuaderno de Cultura Científica.
Día de pi 2024: El tamaño importa… ¿o no?

El número Pi, representado por la letra griega π, es una de las constantes matemáticas más famosas e importantes que existen en el mundo. Este número irracional, que determina la relación entre la longitud de una circunferencia y su diámetro, concierne a múltiples disciplinas científicas como la física, la ingeniería y la geología, y tiene aplicaciones prácticas sorprendentes en nuestro día a día.
La fascinación que ha suscitado durante siglos es tal, que se viene estudiando desde hace más de 4.000 años e, incluso, cuenta con su propio día en el calendario: el 14 de marzo. Este evento internacional vino de la mano del físico estadounidense Larry Shaw, quien en 1988 lanzó la propuesta de celebrar esta efeméride. La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática: 3-14 martxoaren 14 en euskara / 3-14 March, 14th en inglés. En los últimos años, la conmemoración del Día de Pi se ha ido extendiendo, hasta tal punto que el 26 de noviembre de 2019 la UNESCO proclamó el 14 de marzo Día Internacional de las Matemáticas.
Un año más, el Basque Center for applied Mathematics-BCAM y la Cátedra de Cultura Científica de la UPV/EHU nos sumamos a la celebración, organizando la quinta edición del evento BCAM NAUKAS, que se desarrolló a lo largo del 14 de marzo en el Bizkaia Aretoa de UPV/EHU.
En esta charla, Raquel Villacampa parte del hecho de que, desde la antigüedad, se ha querido cuantificar la belleza, incluida y especialmente la del cuerpo humano. Incluso hoy día se entrena a las máquinas para ello.
Raquel Villacampa Gutiérrez es profesora del Departamento de Matemáticas de la facultad de Ciencias de la Universidad de Zaragoza. Es miembro del Instituto Universitario de Matemáticas y Aplicaciones de la Universidad de Zaragoza (IUMA). Es una conocida divulgadora de las matemáticas.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Día de pi 2024: El tamaño importa… ¿o no? se ha escrito en Cuaderno de Cultura Científica.
Lo que nunca nos contaron en el colegio sobre el ciclo del agua
El ciclo del agua es uno de los contenidos cruciales para conocer el funcionamiento básico de la hidrosfera en el currículo de la educación obligatoria. ¿Quién no lo recuerda? Precipitaciones que en la superficie continental conforman la escorrentía, o que se infiltran en el suelo y alimentan las aguas subterráneas. La evaporación devuelve este elemento en forma gaseosa a la atmósfera que, tras la condensación, forma las nubes que darán lugar de nuevo a las precipitaciones.
 El ciclo hidrológico o ciclo del agua es el proceso de circulación del agua entre los distintos compartimentos que forman la hidrósfera.
El ciclo hidrológico o ciclo del agua es el proceso de circulación del agua entre los distintos compartimentos que forman la hidrósfera.Servicio Geológico de Estados Unidos / Wikimedia Commons
Menor atención se ha prestado a procesos geofísicos de gran importancia como la evapotranspiración asociada a los seres vivos o la interconexión entre los diferentes componentes del ciclo, fundamentalmente los del suelo, el gran olvidado.
Lo cierto es que lo que aprendimos en el colegio resulta incompleto para comprender el complejo funcionamiento de la hidrosfera. Sobre todo, si no se consideran otros procesos que interfieren directa o indirectamente. En especial, la dominación humana del ciclo del agua está ausente de representaciones y percepciones, a pesar de que las personas dependemos absolutamente del agua para nuestra supervivencia: la ingesta directa, la higiene, la producción de alimentos, los procesos industriales o el ocio y bienestar.
Saqueo en las masas de aguaLas causas centrales de la actual crisis mundial del agua intervienen en el ciclo junto con los procesos geofísicos y comienzan con la sobreexplotación de este recurso. El 70 % de los acuíferos españoles se encuentran sometidos a extracciones superiores a sus recargas. Esto genera sequías de gran magnitud en zonas tan relevantes como los parques nacionales de Doñana o las Tablas de Daimiel.
Asimismo, el excesivo consumo de agua ha transformado nuestros ríos en meros canales, repletos de embalses y trasvases. De este modo, su estado ecológico se ha visto notablemente afectado, lo que pone en riesgo los numerosos servicios ecosistémicos que nos prestan.
La sobreexplotación está relacionada con nuestro modelo socioeconómico, que abarca aspectos como el consumo de alimentos que requieren enormes cantidades de agua para su producción y modelos agroganaderos intensivos con superficies de riego que siguen incrementándose cada día.
 Los nuevos regadíos permiten el cultivo superintensivo de los olivos, una especie tradicionalmente de secano.
Los nuevos regadíos permiten el cultivo superintensivo de los olivos, una especie tradicionalmente de secano.Michelangelo-36 / Wikimedia Commons, CC BY
Los nuevos regadíos se asocian al cultivo de todo tipo de productos, como frutas tropicales (aguacate, mango…), cultivos con altos requerimientos de agua (maíz, alfalfa…) para alimentar al ganado, o el aumento de producción de cultivos tradicionalmente de secano como almendros, olivo o vid.
Turismo, ropa y pesticidasCompletan la ecuación otras actividades económicas, como el turismo (el consumo de agua por turista llega a quintuplicar el consumo per cápita local, asociado a piscinas, saunas, parques temáticos, mantenimiento de zonas ajardinadas o golf) y la moda (un kilo de algodón necesita 10 000 litros de agua para producirse y su cultivo genera problemas de sobreexplotación en numerosos ecosistemas acuáticos del planeta).
 De media, se estima que el consumo de agua para un campo de golf oscila entre los 200 y los 300.000 m3/año.
De media, se estima que el consumo de agua para un campo de golf oscila entre los 200 y los 300.000 m3/año.Lilrizz / Wikimedia Commons, CC BY
Otro factor a tener en cuenta es la contaminación de las masas de agua, que degrada los ecosistemas hídricos y, con ello, los servicios ecosistémicos que ríos, lagos y acuíferos aportan a la biosfera y al ser humano.
Por ejemplo, los nitratos de origen agroganadero provocan que casi el 30 % de las aguas subterráneas y el 50% de las superficiales presenten una mala calidad. Este hecho impide el acceso a agua potable a una buena parte de la población del país. Otro caso alarmante es la presencia de pesticidas en las diferentes masas de agua, especialmente tóxicos para la salud humana.
A ello se suman las alteraciones del medio físico: la intensa ocupación de diferentes zonas de la cuenca mediante cultivos o urbanizaciones modifica aspectos cruciales del ciclo del agua, como la evapotranspiración, la infiltración o la escorrentía. No solo comprometen la disponibilidad del recurso a nivel local, sino que aumentan los riesgos asociados a fenómenos climáticos extremos como las inundaciones.
Injusticia hídricaPor último, la subida de las temperaturas asociada al cambio climático provocado por la acción humana afecta directamente a diferentes procesos del ciclo del agua: aumento de la fusión de glaciares, de las tasas de evaporación y de evapotranspiración y modificación del régimen de precipitaciones.
 El embalse de Barrios de Luna (provincia de León) tras la sequía de 2017 en la Península ibérica. A principios de octubre de 2017 se encontraba en una situación crítica al 5 % de su capacidad.
El embalse de Barrios de Luna (provincia de León) tras la sequía de 2017 en la Península ibérica. A principios de octubre de 2017 se encontraba en una situación crítica al 5 % de su capacidad.Pablox / Wikimedia Commons, CC BY
Como consecuencia, la disponibilidad de agua dulce va en descenso, especialmente en zonas geográficas como la mediterránea. Sin embargo, su uso no hace sino incrementarse, mostrando la nula adaptación de la población a la realidad climática actual y poniendo en mayor riesgo, si cabe, el estado ecológico de nuestras masas de agua y ecosistemas.
Por tanto, la exclusión de actividad humana de las representaciones del ciclo del agua camufla algunas de las crisis socioecológicas más acuciantes, incluidas la seguridad y la justicia hídrica. Urge solventar estas carencias y activar recursos y métodos educativos como primer paso hacia la formación de las personas y hacia una gobernanza equitativa de este recurso esencial desde una visión planetaria, pero con el foco puesto en lo cotidiano.![]()
Sobre los autores: Rubén Ladrera Fernández, Profesor de Enseñanza Secundaria y Profesor Asociado del Área de Didáctica de las Ciencias Experimentales, Universidad de La Rioja y José Ramón Díez López, Profesor de Didáctica de Ciencias Experimentales, Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Lo que nunca nos contaron en el colegio sobre el ciclo del agua se ha escrito en Cuaderno de Cultura Científica.
¡Es una trampa (paleontológica)!
Cuando encontramos un yacimiento fósil, una de las primeras preguntas que nos hacemos es ¿por qué esos restos están ahí? ¿Los organismos que los produjeron vivían en ese lugar, estaban de paso o alguna otra entidad los arrastró hasta esa zona? Responder a esta pregunta no siempre es fácil, incluso, a veces, resulta imposible. Pero encontrar la solución nos permite contar fantásticas historias ocurridas hace millones de años. Y si no damos con la respuesta correcta, al menos generaremos hipótesis que, en muchas ocasiones, resultan apasionantes. Lo que sí es seguro es que, en todo ese proceso, las personas profesionales de la paleontología nos convertimos en detectives del pasado, al más puro estilo de miss Marple o monsieur Poirot y, al igual que estos inmortales personajes de Agatha Christie, muchas veces nos encontramos con trampas en nuestra búsqueda de la verdad.
 Fotografía aérea del enorme socavón producido en mayo de 2021 en la ciudad de Puebla, México, por un colapso del terreno, posiblemente provocado por un cambio en la compactación del suelo, fruto de variaciones en su humedad relativa. Imagen: Juan Carlos Sánchez Díaz / poblanerias.com / Wikimedia Commons
Fotografía aérea del enorme socavón producido en mayo de 2021 en la ciudad de Puebla, México, por un colapso del terreno, posiblemente provocado por un cambio en la compactación del suelo, fruto de variaciones en su humedad relativa. Imagen: Juan Carlos Sánchez Díaz / poblanerias.com / Wikimedia CommonsEn ocasiones nos topamos con noticias sorprendentes de que, de repente, el suelo se ha abierto bajo nuestros pies, quedando como testigo un enorme agujero que se traga todo lo que se encuentra sobre la superficie. La explicación a este evento, como no podía ser de otra manera, se encuentra en la Geología. La subsidencia es un término geológico con el que se define el hundimiento progresivo y relativamente lento del terreno. Aunque este hundimiento también se puede producir de manera súbita, provocando lo que se conoce como un colapso, que son los que abren los telediarios por su espectacularidad y peligro cuando suceden en zonas urbanizadas. Estos hundimientos generalmente están provocados por procesos naturales, tales como la compactación del sedimento superficial, el hundimiento del techo de una cavidad subterránea o un deslizamiento de tierra producido tras un terremoto. Pero también pueden ser inducidos o, al menos, acelerados por las acciones del ser humano: la extracción desmesurada del agua de los acuíferos desencadena una pérdida de la compactación de los materiales porosos subterráneos, que da lugar al desmoronamiento de los que tienen por encima; o una minería de interior mal planificada puede acabar con derrumbes de los techos de las galerías.
Os estaréis preguntando que a qué viene un cambio tan radical de tema entre el primer párrafo y el segundo. Pues aquí es donde os he puesto la trampa. Una trampa natural y muy geológica, por supuesto. Porque resulta que, en paleontología, denominamos trampa a hendiduras, socavones o fosas generadas por el hundimiento del terreno que actúan como grandes tumbas de animales, terminando, si todo va como esperamos, por dar lugar a un yacimiento fósil en el que se acumulan abundantes restos de organismos.
El proceso es el siguiente. De repente, y por motivos naturales, se produce un colapso del terreno generando un gran socavón o una amplia hendidura en el suelo. En el momento del hundimiento, algunos animales podían encontrarse justo encima de la porción de terreno que colapsó, siendo literalmente tragados por la tierra. Esta cavidad también se convertirá en un depósito de agua, acumulando tanto la de la lluvia como el agua de las avenidas de arroyos y riachuelos, atrayendo a sus profundidades a animales sedientos. O simplemente actuará como un agujero en el camino al que caerán aquellos animales que pasen despistados junto a él. Sea como fuere, todos aquellos animales, grandes y pequeños, que se precipiten en el socavón, quedarán atrapados en su interior, sin posibilidad de salir. Y esta acumulación de presas indefensas se convertirá en un imán para depredadores hambrientos, que no durarán en precipitarse al agujero para darse un festín, sin saber que será su última comida. Incluidos los carroñeros, atraídos en este caso por el olor de la carne en descomposición, también desconocedores de que correrán la misma suerte que sus presas, caerán de cabeza en la trampa. Con el paso del tiempo, todos estos restos quedarán enterrados por la acumulación de los sedimentos que, poco a poco, rellenan el socavón. Y, miles o millones de años después, acabarán preservados en forma de fósiles. Vamos, que el nombre de trampas naturales les viene que ni pintado a estos agujeros del terreno en los que se produce el depósito de multitud de animales.
Identificar si el yacimiento fósil que hemos encontrado es una trampa o no es relativamente fácil. El estudio geológico nos da muchas pistas, ya que se trata de zonas de acumulación de sedimentos con unos límites bien definidos y que se encuentran rodeados por rocas sólidas. Además, en ambientes naturales, hay una mayor presencia de microorganismos frente a organismos de mayor tamaño y un mayor porcentaje de herbívoros que de carnívoros. Sin embargo, en las trampas se encuentran grandes acumulaciones de animales macroscópicos y están invertidas las proporciones, apareciendo una gran abundancia de carnívoros (el anhelo de una presa fácil atrae a muchos depredadores, pero terminan convirtiéndose en el cazador cazado). Incluso el estado de conservación de los restos es casi excepcional en la mayoría de los casos, apareciendo esqueletos muy completos y con los huesos en conexión anatómica (muchos de los animales morían al caer al agujero y cuando llegaban los depredadores no les daba tiempo a desperdigar los restos porque terminaban corriendo la misma suerte que sus presas).
 Recreación de la trampa natural del yacimiento paleontológico del Cerro de los Batallones, Madrid, con los animales atrapados en su interior. Ilustración: David Zurita Gómez /behance.net
Recreación de la trampa natural del yacimiento paleontológico del Cerro de los Batallones, Madrid, con los animales atrapados en su interior. Ilustración: David Zurita Gómez /behance.netLos yacimientos paleontológicos de tipo trampa natural son más comunes de lo que pensamos. Un ejemplo son los yacimientos paleontológicos del Cerro de los Batallones, en Madrid, donde aparecen abundantes fósiles de macrovertebrados de finales del Periodo Mioceno que permiten conocer la fauna que hábito en el centro peninsular hace entre unos 11 y 9 millones de años. O el yacimiento del Complejo Galería, en la Sierra de Atapuerca, una trampa natural que aprovechaban las poblaciones de preneandertales para aprovisionarse de la carne de los animales que caían en ella.
Aunque la naturaleza hace trampas, también nos da una herramienta para evitarlas, la Geología. No es necesario esperar a ver como se abre la tierra y se traga un coche o una casa para saber que el terreno se puede hundir y engullir lo que se encuentre en su camino. Mientras paseamos por el campo, si miramos alrededor, las rocas, el paisaje, el tipo de sedimento e, incluso, los cambios de vegetación nos están dando pistas sobre la posibilidad de encontrarnos con socavones o hendiduras en donde podríamos caernos si damos un mal paso. Así que, si no queremos terminar formando parte de un yacimiento paleontológico muy particular en unos miles de años, más nos vale mirar bien donde pisamos para no caer en la trampa.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo ¡Es una trampa (paleontológica)! se ha escrito en Cuaderno de Cultura Científica.
Warren Weaver, de la física matemática a la traducción automática
No sobreestiméis la ciencia, no penséis que la ciencia es todo lo que hay, no os concentréis tanto en la ciencia que acabéis viviendo una vida deformada. La ciencia no es todo lo que hay, y la ciencia no es capaz de resolver todos los problemas de la vida. También hay muchos otros problemas muy importantes que la ciencia no puede resolver. Así que espero que no haya nadie en esta sala que vaya a pasar los próximos siete días sin leer algo de poesía. Espero que no haya nadie en esta sala que vaya a pasar los próximos siete días sin escuchar algo de música, algo de buena música, algo de música moderna, algo de música. Espero de verdad que no haya nadie aquí que no esté interesado en las artes creativas, interesado en el teatro, interesado en la danza. Espero que os intereséis seriamente por la religión, porque si no abrís vuestras mentes y vuestras actividades a esta gama de cosas, vais a llevar una vida demasiado estrecha.
Warren Weaver, Four Pieces of Advice to Young People, 1966.
 Warren Weaver (1940). Fuente: Wikimedia Commons.
Warren Weaver (1940). Fuente: Wikimedia Commons.
Warren Weaver nació el 17 de julio de 1894 en la ciudad de Reedsburg (Wisconsin, Estados Unidos). Era el pequeño de los dos hijos de Kittie Belle Stupfel e Isaiah Weaver, un farmacéutico. La familia se mudó a Madison en 1904. Allí Weaver asistió a la escuela secundaria e inició sus estudios superiores en la Universidad de Wisconsin.
Cuando era solo un niño, se divertía montando aparatos mecánicos y eléctricos, por ello, cuando ingresó en la universidad, deseaba convertirse en ingeniero. Pero algunos de sus profesores, en particular los matemáticos Max Mason (1877-1961) y Charles Slichter (1864-1946), le animaron para que se formara en física matemática.
Weaver se licenció en 1916 y comenzó a preparar su doctorado, que completó en 1921. Con Mason colaboró al principio de su carrera. De hecho, publicaron conjuntamente el libro The Electromagnetic Field en 1929.
En 1919 contrajo matrimonio con Mary Hemenway, una compañera de estudios, que fue profesora de latín e historia antigua y después ama de casa tras el nacimiento de su hijo Warren Jr. y su hija Helen.
De las matemáticas a la biología molecularWarren Weaver comenzó su carrera como profesor de matemáticas en varios centros universitarios, en particular en la Universidad de Wisconsin.
En 1931, Mason presidía la Fundación Rockefeller e invitó a Weaver a unirse a su equipo como responsable de la División de Ciencias Naturales. En ese momento, en muchas universidades del mundo se hablaba de la necesidad de un enfoque interdisciplinar en la investigación en ciencias biológicas.
Tras muchas dudas, entre otros motivos porque lamentaba dejar el mundo de la docencia y de la investigación, aceptó el puesto. Y sugirió que el programa científico de la fundación abandonara su anterior preocupación por las ciencias físicas hacia un «interés en estimular y ayudar a la aplicación a problemas biológicos básicos, de las técnicas, procedimientos experimentales y métodos de análisis tan eficazmente desarrollados en las ciencias físicas». La Fundación aceptó esta propuesta y, desde ese nuevo puesto, Weaver ejerció una profunda influencia en el desarrollo de la biología a nivel mundial.
Años más tarde, en una carta dirigida a J. M. H. Carson en junio de 1949, Warren Weaver expresaba su confianza en la relevancia de la investigación en biología molecular:
El siglo de la biología en el que estamos embarcados ahora ya no es cuestión de trivialidades. Es un movimiento de dimensiones realmente heroicas, uno de los grandes episodios de la historia intelectual del hombre. Los científicos que impulsan este movimiento hablan en términos de nucleoproteínas, de ultracentrifugadoras, de genética bioquímica, de electroforesis, de microscopía electrónica, de morfología molecular, de isótopos radiactivos. Pero no hay que confundirse por estos terribles términos y, sobre todo, no hay que dejar engañarse pensando que esto es mero artilugio. Ésta es la manera fiable de buscar una solución a los problemas del cáncer y la polio, los problemas del reumatismo y del corazón. Este es el conocimiento en el que debemos basar nuestra solución de los problemas de la población y alimentarios. Esto es el conocimiento de la vida.
Weaver también se desempeñó como asesor científico (1947-1951), administrador (1954) y vicepresidente (desde 1958) del Instituto Sloan-Kettering para la Investigación del Cáncer.
Incursiones en la teoría de la comunicaciónA Weaver le entusiasmaban la teoría de la probabilidad y la estadística. En 1963 publicó Lady Luck. The Theory of Probability, un pequeño libro sobre probabilidad dirigido a un público no experto. Aunque tenía una enorme habilidad con las palabras, estimaba que su aportación matemática durante su etapa universitaria se reducía a soluciones rutinarias de algunos problemas, pero que no eran contribuciones imaginativas reales al avance del conocimiento matemático.
Sin embargo, escribió una introducción expositiva a la teoría matemática de la comunicación en un artículo aparecido en The Mathematical Theory of Communication (1949) en el que Weaver sugería que había tres niveles de problemas en la comunicación:
- Un problema técnico: ¿con qué precisión se pueden transmitir los símbolos de la comunicación?
- Un problema semántico: ¿con qué precisión los símbolos emitidos transmiten el significado deseado?
- Un problema de efectividad: ¿en qué medida el significado recibido afecta la conducta de la manera deseada?
El primer artículo de este libro (que ocupa prácticamente dos tercios de la obra) tiene como autor al matemático y criptógrafo Claude E Shannon (1916-2001) recordado como «el padre de la teoría de la información».
La pasión por la traducción automáticaTambién en 1949 promovió la investigación para el desarrollo de sistemas de traducción automática tras un informe para la Fundación Rockefeller en el que señalaba que existía una analogía entre la decodificación mecánica y la traducción.
Naturalmente, uno se pregunta si el problema de la traducción podría ser tratado como un problema de criptografía. Cuando veo un artículo en ruso, digo: «Esto está escrito en inglés, pero ha sido codificado con algunos símbolos extraños. Ahora procederé a descifrarlo».
Carta de Warren Weaver a Norbert Wiener, 1947
En este sentido, y fascinado por Las aventuras de Alicia en el país de las maravillas de Lewis Carroll (1832-1898), Weaver acumuló 160 versiones del libro en 42 idiomas. En 1964, escribió el libro Alice in many tongues; the translations of Alice in Wonderland, sobre la historia de las diferentes traducciones de esta obra, y diseñó una manera de evaluar la calidad de diferentes versiones, estudiando las bromas y giros de Una merienda de locos.
 Páginas 108 y 109 de Alice in many tongues; the translations of Alice in Wonderland. Fuente: Captura de pantalla de Internet Archive.
Páginas 108 y 109 de Alice in many tongues; the translations of Alice in Wonderland. Fuente: Captura de pantalla de Internet Archive.
Gracias a sus numerosos contactos, para llevar a cabo esta tarea consiguió la colaboración de un importante grupo de colaboradores en el ejercicio de evaluación. Entre estas personas destacamos a la antropóloga Margaret Mead (para valorar la traducción a la lengua pidgin del Pacífico Sur), el alcalde de Jerusalén Teddy Kollek o el bioquímico y Premio Nobel Hugo Theorell (para la traducción al sueco).
Aunque Wiener falleció el 24 de noviembre de 1978, el proyecto Alice in a World of Wonderlands: the Translations of Lewis Carroll’s Masterpiece (2015) continuó con el análisis de las traducciones de Alicia… en 174 idiomas, en una línea similar a la del matemático y administrador científico.
Referencias
- Warren Weaver, MacTutor History of Mathematics Archive, St Andrews University
- Mina Rees, Warren Weaver (1894-1978), Bibliographical Memoir, National Academy of Sciences, 1987
- Warren Weaver, Wikipedia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
El artículo Warren Weaver, de la física matemática a la traducción automática se ha escrito en Cuaderno de Cultura Científica.

