Naukas Bilbao 2024: 18 de enero de 1902
La decimocuarta edición del mayor evento de divulgación científica volvió al Palacio Euskalduna de Bilbao durante los días 19, 20, 21 y 22 de septiembre de 2024.

Oskar González Mendía (autor de kimikArte) doctor en químicas y profesor en la Facultad de Bellas Artes de la UPV/EHU se dedica, entre otras cosas, a resolver misterios. Entre ellos por qué el 18 de enero de 1902, un día en el que no pasó absolutamente nada, es interesante.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2024: 18 de enero de 1902 se ha escrito en Cuaderno de Cultura Científica.
Las ballenas ven en blanco y negro
 Ojo de una ballena yubarta, de la familia Balaenopteridae Foto: Rachel Moore via Instagram
Ojo de una ballena yubarta, de la familia Balaenopteridae Foto: Rachel Moore via InstagramEn la Facultad de Medicina de la Universidad del País Vasco hemos analizando los ojos de tres rorcuales varados en diferentes playas de España entre 2019 y 2021. Y su estudio nos ha ayudado a saber cómo ven las ballenas.
Las tres ballenas que han servido para nuestra investigación tenían medidas similares, alrededor de 18 metros de largo, y pesaban 20 toneladas. Cada ojo era del tamaño de una pelota de balonmano (13 cm de diámetro) y pesaba un kilo.
Ojos para sobrevivir en las profundidadesLos rorcuales, pertenecientes a la familia Balaenopteridae, son cetáceos conocidos por su velocidad e hidrodinámica, lo que les ha valido el apodo de “galgos de los mares”.
Estos animales marinos carecen de dientes y se alimentan filtrando krill en las zonas superficiales del océano. Su adaptación al medio marino ha dotado a sus órganos, especialmente los ojos, de características únicas que les permiten sobrevivir en las profundidades.
Ballenas varadasEl primer ojo provenía de un rorcual común que varó en Sopelana (Vizcaya, País Vasco) tras la borrasca Helena en febrero de 2019. Tener acceso a sus ojos nos permitió realizar estudios anatómicos y moleculares, además de cultivar las neuronas ganglionares y las células gliales de la retina, conocidas como glía de Müller.
El segundo ojo, de un rorcual boreal, se obtuvo en la playa de Tapia de Casariego (Asturias) durante la borrasca Filomena en enero de 2021. Este material permitió confirmar los hallazgos previos e inmortalizar las células de Müller para investigaciones futuras.
El tercer ojo correspondía a un rorcual que varó en Tavernes (Valencia) en mayo de 2021. En este caso, el ojo de la ballena nos sirvió para corroborar nuevamente los estudios anatómicos y moleculares realizados con los otros ejemplares. Los resultados se publicaron en varias revistas científicas.
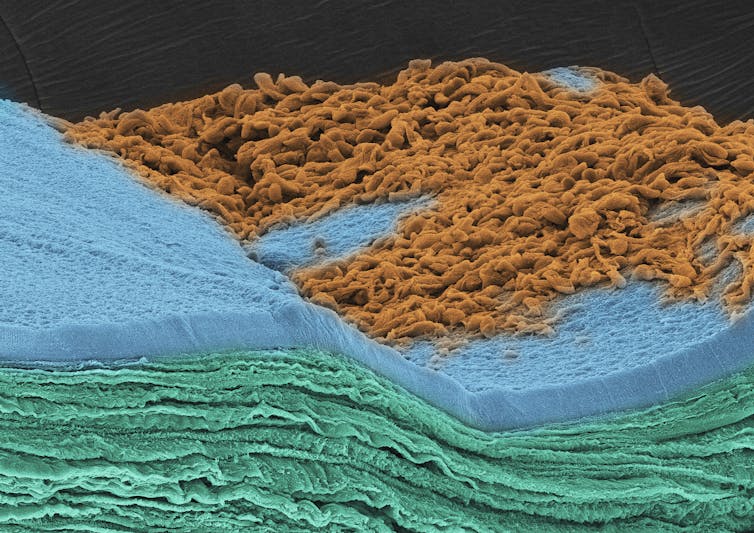 Fotografía de microscopía electrónica de barrido de la córnea del ojo de una de las ballenas. Fotografía premio de la Sociedad Española de Oftalmología.
Fotografía de microscopía electrónica de barrido de la córnea del ojo de una de las ballenas. Fotografía premio de la Sociedad Española de Oftalmología.Elena Vecino y Luis LópezAdaptaciones anatómicas del ojo
En los ojos de los rorcuales encontramos adaptaciones extraordinarias que les permiten resistir las altas presiones y la escasa luz de las profundidades marinas:
- La córnea, que permite la entrada de luz al ojo, es hasta cuatro veces más gruesa que la humana. Este refuerzo, junto con la esclera, protege al órgano visual contra las presiones extremas en el hábitat marino profundo.
- El cristalino en los rorculaes es esférico, para facilitar la visión bajo el mar, a diferencia de los mamíferos terrestres, que es lenticular.
- La esclera, o parte blanca del ojo, es extremadamente gruesa en estos cetáceos: llega a medir hasta 4 centímetros, en contraste con el medio milímetro en humanos. Está formada por colágeno endurecido, lo que protege la retina como si estuviera dentro de un cofre.
- El cuerpo cavernoso es un tejido que rodea el nervio óptico y contiene numerosos vasos sanguíneos y músculo liso. En la ballena, cuando se llena de sangre, impulsa el ojo hacia el exterior, permitiendo enfocar de un modo similar a como lo hace un telescopio.
Estos resultados han sido publicados en el capítulo ¿Cómo ven las ballenas? del libro Mamíferos marinos.
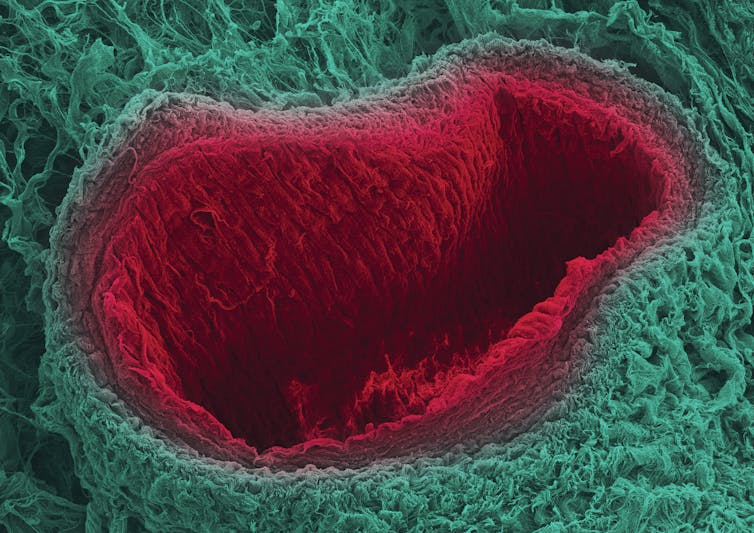 Vaso del cuerpo cavernoso del ojo de la ballena, rodeado de fibras de colágeno. Fotografía de microscopía electrónica de barrido.
Vaso del cuerpo cavernoso del ojo de la ballena, rodeado de fibras de colágeno. Fotografía de microscopía electrónica de barrido.Elena Vecino y Luis LópezCaracterísticas visuales: visión en blanco y negro
Nuestro análisis reveló que la retina de los rorcuales carece de conos, las células responsables de percibir colores y luz intensa. Por el contrario, está compuesta únicamente por bastones, que son sensibles a bajas intensidades lumínicas y funcionan en condiciones de poca luz.
Esto indica que las ballenas solo ven en blanco y negro, una adaptación al entorno oscuro del océano.
Además, las neuronas melanopsínicas, responsables de informar al cerebro sobre los ciclos de luz/oscuridad (denominados ritmos circadianos), están muy desarrolladas en las ballenas. Esto nos revela que tienen alta sensibilidad a la luz y pueden percibir las intensidades lumínicas variables en los distintos hemisferios, lo que les podría ayudar a orientarse.
Aunque los ojos de las ballenas son grandes, su densidad de neuronas ganglionares, encargadas de procesar la información visual y enviarla al cerebro, es muy baja. Esto significa que la cantidad de señales visuales que llegan al cerebro es limitada y da como resultando una visión reducida, como indicamos en el estudio publicado en Frontiers in Anatomy. Metafóricamente hablando, las ballenas podrían llevar el pin de baja visión.
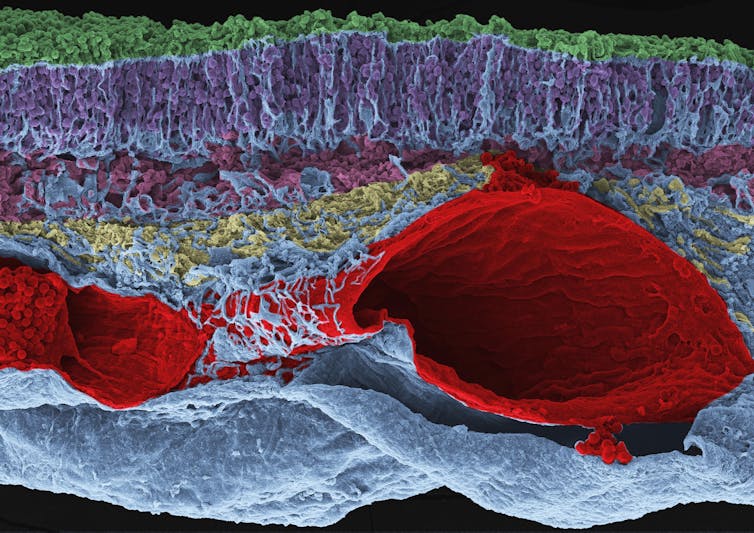 Microscopía electrónica de barrido de la retina de una ballena, coloreada digitalmente. Premio Scientific American NeuroArt de la SENC.
Microscopía electrónica de barrido de la retina de una ballena, coloreada digitalmente. Premio Scientific American NeuroArt de la SENC.Elena Vecino Cordero y Luis López VecinoReconocimientos artísticos
Además de su valor científico, las imágenes obtenidas durante esta investigación han sido reconocidas por su belleza y han ganado varios premios nacionales e internacionales, entre ellos, el de Scientific American NeuroArt.
Estas fotografías se han expuesto en siete museos marítimos, de fotografía y galerías de arte nacionales e internacionales. En la actualidad está en el Museo Nacional de Ciencias Naturales de Madrid, donde permanecerá hasta finales de mayo.
Las exposiciones han sido adaptadas a personas invidentes y con baja visión, incorporando fotografías texturizadas, audioguías y recorridos señalizados con cintas podotactiles. Además, hemos editado tres vídeos que cuentan la historia de la investigación desde el comienzo hasta la exposición: Elena y la ballena; ¿Cómo ven las ballenas? y Cómo adaptar una exposición fotográfica a personas que no ven.
El estudio de los ojos de estos tres rorcuales ha permitido conocer en profundidad las adaptaciones anatómicas y funcionales que posibilitan su vida en el medio marino. Estas investigaciones no solo arrojan luz sobre la biología de estos cetáceos: llevadas al museo, permiten destacar la importancia de preservar y estudiar la biodiversidad de nuestros océanos.![]()
Sobre las autoras: Elena Vecino Cordero, Catedrática de Biología Celular (UPV/EHU), Licenciada en Bellas Artes, Life Member, Clare Hall Cambridge (UK). Directora del Grupo Oftalmo-Biología Experimental (GOBE), Universidad del País Vasco / Euskal Herriko Unibertsitatea y Luis López Vecino, Profesor asociado del Grado en desarrollo de aplicaciones 3D interactivas y videojuegos, Universidad de Salamanca
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Las ballenas ven en blanco y negro se ha escrito en Cuaderno de Cultura Científica.
La impredecibilidad de la sencillez: autómatas celulares
Pocos, como el matemático húngaro John von Neumann, fueron capaces de vislumbrar que el próximo gran giro de guion de la ciencia no vendría de la mano, esta vez, de los campos de la «energía, el trabajo, la fuerza o el movimiento», sino del «control, la programación, el procesamiento de la información, las comunicaciones, la organización y los sistemas» (Burks 1969). Con la llegada de los primeros computadores tras la Segunda Guerra Mundial, o, en otras palabras, las primeras máquinas sofisticadas utilizadas para ayudarnos con tareas mentales en lugar de físicas, se puso sobre la mesa, de manera realista, la posibilidad de recrear artificialmente la vida. Así nació la cibernética, propuesta por Norbert Wiener durante la década de los años cuarenta del siglo XX, y así nacieron los primeros modelos computacionales que buscaban simular procesos que solo se encontraban en la naturaleza a través de operaciones lógicas.
Konrad Zuse, ingeniero alemán y pionero de la computación moderna ya hizo alguna aproximación al problema. Poco después, en el Laboratorio Nacional de Los Álamos, John Von Neumann, por un lado, empezó a explorar la idea de que un sistema computacional pudiera replicarse a sí mismo de forma autónoma; y Stanislaw Ulam, por otro, trató de averiguar si era posible que, de reglas matemáticas sencillas, pudieran surgir estructuras, patrones o comportamientos complejos. Ulam utilizó para ello cuadrículas bidimensionales en las que representaba datos marcando —o no— diferentes celdas. Raúl Ibánez puso, recientemente, un magnífico ejemplo del trabajo del matemático de origen polaco en «Números felices para siempre». Von Neumann utilizó el método de Ulam para crear uno de sus sistemas autorreplicantes. No obstante, y aunque fue el primer autómata celular que se conoce, aquel modelo pasó sin pena ni gloria y quedó olvidado durante décadas.
 Hay pocas ramas de las matemáticas, la física y la computación en las que John von Neumann (1903-1957) no realizara aportaciones fundamentales. En este caso, junto con su colega en Los Álamos Stanislaw Ulam.
Hay pocas ramas de las matemáticas, la física y la computación en las que John von Neumann (1903-1957) no realizara aportaciones fundamentales. En este caso, junto con su colega en Los Álamos Stanislaw Ulam.Créditos: Los Álamos National Laboratory y dominio público
No fue hasta la década de los setenta cuando, en la sección de matemática recreativa de Scientific American, Martin Gardner planteó, a modo de juego, una ocurrencia, sencilla pero fascinante, que había tenido el matemático inglés John Conway. Con el nombre de «juego de la vida», por su semejanza con las dinámicas de evolución de poblaciones de organismos, se regía por unas reglas muy sencillas.
Para jugar al juego de la vida solo se necesita una cuadrícula en la que podamos marcar casillas —puede ser un tablero de ajedrez o de go y algunas piezas, papel y lápiz… aunque lo más fácil e ilustrativo a día de hoy es utilizar un ordenador—. Las casillas marcadas serían el equivalente a organismos o células que podemos hacer evolucionar de forma completamente autónoma en nuestro Mundo Cuadrícula, a partir de una configuración geométrica inicial, con tan solo aplicar una y otra vez las siguientes reglas:
-
Supervivencia: una célula con dos o tres vecinas sobrevivirá en la próxima generación.
-
Muertes:
-
Una célula con cuatro o más vecinas morirá por superpoblación.
-
Una célula con una o ninguna vecina morirá por aislamiento.
-
-
Nacimientos: si una celda vacía está rodeada por tres células, en la siguiente generación nacerá ahí una nueva.
Y nada más, si nos fijamos, en realidad el juego «se juega a sí mismo». Nosotros solo decidimos la configuración inicial de células.
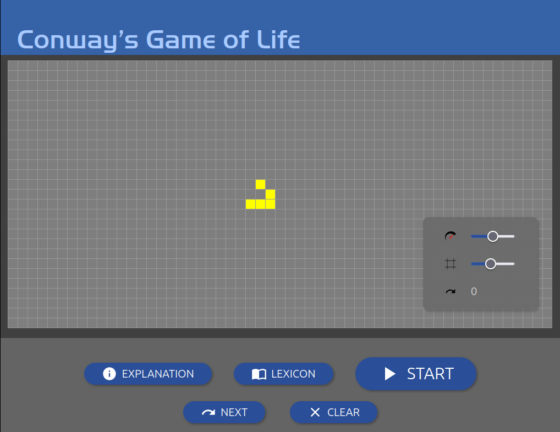 Existen numerosos sitios de internet en los que se puede jugar al juego de la vida, como https://playgameoflife.com/. Existen también librerías de patrones y todo un universo alrededor de las posibles evoluciones que se pueden conseguir a partir de diversas configuraciones iniciales.
Existen numerosos sitios de internet en los que se puede jugar al juego de la vida, como https://playgameoflife.com/. Existen también librerías de patrones y todo un universo alrededor de las posibles evoluciones que se pueden conseguir a partir de diversas configuraciones iniciales.Como el modelo que planteó Von Neumann, el juego de la vida es un autómata celular, aunque algo más sencillo. La popularización de la idea a través de una revista de divulgación científica llevó a matemáticos tanto aficionados como profesionales a experimentar con infinitud de configuraciones iniciales y a descubrir fenómenos muy interesantes; desde patrones estables —no cambian de una generación a otra— y ciclos que se repiten, hasta figuras —«planeadores»— que se deslizan por la cuadrícula dando la sensación de movimiento e incluso estructuras que se replican a sí mismas. Hay auténticas obras de arte geométricas generadas con este sencillo juego en internet —huevo de Pascua: probad a buscar en Google «juego de la vida»—.
 De izquierda a derecha: a) Configuración estable. b) Configuración cíclica (púlsar). c) Planeador (da la sensación de deslizarse por la pantalla). d) Cañón de planeadores de Gosper. Existen numerosos archivos de patrones, por ejemplo: https://conwaylife.appspot.com/library/. Créditos: a), b), c) Dominio público. d) CC BY-SA 3.0/Lucas Vieira.
De izquierda a derecha: a) Configuración estable. b) Configuración cíclica (púlsar). c) Planeador (da la sensación de deslizarse por la pantalla). d) Cañón de planeadores de Gosper. Existen numerosos archivos de patrones, por ejemplo: https://conwaylife.appspot.com/library/. Créditos: a), b), c) Dominio público. d) CC BY-SA 3.0/Lucas Vieira.
Los trabajos de Von Neumman, Ulam y Conway llevaron en los años ochenta al físico Stephen Wolfram a investigar estos autómatas celulares, en esta ocasión, unidimensionales —consisten únicamente en una fila de celdas y se conocen como «elementales»—, y los clasificó en función de la complejidad de su comportamiento en:
-
Clase 1: alcanzan estados estables.
-
Clase 2: generan patrones oscilatorios o periódicos.
-
Clase 3: generan patrones seudoaleatorios o caóticos.
-
Clase 4: generan estructuras complejas pero ordenadas.
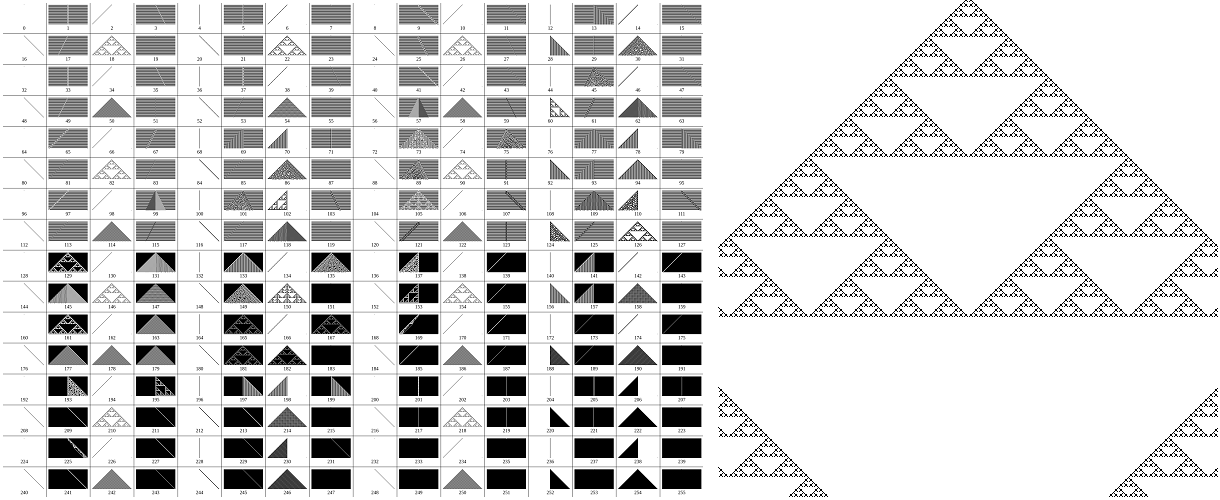 Stephen Wolfram hizo una clasificación de diversas reglas para los autómatas celulares elementales. De algunas de ellas se pueden obtener patrones realmente complejos y, por qué no, bellos, como el fractal que se obtiene tras aplicar la regla 90 (ampliado la derecha). Créditos: CC BY-SA
Stephen Wolfram hizo una clasificación de diversas reglas para los autómatas celulares elementales. De algunas de ellas se pueden obtener patrones realmente complejos y, por qué no, bellos, como el fractal que se obtiene tras aplicar la regla 90 (ampliado la derecha). Créditos: CC BY-SADe nuevo quedó patente que un sistema de reglas muy sencillo en una cuadrícula podía dar lugar a patrones complejos. Esto llevó a Wolfram a aplicar la teoría de autómatas celulares, de una forma cada vez más elaborada, al campo de la física, y a plantear que tal vez el universo podría describirse con un modelo computacional de este tipo… no sin la controversia que suelen despertar este tipo de aseveraciones en el mundo de la física.
Ya se tomen los autómatas celulares como un juego o se pretendan aplicar a campos más tangibles, lo cierto es que son una fuente de sorpresas matemáticas. Su potencial y, seguramente, también su belleza inspiraron al escritor de ciencia ficción Greg Egan para escribir en 1994 su novela Ciudad Permutación, un espectacular homenaje a las matemáticas, la computación y la vida.
 Última edición en inglés de Ciudad Permutación, de Greg Egan (Gollancz). Se publicó en español en 1998, lamentablemente, está descatalogada.
Última edición en inglés de Ciudad Permutación, de Greg Egan (Gollancz). Se publicó en español en 1998, lamentablemente, está descatalogada.
Bibliografía
Burks, A. W. (1969). Von Neumann’s self-reproducing automata. University of Michigan. Computer and Communication Sciences Department. https://fab.cba.mit.edu/classes/MAS.865/topics/self_replication/Burks.pdf
Gardner, M. (octubre de 1970). The fantastic combinations of John Conway’s new solitaire game “life”. Scientific American, 223(4), 120-123.
Wolfram, S. (2002). A new kind of science. Wolfram Media.
.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo La impredecibilidad de la sencillez: autómatas celulares se ha escrito en Cuaderno de Cultura Científica.
Números felices para siempre
Como comentaba en mi anterior entrada del Cuaderno de Cultura Científica, titulada Algunas propiedades matemáticas del número 2025, algunas personas del ámbito de las matemáticas nos dedicamos a buscar propiedades matemáticas del número al que corresponde el nuevo año, en este caso le tocaba el turno al 2.025, para incluir alguna de ellas en nuestras felicitaciones navideñas para compartir en las redes sociales, enviar a nuestros contactos por whatsapp o para diseñar nuestras tarjetas navideñas físicas. Por este motivo, dediqué esa entrada a algunas propiedades matemáticas del mencionado número, el dos mil veinticinco.
En particular, utilicé para mi tarjeta de año nuevo que el número 2.025 puede escribirse como la suma de los cubos de todas las cifras básicas de nuestro sistema de numeración, es decir, todos los números de un solo dígito:
13 + 23 + 33 + 43 + 53 + 63 + 73 + 83 + 93 = 2.025,
donde no incluí el cero ya que cero elevado al cubo es cero. Pero, además, se comentaba en dicha entrada que este número es un número cuadrado (de hecho, es el cuadrado de un número triangular, 45), suma de números triangulares consecutivos, un número trapezoidal (o cortés), que puede expresarse como suma de números naturales consecutivos de catorce maneras distintas, un número octogonal centrado, un número deficiente, un número tau, un número duffiniano o un número de Harshad. Sin embargo, se podría haber ampliado esta familia de propiedades a otras, como escribir el 2.025 con todas las cifras básicas no nulas (1, 2, 3, 4, 5, 6, 7, 8, 9) en orden creciente, o decreciente, intercalando los signos de las operaciones aritméticas básicas (+, –, x, /) y potencias, como aparece en la siguiente imagen, que es el típico problema de ingenio, aunque para diferentes números.
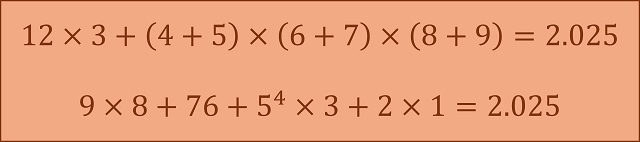 El número 2.025 expresado con todas las cifras básicas no nulas (1, 2, 3, 4, 5, 6, 7, 8, 9) en orden creciente, o decreciente, intercalando los signos de las operaciones aritméticas básicas (+, –, x, /) y potencias
El número 2.025 expresado con todas las cifras básicas no nulas (1, 2, 3, 4, 5, 6, 7, 8, 9) en orden creciente, o decreciente, intercalando los signos de las operaciones aritméticas básicas (+, –, x, /) y potenciasEl año 2.026 también tendrá su tarjeta de año nuevo
Cuando compartí en las redes sociales el enlace de la entrada titulada Algunas propiedades matemáticas del número 2025, algunas personas me comentaron que sería difícil encontrar otro año con tantas propiedades matemáticas como el 2.025. Lo cierto es que, aunque haya años, bueno, los números de los años, con más propiedades matemáticas o propiedades más sorprendentes que otros, podemos obtener curiosas propiedades para todos los números. Así, de cara al año que viene, el 2.026 también verifica algunas curiosas propiedades. Por ejemplo, podemos expresar el 2.026 con todas las cifras básicas no nulas (1, 2, 3, 4, 5, 6, 7, 8, 9) en orden creciente, o decreciente, intercalando los signos de las operaciones aritméticas básicas (+, –, x, /) y potencias, que podéis ir reservando para dentro de un año.
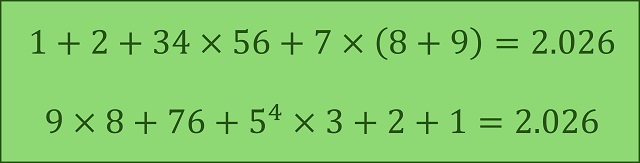 El número 2.026 expresado con todas las cifras básicas no nulas (1, 2, 3, 4, 5, 6, 7, 8, 9) en orden creciente, o decreciente, intercalando los signos de las operaciones aritméticas básicas (+, –, x, /) y potencias
El número 2.026 expresado con todas las cifras básicas no nulas (1, 2, 3, 4, 5, 6, 7, 8, 9) en orden creciente, o decreciente, intercalando los signos de las operaciones aritméticas básicas (+, –, x, /) y potencias
Pero como comentaba, este número tiene muchas otras propiedades. Por ejemplo, puede expresarse como suma de números naturales consecutivos
2.026 = 505 + 506 + 507 + 508,
o también pertenece a la familia de números naturales de la que vamos a hablar en esta entrada, los números felices. Es decir, el 2.026 es un número feliz.
Números felicesDefinición: Un número es feliz (en algunos textos también se han sido llamados números elegantes) si al sumar los cuadrados de sus dígitos, repetir esta misma operación sobre el resultado obtenido e iterar el proceso suficientes veces, la sucesión de números resultante alcanza en algún momento el número 1. En caso contrario, se dice que el número es infeliz o triste.
Por ejemplo, el número 7 es un número feliz ya que si consideramos la sucesión de resultados del algoritmo “sumar los cuadrados de sus dígitos” de manera recursiva nos queda lo siguiente:
7, 49, 97 (= 42 + 92), 130 (= 92 + 72), 10 (= 12 + 32 + 02), 1 (= 12 + 02),
es decir, la sucesión se estaciona en el número 1. Sin embargo, si consideramos el número 5 la sucesión que se genera con el anterior algoritmo es
5, 25, 29 (= 22 + 52), 85 (= 22 + 92), 89 (= 82 + 52), 145 (= 82 + 92), 42 (= 12 + 42 + 52), 20 (= 42 + 22), 4 (= 22 + 02), 16 (= 42), 37 (= 12 + 62), 58 (= 32 + 72), 89 (= 52 + 82), …
que, como podemos observar, se mete en un ciclo sin fin, formado por los números 89, 145, 42, 20, 4, 16, 37 y 58, por lo tanto, el número 5 no es un número feliz.
Más aún, como comentábamos más arriba, el número 2.026 es un número feliz, puesto que la sucesión de resultados de aplicar de manera recursiva el algoritmo “sumar los cuadrados de sus dígitos” al 2.026 y después a los respectivos resultados que se van obteniendo es 2.026, 44, 32, 13, 10 y 1. Por lo tanto, la sucesión llega al 1, donde se estanca, en cinco pasos. De manera que las próximas navidades se podría decir que el nuevo año “es un año feliz”, trasladando la propiedad del número al año. El anterior año feliz fue el 2.019 y el siguiente será el 2.030.
Además, de la definición se deduce fácilmente que, dado un número feliz, cualquier otro número que se obtenga como permutación de sus dígitos sigue siendo feliz. Por ejemplo, como 2.026 es un número feliz, también lo son 226, 262, 622, 2.062, 2.206, 2.260, 2.602, 2.620, 6.022, 6.202 y 6.220.
El origen de estos números es incierto. En una de las referencias clásicas sobre los mismos, el libro de Richard Guy Unsolved Problems in Number Theory, se menciona que llamaron la atención del matemático inglés Reg Allenby, cuando su hija le mostró que se los habían enseñado en la escuela. Aunque parece ser que tienen su origen en Rusia.
No es difícil calcular, a mano o con una calculadora, los primeros números felices. En concreto, los menores de 200 son 1, 7, 10, 13, 19, 23, 28, 31, 32, 44, 49, 68, 70, 79, 82, 86, 91, 94, 97, 100, 103, 109, 129, 130, 133, 139, 167, 176, 188, 190, 192, 193. De hecho, los números felices son la sucesión A007770 de la enciclopedia on-line de sucesiones de números enteros. Al realizar el algoritmo para los números menores de 200 se observará que para los demás números, los infelices, la sucesión termina siempre en el bucle del 89. De hecho, estas son las dos únicas posibilidades que existen, como aparece mencionado en el libro de Richard Guy, aunque demostrado mucho antes, en 1945, en el artículo de Arthur Porges titulado A Set of Eight Numbers (Un conjunto de ocho números).
Teorema: Si para cada número natural se considera la sucesión de números formada por los resultados del algoritmo “sumar los cuadrados de sus dígitos” considerado de forma iterada a partir de dicho número, esta se estacionará en el número 1 o entrará en el ciclo infinito formado por los ocho números 89, 145, 42, 20, 4, 16, 37 y 58.
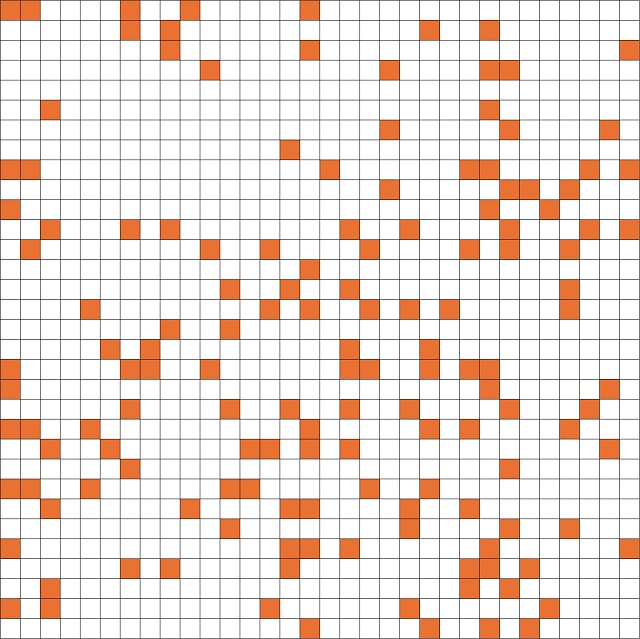 Números felices en la espiral de Ulam. La espiral de Ulam es una estructura geométrica plana, de tipo reticular, en la que los números naturales son escritos en espiral, empezando en el 1 y en el sentido contrario a las agujas del reloj, destacando los números primos (en este caso, los números felices), de tamaño 32 x 32, 1.024 celdas
Números felices en la espiral de Ulam. La espiral de Ulam es una estructura geométrica plana, de tipo reticular, en la que los números naturales son escritos en espiral, empezando en el 1 y en el sentido contrario a las agujas del reloj, destacando los números primos (en este caso, los números felices), de tamaño 32 x 32, 1.024 celdas
Otra curiosa propiedad del algoritmo “sumar los cuadrados de sus dígitos” es que para cualquier número natural n siempre existe otro número natural m tal que el resultado de aplicar el algoritmo “sumar los cuadrados de sus dígitos” a m nos genera n. Esto es muy fácil de demostrar puesto que, en particular, podemos tomar m igual al número formado por n unos (111…111), que trivialmente nos da n al aplicarle el algoritmo.
¿Cuántos números felices hay?Lo primero que nos podríamos plantear es si existe un número infinito de números felices. La respuesta es trivialmente afirmativa, ya que es muy fácil construir familias infinitas de números felices, sin más que añadir ceros a un número que es feliz. Por ejemplo, el 1 es feliz, así como los números 10, 100, 1.000, 10.000, 100.000, …, en general, 10n es un número feliz para cualquier número natural n, que es una familia infinita.
La siguiente cuestión relacionada con esta pregunta es la densidad de números felices dentro de los naturales, es decir, cuál es el porcentaje de números felices dentro de los números naturales. Si miramos la anterior lista de números felices, hay 20 dentro de los 100 primeros, luego un porcentaje del 0,2. Si continuamos con los números felices menores, o iguales, que las potencias de 10, tenemos que hay 143 dentro de los 1.000 primeros (un porcentaje del 0,143); 1.442 dentro de los 10.000 primeros (un porcentaje del 0,1442); 14.377 dentro de los 100.000 primeros (un porcentaje del 0,14377); 143.071 dentro de los 1.000.000 primeros (un porcentaje del 0,143071); y así podemos continuar con los primeros datos, que aparecen en la siguiente tabla.
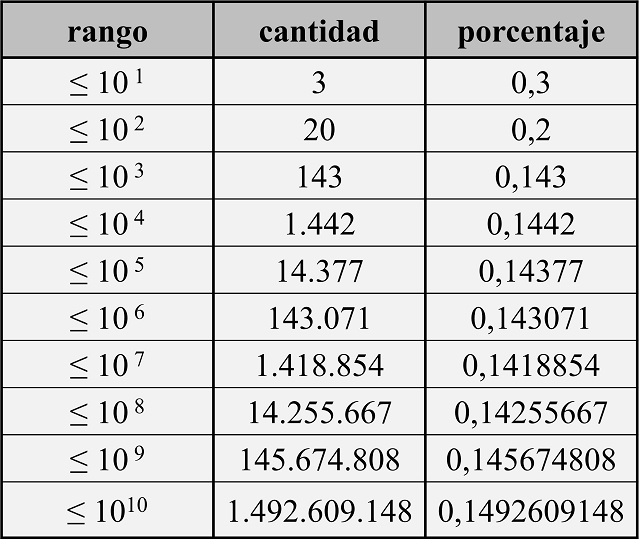
La lista de los porcentajes para números menores, o iguales, que las potencias de 10 (lo que podríamos denominar densidad relativa) empieza con las siguientes cantidades:
1; 0,3; 0,2; 0,143; 0,1442; 0,14377; 0,143071; 0,1418854; 0,14255667; 0,145674808; 0,1492609148; 0,15091199357; 0,149121303586; 0,1443278000870; 0,13770853279685; 0,130660965862333; 0,1245219117260664; 0,12024696404768025; 0,118226055080025491; 0,1183229962059381238; 0,12005034444292997294; etc…
que, salvo las primeras, está en un rango entre 0,118 y 0,151. Richard Guy mencionaba en su libro Unsolved Problems in Number Theory que “parece que 1/7 de los números naturales es feliz” (1 de cada 7), sin embargo, no parece que esto sea realmente así, no existe una densidad “límite”. De hecho, en el artículo On the density of happy numbers, del matemático estadounidense Justin Gilmer, publicado en la revista Integers (2013), se muestra un gráfico (véase la siguiente imagen) en el que se muestra cómo el porcentaje de números felices crece y decrece sin confluir a una cantidad fija.
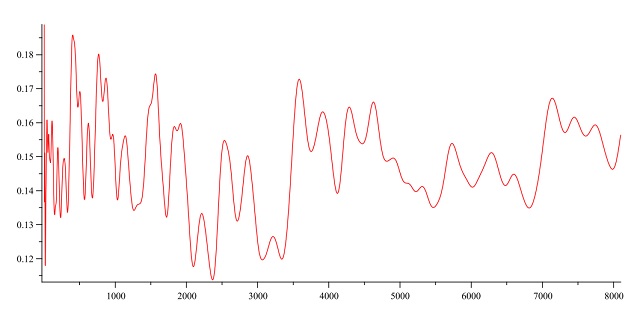 Densidad relativa de números felices menores que 10n
Densidad relativa de números felices menores que 10nDe hecho, Gilmer demuestra que la densidad superior está por encima de 0,18577 y la densidad inferior por debajo de 0,1138.
Números felices consecutivosSi se mira la lista anterior de los números felices menores que 200, se puede observar que existen algunos números felices consecutivos, como 31-32, 129-130 y 192-193, de hecho, existen infinitas parejas de números felices consecutivos. En el libro La gran familia de los números se incluye una actividad relacionada con esto mismo, que ya apareció en el libro Desafíos Matemáticos, propuestos por la Real Sociedad Matemática Española (SM-RSME, 2012), el siguiente sencillo y divertido desafío, que dejo aquí para vuestra diversión.
Problema: Encontrar infinitas parejas de números felices consecutivos.
Si se continuan buscando cadenas de números felices consecutivos se descubrirá que el primer trío es el formado por los números 1.880, 1.881 y 1.882, los tres números felices, como puede comprobarse; el primer cuarteto es el formado por los números 7.839, 7.840, 7.841 y 7.842; mientras que el primer quinteto de números felices consecutivos es el formado por los números 44.488, 44.489, 44.490, 44.491 y 44.492, que aparecen citados por Richard Guy en su libro Unsolved Problems in Number Theory, quien se cuestiona además si existen cadenas de números felices consecutivos de cualquier longitud.
Los matemáticos saudíes Esam El-Sedy y Samir Siksek demostraron, en su artículo On happy numbers, publicado en la revista Rocky Mountain Journal of Mathematics (2000), que la respuesta es afirmativa, es decir, existen cadenas de números felices consecutivos de cualquier longitud.
Una reflexión finalVamos a terminar aquí esta entrada del Cuaderno de Cultura Científica, aunque podríamos haber continuado por dos caminos distintos. El primero hablando de números felices que además satisfacen otras propiedades matemáticas, como ser primos, cuadrados, triangulares, capicúas, de Fibonacci u otras propiedades.
Por ejemplo, los números felices primos menores que 500 son: 7, 13, 19, 23, 31, 79, 97, 103, 109, 139, 167, 193, 239, 263, 293, 313, 331, 367, 379, 383, 397, 409 y 487, sucesión que aparece mencionada en el episodio titulado 42 (el séptimo de la tercera etapa) de la serie británica Doctor Who, emitido en 2017, donde se necesita introducir un número para abrir una puerta, que es el siguiente a la sucesión 313, 331, 367… (véase la siguiente imagen) y la respuesta es 379, que es el siguiente número feliz primo.
 Fotograma del episodio 42 de la serie británica Doctor Who
Fotograma del episodio 42 de la serie británica Doctor WhoMientras que el segundo camino, interesante también, hablando de que la felicidad de los números depende de la base de numeración en la que estén representados (hasta ahora nosotros hemos trabajado en la base natural, la base 10) y no es una característica del propio número. Por ejemplo, el número 160 que no es feliz en la base 10, sí lo es en base 6. Como 160 = 4 36 + 2 6 + 4 1, se representa en dicha base como 424, que al hacer la suma de sus dígitos al cuadrado sale 10 (36 en base decimal) y repitiendo la operación queda 1. El número 5, que no era feliz en base 10, tampoco lo es en base 6, ya que la sucesión asociada, expresada en la base 6, es 5, 41, 25, 45, 105, 42, 32, 21, 5, produciéndose un bucle infinito, que es el único que existe para esta base. O el 7, que es un número feliz en base decimal, no lo es en base senaria, ya que cae en el ciclo del 5.
Bibliografía
1.- Ibáñez, La gran familia de los números, Libros de la Catarata, 2021.
2.- Página web: Numbers Aplenty.
3.- Richard Guy, Unsolved problems in number theory, Springer-Verlag, Berlin, 1994.
4.- Arthur Porges, A Set of Eight Numbers, American Mathematical Monthly 52, p. 379-382, 1945.
5.- Justin Gilmer, On the density of happy numbers, Integers, vol, 13, n. 2, pp. 689-713, 2013.
6.- Esam El-Sedy y Samir Siksek, On happy numbers, Rocky Mountain Journal of Mathematics, vol. 30, n.2, pp. 565-570, 2000.
7.- R. Ibáñez, Números elegantes, en el libro Desafíos Matemáticos, propuestos por la Real Sociedad Matemática Española (coordinado por A. Quirós), SM-RSME, 2012.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Números felices para siempre se ha escrito en Cuaderno de Cultura Científica.
La temperatura en el límite entre el núcleo interno sólido y el núcleo externo líquido de la Tierra
En ocasiones, experimentos hechos en un laboratorio, combinados con un poco de lógica nos permiten tener una idea bastante aproximada de lo que ocurre en lugares inaccesibles para el ser humano y su tecnología. Como el interior del núcleo de la Tierra. Al medir la temperatura de fusión del hierro sometido a una alta presión transitoria, un equipo de investigación ha establecido un valor máximo a la temperatura en el límite entre los núcleos interno y externo.
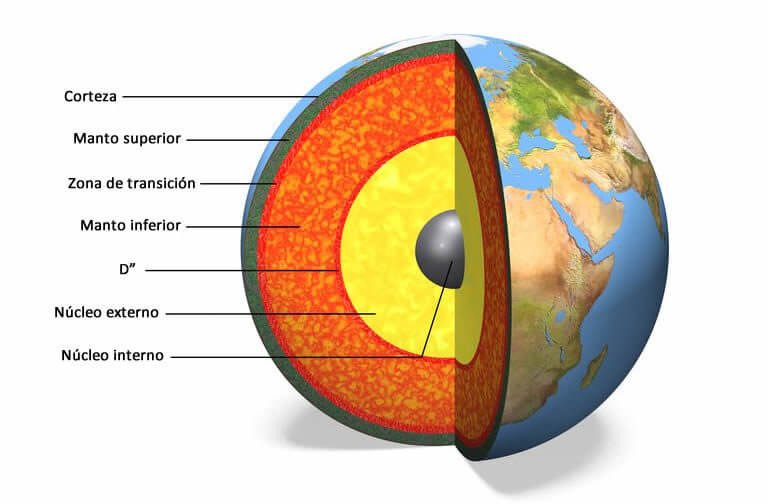 Fuente: capasdelatierra.org
Fuente: capasdelatierra.orgPara comprender el funcionamiento de la dinamo de la Tierra y otros procesos internos del planeta es necesario saber cómo se comporta el hierro (el componente principal del núcleo de la Tierra) bajo altas presiones y temperaturas. Sucesivos estudios han permitido obtener partes del diagrama de fases de presión y temperatura para el hierro utilizando una combinación de teoría y experimentación, pero como las condiciones más extremas solo se pueden producir en el laboratorio de manera fugaz (si es que se pueden producir), aún quedan grandes lagunas e incertidumbres.
Ahora, Sofia Balugani, del Centro Europeo de Radiación Sincrotrón (Francia), y sus colegas han sometido una muestra de hierro puro a una presión de 270 gigapascales (GPa), cerca de los 330 GPa que se encuentran en el límite del núcleo interno de la Tierra, y han medido su temperatura a medida que se fundía. Dado que el hierro del núcleo está mezclado con níquel y otros elementos que reducen su punto de fusión, el resultado establece un límite superior para la temperatura en el límite entre el núcleo interno sólido y el núcleo externo líquido.
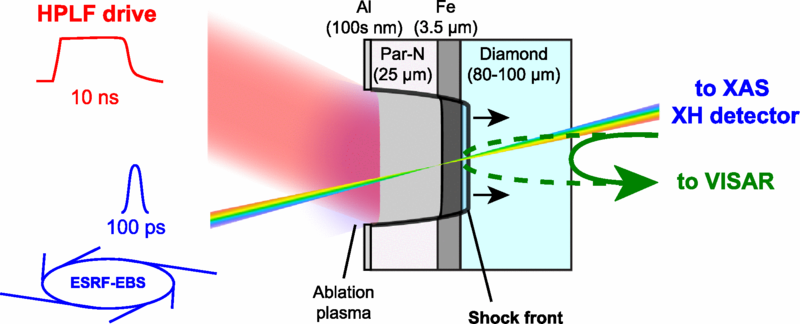 Fuente: S. Balugani et al. (2024)
Fuente: S. Balugani et al. (2024)Los investigadores suelen producir presiones estáticas de cientos de gigapascales utilizando celdas de yunque de diamante. Sin embargo, combinar estas presiones con altas temperaturas requiere un enfoque dinámico. En estudios anteriores los investigadores comprimieron las muestras aplicándoles pulsos láser breves e intensos mientras caracterizaban su estructura mediante difracción de rayos X. Balugani y sus colegas también utilizaron compresión láser, pero la combinaron con espectroscopia de absorción de rayos X, una técnica que es sensible tanto a la estructura como a la temperatura.
La muestra comenzó a fundirse sometida a 240 GPa a 5345 K. Extrapolando, los investigadores dedujeron que la temperatura en el límite del núcleo interno no debe ser mayor que 6202 K. También descartaron una transición cristalina (de empaquetamiento compacto hexagonal a cúbico centrado en el cuerpo) que se había predicho que ocurriría cerca de esa temperatura.
Referencias:
S. Balugani et al. (2024) New constraints on the melting temperature and phase stability of shocked iron up to 270 GPa probed by ultrafast x-ray absorption spectroscopy Phys. Rev. Lett. doi: 10.1103/PhysRevLett.133.254101
M. Stephens (2024) Taking the Temperature of Earth’s Core Physics 17, s139
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La temperatura en el límite entre el núcleo interno sólido y el núcleo externo líquido de la Tierra se ha escrito en Cuaderno de Cultura Científica.
¿Cuál es la verdadera edad de la Luna?
Damos por hecho que, aparte de la Tierra, la historia geológica de la Luna es la que mejor conocemos. Al fin y al cabo, puesto que es el objeto astronómico más cercano a la Tierra ha facilitado que también sea el más visitado ya no solo por misiones robóticas, sino también por el propio ser humano. Y al mismo tiempo es también uno de los pocos de los que hemos podido traer muestras de su superficie de vuelta a nuestro planeta, algo fundamental para poder estudiarlas en los mejores laboratorios y exprimir los párrafos de su historia escritos en sus rocas.
A pesar de esta mayor facilidad para estudiar la Luna en comparación con otros cuerpos astronómicos, existe una discrepancia en los distintos cálculos de su edad, que abarcan más de 150 millones de años entre unas dataciones y otras, y que es francamente difícil de explicar. Y no, no tiene nada que ver con que las dataciones de las rocas estén mejor o peor hechas, sino de que quizás la historia geológica de nuestro satélite haya sido más turbulenta de lo que pensábamos. Y un nuevo estudio publicado en Nature por Nimmo et al. (2024) parece dar una explicación a esta discrepancia. Pero antes, empecemos por el nacimiento de la Luna…
 La superficie de la Luna vista desde la misión Apolo 17. En esta imagen podemos ver el fuerte contraste en color entre los “mares” lunares, de color gris oscuro, y las tierras altas, con unos tonos mucho más claros y cubiertas de cráteres. Cortesía de NASA/JSC.
La superficie de la Luna vista desde la misión Apolo 17. En esta imagen podemos ver el fuerte contraste en color entre los “mares” lunares, de color gris oscuro, y las tierras altas, con unos tonos mucho más claros y cubiertas de cráteres. Cortesía de NASA/JSC.La teoría más aceptada sobre el origen de nuestro satélite es la “teoría del gran impacto”, en la cual, durante la infancia de nuestro sistema solar, un objeto del tamaño aproximado al de Marte -y que conocemos como Tea- chocó con nuestro planeta. Este impacto lanzó al espacio una gran cantidad de material a la órbita de la Tierra y, parte de esa materia, iría uniéndose hasta formar nuestra Luna.
Esta teoría explica algunas características de nuestra Luna, como una menor densidad de la Luna -en comparación con la Tierra- y la similitud entre las proporciones isotópicas entre las rocas lunares y terrestres, lo que indicaría un origen “común” para la mayor parte de los materiales. Pero, ¿Cuándo ocurrió realmente este impacto? ¿Fue muy pronto o quizás un poco más tarde?
Para conocer la edad de la Luna, los científicos se basan en la datación radiométrica de las muestras lunares y de los meteoritos procedentes de esta. Esta técnica se basa en medir la desintegración de los elementos radioactivos que forman parte de los minerales de las rocas y que, de algún modo, son un reloj natural. Si nada altera -a nivel químico- esos minerales, podemos confiar en que nos den una fecha fiable.
¿Y qué rocas podrían representar la edad de formación de la Luna? Suponemos que nuestro satélite, al igual que nuestro planeta, después de su formación estaba, si no por completo, mayormente en un estado fundido, en lo que conocemos como la etapa del océano de magma, que podría ser una fase común entre los planetas rocosos de nuestro sistema solar.
Conforme este océano fue enfriándose y formando la primera corteza lunar, aparecieron una serie de rocas de tonos muy claros y que en geología conocemos como anortositas. La edad de estas rocas, junto con la de otras similares, indicaban una formación tardía de la Luna, situando su nacimiento en hace aproximadamente 4350 millones de años, casi 200 millones de años después de la propia formación de nuestro sistema solar.
 Una anortosita traída a la Tierra por la misión Apolo 15. A esta roca se la conoce la roca del “Génesis”, porque se pensaba que formaba parte de la corteza original de la Luna, pero resultó ser un poco más joven, de tan solo unos 4100 millones de años. Imagen cortesía de NASA/JSC.
Una anortosita traída a la Tierra por la misión Apolo 15. A esta roca se la conoce la roca del “Génesis”, porque se pensaba que formaba parte de la corteza original de la Luna, pero resultó ser un poco más joven, de tan solo unos 4100 millones de años. Imagen cortesía de NASA/JSC.Bien, si la edad de esas rocas es la que es, asunto zanjado. Esa sería la edad de nuestro satélite. Al fin y al cabo, la datación radiométrica es una técnica que conocemos bastante bien y, al mismo tiempo, bastante precisa. Pero no vayamos tan rápido porque hay un pero.
Hay un mineral muy resistente -y a veces diminuto- que aparece dentro de algunas rocas lunares y que nos cuenta una historia un tanto diferente: los circones. Estos minerales, gracias a su resistencia a la meteorización y a la temperatura, pueden guardar el registro de su formación, incluso aunque sufran grandes eventos geológicos, hasta cierto límite. Y es precisamente en estos donde aparece la discordia: algunos de los circones tienen una fecha de unos 4510 millones de años… y para que estén ahí la Luna ya tenía que haberse formado o, al menos, parte de esta haberse enfriado lo suficiente para que los minerales se hubiesen podido formar a partir del magma.
¿Cómo es posible resolver esta discrepancia? Porque está claro que la Luna no puede haber cambiado su partida de nacimiento. Aquí es donde los autores del artículo explican cómo es posible que se hayan calculado dos edades diferentes, pero solo una apunte al verdadero nacimiento de nuestro satélite.
Viajemos de nuevo al pasado, hasta hace unos 4350 millones de años aproximadamente. En este momento, nuestra Luna estaba experimentando un fenómeno que conocemos “calentamiento de mareas”, un proceso fruto de la interacción gravitatoria entre dos o más cuerpos.
Para comprender mejor como es este fenómeno, pensemos en la órbita de la Luna: Aunque nos parezca un círculo perfecto, no es así, sino que es ligeramente elíptica, de tal manera que, al recorrer la órbita, la distancia entre la Tierra y la Luna va cambiando y, por lo tanto, la atracción gravitatoria que ejerce nuestro planeta sobre ella.
Básicamente, es como si estrujásemos y dejásemos de estrujar una pelota antiestrés. Solo que con este ciclo repetido en el que la Luna se ve obligada a cambiar de forma, se generan unas enormes fricciones en las rocas de su interior que acaban transformándose en calor, algo similar a lo que ocurre en Ío, el satélite de Júpiter.
En este momento, el gran calentamiento de mareas que estaba sufriendo la Luna, habría sido suficiente para crear un importante porcentaje de volumen de roca fundido en su interior, que continuamente ascendía hasta la corteza, calentando las rocas ya frías de la corteza y reiniciando el reloj -en este caso los relojes radioactivos que nos permiten datar las rocas- de muchas de las rocas de la Luna, haciendo pasar las rocas por más jóvenes.
Esto explicaría por qué encontramos tantas rocas con una edad de alrededor de 4350 millones de años, y que los científicos de este estudio interpretan no como la edad de formación de la Luna, sino el momento en el que la Luna sufrió este periodo de gran calentamiento por mareas que alteró los sistemas geoquímicos de algunos minerales, como el de los circones.
 El astronauta Harrison Schmitt recoge muestras de lo que parece un bloque de roca lanzado por el impacto de un cuerpo contra la superficie de la Luna durante la misión Apolo 17. Imagen cortesía de NASA/JSC.
El astronauta Harrison Schmitt recoge muestras de lo que parece un bloque de roca lanzado por el impacto de un cuerpo contra la superficie de la Luna durante la misión Apolo 17. Imagen cortesía de NASA/JSC.Esto tiene una consecuencia y es que, si están en lo cierto, la Luna se formó mucho antes y su edad podría coincidir con la de los circones que tienen una edad de alrededor de 4510 millones de años, colocando su “nacimiento” dentro del calendario de nuestro sistema solar en las primeras decenas de millones de años tras la formación de este. Los circones de esta edad serían los minerales relictos de esas primeras rocas que no habrían sufrido un reinicio de su edad como consecuencia del calentamiento.
Aun así, queda mucho trabajo por hacer. Trabajo que probablemente necesite de nuevas muestras lunares, nuevos modelos matemáticos y estudios geológicos que puedan llevar a los científicos a encontrar rocas que hayan sobrevivido a esa vigorosa etapa de la Luna y que nos permita, en definitiva, dar una edad certera para su origen.
Referencias:
Nimmo, Francis, et al. (2024) Tidally Driven Remelting around 4.35 Billion Years Ago Indicates the Moon Is Old Nature doi: 10.1038/s41586-024-08231-0
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo ¿Cuál es la verdadera edad de la Luna? se ha escrito en Cuaderno de Cultura Científica.
Naturaleza humana con números complejos
La Humanidad ha estudiado su propia naturaleza desde tiempo inmemorial. La Naturaleza Humana es uno de los saberes más complejos y fascinantes para cualquier persona dedicada al pensamiento, sea desde las Humanidades, las Artes, las Ciencias Sociales o las Ciencias Naturales. Los porqués de nuestras formas de pensar, sentir y actuar se han intentado explicar desde nuestra codificación genética, pero resulta evidente que la expresión de nuestros genes depende tanto o más de nuestra interacción con la sociedad en la que vivimos, el ejemplo familiar que observamos al crecer, o la educación que recibimos, en el sentido amplio de la palabra.
A los científicos nos gusta medir los fenómenos naturales. De momento, no parece posible medir la naturaleza humana, pero podemos intentar aportar alguna pequeña idea a este campo.
 Foto: Jake Nackos / UnsplashLa ecuación de onda
Foto: Jake Nackos / UnsplashLa ecuación de onda
Personas dedicadas a la matemática, la física y otras ciencias pudieron modelar matemáticamente el fenómeno de las ondas a lo largo de la historia de la ciencia. Resulta que explicar las ondas mecánicas que se observan lanzando una piedra a un estanque o tocando un instrumento musical, permitió en el siglo XVIII establecer una ecuación diferencial en derivadas parciales que describía muy bien las ondas medidas. A mediados del siglo XIX, las ecuaciones del electromagnetismo de J.C. Maxwell incluyeron la predicción de la existencia de ondas electromagnéticas, sorprendentes entidades que nadie había medido aún. Poco después, H. Hertz observó en su laboratorio la existencia real de dichas ondas electromagnéticas que seguían la ecuación de onda que puede deducirse de las ecuaciones de Maxwell.
En 1926, E. Schrödinger postuló su ecuación de onda, cuya solución permite describir el estado cuántico de ciertas partículas, y dos años después P. Dirac propuso la primera ecuación de onda capaz de conjugar la mecánica cuántica con la relatividad especial. Por otro lado, la relatividad general de A. Einstein predijo la existencia de ondas gravitatorias, que se lograron medir directamente en septiembre de 2015, a través del experimento internacional LIGO, quizás el más emocionante de los desarrollados en el primer cuarto del siglo XXI.
FasoresEn su época de Berlín en 1748, L. Euler publicó una de sus más importantes obras: “Introductio in analysin infinitorum”. De entre sus numerosísimas aportaciones al análisis matemático, nos centramos aquí en el capítulo VIII “De quantitatibus transcendentibus ex Circulo ortis”, en donde Euler extrae casi mágicamente “cantidades transcendentales” del Círculo. Nos referimos aquí a la exponencial compleja, quizás la fórmula más famosa y útil para todas las ciencias e ingenierías. Además, expresada en el caso particular para el ángulo llano, estamos ante la ecuación más bella de las de Euler: eiπ+1=0.
Usando la fórmula de Euler para cualquier ángulo en un círculo, podemos expresar gráficamente los números complejos a través de vectores de fase. Componiendo ambos lexemas, a esas entidades las llamamos Fasores. Todas las ecuaciones de onda se benefician de los números complejos y de la exponencial compleja de Euler, para poder caracterizar las magnitudes que definen las ondas, como la amplitud, la frecuencia y en el caso que ahora nos ocupa, la fase.
Conflicto de visionesEn su blog “Lecturas y Conjeturas” J.I. Pérez Iglesias publicó en mayo de 2024 una excelente y muy ilustrativa reseña [1] sobre las visiones humanas en conflicto que el economista Thomas Sowell describía en su interesantísimo libro [2]. Este estudio de la naturaleza humana trata de describir las diferencias ideológicas de las personas. Se trata de un problema muy complejo pero apasionante, para discutir las razones de las diferencias de lo que llamamos “progresismo” o “conservadurismo”, “izquierda” o “derecha”, “social” o “individual”. Sowell presenta unas bases muy convincentes del fondo de esta cuestión.
Aunque las explicaciones de Sowell pueden ser incompletas, y no se trata de un teorema matemático, su tratamiento científico de la naturaleza humana es brillante, y nos permite concebir una cierta posibilidad de clasificar la ideología humana e incluso podemos intentar explicar algunas de nuestras propias contradicciones.
Escala de naturaleza humanaNo sabemos aún medir la naturaleza humana, pero sí podemos establecer una posible escala de medida usando algunas de las ideas de Sowell. Si tomamos el plano complejo con el círculo de Euler y lo reorientamos, podemos hacer coherentes las indicaciones de un simple fasor con nuestro lenguaje ordinario al describir las ideologías humanas.
En la Figura ilustramos una manera de ordenar el conflicto de visiones, junto con alguna terminología más clara del psicólogo Steven Pinker, que prefiere utilizar la visión “Trágica” vs la visión “Utópica” en lugar de la denominación menos ilustrativa de Sowell (“Restringida” vs “No restringida”).
Si partimos del extremo superior de la ilustración (medida 0º), estamos en una ideología central, moderada y humanista, conscientes de que nuestra sociedad requiere cierto mercado y una imposición. Si somos partidarios de que el mercado se liberalice y nos bajen los impuestos, nos alejamos por la derecha (medida >0º). En caso contrario, si queremos que el mercado se regule más y creemos en los impuestos, nos vamos por la izquierda (medida <0º).
Claramente, a +90º tenemos visión Trágica, lo que llamamos conservadora, de derecha o de visión individual. A -90º nuestra visión es Utópica, lo que denominamos progresista, de izquierda o de visión social.
Si recorremos más allá la medida hacia la parte inferior de la ilustración y nos acercamos a los +180º o a los -180º, somos extremistas. Desaparece nuestro carácter Trágico o Utópico, y somos de la misma ideología: autoritaria, violenta, irracional y antidemocrática. La fórmula de Euler nos indica que, a todos los efectos, en un oscilador la fase +180º o -180º (+π, -π) es idéntica.
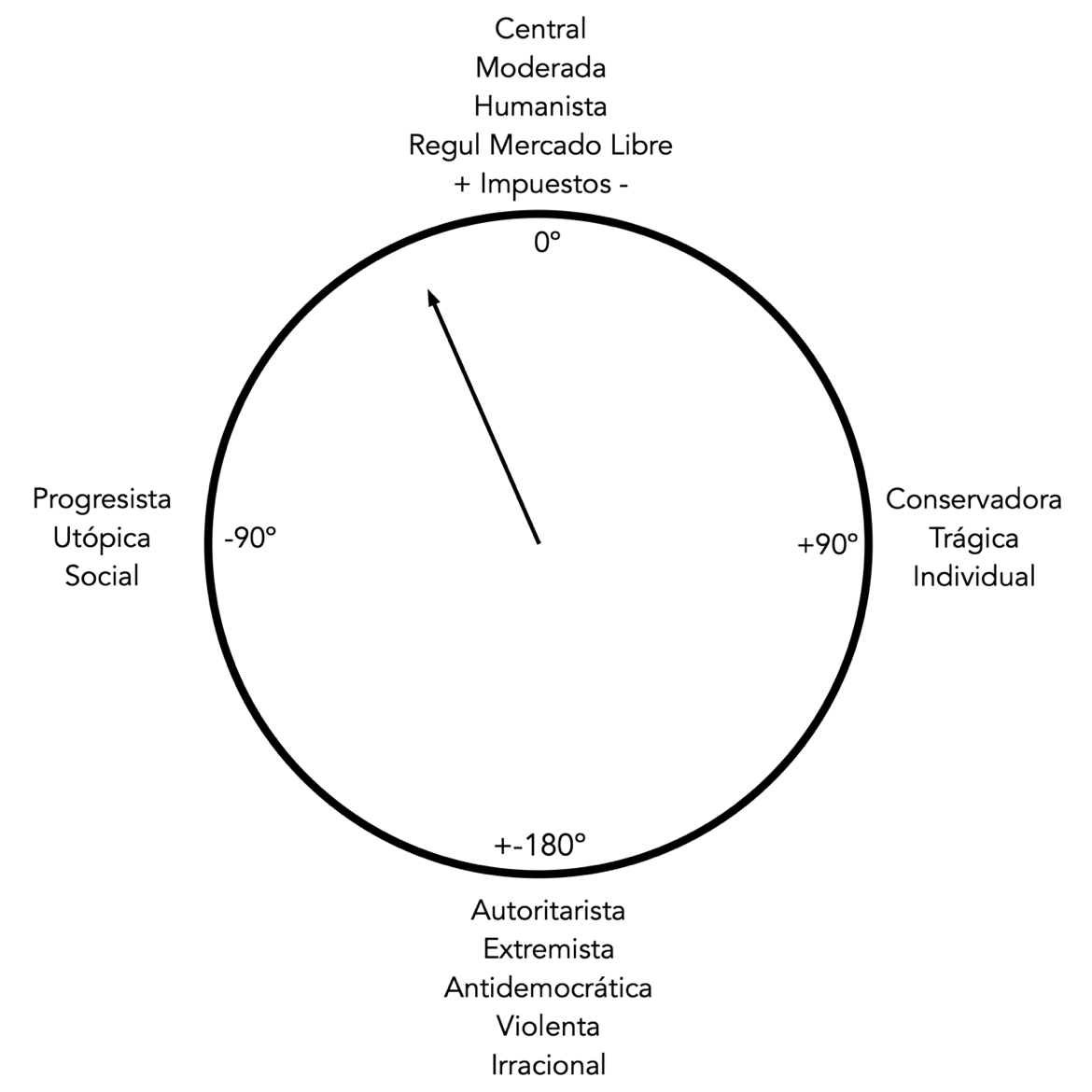 Posible escala de visiones humanas. Nótese que la flecha indicadora de este “naturalezómetro humano” es un vector de fase (fasor)
Posible escala de visiones humanas. Nótese que la flecha indicadora de este “naturalezómetro humano” es un vector de fase (fasor)
No tenemos un instrumento para medir exactamente la naturaleza de una persona, pero aun con cierto nivel de ruido en nuestra propia medida, si somos sinceros con nosotros mismos, el nivel señal/ruido de nuestro medidor puede ser suficiente como para podernos colocar en un cierto sector del círculo.
Si simpatizamos con una tendencia ideológica, podemos criticar fuertemente el extremismo contrario, pero a veces justificamos o comprendemos el extremo propio. Esta es una contradicción humana muy común, pero recordemos que ambas visiones, si son extremas, no están en conflicto: son la misma.
Referencias
[1] Juan Ignacio Pérez Iglesias (2024) Dos visiones en conflicto de la naturaleza humana. Substack.
[2] Thomas Sowell (2007) A conflict of visions. Basic Books ISBN: 978-0465004669
Sobre el autor: Victor Etxebarria Ecenarro es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (UPV/EHU)
El artículo Naturaleza humana con números complejos se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2024: El verdadero valor de un traje espacial
La decimocuarta edición del mayor evento de divulgación científica volvió al Palacio Euskalduna de Bilbao durante los días 19, 20, 21 y 22 de septiembre de 2024.

La doctora en biología molecular del cáncer Sara García Alonso consiguió la fama mediática al ser seleccionada como astronauta de reserva por la ESA. En Naukas Bilbao 2024 algunos descubrimos, además, que es una fantástica comunicadora científica. En El verdadero valor de un traje espacial explica la importancia de la investigación y desarrollo tecnológico espaciales.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2024: El verdadero valor de un traje espacial se ha escrito en Cuaderno de Cultura Científica.
¿Dónde están las calzadas romanas que impulsaron la civilización mediterránea?
 Puente de Alcántara, Cáceres (España). Fuente: Estevoaei/Shutterstock, CC BY-SA
Puente de Alcántara, Cáceres (España). Fuente: Estevoaei/Shutterstock, CC BY-SA
En el colegio se nos decía en clase de historia que la mayor aportación que había dejado la civilización romana en la península ibérica había sido su red de carreteras, un tejido de comunicaciones que permitió el desarrollo de la civilización mediterránea.
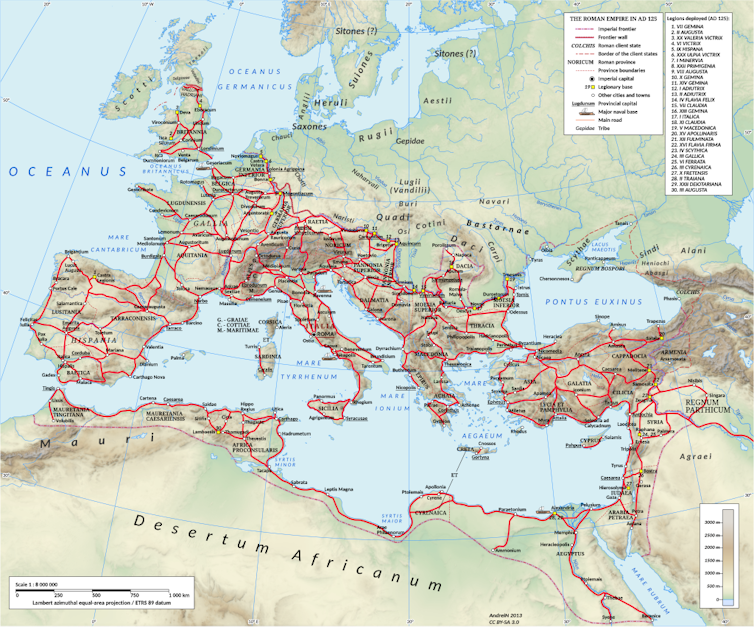 El imperio romano en tiempos de Adriano (117-138), con la red de las principales calzadas romanas. Fuente: DS28/Wikimedia Commons, CC BY-SA
El imperio romano en tiempos de Adriano (117-138), con la red de las principales calzadas romanas. Fuente: DS28/Wikimedia Commons, CC BY-SAA pesar de ello, la mayor parte de aquellas han desaparecido o han sido profundamente alteradas. Pero no todo está perdido. Algunos estudios recientes han impulsado su conocimiento y se han descubierto nuevos tramos.
Solo se conserva un 10 % de las calzadasUn nuevo estudio de la Universidad de Copenhague ha demostrado que los lugares con una mayor densidad de calzadas romanas poseen una mayor actividad económica actual. Esto se debe a que la perduración de dichas infraestructuras incentivó el surgimiento de las ciudades de mercado medievales, siendo éstas el origen de la mayor parte de las ciudades modernas europeas.
A pesar de la importancia que han tenido, no han sido tratadas como elementos patrimoniales de relevancia y se conservan pocos kilómetros de ellas. Isaac Moreno, ingeniero e historiador galardonado con la medalla Frontino por sus investigaciones sobre ingeniería romana, ha constatado que solo se conservan en torno a un 10 % de las mismas.
Por una parte, existen caminos que no siendo romanos han sido señalizados como tales por algunas administraciones. La razón es que se ha denominado calzada romana o puente romano a las calzadas y puentes de piedra, aunque no fueran de ese origen. Es cierto que la piedra fue un material importante en las construcciones romanas, pero para que una estructura sea considerada “romana”, las técnicas y métodos de construcción empleados en ella deben ser romanos también.
Por otra parte, los caminos verdaderamente romanos han sufrido la aceleración de su destrucción durante los últimos cien años debido a la ejecución de obras modernas. Dichas acciones se han producido por el desconocimiento de la composición de las calzadas romanas y las características de su trazado.
Herramientas usadas para localizar calzadas desconocidasLas fuentes geográficas históricas que se han utilizado para el estudio de las vías romanas en la península ibérica han sido fundamentalmente los itinerarios romanos. Estos itinerarios han llegado a nuestros días en códices manuscritos medievales.
Los itinerarios romanos son una serie de rutas que discurrían por las calzadas del Imperio y que se describen a partir de las ciudades por las que transcurren, conocidas como estaciones o mansiones. En el caso de algunos itinerarios aparecen también las distancias entre ellas.
Sirva como ejemplo el primer tramo de la ruta entre Asturica (Astorga) y Caesaraugusta (Zaragoza) del Itinerario de Antonino, que pasaba por:
- Brigeco (?), a 40 m.p. (millas romanas, unos 1 480 metros)
- Intercatia (?): 20 m.p.
- Tela (?): 22 m.p.
- Pintiam (Padilla de Duero): 24 m.p.
- Raudam (Roa): 11 m.p.
- Cluniam (Peñalba del Castro): 26 m.p., 16 m.p.
Para saber por dónde iban los itinerarios se necesita conocer la posición de las estaciones por las que pasaban. Y como se ve en las interrogaciones anteriores, hay muchas estaciones de ubicación desconocida. La razón es que las coordenadas geográficas que dan los códices antiguos no son suficientemente precisas.
Además, en algunas rutas existen errores en las distancias y ausencia de estaciones. Esto hace que algunos de estos itinerarios sean interpretados de maneras diferentes por los investigadores, de tal manera que las rutas propuestas por distintos autores para un mismo itinerario pasan por distintas localidades.
Nuevas formas de localizar las calzadas romanasEn el trabajo “Vías romanas en Castilla y León”, dirigido por Isaac Moreno, se realizó un proyecto pionero para la localización de vías romanas en esta comunidad española.
Así, para la interpretación de los itinerarios se realizó un estudio de arqueología apoyado en conocimientos de ingeniería y se analizaron fotos aéreas de la zona en diferentes años y épocas del año para visualizar la huella de las vías bajo los campos. Esto se completó con excavaciones arqueológicas en la propia calzada.
La mayoría de los trabajos dedicados al estudio de las calzadas romanas que han realizado excavaciones arqueológicas se habían centrado en un tramo de una vía. En este caso, el estudio se extendió a una localización geográfica amplia: la submeseta norte.
Gracias a ello ahora conocemos más kilómetros de vías romanas verdaderas y sabemos cuál es la composición y técnica constructiva de la vía.
En los últimos años otros autores han hecho estudios similares para la identificación de tramos de vías romanas en la península ibérica. Entre ellos, cabe destacar los estudios de la Sociedad de Ciencia Aranzadi sobre la carretera romana de Roncesvalles y los realizados sobre la Vía Augusta en Ciudad Real.
Beneficios del conocimiento de la red viaria romanaEl conocimiento de los vestigios que nos quedan de este patrimonio de la ingeniería civil permite tenerlos en cuenta en las obras civiles actuales.
En este sentido, en España se ha llevado a cabo una actuación pionera en Europa. En la construcción de la autovía de Soria (Castilla y León) se modificó el proyecto para reducir su afección a la calzada romana que pasa por allí y se acondicionó esta última para poder ser disfrutada por los turistas culturales. Esto permite que los viajeros que se acercan a Soria para visitar la mítica Numancia se den un paseo por una calzada romana auténtica.
Para evitar la destrucción de los escasos kilómetros de vías romanas verdaderas que se conservan sería interesante un estudio similar a los arriba mencionados aplicado al resto de comunidades de España. Y lo que es no menos importante, la defensa por parte de las administraciones públicas de las vías identificadas por el mismo.![]()
Sobre las autoras: Jesús María Romera Aguayo, Profesor agregado de la Escuela de Ingeniería, UPV/EHU; Amaia Santamaría León, Profesora Titular de Universidad en Hormigón, UPV/EHU y Marcos Larrauri Gil, Profesor en ingeniería de la construcción, UPV/EHU.
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Dónde están las calzadas romanas que impulsaron la civilización mediterránea? se ha escrito en Cuaderno de Cultura Científica.
Soy un computador HAL de la serie 9000…
…me pusieron en funcionamiento en la fábrica H A L de Urbana, Ilinois, el 12 de enero de 1992. Mi instructor fue el señor Langley; me enseñó una canción, si usted quisiera, podría cantársela. Se llama Daisy.
Así es la sobrecogedora despedida de HAL 9000 en 2001: Una odisea del espacio; seguramente, una de las inteligencias artificiales más… ¿queridas? del mundo del cine —HAL tiene sus cositas de psicópata, pero creo que, en el fondo, todos le tenemos cariño—. A medida que Dave Bowman va desconectándole módulos de memoria, el computador, ya en esta escena más humano que los propios humanos de la película, va perdiendo facultades, su voz se ralentiza, se vuelve más grave y se va apagando al son de una canción que, en principio, parece no tener ningún sentido:1
Daisy, Daisy, give me, give me your answer do
I’m half crazy all for the love of you
It won’t be a stylish marriage
I can’t afford a carriage
But you’ll look sweet upon the seat
Of a bicycle built for two.
Pero lo tiene, y mucho. Años antes de la grabación de 2001, en 1961, Daisy Bell le había puesto banda sonora a uno de los grandes hitos de la historia de la computación.
 El astronauta Dave Bowman desconectando a HAL 9000 en 2001: Una odisea del espacio. Las últimas palabras de computador son unos versos de la canción Daisy Bell. Fuente: Metro-Goldwyn Mayer / Fair use
El astronauta Dave Bowman desconectando a HAL 9000 en 2001: Una odisea del espacio. Las últimas palabras de computador son unos versos de la canción Daisy Bell. Fuente: Metro-Goldwyn Mayer / Fair use
Esta canción tan naíf, en la que un joven le declara el amor a su dama, se remonta a 1892 y también tiene su propia historia. En un viaje a Estados Unidos, a Harry Dacre, el autor, se le ocurrió llevar consigo una bicicleta y, al tratar de pasarla por la aduana, se encontró con la sorpresa de que le cobraron aranceles. Cuando se lo comentó a otro compositor y amigo suyo, William Jerome, este le comentó que menos mal que no era «una bicicleta hecha para dos» (a bicycle built for two) o le habrían cobrado el doble. Parece que la frase llamó la atención de Dacre, que se propuso utilizarla en una canción: esa canción fue Daisy Bell.
 Portada australiana de la partitura de Daisy Bell. Fuente: Dominio público.
Portada australiana de la partitura de Daisy Bell. Fuente: Dominio público.
Fue precisamente lo sencillo de la letra y de la melodía, además de que, en aquel momento, ya no estuviera protegida por derechos de autor, lo que llevó al ingeniero eléctrico —y violinista— Max Mathews y a los programadores John L. Kelly y Carol Lochbaum a elegirla para el proyecto que estaban llevando a cabo en los Laboratorios Bell en Murray Hill (Nueva Jersey): querían que un ordenador cantara o, en otras palabras, querían digitalizar el sonido.
En los Bell Labs se llevaba trabajando en el análisis y codificación de la voz desde los años treinta; el objetivo que el ingeniero Homer Dudney tenía en mente cuando creó el vocoder en 1938 era desarrollar un dispositivo capaz de analizar y modificar señales habladas, con el fin de mejorar las transmisiones de voz. Lo hizo prácticamente a la par que otro dispositivo, el voder, uno de los primeros sintetizadores del habla —el resultado, a decir verdad, fue un tanto siniestro—. Ambos inventos serían fundamentales para el desarrollo de la codificación de música por ordenador.
Demostración del voder de Homer Dudney en la Feria Universal de Nueva York de 1939. Fuente: Dominio públicoKelly conocía bien los entresijos del vocoder, con el que había trabajado durante mucho tiempo. Por su parte, Mathews había creado en 1957 el primer programa para generar música por ordenador: MUSIC. En el proyecto de conseguir hacer cantar a una máquina, Kelly y Lochbaum se encargaron de la parte de la voz, mientras Mathews se encargaría de sintetizar el acompañamiento musical con su software. El intérprete fue un flamante IBM 704 de válvulas de vacío que funcionaba con tarjetas perforadas, y sonaba así:
Max Mathews, John L Kelly y Carol Lochbaum programaron un IBM 704 para que cantara Daisy Bell.¡Y ahora es cuando llega el crossover! El interés de Max Mathews por la música por ordenador no surgió por generación espontánea, sino que fue idea de su jefe, con el que mantenía una magnífica relación y con el que solía ir a conciertos de vez en cuando. En 1957, en uno de esos conciertos, este le sugirió a Mathews que siguiera esa línea de trabajo. Este jefe, como él mismo se definió a sí mismo una vez, era «un oscuro personaje» llamado John R. Pierce que, casualmente, también era escritor de ciencia ficción y un habitual de revistas como Astounding Science Fiction, donde solía aparecer bajo el pseudónimo de J. J. Coupling —guiño, guiño a los físicos —. Como escritor de ciencia ficción era, por supuesto, amigo de otros escritores de ciencia ficción, entre ellos, Arthur C. Clarke.
En uno de los viajes que Clarke hizo a Estados Unidos a principios de los sesenta, Pierce lo invitó a visitar los Bell Labs. Una de las atracciones estrella de aquellos tours que se les hacía a los visitantes era, por supuesto, escuchar al IBM 704 cantando Daisy Bell… Y el resto es historia del cine.
Impresionado por lo que había presenciado, Clarke incluyó la canción en el guion de 2001. De esta manera, en la escena en que el ordenador pierde facultades mientras Dave lo desconecta, HAL no solo vuelve a su infancia, sino a la infancia de la historia de la computación y la inteligencia artificial.
Bibliografía
Clarke, A. C. (1980). The lost worlds of 2001. New American Library.
Hass, J. (s. f.) Introduction to computer music. Universidad de Indiana.
O’Dell, C. (2009). «Daisy Bell (Bicycle Built for Two)»—Max Mathews, John L. Kelly, Jr., and Carol Lochbaum (1961). Library of Congress.
Nota:
1 La traducción un poco libre al español fue: «Daisy, Daisy, tú eres mi ilusión. / Dulce sueño, por ti yo loco estoy. / Por un beso tuyo diera feliz la vida entera»… y se volvía a repetir desde el principio.
.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo Soy un computador HAL de la serie 9000… se ha escrito en Cuaderno de Cultura Científica.
Puntos reticulares sobre circunferencias
Leyendo sobre sucesiones fractales, tema al que he dedicado algunas entradas del Cuaderno de Cultura Científica, como Sucesiones fractales, La sucesión fractal de Thue-Morse y la partida infinita de ajedrez, Sucesiones fractales: del número a la nota musical o La sucesión del infinito del compositor Per Nørgård, llamó mi atención una sucesión que se definía como el “número de puntos reticulares sobre las circunferencias de radio n centradas en el origen (0,0)”.
 Portada del disco Per Nørgård: Iris/Voyage into the Golden Screen (1973), de la Danish National Symphony Orchestra, dirigida por Herbert Blomstedt y Tamás Vetö, en cuya imagen podemos observar la sucesión del infinito en formato musical y dibujada en espiralPuntos reticulares
Portada del disco Per Nørgård: Iris/Voyage into the Golden Screen (1973), de la Danish National Symphony Orchestra, dirigida por Herbert Blomstedt y Tamás Vetö, en cuya imagen podemos observar la sucesión del infinito en formato musical y dibujada en espiralPuntos reticulares
Empecemos explicando los conceptos relacionados con la generación de esta sucesión de números, en particular, qué son los puntos reticulares.
Aunque podemos trabajar con una retícula infinita cualquiera, es decir, un conjunto infinito de líneas verticales y horizontales equidistantes cada una con la siguiente y con la anterior, lo mejor es trabajar con el plano coordenado y la retícula formada por las rectas paralelas a los ejes de coordenadas (verticales y horizontales) que pasan por los puntos de la forma (n,0), las primeras, y de la forma (0,m), las segundas, para n y m números enteros (como en la siguiente imagen).
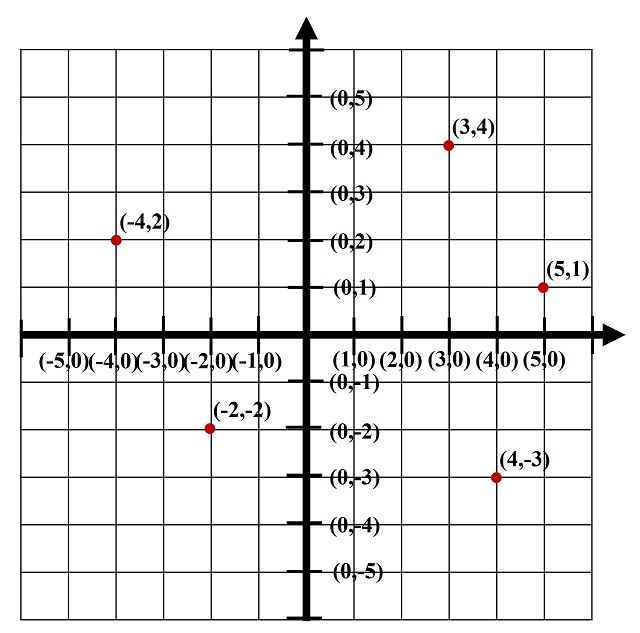 El plano coordenado y el retículo de líneas verticales y horizontales
El plano coordenado y el retículo de líneas verticales y horizontales
Los puntos reticulares, o puntos de la retícula, son aquellos puntos que son intersección de las líneas horizontales y las verticales de la retícula. En el caso de la retícula del plano coordenado los puntos reticulares son aquellos puntos de la forma (n, m), donde n y m son números enteros (como los puntos (3,4), (5,1), (4,–3), (–2,–2) y (–4,2) de la anterior imagen).
No es la primera vez que se habla en el Cuaderno de Cultura Científica sobre puntos reticulares, ya lo hicimos en la entrada Calcular el área contando puntos, dedicada al conocido teorema de Pick, que permite calcular el área de la región encerrada por un polígono reticular (un polígono trazado sobre una retícula y cuyos vértices son puntos reticulares) contando puntos, en concreto, mediante la expresión Área = I + B/2 – 1, donde I es el número de puntos del retículo que están en el interior del polígono y B la cantidad de los puntos del retículo que están en la frontera, es decir, en el polígono.
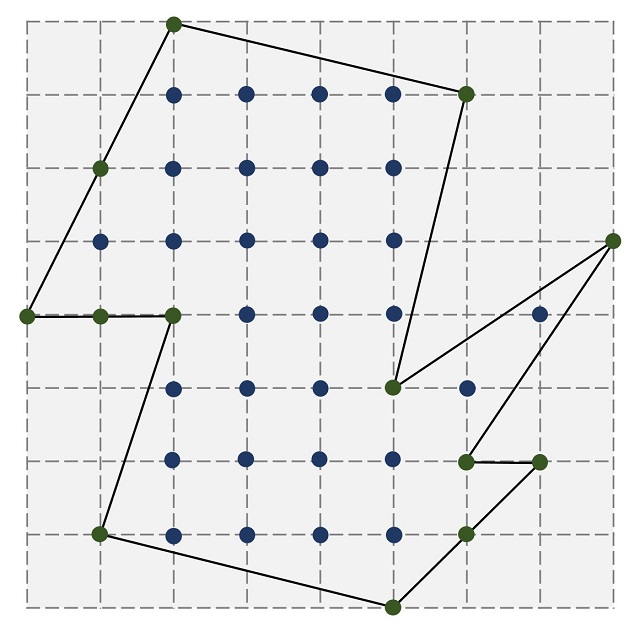 Aplicando el teorema de Pick, el área encerrada por este polígono reticular es igual a A = I + B/2 – 1 = 29 + 13/2 – 1 = 34,5 u.c.
Aplicando el teorema de Pick, el área encerrada por este polígono reticular es igual a A = I + B/2 – 1 = 29 + 13/2 – 1 = 34,5 u.c.
Aprovechemos que tenemos ante nosotros el teorema de Pick para mencionar a un artista que lo utiliza en una de sus obras, el estadounidense Nelson Saiers, quien después de doctorarse en matemáticas estuvo trabajando en el mundo de las finanzas hasta 2014, año en el que decide dedicarse al arte, en concreto, realiza obras de arte basadas en las matemáticas. Una de sus obras más conocidas es la instalación Acortando: hacer racional lo irracional (2017), en la cárcel de Alcatraz (San francisco, California).
La obra de Nelson Saiers relacionada con el teorema de Pick es Genocide is Evil (2014). En la misma, Saiers escribe en Braille la frase que da título a la obra “Genocide is Evil”, dando color a cada uno de los puntos, que luego conecta formando un polígono reticular. Debajo, a la derecha, aparece la fórmula de Pick que permite calcular el área de esa región contando puntos. La elección del teorema de Pick no es casual, ya que Georg Alexander Pick (1859-1942) fue un matemático austriaco judío que murió en el “campo de concentración-ghetto” de Theresienstadt (Terezín, República Checa).
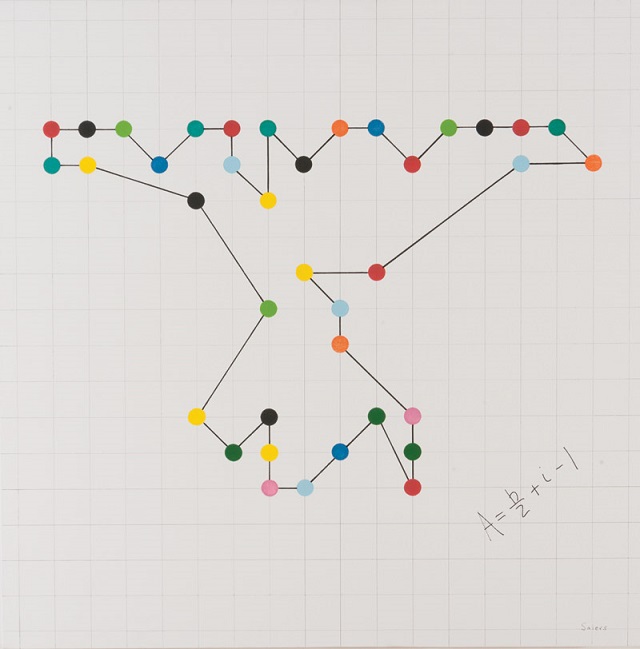 Genocide is Evil (2014), del artista estadounidense Nelson SaiersNúmero de puntos reticulares sobre circunferencias
Genocide is Evil (2014), del artista estadounidense Nelson SaiersNúmero de puntos reticulares sobre circunferencias
Conocido el concepto de punto reticular, estamos en condiciones de introducir esta sucesión de números que consiste en la cantidad de puntos reticulares sobre las circunferencias de radio n centradas en el origen (0,0), para n números enteros no negativos.
Recordemos que una circunferencia de centro un punto c = (a,b) y radio r está formado por todos los puntos del plano que están a distancia r de dicho centro c, es decir, aquellos puntos (x,y) del plano que satisfacen que (x – a)2 + (y – b)2 = r2.
En la siguiente imagen tenemos la construcción geométrica de los primeros términos, es decir, para n = 0, 1, 2, 3, 4 y 5, es decir, circunferencias centradas en el origen de radio 0 (un punto), 1, 2, 3, 4 y 5.
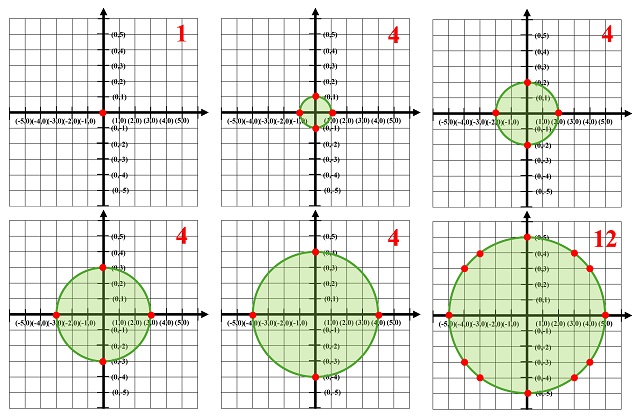 Primeros términos de la sucesión de las cantidades de puntos reticulares sobre las circunferencias de radio n centradas en el origen (0,0), para n = 0, 1, 2, 3, 4, 5
Primeros términos de la sucesión de las cantidades de puntos reticulares sobre las circunferencias de radio n centradas en el origen (0,0), para n = 0, 1, 2, 3, 4, 5El caso extremo de una circunferencia de radio 0, centrada en el origen (0,0), se entiende que está formada solo por el punto (0,0), luego la cantidad es de 1 punto reticular; para los radios iguales a n = 1, 2, 3 y 4, solo hay 4 puntos reticulares, a saber, (n,n), (n,–n), (–n,–n) y (–n,n), los que están en los ejes de coordenadas. En el caso de n = 5, la circunferencia de radio 5, no solo existen los cuatro puntos reticulares similares a los anteriores, los que están en los ejes, (5,5), (5,–5), (–5, –5) y (–5,5), sino que además hay otros 8 puntos reticulares más, que son (3,4) y (4,3), en el primer cuatrimestre, más los otros seis simétricos a estos. En conclusión, los primeros miembros de esta sucesión son 1, 4, 4, 4, 4, 12.
Analicemos brevemente el caso particular de los 8 puntos nuevos, que no son los cuatro de los ejes coordenados, que aparecen en el caso del radio n = 5. Estos se corresponden con el triple pitagórico (3, 4, 5), es decir, 32 + 42 = 52 (sobre triples pitagóricos pueden leerse las entradas El teorema de Pitágoras y los números congruentes [https://culturacientifica.com/2022/02/23/el-teorema-de-pitagoras-y-los-numeros-congruentes/] y Construir un triángulo pitagórico doblando papel [https://culturacientifica.com/2021/11/17/construir-un-triangulo-pitagorico-doblando-papel/]). Por lo tanto, la expresión 32 + 42 = 52 significa, en particular, que los puntos (3,4) y (4,3) están a una distancia 5 del origen (0,0), es decir, están sobre la circunferencia centrada en el origen y de radio 5. Por lo tanto, la construcción de esta sucesión está relacionada con los triples pitagóricos, aunque hoy no vamos a profundizar en esta cuestión.
 El óleo Pythagoraisches dreieck im quadrat II / Triángulo pitagórico en un cuadrado II (1974-1980), del artista concreto suizo Max Bill, en el que aparece un triángulo pitagórico de lados 3, 4 y 5
El óleo Pythagoraisches dreieck im quadrat II / Triángulo pitagórico en un cuadrado II (1974-1980), del artista concreto suizo Max Bill, en el que aparece un triángulo pitagórico de lados 3, 4 y 5Para los siguientes radios n = 6, 7, 8 y 9, solamente hay 4 puntos reticulares en las correspondientes circunferencias, que son los que se encuentran en los ejes coordenados. De nuevo, surgen más puntos para n = 10, ya que tenemos el triple pitagórico (6, 8, 10), que se obtiene multiplicando el triple (3, 4, 5) por 2, es decir, para n = 10 hay 12 puntos reticulares. Para n = 11 y 12, se vuelve a los cuatro puntos de la retícula están en los ejes. Sin embargo, para n = 13 se obtiene otro triple pitagórico (5, 12, 13), ya que 52 + 122 = 132, luego para n = 13 hay de nuevo 12 puntos reticulares (los cuatro de los ejes, más (5,12) y (12,5), junto con sus simétricos).
Por lo tanto, la sucesión de la cantidad de puntos reticulares sobre las circunferencias de radio n centradas en el origen (0,0), para los números enteros no negativos, que empezaba por 1, 4, 4, 4, 4, 12, se continua con 4, 4, 4, 4, 12, 4, 4, 12. Después de estos siguen los términos 4, 12, 4, 12, 4, 4, 12, 4, 4, 4, 4, para n entre 14 y 24. En todos esos casos están los cuatro puntos reticulares de los ejes coordenados, pero para n = 15, 17 y 20 volvemos a tener triples pitagóricos, (9, 12, 15), (8, 15, 17) y (12, 16, 20).
Para n = 25, tenemos otro pequeño salto, ya que ahora disponemos de dos triples pitagóricos, que son (15, 20, 25) y (7, 24, 25). Por lo tanto, en este caso hay 20 puntos reticulares (4 + 8 + 8) sobre la circunferencia de radio 25, centrada en el origen, que se muestran en la siguiente imagen.
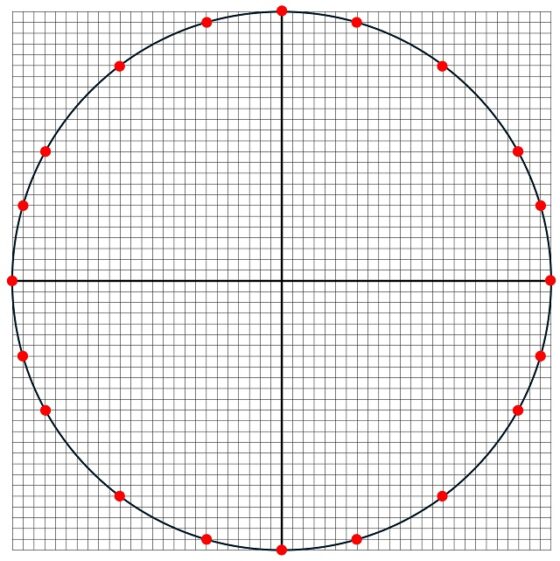 Los 20 puntos reticulares sobre las circunferencias de radio 25 centrada en el origen (0,0)
Los 20 puntos reticulares sobre las circunferencias de radio 25 centrada en el origen (0,0)
Y así podríamos continuar con los demás miembros de la sucesión del número de puntos reticulares sobre las circunferencias de radio números enteros no negativos centradas en el origen (0,0), que es la sucesión A046109 de la Enciclopedia on-line de Sucesiones de Números Enteros – OEIS, y cuyos primeros términos son
1, 4, 4, 4, 4, 12, 4, 4, 4, 4, 12, 4, 4, 12, 4, 12, 4, 12, 4, 4, 12, 4, 4, 4, 4, 20, 12, 4, 4, 12, 12, 4, 4, 4, 12, 12, 4, 12, 4, 12, 12, 12, 4, 4, 4, 12, 4, 4, 4, 4, 20, 12, 12, 12, 4, 12, 4, 4, 12, 4, 12, 12, 4, 4, 4, 36, 4, 4, 12, 4, 12, 4, 4, 12, 12, 20, 4, 4, 12, 4, 12, 4, 12, 4, 4, 36, …
La sucesión A046109 es una sucesión fractalPara empezar, recordemos que una sucesión infinita de números enteros es una sucesión fractal, también llamada sucesión autosemejante, si una parte de la sucesión es igual a toda la sucesión, es decir, si se eliminan algunos miembros de la sucesión los miembros de la sucesión que quedan siguen siendo toda la sucesión. Además, se dice que una sucesión es una sucesión fractal de razón d si el subconjunto de términos de la sucesión que no se eliminan son los que van apareciendo cada d posiciones.
La sucesión A046109 (en la OEIS) de la cantidad de puntos reticulares sobre las circunferencias de radio números enteros no negativos centradas en el origen (0,0), es una sucesión autosemejante de razón 3, como puede observarse, ya que si se empieza en el 1, luego se eliminan los dos siguientes términos y se mantiene el tercero, y así se continúa de forma infinita, se eliminan dos seguidos y se mantiene el tercero, la sucesión infinita de los términos que quedan sigue siendo la sucesión original, la sucesión A046109:
1, 4, 4, 4, 4, 12, 4, 4, 4, 4, 12, 4, 4, 12, 4, 12, 4, 12, 4, 4, 12, 4, 4, 4, 4, 20, 12, 4, 4, 12, 12, 4, 4, 4, 12, 12, 4, 12, 4, 12, 12, 12, 4, 4, 4, 12, 4, 4, 4, 4, 20, 12, 12, 12, 4, 12, 4, 4, 12, 4, 12, 12, 4, 4, 4, 36, 4, 4, 12, 4, 12, 4, 4, 12, 12, 20, 4, 4, 12, 4, 12, 4, 12, 4, 4, 36, …
El teorema de SchinzelEn relación con la construcción de la anterior sucesión infinita de números, la búsqueda de los puntos reticulares que están sobre ciertas circunferencias, el matemático polaco Andrzej Schinzel (1937-2021) demostró el siguiente resultado.
Teorema de Schinzel: Para todo número entero positivo n, existe una circunferencia sobre el plano coordenado que pasa exactamente por n puntos reticulares.
Veamos qué ocurre para los primeros casos.
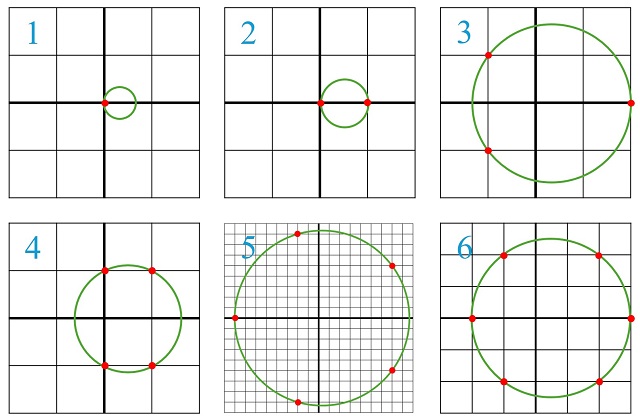 Circunferencias sobre el plano coordenado que pasan por 1, 2, 3, 4, 5 y 6 puntos de la retícula
Circunferencias sobre el plano coordenado que pasan por 1, 2, 3, 4, 5 y 6 puntos de la retícula
La demostración que realizó Schinzel de este resultado, publicada en el artículo Sur l’existence d’un cercle passant par un nombre donné de points aux coordonnées entières (L’Enseignement Math. Ser. 2, n. 4, 71-72, 1958), consistía en la contrucción de circunferencias concretas en función de si n era par o impar. En concreto, si n era par, de la forma n = 2k, entonces consideró la circunferencia de centro (1/2,0) y radio 5(k – 1)/2/2, cuya ecuación es
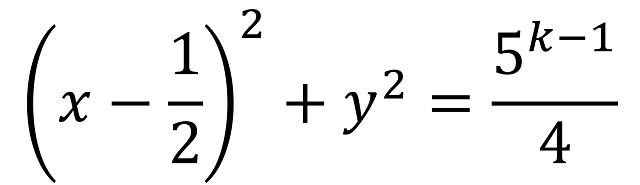
construida para tener exactamente 2k puntos reticulares, mientras que, si n era impar, de la forma n = 2k + 1, entonces consideró la circunferencia de centro (1/3,0) y radio 5k/3, cuya ecuación es
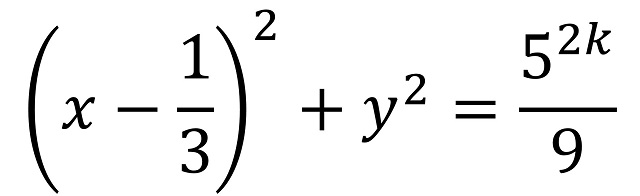
construida para tener exactamente 2k + 1 puntos reticulares.
La construcción de las circunferencias de la demostración de Schinzel proporciona circunferencias con la cantidad deseada n de puntos reticulares, aunque no son las circunferencias de radio más pequeño que cumplen que tienen n puntos de la retícula. Por ejemplo, el matemático recreacional Ed Pegg Jr en la página de Wolfram Demonstrations Project construye algunas circunferencias minimales con n puntos reticulares, siendo n = 4, 5, …, 12 (puede verse aquí).
 Dibujo sin papel 76/1 (1976), de la artista venezolana Gego, Gertrud Goldschmidt (1912-1994)
Dibujo sin papel 76/1 (1976), de la artista venezolana Gego, Gertrud Goldschmidt (1912-1994)Bibliografía
1.- Clifford A. Pickover, El prodigio de los números. Desafíos, paradojas y curiosidades matemáticas, Ma Non Troppo (ediciones Robinbook), 2002.
2.- Ron Honsberger, Mathematical Gems I, MAA, 1973.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Puntos reticulares sobre circunferencias se ha escrito en Cuaderno de Cultura Científica.
Los fotones entrelazados que tienen distinta velocidad
En óptica cuántica los científicos suelen crear fotones entrelazados mediante la llamada conversión descendente paramétrica espontánea. En este proceso los fotones individuales se convierten en pares de fotones entrelazados cuando se proyecta luz sobre un cristal diseñado específicamente para ello. Ahora, Guillaume Thekkadath, del Consejo Nacional de Investigación de Canadá, y sus colegas han identificado un retraso entre los tiempos de detección de cada fotón entrelazado que depende de la intensidad de la luz que incide sobre el cristal. Este hallazgo podría afectar al diseño de ordenadores y sensores cuánticos porque estas tecnologías a menudo requieren fotones sincronizados con precisión.
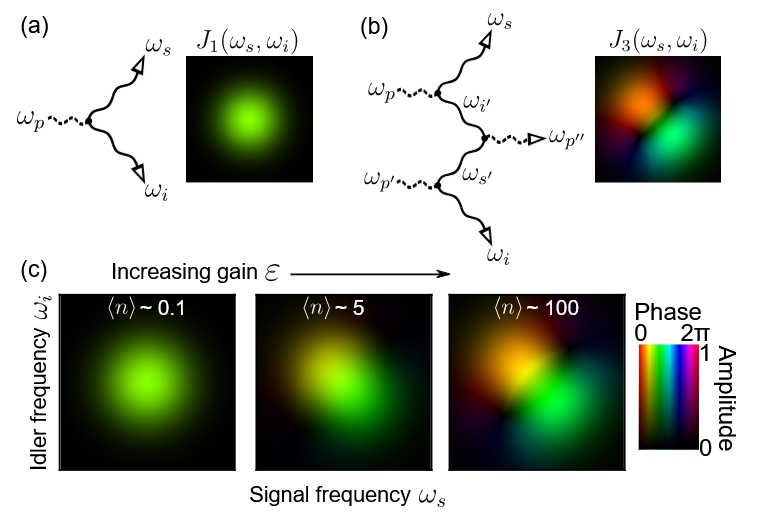 El proceso de conversión descendente paramétrica espontánea
El proceso de conversión descendente paramétrica espontáneaLos investigadores descubrieron que podía existir una diferencia temporal en la detección de forma teórica primero. Analizaron la conversión descendente paramétrica espontánea utilizando la teoría de perturbaciones más allá del primer orden, que es el que se considera habitualmente. A continuación, desarrollaron un modelo numérico del proceso de generación de fotones que han puesto a disposición pública para otros científicos. Para comprobar experimentalmente el modelo teórico construyeron un sistema en el que los tiempos de detección se pueden medir con precisión empleando interferometría.
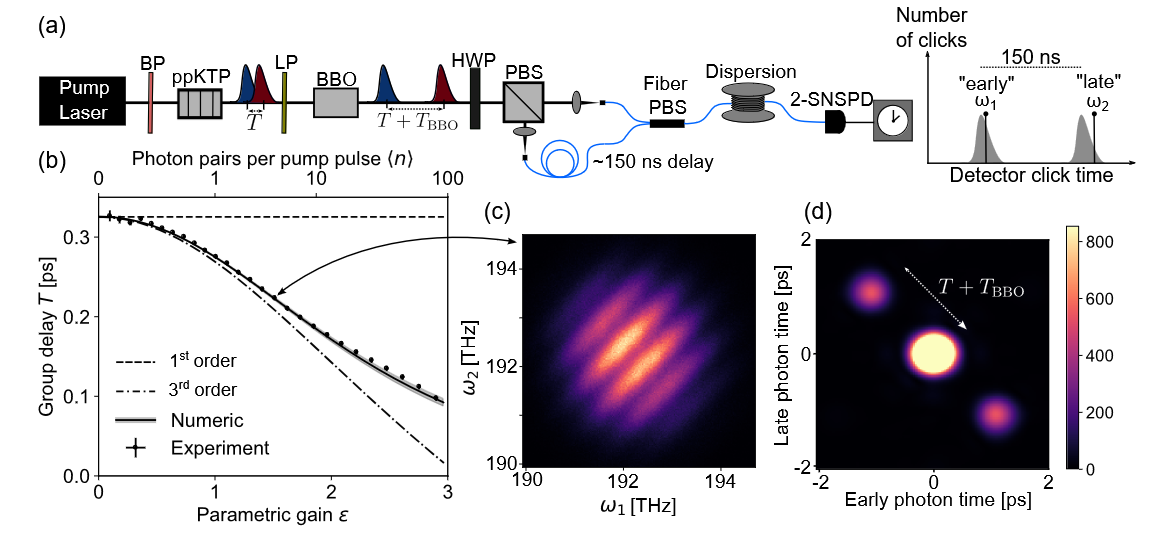 Un esquema del dispositivo experimental
Un esquema del dispositivo experimentalEl equipo descubrió que, en el caso de una luz de entrada de baja intensidad, el fotón inicial recorre la mitad del cristal, en promedio, antes de convertirse en un par entrelazado. Debido a sus diferentes longitudes de onda y polarizaciones, cada fotón de este par se propaga a diferentes velocidades por el resto del cristal, lo que genera una diferencia relativamente grande entre sus tiempos de detección.
En comparación, en el caso de una luz de entrada de alta intensidad, el fotón inicial suele penetrar hasta cerca del extremo del cristal. Los fotones de cada par tienen que recorrer una distancia menor a través del cristal, lo que da como resultado un retraso más corto.
Los investigadores dicen que, aunque este retraso se puede compensar en configuraciones ópticas a gran escala, plantea complicaciones para la fabricación de sistemas en chip, esto es, integrar todos o gran parte de los módulos que componen un ordenador o cualquier otro sistema informático o electrónico en un único circuito integrado.
Referencias:
Guillaume Thekkadath, Martin Houde, Duncan England, Philip Bustard, Frédéric Bouchard, Nicolás Quesada, & Ben Sussman (2024) Gain-Induced Group Delay in Spontaneous Parametric Down-Conversion Phys. Rev. Lett. doi: 10.1103/PhysRevLett.133.203601
Ryan Wilkinson (2024) Delay Detected in Photon Generation Physics 17, s130
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Los fotones entrelazados que tienen distinta velocidad se ha escrito en Cuaderno de Cultura Científica.
Una nueva perspectiva sobre el origen de los satélites de Marte
Los minúsculos satélites de Marte -Fobos y Deimos- han sido un verdadero quebradero de cabeza para los científicos, especialmente cuando han intentado resolver cual fue su origen, un tema que ya tratamos aquí en “El misterio de Fobos y Deimos”. A fecha de hoy todavía no tenemos muy clara la respuesta, pero aspira a ser uno de esos interrogantes que, si no se resuelven en la próxima década, sí se podrán acotar mucho las posibilidades.
A lo largo del tiempo se han propuesto distintas teorías para poder explicar su formación: Un par de asteroides capturados, la destrucción de un antiguo satélite en órbita y posterior formación de los dos nuevos satélites a partir de sus restos, material expulsado de la superficie del planeta por un gran impacto que acaba coalesciendo en órbita… pero lo cierto es que ninguna termina de convencer por completo a la comunidad científica. Y es que el hecho de que sus propiedades espectrales sean muy similares a la de algunos asteroides, junto con su forma irregular y una densidad relativamente baja los harían candidatos excepcionales para simplemente ser un par de cuerpos capturados.
 Fobos observado por la cámara HRSC de la sonda europea Mars Express. Cortesía de ESA/DLR/FU Berlin (G. Neukum).
Fobos observado por la cámara HRSC de la sonda europea Mars Express. Cortesía de ESA/DLR/FU Berlin (G. Neukum).Respecto a este último punto hay una pieza del puzle que nunca ha terminado de encajar: las órbitas casi circulares y ecuatoriales son algo muy difícil de explicar si suponemos que los asteroides se acercan al planeta desde direcciones aleatorias y que su captura tendría que, en los escenarios más probables, haber dado lugar a órbitas con distinta inclinación y una forma elíptica.
Pero, ¿y si realmente procediesen de un asteroide? Un nuevo estudio publicado por Kegerreis et al. (2024) propone un escenario a caballo entre la captura de un asteroide y el ensamblaje de los nuevos satélites a partir de los restos de este… ¿Cómo puede ocurrir tal cosa? Te lo explico.
Imaginemos un asteroide que se aproxima a Marte, pasando tan cerca que la gravedad del planeta es capaz de romper su cohesión, fragmentándolo. Ojo, en este punto es importante recordar que los asteroides no tienen que ser monolíticos, sino que pueden estar compuestos por fragmentos que viajan unidos por efecto de la gravedad.
Estas piezas desgajadas del asteroide podrían entonces dispersarse formando un disco de materiales que orbitase a Marte y, parte de este material, quedar “atrapado” en órbitas estables alrededor del planeta. Con el paso del tiempo, un porcentaje de estos fragmentos podrían colisionar entre ellos y dar lugar a protosatélites que, posteriormente, darían lugar a los satélites que conocemos hoy a partir de sucesivas colisiones.
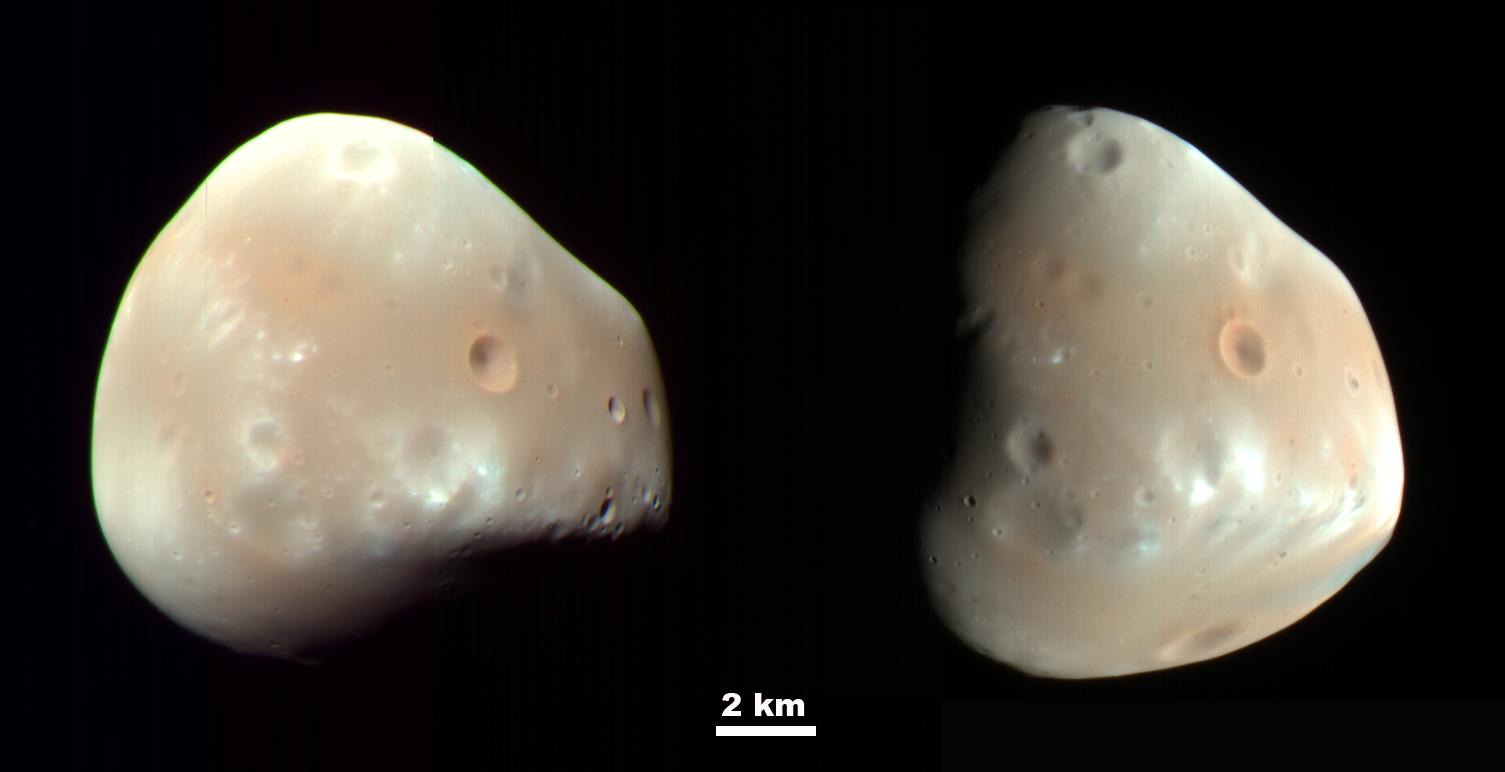 Deimos, el satélite más pequeño de Marte, observado con la cámara HiRISE que viaja a bordo de la Mars Reconaissance Orbiter. Cortesía de NASA/JPL-Caltech/University of Arizona.
Deimos, el satélite más pequeño de Marte, observado con la cámara HiRISE que viaja a bordo de la Mars Reconaissance Orbiter. Cortesía de NASA/JPL-Caltech/University of Arizona.Las simulaciones realizadas en este estudio del que hoy hablamos, muestran que un porcentaje significativo (hasta varias decenas porcentuales de la masa original del asteroide) podrían ser capturadas por la gravedad de Marte y alrededor de un uno por ciento de su masa podría acabar en órbitas circulares.
Y volvemos al mismo problema: las órbitas circulares. ¿Cómo es posible que los fragmentos del asteroide acabasen en órbitas casi circulares cuando al principio mencionábamos que esto es muy difícil? Pues probablemente el mecanismo más eficiente para lograr estas órbitas fuesen las propias colisiones entre los fragmentos, que no solo serían capaces de crear nuevos fragmentos, sino también de alterar sus velocidades y progresivamente logrando formar un disco de materia estable a partir del que se formarían los satélites.
 Detalle de la superficie de Fobos donde se puede apreciar un elevado número de cráteres y sistemas de surcos que cruzan su superficie. Cortesía de ESA/DLR/FU Berlin.
Detalle de la superficie de Fobos donde se puede apreciar un elevado número de cráteres y sistemas de surcos que cruzan su superficie. Cortesía de ESA/DLR/FU Berlin.Este modelo serviría también para explicar por qué la composición de los satélites, es compatible con la de los asteroides de tipo C que, por cierto, son los más abundantes de todos los existentes en nuestro Sistema Solar y otros aspectos, como las cadenas de cráteres y los sistemas de “surcos”, que podrían haberse formado durante el propio proceso de acreción que dio lugar a los satélites.
Si todo va bien, en 2026 despegará la misión Mars Moons eXploration (MMX) de la JAXA, que gracias a sus instrumentos y al retorno de muestras de Fobos -aunque solo sea una pequeña cantidad en el entorno de los 10 gramos ya será un gran hito científico- podrá traernos nueva información sobre estos satélites y quien sabe si cerrar definitivamente la historia sobre su origen.
Referencia:
Kegerreis, Jacob A. et ál (2024) “Origin of Mars’s Moons by Disruptive Partial Capture of an Asteroid.” Icarus, Oct. 2024, p. 116337 doi: 10.1016/j.icarus.2024.116337.
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Una nueva perspectiva sobre el origen de los satélites de Marte se ha escrito en Cuaderno de Cultura Científica.
No tiene que ser nuevo para estrenarlo
 The Golden Book Gown / El vestido del libro de oro de Ryan Jude Novelline. Confeccionado a partir de libros infantiles reciclados. Fuente: Ryan Jude Novelline / Wikimedia Commons
The Golden Book Gown / El vestido del libro de oro de Ryan Jude Novelline. Confeccionado a partir de libros infantiles reciclados. Fuente: Ryan Jude Novelline / Wikimedia CommonsA la protagonista de esta historia le tocó ser la cuarta hija de una familia de cuatro. Sus hermanas se llevan uno o un año y medio entre ellas. Después llegó ella, pero después de seis años. Así que como coloquialmente se dice, fue un pilón.
La madre traía a las hermanas mayores vestidas iguales. Todas bonitas y bien peinadas, vistiendo el mismo vestido o el mismo traje de pantalones cortos y blusas coloridas. Eso sí, cada una vestía un color diferente. Eso dejó en casa varias prendas en tres diferentes tallas y colores. Obviamente, como la última en casa, le tocaba estrenar el mismo modelo en tres diferentes ocasiones. Había talla 5, talla 7 y talla 8. Por lo tanto, cuando usó esas tallas, portaba el mismo modelito, pero en diferentes colores.
En su mente hay un recuerdo sobre una prenda a la cual le tenía un particular cariño. Un hermoso conjunto de pantalones cortos, o shorts como se dice en el Norte de México. Eran de lino y la blusa se abotonaba por la parte de atrás con unos botones forrados de la misma tela. Al frente tenían un gracioso pulpo con la cabeza rellena y unos ojos saltones, lo que lo hacía muy divertido. Los tentáculos estaban por toda la parte de enfrente y también estaban rellenos, aunque no tanto como la cabezota del pulpo.
Nuestra protagonista estrenó su traje de pulpo cabezón en color morado a los cinco años, el color verde a los siete y el color azul a los ocho. En ese momento no estaba ni de broma en la cabeza de nadie aquello de “moda sustentable”, pero ella tenía muy claro que estaba estrenando, aun cuando no fuera nuevo. La práctica de pasar la ropa de los hermanos mayores a los más pequeños se mantiene hasta ahora. Incluso cambiar ropa con las amigas podría decirse que es común, especialmente en la adolescencia, tiempos en que se quiere más a las amigas que a la propia familia. Sin embargo, comprar ropa de segunda mano en bazares o tiendas especializadas, por todo tipo de personas, es decir, sin distinguir clases sociales, no había sido tan común hasta hace solamente un par de años.
Como se mencionaba en el párrafo anterior, los bazares de segunda mano son actualmente mucho más comunes de lo que se puede pensar. Las nuevas generaciones tienen claro que se necesita cuidar al planeta y son conscientes de varios conceptos que generaciones atrás no tenía ni idea. Aquí algunos de esos conceptos que no estaban comúnmente incluidos en los cursos de nivel básico ni medio superior a los que asistió la protagonista.
Regla de las tres erres (3R)Regla para cuidar el medio ambiente, específicamente para reducir el volumen de residuos o basura generada. Se espera que cualquier empresa socialmente responsable deba considerarla.
Reducir Reciclar y Reutilizar. Tres verbos importantes que, si se siguen, ayudan a ser un consumidor responsable además de generar menos basura y ahorrar dinero. Aquí las definiciones, de acuerdo a Editorial RSyS, una plataforma de comunicación y difusión que ofrece servicios de asesoría y consultoría en temas afines para el sector social, educativo y empresarial [1].
– Reducir. Disminuir o simplificar el consumo de los productos directos.
– Reutilizar. Volver a utilizar las cosas y darles la mayor utilidad posible antes de que llegue la hora de deshacernos de ellas. Esto disminuye directamente el volumen de la basura.
– Reciclar. Someter los materiales a un proceso en el cual se puedan volver a utilizar, evitando la necesidad de utilizar nuevos materiales.
Calentamiento globalDe acuerdo con la Organización de las Naciones Unidas (ONU), el cambio climático se refiere a los cambios a largo plazo de las temperaturas y los patrones climáticos. Estos cambios pueden ser naturales, por ejemplo, a través de las variaciones del ciclo solar. Pero desde el siglo XIX, las actividades humanas han sido el principal motor del cambio climático, debido principalmente a la quema de combustibles fósiles [2]. La principal causa del cambio climático es el calentamiento global y tiene múltiples consecuencias negativas en los sistemas físicos, biológicos y humanos.
La temperatura media del planeta aumente al verse afectada por la emisión de gases de efecto invernadero a la atmósfera ya que retiene más calor del que se disipa al exterior. Estos gases emitidos aumentan como consecuencia de las actividades del ser humano. En la Figura 1 se muestra la temperatura del planeta en diferentes años de nuestra era [3]. Según los últimos informes de la ONU, miles de científicos y revisores gubernamentales coincidieron en que limitar el aumento de la temperatura global a no más de 1.5 °C ayudaría a evitar los peores impactos climáticos y a mantener un clima habitable. Sin embargo, las políticas actuales apuntan a un aumento de la temperatura de 2.8 °C para finales de siglo [2].
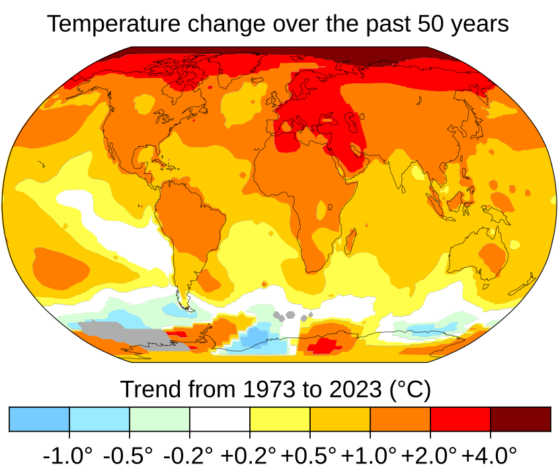 Figura 1. Cambio en las temperaturas globales entre 1973 y 2023. Fuente: NASA’s Scientific Visualization Studio /Wikimedia Commons
Figura 1. Cambio en las temperaturas globales entre 1973 y 2023. Fuente: NASA’s Scientific Visualization Studio /Wikimedia CommonsExiste otro término con relación a la industria del vestido, tema principal de este escrito: Moda sustentable. Se puede encontrar en una página del gobierno y la verdad es reconfortante saber que es un tema que se aborda en páginas oficiales. Eso indica que ya lo consideran en las agendas políticas.
Moda sustentable o sostenibleEs aquella que aboga por la reducción de los recursos necesarios para la producción y la reutilización de los mismos en prendas de vestir y complementos que cumplan criterios de respeto por el medio ambiente y con materiales naturales u orgánicos. [4]
Existe a la fecha un amplio catálogo de tiendas de moda sustentable y bazares que se dedican a reunir a estas emprendedoras que creen en la moda sustentable. Es un fenómeno a nivel mundial. En la Figura 2 se muestra una de estas tiendas.
 Una tienda de ropa de segunda mano. Fuente: Rex Roof / Wikimedia Commons
Una tienda de ropa de segunda mano. Fuente: Rex Roof / Wikimedia CommonsLa industria textil es un sector que utiliza grandes cantidades de agua y es una de las que genera mayor contaminación. Esta industria genera el 20% del total de las aguas residuales del planeta. Además, genera una gran cantidad de basura, ya que un alto porcentaje de las fibras son incineradas y, tristemente, arrojadas a vertederos.
Las sociedades del mundo siempre han producido residuos, pero es ahora, en la sociedad de consumo, cuando el volumen de las basuras ha crecido de forma desorbitada. Además, se ha incrementado su toxicidad hasta convertirse en un gravísimo problema.
La llamada “fast fashion” ha incrementado este problema ya que existen algunas marcas que lanzan una enorme cantidad de colecciones anualmente. Estas colecciones y prendas de “precios bajos” son producto de la necesidad creciente entre los consumidores, quienes tienen que estrenar lo último de los aparadores de estas marcas. De acuerdo con Bloomberg, en Estados Unidos, cada ciudadano desecha al año una cantidad de ropa equivalente a 70 pares de pantalones. Suena a un enorme desperdicio, pero también señala que uno de cada tres británicos considera que una prenda está vieja después de usarla solo una o dos veces.
Lo importante es que al menos ya se conoce lo que está pasando. ¿Cuántos años se tardó la humanidad en aceptar que quemar combustibles fósiles estaba contribuyendo al cambio climático? Como dicen, aceptar el problema es lo primero, ahora hay que buscarle solución. Reciclar la ropa es un buen inicio. Existen personas de varias generaciones que se preocupan por el futuro. Acostumbran a reciclar, guardan y llevar a los contenedores aquellos residuos que posteriormente pueden convertirse en nuevos productos y utilizarse de nuevo. Con esto contribuyen al desuso de materiales y reducen los consumos de agua y energía que se usarían en fabricarlos.
La esperanza está puesta en estas nuevas generaciones que tienen conciencia sobre lo que se le ha hecho al planeta Tierra y quieren evitar continuar con los malos hábitos para buscar mejorar el medio ambiente en el futuro. Algunas personas están en la transición. Ya juntan algunos materiales para llevarlos a contenedores especiales como lo es el PET, (polietilentereftalato para los conocedores). El PET es un polímero o plástico producido a grandes escalas para diferentes usos, pero el principal y más conocido es en la industria alimentaria para contener algunos productos, principalmente refrescos y agua embotellada. Este material es reciclable y existen muchas industrias que se dedican a este proceso. Así que no lo tiren a la basura. Es mejor llevarlo a un punto de recolección al igual que los botes de aluminio, el papel y cartón. Si se empieza hoy mismo en casa en una familia, los hijos verán esto como una acción cotidiana y para los hijos de los hijos, serán actividades regulares.
Además, cada vez más personas compran su vestimenta en los bazares de ropa de segunda mano. Esperemos que cada vez existan menos prejuicios para comprar en estos lugares y que se haga habitual intercambiar la ropa con las amigas y familiares no solamente porque se ha heredado, sino por el deseo de cuidar al planeta. ¿Y ustedes? Después de leer esto, ¿van a empezar a reciclar en casa y a comprar ropa de segunda mano? Ojalá que sí.
Referencias:
[1] Responsabilidad Social Empresarial y Sostenibilidad
[2] Naciones Unidas – Acción por el clima
[3] Acciona – Canbio climático
[4] Gobierno de México – Moda sostenible
Sobre la autora: Norma Flores-Holguín es investigadora en el Departamento de Medio Ambiente y Energía del CIMAV (CONAHCYT, México)
El artículo No tiene que ser nuevo para estrenarlo se ha escrito en Cuaderno de Cultura Científica.
Naukas Pro 2024: Euskadi punta de lanza en energías renovables marinas

Los últimos avances en el ámbito de las energías renovables marinas o la proliferación de los microplásticos fueron algunos de los temas que componen la última edición de NAUKAS PRO. Una cita en la que el personal investigador se sube al escenario del Euskalduna Bilbao para hablar de las investigaciones más destacadas del momento en un ámbito concreto.
En esta ocasión el personal investigador de la Universidad del País Vasco, de la Estación Marina de Plentzia (PiE-UPV/EHU), AZTI, Tecnalia o el CSIC acercaron las últimas investigaciones relacionadas en el ámbito marítimo.
La conferencia Euskadi punta de lanza en energías renovables marinas corre a cargo de Eider Robles Sestafe, investigadora del Centro de Investigación Aplicada y Desarrollo Tecnológico TECNALIA.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Pro 2024: Euskadi punta de lanza en energías renovables marinas se ha escrito en Cuaderno de Cultura Científica.
Las discordancias entre las diferentes etiquetas nutricionales
El grupo de investigación en Enfermería y Promoción de la Salud de la Universidad del País Vasco ha comparado siete sistemas de etiquetado nutricional de Europa, Oceanía y América del Sur y ha determinado que apenas coinciden a la hora de definir si los alimentos cocinados son saludables. Las investigadoras concluyen que hace falta desarrollar un nuevo sistema para evaluar la calidad alimentaria de los platos preparados.
 Fuente: Tamorlan / Wikimedia Commons
Fuente: Tamorlan / Wikimedia CommonsEn respuesta a la creciente preocupación por los hábitos alimentarios de la población, gobiernos de todo el mundo han implementado diferentes sistemas de etiquetado nutricional para ayudar a los y las consumidoras a elegir productos saludables cuando hacen la compra. El grupo de investigación en Enfermería y Promoción de la Salud de la UPV/EHU se ha propuesto dar un paso más. En vista de que cada vez comemos más fuera de casa, plantea la posibilidad de que los restaurantes también incluyan en sus cartas información sobre si los platos son sanos o no: “De la misma manera que marcan si las recetas contienen alérgenos o si son aptas para veganos, creemos que estaría bien indicar si son saludables. En este contexto, queríamos saber si alguno de los sistemas de etiquetado nutricional que ya se emplean a nivel global para evaluar productos procesados podrían ser válidos para evaluar platos cocinados. Para ello hemos comparado siete métodos diferentes y hemos encontrado tan poca coherencia entre ellos que consideramos que ninguno es adecuado para nuestro objetivo”, explica Leyre Gravina, la investigadora principal del trabajo.
Discordancias entre etiquetas nutricionalesLa investigación es novedosa dado que hasta ahora no se había comparado la reproducibilidad y la concordancia de las etiquetas a nivel global con relación a comida cocinada. Para realizar la comparación han seleccionado 178 platos mediterráneos que se sirven en la Escuela de Hostelería de Leioa y los han examinado empleando los siguientes sistemas de etiquetado: Nutri-Score, los semáforos del Reino Unido y Ecuador, el método Mazocco, el sistema HSR de Australia y las etiquetas de advertencia de Uruguay y Chile. Los resultados muestran discordancias entre todas las herramientas. En algunos casos las diferencias son más acentuadas, pero en general, el nivel de acuerdo es reducido. Por ejemplo, en lo que se refiere al número de platos no saludables detectados, los sistemas que más discrepan son Nutri-Score y el de Ecuador. El primero es el método que más recetas califica como insanas (el 38 %), mientras que el segundo es el más laxo, ya que no califica ninguna como tal.
El equipo de la Universidad del País Vasco reconoce que esperaban diferencias porque los sistemas no emplean las mismas metodologías y consideran variables dispares, pero se han sorprendido con el nivel de incoherencia encontrado: “Las herramientas de Uruguay o Ecuador solo tienen en cuenta el contenido de componentes perjudiciales para la salud como el exceso de azúcares o grasas saturadas. Y otros contemplan también nutrientes saludables como las legumbres o las fibras. Por lo tanto, intuíamos que los análisis podían dar resultados diferentes, pero resulta que el desacuerdo es significativo incluso entre los sistemas que valoran componentes similares”, detalla Gravina.
Por ejemplo, Nutri-Score analiza 13 nutrientes y 9 de ellos son todos los que contempla el sistema HSR de Australia: calorías, azúcares, ácidos grasos saturados, fibras, frutas, verduras, frutos secos y proteínas. Sin embargo, aun coincidiendo en muchos de los componentes a analizar, la investigación revela que el acuerdo entre ambas herramientas de evaluación solo es moderado. Una muestra de ello son los resultados del análisis de los postres: Nutri-Score considera que el 6 % son sanos; el sistema australiano, el 25 %.
Las herramientas globales no sirvenSegún las autoras del trabajo, la baja coincidencia entre las diferentes etiquetas nutricionales indica que es necesario desarrollar estrategias más complejas para evaluar la calidad alimentaria de platos preparados. Ante la falta de consenso a la hora de definir lo que es saludable, Gravina propone crear un método que se adapte al contexto geográfico: “De momento no parece que un sistema universal pueda ser efectivo. Sería conveniente empezar por herramientas de etiquetado que tengan en cuenta los alimentos de cada lugar y la realidad culinaria y sociocultural de cada país o región”.
Referencia:
Julia Fernandez-Alonso, María del Mar Lamas-Mendoza, Stuart D. R. Galloway and Leyre Gravina (2024) Assessing the Validity of Front-of-Pack Nutrition Labels for Evaluating the Healthiness of Mediterranean Food Choices: A Global Comparison Nutrients doi: 10.3390/nu16172925
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Las discordancias entre las diferentes etiquetas nutricionales se ha escrito en Cuaderno de Cultura Científica.
La rebelión de las cianobacterias
En los últimos días, ciertos sectores de la sociedad parece que quieren iniciar un retroceso en el conocimiento científico sobre el origen de nuestro planeta y de la vida que habita el mismo, poniendo de nuevo al ser humano en el centro de todo. Cada vez que escucho comentarios de esta índole, recuerdo las palabras que solía decir una profesora ya jubilada del Departamento de Geología de la Universidad del País Vasco (UPV/EHU): “los seres humanos nos creemos el ombligo del mundo y que podemos alterar todo lo que nos rodea. Pues para revolución de verdad, la que montaron unos organismos microscópicos hace más de 2000 millones de años”. Esta sentencia hacía que te sintieses como una pequeña mota de polvo dentro de la historia de nuestro planeta. Pero, ¿qué pudieron hacer estos microorganismos para liarla tan parda?
Para responder a esta pregunta debemos viajar hasta los orígenes de nuestro propio planeta. Se estima que, hace unos 4500 millones de años, la Tierra podría tener una atmósfera primitiva reductora, conformada por gases como dióxido de carbono (CO2), hidrógeno (H2) y agua (H2O), muy inestable y débil, ya que esos gases escaparían al espacio. Pero, cuando nuestro nacimiento planetario se tranquilizó, hace entre 4400 y 3500 millones de años, gracias a procesos como la diferenciación de la corteza y el núcleo, el bombardeo de cuerpos extraterrestres y la aparición de océanos de agua líquida sobre la superficie, la Tierra contaría con una atmósfera secundaria estable. Esta capa atmosférica sería débilmente reductora y estaría compuesta por monóxido y dióxido de carbono (CO y CO2), hidrógeno (H2), agua (H2O), amoniaco (NH3) y metano (CH4).
 Imagen de microscopio de cianobacterias del género Lyngbya encontradas en Baja California (México). Fuente: NASA / Wikimedia CommonsLas cianobacterias y el Gran Evento Oxidativo
Imagen de microscopio de cianobacterias del género Lyngbya encontradas en Baja California (México). Fuente: NASA / Wikimedia CommonsLas cianobacterias y el Gran Evento Oxidativo
Bajo esta atmósfera primitiva, en la Tierra ocurrió uno de los eventos que nos diferencia de nuestros vecinos planetarios más cercanos, la aparición de la vida. Al principio, se trataba de células simples, unas bacterias primitivas sin núcleo diferenciado, que vivían en medios con salinidades y temperaturas extremas alimentándose de metano o compuestos metálicos. Pero rápidamente se les ocurrió la brillante idea de combinarse entre sí para convertirse en organismos más complejos, dando lugar a las cianobacterias. Aparecidas hace entre 3700 y 3400 millones de años, la principal característica de las cianobacterias es que son los primeros organismos fotosintéticos de la historia, por lo que fueron capaces de liberar moléculas de oxígeno (O2) gaseoso a la atmósfera.
Esta actividad bacteriana favoreció que tanto la atmósfera como las capas más superficiales de las aguas oceánicas pasasen a convertirse en débilmente oxidantes. Pero a las cianobacterias no les pareció suficiente. En los siguientes millones de años decidieron proliferar por todo el mundo, convirtiéndose en la forma de vida dominante de nuestro planeta. Esto provocó la liberación de cantidades cada vez mayores de oxígeno a la atmósfera hasta que, hace unos 2400 millones de años, generaron esa revolución de la que os hablaba al principio de este artículo: el Gran Evento Oxidativo, o GOE por sus siglas en inglés (Great Oxidation Event).
 A) Estromatolitos actuales creciendo en las aguas poco profundas de la Hamelin Pool Marine Nature Reserve de Shark Bay (Australia). B) Estromatolitos fósiles en corte longitudinal, donde se observan las capas superpuestas de sedimento, encontrados en Québec (Canadá). Fuentes: A) Paul Harrison / Wikimedia Commons; B) André P. Drapeau / Wikimedia Commons
A) Estromatolitos actuales creciendo en las aguas poco profundas de la Hamelin Pool Marine Nature Reserve de Shark Bay (Australia). B) Estromatolitos fósiles en corte longitudinal, donde se observan las capas superpuestas de sedimento, encontrados en Québec (Canadá). Fuentes: A) Paul Harrison / Wikimedia Commons; B) André P. Drapeau / Wikimedia CommonsEl GOE, ocurrido hace entre 2400 y 2100 millones de años, supuso un cambio radical de todo lo conocido hasta ese momento, así como el comienzo de todo lo que vino después. La atmósfera pasó de ser reductora o ligeramente oxidativa a completamente oxidativa, llegando a tener porcentajes de oxígeno incluso superiores a los de nuestra atmósfera actual; las aguas oceánicas también se convirtieron en oxidativas, tanto las masas más superficiales como las que circulaban por los fondos marinos; el oxígeno gaseoso reaccionó con el metano atmosférico, reduciendo la cantidad de este gas de efecto invernadero y, por tanto, disminuyendo la temperatura de nuestro planeta; y, debido a la disociación de las moléculas de oxígeno producida por la luz solar, se empezaron a combinar tres moléculas de oxígeno para generar la capa de ozono (O3) que recubre nuestro planeta y que lo protege de la radiación solar, efecto que favoreció la colonización de tierra firme, primero por las plantas y después por los animales, millones de años después.
Estas cianobacterias siguen pululando por nuestro planeta, aunque ya no son tan dominantes como en el pasado. Uno de los lugares donde se pueden encontrar en la actualidad son los mares cálidos y poco profundos de Australia, donde forman unas estructuras sedimentarias conocidas como estromatolitos. Precisamente, la presencia de fósiles de estromatolitos de hace casi 3700 millones de años nos aportan una de las evidencias de la aparición de las cianobacterias en la Tierra. Sin embargo, el registro fósil del GOE que a mí más me gusta son las Formaciones de Hierro Bandeado o BIF por sus siglas en inglés (Banded Iron Formations). Se trata de depósitos sedimentarios en los que se alternan capas de minerales de hierro oxidado, como el hematites (Fe2O3), de colores rojizos, con capas de silicio (SiO2) de colores grises y negros, que se formaron hace entre 2500 y 1800 millones de años. En este caso, la existencia de ese hierro oxidado, implica que las masas de agua que atravesaron estas partículas minerales antes de depositarse en los fondos oceánicos eran ya oxidativas y no reductoras.
 Depósito de una Formación de Hierro Bandeado (BIF) generado hace unos 2100 millones de años encontrado en Norteamérica. Fuente: André Karwath / Wikimedia Commons
Depósito de una Formación de Hierro Bandeado (BIF) generado hace unos 2100 millones de años encontrado en Norteamérica. Fuente: André Karwath / Wikimedia CommonsComo os decía al principio, volver la vista atrás en nuestra historia y comprobar que unos simples organismos microscópicos provocaron un cambio tan grande en todo el planeta, hace que se nos bajen mucho los humos. Si no se hubiesen puesto a liberar oxígeno a la atmósfera como si no hubiese un mañana, los seres humanos no estaríamos hoy en día sobre la Tierra, porque la evolución biótica de nuestro planeta es una historia maravillosa repleta de fantásticas casualidades que no debemos dejar que nos arrebaten.
Agradecimientos:
Quiero darle las gracias a Estíbaliz Apellaniz, profesora jubilada de Paleontología del Departamento de Geología de la Universidad del País Vasco (UPV/EHU), tanto por repetir continuamente la frase con la que abro este artículo, como por despertarnos la curiosidad por conocer nuestros verdaderos orígenes a generaciones de estudiantes que pasamos por sus manos.
Para saber más:
J. Pla-García y C. Menor-Salván (2017). La composición química de la atmósfera primitiva del planeta Tierra. Anales de Química 113 (1), 16-26
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo La rebelión de las cianobacterias se ha escrito en Cuaderno de Cultura Científica.
Maddalena y Teresa Manfredi, calculadoras astronómicas
La bella Hipatia escribió varios tratados: profesaba la astronomía en Alejandría cuando fue asesinada por el clero, fue en 415. Maria Cunitz, hija de un médico de Silesia, publicó en 1650 unas tablas astronómicas. Marie-Claire Eimmart Muller, hija y esposa de astrónomos conocidos, también fue astrónoma. Jeanne Dumée presentó en 1680 unas entrevistas sobre el sistema de Copérnico. La esposa de Hevelius realizaba obvervaciones junto a él. Las hermanas de Manfredi calculaban las efemérides de Bolonia; las tres hermanas de Kirch calcularon durante mucho tiempo las efemérides de Berlín; su esposa, nacida Winkelmann, presentó en 1712 una obra de astronomía. La Marquesa de Châtelet ha proporcionado una traducción de Newton. La condesa de Puzynina ha fundado un observatorio en Polonia […]. Madame Lepaute, fallecida en 1788, ha calculado durante más de diez años efemérides de la Academia, y la viuda de Edwards trabaja en Inglaterra en el «Nautical almanac«. Madame du Piery ha realizado numerosos cálculos de eclipses para comprender mejor el movimiento de la Luna; fue la primera que ejerció la astronomía en París. Miss Caroline Herschel trabaja con su hermano. Ya ha descubierto cinco cometas. La Señora Duquesa de Gotha ha realizado gran cantidad de cálculos, pero no desea ser citada. Mi sobrina, Le Français de Lalande, ayuda a su marido en sus observaciones y obtiene conclusiones de ellas mediante cálculos; ha reducido diez mil estrellas, ha preparado trescientas páginas de tablas horarias para la marina, un trabajo inmenso para su edad y sexo. Están en mi “Abrégé de Navigation”.
Joseph-Jérôme Le Français de Lalande, Astronomie des dames (1785): 5-7.
 Portada de Ephemerides motuum coelestium de Eustachio Manfredi. Fuente: Google Books.
Portada de Ephemerides motuum coelestium de Eustachio Manfredi. Fuente: Google Books.
Las hermanas Maddalena y Teresa Manfredi nacieron en 1673 y 1679, respectivamente. Su madre, Anna Maria Fiorini, y su padre, el notario Alfonso Manfredi, no dieron a sus hijas (eran tres, la tercera se llamaba Agnese) la oportunidad de estudiar en la universidad, a diferencia de sus hijos (Eustachio, Gabriele, Eraclito y Emilio). Las hermanas Manfredi recibieron una educación primaria tradicional en un convento de monjas terciarias.
Una familia ilustradaGracias a los conocimientos de sus hermanos y a las amistades que frecuentaban la casa familiar, Maddalena y Teresa pudieron mejorar la escasa formación que habían recibido. En particular, tenían buenos conocimientos de astronomía, matemáticas y latín.
Su hermano Eustachio (1674-1739) fundó la Accademia degli Inquieti (Academia de la Inquietud) en Bolonia alrededor de 1690; buscaba un lugar en el que se pudieran discutir temas científicos. Se dedicó a la observación astronómica; entre sus numerosos trabajos científicos se encuentra Ephemerides motuum coelestium (1715-1725), que completó con la ayuda de sus hermanas Maddalena y Teresa.
Gabriele (1681-1761) y Eraclito (1682-1759), también hermanos de Maddalena y Teresa, estudiaron medicina. Gabriele abandonó esta materia para centrarse en las matemáticas, dedicándose fundamentalmente al cálculo infinitesimal. En su obra De constructionae aequationum differentiationium primi gradu (1707) expuso sus resultados sobre la resolución de problemas relacionados con ecuaciones diferenciales y fundamentos del cálculo. Emilio (1679-1742) se convirtió en sacerdote jesuita. De Agnese no hay datos disponibles.
A pesar de su influencia en la vida cultural de Bolonia, los hermanos Manfredi tenían puestos mal remunerados. Debido a estas limitaciones económicas, la familia se mantuvo muy cohesionada, involucrando a hermanos y hermanas en la creación de una empresa cultural destinada a mejorar el presupuesto familiar.
Así, Maddalena y Teresa, además de ocuparse de las labores domésticas, se dedicaron también a la administración del negocio familiar, a la colaboración científica en la obra de sus hermanos y a la producción de obras literarias para el mercado de la burguesía boloñesa.
En 1701 toda la familia Manfredi se trasladó al palacio del conde Luigi Ferdinando Marsili que deseaba de crear una academia en Bolonia siguiendo el modelo de la Académie des Sciences de París y la Royal Society de Londres; Eustachio ayudó a Marsili a crear la Academia de Ciencias de Bolonia. En 1711, Eustachio fue nombrado astrónomo de la Academia, sus hermanas lo acompañaron a su nuevo destino.
El trabajo de Maddalena y TeresaLa familia Manfredi comenzó a realizar observaciones de las posiciones de los objetos astronómicos en una cúpula astronómica preparada en su casa para crear efemérides. Maddalena y Teresa se encargaron del trabajo computacional; sus avances en las técnicas de cálculo ayudaron a que algunos de ellos pudieran ser realizados por personas no especialistas. Por ello, probablemente, su hermana Agnese también podría haber colaborado en el trabajo.
En 1715, Eustachio publicó Ephemerides motuum coelestium, una referencia ampliamente utilizada por otros astrónomos europeos. Atribuyó a sus hermanas la ayuda con las efemérides desde 1712 y, en particular, a Maddalena el cálculo de la tabla de latitudes y longitudes incluida en la publicación.
Eustachio también contó con la colaboración de sus hermanas para realizar investigaciones bibliográficas para la redacción de su Compendiosa Informazione di facto sopra el confines del Ferrara community di Ariano con il Stato Veneto (1735).
Con el paso de los años, a pesar de permanecer a la sombra de sus hermanos, Maddalena y Teresa adquirieron cierta popularidad. La familia Manfredi cultivó la pasión por la poesía y la literatura dialectal. Como producto adicional de la empresa cultural familiar, publicaron obras literarias para público general, como la traducción de cuentos napolitanos al dialecto boloñés. Aunque los nombres de los traductores no aparecían en la portada, era de conocimiento general que las traducciones de Bertoldo y de Chiaqlira eran obra de Teresa y Maddalena, apoyadas por las hermanas Teresa Maria y Angiola Anna Maria Zanotti, hijas del pintor Giampietro Zanotti (1675-1765).
Maddalena falleció el 11 de marzo de 1744 a la edad de 72 años; Teresa murió 23 años después, el 8 de octubre de 1767.
El asteroide 13225 Manfredi fue nombrado en honor a Eustachio, Gabriele y Eraclito. A pesar de su colaboración en el trabajo de sus hermanos, esta dedicatoria no incluía a Maddalena y Teresa…
Referencias
- Ariane Dröscher, Manfredi Maddalena, Szienza a due voci
- Gabriella Bernardi, Maddalena (1673–1744) and Teresa (1679–1767) Manfredi, en The Unforgotten Sisters, 2016
- Maddalena and Teresa Manfredi, Wikipedia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
El artículo Maddalena y Teresa Manfredi, calculadoras astronómicas se ha escrito en Cuaderno de Cultura Científica.
En el mundo cuántico hasta los marcos de referencia son inciertos
Los marcos de referencia desde los cuales los observadores ven los eventos cuánticos pueden tener múltiples ubicaciones posibles a la vez, un descubrimiento con importantes ramificaciones.
Un artículo de Anil Ananthaswamy. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 La naturaleza cuántica de los marcos de referencia puede incluso afectar el orden percibido de los acontecimientos. Ilustración: Michele Sclafani para Quanta Magazine
La naturaleza cuántica de los marcos de referencia puede incluso afectar el orden percibido de los acontecimientos. Ilustración: Michele Sclafani para Quanta MagazineImagínate que estás de pie en un andén viendo pasar un tranvía. A una chica que está en el tranvía se le cae una pelota roja brillante. Para ella, la pelota cae directamente hacia abajo. Pero desde el andén ves que la pelota describe un arco antes de tocar el suelo del tranvía. Los dos observáis el mismo evento, pero desde diferentes marcos de referencia: uno anclado al tranvía y el otro al andén.
La idea de los marcos de referencia tiene una larga historia en la física clásica: Isaac Newton, Galileo y Albert Einstein se basaron en ellos para sus estudios sobre el movimiento. Un marco de referencia es, en esencia, un sistema de coordenadas (una forma de especificar posiciones y tiempos relativos a un punto cero u “origen”) que puede él mismo estar en movimiento. Einstein utilizó marcos de referencia para desarrollar sus teorías de la relatividad, que revelaron que el espacio y el tiempo no son telones de fondo fijos del universo, sino entidades elásticas que pueden estirarse, contraerse y deformarse.
Pero la física cuántica ha ignorado en gran medida los marcos de referencia. Alice y Bob, los observadores ficticios en muchos experimentos de física cuántica, suelen tener diferentes ubicaciones físicas, pero se supone que tienen un marco de referencia común. Esto está cambiando ahora. Los físicos cuánticos se están dando cuenta de que no pueden ignorar el hecho de que el marco de referencia al que está anclada Alice (similar al tranvía o el andén) puede tener múltiples ubicaciones posibles a la vez. O que el reloj que Bob usa para medir el tiempo puede estar sujeto a la incertidumbre cuántica.
“En el mundo cuántico, los marcos de referencia deberían [también] describirse mediante el formalismo de la teoría cuántica”, explica Renato Renner, físico teórico del Instituto Federal Suizo de Tecnología de Zúrich.
En un artículo publicado este año, el físico Časlav Brukner, del Instituto de Óptica Cuántica e Información Cuántica de la Universidad de Viena, y sus colegas demostraron que los marcos de referencia cuánticos ofrecen una nueva perspectiva a fenómenos cuánticos largamente estudiados, como la superposición y el entrelazamiento. Los hallazgos llevaron a Renner a sospechar que los marcos de referencia cuánticos podrían ayudar a resolver algunas de las extrañas paradojas que surgen en los experimentos mentales cuánticos.
 Časlav Brukner, físico de la Universidad de Viena y director del Instituto de Óptica Cuántica e Información Cuántica, ha explorado los marcos de referencia cuánticos en una serie de artículos recientes. Foto cortesía de Magdalena Zych
Časlav Brukner, físico de la Universidad de Viena y director del Instituto de Óptica Cuántica e Información Cuántica, ha explorado los marcos de referencia cuánticos en una serie de artículos recientes. Foto cortesía de Magdalena ZychMás ambiciosos aun, Brukner y sus colegas esperan que pensar en la lógica de los marcos de referencia cuánticos pueda producir nuevos conocimientos sobre la gravedad cuántica, un programa de investigación que intenta colocar la gravedad en el mismo ámbito teórico que las otras fuerzas fundamentales.
Con esta nueva incursión en los marcos de referencia cuánticos, afirma Renner, “estamos solo en el comienzo de algo muy grande”.
Ubicaciones difusasLa noción de marcos de referencia cuánticos se introdujo por primera vez en 1984, pero varios grupos retomaron la idea alrededor de 2019, lo que ha desencadenado la oleada de estudios recientes. Los argumentos nos desafían a cambiar nuestra forma de pensar sobre dos propiedades cuánticas por excelencia: la superposición, donde un objeto puede estar simultáneamente en múltiples estados posibles, y el entrelazamiento, donde partículas distintas comparten un único estado cuántico, de modo que la medición de una de ellas determina instantáneamente el estado de la otra, independientemente de la distancia entre ellas.
 De izquierda a derecha: Luca Apadula, Anne-Catherine de la Hamette y Viktoria Kabel del Instituto de Óptica Cuántica e Información Cuántica y la Universidad de Viena dirigieron conjuntamente un estudio que muestra que la elección del marco de referencia afecta a los sistemas que parecen estar entrelazados o en superposición. Foto: Andrea Di Biagio
De izquierda a derecha: Luca Apadula, Anne-Catherine de la Hamette y Viktoria Kabel del Instituto de Óptica Cuántica e Información Cuántica y la Universidad de Viena dirigieron conjuntamente un estudio que muestra que la elección del marco de referencia afecta a los sistemas que parecen estar entrelazados o en superposición. Foto: Andrea Di BiagioPara ver cómo, consideremos dos sistemas de referencia; los llamaremos A y B. Digamos que el origen de A está anclado a un objeto cuántico que tiene probabilidades de encontrarse en varias ubicaciones. Desde la perspectiva de B, la ubicación de A está difuminada sobre alguna región. Pero desde la perspectiva de A, la distancia a B está difuminada. Parece como si B fuera el que está en una superposición.
La cosa mejora. ¿Y si B también está anclado a un objeto cuántico que se encuentra en una superposición de dos posiciones? Entonces, el estado cuántico de A se difumina de dos maneras diferentes, dependiendo de las posibles posiciones de B. Como la determinación del estado cuántico de B determina el estado de A, A y B ahora están entrelazados.
 Renato Renner, físico del Instituto Federal Suizo de Tecnología de Zúrich, cree que un análisis cuidadoso de los marcos de referencia cuánticos resolverá las paradojas en nuestra comprensión del mundo cuántico. Foto: Giulia Marthaler
Renato Renner, físico del Instituto Federal Suizo de Tecnología de Zúrich, cree que un análisis cuidadoso de los marcos de referencia cuánticos resolverá las paradojas en nuestra comprensión del mundo cuántico. Foto: Giulia MarthalerEn el ejemplo anterior, dos propiedades esenciales de los sistemas cuánticos (la superposición y el entrelazamiento) resultan depender del marco de referencia. “El mensaje principal es que muchas de las propiedades que consideramos muy importantes y, en cierto modo, absolutas, son relacionales” o relativas, explica Anne-Catherine de la Hamette, coautora del artículo reciente.
Incluso el orden de los acontecimientos sucumbe a los rigores de los marcos de referencia cuánticos. Por ejemplo, desde un marco de referencia, podríamos observar el clic de un detector que se produce en un momento determinado, pero desde un marco de referencia diferente, el clic podría acabar en una superposición de ocurrir antes y después de algún otro evento. El hecho de que observemos el clic como si se produjera en un momento determinado o como si se tratara de una superposición de diferentes órdenes de acontecimientos depende de la elección del marco de referencia.
Un paso hacia la gravedadLos investigadores esperan utilizar estas diferentes perspectivas cuánticas para dar sentido a la desconcertante naturaleza de la gravedad. La relatividad general de Einstein, que es una teoría clásica de la gravedad, dice que la gravedad es la deformación del tejido del espacio-tiempo por un objeto masivo. Pero, ¿cómo se deformará el espacio-tiempo si el propio objeto está en una superposición de dos ubicaciones? «Es muy difícil responder a esa pregunta con la física cuántica y la gravedad habituales», afirma Viktoria Kabel, investigadora del grupo de Brukner y coautora del nuevo artículo.
Sin embargo, si cambiamos a un sistema de referencia cuyo origen se encuentra en una superposición, el objeto masivo puede terminar en una ubicación definida. Ahora es posible calcular su campo gravitatorio. “Al encontrar un sistema de referencia cuántico conveniente, podemos tomar un problema que no podemos resolver [y convertirlo] en un problema para el cual podemos usar la física estándar conocida”, explica Kabel.
Estos cambios de perspectiva deberían ser útiles para analizar futuros experimentos cuyo objetivo sea colocar masas extremadamente pequeñas en superposiciones. Por ejemplo, los físicos Chiara Marletto y Vlatko Vedral, de la Universidad de Oxford, han propuesto colocar dos masas cada una en una superposición de dos posiciones y luego estudiar cómo esto afecta a sus campos gravitatorios. Los crecientes intentos de describir formalmente los marcos de referencia cuánticos podrían ayudar a dar sentido a estas investigaciones sobre la interacción entre la gravedad y la teoría cuántica, un paso esencial hacia una teoría de la gravedad cuántica.
Renner cree que los marcos de referencia cuánticos también pueden ser fundamentales para dilucidar los fundamentos de la física cuántica. Hace unos años, él y su colega Daniela Frauchiger diseñaron un experimento mental cuántico que crea una contradicción lógica. La paradoja resultante parece implicar que los físicos deben renunciar a al menos una de las muchas nociones aceptadas sobre nuestro mundo, por ejemplo, que la teoría cuántica es universal y que se aplica tanto a los seres humanos como a los átomos.
Sin embargo, Renner ahora sospecha que la paradoja surge simplemente porque los físicos no han tenido en cuenta cuidadosamente los marcos de referencia. Nadie ha descubierto aún cómo reescribir este u otros experimentos mentales utilizando marcos de referencia cuánticos, pero hacerlo “es muy probable que nos lleve a la solución de las paradojas”, afirma.
No va a ser fácil, porque los sistemas de referencia cuánticos traen consigo muchos problemas sin resolver. Por ejemplo, con los sistemas de referencia clásicos, si cambias tu punto de vista de un sistema a otro, esta transformación es reversible: puedes volver a tu punto de vista original. No está claro que esto sea posible en la actualidad de forma universal con los sistemas de referencia cuánticos.
Además, en este momento no hay una forma estándar de definir y cambiar entre sistemas de referencia cuánticos. Diferentes grupos de físicos tienen diferentes enfoques. “Todos parecen razonables a primera vista, pero no son equivalentes entre sí”, apunta Renner.
Con el tiempo, sin embargo, los marcos de referencia cuánticos podrían resultar esenciales para dar sentido al mundo cuántico.
El artículo original, In the Quantum World, Even Points of View Are Uncertain, se publicó el 22 de noviembre de 2024 en Quanta Magazine.
Traducido por César Tomé López
El artículo En el mundo cuántico hasta los marcos de referencia son inciertos se ha escrito en Cuaderno de Cultura Científica.
Dormir para reparar el corazón
En 1971, los Bee Gees alcanzaron por primera vez al número 1 en EE. UU. con su canción How Can you Mend a Broken Heart (“Cómo puedes reparar un corazón roto”). Más de medio siglo después tenemos una respuesta que jamás hubieran imaginado los hermanos Gibb: durmiendo. Pero no se trata de hacer un esfuerzo para dormir más. Se acaba de descubrir que el daño cardiaco provoca una inducción de sueño profundo que favorece la reparación de dicho daño. Resulta difícil de creer, así que lo vamos a explicar detenidamente.
El sueño sigue siendo un fenómeno misterioso en muchos aspectos. Sabemos que el sueño es indispensable para la salud, aunque muchas conexiones entre sueño y salud se nos escapan. Un grupo de investigadores estadounidenses acaba de publicar en Nature una conexión que ha resultado ser tan inesperada como sorprendente.
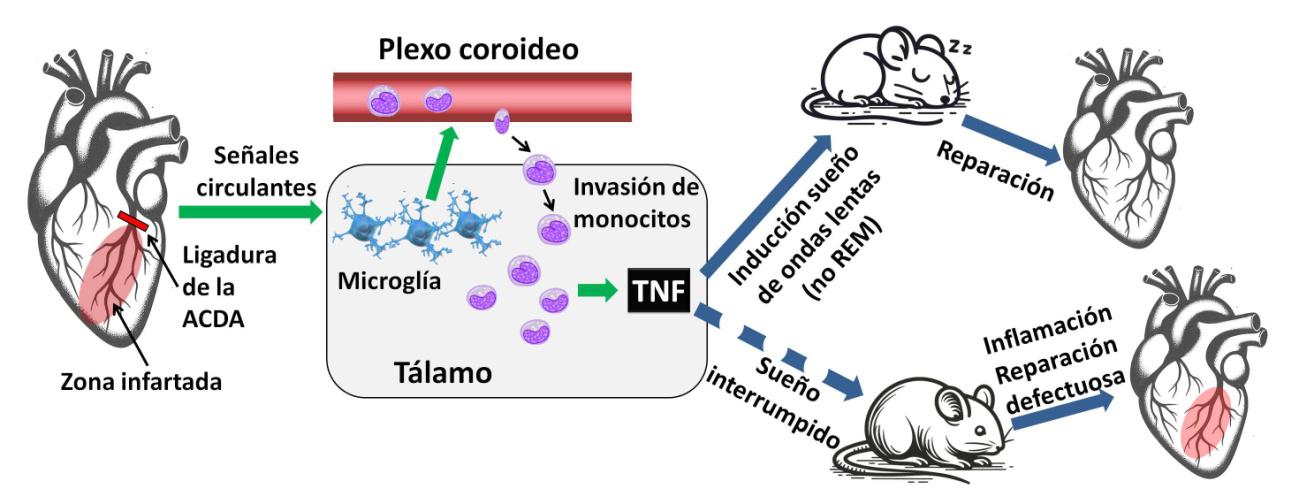 Figura 1. Esquema de los resultados obtenidos por Huynh et al., (2024). Un infarto de miocardio provocado por la ligadura de la arteria coronaria descendente anterior (ACDA) genera señales circulantes que hacen que la microglía del tálamo atraiga monocitos desde el plexo coroideo. Los monocitos invasores secretan factor de necrosis tumoral (TNF) que induce una prolongación de la fase de sueño de ondas lentas. De esta forma se mejora el proceso de reparación del corazón. Si se interrumpe el sueño, se alarga el proceso inflamatorio en el corazón, perjudicando la reparación. Imágenes: Wikimedia Commons, Medical gallery of Blausen y generadas con Microsoft Bing
Figura 1. Esquema de los resultados obtenidos por Huynh et al., (2024). Un infarto de miocardio provocado por la ligadura de la arteria coronaria descendente anterior (ACDA) genera señales circulantes que hacen que la microglía del tálamo atraiga monocitos desde el plexo coroideo. Los monocitos invasores secretan factor de necrosis tumoral (TNF) que induce una prolongación de la fase de sueño de ondas lentas. De esta forma se mejora el proceso de reparación del corazón. Si se interrumpe el sueño, se alarga el proceso inflamatorio en el corazón, perjudicando la reparación. Imágenes: Wikimedia Commons, Medical gallery of Blausen y generadas con Microsoft BingEs posible provocar un infarto de miocardio en los ratones ligando, con microcirugía, la arteria coronaria descendente anterior. Como control de los experimentos se utilizan ratones sometidos al mismo procedimiento de anestesia y toracotomía, pero sin ligar la arteria. Pues bien, los ratones con infarto de miocardio (en adelante ratones-IM) experimentan periodos más largos de sueño de ondas lentas, un tipo de sueño profundo diferente al sueño REM. Esta prolongación del sueño de ondas lentas se mantiene durante siete días tras el infarto.
¿Cómo se induce un mayor periodo de sueño de ondas lentas tras el infarto? La microglía1 de los ratones-IM envía señales que provocan el reclutamiento de monocitos, un tipo de células inmunitarias. Estos monocitos abandonan la circulación en el plexo coroideo e invaden una región del tálamo. La invasión puede ser también inducida inyectando en el líquido cefalorraquídeo de ratones sanos plasma de ratones-IM, lo que indica que se debe a factores circulantes. De hecho, si se inhiben farmacológica o genéticamente ciertos receptores de señales de los monocitos, estos no invaden el tálamo y desaparece el efecto del infarto sobre el sueño.
¿Qué sucede si se inyectan directamente monocitos en el líquido cefalorraquídeo de un ratón normal? Pues si estos proceden de un ratón-IM, se induce la prolongación del sueño de ondas lentas, pero esto no ocurre si los monocitos vienen de ratones control. Por tanto, los monocitos de ratones-IM hacen algo en el tálamo para inducir cambios en el sueño.
Comparando el transcriptoma (conjunto de genes expresados) de monocitos aislados del tálamo de ratones-IM con el de ratones control, se observó en los primeros un aumento en la secreción del factor de necrosis tumoral (TNF), una citoquina2 implicada en procesos de inflamación, entre otros muchos. Todo indicaba que TNF era el elemento inductor del sueño. El sueño de ondas lentas no se prolongaba en ratones-IM si se inyectaban anticuerpos anti-TNF en el líquido cefalorraquídeo. Tampoco si los monocitos procedían de ratones mutantes sin expresión de TNF, o si los ratones-IM carecían de receptores para el TNF.
Resumiendo hasta ahora, un infarto provoca la invasión de monocitos circulantes en el tálamo, estos producen TNF, provocando un aumento del sueño de ondas lentas. Ahora viene lo importante, ese aumento del sueño profundo ¿realmente contribuye a reparar el corazón?
Pues así es. Si se producían interrupciones en el sueño aumentaba la cantidad de troponina3 en sangre pasadas 1-3 semanas desde el infarto. También disminuía la función cardiaca. Me estoy refiriendo ahora solo a ratones hembras, que son los que se utilizaron principalmente en el experimento. Los ratones machos soportan peor la ligadura coronaria y sobreviven menos. Eso sí, la interrupción del sueño en ratones-IM machos resultaba fatal. El 68% de los que habían dormido sin problemas sobrevivían una semana después del infarto. En cambio, solo sobrevivió el 18% de los que habían visto su sueño interrumpido.
Sueño y reparación del corazónEl estudio aventura una hipótesis sobre la relación entre sueño y reparación cardiaca. Los ratones-IM con sueño interrumpido mostraban en sus corazones más células del sistema inmune que los controles. La idea es que el sueño de ondas lentas disminuye la actividad del sistema simpático sobre el corazón, una actividad que contribuye a mantener la inflamación cardiaca post-infarto perjudicando la capacidad reparadora.
Un punto crucial: ¿Este descubrimiento tiene alguna relación con lo que sucede en humanos? Los investigadores realizaron un estudio preliminar sobre 78 pacientes que se habían recuperado de un infarto. Los dividieron en dos grupos atendiendo a indicadores de la calidad del sueño. Dos años después del infarto, los que habían dormido bien tenían una mejor función cardiaca que los que tenían peor calidad de sueño. Estos últimos sufrieron una mayor mortalidad a lo largo de estos dos años y el doble de eventos cardiovasculares adversos que los pacientes “bien dormidos”. Aunque es imprescindible contar con más estudios, esto sugiere que dormir bien contribuye a la recuperación tras un infarto de miocardio.
Los resultados son sorprendentes y contraintuitivos, porque sugieren que un proceso inflamatorio cerebral (invasión de monocitos, secreción de TNF) induce sueño profundo, disminuyendo la inflamación cardiaca. Pero también son estimulantes, ya que proporcionan nuevas vías para el tratamiento del infarto de miocardio y subrayan la importancia de una correcta higiene del sueño en dicho tratamiento.
Referencias
Huynh, P., Hoffmann, J.D., Gerhardt, T., et al. (2024) Myocardial infarction augments sleep to limit cardiac inflammation and damage. Nature. doi: 10.1038/s41586-024-08100-w.
Notas:
1 Células del sistema inmune presentes en el cerebro.
2 Proteína señalizadora producida por células inmunitarias.
3 Un marcador circulante que indica la existencia de daño cardiaco
 
 
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga
El artículo Dormir para reparar el corazón se ha escrito en Cuaderno de Cultura Científica.

