Cómo la química de nuestro cerebro hace que las drogas tomen el control
Las drogas forman parte de nuestra sociedad, con todas sus formas y aplicaciones. Desde el tabaco al alcohol, pasando por los opiáceos, siempre han estado de moda. En los medios vemos constantemente noticias relacionadas con la crisis del fentanilo, la legalización del cannabis y los efectos antioxidantes del consumo de vino. Pero ¿cuál es la base química que hace que estas sustancias sean tan populares y peligrosas?
 Imagen: vat loai / PixabayUna vieja costumbre
Imagen: vat loai / PixabayUna vieja costumbre
La historia del consumo de drogas es prácticamente tan antigua como la de la humanidad. Ya en la Edad Antigua, numerosas drogas como el opio recorrieron ampliamente las civilizaciones de la cuenca mediterránea, principalmente aplicadas como remedios medicinales. Pese al aviso de pensadores como Diágoras de Melos (“es mejor sufrir dolor que volverse dependiente del opio”, siglo V a. e. c.), su aplicación recreativa no tardó en llegar.
Otro ejemplo de droga popular desde la Antigüedad es el alcohol. Persas, griegos, chinos, egipcios, mayas, romanos… Por todos los rincones del mundo la elaboración y el consumo de bebidas alcohólicas formaba parte de la vida social, espiritual y cultural de cada civilización. Hoy en día la situación se mantiene: el consumo moderado de alcohol en la cultura occidental está normalizado, legalizado y extendido a gran parte de la población. En ocasiones, el cine, la televisión y la música incluso glorifican su ingesta, enfatizando sus efectos eufóricos.
¿Cuál es el secreto de estas sustancias? ¿Cómo es posible que afecten a nuestra química cerebral hasta el punto de influir en el devenir de las civilizaciones?
La respuesta se encuentra en un conjunto de áreas interconectadas de nuestro cerebro conocido como sistema mesocorticolímbico.
¿Me está engañando mi dopamina?Para hacernos saber que un estímulo es beneficioso para la supervivencia, nuestro cerebro se encarga de que este nos guste. Ejemplo de ello son las sensaciones de placer que experimentamos a través de una comida calórica, el sexo y la interacción social.
Acompañando a esa sensación, nuestro cerebro también señaliza ese estímulo y hace que aprendamos que nos ha gustado: así es más probable que repitamos esa actividad positiva. De hecho, gracias a este sistema tendremos además una gran motivación, necesaria para poner en marcha nuestro cuerpo y así obtener esos estímulos.
¿Son siempre importantes para la supervivencia las conductas que se ven reforzadas? La respuesta es que no.
Al sistema mesocorticolímbico encargado de la recompensa se le puede hackear.
A nivel celular, las dos regiones más relevantes de este sistema son el área tegmental ventral y el núcleo accumbens. Las neuronas de la primera región conectan con las de la segunda y envían una molécula neurotransmisora llamada dopamina. Esta cumple un rol esencial en la recompensa: cuando se aumenta el nivel de dopamina que se libera se inician una serie de procesos. El resultado final es que aprendemos que ese estímulo es importante para la supervivencia y provoca que estemos más motivados para volver a buscarlo en el futuro.
Este sistema requiere regulación. De esto se encargan unas proteínas en la superficie celular llamadas receptores opioides. Es aquí donde entran en juego las drogas y el hackeo del sistema: este tipo de receptores pueden ser activados tanto por estímulos naturales como por las drogas. Al hacerlo, se intensifica la liberación de dopamina.
El resultado es que a nuestro cerebro le gustan estas drogas, aprende que son estímulos importantes y nos motiva a volver a conseguirlas. Aunque no aporten ventajas para la supervivencia.
De este modo se explican parcialmente los efectos eufóricos y reforzantes del consumo agudo de estas sustancias. Sin embargo, también es la base de su cara más oscura: la adicción. ¿Qué pasa cuando el uso de drogas se cronifica?
La delgada línea entre la euforia y el dolorSi bien el consumo moderado de drogas se normaliza y hasta celebra en contextos sociales, este puede desencadenar problemas graves. El consumo prolongado de alcohol y de otras sustancias no solo afecta a nuestras percepciones y comportamientos, sino que también deja su huella en nuestro cerebro de una manera que puede ser difícil de revertir.
Recordemos que nuestro sistema mesocorticolímbico es un sistema de recompensa, diseñado para hacernos sentir bien cuando realizamos acciones beneficiosas. No obstante, el consumo repetido de estas sustancias puede hacer que su funcionamiento cambie y que aquello que solía producir placer ya no lo haga en la misma medida.
Estos cambios en las capacidades reforzantes del alcohol y los opioides se deben, entre otras cosas, a reducciones en la liberación de dopamina. Pero ¿quién es responsable de estas alteraciones?
Igual que hay receptores opioides –receptor Mu opioide– que provocan un incremento en la liberación de dopamina y son responsables del refuerzo positivo, existen otros –receptor Kappa opioide– que actúan de forma opuesta. Es decir, su actividad hace que disminuya la liberación del neurotransmisor y da lugar a efectos opuestos: disforia, aversión y pérdida de motivación.
Durante el consumo repetitivo de sustancias como alcohol y opioides tienen lugar cambios en la expresión de estos receptores. Mientras que los Mu están cada vez menos activos, los Kappa lo están cada vez más.
La disminución de la capacidad de las drogas para generar sensaciones placenteras hace que estas se vuelvan menos gratificantes con el tiempo. Este hecho, junto a los estados disfóricos que se manifiestan en ausencia de la sustancia, conducen a escaladas en el consumo con la finalidad de autotratar dicho malestar.
Es tan importante este mecanismo en la adicción que hasta se ha acuñado un nuevo término: hyperkatifeia, del griego katifeia, que significa “abatimiento” o “estado emocional negativo”. Curiosamente, estas alteraciones en los receptores opioides son similares a las que ocurren en situaciones de dolor crónico y pueden desencadenar estados negativos como falta de motivación, ansiedad y depresión.
La conclusión es que el consumo continuado de ciertas sustancias puede tener consecuencias físicas, mentales y sociales graves, y alterar la manera en que nuestro cerebro experimenta el placer y el dolor. No es de extrañar que la adicción a las drogas haga tocar fondo. Aunque se disfracen como aliadas para sobrellevar los problemas, acaban convirtiéndose en el mayor de ellos.![]()
Sobre las autoras: María Ros Ramírez de Arellano, Doctorando en Neurociencias, Lucía Hipólito Cubedo, Profesora en el área de Farmacia y Tecnología Farmacéutica y Víctor Ferrís Vilar, Doctorando en Neurociencias. Los tres de la Universitat de València.
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Cómo la química de nuestro cerebro hace que las drogas tomen el control se ha escrito en Cuaderno de Cultura Científica.
Cómo viajar en el tiempo sin destruir el universo
Dijo una vez Ursula K. Le Guin que no somos nosotros los que viajamos en el tiempo, sino que es el tiempo el que viaja a través de nosotros, y tal vez ese sea el el motivo por el que todo lo relacionado con él nos fascina tanto: no lo controlamos, nos controla y lo hace, además, sin que podamos evitarlo y sin que, desde un aspecto puramente científico, tengamos todavía muy claro qué es. Sabemos que el tiempo, o la dirección en la que casi siempre lo vemos transcurrir, se manifiesta a través de los procesos irreversibles de la naturaleza, ya sean termodinámicos, cuánticos, cosmológicos… El universo que nos rodea parece tener claro hacia dónde va; resta averiguar por qué.
Más allá de la física, el tiempo determina prácticamente todos los aspectos de la experiencia humana, de ahí que haya sido un tema omnipresente en nuestras narraciones desde hace miles de años. Primero, en los mitos y leyendas, después, en la ciencia ficción. En el Mahabharata, texto hindú de alrededor del siglo III a. C, el rey Kakudmi experimenta los «efectos relativistas» de abandonar por un momento la Tierra para visitar a Brahma, el creador, y encontrarse al volver que han transcurrido varias generaciones desde su partida; algo similar a lo que le pasa a Urashima, el pescador protagonista de una leyenda japonesa del siglo XV, quien, cuando regresa a su aldea tras estar tres años en el palacio del dios dragón en el fondo del mar, se da cuenta de que, en realidad, han pasado casi trescientos cincuenta. Quedarse dormido y despertarse varios siglos en el futuro también es una forma muy típica de viajar en el tiempo en muchas historias fantásticas, o a través de la ingesta de algún tipo de sustancia con poderes milagrosos. Pero ¿en qué momento esos relatos de viajes dejaron la fantasía a un lado para intentar convertirse en ciencia? ¿Es que acaso la física permitiría algo así? ¿Existe alguna teoría que respalde la posibilidad de viajar en el tiempo, no solo hacia el futuro y más allá de la dilatación relativista? En otras palabras: ¿es posible viajar en el tiempo de alguna forma «no sobrenatural» o este tipo de historias están condenadas a existir en el ámbito de la fantaciencia para siempre?
Ha habido innumerables intentos de justificar de una manera racional la existencia de viajeros temporales en la literatura de ciencia ficción. Enrique Gaspar y Rimbau identificó el tiempo con algún tipo de fluido manipulable —algo similar al éter, aunque no exactamente eso—, en El anacronópete (1887) cuando trató de despojarlo de su halo místico. H. G. Wells, por su parte, habló de una cuarta dimensión en La máquina del tiempo (1895) —algo muy similar a lo que ya había hecho en «Los ojos del señor Davidson» (1894) con el espacio para conectar dos lugares muy alejados entre sí utilizando una especie de agujero de gusano—. Sorprendentemente, ambos vislumbraron de alguna manera el camino por el que luego iría la teoría de la relatividad general y algunas de las soluciones a las ecuaciones de Einstein. Y, así, podríamos seguir enumerando relatos y novelas hasta llegar a 1958, cuando Robert A. Heinlein escribió el que, al menos para mí, es uno de los relatos más verosímiles de viajes en el tiempo o, al menos, uno que no escandalizaría a la ciencia tanto como otros: «All you zombies—», publicado en The Magazine of Fantasy and Science Fiction en marzo del año siguiente y adaptado a la gran pantalla por Michael y Peter Spierig en 2014 con el título de Predestination.
 Primera página de «All you zombies—», de Robert Heinlein. publicada por primera vez en The Magazine of Fantasy and Science Fiction. Se adaptó al cine con el título de Predestination en 2014.
Primera página de «All you zombies—», de Robert Heinlein. publicada por primera vez en The Magazine of Fantasy and Science Fiction. Se adaptó al cine con el título de Predestination en 2014.
Al que no haya leído el relato o visto la película y no le gusten los spoilers —y este es uno de esos casos en los que un mínimo destripe puede echar a perder toda la experiencia— le recomiendo que lo haga, y que vuelva más adelante a este artículo. No voy a entrar en los detalles fundamentales de la trama, pero, entre solución y solución relativista, sí es posible que haya suficientes pistas como para que alguien pueda ser capaz de desvelar el truco del prestidigitador.
Dicho esto, convirtamos la ciencia ficción en ciencia.
Entre todas estas historias de viajes temporales al pasado, al futuro, con máquina, sin máquina, de paradojas y quebraderos de cabeza con el libre albedrío hay unas de un tipo concreto que, en principio, la física no prohíbe: las de bucles temporales o, en lenguaje científico, las curvas cerradas de tipo tiempo.
En la teoría de la relatividad de Einstein, cualquier objeto que se mueve a través del espacio-tiempo tetradimensional sigue una trayectoria denominada «línea de universo». Ese espacio-tiempo normalmente lo representamos de forma geométrica con el conocido cono de luz, que, además, describe la estructura causal de determinado evento. Esto es: sus posibles pasados —causas—, su momento presente y sus posibles futuros —consecuencias—.
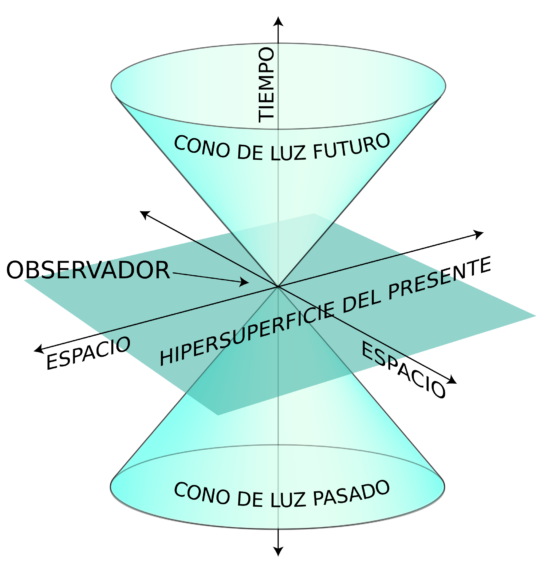 El cono de luz describe las relaciones causales de cualquier evento, tanto hacia el pasado como hacia el futuro. La propia superficie viene determinada por la velocidad de la luz. Como nada puede ir más rápido según la teoría de la relatividad, todo lo que sucede en el universo se encuentra dentro de sus límites. Créditos: CC BY-SA 3.0/Stib, K. Aainsqatsu e Ignacio Icke.
El cono de luz describe las relaciones causales de cualquier evento, tanto hacia el pasado como hacia el futuro. La propia superficie viene determinada por la velocidad de la luz. Como nada puede ir más rápido según la teoría de la relatividad, todo lo que sucede en el universo se encuentra dentro de sus límites. Créditos: CC BY-SA 3.0/Stib, K. Aainsqatsu e Ignacio Icke.
Existen, además, varios tipos de líneas de universo en función de la posición que ocupen respecto al cono de luz:
-
De tipo tiempo: siempre están dentro del cono, lo que significa que describen las trayectorias de partículas que viajan a menor velocidad que la de la luz o que tienen masa.
-
De tipo nulo o tipo luz: se encuentran sobre la superficie del cono y describen las trayectorias de partículas sin masa, como los fotones, que viajan a la velocidad de la luz.
-
De tipo espacio: estarían fuera del cono de luz; representarían eventos desconectados causalmente o, por decirlo de otra manera, completamente «incomunicados» entre sí.
Lo que sucede en nuestro mundo se encuentra, por tanto, dentro del cono de luz y, en principio, todo tiene un punto de inicio y un punto final. Pero ¿es esa la única opción posible? Según la teoría de la relatividad general, no. Matemáticamente no hay inconveniente en que existan líneas de universo «cerradas» o bucles que empiecen y acaben en el mismo punto y se retroalimenten a sí mismos. Eso son las curvas cerradas de tipo tiempo que mencionamos antes. Y es cierto que podrían provocar algunos problemas causales, pero no siempre. En la práctica, como es obvio, este tipo de soluciones son bastante impracticables, pero ¿cuándo los límites de la realidad supusieron algún problema para un físico teórico?
Este tipo de soluciones de las ecuaciones de Einstein fueron, de hecho, de las primeras en aparecer. El físico holandés Willem Jacob van Stockum las encontró en 1937 al tratar de describir cómo sería el campo gravitacional generado por un cilindro infinito compuesto por un fluido —Gaspar y Rimbau no iba tan desencaminado— que gira alrededor de un eje. La contraposición entre fuerzas gravitacionales y centrífugas haría que, en zonas de curvatura intensa, los conos de luz se inclinaran en la dirección de rotación y… Voilà! Las líneas de universo se cerraran sobre sí mismas. Kurt Gödel encontró una solución muy similar en 1949, pero él puso a girar todo el universo, tejido del espacio-tiempo incluido, en lugar de solo una región, como Van Stockum. De nuevo, la rotación permitía la inclinación de los conos de luz y la existencia de curvas cerradas de tipo tiempo. En 1963, llegarían los agujeros negros rotatorios de Kerr, que también permitirían la existencia de bucles temporales en sus inmediaciones; en 1974, el cilindro rotatorio de Tipler…
Para entender un poco mejor qué es lo que estaría pasando en este tipo de geometrías y universos —estos últimos nada tienen que ver con el nuestro, por cierto— basta pensar en cómo los campos gravitatorios intensos afectan al tiempo dentro del marco de la relatividad general: a mayor curvatura, más lento pasa el tiempo, como ya nos enseñó la película Interstellar. Si, además, los ponemos a rotar, se produce una distorsión adicional que provoca un efecto llamado «arrastre de marcos de referencia», que como si nos lleváramos por delante el propio espacio-tiempo, pudiendo poner patas arriba su estructura causal.
 Este remolino de tela sería lo más parecido a cómo se verían las zonas que podrían albergar curvas cerradas de tipo tiempo en geometrías rotatorias. Si la tela fuera plana, imaginemos los conos de luz cosidos a ella verticalmente. Al poner la tela a girar a grandísimas velocidades, los conos, con las arrugas, se inclinarían y las líneas de universo que contienen, se acabarían cerrando sobre sí mismas.
Este remolino de tela sería lo más parecido a cómo se verían las zonas que podrían albergar curvas cerradas de tipo tiempo en geometrías rotatorias. Si la tela fuera plana, imaginemos los conos de luz cosidos a ella verticalmente. Al poner la tela a girar a grandísimas velocidades, los conos, con las arrugas, se inclinarían y las líneas de universo que contienen, se acabarían cerrando sobre sí mismas.Créditos: Pixabay/Mohamed_hassan
No son conceptos fáciles de visualizar, ni siquiera para un físico teórico y ni siquiera con las ecuaciones y los diagramas delante, por no mencionar los quebraderos de cabeza que podría dar que se demostrara que existiera algo así. Imaginemos, simplemente, un sistema cuántico atrapado en uno de esos bucles temporales, ¿dónde quedarían su naturaleza estadística y el principio de indeterminación si, para no violar la causalidad, estuviera condenado a encontrarse siempre en el mismo estado al pasar por determinado punto?
Por si acaso, y para curarse en salud, Stephen Hawking planteó, en 1992, su conjetura de protección cronológica, que dice, básicamente, que el universo se protege a sí mismo de inconsistencias. No elimina la posibilidad de la existencia de curvas cerradas de tiempo tiempo, pero sí de aquellas que puedan provocar «¡…una paradoja temporal, lo que produciría una reacción en cadena que seguramente desarticularía el continuo espacio-tiempo y destruiría todo el universo!», como explicaría el doctor Emmett Brown en Regreso al futuro II. ¿Vas a intentar viajar al pasado para matar a tu abuelo? No pasa nada, se te encasquillará el revólver; te resbalarás con una cáscara de plátano al intentarlo, frustrando el homicidio, o descubrirás, al no desaparecer de la existencia, que hubo una infidelidad marital, pero el universo siempre evitará que se produzca una paradoja.
En junio de 2009, Stephen Hawking organizó una fiesta para viajeros del tiempo… pero envió las invitaciones después. Como no fue nadie, dio por demostrado que viajar en el tiempo es imposible. Pero ¿demostró con esta maniobra la conjetura de protección cronológica? Créditos: Discovery CommunicationsEstá claro que los físicos se han comido bastante la cabeza para, en primer lugar, buscar maneras de que los viajes en el tiempo sean algo loquísmo, pero no tanto como podría parecer de primeras. Y, en segundo, buscarse las mañas para que esa posibilidad no provoque paradojas que destruyan el universo. ¿Sabéis quién lo hizo también? Robert A. Heinlein.
Bibliografía
Gaspar y Rimbau, E. (1887). El anacronópete. Daniel Cortezo. Biblioteca «Arte y letras».
Gödel, K. (1949). An example of a new type of cosmological solutions of Einstein’s field equations of gravitation. Reviews of Modern Physics, 21(3), 447–450
Hawking, S. W. (1992). The Chronology Protection Conjecture. Physical Review D, 46(2), 603-611.
Hawking, S., y Ellis, G. F. R. (1973). The large scale structure of space-time. Cambridge University Press.
Heinlein, R. A. (marzo de 1959). All you zombies—. The Magazine of Fantasy and Science Fiction.
Kerr, R. P. (1963). Gravitational field of a spinning mass as an example of algebraically special metrics. Physical Review Letters, 11(5), 237–238
Le Guin, U. K (2021 [1995]). Ether, OR. En Lo irreal y lo real. Minotauro.
Thorne, K. (1992). Closed timelike curves. Proceddings of the 13th International Conference on General Relativity and Gravitation.
Tipler, F. J. (1974). Rotating cylinders and the possibility of global causality violation. Physical Review D, 9(8), 2203–2206
Stockum, W. J. van (1937). The gravitational field of a distribution of particles rotating around an axis of symmetry. Proceedings of the Royal Society of Edinburgh, 57, 135.
Wells, H. G. (1895). La máquina del tiempo. William Heinemann.
.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo Cómo viajar en el tiempo sin destruir el universo se ha escrito en Cuaderno de Cultura Científica.
El rompecabezas IQ-Block
En el libro El prodigio de los números, del divulgador científico estadounidense Clifford A. Pickover (1957) se muestra un rompecabezas geométrico, conocido con el nombre de IQ-Block, que está formado por piezas geométricas pertenecientes a la versátil familia de los poliominós. Vamos a dedicar esta entrada del Cuaderno de Cultura Científica a este juego geométrico.
 Caja y piezas del rompecabezas geométrico conocido con el nombre de IQ-Block
Caja y piezas del rompecabezas geométrico conocido con el nombre de IQ-Block
El juego fue fabricado y comercializado por la empresa británica Hercules, aunque manufacturado en Hong-Kong, hacia la década de 1980.
Los poliominós, juntando cuadradosLos poliominós son unos curiosos objetos geométricos que fueron introducidos formalmente por el matemático e ingeniero estadounidense Solomon W. Golomb (1932-2016) en una conferencia en el Harvard Mathematics Club en 1953, y en su posterior artículo Checkers Boards and Polyominoes publicado en la revista American Mathematical Monthly, revista matemática de la MAA (Asociación Matemática de América) dirigida a un amplio público dentro de las matemáticas, desde estudiantes de grado hasta investigadores punteros, que se ha convertido en la revista matemática más leída del mundo. Pero serían descubiertos para el público general por el gran divulgador de las matemáticas Martin Gardner (1914-2010), en su columna de juegos matemáticos de Scientific American (1957). Poco después, en 1965, Golomb publicaría un extenso libro que analizaba en profundidad estos objetos geométricos, con el sencillo título Polyominoes (Poliominós). Al introducir los poliominós, el matemático abrió un fructífero campo para las matemáticas, las ciencias de la computación y la creación de juegos. Están relacionados con conceptos matemáticos como las teselaciones (o embaldosados), los patrones geométricos, los empaquetamientos o la medida (área), y de ellos han surgido infinidad de juegos de ingenio y rompecabezas geométricos, como el juego de los pentominós y sus derivados (véase la entrada Tetris, embaldosados y demostraciones), el Tetris o el Vee-21 (véase la entrada Embaldosando con L-triominós (Un ejemplo de demostración por inducción)), por citar algunos.
 Katamino es el nombre comercial de la empresa francesa Gigamic para el juego de los pentominós
Katamino es el nombre comercial de la empresa francesa Gigamic para el juego de los pentominós
Un poliominó es una figura geométrica plana formada conectando dos o más cuadrados por alguno de sus lados. Los cuadrados se conectan lado con lado, pero no se pueden conectar ni por sus vértices, ni juntando solo parte de un lado de un cuadrado con parte de un lado de otro. Si unimos dos cuadrados se obtiene un dominó, si se juntan tres cuadrados se construye un triominó, o trominó, con cuatro cuadrados se tiene un tetraminó, con cinco un pentominó, y así se puede continuar para cualquier número de cuadrados, hexaminó, heptaminó, octominó. etcétera. Podemos considerar que un único cuadrado es también un poliominó, que denominamos monominó.
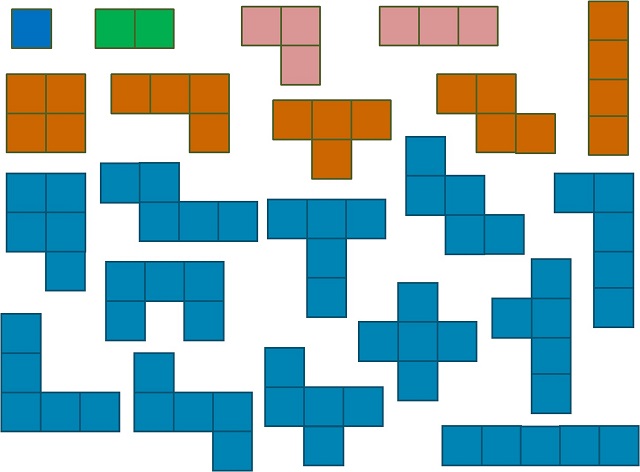 Todos los poliominós formados por 1, 2, 3, 4 o 5 cuadrados
Todos los poliominós formados por 1, 2, 3, 4 o 5 cuadrados
Como podemos ver en la anterior imagen, existen un monominó, un dominó, dos triominós, cinco tetraminós y doce pentominós. Si pasamos al orden seis, la familia de los poliominós se extiende con 35 hexominós, poliominós formados con seis cuadrados.
Antes de seguir adelante con el rompecabezas, una pequeña aclaración sobre estas piezas. Como estamos trabajando con piezas geométricas que vamos a poder manipular, se considera que podemos darles la vuelta, luego poliominós como los de la imagen (que son dos tetraminós) se consideran iguales, ya que dando la vuelta a uno se obtiene el otro (que es su imagen especular). Si estuviésemos trabajando con juegos o cuestiones simplemente planas, con en el Tetris, serían poliominós distintos, en cuyo caso podríamos hablar de “poliominós planos” o “poliominós de una cara”, como los denomina Golomb. Por ejemplo, hay 5 tetraminós (poliominós construidos con cinco cuadrados), como se muestra en la imagen de arriba, pero existen siete si hablamos de poliominós de una cara.
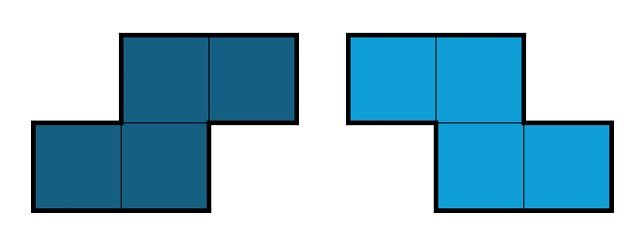 Dos tetraminós que son iguales como poliominós, ya que podemos pasar de uno a otro dándole la vuelta (uno es la imagen especular del otro), pero diferentes como poliominós de una cara (planos)
Dos tetraminós que son iguales como poliominós, ya que podemos pasar de uno a otro dándole la vuelta (uno es la imagen especular del otro), pero diferentes como poliominós de una cara (planos)
Aunque para lo que nos ocupa en esta entrada del Cuaderno de Cultura Científica seguiremos con los poliominós normales, los que se pueden voltear.
Las piezas del rompecabezas IQ-BlockEste rompecabezas geométrico está formado por diez piezas, diez poliominós, en concreto, un tetraminó, dos pentominós, dos hexominós, dos heptominós y tres octominós, una de ellas con forma de rectángulo, otra con forma de Z y las demás con formas que son, más o menos, una L, como aparece en la siguiente imagen.
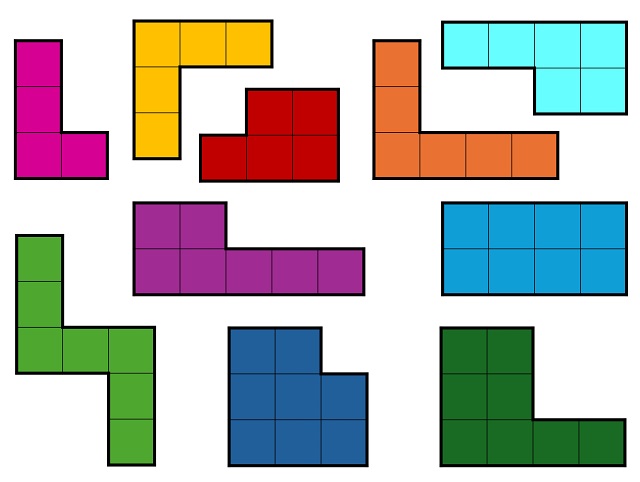 Las diez piezas del juego IQ-Block
Las diez piezas del juego IQ-Block
El número total de cuadrados implicados en las diez piezas del juego son 64 (1 x 4 + 2 x 5 + 2 x 6 + 2 x 7 + 3 x 8), luego, a priori, se podría, y se puede, formar un cuadrado de lado 8, como se muestra en la siguiente imagen.
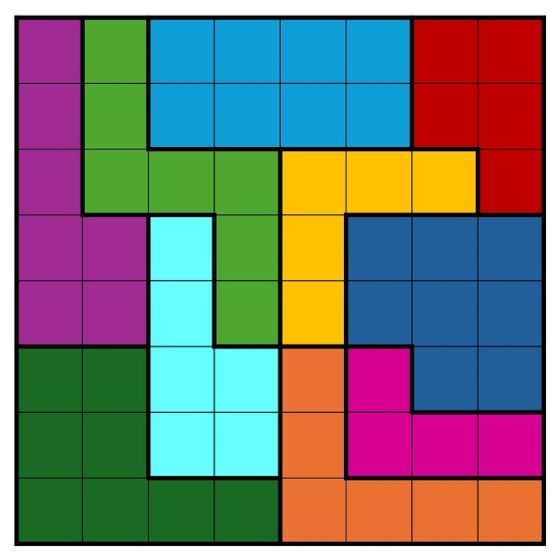 Con las diez piezas del juego IQ-Block puede formarse un cuadrado grande de lado igual a 8 cuadrados, luego cuya superficie es de 64 cuadrados
Con las diez piezas del juego IQ-Block puede formarse un cuadrado grande de lado igual a 8 cuadrados, luego cuya superficie es de 64 cuadrados
Este es esencialmente el objetivo de este rompecabezas, construir un cuadrado grande 8 x 8, un cuadrado de lado 8, es decir, formado por 64 cuadrados, con las diez piezas del juego. Tengamos en cuenta que las piezas del rompecabezas se pueden rotar y dar la vuelta.
Antes de seguir adelante, mi recomendación es construirse uno mismo las piezas de este rompecabezas, ya sea con papel, cartulina, papel maché, madera o piezas de algún juego de construcción, como he hecho yo, que he utilizado piezas cuadradas del LiveCube, para poder disfrutar jugando con las mismas, tanto mientras se lee esta entrada, como después.
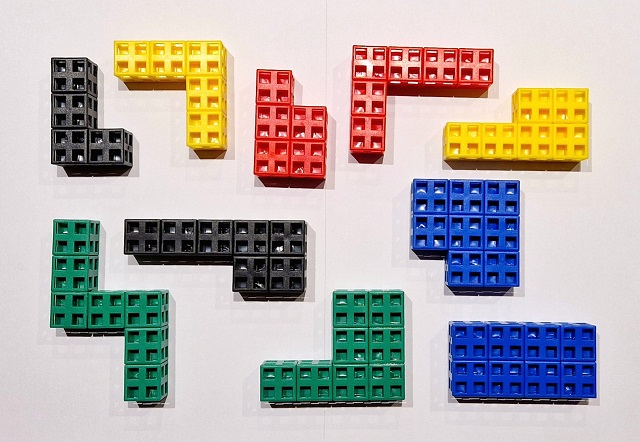 Las diez piezas del rompecabezas IQ-Block construidas con las piezas cuadradas del LiveCube
Las diez piezas del rompecabezas IQ-Block construidas con las piezas cuadradas del LiveCubeEl rompecabezas IQ-Block
Como acabamos de comentar, el objetivo de este rompecabezas es formar un cuadrado grande 8 x 8 con las diez piezas que acabamos de describir, un tetraminó, dos pentominós, dos hexominós, dos heptominós y tres octominós.
Aunque, en el juego comercializado por la empresa Hercules las reglas del rompecabezas estaban escritas de la siguiente forma.
Primero debes elegir una de las piezas del juego, la que desees, que es la que va a estar colocada en la esquina superior izquierda (véase imagen inferior). Después, coloca las otras nueve piezas para que formen un cuadrado 8 x 8, sin mover de la esquina superior izquierda la pieza elegida.

Como vemos el objetivo del juego es formar un cuadrado grande de tamaño 8 x 8, con las diez fichas del juego, aunque en las reglas del juego comercial se plantea que se obtenga al menos una solución para cada una de las fichas colocada en la esquina superior izquierda. Por una parte, se amplia el reto a encontrar al menos diez soluciones, una por cada una de las diez fichas colocadas en la esquina. Pero además si se tiene en cuenta que cada ficha elegida para la posición de la esquina superior izquierda puede ser colocada de varias maneras distintas, se puede buscar al menos una solución para cada ficha y para cada una de sus posiciones posibles en la esquina superior izquierda. Quizás, este es el motivo por el cual en las reglas se menciona que hay bastantes soluciones distintas, en concreto:
Existen más de sesenta soluciones distintas que puedes encontrar. Se muestran dos soluciones a modo de ejemplo.
Las dos soluciones mostradas en las reglas del juego comercial son las siguientes.
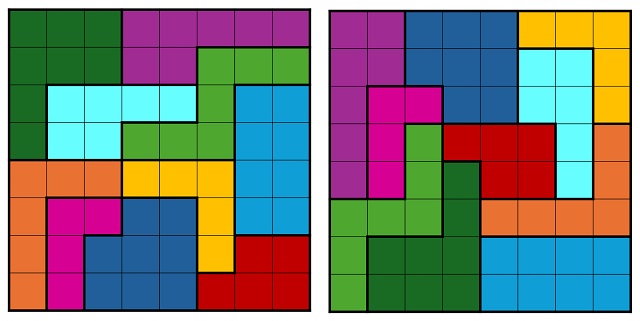 Dos soluciones del rompecabezas IQ-Block mostradas en las reglas del juego
Dos soluciones del rompecabezas IQ-Block mostradas en las reglas del juego
Es cierto que, al plantearse en las reglas del rompecabezas IQ-Block obtener soluciones para cada ficha, y para cada una de sus posiciones posibles, colocada en la esquina superior izquierda, esto nos anima a obtener muchas más soluciones, que solamente una, pero también a clasificarlas a la hora de encontrarlas, según cual sea la ficha y la posición de esa esquina.
Y la parte de las reglas del juego termina con la siguiente frase.
Trata de encontrar la mayor cantidad de soluciones posibles. Únete a nosotros para desafiar a tu I. Q. (Intelligence Quotient / Cociente intelectual).
Las soluciones del IQ-BlockUna pregunta lógica, tanto de quien idea y construye el rompecabezas, como de quien pretende solucionarlo, es cuántas soluciones distintas existen. En las reglas del juego afirman que existen más de 60 soluciones, pero no sabemos, al leer eso, cuántas más hay, es decir, cuántas son realmente todas las soluciones del rompecabezas.
Antes de seguir con esta cuestión observemos las dos soluciones que nos ofrecen como ejemplos en las reglas del juego. La primera de ellas es exactamente la misma que la que se había mostrado antes, pero girada 90 grados en el sentido de las agujas del reloj. Desde el punto de vista de las soluciones estas dos se consideran “esencialmente” la misma, al igual que las obtenidas si seguimos girando 90 grados, e incluso si diésemos la vuelta a la solución, luego todas ellas cuentan como una en el cómputo de soluciones.
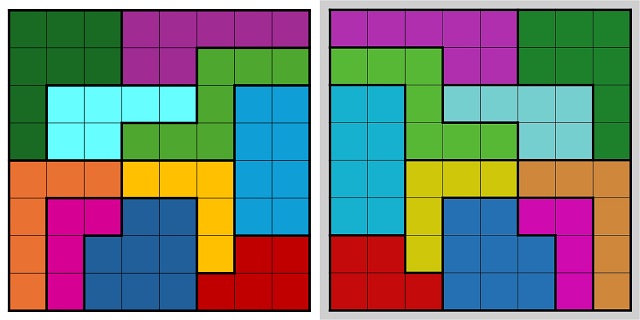 Una solución del rompecabezas, la primera de los dos ejemplos de las reglas, y la solución obtenida al dar la vuelta a esta (que es su imagen especular), y que se considera que son “esencialmente” la misma solución
Una solución del rompecabezas, la primera de los dos ejemplos de las reglas, y la solución obtenida al dar la vuelta a esta (que es su imagen especular), y que se considera que son “esencialmente” la misma solución
El matemático estadounidense Charles Ashbacher, que fue co-editor de la revista Journal of Recreational Mathematics, revista en la cual Pickover había publicado un par de artículos sobre el rompecabezas IQ-Block, escribió un programa de ordenador que rápidamente obtuvo mil soluciones distintas del rompecabezas. Sin embargo, hay más soluciones aún. El alemán Hartmut Blessing, miembro de MENSA e INTERTEL, sociedades de personas con alto cociente intelectual, afirma que existen 12.724 soluciones, lo cual ha sido comprobado con el programa PolySolver, que es un programa de Jaap Scherphuis que resuelve una gran variedad de rompecabezas geométricos.
Algunos retos con las piezas del IQ-BlockEl autor de libros como El prodigio de los números (2000), La maravilla de los números (2001), Las matemáticas de Oz (2002), La banda de Moebius (2006), El libro de las matemáticas, de Pitágoras a la 57ª dimensión (2009) o Inteligencia artificial (2019), entre muchos otros, planteaba en su libro El prodigio de los números algunos retos relacionados con este rompecabezas.
Pregunta 1: ¿Puede construirse una estructura cuadrada eliminando una pieza y utilizando todas las restantes?
La respuesta a esta cuestión es sencilla. Al eliminar una pieza, que tendrá 5, 6, 7 u 8 cuadrados, nos quedarán nueve piezas que sumarán entre todas entre 56 y 59 cuadrados, lejos del siguiente número cuadrado más bajo 49 (que correspondería con un cuadrado 7 x 7), luego la respuesta es negativa.
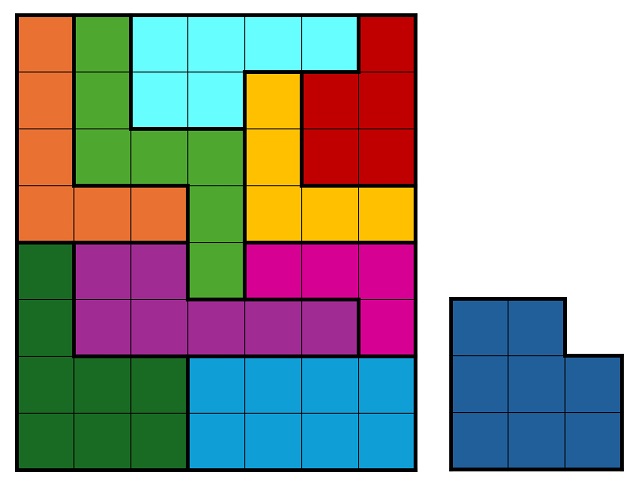
Pero podemos ir un poco más allá, analizando caso por caso. Si se elimina la pieza con 5 cuadrados (pentominó) quedarían nueve piezas con 64 – 5 = 59 cuadrados, pero 59 es un número primo, luego es imposible formar una estructura rectangular, no solo cuadrada, con las nueve piezas restantes. Si se quita una de las dos piezas con 6 cuadrados (hexaminós) las otras nueve piezas sumarían 64 – 6 = 58, que es igual a 2 x 29, luego a priori podría formarse un rectángulo de tamaño 2 x 29, lo cual es imposible en este caso ya que hay varias piezas cuya anchura mínima es tres, luego imposible colocarlas para formar un cuadrado de anchura 2. Si se elimina una pieza de 7 cuadrados (heptominós), quedarían nueve piezas con 64 – 7 = 57, que es igual a 3 x 19, luego se podría construir un rectángulo de tamaño 3 x 19, lo cual es posible como he podido comprobar por mí mismo (si tenéis construidas las piezas del rompecabezas podéis buscar alguna distribución posible). Finalmente, si se deja fuera una pieza de 8 cuadrados quedan nueve piezas con 56 cuadrados en total, pero como 56 = 7 x 8, se podría formar un rectángulo de tamaño 7 x 8, lo cual es posible, como se muestra en la siguiente imagen.
 Estructura rectangular de tamaño 7 x 8 obtenida por todas las piezas del IQ-Block menos el octominó que aparece a la derecha
Estructura rectangular de tamaño 7 x 8 obtenida por todas las piezas del IQ-Block menos el octominó que aparece a la derecha
En este último caso, si se elimina una pieza de 8 cuadrados, ya hemos explicado que quedan nueve piezas con 56 cuadrados entre todas y se puede construir un rectángulo de tamaño 7 x 8, pero pensemos … ¿también se podría construir de tamaño 14 x 4? La respuesta a esta cuestión también la dejo para que la penséis quienes estáis leyendo esta entrada.
La cuestión anterior puede ampliarse a dos piezas (o más).
Pregunta 2: ¿Puede construirse una estructura cuadrada eliminando dos piezas y utilizando todas las restantes?
Como el siguiente número cuadrado, más pequeño que 64, es 49, como hemos comentado arriba, y la diferencia entre ambos es 64 – 49 = 15, hay que eliminar una pieza con 7 cuadrados y otra con 8, solo para esta opción podría ser posible construir una estructura cuadrada con el resto de piezas. Teniendo en cuenta esta información podéis buscar vosotros mismos dichas estructuras.
Si hasta ahora la diversión consistía en construir un cuadrado 8 x 8 (o más pequeños si se eliminan piezas), ahora vamos a darle la vuelta a la tortilla, ahora se tratará de formar, con las diez piezas del IQ-Block, el perímetro alrededor de un cuadrado 8 x 8, o si se elimina una pieza, un cuadrado 7 x 7.
Pregunta 3: ¿Puede construirse el perímetro de una estructura cuadrada vacía de tamaño 8 x 8 con todas las piezas del rompecabezas? ¿Y si se elimina una pieza puede construirse el perímetro de una estructura cuadrada vacía de tamaño 7 x 7?
Veamos una posible solución a la primera cuestión.
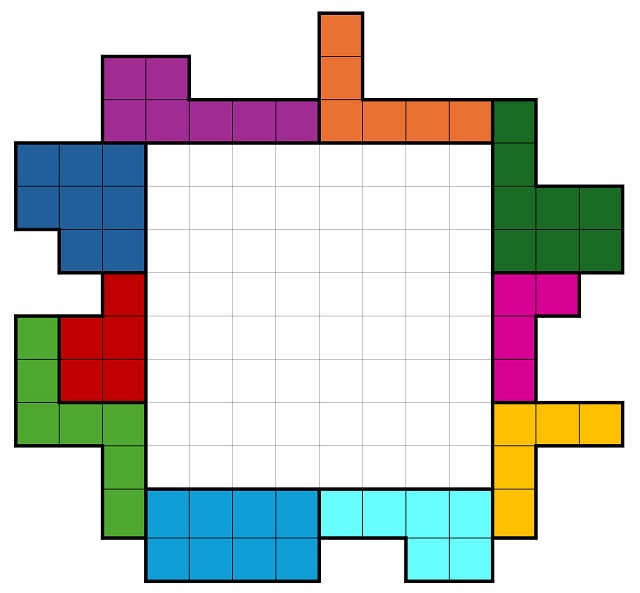
Dejo para diversión de las personas que estáis leyendo esta entrada la búsqueda de soluciones, que las hay, para el caso en el que se quita una de las piezas del rompecabezas y se utilizan las otras nueve piezas.
 Otro de los formatos comercializados del IQ-Block
Otro de los formatos comercializados del IQ-Block
Bibliografía
1.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, El mundo es matemático, RBA, 2015.
2.- Solomon W. Golomb, Polyominoes: Puzzles, Patterns, Problems, and Packings, Princeton University Press, 1994.
3.- Clifford A. Pickover, El prodigio de los números. Desafíos, paradojas y curiosidades matemáticas, Ma Non Troppo (ediciones Robinbook), 2002.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El rompecabezas IQ-Block se ha escrito en Cuaderno de Cultura Científica.
El agua tiene un punto crítico líquido-líquido
El agua, una molécula esencial para la vida, presenta unas propiedades inusuales —conocidas como anomalías— que definen su comportamiento. Sin embargo, todavía hay muchas incógnitas sobre los mecanismos moleculares que explicarían las anomalías que hacen única a la molécula de agua. Descifrar y reproducir este comportamiento particular del agua en diferentes rangos de temperaturas es todavía un gran desafío para la comunidad científica. Ahora, un estudio presenta un nuevo modelo teórico capaz de superar las limitaciones de metodologías anteriores para entender cómo es el comportamiento del agua en condiciones extremas.
La investigación no solo amplía nuestra comprensión de la física del agua, sino que tiene implicaciones en el ámbito de la tecnología, la biología y la biomedicina, en especial para abordar el tratamiento de enfermedades neurodegenerativas y el desarrollo de biotecnologías avanzadas.
Un punto crítico entre dos formas líquidas de agua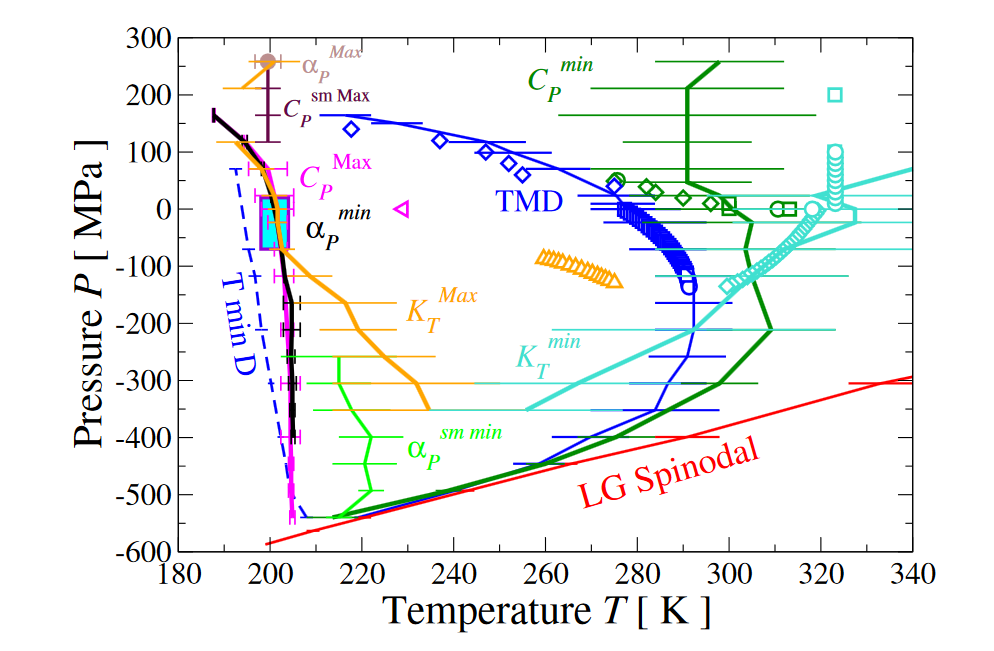
La investigación, que deriva de la tesis doctoral que Luis E. Coronas presentó en 2023 en la Facultat de Física de la UB, muestra un nuevo modelo teórico que responde a las siglas CVF (las iniciales de los apellidos de los investigadores Luis E. Coronas, Oriol Vilanova y Giancarlo Franzese). El nuevo modelo CVF se caracteriza por ser fiable, eficiente, escalable y transferible, e incorpora cálculos cuánticos ab initio que reproducen con precisión las propiedades termodinámicas del agua bajo diferentes condiciones.
Mediante la aplicación del nuevo marco teórico, el estudio revela que «existe un punto crítico entre dos formas líquidas de agua, y este punto crítico es el origen de las anomalías que hacen que el agua sea única y esencial para la vida, así como para muchas aplicaciones tecnológicas», detalla el profesor Giancarlo Franzese, de la Sección de Física Estadística del Departamento de Física de la Materia Condensada.
«Aunque esta conclusión ya se había alcanzado en otros modelos de agua, ninguno de ellos tiene las características específicas del modelo que hemos desarrollado en este estudio», detalla Franzese.
El modelo CVFAlgunos de los modelos actuales para explicar las anomalías del agua no son capaces de reproducir adecuadamente las propiedades termodinámicas del agua, como, por ejemplo, su compresibilidad y capacidad calorífica. «Sin embargo, el modelo CVF lo consigue porque incorpora resultados de cálculos cuánticos ab initio sobre interacciones entre moléculas. Estas interacciones, conocidas como interacciones de muchos cuerpos, van más allá de la física clásica y se deben a que las moléculas de agua comparten electrones de una manera difícil de medir experimentalmente», detalla Franzese.
Según el estudio, «las fluctuaciones de densidad, energía y entropía del agua están reguladas por estas interacciones cuánticas, con efectos que van desde la escala nanométrica hasta la macroscópica», detalla el investigador Luis E. Coronas.
«Por ejemplo —continúa Coronas— el agua regula el intercambio de energía y moléculas, así como el estado de agregación de proteínas y ácidos nucleicos en las células. Se sospecha que defectos en estos procesos pueden causar enfermedades graves como el alzhéimer, el párkinson y la esclerosis lateral amiotrófica. Por lo tanto, entender cómo las fluctuaciones del agua contribuyen a estos procesos podría ser clave para encontrar tratamientos contra estas patologías».
Nuevas biotecnologíasEl modelo CVF también ofrece nuevas ventajas que permiten realizar cálculos donde otros modelos fallan, debido a que son computacionalmente muy pesados o bien porque se desvían significativamente de los resultados experimentales.
En el ámbito del desarrollo tecnológico, algunos laboratorios están desarrollando biotecnologías para reemplazar músculos (actuadores mecánicos) que aprovechan las interacciones cuánticas del agua; memorias a base de agua (water-based memristors) para crear dispositivos de memoria (con una capacidad millones de veces mayor que las actuales), o bien la aplicación de esponjas de grafeno que separan el agua de impurezas gracias a las fluctuaciones de densidad del agua en nanoporos.
También existen implicaciones en la comprensión de la física del agua. «Este modelo puede reproducir las propiedades del agua líquida en prácticamente todas las temperaturas y presiones que se encuentran en nuestro planeta, aunque se desvía en condiciones extremas alcanzadas en laboratorios», detallan los expertos. «Esto demuestra que los efectos no incluidos en el modelo —los efectos cuánticos nucleares— también son importantes a estas presiones y temperaturas extremas. Así, las limitaciones del modelo nos guían hacia dónde mejorar para llegar a una formulación definitiva del mismo», concluyen.
Referencia:
Luis Enrique Coronas, Giancarlo Franzese (2024) Phase behavior of metastable water from large-scale simulations of a quantitatively accurate model near ambient conditions: The liquid–liquid critical point. J. Chem. Phys. doi: 10.1063/5.0219313
Edición realizada por César Tomé López a partir de materiales suministrados por la Universitat de Barcelona
El artículo El agua tiene un punto crítico líquido-líquido se ha escrito en Cuaderno de Cultura Científica.
El colapso atmosférico y los periodos húmedos de Marte
Marte es uno de esos lugares de nuestro sistema solar que al mismo tiempo nos resulta aterradoramente parecido a la Tierra, pero, por otro, nos parece totalmente diferente. Lo que hoy es un desierto helado y yermo dominado por una ubicua capa de polvo rojo, hace miles de millones de años era un planeta vivo -en el sentido geológico de la palabra, no me malinterpreten- donde los volcanes todavía entraban en erupción con cierta regularidad y el agua en estado líquido esculpía su superficie.
Todavía hoy seguimos discutiendo las causas y los procesos que transformaron de una manera tan radical al planeta. ¿Fue un cambio gradual o acaso cambió de manera brusca? ¿O quizás la historia de Marte ha sido mayoritariamente fría, pero con periodos cálidos donde la existencia de una atmósfera más densa permitía que el agua líquida fuese estable en su superficie? Todavía nos quedan muchos detalles -y límites temporales- que marcar en Marte para poder responder a estas preguntas.
 ¿Tuvo Marte en algún momento de su historia este aspecto? Es una de las preguntas que esperamos responder en el futuro, cuando dispongamos de más datos sobre la geología del planeta rojo. Cortesía de ESO/M. Kornmesser.
¿Tuvo Marte en algún momento de su historia este aspecto? Es una de las preguntas que esperamos responder en el futuro, cuando dispongamos de más datos sobre la geología del planeta rojo. Cortesía de ESO/M. Kornmesser.Por estudios más recientes -como el publicado por Thomas et al. (2023)- el rango de composición y densidad atmosférico hace unos 3800 millones de años indican una atmósfera mayoritariamente compuesta por dióxido de carbono (0.3-1.5 bares de presión) y nitrógeno (0.2-0.4 bares), composición que quizás no era tan diferente a la segunda atmósfera de nuestro planeta, antes de la aparición de la fotosíntesis -al menos en las proporciones de los gases- y que probablemente tuvo su origen principal en la degasificación del magma fruto de importante actividad volcánica que tendría el planeta al principio de su historia.
Pero bueno, ¿por qué dejar la geología hoy para hablar del agua? Lo cierto es que podemos considerar al agua como un recurso geológico, pero también es un importante agente de modelado del relieve, así como de transporte de sedimentos tanto en su fase líquida como en la de hielo, y de ahí que desde el punto de vista de la geología también sea extremadamente interesante y fundamental para explicar Marte tal y como lo entendemos hoy día.
Un nuevo artículo publicado por Buhler (2024) propone un interesante mecanismo para generar periodos “húmedos” en Marte. Para ello tenemos que viajar en el tiempo a la transición entre el periodo Noeico y el Hespérico, hace aproximadamente 3600 millones de años. Probablemente en este momento prácticamente toda el agua superficial de Marte se encontraría congelada en distintas reservas: suelos, casquetes glaciares, escarcha…
Sería este momento cuando, según esta nueva investigación, comienza a producirse una serie de eventos de manera periódica: los colapsos atmosféricos. Este proceso ocurriría cuando la inclinación del eje del planeta cruzase cierto umbral, de tal manera que el dióxido de carbono de la atmósfera, debido a las bajas temperaturas, se condensaría y congelaría sobre los polos, cubriendo estos con un gran casquete de hielo de dióxido de carbono. Este proceso, como hemos dicho más arriba, sería periódico y ocurriría durante millones de años.
 Detalle de los depósitos de hielo y polvo presentes en el polo norte de Marte, donde se puede apreciar cierta alternancia y distintos ciclos donde ha habido más depósito de hielo y, en otros, de polvo. Cortesía de NASA/JPL-Caltech/UArizona.
Detalle de los depósitos de hielo y polvo presentes en el polo norte de Marte, donde se puede apreciar cierta alternancia y distintos ciclos donde ha habido más depósito de hielo y, en otros, de polvo. Cortesía de NASA/JPL-Caltech/UArizona.En el punto álgido de este ciclo de colapsos, la mayor parte del agua de la superficie de Marte se encontraba congelada, pero en concreto, en el hemisferio sur, formando grandes casquetes de hielo o glaciares. Sobre estos habría “nevado” una gran parte del dióxido de carbono congelado desde la atmósfera durante los procesos de colapso atmosférico.
¿Qué efecto tendría este hielo de dióxido carbono depositado sobre el hielo de agua? Pues actuaría como una manta térmica que no dejaría escapar el calor… pero, ¿de qué calor hablamos? El autor sugiere que el calor geotérmico -el que sale del interior del planeta- sería suficiente como para comenzar la fusión de los hielos en la interfaz entre la corteza y el hielo, o lo que es lo mismo, en la base de los casquetes glaciares.
Esto habría provocado una gigantesca cantidad de agua líquida, suficiente para alimentar ríos de cientos de kilómetros que llegarían a la cuenca de Argyre, una enorme depresión que se transformaría en un lago del tamaño del mar Mediterráneo y que, en ocasiones, acabaría desbordándose con la gran cantidad de agua que llegaba hasta él.
 Imagen de uno de los extremos de la cuenca de Argyre, en Marte, tomada por la sonda Europea Mars Express. Se aprecian unas zonas de terreno caótico que podrían haberse formado por la fusión del hielo a gran escala. Cortesía de ESA/DLR/FU Berlin.
Imagen de uno de los extremos de la cuenca de Argyre, en Marte, tomada por la sonda Europea Mars Express. Se aprecian unas zonas de terreno caótico que podrían haberse formado por la fusión del hielo a gran escala. Cortesía de ESA/DLR/FU Berlin.Pero no todo acaba aquí, porque nos estamos saltando una parte muy importante y de la que debemos hablar para comprender mejor este fenómeno: el ciclo del agua. Hace 3600 millones de años, no solo hacía más frío en Marte, sino que la atmósfera era, probablemente, mucho más tenue, haciendo difícil la presencia de masas de agua estable -a escala geológica- en su superficie.
Pues bien, el agua se iba moviendo -principalmente por las redes fluviales- desde el polo sur hasta el ecuador, pero durante este tránsito, los procesos de sublimación del hielo y evaporación del agua devolverían parte de esta a la atmósfera y de ahí, de nuevo, a los polos. Este ciclo podría haberse repetido entre 100.000 años y 10 millones de años y ocurrido varias veces a lo largo de una ventana temporal de 100 millones de años.
Esta nueva interpretación desafía a esa imagen que tenemos del clima de Marte que es necesario para la presencia de masas de agua y redes fluviales en el planeta y que normalmente asociamos a periodos cálidos, pero también podrían haberse dado en periodos fríos, rompiendo de algún modo esa paradoja que existía a la hora de interpretar las formas de modelado del relieve creadas por el agua en la transición entre el Noeico y el Hespérico, cuando la atmósfera de Marte era más tenue y el planeta más frío.
Y una cosa más: esta presencia de agua líquida en la superficie podría también tener repercusiones a nivel astrobiológico y haber extendido la ventana de habitabilidad en el planeta no solo en la propia superficie de este, sino en los posibles lagos y ríos subglaciales que se habrían formado durante la fusión de los hielo y que estarían menos expuestos a las condiciones más extremas de radiación… ¿Fue la superficie de Marte, quizás, un lugar habitable durante más tiempo del que pensamos?.
Referencias:
Thomas, Trent B, et al (2023) Constraints on the Size and Composition of the Ancient Martian Atmosphere from Coupled CO2–N2–Ar Isotopic Evolution Models The Planetary Science Journal, vol. 4, no. 3, 1 Mar. 2023, pp. 41–41 doi: 10.3847/psj/acb924
Buhler, P B. (2024) Massive Ice Sheet Basal Melting Triggered by Atmospheric Collapse on Mars, Leading to Formation of an Overtopped, Ice‐Covered Argyre Basin Paleolake Fed by 1,000‐Km Rivers Journal of Geophysical Research Planets, vol. 129, no. 11, 1 Nov. 2024 doi: 10.1029/2024je008608
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo El colapso atmosférico y los periodos húmedos de Marte se ha escrito en Cuaderno de Cultura Científica.
La música y el entorno natural
José Manuel González Gamarro
La música y la naturaleza es un binomio estudiado desde casi los primeros tratados sobre música. La poética subyacente de la observación del medio ambiente puede casar perfectamente con las emociones que logra provocar la escucha musical. También ha habido múltiples ejemplos de compositores, teóricos e investigadores que han intentado plasmar o transcribir los sonidos de la naturaleza, como el caso paradigmático de Oliver Messiaen con el canto de los pájaros u otros anteriores como fueron Athanasius Kircher o William Gardiner.
 Foto: Erica Li / Unsplash
Foto: Erica Li / UnsplashSin embargo, existen otro tipo de investigaciones que no intentan fijar en una partitura aquello que se escucha en el entorno natural, sino más bien averiguar cómo puede influir la música que se escucha en nuestra percepción de ese entorno. Las personas escuchan cada vez más música con auriculares al aire libre, en la naturaleza, mientras pasean o practican algún deporte, así que estudiar las interacciones audiovisuales entre la música y el entorno es significativo tanto para la psicología musical como para la investigación del paisaje sonoro. Es por esto que investigadores como Marek Franěk y Jan Petružálek han profundizado en la influencia que tiene la música que se escucha en la percepción de los entornos naturales1. Tal y como indican estos investigadores, el objetivo de profundizar en esta relación es averiguar si la música que ellos denominan feliz puede aumentar la preferencia ambiental y los sentimientos agradables al ver entornos en comparación con la observación bajo música triste o simplemente sin música.
Para ello se plantearon un experimento donde personas visualizaban diferentes tipos de entornos bajo música feliz, música triste y sin música. Los entornos los clasificaron mediante cuatro tipologías: ambientes atractivos abiertos, ambientes atractivos cerrados, ambientes poco atractivos abiertos y ambientes poco atractivos cerrados.
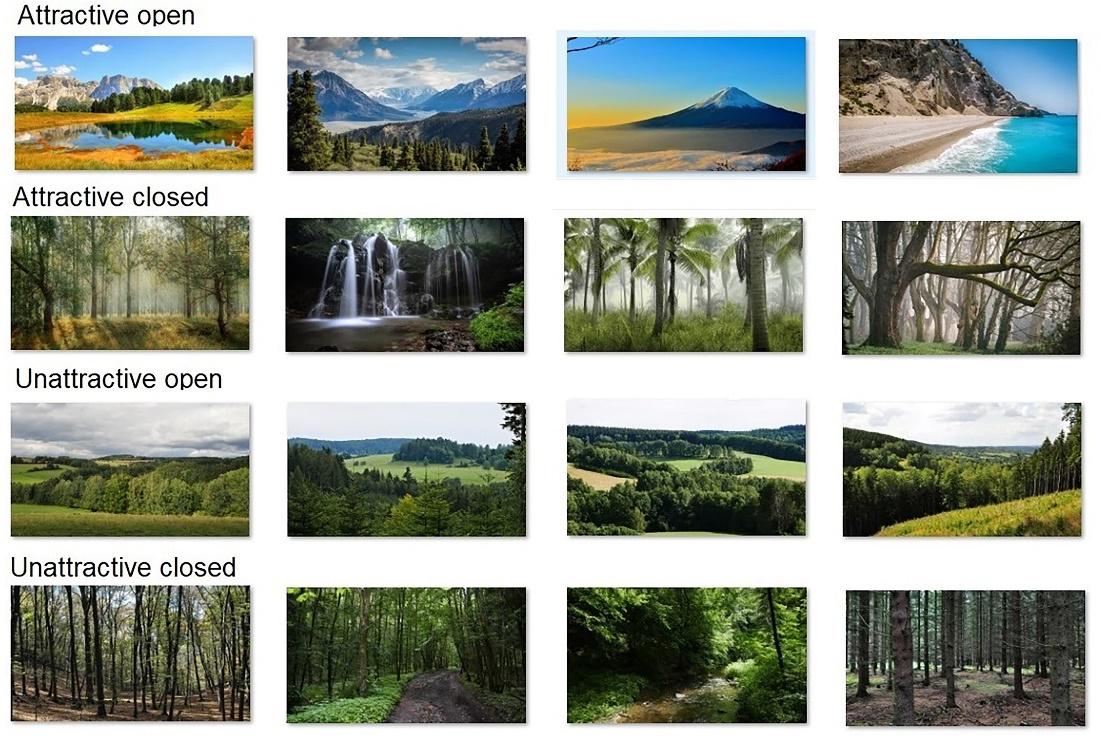 Ilustración 1. Estímulos visuales utilizados en el estudio: entornos abiertos atractivos, entornos cerrados atractivos, entornos abiertos poco atractivos y entornos cerrados poco atractivos. Fuente: Franěk, M., & Petružálek, J. (2024)
Ilustración 1. Estímulos visuales utilizados en el estudio: entornos abiertos atractivos, entornos cerrados atractivos, entornos abiertos poco atractivos y entornos cerrados poco atractivos. Fuente: Franěk, M., & Petružálek, J. (2024)La música feliz estuvo representada por One Fine Day mientras que para la música triste fue usada la canción Mad World de Michael Andrews Estos dos ejemplos salen de una selección de otro estudio anterior donde se pidió a los participantes que seleccionaran y enviaran dos archivos de diferentes tipos de música que les gustaban. Para evaluar en qué medida influía el tipo de música (o la no música) en la visualización y preferencia de los ambientes se usó, por un lado, una autoevaluación con escala tipo Likert para evaluar el gusto por el medio ambiente y los sentimientos al visualizar las imágenes. Por otro lado, se midieron las expresiones faciales mediante grabaciones en vídeo y el posterior análisis con un software capaz de determinar siete emociones básicas (alegría, ira, sorpresa, miedo, desprecio, tristeza y disgusto).
La paradoja de la tristeza agradableLos resultados sacaron a la luz algo nada sorprendente en cuanto a la música feliz, puesto que escuchar música que es agradable y gustada generalmente resulta en respuestas emocionales positivas. El emparejamiento de música alegre con imágenes naturales resultó en un aumento significativo en la preferencia ambiental y sentimientos agradables en todos los entornos. Sin embargo, la música triste no redujo la preferencia ambiental o los sentimientos agradables en comparación con el grupo control al que no se le expuso a música alguna. La explicación más probable a esto es la paradoja de la «tristeza agradable»2, ya que la tristeza evocada por la música puede ser placentera cuando se percibe como no amenazante, es estéticamente agradable o produce beneficios psicológicos como la regulación del estado de ánimo y sentimientos empáticos causados, por ejemplo, por el recuerdo y la reflexión sobre eventos pasados. La música tampoco tuvo el poder de cambiar las preferencias ambientales de los participantes, por lo que la música feliz aumentó las calificaciones de todos los entornos, pero no suprimió las características ambientales. En cualquier caso, la música sí que intensificó la experiencia emocional de la visualización de los entornos.
¿Que ocurriría en un entorno real?Además del debate que puede suscitar la fiabilidad de los métodos de análisis de las expresiones faciales mediante software o la subjetividad del autoinforme, no hay que olvidar que esto es un experimento de laboratorio donde el entorno real no es la imagen que se visualiza. A estímulos visuales se le añaden estímulos sonoros, pero la experiencia en un entorno natural es multisensorial, además de que la música también lo es o puede serlo3. Este tipo de investigación puede ser muy útil para la realización de vídeos relajantes o realidad virtual donde se combinan el entorno natural con la música. Sin embargo, la realidad es bastante más compleja, donde analizar y controlar todas las variables es una tarea muy difícil. La visualización de diferentes entornos naturales no influyó en las preferencias musicales, lo cual en la realidad del entorno podría no ser así. El entorno acústico medioambiental es determinante en muchas cuestiones evolutivas musicales, hasta el punto de haber podido influir en el desarrollo del lenguaje4, por lo que reducir a una visualización la precepción del medio ambiente es un primer paso necesario para la investigación de la interacción de música y entorno natural. Un primer paso que nos adentra en el océano de un nuevo conocimiento en el que, sin embargo, nos hallamos todavía en la orilla.
Referencias:
1 Franěk, M., & Petružálek, J. (2024). Audio-Visual Interactions Between Music and the Natural Environment: Self-Reported Assessments and Measures of Facial Expressions. Music & Science, 7. doi: 10.1177/20592043241291757
 
2 Sachs, M. E., Damasio, A., & Habibi, A. (2015). The pleasures of sad music: a systematic review. Frontiers in human neuroscience, 9, 404. doi: 10.3389/fnhum.2015.00404 
3 Zatorre, R. J., Chen, J. L., & Penhune, V. B. (2007). When the brain plays music: auditory–motor interactions in music perception and production. Nature reviews neuroscience, 8(7), 547-558.doi: 10.1038/nrn2152 
4 Gannon, C., Hill, R. A., & Lameira, A. R. (2023). Open plains are not a level playing field for hominid consonant-like versus vowel-like calls. Scientific Reports, 13(1), 21138. doi: 10.1038/s41598-023-48165-7 
Sobre el autor: José Manuel González Gamarro es profesor de guitarra e investigador para la Asociación para el Estudio de la Guitarra del Real Conservatorio Superior de Música “Victoria Eugenia” de Granada.
El artículo La música y el entorno natural se ha escrito en Cuaderno de Cultura Científica.
Naukas pro 2024: SAREUS: Red de Varamientos de cetáceos y pinnípedos de Euskadi

Los últimos avances en el ámbito de las energías renovables marinas o la proliferación de los microplásticos fueron algunos de los temas que componen la última edición de NAUKAS PRO. Una cita en la que el personal investigador se sube al escenario del Euskalduna Bilbao para hablar de las investigaciones más destacadas del momento en un ámbito concreto.
En esta ocasión el personal investigador de la Universidad del País Vasco, de la Estación Marina de Plentzia (PiE-UPV/EHU), AZTI, Tecnalia o el CSIC acercaron las últimas investigaciones relacionadas en el ámbito marítimo.
La conferencia SAREUS: Red de Varamientos de cetáceos y pinnípedos de Euskadi corre a cargo de Denis Benito Fernández, investigador de la Estación Marina de Plentzia-Plentziako Itsas Estazioa.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas pro 2024: SAREUS: Red de Varamientos de cetáceos y pinnípedos de Euskadi se ha escrito en Cuaderno de Cultura Científica.
Aceite de palma: ¿aliado tecnológico o enemigo de la salud?
Es probable que haya escuchado hablar sobre el aceite de palma en más de una ocasión, casi siempre acompañado de una connotación negativa. Sin embargo, ¿es tan perjudicial como se dice, o parte de su mala reputación proviene de mitos y/o desinformación?
 Foto de Marcelo Verfe / PexelsAceite de palma “hasta en la sopa»…
Foto de Marcelo Verfe / PexelsAceite de palma “hasta en la sopa»…
El principal problema del aceite de palma es que se encuentra como ingrediente en muchos alimentos procesados. Estos van destinados tanto a la población general (sopas instantáneas, helados, galletas y pan de molde) como a colectivos específicos (fórmulas infantiles).
Esta popularidad se debe a que el aceite de palma tiene una composición de ácidos grasos que lo hace estable y semisólido a temperatura ambiente. Además, cuenta con un punto de fusión elevado (temperatura a la que se derrite) y un sabor neutro.
Dichas características lo convierten en un ingrediente ideal para la elaboración de productos de panadería, confitería y aperitivos, donde es frecuente su uso como sustituto de grasas sólidas de mayor valor económico (mantequilla, manteca de cacao) o menos saludables, como las grasas parcialmente hidrogenadas (margarina). La industria alimentaria puede incluso emplearlo como medio de fritura de alimentos que, en principio, no lo contienen.
Todo ello explicaría la omnipresencia del aceite de palma en una gran variedad de alimentos de consumo más o menos habitual.
Pero ¿qué es y de dónde viene el aceite de palma?El aceite de palma es el aceite vegetal más utilizado a nivel mundial y se obtiene a partir del fruto de diferentes ejemplares de plantas del género Elaeis (E. guineensis, E. oleífera o el híbrido entre ambas). Todas ellas son comúnmente conocidas como palma de aceite o palma aceitera. Son originarias de África Occidental, pero en la actualidad los mayores productores a nivel mundial son Indonesia y Malasia.
Aunque solemos hablar de «aceite de palma” de forma general, en realidad se pueden obtener dos tipos diferentes de aceite según la parte del fruto que se utilice.
- El aceite de almendra de palma o aceite de palmiste, que se obtiene de la semilla del fruto.
- El aceite de palma propiamente dicho, que se extrae del mesocarpio (de la pulpa del fruto).
Estos aceites no solo difieren en su procedencia, sino también en su composición lipídica. Así, el aceite de palmiste es rico en ácidos grasos saturados (entre un 72 y un 98 % del total), principalmente ácidos láurico, mirístico y palmítico. En cambio, el aceite de palma presenta una composición mucho más equilibrada de ácidos grasos: casi la mitad de ellos son saturados y la otra mitad son insaturados. Entre los saturados destaca el palmítico (entre un 32 y un 47 %) y entre los insaturados destaca el oleico (ácido monoinsaturado, entre un 40 y un 52 %).
Aparte de su perfil de ácidos grasos, tanto el aceite de palmiste como el de palma contienen elevadas cantidades de componentes lipídicos minoritarios con propiedades antioxidantes, como la vitamina E (especialmente tocotrienoles) y carotenoides precursores de la vitamina A, que le confieren su característico color anaranjado.
Su contenido en estos compuestos lo ha posicionado como alternativa para paliar las deficiencias de vitamina E y A en poblaciones de Asia y África. Sin embargo, el proceso de refinamiento previo a su comercialización provoca que estos componentes bioactivos se pierdan casi en su totalidad, por lo que esta aparente ventaja nutricional en realidad no lo es tanto.
¿Por qué se dice que el aceite de palma es malo?En los últimos años el uso y consumo de aceites y grasas derivados de la planta de la palma de aceite ha causado gran controversia, dado que su alto contenido en ácidos grasos saturados (especialmente ácido palmítico) lo hace difícilmente recomendable desde un punto de vista nutricional.
La capacidad del ácido palmítico para aumentar los niveles circulantes de colesterol LDL (lipoproteína de baja densidad, popularmente conocido como “colesterol malo”) es bien sabida. Dada la relación existente entre niveles aumentados de colesterol LDL y el riesgo de padecer enfermedades cardiovasculares, las recomendaciones dietéticas sugieren reducir o limitar la ingesta de ácidos grasos de la dieta, incluido el ácido palmítico.
También es necesario recalcar la detección de glicidol, 3-monocloropropano-1,2-diol (3-MCPD) y sus ésteres en el aceite de palma refinado, compuestos que resultan tóxicos y para los cuales las autoridades ya han implantado medidas con el fin de reducir su contenido. Cabe recordar que estos compuestos se pueden generar durante el proceso de refinado de cualquier aceite vegetal a temperaturas excesivas (no solo en el procesado del aceite de palma).
No compensaEn conclusión, parece que a día de hoy las ventajas que puede aportar el aceite de palma por sus propiedades tecnológicas no son suficientes para contrarrestar los efectos que puede tener sobre la salud. Por ello, es necesario recalcar la importancia y suerte que tienen países mediterráneos como España de contar con el aceite de oliva virgen extra, que representa una opción mucho más interesante a nivel nutricional por ser rico en ácido oleico y en compuestos fenólicos únicos. Estos son potentes agentes bioactivos antioxidantes que no están presentes en otros aceites y grasas, cuyo consumo se ha relacionado con numerosos beneficios para la salud.![]()
Sobre las autoras: Laura Isabel Arellano García, Investigadora predoctoral del Grupo Nutrición y Obesidad del Centro de Investigación Biomédica en Red de la Fisiopatología de la Obesidad y Nutrición (CiberObn), Universidad del País Vasco / Euskal Herriko Unibertsitatea; Alfredo Fernández-Quintela, Profesor de Nutrición e Investigador del CiberObn; Bárbara Nieva Echevarría, Profesora Ayudante Doctora en el área de Tecnología de Alimentos, UPV/EHU; Encarnación Goicoechea Osés, Profesora Titular de Tecnología de los Alimentos, UPV/EHU; Iñaki Milton Laskibar, Profesor Investigador del CiberObn y del Instituto de Investigación Sanitaria Bioaraba, UPV/EHU, y María Puy Portillo, Catedrática de Nutrición, CIBERobn.
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Aceite de palma: ¿aliado tecnológico o enemigo de la salud? se ha escrito en Cuaderno de Cultura Científica.
¿Y si cae un meteorito?
Los meteoritos son fragmentos de cometas y asteroides que consiguen atravesar la atmósfera terrestre sin destruirse y caen en la superficie de nuestro planeta. Este proceso es mucho más común de lo que nos imaginamos, ya que se ha estimado que miles de estos visitantes extraterrestres llegan a la Tierra cada año, la mayoría de ellos de muy pequeño tamaño, lo que hace que ni nos enteremos de su presencia, aunque alguno consigue alcanzar un tamaño considerable pudiendo provocar ciertos daños materiales al caer en zonas pobladas.
 Meteorito de Hoba, encontrado en Namibia. Foto: Patrick Giraud / Wikimedia Commons
Meteorito de Hoba, encontrado en Namibia. Foto: Patrick Giraud / Wikimedia CommonsSin embargo, cuando oímos la palabra meteorito, lo que nos viene a la cabeza es un enemigo gigantesco e implacable acercándose a la Tierra para sembrar caos y destrucción. Esta imagen se nos ha quedado marcada debido a los eventos desencadenados por el impacto meteorítico más famoso de la historia, el acontecido hace unos 66 millones de años, cuando un cuerpo extraterrestre de más de 10 km de diámetro cayó en el actual Golfo de México y provocó la última gran extinción masiva de la historia de la Tierra, en la que desaparecieron el 75% de las especies del planeta, incluidos los dinosaurios no avianos. Y este miedo a que se repita la misma historia ha llegado a formar parte de la cultura popular en forma de numerosas películas de ciencia ficción, como “Deep Impact”, o novelas de terror como “El color surgido del espacio”, de H. P. Lovecraft.
Pero, si echamos un vistazo a la historia geológica de la Tierra, los impactos meteoríticos no han sido siempre tan catastróficos, más bien todo lo contrario. Y para comprobarlo viajaremos a nuestros orígenes… como planeta.
La Tierra se formó hace unos 4567 millones de años gracias a lo que se conoce como acreción de planetesimales. Este proceso consistió en la colisión de varios objetos sólidos con diámetros kilométricos (los planetesimales) que estaban dispersos en una nube de polvo y gases que orbitaba alrededor de una protoestrella que acabó convirtiéndose en nuestro Sol. Tras unos cuantos millones de años de impactos de planetesimales, hace unos 4538 millones de años tuvimos ya formada la Proto-Tierra, una gran bola semisólida cubierta por un océano de lava fruto del enorme calor generado por las colisiones.
 Recreación del aspecto de la Tierra primitiva, hace unos 4000 millones de años, mostrando la caída de meteoritos sobre una superficie parcialmente fundida. Ilustración: Simone Marchi & Dan Durda / Southwest Research Institute
Recreación del aspecto de la Tierra primitiva, hace unos 4000 millones de años, mostrando la caída de meteoritos sobre una superficie parcialmente fundida. Ilustración: Simone Marchi & Dan Durda / Southwest Research InstituteMientras nuestro joven planeta recién formado empezaba a enfriarse y parecerse más a lo que vemos hoy en día a nuestro alrededor, no estuvo a salvo de la caída de más meteoritos. En concreto, sufrió un auténtico ataque indiscriminado de proyectiles extraterrestres en dos fases temporales muy concretas: hace entre unos 4400 y 4100 millones de años, en lo que se conoce como Gran Bombardeo Temprano, y hace entre 4100 y 3900 millones de años, durante el Gran Bombardeo Tardío.
Los meteoritos que bombardearon esa Tierra primitiva eran de diferentes tipos: aerolitos o condritas, sideritos, litosideritos y fragmentos de asteroides carbonáceos. Y son los culpables de que, hoy en día, nuestro planeta sea un vergel de vida, ya que aportaron los componentes principales que la caracterizan, elementos químicos como hierro (Fe), níquel (Ni), silicio (Si), oxígeno (O), carbono (C) o hidrógeno (H), algunos de cuales se combinaron para generar moléculas tan importantes como dióxido de carbono (CO2), agua (H2O) y ozono (O3). Sin los cuales, la evolución geológica de nuestro planeta no se habría producido de la manera que lo hizo, propiciando que ahora mismo yo esté escribiendo este texto que estáis cómodamente leyendo.
Si todavía no os he convencido de que los impactos meteoríticos acontecidos en la historia geológica de nuestro planeta han sido más beneficiosos que perjudiciales para el ser humano, quiero que sepáis que, si no se hubiese producido esa extinción de los dinosaurios hace 66 millones de años, los mamíferos no habrían evolucionado hasta dar lugar al ser humano, millones de años después. Así que, ese grandullón surgido del espacio, nos hizo un enorme favor. Además, los meteoritos no dejan de ser fragmentos de cuerpos extraterrestres que nos permiten conocer de primera mano cómo debió ser la Tierra primigenia, aparte de que tener un siderito en las manos, formado principalmente por hierro y níquel, es lo más parecido a poder tocar el propio núcleo de nuestro planeta.
La próxima vez que miréis al cielo en una noche estrellada y veáis una estrella fugaz no quiero que penséis un deseo, sino que os acordéis de que fueron los meteoritos los que pusieron los primeros ladrillos tanto de nuestro planeta como de la vida tal y como la conocemos. Y sí, es posible que, algún día, vuelva a caernos uno lo suficientemente grande como para que la era del ser humano llegue a su fin, pero de eso no tenemos tanta certeza.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo ¿Y si cae un meteorito? se ha escrito en Cuaderno de Cultura Científica.
Benoît Mandelbrot, el padre de los fractales
El matemático Benoît Mandelbrot (1924- 2010) nació tal día como hoy, hace cien años. En un día tan especial, le dedicamos este retrato alfabético.
 Benoît Mandelbrot. Fuente: Wikimedia Commons.
Benoît Mandelbrot. Fuente: Wikimedia Commons.
Autosimilitud
En matemáticas, la autosimilitud es la propiedad de un objeto (denominado autosimilar) en el que el todo es exactamente (como, por ejemplo, la curva de Koch) o aproximadamente similar (como en el caso del brócoli) a una parte de sí mismo. La autosimilitud es una propiedad de los conjuntos fractales.
 Curva de Koch. Fuente: Wikimedia Commons.
Curva de Koch. Fuente: Wikimedia Commons.
Bourbaki
Aunque formado en Francia, los gustos científicos de Mandelbrot no encajaban con el enorme predominio de la escuela fundacional francesa de Bourbaki; por ello, en 1958, emigró a Estados Unidos de forma permanente.
Conjunto (de Mandelbrot)
Benoît Mandelbrot descubrió el conjunto que lleva su nombre en 1980; es un subconjunto del plano complejo.
 Conjunto de Mandelbrot. Fuente: Wikimedia Commons.
Conjunto de Mandelbrot. Fuente: Wikimedia Commons.
Diferentes (aspectos y cosas)
En una entrevista realizada en 2004, Mandelbrot cuestionaba la aplicabilidad de la teoría fractal:
¿Cómo es posible que la misma técnica se aplique a Internet, al clima y a la bolsa? ¿Por qué, sin esforzarme demasiado, estoy tocando tantos aspectos diferentes de muchas cosas diferentes?
Escalamiento (en las finanzas)
A finales de los años 1980, Mandelbrot aplicó la teoría fractal al estudio de los mercados. Publicó varios trabajos sobre la ley de escalamiento en las finanzas, ley que muestra propiedades similares a distintas escalas de tiempo.
Fractal (Geometry of Nature)
En 1982 Mandelbrot publicó su libro Fractal Geometry of Nature en el que explicaba sus investigaciones en este área. En 1997 se publicó su traducción al español.
Gran (Bretaña)
En 1967 Mandelbrot publicó en la revista Science su famoso artículo ¿Cuánto mide la costa de Gran Bretaña? donde se exponen sus primeras ideas sobre los objetos fractales. El trabajo examina la paradoja de que la longitud de una línea costera depende de la escala de medida.
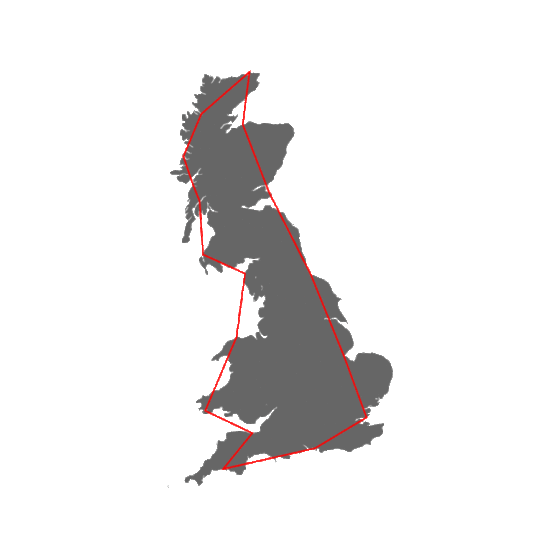 ¿Cuánto mide la costa de Gran Bretaña? Fuente: Wikimedia Commons.
¿Cuánto mide la costa de Gran Bretaña? Fuente: Wikimedia Commons.
Hausdorff (dimensión)
La dimensión de Hausdorff generaliza el concepto de dimensión topológica y permite definir una dimensión no entera para un objeto fractal. Por ejemplo, la dimensión de Hausdorff del conjunto de Cantor es log(2)/log(3), que es aproximadamente 0,63.
IBM
Desde 1958, y durante 35 años, Mandelbrot trabajó en IBM.
Julia (conjuntos de)
Mandelbrot estudió los llamados conjuntos de Julia que son invariantes bajo ciertas transformaciones del plano complejo. Basándose en trabajos previos de los matemáticos Gaston Julia y Pierre Fatou, Mandelbrot representó gráficamente imágenes de estos conjuntos con ayuda de un ordenador.
Kagan (Aliette)
Mandelbrot se casó con Aliette Kagan en 1955 y se mudó a Ginebra para colaborar con Jean Piaget en el Centro Internacional de Epistemología Genética. En 1958, la pareja se mudó a Estados Unidos, donde Mandelbrot se unió al personal de investigación de IBM.
Lévy (Paul)
Tras realizar sus estudios en la Universidad de Lyon, en 1944, Mandelbrot ingresó en la École polytechnique donde fue tutorizado por el matemático Paul Lévy.
Mandelbrojt (Szolem)
Szolem Mandelbrojt, su tío, fue también matemático. Nació en Varsovia en 1899 en una familia judía procedente de Lituania. En 1920 emigró a Francia y en 1936 ayudó al resto de su familia a dejar Polonia para encontrarse con él. Influyó enormemente en la formación de su sobrino.
Nubes
En su libro Introduction to The Fractal Geometry of Nature, Mandelbrot escribió esta conocida frase sobre las formas geométricas en la naturaleza, comenzando por las nubes:
Las nubes no son esferas, las montañas no son conos, las costas no son círculos, y las cortezas de los árboles no son lisas, ni los relámpagos viajan en una línea recta.
Ordenadores
Gracias a su acceso a los ordenadores de IBM, Mandelbrot fue uno de los primeros en usar gráficos para crear y mostrar imágenes fractales como el conjunto de Mandelbrot y los conjuntos de Julia.
Precios
En sus primeros trabajos sobre mercados financieros, Mandelbrot descubrió que los cambios de precios no seguían una distribución gaussiana, sino distribuciones estables de Lévy con varianza infinita.
Rugosidad
Mandelbrot creó la primera «teoría de la rugosidad» al observar rugosidad en las formas de las montañas y costas, en las estructuras de las plantas, en los vasos sanguíneos y pulmones o en la agrupación de galaxias. Su deseo era establecer matemáticamente una medida de esa rugosidad.
Science
En esta revista, en 1967, publicó ¿Cuánto mide la costa de Gran Bretaña?.
Teoría (Big Bang vs. fractal)
Mandelbrot ofreció en 1974 una nueva explicación de la paradoja de Olbers (¿por qué la noche es oscura?). Postuló que, si las estrellas del universo estuvieran distribuidas de manera fractal (por ejemplo, como el conjunto de Cantor), no sería necesario recurrir la teoría del Big Bang para explicar la paradoja. Su modelo no descartaba un Big Bang, pero permitía un cielo oscuro incluso si el Big Bang no hubiera ocurrido.
Universidades
Fue profesor de diferentes materias en diferentes centros universitarios: impartió docencia en economía en la Universidad Harvard, en ingeniería en la Universidad de Yale, en fisiología en el Colegio Albert Einstein de Medicina y en matemáticas en París y Ginebra.
von Neumann
Mandelbrot defendió su tesis doctoral Contribution à la théorie mathématique des communications en la Universidad de París en 1952, supervisado por Paul Lévy. Después se fue al Instituto Tecnológico de Massachusetts y luego al Instituto de Estudios Avanzados de Princeton, donde fue el último estudiante de postdoctorado del matemático John von Neumann.
Wolf (premio)
Entre muchos otros galardones y reconocimientos, Mandelbrot recibió el Premio Wolf en física en 1993, ya que, según la Fundación Wolf, “al reconocer la aparición generalizada de fractales y desarrollar herramientas matemáticas para describirlos, ha cambiado nuestra visión de la naturaleza”.
XYZ (el final de su carrera y el final de este retrato alfabético)
Benoît Mandelbrot comentaba al final de su carrera:
Ahora que me acerco a los 80, me doy cuenta con melancólico placer de que, en muchas ocasiones estuve diez, veinte, cuarenta, incluso cincuenta años adelantado a mi tiempo.
Referencias
- J J O’Connor and E F Robertson, Benoit Mandelbrot, MacTutor History of Mathematics archive, University of St Andrews
- Benoît Mandelbrot, IBM
- Benoit Mandelbrot, Wikipedia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
El artículo Benoît Mandelbrot, el padre de los fractales se ha escrito en Cuaderno de Cultura Científica.
Detectados tornados cuánticos girando en un “supersólido”
Nuevas observaciones de vórtices microscópicos confirman la existencia de una fase paradójica de la materia que también puede surgir en el interior de las estrellas de neutrones.
Un artículo de Zack Savitsky. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
https://culturacientifica.com/app/uploads/2024/11/Supersolids-comprimido.mp4 Cuando se hace girar un supersólido, se forman vórtices de forma espontánea. Vídeo: Ibrahim Rayintakath y Rui Braz para Quanta MagazineEn un laboratorio situado entre los picos escarpados de los Alpes austríacos, los metales de tierras raras se vaporizan y salen de un horno a la velocidad de un avión de combate. Luego, una combinación de láseres y pulsos magnéticos frena el gas hasta casi detenerlo, volviéndolo más frío que las profundidades del espacio. Los aproximadamente 50.000 átomos del gas pierden todo sentido de identidad y se fusionan en un solo estado. Finalmente, con un giro del campo magnético ambiental, pequeños tornados cobran vida y dan vueltas en la oscuridad.
Durante tres años, la física Francesca Ferlaino y su equipo de la Universidad de Innsbruck han trabajado para obtener imágenes de estos vórtices a escala cuántica en acción. “Mucha gente me dijo que esto sería imposible”, contaba Ferlaino durante una visita a su laboratorio este verano. “Pero estaba convencida de que lo lograríamos”.
Ahora, en un artículo publicado en Nature, han publicado instantáneas de los vórtices, confirmando la señal largamente buscada de una fase exótica de la materia conocida como supersólido.
El supersólido, una fase paradójica de la materia que es al mismo tiempo el más rígido de los sólidos y el más fluido de los fluidos, ha fascinado a los físicos de la materia condensada desde su predicción en 1957. Los indicios de esta fase habían ido aumentando, pero el nuevo experimento asegura la última pieza importante de la evidencia de su existencia. Los autores creen que los vórtices que se forman en los supersólidos pueden ayudar a explicar las propiedades en una variedad de sistemas, desde superconductores de alta temperatura hasta cuerpos astronómicos.
Los vórtices podrían mostrar cómo se comporta la materia en algunas de las condiciones más extremas del universo. Se sospecha que los púlsares, que son estrellas de neutrones giratorias (los cadáveres extraordinariamente densos de estrellas quemadas) tienen interiores supersólidos. “En realidad, este es un sistema análogo muy bueno” para las estrellas de neutrones, explica Vanessa Graber, física de Royal Holloway, Universidad de Londres en el Reino Unido, que se especializa en estas estrellas. “Estoy muy emocionada con esto”.
Rígido y fluidoImagina que haces girar un cubo lleno de distintos tipos de materia. Un sólido girará junto con el recipiente debido a la fricción entre el cubo y la red rígida de átomos del material. Un líquido, por otro lado, tiene menos fricción interna, por lo que formará un gran vórtice en el centro del cubo. (Los átomos externos giran con el cubo mientras que los internos se van quedando atrás).
Si se enfrían y dispersan lo suficiente ciertos líquidos, sus átomos comienzan a interactuar a lo largo de distancias mayores y terminan uniéndose en una ola gigante que fluye perfectamente sin fricción alguna. Estos llamados superfluidos fueron descubiertos por primera vez en el helio en 1937 por físicos rusos y canadienses.
 Francesca Ferlaino, física de la Universidad de Innsbruck, ha observado la característica distintiva de los supersólidos. Foto: M Vandory/Universidad de Innsbruck
Francesca Ferlaino, física de la Universidad de Innsbruck, ha observado la característica distintiva de los supersólidos. Foto: M Vandory/Universidad de InnsbruckIntenta hacer girar un cubo lleno de superfluido y este permanecerá en reposo incluso mientras el cubo gira a su alrededor. El superfluido sigue rozando el cubo, pero el material es totalmente impermeable a la fricción hasta que el recipiente alcanza una determinada velocidad de rotación. En este punto, al resistir el impulso de girar, el superfluido genera de repente un único vórtice cuántico: un remolino de átomos que rodea una columna de nada que se extiende hasta el fondo del cubo. Continúa acelerando el recipiente y más de estos tornados perfectos se deslizarán desde el borde.
Veinte años después de que se descubrieran los superfluidos, el físico estadounidense Eugene Gross sugirió que el mismo colectivismo cuántico podría surgir en los sólidos. Los físicos debatieron durante décadas si este extraño híbrido de superfluido y sólido podría existir. Finalmente, surgió una imagen teórica del supersólido. Al ajustar el campo magnético alrededor de un superfluido se puede reducir la repulsión entre los átomos de tal manera que comiencen a agruparse. Todos esos grumos se alinearán con el campo magnético pero se repelerán entre sí, autoorganizándose en un patrón cristalino mientras conservan su extraño comportamiento sin fricción.
Si se coloca un supersólido en un recipiente giratorio, los átomos se desplazarán en sincronía, de modo que la red de grumos parecerá girar con el recipiente, como un sólido. Pero, al igual que un superfluido, al girar lo suficientemente rápido, el material se romperá en vórtices, que quedarán atrapados entre los grumos de átomos. El supersólido será rígido y fluido a la vez.
La predicción de Gross dio inicio a una larga búsqueda de los supersólidos en el laboratorio.
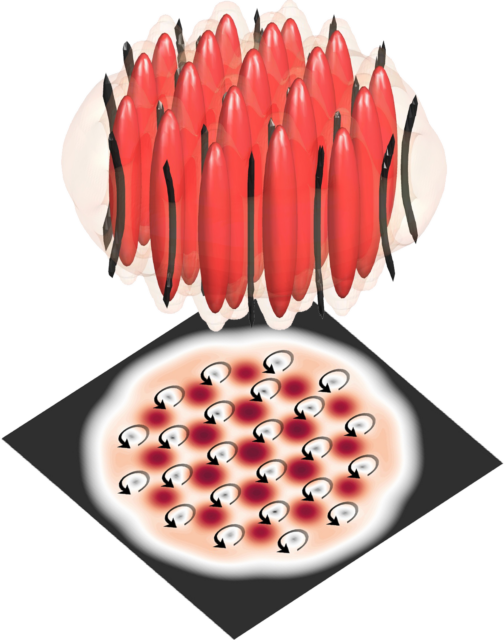 Ferlaino Group
Ferlaino GroupLos investigadores anunciaron por primera vez un descubrimiento en 2004, pero luego se retractaron de su afirmación. En 2017 y 2019 se produjeron nuevos estallidos de actividad, cuando grupos de Stuttgart, Florencia e Innsbruck encontraron señales prometedoras de supersolidez en sistemas unidimensionales. Los grupos comenzaron con gases de átomos de disprosio y erbio, que son lo suficientemente magnéticos como para actuar como pequeños imanes de barra. La aplicación de un campo magnético hizo que los átomos se agruparan de forma natural en grupos espaciados regularmente, formando una red cristalina. Luego, cuando los investigadores redujeron la temperatura y la densidad, las interacciones entre los átomos hicieron que oscilaran de forma natural como una onda coherente, con todas las características de un superfluido.
Los experimentos de 2019 vislumbraron las “dos naturalezas en competencia” del supersólido, explica Elena Poli, una estudiante de posgrado del equipo de Innsbruck. Desde entonces, el grupo ha expandido su supuesto supersólido de una dimensión a dos y lo ha investigado para detectar las diferentes propiedades predichas.
Pero “lo que faltaba era básicamente la evidencia irrefutable” de los supersólidos, dice Jens Hertkorn, físico del Instituto Tecnológico de Massachusetts y ex miembro del equipo de Stuttgart. El sello distintivo de la superfluidez es la serie de vórtices que se generan durante la rotación. A pesar de años de intentos, “nadie había logrado hacer girar un supersólido con éxito antes”, cuenta Hertkorn.
Girando un supersólidoPara observar cómo responde su supersólido a la rotación, el equipo de Innsbruck utilizó un campo magnético como una cuchara para retirar los campos magnéticos internos de los átomos unas 50 veces por segundo. Eso es lo suficientemente rápido como para desencadenar vórtices, pero lo suficientemente suave como para preservar la fase cuántica. «Es un estado muy, muy delicado: cualquier pequeño cambio lo destruiría», explica Ferlaino.
Detectar esos pequeños ciclones fue un desafío mayor. El grupo pasó tres años persiguiendo tormentas cuánticas. Finalmente, ejecutaron una propuesta de 2022 de Alessio Recati, un físico de la Universidad de Trento. Sugería formar vórtices en la fase supersólida y luego fundir el material nuevamente en un superfluido para obtener imágenes de los vórtices con mayor contraste.
 El laboratorio de Francesca Ferlaino en la Universidad de Innsbruck. Foto: Patscheider
El laboratorio de Francesca Ferlaino en la Universidad de Innsbruck. Foto: PatscheiderUn viernes por la noche, a principios del año pasado, tres estudiantes de posgrado irrumpieron en un pub oscuro cerca del campus de Innsbruck con un ordenador portátil en la mano. Buscaban a dos de los posdoctorados del equipo, quienes verificaron que habían capturado un tornado en su gas cuántico. “Fue excepcionalmente emocionante”, narra Thomas Bland, uno de los posdoctorados. Los estudiantes de posgrado regresaron al laboratorio, y Bland y su colega se quedaron para una ronda de celebración.
“Todos creemos que se trata de un vórtice cuántico”, dice Recati, que no participó en el experimento. Está esperando que los investigadores midan la velocidad de rotación de los tornados para corroborar plenamente las predicciones teóricas, pero las imágenes por sí solas son una validación satisfactoria, afirma. “Esto es muy relevante para toda la comunidad física”.
Hertkorn quiere que otros grupos repitan los resultados y que se haga un seguimiento de cómo cambian las señales en diferentes condiciones experimentales. Aun así, elogia al equipo de Innsbruck por su persistencia a la hora de realizar una medición tan difícil. “Es realmente impresionante, desde el punto de vista experimental, que esto sea observable”, concluye.
Conexiones cósmicasEl pasado mes de mayo, Ezequiel Zubieta estaba almorzando un estofado en un pequeño pueblo de las afueras de Buenos Aires cuando vio cómo una estrella muerta convulsionaba en la pantalla de su portátil. Zubieta, estudiante de posgrado en astronomía de la Universidad Nacional de La Plata, había estado siguiendo la rotación impresionantemente estable del púlsar Vela, el remanente magnetizado de una estrella masiva que explotó hace aproximadamente 11.000 años.
Mientras gira, Vela emite rayos de radiación desde sus polos que destellan en la Tierra 11 veces por segundo, con una regularidad que rivaliza con los mejores relojes que los humanos pueden construir. Pero ese día, la estrella giró 2,4 mil millonésimas de segundo más rápido de lo habitual.
https://culturacientifica.com/app/uploads/2024/11/VelaPulsarTimelapse-comprimido.mp4 Una película del Observatorio de rayos X Chandra de la NASA muestra un chorro de partículas que sale disparado del púlsar Vela, una estrella de neutrones situada a unos 1.000 años luz de la Tierra que gira 11 veces por segundo. Se cree que las formas en forma de arco son ondas expansivas de materia que se aleja de la estrella. Vídeo: NASA/CXC/Universidad de Toronto/M. Durant et alDurante décadas, los astrónomos se han preguntado qué podría provocar que estos objetos masivos aceleren repentinamente su rotación. Muchos esperan que estos fallos técnicos en los púlsares puedan ayudarlos a descifrar el funcionamiento interno de estos peculiares faros cósmicos.
Los científicos saben que los cadáveres estelares están densamente poblados de neutrones (una cucharadita de material de una estrella de neutrones pesaría tanto como el Monte Everest). Nadie está seguro de qué les sucede a los neutrones en esas condiciones, pero los astrónomos sospechan que, en una capa debajo de la corteza sólida exterior de la estrella, los neutrones presurizados forman grumos que adoptan formas inusuales, a las que a menudo se refieren como “pasta nuclear”. Los modelos principales presentan fases que se parecen a ñoquis, espaguetis y lasaña.
En una conferencia celebrada en 2022, Ferlaino escuchó a unos astrónomos hablar sobre las supuestas cualidades de la pasta nuclear. Muchos creen que los grumos de neutrones, parecidos a la pasta, se fusionarían para formar un superfluido, pero no está claro cómo ese material podría dar lugar a los fallos técnicos. Ferlaino sospechó que estos podrían ser una señal de los supersólidos que había estado preparando en su propio laboratorio, por lo que decidió investigar.
 Se cree que los neutrones presurizados que llenan las estrellas de neutrones adoptan una variedad de formas posibles conocidas como “pasta nuclear”. Fuente: Grupo Ferlaino
Se cree que los neutrones presurizados que llenan las estrellas de neutrones adoptan una variedad de formas posibles conocidas como “pasta nuclear”. Fuente: Grupo FerlainoEl año pasado, su equipo utilizó una simulación por ordenador de su supersólido para modelar lo que sucedería si existiera un material similar dentro de una estrella de neutrones giratoria. Descubrieron que, después de formarse los vórtices, uno de ellos puede desprenderse y chocar con su vecino, lo que desencadena un tornado y una avalancha que transfiere su energía al contenedor. Según propusieron, una cantidad suficiente de estas colisiones de tornados podría acelerar brevemente la rotación de la estrella de neutrones, lo que daría lugar a un fallo técnico.
Graber, que había publicado una revisión de análogos de laboratorio para estrellas de neutrones varios años antes, se emocionó al encontrar el artículo. “Dios mío, hay algo más por ahí que puedo usar”, recordó que pensó sobre las diversas propiedades de los supersólidos rotatorios descritos en el artículo. “Solo leyendo el texto, pensé: ‘Esto es lo que tengo, y esto es lo que tengo, y esto es lo que tengo’”.
Ahora que el grupo de Ferlaino ha identificado vórtices en su supersólido, planean investigar cómo se forman, migran y se disipan los tornados. También quieren replicar el supuesto mecanismo de los fallos técnicos de los púlsares, para demostrar cómo una avalancha de vórtices podría provocar que un supersólido del mundo real acelere su giro. Los físicos también esperan utilizar estos estudios para descifrar otras fases exóticas de la materia en las que se espera que los vórtices desempeñen un papel clave, como en los superconductores de alta temperatura.
Mientras tanto, astrónomos como Graber y Zubieta esperan que este trabajo permita desarrollar una nueva herramienta de diagnóstico para los púlsares. Con una mejor comprensión de la dinámica de los vórtices, podrían utilizar las observaciones de los fallos técnicos de los púlsares para inferir la composición y el comportamiento de la pasta nuclear.
“Si podemos entender cómo funciona esa física a pequeña escala, eso es realmente valioso para nosotros”, dice Graber. “No puedo usar un telescopio y mirar dentro de la corteza de una estrella de neutrones, pero ellos básicamente tienen esa información”.
Ferlaino, cuyo grupo está buscando otros sistemas que puedan presentar supersolidez, ve las aplicaciones como un reflejo de la conectividad fundamental de la naturaleza. “La física es universal”, afirma, y “estamos aprendiendo las reglas del juego”.
El artículo original, Physicists Spot Quantum Tornadoes Twirling in a ‘Supersolid’, se publicó el 6 de noviembre de 2024 en Quanta Magazine.
Traducido por César Tomé López
El artículo Detectados tornados cuánticos girando en un “supersólido” se ha escrito en Cuaderno de Cultura Científica.
Los tardígrados resisten radiaciones letales para cualquier otro organismo. Y ya sabemos cómo lo logran
No hay animales tan resistentes a condiciones ambientales extremas como los tardígrados. Estos minúsculos organismos (<1 mm), relacionados filogenéticamente con los artrópodos, viven en ambientes húmedos de todo tipo de climas, especialmente sobre musgos o líquenes como podemos ver en este vídeo:
En condiciones ambientales desfavorables los tardígrados entran en un estado denominado criptobiosis. De un 85% de agua en sus tejidos pasan a tener solo un 3%, y prácticamente detienen su metabolismo. Así pueden resistir sin problemas temperaturas extremas (entre ─200ºC y más de 100ºC) o presiones de 6000 atmósferas. En 2007, la sonda espacial Foton-M3 (Rusia/Agencia Espacial Europea), expuso tardígrados al vacío y a la radiación ultravioleta del espacio exterior en el proyecto TARDIS (tardigrades in space). A su regreso algunos ejemplares sobrevivieron e incluso se reprodujeron. En 2016, investigadores japoneses revivieron tardígrados que habían permanecido congelados durante treinta años en la Antártida.
Pero lo que nos interesa hoy es su increíble resistencia a las radiaciones ionizantes. Son capaces de sobrevivir a una dosis de 3000-5000 grays (Gy). Para hacernos una idea, la dosis letal para un ser humano está entre 5-10 Gy. No hay ser viviente (exceptuando a las bacterias) que pueda sobrevivir a estos niveles de radiación. ¿Cómo es posible? La investigación de un grupo de científicos chinos, recién publicada en Science, parece haber dado con las claves.
 Figura 1. El tardígrado Hypsibius dujardini, muy similar a la nueva especie Hypsibius henanensis descrita en el artículo de Science. Su longitud no llega a 1 mm. De Willow Gabriel, Goldstein Lab, CC BY-SA 2.5
Figura 1. El tardígrado Hypsibius dujardini, muy similar a la nueva especie Hypsibius henanensis descrita en el artículo de Science. Su longitud no llega a 1 mm. De Willow Gabriel, Goldstein Lab, CC BY-SA 2.5Los investigadores secuenciaron el genoma de una nueva especie de tardígrado, Hypsibius henanensis (Figura 1). El grupo identificó un total de 14 701 genes codificantes de proteínas. Tras someter a los tardígrados a dosis de radiación entre 200 y 2000 Gy, comprobaron qué genes habían modificado su nivel de expresión. En total, 2801 genes (un 19%) modificaron su actividad, generalmente con un aumento. Estos genes diferencialmente expresados se podían clasificar en tres grupos (Figura 2).
El primer grupo, podríamos decir el más sorprendente, estaba formado por 459 genes que probablemente derivaban de otros organismos por transferencia genética horizontal. Esto ocurre cuando un organismo incorpora a su genoma genes procedentes de otros seres vivos. Se calculó que entre un 0,5 y un 3% de todo el genoma tardígrado había sido “robado” a otros organismos, 54% a bacterias, 29% a hongos y un 9% a plantas.
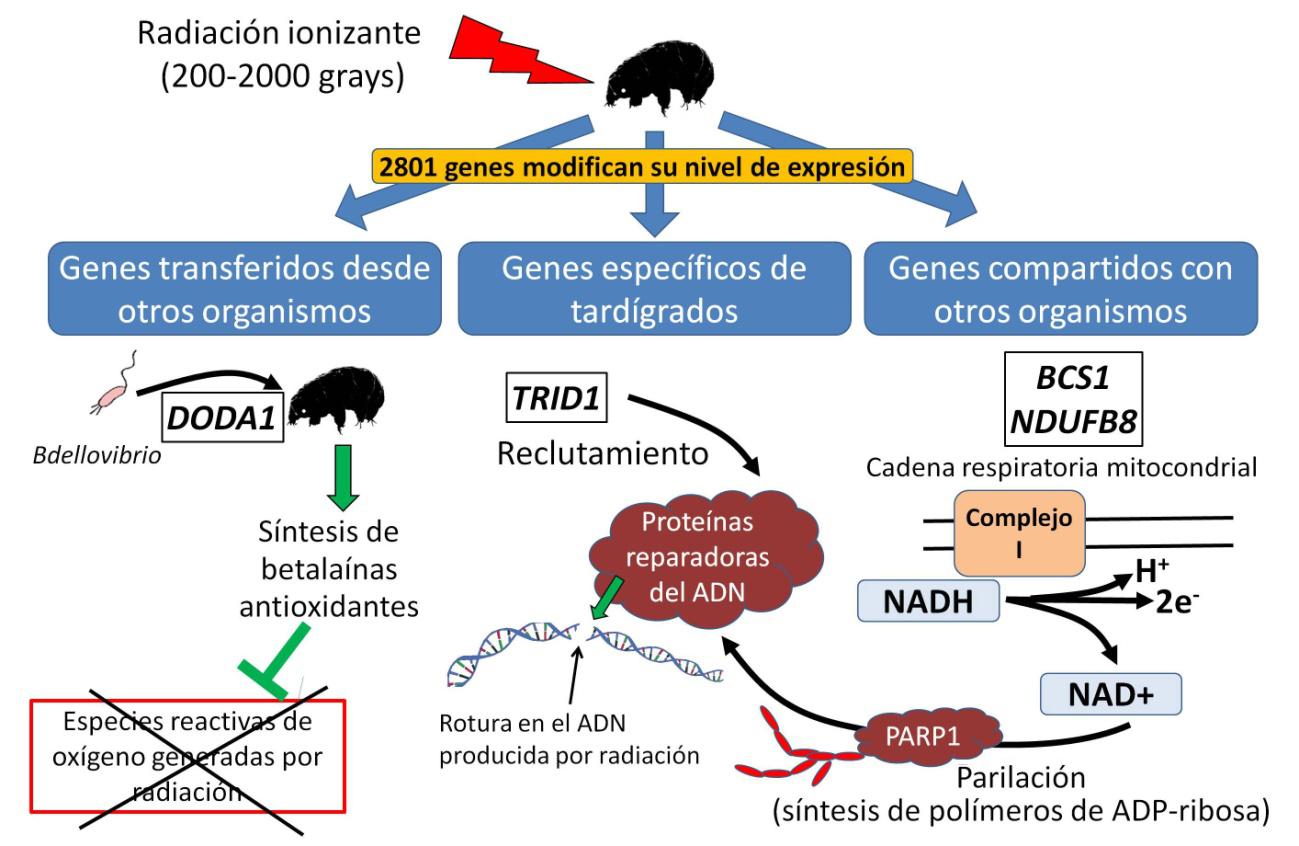 Figura 2. Esquema de los resultados obtenidos por Li et al., (2024). La irradiación de Hypsibius henanensis provoca cambios en la expresión de 2801 genes. Un grupo de genes derivan de transferencias desde otros organismos. Entre ellos, DODA1, derivado de una bacteria, permite sintetizar betalaínas antioxidantes que protegen contra la radiación. Entre los genes específicos de tardígrados destaca TRID1, que recluta proteínas reparadoras del ADN a los sitios de rotura de la cadena. Por último, un aumento en la expresión de genes de la cadena respiratoria mitocondrial permite generar grandes cantidades de NAD+, que es usado como sustrato por la enzima PARP1 para sintetizar poli-ADP-ribosa y activar mecanismos de reparación del ADN.
Figura 2. Esquema de los resultados obtenidos por Li et al., (2024). La irradiación de Hypsibius henanensis provoca cambios en la expresión de 2801 genes. Un grupo de genes derivan de transferencias desde otros organismos. Entre ellos, DODA1, derivado de una bacteria, permite sintetizar betalaínas antioxidantes que protegen contra la radiación. Entre los genes específicos de tardígrados destaca TRID1, que recluta proteínas reparadoras del ADN a los sitios de rotura de la cadena. Por último, un aumento en la expresión de genes de la cadena respiratoria mitocondrial permite generar grandes cantidades de NAD+, que es usado como sustrato por la enzima PARP1 para sintetizar poli-ADP-ribosa y activar mecanismos de reparación del ADN.De todos estos genes destacó por su fuerte expresión el denominado DODA1 (DOPA dioxygenase-1), probablemente derivado de una bacteria (Bdellovibrio). DODA1 participa en la síntesis de las betalaínas, pigmentos que aparecen en bacterias y plantas del orden cariofilales. Estas moléculas son las que dan su color rojo a la remolacha. En el caso de los tardígrados, las betalaínas actúan como potentes antioxidantes, eliminando las especies reactivas de oxígeno generadas por la radiación y protegiendo de esta forma al ADN.
El segundo grupo de genes activados por la radiación eran específicos de los tardígrados, ya que no se encontraron equivalentes en otros animales. Constituían el 30% del genoma, y entre ellos destacó TRID1 (por tardigrade-specific radiation-induced disordered protein-1). Se trata de una proteína desestructurada, es decir, sin estructura tridimensional fija, que actúa reclutando proteínas reparadoras del ADN a sitios en los que se ha producido una rotura doble de su cadena. Esta función es tan importante que la inactivación de TRID1 mediante ARN interferente disminuye drásticamente la supervivencia de los tardígrados tras ser irradiados.
Por último, el tercer grupo de genes activados por la radiación se encuentra también en otros animales. Dos de ellos, BCS1 y NDUFB8, destacaron especialmente. Son genes que codifican proteínas de la cadena respiratoria mitocondrial, responsable de la producción de energía en la célula. En el caso de BCS1, se localizaron en distintas especies de tardígrados entre 7-9 copias del gen, frente a la única copia presente en los animales. Todo esto indica una potente aceleración de la fosforilación oxidativa en las mitocondrias tras la irradiación. El objetivo de este proceso sería la regeneración del NAD+ (nicotinamina adenina dinucleótido), una molécula usada como sustrato por la enzima PARP1 para generar polímeros de ADP-ribosa. Estos polímeros facilitan la reparación de daños en el ADN por un proceso llamado parilación.
Lo que resulta intrigante es la razón de que los tardígrados estén equipados con un complejísimo y excepcional sistema de reparación de ADN, teniendo en cuenta de que no se trata de organismos extremófilos. Normalmente no viven sometidos a temperaturas extremas, ni están expuestos al vacío o a la radiación. Es cierto que eventualmente soportan tanto la congelación como la desecación, pero esto también ocurre en otros animales. En cambio, los tardígrados parecen estar preparados para sobrevivir a auténticos cataclismos. En cualquier caso, los nuevos descubrimientos podrían ser valiosos para comprender mejor los mecanismos de supervivencia celular en condiciones de estrés ambiental.
Referencias
Li, L., Ge, Z., Liu, S. et al. (2024) Multi-omics landscape and molecular basis of radiation tolerance in a tardigrade Science doi: 10.1126/science.adl0799.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga
El artículo Los tardígrados resisten radiaciones letales para cualquier otro organismo. Y ya sabemos cómo lo logran se ha escrito en Cuaderno de Cultura Científica.
Las ranas de Chernóbil envejecen bien
 Macho de Rana de San Antonio oriental (Hyla orientalis). Chernóbil (Ucrania), 2018.
Macho de Rana de San Antonio oriental (Hyla orientalis). Chernóbil (Ucrania), 2018.Germán Orizaola, CC BY
Han transcurrido casi cuatro décadas desde el accidente en la central nuclear de Chernóbil (Ucrania). Durante este tiempo, y para sorpresa de muchos, este lugar se ha convertido en una de las mayores reservas naturales de Europa. A lo largo de los últimos ocho años hemos trabajado para entender la situación de la fauna en el área afectada por este desastre medioambiental.
La radiación es capaz de dañar las células y, en exposiciones extremas, puede incluso causar la muerte de los organismos. Pero la situación de Chernóbil ha cambiado mucho desde el accidente. Allí queda hoy en día menos del 10 % del material radiactivo liberado en 1986. Los isótopos más peligrosos, como los de yodo, desaparecieron hace muchos años.
Estos factores pueden explicar la gran abundancia y diversidad de animales que viven hoy en Chernóbil. Sin embargo, es imprescindible examinar si los organismos experimentan daños que no vemos. Por ejemplo, si acumulan daños que acaben reduciendo su esperanza de vida.
Las ranas de ChernóbilDesde 2016 estudiamos las poblaciones de la rana de San Antonio oriental (Hyla orientalis) en Chernóbil, visitando la zona durante varias semanas cada primavera. Aprovechando la temporada de cría, capturamos machos durante la noche y los llevamos a nuestro laboratorio.
Además de en la zona de exclusión de Chernóbil, trabajamos en otras áreas del norte de Ucrania sin contaminación radiactiva. Estos lugares nos sirven como control para comparar nuestros resultados allí con los de la parte afectada por el accidente.
Durante años hemos examinado la morfología, el estado fisiológico e inmunitario y muchos otros rasgos de estas ranas. Nuestros trabajos han mostrado el aparente buen estado de salud de los anfibios en Chernóbil. Además, descubrimos un ejemplo de evolución rápida en las ranas, que son más oscuras que las de otras zonas sin radiación. Esto se debe, posiblemente, al papel protector de la melanina frente a la radiación.
Quedaba por investigar el efecto a largo plazo de la radiación sobre estos animales. Por eso analizamos la relación entre la radiación, la edad y el envejecimiento de las ranas.
¿Cuánto vive una rana?Podemos calcular la edad de un anfibio contando las líneas de crecimiento en sus huesos. Igual que ocurre con los anillos de los árboles, cada año de vida de una rana queda marcado. Sabemos que algunas especies en zonas de alta montaña pueden vivir más de 20 años. Otras especies, en cambio, apenas llegan a los 2 años.
En nuestro trabajo en Chernóbil examinamos unos 200 ejemplares a lo largo de tres años. Encontramos una edad máxima de 9 años en los machos de rana de San Antonio oriental. La mayoría de individuos que estudiamos tenían entre 3 y 4 años.
Además, queríamos saber si la radiación afectaba al ritmo de envejecimiento de las ranas. Para ello, medimos la longitud de los telómeros, un marcador asociado con la tasa de envejecimiento. Se trata de secuencias de ADN que se encuentran en el extremo de los cromosomas. Su función es proteger el material genético y se van acortando con cada división de la célula.
Para completar nuestro estudio, examinamos también los niveles de hormonas relacionadas con estrés en estas ranas. Medimos el contenido en sangre de corticosterona, una hormona que participa en la regulación del metabolismo y en la activación de la respuesta frente a estrés.
En todas las ranas calculamos también los niveles de radiación absorbida por cada individuo. Medimos el nivel de cesio de sus músculos y de estroncio de sus huesos. Este es uno de los estudios más detallados sobre la exposición actual a radiación en animales de Chernóbil. A nosotros nos permite relacionar de manera precisa los rasgos que medimos con la exposición a radiación en las ranas estudiadas.
El envejecimiento de las ranas de ChernóbilNuestro trabajo revela que vivir en Chernóbil no afecta ni a la edad ni al ritmo de envejecimiento de las ranas estudiadas.
La edad media de los individuos que capturamos fue de 3,6 años y fue similar en los individuos con mayor nivel de radiación y en aquellos de zonas sin radiación. Estos valores son normales para la especie y parecidos a los de otras poblaciones lejos de Chernóbil.
Tampoco observamos ningún efecto de la radiación sobre la velocidad de envejecimiento de las ranas. No detectamos ninguna relación entre la radiación absorbida por las ranas y la longitud de sus telómeros. Ésta se mantuvo bastante constante a lo largo de todos los niveles de radiación estudiados.
Además, los niveles de la hormona corticosterona no se vieron afectados por la radiación absorbida. Las ranas de Chernóbil tampoco parecen estar estresadas.
Estos resultados sugieren que los niveles de radiación presentes hoy en Chernóbil no son suficientes para causar daño crónico en estos organismos. Estas investigaciones son imprescindibles para desmontar el mito de que la Zona de exclusión es un infierno para la vida. En su lugar, estudios como el nuestro demuestran que se ha convertido en un refugio de gran relevancia para la fauna amenazada de Europa.![]()
Sobre los autores: Germán Orizaola, Profesor Titular de Zoología, Universidad de Oviedo y Pablo Burraco, Investigador postdoctoral Juan de la Cierva, Estación Biológica de Doñana (EBD-CSIC)
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Las ranas de Chernóbil envejecen bien se ha escrito en Cuaderno de Cultura Científica.
Naukas Pro 2024: Las batimetrías, los ojos del fondo marino

Los últimos avances en el ámbito de las energías renovables marinas o la proliferación de los microplásticos fueron algunos de los temas que componen la última edición de NAUKAS PRO. Una cita en la que el personal investigador se sube al escenario del Euskalduna Bilbao para hablar de las investigaciones más destacadas del momento en un ámbito concreto.
En esta ocasión el personal investigador de la Universidad del País Vasco, de la Estación Marina de Plentzia (PiE-UPV/EHU), AZTI, Tecnalia o el CSIC acercaron las últimas investigaciones relacionadas en el ámbito marítimo.
La conferencia Las batimetrías, los ojos del fondo marino corre a cargo de Gemma Ercilla Zarraga, investigadora del Instituto de Ciencias del Mar-ICM-CSIC.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Pro 2024: Las batimetrías, los ojos del fondo marino se ha escrito en Cuaderno de Cultura Científica.
El impacto en la Amazonía del petróleo que consumes aquí
Del petróleo extraído en la Amazonía ecuatoriana por una empresa española, Ecuador apenas se queda con el 21 % de los ingresos. Y ello a pesar de soportar buena parte de los impactos ambientales y las transformaciones culturales en las comunidades indígenas como consecuencia de las extracciones.
 Vista aérea de parte de las intalaciones de estracción de petróleo en la Amazonía ecuatoriana. Fuente El Santo Films / Izar Films
Vista aérea de parte de las intalaciones de estracción de petróleo en la Amazonía ecuatoriana. Fuente El Santo Films / Izar FilmsEl último trabajo del grupo de investigación Life Cycle Thinking de la UPV/EHU muestra que el 79 % del dinero procedente del petróleo de los bloques 16 y 67 de Ecuador va a países enriquecidos: el 20 % lo ganan las empresas de extracción, el 21 % las refinerías y los intermediarios en la distribución y el 38 % el gobierno de España a través del impuesto especial sobre hidrocarburos que se aplica por la falta de sostenibilidad. “El hecho de que en el país de origen del recurso, Ecuador, solo se quede el 21 % de los ingresos demuestra que la distribución de beneficios y daños no es equitativa. Nuestro estudio ha convertido en cifras el desigual reparto de los impactos económicos y ambientales de la explotación del petróleo en el norte y en el sur global”, ha explicado Ortzi Akizu Gardoki, investigador de la Escuela de Ingeniería de Vitoria-Gasteiz de la UPV/EHU.
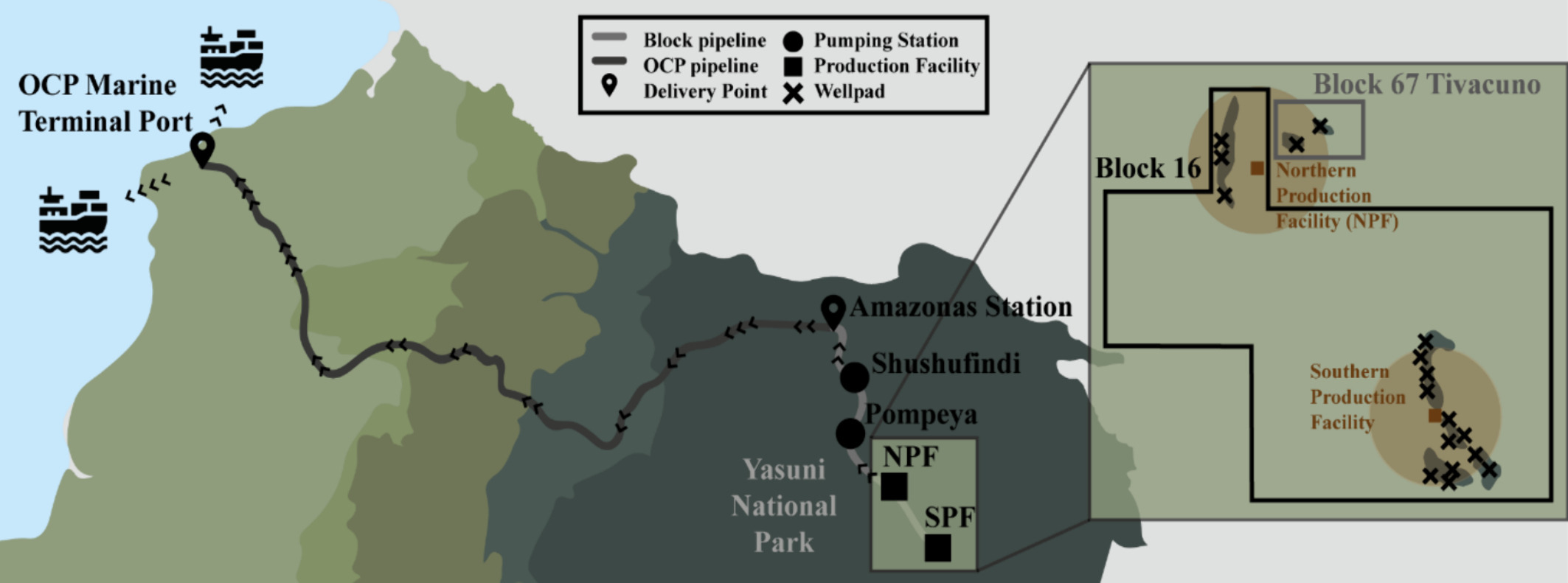 Fuente: Eugenio, C. et al (2024)
Fuente: Eugenio, C. et al (2024)Ecuador produce anualmente unos 175 millones de barriles de petróleo, cuya exportación constituye la principal fuente de ingresos del país. Hay más de 80 bloques repartidos por todo el país, pero los que más polémica generan son los de la selva amazónica, por los daños sociales y ecológicos que provocan. En concreto, los bloques 16 y 67 sobre los que ha incidido la labor de la Universidad del País Vasco se encuentran en el Parque Nacional Yasuní, situado en esa zona, uno de los lugares del mundo con una mayor biodiversidad. Estos pozos han sido elegidos para la investigación por la urgencia de cuantificar el equilibrio entre los impactos y los beneficios que generan las extracciones sobre la naturaleza y sus comunidades indígenas. También porque Repsol ha sido quien ha explotado estos dos bloques durante 24 años: «No se sabe si el combustible que compramos procede de uno de esos dos bloques, pero sí tenemos gasolineras de esa compañía en el País Vasco. El estudio ha servido para impulsar el objetivo de concienciar a los usuarios finales de aquí sobre la responsabilidad que tenemos en los impactos del petróleo que se extrae en la Amazonia”, ha aclarado Akizu Gardoki.
La investigación ha llenado una laguna existente al respecto. De hecho, es la primera vez que se cruzan los datos relativos a los beneficios obtenidos de la explotación de estas dos zonas con la huella ecológica. Se concluye que, de media, la propia Amazonia soporta directamente el 19,6 % de las emisiones equivalentes de CO2 producidas por la producción y el consumo.
El ciclo de vida del petróleoPara lograr estos resultados, el equipo de investigación ha utilizado el análisis del ciclo de vida del petróleo. Con el fin de poder comparar los datos, se ha tenido en cuenta la huella de carbono que se produce cuando lo utilizamos como combustible en vehículos particulares. Es decir, han cuantificado las emisiones de CO2 que se producen desde el momento en que se extrae el petróleo de los dos bloques del Parque Nacional Yasuní, se transporta a las refinerías, se trata y se distribuye a las gasolineras, hasta que sale por el tubo de escape de los coches. Los resultados indican que el 38,7 % de las emisiones se producen directamente por mantener el motor en marcha, el 37,1 % durante la construcción del vehículo y las infraestructuras, y el 24,3 % en los procesos de extracción, refinamiento y distribución.
Akizu Gardoki desea despertar la conciencia de los consumidores finales a través de los siguientes datos: “Se pone de manifiesto la gran responsabilidad de las personas que van al volante. En muchas ocasiones solo miramos el CO2 que sale por el tubo de escape, pero debemos ser conscientes de que la huella ambiental que genera la acción de conducir es más larga y de que también se producen daños en otros países. No somos responsables de los modelos energéticos creados por empresas privadas y gobiernos, pero podemos ser agentes de cambio”.
Impacto social en las comunidades indígenas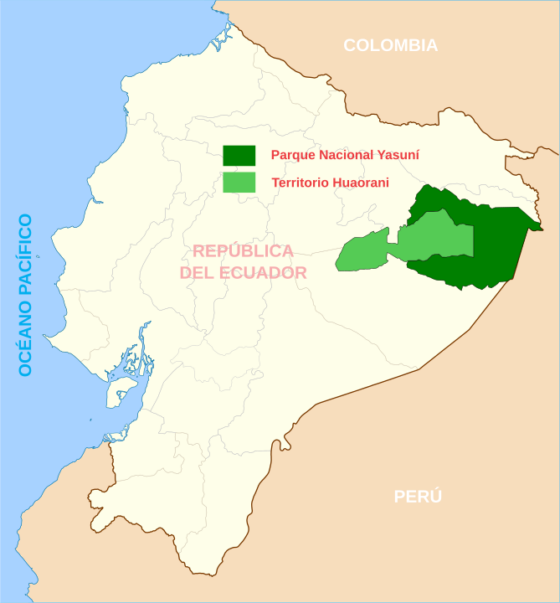 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsAdemás del impacto medioambiental, el estudio de la UPV/EHU también ha analizado el impacto social de las extracciones del Parque Nacional Yasuní en los grupos indígenas locales. “Hemos mantenido largas entrevistas con representantes de grupos de la etnia huaorani —señala el investigador— y hemos detectado impactos graves en la calidad de vida. También transformaciones culturales, que no tienen vuelta atrás. Entre otras cosas, hemos visto que se ha producido la dependencia del modelo económico y la pérdida de algunos hábitos, como consecuencia de la civilización”. Por otra parte, el estudio concluye que la explotación del petróleo en la Amazonia ha provocado la aparición del alcoholismo y el aumento de los casos de violencia de género.
Sin embargo, según el líder de Life Cycle Thinking, en el análisis se ha comprobado que las empresas y los gobiernos no cuantifican los daños sociales y ecológicos: “Lo hacen de forma intencionada, porque la falta de medición permite seguir generando impactos y permite pagar una compensación arbitraria por daños no cuantificados”.
El estudio de la Universidad del País Vasco supone una aportación a este primer paso para conocer la relación entre los beneficios y los impactos, pero el autor ha subrayado que es necesario dar más pasos. Por ejemplo, con vistas a reducir los impactos, propone empezar a indicar el origen del petróleo en las gasolineras: “Así como nos hemos acostumbrado a preguntar de dónde procede la fruta que compramos y estamos dispuestos a pagar el doble por las manzanas de productores locales, miremos de dónde viene el combustible que ponemos en los vehículos y de qué manera se produce. La sociedad vasca tiene el potencial de generar cambios en el actual modelo energético”.
Referencia:
Cinta Eugenio, Jacid Montoya-Torres, Ortzi Akizu-Gardoki, Leire Urkidi, Unai Villalba-Eguiluz , Carlos Larrea, Sylvia Pappuccio, Angélica Calle-Calderón, Dania Quirola (2024) Environmental impacts of oil extraction in blocks 16 and 67 of the Yasuní Reserve in the Amazonian Forest: Combined qualitative and Life-Cycle Assessment Science of The Total Environment doi: 10.1016/j.scitotenv.2024.175189
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo El impacto en la Amazonía del petróleo que consumes aquí se ha escrito en Cuaderno de Cultura Científica.
Mars Phoenix: la primera biblioteca de Marte
El 25 de mayo de 2008 aterrizó sobre la superficie de Marte la sonda Phoenix y, con ella, muchos de los sueños sobre el planeta rojo que habían alimentado, hasta entonces, la imaginación de varias generaciones. No era la primera vez que llegábamos allí, ni fue la última, pero Phoenix sí fue nuestra Cook o nuestra Peary, esto es, nuestra pionera de la exploración polar marciana.
 Impresión artística de la sonda Phoenix.
Impresión artística de la sonda Phoenix.Créditos: NASA/JPL/Corby Waste
El objetivo de la misión Mars Phoenix Lander era ayudar a reconstruir la historia geológica del agua en Marte, así como su pasado climático, y estudiar la química del suelo para dilucidar si en algún momento fue capaz de albergar vida. Desde 2001 se sabía, gracias al orbitador Odyssey, que había grandes cantidades de hielo en el subsuelo marciano a latitudes superiores a 55 º, Phoenix —tras el fracaso de la Mars Polar Lander que, en 1999, trató de aterrizar en el polo sur marciano— fue hasta Green Valley, en las planicies septentrionales de Vastitas Borealis, para comprobarlo, pero no solo iba equipada con instrumentos científicos. También llevaba consigo testimonios, historias, visiones y melodías.
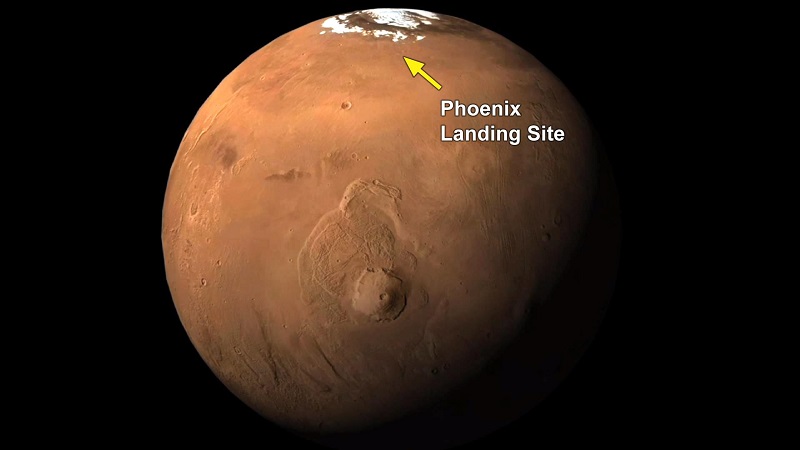 Lugar de aterrizaje de la sonda Phoenix: Green Valley, en las tierras bajas septentrionales de Vastitas Borealis, muy cerca del casquete polar norte.
Lugar de aterrizaje de la sonda Phoenix: Green Valley, en las tierras bajas septentrionales de Vastitas Borealis, muy cerca del casquete polar norte.Créditos: NASA/JPL-Caltech/University of Arizona/MSSS
En algunas fotos de la sonda se puede observar sobre la cubierta un miniDVD con el título Visiones de Marte; una versión actualizada —y mucho menos mítica, aunque no menos interesante— del disco dorado de las Voyager. Y sí… como era de esperar, el científico y divulgador Carl Sagan tuvo algo que ver en el proyecto.
 El miniDVD Visiones de Marte sobre la cubierta de la Mars Phoenix, fotografiado desde la superficie del planeta.
El miniDVD Visiones de Marte sobre la cubierta de la Mars Phoenix, fotografiado desde la superficie del planeta.Créditos: NASA/Jet Propulsion Lab-Caltech/University of Arizona
La idea, en esta ocasión, nació en 1991 de la mano del ingeniero Louis Friedman, confundador de la Planetary Society junto con el propio Sagan, que en aquel momento era el presidente, y Bruce Murray. Desde finales del siglo XIX y durante gran parte del siglo XX, Marte había sido el protagonista de innumerables aventuras e historias de ciencia ficción y estas, a su vez, habían inspirado a la generación de científicos que había hecho posible que llegáramos hasta nuestro vecino planetario, así que, ¿por qué no recopilar las más significativas y enviarlas allí? Quince años después de las Voyager, la tecnología había avanzado lo suficiente como para poder hacerlo sin un coste prohibitivo: del vinilo se había pasado a las cintas magnéticas, de las cintas magnéticas, al CD y, del CD, al DVD. Ahora se podía almacenar una cantidad de información mucho mayor en mucho menos espacio.
La primera versión de Visions of Mars, cuyo desarrollo corrió a cargo del artista y divulgador Jon Lomberg —colaborador habitual de Carl Sagan y director artístico de Cosmos—, partió a bordo de la misión soviética Mars 96, que acabó en el fondo del Pacífico poco después del despegue. Sin embargo, el proyecto resurgiría de sus cenizas —y no se me ocurre mejor forma de expresarlo— poco más de una década después, cuando se actualizaron y remasterizaron los contenidos para enviarlos al planeta rojo en la misión Mars Phoenix Lander.
Jon Lomberg y John Robert Colombo, con la inestimable ayuda y asesoramiento de la escritora Judith Merril —así como acceso a su extensa biblioteca—, hicieron una selección de obras de ciencia ficción con la que intentaron representar, de la manera más global posible, la historia de nuestras percepciones de Marte a través del tiempo y su influencia en la cultura popular. Así, volvieron a su hogar clásicos anglosajones como Una princesa de Marte, de Edgar R. Burroughs; La guerra de los mundos, de H. G. Wells, o Crónicas marcianas, de Ray Bradbury. Pero también la soviética Estrella Roja, de Alexander Bogdanov (Rusia); Il tre cosmonauti, de Umberto Eco (Italia); Auf zwei Planeten, de Kurd Lasswitz (Alemania), o El atardecer, 2217 d. C., de Ryu Mitsuse (Japón). Y no solo obras de ficción; también se incluyeron algunos de los ensayos más influyentes de la historia de la investigación marciana, como los escritos por Giovanni Schiaparelli y Percivall Lowell. El propio Jon Lomberg diría:
Esta asociación [entre el programa espacial y la ciencia ficción] es lo que nos ha inspirado a enviar este disco a Marte, para honrar y conmemorar el papel que ha desempeñado la ciencia ficción a la hora de alimentar los sueños de las personas que diseñaron, construyeron, volaron y financiaron las misiones que finalmente cruzaron el espacio. ¿Habríamos llegado tan lejos sin estas visiones que nos inspiraron?
Sin embargo, Visiones de Marte no incluía solo textos, sino que en él podemos encontrar todo tipo de expresiones culturales: ilustraciones y fotografías, emisiones de radio —no podía faltar la famosa retransmisión de Orson Welles de La guerra de los mundos, de 1938—… y una lista con los nombres de las 250 000 personas que quisieron formar parte, de alguna manera, de esta misión, incluidos todos los miembros de la Sociedad Planetaria.
 Ilustración de 1906 de la edición belga de La guerra de los mundos de H. G. Wells incluida en Visions of Mars.
Ilustración de 1906 de la edición belga de La guerra de los mundos de H. G. Wells incluida en Visions of Mars.
Como si una cápsula del tiempo se tratara, Arthur C. Clarke, Louis Friedman y Judith Merrill dejaorn mensajes para los colonos del futuro. También otra persona que, de haber seguido todavía entre nosotros, hubiera cumplido noventa años el pasado 9 de noviembre:
Cualquiera que sea la razón por la que estáis en Marte, me alegro de que sea así. Y desearía estar con vosotros.
Carl Sagan
Bibliografía
NASA (2008). Phoenix Landing. Mission to the Martian Polar North [press kit].
The Planetary Society (s. f.). Visions of Mars.
The Planetary Society (s. f.). Visions of Mars. Then and now.
.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo Mars Phoenix: la primera biblioteca de Marte se ha escrito en Cuaderno de Cultura Científica.
La sucesión del infinito del compositor Per Nørgård
Los fractales son unos curiosos objetos matemáticos que gozan de una cierta popularidad fuera de la comunidad matemática, y científica, desde que el matemático polaco, nacionalizado francés y estadounidense, Benoît Mandelbrot (1924-2010), considerado el padre de la geometría fractal, realizara una importante labor divulgativa sobre ellos, primero con el artículo ¿Qué longitud tiene la costa de Gran Bretaña? (Revista Science, 1967) y posteriormente con los libros Los objetos fractales: forma, azar y dimensión (1975) o La geometría fractal de la naturaleza (1982), entre muchos otros.
En la entrada del Cuaderno de Cultura Científica titulada Sucesiones fractales hablábamos de un tipo de sucesiones de números enteros que compartían con los objetos fractales una de sus propiedades definitorias, la autosemejanza (para una explicación divulgativa de las mismas puede leerse la entrada Fractus, arte y matemáticas). Más aún, en una entrada posterior, titulada Sucesiones fractales: del número a la nota musical, explicábamos como el compositor minimalista estadounidense Tom Johnson (1939) las había utilizado en algunas de sus composiciones musicales, por ejemplo, La melodía racional XV y la pieza La vie est si court, las cuales fueron explicadas en dicha entrada.
 Fotograma del video “Illustrated Music #6, Rational Melody XV” del canal de YouTube del compositor Tom Johnson, al que podemos ver en el mismo
Fotograma del video “Illustrated Music #6, Rational Melody XV” del canal de YouTube del compositor Tom Johnson, al que podemos ver en el mismo
La “sucesión del infinito” que, en particular, es una sucesión fractal y de la que vamos a escribir en esta entrada, fue descubierta por el músico danés Per Nørgård, que la utilizó como base matemática de muchas de sus composiciones musicales.
Per Nørgård, descubridor de la sucesión del infinitoEl compositor, teórico de la música y profesor danés Per Nørgård (1932) es una figura fundamental en la música danesa contemporánea. Ha escrito alrededor de 400 composiciones, que incluyen seis operas, ocho sinfonías, tres ballets, música para orquesta, conciertos, obras corales y vocales, música de cámara, piezas para instrumentos solistas y también bandas sonoras para películas. Entre sus composiciones más importantes se podrían citar Voyage into the Golden Screen / Viaje a la pantalla dorada (1968), para orquesta, la Sinfonía no. 2 (1970), para orquesta, la ópera Gilgamesh (1972), premiada con el Nordic Music Prize en 1974, la Sinfonía no. 3 (1972), para dos coros y orquesta, la ópera Siddharta (1979), la pieza para un solo instrumento de percusión I Ching (1982) o la ópera Det Guddommelige Tivoli / El circo divino (1982). Además, ha recibido muchos reconocimientos a lo largo de su extensa carrera, como el Premio (internacional) Ernst von Siemens, conocido como el Premio Nobel de la Música, en 2016, o el Premio (internacional) Wihuri Sibelius, en 2006, por mencionar algunos.
 Fotografía del compositor danés Per Nørgård (1932)
Fotografía del compositor danés Per Nørgård (1932)
Si consultamos la biografía de Per Nørgård que aparece en la base de datos sobre compositores del Institut de Recherche et Coordination Acoustique/Musique (IRCAM), un instituto francés de investigación sobre música y acústica, asociado al Centro Nacional de Arte y Cultura Georges Pompidou de París (cuya dirección web es brahms.ircam.fr), se mencionan las siguientes cuestiones respecto a su música. “Tras experimentar con collages musicales a finales de la década de 1950, Per Nørgård centró su atención en la música serial en los primeros años de la nueva década, desarrollando su propia técnica conocida como sucesión del infinito”, que es una de las herramientas musicales más importantes del conjunto de su producción musical. Además, no podemos olvidar que esta sucesión del infinito es un objeto matemático, una sucesión de números enteros con una serie de propiedades que la hacían interesante para las composiciones musicales que Per Nørgård quería componer y que utilizó en obras como Viaje a la pantalla dorada (1968), la Sinfonía no. 2 (1970), la Sinfonía no. 3 (1972) o I Ching (1982). Además de la sucesión del infinito, también utilizó el número de oro y la sucesión de Fibonacci, aunque en menor medida.
Por otra parte, “en 1979, durante una exposición en el Museo de Arte Moderno de Luisiana (Dinamarca), el compositor descubrió la obra del pintor suizo, uno de los primeros artistas asociados con el Art Brut (arte marginal), Adolf Wölfli. La interpretación de los criptogramas del artista esquizofrénico atrajo la práctica compositiva de Nørgård hacia el expresionismo. El resultado es un juego de intensidades, cambios bruscos de humor y modificaciones violentas del sonido y, además, un desbordamiento del flujo musical. Esta aparición del conflicto y la irracionalidad en su obra es una respuesta directa a la última década de composiciones matemáticamente regulares”. Entre las obras que pertenecen a este periodo están la Sinfonía no. 4 (1981) y la ópera sobre la vida de Wölfli, El circo divino (1982).
 Portada del disco Per Nørgård: Iris/Voyage into the Golden Screen (1973), de la Danish National Symphony Orchestra, dirigida por Herbert Blomstedt y Tamás Vetö, en cuya imagen podemos observar la sucesión del infinito en formato musical y dibujada en espiralLa sucesión del infinito
Portada del disco Per Nørgård: Iris/Voyage into the Golden Screen (1973), de la Danish National Symphony Orchestra, dirigida por Herbert Blomstedt y Tamás Vetö, en cuya imagen podemos observar la sucesión del infinito en formato musical y dibujada en espiralLa sucesión del infinito
El compositor Per Nørgård descubrió (utilizamos este término y no “inventó”, ya que es el que utilizaba el propio Nørgård) la sucesión de números enteros que bautizó con el nombre de Uendelighedsrækken (en danés), que he traducido para esta entrada como sucesión del infinito, en 1959, años antes de que los fractales se hicieran conocidos a través de la labor divulgativa del matemático Benoit Mandelbrot, y que utilizó en muchas de sus composiciones, especialmente de las décadas de 1960 y 1970. La primera obra en la que utiliza la sucesión del infinito es su obra Viaje a la pantalla dorada (1968), en la cual utiliza 1.024 elementos de la sucesión en su versión musical. La siguiente obra en la que la utilizaría es la Sinfonía no. 2 (1970), con una utilización más compleja con 4.096 elementos de la sucesión.
Si consultamos la partitura de la obra Viaje a la pantalla dorada podemos ver una versión musical de la sucesión del infinito, cuyas primeras 64 notas (interpretadas en esta obra por las dos flautas) aparecen en la siguiente imagen.
 Las primeras 64 notas de la sucesión musical del infinito extraída de la composición Viaje a la pantalla dorada (1968), de Per Nørgård
Las primeras 64 notas de la sucesión musical del infinito extraída de la composición Viaje a la pantalla dorada (1968), de Per NørgårdA partir de la anterior imagen, extraída de la partitura de la obra Viaje a la pantalla dorada, vamos a escribir la sucesión de números enteros, que Nørgård descubrió, realizando el proceso inverso al que realizó el compositor al pasar de la sucesión de números a la sucesión de notas musicales. Para ello empezamos indicando que el punto inicial es la primera nota de la sucesión musical, que en este caso es “Sol” y que se corresponde con el número 0. A partir de ahí los números enteros de la sucesión van a indicar, para cada nota, la cantidad de semi-tonos que esa nota está por encima (positivo) de “Sol”, luego es más aguda, o por debajo (negativo), luego es más grave. Así, el segundo número es un 1 puesto que la siguiente nota es “La bemol” que es un semi-tono más alta (aguda) que “Sol” (de “Sol” a “La” subimos un tono, pero el bemol indica que baja un semi-tono, luego de “Sol” a “La bemol” sube un semi-tono). Como la tercera nota es “Fa sostenido”, que es un semi-tono más baja (grave) que “Sol” (de “Sol” a “Fa” se baja un tono, pero el sostenido indica que la nota sube un semi-tono, entonces el “Fa sostenido” es un semi-tono más bajo que “Sol”), el siguiente número de la sucesión es -1. El cuarto número es 2, ya que la cuarta nota es un “La”, un tono, luego dos semi-tonos, por encima de “Sol”. De esta manera descubrimos que los 64 primeros números de la sucesión del infinito, en correspondencia con las notas musicales de la partitura, son los siguientes.

De hecho, los 86 primeros términos de la sucesión del infinito, que es la sucesión A004718 de la Enciclopedia online de sucesiones de números enteros, son los siguientes.
0, 1, -1, 2, 1, 0, -2, 3, -1, 2, 0, 1, 2, -1, -3, 4, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, -1, 2, 0, 1, 2, -1, -3, 4, 0, 1, -1, 2, 1, 0, -2, 3, 2, -1, -3, 4, -1, 2, 0, 1, -3, 4, 2, -1, 4, -3, -5, 6, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, 0, 1, -1, 2, 1, 0, …
Existen varias formas de generar esta sucesión de números enteros. La más simple es mediante una fórmula recursiva.
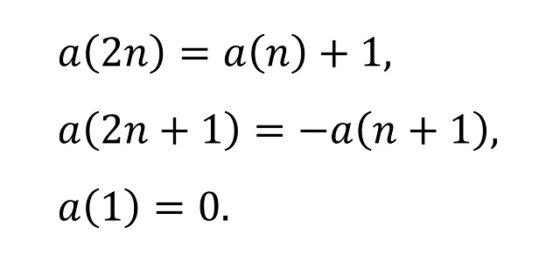 Fórmula recursiva de la sucesión del infinito
Fórmula recursiva de la sucesión del infinito
En la propia fórmula recursiva ya podemos percibir las propiedades relacionadas con la autosemejanza, de hecho, la sucesión del infinito es una sucesión fractal, que buscaba el compositor y que veremos más adelante.
Un proceso iterativo infinitoOtro método de construcción de esta sucesión es un proceso iterativo infinito proyectando un “segmento” inicial de dos números, o dos notas. El segmento inicial es 0 y 1 (“Sol” y “La bemol”) y la variación entre los dos (segundo menos primero) es + 1, entonces vamos a proyectar los dos primeros términos de la sucesión utilizando esa variación de la siguiente forma. Al segundo término le aplicamos la variación 1 + 1 y se convierte en el cuarto término 2, mientras que al primer término le aplicamos el opuesto 0 – 1 y se convierte en el tercer término – 1, como se muestra en la siguiente imagen. Por lo tanto, tenemos los cuatro primeros términos de la sucesión 0, 1, -1, 2.

A continuación, avanzamos una posición y el segmento que nos va a determinar las dos siguientes notas es el segmento 1 y -1, y la variación entre los dos es -2. Ahora aplicaremos esta variación a los dos últimos términos de la sucesión que vamos construyendo, – 1 y 2. Al segundo de esos dos términos le aplicamos la variación 2 – 2 y se convierte en el sexto término de la sucesión 0, mientras que al primero le aplicamos el opuesto -1 + 2 = 1 y se convierte en el quinto término de la sucesión, como se muestra en la siguiente imagen. De esta forma quedan determinados los seis primeros términos de la sucesión 0, 1, -1, 2, 1, 0
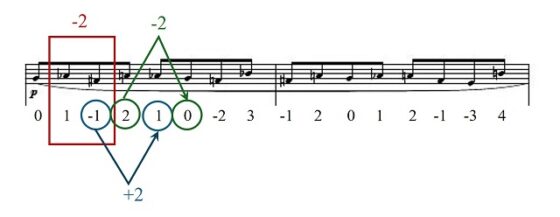
Volvemos a avanzar una posición y el segmento que nos va a determinar ahora las dos siguientes notas es el segmento -1 y 2, por lo que la variación es +3. Aplicando, como en los casos anteriores, esta variación a los dos últimos términos construidos 1 y 0, se obtienen los dos siguientes, séptimo y octavo, -2 y 3, como se puede ver en la siguiente imagen.
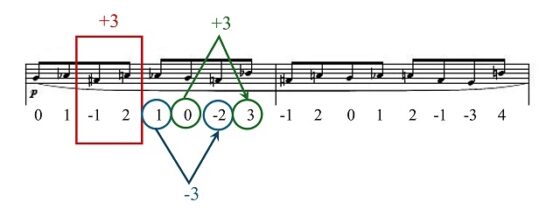
Y así se continuaría, podéis observar el siguiente paso en la siguiente imagen, en un proceso iterativo infinito que nos genera la sucesión del infinito.
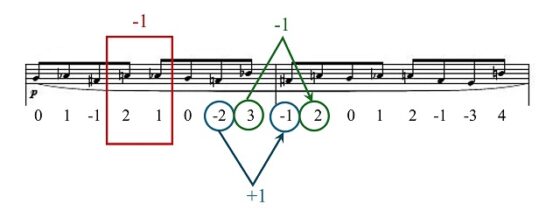
Existe otro proceso iterativo infinito para generar la sucesión del infinito denominado “desplegado”, pero que no vamos a explicar en esta entrada.
Construcción con números binariosEn la entrada Sucesiones fractales mostrábamos un ejemplo de una sucesión fractal construida a partir de la representación binaria de los números naturales (sobre la representación binaria puede leerse la mencionada entrada Sucesiones fractales, o con una explicación más extensa y detallada la entrada Las bases de numeración o cómo hacer trucos de magia binarios), incluido el 0, en concreto, la sucesión consistía en la cantidad de unos (1s) de la expresión binaria de los números enteros no negativos. Así mismo, en la entrada La sucesión fractal de Thue-Morse y la partida infinita de ajedrez se mostraba un proceso de construcción de la conocida sucesión fractal de Thue-Morse a través de las representaciones binarias de los números, en concreto, sumando los unos (1s) de la representación binaria de los números, empezando en 0, si es una cantidad par se considera el número 0 y si es impar el número 1.
También existe un método de construcción de la sucesión del infinito mediante la representación binaria de los números naturales, empezando en cero. Por lo tanto, empecemos considerando la representación binaria de los números, que mostramos en la siguiente imagen entre el 0 y el 38.
 Representación binaria de los números, desde 0 hasta 38
Representación binaria de los números, desde 0 hasta 38
Expliquemos, a continuación, cómo se construye la sucesión del infinito a partir de esas representaciones binarias. Para obtener los términos de la sucesión del infinito se realiza la “suma” de los unos (1s), pero teniendo en cuenta “cambios de signo” cuando aparecen ceros (0s) en la representación binaria, leyendo estas de izquierda a derecha. Así, para la representación 1111 (del número 15) se obtiene el término 4 (suma de los cuatro 1s); para la representación 1110 (del número 14) se obtiene -3 (suma de tres 1s, más un 0 que cambia el signo); para la representación 1101 (del número 13) se obtiene -1 (suma de dos 1s, luego 2, con el 0 se cambia el signo a -2 y luego se suma el último 1, luego -2 + 1 = -1); para 1010 (número 10), se obtiene 0 (se empieza sumando 1, que cambia de signo con el 0, a -1, se suma 1, luego 0, y el cambio de signo, del último 0, no modifica nada); o para 1001 (número 9), se obtiene 2 (primero 1, que cambia de signo con el primer 0, luego -1, que vuelve a cambiar de signo con el segundo 0, luego 1, al que se le suma el último 1, finalmente 2). Veamos ahora la tabla de dicha construcción.
 Construcción de la sucesión del infinito mediante las representaciones binarias de los números
Construcción de la sucesión del infinito mediante las representaciones binarias de los númerosSucesiones fractales
Vamos a terminar esta entrada viendo las propiedades que hicieron que la sucesión del infinito fuera importante como herramienta de creación musical para el compositor Per Nørgård, propiedades de autosemejanza. Aunque antes recordemos la definición de sucesión fractal o autosemejante.
 Doble página del libro Seeing New Music – Contemporary classical music through the eyes of a graphic designer (2015), de Denise Burt, en el que se recoge la explicación del diseño de la portada del álbum Libra (2012) de Per Nørgård
Doble página del libro Seeing New Music – Contemporary classical music through the eyes of a graphic designer (2015), de Denise Burt, en el que se recoge la explicación del diseño de la portada del álbum Libra (2012) de Per NørgårdUna sucesión (infinita) de números enteros es una sucesión fractal, también llamada sucesión autosemejante, si una parte de la sucesión es igual a toda la sucesión, es decir, si eliminamos algunos miembros de la sucesión infinita los miembros de la sucesión que quedan constituyen de nuevo toda la sucesión.
Veamos un ejemplo. Consideremos la sucesión finita de números 1, 2, 2, 3, 2, 3, 3 y construyamos la sucesión infinita que consiste en repetir la secuencia anterior de forma infinita, es decir, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, … Ahora si eliminamos de la sucesión infinita todos los números que están en posiciones pares, los que nos quedan, que son los que están en las posiciones impares, siguen siendo la sucesión original, como queda de manifiesto en la siguiente imagen.
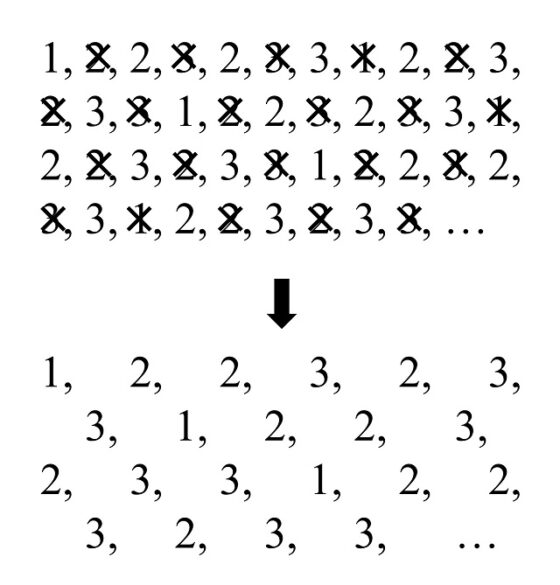
Volvamos a la sucesión inventada, o descubierta, por el compositor danés Per Nørgård. Empecemos recordando los primeros términos de la sucesión, que ya mostramos antes.
0, 1, -1, 2, 1, 0, -2, 3, -1, 2, 0, 1, 2, -1, -3, 4, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, -1, 2, 0, 1, 2, -1, -3, 4, 0, 1, -1, 2, 1, 0, -2, 3, 2, -1, -3, 4, -1, 2, 0, 1, -3, 4, 2, -1, 4, -3, -5, 6, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, 0, 1, -1, 2, 1, 0, …
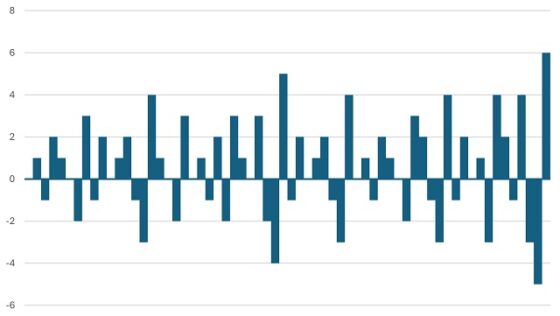 Visualización de la sucesión del infinito mediante un gráfico de barras
Visualización de la sucesión del infinito mediante un gráfico de barras
Ahora, vamos a eliminar los términos que están en posiciones pares, quedarnos con los que están en posiciones impares y veamos qué ocurre.
0, 1, -1, 2, 1, 0, -2, 3, -1, 2, 0, 1, 2, -1, -3, 4, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, -1, 2, 0, 1, 2, -1, -3, 4, 0, 1, -1, 2, 1, 0, -2, 3, 2, -1, -3, 4, -1, 2, 0, 1, -3, 4, 2, -1, 4, -3, -5, 6, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, 0, 1, -1, 2, 1, 0, …
Si nos fijamos bien en el resultado, lo que nos ha quedado es la sucesión del infinito original (0, 1, -1, 2, 1, 0, -2, 3, …) pero invertida, es decir, con el signo opuesto (0, -1, 1, -2, -1, 0, 2, -3, …). Por lo tanto, la sucesión del infinito tiene una cierta propiedad de autosemejanza, pero con inversión del signo. Esta propiedad está reflejada en la fórmula recursiva, a(2n + 1) = – a(n + 1).
Por otra parte, si eliminamos los términos que están en posiciones impares y nos quedamos con los términos de las posiciones pares, ocurre lo siguiente.
0, 1, -1, 2, 1, 0, -2, 3, -1, 2, 0, 1, 2, -1, -3, 4, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, -1, 2, 0, 1, 2, -1, -3, 4, 0, 1, -1, 2, 1, 0, -2, 3, 2, -1, -3, 4, -1, 2, 0, 1, -3, 4, 2, -1, 4, -3, -5, 6, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, 0, 1, -1, 2, 1, 0, …
De nuevo, si nos fijamos en el resultado, lo que queda es la sucesión del infinito original (0, 1, -1, 2, 1, 0, -2, 3, …) pero desplazada en una unidad, es decir, se suma 1 a cada término de la sucesión del infinito (1, 2, 0, 3, 2, 1, -1, 4, …). Otra propiedad del tipo de autosemejanza, pero con traslación de una unidad. También esta propiedad está reflejada en la fórmula recursiva, a(2n) = a(n) + 1.
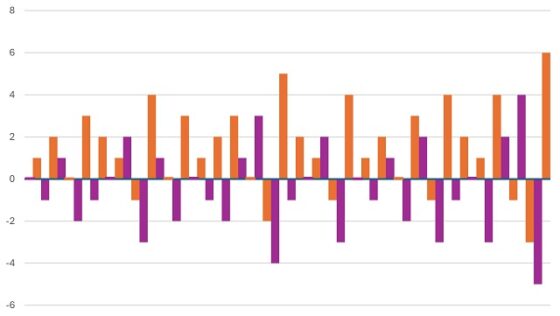 Visualización de los términos pares (naranja) e impares (ciruela) de la sucesión del infinito mediante un gráfico de barras
Visualización de los términos pares (naranja) e impares (ciruela) de la sucesión del infinito mediante un gráfico de barras
Podemos cuestionarnos si la sucesión del infinito es una sucesión fractal en sentido estricto y la respuesta es, claramente, afirmativa. De hecho, es lo que se llama una sucesión fractal de razón d = 4, es decir, el subconjunto de la sucesión que no eliminamos son el primer número de la sucesión y los que van apareciendo cada d posiciones, es decir, los números que están en las posiciones que son múltiplos de d más 1 y de esta forma obtenemos de nuevo la sucesión original. Veamos si es así para la sucesión del infinito.
0, 1, -1, 2, 1, 0, -2, 3, -1, 2, 0, 1, 2, -1, -3, 4, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, -1, 2, 0, 1, 2, -1, -3, 4, 0, 1, -1, 2, 1, 0, -2, 3, 2, -1, -3, 4, -1, 2, 0, 1, -3, 4, 2, -1, 4, -3, -5, 6, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, 0, 1, -1, 2, 1, 0, …
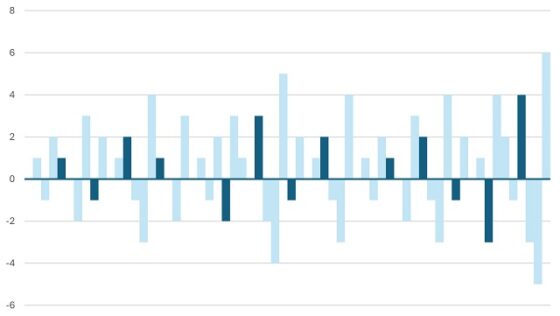 Visualización mediante un gráfico de barras de la propiedad de que la sucesión del infinito es una sucesión fractal de razón 4
Visualización mediante un gráfico de barras de la propiedad de que la sucesión del infinito es una sucesión fractal de razón 4
La propiedad de ser una sucesión fractal de razón 4 también se podía observar en la fórmula recursiva, ya que a(4n + 1) = – a(2n + 1) = a(n + 1).
La sucesión del infinito es una sucesión con muchas más propiedades matemáticas, pero en las que no vamos a entrar ahora. Simplemente terminaremos esta entrada viendo la relación que tiene con la sucesión de Thue-Morse.
La sucesión de Thue-MorseEn la entrada del Cuaderno de Cultura Científica titulada La sucesión fractal de Thue-Morse y la partida infinita de ajedrez [https://culturacientifica.com/2023/04/05/la-sucesion-fractal-de-thue-morse-y-la-partida-infinita-de-ajedrez/] presentamos la sucesión de Thue-Morse, o sucesión de Prouhet-Thue-Morse, que es una curiosa sucesión de números enteros que aparece en diferentes ramas de las matemáticas, desde la combinatoria de palabras a problemas de ajedrez, pasando por la geometría diferencial, la teoría de números, el análisis matemático de funciones, la física matemática, los cuasi-cristales o la teoría de grupos.
Los primeros términos de la sucesión de Thue-Morse (que es la sucesión A010060 en la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS) son los siguientes.
0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, …
Resulta que si consideramos la sucesión del infinito módulo 2, es decir, los números pares serán 0 y los números impares 1, entonces se obtiene la sucesión de Thue-Morse. A continuación, volvemos a mostrar los primeros términos de la sucesión del infinito, para que podáis comprobar que los números pares coinciden con los 0s de la sucesión de Thue-Morse y los impares con los 1s.
0, 1, -1, 2, 1, 0, -2, 3, -1, 2, 0, 1, 2, -1, -3, 4, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, -1, 2, 0, 1, 2, -1, -3, 4, 0, 1, -1, 2, 1, 0, -2, 3, 2, -1, -3, 4, -1, 2, 0, 1, -3, 4, 2, -1, 4, -3, -5, 6, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, 0, 1, -1, 2, 1, 0, …
 Portada, con una obra del artista Adolf Wölfli, del álbum Per Nørgård, Symphony no. 2 & Symphony no. 4, de la Aarhus Symphony Orchestra, dirigida por Jorma Panula
Portada, con una obra del artista Adolf Wölfli, del álbum Per Nørgård, Symphony no. 2 & Symphony no. 4, de la Aarhus Symphony Orchestra, dirigida por Jorma PanulaBibliografía
1.- Benoît Mandelbrot, Los objetos fractales: forma, azar y dimensión, colección Metatemas, Tusquets, 1984.
2.- Benoît Mandelbrot, La geometría fractal de la naturaleza, colección Metatemas, Tusquets, 1982.
3.- Clifford A. Pickover, La maravilla de los números, MA NON TROPPO, 2002.
4.- Tom Johnson, Self-similar Melodies, Editions 75, 2014.
5.- Tom Johnson, Rational Melodies, Editions 75, 1982.
6.- Página web del compositor Per Nørgård [http://www.pernoergaard.dk/] (enlace roto)
7.- Jørgen Mortensen, Uendelighedsrækken / La serie del infinito
8.- Yu Hin (Gary) Au, Christopher Drexler-Lemire, Jeffrey Shallit, Notes and note pairs in Nørgård’s infinity series, Journal of Mathematics and Music, vol. 11, no. 1, pp. 1-19, 2017.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo La sucesión del infinito del compositor Per Nørgård se ha escrito en Cuaderno de Cultura Científica.
El infanticidio íbero que no fue
Los bebés de la cultura íbera (VIII-I a. C.) que aparecen inhumados en contextos domésticos habrían muerto por causas naturales, como complicaciones en el parto o prematuridad, y no por prácticas rituales.
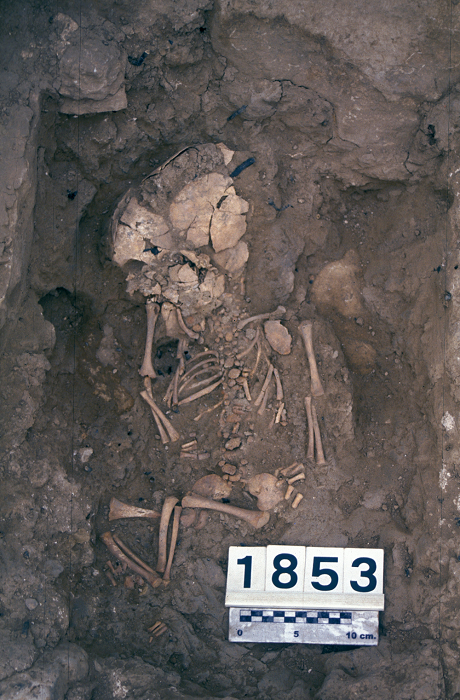 Entierro de un individuo con muerte perinatal del yacimiento de la Fortaleza de Els Vilars (Arbeca, Lleida). Fuente: ARQHISTEC-GIP, UdL
Entierro de un individuo con muerte perinatal del yacimiento de la Fortaleza de Els Vilars (Arbeca, Lleida). Fuente: ARQHISTEC-GIP, UdLLa cultura ibérica habitó las regiones costeras orientales y meridionales de la península Ibérica durante la Edad del Hierro (siglos VIII-I a. C.). El ritual funerario más común de los íberos era la cremación de los difuntos y posterior depósito de los restos en urnas que se enterraban en necrópolis. Pero los arqueólogos han descubierto también entierros con restos de recién nacidos, que no habían sido quemados, en áreas destinadas a vivienda o producción. Tres tipos de hipótesis podían explicar este hecho: que fuesen muertes por causas naturales, infanticidio o sacrificios rituales.
Un nuevo estudio aporta ahora evidencias muy precisas a favor de la hipótesis de que estos recién nacidos enterrados en contextos domésticos murieron principalmente por causas naturales y que, por lo tanto, son un reflejo de la elevada mortalidad infantil durante el primer año de vida en el mundo íbero.
Los autores han llegado a esta conclusión después de estudiar 45 esqueletos de bebés de cinco yacimientos arqueológicos de época íbera en Cataluña: Camp de les Lloses (Osona), Olèrdola (Alt Penedès), Puig de San Andreu e Illa d’en Reixac (Baix Empordà) y la Fortaleza de Els Vilars d’ Arbeca (Lleida).
 Reconstrucción digital del aspecto de la Fortaleza de Els Vilars d’ Arbeca (Lleida). Fuente: Universitat de Lleida.
Reconstrucción digital del aspecto de la Fortaleza de Els Vilars d’ Arbeca (Lleida). Fuente: Universitat de Lleida.El equipo de investigación ha aplicado una metodología innovadora, basada en el análisis histológico y elemental (tejido y composición química) de los dientes deciduos o temporales (dientes de leche) presentes en los esqueletos de los bebés. El estudio ha permitido visualizar mediante microscopia óptica las líneas de crecimiento de la corona dental que se generan al formarse los dientes durante la vida intrauterina y hasta poco después del nacimiento, e identificar así la presencia de la línea neonatal que se produce en el momento de nacer. De esta manera los investigadores han podido identificar el momento del nacimiento de los individuos y su supervivencia, así como determinar con mucha precisión la edad cronológica en el momento de la muerte. La edad cronológica se refiere al tiempo transcurrido desde el nacimiento y no el desarrollo biológico del esqueleto.
Muertes perinatales naturalesCasi la mitad de los bebés murieron durante el periodo perinatal, concretamente entre la semana 27 de gestación y la primera semana de vida. La gran mayoría de las muertes perinatales no sobrevivieron al momento del nacimiento, y muchos de estos bebés murieron a causa de nacimientos prematuros. «Estos datos refuerzan la hipótesis de que la mayoría de muertes perinatales fueron causadas por factores naturales, como complicaciones en el parto o problemas de salud asociados a la prematuridad, y no por prácticas culturales como infanticidios o sacrificios rituales, tal como algunas hipótesis habían sugerido», señala Xavier Jordana, profesor de la Unidad de Antropología Biológica del Departamento de Biología Animal, de Biología Vegetal y de Ecología de la UAB.
Los investigadores han observado también que de la veintena de bebés que sobrevivieron más allá de la primera semana de vida, el más longevo solo llegó a los 67 días. «En los yacimientos estudiados no se ha identificado ningún entierro de un bebé más allá de los dos meses de vida. Esto nos hace pensar que probablemente podría obedecer a una práctica cultural, que sería la de enterrar en los espacios domésticos a los bebés que morían en las etapas más tempranas», apunta Assumpció Malgosa, investigadora de la UAB y coautora del estudio.
Una técnica única para precisar el nacimiento y la muerteEl análisis histológico que han aplicado los investigadores es una innovación importante para calcular con mucha precisión la edad a la muerte de los individuos a partir del estudio de la corona de los dientes. Los dientes temporales se empiezan a formar durante la vida intrauterina y acaban de formarse en la etapa postnatal, alrededor del nacimiento, un periodo en el que graban su crecimiento debido a la propiedad singular de formar líneas de crecimiento. Estas líneas pueden formarse diariamente, pero también se pueden formar líneas más gruesas por un hecho puntual y estresante. Una de las líneas puntuales que se pueden visualizar con microscopia óptica en los dientes de los niños que han sobrevivido al nacimiento es la línea neonatal, que se forma por el estrés fisiológico resultante del cambio brusco de la vida intrauterina a la extrauterina.
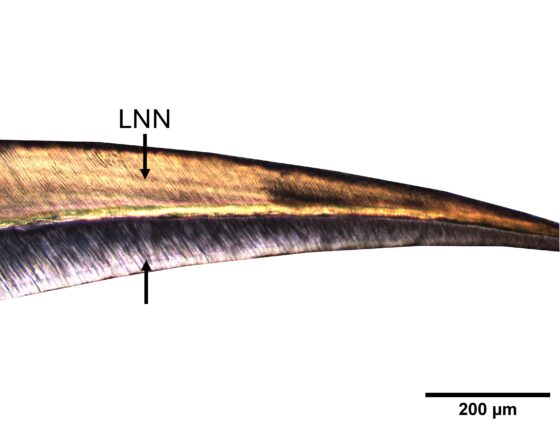 Línea neonatal en el diente incisivo central de un bebé del yacimiento de Olèrdola (Alt Penedès). Fuente: Unidad de Antropología Biológica, UAB.
Línea neonatal en el diente incisivo central de un bebé del yacimiento de Olèrdola (Alt Penedès). Fuente: Unidad de Antropología Biológica, UAB.«La técnica que hemos empleado es única, porque permite identificar el momento del nacimiento y calcular la edad cronológica en restos esqueléticos. Las técnicas convencionales estiman la edad biológica del individuo a partir del crecimiento y desarrollo esquelético, por lo que tienen una gran variabilidad en la determinación de la edad, y no permiten identificar el momento del nacimiento», señala Ani Martirosyan, investigadora predoctoral de la UAB y primera autora del artículo.
La innovación metodológica les ha permitido diferenciar los individuos que murieron en el nacimiento de los que sobrevivieron. De los que murieron al nacer, han identificado los que fueron a término (entre la semana 37 y 42 de gestación) y los que fueron prematuros (antes de la semana 37). También han podido determinar la edad cronológica de los bebés que sobrevivieron.
El papel del zinc y la luz sincrotrónLos investigadores han confirmado la precisión de su técnica en dientes actuales en los que se conoce la edad cronológica de muerte del individuo. Además, han empleado también microfluorescencia de rayos X a partir de luz sincrotrón en el Sincrotrón ALBA (Cerdanyola del Vallès), concretamente en la línea de luz Xaloc, para analizar la composición elemental a la línea neonatal, y en particular la cuantificación de zinc en los casos en los que la visualización histológica de la línea era incierta.
«El zinc es un elemento importante en el momento del nacimiento, relacionado particularmente con el inicio de la lactancia materna, pero por su bajo contenido no se pueden detectar por microscopia electrónica variaciones de concentración en el esmalte y la dentina. La luz sincrotrón nos permite aplicar un haz de rayos X de solo diez micras para analizar diferentes elementos en el esmalte y la dentina en concentraciones extremamente bajas», señala Judit Molera, investigadora de la UVic-UCC y también coautora de la investigación. Los resultados del experimento han mostrado un aumento de la cantidad de zinc y una disminución del calcio, un elemento principal del esmalte dental, coincidiendo con la presencia de la línea neonatal, lo que ha servido a los investigadores para corroborar los resultados histológicos.
«Los datos de nuestro estudio aportan información mucho más detallada y concreta que la que teníamos hasta ahora para establecer el patrón de mortalidad infantil en las poblaciones íberas y contribuyen a descifrar aspectos importantes de su historia de vida y prácticas culturales. Confiamos en que la metodología que hemos aplicado sirva para continuar desvelando otros misterios que todavía quedan por conocer en poblaciones antiguas», concluye Xavier Jordana.
Referencia:
Ani Martirosyan, Carolina Sandoval-Ávila, Javier Irurita, Judith Juanhuix, Nuria Molist, Immaculada Mestres, Montserrat Durán, Natàlia Alonso, Cristina Santos, Assumpció Malgosa, Judit Molera, Xavier Jordana (2024) Reconstructing infant mortality in Iberian Iron Age populations from tooth histology Journal of Archaeological Science doi: 10.1016/j.jas.2024.106088
Edición realizada por César Tomé López a partir de materiales suministrados por la Universitat Autònoma de Barcelona
El artículo El infanticidio íbero que no fue se ha escrito en Cuaderno de Cultura Científica.
Miranda, ¿otro mundo océano?
Miranda es uno de los satélites más misteriosos de nuestro sistema solar, quizás porque todavía sabemos muy poco sobre este -solo ha sido visitado por la Voyager 2- y su aspecto nos evoca una tortuosa historia en la que su superficie nos recuerda al cascarón de un huevo agrietado y reconstruido a partir de remiendos de su propia cáscara. Y sin una misión en el horizonte que nos permita volver a visitarlo y tomar datos más detallados, nuestra única alternativa para conocerlo un poco mejor es la reinterpretación de los datos de nuestra única visita y la confección de modelos numéricos cada vez más avanzados para explicar a lo que vemos.
Este satélite de Urano ostenta el título de ser el más pequeño de los satélites “esféricos” del planeta y uno de los más pequeños -tiene tan solo un radio de 236 kilómetros- de todo el Sistema Solar que probablemente haya alcanzado el equilibrio hidrostático. Algo a lo que probablemente haya ayudado su composición, que se estima podría superar el 60% de hielo de agua.
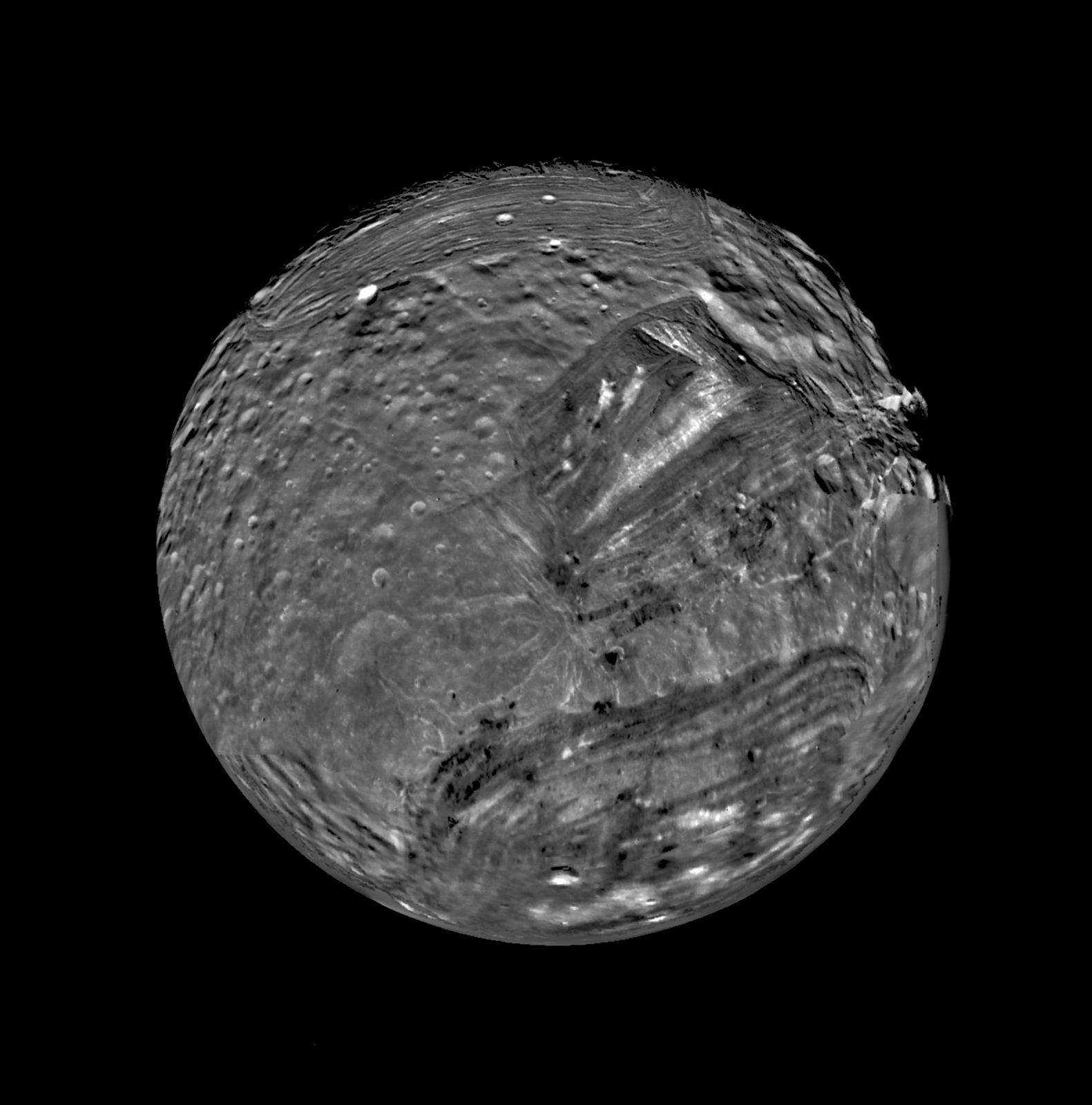 Figura 1. mosaico de imágenes de Miranda en la que podemos apreciar perfectamente la presencia de zonas más antiguas -y cubiertas de cráteres- y otras más recientes, con muchos menos cráteres, indicando procesos de rejuvenecimiento de la superficie del satélite. Cortesía de NASA/JPL/USGS.
Figura 1. mosaico de imágenes de Miranda en la que podemos apreciar perfectamente la presencia de zonas más antiguas -y cubiertas de cráteres- y otras más recientes, con muchos menos cráteres, indicando procesos de rejuvenecimiento de la superficie del satélite. Cortesía de NASA/JPL/USGS.Con toda esta cantidad de hielo de agua cabría preguntarse si Miranda podría albergar -o albergó en el pasado- un océano subterráneo, al igual que otros cuerpos de nuestro Sistema Solar exterior, a pesar de que su tamaño hace muy difícil, al menos en principio, albergar un océano capaz de aguantar sin congelarse una gran cantidad de tiempo. La primera pista de que esta puede ser una posibilidad real es que, si hacemos un esfuerzo y miramos con detalle su superficie, observaremos que hay zonas de su superficie más antiguas y más modernas, algo que reconocemos por el número y tamaño de sus cráteres, entre otras cosas de las que ahora hablaremos.
Este hecho nos indica que Miranda habría sufrido un proceso, o quizás procesos, de rejuvenecimiento activo de su superficie con la capacidad suficiente de cambiar su aspecto desde dentro y borrar o transformar los cráteres y otras formas del relieve, indicándonos la existencia de una cierta dinámica que a su vez apuntaría a la posibilidad de la presencia de un océano subterráneo como correa de transmisión de la energía interna del satélite hacia el exterior.
Aunque vamos a centrarnos en las pistas más puramente geológicas, este año, Hemingway et al. (2024) han propuesto usar las libraciones para comprobar si los satélites de Urano albergan un océano subterráneo. Las libraciones son un movimiento de oscilación y bamboleo que muestran algunos cuerpos celestes, como nuestra Luna, cuando los observamos desde un punto “fijo” como puede ser la superficie de nuestro planeta. Este fenómeno es el que nos permite, desde la Tierra, ver parte de la “cara oculta” de nuestra Luna.
Pues bien, analizando la amplitud de estas oscilaciones, podríamos conocer mejor la distribución de masas en el interior de los satélites de Urano, de tal manera que podríamos inferir detalles como, por ejemplo, si el núcleo está en estado sólido o líquido o si hay un océano subterráneo, entre otros.
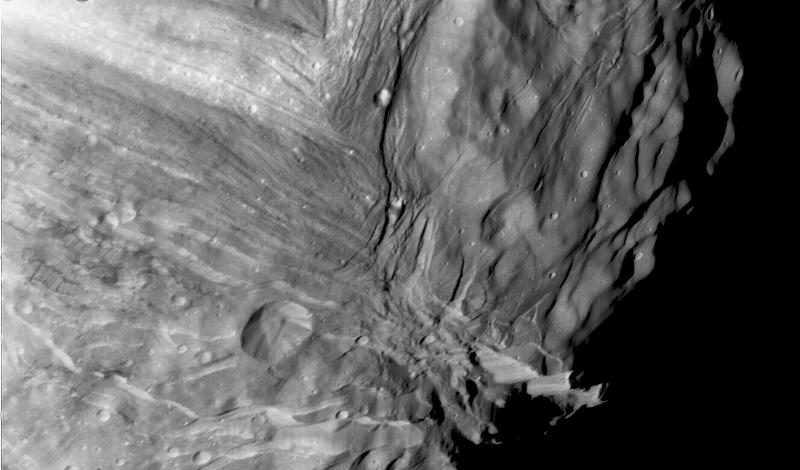 Figura 2. Detalle de la superficie de Miranda en el entorno de Verona Rupes, uno de los acantilados más altos de todo el Sistema Solar. Cortesía de NASA/JPL.
Figura 2. Detalle de la superficie de Miranda en el entorno de Verona Rupes, uno de los acantilados más altos de todo el Sistema Solar. Cortesía de NASA/JPL.En el caso de Miranda (también en el de Ariel y Umbriel), si la capa de hielo que hay por encima del océano subterráneo tiene unos 30 kilómetros de espesor o potencia, la amplitud de las libraciones en el ecuador superarían los 100 metros y cuanto más fina fuese la capa de hielo que sirve como corteza, más precisa podrá ser la detección de un posible océano.
Y cuanto menos “profundo” sea el océano, más difícil será de detectar mediante las libraciones, por lo que habría que usar también datos como las medidas del campo gravitatorio, que permitan complementar los modelos y dar una respuesta fiable a la pregunta de si hay un océano bajo el hielo de la superficie o no. Este caso sería aplicable a los satélites que tengan ya un océano en proceso de congelación. Cabe decir que tanto las libraciones como las medidas del campo gravitatorio habría que hacerlas in situ, desde el propio sistema de Urano.
Pero volvamos a las pruebas geológicas que apuntarían a la existencia de un océano subterráneo: En Miranda se han observado unas formas circulares u ovaladas sobre su superficie que conocemos como coronas -también observadas en planetas como Venus- y que son unas regiones que muestran una intensa actividad geológica marcada por sistemas de fracturas concéntricos.
En Miranda hay al menos tres de estos sistemas: Arden Corona, Inverness Corona y Elsinore Corona, identificados gracias a las imágenes tomadas en 1989 por la Voyager 2 y que muestran algunas diferencias morfológicas entre sí, aunque en el fondo podrían representar un mismo mecanismo de formación.
¿Y qué tienen que ver las coronas con los océanos subterráneos? Los científicos proponen dos posibles orígenes para estas. Por un lado, procesos diapíricos en los cuales materiales más calientes y menos densos -como un hielo a mayor temperatura que el que compone la corteza- asciende a través de la corteza, deformándola y provocando la formación de los sistemas de fracturas. La convección de las aguas dentro del océano podría facilitar este tipo de fenómenos.
Por otro lado, si el océano se congeló -o está en proceso de congelación actualmente- el aumento de volumen que sufriría tendría la capacidad de generar unos importantes esfuerzos en la corteza helada de Miranda y, de nuevo, dando lugar a los sistemas de fracturas que vemos.
 Figura 3. Detalle de la superficie de Miranda donde podemos apreciar tipos de terreno diferentes: Uno más rugoso y antiguo con cráteres en distintos grados de preseveración y otro más reciente y con menos cráteres. Cortesía de NASA/JPL.
Figura 3. Detalle de la superficie de Miranda donde podemos apreciar tipos de terreno diferentes: Uno más rugoso y antiguo con cráteres en distintos grados de preseveración y otro más reciente y con menos cráteres. Cortesía de NASA/JPL.Si echamos un vistazo al artículo publicado por Strom et al. (2024), los resultados de los modelos de estos autores sugieren que la corteza es bastante delgada, de 30 kilómetros o menos de espesor y que ha existido un océano de unos 100 kilómetros -una barbaridad, ya que supondría ocupar casi la mitad del radio del satélite- de potencia en los últimos 100 a 500 millones de años.
Y, si es un cuerpo con esta elevada proporción de hielo en su composición, ¿Cómo es posible que haya estado a una temperatura suficiente para sostener un océano de agua líquida a lo largo del tiempo geológico? Pues esto podría explicarse por las interacciones gravitatorias entre Miranda y el resto de grandes satélites, que podrían generar suficiente fricción en su interior como para elevar la temperatura y fundir parte del hielo de Miranda. Y este proceso podría haberse repetido varias veces desde la formación del Sistema Solar.
Es posible que hoy día ese mecanismo haya dejado de funcionar y el interior de Miranda esté casi totalmente congelado, aunque todavía podría quedar un pequeño océano atrapado entre la corteza y su núcleo algo que, como ocurre en estos casos, eleva mucho el interés astrobiológico de este satélite.
Pero de momento, y hasta que nuevas misiones sean capaces de llegar al sistema de Urano, tendremos que seguir esperando para conocer si Miranda – y quizás alguno de los otros satélites- alberga un océano subterráneo incluso hoy en día.
Referencias:
Hemingway, D. J., & Nimmo, F. (2024). Looking for Subsurface Oceans Within the Moons of Uranus Using Librations and Gravity. Geophysical Research Letters, 51(18), e2024GL110409. doi: 10.1029/2024GL110409
Leonard, E. J., Beddingfield, C. B., Elder, C. M., & Nordheim, T. A. (2023). Unraveling the Geologic History of Miranda’s Inverness Corona. The Planetary Science Journal, 4(12), 235. doi: 10.3847/PSJ/ad0552
Strom, C., Nordheim, T. A., Patthoff, D. A., & Fieber-Beyer, S. K. (2024). Constraining Ocean and Ice Shell Thickness on Miranda from Surface Geological Structures and Stress Modeling. The Planetary Science Journal, 5(10), 226. doi: 10.3847/PSJ/ad77d7
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Miranda, ¿otro mundo océano? se ha escrito en Cuaderno de Cultura Científica.
Una aldea global en Marte, con escala en la Luna
Colonizar nuestro satélite será el primer paso para llegar a Marte y más allá. Cultivar sus propias verduras allí arriba será una de las cosas que harán los astronautas gracias a proyectos como el español Green Moon. Pero ese no será el único reto al que tendrán que enfrentarse.
 Ilustración artística de una posible colonización futura de la Luna. / ESA
Ilustración artística de una posible colonización futura de la Luna. / ESA“Queremos convertir a la especie humana en una especie interplanetaria”, dice Jorge Pla García, investigador en el Centro de Astrobiología (CAB-INTA-CSIC). “El próximo paso es explorar Marte. La idea es usar antes la Luna como entrenamiento y aprendizaje para dar el salto a otros planetas”.
En eso está la misión Artemis, una colaboración de la NASA con la Agencia Espacia Europea (ESA), la japonesa JAXA, la canadiense CSA, la israelita ISA y la australiana ASA, que en su tercera fase propone llevar al polo sur de nuestro satélite a la primera mujer y al próximo hombre en septiembre de 2026. Su objetivo, sentar la bases para que las empresas privadas afiancen una economía lunar y hacer lo mismo en Marte a partir de 2033.
Es un objetivo arraigado en la comunidad astrocientífica, que desde hace un década acaricia el sueño de una aldea lunar global. El concepto de Moon Village, introducido en 2015 por Jan Woerner, director general de la ESA, se centra en la cooperación entre países y actores privados. “No es un único proyecto, ni un plan fijado con un calendario definido. Es una visión para una iniciativa comunitaria internacional. Su naturaleza abierta permitirá que muchas nacionalidades vayan a la luna, dejando atrás, en Tierra, sus diferencias de opiniones”, dijo Woerner.
Irresistible instinto colonizadorPero si tenemos la Tierra, que es cómoda y tiene todo lo que necesitamos, ¿por qué tanto ímpetu –y tantos recursos– en colonizar el espacio? “Queremos seguir expandiendo nuestras fronteras”, recalca Pla. Y las razones son muchas.
Por una parte, en el campo de la exploración y la investigación, “cuanto más conocemos los planetas rocosos del sistema solar, mejor conocemos el nuestro. Por ejemplo, las atmósferas de Venus o Marte parece que son similares a la de la Tierra primitiva, pero los tres se han transformado de formas muy diferentes. Entender esto nos ayuda a comprender cómo evolucionará la Tierra”, apunta Pla. En este sentido, “nuestros robots están muy limitados y no pueden hacer el mismo trabajo que hace un astronauta”, añade.
 Primera pisada del hombre en la Luna, con la misión Apolo. / NASA
Primera pisada del hombre en la Luna, con la misión Apolo. / NASAEn opinión de este experto, “dentro de dos o tres décadas, las sondas que ahora enviamos al espacio más allá de Marte podrán ir tripuladas por humanos. La experiencia nos dice que la ciencia ficción termina convirtiéndose en realidad”.
Por otro lado, está el poderoso tema económico, que mueve montañas y cohetes: “la Luna, Marte, los asteroides y los cometas son fuente de recursos muy valiosos para nuestro avance como sociedad. Poseen metales preciosos, minerales de tierras raras que son escasos en la Tierra”, indica Pla. Nuestro satélite, sin ir más lejos, es rico en helio-3, un isótopo de este elemento que se forma cuando el Sol interacciona con el suelo lunar –algo que no pasa en la Tierra porque nuestra atmósfera actúa como escudo–. Y resulta que el helio 3 que campa por toneladas sobre la superficie de la Luna, promete ser un supercombustible: su reacción en centrales de fusión produciría grandes cantidades de energía; encima, sin emitir radiaciones peligrosas.
“Estos elementos críticos se podrían extraer y traer a la Tierra o empezar a emplearse in situ, en el espacio”, observa este investigador, a quien no le cuesta visualizar asentamientos humanos fuera de nuestro planeta, con sus propias necesidades energéticas y tecnológicas.
Otra necesidad básica de los intrépidos colonos espaciales será comer. No solo los alimentos disecados y empaquetados que vemos en las películas, sino también una ensalada de lechuga recién cortada y cultivada en un huerto extraterrestre. Es la idea que inspira el proyecto español Green Moon, formado en 2016 por tres estudiantes malagueños y hoy integrado por científicos de los campos de la ingeniería espacial, la geología planetaria y la biología vegetal. Algunos de ellos, como Pla, su coordinador técnico y científico, ya han participado en varias misiones de la NASA.
Invernaderos extraterrestresPor el momento, la única planta que ha conseguido crecer en un cuerpo celeste distinto al nuestro es una especie de algodón que germinó en la Luna, como parte de la misión china Chang´e 4, en 2019. “Estaba dentro de una microsfera, pero el instrumento no realizó bien el control térmico y el brote murió en 24 horas. La idea era buena, pero pretenciosa. Proponían que la planta generara el oxígeno que consumían unas larvas de mosca y, a cambio, los desechos producidos por estas proveerían del CO2 a la planta”, nos comenta Pla.
En la cápsula-huerto diseñada por los investigadores de Green Moon, las plantitas estarían a salvo de las inclemencias del tiempo. Han probado diferentes productos hortofrutícolas, “de porte pequeño y ciclos cortos, que germinan en 24-72 horas desde que se humedece la semilla, para ver cuáles pueden germinar en esas condiciones extraterrestres”, explica a SINC Eva Sánchez, coordinadora biológica del proyecto. Entre ellas, distintas variedades de lechugas, pimiento, tomate, rábano o zanahoria.
 Experimento con plantas sobre un simulante del suelo lunar, con condiciones ambientales controladas en la cápsula Green Moon. / Green Moon Project
Experimento con plantas sobre un simulante del suelo lunar, con condiciones ambientales controladas en la cápsula Green Moon. / Green Moon ProjectSalvando las distancias, será como un invernadero. Tendrá regulada la luz que recibe, el suministro de agua y el rango de temperatura (constante entre 15ºC y 28ºC) y estará protegida de las radiaciones solares y cósmicas. La electricidad para mantener en funcionamiento todos esos procesos la lleva incorporada. “Nuestra cápsula es muy adaptable. Se puede incluir en cualquier tipo de misión y, aunque es autosuficiente porque incluye sus propios paneles solares, puede aprovechar cualquier tipo de de fuente de energía”, apunta Pla.
Una cuestión de sueloPor si el reto fuera pequeño, las plantas de Green Moon también tendrán que sobrevivir en el suelo de la Luna, cuya tierra arenosa y estéril recibe el nombre de regolito. Para ensayar, el equipo buscó un suelo parecido a la muestra que trajo a la misión Apolo 14. Lo encontraron en Lanzarote: procesando restos volcánicos, han elaborado un ‘simulante lunar’, que coincide en un 99,5% con el suelo de nuestro satélite.
“Por su composición, tiene unas características muy complicadas para que crezca cualquier planta. Posee gran cantidad de metales pesados y apenas nada de nitrógeno y fósforo, indispensables para la vegetación”, nos explica Eva Sánchez, que también es directora y fundadora, desde hace nueve años, de la empresa granadina de investigación agrícola Innoplant.
Es aquí donde entran en juego ciertas bacterias de suelo extremófilas, capacitadas para sobrevivir en condiciones muy hostiles. Algunas, por ejemplo, fueron aisladas del suelo de las minas de Riotinto, en Huelva. “Colaboramos para eso con la empresa española de fertilizantes Herogra, que nos ha suministrado los microorganismos. Los hemos probado de forma individual y combinados, para ver cómo podían fertilizar la tierra. De la batería inicial de 20 cepas candidatas, hemos detectado tres que, cuando se ponen juntas, tienen un efecto positivo. A través de su metabolismo, digieren esos metales pesados y generan nitrógeno y fósforo”, explica Sánchez.
La siguiente fase sería aportar materia orgánica al suelo, que funcione como una especie de estiércol. “Queremos usar algo que esté presente en las bases lunares. Para eso, tenemos que hacer un estudio sobre las características de los residuos que encontraremos allí”, observa. Además, partiendo de la misma idea de los chinos con sus brotes de algodón, se podría lograr, por qué no, un aprovechamiento circular de los gases vitales para las plantas y los humanos, de forma que el oxígeno que desprenden las primeras en la fotosíntesis fuera desviado a la microatmósfera donde vivan las personas y, al revés, el CO2 que exhalan los astronautas sirviera de sustento a las plantas.
¿Y de dónde van a sacar el agua para regarlas? El proyecto plantea un sistema de hidroponía para necesitar cantidades mínimas. Además, “la propia planta, por su transpiración, permite hacer un mecanismo cerrado de agua, que se puede reaprovechar. Del agua que se aporta a un vegetal, el 95 % lo pierde o lo transpira a la atmósfera”, afirma esta científica.
Otro detalle con el que tendrán que enfrentarse las lechugas y las zanahorias será la microgravedad de la Luna, que es un sexto de la que tenemos en la Tierra. ¿Cómo alterará su metabolismo? Para dar una respuesta, los científicos tienen que simular esas mismas condiciones, algo que puede hacerse con los vuelos parabólicos, cuando sobrepasan las capas altas de la atmósfera. “Lo malo es que es en un tiempo muy corto y son muy caros: uno puede costar 40.000”, nos dice Sánchez. Luego están los ciclostatos, unos aparatos que reproducen la microgravedad. “Necesitamos llegar a un acuerdo con alguno de los centros privados que los tienen para meter ahí dentro las plantitas y ver cómo crecen”.
Por lo pronto, los investigadores tienen sus propias hipótesis y ya hay algo de literatura científica al respecto, con algunos experimentos que se han hecho con una especie no hortícola muy versátil, la Arabidiopsis thaliana. “Creemos que van a crecer más alto, porque no hay gravedad que las retenga. Y más rápido, porque es lo que pasa en situaciones de estrés. Si la lechuga tiene un ciclo de 45 días, igual crece en 28. A nivel metabolico, en cuanto a su sabor color, nutrientes… también cambiarán, aunque no sabemos cómo. Eso es lo que queremos estudiar”, señala.
También aprovechable en la TierraPara Eva Sánchez, los beneficios de implementar cápsulas como la que están desarrollando en Green Moon van más allá del cultivo de hortalizas en la Luna o en Marte. Su invento se podría utilizar para cultivar en zonas extremas donde apenas hay agua, como los desiertos. De igual manera, la misma combinación de bacterias fertilizantes sería una opción interesante para tratar suelos que han sufrido una erupción volcánica, como La Palma. “Se acortaría mucho el tiempo de regeneración”, apunta.
Para pasar de ser un modelo digital en 3D a una realidad, por el momento, lo único que le falta a la cápsula de Green Moon es financiación. En concreto, nada menos que un millón de euros. “La construcción sería por parte de empresas privadas especializadas en instrumentación espacial”.
Buen viaje a MarteCuando el ser humano esté preparado para la aventura de pisar el planeta rojo, tendrá que aprovechar una ventana óptima de lanzamiento que, según Pla, ocurre cada dos años. Será, además, una travesía de casi dos años, si contamos la ida y la vuelta. Los retos más acuciantes serán la radiación procedente del Sol –“habrá que apantallar bien y protegerse con escudos, como el agua o la vegetación”, dice Pla– y la radiación cósmica que proviene de protones cargados energéticamente, expelidos por la muerte de estrellas. “La probabilidad de contraer cáncer debido a esta radiación obliga a reducir el tiempo de las misiones. La solución que tenemos por ahora es la protección pasiva”, añade. Sin embargo, la ciencia no deja de investigar. Por ejemplo, “hemos descubierto que, cuanto mayor es la edad del astronauta, menos es su posibilidad de desarrollar tumores”.
 Esquema del proyecto Green Moon para cultivar plantas en la Luna y planetas fuera de la Tierra. / J.M. Ortega et al / Resources, Environment and Sustainability
Esquema del proyecto Green Moon para cultivar plantas en la Luna y planetas fuera de la Tierra. / J.M. Ortega et al / Resources, Environment and SustainabilitySon escollos que afectarán a las personas, pero también a las plantas. En este sentido, en el invernadero del Centro de Astrobiología (CAB-CSIC), un equipo liderado por el biólogo molecular Eduardo González Pastor está estudiando cómo modificar genéticamente la Arabidiopsis thaliana con genes de microorganismos resistentes a las radiaciones. Por el momento, se está probando su efectividad en simuladores de radiación espacial y de microgravedad, con resultados muy prometedores. Es algo que, en opinión de Pla, quizá podría algún día hacerse con los astronautas.
Mientras, lo que ya se está haciendo es la medición y evaluación del clima marciano, una fase previa importante porque, cuanto mejor conozcamos el entorno al que pensamos enviar humanos en el futuro, mejor podrán minimizarse los riesgos. “El Centro de Astrobiología es líder en meteorología planetaria”, recalca Pla. Y es que, en la actualidad, las únicas estaciones meteorológicas que hay en suelo del planeta rojo, REMS y MEDA, son españolas.
“Nos sirven para entender las temperaturas de Marte, la presión, la humedad atmosférica, la radiación que llega al suelo… Y, sobre todo, para estudiar el actor principal de su atmósfera, el polvo, que tiene un papel clave en los cambios de sus condiciones meteorológicas. Además, es un polvo fino y tóxico, que puede penetrar en los instrumentos y estropearlos, o enfermar a los astronautas”, apunta.
Llegar hasta allí será, sin duda, una epopeya con lucha contra los elementos incluida. Aunque Pla insiste en que, tal vez, la prueba más difícil será la psicológica. “Al final, de una forma u otra puedes generar oxígeno, alimentarte, protegerte de la radiación… pero pasar tanto tiempo en soledad en el espacio es algo a lo que los astronautas les cuesta acostumbrarse”.
El espacio no es un plan BEn opinión de este astrobiólogo, el motivo que subyace a todas estas aventuras conquistadoras del espacio no es encontrar un nuevo hogar para salvarnos de un cataclismo inevitable en el nuestro. “Marte no es un plan B”, recalca. “Hay que proteger lo que tenemos y, al mismo tiempo, seguir explorando”.
No seremos nosotros quienes terminemos con la Tierra, dice, que “estará aquí hasta que el Sol se inflé y acabe engulléndola, dentro de por lo menos 5.000 millones de años. Lo que sí puede pasar si seguimos así, aumentando la temperatura, es que muchas especies desaparezcan. Pero la edad de nuestro planeta será más larga que la de nuestra especie, a no ser que nos convirtamos en una especie interplanetaria”.
¿Y después de Marte? El próximo escalón son las lunas heladas de Júpiter y Saturno: Europa, Encelado, Titán. “Desde el punto de vista biológico, las probabilidades de encontrar actividad biológica allí son mucho más altas que en Marte, que es una roca estéril flotando en el sistema solar en comparación”, apunta. Y es que los satélites de Júpiter tienen agua líquida en sus océanos internos, bajo una gruesa capa de hielo. Además, es agua en movimiento, que tiene actividad, como demuestran los géiseres que fueron captados por primera vez en Europa, en 2013, por el telescopio espacial Hubble.
Y el agua, como sabemos, es un ingrediente fundamental para la vida –aunque no el único–. Por el momento, están a punto de despegar varias misiones no tripuladas: Europa Clipper de la NASA este mes de octubre, Dragon Fly, también de la NASA, partirá hacia Titán en julio de 2028 y la misión Juice de la ESA planea llegar a Júpiter en 2031 para explorar Ganímedes, Calisto y Europa…
Según Pla, es solo el inicio. “Conociendo su capacidad de progreso, el ser humano también llegará hasta allí en persona, seguro. Hemos conseguido explorar todos los rincones del planeta, desde el Polo Norte al Polo Sur, pasando por las Américas y todas las islas de los océanos. No solo se trata de crear nuevas vías comerciales, sino de conocer nuestro entorno mejor”.
Por ahora, como señala Eva Sánchez, antes de soñar con Marte y más allá, “tenemos que pisar bien la Luna, que ya es mucho”.
Sobre la autora: Laura G. De Rivera es periodista especializada en ciencia
Una versión de este artículo apreció originalmente en SINC el 1 de noviembre de 2024
El artículo Una aldea global en Marte, con escala en la Luna se ha escrito en Cuaderno de Cultura Científica.

