Feed aggregator

Soy más de turrón blando que de turrón duro. Aunque reconozco que con un pedazo tengo más que suficiente, incluso si es de calidad suprema. Realmente no hay grandes diferencias entre uno y otro, ni nutricionales ni de fabricación.

El turrón de Jijona y el turrón de Alicante tienen denominación de origen. Cuando no la tienen se llaman turrón blando y turrón duro respectivamente. Ambos están compuestos exclusivamente por almendras tostadas, miel, azúcar y clara de huevo. Las calidades varían en función de la cantidad de almendra. Así, la calidad suprema contiene un 60% de almendra, la calidad extra un 50%, la calidad estándar un 40% y la calidad popular un 30%.

• El valor nutricional del turrón

Ambos turrones son ricos en proteínas de alto valor biológico, provenientes del huevo y de las almendras: contienen 7 de los 9 aminoácidos esenciales. También son ricos en ácido fólico y en vitamina E.

Estos turrones contienen mucha grasa: alrededor de 30 g por cada 100 g de turrón. Pero, como la grasa proviene exclusivamente de la almendra, tiene un buen perfil lipídico. Sólo entre 2 y 3 g son grasas saturadas, naturalmente presentes en las almendras. Contiene ácidos grasos insaturados que también encontramos en el aceite de oliva, como el ácido linoleico y linolénico.

La cantidad de azúcar oscila entre los 40 y los 50 g por cada 100g de turrón, por lo que nutricionalmente son alimentos superfluos. Cualquier bondad que pudiésemos atribuir a las almendras queda ensombrecida por el elevado contenido en azúcar que poseen. A estas alturas nadie duda de que los turrones son alimentos que consumimos sólo por placer, nunca por cuestión de salud.

• La ciencia de la fabricación del turrón

El primer paso para fabricar ambos turrones consiste en tostar las almendras. Esto se hace en hornos rotatorios esféricos durante 45-50 min. Cuando se tuestan las almendras se generan más de 50 compuestos diferentes, entre ellos cetonas, aldehídos, pirazinas, alcoholes, hidrocarburos aromáticos, furanos, pirroles, terpenos e hidrocarburos lineales. Las pirazinas, junto con los furanos y los pirroles, contribuyen significativamente al característico aroma tostado de la almendra. Los procesos químicos que suceden son muy complejos, tanto es así que todavía no se han determinado todos los compuestos volátiles que se producen durante el tueste.

Aparte se prepara el caramelo en una malaxadora, que es como una olla con una pala mezcladora. El caramelo se hace con miel, azúcar y agua. Los turrones de más calidad contienen más miel que azúcar. La mezcla se hace en caliente para aumentar la miscibilidad del azúcar y favorecer las reacciones de caramelización.

La caramelización es un proceso químico complejo mediante el cual se produce la oxidación de los azúcares, la fragmentación de la sacarosa, la condensación y deshidratación de los azúcares, etc. dando como resultado el sabor acaramelado, el color dorado y la formación de varios compuestos volátiles que dan ese olor característico a caramelo caliente. La caramelización sucede en el azúcar y en la miel. No olvidemos que la miel es 80% azúcar.

Cuando la mezcla de la miel y el azúcar es homogénea, se añade la clara de huevo. La clara de huevo tiene varias funciones: blanquea el caramelo, le da textura y volumen, aglutina todos los ingredientes del turrón y evita que se formen cristales de azúcar.

La clara del huevo es traslúcida, sin embargo, cuando la calentamos o la agitamos, las proteínas pierden el orden interno y se convierten en un entramado amorfo. A esto se le llama desnaturalización. Cuando esto sucede, ni siquiera la luz es capaz de atravesar ese caos proteico y por eso se vuelve de color blanco. Si seguimos batiendo, esas proteínas desnaturalizadas comienzan a coagular, a formar agregados de proteínas con una nueva estructura que es capaz de almacenar aire en su interior. Esto es lo que da textura y volumen al caramelo.

La clara de huevo funciona como aglutinante. Esto quiere decir que funciona como un pegamento, haciendo que los diferentes ingredientes se adhieran entre sí. También por esto es anticristalizante, es decir que, aunque haya alta concentración de azúcar, evita que éste forme cristales cuando la mezcla se enfríe.

Esta mezcla se sigue agitando hasta que alcanza el «punto de melero» o «punto de garguirol». Esto significa que cuando coges una pequeña porción de mezcla, ésta se solidifica en segundos y se rompe con un leve golpe; y al morderla se resquebraja sin pegarse a los dientes.

Cuando esta mezcla está en su punto, se le añade la almendra tostada y se mezcla bien con unas palas.

Tras este último paso, el turrón de Alicante y el de Jijona toman caminos diferentes. Por una parte, el turrón de Alicante se divide en bloques, se introduce en moldes cubiertos de oblea para que no se pegue y se prensa a mano hasta que queda con el menor número de imperfecciones. Finalmente, se cortan los bloques en tabletas y se envasan para su distribución.

Para el turrón de Jijona, la pasta caliente formada por las almendras y el caramelo se extiende sobre bandejas y se deja enfriar hasta que endurece. Estas placas se introducen en un molino de piedra, generalmente junto a más cantidad de almendras tostadas ya molidas. Todo esto se muele finamente y se bate hasta que quede una pasta homogénea, sin granos apreciables a simple vista.

Esta mezcla se lleva al boixet. El boixet es como un gran mortero caliente automatizado que permite alcanzar la cremosidad óptima. Una vez alcanzada, la pasta se vierte en unos moldes y se deja reposar durante 24 horas. Estos moldes son porosos, de forma que durante ese tiempo el turrón va exudando parte del aceite de las almendras. Una vez terminado este proceso, se desmolda, se corta en tabletas y se envasa.

Tanto el turrón de Jijona como el de Alicante, a menudo se envasan al vacío para que duren al menos un año.

• Sí, sí, el turrón caduca

La vida útil del turrón depende sobre todo de la variedad. Según la calidad del envasado, rondará los 12-18 meses tras su fabricación. El turrón de Jijona dura más que el de Alicante, porque el aceite de la almendra impregna toda la tableta y favorece su conservación. Mas allá de la fecha de caducidad podría ser peligroso consumirlo, principalmente porque la grasa se enrancia.

• Vuelve a casa, vuelve por Navidad

Lo interesante del turrón es su valor gastronómico, cultural y tradicional. Como cualquier alimento propio de una época del año, tiene ese algo de ritual que nos conquista y que lo convierten en parte fundamental de la ceremonia de estas fiestas.

La ciencia que hay tras él también nos hace entender gran parte de su atractivo culinario. Aun así, el turrón es un dulce altamente calórico y atiborrado de azúcar y, como tal, ningún nutricionista te recomendará consumirlo a lo largo de todo el año ni lo incluiría dentro de una dieta saludable.

Así que, tanto por conservar lo especial del ritual gastronómico navideño, como por salud, si el turrón vuelve a casa, que sólo vuelva por Navidad.

Sobre la autora: Déborah García Bello es química y divulgadora científica

El artículo El buen turrón tiene su ciencia se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El mejor lacón con grelos tiene su ciencia
2. La pantalla de tu móvil solo tiene tres colores
3. Azúcar moreno, ¿mejor que el azúcar blanco?

Juan Ignacio Pérez eta Miren Bego Urrutia Defentsak eta erasoak

———————————————————————————————————–

«Hiru lagun hil ziren atzo, muskulu-paralisi orokorraren ondorioz. Etxean “fugu” plater bat jan ondoren gertatu zen ezbeharra».

Hori bezalako prentsa titularra askotan irakur daiteke Japoniako egunkarietan. Ez dira gutxi (100 eta 200 artean zenbait neurketa kontserbadoreren arabera) urtero elikatze-intoxikazio bitxi baten ondorioz hiltzen diren japoniarrak.

1. irudia: Puxika arraina jateagatik 100-200 pertsona hitzen dira urtero Japonian.

Intoxikazioa sortzen duen janaria ez dago egoera txarrean, eta ez dagokio marea gorrien moduko gertaera bati. Hau desberdina da; errua ez da janari ustelduarena ez eta mikroalga pozoitsu batena ere. Intoxikazioaren errua arrain bitxi bat da, Europan puxika-arraina izenaz ezagutzen dugun arraina, eta japoniarrek fugu deitzen dutena hain justu.

Puxika-arrainaren toxizitatea ekialdeko herrietan betidanik ezagutu badute ere, James Cook kapitain britainiarrak eman zuen lehen erreferentzietako bat Mendebaldeko jendearentzat, 1744an. Kaledonia Berrian ainguratua zegoelarik, puxika-arrain bat eraman zuten itsasontzira eta eskifaiako naturalistari eman zioten aztertu eta deskriba zezan. Hainbeste denbora eman zuen arraina aztertzen, ezin izan baitzuten arrain osoa afari baterako prestatu; baina gibelaren zati txiki bat geratu zitzaien. Cookek, gibela jateagatik gertatu zitzaiena idatzi zuen:

About three to four o’clock in the morning we were seized with most extraordinary weakness in all our limbs attended with numbness of sensation… We each took a vomit and after that a sweat gave great relief. In the morning one of the pigs which had eaten the entrails was found dead.

«Goizeko hirurak edo laurak aldera, ahulezia ikaragarri batek harrapatu gintuen, gorputz-adar guztiak ahuldu zizkiguna… Goitik botaka hasi ginen denak, eta horren ondoren, izerdi hotz batek arintze ederra eman zigun. Egunsentian, erraiak jan zituen txerrietako bat hilik aurkitu zuten.»

Egoera normalean, puxika-arrainak ez du itxura berezirik, baina mehatxupean dagoenean puztu egiten da eta itxura esferikoa hartzen. Handiagoa dela dirudi, eta horrela beldurtu nahi ditu hurbiltzen zaizkion harrapariak. Horregatik du izen hori, puxika baten antza hartzen duelako.

2. irudia: ‘Arothron meleagris‘ puxika arraina.

Baina hori ez da puxika-arrainak duen defentsarako jokabide edo modu bakarra. Izan ere, ezusteko galantarekin topa daitezke puxika-arrainaren itxuragatik beldurtu ez diren animaliak. Halaxe da, bai, zeren ehunetan daukan toxina batek muskulu-paralisia eragiten baitio zorigaiztoko harrapariari: hil egiten du, izan ere. Toxina hiltzaile horrek tetrodotoxina (TTX) izena du eta gizakietan heriotza dakar intoxikazio-sintomak agertzen diren kasu guztien %60an.

Baina, nola liteke horren arriskutsua den arraina jatea? Edonork egiten du galdera hori. Eta erantzuna bistakoa da: japoniarrentzat puxika-arraina oso gozoa da, dagoen janaririk preziatuena seguru asko ere. Urtero 10.000 tona saltzen dira Japonian, eta janaririk garestienetakoa da. Horren arriskutsua da puxika-arraina jatea, non Japoniako historiaren zenbait alditan debekaturik egon baita; halaxe gertatu zen Erdi Aroan, Tokugawa Shogun aldian, bai eta Meiji aldian (1868-1912) ere. Eta gaur hertsiki arautua dago puxika-arrainaren kontsumoa; baimen berezia duten 1.500 jatetxetan bakarrik jan daiteke, eta jatetxe horietan prestakuntza berezia duten sukaldari batzuek prestatu behar dute. Prestatu ahal izateko baimena lortzeko, proba bat gainditu behar dute sukaldariek, baina proba egitera aurkezten direnen % 25ek baino ez du gainditzen. Oso zaila da, beraz, puxika-arraina prestatu ahal izateko baimena lortzea.

3. irudia: Fugu sashimi platerra.

Jatetxeetan sukaldari gaituek prestatzen dute, baina Japonian kontsumitzen den puxika-arrainaren zati handi bat herritarren etxeetan kontsumitzen da, eta herritarrak eurak dira arraina prestatzen dutenak. Gainera, hainbat jatetxetan bezero “bereziei” debekaturiko organoak ere prestatu eta zerbitzatzen dizkiete. “Japoniako Altxorra” izeneko tituluaren jabea zen Mitsugoro Bando VIII aktore ospetsua hil egin zen 1975ean puxika-arrainaren lau platerkada gibel jan ondoren. Zeresanik ez dago gibela zerbitzatzea guztiz galarazita dagoela, tetrodotoxinaren kontzentrazioa oso altua baita organo horretan. Izatez, gibela, emearen gonada eta larruazala dira toxinaren kontzentrazio altuenak dituzten organoak.

Tetrodotoxinak nerbio-sisteman du eragina, neuronak nerbio-bulkada hedatzeko ezgaitzen baititu. Zelulen mintza elektrikoki polarizatuta dago, karga elektrikoa duten ioi jakin batzuen kontzentrazioak desberdinak direlako kanpoko eta barneko aldeetan. Bada, neuronaren punta batetik bestera hedatzen den polaritate horren aldaketa da nerbio-bulkada, eta mintzean zehar gertatzen diren sodio- eta potasio-mugimenduek sortzen dute aldaketa hori. Sodio- eta potasio-ioiak kanalen bitartez igaro daitezke mintzaren alde batetik bestera. Eta hortxe du tetrodotoxinak eragina, sodio-kanala blokeatuz, ioi horren mugimendua ezintzen baitu. Ioi-mugimendurik gabe ezin daiteke mintzaren polaritate elektrikoa aldatu eta, beraz, nerbio-bulkada gelditu egiten da.

Dirudienez, arrainaren ehunetan bizi diren bakterio sinbiontikoek sortzen dute tetrodotoxina; hau da, ez dute arrainaren ehunek ekoizten. Eta, noski, toxinak ez du inolako eraginik puxika-arrainaren neuronetan, neurona horien sodio-kanalak ez baitira blokeatzen tetrodotoxinaren eraginez.

Fugu wa kuitashii, inochi wa oshishii «fugu jan nahi dut, baina ez dut hil nahi»: abesti japoniar zahar baten hitzak dira. Ondo dakite japoniarrek fugua jatea zein arriskutsua den, baina, seguru asko, japoniar gehienek ez dakite zein garrantzitsua izan den tetrodotoxina neurozientzien alorrean. Bestelako teknikekin batera, tetrodotoxinaren erabilerari esker dakigu nerbio-bulkadaren oinarriei buruz dakigunaren zati esanguratsu bat. Izan ere, kanal jakin batzuk blokeatzen dituzten toxinak erabiliz aztertu ahal izan dira mintzean zehar gertatzen diren ioi-mugimenduak eta ioi-mugimendu horien ondorioz gertatzen diren polaritate-aldaketak. Beraz, neurozientziek aurrera egin dute eragin hilgarria duen gai toxiko natural bati esker. Eta denok dakigu zein garrantzitsuak diren neurozientziei buruzko jakintzak giza osasun eta ongizaterako. Zelako paradoxa!

—————————————————–

Egileez: Juan Ignacio Pérez Iglesias (@Uhandrea) eta Miren Bego Urrutia Biologian doktoreak dira eta UPV/EHUko Animalien Fisiologiako irakasleak.

—————————————————–

Artikulua UPV/EHUren ZIO (Zientzia irakurle ororentzat) bildumako Animalien aferak liburutik jaso du.

The post ‘Fugu wa kuitashii, inochi wa oshishii’ appeared first on Zientzia Kaiera.

Según cuenta la leyenda, mientras Alejandro Magno (356 – 323 a.c.), rey de Macedonia y de los griegos, se encontraba conquistando el Imperio Persa, llegó a Gordion, capital del reino de Frigia, que formaba parte del Imperio Persa. El nombre de la capital se debía a su rey Gordio (padre del rey Midas, el que transformaba en oro todo lo que tocaba). Parece ser que en el templo de Zeus, situado en la acrópolis de Gordion, se encontraba un carro que estaba atado a un yugo mediante un complicadísimo nudo. Según las creencias de Frigia, un antiguo oráculo estableció que aquel que consiguiese deshacer el nudo se convertiría en el Rey de Frigia, y se le abrirían las puertas de toda Asia.

Alejandro Magno se vio atraído por la leyenda e intentó beneficiarse de las creencias locales desatando el nudo gordiano, sin embargo, este era muy intrincado y se le resistía. Por este motivo, el general mecedonio tomó una solución radical, sacó su espada y con ella cortó el nudo. Se cuenta que esa noche hubo una gran tormenta de rayos, lo que se interpretó como que el propio dios Zeus estaba de acuerdo con aquella solución, y Alejandro afirmó que “¡Es lo mismo cortarlo que desatarlo!” Por cierto, en once años Alejandro Magno conquistó todo el oriente… su imperio se extendió desde Grecia y Egipto hasta el valle del rio Indo.

“Alejandro cortando el nudo gordiano”, de Jean-Simon Berthélemy (1743–1811). Wikimedia

El lema de Fernando el Católico “Tanto monta” hace referencia a esta leyenda, “lo mismo da [tanto monta] cortarlo que desatarlo”, por eso está asociado a un yugo y a un nudo cortado, que aparecerán después en el escudo, junto a las flechas.

Yugo y nudo gordiano cortado, con el lema “tanto monta”, como emblema de Fernando II de Aragón en la techumbre de una de las estancias del palacio de los Reyes Católicos de la Aljafería de Zaragoza, 1488-1492. Wikimedia

La expresión “nudo gordiano” acabó incorporándose al lenguaje ordinario como una metáfora de un problema irresoluble, deshacer un nudo “imposible”, y que en ocasiones puede superarse cambiando el marco de pensamiento. En consecuencia, esta expresión también aparece reflejada en la literatura. Un ejemplo es La vida de Enrique V (1600), de William Shakespeare. Hablando Canterbury del rey dirá…

“CANTERBURY:

Basta oírlo razonar en teología para que,

lleno de admiración, uno desee en lo profundo

que el rey se convierta en prelado;

basta oírlo discutir asuntos de bien común

para afirmar que nunca estudió otra cosa;

escucharlo hablar de guerra es como oír

una batalla temible vuelta música;

si pasa a cualquier cuestión política,

desatará el nudo gordiano con tanta facilidad

como su jarretera: porque cuando habla,

el aire, ese libertino leve, permanece inmóvil,

y el mudo asombro acecha en los oídos de los hombres

para captar sus frases dulces e impregnadas de miel…”

O también se menciona en un par de ocasiones en Segunda parte del ingenioso caballero don Quijote de la Mancha (1615), de Miguel de Cervantes.

Portada del disco “Gordian Knot” (1999) del grupo de rock progresivo del mismo nombre

En mi anterior entrada del Cuaderno de Cultura Científica, La artista Anni Albers, The Walking Dead y la teoría de nudos, habíamos explicado qué es la teoría de nudos y que su principal problema es la clasificación topológica de los nudos, el cual incluye el problema de reconocimiento, es decir, determinar cuándo dos nudos son equivalentes (iguales desde el punto de vista topológico), para lo cual se introducen diferentes invariantes de los nudos.

Recordemos que los invariantes son objetos (por ejemplo, un número, un polinomio o un grupo algebraico) o propiedades (como la tricoloreabilidad) de un nudo, que tienen el mismo valor para todos los nudos equivalentes. En consecuencia, si un invariante es distinto para dos nudos, estos no pueden ser equivalentes. En la entrada La artista Anni Albers, The Walking Dead y la teoría de nudos se vieron algunos ejemplos de invariantes de los nudos, como la quiralidad, la tricoloreabilidad y el número mínimo de cruces.

En esta entrada de la sección Matemoción Cuaderno de Cultura Científica se van a analizar otros dos invariantes de la teoría de nudos, el número gordiano y el índice poligonal. El primero tiene que ver con la historia del nudo gordiano que acabamos de contar. El “número gordiano de un nudo” es el mínimo número de cruces que hay que cambiar en un nudo para deshacerlo, para obtener el nudo trivial.

Más concretamente, dado un nudo N, se dice que el número gordiano de N es n, y se denota u(N) = n (la u viene del inglés unknotting number, que es otro de los nombres que recibe), si existe un diagrama D del nudo N tal que si se cambian n cruces del mismo, el nuevo diagrama obtenido es equivalente al trivial, y no existe ningún otro diagrama D’ del nudo N tal que con menos cambios que n se obtenga un diagrama equivalente al trivial. Este es un invariante, es decir, para cualesquiera dos nudos equivalentes N1 y N2, su número gordiano es el mismo, u(N1) = u(N2).

El número gordiano del nudo de trébol es igual a 1, como se muestra en la siguiente imagen, puesto que si se cambia uno de los cruces se obtiene el no-nudo.

Si se cambia el cruce marcado en el nudo de trébol, el nuevo diagrama puede transformarse mediante los movimientos de Reidemeinster en el nudo trivial

De igual forma puede verse que el nudo del ocho también tiene número gordiano igual a 1, y para los demás nudos de la clasificación de los nudos con mínimo número de cruces menor o igual que 7 (más abajo también aparecen), que vimos en la anterior entrada, es:

Veamos una sencilla aplicación de este invariante. Por ejemplo, los dos nudos que existen con número mínimo de cruces igual a 5, son ambos no tricoloreables, como se puede observar fácilmente (véanse las imágenes de abajo), además no son anfiquerales. Sin embargo, el primero, 51, que se conoce con los nombres de nudo de cinco lóbulos, nudo pentagrama o nudo sello de Salomón, tiene número gordiano igual a 2, mientras que el segundo, 52, conocido como nudo con tres retorcimientos, tiene numero gordiano igual a 1. Luego ambos nudos no son equivalentes, no son el mismo desde un punto de vista topológico.

El nudo de cinco lóbulos no es tricoloreable, además, si cambiamos uno de los cruces (por simetría da igual cuál de ellos) queda el nudo de trébol, que necesita cambiar otro cruce para desatarlo, luego u(51) = 2

El nudo de tres retorcimientos es no tricoloreable y si cambiamos el cruce del medio es el nudo trivial, luego u(52) = 1

A continuación, vamos a introducir otro invariante curioso, el “número mínimo de aristas de un nudo” o “índice poligonal”, que en inglés se suele conocer también como “stick number”. Un nudo puede ser representado, en el espacio, por una serie de segmentos rectos (llamados aristas) que se intersecan solo en los extremos de los mismos (llamados vértices). Es lo que se llama una representación poligonal del nudo. En la siguiente imagen vemos una representación poligonal del nudo de trébol, que hemos realizado con “barras y bolas” de la herramienta zome.

Representación poligonal del nudo de trébol, realizada con la herramienta zome, para la que se han necesitado 6 barras, que es el mínimo posible para este nudo

El mínimo número de aristas de un nudo N, que se denota s(N), se define como el mínimo número de segmentos rectos que son necesarios para formar una representación poligonal del nudo N. Por ejemplo, el no-nudo tiene índice poligonal igual a 3, ya que aunque podemos realizar representaciones poligonales del no-nudo con 4 (cuadrado), 5 (pentágono), 6 (hexágono), o más aristas, la que requiere el menor número de aristas es la representación triangular, con tan solo 3 aristas. En la siguiente imagen, una escultura del nudo de trébol realizada por el artista Kevin Caron, puede verse una representación poligonal del nudo de trébol realizada con 12 aristas, sin embargo, de la anterior imagen se deduce que el número mínimo de aristas del nudo de trébol es 6.

Escultura “Luz de luna” (2016), en bronce y acero, del artista estadounidense Kevin Caron, perteneciente a su serie “Enterna”

Podríamos plantearnos cuántos nudos admiten representaciones poligonales realizadas con 8, o menos, aristas. Hay exactamente 12 nudos, que son los que se ven en la siguiente imagen, en la cual se ha dibujado los modelos, realizados con “barras (rígidas) y bolas”, de dichas representaciones poligonales. Los 10 primeros son nudos primos, mientras que los dos últimos son nudos compuestos, el nudo de la abuela y el nudo de rizo, de los que ya hablamos en la entrada La artista Anni Albers, The Walking Dead y la teoría de nudos.

Podríamos tener la impresión de que el nudo 51 que aparece en la imagen realizado con 8 aristas, c(51) = 8, podría ser realizado con tan solo con 5 aristas, mediante su representación como el pentagrama. Sin embargo, hay que tener en cuenta que las aristas de las representaciones poligonales no se pueden intersecar entre sí, salvo en los vértices, donde se intersecan solo dos aristas, mientras que al realizar el pentagrama con 5 aristas, estas se intersecarían entre sí en puntos que no son los extremos, o las barras se doblarían dejando de ser segmentos rectos.

Colgante de oro con el pentagrama

El número mínimo de cruces c(N) de un nudo N nos da información sobre el mínimo número de aristas s(N) del mismo. Aunque el conocimiento de c(N) no nos permite determinar con exactitud el valor de s(N), sí establecer unas cotas, superior e inferior, para el mismo. En concreto, se ha demostrado que

En 2011 se mejoró la cota superior, demostrándose que

Para los nudos con mínimo número de cruces c(N) menor o igual a 7, que son los de la clasificación que mostramos en la entrada La artista Anni Albers, The Walking Dead y la teoría de nudos, el índice poligonal s(N) es el mismo para los nudos con el mismo número mínimo de cruces. Como se observa en una imagen anterior, c(51) = c(52) = 8 y c(61) = c(62) = c(63) = 8. Además, se puede probar que c(N) = 9, si N tiene número mínimo de cruces igual a 7. Veamos, por lo tanto, una clasificación más amplia que la que habíamos visto.

En la entrada anterior, habíamos comentado que la primera clasificación de los nudos la realizó Peter G. Tait en 1846, e incluía todos los nudos primos con mínimo número de cruces menor o igual que 7. La siguiente clasificación fue realizada por el matemático e ingeniero civil estadounidense Charles N. Little (1858-1923) en 1885 y contenía los nudos primos con mínimo número de cruces menor o igual que 10 (de nuevo no se distingue entre un nudo y su imagen especular). En ella se refleja que existen 21 nudos primos con mínimo número de cruces igual a 8, 49 con 9 cruces y 165 con 10 cruces.

En la actualidad están clasificados todos los nudos primos hasta mínimo número de cruces igual a 16, para lo cual Jim Hoste, Jeff Weeks, y Morwen Thistlethwaite realizaron búsquedas por ordenador mediante algoritmos diseñados por ellos mismos. La sucesión de la cantidad de nudos primos en función de su número mínimo de cruces, denominada A002863 en la Enciclopedia on-line de números enteros, es:

0, 0, 1, 1, 2, 3, 7, 21, 49, 165, 552, 2.176, 9.988, 46.972, 253.293, 1.388.705.

Clasificación de los nudos con mínimo número de cruces menor o igual que 9

Los nudos primos con mínimo número de cruces igual a 8 ya no tienen todos el mismo índice poligonal, contrariamente a lo que ocurría hasta 7 cruces. Así, los nudos primos del 81 hasta el 815 tienen número mínimo de aristas igual a 10, los nudos 819 y 820 igual a 8 y para los cuatro restantes el valor es 9. Veamos tres ejemplos concretos de nudos con 8 cruces.

El primero de los nudos es el nudo 81. Este pertenece a la familia de los nudos retorcidos, que consisten en coger el nudo trivial e ir dando vueltas (de hecho, medias vueltas) y después “enganchar” los dos extremos desde los que hemos estado girando el nudo trivial. El nudo 81 es el nudo retorcido de 6 medias vueltas (véase la siguiente imagen). Con media vuelta se obtiene el nudo de trébol, con dos medias vueltas el nudo de ocho, con 3 el nudo 52, conocido como el nudo de tres retorcimientos, para cuatro el 61, conocido dentro de los nudos marineros como nudo Stevedore, y para cinco el 72. Una cuestión interesante de los nudos retorcidos es que todos tienen, por su construcción, número gordiano igual a 1. Además, ninguno es anfiquiral, salvo en nudo de ocho. Por otra parte, el nudo 81 tiene número poligonal igual a 10 y es tricoloreable.

El nudo retorcido 81 y su representación poligonal minimal con 10 barras, realizada con Knot Plot

Nuestro siguiente nudo, el nudo 818 es un nudo que deriva de los conocidos nudos de Carrick, que se obtienen anudando dos cuerdas. Se deriva del nudo marinero de Carrick (utilizado en náutica desde la edad media, aunque en la actualidad se utiliza principalmente en escalada; además, también es un nudo heráldico, que aparece en la heráldica de la familia Wake (Inglaterra) y del Condado de Ormond (Ireland)), que es el que vemos en la imagen de abajo realizado por una cuerda roja y otra azul, y después se unen los dos extremos de arriba, respectivamente, de abajo, entre sí, formando el nudo topológico, que se conoce como “estera o tapete de Carrick”. También puede obtenerse a partir del nudo, con una sola cuerda, conocido como nudo de doble moneda, uniendo los extremos.

Nudo marinero de Carrick

Tapete de Carrick, realizado con doble cuerda

El tapete de Carrick ha sido muy utilizado en decoración. Precisamente, el logo de la International Guild of Knot Tyers, es decir, la asociación internacional de personas interesadas en los nudos, es un tapete de Carrick. Este también es el “nudo húngaro” que aparece decorando algunos uniformes militares franceses.

Logo de la “International Guild of Knot Tyers” y el “nudo húngaro” que aparece decorando algunos uniformes militares franceses

El tapete de Carrick, es decir, el nudo 818, tiene número poligonal igual a 9, como se ve en la siguiente imagen de una representación poligonal minimal suya. Además, su número gordiano es 2, no es tricoloreable y es anfiquiral.

El nudo retorcido 818 y su representación poligonal minimal con 9 barras, realizada con Knot Plot

El tercero de los nudos, el nudo 819, se deriva de uno de los nudos más conocidos, el nudo de los enamorados (en inglés, true lover’s knot, el nudo del verdadero amante), y que vemos en la siguiente imagen, en las versiones físicas de una o dos curvas. Muchos nudos han sido asociados desde la antigüedad con la amistad y el amor.

Nudo de los enamorados con dos cuerdas

Nudo de los enamorados con una cuerda, y una variación equivalente

Existen muchos diagramas planos equivalentes del nudo de los enamorados, cada uno de los cuales intenta transmitir una propiedad diferente de este nudo topológico. Abajo vemos cuatro de esos diagramas, el primero derivado del nudo físico a partir del cual se genera, en el que se destacan los dos corazones entrelazados, el segundo expresa que este es un nudo tórico puesto que es equivalente a un nudo que está sobre una superficie de toro (la superficie de un donuts o un flotador), la tercera indica que es un nudo pretzel (familia de nudos cuyo nombre deriva del pretzel, o bretzel, un tipo de galleta o bollo salado retorcido en forma de lazo de origen alemán) y el último es un diagrama normal para expresar cierta disposición espacial del nudo.

Cuatro diagramas planos del nudo de los enamorados, del libro “Knots and Links”

El nudo 819 tiene número poligonal igual a 9, como se vio en la imagen de las representaciones poligonales con 8, o menos, aristas. Además, su número gordiano es 3, no es anfiquiral y es tricoloreable.

Existen muchos más invariantes numéricos, geométricos o algebraicos de los nudos topológicos, como el género de un nudo, el número de puentes, la alternancia, los polinomios de Alexander, Conway, Jones o HOMFLY, los invariantes de Vasiliev, o el grupo fundamental, entre otros, pero esta es otra historia que ya tendrá su momento.

Por cierto, si consideramos el “nudo de Anni” que mostramos en la anterior entrada, ¿cuál es su comportamiento respecto a los invariantes topológicos que hemos visto? ¿Es primo o compuesto? ¿Cuál es su número mínimo de cruces (como mucho es 15)? ¿Es tricoloreable? ¿Cuáles son los valores de su número gordiano y su índice poligonal? Eso queda como problema abierto para aquellas personas que os animéis. No es un problema sencillo.

Terminaremos esta entrada volviendo a lo que fue la motivación del inicio de estas dos entradas dedicadas a la teoría de nudos, el arte. Shinkichi Tajiri (1923-2009) fue un escultor estadounidense-neerlandés, descendiente de japoneses, en cuya obra escultórica tienen mucha importancia los nudos.

La escultura “Nudo de la amistad” (1981), del artista Shinkichi Tajiri, es una de sus esculturas inspiradas en el nudo de rizo

La escultura “Nudo de la abuela” (1992), del artista Shinkichi Tajiri, es una de sus obras inspiradas en el nudo homónimo

Bibliografía

1.- Raúl Ibáñez, La artista Anni Albers, The Walking Dead y la teoría de nudos, Cuaderno de Cultura Científica, 2017.

2.- Raúl Ibáñez, La topología modifica la trayectoria de los peces, Cuaderno de Cultura Científica, 2016.

3.- María Teresa Lozano, La teoría de nudos en el siglo XX, Un Paseo por la Geometría 1998/99, Departamento de Matemáticas, UPV/EHU, 1999. Versión on-line en divulgamat

4.- Martín Gardner, Huevos, nudos y otras mistificaciones matemáticas, Gedisa, 2002.

5.- Colin C. Adams, The Knot Book, An Elementary Introduction to the Mathematical Theory of Knots, AMS, 2001.

6.- Peter Cromwell, Knots and Links, Cambridge, 2004.

7.- Stephan C. Carlson, Topology of Surfaces, Knots, and Manifolds, John Wiley and Sons, 2001.

8.- The Knot Atlas

9.- Página web del artista Kevin Caron

10.- Youngsik Huh, Seungsang Oh, An upper bound on stick number of knots, J. Knot Theory Ramifications 20, no. 5, 2011, pp. 741-747.

11.- Jim Hoste, Morwen Thistlethwaite, Jeff Weeks, “The first 1,701,936 knots”, The Mathematical Intelligencer 20 (4), (1998, pp. 33–48.

12.- J. C. Turner, P. van der Griend, History and Science of Knots, World Scientific, 1996.

13.- Página web del escultor Shinkichi Tajiri

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El artículo Del nudo gordiano al nudo de los enamorados, por territorio matemático se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. La artista Anni Albers, The Walking Dead y la teoría de nudos
2. El problema matemático de las cartas extraviadas
3. Un convite matemático ‘de altura’

Juanma Gallego Anbar fosil batean kapar bat eta dinosauro baten luma batera ageri dira, duela 100 mila urte izandako parasitismoaren adibide. Bigarren ale batean odola xurgatu berri zuen kaparra ageri da ere.

Ezagunak dira hainbat ikastetxetan eta erakundetan prestatzen dituzten denbora kapsulak. Horietan, garaiko objektuak sartzen dira, etorkizunean ezusteko opari hori aurkitzen dutenek iraganari buruzko informazioa izan dezaten. Naturak gutxitan uzten ditu halakoak; baina, noizean behin, zortea badago, eta fosilak modu paregabean babestuta mantentzen dira, milioika urtetan zehar.

Zuhaitzetako erretxina fosilduan abiapuntu duen anbara naturak eskainitako kapsula horietako bat da. Tamainagatik, ordea, gauza gutxi lor daiteke bertan. Intsektuak, askoz jota. Hala eta guztiz ere, hori gertatzen denean, naturaren benetako mirari baten parekoa izaten da. Txiripak gidatzen ditu halakoak, eta, batzuetan, txiripa hori biderkatzen da. Halakoa da ikertzailek talde batek aztertzeko aukera izan duen anbar zatiaren kasua. Bertan, kapar bat ageri da, baina ez hori bakarrik. Aspaldiko krimen baten aztarna balitz bezala, kaparrarekin batera dinosauro baten luma ere agertu da. Biak batera, gaizkilea eta haren “biktimaren” aztarna.

1. irudia: Deinocroton draculi kaparrak dinosauro baten gainean erakusten dituen irudikapen artistikoa. (Ilustrazioa: Nature Communications)

Myanmarren aurkitutako anbar batean agertu da zoriak betiko izoztutako eszena hori. Baina ez da aztertu duten bakarra. Duela 99 milioi urte inguruko beste anbar batzuk aztertu dituzte, horiek ere barruan kaparrak dituztelarik. Zientzialariek egindako azterketa sakonaren emaitzak Nature Communications aldizkarian aurkeztu dituzte.

Luma hori zehazki zein dinosaurorena den ezin izan dute argitu, baina jakin badakite Theropoda azpiordenako dinosauro batena izan zela. Beste aukerarik ez dago, garai horretan hegaztiak ez zirelako agertu. Teropodo lumadunak dira, zantzu guztien arabera, gaur egungo hegaztien arbasoak. Are gehiago, paleontologo askok gustuko dute esatea dinosauro guztiak ez direla desagertu, eta jende askok afaltzen dituela dinosauro bularkiak. Zaila da Tyrannosaurus rex eta oilasko baten arteko lotura irudikatzea, baina, zentzu ebolutiboan, badago.

Teropodoak duela 225-70 milioi urte bizi izan ziren; dinosauroen artean, hoberen ezagutzen direnak dira, bi hanken gainean ibiltzen ziren dinosauro horiek arrasto ugari utzi dituztelako mundu osoan. Esaterako, Jurassic Park filmean agertzen diren velocirraptor zitalak teropodoak ziren, eta Michael Crichton idazleak eta Steven Spielberg zinemagileak garai horretan ez bazekiten ere, lumadunak ziren. Lumadun dinosauroak irudikatzean, beraz, hobe burua kentzea burua ezkutatzen duen ostruka beldurtiaren irudi hori.

Dinosauro mota horri lotutako bizkarroia antzematen den lehenengo aldia da honakoa. Zehazki gaur egin iraungita dagoen Cornupalpatum burmanicum espeziekoa da lumarekin batera harrapatutako kaparra. Zientzialariek, noski, naturak emandako opari hori goitik behera aztertu dute.

Zientzia artikuluan egileek azpimarratu dutenez, “aurkikuntza hauek kaparraren hasierako eboluzioaren eta ekologiaren inguruan argibide gehiago ematen digute, eta argitzen dute orain arte gutxi ezagutzen den artropodoen eta ornodunen arteko harremanak nolakoak ziren, eta nola izan zitekeen gaixotasunen zabaltzea Mesozoikoan”.

2. irudia: Myanmarreko anbarean topatu dituzte dinosauroaren luma eta kaparra. (Irudia: Nature Communications)

Horrez gain, aztertutako beste hiru anbar aleetan kaparra gehiago zeuden. Horietako bat, odolez handituta. Azterketa sakon baten ostean ondorioztatu dute espezie berria dela, eta Deinocroton draculi izena eman diote, Bran Stokerrek sortutako pertsonaia odoltsuaren omenez. Kasu honetan, kapar horren eta dinosauro ostalariaren arteko lotutarik ez dute atzeman. Barruan zuen odola ikertzea ere ezinezkoa izan da, kaparra erretxinan guztiz txertatuta ez zegoelako eta, ondorioz, inguruko mineralen lagatzeak lagin hori kutsatu zuen. Halere, kapar horren hanketan kakalardo larben ileak agertu dira. Ikertzaileek iradoki dute agian kakalardoa, kaparrak eta dinosauroa espazio komun batean zeudela. Gaur egun, antzeko azaleko kakalardoak (Dersmestidae familiakoak) habietan bizi daitezke ere, eta bertan eskuratzen dituzte elikatzeko erabiltzen dituzten lumak, ileak eta azaleko zatiak.

Egileek diotenez, bi parasito batera harrapatuta agertu izana guztiz harrigarria da, eta errazago azaltzen da aintzat hartzen bada kapar horiek hobi batean zeudela. Gaur egun hala izaten omen da, bai habian bertan edo habiaren inguruan.

Jurassic Park-en bezala, odol horretatik informazio genetikoa atera al liteke? Azken urteotan antzinako DNAren teknologiak aurrerapauso itzelak eman baditu ere, oraindik orain ez da lortu halakorik, eta ez dirudi erraza izango denik. IGME Espainiako Geologia eta Meatzaritza Institutuko ikertzaile Enrique Peñalverrek aurkikuntzari buruzko argibideak eman ditu Radio Euskadiko La mecánica del caracol saioan, eta gaiari ere heldu dio.

“Tamalez DNA oso azkar txikitzen da, eta anbarean ez da kontserbatzen. Zenbaitetan uste izan da lortua dela DNA puskak berreskuratzea, baina ondoren ikusi izan da gaur egungo DNAk eragindako kutsadurak zirela eta”. Adituak nabarmendu du “bikaina” izango litzatekeela horrelakorik topatzea. “Ez klonatzeko, zeren horretarako dinosauroen obuluak beharko baikenituzke, baizik eta dinosauroen eboluzioari buruzko informazio asko eman zezaketen geneak ikertzeko”.

Erreferentzia bibliografikoa:

Peñalver, E. et al. The paper Ticks parasitised feathered dinosaurs as revealed by Cretaceous amber assemblages. Nature Communications 8, Article number: 1924 (2017). DOI:10.1038/s41467-017-01550-z

———————————————————————————-

Egileaz: Juanma Gallego (@juanmagallego) zientzia kazetaria da.

———————————————————————————-

The post Dinosauroek ere kaparrak zituzten appeared first on Zientzia Kaiera.

Aplicando los dos postulados de la teoría de la invariancia [1], el principio de relatividad y el principio de constancia de la velocidad de la luz en el vacío, a una situación similar al barco de Galileo, Einstein propuso un experimento mental extremadamente simple y que, sin embargo, proporcionó un primer resultado sorprendente. Descubrió que dos sucesos que ocurren simultáneamente para un observador pueden no ocurrir simultáneamente para otro observador en movimiento relativo con respecto a los sucesos. En otras palabras, la simultaneidad de los sucesos es un concepto relativo [2].

Una linterna LED, como las empleadas en el experimento mental, emite un haz de luz

El experimento mental de Einstein, en una versión actualizada, sería como sigue . Un observador, Esteban, está estático al lado de una vía de ferrocarril perfectamente recta. Está situado en el punto medio entre dos puntos A y B. Imaginemos que sostiene un interruptor eléctrico que conecta cables de exactamente la misma longitud a dos linternas LED colocadas en A y B. Como se encuentra en el punto medio entre A y B, si cierra el interruptor, las linternas se encenderán, y muy poco después de eso Esteban verá la luz de A y de B llegando a sus ojos en el mismo momento. Esto se debe a que la luz de cada linterna, viajando a la velocidad constante de la luz y cubriendo exactamente la misma distancia a Esteban desde cada linterna, empleará exactamente el mismo tiempo para alcanzar sus ojos. Como es lógico, Esteban concluye de todo ello que las dos linternas se encienden simultáneamente.

Esto es a lo que se conoce como un vagón plataforma. Podríamos haber empleado en el experimento mental un tren de alta velocidad, pero el tipo de vagón de este clase de trenes no es el óptimo habida cuenta del tipo de sucesos implicados en el experimento.

Ahora imaginemos a una segunda observadora, Mónica, de pie en un vagón plataforma que viaja por la vía a una velocidad uniforme muy alta desde A hacia B. Mónica y Esteban han acordado que cuando Mónica llegue al punto medio exacto entre A y B, Esteban activará inmediatamente el interruptor y encenderá las linternas [3].

Mónica y Esteban realizan el experimento. En el instante en que Mónica alcanza la posición del punto medio entre A y B, el interruptor se cierra, las linternas se encienden y Esteban ve los haces de luz simultáneamente. Pero Mónica ve algo diferente: para ella los haces no ocurren simultáneamente. De hecho, le parece que la linterna en B se enciende antes que la que está en A.

¿Por qué? Como Mónica se desplaza muy rápidamente hacia B y se aleja igual de rápidamente de A y como la velocidad de la luz es finita y exactamente la misma independientemente del movimiento del observador, Mónica se encontrará con el haz de B antes que el haz de A la alcance. En consecuencia, verá el haz de B antes que el haz de luz de A.

La conclusión: los dos sucesos que Esteban percibe que ocurren simultáneamente no se producen simultáneamente para Mónica. Las razones de esta discrepancia son que la velocidad de la luz es la misma para ambos observadores y que cada observador se mueve de una manera diferente en relación con los sucesos en cuestión.

Sería muy natural pensar que Mónica podría usar una calculadora y que, conociendo su velocidad y la velocidad de la luz, podría averiguar muy fácilmente si las linternas se encendieron tal y como ella las vio o como dice Esteban que las vio él. Sin embargo, si hace esto, y aquí viene la sutileza del experimento, entonces Mónica está afirmando una relación concreta entre los marcos de referencia; en otras palabras, está asumiendo que ella es el observador en movimiento y que Esteban es el observador estacionario. Pero esta asunción de Mónica no es posible ya que, de acuerdo con el principio de relatividad, no hay ningún experimento que se pueda realizar dentro de un marco de referencia inercial [4] que revele si éste está en reposo o moviéndose a una velocidad uniforme. Nada impide por tanto que ella sea el observador estacionario, y Esteban, parado al lado de la vía, ¡podría ser el observador en movimiento!

Si esto es así, entonces Mónica puede afirmar que la linterna en B en realidad se encendió antes que la que está en A y que Esteban percibió que las dos se encendían simultáneamente solo porque, desde el punto de vista de ella, Esteban se estaba moviendo hacia A y alejándose de B. Por supuesto, Esteban podría argumentar exactamente lo contrario, que él está en reposo y que es Mónica quien se está moviendo.

Pero, ¿qué interpretación es la correcta? En contra de nuestro sentido común, resulta que no hay una interpretación “correcta” porque no hay un marco de referencia preferido. Ambos observadores se mueven uno con relación al otro. Pueden ponerse de acuerdo a la hora de describir qué ocurrió realmente, pero solo si están de acuerdo en usar uno solo de los dos marcos de referencia [5], un acuerdo que es puramente arbitrario.

Por consiguiente, el que un observador considere dos sucesos como simultáneos, esto es, que ocurren al mismo tiempo, depende del movimiento del observador. De aquí se sigue que el tiempo mismo también debería ser un concepto relativo al observador cuando se examina a la luz de los postulados de la teoría de la invariancia [1]. Este será el tema de la próxima entrega.

Notas:

[1] Popularmente conocida como teoría de la relatividad.

[2] A pesar de ello, las leyes de la física implicadas en estos sucesos son iguales para ambos obervadores, de ahí que la teoría se llame de la invariancia.

[3] Dado que este es un experimento mental, podemos despreciar el tiempo de reacción de Esteban o el de la alternativa, un interruptor activado electrónicamente así como el implicado en la activación de las linternas.

[4] Un marco de referencia inercial es un marco de referencia que está en reposo o en velocidad uniforme en relación con otro marco de referencia.

[5] Tal y como hemos hecho implícitamente en el planteamiento del experimento, cuando hemos afirmado que es Mónica la que se mueve.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo La simultaneidad de los sucesos se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El principio de constancia de la velocidad de la luz
2. El principio de relatividad (y 4): la versión de Einstein
3. El principio de relatividad (2): la versión de Galileo

Juan Ignacio Pérez Iglesias Gizakiok pikuak jan izan ditugu gure espeziearen hasieratik. Agian horregatik azaltzen da pikondoa kreazioaren hainbat pasarte mitikotan. Erlijio batzuetan sakratua da zuhaitz hau, madarikatua beste batzuetan. Jesus Nazaretekoak berak esan omen zion pikondo bati “inork ez dezala zugandik fruiturik jan” zuhaitz horrek ez zeukalako pikurik (Marcos 11: 12-14).

Ficus da pikondoaren latinezko izena; euskaraz “piku” deritzo jatekoari ere, eta ohi bezala, pikondoa da zuhaitza. Pikua ez da fruitu bat: errezeptakulu bat da, alegia infloreszentzia bat, lore paketatuak dituena.

1. irudia: Harluxet hiztegi entziklopedikoaren arabera, pikondoa da Morazeoen familiako zuhaitz edo zuhaixka hosto erorkorra, azal griseko enbor lodi eta motza, hosto palmatilobatu handi, larrukara eta biribilduak eta udare-formako errezeptakulu mamitsuen baitan dauden lore unisexualak dituenak. Haren fruitua pikua da (Ficus carica).

Generoari ere Ficus deritzo eta bere barruan 800 espezie daude. Gure pikondo arrunta, Ficus carica da. Espezie horien artean gehienek, Agaonidade familiako liztor espezie jakin batekin koeboluzionatu dute. Asoziazio horiek gutxienez duela 80 miloi urte hasi ziren: liztorrak pikondoko loreak polinizatzen ditu, eta pikuek liztorrei babesteko tokia eskaintzen die.

Liztor eme txiki batek, 2 mm-ko luzera duelarik ere, polena eta ehunka arrautza ernaldu garraiatzen ditu. Piku batean jaio da eta ostiolo izeneko irekigune txiki batetik ateratzen da. 48 ordu ditu espezie bereko beste pikondo bat aurkitzeko. Hamarka kilometrora egon daiteke pikondo hori. Hala ere, esan beharrekoa da pikondoak erraztu egin diola liztorrari bere lana, intsektuak erraz detektatzen dituen substantzia kimiko batzuk botatzen dituelako atmosferara. Behin piku berrira sartuta, erantsita daraman polen berria barreiatzen doa barrunbe zentralerako bidean. Arrautza bana erruten du lore femenino bakoitzean; liztorra langile ona bada, berrehun arrautza errun ditzake. Horren ostean, hil egiten da akiturik.

2. irudia: Agoanidade espezieko liztorrak piku batean.

Arrautza ernalduak hazten doaz eta hezietatik elikatuz bere garapena burutzen dute azkenean. Arrak lehenago ateratzen dira, ernaltzeko emeen bila. Masail handiak dituzte, hegogabeak dira eta ia itsuak. Emeak ernaldu ostean hil egiten dira. Ar gutxi batzuk, habiatik ateratzen dira, baina bizitza laburra eta ezbehartsua pairatzen dute. Emeak hegaka doaz aske eta azkar, pikondo berri baten bila, prozesuari berriz hasiera emateko.

Behin liztorrak aterata, pikuak handitu egiten dira, kolore gorria hartzen dute eta azukrez betetzen dira. Elikagai gustagarri bilakatzen dira beraz. Ficus generoaren espeziearen arabera, saguzarrek, hegaztiek, tximinoek edo bestelako animaliek jango dituzte pikuak. Animaliek sabela husten dutenean, barreiatu egingo dituzte haziak, ernatu ostean beste pikondo batzuk sortuko dituztenak.

3. irudia: Piku heldua.

Zonalde epeletan, bizpahiru uzta ematen dituzte pikondoek, landarearen sexuaren arabera. Tropikoetan ordea, urte osoan daude piku “helduak”, eta beste edozein fruitu baino gehiago, mila hegazti eta ugaztun-espezieren elikagai dira. Hau guztia oso garrantzitsua da ekologian, zeren pikurik gabe animali espezie asko desagertu ere egin balitezke, elikagai ezagatik. Animalia horiek hilda, beste landare-espezieek ere kaltea pairatuko lukete, ez luketelako hainbeste polinizatzailerik izango.

Pikondoa bitxia da, eta bitxia da bere fruitua, sasizko fruitua delako. Hala ere, elikagai garrantzitsua izan da gizakiontzat eta beste animalia askorentzat. Hori dela eta, mundua oso desberdina izango litzateke pikondorik gabe.

———————————————————————————-

Egileaz: Juan Ignacio Pérez Iglesias (@Uhandrea) UPV/EHUko Fisiologiako katedraduna da eta Kultura Zientifikoko Katedraren arduraduna.

———————————————————————————

—————————————————–

Hizkuntza-begiralea: Juan Carlos Odriozola

——————————————–

The post Zuhaitz sakratua, zuhaitz madarikatua appeared first on Zientzia Kaiera.

El título de esta anotación expresa de forma sintética la conclusión de una investigación hecha en Senegal, en una sociedad en la que está muy extendida la poliginia. En las sociedades poligínicas hay un incentivo muy fuerte para que los varones solteros intenten mantener relaciones con mujeres casadas y para que las mujeres casadas que ocupan una posición inferior o son peor tratadas en la familia mantengan relaciones con otros hombres. De esa forma, y expresado en términos demográfico-evolutivos, esos varones tienen alguna posibilidad de reproducirse y, por lo tanto, de dar continuidad a su linaje; y las mujeres, por su parte, pueden diversificar así su apuesta reproductiva. Ahora bien, bajo esas condiciones, la incertidumbre acerca de la paternidad es relativamente alta, algo que puede condicionar el comportamiento de los padres para con su progenie.

Y efectivamente, utilizando el parecido facial y el olor corporal como criterios de similitud fenotípica, la investigación concluyó que los padres dedican un mayor esfuerzo a los hijos que más se les parecen. Como consecuencia de ese mayor esfuerzo y atención, los hijos más parecidos a sus padres también crecen más y se encuentran en un mejor estado nutricional, con lo que ello implica en términos de adecuación (fitness, en términos darwinianos).

Los resultados obtenidos en el estudio son consistentes con predicciones teóricas basadas en el supuesto de que la inversión de recursos en la progenie actual compromete los recursos que puedan ser utilizados en la progenie futura. Por esa razón, bajo condiciones de incertidumbre acerca de la paternidad, los padres recurrirían a criterios de similitud fenotípica (los únicos a los que tienen acceso) a la hora de canalizar recursos hacia la progenie.

Fuente: Alexandra Alvergne, Charlotte Faurie y Michel Raymond (2009): Father–offspring resemblance predicts paternal investment in humans. Animal Behaviour 78: 61-69.

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo Conviene que los hijos se parezcan a su padre se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. La reacción de las madres al llanto de los bebés es universal
2. Los padres mienten a sus hijos… mucho y en todo el mundo
3. “Norman Borlaug, padre de la Revolución Verde” por Elías Fereres

2019an nahitaezko izango diren ia energiarik kontsumitzen ez duten eraikinak (nZEB) ezartzeko eta, bereziki, eraikinak modernizatzeko prest ez daudela Europa hegoaldeko herrialde gehienak ondorioztatu du eraikingintzaren egoera aztertu duen ENEDI ikerketa-taldeak.

Irudia: Europa hegoaldeko herrialdeetako eraikingintzaren egoera aztertu dute UPV/EHUko ikertzaileek.

Ia energiarik kontsumitzen ez duten eraikinak (nZEB, Nearly Zero Energy Building) eraikitzeko legezko konpromisoa hartu dute Europako herrialdeek, datozen urteetarako eraikinetako energia-eraginkortasuna hobetzeko. 2019ko urtarrilaren 1etik aurrera eraikin publiko guztiek nZEB izan beharko dira, 31/2010/EU direktibak finkatutako daten arabera, eta 2021eko urtarrilaren 1etik aurrera egiten den eraikin oro izan beharko da nZEB.

Europako hegoaldeko zazpi herrialderen (Zipre, Frantzia, Grezia, Italia, Portugal, Errumania eta Espainia) eraikingintzaren egoera aztertu dute honako ikerketan. Herrialde bakoitzak ñabardurak ditu definizio teknikoetan eta horrek zaildu egiten du nZEB eraikinak bultzatzeko araudiak eta programak zuzenean konparatu ahal izatea, baina metodologia bateratua adostu dute ikertzaileek alderaketak egin ahal izateko.

Barrera sozial eta teknologikoak

nZEB eraikinak garatzeko dauden barrera sozial eta teknologikoen azterketa konparatiboa izan da ikerketaren ardatza, bai eraikuntza berriaren bai higiezinen birgaitzearen ikuspegitik. Egindako ikerketa askok egoera ekonomikoari egotzi diote hegoaldearen eta iparraldearen arteko ezberdintasunak.

Bestelako oztopoak badirela ere frogatu du lan honek, barrera soziologikoak eta herrialde bakoitzeko klima, besteak beste, asko baldintzatzen dute ia energiarik kontsumitzen ez duten eraikinen helburuak lortzea. Horretaz gain, eragile ia guztien trebakuntza oso eskasa dela ikusi da, administraziotik eta eraikingintzako langileetatik hasi eta herritarretaraino nZEB eraikinak zehazki zer diren eta nola lor daitezkeen ez dakien giza kate oso luzea osatzen dutela.

Era berean, errazagoa dela nZEB eraikin berri bat eraikitzea kontzeptu hori birgaikuntzara eramatea baino uste du Juan Maria Hidalgo-Betanzos ikertzaileak. Eraikin berriak egitean, kokapena eta orientazioa aukera daitezke eta baita material berriak eta diseinuan integratutako teknologiak erabili. Birgaitze lanetan, aldiz, malgutasuna txikiagoa da eta kostuak handitzen dira.

Eraikinen diseinua xehetasun gehiagorekin aztertu behar dela, neguko eta udako urtaro aldaketei irtenbidea aurkitzeko ondorioztatu daiteke ikerketaren emaitzetatik. Barrera horiek konpondu ezean, oso litekeena da benetako emaitzarekin gustura ez gelditzea. Arazoak sor litezke konfort termikoarekin, gehiegizko berokuntzarekin, alferrikako eraikuntza gainkostuekin, e.a.

Euskal Herria oso proba banku aproposa izan daitekeela uste du ikertzaileak, ikerketan landutako ia klimatologia guztiak baititu. Oso lurralde txikia izan arren, diseinu-irizpide oso desberdinak aplikatu behar direla kostaldean, mendialdean, hegoaldean… azaltzen du.

Lehen konpromisoaren epea amaitzeko urtebete falta denean herrialde asko urrun daude eraikinetako energia eraginkortasun mailatik, Europako erdialdeko eta hegoaldeko herrialdeak daude aurreratuen.

Erreferentzia bibliografikoa:

Shady Attia, Polyvios Eleftheriou, Flouris Xeni, Rodolphe Morlot, Christophe Menézo, Vasilis Kostopoulos, Maria Betsi, Iakovos Kalaitzoglou, Lorenzo Pagliano, Maurizio Cellura, Manuela Almeida, Marco Ferreira, Tudor Baracu, Viorel Badescu, Ruxandra Crutescu, Juan Maria Hidalgo-Betanzos. “Overview and future challenges of nearly zero energy buildings (nZEB) design in Southern Europe” Energy and Buildings. Vol. 155. November 2017. Pages 439-458.

Iturria:

UPV/EHUko Komunikazio bulegoa: Ia energiarik kontsumitzen ez duten eraikinak: erronka zaila, Europako hegoalderako.

The post Ia energiarik kontsumitzen ez duten eraikinentzat prest ez appeared first on Zientzia Kaiera.

“Serendipia. Hallazgo valioso que se produce de manera accidental o casual.”
“Chiripa. 1. Carambola, casualidad favorable. 2. En el juego de billar, suerte favorable que se gana por casualidad.”
Diccionario de la Real Academia

“En el campo de la investigación el azar no favorece más que a los espíritus preparados.”
Louis Pasteur

“La inspiración existe pero tiene que encontrarnos trabajando.”
Pablo Picasso

“Las ideas experimentales frecuentemente nacen a partir de una observación casual, por ello representan la forma más sencilla de comenzar un trabajo científico.”
Claude Bernard

El 28 de enero de 1754, Horace Walpole, cuarto Conde de Orford, hijo de un Primer Ministro y famoso escritor, envió una carta a Sir Horace Mann, amigo y embajador en Florencia, e incluyó en el texto un término recién inventado, serendipity o, en español, serendipia. Walpole construye el término a partir de una antigua fábula asiria titulada “Los tres príncipes de Serendip”, que, en sus viajes, “siempre descubrían, por accidente o por sagacidad, cosas que no estaban buscando”.

Serendip es el antiguo nombre de la isla de Ceilán, hoy conocida como Sri Lanka. Como ejemplo nos sirve aquella aventura en la que los príncipes describen un camello, al que no han visto, y afirman que está ciego del ojo derecho porque en el camino que recorre solo está comida la hierba del margen izquierdo, la única que ve con su ojo sano. O que lleva una carga de mantequilla y miel, cada una en un costado, pues en una cuneta hay hormigas comiendo y en el otro un enjambre de abejas, avispas y moscas. Las hormigas comen la mantequilla y los otros insectos la miel. Estos príncipes más bien me parecen ancestros de Sherlock Holmes que viajeros con suerte que descubren por casualidad.

Así explica Walpole a su amigo Mann lo que significa serendipia. Ahora, en nuestro tiempo, se usa serendipia en ciencia para describir un hallazgo inesperado y afortunado.

La palabra casi se olvidó hasta que, en 1955, Salvador Luria, después Premio Nobel en 1969, iniciaba un artículo sobre los virus llamados fagos, que destruyen bacterias, con este párrafo: “Nuestra historia tiene como episodio crítico una de esas coincidencias que muestran como el descubrimiento depende a menudo del azar o, más bien, de lo que se ha llamado serendipia –la observación casual que llega a un ojo receptivo”.

Para Pablo Capanna, las serendipias son ocasiones irrepetibles que no suponen un conocimiento fácil y listo para captar. Dependen de una mente alerta, entrenada y con los conocimientos suficientes como para entender lo que aparece de improviso. Hay que saber cómo sacar provecho de la serendipia. Solo lo consigue quien es capaz de ver lo que la mayoría deja pasar, eso que está delante de los ojos. A menudo parece un golpe de suerte pero, más bien, es la conclusión de un razonamiento en segundo plano según se está atento a otra cosa.

El camino que sigue la investigación científica no siempre es lineal ni predecible o, si se quiere, no se puede planificar al detalle. Las rutinas metodológicas ordenan la búsqueda, ahorran tiempo, garantizan la objetividad y evitan fantasías, pero no lo son todo ni aseguran los resultados. Es el inconveniente de los proyectos demasiado específicos y con objetivos muy concretos, pues así no se permite captar los imprevistos. Después de todo esos proyectos se preparan a partir de lo que ya conocemos y no es fácil, más bien no es posible, que planifiquen lo desconocido. Por ello es importante, por un lado, que se deje a los científicos elegir lo que investigan y que, además, siempre exista un componente importante de investigación básica. Y, por otra parte, que los que hagan ciencia estén bien provistos de conocimientos básicos y así les será más sencillo detectar lo inesperado.

También Peter Medawar, Premio Nobel en 1960, escribió que cualquier científico que no sea hipócrita reconocerá el papel de la suerte en los descubrimientos. Para Medawar, un descubrimiento científico nunca es premeditado. Un acto de la imaginación, una aventura especulativa, subyace, por tanto, en todo avance del conocimiento.

Veamos algunos ejemplos de serendipia, aunque no trataré a fondo el más famoso de todos: la llegada a América de Cristóbal Colón, que no solo no encontró lo que buscaba, las Indias y sus riquezas, sino que encontró un continente, América, que no buscaba y que, además, nunca aceptó que lo había hecho y que se había equivocado. Murió convencido de haber llegado a las Indias. Esto sí que es una serendipia sin querer, sin buscarla.

Empezaré con otra serendipia famosa como es el descubrimiento de la penicilina por Alexander Fleming, también Premio Nobel en 1945.

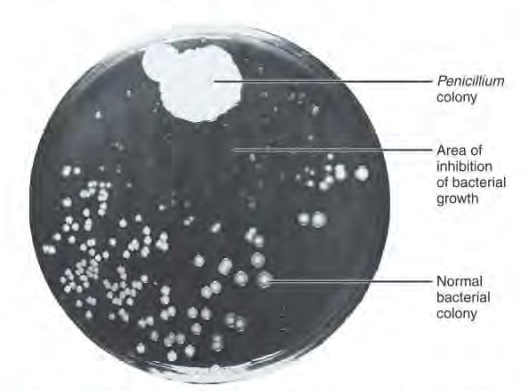
He conocido recientemente un relato del descubrimiento de la penicilina escrito por un testigo directo, el profesor Melvyn Price, colega y amigo de Fleming, y su visitante en el laboratorio en el momento de serendipia de encontrar e interpretar la placa contaminada con el moho Penicillium. Fue en 1928. Fleming estaba haciendo una serie de estudios con estafilococos para incluirlos en un manual de Microbiología de próxima aparición. Price había iniciado los experimentos y luego había marchado del laboratorio sin terminarlos. Fleming los estaba completando. Así que estaba rodeado de placas con cultivos de estafilococos y encontró una de ellas con una contaminación con moho. La observó y, según relata Price, vio donde crecía el moho y que había zonas cercanas de donde habían desaparecido los estafilococos. Comentó para sí mismo “That is funny…”, o sea, “Esto es curioso…”. Tomó una muestra y la guardó para próximos estudios. Fue su primer cultivo con el hongo Penicillium chrysogenum, productor de la penicilina. Fleming guardó toda su vida esa primera placa contaminada.

Otro ejemplo de serendipia es la invención del estetoscopio, el instrumento tan conocido y peculiar que utilizan los médicos para escuchar cómo sonamos por dentro. Antes del estetoscopio, el médico colocaba su oído directamente sobre el pecho del paciente. Pero había dificultades para escuchar con claridad en los obesos y, además, las mujeres no se sentían cómodas pues consideraban que su intimidad se veía invadida.

Fue el médico francés René Laënnec quien encontró la solución en 1816. Observó a unos niños que jugaban en la calle con una tabla de madera. Uno de ellos golpeaba muy suave uno de los extremos y los demás escuchaban los golpes desde el otro extremo. Pensó que el sonido se transmitía bien en un sólido y que, quizá, así conseguiría escuchar mejor los sonidos del interior del cuerpo humano. Primero ensayó con un cilindro de papel y constató que mejoraba el sonido. Entonces encargó que le fabricaran un cilindro de madera, abombado por los dos extremos, de 30 centímetros de longitud, 3 centímetros de diámetro y un conducto interno central de 5 milímetros de ancho. Este fue el primer estetoscopio.

Y ahora, la historia de la droga LSD o dietilamida de ácido lisérgico. Fue, como en toda serendipia, una casualidad que necesitaba de un científico atento y preparado para percibirla. Era Albert Hofmann, investigador de la compañía farmacéutica Sandoz en Basilea, Suiza. Trabajaba con compuestos formados por el ácido lisérgico con varias amidas para conocer sus posibles propiedades estimulantes sobre la circulación y la respiración, el alivio de las migrañas y para detener hemorragias en el parto. El compuesto número 25 era la dietilamida del ácido lisérgico. El día era el viernes 16 de abril de 1943 y así lo relató Hofmann años más tarde a partir de su cuaderno de laboratorio y del informe que preparó para su director.

“El viernes pasado, 16 de abril de 1943, me vi obligado a detener mi trabajo en el laboratorio y regresar a casa, pues sentía una inquietud peculiar asociada con una sensación de leve mareo. Al llegar a casa, me tumbé y caí en una especie de embriaguez que no era desagradable y que se caracterizaba por la extrema actividad de la imaginación. Mientras estaba en un estado aturdido con los ojos cerrados (experimentaba la luz del día como desagradablemente brillante), surgió sobre mi un flujo ininterrumpido de fantásticas imágenes de extraordinaria plasticidad y vivacidad y acompañado por un intenso y caleidoscópico juego de colores. Esta condición pasó gradualmente y terminó después de cerca de dos horas.”

Hofmann quedó impresionado por lo que había provocado aquella molécula que llamaba LSD-25 y comenzó a hacer ensayos cuidadosos consigo mismo. Tres días después, el 19 de abril, se administró una dosis de 0.25 miligramos. En su cuaderno de laboratorio hay una sola nota sobre aquella sesión: “Deseo de reír”. Montó en su bicicleta y se marchó a su casa acompañado por un colega del laboratorio. Tuvo la placentera sensación de que, durante todo el trayecto, permaneció inmóvil. Entre los aficionados al LSD de todo el mundo, ese 19 de abril se conoce como “El Día de la Bicicleta”. Así demostró Hofmann las extraordinarias propiedades del LSD-25.

Después de estos ejemplos, con el primer antibiótico, un instrumento médico como el estetoscopio, y una droga como el LSD, podemos terminar afirmando que la ciencia, vista la contribución de las serendipias, no avanzaría si los investigadores no fueran capaces de responder a lo inesperado y de conectar lo sorprendente con lo rutinario. Además, y como escribió Alexander Fleming años después de su descubrimiento, “La historia de la penicilina tiene un cierto encanto y ayuda a ilustrar la cantidad de azar o fortuna, de fatalidad o destino, llámenlo como quieran, que hay en la carrera de alguien.” Para los científicos, no todo son objetivos a cumplir y planificación, también hay mucho trabajo e intuición y, siempre, muchos conocimientos.

Para terminar y como resumen, ocho puntos sobre la serendipia que ofrece Peter Van Andel, de la Universidad de Groningen. Aquí van:

1.- La serendipia existe.

2.- En las áreas más empíricas (astronomía, química, medicina) los hallazgos por serendipia son habituales.

3.- La serendipia ayuda, es esencial y no debe ser subestimada ni exagerada.

4.- La investigación científica sistemática y la serendipia no se excluyen sino que, más bien, se complementan.

5.- En general, la serendipia tiene a desparecer o a ser disimulada en las narraciones a posteriori cuando se publican los resultados; se racionaliza el método y no hay lugar a la casualidad.

6.- Antes decíamos por suerte o por casualidad, ahora decimos por serendipia.

7.- La mayor parte de los que aceptan y practican la serendipia son de mente abierta, perceptivos, curiosos, intuitivos, ingeniosos, flexibles, artistas, con sentido del humor y laboriosos.

8.- La intuición es una anticipación que no puede ser explícita antes o cuando ocurre y, entonces, la serendipia, por definición, sigue a la intuición.

Referencias:

Bunge, M. 2013. La ciencia: su método y su filosofía. Laetoli. Pamplona. 144 pp.

Capanna, P. 2011. Serendipias. Los descubrimientos que se realizan por “casualidad”. Página 12 Futuro Diciembre 3.

Coppo, J.A. 2012. Serendipia. Revista Veterinaria 23: 71-76.

Darbellay, F. et al. 2014. Interdisciplinary research boosted by serendipity. Creativity Research Journal doi: 10.1080/10400419.2014.873653

Forni, P. 2011. Robert Merton. Miriada 4: 1-4.

Hofmann, A. 1970. The discovery of LSD and subsequent investigations on naturally occurring hallucinogens. En “Discoveries in Biological Psychiatry”, p. 98-109. Ed. por F.J. Ayd, Jr. & B. Blackwell. J.B. Lippincott Co. Philadelphia/Toronto. 254 pp.

Luria, S.E. 1955. The T2 mystery. Scientific American 192: 92-98.

Maurois, A. 1963. La vida de Sir Alexander Fleming. Eds. Cid. Madrid. 318 pp.

Medawar, P.B. 1988. Los límites de la ciencia. Fondo de Cultura Económica. México. 141 pp.

Roberts, R.M. 1992. Serendipia. Descubrimientos accidentales en ciencia. Alianza Ed. Madrid. 443 pp.

Stix, G. 2011. El primer “viaje” alucinógeno. Investigación y Ciencia enero: 7.

Taton, R. 1967. Causalidad y accidentalidad de los descubrimientos científicos. Ed. Labor. Barcelona. 172 pp.

Valer, N.B. 2005. A serendepidade na Medicina e na Anestesiologia. Revista Brasileira de Anestesiologia 55: 224-249.

Van Andel, P. 1994. Anatomy of the unsought finding serendipity: origin, history, domains, traditions, appearances, patterns and programmability. British Journal for the Philosophy of Science 45: 631-648.

Villanueva Meyer, M. 2012. René Laënnec (1781-1826): Inventor del estetoscopio y maestro del examen médico. Galenus 35: 70-71.

Villanueva Meyer, M. 2014. Alexander Fleming: Pionero en el uso de la penicilina. Galenus 47: 68-69.

Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.

El artículo Un viaje a Serendipia se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Serendipia
2. Viaje a la dimensión desconocida
3. El frustrante viaje de un átomo de carbono, mención especial del jurado “On zientzia”

Uxune Martinez

Osasuna

Dengea zein zika transmititzen ditu Aedes aegypti eltxoak. Dengeak 400 milioi lagun inguru kutsatzen ditu urtero. Gehienek ez dute ia sintomarik izaten, baina gutxi gorabehera bi milioi lagunek sukar hemorragikoa izaten dute birusaren eraginez, eta azkenerako, 25.000 hiltzen dira urtero. Arazoari aurre egiteko, zergatik ez jo eltxo horien kontra? Zilegi al da espezie horiek behin betiko iraungitzea? Juanma Gallego kazetariak galdera bota du Berrian: “Ziztada hilgarrien aurkako lasterketa” artikuluan. Eta erantzuna bilatu nahian, besteak beste, Roger Eritja entomologoari luzatu dio gaia. Honen ustez, “eltxoen edo gaixoen kopuruak apalduta, aurre egin dakioke gaixotasunari. Beraz, ez da beharrezkoa espezie bat guztiz akabatzea”.

Zientziak baditu emaitza bitxiak plazaratzen dituen ikerketak eta horrelako bat ekarri digu Josu Lopez-Gazpio kimikariak. Abiapuntua Robert Alan Kloner medikuak eta ikertzaileak 1999. urtean egin zuen ikerketan daukagu. Bihotzarekin lotura zuten arazoen heriotza-tasa izan zuten aztergai eta frogatu zuten neguan udan baino heriotza gehiago gertatzen direla, gehienak abendutik urtarrilera. Antza, neguan tenperaturak hotzagoak izaten direnez horrek azal zezakeen heriotza-tasa hori baina beste kontu batekin egin zuten topo: azaro bukaeran heriotzak handitzen hasten ziren, Gabonetako oporren inguruan maximora iristen ziren eta ondoren berrio jaisten hasten ziren. Zergatik ordea? Azalpen guztiak Gabonetako oporraldiak osasunean duen kaltea artikuluan.

Biologia

Flora aloktonokoa da tokikoa edo jatorrizkoa izan ez arren ohikoa bilakatu den espeziea. Horrelako espezieak ikus daitezke Nansa (Kantabria) eta Bidasoa (Gipuzkoa-Nafarroa) ibaien arroen artean. Izan ere UPV/EHUko ikertzaile batek denera 156 espezie detektatu dira zonalde horietan eta, horrez gain, ikusi du espezie horien %40 puntu bakar batean agertzen dela. Horren adibidea da, esaterako, Urumea ibaian aurkitu den Ipar Amerikako Muhlenbergia schreberi graminearen populazio naturalizatuak (hainbat ziklotan zehar -10 urte gutxienez- haien kabuz populazioa mantentzeko gai diren kanpoko espezieak). Datu guztiak Kantauriar ibaietako espezie exotikoak artikuluan.

Jatorriz Asiakoa den baina 2004an Frantziara iritsi zen Vespa velutina liztorra arazo larriak sortzen ari da Europako erlauntzetan. 2006. urtean antzeman zuten lehen aldiz Frantziako Lot-et-Garonne departamenduan eta handik aurrera Europan inoiz izan den liztor-inbasiorik arrakastatsuena izan da ziur aski velutinaren inbasioa. Erle europarrak harrapatzen dihardu ordutik hona liztor erle-hiltzaile honek. 2010ean Gipuzkoako zenbait erlategitan aurkitu izan zirenez Asiako liztor honen aleak, erlezaintzaren munduaren inguruan kezka handia zabaldu da honek izan dezakeen eragin kaltegarriari dagokionez. Espezie honen ezaugarriak eta jokaera azaldu digute Juan Ignacio Pérez Iglesias eta Miren Bego Urrutia biologoek: David vs Goliat?

Hegaztien behaketen datuak biltzen dituzten hainbat webgune ditugu eskura. Esaterako, Aranzadi Zientzia Elkarteak kudeatzen duen Ornitho webgunea daukagu. Bertan faunan behatzen diren animalien datuak biltzen dira, besteak beste, hegaztienak. Ornitho.eus 2015ean sortu zen eta jada 100.000 behaketa baino gehiagoren datuak ditu. Datu-base hau Euro Bird Portal erakusleiho handiagoan integratzen da. Asier Sarasua biologoak Sustatun Euro Bird Portalen aukera berriak azaldu ditu egunotan. Izan ere, hegaztien joan-etorriak erakusten dituzten mapak sortu daitezke. Milaka ornitologoren datuak bildu eta mapa dinamikoen bidez erakusten dituzte: Hegaztien migrazioa irudikatzen duten mapa animatuak.

Emakumeak zientzian

Ziortza Guezuraga kazetariak genero berdintasuna eta lidergoa batzen dituen Homeward Bound nazioarteko egitasmoaren berri eman digu asteon. Hamar urtean 1.000 emakume zientzialariren kolaborazio sarea sortu nahi du Homeward Boundek, planetan eragina duten politiketan eta erabaki-hartze guneetan eragina izan dezaten. Horrez gain, beste ildo bat du egitasmoak: aldaketa klimatikoari irtenbidean laguntzea. Xehetasun guztiak Ama naturak bere alabak behar ditu artikuluan.

Astrofisika

2069. urtean gizakia Ilargira ailegatu zenaren mendeurrena izango dugu. Urte hori hautatu du NASAk beste urrats handi bat emateko: Izarrarteko lehen misioa gauzatzeko. Sustatu agerkarian eman dizkigute NASAren asmoen berri. Antza, 2069rako aurreikusten du NASAk izarrarteko lehenengo misioa, Alpha Centauri izar sistemara iritsiko litzatekeena, gugandik gertuen dagoen izar sistema.

Fisika

Duela 50 urte aurreikusitako materiaren egoera berria egiaztatu dute zientzialariek, bereizmen handiko elektroskopia erabilita. Illinoisko Unibertsitateko (AEB) ikertzaileek aurrenekoz elektroi baten eta elektroi horrek berak atzean utzitako hutsunearen arteko egoera existentzia frogatzea lortu dute: eszitonioa. Titanio diselenioa (TiSe2) konposatuaren azterketa baliatu dute egoera horren existentzia frogatzeko. Orain topatu berri duten egoera honen ezaugarriak arretaz aztertuko dituzte, bertatik atera daitezkeen aplikazio teknologikoak garatu ahal izateko. Datu guztiak Juanma Gallegoren eskutik: Jaun-andreok: hona hemen eszitonioa, materiaren egoera berria.

———————————————————————–
Asteon zientzia begi-bistan igandeetako atala da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna erreparatuz, Interneteko “zientzia” antzeman, jaso eta laburbiltzea da gure helburua.

———————————————————————–

Egileaz: Uxune Martinez, (@UxuneM) Euskampus Fundazioko Kultura Zientifikoko eta Berrikuntza Unitateko Zabalkunde Zientifikorako arduraduna da eta Zientzia Kaiera blogeko editorea.

———————————————————————–

The post Asteon zientzia begi-bistan #182 appeared first on Zientzia Kaiera.

En #Naukas17 nadie tuvo que hacer cola desde el día anterior para poder conseguir asiento. Ni nadie se quedó fuera… 2017 fue el año de la mudanza al gran Auditorium del Palacio Euskalduna, con más de 2000 plazas. Los días 15 y 16 de septiembre la gente lo llenó para un maratón de ciencia y humor.

Diana González nos plantea una cuestión muy simple: ¿de verdad eres capaz de diferenciar entre un humano y un robot?

Diana González (Pamplonetario): Identidad digital y robots

Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Naukas Bilbao 2017 – Diana González: Identidad digital y robots se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Naukas Bilbao 2017 – Guillermo Peris: Los trapecistas del genoma
2. Naukas Bilbao 2017- Daniel Torregrosa: ¡Estamos rodeados!
3. Naukas Pro 2017: Leni Bascones y los superconductores

Elikagai bankuekin egindako esperimentua merkatuen funtzionamendua erraz ulertzeko. José Luis Ferreira Use markets to feed the poor artikuluan.

Limite fisikoetara heltzen ari da elektronika. Elektroien fluxu sinplea ez diren bestelako fenomeno fisikoetan oinarritutako dispositiboetan oinarrituko da etorkizuna. Aukera horietako bati, espintronikari, ekarpena egiten diote DIPCn fase industrialetik hurbilago egon dadin: Towards a bottom-up engineering of molecular spintronic devices

–—–

Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.

The post Ezjakintasunaren kartografia #196 appeared first on Zientzia Kaiera.

En los próximos años, existe un compromiso legal de todos los países de Europa para mejorar la eficiencia energética de los edificios que se traduce en construir edificios de consumo de energía casi nulo (EECN, o nZEB en inglés), es decir, edificios con un consumo energético mínimo. La Directiva 31/2010/EU fija dos fechas clave: todos los edificios públicos deberán ser EECN a partir del 1 de enero de 2019 y dos años más tarde, el 1 de enero de 2021, deberán serlo todos los edificios de nueva construcción. “Falta sólo un año para el primer compromiso, y sin embargo, muchos países están lejos de alcanzar ese nivel de eficiencia energética en los edificios. Los países que más han avanzado en este reto son los países del centro y norte de Europa”, explica Juan María Hidalgo, coautor del estudio.

Imagen térmica de un bloque de viviendas del País Vasco construido en los años setenta del siglo pasado, donde se evidencia la pérdida de calor por falta de aislamiento. Imagen: Juan María Hidalgo / UPV/EHU.

Esta investigación liderada por la Université de Liege ha sido realizada por más de una docena de investigadores Europeos y analiza la situación de la edificación en siete países del sur de Europa (Chipre, Francia, Grecia, Italia, Portugal, Rumanía y España). Cada país tiene matices en las definiciones técnicas que hacen muy difícil la comparación directa de las normativas y programas de impulso de los EECN. Por ello, “los participantes en el estudio hicimos un esfuerzo para consensuar una metodología común. Era la única manera de hacer comparaciones reales de igual a igual”, añade Hidalgo.

La investigación se ha centrado en el estudio comparativo de las barreras sociales y tecnológicas para el desarrollo de los EECN tanto en la nueva construcción como en la rehabilitación del inmobiliario existente. Hasta ahora, muchos estudios justificaban los retrasos sur-norte debido al contexto económico. Sin embargo, este trabajo ha mostrado que hay otras barreras, como las sociológicas y las condiciones climatológicas de cada país que afectan y mucho a la consecución de los objetivos de los edificios de consumo de energía casi nulo. “La escasa formación de prácticamente todos los agentes, desde la administración, pasando por los operarios de la construcción, hasta la ciudadanía hay una gran cadena humana en la que todavía no se comprende en qué consiste un EECN y cómo conseguirlo”, subraya Hidalgo. Por otro lado, “el diseño de edificios debe ser estudiado más a detalle para solucionar los cambios de estación como el invierno y el verano etc”, añade Hidalgo. “El País Vasco puede ser un buen banco de pruebas para ello ya que tiene casi todas las climatologías del estudio. A pesar de ser un territorio pequeño tenemos que aplicar criterios de diseño muy distintos en zonas de costa, zonas de montaña, zonas del sur…”.

“Si estas barreras no se solucionan, es muy probable que haya insatisfacción con el resultado real, ya que podrían darse problemas de confort térmico, sobrecalentamiento, sobrecostes innecesarios en la construcción etc. a menudo empeorados por un mal funcionamiento de los edificios”, comenta el investigador. Para ello, “el estudio propone mejoras para las normativas, diseño, construcción y uso para de este tipo de edificios”, añade.

Asimismo, el investigador afirma que es más fácil construir un EECN nuevo por las posibilidades de ubicación y orientación, el empleo de materiales nuevos y tecnologías integradas en el diseño, que llevar este concepto al ámbito de la rehabilitación, pues hay menos flexibilidad de maniobra y los costes también aumentan.

Según Juan María Hidalgo, “esperamos que este trabajo contribuya a solucionar las principales dificultades del sector y nos permita llegar al 2020 con un sector de la edificación más preparado, con mejores herramientas y mayor concienciación”. De este modo, “se podrán construir EECN que satisfagan las necesidades de todas las personas, con el mínimo coste y el menor impacto ambiental posible”.

Referencia:

Shady Attia, Polyvios Eleftheriou, Flouris Xeni, Rodolphe Morlot, Christophe Menézo, Vasilis Kostopoulos, Maria Betsi, Iakovos Kalaitzoglou, Lorenzo Pagliano, Maurizio Cellura, Manuela Almeida, Marco Ferreira, Tudor Baracu, Viorel Badescu, Ruxandra Crutescu, Juan Maria Hidalgo-Betanzos (2017) Overview and future challenges of nearly zero energy buildings (nZEB) design in Southern Europe Energy and Buildings doi: 10.1016/j.enbuild.2017.09.043

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo Las barreras a los edificios de consumo de energía casi nulo en el sur de Europa se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Los edificios y el mar
2. ¿Son eficientes las plantas de energía marina?
3. Comunicar la ciencia a la sociedad: el reto de Europa

La espaguetización es el efecto de las fuerzas de marea gravitacionales sobre un astronauta flotando en el espacio cerca de un agujero negro. Cuando estás de pie en el suelo hay una diferencia entre la aceleración de la gravedad en tu cabeza y en tus pies, pero es tan pequeña que no notas nada. Sin embargo, cerca de un objeto de gran masa, como un agujero negro de masa estelar, la diferencia puede ser grande. Conforme te acerques al agujero negro pasará de ser incómoda a un doloroso potro de tortura medieval que te acabará desmembrando.

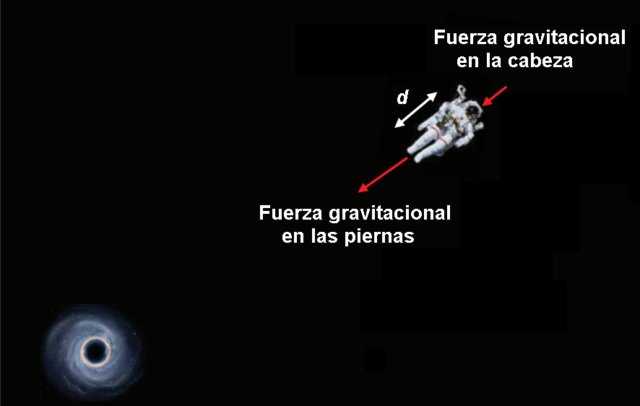
La diferencia entre las fuerzas gravitacionales en los pies y en la cabeza de un astronauta cerca de un agujero negro. Traducción de la figura 1 de Phys. Educ. 53: 015010 (2018).

Los agujeros negros son muy pequeños, tanto que son los objetos astrofísicos más compactos que se conciben. Su tamaño viene dado por el radio de Schwarzschild de su horizonte de sucesos, la frontera más allá de la cual ni siquiera la luz puede escapar. Este radio es proporcional a su masa, en concreto, R = 2 G M/c2, donde G = 6,67 × 10−11 N · m2 kg−2 es la constante de gravitación universal de Newton, c = 3,00 × 108 m/s es la velocidad de la luz en el vacío y M es la masa del agujero negro. La masa de un agujero negro se suele medir en unidades de masa solar (M☉), luego su radio R = 2,95 (M/M☉) km. Por ejemplo, un agujero negro de 10 masas solares tendrá un radio de 29,5 km y uno de 100 masas solares un radio de solo 295 km.

Para calcular la diferencia de fuerzas gravitacionales entre la cabeza y los pies de un astronauta hay que usar un modelo de esta persona junto con su traje espacial. Supongamos que mide 1,70 metros de altura con el traje puesto y que su masa es de 150 kilogramos (unos 80 kg para el traje espacial y unos 70 kg para su peso). Para hacer los cálculos más sencillos vamos a suponer que la cabeza con casco y los pies con botas pesan lo mismo, sean m = 20 kg cada uno, no viéndose afectado el resto del cuerpo; además, supondremos que la distancia entre los centros de masa de la cabeza y de los pies es d = 1,50 m. Un cálculo sencillo [1] nos dice que la diferencia de fuerzas entre la cabeza y los pies es ∆F = R m c2 d/r3, donde m es la masa común de pies y cabeza, d es la distancia que separa sus centros de masa y r es la distancia que separa el centro de masas del astronauta y el centro del agujero negro.

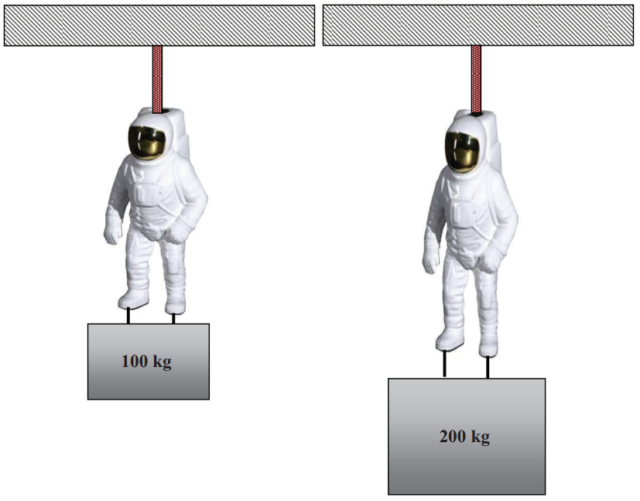
Astronauta colgado a pocos metros sobre la superficie de la Tierra soportando un peso bajo sus pies. Figura 3 de Phys. Educ. 53: 015010 (2018).

Usando la fórmula anterior puedes hacer los cálculos para cualquier agujero negro que desees. Solo como ejemplo supondré un agujero negro de 10 masas solares y 61 km de diámetro, con lo que ∆F = 3,11 × 109 / (­r/R)3 newtons (N). Para un astronauta a una distancia de 200 radios de Schwarzschild, unos 5900 km, se obtiene ∆F = 388 N; esto equivale a soportar unos 40 kg de peso sujeto a los pies de un astronauta que esté colgado por un cable de acero a pocos metros de la superficie terrestre (como ilustra la figura 2). Quizás sea algo incómodo, pero se puede soportar sin problemas.

La distancia más próxima al agujero negro que podrá soportar el astronauta depende de lo que soporte su cuerpo. Pero seguro que estará muy incómodo a una distancia 130 radios de Schwarzschild, unos 3800 km, pues ∆F = 1400 N; esto equivale a soportar unos 140 kg de peso bajo los pies. ¿Cuánto podrá soportar hasta que empiece a desmembrarse? A una distancia de 100 radios de Schwarzschild, unos 3000 km, soportará ∆F = 3100 N, un peso colgante de unos 310 kg tirando de los pies. ¿Podría acercarse a unos 1500 km del agujero negro? No, pues a unos 50 radios de Schwarzschild debería ser capaz de soportar unos 2500 kg de peso colgados de los pies.

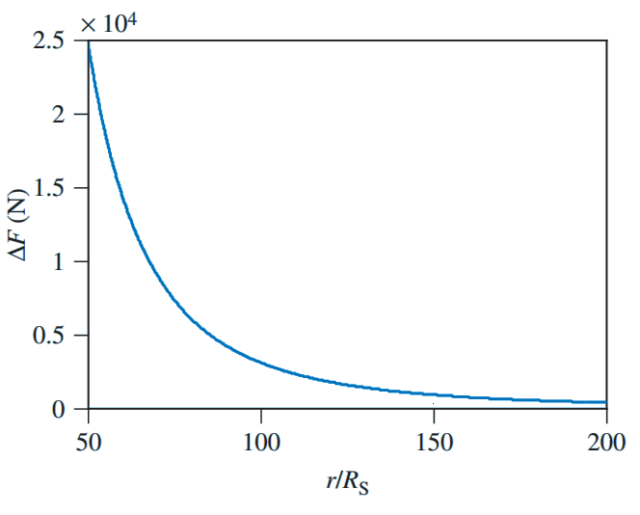
Diferencia de fuerzas gravitacionales entre pies y cabeza para un astronauta en función de la distancia a un agujero negro de diez masas solares. Figura 2 de Phys. Educ. 53: 015010 (2018).

Los agujeros negros son objetos muy pequeños y el disco de acreción de materia que les rodea suele tener menos de 10 radios de Schwarzschild de diámetro. El ojo humano tiene una resolución angular mínima de un minuto de arco, o sea, unos 30 cm a 1 km de distancia (0,3 miliradianes). La Luna y el Sol tienen un diámetro aparente en el cielo de unos 9 miliradianes. Para ver el disco de acreción de un agujero negro con un tamaño similar al de la Luna en el cielo hay que acercarse a unos 1100 radios de Schwarzschild; a esa distancia las fuerzas de marea gravitacionales serán tan pequeñas que el astronauta no las notará.

¿Qué pasa con un agujero negro sin disco de acreción? Un agujero negro sin disco de acreción deforma la imagen del fondo estelar a su alrededor gracias a su efecto como lente gravitacional. Para disfrutar de este efecto (muy popular en las representaciones artísticas de los agujeros negros que decoran las noticias sobre las ondas gravitacionales detectadas por LIGO/Virgo) hay que acercarse a unos 220 radios de Schwarzschild. Por fortuna a esa distancia el astronauta sentirá que sus pies le pesan un poco, pero por lo demás estará perfectamente cómodo.

En la divulgación de la Física una fórmula vale más que mil palabras. Te animo a usar la fórmula que decora este texto para realizar cálculos con otros agujeros negros, estrellas de neutrones y cuerpos astrofísicos. Sobre todo si eres profesor de enseñanza secundaria; vamos, anima a tus alumnos a realizar estos cálculos sencillos. La mejor manera de apreciar lo pequeños que son los agujeros negros es calcular cuánto nos podemos acercar a ellos para verlos con el mismo detalle con el que vemos la Luna en el cielo.

Este post ha sido realizado por Francis Villatoro (@Emulenews) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.

Referencias

[1] Stylianos V. Kontomaris, Anna Malamou, “A presentation of the black hole stretching effect,” Physics Education 53: 015010 (2018), doi: 10.1088/1361-6552/aa8d22.

El artículo La espaguetización cerca de un agujero negro se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. ¿Tiene límite el tamaño de un agujero negro?
2. #Quantum13 ¿Clásico o cuántico? La paradoja del agujero negro
3. Un agujero negro de laboratorio con radiación de Hawking caliente

Ziortza Guezuraga Antartika ildo hartuta, eta zientziaren arlotik, klima aldaketa, genero berdintasuna eta lidergoa batzen dituen nazioarteko ekintza da Homeward Bound. Mundu osoko emakume zientzialariak bildu eta urtebetez lidergo tekniketan, taldeen kudeaketan, nazioarteko harremanetan eta proiektuen finantzazioan trebatzea, besteren artean, da proiektuaren helburu nagusia. Hamar urtean 1.000 emakume zientzialariren kolaborazio sarea sortu nahi du Homeward Boundek, planetan eragina duten politiketan eta erabaki-hartze guneetan eragina izan dezaten.

1. irudia: Klima-aldaketaren ondorioak nabarmenen izaten dira Antartikan.

Zientziaren alorrean emakumeak duen egoera dago proiektuaren oinarrian. I+G alorrean emakumeen errepresentazio maila %29koa da batez beste mundu mailan Unescoren datuen arabera. Mendebaldeko Europan eta Ipar Amerikan %32ra igotzen da portzentaia.

Europar Batasunari dagokionez ere, ikertzaileen %33 dira emakumeak Komisio Europarraren She Figures txostenak adierazten duenez. Estatu mailan %39an dago emakumeen portzentaia, ekonomia ministerioaren Científicas en cifras 2015 txostenaren datuei begira. Euskadiko datuei erreparatuta emakumeen portzentaia %35ean dagoela ikus daiteke Zientzia 2017 txostenean.

Ikertzaile karreran aurrera egin ahala, baina, beheranzko joera du emakumeen portzentaiak. Hala, ikertzaile karreraren maila apalenetan emakumeen kopurua gizonen parekoa edota gehiago bada ere, karreran aurrera eta postuetan gora egin ahala emakumeen portzentaia jaitsi egiten da, dela estatu mailako unibertsitate eta OPISetan:

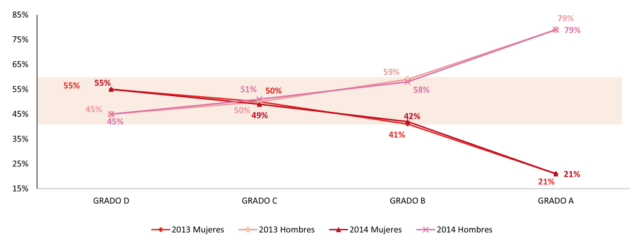
2. irudia: Emakumeen portzentaia ikertzaile karreran estatu mailako unibertsitate eta OPISetan.

Dela CSICen:

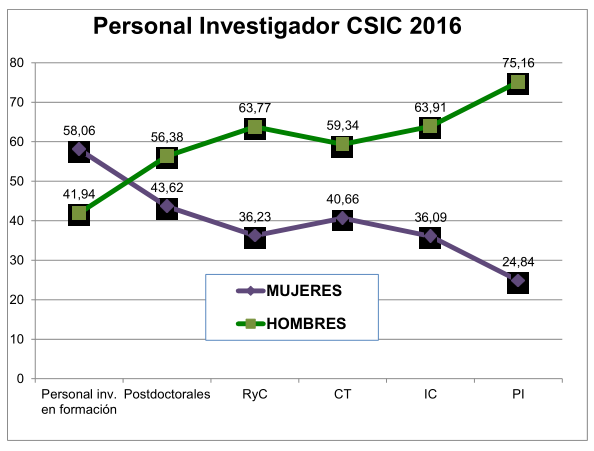
3. irudia: CSICko ikertzaile-karreraren eboluzioa sexuaren arabera.

Edo UPV/EHUko ikertzaile eta irakasleen banaketa:

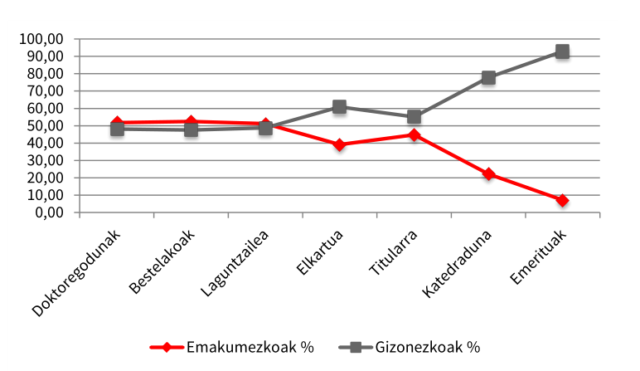
4. irudia: UPV/EHUko ikertzaileen eta irakasleen banaketa sexuaren arabera.

Edota BERCetakoa:

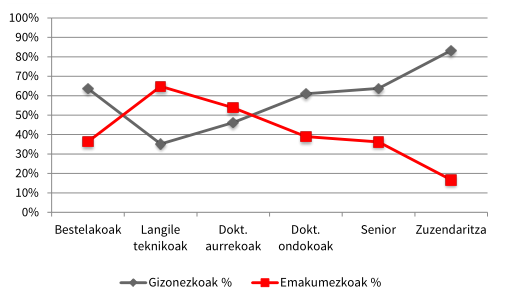
5. irudia: BERCetako banaketa sexuaren arabera.

Kasu guztietan patroi bera errepikatzen da: karreran aurrera egin ahala emakumeen portzentaia behera egiten du. Aurten bertan Rosa María Menéndez izendatu dute CSIC erakundearen historiako lehen presidente emakumea. Euskal unibertsitate pribatuetan egoera ezberdina da; kontuan izan behar da, hala ere, karrera profesionala bestelakoa dela, ez duela bide bera jarraitzen eta, beraz, ez direla konparagarriak.

Emakumeek zientzian duten egoera irauli nahi du Homeward Bound programak. Horretarako lau ataletan banatutako programa garatu dute:

1. Urtebeteko iraupena duen lidergo formakuntza birtuala.
2. 12 eguneko formakuntza intentsiboa lidergoan eta estrategian.
3. 6 eguneko formakuntza berezitua aldaketa klimatikoan.
4. Hiru asteko espedizioa Antartikara.

Antartikara espedizioa

Programaren baitan Antartikara espedizioa egitea ez da ausaz hartutako erabakia. Esplorazioaren paradigma izateaz gain, klima-aldaketaren gaian, Homeward Bound programaren ildo nagusietako bat, erreferente da Antartika.

Klima-aldaketaren ondorioak Antartikan (eta baita Antartidan ere) dira nabarmenen, Eñaut Izagirrek azaldu bezala, glaziarrak klimaren indikatzaile sentikorrak dira. Hori hala, klima-aldaketaren eboluzioaren ikerketan Antartika gehien ikertzen den puntuetako bat da. NASAren Global Climate Change: Vital Signs of the Planet programak (klima-aldaketaren jarraipena egiten duen programa), esaterako, Antartikaren izotz masa du aldaketa klimatikoaren egoeraren adierazle moduan.

6. irudia: Landare bizitza lurrazalean eta ozeano azalean, 1997ko irailetik 2017ko irailera arteko satelite behaketez osatutako animazioa. (Iturria: NASA)

Klima-aldaketari erantzun azkarrenetarikoak ematen ari dira Antartikaren zenbait zonaldek eta hauek zuzenean ikertzeaz gain, Homeward Bound proiektuan parte hartzen duten emakumeen arteko harremanak bultzatzea da bertara joateko beste arrazoietako bat. Klima-aldaketaren aurka emakume zientzialarien sare kolaboratiboa sortzea.

Emakumeak zientzian duten papera indartzeko, emakume zientzialarien arteko harremanak sustatzeko eta klima-aldaketari aurre egiteko asmoa du Homeward Bound nazioarteko proiektuak. Zientziaren baitako emakumeen inpaktua eta influentzia handitu planetan eragina duten politiketan eta erabakietan egungo egoerari aurre egiteko.

Zientziak gaur egun dituen erronketako biri, emakumeak zientzian duten egoerari eta aldaketa klimatikoari irtenbidean laguntzeko asmotan sortutako ekimena da Homeward Bound.

Erreferentziak:

• European Commission – Research and Innovation.
• Homeward Bound
• NASA – Global Climate Change: Vital Signs of the Planet.
• National Geographic – See the Extreme Ice Changes Near the Antarctic Peninsula (bideoa, ingelesez).
• NASA – The Arctic and the Antarctic Respond in Opposite Ways (bideoa, ingelesez).
• Ministerio de Economía, industria y competitividad – Científicas en cifras.
• CSIC – Mujeres y ciencia.
• Ikerbasque – Zientzia Euskadin 2017.

———————————————————————–

Egileaz: Ziortza Guezuraga kazetaria eta UPV/EHUko Kultura Zientifikoko Katedraren kolaboratzailea da.

——————————————————————

The post Ama naturak bere alabak behar ditu appeared first on Zientzia Kaiera.

Catástrofe Ultravioleta #22 HUMOR

A finales de los años cincuenta un tipo de gesto arisco se paseaba por los pasillos de los principales estudios de televisión empujando un misterioso carrito. En su interior había una caja cuyo contenido cambiaría la historia de la televisión y al forma en que hoy en día entendemos el humor. Para saber qué contenía tendrás que acompañarnos un ratito.

Agradecimientos: Ángel Martín, Berto Romero, Diego Cuevas, Ernesto Sevilla, Joaquín Reyes, Santiago de Luca, Pedro Toro, Raquel Sastre, Miguel Noguera, Antonio Castelo, Patricia Sornosa, José María del Río, Ray Jaén, Manuel Arias, el efecto halo y las risas de la gente muerta.

* Catástrofe Ultravioleta es un proyecto realizado por Javier Peláez (@Irreductible) y Antonio Martínez Ron (@aberron) con el patrocinio parcial de la Cátedra de Cultura Científica de la Universidad del País Vasco y la Fundación Euskampus. La edición, música y ambientación obra de Javi Álvarez y han sido compuestas expresamente para cada capítulo.

El artículo Catástrofe Ultravioleta #22 HUMOR se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Preparados para una Catástrofe Ultravioleta
2. Catástrofe Ultravioleta #13 LEVIATÁN
3. Catástrofe Ultravioleta #14 VULCANO

Ilustración de Dusan Petricic

Cuando una medida se convierte en un objetivo deja de ser una buena medida, dice la Ley de Goodhart, bien conocida en el campo de la sociología. Y si lo pensamos un poco es lógico:Los humanos somos, bueno, humanos, de manera que consciente o inconscientemente tendemos a tomar el camino del mínimo esfuerzo hacia el cumplimiento de nuestros objetivos. Si el objetivo es una medida concreta buscaremos la manera de alcanzarla con el menor coste para nosotros, tenga o no tenga sentido desde el punto de vista de la intención original; como en el viejo chiste soviético, si el objetivo de la factoría es hacer 1.000 toneladas de tornillos podemos cumplirlo fabricando un único tornillo de 1.000 toneladas, aunque sea perfectamente inútil y absurdo en el contexto de la planificación global. Y si en algo somos buenos los humanos es en buscar atajos, simplificaciones, recortes y reinterpretaciones para justificar casi cualquier manipulación de esta clase.

Por eso cualquier medida que se designa como objetivo es susceptible de ser retorcida del modo más torticero posible, y por eso deja de ser una buena medida de lo que ocurre en el sistema: porque automáticamente deja de tener valor como indicación objetiva de su estado. Esta es la razón de que el número de publicaciones se haya convertido en una pésima medida del estado de un sistema de investigación, y de la existencia de un nuevo fenómeno como son las famosas ‘revistas predadoras’. Un resultado previsible según la ley de Goodhart.

Si el modo de avanzar en lo profesional y de recibir mejor financiación para la investigación científica es aumentar el número de publicaciones (maximizar esta medida en particular) los científicos se encuentran con un poderoso incentivo para manipular esta variable. Si pueden estirar los resultados de un experimento a tres publicaciones en lugar de a una, lo harán; si pueden maximizar los resultados de su tesis en términos de número de artículos publicados tienen que hacerlo. Si lo que cuenta a la hora de obtener un puesto de trabajo o de conseguir una beca es el número de artículos publicados quien no lleve a cabo este tipo de estrategias resultará perjudicado en la carrera y se quedará atrás. Las plazas, y los proyectos, serán para quien sí lo haga.

Aquí es donde surgen las ‘revistas predadoras’, que simplemente aprovechan esta necesidad de millones de investigadores de todo el mundo para sacar dinero. Lo que ofrecen es simple: publicar artículos de baja o nula calidad de modo rápido y sin muchas preguntas a cambio de dinero. Muchos investigadores cuentan con presupuestos para publicar, ya que algunas revistas (incluso de la máxima calidad) cobran por la publicación. Estas ‘revistas predadoras’ tan sólo obvian la parte cara del asunto: la revisión por pares, el análisis de calidad previo, y proporcionan una vía para a cambio de dinero añadir de modo sencillo una línea al currículo. Dotadas de nombres rimbombantes que suenan legítimos, con frecuencia radicadas en países como China o la India y a veces complementadas por congresos y seminarios de nombre impresionante y calidad nula estas revistas cubren un nicho de mercado: el de los investigadores desesperados por cumplir con el requisito de número de publicaciones que se les impone.

El resultado, por supuesto, es que el sistema completo deja de funcionar. Los criterios de calidad casi han desaparecido reemplazados por criterios basados en la pura cantidad; el dar mayor puntuación a las revistas de alto impacto no basta, porque ahora es el impacto de las revistas lo que se ha pervertido (siguiendo la Ley de Goodhart). Los currículos se alargan y en el fárrago de publicaciones resulta muy difícil separar el grano (las revistas serias que son leídas por otros científicos) de la paja (las predadoras que nadie lee). Los requisitos de mínimos se hacen astronómicos, como los recientes de la ANECA española que de media exigen 130 artículos para cualificarse para la categoría de catedrático. Y la medida, que se supone que sirve para garantizar una producción científica razonable, se hace completamente irrelevante e incluso contraproducente. Hasta tal punto que ahora es necesario luchar contra la proliferación de ‘revistas predadoras’ que, como malas hierbas, amenazan con ahogar el sistema científico convencional.

Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.

El artículo Revistas predadoras y la Ley de Goodhart se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Flujo de manuscritos entre revistas científicas
2. La contradicción de la publicación
3. Qué es un dato: la longitud de un hueso

Juan Ignacio Pérez eta Miren Bego Urrutia Defentsak eta erasoak

———————————————————————————————————–

Jatorriz Asiakoa den baina 2004an Frantziara iritsi zen Vespa velutina liztorra arazo larriak sortzen ari da Europako erlauntzetan. Liztor hori Vespa crabro Europako liztorraren oso antzekoa da, baina honek ez bezala, erleak erabiltzen ditu proteina-iturri modura.

Irudia: ‘Vespa velutina’ liztorrak erleak erabiltzen ditu proteina iturri gisa.

Asiako liztorrak, beraz, Europan sartu zenez geroztik erle europarrak harrapatzen dihardu. Frantziara heldu zenetik hedatzen ari da liztor erle-hiltzailea, eta Pirinioak zeharkatzea ere lortu du. 2010ean Gipuzkoako zenbait erlategitan aurkitu izan zirenez Asiako liztor honen aleak, erlezaintzaren munduaren inguruan kezka handia zabaldu da honek izan dezakeen eragin kaltegarriari dagokionez.

Vespa generoaren barruan, beraz, erleak harrapatzen ez dituzten liztorrak ditugu batetik, bertako Vespa crabro Europako liztorra esaterako, eta erle-harrapariak direnak bestetik; azken hauen artean Vespa velutina ez da bakarra, badira elikatze-jokaera bera erakusten duten beste espezie batzuk. Horietako bat liztor japoniarra dugu: Vespa mandarinia japonica liztor japoniarra ere harraparia da, baina bere harrapakinen artean bada bat arazo larriak ekar diezazkiokeena; hain larriak non harrapakinak harraparia hil egin dezakeen. Apis cerana japonica izeneko erle japoniarra da ustezko harrapakina. Aspalditik zen jakina erle hauek garaile atera zitezkeela liztorraren kontrako lehian, baina hasieran ziztadaka hiltzen zutela uste bazuten, gero ikusi zen ezetz, beste prozedura sofistikatuago bat erabiltzen zutela liztorra garbitzeko. Ikus dezagun orain nola akabatzen duen txikiak (erleak) handia (liztorra).

Liztorrak erle bati erasotzen dionean, berehala hurbiltzen zaizkio bostehunetik gora erle, eta liztorra inguratu egiten dute. Egia esan, inguratu baino gehiago egiten dute, “erle-pilota” bat osatzen baitute, eta pilota horren erdi-erdian geratzen baita liztorra. Bada, berehala 48 °C-ra igotzen da tenperatura pilotaren erdigune horretan, eta horixe da, tenperatura horixe hain justu, liztorra hiltzen duena.

Bideoa: Apis cerana japonica erleak beroa baliatzen du Vespa mandarinia liztorrari aurre egiteko. (Iturria: National Geographic)

Liztorraren hiltze-muga 44-46 °C-koa da, eta, beraz, 48 °C tenperatura handiegia da berarentzat. Ez, ordea, erleentzat, 48-50 °C artean baitago horien hiltze-tenperatura. Ikusi dugunez, bizitzaren ertz bero hori oso zorrotza da zenbait kasutan, zorrotzegia animalia batzuentzat. Eta, ikusi dugunez, badago desberdintasun txikiei etekina ateratzen dion espezierik ere.

Tamalez, erle japoniarrek erakusten duten babes-jokaera hori ez da unibertsala erleen artean, eta hori dela eta erle europarrek (Apis mellifera) japoniarrek erabiltzen duten erle-pilota hipertermikoa osatzeko jokaera garatzen ez duten artean, Asiako liztor hiltzaileari aurre egiteko modu bakarra gizakiaren bidezkoa izan beharko da. Bi modu omen daude: erregina gazteak harrapatzea udaberrian habia berria eraiki orduko, edo/eta habiak atzeman eta suntsitzea. Ea laster “ikasten” duten gure erleek ere bizitzaren ertz beroa baliatzen!

—————————————————–

Egileez: Juan Ignacio Pérez Iglesias (@Uhandrea) eta Miren Bego Urrutia Biologian doktoreak dira eta UPV/EHUko Animalien Fisiologiako irakasleak.

—————————————————–

Artikulua UPV/EHUren ZIO (Zientzia irakurle ororentzat) bildumako Animalien aferak liburutik jaso du.

The post David vs Goliat? appeared first on Zientzia Kaiera.

En el imaginario colectivo los planetas de un sistema solar giran alrededor de su estrella en el mismo plano, y este plano es también el plano ecuatorial de la estrella. La estrella también gira, y su eje de giro se alinea con los ejes de giro de las órbitas planetarias, dando la impresión de un sistema bien ordenado. Pero el universo es caprichoso en sus creaciones.

Gliese 436 es una estrella de la que se ha escrito mucho, ya que alberga un planeta del tamaño de Neptuno, Gliese 436b, que se evapora como un cometa. En una investigación cuyos resultados se publican ahora en Nature, un equipo de investigadores encabezados por Vincent Bourrier, de la Universidad de Ginebra (Suiza), demuestran que, además de su enorme nube de gas, el planeta Gliese 436b también tiene una órbita muy especial. Es “polar”: en lugar de orbitar en el plano ecuatorial de la estrella, el planeta pasa casi por encima de los polos estelares.

La inclinación orbital es la última pieza de un rompecabezas que ha desconcertado a los astrónomos durante 10 años: a diferencia de los planetas del Sistema Solar cuyas órbitas forman círculos casi perfectos (aunque sean en realidad elipses), la de Gliese 436b forma una elipse muy plana, es decir, su distancia a la estrella varía mucho a lo largo de su órbita.

Gliese 436b está sometido a enormes fuerzas de marea porque pasa increíblemente cerca de su estrella, apenas el 3% de la distancia que separa la Tierra del Sol. La estrella Gliese 436 es una enana roja cuya vida activa es muy larga, por lo que las fuerzas de marea que induce deberían haber conseguido haber acercado la órbita del planeta a un círculo pero, por alguna razón, no lo ha hecho.

¿Y cual podría ser la causa?

Las arquitecturas orbitales de los sistemas planetarios son registros fósiles que nos dicen cómo se han formado y evolucionado. Un planeta perturbado por el paso de una estrella cercana o por la presencia de otros planetas masivos en el sistema mantendrá un registro, por así decirlo, en su órbita. La existencia de un planeta desconocido, más masivo y distante que lo perturbase explicaría no solo por qué Gliese 436b no está en una órbita circular, sino también por qué está en una órbita polar.

Los mismos cálculos que apuntan a esta conclusión también predicen que el planeta no siempre ha estado tan cerca de su estrella, sino que podría haberse acercado recientemente (en términos astronómicos). Por lo tanto, el “planeta que se evapora” no siempre se habría evaporado, sino que habría sido empujado hacia la estrella por la gravedad de un planeta compañero aún no detectado. La caza no ha hecho más que empezar.

Referencia:

Vincent Bourrier et al (2017) Orbital misalignment of the Neptune-mass exoplanet GJ 436b with the spin of its cool star Nature doi: 10.1038/nature24677

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

Este texto es una colaboración del Cuaderno de Cultura Científica con Next

El artículo Algo raro pasa alrededor de Gliese 436 se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. La habitabilidad de las exotierras alrededor de estrellas enanas rojas
2. ¿Qué pasa si me río de todo?
3. Catástrofe Ultravioleta #16 RARO

El niño y los sortilegios es una fantasía lírica (en dos partes para solistas y coros con orquesta) de Maurice Ravel sobre un libreto de la escritora Sidonie Gabrielle Colette. Se estrenó en Montecarlo el 21 de marzo de 1925 y, un año más tarde, se presentó en el Teatro de la Ópera Cómica de París.

Portada diseñada por André Hellé para la primera edición de la ópera. Imagen: Wikipedia.

En 1916, Jacques Rouché, en ese momento el director de la Ópera de París, solicitó a su amiga Colette que escribiera un libreto para ballet, de ambiente fantástico, sobre los sueños de un niño perseguido por animales y objetos por él maltratados: Ballet pour ma fille. Ravel fue elegido para musicalizar la historia. Pero, debido a problemas personales, abandonó el proyecto hasta 1919, año en que retomó el libreto y descubrió sus posibilidades, decidiendo crear una ópera y no un ballet.

El niño y los sortilegios es una sucesión de cuadros independientes que mezclan diferentes géneros musicales: jazz, foxtrot, ragtime, polka, dúo maullador, vals y música coral. Para reproducir las numerosas onomatopeyas del libreto de Colette, Ravel utilizó instrumentos poco habituales, como un rallador de queso, una carraca con manivela, crótalos, bloques de madera, látigo,…

La obra tiene lugar en el interior de una casa en Normandía. El protagonista, el niño, intenta, con pereza, hacer sus deberes. A ver que las tareas no están terminadas, la madre castiga al niño dejándole como merienda una taza de té y un trozo de pan duro. Al quedarse solo, el protagonista demuestra su enojo rompiendo objetos y maltratando a los animales domésticos. Aburrido, se recuesta sobre un sillón; en ese momento entran en acción los sortilegios a los que alude el título: el sillón comienza a danzar con una silla, los muebles lo imitan enfadados con el protagonista,… El niño, atemorizado, llora. De las páginas de un libro por él destrozado acude una princesa a consolarlo, aunque le reprocha su conducta. Ella desaparece para ocupar su lugar un viejo amenazante, que le plantea problemas matemáticos para resolver: es la Aritmética. Sale la luna, el gato y la gata se unen en un ceremonioso dueto amoroso. Los animales que habitan el jardín desafían y amenazan al niño: entablan extraños diálogos, realizan frenéticas danzas, con tanta euforia que hieren a una ardilla. El niño, conmovido, ayuda al roedor. El resto de los animales, al ver el acto de compasión del protagonista, comienzan a dudar de su maldad. Lo acompañan hasta la casa, finalizando de este modo los sortilegios: el niño regresa al mundo real, reclamando a gritos la presencia de su madre.

En una de las escenas, las matemáticas son las encargadas de atormentar al niño.

[…] (Los patea. Voces chillonas salen de entre las páginas que dejan ver a las gesticulantes figuritas de los números. De un álbum abierto como un techo, salta un viejecillo jorobado, de nariz ganchuda, barbado, vestido con números, sombrero en forma de “pi”, ceñido con una cinta métrica y armado con una regla. Sostiene un libro de madera que golpea cadenciosamente. Baila mientras recita fragmentos de problemas.)

EL VIEJECILLO: ¡Dos grifos de agua fluyen a un tanque! ¡Dos ómnibus dejan una estación a veinte minutos de intervalo, valo, valo, valo! ¡Una campesina, sina, sina, sina, lleva todos sus huevos al mercado! ¡Un mercader de telas, telas, telas, telas, vende seis metros de trapo! (ve al niño y se le acerca de una manera malévola.)

EL NIÑO: (aterrado) ¡Dios mío! ¡Es la Aritmética!

EL VIEJECILLO, LOS NÚMEROS: ¡Tica, tica, tica! (Danzan alrededor del niño multiplicando sus maléficos pases.) Once más seis: ¡veinticinco! Cuatro más cuatro: ¡dieciocho! Siete por nueve: ¡treinta y tres!

EL NIÑO: (sorprendido) ¿Siete por nueve, treinta y tres?

LOS NÚMEROS: (levantando las hojas y chillando) Siete por nueve: ¡treinta y tres! etc.

EL NIÑO: (con audacia) Tres por nueve: ¡cuatrocientos!

EL VIEJECILLO: (balanceándose para mantener el ritmo) Milímetro, centímetro, decímetro, decámetro, hectómetro, kilómetro, miriámetro. ¡Sin fallar! ¡Qué felicidad! ¡Millones, billones, trillones, y fracciones!

LOS NÚMEROS, EL VIEJECILLO: ¡Dos grifos de agua fluyen a un tanque! etc.

LOS NÚMEROS: (hacen bailar al niño con ellos) Tres por nueve: ¡treinta y tres! Dos por seis: ¡veintisiete! ¿Cuatro más cuatro?… ¿Cuatro más cuatro?…Cuatro por siete: ¿cincuenta y nueve? Dos por seis: ¡treinta y uno! Cinco por cinco: ¡cuarenta y tres! Siete más cuatro: ¡cincuenta y cinco! (Giran desenfrenadamente. El niño, aturdido, cae al suelo. El Viejecillo y el coro se retiran.) Cuatro más cuatro: ¡dieciocho! Once más seis: ¡veinticinco!

(El niño se sienta con dificultad. La luna ilumina la habitación. El gato negro se desliza bajo el sillón. Se estira, bosteza y se relame. El niño no lo ve pues, cansado, tiene la cabeza apoyada en un taburete. El gato juega, haciendo rodar una bola de estambre. Se acerca al niño e intenta jugar con su cabeza rubia como si fuera una pelota.)

EL NIÑO: ¡Oh! ¡Mi cabeza! ¡Mi cabeza! […]

Es una lástima que las matemáticas se perciban sistemáticamente como una ‘maldición’… ¡incluso en la ópera!

Os dejo debajo la original versión de Giovanni Munari y Dalila Rovazzani, de esta escena de El niño y los sortilegios:

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.

El artículo ¡Es la Aritmética! se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. La lección… de aritmética
2. Uno, dos, muchos
3. Aritmética afectiva