Feed aggregator

Juanma Gallego Duela 50 urte aurreikusitako materiaren egoera berria egiaztatu dute zientzialariek, bereizmen handiko elektroskopia erabilita. Elektroi baten eta elektroi horrek berak atzean utzitako hutsunearen arteko lotura bitxian oinarritzen da eszitonioa.

Denbora gutxian, gauzak asko konplikatu dira unibertsoaren eskala txikienetan. 1930eko hamarkadara arte protoiak, neutroiak, elektroiak eta fotoiak baino ez zeuden testu liburuetan. Partikula horien bitartez, zientzialariak gai ziren natura bere osotasunean azaltzeko. Fotoiak alde batera utzita, kalean inkesta bat eginez gero, seguruenera horiek izango dira “nola osatuta dago materia?” galderari gehienek emango geniokeen erantzuna. Eskola garaietako eskemak berehala datoz burura; eguzki sistema baten antzera osatuta dagoen atomoaren irudi polit hori: protoiak eta neutroiaz osatutako “eguzki” bat, eta inguruan dantzan dabiltzan elektroiak, planetak balira bezala.

1. irudia: Eszitonioaren irudikapena. Egoera ordenatua urdinez marraztu dute, eta, eszitoiak, hori kolorez. (Argazkia: Peter Abbamonte / Ilinoisko Unibertsitatea)

Fisikariek badakite, ordea, gauzak askoz konplexuagoak direla. Bai protoiak zein neutroiak quark izeneko oinarrizko partikula txikiez osatuta daudelako, baina askoz partikula gehiago daude. Horrenbeste, ezen “partikulen zooa” kontzeptua asmatu baitzen.

Gehienak, laborategian fisikariek marraztutako koadernotan ageri ziren, eta esperimentuen bitartez horien existentzia frogatzen aritu dira. Matematika baliatuz, mundua osatzen duten adreiluak zeintzuk diren asmatzen eta ordenatzen aritu dira fisikariak. Horrela jaio zen gaur eredu estandar gisa ezagutzen duguna.

Eredu estandarrean, oinarrizko 12 partikulek osatzen dute materia, eta horiek loturik egotea ahalbidetzen duten indarren partikulak ere badira. “Ez da munduaren errepresentaziorik garbiena, baina datu guztiek bat egiten dute”, Sean Carroll fisikari ezagunaren esanetan. Hori guztia Lurreko eskalei dagokienean, Carrollek berak The Particle at the End of the Universe liburuan aitortzen duenez. Izan ere, unibertsoaren handitasunean gertatzen diren fenomenoak azaltzeko materia eta energia ilunaren kontzeptuetara jo beharra dago, ezinbestean.

2012an LHC Hadroien Talkagailu Handian Higgs bosoia aurkitu zutenean, eredu estandar horretan aurkitzeko zegoen azken partikula bezala aurkeztua izan zen. Baina argitu gabeko eremuak geratzen ziren. Ezagunenak, arestian aipatutako materia eta energia ilunak. Argitzeko dauden beste eremu zehatzagoak badira. Tartean, gaurkoan mintzagai daukagun exzitonioa.

Elektroiaren dantza

Ezagunak dira materiaren egoera arruntak: solidoa, likidoa eta gasa. Hain ezaguna ez bada ere, plasma ere materiaren laugarren egoera bezala ezagutzen da. Gasak tenperatura altua hartzen duenean, bertako atomo gehienak ionizatu egiten dira. Egoera horretan daude izarrak, gure Eguzkia barne.

Horietaz gain, ordea, beste egoera bereziak ere badira: fluido superkritiko deritzenak, edota Bose-Einsteinen eta Fermiren kondentsatuak. Baina orain, zerrenda horri egoera berri bat gehitu behar zaio: eszitonioa.

Harvardeko Unibertsitateko (AEB) fisikari Bert Halperin matematikariak materiaren egoera hau aurreikusi zuen 1960ko hamarkadan, beti ere maila teorikoan. Halperinen proposamenaren arabera, elektroi batek eta elektroi horrek utzitako eremu hutsak osatutako egoera bat egon behar zen. Halere, lehen hurbilpena Yakol Frenkel fisikariak egin zuen, 1931n.

2. irudia: 2. irudia. Aurkikuntzan parte hartu duten ikertzaileak: Mindy Rak, Peter Abbamonte eta Anshul Kogar. Irudia: (Argazkia: Brian Stauffe / Illinoisko Unibertsitatea)

Proposamena mahai gainean jarri zenetik, fisikariak ez dira ados jarri materiaren egoera berri horrek izan beharko lituzkeen ezaugarrien inguruan. Batzuen ustez, isolatzailea izango litzateke; beste batzuek eroalea edo superfluidoa izango litzatekeela esan zuten. Orain, Illinoisko Unibertsitateko (AEB) ikertzaileek aurrenekoz egoera horren existentzia frogatzea lortu dutela jakinarazi dute Science aldizkarian.

Duela 50 urte inguru Halperinek aurreikusi zuen bezala, erdieroale diren materialetan, kitzikatuak direnean, elektroiek atomoaren hurrengo energia mailara jauzi egiteko gaitasuna dute. Alabaina, atzean utzitako tarte horretan hutsune bat uzten dute. Hutsune horrek karga positiboa duen partikula baten funtzioa betetzen du, eta jauzi egin duen elektroia erakartzen du. Indar elektrostatikoari esker, lotuta mantentzen dira bai elektroia zein atzean utzitako hutsunea. Karga negatiboaren eta positiboaren arteko lotura honek konposatutako partikula osatzen du: eszitoia.

Titanio diselenioa (TiSe2) konposatuaren azterketa baliatu dute egoera horren existentzia frogatzeko. Orain arte halako estrukturak ongi bereizteko moduko teknologiarik ez zegoela eta, bereizmen handiagoko elektroskopia berezia garatu behar izan dute. Seguruenera, ez da halako materiala lortu den aurreneko aldia, zientzialariak aspaldi dabiltzalako horren bila, baina bai da aurreneko aldia ziurtasunez frogatu dela. Ikertzaileek diotenez, bost aldiz lortu dute emaitzak errepikatzea, kristal mota desberdinak erabilita. Batez ere, aurrean zeukatena Peierls-en fasea izenekoa ala eszitonioa ote zen bereiztea ezinezkoa izan da orain arte, bi fenomenotan kristaletan antzeko simetriak marrazten direlako.

Ikertzaileek orain aurrean duten erronka da topatu berri duten egoera honen ezaugarriak arretaz aztertzea, bertatik atera daitezkeen aplikazio teknologikoak garatu ahal izateko. Halere, egileek aitortu dutenez, aplikazio hauek “guztiz espekulatiboak” dira, eta, batez ere, mekanika kuantikoaren misterioak argitzeko baliagarria izango dela aurreratu dute.

Erreferentzia bibliografikoa:

Kogar, Anshul et a. Signatures of exciton condensation in a transition metal dichalcogenide. Science, 2017; 358 (6368): 1314 DOI: 10.1126/science.aam6432

———————————————————————————-

Egileaz: Juanma Gallego (@juanmagallego) zientzia kazetaria da.

———————————————————————————-

The post Jaun-andreok: hona hemen eszitonioa, materiaren egoera berria appeared first on Zientzia Kaiera.

Cangrejo (Cancer productus ) visto desde abajo. El color púrpura lo proporciona la hemocianina, un pigmento respiratorio.

Llamamos pigmentos respiratorios a un grupo de proteínas que tienen la propiedad de combinarse de forma reversible con oxígeno molecular. Por esa razón, pueden transportar oxígeno, captándolo en un lugar y liberándolo en otro. Todos los pigmentos respiratorios son metaloproteínas, o sea, proteínas que contienen átomos metálicos. Y los llamamos pigmentos porque, al menos en algunos momentos, tienen un color intenso.

El O2 tiene una solubilidad relativamente baja en agua, por lo que es muy limitada la capacidad de las disoluciones acuosas, como son la hemolinfa o el plasma sanguíneo, para transportar oxígeno. Gracias a los pigmentos respiratorios de los que los animales se han dotado, la capacidad de la sangre o equivalente para transportarlo es muy superior a la que tendrían sin ellos, y pueden satisfacer las necesidades que se derivan de altos niveles de actividad metabólica. Para hacernos una idea de lo que representa su contribución, 100 ml de sangre humana contienen, al salir del pulmón, 0,4 ml de O2 en forma disuelta y 19,6 ml combinados con la hemoglobina. O sea, la denominada capacidad de oxígeno de la sangre se multiplica por cincuenta gracias a su pigmento. Es cierto que los mamíferos somos los animales en los que la contribución del pigmento es máxima y que en otros puede ser muy inferior, pero en cualquier caso, se trata de una contribución importante.

Cuando un pigmento respiratorio se encuentra combinado con el oxígeno decimos que está oxigenado y, en caso contrario, que está desoxigenado. No utilizamos los términos oxidado y reducido para denominar esos dos estados alternativos. La combinación del oxígeno con un pigmento no es químicamente equivalente a una oxidación. En una oxidación los electrones de los átomos metálicos del pigmento son parcialmente transferidos a la molécula de oxígeno, pero no es una transferencia completa como la que ocurre en una oxidación. De hecho, si la molécula de pigmento se oxidase realmente perdería su capacidad para transportar oxígeno. Utilizamos los prefijos oxi- y desoxi- para denominar a las dos formas del pigmento: oxihemoglobina y desoxihemoglobina, por ejemplo. Hay cuatro tipos o categorías de pigmentos respiratorios: hemoglobinas, hemocianinas, hemeritrinas y clorocruorinas. Cada una de esas categorías agrupa a compuestos relacionados, no a estructuras químicas únicas.

Existen notables similitudes entre la forma en que los pigmentos respiratorios se unen al oxígeno y la forma en que las enzimas se unen a sus sustratos. En ambos casos la unión ocurre en sitios específicos, y se produce mediante enlace débil no covalente. Al unirse el O2 con el pigmento, este modifica ligeramente su conformación, como ocurre con las enzimas. Igualmente, en ambos casos cabe hablar de afinidad, que en este caso refleja la facilidad con la que el oxígeno se une al pigmento. Los pigmentos se puede unir con otras sustancias, también en sitios específicos, y esa unión modifica sus propiedades y la facilidad con que se combina con el oxígeno; a esas sustancias se las denomina moduladores alostéricos. Las moléculas de pigmento suelen estar formadas por dos o más subunidades. Las subunidades son proteínas unidas entre sí mediante enlaces no covalentes. Cada subunidad tiene un sitio de unión para el oxígeno y muestran cooperatividad entre los sitios de unión de las diferentes subunidades. Quiere ello decir que la unión de una molécula de oxígeno al sitio de unión de una subunidad, modifica la facilidad con la que otros sitios se combinan con otras moléculas de O2. Esas variaciones se producen como consecuencia de los cambios conformacionales antes citados.

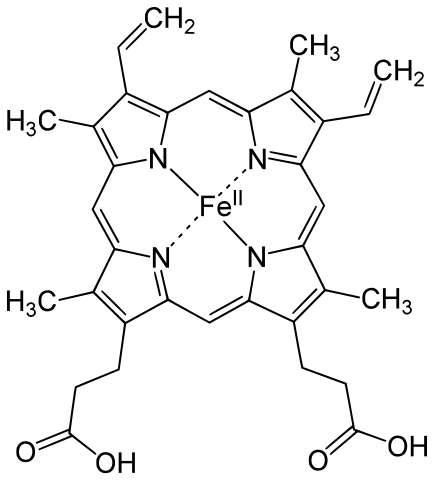
Grupo hemo

Las hemoglobinas y las clorocruorinas consisten en largas cadenas de aminoácidos (globinas) unidas de forma no covalente a sendos grupos prostéticos (grupos hemo) que son metaloporfirinas. El grupo prostético es común a todos los pigmentos de una misma categoría, ya sean hemoglobinas o clorocruorinas, y es ahí donde se produce la unión con el oxígeno. Los pigmentos de una misma categoría difieren en las cadenas polipeptídicas. De hecho, la diversidad de propiedades y funciones de unas y otras hemoglobinas, por ejemplo, tiene su origen en las diferentes estructuras de sus cadenas. Los grupos hemo de las hemoglobinas y de las clorocruorinas son metaloporfirinas en las que el metal es el hierro. Las clorocruorinas tienen la particularidad de ser verdes en disoluciones diluidas y rojas en concentradas. Las hemoglobinas son rojas. Las hemocianinas son la segunda categoría pigmentaria más común. A diferencia de hemoglobinas y clorocruorinas, no tienen grupo hemo. Y además, en vez de hierro contienen cobre, que se encuentra unido directamente a la proteína. El sitio de unión con la molécula de O2 contiene dos átomos de metal. Cuando se encuentran desoxigenadas carecen de color, y cuando están combinadas con el O2 son azules. Por último tenemos las hemeritrinas, que, como las hemocianinas, carecen de grupo hemo. El metal de estas es el hierro, también ligado directamente a la proteína.

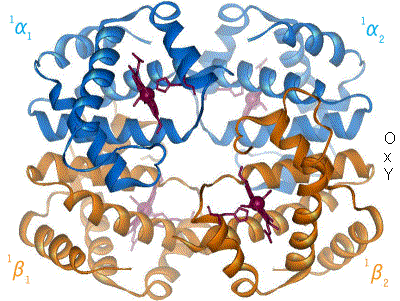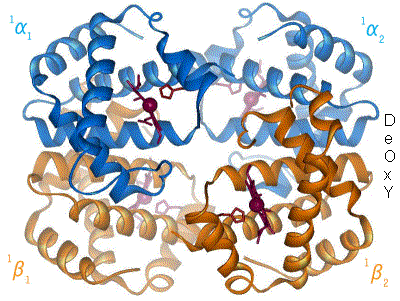
Esquema básico de la hemoglobina humana. Se muestran las dos parejas de globinas, α y β, y los cambios de estructura al enlazarse el oxígeno (no mostrado)

El pigmento respiratorio mejor conocido es la hemoglobina humana. La de un individuo adulto consta de cuatro subunidades (se dice que es tetramérica) cuyas globinas están formadas por algo más de 140 aminoácidos. Se conocen más de un centenar de formas mutantes, la mayoría de las cuales solo difiere de la forma normal en un único aminoácido. El peso molecular de las subunidades se encuentra entre 16000 y 17000 daltons. La sangre adulta contiene dos tipos de globinas, denominadas α (141 aminoácidos) y β (146 aminoácidos), de manera que en una molécula de hemoglobina hay dos de cada tipo. Hemos especificado que los datos anteriores corresponden a la hemoglobina de personas adultas, porque a lo largo del desarrollo, desde la fase embrionaria hasta semanas después del nacimiento, cambian de manera notable su composición y características. En otras especies no es raro que coexistan más de una variedad de hemoglobina en la sangre, cada una con diferentes características en lo relativo a su unión con el O2; esa variedad permite a los animales que la poseen transportar oxígeno en un amplio rango de condiciones ambientales.

Fuentes:

Richard W. Hill, Gordon A. Wyse & Margaret Anderson (2004): Animal Physiology. Sinauer Associates, Sunderland

John D. Jones (1972): Comparative physiology of respiration. Edward Arnold, Edinburgh

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo Sistemas respiratorios: los pigmentos respiratorios se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Sistemas respiratorios: los límites a la difusión de los gases
2. Sistemas respiratorios: la emergencia de un doble sistema circulatorio
3. Sistemas respiratorios: la ventilación de los pulmones de mamíferos

El principio de relatividad es uno de los dos postulados a partir de los cuales Einstein derivó las consecuencias de la teoría de la invariancia, popularmente llamada de la relatividad. El otro postulado se refiere a la velocidad de la luz, y es especialmente importante cuando se comparan las observaciones entre dos marcos de referencia inerciales, aquellos marcos de referencia que están en reposo o se mueven con una velocidad uniforme relativa entre sí, ya que dependemos principalmente de la luz para hacer observaciones.

Cuando Einstein dejó la secundaria a la edad de 15 años, estudió por su cuenta para poder ingresar en el Instituto Politécnico Federal de Zúrich (Suiza). Probablemente fue durante esta época cuando Einstein consideró por primera vez un experimento mental importante. Se preguntó qué pasaría si pudiera moverse lo suficientemente rápido en el espacio como para alcanzar un rayo de luz. Maxwell había demostrado que la luz es una onda electromagnética que se propaga a la velocidad de la luz. Si Albert pudiera viajar en paralelo y a su misma velocidad no vería una onda propagándose. En cambio, vería los “valles” y las “crestas” de la onda fija y estacionaria con respecto a él. Esto contradecía la teoría de Maxwell, en la que no era posible ese paisaje “estacionario” en el espacio libre. De estas y otras consideraciones principalmente teóricas, Einstein concluyó en 1905 que la teoría de Maxwell debía ser reinterpretada: la velocidad de la luz tiene que ser exactamente la misma, debe ser una constante universal, para todos los observadores, independientemente de si se mueven (con velocidad constante) respecto a la fuente de la luz. Esta idea revolucionaria se convirtió en el segundo postulado de la relatividad especial de Einstein, el principio de constancia de la velocidad de la luz:

La luz y todas las demás formas de radiación electromagnética se propagan en el espacio vacío con una velocidad constante c que es independiente del movimiento del observador o del cuerpo emisor.

Lo que Einstein está diciendo es que ya estemos moviéndonos a una velocidad uniforme hacia, o alejándonos de una la fuente de luz, o de si nos movemos en paralelo o no a un haz de luz, siempre mediremos exactamente el mismo valor para la velocidad de la luz en el vacío, que es exactamente de 299.792.458 m/s [1] . A esta velocidad se le dio el símbolo c de “constante”. Si la luz viaja a través del vidrio o el aire su velocidad será algo más lenta, pero la velocidad de la luz en el vacío es una de las constantes físicas universales.

Es importante recordar que este principio solo se aplica a los observadores y las fuentes que están en marcos de referencia inerciales. Esto significa que se están moviendo a una velocidad uniforme o están en reposo uno con relación al otro [2].

Veamos una implicación inmediata de este principio tan simple, en el que empiezan a intuirse las peculiaridades de la teoría de la invariancia que la apartan de nuestro sentido común. Para ello hagamos unos pocos experimentos mentales muy sencillos.

Imaginemos que Mónica está sobre una plataforma con ruedas moviéndose a una velocidad uniforme de 5 m/s hacia Esteban, que permanece estático en el suelo. Mientras Mónica se mueve, arroja una pelota de tenis a Esteban a una velocidad para Mónica de 7 m/s. Esteban la atrapa, pero justo antes de hacerlo, rápidamente mide su velocidad [3]. ¿Qué velocidad obtiene? La respuesta, obviamente, es 5 +7 = 12 m/s, ya que las dos velocidades se suman.

Hagamos otro experimento. Mónica está en la plataforma alejándose a 5 m/s de Esteban. Nuevamente lanza la pelota a 7 m/s para ella a Esteban, quien nuevamente mide su velocidad antes de atraparla. ¿Qué velocidad mide ahora? Esta vez es -5+7 = 2 m/s, donde hemos adoptado la convención de que las cosas que se mueven hacia Esteban tienen velocidad de signo positivo y las que se alejan de signo negativo. Las velocidades se suman de nuevo [4]. Todo muy convencional e intuitivo.

Ahora intentemos estos mismos experimentos usando rayos de luz en lugar de pelotas de tenis. Cuando Mónica se mueve hacia Esteban, le apunta con el haz de un lápiz láser [5]. Esteban tiene un detector de luz que también mide la velocidad de la luz. ¿Qué velocidad de la luz mide? Mónica y Esteban se sorprenden al descubrir que Einstein tenía razón: la velocidad es exactamente la de la luz, ni más ni menos [6]; la velocidad de la plataforma no se ha añadido a c. Obtienen la misma velocidad c cuando la plataforma se aleja de Esteban. De hecho, incluso si aumentan la velocidad de la plataforma hasta casi la velocidad de la luz misma [3], la velocidad de la luz medida sigue siendo la misma, c,en ambos casos. Por extraño que parezca, la velocidad de la luz (o de cualquier onda electromagnética) siempre tiene el mismo valor, c,sin importar la velocidad relativa de la fuente y el observador.

En las próximas entregas veremos algunasde las consecuencias a las que llegó Einstein cuando juntó los dos postulados fundamentales de la teoría de la relatividad especial, el principio de relatividad y el principio de constancia de la velocidad de la luz en el vacío.

Notas:

[1] La exactitud de esta cifra es una convención moderna, ya que la unidad de longitud se deriva de la velocidad de la luz.

[2] El autor comprende que se pone pesado con estas repeticiones, y pide disculpas por ello. Pero considera imprescindible que la persona que lea cualquiera de estas entregas independientemente del resto sea en todo momento consciente de los límites de aplicación de las ideas que se discuten.

[3] Una licencia que permite el hecho de que esto solo sea un experimento mental

[4] Las restas no existen, son siempre sumas, lo que cambia es el signo de los factores.

[5] Asumimos que Mónica evita los ojos de Esteban y que ambos usan protección ocular adecuada durante el experimento.

[6] Despreciamos el pequeñísimo, pero no nulo, efecto del aire sobre la velocidad de la luz para no tener que realizar el experimento en el espacio.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo El principio de constancia de la velocidad de la luz se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El principio de relatividad (y 4): la versión de Einstein
2. El principio de relatividad (2): la versión de Galileo
3. El principio de relatividad (1): movimiento relativo

Josu Lopez-Gazpio 1999an Robert A. Kloner zientzialariaren ikerketa-taldeak bihotzarekin lotura zuten arazoen heriotza-tasa izan zuen aztergai. Pentsa zitekeen modura, frogatu ahal izan zuten neguan udan baino heriotza gehiago gertatzen direla eta gehienak abendutik urtarrilera gertatzen zirela.

Hasiera batean azalpen errazenera jo zuten eta ondorio horrekin argitaratu zuten haien lana: neguan tenperaturak hotzagoak dira, eta fenomeno horrek azaltzen du neguan heriotza-tasa handiagoa izatea. Guztiak zentzua zuen: tenperatura hotzagoa denean odol-presioa, hemostasia, basoespasmo koronarioa, eta abar handitu egiten dira eta errazagoa da bihotz-arazoak izatea.

1. irudia: Eguberrietako oporraldia ez da beti zoriontasunen iturri, zientziaren arabera; izan ere, hiltzeko egunik probableenak Gabonetako egun seinalatuak dira. (Argazkia: jill111 – domeinu publikoko irudia. Iturria: Pixabay.com)

Datuak grafikoetan irudikatu zituztenean, ordea, bazen zentzurik ez zuen datu bat: azaro bukaeran heriotzak handitzen hasten ziren, Gabonetako oporren inguruan maximora iristen ziren eta ondoren berrio jaisten hasten ziren. Alabaina, gorabehera hauek ezin ziren azaldu tenperaturaren bilakaerarekin; izan ere, tenperatura baxuak konstanteak dira abenduan eta urtarrilean -zergatik gertatzen zen orduan Eguberri inguruan igoera eta gero jaitsiera?-.

Azken galdera hori erantzunik gabe egon behar izan zen David P. Phillips eta bere lankideak gaia ikertzeari ekin zioten arte. Haien ikerketen emaitzen berri 2004an eman zuten eta ordura arte ezagutzen zena jaso zuten. Alde batetik, frogatuta zegoen neguko oporraldian suizidioak, hilketak eta heriotza eragiten duten auto-istripuak areagotu egiten zirela -baina, ez zen ikertu heriotza naturalak ere neguko oporraldian areagotzen ziren edo ez -. Bestetik, ezaguna zen neguan heriotza-tasa handiagoa zela neguan udan baino. Nolanahi ere, aurreko ikerketetan ez zen kontuan hartu Gabonetako oporraldiak heriotza naturaletan eragina zuen edo ez, neguaren efektua kendu ondoren -alegia, Eguberriak berak efekturik ba ote zuen-.

Phillips eta bere lankideek hainbat galdera erantzun nahi zituzten: Gabonetako oporraldian espero direnak baino heriotza gehiago gertatzen al dira? Heriotzen gehikuntza hori bihotz-arazoekin lotzen da bakarrik edo heriotza mota guztiak handitzen dira? Neguaren efektuaz gainera, zenbaterainokoa da Eguberrien efektua? Eguberrien efektu hori handitzen ari al da urtez urte? Bada, galdera horiei guztiei erantzuna emateko Ameriketako Estatu Batuetan 1973tik 2001era gertatutako 53 milioi heriotza aztertu zituzten eta ondorio aztoragarri batera iritsi ziren.

Eguberrietan hiltzea probableena da

Urtean zeharreko datu guztiak irudikatuta, urte-sasoien tenperaturaren arabera espero den irudikapena lortu zuten ikertzaileek. Neguan jende gehiago hiltzen da udan baino, espero zuten bezala. Baina abendu bukaeran eta urtarrila hasieran, Eguberrietako oporrekin batera, tenperaturarekin bat ez datorren igoera bat nabaritzen da eta, bitxiagoa dena, heriotza-tasak bi tontor ditu oporraldi horren barruan: Eguberri- Urteberri-egunetan, hain zuzen ere. Bihotzeko arazoen kausaz gertatutako heriotzei dagokienez, urte guztia kontuan hartuta, heriotza gehien gertatzen diren eguna abenduaren 25a da, bigarrena abenduaren 26a eta hirugarren postuan urtarrilaren 1a dago. Ikertzaileek aztertutako 26 urteetatik, 24 urtetan betetzen zen hori eta, gainera, urtetik urtera egun horietako heriotza-tasaren tontorra geroz eta handiago zen.

2. irudia: Olentzero edo Aita Noelen oparia ez da beti gustukoa izaten, izan ere, arrazoi naturalez hiltzeko egunik probableenak abenduaren 25a eta 26a dira. (Argazkia: Free-photos – domeinu publikoko irudia. Iturria: Pixabay.com)

Bihotzarekin zerikusirik ez duten heriotza naturalen kasuan ere, antzeko patroia betetzen zela ikusi zuten. Heriotza naturala gertatzeko urteko egunik probableena abenduaren 26a da, gero abenduaren 25a eta, hirugarren postuan, urtarrilaren 1a. Berriro ere, Eguberrietako oporraldi horretan heriotza-tasak bi tontor ditu egun berezi horien inguruan. Neguko tenperatura baxuen hipotesiak ezin du azaldu tontor horien agerpena; izan ere, tenperaturaren aldaketa garrantzitsurik ez da gertatzen abenduaren 25ean edo urtarrilaren 1ean. Phillipsen analisian, urteko-sasoiaren kausazko heriotza-tasaren fluktuazioak kentzen zirenean Eguberri- eta Urteberri-eguneko igoerak ere mantendu egiten ziren eta, gainera, AEBtako zonalde hotzetan tontorra txikiagoa zen zonalde epeletan baino ¾hortaz, tenperatura baxuen eragina ez da gakoa¾. Datuak aztertu ondoren, Phillips eta bere kolaboratzaileek argi ikusi zuten zer gertatzen zen: Eguberrietako oporraldian bada heriotzak areagotzen dituen faktoreren bat, eta faktore hori ez da neguko tenperatura baxua.

Olentzerok ekarritako bihotzekoaren balizko azalpenak

Neguko tenperatura hotzen hipotesia baztertu ondoren, beste bederatzi azalpen proposatu izan dira zientzia-bibliografian Eguberrietako oporraldiaren heriotza-tasaren handitze anormala argitzen saiatzeko. Klonerren taldeak balizko lau azalpen eman zituen: neguko arnasketa-arazoen areagotzea, oporraldi horretan gertatzen den kutsadura-maila handiagoa, dieta aldaketa eta alkohol kontsumoa eta oporraldiarekin lotutako estresa. Phillipsen taldeak lau hipotesi horiek baztertu zituen. Lehen bi hipotesiek ezin ditu azaldu bi egun berezietan gertatzen den tontorra eta beste biak baztertzeko ikerketak ere egin zituzten. Oporraldiarekin lotutako estresa baztertzeko, Alzheimerra zuten gaixoen heriotza aztertu zuten; izan ere, Alzheimerra duten gaixoek ez dira hain kontziente Eguberrietako oporraldiaren estresaz. Datuak aztertuta, ikusi zuten Alzheimerra zuten gaixoen artean ere heriotza naturala probableagoa zela Eguberri- zein Urteberri-egunean. Dieta eta alkohol kontsumoaren azalpena baztertzeko, ospitaleratutako gaixoen heriotza aztertu zuten; izan ere, ospitaletan dieta ez da nabarmenki aldatzen Eguberrietako egunetan. Gaixo horien kasuan ere, probableago zen abenduaren 25ean eta urtarrilaren 1ean hiltzea.

3. irudia: Eguberrietako oporraldian heriotza-tasa handiagoa izatearen arrazoiak asko dira: oporraldiaren estresa, dieta aldaketa, alkohol kontsumoa, gaixotasunei arretarik ez egitea, bidaia luzeak egin beharra eta tenperatura hotzak proposatu dira, besteak beste, azalpen gisa. (Argazkia: jill111 – domeinu publikoko irudia. Iturria: Pixabay.com)

Phillipsen taldeak beste bost azalpen luzatu zituen: hilabete aldaketetan heriotza gehiago gertatu daitezkeela, jaiegunetan heriotzak ez direla jakinarazten, gaixoek heriotza atzeratzen dutela egun garrantzitsuak iritsi arte, egun berezi horiek heriotza azkartzen dutela, edota jaiegunetan gaixoek ez dituztela tratamenduak behar bezala hartzen edo ez dutela medikuengana jotzen. Ikertzaileek ezin izan zuten aurkitu azalpen horietako gehienak babesteko frogarik, baina, bai azkenekoaren kasuan. Hau da, gaixoek modu desegokian jarraitzen dituzte medikuen aholkuak eta medikuarengana joatea atzeratu egiten dute Gabonetako oporraldiaren egun seinalatuetan. Ikertzaileen arabera, arrazoi horrek abenduaren 25eko, 26ko eta urtarrilaren 1eko heriotza-tasaren handitzea azaltzen du. Hala ere, azalpenak hutsen bat ere baduela adierazi zuten; izan ere, ospitaleratutako gaixoek ere heriotza-tasa handiagoa dute egun horietan -eta egun horietan medikuen arreta bera izatea espero da, ospitalean baitaude-.

Eguberrietarako zenbait gomendio

Nolanahi ere, frogatuta dago Eguberrietan heriotza naturala izatea probableago dela, baina, oraingoz ez da azalpen zientifiko bat aurkitu datuek erakusten dutena azaltzeko. Zerk eragingo ote du Eguberri- eta Urteberri-egunak hiltzeko urteko egunik probableenak izatea? Baliteke oraindik aztertu gabeko azalpenen bat egotea, edo literaturan proposatutako azalpen guztien bateratzea izatea arrazoia. Oraingoz, ez da lortu horietako hipotesirik zientifikoki frogatzea. Edozein kasutan, arrazoi hori aurkitzen den bitartean, zientzia-literaturan Eguberrietako oporraldiari aurre egiteko zenbait gomendio aurki ditzakegu.

Gomendioetako batzuk gaixoei edo arrisku handiagoan dagoen populazioari zuzendutakoak dira: batez ere, Eguberrietako gehiegikerietatik alde egitea eta kalterik eragingo ez duen dietarekin jarraitzea, tenperatura hotzak saihestea eta beharrezkoa den atsedena hartzea Eguberrietako oporraldi izanik ere. Osasun zerbitzuei ere zuzentzen zaizkie gomendioak, alegia, urtean zeharreko beste edozein egunetan bezala jarraitzea eta salbuespenik ez egitea jaiegunak izanik ere -osasun-zerbitzuak, langileria eta beharrezkoak diren arretak aldatu gabe-. Populazio osoarentzat gomendiorik ere bada: Eguberrietako oporraldia izanik ere, ondoeza edo bestelako sintomarik sentitzen bada medikuarengana jotzea urteko beste edozein egunetan egingo litzatekeen bezala. Egun seinalatuetan bazkarian edo afarian egon nahi izateagatik, agian, Urtezahar-gaueko mahatsak kontrako eztarritik joango zaizkizu koinatuari bihotzekoak ematen badio. Hori gertatzeko egunik probableenetakoa da, behintzat, zientziaren arabera.

Informazio osagarria:

• Christmas and New Year as risk factors for death, D.P. Phillips et al., Social Science & Medicine 71(8), 1463-1471, 2010.
• The “Merry Christmas Coronary” and “Happy New Year Heart Attack” phenomenon, R. A. Kloner, Circulation 110, 3744-3745, 2004.
• Cardiac mortality is higher around Christmas and New Year’s than at any other time, D.P. Phillips et al., Circulation 110, 3781-3788, 2004.

—————————————————–
Egileaz: Josu Lopez-Gazpio (@Josu_lg) Kimikan doktorea eta zientzia dibulgatzailea da. Tolosaldeko Atarian Zientziaren Talaia atalean idazten du eta UEUko Kimika sailburua da.
—————————————————–

The post Gabonetako oporraldiak osasunean duen kaltea appeared first on Zientzia Kaiera.

Antonio Martínez Ron, lector

Encontrar un libro de filosofía que se entienda y que además te atrape con su lectura no es fácil en los tiempos que corren. Y eso es lo que consigue Peter Godfrey-Smith con “Otras mentes. El pulpo, el mar y los orígenes profundos de la consciencia”, publicado por Taurus. Uno de los principales méritos del libro es precisamente el de centrarse en un asunto que no suele ser tema de conversación en el ascensor y convertirlo en algo apasionante. Durante más de 200 páginas el autor nos adentra en la evolución de los sistemas nerviosos y la naturaleza misma de la consciencia a partir de su experiencia con los cefalópodos. ¿Se imagina usted enfrascado en las andanzas de pulpos y sepias en el fondo del mar? Al principio yo tampoco, y terminé lamentando que se el libro se acabara tan rápido.

“Otras mentes” es un libro escrito por alguien que sabe de biología y además sabe pensar, una tarea para lo que la mayoría de nosotros ni sacamos tiempo ni estamos entrenados. Se agradece su sencillez y lucidez a la hora de explicar los procesos evolutivos que han llevado a los seres vivos a desarrollar diferentes soluciones para navegar por el mundo e interactuar con el entorno. Su comprensión sobre estos procesos es tan profunda que uno tiene la impresión de que los explica con más destreza que muchos especialistas con años de divulgación a sus espaldas.

El libro es un soplo de aire fresco por muchos motivos, pero el principal es la magistral mezcla entre dos campos del conocimiento, biología y filosofía, que deberían solaparse con más frecuencia de lo que estamos acostumbrados. A partir de lo que le han enseñado los pulpos en sus horas de inmersión en aguas australianas, Godfrey-Smith es capaz de hacernos pensar en lo que somos nosotros mismos y en lo que otorga al pensamiento consciente su singularidad. Para ello no nos habla de las frías abstracciones y enrevesadas entelequias a las que nos tienen habituados la mala filosofía y la mala neurociencia, sino que toma un punto de partida terrenal y cercano: ¿cómo integran otros seres sus experiencias sensoriales? ¿Cómo sería estar dentro del cuerpo de otra criatura, si es que acaso esto significa algo?

El resultado es como asomarse a un abismo en el que el artificio del “yo” se desvanece por momentos ante la certidumbre de que existen otras integraciones sensoriales cuya naturaleza no terminamos de entender, un viaje fascinante entre sepias con nombres de pintores expresionistas, pulpos que escupen a sus captores y calamares que nos miran con el interés que lo haría un alienígena. Y, sobre todo, un pequeño ejercicio de humildad para recordarnos que no somos únicos y que quizá la vida muestra una particular tendencia a crear sistemas conscientes, no solo aquí, sino en otros rincones del universo.

Ficha:

Autor: Peter Godfrey-Smith

Título: Otras mentes. El pulpo, el mar y los orígenes profundos de la consciencia

Año: 2017

Editorial: Taurus / Colección: Pensamiento

En Editoralia personas lectoras, autoras o editoras presentan libros que por su atractivo, novedad o impacto (personal o general) pueden ser de interés o utilidad para los lectores del Cuaderno de Cultura Científica.

El artículo El filósofo que baila con las sepias se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Jan van Helmont, filósofo por el fuego (1)
2. Las cartas de Darwin: El capitán y el filósofo
3. ¿Es el universo un holograma?, y otras grandes preguntas de la ciencia actual

Foto: Pxhere

Tienen las personas nacidas en el sur de España fama de ser alegres, abiertas a lo nuevo, amistosas y ‘echás p’alante’, especialmente comparadas con las del norte, más reservadas, calmadas, y conservadoras. En esto se mezclan los tópicos y las costumbres. También se mezcla la ciencia: según un estudio reciente, la temperatura del lugar en el que crecemos modela nuestro hábitos y con ello nuestra personalidad.

Esto nos sorprende apenas, porque la idea de que el clima afecta a nuestro estado de ánimo no es una novedad: está demostrado que los meses de invierno, más fríos y oscuros, generan estados similares a la depresión, especialmente en países nórdicos donde la luz del sol pasa meses en los que apenas brilla, mientras que al volver el calor los ánimos se elevan y nos sentimos llenos de energía.

El nuevo estudio sugiere que la cosa tiene mucha más miga de la que creíamos, y que el clima puede incluso modelar nuestra personalidad, y esto tendría una consecuencia inesperada: ¿si sigue avanzando el cambio climático, cambiará también nuestra personalidad?

Si tuviésemos que quitar paladas de nieve para salir de casa por las mañanas, ¿seríamos más huraños? Foto: US Air Force.

Pero vayamos por partes. Investigaciones anteriores ya habían señalado que muchos aspectos de la personalidad humana varían de una región geográfica a otra: unas culturas son más acogedoras que otras, unas disfrutan más las actividades en el exterior que otras, unas disfrutan más relacionándose con otras personas que otras… Las causas de estas diferencias era lo que aun estaba por aclarar.

Una posible explicación es la temperatura media a la que viven las distintas culturas. Eso es lo que apunta este estudio, realizado por científicos de la Universidad de Pekín: que puesto que la temperatura es una cosa que varía de forma muy marcada a lo ancho y sobre todo a lo alto del globo, impacta en la personalidad de la gente a través de su influencia en sus hábitos cotidianos. No se trata, según los autores, de mirar simplemente si las personas han crecido en climas fríos o calientes; también de si lo han hecho en climas templados (unos 22 grados de media) o extremos, ya sea por arriba o por abajo.

El paper contempla de hecho dos estudios distintos, llevados a cabo en dos países enormes pero muy diferentes, Estados Unidos y China, para evitar que en las conclusiones se mezclasen otros factores, como las diferencias culturales o económicas que también pudiesen afectar a la personalidad de las personas. Analizaron datos de 5.500 personas de 59 ciudades chinas diferentes, y de 1,66 millones de personas de 12.500 códigos postales estadounidenses. Trazaron relaciones entre sus respuestas a tests de personalidad y las temperaturas medias de los lugares donde habían crecido.

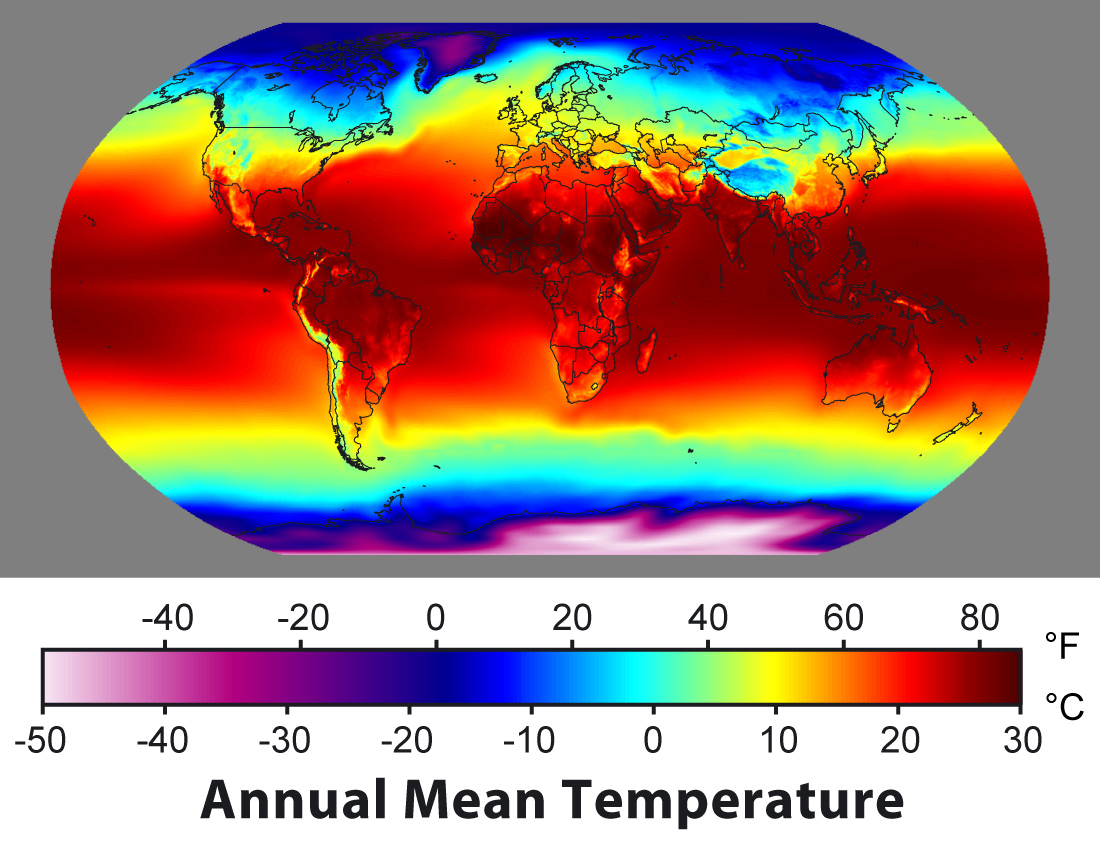
Mapa mundial de temperaturas medias

Los resultados mostraron que las personas crecidas en climas con temperaturas templadas eran generalmente más afables, responsables, emocionalmente estables, extrovertidos y abiertos a nuevas experiencias, y que lo eran en ambos países sin importar su edad, género o ingresos económicos.

“Crecer en temperaturas cercanas a la comodidad psicofisiológica óptima anima a los individuos a pasar más tiempo en el exterior, y por tanto influye en su personalidad”, concluyen los autores.

Claro que aun hay algunas cosas a tomar con cautela en este tema. Por ejemplo, el estudio señala los habitantes de regiones chinas con climas más duros (Heilongjiang, Xinjang o Shandong ) son más colectivistas y se preocupan más por la comunidad, en comparación con sus compatriotas de zonas más templados (Sichuan, Guangdong o Fujian); mientras que los habitantes estadounidenses de zonas más extremas (Dakota del Norte y del Sur, Montana o Minnesota) son más individualistas que sus compatriotas de zonas más templadas (Hawaii, Luisiana, California o Florida).

¿Nos hará el cambio climático más simpáticos, abiertos y emocionalmente estables? Foto: Pxhere

Esto pone de manifiesto que el clima no es la única variable, y que también las condiciones económicas, entre otras muchas cosas, parecen tener algún impacto en cómo somos.

No es solamente que la relación entre clima y personalidad no sea todopoderosa. Es que insinuar que lo es nos pone ante una situación un poco incómoda: ¿si el clima moldea nuestra personalidad, y el clima está cambiando, cambiará nuestra personalidad con él? ¿Nos encaminamos hacia un mundo en el que todos seremos más afables, extrovertidos y aventureros? ¿Tan maleables resultamos por la temperatura?

Los autores son conscientes de este problema, y dejan la puerta abierta a seguir investigando: “a medida que el cambio climático continúa a través del mundo, podríamos observar cambios asociados en la personalidad humana. Las preguntas sobre la extensión de esos cambios esperan respuesta en futuras investigaciones”.

Referencia:

Wenqi Wei, Jackson G. Lu, Lei Wang. Regional ambient temperature is associated with human personality. Nature Human behaviour, 27 de noviembre de 2017. doi: 10.1038/s41562-017-0240-0

Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista

El artículo ¿Y si el cambio climático nos termina haciendo a todos más simpáticos? se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Del cambio climático
2. Verdín, eucaliptos y cambio climático
3. “El cambio climático: ciencia, política y moral” por José Manuel Sánchez Ron

Gehienbat jatorri amerikarra eta asiarra duten flora exotikoko 156 espezie aurkitu ditu Diego Liendo ikertzaileak Kantauriko erlaitzeko ibaietan egindako ikerketan.

Flora aloktonoko (jatorrizkoa ez dena) espezieak bilatu dira Nansa (Kantabria) eta Bidasoa (Gipuzkoa-Nafarroa) ibaien arroen artean. Denera 156 espezie detektatu dira, espezie horien %40 puntu bakar batean agertu delarik.

Detektatu diren zenbait espezie, hala nola ‘Fallopia japonica’, oso maiz agertu ez arren, zati handiak estaltzera iristen dira. Beste batzuk, ‘Paspalum distichum’ kasu, ibai-hondartzak (ibaian zehar sortzen diren metakinak -harrizkoak, hareazkoak edo lohizkoak-) ia osorik estaltzera irits daitezke.

1. irudia: ‘Fallopia japonica’ (ezk.) oso maiz agertu ez arren, zati handiak estaltzera iristen da. ‘Paspalum distichum’ (esk.) ibai-hondartza batzuk ia osorik estaltzera irits daiteke.

Ipar Amerikan jatorria duen ‘Muhlenbergia schreberi’ graminearen populazio naturalizatuak (hainbat ziklotan zehat -10 urte gutxienez- haien kabuz populazioa mantentzeko gai diren kanpoko espezieak) aurkitu dira Urumea ibaian. Espezie honen bigarren erreferentzia da Iberiar penintsulan, orain arte Kataluniako leku jakin batean soilik zegoen aipatuta. Deigarria da emaitza, arro horretan maiztasun handiarekin aurkitu baita. Espero zen baino askoz zabalduago dagoela azaltzen du ikertzaileak eta espezie horren populazioari segimendua egin behar zaiola uste du haren inbasio potentziala ebaluatu ahal izateko.

2. irudia: ‘Muhlenbergia schreberi’ren populazio naturalizatuak topatu dira bigarrenez Iberiar penintsulan.

Landare exotikoei dagokienez Kantauriko ibaiak zer egoeratan dauden azaltzen du ikerketak. Ekosistema hauen kudeaketarako garrantzitsua izan daiteke informazioa, ekosistema guztiek ez baitute kalteberetasun bera espezie exotikoen inbasioa jasateko.

Inbasio biologikoa

Ibai ekosistemak bereziki sentiberak dira espezie exotikoen inbasioarekiko, ibaien beren ezaugarriengatik, ibai ingurunea oso dinamikoa baita. Noizbehinka izaten diren uholdeek landarediaren parte bat eramaten dute eta beste espezie horiek sartzea errazten da. Nahiko ingurune egokia da, gainera, nutriente ugari eta ura eskuragarri baititu.

Inbasio gradua zenbait aldagairen araberakoa da, ikerketan azaltzen denez:

• Aldagai klimatikoak (tenperatura).
• Inguruneari dagozkion aldagaiak (ibilguaren batezbesteko zabalera eta landare-komunitateen kopurua).
• Aldagai antropikoak (ibai-zatiaren inguruko hiri-lurraren proportzioa eta hurbilen dagoen hirigunerako distantzia).

Halaber, ibai-arro industrializatuetan inbasio maila askoz ere handiagoa dela ikusi da. Jatorriz bertakoak ez diren landareen inbasio handiagoa dago ibaiaren luzeraren %50ean edo gehiagoan hiri edo industria lurra duten arroetan.

Inbasio biologikoen fenomenoa, gizakiak espezieak beren banaketa eremu naturaletatik kanpo mugitzea eta huek bertan ezartzea, ingurumen arazo nagusietako bat da mundu mailan. Kontinente arteko garraio sareetan izan diren hobekuntzen eta nazioarteko merkataritzaren gorakadaren ondorioz areagotu egin da fenomenoa, bereziki azken hamarkadetan.

Munduko edozein lurraldeko ia edozein ekosistematan aurki daitezke kanpotik ekarritako espezie exotikoak eta espezie horiek gai dira leku horretan ezarri eta arazo ekologiko eta ekonomikoak eragiteko. Jatorriz bertakoak ez diren espezie batzuek alboratu egin dezakete bertako landaredia, portaera inbaditzailea baitute. Eta gaur egun portaera inbaditzailerik ez badute ere, aurrerago izan dezakete, ikertzaileak azaltzen duenez inbasio biologikoen fenomenoa denbora luzea hartzen duen prozesu bat baita.

Kantauriko ibaietako bi habitat nagusietan oinarritutako beste ikerketa bat ere egin da. Ibaiertzean hazten diren baso naturalak eta ibai-hondartzak aztertu dira eta ibai-hondartzetan espezie aloktonoen kopurua basoetakoa baino askoz handiagoa dela aurkitu da.

Iturria:

UPV/EHUko Komunikazio bulegoa: Ehun espezie baino gehiagotako landare exotikoek inbaditzen dituzte kantauriar ibaiak

Erreferentzia:

Diego Liendo Pérez ‘Plant Invasion in Cantabrian rivers: drivers and effects on plant diversity and riparian habitats’. ADDI.

The post Kantauriar ibaietako espezie exotikoak appeared first on Zientzia Kaiera.

“La plaga de Atenas” de Michiel Sweerts. Alrededor de 1652.

Tras las guerras médicas, finalizadas en 448 a.e.c. con la derrota del ejército persa de Artajerjes I y la Paz de Calias, Atenas se encontraba en su máximo apogeo. Pericles, seguramente la máxima figura política de la Grecia clásica, gobernaba un imperio marítimo y, a decir del historiador Tucídides, lo hacía con talento y prudencia. Y sin embargo, la era de Pericles llegaría a su fin 17 años después, en parte al menos, por una serie de malas decisiones promovidas por el “primer ciudadano”.

En 431 a.e.c. Esparta, que lideraba una confederación de ciudades del Peloponeso, tuvo que apoyar a sus aliadas Mégara y Corinto que habían sido perjudicadas por Atenas, y atacó por tierra con sus hoplitas. Pericles había preparado a Atenas fortificando la ciudad y construyendo los dos “Muros Largos” que protegían el corredor hasta el Pireo, el puerto por el que afluían a la ciudad los suministros que necesitaba. Atenas era inferior a Esparta en tierra, pero tenía la flota más poderosa del Egeo y era, además, muy rica. Cuando la coalición lacedemonia atacó el Ática, las gentes de toda la región se refugiaron en el interior del recinto amurallado. A los 150.000 atenienses se les unieron entre 200.000 y 250.000 nuevos pobladores. En el verano de 430 se declaró una epidemia terrible que asoló la ciudad.

Tenemos noticias precisas de la epidemia gracias a Tucídides, quien sufrió en su persona la enfermedad. Los enfermos se arrastraban por las calles y morían cerca de las fuentes –a donde iban a beber-, y en los templos, donde se hacinaban los refugiados. “Morían como ovejas” escribe Tucídides. Pericles perdió a sus dos hijos legítimos, y él mismo también cayó enfermo y murió en el otoño de 429.

Se desconoce cuál es el patógeno que causó la epidemia. El mal surgió, según Tucídides, en Etiopía; se desplazó por el valle del Nilo hasta Egipto; y desde allí, por mar, llegó a Atenas a través del Pireo. Acabó con la vida de un tercio de los atenienses.

Según el epidemiólogo Paul Ewald, de la Universidad de Louisville (EEUU), la conocida como Gran Plaga de Atenas puede darnos una idea de cómo pueden desarrollarse las enfermedades más peligrosas para los seres humanos en el futuro. Frente a la extendida creencia de que las peores pandemias serán las que causen patógenos procedentes de animales –como el ébola o las gripes aviares- Ewald sostiene que esos patógenos no han convivido suficiente tiempo con los seres humanos como para haber desarrollado mecanismos eficaces para transmitirse entre personas. Los virus y bacterias con que convivimos producen síntomas e inducen respuestas por nuestra parte que facilitan mucho su dispersión.

Por esa razón, Ewald piensa que, en buena lógica evolutiva, es más probable que sean los virus y bacterias con los que más tiempo llevamos coevolucionando, y que han desarrollado buenos mecanismos de dispersión los que, bajo determinadas condiciones, puedan generar peligrosas epidemias. Enfermedades como el cólera, la viruela y las causadas por Staphylococcus aureus serían las mejores candidatas a protagonizar una pandemia peligrosa. Para que eso ocurra bastaría con que su capacidad de transmisión y virulencia se vieran favorecidas, tanto por las condiciones ambientales –grandes números de personas hacinadas- como por la aparición de alguna cepa de especial peligrosidad. Por esa razón, Ewald considera importante evitar condiciones que faciliten a los patógenos aumentar su virulencia y transmisibilidad, como las que se dan en hospitales hacinados o en grandes campos de refugiados. Porque puede que las epidemias del futuro se produzcan de modo similar a como lo hicieron en el pasado.

Fuentes:

Javier Murcia Ortuño (2007): De banquetes y batallas, Alianza Editorial, Madrid.

Wendy Orent (2017): How plagues really work Aeon.

El artículo Las epidemias del pasado… y del futuro se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Otra ventana al futuro
2. ¿Se puede predecir el éxito futuro de un científico?
3. El futuro ya no es lo que era

Uxune Martinez

Klima-aldaketa

Lurra da, bere bizi guztiarekin, gure aterpe bakarra. Ez dugu besterik. 1992. urtean zientzialariek ohartarazi ziguten Lurraren egoera ez zela ona eta gizakion eragina zela nagusi horretan. 25 urte beranduago planetaren egoerak txarrera jo du aztertutako adierazle gehienetan, eta horrela jarraituz gero atzera bueltatzeko aukerarik ez dela izango nabarmendu dute oraingoan mundu osoko 15.000 zientzialarik BioScience aldizkarian argitaratutako ohar batean. Juanma Gallego kazetariak aldarriarekin bat egin duten ikertzaile euskaldunen hitzak batu ditu Berrian: Planeta babesteko bigarren aldarria.

Meteorologia

Urakanek eta tifoiak izenak dituzte. Eta badakizue zer dioen esaera zaharrak: “Izanaren itzala, izena“. Izan ere, arreta gehiago jartzen diogu urakan, tifoi edo ekaitz gogorrei hauek izena badute. Urakanen eta tifoien kasuan 1979. urtetik aurrera emakume eta gizonezkoen izen propioak tartekatzea adostu zuten Nazioarteko Meteorologia Erakundeak (WMO-k) eta Estatu Batuetako Meteorologia Zerbitzuak (NWS-k). Bestalde, 1954. urtetik aurrera Berlingo unibertsitate batek, Freie Universität Berlin, antizikloiak eta ekaitz gogorrei izena jarri izan diete. Hariari jarraituz, Espainiako, Frantziako eta Portugalgo meteorologia zerbitzuek iragarri dute hemendik aurrera ekaitz gogorrak edo behe presio sakonak izendatzen hasiko direla. Datu guztiak Sustatu agerkarian bildu dituzte: Borraska sakonak izendatzen hasi dira Aemet, MéteoFrance eta IMPA. “Ana” izan da lehenengoa.

Teknologia

Gure inguruan gertatzen dena ezagutzeko teknologiak hainbat tresna garatu ditu. Horrenbestez, buia, radar, sismografo eta meteorologia estazioetan bildutako datuek datorrenaren berri ematen digute. Euskal Herrian baditugu arestian aipatutako erremintak eta Edu Lartzanguren kazetariak aurkeztu dizkigu Berrian: Euskal Herriaren zentzumenak.

Matematika

Josu Doncel matematikariak Galileoren esaldi bat dakarkigu gogora asteon: “Natura matematika erabiliz sortua da“. Eta, antza, zuzen zegoen. Gure matematikariak oso kontu bitxia eta interesgarria azaldu digu Zientzia Kaieran, kilkerren kantuak tenperatura adierazten duela. 15 graduko tenperatura dagoenean hasten dira kantuan kilkerrak eta zenbat eta gehiago abestu, are eta tenperatura beroagoa dago. Hori ba, 36 gradutik aurrera moteldu egiten duten euren txirtxirra eta 40 gradutik aurrera ez dira entzuten. Tenperatura kalkulatzeko formula matematikoa sortu zuen Amos Dolbear fisikariak 1897. urtean “Kilkerra termometro gisa” izeneko artikuluan.

Astronomia

ULAS J1342+0928 du izena, Eguzkiak baino 800 milioi masa handiagoa du eta Unibertsoak 690 milioi urte zituenean sortutako quasarra da. Quasarra honek badu berezitasun bat, urrunen detektatutako quasarra da eta gugandik argiarena baino 7,54 aldiz abiadura handiagoan urruntzen ari dela ere zehaztu dute berarekin topo egin duten Carnegie Institutuko astronomoek. Ana Galarragak ematen digu honen berri Elhuyar aldizkarian: Urruneneko zulo beltza detektatu dute.

Genetika

Francis Galton zientzialariak hainbat esparru jorratu zituen, esaterako estatistika. Berak sortu zuen korrelazio kontzeptua. Baina bada ere ezaguna antropologiarekin eta genetikarekin lotura duen beste termino bat sortzeagatik: eugenesia. Eugenesiak herentziazko giza ezaugarrien hobekuntza du helburu, teknika biologiko eta genetikoak erabiliz. Eugenesiaren historia ardatz hartuta Koldo Garcia genetistak edizio genomikoari so egiten dio eta haren erabilerari: Eugenesiaz hitz egin behar dugu.

Robotika

Robot biohibridoak osagarri organikoak dituzten gailuak dira. Ehunen ingeniaritzan izan diren aurrerapenei esker, mota honetako robotek garapen handia izan dute azken urteotan eta etorkizunean ere bide oparoa izan dezakete. Hori dela eta, robotak sailkatzeko proposamena egin du zientzialari talde batek, beren taxonomia finkatzeko asmoz. Juanma Gallegok hurbiltzen dizkigu datu guztiak: Ate-joka ari diren roboten landa gida.

Biologia

Laktosa digeritzeko ezintasunari laktosarekiko intolerantzia deitzen zaio. Digeritu ezean, hestearen argian gelditzen da laktosa eta ondorioz hestean dagoen mikroflorak hartzitu egiten du, hartziduraren ondorioz gasak sortzen dira eta horiek eragiten dute ondoeza. Baina ba al dakizue ondoezaz gain, deshidratazioa ere ekar dezakeela laktosa digeritu ezin izateak? Juan Ignacio Pérez Iglesias eta Miren Bego Urrutia biologoek azaltzen digute kontua: Esnea denontzat?

Zientziarekiko pertzepzioa

Eusko Jaurlaritzaren Prospekzio Soziologikoen Kabineteak “Zientziaren eta teknologiaren gizarte pertzepzioa“ri buruzko soziometroaren emaitzak plazaratu berri ditu. Txostena aztertu du Ana Galarraga kazetariak eta emaitzen berri eman digu Elhuyar aldizkarian: Zientzia eta teknologiari buruzko pertzepzioa: oro ez da urre. Plazaratu diren datuen arabera 2012tik hona hazi egin da gizarteak duen zientziarekiko interesa, baina galdetutakoen artean, hamarretik ia hiruk nahiko uste du ikerketa zientifikoaren zati handi bat ez dela fidagarria, finantziazio pribatuaren mende omen dagoelako.

———————————————————————–
Asteon zientzia begi-bistan igandeetako atala da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna erreparatuz, Interneteko “zientzia” antzeman, jaso eta laburbiltzea da gure helburua.

———————————————————————–

Egileaz: Uxune Martinez, (@UxuneM) Euskampus Fundazioko Kultura Zientifikoko eta Berrikuntza Unitateko Zabalkunde Zientifikorako arduraduna da eta Zientzia Kaiera blogeko editorea.

———————————————————————–

The post Asteon zientzia begi-bistan #181 appeared first on Zientzia Kaiera.

En #Naukas17 nadie tuvo que hacer cola desde el día anterior para poder conseguir asiento. Ni nadie se quedó fuera… 2017 fue el año de la mudanza al gran Auditorium del Palacio Euskalduna, con más de 2000 plazas. Los días 15 y 16 de septiembre la gente lo llenó para un maratón de ciencia y humor.

Guillermo Peris nos habla de la consecuencias que tienen para los humanos los saltos que pegan dentro del genoma algunos genes, unos trapecistas llamados transposones.

Guillermo Peris ''Los trapecistas del genoma''

Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Naukas Bilbao 2017 – Guillermo Peris: Los trapecistas del genoma se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Naukas Bilbao 2017- Daniel Torregrosa: ¡Estamos rodeados!
2. Naukas Pro 2017: Carlos Briones y el origen de la vida
3. Naukas Bilbao 2017, en directo

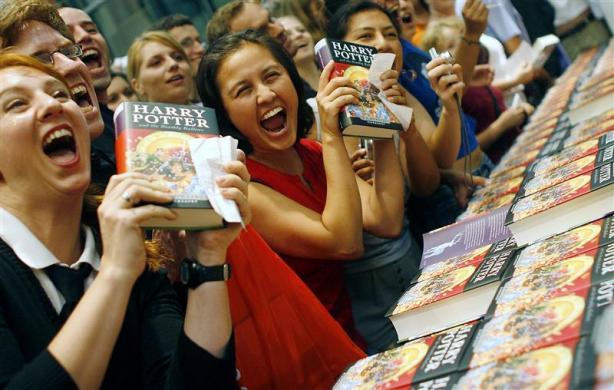
Humanitateak babestu behar dira, zalantza barik, baina arrazoi zuzenengatik. Jesús Zamora Humanities: how not to defend them, and how to do it (2) artikuluan.

Duela urte batzuk pentsaezinak ziren efektuak lortzeko gai diren literalki atomoz atomo diseinatutako egituren eraikuntzan parte hartzen du DIPCko jendeak. Adibibez, A Kondo effect by manipulating spin chains

–—–

Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.

The post Ezjakintasunaren kartografia #195 appeared first on Zientzia Kaiera.

La planta de energía marina o planta undimotriz de Mutriku es la única instalación comercial (no es un prototipo) en el mundo que funciona inyectando energía eléctrica generada por las olas a la red de manera regular. Está en funcionamiento desde el año 2011 y el estudio del grupo EOLO de la UPV/EHU ha analizado su comportamiento en el periodo 2014-2016. “Es importante conocer el funcionamiento real de la planta undimotriz, analizar cómo se comporta la tecnología empleada, y observar qué carencias y ventajas presenta para contribuir en su mejora”, afirma Gabriel Ibarra Berastegi, el autor principal del estudio. “La extracción de energía de las olas se encuentra en sus inicios y varios tipos de dispositivos y tecnologías se encuentran actualmente en desarrollo. Entre ellas, la tecnología OWC (Oscillating Water Column) empleada en Mutriku”, añade.

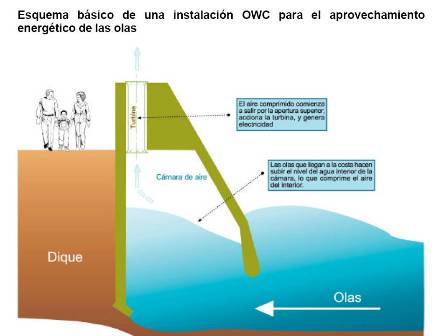
En la tecnología OWC, no son las olas las que mueven las turbinas directamente, sino una masa de aire comprimido que estas empujan. Se trata de una estructura cuya parte superior forma una cámara de aire y cuya parte inferior está sumergida en el agua. De esta manera, la turbina aprovecha el movimiento provocado por la ola tanto cuando viene como cuando se va, y el generador al que está acoplada inyecta la energía en la red. “Las turbinas generan electricidad que se vende de manera regular a la red eléctrica. En el caso de Mutriku, sucede en el 75% del tiempo. Hay ciertos parones cuando las olas son muy calmadas o incluso cuando son demasiado fuertes”, explica Ibarra.

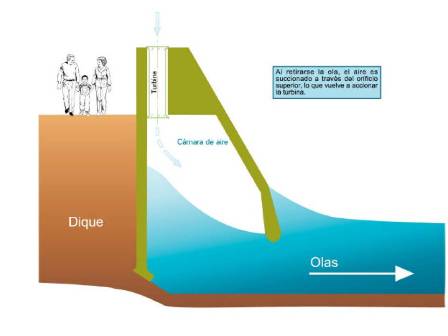
La investigación se ha centrado en el estudio y análisis de los datos operacionales facilitados por el Ente Vasco de la Energía, que es quien gestiona la planta.

Una vez analizados y ordenados esos datos, “hemos visto que un indicador de rendimiento es el Factor de Capacidad (FC), que permite comparar distintas tecnologías de producción eléctrica”, explica el investigador principal del artículo. “En este caso, hemos calculado el FC de la planta de Mutriku y su valor es de 0,11, mientras que las instalaciones de energía eólica tienen un FC del orden de 0,2-0,3 y las solares de 0,4. Ello indica —apunta Ibarra— que la tecnología OWC de Mutriku necesita mejorar su FC para poder lograr situarse al nivel de los valores del resto de las fuentes de energías renovables”. “Creemos que la manera de lograrlo es mejorar la regulación y control de la velocidad de giro de las turbinas, es decir, gestionar adecuadamente la velocidad con la que gira la turbina en relación a las olas que vienen”, concluye.

Según Gabriel Ibarra, “estas conclusiones obtenidas a partir de los datos de una planta real como la de Mutriku, representan un avance que permite enfocar e identificar los siguientes pasos a dar para que la tecnología OWC alcance su madurez, facilitando así su penetración e implementación”.

Referencia:

G. Ibarra-Berastegi, J. Sáenz, A. Ulazia, P. Serras, G. Esnaola, C. García-Soto (2017) Electricity production, capacity factor, and plant efficiency index at the Mutriku wave farm (2014-2016) Ocean Engineering doi: 10.1016/j.oceaneng.2017.10.018

El artículo ¿Son eficientes las plantas de energía marina? se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Robots más eficientes energéticamente sin pérdida de precisión
2. Se intuye la conservación de la energía (1)
3. Se establece el principio de conservación de la energía

Uno de mis objetivos como divulgador científico es mostrar a la sociedad que la ciencia forma parte de sus vidas. Para ello divulgo la importancia del progreso científico en el desarrollo de fármacos, alimentos, ropa, dispositivos móviles y otro instrumentos sin los cuales sería imposible disfrutar de la calidad de vida que tenemos. Creo que entre muchos lo hemos conseguido. Una parte mayoritaria de la sociedad tiene claro que detrás de cada uno de los ejemplos que he citado se encuentra la ciencia. En los últimos tiempos he dado un paso más allá e intento mostrar al ciudadano como el progreso científico y tecnológico también se encuentra en lugares aparentemente alejados del mismo como, por ejemplo, una procesión de Semana Santa, un simple sándwich de queso o la embestida de un toro de lidia. Con ese objetivo hoy toca hablar de la ciencia y tecnología que esconde el deporte rey: el fútbol.

Todos nosotros nos acordamos lo que hicimos en momentos puntuales de nuestras vidas. El atentado de las Torres Gemelas o el golpe de Estado del 23-F son fechas que jamás se nos olvidarán. Tampoco donde estábamos la noche del 11 de julio de 2010, el día que la Selección Española se proclamó por primera y única vez en su historia Campeona del Mundo de Fútbol.

Iniesta celebrando el gol durante la final

Aquel día vi el partido con los ojos del gran aficionado al fútbol que soy pero también, y aunque ustedes no lo crean, con los ojos de un científico. Mi reacción como aficionado no creo que les interese pero sí las dos conclusiones científico-tecnológicas que saqué tras el partido. La primera es que la ciencia se encuentra muy presente en el fútbol moderno. La segunda es que sin el progreso científico y tecnológico poco de lo ocurrido aquella noche en Johannesburgo hubiese sido posible. Se lo demostraré analizando desde el punto de vista de la ciencia y la tecnología lo que ocurrió en el minuto 116 de partido, momento en el que Andrés Iniesta marcó el gol que nos hizo campeones del mundo.

La presencia de la ciencia en el gol de Iniesta comenzó mucho antes de la final de Sudáfrica. Disciplinas como la medicina, la fisioterapia y, sobre todo, la psicología, fueron cruciales para que Andrés marcara el gol que jamás olvidaremos. Los tratamientos psicológicos no solo ayudan a motivar al futbolista. También a mantener la frialdad en momentos de máxima tensión como los muchos que hubo en el Mundial de 2010 donde ganamos casi todos los partidos por la mínima.

¿Y cómo ayudó la psicología a Andrés Iniesta? Ayudándolo a recuperarse muscular y mentalmente de un año dificilísimo. La lesión que sufrió meses antes Iniesta en el Barça y la muerte de su gran amigo Dani Jarque erosionó tanto su estado físico y mental que estuvo a punto de no ser convocado para ir al Mundial. Como Andrés reconoce en este fantástico capítulo del programa “Informe Robinson” el apoyo de médicos y fisioterapeutas, tanto del Barça como de la selección española, fueron vitales para que se recuperara a tiempo… y también para que superara la pequeña lesión que tuvo en el primer partido del Mundial ante Suiza que le impidió jugar el siguiente contra Honduras.

Un partido del que pocos se acuerdan pero que pudo dejarnos sin la copa de campeones del mundo fue el de octavos de final contra Paraguay. Aquel día otra disciplina científica, la estadística, tuvo un papel prioritario. A falta de media hora para el final el árbitro pitó un claro penalti contra España. Si hubiese marcado Cardozo, el jugador paraguayo encargado de lanzar la pena máxima, habría sido dificilísimo remontar. Sin embargo Casillas se lanzó al lado adecuado y detuvo el balón con una seguridad pasmosa.

La intuición y el azar tuvieron mucho que ver pero la ciencia también. Como se observa en el siguiente vídeo Casillas, tras detener el penalti, miró al banquillo y dedicó su decisiva parada a Pepe Reina, el portero suplente. ¿Por qué? Porque antes del partido Reina había estudiado detenidamente la forma de tirar los penaltis de Cardozo. Tras visionar muchos vídeos del jugador paraguayo había llegado a la conclusión de que casi todos los tiraba a la izquierda del portero. Se lo dijo a Iker desde el banquillo antes del lanzamiento, Casillas le hizo caso y atrapó el balón. Pura estadística.

Centrémonos en el gol de Iniesta en la final. La jugada más importante de la historia del fútbol español comenzó en el área española con un pase de Carles Puyol a Jesús Navas que recibió el esférico muy lejos de la portería rival. El balón que se empleó en el Mundial de Sudáfrica 2010, el controvertido Jabulani, ha sido uno de los más discutidos en la historia de los mundiales. Su inestable vuelo fue criticado por muchos porteros que no veían la forma de controlarlo… y es que en el diseño de los balones modernos la aerodinámica tiene mucho que decir. Polímeros como el poliuretano o el etiilvinilacetato se han sumado (y en algunos casos sustituido) al nailon, poliéster, caucho y algodón. Las modernas tecnologías de unión de los materiales que forman los balones les otorgan mayor redondez y mejor resistencia al agua. Además, las ranuras integradas de los modernos balones proporcionan buenas características de vuelo, corrigiendo los errores del Jabulani y haciéndolos más estables.

Jabulani

Tras recibir el esférico de Puyol, Jesús Navas hizo una carrera por la banda de más de 30 metros gracias a su potente zancada… y a la química de los nuevos materiales de las camisetas que mejoran el rendimiento deportivo de los futbolistas. Los jugadores holandeses, al ver que eran mas lentos que el extremo andaluz, intentaron agarrarlo pero no pudieron con la fuerza del sevillano ni con la elasticidad de la camiseta. La presencia en las equipaciones actuales de un compuesto químico como el elastano, también llamado lycra o spandex, las hace más elásticas. Sin esta fibra sintética, que en realidad es un copolímero uretano-urea, Navas no hubiese podido seguir corriendo al ser agarrado. Además, la ausencia de este material o un defecto en la fabricación provoca que las camisetas terminen desgarradas como le ocurrió en la pasada Eurocopa a 7 jugadores de la selección Suiza, lo que trajo nefastas consecuencias para la empresa responsable de la equipación.

El poliéster de las camisetas modernas provoca que sean transpirables y no retengan tanto el sudor como ocurría antiguamente con la ropa de algodón. La final del Mundial de Sudáfrica fue intensísima y tras 120 minutos trepidantes los jugadores acabaron casi deshidratados. ¿Se imaginan que todo el sudor hubiese quedado retenido en la camiseta? Muchos de ellos no hubiesen acabado el partido. Tampoco podemos olvidar la importancia de la presencia en las camisetas del poliuretano, compuesto que actúa como aislante térmico y es resistente al agua. En el Mundial de Fútbol 2010, donde la selección española jugó muchos partidos en condiciones climáticas muy diferentes, su papel fue fundamental.

La química de una camiseta de fútbol

La fantástica conducción del balón que hizo Navas fue posible gracias a la calidad del jugador pero también al buen césped del Soccer City, el campo de fútbol de Johannesburgo donde se jugó la final. La botánica, la biotecnología y la química agrícola ayudan a que los campos actuales se encuentren en perfecto estado y no tengan nada que ver con los irregulares terrenos donde se jugaron otros mundiales anteriormente. Las nuevas variedades de hierba, los fertilizantes y los modernos sistemas de regadío hacen que el balón circule a las mil maravillas.

Sin lugar a dudas, una de las grandes revoluciones del fútbol moderno reside en los campos con césped híbrido. De hecho el Mundial de Sudáfrica 2010 fue el primero donde se empleó este tipo de césped en varias sedes. En el césped híbrido predomina el natural (95%) sobre el sintético (5%) pero las millones de fibras artificiales implantadas por todo el campo tienen un efecto trascendental. Estas fibras se entrelazan con el césped natural logrando que el terreno de juego sea más resistente y más estable a la degradación, permitiendo una frecuencia de juego superior. Además, el césped híbrido tiene una mayor densidad vegetal por lo que el color verde es mucho más intenso. Pero la característica más importante para el futbolista de los céspedes híbridos es que tienen mayor capacidad de amortiguación, lo que reduce el número de lesiones.

Tras su maravillosa carrera Jesús Navas, exhausto, entregó el balón a Andrés Iniesta. El manchego hizo algo de lo que poco se ha hablado pero que fue crucial en el gol. Cuando recibió el balón se encontró rodeado de cuatro jugadores holandeses pero se deshizo de ellos dando un taconazo. Cesc Fábregas, que estaba a su espalda, quedó completamente solo con el esférico. La visión periférica de Iniesta es uno de sus valores añadidos… y también se entrena.

El equipo alemán del Hoffenheim utiliza en sus entrenamientos un sistema llamado ‘Helix’ que pone a prueba la visión periférica de los futbolistas. Se trata de una especie de simulador formado por una pantalla circular de 180 grados en la que van apareciendo jugadores realizando diferentes acciones del juego. Los jugadores, que emplean unas Google Glass en los entrenamientos, deben reconocer quiénes son los oponentes, quiénes son sus compañeros y definir sus acciones para pensar rápidamente cómo crear una situación de pase o cómo dejar atrás a sus rivales.

Cesc Fábregas, el jugador que recibió el balón procedente del taconazo de Iniesta gracias a su visión periférica, es uno de esos jugadores procedentes de La Masía que tienen lo que se conoce como el “ADN azulgrana”. Me refiero a intentar tener la posesión del balón el máximo tiempo posible. Desde que Cruyff fue nombrado entrenador del Barca ese es el sello de identidad del equipo azulgrana que luego adaptaron a la sección española Luis Aragonés y Vicente del Bosque.

Hay dos grandes culpables de que durante todos los partidos de la selección en el Mundial de Sudáfrica la posesión del balón cayera del lado español. Uno de ellos es la gran calidad de sus jugadores… el otro, las matemáticas. La disposición geométrica de los jugadores de “la Roja” a lo largo del terreno de juego fue perfecta y los diagramas de Voronoi (una construcción geométrica que permite construir una partición del plano euclídeo y que en el caso del fútbol muestran el espacio controlado por cada jugador) y las triangulaciones de Delaunay (una red de triángulos conexa y convexa que en el deporte rey conecta los jugadores con líneas), estaban presentes por todo el campo.

La aplicación al fútbol de estos conceptos matemáticos, asociados a la geometría computacional, es la clave de los famosos rondos de la selección que tanto daño hicieron a los rivales. Potentes selecciones como Portugal o Alemania sufrieron muchísimo ante “las matemáticas de la roja”. En el siguiente vídeo, del que tuve conocimiento gracias al blog del gran divulgador Francisco Villatoro, se aprecia la importancia de la geometría en la presión y posterior robo del balón, dos aspectos importantísimos en el juego de la selección española. Tras el saque inicial el equipo rojo presiona, fuerza un error del equipo azul y gana el control del balón. El centrocampista del equipo rojo abre espacio en el centro del campo, logrando tras un par de pases crear una oportunidad que acaba en gol.

Pero además de las matemáticas se necesita algo más para tener la posesión del balón: calidad técnica en los jugadores. Pocas veces se han juntado en un mismo equipo futbolistas con la técnica de Xavi Hernández. Busquets, Silva, Xabi Alonso, Navas, Iniesta, Fábregas, Villa, etc. Sus grandes virtudes son el perfecto control del balón, la rapidez de desplazamiento que imprimen al esférico y la precisión en el pase al “primer toque”, cualidades que muchos equipos entrenan con ayuda de modernas tecnologías.

En el siguiente vídeo se observa cómo hay equipos que emplean el innovador “Footbonaut” en sus centros de entrenamiento. Se trata de una caja de 20 metros cuadrados con cuatro máquinas que ‘disparan’ balones a diferentes velocidades y trayectorias hacia los futbolistas. El jugador tiene que recibir la pelota y en dos toques enviarla hacia el panel indicado de los 64 que tiene la estructura. Este instrumento es fundamental a la hora de realizar transiciones rápidas, con un máximo de dos toques seguidos de pase o tiro.

Mediante aplicaciones informáticas la máquina recoge los aciertos y errores de cada jugador y almacena la información. Posteriormente el entrenador analiza los resultados y elige qué jugadores son los que mejor se adaptan a su sistema de juego… y es que el fútbol no es ajeno al Big Data. Gracias al mismo los entrenadores conocen al instante cuantos pases correctos e incorrectos han dado sus jugadores, la distancia recorrida por cada uno, los futbolistas que mejor se acoplan al sistema defensivo u ofensivo diseñado, etc. El Big Data, que ha entrado de lleno en el fútbol moderno, también le sirve a los clubes para recoger información sobre futuros fichajes.

Sigamos con el gol de Iniesta. Fábregas, tras recibir el taconazo del jugador de Fuentealbilla, devolvió con ese primer toque que ya hemos visto como se entrena el balón a Jesús Navas. El sevillano, exhausto, dio un pase a Fernando Torres. El “Niño” realizó un centro al área buscando a Iniesta que se había desmarcado… pero se equivocó. Torres golpeó el balón suavemente y con el empeine de su pie derecho. El esférico salió en línea recta siguiendo la primera Ley de Newton, según la cual un cuerpo se mueve en la misma dirección y a la misma velocidad hasta que se le aplica una fuerza que lo haga variar de dirección. Como no apareció ninguna fuerza, el balón siguió su trayectoria rectilínea hasta que fue interceptado por un rival.

¿Qué hubiese ocurrido si Fernando Torres hubiese golpeado el esférico con el exterior del pie derecho (en lugar de con el empeine) imprimiéndole más fuerza, elevación y, sobre todo, mayor efecto? Que gracias al Efecto Magnus la pelota hubiese llegado a Iniesta, que se había desmarcado perfectamente buscando la región óptima de Voronoi.

En un lado del balón el aire se hubiese movido en dirección contraria al giro del mismo, aumentando la presión. En el otro lado el aire se movería en la misma dirección del giro de la pelota, creando un área de baja presión. Como consecuencia de la diferencia de presiones hubiese aparecido una fuerza perpendicular a la dirección de la corriente de aire. Esto hubiese provocado que el balón se curvara hacia la zona de baja presión y cambiara su trayectoria, superando a la defensa holandesa y dejando solo a Andrés Iniesta delante del portero gracias a la física del Efecto Magnus.

Para explicar el Efecto Magnus en el fútbol tradicionalmente se muestra el mítico gol de Roberto Carlos a la selección francesa que pueden observar aquí. También se aprecia en un gol de la selección española en el Mundial de Sudáfrica, concretamente en el que marcó David Villa a Chile en el tercer partido del Mundial y que nos dio el pase a octavos de final. En este enlace pueden verlo.

Pero hoy les voy a mostrar una joya donde se aprecia mucho mejor el Efecto Magnus. Se trata del gol que marcó Mohd Faiz Subri, jugador del Penang que milita en la liga de Malasia, y que ganó el Premio Puskas al mejor gol del 2016. Alucinante.

Desgraciadamente en Sudáfrica Torres no golpeó correctamente el balón y este fue interceptado por un defensa holandés. Por fortuna para el equipo español el esférico cayó de nuevo en los pies de Cesc Fábregas que, haciendo gala de su entrenada precisión, dio un pase perfecto a Andrés Iniesta dejándolo solo ante el portero holandés… y se armó la mundial, nunca mejor dicho.

Iniesta golpeó con fuerza el balón, que salió con una aceleración tremenda de su bota derecha y se coló en la portería holandesa… lo que tampoco hubiese ocurrido sin ayuda de los nuevos materiales con los que se fabrican las botas actuales y de su avanzada tecnología. Las botas modernas, mucho más ligeras que las antiguas, han mejorado la fricción entre el pie y la pelota favoreciendo el control, el pase y la precisión del tiro. Además de ser muy ligeras, las nuevas zapatillas se adaptan al pie como un guante y tanto las lengüetas, las suelas y los tacos están preparados para los innumerables disparos, giros y cambios de ritmo del fútbol moderno. Incluso para conseguir que el balón adquiera una gran aceleración ya no hace falta la fuerza con la que los jugadores de épocas pasadas golpeaban el esférico. Los innovadores materiales con los que se elaboran las botas son capaces de conseguir gran aceleración con mucho menor potencia de disparo. El balón disparado por Iniesta salió con tal aceleración de su bota derecha que dobló las manos del portero.

Lo que ocurrió después ya lo saben. Yo me abalancé sobre mi vecino rompiéndole una costilla y mi paisano José Antonio Camacho, en la retransmisión que hizo televisión de la final, gritó la célebre frase que ha quedado grabada para la eternidad: “¡¡Iniesta de mi vida!!”.

Estimados lectores, lo ocurrido en el gol de Iniesta en la final del Mundial de 2010 demuestra que la ciencia, la tecnología y el fútbol van cogidos de la mano… y es necesario que la sociedad sepa que el progreso científico y tecnológico se encuentra presente hasta en los sitios más insospechados. Disciplinas como la medicina, la química, la física, la informática, la fisioterapia, la óptica, las matemáticas, la botánica, el big data, la psicología y muchas otras aparecieron en el momento más importante de la historia del fútbol español que hizo feliz a millones de personas. Más de diez años después los avances científicos y tecnológicos siguen revolucionando el fútbol.

Sin embargo, después de Sudáfrica 2010 no hemos vuelto a ganar un Mundial. ¿Por qué? Porque en el fútbol, al igual que en el mejor de los laboratorios, el progreso científico no se pone de manifiesto si no está detrás el talento humano. A buen entendedor…

Este post ha sido realizado por José M. López Nicolás (@ScientiaJMLN) y es una colaboración de Naukas.com con la Cátedra de Cultura Científica de la UPV/EHU.

El artículo ¡Iniesta de mi vida! se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Saturno en un vaso de aceite
2. Vida bajo la luz cenicienta
3. El demonio de Maxwell

Plentziako Itsas Estazioa UPV/EHUko goi mailako ikerketa eta irakaskuntza zentro bat da. Bertan, zientzian eta teknologian oinarritutako ikerketa gauzatzen da, itsas ekosistemak giza osasunean duen eragina aztertzeko helburuarekin.

Biologo zelularrak, zoologoak, ekologoak, botanikoak, fisikariak, geologoak, mikrobiologoak eta kimikariak elkarlanean dabiltza itsas estazioetan. Zientzialariek modu integratuan ikertzen dute itsasoa, ekosistema honek gizarteari eskaintzen dizkion baliabideak aztertzeko xedearekin.

Besteak beste, itsaso sakonean minbiziaren aurkako farmakoak aztertzeko edo hainbat prozedura industrialetan erabiltzeko konposatu aktiboak aurkitu daitezke.

Zertan datza Itsas Estazio baten jarduera? Zeintzuk dira itsasoak eskaintzen dizkigun baliabide nagusiak? Lotura ote dago itsasoaren eta giza osasunaren artean? Itsasoa eta giza osasunari buruz gehiago jakiteko, Manu Soto Plentziako Itsas Estazioko zuzendariordearekin izan gara. Bere esanetan itsas ekosistema osasungarriak dira giza ongizatearen euskarri.

‘Zientzialari’ izeneko atal honen bitartez zientziaren oinarrizko kontzeptuak azaldu nahi ditugu euskal ikertzaileen laguntzarekin.

The post Manu Soto: “Ziurtatzen baldin badugu osasuntsua dela ekosistema, gizartea askoz osasuntsuagoa izango da” #Zientzialari (84) appeared first on Zientzia Kaiera.

“El frustrante viaje de un átomo de carbono” de Julio Ruiz Monteagudo recibió la mención especial del jurado en la 7ª edición de los premios On zientzia. El ciclo del carbono puede explicarse de muchas maneras, pero pocas serán tan musicales, divertidas y didácticas como este vídeo de poco más de 4 minutos.

¿Tienes una idea genial para explicar un concepto científico en un vídeo? ¿Quieres ver tu trabajo emitido en televisión? La Fundación Elhuyar y el Donostia International Physics Center (DIPC) han organizado la octava edición de On zientzia, un concurso de divulgación científica y tecnológica enmarcado en el programa Teknopolis, de ETB. Este certamen pretende impulsar la producción de vídeos cortos y originales que ayuden a popularizar el conocimiento científico.

On zientzia tendrá tres categorías. El mejor vídeo de divulgación recibirá un premio de 3.000 euros. Para impulsar la producción de piezas en euskera, existe un premio de 2.000 euros reservado a la mejor propuesta realizada en ese idioma. Por último, con el objetivo de impulsar la participación de los estudiantes de ESO y Bachillerato, hay un premio dotado con 1.000 euros para el mejor vídeo realizado por menores de 18 años.

Los vídeos han de tener una duración inferior a los 5 minutos, se pueden realizar en euskera, castellano o inglés y el tema es libre. Deben ser contenidos originales, no comerciales, que no se hayan emitido por televisión y que no hayan resultado premiados en otros concursos. El jurado valorará la capacidad divulgativa y el interés de los vídeos más que la excelencia técnica.

Las bases las encuentras aquí. Puedes participar desde ya hasta el 25 de abril de 2018.

Edición realizada por César Tomé López

El artículo El frustrante viaje de un átomo de carbono, mención especial del jurado “On zientzia” se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Fallos científicos en el cine, mejor vídeo de divulgación joven “On zientzia”
2. El mecanismo de la vida, mejor vídeo de divulgación joven “On zientzia”
3. Soy esa bacteria que vive en tu intestino, mejor vídeo de divulgación “On zientzia”

«La potencia sin control no sirve de nada». Este es el eslogan de la que, con toda probabilidad, ha sido la campaña publicitaria de neumáticos más exitosa de la historia. Fue realizada en 1995 por la agencia de publicidad Young & Rubicam para Pirelli.

Uno de los cometidos pretendidos en el diseño de automóviles es que se mantengan pegados a la carretera. Esto se logra sobre todo gracias a la aerodinámica, de manera que, al aumentar la potencia el automóvil no se separe del suelo. Podríamos decir que la aerodinámica de un automóvil sería la contraria a la de un avión.

La aerodinámica es fundamental, sobre todo en los coches deportivos y de competición, pero, no hay que olvidar la importancia de los neumáticos. Mi padre, que se dedicó durante años a la industria del neumático, siempre dice que «los neumáticos son la única parte del coche que está en contacto directo con la carretera», por eso son tan importantes. No le falta razón.

Utilizamos ruedas desde hace miles de años, pero la idea de ponerle caucho en el borde exterior es relativamente nueva. Fue a principios del siglo XIX cuando por primera vez se utilizó este polímero natural para recubrir las ruedas de madera. Antiguamente se enfundaban en cuero o metal.

El caucho se obtiene de varios tipos de plantas, pero principalmente se extrae del látex que surge de los cortes hechos del tronco de Hevea brasiliensis. En la década de 1920 los laboratorios de Bayer inventarían el caucho sintético.

El caucho natural se somete a varios procesos sucesivos como la coagulación, el lavado y el refinado. El caucho natural resulta poco elástico y se reblandece fácilmente con el calor. Se desgasta con rapidez, así que su futuro no parecía muy prometedor.

El químico Charles Goodyear dedicó varios años de su vida a investigar el caucho. En 1839 descubrió el vulcanizado, que es un procedimiento que consiste en calentar el caucho en presencia de azufre en polvo. En resultado final es que las moléculas elásticas de caucho se quedan unidas entre sí mediante puentes de azufre. De esta manera se consigue un caucho más duro y resistente sin perder elasticidad. El vulcanizado es el proceso químico que dio origen a los neumáticos que utilizamos hoy en día.

Desgraciadamente Charles Goodyear no patentó su invento. El ingeniero Thomas Hancock, habiendo llegado más tarde a la misma conclusión se hizo con la patente en 1843. Fue entonces cuando se hicieron populares las ruedas de goma maciza.

Charles Goodyear sigue estando asociado al mundo del neumático debido a que una empresa de éxito de la industria de la automoción tomó su nombre. Sin embargo, esta compañía no tiene ninguna relación con él.

Hasta entonces los neumáticos eran de color claro, por lo que se ensuciaban con facilidad y comprometían la estética. En 1885 la empresa Goodrich decidió fabricar ruedas de color negro. Al tintar el caucho se hizo un descubrimiento sorprendente, los neumáticos negros duraban más. Esto es debido a que el tinte negro absorbe los rayos ultravioletas que son, en parte, los causantes del agrietamiento del caucho.

La primera rueda neumática —llena de aire— fue patentada en 1845 por el ingeniero Robert W. Thomson. Sin embargo, no fue hasta 1888 que el ingeniero John Boyd Dunlop, desarrolló el primer neumático con cámara de aire. Lo inventó para envolver las ruedas del triciclo que su hijo de nueve años usaba para ir a la escuela por las calles bacheadas de Belfast. Esas precarias cámaras de aire consistían en unos tubos de goma hinchados. Envolvió los tubos con una lona y los pegó sobre las llantas de las ruedas del triciclo. Patentó el neumático con cámara de aire en 1889. Había ganado en comodidad, aun así, al neumático le faltaban algunos obstáculos por vencer. Era muy trabajoso repararlos, ya que estaban adheridos a la llanta.

En 1891, Édouard Michelin, quien era conocido por su trabajo con el caucho vulcanizado, decidió desarrollar un neumático que pudiera separarse de la llanta y así facilitar el trabajo. Los neumáticos de Michelin resultaron tan prácticos que al año siguiente ya eran los que utilizaban la mayoría de ciclistas. Poco después también los llevarían los carruajes. En 1946, la compañía Michelin desarrolló el método de construcción de neumáticos radiales que supusieron un antes y un después en la conducción deportiva.

En los años 40 se incluyeron nuevos materiales en la composición del neumático, como el rayón, el nailon y el poliéster. Cuando terminó la segunda guerra mundial, se empezó a trabajar en la fabricación de un neumático que sellara herméticamente sobre la rueda, lo que al fin eliminó la necesidad de acompañarlos de cámara de aire. La evolución fue vertiginosa, propiciada en gran medida por la Fórmula 1. En los neumáticos modernos se utilizan más de doscientos materiales distintos, entre ellos el acero, la fibra de carbono o el kevlar. En la actualidad el caucho vulcanizado lo encontramos, sobre todo, en la superficie del neumático.

En automoción —y en otros aspectos de la vida— sigue siendo muy certero eso de que «la potencia sin control no sirve de nada». En las vallas publicitarias y en prensa, bajo este eslogan de Pirelli salía una magnífica imagen del deportista Carl Lewis con zapatos de tacón. En la versión televisiva del anuncio, la planta de sus pies estaba cubierta de caucho.

Y es que, entre otros aspectos ingenieriles, los neumáticos y en consecuencia la ciencia del caucho es fundamental para el control de la conducción. Al fin y al cabo, como dice mi padre, es la única parte del coche que está en contacto directo con el asfalto. Cuando vamos en coche los neumáticos son nuestros pies en el suelo.

Sobre la autora: Déborah García Bello es química y divulgadora científica

El artículo La potencia sin control no sirve de nada se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. ¿La publicidad no sirve para nada?, ¡ja!
2. Potencia y eficiencia de una máquina
3. Fotovoltaicos siempre a máxima potencia

Juan Ignacio Pérez eta Miren Bego Urrutia Janaria

———————————————————————————————————–

1. irudia: Esnearen laktosa digeritzeko ezintasunari laktosarekiko intolerantzia deritzo.

Batzuek gustukoa dute esnea; beste batzuek, berriz, ezin dezakete edan. Jende helduaren artean asko dira esneak kalte egiten dietela diotenak, digeritu ezin dezaketelako. Zehatzak izateko, esnearen laktosa da digeritu ezin dezaketena. Laktosa digeritzeko ezintasun horri laktosarekiko intolerantzia deitzen zaio.

Laktosa disakarido bat da, bi hexosaz osatua dagoen azukrea. Horrelako azukreak digeritu ahal izateko, disakaridasak behar dira, disakaridoak hidrolizatzen laguntzen duten entzimak. Laktosaren kasuan laktasa da disakaridasa hori. Laktasa, beste disakaridasak bezala, hestearen epitelioko zelulen mintzean dago, hestearen argira begira dagoen aldean. Mintzean egotea garrantzitsua da: laktosaren digestioaren ondorioz sortzen diren bi monosakaridoak (glukosa eta galaktosa) xurgatzen baitira digestioaren prozesu berean.

Zer gertatzen da, baina, laktosa digeritu ezin daitekeenean? Digeritu ezean, hestearen argian gelditzen da laktosa. Hori dela eta, hestean dagoen mikroflorak hartzitu egiten du, eta hartziduraren ondorioz gasak sortzen dira; gas horiek eragiten dute ondoeza. Baina, horrez gain, eragile osmotikoa da disakarido hori; hau da, hestearen argian xurgatu gabe dagoen bitartean ura erakartzen du eta, horren ondorioz, ura iragaten da barne-mediotik hestearen argira. Ur hori digestioaren hondakinekin batera galtzen da, gorotzekin batera, eta beherakoa gertatzen da. Ondoeza alde batera utzirik, deshidratazioa ere ekar dezake laktosa digeritu ezin izateak. Esnearekiko nazka eta errefusa dira ezintasun horren ondorioak eta, beraz, esneak dituen makro eta mikroelikagaiak baliatzeko aukera galtzea.

Laktosarekiko intolerantziak jatorri bi izan ditzake. Lehen mailako intolerantzia deitzen duguna oso arrunta da, eta gizabanako askori gertatzen zaio amaren bularretik bereizi ondoren. Geroago arituko gara intolerantzia mota horretaz. Bigarren mailako intolerantzia, berriz, heste-hodiaren gaixotasunek sortua da. Zenbaitetan, heste-hodiaren gaixotasun batek laktasaren gabezia ekar dezake. Gaixotasun zeliakoa, Crohn gaitza, edo hantura-gaixotasunak egon daitezke intolerantzia mota horren oinarrian. Zenbaitetan, birus- edo bakterio-infekzioak dira bigarren mailako intolerantzia sorrarazten dutenak. Oso arruntak dira horiek, haurren artean esaterako. Infekzio-gaitz batek heste-hodiaren mukosa kaltetzen duenean epitelio-zelula asko galtzen dira, eta, beraz, zelula horien mintzetan dagoen laktasa ere galtzen da. Hortik dator esnea digeritu ezin izatea.

2. irudia: Ugaztun gehienek laktosarekiko intolerantzia garatzten dute edoskitze aldiaren ostean (Dehesadevaldelazarzaren irudia).

Baina askoz hedatuago dago lehen mailako laktosarekiko intolerantzia, intolerantzia mota horrek gizabanako gehienei eragiten baitie. Lehen mailako intolerantzia, berez, ugaztun gehienei gertatzen zaie amagandiko edoskitze-aldia bukatu ondoren. Esnea, azken batean, ugaztunen lehen hilabete edo lehen urteetako elikagaia da, eta ez luke zentzu handirik bizitza osoan zehar beharrezkoa ez den entzima bat, laktasa, ekoiztea. Izan ere, ume batzuengan bigarren urtetik aurrera hasten da laktasa-jarduera jaisten.

Zenbait herritako gizakiek, baina, esnea digeritzeko ahalmena bizitza osoan zehar mantentzen dute, edoskitzeari utzi ondoren ere laktasa sortzen baitute. Ahalmen hori, esan bezala, ez da unibertsala eta duela 8.000 urte[1] sortu zen abereak etxekotu zituzten zenbait herritan. Horri esker, elikatze-balio handia duen elikatze-baliabidea erabili ahal izan dute, eta, bereziki, D bitamina- eta kaltzio-emari egokia bermatu. Gogoan izan behar dugu kaltzioa eta D bitamina hezurrak osasuntsu hazteko ezinbesteko elikagaiak direla.

Hortaz, goi-latitudeak kolonizatzeko moldaera baliotsua izan da esnea digeritu ahal izatea, latitude horietan argi gutxi baitago, eta argi gutxi egonda D bitamina gutxiago sor baitaiteke. Eguzki-argiaren izpi ultramoreei esker sortzen dira D2 bitamina (ergosteroletik) eta D3 bitamina (kolesteroletik). Interes handikoa da laktosarekiko intolerantziari dagozkion herrien arteko desberdintasunei begiratu bat ematea. Hona zenbait datu: herbeheretarrak, % 0; suediarrak, % 1; danimarkarrak, % 3; ingelesak, % 6; errusiarrak, % 15; espainiarrak, % 15; europar jatorriko estatubatuarrak, % 24; grekoak, % 53; Australiako aborigenak, % 67; italiarrak, % 71; arabiarrak, % 80; afrikar jatorriko estatubatuarrak, % 81; inuitak, % 83; afrikarrak, % 83; mexikarrak, % 83; nigeriarrak, % 89; Estatu Batuetako aborigenak, % 95; tailandiarrak, % 98; asiar jatorriko estatubatuarrak, % 100. Oso esanguratsua da inuitei dagokien datua, frogatzen baitu aldaketaren joera ez dela latitudearen araberakoa. Aipagarria da, halaber, Estatu Batuetako aborigen eta europar jatorrikoen arteko aldea. Argi dago herri europarretan gertatzen dela laktosarekiko tolerantzia-maila handiena, Europan esne-abereek beste inon baino garrantzi handiagoa izan dute-eta historia osoan zehar.

Oharrak:

[1] 2010ean egin diren aurkikuntza berrien arabera, baliteke ahalmen hori lehenago ere (duela 12.000 urte) sortu izana.

—————————————————–

Egileez: Juan Ignacio Pérez Iglesias (@Uhandrea) eta Miren Bego Urrutia Biologian doktoreak dira eta UPV/EHUko Animalien Fisiologiako irakasleak.

—————————————————–

Artikulua UPV/EHUren ZIO (Zientzia irakurle ororentzat) bildumako Animalien aferak liburutik jaso du.

The post Esnea denontzat? appeared first on Zientzia Kaiera.

Imagina que te digo que existe una lente óptica tan potente, una hiperlente, que permite ver detalles del tamaño de un pequeño virus en la superficie de una célula viva en su entorno natural. Suena increíble, tanto más cuanto más sepas de biología o de física, pero existe realmente.

Una representación artística de una hiperlente que permite ver una célula viva con detalle. Arriba a la izquierda, la estructura cristalina del nitruro de boro hexagonal (hBN). Imagen de Keith Wood, Vanderbilt University

La ciencia y la ingeniería han desarrollado muchos instrumentos capaces de producir imágenes con resolución a nanoescala, como microscopios basados en flujos de electrones y otros llamados de fuerza atómica. Sin embargo, estos instrumentos son incompatibles con organismos vivos, ya que, o bien operan bajo un alto vacío, o exponen las muestras a niveles nocivos de radiación, o requieren técnicas letales de preparación de muestras como la liofilización o extraen las muestras de su entorno natural basado en disoluciones.

La razón principal para desarrollar las llamadas hiperlentes (lentes ópticas con una resolución mucho menor que la longitud de onda de la luz empleada) es la posibilidad de que pudiesen proporcionar imágenes detalladas de las células vivas en sus entornos naturales utilizando luz de baja energía que no las dañe. El trabajo realizado por un equipo de investigadores encabezado por Alexander Giles, del Laboratorio de Investigación Naval de los Estados Unidos, ha llevado la construcción de hiperlentes un paso más allá simplemente purificando el material a niveles que hace unas décadas eran inimaginables.

El material óptico empleado es el nitruro de boro hexagonal (hBN), un cristal natural con propiedades de hiperlente. La mejor resolución que se había conseguido previamente usando hBN fue de 36 veces más pequeña que la longitud de onda infrarroja utilizada: aproximadamente el tamaño de la bacteria más pequeña. El nuevo trabajo describe mejoras en la calidad del cristal que mejoran su capacidad en un factor de diez.

Los investigadores lograron esta mejora al fabricar cristales de hBN usando boro isotópicamente purificado. El boro natural contiene dos isótopos que difieren en peso en aproximadamente un 10 por ciento, una combinación que degrada significativamente las propiedades ópticas del cristal en el infrarrojo.

Los científicos calculan que una lente hecha de su cristal purificado puede, en principio, capturar imágenes de objetos de 30 nanómetros de tamaño. Para poner esto en perspectiva, un pelo humano tiene entre 80.000 y 100.000 nanómetros de diámetro. Un glóbulo rojo humano tiene aproximadamente 9.000 nanómetros y los virus varían de 20 a 400 nanómetros.

La física de las hiperlentes es bastante compleja. El nivel de detalle con el que los microscopios ópticos pueden generar imágenes está limitado por la longitud de onda de la luz y el índice de refracción del material de la lente. Cuando esto se combina con los factores de apertura de la lente, la distancia desde el objeto a la lente y el índice de refracción del objeto bajo observación, se traduce en un límite óptico típico de aproximadamente la mitad de la longitud de onda utilizada para la obtención de las imágenes.

En las longitudes de onda infrarrojas utilizadas en este experimento, este “límite de difracción” es de aproximadamente 3.250 nanómetros. Este límite puede superarse mediante el uso de hBN debido a su capacidad para soportar polaritones de fonones superficiales, partículas híbridas formadas por fotones de luz que se acoplan con átomos del cristal que poseen carga y vibran. Estos polaritones tienen longitudes de onda mucho más cortas que la luz incidente.

El problema con el uso de polaritones ha sido siempre la rapidez con la que se disipan. Mediante el uso de cristales de hBN hechos con un 99% de boro isotópicamente puro, los investigadores han podido comprobar que existe una reducción drástica de las pérdidas ópticas en comparación con los cristales naturales, es decir, que aumenta el tiempo de vida del polaritón, lo que les permite viajar el triple de distancia. Este mayor recorrido se traduce en una mejora significativa en la resolución de las imágenes. El análisis teórico de los investigadores sugiere que es posible incluso otro factor de mejora de diez adicional.

En 1654, Anton van Leeuwenhoek utilizó uno de los primeros microscopios para descubrir el mundo desconocido hasta ese momento de la vida microscópica. Este resultado en el desarrollo de hiperlentes es un paso importante para llevar el descubrimiento de van Leeuwenhoek a un nivel completamente nuevo, que permitirá a los biólogos observar directamente los procesos celulares en acción, como virus invadiendo células o células inmunes que atacan invasores extraños, abriendo innumerables posibilidades en la investigación biomédica.

Referencia:

Alexander J. Giles et al (2017) Ultralow-loss polaritons in isotopically pure boron nitride Nature Materials doi: 10.1038/nmat5047

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

Este texto es una colaboración del Cuaderno de Cultura Científica con Next

El artículo Una hiperlente que permite ver un virus en la superficie de una célula viva se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Otra pieza en el puzle de la fotosíntesis
2. Cómo fabricar hielo extraterrestre y verlo molécula a molécula
3. Estroncio en la leche

Las personas que han visitado durante las últimas semanas el Museo Guggenheim de Bilbao han tenido la suerte de poder disfrutar de una exposición interesante e inspiradora, “Anni Albers, tocar la vista” (6 de octubre de 2017 – 14 de enero de 2018). Esta exposición nos acerca a la obra de la artista de origen alemán, afincada en Estados Unidos, Anni Albers (1899-1994), quien seguramente sea la artista textil más importante del siglo XX, aunque también trabajó otras técnicas como el grabado, la pintura o el diseño de joyas.

Anni Albers, “Estudio para Colgadura no realizada” (sin fecha), Gouache sobre papel, The Josef and Anni Albers Foundation

La exposición está compuesta por alfombras y colgaduras textiles, telas, diagramas geométricos, dibujos y estudios para el diseño de obras textiles, joyas, aguatintas, litografías, serigrafías e impresiones offset, acuarelas y otros tipos de pinturas, en las cuales la geometría juega un papel fundamental.

Las personas que deseen más información sobre la exposición pueden visitar la página del Museo Guggenheim-Bilbao Anni Albers, tocar la vista o ver los cuatro videos que el museo ha colgado en su canal de youtube y que están aquí.

Anni Albers, “Segundo movimiento V” (1972), Aguatinta, The Josef and Anni Albers Foundation

La visita a la exposición Anni Albers, tocar la vista fue una experiencia enriquecedora. Descubrí a una artista excepcional y disfruté de unas creaciones artísticas increíbles. Tengo ganas de volver para sumergirme de nuevo en el arte de Anni Albers, y descubrir más sobre los procesos creativos, claramente conectados con las matemáticas, de esta artista. Aunque muchas de las obras de la exposición despertaron la curiosidad de mi mirada matemática, me gustaría destacar aquí la serie de obras dedicadas a los “nudos”, como su litografía Enredada (1963),

Anni Albers, “Enredada” (1963), litografía, The Josef and Anni Albers Foundation

o su, también litografía, Sin título (1963),

Anni Albers, “Sin título” (1963), litografía, The Josef and Anni Albers Foundation

que rápidamente me recordaron a la teoría de nudos de las matemáticas. De hecho, esta última obra me hizo recordar la fotografía realizada por un microscopio electrónico de un fragmento anudado del ácido desoxirribonucleico, ADN, cuyo estudio es uno de los campos de aplicación de la teoría de nudos.

Fotografía de un fragmento de ADN anudado visto con un microscopio electrónico, realizada por Steven A. Wasserman y Nicholas R. Cozzarelli

La teoría de nudos, que ya mencionamos brevemente en la entrada del Cuaderno de Cultura Científica La topología modifica la trayectoria de los peces, es una rama de la topología que se dedica al estudio matemático de los nudos, que surgió en el siglo XX, aunque tiene sus orígenes en el siglo XIX con el trabajo de matemáticos como el alemán Carl Friedrich Gauss (1777-1855), su alumno Johann B. Listing (1808-1882) o el inglés Peter G. Tait (1831-1901). La teoría de nudos tiene numerosas e importantes aplicaciones fuera de las matemáticas, como por ejemplo en biología molecular, medicina, mecánica estadística, física de polímeros y de cristales, teoría física de cuerdas, criptografía, o ciencias de la computación.

La idea matemática de nudo es una abstracción matemática de lo que sería un nudo físico. Se coge una cuerda, se anuda de una forma más o menos enrevesada y se pegan los extremos. Desde el punto de vista matemático nos interesa la línea cerrada que describe la cuerda, sin tener en cuenta el grosor de la misma, es decir, un nudo es una línea curva anudada cerrada, que no tiene puntos de intersección, en nuestro espacio tridimensional.

Como estamos hablando de nudos en topología, esto significa que podemos deformar estirando o encogiendo la línea, es decir, la cuerda, y cambiándola de forma en el espacio, lo cual no altera el nudo, siempre que no se corte o pegue la misma. De hecho, se dice que dos nudos son equivalentes, que para nosotros es tanto como decir que “son iguales desde el punto de vista topológico”, cuando se puede deformar un nudo en el otro de forma continua, es decir, sin realizar cortes, ni pegar.

El nudo más simple es cuando cogemos la cuerda y unimos los extremos sin anudar, es decir, es la circunferencia, en la que no existe un nudo como tal, podríamos decir que es el no-nudo. Cualquier deformación espacial de la circunferencia, como en la imagen de abajo realizada con el juguete Tangle, sigue siendo el no-nudo.

Cuatro deformaciones en el espacio del nudo trivial, realizadas con el juguete Tangle, luego los cuatro nudos resultantes son equivalentes entre sí, son el mismo nudo, el no-nudo

El nudo más sencillo no trivial es el nudo de trébol, que es cuando hacemos un nudo sencillo a la cuerda y después anudamos los extremos. Es imposible deformarlo al nudo trivial sin cortar la cuerda y volver a pegarla, luego topológicamente el no-nudo y el nudo de trébol no son el mismo, no son equivalentes.

Nudo de trébol en el espacio tridimensional. Jim Belk, de wikimedia

El nudo de trébol es un símbolo muy común desde la antigüedad, ya que su versión plana es la triqueta, o triquel, que fue ampliamente utilizada, por ejemplo, en el arte celta, en la religión cristina, como símbolo de la trinidad (padre, hijo y espíritu santo), en una de las versiones del Valnout alemán, que se relaciona con el dios Odín, o en el Mjolnir, martillo del dios Thor de la mitología nórdica. Y hoy en día nos la encontramos con mucha frecuencia en la cultura popular, por ejemplo, en la katana de Michonne de la serie de TV Walking Dead, así como en muchas otras series, películas o video juegos.

La katana de Michonne, de la serie The Walking Dead, tiene el símbolo de la triqueta, que es el nudo de trébol

Para estudiar los nudos se utilizan representaciones gráficas planas de los mismos, que son proyecciones sobre el plano de los nudos tridimensionales, como si les hiciéramos una fotografía. Se utilizan solo las proyecciones buenas, las llamadas regulares, en las que solamente hay un número finito de puntos dobles (cruces) como puntos singulares. En las proyecciones no regulares perderíamos parte de la información del nudo. Estas representaciones se llaman diagramas del nudo. Son líneas continuas en el plano, que solo se pintan discontinuas cuando esa parte del nudo pasa por debajo de la que ya está pintada, como se muestra en los siguientes ejemplos. También podemos pensar en los diagramas de los nudos, como la representación de un nudo, como cuerda anudada, que apoyamos en una superficie plana.

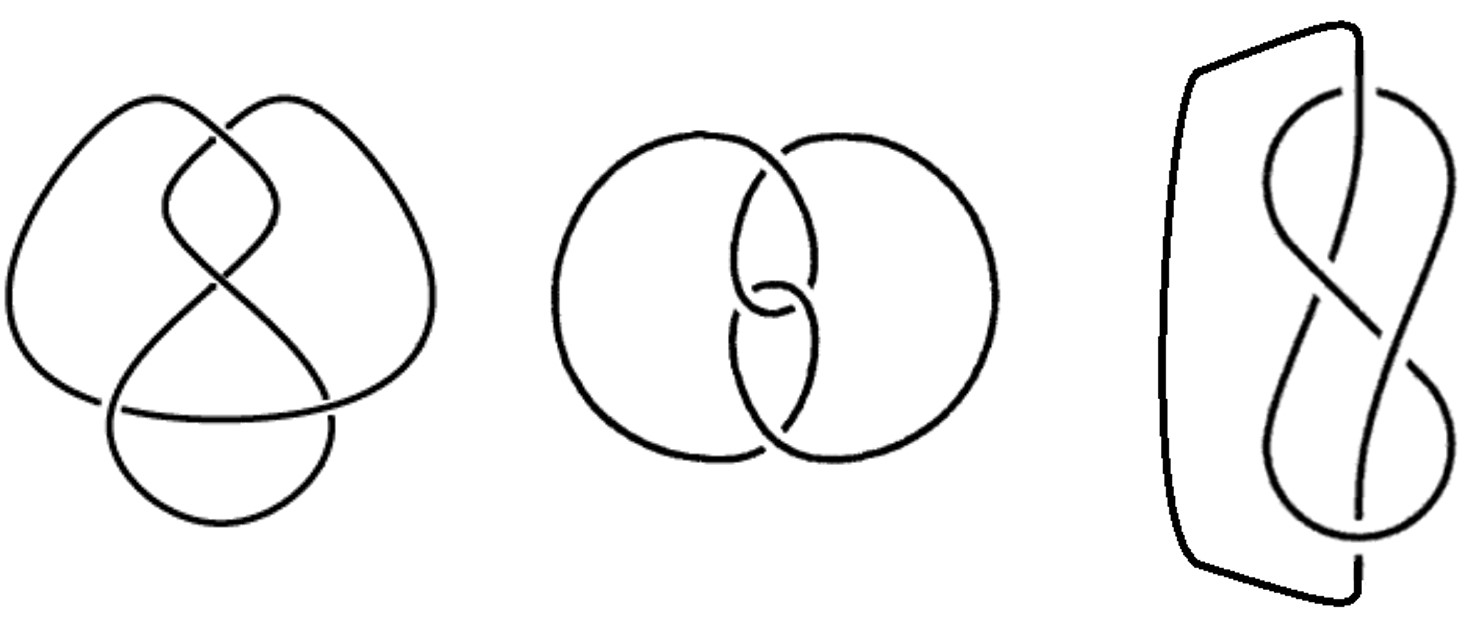
Tres diagramas diferentes del nudo de Saboya, o nudo del ocho

El nudo de Saboya, o nudo del ocho, que aparece en la anterior imagen, es un nudo cuyo diagrama tiene cuatro cruces, el diagrama del trébol tenía solamente tres, y se llama así porque aparece en el escudo de armas de la Casa de Saboya.

Escudo de armas de la Casa de Saboya con distintas copias del diagrama del nudo de ocho, o de Saboya

A continuación, mostramos el diagrama del nudo de la obra Sin título (1963), de Anni Albers.

La teoría de nudos estudia las propiedades topológicas de los nudos, en particular, el problema más importante es la clasificación de los diferentes nudos que existen, el cual incluye el problema de reconocimiento, es decir, determinar cuándo dos nudos son equivalentes, para lo cual se desarrollan herramientas matemáticas que nos permitan saber cuándo dos nudos son, o no, equivalentes (el mismo desde el punto de vista topológico).

En particular, deberemos de estudiar cuando dos diagramas corresponden a nudos equivalentes. Por ejemplo, nos podemos preguntar si un diagrama complejo como el que aparece en la imagen de abajo, y que se conoce como nudo gordiano de Haken, es topológicamente equivalente al no-nudo, es decir, que no hay nudo, solamente está enmarañado. El propio matemático alemán Wolfgang Haken, conocido por demostrar junto al matemático estadounidense Kenneth Appel el teorema de los cuatro colores, demostró que efectivamente dicho nudo es equivalente al no-nudo.

Nudo gordiano de Haken

En la década de 1920, que fueron los inicios de la teoría de nudos, el matemático alemán Kurt Reidemeister (1893-1971), dio una primera herramienta para determinar cuándo dos diagramas correspondían a nudos equivalentes. Demostró que:

“Dos diagramas representan nudos equivalentes si, y sólo si, se puede pasar de uno a otro mediante un número finito de transformaciones del tipo I, II y III (que se muestran a continuación).”

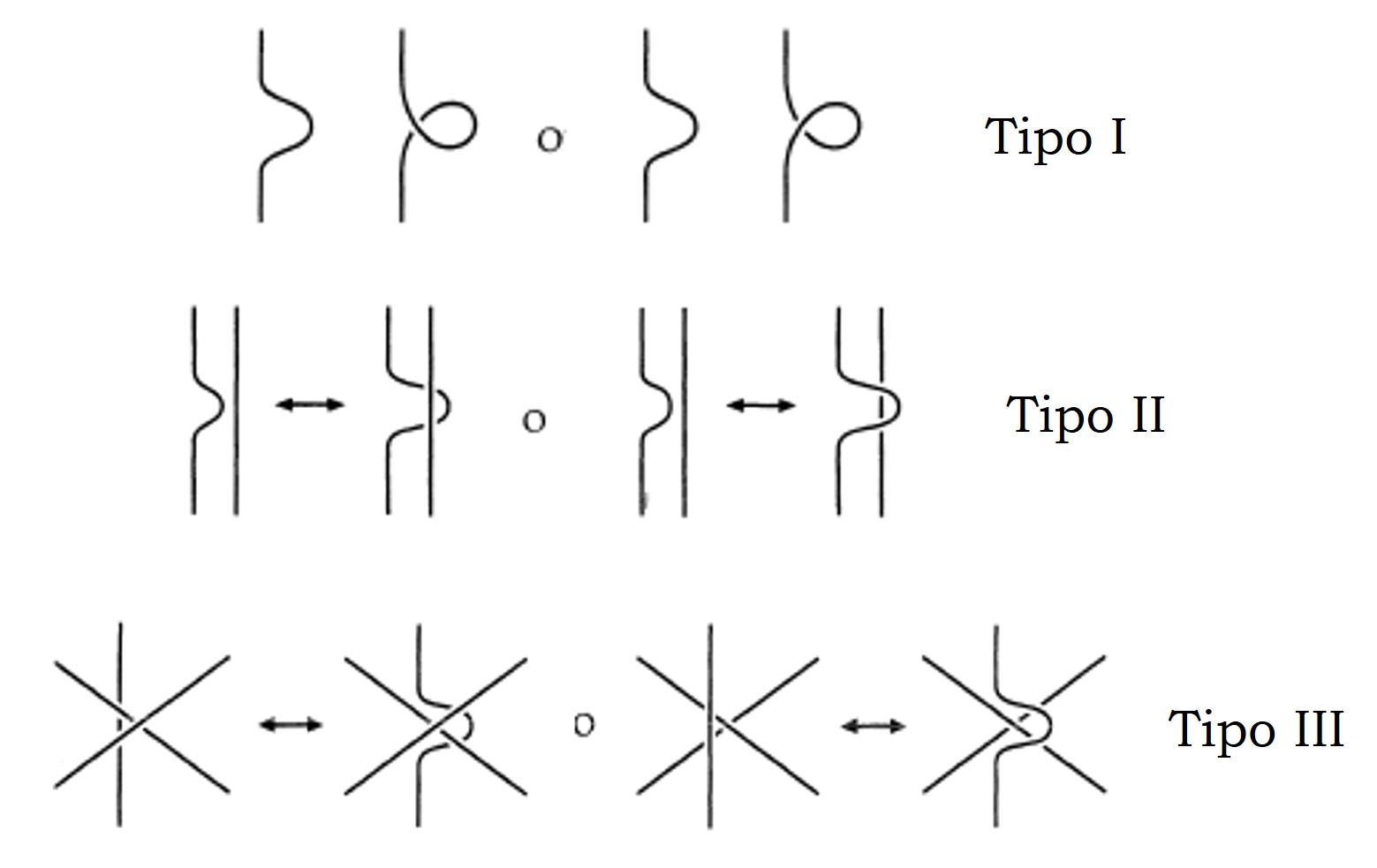
Transformaciones de Reidemeister de tipo I, II y III de los diagramas de nudos

A continuación, vemos un nudo con tres cruces que es equivalente al nudo de trébol, puesto que mediante una serie de movimientos de Reidemeister puede transformarse uno en otro, como se muestra en la siguiente imagen.

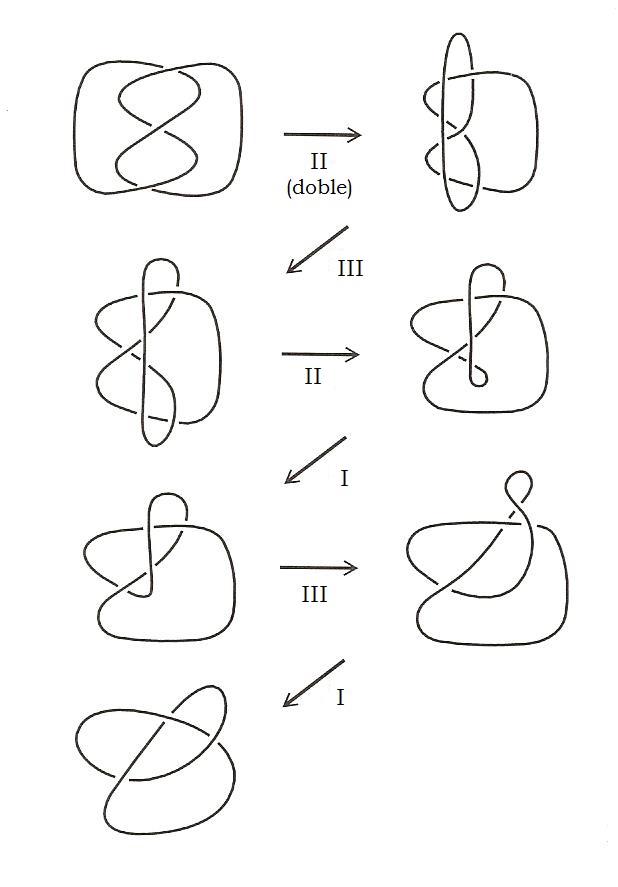
Los movimientos de Reidemeister transforman el diagrama con tres cruces inicial en el diagrama del nudo de trébol, luego ambos son equivalentes, corresponden al mismo nudo topológico

Existe un tipo especial de nudos, aquellos que son equivalentes a su imagen especular. Se llaman nudos anfiquirales. La imagen especular de un nudo es aquella que se obtiene como reflejo en un espejo, es decir, es el nudo simétrico respecto a un plano del espacio. Dado el diagrama de un nudo, entonces el diagrama del nudo imagen especular del primero es igual salvo que tiene los cruces dados la vuelta, es decir, la línea continua se convierte en discontinua, y la discontinua en continua.

El nudo de Saboya es un nudo anfiquiral, como se muestra en la siguiente imagen, mientras que el nudo de trébol puede demostrarse que no es anfiquiral.

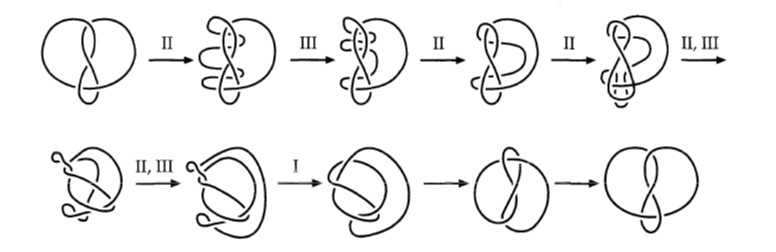
Otra división importante de los nudos de cara a su estudio y clasificación es en nudos primos y nudos compuestos. La idea es descomponer los nudos en otros más simples, los llamados nudos primos, que son los que no se pueden descomponer en otros más simples aún y a partir de los cuales se generan todos los demás, y entonces centrar el estudio general de los nudos en estos.

Por lo tanto, tenemos dos “operaciones” con nudos, que son una inversa de la otra, la descomposición y la suma conexa. Un nudo se descompone mediante una esfera (en el diagrama plano sería una circunferencia) que corta transversalmente al nudo en dos puntos, por los que se corta el nudo generándose dos partes disjuntas, cada una de las cuales se cierra de nuevo al pegar los dos puntos extremos mediante un segmento, generándose así dos nudos. Un nudo es primo si no se puede descomponer en dos nudos no triviales.

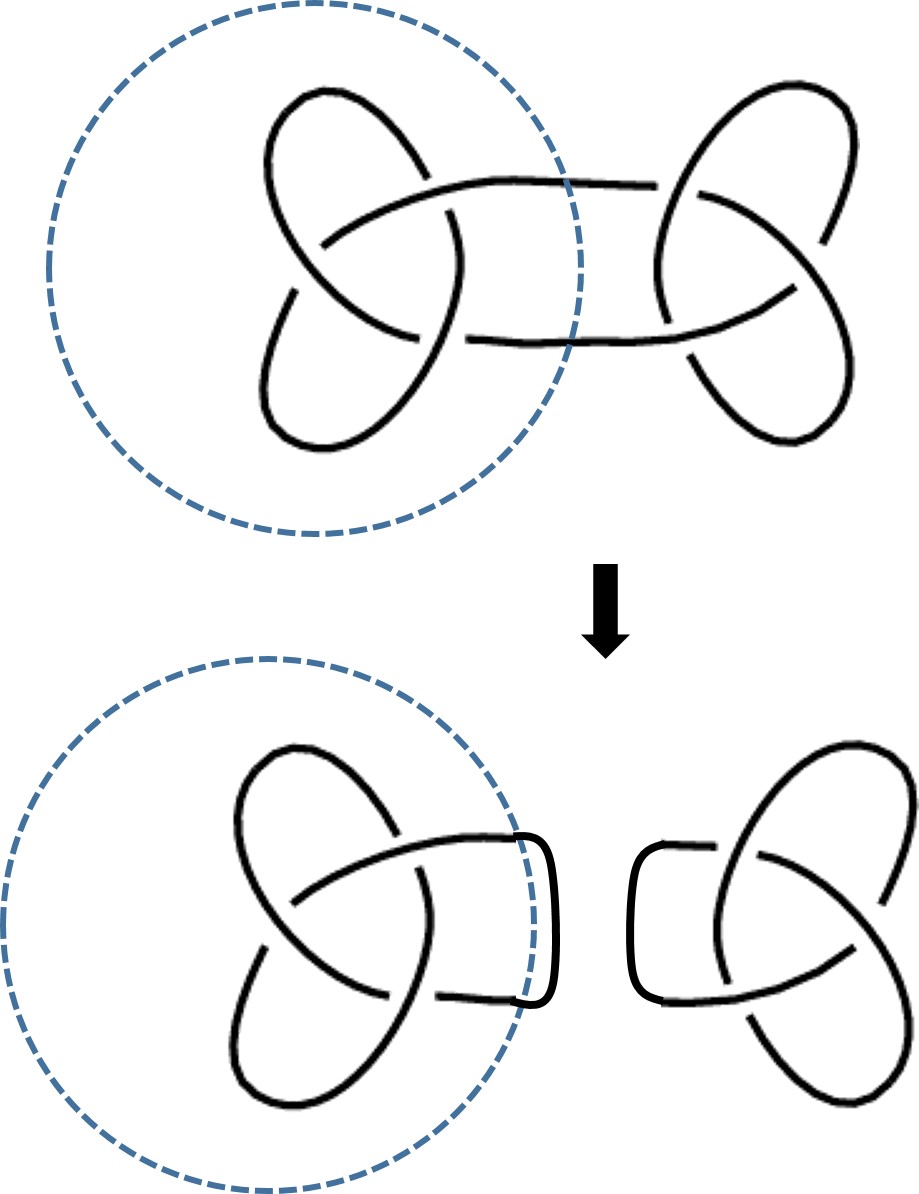
Descomposición del conocido como nudo de la abuela en dos copias del nudo de trébol

Cualquier nudo no primo se obtiene mediante la operación inversa a la anterior, la suma conexa, a partir de un número finito de nudos primos. En la imagen siguiente vemos la suma conexa del nudo de trébol y de su imagen especular, que es el nudo de rizo o nudo cuadrado.

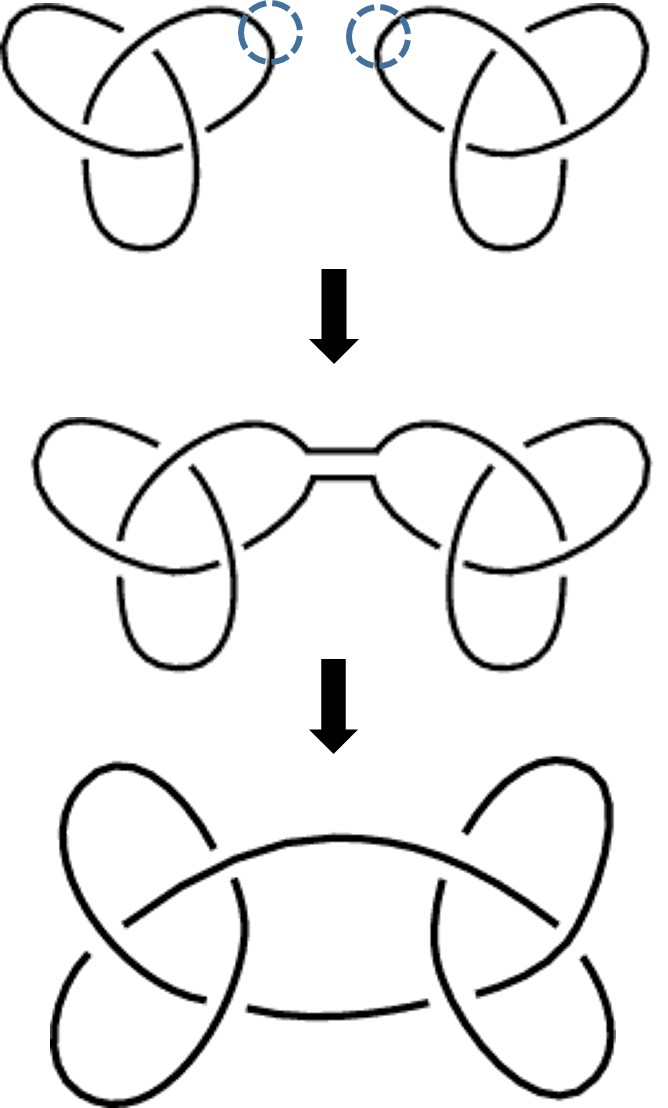
Suma conexa del nudo de trébol y su imagen especular, que es el nudo de rizo, o nudo cuadrado

El nudo de la abuela, que es la suma conexa de dos copias del nudo de trébol, es un nudo no anfiquiral, mientras que el nudo de rizo, que es la suma conexa del nudo de trébol y su imagen especular, sí es anfiquiral. En consecuencia, ambos nudos no son equivalentes.

Algunos de los nombres de los nudos matemáticos, como el nudo del ocho, el nudo de la abuela, el nudo de rizo, el nudo del cirujano o el nudo del amor verdadero, entre otros, derivan de los nombres de los nudos físicos, los nudos utilizados en la navegación y en muchas otras actividades de nuestra sociedad, como la escalada, la medicina, la costura o la decoración, desde la antigüedad.

Según el diccionario de la RAE, un nudo (físico) es un “lazo que se estrecha y cierra de modo que con dificultad se pueda soltar por sí solo, y que cuanto más se tira de cualquiera de los dos cabos, más se aprieta”. En matemáticas, para estudiar cómo de anudado está un nudo se unen los dos cabos del mismo, cerrando el nudo y no dejando que se pueda deshacer.

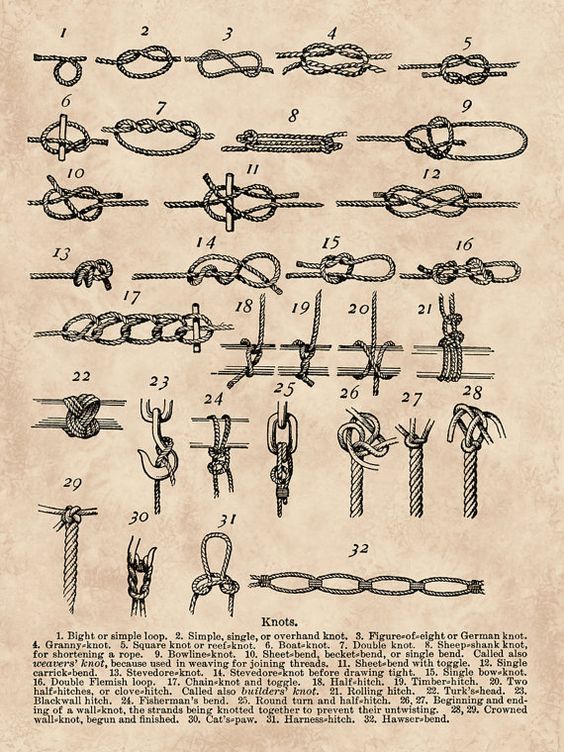
Poster de estilo vintage con nudos marineros, entre los que están el nudo simple (2), que da lugar al nudo de trébol, el nudo de ocho (3), el nudo de la abuela (4), el nudo de rizo o cuadrado (5) o el nudo doble (7), relacionado con el nudo del cirujano

Pero continuemos con el estudio topológico de los nudos. Con el fin de resolver el problema de la clasificación de los nudos se introducen invariantes de los mismos. Los invariantes son objetos (por ejemplo, un número, un polinomio o un grupo) o propiedades (como la tricoloreabilidad) de un nudo, que tienen el mismo valor para todos los nudos equivalentes. En consecuencia, si un invariante es distinto para dos nudos, estos no pueden ser equivalentes.

Un primer ejemplo de invariante sería el “mínimo número de cruces de un nudo”. Consideremos un nudo N, se define el mínimo número de cruces c(N) del nudo N, como el menor número de cruces que puede tener un diagrama D de N, es decir, si denotamos por c(D) el número de cruces de un diagrama D, sería el mínimo valor de c(D), para todos los diagramas D del nudo N.

Si c(N) = 0, entonces N es el nudo trivial. No existen nudos para los cuales el mínimo número de cruces sea 1 o 2, cualquier diagrama que dibujemos con 1 o 2 cruces se puede transformar mediante movimientos de Reidemeister en el no-nudo. Los únicos nudos con c(N) = 3 son el nudo de trébol, y su imagen especular, mientras que el único con c(N) = 4 es el nudo de Saboya.

La primera clasificación de los nudos la realizó el matemático inglés Peter G. Tait en 1846, sin las herramientas aún de la topología, e incluía todos los nudos primos con mínimo número de cruces menor o igual que 7, que son el no-nudo y los 14 que aparecen en la imagen de abajo (obsérvese que en dicha clasificación no se está distinguiendo entre un nudo y su imagen especular).

Clasificación de los nudos con mínimo número de cruces menor o igual que 7. Cada color se corresponde con los nudos con el mismo número mínimo de cruces, desde 3 hasta 7

Un invariante sencillo, que nos permitirá distinguir entre algunos nudos que no son equivalentes, es la tricoloreabilidad. Un diagrama se dice que es tricoloreable si, dado un conjunto de tres colores, se puede asignar un color a cada arco del diagrama de forma que: i) se utilizan al menos dos de los tres colores; ii) si en un cruce aparecen dos de los colores, entonces también aparece el tercero.

Se puede demostrar fácilmente que la coloreabilidad no varía con los tres tipos de movimientos de Reidemeister, por lo que, si un diagrama es tricoloreable, lo es cualquier otro equivalente. Es decir, si un diagrama es tricoloreable y otro no, entonces se corresponden con nudos no equivalentes.

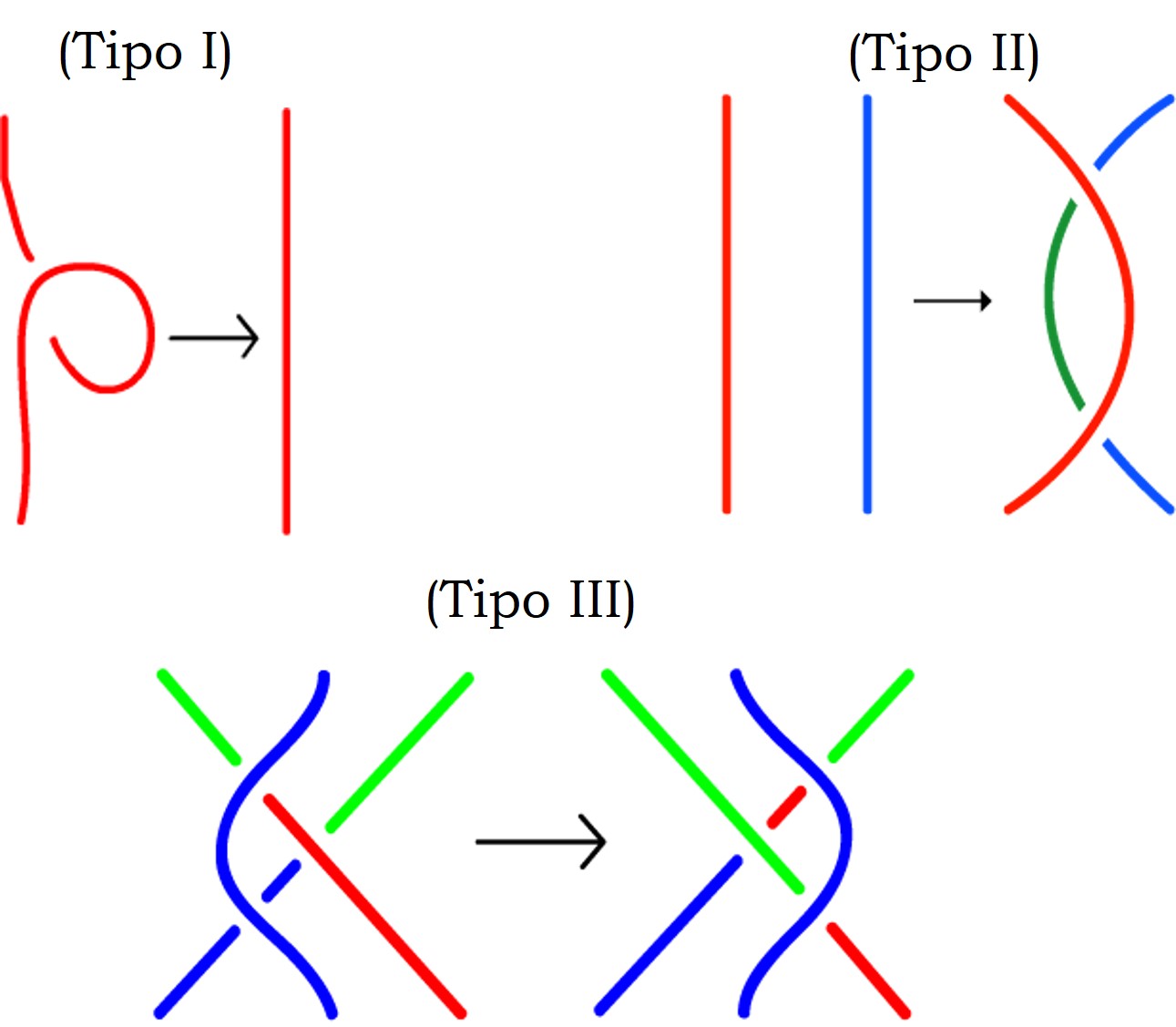
La tricoloreabilidad no varía con los tres movimientos de Reidemeister

El no-nudo es trivialmente no tricoloreable, ya que no se puede utilizar más de un color, el nudo de trébol sí es tricoloreable y el nudo de Saboya no.

Veamos un ejemplo de cómo distinguir nudos, con el mismo número mínimo de cruces, mediante la tricoloreabilidad. Los nudos 71 y 74, que podemos ver en la clasificación anterior (el primero y cuarto de los nudos con mínimo número de cruces 7), y que tienen mínimo número de cruces, no son equivalentes, ya que 71 no es tricoloreable, mientras que 74 sí lo es.

Claramente el nudo 71 no es tricoloreable, puesto que, si pintamos uno de los segmentos de un color, por ejemplo, rojo, solo pueden ocurrir dos cosas, o todos los demás son también rojos, con lo cual no se utilizan al menos dos colores, o los colores de los demás segmentos quedan determinados y al llegar de nuevo al segmento rojo inicial habrá tres cruces cada uno con dos colores y por cada color elegido para el segmento que falta por marcar se obtienen dos cruces con solo dos colores, como se muestra en la siguiente imagen.

El nudo 71 no es tricoloreable

Mientras que el nudo 74, que es un nudo celta y también el nudo infinito del Budismo, es tricoloreable, como se muestra en la siguiente imagen.

El nudo 74 es tricoloreable

Continuará en mi siguiente entrega de la sección Matemoción del Cuaderno de Cultura Científica…

…CONTINUARÁ…

Colgante con el nudo infinito del budismo

Bibliografía

1.- Museo Guggenheim-Bilbao, Anni Albers, tocar la vista, 6 de octubre de 2017 – 14 de enero de 2018.[]

2.- The Josef and Anni Albers Foundation

3.- Canal de youtube del Museo Guggenheim-Bilbao, Anni Albers, Tocar el viento.

4.- Raúl Ibáñez, La topología modifica la trayectoria de los peces, Cuaderno de Cultura Científica, 2016.

5.- María Teresa Lozano, La teoría de nudos en el siglo XX, Un Paseo por la Geometría 1998/99, Departamento de Matemáticas, UPV/EHU, 1999. Versión on-line en divulgamat

6.- Sergio Ardanza Trevijano, Excursiones matemáticas en biología, Un Paseo por la Geometría 2005/06, Departamento de Matemáticas, UPV/EHU, 2006. Versión on-line en divulgamat

7.- Martín Gardner, Huevos, nudos y otras mistificaciones matemáticas, Gedisa, 2002.

8.- Colin C. Adams, The Knot Book, An Elementary Introduction to the Mathematical Theory of Knots, AMS, 2001.

9.- Stephan C. Carlson, Topology of Surfaces, Knots, and Manifolds, John Wiley and Sons, 2001.

10.- The Knot Atlas

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El artículo La artista Anni Albers, The Walking Dead y la teoría de nudos se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. La teoría de grafos y “Così Fan Tutte”
2. Arthur Cayley, la teoría de grafos y los isómeros químicos
3. El quipu: ¿algo más que un registro numérico?

Juanma Gallego Osagarri organikoak dituzten robotak sailkatzeko proposamena egin du zientzialari talde batek. Robot hauen hedapena hain handia izan da, ezen beharrezkoa baita beren taxonomia finkatzea.

Kolaborazioan oinarritutako edozein sisteman funtsezkoa da hizkuntza komuna erabiltzea. Bestela, arazoak suerta daitezke. Esaterako, 1999an Mars Climate Orbiter espazio ontziak planeta gorriaren kontra talka egin zuenean, mundu guztiak ulertu zuen komenigarria zela kalkuluak burutzeko neurri unitate berdinak erabiltzea. Jakina denez, zunda ekoiztu zuen enpresako ingeniariek sistema anglo-saxoia erabili zuten, baina NASAk Nazioarteko Unitate Sistema erabili zuen.

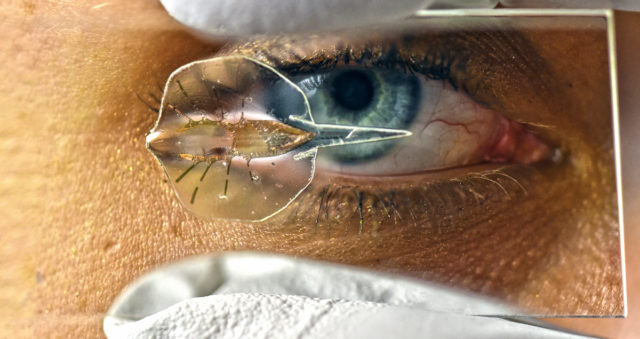
1. irudia: Orain arte, Wyss Institutuak garatutako arraia-robota da gailu biohibridoen artean ospe gehien eskuratu duena. Iaz ‘Science’ aldizkariak azal bat eskaini zion. (Argazkia: K. Hudson and M. Rosnach / Science Robotics)

Robotika bezalako arlo batean, gainera, are garrantzitsuagoa da komunikazioan batasun hori mantentzea. Izan ere, aurrerapenak hain bizkor suertatzen ari dira, ezen beharrezkoa bihurtu baita adostasun terminologikoa lortzea. Hala pentsatu du, bederen, Victoria Webster-Wood ikertzaileak gidatutako lan taldeak. Horregatik, Science Robotics aldizkarian robot biohibridoen sailkapen sistema berria proposatu dute.

Ehunen ingeniaritzan izan diren aurrerapenei esker, mota honetako robotek garapen handia izan dute azken urteotan, eta litekeena da etorkizunean ere bide oparoa izatea. Izenak dioenari jarraituz, osagarri organikoak dituzten gailuak dira robot biohibridoak. 2016an Harvardeko Unibertsitateko Wyss Institutuko ikertzaileek aurkeztu zuen tramankulua adibideetako bat da: alga baten eta arratoi baten ehunak biltzen zituen arraia-robota egin zuten. Optogenetika baliatuz, algaren geneak arratoiaren muskuluetan sartu zituzten, eta, horrekin, argiaren poderioz mugitzen zen arraia antzeko bat lortu zuten.

Momentu honetan halako burutazioek aplikazio askorik ez badute ere, argi dago teknologia honen garapena funtsezkoa izan daitekeela, besteak beste, medikuntzaren alorrean. Giharren mugimenduari dagokionez, bederen, bihotzari lotutako gaixotasunak berehala datoz burura.

Ikertzaileek artikuluan argudiatu dutenez “ohiko ingeniaritza sistemekin alderatuz, osagarri organikoek etorkizun oparoko alternatiba suposatzen dute sistema robotiko autonomo konplexuak garatu aldera”. Ohiko roboten sentsoreak mugatuta daudela diote (txakurrek droga edo lehergaiak atzemateko duten gaitasun paregabea jarri dute adibidetzat). Bestetik, efizientziari dagokionean, oraindik ere eskala txikiko robotetan ez da lortu animaliek duten gihar eta eskeleto sistemaren parekorik, eta ehunak erabiltzea aukera bikaina izan daiteke.

Taxonomia baterantz

Robotic Taxonomic Key (Roboten Gako Taxonomikoa) izena eman diote proposamenari. Horren bitartez, robotak deskribatzeko eta sailkatzeko modua garatu nahi izan dute. Eurena ingeniaritzari lotutako arloa dirudien arren, profesional asko inplikatuta daude bertan: biologia, farmakologia, neurologia edota adimen artifiziala, besteak beste. Hortaz ere sailkatze honen beharra. Sailkapena egiteko, gaiaren ingurua dagoen bibliografia hartu dute abiapuntutzat. Lau parametrotan oinarritu dira: estruktura, jokaera (edo mugimendua), sentsoreak eta kontrola.

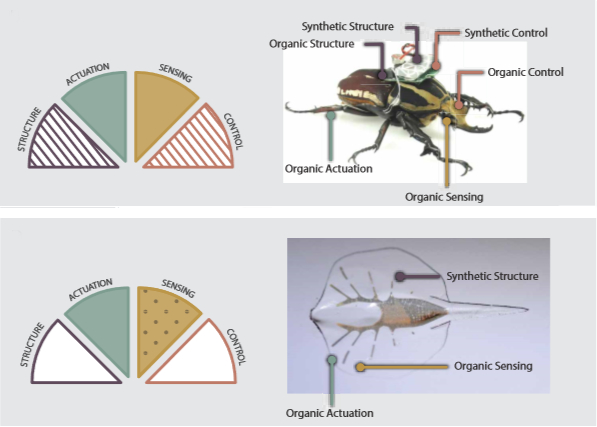
2. irudia. Taxonomia berriaren bi adibide: intsektu batean txertatutako gailuaz garatu duten robot hibridoa, eta arraia-robota. (Argazkia: Webster-Wood / Science Robotics)

Zuhaitzak, hegaztiak edo onddoak identifikatzeko gakoa balitz bezala, robotak identifikatzeko bidea proposatu dute. Halako “espezimen” baten aurrean, galdera hau egin beharra dago: parametro bakoitzari dagokionean, osagarria organikoa, hibridoa ala sintetiko al da? Era eskematiko batean aurkeztuta, horrelakoa da sailkapena:

1. Estruktura a) Organikoa b) Hibridoa c) Sintetikoa 2. Jokaera a) Organikoa b) Hibridoa c) Sintetikoa 3. Sentsoreak a) Organikoa b) Hibridoa c) Sintetikoa 4. Kontrola a) Organikoa b) Hibridoa c) Sintetikoa

Gako hau modu grafiko batean era errazean irudikatzeko bidea eman dute, gainera. Organikoa bada, margo solidoarekin adierazten da. Hibridoa bada, marratuta; azkenik, sintetikoa bada, hutsik irudikatzen dute. Osagarri organikoa genetikoki eraldatua izan bada, puntutxoak jartzea proposatu dute.

Wyss Institutuak garatutako arraia-robotak, esaterako, honako klasifikazioa izango luke: estruktura sintetikoa, jokaera organikoa, sentsore organikoa (genetikoki eraldatua) eta kontrol sintetikoa.

Arraia-robotari buruzko bideoa.

Organobotak

Taxonomia berezi hau landu duten honetan, terminologiaren alorrean ere proposamen bat egin dute. Artikuluan “organoboten” aukera ere kontuan hartu dute, nahiz eta oraindik halakorik ez den garatu. Izan ere, termino hori proposatu dute “soilik osagarri organikoez osatutako robotak” definitzeko. Teknologiaren garapena ikusita, argi dago laster bioteknologiaren eta ingeniaritzaren arteko mugak are lausoagoak izango direla, eta egunen batean “organobotak” errealitate bat izango direla.

Alde etikoak ere jaso dituzte: “Robot biohibridoen eta organoboten garapenean ehunen ingeniaritzari lotuta doazen kezka berdinak agertzen dira”. Horren adibide jarri dituzte ehunen eta zelulen jatorria, edota lagin horiek eskuratzeko erabili diren animalien zaintza egokia. Harago joan dira, etorkizunean “izaki” berri hauen inguruan sor daitezkeen bestelako kezkak aurreikusita. “Periferia garatuak dituzten gailu autonomoen garapenarekin, agertzen hasi dira kezkak gailuak mina edota estresa sentitzeko ote dituzten, edota organismo bizi bezala existitzen hasiko ote diren”. Bestalde, baliteke robot horiek bakterioen edo bestelako kutsatzaile biologikoen arriskua jasan behar izatea, eta horrek erronka berria ekarriko du etorkizunean: birus informatikorik ez, baizik benetako birusak izan ditzakete lagun.

Erreferentzia bibliografikoa:

Webster-Wood V.A. et al. Organismal engineering: Toward a robotic taxonomic key for devices using organic materials. Science Robotics, 29 Nov 2017: Vol. 2, Issue 12, eaap9281 DOI: 10.1126/scirobotics.aap9281

———————————————————————————-

Egileaz: Juanma Gallego (@juanmagallego) zientzia kazetaria da.

———————————————————————————-

The post Ate-joka ari diren roboten landa gida appeared first on Zientzia Kaiera.