Elektroiaz (eta II)
 Irudia: Fenomeno fisikoetan askotan, esaterako, elektrizitatean, magnetismoan edo eroankortasun termikoan, elektroiek funtsezko zeregina dute. (Argazkia: Gerd Altmann – Pixabay lizentziapean. Iturria: pixabay.com)
Irudia: Fenomeno fisikoetan askotan, esaterako, elektrizitatean, magnetismoan edo eroankortasun termikoan, elektroiek funtsezko zeregina dute. (Argazkia: Gerd Altmann – Pixabay lizentziapean. Iturria: pixabay.com)George Francis Fitzgerald fisikariaren proposamena, hau da, katodo-izpiak elektroi askeak zirela −à la Larmor elektroiak−, erradioaktibitatearen arloko ikerketek egiaztatu zuten. Hain zuzen, ikerketok beta erradiazioaren zein katodo-izpien izaera ezagutarazi zuten, eta atomoak prozesuan zatitzeko eta barneko izaera kimikoa aldatzeko gai zirela ere erakutsi zuten, bai eta hori egin egiten zutela frogatu.
Fitzgeralden hipotesia arras interesgarria izan zen garaiko komunitate zientifikoarentzat, lotu egiten baitzituen bai Thomsonen katodo-izpiak, bai Lorentz, Henri Poincaré, Kaufmann eta beste zientzialari batzuen saiakerak materiaren teoria guztiz elektromagnetiko bat garatzeko. Saiakera horiek ireki zioten bidea Einsteinen erlatibitatearen teoriari, eta, aldi berean, haiek postulatzen zutenarekin bateraezina zela frogatu zuten.
Thomsonen ideiarengatik bihurtu zen elektroia funtsezkoa atomoaren eta lotura kimikoaren teoria berrietan, geroago Ernest Rutherford eta Niels Bohr fisikariek emango zioten interpretazio berriari esker. Horrez gain, mekanika kuantikoarekin eta erlatibitatearekin batera berebiziko rola izan zuen materiaren izaera bera ulertzeko garatuko ziren ikuskera berrietan.
Ikuskera berri horien garapena estuki lotu zitzaion elektroiaren ezaugarriak zein ziren argitzeko bideari. Hasiera batean, John S. Townsend eta H.A. Wilson fisikariek elektroiaren karga neurtu zuten (1899 eta 1903an, hurrenez hurren), eta Robert A. Millikan fisikariaren esperimentuek finkatu zuten kargaren neurketa, 1907tik aurrera. Elektroiaren spina Samuel Goudsmit eta George Uhlenbeck fisikariek proposatu zuten 1925ean, espektroen egitura mehearen azalpena, eta, beraz, «teoria kuantiko zaharraren» azken etapa erabat osatzeko. Elektroiaren uhin-izaera, gerora mikroskopio elektronikoa garatzeko ezinbestekoa, egiaztatu zuten 1927an Clinton Davisson eta Lester Germer fisikariek, eta, urte berean baina bere aldetik lanean, George P. Thomsonek. 1928an, Paul Adrien Maurice Dirac fisikariak elektroi erlatibista deskribatu zuen, mekanika kuantiko berriaren beste zutabea, alegia.
Dirac, Werner Heisenberg, Ernst Pascual Jordan eta Wolfgang Pauli arduratu ziren elektrodinamika kuantikoa garatzeaz 1920ko hamarkada bukaeran, erradiazio elektromagnetikoaren eta kargadun partikulen (adibidez, elektroien) arteko interakzioak deskribatzeko asmoz. Ahalegin hori 50eko hamarkadan burutu zen, Freeman Dyson, Richard Feyman, Julian Schwinger eta Shin’ichirō Tomonaga fisikariaren eskutik, birnormalizazioa onartu zenean. Prozedura horri esker, elektroi baten −nahiz bestelako kargadun partikula baten− uhin-funtzioak kalkulatzean aldagai batzuetan agertzen diren balio infinituak kudeatu daitezke, ikuspuntu erlatibistatik inbarianteak izan daitezen.
Diracek elektroiaz ikuspuntu erlatibistatik egin zuen deskribapenak espero gabeko emaitza bat ekarri zuen: energia-balio negatiboko egoerak zeudela. Hari horri tiraka helduko zen antimateriaren existentzia posiblea zelako ideia. Fisikaren aro oso bat bukatu zen horrela: partikulak ez ziren jada beti kontserbatzen. Hasiera batean egoera negatibo horiek protoitzat jo ziren, harik eta 1930ean argi geratu zen arte elektroiaren masa izan behar zutela nahitaez. Ideia hori Carl D. A. Anderson fisikariak baieztatu zuen positroi edo antielektroia aurkitu zuenean.
1950eko hamarkadan, elektroi-bonbardaketa ugari egin zen nukleoen eta elektroien arteko talka eragiteko, eta ondorioztatzen zen neutroi eta protoiek egitura konplexua zeukatela. Ideia horren garapenak partikulen eredu estandarra sorrarazi zuen. Eredu horren arabera, elektroia arinena eta egonkorrena da –dagozkion neutrinoekin batera osatzen dituen– leptoi deituriko karga negatibodun hiru partikulen artean. Elektroiak barne egitura duela frogatzeak arrakalatu egingo luke partikulen fisikaren eraikina.
Egileaz:Cesár Tomé López (@EDocet) zientzia dibulgatzailea da eta Mapping Ignorance eta Cuaderno de Cultura Cientifica blogen editorea.
Itzulpena:Lamia Filali-Mouncef Lazkano
Hizkuntza-begiralea:Xabier Bilbao
Elektroiari buruz idatzitako artikulu-sorta:- Elektroiaz (I)
- Elektroiaz (eta II)
The post Elektroiaz (eta II) appeared first on Zientzia Kaiera.
Lluvia, hoy no te siento
Lluvia, hoy no te siento.
Hoy no eres nada
más que agua vertical.
Apenas si te escucho
golpear el pavimento
y llamar con tu clave
sobre mi ventanal
Lluvia, hoy no eres nada
para mi desaliento
nocturno y abismal.
Cuando era niña hallaba
en tu canción un cuento,
y ya en mi adolescencia
me diste un madrigal.
Ahora, lluvia, tengo
tanta tristeza adentro,
que no me dices nada,
solo te oigo golpear.
Lluvia, Matilde Alba Swan
Hoy planteamos un juego para ejercitar un poco la lógica. Fue propuesto por el matemático Howard C. Saar y apareció publicado en el Recreational Mathematics Magazine en octubre de 1962.
Reto meteoro-lógico
«Anteayer, Matilde, la mujer del tiempo, decidió dar su predicción meteorológica de una manera poco habitual, apelando a las capacidades lógicas de sus oyentes:
El tiempo de hoy es diferente al de ayer. Si el tiempo de mañana es el mismo que el de ayer, entonces pasado mañana hará el mismo tiempo que anteayer. Pero si el tiempo de mañana es el mismo que el de hoy, entonces pasado mañana hará el mismo tiempo que ayer.
Hoy llueve y llovió anteayer. ¿Podrías decir que tiempo hizo ayer?».
Solución
Por favor, piensa un poco antes de leer el razonamiento y la respuesta.

Reescribimos los datos fijando fechas, para que sea más sencillo el razonamiento. Además, cuando hablamos del tiempo, estamos pensando en lluvia o sol.
Hoy es 9 de junio, así que la predicción meteorológica de Matilde es de fecha 7 de junio. Y lo que dice es:
-
El tiempo del 7 de junio es distinto que el del 6 de junio.
-
Si el tiempo del 8 de junio (Matilde habla de “su mañana”) es el mismo que el del 6 de junio, entonces el tiempo del 9 de junio y el del 5 de junio serán iguales.
-
Pero, si el tiempo del 8 de junio es el mismo que el del 7 de junio, entonces el tiempo del 9 de junio y el del 6 de junio serán iguales.
Como dato adicional (ya no habla Matilde, la mujer del tiempo), se nos informa que:
-
Hoy, 9 de junio, llueve y llovió el 7 de junio.
La pregunta es: ¿qué tiempo hizo el 8 de junio?
Hay dos respuestas posibles, o bien 8 de junio hizo sol o bien llovió. Razonemos ambas posibilidades.
Supongamos que el 8 de junio llovió. Por 4), llovió el 7, el 8 y el 9 de junio. Aplicando 1), el 6 de junio hizo sol. No tiene sentido aplicar la condición 2). Pero si puede aplicarse 3), ya que el 7 y el 8 de junio llovió. Así, se deduce que el tiempo del 6 y del 9 de junio debería ser el mismo. ¡Pero esto no es verdad! Como hemos llegado a una contradicción, necesariamente el 8 de junio debió de lucir el sol.
De cualquier manera, quizás Matilde ha planteado mal su adivinanza… No hay que fiarse de todo lo que nos dicen. Así que vamos a comprobar si, efectivamente, con las condiciones planteadas por la meteoróloga, el 8 de junio no llovió. Las conclusiones de 1) y 4) son las mismas de antes. Ahora no podemos aplicar 3) ya que el día 7 llovió, mientras que el día 8 hizo sol. Pero podemos aplicar 2), que afirma que (ya que los días 6 y 8 de junio lució el sol), el 5 y el 9 de mayo tuvieron el mismo tiempo. Así, nos enteramos, de paso, que el 5 de junio también llovió. No hay contradicción alguna, así que, efectivamente, el 8 de junio hizo sol…
Por cierto, el título no es engañoso, porque hoy 9 de junio llueve, y el poema habla de sensaciones: «Lluvia, hoy no te siento. / Hoy no eres nada / más que agua vertical».
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Lluvia, hoy no te siento se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #Naukas13 Lo siento Planck, pero no me lo creo
- Plattner y la cuarta dimensión
- El teorema de los cuatro colores (1): una historia que comienza en 1852
Pi, zenbaki agortezina
Zenbaki ospetsurik bada matematikan, hori pi da, letra (greko) baten izena duen zenbakia. Aurreko artikulu batean Pi eguna aipatu genuen, martxoaren 14a, alegia, π = 3.14 izateagatik aukeratua. Baina 3.14 ez da π-ren balio zehatza, haren adierazpen hamartarreko lehen zifra dezimal biak hartuta lortzen den zenbakia da, ez besterik. Idatz daiteke garapen hamartar osoa?
Duela bi mende eta erdi Johann H. Lambert-ek frogatu zuen π irrazionala dela. Horren ondorioz, garapen hamartarrak infinitu zifra dezimal ditu eta, gainera, ez dago bloke bat behin eta berriro errepikatzen dena (periodoa), bestela zenbaki arrazionala izango bailitzateke. Hortaz, garapeneko zifra pilo bat idatzita ere, beti daude gehiago eta, gainera, ezin dugu aurresan zein izango den jarraipena. Garapeneko dezimalak kalkulatzeko, formula on bat eta denbora edo/eta tresna egoki bat behar dira. Duela urtebete, 50 bilioi (5 x 1013) zifra dezimal kalkulatzeraino heldu ziren. Zer esanik ez, teknologiaren aurrerapen izugarriaren eskutik etorri da halako lorpena. Ikus dezagun π-ren dezimalen kalkuluaren bi mila urte eta gehiagoko bilakaera hori.
 1. irudia: Pariseko Palais de la Découverte 1937an inauguratu zen eta π-ren 707 zifra dezimal —artean ezagutzen zirenak— idatzi zituzten areto batean. Azken 180 zifrak oker zeuden eta 1950ean zuzendu zituzten. (Iturria: Palais de la découverte)Arkimedesen bidea
1. irudia: Pariseko Palais de la Découverte 1937an inauguratu zen eta π-ren 707 zifra dezimal —artean ezagutzen zirenak— idatzi zituzten areto batean. Azken 180 zifrak oker zeuden eta 1950ean zuzendu zituzten. (Iturria: Palais de la découverte)Arkimedesen bidea
Zirkunferentziaren luzeraren eta diametroaren arteko erlazioa da π. Ikuspegi geometriko hori zen nagusi Antzinatean eta ez zuten erlazioa berez zenbaki gisa ikusten. Geometrian oinarritu zuen Arkimedesek proportzio horren bilaketa (π-ren balioarena guretzat) K.a. III. mendean. Ia bi mila urtez erabili zen Arkimedesen metodoa π-ren hurbilketak lortzeko.
Hasteko, zirkunferentzia baten barruan eta kanpoan hexagono erregularrak kokatu zituen, zirkunferentzian inskribatutako eta zirkunskribatutako poligonoak, alegia. Zirkunferentziaren luzera hexagono horien perimetroen artean dago. Gero, alde-kopurua bikoiztuz, dodekagonoak kokatu zituen. Barruko poligonoaren luzera handitu eta kanpokoarena txikitu egiten zen horrela, eta π tarte estuago batean kokatu. Behin eta berriro alde-kopurua bikoiztuz, geroz eta hurbilketa hobea lortzen da. Arkimedesek berak 96 aldeko poligonoraino eraman zituen kalkuluak; horrela, 3 10/71 eta 3 1/7 artean kokatu zuen π-ren balioa. Idazkera hamartarrera pasatuz, 3.140845…
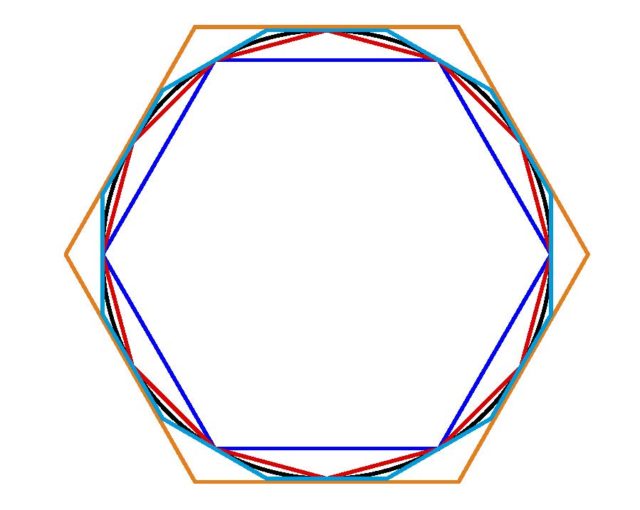 2. irudia: Arkimedesen metodoaren lehen urratsak (hexagonoa eta dodekagonoa). Alde-kopurua handitzean poligonoak zirkunferentziatik hurbilago daude. (Irudia: Javier Duoandikoetxea)
2. irudia: Arkimedesen metodoaren lehen urratsak (hexagonoa eta dodekagonoa). Alde-kopurua handitzean poligonoak zirkunferentziatik hurbilago daude. (Irudia: Javier Duoandikoetxea)
Hurrengo mendeetan etekina atera zioten Arkimedesen metodoari alde gehiago kontuan hartuz. Ptolomeok II. mendean 377/120 balioa eman zuen eta horrek hiru dezimal zuzen ditu. Gero, Asian aurkitzen ditugu ekarpenik aipagarrienak, zientziaren arrastoa ia desagertuta egon baitzen mendebaldean denbora luzean. Bereziki Txinako emaitza batzuk nabarmentzen dira: Liu Huiren algoritmoa (III. mendea) eta Zu Chongzhiren hurbilketa (V. mendea). Azken honek 3.1415926 eta 3.1415927 artean kokatu zuen π.
Arkimedesen poligonoen metodoa erabiliz azken emaitza garrantzitsua Ludolph van Ceulen alemaniarrak eman zuen XVII. mendearen hasieran: 35 zifra dezimal lortu zituen, 262 aldeko poligonoen bidez, urte askoko lanaren ondoren. Holandan izan zen irakasle eta Leidenen hil zen. Kalkulaturiko π-ren balioa Leidengo hilobian ipini zioten (3. irudia). Denbora luzez Alemanian Ludolphsche Zahl (Ludolphen zenbakia) esan zioten π-ri.
 3. irudia: Leidengo Pieterskerk-en, Ludolph van Ceulenen hilobian, π-ren balioa jarri zuten. Jatorrizkoa desagertu egin zen eta 2000 urtean kopia bat jarri zuten. (Iturria: Wikimedia Commons)Kalkuluaren aroa
3. irudia: Leidengo Pieterskerk-en, Ludolph van Ceulenen hilobian, π-ren balioa jarri zuten. Jatorrizkoa desagertu egin zen eta 2000 urtean kopia bat jarri zuten. (Iturria: Wikimedia Commons)Kalkuluaren aroa
Kalkulu infinitesimala XVII. mendean sortu zen eta aro berri bat ekarri zuen matematikara. Handik aurrera funtzioen garapen infinituak ohiko egin ziren eta π-ren balio hurbilduak lortzeko ere baliatu ziren. Horren adibide,
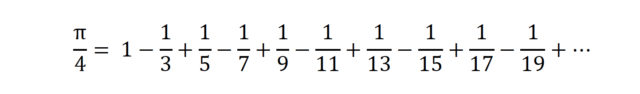
formula daukagu. Puntuek adierazten dute infinituraino jarraitu beharko genukeela gaiak jartzen berdintza gertatzeko. Berez, batura partzialen limitea hartu behar da eta, horregatik, nahi beste hurbildu gaitezke ezkerreko baliora behar adina gai hartuta eskuinean. Guregana Gottfried W. Leibniz (1676) eta James Gregory (1671) izenei lotuta heldu den formula da, baina Sangamagrama-ko Madhava astronomo indiarrak jada ezagutzen zuen haiek baino 250 urte lehenago. Formula bera ez da oso erabilgarria praktikan, gai gehiegi behar direlako zehaztasun egoki bat lortzeko. Baina hobetu daiteke, eta Madhavak berak antzeko serie hobe bat erabiliz, 11 dezimal lortu zituen π-rako.
Goiko formula hori, berez, arku tangente funtzioaren seriezko garapenaren kasu bat da. Oro har,
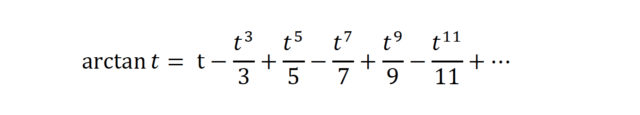
dugu eta t = 1 eginez gero, Madhavaren formula lortzen da, arctan 1 = π/4 baita. (arctan t = x izateak esan nahi du x radianeko neurria duen angeluaren tangente trigonometrikoak t balio duela.) Serieak arinago konbergitzen du t txikiago izanda eta, horregatik, beste formula batzuk baliatuz, hala nola,
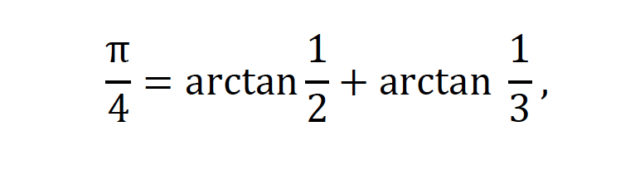
beste garapen hau lortuko genuke:
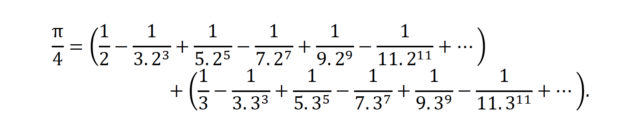
Lehengoak ez bezala, honek arin ematen ditu zifra dezimal zehatzak. Eskuineko atalean idatzi ditugun apur horiek batuta 3.14156158… lortzen da, lau zifra dezimal zehatz, alegia.
Hortik aurrera, π-ren dezimal ezagunen zerrenda asko hazi zen. Bereziki aipagarria da John Machin ingelesaren ekarpena,
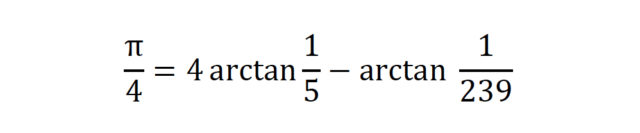
formula lortu ondoren, 100 zifra dezimal kalkulatu baitzituen 1706an. Ez zen hor gelditu kalkulua eta aro horretako ekarpenik luzeena William Shanks ingelesak eman zuen 1873an: Machinen algoritmoa erabiliz eta urte asko kalkuluari emanda, 707 dezimal plazaratu zituen. Handik 70 urtera, mahai gaineko kalkulagailu batekin lanean, konturatu ziren bakarrik lehenengo 527ak zirela zuzenak. Horregatik aldatu behar izan zituzten goiko 1. irudian agertzen direnak.
Ordenagailuen aroaOrdenagailuak kalkuluak arinago egiteko sortu ziren eta horrek erabat aldatu zituen π-ren dezimalak lortzeko aukerak. Lehen ordenagailua, ENIAC ospetsua, 1949an jarri zuten eginkizun horretan, eta 70 orduko lanaren ondoren π-ren 2037 dezimal kalkulatu zituen. Handik aurrera, eten gabe egin du gora dezimal-kopuruak, besteak beste, makinen ahalmenari formula hobeak elkartu zaizkiolako.
Hurrengo taula honek laburbiltzen du azken 70 urteetako bilakaera:
Urtea Makina Denbora Dezimal-kopurua 1958 IBM 704 1.7 ordu 10 000 1961 IBM 7090 8.7 ordu 100 265 1967 CDC 6600 28 ordu 500 000 1973 CDC 7600 23.3 ordu 1 001 250 1987 NEC SX-2 36 ordu 134 217 700 1989 IBM 3090 1 011 196 691 1997 HITACHI SR2201 91 ordu 51 539 600 000 1999 HITACHI SR8000 83.5 ordu 206 158 430 000 2002 HITACHI SR8000 600 ordu 1 241 100 000 000 2011 etxekoa 371 egun 10 000 000 000 050 2020 etxekoa 303 egun 50 000 000 000 000
Uneko errekorraren jabe den Timothy Mullican-ek azaltzen duenez, piezak erosita muntatu zuen ordenagailua (ikus 4. irudia) eta, behin kalkulurako programa prestatuta, 303 egun mantendu zuen makina lanean, 2020ko urtarrilaren 29an gelditu arte, orduan lortu baitzuen 50 bilioigarren tokiko dezimala.
 4. irudia: Timothy Mullicanek errekorra lortzeko eraiki zuen ordenagailua. Gorriz markatuta daude π-ren kalkulurako erabili ziren atalak. (Iturria: Timothymullican.com)
4. irudia: Timothy Mullicanek errekorra lortzeko eraiki zuen ordenagailua. Gorriz markatuta daude π-ren kalkulurako erabili ziren atalak. (Iturria: Timothymullican.com)Ordenagailuen gaitasunaz gain, formula berriak aipatu behar dira. Ramanujan matematikari indiar harrigarriak formula sinestezinak aurkitu zituen π-rako, hala nola 5. irudian agertzen den lehen hori. Formula zaharrak baino arinago ematen ditu π-ren dezimalak, eta geroago beste aldaera batzuk asmatu dira. Chudnosky anaiek emandako aldaera batekin (hori ere 5. irudian) mila milioi dezimal lortu zituzten 1989an. Azken aldiko errekor batzuetan algoritmo bera erabili dute, batugai bakoitzak 14 dezimal zuzen gehitzen dituelako. Bestalde, 5. irudian agertzen den hirugarren formulak (BBP deitzen zaio, egileen abizenak hartuta) badu berezitasun bat: 16 oinarriko sisteman, eta ondorioz sistema bitarrean ere, toki zehatz bateko dezimala kalkula daiteke, aurrekoak ezagutu barik.
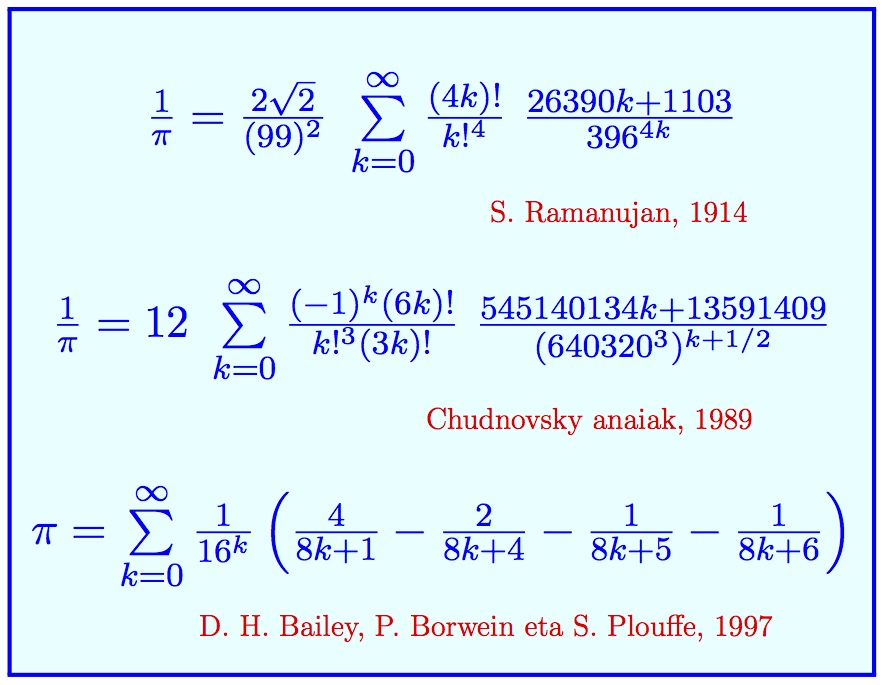 5. irudia: Formula berriak agertu dira XX. mendean eta ordenagailuan kalkuluak egiteko erabili dira. (Irudia: Javier Duoandikoetxea)Eta hori guztia, zertarako?
5. irudia: Formula berriak agertu dira XX. mendean eta ordenagailuan kalkuluak egiteko erabili dira. (Irudia: Javier Duoandikoetxea)Eta hori guztia, zertarako?
Zertarako balio du π zenbakiaren hainbeste zifra dezimal ezagutzeak? Egia esateko, ezertarako ere ez… Benetan π-ren balioa mundu errealean erabiltzen denean, kalkulurik zorrotzenetan ere, duela 500 urte ezagutzen zen zehaztasuna nahikoa eta sobera da. Orduan, zerk pizten du batzuen interes hori? XVIII. mendera arte pentsa zitekeen garapen hamartarra amaitu egingo zela edo periodiko bihurtu, hots, π zenbaki arrazionala izango zela. Norbaitek esperantza hori bazuen, Lamberten emaitzak zapuztu zion: π irrazionala da.
Garai modernoetan, ordenagailua kalkuluetan sartu zutenean, makinaren gaitasuna probatzeko balio dezakeela esan ohi dute. Hala zioen Timothy Mullicanek, esaterako, orain arteko errekorra lortu zuenean. Dena dela, beste errekor batzuen antzera, badirudi honek ere ez duela pizten Guinness World of Records ospetsuan agertzetik aparteko interesik.
Gehiago jakiteko edo ikusmiran ibiltzeko- π-ren hurbilketaren historia eta haren kronologia.
- Timothy Mullicanen bloga: gaur egungo errekorra ezarri zuen lana azaltzen du.
- Milioi bat dezimal orrialde bakar batean: https://www.piday.org/million/.
- π kalkulatzeko erabili diren formulak eta algoritmoak aurkezten dituen Jesús Guilleraren artikulu bat.
- π-ren zenbat zifra dezimal gogoratzen dituzu? Horretan ere bada lehia bat, ea nork gehiago esan. Orain arte buruz zifra dezimal gehien esan duena Suresh Kumar Sharma indiarra da: 2015ean 70 030 eman zituen, 17 ordu eta 14 minutuan. Harrigarria! Hori guztia eta gehiago, Pi World Ranking List webgunean.
- Pifilologia deitzen da π-ren zifra dezimalak gogoratzeko baliabide mnemoteknikoen alorra.
- Azken hamarkadako errekorrak egiteko y-cruncher programa erabili dute. Alexander J. Yee da programaren sortzailea eta beste konstante matematiko ezagun batzuk kalkulatzeko ere erabili dute. Programaren webgunean informazio guztia duzue.
- Zure jaioteguna edo nahi duzun data aurkituko dizu π-ren zifra dezimalen artean Find Your Pi Day webguneak.
Egileaz:
Javier Duoandikoetxea Analisi Matematikoko Katedradun erretiratua da UPV/EHUn.
The post Pi, zenbaki agortezina appeared first on Zientzia Kaiera.
Actua localmente: inteligencia artificial en procesos para la industria 4.0

Una famosa introducción a algunas producciones de Disney cantaba que “el mundo es cascada de colores” y eso, que queda muy mono en una pantalla, es inexacto. Vivimos en un mundo que es una cascada de datos de la que nuestros encéfalos intentan obtener información relevante, no siempre con éxito.
La consciencia de que los datos son un activo económico toma cuerpo en empresas como Facebook, que se dedican a recabar datos de multitud de usuarios, organizarlos y clasificarlos, y servirlos en bandeja de plata a los anunciantes que buscan determinado público para sus productos.
La cantidad de datos que se generan a diario en el mundo es abrumadora. Y obtener información de ellos es cualquier cosa menos fácil, tanto por la capacidad que se requiere para manejar esa cantidad de datos como por el diseño e implementación de unos algoritmos que sean capaces de extraer información útil. Por eso Facebook gana dinero.
Pero no todo van a ser redes sociales. Actualmente se están desarrollando de forma masiva productos y servicios en los ámbitos del internet de las cosas, la robótica, el desarrollo de gemelos digitales [1]*, la fabricación aditiva (impresión 3D), la realidad aumentada y muchos otros. Todos tienen en común una cosa: datos, más datos y analítica de datos. Consideremos que una fábrica que sea algo más que un taller genera teras de datos por día.
El tratamiento inteligente de los datos está revolucionando la fabricación de cosas: es parte de lo que se llama la industria 4.0. Lo que se suele llamar Big Data, sería conveniente llamarlo mejor Huge Data, debido a la enorme cantidad de ellos que pueden recogerse y procesarse. Decíamos antes que cualquier fábrica emite teras de datos por día. Nos enfrentamos a unas cantidades de datos tan grandes, que es muy difícil procesarlos con un fin útil. Como si esto fuese poca dificultad nos encontramos con la granularidad del origen de los datos: diferentes procesos industriales obedecen a diferentes ciclos temporales, incluso muchos de ellos pueden no ser deterministas, lo cual implica la redefinición de las series temporales [2].
En una industria 4.0, además, hay que pensar en diferentes niveles de procesamiento de datos:
- A nivel de dispositivo/máquina/etapa. Los datos los proporcionan sensores y actuadores que interaccionan físicamente con el proceso. Esto va más allá de la internet de las cosas y requiere de desarrollos específicos que en algunos casos pueden requerir conexión con la nube (más abajo hablamos de ella). Tiene hasta nombre, edge computing, porque es la interfase entre el mundo físico y el digital.
- A nivel de línea de producción (conjunto de dispositivos/máquinas/etapas coordinadas que producen una cosa concreta). Las diferentes fases de una fabricación se comunican unas con otras creando la oportunidad de optimizar el proceso industrial. De nuevo tenemos nombre específico, fog computing, computación en la niebla que, como es sabido, es una nube pegada al terreno.
- A nivel de fábrica/empresa. Todas las líneas de producción deben coordinarse con los distintos departamentos de la empresa (compras, ventas, administración, personal, calidad, seguridad e higiene) generando multitud de interacciones cruzadas y más oportunidades de optimización. Aquí es donde entra el cloud computing [3], la computación en la nube, donde grandes cantidades de datos se extraen de diferentes fuentes y se procesan todas ellas en un servidor dedicado. Estas operaciones generalmente se enfocan hacia el direccionamiento de la empresa y de la producción.
¿Qué hacemos con todos estos datos? Buscamos en ellos la información que nos ayude a fines muy diversos como: fabricar mejor, vender mejor, optimizar la calidad y aumentar con todo ello el beneficio de la empresa [4]. Se recurre para ello a las ciencias de los datos, para ayudar a encontrar correlaciones, patrones y pautas en los datos.
Un ejemplo de vanguardia de edge computing. La fusión de lecho de polvo es la tecnología preferida para la fabricación de objetos metálicos de precisión y con geometrías complejas. Existen distintos procesos en función de la fuente de calor empleada (haz láser o de electrones) y del grado de fusión del material (sinterizado o fusión). El proceso más extendido para la fabricación de piezas metálicas es la denominada fusión selectiva por láser (Selective Laser Melting o SLM). Se pueden procesar mediante SLM materiales como aceros inoxidables, aceros de herramienta, aleaciones de titanio, aleaciones de base níquel y aleaciones de aluminio, entre otros.
Una cooperativa como Lortek usa para SLM una máquina que trabaja con 4 láseres simultáneamente. Monitorizar los datos en tiempo real es ya un ejercicio de emisión de gran cantidad de datos (big bata streaming), análisis de los mismos (data analytics) e inteligencia artificial con la idea de fabricar sin defectos. Respecto a esta última hay que decir que Lortek usa deep learning (aprendizaje profundo) desarrollando algoritmos de descubrimiento de conocimiento que aprenden desde cero. Estos algoritmos son capaces de detectar estados de estrés en el proceso, predecir la probabilidad de cometer fallos bajo ciertas condiciones, y hasta aconsejar cómo evitarlas.
Y esto solo en una máquina…
Notas:
[1] Un gemelo digital es una réplica virtual de un producto, servicio o sistema real que permite adelantarse a posibles problemas y experimentar sin correr riesgos antes de lanzar nuevas funcionalidades.
[2] Una serie temporal es una sucesión de datos medidos en determinados momentos y ordenados cronológicamente.
[3] El peatón común (un mamífero bípedo que vive conectado a intenet) piensa que Amazon gana dinero con sus grandes almacenes online. Gana, sí, pero muy poco, apenas un 2 % de margen. El gran negocio de Amazon es el cloud computing.
[4] Combiene recordar que las empresas se crean para obtener beneficios. Si no hay beneficios desaparecen y, con ellas, el empleo y los impuestos que pagan tanto la propia empresa como sus trabajadores. La persona informada se alegra de que las empresas tengan beneficios.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Actua localmente: inteligencia artificial en procesos para la industria 4.0 se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Actúa localmente: robots inteligentes autoadaptativos para la producción industrial
- Actúa localmente: blockchain para la cadena de suministros
- Actúa localmente: el dron espía del cambio climático
Hezurretan idatzitako erasoak, liskarrak, segadak…
Jebel Sahabako hilerria da Niloko ibarreko hilobi-gunerik zaharrena. Gune hau duela 13 400 eta 18 600 urte bitartekoa da. Eskeletoen lehen azterketak duela sei hamarkada egin ziren eta emaitzek indarkeriaren arrastoak erakutsi zituzten, lurperatutako banakoen erdien kasuan, gutxienez.
 Irudia: Hilobi bikoitzaren irudia. Bertan arkatzen bidez tresna litikoak aurkitzen ziren kokapena adierazten da. (Argazkia: © British Museum, Wendorf Artxiboa. Iturria: CNRS)
Irudia: Hilobi bikoitzaren irudia. Bertan arkatzen bidez tresna litikoak aurkitzen ziren kokapena adierazten da. (Argazkia: © British Museum, Wendorf Artxiboa. Iturria: CNRS)Jebel Sahabako hilobietan Qadan kulturan ohikoak ziren harrizko tramankuluak ere bazeuden. Hauek, gorputzean ehun bigunek hartu zuten tokietan zeuden eta, batzuetan, hezurretan bertan sartuta. Posizio honen arabera, tresnak ez ziren hilobi-objektuak; gainera, lurperatutako gizabanakoak ez ziren Qadan kulturakoak, beste kultura batekoak baizik.
Hilerria 1960ko hamarkadan induskatu zen lehen aldiz, eta indarkeria eta gerra antolatuaren lekukotzat hartu da. Duela gutxi aztertu dituzte berriz ehorzketaren aztarnak eta ondorio interesgarriak atera dituzte.
Besteak beste, egiaztatu dute identifikatutako lesioen jatorria pertsonen arteko indarkeria izan zela, eta gehienak jaurtigaiek eragin zituztela. Gutxi gorabehera, indibiduoen laurden batek traumaren baten zantzuak zituen hil baino lehentxeago, eta ia bi herenek aurreko traumak erakusten zituzten, sendatuak edo sendatu gabeak (seinale hauek sexu edo adinarekiko independenteak ziren, lau urte baino gutxiagoko haurrak barne zeudelarik). Bestalde, hobi bakoitzari lotutako harrizko objektuak jaurtigai baten parte izandakoak ziren (geziak edo lantzak). Behaketek iradokitzen dute agresioak ez zirela gertatu talde berbereko kideen artean edo familien barruan, baizik eta beste giza talde batzuen erasoen ondorioz izan zirela.
Hobi batzuk bikoitzak edo aniztunak ziren arren, eta, seguruenik, hilobietan ehortzitako subjektuak aldi berean hildakoak izan, datu demografikoek eta geroago ehorzketa berriek eragindako aldaketak iradokitzen dute hilerriak ez dituela soilik gerra bakar bateko giza aztarnak.
Ezin da baztertu Jebel Sahabako hilerria indarkeriaren biktimak ehorzteko tokia izatea, baina lurperatutako gizabanakoek zituzten sendatutako zauri ugariek adierazten dute behin baino gehiagotan eraso zituztela. Horrez gain, hileta-espazioa berrerabiltzeak ideia hau indartzen du: pertsonen arteko noizbehinkako indarkeria kasuak jazo zirela behin eta berriz. Gainera, zauriak gorputzaren aurreko eta atzeko aldean gertatu ziren, beraz, ez dirudi jatorria bi talderen arteko aurrez aurreko liskarretan zegoenik. Horregatik, litekeena da gehienak liskarren, razzien (erasoaldi) edo segaden ondorio izatea.
Pleistozenoaren amaieran eta Holozenoaren hasieran Niloko ibarrean aurkitutako objektuek erakusten dute tradizio kultural desberdinak zeudela inguruan, eta horrek iradokitzen du giza taldeen nolabaiteko zatiketa eta isolamendua.
Gainera, ehorzketa handien esan nahi du sedentarismo maila bat hedatu zela, eta oso litekeena da lehia handia egotea ehizatik, arrantzatik eta fruituen bilketatik bizi ziren taldeen artean, Azken Maximo Glaziarraren amaieran (duela 20 000 urte inguru) eta Afrikako Periodo Hezearen hasieran (duela 16 000-6 000 urte) gertatu ziren ingurumen-aldaketei aurre egin behar izan zietenean.
Ezaugarri kultural desberdinak zituzten giza taldeen arteko indarkeriazko gertaera errepikakorrak, lehia gogor horren ondorio zuzena izango ziren. Hau da, sasoi hartan izandako ingurumen-aldaketen eraginez. Aipatutako gertakariak duela 15 000 urte inguru jazo ziren, baina etengabe suertatu dira hainbat modutan eta eskala desberdinetan.
Erreferentzia bibliografikoa:Crevecoeur, I., Dias-Meirinho, MH., Zazzo, A. et al. (2021). New insights on interpersonal violence in the Late Pleistocene based on the Nile valley cemetery of Jebel Sahaba. Scientific Report, 11 (1), 9991. DOI: 10.1038/s41598-021-89386-y
EgileaJuan Ignacio Pérez Iglesias (@Uhandrea) UPV/EHUko Fisiologiako katedraduna da eta Kultura Zientifikoko Katedraren arduraduna.
The post Hezurretan idatzitako erasoak, liskarrak, segadak… appeared first on Zientzia Kaiera.
Miltos, un pigmento muy preciado, pero no por su color
El ocre rojo de óxido de hierro, también conocido como miltos, fue uno de los minerales de uso clínico más populares de la literatura médico-científica de la antigüedad grecoromana. Sin embargo, también tenía usos decorativos, era útil en la agricultura, en el mantenimiento de barcos, o se empleaba como cosmético. Curiosamente, según donde se extrajese se le daba un uso u otro.
Un grupo de investigadores de distintas universidades de Reino Unido y Grecia decidieron colaborar para estudiar este mineral. Para ello extrajeron muestras de cinco enclaves de Grecia, destacados en los textos de la época, cuatro provenientes de la isla de Kea y una de la isla de Lemnos.
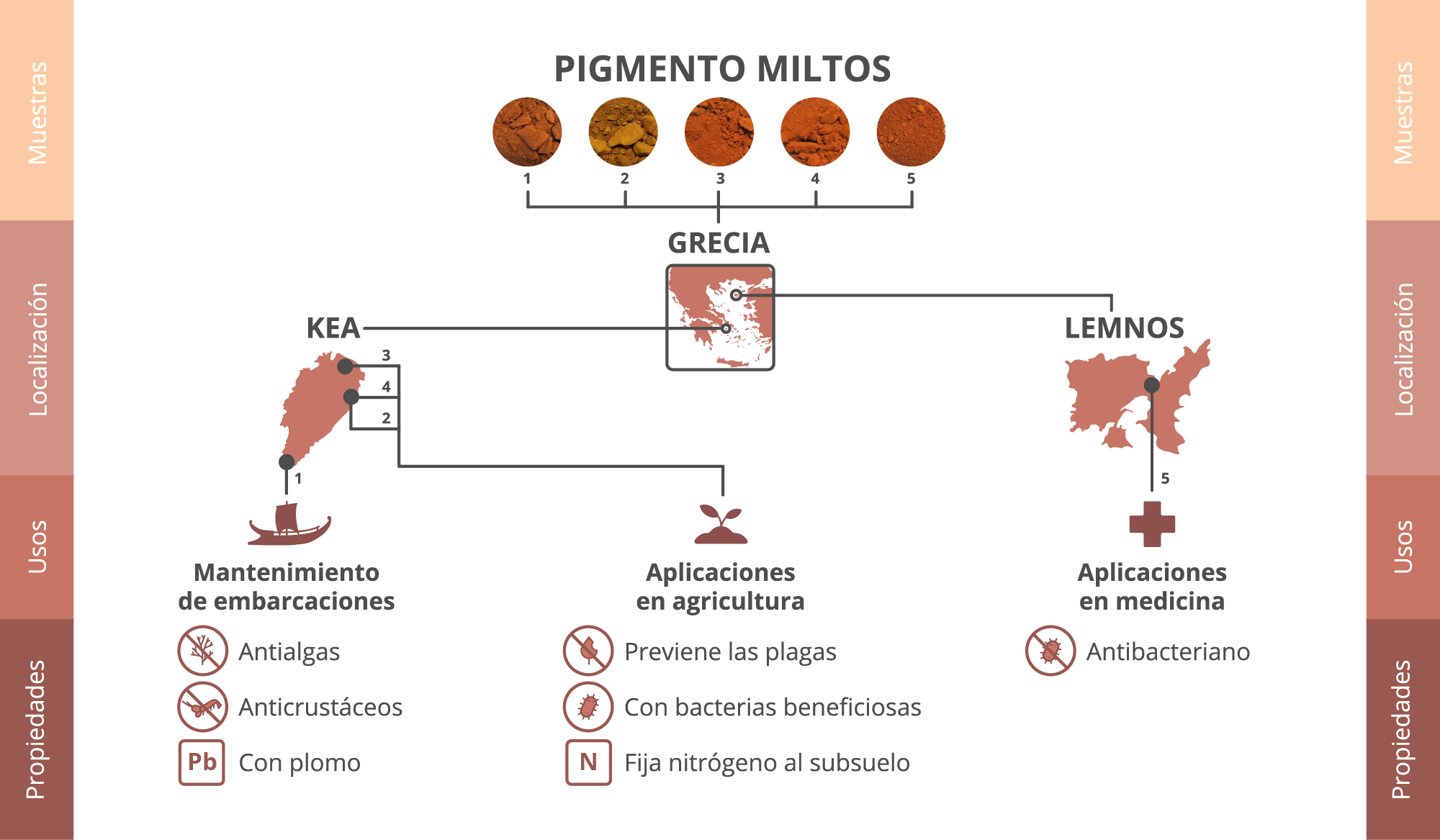 Imagen: Localizaciones populares de miltos en la antigüedad clásica, usos y propiedades. Ilustración: María Candamil López
Imagen: Localizaciones populares de miltos en la antigüedad clásica, usos y propiedades. Ilustración: María Candamil LópezEl análisis geoquímico, microbiológico y mineral determinó que no había una fórmula única de ocre rojo. La variación de la composición química favorecía el desarrollo de microbiotas diferentes y la combinación de ambos factores, determinaba sus propiedades. Esto explicaba por qué la localización determinaba el uso.
El miltos de Kea obtenido en Petroussa contenía plomo. El plomo es tóxico, por lo que la pintura para barcos fabricada con ese ocre impedía que las algas y los invertebrados pudieran adherirse al casco de la embarcación y dificultar la navegación. Sin embargo, si se extraía de otras zonas de la isla, tenía bacterias fijadoras del nitrógeno del subsuelo. Al diluirlo en soluciones acuosas se convertía en un gran fertilizante, mientras que aplicándolo en polvo sobre las raíces de los árboles prevenía la aparición de enfermedades. En cambio, el miltos de Lemnos era el mejor para uso médico, ya que la alunita, el óxido de titanio y una ausencia total de metales tóxicos, le otorgaban propiedades antibacterianas.
El miltos no era apreciado solo por ser un efectivo pigmento rojo. De hecho, los griegos ya habían descubierto su versatilidad de forma empírica, pero gracias a estos recientes estudios conocemos los motivos.
Referencias consultadas:Photos-Jones, E., Knapp, C. W., Vernieri, D., Christidis, G. E., Elgy, C., Valsami-Jones, E., Gounaki, I., Andriopoulo, N. C. (2018). Greco-Roman mineral (litho)therapeutics and their relationship to their microbiome: The case of the red pigment miltos. Journal of Archaelogical Science, 22, 179-192. DOI: https://doi.org/10.1016/j.jasrep.2018.07.017
Autora: María Candamil López, alumna del Postgrado de Ilustración Científica de la UPV/EHU – curso 2019/20
Artículo original: El ocre rojo de la antigüedad y los porqués de sus propiedades. Juan Ignacio Pérez Iglesias, Cuaderno de Cultura Científica, 20 de enero de 2019.
“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.
El artículo Miltos, un pigmento muy preciado, pero no por su color se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El ocre rojo de la antigüedad y los porqués de sus propiedades
- ¿Es posible el arte sin ciencia?
- ¿Azúcar moreno o azúcar milagro?
Planktona Bilboko itsasadarrean, kate trofikoaren oinarri
Ibaizabal Itsasadarra zientziak eta teknologiak ikusita
Bilboko itsasadarra berreskuratzeko plana abiatu zenean itsasadarraren egoera leheneratzea zen helburua. Ikusgarriak dira lortutako emaitzak. Baita ikusgarri ez den planktonean ere. Berebiziko garrantzia du honek, izan ere, planktona dago itsasadarraren kate trofikoaren oinarrian.
Planktona izan da Bilboko itsasadarreko kutsadura maila kezkagarria jasan duen parametroetako bat. Bestelako bizidunek jasandakoen parekoa izan da, baina ez hain nabarmena populazioarentzat.
Uretan esekita dauden organismo txikiek osatzen dute planktona. Fernando Villate eta Aitor Laza-Martínez azaldu zituzten planktonaren nondik-norakoak eta klasifikazio ezberdinak honako artikuluan.
Garrantzi handia du ekosistemetan planktona, kate trofikoaren oinarria osatzen baitu. Karbonoaren zikloak, fitoplanktona oinarrian duenak, fotosintesia erabiltzen du co2-a finkatzeko. Karbono hori kate trofikoan zehar bidaiatzen du, gizakiraino.
Esan bezala, itsasadarraren saneamendu planari esker, planktona berreskuratzen ari da, bai fitoplanktona (landare mikroskopikoz osatua), bai zooplanktona (animalia mikroskopikoak).
Bilboko itsasadarrera bizia itzuli izanaren oinarrian planktona egon da eta hau berreskuratzeko ezinbestekoak izan dira zientzia eta teknologia.
Ibaizabal Itsasadarra zientziak eta teknologiak ikusitaIbaizabal Itsasadarra zientziak eta teknologiak ikusita / La Ría del Nervión a vista de ciencia y tecnología proiektua infografia sorta bat izan zen hasieran, Ibaizabal itsasadarra eta bere inguru metropolitarra zientziaren eta teknologiaren begiez erakusten duten infografia bilduma batekin osatutako erakusketa.
Ondoren, zientziaren arlotik landutako artikulu sorta etorri zen euskaraz blog honetan bertan irakurgai eta gaztelaniaz Cuaderno de Cultura Científica blogean.
Proiektu honen (orain arteko) azken atala dugu honakoa, azalpen bideoak.
The post Planktona Bilboko itsasadarrean, kate trofikoaren oinarri appeared first on Zientzia Kaiera.
Trampas de CO2 más baratas
 Foto: Patrick Hendry / Unsplash
Foto: Patrick Hendry / UnsplashHasta ahora, al pensar en las medidas más eficaces para combatir el calentamiento del planeta, se ha puesto especial énfasis en la limitación de la emisión de gases con efecto invernadero, CO2 especialmente, por ser el que más se emite a la atmósfera. Ese efecto consiste en la retención, por esos gases, de radiaciones infrarrojas en el interior de la atmósfera, del mismo modo a como lo hacen los vidrios de un invernadero. Como consecuencia, la temperatura de la atmósfera aumenta.
La combustión de materiales orgánicos fósiles para obtener energía es la fuente principal de producción de los gases en cuestión, por lo que no es de extrañar que se promueva la limitación de las emisiones como forma de evitar o mitigar el calentamiento. Para ello es necesario limitar el consumo de energía, por un lado, y recurrir cada vez en mayor medida a fuentes de energía inagotables (hidráulica, eólica, solar u otras) o, cuando menos, que no conlleven la emisión de esos gases. Sin embargo, eso no es nada fácil. Por un lado, quemar carbón y otros combustibles fósiles sigue siendo la forma más barata de obtener energía. La nuclear cuenta con muy mala prensa en los países occidentales. Los métodos alternativos son caros y su uso no ha crecido lo suficiente como para que sean una solución a corto plazo.
Por esas razones también se trabaja en el diseño de métodos que permitan retirar de la atmósfera parte del CO2 presente en ella. De esa forma, combinando limitaciones a la emisión con su retirada, podría conseguirse estabilizar la concentración atmosférica del gas y evitar que siga intensificándose el efecto. Podría, incluso, llegar a revertirse la tendencia y disminuir su concentración.
El problema es que los métodos para retirar CO2 son muy caros. La tecnología que se utiliza en la actualidad se sirve de aminas disueltas en agua. Las aminas son derivados del amoniaco (NH3) en el que uno, dos o los tres átomos de hidrógeno han sido sustituidos por un radical. Una de las formas de atrapar CO2 consiste en rociar los gases emitidos con una disolución acuosa de aminas. La disolución cargada con el CO2 se procesa de manera tal que puede recuperarse aquella a la vez que el gas es retirado y almacenado. El método es caro porque requiere llevar la disolución de aminas a ebullición y su posterior condensación para volverla a utilizar. Requiere mucho gasto de energía.
Recientemente, sin embargo, se ha ensayado un procedimiento que permite reducir los costes en cerca de un 20%. No utiliza agua, sino un disolvente orgánico pobre en agua basado en la amina 2-EEMPA (N-(2-etoxietil)-3-morfolinopropan-1-amina). La ventaja de este método es que, una vez el CO2 ha quedado atrapado por la amina, no es necesario llevar el disolvente a ebullición para recuperarlo y, tras retirar el gas, volver a ser utilizado. Basta con calentarlo. Y eso reduce el coste de forma significativa.
Se ha investigado mucho para hallar procedimientos para capturar el CO2 contenido en las emisiones gaseosas industriales y utilizarlo o almacenarlo después. En 2020 se capturaron 40 millones de toneladas (en adelante, M t) de CO2 procedente de emisiones industriales. Se calcula que las 30 instalaciones de captura ya proyectadas en el mundo permitirán retirar hasta 140 M t anuales. Pero las emisiones globales ascienden a 35000 M t en la actualidad. Por lo tanto, para acercar la captura al volumen de emisiones, es necesario multiplicar el esfuerzo actual y, para ello, va a ser necesario reducir los costes prácticamente a la mitad, de los actuales 50€ a 25€ por tonelada.
Referencias:
Robert F. Sevice (2021) New generation of carbon dioxide traps could make carbon capture practical Science News
Richard Zheng et al. (2021) A single-component water-lean post-combustion CO2 capture solvent with exceptionally low operational heat and total costs of capture – comprehensive experimental and theoretical evaluation Energy & Environmental Science doi: 10.1039/D0EE02585B
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Trampas de CO2 más baratas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La ley del gas ideal y la tercera ley de la termodinámica
- África arde más de lo que se pensaba
- Carnot y los comienzos de la termodinámica (2)
Asteon zientzia begi-bistan #353
Asteon zientzia begi-bistan igandeetako gehigarria da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna jaso eta laburbiltzea da gure helburua.

Klima-aldaketak giza osasunari eragiten dio, baina ez da eskala handiko azterketarik egin beroak gure osasunean duen eragina zenbatzeko. Ikerketa batek 43 herrialdetako datuak jaso ditu, 1991-2018 aldian berotze globalak eragin duen beroaren esposizio gehigarriaren ondoriozko hilkortasun-tasa ezagutzeko. Emaitzen arabera, urte-sasoi beroenean hildakoen % 37a klima-aldaketa antropogenikoari egotz dakizkioke. Xehetasun guztiak, Berrian: Klima-aldaketak eragindako beroaldiek urtero 33 lagun hiltzen dituzte Hegoaldeko hiriburuetan.
HistoriaMartiodako elizan (Araba) erlikia multzo garrantzitsu bat izan dute gordeta. Juanma Gallego kazetariak kontatu duenez Alea aldizkarian, erlikiez harago joanez gero ezkutuko altxorra da material hori. Arabako Zaharberrikuntza Zerbitzuak hainbat teknika erabiliz aztertu ditu piezak eta publikoak ezagutu ditzan erakusketa bat antolatu du.
NeurozientziaTeknologia berriak funtsezkoak dira garuneko zirkuitu eta neurona-sistemaren dinamika ulertzeko. Ultrasoinuetan oinarritutako neuroirudi teknika baten bidez, makako baten gorputz atalen mugimenduak eta begiradaren norabidea aurreikusi dituzte ikerketa baten. Juan Ignacio Pérez Iglesias biologoak azaldu du: Ultrasoinuak, entzefaloaren barrualdera begiratzeko.
OsasunaCovid-19a modu arinean pasatu zuten 77 gaixoren azterketak emandako datuak argitaratu dituzte Nature aldizkarian. Emaitzek iradokitzen dutenez, gaixotasuna pasatu duen pertsona batek, nahiz eta arina izan, epe luzerako babesa eman diezaioketen antigorputzak gara ditzake. Egoitz Etxebestek azaldu du Elhuyar aldizkarian: COVID-19tik epe luzean babesten duten zelulak topatu dituzte hezur-muinean.
Ana Galarragak Elhuyar aldizkarian jakitera eman digu, Gaixotasun Infekziosoen Europako Zentroak (ECDC) osasun publikoko agintarientzako lagungarria izan daiteken txosten tekniko bat argitaratu dutela. Bertan, 12 eta 18 urte bitarteko nerabeei Covid-19aren txertoa emateari buruzko erabakia hartzeko lagungarria izan daitezken irizpideak eskaintzen zaizkie.
Euskal Herriko Unibertsitateko ikertzaileek ikerketa bat abiarazi dute, trebatutako txakurren laguntzarekin Covid-19arekin kutsatutako pertsonak usainaren bidez antzemateko. Maialen Arteaga kazetariak azaltzen du Berrian: Txakurrak birusa antzematen.
AstrofisikaMartek gure arreta erakartzen duela gauza jakina da. Azkenaldian planeta gorriari buruzko hainbat gauza ezagutzen ari gara bertan dauden ibilgailu robotikoei esker. Esaterako, Nagore Arin kazetariak Berrian jakitera eman digu izotz lehorrez konposatutako hodei koloretsu eta distiratsuak antzeman dituztela Marten. Hodei bitxiak dira, ilunabarrean eguzkiaren azken izpien koloreak xurgatu eta distira nabarmena egiten dute.
GenetikaPandemiak zaintza genomikoko aro bati eman dio hasiera. Izan ere, zientzialariak SARS-CoV-2 birusaren aldaerak aztertzen dihardute inoiz ikusi gabeko abiadura eta eskalan. Baina lan hau ez da modu berean ematen munduan zehar eta zientzialariek ohartarazi dute litekeena dela diru-sarrera txiki eta ertaineko herrialde askotan birusaren aldaerak modu kezkagarrien zabaltzea, inork atzeman gabe. Koldo Garcia genetistak ohartarazi digu asteon auziaz: Gene informazioa, denon onurarako?
MikrobiologiaEztabaida publikoetan laguntzeko, OMEk letra greziarrak erabiliko ditu SAR-COV-2 birusaren aldaerak izendatzeko. Osasun erakundearen esanetan, hauek errazagoak eta praktikoagoak izango dira zientzia gaietan trebatua ez dagoen audientzia batek informazioa kudeatu dezan. Aitziber Agirreren eskutik, Elhuyar aldizkarian: Alfa, Beta, Gamma eta Delta: SARS-CoV-2aren aldaerentzako izen berriak.
BiologiaHerpetologia narrastiak eta anfibioak aztertzen dituen zoologiaren adarra da. Besteak beste, sugeak dira herpetologoen ikergaia eta Berrian Enekoitz Telleria kazetariak animalia hauek protagonista duen egitasmo baten berri eman digu: #sugebizi proiektua. Aranzadi Elkarteak martxan jarritako egitasmoa da eta herritarrek Twitter bidez partekatutako argazki eta datuen bidez, sugeei buruzko ezagutza eta sentsibilizazioa handitzea izan du helburu.
NeurozientziaGaruna neuroirudien bidez aztertzen espezializatu zen Ileana Quiñones ikertzailea eta, egun, kognizioa, garuna eta hizkuntza ikertzen dituen BCBL zentroan ari da lanean. Bere ibilbideari buruz hitz egin du Ana Galarragarekin eta Quiñones neurozientzialariak azpimarratu dio zaila dela emakume izatea eta ikerketan lan egitea.
Egileaz:Uxune Martinez (@UxuneM), Euskampus Fundazioko Kultura Zientifikoko eta Berrikuntza Unitateko Zabalkunde Zientifikorako arduraduna da eta Zientzia Kaiera blogeko editorea.
The post Asteon zientzia begi-bistan #353 appeared first on Zientzia Kaiera.
Aitziber López-Cortajarena – P4K 2019: Ingeniería de proteinas: nuevas terapias y biomateriales
 Imagen: National Cancer Institute / Unsplash
Imagen: National Cancer Institute / UnsplashAitziber López-Cortajarena dirije el Laboratorio Cortajarena del CIC biomaGUNE especializado en nanotecnología biomolecular. Dicho así puede sonar entre raro y directamente de ciencia ficción. Pero cuando Aitziber nos cuenta en cómo pretenden construir biomateriales y nanoestructuras funcionales prediseñadas partiendo de como se ensamblan proteínas simples, la cosa pasa a oscilar entre la psicodelia y la más pura fascinación. Las posibilidades y aplicaciones de esta tecnología son increíbles.
Aitziber López-Cortajarena se doctoró en bioquímica por la Universidad del País Vasco en 2002. Fue becaria postdoctoral y, posteriormente, investigadora asociada en el Departamento de Biofísica Molecular y Bioquímica de la Universidad de Yale (New Haven, Connecticut, Estados Unidos) hasta 2010, cuando estableció su propio grupo de investigación en la Fundación IMDEA Nanociencia de Madrid. Desde 2016 es profesora de investigación Ikerbasque en Cic biomaGUNE.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Aitziber López-Cortajarena – P4K 2019: Ingeniería de proteinas: nuevas terapias y biomateriales se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ana María Zubiaga – Naukas Pro 2019: La difícil búsqueda de terapias contra el cáncer
- Ignacio López Goñi – Naukas P4K 2019: La sopa amarilla de la dinastía Ming
- Virginia Arechavala – Naukas Pro 2019: Buscando terapias para enfermedades poco frecuentes
Ezjakintasunaren kartografia #354

Nukleo zelularren edizio genetikoaren ostean, mitokondrien edizio genetikoa dator. Geldiezina da hau guztia. Mitochondrial gene editing is now possible, thanks to a bacterium Rosa García-Verdugoren eskutik.
Bizidun oso txikien inguruan, posible litzateke mikroorganismo batek estralurtar batekin komunikatzea. Predrag Slijepcevic eta Nalin Chandra Wickramasinghe azaltzen dute: Seti: how microbes could communicate with alien species
Molekula organikoetan gauzak di-da gertatzen dira, femtosegundutan. Baina ez berdin norabide guztietan. DIPCk: The anisotropic behaviour of ultrafast electron transfer at the metal/organic interface
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #354 appeared first on Zientzia Kaiera.
25 años del escándalo Sokal: la culpa de todo la tienen los posmodernos
Urko Gorriñobeaskoa y Ekai Txapartegi
 Imagen: Shutterstock / paseven
Imagen: Shutterstock / paseven
“El objetivo de este libro es hacer una contribución limitada pero original a la crítica del ‘Zeitgeist’ ciertamente obscuro que hemos llamado ‘posmodernismo’”.
Con esta firme declaración, Alan Sokal y Jean Bricmont inauguraban el primer epígrafe de su polémica obra de 1996, Imposturas intelectuales. En ella, los autores acusan a los editores y académicos posmodernos de falta de rigor, de dejarse llevar por sus sesgos ideológicos y de mala praxis académica. Cabe preguntarse, ¿es realmente el posmodernismo un enemigo natural de las ciencias? ¿Esta clase de imposturas son exclusivas de los estudios posmodernos y de las humanidades? Analizar algunas de las polémicas académicas más sonadas de los últimos años puede arrojar algo de luz a estas preguntas.
Echemos un vistazo al suceso con el que empezó todo: el escándalo Sokal. Fue en 1996 cuando Social Text, revista académica centrada en estudios culturales, publicó el artículo Transgressing the Boundaries: Towards a Transformative Hermeneutics of Quantum Gravity, de Alan Sokal. Este artículo había sido redactado por su autor a modo de broma y engaño.
Plagado de sinsentidos, el artículo fue aceptado por la revista posmoderna, y confirmó así las sospechas de Sokal: estas publicaciones aceptarían cualquier cosa que sonase bien y estuviese dentro de su línea ideológica. Poco después de su salida al público, Sokal admitió que se trataba de un engaño y reveló sus motivos.
Las respuestas al escándalo y al libro de Sokal no tardaron en llegar. Jacques Derrida escribió que la lectura de Sokal y Bricmont en el libro era exageradamente simplista. Según el autor francés, Sokal hizo un hombre de paja del posmodernismo y sus argumentos no se sostenían.
Baudouin Jurdant, filósofo de la ciencia francés, reunió a un grupo de científicos de distintas ramas para comprobar el rigor de las acusaciones de Sokal y Bricmont. Estos científicos eran, además, especialistas en los autores citados en Imposturas intelectuales. En conjunto, escribieron un artículo mostrando que Sokal y Bricmont no conocían con la profundidad suficiente las ideas que trataban de criticar. Por otra parte, científicos como Richard Dawkins y filósofos como Thomas Nagel alabaron el trabajo de Sokal y Bricmont, y coincidieron en que muchas revistas de humanidades se dejaban influenciar por sus sesgos políticos.
Este no es el único bulo intelectual que ha avergonzado a la academia en las últimas décadas. En 2018, James Lindsay, Peter Boghossian y Helen Pluckrose dieron a conocer un engaño similar que habían estado urdiendo. Los tres autores escribieron una veintena de artículos de corte posmoderno plagados de sinsentidos y tesis insostenibles, pero que empleaban de manera correcta la terminología habitual de estos campos.
De todos sus artículos, aproximadamente un tercio fueron publicados o aceptados; otro tercio fue rechazado y los restantes seguían pendientes de revisión en el momento en el que se destapó la mentira. Igual que en el caso Sokal, este escándalo desencadenó tanto elogios como críticas por parte de los académicos.
Las ciencias ‘de verdad’ también pican
Quienes alaban los resultados de ambos bulos tienden a leer estos episodios como parte de una polémica mayor: el problema de las dos culturas. Aparentemente, engaños de este estilo solo podrían darse en disciplinas relacionadas con los estudios sociales y culturales, en revistas de humanidades posmodernas donde el rigor brilla por su ausencia. Al contrario, quienes investigan y publican acerca de ciencias de verdad, como la física o la biología, jamás se dejarían embaucar por una treta tan simple.
Sin embargo, la historia reciente nos enseña que esto no es necesariamente cierto.
Alrededor del año 2002 distintos medios comenzaron a hacerse eco de una controversia similar que amenazó, en este caso, al campo de la cosmología. Los protagonistas de esta polémica fueron los hermanos Igor y Grichka Bogdanov, dos divulgadores científicos que trabajaban para la televisión francesa. Al parecer, varias dudas acerca de su legitimidad como físicos llevaron a los hermanos a perseguir sendos títulos de doctorado en la Universidad de Borgoña. Tras un periodo extraordinariamente largo, consiguieron graduarse bajo la condición de que publicasen algunos artículos en revistas de su campo.
Una vez las tesis y artículos de los Bogdanov fueron abiertas al público, diversos especialistas comenzaron a analizarlas. Muchos autores apreciaron que sus trabajos eran más bien pobres, que sus tesis no tenían sentido y que podrían encontrarse ante un escándalo à la Sokal, pero a la inversa. Sin ir más lejos, John Baez, reputado matemático estadounidense, afirmó que su trabajo “es una mezcolanza de frases aparentemente plausibles que contienen las palabras técnicas correctas en el orden aproximadamente correcto. Pero no hay lógica ni cohesión en lo que escriben.” Curiosamente, el diagnóstico es muy similar a aquel que hiciera Sokal de las revistas posmodernas de humanidades.
Pero esto no acaba aquí. En 2005 tres estudiantes del MIT gastaron una broma pesada a una escena académica que consideraban plagada de intereses económicos. Para Jeremy Stribling, Dan Aguayo y Max Krohn, muchos congresos científicos se organizaban con el objetivo principal de aprovecharse económicamente de los investigadores jóvenes ansiosos por hacer currículum. Es por ello por lo que los tres jóvenes desarrollaron un programa informático de IA que generaba artículos académicos automáticamente mezclando frases y tecnicismos aleatorios de otros trabajos. La polémica estalló cuando uno de esos artículos fue aceptado en una conferencia de informática ese mismo año.
Dada la abundancia y diversidad de casos de bulos académicos en los últimos años, creo que podemos sugerir que esta clase de imposturas no se deben exclusivamente a los sesgos de los editores. Casos como el de los Bogdanov y los chicos del MIT parecen indicar que esta clase de engaños son fenómenos poliédricos y que atienden a una variedad de motivos. Tal vez algunos editores de revistas posmodernas den demasiada manga ancha a artículos pobres solo porque suenan bien. Pero esto no debe enmascarar el hecho de que la realidad académica actual está repleta de fallos, métodos de revisión deficientes e intereses extraacadémicos. Además, tal y como muestran algunos de los ejemplos comentados, esta clase de intereses y deficiencias también se dan en las ciencias de verdad.
En un mundo donde publicar es cada vez más necesario para labrarse una carrera, y donde la labor editorial y la organización de conferencias pueden llegar a ser negocios muy lucrativos, ¿cómo no va a primar la cantidad sobre la calidad?![]()
Sobre los autores: Urko Gorriñobeaskoa es doctorando en historia y filosofía de la ciencia y Ekai Txapartegi, profesor de filosofía, ambos en la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo 25 años del escándalo Sokal: la culpa de todo la tienen los posmodernos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un cómic de hace dos mil años a todo color
- Todo lo que se puede medir en un río
- ¿Por qué los átomos tienen el tamaño que tienen?
Ileana Quiñones, neurozientzialaria: “Zaila da emakume izatea eta ikerketan lan egitea”
Kognizioa, garuna eta hizkuntza ikertzen dituen BCBL zentroko ikertzailea da Ileana Quiñones González. Horra iristeko, bide zuzena egin du gaztetik, beti izan baitzuen argi ikertzaile izan nahi zuela: “Batxilergoa ere zientzietan espezializatutako zentro batean egin nuen, eta gero, medikuntza ikastekotan ere egon nintzen, baina banekien, mediku izanda, ez zela erraza izango ikerketan aritzea. Hortaz, biologia ikasi, eta masterra egin nuen, neurozientzia kognitiboen arloan. Garuna neuroirudien bidez aztertzen espezializatu nintzen, eta tesiaren zati bat Eskozian egin nuen. Habanara itzuli, eta BCBLren oso antzeko zentro batean hasi nintzen lanean, tesia bukatu bitartean”.
Gaur egun BCBLren zuzendari den Manuel Carreiras Valiñari esker igaro zen handik BCBLra: “Nazioarteko mintegi batean ezagutu genuen elkar, Habanan. Orduantxe sortu zen BCBL zentroa, 2010ean, eta tesia Donostian amaitzea proposatu zidan. 2011tik nago hemen”.

Aitortu du hasieran erreparo pixka bat izan zuela, euskara ez jakiteagatik; baina ikerketen funts nagusietako bat elebitasuna duen zentro batean lan egitea oso erakargarria egiten zitzaion, bi hizkuntza ezagutzeak eragin handia baitu garunean.
Gainera, ikerketa-zentro guztietan lantaldeak nazioartekoak dira, eta ingelesa erabiltzen dute elkarren artean hitz egiteko. “Ez du axola non zauden. Ikertzaile izateak mugitzea dakar, nazioartekotasuna eta ingelesez komunikatzea. Hortaz, euskara ez jakitea ez da arazo bat”.
Quiñonesek gidatzen duen proiektua neuroplastikotasuna ikertzean datza, buruko tumoreak dituzten pertsonetan. “Beste leku askotan ere ikertzen da hori, baina BCBLn elebitasuna aintzat hartzen dugu. Kontuan izan behar da paziente gehienak, normalean, beti gaztelaniaz testatu dituztela, eta, batzuentzat, ez da hori beren jatorrizko hizkuntza. Beraz, pazienteak hitz egiten dituen hizkuntza guztiak aintzat hartzen dituzten test berriak diseinatu ditugu, eta elebitasunak plastikotasunean nola eragiten duen ere ikertzen dugu”.
Horren garrantzia nabarmentzeko, kasu ezagun baten adibidea jarri du: “Gizon batek bi hizkuntza hitz egiten zituen, gaztelania, jatorrizkoa, eta ingelesa, gero ikasia. Bada, istripu baten ondorioz, operazio kirurgiko bat egin behar izan zioten garunean. Ondoren, ez zen gaztelaniaz hitz egiteko gai, baina bai ingelesez. Horrenbestez, neurozientzialariontzat oso da interesgarria elebidunak ikertzea”.
Lana eta familia bateragarri egiteko zailtasunaQuiñonesek guztiz bokaziozkoa du bere lana, baina horrek ez du esan nahi ez dituela alderdi txarrak. Adibidez, bereziki zaila egiten zaio finantziazioa bilatzeko lana, ikerketa, eta familia uztartzea. “Gauza jakina da, eta BCBLn, gainera, egiten ditugu saioak kontziliazioa nola hobetu dezakegun aztertzeko. Alegia, gaiarekiko sentiberatasuna eta ulerkortasuna badago; baina, praktikan, ez da erraza irtenbideak topatzea, eta lan-kargak banatzea ez da nahikoa. Zaila da emakume izatea eta ikerketan lan egitea”.
Dioenez, haurrak izatea erabakitzen duen emakumeak zailtasun batzuk izango ditu, beraz: “Biologiak agintzen du. Haurdunaldiak emakumeari eragingo dio, beti; hori ezin dio beste inori esleitu. Eta haurra izan ondoren ere, hasieran, badaude amak baino egin ezin dituen gauzak. Nire ustez, lagungarria izango litzateke, hori kontuan hartuta, aldez aurretik egotea zerbait aurreikusita, amaren gain utzi beharrean laguntza eskatzeko ardura”.
Bestelakoan, BCBLn ez du inoiz arazorik izan haurrak berekin eramateko lan-bidaietan eta abar, eta lankideek ere beti izan dute kontziliazioan laguntzeko jarrera. Baina, hala ere, zaila dela onartu du: “Konfinamenduan, adibidez, gogorra egin zitzaidan etxekoek ni lanean ikustea, ordenagailuarekin eta abar. Izan ere, beti saiatu izan naiz etxean pantailarik ez erabiltzen: ez mugikorrik, ez ordenagailurik… Konfinamenduan ezinezkoa izan zen, eta asko kostatu zait”. Nolanahi ere, garbi du etorkizunean ikertzen jarraitu nahi duela: “Ikerketa nire bizitzaren zati bat da”.
Fitxa biografikoa:Ileana Quiñones González 1981ean jaio zen, Kuban. Biologia ikasi ondoren, masterra egin zuen, neurozientzia kognitiboen arloan. Garuna neuroirudien bidez aztertzen espezializatu zen, eta, tesia amaitzen ari zela, 2011n, Donostiara etorri zen, BCBLra. Geroztik, bertan ari da lanean, eta, gaur egun, ikerketa-lerro bat gidatzen du.
Egileaz:Ana Galarraga Aiestaran (@Anagalarraga1) zientzia-komunikatzailea da eta Elhuyar Zientzia eta Teknologia aldizkariko erredaktorea.
Elhuyar Zientzia eta Teknologia aldizkariarekin lankidetzan egindako atala.
The post Ileana Quiñones, neurozientzialaria: “Zaila da emakume izatea eta ikerketan lan egitea” appeared first on Zientzia Kaiera.
Toman agua por la piel
 Hyla versicolor. Ilustración: María Lezana
Hyla versicolor. Ilustración: María LezanaRanas y sapos pueden respirar a través de la piel. En determinadas épocas del año la piel es, de hecho, su principal órgano respiratorio. Pero no son gases lo único que intercambian con el medio externo por esa vía. También incorporan agua.
La mayoría de los anfibios terrestres no beben agua. La necesitan, por supuesto, pero la absorben a través de la piel, gracias a su gran permeabilidad. Eso tiene sus contrapartidas, ya que, de la misma forma que la adquieren, también la pueden perder. Por eso han desarrollado estrategias especiales para almacenarla. El medio interno o la misma vejiga, incluso, pueden funcionar como depósitos, de manera que pueden reutilizar el agua en ellos contenida en caso de riesgo de deshidratación.
Algunas ranas y sapos tienen una zona – la pélvica- especializada para facilitar la incorporación de agua. Es una zona comprendida entre la pelvis y el abdomen, la situada entre las inserciones de las extremidades posteriores al tronco. De hecho, los anfibios terrestres, cuando necesitan hidratarse, no tienen por qué sumergirse en una masa de agua; les basta con colocarse, sentados, sobre un sustrato húmedo o mojado, o aplastar la zona pélvica contra ese sustrato. El epitelio de esa zona está lleno de capilares sanguíneos, por lo que puede llegar a absorberse un volumen importante de agua. La cantidad que una rana puede absorber de ese modo en un día es equivalente al triple de su masa corporal.
La fuerza que impulsa la absorción de agua es un gradiente osmótico. El agua que se absorbe está muy diluida, casi no tiene sales. La sangre del sapo es de mayor concentración osmótica que el agua; tiene muchas más sales disueltas. Por esa razón, el agua del exterior tiene una fuerte tendencia a penetrar a través de la piel que, al fin y al cabo, es una membrana semipermeable, ya que permite el paso de agua a su través, pero no el de las sales. Eso sí, la sangre ha de circular rápidamente para que pueda ser absorbida el agua. Veamos esto con algún detenimiento.
Cuando penetra el agua y se mezcla con la sangre, ésta se diluye, puesto que la misma cantidad de solutos pasa a estar disuelta en un volumen mayor de agua, de plasma, en este caso. Por lo tanto, la fuerza que impulsa la absorción disminuye, y disminuirá en mayor medida cuanto más lenta sea la renovación de la sangre. Por esa razón, la sangre ha de circular con rapidez, porque si lo hiciese lentamente, la concentración de sales disueltas bajaría demasiado poco. Circulando rápidamente, la diferencia de concentración osmótica entre el interior y el exterior disminuye muy poco, por lo que la fuerza de absorción prácticamente se mantiene constante. En virtud de ese mecanismo, el flujo sanguíneo es proporcional a las necesidades hídricas. Esto es, cuando la deshidratación es baja, la sangre circula lentamente por la zona pélvica, pero la velocidad se eleva cuando el sapo tiene necesidad de agua.
Las hormonas que intervienen en la regulación de la economía del agua y los electrolitos en los vertebrados juegan un papel importante en este proceso. El péptido angiotensina II provoca que aumente la tendencia del sapo a sentarse y la hormona antidiurética (ADH) eleva la permeabilidad del epitelio de la zona pélvica. Por ello, el volumen de agua absorbido puede aumentar mucho como consecuencia de la acción de esas dos hormonas.
No quiero terminar la descripción de este fenómeno sin hacer notar el hecho de que la angiotensina II forma parte del sistema renina-angiotensina que interviene en la regulación de la actividad de la aldosterona en mamíferos y que la hormona antidiurética actúa en el epitelio de los tubos colectores de las nefronas aumentando, precisamente, su permeabilidad al agua. Como vimos aquí, esos sistemas hormonales promueven el ahorro y la recuperación de agua, esto es, lo mismo que promueven en las ranas y sapos que “beben” por su piel abdominal.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Toman agua por la piel se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los intercambios de agua y sales en los tetrápodos acuáticos
- La distribución del agua animal y el curioso caso del potasio
- Los animales que respiran en agua
Isotopo egonkorrak elikadura eta mugikortasun ikerketetan: Erdi Aroko zenbait aztarnategien kasuak
Azken hamarkadetan izan den teknologiaren aurrerapenari esker, isotopo egonkorren analisia eskeleto-aztarnetan geroz eta garrantzitsuagoa bihurtu da gure arbasoen bizimodua ikertzeko. Isotopoek antzinako gizakien bizimoduari buruz eman dezaketen informazioa populazio mugikortasun eta elikadura patroiei buruzkoa da. Gainera patroi hauen ezagutzak, besteak beste gizarte-egituraketa sozial eta ekonomikoaren inguruko informazioa lortzea ahalbidetzen du ere.
 1. irudia: Isotopo egonkorren analisiak arbasoen elikadura ikertzeko baliagarriak izan daitezke.
1. irudia: Isotopo egonkorren analisiak arbasoen elikadura ikertzeko baliagarriak izan daitezke.Isotopoak zenbaki atomiko berdina baina masa-zenbakia ezberdina duten elementu kimiko baten atomoak dira. Elementu baten isotopoek propietate kimiko berberak dituzte, baina masa atomikoan duten desberdintasunaren eraginez, propietate fisiko desberdinak azaltzen dituzte. Ikerketa hauetan isotopo-egonkorrak dira erabiliak. Egonkorrak dira ez dutelako desintegraziorik jasaten, baina isotopo-frakzionazioa deritzon fenomenoa pairatzen dute. Hau da edozein prozesu kimiko, fisiko edo biologikoen aurrean isotopo arinak eta astunak (masaren araberakoa) jokaera desberdina dute, izan ere prozesu mota batean isotopo batek bestearekiko lehentasuna izaten du.
Gizakiaren edozein ehunetan neurtu daitezke isotopo erlazioak (isotopo arin eta astunaren arrazoia), bizitzan zehar jan eta edan dugunaren isotopo-konposizioa gizaki eta animalien gorputz ehunetan islatzen baita. Ekosistema bateko isotopo-konposizioa elikagaietara pasatzen da, eta elikatzean gure gorputzak jasotzen du konposizio hori. Horrela gure ehunak aztertzerakoan atzerako ibilbidea egiten da, alegia gizakian neurtutako isotopo-erlazioetatik abiatuta bizi izan ziren eskualdea eta elikagai motak bereizten dira.
Antzinako gizakien elikadura eta mugikortasun ikerketetan hezurretako kolagenoan eta hortzetako esmaltean neurtzen diren karbono (δ13C), nitrogeno (δ15N), oxigeno (δ18O) eta estrontzio isotopo arrazoiak (87Sr/86Sr) erabiltzen dira. Karbono eta nitrogeno isotopo-erlazioek elikaduraren berri ematen dute. Karbono 13C eta 12C isotopo-erlazioak landaretza motak bereizteko erabiltzen dira, izan ere landareen δ13C balioak burutzen duten fotosintesi-bide moduaren araberakoak dira (C3 eta C4 landare motak). Nitrogeno isotopoen 15N eta 14N arrazoien kasurako, kontsumitzen den animalia-proteinen maila trofikoa islatzen du, zenbat eta animalia-proteina sarrera ugariagoa izan, δ15N balioak aberatsagoak dira. Bestalde, oxigeno 18O eta 16O isotopo egonkorren erlazioa edaten den eskualde geografiko bateko ur meteorikoaren oxigeno isotopo konposizioaren arabera aldatzen da, aldiz estrontzio isotopoen arrazoiak (87Sr/86Sr), arroka motaren isotopo-erlazioaren araberakoak dira. Ondorioz, bi isotopo-sistema hauen informazio-konbinaketak gizakiaren jatorri eskualde geografikoa mugatuko du.
Iberiar Penintsulako hainbat aztarnategi arkeologikoetako gizaki aztarnak erabili dira isotopo-egonkorrak populazioaren mugikortasun eta elikaduraren azterketa burutzeko: Momoitioko San Juan (Bizkaia), Tauste (Zaragoza), eta Las Gobas (Trebiñuko Konderria). Aztarnategi hauek Iberiar Penintsulako iparraldean kokatzen dira, eta VI-XIII. mendeen artekoak dira. Aipatzekoa da Momoitioko San Juan eta Las Gobas aztarnategiak kristauak direla, aldiz Tauste musulmana da.
Elikadurari dagokionez, elikadura orojaleak zuten, eta batez ere zereal, lekale eta barazkietan oinarritzen zen. Tauste aztarnategiaren kasurako, sexu zein adinaren araberako bereizketa dago. δ15N balio altuek adierazten dutenaren arabera, gizon helduek emakume eta gazteek baino haragi gehiago jaten zuten. Haragia jatea estatus maila altuagoa izateari lotu da betidanik, beraz gizonezkoak pribilegiatuagoak ziren aztarnategi musulman honetan. Bereizketa hau ez da antzeman aztertutako aztarnategi kristauetan.
δ18O eta 87Sr/86Sr arrazoien arabera populazio mugikortasuna urria zen Erdi Aroan zehar, genero eta adinaren araberako desberdintasunik ez zegoen eta bertan bizitakoak ziren gehienetan. Kanpotarrak ziren gizakiak ere identifikatu dira baina hauen jatorri geografikoa ezin izan da ezarri, baina orokorrean aztarnategiarekiko nahiko hurbila izan behar zuela ondorioztatu da.
Iturria:
Guede, Iranzu; Alonso-Olazabal, Ainhoa; Zuluaga Maria Cruz; Ortega, Luis Angel (2019). «Isotopo egonkorrak elikadura eta mugikortasun ikerketetan: Erdi Aroko zenbait aztarnategien kasuak»; Ekaia, 36, 2019, 255-274. (https://doi.org/10.1387/ekaia.20841). Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: Ekaia 36
- Artikuluaren izena: Isotopo egonkorrak elikadura eta mugikortasun ikerketetan: Erdi Aroko zenbait aztarnategien kasuak
- Laburpena: Gizakien hezur eta hortzetan neurtutako isotopo-erlazioak (87Sr/86Sr, δ13C, δ15N eta δ18O) antzinako gizakien elikadura eta mugikortasun-ereduak berreraikitzeko erabiltzen dira. Gizakien elikaduraren berri izateko, gizaki eta faunaren hezurretik lortutako kolagenoan karbono eta nitrogeno isotopoen analisiak egiten dira. Gainera, gizaki eta animalien mugikortasunari buruzko informazioa lortzeko, hezur eta hortzetan neurtutako estrontzio eta oxigenoen isotopo-erlazioak erabiltzen dira. Isotopo hauek duten aplikazioa ikusteko Erdi Aroko hiru aztarnategiren emaitzak deskribatuko dira, Momoitioko San Juan (Bizkaia), Tauste (Zaragoza) eta Las Gobasekoak (Trebiñuko Konderria), hain zuzen ere.
- Egileak: Iranzu Guede, Ainhoa Alonso-Olazabal, Maria Cruz Zuluaga eta Luis Angel Ortega
- Argitaletxea: UPV/EHUko argitalpen zerbitzua.
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 255-274
- DOI: 10.1387/ekaia.20841
————————————————–
Egileaz:
Iranzu Guede, Ainhoa Alonso-Olazabal, Maria Cruz Zuluaga eta Luis Angel Ortega UPV/EHUko Zientzia eta Teknologia Fakultateko Mineralogia eta Petrologia Sailekoak dira.
———————————————–
Ekaia aldizkariarekin lankidetzan egindako atala.

The post Isotopo egonkorrak elikadura eta mugikortasun ikerketetan: Erdi Aroko zenbait aztarnategien kasuak appeared first on Zientzia Kaiera.
36 días de tipos (de números)
En esta entrada del Cuaderno de Cultura Científica me gustaría hablaros de un proyecto interesante y hermoso que descubrí en la cuenta de Instagram de Calpurnio (creador de El bueno de Cuttlas) el pasado mes de abril. Se trata del proyecto 36 Days of Type (36 días de tipos).
 El bueno de Cuttlas en la cuarta dimensión, de Calpurnio, publicado el 29 de marzo de 2021 en Valencia Plaza
El bueno de Cuttlas en la cuarta dimensión, de Calpurnio, publicado el 29 de marzo de 2021 en Valencia Plaza
Este es un proyecto creado en 2014 por la diseñadora gráfica Nina Sans y el diseñador gráfico Rafa Goicoechea, del estudio de diseño gráfico treintayseis, de Barcelona. Como cuentan sus creadores en la página web del proyecto 36 Days of Type, ellos decidieron desafiarse a sí mismos creando algo nuevo cada día, nuevos diseños personales en torno a la tipografía y el diseño gráfico. Entonces decidieron invitar a más personas a sumarse a este desafío. Para ello crearon el proyecto 36 Days of Type: “Una celebración de 36 días de la tipografía y la creatividad, animando a diseñadores, artistas visuales y creativos de todos los campos en un acto global y simultáneo de creatividad alrededor de la tipografía y la forma de las letras (y números)”.

¿En qué consistía el proyecto 36 Days of Type? El objetivo del mismo era animar a diseñadores, ilustradores y artistas gráficos a crear nuevos diseños, o interpretaciones personales, de las letras del alfabeto y los números (cifras básicas) del alfabeto latino, durante 36 días consecutivos. Cada día estaría dedicado a una letra del alfabeto o a un número, siguiendo un calendario prefijado (como el que aparece en la siguiente imagen, correspondiente a la edición de 2021). Los participantes en el proyecto debían de subir su diseño de la letra o número correspondiente a ese día en Instagram, etiquetando la imagen convenientemente, según las instrucciones indicadas en la página del proyecto.
 Calendario de la edición de 2021 del proyecto 36 Days of Type
Calendario de la edición de 2021 del proyecto 36 Days of Type
Cada día, durante los treinta y seis que duraba el reto gráfico, la organización del proyecto seleccionaba algunos de los diseños presentados y los publicaba en su página oficial de Instagram (36daysoftype), así como en Facebook y Twitter. Además, a lo largo del año se irán publicando el resto de diseños que se han presentado al proyecto, para mostrar el trabajo de los artistas gráficos involucrados.
 Diseños de Calpurnio de algunas de las letras, una D geométrica, una G áurea, una H imposible o una K poliédrica
Diseños de Calpurnio de algunas de las letras, una D geométrica, una G áurea, una H imposible o una K poliédrica
En la cuenta de Instagram del proyecto 36 Days of Type podéis encontrar los hermosos e interesantes diseños seleccionados cada día, de letras y números. Aunque en esta entrada del Cuaderno de Cultura Científica os mostraré algunos de los diseños de números que fueron seleccionados por la organización. Iremos día a día o, mejor dicho, cifra a cifra.
La parte numérica del proyecto se inició el día 1 de mayo, con el número 0. El primer diseño que he seleccionado es del diseñador brasileño Daniel Escudeiro (aquí podéis ver parte de su trabajo, en la página del diseñador en Behance: Daniel Escudeiro).
 Diseño del número 0 realizado por el diseñador Daniel Escudeiro
Diseño del número 0 realizado por el diseñador Daniel Escudeiro
El siguiente diseño del número 0, que es un delicado diseño hecho a mano, es de la letrista finlandesa Monika Fällman.
 Diseño a mano del número 0 realizado por la finlandesa Monika Fällman
Diseño a mano del número 0 realizado por la finlandesa Monika Fällman
El primer diseño que os muestro del número 1 es un diseño geométrico del artista valenciano Tormius, Adrià Tormo (aquí podéis ver parte de su trabajo, en la página del artista, Tormius).
 Diseño geométrico del número 1 realizado por el valenciano Tormius
Diseño geométrico del número 1 realizado por el valenciano Tormius
El siguiente diseño del número 1 lleva el título Gender Equality 1+1=1 (Igualdad de género, 1+1=1), de la artista francesa Katell (página en Etsy, Quatelle [https://www.etsy.com/fr/shop/QUATELLE]).
 Diseño del número 1, Gender Equality 1+1=1, realizado por la artista francesa Katell
Diseño del número 1, Gender Equality 1+1=1, realizado por la artista francesa Katell
Siguiendo la cuenta creciente de los números, ahora nos toca el número 2. El primer diseño que vamos a mostrar corresponde a la agencia creativa estadounidense Swoon Studios (cuya página web es Swoon Studios).
 Diseño del número 2 de Swoon Studios
Diseño del número 2 de Swoon Studios
El segundo diseño del número 2 es un diseño plumífero de la artista finlandesa Jenni Pasanen (podéis acceder a sus diferentes páginas en esta dirección Jenni Pasanen).
 Diseño del número 2 de la artista finlandesa Jenni Pasanen
Diseño del número 2 de la artista finlandesa Jenni Pasanen
Podéis ver más diseños de este número, y de los demás números, en las diferentes cuentas del proyecto, por ejemplo, en Facebook, de donde estamos seleccionando los diseños, sus imágenes, para esta entrada del Cuaderno de Cultura Científica.
Para el número 3 os traigo un diseño muy festivo, esta creación de la diseñadora gráfica Jessie Noble (podéis ver algunos trabajos de esta artista en la página de Dribbble).
 Diseño del número 3 de la artista Jessie Noble
Diseño del número 3 de la artista Jessie Noble
La siguiente propuesta es de la diseñadora y letrista rusa Olemie (cuya página es Olemie).
 Diseño del número 3 de la artista rusa Olemie
Diseño del número 3 de la artista rusa Olemie
El juego “cuatro en raya” es la idea generadora del interesante diseño seleccionado para el número 4, del artista gráfico y creador de videos estadounidense Dylan Blau (podéis disfrutar de sus trabajos en la página del artista Dylan Blau).
 Diseño del número 4 del artista estadounidense Dylan Blau
Diseño del número 4 del artista estadounidense Dylan Blau
Y la artista gráfica, afincada en Beirut, Nancy Kouta (cuya página web es Nancy Kuota) propuso la siguiente imagen.
 Diseño del número 4 de la artista Nancy Kouta
Diseño del número 4 de la artista Nancy Kouta
Entre los hermosos diseños del número 5, hemos elegido este de la diseñadora colombiana Lagabrie, Gabriela Parra.
 Diseño del número 5 de la artista colombiana Lagabrie, Gabriela Parra
Diseño del número 5 de la artista colombiana Lagabrie, Gabriela Parra
Y otro hermoso diseño de la artista gráfica y letrista chilena Flor Flay (Florencia Study), algunos de cuyos trabajos podéis apreciar en su página web Florencia Study.
 Diseño del número 5 de la artista chilena Flor Flay
Diseño del número 5 de la artista chilena Flor Flay
Seguimos con el número 6. Como para otros números, y letras, hay diseños que son animaciones. Podéis visitar las diferentes cuentas del proyecto 36 Days of Type para ver estos diseños también, algunos son impresionantes. El primer diseño que he seleccionado para el número 6 es de la artista británica Amber Maxwell, que, aunque es una imagen animada, mostramos aquí el inicio del diseño.
 Diseño del número 6 realizado por la artista británica Amber Maxwell
Diseño del número 6 realizado por la artista británica Amber Maxwell
Y la segunda elección para el número 6 es este diseño del artista afincado en Estados Unidos Zsolt M, Zsolt van den Már (aquí tenéis su página en Dribble, Zsolt).
 Diseño del número 6 del artista Zsolt M
Diseño del número 6 del artista Zsolt M
Seguimos avanzando en los números y ya llegamos al número 7 (sobre este número podéis leer la entrada del Cuaderno de Cultura Científica dedicada al mismo: Siete, un número muy popular). El primer diseño que traemos a esta entrada, de entre los seleccionados por el proyecto, es de la artista gráfica y letrista suiza Océane Haenni (cuya página en Behance es Océane Haenni). Es un diseño para las personas amantes de los gatos.
 Diseño del número 7 de la artista suiza Océane Haenni
Diseño del número 7 de la artista suiza Océane Haenni
El segundo diseño del número 7 es de la diseñadora gráfica india Seema Surana (podéis disfrutar de más trabajos suyos en la página de Behance de Seema Surana).
 Diseño del número 7 de la artista india Seema Surana
Diseño del número 7 de la artista india Seema Surana
El diseñador afincado en Berlín, Christian Pietrzok, que en Instagram tiene la cuenta A letter a day donde publica desde 2017 cuando empezó el reto de publicar un nuevo diseño de una letra, o un número, cada día de ese año, nos propone el siguiente diseño para el número 8.
 Diseño del número 8 de Christian Pietrzok
Diseño del número 8 de Christian Pietrzok
El segundo diseño que os traemos del número 8 es del diseñador gráfico danés Aggerhomes (Martin Aggerholm), cuya página web es Aggerhomes.
 Diseño del número 8 del diseñador gráfico suizo Aggerhomes
Diseño del número 8 del diseñador gráfico suizo Aggerhomes
El último número del proyecto con el que finalizaba la octava edición del proyecto 36 Days os Type, fue el número 9 (al que también dediqué una entrada con el título El número nueve en una noche de verano). El diseñador gráfico de Barcelona, Loor Nicolas (del que podéis disfrutar de más trabajos en su página de Behance, Loor Nicolas), propuso un diseño de ficción.
 Diseño del número 9 del diseñador gráfico de Barcelona Loor Nicolas
Diseño del número 9 del diseñador gráfico de Barcelona Loor Nicolas
Y terminamos con una propuesta muy africana de la diseñadora británica Ella Smith, a través de su cuenta Ella Create.
 Diseño del número 9 de la diseñadora gráfica británica Ella Smith
Diseño del número 9 de la diseñadora gráfica británica Ella Smith
Espero que hayáis disfrutado de este pequeño paseo por algunos diseños de los números, de las diez cifras básicas, de nuestro sistema de numeración, del 0 al 9, dentro del proyecto 36 Days of Type. Podéis admirar, como ya hemos comentado, los demás diseños en Instagram. Facebook o Twitter.
Me gustaría terminar con una propuesta personal muy sencilla. Está basada en la hipótesis fantástica sobre el origen de la grafía de los números del astrólogo árabe Aben Ragel (siglo X-XI), que mostré en mi entrada Teorías fantásticas del origen de la grafía de las cifras y en los colores del artista neerlandés Piet Mondrian (1872-1944). El diseño de las diez cifras básicas sería el siguiente.










¿Se os ocurre a vosotras algún otro diseño para los números? Podéis animaros con los vuestros.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo 36 días de tipos (de números) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los números apocalípticos
- Los números que proporcionan alegría
- El secreto de los números que no querían ser simétricos
Gene-informazioa, denon onurarako?
COVID-19 gaixotasunaren pandemian argi ikusi dugu zeinen garrantzitsua den SARS-CoV-2 birusaren aldaeren zainketa. Zainketa hori gauzatzeko, ezinbesteko da birusen genoma sekuentziatzea eta sekuentzia horiek komunitate zientifikoan zabaltzea. Hala, toki bakoitzean zirkulazioan dauden birusaren aldaerak ezagutu daitezke eta kezkagarriak izan daitezkeen aldaeren kontrola areagotu. Baina oro ez da urre.
Gene-informazioa eskuragarri jarri ohi da datu-base publikoetan. Zientzia-artikulu baten baitan gene-informazio berria sortzen denean, zientzia-aldizkariek gene-informazio hori modu publikoan jartzea eskatu ohi dute artikulua argitaratzeko. Hala, zientzia-komunitateak ikuska dezake gene-informazio hori eta berrerabili lan berriak egiteko. SARS-CoV-2 birusaren gene-informazioaren kasuan, zientzia-artikuluak argitaratu baino lehenago eskuragarri jarri dira, pandemiaren ezagutzan arinago sakontzeko. Baina prozedura horrek arazoak izan ditu.
 1. irudia: Gene-informazioa datu-baseetan gordetzen da (Argazkia: ColossusCloud – Pixabay lizentziapean. Iturria: pixabay.com)
1. irudia: Gene-informazioa datu-baseetan gordetzen da (Argazkia: ColossusCloud – Pixabay lizentziapean. Iturria: pixabay.com)COVID-19 gaixotasunean positibo eman duten pertsonen birusak sekuentziatu dira, baina herrialde guztiek ez dute modu berdinean egin. GISAID datu-basea izan da SARS-CoV-2 birusaren sekuentzia horiek partekatzeko biderik erabiliena. Datu-base hori 2008. urtean sortu zen gripearen birusaren sekuentziak bidezkoa den modu batean partekatzeko; eta bermatzeko dagokien aitortza emango zitzaiela sekuentzia horiek sortzen dituzten ikertzaileei eta zentroei. GISAIDeko datuak erabili ahal izateko, izena eman behar da bertan eta hitzeman egiten da datuei bidezko erabilera emango zaiela, GISAIDeko gidalerroak jarraituta. COVID-19aren pandemiari aurre egiteko, GISAID datu-baseak aukera eman zuen SARS-CoV-2 birusaren sekuentzien gordailu izateko eta gene-datu horietan oinarrituta analisiak egiteko.
GISAID datu-basean biltzen diren sekuentziak berebizikoak bilakatu dira COVID-19 birusaren aldaeren zainketa egiteko. Bertan COVID-19 birusaren 1,5 milioi sekuentzia gordetzen dira, baina herrialde guztiek ez dute informazioa modu berean bidali. Ezberdintasun horren oinarria da herrialde bakoitzean ez direla berdinak izan jarritako baliabideak eta pandemiari aurre egiteko hartutako neurriak. Adibidez, sekuentzien %45 Erresuma Batuak bidali ditu eta %7 Danimarkak. Horrez gain, esan behar da herrialde batzuk kasu gutxiago izan dituztenez, sekuentzia gutxiago bidaltzeko aukera izan dutela baina kasuen ehuneko handi bat direla. Adibidez, Australiak izan dituen kasuen %58ren sekuentziak bidali ditu, eta Zeelanda Berriak %48. Desberdintasun hauek zailtzen dute munduko eskualde batzuetan zirkulazioan dauden birusak zeintzuk diren jakitea eta, ondorioz, aldaera berrien zaintza.
 2. irudia: Txertoak garatzeko, birusen gene-informazioa erabiltzen da (Argazkia: whitesession – Pixabay lizentziapean. Iturria: pixabay.com)
2. irudia: Txertoak garatzeko, birusen gene-informazioa erabiltzen da (Argazkia: whitesession – Pixabay lizentziapean. Iturria: pixabay.com)Aipatutako mugak direla eta, gero eta ikertzaile gehiagok esaten dute SARS-CoV-2 birusaren gene-informazioa inolako baldintzarik ez duten datu-baseetan partekatu beharko litzatekeela. Horrela, ahalbidetu egingo litzateke datuen analisi konplexuak egitea eta emaitza baliagarriak arinago lortzea. Bestalde, SARS-CoV-2 birusaren sekuentzien eskuragarritasuna errazteko, 800 ikertzaile inguruk sinatutako gutun batean eskatzen da gene-informazio hori domeinu publikoan jartzea. Ikertzaile horien %99 Europako, AEBko eta Kanadako ikertzaileak dira. Baina, zer iritzi dute hainbeste baliabiderik ez duten herrialdeetako ikertzaileek?
Christian Happi-k –Nigerian kokatutako Genomikarako eta Gaixotasun Infekziosoetarako Afrikako Bikaintasun Zentroko mikrobiologoak– adibide argi bat ematen digu “Imajinatu afrikarrak lan ta lan egiten datu-base bat elikatzeko, zeina erabiltzen den txertoak egiteko edo eguneratzeko, eta gero txertoetara sarbiderik ez izatea. Etsigarria da.” Baliabideak mugatuak izanda eta aitortzarik lortzen ez badute, beren lanak ez die onurarik sortzen. Horregatik, lasaitasuna ematen die GISAID datu-basearen funtzionamenduak. Nnaemeka Ndodo-k –Nigeriako Gaixotasunen Kontrolerako Zentroko bioingeniaritza molekularrerako adituak– eta bere lankideek egun osoan zehar egiten dute lan birusaren sekuentziak lortzeko eta gauez GISAIDera igotzen dituzte. Horrela egunero. Ndodo-ren kezka da sortzen dituzten datuak mugarik gabe eskuragarri jartzen badituzte, baliabide gehiago dituzten ikertzaileek datu horiek erabili ditzaketela eta zientzia-aldizkari garrantzitsuetan analisiak argitaratu edo teknologiak patentatu, datu-biltzaileek inolako onura eta aitortzarik jaso gabe. Nolabait, GISAIDen ereduak bermatu egiten ditu baliabide gutxi dituzten laborategien aitortza eta parte-hartzea, babestu egiten du egin duten lana.
Gene-datuen partekatzeari buruzko kezka aspalditik datorren auzia da. Hego Afrikako IOL agerkarian editorial anonimo batek deskribatzen duen bezala, “zientzia-komunitatea aspalditik blaituta dago mentalitate neokolonial batekin”. Afrikarren kezkei oinarri ematen die 2014 eta 2016 urteen artean Ginean gertatutako Ebolaren agerraldian jazotakoak. Garai hartan, Afrikako ikertzaileek lortu zituzten laginak Gineatik kanpo bidali ziren; eta lagin horiek erabilita argitaratu ziren zientzia-artikuluen eta lortu ziren patente gehienen egileak herrialde aberatsetakoak izan ziren. Bitartean, Gineako laborategiek ez zuten lan horretatik onurarik jaso eta gaur egun ez dute gaitasunik laginak sekuentziatzeko.
 3. irudia: SARS-CoV-2 birusaren aldaeren zaintza beharrezkoa da pandemiari aurre egiteko (Argazkia: OliverKepka – Pixabay lizentziapean. Iturria: pixabay.com)
3. irudia: SARS-CoV-2 birusaren aldaeren zaintza beharrezkoa da pandemiari aurre egiteko (Argazkia: OliverKepka – Pixabay lizentziapean. Iturria: pixabay.com)Auzi garrantzitsua da SARS-CoV-2 birusaren gene-informazioa non gordetzen den. Birusaren aldaeren zaintza eraginkorra izan dadin, beharrezkoa da baliabide mugatuak dituzten herrialdeetako ikertzaileak prest egotea gene-informazioa partekatzeko. Txertaketa-prozesuaren onurak jaso ez dituztenez, gerta liteke birusaren aldaera kezkagarriak herrialde horietan agertzea. Ondorioz, herrialde horietan dauden birusen sekuentziak beharrezkoak izango dira pandemiaren zaintza eraginkor bat egiteko. Horretarako, herrialde horiek baliabideak izatea bezain garrantzitsua da beren lana aitortzea.
Aurreko batean azaldu genuen gizatalde guztiek ez dituztela gene-informazioaren onurak modu berean jaso. Orduan gizakion gene-informazioaz ari ginen, baina argi dago joera orokorra dela, bai edozein gene-informazio eskuratzeko, bai edozein gene-informazio erabiltzeko. Herrialde batzuek onura gehiago lortzen dituzte gene-informaziotik beste batzuek baino eta denon ardura izan beharko luke herrialde guztiek gene-informazioaren onurak modu bidezko batean jasotzeak.
Erreferentzia bibliografikoak:Cyranoski, D. (2021). Alarming COVID variants show vital role of genomic surveillance. Nature, 589, 337-338. DOI: https://doi.org/10.1038/d41586-021-00065-4
Maxmen, A. (2021). Why some researchers oppose unrestricted sharing of coronavirus genome data. Nature, 593, 176-177. DOI: https://doi.org/10.1038/d41586-021-01194-6
Egileaz:Koldo Garcia (@koldotxu) Biodonostia OIIko ikertzailea da. Biologian lizentziatua eta genetikan doktorea da eta Edonola gunean genetika eta genomika jorratzen ditu.
The post Gene-informazioa, denon onurarako? appeared first on Zientzia Kaiera.
Actúa localmente: robots asistentes en cirugía
 Foto: Artur Tumasjan / Unsplash
Foto: Artur Tumasjan / UnsplashLa automatización era el futuro hace 50 años. Lo robotización es un futuro tan próximo que es presente. Y lo que parece una tendencia imparable es la robotización de todos los ámbitos de la actividad humana. Pero no hay que pensar necesariamente en robots completamente autónomos, como los de la película Yo Robot (Alex Proyas, 2004) basada en el libro homónimo de 1950 de Isaac Asimov. La integración de los robots en nuestro día a día será como colaboradores. Un ejemplo ilustrativo es el robot como asistente en intervenciones quirúrgicas muy delicadas.
Pongamos el caso de las intervenciones de columna que se quiere que sean mínimamente invasivas. En términos muy simples, en este tipo de intervenciones hay que saber con precisión donde colocar los tornillos para maximizar su efecto y asegurarse de que no se hace más daño del que se pretende solucionar al tocar la médula espinal.
Ceit y Egile colaboran en el proyecto ELCANO que lo que pretende es, precisamente, desarrollar una solución integrada y robotizada para este tipo de intervenciones. La persona encargada de la cirugía es la que decide y realiza la operación; el robot le ayudará en los cálculos y en evitar que se produzcan daños. Esta ayuda se concreta en tres aspectos, los dos primeros son los que permiten el tercero, que es la actuación del robot:
Planificación virtual de la intervención*
Los hospitales suelen contar con un Sistema de Comunicación y Archivado de Imágenes (PCAS, por sus sigles en inglés). Su función primordial es almacenar imágenes y facilitar la comunicación entre los servicios del hospitale. Un sistema PACS ideal debe atender todo el flujo de imagen, desde la adquisición del examen, hasta el diagnóstico, proceso de informe y monitoreo.
Antes de la intervención*, un programa software planificador (viewIT-spine) extrae información del historial del paciente desde el sistema PACS y reconstruye un modelo virtual del paciente basado en las imágenes de TAC disponibles que permitirá al cirujano hacer una planificación de la intervención, definiendo la posición y orientación de los tornillos que desea introducir en el paciente, desde su despacho. Una vez terminada la planificación, ésta se envia al quirófano.
Sistema de navegación/tracking
Un dispositivo instalado en quirófano es capaz de monitorizar en tiempo real la posición real del paciente de forma que pueda hacerse una correlación de la disposición del paciente real con el modelo virtual construido con el planificador. Para ello un módulo del software viewIT-spine se ejecuta en tiempo real en quirófano.
 Prototipo de laboratorio, basado en un robot de 7 grados de libertad.
Prototipo de laboratorio, basado en un robot de 7 grados de libertad.Asistente colaborativo robotizado (COBOT)
Un COBOT es un sistema robótico capaz de recibir información del planificador. Este robot es capaz de configurar unas restricciones activas de movimiento y trabajar de forma colaborativa con el cirujano (COllaborative roBOT) para facilitar la intervención. A la vez, las restricciones de movimiento limita los movimientos del cirujano para impedir el acceso a las zonas de riesgo.
 Prototipo de quirófano, basado en un robot de 6 grados de libertad
Prototipo de quirófano, basado en un robot de 6 grados de libertad
* Nota para profesionales:
Intervenciones de fusión instrumentada con tornillos transpediculares. El concepto es aplicable a otro tipo de intervenciones, como artrodesis intersomática por vía lateral ALIF o TLIF.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Actúa localmente: robots asistentes en cirugía se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Actúa localmente: robots inteligentes autoadaptativos para la producción industrial
- Actúa localmente: blockchain para la cadena de suministros
- Actúa localmente: electrónica de papel
Ultrasoinuak, entzefaloaren barrualdera begiratzeko
Makako baten gorputz atalen mugimenduak eta begiradaren norabidea aurreikusi daitezke, bere entzefaloaren hainbat eremutako neuronen jarduera zehaztasun espazial eta tenporal handiarekin “ikustea” ahalbidetzen duen teknika nahiko berri baten bidez.
Teknika horren bidez erregistratutako garun jarduera gailu robotikoei edo, oro har, makinei aginduak emateko erabil daiteke, dagokion subjektuak bere kabuz egin ahalko ez lituzkeen gauzak egiteko. Pentsatu, adibidez, elbarritasun baten eraginez besoak mugitu ezin dituen edo, besterik gabe, besorik ez duen pertsona batengan. “Ultrasonika funtzionala” izeneko neuroirudi teknika bat erabiltzen da metodo gisa (edo fUS, ingeleseko functional UltraSound imaging-etik hartua).
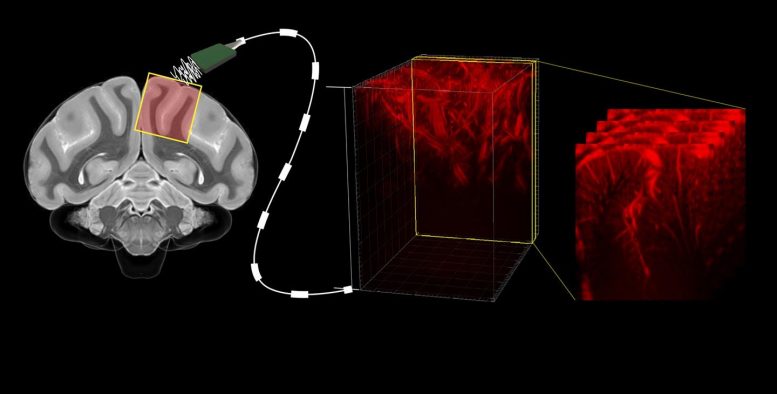 Irudia: Zer gertatzen da zure garunean artikulu hau irakurtzeko orrialdea goitik behera mugitzen ari zarela?
Irudia: Zer gertatzen da zure garunean artikulu hau irakurtzeko orrialdea goitik behera mugitzen ari zarela?Hori da garuna-makina interfazeak helburu dituzten neurozientzialariek jakin nahi dutena: garunaren jarduera irakurri eta interpretatzen duten eta ordenagailu edo makina bati jarraibideak transmititzen dizkioten gailuak garatzeko. (Argazkia: Caltech)
Hau ez da interfaze baten bidez buruko aginduak makina baten ekintza edo mugimendu bihurtzen diren lehenengo aldia. Dagoeneko lortuta zegoen beso robotiko batek garunean elektrodoak ezarrita zituen pertsona paraplegiko baten ahora kopa bat eramatea. Subjektuaren gorputz atalek esku hartu gabe garunak aginduak emateko ahalmena ez da berria, horretarako erabilitako teknika baizik.
Orain arte, entzefaloan neuronen jarduera erregistratzeko zenbait metodo zuzen erabili dira. Elektroentzefalografia da (EEG) zaharrena; garuneko potentzial elektrikoaren aldaketak detektatzen ditu, garezurrean kokatutako elektrodoen bitartez. Ez da inbasiboa, baina bereizmen espazial txikia du. Horren aldaeretako bat elektrokortikografia da (ECoG): neuronen seinale elektrikoetarako irisgarritasun zuzena ematen du; bereizmen tenporal eta espazial handia du. Arazoa da kirurgia eskatzen duela eta arriskuak eragiten dituela, elektrodoak jarri behar direlako, horiek hartzen dituzten ehunak kaltetzen dituztelako eta denborarekin elektrodoak biltzen dituen materiala hondatu egiten delako.
Zeharkako metodoak ere badaude. Erresonantzia magnetiko funtzionala da (FMRi) azken urteetan neuronen jarduera “ikusteko” gehien erabiltzen ari den alternatiba ez inbasiboa. Oxigenoarekin konbinatutako hemoglobinaren maila erlatiboaren aldaketa lokala neurtzen du, maila horrek eremu horretako odol fluxua islatzen duelako eta hori, era berean, neuronen metabolismoaren mende dagoelako. Positroi igorpenezko tomografia (PET) ere ez da inbasiboa; isotopo erradioaktiboak erabiltzen ditu jarduera metabolikoko mailak detektatzeko, adierazle metabolikoen edo odol fluxuaren adierazleen bitartez. Teknika horien arazoa da, batez ere bigarrenarena, ez dutela ez bereizmen espazial ez tenporal handirik eskaintzen eta gailuak ekipo handiak direnez ezin direla erraz lekualdatu; are gutxiago, soinean eraman.
Neuroirudi ultrasoniko funtzionalak, ultrasoinuak erabiliz, odol fluxuaren aldaketak detektatzen ditu, zeinak, adierazi dugun bezala, xede dituen neuronen jarduera metabolikoaren mailaren berri ematen duen. Aurrekoek baino bereizmen tenporal handiagoa du eta bere bereizmen espaziala EEGarenaren eta ECoGarenaren artean dago (FMRi-arenaren antzekoa da). Gainera, gailu eramangarrien bidez erabil daiteke. Desabantaila honako hau da: teknika hori erabiltzeko garunaren zati txiki bat kendu behar dela, entzefaloaren barrura sartzeko “leiho” moduko bat egin behar dela, baina ECoGaren elektrodoen kasuan ez bezala, detektagailua ez da nerbio ehunaren barrura sartzen eta ez ditu berau babesten duten ehun konektiboaren mintzak zeharkatzen ere.
Neuroirudi ultrasonikoko teknikak adibide bikain bat dira; bai desgaitasuna duten pertsonei autonomia funtzionala izateko tresnak emateko bai haien barrura begiratuz entzefaloaren, buruko makinaren, funtzionamenduaren misterioak argitzeko gaur egun dauden teknologia itxaropentsuenen adibide bikaina.
Erreferentzia bibliografikoa:Sumner L. Norman, David Maresca, Vassilios N. Christopoulos, Whitney S. Griggs, Charlie Demene, Mickael Tanter, Mikhail G. Shapiro, Richard A. Andersen (2021). Single-trial decoding of movement intentions using functional ultrasound neuroimaging. Neuron, 109 (9), 1554-1566.e4. DOI: https://doi.org/10.1016/j.neuron.2021.03.003
Egileaz:Juan Ignacio Pérez Iglesias (@Uhandrea) UPV/EHUko Fisiologiako katedraduna da eta Kultura Zientifikoko Katedraren arduraduna.
The post Ultrasoinuak, entzefaloaren barrualdera begiratzeko appeared first on Zientzia Kaiera.
Virus con ADN «extraterrestre»
María Teresa Tejedor Junco
 Shutterstock / Zita
Shutterstock / Zita
El lenguaje de la vida se escribe con un código de cuatro letras: A, G, C y T. Son las abreviaturas de adenina, guanina, citosina y timina, las bases nitrogenadas que se encuentran en la mayoría de los genomas. En la doble hélice de ADN se aparean las bases, G con C y A con T.
El ADN almacena la información, que posteriormente es transcrita a ARN mensajero y este se traduce a proteínas. Este esquema de flujo de la información genética fue denominado por Crick como “dogma central de la biología molecular”.
La biología no es una ciencia exacta
Como el propio Crick reconocía, emplear el término “dogma” no fue una buena idea. Un dogma es una idea que no se puede cuestionar. Pero en biología parece que siempre se puede encontrar una excepción a las reglas generales: desde mamíferos que ponen huevos a células eucariotas sin mitocondrias.
En el caso del “dogma central de la biología molecular”, poco a poco fueron describiéndose excepciones. Casi todas ellas en microorganismos.
Una de las principales fue la descripción de los Retrovirus, cuyo genoma no es ADN sino ARN. Poseen una enzima, la transcriptasa inversa, que copia ese ARN a ADN, cambiando así el sentido del flujo de información genética. Muchos virus tienen genomas de ARN, lo que añadiría una nueva letra (U = uracilo) al alfabeto genético, pero siempre son cuatro, ya que U reemplaza a T.
También se describen los viroides y los priones. Los primeros, son simples moléculas de ARN. Los priones, carecen de ácidos nucleicos y son proteínas capaces de replicarse.
Nuevas letras en el alfabeto genético
La biología sintética se enfoca a la síntesis de nuevas biomoléculas y a la ingeniería de sistemas biológicos para dotarlos de funciones nuevas que no se encuentran en la Naturaleza. Uno de los campos de investigación es la expansión del código genético, a fin de obtener proteínas con características novedosas.
Incorporar nuevas bases al ADN no es una tarea sencilla. La estructura de la doble hélice no debe alterarse, y las enzimas que desarrollan diversas tareas deben reconocer a las nuevas moléculas, a fin de que el flujo de información, desde genes hasta las proteínas, siga funcionando.
Un equipo de investigadores consiguió crear un ADN que utiliza ocho bases diferentes, en vez de cuatro. Inicialmente no se podía considerar un nuevo alfabeto genético, ya que no se traducía a nuevos aminoácidos. Pero se transcribe a un ARN que es capaz de reconocer y “pegarse” a las células cancerígenas, lo que se podría aplicar a nuevas técnicas de diagnóstico.
En 1977, científicos rusos describieron un bacteriófago (virus que infecta a las bacterias) que, en lugar de adenina, tenía en todos los casos 2-aminoadenina (abreviada como Z). Ahora bien, a diferencia del ADN sintético, las bases siguen siendo cuatro. Parece que la naturaleza se había adelantado a las ideas de los investigadores, creando virus con un “alfabeto” genético alternativo.
En ese ADN, Z se une a T por 3 enlaces de puente de hidrógeno, en vez de por los dos que forman la unión entre T y A. El ADN resultante es mas estable frente al calor y a otros factores ambientales.
Z, la 2-aminoadenina, es un compuesto que se encuentra en la naturaleza, proveniente de restos de meteoritos. Nunca se había descrito como parte de un organismo. Debido a eso, empezaron a llamar a este ADN, “ADN extraterrestre”.
Varios grupos de investigadores comenzaron a analizar bases de datos, buscando otros fagos que pudieran tener las mismas características, y encontraron bastantes casos.
Durante décadas nadie había conseguido averiguar cómo sucedía esto y la importancia que podría tener.
¿Cómo se sintetiza ese ADN diferente, si Z no existe en las bacterias?
Tres trabajos publicados (este, este y este) en 2021 en la revista Science y en Nature Communications explican este proceso.
Podemos leer un estupendo artículo de la doctora Gemma Marfany y ver el vídeo explicativo del doctor Lluis Montoliu, que resumen los aspectos más importantes relacionados con este tema.
Lluís Montoliu explica el nuevo nucleótido Z encontrado en el ADN de algunos virus de bacterias.Estos fagos codifican en su genoma enzimas que retiran la adenina del ADN y la sustituyen por Z. También codifican enzimas que pueden sintetizar Z a partir de precursores existentes en las bacterias.
Como indica la doctora Zhao, investigadora principal de uno de los grupos que trabajan en este tema, todavía no está del todo claro como se produce la síntesis del ADN con esta nueva base en las bacterias, ni como interactúan todas las enzimas implicadas en la replicación y transcripción del ADN, con esta nueva molécula.
Beneficios para los virus que usan Z
Los fagos son virus que infectan bacterias. Las bacterias poseen mecanismos que les permiten luchar contra estas infecciones, ya que pueden reconocer el ADN del fago y degradarlo.
Pero las defensas de las bacterias no pueden reconocer a este nuevo ADN, por lo que el fago puede escapar de ellas. Esto también podría suponer una ventaja en los tratamientos por fagoterapia, ya que la bacteria causante de la infección no podría destruir los fagos usados como tratamiento.
Al ser un ADN más estable, permite la persistencia del virus en condiciones adversas, ampliando el rango de hospedadores que puede colonizar.
Aplicaciones de este nuevo ADN
Actualmente se investigan numerosas aplicaciones de biología sintética para las que este nuevo ADN sería muy útil, dada su mayor estabilidad.
Por ejemplo, contribuiría a mejorar el almacenamiento de datos en ADN. También sería aplicable a las técnicas que utilizan papiroflexia de ADN para la administración dirigida de medicamentos.
Por ahora no se han descubierto organismos celulares que posean Z en su ADN, pero se trabaja en dicha posibilidad, intentando incorporarla en E. coli y que la célula siga siendo funcional.
¿Qué implicaciones tiene?
El descubrimiento de estos virus con un código genético diferente no solo tiene aplicaciones desde el punto de vista de la biología sintética. Nos plantea también numerosos interrogantes sobre el origen de la vida en la Tierra y sobre la posibilidad de vida en otros planetas.
Es discutible si los fagos que contienen Z en su ADN son nuevas formas de vida, ya que incluso se discute si los virus son seres vivos o no. Pero está claro que esta nueva codificación genética, que permite la síntesis de proteínas funcionales, influirá en la búsqueda de vida en otros planetas. No solo habrá que buscar este nuevo compuesto sino que también, dado que este nuevo ADN tolera condiciones ambientales más extremas que las convencionales, se amplían las opciones de búsqueda.![]()
Sobre la autora: María Teresa Tejedor Junco es profesora titular de microbiología en la Universidad de Las Palmas de Gran Canaria
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Virus con ADN «extraterrestre» se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Puede el virus SARS-CoV-2 integrarse en nuestro genoma?
- Quince virus que han cambiado la historia de la Humanidad
- Virus, selección natural y vacunas

