El sistema de la difusión social de la ciencia: Medios (II)

Xurxo Mariño durante la representación del discurshow Código Sapiens en Naukas 16. Imagen tuiteada por @Perestupinya durante la misma.
Medios presenciales
Exposiciones y presentaciones especiales
Diferentes instituciones, universitarias principalmente (pero no exclusivamente), suelen organizar presentaciones públicas de sus actividades fuera de los entornos que les son propios. Un ejemplo típico de estas actividades es la Semana de la ciencia que organizan diferentes universidades y otras entidades, en cuyo marco se presenta la actividad investigadora que desarrollan en sus departamentos.
Se trata de actividades dirigidas también a públicos amplios. Normalmente muchos centros escolares incluyen visitas a estas presentaciones dentro de su programación académica fuera de las aulas.
Conferencias o similares
Las conferencias también forman parte de las actividades cuyos destinatarios son personas interesadas en temas científicos. Suelen estar organizadas por organismos públicos o asociaciones de particulares. Dado que las conferencias pueden ser grabadas, se prestan a su difusión por internet, tanto en directo como a través de la inserción en bitácoras científicas. Esa posibilidad amplía enormemente el alcance de un tipo de actividad que, de otra forma, tendría un impacto muy limitado.
Últimamente se están llevando conferencias de ciencia a bares. Pint of Science es un movimiento internacional que promueve y organiza conferencias de ciencia en bares y tabernas durante una semana concreta del año y lo hace, además, en un buen número de países (en todos ellos se celebran las conferencias en los mismos días).
En los últimos años se han producido cambios importantes en el modelo tradicional de conferencias. Por una parte, se han empezado a impartir conferencias de duración más corta (de hasta 10 min). Y por la otra, de la conferencia magistral se transita en numerosas ocasiones hacia el monólogo, a menudo en clave de humor.
Visitas guiadas y jornadas de puertas abiertas
De la misma forma que algunas instituciones realizan exposiciones o ferias extramuros, también las hay que convocan jornadas de puertas abiertas y organizan visitas guiadas a sus propias instalaciones. Se trata de que las personas interesadas, en numerosos casos estudiantes, tengan la oportunidad de conocer in situ en qué consiste la actividad que se desarrolla en las instituciones que se visitan.
Cada vez son más los centros tecnológicos y de investigación que organizan este tipo de actividades.
Representaciones escénicas
Las representaciones teatrales o los monólogos de contenido científico son quizás la última incorporación al universo de actividades de divulgación científica. Los monólogos (no siempre de humor) empezaron a ofrecerse a partir del concurso FameLab, otro fenómeno de carácter internacional que impulso en España la FECyT. Después, un grupo de participantes en el certamen se organizó y constituyó en grupo estable –Big Van, científicos sobre ruedas-, que viene actuando desde entonces por toda la geografía española, y muy especialmente en representaciones para público infantil y adolescente.
Medios participativos
Los últimos años han sido pródigos en novedades en formas de expresión en comunicación y divulgación científica. Y quizás la principal novedad ha consistido en la puesta en marcha de iniciativas en las que el público se convierte en protagonista de la difusión, dejando de ser receptor pasivo para pasar a ser emisor o agente. En el lenguaje que se ha generalizado en los últimos años, se trataría de que los receptores se apropien del hecho científico, lo hagan suyo. Se trata de un planteamiento que pretende superar el “modelo del déficit”. Simplificando, el modelo del déficit presupone que la ciudadanía presenta déficits de conocimiento científico y que esos déficits pueden subsanarse gracias a la actividad de transmisión que realiza un selecto conjunto de expertos. El modelo de la apropiación no se basa en esa idea, sino en la de que la ciudadanía ha de ser protagonista en la adquisición de ese conocimiento (ha de apropiarse del mismo), porque de esa forma dicha adquisición será más efectiva y le ayudará mejor a disponer de criterio propio.
Certámenes
Los certámenes o concursos empezaron a celebrarse, como se ha señalado en el párrafo anterior, con la intención de que el conocimiento científico se difundiese haciendo que los receptores tuvieran un papel más activo en el proceso, que no se limitasen a ser meros receptores. La primera, o una de las primeras iniciativas de esta naturaleza fue el concurso FameLab de monólogos científicos. Se trata de un concurso de carácter internacional en el que investigadores en activo cuentan una historia de contenido científico mediante un monólogo (humorístico o no) en un tiempo breve. Han de hacerlo, además, en un teatro y ante los espectadores.
Otras modalidades de certámenes tienen como destinatario principal al alumnado de enseñanza secundaria obligatoria y bachillerato, y suelen incorporarse en las actividades complementarias de los centros que se prestan a participar o que facilitan la participación de sus estudiantes. Merecen ser nombrados aquí LocosxCiencia (aunque en su próxima edición cambiará, previsiblemente, de nombre), que es muy similar a FameLab, pero sus concursantes son estudiantes de 4º de la ESO. Y también CienciaClip, el concurso de youtubers de ciencia en el que pueden participar estudiantes de secundaria obligatoria y de bachillerato, y que tuvo en 2016 su primera edición.
Ciencia ciudadana
Aunque, en rigor, no se trate de un medio de difusión científica, lo que se conoce como ciencia ciudadana tiene un indudable y muy efectivo componente de difusión social de la ciencia. Por esa razón se ha incluido aquí.
Se entiende por ciencia ciudadana a la investigación científica llevada a cabo por un amplio grupo de personas, incluyéndose profesionales científicos, así como público en general. Formalmente, la ciencia ciudadana ha sido definida como “la recopilación y análisis sistemático de datos, el desarrollo de la tecnología, las pruebas relativas a fenómenos naturales, y la difusión de estas actividades sobre una base principalmente vocacional”.
Sobre ciencia ciudadana pueden consultarse estos textos de Pilar Perla y de Ana Ribera. Y también se puede visitar la web Ciencia Ciudadana. Uno de los proyectos de esta modalidad que más alcance han tenido en España ha sido Mosquito Alert. Y el más reciente del que hemos tenido conocimiento, Small World Initiative.
————————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El sistema de la difusión social de la ciencia: Medios (II) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El sistema de la difusión social de la ciencia: Motivaciones y agentes
- El sistema de la difusión social de la ciencia: Introducción
- El sistema de la difusión social de la ciencia: Receptores y contenidos
#Naukas16 De profesión, futurólogo

Pablo Rodríguez, futurólogo profesional, demuestra, más allá de toda duda razonable, que el futuro puede predecirse (bastante).
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo #Naukas16 De profesión, futurólogo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #Naukas16 Conviviendo con robots
- #Naukas16 ¿Que te chupe la qué?
- #Naukas16 Alucinaciones lingüísticas: los engaños de tu lengua materna
Saliva, bacterias y oxitocina: ¿por qué nos gusta tanto besarnos?

Imagina que estás en un bar con tus amigos y a lo lejos ves a una persona, elija cada uno hombre o mujer según sus gustos, que te resulta atractiva. Intercambiáis miraditas y tras un rato el sujeto de tu interés se acerca a ti, escupe un poco de saliva en su mano y te ofrece probarla. Asqueroso, ¿verdad? Enormemente, responderá la mayoría.
Pues no se pongan tan exquisitos porque algo así es lo que hacemos al besarnos. Según un artículo publicado en el American Journal of Medicine, durante un beso (uno bien dado, se entiende) una pareja intercambia de media 0,9 mililitros de agua, 0,7 miligramos de proteína y 0,71 mg de diferentes grasas entre otras sustancias.
También cambian de huésped entre 10 y 1.000 millones de bacterias de casi 300 especies distintas. El 95% de estos organismos no son una amenaza para la salud de cualquier persona con un sistema inmunológico que funcione correctamente, pero algunos de ellos sí pueden serlo, incluyendo virus que afectan al sistema respiratorio superior o herpes, entre otros.
Es decir, que besarse no solo es objetivamente algo un poco asqueroso, sino que también supone cierto riesgo para la salud. Y sin embargo nos encanta, ¿por qué? Algún beneficio debemos obtener de ello, y la ciencia lleva décadas intentando aprender más sobre los besos para averiguar qué es. El estudio científico de los besos recibe el nombre de filematología, comenzó en el siglo XIX y, además de las cantidades de saliva, compuestos orgánico y bacterias, estas son las preguntas que ha conseguido responder hasta ahora.

¿Los besos son instintivos o aprendidos?
¿Besamos porque nos sale de dentro o porque lo hemos aprendido de fuera? Pues empezamos con una pregunta sin respuesta hasta el momento, porque, por un lado, según un estudio menos de la mitad de las culturas del mundo practican los besos románticos según los entendemos en la cultura occidental, lo cual querría decir que es una cuestión cultural y social; mientras que, por otro, comportamientos parecidos a los besos se han observado en otros primates, que los usan como método para solucionar un conflicto y hacer las paces. Ya saben, hacer el amor y no la guerra.
¿De dónde surgieron los besos?
Aunque no todas las culturas se besen, prácticamente en todas hay algún comportamiento parecido que involucre el acercamiento de las caras hasta entrar en contacto directo y muchas veces prolongado, con significados relacionados con la cercanía, la intimidad, la protección o el cariño. ¿Cuál es el origen de estos comportamientos?
Una de las hipótesis más comunes es que se trata de una derivación de la costumbre de pasar comida a medio masticar de la boca de la madre a la de sus hijos pequeños, cuando están dejando la lactancia pero aun no tienen los dientes para masticar. En algunas especies se observa el mismo comportamiento de los machos hacia las hembras como parte de los ritos de cortejo.
Nada de esto explica por qué nos besamos
Ya llegamos a eso. La explicación más sencilla y sincera a eso sería que nos encanta.

No es una explicación muy científica
Aquí va la versión científica: nuestros labios están dotados de muchísimas terminaciones nerviosas, y cuando besamos a alguien las activamos, lo cual desencadena una serie de reacciones en el cerebro, que crea un cóctel de sustancias que nos hace sentirnos bien y quedarnos con ganas de más. Esas sustancias son las siguientes:
– Dopamina: estimula las mismas zonas del cerebro que la heroína y la cocaína, y como resultado nos deja un sentimiento de euforia y de adicción.
– Oxitocina: favorece sentimientos de afecto y apego. Es la misma hormona que se segrega durante el parto y la lactancia.
-Serotonina: los niveles de esta hormona presentes en el cerebro al besarse se parece a los que presentan las personas que padecen un trastorno obsesivo compulsivo.
Resultado de esta combinación es esa sensación de euforia, afecto y adicción que deja un beso.

Entonces… ¿besarse sirve para algo?
Puesto que habitualmente nuestro cuerpo nos recompensa con buenas sensaciones por aquellos comportamientos de los que saca algún beneficio (el alivio de un estornudo llega tras haberse librado de miles de microbios, por ejemplo), es lógico pensar que el subidón de hormonas con el que nos premia al besarnos responde a alguna utilidad que tienen para nosotros los besos.
Se trata de una cuestión aun por terminar de aclarar, Rafael Wlodarski, investigador de la Universidad de Oxfrord, explicaba en este artículo para la revista del Smithsonian, que los besos son una forma de evaluar a un posible compañero de reproducción. Al fin y al cabo, la saliva está llena de hormonas y otros elementos químicos que sirven para determinar, de forma inconsciente, lo apropiado de otro individuo para seguir adelante con los comportamientos sexuales.
Una vez establecida una pareja, los besos han demostrado tener un efecto relajante: según un estudio, están relacionados con el aumento de la sensación de satisfacción en una relación, más que las relaciones sexuales, además de disminuir el estrés y los niveles de colesterol.
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista en El Confidencial
El artículo Saliva, bacterias y oxitocina: ¿por qué nos gusta tanto besarnos? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Mientras tanto, en Crimea…
- ¿Dónde van las bacterias marinas en invierno?
- Bacterias emisoras de rayos X
El sistema de la difusión social de la ciencia: Medios (I)

En esta primera parte del capítulo dedicado a presentar los medios de difusión, se tratará de los medios no presenciales. En la segunda parte se abordarán los medios presenciales, así como los que implican la participación del público.
Productos radiofónicos
Englobamos bajo este epígrafe todos los medios que transmiten contenidos de audio y muy en particular, programas de radio o podcasts [ejemplo].
Los medios audiovisuales tradicionales siguen siendo una vía efectiva de transmisión de información y conocimiento. Y, sobre todo los medios de titularidad pública, incluyen programas específicos o secciones de ciencia en programas generalistas. La radio es una herramienta excelente para llegar a numerosas personas, y hacerlo, además, en las más variadas circunstancias (se puede escuchar radio mientras se conduce o se cocina), lo que le da un gran alcance al medio. Por otro lado y por comparación con la televisión, los horarios de emisión de contenidos científicos son buenos o aceptables.
Tanto la radio como la televisión disponen de sus canales en internet, de manera que se puede acceder a los contenidos de esos medios a través de sus canales “a la carta”. Una variante de la radio propia de internet es el podcast, programa de audio de extensión variable que se publica y emite a través de la web [ejemplo, ejemplo]. La gran ventaja de disponer en la red de programas de radio o audios de emisoras propias de internet es que permite salvar las limitaciones que establece el horario de emisión en el formato tradicional, de manera que las personas que, por lo que sea, no se encuentran en condiciones de escuchar o ver un programa en el momento de su emisión, pueden acceder al mismo en cualquier otro momento.
Materiales televisivos y videográficos en general
Lo señalado en relación con la potencia de la radio sirve igualmente, solo que en mayor medida aún, para la televisión. La televisión es una herramienta valiosísima para llegar a un gran volumen de personas, pues es el medio de mayor consumo; no obstante, los canales de televisión más importantes incluyen muy pocos contenidos científicos en su programación o en sus informativos. Y cuando hay programas de contenido científico suelen ocupar franjas horarias de escasa audiencia. [Algunas consideraciones al respecto, aquí y aquí.]
Al igual que la radio, las cadenas de televisión disponen de sus sitios en internet, de manera que se puede acceder a los contenidos de esos medios a través de sus canales “a la carta”. También en este caso quienes, por lo que sea, no se encuentran en condiciones de ver un programa en el momento de su emisión, pueden acceder al mismo en cualquier otro momento.
Tradicionalmente ha habido una importante oferta de productos audiovisuales de contenido científico en formato de video (cinta magnética, DVD, blue ray, etc.). Se trata de productos realizados para la televisión y que, posteriormente, se han distribuido en esos soportes, normalmente por haber sido de gran aceptación por parte del público. El ejemplo más sobresaliente es la serie Cosmos de Carl Sagan, pero hay un buen ramillete de ejemplos.
En la actualidad, esos formatos han dado paso a los canales en internet, sobre todo YouTube. Dichos canales son cada vez más utilizados para acceder a todo tipo de contenidos, especialmente por jóvenes y adolescentes.
A diferencia de la radio y la televisión, el consumo de los vídeos, tanto en soporte material como en la web, no tiene el carácter universal y pasivo de aquéllos. Quienes recurren a los vídeos como forma de acceder a contenidos científicos lo hacen de forma activa; se trata, por ello, de medios utilizados principalmente por personas interesadas en los contenidos.
Prensa generalista
Hay prensa generalista que mantiene secciones especiales dedicadas a publicar contenidos científico-tecnológicos. Pero es la excepción y suele tratarse de grandes medios [ejemplo]. No obstante, prácticamente todos ellos suelen incluir en su oferta informativa noticias de ciencia y tecnología.
La prensa llega a menor número de personas que los medios audiovisuales, pero tiene, como los anteriores, un público muy amplio.
Lo anterior vale, especialmente, para las ediciones en papel de prensa diaria. No obstante, todos los medios mantienen una edición en internet y en ésta no es raro encontrar una mayor frecuencia de informaciones de carácter científico. Y por otro lado, existen medios exclusivamente digitales y algunos de ellos cuentan con una importante sección dedicada a tratar temas científicos [ejemplo].
Publicaciones especializadas
Las publicaciones especializadas tradicionales son las revistas de divulgación científica [ejemplo]. Pero ahora los medios digitales han adquirido una gran importancia. La edición de un medio digital (una bitácora o blog) está al alcance de cualquiera. Es por eso por lo que ha surgido una potente blogosfera que protagoniza en gran medida la divulgación científica en internet. Dada la facilidad con que se puede editar un blog, la blogosfera es un entorno muy cambiante; algunos tienen una vida muy corta, pero en ese panorama hay medios que se han consolidado como verdaderas referencias. CienciaSfera recoge todos los blogs publicados en español que acreditan un buen nivel científico y cuyos autores han solicitado su incorporación al agregador.
Un rasgo interesante de las publicaciones digitales que resulta especialmente fructífero en divulgación científica es la posibilidad de embeber grabaciones visuales de conferencias, documentales o animaciones, y también de podcasts. Se convierten así en verdaderas herramientas multimedia de comunicación.
Como ocurre con los vídeos, los blogs, a pesar de la facilidad para acceder a ellos, son utilizados, sobre todo, por personas interesadas en la ciencia, aunque también cumplen un papel de importancia creciente en entornos formativos.
En este apartado merecen mención especial las agencias de noticias. De la misma forma que hay agencias de información general, también las hay que se dedican de forma exclusiva a informar acerca de temas científicos y tecnológicos [ejemplo].
Libros
Los libros de contenido científico son, en realidad, publicaciones especializadas. Pero se les ha dedicado un apartado diferenciado aquí porque, junto con las exposiciones (en museos o de carácter especial), son los únicos vehículos de comunicación que no se benefician de internet para su consumo directo.
Como en el caso de las demás publicaciones especializadas, el público de los libros son personas interesadas en su contenido.
Redes sociales
Se recogen en apartado independiente las redes sociales porque así como el resto de medios de internet tienen su modalidad en soporte material, las redes sociales constituyen un medio genuinamente virtual. Salvo las relaciones interpersonales “tradicionales”, estas redes carecen de formato material. Las redes sociales tienen un alto poder de viralización, lo que las convierte en vehículos de transmisión de información de gran potencialidad. Además, lo hacen con carácter instantáneo o muy rápido. Pero pueden, por lo mismo, tener efectos relativamente efímeros.
El principal uso que se les da como transmisoras de contenidos es el de compartir enlaces de páginas web. Y son, por ello, complementos ideales de los medios digitales. Para quien estén interesados, Lydia Gil ofrece, en su blog, información muy interesante, con estudios cuantitativos incluidos, acerca del uso de las redes sociales de internet como medios para difundir ciencia.
Por su interés y novedad, merece la pena recoger aquí el uso que han hecho de tuiter un grupo de microbiólogos españoles para impartir un curso sobre microbiología. Su principal promotor, Nacho López Goñi, ha relatado y analizado la experiencia aquí.
————————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El sistema de la difusión social de la ciencia: Medios (I) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El sistema de la difusión social de la ciencia: Receptores y contenidos
- El sistema de la difusión social de la ciencia: Introducción
- El sistema de la difusión social de la ciencia: Motivaciones y agentes
Los meteoritos ya no son lo que eran desde hace 466 millones de años

Impresión artística del meteorito que provocó la extinción de los dinosaurios mayores.
La Tierra de formó hace unos 4.500 millones de años, y la vida en su forma más elemental apareció sobre ella unos 500 millones de años después. La vida pluricelular era una realidad hace 2.000 millones de años y la mayor parte de las ramas del árbol de la vida de los animales surgió hace 541 millones de años, en lo que se llamó la explosión cámbrica.
El resto es historia. ¿O no? Parece ser que no: los meteoritos recientemente estudiados por un equipo internacional de investigadores nos dicen que pasó algo muy importante en el Sistema Solar poco después (en términos geológicos) de la explosión cámbrica. La cuestión es que no sabemos el qué.
Los meteoritos son trozos de roca que caen a la Tierra desde el espacio exterior. Se forman a partir de los restos de las colisiones entre asteroides, lunas e incluso planetas. Hay de muchos tipos diferentes que reflejan la composición de los cuerpos a partir de los que se formaron. Estudiando los distintos meteoritos que han llegado a la Tierra los científicos pueden comprender mejor cómo evolucionaron los materiales con los que se formó el Sistema Solar.

La Luna durante el bombardeo intenso tardío (arriba) y en la actualidad
En la narración del origen e historia de la Tierra los meteoritos aparecen dos veces de forma estelar. La primera es poco antes y quizás a la vez de cuando surge la vida, con el bombardeo intenso tardío y, aún sabiendo que siguieron cayendo, no vuelven a ser relevantes hasta hace 65 millones de años cuando un meteorito acaba con los grandes dinosaurios. Aparte de esto según narran las historias, en el Sistema Solar no debió ocurrir nada importante, aparte de un meteorito aquí y otro allá y la evolución de los propios planetas.
Sin embargo, un grupo de investigadores, encabezados por Phillipp Heck del Museo Field de Historia Natural (Chicago, EE.UU.), ha analizado 43 micrometeoritos llegados a la Tierra hace unos 470 millones de años y han encontrado algo sorprendente: más de la mitad de los granos minerales encontrados corresponden a composiciones completamente desconocidas o extremadamente raras en los meteoritos que llegan hoy día a la Tierra. Por ejemplo, el 34 % de los meteoritos analizados pertenecen a lo que se conoce como acondritas primitivas: hoy día solo el 0,45 % de los meteoritos que caen a la Tierra son de este tipo.

Esto implica que algo extraordinario que no sabemos qué es, aunque se puede sospechar que fue una colisión gigantesca, ocurrió en el Sistema Solar, alrededor de este periodo; algo tan grande que cambió la composición de los asteroides.
Un descubrimiento así, implica que hay que revisar la historia del Sistema Solar tal y como la conocemos. De entrada hay que incluir posiblemente la colisión de algo con un bastante grande asteroide hace 466 millones de años que es la que envia los trozos de roca que caen como meteoritos en los planetas y lunas del Sistema Solar interior desde entonces. También habrá que tener en cuenta que los meteoritos llegados y recogidos en los últimos 300 años no son representativos de los que llegaron a la Tierra en periodos anteriores.
Referencia:
Heck et al (2017) Rare meteorites common in the Ordovician period Nature Astronomy doi: 10.1038/s41550-016-0035
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Los meteoritos ya no son lo que eran desde hace 466 millones de años se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los misterios que rodean al máximo térmico de hace 56 millones de años
- Constantes durante al menos 12 mil millones de años
- Relaciones a distancia desde hace 16.000 años
La ratonera, el juego de Cayley
El matemático inglés Arthur Cayley (1821-1895) fue uno de los matemáticos teóricos más importantes de la Inglaterra del siglo XIX. Escribió 967 artículos, recogidos en los 13 volúmenes de la publicación The Collected Mathematical Papers of Arthur Cayley (obra de acceso libre en la página Internet Archive), y un libro sobre funciones elípticas, An Elementary Treatise on Elliptic functions (1876).
Trabajó en todas las ramas de la matemática pura, e incluso en cuestiones de matemática aplicada. Su nombre está asociado a muchos conceptos y resultados matemáticos, desde la superficie de Cayley, la métrica de Cayley-Klein, el grafo de Cayley o la construcción de Cayley Dickson, hasta el teorema de Cayley-Hamilton en álgebra lineal, el teorema de Cayley en teoría de grupos o la fórmula de Cayley de teoría de grafos.

Retrato de Arthur Cayley realizado por el pintor William Henry Longmaid (1835–1919) en 1884
En 1857, el matemático inglés, que había sido Senior Wrangler de Cambridge en 1842, se inventó un juego de cartas relacionado con las permutaciones al que llamó la ratonera y que publicó en una pequeña nota titulada Un problema sobre permutaciones, en la revista Quarterly Journal of Pure and Applied Mathematics (vol. 1, página 79).
Para este juego se necesitan n cartas numeradas del 1 a n. Por ejemplo 13 cartas, como menciona Cayley en su nota, que pueden ser las cartas de cada palo en la baraja francesa que se utiliza para jugar al póker. Para empezar se barajan bien las n cartas, lo cual forma una permutación de las cartas, o lo que es lo mismo, del conjunto de los n números, {1, 2, …, n}.
Se coge el mazo de las n cartas barajadas, con los números hacia abajo, y se empiezan a coger las cartas, una a una, por la parte de arriba, a la vez que se va contando. Primera carta “1”, segunda carta “2”, tercera carta “3”, etcétera. Si el número de la carta que se coge coincide con el número que se está contando se retira dicha carta y se empieza a contar de nuevo desde “1” con la siguiente carta de arriba. En caso contrario, se coloca la carta en la parte de abajo del mazo y se continua contando. Se gana en la ratonera si se terminan retirando todas las cartas, pero si se llega a contar hasta n + 1 (14 en el caso de 13 cartas) se habrá perdido.
Cayley lo explica de una forma un poco distinta. Una vez barajadas las cartas, estas son colocadas, según su versión original, boca arriba formando un círculo, pero el procedimiento es el mismo.

Imagen de la nota “Un problema sobre permutaciones” publicada por Arthur Cayley en el primer volumen de la revista “Quarterly Journal of Pure and Applied Mathematics”
Veamos un par de ejemplos con tan solo 5 cartas, como se muestra en la imagen.

Dos permutaciones iniciales de las 5 cartas del juego la ratonera con 5 cartas, 4, 2, 5, 3, 1 y 4, 2, 3, 5, 1. En la imagen se han utilizado cartas del proyecto artístico colectivo Playing Arts, pertenecientes a los artistas Peter Olschinsky, Mattias Adolfsson, Ann Chua, Osacar Ramos, Studio Blup, Foreal, Kate Ohara, David McLeod, Bram Vanhaeren y Omaraquil
Con la primera posición inicial de las cartas, 4, 2, 5, 3, 1, se descarta primero la carta 2, después la carta 4 y finalmente no se puede descartar ninguna carta más. Mientras que con la posición inicial 4, 2, 3, 5, 1, se van descartando las cartas 2, 4, 5, 1 y finalmente la carta 3, con lo que se gana en el juego.
Los problemas que interesaban a Cayley en relación a este juego eran conocer para cuántas de las permutaciones de los n números, es decir, posiciones iniciales de las cartas barajadas, se puede ganar en la ratonera, y en general, para cuántas permutaciones quedarán solamente un número k de cartas. Por ejemplo, para n = 4, las permutaciones {1, 2, 4, 3} y {2, 1, 3, 4} son ganadoras, mientras que {1, 2, 3, 4} y {3, 2, 1, 4} no, en la primera solo se elimina la carta 1 y en la segunda las cartas 2 y 1.
Además, en ese primer artículo Cayley muestra las permutaciones para las que las cartas se van retirando en el orden creciente natural, hasta n = 8, que son:
{1}, {1, 2}, {1, 3, 2}, {1, 4, 2, 3}, {1, 3, 2, 5, 4}, {1, 4, 2, 5, 6, 3},
{1, 5, 2, 7, 4, 3, 6} y {1, 6, 2, 4, 5, 3, 7, 8}.

Cartas de la baraja francesa diseñadas con el estilo steampunk, por la compañía Bicycle de EE.UU.
Arthur Cayley, en su siguiente nota sobre la cuestión, Sobre el juego de la ratonera (Quarterly Journal of Pure and Applied Mathematics, 1878) insiste en el interés matemático de estudiar el comportamiento del juego en función de las permutaciones de las n cartas, es decir, de los n números. Como ejemplo, analiza todas las posibles situaciones de la ratonera para 4 cartas, aunque comete algunos errores de cálculo.
Para las 24 permutaciones de las 4 cartas (recordemos que el número de permutaciones de un conjunto con n elementos, por ejemplo, {1, 2, 3, …, n} es el factorial de n, n! = n ∙ (n – 1) ∙ (n – 2) ∙∙∙ 2 ∙ 1, como se vio, por ejemplo, en el artículo Cuadrados latinos, matemáticas y arte abstracto) se dan las siguientes posibilidades.
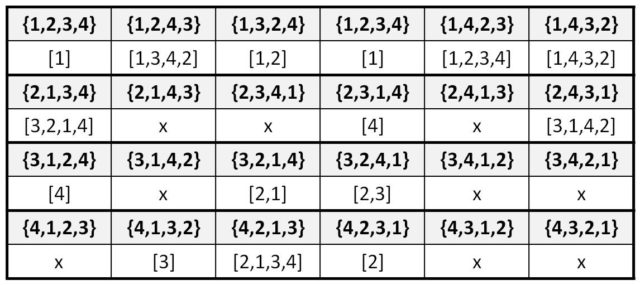
Resultados del juego de la ratonera para 4 cartas. Para cada permutación inicial se indica qué cartas se retiran del mazo
Existen 6 juegos ganadores para la ratonera de 4 cartas, 3 para los que se descartan 2 cartas, 6 para los que se retira una sola carta y 9 para los que no se puede retirar ni una sola carta.
Como podemos observar en la tabla anterior, pero ocurre para cualquier cantidad de cartas n cualquiera, para los desarreglos, que son las permutaciones en las que ninguno de sus elementos aparece en su posición original, obviamente no se puede descartar ninguna carta.
En el mismo volumen de la revista Quarterly Journal of Pure and Applied Mathematics en el que Cayley publica su nota Sobre el juego de la ratonera, el matemático y político danés Adolph Steen (1816-1886) publicó el artículo Algunas fórmulas relacionadas con el juego la ratonera. En este artículo se obtenían fórmulas que permitían calcular el número de permutaciones para las cuales una cierta carta j concreta, para 1 ≤ j ≤ n, era la primera en ser descartada, así mismo se obtenían fórmulas para las permutaciones en las que primero se descartaba la carta 1 y después la carta j. Este artículo contenía algunos errores que fueron posteriormente corregidos por Guy y Nowakowski (1993) y Mundfrom (1994).
La ratonera se ha mostrado como un juego difícil de analizar. Los problemas planteados por Cayley sobre este juego siguen estando abiertos hoy en día y se sigue investigando en ellos en la actualidad.

Mientras preparaba esta entrada he estado jugando a la ratonera con 13 cartas, y esta ha sido mi primera partida ganadora. En la imagen se han utilizado cartas del proyecto artístico colectivo Playing Arts, pertenecientes a los artistas Van Schneider, Antonio Rodrigues Jr., Alexander Grahovsky, Nikita Kaun, Antoni Tudisco, Chuck Anderson, Mr Kone, Justin Poulter, Edgar Rozo, Jilipollo, Zutto, Grzegorz Domaradzki y Denis Zilber
Para el juego de 13 cartas, existen 6.227.020.800 permutaciones diferentes, lo que da una idea de la complicación de abordar el análisis de este juego, salvo que se empleen potentes herramientas matemáticas. Aunque por otra parte, hace que como solitario sea divertido jugar para ver si se consigue ganar la ratonera de 13 cartas y si son muchas veces.
En la Enciclopedia on-line de sucesiones de enteros, de N.J.A. Sloane, aparece la sucesión de los números de permutaciones ganadoras de la ratonera para los n (número de cartas) para los que el resultado es conocido, la sucesión A007709:
1, 1, 2, 6, 15, 84, 330, 1812, 9978, 65503, 449719, 3674670, 28886593, 266242729, 2527701273, 25749021720.
Los matemáticos Guy y Nowakowski han propuesto, y estudiado, algunas generalizaciones del juego de la ratonera, como la ratonera modular, en la que no se para de contar, es decir, al llegar a n se vuelve a empezar por el 1 y así de forma infinita. Han demostrado que si n es un número primo entonces solo hay dos tipos de permutaciones, desarreglos o permutaciones ganadoras. Y para el caso de los números no primos han estudiado solamente los juegos para n pequeños. Otra variación es jugar con varias copias de las cartas, por ejemplo, las 52 cartas de la baraja francesa, 4 copias desde 1 hasta 13.
Y terminaremos con la cita con la que empiezan su artículo Ratonera (mousetrap) los matemáticos Guy y Nowakowski:
Seguramente no tiene importancia. Ninguna. Por eso es tan interesante —declaró Poirot.
Agatha Christie, El asesinato de Roger Ackroyd (1926)

Cartas de la baraja francesa diseñadas con imágenes de zombies, por la compañía Bicycle de EE.UU.
Bibliografía
1.- Raúl Ibáñez, Arthur Cayley, explorador victoriano del territorio matemático, RBA, 2017 (pendiente de publicación).
2.- Arthur Cayley, The Collected Mathematical Papers, Internet Archive [archive.org].
3.- Arthur Cayley, A problem in permutations, Quarterly Journal of Pure and Applied Mathematics I (1857), p. 79.
4.- Arthur Cayley, On the game of Mousetrap, Quarterly Journal of Pure and Applied Mathematics XV (1878), p. 8-10.
5.- Playing Arts, proyecto artístico colectivo
6.- Raúl Ibáñez, Cuadrados latinos, matemáticas y arte abstracto, Cuaderno de Cultura Científica, 2015.
7.- Adolph Steen, Some formulae respecting the game of Mousetrap, Quarterly Journal of Pure and Applied Mathematics, XV(1878), p. 230–241.
8.- R. K. Guy and R. J. Nowakowski, Mousetrap, in D. Miklós, V. T. Sós y T. Szonyi (editores), Combinatorics, Paul Erdös is Eighty, volume 1 (1993), p. 193–206.
9.- D. J. Mundfrom, A problem in permutations: the game of ‘Mousetrap’, European Journal of Combinatorics, 15 (1994), p. 555–560.
10.- M.Z. Spivey, Staircase Rook Polynomials and Cayley’s Game of Mousetrap, European Journal of Combinatorics, 30 (2009), p. 532-539.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo La ratonera, el juego de Cayley se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Matemáticas en el juego de cartas SET (1)
- Arthur Cayley, la teoría de grafos y los isómeros químicos
- Matemáticas en el juego de cartas SET (2)
El sistema de la difusión social de la ciencia 3. Receptores y contenidos

Público, conferenciantes y organizadores tras NaukasCoruña Neurociencia (2016)
Receptores
En una primera aproximación, cabe afirmar que los receptores de las actividades de difusión social del conocimiento científico son todas la personas, el conjunto del cuerpo social. Sin embargo, esa afirmación necesita importantes matices, porque dentro de ese cuerpo social hay diferentes públicos potenciales, y tanto los contenidos como los medios que han de utilizarse varían en función de cuál sea ese público receptor.
Hay, en concreto, cuatro grupos que deben ser considerados de forma diferenciada. En una posición extrema se encuentra el personal científico; son personas que se dedican a la ciencia de forma profesional. Son receptores muy minoritarios y muy especiales; a estos interesa estar al día en campos diferentes del propio. Luego tenemos el público aficionado a la ciencia. De acuerdo con los resultados de las encuestas de percepción social de la ciencia y la tecnología, hay entre un 10% y un 15% de personas a las que interesan de forma activa esas disciplinas. La variación del 10% al 15% refleja, en realidad, diferentes grados de interés, mayor cuanto menor es el porcentaje. Por otro lado, está el profesorado de materias científicas, principalmente de educación secundaria y bachillerato. Lógicamente, este grupo representa un porcentaje pequeño de la población, pero de gran importancia, puesto que son vectores de conocimiento científico cuyos destinatarios últimos son sus estudiantes. Como es natural, muchas de estas personas pertenecen también al grupo de quienes tienen alto interés por la ciencia y la tecnología. Y, por último, están los estudiantes que, además de ser sujetos de la formación que reciben en sus centros de enseñanza, son también receptores potenciales de las actividades de comunicación social de la ciencia, y lo son de una manera especial. Por una parte, se encuentran en una etapa en la que el conocimiento que adquieren puede ejercer un mayor impacto sobre sus decisiones posteriores y, por lo tanto, sobre sus vidas. Y por el otro, también es la época en que con más facilidad se incorporan nuevos conocimientos.
Dentro del público general, por otro lado, cabría establecer otras distinciones, en virtud del interés que unas personas y otras tienen por temas diferentes relacionados con la ciencia, como pueden ser el medio ambiente, la alimentación, salud, etc. De hecho, es relativamente frecuente que personas que afirman tener escaso interés en temas científicos, se muestran muy interesadas en los temas citados, sin ser conscientes de que también tienen alto contenido científico.
Contenidos
Los contenidos que se comunican dependen de cuál es la motivación que anima a los agentes, del público al que están dirigidos y del fin que se pretende alcanzar.
Información
Cuando se trata de contenidos de carácter informativo, suelen tener, como es lógico, las características propias de los mismos. Los descubrimientos científicos de cierta importancia tiene la componente de actualidad que han de tener las noticias para serlo. Medios de comunicación, periodistas y los organismos públicos de investigación que han hecho el descubrimiento son los agentes interesados en difundir ese tipo de contenidos. Y además de los descubrimientos de importancia, catástrofes (terremotos, erupciones volcánicas, huracanes, etc.), incidentes con resultados sanitarios graves (intoxicaciones alimentarias, por ejemplo), y otras informaciones con matiz escandaloso o de cierta gravedad, también tienen su acomodo en los medios de información.
En numerosas ocasiones se transmiten contenidos informativos de carácter científico bajo epígrafes o secciones que no están identificadas de forma específica como “científicos”. Me refiero, principalmente, a información sobre el medio ambiente, alimentación, salud o consumo en general. Se trata de informaciones que despiertan un gran interés en la audiencia pero que no suelen etiquetarse como científicas.
Igualmente, además de lo que en rigor debe considerarse información, también se transmite opinión, pues un buen número de asuntos de carácter científico se prestan al debate público y suelen manifestarse posturas dispares e, incluso, enfrentadas.
Conocimiento
Aparte de los conocimientos científicos básicos que suelen ser difundidos por editoriales, instituciones, personal científico y divulgadores en general, son objeto de especial atención dos ámbitos de conocimiento. Las tecnologías cuyo uso genera controversia social concitan con facilidad la atención de la ciudadanía; buenos ejemplos son los organismos modificados genéticamente o todo lo relativo a la telefonía móvil. Y los conocimientos relativos a temas relacionados con la experiencia cotidiana de las personas, también despiertan mucho interés. Nos referimos a cuestiones citadas en el apartado anterior, tales como la salud, la alimentación, productos de consumo o el medio ambiente. Como ya se ha señalado, lo normal es que muchos receptores no sean del todo conscientes de que se trata de materias de índole científica, o no han reparado en ello.
Por su adscripción disciplinar, hay divulgadores e instituciones que se dedican de manera específica a la divulgación sobre algunos de esos temas concretos.
————————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El sistema de la difusión social de la ciencia 3. Receptores y contenidos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El sistema de la difusión social de la ciencia: 1. Introducción
- Sobre la difusión social de la ciencia y su función
- Presentación del estudio “Percepción social de la ciencia y la tecnología en el País Vasco”
#Naukas16 Improbable-mente

El común de los mortales piensa que la mente puede hacer cosas maravillosas. Eparquio Delgado sostiene no solo que esto no es así, sino que la mente es un mito.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo #Naukas16 Improbable-mente se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Para qué nos sirve la mente?
- #Naukas16 ¿Que te chupe la qué?
- #Naukas16 Alucinaciones lingüísticas: los engaños de tu lengua materna
El lenguaje de los libros de alquimia oscura y el misterio de la existencia de éstos

Imagen de “El libro de Abraham el judío” de Nicolas Flamel
Decíamos en El oscurecimiento de la alquimia que en los siglos XIV y XV el simbolismo y el misterio se convirtieron en un arma de defensa, más que una forma de guardar “el gran secreto”, que no era otra cosa que lo que ya circulaba libremente en siglos anteriores. Esta oscuridad servía también como cortina frente a las acusaciones de falta de ortodoxia. No te podían acusar de nada concreto si todo era interpretable…
Pero, ¿qué aspecto tenía este oscurecimiento? ¿En qué se traducía? Bien, veamos un ejemplo muy característico: el mercurio, la hydrárgyros (de ahí su símbolo actual, Hg), el agua de plata, el metal líquido.
Si al leer un texto de un alquimista te encuentras con referencias al portero, a nuestro bálsamo o nuestra miel (en estos casos “nuestro/a” hace referencia al colectivo de alquimistas), te están hablando del mercurio. Pero también lo pueden estar haciendo si lees que tratan de aceite, orina, rocío de mayo (el rocío que se recoge el primer día de mayo, al que se atribuyen propiedades mágicas), huevo madre, horno (de fundición) secreto, horno (a secas), fuego verdadero, dragón venenoso, triaca (un antídoto contra venenos que ya usaban los griegos clásicos), mina ardiente, león verde, pájaro de Hermes o de la espada de doble filo que guarda el árbol de la vida.

Imagen de “Alquimia” de Libavius
Los procesos también tenían un simbolismo concreto. Así, los pájaros que suben al cielo señalan que se realiza una sublimación; pero si los pájaros van y vuelven del cielo, una destilación. El efecto de un ácido mineral no es otra cosa que un león devorando lo que sea.
Otros símbolos habituales eran la serpiente o el dragón para representar la materia en su estado imperfecto, un símbolo que se remonta a la época de Zósimos de Panópolis (s. IV). El propio proceso alquímico era simbolizado por el matrimonio, en general, y por la unión sexual, en particular, desde los tiempos de la alquimia alejandrina de María la Judía (s. II).
Pero salpimentar el texto de lenguaje cristiano no parecía mala idea, más que nada para confundir al extraño. La muerte y resurrección de Jesús no eran otra cosa que la muerte (digestión) y resurrección (aislamiento, separación, precipitación) de los metales. La Santísima Trinidad no solo eran las tres personas del dios único, también eran la sal, el mercurio y el azufre que se suponía estaban presentes en todos los metales.
Todo este lenguaje misterioso está muy bien y es muy ingenioso, pero hay un misterio aún mayor: ¿Por qué escribir un libro, lo que te puede llevar a perder la vida, si se trata de esconder un secreto?
Quizás la solución la tiene el viejo principio de los detectives a la hora de iniciar la investigación de un delito: Cui prodest? (¿quién se beneficia?).

Página de “Alquimia” de Flamel
El que se beneficia de escribir un libro de alquimia es quien lo escribe. Pero no por ningún motivo romántico, sino porque lo puede vender a otros alquimistas o a aspirantes a serlo. Y los alquimistas necesitaban un flujo constante de dinero.
La mayor parte de los alquimistas eran religiosos (el grupo más alfabetizado de la sociedad) pobres (por circunstancias personales o votos profesados). Si bien afirmaban que seguían con el estudio de la alquimia para mayor gloria de la Iglesia, la Iglesia no sufragaba precisamente estas investigaciones bastante cuestionables que rozaban lo ilegal tras el decreto de Juan XXII.
El estudio de la alquimia era caro: los utensilios se consumían o rompían con suma facilidad y para reemplazarlos algunas veces era necesario pagar un extra al artesano para que trabajase en secreto si los superiores del alquimista no veían su práctica con buenos ojos o, más temible aún, por si alguien se enteraba en lo que trabajaba y quería sacarle su “secreto” por métodos violentos.
Esta combinación de misticismo y secretos llevó a una desconfianza generalizada en la práctica alquímica, por una parte y, por otra, creo oportunidades para que oportunistas se aprovechasen de la avaricia de algunos, creando la figura del alquimista estafador profesional durante siglos.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El lenguaje de los libros de alquimia oscura y el misterio de la existencia de éstos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:El sistema de la difusión social de la ciencia: 2. Motivaciones y agentes

Motivaciones de los agentes
Los motivos por los que diferentes agentes desarrollan actividades de comunicación científica se pueden resumir en tres grandes epígrafes. Ciertos agentes las realizan por los beneficios que reportan, que pueden ser materiales (económicos) o inmateriales (prestigio). La comunicación científica es una actividad económica como cualquier otra ya que hay personas dispuestas a comprar –en formato divulgativo o informativo- contenidos de ciencia. El prestigio, como bien inmaterial, se identifica en muchos casos con una buena imagen y ésta puede conseguirse como consecuencia del desempeño de las actividades de difusión social de la ciencia. Otros agentes actúan por responsabilidad social, por los beneficios sociales que se le atribuyen. Y otros por placer (o afición), porque hay personas que disfrutan desarrollando esa labor. No hay fronteras absolutas entre esas motivaciones. Un agente puede disfrutar con una actividad que la empezó a desarrollar por responsabilidad social y que, además, le reporta un beneficio económico. Y no es extraño que quienes empiezan haciendo divulgación científica por afición acaben haciendo de ello un modo de vida.
Los agentes
Cada uno de los agentes que se señalan a continuación desarrollan su labor en el ámbito de la comunicación científica. Por regla general no actúa de forma aislada, sino que se benefician mutuamente de la colaboración de otros. Y cada uno de ellos desarrolla esa labor debido a un motivo o a un conjunto de ellos.
Medios de comunicación
Dependiendo de su carácter público o privado, la motivación para comunicar ciencia es o puede ser diferente. Los medios privados –normalmente prensa, pero también radio, principalmente- informan sobre ciencia porque interesa a cierto público y son consumidores de información científica (receptores). Para los medios se trata de lograr un rendimiento económico a esa actividad. En el caso de los medios públicos, aparte de satisfacer el interés de una parte de su audiencia, también opera la responsabilidad social. Los medios de comunicación de titularidad pública tienen una función social que cumplir como agentes al servicio de la transmisión de cultura, y la cultura científica es parte inseparable de la cultura humana.
Periodistas independientes
Los periodistas independientes actúan en el sistema de la comunicación científica por razones económicas, con independencia de que, además, consideren que se trata de una actividad socialmente necesaria y gratificante. Los diferenciamos de los medios de comunicación porque aunque su motivación es también económica, las condiciones en que desarrollan su actividad son muy diferentes. Suelen ser periodistas freelance que en ocasiones trabajan para más de un medio de comunicación.
Divulgadores profesionales
Aunque pocos, existen divulgadores científicos profesionales que trabajan de forma independiente. Son autores de libros, mantienen blogs, participan en proyectos de comunicación de empresas del sector, dictan conferencias, etc.
Museos
Hay una gran diversidad de museos e infraestructuras equivalentes. También los hay de concepciones muy distintas, variando desde planteamientos expositivos tradicionales hasta centros concebidos para interactuar con el público visitante. [Ejemplos: MUNCYT, Eureka Zientzia, Planetario, Laboratorium]
Los museos también están dirigidos a públicos amplios y, como ocurre con las exposiciones especiales, también reciben la visita de grupos de estudiantes.
Editoriales
Numerosas editoriales mantienen una colección de libros de divulgación, en ocasiones no sólo del ámbito científico, pero sí principalmente. Al igual que los medios privados de comunicación, su motivación es económica, aunque también puede serlo la búsqueda de prestigio.
Organismos públicos
Dentro de este apartado se incluyen universidades, centros de investigación y otras entidades relacionadas con el mundo de la ciencia o, en general, del conocimiento. La motivación principal es la responsabilidad social, motivación que tiene, a su vez, dos componentes. Una tiene que ver con el interés que se atribuye a la alfabetización científica de la sociedad. Y la otra es un ejercicio de transparencia, pues se entiende que la ciudadanía tiene derecho a conocer el destino que esos organismos dan a los recursos públicos que se destinan a la investigación.
Y a la responsabilidad social habría que añadir el prestigio o, quizás en el caso de estas instituciones, la imagen, que al fin y al cabo es una forma de prestigio o reputación. En la medida en que las actividades de difusión social de la ciencia tienen un alcance importante y llegan a amplios sectores de la sociedad, ello genera una buena imagen de la institución, pues para el público, el correcto desempeño de esa función es un indicador de competencia y de responsabilidad social.
Agencias de comunicación
Numerosas instituciones públicas del ámbito del conocimiento y de la ciencia -universidades y centros de investigación, principalmente- disponen de sus propios gabinetes de comunicación. Además, tanto si disponen de su propio servicio y requieren apoyo adicional como si carecen del mismo, cada vez son más las entidades que recurren a los servicios de agencias especializadas de comunicación. Aunque una agencia generalista puede ofrecer servicios de difusión científica, cada vez es más frecuente encontrarnos con agencias especializadas en materias científicas y tecnológicas.
Empresas de divulgación
Al igual que ocurre con la comunicación, y si bien por el momento se trata de un sector de escasa entidad, también en el terreno de la divulgación científica hay empresas. En algunos casos se trata de compañías especializadas en la organización de eventos; en otros, ofrecen productos de divulgación dirigidos a sectores o segmentos determinados (infancia, por ejemplo), y en otros realizan tareas de producción audiovisual, de edición de medios digitales, etc.
Asociaciones
Existen numerosas asociaciones que desarrollan tareas de difusión social de la ciencia. Unas son asociaciones culturales de carácter general [ejemplo], otras se dedican a la difusión de las ciencias experimentales [ejemplo] y otras, incluso, trabajan campos muy especializados [ejemplo]. Son asociaciones de particulares cuya principal motivación es la afición o, también, la responsabilidad social. Ejemplos especiales de asociaciones con una clara motivación de responsabilidad social son las asociaciones de escépticos, como Círculo Escéptico y ARP Sociedad para el Avance del Pensamiento Crítico.
Investigadores y docentes
Un buen número de investigadores, así como docentes de diferentes niveles formativos (universitarios y de bachillerato, principalmente) realizan actividades de divulgación científica. Para algunas de estas personas la actividad divulgadora ocupa una parte significativa de su tiempo y otras lo hacen de forma muy esporádica. La motivación de estas personas es la responsabilidad social, el prestigio social y el placer. Raramente se trata de una actividad remunerada. En muchas ocasiones esta tarea se enmarca en la actividad de otros agentes, como organismos públicos o medios de comunicación.
Divulgadores aficionados
Aunque no es el caso más habitual, también hay personas ajenas a las instituciones académicas u organismos de investigación que desarrollan, por placer y también por responsabilidad social, una cierta actividad de divulgación científica. Un buen número de investigadores, docentes y divulgadores aficionados engrosan las filas de las asociaciones a que se ha hecho referencia antes.
————————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El sistema de la difusión social de la ciencia: 2. Motivaciones y agentes se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El sistema de la difusión social de la ciencia: 1. Introducción
- Sobre la difusión social de la ciencia y su función
- Presentación del estudio “Percepción social de la ciencia y la tecnología en el País Vasco”
La sinergia prebiótica de aminoácidos y ácidos grasos

El ADN, el ARN, las proteínas, las membranas, los azúcares… las células están compuestas por diversidad de componentes. En biología, y, concretamente, en los estudios sobre el origen de la vida, es muy común centrarse en una de esas moléculas, y postular hipótesis sobre cómo se originó la vida mediante el análisis de los mecanismos específicos relacionados con ella. “Estos estudios, básicamente, buscan “la molécula de la vida”, es decir, establecer cuál fue la molécula más importante para que fuera posible este hito, comenta Kepa Ruiz-Mirazo, investigador de la Unidad de Biofísica y del departamento de Lógica y Filosofía de la Ciencia de la UPV/EHU. No obstante, teniendo en cuenta que “la vida es un juego entre una gran variedad de moléculas y componentes, en los últimos años está habiendo un cambio de planteamiento, y están tomando fuerza las investigaciones que tienen en cuenta diferentes moléculas al mismo tiempo”, añade.
Además de mostrarse a favor de este nuevo planteamiento, el grupo de Ruiz-Mirazo, en colaboración con la Universidad de Montpellier, mediante la estancia de la doctoranda de la UPV/EHU Sara Murillo-Sánchez, ha podido demostrar que existe interacción entre unas moléculas y otras. “Nuestro grupo es experto en la investigación de las membranas que se crearon en los entornos prebióticos, es decir, en el estudio de las dinámicas que pudieron haber tenido los ácidos grasos, los precursores de los lípidos actuales. El grupo de Montpellier, por su parte, está especializado en la síntesis de los primeros péptidos. Así, al juntar el conocimiento de unos y otros, y cuando experimentalmente mezclamos los ácidos grasos y los aminoácidos, pudimos ver que se da una fuerte sinergia entre ambos”.

Imagen de las estructuras supramoleculares formadas por los ácidos grasos en entorno acuoso, tomada mediante la técnica microscópica cryo-TEM (Adela Rendón, en colaboración con el CIC-BioGUNE).
Según pudieron observar, la catálisis de la reacción se produjo cuando los ácidos grasos formaron compartimentos. Al estar en un medio acuoso, y debido al carácter hidrófobo de los lípidos, estos tienden a unirse entre sí y formar compartimentos cerrados; es decir, toman la función de membrana; “en aquella época, obviamente, las membranas no eran biológicas, sino químicas”, aclara Ruiz-Mirazo. En sus experimentos pudieron ver que las condiciones que ofrecen estas membranas son favorables para los aminoácidos: “El grupo de Montpellier tenía muy bien caracterizadas las reacciones prebióticas de formación de dipeptidos; así, pudieron ver que en presencia de los ácidos grasos, esta reacción se daba con una eficiencia mayor”, añade.
Además de demostrar la sinergia entre los ácidos grasos y aminoácidos, Ruiz-Mirazo considera muy importante haber realizado el estudio partiendo de componentes químicos básicos, es decir, con precursores moleculares: “La vida surgió a partir de esas moléculas básicas; por tanto, para estudiar su origen no podemos partir de los fosfolípidos complejos que se encuentran en las membranas de hoy en día. Hemos demostrado la formación de las primeras uniones y cadenas partiendo de precursores moleculares. O dicho de otro modo, hemos demostrado que es posible llegar a la diversidad y complejidad de la biología, partiendo de la química”.
En sus estudios, además del trabajo experimental, Ruiz-Mirazo trabaja en otros dos ámbitos, por lo que al final estudia el origen de la vida desde tres pilares o perspectivas: “por un lado, está el campo experimental; otro, está basado en modelos teóricos y simulaciones computacionales, que utilizamos para analizar los resultados obtenidos en los experimentos, y el tercero es un poco más amplio, ya que estudiamos desde el punto de vista filosófico qué es la vida, la influencia que tiene en el campo experimental la concepción que se tiene de la vida, ya que cada concepción te lleva a realizar un tipo de experimentos —aclara—. Estas tres metodologías se alimentan mutuamente: una idea que pueda surgir en el análisis filosófico te lleva a realizar una nueva simulación, y los resultados de esas simulaciones marcan el camino para diseñar los experimentos. O al revés. Seguramente, nunca llegaremos a resolver el inicio de la vida, pero trabajamos en ello: todos los seres vivos de la Tierra tenemos el mismo origen, y queremos conocer cómo sucedió”.
Referencia:
Murillo-Sánchez, S., Beaufils, D., González Mañas, J. M., Pascal, R. & Ruiz-Mirazo, K. (2016): Fatty acids’ double role in the prebiotic formation of a hydrophobic dipeptide. Chemical Science 7: 3406-3414 DOI 10.1039/C5SC04796J.
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La sinergia prebiótica de aminoácidos y ácidos grasos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- De los ácidos y las bases (y II)
- Ácidos minerales y alquimistas europeos
- De los ácidos y las bases (I)
El sistema de la difusión social de la ciencia: 1. Introducción

La difusión social de la ciencia, objeto de debate
Empieza con esta anotación una serie de siete entregas en las que se presentará la noción de “sistema de la difusión social de la ciencia” y se describirán los elementos que lo conforman, así como las relaciones funcionales que se establecen entre ellos.
Como seguramente ocurre con otros, el mundo de la difusión científica y aledaños es pródigo en debates. Sus términos y las materias objeto del mismo son, a la vez, variados y recurrentes, surgen una y otra vez. Muestra del interés que suscitan en la comunidad que conforman quienes se dedican, como profesionales o como aficionados, a este tipo de actividades son los artículos que se publican al respecto, principalmente en medios digitales. A continuación recojo unas muestras de lo mucho que se ha publicado, con el único propósito de proporcionar algunas referencias e ilustrar la amplitud de las reflexiones pero –quede claro- sin ninguna intención de ser exhaustivo.
Sobre la relación entre el mundo del periodismo y el de la ciencia han escrito Ana Ribera. Pampa García Molina, Francis Villatoro, Lourdes López y Pere Estupinyá lo han hecho sobre el periodismo científico (y sus limitaciones y problemas). Francis también se ha referido al dilema entre periodistas científicos y científicos divulgadores, a la divulgación como actividad propia e irrenunciable del personal científico y a ciertas licencias que se permiten los divulgadores científicos.
Pere Estupinya se muestra crítico con algunas facetas de la divulgación, tanto en lo concerniente a sus aspectos formales, como a la virtual ausencia de evaluación del impacto de las actividades de divulgación (un punto de vista diferente, aquí).
Manuel Herman ha reflexionado acerca de la importancia creciente de internet en la divulgación científica. José Manuel López Nicolás ha tratado sobre la gran potencialidad de los blogs universitarios como herramientas de divulgación. El papel de las universidades y de sus unidades de cultura científica e innovación en la comunicación científica ha sido motivo de reflexión por parte de Elena Lázaro. Y José Luís Vicente también ha escrito acerca de la importancia de difundir los resultados de la investigación que se realiza en universidades y centros de investigación.
La noción de sistema
Hace tres años publiqué aquí el que podría considerarse primer intento por mi parte de sistematización de las actividades de difusión social de la ciencia. Aquella primera aproximación sirvió para iniciar una línea de reflexión que ha dado lugar a diferentes presentaciones públicas en cursos y seminarios (UEU, UPV/EHU, UPNA-Planetario y Universitat de Vic). Y han sido esas presentaciones y el contraste con puntos de vista diferentes las que han conducido a la preparación del texto cuya primera entrega es esta anotación. Aunque quizás no resulte evidente en primera instancia, creo que la sistematización a que he aludido y que considero útil –no me atrevo a calificarla de necesaria- será de ayuda a la hora de clarificar los debates a que he aludido antes. Con esa confianza me he animado a redactar este texto.
La difusión social de la ciencia se produce mediante flujos de información y conocimiento (contenidos científicos) que ocurren en un determinado ámbito (geográfico, cultural, administrativo, etc.) y en un tiempo determinado. A tal ámbito puede dársele la consideración de sistema, en el sentido que se utiliza esa palabra en ecología, por ejemplo. El sistema lo forman dos tipos de elementos, los agentes (o emisores) y los receptores. Los agentes actúan en virtud de unas motivaciones y, haciendo uso de los medios de los que disponen, transmiten unos contenidos (información y conocimiento) al público receptor. La transmisión de esos contenidos ejerce unos efectos que no tienen por qué corresponder a las motivaciones que impulsan estas actividades.
————————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El sistema de la difusión social de la ciencia: 1. Introducción se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sobre la difusión social de la ciencia y su función
- Presentación del estudio “Percepción social de la ciencia y la tecnología en el País Vasco”
- La responsabilidad social de la investigación
El futuro ya no es lo que era

futuro
A estas alturas desconozco si fue Niels Bohr, Enrico Fermi o el mismísimo Yogi Berra quien dijo que “hacer predicciones es muy difícil, sobre todo las del futuro”. Pero fuese quien fuese, acertó de pleno.
Son especialmente conocidas las predicciones negativas que resultaron fallidas. El británico Sir John Eric Ericson, cirujano de la Reina, dijo en 1873 que “el abdomen, el pecho y el cerebro estarían para siempre vedados a la intrusión del cirujano sabio y humano”. De ser ciertas todas las que se le atribuyen, el físico británico William Thomson (Lord Kelvin) se lleva la palma de predicciones incumplidas: sostuvo que la radio no tenía futuro, que era imposible que volaran máquinas más pesadas que el aire, y que se acabaría demostrando que los rayos X eran falsos. Einstein dijo en 1932 que “no hay el más mínimo indicio de que pueda llegar a obtenerse energía atómica; significaría que podría desmenuzarse el átomo a voluntad”. Y sir Harold Spencer Jones, Astrónomo Real del Reino Unido afirmó, en 1957 que “los viajes espaciales eran un disparate”; dos semanas después el Sputnik orbitaba la Tierra.
Lo anterior viene a cuento de las listas que han publicado los primeros días de enero numerosos medios de comunicación con lo que será noticia en ciencia y tecnología en 2017. No deja de sorprenderme, porque aunque es cierto que hay temas –tecnológicos, sobre todo- acerca de los cuales es posible aventurar logros, no es raro que surjan imponderables que impidan que se cumplan las expectativas. Antes hemos visto algunas predicciones negativas incumplidas. También se hacen predicciones positivas que acaban resultando fallidas; al contrario que con las anteriores, rara vez se comprueba su cumplimiento, por lo que no solemos tener constancia de ellas.
En realidad, el mismo hecho de hacer predicciones en estos ámbitos es contradictorio con la naturaleza del progreso científico. El motor de la ciencia es la ignorancia. Cuando se aborda una investigación y tras las observaciones o experimentos se obtiene lo que se esperaba, el conocimiento experimenta un pequeño avance. El físico Enrico Fermi decía a sus estudiantes que un experimento que verifica una hipótesis es una medida, y el que no la verifica, un descubrimiento. Así es: un des-cubrimiento de nueva ignorancia. Es cuando se obtienen resultados inesperados cuando realmente se abren nuevos caminos para el progreso del saber. Porque los resultados inesperados iluminan el límite que separa lo que conocemos y lo que ignoramos, y por lo tanto, muestran áreas desconocidas en las que podemos aventurarnos en busca de aspectos ignotos de la realidad.
Cuando los medios informan de “grandes descubrimientos científicos”, lo que hacen normalmente es dar cuenta de la verificación de hipótesis célebres o de algún desarrollo tecnológico de consecuencias espectaculares. En alguna ocasión han informado de resultados que cuestionan nociones sólidamente establecidas (neutrinos supuestamente superlumínicos, por ejemplo). Y rara vez lo harán de alguna conjetura revolucionaria, cuya comprobación, quizás años más tarde, abra nuevos caminos. Sospecho que ningún medio informó en 1928 de que Paul Dirac había desarrollado una ecuación que describía la dinámica del electrón en términos de la mecánica cuántica, incluyendo también los efectos relativistas. La ecuación predecía además la existencia de antielectrones (positrones), o sea, de antimateria. Y desde luego, a nadie se le ocurrió entonces que aquella ecuación, aparte de iluminar una nueva frontera del conocimiento, acabaría siendo el origen de una técnica de diagnóstico médico tan útil como la tomografía por emisión de positrones (PET). Y es que, como dijo Yogi Berra, “el futuro ya no es lo que era”. De hecho, nunca lo fue.
—————————————————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————————————–
Este artículo fue publicado en la sección #con_ciencia del diario Deia el 15 de enero de 2017.
El artículo El futuro ya no es lo que era se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Se puede predecir el éxito futuro de un científico?
- Otra ventana al futuro
- Por qué no podemos recordar el futuro
#Naukas16 Drogas y falsas promesas

Escuchar a Ohiana Iturbide hablar de adicción a la droga impresiona. No importa el número de veces que lo hayas hecho. En los diez minutos de esta charla el público presente no rio, no aplaudió, no tuiteó, no se movió. Solo guardó un atentísimo silencio.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo #Naukas16 Drogas y falsas promesas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #Naukas15 Falsas memorias
- #Naukas16 ¿Que te chupe la qué?
- #Naukas16 Cuando Indiana Jones se hizo astrónomo
El hidrógeno en el Universo (I): La emisión del hidrógeno neutro a 21 cm.

Imagen en falso color de la Nebulosa de Orión, M 42, y la Nebulosa de Marian, M 43, usando datos obtenidos con el Telescopio Isaac Newton, de 2.5m, en el Observatorio del Roque de los Muchachos en la isla de La Palma (España) usando el instrumento de gran campo Wide Field Camera (WFC). Las líneas verticales negras corresponden a la separación entre distintas CCDs. El color rojo codifica la emisión del hidrógeno ionizado, Hα 6563 Å, mientras que en verde de muestra la emisión de oxígeno dos veces ionizado, [O III] 5007 Å. En color azul sólo se muestra el campo estelar. Esta imagen es la típica que se obtiene mediante CCD o película fotográfica sin filtros, donde destaca especialmente el hidrógeno de la nebulosa. Crédito de la imagen: Ángel R. López-Sánchez (AAO/MQU), Sergio Simón-Díaz (IAC) y Jorge García-Rojas (IAC).
El hidrógeno es, con diferencia, el elemento químico más abundante del Universo. Creado durante los procesos que sucedieron al Big Bang, particularmente durante la recombinación de los núcleos atómicos (protones en su mayoría) con los electrones unos 380 mil años después del inicio del Cosmos, el hidrógeno es el “padre” del que provienen el resto de elementos químicos. La transformación del hidrógeno en otros elementos ocurre sobre todo dentro de las estrellas (por fusión termonuclear, por ejemplo formando núcleos de helio a partir del hidrógeno, que luego se fusiona en núcleos de oxígeno, silicio, azufre o hierro en las estrellas más masivas) o por la acción de éstas en sus alrededores (explosiones de supernova, que típicamente producen los elementos químicos más pesados que el hierro). Así, deberíamos esperar que los astrofísicos invirtieran gran parte de su esfuerzo en conocer dónde se encuentran las nubes de hidrógeno dentro de las galaxias y dentro de la estructura a gran escala del Cosmos, y qué características tienen.
Pero la cosa no es sencilla. Desgraciadamente los telescopios convencionales no pueden detectar el hidrógeno neutro y frío. Los átomos de hidrógeno sólo pueden emitir luz en los colores “visibles” cuando son excitados por radiación energética (particularmente emisión ultravioleta emitida por estrellas masivas, enanas blancas, y otros procesos violentos). Es así como “vemos” las nebulosas difusas de emisión, nubes gigantescas constituidas sobre todo de hidrógeno, como la Gran Nebulosa de Orión (Figura 1). El color rojizo que típicamente domina estas nubes de gas proviene de la emisión del hidrógeno ionizado (línea H-alpha). Pero, obviamente, este tipo de excitación del hidrógeno no ocurre en las frías profundidades del espacio, particularmente en el casi vacío espacio extragaláctico.
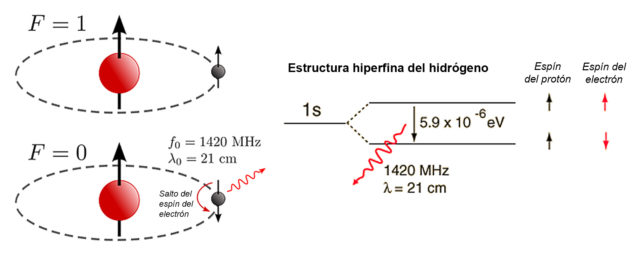
La emisión de 21cm (1420 MHz) del hidrógeno atómico ocurre cuando se produce el cambio del espín del electrón de ser paralelo al espín del protón (arriba) al ser anti-paralelo al protón (abajo). La estructura hiperfina del nivel 1s del átomo de hidrógeno indica que en el primer caso se tiene un poco más de energía (5.9 x 10-6 eV) que en el segundo.
Sin embargo, se da la peculiaridad de que el hidrógeno neutro sí emite cierto tipo de luz. Esta radiación no ocurre en los “colores” que nosotros vemos sino en el dominio de las ondas de radio. La emisión del hidrógeno neutro en radio sucede como consecuencia de la transición atómica entre los dos niveles hiperfinos del estado fundamental del hidrógeno.
¿Qué quiere decir esto? La energía del átomo de hidrógeno, que consta de un protón y un electrón, es ligeramente diferente dependiendo si el espín (análogo al “giro”) del protón y del electrón están en la misma dirección (un poco más de energía) que en direcciones opuestas (un poco menos de energía). Un átomo de hidrógeno en el que el protón y el electrón tengan sus espines paralelos puede emitir un fotón (liberar energía) para pasar al estado en el que ambos espines apuntan en direcciones opuestas (Figura 2). Como la diferencia de energía es muy pequeña (5.9 x 10-6 eV), el fotón emitido tiene una frecuencia baja (1420.4 MHz) y, por tanto, una longitud de onda relativamente larga (21.1 cm).
A esta emisión en radio se la designa como “H I”, la emisión del hidrógeno atómico a 21 cm. No obstante es muy raro que ocurra en un átomo en concreto: la vida media del estado excitado es de unos 10 millones de años. Así, cuando en 1944 el astrónomo holandés Hendrik van de Hultz propuso por primera vez que se usaran radiotelescopios para captar la emisión del H I a 21 cm y así detectar nubes de gas hidrógeno en la Vía Láctea no muchos le hicieron caso. Pero, en realidad, como hay tal enorme cantidad de hidrógeno aún disponible en el Cosmos, la emisión a 21 cm del hidrógeno atómico es, en efecto, no sólo observable, sino fundamental para la Astrofísica contemporánea.

Radiotelescopio de Parkes (NSW, Australia), de 64 metros de tamaño, durante la puesta de Sol. Crédito: Ángel R. López-Sánchez (AAO/MQU).
No fue hasta 1951 cuando los astrónomos Harold Ewen y Edward Purcell de la Universidad de Harvard (EE.UU.) detectaron por primera vez la emisión a 21 cm del hidrógeno atómico, que fue rápidamente corroborada por observaciones independientes desde Europa y Australia. En la actualidad, este tipo de observaciones son rutinarias y otorgan a los astrofísicos piezas claves a la hora de entender nuestro Universo.
Precisamente, una de las grandes ventajas que propiciaban las observaciones en la línea de 21 centímetros del hidrógeno atómico es que, al estar en el rango de las ondas de radio, la extinción de la luz por el polvo y gas interestelar es completamente despreciable. Esto no ocurre en “los colores que nosotros vemos” (el rango óptico del espectro electromagnético), que son fuertemente absorbidos por el polvo y el gas difuso. Así, las observaciones en HI a 21 centímetros permitieron por primera vez “ver” la Vía Láctea en su totalidad.
Fue así como, en 1952 y tras conseguir los primeros mapas de la Galaxia, se encontró que la Vía Láctea tiene una estructura espiral. En este punto hay que insistir en que las observaciones radioastronómicas en la línea de 21 cm no son imágenes, sino espectros. Es una línea de emisión más, y como tal no sólo su intensidad máxima (su brillo) sino también otras propiedades, como la anchura, la velocidad o un análisis de componentes, pueden estudiarse en detalle.
Las observaciones en H I permiten, por efecto Doppler, calcular las distancias a las galaxias o inferir a qué velocidad relativa se mueve el gas dentro de una galaxia. Y, en efecto, ha sido usando observaciones H I a 21 cm de otras galaxias (normalmente el gas es mucho más fácil de observar en las partes externas de las galaxias que las estrellas) como se confirmó definitivamente que las partes externas se movían extremadamente rápido contabilizando la cantidad de masa (estrellas, polvo y gas difuso incluyendo hidrógeno atómico) que contenían, necesitando la componente extra de un amplio pero homogéneo halo de materia oscura para poder mantener las galaxias como entidades estables.

Mapa de todo el cielo observando en la línea de 21 cm del hidrógeno atómico, HI, mostrando la emisión de gas neutro de nuestra Galaxia y las Nubes de Magallanes y la velocidad con la que lo vemos moverse (en color). Esta fantástica imagen ha sido conseguida en la colaboración HI 4π survey (HI4PI), que usa datos obtenidos con el cartografiado Effelsberg-Bonn HI Survey (EBHIS), que usa el radiotelescopio Effelsberg (Alemania), de 100 metros de tamaño, y los datos del cartografiado Galactic All-Sky Survey (GASS), que usa “The Dish”, el radiotelescopio de Parkes (Australia), de 64 metros de tamaño. Crédito: Benjamin Winkel & the HI4PI Collaboration.
El mapa más profundo de la Vía Láctea usando la emisión del hidrógeno atómico a 21 centímetros fue obtenido recientemente mediante la colaboración “HI4PI” (acrónimo de “H I 4π”), que usa datos obtenidos por dos de los radiotelescopios más potentes de la Tierra: el radiotelescopio Effelsberg (Alemania), de 100 metros de tamaño, y el famoso radiotelescopio de Parkes, ”The Dish”, (Australia), de 64 metros de tamaño (Figura 3). En esta proyección de todo el cielo, el plano de la Vía Láctea se encuentra en el ecuador, mientras que el centro de nuestra Galaxia corresponde al amasijo de gas brillante hacia la derecha.
La espectacular imagen del hidrógeno atómico de la Vía Láctea obtenida por la colaboración HI4PI (Figura 4) no sólo muestra la distribución de gas difuso (muy asimétrica) sino que codifica en colores la velocidad a la que se mueve dicho gas. Colores azules indican gas que se acerca al observador, mientras que los colores verdosos corresponden a gas que se aleja. Así se puede apreciar la misma rotación de la Vía Láctea, pero aparecen estructuras más complicadas: filamentos, burbujas, grumos, huecos, capas de gas, que narran la dinámica evolución de nuestra Galaxia. Muchos de los huecos, por ejemplo, corresponden a zonas liberadas de gas por explosiones de supernova. El mismo Sol se encuentra cerca de una de estas zonas irregulares, la Burbuja Local, que brilla particularmente en rayos X. La Burbuja Local, de al menos 300 años luz de tamaño. se originó hace poco tiempo (pocos millones de años, algunos estudios apuntan que incluso menos).
Por otro lado, la mayor densidad de gas corresponde precisamente a las regiones donde se están formando las estrellas. Las nebulosas de emisión aparecen justo en estas zonas donde el gas difuso está condensando para crear nuevos soles. Estas regiones de formación estelar se localizan sobre todo si se mira cerca del centro galáctico
Los colores de la imagen también muestran algo muy interesante: aparecen nubes de gas difusas en colores violetas y amarillos (altas velocidades). Estas “nubes de alta velocidad” corresponden a gas que está cayendo sobre la Vía Láctea (quizá por acreción de alguna galaxia enana) o es gas que ha sido expulsado del disco de nuestra Galaxia por las explosiones de supernovas. La más evidente de estas nubes de alta velocidad es la que corresponde a las galaxias enanas satélite de la Vía Láctea, las Nubes de Magallanes (abajo derecha, en colores naranjas). La imagen de la colaboración “HI4PI” permite distinguir que ambas galaxias enanas se encuentran dentro de esta gigantesca nube de hidrógeno neutro. Es más, permite apreciar su estructura alargada apuntando al centro de la Vía Láctea, además de muchas otras de sus características.
Las observaciones tanto de la Vía Láctea como de otras galaxias usando radioastronomía para “ver” la línea de 21 cm del hidrógeno atómico está proporcionando enorme información a los astrofísicos a la hora de entender la formación de las estrellas, la estructura de las galaxias, la interacción con su entorno, la evolución de las galaxias y la propia evolución del Universo. Sin embargo, quizá porque las imágenes en radioastronomía muchas veces no son atractivas para nuestros ojos (o, pensando mal, que la radioastronomía es el único rango espectral que la Agencia Espacial Estadounidense, NASA, no lidera), muchos de estos detalles no suelen conocerse por el público. En próximas entregas indagaremos en algunos de los sorprendentes detalles que, gracias a la radioastronomía y a la línea de H I a 21 cm, hemos conseguido arrancar al Universo.
Este post ha sido realizado por Ángel López-Sánchez (@El_lobo_rayado) y es una colaboración de Naukas.com con la Cátedra de Cultura Científica de la UPV/EHU.
El artículo El hidrógeno en el Universo (I): La emisión del hidrógeno neutro a 21 cm. se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La fusión a un paso gracias al hidrógeno líquido
- Hidrógeno a partir de cualquier biomasa
- El grafeno distingue entre isótopos del hidrógeno
#Naukas16 La fiesta de las moléculas

Los químicos, algunos, son frikis, pero muy frikis. Daniel Torregrosa es de estos últimos y nos trae una colección de moléculas bautizadas o sintetizadas por químicos frikis.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo #Naukas16 La fiesta de las moléculas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #Naukas16 Astrofotografía
- #Quantum13 Moléculas en el espejo
- #Naukas16 Exoplanetas: mundos de ciencia ficción
Ciencia y tecnología
Aunque se las suele confundir o al menos tratar por igual el objetivo de las ciencias y el de las tecnologías no es el mismo, y eso hace a la verdadera ciencia más resistente a interferencias de poderes externos de lo que pudiera parecer. Buena parte de los ataques a las ciencias en realidad lo que están rechazando es alguna determinada tecnología, o incluso decisiones que no son técnicas sino políticas y económicas. Por eso quizá convenga separar con claridad conceptos y campos de actuación, para delimitar las responsabilidades.

Las ciencias y las tecnologías se diferencian en su objetivo final, que es clara y contundentemente diferente. Las ciencias buscan comprender el universo y su funcionamiento; dilucidar las reglas, los procedimientos y sistemas que hacen que el cosmos exista tal y como es. Son descriptivas en el sentido de que contemplan los fenómenos existentes e intentan explicar sus mecanismos; todas sus intervenciones (experimentos) tienen por objeto ayudar al entendimiento, y por tanto en condiciones ideales las modificaciones que se introducen en el funcionamiento natural están reguladas y son mínimas. El resultado final de las ciencias son las teorías que explican qué hay ahí fuera y de qué manera funciona.
Las tecnologías, sin embargo, no describen el mundo, sino que lo modifican para adaptarlo a las necesidades humanas. Su objetivo no es entender el universo, sino moldearlo para hacerlo mejor para nosotros; el conocimiento que buscan y emplean tiene como objetivo su aplicación en este empeño, no el conocimiento mismo. Las tecnologías siempre son ‘para’ algo: crear vías de comunicación u otras obras públicas, curar enfermedades, extraer minerales, fabricar objetos. La finalidad es utilitaria, y la razón de su existencia es en última instancia mejorar la existencia de la Humanidad.
La relación entre ambos campos es íntima, retorcida y a veces mal entendida; la extensión de conceptos como ‘ciencia aplicada’ no hace más que complicarla todavía más. Las tecnologías emplean el conocimiento del universo generado por las ciencias para mejorar sus técnicas, mientras que la ciencia precisa echar mano de la tecnología más avanzada (y a veces impulsarla más allá de sus límites) para poder llevar a cabo sus experimentos. Hay veces que la investigación científica en una dirección concreta o en un campo específico es dirigida y favorecida para ayudar a resolver una cuestión tecnológica, como ocurre con la biología celular y la cura del cáncer. Otras veces nuevas tecnologías aparecen de pronto surgidas de avances científicos relativamente recónditos o incluso inesperados, como acaba de ocurrir con la ingeniería genética y el sistema CRISPR-Cas. Cuando se habla de ‘ciencia aplicada’ se mezclan conceptos y se diseñan actividades que están a medio camino entre ambas orillas.
Pero se trata de empeños diferentes con objetivos distintos, y mezclarlos conceptualmente tiene consecuencias que pueden ser graves. Porque si en la tecnología entra, por definición, la economía y por tanto la política, en ciencia no es así. Un chiste de ingenieros dice que a la pregunta ‘¿Esto se puede hacer?’ la respuesta siempre es: ‘Depende del presupuesto’, porque en cualquier ámbito tecnológico la clave para la toma de decisiones es la rentabilidad y el acceso a los recursos. En muchas ocasiones las discusiones sobre temas de tecnología no analizan la posibilidad de hacer algo, sino si la solución elegida es la mas conveniente, económica, interesante, rentable: no se discute si es o no posible, sino la conveniencia de hacerlo. No es una decisión sobre hechos, sino sobre política, y así es como debe ser.
El problema surge cuando las cuestiones políticas saltan desde las tecnologías a las ciencias y se intenta doblegar el conocimiento para adaptarlo a las necesidades de la conveniencia social. Se puede (se debe) discutir cuál es la mejor manera de poner límites al cambio climático, si una determinada decisión política será suficiente, o si no habrá otras tecnologías que puedan resolver el problema de modo más económico, ya que hablamos de una cuestión tecnológica (cambiar la realidad). Lo que no es razonable es negar la existencia del calentamiento global medido por la ciencia (describir la realidad). Es posible analizar si los actuales calendarios y sistemas de vacunación son los más eficientes para mantener a raya a las enfermedades contagiosas, pero para ello es absurdo afirmar que las vacunas tienen efectos secundarios que no se han descrito. La decisión política de usar o no usar Organismos Modificados Genéticamente para mejorar el rendimiento de la agricultura debe ser discutida en público para determinar si es la más conveniente o qué sacrificios y de quién estamos dispuestos a hacer para emplearla o no, pero sin usar en la discusión acusaciones infundadas y hechos falsos. La tecnología y en especial sus componentes económico y político siempre puede, y deben, discutirse con pasión, porque todas las decisiones de actuar sobre la naturaleza tienen costes además de beneficios y contrapesarlos es derecho y deber de una sociedad libre.
Lo que no quiere decir que los hechos, los datos, los conocimientos de la ciencia sobre el funcionamiento del universo sean maleables: la ciencia no cambia porque sus resultados sean inconvenientes para una postura política u otra. El planeta se calentará o no; las vacunas causarán autismo o no, y los OMGs serán dañinos o no, y a esa pregunta debe contestar la ciencia y su respuesta debe ser respetada. Después la tecnología determinará si podemos hacer algo para reducir las emisiones de CO2 y cómo, si es mejor vacunar a una edad u otra o si el mejor modo de acabar de una vez con el hambre en el mundo es usar OMGs o no, y la política asignar recursos económicos a la decisión que la sociedad tome. Pero partiendo de una descripción lo más certera posible de la realidad, es decir, de la mejor ciencia disponible. Porque si permitimos que la ideología o la rentabilidad determinen los hechos a partir de los cuales tomamos decisiones nos estaremos haciendo trampas al solitario, que es el modo más estúpido de autoengañarse que existe. Si confundimos la ciencia con la tecnología y ésta con la política no sólo nos irá mal en el futuro, sino que nos habremos merecido que nos pase.
Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.
El artículo Ciencia y tecnología se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Presentación del estudio “Percepción social de la ciencia y la tecnología en el País Vasco”
- Visión de los jóvenes vascos sobre la ciencia y la tecnología
- Ciencia, poder y comercio
La fascinación del oro

Este espejo del futuro telescopio espacial James Webb está recubierto de oro
Desde comienzos del año el oro está subiendo de precio forma sostenida. Eso es indicio de que la incertidumbre aumenta y los inversores buscan refugio en el metal amarillo. Increíblemente es su mera posesión lo que da tranquilidad financiera, aunque el oro no produzca intereses, ni dé nada que se pueda comer, su uso industrial sea limitado, y solo aparezca espectacularmente en naves y sondas espaciales como recubrimiento capaz de reflejar la radiación infrarroja. El oro fundamentalmente encarna la importancia que los humanos damos a los simbólico.
Y es que el oro es un metal raro. De entrada se puede encontrar en estado puro en la naturaleza, ya que hoy sabemos que no se combina con el oxígeno, por lo que es más difícil que entre a formar parte de compuestos como los que forman las rocas. No solo eso, encima es amarillo, brilla y mantiene ese brillo con el tiempo, coloración que no ocurre con ningún otro metal; el cobre es rojo, pero se oxida fácilmente. Por si esto fuese poco, el oro es maleable, por lo que se pueden hacer adornos complejos y fundirlo para hacer monedas. No es de extrañar la fascinación de los humanos con el metal noble desde tiempos inmemoriales.

Corona de Kritonios, s. IV a.e.c.
Pero las maravillas del oro solo aumentan cuando intentamos comprender sus características.
De entrada, su color amarillo está íntimamente relacionado con la teoría de la relatividad de Einstein; son los llamados efectos relativistas debidos a las altísimas energías de los electrones en estos átomos. Estos mismos efectos son los que complican los cálculos teóricos de las propiedades electrónicas del oro. De hecho, los teóricos que se han dedicado durante décadas a intentar describir las características del metal desde primeros principios han encontrado muy difícil explicar las discrepancia entre sus predicciones y las observaciones experimentales. Ahora, un equipo de investigadores ha conseguido resolverlas con un nivel de precisión desconocido incorporando la existencia de interacciones “quíntuples” entre 5 electrones.
Estructura electrónica simplificada del oro
Calcular las propiedades electrónicas de un átomo nunca es fácil, especialmente para los átomos pesados en los que el elevado potencial de Coulomb implica que existen niveles de energías de los electrones para los que la teoría de la relatividad es de aplicación. En el caso del oro, los efectos relativistas son la causa de que exista un salto de energía más pequeño entre los orbitales (regiones en las que puede encontrarse un electrón en un átomo) 6s y 5d, lo que explica que el oro absorba las frecuencias más azules del espectro, y el resultado sea que refleje los tonos amarillo-rojizos.
Pero no todo es tan fácil de explicar. Los cálculos de la energía de ionización (la energía necesaria para arrancar un electrón del átomo) y la afinidad electrónica (la energía necesaria para incorporar un electrón) han resultado siempre en valores inferiores a los experimentales en decenas de mili-electrón-voltios, una discrepancia significativa, aunque no escandalosa.
El equipo que encabeza Lukas Pašteka, de la Universidad Massey (Nueva Zelanda), han conseguido realizar los cálculos más precisos conocidos hasta la fecha para el oro. Su modelo incorpora los efectos relativistas, las correlaciones entre electrones y la electrodinámica cuántica. Las correlaciones entre electrones incluyen todas las interacciones electrón-electrón que tienen lugar en un átomo que tiene 79 electrones.
Una de las principales novedades de este estudio está precisamente en que, a la hora de estudiar estas correlaciones se asumía que un electrón interaccionaba con otros 2, interacciones triples. Pašteka y sus colaboradores lo han ampliado a cuádruples y quíntuples. Al hacerlo así han reducido la discrepancia en las energías de ionización y la afinidad electrónica a tan solo unos pocos de milielectronvoltios, mejorando los resultados anteriores en 10 veces.
Esta metodología, que puede aplicarse a otros átomos pesados, es un indicio de hasta qué punto una creciente capacidad de cálculo nos puede permitir comprender mucho mejor el funcionamiento de la materia y poder predecir características en materiales que ahora son inimaginables.
Referencia:
L. F. Pašteka, E. Eliav, A. Borschevsky, U. Kaldor, and P. Schwerdtfeger (2017) Relativistic Coupled Cluster Calculations with Variational Quantum Electrodynamics Resolve the Discrepancy between Experiment and Theory Concerning the Electron Affinity and Ionization Potential of Gold Phys. Rev. Lett. doi: 10.1103/PhysRevLett.118.023002
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo La fascinación del oro se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- 30 milésimas por encima del cero absoluto, electrónicamente
- La suave piel del núcleo
- Un minuto eterno: pares de Majorana y computación cuántica
Círculo vicioso
“Tomen un círculo, acarícienlo, y se hará un círculo vicioso.”
Eugène Ionesco, La cantante calva

Círculo vicioso
Etienne Lécroart es un artista del cómic. Ya hablamos de uno de sus magníficos trabajos en Interpretando mensajes cifrados.
Es miembro, y uno de los pilares, del grupo OuBaPo (Ouvroir de Bande dessinée Potentielle, Obrador del Tebeo Potencial), que crea sus cómics obedeciendo determinadas trabas formales (muchas de ellas matemáticas), al igual que hace con sus textos el grupo OuLiPo.
Lécroart es un maestro del tebeo; basta con recorrer su trabajada página web para observar sus dotes creativas, sus grandes dosis de humor y sus sorprendentes juegos. Destacan los cómics en los que la lectura puede realizarse en horizontal, en vertical y oblicuamente, o en los que se puede progresar según la numeración de la página o en sentido inverso.
En mi opinión, Cercle Vicieux (Círculo vicioso) es una joya dentro de esta familia de tebeos. Es un enorme palíndromo, es decir, Cercle Vicieux puede leerse desde la primera viñeta hasta la última, o viceversa… y la historia narrada es exactamente la misma en cualquiera de los dos sentidos.
El tebeo tiene treinta páginas, con seis viñetas en cada una de ellas. La última viñeta de la página 15 (la número 90) es la que marca el punto de inflexión de este magnífico palíndromo: la imagen que aparece es simétrica respecto al eje vertical, y marca el centro de este enorme palíndromo.

La viñeta central de Cercle Vicieux, con el ayudante del científico protagonista.
A partir de esta viñeta central se observa que la casilla 91 (página 16) es la misma que la 89 (página 15), y se van comprobado sucesivamente estas identificaciones entre viñetas: 92 (página 16) = 88 (página 15), 93 (página 16) = 87 (página 15), …, 100 (página 17) = 80 (página 14),…, 179 (página 30) = 1 (página 1), hasta llegar a la casilla final, la 180 (página 30), que se reserva para la palabra FIN ¿o es el principio?
He puesto el signo de igualdad entre los números de las viñetas, para insistir en que son idénticas, tanto la imagen como el texto sobre ellas.
La historia trata de un sabio un tanto excéntrico y nervioso que trabaja en su laboratorio diseñando una máquina del tiempo. Le acompañan su paranoico asistente y su ingenua secretaria.
En las quince primeras páginas de Cercle Vicieux se habla de la máquina del tiempo, que el profesor y su ayudante no consiguen poner en marcha; quieren invertir el tiempo para salvar a la secretaria que ha sufrido un colapso. El nerviosismo y la desesperación son las claves en esta primera mitad del tebeo. Los mandos de la máquina envían mensajes extraños, uno de los interruptores de la máquina está apagado… Pero algo sucede de repente –exactamente en la viñeta 90, de las 180 de las que consta el tebeo–, algo que hace cambiar el ritmo y el tema de la trama.
En efecto, la acción de la viñeta central tiene lugar en una hora capicúa, son exactamente las 12h21…, y como se ha indicado, el cómic empieza a escribirse en sentido inverso. La desesperación lleva a la calma, la secretaria ‘resucita’, aparece la atracción entre el sabio y la mujer…
Insistimos en que Lécroart narra la segunda parte de la historia invirtiendo el sentido de las viñetas, pero sin ningún otro cambio, ni en las imágenes ni en los diálogos. El autor consigue crear una historia coherente, tanto en la primera parte como en la segunda, como en su conjunto: a partir de la página central se construye una trama diferente, ‘deshaciendo’ el camino trazado al ir recorriendo las viñetas en sentido inverso…
Si leyéramos la historia desde el final –casillas 179, 178, 177, etc.– comenzaríamos de nuevo la historia del sabio que dice desesperado a su secretaria que no consigue poner en marcha su máquina del tiempo… se trata, sin duda, de un auténtico Círculo Vicioso…
Referencias
- Etienne Lécroart, Cercle Vicieux, l’Association, 2000
-
Marta Macho Stadler, Cercle Vicieux, de Etienne Lécroart, DivulgaMAT, Literatura y Matemáticas, 2012
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Círculo vicioso se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ” El círculo de los nueve puntos “, una sociedad científica singular
- Repasando algunos objetos matemáticos notables
- Interpretando mensajes cifrados
#Naukas16 Tiene bigote, carga eléctrica y no lleva gafas

Partículas. Ilustración de Raquel Garcia Ulldemolins.
Mario Herrero Valea nos explica cómo se juega a un quién es quién muy particular.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo #Naukas16 Tiene bigote, carga eléctrica y no lleva gafas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #Naukas16 La transferencia de conocimiento, ¿nos lleva a la pobreza?
- #Naukas16 Si Rajoy fuese nutricionista
- #Naukas16 Conviviendo con robots

