Magdalena Mouján Otaño, la matemática que escribía relatos de ciencia ficción
Es un problema que con la lógica común no podemos manejar. Demasiadas paradojas. Otra lógica necesitamos, que aún no ha sido construida.
Extracto de Gu ta Gutarrak de Magdalena Mouján Otaño
 Magdalena Mouján Otaño. Fuente: Zientzia Kaiera.
Magdalena Mouján Otaño. Fuente: Zientzia Kaiera.
Magdalena Mouján Otaño nació en la localidad de Pehuajó (provincia de Buenos Aires, Argentina) el 26 de marzo de 1926. Era hija de Armando Mouján y María Teresa Otaño Alberdi.
El abuelo materno de Magdalena, Pedro Mari Otaño (1857-1910), fue un famoso poeta descendiente de una dinastía de bertsolaris y natural de Zizurkil (Gipuzkoa). Por avatares de la vida, emigró a Argentina en 1898 junto a su esposa, María Magdalena Alberdi Descarga, y tres hijos. María Teresa, la madre de Magdalena, nació en Argentina en 1899. Aunque Mouján Otaño nació 16 años después del fallecimiento de su abuelo materno, estuvo muy influenciada por su poesía y sus raíces vascas; su madre le enseñó el idioma de sus antepasados, el euskera.
Magdalena asistió a las escuelas primaria y secundaria en Pehuajó. Posteriormente ingresó en la Universidad Nacional de La Plata, donde tuvo como profesores a los matemáticos Manuel Sadosky (1914-2005) –considerado por algunas personas como el padre de la computación en Argentina– y a Luis Santaló (1911-2001) –quien había abandonado España por motivos políticos durante la Guerra Civil Española–.
Se graduó en matemáticas en la Universidad Nacional de La Plata y consiguió un doctorado en esta área en 1950.
Mouján Otaño comenzó a enseñar matemáticas, área en la que también investigó, y escribió algunos artículos de divulgación para la revista Mundo Atómico entre los años 1952 y 1955.
Investigación operativa: una nueva disciplinaEn 1957, el matemático Agustín Durañona y Vedia (1904-1980) propuso a la Junta de Investigaciones Científicas y Experimentaciones de las Fuerzas Armadas (JICEFA) la creación de un Grupo de Investigación Operativa –que lideraría él mismo– al que se incorporaron Magdalena Mouján Otaño, el ingeniero de estructuras Horacio C. Reggini (1933-2022) y el ingeniero de caminos Isidoro Marín (1921-2020). Tras dos años de estudio e investigación en esta nueva disciplina, los componentes de grupo publicaron más de veinte trabajos teórico-prácticos, asesoraron a organismos del estado, e impartieron cursos y conferencias. Con su trabajo, los miembros de este equipo ayudaron a introducir la investigación operativa en Argentina.
Durante su trayectoria docente, Magdalena Mouján Otaño enseñó matemáticas y estadística en varias universidades públicas y privadas de Argentina, como la Universidad Católica de la Plata, la Universidad Nacional de Córdoba, la Universidad Nacional del Comahue o la Universidad Nacional de Luján.
La computadora ClementinaEn 1966, Mouján Otaño entró a formar parte de la Comisión Nacional de Energía Atómica y fue una de las primeras personas en trabajar con la computadora Clementina, ubicada en el Instituto de Cálculo dependiente de la Universidad de Buenos Aires. Este ordenador, un Ferranti Mercury, fue la primera computadora en instalarse en Argentina con fines científicos. Su nombre se debía a que había sido programada para reproducir la canción Oh My Darling, Clementine.
Sadosky fue el responsable de llevar ese ordenador a Argentina; el equipo que lideraba el trabajo de la computadora Clementina contaba, además, con dos amigas y compañeras de estudios de Magdalena, la matemática Rebeca Guber (1916-2020) y la matemática y programadora Cecilia Berdichevsky (1925-2010).
 Cecilia Berdichevsky trabajando con la computadora Clementina. Fuente: Wikimedia Commons
Cecilia Berdichevsky trabajando con la computadora Clementina. Fuente: Wikimedia Commons
Parte de los cálculos realizados con ayuda de ese ordenador se utilizaron en la construcción del reactor RA1.
Mouján Otaño, escritora de ciencia ficciónEn 1966, tras el golpe de estado del general Juan Carlos Onganía, Magdalena abandonó temporalmente la docencia universitaria, al no apoyar al golpista. Al cabo de unos años, Mouján Otaño regresó a su trabajo de profesora y comenzó a crear relatos de ciencia ficción bajo el seudónimo de Inge Matquim, consiguiendo un gran éxito como escritora.
Uno de sus relatos más conocidos es Gu ta Gutarrak –Nosotros y los nuestros, en euskera–. Trata de una familia vasca que realiza un viaje en el tiempo para encontrar sus orígenes. Este cuento se lo dedicó a su abuelo, quién escribió en 1899 el poema del mismo título en el que se preguntaba –lejos del lugar en el que había nacido– sobre el origen del euskera y del pueblo vasco.
En esta divertida historia, uno de los hijos del protagonista –Xaviertxo, que es superdotado– se convierte en físico para «estudiar la estructura del continuo espacio-tiempo». Sus conocimientos le permiten construir una máquina del tiempo –bautizada como Pimpilimpausa (mariposa, en euskera)– con la ayuda de su hermana pequeña –Malentxo– que inventa una nueva lógica, la necesaria para evitar las paradojas producidas por los saltos en el tiempo. Esta máquina supone «… la gran revolución en la física, algo mucho más importante que la relatividad, y que la teoría cuántica y la bomba atómica…». Gu ta Gutarrak puede leerse en este enlace.
Magdalena Mouján Otaño falleció el 16 de julio de 2005, a los 79 años. Pidió ser enterrada junto a su abuelo, el bertsolari, en el cementerio de Mar del Plata.
Referencias-
Carlos Domingo, Construcción, uso y reforma del Reactor Argentino 1 (RA1), 2005
-
Marta Macho Stadler, Magdalena Mouján Otaño: matemáticas y ciencia ficción, Mujeres con ciencia, Vidas científicas, 29 marzo 2018
-
Isidoro Marín, Investigación Operativa en Argentina, Investigación Operativa no. 38 (2015) 2-17
- John J. O’Connor and Edmund F. Robertson, Magdalena Mouján, MacTutor History of Mathematics archive, University of St Andrews
-
Uxune Martinez, Magdalena Mouján (1926-2005): Argentinako matematikari gutarra, Zientzia Kaiera, 26 diciembre 2014
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Magdalena Mouján Otaño, la matemática que escribía relatos de ciencia ficción se ha escrito en Cuaderno de Cultura Científica.
Einstein y Werner Heisenberg
El físico alemán Werner Heisenberg fue uno de los primeros investigadores de la mecánica cuántica, ayudando a establecer sus ecuaciones y contribuyendo a la interpretación más extendida de éstas, la que se conoce como interpretación de Copenhague. Einstein fue uno de los ídolos de Heisenberg, y los dos científicos se reunieron en múltiples ocasiones para discutir las implicaciones de la mecánica cuántica, pero discreparon a menudo y en multitud de temas, desde la ciencia a la política.
 Asistentes a la Conferencia Solvay de 1927. Sentado, en el centro de la primera fila, Einstein. De pie, tercero por la derecha, Heisenberg.
Asistentes a la Conferencia Solvay de 1927. Sentado, en el centro de la primera fila, Einstein. De pie, tercero por la derecha, Heisenberg.Werner Heisenberg descubrió el trabajo de Einstein mientras estudiaba en la Universidad de Múnich, donde asistió a un curso sobre la relatividad que impartió Arnold Sommerfeld. A Heisenberg le encantó la insistencia de Einstein en que sólo debemos teorizar sobre lo que podemos percibir (posición que tenía su origen en la influencia de Ernst Mach): toda la relatividad surgía de la insistencia en que, si bien diferentes personas observan diferentes sucesos, todas esas observaciones son válidas. Este concepto se grabó en el cerebro de Heisenberg, y se convertiría en una de las creencias fundamentales que darían forma a su ciencia posterior.
Heisenberg quería escribir su tesis doctoral sobre la relatividad, pero fue disuadido de ello por su compañero de estudios Wolfgang Pauli. En esa época Pauli estaba escribiendo lo que llegaría a ser el primer gran ensayo sobre la teoría de la relatividad, que para él era un campo de la ciencia que ya había sido bastante bien establecido. El verdadero futuro está, le dijo Pauli a Heisenberg, en la física atómica.
Heisenberg, sin embargo, se sentía intrigado por la figura de Einstein. En 1922, el joven alemán se dirigió a Leipzig para asistir a una conferencia de su ídolo. Habría sido la primera vez que Heisenberg se encontrase con el hombre al que tanto respetaba, pero no sería así. La fecha de la conferencia coincidió con el comienzo de los ataques antisemitas contra Einstein: es el año de publicación de La crisis actual de la física alemana de Johannes Stark. Nada más llegar a la sala donde tendría lugar la conferencia, a Heisenberg le entregaron un folleto en el que, según Heisenberg escribiría en su libro La parte y el todo, se denunciaba a Einstein como “un extraño al espíritu alemán, y exagerado por la prensa judía”. Heisenberg, cristiano luterano y “ario”, había pertenecido al movimiento juvenil nacionalista de Alemania casi toda su vida, por lo que se vio sorprendido por este ataque nacionalista a un campo exclusivamente científico. Ese día, habida cuenta de las tensiones existentes y los previsibles incidentes, se buscó un sustituto: Max von Laue fue el conferenciante.
Einstein y Heisenberg se encontraron por primera vez en 1924, durante una visita que Einstein hizo a la Universidad de Gotinga. En esta universidad defendería Heisenberg ese mismo año su tesis doctoral, codirigida por Max Born y Arnold Sommerfeld, tras haber ampliado sus conocimientos de matemáticas con David Hilbert. En ese período, se estaba desarrollando la teoría de la mecánica cuántica, y a Einstein no le gustaba el rumbo que esas teorías estaban tomando: conforme los físicos intentaban aportar nuevas explicaciones a cómo los átomos emitían radiación, desarrollaban teorías que sólo ofrecían respuestas probabilísticas. Sus teorías podían predecir un rango de posibilidades para cómo se comportaría un átomo, pero una y otra vez, los científicos se veían forzados a creer que no había un resultado definido para un suceso dado. Cuando se trataba de partículas, decían estos físicos, simplemente no hay una perfecta correlación entre causa y efecto. Heisenberg fue arrastrado por el entusiasmo de crear un nuevo campo científico. Einstein, por otro lado, no podía creer la alocada dirección que estaba tomando la física. Por tanto el encuentro entre Einstein y Heisenberg fue interesante: el joven de 23 años conoció a su ídolo solo para descubrir que tenían ideas opuestas. Fue el comienzo de una separación creciente entre Einstein y la mayoría de sus contemporáneos, pero Heisenberg todavía tenía la esperanza de convencer a Einstein de la corrección de la nueva ciencia.
Fue en septiembre de 1925 cuando Heisenberg hizo su primera aportación asombrosa a la física. Publicó un artículo en el que se exponían las matemáticas necesarias para crear las predicciones probabilísticas que otros estaban estudiando. Básicamente esta fue la primera formulación de la mecánica cuántica. Esta formulación se llama álgebra de matrices [1], y conseguía lo mismo que la famosa ecuación de Schrödinger, que éste desarrollaría el año siguiente. Hubo una gran rivalidad entre los dos hombres sobre qué método debería ser usado. Hoy día se usan ambos, pero la mayoría de los científicos prefieren la mecánica ondulatoria de Schrödinger por ser más simple.
Años después, Heisenberg diría que desarrolló sus teorías basándose en lo que él veía como la filosofía de Einstein de solo analizar observables. Pero el artículo de las matrices de Heisenberg no consiguió que Einstein cambiara sus posiciones ni un ápice. Casi inmediatamente Einstein replicó con una carta a Heisenberg en la que planteaba numerosas objeciones, y que Heisenberg respondió en noviembre rebatiendo cada una de ellas. En esta carta parece que Heisenberg todavía creía que sus dos puntos de vista podrían reconciliarse algún día.
El abismo entre los dos científicos era más grande de lo que Heisenberg creía. En abril de 1926, los dos físicos se encontraron cara a cara por segunda vez tras la conferencia que Heisenberg había dictado en la Universidad de Berlín y a la que Einstein asistió. Heisenberg contaría después la historia de cómo cuando Einstein planteó una objeción al álgebra matricial de Heisenberg, éste intentó usar la filosofía de Einstein contra el propio Einstein, señalando que él había hecho lo mismo que Einstein con la relatividad, usando sólo lo que uno podía percibir directamente para formular sus teorías. Después de todo, esta filosofía, conocida como positivismo, era la preferida por Heisenberg. Einstein, sorprendido, dijo: “Pero, ¿no creerás de verdad que sólo las magnitudes observables deben aparecer en una teoría física?” Pasmado por la respuesta, Heisenberg dijo: “Pensaba que fue precisamente usted el que hizo de esta idea la base de su teoría de la relatividad”. Einstein replicó: “Quizás usé este tipo de filosofía; pero en cualquier caso es una tontería. Solo la teoría decide lo que uno puede observar”.
El punto de vista de Einstein había claramente cambiado en los últimos veinte años. Ahora creía que uno tenía que usar algo más que sólo lo observable para construir una teoría válida. Heisenberg tuvo que afrontar el hecho de que el hombre que él veía como el pionero de la física moderna no le apoyaba.
En 1927, Heisenberg desarrolló el concepto por el que es más famoso, el Principio de Incertidumbre. Basándose en lo difuso del comportamiento de las partículas, Heisenberg postuló que ciertas propiedades atómicas nunca podrían conocerse con exactitud. Si, por ejemplo, uno sabía la posición exacta de un electrón, no podía saber su velocidad exacta. Al principio, Heisenberg explicaba esta idea diciendo que uno simplemente no puede medir la posición sin afectar a la velocidad; medir la posición cambia la velocidad, y viceversa. Por lo que no se pueden conocer ambas variables al mismo tiempo. Pero poco después, Heisenberg y la mayor parte de los físicos dieron una interpretación más profunda: no se trataba de una cuestión de medir simultáneamente, sino de que ambas variables simplemente no podían ser precisas al mismo tiempo. Si el electrón tuviese una velocidad definida entonces estaría difuminado en el espacio, sin una posición definida, y viceversa. A Einstein, como era de esperar, le gustó esta teoría de Heisenberg tan poco o menos que las anteriores.
Ese año de 1927 la Conferencia Solvay se celebró en octubre sobre “Electrones y fotones”, fue durante la misma que Einstein, desencantado con el principio de incertidumbre que Heisenberg había presentado, exclamó “Dios no juega a los dados”, a lo que Niels Bohr replicó “Einstein, deja de decirle a Dios lo que tiene que hacer”.
A pesar de las discrepancias en lo científico, el respeto entre Einstein y Heisenberg era enorme. Einstein se dio cuenta rápidamente de lo adecuadamente que la mecánica cuántica, incluyendo las “extrañas matemáticas” de Heisenberg, predecían el comportamiento de los átomos. Pensaba que la nueva ciencia era valiosa, solo que no estaba completa. De hecho, Einstein nominó a Heisenberg para el premio Nobel a la primera oportunidad tras la conferencia Solvay, en 1928, y también en 1931 y 1932. En la nominación de 1931 escribió: “Esta teoría contiene sin duda un trozo de la verdad última”. Heisenberg ganó el premio Nobel de 1932.
En frentes opuestosEinstein y Heisenberg estaban unidos por razones distintas a la ciencia. Ambos experimentaron la persecución nazi, y ambos se vieron obligados a tomar decisiones difíciles durante la Segunda Guerra Mundial. En los años 30, toda la física moderna se convirtió en tabú en Alemania, a la que se llamaba despreciativamente “ciencia judía”. Practicarla era arriesgarse al ostracismo, y Heisenberg se encontró con que, por el hecho de ser un fundador de la mecánica cuántica, se le prohibía el acceso a varias universidades alemanas.
También se le puso a Heisenberg la etiqueta de “judío blanco”, aunque él era luterano y “ario”, y se le emparejaba con Einstein en los ataques de los medios alemanes y de los físicos antisemitas alemanes Philipp Lénárd y Johannes Stark. Un periódico nazi escribió en julio de 1937: “Heisenberg es sólo un ejemplo entre otros muchos […] Son todos representantes del judaísmo en la vida espiritual alemana que deben ser eliminados igual que los mismos judíos”.
Si bien Heisenberg rechazaba la ideología nazi, era un nacionalista y, a pesar de todas las invitaciones que recibió por parte principalmente de científicos estadounidenses para emigrar a Estados Unidos, tomó la decisión de permanecer en Alemania. Por otra parte, una visita de la madre de Heisenberg a la madre del Reichsführer SS (jefe máximo de la SS) Heinrich Himmler, acabó con los ataques a Heisenberg.
Aunque la relatividad era públicamente menospreciada por los Nazis, el hecho cierto es que nadie ponía en duda la validez de E = mc2, la ecuación que haría posible la construcción de una bomba atómica. En 1939 Einstein estaba viviendo en los Estados Unidos y, sabiendo lo destructiva que una bomba como esa podría ser, escribió una carta al presidente Franklin Roosevelt advirtiéndole del peligro.
 Heisenberg durante la Segunda Guerra Mundial. Fuente: Wikimedia Commons
Heisenberg durante la Segunda Guerra Mundial. Fuente: Wikimedia CommonsHeisenberg, sin embargo, estaba aún en Alemania, y como físico con capacidades útiles se encontró de repente con el favor del gobierno nazi, y se le pidió que trabajase en la construcción de la bomba atómica. El hecho cierto es que Heisenberg pasó la mayor parte de la guerra trabajando en física nuclear, pero para usos energéticos, no armamentísticos. Años más tarde Heisenberg diría que esto fue así debido a sus propias manipulaciones: había hecho su contribución a la paz mediante la confusión, quitando importancia delante de los nazis a los usos prácticos de una bomba como esa y llevándoles a creer que probablemente no podría hacerse. Heisenberg afirma que dijo a sus superiores que creía que la guerra habría terminado antes de que nadie pudiera construir una bomba.
Solo tenemos la versión de Heisenberg de esta historia [2]. Hay quien no cree esta versión y afirma que Heisenberg intentó ocultar sus errores. Su fuerza estaba en la física teórica, no en la experimentación, quizás creyese realmente que no podía construirse. Sea como fuese, el hecho cierto es que después de la guerra trabajó para limitar el uso de las armas nucleares y para reparar las relaciones entre Alemania y el resto del mundo.
La última vez que Einstein y Heisenberg se encontraron fue en 1954 en Princeton, pero sus diferencias científicas eran las mismas de siempre. Heisenberg trató una vez más de convencer a Einstein de la validez de los planteamientos de la mecánica cuántica, pero Einstein fue contundente: “No me gusta vuestro tipo de física. Pienso que os va muy bien con los experimentos…pero no me gusta”. Einstein murió en 1955, sin admitir la mecánica cuántica que Heisenberg simbolizaba.
Tras la muerte de Einstein, Heisenberg escribió un artículo en el que atacaba a Einstein por su carta a Roosevelt, diciendo que un auténtico pacifista nunca debería haber iniciado el esfuerzo para construir una bomba que terminaría resultando en la muerte de miles. Pero culpar a Einstein por haber empezado, de alguna manera, el Proyecto Manhattan parece evidentemente injusto, a la par que incierto. El artículo de Heisenberg estaba probablemente más inspirado por los temas pendientes que tuviese con Einstein, sugiriendo que había más problemas entre los dos de lo que Heisenberg nunca llegase a admitir.
Notas:
[1] Un relato fantástico (porque intervienen dioses nórdicos) de las vicisitudes de la creación del algebra matricial de la mecánica cuántica es La leyenda de Helgoland.
[2] Obviamente, durante la guerra la gente en el otro bando creía cosas distintas. Una narración basada en las consecuencias de algunas de estas creencias es Hay que secuestrar a Heisenberg. El seguimiento en Suiza que se menciona daría lugar a un libro y este a una película.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 13 de noviembre de 2009.
El artículo Einstein y Werner Heisenberg se ha escrito en Cuaderno de Cultura Científica.
La extraña paradoja tras los suplementos de vitamina D
 Foto: Pixabay
Foto: PixabayLa vitamina D es una molécula especial en muchos sentidos. En primer lugar, se trata, en realidad, de una prohormona (una molécula precursora de una hormona) que ejerce efectos muy variados sobre diferentes tejidos. Su papel más destacado es la mineralización de los huesos, pero también está involucrada en el funcionamiento del sistema inmunitario, la función endocrina del páncreas, el desarrollo cerebral… Por si esto fuera poco, la vitamina D tiene la peculiaridad de que su forma activa se sintetiza en la piel tras la exposición directa a los rayos ultravioleta del sol. Así, en circunstancias normales, la principal fuente de esta molécula no son los alimentos, sino la radiación solar (un 80-90 % del total).
Es precisamente esta particular forma de obtener la vitamina D la que ocasiona que el déficit de esta molécula sea, en apariencia, algo relativamente frecuente. Este déficit no solo aparece en países con limitada radiación solar, como los nórdicos, sino también en naciones en las que no esperaríamos que se diese por contar con abundantes días soleados y una radiación solar importante. Este es el caso de España.
Aunque existe muchísima controversia al respecto, si se considera que existe deficiencia de vitamina D cuando los niveles en suero sanguíneo de 25-hidroxivitamina D son menores a 20 ng/ml, entonces, según la Sociedad Española de Endocrinología y Nutrición (SEEN), el 40 % de la población española y más de un 80 % de las personas mayores de 65 años tendría déficit de esta molécula.
Ante esta alarmante magnitud de déficit vitamínico en nuestra sociedad, cualquier profano en la materia esperaría que los médicos solicitasen, de rutina, análisis de sangre entre sus pacientes para detectar si, efectivamente, alguno de ellos sufre este déficit y así recetar suplementos de vitamina D. Sería lo lógico, ¿no? Pues no. De hecho, no se recomienda realizar cribados universales en las consultas médicas para detectar los niveles de vitamina D en la población general, salvo que existan factores de peso para ello en casos de riesgo (osteoporosis, ancianos de edad avanzada…).
Aun en el caso de que se detectase deficiencia leve de vitamina D, las diferentes guías clínicas y sociedades médicas no aconsejan dar suplementos de esta molécula por sistema. En su lugar, y si es posible, se aconseja al paciente aumentar la exposición al sol y consumir más alimentos ricos en esta vitamina (pescado azul, huevos, hígado…).
Entonces, si el déficit de vitamina D es tan frecuente en nuestro país y en otros muchos, ¿por qué no se hacen screenings ni se pautan suplementos? La razón es sencilla: porque los ensayos clínicos muestran, una y otra vez, que el consumo de complementos o suplementos dietéticos con vitamina D no aporta ningún beneficio para la salud a la población sana sin déficits y, en muchas ocasiones, ni siquiera a las personas con déficits.
La ausencia total de beneficio de la suplementación de vitamina DUn ensayo clínico reciente en este sentido, que llama la atención por la ausencia total de beneficio de la suplementación de vitamina D, se realizó en Mongolia sobre 8.851 niños con déficit de esta molécula (menos de 20 ng/ml en suero). Los investigadores querían averiguar si el consumo de suplementos de vitamina D3 (14.000 unidades internacionales cada semana, durante 3 años) en este colectivo tendría algún efecto positivo sobre la salud, en comparación con el grupo placebo. No encontraron ninguna diferencia entre ambos grupos, salvo por el hecho de que el grupo de niños que recibió vitamina D a lo largo de los años ya no tenía déficits. No hubo ningún efecto sobre la altura, la masa corporal o el desarrollo en la pubertad. Nada. Y esto no solo ocurría entre los niños con un déficit normal previo (menos de 20 ng/ml de vitamina D en suero), sino también incluso en aquellos con un déficit grave (menos de 10 ng/ml) al comienzo del estudio.
Resultados decepcionantes como los anteriores se dan constantemente en ensayos clínicos. La suplementación de vitamina D tampoco ofrece beneficio para disminuir el riesgo de tuberculosis en niños con déficits, no mejora la mineralización de los huesos en la población general, no previene fracturas ni caídas, y no reduce el riesgo de muerte por todas las causas, de cáncer o de enfermedades cardiovasculares.
Además de la ausencia generalizada de beneficios por el consumo de suplementos de vitamina D, algunos estudios han observado incluso riesgos para la salud. Un estudio observacional de casi 31.000 participantes detectó que el consumo de dosis mayores de 10 microgramos al día en personas sin déficits se asociaba con un incremento de mortalidad por todas las causas y por cáncer en particular. Por otro lado, un exceso de este nutriente puede provocar daños en los riñones y en otros órganos y tejidos.
¿A qué se debe esta paradoja en torno a la vitamina D? Hay dos explicaciones principales. La primera, que realmente los umbrales actuales para definir cuando existe un déficit por esta molécula no son correctos (son demasiado altos) y eso nos lleva a diagnosticar deficiencias que, en realidad, no existen porque no provocan daños sobre la salud. Por eso, añadir más vitamina D no aporta beneficio. De hecho, existe desde hace un tiempo mucha discusión científica sobre por debajo de qué nivel se puede considerar una deficiencia de vitamina D.
Otra posible explicación sobre por qué no se ven efectos saludables por el consumo de suplementos de vitamina D, incluso en personas con claros déficits, es que existe algún problema en el organismo que impide la transformación de esta molécula a su forma activa (el calcitriol), que es la que realiza las diversas funciones, o existe otro factor que no conocemos y que limita sus efectos aún en la forma activa.
Sea la razón que sea, lo que el conjunto de la evidencia científica nos sugiere es que no hay razón para consumir complementos de vitamina D, salvo casos muy definidos. Si lo que se quiere es tener unos buenos niveles, exponerse al sol de forma moderada, hacer ejercicio físico y comer alimentos ricos en este nutriente son una opción más recomendable, por ofrecer numerosos beneficios para la salud, además de más asequible.
Para saber más:
A tomar el sol
El enigma de los suplementos nutricionales
Sobre la autora: Esther Samper (Shora) es médica, doctora en Ingeniería Tisular Cardiovascular y divulgadora científica
El artículo La extraña paradoja tras los suplementos de vitamina D se ha escrito en Cuaderno de Cultura Científica.
El violín bien temperado
Los 24 preludios y fugas en todas las tonalidades musicales son una de las más conocidas e importantes obras docentes e investigadoras del gran Johann Sebastian Bach. Por medio de “El clave bien temperado” Bach nos explica y demuestra en la práctica cómo funcionan los posibles temperamentos en un teclado. En los violines, las notas musicales se afinan de forma directa pisando sobre las cuerdas, en cualquier tono o microtono. Esto da total libertad al músico para interpretar en cualquier tonalidad, pero el lutier debe construirle un instrumento cuya caja de resonancia quede bien afinada: el violín bien temperado.
Savart, Chladni y Vuillaume Hilary Hahn es una de los mejores intérpretes de violín en activo. En la imagen con su Vuillaume de 1865 (construido tomando como referencia el Stradivarius «Alard» de 1715). Foto: Dana van Leeuwen. Fuente: Tarisio
Hilary Hahn es una de los mejores intérpretes de violín en activo. En la imagen con su Vuillaume de 1865 (construido tomando como referencia el Stradivarius «Alard» de 1715). Foto: Dana van Leeuwen. Fuente: TarisioA mediados del siglo XVIII la edad de oro de la lutería cremonense tocó a su fin. Los gremios familiares mantuvieron celosamente sus secretos durante más de dos siglos y gran parte de su conocimiento se consideró olvidado. Por fortuna, la era de la Ilustración recogió los medios científicos para redescubrir el saber de los antiguos constructores de instrumentos. El físico Félix Savart, aplicó los métodos de su amigo Ernst Chladni junto con su dispositivo para medir frecuencias en las tablas armónicas de múltiples violines históricos, desmontadas y prestadas por el gran lutier francés Jean-Baptiste Vuillaume.
Los elementos constituyentes más importantes de la caja de resonancia de un violín son las tapas y los fondos, tablas armónicas construidas en abeto (picea abies) y en arce (acer platanoides), respectivamente. Savart propuso estudiar qué sonidos deberían tener la tapa y el fondo de un violín antes de unirse en una caja de resonancia, con la idea de explicar y publicar la ciencia de los grandes lutieres. Savart observó que la frecuencia de los modos normales de vibración por parejas (tapas y fondos) de los mejores instrumentos coincidían entre sí a intervalos cercanos. Estas medidas permitieron a Vuillaume no solamente reparar en su taller de París los mejores instrumentos de todos los tiempos, sino construir nuevos violines, verdaderas copias tonales indistinguibles de los apreciados Stradivarius y Guarnerius.
Las tablas armónicas de Carleen Maley HutchinsLa gran científica y lutier Carleen Hutchins publicó en 1981 otro importante hallazgo de acústica musical describiendo en detalle métodos para construir cajas resonantes de violines de gran calidad [1]. Hutchins modernizó los experimentos de Savart y Chladni mediante un sencillo generador y amplificador electrónico de audio, para excitar los modos normales de vibración de sus tablas armónicas, trazar las líneas nodales de Chaldni, así como medir las frecuencias de dichos modos de vibración.
Cientos de experimentos realizados por Hutchins confirmaron las observaciones de Savart: cuando las frecuencias principales de la tapa y del fondo de un violín están separadas menos de un tono, el instrumento tiene buenas cualidades musicales. No solamente verificó estos resultados, sino que además descubrió que tres modos normales de vibración de las tablas armónicas tienen especial importancia para poder fabricar instrumentos bien temperados.
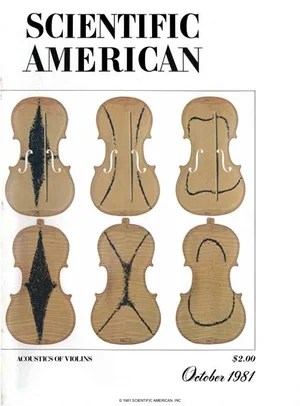 Portada de Scientific American de octubre de 1981
Portada de Scientific American de octubre de 1981La portada de Scientific American de octubre de 1981 ilustra precisamente los modos normales de vibración más importantes medidos por Hutchins: modos #1, #2 y #5, de sus tapas (fila superior) y sus fondos (fila inferior). Tal y como describe la autora, estos tres modos eran ajustados por los grandes lutieres golpeando las tablas armónicas y escuchando su sonido. Estos experimentos de golpeos son muy sencillos de efectuar observando las figuras de Chladni: para excitar un modo de vibración concreto, basta con sujetar una tabla en un punto nodal (zona oscura en el patrón de Chladni) y golpear seguidamente en un punto ventral (zona clara en el patrón de Chaldni). Esto nos permite escuchar el sonido de las tablas armónicas, tal y como hacían los antiguos constructores en una época en la que no existían sistemas de medida más allá de sus manos y sus oídos.
Los secretos de la lutería al descubiertoUna de las funciones más importantes de la ciencia es descubrir y publicar el conocimiento para su uso, avance y disfrute general. Los secretos de los antiguos constructores de instrumentos quedaron por fin al descubierto por parte de la ciencia. Hoy en día ninguna autoridad experta en música, instrumentistas o lutieres, es capaz de distinguir o juzgar como superior la calidad sonora y expresión musical de los antiguos violines con respecto a los buenos nuevos instrumentos desarrollados en la actualidad [2].
Sabemos ya hoy cómo construir violines basados en la ciencia, no en los secretos. La acústica musical nos ha enseñado que el tallado de las tablas armónicas de un violín reduce claramente tanto su masa como su rigidez y también altera la capacidad de las placas para absorber energía. Así pues, la frecuencia y la forma de un modo normal de vibración determinado puede ajustarse selectivamente. El adelgazamiento de las tablas armónicas en una zona de flexión pronunciada reduce la rigidez más que la masa, de modo que la frecuencia disminuye. Por otro lado, la eliminación de madera en una zona de poca flexión reduce la masa más que la rigidez, de forma que la frecuencia aumenta. Estos procedimientos científicos se explican hoy día en las mejores escuelas de lutería internacionales y ello nos ha permitido producir excelentes violines bien temperados en todo el mundo.
Referencias
[1] Caleen M. Hutchins (1981) The acoustics of violin plates. Scientific American, vol 245, n. 4, pp: 170-186.
[2] Adrian Cho (2017) Million-dollar Strads fall to modern violins in blind ‘sound check’. Science. doi: 10.1126/science.aal1163
Sobre el autor: Victor Etxebarria Ecenarro está diplomado como lutier por el Conservatorio Juan Crisóstomo de Arriaga (Bilbao) y es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (UPV/EHU)
El artículo El violín bien temperado se ha escrito en Cuaderno de Cultura Científica.
Amanda Sierra Saavedra – Vida tras la muerte (de las neuronas)

Las neuronas con las que nacemos no nos acompañan durante toda nuestra vida, sino que se van perdiendo de manera natural tanto en el proceso de desarrollo como durante el envejecimiento. Pero, ¿qué pasa en nuestro cerebro cuando estas neuronas mueren? ¿Cómo reaccionan las otras neuronas que siguen con vida?
Para evitar que estas neuronas muertas “contaminen” el entorno, liberando sustancias tóxicas que puedan afectar a las células circundantes, el cerebro dispone de un sistema de autolimpieza que elimina los residuos de manera rápida y eficaz mediante un proceso conocido como fagocitosis (del griego “fago”, comer)
En el encéfalo las células que se encargan de este proceso como fagocitos profesionales son las microglías. Son células pequeñas, muy ramificadas, y altamente móviles, descubiertas en 1919 por el médico e investigador vallisoletano Pío del Río Hortega. Discípulo del médico bilbaíno Nicolás Achúcarro, realizó aportaciones fundamentales en el campo de la histología y, en especial, en el de las células gliales, como la micrología, que forman parte del sistema inmunitario del sistema nervioso central.
En este contexto, en el Laboratorio de Biología Celular Glial del Achucharro Basque Center of Neuroscience trabajan desde más de una década en el estudio del proceso de fagocitosis cerebral, lo que les ha permitido desarrollar nuevas herramientas terapéuticas que permiten controlar este proceso y acelerar la regeneración del cerebro enfermo.
Con el objetivo de mostrar cómo funciona este proceso y coincidiendo con el aniversario del nacimiento de Nicolás Achúcarro, Amanda Sierra Saavedra, directora del Laboratorio e investigadora Ikerbasque de la UPV/EHU, ofreció esta charla, que tuvo lugar el 16 de junio de 2021 en la Biblioteca Bidebarrieta de Bilbao.
Además de mostrar el proceso de fagocitosis cerebral, durante esta conferencia la investigadora explica cómo estudian el proceso de la fagocitosis cerebral dentro del Laboratorio de Biología Celular Glial, el impacto de estas células en su entorno, así como la posible implicación de este proceso en la regeneración celular en enfermedades como la epilepsia o el infarto cerebral. Finalmente, Sierra Saavedra expone la investigación que se realiza dentro del Laboratorio para avanzar en el desarrollo de nuevas herramientas terapéuticas y su aplicación en la regeneración celular del cerebro.
(Si no se reproduce el vídeo en su navegador, pulse el enlace)
Edición realizada por César Tomé López
El artículo Amanda Sierra Saavedra – Vida tras la muerte (de las neuronas) se ha escrito en Cuaderno de Cultura Científica.
Reconocimiento automático de la lengua de signos
Las personas con problemas de audición suelen tener dificultades para comunicarse en entornos sin un intérprete. Últimamente se han desarrollado diferentes enfoques para tratar de resolver este problema. Un grupo de investigadores de la Facultad de Informática de la UPV/EHU ha desarrollado un sistema de reconocimiento de la lengua de signos argentina que utiliza puntos de referencia de la mano extraídos de vídeos con el fin de distinguir entre diferentes signos sin necesidad de que el signante use equipos especiales.
 Fuente: Basilio Sierra – UPV/EHU
Fuente: Basilio Sierra – UPV/EHU“Según los datos de la Organización Mundial de la Salud-expome Basilio Sierra, catedrático del Departamento de Ciencias de la Computación e Inteligencia Artificial de la UPV/EHU-, más del 5% de la población mundial tiene problemas de audición. Esto supone unos 466 millones de personas (432 millones de adultos y 34 millones de niños), y se prevé que esta cantidad aumente. Para 2050 se espera que alrededor de 700 millones de personas (una de cada diez personas) sufran deficiencias auditivas. Entre estas personas, más o menos 70 millones utilizan una de las más de 300 lenguas de signos que existen como primera lengua. Sin embargo, como el conocimiento de las lenguas de signos no está extendido por todo el mundo, estas personas suelen tener dificultades para comunicarse en diferentes escenarios, y su interacción en la vida diaria se complica cuando no hay un intérprete que les ayude con la traducción. Para tratar de resolver estos problemas, últimamente se han desarrollado muchos enfoques diferentes en el campo del reconocimiento automático del lenguaje de signos. Algunos de estos enfoques son un poco intrusivos, ya que requieren que el signante (persona que usa el lenguaje de signos) utilice algún tipo de dispositivo para que el sistema sea capaz de interpretar lo que está diciendo.”
“Las lenguas de signos-apunta Itsaso Rodríguez, estudiante de doctorado-, como lenguas orales, tienen sus propias estructuras lingüísticas y son bastante difíciles de traducir a lenguas habladas debido a diferentes aspectos. Cada lengua de signos está compuesta por miles de signos diferentes que muchas veces difieren por pequeños cambios. Por ejemplo, algunos signos tienen la misma configuración de manos, pero diferente orientación. Además, a veces el significado de un signo puede cambiar según el contexto o la frase en la que se utilice. La expresión facial también es crucial para diferenciar algunos de los signos, lo que es muy importante, por ejemplo, a la hora de hacer frases interrogativas. Por lo tanto, algunos signos difieren solo en pequeños detalles, como la configuración de la mano, el movimiento, la posición, la expresión facial o incluso el contexto.”
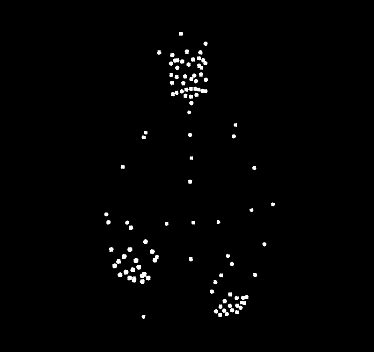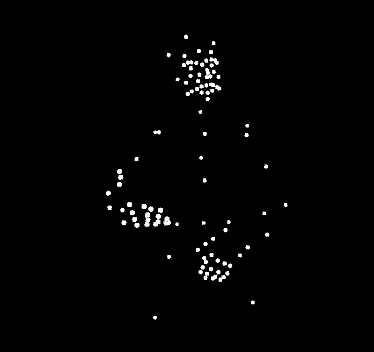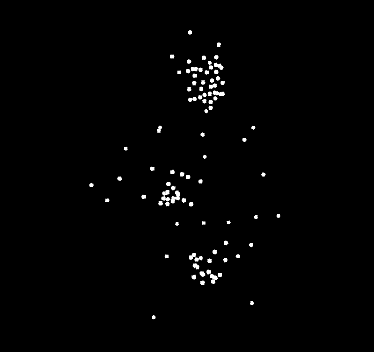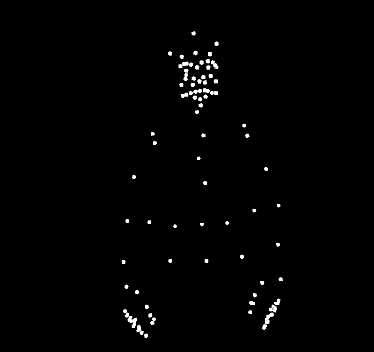 Análisis de puntos de una frase en lengua de signos estadounidense. Este enfoque analiza los gestos del signante usando un equipo especial. En el nuevo enfoque se pretende analizar un vídeo de la persona signante sin que esta use equipo adicional alguno. Fuente: Wikimedia Commons
Análisis de puntos de una frase en lengua de signos estadounidense. Este enfoque analiza los gestos del signante usando un equipo especial. En el nuevo enfoque se pretende analizar un vídeo de la persona signante sin que esta use equipo adicional alguno. Fuente: Wikimedia CommonsSin embargo, varios signos se parecen mucho a los gestos que realizaría un oyente no experto para describir una acción. Y, en la mayoría de los casos, la relación signo-objeto es arbitraria y no tienen ninguna referencia visual. “Otras características de las lenguas de signos son, por ejemplo, que el orden de las palabras puede ser diferente según el contexto o que algunos verbos no se signan. También hay que tener en cuenta la ortografía dactilar, en la que las palabras se deletrean si no se conoce el signo de esa palabra. El deletreo con los dedos se utiliza sobre todo para los nombres propios. Hay muchas otras características que hacen que el reconocimiento del lenguaje de signos sea una tarea compleja, aunque no mencionamos todas en el estudio”, explica Sierra.
En este trabajo se presenta un enfoque para el reconocimiento de la lengua de signos basado en vídeo. “Como primer paso del proceso, se componen unas señales con las posiciones extraídas por MediaPipe (solución de detección facial ultrarápida), que representan un conjunto de articulaciones de la mano que está realizando el signo. A continuación, estas señales se transforman utilizando el algoritmo Common Spatial Patterns, un algoritmo de reducción de la dimensionalidad ampliamente utilizado en las señales de electroencefalograma. Common Spatial Patterns también se ha aplicado en el campo de la electrocardiografía, la electromiografía o incluso en imágenes astronómicas para la detección de planetas, y recientemente se ha utilizado en tareas de reconocimiento de acciones en vídeo obteniendo resultados alentadores. Este enfoque permite un cálculo de forma cerrada y por lo tanto no es necesario decidir los criterios de terminación como ocurre en métodos iterativos ampliamente aplicados, por ejemplo, el descenso de gradiente en el aprendizaje profundo.”
Los investigadores han utilizado vídeos de un conjunto de datos de la lengua de signos argentina. “Para cada fotograma de vídeo se obtienen varios puntos de referencia de la mano mediante la mencionada tecnología MediaPipe. Estos puntos de referencia de la mano se utilizan para crear un conjunto de señales para cada vídeo. El algoritmo Common Spatial Patterns se utiliza para transformar estas señales y después de extraer algunas características de las mismas (valores de varianza, máximo, mínimo y rango intercuartílico) se realiza la clasificación. Para la clasificación se han utilizado diferentes clasificadores. Hay que mencionar que el enfoque presentado no es intrusivo, no es necesario colocar ningún tipo de dispositivo a los signantes, lo que hace que el sistema sea más cómodo para ellos. Los resultados obtenidos tienen entre 0,90 y 0,95 de precisión, alcanzando valores más altos tras convertir los vídeos originales al espacio de color blanco y negro. Son resultados de clasificación muy prometedores”, concluye Itsaso Rodríguez.
Referencia:
Rodríguez-Moreno I, Martínez-Otzeta JM, Goienetxea I, Sierra B (2022) Sign language recognition by means of common spatial patterns: An analysis. PLoS ONE doi: 10.1371/journal.pone.0276941
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Reconocimiento automático de la lengua de signos se ha escrito en Cuaderno de Cultura Científica.
La mente de una abeja
¿Qué se siente al ser un murciélago? Se preguntaba el filósofo Thomas Nagel1. Nuestra intuición nos dice que la rica conducta de los mamíferos solo puede explicarse si éstos tienen una “experiencia subjetiva”, aunque no necesariamente parecida a la nuestra. La mayoría de los dueños de perros y gatos están convencidos de que sus mascotas tienen algún tipo de vida interior. ¿Pero, qué se siente al ser una abeja? Este es el reto que lanza el entomólogo Lars Chittka en su libro “The Mind of a Bee”2, en el que afirma que ellas también poseen alguna forma de consciencia. Para la mayoría de nosotros esta idea resulta contraintuitiva, pero hay que reconocer que la mera intuición es una base muy pobre para construir un argumento. Deberíamos comenzar considerando los retos cognitivos que tienen que resolver las abejas en su vida cotidiana.
 Foto: Carolien van Oijen / UnsplashIdentificar flores
Foto: Carolien van Oijen / UnsplashIdentificar flores
Una abeja tiene que visitar cien mil flores para producir una sola cucharada de miel; en ese proceso habrá rechazado unas quinientas mil que no parecían prometedoras; para ello tiene que aprender a reconocer la flora habitual de su región. Además, cada flor ‘esconde’ el néctar con objeto de que la abeja se impregne de polen y lo traslade a otra flor, de manera que constituye una especie de puzzle tridimensional, que la abeja tiene que resolver caso a caso3. La capacidad visual de las abejas es muy diferente de la nuestra4: su visión es menos nítida, pero, a cambio, el procesamiento visual es mucho más rápido. Su percepción del color es muy diferente ya que pueden ver en el espectro ultravioleta, pero no en el rojo. Realmente, las plantas con flores han coevolucionado con sus polinizadores, así que sus patrones de color “están hechos” para ellas, no para nosotros. La vista no es el único sentido que interviene en este proceso. Sus antenas pueden percibir campos electrostáticos5: las abejas en vuelo tienen carga positiva mientras que las flores la tienen negativa, de manera que cuando se produce una visita, la carga de la flor cambia de forma temporal; esto permite a las abejas “saber” si la flor ha sido visitada recientemente y no merece la pena detenerse. Y, por supuesto, las abejas pueden percibir olores y sabores y esto constituye otra pista importante para ellas6.
Conocer el terrenoLas abejas tienen que conocer el territorio en el que viven para poder regresar a la colmena7, para ello cuentan con una prodigiosa memoria y con algunos “superpoderes”. Por ejemplo, son capaces de percibir la polarización de la luz solar; esto se traduce en que ven una banda en el cielo en la trayectoria del sol, lo que les ayuda a saber su posición incluso en días parcialmente nublados. También pueden percibir el campo magnético de la Tierra. Su forma de orientarse depende en primer lugar de un vector construido con respecto al ángulo con el sol. Adicionalmente, son capaces de reconocer determinadas características del terreno que le sirven para orientarse. Los científicos han visto que si capturan a una abeja y la liberan en otro lugar (no demasiado lejano), el animal utiliza primero el vector solar para regresar, lo que lógicamente le lleva a un lugar diferente. En ese caso realiza una serie de vuelos en redondo hasta que reconoce el lugar en el que se encuentra y, acto seguido, se dirige a la colmena en línea recta.
Comunicarse con otras abejas y trabajar en equipoLas abejas tienen un sistema de comunicación simbólica8, en forma de danza, que no tiene parangón en el reino animal y que permite a una obrera comunicar a las otras la situación de una fuente sustanciosa de alimento. Más aún, cuando se mezclan artificialmente abejas de distintas especies, se ha visto que son capaces de aprender la danza (algo diferente) de la otra, presumiblemente, mediante ensayo-error9. Un tipo diferente de danza comunicativa se produce cuando el enjambre se encuentra buscando una nueva localización para construir una colmena. Las obreras exploran el terreno y cuando encuentran un sitio apropiado se lo cuentan a las otras. Cuando un porcentaje significativo de obreras coincide en comunicar el mismo lugar, la colmena en pleno se dirige a él, lo que constituye una insólita forma de democracia entre los insectos: las abejas votan dónde quieren establecerse10. En condiciones naturales elegirán cavidades para la construcción del panal de cera. Este proceso también es asombroso porque requiere una gran coordinación entre individuos. Los científicos han comprobado, en un ambiente artificial, que si durante el proceso de construcción se sustituye una de las paredes por un vidrio (un tipo de superficie poco adecuada), las abejas cambian sobre la marcha la forma del panal, haciendo que gire 90 grados hasta terminar en otra pared. Esto requiere un ajuste exquisito y coordinado del tamaño de las celdillas11.
Aprendizaje rápido y metacogniciónLas abejas se encuentran entre los animales que más rápido aprenden a asociar un color u otro estímulo a una recompensa azucarada; de la misma forma, aprenden en seguida a asociar estímulos con sustancias amargas o nocivas. Pero van más lejos: son capaces de saber lo que no saben12. En estos experimentos, los científicos confrontaban a los insectos a una tarea difícil de discriminación visual, pero les daban una tercera opción que les permitía evitar dicha tarea; a medida que la prueba se iba haciendo más difícil, las abejas elegían con mayor frecuencia esta tercera opción, lo que sugiere que son capaces de reconocer su propia incertidumbre.
Emociones o algo parecidoEl hecho conocido de que las abejas prefieran visitar flores con cierto contenido en cafeína, que no tiene valor nutricional, sugiere que son susceptibles a los estimulantes y reaccionan de forma parecida a nosotros. Más interesante aún es el hecho de que las abejas estresadas se vuelven más pesimistas13. Para estudiar este fenómeno, los científicos las enseñaron a asociar una mezcla 9:1 de dos olores con una recompensa azucarada y una mezcla 1:9 de los mismos olores con una sustancia amarga desagradable para ellas. En la segunda parte del experimento las sometían a un estímulo ambiguo: una mezcla 1:1 de ambos. Previamente, la mitad de las abejas habían sido sometidas a una circunstancia estresante. El resultado fue que las abejas estresadas eligieron en menor proporción el estímulo ambiguo que las no estresadas; en esencia, se volvieron más pesimistas.
¿Tienen las abejas consciencia?En resumen, las abejas disponen de un rico arsenal sensorial y son capaces de integrarlo para realizar tareas muy diversas. Pueden de recordar detalles del territorio que habitan y, posiblemente, tienen algún tipo de representación mental del mismo. Aprenden rápidamente, tienen conciencia del espacio que les rodea14, se comunican con otras y trabajan en equipo. Además, tienen memorias autobiográficas y las utilizan es su día a día. Aunque nadie duda que muchas de las capacidades de las abejas son innatas, también es evidente que una parte significativa de su conducta tiene que ser aprendida ¿Sería posible realizar este abanico de tareas cognitivas sin algún tipo de sensación subjetiva? Es evidente que su percepción del mundo es completamente diferente de la nuestra, pero creo que Chittka consigue armar un buen argumento en favor de que las abejas necesitan algún tipo de consciencia para sobrevivir. Se debe sentir algo al ser una abeja.
Referencias:1. Nagel T. WHAT IS IT LIKE TO BE A BAT? In: Journey into Philosophy: An Introduction with Classic and Contemporary Readings. ; 2016. doi:10.1017/s1477175616000336
2. Chittka L. The Mind of a Bee. Princeton University Press; 2022.
3. Laverty TM. Bumble bee learning and flower morphology. Anim Behav. 1994;47(3). doi:10.1006/anbe.1994.1077
4. Aurore AW, Mota T, Giurfa M. New vistas on honey bee vision. Apidologie. 2012;43(3). doi:10.1007/s13592-012-0124-2
5. Clarke D, Whitney H, Sutton G, Robert D. Detection and learning of floral electric fields by bumblebees. Science (80- ). 2013;340(6128). doi:10.1126/science.1230883
6. Robertson HM, Wanner KW. The chemoreceptor superfamily in the honey bee,. Genome Res. 2006;(16).
7. Menzel R, Greggers U, Smith A, et al. Honey bees navigate according to a map-like spatial memory. Proc Natl Acad Sci U S A. 2005;102(8). doi:10.1073/pnas.0408550102
8. Simpson J, von Frisch K. The Dance Language and Orientation of Bees. J Anim Ecol. 1969;38(2). doi:10.2307/2785
9. Su S, Cai F, Si A, Zhang S, Tautz J, Chen S. East learns from west: Asiatic honeybees can understand dance language of European honeybees. PLoS One. 2008;3(6). doi:10.1371/journal.pone.0002365
10. Ratnieks FLW. Honeybee Democracy. Anim Behav. 2011;82(1). doi:10.1016/j.anbehav.2011.02.020
11. Gallo V, Chittka L. Cognitive aspects of comb-building in the honeybee? Front Psychol. 2018;9(JUN). doi:10.3389/fpsyg.2018.00900
12. Perry CJ, Barron AB. Honey bees selectively avoid difficult choices. Proc Natl Acad Sci U S A. 2013;110(47). doi:10.1073/pnas.1314571110
13. Bateson M, Desire S, Gartside SE, Wright GA. Agitated honeybees exhibit pessimistic cognitive biases. Curr Biol. 2011;21(12). doi:10.1016/j.cub.2011.05.017
14. Ravi S, Siesenop T, Bertrand O, et al. Bumblebees perceive the spatial layout of their environment in relation to their body size and form to minimize inflight collisions. Proc Natl Acad Sci U S A. 2020;117(49). doi:10.1073/pnas.2016872117
Para saber más:
Qué puedes hacer tú para proteger a las abejas
Sobre el autor: Pablo Rodríguez Palenzuela es catedrático de Bioquímica en la Universidad Politécnica de Madrid y autor del libro “Cómo entender a los humanos” (Editorial Next Door, 2022).
El artículo La mente de una abeja se ha escrito en Cuaderno de Cultura Científica.
Cuadrados mágicos geométricos
Hace unos días estaba yo visitando el canal de YouTube del compositor minimalista estadounidense, afincado en París, Tom Johnson (Greeley, Colorado, EE.UU., 1939). En particular, estaba viendo algunos de sus videos de la serie Illustrated Music, en la que el compositor explica la manera en la que crea sus composiciones musicales utilizando conceptos matemáticos, como permutaciones, combinaciones, sucesiones numéricas, teselaciones rítmicas perfectas, el triángulo de Pascal, el problema de las estudiantes de Kirkman o diseños combinatorios, entre muchos otros (podéis leer las entradas Las vacas de Narayana, la versión hindú de los conejos de Fibonacci y Teselaciones rítmicas perfectas, para conocer las matemáticas que utiliza en dos de sus composiciones). En uno de los videos de la serie, el número 19, Tom Johnson explica su obra para guitarra Tinkelenberg Rhythms (2014) y cómo utiliza un cuadrado mágico geométrico, encontrado por el programador de software, mago matemático y creador de rompecabezas matemáticos holandés Frank Tinkelenberg, para realizar su composición musical.
 Portada y primera página de la composición para guitarra Tinkelenberg Rhythms (2014), de Tom Johnson. Imagen de la página Editions 75.
Portada y primera página de la composición para guitarra Tinkelenberg Rhythms (2014), de Tom Johnson. Imagen de la página Editions 75.
Si hablamos de “cuadrados mágicos geométricos”, se ponen en juego dos cuestiones. La primera es que estamos hablando de “cuadrados mágicos”, que están relacionados con los números, y la segunda es que el término “geométricos” nos indica que se están modificando los elementos que componen los cuadrados mágicos, ya no son números. Pero vayamos por partes.
Los cuadrados mágicos son unos objetos matemáticos que han cautivado a matemáticos y no matemáticos a lo largo de la historia. Se pueden encontrar, normalmente, en libros de divulgación de las matemáticas, de matemática recreativa o incluso de magia, pero también, en libros de ajedrez (como vimos en la entrada ¿Existen recorridos mágicos del caballo en el tablero de ajedrez?). Sobre ellos investigaron grandes matemáticos como el francés Pierre de Fermat (1607-1665) o el suizo Leonhard Euler (1707-1783), y hasta personalidades como el político, científico e inventor estadounidense Benjamin Franklin (1706-1790), se atrevieron con ellos. Los cuadrados mágicos ya se conocían desde la antigüedad (quizás más allá del año 2.200 a.n.e.), y se les relacionaba con los planetas y con la alquimia, con la magia y la astrología, con la numerología, y también se utilizaban para sanar o como amuletos.
Definición: Un cuadrado mágico de orden n es una distribución de los primeros n2 números sobre las casillas de un retículo cuadrado n × n, de forma que la suma de cada fila, cada columna y cada diagonal principal sea siempre la misma, la cual se conoce con el nombre de constante mágica.
Pero nada mejor que poner un ejemplo. El siguiente cuadrado mágico de orden 4 aparece en la obra Still Life with Magic Square / Naturaleza muerta con cuadrado mágico (2011) de la artista francesa Sylvie Donmoyer.
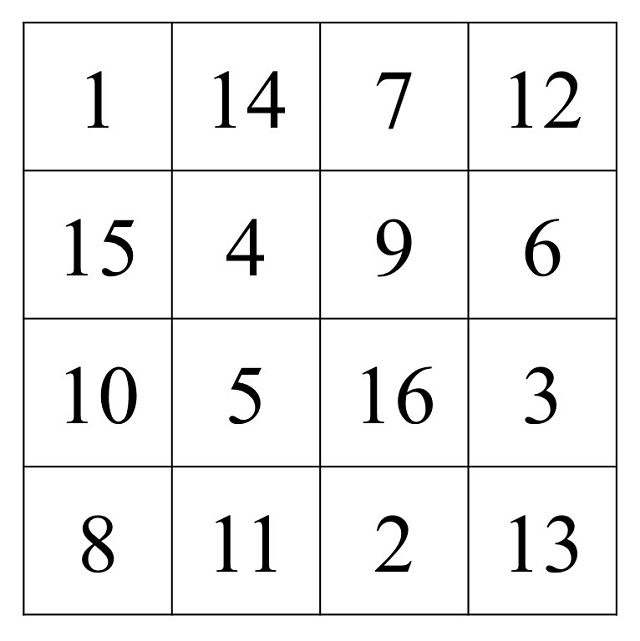
Como podemos observar la suma de los números de cada una de las cuatro filas {1, 14, 7, 12}, {15, 4, 9, 6}, {10, 5, 16, 3} y {8, 11, 2, 13}, de las cuatro columnas {1, 15, 10, 8}, {14, 4, 5, 11}, {7, 9, 16, 2} y {12, 6, 3, 13}, y de las dos diagonales principales {1, 4, 16, 13} y {8, 5, 9, 12}, es siempre la misma, 34, la constante mágica para el orden 4. Por lo tanto, la retícula cuadrada anterior es un cuadrado mágico de orden 4.
Pero este cuadrado mágico tiene más propiedades mágicas, ya que es lo que se denomina un cuadrado mágico pandiagonal (también llamados cuadrados perfectos o cuadrados panmágicos), es decir, que la suma de los números de las diagonales quebradas también es 34, como se muestra en la siguiente imagen (indicando las diagonales, en cada sentido, con colores).
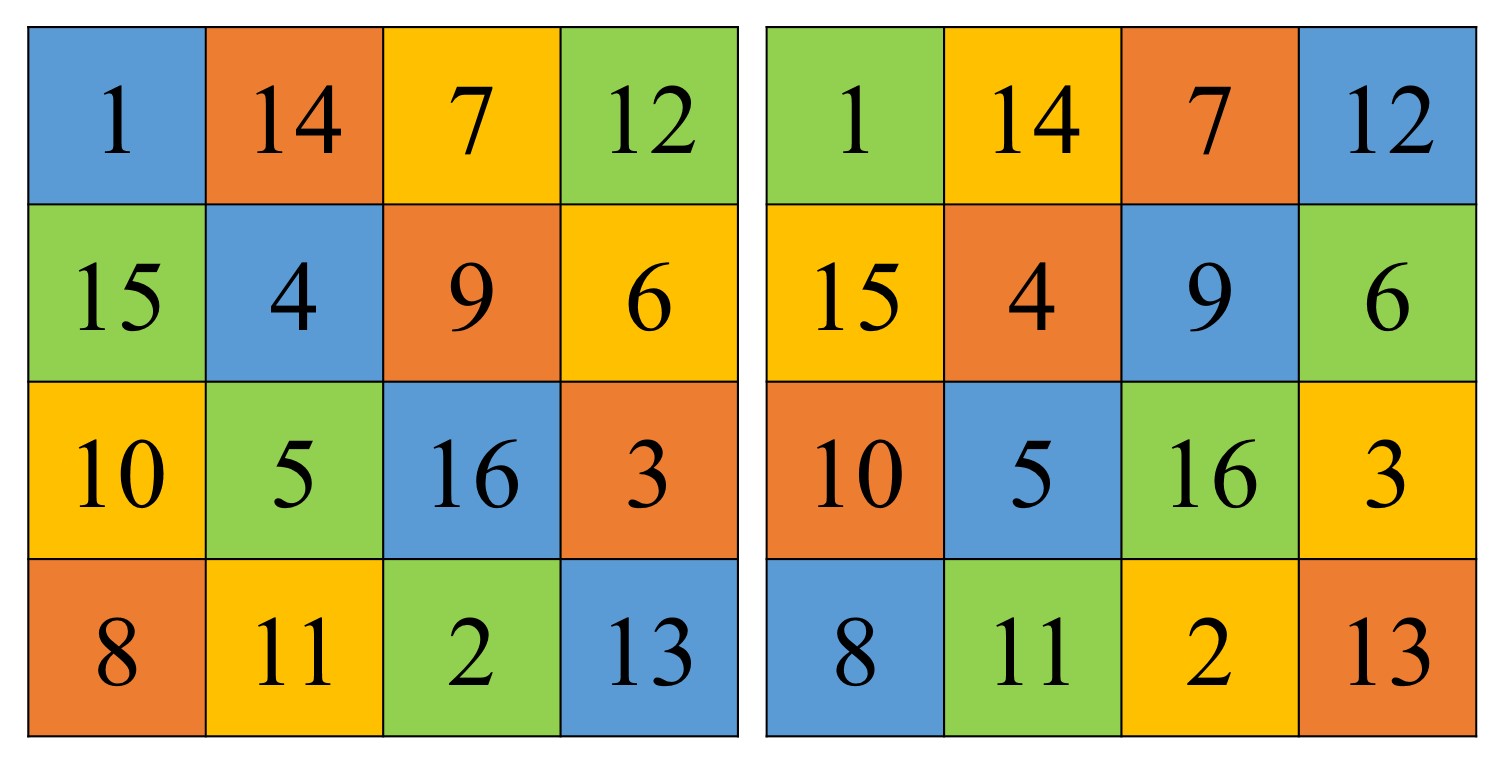
Pero aún tiene más propiedades mágicas. Veamos diferentes grupos de cuatro números que siguen sumando la constante mágica, 34. Un cuadrado mágico que cumplen todas estas condiciones (véase la siguiente imagen, en la que, de nuevo, se indica mediante colores los grupos de casillas cuya suma es 34) se dice que pertenece al grupo de cuadrados mágicos más perfectos.
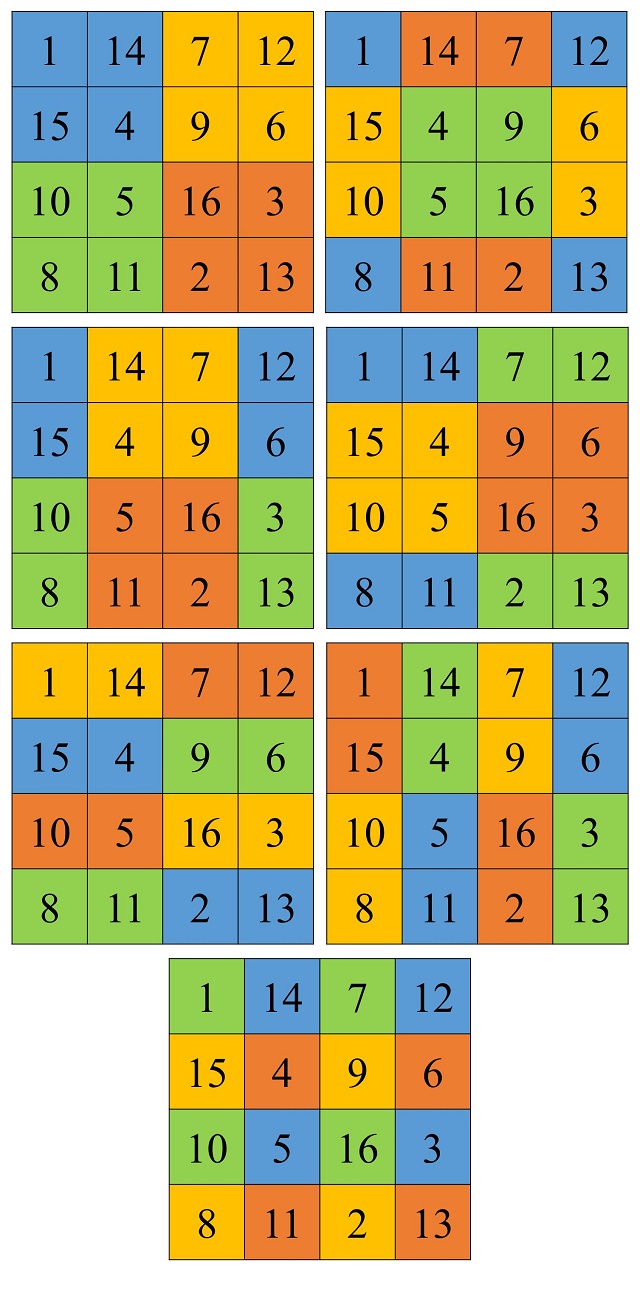
No nos olvidemos de disfrutar de la hermosa obra Still Life with Magic Square / Naturaleza muerta con cuadrado mágico (2011) de la artista Sylvie Donmoyer que recoge este cuadrado mágico.
 Still Life with Magic Square / Naturaleza muerta con cuadrado mágico (2011), de la artista francesa Sylvie Donmoyer, que ganó el primer premio de la exposición de Arte Matemático del congreso organizado en 2012 por la American Mathematical Society de su serie de congresos Joint Mathematics Meetings. Imagen de la página de Sylvie Donmoyer
Still Life with Magic Square / Naturaleza muerta con cuadrado mágico (2011), de la artista francesa Sylvie Donmoyer, que ganó el primer premio de la exposición de Arte Matemático del congreso organizado en 2012 por la American Mathematical Society de su serie de congresos Joint Mathematics Meetings. Imagen de la página de Sylvie Donmoyer
Este es un cuadrado mágico con muchos grupos de cuatro casillas sumando la constante mágica, en este caso, 34, que como se ha comentado son las condiciones para que un cuadrado mágico sea considerado del grupo de cuadrados mágicos más perfectos. Otro cuadrado mágico famoso es el que está en el cuadro Melancolia (1514) del artista alemán Alberto Durero (1471-1528), que, si os fijáis bien, aparece en la parte superior derecha del cuadro de Sylvie Donmoyer, y que es lo que se define como un cuadrado supermágico, ya que posee también muchos grupos de cuatro casillas que suman 34, algunos grupos compartidos con los cuadrados mágicos más perfectos y otros diferentes, aunque no es pandiagonal.
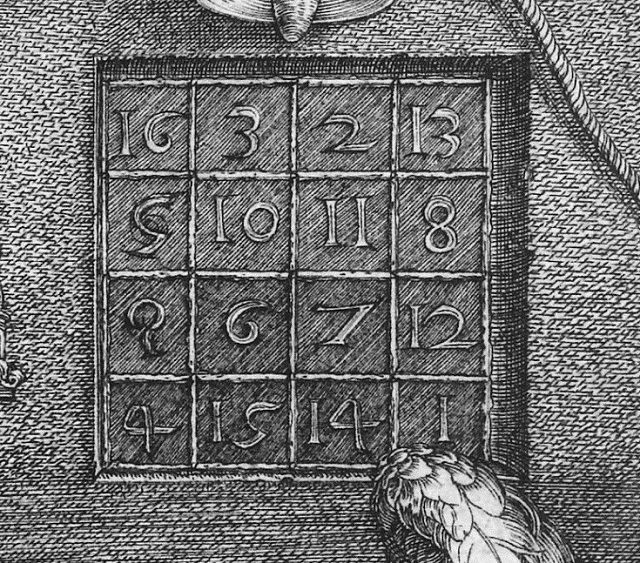 Cuadrado mágico (de hecho, supermágico) que aparece en la obra Melancolia (1514) del artista alemán Alberto Durero. Como curiosidad obsérvese que el año en el que se pintó el cuadro, 1514, aparece reflejado en el cuadrado mágico *1514
Cuadrado mágico (de hecho, supermágico) que aparece en la obra Melancolia (1514) del artista alemán Alberto Durero. Como curiosidad obsérvese que el año en el que se pintó el cuadro, 1514, aparece reflejado en el cuadrado mágico *1514
Pero volvamos a los objetos que son el centro de esta entrada del Cuaderno de Cultura Científica, los cuadrados mágicos geométricos, que fueron introducidos en 2001 por el ingeniero electrónico británico, apasionado de la matemática recreativa, Lee C. F. Sallows (1944). La idea base de estos objetos es sustituir los números en el concepto de cuadrado mágico por formas geométricas.
Para entender lo que son los cuadrados mágicos geométricos, empecemos por un ejemplo sencillo.
Definición: Un cuadrado mágico geométrico (también llamado cuadrado geomágico) de orden 3 está formando por una cuadrícula 3 x 3 de formas geométricas tales que se pueden unir las formas de cada fila, cada columna o cada diagonal principal para formar la misma figura geométrica, llamada forma objetivo.
Veamos un ejemplo en el que las figuras geométricas son poliominós y la forma objetivo es un cuadrado. Recordemos (de la entrada Embaldosando con L-triominós (Un ejemplo de demostración por inducción) que un poliominó es una figura geométrica plana formada conectando dos o más cuadrados por alguno de sus lados. Los cuadrados se conectan lado con lado, pero no se pueden conectar ni por sus vértices, ni juntando solo parte de un lado de un cuadrado con parte de un lado de otro. Si unimos dos cuadrados se obtiene un dominó, si se juntan tres cuadrados se construye un triominó, o trominó, con cuatro cuadrados se tiene un tetraminó (véase la entrada Tetris, embaldosados y demostraciones), con cinco un pentominó, y así se puede continuar para cualquier número de cuadrados.
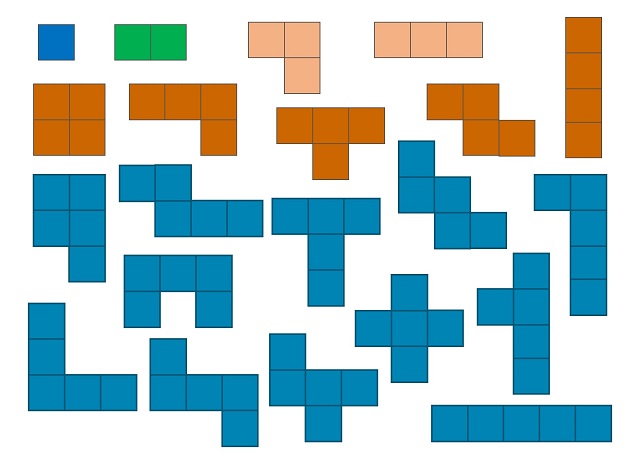 Todos los poliominós formados por 1, 2, 3, 4 o 5 cuadrados
Todos los poliominós formados por 1, 2, 3, 4 o 5 cuadrados
Volvamos al ejemplo de cuadrado mágico geométrico de orden 3 formado por poliominós (creado por Lee Sallows). El cuadrado mágico es el que aparece en la siguiente imagen.
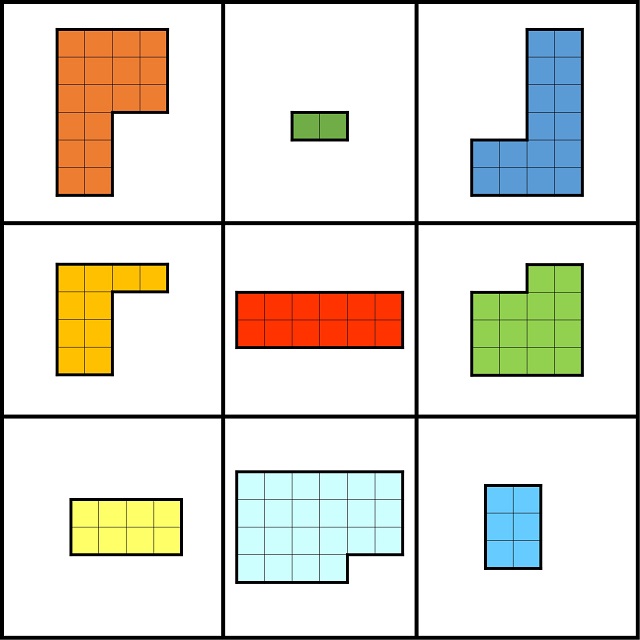
Lo forman 9 poliominós de 18, 2 y 16 cuadrados (la primera fila), de 10, 12 y 14 cuadrados (la segunda fila) y de 8, 22 y 6 cuadrados (tercera fila).
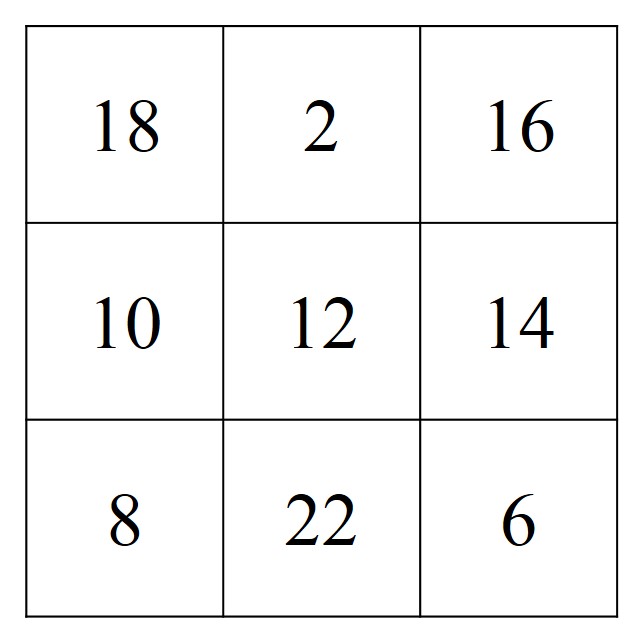
Una primera observación que podemos realizar, a partir de la definición que hemos dado, es la siguiente. Como la unión de las formas de cada fila, cada columna y cada diagonal principal es la misma (lo cual comprobaremos en breve), el número de cuadrados de todas esas uniones, que es la figura objetivo, tiene que ser la misma (de hecho, va a ser un cuadrado 6 x 6, que tiene 36 pequeños cuadrados), por lo tanto, el número de cuadrados de cada una de las figuras geométricas del retículo 3 x 3 forma un cuadrado mágico de orden 3, en sentido general, es decir, una colección de nueve números (no necesariamente los primeros nueve números) tales que la suma de las filas, las columnas y las diagonales principales es la misma. El cuadrado mágico asociado a este cuadrado mágico geométrico es el de la siguiente imagen, y su constante mágica es 36.
Pero veamos que efectivamente estamos ante un cuadrado mágico geométrico, mostrando la unión de cada fila, cada columna y cada diagonal principal. Para entender bien la siguiente imagen debemos de tener en cuenta dos cuestiones. La primera es que, a la hora de unir las piezas de una fila, columna o diagonal principal, las piezas pueden girarse e incluso voltearse (por ejemplo, las piezas de la tercera columna se juntan en la pieza de arriba y para ello se ha tenido que dar la vuelta a la pieza verde). Por otra parte, hemos colocado en los extremos de cada fila, columna o diagonal principal dos uniones de las tres piezas, que son una la imagen especular de la otra (como si volteamos la figura objetivo), lo cual es simplemente decorativo.
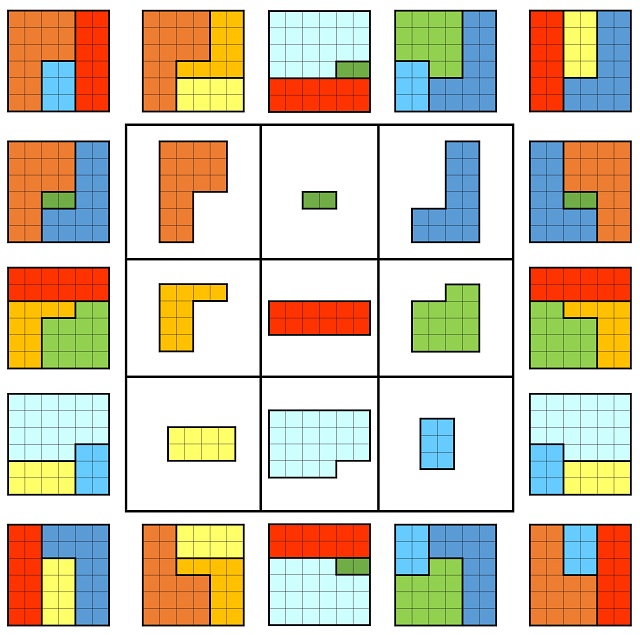
Mostremos un segundo ejemplo de cuadrado geomágico, de Lee Sallows, que aparece en un sello de Macao (China).
 Sello de Macao (China) que contiene un cuadrado mágico geométrico de orden 3 formado por poliominós y creado por Lee Sallows. Imagen de la página de Lee Sallows
Sello de Macao (China) que contiene un cuadrado mágico geométrico de orden 3 formado por poliominós y creado por Lee Sallows. Imagen de la página de Lee Sallows
El “cuadrado mágico” que subyace a este cuadrado mágico geométrico es trivial, ya que el número 5 está en todas las casillas.
A continuación, mostremos un ejemplo que no está formado por poliominós, sino por los análogos con triángulos equiláteros (que Lee Sallows llama cristales mágicos, pero se suelen llamar polidiamantes), y cuya forma objetivo es un hexágono. De hecho, vamos a mostrar dos cuadrados geomágicos complementarios. En concreto, cada grupo de piezas de un color, azul y marrón, forman un cuadrado mágico geométrico en sí mismas, pero, además, las piezas azul y marrón de cada casilla se juntan dando lugar a una pieza con la misma forma en todas las casillas.
 Cuadrados geomágicos de orden 3 complementarios formados por polidiamantes y cuya figura objetivo es un hexágono, creados por Lee Sallows. Imagen de la página de Lee Sallows
Cuadrados geomágicos de orden 3 complementarios formados por polidiamantes y cuya figura objetivo es un hexágono, creados por Lee Sallows. Imagen de la página de Lee Sallows
Para comprobar que efectivamente las figuras geométricas utilizadas son cristales mágicos vamos a mostrar el cuadrado mágico geométrico de las figuras marrones, pero dibujadas estas con sus triángulos equiláteros.
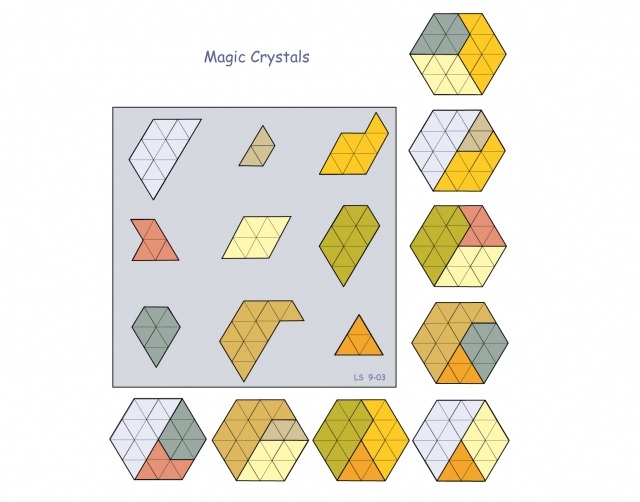 Imagen de la página de Lee Sallows
Imagen de la página de Lee Sallows
Os recomiendo que visitéis la página Geomagic Squares de Lee Sallows, que contiene una galería con 65 ejemplos de cuadrados geomágicos, algunos con curiosas propiedades. Así mismo, este autor ha publicado el libro Geometric Magic Squares: A Challenging New Twist Using Colored Shapes Instead of Numbers (Dover, 2013).
A continuación, vamos a mostrar un ejemplo de cuadrado mágico geométrico de orden 4, también de la página de Lee Sallows. Las figuras geométricas son de nuevo poliominós, más concretamente, cada línea mágica (fila, columna y diagonal principal) posee tres hexominós y un heptaminó, luego en total cada línea suma 6 x 3 + 7 = 25 cuadrados, que dan lugar a la figura objetivo, un cuadrado de tamaño 5 x 5, luego con 25 cuadrados.
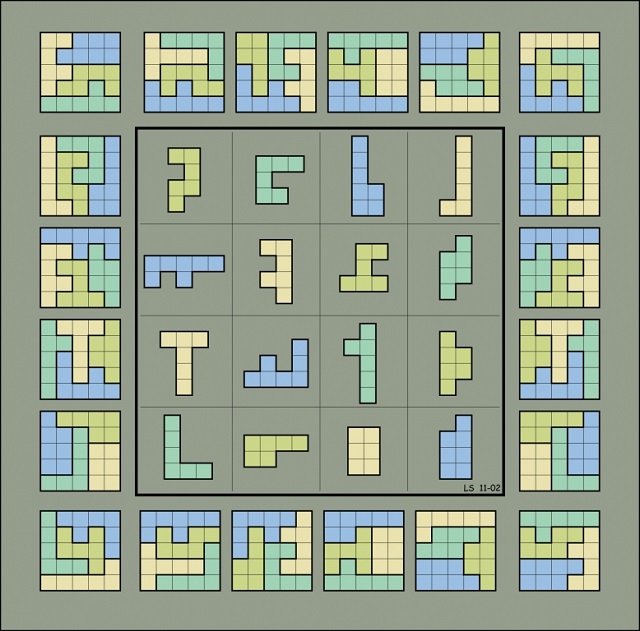 Cuadrado geomágico de orden 4, obtenido por ordenador, formado por poliominós y cuya figura objetivo es un cuadrado. Imagen de la página de Lee Sallows
Cuadrado geomágico de orden 4, obtenido por ordenador, formado por poliominós y cuya figura objetivo es un cuadrado. Imagen de la página de Lee Sallows
Una cuestión interesante es si existen cuadrados geomágicos de orden 2. Lo primero que podemos hacer es pensar si existen cuadrados mágicos (con números) de orden 2. Supongamos que nuestro cuadrado mágico de orden 2 está formado por los números A, B, C y D. Por ejemplo, si la primera fila A y B, y la segunda fila C y D, las condiciones para que sea un cuadrado mágico son A + B = C + D = A + C = B + D = A + D = C + B. Despejando estas ecuaciones se obtiene que A = B = C = D. Es decir, la única opción para que sea un cuadrado mágico es que sea trivial, con todas las entradas iguales.
Por lo tanto, las figuras geométricas utilizadas deben tener la misma cantidad de elementos básicos. El propio Lee Sallows, en la introducción sobre cuadrados geomágicos de su página Geomagic Squares, comentaba la dificultad de encontrar un ejemplo de cuadrado geomágico de orden 2. El primero, de 2011, se debe precisamente a Frank Tinkelenberg y se muestra en la siguiente imagen. Las cuatro figuras geométricas del cuadrado geomágico son la unión de 6 secciones de un polígono de 16 lados y la figura objetivo es el polígono de 16 lados, menos 4 secciones.
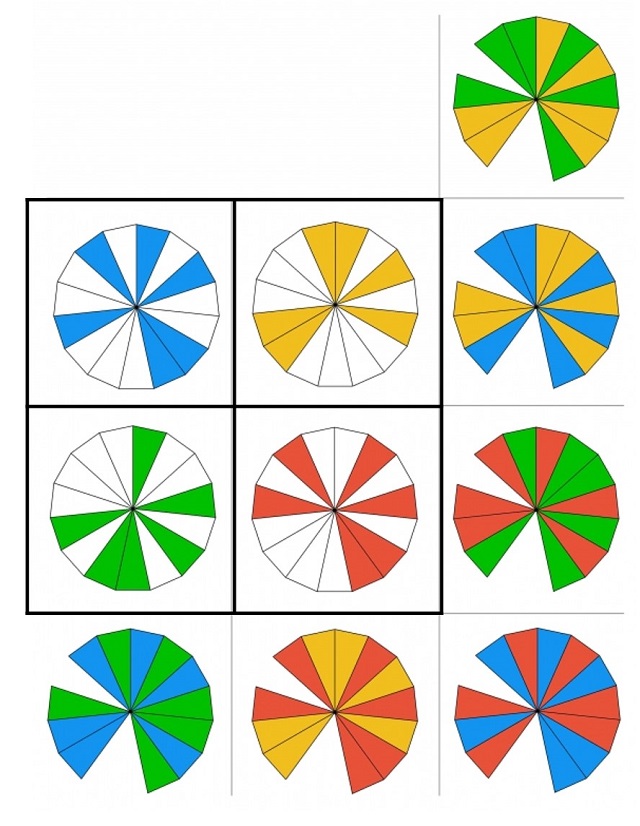 Cuadrado geomágico de orden 2, obtenido por Frank Tinkenlenberg. Imagen de la página de Lee Sallows
Cuadrado geomágico de orden 2, obtenido por Frank Tinkenlenberg. Imagen de la página de Lee SallowsVamos a finalizar esta entrada del Cuaderno de Cultura Científica con el cuadrado mágico geométrico de Frank Tinkelenberg, que utiliza el compositor Tom Johnson para crear su pieza para guitarra Tinkelenberg Rhythms (2014), que podéis escuchar como parte del proyecto Tom Johnson for Six (parte IV) en la página de Editions 75.
El cuadrado mágico geométrico de orden 3 de Frank Tinkelenberg (del año 2011) tiene 28 grupos de tres casillas con figuras geométricas cuya unión es la figura objetivo. Recordemos que para un cuadrado geomágico de orden 3 normal se tienen exactamente 8 grupos de tres casillas (3 filas, 3 columnas y 2 diagonales principales). Para empezar, la construcción de Tinkelenberg es un cuadrado mágico geométrico pandiagonal (o cuadrado pangeomágico), ya que las diagonales quebradas también generan la figura objetivo. Así ya son 8 + 4 = 12 grupos. El resto de grupos, 28 – 12 = 16, está formado por los grupos de tres figuras geométricas que se pueden elegir en cada uno de los cuatro sub-retículos cuadrados 2 x 2. Todos ellos se pueden ver en la siguiente imagen.
 Cuadrado geomágico de orden 3, obtenido por Frank Tinkenlenberg en 2011, que es pandiagonal, además de cumplir algunas condiciones adicionales (hasta 28 grupos de tres casillas distintas tales que la unión de sus figuras geométricas forma la figura objetivo). Imagen de la página de Lee Sallows
Cuadrado geomágico de orden 3, obtenido por Frank Tinkenlenberg en 2011, que es pandiagonal, además de cumplir algunas condiciones adicionales (hasta 28 grupos de tres casillas distintas tales que la unión de sus figuras geométricas forma la figura objetivo). Imagen de la página de Lee Sallows
Podéis entreteneros comprobando cada una de las 28 uniones de las figuras geométricas de las triadas de casillas mencionadas. Aunque, si os fijáis un poco podéis descubrir que aún hay alguna más. Según su creador, Frank Tinkelenberg, hay hasta 62 grupos distintos de tres casillas (de las C(9, 3) = 84 formas distintas de elegir tres casillas de las 9 que forman el retículo cuadrado), aunque eso yo ya no lo he comprobado.
Para finalizar, un ejemplo en el cual las figuras geométricas y la figura objetivo no son planas, sino tridimensionales. De hecho, las figuras geométricas con las que está formado el cuadrado mágico geométrico son policubos (como los poliominós, pero con cubos que se unen por sus caras) y la figura objetivo es un cubo 3 x 3 x 3 (luego formado con 27 cubos).
 Cuadrado geomágico de orden 3 formado por policubos y cuya figura objetivo es un cubo 3 x 3 x 3, creado por Lee Sallows. Imagen de la página de Lee Sallows
Cuadrado geomágico de orden 3 formado por policubos y cuya figura objetivo es un cubo 3 x 3 x 3, creado por Lee Sallows. Imagen de la página de Lee Sallows
Bibliografía:
1.- Tom Johnson, Finding Music Writtings – Schriften, MusikTexte, 2019.
2.- Lee Sallows, Geometric Magic Squares, Mathematical intelligencer, vol.33, n. 4, pp. 25-31, 2011.
3.- Lee Sallows, Geomagic Squares
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Cuadrados mágicos geométricos se ha escrito en Cuaderno de Cultura Científica.
Einstein y el comunismo
Einstein tenía unas ideas políticas muy claras y las expresaba sin ambages. No tenía miedo de prestar su apoyo a cualquier causa que pensara que mereciese la pena. Pero no le gustaba “pertenecer” a nada, por lo que permanecía en la periferia de cualquier grupo al que respaldase, a menudo criticándolo tanto como lo alababa. Si bien nunca fue miembro del partido comunista, sus ideas de izquierdas le hicieron frecuentar la compañía de numerosos grupos de tendencias comunistas.
 Primera página de un artículo de la revista Life del 5 de abril de 1949. Fuente: The Einstein File
Primera página de un artículo de la revista Life del 5 de abril de 1949. Fuente: The Einstein FileEinstein fue muy cuidadoso con sus filiaciones políticas. Se sabe que reusó unirse a ciertas organizaciones específicamente porque estaban regidas por lo que el interpretaba que era un ideario comunista y, sin embargo, es evidente que, al menos en el último tercio de su vida, estuvo claramente alineado con una visión marxista del mundo. En la Alemania de comienzos de los años treinta Einstein firmaba a menudo peticiones del Rote Hilfe Deutchlands (Socorro Rojo de Alemania, RHD; entidad de ayuda humanitaria dependiente del Partido Comunista de Alemania, KPD) y llegó a formar parte del consejo de administración de dos casas de acogida de menores del RHD, junto con otras personalidades alemanas como Thomas Mann. También fue conferenciante en el Marxistischen Arbeiterschule (Escuela de los trabajadores marxistas), también afiliada al KPD [1].
Su traslado a Estados Unidos no influyó en sus posiciones de izquierda. En mayo de 1949, escribió para Monthly Review (un medio socialista [2]) un artículo titulado “¿Por qué socialismo?” en el que describía los problemas que él veía en el mundo, desde el racismo a la pobreza, y cómo el socialismo podía representar una vía de solución (aquí el original en inglés). En él afirmaba:
“Estoy convencido de que hay solamente un camino para eliminar estos graves males: el establecimiento de una economía socialista, acompañado por un sistema educativo orientado hacia metas sociales. En una economía así, los medios de producción son poseídos por la sociedad y utilizados de una forma planificada. Una economía planificada que ajuste la producción a las necesidades de la comunidad, distribuiría el trabajo a realizar entre todos los capacitados para trabajar y garantizaría un sustento a cada hombre, mujer, y niño. La educación del individuo, además de promover sus propias capacidades naturales, procuraría desarrollar en él un sentido de la responsabilidad para sus compañeros-hombres en lugar de la glorificación del poder y del éxito que se da en nuestra sociedad actual.”
Unas afirmaciones que, en un tiempo de patriotismo exacerbado y en plena Guerra Fría, no estaban destinadas a ser del gusto de la opinión pública estadounidense, a pesar de la crítica velada a la Unión Soviética de su último párrafo:
“Sin embargo, es necesario recordar que una economía planificada no es todavía socialismo. Una economía planificada puede estar acompañada de la completa esclavitud del individuo. La realización del socialismo requiere solucionar algunos problemas sociopolíticos extremadamente difíciles: ¿cómo es posible, con una centralización de gran envergadura del poder político y económico, evitar que la burocracia llegue a ser todopoderosa y arrogante? ¿Cómo pueden estar protegidos los derechos del individuo y cómo asegurar un contrapeso democrático al poder de la burocracia?”
Este artículo atrajo la atención del FBI, que ya tenía un expediente sobre las actividades relacionadas con el comunismo de Einstein. El expediente había sido abierto por el FBI en 1932, con una denuncia de la Corporación Patriótica de Mujeres, antes incluso de que Einstein se mudase a Estados Unidos. La carta de denuncia había sido escrita por “la señora de Randolph Frothingham” [sic.] y enviada al Departamento de Estado (equivalente al Ministerio de Asuntos Exteriores). Muy bien escrita e inteligentemente organizada como un documento judicial, pero llena de información cuestionable, acusaba a Einstein de pertenecer a más organizaciones anarcocomunistas que Stalin o Trotsky, y de que deseaba destruir el gobierno de los Estados Unidos así como a “la iglesia americana”. Si bien la descripción de Einstein era tan incorrecta como demasiado dramática, llegó en un momento de la historia en el que la amenaza que suponía el espionaje soviético era algo muy real, por lo que la carta no fue despreciada por el FBI. Desde ese momento siempre consideró la posibilidad de que Einstein fuese un espía soviético.
Está claro que Einstein no era un espía. También es cierto que nunca ocultó sus simpatías hacia los partidos, asociaciones y personas de izquierdas. De hecho, defendió públicamente a los acusados por ser comunistas. Con tantas declaraciones públicas, un observador interesado en ver en él a un prosoviético tenía toda la munición necesaria. El número de la revista Life del 5 de abril de 1949 mostraba varias fotografías de personajes públicos que, según la revista, bien porque eran unos ingenuos o porque eran criptocomunistas, prestaban su imagen para disfrazar el monstruo comunista. Bajo el titular “Dupes and Fellow Travelers Dress Up Communist Fronts” (“Primos y compañeros de viaje disfrazan los frentes comunistas”) aparecía el retrato de Einstein en posición central [3].
Su asociación con los comunistas estadounidenses no implica que pensase que las políticas de la Unión Soviética no fuesen problemáticas. Los ataques de Stalin a los derechos humanos no pasaron desapercibidos para Einstein; y la angustiosa situación de los judíos en Rusia era una preocupación adicional. Por otra parte, por alguna razón, siguió percibiendo el gobierno de Stalin como menos maligno que el de Hitler. Muchos colegas se sentían asombrados y consternados por esto, y a pesar de sus esfuerzos por convencerle, Einstein nunca igualó los dos regímenes.
El expediente del FBI afirma que Einstein estuvo relacionado con 34 frentes comunistas entre 1937 y 1954 y que era consejero honorario de 3 de ellos. Si bien el concepto de frente comunista empleado por el FBI por aquella época era muy amplio, y considerando que el número real no fuese tan alto, Einstein claramente tenía conexiones con organizaciones que, a su vez, mantenían relaciones con el Partido Comunista. Sin embargo, no parece que tuviese más que otras personalidades significadas políticamente en aquella época.
Notas:
[1] Como no podía ser de otra manera, su conferencia se tituló “Lo que un obrero debería saber sobre la teoría de la relatividad”.
[2] Hay que ser conscientes del contexto y no juzgar el pasado con criterios del presente: el socialismo era en esta época marxista, no socialdemócrata. Por ejemplo, el PSOE mantuvo su definición marxista fundacional hasta el congreso extraordinario de 1979.
[3] “Communist front”, frente comunista, era el término usado por el partido Comunista de los Estados Unidos, CPUSA, para referirse a las organizaciones relacionadas con el Komintern, la Internacional Comunista.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 25 de julio de 2010
El artículo Einstein y el comunismo se ha escrito en Cuaderno de Cultura Científica.
Pero, entonces, ¿de dónde vino el agua de Marte?
Aunque pueda sorprenderles -o cuanto menos parecerles duplicado el título del artículo- lo cierto es que hace apenas dos semanas hablábamos en este mismo espacio sobre como el uso de técnicas como los rayos X o la imagen con neutrones podrían ayudarnos a estudiar de dónde vino el agua de nuestro planeta al mostrarnos las regiones de los meteoritos con mayor contenido en esta, especialmente en minerales hidratados, y de ahí tomar muestras para su análisis con una mayor precisión.
Pero no toda el agua del Sistema Solar se encuentra en nuestro planeta, ni mucho menos, y sin duda, uno de los planetas de los que más nos interesa conocer su historia por sus fuertes implicaciones geológicas y también astrobiológicas es Marte, especialmente porque sabemos que hubo masas de agua estable en su superficie durante periodos prolongados – quizás incluso durante los mil primeros millones de años de existencia- y porque quizás responder a la pregunta sobre el origen de su agua nos ayude a comprender mejor de donde pudo venir la de la Tierra ya que, al fin y al cabo, ambos son planetas rocosos y podría haber ciertas similitudes en el modo de llegada de esta a los planetas interiores.
 Imagen del meteorito ALH84001, encontrado en la Antártida en el año 1984 en la zona de Allan Hills. De lado a lado mide unos 9 centímetros. Imagen cortesía de NASA/JSC/Stanford University.
Imagen del meteorito ALH84001, encontrado en la Antártida en el año 1984 en la zona de Allan Hills. De lado a lado mide unos 9 centímetros. Imagen cortesía de NASA/JSC/Stanford University.En un nuevo estudio -publicado el pasado día 16 de noviembre- un equipo formado por científicos de las universidades de Copenhague, Paris, Zúrich y Bern han analizado 31 meteoritos marcianos, entre ellos el famoso ALH84001, que en 1996 saltó a la fama por las posibles formas de vida que había descubierto un equipo de investigadores de la NASA y que a día de hoy siguen siendo cuestionadas.
Como decíamos en el anterior artículo, el origen del agua en los planetas sigue también bajo una gran controversia, pero por norma general se aceptaba que el agua de las superficies planetarias y sus atmósferas venía principalmente de la degasificación fruto del enfriamiento y actividad volcánica de estos y que, de algún modo, esta agua venía ya incluida en la receta de la formación planetaria.
 Así podría haber lucido Marte con un gran océano boreal, sumando el agua interna más la aportada por los impactos de meteoritos. Cortesía de NASA’s Goddard Space Flight Center.
Así podría haber lucido Marte con un gran océano boreal, sumando el agua interna más la aportada por los impactos de meteoritos. Cortesía de NASA’s Goddard Space Flight Center.Pero este nuevo artículo parece sugerir justo lo contrario -al menos en el caso de Marte- y es que la mayor parte del agua habría llegado al planeta tras su formación, especialmente a partir de condritas carbonáceas, un tipo de meteoritos ricos en carbono, pero que también pueden contener un alto porcentaje en agua y provenientes del Sistema Solar exterior, donde los volátiles podrían condensarse con una mayor facilidad, formando parte de los cuerpos que posteriormente impactarían contra los planetas, especialmente en las primeras etapas del Sistema Solar tras su formación, donde las colisiones fueron un fenómeno muy habitual y como atestiguan las superficies de los cuerpos que menos han cambiado, como la Luna o Mercurio.
¿Cómo han llegado a esta conclusión? Pues gracias al estudio de las concentraciones de dos isótopos del cromo, el cromo-54 y el cromo-53, en los meteoritos marcianos, y comparándolas con las de las condritas carbonáceas, observando que las ratios isotópicas en ambos son muy parecidas, por lo que la fuente de el cromo-54, muy raro en Marte, podría provenir de este tipo de meteoritos.
Calculando aproximadamente un 10% de contenido en agua en las condritas carbonáceas, y haciendo un balance de cuantos impactos fueron necesarios para conseguir estos ratios isotópicos que observamos en los meteoritos marcianos, los científicos han calculado que a través del impacto de meteoritos que proviniesen del exterior del Sistema Solar podría haberse formado una capa de agua de más de 300 metros de profundidad que cubriese todo el planeta (si fuese llano, claro), a lo que habría que sumarle el agua que si se habría formado por el enfriamiento del planeta y la actividad volcánica, pudiendo llegar a formar océanos de hasta 1.5 kilómetros de profundidad.
Aunque este estudio es muy interesante, todavía quedaría por calcular los porcentajes de las aguas con diferente procedencia que han existido en Marte, aunque está claro que el agua llegada tras la formación del planeta es un porcentaje significativo.
No cabe la menor duda que el estudio de los meteoritos y las mejores técnicas analíticas que van surgiendo, nos van a posibilitar el descifrar, aunque sea paso a paso, la historia del agua en nuestro Sistema Solar.
Referencias:
Zhu, K. et al. (2022) Late delivery of exotic chromium to the crust of Mars by water-rich carbonaceous asteroids Science Advances, 8(46). doi: 10.1126/sciadv.abp8415.
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Pero, entonces, ¿de dónde vino el agua de Marte? se ha escrito en Cuaderno de Cultura Científica.
El entorno político puede afectar seriamente a su salud
 Foto: Isai Ramos / Unsplash
Foto: Isai Ramos / UnsplashLa frase que encabeza estas líneas resume las conclusiones de un estudio realizado en Estados Unidos que ha publicado hace unos meses The British Medical Journal. Las consecuencias son obvias, porque si se deteriora su salud a causa de las condiciones sociopolíticas, vivirá peor. Además, como la salud también determina la probabilidad de fallecimiento, una salud peor puede dar lugar a que aumente la probabilidad de que usted muera.
En el estudio en cuestión se analizó la variación, desde 2001 hasta 2019, de la probabilidad de fallecer relacionando la tendencia con el color político del condado de residencia y una serie de variables demográficas con efectos demostrados sobre la salud. Considerados los datos en su conjunto, la tasa de mortalidad en los EEUU en 2001 fue de 850 personas por cada cien mil habitantes en los condados que habían votado candidatos demócratas en las anteriores elecciones presidenciales y de 867 en los que habían votado candidatos republicanos. En 2019 esas tasas fueron, respectivamente, 664 y 771. El equipo investigador comprobó que los resultados eran los mismos si, en vez del resultado de las elecciones presidenciales, se consideraba el partido del gobernador del Estado.
Es más probable morir en un condado republicano que en uno demócrata, la mortalidad ha disminuido en las últimas dos décadas, pero la diferencia entre los condados de uno y otro color ha aumentado con el tiempo. En términos estrictos, la mera existencia de asociación no permite hablar de relación causal, por supuesto, pero sería realmente extraño que tal relación no existiese. Los cambios en la mortalidad se produjeron debido, fundamentalmente, a la reducción de las enfermedades cardíacas, el cáncer y los accidentes cerebrovasculares, que son, precisamente, los males causantes de un mayor número de muertes.
Los autores del estudio sugieren que las diferencias observadas entre condados demócratas y republicanos pueden deberse a las diferentes políticas que se aplican en los estados en que se encuentran los condados. En estudios anteriores, a las políticas más “liberales” (en la jerga política norteamericana, liberal es lo que en Europa denominamos “progresista”) en materia de control del tabaco, trabajo, inmigración, derechos civiles y protección ambiental se han asociado, estadísticamente, una esperanza de vida más larga, mientras que se ha asociado una menor esperanza de vida a las políticas más conservadoras, como las restricciones al aborto y un menor control del uso de armas de fuego.
El entorno político también influye en otros elementos, como la prodigalidad del estado de bienestar en lo relativo a asuntos tales como el alcance de los seguros de desempleo o las ayudas a familias necesitadas. Dado que los estados se diferencian en ese tipo de materias, tanto la mortalidad como las tendencias de reducción observadas se pueden ver afectadas por el entorno político. Los estados más progresistas suelen implantar medidas de salud pública –como mayores coberturas para familias de pocos ingresos– que actúan como una red de seguridad para las poblaciones vulnerables. El acceso a la atención primaria y preventiva también es más amplio en esos estados, lo que mejora la identificación y tratamiento de enfermedades crónicas y, como consecuencia, la supervivencia. Igualmente, el gasto en salud suele ser más alto en los estados con gobernadores demócratas.
Este estudio se ha basado en el 98% de la población norteamericana. Sus conclusiones son muy sólidas. Y no limitan su valor a los Estados Unidos; son de interés también para los países en que las políticas sanitarias son competencia de las regiones, estados federales o comunidades autónomas. Diría que, en estos tiempos, España es uno de esos países.
Fuente: Warraich H J, Kumar P, Nasir K, Joynt Maddox K E, Wadhera R K. Political environment and mortality rates in the United States, 2001-19: population based cross sectional analysis BMJ 2022; 377: e069308 doi:10.1136/bmj-2021-069308
Para saber más:
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El entorno político puede afectar seriamente a su salud se ha escrito en Cuaderno de Cultura Científica.
Inma Hernáez Rioja – Voces sintéticas personalizadas
¿Es posible reemplazar nuestra voz? Aunque parezca una utopía, los avances tecnológicos invitan a pensar que las personas que pierden su voz puedan recobrarla en un futuro y volver a comunicarse a través de voces sintéticas.
 Foto: Jason Rosewell / Unsplash
Foto: Jason Rosewell / UnsplashEl sistema de voces sintéticas es un método más habitual de lo que parece. Las voces artificiales han ido apareciendo los últimos años en diferentes servicios: en el aeropuerto anunciando los próximos vuelos, en la atención de llamadas telefónicas a determinadas compañías o en las indicaciones del navegador. En muchos casos parecen tan naturales que ni nos hemos planteado la opción de que se trate de voces sintéticas. Pero, ¿qué ocurriría si nosotros perdiéramos nuestra voz? ¿Nos atreveríamos a usar esta tecnología para comunicarnos? ¿Sería posible?
Estas cuestiones son a las que trata la ingeniera Inma Hernáez Rioja en la charla “Voces sintéticas personalizadas para dar la palabra a quienes han perdido la voz”, que tuvo lugar el 21 de abril de 2021 en la Biblioteca Bidebarrieta de Bilbao. La charla se enmarca en el ciclo de conferencias Bidebarrieta Científica, impulsada por la Cátedra de Cultura Científica de la UPV/EHU y la Biblioteca Bidebarrieta.
Inma Hernáez Rioja es directora del Aholab Signal Processing Laboratory, especializado en el proceso digital de la voz y creador del sistema de síntesis de voz para el euskera AhoTTS. Inma Hernáez Rioja estudió Ingeniería de Telecomunicación en la Universidad Politécnica de Catalunya y en 1987 se incorporó como profesora en la Escuela de Ingeniería de Bilbao para colaborar en la implantación de la titulación de Ingeniería de Telecomunicación en la UPV/EHU. Profesora e investigadora, es catedrática de Teoría de la Señal y Comunicaciones en la Universidad del País Vasco.
Sus líneas de investigación en Aholab Signal Processing Laboratory incluyen técnicas de síntesis, conversión y transformación de la voz; la aplicación de las tecnologías del habla (reconocimiento, verificación, evaluación de la pronunciación) en la enseñanza de segundas lenguas; y el desarrollo de estrategias que permitan el aprovechamiento de las tecnologías del habla por personas con discapacidades.
Edición realizada por César Tomé López
El artículo Inma Hernáez Rioja – Voces sintéticas personalizadas se ha escrito en Cuaderno de Cultura Científica.
El perro de Erralla es uno de los más antiguos encontrados en Europa
El perro es la primera especie domesticada por los humanos, aunque el origen geográfico y temporal de la domesticación del lobo es aún objeto de debate. En 1985, en una excavación dirigida por Jesus Altuna en la cueva de Erralla (Zestoa, Gipuzkoa), se recuperó un húmero casi completo de un cánido, una familia de carnívoros que abarca lobos, perros, zorros y coyotes, entre otros. En aquel momento era difícil identificar a qué especie de cánido pertenecía.
 Húmero de Erralla. Fuente: UPV/EHU
Húmero de Erralla. Fuente: UPV/EHUAhora el equipo de Biología Evolutiva Humana de la Universidad del País Vasco, que dirige la profesora Conchi de la Rúa, ha realizado un estudio en profundidad del resto óseo. El análisis morfológico, radiométrico y genético realizado ha permitido confirmar la identificación genética de la especie como Canis lupus familiaris (perro doméstico). La datación directa del húmero mediante carbono-14 le otorga una antigüedad de entre 17.410 y 17.096 años antes del presente (los resultados obtenidos se ajustan teniendo en cuenta los cambios en la concentración global de radiocarbono a través del tiempo). Esto es, el perro de Erralla vivió en el periodo Magdaleniense del Paleolítico Superior, lo que le sitúa como uno de los perros domésticos más antiguos encontrados hasta el momento en Europa.
 Reproducción artística del posible aspecto de un perro paleolítico. Fuente: Dinopedia
Reproducción artística del posible aspecto de un perro paleolítico. Fuente: DinopediaEl perro de Erralla comparte el linaje mitocondrial con los escasos perros magdalenienses analizados hasta ahora. El origen de este linaje se vincula a un periodo de clima frío coincidente con el Último Máximo Glacial, que ocurrió en Europa hace unos 22.000 años. “Estos resultados plantean la posibilidad de que la domesticación del lobo se produjera antes de lo que se había propuesto hasta ahora, al menos en Europa occidental, donde la interacción de los cazadores-recolectores paleolíticos con especies salvajes, como el lobo, pudo verse potenciada en las áreas de refugio glacial (como el Franco-Cantábrico) durante este periodo de crisis climática”, explica de la Rúa.
Para saber más:
La evolución de los perros
Domesticados
Origen y legado genético de los perros prehistóricos
Referencia:
M. Hervella, A. San-Juan-Nó, A. Aldasoro-Zabala, K. Mariezkurrena, J. Altuna, C. de-la-Rua (2022) The Domestic dog that lived ~17,000 years ago in the Lower Magdalenian of Erralla site (Basque Country): A Radiometric and Genetic Analysis Journal of Archaeological Science: Reports doi: 10.1016/j.jasrep.2022.103706
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo El perro de Erralla es uno de los más antiguos encontrados en Europa se ha escrito en Cuaderno de Cultura Científica.
Tablas de colores con chinchetas doradas
Hace unos días, la Comisión Internacional de Estratigrafía (ICS por sus siglas en inglés), perteneciente a la Unión Internacional de Ciencias Geológicas (IUGS, también por sus siglas en inglés), publicó la última actualización de la Tabla Cronoestratigráfica Internacional (ICC para no abandonar el inglés).
Dejando el párrafo redactado de esta manera, es probable que hayáis entendido aproximadamente una cuarta parte de lo que he escrito, pero suena como algo muy importante. Pues lo he hecho a posta, ya que, para todas las personas que nos dedicamos a la Geología, realmente esto es de vital importancia.
 Última versión de la Tabla Cronoestratigráfica Internacional, actualizada en octubre de 2022, en inglés. Créditos: International Commission on Stratigraphy. Disponible para su descarga gratuita, así como las versiones previas traducidas, aquí.
Última versión de la Tabla Cronoestratigráfica Internacional, actualizada en octubre de 2022, en inglés. Créditos: International Commission on Stratigraphy. Disponible para su descarga gratuita, así como las versiones previas traducidas, aquí.La Tabla Cronoestratigráfica Internacional es el pilar fundamental en el que se sustentan todas nuestras investigaciones, ya que se trata de la tabla de los tiempos geológicos unificada para todo el mundo. Y, sin el concepto tiempo, no se puede hacer nada en Geología. Cuando queremos describir algún proceso, estructura, material o evento geológico hay que especificar cuándo pasó, es decir, darle una edad, ya sea absoluta (numérica, por ejemplo, esto ocurrió hace 20 millones de años) o relativa (relacionando eventos de acuerdo a su temporalidad, por ejemplo, esto sucedió antes de que se extinguieran los trilobites) para poder situarlo en la historia geológica de nuestro planeta.
Antiguamente, cada país construía sus propias escalas de tiempo para reflejar la historia geológica de su territorio. Pero cuando querían comparar estos resultados con otros países vecinos, aparecían los problemas. Lo que en un lado habían definido como una de sus divisiones temporales, con un rango de edad concreto y un nombre determinado, no tenía nada que ver con las divisiones que habían definido en otra parte del mundo y ya no sabían ni de lo que estaban hablando.
Para solucionar esta “pequeña eventualidad” surgió la ICS en el seno de la IUGS, convirtiéndose en la institución responsable de unificar todas las divisiones temporales de la historia geológica de nuestro planeta para que pueda ser empleada, de manera unánime, por todos los servicios geológicos mundiales. Así es como nació la primera Tabla Cronoestratigráfica Internacional, que cada año se va afinando y corrigiendo sobre la marcha de acuerdo a los últimos avances geológicos.
Si nos fijamos en la última versión de la tabla de los tiempos geológicos, vemos que se trata de una especie de columna que ordena la historia geológica de la Tierra desde su formación, hace aproximadamente 4600 millones de años, hasta la actualidad y que presenta varias divisiones y subdivisiones (sí, como en cualquier otra ciencia, en Geología nos encanta subdividirlo todo hasta la saciedad). Pero hay tres aspectos que centran un poco más nuestra atención:
1- Todas las divisiones, por pequeñas que sean, tienen un nombre que no se repite y que, independientemente del idioma al que lo traduzcamos, comparte siempre la misma raíz, adaptando únicamente la terminación de la palabra. Por ejemplo, Cretaceous en inglés es Cretácico en castellano, mientras que Cenomanian lo traducimos como Cenomaniense.
2- Cada división presenta un color característico y que tampoco se repite. Estos colores no están puestos al azar para que quede más bonita, sino que responden a un código consensuado internacionalmente dentro de la Comisión del Mapa Geológico Mundial (para seguir con los anglicismos, la CCGM). Es decir, este código de colores es el que se utiliza en cualquier mapa geológico que se realice en todo el mundo para representar los materiales de esa determinada edad, de tal manera que, con un simple vistazo, podamos situarnos geológicamente hablando allí donde vayamos. Así, el Cretácico siempre se pintará en tonos vedes, ya sea un mapa del País Vasco o de California.
3- Por último, en cada división aparece un número al lado que representa la edad, en millones de años con respecto a la actualidad, en la que empieza. Y, si nos fijamos con detalle, podemos ver que en muchos de esos comienzos hay dibujada una especie de chincheta de color amarillo, que son las que van a merecer toda mi atención a partir de ahora.
 Clavos dorados de la playa de Itzurun, Zumaia. A) Límite del Selandiense; B) límite del Thanetiense.
Clavos dorados de la playa de Itzurun, Zumaia. A) Límite del Selandiense; B) límite del Thanetiense.Este símbolo indica que para el comienzo de la subdivisión junto a la que se encuentra se ha definido una Sección Estratotipo y Punto de Límite Global (GSSP, de nuevo en inglés). Con este nombre tan sencillo se define a aquella sección geológica que representa el mejor afloramiento en el que se registra el límite entre dos de las subdivisiones menores de la tabla de tiempos geológicos, los Pisos o Edades, y que sirve de referencia a nivel mundial. Y, para que quede constancia de su importancia y señalarla sobre las demás secciones, se coloca un clavo dorado en las rocas marcando el punto concreto del límite y una placa identificativa a su lado.
El origen de esta tradición procede de una puesta en escena muy estadounidense. Cuando en 1869 la Union Pacific y la Central Pacific unieron sus vías para crear el primer ferrocarril transcontinental de Estados Unidos, se realizó una ceremonia donde se colocó un último clavo de oro, que obviamente fue rápidamente retirado y sustituido por uno normal en cuanto se fueron los medios de comunicación.
Pues la ICS emula esa ceremonia actualmente al declarar una nueva sección tipo de referencia. Pero colocando un clavo de acero inoxidable con un baño de pintura dorada, nada de oro de verdad. Por eso los denominamos Clavos Dorados o Golden Spykes.
En España podemos encontrar cinco de esos clavos dorados: uno en Fuentelsaz (Guadalajara) marcando el comienzo del Aaleniense; otro en Olazagutía (Navarra) que señala la base del Santoniense; dos en Zumaia (Gipuzkoa) indicando los inicios del Selandiense y del Thanetiense; y uno en Gorrondatxe (Bizkaia) en el comienzo del Luteciense.
 Ceremonia de colocación del clavo dorado marcando la base del Luteciense en la playa de Gorrondatxe, con las autoridades de la ICS-IUGS y el personal investigador de la Universidad del País Vasco y la Universidad de Zaragoza, gracias a cuyos trabajos se pudieron conseguir la declaración de sección tipo. Imágenes cedidas por Estíbaliz Apellaniz, Catedrática jubilada de Paleontología de la UPV-EHU.
Ceremonia de colocación del clavo dorado marcando la base del Luteciense en la playa de Gorrondatxe, con las autoridades de la ICS-IUGS y el personal investigador de la Universidad del País Vasco y la Universidad de Zaragoza, gracias a cuyos trabajos se pudieron conseguir la declaración de sección tipo. Imágenes cedidas por Estíbaliz Apellaniz, Catedrática jubilada de Paleontología de la UPV-EHU.Como la Geología es una ciencia viva cuyos avances se producen de manera continua, os aseguro que, en unos meses, veréis algunos cambios en la tabla de tiempos geológicos. Pero eso es lo divertido de la investigación, tener que ir evolucionando al momento.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Tablas de colores con chinchetas doradas se ha escrito en Cuaderno de Cultura Científica.
Cecily Tanner, la desconocida matemática de la familia Young
Desde la infancia sufrió problemas de audición, que se hicieron más graves con los años y restringieron sus contactos fuera de su familia, aunque aprendió a leer los labios y tuvo muchos amigos, especialmente entre sus compañeros matemáticos.
 Cecily Young (situada a la izquierda, en segunda fila) en el Congreso Internacional de Matemáticos de Zúrich de 1932. Imagen: Wikimedia Commons.
Cecily Young (situada a la izquierda, en segunda fila) en el Congreso Internacional de Matemáticos de Zúrich de 1932. Imagen: Wikimedia Commons.
Rosalind Cecilia Hildegard (Cecily) Young nació el 15 de febrero de 1900 en Gotinga (Alemania). Era una de las seis hijas e hijos de los matemáticos británicos William Henry Young y Grace Emily Chisholm.
Aprendiendo matemáticas al estilo YoungLa madre de Cecily, Grace Chisholm Young (1868-1944), trabajó en Gotinga bajo la tutela de Felix Klein. Se doctoró en 1895 con una tesis sobre grupos algebraicos en trigonometría esférica. Y tuvo que regresar a Inglaterra, su país natal, para cuidar de sus padres de avanzada edad. Grace se casó en junio de 1986 con William Henry Young (1863-1942) que había sido su tutor durante un trimestre en Cambridge.
En 1897, Felix Klein llegó a Cambridge para recibir un título honorífico y animó al matrimonio a viajar a Gotinga para proseguir sus investigaciones. El primer hijo de Grace y William (Francis) nació en junio de 1897. Y, en septiembre, desanimados por la manera en la que se orientaba la enseñanza en su país, los Young se desplazaron a Gotinga, aceptando la invitación de Klein. En septiembre de 1899 nació Cecily. Los otros cuatro hijos del matrimonio también nacieron en Gotinga: Janet Dorothea Ernestine (1901), Helen Marian Kinnear (1903), Laurence (1904, que también se dedicó con éxito a las matemáticas) y Patrick (1908).
En 1905 Grace y William publicaron el libro First book of geometry, que Godfrey Harold Hardy describía de este modo en el obituario de Young:
El libro es un auténtico «libro para niños» de un tipo muy interesante y original. La idea central es que se debe motivar a los niños a pensar en objetos geométricos en tres dimensiones, a pensar en un plano, por ejemplo, como un límite de un sólido, y en una recta como una intersección de dos planos, o como un pliegue en uno de ellos. No soy una autoridad en esta materia, pero debería haber pensado que la idea era sensata, y que un libro basado en ella debería ser más concreto y más estimulante, para la mayoría de los estudiantes, que los del patrón más convencional y abstracto. Los autores, sin embargo, estaban pidiendo demasiado a los profesores ingleses. Parecía que no podían, o no querían, doblar el papel, y el libro no tuvo éxito en Inglaterra. Tuvo mucho más éxito en el extranjero, ha sido traducido al alemán, italiano, húngaro y sueco, y utilizado con éxito en las escuelas alemanas.
Con estas ideas como guía, Grace y William iniciaron a sus hijas e hijos en el aprendizaje de las matemáticas. Grace escribió otros dos libros infantiles para interesar a su prole por la ciencia: Bimbo (1906) y Bimbo and the Frogs (1907); Bimbo era el nombre familiar de su hijo mayor, Frank.
Traductora, investigadora e historiadoraEn 1908 la gran familia se mudó a Ginebra. La mayor parte del tiempo Young estaba lejos de casa, ocupando diferentes puestos docentes y de gestión en Gran Bretaña. Así, Grace se ocupaba de educar a sus hijas e hijos ella sola.
La familia se mudó a Lausana en 1915. Tras completar sus últimos años de educación secundaria, en 1917, Cecily ingresó en la Universidad de Lausana. En ese momento, Young fue nombrado profesor de matemáticas puras en Aberystwyth (Gales). Aunque matriculada en Lausana, durante gran parte de los cuatro años de estudio para completar su licenciatura, Cecily permaneció en Aberystwyth trabajando como ayudante no oficial de su padre.
Edward Collingwood formaba parte del personal de Aberystwyth. Entre 1921 y 1924 Cecily le ayudó a traducir las conferencias del matemático francés Georges Valiron que se publicaron bajo el título de Lectures on the General Theory of Integral Functions. El prefacio del libro fue escrito por William Young, pero fue el único Young que apareció en el libro, ya que la colaboración de Cecily fue invisibilizada.
Finalmente, en 1925, Cecily recibió su Licence ès sciences (mathématique et physique) en Lausana. En ese año también escribió su primer artículo, Les fonctions monotones et l’intégration dans l’espace à n dimensions, que se publicó en la revista L’Enseignement Mathématique.
Se matriculó entonces en el Girton College para realizar su doctorado. Su madre también había estudiado en esta universidad para mujeres. Su director de tesis fue el matemático Ernest William Hobson y, bajo su tutela, Cecily defendió la memoria Foundations For The Generalisation Of The Theory Of Stieltjes’ Integration And Of The Theory Of Length, Area And Volume. An N-Dimensional Treatment en 1929 y publicó algunos artículos relacionados con su trabajo de doctorado entre 1928 y 1932.
Además de traducir textos franceses al inglés, Cecily también tradujo textos del alemán al inglés, como un libro de Konrad Knopp que fue publicado en inglés en 1928 bajo el título de Theory and Application of Infinite Series.
En 1932, la beca del Girton College con la que sobrevivía finalizó y durante un año no pudo encontrar otro puesto. Finalmente, en 1933, ingresó en el Imperial College of Science and Technology de la Universidad de Londres, donde pasó el resto de su carrera. Sus últimas publicaciones sobre temas cercanos a su tesis fueron dos artículos en 1936. Después de esto, se dedicó de lleno a la historia de las matemáticas y a la educación matemática. Se interesó, en particular, por la difusión de los trabajos del matemático Thomas Harriot, el creador de algunas notaciones matemáticas como los símbolos > (mayor que) y
En 1953, Cecily se casó con Bernard William Tanner, un ingeniero de 72 años que falleció un año más tarde.
Cecily Tanner heredó de su madre y de su padre su amor por las matemáticas. Desde pequeña, gracias a ellos, aprendió esta materia de una manera sugerente. Trabajó con su padre en sus comienzos, pero admiró de especial manera a su madre:
[…] Mi padre tenía ideas y una amplia comprensión de los temas, pero por naturaleza era indeciso; su mente funcionaba solo cuando era estimulada por las reacciones de una audiencia comprensiva. Mi madre tenía decisión, iniciativa y la fortaleza para llevar un proyecto hasta su conclusión. Su habilidad para comprender y responder, y su placer en ejercer esta habilidad la llevaron naturalmente a la posición que ocupó de manera tan única. Si ella no hubiera tenido esa habilidad, el genio de mi padre probablemente habría sido frustrado, y no habría eclipsado el de mi madre y el nombre que ya se había hecho por sí misma.
Su sobrina Sylvia Wiegand (1945), hija de su hermano Laurence, es también matemática, especializada en álgebra conmutativa.
Referencias
-
O’Connor, John J.; Robertson, Edmund F., Rosalind Cecilia Hildegard Tanner, MacTutor History of Mathematics archive, University of St Andrews.
-
I. Grattan-Guinness, Dr. R. C. H. Tanner (1900-92), The British Journal for the History of Science 26 (2) (1993), 229-231.
-
Rosalind Tanner, Wikipedia.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Cecily Tanner, la desconocida matemática de la familia Young se ha escrito en Cuaderno de Cultura Científica.
Einstein y la religión
El Albert Einstein adulto nunca abrazó ninguna religión organizada. Nacido judío, abandonó las costumbres y tradiciones del judaísmo cuando tenía doce años, y nunca volvió a relacionarse con un culto establecido. Sin embargo, no sería cierto decir que Einstein no era religioso, si bien en un sentido muy concreto. Expresó a menudo agradecimiento y un profundo sobrecogimiento ante lo que él describió como “esa fuerza que está más allá de lo que podamos comprender”, la esencia según Einstein de cualquier religión.
 Imagen del espacio profundo (agrupación galáctica SMACS 0723) captada por el Telescopio Espacial James Webb en 2022. Fuente: NASA, ESA, CSA & STScI
Imagen del espacio profundo (agrupación galáctica SMACS 0723) captada por el Telescopio Espacial James Webb en 2022. Fuente: NASA, ESA, CSA & STScILa legislación del Imperio Alemán (el Segundo Reich) exigía que todo estudiante a partir de doce años tuviese una educación religiosa oficial, fuese esta la que fuese siempre que estuviese reconocida por el estado. Así, los padres judíos de Einstein, por lo demás nada religiosos, contrataron a un pariente lejano para educarle en su tradición. Con once años, el joven Albert abrazó el judaísmo con furia. Para sorpresa de sus padres (y quizás, disgusto) Einstein se convirtió en un judío practicante, incluso rehusando comer cerdo. Más tarde describiría esta fase como su “paraíso religioso”. Pero, la fase no duraría mucho.
A la edad de doce años, Einstein descubrió el mundo de la ciencia y las historias de la Torá que tanto había disfrutado ahora le sonaban como cuentos para niños. En un movimiento pendular, rechazó su anterior religiosidad y una visión del mundo que ahora percibía como correspondiente a un cuento de hadas. Durante el resto de su vida Einstein mantuvo esa misma opinión de la religión organizada, describiendo la creencia en un dios personal o la creencia en una vida después de la vida como muletas para supersticiosos o miedosos. No participó nunca en un ritual religioso tradicional: rehusó celebrar en un bar mitzvah (la celebración del reconocimiento como adulto desde el punto de vista de la ley judía) a los trece años, sus bodas fueron civiles, nunca acudió a un servicio religioso y eligió que su cuerpo fuese incinerado, algo expresamente contrario a la tradición judía.
Y sin embargo, Einstein se describía a sí mismo como religioso. Se cuenta la anécdota de que en una fiesta en Berlín en 1927 había un invitado que había estado haciendo comentarios sarcásticos acerca de la religión durante toda la velada. Al hombre, un crítico literario llamado Alfred Kerr, se le advirtió de que no hiciese esos comentarios delante de Einstein. Kerr fue a buscar a Einstein incapaz de creer que el gran hombre de ciencia fuese tan religioso. Einstein replicó, “Sí, puedes llamarlo así. Intenta penetrar en los secretos de la naturaleza con tus limitados medios y encontrarás que […] queda algo sutil, intangible e inexplicable. La veneración por esta fuerza que está más allá de lo que podemos comprender es mi religión. Hasta ese punto soy, de hecho, religioso”.
El sentimiento religioso cósmicoEinstein creía en algo que él llamaba “el sentimiento religioso cósmico”. Al estudiar el universo sentía que los humanos estamos intrínsecamente limitados a un conocimiento solo parcial de la naturaleza. Habría un nivel de la existencia que nunca podríamos comprender. Algo complejo, inexplicable y sutil. El sentimiento religioso cósmico se expresaba como respeto y amor por este misterio.
Como buen científico Einstein analizó esta creencia. En un artículo del 9 de noviembre de 1930 que escribió para New York Times Magazine titulado “Religión y ciencia” argumentaba que existían tres etapas en la evolución de la religión. Al comienzo, decía, la gente se enfrentaba al miedo básico ante los peligros del universo y esto llevó a la creencia de que debe haber algo poderoso cuyos caprichos marcan el destino humano. A continuación aparece la idea del dios antropomorfo que puede castigar y recompensar, lo que conduce a los conceptos de moralidad, así como a generar respuestas acerca de la vida después de la muerte. Más allá de esto, continuaba Einstein, está el sentimiento religioso cósmico, un sentimiento de la impotencia e inutilidad humanas ante la naturaleza y el “mundo del pensamiento”.
Escribió que el universo y su funcionamiento es lo que inspira este sentimiento. En este tipo de religiosidad, el practicante desea experimentar ser parte del universo en un sentido holístico del término, en contraposición a ser un individuo separado de él. Einstein citó desde los escritos de Schopenhauer hasta los Salmos de David, pasando por las escrituras budistas, como ejemplos de esta experiencia casi mística. Por último, insistió en que este sentimiento era tan universal, tan libre de dogmas, que ninguna religión en concreto lo podía abarcar y, por lo tanto, estaba intrínsecamente separado de la religión organizada. De hecho, el fin último de toda la ciencia y el arte era inspirar este sentimiento tan intenso, y fruto de él era la dedicación solitaria durante años a la ciencia de gente como Kepler o Newton. Claramente, la religión, si bien una definición muy específica de religión, era crucial en el pensamiento de Einstein.
No es de extrañar, pues, que Einstein siempre mantuviese que la ciencia y la religión se beneficiaban de su mutua asociación. En su opinión, lo mejor de la religión surgía directamente del impulso científico. Escribió: “Cuanto más avance la espiritualidad de la humanidad, más cierto me parece que el camino hacia la genuina religiosidad no pasa por el miedo a la vida, o por el miedo a la muerte, y la fe ciega, sino en esforzarse por alcanzar el conocimiento racional”. Era la búsqueda del conocimiento mismo lo que Einstein consideraba la base de la religión.
La visión habitual del público de la posición de Einstein con respecto a la religión parece indicar que esta está llena de aparentes contradicciones. Si bien Einstein siempre mantuvo este sentimiento religioso cósmico y, en este sentido, sus menciones a dios se referían a un dios próximo al de Spinoza [*], los líderes religiosos se afanaban por atraerse a Einstein, si no a su religión, si a un “marco conceptual” próximo. Así, es fácil (si uno es religioso) ver el desarrollo de la física del siglo XX como indiciario de la existencia de “lo misterioso” en lo que, de otra forma, habría sido un universo completamente determinista. Einstein negó este extremo con toda contundencia. Cuando en 1921 el Arzobispo de Canterbury le preguntó cómo afectaba la relatividad a la religión, contestó que no le afectaba. La relatividad, insistió, era totalmente científica y no tenía nada que ver con la religión.
Nota:
[*] Próximo, pero no igual. Einstein suele referirse al “orden” del universo como una de sus características más maravillosas; Spinoza afirma que el orden, cualquier orden, es una creación humana. Esta distinción hace al “dios o naturaleza” de Spinoza mucho más ilimitado que el “dios” de Einstein.
Para saber más:
Einstein y la belleza matemática
Ciencia, arte, religión
Kelvin, padre de la termodinámica: cuando la religión inspira a la ciencia
La neurociencia como religión
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 18 de julio de 2010.
El artículo Einstein y la religión se ha escrito en Cuaderno de Cultura Científica.
RCP-ECA: Una nueva reanimación cardiopulmonar, para salvar más vidas
Según el informe Muerte súbita y cardioprotección de la Sociedad Española de Cardiología (SEC), cada año en España se dan en torno a 30.000 casos de muerte súbita fuera de centros sanitarios y 15.000 intentos de reanimación por parte de los servicios de emergencia. Estos fallecimientos repentinos e inesperados suelen estar provocados, en la gran mayoría de los casos, por alteraciones del ritmo cardíaco que llevan a una parada. Una actuación rápida y adecuada, en los primeros 8 minutos, resulta vital para poder salvar la vida al paciente con paro cardíaco y disminuir el riesgo de secuelas. Cada minuto que pasa sin ninguna intervención implica un 10 % menos de probabilidad de que la persona sobreviva.
 Foto: Michel E / Unsplash
Foto: Michel E / UnsplashLa reanimación cardiopulmonar (RCP) es una maniobra fundamental ante paros cardíacos y su realización adecuada duplica o incluso triplica las probabilidades de que el paciente pueda seguir viviendo. Sin embargo, solo un 30 % de los españoles sabe realizar una RCP. Los cardiólogos estiman que se podrían salvar entre 1.5000 y 3.000 vidas cada año si la población española contara con la formación necesaria para realizar esta maniobra. Según la ley, educar en la RCP debería ser obligatorio en Educación Primaria, pero la realidad es que la enseñanza de primeros auxilios en la escuela es minoritaria en nuestro país. Esto determina que, mientras que en los países nórdicos las probabilidades de supervivencia ante una parada cardíaca en la calle son del 30 %, en España estad se encuentran entre el 5 y el 10 %.
Las maniobras de reanimación cardiopulmonar han evolucionado radicalmente a lo largo de los siglos. Por ejemplo, antes del siglo XX, la técnica predominante se centraba solo en la ventilación asistida, ya fuera con un fuelle o boca a boca. Sin embargo, más adelante se observó que la supervivencia era mayor cuando se realizaban compresiones torácicas, lo que permitía que la sangre siguiera circulando. La RCP, tal como la conocemos en la actualidad, se implantó no hace mucho: en los años 60 del siglo pasado. Los médicos Kouwenhoven, Safar y Jude defendieron las insuflaciones boca a boca junto a las compresiones torácicas y esta técnica fue la que se expandió a lo largo del mundo.
La RCP sigue en constante evolución, conforme van surgiendo nuevas evidencias científicas que nos muestran qué criterios aportan una mayor supervivencia o aparecen nuevas tecnologías. Así, factores como la rapidez y el número de compresiones, la alternancia de compresiones con insuflaciones o el uso del desfibrilador son detalles que se han ido actualizando o incorporando con el tiempo.
De hecho, hace menos de 20 años se defendía que la población general debía realizar 15 compresiones torácicas por cada 2 insuflaciones seguidas. No obstante, investigaciones al respecto detectaron que era mucho más importante para la supervivencia las compresiones torácicas y esto llevó a defender que se hicieran 30 compresiones por cada 2 insuflaciones. Hace pocos años, esto volvió a cambiar. En la actualidad, se defiende que la población general sin formación en primeros auxilios debe realizar solo compresiones torácicas ante una parada cardíaca en adultos (entre 100 y 120 por minuto, más o menos al ritmo de la Macarena), porque las insuflaciones que realizan no suelen ser efectivas y, por ello, es mejor para la supervivencia que realicen exclusivamente compresiones. Eso sí, para bebés, se siguen recomendando las insuflaciones.
No es fácil recopilar pruebas científicas de calidad sobre maniobras de urgencia vital como la RCP. Esto lleva a que su mejora, aunque constante, sea lenta. Recientemente, varios estudios científicos han aportado nuevos datos que probablemente cambien la forma en la que se realiza esta maniobra entre el personal sanitario en un futuro próximo. Una RCP «refinada» mejora hasta un 50 % la supervivencia de los pacientes con parada cardíaca, atendidos fuera del hospital por los servicios de emergencia médica, en comparación con la RCP convencional. Esta novedosa maniobra se denomina RCP-ECA, que significa reanimación cardiopulmonar con elevación controlada automática de la cabeza y el tórax.
Una de las desventajas de la RCP convencional, como explica el director médico de los Servicios de Emergencias Médicas del distrito de Dallas, Paul Pepe, es que esta no solo hace fluir la sangre hacia adelante en las arterias, sino que también provoca una presión hacia atrás en las venas. Esto implica una mayor presión intracraneal, que compromete el flujo sanguíneo en el cerebro. Para remediarlo, a la RCP convencional se añade el uso de un dispositivo que eleva de forma gradual tanto la cabeza como el tórax.
Además, también se usa un aparato, denominado dispositivo de umbral de impedancia, que se acopla a la vía aérea, en combinación con un sistema de compresión y descompresión del tórax. La función del artilugio es regular la presión del tórax durante las fases de descompresión de la RCP, al restringir de forma selectiva el flujo innecesario de aire al interior del tórax, se reduce la presión intracraneal y, con ello, mejora el flujo sanguíneo al cerebro.
En resumen, la RCP-ECA mejora el flujo sanguíneo hacia el cerebro, lo que disminuye el riesgo de daño neuronal con el paso del tiempo y aumenta de forma significativa la supervivencia. Aunque no es posible saber cuándo se extenderá su uso entre los equipos de emergencias de distintos países, los beneficios parecen claros en los ensayos clínicos con miles de pacientes. Otro ejemplo más en la constante evolución de la RCP.
Para saber más:
¿Puede un muerto regresar a la vida?
Sobre la autora: Esther Samper (Shora) es médica, doctora en Ingeniería Tisular Cardiovascular y divulgadora científica
El artículo RCP-ECA: Una nueva reanimación cardiopulmonar, para salvar más vidas se ha escrito en Cuaderno de Cultura Científica.
La nueva familia de violines de Carleen Maley Hutchins
Michael Praetorius (1571-1621) fue el mayor académico musical de su época. Aparte de sus notables composiciones y mejoras en la práctica del bajo cifrado en el órgano, recopiló un registro enciclopédico de las prácticas musicales contemporáneas. Como musicólogo son de gran importancia sus discusiones sobre el uso de los instrumentos y las voces en los conjuntos, la afinación estándar de la época y la teoría modal, métrica y contrapuntística. Su obra Syntagma Musicum incluye en su segundo volumen un tratado de organología así como un suplemento de ilustraciones [1]. En la grabado XXI, Praetorius muestra un octeto de instrumentos de cuerdas para poder cubrir todas las voces musicales, de las más agudas a las más graves.
 M. Praetorius, Syntagma musicum vol. II, figura XXI. Fuente
M. Praetorius, Syntagma musicum vol. II, figura XXI. Fuente
La sección de cuerda de las orquestas incluye desde el Renacimiento hasta nuestros días los conocidos cuatro instrumentos de la familia del violín (violín, viola, violonchelo y contrabajo). Es llamativo que, salvo el violín que siempre se construye siguiendo unos parámetros fijos y únicos, el resto de los instrumentos se han ido modificando múltiples veces a lo largo de la historia, y el propio tamaño de las violas, el grosor de los violonchelos o las dimensiones generales de los contrabajos no se han mantenido fijas ni tampoco bien definidas.
La nueva familia de violines Hutchins Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsEl compositor Henry Brant sugirió en 1958 el diseño y construcción de una nueva y completa familia de instrumentos de violines escalados científicamente para poder cubrir de forma global y coherente todo el rango musical audible. Los investigadores Frederick Saunders y Carleen Maley Hutchins entraron de lleno en el problema y estudiaron su solución como científicos y lutieres. Después de casi ocho años de incansable trabajo, en 1965 Carleen Hutchins presentó su nuevo y completo octeto de violines. Cada miembro de la nueva familia se basa en el violín ordinario y todos comparten sus propiedades acústicas, con el objetivo de obtener sonido homogéneo en todos los rangos musicales. Todos los instrumentos de Hutchins incorporan un carácter tonal más rico y se basan en parte en las ideas presentadas por Michael Praetorius.
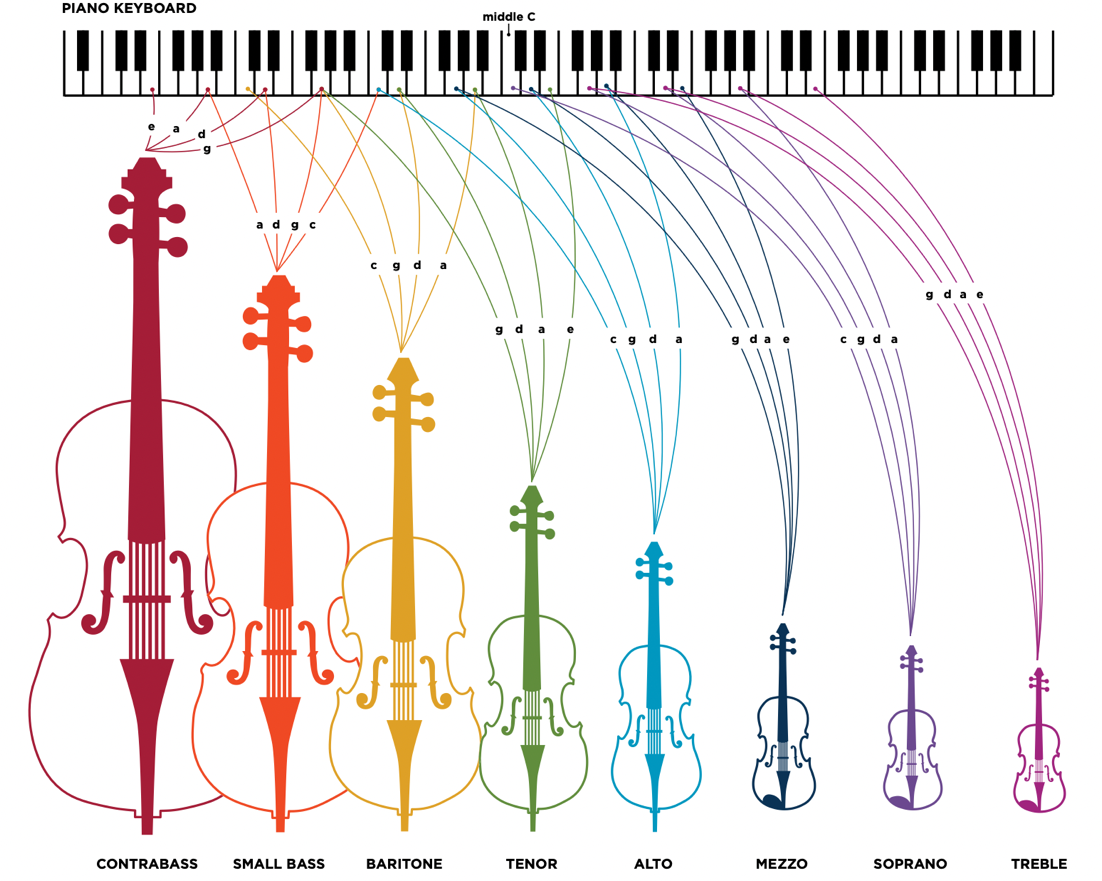 La Nueva Familia de Violines creada por Carleen Maley Hutchins en 1965. Fuente
La Nueva Familia de Violines creada por Carleen Maley Hutchins en 1965. Fuente
A diferencia de los cuatro instrumentos de cuerda estándar, la caja de resonancia de cada nuevo instrumento se construye de modo escalable dependiendo de su rango de frecuencias de funcionamiento. Así, la resonancia de aire y la principal del cuerpo de cada instrumento del octeto de violines están, respectivamente, en un tono cercano a las dos cuerdas centrales de cada violín, lo cual confiere a los nuevos instrumentos un sonido mucho más claro y equilibrado.
Análisis modal de la nueva generaciónEl Violín Mezzo de la nueva familia coincide con el violín ordinario creado por los clásicos lutieres de Cremona. Las 4 cuerdas de un violín se afinan a intervalos de quintas (frecuencias crecientes con factor aproximado 3/2). En el moderno temperamento igual, ello da lugar a que las cuerdas libres suenen a frecuencias Sol3=196.0 Hz; Re4=293.7 Hz; La4=440.0 Hz; Mi5=659.3 Hz (G D A E en terminología anglosajona).
Si observamos los modos de vibración medidos en el cuerpo del famoso violín “Leonora Jackson” de Antonio Stradivari (1714) encontramos que la primera resonancia de aire (A0) de este instrumento se encuentra en el rango 270-280 Hz, muy cerca de la cuerda central Re4=293.7 Hz. Asimismo, encontramos que la primera resonancia de madera (CBR) se encuentra en el rango 390-400 Hz, también cerca de la otra cuerda central La4=440 Hz.
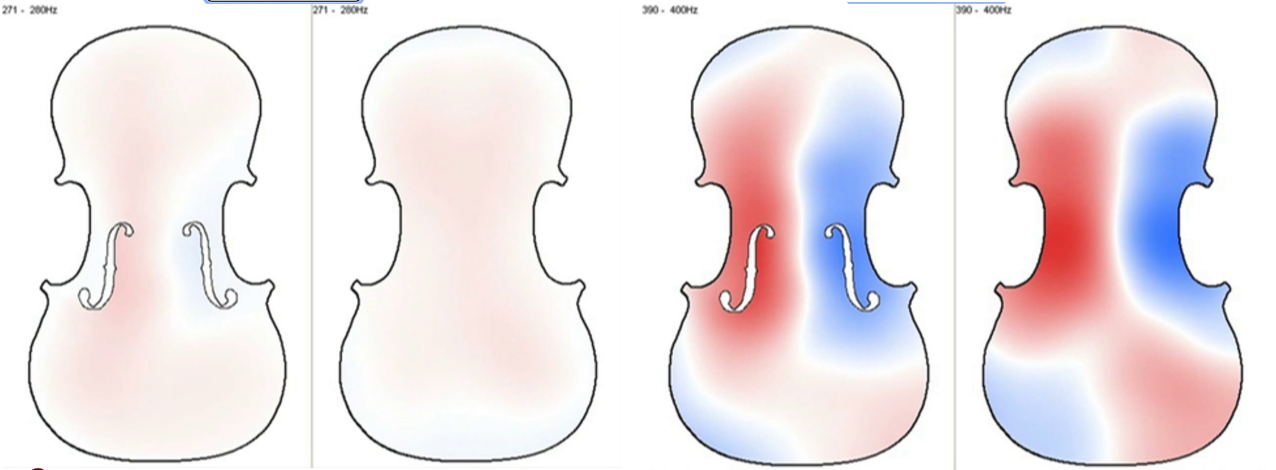 Primeras resonancias y vibraciones asociadas de la caja del “Jackson” Stradivarius: A0 (270-280Hz) y CBR (390-400Hz). Fuente
Primeras resonancias y vibraciones asociadas de la caja del “Jackson” Stradivarius: A0 (270-280Hz) y CBR (390-400Hz). FuenteNotemos que el diapasón de la nota La4 en la época barroca se afinaba en torno aproximado de 415 Hz (en lugar de los actuales 440-442 Hz de las orquestas modernas). Así pues, las dos cuerdas centrales de los violines históricos de Cremona se afinaban con un Re4=277.0 Hz y un La4=415.0 Hz, respectivamente. Esto indica que las resonancias del aire y madera medidas en el “Jackson” Strad 1714, se encuentran aún más cerca de las frecuencias vibratorias de las dos cuerdas libres centrales del violín.
Carleen Hutchins ajustó todas las cajas de resonancia de su octeto a las frecuencias de las cuerdas centrales y escaló todos los instrumentos de forma coherente y brillante. Aunque la tradición e historia musical clásica siempre ha evolucionado lentamente, la innovadora nueva familia de violines creada por Carleen Hutchins supuso un importante hito en lutería y acústica musical, e influyó a múltiples científicos, constructores de instrumentos, e importantes músicos. Como simple ejemplo histórico de estos hechos, podemos citar al director de orquesta Leopold Stokowski , el violonchelista Yo-Yo Ma o a la organización musical The Hutchins Consort, que desarrolla en este ámbito su importante actividad docente, investigadora y cultural.
Referencias
[1] Michael Praetorius (1620) Syntagma musicum vol. II. Suplemento ilustrado Theatrum Instrumentorum
[2] Quincy Whitney (2020) American luthier: the art and science of Carleen Hutchins. Acoustics Today, vol 16, n.1, pp. 10-19.
El artículo La nueva familia de violines de Carleen Maley Hutchins se ha escrito en Cuaderno de Cultura Científica.
Maia García Vergniory y Kepa Acero – Historia de una ola
 Foto: Tim Marshall / Unsplash
Foto: Tim Marshall / UnsplashEl pasado 21 de septiembre se impartió la conferencia «Historia de una ola» en la Biblioteca Bidebarrieta dentro del ciclo Bidebarrieta Científica, en el marco de Bilbo Zientzia Plaza.
La física Maia García Vergniory y el surfista Kepa Acero explican en esta charla por qué unas olas se abren y otras se cierran, por qué algunas veces vienen en serie y otras no, o qué papel juegan las mareas, el viento y el fondo marino en las olas que surfeamos. De hecho, cada vez que alguien que practica surf mira las tablas de predicción está analizando fenómenos físicos, y en esta charla se demuestra que para tener una actitud científica no hace falta ser profesional de la ciencia.
Maia García Vergniory es investigadora principal en el Instituto Max Planck de Fisicoquímica de Sólidos en Dresde (Alemania). Maia ha sido elegida muy recientemente como APS Fellow de la American Physical Society por sus contribuciones al descubrimiento de la química cuántica topológica. Kepa Acero es surfista profesional y documentalista, conocido por documentar sus viajes en solitario en busca de las olas más aisladas del planeta.
Edición realizada por César Tomé López
El artículo Maia García Vergniory y Kepa Acero – Historia de una ola se ha escrito en Cuaderno de Cultura Científica.
¿Es posible acabar con el dolor sin efectos adversos?
 Foto: Aarón Blanco Tejedor / Unsplash
Foto: Aarón Blanco Tejedor / UnsplashHay pocas cosas tan necesarias y al mismo tiempo tan indeseables como el dolor. Nos advierte y defiende de algo que nos perjudica o nos puede perjudicar. Hay dolores nociceptivos, debidos a estímulos dañinos; psicógenos, con gran componente emocional; e incluso neuropáticos, cuando el daño lo sufre el propio sistema nervioso. Hay dolores que solo pasan y dolores que se quedan, como el crónico, aquel que dura más de tres meses y puede vincularse a cuadros de ansiedad, depresión e incluso al suicidio.
Acabar con el dolor y aliviar al que lo sufre es un acto de humanidad encomendado a la ciencia y a los profesionales sanitarios, y los fármacos analgésicos disponibles actualmente ayudan al paciente a vivir con mejor calidad de vida. Incluyen antiinflamatorios no esteroideos como el ibuprofeno, opioides menores como la codeína y opioides mayores como la morfina, el fentanilo y la oxicodona.
En los últimos años, la prescripción de opioides ha crecido considerablemente debido a que ha disminuido el miedo a su uso. Sin embargo, a pesar de su eficacia, su empleo prolongado no está exento de problemas, por lo que la búsqueda de alternativas resulta de gran interés.
Limitaciones de los analgésicos actualesEl consumo crónico de opioides produce, entre otros problemas, la aparición de tolerancia –una necesidad de mayor dosis para lograr el efecto deseado– y cuadros de adicción. De modo que ciertos pacientes que comienzan a tomarlos pueden terminar abusando de ellos.
Y a pesar de los perjuicios que generan los opioides, no se ha encontrado nada mejor para el tratamiento del dolor moderado y severo. De hecho, tan malo es sobretratar como infratratar con ellos. La clave está en realizar un uso racional de los mismos ayudando al paciente a aliviar su malestar, pero vigilando los problemas derivados de su consumo crónico.
La OMS aboga por un tratamiento escalonado que consiste en añadir opioides menores o mayores solo cuando los antiinflamatorios no esteroideos, considerados más seguros, sean insuficientes.
No obstante, la utilización de estos últimos tampoco está exenta de efectos perniciosos, sobre todo cuando se consumen dosis altas y de forma crónica. Su empleo prolongado podría producir problemas gastrointestinales y renales.
¿Es posible separar los efectos terapéuticos de los adversos?La mayoría de los medicamentos funcionan gracias a la interacción con macromoléculas presentes en nuestro organismo, a las que denominamos dianas farmacológicas. Fruto de esta interacción fármaco-diana, se altera la función de esas macromoléculas, lo que da lugar a eventos bioquímicos y fisiológicos conocidos como efectos farmacológicos. Algunos son de carácter terapéutico y otros, adversos.
Los antiinflamatorios no esteroideos y los opioides reducen el dolor a través de la interacción con dos dianas concretas, denominadas enzimas ciclooxigenasas y el receptor opioide µ, respectivamente. El problema es que dichas dianas participan también en numerosas funciones fisiológicas en el sistema gastrointestinal, los riñones o el cerebro. Así, al actuar sobre esos compuestos, los fármacos pueden producir también daños colaterales.
Esto nos lleva a la conclusión, un tanto pesimista, de que los efectos terapéuticos difícilmente podrán separarse de los adversos: el riesgo de daño renal, gastrointestinal, tolerancia, adicción e incluso depresión respiratoria, serán peajes a pagar por el uso de analgésicos. No obstante, prometedoras herramientas como los llamados moduladores alostéricos y agonistas sesgados –que explicaremos más adelante– o la combinación de varios fármacos abren la puerta a la esperanza.
¿Qué nuevos tratamientos se están investigando?La adenosina es una sustancia muy interesante para quienes buscan nuevas armas contra el dolor. Producida por nuestro organismo, tiene propiedades analgésicas cuando actúa sobre la diana denominada receptor de adenosina 1 (A1). Por ello, en el caso del dolor neuropático –resistente a los opioides– se han probado fármacos agonistas (activadores) del receptor A1.
Estos compuestos alivian efectivamente el dolor pero, al actuar también sobre el A1 presente en el corazón, pueden reducir la frecuencia cardíaca. Ante este problema, los farmacólogos han recurrido a un modulador alostérico del receptor A1.
En este caso, los moduladores alostéricos son fármacos que se unen al receptor A1 en un punto diferente al que lo hace la propia adenosina. Pueden ser positivos y negativos en función de si colaboran o no con ella. Así, actuando de manera cooperativa junto a la adenosina presente en el tejido dañado, los moduladores alostéricos positivos potencian su acción contra el dolor.
Los agonistas sesgados son otras herramientas esperanzadoras ya que, al unirse a un receptor diana, pueden activar ciertas funciones de manera más eficiente que otras. Esta capacidad haría realidad el objetivo de producir solo efectos terapéuticos, sin los adversos.
Recientemente, se ha hallado un agonista sesgado del receptor A1 que activa preferentemente ciertas vías celulares, aliviando el dolor sin provocar depresión cardiorrespiratoria. También se han encontrado agonistas sesgados que al actuar sobre otra diana, denominada adrenoceptor α2A, producen analgesia sin el efecto sedante que limita a otros fármacos que actúan sobre dicha diana.
Y tendríamos, por último, la estrategia de asociar opioides y compuestos con efecto analgésico para reducir la dosis de los primeros y evitar así sus efectos perniciosos. Un ejemplo sería la combinación con el cannabis medicinal.
Aunque de manera prudente, podemos decir que avanzamos en el descubrimiento de nuevos tratamientos analgésicos eficaces que mejorarían el perfil de seguridad del arsenal existente. Sabemos que el camino es largo, pero el trabajo cooperativo, como el que realizan ciertos fármacos, nos llevará a nuestra meta.![]()
Sobre las autoras: Guadalupe Rivero Calera y Aitziber Mendiguren Ordorica son profesoras agregadas del Departamento de Farmacología en la Facultad de Medicina y Enfermería de la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Es posible acabar con el dolor sin efectos adversos? se ha escrito en Cuaderno de Cultura Científica.

