Gemma del Caño – Naukas P4K 2019: ¡Que si quiere bolsa!
 Foto: Maria Lin Kim / Unsplash
Foto: Maria Lin Kim / UnsplashTras el uso de una bolsa en la que poder transportar nuestra compra del supermercado hay todo un mundo de química, industria, salud y legislación da igual el material de que esté hecha. Gemma del Caño, farmacéutica especialista en I+D+i y seguridad alimentarias en la industria, nos revela algunos de los intríngulis de ese mundo.
La conferencia se impartió dentro del marco del festival Passion for Knowledge 2019 (P4K) organizado por el Donostia International Physics Center (DIPC).
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Gemma del Caño – Naukas P4K 2019: ¡Que si quiere bolsa! se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ambrosio Liceaga – Naukas P4K 2019: Nunca quisimos coches voladores
- Gemma Del Caño y Marián García – Naukas Bilbao 2018: Sandwich mixto en tres actos
- César Tomé López – Naukas P4K 2019: ¿Eureka?¿En serio?
Mascarilla y COVID-19: ¿dilema del prisionero o juego de coordinación?
Annick Laruelle
 Grafiti en una calle de Varsovia (Polonia). Foto: Adam Nieścioruk / Unsplash
Grafiti en una calle de Varsovia (Polonia). Foto: Adam Nieścioruk / UnsplashEn seis meses la mascarilla se ha vuelto un objeto cotidiano en todo el mundo. Los gobiernos de China, Hong Kong o Taiwán fueron los primeros en recomendar su uso. Desde junio de 2020 la posición de Organización Mundial de la Salud es que los gobiernos deberían alentar al público a que use la mascarilla en situaciones específicas (como el transporte público). La decisión acerca de recomendar o hacer obligatorio el uso de mascarilla varía según los países.
Si el uso de la mascarilla no es obligatorio, los individuos se enfrentan a la decisión de ponérsela o no. Las preferencias individuales pueden depender de las circunstancias, de las personas con quienes uno se encuentra… y de lo que deciden los demás individuos.
Se puede analizar la situación con la teoría de juegos: cada persona tiene que decidir si llevar la mascarilla o no. El resultado final depende de lo que han decidido todos. En un encuentro con otra persona, cada uno tiene dos acciones posibles y evalúa cuatro resultados.
 Los cuatro resultados en un encuentro entre dos personas.
Los cuatro resultados en un encuentro entre dos personas.La teoría de juegos no realiza ningún juicio ético o moral sobre las preferencias de los individuos. Solamente intenta determinar las decisiones de equilibrio en función de ellas. En el equilibrio, ningún individuo se arrepiente de la decisión que ha tomado: el resultado es estable.
La situación puede dar lugar al conocido “dilema del prisionero”. Si llevar la mascarilla constituye más una protección para los demás que para los que la llevan y llevarla conlleva un cierto esfuerzo, la mejor opción para una persona que se preocupa exclusivamente de su bienestar individual es no llevar la mascarilla y que el otro la lleve.
La segunda mejor opción es que los dos lleven la mascarilla; la tercera opción que ninguno la lleve y la cuarta llevar la mascarilla y que el otro no la lleve. Una persona con estas preferencias es un free-rider, en el sentido de que intenta aprovecharse de los esfuerzos de los demás y no llevar la mascarilla – aunque no le gustaría que los demás hagan lo mismo.
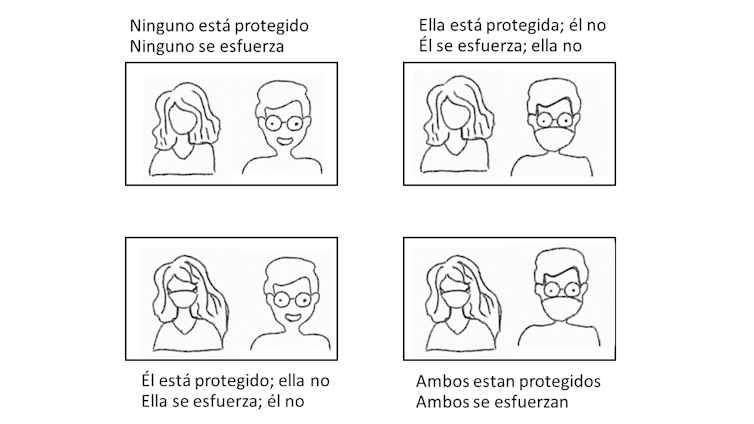 Dilema del prisionero.
Dilema del prisionero.En un encuentro entre dos free-riders, si ambos no llevan la mascarilla ninguno de los dos se arrepiente de su decisión. Es la tercera mejor opción para cada uno, pero cambiar de decisión significaría ser el único de los dos en llevar la mascarilla, la peor opción de todas para un free-rider. Es el único equilibrio. En cambio, si ambos llevan la mascarilla, cada uno se arrepiente de su decisión: preferiría quitársela si el otro la lleva. Que ambos lleven la mascarilla no es un equilibrio, aunque es la segunda mejor opción para cada uno.
¿Se puede justificar el uso obligatorio?
El dilema del prisionero tiene esta característica paradójica: un resultado mejor que el resultado del equilibrio no se puede alcanzar de manera descentralizada. En una sociedad de free-riders se puede justificar el uso obligatorio de la mascarilla.
En la práctica es (afortunadamente) poco probable que todos los individuos de un grupo social sean free-riders con respecto a la mascarilla. Un experimento realizado en Alemania con unos 925 participantes sugiere que el uso de la mascarilla está visto como un contrato social: los participantes perciben de manera positiva a los que llevan la mascarilla. Tienden a recompensar a los que la llevan y castigar a los que no la llevan. Este comportamiento se podría justificar por preferencias para la reciprocidad: si la otra persona lleva la mascarilla uno prefiere llevarla y prefiere no llevarla si el otro no la lleva.
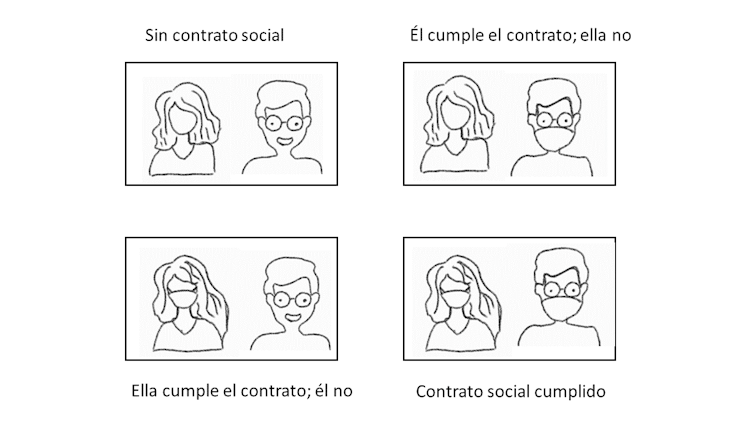 Juego de coordinación.
Juego de coordinación.En este caso la situación corresponde a un juego de coordinación con dos equilibrios. En un equilibrio ambos llevan la mascarilla o ambos no la llevan.
La teoría de juegos no puede predecir cuál de los equilibrios puede emerger. Las circunstancias (espacio cerrado o no; con distancia o no) podrían ayudar a las personas a coordinarse en un equilibrio o el otro.
El uso obligatorio de la mascarilla se justifica en sociedades de free-riders: resuelve el dilema social.
A cambio, si el uso de la mascarilla es un contrato social, el uso de la mascarilla por parte de todos es un equilibrio posible.
Dilemas sociales
Las medidas para luchar contra la pandemia generan dilemas sociales. El uso de la mascarilla es una de ellas, como lo son también el confinamiento o la vacuna.
En este ultimo caso, dado que los beneficios son bienes públicos, los individuos “free riders” tienen el incentivo de no contribuir y beneficiarse de los esfuerzos de los demás. Con respecto a la futura vacuna contra la COVID-19, el epidemiólogo de la Organización Mundial de la Salud advirtió en agosto que los países tomarían la decisión de hacerla obligatoria o no.
La encuesta del CIS realizada a principios de octubre (pregunta 6) revela que el 43,8% de los encuestados no están dispuestos a vacunarse.
Sobre la autora: Annick Laruelle es profesora Ikerbasque de Fundamentos del Análisis Económico en la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Mascarilla y COVID-19: ¿dilema del prisionero o juego de coordinación? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Relación entre genoma y las formas graves de COVID-19
- El dilema de la hepatitis C
- Un extraño juego de dados
Los invasores: Invasiones biológicas
“Los invasores. Seres extraños de un planeta que se extingue. Destino: la Tierra. Propósito: adueñarse de ella.”
En los créditos de la serie de televisión “Los invasores”. 1967-1968.
“Hoy en día vivimos en un mundo muy explosivo, y aunque no sepamos dónde o cuándo será el próximo estallido, esperamos encontrar formas de detenerlo o, en cualquier caso, de mitigar su fuerza”.
Charles Elton, La ecología de las invasiones de animales y plantas, 1958.
“En el fondo, bajo los rayos perpendiculares del sol, brillaba un pequeño lago, que el aburrimiento de un inglés pobló de ciprínidos con escamas de oro o de plata.”
Julio Verne. En el lago del volcán Caldeira en la isla Fayal de las Azores. Agencia Thompson y Cía, 1907. Allí siguen los ciprínidos (Filipe Ribeiro y su grupo, Universidade de Lisboa).
La introducción de agentes de control biológico en una nueva región es un ejemplo de los efectos peligrosos de las especies invasoras. Así, Diana Kimberling, de la Universidad Estatal de Oregon, revisa los efectos de 87 especies de insectos introducidas en Estados Unidos entre 1900 y 1981. De ellas, 57 no funcionaron como control biológico de la especie a vigilar. Y 24 actúan sobre especies diferentes al blanco original.
Hay 18 especies típicas de mamíferos terrestres que viven en entornos húmedos en Francia, y siete de ellas son introducidas. La mayor parte son ejemplares escapados de granjas de cría para comercializar su piel, como ha ocurrido con el visón y el castor americanos.
En 1869 se inauguró el Canal de Suez. En el sistema de canales que lo forman hay un lago con baja salinidad que funciona como barrera para el paso de especies entre los mares Rojo y Mediterráneo, pero para el 2000, más de 250 especies habían llegado al Mediterráneo.
Cuando la isla de Krakatoa estalló en 1883, las cenizas del volcán destruyeron toda la vida de la isla. Pero, 50 años más tarde era recolonizada por especies llegadas de islas cercanas, al menos a 40 kilómetros de distancia. En 1933, medio siglo después de la destrucción, se encontraron en Krakatoa 720 especies de insectos y 30 de aves. También había reptiles y mamíferos.
El número de especies de peces introducidas en Estados Unidos fue de 67 entre 1850 y 1900, de 140 entre 1901 y 1950, y de 488 entre 1951 y 1996.
Las especies invasoras en la Bahía de San Francisco fueron, de media, una por año entre 1851 y 1960, y de más de tres por año entre 1961 y 1995.
Entre 2000 y 2008, una media de 196 especies no nativas se estableció en Europa cada año. En 2009, los insectos no nativos eran cerca de 1300, pero diez años después, en 2019, alcanzaban las 2500 especies. Uno de los caminos de entrada es el tráfico marítimo de contenedores. Entre febrero y agosto de 1996, se inspeccionaron 1174 contenedores y se encontraron más de 7400 especies de insectos. En Nueva Zelanda, y en 2001 y 2002, se inspeccionaron 11200 contenedores. El 4.1% de los contenedores con carga y el 3.6% de los contenedores vacíos llevaban insectos.
Según EASIN, European Alien Species Information Network, a 21 de octubre de 2019, en Europa hay censadas 14165 especies no nativas.
 Conejo silvestre en Australia. Fuente: Wikimedia Commons
Conejo silvestre en Australia. Fuente: Wikimedia CommonsLas invasiones biológicas son una de las consecuencias más serias de la actividad de la especie humana. La globalización de la biota del planeta está transformando las floras y faunas regionales y locales. Anthony Ricciardi comentó que, en 2008, la especie humana movía unas 7000 especies cada día. Es lo que algunos autores denominan neozoismo: introducir especies no nativas y homogeneizar faunas y floras. Desde la más pequeña y remota isla hasta el continente más extenso, la introducción intencionada o accidental de nuevas especies está alterando la composición y el entorno de las especies allí establecidas. Los problemas potenciales asociados con la introducción de especies no indígenas se conocen desde hace tiempo. Este es el aviso de peligro que un grupo de investigadores de trece países, liderado por Petr Pysek, de la Academia Checa de Ciencias, publicó hace unos meses, y en el que participó Montserrat Vilá, de la Estación Biológica de Doñana.
En general, las especies extrañas se perciben como problemas ambientales potenciales. Por supuesto, la especie invasora con más éxito es Homo sapiens, la especie humana, que ha llegado a todo el planeta y, con ella, han viajado muchas otras que ahora llamamos invasoras.
Para ilustrar la peligrosidad de las especies invasoras nos sirve el estudio reciente de Xuan Liu y su equipo, de la Academia China de Ciencias, sobre la presencia de especies invasoras cerca de áreas protegidas. Han revisado 894 especies invasoras terrestres en casi 200000 áreas protegidas de todo el planeta. Encuentran que hay especies invasoras en menos del 10% de las áreas protegidas pero hay al menos una en el entorno. El 84% de las áreas protegidas tienen especies invasoras a menos de 10 kilómetros, y el 99% a menos de 100 kilómetros.
Algunos ejemplos de esas especies invasoras cercanas son la paloma doméstica, el faisán, el gorrión común, el conejo, el visón americano, el ratón doméstico, la rata, la abeja africana o el mosquito de la fiebre amarilla.
El hombre siempre ha mantenido relaciones privilegiadas con un buen número de especies animales y vegetales. Muchos ejemplos lo demuestran: las representaciones en las pinturas rupestres, los bestiarios de la Edad Media o, más cercano a nosotros y en otro registro, las movilizaciones mundiales para salvar a las focas o las ballenas de la extinción. La domesticación de animales y plantas para la ganadería y la agricultura constituyen un ejemplo evidente de esas relaciones.
Pero la armonía no ha sido siempre, ni mucho menos, la regla de conducta entre humanos y fauna y flora en la medida en que, en primer lugar, la relación ha sido trófica, es decir, por su utilidad para comer, vestir, etc. En la época histórica, está documentada la desaparición de especies porque competían, de una u otra manera, con la especie humana o con sus especies animales y vegetales acompañantes.
Es James Carlton, del Colegio Williams de Mystic, en Estados Unidos, el que plantea los procesos de cambio que puede ser la causa del movimiento de especies a nuevos entornos. Menciona transformaciones en la región de origen, la aparición de nuevas regiones con especies disponibles para moverse, cambios en la región de recepción que atraigan especies de otras zonas, combinaciones de estos factores que supongan la apertura de nuevas ventanas a la invasión, y la presencia de vectores que ayuden a la invasión en cualquiera de sus fases como, por ejemplo, las actividades de la especie humana.
Pueden provocar importantes modificaciones en la estructura y funcionamiento de los ecosistemas, llegando a la extinción de especies nativas. Los mecanismos más habituales son la competición, la depredación, el parasitismo y las alteraciones en la cadena trófica o en ciclos de nutrientes. Son menos frecuentes los cambios en el propio hábitat. Sin embargo, Mark Davis, del Colegio Macalester, de St. Paul, en Estados Unidos, comenta que la extinción rara vez ocurre por una competición directa con la especie invasora, más bien es por cambios en el entorno o en otras especies relacionadas de alguna manera con la especie que desaparece.
 Presa realizada por castores oriundos de Amética del Norte en Tierra del Fuego. Fuente: Wikimedia Commons
Presa realizada por castores oriundos de Amética del Norte en Tierra del Fuego. Fuente: Wikimedia CommonsPero el grupo de Gyan Sharma, de la Universidad Hindu Baranas, en la India, afirma que más del 40% de las especies en riesgo de extinción lo están por la acción de especies invasoras. El 20% o más de las especies de plantas son, de media, no nativas en algunas áreas continentales y el 50% en algunas islas. Calculan que el 10% de las 260000 especies de plantas vasculares que conocemos tiene el potencial de convertirse en invasoras.
Cada una de las especies invasoras es un capítulo más en la larga historia de transgresiones ecológicas que provoca la especie humana. Poner y quitar especies, llevarlas y traerlas, depara siempre consecuencias casi siempre imprevisibles y, a veces, no beneficiosas. Aunque, no hay que olvidarlo, no todas las plantas invasoras son peligrosas. La introducción en un determinado entorno de especies no nativas puede suponer tanto un desastre ecológico como algún beneficio. De esas especies invasoras se alimenta la especie humana pues suministran el 70% de la dieta con solo nueve cultivos: trigo, maíz, arroz, patata, cebada, mandioca, soja, caña de azúcar y avena. Todas ellas han sido transportadas por la especie humana a todo el planeta y se cultivan lejos de su lugar de origen. O, también, el 85% de las plantaciones forestales industriales son especies de tres géneros: Eucalyptus, Pinus y Tectona (teca). En resumen, las especies no nativas tienen un papel integral en la economía y en los cultivos de todas las regiones.
Hay un grupo de ecólogos expertos en invasiones, liderados por Mark Davis, que proponen que no hay que diferenciar entre especies en un hábitat según su origen, nativas o invasoras, sino por su impacto en el entorno, por su integración y por su contribución a la biodiversidad del área a la que llegan. Debe aplicarse un enfoque dinámico y pragmático a la conservación y gestión de las especies. Hasta ahora, lo prioritario ha sido la preservación de la biodiversidad original y a su restauración ecológica. Para Davis y su grupo, estos objetivos se han convertido, más bien, en metáforas militares de lucha contra invasores. En conclusión, hay que centrarse en las funciones de las especies más que en su origen. Por todo ello, Martin Schlaepfer, de la Universidad de Ginebra, propone que las especies introducidas e invasoras deben incluirse en los índice de biodiversidad y sostenibilidad del hábitat en el que se encuentran.
 Lantana, oriunda de América, invadiendo un campo de cítricos en Israel. Fuente: Wikimedia Commons
Lantana, oriunda de América, invadiendo un campo de cítricos en Israel. Fuente: Wikimedia CommonsUno de los objetivos más actuales de la investigación sobre especies invasoras con éxito es el análisis de sus propiedades biológicas y ecológicas en la búsqueda de características generales que permitan identificarlas. No conocemos un carácter morfológico, fisiológico o ecológico sencillo que podamos relacionar con la capacidad invasora de una especie o de un grupo de especies. Sin embargo, debemos precisar los conceptos y la terminología utilizados en la biología de las invasiones. En una revisión publicada en 2006, Jannike Falk-Petersen y su grupo, de la Universidad de Tromso, en Noruega, recopilan nada menos que 145 definiciones que se utilizan en este tema, y concluyen que no encuentran una definición concreta, sencilla y rápida cuando se investigan especies invasoras. Piden algo así: una especie invasora es un organismo extranjero (alien) que se ha establecido en un área nueva y está expandiendo su rango de distribución.
La teoría ecológica no está suficientemente desarrollada para tratar el problema de las invasiones biológicas, escribe Kristin Shrader-Frechette, de la Universidad de Notre Dame, en Estados Unidos. En primer lugar, no hay concepto y definición claros y precisos de especie invasora y, por tanto, los expertos pueden utilizar el mismo término para distintos conceptos o, por el contrario, el mismo concepto para diferentes procesos. Esta confusión no permite comparaciones, debates y generalizaciones teóricas. En segundo lugar, las teorías más utilizadas tienen poca o ninguna capacidad predictiva y no permiten asegurar si una especie puede promover o dañar la diversidad del hábitat invadido. Y, en tercer lugar, las teorías no predicen si una especie puede vivir en el nuevo hábitat o fracasará en el intento.
Las etapas de la invasión, según Alfredo Vilches y sus colegas, de la Universidad Nacional de La Plata, en Argentina, son, en primer lugar, el transporte de la especie al nuevo entorno, con el resultado de muerte, captura o introducción. Después está el establecimiento o naturalización que, también, puede fallar. En tercer lugar, hay un aumento de la población y su dispersión. Y, después, llega la percepción de la presencia de la nueva especie por la especie humana y se estudia el impacto creado, bajo o alto.
Desde la UPV/EHU, Ana Rallo y Loreto García-Arberas propusieron las siguientes definiciones para aclarar los problemas en conceptos y terminología tan habituales en los estudios de la biología de las invasiones. He añadido algunas aportaciones de Petr Pysek, de la Universidad Agrícola de Praga, y del grupo de expertos liderado por David Richardson, de la Universidad de Ciudad del Cabo.
.- Especie nativa o autóctona: la que se encuentra en su área habitual de distribución.
.- Especie exótica o alóctona o no nativa: fuera del área de distribución habitual, por acción directa o indirecta de la especie humana.
.- Especie exótica o alóctona o no nativa con potencial invasor: que podría convertirse en invasora, sobre todo si ya lo ha conseguido en otras regiones.
.- Especie exótica o alóctona o no nativa invasora: establecida en un hábitat diferente al suyo natural y que puede ser un peligro para la biodiversidad local, y se reproducen en cantidad, a veces, a distancia de los progenitores y con capacidad para extenderse.
.- Especie exótica o alóctona o no nativa aclimatada o casual: en un hábitat diferente al suyo pero sin reproducción establecida, aunque lo haga ocasionalmente.
.- Especie exótica o alóctona o no nativa establecida: con poblaciones reproductoras durante varios ciclos vitales y sin intervención humana.
Por otra parte, Brandon Larson propone un lenguaje más neutro, no tan hiperbólico y catastrofista como el que se usa habitualmente. Sin embargo, este lenguaje más neutro presenta dos inconvenientes. En primer lugar, separa los resultados científicos de los debates sociales entre los ciudadanos interesados. Y, en segundo lugar, no es consistente con los valores conservacionistas evidentes y mayoritarios que animan a muchos científicos a investigar las invasiones biológicas.
En los últimos años, las investigaciones se han centrado en los procesos y patrones de las invasiones. Es importante conocer las causas del éxito invasor de una especie. En 1994, Sarah Reichard publicó una propuesta, en diez apartados, como observaciones preliminares, no todas probadas y, según la autora, alguna puede ser falsa. Anthony Ricciardi y Joseph Rasmussen, de las universidades Laval y McGill de Canadá, plantean características parecidas para especies invasoras del medio acuático.
En general, una especie invasora se caracteriza por:
1.- Tiene una distribución amplia y abundante en su hábitat nativo; es generalista, y con facilidad para ser trasladada e introducida, especialmente de manera accidental.
2.- Gran variabilidad genética, con más posibilidades a nuevas condiciones del entorno.
3.- Existe una correspondencia estrecha en cuanto a las condiciones climáticas entre su hábitat nativo y el invadido; ha evolucionado en determinadas condiciones y no es fácil que prospere en otras radicalmente diferentes.
4.- Generalista en su dieta o tolerante a diferentes condiciones del entorno, y más adaptables a condiciones no habituales del hábitat invadido.
5.- Tienen éxito invasor porque huyendo evitan a los depredadores del hábitat original, lo que supone más individuos en la reproducción. Así, Lorne Wolfe de la Universidad del Sur de Georgia, menciona la planta Silene latifolia, que invadió Norteamérica a principios del siglo XIX y que ha calculado que tiene 17 veces más probabilidades de ser dañada por alguna especie enemiga en su hábitat original de Europa que en Norteamérica.
6.- Se asocian con la especie humana para su dispersión, para conseguir más alimentos o aprovechar la degradación del hábitat a invadir por la actividad humana. Muchas especies introducidas tienen éxito en la invasión porque los ambientes modificados por la actividad humana permiten su instalación. Y, además, la especie humana puede ayudar con un número alto de individuos o con repetidos episodios de transporte.
7.- Tienen mecanismos de dispersión muy efectivos para formar poblaciones viables lejos de la población de origen.
8.- Con fases juveniles cortas, alcanzan la madurez sexual con rapidez.
9.- Pueden colonizar a partir de uno o de muy pocos individuos con, por ejemplo, una hembra fertilizada o por partenogénesis.
10.- Tienen una tasa reproductora alta y pueden construir poblaciones con rapidez y, así, la invasión progresa rápida y potente. Incluso, como menciona Petr Pysek, de la Academia de Ciencias de la República Checa, una característica importante es la posibilidad de la reproducción clonal, como ocurre con el alga Caulerpa en el Mediterráneo.
Algunas de las plagas más conocidas y extendidas por el planeta se deben a especies introducidas. Es un asunto en debate cuántas de las especies pueden ser invasoras y cuántas llegarán a provocar una plaga. Es la famosa regla del 10%. Mark Williamson apoya esta regla. De 10 especies nuevas que llegan a un área geográfica concreta, solo una aparece en el entorno natural; una de cada 10 introducidas se establece y una de cada 10 de las establecidas se convierte en un peligro, en una plaga. Hay datos que no coinciden con este 10% como, por ejemplo, los que publicó Max Wade, de la Universidad de Loughborough, en Inglaterra. De los árboles introducidos en el centro de Alemania en la década de los noventa, unas 3150 especies, el 10% aumenta su área de distribución y se expande, el 2% se establece, y el 1% acaba formando parte de la vegetación habitual de la región. Aquí los porcentajes siguen la regla de 10:2:1. No es el 10% sin más.
Fue David Lodge, de la Universidad de Notre Dame, en Estados Unidos, quien propuso, en la década de los noventa, una nueva línea de investigación para la búsqueda de las características de los hábitats susceptibles de ser invadidos. Incluye, en parte, la propuesta de Sarah Reichard de 1994. Como una primera aproximación enumera que el clima sea parecido al de la región de origen de la especie invasora, que, en la región nueva, haya una diversidad baja y escasa presencia de depredadores y, además, que sea un hábitat perturbado, con recursos escasos o alterados. Si el nivel de recursos es estable, hay menos probabilidad de que se convierta en un hábitat invadido. A todo ello, añaden Luis Espínola y Horacio Ferreira, de las universidades Estatal de Maringá y de Sao Paulo, el aislamiento geográfico e histórico de la región invadida.
 Kudzu, una planta trepadora oriunda de Asia Oriental, creciendo sobre los árboles en Atlanta (Georgia, Estados Unidos). Fuente: Wikimedia Commons
Kudzu, una planta trepadora oriunda de Asia Oriental, creciendo sobre los árboles en Atlanta (Georgia, Estados Unidos). Fuente: Wikimedia CommonsEn conclusión, y como John Ewel y otros veinte expertos de todo el planeta escribían en 1999, hay varios temas de investigación sobre especies invasoras sobre los que existe un amplio consenso. No hay que olvidar que, aunque a la ciencia se le piden bases científicas detalladas y certezas de los efectos que provocan las especies invasoras, siempre es adecuado partir del principio de precaución al tomar decisiones.
Según Ewel, las especies invasoras tienen un gran potencial para dar grandes beneficios económicos y ecológicos a la sociedad; además, continuará la introducción de especies aunque se debe vigilar su impacto que tendrá una distribución desigual; la actividad humana facilita el movimiento de especies y también su establecimiento; puede pasar mucho tiempo entre la introducción de una especie y su expansión; una vez establecida es casi imposible de erradicar; una especie invasora que se ha establecido con éxito en un determinado hábitat predice su potencial invasivo en otros hábitats.
Para las invasiones biológicas también hay mitos, y Stephen Gollasch, de GoConsult de Hamburgo, y James Carlton, del Colegio Williams de Williamstown, en Estados Unidos, nos comentan algunos.
El primero se puede resumir en la optimista afirmación de “todas las especies que podrían haberse introducido ya están aquí” y, por tanto, no hay peligro de que lleguen más. No es así y, cuando se dé la combinación adecuada de factores, sobre todo el número suficiente de individuos de la especie invasora para conseguir una población viable puede llegar la nueva invasión.
Otro mito es preguntarnos “por qué necesitamos estar atentos ahora”, ya lo haremos cuando llegue la invasión. Hay que estar atentos porque llegará, con la globalización otras especies pueden ser invasoras y hay que responder de inmediato.
El tercer mito que mencionan Gollasch y Carlton es que “las invasiones son parte de la naturaleza y sucederán de todos modos; lo único es que ahora se acelera el proceso”. No es cierto, no es fácil que una especie llegue de manera natural, por ejemplo, del Pacífico a Europa occidental. Pero lo puede conseguir, y con rapidez, por la intervención de la especie humana. Nos sirven de ejemplo los ciclos de vida del zooplancton, demasiado cortos como para poder atravesar un océano, pero la intervención humana puede acelerar la velocidad del viaje y, transportada en el agua de lastre de los barcos, llegar viables a otro continente.
El siguiente mito afirma que “los humanos no deben interferir con la distribución de las especies como fenómeno natural que es”. Sin embargo, la actividad humana ha adquirido tal importancia que sobrepasa con mucho un fenómeno natural.
Y, para terminar, “solo el 10% de las invasiones tiene un impacto significativo”. Es la típica regla del 10% que, cuando se entra en el debate, no tiene ninguna evidencia clara. A menudo, el impacto más visible de una especie invasora es evidente cuando la población ha aumentado de manera notable, incluso tiempo después de su introducción. Soplo hay que recordar, en nuestro entorno, del plumero de la Pampa.
La dispersión de especies por la actividad humana no es simplemente una cuestión de aceleración de un proceso normal que siempre ha ocurrido o que ocurrirá antes o después. Los movimientos naturales de especies suceden por corredores predecibles: márgenes continentales, corrientes oceánicas o caminos que se abren y cierran en una escala temporal geológica. Por el contrario, los movimientos de especies mediados por la especie humana a menudo suponen procesos impredecibles e instantáneos independientes de barreras en el espacio o en el tiempo. No existe un flujo natural de especies entre, por ejemplo, los estuarios templados del sur de Australia y los de Europa occidental. Sin embargo, por el transporte de especies de interés comercial, o por accidente, una especie puede ser transportada entre Australia y Europa en cuestión de días e, incluso, de horas.
Referencias:
Carlton, J.T. 1996. Pattern , process, and prediction in marine invasion ecology. Biological Conservation 78: 97-106.
Carlton, J.T. 1999. Molluscan invasions in marine and estuarine communities. Malacologia 41: 439-454.
Davis, M.A. et al. 2000. Fluctuating resources in plant communities: a general theory of invasibility. Journal of Ecology 88: 528-534.
Davis, M.A. 2003. Biotic globalization: Does competition from introduced species threaten biodiversity? BioScience 53: 481-489.
Davis, M. et al. 2011. Don’t judge species on their origins. Nature 474: 153-154.
Espínola, L.A. & H. Ferreira Júlio Junior. 2007. Espécies invasora: Conceitos, modelos e atributos. Interciencia 32: 580-585.
Ewel, J.J. et al. 1999. Deliberate introductions of species: research needs. BioScience 49: 619-630.
Falk-Petersen, J. et al. 2006. On the numerous concepts in invasión biology. Biological Invasions DOI: 10.1007/s10530-005-0710-6
Gollasch, S. & J. Carlton. 2004. To whom it may concern “Invasion on myths” – GoConsult. 2004-06-09, 2.
Kimberling, D.N. 2004. Lessons from history: predicting successes and risks of intentional introductions for arthropod biological control. Biological Invasions 6: 301-318.
Kinzelbach, R. 1995. Neozoans in European waters – Exemplifying the worlwide process of invasion and species mixing. Experientia 51: 526-538.
Kolar, C.S. & D.M. Lodge. 2001. Progress in invasion biology: predicting invaders. Trends in Ecology & Evolution 16: 199-204.
Larson, B.M.M. 2007. An alien approach to invasive species: objectivity and society in invasion biology. Biological Invasions 9: 947-956.
Levine, J.M. & C.M. D’Antonio. 1999. Elton revisited: a review of evidence linking diversity and invasibility. Oikos 87: 15-26.
Liu, X. et al. 2020. Animal invaders threaten protected areas worldwide. Nature Communications 11: 2892.
Lodge, D.M. 1993. Biological invasions: Lessons for Ecology. Trends in Ecology & Evolution 8: 133-137.
Marchioro, M. et al. 2020. Light traps in shipping containers: A new tool for the early detection of insect alien species. Journal of Economic Entomology doi: 10.1093/jee/toaa098.
Maurin, H. 1997. L’homme et les mamifères de France métropolitaine: Évolution historique et introductions d’espèces dans les milieux humides et aquatiques. Bulletin Français de la Pêche et de la Pisciculture 344/345: 117-132.
Mooney, H.A. & E.E. Cleland. 2002. The evolutionary impact of invasive species. Proceedings of the National Academy of Sciences USA 98: 5446-5451.
Morton, B. 1997. The aquatic nuisance species problema: A global perspective and review. En “Zebra mussel and aquatic nuisance species”, p. 1-54. Ed. Por F.M. D’Itri. Ann Arbor Press Inc. Chelsea, Michigan.
Pysek, P. 1995. On the terminology used in plant invasion studies. En “Plant invasions – General aspects and special problems”, p. 71-81. Ed. por P. Pysek et al. SPB Academic Publ. Amsterdam.
Pysek, P. 1997. Clonality and plant invasions: Can a trait make a difference? En “The ecology and evolution of clonal plants”, p. 405-427. Ed. Por H. de Kroon & J. van Groenendael. Backhuys Publ. Leiden.
Pysek, P. 1998. Is there a taxonomic pattern to plant invasions? Oikos 82: 282-294.
Pysek, P. et al. 2020. Scientists’ warning on invasive alien species. Biological Review doi: 101111/brv.12627
Rallo, A. & L. García-Arberas. 2012. Fauna exótica invasora en Bizkaia. Diputación Foral de Bizkaia. Bilbao. 330 pp.
Reichard, S. 1994. What makes a species a successful invades? En “Biological invasion as a global change”, p. 63-64. Ed. Por S.J. Hassol & J. Katzeberger. ASPEN Global Change Institute. Aspen, Colorado.
Reise, K. et al. 2006. Are aliens threatening European aquatic coastal ecosystems? Helgoland Marine Research 60: 77-83.
Ribeiro, F. et al. 2009. Non-native fish in the fresh waters of Portugal, Azores and Madeira Islands: a growing threat to aquatic biodiversity. Fisheries Management and Ecology 16: 255-264.
Ricciardi, A. & J.B. Rasmussen. 1998. Predicting the identity and impact of future biological invaders: a priority for auqtic resource management. Canadian Journal of Fisheries and Aquatic Sciences 55: 1759-1765.
Richardson, D.M. et al. 2000. Naturalization and invasion of alien plants: concepts and definitions. Diversity and Distributions 6: 93-107.
Schlaepfer, M.A. 2018. Do non-native species contribute to biodiversity? PLOS Biology 16: e2005568.
Sharma, G.P. et al. 2005. Plant invasions: Emerging trends and future implications. Current Science 88: 726-734.
Shrader-Frechette, K. 2001. Non-indigenous species and ecological explanation. Biology and Philosophy 16: 507-519.
Vilches, A. et al. 2010. Introducción a las invasiones biológicas. Boletín Biológica 17: 14-19.
Wade, M. 1997. Predicting plant invasions: making a start. En “Plant invasions: Studies from North America and Europe”, p. 1-18. Ed. por J.H. Brock et al. Backhuiys Publ. Leiden, Holanda.
Williamson, M. & A. Fitter. 1996. The varying success of invaders. Ecology 77: 1661-1666.
Wolfe, L.M. 2002. Why alien inveders succeed: Support for the Escape-from-Enemy Hypothesis. American Naturalist 160: 705-711.
Zimmer, C. 2008. Una especie exótica puede ayudar, no asfixiar, a la diversidad. New York Times 25 septiembre.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Los invasores: Invasiones biológicas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La cooperación no favorece a los invasores rápidos
- Los invasores
- Catástrofe Ultravioleta #18 INVASORES
Rompecabezas matemáticos con números
El sudoku es sin lugar a dudas uno de los rompecabezas más populares de los últimos tiempos, que ha tenido además un desarrollo vertiginoso. Todo el mundo lo relaciona con las matemáticas porque hay que colocar números en sus casillas, aunque su relación con esta ciencia es más profunda.
Desde que se diera a conocer internacionalmente el verano de 2005, el sudoku se ha convertido en todo un fenómeno de masas. Tenemos sudokus en los periódicos, revistas de sudokus, libros de sudokus, sudokus en todos los dispositivos electrónicos existentes (móviles, tabletas, ordenadores, etc), juegos de sudokus en las tiendas de juguetes, programas de ordenador para crear sudokus, colecciones por entregas relacionadas con el sudoku en los estancos, sudokus infantiles y una enorme cantidad de variantes del original.
 Sudoku 3 9×9-63 Typesetting F (2014), del artista esloveno Jaka Bonča (conocido también como Rototype). Imagen de la página web de Jaka Bonča
Sudoku 3 9×9-63 Typesetting F (2014), del artista esloveno Jaka Bonča (conocido también como Rototype). Imagen de la página web de Jaka BončaAunque seguramente las personas que estén leyendo esta entrada del Cuaderno de Cultura Científica ya conocerán perfectamente qué es un sudoku, empezaremos recordando las reglas de este pasatiempo matemático. El sudoku normal consiste en una cuadrícula de 9 x 9 celdas, dividida en 9 regiones de 3 x 3 celdas, y hay que rellenar las 81 celdas con las cifras del 1 al 9 (partiendo de una situación inicial en la que algunos números ya están colocados en algunas de las celdas), de manera que no se puede repetir ninguna cifra en una misma fila, columna o región. El sudoku está relacionado con los cuadrados latinos (véase la entrada Cuadrados latinos, matemáticas y arte abstracto o el libro Del ajedrez a los grafos, la seriedad matemática de los juegos) estudiados por el matemático Leonard Euler (1707-1783), aunque el juego moderno fue creado en la década de 1970 por el arquitecto jubilado y diseñador de pasatiempos Howard Garns (1905-1989) y publicado bajo en nombre number place en la revista Dell Pencil Puzzles & Word Games.
Maki Kaji, presidente de la editorial Nikoli, especializada en juegos y pasatiempos, en particular, rompecabezas lógicos, lo exportó a Japón y empezó a publicarlo en 1984 en su revista Monthly Nikolist bajo el nombre Suji wa dokushin ni kagiru (los números deben estar solos), que se abrevió a Su Doku. Su expansión por el resto del mundo vino de la mano del juez retirado neozelandés, residente en Hong Kong, Wayne Gould, quien desarrolló un programa de ordenador para crear rápidamente sudokus. En 2004 empezaron a publicarse sudokus en periódicos británicos, como The Times y The Guardian, y acabó convirtiéndose, desde 2005, en un rompecabezas muy popular que aparecía en la mayoría de los periódicos del mundo.
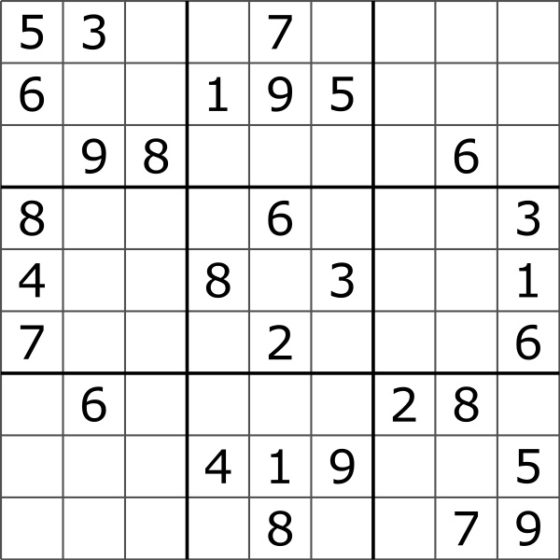 Un típico sudoku, en el que aparecen algunos números, pero las demás casillas están vacías y hay que rellenarlas siguiendo las reglas del rompecabezas. Imagen de Wikimedia Commons
Un típico sudoku, en el que aparecen algunos números, pero las demás casillas están vacías y hay que rellenarlas siguiendo las reglas del rompecabezas. Imagen de Wikimedia Commons
 Solución del sudoku anterior. Imagen de Wikimedia Commons
Solución del sudoku anterior. Imagen de Wikimedia Commons
La relación del sudoku con las matemáticas no es que se utilicen números, ya que se podrían utilizar letras, colores o cualesquiera otros símbolos, sino que es de tipo combinatorio, está basada en la relación entre las diferentes posiciones de los símbolos (números) en las filas, columnas y regiones. Si observamos la solución de un sudoku, como la anterior imagen, se trata de un tipo particular de cuadrado latino (recordemos que un cuadrado latino de orden n es un retículo cuadrado de tamaño n x n en el que cada entrada es un número del 1 al n, de tal forma que cada número de {1, …, n} aparece una vez, y sólo una vez, en cada fila y cada columna) de tamaño 9 x 9, en el que se verifica también que los números del 1 al 9 aparecen solo una vez en cada una de las nueve regiones 3 x 3.
 Cuadro del pintor suizo Richard Paul Lohse, que bajo el título “Komplementäre Gruppen durch sechs horizontale systematische Farbreihen” -Grupos complementarios formados por seis series sistemáticas horizontales de color- (1950 y 1976), recoge un cuadrado latino de orden 6 cuyos símbolos son los colores
Cuadro del pintor suizo Richard Paul Lohse, que bajo el título “Komplementäre Gruppen durch sechs horizontale systematische Farbreihen” -Grupos complementarios formados por seis series sistemáticas horizontales de color- (1950 y 1976), recoge un cuadrado latino de orden 6 cuyos símbolos son los colores
Existen diferentes cuestiones matemáticas implicadas en este rompecabezas, como cuántas estructuras de solución, es decir, cuadrados latinos de orden 9 que cumplen la regla de las regiones diferentes, hay (que resultan ser 6.670.903.752.021.072.936.960, aunque si tenemos en cuenta las simetrías, estas se reducen a 5.472.730.538 soluciones de sudokus distintas); dado un cuadrado latino de orden 9 que es solución de sudoku, cuántos rompecabezas sudokus distintos se pueden generar a partir del mismo (es decir, eliminando los números de las casillas hasta dejar una pequeña cantidad inicial que es el punto inicial del juego, las pistas) y cuál es la cantidad mínima de números iniciales (pistas) que se necesitan para que el sudoku esté bien definido, esto es, que exista una solución única (que resultan ser 17 pistas), entre otras.
Sin embargo, mi intención en esta entrada de la sección Matemoción del Cuaderno de Cultura Científica no es hablar de las matemáticas de los sudokus (puede verse, por ejemplo, el artículo Sudokus y modelización, de María Merino), sino presentar otros rompecabezas matemáticos similares a este, en el sentido de que se colocan números sobre una estructura reticular.
En el año 2010, Jai Gomer, de Kobayaashi Studios, desarrolló una serie de rompecabezas numéricos, llamados sujiko y suko, herederos de los sudokus, pero que ya implican algo de aritmética –en concreto la suma– en sus reglas. Estos aparecieron primero en los periódicos ingleses como The Times y The Telegraph, y posteriormente en periódicos de todo el mundo, como, por ejemplo, El País.
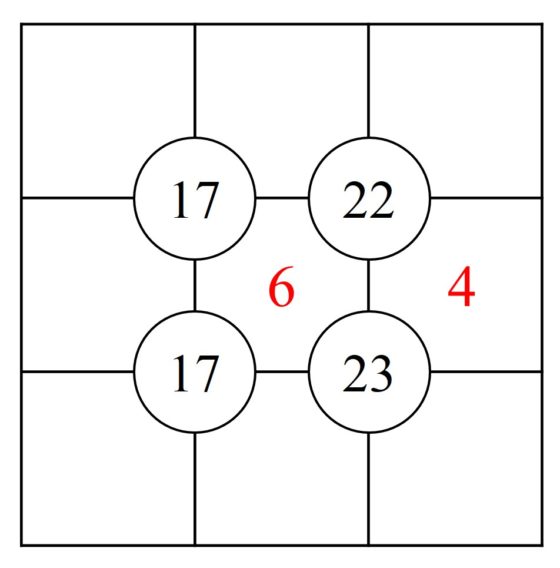
El tablero del sujiko es una cuadrícula 3 x 3, con cuatro espacios circulares colocados en las cuatro intersecciones de las líneas horizontales y verticales de la cuadrícula, en los cuales hay escritos cuatros números (por ejemplo, 17, 22, 17, 23, en la imagen anterior). El objetivo del pasatiempo es colocar los números del 1 al 9 en las celdas –aunque puede haber ya alguno colocado, como pista (en el sujiko anterior 6 y 4)– de forma que la suma de los números que estén en los recuadros alrededor de cada círculo es exactamente el número escrito en el mismo.
Este rompecabezas de resuelve de forma lógica, como el sudoku, pero teniendo en cuenta su regla, que la suma de los números de las celdas alrededor de un círculo es el valor del mismo. Veamos cómo resolver el sujiko anterior, que es de los sencillos.
Los números de las dos casillas de arriba a la derecha deberán sumar 12, ya que 6 y 4 están también alrededor del 22 y su suma es 6 + 4 = 10. Como en esas casillas no pueden estar 6 y 4, que ya están colocados, las dos opciones son 9 y 3, o 7 y 5, sin determinar aún cual va en cada una de las dos casillas. Si realizamos el mismo razonamiento para las dos celdas de abajo a la derecha, que deberán sumar 13, la única posibilidad es 8 y 5. Como aquí estaría el número 5, en las dos celdas de arriba tendrían que ser los números 9 y 3.
Veamos el orden arriba. En la casilla central de la fila de arriba va el 3 o el 9, si fuese el 9 tendríamos que alrededor de la casilla del 17 ya se sumaría 9 + 6 = 15, luego las otras dos casillas deberían sumar 2, lo cual es imposible, puesto que la suma más baja posible sería 1 + 2 = 3. En conclusión, en la primera fila, el número 3 iría en la casilla central y el 9 en la derecha.
Antes de seguir, pensemos en que tres números nos faltan de utilizar para las celdas de la columna de la izquierda. Serían 1, 2 y 7. Entonces, alrededor del 17 de arriba tenemos 3 + 6 = 9, más la suma de los números de las dos celdas, que deberá ser 8, luego los números de esas dos celdas son 1 y 7. Si seguimos este razonamiento un poco más, obtendremos la solución definitiva, que aparece en la imagen de abajo.
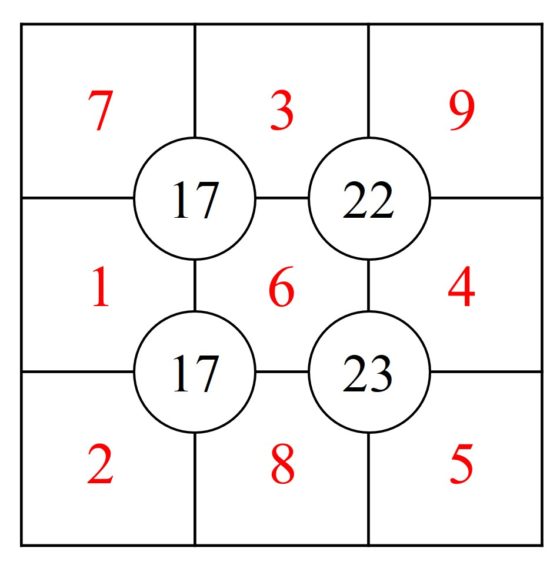
Podemos presentar este problema de la siguiente forma. La información del mismo está dada en el siguiente esquema, donde en las celdas tenemos las variables del juego y en los círculos los datos del mismo.
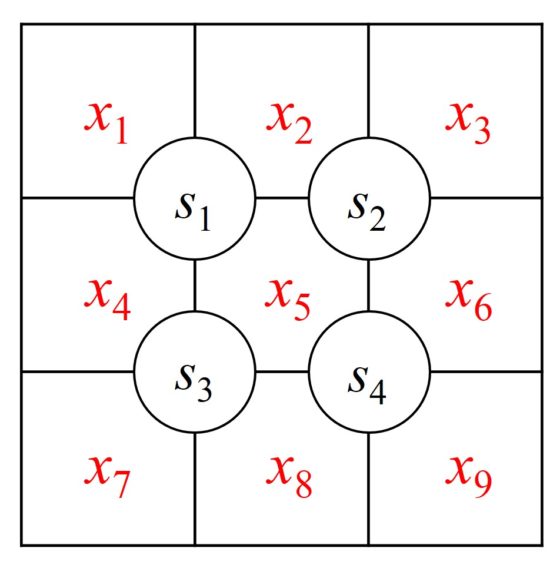
Luego la solución del sujiko es la solución de un sistema de cuatro ecuaciones y nueve incógnitas, aunque con las siguientes restricciones, las variables solo toman valores entre los números 1, 2, 3, 4, 5, 6, 7, 8, 9 y cada variable toma un valor distinto a las otras.
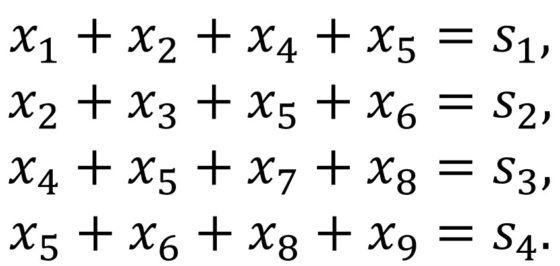
Aunque la diversión del sujiko está en obtener la solución de forma lógica, se puede utilizar también el planteamiento algebraico como ejemplo para estudiantes que estén trabajando el álgebra lineal de la resolución de los sistemas de ecuaciones lineales.
Os dejo con dos sujikos, de niveles medio y alto, que he sacado de la página Sudokasana, donde se denominan Minisum puzzles. Aunque también podéis encontrar sujikos en la página de pasatiempos del periódico The Times.
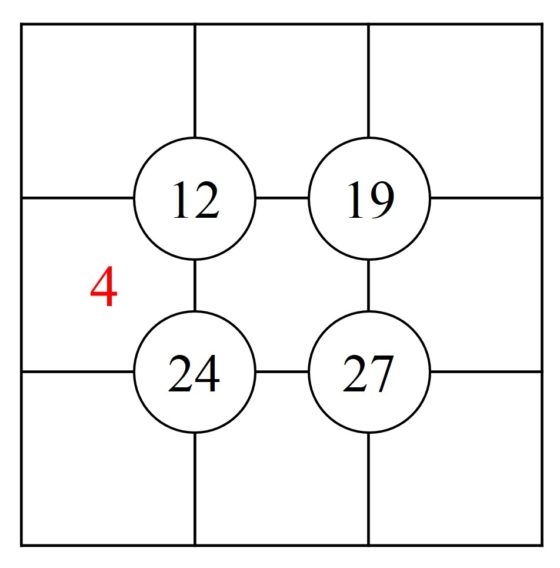
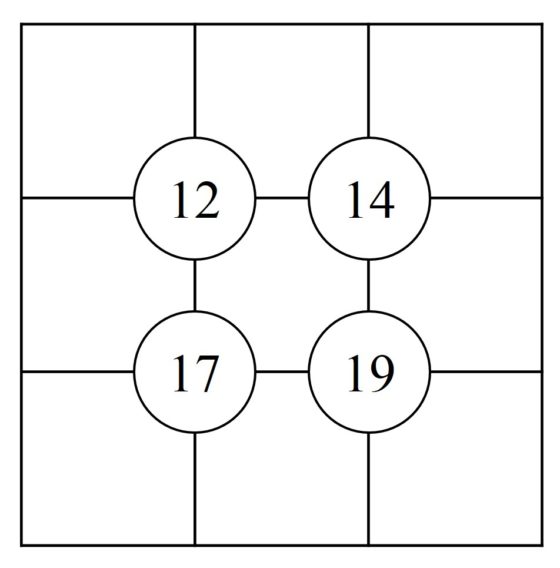
Por otra parte, el rompecabezas suko es como el sujiko, pero al que se le añade una nueva condición relacionada con regiones del retículo 3 x 3. La condición es que la suma de los números de las casillas de un mismo color suman la cantidad indicada en el pasatiempo, como aparece en la siguiente imagen (suko que hemos tomado de la página de pasatiempos de The Times).
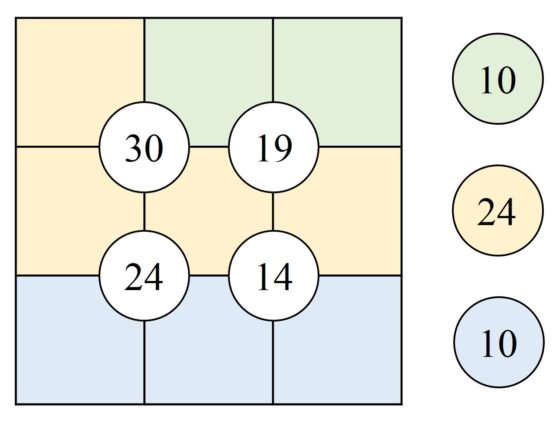
Desde el punto de vista algebraico, en el suko añadimos tres ecuaciones lineales más, luego tenemos un sistema de siete ecuaciones lineales con nueve incógnitas, y la solución del rompecabezas es la solución del sistema de ecuaciones.
Otro rompecabezas relacionado con el sudoku, o más bien con los cuadrados latinos, pero que añade aritmética –aunque ahora las cuatro operaciones aritméticas, no solo la suma– a sus reglas es el KenKen.
El rompecabezas KenKen, también conocido con los nombres KenDoku, MathDoku o CalcuDoku, fue inventado por el profesor de matemáticas japonés Tetsuya Miyamoto como una herramienta para ejercitar el cerebro. Su nombre se deriva del vocablo japonés Ken que significa inteligencia o ingenio.
En 2007 el inventor de juguetes Robert Fuhrer, propietario de la empresa de juguetes Nextoy, descubrió en Japón varios libros con este pasatiempo y su interés por el mismo haría que el rompecabezas lógico acabara en las páginas del periódico británico The Times y después en muchos otros periódicos de todo el mundo.
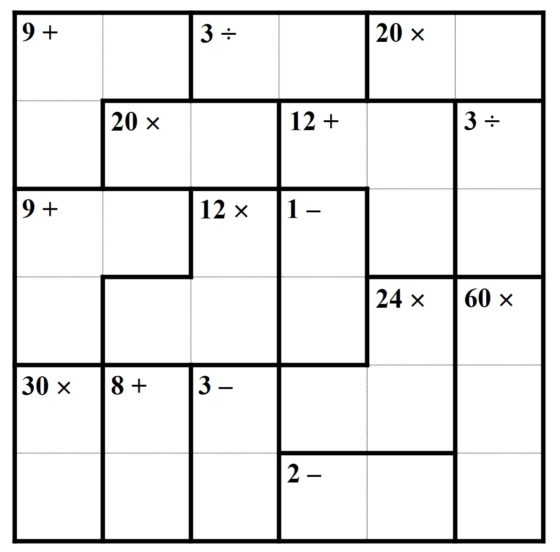
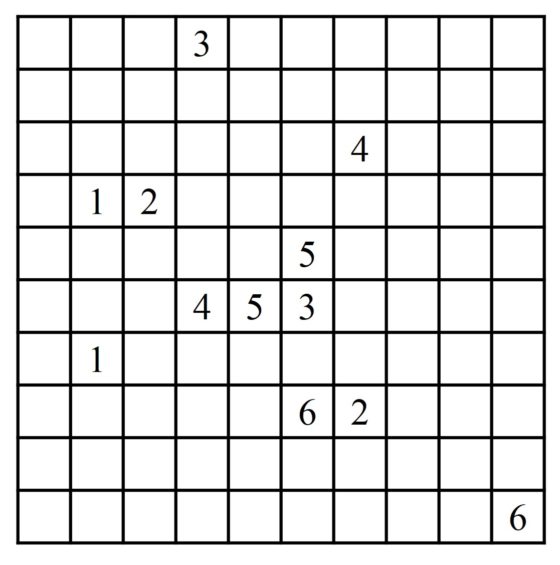
Las reglas del KenKen son las siguientes. Se parte de una cuadrícula n x n sobre la que hay que colocar los números de 1 a n de forma que en cada fila y cada columna estén todos los n números y no se repita ninguno (luego será un cuadrado latino de orden n), pero además la retícula está dividida en una serie de regiones, en cada una de las cuales aparecen una operación aritmética (suma, resta, multiplicación o división) y un número, que será el resultado de aplicar la operación aritmética indicada a los números de las celdas de esa región.
En el siguiente ejemplo de rompecabezas KenKen tenemos una cuadrícula 4 x 4, luego hay que escribir los números 1, 2, 3 y 4 en las celdas de la misma, de forma que se constituya un cuadrado latino –en cada fila y cada columna aparece cada uno de los cuatro números una y solo una vez– y se cumplan las condiciones aritméticas de las regiones –por ejemplo, en la región de arriba a la izquierda la división de los dos números es 2, o en la región de la derecha la resta de los dos números es también 2–.
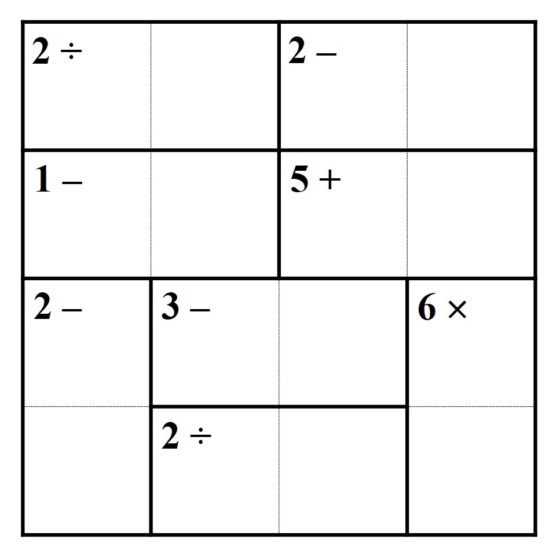
La solución de este KenKen viene dada en la siguiente imagen.
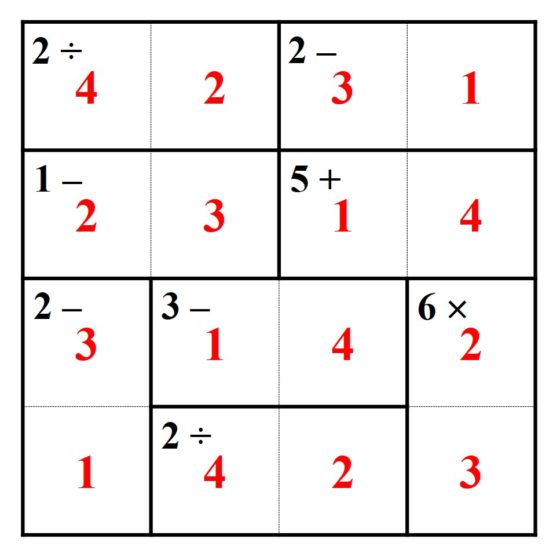
En la página KenKen, puzzles that make you smarter se pueden encontrar rompecabezas con cuadrículas desde 3 x 3 hasta 9 x 9, de diferentes niveles de dificultad. Os dejamos con uno para que os divirtáis de tamaño 6 x 6 y dificultad media.
Otro de los juegos de la editorial Nikoli, famosa internacionalmente por el Sudoku, es el Hitori, término que en japonés significa “solitario”. Este pasatiempo consiste en una retícula con números en todas sus celdas y la acción del mismo consiste en eliminar una serie de números, o pintar de negro las celdas correspondientes, de forma que se cumplan las siguientes reglas:
i) en cada fila y cada columna no se repite ningún número;
ii) las celdas tachadas o negras no pueden ser adyacentes (pueden tocarse esquina con esquina, pero no lado con lado);
iii) el resto de las celdas con números tienen que estar conectadas, vertical u horizontalmente, entre sí, es decir, no pueden quedar celdas aisladas.
Veamos en qué consiste el juego mediante un ejemplo concreto de tamaño 5 x 5.
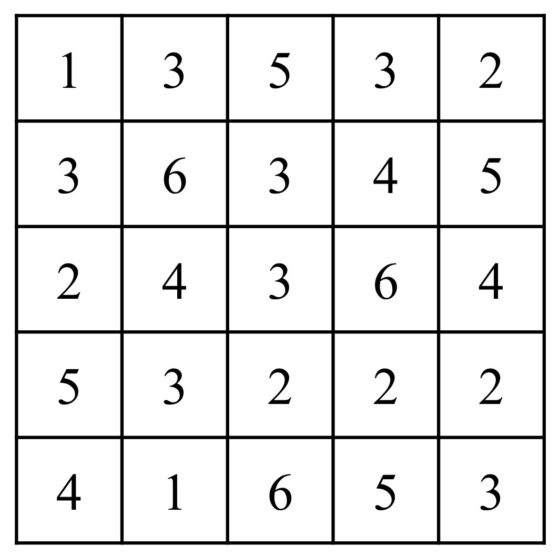
La solución aparece en la siguiente imagen. Como podemos observar, se cumplen las tres condiciones de este rompecabezas lógico. En cada fila y cada columna de la solución no se repite ningún número, por ejemplo, en la primera fila había dos celdas con el número 3, luego se ha tenido que tachar una. Las celdas tachadas solo se tocan por los vértices o no se tocan. Y no hay celdas aisladas de las demás.

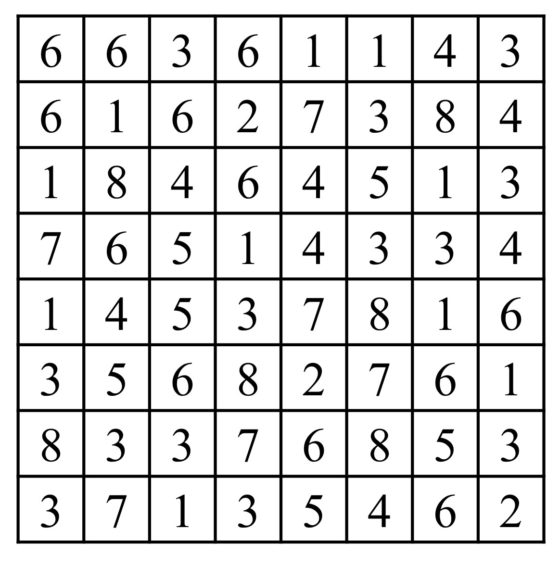
En la página Hitori Conquest [www.hitoriconquest.com/] pueden encontrarse más rompecabezas Hitori de tamaños 5 x 5, 8 x 8 y 12 x 12, como el que dejamos a continuación para aquellas personas que queráis pasar un buen rato resolviéndolo.
Vamos a concluir esta entrada del Cuaderno de Cultura Científica con otro de los rompecabezas lógicos popularizado por la editorial japonesa Nikoli, el conocido como Numberlink (que podríamos traducir como “conecta los números”). Este juego tiene su origen en la matemática recreativa clásica, ya que una versión del mismo fue propuesta por el matemático recreativo estadounidense Sam Loyd (1841-1911) en 1897 y también por el matemático recreativo inglés Henry Dudeney (1857-1930), en su libro Amusements in Mathematics (1917), el problema 252, que vemos en la siguiente imagen.

El rompecabezas consiste en una retícula en la que aparecen parejas de números (aunque también podrían ser letras, colores u otros símbolos), dos unos, dos doses, dos tres, etcétera. El jugador tiene que conectar cada número con su igual mediante una línea que pasa de una celda a otra, horizontal o verticalmente, de tal forma que las líneas no se pueden cruzar entre sí, ni volver hacia atrás a celdas ya recorridas y no debe de quedar ninguna celda sin ser recorrida por alguna línea (aunque hay algunos diseñadores de juegos que se saltan esta regla).
Veamos un sencillo ejemplo y su solución.
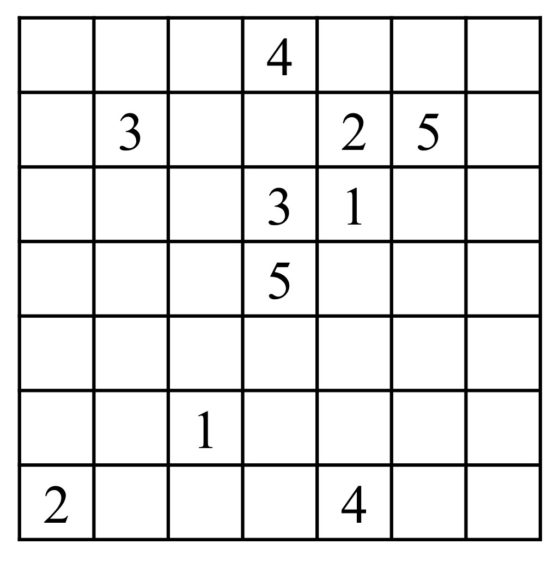
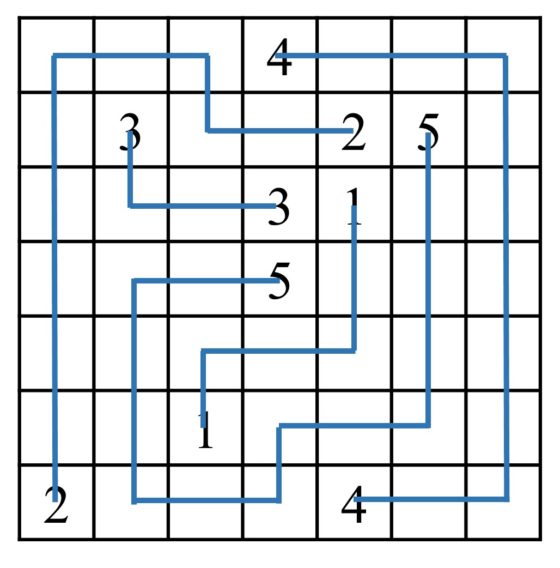
Os dejamos propuesto un rompecabezas lógico conecta los números, sacado de la página Puzzle’s Baron Numberlinks, para vuestro disfrute.
Para todos los rompecabezas lógicos presentados en esta entrada existen aplicaciones para móviles que os podéis bajar y jugar en cualquier momento. Yo mientras escribía esta entrada me he bajado algunas a mi móvil para poder jugar tranquilamente.
 2x Sudoku I (2006), de la artista polaca Eliza Kopec. Imagen de la página Affordable Art Fair
2x Sudoku I (2006), de la artista polaca Eliza Kopec. Imagen de la página Affordable Art FairBibliografía
1.- Raúl Ibáñez, Sudoku, Las matemáticas en la publicidad, DivulgaMAT, 2011.
2.- María Merino, Sudokus y modelización, Un paseo por la Geometría 2009/2010, UPV/EHU, 2010.
3.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, colección El mundo es matemático, RBA, 2015.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Rompecabezas matemáticos con números se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Locura instantánea, un rompecabezas con cubos de colores
- Números errores de impresión
- Quipu y yupana, instrumentos matemáticos incas (II)
Historia de Uri Geller
Hay personas que son capaces de hacer cosas extraordinarias. Entre ellas, por ejemplo, se encuentran las y los deportistas de élite, que son capaces de realizar proezas imposibles para el resto de los mortales. Pero también nos encontramos con otras que realizan cosas, en apariencia, imposibles y que se escapan a nuestra compresión.
Una de ellas es Uri Geller. Un ilusionista que se hizo famoso hace unas cuantas décadas porque doblaba las cucharas con el supuesto poder de su mente. Sí, Uri acudió a distintos programas de televisión haciendo su número de las cucharas. Pero… ¿tenía realmente poderes mentales para hacer tal cosa?
Los vídeos de Historias de la Ciencia presentan de forma breve y amena pasajes de la nuestra historia científica y tecnológica. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.
El artículo Historia de Uri Geller se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Historia de la quinina
- La historia del bolígrafo más famoso del mundo
- Ciencia y Misterio, la webserie
Las reglas de desplazamiento radiactivo
 Foto: Sebastian Yepes / Unsplash
Foto: Sebastian Yepes / UnsplashEl concepto de isótopo fue un avance muy significativo en la comprensión de la radiactividad. Pero aun estaban sobre la mesa dos cuestiones fundamentales, a saber, ¿cómo se producen los cambios en la naturaleza química cuando un átomo sufre una desintegración radiactiva? y ¿qué determina si el número atómico Z aumenta o disminuye en una transformación radiactiva dada?
En 1913, Soddy en Inglaterra y Kazimierz Fajans [1] en Alemania respondieron estas preguntas de forma independiente. Ambos propusieron dos reglas que sistematizaban todas las observaciones relevantes de la radiactividad natural. Se llaman reglas (hay quien las llama leyes) de Fajans-Soddy, reglas de transformación de la radiactividad o reglas de desplazamiento radiactivo.
Para 1913 el modelo nuclear del átomo de Rutherford estaba generalmente aceptado. Usando este modelo se podía considerar que un átomo radiactivo tiene un núcleo inestable que emite una partícula alfa o una partícula beta (a veces con emisión de un rayo gamma). Cada núcleo tiene una carga positiva dada por Ze, donde Z es el número atómico y e es la magnitud de la carga de un electrón. El núcleo está rodeado por Z electrones que hacen que el átomo en su conjunto sea eléctricamente neutro y determinan el comportamiento químico del átomo.
Por otra parte, sabemos que una partícula alfa tiene una masa atómica de aproximadamente cuatro unidades y una carga positiva de dos unidades, +2e. Una partícula beta tiene una carga negativa de una unidad, -e, y muy poca masa en comparación con una partícula alfa.
Con esta información en mente, las reglas de transformación radiactiva [2] dicen lo siguiente:
1. Cuando un núcleo emite una partícula alfa, la masa del átomo disminuye en cuatro unidades de masa atómica y el número atómico Z del núcleo disminuye en dos unidades; el átomo resultante pertenece a un elemento dos espacios hacia atrás en la tabla periódica.
2. Cuando un núcleo emite una partícula beta, la masa del átomo cambia muy poco, pero el número atómico Z aumenta en una unidad; el átomo resultante pertenece a un elemento un espacio hacia delante en la tabla periódica.
3. Cuando solo se emite un rayo gamma, no hay cambio en el número correspondiente a la masa atómica, ni en el número atómico.
 La tabla de la serie radiactiva que venimos usando como ejemplo muestra cómo se aplican estas reglas de desintegración radiactiva a esa serie, al menos en lo que respecta al número atómico.
La tabla de la serie radiactiva que venimos usando como ejemplo muestra cómo se aplican estas reglas de desintegración radiactiva a esa serie, al menos en lo que respecta al número atómico.
Estas reglas, usando ahora el modelo del átomo de Rutherford-Bohr-Sommerfeld, ayudan a explicar por qué se produce un cambio en la naturaleza química como resultado de la emisión de una partícula alfa o beta. La emisión de una partícula alfa requiere dos cargas positivas del núcleo y cuatro unidades de masa atómica del átomo. Un ejemplo es el siguiente:
21884Po → 21482Pb + α
El nuevo átomo resultante (82Pb) con su núcleo menos positivo puede contener en sus capas externas dos electrones menos que antes, por lo que los dos electrones en exceso se pierden. El comportamiento químico de los átomos está controlado por el número de electrones; por lo tanto, el nuevo átomo actúa químicamente como un átomo de un elemento con un número atómico dos unidades menor que el del átomo original.
Por otro lado, en el caso de la emisión beta, el núcleo, y con él todo el átomo, adquiere una carga positiva. Un ejemplo es el siguiente:
23490Th → 23491Pa + β
El número de electrones que el átomo puede contener alrededor del núcleo ha aumentado en uno. Después de que ha recogido un electrón extra para volverse neutral nuevamente, el átomo actúa químicamente como un átomo con un número atómico una unidad mayor que el del átomo antes de que ocurriera el cambio radiactivo.
Usando estas reglas de transformación, Soddy y Fajans pudieron determinar el lugar en la tabla periódica para cada una de las sustancias (o nucleidos) en la serie radiactiva; no era necesaria ninguna revisión de la tabla periódica existente. Ahora se sabe que muchos de los elementos entre Z = 82 (plomo) y Z = 92 (uranio) contienen varios isótopos cada uno. Estos resultados se podían deducir de la hipótesis de la existencia de isótopos, pero también se buscaron, y se obtuvieron, pruebas directas e independientes en 1914.
Notas:
[1] Unos de esos científicos olvidados de la primera mitad del siglo XX , a los que el Nobel pasó rozando y que lo hubieran merecido. Hoy sus descubrimientos están en libros de texto de física y química, muchas veces de forma anónima.
[2] A estas alturas de la serie, la lectora atenta posiblemente encontrará las reglas dignas de Pero Grullo, pero en 1913 fueron un gran avance.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Las reglas de desplazamiento radiactivo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:¿Se pueden ver los átomos?
Javier Fernández Panadero
Hay preguntas muy fáciles de hacer y no tan fáciles de contestar… pero vamos a intentarlo.
Repuesta simple: ¿Ves este plátano? ¿Sí? Pues está hecho de átomos. Conclusión: ves los átomos.
¿Seguro? No sé vosotros, pero mis ojos no ven “plátanos”. Mi retina es sensible a la luz, no a la fruta.
Eso significa que, cuando hablo de que veo algo, en realidad, lo que estoy haciendo es detectar luz que proviene de aquello que digo ver. Bien porque ese objeto la emita o bien porque la refleje o disperse.
En el caso del plátano, una parte de la luz incidente se absorbe y otra parte se refleja, pero no de forma igual para todos los colores. Las frecuencias próximas al “amarillo” resultan reflejadas en mayor cuantía. De esta forma, la luz reflejada llega a mi retina y así percibo la forma, “su” color, si la piel es suave o rugosa y otras características que son capaces de alterar de alguna manera la radiación incidente, para que la reflejada “transporte” información sobre ellas.
Bien, ¿es eso, entonces, VER?
Este… no.
VER es un proceso que quizá comience en el ojo, pero que sin duda termina en el cerebro.
Contestadme a esta pregunta: ¿Qué es esto?
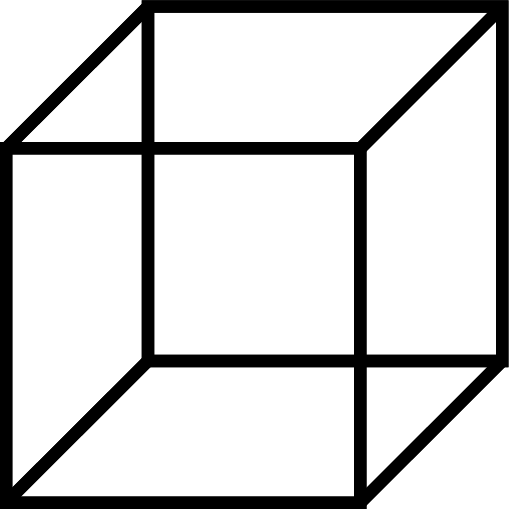 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsSi habéis dicho “Un cubo”, estáis hablando de algo más allá de lo que ven los ojos. Un cubo es una figura tridimensional, pero esto que ves es un dibujo PLANO. Son unas líneas sobre un plano que te “hacen pensar” en un objeto tridimensional, es lo que llamamos perspectiva. De hecho, si os concentráis podéis conseguir ver el “cubo” de dos formas distintas, según escojáis en vuestra mente si son los vértices inferiores los que están “delante” o son los superiores.
Por lo tanto, el acto de VER se completa cuando la mente modeliza el patrón de puntos e interpreta un modelo de lo que está percibiendo.
A veces “viendo” cosas que no existen, por ejemplo “completando” la imagen percibida, como en este caso, donde el triángulo blanco, que todos “vemos”, no existe.
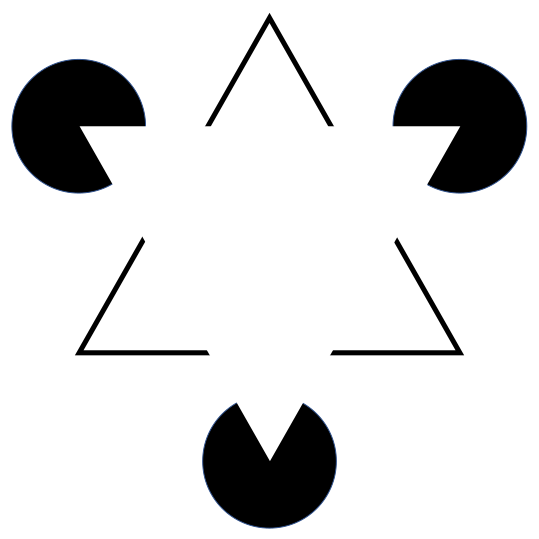 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsMirad esta otra.
 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsEn este caso, nuestra mente interpreta que las “vías” son paralelas, y están alejándose, por lo que esa barra amarilla que hay “a lo lejos” debe de ser más grande que la que está “delante”. Pero todo eso son interpretaciones de nuestro cerebro para adecuar la percepción en el modelo del mundo que nos hemos ido construyendo… y esto supera con creces la información que está contenida en la imagen, de hecho, nos puede llevar a conclusiones erróneas sobre ella, como en este caso.
Bien, pero volvamos a la pregunta inicial.
Asumiendo todas estas limitaciones sobre el acto de VER, ¿podemos ver los átomos, Javi?
No, son muy pequeños, tus ojos no llegan a tanto. Si pensamos en la parte óptica de tu ojo: el cristalino, la pupila, los humores, la resolución de la retina… No, no llegas a resolver algo tan pequeño.
Muy bien -protestas, pero, ¿qué me dices de esto?
https://culturacientifica.com/app/uploads/2020/10/Espermatozoides.ogvSon espermatozoides, muy pequeños como para verlos al ojo desnudo, pero visibles a través de métodos ópticos, interponiendo lentes de suficiente potencia como para ampliarlos hasta que pueda percibirlos usando los ojos.
Por lo tanto, usando “lupas gordas” podemos “ver con los ojos” cosas muy pequeñas. ¿Podríamos, entonces, poner una enorme lente y ver los átomos?
No. Son demasiado pequeños. Pero, tenme paciencia, de verdad que quiero contestar a tu duda inicial. Mira la siguiente imagen y contéstame a una pregunta.
 Fuente: Wikimedia Commons
Esto es lo que llamamos una imagen térmica. Nuestros ojos no pueden ver la radiación infrarroja, pero esta cámara sí es capaz de detectarla y “crear” una imagen en una pantalla.
Fuente: Wikimedia Commons
Esto es lo que llamamos una imagen térmica. Nuestros ojos no pueden ver la radiación infrarroja, pero esta cámara sí es capaz de detectarla y “crear” una imagen en una pantalla.
Podéis hacer un experimento sobre esto con la cámara de vuestro teléfono móvil y un mando a distancia. Mirad la “bombillita” del mando a distancia. Cuando pulsáis un botón no se ve nada… porque la emisión es infrarroja. Ahora, miradla a través de la cámara de vuestro móvil y pulsad algún botón del mando. A través del móvil veréis que emite un parpadeo, un código con la orden que está mandando el mando. Según tu teléfono lo veréis de un color ligeramente diferente, por ejemplo violeta o blanco (funciona en casi todos los modelos de teléfono). Pero si miráis directamente al mando veréis… que no veis nada. Aquí puedes ver un vídeo con esta demostración de mi libro Experimentos para entender el mundo. La ciencia para todos.
Tengo una pregunta para ti. Ese color violeta que veo a través de la cámara, ¿es violeta? Quiero decir: ¿Es el color violeta de la luz visible que veo normalmente? No, ¿verdad? Si esa “bombillita” emitiese luz violeta, de la de “verdad”, la podría ver sin necesidad de la cámara. Ese color se lo “inventa” la cámara del móvil, ha convertido esa radiación infrarroja en luz visible con el color que le ha parecido. A eso lo llamamos falso color.
Volvamos a la foto del gato. Ese gato no tiene partes naranja, blancas o moradas. Eso son códigos de colores que elige el sistema de imagen térmica para representar distintas temperaturas. De hecho, tenéis la correspondencia entre color y temperatura a la derecha de la imagen. Como os podréis imaginar, esas escalas pueden modificarse, según lo que queramos medir.
Y ahora te pregunto yo, a la vista de esta imagen, ¿dirías que estamos VIENDO la temperatura?
Hay quien contestaría que no, que solo podemos hablar de VER si estamos usando sistemas ópticos y el ojo. Para ellos, aquí termina su viaje. No podemos ver los átomos.
Pero si eres más flexible en tu definición y te permites llamar VER a esto que hemos hecho con la temperatura, digamos a cambiar tu retina por un sistema de sensores y tu mente por un procesador que lo convierta en una imagen, te diré que sí, que podemos ver los átomos.
Para ello vamos a necesitar un sistema que sea capaz de medir a escala suficientemente pequeña, para luego componer, crear, inventarse una imagen a partir de esos datos, una representación. Lo mismo que hicimos con el gato y el mapa de falso color de temperaturas. Es importante que recuerdes que esa imagen coloreada del gato no existe, no es “real”, está construida a partir de datos.
Pero además con el átomo tenemos otro problema… un átomo no es “sólido”. Se parece más a una pequeña partícula (el núcleo) rodeada de un enjambre de electrones que, debido a su movimiento dan la impresión de formar una pequeña “bola”, pero no es algo macizo.
Así que de nuevo tenemos un problema. ¿Qué es lo que vamos a intentar “ver” del átomo? Pues vamos a intentar “percibir” ese enjambre de electrones, que, aunque sólo sea uno, se mueve por una región tan amplia y a tanta velocidad que da la impresión de una distribución de carga negativa esférica alrededor de ese núcleo, de una “nube”.
Un aparato capaz de esto es el microscopio de efecto túnel. Y este es un esquema de su funcionamiento:
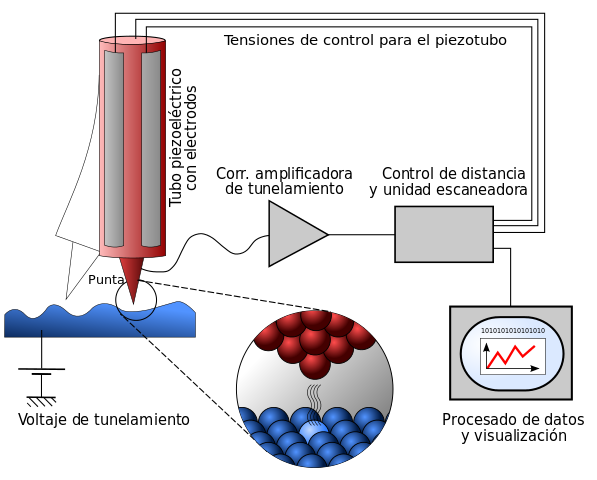 Fuente: Wikimedia CommonsLas “bolitas” rojas representan los átomos finales de la punta que escanea el material y las azules, los de la muestra del material que queremos medir.
Fuente: Wikimedia CommonsLas “bolitas” rojas representan los átomos finales de la punta que escanea el material y las azules, los de la muestra del material que queremos medir.
Se dispone un voltaje suficientemente pequeño para que, según la física clásica, no se establezca una corriente entre la punta y el material… pero por una curiosa propiedad cuántica, sí se producirá una corriente. Y esa corriente tiene una relación muy estrecha con la anchura de la separación entre punta y material. De esta forma, midiendo la corriente, podemos estimar esa distancia.
Como habrás notado, esto se diferencia mucho de lo que solemos llamar “ver”.
Si vamos moviendo la punta por toda la superficie del material y vamos calculando las distancias… podríamos DIBUJAR un “mapa” de ese material, ponerlo en una pantalla y… verlo.
Efectivamente, aquí tenéis:
 Fuente: Wikimedia Commons
Y, efectivamente, esto es oro… y esas bolitas, los átomos de oro.
Fuente: Wikimedia Commons
Y, efectivamente, esto es oro… y esas bolitas, los átomos de oro.
Bueno, en realidad, son las “cortezas”, las nubes electrónicas de esos átomos, interaccionando con la punta del microscopio de efecto túnel.
Bueno, en realidad, son las medidas de distancias, calculadas a partir de las medidas de corriente eléctrica que hemos obtenido al ir paseando la punta del microscopio por la muestra de oro.
Bueno, en realidad, es la representación gráfica de esas distancias, (que han PINTADO de amarillo para que te parezca más oro, qué tramposos), en una foto, hecha pixel a pixel.
Así que, por fin, hemos llegado al final del camino y voy a contestar a la pregunta con que empezamos…
Los átomos son tan pequeños que no podemos verlos con nuestros ojos desnudos.
Los átomos son tan pequeños que no podemos verlos con sistemas ópticos.
Los átomos ni siquiera tienen un “cuerpo macizo” que pudiéramos ver, así que nos conformamos con poder “sentir” su corteza electrónica.
Así que lo que hacemos es usar unos aparatos que midan con más precisión que nuestros sentidos y poner todos esos datos en forma de una imagen.
Para mí, eso es VER. Medir y organizar datos para poder hacerme un modelo del mundo.
Por lo tanto, yo veo los átomos.
¿Qué opinas tú? ¿Crees que acabas de ver átomos?
Sobre el autor: Javier Fernández Panadero es físico y profesor de secundaria además de un prolífico autor de libros de divulgación científica.
El artículo ¿Se pueden ver los átomos? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Entrelazamiento cuántico entre dos nubes de átomos ultrafríos
- ¿Por qué los átomos tienen el tamaño que tienen?
- De cómo se formaron los átomos de mi mano
De la química al tratado internacional o de por qué la ciencia cambia cosas
Mikel Mancisidor
Hace unos días el Comité Nobel anunció que este año las premiadas en su modalidad de Química serían la francesa Emmanuelle Charpentier y a la estadounidense Jennifer A. Doudna “por el desarrollo de un método para la edición del genoma”. Ese mismo día, el azar a veces tiene estas cosas, moría quien había ganado ese mismo premio 25 años antes: el mexicano Mario Molina.
 José Mario Molina Pasquel y Henríquez (1943-2020). Fuente: nobelprize.org Foto: © University of California, San Diego / Donna Coveney / MIT
José Mario Molina Pasquel y Henríquez (1943-2020). Fuente: nobelprize.org Foto: © University of California, San Diego / Donna Coveney / MIT
Molina obtuvo el Nobel de Química en 1995 por su participación en el descubrimiento del agujero de la capa de ozono y por sus trabajos sobre los compuestos de cloro como causante de ese agujero. Gracias a su trabajo (y el de otros, claro está, que la ciencia acostumbra a ser una empresa colectiva) la comunidad internacional pudo conocer el problema, se hizo consciente de su gravedad y de la necesidad de combatirlo. A raíz de ello se adoptó el Convenio de Viena para la protección de la capa de ozono (1985) y posteriormente su Protocolo de Montreal (1989), que prohibió la producción y emisión de los CFC causantes de ese deterioro. Este Protocolo incluía compromisos concretos y diferenciados por parte de los países y fechas concretas para su cumplimiento. Se incluyeron medios técnicos, jurídicos y financieros. Los estados y los agentes industriales y comerciales cumplieron. Como resultado de todo ello, la emisión de esos productos se eliminó en unos años, permitiendo que su concentración se vaya poco a poco reduciendo. El Convenio y su Protocolo han sido un éxito: la situación está ya revirtiendo y se espera que en 35 años la capa de ozono se haya recuperado prácticamente por completo.
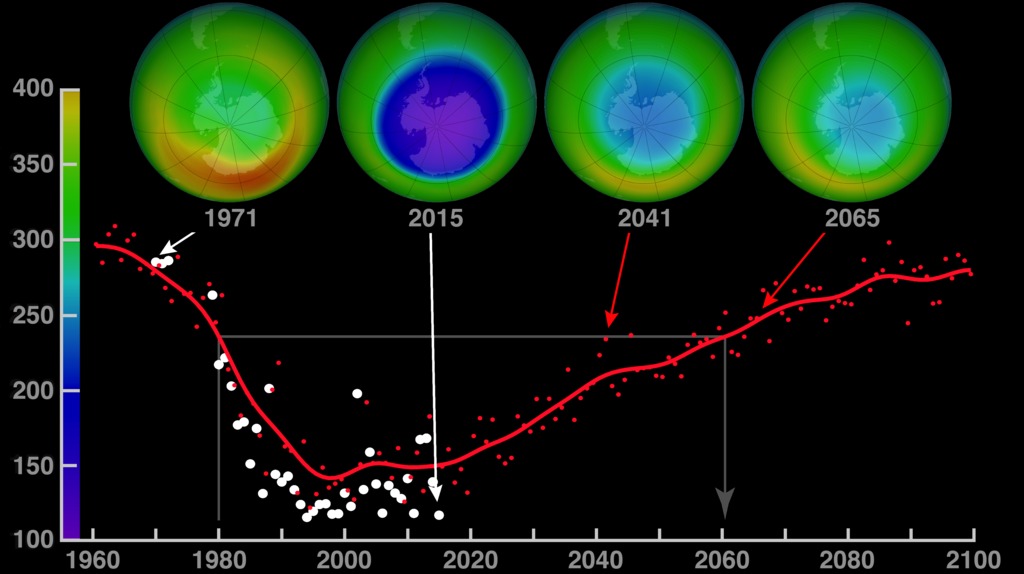 Evolución del agujero antártico de la capa de ozono desde 1960 y proyección a 2100. Fuente: NASA
Evolución del agujero antártico de la capa de ozono desde 1960 y proyección a 2100. Fuente: NASANo sé si ustedes lo han observado, pero de vez en cuando uno lee o escucha a comentaristas que emplean este caso de éxito para defender exactamente lo contrario de lo que a mi juicio podría enseñarnos. Hace no mucho, por poner un ejemplo entre tantos, un medio online de los más importantes del país publicaba un artículo de uno de sus colaboradores que decía: “el cambio climático está de moda. Yo, que he vivido la moda del agujero en la capa de ozono (¿alguien sabe qué pasó con el agujero y, mayormente, con el ozono?), debo reconocer que duermo muy tranquilo por las noches mientras el planeta se dirige hacia su destrucción total. Lo siento: duermo por las noches arrullado por mil problemas personales y ninguno es el cambio climático. En cierta medida, les envidio. Envidio que ustedes tengan tiempo de salvar un planeta mientras yo apenas puedo salvar mi matrimonio.”
Como gracieta tampoco es tan original, de hecho no es la primera vez que oigo o leo que esto del cambio climático es una distracción de ociosos y diletantes como lo fue, al aparecer, la moda de la emergencia del agujero de la capa de ozono que, según parece, surgió de la nada, alarmó gratuitamente un par de temporadas (coincidiendo con la no menos alarmante moda de las hombreras) y por arte de magia desapareció de la agenda sin dejar rastro. En algo estoy de acuerdo: debemos recordar el caso del agujero de la capa de ozono. Pero yo leo aquí justo lo contrario que quienes creen que son modas que vienen y se van. «¿Alguien sabe qué pasó con el agujero y con el ozono?», se pregunta el articulista como queriendo dar a entender que nadie lo sabe. Pero sí se puede saber: basta con interesarse un poco y dedicarle unos minutos de atención en fuentes rigurosas.
No estamos ante una graciosa historia de una moda tonta que vino y se fue. Estamos ante un problema que muy justificadamente alarmó y que la comunidad internacional fue capaz de revertir reaccionando con conocimiento científico, implicación social y voluntad política. Este es un buen ejemplo para otros problemas, especialmente para el cambio climático y de alguna forma también para la pandemia de la COVID-19. Estos retos, como aquel, solo se pueden afrontar sumando conocimiento científico riguroso, responsabilidad ciudadana y buena dirección política.
Los problemas citados son diferentes, sin duda. El problema de los CFC se pudo atajar de una forma tan eficaz, entre otras cosas, porque se trataba de un problema bien definido, sobre el que había alternativas técnicas maduras que eran económicamente asumibles y no presentaban dificultades políticas insalvables. Pero no por ello fue un problema menor, ni fácil, ni una experiencia que podamos despreciar o de la que podamos darnos el lujo de no querer aprender.
Cierto que el problema del cambio climático es más complejo técnica y científicamente, con alternativas más difíciles, mucho más caras, con implicaciones endiabladas. No quiero decir por tanto que la forma de afrontar el problema del Cambio Climático pueda seguir los mismos pasos o al mismo ritmo que el problema de la capa de ozono, pero sí que, tanto en un caso como en otro, nada podrá hacerse si no es en alianza entre la ciencia, la sociedad, la economía y la política.
Mario Molina lo dijo recientemente en una de sus últimas entrevistas: «La capa de ozono es un ejemplo importantísimo de un problema global que se pudo resolver con éxito». Y lo dijo mucho antes, con enorme visión, en su discurso de recepción del Nobel en 1995:
“[…] este problema global nos ha mostrado que diferentes sectores de la sociedad pueden trabajar juntos – la comunidad científica, la industria, las organizaciones medioambientales, los representantes gubernamentales y los gestores públicos- para llegar a acuerdos internacionales: el protocolo de Montreal ha establecido un importante precedente para la solución de problemas medioambientales globales”.
Hemos tenido estas últimas semanas polémicas, no siempre constructivas, sobre la relación entre la ciencia y la política. Molina también habló en su momento de estas cosas: «los científicos pueden plantear los problemas con base en la evidencia disponible, pero su solución no es responsabilidad de los científicos, es de toda la sociedad».
¿Puede usted imaginar mensajes más actuales, más ambiciosos, más inspiradores? Mis respetos a un gran científico que con su trabajo y su visión nos ha legado un mundo mejor.
La buena noticia para terminar este escrito es que en nuestra sociedad hay cada vez más molinas trabajando en diferentes problemas: ¡cuidemos nuestra ciencia y a nuestros científicos si queremos un mundo mejor! Y es que hoy más nunca #SinCienciaNoHayFuturo.
Sobre el autor: Mikel Mancisidor (@MMancisidor1970) es miembro del Comité de Derechos Económicos, Sociales y Culturales de la ONU y Adjunct Professor of International Human Rights Law, Washington College of Law, American University (Washington D. C.)
El artículo De la química al tratado internacional o de por qué la ciencia cambia cosas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La química analítica como base para el estudio de las prácticas pastoriles prehistóricas
- Un camaleón plasmónico que cambia de color en función del entorno
- De la materia a la vida: ¿Química? ¡Química!, por Jean-Marie Lehn
Javier Armentia – Naukas P4K 2019: La vie en rose (ciencia y sociedad de un color muy suyo)
 Imagen: Stephane YAICH / Unsplash
Imagen: Stephane YAICH / UnsplashJavier Armentia, director del Planetario de Pamplona y conocido divulgador, nos ofrece una charla sobre el color más heteropatriarcal que imaginarse pueda.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Javier Armentia – Naukas P4K 2019: La vie en rose (ciencia y sociedad de un color muy suyo) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Pro 2017: Javier Burgos y el alzhéimer
- Ambrosio Liceaga – Naukas P4K 2019: Nunca quisimos coches voladores
- Francisco Villatoro – Naukas Bilbao 2019: El abrazo de la plata
La posverdad es más peligrosa que la mentira
Agustín Arrieta Urtizberea
 Foto: Ryoji Iwata / Unsplash
Foto: Ryoji Iwata / UnsplashDe la posverdad se habla tanto que, en el año 2016, “posverdad” fue nombrada palabra del año por los diccionarios Oxford. ¿Pero a qué fenómeno se refiere esa palabra? En un principio, cabría decir que en tiempos de posverdad se ha dejado atrás la verdad, como en la posmodernidad se pretendía superar la modernidad. ¿En qué consiste eso de dejar atrás la verdad?
Tiempos de posverdad, tiempos de engaño
Son varios los fenómenos que circundan o acompañan a la posverdad. Mentira, ignorancia, charlatanería, desinformación, fake news, populismo, redes sociales, propaganda, negacionismo… Son fenómenos heterogéneos que suscitan la idea de engaño masivo.
Pero lo que mejor caracteriza a la posverdad es la falta de respeto por la verdad o el desprecio hacia la misma. Esta característica no hay que identificarla con la mentira. La mentira y el desprecio a la verdad son diferentes formas de engaño. El mentiroso sabe cuál es la verdad, juega la partida de la verdad, pero la oculta intencionadamente. Sin embargo, la posverdad va más allá (o más acá). Ignora el juego de la verdad, se desentiende: la verdad es ignorada, obviada.
El charlatán como origen
Quiero mencionar a dos autores que hurgaron en el fenómeno de la posverdad, si bien la palabra todavía no estaba en circulación. El más cercano en el tiempo es Harry G. Frankfurt. En el año 2005, en un breve texto titulado On Bullshit, Frankfurt analiza el fenómeno de la charlatanería y contrapone dicho fenómeno con la mentira. Sobre esta contraposición se debate actualmente con gran intensidad, por ejemplo, en el ámbito de la pragmática.
Este filósofo estadounidense está preocupado por una figura que en ese momento, con los cambios sorprendentes en el universo de la comunicación, se está expandiendo sin cesar en distintos foros: el charlatán. El charlatán menosprecia la verdad, ignorándola, pasando por encima de ella. Habla sin cesar, produce discursos. Su actitud no es la del mentiroso.
Sin embargo, subraya Frankfurt, hay algo perturbador en su figura. Y es que históricamente se ha sido menos tolerante con el mentiroso que con otra formas de engaño. El mentiroso siempre ha sido perseguido y castigado (“¡No darás falso testimonio ni mentirás!”, rezaba el mandamiento católico). El charlatán, a lo sumo, ha sido objeto de mofa. Frankfurt, en cambio, ve una terrible amenaza en esta última figura: es el comienzo de la posverdad, aun antes de que se creara un nombre para este fenómeno.
La verdad y la política: Hannah Arendt
Con anterioridad (finales de los 60, principios de los 70 del siglo XX), Hannah Arendt también habla de este fenómeno. Arendt realiza un análisis muy interesante acerca de las relaciones intrínsecas entre la política y la mentira, y vislumbra novedades en dicha relación.
Comprueba que las mentiras de su época (entre otros casos, se ocupa de los famosos Papeles del Pentágono) ya no son sobre cuestiones secretas sino sobre cuestiones de sobra conocidas. Comprueba que la política sigue estrategias propias de la publicidad. Señala ese menosprecio hacia la verdad que nos está dejando sin la brújula requerida para poder caminar y avanzar en nuestras vidas con una orientación mínima.
Estas estrategias publicitarias de los poderes públicos abren las puertas a nuevos totalitarismos (Arendt es una gran conocedora y analista de los totalitarismos de Hitler y Stalin). Se trata, pues, de una auténtica amenaza. Considera que el fenómeno del menosprecio está afectando a lo que denomina “repositorios de la verdad” (reservas de la verdad): el sistema judicial, la universidad y el sistema educativo en general; la ciencia (que, en sus palabras, ha sido posible gracias a un ansia de objetividad) y finalmente el periodismo (que ella ejerció, por ejemplo, en el caso Adolph Eichmann).
La posverdad no es de derechas o de izquierdas
Hay un gran debate sobre los orígenes, las raíces y la evolución de esta actitud de menosprecio. Numerosos autores (véase McIntyre 2018, cap. 6) han argumentado que dicha actitud ha ido trasladándose de vertiente ideológica: de ser propia de un pensamiento político de izquierdas (crítico con el carácter absoluto de la verdad o del conocimiento o de la ciencia), a vincularse con la derecha (Trump es el gran modelo).
Sin embargo, por interesante que sea este debate desde un punto de vista histórico, político y conceptual, lo realmente problemático es que la posverdad está empapando todo lo que nos rodea, desde lo más cercano a lo más remoto. No es una cuestión de izquierdas y derechas.
Menosprecio de la verdad
Lo novedoso no es que se mienta o se engañe acerca de esto o de aquello. Lo novedoso es que la verdad misma se menosprecia. Es inquietante ver a la ignorancia manifestándose arrogantemente frente a la estupefacción del que investiga. Piénsese en las protestas negacionistas relacionadas con la pandemia, o en el negacionismo con respecto al evolucionismo o al cambio climático, o en las concepciones ligadas a los movimientos antivacunas.
Lo novedoso es que los conceptos sobre los que giran “necesariamente” determinadas actividades humanas son menospreciados. Por ejemplo, no se trata ya de debatir sobre si un artículo o trabajo periodístico es más o menos objetivo (debate interesante, difícil e irrenunciable, según mi parecer), sino que con el eslogan “la objetividad no existe” se paraliza dicha reflexión, se abre la puerta a otra concepción de la actividad “periodística”. ¿Dónde queda el periodismo representado en la excelente película “Spotlight”? Retomando las palabras de Arendt y aplicándolas en otro contexto, negar “el ansia por la objetividad” es abrir la veda a otro “periodismo”.
Por supuesto, reflexiones y preocupaciones análogas pueden aplicarse a otros ámbitos. En tiempos de COVID e incertidumbre, ¿qué no hemos oído acerca de la ciencia? ¿Qué idea de la ciencia transmite el negacionismo?
La importancia de los repositorios de la verdad
Hemos subido un escalón en la vía del engaño. Se menosprecia la verdad misma y toda una serie de conceptos (denominados “conceptos epistémicos”) que son satélites de aquella: la objetividad, la consistencia, la imparcialidad, la sinceridad, contrastar las creencias (hipótesis o teorías), el respeto a las evidencias, la precisión, el reconocimiento de la falibilidad y la búsqueda de la minimización de errores, la autocorrección…
En la actualidad hay más medios que nunca para el despliegue masivo de un ambiente de posverdad. Entre otros elementos, las nuevas tecnologías y las redes sociales proporcionan un hábitat adecuado para su desarrollo.
¿Qué hacer? Recordando a Arendt, protejamos los repositorios de la verdad. ¿Cómo? Siendo fieles a los valores arriba mencionados, por lo menos en las actividades humanas donde esos valores son requeridos. Por supuesto, esa fidelidad está acompañada de numerosos obstáculos y fracasos. La posverdad ignora todo ello, juega (o pretende jugar) en otro terreno.
Sobre el autor: Agustín Arrieta Urtizberea, Profesor de Filosofía en la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Lea el original.
El artículo La posverdad es más peligrosa que la mentira se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Las caracolas de Helmholtz
 Colección de resonadores Helmholtz de 1870. Fuente: Wikimedia Commons
Colección de resonadores Helmholtz de 1870. Fuente: Wikimedia Commons«Aplique un resonador en el oído y deje que cualquier instrumento interprete una pieza de música armonizada, en la que suene con frecuencia el tono del resonador. Siempre que suene ese tono, el oído apoyado contra el instrumento lo oirá contrastar violentamente con todos los demás del acorde.»
Hermann von Helmholtz (1863) Sobre las sensaciones de tono como base fisiológica para la teoría de la música.
Sobre las sensaciones de tono es sin duda la obra más conocida de Hermann von Helmholtz. El libro es, simultáneamente, una introducción a la física del sonido, un estudio anatómico del oído y su funcionamiento, un tratado de armonía y un ensayo sobre la historia de la música desde sus inicios hasta el siglo XIX. Partiendo de lo más básico y con una minuciosidad de artesano, Helmholtz va levantando capas sucesivas de complejidad creciente para responder una pregunta inocente solo en apariencia: ¿por qué nos suenan bien ciertos sonidos y no otros?, o, como él mismo escribe,»¿qué tiene que ver la armonía con los ratios de los primeros números enteros?»
Después de que Pitágoras describiese la base numérica de la consonancia hacia el siglo V a.C., Helmholtz fue el primero en darle una explicación satisfactoria. En su empeño, tuvo que combinar todas las ramas de su polifacético conocimiento. Pero sobre todo, tuvo que convencer a sus contemporáneos de que todos los sonidos de nuestro entorno, todas las notas, todos los ruidos, todos los cláxones de los coches y por supuesto, nuestra propia voz, son en realidad una suma de muchos sonidos, frecuencias de distintas amplitudes y frecuencias que se combinan para formar eso que cotidianamente llamamos “timbre”.
Para descomponer los sonidos, Helmholtz se valió de una caracola… pero no cualquier caracola. Como buen físico, fue el inventor de la primera caracola esférica de la historia.
Cuando acercamos nuestro oído a una cavidad resonante, esta concentra la energía del ruido circundante en torno a ciertas frecuencias. La caracola se comporta, por tanto, como un filtro acústico, capaz de subrayar ciertos sonidos o amortiguar otros. Su efecto es fácil de visualizar con ayuda de un espectrógrafo sonoro. Basta introducir un micrófono dentro de una caracola y comparar la distribución de frecuencias del sonido dentro y fuera. Pero si no tienes una caracola a mano, te recomiendo probar con una simple taza o un bote de garbanzos (vacío). Puedes instalar una aplicación como esta en tu móvil y ver cómo cambia el dibujo del sonido ambiente cuando metes el móvil dentro de la taza. Notarás que aparece una especie de pico tembloroso: la frecuencia fundamental de la cavidad resonante.

Sin embargo, las caracolas y las tazas tienen una forma bastante irregular, por lo que resonarán en muchas frecuencias, además de la fundamental. El pico que generan en el espectro tiene más bien forma de colina. Para seleccionar una frecuencia única, Helmholtz tuvo que construir sus propios resonadores, aprovechando todas las ventajas de una cuidada simetría. Utilizó contenedores rígidos, de forma casi esférica y un volumen conocido. En un extremo, un pequeño orificio permitía apoyarlos sobre el oído. Al otro lado, una cavidad cilíndrica, un poco más ancha, permite la entrada del aire y el ruido del ambiente.
El principio que caracteriza la frecuencia de un resonador Helmholtz es similar al que hace sonar la típica botella de refresco. Existe un volumen de aire encerrado dentro de la botella y otra porción, situada en su cuello que es empujada hacia dentro cuando uno sopla. Estos dos elementos suelen compararse con el muelle y la masa de un oscilador armónico (aunque los físicos son muy de comparar todas las cosas del universo, vacas esféricas incluidas, con un oscilador armónico). La idea básica es que, ante un soplido certero, el aire del cuello de la botella (la masa), presiona el volumen contenido en la botella. Este, por su parte, tiende a restaurar las condiciones iniciales (como un muelle). El resultado es una oscilación armónica, con una frecuencia fácil de calcular conociendo las dimensiones del resonador.
Como el prisma que dividió la luz en colores para Newton, estos resonadores permitieron a Helmholtz seleccionar y escuchar claramente la composición en frecuencias de los sonidos de su entorno. “El tono principal de la esfera, mucho más profundo que cualquier otro de sus tonos normales, puede vibrar por simpatía de manera muy poderosa” explica en su libro. “Si tamponamos un oído […] y aplicamos un resonador al otro, la mayoría de los tonos producidos en el aire circundante se amortiguarán considerablemente. Pero si suena el tono del resonador, este vibrará con más fuerza”. Los resonadores de Helmholtz eran capaces de colorear, para él, todos los sonidos de su ambiente. Gracias a ello, pudo estudiar en detalle la diferencia entre tonos y ruidos, sonidos consonantes o disonantes, las frecuencias que forman la voz humana… y también, cómo no, las presentes en los ruidos cotidianos que llenan todas las caracolas. “El tono del resonador puede escucharse a veces surgir en el silbido del viento, el traqueteo de las ruedas del carro, el chapoteo del agua.”
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Las caracolas de Helmholtz se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Augusto Monterroso: lo breve y lo infinito
«Como Borges, Augusto Monterroso es uno de los narradores cuya lectura, además de ser un verdadero deleite, nos sirve a los escritores para fijarnos mucho en lo que vamos a hacer al sentarnos ante una página en blanco.»
Alfredo Bryce Echenique
 Augusto Monterroso. Efecto creado en Cartoon.Pho.to.
Augusto Monterroso. Efecto creado en Cartoon.Pho.to.
Probablemente el relato más conocido de Augusto Monterroso (1921-2003) es El dinosaurio:
Cuando despertó, el dinosaurio todavía estaba allí.
Y, probablemente, El dinosaurio sea uno de los textos más citados y estudiados de la historia de la literatura. De hecho, el propio Monterroso afirmaba que este relato tiene “interpretaciones tan infinitas como el universo mismo”.
Este “análisis matemático” de Claudio Escobar propone algunas “locas teorías científicas” sobre el propósito de este relato:
Este… no sé qué decir…
Bueno: 7 palabras, 7 es el cuarto número primo, un «número interesante» que se puede descomponer en la suma de otros dos primos, como me dijo a mí —personalmente— Ramanujan, antes de su temprana muerte: 7=5+2.
7=4+3, algo así como un número perfecto para algunas culturas.
Posee 4 palabras temporales: Cuando, todavía, estaba, allí… la verdad es que más bien son palabras espacio-temporales, tal como demostrara Einstein, que las dimensiones son 4: 3 espaciales y una temporal, inseparables, al punto que solo se puede hablar de espacio-tiempo, siendo un mal ejercicio separar estas dimensiones…
Ojo que se alternan adverbios y verbos… 3 y 2 respectivamente, nuevamente 2 números primos…
Para mí que —este cuento— es la odisea y la cosmogonía de todos los pueblos latinoamericanos (y africanos)… ¡despertamos a la esperanza cuando todavía los dinosaurios estaban allí! y tuvimos que organizarnos y luchar para sacar a los dinosaurios… ¡¡¡para que luego vinieran otros dinosaurios, esta vez autollamados «demócratas»!!! Pero el cuento es una «H»elipsis, entonces ojo que nos compete cuestionarnos por/en su ciclo…
Traté de derivar o integrar esta «H»elipsis y nada, hummmmm, yo sospecho que detrás de este cuento hay una fórmula sagrada, un augurio potente, una predicción o desafío FERMÁTICO. Seguro que no tuvo papel para apostillar, para continuar el cuento…
En fin, espero despertar y que mañana el dinosaurio se haya ido o que lo hayamos echado, mejor, por lo menos en mis sueños (utopías), ¡combatiré por ello!
(publicado en un pasquín de la universidad de Harvard)
La fábula de Aquiles y la tortuga, una de las paradojas de Zenón, tiene una estrecha relación con el infinito. Monterroso propone una breve y aguda versión:
Por fin, según el cable, la semana pasada la tortuga llegó a la meta.
En rueda de prensa declaró modestamente que siempre temió perder, pues su contrincante le pisó todo el tiempo los talones.
En efecto, una diezmiltrillonésima de segundo después, como una flecha y maldiciendo a Zenón de Elea, llegó Aquiles.
La cita de Alfredo Bryce Echenique que abre este escrito alude a Jorge Luis Borges. Monterroso admiraba al escritor argentino, como demuestra en su Beneficios y maleficios de Jorge Luis Borgesidel que se incluyen debajo algunos fragmentos en los que el infinito es el protagonista:
Cuando descubrí a Borges, en 1945, no lo entendía y más bien me chocó. […]
Pasar de aquel prólogo a todo lo que viniera de Borges ha constituido para mí (y para tantos otros) algo tan necesario como respirar, al mismo tiempo que tan peligroso como acercarse más de lo prudente a un abismo. […]
Acostumbrados como estamos a cierto tipo de literatura, a determinadas maneras de conducir un relato, de resolver un poema, no es extraño que los modos de Borges nos sorprendan y desde el primer momento lo aceptemos o no. Su principal recurso literario es precisamente eso: la sorpresa. A partir de la primera palabra de cualquiera de sus cuentos, todo puede suceder. Sin embargo la lectura de conjunto nos demuestra que lo único que podía suceder era lo que Borges, dueño de un rigor lógico implacable, se propuso desde el principio. […]
Y por último, el gran problema: la tentación de imitarlo era casi irresistible; imitarlo, inútil. Cualquiera puede permitirse imitar impunemente a Conrad, a Greene, a Durrel; no a Joyce, no a Borges. Resulta demasiado fácil y evidente.
El encuentro con Borges no sucede nunca sin consecuencias. He aquí algunas de las cosas que pueden ocurrir, entre benéficas y maléficas:
-
Pasar a su lado sin darse cuenta (maléfica).
-
Pasar a su lado, regresarse y seguirlo durante un buen trecho para ver qué hace (benéfica)
-
Pasar a su lado, regresarse y seguirlo para siempre (maléfica).
-
Descubrir que uno es tonto y que hasta ese momento no se le había ocurrido una idea que más o menos valiera la pena (benéfica).
-
Descubrir que uno es inteligente, puesto que le gusta Borges (benéfica).
-
Deslumbrarse con la fábula de Aquiles y la Tortuga y creer que por ahí va la cosa (maléfica).
-
Descubrir el infinito y la eternidad (benéfica).
-
Preocuparse por el infinito y la eternidad (benéfica).
-
Creer en el infinito y en la eternidad (maléfica).
-
Dejar de escribir (benéfica).
Referencia:
i En “Movimiento perpetuo”, Seix Barral, 1981, págs.53-58
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Augusto Monterroso: lo breve y lo infinito se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una paradoja del infinito: la oferta del diablo
- A infinito
- Una paradoja del infinito: ¿riqueza o ruina?
Historia de la quinina
La malaria es una enfermedad infecciosa que durante siglos ha sido una de las enfermedades más temidas y devastadoras. Su nombre proviene del italiano y está compuesta por “mal” y “aria”, es decir, “mal aire”.
Esta enfermedad está provocada por protozoos del género Plasmodium que infectan los glóbulos rojos de la sangre y se transmiten por las picaduras de las hembras infectadas de varias especies de mosquitos del género Anopheles.
La cura de la malaria llegó de la mano de la quinina, que sabemos que destruye al Plasmodium dentro de los glóbulos rojos, aunque todavía se desconoce el mecanismo preciso.
Los vídeos de Historias de la Ciencia presentan de forma breve y amena pasajes de la nuestra historia científica y tecnológica. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.
El artículo Historia de la quinina se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Afecta el sexo a los síntomas de una enfermedad?
- Historias de la malaria: La guerra y la historia
- ¿Podría un humano vivir en el mar?
El concepto de isótopo
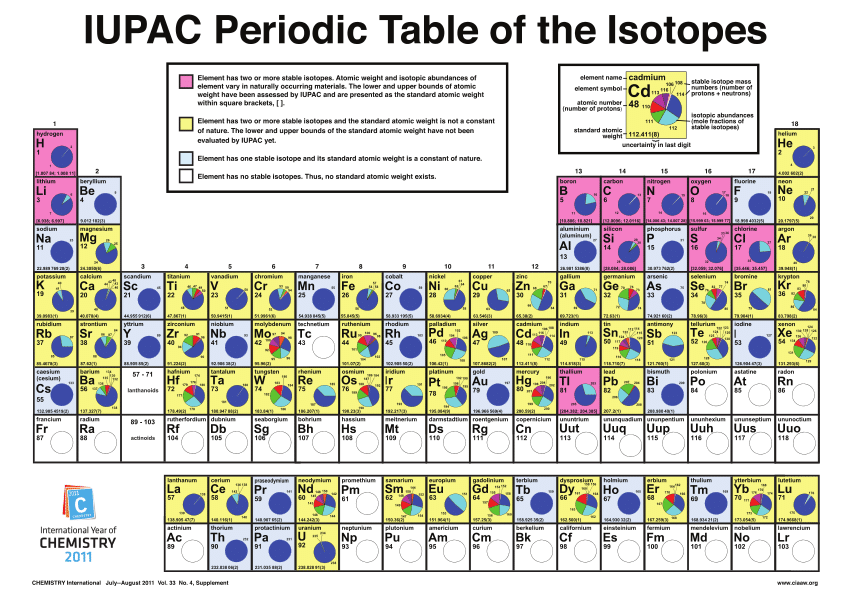 Tabla periódica de los isótopos (2011). Fuente: IUPAC
Tabla periódica de los isótopos (2011). Fuente: IUPACLa idea de que un elemento químico puede ser en realidad una mezcla de átomos con diferente comportamiento radiactivo y diferentes masas atómicas, pero todos con las mismas propiedades químicas, significaba que habría que cambiar uno de los postulados básicos de la teoría atómica de Dalton, a saber, el postulado de que los átomos de un elemento puro son iguales en todos los aspectos.
Según Soddy, los átomos de un elemento dado son idénticos solo en las propiedades químicas [1]. Las distintas especies de átomos físicamente diferentes que componen un elemento en concreto ocupan el mismo lugar en la tabla periódica, es decir, tienen el mismo número atómico Z. Por eso, Soddy los llamó isótopos del elemento, del griego mismo-lugar, en referencia a que ocupan el mismo lugar en la tabla periódica.
Así, el uranio-238 (238U) y el uranio-234 (234U) son isótopos del uranio (92U); el plomo-214 (214Pb) y el plomo-206 (206Pb) son isótopos del plomo (82Pb). Son químicamente iguales; ocupan el mismo lugar en la tabla periódica y tienen el mismo número atómico Z, que se suele escribir como subíndice. Pero son físicamente diferentes, porque tienen diferentes masas atómicas A, que se suele escribir como superíndice en unidades de masa atómica [2].
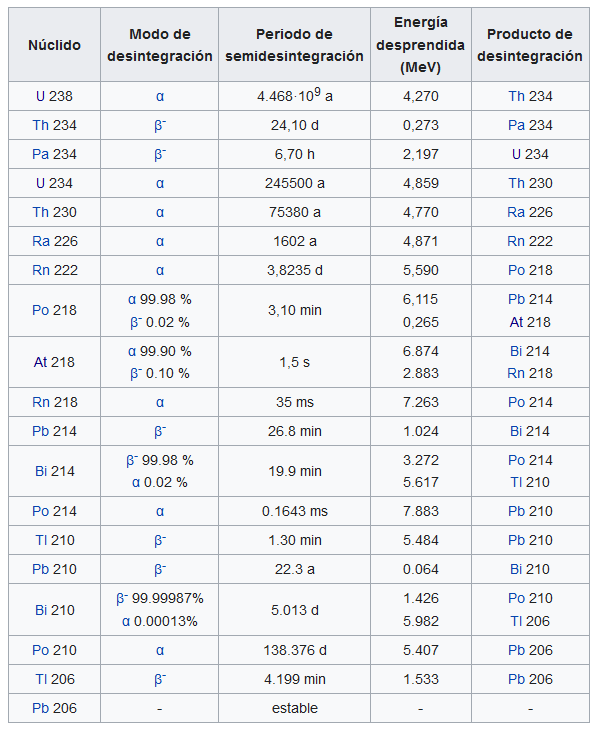 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsCon esta idea en mente, el análisis químico pronto demostró que las muchas especies de átomos radiactivos de las series radiactivas eran isótopos de uno u otro de los últimos 11 elementos naturales de la tabla periódica, desde el plomo (Z = 82) hasta el uranio (Z = 92). Por ejemplo, se demostró que el segundo y el quinto miembro de la serie del uranio (ver la tabla) eran isótopos del torio, con Z = 90; los miembros 8, 13 y 17 resultaron ser isótopos del polonio (Z = 84). Los antiguos nombres y símbolos dados a los miembros de las series radiactivas tras su descubrimiento se sustituyeron para representar tanto la similitud química como la diferencia física entre isótopos [3].
Es importante recalcar que al escribir el símbolo de un nucleido [2], la masa atómica siempre se da como un número natural positivo (por ejemplo, U-238); pero la consulta de cualquier tabla periódica nos dará un valor de la masa atómica de un elemento que es un número racional (para el uranio, 238.02891). Esto se debe a que la masa atómica dada en la tabla periódica se refiere a la masa del elemento en su estado natural, que es una mezcla de los diversos isótopos naturales del elemento, con sus respectivos electrones. La masa atómica del elemento natural es por tanto un promedio de las masas atómicas de los isótopos individuales, ponderadas según su abundancia en relación con las de los otros isótopos.
Notas:
[1] Esto no es del todo cierto en los elementos más ligeros, pero se puede aceptar como regla general.
[2] Cualquier especie de átomo, llamada nucleido, se representa como, por ejemplo, 23490Th y 23090Th para dos de los isótopos del torio. El subíndice (90 en ambos casos para el torio) es el número atómico Z, el número que asigna el lugar en la tabla periódica; el superíndice (234 o 230) es el número de masa A, la masa atómica aproximada en unidades de masa atómica.
[3] Por ejemplo, el uranio X1 y el ionio pasaron a ser torio-234 y torio-230.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El concepto de isótopo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los nuevos ‘elementos’ de las series radiactivas
- Las series de desintegración radiactiva
- No solo el uranio emite rayos
Los componentes genéticos del atractivo
Koldo Garcia Etxebarria
Viajas en metro, o en autobús, y vas leyendo este artículo cuando el vehículo se detiene en una nueva parada. Levantas la cabeza y observas a la gente que entra. Ves una cara, posas tu mirada en ella y algo en tu interior te dice que ese rostro es atractivo. No sabes por qué, pero es así. Llegas a tu destino y continúas con tu día, sin embargo, no te puedes quitar de la cabeza esa imagen, ese rostro te ha hechizado. Podría ser el principio de una novela, pero, en cierta medida, es una cuestión de genética.
 Imagen 1: Viajeros en el metro. (Fotografía: Engin_Akyurt – bajo licencia Pixabay. Fuente: pixabay.com)
Imagen 1: Viajeros en el metro. (Fotografía: Engin_Akyurt – bajo licencia Pixabay. Fuente: pixabay.com)A lo largo de la historia, se ha escrito mucho sobre la belleza y cientos de obras de arte han tratado de representarla. El ser humano vive obsesionado con la belleza y, hoy en día, es el pilar de una industria gigantesca. Aunque sea de forma inconsciente, prestamos atención a diferentes características para medir la belleza. Algunas de las que se han estudiado en profundidad son la juventud, el estado de salud, la cantidad de grasa, la complexión, la coloración, la simetría y el carácter. Si bien el concepto de atractivo varía en función de los individuos y de la cultura, si se muestra el mismo conjunto de caras a diferentes personas, aparecen consensos en torno al atractivo tanto dentro de una cultura como entre diferentes culturas. Esto indica que puede haber una base biológica a la hora de decidir qué es bello.
La base evolutiva que puede haber alrededor del atractivo ha dado, y seguirá dando, mucho que hablar. Es un tema complejo analizar si, a la hora de elegir pareja, el atractivo y sus componentes sirven para medir la «calidad» de la posible pareja. Por ejemplo, el hecho de ver a mujeres con rostros jóvenes puede asociarse a la capacidad de reproducción; la cantidad de grasa y la complexión pueden relacionarse con el estado de salud; u otras características pueden indicar que la persona es portadora de genes que pueden garantizar la supervivencia. Sin embargo, la relación entre las características y los genes «deseables» no es tan clara: aunque la simetría, la masculinidad, el peso y/o la habitualidad se han puesto como ejemplo de estas asociaciones, realmente existen muchas dudas al respecto. Se ha sugerido que las características que resultan atractivas para encontrar una pareja «adecuada» han sido seleccionadas por la evolución, pero eso no es más que una especulación. Aunque en el campo de la sociología y/o la psicología se ha estudiado qué es lo que hace atractiva una cara, su base genética, de existir, es poco conocida.
Un estudio reciente ha analizado los componentes genéticos que pueden influir en el atractivo facial. Hay que tener en cuenta que no es fácil obtener remesas de datos con datos genéticos e información sobre el atractivo, ya que resulta muy costoso. En este trabajo se han utilizado los datos del estudio denominado Wisconsin Longitudinal Study, que recoge estos datos. Los participantes fueron un tercio de los estudiantes graduados en 1957 en los institutos de Wisconsin (EE. UU), cuyos datos genéticos se recopilaron entre los años 2006 y 2007 utilizando su saliva. Su atractivo fue medido por doce participantes (seis mujeres y seis hombres) entre los años 2004 y 2008, a partir de fotografías del anuario del instituto de 1957. Hay que decir que, si bien la fotografía de cada uno de los estudiantes fue valorada por los doce participantes, no todas las fotografías fueron analizadas por los mismos doce participantes, ya que en las labores de valoración trabajaron ochenta personas aproximadamente. Tras la recogida y adaptación de los datos, se analizaron más de siete millones de marcadores genéticos que podrían influir en el atractivo de casi cuatro mil personas, a través del estudio asociativo de todo el genoma.
 Imagen 2: Aunque el impacto puede ser limitado, parece que los genes influyen en la clasificación de las caras. (Fotografía: Grae Dickason – bajo licencia Pixabay. Fuente: pixabay.com)
Imagen 2: Aunque el impacto puede ser limitado, parece que los genes influyen en la clasificación de las caras. (Fotografía: Grae Dickason – bajo licencia Pixabay. Fuente: pixabay.com)Considerando que el atractivo es una característica compleja, conviene preguntarse en qué medida influyen los genes. En este nuevo trabajo han observado que la influencia de los genes es menor de lo que se había calculado anteriormente. Sin embargo, han tenido la oportunidad de relacionar varias regiones del genoma con el atractivo: dos de ellas tuvieron una relación clara y, otras diez, bastante fuerte. Se debe mencionar que la conexión de algunas de estas regiones estaba ligada, en algunos casos, al sexo, tanto al de las personas observadoras como al de las personas cuyo atractivo se estaba midiendo. Por tanto, los autores sugieren que el gen del atractivo facial puede ser específico del sexo.
Analizando los componentes genéticos que se ubicaban en estas regiones del genoma, observaron que previamente se habían relacionado estos componentes genéticos con el color de la piel, el índice de masa corporal, la altura, la proporción cintura-cadera y la morfología facial. Además, observaron que el gen del atractivo tenía correlación con el de otras características: el índice de masa corporal en las mujeres y la grasa en los hombres. Es decir, que la genética del atractivo tenía relación con la genética de los factores que pueden condicionar el atractivo.
Este trabajo ha aportado nuevos datos para profundizar en la base genética del atractivo, pero también tiene sus limitaciones. Por un lado, las personas observadoras mostraron una gran volubilidad a la hora de medir el atractivo de cada persona; es decir, hubo disparidad de opiniones a la hora de decidir cuál es el atractivo. Esto pone de manifiesto la influencia del observador, y no hay que olvidar que el atractivo de cada persona no ha sido valorado por el mismo grupo de observadores. Por otra parte, este trabajo se realizó únicamente con población de origen europeo, por lo que cabe preguntarse si los componentes genéticos son similares en otras poblaciones o hay otras características más deseables. No será fácil resolver estas limitaciones, ya que, como hemos comentado, es difícil obtener este tipo de datos y resulta complicado determinar todos los factores que pueden condicionar el atractivo.
En resumen, parece que puede haber una base genética en las características que nos resultan atractivas; y aunque tiene sus limitaciones, este trabajo es un nuevo paso para entender por qué no puedes quitarte de la cabeza esa cara que acabas de ver en el metro o en el autobús: son sus genes.
Referencia bibliográfica:
White, Julie D., Puts, David A. (2019). Genes influence facial attractiveness through intricate biological relationships. PLoS Genetics, 15 (4), e1008030. DOI: 10.1371/journal.pgen.1008030
Sobre el autor: Koldo Garcia Etxebarria (@koldotxu) es doctor en Genética, investigador en Biodonostia-Instituto de Investigación Biosanitaria y divulgador científico.
Este artículo se publicó originalmente en euskara el 19 de mayo de 2019 en el blog Zientzia Kaiera. Artículo original.
El artículo Los componentes genéticos del atractivo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Colonialismo científico: los investigadores africanos se rebelan contra el expolio de datos genéticos
- Historias genéticas de un fósil viviente
- La CRISPR más precisa hasta la fecha convierte la tijera genética en una navaja suiza
Del origen de gallos, gallinas y pollos
 Foto: Zosia Korcz / Unsplash
Foto: Zosia Korcz / UnsplashCharles Darwin pensaba que los gallos actuales proceden del gallo salvaje rojo, Gallus gallus, una especie tropical de las selvas del sudeste asiático. Se parecen mucho e hibridan, de hecho. La especie tiene cinco subespecies salvajes que se distribuyen en una amplia zona geográfica que va desde las selvas de Indonesia hasta las estribaciones del Himalaya, en Paquistán. De hecho, el naturalista inglés creía que el gallo fue domesticado en la India.
Darwin estaba en lo cierto en lo primero, pero se equivocaba en lo segundo. Gallus gallus es, en efecto, la especie de la que proceden nuestros pollos, pero parece que no fueron domesticados en el subcontinente indio. A partir de restos óseos encontrados en diferentes lugares de Asia, muchos arqueólogos pensaban que los pollos fueron domesticados hace unos 9000 años en el norte de China, en primer lugar, y hace unos 4000 en el Paquistán -en el valle del Indo-, por segunda vez.
Recientemente se han publicado los resultados de una investigación en la que han analizado el genoma de 863 individuos pertenecientes a diferentes variedades de gallos domésticos, a las cuatro especies salvajes y a las cinco subespecies del gallo rojo salvaje. El equipo de investigación ha concluido que los gallos domésticos actuales proceden de una subespecie de este último, Gallus gallus spadiceus, que se distribuye en la actualidad en el sudoeste de China, norte de Tailandia y Birmania. Pero tras la domesticación, fueron trasladados hacia el sudeste y sur de Asia. En las zonas a las que los llevaron había (y sigue habiendo) poblaciones de otras especies de gallo salvaje y de otras variedades (o subespecies) del gallo rojo, y con muchos de ellos se cruzaron y dejaron descendencia fértil. Por lo tanto, los actuales pollos tienen un pasado genético muy enrevesado, porque al original se le han añadido linajes de otras especies y subespecies. Todos los gallos domésticos en China, Sudeste de Asia y Sur de Asia poseen genomas híbridos, en los que hasta casi una cuarta parte procede de subespecies de Gallus gallus distintas de la originaria.
También han encontrado que los gallos domésticos divergieron del gallo rojo salvaje hace unos 9500 años y, por lo tanto, antes de que empezase la domesticación, por lo que esta no habría sido el factor desencadenante de la divergencia entre los dos linajes, el salvaje y el doméstico. El momento en que se produjo esa separación de linajes coincidió con una época de intenso cambio climático, tras la transición del Pleistoceno al Holoceno, cuando se elevaron las temperaturas y se produjo un aumento en la actividad de los monzones en el Sudeste de Asia. Es posible que las condiciones ambientales cambiantes propiciasen la diversificación del linaje original (Gallus gallus spadiceus) y que alguna o algunas de sus variantes fuera domesticada más adelante.
Como suele ocurrir con las especies utilizadas para consumo humano, los genes relacionados con la producción han experimentado una fuerte selección positiva, lo que, lógicamente, es el resultado de la búsqueda de crecimiento rápido y elevada producción de huevos. Al fin y al cabo, los pollos se han convertido en los animales de granja más abundantes del planeta; hay alrededor de tres por cada ser humano.
La variedad de gallo salvaje está en peligro de extinción en la actualidad, porque puede acabar diluyendo su bagaje genético en los muchísimos más numerosos gallos domésticos con los que hibridan, perdiéndose así una fuente valiosa de diversidad genética. Se cumpliría, de forma quizás insólita, esa paremia del castellano que dice que no hay peor astilla que la de la misma madera.
Fuente: Ming-Shan Wang (2020): 863 genomes reveal the origin and domestication of chicken. Cell Research 0:1–9
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Del origen de gallos, gallinas y pollos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los amiloides y el origen de la vida
- Sobre el origen del uso de herramientas en aves
- Naukas Pro 2017: Carlos Briones y el origen de la vida
Helena Matue – Naukas P4K 2019: Vulnerable-mente
 Foto: Edwin Andrade / Unsplash
Foto: Edwin Andrade / UnsplashSomos vulnerables. Cometemos errores y, lo que es peor, se trata de errores predecibles, lo que da lugar a que puedan ser explotados en beneficio de terceros, desde estafadores de barrio a políticos tan ambiciosos como poco escrupulosos. Helena Matute, catedrática de psicología experimental de la Universidad de Deusto, nos asoma a esta inquietante realidad.
La conferencia se impartió dentro del marco del festival Passion for Knowledge 2019 (P4K) organizado por el Donostia International Physics Center (DIPC).
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Helena Matue – Naukas P4K 2019: Vulnerable-mente se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ambrosio Liceaga – Naukas P4K 2019: Nunca quisimos coches voladores
- César Tomé López – Naukas P4K 2019: ¿Eureka?¿En serio?
- Joaquín Sevilla – Naukas P4K 2019: Lo que esconden unos champiñones al ajillo
¿Por qué matan las pocas mujeres que matan?
César San Juan
 Blancanieves recibiendo un regalo envenenado de su madrastra en una ilustración del siglo XIX. Fuente: Wikimedia Commons
Blancanieves recibiendo un regalo envenenado de su madrastra en una ilustración del siglo XIX. Fuente: Wikimedia CommonsLa noticia del presunto intento de asesinato del productor y ex miembro del grupo humorístico “La Trinca” Josep María Mainat por parte de su esposa ha traído a la actualidad una casuística con mucha literatura y poca investigación criminológica, los asesinatos cometidos por mujeres.
Lo que se sabe, porque lo dicen los datos, es que son muchísimos menos que los perpetrados por hombres, como veremos, y las motivaciones son con frecuencia diferentes.
Desde que Gesche Gottfried fue sentenciada a muerte en 1831 por envenenar con arsénico a 15 personas, todas ellas próximas a su círculo social, se diría que este elemento químico ha tenido cierta popularidad en asesinas en serie posteriores.
Nannie Doss, seducida por el afán de lucro, envenenó con arsénico a sus cuatro maridos. Así como Judy Buenoano, que con idéntico móvil y con la misma sustancia, acabó con la vida de su marido, un novio y su hijo de 19 años.
Además de los casos citados, podemos recordar a Kristen Gilbert, enfermera condenada por matar a cuatro pacientes inyectándoles epinefrina. O Dorothea Puente, que envenenó a sus inquilinos más ancianos con el fin de cobrar sus pensiones.
Hay notables excepciones a estos patrones, como es el caso de Aileen Wuornos, que disparó a seis hombres a sangre fría. O Rosemary West y Karla Homolka que, con la connivencia de sus respectivos maridos, violaron y asesinaron brutalmente a varias chicas adolescentes.
Como podemos constatar, las asesinas en serie existen, pero sus motivaciones difieren significativamente de las de sus homólogos varones, para quienes el sexo y el sadismo tienen un mayor protagonismo.
Las asesinas son más pragmáticas
Ellas tienden a adoptar un enfoque más pragmático en sus crímenes, ya que son más propensas que los hombres a matar por lucro o venganza. Asimismo, a diferencia de los asesinos en serie masculinos, que suelen atacar a víctimas desconocidas, las mujeres tienden a matar a personas dentro de su círculo familiar y social.
Y finalmente, siguiendo con la descripción de un patrón típicamente femenino, también podemos señalar la tendencia de las asesinas seriales al envenenamiento.
La educación y el contexto sociocultural
Sea como fuere, parece que referirse al comportamiento violento de la mujer supone poner el foco de atención en un fenómeno extraordinario, ya que, efectivamente, si atendemos al informe sobre homicidios en España, podemos comprobar que solo un 11 % ha sido perpetrado por mujeres.
La ratio de género que de forma abrumadora señala el ser “varón” como principal factor de riesgo del comportamiento violento ha propiciado que hoy día sepamos tan poco acerca de la etiología del comportamiento agresivo en las mujeres.
Este déficit de conocimiento es debido a que, por lo general, se ha intentado explicar la delincuencia femenina desde la perspectiva de las teorías existentes en relación a la delincuencia en general, lo que podría resultar poco pertinente considerando las diferencias de género existentes en lo que concierne, cuando menos, a la gestión de las emociones y los conflictos, o a las diferencias de crianza familiar con las niñas y con los niños.
Por ejemplo, parece indiscutible que se ejerce más control en muchos aspectos de la vida de las niñas, en particular, en cómo pasan su tiempo libre y la clase de riesgos que se les permite asumir.
Así, resulta evidente que para entender la etiología del comportamiento violento en las mujeres precisamos diferentes niveles de análisis y fijarnos en ellas, no en los hombres.
En lo que se refiere a las causas…
En este sentido, es particularmente interesante la revisión realizada por Denson, O´Dean, Blake & Beames (2018) en la que se pone en evidencia que la magnitud de lo que ignoramos es muy superior a lo que verdaderamente sabemos.
A pesar de todo lo que popularmente se da por sentado y asumimos sin margen de réplica, incluso desde las ciencias criminológicas, estos autores constatan que los mecanismos neuronales que subyacen a la agresión siguen siendo poco conocidos en las mujeres.
Dado que en la mayor parte de los estudios no se exploraron las diferencias de género, es imposible llegar a conclusiones firmes en este momento.
El mismo problema comparten los estudios de ERP (potencial relacionado con evento) medidos con electroencefalografía y las investigaciones que analizan el papel de determinadas hormonas (testosterona, cortisol, estradiol, progesterona y oxitocina).
Efectivamente, no son concluyentes los mecanismos hormonales que subyacen a la agresión en las mujeres y serían precisos más estudios sobre las condiciones sociales específicas en las que algunas hormonas aumentan o inhiben su conducta agresiva.
…y a las consecuencias
Algunos autores sostienen que las mujeres tienen la misma probabilidad que los hombres de cometer VCP (violencia contra la pareja) aunque, obviamente, los hombres cometen un mayor número de agresiones graves.
En el caso de las agresiones sexuales, aunque son perpetradas principalmente por los hombres, Denson y sus colaboradores constatan que una pequeña proporción de estos delitos son perpetrados por mujeres, y es una casuística sobre la que no sabemos nada.
Es fundamental que las investigaciones futuras confirmen o descarten lo que tal vez sean suposiciones simplistas sobre estos fenómenos y consideren el papel de la mujer en las relaciones agresivas.
Y qué decir del filicidio. Pese a que es constatable la alta prevalencia de asesinatos de menores a manos de sus padres, también existen mujeres que matan a sus hijos. Sin embargo, por ser actos tan execrables que se escapan a nuestra comprensión, se tiende a pensar que ellos son intrínsecamente “asesinos” y ellas intrínsecamente “enfermas”, por lo que es más probable encontrar padres filicidas en la cárcel y madres filicidas en el psiquiátrico.
Si seguimos renunciando a explorar nuestra propia naturaleza por inercias ideológicas o por irrelevancia estadística, estaremos un poco más lejos de entender la etiología de la respuesta violenta en las mujeres y diseñar estrategias de prevención eficaces basadas en la evidencia.
Sobre el autor: César San Juan es profesor de psicología criminal en departamento de Psicología Social de la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Por qué matan las pocas mujeres que matan? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La menor influencia de las mujeres en Internet
- La mitad de las mujeres embarazadas son fumadoras pasivas
- La gestión de la salud y seguridad en el trabajo de las mujeres
Campañas de salud pública con efecto bumerán
Uxune Martinez
Ante una crisis de salud pública, la mayor parte de la población se adapta y cambia su comportamiento, siguiendo las recomendaciones sanitarias y las nuevas normas propuestas. Sin embargo, si las nuevas pautas se implantan para periodos largos de tiempo, los cambios no se normalizan con facilidad, menos aún cuando conllevan una modificación en las prácticas habituales e inciden en las relaciones sociales.
Para hacer frente a esas situaciones, se ponen en marcha campañas dirigidas a alertar y sensibilizar a la ciudadanía, así como a minimizar los posibles daños. Muchas de esas campañas utilizan los sentimientos (pena, miedo, vergüenza) para captar la atención y promover la colaboración ciudadana. No obstante, aunque esa estrategia se utiliza con la mejor intención, puede provocar precisamente el efecto contrario del que se pretendía, y dar pie, por ejemplo, a la resistencia al cambio y a actitudes transgresoras.
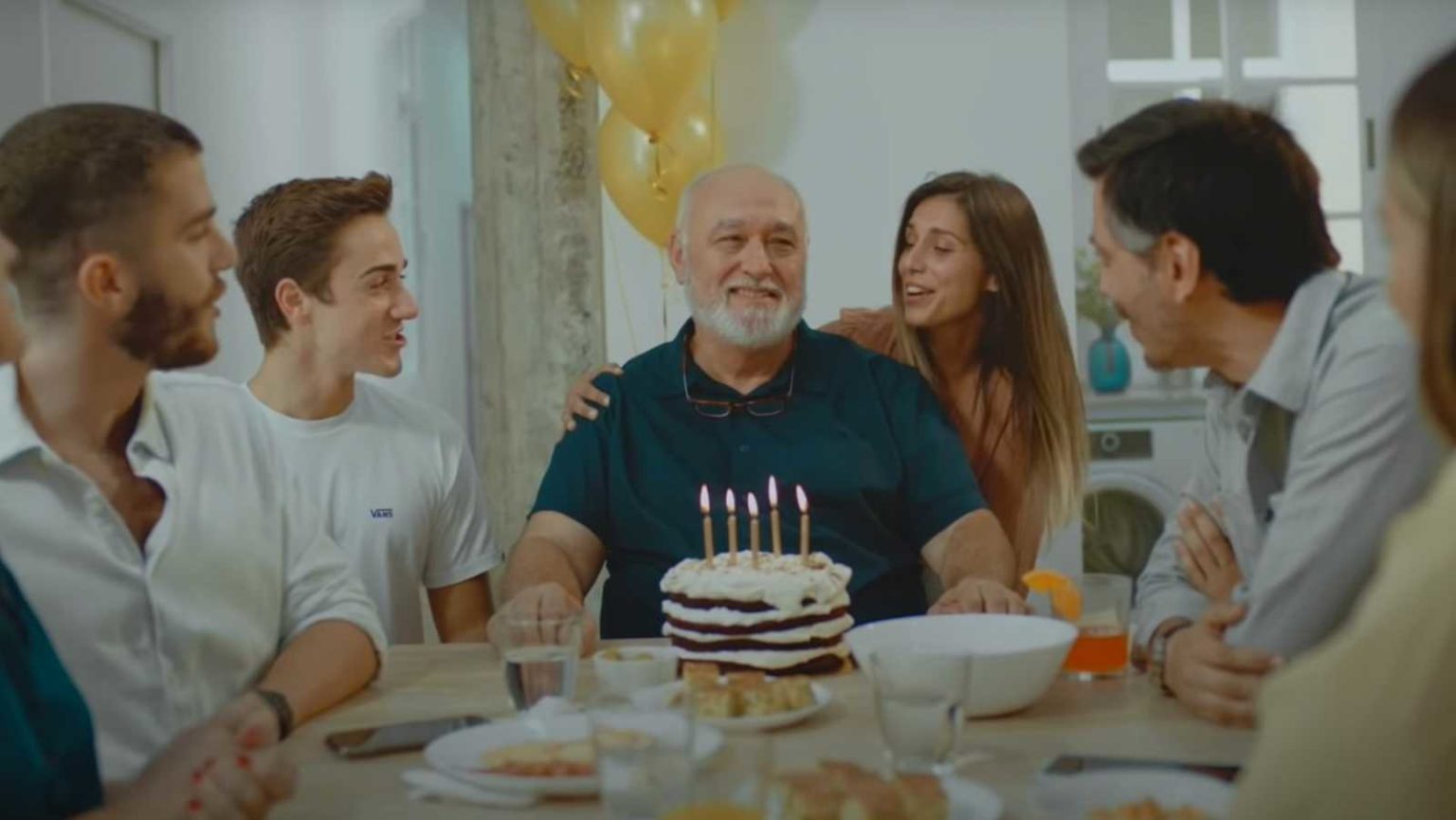 Imagen 1: imagen de la campaña publicitaria de la Consejería de Sanidad del Gobierno de Canarias puso en marcha en julio. La campaña tenía como finalidad concienciar a la ciudadanía, por ejemplo, advirtiendo sobre los riesgos de incumplir las recomendaciones en las reuniones familiares o con amigos. (Fotografía: Consejería de Sanidad de Canarias)
Imagen 1: imagen de la campaña publicitaria de la Consejería de Sanidad del Gobierno de Canarias puso en marcha en julio. La campaña tenía como finalidad concienciar a la ciudadanía, por ejemplo, advirtiendo sobre los riesgos de incumplir las recomendaciones en las reuniones familiares o con amigos. (Fotografía: Consejería de Sanidad de Canarias)El Gobierno de Canarias puso en marcha en julio una campaña publicitaria para informar y sensibilizar a la población sobre los riesgos de la COVID-19. En el marco de esta campaña, se han publicado una serie de vídeos. En el primero se muestra una celebración familiar en la que se festeja el cumpleaños del abuelo. En el encuentro no faltan la tarta, las velas y los regalos, pero la reunión familiar tiene consecuencias no deseadas, el ingreso del abuelo en la UCI tras ser contagiado en su fiesta de cumpleaños. El último vídeo se centra en la vuelta al cole. Una niña de 10-12 años conversa con su madre sobre el inicio del curso escolar y la tranquiliza repasando junto a ella muchas de las cosas que le ha inculcado a lo largo de su vida: esperar en la acera cuando el semáforo está en rojo, tener valor para decir lo que siente y adoptar medidas de seguridad ante el coronavirus. Los vídeos duran poco más de un minuto y pretenden remover los sentimientos de la gente a través de un llamamiento audiovisual.
Apenas tres meses después, los ciudadanos han empezado a mostrar cierto hartazgo y a expresar opiniones negativas por la estrategia de marketing que se ha adoptado (sobre todo en las redes sociales). Son varios los argumentos de quienes critican la campaña: que los vídeos transmiten mensajes pesimistas y fomentan el miedo, que son demasiado «ejemplares», que no han acertado en las formas, que los modelos de familia que aparecen en los vídeos están lejos de la realidad local o que no resultan de gran ayuda para apoyar a quienes trabajan en la lucha contra el coronavirus (por ejemplo, personal de centros educativos, profesorado, equipos directivos, etc.).
Por tanto, cabe preguntarse ¿son eficaces estas campañas?
Nosotros frente a los demás
La mayoría de las campañas de marketing social en materia de salud buscan incidir en el comportamiento de las personas para que tomen determinadas medidas. Se dan a conocer las consecuencias que acarrea el no seguir las indicaciones recomendadas: muertes prematuras, discapacidades físicas, el sufrimiento de los seres queridos o el perjuicio a nuestro bienestar. De esta manera, en las campañas para promover el uso del cinturón de seguridad y en las que inciden en las consecuencias del consumo de tabaco, por ejemplo, se ha puesto de manifiesto el impacto de la no adopción de las recomendaciones en el día a día de la gente y en su salud. Sin embargo, diversas campañas en torno al coronavirus han hecho hincapié en el efecto del comportamiento propio en la salud de los demás. Es decir, en las campañas del primer tipo, los beneficiarios directos del cambio de actitud somos «nosotros», mientras que en el segundo caso los beneficiarios son «los demás»; porque es nuestra conducta la que protege a las personas más vulnerables frente al coronavirus.
 Imagen 2: imagen de la campaña de prevención y diagnóstico precoz del VIH y otras infecciones de transmisión sexual puesta en marcha por el Ministerio de Sanidad en el año 2008. (Foto: Ministerio de Sanidad)
Imagen 2: imagen de la campaña de prevención y diagnóstico precoz del VIH y otras infecciones de transmisión sexual puesta en marcha por el Ministerio de Sanidad en el año 2008. (Foto: Ministerio de Sanidad)Recientemente, la epidemióloga Julia Marcus hacía referencia a este hecho como factor condicionante en el uso de las mascarillas en EE.UU. Marcus considera que, las dudas y opiniones contrarias que han surgido en este país sobre el uso de las mascarillas, se deben al mensaje emitido. Un mensaje que ha hecho hincapié en la idea de que las mascarillas «son para proteger a los demás». En otras palabras, los mensajes públicos han destacado que el uso de la mascarilla protege al de al lado y no han mostrado el beneficio que su uso comporta para quien la lleva puesta. Este planteamiento ha incidido negativamente en su uso; y en muchos casos ha generado una respuesta opuesta a la pretendida. Porque, si la mascarilla no nos protege, no usarla nos deja en la misma situación, así que un gran número de estadounidenses han dejado de lado su uso.
En este binomio de «nosotros» y «los demás» hay otro elemento que requiere atención. Deborah Lupton, socióloga experta en comunicación en el ámbito de la sanidad pública, señala que estas campañas plantean una clara dicotomía. «Los demás» aparecen como si fueran diferentes: el que no usa el cinturón de seguridad; el que bebe alcohol, coge el coche y provoca un accidente; el que no adopta medidas de higiene y contagia a quienes tiene cerca… Esos son «los demás». A simple vista parecen ser las y los «culpables», ya que su comportamiento supone un riesgo para nosotros. Eso genera la marginación y estigmatización de algunos grupos, y también vergüenza, ansiedad y miedo ante el rechazo que pueden sufrir quienes sean vistos como diferentes.
Los expertos creen que debería tenerse en cuenta que, en algunos casos, esos comportamientos responden a una compleja interacción de factores sociales y económicos. Es más, el presentar el «yo» y el «otro» como figuras contrapuestas puede marginar aún más a grupos ya de por sí marginados. De hecho, los grupos en situación de vulnerabilidad pueden tener dificultades para adoptar las medidas que proponen las campañas publicitarias de salud pública, lo que les perjudica aún más.
Por tanto, deberían analizarse previamente, por un lado, los mensajes que van a transmitir en este tipo de campañas y, por otro, las imágenes e historias que se difunden junto con el mensaje.
Efecto bumerán
Si una campaña no tiene en cuenta lo señalado anteriormente, es posible que el resultado que obtenga sea el contrario al perseguido.
En psicología social llamamos efecto bumerán al hecho de que una persona adopte la actitud contraria al objetivo perseguido cuando tratamos de convencerla de algo. Por ejemplo, el efecto bumerán puede aparecer cuando sentimos que se nos restringe la libertad, cuando el cambio nos provoca una pérdida económica o cuando no tenemos recursos suficientes para poner en práctica las medidas que se nos piden. En estos casos, mostramos nuestra disconformidad o imposibilidad renunciando a adoptar las normas o infringiéndolas.
 Imagen 3: imagen de la campaña de información y sensibilización «12 cucharadas» para alertar sobre los efectos del consumo de refrescos, una de las principales causas de la diabetes y la obesidad en niños y adultos en Méxic. (Fotografía: Alianza por la Salud Alimentaria)
Imagen 3: imagen de la campaña de información y sensibilización «12 cucharadas» para alertar sobre los efectos del consumo de refrescos, una de las principales causas de la diabetes y la obesidad en niños y adultos en Méxic. (Fotografía: Alianza por la Salud Alimentaria)Así, podríamos considerar efectos bumerán, por ejemplo, la resistencia que vemos estos días a las prohibiciones de reunirnos grupos de más de 6 o 10 personas, de beber en la calle… a causa del coronavirus. El cumplimiento de ambas recomendaciones supone para muchas personas el cambiar hábitos muy arraigados y renunciar a las relaciones sociales. Una renuncia difícil, más aún después de varios meses de confinamiento. En este sentido, cumplir las normas puede verse como una restricción de la libertad y, en consecuencia, hay quien hace pantente su discrepancia y su resistencia adoptando comportamientos contrarios a los que desean promover las instituciones.
Lo que muestran las respuestas negativas
Las reacciones negativas que obtienen las campañas de salud pública pocas veces reciben la atención que merecen, pero resultan muy útiles para conocer el contexto en el que nos movemos. Es decir, permiten entender por qué no se aceptan los criterios y las pautas recomendadas, y dan cuenta de la situación en la que se encuentran las personas destinatarias de los mensajes. De esa forma, si se estimase conveniente podrían adoptarse otras medidas de apoyo a las campañas.
Por ejemplo, en la situación que vivimos ahora, se podría informar a los jóvenes de las opciones que tienen para pasar un rato juntos, más allá del botellón, a través de anuncios breves en medios como TikTok o Instagram, donde se den a conocer las agendas culturales de los municipios, las actividades de tiempo libre organizadas en su entorno, las propuestas de ocio, etc. A los adultos se les podrían mostrar los beneficios que tiene el cumplimiento de la distancia de seguridad y las medidas de higiene, pero aportando un dato positivo y a ser posible cuantificable, como mostrar cómo ayudan a minimizar la carga del sistema sanitario y exponer el beneficio económico que conllevan.
Al fin y al cabo, detectar aquello que al público objetivo no le gusta de la estrategia de salud pública ayuda a ver dónde están los obstáculos y a entender las dificultades. Y como bien sabemos, una vez se comprende un problema, resulta más fácil abordar su solución.
Referencias:
Dillard, James P., Shen, Lijiang (2005). On the Nature of Reactance and its Role in Persuasive Health Communication. Communication Monographs, 72 (2), 144-168. DOI: 10.1080/03637750500111815
Lupton, Deborah (2015).The pedagogy of disgust: the ethical, moral and political implications of using disgust in public health campaigns. Critical Public Health, 25 (1), 4-14. DOI: 10.1080/09581596.2014.885115
Ringold, Debra J. (2002). Boomerang Effects in Response to Public Health Interventions: Some Unintended Consequences in the Alcoholic Beverage Market. Journal of Consumer Policy, 25, 27-63. DOI: 10.1023/A:1014588126336
Marcus, Julia (23 de junio de 2020). The dudes who won’t wear masks. The Atlantic.
Ophir, Yotam (21 de agosto de 2018). Los medios de comunicación fallan a la hora de informar sobre epidemias. The Conversation.
Sobre la autora: Uxune Martinez (@UxuneM) es resposanble de difusión científica de la UCC+i de Euskampus Fundazioa y editora del blog Zientzia Kaiera.
Este artículo se publicó originalmente en euskara el 23 de septiembre de 2020 en el blog Zientzia Kaiera. Artículo original.
El artículo Campañas de salud pública con efecto bumerán se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:El problema de las flechas de Mahavira
Uno de mis libros preferidos de problemas y rompecabezas matemáticos es el libro Famous Puzzles of Great Mathematicians (Rompecabezas famosos de grandes matemáticos) del matemático Miodrag Petrovic. Uno de los problemas que aparecen en el apartado de aritmética es el siguiente problema del matemático indio del siglo IX Mahavira (o Mahaviracharya, es decir, “Mahavira el maestro”), que aparece en su libro Ganatasarasamgraha – Compendio de la esencia de las matemáticas–, del año 850:
Problema: Las flechas, con forma de cilindros de sección circular, pueden ser empaquetadas formando un haz hexagonal. Si hay 18 flechas en la parte exterior del haz, determinar el número total de flechas que hay (en el haz) dentro del carcaj.
Este problema lo podemos resolver de una forma sencilla dibujando flechas (sus secciones circulares) formando una estructura hexagonal, como en la imagen siguiente. Podríamos proceder de forma ordenada. Primero 1 flecha en el centro, luego 6 alrededor formando un hexágono, después 12 en el siguiente hexágono alrededor del anterior, y finalmente 18 flechas en el hexágono exterior. Por lo tanto, la respuesta al problema es 1 + 6 + 12 + 18 = 37 flechas en total.
 Distribución hexagonal de las flechas con 18 flechas en la parte exterior
Distribución hexagonal de las flechas con 18 flechas en la parte exterior
La solución de este problema está relacionada con los llamados números poligonales centrados. Como es bien conocido, los números poligonales (triangulares, cuadrados, pentagonales, hexagonales, etcétera) son aquellos números que se obtienen al representar el número como una disposición poligonal de puntos o piedras, como puede verse en la entrada El asesinato de Pitágoras, historia y matemáticas (y II). Sin embargo, existen otras disposiciones geométricas de puntos o piedras con forma poligonal, pero con un punto en el centro y los polígonos alrededor del mismo, son los números poligonales centrados (triangulares centrados, cuadrados centrados, pentagonales centrados, hexagonales centrados, etcétera).
Como puede verse en la siguiente imagen, los primeros números triangulares centrados son 1, 4, 10, 19, los cuadrados centrados son 1, 5, 13, 25, los pentagonales centrados 1, 6, 16, 31 y los hexagonales centrados, llamados por Martin Gardner números hex, 1, 7, 19, 37.
 Los primeros números triangulares centrados, cuadrados centrados, pentagonales centrados y hexagonales centrados
Los primeros números triangulares centrados, cuadrados centrados, pentagonales centrados y hexagonales centrados
Si nos fijamos en la construcción de los números poligonales centrados, se ve rápidamente que se empieza por un punto, después se representa el polígono alrededor del punto y se van añadiendo polígonos cada vez más grandes. Por lo tanto, es fácil calcular el número de puntos que se necesitan para representar los polígonos centrados. En concreto, para un polígono de k lados, la fórmula para calcular los números poligonales centrados es:
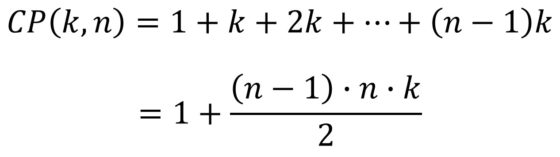
Pueden construirse fácilmente demostraciones sin palabras (véanse Matemáticas para ver y tocar y Más matemáticas para ver y tocar) de algunas primeras identidades de los números poligonales centrados.
Por ejemplo, se pueden relacionar los números cuadrados, pentagonales y hexagonales centrados con los números triangulares (los clásicos, no los centrados, sobre los que puede leerse en la entrada El asesinato de Pitágoras, historia y matemáticas (y II)): CCn = 1 + 4Tn – 1, PCn = 1 + 4Tn – 1, hexn = 1 + 6Tn – 1, con la notación evidente.
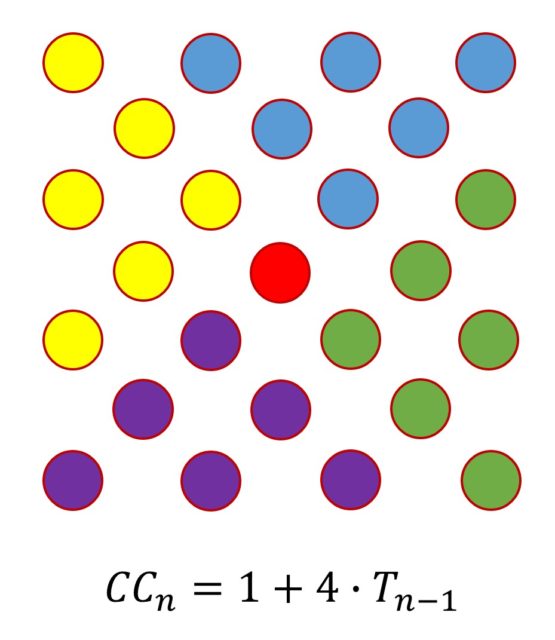
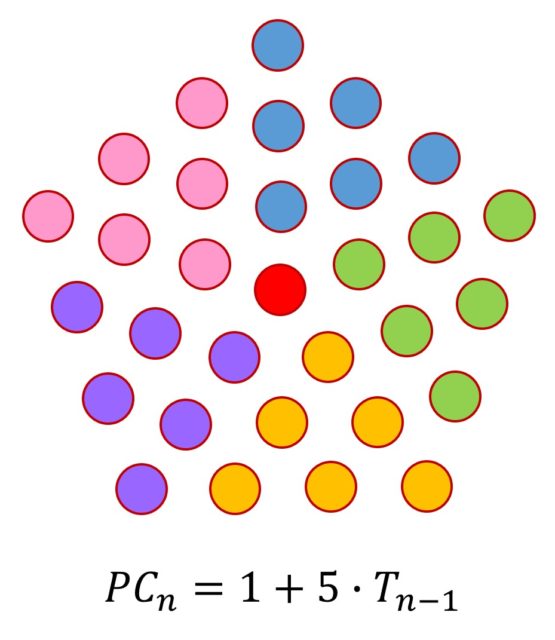
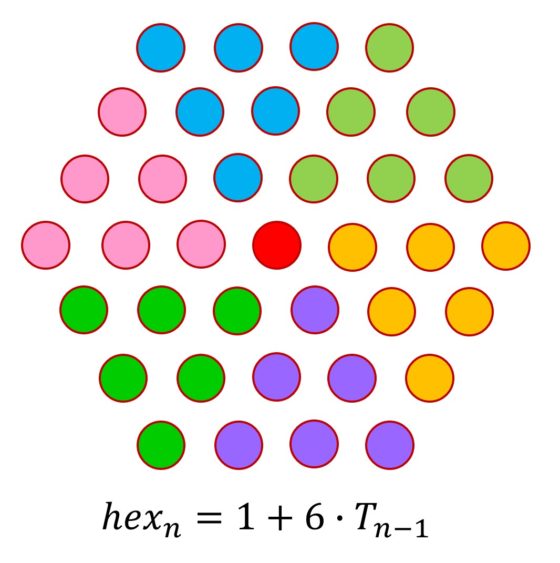
De hecho, esa es una identidad que se cumple para todos los números poligonales centrados, en concreto:
![]()
Pueden verse más identidades relacionadas con los números poligonales centrados. Para empezar, los números triangulares centrados (que forman la sucesión denominada A005448 en la Enciclopedia online de sucesiones de enteros, cuyos primeros veinte términos son 1, 4, 10, 19, 31, 46, 64, 85, 109, 136, 166, 199, 235, 274, 316, 361, 409, 460, 514, 571, etcétera), pueden ser expresados como suma de tres números triangulares normales: TCn = Tn + Tn – 1 + Tn – 2, para n mayor o igual que 3.
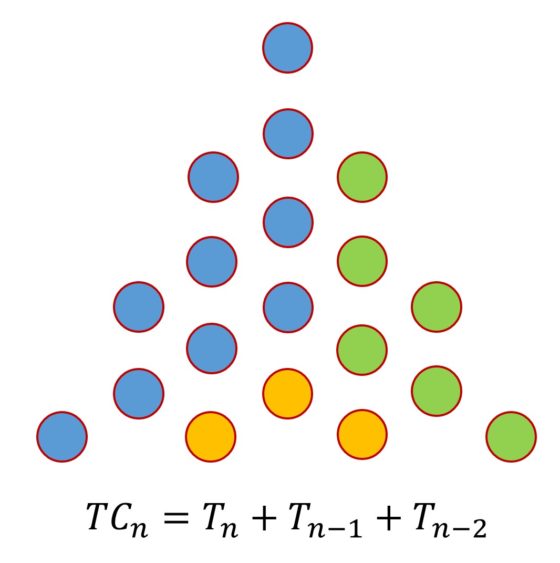
O los números cuadrados centrados (que forman la sucesión denominada A001844 en la Enciclopedia online de sucesiones de enteros, cuyos primeros veinte términos son 1, 5, 13, 25, 41, 61, 85, 113, 145, 181, 221, 265, 313, 365, 421, 481, 545, 613, 685, 761, etcétera) pueden expresarse como suma de dos números cuadrados normales: CCn = Cn + Cn – 1.
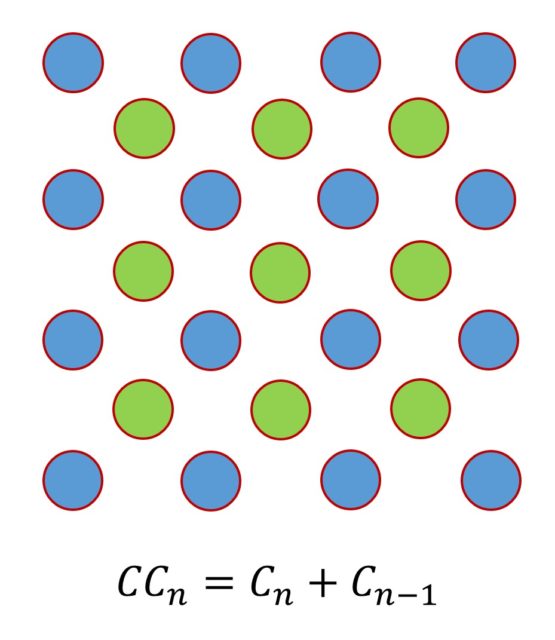
Los veinte primeros números pentagonales centrados, que es la sucesión A005891 en la Enciclopedia online de sucesiones de enteros son 1, 6, 16, 31, 51, 76, 106, 141, 181, 226, 276, 331, 391, 456, 526, 601, 681, 766, 856, 951, etcétera. O la sucesión A003215 es la de los números hex, cuyos veinte primeros términos son 1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, 397, 469, 547, 631, 721, 817, 919, 1027, 1141, etcétera.
Pueden obtenerse también fórmulas para números poligonales centrados con una mayor cantidad de lados, por ejemplo, para los números octogonales centrados, se puede demostrar que son números cuadrados: OCn = C2n – 1.
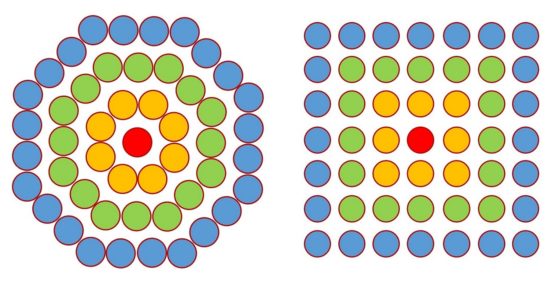
Vamos a terminar esta entrada del Cuaderno de Cultura Científica con otro rompecabezas que aparece en el apartado de aritmética del libro Famous Puzzles of Great Mathematicians. Esta configuración mágica está contenida originalmente en el libro del matemático chino Yang Hui (aprox. 1238-1298) Xugu Zhaiqi Suanfa (Continuación de la tradición de extraños métodos de computación), de 1275.
Problema: Colocar los números del 1 al 33 en los pequeños círculos de la siguiente imagen, de forma que todos los números de las circunferencias concéntricas, incluido el centro, así como todos los números de los diámetros, sumen lo mismo.
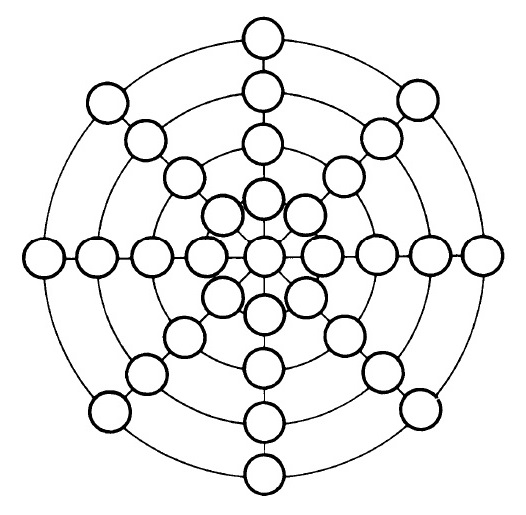
Este problema os lo dejo para quienes queráis enfrentaros al reto. ¡Que os divirtáis!
Bibliografía
1.- Miodrag S. Petrovic, Famous Puzzles of Great Mathematicians, AMS, 2009.
2.- David Well, The Penguin Book of Curious and Interesting Puzzles, Penguin Books, 1992.
3.- John Conway, Richard K. Guy, The book of numbers, Springer-Verlag, 1996.
4.- Elena Deza, Michel Marie Deza, Figurative Numbers, World Scientific, 2012.
5.- Raúl Ibáñez, La gran familia de los números (título provisional), Catarata, 2020.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El problema de las flechas de Mahavira se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El problema de la plantación de árboles en filas (2)
- Un dulce problema de Paul Erdös
- El problema matemático de las cartas extraviadas

