La carga de las partículas radiactivas
 Foto: Divjot Ratra on Unsplash
Foto: Divjot Ratra on UnsplashOtro experimento realizado para estudiar los rayos emitidos en la radioactividad fue hacerlos pasar por un campo magnético para ver hasta qué punto se desviaban de sus direcciones iniciales por la acción del campo. Este método llegó a proporcionar una de las herramientas más utilizadas para el estudio de eventos atómicos y nucleares. Se basa en el hecho ahora familiar de que actúa una fuerza sobre una partícula cargada cuando esta se mueve a través de un campo magnético. Esta fuerza siempre actúa en ángulo recto con respecto a la dirección de movimiento de la partícula cargada. De aquí que la partícula experimente una desviación continua y, si pasa a través de un campo uniforme en ángulo recto, se mueva siguiendo un arco de círculo.
Esta propiedad había sido utilizada en la década de 1890 por J.J. Thomson en sus estudios sobre los rayos catódicos. Demostró que estos rayos consisten en partículas muy pequeñas cargadas negativamente, o electrones. Becquerel, los Curies y otros descubrieron que los rayos alfa, beta y gamma se comportaban de manera diferente en un campo magnético. El comportamiento de los rayos se ilustra en la figura siguiente.
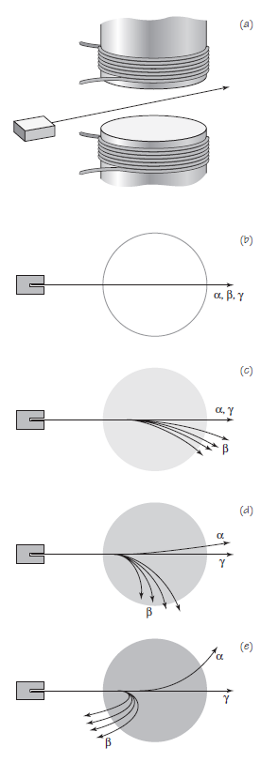 Efectos de un campo magnético sobre las partículas radiactivas. a) Los rayos alfa, beta y gamma de una muestra radiactiva se hacen pasar por un campo magnético uniforme y en ángulo recto a la dirección de propagación. b) Sin campo magnético. c) Con un campo magnético débil. d) Con un campo magnético más fuerte. e) Con un campo magnético muy fuerte. Fuente: Cassidy Physics Library
Efectos de un campo magnético sobre las partículas radiactivas. a) Los rayos alfa, beta y gamma de una muestra radiactiva se hacen pasar por un campo magnético uniforme y en ángulo recto a la dirección de propagación. b) Sin campo magnético. c) Con un campo magnético débil. d) Con un campo magnético más fuerte. e) Con un campo magnético muy fuerte. Fuente: Cassidy Physics LibrarySupongamos que colocamos una muestra de material radioactivo, uranio por ejemplo, en el fondo de un agujero estrecho y algo profundo que hemos hecho en un bloque de plomo. Por la boca del agujero saldrá un haz estrecho de rayos alfa, beta y gamma. Si colocamos un campo magnético lo suficientemente fuerte y uniforme (como en los últimos dos dibujos), los tres tipos de rayos seguirán trayectorias diferentes. Los rayos gamma continúan en línea recta sin ninguna desviación. Los rayos beta se desviarán hacia un lado, moviéndose en arcos circulares de radios diferentes. Los rayos alfa se desviarán ligeramente hacia el otro lado, moviéndose en un arco circular de gran radio [1]
La dirección de la desviación de los rayos beta en dicho campo magnético es la misma que se observó anteriormente en los estudios de Thomson sobre las propiedades de los rayos catódicos. Se concluyó, por lo tanto, que los rayos beta, como los rayos catódicos, consisten en partículas cargadas negativamente. [2]
Como la dirección de la desviación de los rayos alfa era opuesta a la de los rayos gamma, se deduce que los rayos alfa consisten en partículas cargadas positivamente. Como los rayos gamma no se desvían en absoluto, se sigue que son neutros, es decir, no tienen carga eléctrica neta.[3][4]
Notas:
[1] El experimento no se hace en el vacío, por lo que tras pasar por el campo magnético el aire los absorbe rápidamente.
[2] Los Curies confirmaron la carga negativa de los rayos gamma en 1900 usando un electroscopio.
[3] La radiación electromagnética es neutra, al igual que las partículas que transportan cantidades iguales de carga positiva y negativa.
[4] No se puede sacar ninguna conclusión de este tipo de experimento sobre si los rayos gamma son, o no, partículas.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La carga de las partículas radiactivas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Rayos alfa, beta y gamma
- Trayectorias de las partículas cargadas en un campo magnético
- Las partículas de los rayos catódicos
Preparados para matar: a modo de conclusión
“Nada tiene sentido en biología excepto a la luz de la evolución”.
Theodosius Dobzhansky, 1973.
“El tiro lo pega el asesino, no sus genes”.
Reyes Calderón. En una entrevista en El Norte de Castilla, 10 de octubre de 2010.
“Una vez explicado por todos los factores sociopsicológicos imaginables, el crimen sigue siendo el misterio de nuestra especie”.
Daniel Pennac.
“Así podría razonar tanto a priori como a posteriori”.
Bert Leston Taylor (1866-1921), poeta y escritor, al comentar los dos cerebros de los dinosaurios, uno en la cabeza y otro en la cola.
 Foto: Tbel Abuseridze / Unsplash
Foto: Tbel Abuseridze / UnsplashYa que nunca he comprendido por qué nos matamos unos a otros, y la única explicación que me parece plausible viene de la psicología evolutiva y de los mecanismos de selección natural aplicada a la conducta humana, permítanme presentar los siguientes argumentos en defensa de un enfoque que, lo he experimentado, tanto molesta.
Una de las características más sorprendentes de la violencia, y en último término, del asesinato en nuestra especie es que nadie pone en duda este comportamiento. La violencia es algo asumible, consustancial a nuestra especie y muchos, aunque haya quien lo niegue, la usan, o la usamos, con mayor o menor intensidad y frecuencia, si se dan las circunstancias adecuadas.
Cerca de la aldea de Koszyce, en el sur de Polonia, Hace unos 5000 años
El grupo que excavó el yacimiento, dirigido por Hannes Schroeder, de la Universidad de Copenhague, encontró una tumba con 15 cadáveres de hombre mujeres y niños, muertos con golpes en la cabeza. El análisis de ADN demostró que eran miembros de una misma familia. Son siete mujeres y ocho hombres y, entre ellos, hay tres niñas.
Los hallazgos en la ciencias de la evolución pueden ayudar a entender y a formar y guiar las decisiones colectivas que debemos tomar sobre los actos de violencia. La perspectiva evolutiva nos da un enfoque útil para conocer la violencia en nuestra especie. Somos seres biológicos que se relacionan entre sí y coevolucionan con otros humanos y con otras especies. Un paradigma evolutivo puede enriquecer el conocimiento de uno mismo, de nuestra especie y de nuestro entorno. El futuro sin violencia pasa por conocer sus causas con nuevos conocimientos en neurociencias y en genética, y por cambios en las conductas. Así, quizá podamos mitigar y, finalmente, erradicar la violencia, por lo menos entre individuos. Soy poco optimista sobre acabar con la violencia entre grupos, pero se puede conseguir que esté controlada y sea menos dañina y letal.
Biblia de Jerusalén, Josué 6: 21.
“Consagraron al anatema todo lo que había en la ciudad, hombres y mujeres, jóvenes y viejos, ovejas y asnos, a filo de espada”.
Josué 8: 25.
“El total de los que cayeron aquel día, hombres y mujeres, fue 12000, todos los habitantes de Ay”.
Josué 8: 28.
“Josué incendió Ay y la convirtió para siempre en una ruina, en desolación hasta el día de hoy”.
La eliminación de la violencia se ha intentado en nuestra historia por muchos individuos e instituciones. Incluso hay quienes han promovido movimientos a favor de la paz que, de inmediato, han sido despreciados y deshumanizados por quienes se oponen a ellos y han procurado eliminarlos. A veces, se ha conseguido la paz por quienes han luchado para ello pero, a la larga, la violencia ha vuelto al comportamiento de nuestra especie.
Pero, ya lo he mencionado, hay datos, muchos datos que demuestran que el número de asesinatos está disminuyendo en países de todo el mundo. Sergio Parra, en el blog Yorokobu, recoge que, en España, en 2003 hubo 587 homicidios y en 2013 fueron 302. O, en Nueva York, en 1975 fueron 22 muertos por cada 100000 habitantes, y en 2005 fueron 6. Por su parte, el historiador Ian Morris apunta que el porcentaje de muertes violentas fue entre el 10% y el 20% en el Neolítico, entre el 2% y el 5% en imperios clásicos como el romano o los persas, y del 1%-2% en el siglo XX.
Primera Cruzada, 1096-1099.
Karen Armstrong, en sus Campos de sangre, transcribe que “mataron a todos los turcos y sarracenos que encontraron”. Los mataron a todos, hombres y mujeres. La sangre corría por las calles. Se reunió a los judíos en la sinagoga y se les pasó por la espada, y unos diez mil musulmanes que buscaron la salvación en el santuario en el Haram-al-Sharif fueron brutalmente masacrados. “Se veían montañas de cabezas, manos y pies: la sangre llegaba a las rodillas. De hecho, que el lugar estuviera empapado por la sangre de los infieles constituía el justo y espléndido juicio de Dios”.
Estos porcentajes se han corroborado desde otro enfoque muy distinto. El grupo de José María Gómez, de la Universidad de Granada, revisó los datos de violencia letal en mamíferos y su legado filogenético hasta nuestra especie. Calcularon que el porcentaje de muertes en Homo causadas por violencia entre individuos está en el 2%, con un descenso paulatino hasta la actualidad, como propone Morris.
La violencia es el producto de la evolución de mecanismos que ayudaban a nuestros antepasados a conseguir recursos para la supervivencia y la reproducción. Así, sus genes, violentos, pasaban a las siguientes generaciones. Contaba Napoleon Chagnes que, entre los yanomamis del Amazonas, uno de cada cuatro muere violentamente, y dos de cada cinco participan en al menos un homicidio. Y los asesinos, los que matan, tienen tres veces más hijos que los que no lo hacen. Fue así durante millones de años, y pretender que desaparezcan sin más y sin mucho esfuerzo es una ilusión.
Matanza de los indios pequot, 1637
Lo cuenta William Bradford y lo transcribe Karen Armstrong: “Quienes escaparon al fuego perecieron por la espada; algunos fueron despedazados, y muy pocos escaparon. En aquella ocasión mataron a unos cuatrocientos. Verlos quemarse en el fuego era una terrible visión, y los ríos de sangre enfriándose, y era horrible el hedor, pero la victoria parecía un dulce sacrificio, y se ofrecieron plegarias a Dios, que tan maravillosamente se había portado con ellos”.
La violencia puede ser una necesidad para defendernos a nosotros mismos, a los más cercanos, a nuestro grupo o a otros individuos que consideremos débiles y oprimidos. Si eliminamos la violencia, algunos opinan que dejamos de lado nuestros mecanismos de defensa contra aquellos que clasificamos como criminales, opresores o genocidas. Siempre hay quien está dispuesto a atacar a los buenos, a los débiles, a los pacíficos, en otra de las conductas humanas típicas y habituales. Incluso si se controla la violencia, siempre habrá violentos que deban controlarla y, antes o después, volverán esa violencia contra quienes dicen que defienden. Así, desde la evolución ganarán pues tendrán más recursos para sobrevivir y para reproducirse. Opino que, como ven, solo hay dos alternativas: o eliminamos la violencia o no hacemos nada. Y todavía, ni como especie ni como cultura, hemos encontrado un camino aceptable contra la violencia entre humanos.
Rebelión en La Vendée, 1793-1796
Nos lo cuenta Karen Armstrong:
“Atravesad con las bayonetas a todos los que encontréis en vuestro camino. Sé que puede haber algunos patriotas en la región: no importa, hemos de sacrificarlos a todos”. “Todos los bandidos en posesión de armas o sospechosos de haberlas poseído serán pasados por la bayoneta. Actuaremos igual con mujeres, muchachas y niños … no se perdonará a los sospechosos. La Vendée ya no existe. Siguiendo las órdenes que he recibido, he aplastado a niños bajo las pezuñas de nuestros caballos, y masacrado a mujeres … Los caminos están atestados de cadáveres”.
La Revolución Francesa asesinó a doscientas cincuenta mil personas.
Hay, sin embargo, un camino para atenuar la violencia, por lo menos cierto tipo de violencia. En general, en los países desarrollados hay menos violencia, menos asesinatos y menos delitos. Por lo menos en muchos países y culturas aunque, es evidente, no en todos los países ricos. No olvidemos Estados Unidos, con su escaso control de armas y la pena de muerte, Rusia en Chechenia, China y sus ejecuciones o Brasil y Filipinas y la violencia mafiosa e institucional o la destrucción de tribus en el Amazonas.
Es evidente que se ha conseguido mitigar el uso de la violencia porque la riqueza de algunos países permite que todos los miembros del grupo reciban suficientes recursos para sobrevivir y reproducirse y, por tanto, a atenuar sus impulsos evolutivos como especie. Además, en estas sociedades, más grandes y pacíficas hacia adentro, hay educación para el control de las conductas violentas, aunque, en realidad, no sea contra la violencia en sí. Por ejemplo, son estos países ricos los que tienen los ejércitos más potentes y con armamento más mortífero y personal entrenado más letal. Disminuye la violencia en el interior de sus sociedades pero, hacia el exterior, está institucionalizada y produce muchas muertes. Estos grandes estados tienen las armas nucleares y algunos todavía mantienen la pena de muerte. Lo que ocurre con la guerra, sobre todo con las guerras mundiales del siglo XX, ha provocado que algunos investigadores nieguen que la violencia haya disminuido. Es un debate todavía abierto. Quizá la tasa de muertes ha disminuido pero es indudable que, llegado el caso, son igualmente violentos los que viven en pequeños grupos como los que pertenecen a grandes estados.
Ejecución en Roma, 1844, El Conde Montecristo
Alejandro Dumas describe una ejecución en la Plaza del Popolo de Roma:
“El condenado intentó levantarse, pero antes de que le diera tiempo, la maza se abatió sobre su sien izquierda; se oyó un ruido sordo y velado, el ajusticiado cayó como un buey, con la cara pegada al suelo, después de un contragolpe, se dio la vuelta sobre la espalda. Entonces el verdugo dejó caer la maza, sacó el cuchillo del cinturón, y de un solo tajo le abrió la garganta, y, subido sobre el vientre del condenado, se puso a aprisionarle con los pies. A cada presión, un surtidor de sangre salía del cuello”.
Y, para terminar, hay que corregir la idea equivocada de que unos mecanismos psicológicos evolucionados, como los que son la base de la violencia, implican, sin más, un determinismo biológico. Según Steven Pinker, cinco serían las conductas que llevan a la violencia: depredación, dominación, venganza, sadismo e ideología.
Como decía Reyes Calderón, quien mata no son los genes, son los asesinos. Nuestra especie siempre tiene capacidad de elegir, sobre todo si a los individuos se les educa para hacerlo. Los genes reaccionan cuando son estimulados por la información externa adecuada. En el caso de la violencia, utilizarla de manera habitual es enormemente costoso, tanto para quien la usa como para quien la sufre, y, desde la evolución, se ha seleccionado que solo se active con estímulos muy concretos y específicos. Y, de nuevo Steven Pinker, hay cuatro conductas que moderan la violencia: compasión, autocontrol, moralidad y razonamiento.
En el Amazonas, a principios del siglo XX.
El periodista y viajero estadounidense Fritz W. Up de Graff nos cuenta:
“La victoria es para los indios del Alto Amazonas la señal para dar principio al más odioso e importante de todos sus ritos … Habiendo dejado el enemigo tras de sí los muertos y moribundos los vencedores avanzaban para apoderarse de los despojos más preciados de la batalla, las cabezas. Con hachas de piedra, machetes de madera de chonta y conchas afiladas en la arena, iban de un cadáver a otro cortando y reuniendo sus horrendos emblemas de victoria … Yo mismo tuve ocasión de presencias la suerte de una mujer huambisa que cayó al suelo herida por tres lanzas … Los aguarunas, ansiosos por cortar su cabeza, empezaron la obra cuando la infeliz estaba aún viva, aunque incapaz de defenderse. Mientras uno le retorcía la cabeza, otro la sujetaba en tierra y un tercero empezó a darle tajos en el cuello con su hacha de piedra. Por último, me llamaron para que les prestara mi machete, arma mucho más a propósito para ejecutar la operación empezada … Cualquier intervención por mi parte hubiera equivalido a un suicidio”.
No podemos justificar la violencia actual porque sirvió como adaptación y por selección natural a nuestros antepasados. Ya he mencionado que una explicación evolutiva de la violencia no implica que sea inevitable o imposible de prevenir. Comprender las causas de la violencia y de los asesinatos no implica que sea deseable, inevitable o que no deba ser erradicada. El estudio de la violencia desde una perspectiva evolutiva, analizar los contextos en que aparece, y los estímulos que la provocan puede llevarnos a conocer mejor los mecanismos que llevan a la violencia, lo que nos colocará en una posición mejor para controlar la activación de esos mecanismos.
Acabemos. Somos lo que somos y aceptamos que venimos, aunque haya todavía quien lo dude, de ancestros del grupo de los primates. Nuestros pies y el andar bípedo, nuestras manos y su capacidad de, nunca mejor dicho, manipulación, el cerebro, nuestros estómago y nuestro hígado y nuestra digestión, los riñones y el pene o la vagina, los ojos y las orejas, hasta el pelo, si algo queda, son el resultado de la selección natural y de la evolución y, todo ello, lo encontramos en los primates. Todo lo aceptamos excepto, para muchos, que nuestra psicología, el pensamiento, las emociones y las conductas tengan el mismo origen. Incluso se puede decir que aceptamos el cerebro pero en absoluto aceptamos las funciones de ese cerebro, o sea, lo que hace. Entre lo que no aceptamos es que la violencia también sea el resultado de los procesos evolutivos.
Somos unos 10 millones de especies en el planeta, y quizá muchos cientos de millones en la historia de la vida, y todas las especies, lo aceptamos, son consecuencia de la evolución. Todas menos, para muchos, nuestra mente. Es un hecho extraordinario afirmar que nuestra mente no es resultado de la evolución. Es el único caso. Y como se les exige a los que practican las pseudociencias, una afirmación extraordinaria debe ser probada con un experimento extraordinario. Es lo que debemos exigir, lo que exijo, a los que defienden la extraordinaria exclusividad de la mente humana. Adelante con ello. Mientras tanto, aprendamos de la violencia para conocernos mejor.
 Foto: Luz Fuertes / Unsplash
Foto: Luz Fuertes / UnsplashOrdizia, 1986: Yoyes y Kubati en la Plaza Nueva
El 10 de septiembre de ese año, Yoyes paseaba por la Plaza Nueva de su pueblo, Ordizia, con su hijo de tres años, Akaitz. Se acercan dos hombres. Uno de ellos, José Miguel Latasa, “Fermín”, la señala: “Es Yoyes”. El segundo, José Antonio López Ruiz, “Kubati”, le pregunta: “¿Eres Yoyes?”. A la respuesta afirmativa, dice “¿Sabes quién soy?”. “No”.- responde Yoyes. “Soy militante de ETA y vengo a ejecutarte”. Suenan dos tiros, Yoyes cae al suelo, y otro tiro más en la cabeza para rematarla. El hijo, Akaitz, le grita poco después a su abuela: “Abuela, dos hombres la han matado”.
El 21 de septiembre de 1994, en el diario Egin aparece una carta de Kubati:
“¡Cómo os gustaría que al que acusáis de matar a Yoyes os fuera pidiendo perdón de rodillas! No os preocupéis … que nunca pediré salir de la cárcel si antes tengo que hacerme merecedor de vuestro perdón y/o renunciar a mis ideas … Me despido de todos vosotros con desprecio y con el deseo esperanzador de que algún día, al poner la radio, oiga por ella una buena noticia que me alegre el día .. Por todo ello, y por mucho más: os odio”.
Guerra de Iraq: a principios de los noventa
Lo cuenta Tim Kelsey en el Independent on Sunday: un oficial iraquí dijo a sus padres que iban a liberar a su hijo y ”estaban llenos de alegría, cocinaron exquisiteces, y cuando oyeron que se aproximaban coches fueron a la puerta. Cuando sacaron del coche a Ahmad Quazabard, los padres vieron que le habían extirpado las orejas, la nariz y los genitales. Salió del coche con los ojos en las manos. Luego los iraquíes le dispararon, una bala de lleno en el estómago y otra en la cabeza, y dijeron a la madre que se cuidara de no mover el cadáver durante tres días”.
Bosnia, en diciembre de 1992
Lo cuentan José Antonio Marina y Javier Rambaud, según una noticia del 13 de diciembre de 1992 en el New York Times:
“En Bosnia, unos soldados detienen a una muchacha con su hijo. La llevan al centro del salón. Le ordenan que se desnude. Puso el bebé en el suelo, a su lado. Cuatro chetniks la violaron. Ella miraba en silencio a su hijo, que lloraba. Cuando terminó la violación, la joven preguntó si podía amamantar al bebé. Entonces, un chetnik decapitó al niño con un cuchillo y dio la cabeza ensangrentada a la madre. La pobre mujer gritó. La sacaron del edificio y no se la volvió a ver más”.
Referencias:
Antolín, M. 2002. Mujeres de ETA. Piel de serpiente. Ed. Temas de Hoy. Madrid. 245 pp.
Ardrey, R. 1969. Génesis en África. La evolución y el origen del hombre. Ed. Hispano Europea. Barcelona. 457 pp.
Arjona, D. 2017. Hobbes contra Rousseau: ¿somos buenos salvajes o lobos? Una solución inesperada. El Confidencial 10 agosto.
Armstrong, K. 2015. Campos de sangre. La religión y la historia de la violencia. Paidós. Barcelona. 575 pp.
Bartlett, T.Q. et al. 1993. Infant killing in primates: A review of observed cases with specific reference to the sexual selection hypothesis. American Anthropologist 95: 958-990.
Baumeister, R.F. 2001. Raíces de la violencia. Investigación y Ciencia junio.
Blanco, A. 2012. La zona gris: aproximación psicosocial a la violencia. Mente y Cerebro 52: 68-74.
Boutwell, B.B. et al. 2015. A unified crime theory: The evolutionary taxonomy. Aggression and Violent Behavior 25: 343-353.
Buss, D.M. 2005. The murdered next door: Why the mind is designed to kill. Penguin Books. New York. 278 pp.
Buss, D.M. 2012. The evolutionary psychology of crime. Journal of Theoretical and Philosophical Criminology Special Edition January: 90-98.
Crego, A. 2015. La seducción del lado oscuro. Investigación y Ciencia Scilogs 14 enero.
Dobzhansky, T. 1973. Nothing in Biology makes sense except in the light of Evolution. American Biology Teacher 35: 125-129.
Duntley, J.D. & D.M. Buss. 2004. The plausability of adaptations for homicide. En “The structure of the innate mind”. Ed. por P. Carruthers, S. Laurence & S. Stich. Oxford University Press. New York.
Duntley, J.D. & D.M. Buss. 2011. Homicide adaptations. Aggression and Violent Behavior 16: 399-410.
Falke, D. & C. Hildebott. 2017. Annual war deaths in small versus state societies scale with population size rather than violence. Current Anthropology DOI: 10.1086/694568
García, J.E. 2015. El comportamiento criminal desde un punto evolucionista. Persona 18: 27-46.
Geher, G. 2006. Evolutionary psychology is not evil! (… and here’s why…). Psychological Topics 15: 181-202.
Gómez, J.M. et al. 2016. The phylogenetic roots of human lethal violence. Nature 538: 233-237.
Gorelik, G. et al. 2012. Human violence and evolutionary consciousness. Review of General Psychology 16: 343-356.
Kelly, R.C. 2005. The evolution of lethal intergroup violence. Proceedings of the National Academy of Sciences USA 102: 15294-15298.
Liddle, J.R. et al. 2012. Why can’t we all just get along? Evolutionary perspectives on violence, homicide, and war. Review of General Psychology 16: 24-36.
Marina, J.A. & J. Rambaud. 2018. Biografía de la Humanidad. Historia de la evolución de las culturas. Ed. Ariel. Barcelona. 592 pp.
Morris, I. 2017. Guerra, ¿para qué sirve? Ático de los LIbros. Barcelona. 639 pp.
Moya Albiol, L. 2011. La violencia: la otra cara de la empatía. Mente y Cerebro 47: 14-21.
Oka, R.C. et al. 2017. Population is the main driver of war group size and conflicto casualties. Proceedings of the National Academy of Sciences USA DOI: 10.1073/pnas.1713972114
Parra, V. 2016. Aunque no lo parezca, cada vez hay menos asesinatos en el mundo. Yorokobu Blog 24 octubre.
Pinker, S. 2012. Los ángeles que llevamos dentro. El declive de la violencia y sus implicaciones. Paidós. Barcelona. 1152 pp.
Schroeder, H. et al. 2019. Unraveling ancestry, kinship, and violence in a Late Neolithic mass grave. Proceedings of the National Academy of Sciences USA DOI: 10.1073/pnas.1820210116
Up de Graff, F.W. 1961 (1921). Cazadores de cabezas del Amazonas. Siete años de exploración y aventuras. Espasa-Calpe. Madrid. 255 pp.
Victoroff, J. 2012. Emotional and evolutionary aspects of contagious violence. Forum on Global Violence Prevention, Washington DC, April 30.
Wilson, C. 1984. A criminal history of Mankind. Granada Publ. Ltd. London. 702 pp.
Winter, D.A. 2016. Construing homicide. En “The Wiley handbook of personal construct psychology”, p. 416-425. Ed. Por D.A. Winter & N. Reed. John Wiley & Sons. New York.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Preparados para matar: a modo de conclusión se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Preparados para matar: algunas ideas para el debate
- Preparados para matar: Guerra
- Preparados para una Catástrofe Ultravioleta
La barba humana
 Foto: Logan Troxell / Unsplash
Foto: Logan Troxell / Unsplash¿Se ha preguntado alguna vez acerca de la razón de ser de la cola del pavo real? Es espectacular, mucho más grande y colorida que la de la hembra. ¿Qué presión selectiva ha propiciado algo tan grande, aparatoso y lleno de color? Cuesta mantener un adorno de esas dimensiones y el coste van en detrimento de la satisfacción de otras necesidades.
La cola del pavo real, como muchos otros atributos, principalmente masculinos, se ha desarrollado en el mundo animal porque ha sido seleccionado por las parejas reproductivas, principalmente las hembras. Son rasgos que, al imponer un hándicap para la supervivencia y el potencial reproductor del macho, exigen a su poseedor un excelente estado de salud y forma física. Informarían, por ello, de su “aptitud” (fitness en términos darwinianos), de manera que las hembras se emparejarían con los machos que exhiben ese tipo de rasgos en sus versiones más exageradas. Serían los machos con “los mejores genes”, por así decir, los que mejor bagaje biológico pueden legar a su descendencia. Nada de esto es consciente, por supuesto. Se trata de mecanismos que operan de forma automática. A este proceso se le denomina selección sexual.
¿Se ha preguntado alguna vez por qué somos tan diferentes hombres y mujeres en lo relativo a la densidad del vello facial? Cuando un rasgo es muy diferente en los machos y las hembras de una especie, decimos que presenta dimorfismo sexual. Pues bien, en nuestra especie hay dimorfismo en lo relativo al vello facial. Formulemos ahora la pregunta en otros términos: ¿Se ha preguntado por qué los hombres tenemos barba y las mujeres no?
Probablemente responda que, como la cola del pavo real, la barba humana es el resultado de la selección sexual. Pensará, quizás, que las mujeres heterosexuales prefieren a los hombres barbudos como parejas. También una barba tiene sus contrapartidas: tiende a acumular restos de comida, atrae parásitos y, en algunos casos, dificulta la comunicación. Sin embargo, los hombres con barba son percibidos como más masculinos, dominantes y agresivos que los que vamos afeitados. Darwin, de hecho, pensaba que la barba era un ejemplo de selección sexual.
Seguramente no debe descartarse que la barba haya surgido en virtud de ese mecanismo. Sin embargo, hay posibilidades alternativas. La violencia física es mucho más frecuente entre hombres que entre mujeres, y cuando se pelean dos hombres, lo normal es que la cara sea el objetivo de los golpes. Le sonará eso de “le voy a partir la cara”, ¿no? De hecho, a eso se atribuye la anatomía ósea de la cara masculina, más robusta que la femenina.
Por esa razón se ha considerado la posibilidad de que la barba ofrezca protección física. Y lo que se ha observado mediante experimentos es que, efectivamente, protege los huesos de la mandíbula, que son los que con más facilidad se fracturan en las peleas entre dos individuos y cuyas consecuencias, antes de la llegada de la cirugía moderna, podían costar la vida. La protección se produce al reducir la fuerza del impacto sobre los tejidos subyacentes, gracias a la absorción y dispersión de la energía del golpe. El vello facial puede absorber hasta un 30% de la energía transferida mediante un impacto, una diferencia que puede resultar determinante de que se produzca o no la fractura de la mandíbula.
Estas conclusiones, no obstante, han de tomarse con cautela. Porque no siempre es posible deslindar el efecto de diferentes factores. Y esto es especialmente cierto si nos referimos a diferentes posibles presiones selectivas, que pudieron haber actuado a la vez, o también haberse sucedido en el tiempo.
Fuente: E A Beseris, S E Naleway, D R Carrier (2020): Impact Protection Potential of Mammalian Hair: Testing the Pugilism Hypothesis for the Evolution of Human Facial Hair Integrative Organismal Biology 2 (1) obaa005, https://doi.org/10.1093/iob/obaa005
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La barba humana se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Límite energético a la actividad humana
- La cara más emocionante, humana y filosófica de la ciencia
- La civilización ha transformado la especie humana
Juan Ignacio Cirac – P4K 2019: ¿Cómo serán los ordenadores cuánticos?
 Imagen: Michael Dziedzic / Unsplash
Imagen: Michael Dziedzic / Unsplash¿Qué es un ordenador cuántico? ¿Qué hace que sea diferente? Y, de ser posible, ¿cuándo es razonable esperar que podamos tener uno que haga cosas que no haga uno convencional? Juan Ignacio Cirac, director de la División Teórica del Instituto Max-Planck de Óptica Cuántica y uno de los mayores expertos mundiales en información cuántica, responde a estas preguntas en esta excepcional conferencia.
La conferencia se impartió dentro del marco del festival Passion for Knowledge 2019 (P4K) organizado por el Donostia International Physics Center (DIPC).
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Juan Ignacio Cirac – P4K 2019: ¿Cómo serán los ordenadores cuánticos? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Superordenadores del futuro, por Juan Ignacio Cirac
- Juan Ignacio Cirac entrevistado por José María Pitarke
- Curso de verano “La ciencia de nuestras vidas”: La cultura como factor evolutivo, por Juan Ignacio Pérez
El precio de la electricidad es más volátil en épocas de incertidumbre en la regulación de renovables
 Foto: Macau Photo Agency / Unsplash
Foto: Macau Photo Agency / UnsplashTres miembros del grupo de investigación BiRTE de la Facultad de Economía y Empresa de la UPV/EHU han analizado la evolución del precio de la electricidad durante un periodo de 16 años (desde el 2002 al 2017). El objetivo del estudio ha sido ver el efecto de distintos factores relacionados con la energía renovable en el precio de la electricidad. Como punto de partida, “es conocido que la incorporación de esta energía tiene un doble efecto: por un lado es que baja el precio, es decir, la energía que se transacciona es más barata, porque la energía renovable tiene un coste unitario de producción muy cercano a cero. Pero por el otro lado, aumenta la volatilidad del precio, las fluctuaciones que se dan en el precio, porque como es una energía intermitente, no siempre se puede garantizar la generación, y por tanto, la disponibilidad”, explica Aitor Ciarreta Antuñano, investigador principal del grupo de investigación BiRTE y coautor de la presente publicación.
Sin embargo, el grupo de investigación quiso dar un paso más en el análisis de la volatilidad, e incorporar en el análisis la influencia que tiene el marco regulatorio, las políticas que regulan la instalación de plantas de energía renovable y las ayudas con las que se incentivan. “El marco regulatorio es muy importante en el mercado eléctrico, y además está muy influenciado por las directivas europeas. Hemos querido ver si los periodos en los que ha habido incertidumbre en este aspecto han influido en la volatilidad del precio de la electricidad”, comenta Ciarreta. Para ello, “construimos un modelo estadístico con los datos de los precios eléctricos del mercado español, que abarcaba los datos de un periodo de 16 años”, para poder ver en base a qué indicadores variaba la volatilidad.
El análisis estadístico de los datos puso de manifiesto “un agrupamiento o cluster de volatilidad en el periodo concreto en el que hubo una incertidumbre en el marco regulatorio en España”. En el periodo analizado, desde el 2002 al 2017, el doctor en Economía destaca que se diferencian “fases en las que existe un marco regulatorio muy estable, como la que se dio entre el 2007 y el 2012, donde se ofrecían unas ayudas directas a la generación de energía eléctrica renovable. En el año 2012, sin embargo, hubo un cambio en la reglamentación, que no se estabilizó hasta el 2014, y esos dos años de incertidumbre regulatoria coinciden con el periodo en el que se registró el mayor nivel de volatilidad de los precios de la electricidad, que nada tiene que ver con el hecho de que las energías renovables provoquen cierta volatilidad por su naturaleza intermitente. A los agentes económicos les perturba más la incertidumbre asociada a las políticas reguladoras”.
El periodo de incertidumbre regulatoria descrito fue provocado por diferentes factores, tal como describe Ciarreta: “A partir del año 2010 la crisis económica llegó también al mercado eléctrico, y esta crisis se vio acentuada por el alto crecimiento de déficit que se había producido en el periodo anterior, donde estaba regulado un nivel de financiación de renovables tal, que llegó a representar casi el 3 % del PIB. Además, la Unión Europea también estaba presionando bastante a España para que controlara ese déficit”.
Ante esa situación el gobierno intentó articular un nuevo sistema que promoviera las energías renovables, porque, por otra parte, España tenía que cumplir con los objetivos de disminución de emisiones de CO2. Encontrar y establecer el nuevo sistema le llevó dos años, y cuando se implantó, volvió la certidumbre a los mercados. “La tasa de retorno que ofrece el nuevo sistema regulatorio es menor, y se puede estar más o menos de acuerdo con lo establecido, pero vemos que eso no afecta a la volatilidad del precio de la electricidad, afecta mucho más la incertidumbre. A los inversores les da mayor seguridad saber a qué deben atenerse —comenta el investigador—. Y a fin de cuentas, también nos afecta a la ciudadanía, porque la mayoría estamos acogidos a tarifas que dependen del precio de mercado diario”, añade.
El investigador considera que los resultados obtenidos en este análisis deberían servir “como llamada de atención a los reguladores, para que no tomen medidas de cambio de regulaciones a la ligera, y que mantengan la regulación lo más estable posible. Y si van a hacer algún cambio, que permitan a los agentes reaccionar de tal manera que no introduzcan incertidumbre en los mercados eléctricos”.
Referencia:
Aitor Ciarreta, Cristina Pizarro-Irizar, Ainhoa Zarraga (2020) Renewable energy regulation and structural breaks: An empirical analysis of Spanish electricity price volatility Energy Economics doi: 10.1016/j.eneco.2020.104749
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo El precio de la electricidad es más volátil en épocas de incertidumbre en la regulación de renovables se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una red electrica global basada en corriente continua para optimizar el uso de energías renovables
- El principio de incertidumbre, cuantitativamente
- El carácter fundamental de las relaciones de incertidumbre
La caracola más grave del mundo
«El caracol debía tocar el trombón que lleva a cuestas.»
Ramón Gómez de la Serna. Greguerías.
Steve Turre es un virtuoso del trombón, arreglista y compositor de jazz estadounidense. Con más de cincuenta años de carrera a sus espaldas, veinte discos liderados por él e incontables colaboraciones, se ha convertido en uno de los trombonistas más prolíficos de la historia del jazz. Sin embargo, cuando uno busca su nombre en internet es mucho más fácil asociarlo a sus sorprendentes habilidades con otro instrumento de viento metal: la caracola. O, mejor dicho, las caracolas. En cada concierto, Turre alterna entre conchas vacías como un pulpo avaricioso en una mariscada. No es por presumir de instrumentos, ni un síntoma de indecisión. Cada una le ofrece un color propio, un timbre nuevo y, sobre todo, la capacidad de tocar una nota distinta.
 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsEl tono de un instrumento depende de su forma y, sobre todo, de su tamaño. En una caracola grande, el aire tarda más en recorrer la cámara de resonancia, por lo que las ondas estacionarias que se forman en su interior son más largas o, lo que es lo mismo, tienen un sonido más grave. Las caracolas pequeñas, en cambio, producen sonidos más agudos. Por ese mismo motivo, casi todos los instrumentos de una orquesta se estructuran en familias: un mismo artilugio que, a distintas escalas, consigue producir rangos de frecuencias diferentes.
 Octobajo y violino piccolo. Créditos: Fotografía de Henrik Beck / nyMusikk.
Octobajo y violino piccolo. Créditos: Fotografía de Henrik Beck / nyMusikk.La familia orquestal más conocida es, sin duda, la de la cuerda frotada. Probablemente, porque todos sus miembros tienen un nombre propio y ocupan un montón de hueco en el escenario. Mientras que los distintos saxofones, por poner ejemplo, se distinguen únicamente mediante su apellido (saxofón tenor, alto, soprano…), los violines mutan en violas, violonchelos y contrabajos según van aumentando de peso1. Pero existen también otros miembros menos conocidos dentro de esta gran familia. Los luthiers fabrican violines fraccionarios para los violinistas de brazos diminutos. En el extremo opuesto encontramos el gigantesco octabajo de 4 metros de altura. No existen gigantes que puedan trepar por sus cuerdas, así que el instrumento cuenta con una serie de trastes y palancas que permiten pulsarlas. Fue inventado a finales del siglo XIX por Jean Baptiste Vuillaume y se llama así por producir sonidos una octava más graves que los de un bajo. Como resultado, el octabajo suena a truenos y a rugir de tripas. Alcanza, de hecho, el límite de nuestro rango auditivo.
No existe un equivalente del tamaño del octabajo en la familia de las caracolas. Pero si hubiese que elegir uno, sin duda sería miembro de la especie Syrinx aruanus. Estos gasterópodos pueden alcanzar casi un metro de altura y llegar a pesar 18 kg. El espécimen más grande conocido se encuentra en el Museo de Ciencias Naturales de Houston y tiene una altura de 91 centímetros. Con este dato y gracias a las propiedades geométricas de su espiral logarítmica podemos calcular la longitud de su cavidad interna: unos 3 metros, según la foto que se encuentra en la Wikipedia. Ahora, para calcular su frecuencia, debemos modelar la caracola como un cono cerrado en un extremo (la punta desde donde se sopla) y abierto en el opuesto. En ese sentido, sería parecida a un saxofón o a una tuba. En un tubo cónico, la frecuencia fundamental se calcula como f=c/2L, siendo c la velocidad del sonido y L, la longitud del tubo.
Otros instrumentos cónicos son el saxofón y la tuba. El saxofón más grave del mundo, de apellido subcontrabajo y con una altura superior a 2 metros (lo que equivale a una longitud de unos 6 metros según calculo a ojo), alcanza sonidos de 29 Hz. No fue posible construirlo hasta 1999. La tuba de la misma tesitura, cuyo tubo se pierde en un nido de espirales mucho más difícil de seguir, retumba hasta una frecuencia parecida. La caracola más grave del mundo, en cambio, se parece mucho más a una trompa alpina; se podría decir que no es más que su versión desenrollada. Aunque este instrumento tiene una tesitura menos estandarizada que la del saxofón o la tuba, su voz resuena en los graves sin llegar a la tenebrosa caverna de los subcontrabajos. Más o menos, a partir del do2 o 65 hercios: la nota más grave del bajo más profundo; el sonido más grave que un ser humano puede cantar.
 Trompa alpina. Fuente: Wikimedia Commons
Trompa alpina. Fuente: Wikimedia Commons
Nota:
1Por motivos históricos, existen diferencias entre las propiedades acústicas de estos instrumentos. Ha habido propuestas en el siglo XX para cambiar esto, como el octeto de violín.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo La caracola más grave del mundo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Las curiosas reglas de divisibilidad (II)
En la anterior entrada del Cuaderno de Cultura Científica titulada Las curiosas reglas de divisibilidad presentamos algunos criterios de divisibilidad de los números de un solo dígito, es decir, de las cifras básicas -no nulas- de nuestro sistema de numeración, y de algún número más, como 11, 12, 13 o 15.
En esta entrada vamos a seguir analizando las reglas de divisibilidad de la aritmética. Algunos son nuevos criterios para números ya vistos, como 7, 8 u 11, mientras que otros serán de números nuevos, como el 17. Además, muchos de estos criterios, incluidos algunos de los vistos en la entrada anterior, emanan de una idea general de la divisibilidad, el criterio de Pascal.
 Infinito a Cannaregio (2019), del artista italiano Tobia Rava. Imagen de la galería Sist’Art
Infinito a Cannaregio (2019), del artista italiano Tobia Rava. Imagen de la galería Sist’Art
Reglas de divisibilidad del número 7. En la anterior entrada ya vimos un criterio para el número 7, que la suma alternada de los grupos de tres dígitos del número, empezando por la derecha, también sea divisible por 7. Por ejemplo, sabemos que el número 417.885.713 es divisible por 7 porque 713 – 885 + 417 = 245 también lo es, 245 = 7 x 35.
Pero existen más reglas de divisibilidad para este número. Los primeros criterios que vamos a mostrar son bastante sencillos de aplicar, si se hace de forma recursiva. La primera regla dice:
Un número es divisible por 7 si, y sólo si, la resta de dos veces el dígito de las unidades del resto de los dígitos del número es divisible por 7.
Por ejemplo, si tomamos el número 539, como 53 – 2 x 9 = 35, entonces es divisible por 7, mientras que 713 no lo es, ya que 71 – 2 x 3 = 65. Y para números grandes se puede utilizar de forma recursiva, así el número 4.357 será divisible por 7 si lo es 435 – 2 x 7 = 421, pero este lo será si 42 – 2 x 1 = 40 lo es. Pero 40 no es divisible por 7, luego tampoco 421, ni 4.357. Para números con muchos dígitos puede ser un criterio un poco largo, aunque efectivo.
El motivo por el que funciona este criterio es que el 21 es divisible por 7. Dado un número N, este puede escribirse de la forma N = 10 a + b, donde b son las unidades, y si fuese múltiplo de 7 se podría expresar de la forma 7k. Por lo tanto, si le restamos la cantidad 21b, entonces se obtiene que 10a – 20b = 7k – 21b, es decir, la igualdad
10 (a – 2b) = 7 (k – 3b),
de donde sale el criterio, ya que N es divisible por 7 si, y sólo si, a – 2b lo es.
Un razonamiento similar, pero utilizando que 49 es divisible por 7, nos permite obtener otro criterio muy parecido:
Un número es divisible por 7 si, y sólo si, la suma de cinco veces el dígito de las unidades y el resto de los dígitos del número también lo es.
Es decir, si escribimos el número como 10 a + b, este es divisible por 7 si, y sólo si, a + 5b lo es. Por ejemplo, tomemos el número 3.791, este será divisible por 7 si lo es 379 + 5 x 1 = 384, que a su vez es divisible por 7 si lo es 38 – 5 x 4 = 18, que como no lo es, en consecuencia, no lo es ninguno de los anteriores, ni 384, ni 3.791.
Y el mismo tipo de argumento nos lleva, por ejemplo, a obtener el siguiente criterio:
Un número es divisible por 7 si, y sólo si, la suma del dígito de las unidades y tres veces el resto de los dígitos del número es divisible por 7.
Es decir, si escribimos el número como 10 a + b, este es divisible por 7 si, y sólo si, 3a + b lo es. Curiosamente, en el Talmud, que como señala el diccionario de la RAE es el “libro que contiene la tradición oral, doctrinas, ceremonias y preceptos de la religión judía”, está escrito otro criterio similar a los anteriores, basado en el hecho de que 98 es divisible por 7, que dice que 100 a + b es divisible por 7 si, y sólo si, 2a + b lo es.
Un reto sencillo para las personas que estáis leyendo esta entrada del Cuaderno de Cultura Científica consiste en probar estas tres últimas reglas de divisibilidad, de forma paralela a como hemos hecho para la primera.
 Número 7 (2011), del artista conceptual danés de origen vietnamita Danh Vô. Imagen de la página web de Sotheby’s
Número 7 (2011), del artista conceptual danés de origen vietnamita Danh Vô. Imagen de la página web de Sotheby’sPara la siguiente regla de divisibilidad se necesitan los restos de dividir por 7 las potencias de 10, asociadas a la representación decimal de los números. Como 100 = 1, 101 = 7 + 3, 102 = 7 x 14 + 2, 103 = 7 x 142 + 6, 104 = 7 x 1.428 + 4 y 105 = 7 x 14.285 + 5, los restos de dividir las anteriores potencias de 10 por 7 son 1, 3, 2, 6, 4, 5 y para las siguientes potencias de 10 los restos se repiten de forma cíclica 1, 3, 2, 6, 4 y 5.
El criterio dice lo siguiente:
Un número es divisible por 7 si, y sólo si, al multiplicar los dígitos del número por el resto correspondiente a la potencia de 10 de su posición, el resultado es divisible por 7.
Veamos el criterio mediante un ejemplo concreto. El número 234.647 será divisible por 7 si lo es 2 x 5 + 3 x 4 + 4 x 6 + 6 x 2 + 4 x 3 + 2 x 1 = 77, luego sí lo es (77 = 7 x 11).
Veamos la justificación de esta regla de divisibilidad del 7 para números de seis dígitos, aunque realmente funciona para cualquier cantidad de dígitos. Sea un número de seis dígitos a5a4a3a2a1a0, entonces
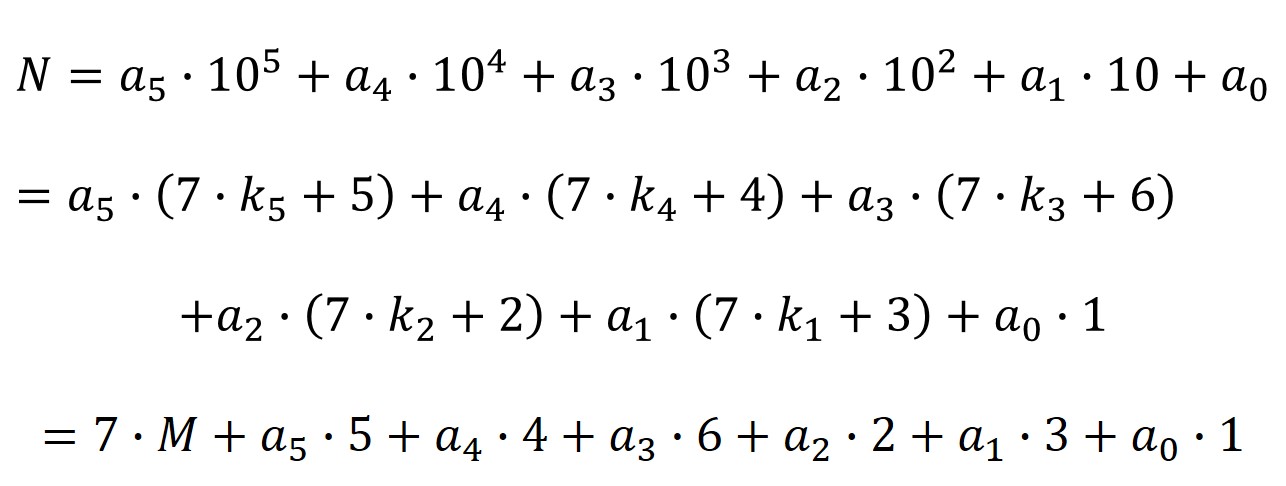
Por lo tanto, N es divisible por 7 si, y sólo si, (a5 x 5) + (a4 x 4) + (a3 x 6) + (a2 x 2) + (a1 x 3) + (a0 x 1) también es divisible por 7.
De hecho, podríamos ir un poco más allá para simplificar esta regla. Como 7 = 7 + 0, 8 = 7 + 1 y 9 = 7 + 2, podemos sustituir, a la hora de aplicar la regla al número, el 7 por 0, el 8 por 1 y el 9 por 2, en el número original. Así, para saber si el número 144.879, basta verlo para el número 144.102, así como 1 x 5 + 4 x 4 + 4 x 6 + 1 x 2 + 0 x 3 + 2 x 1 = 49, entonces sí es divisible por 7.
 Litografía de Blaise Pascal. Imagen de Wellcome Collection
Litografía de Blaise Pascal. Imagen de Wellcome Collection
De hecho, este es solamente un caso particular del criterio de Pascal, que introdujo el matemático francés Blaise Pascal (1623-1662), de quien ya hablamos en la entrada Blaise Pascal, Dios y la cicloide, en su libro De Numeris Multiplicibus. El criterio de Pascal es el siguiente.
Criterio de Pascal: Un número N = an an–1 … a2 a1 a0, es decir,
![]()
es divisible por un número m si, y sólo si, el número
![]()
es divisible por m, donde rk es resto de dividir 10k por m (r0 = 1).
La demostración del criterio de Pascal es similar a la explicación que hemos dado para la última regla de divisibilidad del 7.
Muchas de las reglas vistas en la entrada Las curiosas reglas de divisibilidad son realmente consecuencia del criterio de Pascal. Por ejemplo, si miramos de nuevo a la regla de divisibilidad del 3, realmente se utiliza que el resto de dividir las potencias de 10 por 3 es siempre 1, por eso sale que la suma de los dígitos del número debe ser divisible por 3.
A continuación, vamos a mostrar un pequeño truco de magia que el divulgador estadounidense Martin Gardner (1914-2010) nos enseñó en su columna de juegos matemáticos en la revista Scientific American. Aunque no es una aplicación de las reglas de la divisibilidad, si tiene que ver con la divisibilidad. En concreto, está relacionado con el hecho, visto en la anterior entrada, de que 1.001 = 7 x 11 x 13.
 Portada de la revista Scientific American de 1958 con una ilustración del artículo “How rectangles, including squares, can be divided into squares of unequal size” de la columna de juegos matemáticos de Martin Gardner
Portada de la revista Scientific American de 1958 con una ilustración del artículo “How rectangles, including squares, can be divided into squares of unequal size” de la columna de juegos matemáticos de Martin GardnerEl truco conocido como El misterio de las mil y una noches consiste en lo siguiente. Se le pide a una persona de nuestro “público” que piense en un número de tres cifras –ABC– y que lo escriba en una calculadora, que tendremos preparada para el truco. Después se le pide que vuelva a escribir, seguido, el mismo número, quedando entonces en la calculadora ABCABC. Nosotros no debemos saber el número y lo mejor es que estemos de espalda al “público” para que no haya sospechas.
Luego llega el momento de adivinar el número que ha pensado esa persona y hay que hacerlo con teatralidad. Puede empezar diciéndose algo así como “esperad que me concentre en el número que está escrito en la calculadora, estoy captando algo, sí creo que sí, … si no me equivoco es divisible por el número de la mala suerte, el 13”. Le pedimos que lo compruebe, que divida el número que está en la calculadora –ABCABC– por 13. Y se le pregunta, “¿Es cierto? ¿Era divisible por 13?” y cuando nos diga que sí, volvemos al teatro de mentalista.
Se puede seguir diciendo algo así como “sigo teniendo una sensación extraña, me parece que … sí, también creo que es divisible por el número de la buena suerte, el 7. ¿Estaré equivocado? ¿Divide el número que tienes en la calculadora por 7?¿Se ha podido dividir?”. Realizará la división –el resultado de dividir ABCABC por 13, lo divide ahora por 7– y contestará que sí.
Llega entonces el momento final del truco. El mago debe seguir ejerciendo de mentalista y decir algo así como “Percibo más cosas… percibo un uno, qué raro … espera … no, son dos unos, es el número 11 … divide el número que te ha quedado por 11”. Cuando la persona del “público” realice esa división, llega el efecto final… “fíjate bien en la pantalla de la calculadora, ¿no es ese el número que habías pensado?” y efectivamente, ahí está el número que había pensado, ABC.
El truco es muy sencillo y funciona porque ABCABC = 1.001 x ABC, pero 1.001 = 7 x 11 x 13.
 Lucky number 8 (2012), de la artista Belinda Capol. Imagen de la página web de Belinda Capol
Lucky number 8 (2012), de la artista Belinda Capol. Imagen de la página web de Belinda CapolLas reglas de divisibilidad del 8. Con el número 8 también podemos dar criterios de los dos tipos que hemos mostrado para el número 7, además del que mostramos ya en la anterior entrada. Un criterio de la primera clase es:
Un número 10 a + b es divisible por 8 si, y sólo si, 2a + b es divisible por 8.
Veamos un ejemplo. El número 5.176 será divisible por 8 si lo es 2 x 517 + 6 = 1.040, que a su vez es divisible por 8 si lo es 2 x 104 + 0 = 208, que claramente es divisible por 8, aunque podríamos volver a usar el criterio, ya que 2 x 20 + 8 = 48, divisible por 8.
Si ahora adaptamos el criterio de Pascal al número 8, necesitamos los restos de dividir las potencias de 10 por 8, que son 1, 2, 4 y el resto 0, ya que 1.000 y las potencias mayores son todas múltiplos de 8 (pensemos que cada 10 aporta un 2). Por lo tanto, el criterio de Pascal para el 8 queda:
Un número es divisible por 8 si, y sólo si, el resultado de sumar el dígito de las unidades, dos veces el de las decenas y cuatro veces el de las centenas es divisible por 8.
Veámoslo con el número anterior, 5.176, para el que 6 + 2 x 7 + 4 x 1 = 24, divisible por 8, como ya sabíamos.
Las reglas de divisibilidad del 11. El criterio visto en la anterior entrada, la suma alternada de sus dígitos (es decir, se va alternando suma y resta) es divisible por 11, no es el criterio de Pascal, pero está muy cerca, puesto que como demostramos entonces las potencias de 10 son casi múltiplos de 11, un número arriba o debajo de un múltiplo de 11.
Como 11 es mayor que 10, podemos aplicar la misma idea del criterio de Pascal, pero para la expresión del número como potencias de 100 y tomar los restos de dividir estas potencias por 11 (aunque también nos valdría para otros números de dos dígitos). Por ejemplo, el número 979.957 lo podemos expresar de la forma 97 x 1002 + 99 x 100 + 57. De esta forma, se puede demostrar un nuevo criterio de tipo Pascal:
Criterio de tipo Pascal: Un número N = an an–1 … a2 a1 a0(con una cantidad par de dígitos, en caso contrario es como si tuviese el dígito 0 a la izquierda, para que sea par), es decir,

es divisible por un número m si, y sólo si, el número
![]()
es divisible por m, donde rk es resto de dividir 102k por m (r0 = 1).
Como el resto de dividir las potencias de 100 por 11 siempre es 1, la regla de divisibilidad que se genera es:
Un número es divisible por 11 si, y sólo si, también lo es el resultado de sumar los grupos de dos dígitos (desde la derecha) del número.
Por ejemplo, 3.719 no es divisible por 11 ya que 37 + 19 = 56 no lo es. Sin embargo, el número anterior, 979.957, sí lo es ya que 97 + 99 + 57 = 253 es divisible por 11, para lo cual volvemos a utilizar el criterio, 53 + 2 = 55, múltiplo de 11.
O podemos dar algún criterio del otro tipo, como:
Un número 10 a + b es divisible por 11 si, y sólo si, a – b es divisible por 11.
 Once, del artista Kevin P. Robinson. Imagen de la página web de Kevin P. Robinson
Once, del artista Kevin P. Robinson. Imagen de la página web de Kevin P. RobinsonAntes de ver más criterios, incluyamos uno de esos problemas de ingenio que tanto nos gustan, relacionado con este tema.
Problema: Encontrar el número capicúa más pequeño que es divisible por 3, 5 y 11.
Os animo a que lo resolváis por vosotros mismos, ya que es sencillo y lo divertido con los juegos es intentarlo uno mismo. De todas formas, damos a continuación la solución al mismo.
Como se trata de un número divisible por 5, debe terminar en 0 o 5, pero como no hay números que empiecen por 0 (a la izquierda), necesariamente el primer y último dígitos debe ser 5. Solo hay uno con dos dígitos –55–, pero no es divisible por 3. De tres dígitos que sean múltiplos de 3, por la regla de divisibilidad del 3, están 525, 555, 585, pero ninguno es múltiplo de 11, ya que la suma alternada de sus dígitos –8, 5 y 2, respectivamente– no es en ningún caso múltiplo de 11. Cualquier número capicúa de cuatro dígitos es divisible por 11 (en general, todos los números capicúas con una cantidad par de dígitos, como vimos en la entrada Las curiosas reglas de divisibilidad, son divisibles por 11), luego solo hay que buscar el número más pequeño de la forma 5aa5, divisible por 3, es decir, 5.115.
 Toro algorítmico (2018), del artista italiano Tobia Rava. Imagen de la galería Sist’Art
Toro algorítmico (2018), del artista italiano Tobia Rava. Imagen de la galería Sist’ArtLas reglas de divisibilidad del 13. La regla de divisibilidad del 13 vista en la anterior entrada del Cuaderno de Cultura Científica es la misma que para 7 y 11, que la suma alternada de los grupos de tres dígitos del número, empezando por la derecha, también sea divisible por 13. Pero podemos dar algunos criterios similares a los del primer tipo estudiados para el 7.
Criterio 1: Un número 10 a + b es divisible por 13 si, y sólo si, a + 4b es divisible por 13.
Criterio 2: Un número 100 a + b es divisible por 13 si, y sólo si, 4a – b es divisible por 13.
Criterio 3: Un número 10 a + b es divisible por 13 si, y sólo si, a – 9b es divisible por 13.
Veamos la divisibilidad por 13 del número 8.333. Por el criterio 1 sería divisible si lo es 833 + 4 x 3 = 845, que a su vez lo será si lo es 84 + 4 x 5 = 104, que es divisible por 13 ya que 10 + 4 x 4 = 26.
Aplicando el criterio 2, 8.333 es divisible por 13 si lo es 4 x 83 – 33 = 299, que es múltiplo de 13, puesto que 4 x 2 – 99 = 91, que es siete veces 13.
Y mediante el criterio 3, tenemos 833 – 9 x 3 = 806 y a partir de este, 80 – 9 x 6 = 26.
 Casa no. 13, del artista alemán Jack N. Mohr. Imagen de la página Saatchi Art
Casa no. 13, del artista alemán Jack N. Mohr. Imagen de la página Saatchi ArtLas reglas de divisibilidad del 17. Para este número se pueden encontrar, de nuevo, varios criterios de divisibilidad del primer tipo, aunque vamos a citar solamente uno.
Un número 10 a + b es divisible por 17 si, y sólo si, a – 5b es divisible por 17.
Por ejemplo, el número 289 es divisible por 17 ya que 28 – 5 x 9 = – 17, lo es.
Como hicimos para el número 11 podemos intentar aplicar el criterio de tipo Pascal anterior para el número 17. Para lo cual necesitamos conocer los restos de dividir las potencias de 100 por 17, que son (además del resto inicial 1) los siguientes: el resto de dividir 100 por 17 es 15, pero como es muy grande y nos interesa los múltiplos de 17, podemos restarle 17, quedando – 2; el resto para 1002 es 4; el resto para 1003 es 9; el resto para 1004 es 16, que restándole 17 queda – 1; el resto para 1005 es 2; y así podríamos seguir.
Veamos un ejemplo de aplicación de este criterio de tipo Pascal para el número 17. Tomemos el número 333.333.331 (más adelante entenderemos el motivo de elegir este), será divisible por 17 si lo es
3 x (– 1) + 33 x 9 + 33 x 4 + 33 x (– 2) + 31 x 1 = 391,
que es múltiplo de 17 (al multiplicarlo por 23), aunque podemos utilizar una vez más el criterio, por lo que 391 es múltiplo de 17 si lo es
3 x (– 2) + 91 x 1 = 85,
que es 17 x 5. Por lo tanto, el número 333.333.331 se puede dividir por 17.
 Instalación con post-its del número 17 en el Centro Comercial de Munich, en 2011, del artista Andreas Kopp, dentro de un proyecto de post-it-art
Instalación con post-its del número 17 en el Centro Comercial de Munich, en 2011, del artista Andreas Kopp, dentro de un proyecto de post-it-artVeamos una cuestión sobre patrones de números primos que se puede leer en el libro de Martin Gardner, Huevos, nudos y otras mistificaciones matemáticas.
Si se observa la sucesión de números 31, 331, 3.331, 33.331, 333.331, 3.333.331, 33.333.331… se verá que esos primeros miembros son todos números primos, la cuestión es si toda la sucesión será de números primos y en caso contrario, cuál es el primero que no lo es.
Las reglas de la divisibilidad no son la mejor herramienta para resolver este problema, ya que con una calculadora podemos hacer rápidamente algunas cuentas y observar la solución. Además, ya hemos probado más arriba que el siguiente miembro de la sucesión 333.333.331 es divisible por 17, luego no primo. De hecho,
333.333.331 = 17 x 19.607.843.
Sin embargo, podemos utilizar las reglas de la divisibilidad para obtener algunas conclusiones generales sobre esta sucesión de números, 31, 331, 3.331, etc.
Claramente, los miembros de esa sucesión no son múltiplos de 2 o 5, ya que el dígito de las unidades es 1. Tampoco ningún miembro es múltiplo de 3, ya que la suma de sus dígitos es de la forma 3 k + 1, donde k es el número de treses que tiene el número, luego nunca puede ser múltiplo de 3.
Veamos qué pasa con el siguiente primo, el 7. Si utilizamos el criterio de que un número 10 a + b es divisible por 7 si, y sólo si, lo es a – 2b, se observa que, para cada miembro de la sucesión, al aplicar el criterio se genera el miembro anterior. Por ejemplo, dado 3.331, este sería divisible por 7 si lo fuese 333 – 2 x 1 = 331, que es el elemento anterior. Por lo tanto, como los primeros miembros de la sucesión son primos, ningún elemento de esta sucesión es múltiplo de 7.
Si utilizamos la regla de divisibilidad del 11 de las sumas alternadas, observaremos que las sumas alternadas de los miembros de la sucesión 31, 331, 3.331, 33.3331, … son siempre 2 y 1, repitiéndose de forma cíclica, luego nunca múltiplos de 11. De la misma forma, si se utiliza el criterio de divisibilidad del 13 de las sumas alternadas de los grupos de tres dígitos, se obtienen siempre las sumas – 328, – 298, 2, 1, 31 y 331, repitiéndose de forma cíclica, luego tampoco son múltiplos de 13.
Resumiendo, con estos criterios de divisibilidad, hemos probado que los miembros de la sucesión infinita
31, 331, 3.331, 33.331, 333.331, …
no son divisibles por los números primos 2, 3, 5, 7, 11 y 13.
Podríamos dar reglas de divisibilidad para más números, pero “creo que lo dejaré aquí” (véase la entrada Euler y el último teorema de Fermat, para ver donde esta última expresión tuvo un sentido muy especial).
 Sidewalk white, del artista canadiense Michael Soltis. Imagen de la página web de Michael Soltis
Sidewalk white, del artista canadiense Michael Soltis. Imagen de la página web de Michael SoltisBibliografía
1.- Martin Gardner, The Unexpected Hanging and other Mathematical Diversions, University of Chicago Press, 1991.
2.- Branislav Kisacanin, Mathematical Probems and Proofs, Kluwer, 2002.
3.- Wikipedia: Divisibility rule
4.- James J. Tattersall, Elementary Number Theory in Nine Chapters, Cambridge University Press, 1999.
5.- Página web del artista Tobia Ravá
6.- Página web del artista Andreas Kopp
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Las curiosas reglas de divisibilidad (II) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las curiosas reglas de divisibilidad
- Los institutos Isaac Newton y Oberwolfach, dos curiosas instituciones de investigación matemática
- Los números que proporcionan alegría
Rayos alfa, beta y gamma
Una vez que se conocieron las extraordinarias propiedades del radio, el interés en ellas se disparó tanto dentro como fuera del mundo científico, y el número de personas que pasaron a estudiar el fenómeno aumentó rápidamente, tanto desde el punto de vista puramente científico como en sus aplicaciones, digamos, “prácticas”.
 Desde que el mundo es mundo los estafadores han intentado hacer negocio con la incultura científica popular, con base en lo último que asomaba a los medios generalistas. Parche de mineral de radio curalotodo. Completamente natural porque solo contiene mineral de radio silvestre. En fin. Fuente: Oobject
Desde que el mundo es mundo los estafadores han intentado hacer negocio con la incultura científica popular, con base en lo último que asomaba a los medios generalistas. Parche de mineral de radio curalotodo. Completamente natural porque solo contiene mineral de radio silvestre. En fin. Fuente: OobjectLa cuestión principal que atrajo la atención científica fue: ¿qué son las misteriosas radiaciones emitidas por los cuerpos radiactivos?
En 1899, Ernest Rutherford, en lo que serían los primeros pasos de lo que después resultaría en su teoría del átomo nuclear, comenzó a buscar respuestas a esta pregunta. Rutherford descubrió que una muestra de uranio emite al menos dos tipos distintos de rayos: uno que se absorbe muy fácilmente, que llamó rayos α (rayos alfa) [1], y el otro más penetrante, que llamó rayos β (rayos beta) . Un año después, en 1900, Paul Ulrich Villard observó que la emisión del radio contenía rayos mucho más penetrantes que incluso los rayos β; este tipo de emisión recibió el nombre de rayos γ (gamma). El poder de penetración de los tres tipos de “rayos”, como se conocían en ese momento, lo midió Rutherford en términos del espesor necesario que tenía que tener una lámina de aluminio para absorberlos completamente. En 1903 publicó una tabla fiable de valores:
Rayos alfa → 0,0005 cm
Rayos beta → 0,05 cm
Rayos gamma → 8 cm
Por lo tanto, los «rayos Becquerel» eran más complejos de lo que se había pensado. Y eso que aún no se había determinado la naturaleza de los distintos tipos de rayos. De los tres tipos de rayos, los rayos alfa son los más fuertemente ionizantes y los rayos gamma los menos. El poder de penetración es inversamente proporcional al poder de ionización. Esto es lógico: el poder de penetración de los rayos alfa del uranio es bajo porque “gastan” su energía muy rápidamente en causar una ionización intensa.
Los rayos alfa emitidos por una fuente son casi todos [2] absorbidos por aproximadamente 0.0005 cm de aluminio, o por una hoja de papel de escribir ordinario o por unos pocos centímetros de aire. Los rayos beta se detienen por completo solo después de viajar muchos metros en el aire, o 0.05 cm en aluminio. Los rayos gamma pueden atravesar muchos centímetros de aluminio o plomo, o un metro de hormigón, antes de ser absorbidos casi por completo [2].
Una consecuencia de estas propiedades de los rayos es que a veces se necesita un blindaje muy pesado y muy caro para proteger a las personas de los efectos nocivos de los rayos cuando estudian o usan estas radiaciones, ya sea en aceleradores, reactores nucleares o instalaciones radioterápicas o de radiodiagnóstico. En algunos casos estos blindajes alcanzan los 3 metros de grosor.
Los rayos de las sustancias radiactivas ionizan y, en consecuencia, descomponen las moléculas que constituyen las células vivas, causando «quemaduras» por radiación, y lesiones fatales en las células. Estos daños pueden conducir al crecimiento de células cancerosas y a la aparición de mutaciones peligrosas en la estructura de las moléculas de ADN. [3]
Notas:
[1] De alguna forma tenía que llamarlos. Así que, como había varios tipos pero no sabía a priori cuantos decidió usar el alfabeto griego, por llevar una sistemática: alfa, beta, gamma, delta, épsilon, etc.
[2] Esto es un valor estadístico. Es decir, si le das el tiempo suficiente algún rayo va a atravesar lo que sea. Por lo tanto hay que poner un límite: si en determinado tiempo la cantidad de rayos que se detectan es menor que cierto valor umbral, entonces podemos decir que, a efectos prácticos, los rayos no atraviesan.
[3] No, ni la wifi, ni el 5G, ni la televisión ionizan. No tienen energía para ello. Rock FM provoca la ionización del pelo, pero eso es solo porque los melenudos que tocan la guitarra de aire mientras la escuchan sacuden la cabeza.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Rayos alfa, beta y gamma se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Rayos X y gamma
- No solo el uranio emite rayos
- Un trio de supernovas con brotes de rayos gamma asociados
La Covid-19 revoluciona el sistema de publicación científica
Elea Giménez Toledo y Antonio Lafuente
 Foto: REVOLT / Unsplash
Foto: REVOLT / UnsplashEn los últimos meses hemos visto abundancia de prepublicaciones y estudios sobre la COVID-19 y el coronavirus que la provoca. El motivo está en la necesidad de contar de manera inmediata con evidencias y resultados fiables.
En este periodo se han detectado tres tipos de reacciones en la comunidad científica: la de la propia comunidad académica, la de la editorial y la de los especialistas en Inteligencia Artificial (IA), tecnología semánticas y recuperación de información.
Más de una veintena de artículos sobre la COVID-19 han sido retractados, según The Retraction Watch.
Algunos de los estudios retirados habían sido publicados en revistas muy prestigiosas del área –The Lancet y The New England Journal of Medicine–, lo que ha provocado que se cuestionara de nuevo el sistema de revisión por expertos (peer review).
Este sistema representa el primer filtro y la validación por parte de especialistas de los contenidos de un artículo. Las críticas a este proceso han existido siempre, pero en esta ocasión, por el impacto social de la pandemia, han traspasado la frontera de la comunidad científica y alcanzado la esfera pública a través de los medios de comunicación.
La propia comunidad científica ha reivindicado durante la pandemia la necesidad de velar por la calidad de los contenidos y su solidez antes de la publicación.
En este tema, se identifican posiciones para todos los gustos. Vincent Lariviére, un especialista en estudios de la ciencia, dijo recientemente:
Si la revisión por pares fuera un fármaco no llegaría al mercado, ya que no tenemos claras sus ventajas pero conocemos muchos efectos adversos.
Otros defienden el método, aceptando sus limitaciones. Tal y como lo ven algunos expertos, estas retractaciones son la muestra de que la comunidad científica cuida constantemente de los resultados que se producen y se autocorrige.
El peer review no acaba cuando se publica un artículo. Implica un primer control sobre los contenidos, que se produce dentro del equipo editorial de una revista, y con el peso específico de dos o tres evaluadores para cada artículo. Naturalmente, no es un proceso exento de errores. Pero allí donde falla el sistema está la propia comunidad académica que detecta fallos, identifica carencias y descubre debilidades.
Por otra parte, no es solo que los ojos de los académicos estén alerta ante lo que se publica. La publicación científica forma parte de un complejo ecosistema, en el que cada vez hay más herramientas y prácticas científicas recomendadas que permiten incrementar las garantías sobre lo que se publica.
Una de ellas, especialmente relevante en estos días, es la vinculación de un artículo a datos abiertos en los que se basa y su cumplimiento de los principios FAIR (Encontrable, Accesible, Interoperable y Reusable, por sus siglas en inglés, que significan “justo”).
Las reacciones de la comunidad editorial
Más allá de los naturales llamamientos por parte de las asociaciones de editoriales para asegurar la calidad y la agilidad en la evaluación de originales, han sido especialmente destacadas las iniciativas colaborativas entre editoriales.
Se ha visto que la solución al problema de contar con artículos de rápida publicación, pasaba por compartir procesos y recursos. También por crear vasos comunicantes entre estructuras que antes no estaban comunicadas, precisamente por cuestiones de mercado, de competencia entre revistas.
Acelerar las revisiones de los artículos y facilitar el intercambio de informes de revisión entre revistas han sido fórmulas para garantizar revisiones rápidas, pero con garantías.
Si ha habido un foco de interés en esta época de pandemia, que además ha marcado un cambio en la comunicación científica, han sido los servidores de prepublicaciones como MedRxiv y BioRxiv.
Con un crecimiento imprevisto e inundados de artículos (5071 medRxiv, 1317 bioRxiv) han tenido que comenzar a filtrar y rechazar de partida algunos artículos que derivaban a revistas científicas para que los trabajos pasaran por los correspondientes procesos de revisión. Eso hizo bioRxiv con los estudios predictivos basados en cálculo computacional. El riesgo de hacer públicas investigaciones no contrastadas puede causar mucho daño.
Al margen de la gestión de los repositorios de prepublicaciones, son destacables las nuevas iniciativas entre editoriales, por cuanto cambian las dinámicas de lo editorial. PreReview es un ejemplo: una plataforma que permite a cualquier investigador identificado mediante su ORCID solicitar la revisión de una prepublicación.
Esa petición será atendida por toda una red de evaluadores que se han comprometido a realizar evaluaciones rápidas, basadas en un cuestionario estructurado y que conducen a decidir si ese texto debe pasar a revisión por expertos, ya en el marco de una revista científica.
Así se crea el vaso comunicante, pues se produce un trasvase de textos desde los servidores de prepublicaciones a las revistas científicas, impulsado por los propios investigadores. Es una iniciativa que trasciende a los sellos editoriales particulares. Se trata de una acción editorial conjunta, infrecuente en un mercado tan competitivo como el de la edición académica.
Merece la pena detenerse en cómo la gobernanza de la ciencia se modifica en parte. Sale un poco del radio de acción de las grandes editoriales académicas y reposa un poco más en las necesidades reales de la comunidad académica, en la acción colectiva editorial, en los principios de la ciencia abierta y, desde luego, en los grupos y entidades que promueven la integridad de la investigación y las nuevas formas de evaluación científica. Todo ello muy relacionado entre sí.
Colaboración, intercambio de datos e IA
La Inteligencia Artificial es una aliada clave en el tratamiento de grandes corpus de textos científicos, en la búsqueda sobre ellos para localizar datos, hallazgos relevantes o asociaciones entre temas. Ha permitido de algún modo ordenar y filtrar entre el maremágnum de literatura científica que se ha producido durante la pandemia.
Un desarrollo anunciado por Nature, scite.ai, permite ver la red de citas que recibe una prepublicación, ya sea para validarla o refutarla. Esto ayuda a discernir entre lo que puede ser valioso y lo que no.
Lo abierto, ya sean textos, datos o citas, es crítico en la comunicación científica actual. Porque textos, datos o citas son bases también del trabajo realizado por los equipos de Semantic Scholar y el Instituto Allen: están compartiendo miles de textos aunados en el corpus CORD-19 (COVID-19 Open Research Dataset). Equipos de IA de todo el mundo desarrollan herramientas para responder a preguntas de la comunidad científica que pueden ser respondidas a partir del análisis de ese inmenso corpus.
Uno de ellos ha sido el grupo Ontology Engineering Group (Universidad Politécnica de Madrid), que ha desarrollado un buscador terminológico para contribuir a esta tarea.
Estas aplicaciones, que han constituido una solución ante la avalancha de publicaciones científicas, hacen pensar de algún modo que la ciencia abierta ha acabado de arraigar con la COVID-19.
Ya no basta, además, con disponer de literatura científica y datos en abierto. Su estructura y su marcado semántico son esenciales para poder analizar y encontrar aquello que la comunidad científica -y la sociedad– quiere encontrar. Muchas grandes editoriales y productores de contenidos de perfil internacional lo tienen claro desde hace tiempo y han afrontado con determinación su transformación digital. De ello depende, por ejemplo que recibamos con puntualidad lo que publican, que lo encontremos fácilmente y bien posicionado en buscadores y que puedan ofrecer contenidos de manera inmediata.
Así ha sucedido durante la pandemia: la comunidad académica ha podido acceder a miles de artículos científicos para su consulta pero también para su tratamiento mediante técnicas de minería de datos.
De la transformación digital de las editoriales seremos beneficiarios todos los académicos, tanto para el acceso a la literatura científica y a los datos, como para su uso con fines de investigación. Pero es necesario considerar un factor crítico, relacionado con el hecho de que la comunicación de la ciencia es multilingüe.
El inglés es necesario para difundir, hacer visibles e intercambiar resultados de investigación con académicos de todo el mundo. Eso está fuera de toda duda. Sin embargo, tanto para la comunicación entre especialistas dentro de un país o de una región, como para la comunicación con la sociedad, las lenguas nacionales y locales son necesarias.
Por ello, además de admirar y valorar las innovaciones que se están produciendo en la comunicación científica, debemos preguntarnos hasta qué punto esas transformaciones pueden darse y proponerse en las estructuras editoriales del conjunto de países de habla hispana.
Apenas ha habido artículos científicos en español sobre la COVID-19 en revistas científicas de España. Esto se relaciona con que los artículos españoles han sido enviados a revistas internacionales. La ciencia producida en español, los nuevos hallazgos y los nuevos datos no se han publicado en revistas científicas nacionales, sino en medios de comunicación generalistas y más especializados, como SINC o The Conversation.
Los ritmos de evaluación, la publicación de números cerrados que no permiten la publicación según finaliza la evaluación, la falta de dinamismo en redes, lo “estático” de las estructuras editoriales y los formatos de los contenidos son algunos de los factores que han influido en esta situación.
Al mismo tiempo cabe preguntarse de qué forma las comunidades académica y editorial españolas participan en las redes internacionales que se organizan para agilizar la evaluación y mejorar la disponibilidad de contenidos científicos rigurosos. ¿Participamos en las infraestructuras y organizaciones internacionales? ¿Qué implica eso para la comunicación científica en español? ¿Debe la comunidad iberoamericana participar más activamente o proponer sistemas cooperativos y colectivos para afrontar el desafío de comunicar la ciencia en español?
Quizá debería haber un mayor compromiso de la comunidad académica por cuidar la comunicación científica en español, como una derivada más de la difusión de su actividad. Pero también debería haber una reflexión colectiva, seguida de acciones, por parte las instituciones de política científica y lingüística para que las estructuras editoriales de nuestros países pudieran afrontar una verdadera transformación digital. Así lograremos que los contenidos científicos en español puedan ser versátiles, valiosos y visibles para la comunidad académica hispanoblante y para nuestras sociedades.
Sobre los autores: Elea Giménez Toledo es científica titular del CSIC y Antonio Lafuente, investigador científico, en el Instituto de Historia, Centro de Ciencias Humanas y Sociales (CCHS – CSIC)
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo La Covid-19 revoluciona el sistema de publicación científica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El sistema de la difusión social de la ciencia: Efecto de las actividades de difusión científica
- El ferrocarril metropolitano ante la COVID-19
- El sistema de la difusión social de la ciencia: Catalizadores del sistema y consideraciones finales
Un paseo por la ciudad
“Caminar es la mejor medicina para el hombre”.
Hipócrates, hace 2400 años.
“El buen paseante sale a pasear cuando le apetece”.
Ramón Juventeny, 2014.
“Andar no es un deporte”.
Frédéric Gros, 2014.
Lo afirmaba Hipócrates hace casi 2500 años, pasear, caminar, deambular, es bueno para la salud. Sabemos que reduce el riesgo y ayuda en el tratamiento y la rehabilitación de las enfermedades no transmisibles. David Boatman menciona la diabetes tipo II, el infarto de miocardio, el derrame cerebral, el cáncer y la obesidad.
 Foto: Tomas Llorente / Pixabay
Foto: Tomas Llorente / PixabayEl caminar se puede cuantificar con el número de pasos por día o por semana. Wattanapisit y Thanamee, de Tailandia, clasifican el tipo de vida según el número de pasos por día: sedentario con menos de 5000 pasos al día; activo bajo, entre 5000 y 7499 pasos al día; algo activo, entre 7500 y 9999; activo, con más de 10000; y muy activo, con más de 12500 pasos al día.
Los autores publican un meta análisis de los beneficios para la salud al caminar 10000 pasos al día o, según la clasificación anterior, de tener un tipo de vida activo. Después de revisar las bases de datos, encuentran 49 artículos, publicados entre 2006 y 2016. Después de su revisión, hay 17 que cumplen los requisitos metodológicas para su inclusión en la revisión.
Con 10000 pasos al día disminuye la circunferencia corporal, el peso, el Índice de Masa Corporal (IMC), y la grasa corporal. También baja la tensión sanguínea y sube la concentración en sangre del colesterol “bueno”. Además, se mantiene la densidad ósea en adultos entre 49 y 64 años.
En conclusión, con 10000 pasos al día, como afirmaba Hipócrates, caminar es bueno para la salud. Y, si parece necesario, podemos mencionar lo escrito por Frédéric Gros cuando aconsejaba que “para ir más despacio no se ha encontrado nada mejor que andar”.
Pero hay que recordar que no siempre que se camina se hace por el ejercicio físico que supone. Por ejemplo, Prabasaj Paul y su grupo, del Centro de Control y Prevención de Enfermedades de Atlanta, han revisado una encuesta nacional de salud de Estados Unidos, de 2010, y encuentran que se camina por obligación, por transporte o por tiempo libre, que sería el paseo sin objetivo. Tienen datos de 24017 voluntarios.
Los resultados indican que por obligación caminan el 29.4% de los voluntarios, y por tiempo libre lo hacen el 50%. Por obligación, lo hacen más los hombres que las mujeres, y por tiempo libre es al contrario, y lo hacen más las mujeres que los hombres. El paseo por obligación, para más del 50% de los voluntarios, dura entre 10 y 15 minutos. En cambio, el 17% del paseo por tiempo libre dura entre 41 y 60 minutos. En los hombres, si pasean por obligación, la duración del paseo es menor si tienen el IMC alto, y, en general, el paseo por tiempo libre crece con la edad y con el IMC bajo.
Un meta análisis publicado en 2017 por Tessa Pollard y Janelle Wagnild, de la Universidad de Durham, en Inglaterra, revisa 33 estudios sobre las diferencias en el paseo según el género. La primera conclusión es que las mujeres pasean más que los hombres. Sobre todo las más jóvenes pasean más que los jóvenes de su edad, pero es una tendencia que se invierte con los años y los hombres de más edad pasean más que las mujeres de su edad.
Después de entrevistar, en 2017, a cinco grupos de mujeres caminantes del nordeste de Inglaterra, con 51 mujeres en total, Stephanie Morris y su grupo, detectan los importancia de estos paseos para los mujeres y, en primer lugar, supone, para ellas, una pausa en su vida cotidiana. Les gusta el ambiente entre las paseantes y, por ello, los valoran muy alto, son espacios de intercambio, de buena salud y disfrute, son un recurso positivo para su vida y, también, de su contacto con el entorno social.
En Estados Unidos, y con una muestra de 3653 voluntarios, con el 52.4% de mujeres, y un rango de edad de 18 a 65 años, según Kathleen Watson y su grupo, del Centro de Control y Prevención de Enfermedades de Atlanta, es que el 43% considera que caminar una milla, o 1609 metros, o hacerlo durante 20 minutos, es razonable.
El ambiente del lugar de paseo anima a caminar, a pasear a gusto, y, como estudiaron Inés Ferreira y sus colegas, de la Universidad de Lund, en Suecia, la emoción y las ganas de caminar las provoca el entorno, la vecindad más cercana, tanto el lugar físico como el contexto social.
Entrevistaron a 110 vecinos de Malmoe, con el 64.5% de mujeres, y edad media de 38 años. Los resultados muestran que las mujeres y los adultos de edad evitan las calles menos seguras, buscan las menos solitarias y las que facilitan el trato con otros paseantes y la sociabilidad entre vecinos. Son los vecinos con el nivel económico más bajo los que más tiempo dedican a pasear.
En conclusión, anima a caminar, en primer lugar, sentirse con seguridad y a gusto en el barrio y, además, el paseo relaja y elimina el estrés y estimula al paseante frente al aburrimiento.
Incluso se ha investigado que caminar juntos ayuda a resolver conflictos pues, según Christine Webb y su grupo, de la Universidad Columbia de Nueva York, implica que los caminantes deben cooperar para hacer el paseo en conjunto. Comparten experiencias sobre lo que hacen y ven en entornos nuevos y, todo ello, ayuda a la conversación y al debate.
Creo que es evidente que caminar no es solo un deporte, es algo más. Carlos García Gual, en 2014, y después de revisar varios libros sobre caminar, termina con que “caminar invita a pensar e imaginar con frescor, temple airoso y libertad”. O sea, lo que el título del texto da García Gual afirma con claridad: “Pasear y pensar”. Jean-Jacques Rousseau lo confirma en su escrito en que nos cuenta que ha descubierto lo que, ahora, consideraríamos una nueva especie, el Homo viator.
Y este Homo viator nos introduce en los paseos del llamado, en francés, flâneur, el que deambula por la ciudad. Es un descubrimiento del París del siglo XIX, y ahora es un término y un concepto habitual en muchos idiomas y culturas. Beatriz Sarlo lo define como “paseante urbano, consumidor, neurasténico y un poco dandy que … sintetiza una idea: la del anonimato en la ciudad moderna y en el mercado”.
Para el flâneur inicial, el del París del XIX, comprar va acompañado de una actividad novedosa: deambular por los espacios comerciales. El flâneur deambula sin un propósito concreto, pasea por la ciudad porque es un concepto adaptado a lo urbano, y lo hace, sobre todo, por las zonas comerciales. En tiempos recientes y para algunos autores, el flâneur ha perdido su deambular y se ha quedado, como mucho, en un consumidor o, más fácil, en un comprador. Tampoco es un turista que pasea por la ciudad con un objetivo concreto: conocerla y, en los últimos tiempos, fotografiarla para demostrar que allí se ha paseado. Lo importante no es comprar o acumular imágenes sino disfrutar de lo que la ciudad ofrece y, así, ver a otros, ser visto y lo habitual debe ser no comprar nada. Es el nuevo pasatiempo de la burguesía para su tiempo libre.
Referencias:
Abad, M. 2014. Caminar como técnica para pensar. Yorokobu Blog 6 octubre.
Boatman, D.C. 2012. Hippocrates: “Walking is man’s best medicine!”. Occupational Medicine 62: 320-324.
Ferreira, I.A. et al. 2016. Transport walking in urban neighbourhoods – Impact of perceived neighbourhood qualities and emotional relationship. Lanscape and Urban Planning 150: 60-69.
García Gual, C. 2014. Pasear y pensar. El País 29 diciembre.
Gros, F. 2014. Andar, una filosofía. Taurus. Barcelona. 248 pp.
Hiernaux-Nicolás, D. 2006. De flâneur a consumidor: reflexiones sobre el transeúnte en los espacios comerciales. En “Pensar y habitar la ciudad: afectividad, memoria y significado”, p 145-156. Ed. por Ramírez-Kuri et al. Anthropos Ed. Barcelona.
Morris, S. et al. 2019. Group walking as a “lifeline”: Understanding the place of outdoor walking groups in women’s lives. Social Science & Medicine 238: 112489.
Paul, P. et al. 2015. Walking for transportation and leisure among U.S. adults – National Health Interview Survey 2010. Journal of Physical Activity and Health 12, Suppl. 1: S62-S69.
Pollard, T.M. & J.M. Wagnild. 2017. Gender differences in walking (for leisure, transport and in total) across adult life: a systematic review. BMC Public Health 17: 34.
Quijano, E. 2018. El flâneur bogotano contemporáneo: reflexiones sobre el deambular en los espacios comerciales de Bogotá. Cuadernos de Vivienda y Urbanismo doi: 10.11144/Javeriana.cvu11-22.fbcr
Sarlo, B. 2000. Siete ensayos sobre Walter Benjamin. Fondo de Cultura Económica. México. 108 pp.
Walson, K.B. et al. 2015. Walking for transportation: What do U.S. adults think is a reasonable distance and time? Journal of Physyical Activity and Health 12, Suppl. 1: S53-S61.
Wattanapisit, A. & S. Thanamee. 2017. Evidence behind 1.000 steps walking. Journal of Health Research 31: 241-248.
Webb, C.E. et al. 2017. Stepping forward together: Could walking facilitate interpersonal conflicto resolution? American Psychologist 72: 374-385.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Un paseo por la ciudad se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:María Martinón-Torres – P4K 2019: Homo sapiens y la sombra del ciprés
 Imagen: Rudy & Peter Skitterians / Pixabay
Imagen: Rudy & Peter Skitterians / PixabayLa consciencia de su vulnerabilidad es una de esas cosas que hacen a los humanos, humanos. María Martinón- Torres, doctora en medicina, paleoantropóloga y directora del Centro Nacional de Investigación sobre la Evolución Humana (CENIEH) expone en esta estupenda charla cuando aparece esa consciencia y si esto supone alguna ventaja.
La conferencia se impartió dentro del marco del festival Passion for Knowledge 2019 (P4K) organizado por el Donostia International Physics Center (DIPC).
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo María Martinón-Torres – P4K 2019: Homo sapiens y la sombra del ciprés se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ambrosio Liceaga – Naukas P4K 2019: Nunca quisimos coches voladores
- Neandertales ¿crónica de una muerte anunciada?, por María Martinón-Torres
- Naukas Bilbao 2017 – Aberrón entrevista a María Martinón y a José Mª Bermúdez de Castro
Un estudio paleoceanográfico apunta a que los ciclos naturales de cambio climático están siendo alterados
Un estudio paleoceanográfico de la UPV/EHU ofrece una descripción detallada de los cambios climáticos ocurridos en el golfo de Bizkaia en los últimos 37.000 años y apunta a que se está alterando el ciclo natural.
 Gofo de Vizcaya. Foto: Envisat / ESA
Gofo de Vizcaya. Foto: Envisat / ESAEl clima representa el conjunto de condiciones atmosféricas que caracterizan una región. Esas condiciones, no obstante, son consecuencia de una interacción global entre la tierra emergida, la vegetación, el hielo, la atmósfera y el océano. “Teniendo en cuenta que los océanos ocupan el 75 % de la superficie terrestre, la influencia que estos tienen sobre el clima es muy fuerte, y viceversa, los cambios en el clima influyen fuertemente en los océanos. En nuestro grupo nos dedicamos al estudio de la paleoceanografía, donde buscamos y analizamos las evidencias de cómo ha cambiado el océano en los diferentes periodos o intervalos climáticos. Nuestro estudio se centra en el golfo de Bizkaia, que es el trozo de océano que tenemos delante de nuestras costas”, describe Julio Rodríguez Lázaro, catedrático del Departamento de Estratigrafía y Paleontología de la Facultad de Ciencia y Tecnología de la UPV/EHU, y uno de los autores del estudio.
Un trabajo de este grupo ha detallado con gran precisión muchos de los eventos climáticos que han sucedido en los últimos 37.000 años. Para ello, los investigadores han recurrido al estudio de los microfósiles de 176 especies de foraminíferos bénticos, obtenidos de sondeos del fondo oceánico. Los foraminíferos estudiados son unos pequeños seres marinos (de una sola célula, pero muy grande), caracterizados por una concha de carbonato, del tamaño de granos de arena, muy utilizados en paleoceanografía, porque dependiendo de las especies que abundan en una época geológica u otra, “conocemos las condiciones que se daban en ese lugar y en ese periodo concreto. Este análisis faunístico es posible porque muchas de las especies de foraminíferos son muy sensibles a los parámetros medioambientales básicos, como la temperatura, la concentración de oxígeno o el contenido de materia orgánica”, relata el investigador.
Así, han podido identificar en el sedimento del golfo de Bizkaia analizado, evidencias de los episodios climáticos conocidos, tanto los periodos fríos, como el Younger Dryas, o eventos Heinrich, como los intervalos cálidos, Bolling-Allerod, o el Holoceno, sucedidos a lo largo de la historia geológica reciente, que comprende los últimos milenios. Además, consideran la identificación de las 176 especies de foraminíferos bentónicos descritas como “una contribución al conocimiento de la biodiversidad existente en el golfo de Bizkaia durante el periodo Cuaternario”.
Este estudio se enmarca en un proyecto cuyo objetivo es la detección de los cambios climáticos habidos en el golfo de Bizkaia en los últimos 150.000 años. Rodríguez lo resume de la siguiente manera: “El clima del planeta en este periodo de tiempo se caracteriza por la alternancia brusca de periodos cálidos y fríos, y estos cambios climáticos parecen haber ocurrido cada 1.500 años, aproximadamente. El calentamiento (hasta 10 °C) se produce en pocas décadas, mientras que el enfriamiento ocurre a lo largo de varios siglos. Cuando ocurre un enfriamiento, la consecuencia es que el agua del océano Atlántico norte se enfría a la vez que ocurre una descarga masiva de icebergs procedentes de la fragmentación de las capas de hielo en el Océano Ártico, y esto conlleva un periodo climático frío en el hemisferio norte”.
Estos cambios climáticos rápidos son producidos por alteraciones de la llamada AMOC (Atlantic Meridional Overturnig Circulation) que es el transporte de calor que se da desde el Atlántico sur hacia el norte a través de los movimientos de las masas de agua oceánicas, donde las aguas cálidas tropicales, menos densas, se mueven hacia el norte, mientras que las frías y densas aguas del Atlántico norte se dirigen en profundidad hacia el sur. Estos movimientos de agua modifican en su tránsito no solo el clima de Europa (templándolo), sino del conjunto del planeta. La AMOC se altera cuando hay entrada de aguas poco salinas en el Ártico, por el deshielo del permafrost, así como por cambios del espesor del hielo en estas latitudes árticas.
El momento geológico que estamos viviendo ahora es una época interglaciar “o cálida” (Holoceno), y “si fuéramos al ritmo que ha transcurrido en los intervalos de frío y calor anteriores, deberíamos estar yendo hacia un enfriamiento, pero esto no está ocurriendo —advierte Rodríguez—. Debido a la actividad humana, estamos alterando ese ciclo, estamos modificando el equilibrio natural. Y esto podría tener consecuencias graves en los siguientes ciclos climáticos de un futuro próximo”.
Referencia:
Ana Pascual, Julio Rodríguez-Lázaro, Blanca Martínez-García, Zeltia Varela (2020) Palaeoceanographic and palaeoclimatic changes during the last 37,000 years detected in the SE Bay of Biscay based on benthic foraminifera. Quaternary International doi: 10.1016/j.quaint.2020.03.043
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Un estudio paleoceanográfico apunta a que los ciclos naturales de cambio climático están siendo alterados se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Verdín, eucaliptos y cambio climático
- Los ecosistemas acuáticos de África y el cambio climático
- Geología, Antropoceno y cambio climático
Gustave Bémont, el fantasma de la rue Vauquelin
 Foto: Erik Müller / Unsplash
Foto: Erik Müller / UnsplashEn 1911 el comité Nobel concedía el premio de química a Marie Curie “como reconocimiento a sus servicios en el avance de la química por el descubrimiento de los elementos radio y polonio, por el aislamiento del radio y el estudio de la naturaleza y compuestos de este elemento extraordinario.”
Que Marie Curie merecía el premio nadie lo discute, ni lo haremos nosotros en lo que sigue. Ahora bien, también es cierto, que nada de lo relacionado con el descubrimiento del polonio y el radio hubiese sido posible sin los conocimientos químicos de Gustave Bémont. Es nuestro objetivo en este breve texto exponer algo de la química del descubrimiento, la mejor forma, creemos, de comprender la verdadera dimensión de las aportaciones de Gustave Bémont. Por otra parte quizás también sería interesante desmitificar la imagen del trabajo aislado de la pareja Curie en sus primeros años de colaboración, por lo que mencionaremos a todo aquel que nos conste que ayudó de alguna manera relevante (que fueron, mire usted, mayoritariamente químicos).
 El fantasma, Pierre y Marie Curie en el laboratorio de rue Vauquelin / Foto tal cual aparece en Wikimedia Commons
El fantasma, Pierre y Marie Curie en el laboratorio de rue Vauquelin / Foto tal cual aparece en Wikimedia CommonsUn tema para la tesis
La anécdota de la vida de Marie Curie es tan conocida que no abundaremos en ella. Baste decir que Marie Curie obtuvo su segunda licenciatura (en matemáticas) en 1894, tras haber obtenido la de física en 1893 y haber comenzado a trabajar bajo la supervisión de Gabriel Lippmann (quien a la postre sería su director de tesis y su primera conexión con la Academia de Ciencias; curiosamente obtendría el Nobel en 1908, después de que su pupila lo consiguiese en 1903). En 1895 se casó con Pierre Curie, un físico conocido por sus estudios en magnetismo y simetría cristalina que, junto a su hermano Jacques, había descubierto el efecto piezoeléctrico en 1882. Pierre era en ese momento profesor en la Escuela Municipal de Física y Química Industriales (EMFQI), sita en el número 10 de la rue Vauquelin de la ciudad de París.
El descubrimiento de la radioactividad por parte de Becquerel había planteado un problema desconcertante: las sales de uranio mantenían en el tiempo, sin una fuente de energía externa, la capacidad de ennegrecer una placa fotográfica. Marie, que buscaba tema para su tesis decidió investigar el fenómeno.
El 11 de febrero de 1898 Marie comienza una búsqueda sistemática de elementos y compuestos con la capacidad de conferir conductividad eléctrica al aire (lo que hoy llamaríamos elementos y compuestos radioactivos). Comprobó, usando para ello una antigua leñera, luego sala de usos múltiples (vulgo, trastero), anexa a las instalaciones de la EMFQI, todas las muestras de que disponía en la escuela más las que pidió prestadas a distintos laboratorios de la ciudad. La lista de materiales analizados es bastante extensa y puede ser agrupada en tres grandes grupos:
1) Metales y metaloides disponibles habitualmente (de la colección mantenida por el profesor Etard, EMFQI)
2) Sustancias raras: galio, germanio, neodimio, praseodimio, niobio, escandio, gadolinio, erbio, samario y rubidio (proporcionadas por Demarçay); itrio, iterbio junto con un “nuevo erbio” (proporcionadas por Urbain)
3) Rocas y minerales (colección de la EMFQI)
Los resultados obtenidos fueron lo suficientemente interesantes como para que el profesor Lippmann presentase una nota de Marie (ella sola, sin Pierre como coautor) a la Academia de Ciencias y para que Pierre abandonase sus propias investigaciones cristalográficas para dedicarse de lleno al nuevo fenómeno.
El uranio y algo más
Marie descubrió que todos los minerales que eran activos contenían o bien uranio o bien torio (esto último lo había descubierto independientemente dos meses antes Gerhard Schmidt; en esta época de efervescencia los descubrimientos se atribuían por diferencias de meses, si no semanas, como bien supo un hoy olvidado Silvanus Thompson que descubrió la “hiperfosforescencia” del nitrato de uranio en febrero de 1896, exactamente a la vez que Becquerel, pero éste lo comunicó públicamente antes. De ahí la prisa de Marie y Lippmann por comunicar resultados parciales).
Pero el resultado más importante de Marie fue que la pechblenda, una variedad de uraninita (UO2), era (es) cerca de cuatro veces más activa que el uranio metálico, que la chalcolita (hoy metatorbernita), Cu(UO2)2(PO4)2·8 H2O, lo era alrededor de dos veces y que la autunita, Ca(UO2)2(PO4)2·12H2O, aunque menos marcado que los anteriores, también presentaba una actividad anómala. Tras sintetizar chalcolita en el laboratorio a partir de sus constituyentes puros, Marie comprobó que en la chalcolita sintética la actividad era proporcional al contenido de uranio. Esto la llevó a una conclusión que aparece en la nota a la Academia en una frase clave: “Este hecho es muy notable y sugiere que estos minerales podrían contener un elemento mucho más activo que el mismo uranio”.
De la física a la química
El matrimonio Curie se enfrentaba ahora a la necesidad de investigar la pechblenda. Si bien podía usar el dispositivo inventado por Pierre para medir la actividad de los compuestos y guiar el trabajo, los conocimientos necesarios de química sobrepasaban de manera notable los que la pareja pudiese tener.
Afortunadamente estaban en el lugar ideal para encontrar la ayuda que necesitaban. Como centro de formación en química industrial la EMFQI contaba con grandes especialistas en el tratamiento de minerales. Pierre recurrió al mejor: Gustave Bémont, el chef de travaux de chimie , el responsable de las prácticas de química en la Escuela. Él, tras muchas pruebas, terminó diseñando para ellos la siguiente marcha analítica (que es la que aparece en la nota de Pierre y Marie, no Bémont, que Becquerel presentó a la Academia con el descubrimiento del polonio):
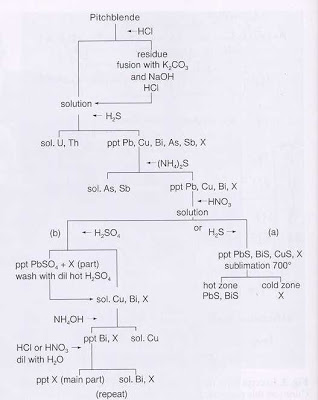 Marcha analítica para el polonio. Véase el texto para una explicación / Tomado de Adloof & McCordick «The Dawn of radiochemistry» (1995) Radiochimica Acta 70/71, 13-22
Marcha analítica para el polonio. Véase el texto para una explicación / Tomado de Adloof & McCordick «The Dawn of radiochemistry» (1995) Radiochimica Acta 70/71, 13-22
El tratamiento de los primeros 100 g de pechblenda comenzó el 14 de abril de 1898. Lo que sigue da una idea de la pericia analítica necesaria para llevarlo a cabo.
La muestra se molió y fue tratada con HCl. Los residuos insolubles aún eran muy activos, por lo que tras fundirlos con una mezcla de carbonato potásico e hidróxido sódico se solubilizaron con ácidos.
El tratamiento de la disolución ácida con H2S fue un paso muy importante, digno de una gran experiencia química, ya que los sulfuros precipitados eran más activos que el resto de la disolución residual. La actividad en los sulfuros era insoluble en sulfuro de amonio, por lo que pudo separarse de As y Sb. El resto de sulfuros insolubles se disolvieron con nítrico tras la adición de sulfúrico y parte de la actividad acompañaba al sulfato de plomo. Finalmente se encontró la actividad mayoritariamente concentrada en la última fracción, que contenía “sólo” bismuto y plomo.
Separar la sustancia activa del bismuto y el plomo por métodos húmedos resultó tremendamente laborioso. Esta frase tan sencilla nos debe dar una idea de la inmensidad del trabajo llevado a cabo: cada ensayo significaba tratar una muestra no pequeña del residuo al que se llega tras todos los pasos anteriores. Finalmente encontraron que la precipitación fraccionada repetida podía ser una vía, angustiosamente lenta, pero segura. Al añadir agua a una disolución ácida del residuo las fracciones que precipitaban antes eran las que portaban la mayor parte de la actividad. De esta forma el 6 de junio tenían un sólido 150 veces más radioactivo que el uranio.
Mientras tanto Pierre probaba cosas nuevas, a ver si alguna podía ser útil. El mismo 6 de junio se le ocurrió calentar el residuo en un tubo de vacío a varios cientos de grados: los sulfuros de bismuto y plomo se quedaron en la parte caliente del tubo, mientras que en la parte fría (entre 250 y 300ºC) condensaba una capa negra con la actividad. Ese día el equipo consiguió una muestra 330 veces más activa que el uranio. Tras reiterar el proceso, purificando la muestra, consiguieron llegar a 400 veces.
La nota presentada por Becquerel, y firmada por Pierre y Marie (no por Bémont, reiteramos) termina diciendo: “Creemos que la sustancia que hemos recuperado de la pechblenda contiene un hasta ahora metal desconocido, similar al bismuto en sus propiedades analíticas. Si la existencia de este nuevo metal se confirma proponemos que se le llame polonio en honor de la tierra natal de uno de nosotros”.
Por primera vez en la historia se anunciaba el descubrimiento de un elemento sin aislarlo y sin medir sus propiedades físicas. Demarçay, renombrado espectroscopista, fue incapaz de detectarlo, lo que no es de extrañar habida cuenta de la bajísima concentración en la muestra (del orden de nanogramos). Hubo que esperar al tratamiento de varias toneladas de pechblenda en 1910 (cosa que hicieron Marie y André Debierne; ese mismo año Debierne, descubridor del europio, ayudó a Marie a obtener el radio metálico) para obtener una muestra de 2 mg de producto que contendría aproximadamente 0,1 mg de polonio.
 Gustave Bémont, Pierre y Marie Curie en el laboratorio de rue Vauquelin
Gustave Bémont, Pierre y Marie Curie en el laboratorio de rue VauquelinEl equipo siguió trabajando en lo que después sería el descubrimiento del radio a finales de año. En esta ocasión la nota a la Academia sí aparece firmada por los Curie y Bémont, como era de justicia. Sin embargo, la historia ha querido que Gustave Bémont (1857-1937), que podría haber justamente compartido el Nobel de química con Marie, quedase reducido a una mención en una placa en el 10 de la rue Vauquelin que casi nadie termina de leer.
 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsSobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto se publicó originalmente el 12 de junio de 2013 y reeditado el 12 de febrero de 2018 en el blog personal del autor.
La historia de la radiactividad es el hilo conductor que permite introducirse fácilmente a los conceptos científicos básicos sobre la estructura nuclear en la serie El núcleo.
El artículo Gustave Bémont, el fantasma de la rue Vauquelin se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Las emocionantes aventuras de Lovelace y Babbage
Las emocionantes aventuras de Lovelace y Babbage (UOC, 2016) es una novela gráfica de Sydney Padua en la que se entremezclan texto e imagen, historia y ficción, ciencia y arte.
 Portada del libro.
Portada del libro.La autora comenzó a escribir las hazañas de Ada Lovelace y Charles Babbage en 2009, en formato webcómic, bajo el título de The Thrilling Adventures of Lovelace and Babbage. En 2015 recopiló esas ‘emocionantes aventuras’ en este divertido e informativo libro en el que puede encontrarse una pequeña crónica de la historia de la Inglaterra victoriana, un libro de aventuras que van más allá de lo real, una biografía de la matemática Ada Lovelace (1815-1852) y del ingeniero Charles Babbage (1791-1871), un repaso de algunas de las matemáticas que se hacían en ese momento en Inglaterra y, por supuesto, un bello libro ilustrado.
Cada página del libro consta de algunas viñetas que hablan sobre los esfuerzos de la matemática y el ingeniero para construir y hacer funcionar esa soñada Máquina Analítica y que se complementan con extensos y muy documentados pies de página que introducen la historia real de esa empresa científica. En estas ‘emocionantes aventuras’ se combinan las imágenes y el texto, la fantasía y la realidad, el humor y la precisión histórica.
El libro está dividido en diez capítulos, dos apéndices y un epílogo. En todos ellos la Máquina Analítica es el centro de la acción de una u otra manera:
-
Ada Lovelace: ¡El origen secreto!
La autora presenta a Ada, el motivo por el que su madre –la aristócrata Annabella Milbanke (1792-1860)– optó por incluir las matemáticas en la educación de su hija, cómo conoció a Charles Babbage, y cómo trabajaron juntos hasta su triste final. Esta parte del tebeo va acompañada de numerosas notas sobre las personas que rodearon a Ada Lovelace y Charles Babbage.
-
El Universo de bolsillo
De este modo denomina la autora las páginas de su libro, un mundo de dimensión dos en el que todo funciona de una manera un poco diferente a la del mundo real. En ese universo plano, es posible mezclar historias sucedidas en diferentes momentos; aunque «algo de la información real debe de conservarse sin renunciar al entretenimiento».
-
La persona de Porlock
La autora se permite una licencia poética: ¿quizás fue Ada la persona –el visitante de Porlock– que interrumpió al poeta Samuel Taylor Coleridge (1772-1834) mientras redactaba su conocido poema Kubla Khan? Recordemos que, según el prefacio de Coleridge, concibió el poema durante un sueño, bajo la influencia del opio y tras haber leído una biografía del último Gran Kan del Imperio mongol Kublai Khan. Al despertar, comenzó a transcribir los 300 versos soñados hasta que fue interrumpido por un visitante procedente de Porlock. Cuando esa persona se marchó, el poeta solo consiguió escribir unos pocos versos más, olvidando el resto.
-
¡Lovelace y Babbage contra la clienta!
La clienta es la Reina Victoria (1819-1901), que financiaba el trabajo de Babbage.
-
Fuentes principales
En este corto capítulo se habla de los diarios de la Reina Victoria.
 Ada Lovelace y Charles Babbage se conocen. Imagen: Sydney Padua (Licencia CC BY-NC).
Ada Lovelace y Charles Babbage se conocen. Imagen: Sydney Padua (Licencia CC BY-NC).
-
¡Lovelace y Babbage contra el modelo económico!
La autora habla de inventos, de modelos económicos y de la afición de Ada por las carreras de caballos –a finales de la década de 1840, Ada se volvió adicta a las carreras de caballos. Intentó crear un modelo matemático para ganar las apuestas en esas carreras. El evidente fracaso de ese proyecto generó cuantiosas deudas a la aristócrata–.
-
¡Luditas!
Los luditas eran los componentes de un movimiento de artesanos que protestaron contra los telares industriales que amenazaban sus empleos. La soñada máquina de Babbage se basaba precisamente en el sistema de tarjetas perforadas de los telares de Jacquard.
-
¡Experiencia de usuario!
Aparece en la historia la escritora George Eliot (1819-1880) como usuaria de la ‘Gran Máquina’ correctora de errores ortográficos.
-
El Sr. Boole viene a tomar el té
El lógico George Boole (1815-1864) entra en la historia en el momento en el que se comienza a hablar de la programación de la Máquina Analítica.
-
Cantidades imaginarias
Los números imaginarios y los cuaterniones –y la poesía– se introducen en la historia a través del matemático y astrónomo William Rowan Hamilton (1805-1865). En el ‘Universo de Bolsillo’, al mezclar las matemáticas con la poesía, Ada atraviesa un espejo para entrar en la dimensión tres –una más que la de su mundo plano, por analogía con el mundo de cuatro dimensiones respecto al universo real–. Allí vive aventuras como una Alicia en el País de las maravillas. La autora comenta cómo diferentes biógrafos alaban el intelecto de Ada, mientras que otros afirman que sus contribuciones no fueron tan importantes. Las cartas de Babbage no dejan lugar a dudas –al menos para Sydney Padua– de lo buena matemática que era Ada Lovelace. El ingeniero llega en un corcel mecánico al País de las maravillas para hacer regresar a Ada a su universo de dimensión dos. El capítulo finaliza con una inesperada visita del lógico y escritor Lewis Carroll (1832-1898), autor de Alicia en el País de las maravillas.
-
Apéndice I: Algunos documentos originales entretenidos
Sydney Padua reproduce cartas, artículos y otros documentos hablando de Babbage, de su máquina, de Ada Lovelace, etc.
-
Apéndice II. La Máquina Analítica
La autora describe y dibuja esa ansiada máquina que Babbage nunca llegó a construir.
-
Epílogo
Ada y Babbage caminan juntos, conversando, entre los gigantescos engranajes de la ‘Gran Máquina’.
 Ada Lovelace. Imagen: Sydney Padua (uso libre).
Ada Lovelace. Imagen: Sydney Padua (uso libre).En el ‘Universo de Bolsillo’ –la parte de aventuras de esta historia sobre Ada Lovelace y Charles Babbage– se describen diversas máquinas de la época, algunas de las matemáticas relacionadas con Ada y todos los tutores que la acompañaron –como Mary Somerville (1780-1872) o Augustus de Morgan (1806-1871)–.
Las notas que acompañan al tebeo son una pequeña pero minuciosa recopilación de la historia –y la historia de la ciencia– que sucedía alrededor de los dos protagonistas del libro. Todos los personajes que aparecen convivieron realmente con Lovelace y Babbage, aunque en el ‘Universo de Bolsillo’ se hable de ellos con un poco de humor y grandes dosis de imaginación.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Las emocionantes aventuras de Lovelace y Babbage se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Polonio y radio
 Exterior del «laboratorio» de los Curie en la antigua leñera de la Escuela Municipal de Física y Química Industriales de París en 1898. Fuente: Musée Curie ; coll. ACJC / Cote MCP991
Exterior del «laboratorio» de los Curie en la antigua leñera de la Escuela Municipal de Física y Química Industriales de París en 1898. Fuente: Musée Curie ; coll. ACJC / Cote MCP991Para explorar la hipótesis de que tenía que existir otro elemento en la pechblenda, desconocido, que tenía que ser más radiactivo que el uranio mismo, los Curie aplicaron procesos de separación química [1] a una gran cantidad de pechblenda para tratar de aislar esta hipotética sustancia radiactiva. Después de cada proceso de separación, se comprobaban los productos, descartándose la parte inactiva y analizando de nuevo la parte activa. Finalmente, los Curie obtuvieron un producto altamente radiactivo que era de suponer que consistía principalmente en el elemento desconocido. En una comunicación titulada «Sobre una nueva sustancia radiactiva contenida en la pechblenda» que presentaron a la Academia de Ciencias de Francia en julio de 1898, decían:
Al llevar a cabo estas diferentes operaciones […] finalmente obtuvimos una sustancia cuya actividad es aproximadamente 400 veces mayor que la del uranio. […] Creemos, por lo tanto, que la sustancia que extrajimos de la pechblenda contiene un metal hasta ahora desconocido, similar al bismuto en su propiedades químicas. Si se confirma la existencia de este nuevo metal, proponemos llamarlo polonio, por del nombre del país natal de uno de nosotros.
Seis meses después del descubrimiento del polonio, los Curie separaron químicamente otra sustancia de la pechblenda. Habían encontrado una emisión tan intensa que solo podía explicarse si si existía otro elemento nuevo, más radiactivo aún que el propio polonio. Esta sustancia tenía una actividad por unidad de masa novecientas veces mayor que la del uranio y era químicamente completamente diferente del uranio, del torio y del polonio.
El análisis espectroscópico de esta sustancia mostraba líneas espectrales características del elemento inactivo bario, pero también una línea en la región ultravioleta que no parecía pertenecer a ningún elemento conocido. Los Curie informaron de su creencia de que la sustancia, «aunque en su mayor parte consiste en bario, contiene además un nuevo elemento que produce radiactividad y, además, está muy cerca del bario en sus propiedades químicas». Para este nuevo elemento, tan extraordinariamente radiactivo, propusieron el nombre de radio.
Pero una cosa es predicar y otra dar trigo. Así que el siguiente paso para demostrar la existencia de estos elementos era determinar sus propiedades, especialmente sus masas atómicas. Los Curie aún no habían aislado ni el polonio ni el radio en forma metálica pura, ni habían obtenido una muestra pura de un compuesto de ninguno de los elementos.
De la sustancia que contenía eso fuertemente radiactivo que llamaban radio habían separado una parte que consistía en cloruro de bario mezclado con una cantidad muy pequeña de lo que debía ser cloruro de radio. Separaciones adicionales por medios químicos produjeron una proporción creciente de cloruro de radio. La dificultad de esta tarea está indicada por la observación de Curie de que el radio «está muy cerca del bario en sus propiedades químicas», ya que es muy difícil separar elementos cuyas propiedades químicas son similares [1].
Para obtener las sustancias altamente radiactivas en cantidades utilizables, tuvieron que comenzar con una gran cantidad de pechblenda. Con un envío inicial de 100 kg de pechblenda [2] los Curie se pusieron a trabajar en una leñera abandonada en la Escuela Municipal de Física y Química Industriales, donde Pierre Curie era profesor. Habiendo fracasado en su intento de obtener apoyo financiero, los Curie hicieron sus preparativos sin ayuda manual [1] de otras personas en este «laboratorio». Marie Curie escribiría más tarde:
Llegué a tratar hasta veinte kilogramos de material a la vez, lo que tuvo el efecto de llenar el cobertizo con grandes frascos llenos de precipitados y líquidos. Fue un trabajo agotador transportar los recipientes, verter los líquidos y remover, durante horas seguidas, el material hirviendo en un recipiente de fundición.
A partir de la mezcla de cloruro de radio y cloruro de bario que consiguieron producir produjeron, solo se pudo calcular la masa atómica promedio del bario y el radio. Al principio se obtuvo un valor promedio de 146 unidades de masa atómica [3], en comparación con 137 u para la masa atómica del bario. Después de muchas purificaciones adicionales que aumentaron la proporción de cloruro de radio, el valor promedio de la masa atómica aumentó a 174 u.
No era suficiente. El tedioso proceso de purificación duró 4 años más, durante los que Marie trato varias toneladas de ganga de pechblenda. Finalmente Marie Curie pudo informar, en julio de 1902, que había aislado 0,1 g [4] de cloruro de radio, tan puro que el examen espectroscópico no mostró presencia de bario. Marie calculó que la masa atómica del radio era 225 u. La actividad del radio es más de un millón de veces mayor que la de la misma masa de uranio.
Notas:
[1] Pierre Curie era físico, Marie se acababa de graduar en física y matemáticas. Es sabido que los físicos y matemáticos no saben química, por definición, y encontrar alguno que sepa está considerado milagro mayor de san Alberto el magno. ¿Cómo es posible que los Curie desarrollaran todo un complejísimo sistema químico de separación química de un mineral de la noche a la mañana? Solo hay una explicación: les ayudaron fantasmas.
[2] En puridad habría que hablar de ganga de pechblenda, que es lo que queda después de extraer de ella la mena, es decir, el óxido de uranio que se empleaba para producir vidrio de uranio.
[3] La unidad de masa atómica hoy es la doceava parte de la masa un átomo neutro en reposo de carbono-12. Su símbolo es u, y hay quien la llama Dalton, y la simboliza Da. De lo anterior se deduce que su uso es tolerado por el Bureau international des poids et mesures por tratarse de un submúltiplo de una unidad del sistema internacional de unidades, el kilogramo.
[4] No te engaña la vista ni es un error. Tras tratar toneladas de mineral obtuvo una décima de gramo.
[5] El valor hoy día es está establecido en 226,03 u para la mezcla natural de isótopos de radio.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Polonio y radio se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Los riesgos de la exploración espacial
David Barrado Navascués
 Fuente: TELOS
Fuente: TELOS
El 4 de octubre de 1957 la extinta Unión Soviética lanzó el Sputnik-1, el primer satélite que orbitó alrededor de nuestro planeta. Los primeros sobrevuelos de los planetas Venus y Marte se realizaron en 1962 y 1964 (por las sondas Mariner 2 y Mariner 4), mientras que los primeros aterrizajes sobre estos planetas se produjeron en 1966 y 1971 (las naves Venera 3 y Mars 2, aunque ambas se estrellaron contra la superficie).
En el caso de la Luna, prácticamente carente de atmósfera, el primer aterrizaje de un objeto se produjo en 1959 (el ingenio Luna 2), mientras que un humano holló su superficie en 1969. Otros misiones posteriores han llegado a todos los planetas del Sistema Solar e incluso el módulo Huygens, transportado por la sonda Cassini, se posó en Titán, un satélite de Saturno con mares de hidrocarburos, en 2005.
Por otra parte, los cometas 9P/Tempel 1 y 67P/Churyumov-Gerasimenko han experimentado bien un impacto (por la sonda Deep Impact) o un aterrizaje (Rosetta/Philae). Estas misiones, y otras posteriores, han implicado ciertos riesgos por contaminación biológica. No son los únicos peligros que aparecen en la epopeya de la exploración espacial.
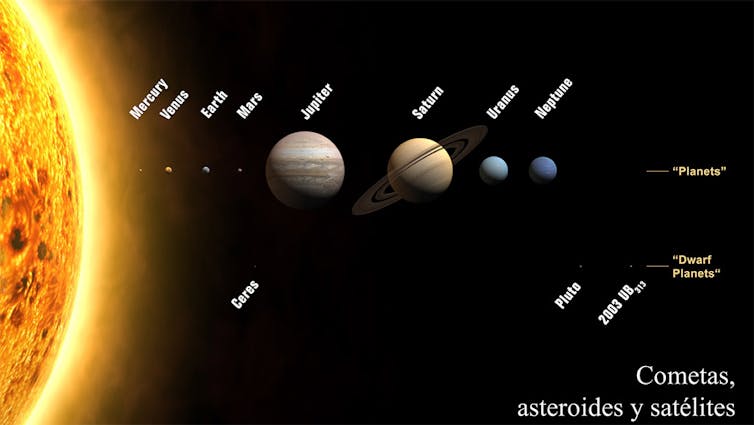 Planetas, planetas enanos y otros cuerpos del Sistema Solar. Fuente: Unión Astronómica Internacional.
Planetas, planetas enanos y otros cuerpos del Sistema Solar. Fuente: Unión Astronómica Internacional.El Planeta Rojo: el hermanastro de la Tierra
De todos los planetas del Sistema Solar, a pesar de ser considerablemente menor a la Tierra, el que posiblemente es más parecido desde el punto de vista astrobiológico es Marte. Por ello ha recibido una atención especial por parte de diversas agencias espaciales.
Entre los aterrizajes con éxito sobre su superficie se encuentran los de las sondas Mars 3 y 6 (1971 y 1973), Viking 1 y 2 (1976), Polar Lander y Deep Space 2 (1999), Phenix (2008), Schiaparelli (2016, un fallo) e Insight (2018), junto con los vehículos Sojouner (1997), Opportunity y Spirit (2004), y Curiosity (2018). En los próximos cuatro años al menos otras cinco misiones serán lanzadas y, de tener éxito, depositarán sobre la superficie de Marte artefactos humanos.
Aunque desde hace décadas existen protocolos para la esterilización de las naves espaciales, la posibilidad de contaminar biológicamente el planeta, lo que podría implicar la posibilidad de eliminar cualquier evidencia de actividad biológica autóctona, no se puede ignorar, como mostró el episodio de contaminación con la cámara de la sonda Surveyor 3, traída por la tripulación del Apollo 12 tras más de dos años sobre la superficie lunar.
Afortunadamente, modernas técnicas han conseguido minimizar esa posibilidad. La organización gubernamental norteamericana National Academies of Sciences, Ingineering and Medicine está llevando a cabo un análisis de múltiples aspectos de la exploración planetaria, incluyendo la perspectiva astrobiológica. La Agencia Espacial Europea (ESA) tiene protocolos análogos.
Las visitas a cometas y asteroides
Dos cometas y un asteoride han sido visitados por naves espaciales: 81P/Wild en 2004 por Stardust, 67P/Churyumov–Gerasimenko en 2014 por Rosetta y 25143 Itokawa en 2005 por Hayabusa. En el primer y último caso ambas naves enviaron muestras a la Tierra que llegaron en 2006 y 2010. La sonda Philae, a bordo de Rosetta, y Hayabusa aterrizaron en sus objetivos, mientras la Stardust tomó muestras del entorno del cometa. Hayabusa 2, que está investigando el asteroide 162173 Ryugu, tiene previsto devolver a la Tierra una muestra tomada de su superficie a finales de 2020.
Como revelaron los resultados de Stardust, los cometas contienen material orgánico, como glicina, un aminoácido esencial para la vida en la Tierra. En los tres casos se implementaron protocolos muy estrictos para evitar contaminación tanto de material terrestre como la posibilidad de traer algún improbable patógeno extraterrestre.
El regreso de muestras de otros cuerpos celestes es especialmente problemático porque el reingreso en la atmósfera terrestre, aterrizaje y recuperación pueden implicar una pérdida de control (desde un reentrada no controlada hasta un pérdida de la estanqueidad del contenedor que aloje la muestra), y por tanto entrañan un riesgo significativo.
Un importante factor a tener en cuenta es el experimento realizado a bordo de la sonda Fotón M3 por parte de las agencias espaciales rusa y europea en 2007. En esa ocasión, se expuso una muestra de tardígrados a las condiciones extremas del entorno espacial. Estos pequeños animales invertebrados, de unos 500 micras de tamaño de medio, sobrevivieron durante diez días a la exposición al vacío y a la intensa radiación ultravioleta del Sol.
Obviamente, los tardígrados son animales que han evolucionado a través de una larga cadena en la Tierra, en ecosistemas mucho más complejos que las situaciones presentes en asteroides y cometas, pero el experimento pone claramente de manifiesto que diferentes seres vivos poseen recursos para resistir incluso las condiciones más adversas. Ese también es el caso de los extremófilos, capaces de vivir y medrar en ambientes verdaderamente hostiles para la inmensa mayoría de seres vivos.
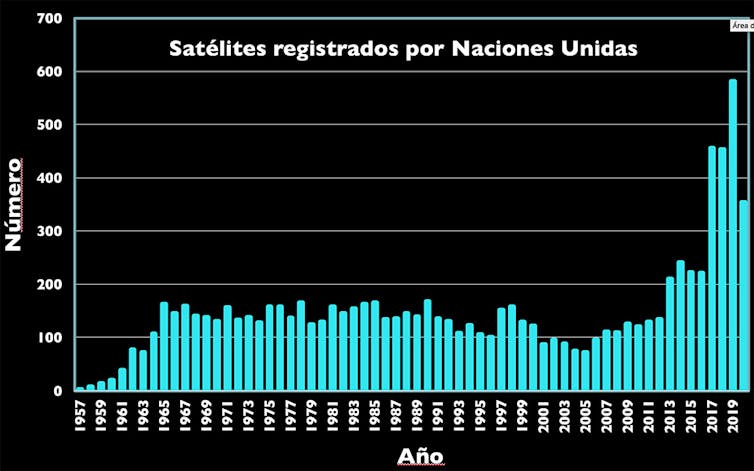 Lanzamientos registrados por United Nations Office for Outer Space Affairs. Nótese el gran incremento durante los últimos años. El histograma incluye datos hasta marzo de 2020.
Lanzamientos registrados por United Nations Office for Outer Space Affairs. Nótese el gran incremento durante los últimos años. El histograma incluye datos hasta marzo de 2020.Riesgos en la órbita terrestre
De diferente cariz son peligros generados por nuestras necesidades tecnológicas. Actualmente los satélites artificiales que orbitan alrededor de la Tierra se han convertido en parte indispensable de nuestra vida, proporcionándonos servicios clave en las comunicaciones (radio, televisión, internet), la logística (navegación por GPS, control de flotas de vehículos o reparto de productos) o la monitorización del planeta (gestión de recursos naturales, vigilancia, predicción meteorológica), además de ser parte integral de la investigación científica.
Según el registro de Naciones Unidas, hasta marzo de 2020 se han enviado al espacio casi 10 000 ingenios, muchos de los cuales siguen orbitando alrededor de nuestro planeta. La gran mayoría se encuentran inactivos y siguen ahí. En el futuro próximo, la empresa SpaceX prevé enviar más de 12 000 mini satélites en los próximos años, mientras que la flotilla de su rival OneWeb estará en el rango de los 650-2 500.
 Basura espacial alrededor de la Tierra.
Basura espacial alrededor de la Tierra.NASA Orbital Debris Program Office at JSC
Por si fuera poco, el mismo proceso de lanzamiento genera residuos y el entorno planetario esta plagado de la denominada “basura espacial”, en muchos casos en órbitas sin control. De hecho, existen varias decenas de miles objetos de tamaño superior a 10 cm orbitando alrededor de la Tierra y 2 000 que intersectan órbitas geoestacionarias, las más valiosas porque son las que albergan a los grandes satélites de telecomunicación.
Más aún, hay casi un millón de fragmentos de más de 1 cm. Por si fuera poco, se tiene constancia de unos 5 000 objetos de más de 1 metro de tamaño. La película Gravity, dirigida por Alfonso Cuarón en 2013, ilustra las consecuencias de impactos en cadena en la red de satélites y sus nefastas consecuencias para la civilización tal y como la concebimos actualmente.
 Impacto de un micrometeorito en el transbordador Endeavour (5,5 mm).
Impacto de un micrometeorito en el transbordador Endeavour (5,5 mm).De hecho, a lo largo de la historia de la exploración espacial ha habido una serie de incidentes muy significativos. En 1977 el satélite Cosmos-954 reentró accidentalmente con 50 kg de uranio enriquecido, afectando a 500 km² en el norte de Canadá. Se aplicó en esta ocasión la UN Space Liability Convention.
La estación espacial Skylab, de unas 170 toneladas, cayó sobre una región desértica de Australia en 1979. En 1996 el satélite Cerise fue golpeado por basura espacial de manera accidental. Por increíble que parezca, probablemente violando la ley internacional, en el año 2007 se produjo la destrucción intencionada del satélite Fengyun 1C por parte de China, generando aproximadamente 2 400 restos de tamaño mayor de 10 cm. La cuenta sigue ascendiendo y en 2009 un satélite de la serie Cosmos (el número 2251) colisionó de manera accidental con el Iridium-33, generando más de 2 000 fragmentos; y a comienzos de 2020 los satélites fuera de uso IRAS y Poppy VII-B se aproximaron a unos 47 m el uno del otro, sin llegar a colisionar en esta ocasión.
Las actividades militares, prohibidas en el espacio, que incluyen el desarrollo de misiones espía a otros satélites o para llegar a inutilizarlos, y que en ocasiones han provocado la posibilidad de impactos, no hacen sino exacerbar la situación de riesgo.
En resumen, nos enfrentamos esencialmente a tres tipos de peligros en la exploración del espacio más próximo, dentro del Sistema Solar: la posibilidad de contaminar con material terrestre otros cuerpos con Marte o los satélites con océanos bajo su superficie, como Europa o Encelado, que orbitan alrededor de Júpiter y Saturno, respectivamente; la llegada accidental e incontrolada de posible material orgánico desde estos cuerpos o de cometas o asteroides a la Tierra; o accidentes en órbita o impactos incontrolados entre la plétora de satélites que orbitan alrededor de la Tierra.
En los dos primeros casos se trata de peligros más hipotéticos que reales, aunque en cualquier caso toda precaución es poca. En el último, los riesgos son reales y los costes económicos y sociales pudieran ser extraordinariamente altos. Solo una gestión global puede ayudar minimizarlos. Nuevamente el multilateralismo y Naciones Unidas son los ámbitos adecuados para lidiar con estos problemas.
Sobre el autor: David Barrado Navascués es profesor de investigación en el Centro de Astrobiología (INTA-CSIC)
Este artículo fue publicado The Conversation (texto). La versión original se publicó en la revista TELOS, de Fundación Telefónica.
El artículo Los riesgos de la exploración espacial se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El sucesor del Hubble: el telescopio espacial James Webb
- La misión espacial Rosetta, por Agustín Sánchez Lavega
- La esponja de grafeno como propulsor espacial
El precio ambiental de la moda rápida
 Venere degli stracci (Venus de los trapos), 1967-1974, de Michelangelo Pistoletto
Venere degli stracci (Venus de los trapos), 1967-1974, de Michelangelo PistolettoA la industria de la moda cabe atribuir el 10% de la contaminación global mundial; es, tras la aviación, el segundo sector económico más contaminante. La razón de que su impacto sea tan grande es doble. Por un lado, su cadena de suministro es larga y compleja; empieza en la agricultura (fibras vegetales) o la fabricación petroquímica (fibras sintéticas), sigue por la manufactura para, pasando por la logística, terminar en la venta al por menor. Y, por otro lado, es un sector que ha experimentado un crecimiento enorme durante los últimos años, debido a la emergencia de lo que se puede denominar fast fashion (“moda rápida”), por analogía con la expresión “fast food”. Su impacto ambiental se produce a través de cuatro componentes: el agua que se consume, los materiales que se emplean (y se desechan), el uso y eliminación de productos químicos de potenciales efectos dañinos, y el gasto de energía.
Veamos unos datos para ilustrar la magnitud de sus efectos. La industria de la moda produce anualmente más de 1.700 millones de toneladas de CO2, lo que representa cerca del 10% de las emisiones globales de este gas. Su consumo de agua es el segundo más grande, con unos 1.500 millones de metros cúbicos; es responsable del 20% de la contaminación industrial de agua, debido a las actividades de tratamiento textil y de tintado. Contribuye en algo más de un tercio a la acumulación de microplásticos de los océanos, con una cantidad anual de 190.000 toneladas. Y genera unos deshechos textiles –incluida ropa que no se llega a vender- de más de 92.000 toneladas anuales, parte importante de las cuales termina en vertederos o es incinerada.
Si nos fijamos en el último medio siglo, la producción de ropa se elevó de forma paralela al aumento de la población hasta aproximadamente el año 2000. Sin embargo, en los veinte años transcurridos desde entonces, la producción textil ha crecido más que la población. De hecho, entre 1975 y 2018 la producción ha pasado de 6 a 13 kg por persona; en otras palabras, se ha más que duplicado. Se estima que la demanda de este tipo de moda crece en la actualidad a razón de un 2% anual.
Ese crecimiento tan grande se ha debido a la capacidad de la industria para ofrecer a los consumidores productos nuevos mucho más baratos y con más frecuencia que antes. Los principales productores han desplazado a compañías tradicionales basadas en la distribución a través de pequeños establecimientos y se han beneficiado de las posibilidades de comercialización a través de internet. Como consecuencia, las marcas de éxito ponen en el mercado hoy el doble de colecciones de las que ponían antes del 2000, cuando comenzó el fenómeno de la moda rápida.
Ha crecido tanto la eficiencia de la producción, que a pesar del aumento en el consumo, el gasto por persona en ropa ha pasado en Europa de representar el 30% de la cesta de la compra en los años 50 del siglo pasado, al 12% en 2009 y al 5% en 2020. Y esa reducción facilita que se compre más ropa porque se adquiere con mayor frecuencia. En los Estados Unidos se adquiere hoy una pieza de ropa cada 5’5 días. Y en Europa se ha reducido el tiempo de uso en un 36% en los últimos quince años.
La industria de la moda ha orientado sus esfuerzos a reducir costes y disminuir los tiempos de entrega, porque ello supone un elemento fundamental de su atractivo y éxito, pero la humanidad paga un precio por ello.
Fuente: Niinimäki, K., Peters, G., Dahlbo, H. et al. The environmental price of fast fashion. Nat Rev Earth Environ 1, 189–200 (2020).
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El precio ambiental de la moda rápida se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sin moda no hay futuro
- Agua cruda, la nueva moda antiprogreso del primer mundo
- Un método para la determinación rápida de especies bacterianas por su código de barras
Ambrosio Liceaga – Naukas P4K 2019: Nunca quisimos coches voladores
 Imagen: Stephane Wootha Richard / Wikimedia Commons
Imagen: Stephane Wootha Richard / Wikimedia CommonsLas leyes de la física limitan lo que la ingeniería puede ofrecer en términos de cosas que vuelen. Por ello, los coches voladores que se ofrecen desde hace décadas son fracasos comerciales. Porque no se parecen a los de las películas. Ambrosio Liceaga, ingeniero industrial y magnífico divulgador de la tecnología, nos explica las posibilidades reales de tener coches voladores.
La conferencia se impartió dentro del marco del festival Passion for Knowledge 2019 (P4K) organizado por el Donostia International Physics Center (DIPC).
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Ambrosio Liceaga – Naukas P4K 2019: Nunca quisimos coches voladores se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Francisco Villatoro – Naukas Bilbao 2019: El abrazo de la plata
- José Ramón Alonso – Naukas Bilbao 2019: Son nuestros amos y nosotros sus esclavos
- #Quantum13 Superhéroes de la ciencia
Desmantelando metódicamente instalaciones nucleares
 La central nuclear Santa María de Garoña (Valle de Tobalina-Burgos) está a la espera de ser desmantelada.
La central nuclear Santa María de Garoña (Valle de Tobalina-Burgos) está a la espera de ser desmantelada.En los últimos años se ha entrado en una fase de desmantelamiento de centrales e instalaciones nucleares, sobre todo en Europa. En 2015, estaban parados o en fase de desmantelamiento 156 reactores de plantas nucleares en todo el mundo, y para 2050 está programado que más de la mitad de la capacidad nuclear actual de 400 GW en todo el mundo tenga que ser clausurada para su desmantelamiento. “En Europa, esto resultará en un aumento de los residuos radiactivos, mientras que las actuales plantas de almacenamiento tienen una capacidad limitada. Es muy importante optimizar esa gestión”, indica la catedrática de ingeniería nuclear de la UPV/EHU Margarita Herranz.
El proyecto europeo H2020 INSIDER —con una financiación de casi cinco millones de euros para cuatro años— aborda la definición de la mejor estrategia para optimizar la producción de los residuos radiactivos durante el desmantelamiento de instalaciones nucleares y radiactivas, incluidas las centrales de producción de energía eléctrica. Se centra tanto en la estrategia de caracterización de los residuos, como en la metodología de desmantelamiento, sobre todo para entornos restringidos, buscando nuevas y mejores soluciones y la remediación del entorno, considerando también situaciones post-accidentales.
“El desmantelamiento de este tipo de instalaciones es un proceso muy caro, los residuos ocupan muchísimo espacio y, además, a la gente no le gusta tener cerca este tipo de repositorios. Y si además hablamos de desmantelar muchas instalaciones nucleares, es muy importante definir qué tiene que ser considerado residuo radiactivo dentro de una central nuclear y qué no, debido a que el coste de la gestión de estos residuos aumenta considerablemente en función de su nivel de actividad y del desmantelamiento de una central nuclear se pueden sacar toneladas y toneladas de residuos”, explica la investigadora de la UPV/EHU. Aunque los desmantelamientos realizados hasta el momento han cumplido exhaustivamente las normas vigentes, “una parte muy importante de lo que se ha considerado residuo nuclear y radiactivo realmente no lo es —afirma. Se está pecando de exceso en ese sentido”.
Margarita Herranz, líder del grupo de trabajo que se encarga de la organización y realización de medidas in situ y posterior análisis de los resultados,asegura que “es fundamental optimizar las medidas de radiactividad in situ de muros, tabiques, maquinaria, blindajes metálicos, etc., debido a la inviabilidad de trasladarlos, en su totalidad, hasta un laboratorio”. Cabe destacar que se trata de mediciones difíciles, “porque hay que buscar qué equipamiento está adaptado para ser utilizado y obtener buenos resultados en función de la atmósfera que hay en cada entorno: radiación, temperatura, presión, humedad, etc.”. En ese contexto, “hemos definido cuáles son los ambientes restrictivos desde el punto de vista de las mediciones in situ en instalaciones nucleares y radiactivas, cómo afectan estas restricciones al tipo de equipo que se va a utilizar y cómo estas restricciones pueden llegar a afectar a los resultados o a la evaluación de los resultados que se van a obtener”, detalla. Asimismo, trabajan en la descripción de diferentes zonas de una instalación nuclear/radiactiva y los problemas que puede haber en ellas, así como en recomendaciones de los tipos de instrumentación a utilizar en cada una de esas zonas.
Herranz indica que este proyecto “contribuye a optimizar los procesos de desmantelamiento, y a que la percepción pública de estos procesos y de estos sistemas mejore. Es decir, demostrar que se controlan y que se trabaja en ello. Hay mucha tecnología puesta al servicio de ese objetivo. Es un objetivo básicamente social”. En el marco del proyecto europeo INSIDER se están publicando numerosos artículos científicos con los que se da a conocer una extensa guía metodológica a la que se puede acceder a través de la página web de INSIDER. El proyecto espera perfeccionar la política de la UE: “Esperamos que este trabajo acabe influyendo en la elaboración de la normativa internacional”, concluye la investigadora.
Referencia:
Frederic Aspe, Raquel Idoeta, Gregoire Auge, Margarita Herranz (2020) Classification and categorization of the constrained environments in nuclear/radiological installations under decommissioning and dismantling processes Progress in Nuclear Energy doi: 10.1016/j.pnucene.2020.103347
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Desmantelando metódicamente instalaciones nucleares se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los residuos nucleares y la memoria de las arcillas
- Mortero reforzado con residuos industriales de acero
- Restos de ensayos nucleares del siglo XX en lo más profundo del océano
Un fósil neuronal de 25 millones de años: los humanos también orientamos las orejas
 Imagen: GIPHY
Imagen: GIPHYEl caracal es una especie de felino con un oído extraordinario. Sus oscuras orejas con tilde son, sin duda, su característica más llamativa. También es la que le da su nombre: “Karrah-kulak” o “Kara-coulac” significa “gato con orejas negras” en turco. Más allá de su llamativo aspecto, como cuenta Juan Carlos Gil en Twitter “cada oreja cuenta con 20 músculos que le permiten orientarlas libremente para localizar a sus posibles presas”. Y hacer la ola, según parece. Cuando yo me concentro mucho, también puedo mover mis orejas. La izquierda, sobre todo, casi 2 milímetros enteros; la derecha, algo menos. No es que se note a simple vista, pero el truco gana bastante si me pongo gafas de sol.
Llama la atención que nuestras orejas estén tan tristemente grapadas a los lados de la cabeza. Muchas especies animales, incluidos perros y gatos, son capaces de dirigirlas hacia una fuente de sonido que les interesa escuchar. Las orejas, con su forma de embudo caprichosa y acaracolada tienen precisamente esta función: recoger la energía sonora y dirigirla hacia el canal auditivo. Sin embargo, los humanos y nuestros parientes evolutivos más cercanos parecemos haber perdido la habilidad de orientarlas. Solo algunos humanos podemos aún ladearlas sutilmente y, para los autores de un estudio publicado recientemente en eLife, esto podría ser lo verdaderamente interesante: el síntoma de que aún existen circuitos neuronales y músculos capaces de desempeñar esa función. Como ellos mismos explican “podría tratarse de una ‘característica vestigial’, una habilidad que se mantiene aunque ya no cumple su propósito original”.
 Imagen: GIPHY
Imagen: GIPHYLo que estos investigadores han descubierto es que, de hecho y sin saberlo ni intentarlo, los humanos también movemos las orejas todo el rato. El equipo dirigido por Daniel Strauss ha demostrado que los músculos alrededor de las orejas se activan en cuanto percibimos sonidos novedosos o sorprendentes. Para estudiar este tipo de reacción refleja, en un primer experimento, le pidieron a varios voluntarios que intentaran leer un texto aburrido, mientras hacían sonar todo tipo de señales para desviar su atención, como un como el sonido de un atasco de tráfico, un bebé llorando o pasos de otro ser humano. En un segundo experimento, les hicieron escuchar un podcast mientras sonaba otro desde una segunda dirección. El objetivo, en este caso, era analizar el comportamiento de los músculos durante una escucha voluntaria, donde la atención se dirige hacia un objetivo. En ambos casos, los investigadores pudieron registrar la actividad eléctrica de los músculos que controlan los diminutos movimientos, casi invisibles, de las orejas. Para ello utilizaron una técnica conocida como electromiografía, mediante electrodos colocados sobre la piel. También grabaron imágenes de vídeo de alta resolución, que luego se trataron digitalmente para amplificar cualquier posible movimiento.
https://culturacientifica.com/app/uploads/2020/07/elife-54536-video1.mp4
Los experimentos revelaron que inconsciente e imperceptiblemente, las orejas de los participantes se activaban en la dirección de los sonidos llamativos. Como explica Strauss “la actividad eléctrica de los músculos del oído indica la dirección en la que el sujeto está enfocando su atención auditiva”. Asimismo, cuando los participantes intentaban escuchar un podcast ignorando el segundo, orientaban inconscientemente sus orejas hacia la fuente de interés.
Nada comparable a las acrobáticas habilidades auriculares del caracal, eso sí. Es difícil saber por qué los humanos perdimos la habilidad de orientar nuestras orejas. La movilidad parece haber ido disminuyendo a lo largo de varios millones de años. Nuestras orejas se fueron volviendo más cortas y rígidas y la musculatura degeneró. Pero sin saberlo, como afirma Strauss, nuestra especie podría haber retenido algún recuerdo de esta habilidad de manera puramente vestigial, ”como un ‘fósil neuronal’ que ha sobrevivido en el cerebro durante unos 25 millones de años”.
Gracias Antonio J. Osuna Mascaró por descubrirme esta historia.
Referencia:
Daniel J Strauss, Farah I Corona-Strauss, Andreas Schroeer, Philipp Flotho, Ronny Hannemann, Steven A Hackley (2020) Vestigial auricular motor activity indicates the direction of auditory attention in humans. eLife, 2020; 9 DOI: 10.7554/eLife.54536
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Un fósil neuronal de 25 millones de años: los humanos también orientamos las orejas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Constantes durante al menos 12 mil millones de años
- Los meteoritos ya no son lo que eran desde hace 466 millones de años
- Los misterios que rodean al máximo térmico de hace 56 millones de años

