Alice Bache Gould, la matemática e historiadora estadounidense con una calle en Simancas
Alice Bache Gould se graduó en matemáticas e inicio una tesis doctoral en geometría que no consiguió terminar. La mayor parte de su vida la dedicó a la historia. Fue precisamente esa ocupación la que la llevó a Simancas (Valladolid) donde descubrió numerosos detalles sobre los viajes de Colón.
 Alice Bache Gould. Fuente: Archivo Digital Nacional de Puerto Rico.
Alice Bache Gould. Fuente: Archivo Digital Nacional de Puerto Rico.Una infancia entre Estados Unidos y Argentina
Alice Bache Gould nació el 5 de enero de 1868 en Cambridge, Massachussets (Estados Unidos). Era la tercera de los cinco hijo e hijas de Mary Apthorp Quincy y Benjamin Apthorp Gould.
Su padre había estudiado matemáticas y astronomía en la Universidad de Harvard. Gracias a la fortuna privada y al apoyo de su esposa Mary pudo llevar adelante su trabajo astronómico. Estaba interesado en observar el cielo del sur por lo que en 1865 se puso en contacto con el gobierno de Argentina para presentarles su plan para establecer un observatorio en Córdoba. Aunque ese proyecto no llegó a buen término por falta de financiación, cuatro años más tarde fue invitado por el entonces presidente de Argentina, Domingo Faustino Sarmiento, para fundar el Observatorio Nacional de Argentina en Córdoba. En mayo de 1870, la familia Gould emprendió el viaje hacia Argentina. A finales de 1871, tras la inauguración oficial del observatorio en Córdoba, Alice fue enviada de nuevo a Massachussets para vivir al cuidado de sus tías maternas.
La educación primaria de Alice tuvo lugar entre Estados Unidos y Argentina; en este último país aprendió la historia, la cultura y la lengua del país. Su educación secundaria se desarrolló en parte en Estados Unidos y en parte en Inglaterra.
La madre de Alice falleció en Boston en 1883, durante una estancia en la que Benjamin Apthorp Gould estaba organizando el estudio de las placas fotográficas que había tomado en el Observatorio de Córdoba. El astrónomo regresó a Córdoba, dejando a Alice y a sus dos hijos pequeños en un internado en Boston (en febrero de 1874 las dos hermanas mayores de Alice fallecieron en un accidente mientras nadaban en un río en Río Primero, Córdoba).
Los estudios de matemáticas y una tesis inacabadaEn 1885, Alice regresó a Estados Unidos y, poco después, ingresó en la Society for the Collegiate Instruction of Women (más tarde pasó a llamarse Radcliffe College), una institución creada para que las mujeres, que no podían estudiar en la Universidad de Harvard, pudieran recibir formación. Allí estudió matemáticas, y un año más tarde ingresó en el Bryn Mawr College, una universidad privada que ofrecía formación de posgrado a mujeres. Alice se graduó con una licenciatura en matemáticas y física en 1889.
Entre 1890 y 1893, estudió matemáticas en el Instituto Tecnológico de Massachusetts y en Inglaterra, en el Newnham College de Cambridge. Aunque este centro permitía a las mujeres asistir a las clases, no recibían ningún título.
Alice enseñó matemáticas en Carleton College en Northfield (Minnesota) durante el curso académico 1893/1894 y dejó la docencia al obtener una beca para estudios de posgrado en matemáticas en la Universidad de Chicago. Allí, en 1894, comenzó sus estudios tutorizada por Eliakim Moore. Gould comenzó a preparar su trabajo de doctorado en geometría con un trabajo de Henri Brocard como punto de partida. Sus avances eran lentos debido a sus problemas de salud.
Benjamin Apthorp Gould falleció en 1896 y Alice dedicó gran parte de sus esfuerzos a crear una beca en la Academia Nacional de Ciencias en honor de su padre y destinada a personas trabajando en astronomía de precisión. Ella misma donó veinte mil dólares a esa institución para conseguir su objetivo.
En 1900, mientras avanzaba lentamente con su tesis (que nunca consiguió finalizar), comenzó a escribir una biografía del naturalista estadounidense Louis Agassiz. Se publicó en 1901 y obtuvo muy buenas reseñas.
Entusiasmada con la historia de la colonizaciónEn 1903, tras sufrir una fuerte gripe, Gould decidió viajar a Puerto Rico y pasar allí un tiempo recuperándose de su afección pulmonar. Finalmente, permaneció durante siete años. Allí se interesó por la historia de la colonización de la isla y comenzó sus investigaciones. También colaboró en la mejora del sistema educativo creando el «Fondo de Maestros de Puerto Rico» que recaudó dinero para fundar una escuela de enfermería.
Tras regresar a Boston, en 1911, emprendió un viaje a Roma con una amiga. Ésta enfermó durante el trayecto y cuando el barco atracó en Gibraltar rumbo a Italia, ambas mujeres decidieron quedarse. Alice encontró allí la oportunidad de continuar sus investigaciones sobre la colonización de las Indias Occidentales y visitó el Archivo General de Indias de Sevilla. Aunque su amiga regresó a Estados Unidos tras recuperarse, Gould se quedó en España y se centró en explorar el recorrido de los viajes de Cristóbal Colón e indagar sobre las personas que le acompañaban.
En 1914, cuando estalló la Primera Guerra Mundial, Gould estaba en España estudiando documentos en el Archivo General de Simancas. Cuando Estados Unidos entró en la guerra en abril de 1917, Alice ofreció sus servicios a la Embajada de su país en Madrid. Debido a la preocupación de su familia, regresó a Boston en marzo de 1918. Para apoyar el esfuerzo bélico, aceptó un puesto en la Universidad de Chicago en el que enseñó matemáticas en un curso de navegación para personal de la Marina.
Gould regresó a España en 1925 y retomó sus investigaciones sobre los viajes de Colón. Durante la guerra civil española volvió a su país y después regresó a España para vivir en Simancas, donde, entre otros, fundó una escuela para niñas y niños sin recursos.
Alice trabajaba en un libro sobre Colón cuando falleció repentinamente en julio de 1953. Aunque no llegó a publicar sus investigaciones, en 1984 salió a la luz el documento Nueva lista documentada de los tripulantes de Colón en 1492 que elaboró tras estudiar los registros del Archivo General de Simancas. Alice buscaba documentos con cualquier información sobre los viajes de Colón, en particular sobre quienes formaban parte de su tripulación. Entre otros, ratificó la presencia judía en los viajes de descubrimiento, como Luis de Torres, el intérprete de Colón, o Rodrigo Sánchez de Segovia. Identificó a 87 de los 90 tripulantes, demostrando que solo cuatro de ellos tenían problemas con la justicia, desmintiendo la versión aceptada hasta entonces que aseguraba que la mayor parte de la tripulación estaba formada por criminales. Se le atribuye, además, haber salvado documentos que de otro modo habrían sido ignorados e incluso destruidos.
 Portada de “Nueva lista documentada de los tripulantes de Colón en 1492”. Fuente: Bibliotheca Sefarad.
Portada de “Nueva lista documentada de los tripulantes de Colón en 1492”. Fuente: Bibliotheca Sefarad.
Entre otros reconocimientos, Gould fue elegida miembro correspondiente de la Real Academia Española de la Historia en 1942, y obtuvo la Orden de Isabel la Católica en 1952.
Tras su repentina muerte (por un derrame cerebral el día 25 de julio de 1953) en el jardín del castillo de Simancas, cerca de los archivos, se colocó en la entrada del edificio una placa en su honor:
A miss Alice B. Gould, ilustre investigadora norteamericana y gran amiga de España. Trabajó en este archivo durante cuarenta años y murió a su entrada el día 25 de julio de 1953.
En Simancas, una calle lleva su nombre.
Referencias
- Alice Bache Gould, MacTutor History of Mathematics Archive, St Andrews University
- Edgardo Ronal Minniti Morgan (2011) Alice Bache Gould. La convergencia de la astronomía, la historia, la matemática y el espionaje, Historia de la astronomía
- Deborah Kent, Alice Bache Gould: mathematician in search of war work, 1918, BSHM Bulletin: Journal of the British Society for the History of Mathematics Volume 27, Issue 1, 2012
- Alice Bache Gould, Wikipedia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Alice Bache Gould, la matemática e historiadora estadounidense con una calle en Simancas se ha escrito en Cuaderno de Cultura Científica.
La mayor parte de la vida en la Tierra está aletargada
Muchos microbios y células están en un sueño profundo, esperando el momento adecuado para activarse. Los biólogos han descubierto una proteína muy extendida que detiene abruptamente la actividad de una célula y la vuelve a activar con la misma rapidez.
Un artículo de Dan Samorodnitsky. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Cuando las cosas se ponen difíciles, muchos microbios quedan inactivos. Una nueva investigación ha descubierto una proteína ubicua que detiene la producción de proteínas de una célula en un instante. Fuente: Nico Roper/ Quanta Magazine
Cuando las cosas se ponen difíciles, muchos microbios quedan inactivos. Una nueva investigación ha descubierto una proteína ubicua que detiene la producción de proteínas de una célula en un instante. Fuente: Nico Roper/ Quanta MagazineSe ha informado recientemente del descubrimiento de una proteína natural, llamada Balon, que puede detener por completo la producción celular de nuevas proteínas. Balon se ha encontrado en bacterias que hibernan en el permafrost ártico, pero también parece ser que es producida por muchos otros organismos y podría ser un mecanismo de letargo pasado por alto en todo el árbol de la vida.
Para la mayoría de las formas de vida, la capacidad de aislarse es una parte fundamental de mantenerse con vida. Las condiciones duras como la falta de alimentos o el clima frío pueden aparecer de la nada. En esta situación desesperada, en lugar de desplomarse y morir, muchos organismos han dominado el arte del letargo. Ralentizan su actividad y metabolismo. Luego, cuando vuelven tiempos mejores, se reaniman.
Permanecer en un estado latente es en realidad la norma para la mayoría de la vida en la Tierra: según algunas estimaciones, el 60% de todas las células microbianas están hibernando en un momento dado. Incluso en organismos cuyo cuerpo entero no está inactivo, como la mayoría de los mamíferos, algunas poblaciones celulares dentro de ellos descansan y esperan el mejor momento para activarse.
«Vivimos en un planeta aletargado», afirma Sergey Melnikov, biólogo molecular evolutivo de la Universidad de Newcastle. «La vida se trata principalmente de estar dormido».
Pero, ¿cómo logran las células esta hazaña? A lo largo de los años, los investigadores han descubierto una serie de «factores de hibernación», proteínas que las células utilizan para inducir y mantener un estado latente. Cuando una célula detecta algún tipo de condición adversa, como hambre o frío, produce un conjunto de factores de hibernación para detener su metabolismo.
Algunos factores de hibernación desmantelan la maquinaria celular; otros impiden que los genes se expresen. Los más importantes, sin embargo, desactivan el ribosoma, la máquina celular para construir nuevas proteínas. La producción de proteínas representa más del 50% del uso de energía en una célula bacteriana en crecimiento. Estos factores de hibernación arrojan arena en los engranajes del ribosoma, impidiéndole sintetizar nuevas proteínas y ahorrando así energía para las necesidades básicas de supervivencia.
A principios de este año, en una publicación en Nature, un equipo de investigadores ha informado del descubrimiento de un nuevo factor de hibernación, al que han llamado Balon. La proteína es sorprendentemente común: una búsqueda de su secuencia genética descubrió su presencia en el 20% de todos los genomas bacterianos catalogados. Y funciona de una manera que los biólogos moleculares nunca antes habían visto.
Anteriormente, todos los factores de hibernación conocidos que alteraban los ribosomas funcionaban pasivamente: esperaban a que un ribosoma terminara de construir una proteína y luego le impedían iniciar una nueva. Balon, sin embargo, tira del freno de mano. Se introduce en cada ribosoma de la célula, incluso interrumpiendo los ribosomas activos en mitad de su trabajo. Antes de Balon, los factores de hibernación sólo se habían observado en ribosomas vacíos.
«El artículo Balon es sorprendentemente detallado», comenta el biólogo evolutivo Jay Lennon, que estudia la latencia microbiana en la Universidad de Indiana y que no ha participado en el nuevo estudio. «Ampliará nuestra visión de cómo funciona el letargo».
 Karla Helena-Bueno descubrió un factor de hibernación común cuando accidentalmente dejó una bacteria del Ártico en el hielo durante demasiado tiempo. «Traté de buscar en un rincón poco estudiado de la naturaleza y encontré algo», cuenta. Fuente: Karla Helena-Bueno
Karla Helena-Bueno descubrió un factor de hibernación común cuando accidentalmente dejó una bacteria del Ártico en el hielo durante demasiado tiempo. «Traté de buscar en un rincón poco estudiado de la naturaleza y encontré algo», cuenta. Fuente: Karla Helena-BuenoMelnikov y su estudiante de posgrado Karla Helena-Bueno descubrieron Balon en Psychrobacter urativorans, una bacteria adaptada al frío nativa de los suelos helados y recolectada del permafrost ártico. (Según Melnikov, la bacteria se encontró por primera vez infectando un paquete de salchichas congeladas en la década de 1970 y luego fue redescubierta por el famoso geneticista Craig Venter en un viaje al Ártico). Estudian P. urativorans y otros microbios inusuales para caracterizar la diversidad de herramientas de construcción de proteínas utilizadas en todo el espectro de la vida y para comprender cómo los ribosomas pueden adaptarse a ambientes extremos.
Debido a que el letargo puede ser desencadenado por una variedad de condiciones, incluyendo el hambre y la sequía, los científicos llevan a cabo esta investigación con un objetivo práctico en mente: «Probablemente podamos usar este conocimiento para diseñar organismos que puedan tolerar climas más cálidos», apunta Melnikov. “y por lo tanto resistir el cambio climático”.
Presentamos: BalonHelena-Bueno descubrió Balon por pura casualidad. Estaba intentando convencer a P. urativorans para que creciera felizmente en el laboratorio. En lugar de eso, hizo lo contrario. Dejó el cultivo en una cubeta de hielo durante demasiado tiempo y logró aplicarle un golpe de frío. Para cuando recordó que estaba allí, las bacterias adaptadas al frío ya estaban en letargo.
No queriendo desperdiciar el cultivo, los investigadores persiguieron de todos modos sus intereses originales. Helena-Bueno extrajo los ribosomas de las bacterias afectadas por el frío y los sometió a crio-EM. Abreviatura de microscopía electrónica criogénica, crio-EM es una técnica para visualizar estructuras biológicas minúsculas en alta resolución. Helena-Bueno vio una proteína atascada en el sitio A del ribosoma paralizado, la «puerta» por donde se entregan los aminoácidos para la construcción de nuevas proteínas.
Helena-Bueno y Melnikov no reconocieron la proteína. De hecho, nunca antes se había descrito. Tenía similitud con otra proteína bacteriana, una que es importante para desmontar y reciclar partes ribosomales, llamada Pelota en referencia al término en español. De ahí que llamaran a la nueva proteína Balon, por el homónimo español a “pelota”, “balón”.
La capacidad de Balon para detener la actividad del ribosoma es una adaptación crítica para un microbio bajo estrés, comenta Mee-Ngan Frances Yap, microbióloga de la Universidad Northwestern que no ha participado en el trabajo. «Cuando las bacterias crecen activamente, producen muchos ribosomas y ARN», continúa. «Cuando se encuentran con estrés, una especie podría necesitar detener la traducción» del ARN en nuevas proteínas para comenzar a conservar energía para un período de hibernación potencialmente largo.
Llamativamente, el mecanismo de Balon es un proceso reversible. A diferencia de otros factores de hibernación, se puede insertar para detener el crecimiento y luego expulsarlo rápidamente como una cinta de casete. Permite que una célula entre rápidamente en estado de letargo en caso de emergencia y que resucite con la misma rapidez para readaptarse a condiciones más favorables.
Balon puede hacer esto porque se adhiere a los ribosomas de una manera única. Cada factor de hibernación ribosómica descubierto previamente bloquea físicamente el sitio A del ribosoma, por lo que cualquier proceso de producción de proteínas que esté en progreso debe completarse antes de que el factor pueda unirse para desactivar el ribosoma. Balon, por otro lado, se une cerca del canal, pero no a través de él, lo que le permite ir y venir independientemente de lo que esté haciendo el ribosoma.

A pesar de la novedad mecánica de Balon, es una proteína extremadamente común. Una vez identificada, Helena-Bueno y Melnikov encontraron parientes genéticos de Balon en más del 20% de todos los genomas bacterianos catalogados en bases de datos públicas. Con la ayuda de Mariia Rybak, bióloga molecular de la Rama Médica de la Universidad de Texas, caracterizaron dos de estas proteínas bacterianas alternativas: una del patógeno humano Mycobacterium tuberculosis, que causa la tuberculosis, y otra de Thermus thermophilus, que vive en el último lugar en el que econtrarías a P. urativorans, en las ultracalientes fuentes hidrotermales submarinas. Ambas proteínas también se unen al sitio A del ribosoma, lo que sugiere que al menos algunos de estos parientes genéticos actúan de manera similar a Balon en otras especies bacterianas.
Balon está notablemente ausente en Escherichia coli y Staphylococcus aureus, las dos bacterias más comúnmente estudiadas y los modelos más utilizados para el letargo celular. Al centrarse sólo en unos pocos organismos de laboratorio, los científicos habían pasado por alto una táctica de hibernación generalizada, afirma Helena-Bueno. «Traté de buscar en un rincón poco estudiado de la naturaleza y encontré algo».
Todo el mundo hibernaCada célula necesita la capacidad de permanecer aletargada y esperar su momento. Melnikov explica que el modelo de laboratorio de la bacteria E. coli tiene cinco modos diferentes de hibernación, cada uno de los cuales por sí solo es suficiente para permitir que el microbio sobreviva a una crisis.
«La mayoría de los microbios se están muriendo de hambre», comenta Ashley Shade, microbióloga de la Universidad de Lyon que no ha participado en el nuevo estudio. “Existen en un estado de necesidad. No se están duplicando. No están viviendo su mejor vida”.
Pero el letargo también es necesario fuera de los períodos de hambruna. Incluso en organismos, como la mayoría de los mamíferos, cuyo cuerpo entero no queda completamente inactivo, las poblaciones celulares individuales deben esperar el mejor momento para activarse. Los ovocitos humanos permanecen inactivos durante décadas esperando ser fertilizados. Las células madre humanas nacen en la médula ósea y luego permanecen inactivas, esperando que el cuerpo las llame para crecer y diferenciarse. Los fibroblastos del tejido nervioso, los linfocitos del sistema inmunitario y los hepatocitos del hígado entran en fases latentes, inactivos y sin división y se reactivan más tarde.
«Esto no es algo exclusivo de bacterias o arqueas», afirma Lennon. “Cada organismo del árbol de la vida tiene una forma de lograr esta estrategia. Pueden pausar su metabolismo”.
Los osos hibernan. Los virus del herpes se lisogenizan. Los gusanos tienen una etapa dauer. Los insectos entran en diapausa. Los anfibios estivan. Los pájaros entran en torpor. Todas estas son palabras para exactamente lo mismo: un estado de letargo que los organismos pueden revertir cuando las condiciones son favorables.
«Antes de la invención de la hibernación, la única forma de vivir era seguir creciendo sin interrupciones», dice Melnikov. “Poner la vida en pausa es un lujo”.
También es un tipo de seguro a nivel poblacional. Algunas células persiguen el estado de letargo detectando cambios ambientales y respondiendo en consecuencia. Sin embargo, muchas bacterias utilizan una estrategia estocástica. «En entornos que fluctúan aleatoriamente, si a veces no entras en estado de letargo, existe la posibilidad de que toda la población se extinga» a través de encuentros aleatorios con desastres, explica Lennon. Incluso en los cultivos de E. coli más sanos, felices y de más rápido crecimiento, entre el 5% y el 10% de las células permanecerán inactivas en cualquier caso. Son los supervivientes designados que vivirán si algo les sucede a sus primos más activos y vulnerables.
En ese sentido, el letargo es una estrategia de supervivencia ante catástrofes globales. Por eso Helena-Bueno estudia la hibernación. Le interesa saber qué especies podrían permanecer estables a pesar del cambio climático, cuáles podrían recuperarse y qué procesos celulares, como la hibernación asistida por Balon, podrían ayudar.
Más fundamentalmente, Melnikov y Helena-Bueno esperan que el descubrimiento de Balon y su ubicuidad ayude a las personas a replantear lo que es importante en la vida. Todos nos quedamos inactivos con frecuencia y muchos de nosotros lo disfrutamos bastante. «Pasamos un tercio de nuestra vida durmiendo, pero no hablamos de ello en absoluto», comenta Melnikov. En lugar de quejarnos de lo que nos perdemos cuando dormimos, tal vez podamos experimentarlo como un proceso que nos conecta con toda la vida en la Tierra, incluidos los microbios que duermen en las profundidades del permafrost del Ártico.
El artículo original, Most Life on Earth is Dormant, After Pulling an ‘Emergency Brake’, se publicó el 5 de junio de 2024 en Quanta Magazine.
Traducido por César Tomé López
El artículo La mayor parte de la vida en la Tierra está aletargada se ha escrito en Cuaderno de Cultura Científica.
Los hongos carnívoros “olfatean” a sus presas
Estoy seguro de que este título ha sorprendido a los lectores. Primero, por el concepto de “hongo carnívoro” bastante opuesto a lo que conocemos sobre estos seres. Segundo, porque atribuimos un cierto sentido del olfato a organismos carentes de sistema nervioso. Lo explicamos a continuación.
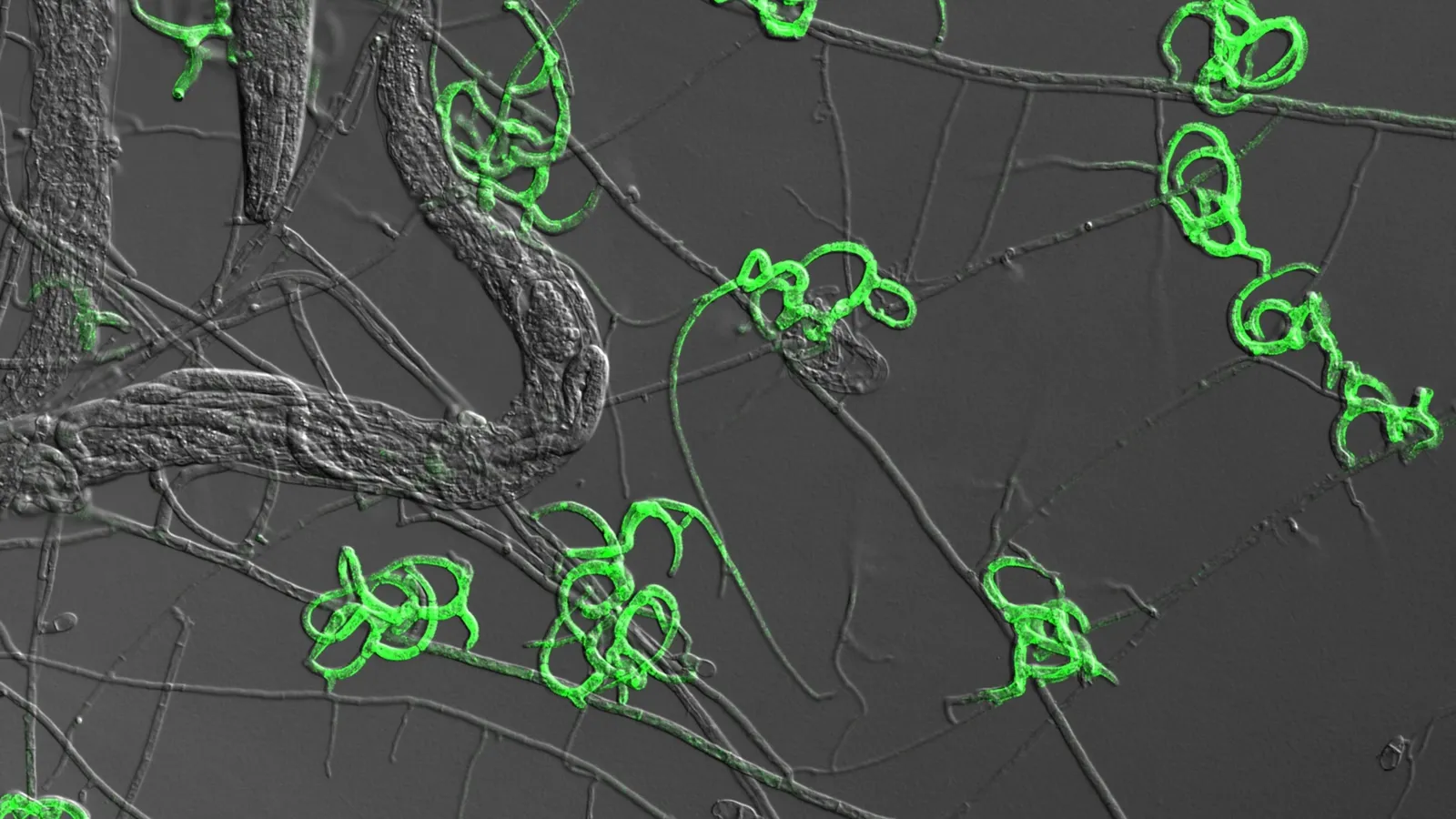 En verde, las células producidas por el hongo hambriento ayudan a atraer y atrapar gusanos nematodos. Las líneas grises en forma de hilo son micelio, las hebras conectivas que forman un solo hongo.
En verde, las células producidas por el hongo hambriento ayudan a atraer y atrapar gusanos nematodos. Las líneas grises en forma de hilo son micelio, las hebras conectivas que forman un solo hongo.Foto: Yen-Ping Hsueh
Los hongos y los animales compartimos algunas características importantes. Somos pluricelulares y heterótrofos. Esto quiere decir que estamos formados por multitud de células organizadas que obtienen su energía a partir de la oxidación de materia orgánica. Esto nos distingue de seres autótrofos como las plantas, que son capaces de utilizar energía de fuentes no orgánicas como la luz.
Hongos y animales también somos diferentes en ambos aspectos. La pluricelularidad se alcanza en los animales a través de un desarrollo embrionario. Esto no sucede en los hongos, cuyo micelio crece a partir de esporas, sin formar tejidos ni órganos. Por otro lado, la alimentación de los hongos es fundamentalmente pasiva, por crecimiento del micelio sobre una fuente de materia orgánica. Los animales (salvo esponjas y placozoos) desarrollamos un sistema nervioso que nos permite desplegar un comportamiento proactivo de detección y obtención del alimento.
La capacidad evolutiva de los seres vivos produce innovaciones insólitas que rompen estos esquemas simples. Hay un grupo de hongos, conocidos genéricamente como NTF (nematode trapping fungi), que en condiciones de inanición y presencia de nematodos son capaces de desarrollar rápidamente unos filamentos adhesivos que atrapan al gusano, causan su muerte y les proporcionan alimento.
Los mecanismos que regulan este sorprendente comportamiento están siendo revelados por una serie de estudios sobre el NTF Arthrobotrys oligospora, liderados por la investigadora taiwanesa Yen-Ping Hsueh. Este hongo ya era conocido por su capacidad de producir compuestos químicos que actuaban como cebo para atraer a los nematodos, simulando el olor de fuentes de alimento o incluso feromonas para la atracción sexual.
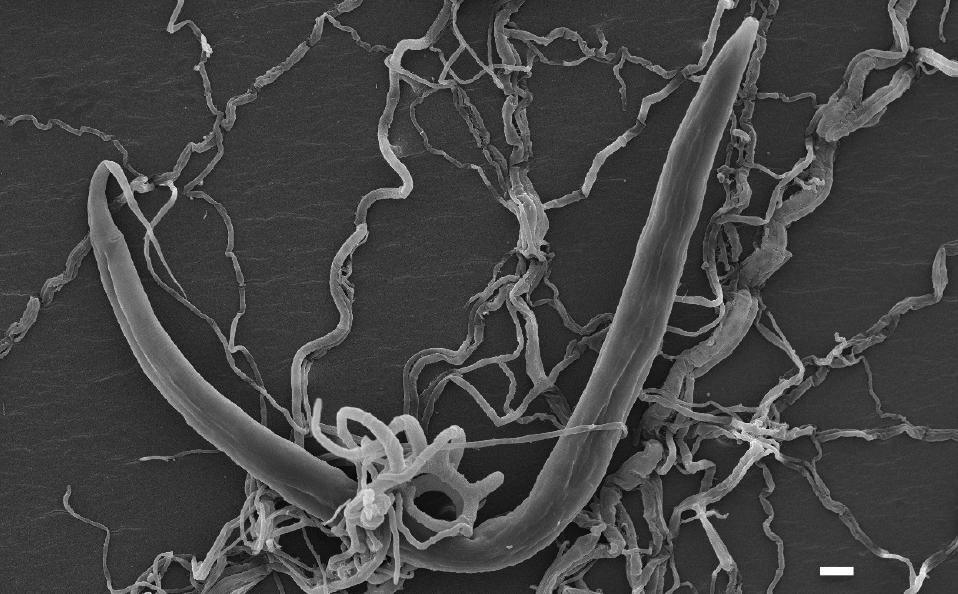 Figura 1. El nematodo C. elegans atrapado por el hongo A. oligospora. Escala=10 μm. Fuente: Hsueh et al. (2017) eLife 2017;6:e20023
Figura 1. El nematodo C. elegans atrapado por el hongo A. oligospora. Escala=10 μm. Fuente: Hsueh et al. (2017) eLife 2017;6:e20023Más recientemente, el grupo de Yen-Ping Hsueh mostró que la presencia del nematodo Caenorhabditis elegans provocaba en el hongo la activación de un gran número de genes. Esta respuesta inducía cambios morfológicos, sobre todo el crecimiento rápido de los filamentos de las trampas (Figura 1). Al mismo tiempo se expresaban proteínas adhesivas para dificultar la huida del gusano, y finalmente se secretaban enzimas, en concreto metaloproteasas, que digerían al infortunado C. elegans haciendo posible su absorción por el hongo. El proceso se puede ver en este espectacular vídeo del laboratorio de la Dra. Hsueh1.
¿Cómo se regula a nivel molecular la rápida respuesta de A. oligospora a la presencia del nematodo? El equipo taiwanés identificó la vía AMPc-PKA como la activadora de este proceso. El adenosín monofosfato cíclico (AMPc) es un “segundo mensajero”. Cuando una célula recibe una señal externa a través de un receptor es habitual que se desencadene una cascada de reacciones en el interior que culmine en una respuesta fisiológica, por ejemplo, la expresión de determinados genes. Este proceso se conoce como “transducción de señales” y en él intervienen muchas veces segundos mensajeros, es decir, pequeñas moléculas como el AMPc o iones como el calcio (Ca2+). En concreto el AMPc activa la proteína kinasa A (PKA), activadora a su vez de otras proteínas que regulan la respuesta celular.
Yen-Ping Hsueh y sus colaboradores mostraron que la inactivación de esta vía de señalización hacía que los hongos fueran indiferentes a la cercanía de sus presas potenciales. Pero todavía quedaba una cuestión por resolver, ¿cómo detecta un hongo sin sistema nervioso la presencia de C. elegans?
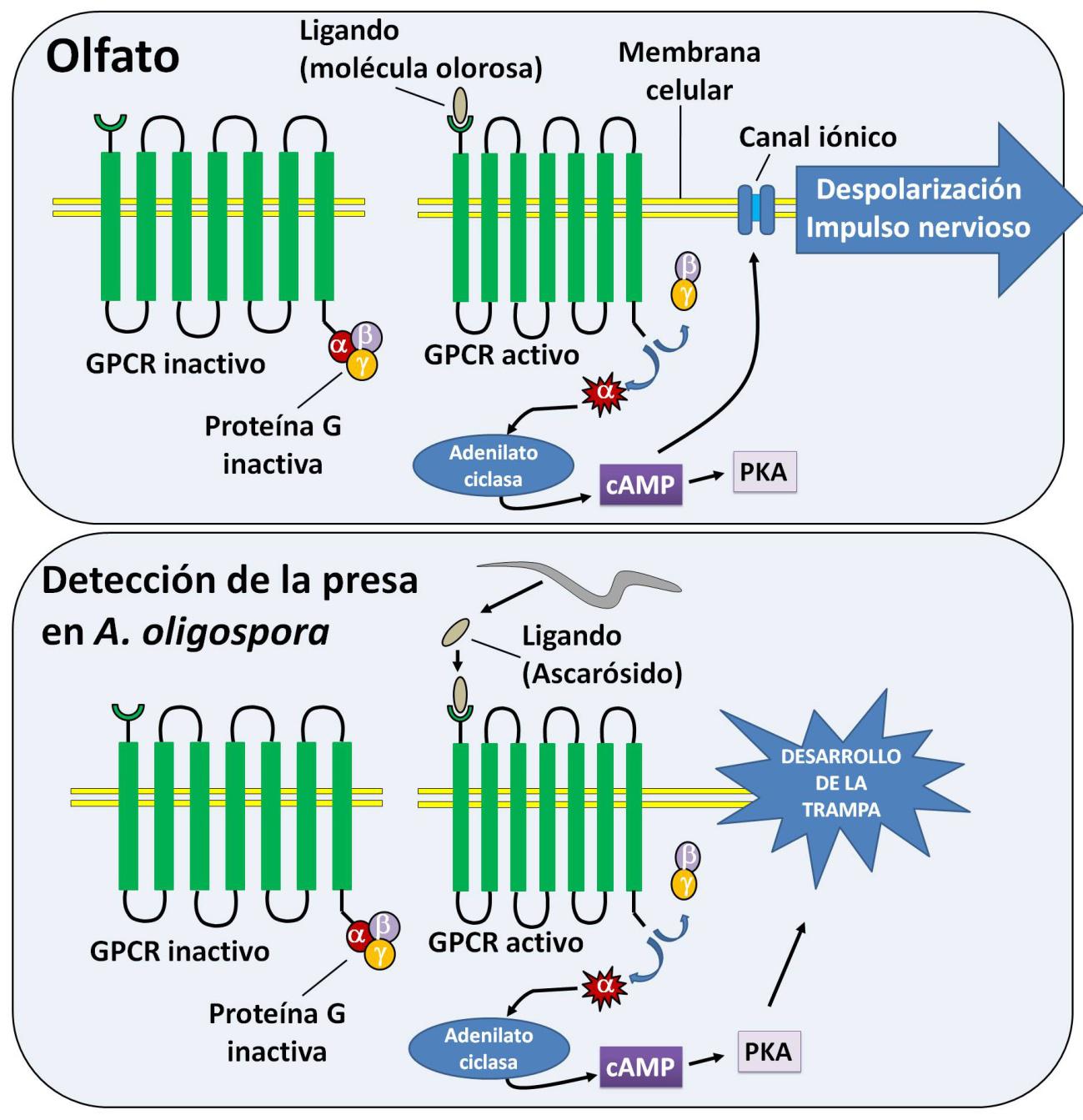 Figura 2. Nuestra sensación olfativa se genera cuando un receptor GPCR del epitelio olfativo capta un ligando (molécula olorosa) y cambia su configuración. Esto provoca la disociación y activación de la proteína G cuya subunidad α activa la enzima sintetizadora de AMPc. Esta molécula provoca la apertura de canales iónicos, la despolarización de la membrana celular y la generación del impulso nervioso. En el caso del hongo A. oligospora el ligando de las GPCRs es un ascarósido segregado por el nematodo. La elevación de los niveles de AMPc activa la proteína kinasa A y se dispara el mecanismo de desarrollo de la trampa
Figura 2. Nuestra sensación olfativa se genera cuando un receptor GPCR del epitelio olfativo capta un ligando (molécula olorosa) y cambia su configuración. Esto provoca la disociación y activación de la proteína G cuya subunidad α activa la enzima sintetizadora de AMPc. Esta molécula provoca la apertura de canales iónicos, la despolarización de la membrana celular y la generación del impulso nervioso. En el caso del hongo A. oligospora el ligando de las GPCRs es un ascarósido segregado por el nematodo. La elevación de los niveles de AMPc activa la proteína kinasa A y se dispara el mecanismo de desarrollo de la trampa
En cierto sentido A. oligospora “huele” al nematodo. Evidentemente no existen órganos olfativos en los hongos, pero el mecanismo que utilizan es sorprendentemente parecido al que usamos nosotros para percibir los olores (Figura 2).
Nuestro sentido del olfato se basa en receptores acoplados a proteína G (GPCRs, por G protein-coupled receptors). Se trata de proteínas cuya cadena atraviesa siete veces la membrana celular. Cuando su porción extracelular detecta las señales adecuadas (hormonas, péptidos, diverso tipo de moléculas…) cambia la configuración del receptor disociando la proteína G unida a su dominio intracelular, lo que desencadena la transducción de la señal.
Estos receptores son importantísimos en la detección de señales. Para hacernos una idea, los humanos tenemos más de 800 GPCRs que intervienen en multitud de procesos sensoriales y de respuesta a hormonas o neurotransmisores. Por esto son la principal diana de los fármacos que utilizamos.
En un reciente artículo, el equipo de Yen-Ping Hsueh acaba de identificar dos familias de GPCRs usadas por A. oligospora para detectar la presencia de nematodos. Una de estas familias detecta ascarósidos, pequeños glicolípidos que secretan continuamente los nematodos a modo de feromonas. La segunda familia detecta otras moléculas segregadas por los nematodos y que todavía no han sido identificadas. En ambos casos la activación de las proteínas G dispara la vía AMPc-PKA y pone en marcha el programa de construcción de las trampas.
En resumen, los hongos NTF no “huelen” al nematodo en un sentido estricto de la palabra, pero el paralelismo entre el uso de GPCRs para la detección de presas y el funcionamiento de nuestro olfato es extraordinariamente llamativo.
Referencias:
Chen SA, Lin HC, Hsueh YP. (2022) The cAMP-PKA pathway regulates prey sensing and trap morphogenesis in the nematode-trapping fungus Arthrobotrys oligospora. G3 (Bethesda). doi: 10.1093/g3journal/jkac217.
Hsueh YP, Gronquist MR, Schwarz EM, Nath RD, Lee CH, Gharib S, Schroeder FC, Sternberg PW. (2017) Nematophagous fungus Arthrobotrys oligospora mimics olfactory cues of sex and food to lure its nematode prey. Elife. doi: 10.7554/eLife.20023.
Kuo CY, Tay RJ, Lin HC, Juan SC, Vidal-Diez de Ulzurrun G, Chang YC, Hoki J, Schroeder FC, Hsueh YP. (2024) The nematode-trapping fungus Arthrobotrys oligospora detects prey pheromones via G protein-coupled receptors. Nat Microbiol. doi: 10.1038/s41564-024-01679-w.
Lin HC, de Ulzurrun GV, Chen SA, Yang CT, Tay RJ, Iizuka T, Huang TY, Kuo CY, Gonçalves AP, Lin SY, Chang YC, Stajich JE, Schwarz EM, Hsueh YP. (2023) Key processes required for the different stages of fungal carnivory by a nematode-trapping fungus. PLoS Biol. doi: 10.1371/journal.pbio.3002400.
Nota:
1 En la primera parte. En una segunda parte se muestra la estrategia de otro hongo carnívoro, Pleurotus ostreatus, que produce una toxina volátil que paraliza al nematodo.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga
El artículo Los hongos carnívoros “olfatean” a sus presas se ha escrito en Cuaderno de Cultura Científica.
Las mentiras visuales de la IA
Federico Kukso
A medida que se expande la inteligencia artificial en cada rincón de nuestras vidas, un cliché se consolida: el de representar visualmente estos sistemas como robots humanoides blancos, cerebros destellantes o con referencias a la ciencia ficción. Un grupo cada vez mayor de especialistas se opone a esta iconografía cargada de sesgos históricos sobre género, etnia y religión que genera expectativas poco realistas y enmascara los efectos sociales de estas tecnologías.
 Las imágenes mediáticas que representan la IA como robots humanoides blancos y sensibles enmascaran la responsabilidad de los humanos que realmente desarrollan esta tecnología. Foto: Jezael Melgoza / Unsplash
Las imágenes mediáticas que representan la IA como robots humanoides blancos y sensibles enmascaran la responsabilidad de los humanos que realmente desarrollan esta tecnología. Foto: Jezael Melgoza / UnsplashEl 25 de abril de 2018, la Comisión Europea publicó un documento que marcó el inicio de su camino hacia la primera ley regulatoria de la inteligencia artificial del mundo. En él, se detallaban las recomendaciones presentadas por un grupo de expertos, se enumeraban los pasos a seguir y se proponían directrices éticas para una IA confiable. Sin llamar mucho la atención, una atractiva imagen acompañaba al texto: una mano humana y una mano robótica –brillante y metálica– se extendían delante de un fondo azul y gris, casi tocándose con las yemas de los dedos.
Inspirada en La creación de Adán de Miguel Ángel, fresco que desde el siglo XVI adorna el techo de la Capilla Sixtina en el Vaticano, esta composición que presenta a la IA como una fuerza creativa divina o como una chispa, una conexión entre lo humano y lo divino, se ha convertido en uno de los pósteres oficiales de la inteligencia artificial.
 Imágenes que recrean ‘La creación de Adán’ de Miguel Ángel son usadas con frecuencia para ilustrar la IA, como hizo la Comisión Europea en 2018. Fuente: Michelangelo / Comisión Europea
Imágenes que recrean ‘La creación de Adán’ de Miguel Ángel son usadas con frecuencia para ilustrar la IA, como hizo la Comisión Europea en 2018. Fuente: Michelangelo / Comisión EuropeaSe la ve una y otra vez en sitios de noticias y revistas, en publicidades, en portadas de libros, en comunicados de empresas, en afiches de cursos y conferencias, a la par de retratos pintorescos de robots humanoides siempre blancos, cerebros azules brillantes, placas de circuitos, código binario y trilladas referencias a personajes de ciencia ficción como Terminator.
Conforman la iconografía actual de la IA, su traducción visual, cada vez más criticada por especialistas que advierten sobre sus peligros y las suposiciones estereotipadas y potencialmente discriminatorias que arrastran sobre género, etnia y religión.
“Estas imágenes tergiversan completamente las realidades de la IA”, advierte a SINC la investigadora en ética Tania Duarte, fundadora de We and AI, una organización sin fines de lucro del Reino Unido que busca mejorar la alfabetización en inteligencia artificial para la inclusión social e impulsar el pensamiento crítico. “Refuerzan mitos sobre la IA –subraya–, ideas falsas sobre la infalibilidad, la sensibilidad y el misticismo religioso que envuelve a estas tecnologías y no ayudan al público a desarrollar una comprensión de lo que está en juego”.
El poder de la imagenComo hace tiempo explicó la escritora Susan Sontag, las imágenes son elementos poderosos. Enmarcan nuestra percepción del mundo, confirman, refuerzan o disipan estereotipos. Influyen en la forma en que la sociedad piensa y comprende temas que retratan. En el caso de la IA, ciertas ilustraciones exageran las capacidades de estos sistemas informáticos cada vez más ubicuos.
Otras, en cambio, siembran miedo, aumentan la desconfianza pública, enmascaran la responsabilidad de los humanos y perpetúan un entendimiento demasiado limitado y temeroso de la IA pero también misterioso, al no mostrar su contexto real, ni sus procesos y ni sus aplicaciones o limitaciones. Y desvían el debate sobre las consecuencias potencialmente significativas para la investigación, la financiación, la regulación y la recepción de estos sistemas cada vez más ubicuos.
Para combatir estos clichés y distorsiones, Duarte y un equipo de más de cien ingenieros, artistas, sociólogos y especialistas en ética impulsan un programa conocido como Better Images of AI.
Con el apoyo del Alan Turing Institute, el Centro Leverhulme para el Futuro de la Inteligencia y del departamento de investigación y desarrollo de la BBC, exponen cómo estas representaciones dominantes refuerzan conceptos erróneos y limitan la comprensión pública del uso y funcionamiento de los sistemas de IA.
“Necesitamos imágenes que retraten de manera más realista la tecnología y las personas detrás de ella y que señalen sus fortalezas, debilidades, contextos y aplicaciones”, indican sus promotores, que ofrecen un repositorio gratuito de mejores imágenes de IA y una guía de consejos para un uso responsable.
 Una de las imágenes del colectivo ‘Better Images of AI’. Fuente: Alan Warburton / BBC / Better Images of AIImperios visuales
Una de las imágenes del colectivo ‘Better Images of AI’. Fuente: Alan Warburton / BBC / Better Images of AIImperios visuales
Una parte importante de las fotografías e ilustraciones que se emplean en publicidades, marketing corporativo, diseño de sitios web y también en sitios de noticias provienen de “fábricas de imágenes”: el negocio de las fotografías de archivo o de stock, una industria global de miles de millones de dólares, dominada por un puñado de corporaciones transnacionales –Getty Images, Corbis, Alamy, Shutterstock, Adobe Stock, Science Photo Library (SPL), entre otras–, con una fuerza poderosa en la cultura visual contemporánea.
Como indican los investigadores Gaudenz Urs Metzger y Tina Braun de la Escuela Superior de las Artes de Zúrich (Suiza) en un estudio publicado en el Journal of Death and Dying, estas imágenes influyen en cómo se imagina un tema, así como en lo que se puede decir y no decir en una sociedad.
A medida que las empresas periodísticas invierten cada vez menos en fotógrafos y diseñadores de infografías, las imágenes de stock expanden su presencia.
Por lo general, se trata de montajes, gráficos o ilustraciones genéricas, con un estilo realista, aunque más simbólico que documental, que buscan atraer la atención del lector al representar visualmente temas complejos como las tijeras moleculares de la técnica CRISPR de edición genética, el mundo subatómico, el interior del cuerpo humano, la computación cuántica, el blockchain (cadena de bloques) o la computación en la nube.
En el caso de la IA, el robot humanoide blanco ha sido elevado en el último tiempo al rol de embajador visual de estas tecnologías complejas por directa influencia de la cultura popular. Como registró el AI Narratives Project de la Royal Society de Londres, existe una fuerte tendencia a concebir las máquinas inteligentes con forma humana.
Una IA con formas hipersexualizadas“Cuando las personas imaginan a otros seres inteligentes, estas imaginaciones tienden a tomar forma humanoide”, destaca el documento principal de esta iniciativa. “Una consecuencia de este antropomorfismo es que los sistemas de IA son con frecuencia representados con género: sus formas físicas a menudo no son andróginas, sino que tienen las características sexuales secundarias estereotipadas de hombres o mujeres. De hecho, a menudo están hipersexualizados: tienen cuerpos masculinos exageradamente musculosos y tendencias agresivas, como Terminator, o formas femeninas convencionalmente hermosas como Ava en la película Ex Machina”.
La IA y sus ramas, como el aprendizaje automático, no son temas sencillos de explicar ni de ilustrar. Pero imaginar estas tecnologías como androides es problemático: desinforma, plantea expectativas demasiado altas, sugiere que su fin último es el de reemplazar a los humanos y dificulta que se consideren sus beneficios reales. Además, cuanto más humanos se ven estas representaciones, más étnicamente blancas son sus características.
De ahí que Stephen Cave y Kanta Dihal, investigadores de la Universidad de Cambridge (Reino Unido), señalen en su ensayo The Whiteness of AI que la representación de la IA sufre de un problema racial. “Imaginar máquinas que sean inteligentes, profesionales o poderosas es imaginar máquinas blancas porque el marco racial blanco atribuye estos atributos predominantemente a la blancura”, dicen los también autores de Imagining AI: How the World Sees Intelligent Machines.
“En las sociedades europeas y norteamericanas, la blancura está normalizada hasta tal punto que la vuelve en gran medida invisible. Al centrar la blancura como el color predeterminado del futuro, estas imágenes contribuyen a imaginar un futuro tecnológico que excluye a las personas de color de la misma manera que lo hacen las grandes empresas tecnológicas en la actualidad”, apuntan.
Clichés visuales y confusión sobre la IALos clichés visuales son varios: placas de circuitos, código binario descendente, brillantes cerebros situados en un espacio oscuro y vacío, aislados de las necesidades de un cuerpo, es decir, una clara alusión a la inteligencia, si bien gran parte de la IA y el aprendizaje automático que se utilizan hoy en día están muy alejados de la inteligencia humana. “Las personas que no entienden qué es la IA no pueden defender las formas en que la tecnología debería o no impactar a la sociedad”, señala Duarte.
 Cerebros brillantes y robots blancos conforman la iconografía actual de la IA. Fuentes: Wiley / Routledge / Apress
Cerebros brillantes y robots blancos conforman la iconografía actual de la IA. Fuentes: Wiley / Routledge / ApressAdemás de la prevalencia de robots blancos, el color favorito de las empresas de tecnología para representar sus sistemas es el azul, usualmente asociado con inteligencia, confianza, seriedad, eficiencia pero también con masculinidad, como destaca la historiadora Alexandra Grieser en Blue Brains: Aesthetic Ideologies and the Formation of Knowledge Between Religion and Science.
“Existe una gran brecha entre la realidad de la IA y la percepción que tiene el público general, que es alimentada por representaciones en los medios y películas que a menudo presentan la IA como robots autónomos con capacidades casi humanas”, indica la desarrolladora de software mexicana Yadira Sánchez, asesora de Better Images of AI.
“Esta distorsión es preocupante porque impide que el público comprenda y participe efectivamente en debates cruciales sobre cómo la IA está remodelando áreas esenciales como la atención médica, la agricultura y la vigilancia estatal. Además –añade–, estas imágenes inexactas crean pensamientos futuristas muy optimistas o muy pesimistas sobre la IA y esto es peligroso porque generan expectativas y miedos en la sociedad”.
Otras imágenes para minimizar la confusiónPara minimizar la confusión, sostienen los investigadores de Better Images of AI, es importante utilizar imágenes que representen honestamente la realidad de la IA, como los recursos naturales y materiales que se consumen en su desarrollo. Por ejemplo, la extracción de litio en América Latina, o el agua y los ríos que se usan para mantener centros de datos en funcionamiento.
“Deberíamos mostrar cómo la IA se integra y afecta nuestros entornos naturales y sociales”, agrega Sánchez, “y cómo su infraestructura impacta directamente en el ecosistema y la vida cotidiana de las personas”.
“La enfermedad de la fotografía de stock de la IA ha alcanzado el estado epidémico”, señaló hace unos años el investigador Adam Geitgey, especialista en aprendizaje automático y reconocimiento facial. Aunque la IA no es la única rama científica que sufre estas tergiversaciones visuales. Más bien, todas las disciplinas, en algún grado u otro, las padecen cuando son representadas en periódicos, avisos publicitarios, campañas públicas o en webs de instituciones.
“Los medios optan por la solución más sencilla: utilizar imágenes que la gente reconozca y asocie rápidamente con la ciencia”, apunta la socióloga portuguesa Ana Delicado, quien estudió las representaciones visuales de la ciencia durante la pandemia de la covid-19 en sitios web de instituciones políticas y medios de comunicación en Portugal y España.
“Las imágenes de stock siempre se basan en estereotipos. Son productos comerciales: su objetivo es vender, no reflexionar sobre los temas que venden. Las imágenes estereotipadas en los medios de comunicación contribuyen a perpetuar representaciones estereotipadas en la opinión pública”, recalca.
En su análisis, publicado en la revista Frontiers in Communication, esta investigadora del Instituto de Ciencias Sociales da Universidad de Lisboa registró el abuso de ilustraciones del coronavirus SARS-CoV-2 con sus púas y pintado de rojo, haciéndolo parecer más amenazador.
También detectó una gran lista de elementos visuales que aluden a la actividad científica: hélices de ADN, células, moléculas, radiografías, equipos de laboratorio como microscopios, tubos, placas de Petri y pipetas, a menudo sostenidos por manos incorpóreas enguantadas, así como la presencia de personas con batas blancas, gafas protectoras y mascarillas, pero sin diversidad étnica, lo que refleja la subrepresentación de las minorías en la comunidad científica.
“La elección de imágenes para ilustrar la ciencia de la covid-19 tiende a reproducir nociones estereotipadas de la investigación científica como una actividad centrada en el laboratorio”, indica Delicado.
Nuevos generadores del imágenesAhora, con el auge de los sistemas de IA generadores de imágenes, como Stable Diffusion, Midjourney y DALL·E, se teme que empeoren las distorsiones sobre la realidad de la IA y la actividad científica en general. Como ya han demostrado algunas investigaciones, estas herramientas que producen imágenes a partir de indicaciones de texto suelen dar resultados racistas y sexistas.
Es decir, reproducen y amplifican sesgos raciales y de género, pues son entrenadas con imágenes utilizadas por medios de comunicación, organizaciones mundiales de salud y bases de datos de internet. “Estas imágenes son utilizadas sin crítica, sin reflexión”, advierte la socióloga portuguesa, “y la IA va a seguir perpetuando los estereotipos sobre la ciencia y las tecnologías”.
Una versión de este artículo fue publicada originalmente en SINC el 3 de mayo de 2024.
El artículo Las mentiras visuales de la IA se ha escrito en Cuaderno de Cultura Científica.
El protagonismo de los cuidados en la evolución humana

Los cambios del cerebro durante el embarazo y la maternidad, cómo el estrés ha pasado de ser un mecanismo de supervivencia a un eventual elemento de riesgo para nuestra salud o cuál ha sido el papel que ha jugado el suicidio en la evolución del ser humano fueron algunos de los temas que se tratarán en la VI Jornada Nacional sobre Evolución y Neurociencias.
La jornada tuvo lugar el Bizkaia Aretoa de la UPV/EHU los pasados 25 y 26 de abril y estuvo dirigida por Eva Garnica y Pablo Malo, de la Red de Salud Mental de Bizkaia, institución que organizó la jornada junto a la Cátedra de Cultura Científica de la UPV/EHU.
El encuentro, cuya primera edición se celebró en 2017, se ha convertido en una cita imprescindible para las y los expertos en ámbitos como la psiquiatría, la psicología o la biología. Una jornada que sirve para analizar el comportamiento humano desde un punto de vista evolutivo y divulgar de un modo accesible para todos los públicos.
¿Cuándo comenzamos a cuidarnos entre los humanos? ¿Cómo se encuadra este comportamiento en nuestra evolución? Los orígenes de los cuidados están estrechamente vinculados al desarrollo de comportamientos que consideramos emblemáticamente humanos: en particular, nuestra disposición a cooperar por un bien mayor y nuestras habilidades de organización social. Explorar cuándo y por qué surgió este rasgo es un reto apasionante, y debe hacernos reflexionar sobre el impacto que su estudio debe producir, y produce, en la ciencia y en la sociedad actual. Estos son los temas que trata la conferencia El protagonismo de los cuidados en la evolución humana. La imparte Roberto Sáez, Doctor en Antropología, Máster en Ingeniería Industrial y divulgador científico, experto en Evolución Humana y en la Bioarqueología del Cuidado. Sáez es el autor del blog Nutcracker man.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo El protagonismo de los cuidados en la evolución humana se ha escrito en Cuaderno de Cultura Científica.
Uso y abuso de la pregabalina
 Envase de Lyrica (pregabalina) comercializado en Finlandia. Fuente: Acdx / Wikimedia Commons
Envase de Lyrica (pregabalina) comercializado en Finlandia. Fuente: Acdx / Wikimedia CommonsEl pasado mes de marzo, una noticia llegada desde Reino Unido generó cierta alarma respecto a la seguridad de la pregabalina, medicamento utilizado frecuentemente para el tratamiento del dolor crónico y la ansiedad. Una investigación del periódico británico The Sunday Times relacionaba el consumo de este fármaco con la muerte de 3 400 personas en los últimos años y describía los problemas de abuso y adicción que puede generar.
Dada la gravedad de la crisis sociosanitaria que sufre EE. UU. por la adicción a los opioides, los problemas de seguridad que puede plantear el uso de medicamentos como la pregabalina constituye un tema de especial interés.
Usos no contemplados en la ficha técnicaLa pregabalina es un medicamento con una estructura química similar a la del neurotransmisor GABA (ácido gamma-amino-butírico), sustancia que regula de forma inhibitoria la actividad del cerebro. Junto con la gabapentina, forma un grupo de medicamentos denominado gabapentinoides.
En España, el primer medicamento con pregabalina lo lanzó al mercado el laboratorio farmacéutico Pfizer, con el nombre comercial Lyrica. Inicialmente, fue aprobado para tratar la epilepsia y el dolor neuropático, y después se autorizó para tratar el trastorno de ansiedad generalizada.
Con el tiempo, el uso de Lyrica se amplió para tratar otras patologías que no contaban con la autorización sanitaria, como el dolor crónico, el dolor lumbar, la prevención del dolor postoperatorio, la fibromialgia y la profilaxis de la migraña. Esta aplicación se conoce como off-label o fuera de ficha técnica. En ocasiones, dichos usos pueden estar médicamente justificados si no existen alternativas terapéuticas autorizadas, y en todo caso se encuentran regulados por ley.
Lo que está prohibido es publicitarlo, y esto condenó a Pfizer a pagos de multas millonarias. Es conveniente recordar que el uso off-label de los medicamentos puede constituir un problema de seguridad, incrementar los costes del tratamiento o, directamente, resultar ineficaz, ya que se ha demostrado que su beneficio terapéutico es insuficiente.
Sin embargo, distintos estudios concluyen que más de la mitad de las recetas de gabapentinoides se realizan para indicaciones no autorizadas; mayoritariamente para tratar distintos tipos de dolor, a pesar de que los estudios científicos no recomiendan su uso.
Un consumo disparadoHoy en día, disponemos de 168 medicamentos que contienen pregabalina, incluidos los llamados genéricos. Los datos de consumo se pueden consultar en la página web de la Agencia Española de Medicamentos y Productos Sanitarios (AEMPS), concretamente en el informe sobre la utilización de analgésicos no opioides.
Esta información se expresa en DHD, es decir, en la dosis diaria definida (DDD) por cada 1 000 habitantes y día. Así sabemos que en los últimos 10 años el consumo de pregabalina se ha incrementado un 66 %, puesto que entre 2012 y 2022 el DHD pasó de 3,56 a 5,92. Este último dato significa que cada día un promedio de 5,92 personas de cada 1 000 recibe una DDD de pregabalina. Actualmente, se encuentra en el tercer puesto de fármacos analgésicos no opioides con mayor consumo en España, por detrás del paracetamol y el metamizol.
¿Es seguro tomar pregabalina?La pregabalina, como todos los medicamentos, no está libre de producir efectos adversos, es decir, efectos que no deseamos pero que en muchos casos no se pueden evitar. Por suerte, los más frecuentes, que aparecen en al menos una de cada 10 personas, son leves. Entre ellos destacan los mareos, la somnolencia y el dolor de cabeza.
También pueden manifestarse otros con menor frecuencia. Todos ellos pueden ser consultados en la ficha técnica en la página web del centro de información de la AEMPS, de acceso abierto, o en el prospecto del medicamento. Es importante señalar que los efectos adversos son más frecuentes cuando la pregabalina se toma en dosis altas y de forma crónica. Y en cualquier caso, este tipo de uso no ha demostrado aliviar mejor del dolor.
Entre los efectos más graves encontramos el riesgo de reducir la respiración, debido a que actúan sobre la zona del cerebro que controla esa función. Es importante tener esto en cuenta si el paciente ya está tomando otros medicamentos que tienen el mismo efecto, ya que su combinación en dosis altas podría llegar a paralizar la respiración y causar la muerte.
Estos otros medicamentos depresores son los analgésicos opioides (como la morfina), que utilizamos para aliviar dolores fuertes, y las benzodiazepinas (como el orfidal), que tomamos para dormir o calmar los nervios. Diversos estudios indican que el 60 % de los pacientes que usa gabapentinoides toma también los otros depresores. Una combinación fatal podría estar detrás del incremento de muertes asociadas al uso de pregabalina que describía el The Sunday Times.
Ese mismo efecto depresor de la pregabalina, pero ejercido sobre el sistema límbico del cerebro, produce una sensación de euforia y bienestar que puede conducir a comportamientos de abuso y dependencia. El concepto de dependencia se refiere a la necesidad de seguir tomando una sustancia para experimentar sus efectos deseados o aliviar el malestar que causa no consumirla (síndrome de abstinencia).
Si no se ingiere el medicamento, aparecen síntomas que provocan malestar y empujan a seguir tomándolo, a pesar de los posibles efectos negativos; es lo que coloquialmente llamamos “estar enganchado”. Son especialmente vulnerables aquellas personas que han sufrido con anterioridad problemas de adicción.
Siempre bajo supervisión médicaLos riesgos asociados al abuso de pregabalina pueden minimizarse con un seguimiento adecuado de la pauta médica, valorando periódicamente la necesidad de mantener o retirar el tratamiento según criterios de eficacia, tolerabilidad, efectos adversos y adherencia. Si la valoración recomienda suspender el tratamiento, se realizará de forma gradual y con supervisión médica.
En todo caso, la pregabalina está autorizada para tratar el dolor neuropático –que se produce por el daño de un nervio–, la epilepsia y la ansiedad porque los estudios indican que los beneficios del tratamiento superan los riesgos. En este contexto, la evaluación de la relación riesgo-beneficio del tratamiento con pregabalina corresponde a los profesionales médicos y cuentan con el apoyo de la AEMPS.
Finalmente, no podemos olvidar el papel de la ciudadanía en la gestión activa de su salud: es fundamental seguir las indicaciones médicas y comunicar si sufrimos efectos adversos y si notamos que el tratamiento no está funcionando. Transmitir toda esta información en las visitas a la consulta es clave para que el médico o la médica evalúe correctamente la utilidad del tratamiento y su seguridad.![]()
Sobre las autoras: María Torrecilla Sesma y Cristina Bruzos Cidón son Profesoras de Farmacología en la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Uso y abuso de la pregabalina se ha escrito en Cuaderno de Cultura Científica.
Un coloso de la informática
El 18 de enero de 1944, llegó a Bletchley Park un camión con una carga muy especial: una máquina de cálculo que pesaba una tonelada, medía 2,13 x 5,18 x 3,35 metros, estaba construida con alrededor de 1600 válvulas termoiónicas y era capaz de operar a una velocidad de 5000 caracteres por segundo. La llamaron Colossus, se considera la primera computadora electrónica, programable y digital de la historia… y estuvo a punto de no existir.
Durante la Segunda Guerra Mundial, Bletchley Park fue uno de los centros neurálgicos de los servicios de inteligencia británicos. Bajo el nombre en clave de Ultra, allí se descifraban todas las comunicaciones que Inglaterra interceptaba al Ejército y la diplomacia de la Alemania nazi y pasó a la historia, sobre todo, por el duelo que tuvo lugar allí entre el matemático inglés Alan Turing y la supuestamente impenetrable Enigma naval de la Kriegsmarine que utilizaban los U-Boote del Atlántico.
 Máquina enigma de cuatro rotores expuesta en Bletchley Park. Funete: Tim Gage / CC BY-SA 2.0
Máquina enigma de cuatro rotores expuesta en Bletchley Park. Funete: Tim Gage / CC BY-SA 2.0
En 1941, casi a la par que la Enigma naval quedaba al descubierto tras un arduo trabajo por parte del barracón 8 que dirigía Turing, las estaciones de escucha británicas comenzaron a interceptar una nueva clase de mensajes indescifrables que no se estaban retransmitiendo en morse, como los de Enigma, sino en el código internacional del teletipo. Alemania había puesto en escena una nueva máquina de cifrado automática y mucho más sofisticada que Enigma para las comunicaciones diplomáticas: la Lorenz SZ, a la que apodaron Tunny.
En este caso, fue el coronel John Tiltman quien consiguió descifrar un mensaje de Tunny por primera vez a finales de aquel mismo año. Con el trabajo de este, el matemático Bill Tutte dedujo cómo debía de ser el funcionamiento de la máquina. Por último, Alan Turing ideó un método algorítmico, la «turingería» ―de «Turing» e «ingeniería»― que permitió acotar sustancialmente las posibles configuraciones de los doce rotores de los que constaba el disposivo y… entonces se marchó a Estados Unidos.
 Máquina de cifrado Lorenz SZ40, sin la carcasa, en el US National Cryptologic Museum. En ella se pueden apreciar los doce rotores. Fuente: Mark Pellegrini / CC BY-SA 2.5
Máquina de cifrado Lorenz SZ40, sin la carcasa, en el US National Cryptologic Museum. En ella se pueden apreciar los doce rotores. Fuente: Mark Pellegrini / CC BY-SA 2.5
Fue Bill Tutte el que continuó trabajando en nuevos métodos de descifrado de Tunny, pero, a medida que Alemania aumentó la extensión aquella red de comunicaciones, que los aliados bautizaron como Fish, y mejoró la seguridad, los cálculos empezaron a volverse inabarcables: se iba a necesitar algún tipo de dispositivo electromecánico para realizarlos, al igual que se habían necesitado las Bombe para poder romper Enigma.
El primer intento de mecanizar el descifrado de Tunny vino de la mano de Max Newman y sus «Heath Robinson» unos cacharros llamados así en honor a William Heath Robinson, un ilustrador que solía hacer dibujos de inventos bizarros dada la lentitud, imprecisión y tendencia al sobrecalentamiento que tenían. Pero un ingeniero eléctrico de Bletchley Park, al que, en un principio, habían reclutado como ayudante de Alan Turing, tenía en mente desde hacía algún tipo una idea de máquina mucho más rápida, precisa y eficiente.
 Réplica de una de las Heath Robinson de Max Newman en el National Museum of Computing, de Bletchley Park. Fuente: TedColes / CC BY-SA 4.0
Réplica de una de las Heath Robinson de Max Newman en el National Museum of Computing, de Bletchley Park. Fuente: TedColes / CC BY-SA 4.0
Tommy Flowers había nacido en una familia humilde en uno de los distritos más pobres de Londres, Poplar, muy cerca de Whitechapel, y ya desde muy pequeño le había llamado la atención la ingeniería. Estuvo durante un tiempo como aprendiz en el Arsenal Real de Londres hasta que encontró trabajo en el departamento de ingeniería de Correos mientras se sacaba el título en la escuela nocturna. Allí conoció y empezó a investigar las posibilidades que ofrecía un nuevo componente electrónico que podía realizar tareas de interruptor a una velocidad mucho más alta de la habitual: la válvula termoiónica o de vacío.
 Tommy Flowers. Fuentes: Dominio público
Tommy Flowers. Fuentes: Dominio público
Aunque ya se estaban utilizando en algunos dispositivos ―y las Heath Robinson eran uno de ellos, aunque solo parcialmente―, el uso de las válvulas de vacío aún era bastante limitado. Tommy Flowers fue el primero al que se le ocurrió que podían utilizarse en un número mucho mayor para fabricar máquinas de computación completamente electrónicas. Pero, como sucede casi siempre que alguien presenta una idea demasiado disruptiva, en Bletchley Park aquello les pareció una locura.
Sin el apoyo que necesitaba, pero convencido de que un computador completamente electrónico era posible, pese a las dificultades de diseño que presentaba, Flowers reunió a cincuenta científicos, ingenieros y técnicos del laboratorio de la oficina de Correos de Dollis Hill donde trabajaba y se pusieron manos a la obra, trabajando doce horas al día, seis días y medio a la semana para crear, en un tiempo récord de diez meses, el primer computador electrónico: Colossus. Cuando se presentaron con él en Bletchley Park y, más aun, cuando lo pusieron en funcionamiento, el personal no daba crédito a lo que tenía delante.
El primer prototipo de Colossus que llegó a Bletchley funcionaba muy bien, pero no lo todo lo rápido que se necesitaba, así que Tommy Flowers y su equipo se pusieron de nuevo a trabajar contrarreloj en una versión mejorada que el Gobierno quería tener lista, como muy tarde, para el 1 de junio: aquella iba a ser la fecha inicial en la que iba a tener lugar el Día-D y se necesitaba que la máquina estuviera ya operativa. Colossus Mark II, con 2400 válvulas y una velocidad de 25 000 caracteres por segundo, lo estuvo y, de hecho, el 5 de junio se descifró con ella un mensaje de Adolf Hitler dirigido al mariscal Erwin Rommel en el que los aliados pudieron confirmar que la maniobras de los servicios secretos para desviar la atención del Führer lejos de las playas de Normandía había funcionado. Al día siguiente, el Ejército aliado tomó la costa francesa y comenzó la ofensiva por la liberación de Europa occidental. Mientras tanto, una Colossus tras otra iba llegando a Bletchley Park a medida que las fuerzas aliadas penetraban en el continente. Veinticuatro horas al día, siete días la semana, un ejército de WRENs ―mujeres pertenecientes al Women’s Royal Naval Service― averiguaba sin descanso la configuración diaria de la las máquinas Tunny y dejaba al descubierto las comunicaciones enemigas.
 Colossus Mark II en Bletchley Park, operada por las WRENs (Women’s Royal Naval Service) Dorothy Du Boisson y Elsie Booker en 1943.
Colossus Mark II en Bletchley Park, operada por las WRENs (Women’s Royal Naval Service) Dorothy Du Boisson y Elsie Booker en 1943.
A menudo se ha tratado de establecer el impacto que todo el trabajo de criptoanálisis de Bletchley Park tuvo sobre el desarrollo de la guerra. Hay quienes dicen que ayudó a acortar el conflicto en unos dos o tres años, por ello, resulta bastante inquietante pensar que Colossus fue posible gracias a una serie de serendipias que podrían, perfectamente, no haber tenido lugar.
A finales de agosto de 1939, y con las tensiones en Europa a punto de hacer estallar todo, algún superior no muy centrado envió a Tommy Flowers a Berlín en viaje de trabajo. Tan pronto como este puso el pie en la capital alemana, la Embajada británica lo llamó para advertirle de que abandonara el país lo antes posible. Flowers consiguió cruzar a Holanda apenas unas horas antes de que se cerraran las fronteras de Alemania, evitando así, seguramente, acabar como prisionero del régimen nazi. También fue providencial que luego la oficina de Correos lo enviara a él, y no a otro, a ayudar a Alan Turing con Enigma y las Bombe, porque cuando alguien iba a consultarle al matemático cualquier tema de ingeniería o problema con los equipos, Alan simplemente respondía: «Flowers»… Lo que llevó a este hasta Newman, luego hasta Tunny, luego hasta Colossus y, finalmente, a marcar ―casualidades que pasan― el primer gran hito de la historia de la computación.
Referencias:
Copeland, B. Jack, et. al. (2006). Colossus. The secrets of Bletchley Park’s codebreaking computers. Oxford University Press.
Copeland, B. Jack (2021 [2013]). Alan Turing. El pionero de la era de la información. Turner.
Para saber más:
Marian Rejewski, el matemático que «rompió» la Máquina Enigma
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo Un coloso de la informática se ha escrito en Cuaderno de Cultura Científica.
El infinito en un segmento (3)
A finales del siglo XIX, el matemático ruso-alemán Georg Cantor (1845-1918) conmocionó al mundo de las matemáticas, rompiendo las creencias existentes sobre el concepto de infinito. Entre los revolucionarios resultados que demostró están que existe más de un infinito o que la cantidad de puntos de un segmento es la misma que la cantidad de puntos de un cuadrado. A esta revolución matemática hemos dedicado, en el Cuaderno de Cultura Científica, la miniserie titulada El infinito en un segmento.
 Página de la novela gráfica Logicomix, de Apostolos Doxiadis y Christos H. Papadimitiou, Bloomsbury, 2009. En la viñeta se muestra una noticia con motivo del Congreso Internacional de Matemáticos de 1900, con una caricatura de dos matemáticos enfrentados, el francés Henri Poincaré, con su frase “¡Le acuso Señor Cantor! ¡La teoría de conjuntos es una enfermedad de la que hay que curar a las matemáticas!”, y el alemán David Hilbert, con su frase “Nadie nos expulsará del paraíso que Herr Cantor ha creado para nosotros”
Página de la novela gráfica Logicomix, de Apostolos Doxiadis y Christos H. Papadimitiou, Bloomsbury, 2009. En la viñeta se muestra una noticia con motivo del Congreso Internacional de Matemáticos de 1900, con una caricatura de dos matemáticos enfrentados, el francés Henri Poincaré, con su frase “¡Le acuso Señor Cantor! ¡La teoría de conjuntos es una enfermedad de la que hay que curar a las matemáticas!”, y el alemán David Hilbert, con su frase “Nadie nos expulsará del paraíso que Herr Cantor ha creado para nosotros”
La primera entrega de esta miniserie, El infinito en un segmento (1), se centró en cómo resolvió el matemático ruso-alemán el problema de comparar dos conjuntos con infinitos elementos. La respuesta es sencilla y está en la base del origen del concepto de número. Dos conjuntos tienen la misma cantidad de elementos cuando se puede establecer una “correspondencia uno-a-uno” entre los elementos de los dos conjuntos. De esta forma, llegamos a la paradoja de que para un conjunto infinito existen subconjuntos propios del mismo que tienen la misma cantidad de elementos que el propio conjunto. Por ejemplo, el conjunto de los números pares tiene la misma cantidad de elementos que el conjunto de los números naturales (que está formado por los números pares y los números impares).
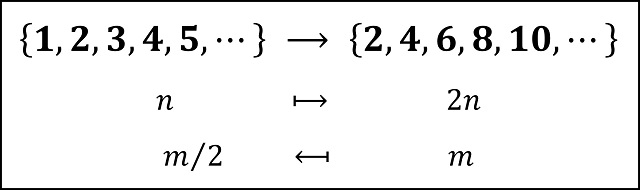 Existe una correspondencia uno-a-uno entre el conjunto de los números pares y el conjunto de los números naturales
Existe una correspondencia uno-a-uno entre el conjunto de los números pares y el conjunto de los números naturales
De hecho, Georg Cantor tomó esta paradoja del ininfito como definición de “conjunto infinito”, es decir, un conjunto es infinito si existe un subconjunto propio suyo que tiene la misma cantidad de elementos que el conjunto.
En esta primera entrega de la serie se demostró también que los conjuntos de los números enteros y de los números racionales son conjuntos numerables, es decir, tienen la misma cantidad de elementos que el conjunto de los números naturales.
En la segunda entrega de esta miniserie, El infinito en un segmento (2), se mostró que el conjunto de los números reales (de forma explícita, en la demostración se consideró el intervalo (0,1), es decir, los números reales entre 0 y 1) no es numerable, no se puede poner en correspondencia uno-a-uno con los números naturales. Por lo tanto, existe más de un infinito, al menos, el infinito de los números naturales (cuyo cardinal se denomina aleph-zero) y el infinito de los números reales (cuyo cardinal se denomina cardinal del continuo, c).
 El bueno de Cuttlas (4MOR, 37 & 99), de Calpurnio, publicado en 20 MinutosEl infinito en un cuadrado
El bueno de Cuttlas (4MOR, 37 & 99), de Calpurnio, publicado en 20 MinutosEl infinito en un cuadrado
Como se comentó al final de la segunda entrada de esta miniserie, una vez demostrado que el cardinal del continuo c (el infinito de los números reales) es mayor que aleph-zero (el infinito de los números naturales), Georg Cantor se planteó si el plano (de dimensión 2) tiene una mayor cantidad de puntos que la recta (de dimensión 1), es decir, si el infinito del plano es mayor que el infinito del continuo. Simplificando la cuestión.
Problema: ¿Hay la misma cantidad de puntos en el segmento unidad [0,1] que en el cuadrado unidad [0,1] x [0,1]?

Para abordar el anterior problema, primero recordemos un par de cuestiones básicas. La primera es que los números reales del intervalo [0,1], es decir, mayores que 0 y menores que 1, se escriben en forma decimal como
donde, si todos los dígitos son 0 se obtendría el número cero (0), y si todos los decimales son 9 se obtendría el número uno (1), ya que, como se comentó en la anterior entrada, el número 1 se puede representar de dos formas distintas 1,00000000… (infinitos ceros) y 0,99999999… (infinitos nueves). Por ejemplo, el número pi menos 3, que es un número real del intervalo (0,1) se expresa como 0,1415926535…
La segunda cuestión básica es que todo elemento del plano real se puede identificar con sus coordenadas cartesianas, es decir, con un par (x, y), donde x e y son números reales, como se muestra en la siguiente imagen (aunque en ella solamente se han utilizado puntos cuyas coordenadas x e y son números enteros).
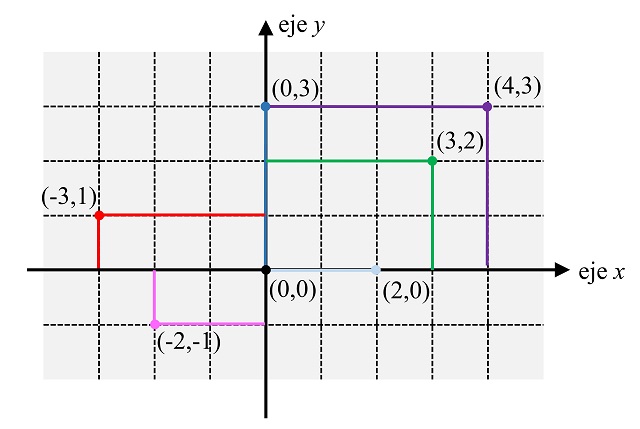
De manera, que los elementos del cuadrado [0,1] x [0,1], serán los puntos del plano (x, y), donde x e y son números reales del intervalo [0,1]. Es decir, son de la forma
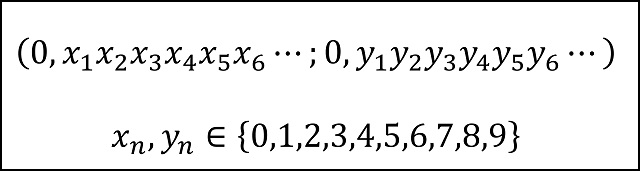 (Nota: hemos utilizado el punto y coma “;” para separar las coordenadas, en lugar de la tradicional coma “,”, con la intención de que quede más clara la separación entre las dos coordenadas)
(Nota: hemos utilizado el punto y coma “;” para separar las coordenadas, en lugar de la tradicional coma “,”, con la intención de que quede más clara la separación entre las dos coordenadas)
Ahora, una cuestión técnica. Antes de entrar en la construcción de la buscada correspondencia uno-a-uno entre el segmento y el cuadrado, vamos a tener en cuenta lo siguiente, de cara a dicha construcción. Como se puede demostrar (aunque no quiero meterme ahora en esta cuestión para no complicar más esta entrada) que los segmentos [0,1], es decir, los números reales mayores o iguales que 0 y menores o iguales que 1; (0,1], es decir, los números reales mayores que 0 y menores o iguales que 1; y (0,1), es decir, los números reales mayores que 0 y menores que 1, tienen la misma cantidad de elementos (existen correspondencias uno-a-uno entre ellos), es equivalente demostrar que existe una correspondencia uno-a-uno entre el segmento [0,1] y el cuadrado [0,1] x [0,1], que entre el segmento (0,1] y el cuadrado (0,1] x (0,1] o que entre el segmento (0,1) y el cuadrado (0,1) x (0,1). Por motivos técnicos, nosotros vamos a centrarnos en construir una correspondencia uno-a-uno entre el segmento (0,1] y el cuadrado (0,1] x (0,1], es decir, los puntos (x, y) tales que sus coordenadas x e y pertenecen a (0, 1].
Por lo tanto, ya estamos en condiciones de mostrar la construcción de Georg Cantor de la correspondencia uno-a-uno entre los elementos del segmento (0,1] y los elementos del cuadrado (0,1] x (0,1], que prueba que ambos conjuntos tienen la misma cantidad de elementos. La idea básica es asignar a cada elemento A del intervalo (0,1], es decir, un número real con su expresión decimal (por ejemplo, 0,1234567891011…), un elemento (B, C) del cuadrado (0,1] x (0,1] tal que los decimales de la primera coordenada B son los decimales en las posiciones impares de A y los decimales de la segunda coordenada C son los decimales en posiciones pares de A, como se muestra en la imagen.
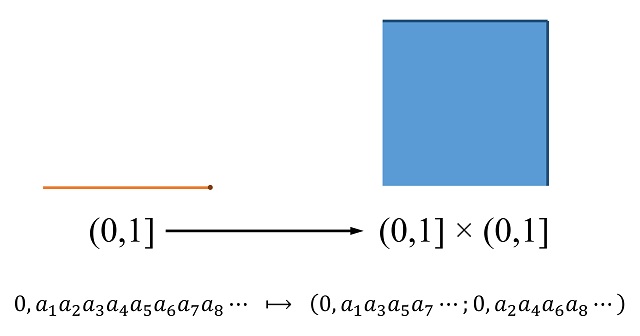
Y cuya aplicación inversa, es decir, que envía los elementos del cuadrado (0,1] x (0,1] en elementos del segmento (0,1], está definida mediante la construcción inversa, juntando los decimales de ambas coordenadas e intercalándolos en posiciones impares y pares.
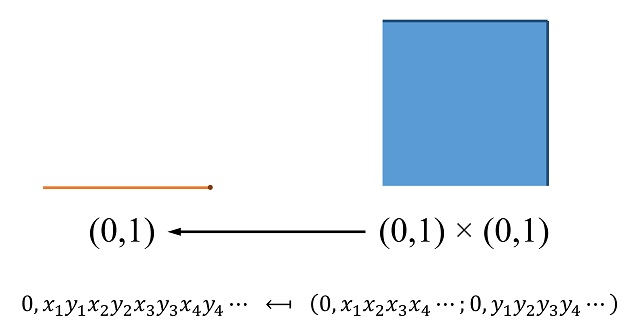
Por ejemplo, la imagen de la conocida “constante de Champernowne”, que es el número real, entre 0 y 1, cuyos decimales son los números naturales ordenados de izquierda a derecha, es decir,
0,123456789101112131415161718192021…
es el punto del cuadrado (0,1] x (0,1] cuyas coordenadas son
(0,135790123456789012…; 0,24681111111111222…).
Por otra parte, si tomamos el punto del cuadrado (0,1] x (0,1] dado por las coordenadas (x, x), donde x es la raíz de 2 menos 1, es decir, el punto
(0, 41421356237309…; 0, 41421356237309…),
su imagen, mediante la aplicación inversa, es el elemento del segmento (0,1] dado por la siguiente expresión
0, 4411442211335566223377330099…
Resolviendo algunas cuestiones técnicasLa idea de Cantor es ingeniosa, sin embargo, el hecho de que haya números reales, en concreto, los números racionales con un número finito de decimales (incluido en caso en el que no hay decimales, es decir, los números enteros) que tienen dos representaciones genera algunos problemas en la anterior aplicación, que hay que resolver.
Problema 1. Como decíamos, hay números que tienen dos representaciones decimales, por ejemplo, el número racional 11/20 se puede representar como 0,55 (o si lo preferimos 0,55000000…) y 0,54999999… Esto es un problema, ya que ese número racional tendría dos posibles imágenes mediante la anterior construcción
(0,500000…; 0,500000…) y (0,599999…; 0,499999…).
Por lo tanto, lo que hizo Cantor fue quedarse con una única representación de las dos, la que tiene infinitos nueves, en este caso, 0,54999999… De esta forma, solo existe, a priori, una imagen en (0,1] x (0,1] de cada número real de (0,1], que, en el ejemplo anterior, es (0,599999…; 0,499999…).
Problema 2. Pero al elegir una única representación de las dos se genera un problema añadido, ya que puede haber números reales de (0,1] cuya imagen contenga una expresión de las primeras y ya no sea válida, como 118/275 = 0,429090909…, cuya imagen sería, por la construcción de Cantor, el punto del cuadrado (0,49999…; 0,20000…), que ya no es un punto válido puesto que para el número 0,2 se ha elegido la representación 0,199999… Notemos que si se admitiesen aquí las dos representaciones se tendría que dos números reales distintos 0,429090909… y 0,4199999999… tendrían la misma imagen (0,49999…; 0,20000…) = (0,49999…; 0,19999…), es decir, la correspondencia no sería uno-a-uno.
Este nuevo problema lo resuelve Cantor de una forma ingeniosa. En la aplicación del segmento (0,1] en el cuadrado (0,1] x (0,1], en lugar de separar dígitos en posiciones pares e impares (y en la aplicación inversa intercalar los dígitos de las dos coordenadas del punto), lo que propone es separar (respectivamente, intercalar) grupos de dígitos, de manera que los ceros consecutivos dentro de la representación decimal se “pegan” al siguiente dígito no nulo. Por ejemplo, los grupos de dígitos de 118/275 = 0,429090909… serían
4 / 2 / 9 / 09 / 09 / 09 …
Por lo tanto, su imagen mediante la aplicación de Cantor sería ahora
(0,49090909…; 0,2090909…).
De hecho, el punto (0,49090909…; 0,2090909…) sería el único punto de (0,1] x (0,1] cuya imagen es 118/275 = 0,429090909…
Veamos otro ejemplo. El número real 0,01002000300004000005… tendría los siguientes grupos de dígitos
01 / 002 / 0003 / 00004 / 000005 …
por lo que su imagen sería el punto del cuadrado de coordenadas (0,010003000005…; 0,002000040000006…). Y ese punto del cuadrado es el único cuya imagen inversa es el número real 0,01002000300004000005…
Por supuesto, los números que no tienen ceros entre sus decimales funcionan como antes. Así, 1/2 = 0,4999999… tiene como imagen (0,4999999…, 0,9999999) y este punto es el único cuya imagen inversa es 1/2 = 0,4999999…
En conclusión, Cantor demostró que existen tantos puntos en el intervalo (0,1], como en el cuadrado (0,1] x (0,1].
 Retrato del matemático ruso-alemán Georg Cantor, de alrededor de 1910. Imagen obtenida de “Library of Congress, courtesy AIP Emilio Segrè Visual Archives”
Retrato del matemático ruso-alemán Georg Cantor, de alrededor de 1910. Imagen obtenida de “Library of Congress, courtesy AIP Emilio Segrè Visual Archives”Bibliografía
1.- R. Ibáñez, La gran familia de los números, Libros de la Catarata – FESPM, 2021.
2.- David Foster Wallace, Todo y más, Breve historia del infinito, RBA, 2013.
3.- J. Stillwell, The Real Numbers: An Introduction to Set Theory and Analysis, Undergraduate Texts in Mathematics, Springer, 2013.
4.- Eli Maor, To infinity and Beyond, A Cultural History of Infinity, Birkhauser, 1987.
5.- José A. Prado-Bassas, Historia del infinito (el apasionante relato de uno de los conceptos más profundos y enigmáticos de las matemáticas), Pinolia, 2023.
6.- Erich Kamke, Theory of Sets, Dover, 1950.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El infinito en un segmento (3) se ha escrito en Cuaderno de Cultura Científica.
La carga efectiva del protón depende del isospín
Al calcular las propiedades de los núcleos pesados los teóricos suelen centrarse en un subconjunto de los nucleones (protones y neutrones) y suponen que estas partículas tienen “cargas efectivas” que de alguna manera compensan todos los nucleones que se ignoran. Sin embargo, elegir las cargas efectivas adecuadas puede resultar complicado. Ahora Andrea Jungclaus, del Instituto de Estructura de la Materia (IEM-CSIC), y sus colegas han proporcionado la primera evidencia experimental clara de que las cargas efectivas dependen del isospín (groseramente, la proporción neutrón-protón) y han medido esta dependencia de forma inequívoca. La nueva información debería mejorar la precisión de los cálculos para núcleos pesados y ricos en neutrones, para los cuales existen datos experimentales limitados.
 El Radioactive Isotope Beam Factory de RIKEN, donde se realizaron los experimentos. Fuente: RIKEN
El Radioactive Isotope Beam Factory de RIKEN, donde se realizaron los experimentos. Fuente: RIKENLas partículas subatómicas que interaccionan a través de la interacción fuerte se conocen como hadrones. Esta categoría incluye a los protones, los neutrones y los piones. El espín isotópico o isospín es un número cuántico que se aplica a los hadrones para diferenciar los elementos de un conjunto de partículas que difieren en sus propiedades electromagnéticas pero que, por lo demás, son indiscernibles. Así, si se ignoran las interacciones electromagnéticas y débiles, el protón no puede distinguirse del neutrón por sus interacciones fuertes: el isospín se introdujo para distinguirlos.
El modelo nuclear de capas asigna a cada nucleón un estado de partícula única que es similar al orbital de un electrón en un átomo. La investigación había demostrado previamente que la carga efectiva es diferente para diferentes núcleos, pero no había quedado claro si la variación era atribuible a diferencias en la configuración orbital de los núcleos o a diferencias en el isospín (o ambas).
Jungclaus y sus colegas aislaron el efecto del isospín comparando las propiedades del estado excitado del cadmio-130 con las medidas previamente en cadmio-98. Estos dos núcleos tienen números muy diferentes de neutrones y, por tanto, una gran diferencia en isospín. Pero tienen configuraciones orbitales similares, ya que ambos tienen capas de neutrones completas y solo les faltan dos protones para tener capas de protones completas.
Los investigadores observaron núcleos de cadmio-130 que se produjeron cuando un haz de uranio colisionó con una diana de berilio en RIKEN (Japón). Combinaron los cálculos del modelo de capas y los nuevos datos junto con datos previos para determinar una carga efectiva de protones de +1,35 para este núcleo rico en neutrones, en comparación con +1,17 para el cadmio-98, lo que sugiere una inesperada dependencia del isospín importante de la carga efectiva.
Para saber más:
Una introducción fácil y paso a paso al núcleo atómico: El núcleo (serie)
Referencias:
A. Jungclaus et al. (2024) Excited-State Half-Lives in 130Cd and the Isospin Dependence of Effective Charges Phys. Rev. Lett. doi: 10.1103/PhysRevLett.132.222501
D. Ehrenstein (2024) Proton Effective Charge Depends on Neutron Population Physics 17, s65
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La carga efectiva del protón depende del isospín se ha escrito en Cuaderno de Cultura Científica.
¿Es esta la (otra) prueba definitiva de que Venus tiene volcanes activos?
Hace poco más de un año, escribíamos en esta sección el artículo “¿Es esta la prueba definitiva de que Venus tiene volcanes activos?” en el cual hablábamos de la que podría ser la primera observación directa de una erupción volcánica en Venus tras el estudio de las imágenes tomadas por el radar de la misión Magellan de la NASA a principios de la década de los 90.
Como también comentábamos en el anterior artículo, y a modo de introducción para quien no lo leyese entonces, no sería extraño que Venus tuviese un nivel de actividad geológica similar a nuestro planeta porque, al fin y al cabo, tienen un tamaño y composición muy parecidos y, por lo tanto, podríamos asumir que todavía mantiene una importante cantidad de calor interno que le permita tener actividad geológica. Si esto no fuese así, deberíamos replantearnos los modelos de evolución planetaria.
Obviamente que sean parecidos no es una razón suficiente para justificar la existencia de actividad geológica, sino que necesitamos pruebas fehacientes de procesos volcánicos y sísmicos que ocurran en Venus a día de hoy. Pero es un planeta terrible tanto para observarlo desde la superficie del planeta como desde la órbita: Una temperatura media superior a los 450ºC -de día y de noche- y una presión atmosférica 90 veces la terrestre hacen muy complicada la supervivencia de la electrónica a largo plazo.
Desde la órbita la dificultad es otra, y es la imposibilidad de estudiar Venus con longitudes de onda visibles, ya que su superficie está completamente cubierta por nubes. Eso sí, este problema tiene una solución más sencilla: El uso de radares de apertura sintética que permitan estudiar la superficie como ya hizo la Magellan en este planeta, la Cassini en Titán o continuamente en la Tierra.
Pero el problema que tenemos es que hasta la próxima década no tendremos nuevas misiones en Venus capaces de estudiar su superficie con radar, la EnVision de la ESA y la VERITAS de la NASA, que nos aportarán una visión mucho más detallada de su superficie de lo que jamás la habíamos visto. Mientras tanto, todavía podemos aprovechar los datos de misiones anteriores para revisitarlos con una mayor capacidad de computación que cuando se tomaron los datos.
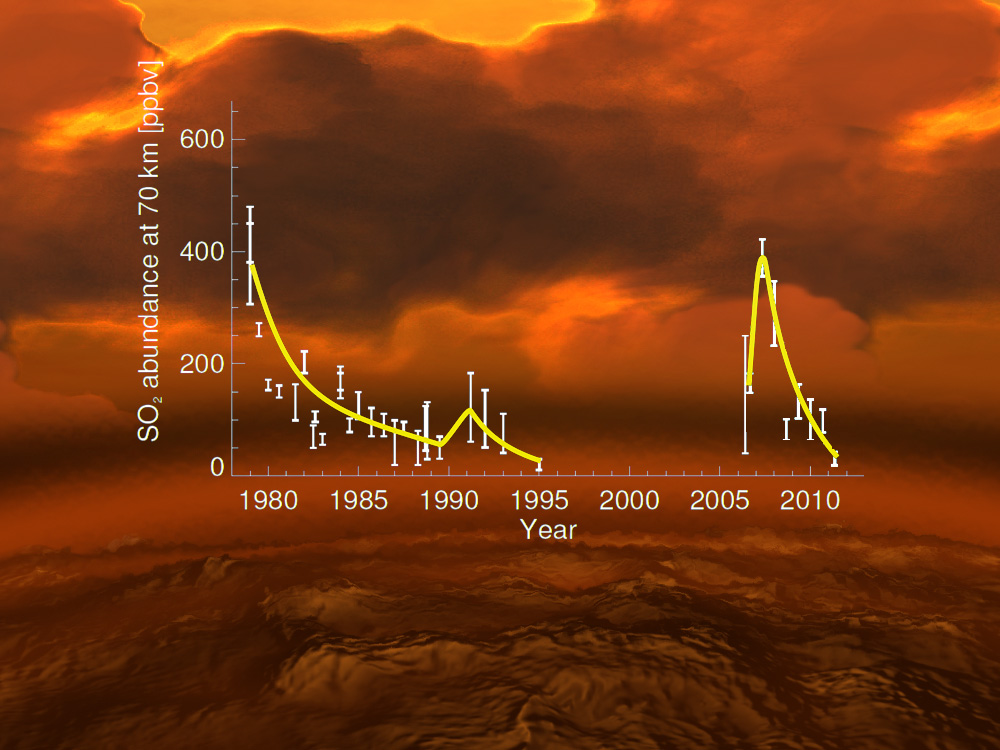 Cambios en la concentración de dióxido de azufre desde 1980 hasta 2011. Estas fuertes variaciones podrían apuntar a inyecciones de este gas a causa de las erupciones volcánicas. Imagen cortesía de E. Marcq et al. (Venus Express); L. Esposito et al. (datos antiguos); imagen de fondo: ESA/AOES Medialab
Cambios en la concentración de dióxido de azufre desde 1980 hasta 2011. Estas fuertes variaciones podrían apuntar a inyecciones de este gas a causa de las erupciones volcánicas. Imagen cortesía de E. Marcq et al. (Venus Express); L. Esposito et al. (datos antiguos); imagen de fondo: ESA/AOES MedialabA pesar de todos estos inconvenientes, ya tenemos una serie de pruebas importantes a favor del vulcanismo activo en Venus: cambios en la concentración de dióxido de azufre -un gas que en nuestro planeta proviene principalmente de la actividad volcánica- en la atmósfera; zonas con muy pocos cráteres de impacto -atestiguando un relieve muy reciente-; anomalías térmicas -en este caso, puntos calientes- sobre la superficie en lugares que parecen volcanes – y que podrían indicar coladas de lava recientes o actividad en los puntos de emisión volcánicos-; y por último, el descubrimiento del fosfano en la atmósfera, que también podría estar relacionado con las erupciones volcánicas y no tanto con la vida como se sugirió inicialmente.
El pasado año, Herrick et al. (2023) publicaban en Science la que podría haber sido la primera evidencia inequívoca de una erupción volcánica en Venus, eso sí, ocurrida treinta años antes y de la que tendríamos una imagen del antes y otra del después, pero que debido al ingente volumen de datos, los cambios entre las dos imágenes habían pasado desapercibidos para los científicos de la época y, solo ahora que podemos procesar y comparar las imágenes con mucha mayor capacidad, había podido detectarse.
Pero, ¿había más erupciones volcánicas escondidas en las imágenes de la Magellan? Parece que sí. Un estudio publicado a finales de mayo por Sulcanese et al. (2024) sugiere que tanto en el flanco occidental de Sif Mons como en Niobe Planitia se aprecian alteraciones compatibles con la ocurrencia de erupciones volcánicas.
Este nuevo artículo se basa en el estudio del fenómeno de la retrodispersión de las ondas de radar que emitía la Magellan para tomar imágenes del planeta. La retrodispersión es la proporción de la señal del radar que se refleja en la dirección de la antena tras rebotar en el suelo. El estudio de esta señal nos aporta detalles sobre la rugosidad topográfica y la composición de la superficie.
Los datos de radar no suelen ser tan fácilmente interpretables como las imágenes en luz visible, lo que supone un reto a la hora de procesar los datos y evitar malentendidos. Para solucionar este problema, los autores del estudio han corregido los datos originales teniendo en cuenta el ángulo de incidencia de la señal del radar, ya que puede tener influencia en el reflejo, así como normalizar los datos para poder comparar mejor los pares de imágenes sin que una de las imágenes tuviese una mayor influencia que la otra y así evitar falsos positivos.
 Reconstrucción tridimensional de Sif Mons realizada con datos de la Magellan. Cortesía de NASA/JPL.
Reconstrucción tridimensional de Sif Mons realizada con datos de la Magellan. Cortesía de NASA/JPL.Pero, ¿qué se ha detectado y en donde? En Sif Mons los autores han encontrado cambios en la retrodispersión de la señal del radar que son compatibles con la aparición de nuevas coladas de lava sobre la superficie. Sif Mons es un gran volcán en escudo, tanto que tiene un diámetro de unos 300 kilómetros y más de 2000 metros de altura. Este tipo de volcanes son como los que forman hoy día la isla de Hawaii en nuestro planeta o la Isla de Fernandina, en las Galápagos, por poner algunos ejemplos.
El otro lugar donde se han detectado cambios es Niobe Planitia, una gran llanura -forma aproximadamente un 13% de la superficie de Venus- donde se existen distintos tipos de volcanes así como evidencias de que muchos de los cráteres de impacto que pueblan su superficie han sufrido cambios posteriores a su formación, como el relleno por coladas de lava. Aquí los científicos también han observado una serie de formas lineales y en abanico que no existían antes y cuyo mecanismo de formación estaría también relacionado con la aparición de nuevas coladas de lava que cubren la superficie.
Por si no fuese suficiente, los investigadores además han realizado un análisis topográfico: Es decir, han estudiado las pendientes de Sif Mons y de Niobe Planitia y comprobado hacia donde tendrían que moverse las coladas de lava, comprobando que los cambios observados en la superficie siguen ese camino y no otro.
 Imagen de la superficie de Venus donde se pueden ver distintas coladas de lava y una aparente ausencia de cráteres de impacto. Cortesía de NASA/JPL.
Imagen de la superficie de Venus donde se pueden ver distintas coladas de lava y una aparente ausencia de cráteres de impacto. Cortesía de NASA/JPL.Un último paso ha sido el comparar los datos de Venus con los de una erupción en la Tierra, en este caso la del volcán Pacaya, en Guatemala, y observar si los cambios relacionados con la erupción del año 2014 -observada con los radares en la órbita de nuestro planeta- sufría una amplificación en la señal retrodispersada, cosa que ocurría también en la Tierra, apoyando con ello las observaciones hechas por los investigadores.
Este nuevo estudio pone de manifiesto que Venus está más activo de lo que pensábamos y que probablemente hemos estado durante décadas ante un sesgo observacional a la hora de cuantificar su actividad de nuestro “gemelo” planetario, ya que los medios de los que disponíamos nos aportaban una visión muy limitada espacial y temporalmente, pero también por una menor capacidad de procesamiento que la que tenemos hoy.
Venus, por lo tanto, es un planeta que requiere repensar nuestra estrategia de exploración espacial puesto que, a la vista de los descubrimientos que se están haciendo en los últimos años, todavía podría guardar muchos secretos sobre la evolución de los planetas a lo largo del tiempo.
Nota:
Gracias a Davide Sulcanese por proveerme de una copia del artículo para poder comentarlo en Planeta B.
Referencias:
Marcq, Emmanuel, Jean Loup Bertaux, Franck Montmessin, and Denis Belyaev (2013) Variations of Sulphur Dioxide at the Cloud Top of Venus’s Dynamic Atmosphere Nature Geoscience doi: 10.1038/ngeo1650.
Zhang, Xi. (2014) On the Decadal Variation of Sulphur Dioxide at the Cloud Top of Venus EPSC Abstracts Vol. 9, EPSC2014-189.
Bains, William, Oliver Shorttle, Sukrit Ranjan, Paul B Rimmer, Janusz J Petkowski, Jane S Greaves, and Sara Seager (2022) Constraints on the Production of Phosphine by Venusian Volcanoes Universe doi: 10.3390/universe8010054
Herrick, Robert R, and Scott Hensley (2023) Surface Changes Observed on a Venusian Volcano during the Magellan Mission Science doi: 10.1126/science.abm7735
Shalygin, E. V., A. T. Basilevsky, W. J. Markiewicz, D. V. Titov, M. A. Kreslavsky, and Th Roatsch. “Search for Ongoing Volcanic Activity on Venus: Case Study of Maat Mons, Sapas Mons and Ozza Mons Volcanoes.” Planetary and Space Science 73, no. 1 (2012): 294–301. https://doi.org/10.1016/j.pss.2012.08.018.
Smrekar, Suzanne E., Ellen R. Stofan, Nils Mueller, Allan Treiman, Linda Elkins-Tanton, Joern Helbert, Giuseppe Piccioni, and Pierre Drossart. “Recent Hotspot Volcanism on Venus from VIRTIS Emissivity Data.” Science 328, no. 5978 (2010): 605–8. https://doi.org/10.1126/science.1186785.
Basilevsky, A. T., E. V. Shalygin, D. V. Titov, W. J. Markiewicz, F. Scholten, Th Roatsch, M. A. Kreslavsky, et al. “Geologic Interpretation of the Near-Infrared Images of the Surface Taken by the Venus Monitoring Camera, Venus Express.” Icarus 217, no. 2 (2012): 434–50. https://doi.org/10.1016/j.icarus.2011.11.003.
Bains, William, Oliver Shorttle, Sukrit Ranjan, Paul B. Rimmer, Janusz J. Petkowski, Jane S. Greaves, and Sara Seager. Only Extraordinary Volcanism Can Explain the Presence of Parts per Billion Phosphine on Venus. Proceedings of the National Academy of Sciences of the United States of America 119, no. 7 (2022): 2–3. https://doi.org/10.1073/pnas.2121702119.
Cordiner, M. A., G. L. Villanueva, H. Wiesemeyer, S. N. Milam, I. de Pater, A. Moullet, R. Aladro, et al. Phosphine in the Venusian Atmosphere: A Strict Upper Limit From SOFIA GREAT Observations. Geophysical Research Letters 49, no. 22 (2022). https://doi.org/10.1029/2022GL101055.
Sulcanese, Davide, Giuseppe Mitri, and Marco Mastrogiuseppe (2024) Evidence of Ongoing Volcanic Activity on Venus Revealed by Magellan Radar 2024. doi: 10.1038/s41550-024-02272-1
Herrick, Robert R., and Scott Hensley. Surface Changes Observed on a Venusian Volcano during the Magellan Mission. Science 379, no. 6638 (2023): 1205–8. https://doi.org/10.1126/science.abm7735.
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario, divulgador científico u autor de la sección Planeta B.
El artículo ¿Es esta la (otra) prueba definitiva de que Venus tiene volcanes activos? se ha escrito en Cuaderno de Cultura Científica.
¡Abre los ojos! La ciencia de la visión y de la mirada
El sistema visual de los mamíferos, y de los vertebrados, en general, es de una complejidad asombrosa. El ojo es una estructura tan complicada y su función, tan relevante, que el mismísimo Charles Darwin lo tenía por la principal amenaza para su teoría sobre el origen de las especies. Y no fue el único; también a Ramón y Cajal le asaltó la duda. El ojo humano, principalmente, pero también los sistemas visuales y las estructuras fotorreceptoras de otras especies son el tema del libro de Conchi Lillo ‘¡Abre los ojos!’.
 Fuente: Next Door Publishers
Fuente: Next Door PublishersEl libro empieza por invocar la evolución y el mecanismo que (a mi juicio) le es más propio, la selección natural. Entiendo que ese es el mejor punto de partida posible para un libro como este, porque si bien el adagio de Theodosius Dobzhansky «En biología nada tiene sentido si no es a la luz de la evolución» –que diese título a su ensayo de 1973– es válido en cualquier caso, resulta especialmente luminoso cuando nos referimos a una modalidad de recepción sensorial con una plasticidad tan grande como la de la visión y con una relación, en general (aunque no en todos sus aspectos), tan evidente con las características del entorno.
A esa inicial contextualización evolutiva de la visión, sigue una descripción del ojo humano. La autora presenta su estructura, tanto del órgano receptor –la retina–, con sus elementos, como de las estructuras accesorias.
Los colores no existen aunque los veasMás adelante se adentra en el mundo de los colores –la visión en color–, para explicar que el fenómeno se basa en la posesión de pigmentos visuales que responden de forma diferente a las distintas longitudes de onda de las radiaciones electromagnéticas que constituyen la luz visible. Es visible, precisamente, porque los pigmentos, al absorber la radiación, reaccionan y desencadenan una secuencia de acontecimientos que desemboca en la generación de señales nerviosas. En definitiva, la energía que portan los fotones se acaba convirtiendo en la energía bioeléctrica propia de los impulsos nerviosos.
El título de este apartado –‘Los colores no existen’– me ha recordado una conversación que tuve hace años con mi madre, a quien se lo dije con esas mismas palabras: «¿Sabes que los colores no existen?» «¿Qué tontería es esa?» me respondió ella. «¿Cómo no van a existir si los estoy viendo?» Traté de explicárselo lo más claramente que pude, pero me resultó imposible. Incluso a mis estudiantes les resulta una noción extraña, y el argumento, un tanto alambicado. Pero Conchi Lillo lo explica muy bien; mi madre, a ella, se lo habría entendido.
El color de los ojos también es objeto de su atención; en el libro se explica la razón por la que unas personas tenemos los ojos oscuros y otras los tienen claros. O, incluso, a qué se debe que, como le ocurría a un compañero de estudios en el instituto de Portugalete, haya quien tiene uno de cada color. Conviví con ese compañero –de clase y de francachelas– en el aula, el patio y los bares, durante meses, sin percatarme de su rareza. Hasta que me lo dijo una compañera. Siempre me había parecido que tenía una mirada extraña, pero me tuvieron que decir que tenía un ojo castaño y otro azul para percatarme. Entendí entonces la razón de mi perplejidad.
Problemas de visiónA los problemas visuales se les dedica un extenso capítulo. Es extenso porque al tratarse de un sistema tan complejo, con tantos elementos, las posibilidades de que funcione de forma anómala se multiplican. Son muchos los fallos posibles del sistema, tanto en los fotorreceptores y sus características pigmentarias, como en el efecto que el paso del tiempo tiene sobre las estructuras retinianas o las averías de algunos componentes accesorios. Cataratas, fatiga visual, miopía, degeneración macular y otros males asoman a las páginas del libro. Y uno no puede dejar de pensar que vemos de milagro. Aunque, en realidad, la reflexión pertinente es otra: qué sistema tan maravilloso es el de la visión que a pesar de tantos elementos constituyentes y potencialmente falibles, lo normal es que durante gran parte de nuestra vida nos preste un servicio excelente.
Tampoco aquí debemos perder de vista la lógica evolutiva. La mayor parte de esos problemas, al menos los que pueden comprometer la supervivencia o capacidad para dejar descendencia, surgen precisamente cuando ya la hemos dejado o, en todo caso, hemos perdido la oportunidad de hacerlo. En otras palabras, la selección natural ha actuado descartando variantes que limitaban a nuestros ancestros; las pocas anomalías que aparecen a edades jóvenes son eso, pocas: excepciones, en realidad.
Los artistas plásticos –me refiero aquí a los pintores, principalmente– también sufren problemas de visión y las consecuencias de esos problemas, de una u otra forma, quedan reflejados en su obra. Es interesantísimo seguir la pista de las deficiencias visuales que delatan los cuadros: miopía, cataratas, estrabismo y otros, son afecciones cuya huella queda impresa en la obra del artista.
Percepción animalUno de los aspectos más interesantes de la visión como modalidad sensorial es el fenómeno perceptivo, la forma en que la información recogida por los sistemas receptores es procesada por los centros superiores del cerebro y el papel que juega en ese procesamiento la memoria, las emociones y, en general, cualquier tipo de información –incluida la que se recibe por otras vías sensoriales– que interactúa con la de origen visual para generar la percepción. De hecho, lo que vemos acaba siendo el resultado de la confluencia, con las señales procedentes de la retina, de expectativas, recuerdos, sentimientos y otros elementos de nuestra experiencia presente o pasada. Por esa razón, nunca dos personas ven lo mismo cuando contemplan una misma escena.
La autora deja para casi el final, un recorrido por los sistemas visuales de diferentes especies, como bivalvos, cefalópodos, crustáceos, insectos o arácnidos. Este es el apartado que mejor ilustra el apotegma antes citado del señor Teodosio. Y es, por eso mismo, el que mejor muestra la asombrosa diversidad de soluciones que ha generado la naturaleza para, sirviéndose de la información contenida en ciertos intervalos de longitudes de onda de las radiaciones electromagnéticas que “bañan” el universo, dotar a las criaturas animales de herramientas mediante las que desenvolverse con éxito en entornos de lo más dispares.
Cierra el libro una breve mirada a lo que nos puede deparar el futuro desde la tecnología electrónica y telemática, en combinación –casi simbiosis– con nuestro sistema visual. Pero el futuro no está escrito y aunque lo que cuenta Lillo es apasionante, estoy seguro de que nos deparará maravillas aún más asombrosas de lo que hoy somos capaces de vislumbrar.
En resumen, querido lector, querida lectora, si tiene curiosidad acerca del funcionamiento de la visión, la nuestra y la de otros seres vivos, ‘¡Abre los ojos!’ es, por claridad, rigor y amenidad, una lectura muy recomendable.
Autora: Conchi Lillo
Título: ¡Abre los ojos!
Ed por Next Door (2023)
En Editoralia personas lectoras, autoras o editoras presentan libros que por su atractivo, novedad o impacto (personal o general) pueden ser de interés o utilidad para los lectores del Cuaderno de Cultura Científica.
Una versión de este texto de Juan Ignacio Pérez Iglesias apareció anteriormente en Lecturas y Conjeturas (Substack).
El artículo ¡Abre los ojos! La ciencia de la visión y de la mirada se ha escrito en Cuaderno de Cultura Científica.
Una (pre)historia de violencia

Los cambios del cerebro durante el embarazo y la maternidad, cómo el estrés ha pasado de ser un mecanismo de supervivencia a un eventual elemento de riesgo para nuestra salud o cuál ha sido el papel que ha jugado el suicidio en la evolución del ser humano fueron algunos de los temas que se tratarán en la VI Jornada Nacional sobre Evolución y Neurociencias.
La jornada tuvo lugar el Bizkaia Aretoa de la UPV/EHU los pasados 25 y 26 de abril y estuvo dirigida por Eva Garnica y Pablo Malo, de la Red de Salud Mental de Bizkaia, institución que organizó la jornada junto a la Cátedra de Cultura Científica de la UPV/EHU.
El encuentro, cuya primera edición se celebró en 2017, se ha convertido en una cita imprescindible para las y los expertos en ámbitos como la psiquiatría, la psicología o la biología. Una jornada que sirve para analizar el comportamiento humano desde un punto de vista evolutivo y divulgar de un modo accesible para todos los públicos.
¿Puede hablarse de violencia en los animales sin suponer que tienen «intención»? Es decir, sin antropomorfizarlos. ¿Qué nos dice esto sobre la violencia entre esos homininos llamados humanos? En Una (pre)historia de violencia, José Miguel Martínez Gázquez, psicólogo y primatólogo, parte de la definición de violencia como el uso intencionado de la fuerza contra otro, para llegar a conclusiones que pueden sorprender a más de uno.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Una (pre)historia de violencia se ha escrito en Cuaderno de Cultura Científica.
Fatiga mecánica en las turbinas eólicas flotantes
Los datos del viento y oleaje de un emplazamiento muy energético en la costa de Irlanda entre 1920 y 2010 han permitido analizar la evolución de las condiciones del mar y generar un modelo de cálculo de la fatiga mecánica que esas condiciones pueden provocar en las turbinas eólicas flotantes. Este método matemático-estadístico permite calcular el tiempo de vida de las turbinas en función de la meteorología de un emplazamiento concreto.
 Fuente: 123rf
Fuente: 123rfEn un estudio realizado por el grupo de investigación EOLO de la Universidad del País Vasco/Euskal Herriko Unibertsitatea, se ha desarrollado un método matemático-estadístico que permite conocer “la conveniencia de instalar parques eólicos flotantes en un emplazamiento concreto. Por ejemplo, si existe una elevada probabilidad de que los aerogeneradores sufran fatiga mecánica o unas condiciones marinas extremas a pesar de ser un lugar muy energético”, explica Alain Ulazia, profesor de la Escuela de Ingeniería de Gipuzkoa (Eibar).
Según el investigador, la pregunta más frecuente en la generación de energía eólica marina es “qué cambios (subidas o bajadas) se sucederán en la producción de energía en función de las condiciones climáticas”; es decir, lo que se mira es cuánta energía se puede producir en función de la climatología. Sin embargo, la investigación dirigida por Ulazia ha ido un paso más allá y se ha centrado en la fatiga mecánica de las turbinas eólicas marinas, es decir, la rotura en última instancia como consecuencia de los choques y las tensiones repetitivas que no son capaces de romper el material individualmente: “Las condiciones del mar (viento y oleaje) pueden influir en la reducción del tiempo de vida de las turbinas flotantes. De hecho, es posible que afecten más a la duración de algunas piezas de las turbinas que a la producción industrial de energía, y que en vez de durar 20 años duren 15 años. Esto puede influir decisivamente en los costes y en la inversión de un proyecto”.
Condiciones marinas en un emplazamientoEl grupo de investigación EOLO lleva años trabajando en proyectos relacionados con la meteorología, el clima y el medio ambiente. “Hemos realizado numerosos estudios sobre la relación a largo plazo entre el cambio climático y la generación de energías renovables. Teniendo en cuenta los cambios producidos a lo largo de varias décadas, hacemos estudios históricos y proyecciones para el futuro”, explica Ulazia.
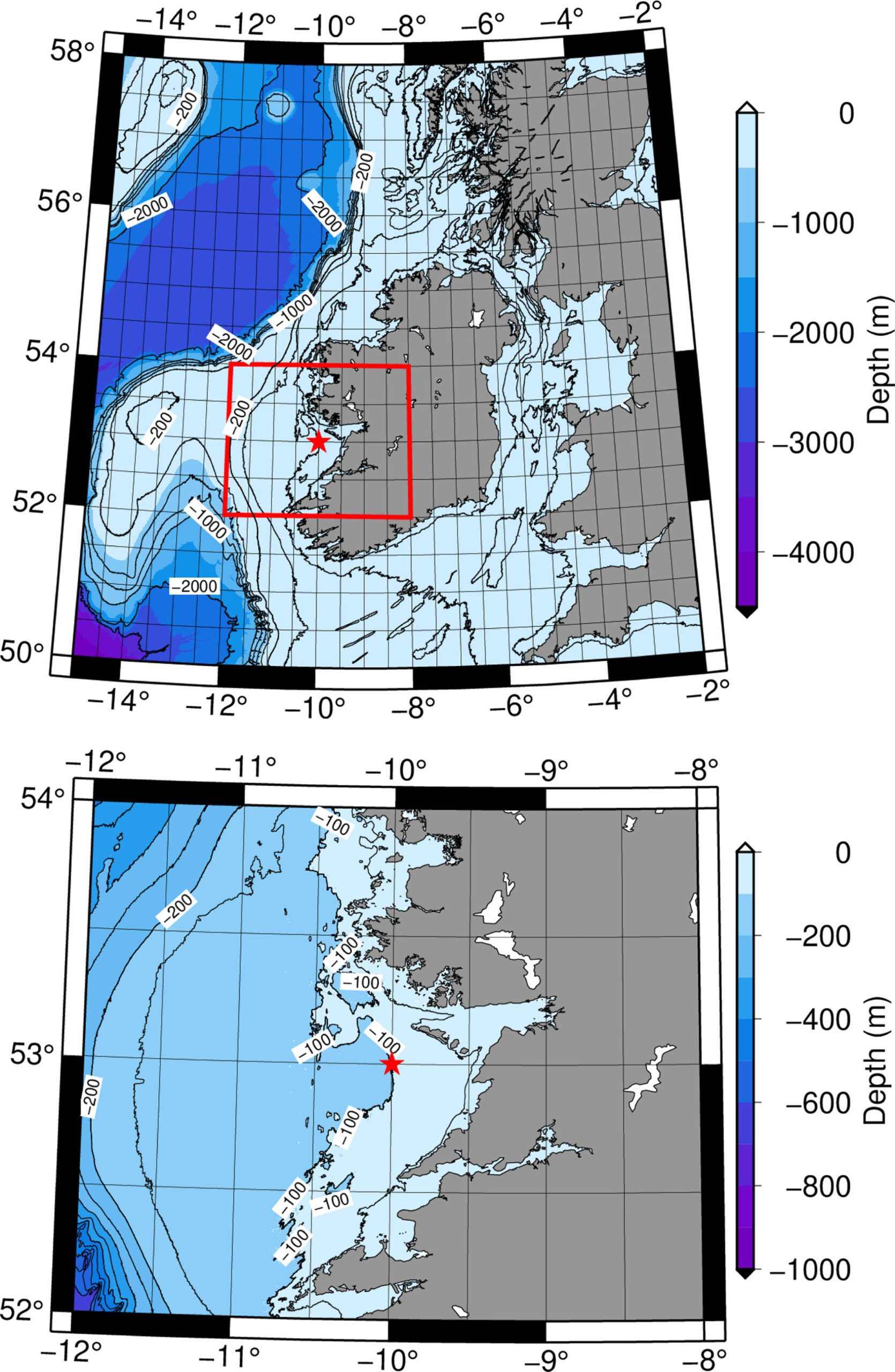 Mapa de la profundidad del mar frente a la costa de Galway (Irlanda)
Mapa de la profundidad del mar frente a la costa de Galway (Irlanda)En este estudio se ha seleccionado un lugar muy energético de Irlanda: a partir de los datos relativos al viento y al oleaje registrados entre 1920 y 2010 en la bahía de Galway, en la costa oeste de Irlanda, han determinado los cambios históricos ocurridos a lo largo de esas décadas mediante la utilización de modelos meteorológicos avanzados, en colaboración con los miembros del Centre for Ocean Energy Research de la Universidad de Maynooth (Irlanda). Estos datos históricos han servido para determinar la evolución de las condiciones marinas y crear un modelo que represente la fatiga a largo plazo que estas provocarán en los aerogeneradores. Este modelo podrá ser utilizado para realizar proyecciones futuras.
La danza de las turbinas eólicas flotantesUtilizando simulaciones, los investigadores han calculado la energía que producirían algunas turbinas flotantes de referencia en las ocho situaciones marinas más probables en la bahía de Galway y, por otro lado, han visto la fatiga mecánica que provocarían en algunos elementos de las turbinas. “Hemos utilizado un simulador que nos ofrece en unos segundos la danza que hace la turbina debido a las olas y el viento, y hemos desarrollado un método matemático-estadístico para implementar cambios en los estados marinos a largo plazo y, en consecuencia, poder determinar la evolución de la fatiga que soportaría la máquina, teniendo en cuenta estos cambios históricos”, explica el investigador del grupo EOLO.
A pesar de que el método ha sido aplicado en esa ubicación irlandesa, “este método es universal. Podemos hacer el análisis en cualquier parte del mundo”, ha señalado. La energía eólica marina es muy apropiada porque “no es turbulenta, como la de las montañas. Sin embargo, hay que invertir mucho más en el mar. Este es el principal problema para la implantación de la energía eólica marina”, explica Ulazia. El cambio climático está provocando acontecimientos extremos, cada vez más, y los inversores se muestran precavidos ante el riesgo de este tipo de proyectos: “Aunque el emplazamiento sea muy energético, ¿merece la pena poner el parque eólico allí si en algún momento puede verse afectado por un fenómeno climatológico o si los elementos de la turbina van a sufrir graves problemas de fatiga?”, afirma. El método desarrollado por el grupo de investigación EOLO de la Universidad del País Vasco ha dado luz a esta cuestión.
Referencia:
Alain Ulazia, Hodei Ezpeleta, Gabriel Ibarra-Berastegi, Jon Sáenz, Nahia Martinez-Iturricastillo, John V. Ringwood (2024) Historical trends of floating wind turbine fatigue loads (Ireland 1920–2010) Ocean Engineering doi: 10.1016/j.oceaneng.2024.117424
El artículo Fatiga mecánica en las turbinas eólicas flotantes se ha escrito en Cuaderno de Cultura Científica.
¿Con qué relleno el arenero de mi gato?
Cuando tenemos una mascota felina en casa, una de las principales cosas en la que tenemos que pensar es en prepararle un lugar en el que pueda hacer sus necesidades. Generalmente, optamos por un cajetín plástico y resistente dentro del cual verteremos un material absorbente en el que nuestra mascota pueda escarbar, hacerse un hueco y sentirse cómoda en esos momentos íntimos, pero que también elimine los olores y la humedad. Es en este momento cuando nos surgen todas las dudas sobre qué elementos utilizar para que cumplan esta función de la manera más eficiente posible. Y, como siempre, la mejor solución nos la aporta la Geología y no es la arena: emplearemos minerales de la arcilla.
 Foto: Lina Angelov / Unsplash
Foto: Lina Angelov / UnsplashEn primer lugar, hay que aclarar lo que significa la palabra arcilla, porque, en Geología, este término tiene dos significados distintos, pero relacionados entre sí. Por un lado, arcilla se refiere a un tamaño de grano del sedimento, incluyendo todas aquellas partículas minerales que midan menos de dos micras de diámetro (es decir, inferiores a 0,002 mm). Y, por otro, tenemos los minerales de la arcilla, que es un término que engloba a minerales del grupo de los filosilicatos que, generalmente, son los principales componentes de los sedimentos de tamaño arcilla, de ahí su nombre.
 Imagen de Microscopio Electrónico de Barrido (SEM) de minerales de la arcilla, en donde se aprecia su disposición en láminas superpuestas. La escala representa 1 micra, que equivale a 0,001 mm. Fuente: Paedona / Wikimedia Commons
Imagen de Microscopio Electrónico de Barrido (SEM) de minerales de la arcilla, en donde se aprecia su disposición en láminas superpuestas. La escala representa 1 micra, que equivale a 0,001 mm. Fuente: Paedona / Wikimedia CommonsLos filosilicatos tienen una particularidad que ya nos está chivando su propio nombre, que deriva del griego phyllon (que podemos traducir como hoja). Químicamente, son moléculas conformadas por átomos de oxígeno y silicio con otros cationes, tales como aluminio o magnesio, que adquieren forma de tetraedros u octaedros. Estas moléculas se disponen en el espacio dando lugar a unas estructuras cristalinas con aspecto de láminas o escamas situadas unas sobre otras. Y, entre cada una de esas láminas, se generan una serie de cavidades o poros de tamaño atómico, es decir, microscópico. Es en esta propiedad química en donde radica uno de sus secretos, su capacidad absorbente.
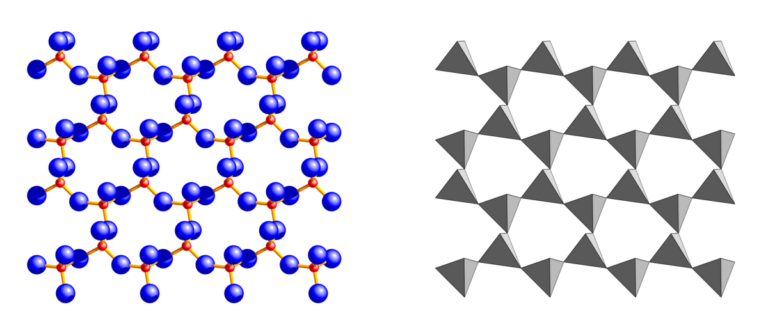 Representación de la estructura cristalina de la moscovita, un mineral del grupo de los filosilicatos, donde los tetraedros de oxígeno y silíceo se van uniendo entre sí formando láminas. Imagen: Finger, L.W., Kroeker, M., Toby, B.H. (2007). DRAWxtl, an open-source computer program to produce crystal-structure drawings. Journal of Applied Crystallography, 40, 188-192 / Wikimedia Commons
Representación de la estructura cristalina de la moscovita, un mineral del grupo de los filosilicatos, donde los tetraedros de oxígeno y silíceo se van uniendo entre sí formando láminas. Imagen: Finger, L.W., Kroeker, M., Toby, B.H. (2007). DRAWxtl, an open-source computer program to produce crystal-structure drawings. Journal of Applied Crystallography, 40, 188-192 / Wikimedia CommonsAsí, los minerales de la arcilla pueden captar nuevos componentes en su estructura cristalina, tanto en forma de partículas sólidas como en estado líquido, dándoles un montón de utilidades en nuestra sociedad. Por ejemplo, esta alta facilidad de absorción los convierte en unas herramientas excelentes para regenerar medios contaminados, como zonas donde se ha producido un derrame de petróleo o suelos afectados por vertidos químicos, ya que, si me permitís el símil, chuparían esas partículas como si fuesen esponjas. También se emplean para potabilizar agua en zonas remotas, al hacer pasar el líquido elemento por membranas recubiertas de estos minerales, que atraen y retienen las partículas sólidas y los contaminantes. Incluso, en la industria se utilizan como soportes de catalizadores o como recubrimiento de superficies para evitar la corrosión por el agua. Y, por supuesto, son el elemento básico en la alfarería y la cerámica, ya que al mezclar los minerales de la arcilla con agua se vuelven una pasta flexible y moldeable que permite deslizar con facilidad las láminas cristalinas una sobre la otra para darle la forma deseada, recuperando su resistencia inicial al desecarlos.
A este elevado nivel de absorción hay que sumarle otra ventaja, ya que también captan las partículas químicas, presentes tanto en estado gaseoso, líquido y sólido, que generan olores. De ahí que los minerales de la arcilla sean los productos favoritos, por encima de materiales vegetales como el serrín, para las camas de los animales domésticos, los suelos de las granjas o las bases de carpas o urinarios públicos temporales colocados en zonas festivas. Y, geológicamente hablando, los minerales de la arcilla no son un producto escaso y difícil de conseguir, en realidad son muy comunes en todo el planeta, encontrándose en diferentes contextos geológicos y no resultando demasiado complicada ni su extracción, ni su procesado para poder emplearlos en nuestro día a día. Por ejemplo, para los areneros de las mascotas simplemente se obtiene el material en canteras, se tritura, se tamiza para elegir el tamaño adecuado, se embolsa y se vende. Esta facilidad en su obtención y tratamiento es la guinda del pastel que convierte a los minerales de la arcilla en materiales tan utilizados, versátiles y con unas aplicaciones industriales y sociales futuras sorprendentes.
 Aspecto de los minerales de la arcilla que se comercializan como arena para gatos.
Aspecto de los minerales de la arcilla que se comercializan como arena para gatos.Para terminar, dejadme daros un consejo para elegir el mejor material absorbente para el aseo de vuestras mascotas. Coged uno de los fragmentos minerales de las distintas bolsas que encontraréis en el mercado, humedeced vuestra lengua y acercad el fragmento a la punta de la misma. Aquel que se quede más pegado, será el elegido. Obviamente, haced esta prueba antes de rellenar el arenero del animal, no después de que Castaño (que así se llama mi gato) haya usado su cuarto de baño. Pero si preferís simplemente mirar la etiqueta del producto sin tener que “chupar piedras”, os recomiendo decantaros por aquellos que contengan fragmentos de sepiolita, ya que este mineral posee la capacidad absorbente más elevada de entre aquellos que podemos encontrar en el mercado.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo ¿Con qué relleno el arenero de mi gato? se ha escrito en Cuaderno de Cultura Científica.
Despedidas matemáticas
 Foto: Scott Rodgerson / Unsplash
Foto: Scott Rodgerson / Unsplash
Poeta de Guardia (1917-1998)
Ya creo que lo he dicho todo
y que todo lo amé.
G. F.
Este epitafio es de la poeta Gloria Fuertes; su hermosa despedida la recuerda y describe impecablemente su carácter y manera de afrontar la vida.
Los que siguen son epitafios de cinco matemáticos y una astrónoma que, como en el caso de la poeta, describen su trabajo o su singular personalidad. Comencemos.
Diofanto de Alejandría (hacia 200-hacia 280)
Se sabe que el matemático Diofanto de Alejandría, el padre del álgebra, vivió 84 años. Y se conoce porque su epitafio tiene forma de enunciado matemático que permite deducir a que edad falleció (aunque se desconoce el año):
Transeúnte, esta es la tumba de Diofanto: los números pueden mostrar, ¡oh maravilla! la duración de su vida. Su niñez ocupó la sexta parte de su vida; después, durante la doceava parte, de vello se cubrieron sus mejillas. Pasó aún una séptima parte de su vida antes de tomar esposa y, cinco años después, tuvo un precioso niño que, una vez alcanzada la mitad de la edad de la vida de su padre, pereció de una muerte desgraciada. Su padre tuvo que sobrevivirle, llorándole, durante cuatro años. De todo esto se deduce su edad.
Efectivamente, si x denota la edad a la que falleció Diofanto, el epitafio afirma que:
x = x/6 + x/12 + x/7 + 5 + x/2 + 4,
y un simple cálculo, lleva a la igualdad x = 84, la edad a la que falleció Diofanto (y su hijo, por supuesto, murió a los 42).
Ludoph van Ceulen (1540-1610)
El matemático Ludolph van Ceulen fue un calculador excepcional. Se le conoce fundamentalmente por haber aproximado el valor del número pi (la relación entre la longitud de una circunferencia y su diámetro) con 35 cifras decimales exactas. Para ello calculó el perímetro de un polígono regular de 262 lados. Estaba tan orgulloso de este logro, que hizo inscribir esta aproximación en su lápida; en ella se indicaba que el número pi estaba comprendido entre los valores 3,14159265358979323846264338327950288 y 3,14159265358979323846264338327950289.
 Copia de la lápida de van Ceulen (perdida hacia 1800). Fuente: Wikimedia Commons.
Copia de la lápida de van Ceulen (perdida hacia 1800). Fuente: Wikimedia Commons.Fundamentalmente en textos alemanes, el número pi fue conocido durante mucho tiempo como número ludolphino.
Johannes Kepler (1571-1630)
El matemático y astrónomo Johannes Kepler proponía en su Mysterium Cosmographicum (1596) que la relación entre las distancias de los seis planetas conocidos en su tiempo (Mercurio, Venus, Tierra, Marte, Júpiter y Saturno) podía entenderse en términos de los cinco sólidos platónicos, encerrados dentro de una esfera que representaba la órbita de Saturno.
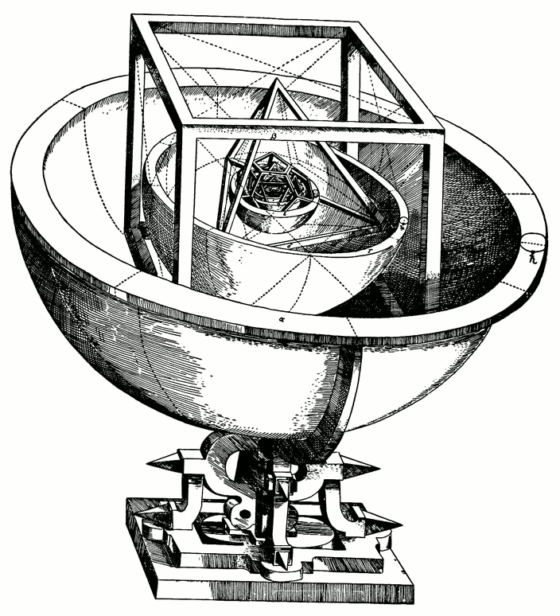 Modelo de Kepler de las órbitas de los planetas del Sistema Solar. Fuente: Wikimedia Commons.
Modelo de Kepler de las órbitas de los planetas del Sistema Solar. Fuente: Wikimedia Commons.Realizó cálculos durante toda su vida para entender cómo se movían los planetas. Así quiso expresar su trabajo en su epitafio escrito en latín:
Mensus eram coelos, nunc terrae metior umbras; Mens coelestis erat, corporis umbra iacet. [Medí los cielos y ahora mido las sombras. Mi mente tenía por límite los cielos, mi cuerpo descansa encerrado en la Tierra.]
Caroline Lucretia Herschel (1750-1848)
La astrónoma Caroline Lucretia Herschel colaboró con su hermano William en el cálculo, diseño y construcción de telescopios, en la anotación de las observaciones nocturnas del astrónomo y en la catalogación, revisión e interpretación de sus análisis. Además, descubrió ocho cometas y tres nebulosas de manera independiente.
Su epitafio, escrito por ella misma, evoca todo el trabajo que realizó, siempre a la sombra de su hermano:
[…] Los ojos de aquella que pasó a la gloria, mientras abajo se volvían hacia los cielos estrellados; sus propios descubrimientos de los cometas y su participación en los trabajos inmortales de su hermano, William Herschel, dan testimonio de ello para épocas posteriores. […]
David Hilbert (1862-1943)
El matemático alemán David Hilbert fue un científico influyente en su época; trabajó y contribuyó en varias áreas de las matemáticas. Durante el Congreso Internacional de Matemáticos que tuvo lugar en París en 1900 propuso 23 problemas matemáticos, algunos de los cuales continúan sin resolverse.
Enterrado en Gotinga, su epitafio parece indicar su certeza de que esos problemas que propuso terminarían por resolverse:
Wir müssen wissen. Wir werden wissen. [ Debemos saber. Sabremos.]
Además, parece ser la respuesta al lema Ignoramus et ignorabimus (Ignoramos e ignoraremos) expresado en 1880 por el médico alemán Emil du Bois-Reymond durante una conferencia ante la Academia Ciencias de Berlín. A lo largo de su discurso definió siete enigmas del mundo que consideraba capitales. En su opinión, tres de estos problemas no podrían nunca ser explicados ni por la ciencia ni por la filosofía.
Paul Erdős (1913-1996)
Paul Erdős fue uno de los más prolíficos matemáticos en cuanto a publicaciones científicas; firmó unos 1500 artículos con más de 500 coautores. Trabajó en problemas de combinatoria, teoría de grafos, teoría de números, análisis clásico, teoría de aproximación, teoría de conjuntos y teoría de probabilidad.
Para su epitafio sugirió una ingeniosa frase (escrita en húngaro) a modo de despedida:
Végre nem butulok tovább. [Finalmente he dejado de hacerme cada vez más tonto.]
Una última despedida
Terminamos como empezamos, con una poeta. Emily Dickinson (1830-1886) escribió su propio epitafio, una despedida breve y contundente:
Called Back. [Me llaman.]
Para saber más:
Muerte entre las ecuaciones (Historias de muerte y matemáticas 1)
Los matemáticos también mueren (Historias de muerte y matemáticas 2)
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Despedidas matemáticas se ha escrito en Cuaderno de Cultura Científica.
Las matemáticas intentan escudriñar más allá del Big Bang
Al estudiar la geometría de los modelos de espacio-tiempo, los investigadores ofrecen visiones alternativas de los primeros momentos del universo.
Un artículo de Steve Nadis. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Ilustración: Nico Roper / Quanta Magazine
Ilustración: Nico Roper / Quanta MagazineHace unos 13.800 millones de años todo el cosmos estaba formado por una pequeña, densa y caliente bola de energía que de repente explotó.
Así empezó todo, según la historia científica estándar sobre el Big Bang, una teoría que tomó forma por primera vez en la década de 1920. La historia se ha perfeccionado a lo largo de las décadas, sobre todo en la década de 1980, cuando muchos cosmólogos llegaron al convencimiento de que en sus primeros momentos el universo pasó por un breve período de expansión extraordinariamente rápida llamado inflación antes de reducir la marcha.
Se cree que ese breve período fue causado por una forma peculiar de materia de alta energía que invierte la gravedad, “inflando” la estructura del universo exponencialmente y provocando que crezca en un factor de un cuatrillón en menos de una milmillonésima de una milmillonésima de una milmillonésima de segundo. La inflación explica por qué el universo parece tan liso y homogéneo cuando los astrónomos lo examinan a gran escala.
Pero si la inflación es responsable de todo lo que podemos ver hoy, eso plantea la pregunta: ¿qué vino antes, si es que hubo algo?
Aún no se ha ideado ningún experimento que pueda observar lo que sucedió antes de la inflación. Sin embargo, los matemáticos pueden plantear algunas posibilidades. La estrategia consiste en aplicar la teoría general de la relatividad de Einstein (una teoría que equipara la gravedad con la curvatura del espacio-tiempo) tan atrás en el tiempo como sea posible.
Esta es la esperanza de tres investigadores: Ghazal Geshnizjani del Perimeter Institute, Eric Ling de la Universidad de Copenhague y Jerome Quintin de la Universidad de Waterloo. El trío ha publicado recientemente un artículo en el Journal of High Energy Physics en el que, explica Ling, «demostramos matemáticamente que podría haber una manera de ver más allá de nuestro universo».
 En colaboración con Jerome Quintin y Eric Ling, Ghazal Geshnizjani, del Perimeter Institute, ha examinado formas en las que el espacio-tiempo podría extenderse más allá del Big Bang. Foto: Evan Pappas /Perimeter Institute
En colaboración con Jerome Quintin y Eric Ling, Ghazal Geshnizjani, del Perimeter Institute, ha examinado formas en las que el espacio-tiempo podría extenderse más allá del Big Bang. Foto: Evan Pappas /Perimeter InstituteRobert Brandenberger, un físico de la Universidad McGill que no ha participado en el estudio, comenta que el nuevo artículo «establece un nuevo estándar de rigor para el análisis» de las matemáticas del comienzo del tiempo. En algunos casos, lo que de primeras parece ser una singularidad (un punto en el espacio-tiempo donde las descripciones matemáticas pierden su significado) puede ser en realidad una ilusión.
Una taxonomía de singularidadesLa cuestión central a la que se enfrentan Geshnizjani, Ling y Quintin es si hay un punto antes de la inflación en el que las leyes de la gravedad se descomponen en una singularidad. El ejemplo más simple de una singularidad matemática es lo que le sucede a la función 1/x cuando x tiende a cero. La función toma un número x como entrada y genera otro número. A medida que x se hace cada vez más pequeño, 1/x se hace cada vez más grande, acercándose al infinito. Si x es cero, la función ya no está bien definida: no se puede confiar en ella como una descripción de la realidad.
 «Hemos demostrado matemáticamente que podría haber una manera de ver más allá de nuestro universo», afirma Eric Ling de la Universidad de Copenhague. Foto: Annachiara Piubello
«Hemos demostrado matemáticamente que podría haber una manera de ver más allá de nuestro universo», afirma Eric Ling de la Universidad de Copenhague. Foto: Annachiara PiubelloA veces, sin embargo, los matemáticos pueden sortear una singularidad. Por ejemplo, consideremos el primer meridiano, que pasa por Greenwich, Inglaterra, en la longitud cero. Si tuvieras una función de 1/longitud, se volvería loca en Greenwich. Pero en realidad no hay nada físicamente especial en los suburbios de Londres: podrías redefinir fácilmente la longitud cero para que pasara por algún otro lugar de la Tierra, y entonces tu función se comportaría con perfecta normalidad al acercarte al Observatorio Real de Greenwich.
Algo similar ocurre en los límites de los modelos matemáticos de agujeros negros. Las ecuaciones que describen los agujeros negros esféricos no giratorios, elaboradas por el físico Karl Schwarzschild en 1916, tienen un término cuyo denominador llega a cero en el horizonte de sucesos del agujero negro: la superficie que rodea un agujero negro más allá de la cual nada puede escapar. Eso llevó a los físicos a creer que el horizonte de sucesos era una singularidad física. Pero ocho años más tarde, el astrónomo Arthur Eddington demostró que si se utiliza un conjunto diferente de coordenadas, la singularidad desaparece. Al igual que el meridiano principal, el horizonte de sucesos es una ilusión: un artefacto matemático llamado singularidad de coordenadas, que solo surge debido a las coordenadas que se han elegido.
En el centro de un agujero negro, por el contrario, la densidad y la curvatura llegan al infinito de una manera que no puede eliminarse utilizando un sistema de coordenadas diferente. Las leyes de la relatividad general empiezan a escupir un galimatías. Esto se llama singularidad de curvatura. Implica que está sucediendo algo que está más allá de la capacidad de descripción de las teorías físicas y matemáticas actuales.
Geshnizjani, Ling y Quintin estudiaron si el inicio del Big Bang se parece más al centro de un agujero negro o más bien a un horizonte de sucesos. Su investigación se basa en un teorema demostrado en 2003 por Arvind Borde, Alan Guth (uno de los primeros en proponer la idea de inflación) y Alexander Vilenkin. Este teorema, conocido por las iniciales de los autores como BGV, dice que la inflación debe haber tenido un comienzo: no puede haber continuado incesantemente hacia el pasado. Debe haber habido una singularidad para comenzar las cosas. BGV establece la existencia de esta singularidad, sin decir de qué tipo de singularidad se trata.
Como dice Quintin, él y sus colegas han trabajado para descubrir si esa singularidad es una pared de ladrillos (una singularidad de curvatura) o una cortina que se puede abrir (una singularidad de coordenadas). Eric Woolgar, un matemático de la Universidad de Alberta que no ha participado en el estudio, comenta que este trabajo aclara nuestra imagen de la singularidad del Big Bang. «Pueden decir si la curvatura es infinita en la singularidad inicial o si la singularidad es más suave, lo que podría permitirnos extender nuestro modelo del universo a tiempos anteriores al Big Bang».
 «Los rayos de luz pueden atravesar la frontera», afirma Jerome Quintin de la Universidad de Waterloo. Foto: Gabriela Secara
«Los rayos de luz pueden atravesar la frontera», afirma Jerome Quintin de la Universidad de Waterloo. Foto: Gabriela SecaraPara clasificar posibles situaciones preinflacionarias, los tres investigadores utilizaron un parámetro llamado factor de escala que describe cómo la distancia entre objetos ha cambiado con el tiempo a medida que el universo se expande. Por definición, el Big Bang es el momento en que el factor de escala era cero: todo quedó comprimido en un punto adimensional.
Durante la inflación, el factor de escala aumentó con una velocidad exponencial. Antes de la inflación, el factor de escala podría haber variado de diversas formas. El nuevo artículo proporciona una taxonomía de singularidades para diferentes situaciones en función de los factores de escala. «Demostramos que bajo ciertas condiciones el factor de escala producirá una singularidad de curvatura, y bajo otras condiciones no», explica Ling.
Los investigadores ya sabían que en un universo con la llamada energía oscura, pero sin materia, el inicio de la inflación identificado en el teorema BGV es una singularidad de coordenadas que puede eliminarse. Pero el universo real tiene materia, por supuesto. ¿Podrían los trucos matemáticos permitir también sortear su singularidad? Los investigadores demuestran que si la cantidad de materia es insignificante en comparación con la cantidad de energía oscura, entonces se puede eliminar la singularidad. «Los rayos de luz pueden atravesar la frontera», aclara Quintin. “Y en ese sentido, puedes ver más allá de la frontera; no es como una pared de ladrillos”. La historia del universo se extendería más allá del Big Bang.
Sin embargo, los cosmólogos creen que el universo primitivo tenía más materia que energía. En este caso, el nuevo trabajo muestra que la singularidad BGV sería una singularidad de curvatura física real, en la que las leyes de la gravedad dejarían de tener sentido.
Una singularidad sugiere que la relatividad general no puede ser una descripción completa de las reglas básicas de la física. Se están realizando esfuerzos para formular tal descripción, que requeriría conciliar la relatividad general con la mecánica cuántica. Ling dice que ve el nuevo artículo como un peldaño hacia dicha teoría. Para dar sentido al universo en los niveles de energía más altos, continúa, «primero necesitamos entender la física clásica lo mejor que podamos».
El artículo original, Mathematicians Attempt to Glimpse Past the Big Bang, se publicó el 31 de mayo de 2024 en Quanta Magazine.
Traducido por César Tomé López
El artículo Las matemáticas intentan escudriñar más allá del Big Bang se ha escrito en Cuaderno de Cultura Científica.
La bacteria que feminiza usando un gen robado
El mundo microbiano es extraordinariamente variado, pero si algún día tuviéramos que elegir a la bacteria más asombrosa, creo que Wolbachia se llevaría muchísimos votos. Esta bacteria (Figura 1) es el parásito reproductivo más abundante en la naturaleza y se calcula que infecta a la mitad de todas las especies de insectos y artrópodos. Solo puede vivir dentro del citoplasma celular y se transmite de una generación a la siguiente a través de los óvulos, no de los espermatozoides. Esta peculiar forma de transmisión ha provocado que Wolbachia desarrolle estrategias diversas para maximizar su propagación. Unas estrategias que no favorecen precisamente a los hospedadores machos, incapaces de contribuir a que la bacteria se extienda.
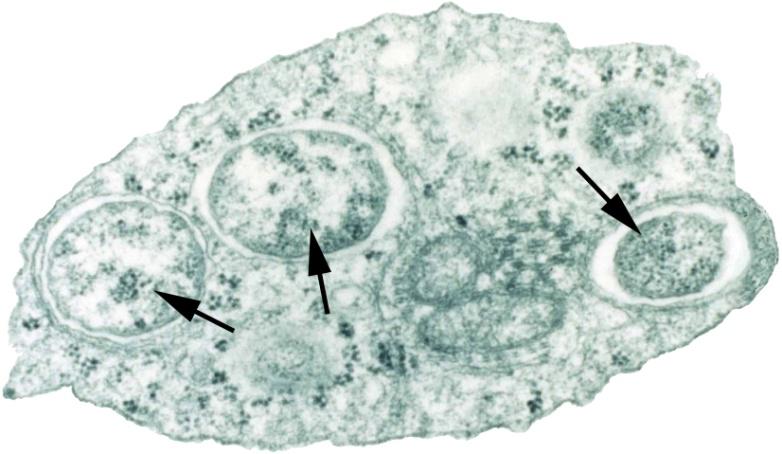 Figura 1. Célula de insecto infectada por Wolbachia (flechas). De Scott O’Neill, doi:10.1371/journal.pbio.0020076, CC BY 2.5.
Figura 1. Célula de insecto infectada por Wolbachia (flechas). De Scott O’Neill, doi:10.1371/journal.pbio.0020076, CC BY 2.5.Wolbachia es capaz de manipular el sistema endocrino de algunos hospedadores para feminizarlos y que solo produzcan óvulos. En otras ocasiones causa la muerte de los hospedadores machos, o hace imposible que espermatozoides de machos infectados fecunden óvulos no infectados por Wolbachia, lo que generaría descendientes sanos. Pueden encontrar más información sobre estas estrategias en un artículo en el que describí algunos de los mecanismos celulares y moleculares desarrollados por la bacteria. También expliqué en ese artículo cómo se está utilizando Wolbachia como aliado en la lucha contra enfermedades transmitidas por insectos.
Una cuarta estrategia es la inducción de partenogénesis, es decir, la reproducción de hembras sin intervención de los machos para producir solo descendientes hembras. En este caso, los mecanismos que utiliza Wolbachia para manipular el sistema reproductivo de sus hospedadores son mucho menos conocidos. Hasta ahora. Un grupo de investigadores de la Universidad Agrícola de Shenyang (China) acaba de desvelar cómo Wolbachia manipula la reproducción de la avispa Encarsia formosa. Este insecto se reproduce por partenogénesis y sus hembras solo producen hembras, sin que aparezcan machos en ningún momento del ciclo reproductivo. Lo relevante del estudio es que Wolbachia utiliza para esta manipulación un gen que ha “robado” a otro insecto.
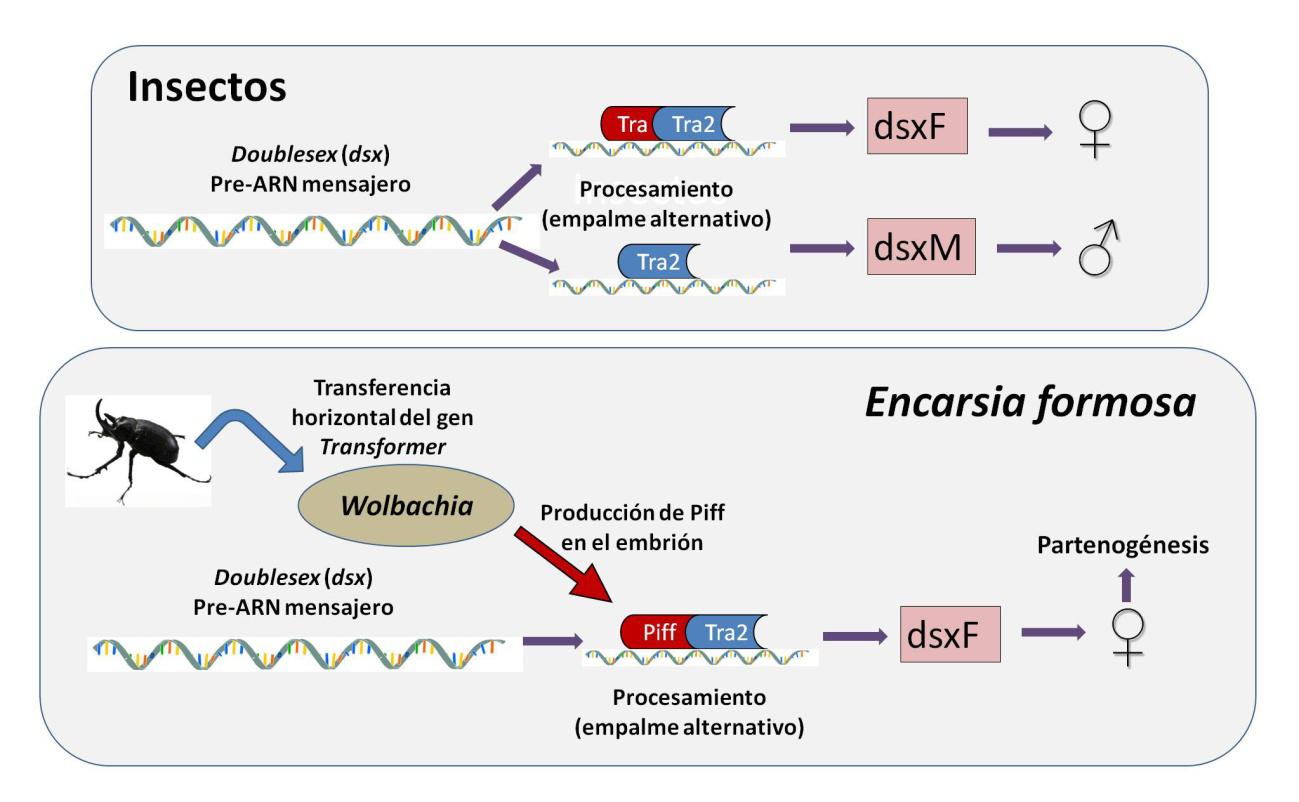 Figura 2. Arriba, determinación del sexo en muchos insectos. El procesamiento del pre-ARNm de Doublesex origina dos mensajeros que generan los polipéptidos dsxF y dsxM, inductores del desarrollo femenino y masculino, respectivamente. La presencia de proteína Transformer (Tra) es esencial para el desarrollo femenino. Abajo, inducción de feminización y partenogénesis en la avispa Encarsia formosa infectada por Wolbachia. Wolbachia ha adquirido en su evolución un gen Transformer de un insecto, con el que produce la proteína Piff, que actúa de la misma forma que Tra. Sólo es posible la diferenciación de hembras, que deben reproducirse obligatoriamente por partenogénesis, contribuyendo a la expansión de Wolbachia.
Figura 2. Arriba, determinación del sexo en muchos insectos. El procesamiento del pre-ARNm de Doublesex origina dos mensajeros que generan los polipéptidos dsxF y dsxM, inductores del desarrollo femenino y masculino, respectivamente. La presencia de proteína Transformer (Tra) es esencial para el desarrollo femenino. Abajo, inducción de feminización y partenogénesis en la avispa Encarsia formosa infectada por Wolbachia. Wolbachia ha adquirido en su evolución un gen Transformer de un insecto, con el que produce la proteína Piff, que actúa de la misma forma que Tra. Sólo es posible la diferenciación de hembras, que deben reproducirse obligatoriamente por partenogénesis, contribuyendo a la expansión de Wolbachia.Para explicar esto necesitamos saber cómo se determina que un insecto sea macho o hembra (Figura 2). En muchos casos esto depende del producto de un solo gen, denominado Doublesex (Dsx). Este gen produce un pre-ARN mensajero que es procesado para dar dos polipéptidos diferentes, dsxF y dsxM. Este procesamiento se conoce como “empalme alternativo” (alternative splicing), un “corta y pega” de segmentos del ARN mensajero. El polipéptido dsxF induce la feminización del embrión, mientras que la forma dsxM origina machos. Para que se produzca la forma dsxF es necesaria la participación de dos proteínas llamadas respectivamente Transformer (Tra) y Transformer2 (Tra2). Si estas dos proteínas aparecen en el desarrollo embrionario se formará un insecto hembra, y en caso contrario tendremos un macho.
Hemos dicho que la avispa E. formosa infectada por Wolbachia sólo produce hembras. Pues bien, si las avispas son tratadas con antibiótico (tetraciclina), la bacteria muere y empiezan a aparecer machos en la descendencia. Eso sí, los machos no son capaces de fecundar a las hembras. E. formosa ha perdido para siempre la capacidad de reproducción sexual, que no se recupera con el tratamiento antibiótico.
Los investigadores chinos estudiaron el sistema de determinación sexual de la avispa y descubrieron que el gen Transformer producía una proteína Tra no funcional. Recordemos que la combinación de Tra con Tra2 es esencial para generar hembras. ¿Cómo se produce entonces la descendencia femenina en las avispas infectadas si Tra no es funcional?
Resulta que Wolbachia produce una proteína llamada Piff (curioso nombre, que viene de parthenogenesis-induction feminization factor). Piff funciona igual que Tra, se une a Tra2 e induce la formación de dsxF, el factor feminizador (Figura 2). Lo sorprendente es que Wolbachia tiene la “inteligencia” de segregar oportunamente el factor Piff justo en el momento del desarrollo en el que se determina el sexo del embrión. Aún más sorprendente es que Piff no aparece en todas las cepas de Wolbachia, y que su secuencia indica que se trata de un gen de insecto, probablemente de un coleóptero. Dicho de otra forma, algunas cepas de Wolbachia se han apoderado de un antiguo gen Transformer de insecto por el fenómeno conocido como “transferencia genética horizontal”. Gracias a esta genialidad evolutiva, suministra a las células del embrión de avispa el producto Piff como complemento de Tra2 y fuerza un desarrollo femenino, dando lugar a un adulto que sólo puede reproducirse por partenogénesis, dada la ausencia de machos. Es importante resaltar que este caso es diferente al de la manipulación del sistema endocrino para feminizar el desarrollo, como hace Wolbachia en otras especies. Lo que hace en este caso es intervenir el propio sistema genético de determinación del sexo.
¿No merece Wolbachia estar en la élite de las bacterias más sorprendentes?
Referencias:
Li C, Li CQ, Chen ZB, Liu BQ, Sun X, Wei KH, Li CY, Luan JB. (2024) Wolbachia symbionts control sex in a parasitoid wasp using a horizontally acquired gene. Curr Biol. doi: 10.1016/j.cub.2024.04.035.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga
El artículo La bacteria que feminiza usando un gen robado se ha escrito en Cuaderno de Cultura Científica.
El ritmo musical y las habilidades comunicativas
José Manuel González Gamarro
Una definición muy recurrente y, hasta cierto punto, comprensible, es la que se hace de la música describiéndola como un lenguaje. Muchas veces se dice que la música es el lenguaje universal, aunque esto no sea más que una alusión a su naturaleza no semántica o bien a un deseo de entendimiento entre seres humanos, como ya expliqué aquí. Lo cierto es que esta comparación tiene su lógica desde el momento en el que se identifica el lenguaje con el habla (aunque no sean lo mismo), puesto que la música y el habla, generalmente, comparten la modalidad auditiva y son de naturaleza comunicativa. Este hecho es especialmente relevante al analizar los primeros años de vida de los seres humanos. La comunicación entre los adultos y sus hijos, cuando aún no se ha adquirido el lenguaje, suele ser efectiva mediante canciones. Cuando se quiere involucrar a los niños en interacciones lúdicas o se pretende calmarlos para hacer que se duerman, se suelen usar canciones. Personalmente he podido comprobar cómo de eficaces son las canciones a la hora de comunicarse con un niño. Por ejemplo, antes de que adquiriera el habla, mi hijo era capaz de identificar los juguetes por la melodía que emitían. Si yo tarareaba una melodía, de todos los que tenía disponibles, centraba toda su atención en el juguete que emitía esa misma melodía. Era una forma de pedirle las cosas antes de que supiera hablar.
 Foto: Sam Moghadam Khamseh / UnsplashEstructuras rítmicas paralelas
Foto: Sam Moghadam Khamseh / UnsplashEstructuras rítmicas paralelas
Las cualidades musicales del habla también se ponen de manifiesto en el desarrollo temprano del lenguaje de los bebés, y una de estas cualidades es el ritmo, que al parecer es una de las primeras propiedades del lenguaje (Nazzi el al., 1998). Esto es debido a que tanto el lenguaje como la música comparten estructuras rítmicas paralelas. Un ejemplo puede apreciarse en los diferentes idiomas. La frecuencia relativa de los ritmos punteados en las canciones populares inglesas en comparación con las francesas es paralela al contraste de los ritmos hablados en los dos idiomas (Huron y Ollen, 2003; Patel y Daniele, 2003), lo que se acentúa en las canciones infantiles (Hannon et al, 2016). La exposición a diferentes patrones de acento en el habla también puede moldear las tendencias perceptuales de agrupación de los bebés. Otro ejemplo con los diferentes idiomas nos lo da la investigadora Katherine A. Yoshida y sus colaboradoras (2010), estudiando las diferencias entre bebés expuestos al idioma japonés en comparación con el inglés. Se ponen de manifiesto diferencias en la manera de agrupar perceptivamente los acentos musicales, lo que probablemente es atribuible a diferencias en los acentos y agrupación en estos idiomas.
La comunicación del afecto es algo trascendental en las canciones que los progenitores cantan a sus bebés, sin embargo, estas canciones también proporcionan un marco temporal sobre el cual se sustentan las habilidades lingüísticas. Es decir, la percepción del ritmo está relacionada con la capacidad del lenguaje en los niños (Gordon et al., 2015; Ladányi, et al., 2020). Esto último tiene mucha relevancia para la observación de las dificultades y trastornos del desarrollo relacionados con la comunicación, es decir, trastornos del habla, el lenguaje y la lectura. Debido a que estos trastornos tienen un gran impacto social y de salud, la investigadora Eniko Ladányi estudia las relaciones profundas entre las dificultades rítmicas en edades tempranas (lo que ella llama “ritmo atípico”) y los posteriores trastornos comunicativos. Estos trastornos presentan en muchas ocasiones comorbilidad con otros trastornos o enfermedades, por lo que identificarlos y comprenderlos para su posterior tratamiento es fundamental para la buena salud de la población. Lo que hace Ladányi es usar el ritmo, sus dificultades o su cualidad de atípico, para predecir y diagnosticar estos problemas comunicativos. Los retrasos o trastornos de la comunicación son sensibles a la intervención temprana, por lo que su pronta identificación puede maximizar la atención terapéutica.
Las habilidades rítmicas como marcador clínicoHay diferentes trastornos de comunicación como pueden ser la dislexia, la tartamudez, el trastorno del desarrollo del lenguaje (conocido como DLD por sus siglas en inglés), etc. que presentan síntomas diferentes, pero existen puntos en común, como un conjunto de posibles “dimensiones” biológicas y conductuales como factores de riesgo que coexisten en todos los trastornos (Nayak et al., 2024). Las habilidades rítmicas podrían proporcionar un marcador clínico para la identificación temprana. Estas habilidades requieren la percepción de pequeñas diferencias entre ritmos, extrayendo tempos de la información rítmica y sincronizando movimientos motores con el puslo, como por ejemplo los golpecitos. El golpeteo isócrono es una forma de medir las habilidades de ritmo musical, el cual se ve afectado en múltiples trastornos del habla y el lenguaje. Las habilidades de sincronización de ritmos están deterioradas en niños con DLD y adultos con dislexia, lo que hace postular una hipótesis a las investigadoras que ellas mismas llaman “hipótesis del riesgo del ritmo atípico”, donde los individuos con deficiencias en muchos aspectos diferentes de las habilidades rítmicas tienen un mayor riesgo de sufrir trastornos del habla y el lenguaje. Para comprobar esta hipótesis se realizaron dos estudios (retrospectivos) principales utilizando datos de cinco cohortes diferentes con un total de 36.950 individuos. Tras estos estudios se pudo concluir que las alteraciones del ritmo son un factor de riesgo transdiagnóstico para los trastornos del desarrollo relacionados con la comunicación. Estas alteraciones rítmicas están relacionadas con una mayor probabilidad de sufrir trastornos de la articulación, tartamudez, dislexia, dificultades con la lectura y el aprendizaje o DLD.
Esto abre una puerta a la ampliación de la comprensión de, por ejemplo, la dislexia ya que, además del estudio del procesamiento del ritmo del habla y la percepción, el papel del ritmo musical parece tener una importancia clave. Los estudios realizados en cuanto al ritmo también lanzaron datos que indican que existe una asociación significativa entre la discriminación del ritmo y las habilidades de lectura. Además, las predisposiciones genéticas para las habilidades de lectura predijeron las puntuaciones en el ritmo, así como las capacidades para sincronizar ritmos predijeron las puntuaciones de lectura, en cohortes diferentes. Esto puede sugerir que la biología subyacente relacionada con el ritmo musical puede ser una fuente adicional de variabilidad entre individuos en los rasgos del habla y el lenguaje.
Posibilidades futurasUna de las consecuencias de estos estudios sobre el ritmo pudiera ser motivar futuros estudios longitudinales que puedan arrojar luz sobre el papel que juega la habilidad rítmica en las distintas etapas del desarrollo y aprendizaje del lenguaje. Además, podrían verse las relaciones entre la genética de los rasgos rítmicos y los diferentes caminos que ha seguido el desarrollo del lenguaje, aunque imagino que esto se verá en un futuro, cuando la hipótesis de las investigadoras se siga sometiendo a su confirmación.
Tal y como deducen las investigadoras, la posibilidad de desarrollar y validar herramientas de detección de los trastornos basadas en ritmos musicales, mejoraría la identificación temprana de personas en riesgo de padecer estos trastornos. Las evaluaciones basadas en el ritmo no requieren ningún cambio ni desarrollo específico para niños multilingües, lo que facilitaría su uso en multitud de países diferentes. Además, usar la evaluación rítmica puede tener un alcance mayor ya que niños que no están en el umbral clínico de estos trastornos, pero presentan (o podrían presentar en un futuro) ciertas dificultades, pueden beneficiarse de este seguimiento por padres, docentes y logopedas. No hace falta decir que este tipo de evaluación rítmico-musical es motivadora y atractiva para los más pequeños, en lo cual reside una gran ventaja. Cómo de eficaces serán estas evaluaciones lo dirá el tiempo, si la investigación avanza en desarrollarlas y llevarlas a cabo.
Todo este asunto del ritmo y las habilidades comunicativas tiene también su lógica desde la perspectiva de la evolución, puesto que hay estudios que postulan que los rasgos de ritmo y comunicación coevolucionaron para respaldar señales creíbles en comportamientos comunicativos claves para la supervivencia, en definitiva, la coordinación entre padres e hijos (Mehr et al., 2020). Esto podría ser una plausible explicación de por qué el ritmo es algo tan primario en los seres humanos. Hay toda una historia biológica, genética, evolutiva, que subyace en un simple repiqueteo de los dedos cuando alguien sigue el tempo o los acentos al oír música. Un primer plano de este simple gesto podría revelarnos una amplia información acerca de nuestra propia manera de comunicarnos.
Que el ritmo no pare.
Gordon, R. L., Shivers, C. M., Wieland, E. A., Kotz, S. A., Yoder, P. J. y McAuley, J. D. (2015). Musical rhythm discrimination explains individual differences in grammar skills in children. Developmental Science, 18(4), 635-644. https://doi.org/10.1111/desc.12230
Hannon, E. E., Lévêque, Y., Nave, K. M. y Trehub, S. E. (2016). Exageration of laguage-specific rhythms in English and French chlidren´s songs. Frontiers in Psychology, 7, 939. https://doi.org/10.3389/fpsyg.2016.00939
Huron, D. y Ollen, J. (2003). Agogic contrast in Frech and English themes: Further support for Patel and Daniele (2003). Music Perception, 21(2), 267-271. https://doi.org/10.1525/mp.2003.21.2.267
Ladányi, E., Persici, V., Fieveash, A., Tillmann, B. y Gordon, R. L. (2020). Is atypical rhythm a risk factor for developmental speech and language disorders? WIREs Cognitive Science, 11(5). https://doi.org/10.1002/wcs.1528
Mehr, S. A., Krasnow, M. M., Bryant, G. A. y Hagen, E. H. (2020). Origins of music in credible signalling. Behavioral and Brain Sciences, 44, e60. https://doi.org/10.1017/S0140525X20000345
Nayak, S., Ladányi, E., Eising, E., Mekki, Y. N., Nitin, R., Bush, C. T., … y Gordon R. L. (2024). Musical rhythm abilities and risk for developmental speech-language problems and disorders: epidemiological and polygenic associations, europepmc.org. https://doi.org/10.31234/osf.io/kcgp5
Nazzi, T., Bertoncini, J. y Mehler, J. (1998). Language discrimination by newborns: Toward an understanding of the role of rythm. Journal of Experimental Psychology: Human Perception and Performance, 24(3), 756-766. https://psycnet.apa.org/doi/10.1037/0096-1523.24.3.756
Patel, A. D. y Daniele, J. R. (2003). An empirical comparison of rhythm in language and music. Cognition, 87(1), B35-B45. https://doi.org/10.1016/S0010-0277(02)00187-7
Yoshida, K. A., Iversen, J. R., Patel, A. D., Mazuka, R., Nito, H., Gervain, J. y Werker, J. F. (2010). The development of perceptual grouping biases in infancy: A Japanese-English cross-linguistic study. Cognition, 115(2), 356-361. https://doi.org/10.1016/j.cognition.2010.01.005
Sobre el autor: José Manuel González Gamarro es profesor de guitarra e investigador para la Asociación para el Estudio de la Guitarra del Real Conservatorio Superior de Música “Victoria Eugenia” de Granada. Una versión anterior de este texto apareció en Substack.
El artículo El ritmo musical y las habilidades comunicativas se ha escrito en Cuaderno de Cultura Científica.
La caza y la evolución del encéfalo humano

Los cambios del cerebro durante el embarazo y la maternidad, cómo el estrés ha pasado de ser un mecanismo de supervivencia a un eventual elemento de riesgo para nuestra salud o cuál ha sido el papel que ha jugado el suicidio en la evolución del ser humano fueron algunos de los temas que se tratarán en la VI Jornada Nacional sobre Evolución y Neurociencias.
La jornada tuvo lugar el Bizkaia Aretoa de la UPV/EHU los pasados 25 y 26 de abril y estuvo dirigida por Eva Garnica y Pablo Malo, de la Red de Salud Mental de Bizkaia, institución que organizó la jornada junto a la Cátedra de Cultura Científica de la UPV/EHU.
El encuentro, cuya primera edición se celebró en 2017, se ha convertido en una cita imprescindible para las y los expertos en ámbitos como la psiquiatría, la psicología o la biología. Una jornada que sirve para analizar el comportamiento humano desde un punto de vista evolutivo y divulgar de un modo accesible para todos los públicos.
La caza, la ingestión regular de carne, un alimento mucho más denso energéticamente, supuso un punto de inflexión en la evolución de nuestro linaje, con profundos cambios fisiológicos y metabólicos, los más trascendentes de los cuales afectaron al encéfalo.
La conferencia «La caza y la evolución del encéfalo humano» corre a cargo de Juan Ignacio Pérez, catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo La caza y la evolución del encéfalo humano se ha escrito en Cuaderno de Cultura Científica.
El negocio de la inteligencia artificial amenaza con convertir la ciencia en pseudociencia
 Elon Musk ha anunciado la introducción de la inteligencia artificial general en sus productos aunque no exista. En la imagen en plena pandemia covid-19. Fuente: Wikimedia Commons.
Elon Musk ha anunciado la introducción de la inteligencia artificial general en sus productos aunque no exista. En la imagen en plena pandemia covid-19. Fuente: Wikimedia Commons.Cuando hablamos de inteligencia artificial (IA) debemos orientarnos con rigor a partir de las bases de las ciencias que la soportan. En otras palabras, nunca debemos apoyarnos en las expectativas generadas artificialmente alrededor de nuevos productos que nos intentan vender, así como en la tremenda hipérbole publicitaria (hype) que arrasa todos los medios. Las afirmaciones exageradas sobre sus éxitos dañan seriamente la reputación de la IA como ciencia y la pueden conducir a ser utilizada casi como una pseudociencia, al modo de la astrología, el terraplanismo y la homeopatía.
El científico Jonathan Grudin publicó en 2009 un artículo en el que ilustraba las bruscas oscilaciones del interés, financiación y avances reales de la IA a lo largo de su historia. En él se recurría a la metáfora de las estaciones del año, que nos permite comprender cómo ha evolucionado la IA desde su nacimiento.
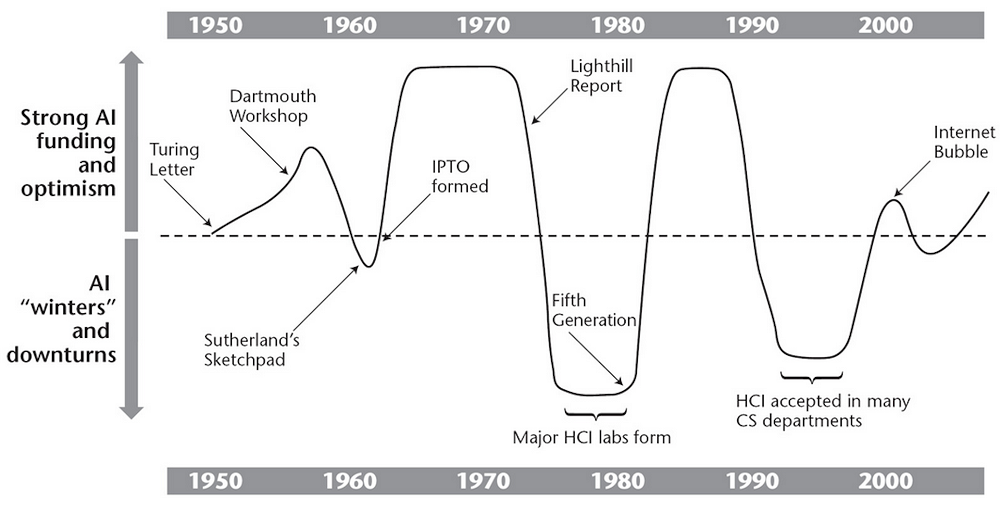 El ciclo estacional de la IA. Fuente: J. Grudin (2009) AI and HCI: two fields divided by a common focus. AI Magazine, vol. 30, n. 4, pp: 48-57. doi: 10.1609/aimag.v30i4.2271.
El ciclo estacional de la IA. Fuente: J. Grudin (2009) AI and HCI: two fields divided by a common focus. AI Magazine, vol. 30, n. 4, pp: 48-57. doi: 10.1609/aimag.v30i4.2271.Ahora, terminando el primer cuarto del siglo XXI nos encontramos en un período álgido, pero no son improbables futuras y profundas simas de inviernos de la IA, dado que aún hay mucho que investigar y comprender sobre esta importante área de conocimiento.
La comunidad científica de este campo es consciente de lo lejos que nos encontramos de modelar verdaderos sistemas nerviosos computacionales o de entender en qué consiste la inteligencia. Estos investigadores también asumen que no hay evidencia –ni matemática, ni física, ni biológica–, ni se conoce la existencia de ningún prototipo equivalente a las capacidades pensantes de un cerebro humano. Por ello aún es necesario gran esfuerzo en múltiples áreas si deseamos avanzar desde la ciencia y con pasos serios y firmes.
Las IA generativas son degenerativasLos productos más populares de la industria IA en estos últimos tiempos son las “IA generativas” basadas principalmente en redes neuronales computacionales entrenadas con modelos de lenguaje de gran tamaño (LLM). Los ejemplos más conocidos son ChatGPT, MidJourney y Sora, capaces de generar texto, gráficos, sonido y vídeos.
Estas herramientas computacionales son entrenadas con enormes cantidades de datos presentes en internet, producidos por personas que tienen derechos legales de autoría de su material, pero que circula libre por la red.
Muchas empresas tienden a evitar demandas judiciales o a ahorrar costes y utilizan datos generados por sus propias IA para seguir entrenando sus máquinas. Desde las matemáticas se demuestra que este entrenamiento recursivo de la máquina con datos generados previamente por la propia máquina produce un efecto estadístico llamado “colapso del modelo”.
Este colapso da lugar a desinformación, degeneración de contenido, modelos de aprendizaje incorrectos crecientes, e incluso a un posible colapso de internet como fuente confiable.
Sabemos que muchas IA generan contenido con buena apariencia, pero falso. Si un buscador web se basa en una IA generativa como ChatGPT el resultado podría ser muy convincente, pero incorrecto. Si lo damos como válido y no lo comprobamos, y además liberamos ese contenido como entrenamiento para la IA, se llenaría de desinformación a una de nuestras fuentes más importantes de información.
Mala praxis en la industria IAEl negocio IA no se para, aunque la ciencia demuestre que no existe la IA fuerte o general (AGI) y que las herramientas particulares existentes (IA débil) necesitan mejoras significativas para asistir correctamente en la resolución de algunos problemas.
Muchas empresas tecnológicas continúan amplificando el hype para seguir haciendo crecer sus resultados económicos. Por poner unos pocos ejemplos de importantes empresarios del sector que saben que no es posible lo que dicen, podemos citar recientes declaraciones o “predicciones” de Elon Musk y de Mark Zuckerberg, quienes anuncian la inminente introducción de esta inexistente inteligencia artificial general en sus productos.
Una praxis quizás aún más censurable es la fundación por parte de Sam Altman (CEO de OpenAI, creadora de ChatGPT) de la empresa Worldcoin, dedicada a las criptomonedas. Muy llamativa ha sido su campaña en todo el mundo de capturar datos biométricos de personas (mayores o menores de edad) por medio de unos “orbes”, dispositivos atractivos para la juventud, que escanean el iris. La clientela capturada por medio de esta campaña cede sus datos a cambio de un token (un vale digital).
La justificación de Worldcoin es intentar ofrecer, en el futuro, una renta universal en criptomonedas para compensar la pérdida de empleos debido al avance de la IA. Afortunadamente, esta declaración tan burda ha permitido a varios países prohibir su actuación, pero muchos han sido captados ya por la empresa.
El culto de la singularidadEl conocido ingeniero e inventor Ray Kurzweil, autor de muchos libros sobre la IA, las máquinas espirituales y el transhumanismo, escribió en 2005 un gran éxito editorial titulado La singularidad está cerca.
La “singularidad tecnológica” es un hipotético acontecimiento por el que las máquinas superarán en inteligencia a la humanidad.
El argumento de Kurzweil se basa en una idea simplista que denominó “ley de los rendimientos acelerados”, en la que postula que el crecimiento científico y tecnológico es exponencial, como una versión generalizada de la ley de Moore de la industria informática.
Relevantes miembros de la industria y ciencia de la computación, como el propio Gordon Moore (cofundador de Intel) y Paul Allen (cofundador de Microsoft) y Mark Greaves expresaron desde hace muchos años una frontal disconformidad con la predicción de la singularidad. Uno de los motivos es que la neurociencia no funciona como los computadores y que ni siquiera hemos empezado a desvelar las capas de complejidad que nos impiden entender cómo funciona nuestra propia mente.
Kurzweil fundó en 2008 la Universidad de la Singularidad, con sede en California, para “reunir, educar e inspirar a un grupo de dirigentes”. Su libro principal, escrito usando términos científicos, pero dogmático y sin expresar ningún tipo de dudas en sus afirmaciones o profecías, es más bien un texto de fe en su transhumanismo. La Universidad de la Singularidad se parece mucho a otros cultos como la cienciología que han ido surgiendo en el último siglo.
Kurzweil pondrá a la venta en verano de 2024 su nueva secuela: The Singularity Is Nearer“, que seguramente se convertirá en un superventas. Anuncia que trata de expandir su universidad con nuevas sedes en Tel Aviv y Sevilla.
El nuevo texto de Kurzweil predice el advenimiento de la singularidad para 2029. Mientras la comunidad científica trata de avanzar en el conocimiento, el negocio de la IA no duda en sembrar la confusión, vender lo que sea y transformar esta ciencia en una peligrosa pseudociencia.![]()
Sobre el autor: Victor Etxebarria Ecenarro es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (UPV/EHU)
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo El negocio de la inteligencia artificial amenaza con convertir la ciencia en pseudociencia se ha escrito en Cuaderno de Cultura Científica.

