La energía oscura evoluciona
 Las estelas de las estrellas toman forma alrededor de la cúpula del telescopio Mayall, en cuyo interior está el Instrumento Espectroscópico de Energía Oscura del experimento DESI
Las estelas de las estrellas toman forma alrededor de la cúpula del telescopio Mayall, en cuyo interior está el Instrumento Espectroscópico de Energía Oscura del experimento DESIFuente: P. Marenfeld y NO, CC BY
Cada nuevo gran experimento para entender el universo es como un capítulo de una novela muy larga. La pieza más reciente puesta a disposición del público ha corrido a cargo de la colaboración DESI, el mayor experimento desde que la humanidad investiga el cosmos.
Con DESI, hemos logrado cartografiar un gran número de galaxias y quásares en el universo, proporcionando una visión sin precedentes de su distribución y estructura. No solo eso: tenemos un mapa de la distribución de materia de los últimos once mil millones de años. No está mal teniendo en cuenta que todo el universo tiene algo menos de catorce mil millones de años.
DESI ha sido capaz de darnos el mejor mapa tridimensional del universo.
Sin incertidumbreImaginemos el universo como un mar lleno de islas de materia. Cada isla tiene un faro, las galaxias. No vemos toda la tierra de cada isla, pero sí sabemos que donde haya un faro, habrá una isla. Esas islas son un poco particulares porque se mueven, cada una a una velocidad distinta tanto en dirección como en cantidad. Pues bien, a partir de esas velocidades podemos saber a qué distancia está de nosotros cada galaxia. Es algo así como saber si se acerca o aleja una ambulancia por como oímos su sirena.
Como todo buen relato, a medida que avanza se pone más interesante. Gracias al mapa que nos ha proporcionado DESI de los últimos mil millones de años, en este momento nuestro conocimiento acerca de la evolución del universo tiene una incertidumbre que no supera el 1 %.
Cambia, todo cambiaEntre la abundante información que nos ha proporcionado DESI, el hallazgo más importante es que la energía oscura parece suscribir una vieja canción, aquella con un verso que decía “cambia, todo cambia”.
Y es que, durante décadas, hemos pensado que la mejor descripción posible de la energía oscura era una constante cosmológica. En ese modelo, la densidad de este ingrediente de la sopa cósmica permanecía inalterada, casi como una fotografía. Aunque, aun siendo constante, la repulsión gravitatoria que ejerce ese tipo de energía oscura hace que el universo se acelere de forma contante.
Así es como hasta ahora nos lo hemos contado. Puede que lo que estemos viendo no sea una fotografía impertérrita en el tiempo, sino una película lenta pero apasionante. Pero es muy posible que, como en una buena novela de Agatha Christie, haya un inesperado giro final y que venga de manos de la energía oscura.
Siguiendo con la analogía literaria, DESI es el Hércules Poirot de esta novela.
Mapeando nuestra ignoranciaUno de los escenarios más populares para explicar la evolución del universo toma como parámetro la rapidez a la que se expande, y un modelo matemático muy sencillo. Tomamos el valor actual (a qué velocidad se mueve el universo más joven) y, por otro lado, el valor de la velocidad que se observa en el universo primitivo. Trazamos una línea que una el valor actual y el más antiguo que podamos tener. DESI se ha encargado de ver la pendiente de la recta. Para ello, los investigadores van reconstruyéndola con sus datos. A veces hay zonas que son inaccesibles a este experimento concreto y recurren a los valores de otros proyectos. En otras ocasiones nos encontramos con un desierto de datos y tenemos que recurrir a rellenar el hueco con ingenio matemático. De alguna manera estamos mapeando nuestra ignorancia.
Las galaxias cuya física ha observado DESI con altísima precisión permiten acotar cada vez más esa incertidumbre.
La energía oscura se diluyeEl resultado de los datos analizados por DESI permite interpretar que la energía oscura en el universo se está diluyendo. Mientras se diluye –eso sí, muy lentamente–, sigue dominándolo todo. Entretanto, el universo sigue y seguirá expandiéndose de forma acelerada.
Pero DESI evidencia algo nuevo, un cambio que no es fácil de encajar: en las etapas más tempranas del universo esto no era así. En aquel periodo la materia, igual que ahora, era un actor secundario, y la energía oscura ni siquiera cotizaba en la gran lonja cósmica. En aquel principio entre los principios, el papel protagonista correspondía a los fotones que hoy forman el fondo cósmico de microondas.
Según DESI, durante aquella etapa la densidad de la energía oscura fue poco a poco aumentando, reclamando su papel relevante.
Podemos aprender algo de este cambio de tendencia. Si el comportamiento actual de la energía oscura difiere mucho del primitivo es porque… ¡se ha producido una evolución! ¡El giro final ha sido descubierto por nuestro Hércules Poirot, DESI!
El revuelo entre físicosEstos hallazgos han suscitado una actividad frenética. Son muchos los investigadores que se han lanzado bien a refutar o bien a respaldar los resultados. Por un lado, la física involucrada es tremendamente compleja. Por otro lado, el tratamiento estadístico de los datos ha de ser intachable. Así que muchos nos ponemos a buscar por los rincones pistas de algo que no acaba de encajar. Algunos cosmólogos nos convertimos en el personaje cotilla de la novela que aporta información al principal responsable de la investigación.
La siguiente cuestión a resolver por nuestro detective cósmico se puede formular así: ¿por qué se ha comportado la energía oscura de forma diferente en dos periodos del universo?
Afortunadamente, DESI no ha acabado aquí, le queda mucha investigación por delante. De hecho, al menos hasta el año 2026 seguirá observando.
¿Quién sabe qué más misterios se plantearán a partir de lo que observe? ¿Y quién sabe si también resolverá algunos de los misterios cosmológicos que ya tenemos entre manos?![]()
Sobre las autoras: Ruth Lazkoz, Profesora de Física Teórica, Universidad del País Vasco / Euskal Herriko Unibertsitatea y David Figueruelo Hernán, Investigador Postdoctoral en Cosmología, Universidad de Salamanca
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo La energía oscura evoluciona se ha escrito en Cuaderno de Cultura Científica.
Un valle de película
Si pregunto por la relación entre los actores William Shatner y Patrick Stewart, las personas fanáticas de la ciencia ficción lo tendrán clarísimo: la capitanía de la nave interestelar USS Enterprise en Star Trek. Ahora bien, si incluyo en el pack al también actor Arnold Schwarzenegger, la cosa se complica. Aunque, si hago yo la pregunta, la respuesta es bastante obvia: la geología. Pero no la geología de manera genérica, me refiero a la geología de una localización muy concreta. Si habéis visto la película Star Trek: Generations, cuando los capitanes Kirk y Picard interaccionan en el planeta Veridian III, y la película Total Recall (Desafío Total en España) cuando Quaid se pasea por Marte, igual os habéis dado cuenta de que ambos paisajes son el mismo. En concreto, esos exteriores se grabaron en el Parque Estatal Valle del Fuego de Nevada.
 A) Fotograma de la película Star Trek: Generations con los dos protagonistas enfrentándose al villano en el planeta Veridian III. Fuente: Paramount Pictures. B) Detalle de la película Total Recall con el protagonista paseando por la superficie de Marte. Fuente: Columbia Pictures / Tri-Star Pictures
A) Fotograma de la película Star Trek: Generations con los dos protagonistas enfrentándose al villano en el planeta Veridian III. Fuente: Paramount Pictures. B) Detalle de la película Total Recall con el protagonista paseando por la superficie de Marte. Fuente: Columbia Pictures / Tri-Star PicturesA unos 80 km al noreste de la capital mundial del juego, Las Vegas, y en pleno desierto de Mojave se encuentra el Valle del Fuego, un lugar con un increíble paisaje formado por rocas bandeadas de tonos rojizos, anaranjados y pardos que brillan con fuerza, incluso cambiando de color, cuando les da el sol, asemejando un enorme lugar llameante, efecto que le ha dado nombre. Característica que lo convierte en un deseado plató de cine no solo para películas de estilo western, sino también para producciones de ciencia ficción como las dos que he comentado previamente. Y esta propiedad se debe a su historia geológica.
 Aspecto general de las rocas presentes en el Valle del Fuego (Nevada, Estados Unidos) con el característico bandeado de colores. Fuente: Nevada State Parks
Aspecto general de las rocas presentes en el Valle del Fuego (Nevada, Estados Unidos) con el característico bandeado de colores. Fuente: Nevada State ParksLa mayoría de las rocas presentes en el Valle del Fuego forman parte de una formación geológica llamada Arenisca Azteca (Aztec Sandstone en el original en inglés). Aunque su nombre ya nos está chivando que, principalmente, nos vamos a encontrar con areniscas formadas por abundantes granos de cuarzo, también aparecen otras rocas detríticas como lutitas y conglomerados de grano fino, además de algunas rocas carbonatadas como las calizas. Estos materiales se formaron hace más de 150 millones de años, durante el Jurásico, cuando el aspecto de esta zona era muy diferente al actual. Por aquel entonces, este lugar era un enorme desierto, mayor de lo que es el Sahara hoy en día, donde el viento movía los granos de cuarzo formando enormes campos de dunas que se movían continuamente. Estas dunas han quedado preservadas en las rocas areniscas, que aún conservan estructuras y lineaciones internas que marcan las crestas y las zonas de máxima pendiente por la que caían los granos de cuarzo.
 Detalle de la arenisca jurásica roja donde se aprecia la lineación interna formada por el movimiento de los granos de cuarzo en las dunas originales. Fuente: Nevada State Parks
Detalle de la arenisca jurásica roja donde se aprecia la lineación interna formada por el movimiento de los granos de cuarzo en las dunas originales. Fuente: Nevada State ParksPor otro lado, en las zonas planas entre las dunas podía acumularse el agua de lluvia, dando lugar a pequeñas charcas y ambientes húmedos que llegaban a convertirse en oasis o lagunas efímeras rodeadas por cierta vegetación y que se han transformado en niveles aislados de rocas carbonatadas o calizas entre las areniscas. Incluso había pequeños cañones por los que el agua podía fluir en forma de arroyos temporales durante episodios tormentosos, arrastrando barro y arena que desparramaba en áreas cercanas cuando perdía la fuerza necesaria para seguir transportándolos. Este último ambiente ha dado lugar a los conglomerados y las lutitas. Pero que esta zona fuese un desierto no implica que no estuviera habitado, ya que se han encontrado fósiles de huellas de artrópodos, reptiles voladores y dinosaurios que se acercaban a las zonas húmedas a beber.
La historia geológica de este lugar no termina aquí. Tras formarse, estas rocas sufrieron grandes procesos tectónicos debido al movimiento las placas litosféricas que culminaron con la creación del actual continente Norteamericano. Primero, a finales de la Era Mesozoica, estuvieron sometidas a esfuerzos compresivos, o de empuje, que dieron lugar a fallas y plegamientos de los materiales. Y, si no habían tenido suficiente, hace entre unos 17 y 14 millones de años sufrieron extensión, es decir, todo lo contrario, generando todavía más fracturación en estas rocas. Pero eso no es todo, ya que en los últimos cientos de miles de años han estado expuestas a la intemperie, siendo modeladas y esculpidas por las inclemencias meteorológicas, cuya erosión ha provocado morfologías como arcos, cañones o cavernas que han despertado la imaginación de la gente que las observaba, creando pareidolias que recuerdan a elefantes o panales de abeja.
Aunque la principal pregunta es, ¿de dónde han salido estos colores? Parece que estas areniscas ya eran rojas cuando se formaron las dunas durante el Jurásico, ya que se han encontrado granos de cuarzo cubiertos por hematites. Este mineral es un óxido de hierro (Fe2O3) que tiene una coloración rojiza brillante que le da nombre (traducido como “parecido a la sangre” del griego). Cuando estas rocas rojas fueron sometidas a los procesos tectónicos posteriores, diferentes tipos de fluidos, tanto subterráneos como superficiales, circularon entre ellas, provocando reacciones químicas que cambiaron las coloraciones, dando lugar a tonos amarillentos, rosados o anaranjados en secuencias bandeadas que destacan sobre los grises de las calizas. Finalmente, las precipitaciones actuales han aportado una pátina marronácea superficial en muchas areniscas debido a la oxidación, pátinas que fueron utilizadas como lienzos por culturas como la anazasi, que las retiraban pacientemente hasta dejar de nuevo a la vista el color rojo de las rocas dibujando así impresionantes petroglifos.
 Petroglifos conservados en la roca arenisca jurásica del Valle del Fuego, formados por el raspado de la pátina de óxido superficial. Foto: Clément Bardot / Wikimedia Commons
Petroglifos conservados en la roca arenisca jurásica del Valle del Fuego, formados por el raspado de la pátina de óxido superficial. Foto: Clément Bardot / Wikimedia CommonsY así es como se crea un escenario de película, teniendo de fondo una historia geológica propia de una gran superproducción de Hollywood. Aunque lo que habéis leído aquí está tan resumido que sería, únicamente, el tráiler promocional de este fantástico film.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Un valle de película se ha escrito en Cuaderno de Cultura Científica.
Muerte de un matemático napolitano
No tengo certezas, a lo sumo probabilidades.
Morte di un matematico napoletano (1992) es el título de una película dirigida por Mario Martone que ganó, entre otros, el premio especial del jurado en la 49a edición del Festival Internacional de Cine de Venecia.
Esta película se basa en un personaje real, el matemático italiano Renato Caccioppoli (1904-1959), y narra los últimos días de su vida, antes de suicidarse, un 8 de mayo, hace 65 años.
 Renato Caccioppoli (hacia 1925). Fuente: Wikimedia Commons.
Renato Caccioppoli (hacia 1925). Fuente: Wikimedia Commons.Roma, 1 de mayo de 1959. Por la noche, en la sala de espera de la estación Termini, la policía ferroviaria detiene a un hombre en evidente estado de embriaguez. Se trata del profesor Renato Caccioppoli, profesor de matemáticas puras en la Universidad de Nápoles, miembro de la Accademia Nazionali dei Lincei, sobrino de Maria Bakunin por parte de madre, célebre científico registrado como comunista. Liberado inmediatamente después de su detención, regresa a la mañana siguiente en el primer tren hacia Nápoles.
Desilusionado y atormentado, ya esclavo del alcohol, de vuelta del hospital psiquiátrico, abandonado por su esposa, distanciado de sus camaradas del Partido Comunista Italiano y de sus colaboradores de la universidad, Caccioppoli vive su última semana de vida: lo vemos con amigos, familia, colegas o solo mientras deambula desencantado a pie por una bochornosa Nápoles. En el ambiente académico se siente un extraño, su genio matemático le atormenta y le agota, el partido ya no confía en él, las relaciones sentimentales le han decepcionado y los lazos familiares le oprimen. El proyecto largamente aplazado se vuelve cada vez más necesario: el suicidio, su último acto como hombre libre.
Caccioppoli, el matemáticoRenato Caccioppoli nació el 20 de enero de 1904 en Nápoles, en el seno de una familia acomodada. Era hijo del cirujano Giuseppe Caccioppoli y de su segunda esposa, la médica Sofia Bakunina, hija del anarquista y filósofo ruso Mijaíl Bakunin. También era sobrino de la química y profesora universitaria Maria Bakunin.
Siguiendo los deseos de su padre, comenzó a cursar estudios de Ingeniería en 1921. Aunque dos años más tarde cambió a la carrera de Matemáticas, graduándose en la Universidad de Nápoles en 1925. Se convirtió inmediatamente en asistente de Mauro Picone, con quien realizó su tesis doctoral en análisis matemático, trabajo codirigido por Ernesto Pascal. Durante los cinco años siguientes publicó una treintena de artículos que le permitieron ganar, en 1931, un puesto de catedrático de Análisis Algebraico en la Universidad de Padua. En 1934 regresó a la Universidad de Nápoles donde ocupó la cátedra de Teoría de Grupos hasta 1943, y después pasó a la cátedra de Análisis Matemático hasta 1959.
Publicó unos ochenta artículos científicos centrados fundamentalmente en análisis funcional y cálculo de variaciones.
En 1930 comenzó a estudiar ecuaciones diferenciales con un enfoque topológico-funcional. Entre otros muchos resultados, demostró el carácter analítico de las soluciones de las ecuaciones elípticas de clase C2, inspirando de este modo la resolución del problema decimonoveno de Hilbert, solucionado en 1957 por el matemático Ennio De Giorgi.
Precisamente fue De Giorgi quien nombró “conjuntos de Caccioppoli” a cierto tipo de conjuntos obtenidos a partir de superficies, y en los que Caccioppoli también trabajó.
Consiguió crear, además, una importante escuela de matemáticos.
Caccioppoli, más allá de las matemáticasA partir de 1938 se convirtió en miembro ordinario de la Academia de Ciencias Físicas y Matemáticas de Nápoles. El 15 de febrero de 1947 fue aceptado como miembro de la Accademia Nazionali dei Lincei, el mismo día de la admisión de su tía Maria Bakunin, un episodio único en la historia de esta academia científica italiana.
Entre 1947 y 1951 dirigió junto a Carlo Miranda la revista Giornale di matematiche, fundada en 1863 por Giuseppe Battaglini.
La anécdota que se comenta a continuación muestra el carácter inconformista Caccioppoli. El 5 de mayo de 1938, coincidiendo con una visita de Adolf Hitler y Benito Mussolini a Nápoles, Caccioppoli contrató una orquestina para que tocara La Marsellesa y pronunció un discurso contra los dictadores. Su tía Maria Bakunin, a la que estaba muy unido, intervino ante las autoridades para impedir el arresto de su sobrino: consiguió convencer a los enfurecidos gobernantes de que Renato estaba desequilibrado, que era incapaz de entender y de querer, y fue enviado temporalmente a un hospital psiquiátrico, evitando la cárcel.
Tras la guerra, Caccioppoli se acercó al Partido Comunista Italiano, sin llegar a afiliarse, entre otros motivos, porque no estaba de acuerdo con la visión oficial soviética de la ciencia.
 Renato Caccioppoli (finales de la década de 1950). Fuente: Wikimedia Commons
Renato Caccioppoli (finales de la década de 1950). Fuente: Wikimedia Commons
En los últimos años de su vida llegaron los desengaños políticos, el abandono por parte de su esposa Sara Mancuso (con la que se había casado en 1939) y probablemente un sentimiento de declive de su intuición y destreza matemáticas. Se refugió en el alcohol: el 8 de mayo de 1959 puso fin a su vida, en su casa, con un disparo en la cabeza.
Referencias
- Faber Renato Fabbris, Renato Caccioppoli, MacTutor History of Mathematics archive, University of St Andrews
- Carlo Sbordone, Renato Caccioppoli, nel centenario della nascita, Bollettino dell unione matematica italiana. Sezione A: la matematica nella società e nella cultura, vol. 7, nº 2 (2004) 193-214
- Angelo Guerraggio, Renato Caccioppoli. Naples: Fascism and the Post-War Period, en Mathematical Lives (2010) 97-107
- Renato Caccioppoli a 100 anni dalla nascita, PRISTEM
- Renato Caccioppoli, Wikipedia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Muerte de un matemático napolitano se ha escrito en Cuaderno de Cultura Científica.
Una piedra Rosetta para las matemáticas
En 1940, André Weil escribió una carta a su hermana, Simone, describiendo su visión para la traducción entre tres áreas distintas de las matemáticas. Ochenta años después, todavía anima muchos de los desarrollos más interesantes en este campo.
Un artículo de Kevin Hartnett. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Ilustración: Kristina Armitage / Quanta Magazine
Ilustración: Kristina Armitage / Quanta Magazine
En 1940, desde una cárcel de Rouen, Francia, André Weil escribió una de las cartas más trascendentales de las matemáticas del siglo XX. Cumplía condena por negarse a alistarse en el ejército francés y ocupaba sus días en parte escribiendo cartas a su hermana, Simone, una consumada filósofa que vivía en Londres.
En una carta anterior, Simone le había pedido a André que le hablara de su trabajo. En medio de la guerra, André comenzó su respuesta con cautela, advirtiendo a su hermana que pasado cierto punto “no entenderás nada de lo que sigue”. En las siguientes 14 páginas esbozó su idea de una “piedra de Rosetta” para las matemáticas. Siguiendo el ejemplo del famoso epígrafe del mismo nombre (un texto trilingüe que hizo que la escritura del antiguo Egipto fuera legible para los lectores occidentales mediante su traducción al griego antiguo), la piedra Rosetta de Weil vinculaba tres campos de las matemáticas: teoría de números, geometría y, en el medio, el estudio de campos finitos.
Otros matemáticos habían propuesto ideas en esta dirección, pero Weil fue el primero en exponer una visión exacta. Su carta presagiaba el programa Langlands, una importante iniciativa en la investigación matemática contemporánea.
«Hay tres mundos que no se comunican directamente entre sí, pero hay ciertas características que tienen en común, y la experiencia muestra que algunas preguntas de un lado pueden interpretarse apropiadamente en otro», explica Brian Conrad, de la Universidad de Stanford.
El primer elemento de la piedra Rosetta de Weil era la teoría de números, el corazón carismático de la investigación matemática durante milenios. La preocupación central de la teoría de números son los números enteros, o números enteros positivos y negativos, y las funciones que dependen de ellos. Los teóricos de los números intentan demostrar resultados sobre cosas como cómo se distribuyen los números primos, utilizando herramientas que pueden extraerse de todo tipo de ramas esotéricas de las matemáticas. También estudian mundos matemáticos llamados campos numéricos que generalizan algunas propiedades importantes de los números enteros.
 André Weil y su hermana Simone fotografiados cuando él tenía 16 años y ella 13. Ambos crecieron hasta convertirse en intelectuales influyentes. Fuente: ARCHIVO GBB / Alamy
André Weil y su hermana Simone fotografiados cuando él tenía 16 años y ella 13. Ambos crecieron hasta convertirse en intelectuales influyentes. Fuente: ARCHIVO GBB / AlamyAl otro lado de la piedra Rosetta de Weil estaba la geometría. Pensaba especialmente en formas como esferas, donuts y pretzels [galletas saladas con forma de nudo] con múltiples agujeros. Estas formas son los conjuntos de soluciones de ciertas ecuaciones que tienen dos variables, como y2 = x3 − x. Se puede considerar que esas soluciones son números «complejos», que tienen una parte «real» (los tipos de números que la gente usa en la vida cotidiana) y una parte «imaginaria», que es un número real multiplicado por la raíz cuadrada de -1, que se escribe i.
Debido a que estas formas son la encarnación geométrica de soluciones a ecuaciones polinómicas, tienen una estructura que puede explotarse utilizando técnicas de análisis complejo, una forma de cálculo. Esta estructura permite un conjunto más rico de herramientas de demostración de teoremas, más allá de las que están inmediatamente disponibles para los teóricos de los números.
Esto estaba claro para los matemáticos del siglo XIX y los motivó a imaginar lo bonito que sería demostrar teoremas sobre las “superficies de Riemann” (las formas que interesaban a Weil) que a su vez pudiesen traducir a teoremas de teoría de números. Pero hay muchas cosas bonitas que no son ciertas, y Weil reconoció ante su hermana que la teoría de superficies de Riemann “está demasiado alejada de la teoría de números. Uno estaría totalmente obstruido si no hubiera un puente entre ambas”.
Entonces llegó al punto principal de su carta: estaba construyendo ese puente. Escribió: “Así como Dios vence al diablo: este puente existe”.
 Robert Langlands, visto aquí en una foto sin fecha, escribiría una carta a Weil que marcó el rumbo de una generación de investigación matemática. Fuente:
Robert Langlands, visto aquí en una foto sin fecha, escribiría una carta a Weil que marcó el rumbo de una generación de investigación matemática. Fuente:Archivo del Instituto de Estudios Avanzados
El puente que proponía Weil era el estudio de los campos finitos: sistemas de números pequeños que se parecen a los números reales al tener dos operaciones que funcionan sin problemas, como la suma y la multiplicación. Lo logran tomando la forma circular que se encuentra en un reloj, con un número primo de horas. Digamos que tienes un reloj con sólo 11 horas; comenzando a las 10 en punto y agregando dos horas, terminarías a la 1 en punto. (El número de horas del reloj tiene que ser primo para que la división funcione como debe).
Los campos finitos son un lugar donde la teoría de números y la geometría comienzan a fusionarse.
To see how, take a finite field with two elements: zero and 1. You can write polynomials — functions that combine sums and products of fixed exponents — in this field. Their coefficients — the numbers in front of the variables — have to be either zero or 1, as in these two polynomials:
Para ver cómo, toma un campo finito con dos elementos: cero y 1. Puedes escribir polinomios (funciones que combinan sumas y productos de exponentes fijos) en este campo. Sus coeficientes (los números delante de las variables) tienen que ser cero o 1, como en estos dos polinomios:
Ejemplo A: 0x3 + 1x2 + 0x + 1
Ejemplo B: 1x3 + 1x2 + 1x + 0
Estos polinomios se pueden representar usando solo sus coeficientes, que forman una cadena de ceros y unos. Los números enteros también se pueden codificar como cadenas de ceros y unos, en lo que se llama forma binaria, donde se expresan como sumas de potencias de 2. El número 1 es igual a 20, 2 es 21, 3 es 21 + 20 y así sucesivamente. Por lo tanto, en binario, los primeros tres números enteros son 00, 01 y 10.
Sobre el campo finito con dos elementos, los coeficientes y los números enteros de polinomios están codificados ambos como cadenas de ceros y unos. Entonces el polinomio del ejemplo A corresponde al número 5, ya que sus coeficientes, 0101, son el número 5 escrito en binario, y el polinomio del ejemplo B corresponde al número 14, ya que 1110 es el número 14 escrito en binario.
También tienen otras similitudes. Algunos números enteros son primos, lo que significa que sus únicos factores son 1 y ellos mismos, y otros son compuestos, lo que significa que son productos de múltiples números primos. Esta misma distinción entre primos y compuestos se aplica a los polinomios. Algunos polinomios se pueden factorizar como producto de polinomios más pequeños que por sí mismos no se pueden factorizar. Estos polinomios más pequeños, conocidos como polinomios irreducibles, son los números primos del mundo polinomial. Y da la casualidad de que los coeficientes de los polinomios irreducibles forman cadenas binarias que codifican números primos. Los polinomios están estrechamente relacionados con las ideas de la geometría, pero en el campo finito con dos elementos su aritmética se vuelve vagamente análoga a la aritmética de los números enteros, abriendo la posibilidad de que, en este contexto, la intuición visual pueda aplicarse a cuestiones de teoría de números.
Escribiendo a su hermana, Weil declaraba que “la analogía con los campos numéricos es tan estricta y obvia que no hay argumento ni resultado en aritmética que no pueda traducirse casi palabra por palabra al campo de función [o finito]”. Sin embargo, admitía que la distancia entre las superficies de Riemann y los campos finitos es mayor. Los polinomios se pueden expresar y factorizar en campos finitos, pero importar toda la maquinaria del análisis complejo a campos finitos era otra cuestión. Sin embargo, Weil afirmaba con confianza: «La distancia no es tan grande como para que un estudio paciente no nos enseñe el arte de pasar de uno a otro». Entonces describía su gran ambición:
Mi trabajo consiste en descifrar un texto trilingüe [de ahí el símil con la piedra Rosetta]; de cada una de las tres columnas solo tengo fragmentos dispares; tengo algunas ideas sobre cada uno de los tres idiomas: pero también sé que hay grandes diferencias de significado de una columna a otra, para las que nada me ha preparado de antemano.
Eso fue en 1940. Durante la siguiente década, Weil desarrolló métodos precisos que descifraron grandes extensiones de su piedra Rosetta. También hizo una serie de conjeturas sobre la relación entre la teoría de números y la geometría. La más audaz de ellas fue una versión de campo finito de la hipótesis de Riemann, una de las cuestiones abiertas más importantes en matemáticas, que se refiere, entre otras cosas, a cómo se distribuyen los números primos. (Demostró un caso unidimensional de esta versión).
 Pierre Deligne demostró la que posiblemente sea la más importante de las conjeturas de Weil sobre la relación entre la teoría de números y la geometría en 1973. Fuente: Archivo del Instituto de Estudios Avanzados
Pierre Deligne demostró la que posiblemente sea la más importante de las conjeturas de Weil sobre la relación entre la teoría de números y la geometría en 1973. Fuente: Archivo del Instituto de Estudios Avanzados«Cuando conviertes la intuición en algo tangible, es cuando se vuelve valiosa», afirma Edward Frenkel de la Universidad de California, Berkeley.
A finales de los años cincuenta y principios de los sesenta, Alexander Grothendieck hizo contribuciones fundamentales al campo de la geometría algebraica en pos de las conjeturas de Weil. En 1973, Pierre Deligne utilizó las técnicas de Grothendieck para demostrar la versión de campos finitos de la hipótesis de Riemann de Weil en dimensiones superiores.
La piedra Rosetta de Weil también ha guiado el progreso del programa Langlands, un gran proyecto para unificar campos dispares de las matemáticas. El proyecto comenzó en 1967 cuando su fundador, Robert Langlands, describió su idea en una carta a Weil, expresando su deseo de conectar diferentes ramas de investigación dentro de la propia teoría de números. Más tarde, a principios de la década de 1980, Alexander Beilinson y Vladimir Drinfeld definieron una versión geométrica del programa Langlands, ampliando la visión de Langlands para abarcar una conexión entre la teoría de números y la geometría.
En los últimos años, algunos de los avances más importantes en el programa Langlands han implicado traducciones entre la visión original de la teoría de números de Robert Langlands y la versión geométrica posterior. Estas traducciones siguen los enfoques establecidos en la piedra Rosetta de Weil.
In 2021 Laurent Fargues and Peter Scholze finalized work on the Fargues-Fontaine curve, which provided one of the first direct translations between the geometric version of the Langlands program and the number-theory version. In recent months, Frenkel, Pavel Etingof and David Kazhdan have sharpened the link between the two versions. They redefined the geometric Langlands program in terms more consistent with Langlands’ initial vision, yielding a more exact translation between the two.
En 2021, Laurent Fargues y Peter Scholze finalizaron el trabajo sobre la curva de Fargues-Fontaine, que proporcionó una de las primeras traducciones directas entre la versión geométrica del programa Langlands y la versión de teoría de números. En los últimos meses, Frenkel, Pavel Etingof y David Kazhdan han agudizado el vínculo entre las dos versiones. Han redefinido el programa geométrico de Langlands en términos más consistentes con la visión inicial de Langlands, produciendo una traducción más exacta entre los dos.
Para Frenkel, el impacto de la piedra Rosetta de Weil resume la forma en que se desarrollan las matemáticas. Algunas ideas nuevas surgen como consecuencia lógica de cosas que ya se conocen. Pero otras –y a menudo los más importantes– son totalmente originales.
“Estas ideas parecen surgir de la nada; no son tangibles ni fácilmente rastreables”, explica Frenkel. Pero la idea de Weil, señala, era más que un sueño. «Todo el mundo tiene un sueño», dijo Frenkel. “Weil no sólo articuló el sueño en la carta, sino que luego lo convirtió en algo concreto”.
El artículo original, A Rosetta Stone for Mathematics, se publicó el 6 de mayo de 2024 en Quanta Magazine.
Traducido por César Tomé López
El artículo Una piedra Rosetta para las matemáticas se ha escrito en Cuaderno de Cultura Científica.
Nitroplasto, un nuevo orgánulo generado por endosimbiosis
Los organismos eucariotas, todos los seres vivos, excepto los procariotas (bacterias y arqueas), deben su propia existencia y su evolución a la endosimbiosis. La simbiosis es la asociación de organismos con beneficio mutuo. Hablamos de endosimbiosis cuando uno de estos organismos vive y se reproduce en el interior de otro. Esto es relativamente frecuente en la naturaleza. Pensemos en las bacterias de nuestra microbiota intestinal o en las zooxantelas fotosintéticas que viven dentro de los corales recibiendo nutrientes de ellos y proporcionándoles carbohidratos.
La gran bióloga Lynn Margulis propuso en 1967 que la endosimbiosis está detrás del origen de las células eucariotas. Según ella, un procariota ancestral se habría asociado con bacterias heterótrofas, es decir, capaces de oxidar la materia orgánica. Esta asociación, ocurrida hace unos 2000 millones de años, se habría consolidado, de forma que las bacterias perdieron su capacidad de vida libre y se convirtieron en las mitocondrias, los orgánulos en los que se genera la energía que necesitan nuestras células. Un segundo evento de endosimbiosis, hace 1500 millones de años, asoció a un eucariota con cianobacterias fotosintéticas, capaces de producir materia orgánica utilizando la energía de la luz. Esas bacterias terminaron por constituir orgánulos celulares, los cloroplastos. De esta forma algas y plantas verdes llegaron a ser capaces de utilizar la luz para sintetizar compuestos orgánicos.
Sin estos dos acontecimientos evolutivos no podemos imaginar cómo habría sido la evolución de los seres vivos en nuestro planeta. La generación de orgánulos celulares a partir de endosimbiosis tiene un enorme potencial evolutivo, y podemos preguntarnos por qué no ha ocurrido más veces. En realidad sí ha ocurrido, al menos en un par de ocasiones más1. Una de ellas, la que vamos a tratar aquí, ha permitido, por primera vez, que un eucariota fije nitrógeno atmosférico.
Antes de explicar este fascinante descubrimiento aclaremos que una modesta ameba de agua dulce, Paulinella chromatophora, es fotosintética gracias a un reciente evento de endosimbiosis. Esto se debe a su asociación con una cianobacteria que, con el paso del tiempo (se calcula unos 120 millones de años), se ha convertido en un orgánulo celular llamado cromatóforo. Insisto en que la asociación simbiótica de organismos fotosintéticos con otros organismos es relativamente frecuente, como el caso de los corales antes mencionado. Pero el caso de Paulinella es diferente. La transición hacia un orgánulo celular implica que el organismo asociado haya perdido su capacidad de vida libre, acople su ciclo al del hospedador, dependa genéticamente e intercambie moléculas e incluso genes con dicho hospedador. Esto es lo que sucede con las mitocondrias, con los cloroplastos y con los cromatóforos de Paulinella. Y esto es lo que sucede también con un alga unicelular, Braarudosphaera bigelowii, un minúsculo organismo que se ha revelado como el primer eucariota capaz de fijar nitrógeno atmosférico.
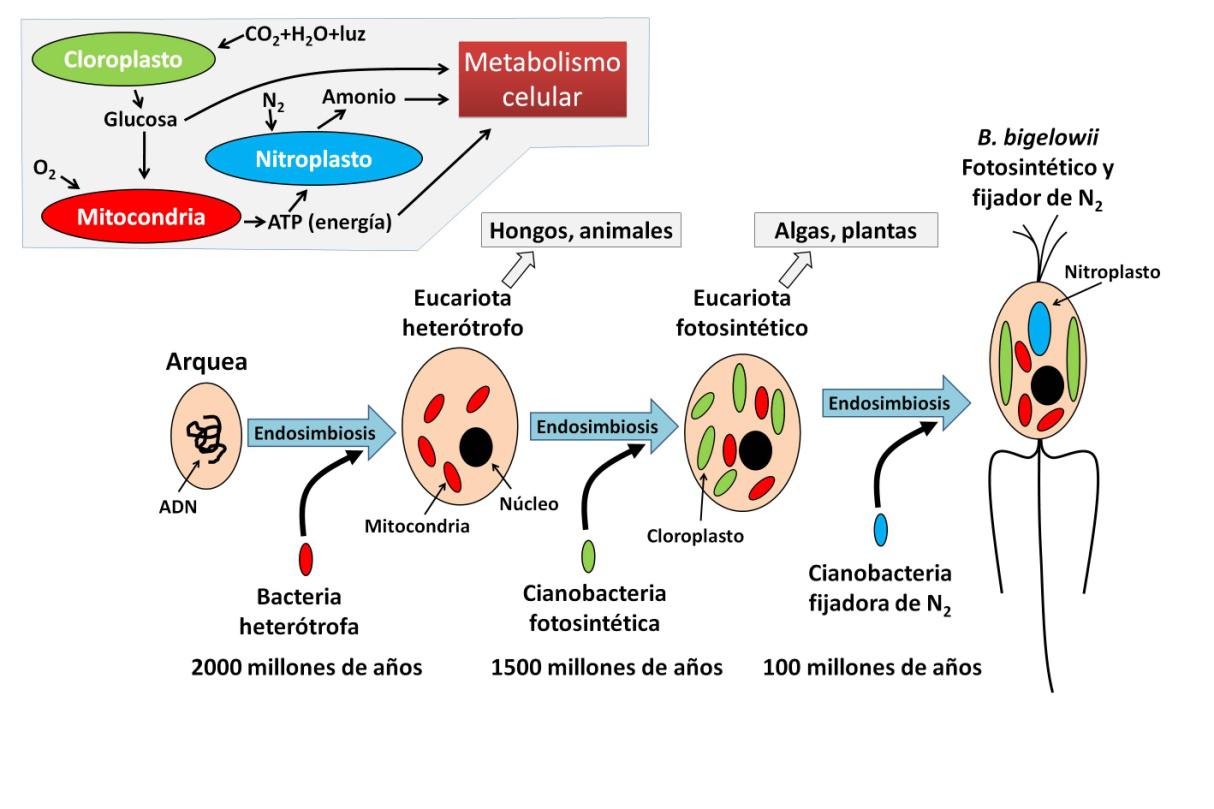 Un largo camino evolutivo ha llevado a Braarudosphaera bigelowii a poseer orgánulos derivados de tres eventos sucesivos de endosimbiosis cuya antigüedad se detalla abajo. Arriba a la izquierda se muestran los intercambios entre los tres tipos de orgánulos y su contribución al metabolismo celular. Ilustración: Ramón Muñoz-Chápuli
Un largo camino evolutivo ha llevado a Braarudosphaera bigelowii a poseer orgánulos derivados de tres eventos sucesivos de endosimbiosis cuya antigüedad se detalla abajo. Arriba a la izquierda se muestran los intercambios entre los tres tipos de orgánulos y su contribución al metabolismo celular. Ilustración: Ramón Muñoz-ChápuliRecordemos que la materia orgánica está formada sobre todo por carbono, hidrógeno y oxígeno. Las proteínas, formadas por cadenas de aminoácidos, requieren también nitrógeno. Carbono, oxígeno e hidrógeno están disponibles en el aire (como dióxido de carbono) y en el agua. La fotosíntesis consiste precisamente en la fijación del carbono atmosférico en moléculas orgánicas, y si las plantas pueden hacerlo es gracias a la endosimbiosis, como hemos dicho. El nitrógeno también es abundante en la atmósfera, pero es muy poco reactivo. Para incorporarlo a la biosfera es necesario combinarlo con otros átomos como oxígeno o hidrógeno. Esto saben hacerlo diversos grupos de bacterias, como las que se asocian a las raíces de las leguminosas o las propias cianobacterias. Pero los eucariotas no son capaces de realizar esta importantísima incorporación del nitrógeno para la síntesis de proteínas.
La minúscula B. bigelowii es capaz de fijar nitrógeno. Lo hace gracias a lo que se consideraba endosimbiosis con una cianobacteria, Atelocyanobacterium thalassa o UCYN-A. Un reciente estudio sobre esta asociación, que acaba de ser portada en la revista Science, muestra que UCYN-A cumple todas las condiciones para ser considerado un orgánulo celular y no un endosimbionte. Es importante destacar que esto ya había sido anticipado en un artículo de la revista Cell, liderado por un investigador del Instituto de Ciencias del Mar-CSIC de Barcelona.
A diferencia de otras cianobacterias, el genoma de UCYN-A es muy reducido (1.44 Mb) y carece de genes imprescindibles para la fotosíntesis o el ciclo de Krebs, por lo que no puede vivir de forma independiente. Recibe compuestos de carbono de su hospedador y le proporciona nitrógeno fijado a cambio. Por otra parte, su ciclo está integrado dentro del ciclo celular de B. bigelowii. Cuandoesta alga va a reproducirse por división, primero se dividen sus mitocondrias, luego lo hace UCYN-A, y por fin el núcleo y los cloroplastos. Además los genes del hospedador sintetizan proteínas marcadas específicamente para la importación por UCYN-A, que depende estrictamente de este aporte.
Los autores del artículo de Science proponen que UCYN-A sea considerado un nuevo orgánulo, para el que proponen el nombre de nitroplasto. El evento de endosimbiosis que originó el nitroplasto habría ocurrido hace “solo” 100 millones de años, mucho más reciente que los que dieron lugar a mitocondrias y cloroplastos. También proponen un excitante escenario para el futuro. Del mismo modo que las algas pardas y otros organismos se hicieron fotosintéticos por endosimbiosis secundaria, es concebible que en el curso de la evolución futura algunas algas o plantas puedan desarrollar la capacidad de fijar nitrógeno por simbiosis secundaria con B. bigelowii o un organismo equivalente. Otra posibilidad es que orgánulos tipo UCYN-A pudieran establecerse artificialmente en plantas de interés agrícola que ya no dependerían del aporte de nitrógeno en forma de abono.
Nota:
1 Estamos hablando sólo de endosimbiosis primaria. Hay casos de endosimbiosis secundaria, por ejemplo las algas pardas que hicieron simbiosis con algas rojas portadoras de cloroplastos.
Referencias:
Duckhyun Lhee et al. (2021) Amoeba Genome Reveals Dominant Host Contribution to Plastid Endosymbiosis Molecular Biology and Evolution doi: 10.1093/molbev/msaa206
Tyler H. Coale et al. (2024) Nitrogen-fixing organelle in a marine algaSciencedoi: 10.1126/science.adk1075
Francisco M. Cornejo-Castillo et al. (2024) Metabolic trade-offs constrain the cell size ratio in a nitrogen-fixing symbiosis Cell doi: 10.1016/j.cell.2024.02.016
El artículo Nitroplasto, un nuevo orgánulo generado por endosimbiosis se ha escrito en Cuaderno de Cultura Científica.
Diferencias en la conducta suicida entre hombres y mujeres: una visión con perspectiva de género
 Foto: Andreea Popa / Unsplash
Foto: Andreea Popa / UnsplashEl suicidio es una de las principales causas de muerte externa o no natural en el mundo. Y aunque se puede prevenir, su incidencia sigue al alza. En España, por ejemplo, se ha registrado un aumento sostenido de los fallecimientos por esta causa desde 2018.
Así, los datos publicados por el Instituto Nacional de Estadística (INE) muestran que en 2022 (último año con información consolidada) la mortalidad por suicidio se incrementó en un 5,6 % con respecto a 2021. Esta subida no es uniforme, ya que la tasa se ha acrecentado casi un 8 % más en menores de 30 años y un 42 % en adolescentes de entre 15 y 19 años.
Las cifras también indican que la proporción de hombres que se quitan la vida es significativamente mayor que la de mujeres: el triple. No obstante, en 2020, el año que estalló la pandemia de covid-19, se constató una igualación de estas tasas (casi un hombre fallecido por mujer fallecida) en adolescentes de 12 a 18 años.
Brecha de sexo: ¿a qué responde?La brecha de sexo también se refleja en las diferentes formas del comportamiento suicida, como la ideación y el intento. Desde este punto de vista, los expertos han identificado un patrón por sexo contrario: las mujeres muestran más presencia e intensidad de ideaciones y un mayor número de intentos.
También se registra una mayor tasa de consultas femeninas en servicios de salud (sobre todo hospitalarios) por esta causa, lo que podría indicar que buscan ayuda antes. ¿A qué podrían deberse las diferencias?
La brecha entre mujeres y hombres atiende a tres variables: método y daño médico (por lo general, los hombres tienden a utilizan formas asociados a mayor severidad de la lesión física) e intentos previos de morir (se percibe el comportamiento de los hombres con mayor intención de morir). Tales disparidades varían según el contexto sociocultural, por lo que estos factores pueden guardar más relación con los roles de género que con el sexo biológico de la persona.
Por otro lado, los estudios indican alta ideación y de justificación del intento de suicidio (ambos estrechamente asociados con el inicio de la conducta suicida) y menor ratio de muerte en las mujeres, mientras que la cifra más abultada de suicidios masculinos se asocia a una ideación más fugaz.
La paradoja del géneroToda esta evidencia apoyaría lo que se conoce como la “paradoja del género” en la conducta suicida. Y aunque tradicionalmente se ha asociado a las diferencias biológicas entre hombres y mujeres, también tiene mucho que ver con las disimilitudes y expectativas culturales en relación al género.
Por ejemplo, las tasas más elevadas de fallecimiento por suicidio en varones suelen estar asociadas a una mayor prevalencia de trastornos externalizantes (asociados a problemas de conducta o dependencia de sustancias), rasgos psicológicos como impulsividad o agresividad y la preferencia por métodos más letales (por ejemplo, saltos desde edificios o uso de armas de fuego).
En contraste, los estudios indican que las mujeres son más propensas a mostrar trastornos de ansiedad, depresión o del estado del ánimo asociados a niveles altos de ideación o intento suicida.
La evidencia es más escasa y contradictoria para los factores que disminuyen la probabilidad de que se produzca esta conducta. Una evaluación centrada en las necesidades, sensibles a la pluralidad y los cambios en las de las circunstancias de las personas, podría aportar luz a dichas diferencias.
Nada es blanco o negroEl problema es que los estudios sobre este asunto en las culturas occidentales han analizado los datos conforme a estructuras de análisis binario: bueno/malo, hombre/mujer, negro/blanco… Desde este punto de vista, mujeres y hombres serían opuestos: ellas lo intentan y ellos lo consiguen.
Además, la conducta suicida en mujeres se ha atribuido erróneamente a la ambivalencia (inestabilidad psicológica), la expresión emocional exacerbada o a la consecuencia de un acto de debilidad precipitado por las turbulencias en sus relaciones. Por contra, los hombres manifestarían un comportamiento suicida firme o calculado o como resultado de una respuesta fuerte a la adversidad.
Adicionalmente, la lectura binaria de los datos puede alimentar la profecía autocumplida (cuando la percepción social sobre las diferencias alienta de forma indirecta a que estas se produzcan) o reproducir estereotipos en las conclusiones sobre frecuencia y letalidad en la conducta suicida.
¿Se puede entonces atribuir la menor incidencia en mujeres a la temprana identificación de casos de riesgo, dado que ellas se muestran más dispuestas a buscar ayuda en los servicios de salud o a expresar sus emociones? ¿Y la mayor mortalidad en hombres al uso de métodos más letales y su menor disposición a buscar apoyo, con tal de no contradecir los estereotipos de masculinidad tradicionales? Pues no únicamente. Y si consideramos que son explicaciones válidas, habría que cuestionarlas, porque evidencian cómo los propios estereotipos ligados a la socialización de nuestra identidad masculina o femenina tienen un efecto en la conducta suicida.
Una mirada única desde el binarismo reproduce clichés de género –tanto para las identidades normativas como para la divergencia–, limita el derecho a la elección de la identidad de género y puede llevar a una contención emocional del malestar. En consecuencia, el sistema de sexo y género binario podría considerarse, en sí mismo, un factor de riesgo de la estigmatización de la conducta suicida. No contribuye a la adopción de una conciencia social amplia para prevenirla.
Hacia una mirada más abiertaDe todo lo anterior se concluye que el análisis binario de los datos o abordar por separado las variables que influyen en la conducta suicida puede llevar a excluir factores relevantes. Y si estos no se tienen en cuenta, las explicaciones sobre un fenómeno tan complejo como es el riesgo de suicidio quedan limitadas.
Incorporar la perspectiva de género en las acciones preventivas y de análisis de datos significa abrir el foco a explorar cómo conectan o se solapan las diversas categorías sociales: etnia, clase social, orientación sexual, estado de salud mental, etc.
Aquí cabe destacar las iniciativas que tienen en cuenta la autodeterminación de género en la comunidad LGTBIQ+, con mayores tasas de riesgo suicida: un 34 % más de ideación y un 18 % más de intentos con respecto al resto de la población. Por otro lado, existen alternativas de cuidado respetuoso que podrían maximizar la prevención, como espacios seguros de acogida, apoyo y aceptación.
La hoja de ruta para evaluar y abordar la conducta suicida contempla considerar la diversidad y la matización propia de cada individuo. Son aspectos cruciales para mejorar la capacidad de detectar el riesgo y poder prevenirlo, un asunto que concierne a toda la sociedad.![]()
Sobre las autoras: Anna Pedrola-Pons es investigadora predoctoral y Alejandro de la Torre Luque, investigador doctor, en el Departamento de Medicina Legal, Psiquiatría y Patología de la Universidad Complutense de Madrid.
Este artículo fue publicado originalmente en The Conversation. Artículo original.
Para saber más:
Podemos prevenir el suicidio
El peor enemigo de la prevención del suicidio
Prevención de la conducta suicida en jóvenes usando perros
El artículo Diferencias en la conducta suicida entre hombres y mujeres: una visión con perspectiva de género se ha escrito en Cuaderno de Cultura Científica.
¡Ups! Darwin y la herencia

Durante el viaje en el Beagle, Charles Darwin se había percatado de que los animales americanos se parecían mucho a los europeos, aunque no eran exactamente iguales. Pensó que esas diferencias podían ser producto de adaptaciones provocadas por los diferentes entornos. Pensó que, tal vez, los animales con capacidades mejor adaptadas a su entorno sobrevivían en mayor número que el resto. Y al hacerlo transmitían esas capacidades a sus hijos por medio de unas células especiales. A ese fenómeno le puso un nombre: Selección natural. Hoy sabemos que la herencia genética no funciona así. A pesar de este error, Darwin lo puso todo patas arriba con su idea.
Producción ejecutiva: Blanca Baena
Guion: José Antonio Pérez Ledo
Grafismo: Cristina Serrano
Música: Israel Santamaría
Producción: Olatz Vitorica
Doblaje: K 2000
Locución: José Antonio Pérez Ledo
Edición realizada por César Tomé López
El artículo ¡Ups! Darwin y la herencia se ha escrito en Cuaderno de Cultura Científica.
Los grandes descubrimientos epigráficos
De vez en cuando los medios de comunicación se hacen eco de espectaculares descubrimientos arqueológicos, en especial rarísimas inscripciones escritas en lenguas y escrituras exóticas, que prometen aclarar misterios o arrojar luz sobre periodos oscuros de la historia.
 Foto: Chris Linnett / Unsplash
Foto: Chris Linnett / UnsplashPosiblemente el hallazgo más famoso de este tipo es la llamada Piedra de Rosetta, hallada en 1799 por las tropas napoleónicas en el delta del Nilo, que le permitió a Jean-François Champollion descifrar la escritura jeroglífica egipcia hacia 1823. Ha habido muchísimos otros descubrimientos importantes que, sin tener la fama de la Piedra de Rosetta, han representado pasos cruciales en el conocimiento del pasado. En noviembre de 2022, toda la prensa vasca y muchos periódicos de difusión española e internacional daban cuenta del hallazgo de un epígrafe sobre bronce, conocido como “La mano de Irulegi”, escrito en un sistema de escritura propio de la península ibérica, que recoge un corto texto presumiblemente redactado en la lengua de los vascones a comienzos del siglo I a.C.
 La Piedra de Rosetta y como podría haber sido originalmente. Ilustración de Claire Thorne. Fuente: British Museum
La Piedra de Rosetta y como podría haber sido originalmente. Ilustración de Claire Thorne. Fuente: British MuseumLimitándonos al campo de los desciframientos de lenguas y escrituras desconocidas, aunque el aporte de algunas inscripciones singulares como la Piedra de Rosetta haya sido crucial, el avance suele venir habitualmente por la comparación y confrontación de varios documentos epigráficos, por limitados o parciales que sean. Muchas veces, la propia inscripción que resulta clave para el desciframiento de una escritura o lengua ha sido, hasta ese momento, un verdadero misterio, que suele empezar a resolverse mediante el recurso al conocimiento de un aspecto o ámbito externo al propio texto. Si Champollion logró descifrar el jeroglífico, antes que el brillante científico inglés Thomas Young, fue gracias a su conocimiento de la lengua copta.
La virtualidad explicativa de los grandes hallazgos epigráficos depende tanto de la propia información aportada como del conocimiento previo existente. Hacia 1925 Manuel Gómez Moreno fue capaz de descifrar la escritura ibérica, una de las escrituras paleohispánicas usadas en la península ibérica antes de la generalización del alfabeto latino, pero aún hoy en día somos incapaces de entender la lengua ibérica. En el desciframiento de la escritura tuvieron un papel importante los hallazgos de dos inscripciones, que curiosamente no estaban redactadas en escritura ibérica: una, aparecida en Ascoli (Italia) en 1908, recogía la concesión de ciudadanía romana a los jinetes ibéricos de una unidad auxiliar que luchó junto a Roma; la otra, aparecida en Alcoy en 1922, contenía un texto en lengua ibérica, pero alfabeto griego. Sin estos dos epígrafes hubiera sido mucho más difícil, por no decir imposible entonces, descifrar la escritura ibérica. Ahora bien, a diferencia de la Piedra de Rosetta, no hay ningún texto bilingüe ibérico-latino o ibérico-griego, de modo que esta limitación en los epígrafes conocidos nos impide pasar por el momento del nivel de la lectura del texto al nivel de su comprensión.
 Cara B del plomo de la Serreta (Alcoy) en alfabeto greco-ibérico. Fuente: Tautintanes / Wikimedia Commons
Cara B del plomo de la Serreta (Alcoy) en alfabeto greco-ibérico. Fuente: Tautintanes / Wikimedia CommonsHay ocasiones en las que la función de un epígrafe no es servir de llave para el desciframiento, sino de prueba posterior de la bondad de la hipótesis. El desciframiento del Lineal B por Michael Ventris en 1952 fue el resultado de un concienzudo trabajo de comparación de muchos textos procedentes de los materiales excavados en Cnossos (Creta) por Evans. De manera marginal le ayudó en la tarea un singular epígrafe en silabario chipriota, escritura descifrada en 1871 que tenía relaciones genéticas con el Linear B, pero la base del desciframiento residía en un análisis detallado de las combinaciones de los signos que parecían cuadrar en la expresión de algunas palabras que podían identificarse con topónimos cretenses y sus derivados. La bondad del desciframiento le quedó clara a Blegen, un arqueólogo norteamericano que había excavado en Pilos (Grecia) en 1939, cuando, aplicando los valores propuestos por Ventris, pudo comprender una tablilla inédita de Pilos, la famosa tablilla de los trípodes.
Un ejemplo muy ilustrativo de diálogo entre conocimiento previo e información aportada por nuevos epígrafes nos proporcionan los avances recientes (2021) sobre el desciframiento de la escritura lineal elamita. Aquí intervienen, por un lado, un conjunto homogéneo de inscripciones conocidas desde el inicio del siglo XX; por otro, el hecho de que la lengua elamita es conocida por un gran número de inscripciones en otra escritura descifrada, la cuneiforme; por último, un nuevo conjunto de textos recién descubiertos que remiten a personajes distintos del primer conjunto. En esencia, se ha ampliado la lista de nombres de reyes, en los que ensayar el análisis combinatorio de los signos.
 La mano de Irulegi. Foto: S.C. Aranzadi. Fuente: Gobierno de Navarra / Nafarroako Gobernua
La mano de Irulegi. Foto: S.C. Aranzadi. Fuente: Gobierno de Navarra / Nafarroako GobernuaCada año se descubren en la península ibérica inscripciones de mayor o menor entidad que vienen a ampliar nuestro conocimiento de las escrituras y las lenguas paleohispánicas. Aunque algunas han sido espectaculares, como los grandes bronces de Botorrita que significaron un avance en nuestro conocimiento del celtibérico, todos los textos nos aportan información valiosa sobre esas lenguas mal conocidas o simplemente inextricables, con tal de que la información aportada sea auténtica y esté bien referenciada arqueológicamente. Desgraciadamente, abundan los epígrafes obtenidos en intervenciones ilegales, en los que se ha perdido toda la información histórica que proporciona el contexto arqueológico, a las que hay que sumar las falsificaciones destinadas al mercado de antigüedades.
Cada epígrafe es un pequeño tesoro, que a veces posee por sí solo una gran virtualidad explicativa y otras, como los fósiles paleontológicos, debe esperar a ser interpretado para proporcionar entonces toda la información, quizá sorprendente, que encierra.
Sobre el autor: Joaquín Gorrochategui es Profesor emérito de Lingüística Indoeuropea en la Facultad de Letras y miembro del Instituto de Ciencias de la Antigüedad de la UPV/EHU
Una versión de este texto apareció originalmente en campusa.
El artículo Los grandes descubrimientos epigráficos se ha escrito en Cuaderno de Cultura Científica.
Elmer, Elsie, una puerta al verano y el aspirador del futuro
 Foto: Denny Müller / Unsplash
Foto: Denny Müller / UnsplashLa idea de crear vida artificial lleva entre nosotros desde prácticamente nuestros orígenes, tal vez como forma de tratar de comprendernos a nosotros mismos y lo que somos. En los mitos de la Antigua Grecia ya aparecen seres como el gigante de bronce Talos, que custodiaba la isla de Creta, y también se mencionan las sirvientas autómatas de oro y plata del dios Hefesto, el encargado de fabricar todo este tipo de artilugios y, probablemente, el primer ingeniero de la historia. Sin embargo, estaremos de acuerdo en que los mitos no son ciencia, y que hace falta algo más que imaginación para poder hablar de «vida artificial» o máquinas que imitan las funciones de los seres vivos.
El cambio de paradigma que hizo posible plantearse la posibilidad real de crear algo así llegó a principios del siglo XX, con la llegada de una idea teórica que, pocas décadas después, se convertiría en algo muy práctico: la máquina universal de Alan Truing. A partir de este momento es cuando el mito empezó a convertirse en una posibilidad y despertó la curiosidad, ya no solo de mecánicos e ingenieros, sino de matemáticos, físicos, filósofos, lingüistas… y, por supuesto, psicólogos y neurólogos.
William Grey Walter pertenecía a esta última categoría. Había visitado el laboratorio de Hans Berger, el inventor del electroencefalograma ―un dispositivo capaz de medir la actividad eléctrica del cerebro― y él mismo había creado algunas versiones mejoradas de este aparato en el Burden Neurological Institute de Bristol que permitieron la detección de nuevos tipos de ondas cerebrales. También, al igual que tantos otros colegas científicos, como el matemático y cibernético Norbert Wiener, participó en la Segunda Guerra Mundial, en su caso diseñando sistemas de detección de radares y guiado de misiles, pero no es realmente por todo esto por lo que más se lo conoce, sino por haber fabricado los dos primeros robots completamente autónomos de la historia.
Tras la guerra, y con el desarrollo de la informática, Grey Walter empezó a preguntarse si alguna de aquellas máquinas que habían empezado a desarrollarse podría ser capaz algún día de simular el sistema nervioso humano. Teniendo en cuenta que gracias a sus trabajos con las máquinas de encefalografía conocía bien la actividad eléctrica del cerebro, aquella idea tenía todo el sentido. La ciencia abría la posibilidad de transformar un antiguo mito en ciencia. Y él lo explicó muy bien:
En los años oscuros antes de la invención de la válvula de vacío había muchas leyendas sobre estatuas vivientes e imágenes mágicas […]. La gran diferencia entre la magia y la imitación científica de la vida es que la primera se contenta con copiar la apariencia externa, la segunda se preocupa más por su desempeño y comportamiento.
Así que se puso a ello y creó la que se podría considerar la primera especie animal artificial: la Machina speculatrix o, como se las suele conocer, las tortugas robóticas Elmer y Elsie, por la forma que tenían. No eran dispositivos muy complicados, estaban fabricados con dos válvulas de vacío, dos sensores ―uno fotoeléctrico y otro antichoque― y dos motores ―uno para desplazarse y otro para girar―. Y esa era precisamente la idea: comprobar qué nivel de complejidad y aleatoriedad en el comportamiento podía conseguirse con el menor número de componentes posible. ¡Y fue bastante! Elmer y Elsie merodeaban por la habitación en la que se encontraban dando vueltas, evitando los muebles y las paredes… Cuando su batería estaba cargada, solían evitar las áreas luminosas y preferían las zonas de penumbra; a medida que la batería se descargaba, hacían justo lo contrario: buscar puntos de luz, que eran los lugares donde Grey Walter había situado los cargadores y, de esta manera, se cargaban solas.
A día de hoy, Elmer y Elsie resultan unos aparatos muy simples y obsoletos, pero en su momento causaron el suficiente impacto como para aparecer en la revista Scientific American, en el número de mayo de 1950, en un artículo escrito por el propio Grey Walter y titulado «An imitation of life».
Es probable que, a estas alturas, cualquiera haya pensado ya en Elmer y Elsie como una suerte de precursoras de los aspiradores robóticos actuales, solo por su aspecto, aunque esa no fuera la intención de su inventor. Suele haber un proceso de maduración intelectual, cultural, científica y tecnológica, que puede durar décadas e incluso siglos, desde que una idea aparece hasta que se le encuentra utilidad y, además, es posible llevarla a cabo. Algo así sucedió en este caso y, una vez más, la ciencia ficción formó parte de ese proceso.
Scientific American, así como otras revistas de divulgación científica, eran publicaciones a las que solían estar suscritos los escritores de ciencia ficción, sobre todo en aquella época, en la que las historias bebían, sobre todo, de los avances científicos y tecnológicos del momento mientras especulaban con otros nuevos: la Edad de Oro de escritores como Isaac Asimov, Arthur C. Clarke y Robert A. Heinlein.
Cualquiera que conozca la biografía de Heinlein, sabrá el impacto que tendría su matrimonio, en 1948, con Virgina Gerstenfeld ―el tercero del autor― tanto en la vida como en la obra de este y tanto para bien como para mal. Si bien es cierto que Heinlein tenía una mentalidad muy liberal en lo referente a las relaciones interpersonales, y en su obra encontramos relaciones homosexuales, heterosexuales, poliamorosas, matrimonios temporales y hasta intergeneracionales, en lo referente a su matrimonio con Virginia seguía defendiendo los roles tradicionales de marido proveedor y esposa ama de casa.1 En cualquier caso, no le restaba ni un ápice de valor al trabajo de su mujer y, no solo eso, sino que trataba de facilitarle todos los medios a su alcance para que le llevara el menor tiempo posible y dispusiera también de tiempo para ella.
Fue por ello que, en cuanto tuvieron la ocasión, diseñaron entre los dos y mandaron construir su casa de Colorado Springs ―y, más adelante, otra en California―, pensada, dentro de las posibilidades de la tecnología de la época, para que tuviera el mínimo mantenimiento posible. Tan moderna fue en ese momento, que Thomas E. Stinton le dedicó un artículo en la revista Popular Mechanics en 1952, «A house to make life easy», donde aparecía el matrimonio Heinlein contando las maravillas de su nuevo hogar. El autor, aunque se le pasó por la cabeza, no pudo dotarla de todo lo que hubiera querido, como un sistema de aspiración automático. No obstante, que no pudiera realizarlo en la vida real, no significa que la idea no apareciera en sus novelas.
Entre noviembre y diciembre 1956 se publicó por entregas en The Magazine of Fantasy & Science Fiction una de las que se convertiría en una de sus obras más conocidas: Puerta al verano, cuyo protagonista, David Boone Davis, era un ingeniero entre cuyos inventos se encontraba uno muy curioso, la «Muchacha de Servicio»:
Lo que la Muchacha de Servicio hacía (el primer modelo, no el robot semiinteligente en que lo transformé) era limpiar suelos; toda clase de suelos, todo el día y sin vigilancia […].
Barría, o fregaba, o limpiaba aspirando, o pulía, consultando cintas en su memoria idiota para decidir qué era lo que tenía que hacer […]. Se pasaba todo el día buscando suciedad, moviéndose infatigablemente según curvas que no dejaban nada por barrer, pasando de largo sobre los pisos limpios, en su incansable búsqueda por los sucios […]. Hacia la hora de comer se iba a su puesto y se tragaba una carga rápida ―eso antes de que le instalásemos la carga permanente―.
No había mucha diferencia entre la Muchacha de Servicio, Marca Uno, y un aspirador doméstico. Pero la diferencia ―que podía limpiar sin vigilancia― fue suficiente; se vendió.
Me apropié del esquema básico de las «Tortugas Eléctricas» descritas en el Scientific American hacia finales de los años cuarenta […].
A través del protagonista de su novela, Robert Heinlein manifestaba que conocía el artículo de William Grey Walter y, seguramente, en su cabeza, la Muchacha de Servicio se parecía más a Elmer y Elsie que a la ilustración que Frank Kelly Freas hizo para la primera entrega de la novela.
 La «Muchacha de Servicio», tal y como la ilustró Frank Kelly Freas en la primera entrega de Puerta al verano en The Magazine of Fantasy & Science Fiction, no se parecía demasiado a Elmer y Elsie ni a un aspirador robótico actual, aunque, según la descripción de Heinlein sí parece que lo era. Ilustración: Frank Kelly Freas
La «Muchacha de Servicio», tal y como la ilustró Frank Kelly Freas en la primera entrega de Puerta al verano en The Magazine of Fantasy & Science Fiction, no se parecía demasiado a Elmer y Elsie ni a un aspirador robótico actual, aunque, según la descripción de Heinlein sí parece que lo era. Ilustración: Frank Kelly Freas
Cabe recalcar, en cualquier caso, que Heinlein no fue el primero en imaginar un aparato de ese estilo. Ya a finales del siglo XIX aparecen robots limpiadores, por ejemplo, en aquella famosa colección de ilustraciones francesas, En L’an 2000, con la que se trataba de festejar la entrada en el año 1900. También Miles J. Breuer habló de algo similar en Paradise and iron, de 1930, aunque su dispositivo era una especie de motor con tubos que surgía del techo:
Alcanzaban aquí y allá, se metían en rincones, debajo de sillas y alrededor de objetos; y podía escuchar el sonido de la succión mientras su aspiradora limpiaba el polvo. Cuando la habitación estuvo completamente limpia, el aparato se retiró hacia una abertura en la pared y se ocultó de la vista.
También Philip K. Dick, casi a la par que Heinlein, mencionó en su relato «La M imposible» algo que se le podría parecer, aunque lo describió de forma muy vaga: «La mayor parte del departamento se había ido a dormir; eran casi las tres de la madrugada y los pasillos y oficinas estaban desiertos. Algunos dispositivos de limpieza automáticos se movían aquí y allá, en la oscuridad».
 Limpiador de suelos robótico imaginado por Jean-Marc Côté en 1899. Ilustración: Jean-Marc Côté
Limpiador de suelos robótico imaginado por Jean-Marc Côté en 1899. Ilustración: Jean-Marc Côté
En cualquier caso fue Heinlein, sin duda, el que más se acercó, y de forma más realista, al tipo de electrodoméstico que conocemos hoy. Su mérito no consistió en imaginarlo, sino en enraizarlo sobre unas bases científicas sólidas y posibles, basándose en lo más novedoso de su época. Tengamos en cuenta que cuando se publicó Puerta al verano el transistor apenas se había empezado a emplear en la tecnología de consumo. John Bardeen, Walter House Brattain y William Shockley lo crearon en 1947, pero no se hizo público hasta el año siguiente, y el primer dispositivo comercial en incluirlo fue una radio: la Regency TR-1, que no salió al mercado hasta 1954. Fabricar un aspirador robótico autónomo tal y como los conocemos hoy era una posibilidad completamente fuera del alcance de los medios de aquella época. La informática, la robótica y la inteligencia artificial todavía tenían que dar sus respectivos saltos cualitativos.
Y lo fueron haciendo en las siguientes décadas. En 1956 se celebró la Conferencia de Dartmouth, el primer encuentro de expertos en inteligencia artificial del que se tiene constancia, y desde entonces y hasta mediados de los años setenta despegó la disciplina. Lo hizo principalmente, en tres instituciones: la Universidad de Stanford, la Universidad de Carnegie Mellon, y el MIT. Por las tres pasó, en ese orden, un estudiante de matemáticas cuyo interés en la computación había germinado, en parte, gracias a las novelas de ciencia ficción que había leído en su adolescencia y a películas como 2001: una odisea espacial, donde HAL 9000 le resultó tan inquietante como fascinante. Ese estudiante era Rodney Brooks.
En un momento en el que la inteligencia artificial estaba mucho más centrada en algoritmos y sistemas simbólicos ―principalmente porque la construcción de «cuerpos» artificiales había resultado más complicada de lo que se pensaba en los tiempos de Grey Walter y la cibernética―, Brooks apostó por la robótica:
Aceptar la hipótesis de la conexión al mundo físico como base para la investigación implica construir los sistemas de abajo arriba, esto es, se deben concretar las abstracciones de alto nivel. Los sistemas que se construyan deben ser capaces, en última instancia, de expresar todas sus metas y deseos como acciones físicas y extraer todo su conocimiento de sensores.
Esto es, en un momento en el que no existía internet y el acceso a los datos era limitado, él pensaba que la mejor manera en la que podían aprender los sistemas de inteligencia artificial era obteniendo la información que necesitaban directamente del entorno, a través de sensores.
Para demostrar su hipótesis construyó numerosos robots en el MIT: Allen, capaz de sortear obstáculos; Herbert, que iba por los despachos recogiendo latas de refresco vacías y las llevaba a la papelera de reciclaje; Genghis, un hexápodo capaz de adaptarse a terrenos irregulares; Squirt, que era capaz de detectar ruidos y esconderse de ellos, o Toto, que se guiaba a través de un sistema de visión artificial. Lo innovador de estos robots fue su programación; para ellos, Brooks desarrolló lo que denominó «arquitectura de subsunción», que determinaba sus comportamientos a través de jerarquías: los comportamiento más sencillos estaban en la base, los más complejos en la cúspide, de tal forma que las jerarquías superiores englobaban las inferiores.
En 1990, Rodney Brooks, Colin Angle y Helen Greiner, también del MIT, fundaron iRobot… y el resto es historia. En 2002 lanzaron la Roomba, el primer aspirador robótico que tuvo éxito comercial y del que ya se han venido millones de unidades en todo el mundo.
Pero, ¿fue casualidad que la Roomba fuera como es y tuviera esa forma tan parecida a Elmer y Elsie y a la Muchacha de Servicio? Sabemos que Rodney Brooks conocía el trabajo de William Grey Walter y que supuso una gran influencia en él, también que leyó a los tres grandes de la Edad de Oro de la ciencia ficción. Asimov, Clarke y Heinlein, porque él mismo lo ha comentado en alguna ocasión, aunque es difícil saber qué papel jugó Puerta al verano y si ejerció alguna influencia directa en el desarrollo de la Roomba como tal. También puede ser que el hecho de que los aspiradores robóticos tengan la forma que tienen hoy tal vez fuera la única posibilidad lógica y por eso muchos los imaginaron así.
 Roomba de primera generación. Otras compañías, como la sueca Electrolux con su Trilobite, crearon antes electrodomésticos similares, pero no consiguieron el mismo éxito comercial. Fuente: Wikimedia Commons/CC-BY 4.0/Larry D. Moore
Roomba de primera generación. Otras compañías, como la sueca Electrolux con su Trilobite, crearon antes electrodomésticos similares, pero no consiguieron el mismo éxito comercial. Fuente: Wikimedia Commons/CC-BY 4.0/Larry D. Moore
Lo que es innegable a varios niveles es que la historia de la Roomba es uno de tantos ejemplos a lo largo de la historia en los que ciencia y ciencia ficción se retroalimentan de maneras que no son siempre conocidas, aunque en muchas ocasiones no es fácil encontrar las conexiones o tal vez no estén tan claras. A lo que, indudablemente, ayuda la ciencia ficción es a crear historias, relatos y visiones del futuro que flotan en el ambiente, que guían nuestra imaginación y que, en última instancia, tienen la capacidad de llevarnos, de manera casi inconsciente, en una dirección o en otra.
Bibliografía
Baños, G. (2024). El sueño de la inteligencia artificial. Shackleton Books.
Breuer, M. (1930). Paradise and iron. Amazing Stories Quarterly.
Brooks, Rodney A. (1990). Elephants don’t play chess. Robotics and Autonomous Systems, 6(1-2).
Davenport, A. (13 de octubre de 2021) The development and significance of cybernetics by William Grey Walter.Cosmonaut Magazine.
Dick, P. K. (2008 [1957]). La M imposible. En: Cuentos completos 4. Minotauro.
Grey Walter, W. (1950). An imitation of life. Scientific American.
Heinlein, R. A. (1956). The door into summer. The Magazine of Fantasy & Science Fiction.
Heinlein, R. A. (2002). Puerta al verano. La Factoría de ideas.
Mayor, A. (2019). Dioses y robots: mitos, máquinas y sueños tecnológicos de la Antigüedad. Desperta Ferro Ediciones.
Polanco Masa, A. (2015). Elmer y Elsie, las tortugas robot de 1948. Tecnología obsoleta. https://alpoma.net/tecob/?p=11359
Stimson, T. E. (1952). A house to make life easy. Popular mechanics.
Nota
1 No le pidamos pidamos peras al olmo en este caso. Robert Heinlein nació en 1907 y no dejaba de ser hijo de su época. No obstante, también es cierto que su segunda mujer, Leslyn, no encajaba para nada en ese perfil y fueron muy felices hasta la aparición de Virginia, pero esa es otra historia.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo Elmer, Elsie, una puerta al verano y el aspirador del futuro se ha escrito en Cuaderno de Cultura Científica.
La curva de Sierpinski, o sobre lo que esconden algunas obras de arte
En la primavera del año 2022 tuve la enorme fortuna de poder asistir a la primera retrospectiva que se ha organizado en España del excepcional artista Bruno Munari, la exposición Bruno Munari, que la Fundación Juan March organizó en Madrid entre el 18 de febrero y el 22 de mayo de 2022, y que posteriormente visitaría Palma de Mallorca y Cuenca.

 Dos vistas generales de la exposición Bruno Munari, en la Fundación Juan March de Madrid (18 de febrero – 22 de mayo de 2022)
Dos vistas generales de la exposición Bruno Munari, en la Fundación Juan March de Madrid (18 de febrero – 22 de mayo de 2022)El italiano Bruno Munari (1907-1998) fue un diseñador, escritor, educador y artista multidisciplinar, para quien la experimentación y el juego son una parte fundamental de la creación, de la educación y de la sociedad. Una de sus frases célebres relacionada con los juegos es la siguiente:
Jugar es algo serio, los niños de hoy son los adultos de mañana. Ayudémosles a crecer libres de estereotipos; ayudémosles a desarrollar todos los sentidos; ayudémosles a ser más sensibles. Un niño creativo es un niño feliz.
(en Direzione Sorpresa (1986), de Bruno Munari y Mario de Biasi)
Por otra parte, la geometría y las matemáticas fueron fundamentales en su obra artística y sus diseños. Este hecho se puede apreciar tanto en sus obras de arte y diseño, como en sus magníficos libros, entre los que podemos destacar: El cuadrado: más de 300 ejemplos ilustrados sobre la forma cuadrada (publicado originalmente en 1960), El círculo (publicado originalmente en 1964), El triángulo. Más de 100 ejemplos ilustrados sobre el triángulo equilátero (1976) o ¿Cómo nacen los objetos? Apuntes para una metodología proyectual (1981).
Entre las muchas obras que llamaron mi atención durante la visita a la exposición Bruno Munari en la Fundación Juan March (Madrid) estaban algunas obras de la serie “curva de Peano” y que tomaban como herramienta de creación artística una conocida curva fractal, de la que vamos a hablar en esta entrada del Cuaderno de Cultura Científica. Por ejemplo, ya en el siguiente cartel de esta exposición, que reproduce la pintura Curva de Peano (1977), se puede observar una estructura geométrica relacionada con la mencionada curva fractal, relación que podemos apreciar, aunque no es evidente, los que ya conocemos este objeto geométrico.
 Cartel realizado con motivo de la exposición Bruno Munari, que reproduce la obra Curva de Peano (1977), del artista Bruno Munari, que es una pintura acrílica sobre óleo, cuyas dimensiones son 120 x 120 cm. Este cartel puede verse y comprarse en la tienda online de la Fundación Juan March
Cartel realizado con motivo de la exposición Bruno Munari, que reproduce la obra Curva de Peano (1977), del artista Bruno Munari, que es una pintura acrílica sobre óleo, cuyas dimensiones son 120 x 120 cm. Este cartel puede verse y comprarse en la tienda online de la Fundación Juan MarchO también, otras dos obras que se podían ver en la exposición, Curva de Peano (1975) y De los colores del papel (1995), en las que se aprecia la forma básica a partir de la cual se crea la curva fractal.
 La pintura acrílica sobre lienzo titulada Curva de Peano (1975) y el óleo sobre lienzo De los colores del papel (1995), del artista Bruno Munari, fotografiadas en la exposición Bruno Munari, de la Fundación Juan MarchCurvas que llenan un cuadrado
La pintura acrílica sobre lienzo titulada Curva de Peano (1975) y el óleo sobre lienzo De los colores del papel (1995), del artista Bruno Munari, fotografiadas en la exposición Bruno Munari, de la Fundación Juan MarchCurvas que llenan un cuadrado
En 1890, el matemático y lógico italiano Giuseppe Peano (1858-1932), en su artículo Sur une courbe, qui remplit toute une aire plane / Sobre una curva que rellena toda una zona plana (publicado en la revista de investigación matemática Mathematische Annalen), construyó el primer ejemplo de una curva continua que llena completamente el cuadrado. La idea de una curva continua (intuitivamente una línea, luego de dimensión 1), que llena el cuadrado (una superficie, de dimensión 2), va completamente en contra de nuestra intuición de lo que es una curva. Pero pongamos este descubrimiento en su contexto.
Once años antes, en 1877, el matemático ruso-alemán George Cantor (1845-1918), que acababa de poner patas arriba al mundo de las matemáticas al demostrar que existía más de un infinito (en su artículo Ueber eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen / Sobre una propiedad de la colección de todos los números algebraicos reales, publicado en 1874, demostró que los números reales eran un conjunto infinito no numerable, es decir, que es un infinito “más grande” que el conjunto de los números naturales, ya que no se puede establecer una correspondencia uno-a-uno entre los números reales y los números naturales, estos últimos son los utilizados para numerar, para contar), demostró que existe una correspondencia uno-a-uno entre el segmento unidad [0,1], es decir, todos los números reales entre 0 y 1, y cualquier espacio de dimensión n, sea quien sea n (1, 2, 3, 4, etc), en particular, el cuadrado unidad [0,1] x [0,1]. Es decir, la cantidad infinita de puntos del segmento unidad, es la misma que la cantidad de puntos del cuadrado unidad. En la carta al matemático alemán Richard Dedekind (1831-1916) en la que le enviaba la demostración de la anterior verdad matemática, el propio Cantor escribió “Je le vois, mais je ne le crois pas” (en francés en el original, aunque la carta estaba escrita en alemán), es decir, “Lo veo, pero no lo creo”.
 Teorema de Cantor: hay la misma cantidad infinita de puntos en el segmento unidad, que en el cuadrado unidad
Teorema de Cantor: hay la misma cantidad infinita de puntos en el segmento unidad, que en el cuadrado unidad
Tras el resultado de Cantor, la comunidad matemática, que estaba perpleja ante los descubrimientos del matemático sobre el infinito, se planteó la siguiente cuestión lógica en este contexto, si es posible definir una tal aplicación uno-a-uno (en matemáticas estas aplicaciones reciben el nombre de aplicaciones “biyectivas”) entre el intervalo unidad y el cuadrado unidad, que fuese “continua” (sin discontinuidades). Rápidamente, en 1879, el matemático alemán Eugen Netto (1848-1919) demostró que esto no era posible, es decir, no existen aplicaciones biyectivas continuas del intervalo unidad en el cuadrado unidad (de hecho, en cualquier espacio de dimensión n).
Como el resultado de Netto establecía que cualquier aplicación uno-a-uno entre el segmento unidad y el cuadrado unidad debía ser discontinua, entonces se plantearon la siguiente cuestión: ¿es posible construir una aplicación continua del intervalo unidad en el cuadrado unidad que cubra todos los puntos del cuadrado (en matemáticas a estas aplicaciones, las que llegan a todos los puntos del conjunto imagen, se las llama sobreyectivas)? Ahora, la aplicación no era biyectiva (uno-a-uno), solo sobreyectiva, puesto que habría puntos del cuadrado que serían imágenes de varios puntos del segmento unidad, lo cual rompe que sea una aplicación uno-a-uno. Puesto que una aplicación continua del segmento unidad [0,1] en el plano es lo que se llama una curva, entonces se estaban preguntando si existían curvas que llenaran completamente el cuadrado unidad.
En este punto es en el que encontramos a nuestro matemático italiano Giuseppe Peano, quien construye el primer ejemplo de curva (continua) que llena completamente el cuadrado unidad, es decir, la primera aplicación continua del intervalo unidad en el cuadrado unidad, que cubre completamente este último, es decir, es sobreyectiva.
 Primera página del artículo Sobre una curva que rellena toda una zona plana, publicado por el matemático italiano Giuseppe Peano, en la revista Mathematische Annalen, en 1890
Primera página del artículo Sobre una curva que rellena toda una zona plana, publicado por el matemático italiano Giuseppe Peano, en la revista Mathematische Annalen, en 1890La demostración de Peano era teórica y no incluía una explicación geométrica que permitiera visualizar, de alguna forma, la curva que llena el cuadrado. El primer artículo en incluir imágenes que ayudasen a entender la construcción de una curva continua que llenase el cuadrado, se publicó, en la misma revista, un año más tarde. El artículo era Ueber die stetige Abbildung einer Linie auf ein Flächenstück / Sobre el mapeo continuo de una línea sobre un trozo de superficie, y su autor, el matemático alemán David Hilbert (1862-1943), construyó otra curva que llenaba el cuadrado, que recibiría el nombre de curva de Hilbert.
 Primera página del artículo Sobre el mapeo continuo de una línea sobre un trozo de superficie, publicado por el matemático alemán David Hilbert, en la revista Mathematische Annalen, en 1891
Primera página del artículo Sobre el mapeo continuo de una línea sobre un trozo de superficie, publicado por el matemático alemán David Hilbert, en la revista Mathematische Annalen, en 1891Otros ejemplos fueron construidos por matemáticos como el estadounidense E. H. Moore (1862-1932), en 1900, el francés Henri Lebesgue (1875-1941), en 1904, el polaco Wacław Sierpiński (1882-1969), en 1912, el húngaro George Pólya (1887-1985), en 1913, entre otros. A este tipo de curvas continuas se las bautizó con el nombre de “space-filling curves”, curvas que rellenan el espacio, pero también se las conoció con el nombre de curvas de Peano.
La curva fractal de PeanoComo acabamos de comentar, la construcción de Peano de una curva continua que llena el cuadrado era teórica, sin embargo, sí existen realizaciones geométricas de la mencionada construcción, como vamos a mostrar a continuación.
Para empezar, comentemos que la curva de Peano es una curva fractal, es decir, es autosemejante, rugosa (de dimensión fractal no entera) y creada mediante un proceso iterativo infinito (véase la entrada Fractus, arte y matemáticas). No vamos a ahondar en esta cuestión, pero sí vamos a construir la curva de Peano mediante un proceso iterativo infinito. El primer paso del proceso iterativo es la pieza básica de la construcción, un 2 tumbado (que estaría en el cuadrado unidad) que aparece en la siguiente imagen.
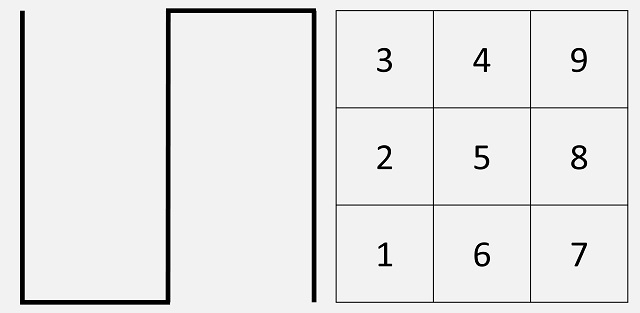
En la anterior imagen, además de la pieza básica, tenemos un cuadrado dividido en 9 zonas cuadradas, marcadas con un número, los cuales nos dan una manera de recorrer los 9 cuadrados, sobre los que vamos a colocar la pieza básica, pero reducida al tamaño de esos cuadrados. La forma de colocar esas 9 copias reducidas de la pieza básica (que también valdrá para los siguientes pasos del proceso iterativo) tiene que seguir unas reglas. En cada cuadrado colocamos una copia de la pieza básica, que puede estar colocada en la misma posición que la original, girada o volteada, con la condición de que un extremo de un cuadrado se pueda conectar de forma directa (añadiendo un pequeño segmento recto) con un extremo del siguiente, para que al final en este segundo paso de la iteración (pero también para el resto) tengamos una curva continua que empieza en el cuadrado 1 y termina en el 9. En la siguiente imagen, podemos apreciar, por ejemplo, que en el cuadrado 1 está la pieza básica (2 tumbado), mientras que en el cuadrado 2 está la pieza básica dada la vuelta (su imagen especular), y podemos conectar los extremos con un pequeño segmento.
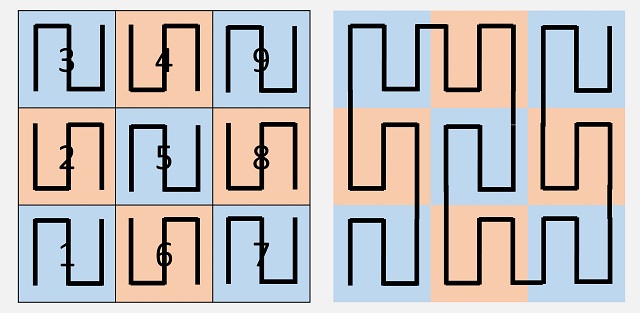 Paso 2 del proceso iterativo de construcción de la curva de Peano
Paso 2 del proceso iterativo de construcción de la curva de Peano
Antes de iniciar el tercer paso del proceso iterativo de construcción de la curva de Peano, debemos de explicar una regla más. En cada paso la pieza básica para utilizar es el resultado del paso anterior y se colocarán sus copias, una vez reducidas de tamaño, en el cuadrado dividido en 9 zonas, de la misma manera que hemos hecho en el segundo paso. Por este motivo, en la imagen anterior, y la siguiente (que se corresponde con el paso 3), hemos dado el mismo color a los cuadrados que tienen la misma posición para la pieza básica. En esta realización que estamos mostrando solo hay dos posiciones, la original (casillas azules) y la volteada (casillas naranjas).
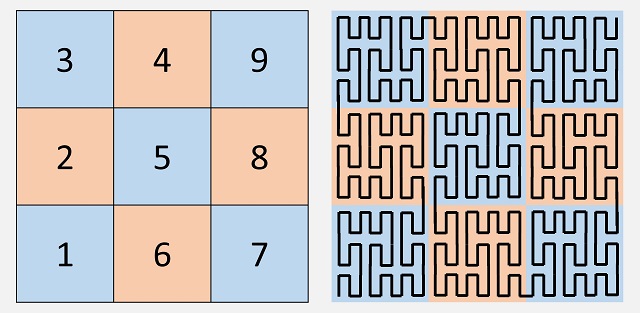 Paso 3 del proceso iterativo de construcción de la curva de Peano
Paso 3 del proceso iterativo de construcción de la curva de Peano
La curva de Peano es el límite de este proceso iterativo infinito. En la siguiente imagen mostramos las tres primeras iteraciones, después del paso 1, es decir, los pasos 2, 3 y 4, de otra elección diferente de posiciones de las piezas básicas.


 Pasos 2, 3 y 4 del otro proceso iterativo de otra construcción geométrica de la curva de Peano. Imagen de Alexander Bogomolny, en su página Cut the KnotLa curva fractal de Sierpinski
Pasos 2, 3 y 4 del otro proceso iterativo de otra construcción geométrica de la curva de Peano. Imagen de Alexander Bogomolny, en su página Cut the KnotLa curva fractal de Sierpinski
La curva fractal que utilizó el artista italiano Bruno Munari como herramienta de creación artística, aunque es una curva de Peano, puesto que es una curva continua que llena el cuadrado, no es “la” curva de Peano, sino otra curva fractal posterior, la conocida como curva de Sierpinski.
Este objeto fractal debe su nombre al matemático polaco Waclaw Franciszek Sierpinski (1882-1969), que nació un 14 de marzo, día que hoy celebramos como Día Internacional de las Matemáticas, por ser el llamado día de pi, 03/14. Este gran matemático del siglo XX, que escribió más de 700 artículos de investigación y 50 libros (entre ellos: Números cardinales y ordinales (1958), Introducción a la topología general (1934), Topología general (1952), Triángulos pitagóricos (1952) o Teoría elemental de números (1914 y 1959)), trabajó en teoría de conjuntos –con contribuciones al axioma de elección y la hipótesis del continuo-, teoría de números, teoría de funciones, topología y lógica matemática. Su nombre se ha asociado a algunos objetos matemáticos, como los fractales denominados curva de Sierpinski, triángulo de Sierpinski (sobre este objeto fractal puede leerse la entrada ¿Conocían los romanos el triángulo fractal de Sierpinski?) y alfombra de Sierpinski, o a los conocidos como números de Sierpinski.
La curva de Sierpinski, también conocida con el nombre de copo de nieve cuadrado de Sierpinski, es una curva continua que rellena el cuadrado, pero que a diferencia de las dos anteriores es una curva cerrada. Como curva fractal se define de forma recursiva.
El primer paso de la construcción de la curva fractal de Sierpinski es el siguiente.
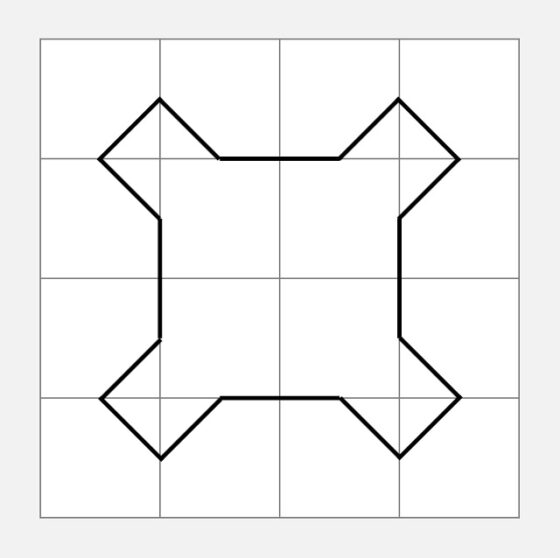 Paso 1 de la construcción del copo de nieve cuadrado de Sierpinski
Paso 1 de la construcción del copo de nieve cuadrado de Sierpinski
En el segundo paso tomamos la imagen anterior, la reducimos en un 25%, una copia se coloca en el centro del cuadrado y se le acopla una nueva copia en cada uno de los extremos, arriba a la izquierda, arriba a la derecha, abajo a la izquierda y abajo a la derecha, obteniendo así la segunda iteración en la construcción de la curva de Sierpinski.
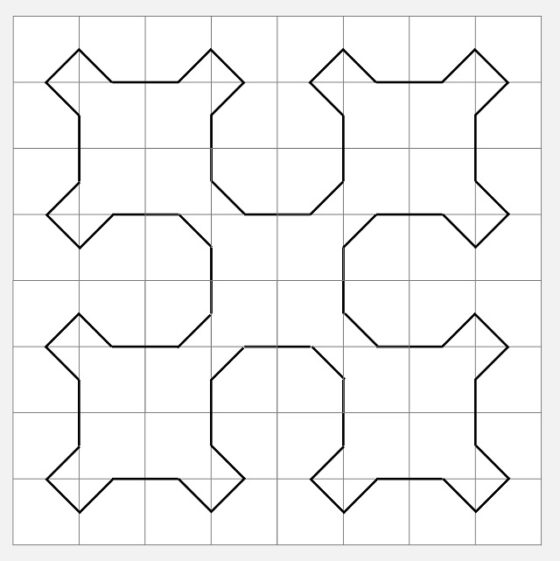 Paso 2 de la construcción del copo de nieve cuadrado de Sierpinski
Paso 2 de la construcción del copo de nieve cuadrado de Sierpinski
Y para los siguientes pasos se actúa de la misma manera. Se toma el paso anterior, se reduce un 25% y se hacen cinco copias que se colocan como antes, una en el centro y cuatro en los extremos. Y la curva de Sierpinski es el límite de este proceso iterativo infinito.
Veamos juntas las cinco primeras iteraciones de la construcción del copo de nieve cuadrado de Sierpinski.
 Primeros cuatro pasos de la construcción del copo de nieve cuadrado de Sierpinski
Primeros cuatro pasos de la construcción del copo de nieve cuadrado de Sierpinski
 Paso 5 de la construcción del copo de nieve cuadrado de Sierpinski
Paso 5 de la construcción del copo de nieve cuadrado de Sierpinski
Si miramos al paso 1 de la construcción de la curva de Sierpinski, llamémosle S1, y calculamos su longitud, simplemente utilizando el teorema de Pitágoras, se obtiene que su longitud es (asumiendo que está dentro del cuadrado unidad):
 Longitud de la primera iteración de la construcción del copo de nieve cuadrado de Sierpinski
Longitud de la primera iteración de la construcción del copo de nieve cuadrado de Sierpinski
De igual forma, puede calcularse la longitud del paso n-ésimo de la construcción, obteniendo la siguiente fórmula.
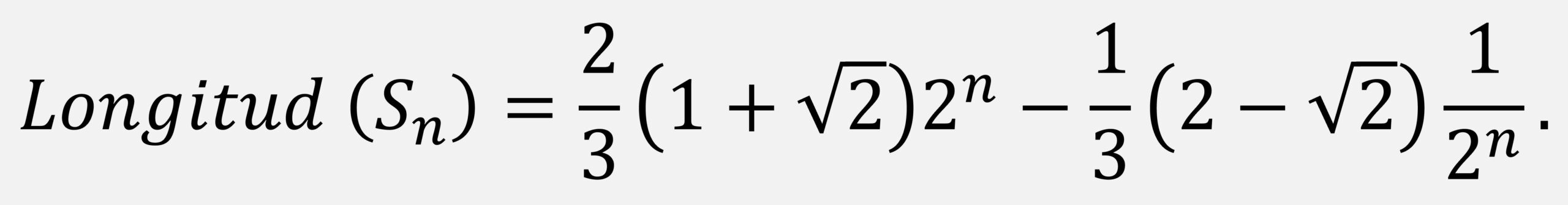 Longitud de la iteración n-ésima de la construcción del copo de nieve cuadrado de Sierpinski
Longitud de la iteración n-ésima de la construcción del copo de nieve cuadrado de SierpinskiComo podemos observar la longitud crece de forma exponencial, luego en su límite, por lo que la curva de Sierpinski tiene longitud infinita.
De la misma forma, podemos calcular el área encerrada por la curva S1, obteniendo que su valor es 11/32 del área del cuadrado. Además, el límite del área encerrada por la curva Sn, es decir, el área encerrada por la curva de Sierpinski es 5/12 del área del cuadrado. Esto es algo que puede sorprender mucho, puesto que podríamos pensar que el área encerrada por una curva que rellena el cuadrado unidad fuese 1, pero no es así.
Por último, mencionar, aunque no vamos a ahondar en esta cuestión, que la dimensión fractal (de Hausdoff) de la curva fractal de Sierpinski, como la de todas las curvas que rellenan el cuadrado, es 2. Como decíamos al principio, esto es algo que rompe nuestros esquemas, ya que es una curva continua cuya imagen tiene dimensión 2. Además, contrariamente a lo que solemos pensar que ocurre con los objetos fractales, la dimensión fractal no es un número no entero, como sí ocurre con fractales como la curva de Koch, cuya dimensión es 1.2619 (sobre la curva de Koch puede leerse la entrada Fractus, arte y matemáticas).
Regreso al arte de Bruno MunariVolviendo a la serie de obras “curva de Peano” del artista italiano Bruno Munari, es cierto que trabaja con una curva fractal de la familia de las curvas de Peano, pero no con la conocida como “la” curva de Peano, sino con la curva de Sierpinski.
El interés artístico de Munari por la curva fractal de Sierpinski no es representar este curioso, e incluso hermoso, objeto geométrico, sino utilizar esta curva fractal, cada una de sus primeras iteraciones, para crear estructuras artísticas que dotadas de color se convierten en hermosas creaciones de arte concreto, movimiento artístico en el que la forma y el color son elementos principales.
Obras como las mostradas al principio, Curva de Peano (1975) y De los colores del papel (1995), que pudimos disfrutar en la exposición de la Fundación Juan March, y en otras obras, como las que mostramos en la siguiente imagen, están basadas en el primer paso de la construcción de la curva de Sierpinski.
 Colores sobre la curva de Peano (1992) y Curva de Peano (1975), del artista Bruno Munari, pintura acrílica sobre lienzo, 30 cm x 30 cm, basada en la primera iteración de la construcción de la curva de Sierpinski
Colores sobre la curva de Peano (1992) y Curva de Peano (1975), del artista Bruno Munari, pintura acrílica sobre lienzo, 30 cm x 30 cm, basada en la primera iteración de la construcción de la curva de SierpinskiEn otras obras trabaja sobre la segunda iteración de la curva de Sierpinski, como las dos que vemos a continuación, entre las muchas que creó.
 Curva de Peano P16-1 (1974), del artista Bruno Munari, pintura acrílica sobre lienzo, 80 cm x 80 cm, basada en la segunda iteración de la construcción de la curva de Sierpinski
Curva de Peano P16-1 (1974), del artista Bruno Munari, pintura acrílica sobre lienzo, 80 cm x 80 cm, basada en la segunda iteración de la construcción de la curva de Sierpinski Colores de la curva de Peano (1985), del artista Bruno Munari, pintura acrílica sobre lienzo, 80 cm x 80 cm, basada en la segunda iteración de la construcción de la curva de Sierpinski
Colores de la curva de Peano (1985), del artista Bruno Munari, pintura acrílica sobre lienzo, 80 cm x 80 cm, basada en la segunda iteración de la construcción de la curva de SierpinskiY en general se basó en diferentes iteraciones de esta curva fractal de la familia de las curvas de Peano, como el cartel que mostramos al principio o la siguiente obra, entre las numerosas obras de esta serie.
 Curva de Peano P64-1 (1974), del artista Bruno Munari, óleo sobre lienzo, 80 cm x 80 cm, basada en la tercera iteración de la construcción de la curva de Sierpinski
Curva de Peano P64-1 (1974), del artista Bruno Munari, óleo sobre lienzo, 80 cm x 80 cm, basada en la tercera iteración de la construcción de la curva de SierpinskiSin lugar a dudas, Bruno Munari es uno de los grandes artistas contemporáneos. Además, sus creaciones alrededor de esta curva continua que llena el cuadrado, es decir, de la familia de las curvas de Peano, la curva de Sierpinski, son de una gran creatividad y belleza.
Bibliografía
1.- Bruno Munari (catálogo de la exposición), Fundación Juan March, 2022.
2.- Hans Sagan, Space-Filling Curves, Universitext, Springer, 1994.
3.- Martin Gardner, Penrose Tiles to Trapdoor Ciphers, … And the Return of Dr Matrix, Cambridge University Press, 1997.
4.- Alexander Bogomolny, Cut the Knot: Plane Filling Curves: All Peano Curves
5.- Wikipedia: Sierpinski curve
6.- R. Ibáñez, Las matemáticas como herramienta de creación artística, Libros de la Catarata – FESPM, 2023.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo La curva de Sierpinski, o sobre lo que esconden algunas obras de arte se ha escrito en Cuaderno de Cultura Científica.
Gaia BH3, un agujero negro supermasivo en la Vía Láctea
La misión Gaia, el proyecto más ambicioso de la Agencia Espacial Europea (ESA) para detallar la cartografía estelar de nuestra galaxia, ha descubierto en la Vía Láctea un agujero negro masivo de origen estelar, el Gaia BH3. Este tipo de agujero negro se había localizado antes en galaxias lejanas mediante observaciones de ondas gravitatorias, y ahora se identifica por primera vez en nuestra galaxia. Se trata de un agujero negro inactivo, es el segundo más cercano a la Tierra —se encuentra a una distancia de 590 pc (o 1926 años luz)—, tiene unas treinta y tres masas solares y forma un amplio sistema binario con su estrella acompañante.
 Fuente: ESA
Fuente: ESAEste descubrimiento excepcional confirma algunas teorías y exige revisar otras. Este es un resultado emocionante para la comunidad astronómica, que hace que nos preguntemos cuántos agujeros negros de este tipo hay en el espacio, o qué rangos de masas de agujeros negros podrá descubrir la misión Gaia.
Cómo detectar un agujero negro inactivoSi el agujero negro está inactivo, ¿no es muy difícil poder detectarlo? Los agujeros negros más conocidos se detectan a través de los rayos X que emiten cuando el material de su compañero estelar es devorado. Con los agujeros negros inactivos, la fuente emite poca o ninguna radiación, por lo que el agujero negro solo puede verse realmente por el efecto gravitatorio que ejerce sobre su estrella acompañante. Los agujeros negros inactivos nunca se habían detectado antes de la misión Gaia. En concreto, después de la publicación de la tercera entrega de datos de Gaia —la Gaia Data Release (DR3)—, se pudieron identificar los primeros agujeros negros inactivos de nuestra galaxia: Gaia BH1 y Gaia BH2.
Durante la validación de los datos preliminares procesados por Gaia Data Release (DR4), y dados los resultados preliminares del análisis de datos para estrellas no individuales, esta fuente galáctica requería más comprobaciones para ver si los datos detectados eran correctos. En un primer momento, el equipo del Consorcio para el Procesamiento y Análisis de Datos (DPAC) consideró que estos resultados no podían ser reales. La sorpresa fue mayúscula cuando, tras muchas verificaciones internas, todos los datos sugirieron que se trataba de una auténtica detección, un hallazgo científico que es importante publicar antes de la difusión de la Gaia Data Release (DR4) para permitir un seguimiento posterior del descubrimiento por parte de la comunidad científica.
El agujero negro de origen estelar más masivo en nuestra galaxiaPero, ¿qué hace que este hallazgo sea tan sorprendente? Sobre todo, la gran masa del agujero negro. Con treinta y tres masas solares, Gaia BH3 no es solo el agujero negro de origen estelar más masivo conocido en nuestra galaxia, sino que también está en línea con los resultados obtenidos por observatorios de ondas gravitacionales como LIGO/VIRGO/KAGRA. Estos equipamientos encontraron a una población de agujeros negros con masas que contradicen los modelos de evolución estelar a través de la observación de las ondas gravitatorias procedentes de fenómenos de fusión de agujeros negros. El hallazgo de Gaia confirma que en nuestra propia Vía Láctea también existen agujeros negros masivos con origen estelar.
La mayoría de los agujeros negros de origen estelar de nuestra galaxia tienen una masa de unas 10 masas solares, y el mayor concido hasta ahora era el agujero negro de Cyg X-1, con una masa calculada de unas veinte veces la del Sol. Gaia BH3 va mucho más allá y es el nuevo récord de nuestra galaxia. Su masa también se fija con una precisión mejorada (32,7 +/- 0,82 Msol), un valor que se sitúa firmemente en el rango de 30 masas solares.
«La distribución de masa de la población de agujeros negros derivada de observaciones de ondas gravitatorias muestra un claro pico en torno a treinta masas solares», explica Tsevi Mazeh, de la Universidad de Tel Aviv, miembro de la Colaboración Gaia. «Es muy interesante ver ahora que Gaia BH3 está justo en este pico con sus treinta y tres masas solares. Esto proporciona un fuerte apoyo científico para la existencia de ese pico».
El segundo agujero negro más cercano a la TierraEste agujero negro, que se encuentra a una distancia de 1926 años luz, es actualmente el segundo más cercano a la Tierra. ¿Por qué ese agujero negro solo se puede ver ahora? El período de tiempo más largo de observaciones que constituirá la base de la Gaia Data Release 4 (DR4) es decisivo para responder a esta cuestión. Se calcula que la órbita de la compañera estelar en torno a su centro de masa común es de 11,6 años. Esto significa que, con 5,5 años de datos que se están procesando para el próximo DR4, Gaia es capaz de mapear la mitad de su órbita. Esto es suficiente para distinguir la oscilación adicional en la posición y movimiento de la estrella acompañante. Se espera que, con un período de tiempo más largo de observaciones de Gaia, se puedan identificar cada vez más sistemas binarios. Por tanto, es de esperar que las próximas publicaciones de datos de Gaia revelen muchos resultados excepcionales.
«En el rango de longitud de onda visible y en el infrarrojo, la luz de la estrella acompañante visible obviamente eclipsa cualquier cosa que pueda provenir de la propia Gaia BH3; de lo contrario, el agujero negro se habría descubierto mucho antes y sin Gaia», detalla Uli Bastian, miembro de la Colaboración Gaia.
Por su especial naturaleza, y para descartar la posibilidad de que la solución sea errónea, se realizó una confirmación del resultado con varios observatorios terrestres. El espectro UVES de este sistema se obtuvo del archivo de la ESO y se realizaron observaciones de seguimiento con el espectrógrafo HERMES en España y el espectrógrafo SOPHIE en Francia. Las velocidades radiales obtenidas con estos observatorios terrestres complementan las velocidades radiales de Gaia, lo que confirma la solución orbital derivada de los datos de Gaia.
«Gaia es una auténtica máquina de detección de agujeros negros porque cada uno de los tres instrumentos puede detectarlos», comenta Laurent Eyer, del Observatorio de Ginebra, miembro de la Colaboración Gaia.
¿Cómo se originó este agujero negro en la Vía Láctea?La fotometría y los espectros de Gaia, así como los espectros obtenidos mediante observaciones en tierra con HERMES, SOPHIE y UVES, permiten desentrañar aún más los secretos de este sistema binario. Como no podemos ver el agujero negro, la mayoría de la información debe deducirse de la estrella acompañante, que es una única estrella gigante antigua. Sin embargo, no es fácil determinar la edad de esta antigua estrella gigante. Al comparar los colores y magnitud con modelos teóricos, se estima que tiene más de 11.000 millones de años.
Sobre el espectro de la estrella acompañante, puede deducirse que tiene una abundancia baja de elementos pesados. Esto sugiere que Gaia BH3 se formó a partir de una estrella masiva pobre en elementos pesados. Tras los hallazgos de la población de agujeros negros extragalácticos en esta gama de masas a partir de observaciones de ondas gravitatorias, se ha propuesto que estos agujeros negros de gran masa son restos de estrellas masivas pobres elementos pesados. Ahora, el agujero negro Gaia BH3 apoya esta teoría.
Un compañero estelar muy particularLa estrella que orbita el Gaia BH3, a unas dieciséis veces la distancia Sol-Terra, es bastante excepcional: es una antigua estrella gigante, que se formó los primeros dos mil millones de años después del Big Bang, en el momento en que nuestra galaxia empezó a crearse. Forma parte de la familia del halo galáctico estelar y se está moviendo en dirección contraria a las estrellas del disco galáctico. Su trayectoria indica que esta estrella probablemente formaba parte de una pequeña galaxia, o un cúmulo globular, que nuestra propia galaxia tragó hace más de ocho mil millones de años.
Esto apoya, por primera vez, la teoría de que los agujeros negros de gran masa observados por los experimentos de ondas gravitacionales fueron producidos por el colapso de estrellas masivas primitivas pobres en elementos pesados. Estas estrellas tempranas podrían haber evolucionado de forma diferente a las estrellas masivas que vemos actualmente en nuestra galaxia. La composición de la estrella acompañante también puede arrojar luz sobre el mecanismo de formación de este sorprendente sistema binario. ««Lo que me llama la atención es que la composición química del acompañante es similar a la que encontramos en las estrellas antiguas pobres en metales de la galaxia»», explica Elisabetta Caffau, del CNRS, Observatorio de París del CNRS, también miembro de la colaboración Gaia.
Por ahora, el proceso de formación de este sistema binario con un agujero negro plantea muchas incógnitas. Este nuevo agujero negro desafía nuestra comprensión de cómo se desarrollan y evolucionan las estrellas masivas. La mayoría de las teorías predicen que, a medida que envejecen, las estrellas masivas arrojan una parte considerable de su material a través de vientos potentes; en última instancia, son parcialmente expulsadas en el espacio cuando explotan como supernovas. Lo que queda de su núcleo se contrae para convertirse en una estrella de neutrones o en un agujero negro, dependiendo de su masa que tenga. Los núcleos lo suficientemente grandes como para acabar siendo agujeros negros de treinta veces la masa de nuestro sol son muy difíciles de explicar.
La estrella compañera tiene muy pocos elementos más pesados que el hidrógeno y el helio, lo que indica que la estrella masiva que se convirtió en Gaia BH3 también podría haber sido muy pobre en elementos pesados. Esto apoya, por primera vez, la hipótesis de que los agujeros negros de alta demasiado observados por los experimentos de ondas gravitacionales fueron producidos por el colapso de estrellas masivas primitivas pobres en elementos pesados. Estas primeras estrellas podrían haber evolucionado de forma diferente a las estrellas masivas que vemos actualmente en nuestra galaxia.
También hay muchas dudas sobre dónde proviene este agujero negro. Aunque actualmente se encuentra en el plano de la Vía Láctea, su movimiento lo sitúa en una órbita retrógrada con una gran inclinación con el plano de la Vía Láctea. El agujero negro puede provenir de un evento de fusión de una pequeña galaxia o de un cúmulo globular con nuestra galaxia. En el futuro, es de esperar que más estudios proporcionen más información sobre cómo Gaia BH3 terminó en la Vía Láctea.
«Un número creciente de agujeros negros que se encuentran en la Vía Láctea con diferentes métodos, incluido a través de microlentes como se documentó en 2022 por OGLE y HST, nos acerca a una imagen más amplia de la población de estos objetos en la galaxia y puede arrojar luz sobre la naturaleza de la materia oscura si se detecta un exceso de estos agujeros negros cerca», comenta Łukasz Wyrzykowski de la Universidad de Varsovia en Polonia y miembro de la colaboración Gaia.
«Desde un punto de vista observacional, descubrir el Gaia BH3 no es demasiado difícil y los instrumentos astronómicos y especializados serán capaces de detectar sus indicios. La dificultad radica en que es necesario saber a cuál de los millones de estrellas debes dirigir tu telescopio. Aquí es donde la enorme capacidad de Gaia entra en juego. La misión Gaia observa todas las fuentes celestes que son suficientemente brillantes para ser vistas por sus detectores, y nosotros pudieron encontrar la aguja en el pajar», dice Johannes Sahlmann, miembro del equipo de operaciones científicos de Gaia del Centro Europeo de Astronomía Espacial Europeo.
Hasta ahora, los datos de la misión Gaia solo han desvelado la punta del iceberg. Los períodos de tiempo más largos de las futuras publicaciones de Gaia revelarán, sin duda, otros sistemas binarios que contienen agujeros negros, pero también exoplanetas y otros sistemas binarios exóticos. La Gaia Data Release (DR4) se basará en 5,5 años de observaciones, casi el doble del período de tiempo de la tercera entrega de datos, con cerca de tres años de observaciones. Actualmente, se espera que la vida útil completa de Gaia sea de unos 10,5 años.
Referencia:
Gaia Collaboration – Panuzzo, P. et al. (2024) Discovery of a dormant 33 solar-mass black hole in pre-release Gaia astrometry Astronomy & Astrophysics doi: 10.1051/0004-6361/202449763
Edición realizada por César Tomé López a partir de materiales suministrados por la Agencia Espacial Europea y la Universidad de Barcelona.
El artículo Gaia BH3, un agujero negro supermasivo en la Vía Láctea se ha escrito en Cuaderno de Cultura Científica.
Kamoʻoalewa, un asteroide con sabor lunar
Asteroides y cometas son los cuerpos más abundantes de nuestro Sistema Solar y, muy probablemente, representen una memoria de aquellos bloques primitivos con los que se construyó. Sabemos que algunos han sufrido ciertos procesos evolutivos posteriores que han podido alterar su estructura y composición a partir de impactos, la radiación o incluso por la presencia de agua. Y en los casos más extremos, algunos podrían haber formado parte de cuerpos planetarios.
¿Cómo es posible seguir ese camino evolutivo al revés? Pues a lo largo de la historia de todo nuestro Sistema Solar, los planetas y los satélites han sufrido violentos impactos que en algunos casos han tenido la fuerza necesaria como para lanzar materiales a una velocidad suficiente como para escapar a su atracción gravitatoria y ponerse en órbita alrededor del Sol.
En abril de 2016, el telescopio Pan-STARRS descubrió un pequeño asteroide de entre 40 y 100 metros de diámetro denominado 469219 Kamoʻoalewa y que tarda algo menos de media hora en girar sobre sí mismo y alrededor de un año en completar una vuelta alrededor del Sol. A pesar de su pequeño tamaño muy pronto comenzó a llamar la atención de los científicos por un par de peculiaridades muy interesantes.
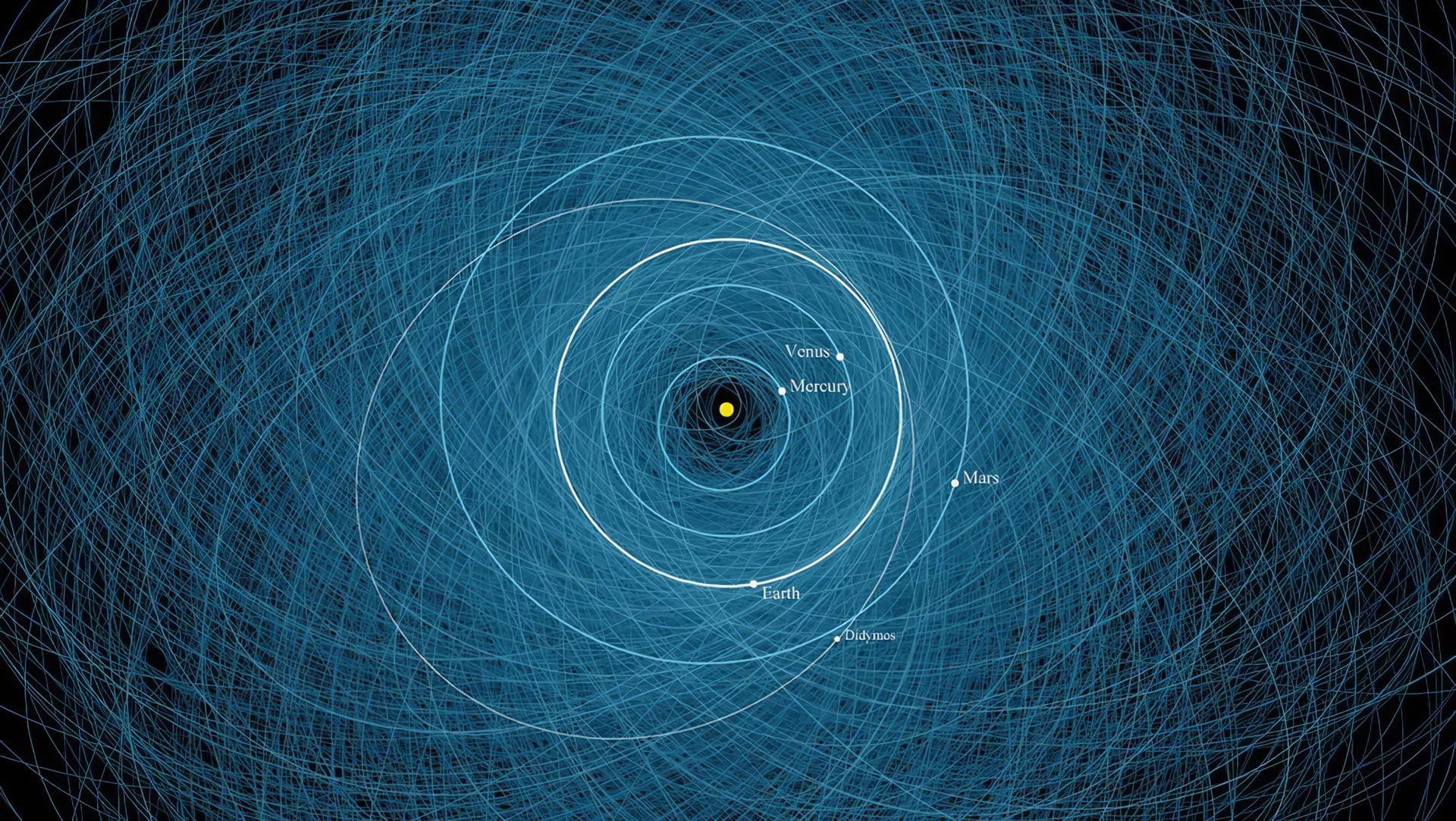 El entorno de la Tierra es un lugar realmente congestionado a nivel orbital, con alrededor de 30000 asteroides cercanos a la Tierra. ¿Y si algunos son fragmentos de la Luna o de nuestro propio planeta? Imagen cortesía de NASA/JPL.
El entorno de la Tierra es un lugar realmente congestionado a nivel orbital, con alrededor de 30000 asteroides cercanos a la Tierra. ¿Y si algunos son fragmentos de la Luna o de nuestro propio planeta? Imagen cortesía de NASA/JPL.La primera es que es un asteroide coorbital de la Tierra, es decir, que comparte una órbita alrededor del Sol muy parecida a la de nuestro planeta, manteniendo una relación más o menos estable a lo largo del tiempo. Pero más concretamente es un cuasisatélite, cuerpos que parecen estar en órbita alrededor de un planeta porque prácticamente tardan lo mismo en completar una órbita alrededor del Sol, aunque en realidad ambos giren alrededor del Sol. De hecho, de los siete cuasisatélites confirmados hasta el momento, probablemente Kamoʻoalewa sea el más estable de todos. De la población de los cuasisatélites se sabe muy poco porque son muy pequeños, lo que hace muy difícil su observación.
En 2021, los datos en luz visible e infrarrojo cercano obtenidos por el Large Binocular Telescope y el Lowell Discovery Telescope permitieron a los científicos (Sharkey et al. 2021) hacerse una idea sobre su composición, descubriendo que estaba formado principalmente por silicatos. Pero, además, el espectro que habían obtenido mostraba un enrojecimiento fruto de la alteración en el espacio, un fenómeno relativamente habitual en los asteroides y otros cuerpos.
Para ver si pertenecía a alguna de las familias de asteroides conocidas, los científicos compararon el espectro con asteroides de tipo S -asteroides con una composición mineralógica formada por silicatos o, de una manera más sencilla, rocosos- y que suelen mostrar ese enrojecimiento que mencionábamos anteriormente. La conclusión: este asteroide estaba más enrojecido de lo que debería. Entonces, ¿pertenecía a este tipo o podría tener otra procedencia?.
Al comparar su espectro con el de muestras lunares y espectros de la superficie lunar tomados por los telescopios se observa que muestra una mayor afinidad a la superficie lunar que a los asteroides de tipo S, por lo que en realidad no sería descabellado pensar que fuese material lunar expulsado durante un impacto y haber sufrido la alteración por los distintos procesos que se dan en el espacio -desde el efecto de la radiación a los micrometeoritos que impactan contra su superficie-.
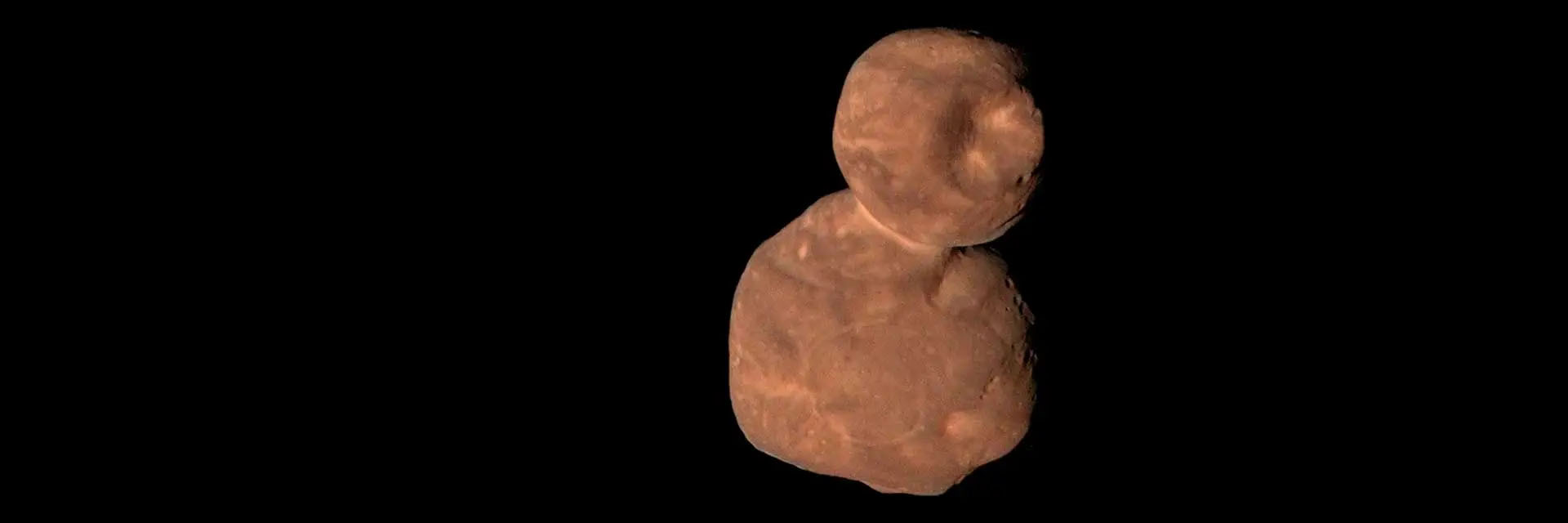 Arrokoth es el objeto más lejano visitado por una sonda, en este caso, la New Horizons. Destaca por intenso color rojo debido a la alteración de los compuestos orgánicos como consecuencia de los rayos cósmicos y la luz ultravioleta. Cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Southwest Research Institute.
Arrokoth es el objeto más lejano visitado por una sonda, en este caso, la New Horizons. Destaca por intenso color rojo debido a la alteración de los compuestos orgánicos como consecuencia de los rayos cósmicos y la luz ultravioleta. Cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Southwest Research Institute.¿Podría este pequeño asteroide ser fruto de una carambola cósmica? Jiao et al. (2024) acaban de publicar en Nature Astronomy como podría haber ocurrido. Para ello han desarrollado un modelo numérico para descubrir que tipos de impactos -tamaño, velocidad, ángulo…- podrían haber lanzado un trocito de la Luna a una órbita como la que vemos hoy en día.
Pues bien, de sus modelos hay dos importantes derivadas que quizás algún día no muy lejano podamos comprobar: La primera es que el impacto ha tenido que ocurrir en el pasado reciente -por reciente hablamos en términos geológicos- para que tenga la órbita que observamos hoy día y las perturbaciones que sufre por efecto de la gravedad del Sol y los demás planetas no la hayan llevado mucho más lejos de nuestro entorno.
 El cráter Giordano Bruno visto desde la Lunar Reconaissance Orbiter. Se aprecia su forma bien definida y el escaso número de cráteres de impacto que pueblan su superficie, lo que atestigua su reciente formación… en términos geológicos. Cortesía de NASA/Goddard/Arizona State University.
El cráter Giordano Bruno visto desde la Lunar Reconaissance Orbiter. Se aprecia su forma bien definida y el escaso número de cráteres de impacto que pueblan su superficie, lo que atestigua su reciente formación… en términos geológicos. Cortesía de NASA/Goddard/Arizona State University.La segunda es: ¿De que cráter podría provenir este asteroide? En este estudio se afirma que uno de los candidatos podría ser el Giordano Bruno, un cráter de unos 20 kilómetros bastante reciente -se estima que en torno a los cuatro millones de años aproximadamente- y que está en el rango de tamaños que coincide con los resultados de las simulaciones realizadas para el estudio, que requerían de un impacto que provocase un cráter de entre 10 y 20 kilómetros de diámetro.
La Agencia Espacial China (CNSA) tiene previsto el despegue, para el mes de mayo de 2025, de una misión denominada Tianwen-2 y cuyo primer destino será el asteroide 469219 Kamoʻoalewa y del que deberá traer a la Tierra al menos cien gramos de muestras con las que podríamos comprobar si efectivamente el origen de este asteroide es realmente la Luna o si en el espacio las apariencias… también engañan.
Referencias:
Castro-Cisneros, Jose Daniel, Renu Malhotra, y Aaron J. Rosengren (2023) Lunar Ejecta Origin of Near-Earth Asteroid Kamo’oalewa Is Compatible with Rare Orbital Pathways Communications Earth & Environment doi: 10.1038/s43247-023-01031-w.
Jiao, Yifei, Bin Cheng, Yukun Huang, Erik Asphaug, Brett Gladman, Renu Malhotra, Patrick Michel, Yang Yu, y Hexi Baoyin (2024) Asteroid Kamo‘Oalewa’s Journey from the Lunar Giordano Bruno Crater to Earth 1:1 Resonance Nature Astronomy doi: 10.1038/s41550-024-02258-z.
Sharkey, Benjamin N. L., Vishnu Reddy, Renu Malhotra, Audrey Thirouin, Olga Kuhn, Albert Conrad, Barry Rothberg, Juan A. Sanchez, David Thompson, y Christian Veillet (2021) Lunar-like Silicate Material Forms the Earth Quasi-Satellite (469219) 2016 HO3 Kamoʻoalewa Communications Earth & Environment doi: 10.1038/s43247-021-00303-7.
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario, divulgador científico u autor de la sección Planeta B.
El artículo Kamoʻoalewa, un asteroide con sabor lunar se ha escrito en Cuaderno de Cultura Científica.
El día que humanos y tigres dientes de sable comieron de la misma mamut
 Recreación de la explotación del cadáver del mamut por parte de los humanos.
Recreación de la explotación del cadáver del mamut por parte de los humanos.Jesús Gamarra, CC BY-NC
Entre los años 2001-2003, en Fuente Nueva 3 (Orce, Granada), se excavaron unos fósiles excepcionales. De entre todos ellos destacó el cadáver casi completo y conectado de una mamut hembra. Tenía un estado de conservación excelente con una antigüedad de 1,2 millones de años. A esta mamut se la llamó Amparo, en honor a un personaje televisivo de la época llamado El Pozí conocida como Amparito.
A Amparito, la mamut, le faltan las patas y el cráneo. Tenía una edad avanzada, de entre 50 y 60 años, cuando murió. Acabamos de publicar el estudio de sus restos y sabemos que fue el menú de humanos y tigres dientes de sable.
Lo que el ojo no veLos yacimientos arqueológicos son, con frecuencia, fruto de la acumulación de múltiples historias. Con el paso del tiempo, éstas, literalmente, se comprimen, dando lugar a una falsa percepción de que todo ocurrió al mismo tiempo. ¿Cómo desvelarlas? Lo logramos magnificando la escala a la que se estudian los sedimentos.
Los especialistas en micromorfología extraen bloques de sedimento que convierten en láminas de 30 micras de grosor (el mismo que las cintas adhesivas de aluminio). Estas microláminas se estudian bajo el microscopio, desvelando características imperceptibles para el ojo humano.
Fuente Nueva 3: las incidencias de un lagoFuente Nueva 3, en Orce (Granada), es un yacimiento conocido por albergar unos de los mejores conjuntos de útiles en piedra tallada de los albores del poblamiento humano del suroeste de Europa. La aplicación de la micromorfología al yacimiento ha puesto de manifiesto que donde, con anterioridad, se proponía una historia al estilo Pompeya –la foto fija de un instante geológico– existe toda una película con situaciones diferentes.
Esto es especialmente visible en el denominado nivel 5. Este intervalo temporal, lejos de ser homogéneo, incluye, de más antiguas a más recientes: arcillas desecadas en el borde de un lago, abanicos fluviales, arcillas formadas en la orilla de un lago, una lámina de agua permanente o semipermanente y arcillas típicas de un lago en regresión.
La muerte de la mamutDe entre todas las escenas propuestas para el nivel 5, hasta hace poco no se sabía en cuál había muerto Amparito. No obstante, había una forma de averiguarlo: aplicando la misma técnica de la micromorfología a alguno de sus huesos.
El resultado fue sorprendente: el relleno del hueso y los restos de sedimento adheridos a él coinciden con el momento en que el lago estaba en transgresión.
Amparito, la hembra de proboscídeo, falleció cuando el entorno del yacimiento estaba aún cubierto por las aguas. Esto también explica el excelente estado de conservación del esqueleto, ya que las aguas y sedimentos protegieron los huesos.
Las marcas de mordedura de humanos y tigresUno de los grandes retos de las ciencias del pasado es dilucidar qué agentes que actuaron sobre los cadáveres de los animales que se encuentran en los yacimientos arqueológicos. Dado que cada especie presenta características dentales diferentes, su reflejo en la superficie de los huesos también lo es. Por tanto, las marcas de mordedura se convierten en un documento identificativo del animal que las mordió.
Para poder reconocer qué carnívoro produjo las marcas de mordedura se utilizan técnicas novedosas de gran resolución. Estas pueden resumirse en un escaneado digital tridimensional de las alteraciones óseas del hueso que ayudan a obtener un modelo digital de las marcas. Los modelos obtenidos se comparan con las marcas que otros carnívoros producen y, tras realizar diferentes test estadísticos, se clasifican.
¿Quiénes comieron del cadáver de mamut?Siempre se ha postulado que los tigres dientes de sable no dejarían marcas sobre los huesos debido a que, supuestamente, estos felinos tenían una dentición muy delicada. Sin embargo, se han encontrado marcas de diente sobre una costilla y la pelvis de Amparo que han podido relacionarse con la acción de un Homotherium, el más grande de los felinos que vivieron en Orce hace 1,2 millones de años, un tigre dientes de sable.
 El momento en que los tigres dientes de sable accedieron al mamut. Posiblemente facilitaron el trabajo a los humanos que llegaron después, quitándole la piel.
El momento en que los tigres dientes de sable accedieron al mamut. Posiblemente facilitaron el trabajo a los humanos que llegaron después, quitándole la piel.Jesús Gamarra, CC BY
En cuanto a la acción humana, se han documentado tres marcas de corte en la pelvis y en una costilla que parecen haberse realizado con un útil de sílex para desarticular y descarnar. Es decir, un “cuchillo” humano.
Implicaciones de este estudioLos yacimientos de Orce ofrecen una ventana a través de la que vislumbrar episodios precisos de la vida en el pasado. En este caso, el escenario de la muerte de una hembra de mamut, que posteriormente sirvió de festín a humanos y tigres dientes de sable. Hay que tener en cuenta que este animal pesaría tres o cuatro toneladas, lo que proporcionaría suficientes recursos a ambos.
Por otra parte, las marcas de corte de la pelvis están en el área de inserción del psoas ilíaco, y pueden asociarse a la desmembración de una pata (la izquierda) o a la extracción de las vísceras del animal.
Además, teniendo en cuenta el utillaje lítico encontrado en Fuente Nueva 3, pequeñas lascas de sílex, cabe la posibilidad de los Homotherium llegaran antes que los humanos y les facilitaran el trabajo rasgando la gruesa piel de mamut con sus dientes. Lo que no se encuentra es evidencia alguna de competencia entre ambos taxones.
Los avances en la técnica y la investigación aplicados a los tiempos profundos de la Prehistoria nos están permitiendo aproximarnos con más detalle a las actividades cotidianas de subsistencia desarrolladas por los primeros pobladores de Orce. Nos permiten conocer cómo era su dieta, y también su interacción con el medio que les rodeaba, los ambientes de lago, los paisajes arbolados mediterráneos, los animales enormes de gran tonelaje o los grandes y peligrosos felinos. Todo sugiere un comportamiento más flexible y adaptado de lo que tal vez pensábamos.
Amparito, la elefante hembra, narra esa pequeña escena en la película de Orce en la que humanos y tigres dientes de sable celebraron un banquete de carne de mamut.![]()
José Yravedra Sainz de los Terreros, Profesor Titular de Prehistoria, Universidad Complutense de Madrid; José A. Solano García, Lecturer in Prehistory and Archaeology, Universidad de Granada y Juan Manuel Jiménez Arenas, Profesor Titular del Departamento de Prehistoria y Arqueología / Instituto Universitario de la Paz y los Conflictos, Universidad de Granada
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo El día que humanos y tigres dientes de sable comieron de la misma mamut se ha escrito en Cuaderno de Cultura Científica.
¡Ups! La edad de la Tierra según Lord Kelvin

Hoy sabemos que la edad de la tierra es de 4540 millones de años, con un margen de error de 50 millones de años, claro. A una cifra muy muy próxima llegó el geofísico estadounidense Clair Cameron Patterson analizando meteoritos con un espectrógrafo de masas. Pero, antes que él, muchos habían intentado calcular la edad de la Tierra. Usando desde la Biblia hasta la datación radiométrica. Aunque todas ellas dieron como resultado cifras muy alejadas de la actual.
Producción ejecutiva: Blanca Baena
Guion: José Antonio Pérez Ledo
Grafismo: Cristina Serrano
Música: Israel Santamaría
Producción: Olatz Vitorica
Doblaje: K 2000
Locución: José Antonio Pérez Ledo
Edición realizada por César Tomé López
El artículo ¡Ups! La edad de la Tierra según Lord Kelvin se ha escrito en Cuaderno de Cultura Científica.
La neurodegeneración de la retina precede al deterioro cognitivo del párkinson
Aunque todavía hay algunos aspectos que se deben confirmar para su uso en el ámbito clínico y mejorar ligeramente su resolución, en un estudio de la UPV/EHU y Biobizkaia se ha comprobado que un método utilizado habitualmente para realizar pruebas oftalmológicas se puede usar también para monitorizar la neurodegeneración que se produce en los pacientes de párkinson. Es probable que la neurodegeneración de la retina preceda al deterioro cognitivo.
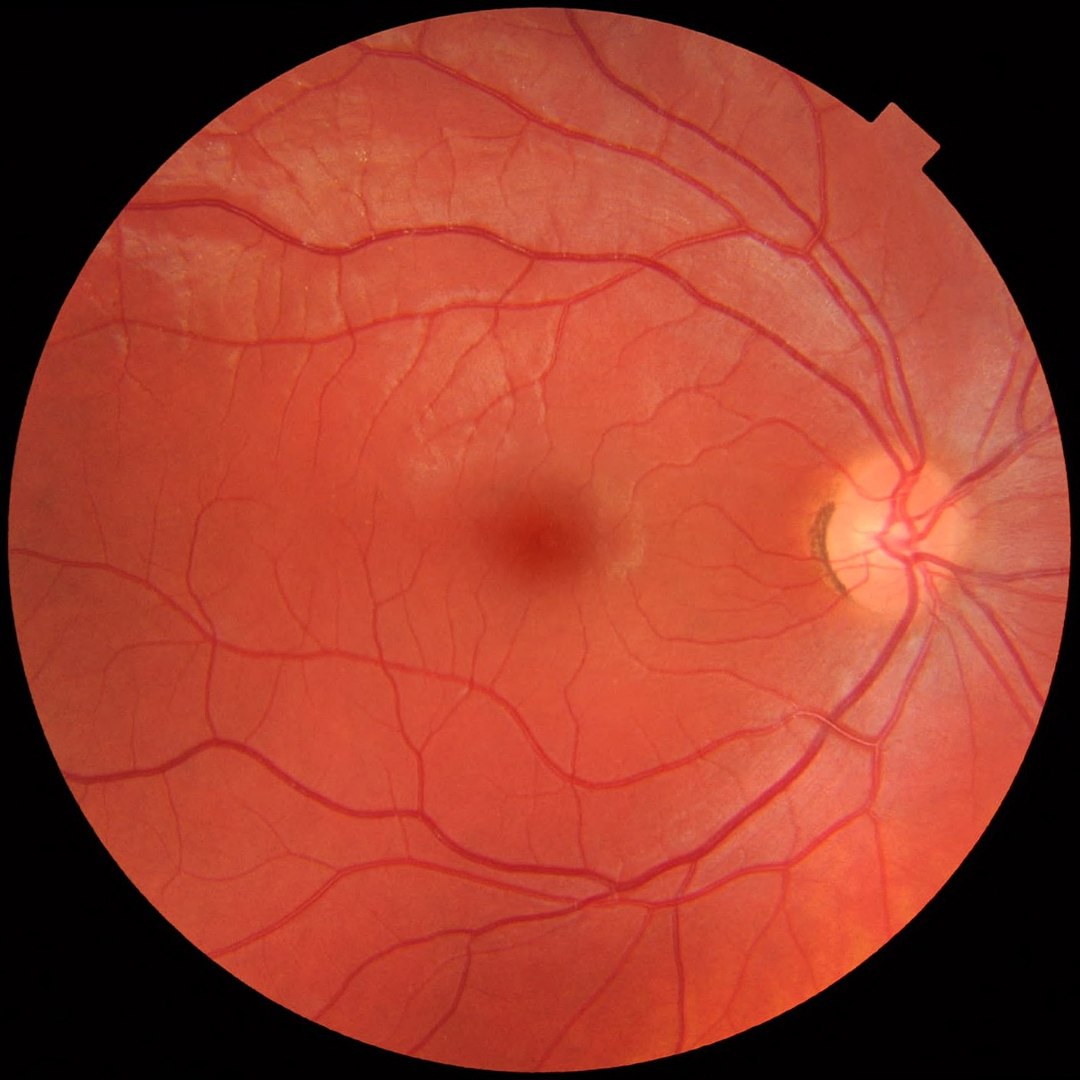 Häggström, Mikael (2014). «Medical gallery of Mikael Häggström 2014». WikiJournal of Medicine 1 (2). doi: 10.15347/wjm/2014.008. ISSN 2002-4436. Public Domain.
Häggström, Mikael (2014). «Medical gallery of Mikael Häggström 2014». WikiJournal of Medicine 1 (2). doi: 10.15347/wjm/2014.008. ISSN 2002-4436. Public Domain.En el momento en que se diagnostica la enfermedad de Parkinson u otra enfermedad neurodegenerativa, los pacientes siempre preguntan: “¿Y ahora qué? ¿Qué pasará? ¿Qué cabe esperar de la enfermedad?”. Para los neurólogos, sin embargo, no es posible responder con precisión a estas preguntas, ya que “la evolución de los pacientes suele ser muy variada: algunos no experimentan cambios con el paso de los años, mientras que otros terminan con demencia o en una silla de ruedas”, explica Ane Murueta-Goyena, investigadora del departamento de Neurociencias de la UPV/EHU.
Hoy en día, la identificación de pacientes de párkinson con riesgo de sufrir deterioro cognitivo supone un gran reto, necesario para proporcionar tratamientos clínicos más eficaces y avanzar en los ensayos clínicos. De hecho, Murueta-Goyena, en colaboración con el personal investigador de Biobizkaia, ha querido ver “si el sistema visual permite predecir ese deterioro, es decir, qué futuro puede tener el paciente en unos años”. Para ello se ha utilizado el grosor de la retina.
La retina es una membrana situada en la parte posterior del globo ocular, relacionada con el sistema nervioso y formada por varias capas. Durante el estudio, a una cohorte o grupo de pacientes de párkinson se les ha medido el grosor de la capa más interna de la retina mediante tomografía de coherencia óptica. Este tipo de tomografía es un instrumento utilizado habitualmente para la realización de pruebas oftalmológicas, ya que permite hacer mediciones de alta resolución, repetibles y precisas. Así, se ha analizado y comparado la evolución de esta capa de la retina en personas con la enfermedad de Parkinson y en personas sin ella durante el periodo 2015-2021. Por otra parte, el análisis de las imágenes de las capas de la retina de pacientes de párkinson en un hospital del Reino Unido ha confirmado los resultados.
Los resultados muestran que la capa de la retina es notablemente más fina en pacientes con párkinson. Además, han observado que “en las fases iniciales de la enfermedad es en la retina donde se detecta la mayor neurodegeneración, y, a partir de un momento dado, cuando la capa es ya muy fina, se produce una especie de estabilización en el proceso de neurodegeneración. La pérdida de grosor de la retina y el deterioro cognitivo no se producen simultáneamente. Los cambios que se producen inicialmente en la retina son más evidentes y luego, con el paso de los años, se observa cómo los pacientes empeoran clínicamente tanto a nivel cognitivo como a nivel motor —explica Murueta-Goya. Es decir, la pérdida de grosor más lenta de la capa de la retina está relacionada con un deterioro cognitivo más rápido; esa lentitud va ligada a una mayor gravedad de la enfermedad”.
La investigadora ha dado mucha importancia a los resultados: “Hemos obtenido información sobre la progresión de la enfermedad, y además la herramienta que proponemos no es invasiva y está disponible en todos los hospitales”. Los resultados deben ser validados internacionalmente y “mejorando ligeramente la resolución de la tecnología, estaremos más cerca de validar el método para monitorizar la neurodegeneración que tiene lugar en la enfermedad de Parkinson”.
Referencia:
Ane Murueta-Goyena, David Romero-Bascones, Sara Teijeira-Portas, J. Aritz Urcola, Javier Ruiz-Martínez, Rocío Del Pino, Marian Acera, Axel Petzold, Siegfried Karl Wagner, Pearse Andrew Keane, Unai Ayala, Maitane Barrenechea, Beatriz Tijero, Juan Carlos Gómez Esteban, Iñigo Gabilondo (2024) Association of retinal neurodegeneration with the progression of cognitive decline in Parkinson’s disease NPJ Parkinson’s disease doi: 10.1038/s41531-024-00637-x
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La neurodegeneración de la retina precede al deterioro cognitivo del párkinson se ha escrito en Cuaderno de Cultura Científica.
Megalodón, el tiburón extinto que alimenta nuestra imaginación
 Póster original de la película Jaws, conocida en España como Tiburón. Imagen propiedad de la Academy Film Archive (Archivo de la Academia de Cine de los Estados Unidos de América) Fuente: www.oscars.org
Póster original de la película Jaws, conocida en España como Tiburón. Imagen propiedad de la Academy Film Archive (Archivo de la Academia de Cine de los Estados Unidos de América) Fuente: www.oscars.orgEn 1975 se estrenó la película Jaws, traducida al español como Tiburón, dirigida por Steven Spielberg. Para mí, una obra maestra de terror que llegó a crear un subgénero particular, el del cine de “bichos comiéndose a la gente”, por llamarlo de alguna forma. Este éxito inicial dio lugar a varias secuelas de la película original, así como a una especie de fiebre por crear películas en las que un gran escualo, o varios, aparecían como protagonistas. Algunas de tinte serio, pero la gran mayoría rozando la parodia, apareciendo tiburones mecanizados, tiburones fantasmas, tiburones moviéndose por la arena o, incluso, tiburones cayendo del cielo desde tornados o huracanes.
Esta evolución del subgénero pronto culminó con la necesidad de que el animal protagonista fuera cada vez más grande, creando monstruos capaces de comerse un buque de guerra o atacar un avión en pleno vuelo, colocando el prefijo “mega” antes de la palabra tiburón en los títulos de las películas, para remarcar que nos encontraríamos ante animales gigantescos. Pero el mundo de Hollywood tardó un poco en darse cuenta de que la realidad siempre supera la ficción y, en la historia geológica de nuestro planeta, ya habían existido enormes tiburones cuyo nombre científico ya incluía el prefijo “mega”. Me refiero al animal protagonista de dos películas relativamente recientes, y también de una canción del grupo musical El Reno Renardo (cuya letra no es apta para menores de edad), el megalodón.
 Póster promocional de la película Meg, conocida en España como Megalodón, inspirado en el póster original de la película Jaws. Imagen propiedad de Warner Bros PicturesEl megalodón era de sangre caliente
Póster promocional de la película Meg, conocida en España como Megalodón, inspirado en el póster original de la película Jaws. Imagen propiedad de Warner Bros PicturesEl megalodón era de sangre caliente
Otodus megalodon, que es el nombre científico de la especie, fue un tiburón prehistórico que apareció en el Mioceno, hace unos 20 millones de años, y se extinguió durante el Plioceno, hace unos 3,6 millones de años. Se estima que llegó a medir más de 18 m de largo y a pesar más de 50 toneladas, teniendo un cuerpo estilizado que le permitía nadar a gran velocidad, convirtiéndole en uno de los principales depredadores marinos de esa época. Con varias hileras de enormes dientes afilados y aserrados, posiblemente acechaba a sus presas en el fondo marino, atacándolas rápidamente atravesando la columna de agua de manera casi vertical, llegando a sobresalir varios metros sobre la superficie marina si fuese necesario. Su comida favorita eran los cetáceos de tamaño medio o grande, a los que acechaba en zonas próximas a la costa. Además, se acercaban a estas zonas litorales para reproducirse y dejar a sus crías en bahías cerradas, donde encontrarían abundante comida basada en reptiles y mamíferos marinos de menor tamaño mientras permanecían protegidas de los depredadores hasta que se hiciesen adultas.
Por otro lado, estudios recientes han demostrado que se trataba de un pez de sangre caliente, es decir, que era capaz de regular su temperatura interior elevándola por encima de la del agua circundante. Esto le permitía desplazarse por todos los océanos del planeta, llegando a acercarse a zonas polares, aunque no habitaba aguas frías, por debajo de 10-5ºC de temperatura. Y esta capacidad de regular su temperatura interna también parece ser la explicación a que alcanzase estos tamaños tan enormes. Finalmente, pasando a las causas de su extinción, se sugieren cambios en el clima y en la circulación oceánica durante el Plioceno, pero recientemente se alude a la competencia con el gran tiburón blanco, que acabaría imponiéndose como el mayor depredador marino desde entonces.
 A) Comparación del tamaño de un ejemplar de Otodus megalodon (clasificado con el antiguo nombre Carcharocles megalodon) con el tamaño de un ser humano y de un ejemplar actual de tiburón blanco (Carcharodon carcharias). B) Reconstrucción de Otodus megalodon a tamaño natural (18 m de longitud). La imagen A es obra de Mary Parrish, ambas son propiedad de la Smithsonian Institution
A) Comparación del tamaño de un ejemplar de Otodus megalodon (clasificado con el antiguo nombre Carcharocles megalodon) con el tamaño de un ser humano y de un ejemplar actual de tiburón blanco (Carcharodon carcharias). B) Reconstrucción de Otodus megalodon a tamaño natural (18 m de longitud). La imagen A es obra de Mary Parrish, ambas son propiedad de la Smithsonian InstitutionComo habéis comprobado, la descripción sobre la biología y ecología del megalodón la he redactado empleando mayoritariamente el condicional. Esto es debido a que los únicos restos fósiles que, de momento, tenemos de esta especie son dientes y vértebras, no se ha encontrado un esqueleto completo. O son evidencias indirectas, como las marcas de sus mordeduras preservadas en los fósiles de sus presas. Por este motivo, los cálculos sobre su tamaño, su forma o su hábitat son estimaciones, muchas veces realizadas a partir de la comparación con otros tiburones recientes que se consideran sus parientes más cercanos. Y, aunque esto es muy habitual en Geología y convierte a la investigación en esta ciencia en algo apasionante y divertido, con constantes cambios en la información que tenemos sobre las especies extintas, muchas veces se convierte en un arma de doble filo dando pie a bulos e ideas fantásticas entre la población. Sobre todo, si existen películas con más ficción que ciencia que puedan ser tomadas como base para la especulación.
 Diente fósil de Otodus megalodon del Mioceno, encontrado en el desierto de Atacama, Chile. Imagen: Lonfat / Wikimedia CommonsExtinto, el megalodón está extinto
Diente fósil de Otodus megalodon del Mioceno, encontrado en el desierto de Atacama, Chile. Imagen: Lonfat / Wikimedia CommonsExtinto, el megalodón está extinto
Así, mucha gente cree que este enorme tiburón puede seguir vivo en los fondos oceánicos, a miles de metros de profundidad, aludiendo a que aún no conocemos todos los organismos que habitan es estas zonas abisales. Y, aunque esta última aseveración es cierta, en el caso del gran escualo es algo totalmente imposible. Como hemos visto, el megalodón no podría soportar la presión de la columna de agua, no habitaba en aguas tan frías como las que encontramos en zonas tan profundas y, además, tendría que acercarse al litoral para reproducirse y alimentarse, además de que no hay restos de su existencia en el registro fósil más moderno de hace unos 3,6 millones de años. ¿De verdad creéis que, si un tiburón de más de 18 m de largo y 50 toneladas de peso llegara a áreas costeras para devorar enormes ballenas u orcas por todo el mundo, no lo habíamos detectado ya? Vivimos en la era digital, con multitud de satélites, boyas oceánicas, barcos navegando continuamente por el mar y todo el mundo con un teléfono móvil en el bolsillo. Si un tiburón de este tamaño estuviera por ahí fuera, tendríamos miles de evidencias circulando por las redes sociales.
En estos casos, hay que tener espíritu crítico y sentido común. Las películas, junto con la novela en la que se basan, son mera ficción que buscan nuestro divertimento, en ningún momento pueden ser tomadas como un documento científico. Al igual que no nos creemos la existencia de un gigantesco tiburón mecanizado capaz de comerse un avión durante su vuelo, tampoco podemos creernos la existencia de un tiburón extinto oculto durante millones de años en las aguas abisales que, de repente, decide comportarse como lo hizo mientras vivió y acercarse a una zona costera a devorar bañistas como si no hubiese un mañana. Por mucho que nos gustase ver, mejor de lejos que de cerca, a estas enormes criaturas extintas, debemos recordar que están, pues eso, extintas.
Agradecimientos:
Quiero dar las gracias a mi colega Jone Mendicoa por aportarme la idea para escribir este artículo y a la iniciativa “Cazabulos”, del Consejo Superior de Investigaciones Científicas (CSIC), por darme la oportunidad de crear un pequeño vídeo sobre este tema.
Referencias:
Cooper, J.A., Hutchinson, J.R., Bernvi, D.C., Cliff, G., Wilson, R.P., Dicken, M.L., Menzel, J., Wroe, S., Pirlo, J., Pimiento, C. (2022) The extinct shark Otodus megalodon was a transoceanic superpredator: Inferences from 3D modeling. Science Advances doi: 10.1126/sciadv.abm9424
Ferrón, H. (2019) Megalodón, un tiburón extinto de sangre caliente. ¡Fundamental! 32, 1-46.
Sternes, P.C., Jambura, P.L., Türtscher, J., Kriwet, J., Siversson, M., Feichtinger, I., Naylor, G.J.P., Summers, A.P., Maisey, J.G., Tomita, T., Moyer, J.K., Higham, T.E., da Silva, J.P.C.B., Bornatowski, H., Long, D.J., Perez, V.J., Collareta, A., Underwood, C., Ward, D.J., Vullo, R., González-Barba, G., Maisch, H.M. IV, Griffiths, M.L., Becker, M.A., Wood, J.J., Shimada, K. (2024) White shark comparison reveals a slender body for the extinct megatooth shark, Otodus megalodon (Lamniformes: Otodontidae) Palaeontologia Electronica doi: 10.26879/1345
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Megalodón, el tiburón extinto que alimenta nuestra imaginación se ha escrito en Cuaderno de Cultura Científica.
Paul Bunyan frente la cinta transportadora
El título de este artículo corresponde al cuento corto Paul Bunyan versus the conveyor belt del escritor norteamericano William Hazlett Upson (1891-1975). Vamos a reproducirlo al completo, analizando las propiedades de las sucesivas transformaciones de la cinta transportadora a la que se refiere el título.
 Una cinta transportadora minera. Foto: Peter Herrmann / Unsplash
Una cinta transportadora minera. Foto: Peter Herrmann / UnsplashEsta cinta transportadora es una banda de Möbius
Uno de los éxitos más brillantes de Paul Bunyan no se debió a un pensamiento brillante, sino a su cautela y cuidado. Fue el famoso asunto de la cinta transportadora.
Paul y su mecánico, Ford Fordsen, habían empezado a trabajar en una mina de uranio en Colorado. El mineral se extraía a través de una cinta sin fin que recorría media milla entrando en la mina y otra media milla saliendo, lo que daba una longitud total de una milla. Tenía cuatro pies de ancho. Se movía sobre una serie de rodillos y era impulsada por una polea montada en la transmisión del gran camión azul de Paul, «Babe». Los fabricantes de la correa la habían hecho de una sola pieza, sin empalmes ni cordones, y habían puesto una media vuelta en la parte de retorno para que el desgaste fuera el mismo en ambos lados.
Por la descripción de esta cinta transportadora, vemos que se trata de una cinta de Möbius. Esta denominación de “cinta sin fin” es la que el artista suizo Max Bill (1908-1994) utilizó para nombrar sus magníficas esculturas en forma de banda de Möbius: “Unendliche Schleife”.
Aunque se alude a que “el desgaste fuera el mismo en ambos lados”, recordemos que una banda de Möbius solo posee una cara. La ventaja de la cinta transportadora del cuento es que duraría más (el doble) que una cilíndrica de la misma longitud y anchura. En efecto, el lado interior de una cinta cilíndrica no se usaría, y por lo tanto no se desgastaría.
Tras varios meses de funcionamiento, la galería de la mina era el doble de larga, pero la cantidad de material que salía era menor. Paul decidió que necesitaba una cinta el doble de larga y la mitad de ancha. Le dijo a Ford Fordsen que cogiera su motosierra y cortara la cinta en dos a lo largo.
“Así tendremos dos correas”, dijo Ford Fordsen. “Tendremos que cortarlas en dos transversalmente y unirlas. Eso significa que tendré que ir a la ciudad a comprar los materiales para dos empalmes”.
“No”, dijo Paul. Esta cinta tiene una media torsión, lo que en geometría se conoce como banda de Möbius«.
“¿Qué más da?», preguntó Ford Fordsen.
“Una banda de Möbius, dijo Paul Bunyan, sólo tiene un lado y un borde, y si la cortamos en dos longitudinalmente, seguirá siendo de una sola pieza. Tendremos una cinta el doble de larga y la mitad de ancha”.
“¿Cómo se puede cortar algo en dos y que siga siendo de una pieza?», preguntó Ford Fordsen.
Paul era modesto. Nunca fue obstinado. “Vamos a probarlo», dijo.
Entraron en el despacho de Paul. Paul cogió una tira de papel engomado de unas dos pulgadas de ancho y una yarda de largo. La colocó sobre el escritorio con el lado engomado hacia arriba. Levantó los dos extremos y los juntó delante de él con los lados engomados hacia abajo. Luego dio la vuelta a uno de los extremos, lo lamió, lo deslizó bajo el otro extremo y pegó los dos lados engomados. Se había hecho una cinta de papel sin fin con una media vuelta, igual que la cinta grande del transportador.
“Esto», dijo Paul, «es una banda de Möbius. Funcionará tal y como he dicho, eso espero».
Paul cogió unas tijeras, clavó la punta en el centro del papel y cortó la tira en dos a lo largo. Cuando terminó, tenía una tira el doble de larga, la mitad de ancha y con una doble torsión.
 Cortando una cinta de Möbius por la mitad.
Cortando una cinta de Möbius por la mitad.
En efecto, cuando se corta una cinta de Möbius longitudinalmente por la mitad, se obtiene una nueva cinta, pero no es de Möbius sino cilíndrica; basta con comprobar que posee dos caras. Como indica Upson, posee una doble torsión que corresponde a la suma de las dos “medias vueltas” de la mitad superior y la mitad inferior de la cinta original.
De este modo, Paul consigue una cinta el doble de larga para llegar al material más alejado de la mina. Pero posee dos caras, así que uno de los lados quedará inutilizado… No es la solución óptima.
Dos apuestas ruinosasFord Fordsen quedó convencido. Salió y empezó a cortar la cinta grande en dos. Y, en ese momento, llegó un hombre llamado Loud Mouth Johnson para ver cómo iba la empresa de Paul, y para ofrecer cualquier crítica destructiva que se le ocurriera. Loud Mouth Johnson, que era el fanfarrón público número uno, encontró muchos motivos de queja.
“Si cortas esa cinta en dos a lo largo, tendrás dos cintas, cada una de la misma longitud que la cinta original, pero sólo la mitad de ancha».
“No», dijo Ford Fordsen, «ésta es una cinta muy especial conocida como banda de Möbius. Si la corto en dos longitudinalmente, obtendré una cinta el doble de larga y la mitad de ancha».
“¿Quieres apostar?», dijo Loud Mouth Johnson. “Claro», dijo Ford Fordsen.
Apostaron mil dólares. Y, por supuesto, ganó Ford Fordsen. Loud Mouth Johnson quedó tan asombrado que se escabulló y permaneció alejado durante seis meses.
Al cabo de algún tiempo, la mina se hizo más profunda y no quedó más remedio que volver a cortar la cinta transportadora…
Cuando finalmente regresó, encontró a Paul Bunyan empezando a cortar el cinturón en dos a lo largo por segunda vez.
“¿Cuál es la idea?», preguntó Loud Mouth Johnson.
Paul Bunyan respondió: «El túnel ha avanzado mucho más y el material que sale no es tan voluminoso como antes. Así que estoy alargando de nuevo la cinta y haciéndola más estrecha”.
¿Dónde está Ford Fordsen?
Paul Bunyan dijo: «Le he enviado a la ciudad a por materiales para empalmar la cinta. Cuando termine de cortarla en dos a lo largo, tendré dos cinturones de la misma longitud, pero sólo la mitad de ancho que éste. Así que tendré que hacer algunos empalmes».
Loud Mouth Johnson apenas podía creer lo que oía. Aquí tenía la oportunidad de recuperar sus mil dólares y dejar en evidencia a Paul Bunyan como un bobo más. Escucha, dijo Loud Mouth Johnson, cuando acabes sólo te quedará una cinta el doble de larga y la mitad de ancha».
¿Quieres apostar?
Claro.
Así que apostaron mil dólares y, por supuesto, Loud Mouth Johnson volvió a perder. No es que Paul Bunyan fuera brillante. Es que era metódico. Lo había probado con aquella tira de papel engomado, y sabía que la segunda vez que cortas una banda de Möbius obtienes dos piezas, unidas entre sí como una cadena de reloj antigua.
Recordemos que, tras el primer corte, la cinta era cilíndrica, y al dividir un cilindro en dos longitudinalmente, se obtienen dos cilindros. En este caso, esos cilindros están enlazados porque la cinta posee (en este momento) dos semigiros. Para comprobarlo, lo mejor es repetir el experimento de Paul y contar cuantas caras tiene cada una de estas piezas.
En realidad, Paul no ha usado la mejor estrategia posible. En ambas ocasiones debería haber cortado la cinta transversalmente para obtener un rectángulo, después debería haber cortado este rectángulo longitudinalmente por la mitad y, finalmente, debería haber soldado los dos lados más cortos tras aplicar en uno de ellos una semivuelta. Así, habrían conseguido una cinta el doble de larga y que seguiría siendo de Möbius. Es decir, su única cara serviría para transportar el material de la mina, y duraría más…
Nota finalLas cintas transportadoras de Möbius se utilizan realmente. En 1957, James O. Trinkle, obtuvo la patente estadounidense 2,784,834 por una transportadora para material caliente. Trinkle trabajaba en la empresa BF Goodrich e inventó esta cinta de Möbius para transportar cenizas o arena de fundición… y se construyó.
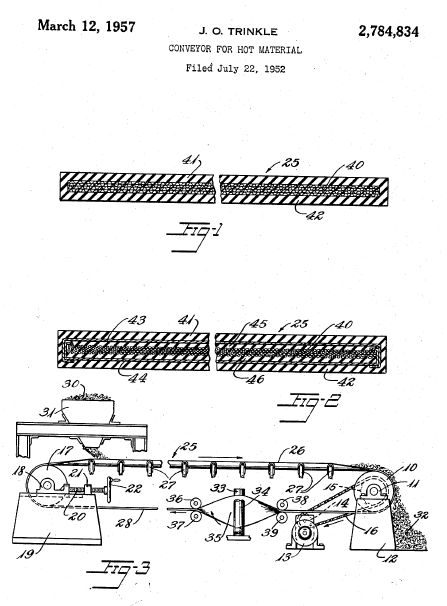 Patente de “Conveyor for hot material”.
Patente de “Conveyor for hot material”.
Referencias
- Paul Bunyan versus the Conveyor Belt, The Open University
- Hazlett W. Upson, Paul Bunyan versus the conveyor belt, John Murray Publishers, 1960
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Paul Bunyan frente la cinta transportadora se ha escrito en Cuaderno de Cultura Científica.
Los insectos y otros animales tienen consciencia
Un grupo de destacados biólogos y filósofos ha anunciado anunció un nuevo consenso: existe “una posibilidad realista” de que insectos, pulpos, crustáceos, peces y otros animales pasados por alto experimenten consciencia.
Un artículo de Dan Falk. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 ¿Qué pasa por la mente de una abeja? Existe «una posibilidad realista» de consciencia, según una nueva declaración. Foto: Dmitry Grigoriev / Unsplash
¿Qué pasa por la mente de una abeja? Existe «una posibilidad realista» de consciencia, según una nueva declaración. Foto: Dmitry Grigoriev / UnsplashEn 2022, investigadores del Laboratorio de Ecología Sensorial y del Comportamiento de las Abejas de la Universidad Queen Mary de Londres observaron que los abejorros hacían algo notable: las diminutas y peludas criaturas participaban en una actividad que solo podía describirse como juego. Cuando les daban pequeñas bolas de madera las abejas las empujaban de un lado a otro y las hacían girar. El comportamiento no tenía una conexión obvia con el apareamiento o la supervivencia, ni era recompensado por los científicos. Al parecer, era sólo por diversión.
El estudio sobre las abejas juguetonas es parte de un conjunto de investigaciones que un grupo de destacados estudiosos de las mentes animales ha citado, apuntalando una nueva declaración que extiende el apoyo científico a la existencia de la consciencia a un conjunto más amplio de animales del que se había reconocido formalmente antes. Durante décadas, ha habido un amplio acuerdo entre los científicos en que los animales similares a nosotros (los grandes simios, por ejemplo) tienen experiencia consciente, incluso si su consciencia difiere de la nuestra. Sin embargo, en los últimos años, los investigadores han comenzado a reconocer que la consciencia también puede estar muy extendida entre animales que son muy diferentes a nosotros, incluidos los invertebrados con sistemas nerviosos completamente diferentes y mucho más simples.
La nueva declaración, firmada por biólogos y filósofos, adopta formalmente ese punto de vista. Dice, en parte: «La evidencia empírica indica al menos una posibilidad realista de experiencia consciente en todos los vertebrados (incluidos todos los reptiles, anfibios y peces) y muchos invertebrados (incluidos, como mínimo, moluscos cefalópodos, crustáceos decápodos e insectos)». Inspirado en hallazgos de investigaciones recientes que describen comportamientos cognitivos complejos en estos y otros animales, el documento representa un nuevo consenso y sugiere que los investigadores pueden haber sobreestimado el grado de complejidad neuronal necesaria para la consciencia.
La Declaración de Nueva York sobre la Conciencia Animal de cuatro párrafos se dio a conocer el 19 de abril en una conferencia de un día llamada “La ciencia emergente de la conciencia animal” que se ha celebrado en la Universidad de Nueva York. Encabezada por la filósofa y científica cognitiva Kristin Andrews de la Universidad de York en Ontario, el filósofo y científico medioambiental Jeff Sebo de la Universidad de Nueva York y el filósofo Jonathan Birch de la Escuela de Economía y Ciencias Políticas de Londres, la declaración ha sido firmada hasta ahora por 39 investigadores, entre ellos los psicólogos Nicola Clayton e Irene Pepperberg, los neurocientíficos Anil Seth y Christof Koch, el zoólogo Lars Chittka y los filósofos David Chalmers y Peter Godfrey-Smith.
La declaración se centra en el tipo más básico de consciencia, conocida como consciencia fenoménica. En términos generales, si una criatura tiene una conciencia fenoménica, entonces ser esa criatura es “como algo”, una idea enunciada por el filósofo Thomas Nagel en su influyente ensayo de 1974, “¿Cómo es ser un murciélago?” Incluso si una criatura es muy diferente de nosotros, escribió Nagel, “fundamentalmente un organismo tiene estados mentales conscientes si y solo si hay algo que se asemeja a ser ese organismo. … Podemos llamar a esto el carácter subjetivo de la experiencia”. Si una criatura es fenoménicamente consciente tiene la capacidad de experimentar sentimientos como dolor, placer o hambre, pero no necesariamente estados mentales más complejos como la autoconsciencia.
«Espero que la declaración [consiga que se preste] mayor atención a las cuestiones de la consciencia no humana y a los desafíos éticos que acompañan a la posibilidad de experiencias conscientes mucho más allá de lo humano», escribe Seth, neurocientífico de la Universidad de Sussex, en un correo electrónico. «Espero que genere debate, informe las políticas y prácticas en materia de bienestar animal y genere una comprensión y apreciación de que tenemos mucho más en común con otros animales que con cosas como ChatGPT».
Una consciencia crecienteLa declaración comenzó a tomar forma el otoño pasado, como consecuencia de conversaciones entre Sebo, Andrews y Birch. «Los tres estábamos hablando de todo lo que ha sucedido en los últimos 10 años, en los últimos 15 años, en la ciencia de la consciencia animal», recuerda Sebo. Ahora sabemos, por ejemplo, que los pulpos sienten dolor y las sepias recuerdan detalles de acontecimientos pasados específicos. Estudios en peces han encontrado que los lábridos limpiadores parecen pasar una versión de la “prueba del espejo”, que indica un grado de autorreconocimiento, y que el pez cebra muestra signos de curiosidad. En el mundo de los insectos, las abejas muestran un aparente comportamiento de juego, mientras que las moscas de la fruta Drosophila tienen distintos patrones de sueño influenciados por su entorno social. Mientras tanto, los cangrejos de río muestran estados similares a los de la ansiedad, y esos estados pueden alterarse con medicamentos ansiolíticos.
 Después de reflexionar sobre investigaciones recientes sobre diversas mentes animales, Jeff Sebo, Kristin Andrews y Jonathan Birch (de izquierda a derecha) decidieron organizar a científicos y filósofos para firmar una declaración que extienda la consciencia a más animales. Fotos, de izquierda a derecha: Kate Reeder; Ben Wulf; María Moore/LSE
Después de reflexionar sobre investigaciones recientes sobre diversas mentes animales, Jeff Sebo, Kristin Andrews y Jonathan Birch (de izquierda a derecha) decidieron organizar a científicos y filósofos para firmar una declaración que extienda la consciencia a más animales. Fotos, de izquierda a derecha: Kate Reeder; Ben Wulf; María Moore/LSEEstos y otros signos de estados conscientes en animales que durante mucho tiempo habían sido considerados menos que conscientes entusiasmaron y desafiaron a biólogos, científicos cognitivos y filósofos de la mente. «Mucha gente acepta desde hace tiempo que, por ejemplo, los mamíferos y las aves son conscientes o es muy probable que lo sean, pero se ha prestado menos atención a otros taxones de vertebrados y especialmente de invertebrados», explica Sebo. En conversaciones y reuniones, los expertos coincidían en gran medida en que estos animales deben tener consciencia. Sin embargo, este consenso recién formado no se comunicaba al público en general, incluidos otros científicos y formuladores de políticas. Así que los tres investigadores decidieron redactar una declaración clara y concisa y hacerla circular entre sus colegas para que la aprobaran. La declaración no pretende ser exhaustiva sino más bien “señalar dónde creemos que está el campo ahora y hacia dónde se dirige”, afirma Sebo.
La nueva declaración actualiza el esfuerzo más reciente para establecer un consenso científico sobre la consciencia animal. En 2012, los investigadores publicaron la Declaración de Cambridge sobre la Consciencia, que decía que una variedad de animales no humanos, incluidos, entre otros, mamíferos y aves, tienen «la capacidad de exhibir comportamientos intencionales» y que «los humanos no son los únicos en poseer los sustratos neurológicos que generan consciencia”.
La nueva declaración amplía el alcance de su predecesora y también está redactada de forma más cuidadosa, escribe Seth. «No intenta hacer ciencia por dictado, sino que enfatiza lo que debemos tomar en serio con respecto a la consciencia animal y la ética relevante dada la evidencia y las teorías que tenemos». Escribe que “no está a favor de avalanchas de cartas abiertas y cosas por el estilo”, pero que finalmente “llegó a la conclusión de que esta declaración merecía mucho ser apoyada”.
Godfrey-Smith, filósofo de la ciencia de la Universidad de Sydney que ha trabajado extensamente con pulpos, cree que los comportamientos complejos que exhiben estas criaturas (incluida la resolución de problemas, el uso de herramientas y el comportamiento de juego) solo pueden interpretarse como indicadores de consciencia. «Tienen esta conexión atenta con las cosas, con nosotros y con objetos novedosos que hace que sea muy difícil no pensar que están sucediendo muchas cosas dentro de ellos», dice. Señala que artículos recientes que analizan el dolor y los estados oníricos en pulpos y sepias «apuntan en la misma dirección… hacia que la experiencia sea una parte real de sus vidas».
Si bien muchos de los animales mencionados en la declaración tienen encéfalos y sistemas nerviosos muy diferentes a los de los humanos, los investigadores dicen que esto no tiene por qué ser una barrera para la consciencia. Por ejemplo, el cerebro de una abeja contiene solo alrededor de un millón de neuronas, en comparación con unos 86 mil millones en el caso de los humanos. Pero cada una de esas neuronas de abeja puede ser tan compleja estructuralmente como un roble. La red de conexiones que forman también es increíblemente densa, y cada neurona contacta quizás con otras 10.000 o 100.000. El sistema nervioso de un pulpo, por el contrario, es complejo en otros aspectos. Su organización está muy distribuida más que centralizada; un brazo cortado puede exhibir muchos de los comportamientos del animal intacto.
 Investigaciones recientes sobre las mentes de los animales (incluidas las de cangrejos de río, pulpos, serpientes y peces) sugieren que la conciencia “puede existir en una arquitectura [neural] que parece completamente ajena” a la nuestra, afirma Peter Godfrey-Smith. Fotos, en el sentido de las agujas del reloj desde arriba a la izquierda: Svetlana123/iStock; Colin Marshal/Biosphoto/Science Source; MATTHIASRABBIONE/iStock; Jim Maley/iStockEl resultado, dice Andrews, es que «quizás no necesitemos tanto equipo como pensábamos» para alcanzar la consciencia. Señala, por ejemplo, que incluso una corteza cerebral (la capa externa del cerebro de los mamíferos, que se cree que desempeña un papel en la atención, la percepción, la memoria y otros aspectos clave de la consciencia) puede no ser necesaria para la consciencia fenoménica más simple a la que se refiere la declaración.
Investigaciones recientes sobre las mentes de los animales (incluidas las de cangrejos de río, pulpos, serpientes y peces) sugieren que la conciencia “puede existir en una arquitectura [neural] que parece completamente ajena” a la nuestra, afirma Peter Godfrey-Smith. Fotos, en el sentido de las agujas del reloj desde arriba a la izquierda: Svetlana123/iStock; Colin Marshal/Biosphoto/Science Source; MATTHIASRABBIONE/iStock; Jim Maley/iStockEl resultado, dice Andrews, es que «quizás no necesitemos tanto equipo como pensábamos» para alcanzar la consciencia. Señala, por ejemplo, que incluso una corteza cerebral (la capa externa del cerebro de los mamíferos, que se cree que desempeña un papel en la atención, la percepción, la memoria y otros aspectos clave de la consciencia) puede no ser necesaria para la consciencia fenoménica más simple a la que se refiere la declaración.
«Hubo un gran debate sobre si los peces son conscientes, y buena parte de él tuvo que ver con que carecían de las estructuras encefálicas que vemos en los mamíferos», explica. “Pero cuando nos fijamos en las aves, los reptiles y los anfibios, vemos que tienen estructuras encefálicas muy diferentes y diferentes presiones evolutivas y, sin embargo, estamos descubriendo que algunas de esas estructuras encefálicas realizan el mismo tipo de trabajo que realiza la corteza cerebral en los humanos.”
Godfrey-Smith está de acuerdo y señala que comportamientos indicativos de consciencia «pueden existir en una arquitectura que parece completamente ajena a la arquitectura de los vertebrados o humana».
Relaciones conscientesSi bien la declaración tiene implicaciones para el tratamiento de los animales, y especialmente para la prevención del sufrimiento animal, Sebo señala que la atención debe ir más allá del dolor. No es suficiente que las personas eviten que los animales en cautiverio experimenten dolor e incomodidad corporal, afrima. «También tenemos que brindarles el tipo de enriquecimiento y oportunidades que les permitan expresar sus instintos y explorar sus entornos y participar en sistemas sociales y, por lo demás, ser el tipo de agentes complejos que son».
Pero las consecuencias de otorgar la etiqueta de “conscientes” a una gama más amplia de animales –particularmente animales cuyos intereses no estamos acostumbrados a considerar– no son sencillas. Por ejemplo, nuestra relación con los insectos puede ser «inevitablemente algo antagónica», dice Godfrey-Smith. Algunas plagas comen cultivos y los mosquitos pueden transmitir enfermedades. «La idea de que podríamos hacer las paces con los mosquitos es una idea muy diferente a la idea de que podríamos hacer las paces con los peces y los pulpos», afirma.
Del mismo modo, se presta poca atención al bienestar de insectos como Drosophila, que se utilizan ampliamente en la investigación biológica. «En la investigación pensamos en el bienestar del ganado y de los ratones, pero nunca pensamos en el bienestar de los insectos», dice Matilda Gibbons, que investiga las bases neuronales de la consciencia en la Universidad de Pensilvania y es firmante de la declaración.
Si bien los organismos científicos han creado algunos estándares para el tratamiento de ratones de laboratorio, no está claro si la nueva declaración conducirá a nuevos estándares para el tratamiento de los insectos. Pero los nuevos hallazgos científicos a veces desencadenan nuevas políticas. El Reino Unido, por ejemplo, ha promulgado una ley para aumentar la protección de los pulpos, cangrejos y langostas después de que un informe de la London School of Economics indicara que esos animales pueden experimentar dolor, angustia o daño.
Si bien la declaración no menciona la inteligencia artificial, la cuestión de la posible consciencia de la IA ha estado en la mente de los investigadores de la consciencia animal. «Es muy poco probable que los sistemas de inteligencia artificial actuales sean conscientes», afirma Sebo. Sin embargo, lo que ha aprendido sobre las mentes animales «me hace reflexionar y me hace querer abordar el tema con precaución y humildad».
Andrews espera que la declaración impulse más investigaciones sobre animales que a menudo se han pasado por alto, una medida que tiene el potencial de ampliar aún más nuestra concienciación sobre el alcance de la consciencia en el mundo animal. «Todos estos gusanos nematodos y moscas de la fruta que se encuentran en casi todas las universidades, estudiad la consciencia en ellos», exhorta. “Ya los tienes. Alguien en tu laboratorio necesitará un proyecto. Haz de ese proyecto un proyecto sobre la consciencia. ¡Imagina eso!»
El artículo original, Insects and Other Animals Have Consciousness, Experts Declare, se publicó el 19 de abril de 2024 en Quanta Magazine.
Traducido por César Tomé López
El artículo Los insectos y otros animales tienen consciencia se ha escrito en Cuaderno de Cultura Científica.
El origen de la cresta neural
Es posible que muchas personas no hayan oído hablar de la cresta neural. Si es así, no pueden imaginarse lo mucho que le deben. Una parte sustancial de nuestro cuerpo se forma a partir de la cresta neural, como ahora veremos. Sucede lo mismo en todos los animales vertebrados, y lo curioso de esta cuestión es que no se conocía nada remotamente parecido en nuestros antepasados invertebrados. Por eso, el origen de la importantísima cresta neural era un enigma. Hasta ahora.
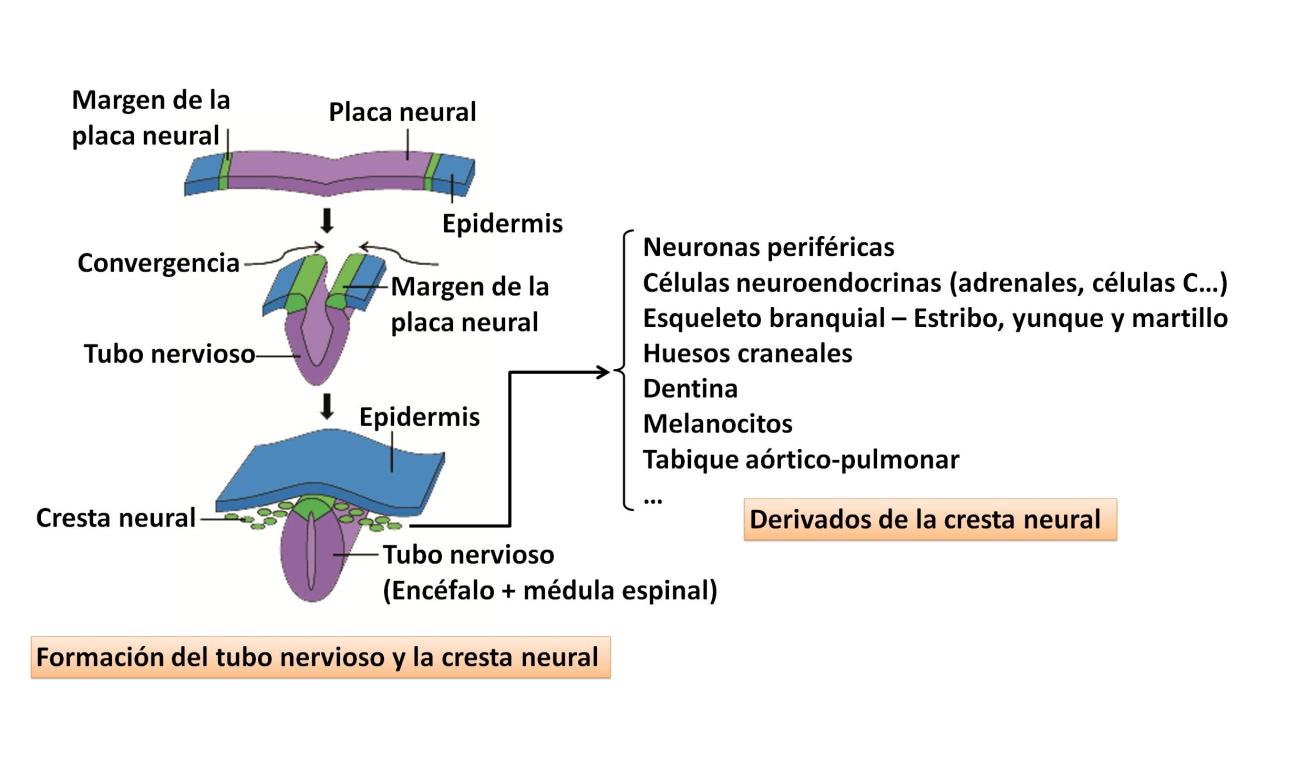 Figura 1. Formación del tubo nervioso embrionario que da lugar al sistema nervioso central de los vertebrados (encéfalo y médula espinal). Los márgenes de la placa neural dan lugar a la cresta neural, un conjunto de células móviles con múltiples destinos. Ilustración: NikNaks / Wikimedia Commons.
Figura 1. Formación del tubo nervioso embrionario que da lugar al sistema nervioso central de los vertebrados (encéfalo y médula espinal). Los márgenes de la placa neural dan lugar a la cresta neural, un conjunto de células móviles con múltiples destinos. Ilustración: NikNaks / Wikimedia Commons.Empecemos por el principio. La cresta neural está formada por células que intervienen en el desarrollo embrionario de todos los vertebrados (Figura 1). Se forman en los márgenes de la placa neural, el conjunto de células superficiales que se va a hundir en el embrión y va a dar lugar a nuestro sistema nervioso central (encéfalo y médula espinal). La cresta neural migra por todo el cuerpo y da lugar a muchos y muy variados derivados. Por ejemplo, todas las neuronas exteriores a dicho sistema nervioso central (sistemas nerviosos simpático y parasimpático) incluyendo las células de Schwann que las protegen. También tejidos endocrinos, como la médula adrenal o las células C de la tiroides. Más sorprendente es su contribución a buena parte de los huesos craneales, la dentina, los huesecillos del oído medio, el músculo liso de grandes arterias o el tabique cardiaco que separa la salida aórtica de la pulmonar. Y por si fuera poco, los melanocitos que dan color a nuestra piel también proceden de la cresta neural.
La importancia de la cresta neural en nuestro desarrollo queda subrayada por la existencia de neurocristopatías. Este término fue creado hace medio siglo para designar a las patologías debidas a anomalías en el desarrollo de la cresta neural. A causa de los múltiples destinos de la cresta neural, sus alteraciones pueden afectar a muchos sistemas orgánicos. Hasta la fecha se han identificado 66 neurocristopatías, que van desde malformaciones craneofaciales o defectos cardíacos hasta alteraciones pigmentarias o tumores como el feocromocitoma. Por citar algunos ejemplos, la enfermedad de Hirschprung produce obstrucciones intestinales graves en 1 de cada 5000-10000 recién nacidos. La prevalencia del síndrome de DiGeorge es mayor (1 de cada 4000 bebés). En estos pacientes, la pérdida de un fragmento del cromosoma 22 produce alteraciones en la migración de la cresta neural, y da lugar a un espectro de patologías, incluyendo infecciones, hipocalcemia, defectos cardíacos y paladar hendido. Más infrecuente es el piebaldismo, extensas alteraciones pigmentarias por defectos en la migración de los melanocitos, derivados como hemos dicho de la cresta neural.
Esta capacidad de originar componentes tan diversos de nuestro cuerpo ha fascinado desde siempre a los biólogos del desarrollo. Pero lo que planteaba más interrogantes era el propio origen evolutivo de la cresta neural. Los invertebrados más emparentados con nosotros, los anfioxos y urocordados (ascidias y salpas) forman un tubo nervioso como el nuestro, pero no desarrollan una cresta neural. En el embrión de las ascidias se habían identificado algunas células de la placa neural que migran para dar células sensoriales y pigmentarias. Pero estas células no dan lugar a derivados esqueléticos o musculares, como sí lo hace la cresta neural.
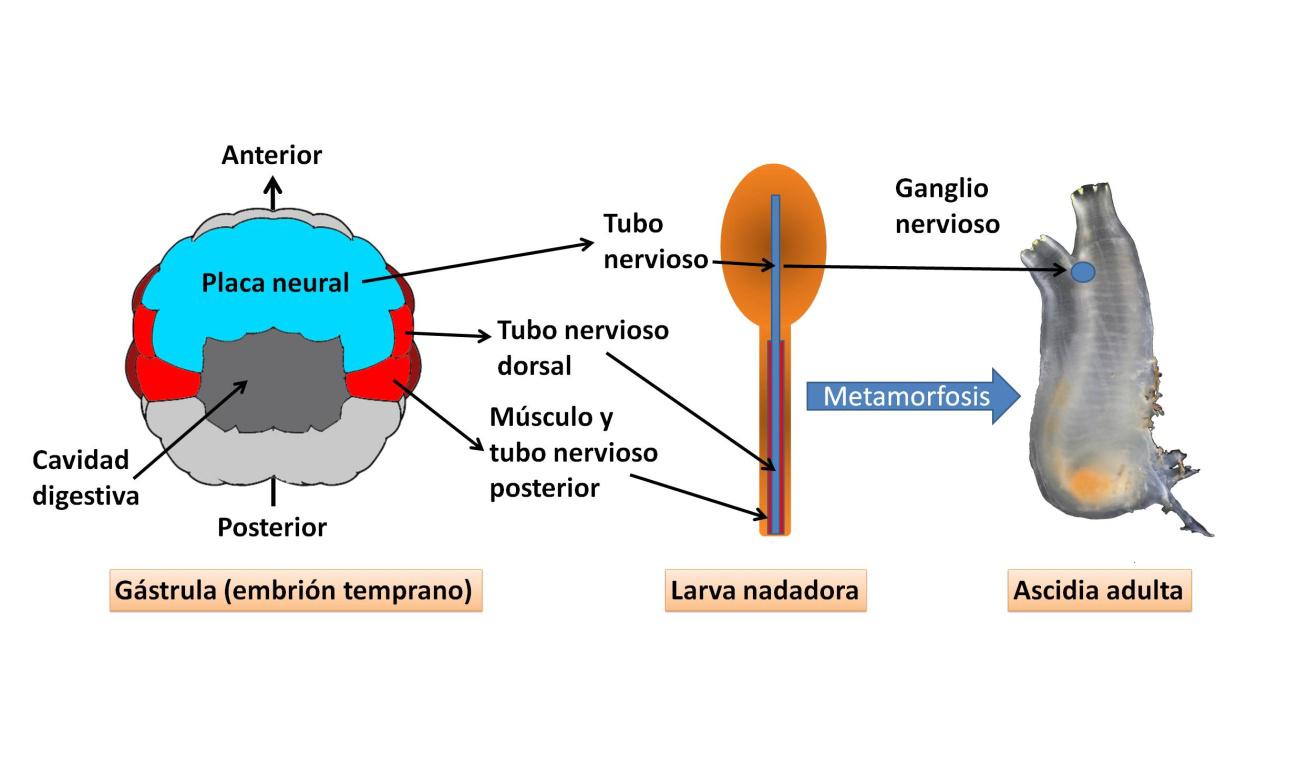 Figura 2. Se muestran en rojo las células de la gástrula de ascidia propuestas por los investigadores japoneses como precursoras de la cresta neural y los progenitores neuromesodérmicos de vertebrados. Estas células originan neuronas y músculo en la cola de la larva nadadora de la ascidia, una cola que se pierde tras la metamorfosis. Imagen de la ascidia realizada por Eric A. Lazo-Wasem, dominio público, CC0 1.0.
Figura 2. Se muestran en rojo las células de la gástrula de ascidia propuestas por los investigadores japoneses como precursoras de la cresta neural y los progenitores neuromesodérmicos de vertebrados. Estas células originan neuronas y músculo en la cola de la larva nadadora de la ascidia, una cola que se pierde tras la metamorfosis. Imagen de la ascidia realizada por Eric A. Lazo-Wasem, dominio público, CC0 1.0.Una investigación realizada por dos biólogos de la universidad de Kyoto sobre la ascidia Ciona intestinalis acaba de mostrar que dos pares de células de su gástrula tienen características que sugieren una relación con la cresta neural de vertebrados. Se localizan en los márgenes de la placa neural, cuando la gástrula cuenta con poco más de un centenar de células (Figura 2). La investigación también sugiere una relación de estas células con los precursores neuromesodérmicos, unos progenitores que contribuyen al tubo nervioso y el mesodermo posterior del embrión de vertebrados.
El linaje de estas cuatro células de las ascidias expresa genes típicos de la cresta neural de vertebrados. Dicho linaje origina tanto neuronas del tubo nervioso más posterior como células musculares de la cola de la larva. El sistema genético que controla la diferenciación hacia neuronas o músculo es el mismo que el que utilizan los precursores neuromesodérmicos de vertebrados. Como evidencia adicional, una comparación del transcriptoma (el conjunto de genes expresados) de las células candidatas de las ascidias con el transcriptoma de un vertebrado (el pez cebra) las relaciona claramente con los precursores neuromesodérmicos.
Los investigadores japoneses concluyen que estas pocas células del embrión de ascidia constituyen el origen evolutivo tanto de la cresta neural como de los precursores neuromesodérmicos del embrión de vertebrados. Lo que hicimos los vertebrados desde el principio fue explotar a fondo la plasticidad de estas células para conducirlas a desempeñar funciones muy variadas, incrementando la complejidad de nuestra organización corporal.
Referencia:
Ishida, T., Satou, Y. (2024) Ascidian embryonic cells with properties of neural-crest cells and neuromesodermal progenitors of vertebrates. Nat Ecol Evol doi: 10.1038/s41559-024-02387-8
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga
El artículo El origen de la cresta neural se ha escrito en Cuaderno de Cultura Científica.
Matando los dragones del dogma y la ignorancia
Se han publicado muchos libros de historia de la ciencia o, en términos más generales, del conocimiento. Cada libro aporta una visión y en conjunto ofrecen una panorámica bastante completa de la evolución de una parte sustancial del patrimonio intelectual de la humanidad. El libro que revisaré en estas líneas es, desde ese punto de vista, uno más. Un libro más para enriquecer la visión que tenemos del conocimiento de la naturaleza y de la forma en que se ha obtenido ese conocimiento.
Empecé a leerlo con esa idea en mente. Sin embargo, ya desde las primeras páginas reparé en que este era algo diferente. Para empezar, sus autores no se han propuesto hacer un repaso exhaustivo de los diferentes saberes. Han abordado un aspecto en particular del progreso científico y, en virtud de ese objetivo, concentrado su esfuerzo en ciertos temas o campos del saber, sin ánimo de ofrecer una visión general de las ciencias de la naturaleza.
El objeto del libro queda reflejado de forma metafórica en su subtítulo: Slaying the Dragons of Dogma and Ignorance («Matando los dragones del dogma y la ignorancia«, el libro aún no ha sido traducido al castellano). Al título principal me referiré más adelante. El subtítulo hace referencia a la leyenda que aparece en el Globo de Hunt-Lenox (1503-1507), HC SVNT DRACONES (hic sunt dracones, ‘aquí hay dragones’), siguiendo la tradición medieval de mencionar la presencia de criaturas míticas en la periferia del mundo conocido, como forma de expresar el desconocimiento acerca de esas zonas marginales y los peligros –reales o imaginados– que aguardaban a quienes osasen aventurarse por ellos.
 Source: World ScientificAquí hay dragones
Source: World ScientificAquí hay dragones
Los autores recurren a la metáfora de los dragones, seres imaginarios, para referirse a entidades cuya existencia se ha postulado a lo largo de la historia del conocimiento, para ofrecer una explicación satisfactoria del mundo real que, andando el tiempo, se han demostrado innecesarias, falsas o erróneas. A ello obedece la voluntad expresada en el subtítulo de “matar” esas criaturas. Siguiendo la metáfora, el avance de la ciencia habría ido eliminando esas entidades para ser sustituidas por explicaciones más satisfactorias.
El primer dragón al que hacen referencia los autores es el éter luminífero, esa sustancia invisible a la que se atribuía la propiedad de transmitir la luz y cuya existencia no pudieron probar Michelson y Morley en uno de los experimentos más importantes en la historia de la física. A ese le siguen unos cuantos dragones más en el libro, aunque no todos los temas que se tratan hacen referencia a alguna entidad imaginaria. Lo que sí tienen en común todos los temas es una descripción del curso de los descubrimientos, las propuestas, las controversias y, en algunos casos, hasta las miserias (humanas) que han jalonado el avance del conocimiento.
La mayor parte de los capítulos tratan de astronomía, cosmología y física, lo que parece lógico dada la adscripción disciplinar de los autores. Pero también se ocupan de asuntos propios de otras disciplinas, como la deriva continental y tectónica de placas (geología), el homúnculo que, hipotética, pero erróneamente, fue considerado portador de la herencia genética, o la extinción de los dinosaurios y el papel que en ese episodio de la historia de la vida jugó –o no– el impacto de un asteroide. Los autores cuentan el modo en que se han eliminado errores y falsas creencias (dragones) de nuestro empeño por comprender la naturaleza.
Con confianzaHe leído con especial interés el capítulo en el que se ocupan de la materia oscura y de la energía oscura. Al respecto, los autores expresan su confianza en que llegaremos a saber en qué consiste la materia no bariónica, pero dicen no tener la misma confianza en lo que se refiere a la energía oscura. Siempre me ha sorprendido la extraordinaria confianza que muestran la mayoría de los físicos que conozco en sus modelos. Son ciertamente optimistas, hasta el punto de que me resulta entrañable la seguridad con la que se expresan acerca de lo que saben. Por eso me ha sorprendido gratamente el apunte acerca de la energía oscura, una entidad cuya existencia se ha postulado porque es necesaria para entender la realidad. Podría, en efecto, acabar siendo uno de esos dragones que nos acechan en los límites de lo conocido.
Me ha gustado esta obra. Es de esos libros que llevan al lector; no requieren un esfuerzo especial para seguir los hilos que entreteje. Por la forma en que está escrito, atrapa desde las primeras líneas. No es fácil dejar de leerlo y deseas volver a sus páginas cuando lo has dejado. Está muy bien escrito.
Los episodios que narra están llenos de información acerca de multitud de aspectos. Pero esa exposición, lejos de resultar aburrida, añaden atractivo al texto. Es, en ese sentido, un magnífico muestrario de la forma en que se ha construido el edificio conceptual de las ciencias. Lo que no sabemos —y eso es algo que señalan los propios autores en el último capítulo— es si se seguirá haciendo como hasta ahora o si la irrupción de la inteligencia artificial cambiará radicalmente la forma en que adquiriremos nuevo conocimiento en adelante.
Al comienzo de la reseña he dejado dicho que haría referencia al título principal del libro más adelante. Ha llegado el momento, pero para señalar que no me corresponde a mí explicarlo aquí. Son los autores quienes deben explicarlo, pero para eso, querido lector, ha de leer el libro. Hay una idea muy poderosa en sus razones.
Título: The Reinvention of Science: Slaying the Dragons of Dogma and Ignorance
Autores: Bernard J. T. Jones, Vicent J. Martínez, Virginia L. Trimble
Ed.: World Scientific, 2024.
En Editoralia personas lectoras, autoras o editoras presentan libros que por su atractivo, novedad o impacto (personal o general) pueden ser de interés o utilidad para los lectores del Cuaderno de Cultura Científica.
Una versión de este texto de Juan Ignacio Pérez Iglesias apareció anteriormente en Lecturas y Conjeturas (Substack).
El artículo Matando los dragones del dogma y la ignorancia se ha escrito en Cuaderno de Cultura Científica.

