Las células cristal transportan oxígeno en Drosophila
Seguro que recuerdan alguna película en la que aparecen insectos gigantescos. Por ejemplo, la espléndida La humanidad en peligro (1954) nos muestra cómo las pruebas nucleares en el desierto han provocado mutaciones en las hormigas, que se convierten en descomunales amenazas.
Este escenario no es demasiado realista, ya que el tamaño de los insectos está constreñido por la forma en que respiran. En los libros de texto se nos explica que los insectos tienen respiración traqueal, mediante un sistema de finísimos tubos huecos que llevan el aire a todos los rincones de su cuerpo. Esto impone un tamaño limitado por los problemas de la difusión del aire dentro de las tráqueas. Curiosamente, el aire rico en oxígeno del periodo Carbonífero permitió que los insectos alcanzaran los mayores tamaños de su historia. La libélula Meganeura, por ejemplo, llegó a los 70 cm de envergadura.
Un reciente descubrimiento, publicado en la revista Nature por un equipo surcoreano, ha revelado que, además de las tráqueas, existen células sanguíneas en la larva de Drosophila capaces de transportar oxígeno mediante un mecanismo sorprendente. Se trata de las células cristal, así llamadas por contener estructuras cristalinas en su interior.
Las células cristal son uno de los tres tipos de hemocitos o células sanguíneas de Drosophila, y representan alrededor del 5% del total. Los más abundantes son los plasmatocitos (95%) una especie de células fagociticas, y el tercer tipo son los lamelocitos que sólo aparecen durante la activación del sistema inmune.
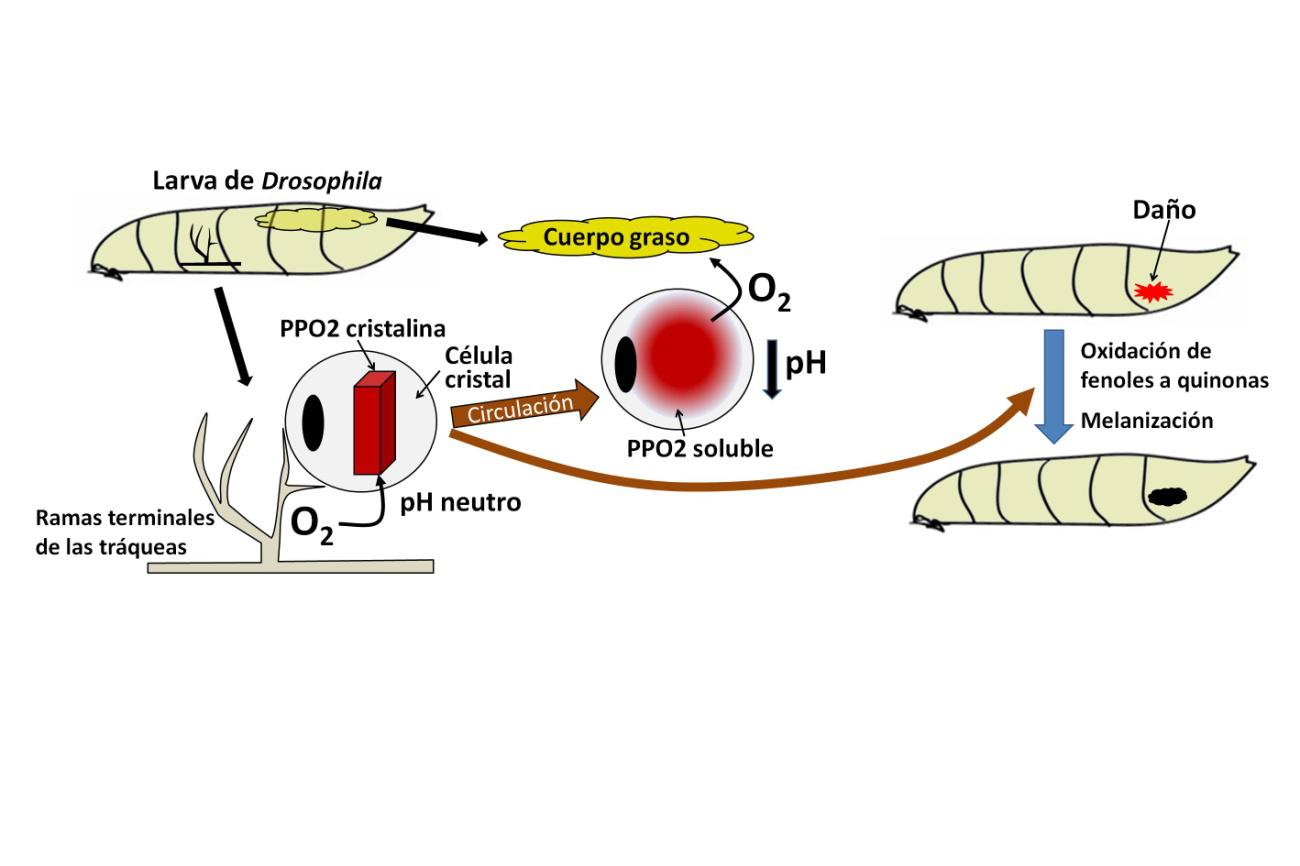 Figura 1. La función hasta ahora atribuida a las células cristal era la melanización, oxidación de fenoles para formar polímeros de melanina capaces de englobar patógenos y cicatrizar heridas (derecha). La nueva función descrita por Shin y cols. consiste en el transporte de oxígeno desde las tráqueas a tejidos como el cuerpo graso, alejados de ellas. El transporte implica un cambio de fase en la profenoloxidasa-2 (PPO2), que almacena oxígeno en estado cristalino y lo libera en la fase soluble, inducida por un descenso del pH.
Figura 1. La función hasta ahora atribuida a las células cristal era la melanización, oxidación de fenoles para formar polímeros de melanina capaces de englobar patógenos y cicatrizar heridas (derecha). La nueva función descrita por Shin y cols. consiste en el transporte de oxígeno desde las tráqueas a tejidos como el cuerpo graso, alejados de ellas. El transporte implica un cambio de fase en la profenoloxidasa-2 (PPO2), que almacena oxígeno en estado cristalino y lo libera en la fase soluble, inducida por un descenso del pH.Los cristales que dan nombre a las células cristal están formados por una proteína que contiene cobre, la profenoloxidasa-2 (PPO2). Esta enzima se encarga de oxidar fenoles y formar polímeros que engloban microorganismos patógenos y contribuyen a la cicatrización de heridas, la función principal que se atribuía a las células cristal hasta ahora (Figura 1). Como los polímeros tienen color oscuro, esta reacción defensiva se conoce como melanización. De hecho, nuestra síntesis de melanina responde a un mecanismo muy similar.
El grupo surcoreano utilizó tres cepas de larvas de moscas mutantes, carentes de células cristal, con ausencia de PPO2 o bien con una PPO2 incapaz de unirse al cobre en su sitio activo. Todas estas larvas muestran alta mortalidad en condiciones de laboratorio y un aumento en el número de ramas terminales de las tráqueas. Este incremento también se produce en larvas normales cultivadas en hipoxia, por lo que se considera una respuesta a la falta de oxígeno.
Estos defectos revierten si se aumenta la concentración de oxígeno en el aire hasta el 60%. De forma más sorprendente, también se rescatan los defectos de las larvas mutantes si se fuerza en las células cristal la expresión de la hemocianina del cangrejo de herradura. Recordemos que esta proteína transporta oxígeno en muchos crustáceos y algunos quelicerados, dando a su sangre color azul debido a su contenido en cobre. Todos estos resultados indican que la PPO2 contenida en las células cristal es indispensable para mantener los niveles de oxígeno en las larvas de las moscas.
Un transportador de oxígeno debe ser capaz de combinarse con esta molécula de forma reversible. En el caso de la hemoglobina o la hemocianina, la fijación se produce en el sitio activo que contiene hierro y cobre, respectivamente. Lo que reveló el estudio de los investigadores surcoreanos es que la combinación reversible de PPO2 con el oxígeno implicaba un cambio de fase en la organización de la proteína (Figura 1). Cuando la célula cristal está próxima a las ramas terminales de las tráqueas, su PPO2 en forma cristalina fija oxígeno. Para ello el pH del interior celular debe ser neutro. Luego, la célula cristal viaja por la cavidad circulatoria y alcanza tejidos alejados de las tráqueas. Allí, el pH citoplasmático disminuye por acción de la enzima anhidrasa carbónica, la proteína pasa de la forma cristalina a una variante soluble, y el oxígeno se libera. La célula cristal regresa a las ramas terminales de las tráqueas y el ciclo comienza de nuevo.
Este proceso ha explicado, por fin, cómo es posible el funcionamiento de un órgano larvario conocido como cuerpo graso, que tiene funciones detoxificadoras y de almacenamiento de lípidos. Su carencia de tráqueas planteaba la cuestión de cómo se satisfacía su demanda metabólica de oxígeno. Ahora sabemos que las células cristal se encargan de transportar el oxígeno desde las tráqueas hasta las proximidades del cuerpo graso.
El sorprendente descubrimiento de células transportadoras de oxígeno en la larva de Drosophila como complemento de la respiración traqueal plantea apasionantes preguntas. ¿Sucede esto en otros insectos, o en insectos adultos? ¿Interviene este tipo de mecanismo en el altísimo consumo de oxígeno que demanda el vuelo de los insectos?
Referencias:
Luschnig, S. (2024) Flies use blood cells to take a deep breath. Nature. doi: 10.1038/d41586-024-01649-6.
Shin, M., Chang, E., Lee, D., et al. (2024) Drosophila immune cells transport oxygen through PPO2 protein phase transition. Nature. doi: 10.1038/s41586-024-07583-x.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga
El artículo Las células cristal transportan oxígeno en Drosophila se ha escrito en Cuaderno de Cultura Científica.
Métodos matemáticos para armonizar la poesía
La Camerata Fiorentina fue un grupo de músicos, poetas y humanistas, bajo el patrocinio en Florencia del conde Giovanni Bardi y reunidos en su palacio entre los años 1572 y 1587 aproximadamente. Algunos de los más importantes miembros de la Camerata, como el músico Vincenzo Galilei, los cantantes Giulio Caccini y Jacopo Peri y el poeta Ottavio Rinuccini fueron quienes fundaron las bases intelectuales, teóricas y prácticas de lo que hoy llamamos la ópera.
 Patio del Palazzo Bardi en Florencia, atribuido a Bruneleschi, lugar de reunión de la Camerata Fiorentina. Foto: Francesco Bini / Wikimedia CommonsArmonizar la poesía: recitativos y tonemas
Patio del Palazzo Bardi en Florencia, atribuido a Bruneleschi, lugar de reunión de la Camerata Fiorentina. Foto: Francesco Bini / Wikimedia CommonsArmonizar la poesía: recitativos y tonemas
La Camerata heredó de la antigüedad importantes poemas o dramas clásicos que querían modernizar, musicalizar y representar en teatros. El recitativo de versos y diálogos fue un extraordinario invento musical de Giulio Caccini y Jacopo Peri, concebido para elevar la voz humana de actores y cantantes. Ello lo basaron en la entonación ordinaria de los lenguajes humanos, pero tratando -por medio de acertadas inflexiones de voz- de dotarles de mejor expresividad, comunicación, sentimiento y musicalidad.
En Fonética podemos sistematizar la entonación de una frase a través de los tonemas, que definen elevaciones o descensos del tono de la voz. La misma frase, entonada con diferentes tonemas, puede dar lugar a una expresión asertiva, o bien introducir una duda o una pregunta, o puede mostrar enfado, alegría, tristeza u otros sentimientos diferentes. Estas importantes inflexiones expresivas de la voz la formalizaron Caccini y Peri escribiendo notas musicales en un texto para recitar musicalmente los versos de un poema o la frase de una obra teatral. La técnica del Recitativo es por tanto el inicio de musicalizar la poesía y la literatura, esencial para desarrollar la ópera.
Matemáticas: melodía, entonación, eufonía y resoluciónSi queremos armonizar un poema, debemos introducir más de una voz, de forma que ambas a la vez suenen eufónicas. Vincenzo Galilei, en su obra Della musica antica et della moderna explicó matemáticamente la disonancia y la consonancia de dos notas sonando simultáneamente, basado en las ideas del teórico musical Gioseffo Zarlino. El discurso de dos frases musicales simultáneas fue descrito a través de unas sencillas reglas matemáticas de resolución de dichas frases. Ello consistía en una progresión ordenada de notas con mayor o menor eufonía que terminaba por medio de un salto tenso entre dos notas seguido por un regreso relajado a la nota final esperada por el lenguaje humano.
Así pues, mediante estas sencillas reglas matemáticas horizontales (melodía y entonación) y verticales (eufonía y resolución), se explica la más simple y conocida armonía entre dos personas cantando intuitivamente a dos voces, mediante intervalos de terceras, quintas, octavas o unísonos, que ya los Pitagóricos atesoraban por su pureza. Para más de dos voces simultáneas se siguen las mismas normas.
El ejemplo de HändelLas personas dedicadas a la música suelen considerarse “de letras”, quizás porque no les han explicado que las artes y especialmente la música beben de las matemáticas. Como ejemplo ilustrativo de cómo armonizar la poesía, mostraremos una sencilla práctica de uno de los pocos grandes compositores que adquirió en vida enorme éxito, reconocimiento y fortuna: Georg Friedrich Händel, que fue venerado en su país de adopción y fue enterrado en la Abadía de Westminster con honores de Estado.
Rinaldo fue la primera ópera que Händel estrenó en Londres el 24 de febrero de 1711 en el Queen’s Theatre de Haymarket. El estilo operístico italiano que el autor había aprendido, y el libreto en italiano del poeta Giacomo Rossi tuvo un éxito arrollador.
En la Figura 1 se muestra un fragmento del manuscrito original del Acto II de Rinaldo. Comienza un Recitativo de Argante: Oscura questo pianto il bel fuoco d’amor, ch’in me s’accese per te, mia cara. Responde Almirena: In questi lacci avvolta, non è il mio cor soggetto d’un amoroso affetto. En ambos recitativos, al puro estilo de la original invención musical de Giulio Caccini y Jacopo Peri, Händel coloca los tonemas mediante notas musicales para apropiada entonación de las frases.
 Figura 1: Manuscrito original de Rinaldo de G.F. Händel (Acto II, Escena IV): recitativos de Argante (Oscura questo pianto) y de Almirena (In questi lacci avvolta) y primeros compases de una de las arias más famosas de Almirena (Lascia ch’io pianga). Wikimedia Commons.
Figura 1: Manuscrito original de Rinaldo de G.F. Händel (Acto II, Escena IV): recitativos de Argante (Oscura questo pianto) y de Almirena (In questi lacci avvolta) y primeros compases de una de las arias más famosas de Almirena (Lascia ch’io pianga). Wikimedia Commons.La parte baja del manuscrito de la Figura 1 es la armonización completa de los primeros compases de una de las arias más famosas de esta ópera y de todo el repertorio operístico de Händel. La simplicísima armonización de los versos
Lascia ch’io pianga mia cruda sorte,
e che sospiri la libertà.
podemos pasarla a limpio para mostrar el ejemplo de ocho compases (cuatro para cada verso). Si no sabe usted leer música, no importa para entender lo escrito que explicaremos a continuación.
 Figura 2: Primer verso del aria a cuatro voces (el violín 1 equivale a la soprano)
Figura 2: Primer verso del aria a cuatro voces (el violín 1 equivale a la soprano)
 Figura 3: Segundo verso del aria a cuatro voces (el violín 1 equivale a la soprano)
Figura 3: Segundo verso del aria a cuatro voces (el violín 1 equivale a la soprano)
Diremos para empezar que el aria de Almirena está en tonalidad de Fa Mayor. La armonización está realizada a cuatro voces, que hemos colocado como si fuera un cuarteto de cuerda, o bien una pequeña orquesta de cuerda, donde la línea más aguda son los primeros violines o la soprano, que canta la letra.
Lectura horizontal y verticalEn las Figuras 2 y 3, leyendo horizontalmente la primera línea, la soprano canta la melodía. Además, sus dos versos cadenciosos están marcados por la combinación de sus importantes acentos de entonación en puntos expresivos clave (cru-da) y sus esenciales pausas rítmicas, que son los silencios.
Si ahora leemos verticalmente la Figura 2, vemos un primer compás con base en la primera nota de la tonalidad (Fa). Este acorde eufónico, muy Pitagórico, es Fa-La-Do, y lo rotulamos con un número romano (I). Las sencillas reglas matemáticas Galileanas -de progresión ordenada de acordes y la resolución de dichas frases- las podemos seguir mirando los números romanos en la parte del bajo de la partitura, que apenas se mueven, salvo algunas ligeras disonancias en el segundo y tercer compás. Ello nos deja el primer verso sin terminar, con carácter casi interrogativo, solicitando una respuesta.
Si ahora vamos a la Figura 3, continuamos leyendo verticalmente y si seguimos los números romanos, vemos que esta progresión del segundo verso cierra la frase con una tríada tensa (V) seguida por un regreso relajado a la nota final (I) esperada por el lenguaje humano, tal y como explicaba la Camerata Fiorentina. Este cierre V-I es lo que en música se llama cadencia (caída) auténtica, y que cierra frases en casi cualquier estilo musical.
Un poema armonizado no es solo “de letras”. Es también “de ciencias”: sus reglas matemáticas expresan sentimientos, y narran una conmovedora historia. Escuchemos el resultado de esta sencilla armonización que explica por qué Händel fue tan apreciado en vida:
Sobre el autor: Victor Etxebarria Ecenarro está diplomado como lutier por el Conservatorio Juan Crisóstomo de Arriaga (Bilbao) y es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (UPV/EHU)
El artículo Métodos matemáticos para armonizar la poesía se ha escrito en Cuaderno de Cultura Científica.
Día de pi 2024: Demostraciones visuales en dimensiones superiores

El número Pi, representado por la letra griega π, es una de las constantes matemáticas más famosas e importantes que existen en el mundo. Este número irracional, que determina la relación entre la longitud de una circunferencia y su diámetro, concierne a múltiples disciplinas científicas como la física, la ingeniería y la geología, y tiene aplicaciones prácticas sorprendentes en nuestro día a día.
La fascinación que ha suscitado durante siglos es tal, que se viene estudiando desde hace más de 4.000 años e, incluso, cuenta con su propio día en el calendario: el 14 de marzo. Este evento internacional vino de la mano del físico estadounidense Larry Shaw, quien en 1988 lanzó la propuesta de celebrar esta efeméride. La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática: 3-14 martxoaren 14 en euskara / 3-14 March, 14th en inglés. En los últimos años, la conmemoración del Día de Pi se ha ido extendiendo, hasta tal punto que el 26 de noviembre de 2019 la UNESCO proclamó el 14 de marzo Día Internacional de las Matemáticas.
Un año más, el Basque Center for applied Mathematics-BCAM y la Cátedra de Cultura Científica de la UPV/EHU nos sumamos a la celebración, organizando la quinta edición del evento BCAM NAUKAS, que se desarrolló a lo largo del 14 de marzo en el Bizkaia Aretoa de UPV/EHU.
Una demostración visual es una prueba matemática que no necesita de manipulación algebraica. En el Cuaderno de Cultura Científica hemos visto este tipo de demostraciones en la serie que hizo Raúl Ibáñez al respecto llamada Teoremas sin palabras. Pero, ¿pueden emplearse en dimensiones mayores que tres? Este es el fascinante (para las personas aficionadas a las matemáticas y matemáticas) tema de esta charla que nos trae Urtzi Bujis Martín.
Urtzi Bujis Martín es profesor de topología algebraica en la Universidad de Málaga y divulgador de las matemáticas en Archimedes Tub.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Día de pi 2024: Demostraciones visuales en dimensiones superiores se ha escrito en Cuaderno de Cultura Científica.
La capacidad de interpretar metáforas se desarrolla por completo a los 6 años
La investigadora de la Universidad del País Vasco Isabel Martín ha analizado con menores de 3 a 9 años la capacidad para interpretar las metáforas, y ha concluido que las comprenden completamente a los 6 años. En edades más tempranas muestran cierta intuición para captar el significado figurado, pero su capacidad no está totalmente desarrollada. La investigadora y sus colaboradoras han llegado a esta conclusión combinando las metodologías de selección de imágenes y de seguimiento de movimientos oculares.
 Fuente: ReferenciaMetáforas en neurotípicas y neurodivergentes
Fuente: ReferenciaMetáforas en neurotípicas y neurodivergentes
Un estudio que ha realizado el equipo de investigación Lindy Lab de la UPV/EHU con 80 niños y niñas de 3 a 9 años ha llegado a la conclusión de que la interpretación total de las metáforas se alcanza a partir de los 6 años. A pesar de ello, los resultados indican que la capacidad para intuir los significados no literales comienza a desarrollarse antes. “Se aprecia que en edades más tempranas captan en cierto modo el lenguaje figurado, pero no lo dominan y su capacidad es limitada. A los 6 identifican correctamente su significado y, es más adelante, hacia los 10, cuando parece que son capaces de explicar las metáforas”, aclara Isabel Martín. Los resultados de esta investigación se enmarcan dentro de la tesis que está realizando la doctoranda sobre la comprensión del lenguaje metafórico en personas tanto de desarrollo típico (neurotípicas) como con el llamado trastorno del espectro autista (neurodivergentes), con el objetivo de comparar lo que sucede en ambos grupos y poder comprender mejor la mente de personas con autismo.
La autora del estudio explica que para llegar a las citadas conclusiones se han servido de una investigación innovadora: “Hemos iniciado una nueva tendencia metodológica en psicología experimental y psicolingüística que nos ha permitido extraer conclusiones más matizadas que los trabajos ya existentes”. Y es que cabe recalcar, que hay diversos estudios que han analizado esta cuestión, pero sus resultados son dispares. El grupo de la Universidad del País Vasco ha logrado aportar información más completa al debate científico combinando dos metodologías diferentes de una manera que no se había hecho antes.
Selección de imágenes y desplazamiento de los ojosPor un lado, han empleado la metodología de la selección de imágenes. Han puesto en práctica un experimento en el que cada niño o niña escucha un audio en el que se dicta una metáfora (p. ej.: “Los saltamontes saltan mucho; ese niño es un saltamontes”), a la vez que visualizan cuatro imágenes (un niño saltando, un niño corriendo, un escarabajo y un saltamontes saltando). Entonces, los y las participantes deben elegir el dibujo que representa el mensaje que han oído (el niño saltando). “Esta metodología nos ha permitido saber que los participantes de 6 años comprenden los significados figurados, porque es en esa edad cuando se ve claramente que eligen la representación adecuada”, indica la investigadora.
Sin embargo, la selección de imágenes no ofrece información sobre cómo ha procesado cada participante los mensajes y en qué medida ha contemplado otras opciones. Para conocer esos detalles, el equipo de investigación de la Universidad del País Vasco ha aprovechado cada ejercicio planteado para analizar también sus movimientos oculares.
Mientras ven las imágenes, escuchan el estímulo auditivo y eligen el dibujo definitivo, una cámara de infrarrojos mide los desplazamientos de los ojos; tanto los sacádicos (movimientos rápidos del globo ocular e imperceptibles a simple vista) como las trayectorias y las fijaciones en cada imagen. Isabel Martín explica que estos datos permiten conocer cómo han procesado lo que han visto y oído: “La cámara capta cómo se han movido los ojos de una imagen a otra y nos da información sobre lo que está pasando dentro de sus cabezas antes de elegir el dibujo que consideran correcto: si han tenido dificultades, entre qué opciones han dudado… Dado que la imagen que finalmente seleccionan es el resultado de una decisión, que ha seguido todo un proceso”. El registro de los movimientos oculares les permite asomarse a ese proceso en sí y matizar los resultados obtenidos a través de la selección de imágenes.
Precisamente es gracias a la combinación de ambas metodologías que han podido saber que, aunque los niños y niñas menores de 6 años no interpretan con claridad las metáforas porque seleccionan con menos frecuencia la imagen correcta, sí que tienen cierta intuición para detectar los significados figurados. Y es que a través del seguimiento ocular han detectado que han dudado a la hora de elegir el dibujo. “Cuando tienen clarísimo qué significa la frase, no le dan más vueltas y fijan su mirada en la opción que consideran correcta. Pero cuando tienen dudas, miran a otros lugares. Y eso es lo que hemos podido percibir en menores de edades tempranas”, concreta la investigadora.
Referencia:
Isabel Martín-González, Camilo R. Ronderos, Elena Castroviejo, Kristen Schroeder, Ingrid Lossius-Falkum, Agustín Vicente (2024) That kid is a grasshopper! Metaphor development from 3 to 9 years of age Journal of Child Language doi: 10.1017/S0305000924000187
El artículo La capacidad de interpretar metáforas se desarrolla por completo a los 6 años se ha escrito en Cuaderno de Cultura Científica.
Un pequeño paso para Neil Armstrong, un gran salto para la ciencia ficción
El 20 de julio de 1969, Neil Armstrong y Buzz Aldrin se convertían en los primeros seres humanos en pisar la Luna, mientras un estoico Michael Collins permanecía, a la espera de la pena o la gloria de la misión, orbitando nuestro satélite. Todos conocemos esta historia, y algunos de los que estén leyendo este artículo, probablemente, también la vivieron en primera persona gracias a la colosal cobertura mediática que recibió el acontecimiento. Se estima que 600 millones personas lo vieron en directo en sus televisores, pero ¿y si no se hubiera retransmitido en vivo ni hubiera habido ese colosal despliegue mediático?, ¿hubiera impactado tan profundamente la llegada a la Luna en nosotros? Para muchos tal vez no, pero para algunos otros sí, y mucho. O, al menos, para los escritores de ciencia ficción que durante décadas habían estado imaginando y esperando ese momento.
 Buzz Aldrin fotografió su propia huella sobre el regolito lunar con fines científicos, pero esta imagen se ha convertido en un símbolo del logro de haber llegado a la luna. Fuente: NASA/Buzz Aldrin
Buzz Aldrin fotografió su propia huella sobre el regolito lunar con fines científicos, pero esta imagen se ha convertido en un símbolo del logro de haber llegado a la luna. Fuente: NASA/Buzz Aldrin
Hubo dos coberturas informativas de la misión Apolo 11 que tuvieron especial relevancia en ese sentido: la de la CBS (Columbia Broadcasting System) y la de la ABC (American Broadcasting Company). La programación especial de CBS News comenzó el 16 de julio de 1969, día del lanzamiento, a las seis de la mañana. Empezaban ocho días de retransmisiones en directo, casi sin descanso, bajo el título de: El hombre en la Luna: el viaje épico del Apolo 11.
La cara visible del despliegue informativo fue Walter Cronkite, uno de los periodistas más respetados del país. Corresponsal en Europa durante la Segunda Guerra Mundial, cubrió el Desembarco de Normandía y otras misiones de bombardeo sobre Alemania, así como los juicios de Núremberg durante los años posteriores. Y su carrera se extendería con éxito durante algunas décadas más. Era la elección lógica por parte de la cadena para cubrir el que sin duda se convertiría en uno de los mayores acontecimientos de la historia de la humanidad.
 El periodista de informativos Walter Cronkite fue el encargado de la cobertura de la misión Apollo 11 para CBS News. Fuente: CC BY-NC-SA 2.0/CBS News
El periodista de informativos Walter Cronkite fue el encargado de la cobertura de la misión Apollo 11 para CBS News. Fuente: CC BY-NC-SA 2.0/CBS News
Pero Walter Cronkite no estuvo solo, el desfile de corresponsales y expertos fue infinito. Y, entre esos expertos, ¿qué mejor que los escritores de ciencia ficción que habían estado especulando durante décadas con ese momento? Arthur C. Clarke apareció en antena hasta en doce ocasiones, pero la intervención más interesante se produjo el día del alunizaje. Aquel día, la CBS hizo una emisión de treinta horas ininterrumpidas, veintisiete de las cuales Cronkite estuvo en directo. En los momentos anteriores y posteriores al aterrizaje tuvo dos acompañantes de lujo: el propio Clarke, que lo acompañaba en el estudio de Nueva York, y Robert A. Heinlein, en conexión desde California, acompañado por Bill Stout.
La entrevista, que se puede ver completa en YouTube (abajo aparece un resumen de 10 minutos), es un documento maravilloso para los amantes de la carrera espacial y la ciencia ficción, sobre todo por el optimismo y la emoción que transmitían ambos escritores en aquel momento. Heinlein llega a decir en un momento de su intervención, visiblemente emocionado:
Este es el acontecimiento más grandioso de la historia de la humanidad hasta el momento. Esto es… hoy es el día de año nuevo del año uno.1 Si nosotros no modificamos el calendario, los historiadores lo harán […]. E iremos allá fuera, no solo a la Luna, sino a las estrellas: nos expandiremos […]. Nos vamos a expandir por todo el universo.
En aquello consistió la magia del momento: la ciencia ficción había soñado durante décadas con lo imposible y lo imposible sucedió el 20 de julio de 1969, ¿qué motivo habría para pensar que, una vez pisada la Luna, nos detendríamos ahí?
La cadena ABC recurrió, por otro lado, a Isaac Asimov, Frederik Pohl y John R. Pierce2 que participaron en una mesa redonda moderada por Rod Serling, guionista y productor televisivo conocido, sobre todo, por la serie The Twilight Zone. Tampoco ninguno de ellos mostró ninguna duda de que, desde que tenían uso de razón, la llegada del ser humano a la luna era una cuestión de tiempo. Parte de aquella intervención se puede ver también en YouTube.
La participación mediática de Isaac Asimov, Arthur C. Clarke, Robert A. Heinlein, Frederik Pohl y John R. Pierce, entre otros, en el que probablemente fue el logro tecnológico más importante del siglo XX fue, por un lado, el testimonio de que el sueño de la Edad de Oro de la ciencia ficción podía cumplirse. Por otro, un ejemplo del poder que la ciencia ficción puede ejercer en la manera en la que entendemos nuestra realidad e imaginamos nuestro futuro. Desde los tiempos de Julio Verne ―incluso antes―, sin las constricciones y formalismo de la ciencia, y con mucho sentido de la maravilla, aquellos escritores, y también divulgadores en muchos casos, inspiraron a varias generaciones de científicos, ingenieros y exploradores de lo desconocido, sembrando en ellos la idea de que un día sería posible pisar la Luna.
 Buzz Aldrin en la superficie de la Luna, fotografiado por Neil Armstrong. Fuente: NASA/Neil Armstrong
Buzz Aldrin en la superficie de la Luna, fotografiado por Neil Armstrong. Fuente: NASA/Neil Armstrong
Aunque es difícil calibrar el grado de influencia que la ciencia ficción de principios a mediados del siglo XX tuvo sobre el desarrollo de la carrera espacial, todo indica que la tuvo. Wernher von Braun y Arthur C. Clarke fueron grandes amigos. Tal vez eso signifique que, al fin y al cabo, la ciencia y la ciencia ficción ―science fact and science fiction― no se encuentren tan alejadas la una de la otra.
Bibliografía
Hsu, T. (15 de julio de 2019). The Apollo 11 mission was also a global media sensation. https://www.nytimes.com/2019/07/15/business/media/apollo-11-television-media.html
Knoll, S. (16 de julio de 1969). First man on the moon has TV network in orbit. Variety. https://variety.com/1969/biz/news/first-man-on-the-moon-has-tv-networks-in-orbit-1201342630/
Jeffrey, J. (11 de julio de 2019). Apollo 11: ‘The greatest single broadcast in television history’. BBC. https://www.bbc.com/news/world-us-canada-48857752
McAleer, N. (1992). Arthur C. Clarke. The authorized biography. Contemporary Books.
NASA (s. f.). Walter Cronkite. NASA. https://www.nasa.gov/people/walter-cronkite/
O’Donell, Norah (16 de julio de 2019). “Say something, I’m Speechless!”: Inside the CBS News coveragie of Apollo 11. CBS News. https://www.cbsnews.com/news/say-something-im-speechless-inside-the-cbs-news-coverage-of-apollo-11/
Patterson, W. H. (2014). Robert A. Heinlein. Vol. 2. The man who learned better. 1948-1988. Tor.
Notas:
1 No fue el único que lo pensó. Ray Bradbury comenzó a fechar su correspondencia de 1969 como «Apolo año 1». Lamentablemente, solo llegó hasta «Apolo año 3».
2 John R. Pierce, además de escritor de ciencia ficción, era ingeniero de los Bell Labs en Nueva York. Fue quien acuñó el término «transistor» para el dispositivo que John Bardeen, Walter Brattain y William Shockley habían desarrollado allí en 1947. Solía escribir bajo el seudónimo de J. J. Coupling.
 
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo Un pequeño paso para Neil Armstrong, un gran salto para la ciencia ficción se ha escrito en Cuaderno de Cultura Científica.
Teorema de los globos oculares
Como se decía en la entrada del Cuaderno de Cultura Científica titulada El teorema de Morley, la geometría euclidiana y, en particular, la geometría plana, está repleta de hermosos y sorprendentes teoremas, sobre algunos de los cuales ya hemos escrito con anterioridad, como el teorema de Pitágoras, el teorema de Napoleón o el teorema de Morley, por citar algunos. En esta entrada estival vamos a disfrutar de un nuevo resultado de la geometría del plano, el conocido teorema de los globos oculares.
 Fotografía de la escultura Ojo (2007), instalada en Dallas (Texas, EE.UU.), del artista estadounidense Tony Tasset. Fotografía realizada por la fotógrafa Carol M. Highsmith / Library of the Congress (USA)Lo que nos dice el teorema
Fotografía de la escultura Ojo (2007), instalada en Dallas (Texas, EE.UU.), del artista estadounidense Tony Tasset. Fotografía realizada por la fotógrafa Carol M. Highsmith / Library of the Congress (USA)Lo que nos dice el teorema
Este es un curioso resultado de geometría elemental sobre dos circunferencias disjuntas y las rectas tangentes a las mismas trazadas desde los centros de las circunferencias opuestas, que ha sido descubierto, o al menos publicado, hace unas décadas, aunque es posible que se conociese desde hace mucho tiempo.
Antes de nada, vayamos con su enunciado.
Teorema: Dadas dos circunferencias disjuntas de centros O y P, se consideran las dos rectas tangentes a la circunferencia de centro P que pasan por O, así como los dos puntos de intersección de estas con la circunferencia de centro O, denotados A y B, y las dos rectas tangentes a la circunferencia de centro O que pasan por P, así como los dos puntos de intersección de las mismas con la circunferencia de centro P, denotados X e Y, entonces los segmentos AB y XY tienen la misma longitud.
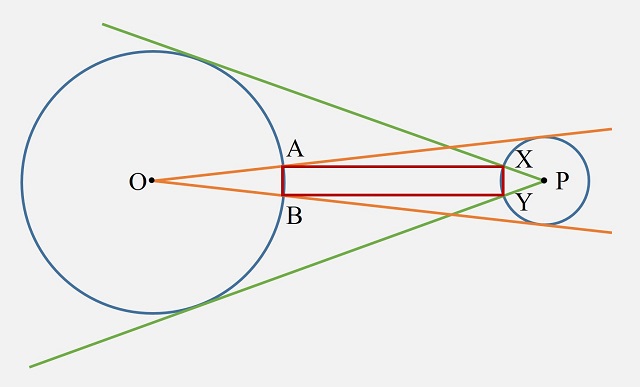 Esquema del teorema de los globos oculares
Esquema del teorema de los globos oculares
Como podemos leer en el libro The Wonder Book of Geometry (El maravilloso libro de la geometría), de David Acheson, este resultado fue descubierto en 1960 por el matemático peruano Antonio Gutiérrez, creador de la página web GoGeometry, aunque es probable, ya que se trata de un resultado elemental, que ya fuese conocido desde la antigüedad. El propio Gutiérrez, en su artículo Eyeball theorems (publicado en el libro The Changing Shape of Geometry. Celebrating a Century of Geometry and Geometry Teaching / La forma cambiante de la geometría: celebrando un siglo de geometría y enseñanza de la geometría), dice “estoy convencido de que este resultado ha sido descubierto en casi todas las culturas”.
No conocemos si efectivamente era un resultado conocido en la antigüedad, aunque podamos sospecharlo. Lo que sí sabemos es que, en 1938 el matemático estadounidense George W. Evans publicó un artículo en la revista The Mathematics Teacher, titulado Ratio as multiplier, en el que se presenta un problema como “más fácil de resolver que de enunciar”, que encontró como problema propuesto en un examen (aunque no cita qué tipo de examen era, ni dónde se realizó) y que resulta ser el teorema de los globos oculares.
El nombre del teorema se debe a que el esquema del mismo nos recuerda a los típicos esquemas que describen la geometría de los rayos de luz en el ojo.
Una demostración simple del teoremaComo hemos comentado, el teorema de los globos oculares es un resultado geométrico elemental y sorprendente, pero además hermoso, motivo por el cual lo he elegido para esta entrada estival del Cuaderno de Cultura Científica. Al ser un resultado elemental, existen bastantes demostraciones relativamente sencillas. Una de ellas es la mostrada por el matemático George W. Evans en su artículo Ratio as multiplier y que explicamos a continuación.
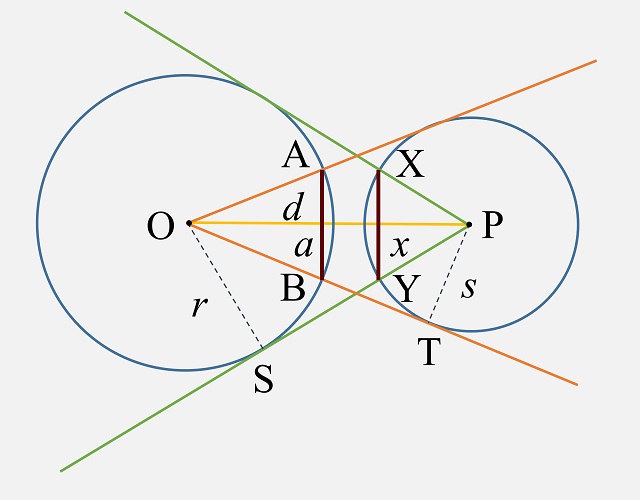 Esquema del teorema de los globos oculares
Esquema del teorema de los globos oculares
En el anterior esquema del teorema de los globos oculares se consideran las siguientes longitudes: a es la mitad de la longitud del segmento AB, x es la mitad de la longitud del segmento XY, d la distancia entre los centros, O y P, y r y s los radios de las dos circunferencias, en particular, r es igual a la longitud de los segmentos OA, OB y OS, y s es la longitud de los segmentos PX, PY y PT. Para demostrar que las longitudes de los segmentos AB y XY son iguales nos basta probar que a = x.
A continuación, consideramos dos triángulos rectángulos. Por una parte, el pequeño triángulo rectángulo formado por el segmento x y los vértices P e Y (coloreado de azul en la siguiente imagen) y el triángulo rectángulo O, S y P (con rayas azules). Como los ángulos de los dos triángulos rectángulos son los mismos, entonces los dos triángulos son semejantes, es decir, tienen la misma forma, pero distinto tamaño (uno es una ampliación/reducción del otro).
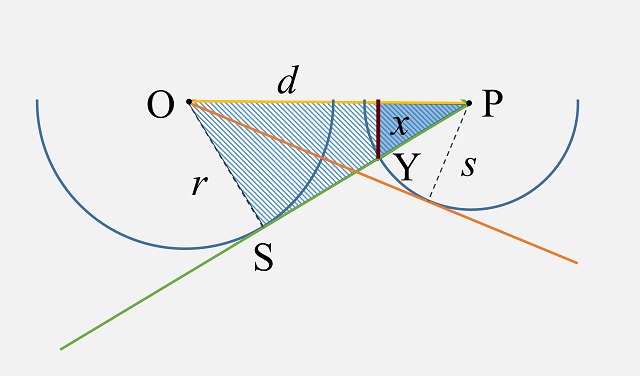 Dos triángulos rectángulos semejantes, luego tienen la misma forma y distinto tamaño
Dos triángulos rectángulos semejantes, luego tienen la misma forma y distinto tamaño
Como los dos triángulos rectángulos seleccionados son semejantes, las longitudes de sus lados serán proporcionales, es decir, existe un factor de proporcionalidad f tal que las longitudes de los lados de uno de los triángulos son iguales a las longitudes de los lados del otro triángulo multiplicadas por ese factor f. En particular, se obtienen las dos igualdades siguientes
![]()
De forma análoga, si miramos a los otros dos triángulos rectángulos similares a los dos anteriores se obtiene que existe un factor de proporcionalidad g y se cumplen igualdades parecidas a las anteriores, en concreto, las siguientes igualdades
![]()
Utilizando las cuatro fórmulas anteriores, es fácil deducir que x = a, como se quería demostrar. Por lo tanto, las longitudes de los segmentos AB y XY son iguales, como afirma el teorema de los globos oculares.
Existen muchas otras demostraciones, desde la propuesta por el matemático peruano Antonio Gutiérrez, que podéis leer en su página GoGeometry, hasta una relacionada con un sangaku (puede leerse más sobre los sangakus en la entrada Sangakus, pasión por los desafíos matemáticos), que podéis leer en la página Cut the knot, del matemático Alexander Bogomolny.
 Portada del número 2, del volumen 53 (2022), de la revista The College Mathematics Journal, en el que se publica el artículo A Variant of the Eyeball Theorem, del ingeniero dominicano Emmanuel Antonio José García
Portada del número 2, del volumen 53 (2022), de la revista The College Mathematics Journal, en el que se publica el artículo A Variant of the Eyeball Theorem, del ingeniero dominicano Emmanuel Antonio José GarcíaBibliografía
1.- David Wells, The Penguin Dictionary of Curious and Interesting Geometry, Penguin, 1991.
2.- David Acheson, The Wonder Book of Geometry. Oxford University Press, 2020.
3.- Chris Pritchard (editor), The Changing Shape of Geometry. Celebrating a Century of Geometry and Geometry Teaching, Cambridge University Press, 2003.
4.- George W. Evans, Ratio as multiplier, The Mathematics Teacher, Vol. 31, No. 3, pp. 114-116, 1938.
5.- Claudi Alsina, Roger B. Nelsen, Icons of Mathematics: An Exploration of Twenty Key Images, MAA, 2011.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Teorema de los globos oculares se ha escrito en Cuaderno de Cultura Científica.
Los primeros homininos de Europa habrían llegado al sur de Iberia
Una de las controversias más importantes sobre la evolución y la expansión humana es cuándo y por qué camino llegaron los primeros homínidos a Europa desde el continente africano. Ahora, unas dataciones con técnicas geológicas de los yacimientos de Orce (cuenca de Baza, Granada) sitúan los restos humanos hallados en esta zona como los más antiguos de Europa, con aproximadamente 1,3 millones de años. Estos resultados refuerzan la hipótesis de la llegada de los seres humanos a Europa por el sur de la península Ibérica, a través del estrecho de Gibraltar, en lugar de dando la vuelta al Mediterráneo por la vía asiática. El trabajo, liderado por Lluís Gibert, investigador y profesor de la Facultad de Ciencias de la Tierra de la Universidad de Barcelona, ha contado con la participación de investigadores del Centro de Geocronología de Berkeley y de la Universidad Estatal de Murray (Estados Unidos).
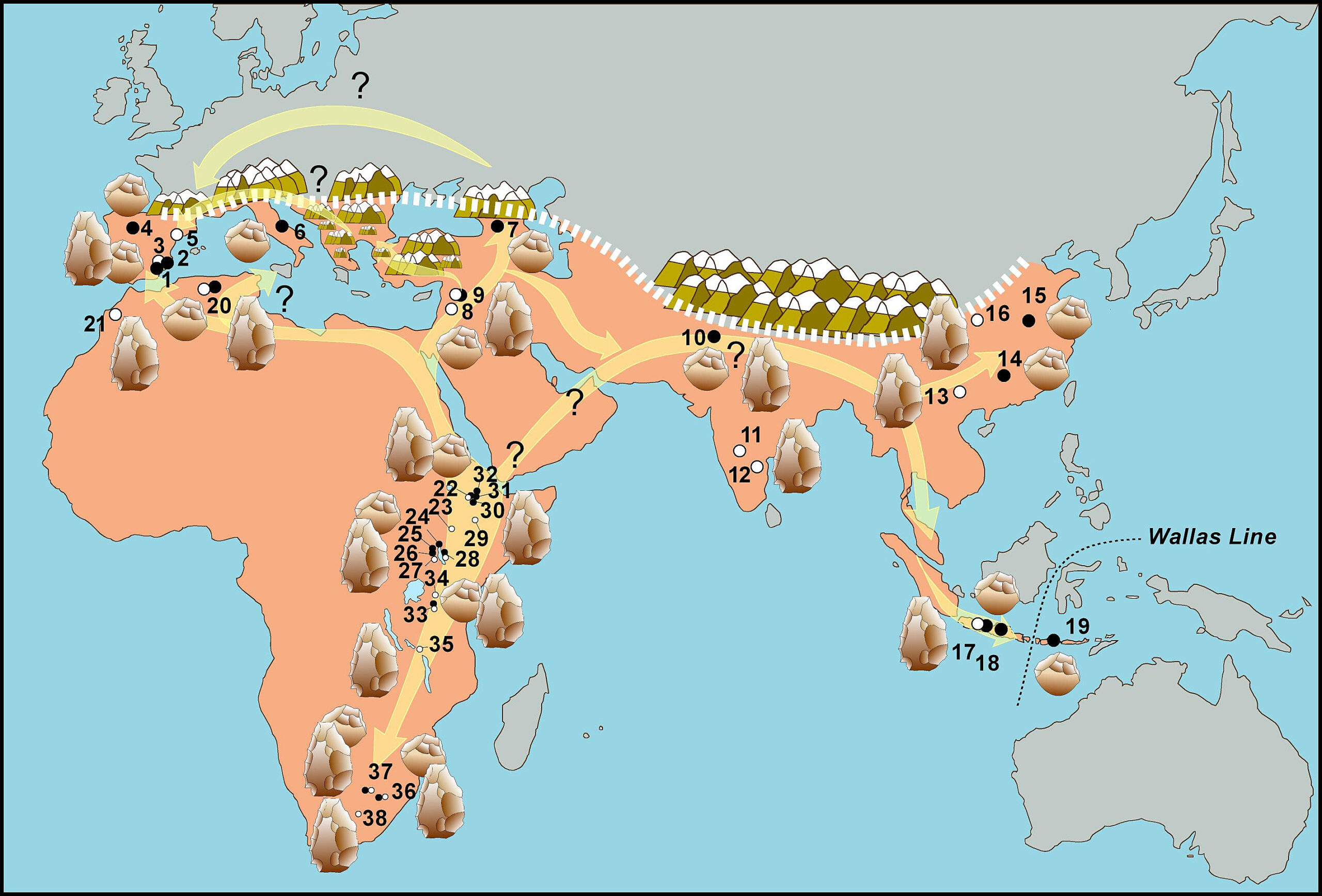 Principales yacimientos datados de homininos con más de 1 millón de años. Europa: 1. Orce, 2. Cueva Victoria, 3 Cueva Negra, 4. Atapuerca, 5. Barranc de la Boella, 6 Pirro Nord. Asia occidental: 7. Dmanisi, 8. Ubeidiya, 9. Gesher Benot. Asia Central: 10. Riwat, 11. Issanpur, 12 Attirampakkam. Asia Oriental: 13. Bose, 14. Yuanmou Basin, 15. Nihewan Basin, 16. Lounan Basin, 17 Sangiran, 18. Mojokerto, 19. Flores. África: 20. Ain Hanech, Ain Ain Boucherit 21. Thomas-1, 22. Gona, 23. Konso Kandula, 24. Omo, 25. Lokalalei, 26 Lomekwi, 27 Kokiselei 28, Kobi Fora, 29 Gaded, 30 M. Awash, 31 Hadar, 32 Ledi Geraru, 33 Olduvai, 34 Peninj, 35 Mwanganda, 36. Sterkfontein, 37 Swartkrans, 38 Vaal River. Fuente: Referencia.El paleomagnetismo de Orce
Principales yacimientos datados de homininos con más de 1 millón de años. Europa: 1. Orce, 2. Cueva Victoria, 3 Cueva Negra, 4. Atapuerca, 5. Barranc de la Boella, 6 Pirro Nord. Asia occidental: 7. Dmanisi, 8. Ubeidiya, 9. Gesher Benot. Asia Central: 10. Riwat, 11. Issanpur, 12 Attirampakkam. Asia Oriental: 13. Bose, 14. Yuanmou Basin, 15. Nihewan Basin, 16. Lounan Basin, 17 Sangiran, 18. Mojokerto, 19. Flores. África: 20. Ain Hanech, Ain Ain Boucherit 21. Thomas-1, 22. Gona, 23. Konso Kandula, 24. Omo, 25. Lokalalei, 26 Lomekwi, 27 Kokiselei 28, Kobi Fora, 29 Gaded, 30 M. Awash, 31 Hadar, 32 Ledi Geraru, 33 Olduvai, 34 Peninj, 35 Mwanganda, 36. Sterkfontein, 37 Swartkrans, 38 Vaal River. Fuente: Referencia.El paleomagnetismo de Orce
La nueva datación se ha basado en analizar el paleomagnetismo de un área de la región de Orce, donde nunca se había muestreado antes y que, ha sido protegida de la erosión que ha sufrido esta cuenca a lo largo de los años. Esta técnica es un método de datación relativo basado en estudiar la inversión de los polos magnéticos del planeta debido a la dinámica interna de la Tierra. Estos cambios no tienen una periodicidad concreta, pero quedan registrados en los minerales y permiten establecer períodos de tiempo a partir de los diferentes eventos magnéticos.
Estos nuevos datos son muy precisos gracias a la larga secuencia sedimentaria que aflora en Orce. «La singularidad de estos yacimientos es que están estratificados y dentro de una secuencia de sedimentaria muy larga, de más de ochenta metros. Normalmente, los yacimientos se encuentran en cuevas o dentro de secuencias estratigráficas muy cortas, que no te permiten desarrollar secuencias paleomagnéticas largas en las que puedas encontrar diferentes inversiones magnéticas», apunta Lluís Gibert.
Los investigadores han podido identificar una secuencia de polaridad magnética «con cinco eventos magnéticos que permiten situar a los tres yacimientos de Orce con presencia humana entre el subcrono Olduvai y Jaramillo, es decir, entre 1,77 y 1,07 millones de años (Ma)», explica el investigador. Posteriormente, han aplicado un modelo estadístico de edad para refinar con precisión la cronología de los distintos niveles estratigráficos con un margen de error de solo 70.000 años. El resultado de esta innovadora metodología es que el yacimiento más antiguo con presencia humana de Europa sería Venta Micena con una edad de 1,32 Ma, seguido de Barranco León, con una edad de 1,28 y finalmente Fuente Nueva 3, con una edad de 1,23 Ma. «Con estos datos, el otro gran yacimiento de la península, el de Sima del Elefante en Atapuerca, quedaría relegado a un segundo puesto, muy detrás de Orce, entre 0,2 y 0,4 Ma más moderno», añade el investigador.
La fauna apuntala la antigüedad del yacimiento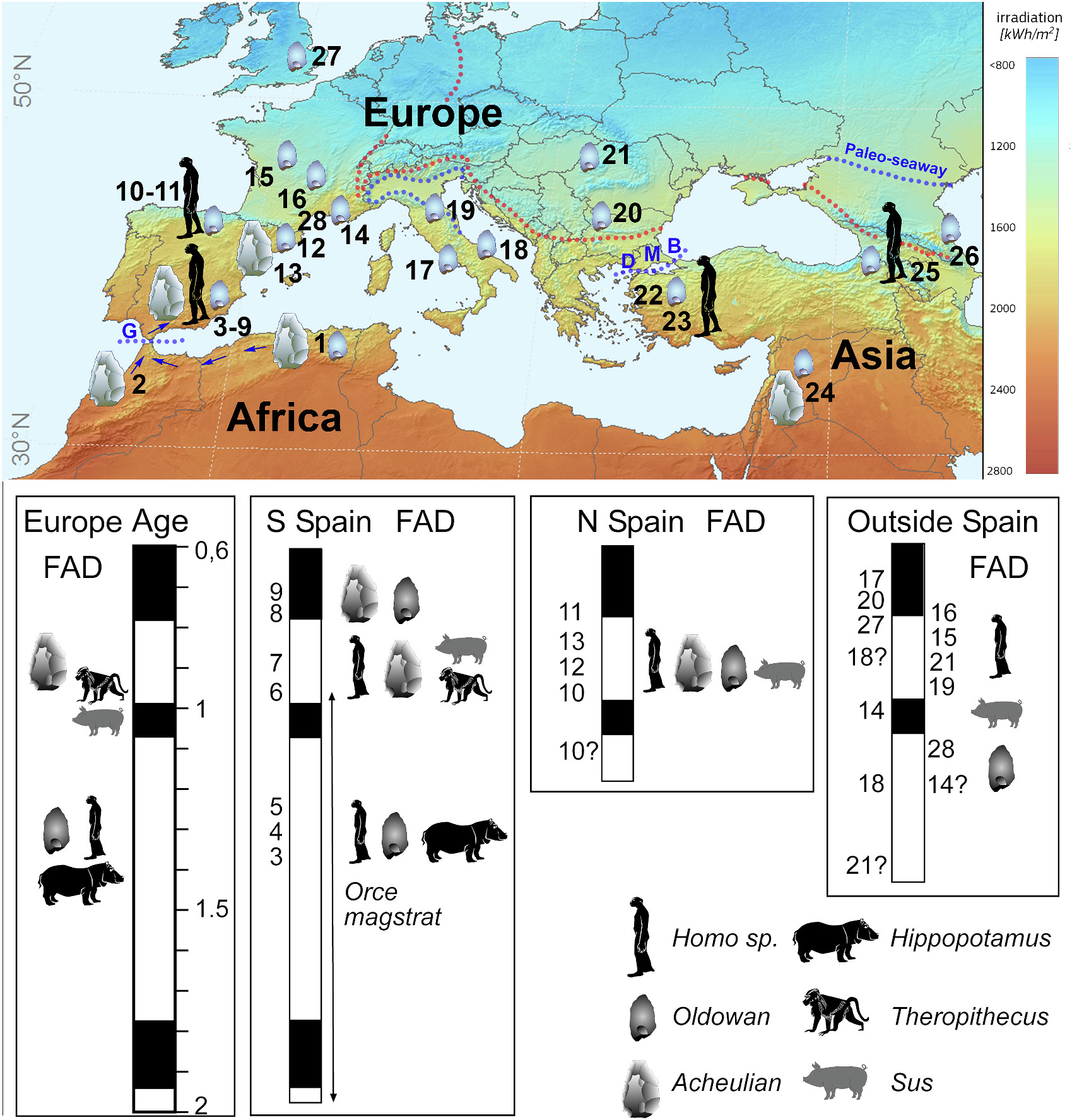 Mapa que muestra la irradiación solar de la región mediterránea mostrando los principales yacimientos con restos de homininos. Fuente: Referencia
Mapa que muestra la irradiación solar de la región mediterránea mostrando los principales yacimientos con restos de homininos. Fuente: ReferenciaPara completar la datación, el estudio también ha analizado la fauna que se encuentra en los diferentes yacimientos de Orce, ya que esta es diferente según el período, y la ha comparado con la que se ha encontrado en otros yacimientos del Pleistoceno temprano situados en otros lugares de Europa.
En este sentido, en el trabajo se presenta un análisis detallado de los micromamíferos y grandes mamíferos de todos los yacimientos de Orce, realizado por el experto Robert Martin, a partir de las colecciones paleontológicas almacenadas en el Museo del Instituto Catalán de Paleontología Miguel Crusafont (IPS) de Sabadell. «Los resultados muestran que la fauna pequeña y grande de Orce es más primitiva que, por ejemplo, la de la Sima del Elefante, donde las evidencias muestran que el roedor Allophaiomys lavocati es más evolucionado que el Allophaiomys recuperado de los yacimientos de Orce», detalla Gibert.
Otro indicador relevante de la antigüedad de los yacimientos de Orce es la ausencia de los antepasados de los cerdos. «Son animales que se consideran inmigrantes asiáticos y que no se han encontrado en ningún yacimiento europeo con una antigüedad de entre 1 y 1,5 Ma, mientras que sí se han encontrado en la Sima del Elefante, apoyando que la fauna de Orce es más antigua», explica el investigador.
Evidencias que apuntan al paso por GibraltarEsta nueva datación se añadiría, según el investigador, a otras evidencias que decantarían, la balanza de la colonización de Europa por el estrecho de Gibraltar, en lugar de la vía alternativa: la vuelta al Mediterráneo por Asia, como por ejemplo «la existencia de una industria lítica con similitudes con la que se ha encontrado en el norte del continente africano y también por la presencia de restos de fauna africana en el sur de la península, como los de Hippopotamus, hallado en los yacimientos de Orce, y las de Theropithecus oswaldi, un primate africano similar a un papión, halladas en la cueva Victoria, un yacimiento cerca de Cartagena (Murcia), inexistentes en ningún otro lugar de Europa».
«También defendemos la hipótesis —añade el investigador— que llegaron desde Gibraltar porque no se han encontrado evidencias más antiguas en ningún otro yacimiento del recorrido alternativo».
Estos nuevos datos son muy precisos gracias a la larga secuencia sedimentaria que aflora en Orce.
Similitud con los homínidos de la isla de FloresCon estos resultados, los investigadores señalan un «diacronismo» entre la ocupación más antigua de Asia, mide 1,8 Ma y la más antigua de Europa, que sería de hace 1,3 Ma, de modo que los homínidos africanos habrían llegado en el suroeste de Europa más de 0,5 Ma después de salir por primera vez de África hace aproximadamente 2 Ma. «Estas diferencias en la expansión humana se explicarían porque Europa está aislada de Asia y de África por barreras biogeográficas difíciles de superar, tanto por el este: (estrecho del Bósforo, Dardanelos, mar de Mármara) como por el oeste (estrecho de Gibraltar). La humanidad llegó a Europa en el momento en que tuvo la tecnología necesaria para cruzar barreras marítimas, tal y como ocurrió antes del millón de años en la isla de Flores (Indonesia)», apunta Gibert. En este sentido, el investigador añade que la ruta de Gibraltar requiere actualmente atravesar hasta catorce kilómetros de vía marítima, pero «quizás en el pasado esta distancia era menor en algunos momentos debido a la alta actividad tectónica en esta región y las fluctuaciones del nivel del mar favoreciendo las migraciones».
«Tal y como se cita en el trabajo —añade—, hemos identificado otras migraciones de fauna africanas a través de Gibraltar en momentos anteriores, hace 6.2 y 5.5 Ma cuando el estrecho de Gibraltar era muy reducido».
Los vestigios humanos en OrceLos restos humanos encontrados en los yacimientos de Orce son un total de cinco, desde que se iniciaron las excavaciones en 1982 por el paleoantropólogo Josep Gibert. En primer lugar, se encontraron en Venta Micena dos fragmentos de húmero mordidos por las hienas y también partes de un fragmento craneal que consiste en dos parietales y un occipital, asociados a una abundante fauna del Pleistoceno temprano. La procedencia humana de estos restos generó una gran controversia durante años, aunque según estudios paleoproteómicos independientes realizados por las universidades de Granada y San Francisco identificaron proteínas humanas en los restos.
El descubrimiento posteriormente en los yacimientos cercanos de Barranco León y Fuente Nueva 3 de dos dientes molares humanos y miles de herramientas líticas olduvayanas —una de las primeras industrias líticas humanas— así como marcas de corte en huesos «sirvieron para consolidar la evidencia de la presencia de homínidos en el Pleistoceno temprano de Orce», concluye Lluís Gibert.
Referencia:
Luis Gibert, Gary Scott, Alan Deino, Robert Martin (2024) Magnetostratigraphic dating of earliest hominin sites in Europe Earth-Science Reviews doi: 10.1016/j.earscirev.2024.104855
Edición realizada por César Tomé López a partir de materiales suministrados por la Universidad de Barcelona
El artículo Los primeros homininos de Europa habrían llegado al sur de Iberia se ha escrito en Cuaderno de Cultura Científica.
Una nueva clase de martemotos
A estas alturas podemos decir sin duda alguna que la misión InSight de la NASA ha sido -y probablemente será en las próximas décadas con la reinterpretación de sus datos- una importante fuente de conocimiento sobre la estructura interna de Marte, pero también sobre procesos que ocurren mucho más próximos a su superficie, como lo fueron la detección de posibles terremotos de origen volcanotectónico o la caída e impacto de meteoroides y asteroides contra la superficie.
Precisamente, los impactos sobre las superficies planetarias nos han aportado una visión muy importante sobre como ha sido la historia y evolución de nuestro Sistema Solar en su conjunto, pero también son capaces de informarnos de manera individual como ha sido la evolución y el grado de actividad de cada uno de los cuerpos que podemos observar con detalle.
 Un impacto reciente sobre la superficie de Marte. Sabemos que es reciente porque todavía se ve la eyecta -el material que sale despedido por el impacto- de un color oscuro sobre la superficie y, en segundo lugar, por la forma todavía marcada del cráter. Conforme pase el tiempo la eyecta irá volviéndose anaranjada por el depósito de polvo y al cráter suavizar su forma. Imagen cortesía de NASA/JPL-Caltech/Universidad de Arizona.
Un impacto reciente sobre la superficie de Marte. Sabemos que es reciente porque todavía se ve la eyecta -el material que sale despedido por el impacto- de un color oscuro sobre la superficie y, en segundo lugar, por la forma todavía marcada del cráter. Conforme pase el tiempo la eyecta irá volviéndose anaranjada por el depósito de polvo y al cráter suavizar su forma. Imagen cortesía de NASA/JPL-Caltech/Universidad de Arizona.Y es que, en Marte, como en cualquier otro lugar, la frecuencia, tamaño y distribución de los cráteres de impacto nos sirven como una herramienta para calcular la edad de las superficies geológicas, permitiéndonos conocer el ritmo de los distintos procesos geológicos que están o estuvieron en funcionamiento y su grado de actividad. Y como hemos dicho más de una vez en esta sección, por norma general, cuanto más antigua es una superficie planetaria y menos ha cambiado, más cráteres acumulará por unidad de superficie, ya que ha estado más tiempo expuesta a la caída de cuerpos sobre esta.
De manera general, este método nos permite mediante el uso de las imágenes tomadas por los satélites en órbita -o que han pasado cerca- del planeta calcular la edad, pero tiene un importante problema relacionado con la formación de los cráteres más pequeños y numerosos, ya que desconocemos el ritmo aproximado de impactos por año capaces de generarlos.
Gracias a los datos sísmicos tomados durante la misión InSight parece que al menos para Marte podríamos tener una respuesta que nos permita una mejor calibración de estas escalas de edad basadas en los cráteres de impacto, ya que ha sido capaz de detectar con su sismógrafo algunos de los impactos ocurridos durante el desarrollo de su misión. Pero además de emplear la extraordinaria visión de la Mars Reconaissance Orbiter, su cámara HiRISE puede tomar imágenes con una resolución en el entorno de los 30 cm/pixel- para poder localizar el punto de impacto y el tamaño del cráter.
 Uno de los impactos detectados por la InSight y observado por la Mars Reconaissance Orbiter. En este caso el impacto ocurrió el 5 de septiembre de 2021. Imagen cortesía de NASA/JPL-Caltech/Universidad de Arizona.
Uno de los impactos detectados por la InSight y observado por la Mars Reconaissance Orbiter. En este caso el impacto ocurrió el 5 de septiembre de 2021. Imagen cortesía de NASA/JPL-Caltech/Universidad de Arizona.En un nuevo artículo publicado por Zenhäusern et al. (2024) los científicos han hecho una búsqueda y un análisis de un tipo de eventos sísmicos muy particulares, los martemotos de muy alta frecuencia o VHF. Este tipo de martemotos -discúlpenme si les disgusta este término- tienen unas características muy diferentes a los terremotos producidos por la actividad tectónica de Marte.
La primera es una liberación de energía muy fuerte en frecuencias que van de los 5 a los 30 Hz; La segunda, una frecuencia de corte o esquina que indica a los científicos que se trata de un evento de muy corta duración y, por último, una fuerte sacudida en la horizontal a frecuencias superiores a los 5 Hz. Estas tres características -que se pueden estudiar gracias a los datos obtenidos por el sismómetro de la InSight- son buenos marcadores de los impactos de meteoroides a hipervelocidad.
Los investigadores han confirmado que todos los impactos detectados durante la misión de la InSight muestran estas características en la señal, por lo que es plausible que todos los eventos de este tipo puedan atribuirse a los impactos contra la superficie de Marte. Y, además, la detección de algunos estos eventos concluyen con un tren de ondas que se interpretan como señales acústicas producidas por la perturbación que el impacto crea en la atmósfera.
 Otros tres impactos muy recientes captados por la InSight y la Mars Reconaissance Orbiter. En este caso, la fecha de los impactos fueron el 27 de mayo de 2020 y el 18 de febrero y 31 de agosto de 2021. Imagen cortesía de NASA/JPL-Caltech/Universidad de Arizona.
Otros tres impactos muy recientes captados por la InSight y la Mars Reconaissance Orbiter. En este caso, la fecha de los impactos fueron el 27 de mayo de 2020 y el 18 de febrero y 31 de agosto de 2021. Imagen cortesía de NASA/JPL-Caltech/Universidad de Arizona.Pero hay un dato más y que es muy importante detallar: la distribución espacial de este tipo de eventos muestra un patrón aleatorio, mientras que los eventos tectónicos detectados por la InSight, como es normal, tienden a agruparse en estructuras tectónicamente activas (como las fallas), al igual que ocurre en nuestro planeta.
El análisis de los datos sísmicos de la InSight ha permitido a los científicos estimar que cada año se forman sobre la superficie de Marte entre 280 y 360 cráteres mayores de 8 metros, coincidiendo este dato con los modelos cronológicos ya publicados, pero, y esto es importante, un ritmo mucho mayor que el que se aprecia a través de las imágenes de satélite… ¿Por qué de esta discrepancia?
Muy probablemente se deba a factores como la resolución de las cámaras, la cobertura en imágenes del planeta a alta resolución -ya que para ver nuevos cráteres las imágenes tienen que tomarse de manera repetida a lo largo del tiempo- y también, quizás, la cantidad de polvo que cubre algunas superficies, puesto que puede complicar la detección de cráteres más pequeños salvo que el ángulo de luz sea muy oblicuo.
¿Qué consecuencias puede tener este estudio? En primer lugar, a nivel científico, el ayudarnos a calibrar mejor las escalas temporales basadas en los cráteres de impacto, lo que a su vez nos permitiría “afinar” mejor las edades de las distintas capas de roca, de las coladas de lava o la duración de algunos eventos que podemos ver en el registro geológico del planeta rojo e, incluso, pone de manifiesto la utilidad de la toma de datos sísmicos en otros lugares de nuestro Sistema Solar para afinar las escalas temporales… ¿Veremos, por lo tanto, más sismómetros montados en sondas de superficie?
Y ya por último, nos puede ayudar a conocer mejor cuál es el riesgo que podrían sufrir las futuras misiones de exploración humana del planeta Marte y qué medidas de protección podrían ser útiles ante este tipo de colisiones que, por ahora, son inevitables.
Referencias:
Zenhäusern, Géraldine, Natalia Wójcicka, Simon C. Stähler, Gareth S. Collins, Ingrid J. Daubar, Martin Knapmeyer, Savas Ceylan, John F. Clinton, y Domenico Giardini (2024) An Estimate of the Impact Rate on Mars from Statistics of Very-High-Frequency Marsquakes Nature Astronomy doi: 10.1038/s41550-024-02301-z.
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Una nueva clase de martemotos se ha escrito en Cuaderno de Cultura Científica.
Alzhéimer, detección precoz con inteligencia artificial
La enfermedad de Alzheimer es la causa más común de demencia y afecta a millones de ancianos en todo el mundo. Solo en España se estima que existen más de 900 000 personas afectadas por esta enfermedad que se ha convertido en una prioridad de salud pública para el Ministerio de Sanidad.
 Imagen del encéfalo de un varón de 56 años generada por tomografía por emisión de positrones. Fuente: Jens Maus / Wikimedia Commons
Imagen del encéfalo de un varón de 56 años generada por tomografía por emisión de positrones. Fuente: Jens Maus / Wikimedia CommonsLa detección precoz es clave para mejorar la calidad de vida de los afectados y sus familias, pero identificarla en sus estadios iniciales no siempre es fácil. Para intentar mejorar en este campo y lograr mejores resultados, investigadores de la Universidad Politécnica de Madrid (UPM) han aplicado técnicas de inteligencia artificial (IA) de aprendizaje automático al análisis de diferentes modalidades de imágenes médicas utilizadas para el diagnóstico de enfermedades neurológicas.
«Desde un punto de vista clínico, la resonancia magnética (RM) y la tomografía por emisión de positrones (PET) son las dos modalidades de imágenes médicas utilizadas en el diagnóstico de este tipo de enfermedades, ya que aportan información complementaria de los aspectos anatómicos y metabólicos de la enfermedad», explica Consuelo Gonzalo, investigadora del Centro de Tecnología Biomédica de la UPM y una de las autoras de este trabajo.
“Pero lamentablemente estas pruebas no se realizan sincrónicamente lo que dificulta su integración y la interpretación adecuada de sus resultados por parte de los profesionales médicos”, continúa.
Abordar este problema es el objetivo que se marcaron los investigadores de la UPM y la propuesta para ello fue desarrollar una metodología que utiliza las redes neuronales convolucionales.
Esta herramienta se trata de una técnica de aprendizaje automático que potencia las tareas de análisis de imágenes y visión por ordenador, permitiendo obtener información significativa de imágenes digitales, vídeos y otras entradas visuales, así como tomar medidas basándose en esas entradas.
Diagnóstico de alzhéimer a partir de datos incompletosPara ello, los investigadores de la UPM realizaron un análisis sistemático de las imágenes de MRI y PET para la evaluación del estado de demencia, utilizando diferentes técnicas de fusión (fusiones temprana, tardía e intermedia).
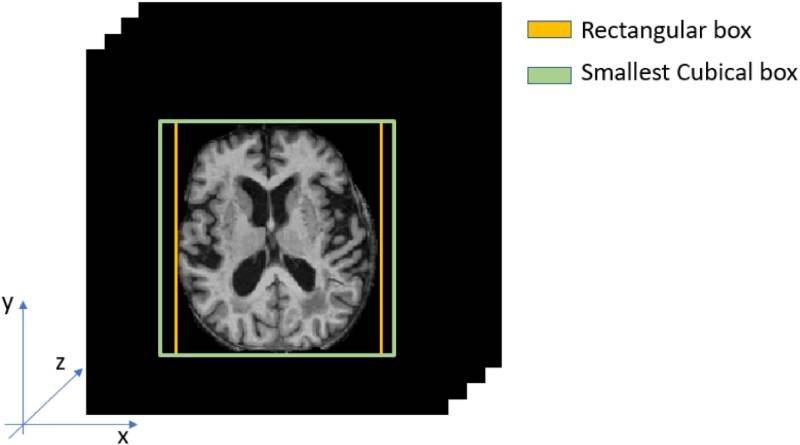 Fuente: Universidad Politécnica de Madrid
Fuente: Universidad Politécnica de MadridA continuación, diseñaron e implementaron una solución completamente basada en redes neuronales convolucionales 3D que extraía características de todo el volumen encefálicol en tres dimensiones. Una vez hecho esto, aplicaron una estrategia de entrenamiento capaz de manejar un conjunto de datos altamente desequilibrado e incompleto.
“Hasta donde sabemos, la metodología propuesta representa el primer trabajo que proporciona un análisis de diferentes técnicas de fusión basada en aprendizaje profundo multimodal para la evaluación de la severidad de la demencia”, explica la investigadora de la UPM.
“El tipo de soluciones que se desarrollan en este trabajo puede ser una herramienta de ayuda a la decisión de enorme interés práctico para los neurólogos”, añade.
En investigaciones futuras, los científicos pretenden seguir explorando la fusión de diferentes modalidades, analizando más a fondo las propiedades de la representación de características compartidas.
“Se deben investigar enfoques que pretendan mejorar la integración de datos heterogéneos, generalizándolos a casos de estudio con más de dos modalidades de imágenes. También se debe abordar la explicabilidad de los modelos implementados, evaluando las decisiones tomadas por las redes en comparación con el diagnóstico clínico», concluyen.
Referencia:
Michela Gravina, Ángel García-Pedrero, Consuelo Gonzalo-Martín, Carlo Sansone, Paolo Soda (2024) Multi input–Multi output 3D CNN for dementia severity assessment with incomplete multimodal data Artificial Intelligence in Medicine doi: 10.1016/j.artmed.2024.102774
Edición realizada por César Tomé López a partir de materiales suministrados por la Universidad Politécnica de Madrid
El artículo Alzhéimer, detección precoz con inteligencia artificial se ha escrito en Cuaderno de Cultura Científica.
Día de pi 2024: El tamaño importa… ¿o no?

El número Pi, representado por la letra griega π, es una de las constantes matemáticas más famosas e importantes que existen en el mundo. Este número irracional, que determina la relación entre la longitud de una circunferencia y su diámetro, concierne a múltiples disciplinas científicas como la física, la ingeniería y la geología, y tiene aplicaciones prácticas sorprendentes en nuestro día a día.
La fascinación que ha suscitado durante siglos es tal, que se viene estudiando desde hace más de 4.000 años e, incluso, cuenta con su propio día en el calendario: el 14 de marzo. Este evento internacional vino de la mano del físico estadounidense Larry Shaw, quien en 1988 lanzó la propuesta de celebrar esta efeméride. La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática: 3-14 martxoaren 14 en euskara / 3-14 March, 14th en inglés. En los últimos años, la conmemoración del Día de Pi se ha ido extendiendo, hasta tal punto que el 26 de noviembre de 2019 la UNESCO proclamó el 14 de marzo Día Internacional de las Matemáticas.
Un año más, el Basque Center for applied Mathematics-BCAM y la Cátedra de Cultura Científica de la UPV/EHU nos sumamos a la celebración, organizando la quinta edición del evento BCAM NAUKAS, que se desarrolló a lo largo del 14 de marzo en el Bizkaia Aretoa de UPV/EHU.
En esta charla, Raquel Villacampa parte del hecho de que, desde la antigüedad, se ha querido cuantificar la belleza, incluida y especialmente la del cuerpo humano. Incluso hoy día se entrena a las máquinas para ello.
Raquel Villacampa Gutiérrez es profesora del Departamento de Matemáticas de la facultad de Ciencias de la Universidad de Zaragoza. Es miembro del Instituto Universitario de Matemáticas y Aplicaciones de la Universidad de Zaragoza (IUMA). Es una conocida divulgadora de las matemáticas.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Día de pi 2024: El tamaño importa… ¿o no? se ha escrito en Cuaderno de Cultura Científica.
Lo que nunca nos contaron en el colegio sobre el ciclo del agua
El ciclo del agua es uno de los contenidos cruciales para conocer el funcionamiento básico de la hidrosfera en el currículo de la educación obligatoria. ¿Quién no lo recuerda? Precipitaciones que en la superficie continental conforman la escorrentía, o que se infiltran en el suelo y alimentan las aguas subterráneas. La evaporación devuelve este elemento en forma gaseosa a la atmósfera que, tras la condensación, forma las nubes que darán lugar de nuevo a las precipitaciones.
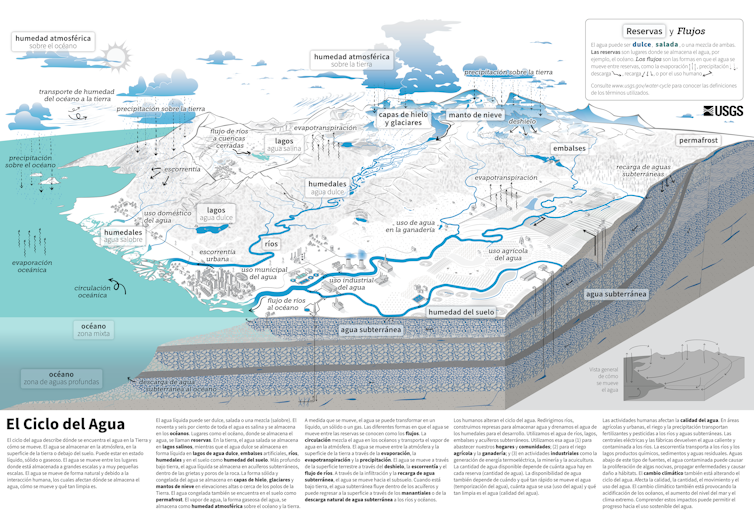 El ciclo hidrológico o ciclo del agua es el proceso de circulación del agua entre los distintos compartimentos que forman la hidrósfera.
El ciclo hidrológico o ciclo del agua es el proceso de circulación del agua entre los distintos compartimentos que forman la hidrósfera.Servicio Geológico de Estados Unidos / Wikimedia Commons
Menor atención se ha prestado a procesos geofísicos de gran importancia como la evapotranspiración asociada a los seres vivos o la interconexión entre los diferentes componentes del ciclo, fundamentalmente los del suelo, el gran olvidado.
Lo cierto es que lo que aprendimos en el colegio resulta incompleto para comprender el complejo funcionamiento de la hidrosfera. Sobre todo, si no se consideran otros procesos que interfieren directa o indirectamente. En especial, la dominación humana del ciclo del agua está ausente de representaciones y percepciones, a pesar de que las personas dependemos absolutamente del agua para nuestra supervivencia: la ingesta directa, la higiene, la producción de alimentos, los procesos industriales o el ocio y bienestar.
Saqueo en las masas de aguaLas causas centrales de la actual crisis mundial del agua intervienen en el ciclo junto con los procesos geofísicos y comienzan con la sobreexplotación de este recurso. El 70 % de los acuíferos españoles se encuentran sometidos a extracciones superiores a sus recargas. Esto genera sequías de gran magnitud en zonas tan relevantes como los parques nacionales de Doñana o las Tablas de Daimiel.
Asimismo, el excesivo consumo de agua ha transformado nuestros ríos en meros canales, repletos de embalses y trasvases. De este modo, su estado ecológico se ha visto notablemente afectado, lo que pone en riesgo los numerosos servicios ecosistémicos que nos prestan.
La sobreexplotación está relacionada con nuestro modelo socioeconómico, que abarca aspectos como el consumo de alimentos que requieren enormes cantidades de agua para su producción y modelos agroganaderos intensivos con superficies de riego que siguen incrementándose cada día.
 Los nuevos regadíos permiten el cultivo superintensivo de los olivos, una especie tradicionalmente de secano.
Los nuevos regadíos permiten el cultivo superintensivo de los olivos, una especie tradicionalmente de secano.Michelangelo-36 / Wikimedia Commons, CC BY
Los nuevos regadíos se asocian al cultivo de todo tipo de productos, como frutas tropicales (aguacate, mango…), cultivos con altos requerimientos de agua (maíz, alfalfa…) para alimentar al ganado, o el aumento de producción de cultivos tradicionalmente de secano como almendros, olivo o vid.
Turismo, ropa y pesticidasCompletan la ecuación otras actividades económicas, como el turismo (el consumo de agua por turista llega a quintuplicar el consumo per cápita local, asociado a piscinas, saunas, parques temáticos, mantenimiento de zonas ajardinadas o golf) y la moda (un kilo de algodón necesita 10 000 litros de agua para producirse y su cultivo genera problemas de sobreexplotación en numerosos ecosistemas acuáticos del planeta).
 De media, se estima que el consumo de agua para un campo de golf oscila entre los 200 y los 300.000 m3/año.
De media, se estima que el consumo de agua para un campo de golf oscila entre los 200 y los 300.000 m3/año.Lilrizz / Wikimedia Commons, CC BY
Otro factor a tener en cuenta es la contaminación de las masas de agua, que degrada los ecosistemas hídricos y, con ello, los servicios ecosistémicos que ríos, lagos y acuíferos aportan a la biosfera y al ser humano.
Por ejemplo, los nitratos de origen agroganadero provocan que casi el 30 % de las aguas subterráneas y el 50% de las superficiales presenten una mala calidad. Este hecho impide el acceso a agua potable a una buena parte de la población del país. Otro caso alarmante es la presencia de pesticidas en las diferentes masas de agua, especialmente tóxicos para la salud humana.
A ello se suman las alteraciones del medio físico: la intensa ocupación de diferentes zonas de la cuenca mediante cultivos o urbanizaciones modifica aspectos cruciales del ciclo del agua, como la evapotranspiración, la infiltración o la escorrentía. No solo comprometen la disponibilidad del recurso a nivel local, sino que aumentan los riesgos asociados a fenómenos climáticos extremos como las inundaciones.
Injusticia hídricaPor último, la subida de las temperaturas asociada al cambio climático provocado por la acción humana afecta directamente a diferentes procesos del ciclo del agua: aumento de la fusión de glaciares, de las tasas de evaporación y de evapotranspiración y modificación del régimen de precipitaciones.
 El embalse de Barrios de Luna (provincia de León) tras la sequía de 2017 en la Península ibérica. A principios de octubre de 2017 se encontraba en una situación crítica al 5 % de su capacidad.
El embalse de Barrios de Luna (provincia de León) tras la sequía de 2017 en la Península ibérica. A principios de octubre de 2017 se encontraba en una situación crítica al 5 % de su capacidad.Pablox / Wikimedia Commons, CC BY
Como consecuencia, la disponibilidad de agua dulce va en descenso, especialmente en zonas geográficas como la mediterránea. Sin embargo, su uso no hace sino incrementarse, mostrando la nula adaptación de la población a la realidad climática actual y poniendo en mayor riesgo, si cabe, el estado ecológico de nuestras masas de agua y ecosistemas.
Por tanto, la exclusión de actividad humana de las representaciones del ciclo del agua camufla algunas de las crisis socioecológicas más acuciantes, incluidas la seguridad y la justicia hídrica. Urge solventar estas carencias y activar recursos y métodos educativos como primer paso hacia la formación de las personas y hacia una gobernanza equitativa de este recurso esencial desde una visión planetaria, pero con el foco puesto en lo cotidiano.![]()
Sobre los autores: Rubén Ladrera Fernández, Profesor de Enseñanza Secundaria y Profesor Asociado del Área de Didáctica de las Ciencias Experimentales, Universidad de La Rioja y José Ramón Díez López, Profesor de Didáctica de Ciencias Experimentales, Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Lo que nunca nos contaron en el colegio sobre el ciclo del agua se ha escrito en Cuaderno de Cultura Científica.
¡Es una trampa (paleontológica)!
Cuando encontramos un yacimiento fósil, una de las primeras preguntas que nos hacemos es ¿por qué esos restos están ahí? ¿Los organismos que los produjeron vivían en ese lugar, estaban de paso o alguna otra entidad los arrastró hasta esa zona? Responder a esta pregunta no siempre es fácil, incluso, a veces, resulta imposible. Pero encontrar la solución nos permite contar fantásticas historias ocurridas hace millones de años. Y si no damos con la respuesta correcta, al menos generaremos hipótesis que, en muchas ocasiones, resultan apasionantes. Lo que sí es seguro es que, en todo ese proceso, las personas profesionales de la paleontología nos convertimos en detectives del pasado, al más puro estilo de miss Marple o monsieur Poirot y, al igual que estos inmortales personajes de Agatha Christie, muchas veces nos encontramos con trampas en nuestra búsqueda de la verdad.
 Fotografía aérea del enorme socavón producido en mayo de 2021 en la ciudad de Puebla, México, por un colapso del terreno, posiblemente provocado por un cambio en la compactación del suelo, fruto de variaciones en su humedad relativa. Imagen: Juan Carlos Sánchez Díaz / poblanerias.com / Wikimedia Commons
Fotografía aérea del enorme socavón producido en mayo de 2021 en la ciudad de Puebla, México, por un colapso del terreno, posiblemente provocado por un cambio en la compactación del suelo, fruto de variaciones en su humedad relativa. Imagen: Juan Carlos Sánchez Díaz / poblanerias.com / Wikimedia CommonsEn ocasiones nos topamos con noticias sorprendentes de que, de repente, el suelo se ha abierto bajo nuestros pies, quedando como testigo un enorme agujero que se traga todo lo que se encuentra sobre la superficie. La explicación a este evento, como no podía ser de otra manera, se encuentra en la Geología. La subsidencia es un término geológico con el que se define el hundimiento progresivo y relativamente lento del terreno. Aunque este hundimiento también se puede producir de manera súbita, provocando lo que se conoce como un colapso, que son los que abren los telediarios por su espectacularidad y peligro cuando suceden en zonas urbanizadas. Estos hundimientos generalmente están provocados por procesos naturales, tales como la compactación del sedimento superficial, el hundimiento del techo de una cavidad subterránea o un deslizamiento de tierra producido tras un terremoto. Pero también pueden ser inducidos o, al menos, acelerados por las acciones del ser humano: la extracción desmesurada del agua de los acuíferos desencadena una pérdida de la compactación de los materiales porosos subterráneos, que da lugar al desmoronamiento de los que tienen por encima; o una minería de interior mal planificada puede acabar con derrumbes de los techos de las galerías.
Os estaréis preguntando que a qué viene un cambio tan radical de tema entre el primer párrafo y el segundo. Pues aquí es donde os he puesto la trampa. Una trampa natural y muy geológica, por supuesto. Porque resulta que, en paleontología, denominamos trampa a hendiduras, socavones o fosas generadas por el hundimiento del terreno que actúan como grandes tumbas de animales, terminando, si todo va como esperamos, por dar lugar a un yacimiento fósil en el que se acumulan abundantes restos de organismos.
El proceso es el siguiente. De repente, y por motivos naturales, se produce un colapso del terreno generando un gran socavón o una amplia hendidura en el suelo. En el momento del hundimiento, algunos animales podían encontrarse justo encima de la porción de terreno que colapsó, siendo literalmente tragados por la tierra. Esta cavidad también se convertirá en un depósito de agua, acumulando tanto la de la lluvia como el agua de las avenidas de arroyos y riachuelos, atrayendo a sus profundidades a animales sedientos. O simplemente actuará como un agujero en el camino al que caerán aquellos animales que pasen despistados junto a él. Sea como fuere, todos aquellos animales, grandes y pequeños, que se precipiten en el socavón, quedarán atrapados en su interior, sin posibilidad de salir. Y esta acumulación de presas indefensas se convertirá en un imán para depredadores hambrientos, que no durarán en precipitarse al agujero para darse un festín, sin saber que será su última comida. Incluidos los carroñeros, atraídos en este caso por el olor de la carne en descomposición, también desconocedores de que correrán la misma suerte que sus presas, caerán de cabeza en la trampa. Con el paso del tiempo, todos estos restos quedarán enterrados por la acumulación de los sedimentos que, poco a poco, rellenan el socavón. Y, miles o millones de años después, acabarán preservados en forma de fósiles. Vamos, que el nombre de trampas naturales les viene que ni pintado a estos agujeros del terreno en los que se produce el depósito de multitud de animales.
Identificar si el yacimiento fósil que hemos encontrado es una trampa o no es relativamente fácil. El estudio geológico nos da muchas pistas, ya que se trata de zonas de acumulación de sedimentos con unos límites bien definidos y que se encuentran rodeados por rocas sólidas. Además, en ambientes naturales, hay una mayor presencia de microorganismos frente a organismos de mayor tamaño y un mayor porcentaje de herbívoros que de carnívoros. Sin embargo, en las trampas se encuentran grandes acumulaciones de animales macroscópicos y están invertidas las proporciones, apareciendo una gran abundancia de carnívoros (el anhelo de una presa fácil atrae a muchos depredadores, pero terminan convirtiéndose en el cazador cazado). Incluso el estado de conservación de los restos es casi excepcional en la mayoría de los casos, apareciendo esqueletos muy completos y con los huesos en conexión anatómica (muchos de los animales morían al caer al agujero y cuando llegaban los depredadores no les daba tiempo a desperdigar los restos porque terminaban corriendo la misma suerte que sus presas).
 Recreación de la trampa natural del yacimiento paleontológico del Cerro de los Batallones, Madrid, con los animales atrapados en su interior. Ilustración: David Zurita Gómez /behance.net
Recreación de la trampa natural del yacimiento paleontológico del Cerro de los Batallones, Madrid, con los animales atrapados en su interior. Ilustración: David Zurita Gómez /behance.netLos yacimientos paleontológicos de tipo trampa natural son más comunes de lo que pensamos. Un ejemplo son los yacimientos paleontológicos del Cerro de los Batallones, en Madrid, donde aparecen abundantes fósiles de macrovertebrados de finales del Periodo Mioceno que permiten conocer la fauna que hábito en el centro peninsular hace entre unos 11 y 9 millones de años. O el yacimiento del Complejo Galería, en la Sierra de Atapuerca, una trampa natural que aprovechaban las poblaciones de preneandertales para aprovisionarse de la carne de los animales que caían en ella.
Aunque la naturaleza hace trampas, también nos da una herramienta para evitarlas, la Geología. No es necesario esperar a ver como se abre la tierra y se traga un coche o una casa para saber que el terreno se puede hundir y engullir lo que se encuentre en su camino. Mientras paseamos por el campo, si miramos alrededor, las rocas, el paisaje, el tipo de sedimento e, incluso, los cambios de vegetación nos están dando pistas sobre la posibilidad de encontrarnos con socavones o hendiduras en donde podríamos caernos si damos un mal paso. Así que, si no queremos terminar formando parte de un yacimiento paleontológico muy particular en unos miles de años, más nos vale mirar bien donde pisamos para no caer en la trampa.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo ¡Es una trampa (paleontológica)! se ha escrito en Cuaderno de Cultura Científica.
Warren Weaver, de la física matemática a la traducción automática
No sobreestiméis la ciencia, no penséis que la ciencia es todo lo que hay, no os concentréis tanto en la ciencia que acabéis viviendo una vida deformada. La ciencia no es todo lo que hay, y la ciencia no es capaz de resolver todos los problemas de la vida. También hay muchos otros problemas muy importantes que la ciencia no puede resolver. Así que espero que no haya nadie en esta sala que vaya a pasar los próximos siete días sin leer algo de poesía. Espero que no haya nadie en esta sala que vaya a pasar los próximos siete días sin escuchar algo de música, algo de buena música, algo de música moderna, algo de música. Espero de verdad que no haya nadie aquí que no esté interesado en las artes creativas, interesado en el teatro, interesado en la danza. Espero que os intereséis seriamente por la religión, porque si no abrís vuestras mentes y vuestras actividades a esta gama de cosas, vais a llevar una vida demasiado estrecha.
Warren Weaver, Four Pieces of Advice to Young People, 1966.
 Warren Weaver (1940). Fuente: Wikimedia Commons.
Warren Weaver (1940). Fuente: Wikimedia Commons.
Warren Weaver nació el 17 de julio de 1894 en la ciudad de Reedsburg (Wisconsin, Estados Unidos). Era el pequeño de los dos hijos de Kittie Belle Stupfel e Isaiah Weaver, un farmacéutico. La familia se mudó a Madison en 1904. Allí Weaver asistió a la escuela secundaria e inició sus estudios superiores en la Universidad de Wisconsin.
Cuando era solo un niño, se divertía montando aparatos mecánicos y eléctricos, por ello, cuando ingresó en la universidad, deseaba convertirse en ingeniero. Pero algunos de sus profesores, en particular los matemáticos Max Mason (1877-1961) y Charles Slichter (1864-1946), le animaron para que se formara en física matemática.
Weaver se licenció en 1916 y comenzó a preparar su doctorado, que completó en 1921. Con Mason colaboró al principio de su carrera. De hecho, publicaron conjuntamente el libro The Electromagnetic Field en 1929.
En 1919 contrajo matrimonio con Mary Hemenway, una compañera de estudios, que fue profesora de latín e historia antigua y después ama de casa tras el nacimiento de su hijo Warren Jr. y su hija Helen.
De las matemáticas a la biología molecularWarren Weaver comenzó su carrera como profesor de matemáticas en varios centros universitarios, en particular en la Universidad de Wisconsin.
En 1931, Mason presidía la Fundación Rockefeller e invitó a Weaver a unirse a su equipo como responsable de la División de Ciencias Naturales. En ese momento, en muchas universidades del mundo se hablaba de la necesidad de un enfoque interdisciplinar en la investigación en ciencias biológicas.
Tras muchas dudas, entre otros motivos porque lamentaba dejar el mundo de la docencia y de la investigación, aceptó el puesto. Y sugirió que el programa científico de la fundación abandonara su anterior preocupación por las ciencias físicas hacia un «interés en estimular y ayudar a la aplicación a problemas biológicos básicos, de las técnicas, procedimientos experimentales y métodos de análisis tan eficazmente desarrollados en las ciencias físicas». La Fundación aceptó esta propuesta y, desde ese nuevo puesto, Weaver ejerció una profunda influencia en el desarrollo de la biología a nivel mundial.
Años más tarde, en una carta dirigida a J. M. H. Carson en junio de 1949, Warren Weaver expresaba su confianza en la relevancia de la investigación en biología molecular:
El siglo de la biología en el que estamos embarcados ahora ya no es cuestión de trivialidades. Es un movimiento de dimensiones realmente heroicas, uno de los grandes episodios de la historia intelectual del hombre. Los científicos que impulsan este movimiento hablan en términos de nucleoproteínas, de ultracentrifugadoras, de genética bioquímica, de electroforesis, de microscopía electrónica, de morfología molecular, de isótopos radiactivos. Pero no hay que confundirse por estos terribles términos y, sobre todo, no hay que dejar engañarse pensando que esto es mero artilugio. Ésta es la manera fiable de buscar una solución a los problemas del cáncer y la polio, los problemas del reumatismo y del corazón. Este es el conocimiento en el que debemos basar nuestra solución de los problemas de la población y alimentarios. Esto es el conocimiento de la vida.
Weaver también se desempeñó como asesor científico (1947-1951), administrador (1954) y vicepresidente (desde 1958) del Instituto Sloan-Kettering para la Investigación del Cáncer.
Incursiones en la teoría de la comunicaciónA Weaver le entusiasmaban la teoría de la probabilidad y la estadística. En 1963 publicó Lady Luck. The Theory of Probability, un pequeño libro sobre probabilidad dirigido a un público no experto. Aunque tenía una enorme habilidad con las palabras, estimaba que su aportación matemática durante su etapa universitaria se reducía a soluciones rutinarias de algunos problemas, pero que no eran contribuciones imaginativas reales al avance del conocimiento matemático.
Sin embargo, escribió una introducción expositiva a la teoría matemática de la comunicación en un artículo aparecido en The Mathematical Theory of Communication (1949) en el que Weaver sugería que había tres niveles de problemas en la comunicación:
- Un problema técnico: ¿con qué precisión se pueden transmitir los símbolos de la comunicación?
- Un problema semántico: ¿con qué precisión los símbolos emitidos transmiten el significado deseado?
- Un problema de efectividad: ¿en qué medida el significado recibido afecta la conducta de la manera deseada?
El primer artículo de este libro (que ocupa prácticamente dos tercios de la obra) tiene como autor al matemático y criptógrafo Claude E Shannon (1916-2001) recordado como «el padre de la teoría de la información».
La pasión por la traducción automáticaTambién en 1949 promovió la investigación para el desarrollo de sistemas de traducción automática tras un informe para la Fundación Rockefeller en el que señalaba que existía una analogía entre la decodificación mecánica y la traducción.
Naturalmente, uno se pregunta si el problema de la traducción podría ser tratado como un problema de criptografía. Cuando veo un artículo en ruso, digo: «Esto está escrito en inglés, pero ha sido codificado con algunos símbolos extraños. Ahora procederé a descifrarlo».
Carta de Warren Weaver a Norbert Wiener, 1947
En este sentido, y fascinado por Las aventuras de Alicia en el país de las maravillas de Lewis Carroll (1832-1898), Weaver acumuló 160 versiones del libro en 42 idiomas. En 1964, escribió el libro Alice in many tongues; the translations of Alice in Wonderland, sobre la historia de las diferentes traducciones de esta obra, y diseñó una manera de evaluar la calidad de diferentes versiones, estudiando las bromas y giros de Una merienda de locos.
 Páginas 108 y 109 de Alice in many tongues; the translations of Alice in Wonderland. Fuente: Captura de pantalla de Internet Archive.
Páginas 108 y 109 de Alice in many tongues; the translations of Alice in Wonderland. Fuente: Captura de pantalla de Internet Archive.
Gracias a sus numerosos contactos, para llevar a cabo esta tarea consiguió la colaboración de un importante grupo de colaboradores en el ejercicio de evaluación. Entre estas personas destacamos a la antropóloga Margaret Mead (para valorar la traducción a la lengua pidgin del Pacífico Sur), el alcalde de Jerusalén Teddy Kollek o el bioquímico y Premio Nobel Hugo Theorell (para la traducción al sueco).
Aunque Wiener falleció el 24 de noviembre de 1978, el proyecto Alice in a World of Wonderlands: the Translations of Lewis Carroll’s Masterpiece (2015) continuó con el análisis de las traducciones de Alicia… en 174 idiomas, en una línea similar a la del matemático y administrador científico.
Referencias
- Warren Weaver, MacTutor History of Mathematics Archive, St Andrews University
- Mina Rees, Warren Weaver (1894-1978), Bibliographical Memoir, National Academy of Sciences, 1987
- Warren Weaver, Wikipedia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
El artículo Warren Weaver, de la física matemática a la traducción automática se ha escrito en Cuaderno de Cultura Científica.
¿Qué es el aprendizaje automático?
Las redes neuronales y otras formas de aprendizaje automático aprenden en última instancia mediante prueba y error, una mejora cada vez.
Un artículo de John Pavlus. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Ilustración: Son of Alan / Quanta Magazine
Ilustración: Son of Alan / Quanta MagazineA estas alturas, muchas personas creen que saben qué es el aprendizaje automático: se “alimentan” los ordenadores con un montón de “datos de entrenamiento” para que “aprendan” a hacer cosas sin que tengamos que especificar exactamente cómo. Pero los ordenadores no son perros, los datos no son chuches y la oración anterior tiene demasiadas comillas. ¿Qué significa realmente todo esto?
El aprendizaje automático es un subcampo de la inteligencia artificial que explora cómo simular (o superar) computacionalmente la inteligencia humana. Si bien algunas técnicas de IA (como los sistemas expertos) utilizan otros enfoques, el aprendizaje automático impulsa la mayor parte del progreso actual en el campo al centrarse en una cosa: usar algoritmos para mejorar automáticamente el rendimiento de otros algoritmos.
Así es como esto puede funcionar en la práctica, para un tipo común de aprendizaje automático llamado aprendizaje supervisado. El proceso comienza con una tarea, por ejemplo, «reconocer gatos en fotografías». El objetivo es encontrar una función matemática que pueda realizar la tarea. Esta función, llamada modelo, tomará un tipo de números como entrada (en este caso, fotografías digitalizadas) y los transformará en más números como salida, que podrían representar etiquetas que digan «gato» o «no gato». El modelo tiene una expresión matemática básica, o forma, que proporciona cierta estructura para la tarea, pero no es probable que produzca resultados precisos al principio.
Ahora es el momento de entrenar el modelo, que es donde otro tipo de algoritmo toma el relevo. Primero, una función matemática diferente (llamada la objetivo) calcula un número que representa la «distancia» actual entre los resultados del modelo y el resultado deseado. Luego, el algoritmo de entrenamiento utiliza la medición de la distancia al objetivo para ajustar la forma del modelo original. No es necesario “saber” nada sobre lo que representa el modelo; simplemente empuja partes del modelo (llamadas parámetros) en ciertas direcciones matemáticas que minimizan esa distancia entre la salida real y la deseada.
Una vez realizados estos ajustes, el proceso se reinicia. El modelo actualizado transforma las entradas de los ejemplos de entrenamiento en resultados (ligeramente mejores), luego la función objetivo indica otro ajuste (ligeramente mejor) del modelo. Y así sucesivamente, adelante y atrás, adelante y atrás. Después de suficientes iteraciones, el modelo entrenado debería poder producir resultados precisos para la mayoría de sus ejemplos de entrenamiento. Y aquí está el verdadero truco: también debe mantener ese desempeño en nuevos ejemplos de la tarea, siempre y cuando no sean muy diferentes de los de entrenamiento.
Usar una función para modificar repetidamente otra función puede parecer más un trabajo intenso que un “aprendizaje automático”. Pero ese es todo el quid de la cuestión. Poner en marcha este proceso mecánico permite que surja automáticamente una aproximación matemática de la tarea, sin que los seres humanos tengan que especificar qué detalles importan. Con algoritmos eficientes, funciones bien elegidas y suficientes ejemplos, el aprendizaje automático puede crear potentes modelos computacionales que hacen cosas que no tenemos idea de cómo programar.
Las tareas de clasificación y predicción, como identificar gatos en fotografías o spam en correos electrónicos, generalmente dependen del aprendizaje automático supervisado, lo que significa que los datos de entrenamiento ya están ordenados de antemano: las fotos que contienen gatos, por ejemplo, están etiquetadas como «gato». El proceso de entrenamiento da forma a una función que puede asignar la mayor cantidad posible de entradas a sus salidas (conocidas) correspondientes. Después de eso, el modelo entrenado etiqueta ejemplos desconocidos.
Mientras tanto, el aprendizaje no supervisado encuentra estructura dentro de ejemplos sin etiquetar, agrupándolos en grupos que no están especificados de antemano. Los sistemas de recomendación de contenido que aprenden del comportamiento pasado de un usuario, así como algunas tareas de reconocimiento de objetos en visión por ordenador, pueden depender del aprendizaje no supervisado. Algunas tareas, como el modelado del lenguaje realizado por sistemas como GPT-4, utilizan combinaciones inteligentes de técnicas supervisadas y no supervisadas conocidas como aprendizajes auto- y semi-supervisado.
Finalmente, el aprendizaje por refuerzo da forma a una función mediante el uso de una señal de recompensa en lugar de ejemplos de resultados deseados. Al maximizar esta recompensa mediante prueba y error, un modelo puede mejorar su desempeño en tareas dinámicas y secuenciales como jugar juegos (como ajedrez y Go) o controlar el comportamiento de agentes reales y virtuales (como los coches sin conductor o los bots conversacionales).
Para poner estos enfoques en práctica, los investigadores utilizan una variedad de algoritmos que suenan exóticos, desde máquinas kernel hasta Q-learning. Pero desde la década de 2010, las redes neuronales artificiales han pasado a ocupar un lugar central. Estos algoritmos, llamados así porque su forma básica está inspirada en las conexiones entre las células cerebrales, han tenido éxito en muchas tareas complejas que antes se consideraban poco prácticas. Los modelos de lenguaje extenso, que utilizan el aprendizaje automático para predecir la siguiente palabra (o fragmento de palabra) en una cadena de texto, se construyen con redes neuronales «profundas» con miles de millones o incluso billones de parámetros.
Pero incluso estos gigantes, como todos los modelos de aprendizaje automático, son solo funciones en el fondo: formas matemáticas. En el contexto adecuado, pueden ser herramientas extremadamente poderosas, pero también tienen debilidades conocidas. Un modelo «sobreajustado» se ajusta tan perfectamente a sus ejemplos de entrenamiento que no puede generalizar de manera fiable, como un sistema de reconocimiento de gatos que falla cuando se pone una foto al revés. Los sesgos en los datos pueden verse amplificados por el proceso de capacitación, lo que lleva a resultados distorsionados, o incluso injustos. E incluso cuando un modelo funciona, no siempre está claro por qué. (Los algoritmos de aprendizaje profundo están particularmente afectados por este problema de «interpretabilidad»).
Aún así, el proceso en sí es fácil de reconocer. En el fondo, todas estas máquinas aprenden de la misma manera: adelante y atrás, adelante y atrás.
El artículo original, What Is Machine Learning?, se publicó el 8 de julio de 2024 en Quanta Magazine.
Traducido por César Tomé López
El artículo ¿Qué es el aprendizaje automático? se ha escrito en Cuaderno de Cultura Científica.
La dieta del padre influye en la salud metabólica del hijo
 Foto: Kelly Sikkema / Unsplash
Foto: Kelly Sikkema / Unsplash
Los genes del espermatozoide contribuyen de forma decisiva al individuo que se formará tras la fecundación del óvulo. En el caso de los humanos, los 23 cromosomas paternos se combinan con el mismo número de cromosomas maternos para originar un nuevo ser. ¿Existe alguna contribución paterna al margen de la cromosómica? Se suele afirmar que las mitocondrias, que también contienen su propio conjunto de genes, no se transmiten por vía paterna, y que la herencia mitocondrial es exclusivamente materna. Esto es algo inexacto, ya que sí hay mitocondrias del espermatozoide que acceden al óvulo, pero tanto ellas como su ADN terminan siendo eliminados por diversos mecanismos.
Desde hace relativamente poco tiempo sabemos que hay otra aportación del espermatozoide cuya importancia empezamos a conocer. Se trata de las moléculas conocidas como sncRNAs (por small non-coding RNA, pequeñas secuencias de ácido ribonucleico no codificante). Tienen una longitud inferior a los 200 nucleótidos y derivan de fragmentos de ARN de transferencia y ribosómico. Estos ARN se encargan, respectivamente, del transporte de aminoácidos para ensamblar el polipéptido y de organizar el ribosoma en el que se produce dicho ensamblaje.
El conjunto de sncRNAs que el espermatozoide entrega al óvulo junto con su núcleo es complejo, dinámico y sensible a influencias ambientales. También sabemos que influye tanto en el desarrollo embrionario como en las características del adulto (su fenotipo). Aquí pueden encontrar una reciente revisión sobre el tema. Esta influencia de los sncRNAs sobre el fenotipo adulto se produce a nivel epigenético, es decir, sin implicar cambios en la secuencia del ADN. Los sncRNAs transferidos desde el espermatozoide pueden modular la expresión de los genes del descendiente provocando cambios fenotípicos. Hablamos por tanto de una herencia epigenética influida por factores ambientales.
Un artículo recién publicado en Nature por un grupo de investigadores alemanes y austríacos ha mostrado que, en ratones, la dieta del padre en el momento del apareamiento tiene influencia en la salud metabólica de los descendientes masculinos, y que esta influencia se produce a nivel epigenético mediante la aportación espermática de sncRNAs.
Un primer experimento consistió en alimentar a ratones macho con una dieta rica en grasa durante dos semanas. Estos ratones se aparearon con hembras y se comprobó que alrededor del 30% de los descendientes masculinos desarrollaban resistencia a la insulina e intolerancia a la glucosa, signos característicos de la diabetes de tipo II. En un segundo ensayo, tras las dos semanas de dieta grasa, los ratones volvieron a recibir una dieta normal durante un mes. Tras el apareamiento, los descendientes no desarrollaron ningún problema metabólico. Los investigadores concluyeron que la influencia de la dieta se ejercía durante el periodo de maduración de los espermatozoides en el epidídimo. Vamos a explicar esto más despacio.
 Figura 1. A la izquierda se muestra la posición del epidídimo sobre el testículo con sus diferentes partes. De KDS444, CC BY-SA 3.0. A la derecha vemos como el epitelio del epidídimo libera epididimosomas, vesículas extracelulares que transportan proteínas, ADN y ARN hasta los espermatozoides en maduración. De ER James et al. Int. J. Mol. Sci. 2020, CC BY 4.0
Figura 1. A la izquierda se muestra la posición del epidídimo sobre el testículo con sus diferentes partes. De KDS444, CC BY-SA 3.0. A la derecha vemos como el epitelio del epidídimo libera epididimosomas, vesículas extracelulares que transportan proteínas, ADN y ARN hasta los espermatozoides en maduración. De ER James et al. Int. J. Mol. Sci. 2020, CC BY 4.0Los espermatozoides se forman en el testículo a partir de las células germinales, unos precursores con gran capacidad proliferativa. Una vez formados, atraviesan una larga estructura tubular llamada epidídimo1. Los espermatozoides del ratón emplean alrededor de una semana en recorrer este tubo de un metro de longitud. Durante el recorrido los espermatozoides incorporan epididimosomas, vesículas cargadas de moléculas procedentes del epitelio del epidídimo, entre ellas los sncRNAs que luego transferirán al óvulo (Figura 1).
El estudio de Nature mostró que si la dieta grasa se suspendía antes del ingreso de los espermatozoides en el epidídimo, no se producían consecuencias en la descendencia. Es decir, la (mala) influencia de la dieta grasa se producía durante el paso por el epidídimo. Y los responsables de esto eran los sncRNAs transferidos. De hecho, la dieta grasa provocaba un aumento precisamente en los niveles de sncRNA de origen mitocondrial en todos los tejidos, epidídimo incluido, un cambio que revertía tras el regreso a la dieta normal.
De forma independiente, los investigadores estudiaron las consecuencias de las mutaciones en dos genes, Mrpl23 y Ndufb8, que causaban aumento de los fragmentos no codificantes de ARN mitocondrial. Los descendientes de los portadores masculinos de estas mutaciones mostraban las mismas alteraciones metabólicas que los descendientes de machos alimentados con dieta grasa.
Los autores de esta investigación indagaron si los resultados obtenidos en ratones podrían tener alguna implicación clínica. Comprobaron que los niveles de fragmentos de ARN de transferencia y de origen mitocondrial estaban correlacionados con el índice de masa corporal de los varones. Al mismo tiempo mostraron que el sobrepeso paterno en el momento de la concepción duplica el riesgo de obesidad de los hijos y compromete su salud metabólica. La carga de sncRNAs en el esperma podría ser el nexo entre estas dos observaciones.
 Figura 2. Modelo propuesto por Tomar et al. para explicar la influencia epigenética de la dieta grasa del padre. El daño mitocondrial provocaría un aumento de la transcripción de los genes mitocondriales y de la carga de sncRNAs en los epididimosomas. La transferencia de estos ARNs al espermatozoide y luego al ovocito modificaría la expresión génica durante el desarrollo aumentando el riesgo metabólico del descendiente
Figura 2. Modelo propuesto por Tomar et al. para explicar la influencia epigenética de la dieta grasa del padre. El daño mitocondrial provocaría un aumento de la transcripción de los genes mitocondriales y de la carga de sncRNAs en los epididimosomas. La transferencia de estos ARNs al espermatozoide y luego al ovocito modificaría la expresión génica durante el desarrollo aumentando el riesgo metabólico del descendienteUn escenario apuntado en el artículo de Nature propone que la exposición a una dieta rica en grasas perjudicaría la función mitocondrial y que esto se intentaría compensar con una mayor transcripción de los genes mitocondriales (Figura 2). El consecuente aumento del contenido celular en ARN produciría un exceso de fragmentos de sncRNAs que, transportados por los espermatozoides, acabarían en el ovocito. Lo que todavía no sabemos es cómo estos fragmentos modulan la expresión de los genes embrionarios, cómo esta modulación epigenética acaba provocando consecuencias en el metabolismo de los descendientes, y por qué los hijos tienen más riesgo metabólico que las hijas.
En resumen, si es aconsejable siempre seguir una dieta saludable y mantener el peso corporal en niveles adecuados, podría serlo de forma especial para los hombres en el momento de la concepción.
Referencias:
Cai, C., Chen, Q. (2024) Father’s diet influences son’s metabolic health through sperm RNA. Nature. doi: 10.1038/d41586-024-01502-w
Tomar, A., Gómez-Velázquez, M., Gerlini, R. et al. (2024) Epigenetic inheritance of diet-induced and sperm-borne mitochondrial RNAs. Nature. doi: 10.1038/s41586-024-07472-3
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga
Nota:
1 Como curiosidad el epidídimo humano, situado sobre el testículo, mide unos 4-5 centímetros, pero si se desenrollase alcanzaría los seis metros de longitud.
El artículo La dieta del padre influye en la salud metabólica del hijo se ha escrito en Cuaderno de Cultura Científica.
El ciclo de la sal en los océanos y su impacto en el colapso de la AMOC
 Foto: Kinø / Unsplash
Foto: Kinø / Unsplash
El bucle de circulación Atlántico (conocido como AMOC, por sus siglas en inglés) transporta eficazmente calor y sal a través del océano global y modula fuertemente el clima de la Tierra. Si colapsara daría lugar a un enfriamiento brusco (a escala de décadas) del clima europeo. Y el ciclo de la sal en los océanos está en el epicentro de ese posible colapso.
La salinidad de los océanos en la historia de la TierraEn promedio, un kilogramo de agua de mar contiene aproximadamente 35 gramos de sales disueltas. Pero no siempre ha sido así: desde la formación de los océanos, hace 3 800 millones de años, la salinidad de los océanos no ha dejado de cambiar.
Concretamente, el océano primitivo tenía entre 1,5 y 2 veces más salinidad que el actual, que hoy oscila entre 32 y 37 gramos de sales por kilogramo de agua.
Quién echa sal al marHay varias maneras indirectas (las llamamos ‘proxies’) de estimar qué salinidad tenía el océano prehistórico. Gran parte de la información la obtenemos del estudio de evaporitas, rocas sedimentarias que se forman por cristalización de sales disueltas. También aporta información útil el estudio de las relaciones isotópicas. Ambos estudios nos llevan a la misma conclusión: que el océano primitivo era más salino que en la actualidad.
A escalas de cientos a miles de millones de años, hay distintos procesos que han añadido o retirado sales del medio. Empezando por los volcanes, principalmente los de los fondos abisales de las dorsales medio-oceánicas, unas elevaciones submarinas situadas en la parte media de los océanos. El magma de estos volcanes es muy rico en sales.
Por otro lado, a lo largo de estos miles de millones de años, cuando la sal sedimenta la concentración global en el océano disminuye. Pero cuando las rocas son erosionadas aumenta de nuevo la concentración salina global.
En nuestros días, la salinidad se mide con una alta resolución espacio-temporal gracias a los satélites y a una pléyade de boyas profundas de deriva.
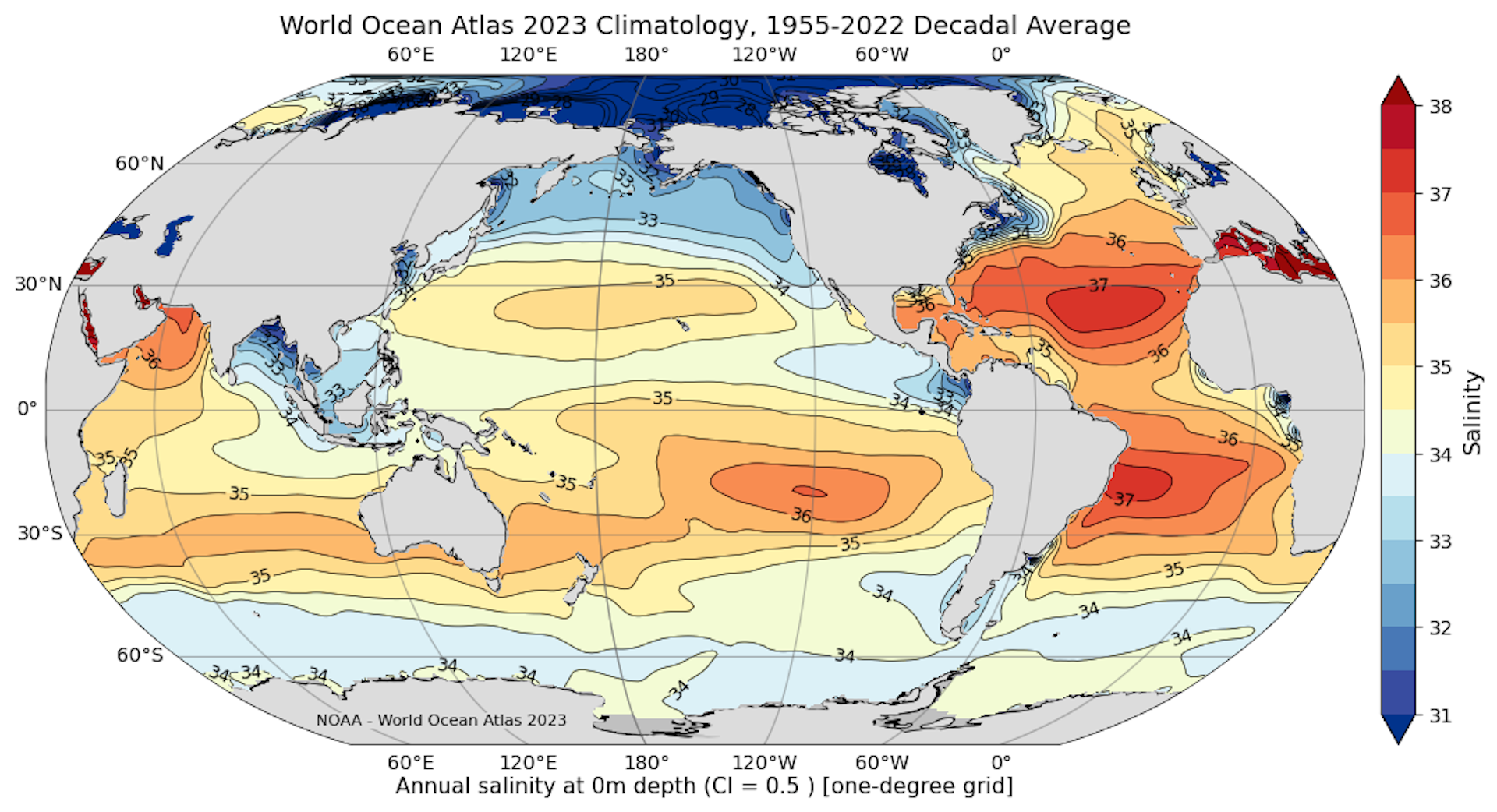
La lluvia, los aportes continentales (escorrentías o fusión de glaciares) y la evaporación son agentes que afectan a la salinidad a escalas climáticas (de cientos-miles de años). De hecho, son las tres componentes del ciclo hidrológico en la Tierra.
La salinidad superficial está relacionada con el balance final resultante de si hay más o menos evaporación, más o menos precipitación, y más o menos aportes continentales: la magnitud de ese balance determina en buena medida la salinidad de cada zona.
En las zonas subtropicales, en las que hay mucha evaporación, la concentración de sal es máxima, mientras que en las zonas ecuatoriales-tropicales es mucho menor. En los mares polares el agua salada se diluye con el agua dulce de los casquetes polares, así que la concentración de sal es baja.
El extraño caso de la cuenca atlánticaLa cuenca atlántica es, con mucho, la más salina. Esto parece contraintuitivo, ya que al Atlántico fluyen los tres ríos más caudalosos: Amazonas, Congo y Orinoco. Su salinidad, a priori, debería ser más baja.
La principal explicación a esta paradoja es que la cuenca atlántica exporta netamente al resto de cuencas a través de los vientos la humedad atmosférica procedente de su evaporación. Es decir, lo que se evapora en el Atlántico no acaba lloviendo sobre el propio Atlántico.
Además, el Atlántico está conectado con el mar Mediterráneo, cuenca fuertemente evaporativa. Y el Mediterráneo le aporta un importante flujo de sal neto a través del estrecho de Gibraltar.
El agua que se hunde: la circulación AMOCLa salinidad afecta a la densidad del agua y juega un papel clave en las corrientes oceánicas, que a su vez influyen en el clima mundial.
El Atlántico tiene un circulación general muy singular, que contribuye a su salinización.
La corriente del Golfo transporta un extra de agua muy salina hacia el norte. Al llegar a los mares nórdicos, aumenta su densidad por enfriamiento y literalmente se hunde. Se forma así en el Atlántico una especie de cinta rodante, la circulación de vuelco meridional del Atlántico (conocida como AMOC, siglas en inglés de Atlantic meridional overturning circulation), que funciona de forma continua. Su rodillo impulsor se encuentra en los mares nórdicos y en el mar de Labrador (sur de Groenlandia), que son muy salinos.
El hundimiento de esta agua con alta concentración de sal hace que las aguas abisales del Atlántico sean también muy salinas, porque provienen de las aguas superficiales. Y así se cierra el circuito de la sal.
Su implicación con el cambio climáticoLa salinidad es sensible a cambios en las precipitaciones, los aportes de agua de los ríos, la evaporación… Y estos cambios en el ciclo hidrológico de la Tierra se están produciendo debido al cambio climático.
En un planeta más cálido, la capacidad de la atmósfera para retener la humedad es mayor (termodinámicamente, un 6,5 % mayor por cada grado centígrado de aumento del clima).
Por ello, se está verificando que en las zonas subtropicales la evaporación se está reforzando, aumentando la aridez continental y la salinidad superficial, y en los trópicos está lloviendo aún más, y más torrencialmente, disminuyendo la salinidad superficial.
El desequilibrio crítico en los océanosEn el océano, estos procesos son aún más críticos que en los continentes. La evaporación y las precipitaciones generan flujos verticales (el agua que asciende del mar y la que regresa por las lluvias). Estos flujos son mayores respecto a lo que corresponde por el área global del océano (que es el 71 % del total): en los océanos se evapora el 85 % y precipita el 77 % del total.
Los cambios de salinidad causan impactos sobre la circulación global de los océanos. La salinización afecta a la densidad del agua, y son los cambios de densidad los motores de la circulación profunda. Además, afecta al incremento del nivel del mar. Si la densidad del agua es menor, el volumen del agua total aumenta.
El calentamiento global también está provocando la fusión de los glaciares continentales de Groenlandia y esto significa agua dulce extra que vierte en los mares noratlánticos. Esto está provocando la desalinización, el agua se va haciendo menos densa y el hundimiento invernal de la columna de agua se está ralentizando (con posible colapso durante este siglo).
Luego en sus cavidades
la sal gema,
montaña de una luz enterrada,
catedral transparente,
cristal del mar,
olvido de las olas.
Oda a la sal, Pablo Neruda.![]()
Sobre el autor: Gabriel Rosón Porto, Catedrático de Oceanografía Física Facultad de Ciencias del Mar Departamento de Física Aplicada, Universidade de Vigo
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo El ciclo de la sal en los océanos y su impacto en el colapso de la AMOC se ha escrito en Cuaderno de Cultura Científica.
Día de pi 2024: La música de los números primos

El número Pi, representado por la letra griega π, es una de las constantes matemáticas más famosas e importantes que existen en el mundo. Este número irracional, que determina la relación entre la longitud de una circunferencia y su diámetro, concierne a múltiples disciplinas científicas como la física, la ingeniería y la geología, y tiene aplicaciones prácticas sorprendentes en nuestro día a día.
La fascinación que ha suscitado durante siglos es tal, que se viene estudiando desde hace más de 4.000 años e, incluso, cuenta con su propio día en el calendario: el 14 de marzo. Este evento internacional vino de la mano del físico estadounidense Larry Shaw, quien en 1988 lanzó la propuesta de celebrar esta efeméride. La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática: 3-14 martxoaren 14 en euskara / 3-14 March, 14th en inglés. En los últimos años, la conmemoración del Día de Pi se ha ido extendiendo, hasta tal punto que el 26 de noviembre de 2019 la UNESCO proclamó el 14 de marzo Día Internacional de las Matemáticas.
Un año más, el Basque Center for applied Mathematics-BCAM y la Cátedra de Cultura Científica de la UPV/EHU nos sumamos a la celebración, organizando la quinta edición del evento BCAM NAUKAS, que se desarrolló a lo largo del 14 de marzo en el Bizkaia Aretoa de UPV/EHU.
En esta charla Francisco R. Villatoro nos habla de la hipótesis de Riemann es la partitura de la música de los números primos. Probablemente uno de los problemas de más difícil resolución.
Francisco R. Villatoro es profesor en la Escuela de Ingeniería Informática de la Universidad de Málaga. Muy conocido como divulgador de la física, no hay que olvidar que, además de licenciado en física, primero es licenciado en informática y doctor en matemáticas, e investiga en matemáticas computacionales.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Día de pi 2024: La música de los números primos se ha escrito en Cuaderno de Cultura Científica.
Cómo migran las células
Un exhaustivo análisis de las trayectorias de movimiento de 700 células individuales indica que sus desplazamientos dependen de una actuación conjunta y autoorganizada de prácticamente todos los procesos fisiológicos que componen la célula.
Esta investigación multidisciplinar en el que han participado diferentes departamentos de la UPV/EHU ha demostrado por primera vez que el movimiento de las células está dirigido y regulado por un proceso autoorganizado fundamental que se origina de forma espontánea en todas las células vivientes.
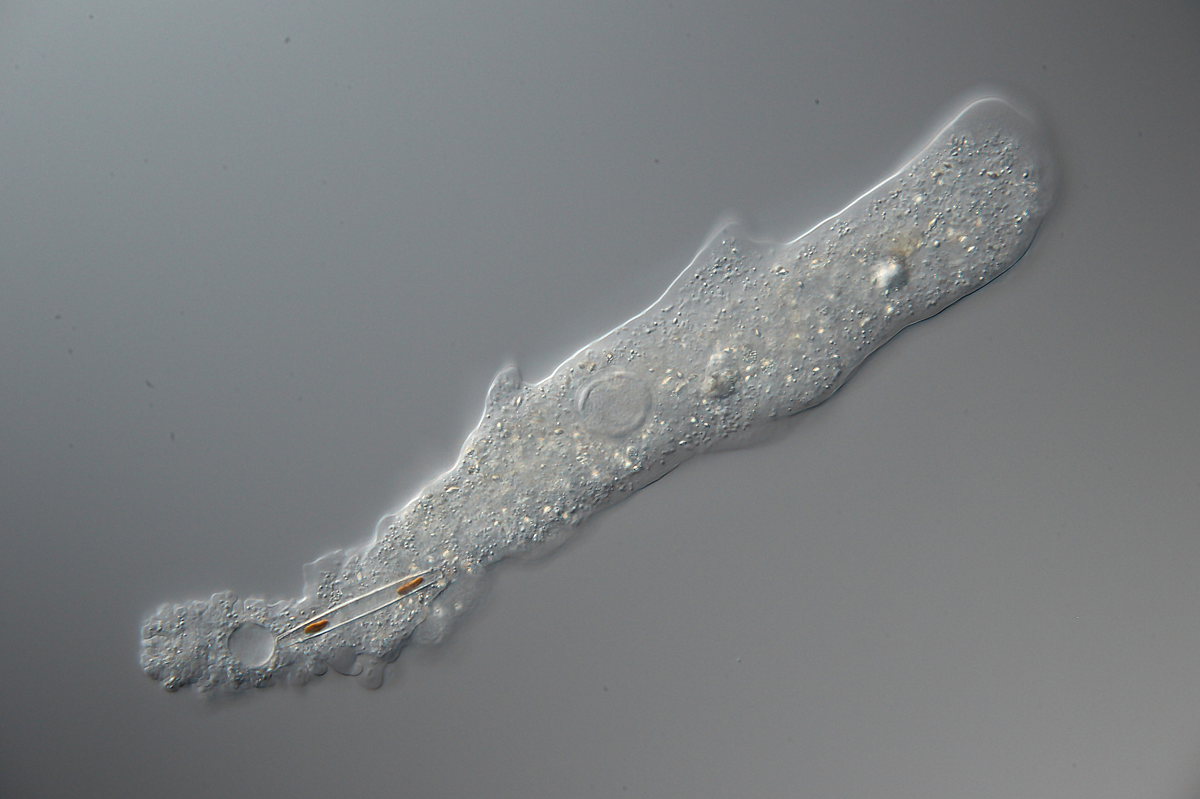 Amoeba proteus desplazándose. Una de las especies analizadas. Fuente: Wikimedia Commons
Amoeba proteus desplazándose. Una de las especies analizadas. Fuente: Wikimedia CommonsSegún Ildefonso Martínez de la Fuente, investigador del departamento de Matemáticas de la Universidad del País Vasco, “estos mecanismos moleculares autoorganizados hacen que los diferentes procesos bioquímico-metabólicos que existen en la célula conformen una unidad funcional, totalmente integrada como un todo único, convirtiendo a miles de procesos fisiológicos en una sola entidad”. “Se trata de una fuerza fundamental que hace emerger en la célula un comportamiento integrado —sostiene Martínez de la Fuente—, y se puede comparar con el movimiento autoorganizado de los miles de estorninos que conforman estructuras altamente ordenadas y coordinadas cuando migran o incluso con la capacidad que tienen las hormigas de estructurar un hormiguero a través de comportamientos colectivos autoorganizados”.
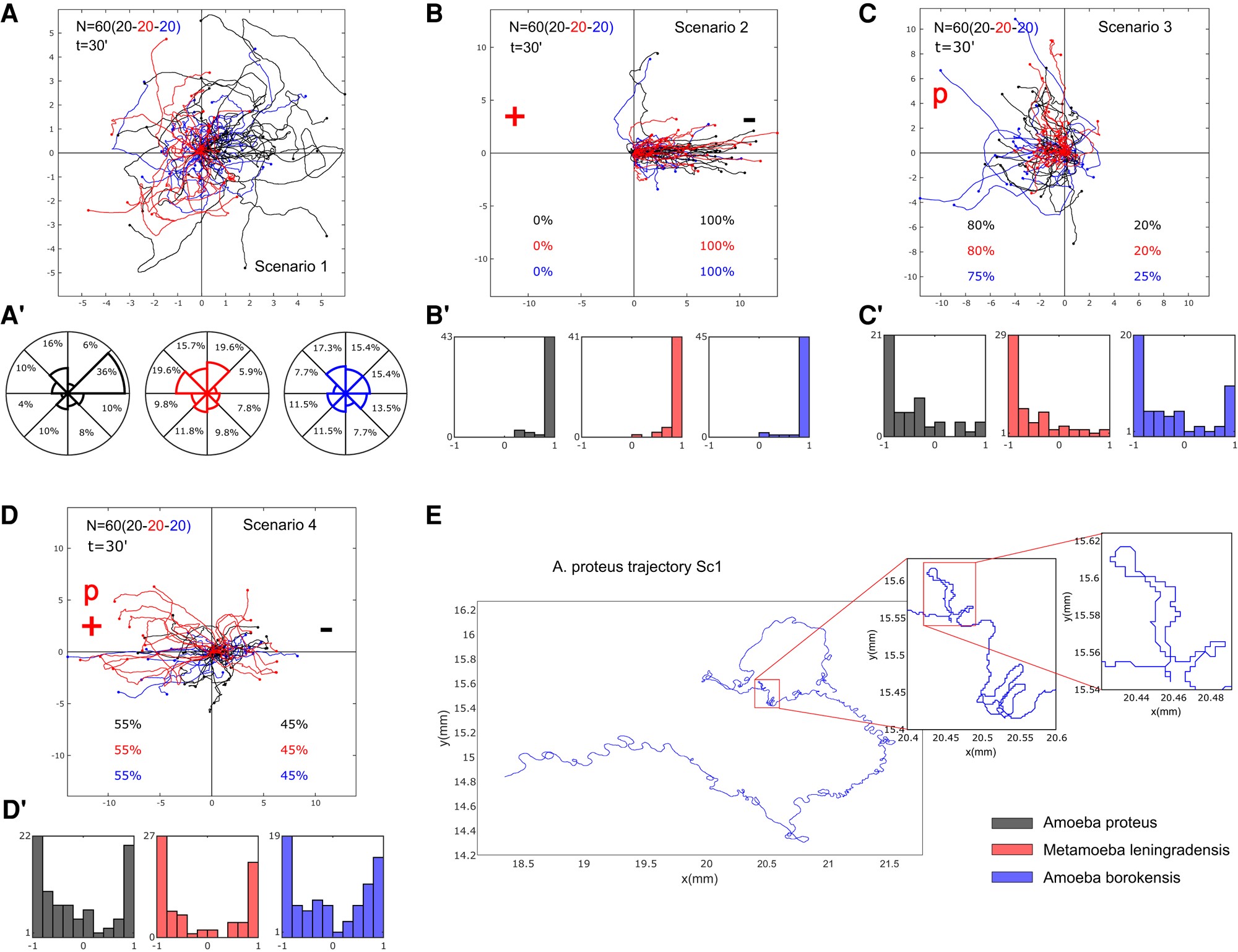 Análisis de los desplazamientos de las especies Amoeba proteus, Metamoeba leningradensis, y Amoeba borokensis. Fuente: Referencia
Análisis de los desplazamientos de las especies Amoeba proteus, Metamoeba leningradensis, y Amoeba borokensis. Fuente: ReferenciaEl autor de la investigación destaca que nunca hasta ahora había sido reconocido científicamente que los movimientos de desplazamiento de las células están gobernados por procesos autorregulados de carácter sistémico que operan a nivel global en la célula. “Este hallazgo científico añade una nueva perspectiva al concepto que se tiene de la propia célula y sus capacidades funcionales”, comenta. Además, “la combinación de estudios de migración celular, desde un punto de vista sistémico, junto con los clásicos estudios moleculares, puede ser crucial para el desarrollo de una nueva generación de terapias eficientes para las patologías relacionadas con las enfermedades originadas por una deficiente migración celular”, indica Martínez de la Fuente.
El movimiento celular es un proceso clave y fundamental para el desarrollo y el óptimo funcionamiento del cuerpo humano. Las células se mueven cuando un organismo se está desarrollando embrionariamente, cuando se produce la cicatrización de una herida o durante la metástasis, por ejemplo. Los errores durante un mal control del movimiento celular pueden tener consecuencias serias en importantes enfermedades, como en la enfermedad Crohn, determinados desórdenes congénitos del cerebro, y diferentes patologías inmunológicas o vasculares, por ejemplo.
Combinación de datos experimentales y análisis cuantitativos
Durante décadas, los trabajos científicos han permitido identificar diferentes mecanismos locales implicados en el movimiento celular, pero a pesar de los esfuerzos realizados, no se ha podido dilucidar la cuestión esencial: cómo las células controlan y gobiernan sus movimientos.
“Descubrir las fuerzas moleculares que dirigen la migración celular representa un desafío científico de enorme dificultad —señala el investigador de la UPV/EHU—, ya que además de confeccionar unos complejos dispositivos especiales de laboratorio creado exprofeso para esta investigación, ha sido necesario utilizar técnicas multidisciplinares que permitan compaginar estudios experimentales con métodos cuantitativos avanzados”.
“Hemos estudiado las características del movimiento de 700 células, y para ello hemos utilizado técnicas que se emplean habitualmente en la mecánica estadística, que es una parte fundamental de la Física. Dos de los métodos que hemos aplicado fueron desarrollados por el premio nobel Albert Einstein. Asimismo, en este trabajo hemos empleado los principios de autoorganización disipativa —estructuras organizadas coherentemente— desarrollados por el premio nobel Ilya Prigogine”, comenta Ildefonso Martínez de la Fuente.
Referencia:
Ildefonso M De la Fuente, Jose Carrasco-Pujante, Borja Camino-Pontes, Maria Fedetz, Carlos Bringas, Alberto Pérez-Samartín, Gorka Pérez-Yarza, José I López, Iker Malaina, Jesus M Cortes (2024) Systemic cellular migration: The forces driving the directed locomotion movement of cells PNAS Nexus doi: 10.1093/pnasnexus/pgae171
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Cómo migran las células se ha escrito en Cuaderno de Cultura Científica.
Inteligencia artificial hasta en la sopa
 El trabajo de Andy Warhol contribuyó a que la marca de sopas enlatadas Campbell se convirtiera en todo un icono pop durante los años sesenta. Fuente: Robert Couse-Baker (CC BY 2.0)
El trabajo de Andy Warhol contribuyó a que la marca de sopas enlatadas Campbell se convirtiera en todo un icono pop durante los años sesenta. Fuente: Robert Couse-Baker (CC BY 2.0)¿Qué tiene que ver la sopa enlatada con la inteligencia artificial? Pese a lo peculiar de esta asociación, lo cierto es que mucho, al menos en una de las historias más curiosas de la historia de esta tecnología.
Aunque el interés por la inteligencia artificial ha experimentado un auténtico boom desde que, en noviembre de 2022, OpenAI presentara ChatGPT, lo cierto es que su desarrollo a un nivel práctico se remonta, al menos, hasta los años cuarenta y cincuenta del siglo XX. Incluso antes, si tenemos en cuenta los intentos pioneros del ingeniero español Leonardo Torres Quevedo. Es más, la historia de la inteligencia artificial se puede resumir en una serie de épocas cíclicas de apogeo y declive desde entonces, con «veranos» de hype desmedidos e «inviernos» de consecuente decepción.
Ahora nos encontramos en el tercero de esos veranos, el de los sistemas generativos, que comenzó en 2011, y solo el tiempo dirá si conseguiremos evitar un nuevo invierno o si, en esta ocasión, la inteligencia artificial iniciará esa transformación social profunda sobre la que se lleva debatiendo tanto tiempo. La diferencia con épocas anteriores es que estos sistemas están, por primera vez, al alcance del usuario doméstico. El primer verano de la inteligencia artificial fue el de los sistemas simbólicos, entre mediados de los años cincuenta y mediados de los setenta del siglo XX, y estuvo más adscrito al mundo académico. El segundo, el de los sistemas expertos, tuvo lugar alrededor de los años ochenta, y en él la inteligencia llegó hasta el mundo profesional y empresarial… y se aplicó incluso en las tareas más inesperadas.
Sistemas expertosUn sistema experto es, básicamente, un programa pensado para emular el desempeño y conocimiento humanos en un dominio muy específico, por ejemplo, el diagnóstico médico, el análisis financiero, asistir al soporte técnico de un producto en concreto… y funcionan muy bien para muchas cosas. Tanto es así que se han seguido desarrollando, mejorando y adaptando a la tecnología disponible a lo largo de las últimas décadas y están más presentes en nuestras vidas de lo que pensamos. El popular AlphaFold de DeepMind para la predicción de la estructura de las proteínas podría ser un ejemplo.
En los años ochenta, cuando los sistemas expertos estuvieron en todo su apogeo, no eran, ni mucho menos, tan avanzados como los actuales. El desarrollo de redes neuronales y algoritmos de aprendizaje automático era muy incipiente, pero eso no impedía que ejercieran entonces una fascinación similar a la que la IA generativa causa hoy en nosotros. Al menos, los miedos que suscitaban parecían muy familiares: ¿nos sustituirían este tipo de algoritmos?, ¿nos robarían el trabajo?, ¿dónde quedaría el factor humano en las labores que hacemos?
Algunos de los primeros sistemas expertos que se crearon fueron DENDRAL, en los años sesenta, para el análisis de moléculas en química orgánica; MYCIN, en los setenta, para el diagnóstico y tratamiento de enfermedades infecciosas, y R1/XCON, de finales de la misma década, un sistema de la compañía DEC que usaban los técnicos y comerciales para asesorar al cliente en cuanto a la configuración más apropiada de sus computadores de la serie VAX.
Los sistemas expertos demostraron ser muy útiles para la resolución de problemas muy concretos, sin embargo, una de las grandes limitaciones que tenían, sobre todo cuando empezaron a llegar a las empresas, es que, como se trataba de algoritmos basados en reglas e inferencias que obtenían la información de una base de datos que había que introducir a mano, era muy engorroso programarlos y, más aún, mantenerlos actualizados. Aun así, se les encontró una aplicación muy valiosa.
En los tiempos anteriores a internet y al acceso masivo a los datos y la información, el conocimiento muy especializado y cualificado se encontraba solo en la mente de personas que tenían años y años de experiencia en su campo. Contar con sistemas en los que ese conocimiento se pudiera guardar, sistematizar y hacerlo accesible podía llegar a suponer una enorme ventaja.
 Computadora VAX 11-750. La compañía DEC creó un sistema experto para que sus comerciales pudieran asesorar a los clientes sobre la configuración más adecuada. Fuente: Donostiako Informatika Fakultatea / Eduardo Mena (CC-BY-SA)
La jubilación de los expertos humanos
Computadora VAX 11-750. La compañía DEC creó un sistema experto para que sus comerciales pudieran asesorar a los clientes sobre la configuración más adecuada. Fuente: Donostiako Informatika Fakultatea / Eduardo Mena (CC-BY-SA)
La jubilación de los expertos humanos
Eso mismo fue lo que sucedió alrededor de 1985 en Sopas Campbell cuando Aldo Cimino, el responsable de mantenimiento de las máquinas de esterilización de los productos de la marca, se encontraba cerca de su jubilación. Tras cuarenta y seis años trabajando allí, sustituirlo no iba a resultar una labor fácil, así que sus superiores se plantearon crear un sistema experto que recogiera todos los años de experiencia y el saber que el empleado había acumulado durante todas aquellas décadas al servicio de la compañía. Un equipo dirigido por Richard Herrods, experto en inteligencia artificial de Texas Instruments, se encargaría de desarrollarlo.
El primer pensamiento de Cimino cuando la compañía le informó de sus intenciones de volcar toda su experiencia en una máquina fue el de que le iban a despedir, «Pero entonces me di cuenta de que tenía sesenta y cuatro años y me iba a jubilar de todas formas. Solo querían salvar parte de lo que yo sabía». El equipo de Herrods tardó siete meses en hacerlo: «Ahora, cuando algo va mal con uno de los esterilizadores, el personal de mantenimiento puede introducir un diskette en un ordenador IBM, arrancar el sistema experto e interaccionar con él de una forma muy parecida a como lo haría con Aldo al teléfono», diría. Aquel programa fue un éxito y Aldo Cimino se jubilaría muy poco tiempo después.
Sopas Campbell no fue la única compañía que había tomado ese camino, General Electric también lo hizo con su sistema DELTA (diesel locomotive troubleshootng aid), creado para la detección y diagnóstico de averías en locomotoras eléctricas, que se basaba en el conocimiento y experiencia de un ingeniero histórico de la compañía a punto de jubilarse: David Smith.
 Captura de pantalla de la primera página del artículo de Piero P. Bonissone y Harold E. Johnson donde se describe el sistema DELTA. Se puede consultar aquí.
Captura de pantalla de la primera página del artículo de Piero P. Bonissone y Harold E. Johnson donde se describe el sistema DELTA. Se puede consultar aquí.
Esto que sucedió con los sistemas expertos tal vez nos dé también pistas acerca de lo que podría suceder con la inteligencia artificial generativa y responda a algunas de las preguntas que se plantearon al principio. ¿Nos sustituirán este tipo de algoritmos? En algunos casos, sí. ¿Nos robarán el trabajo? Probablemente no, pero sí transformará la forma en que lo hacemos o abordamos nuestras tareas. ¿Dónde quedaría el factor humano en las labores que hacemos? Dejemos que Aldo Cimino responda a esto último: «He recopilado muchísima información a lo largo de los años. Hay determinadas cosas que jamás han ido mal en la cocina y que [si surgen] la computadora no sabrá arreglar. Siempre existirá el factor humano»… Pero ha llegado el momento de valorar cómo ese factor humano y nuestro papel en el nuevo mundo que estamos creando también se transforman.
Bibliografía
United Press International/L. A. Times Archives (7 de noviembre de 1989). ‘Expert System’ Picks Key Workers’ Brains : Computers: From airport gate-scheduling to trouble-shooting, technology allows companies to store key employees’ know-how on floppy disks. Los Angeles Times. https://www.latimes.com/archives/la-xpm-1989-11-07-fi-1112-story.html
Baños, G. (2024). El sueño de la inteligencia artificial. Shackleton Books.
Oravec, J. A. (2014). Expert systems and knowledge-based engineering (1984-1991): implicactions for instructional systems research. International Journal of Desings for Learning, 5(2), 66-75.
Sancho Azcoitia, S. (10 de abril de 2019). IA en el mundo de la mecánica: Delta. Telefónica Tech. https://telefonicatech.com/blog/delta-sistemas-expertos-en-el-mundo-de-html
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo Inteligencia artificial hasta en la sopa se ha escrito en Cuaderno de Cultura Científica.
Una elegante demostración del teorema de Morley
El teorema de las trisectrices de Morley es un interesante y atractivo resultado de la geometría del plano, que ha cautivado a muchas personas, en particular, del ámbito de las matemáticas, a lo largo del siglo XX (no es un teorema antiguo) y del que se han desarrollado una cantidad importante de diferentes demostraciones, geométricas, trigonométricas o algebraicas, algunas bastante técnicas, otras de ideas más sencillas y algunas otras de una gran belleza. La entrada del Cuaderno de Cultura Científica titulada El teorema de Morley está dedicada a explicar el significado de este teorema, a acercarnos su historia y a darnos una idea de una de sus demostraciones geométricas. Por otra parte, en esta entrada vamos a mostrar una de las demostraciones más elegantes y sugerentes del teorema de Morley, la demostración que propuso el matemático británico John H. Conway.
 Fotografía del matemático británico John H. Conway, en 2009. Imagen de la Universidad de PrincetonEl teorema de las trisectrices de Morley
Fotografía del matemático británico John H. Conway, en 2009. Imagen de la Universidad de PrincetonEl teorema de las trisectrices de Morley
Empecemos recordado la versión simple del teorema de Morley, que no olvidemos que debe su nombre al matemático británico, que vivió gran parte de su vida en Estados Unidos, Frank Morley (1860-1937).
Teorema de Morley (1899): Los puntos de intersección de las trisectrices adyacentes de los ángulos de un triángulo cualquiera, son los vértices de un triángulo equilátero.
Esto es, dado un triángulo ABC cualquiera, como el de la siguiente imagen, se trazan las trisectrices, es decir, las dos rectas que dividen al ángulo en tres ángulos iguales, de cada uno de los tres ángulos (interiores) del triángulo ABC, se toman los tres puntos que son la intersección de las trisectrices adyacentes, que en la imagen hemos denominado E, F y G, y entonces el teorema de las trisectrices de Morley afirma que el triángulo EFG es un triangulo equilátero (llamado triángulo de Morley), independientemente de la forma del triángulo inicial ABC.
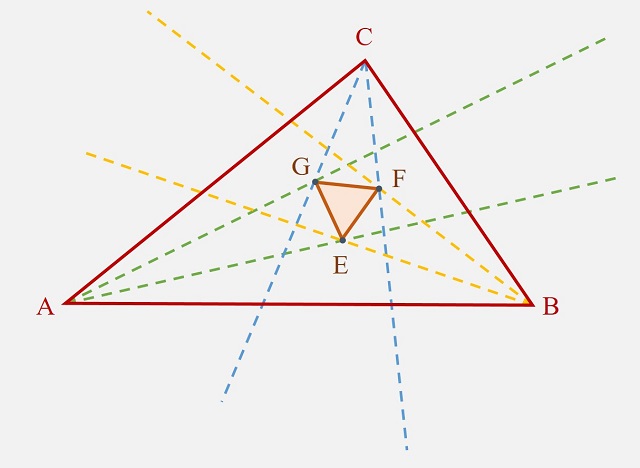
Esta es la versión simple, y más famosa, del teorema, que en su versión completa afirma que existen 18 configuraciones asociadas al triángulo inicial que son también triángulos equiláteros. Por ejemplo, un resultado análogo al anterior se obtiene para las trisectrices de los ángulos exteriores del triángulo.
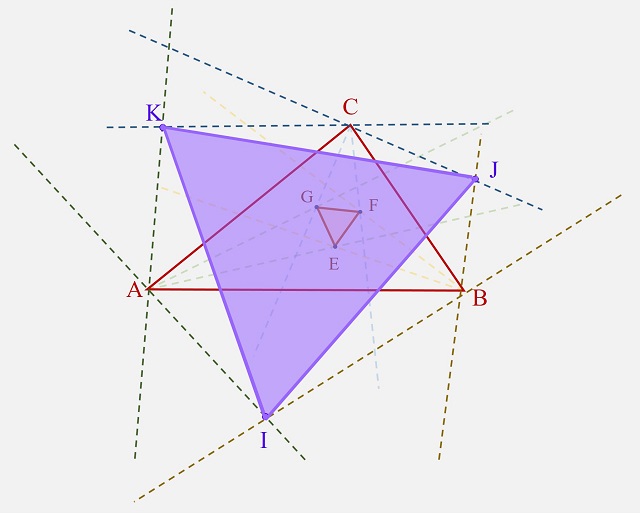 Dado un triángulo ABC, el triángulo EFG, formado por los puntos de intersección de las trisectrices adyacentes de los ángulos interiores de ABC, y el triángulo IJK, formado por los puntos de intersección de las trisectrices adyacentes de los ángulos exteriores de ABC, son equiláterosLa demostración de Conway
Dado un triángulo ABC, el triángulo EFG, formado por los puntos de intersección de las trisectrices adyacentes de los ángulos interiores de ABC, y el triángulo IJK, formado por los puntos de intersección de las trisectrices adyacentes de los ángulos exteriores de ABC, son equiláterosLa demostración de Conway
El matemático británico John Horton Conway (1937-2020), fue un prolífico e imaginativo matemático que trabajó en muchas áreas de las matemáticas, entre ellas la teoría de grupos algebraicos, las matemáticas de los juegos, la teoría de nudos, la teoría de números, la geometría o la teoría de códigos, que escribió interesantes libros, como la trilogía Winning Ways for your Mathematical Plays (Estrategias ganadoras para tus juegos matemáticos), junto a Richard K. Guy y Elwyn Berlekamp, o The Book of Numbers (El libro de los números), con Richard K. Guy, y que es conocido por temas como el autómata celular denominado el juego de la vida, los números surreales o la regla del fin del mundo, entre muchos otros. Os dejo con dos interesantes y profundas opiniones de Conway sobre jugar y educar:
Solía sentirme culpable en Cambridge por pasarme el día jugando a juegos, mientras se suponía que estaba haciendo matemáticas. Luego, cuando descubrí los números surrealistas, me di cuenta de que jugar ES matemáticas.
No se educa a la gente contándole cosas útiles, sino contándoles cosas interesantes.
 El matemático John H. Conway en su despacho de la Universidad de Princeton en 1993. Fotografía de Dith Pran/The New York Times
El matemático John H. Conway en su despacho de la Universidad de Princeton en 1993. Fotografía de Dith Pran/The New York TimesPero vayamos con la demostración de Conway del teorema de las trisectrices de Morley. Empecemos con un poco de notación. Dado un triángulo ABC cualquiera, como el de la siguiente imagen, del que queremos demostrar que los puntos de intersección de las trisectrices adyacentes de los ángulos (interiores) forman un triángulo equilátero, denotamos por alfa, beta y gama los ángulos que son igual a la tercera parte de los ángulos interiores del triángulo ABC, como aparece en la imagen. Como la suma de los ángulos (interiores) de un triángulo plano suman 180 grados, entonces la suma de alfa, beta y gama es igual a 60 grados.
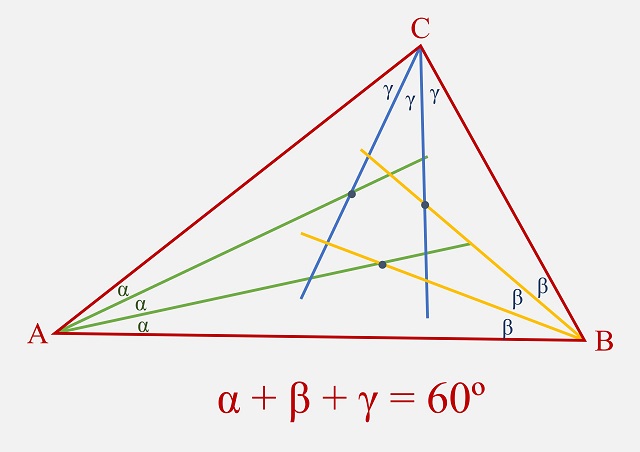
La demostración de Conway se basa en la creación de un rompecabezas con siete piezas triángulares, una de ellas un triángulo equilátero, de un cierto tamaño, que unidas correctamente forman el triángulo ABC y la pieza del triángulo equilátero es precisamente el triángulo de Morley.
La primera parte de la demostración consiste en la construcción de las siete piezas triángulares. Para empezar, se consideran siete triángulos cuyos ángulos interiores son los siguientes siete triples
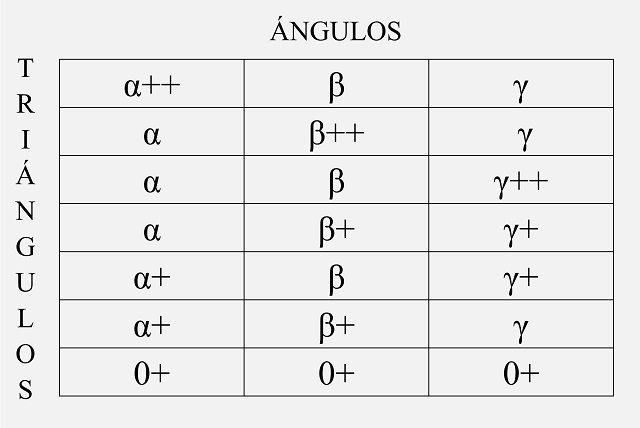
donde el símbolo “+” añadido a un ángulo quiere decir que sumamos 60 grados al ángulo, luego si añadimos dos símbolos “++” querrá decir que se suman 120 grados. Como la suma de alfa, beta y gama es igual a 60 grados, la suma de cada uno de los siete triples de ángulos, de la tabla anterior, es igual a 180 grados, como corresponde a cualquier triángulo. Observemos que uno de los triángulos es equilátero, sus ángulos (interiores) son de 60 grados.
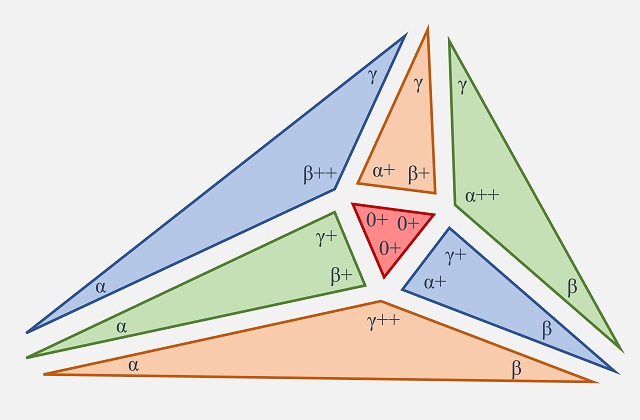
Al determinar los ángulos (interiores) de cada triángulo estamos determinando completamente la forma de dichos triángulos (como se muestra en la anterior imagen), y solo faltaría determinar el tamaño para que puedan encajar convenientemente.
Ahora para decidir el tamaño de las piezas triangulares vamos a proceder de la siguiente manera. Primero fijamos el tamaño del triángulo equilátero, que puede ser de cualquier tamaño, y después iremos adaptando el tamaño del resto de triángulos al de este primero. Para los tres triángulos tales que uno de sus lados se debería apoyar en uno de los lados del triángulo equilátero, que son los tres triángulos agudos (sus tres ángulos son menores de 90 grados), tomamos el tamaño de esos tres triángulos de forma que ese lado sea de la misma longitud que el lado del triángulo equilátero (en la siguiente imagen hemos agrandado y oscurecido esas lados que tienen que tener la misma longitud).
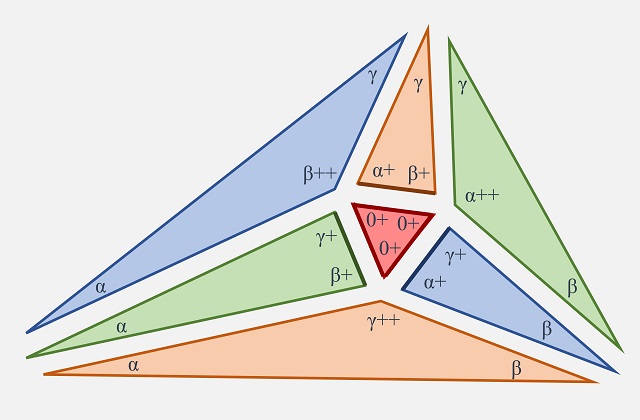
Por otra parte, para determinar el tamaño de los tres triángulos obtusos, es decir, triángulos con un ángulo que mide más de 90 grados, vamos a realizar el procedimiento para el triángulo de la derecha (en el ejemplo que estamos trabajando), el triángulo obtuso verde, procedimiento que se repetirá para los otros dos triángulos obtusos. Se introducen dos segmentos que van del vértice de la izquierda (vértice que se apoyará en uno de los vértices del triángulo equilátero) al lado opuesto, de manera que el ángulo entre estos segmentos y el lado opuesto sea alfa+ (es decir, alfa + 60 grados). Entonces se elige el tamaño del triángulo verde de manera que la longitud de esos dos segmentos (que es la misma, ya que forman un pequeño triángulo isósceles) sea igual al lado del triángulo equilátero.
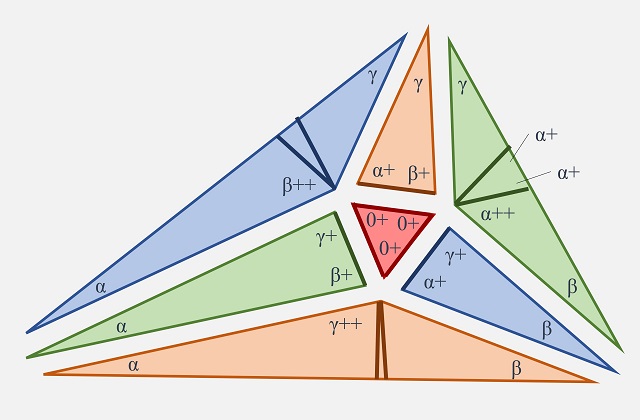
[Observación: Una pequeña aclaración para los más interesados. Si el ángulo en uno de los vértices A, B o C, fuese mayor que un recto, 90 grados, es decir, que uno de los ángulos alfa, beta o gama fuese mayor que 30 grados, entonces al construir ese pequeño triángulo isósceles, el ángulo considerado entre los segmentos y el lado opuesto será el exterior y no el interior]
Por lo tanto, ya tenemos construidos los siete triángulos, con su forma, determinada por los ángulos, y su tamaño, que hemos dispuesto a partir del tamaño del triángulo equilátero central.
El siguiente paso de la demostración consiste en probar que podemos ensamblar bien las siete piezas. Al triángulo equilátero le podemos juntar los tres triángulos agudos, ya que hemos elegido el tamaño de estos para que tengan un lado del mismo tamaño que el lado del triángulo equilátero. Ahora tenemos que comprobar si podemos juntarles además los tres triángulos obtusos, para lo cual tenemos que comprobar que coinciden las longitudes de los lados adyacentes de los triángulos obtusos y agudos. Veamos uno de los lados en cuestión, en concreto, el lado que compartirán el triángulo obtuso verde y el triángulo agudo marrón (arriba a la derecha), los otros cinco se razonan de manera similar.
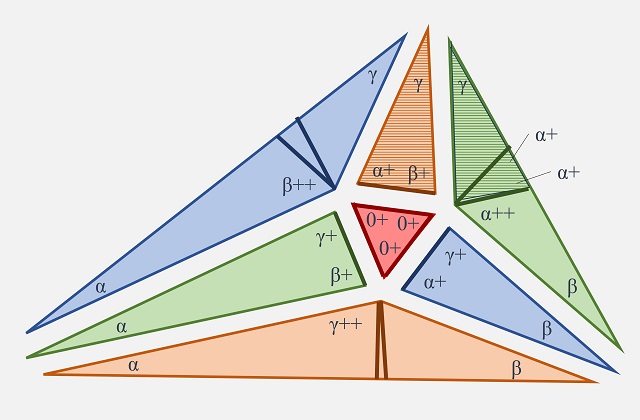
Por la construcción realizada, de ángulos y tamaños, los dos triángulos rayados en la imagen anterior son iguales, sus ángulos son alfa, beta+ y gama+ y tienen un lado de la misma longitud (de hecho, un triángulo rayado es la imagen especular del otro), por lo tanto, los lados adyacentes de ambos son iguales. En consecuencia, el triángulo obtuso verde encaja bien con el triángulo agudo marrón.
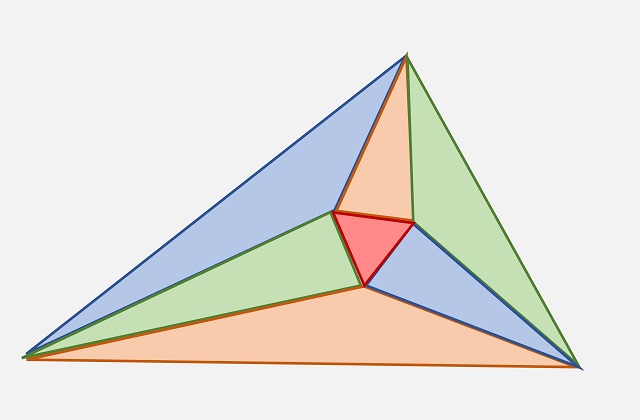
La segunda parte de la demostración queda así concluida al probar que las siete piezas triangulares encajan bien las unas con las otras formando un triángulo más grande entre las siete.
La tercera, y última, parte consiste en comprobar que efectivamente hemos probado el teorema de Morley. Para empezar, el triángulo construido con las siete piezas triángulares tiene ángulos iguales a tres veces alfa, tres veces beta y tres veces gama, como el triángulo ABC, luego ambos tienen la misma forma. Aunque es suficiente, para nuestro propósito, que tengan la misma forma, podemos reescalar el triángulo construido para que coincida, no solo en forma, sino también en tamaño, con nuestro triángulo ABC, basta reescalarlo para que la base tenga la longitud AB.
Por lo tanto, hemos demostrado el teorema de Morley para el triángulo ABC, ya que por la construcción de los triángulos alrededor del triángulo equilátero, los vértices de este son la intersección de las trisectrices adyacentes de los ángulos del triángulo, luego el triángulo que determinan es precisamente nuestra pieza que es un triángulo equilátero. Como decían los matemáticos griegos y seguimos diciendo en la actualidad, QED, es decir, “quod erat demonstrandum” (“lo que se quería demostrar”, literalmente “lo que se iba a mostrar”).
 Morley’s Theorem, del artista Eugent Jost, que aparece recogido en su libro, junto a Eli Maor, Beautiful Geometry (Princeton University Press, 2014). En la pintura aparecen cinco triángulos diferentes con sus respectivos triángulos de Morley asociados, así como tres fechas importantes, nacimiento y muerte del matemático Frank Morley, así como el año del descubrimiento de su resultado geométrico
Morley’s Theorem, del artista Eugent Jost, que aparece recogido en su libro, junto a Eli Maor, Beautiful Geometry (Princeton University Press, 2014). En la pintura aparecen cinco triángulos diferentes con sus respectivos triángulos de Morley asociados, así como tres fechas importantes, nacimiento y muerte del matemático Frank Morley, así como el año del descubrimiento de su resultado geométricoBibliografía
1.- David Wells, The Penguin Dictionary of Curious and Interesting Geometry, Penguin, 1991.
2.- Martin Gardner, Nuevos pasatiempos matemáticos, Alianza editorial, 2018.
3.- H. S. M. Coxeter and S. L. Greitzer, Geometry Revisited, Mathematical Association of America, 1967.
4.- C. O. Oakley, J. C. Baker, The Morley Trisector Theorem, American Mathematical Monthly 85, pp. 737-745, 1978.
5.- Pedro Alegría, Fernando Blasco, John Conway, el genio mágico, Gaceta de la RSME, vol. 23, n. 3, pp. 463–486, 2020.
6.- John Conway, On Morley’s Trisector Theorem, The Mathematical Intelligencer, vol. 36, n. 3, pp. 3, 2014.
7.- John Conway, The Power of Mathematics, publicado en el libro Power (Alan Blackwell, David MacKay, editores), Cambridge University Press, 2006.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Una elegante demostración del teorema de Morley se ha escrito en Cuaderno de Cultura Científica.

