Las ranas de Chernóbil envejecen bien
 Macho de Rana de San Antonio oriental (Hyla orientalis). Chernóbil (Ucrania), 2018.
Macho de Rana de San Antonio oriental (Hyla orientalis). Chernóbil (Ucrania), 2018.Germán Orizaola, CC BY
Han transcurrido casi cuatro décadas desde el accidente en la central nuclear de Chernóbil (Ucrania). Durante este tiempo, y para sorpresa de muchos, este lugar se ha convertido en una de las mayores reservas naturales de Europa. A lo largo de los últimos ocho años hemos trabajado para entender la situación de la fauna en el área afectada por este desastre medioambiental.
La radiación es capaz de dañar las células y, en exposiciones extremas, puede incluso causar la muerte de los organismos. Pero la situación de Chernóbil ha cambiado mucho desde el accidente. Allí queda hoy en día menos del 10 % del material radiactivo liberado en 1986. Los isótopos más peligrosos, como los de yodo, desaparecieron hace muchos años.
Estos factores pueden explicar la gran abundancia y diversidad de animales que viven hoy en Chernóbil. Sin embargo, es imprescindible examinar si los organismos experimentan daños que no vemos. Por ejemplo, si acumulan daños que acaben reduciendo su esperanza de vida.
Las ranas de ChernóbilDesde 2016 estudiamos las poblaciones de la rana de San Antonio oriental (Hyla orientalis) en Chernóbil, visitando la zona durante varias semanas cada primavera. Aprovechando la temporada de cría, capturamos machos durante la noche y los llevamos a nuestro laboratorio.
Además de en la zona de exclusión de Chernóbil, trabajamos en otras áreas del norte de Ucrania sin contaminación radiactiva. Estos lugares nos sirven como control para comparar nuestros resultados allí con los de la parte afectada por el accidente.
Durante años hemos examinado la morfología, el estado fisiológico e inmunitario y muchos otros rasgos de estas ranas. Nuestros trabajos han mostrado el aparente buen estado de salud de los anfibios en Chernóbil. Además, descubrimos un ejemplo de evolución rápida en las ranas, que son más oscuras que las de otras zonas sin radiación. Esto se debe, posiblemente, al papel protector de la melanina frente a la radiación.
Quedaba por investigar el efecto a largo plazo de la radiación sobre estos animales. Por eso analizamos la relación entre la radiación, la edad y el envejecimiento de las ranas.
¿Cuánto vive una rana?Podemos calcular la edad de un anfibio contando las líneas de crecimiento en sus huesos. Igual que ocurre con los anillos de los árboles, cada año de vida de una rana queda marcado. Sabemos que algunas especies en zonas de alta montaña pueden vivir más de 20 años. Otras especies, en cambio, apenas llegan a los 2 años.
En nuestro trabajo en Chernóbil examinamos unos 200 ejemplares a lo largo de tres años. Encontramos una edad máxima de 9 años en los machos de rana de San Antonio oriental. La mayoría de individuos que estudiamos tenían entre 3 y 4 años.
Además, queríamos saber si la radiación afectaba al ritmo de envejecimiento de las ranas. Para ello, medimos la longitud de los telómeros, un marcador asociado con la tasa de envejecimiento. Se trata de secuencias de ADN que se encuentran en el extremo de los cromosomas. Su función es proteger el material genético y se van acortando con cada división de la célula.
Para completar nuestro estudio, examinamos también los niveles de hormonas relacionadas con estrés en estas ranas. Medimos el contenido en sangre de corticosterona, una hormona que participa en la regulación del metabolismo y en la activación de la respuesta frente a estrés.
En todas las ranas calculamos también los niveles de radiación absorbida por cada individuo. Medimos el nivel de cesio de sus músculos y de estroncio de sus huesos. Este es uno de los estudios más detallados sobre la exposición actual a radiación en animales de Chernóbil. A nosotros nos permite relacionar de manera precisa los rasgos que medimos con la exposición a radiación en las ranas estudiadas.
El envejecimiento de las ranas de ChernóbilNuestro trabajo revela que vivir en Chernóbil no afecta ni a la edad ni al ritmo de envejecimiento de las ranas estudiadas.
La edad media de los individuos que capturamos fue de 3,6 años y fue similar en los individuos con mayor nivel de radiación y en aquellos de zonas sin radiación. Estos valores son normales para la especie y parecidos a los de otras poblaciones lejos de Chernóbil.
Tampoco observamos ningún efecto de la radiación sobre la velocidad de envejecimiento de las ranas. No detectamos ninguna relación entre la radiación absorbida por las ranas y la longitud de sus telómeros. Ésta se mantuvo bastante constante a lo largo de todos los niveles de radiación estudiados.
Además, los niveles de la hormona corticosterona no se vieron afectados por la radiación absorbida. Las ranas de Chernóbil tampoco parecen estar estresadas.
Estos resultados sugieren que los niveles de radiación presentes hoy en Chernóbil no son suficientes para causar daño crónico en estos organismos. Estas investigaciones son imprescindibles para desmontar el mito de que la Zona de exclusión es un infierno para la vida. En su lugar, estudios como el nuestro demuestran que se ha convertido en un refugio de gran relevancia para la fauna amenazada de Europa.![]()
Sobre los autores: Germán Orizaola, Profesor Titular de Zoología, Universidad de Oviedo y Pablo Burraco, Investigador postdoctoral Juan de la Cierva, Estación Biológica de Doñana (EBD-CSIC)
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Las ranas de Chernóbil envejecen bien se ha escrito en Cuaderno de Cultura Científica.
Naukas Pro 2024: Las batimetrías, los ojos del fondo marino

Los últimos avances en el ámbito de las energías renovables marinas o la proliferación de los microplásticos fueron algunos de los temas que componen la última edición de NAUKAS PRO. Una cita en la que el personal investigador se sube al escenario del Euskalduna Bilbao para hablar de las investigaciones más destacadas del momento en un ámbito concreto.
En esta ocasión el personal investigador de la Universidad del País Vasco, de la Estación Marina de Plentzia (PiE-UPV/EHU), AZTI, Tecnalia o el CSIC acercaron las últimas investigaciones relacionadas en el ámbito marítimo.
La conferencia Las batimetrías, los ojos del fondo marino corre a cargo de Gemma Ercilla Zarraga, investigadora del Instituto de Ciencias del Mar-ICM-CSIC.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Pro 2024: Las batimetrías, los ojos del fondo marino se ha escrito en Cuaderno de Cultura Científica.
El impacto en la Amazonía del petróleo que consumes aquí
Del petróleo extraído en la Amazonía ecuatoriana por una empresa española, Ecuador apenas se queda con el 21 % de los ingresos. Y ello a pesar de soportar buena parte de los impactos ambientales y las transformaciones culturales en las comunidades indígenas como consecuencia de las extracciones.
 Vista aérea de parte de las intalaciones de estracción de petróleo en la Amazonía ecuatoriana. Fuente El Santo Films / Izar Films
Vista aérea de parte de las intalaciones de estracción de petróleo en la Amazonía ecuatoriana. Fuente El Santo Films / Izar FilmsEl último trabajo del grupo de investigación Life Cycle Thinking de la UPV/EHU muestra que el 79 % del dinero procedente del petróleo de los bloques 16 y 67 de Ecuador va a países enriquecidos: el 20 % lo ganan las empresas de extracción, el 21 % las refinerías y los intermediarios en la distribución y el 38 % el gobierno de España a través del impuesto especial sobre hidrocarburos que se aplica por la falta de sostenibilidad. “El hecho de que en el país de origen del recurso, Ecuador, solo se quede el 21 % de los ingresos demuestra que la distribución de beneficios y daños no es equitativa. Nuestro estudio ha convertido en cifras el desigual reparto de los impactos económicos y ambientales de la explotación del petróleo en el norte y en el sur global”, ha explicado Ortzi Akizu Gardoki, investigador de la Escuela de Ingeniería de Vitoria-Gasteiz de la UPV/EHU.
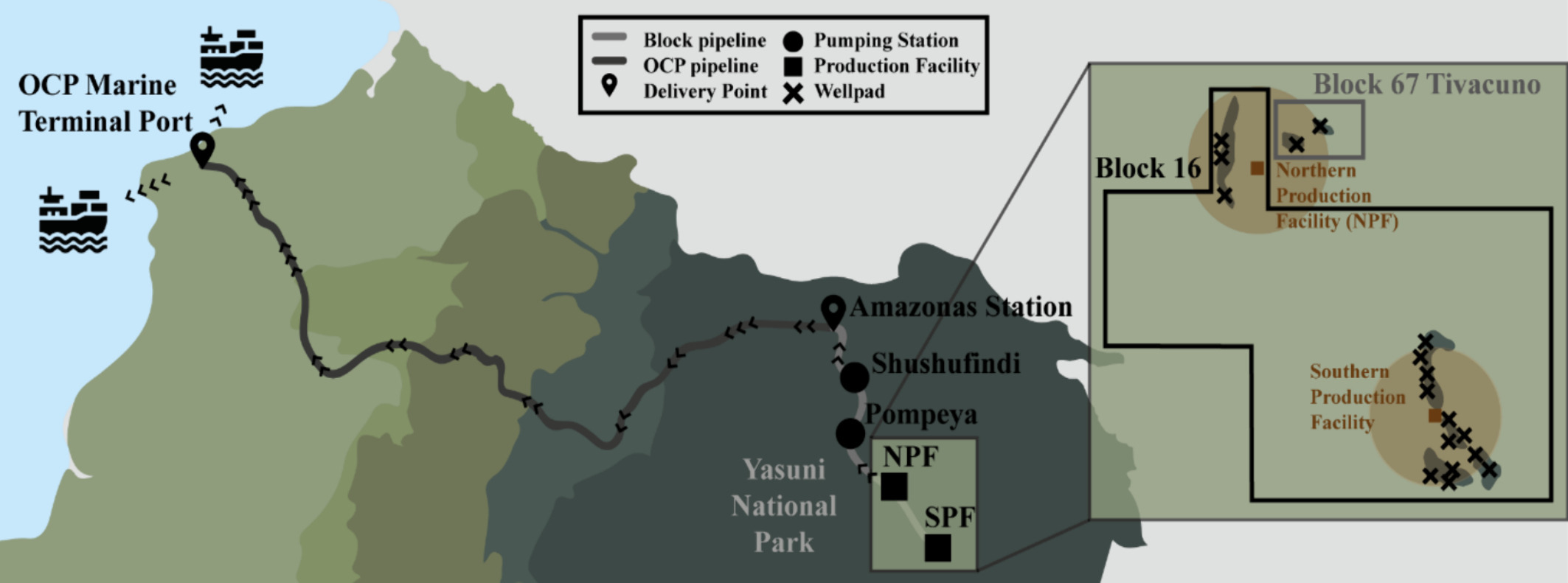 Fuente: Eugenio, C. et al (2024)
Fuente: Eugenio, C. et al (2024)Ecuador produce anualmente unos 175 millones de barriles de petróleo, cuya exportación constituye la principal fuente de ingresos del país. Hay más de 80 bloques repartidos por todo el país, pero los que más polémica generan son los de la selva amazónica, por los daños sociales y ecológicos que provocan. En concreto, los bloques 16 y 67 sobre los que ha incidido la labor de la Universidad del País Vasco se encuentran en el Parque Nacional Yasuní, situado en esa zona, uno de los lugares del mundo con una mayor biodiversidad. Estos pozos han sido elegidos para la investigación por la urgencia de cuantificar el equilibrio entre los impactos y los beneficios que generan las extracciones sobre la naturaleza y sus comunidades indígenas. También porque Repsol ha sido quien ha explotado estos dos bloques durante 24 años: «No se sabe si el combustible que compramos procede de uno de esos dos bloques, pero sí tenemos gasolineras de esa compañía en el País Vasco. El estudio ha servido para impulsar el objetivo de concienciar a los usuarios finales de aquí sobre la responsabilidad que tenemos en los impactos del petróleo que se extrae en la Amazonia”, ha aclarado Akizu Gardoki.
La investigación ha llenado una laguna existente al respecto. De hecho, es la primera vez que se cruzan los datos relativos a los beneficios obtenidos de la explotación de estas dos zonas con la huella ecológica. Se concluye que, de media, la propia Amazonia soporta directamente el 19,6 % de las emisiones equivalentes de CO2 producidas por la producción y el consumo.
El ciclo de vida del petróleoPara lograr estos resultados, el equipo de investigación ha utilizado el análisis del ciclo de vida del petróleo. Con el fin de poder comparar los datos, se ha tenido en cuenta la huella de carbono que se produce cuando lo utilizamos como combustible en vehículos particulares. Es decir, han cuantificado las emisiones de CO2 que se producen desde el momento en que se extrae el petróleo de los dos bloques del Parque Nacional Yasuní, se transporta a las refinerías, se trata y se distribuye a las gasolineras, hasta que sale por el tubo de escape de los coches. Los resultados indican que el 38,7 % de las emisiones se producen directamente por mantener el motor en marcha, el 37,1 % durante la construcción del vehículo y las infraestructuras, y el 24,3 % en los procesos de extracción, refinamiento y distribución.
Akizu Gardoki desea despertar la conciencia de los consumidores finales a través de los siguientes datos: “Se pone de manifiesto la gran responsabilidad de las personas que van al volante. En muchas ocasiones solo miramos el CO2 que sale por el tubo de escape, pero debemos ser conscientes de que la huella ambiental que genera la acción de conducir es más larga y de que también se producen daños en otros países. No somos responsables de los modelos energéticos creados por empresas privadas y gobiernos, pero podemos ser agentes de cambio”.
Impacto social en las comunidades indígenas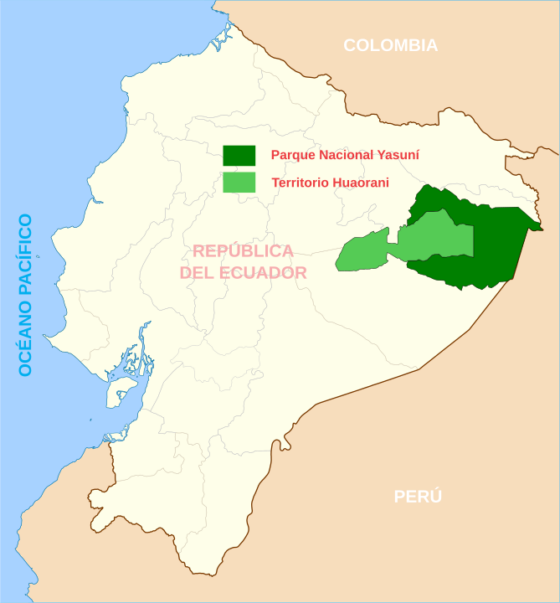 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsAdemás del impacto medioambiental, el estudio de la UPV/EHU también ha analizado el impacto social de las extracciones del Parque Nacional Yasuní en los grupos indígenas locales. “Hemos mantenido largas entrevistas con representantes de grupos de la etnia huaorani —señala el investigador— y hemos detectado impactos graves en la calidad de vida. También transformaciones culturales, que no tienen vuelta atrás. Entre otras cosas, hemos visto que se ha producido la dependencia del modelo económico y la pérdida de algunos hábitos, como consecuencia de la civilización”. Por otra parte, el estudio concluye que la explotación del petróleo en la Amazonia ha provocado la aparición del alcoholismo y el aumento de los casos de violencia de género.
Sin embargo, según el líder de Life Cycle Thinking, en el análisis se ha comprobado que las empresas y los gobiernos no cuantifican los daños sociales y ecológicos: “Lo hacen de forma intencionada, porque la falta de medición permite seguir generando impactos y permite pagar una compensación arbitraria por daños no cuantificados”.
El estudio de la Universidad del País Vasco supone una aportación a este primer paso para conocer la relación entre los beneficios y los impactos, pero el autor ha subrayado que es necesario dar más pasos. Por ejemplo, con vistas a reducir los impactos, propone empezar a indicar el origen del petróleo en las gasolineras: “Así como nos hemos acostumbrado a preguntar de dónde procede la fruta que compramos y estamos dispuestos a pagar el doble por las manzanas de productores locales, miremos de dónde viene el combustible que ponemos en los vehículos y de qué manera se produce. La sociedad vasca tiene el potencial de generar cambios en el actual modelo energético”.
Referencia:
Cinta Eugenio, Jacid Montoya-Torres, Ortzi Akizu-Gardoki, Leire Urkidi, Unai Villalba-Eguiluz , Carlos Larrea, Sylvia Pappuccio, Angélica Calle-Calderón, Dania Quirola (2024) Environmental impacts of oil extraction in blocks 16 and 67 of the Yasuní Reserve in the Amazonian Forest: Combined qualitative and Life-Cycle Assessment Science of The Total Environment doi: 10.1016/j.scitotenv.2024.175189
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo El impacto en la Amazonía del petróleo que consumes aquí se ha escrito en Cuaderno de Cultura Científica.
Mars Phoenix: la primera biblioteca de Marte
El 25 de mayo de 2008 aterrizó sobre la superficie de Marte la sonda Phoenix y, con ella, muchos de los sueños sobre el planeta rojo que habían alimentado, hasta entonces, la imaginación de varias generaciones. No era la primera vez que llegábamos allí, ni fue la última, pero Phoenix sí fue nuestra Cook o nuestra Peary, esto es, nuestra pionera de la exploración polar marciana.
 Impresión artística de la sonda Phoenix.
Impresión artística de la sonda Phoenix.Créditos: NASA/JPL/Corby Waste
El objetivo de la misión Mars Phoenix Lander era ayudar a reconstruir la historia geológica del agua en Marte, así como su pasado climático, y estudiar la química del suelo para dilucidar si en algún momento fue capaz de albergar vida. Desde 2001 se sabía, gracias al orbitador Odyssey, que había grandes cantidades de hielo en el subsuelo marciano a latitudes superiores a 55 º, Phoenix —tras el fracaso de la Mars Polar Lander que, en 1999, trató de aterrizar en el polo sur marciano— fue hasta Green Valley, en las planicies septentrionales de Vastitas Borealis, para comprobarlo, pero no solo iba equipada con instrumentos científicos. También llevaba consigo testimonios, historias, visiones y melodías.
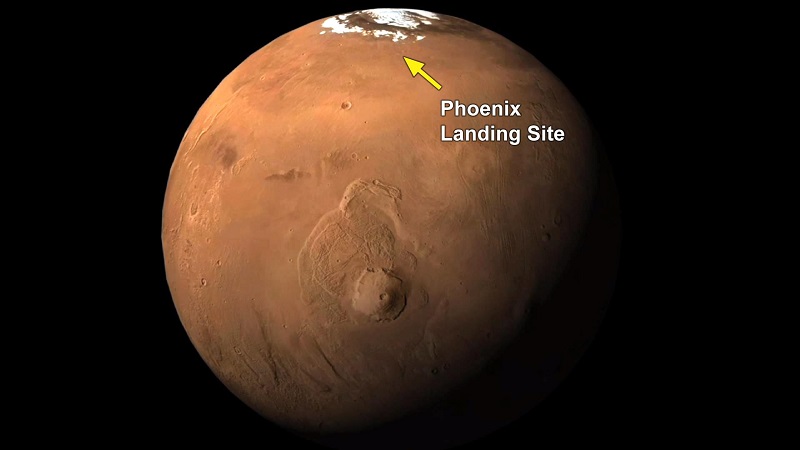 Lugar de aterrizaje de la sonda Phoenix: Green Valley, en las tierras bajas septentrionales de Vastitas Borealis, muy cerca del casquete polar norte.
Lugar de aterrizaje de la sonda Phoenix: Green Valley, en las tierras bajas septentrionales de Vastitas Borealis, muy cerca del casquete polar norte.Créditos: NASA/JPL-Caltech/University of Arizona/MSSS
En algunas fotos de la sonda se puede observar sobre la cubierta un miniDVD con el título Visiones de Marte; una versión actualizada —y mucho menos mítica, aunque no menos interesante— del disco dorado de las Voyager. Y sí… como era de esperar, el científico y divulgador Carl Sagan tuvo algo que ver en el proyecto.
 El miniDVD Visiones de Marte sobre la cubierta de la Mars Phoenix, fotografiado desde la superficie del planeta.
El miniDVD Visiones de Marte sobre la cubierta de la Mars Phoenix, fotografiado desde la superficie del planeta.Créditos: NASA/Jet Propulsion Lab-Caltech/University of Arizona
La idea, en esta ocasión, nació en 1991 de la mano del ingeniero Louis Friedman, confundador de la Planetary Society junto con el propio Sagan, que en aquel momento era el presidente, y Bruce Murray. Desde finales del siglo XIX y durante gran parte del siglo XX, Marte había sido el protagonista de innumerables aventuras e historias de ciencia ficción y estas, a su vez, habían inspirado a la generación de científicos que había hecho posible que llegáramos hasta nuestro vecino planetario, así que, ¿por qué no recopilar las más significativas y enviarlas allí? Quince años después de las Voyager, la tecnología había avanzado lo suficiente como para poder hacerlo sin un coste prohibitivo: del vinilo se había pasado a las cintas magnéticas, de las cintas magnéticas, al CD y, del CD, al DVD. Ahora se podía almacenar una cantidad de información mucho mayor en mucho menos espacio.
La primera versión de Visions of Mars, cuyo desarrollo corrió a cargo del artista y divulgador Jon Lomberg —colaborador habitual de Carl Sagan y director artístico de Cosmos—, partió a bordo de la misión soviética Mars 96, que acabó en el fondo del Pacífico poco después del despegue. Sin embargo, el proyecto resurgiría de sus cenizas —y no se me ocurre mejor forma de expresarlo— poco más de una década después, cuando se actualizaron y remasterizaron los contenidos para enviarlos al planeta rojo en la misión Mars Phoenix Lander.
Jon Lomberg y John Robert Colombo, con la inestimable ayuda y asesoramiento de la escritora Judith Merril —así como acceso a su extensa biblioteca—, hicieron una selección de obras de ciencia ficción con la que intentaron representar, de la manera más global posible, la historia de nuestras percepciones de Marte a través del tiempo y su influencia en la cultura popular. Así, volvieron a su hogar clásicos anglosajones como Una princesa de Marte, de Edgar R. Burroughs; La guerra de los mundos, de H. G. Wells, o Crónicas marcianas, de Ray Bradbury. Pero también la soviética Estrella Roja, de Alexander Bogdanov (Rusia); Il tre cosmonauti, de Umberto Eco (Italia); Auf zwei Planeten, de Kurd Lasswitz (Alemania), o El atardecer, 2217 d. C., de Ryu Mitsuse (Japón). Y no solo obras de ficción; también se incluyeron algunos de los ensayos más influyentes de la historia de la investigación marciana, como los escritos por Giovanni Schiaparelli y Percivall Lowell. El propio Jon Lomberg diría:
Esta asociación [entre el programa espacial y la ciencia ficción] es lo que nos ha inspirado a enviar este disco a Marte, para honrar y conmemorar el papel que ha desempeñado la ciencia ficción a la hora de alimentar los sueños de las personas que diseñaron, construyeron, volaron y financiaron las misiones que finalmente cruzaron el espacio. ¿Habríamos llegado tan lejos sin estas visiones que nos inspiraron?
Sin embargo, Visiones de Marte no incluía solo textos, sino que en él podemos encontrar todo tipo de expresiones culturales: ilustraciones y fotografías, emisiones de radio —no podía faltar la famosa retransmisión de Orson Welles de La guerra de los mundos, de 1938—… y una lista con los nombres de las 250 000 personas que quisieron formar parte, de alguna manera, de esta misión, incluidos todos los miembros de la Sociedad Planetaria.
 Ilustración de 1906 de la edición belga de La guerra de los mundos de H. G. Wells incluida en Visions of Mars.
Ilustración de 1906 de la edición belga de La guerra de los mundos de H. G. Wells incluida en Visions of Mars.
Como si una cápsula del tiempo se tratara, Arthur C. Clarke, Louis Friedman y Judith Merrill dejaorn mensajes para los colonos del futuro. También otra persona que, de haber seguido todavía entre nosotros, hubiera cumplido noventa años el pasado 9 de noviembre:
Cualquiera que sea la razón por la que estáis en Marte, me alegro de que sea así. Y desearía estar con vosotros.
Carl Sagan
Bibliografía
NASA (2008). Phoenix Landing. Mission to the Martian Polar North [press kit].
The Planetary Society (s. f.). Visions of Mars.
The Planetary Society (s. f.). Visions of Mars. Then and now.
.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo Mars Phoenix: la primera biblioteca de Marte se ha escrito en Cuaderno de Cultura Científica.
La sucesión del infinito del compositor Per Nørgård
Los fractales son unos curiosos objetos matemáticos que gozan de una cierta popularidad fuera de la comunidad matemática, y científica, desde que el matemático polaco, nacionalizado francés y estadounidense, Benoît Mandelbrot (1924-2010), considerado el padre de la geometría fractal, realizara una importante labor divulgativa sobre ellos, primero con el artículo ¿Qué longitud tiene la costa de Gran Bretaña? (Revista Science, 1967) y posteriormente con los libros Los objetos fractales: forma, azar y dimensión (1975) o La geometría fractal de la naturaleza (1982), entre muchos otros.
En la entrada del Cuaderno de Cultura Científica titulada Sucesiones fractales hablábamos de un tipo de sucesiones de números enteros que compartían con los objetos fractales una de sus propiedades definitorias, la autosemejanza (para una explicación divulgativa de las mismas puede leerse la entrada Fractus, arte y matemáticas). Más aún, en una entrada posterior, titulada Sucesiones fractales: del número a la nota musical, explicábamos como el compositor minimalista estadounidense Tom Johnson (1939) las había utilizado en algunas de sus composiciones musicales, por ejemplo, La melodía racional XV y la pieza La vie est si court, las cuales fueron explicadas en dicha entrada.
 Fotograma del video “Illustrated Music #6, Rational Melody XV” del canal de YouTube del compositor Tom Johnson, al que podemos ver en el mismo
Fotograma del video “Illustrated Music #6, Rational Melody XV” del canal de YouTube del compositor Tom Johnson, al que podemos ver en el mismo
La “sucesión del infinito” que, en particular, es una sucesión fractal y de la que vamos a escribir en esta entrada, fue descubierta por el músico danés Per Nørgård, que la utilizó como base matemática de muchas de sus composiciones musicales.
Per Nørgård, descubridor de la sucesión del infinitoEl compositor, teórico de la música y profesor danés Per Nørgård (1932) es una figura fundamental en la música danesa contemporánea. Ha escrito alrededor de 400 composiciones, que incluyen seis operas, ocho sinfonías, tres ballets, música para orquesta, conciertos, obras corales y vocales, música de cámara, piezas para instrumentos solistas y también bandas sonoras para películas. Entre sus composiciones más importantes se podrían citar Voyage into the Golden Screen / Viaje a la pantalla dorada (1968), para orquesta, la Sinfonía no. 2 (1970), para orquesta, la ópera Gilgamesh (1972), premiada con el Nordic Music Prize en 1974, la Sinfonía no. 3 (1972), para dos coros y orquesta, la ópera Siddharta (1979), la pieza para un solo instrumento de percusión I Ching (1982) o la ópera Det Guddommelige Tivoli / El circo divino (1982). Además, ha recibido muchos reconocimientos a lo largo de su extensa carrera, como el Premio (internacional) Ernst von Siemens, conocido como el Premio Nobel de la Música, en 2016, o el Premio (internacional) Wihuri Sibelius, en 2006, por mencionar algunos.
 Fotografía del compositor danés Per Nørgård (1932)
Fotografía del compositor danés Per Nørgård (1932)
Si consultamos la biografía de Per Nørgård que aparece en la base de datos sobre compositores del Institut de Recherche et Coordination Acoustique/Musique (IRCAM), un instituto francés de investigación sobre música y acústica, asociado al Centro Nacional de Arte y Cultura Georges Pompidou de París (cuya dirección web es brahms.ircam.fr), se mencionan las siguientes cuestiones respecto a su música. “Tras experimentar con collages musicales a finales de la década de 1950, Per Nørgård centró su atención en la música serial en los primeros años de la nueva década, desarrollando su propia técnica conocida como sucesión del infinito”, que es una de las herramientas musicales más importantes del conjunto de su producción musical. Además, no podemos olvidar que esta sucesión del infinito es un objeto matemático, una sucesión de números enteros con una serie de propiedades que la hacían interesante para las composiciones musicales que Per Nørgård quería componer y que utilizó en obras como Viaje a la pantalla dorada (1968), la Sinfonía no. 2 (1970), la Sinfonía no. 3 (1972) o I Ching (1982). Además de la sucesión del infinito, también utilizó el número de oro y la sucesión de Fibonacci, aunque en menor medida.
Por otra parte, “en 1979, durante una exposición en el Museo de Arte Moderno de Luisiana (Dinamarca), el compositor descubrió la obra del pintor suizo, uno de los primeros artistas asociados con el Art Brut (arte marginal), Adolf Wölfli. La interpretación de los criptogramas del artista esquizofrénico atrajo la práctica compositiva de Nørgård hacia el expresionismo. El resultado es un juego de intensidades, cambios bruscos de humor y modificaciones violentas del sonido y, además, un desbordamiento del flujo musical. Esta aparición del conflicto y la irracionalidad en su obra es una respuesta directa a la última década de composiciones matemáticamente regulares”. Entre las obras que pertenecen a este periodo están la Sinfonía no. 4 (1981) y la ópera sobre la vida de Wölfli, El circo divino (1982).
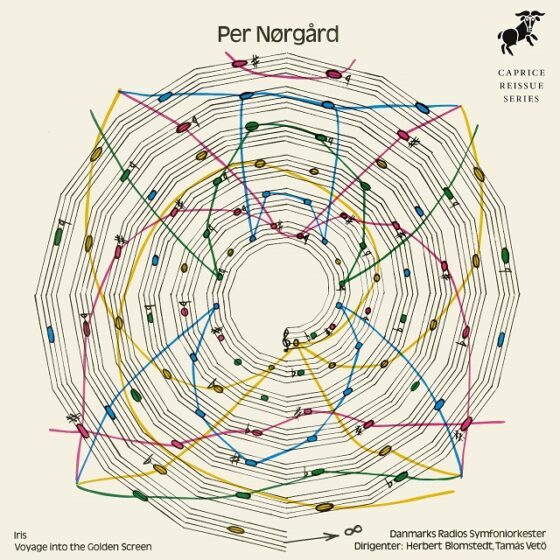 Portada del disco Per Nørgård: Iris/Voyage into the Golden Screen (1973), de la Danish National Symphony Orchestra, dirigida por Herbert Blomstedt y Tamás Vetö, en cuya imagen podemos observar la sucesión del infinito en formato musical y dibujada en espiralLa sucesión del infinito
Portada del disco Per Nørgård: Iris/Voyage into the Golden Screen (1973), de la Danish National Symphony Orchestra, dirigida por Herbert Blomstedt y Tamás Vetö, en cuya imagen podemos observar la sucesión del infinito en formato musical y dibujada en espiralLa sucesión del infinito
El compositor Per Nørgård descubrió (utilizamos este término y no “inventó”, ya que es el que utilizaba el propio Nørgård) la sucesión de números enteros que bautizó con el nombre de Uendelighedsrækken (en danés), que he traducido para esta entrada como sucesión del infinito, en 1959, años antes de que los fractales se hicieran conocidos a través de la labor divulgativa del matemático Benoit Mandelbrot, y que utilizó en muchas de sus composiciones, especialmente de las décadas de 1960 y 1970. La primera obra en la que utiliza la sucesión del infinito es su obra Viaje a la pantalla dorada (1968), en la cual utiliza 1.024 elementos de la sucesión en su versión musical. La siguiente obra en la que la utilizaría es la Sinfonía no. 2 (1970), con una utilización más compleja con 4.096 elementos de la sucesión.
Si consultamos la partitura de la obra Viaje a la pantalla dorada podemos ver una versión musical de la sucesión del infinito, cuyas primeras 64 notas (interpretadas en esta obra por las dos flautas) aparecen en la siguiente imagen.
 Las primeras 64 notas de la sucesión musical del infinito extraída de la composición Viaje a la pantalla dorada (1968), de Per Nørgård
Las primeras 64 notas de la sucesión musical del infinito extraída de la composición Viaje a la pantalla dorada (1968), de Per NørgårdA partir de la anterior imagen, extraída de la partitura de la obra Viaje a la pantalla dorada, vamos a escribir la sucesión de números enteros, que Nørgård descubrió, realizando el proceso inverso al que realizó el compositor al pasar de la sucesión de números a la sucesión de notas musicales. Para ello empezamos indicando que el punto inicial es la primera nota de la sucesión musical, que en este caso es “Sol” y que se corresponde con el número 0. A partir de ahí los números enteros de la sucesión van a indicar, para cada nota, la cantidad de semi-tonos que esa nota está por encima (positivo) de “Sol”, luego es más aguda, o por debajo (negativo), luego es más grave. Así, el segundo número es un 1 puesto que la siguiente nota es “La bemol” que es un semi-tono más alta (aguda) que “Sol” (de “Sol” a “La” subimos un tono, pero el bemol indica que baja un semi-tono, luego de “Sol” a “La bemol” sube un semi-tono). Como la tercera nota es “Fa sostenido”, que es un semi-tono más baja (grave) que “Sol” (de “Sol” a “Fa” se baja un tono, pero el sostenido indica que la nota sube un semi-tono, entonces el “Fa sostenido” es un semi-tono más bajo que “Sol”), el siguiente número de la sucesión es -1. El cuarto número es 2, ya que la cuarta nota es un “La”, un tono, luego dos semi-tonos, por encima de “Sol”. De esta manera descubrimos que los 64 primeros números de la sucesión del infinito, en correspondencia con las notas musicales de la partitura, son los siguientes.

De hecho, los 86 primeros términos de la sucesión del infinito, que es la sucesión A004718 de la Enciclopedia online de sucesiones de números enteros, son los siguientes.
0, 1, -1, 2, 1, 0, -2, 3, -1, 2, 0, 1, 2, -1, -3, 4, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, -1, 2, 0, 1, 2, -1, -3, 4, 0, 1, -1, 2, 1, 0, -2, 3, 2, -1, -3, 4, -1, 2, 0, 1, -3, 4, 2, -1, 4, -3, -5, 6, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, 0, 1, -1, 2, 1, 0, …
Existen varias formas de generar esta sucesión de números enteros. La más simple es mediante una fórmula recursiva.
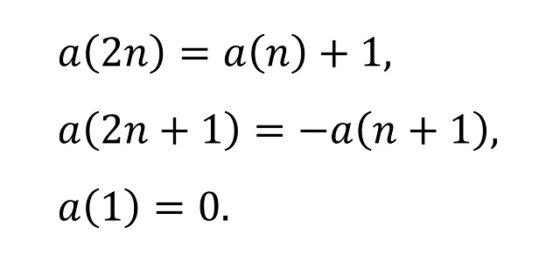 Fórmula recursiva de la sucesión del infinito
Fórmula recursiva de la sucesión del infinito
En la propia fórmula recursiva ya podemos percibir las propiedades relacionadas con la autosemejanza, de hecho, la sucesión del infinito es una sucesión fractal, que buscaba el compositor y que veremos más adelante.
Un proceso iterativo infinitoOtro método de construcción de esta sucesión es un proceso iterativo infinito proyectando un “segmento” inicial de dos números, o dos notas. El segmento inicial es 0 y 1 (“Sol” y “La bemol”) y la variación entre los dos (segundo menos primero) es + 1, entonces vamos a proyectar los dos primeros términos de la sucesión utilizando esa variación de la siguiente forma. Al segundo término le aplicamos la variación 1 + 1 y se convierte en el cuarto término 2, mientras que al primer término le aplicamos el opuesto 0 – 1 y se convierte en el tercer término – 1, como se muestra en la siguiente imagen. Por lo tanto, tenemos los cuatro primeros términos de la sucesión 0, 1, -1, 2.

A continuación, avanzamos una posición y el segmento que nos va a determinar las dos siguientes notas es el segmento 1 y -1, y la variación entre los dos es -2. Ahora aplicaremos esta variación a los dos últimos términos de la sucesión que vamos construyendo, – 1 y 2. Al segundo de esos dos términos le aplicamos la variación 2 – 2 y se convierte en el sexto término de la sucesión 0, mientras que al primero le aplicamos el opuesto -1 + 2 = 1 y se convierte en el quinto término de la sucesión, como se muestra en la siguiente imagen. De esta forma quedan determinados los seis primeros términos de la sucesión 0, 1, -1, 2, 1, 0
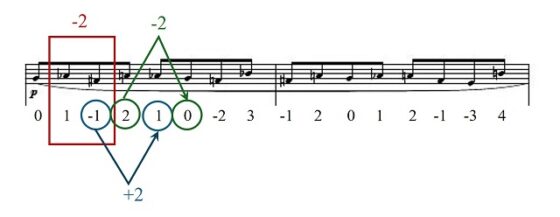
Volvemos a avanzar una posición y el segmento que nos va a determinar ahora las dos siguientes notas es el segmento -1 y 2, por lo que la variación es +3. Aplicando, como en los casos anteriores, esta variación a los dos últimos términos construidos 1 y 0, se obtienen los dos siguientes, séptimo y octavo, -2 y 3, como se puede ver en la siguiente imagen.
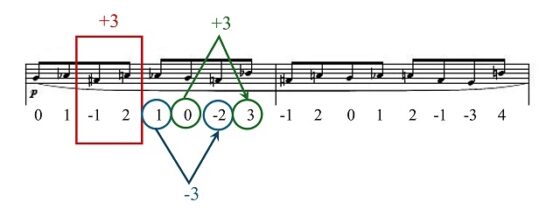
Y así se continuaría, podéis observar el siguiente paso en la siguiente imagen, en un proceso iterativo infinito que nos genera la sucesión del infinito.
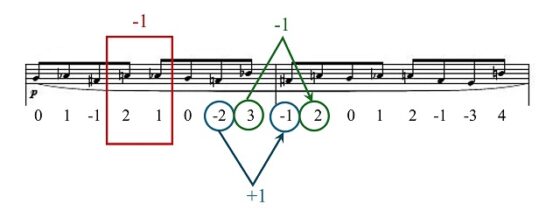
Existe otro proceso iterativo infinito para generar la sucesión del infinito denominado “desplegado”, pero que no vamos a explicar en esta entrada.
Construcción con números binariosEn la entrada Sucesiones fractales mostrábamos un ejemplo de una sucesión fractal construida a partir de la representación binaria de los números naturales (sobre la representación binaria puede leerse la mencionada entrada Sucesiones fractales, o con una explicación más extensa y detallada la entrada Las bases de numeración o cómo hacer trucos de magia binarios), incluido el 0, en concreto, la sucesión consistía en la cantidad de unos (1s) de la expresión binaria de los números enteros no negativos. Así mismo, en la entrada La sucesión fractal de Thue-Morse y la partida infinita de ajedrez se mostraba un proceso de construcción de la conocida sucesión fractal de Thue-Morse a través de las representaciones binarias de los números, en concreto, sumando los unos (1s) de la representación binaria de los números, empezando en 0, si es una cantidad par se considera el número 0 y si es impar el número 1.
También existe un método de construcción de la sucesión del infinito mediante la representación binaria de los números naturales, empezando en cero. Por lo tanto, empecemos considerando la representación binaria de los números, que mostramos en la siguiente imagen entre el 0 y el 38.
 Representación binaria de los números, desde 0 hasta 38
Representación binaria de los números, desde 0 hasta 38
Expliquemos, a continuación, cómo se construye la sucesión del infinito a partir de esas representaciones binarias. Para obtener los términos de la sucesión del infinito se realiza la “suma” de los unos (1s), pero teniendo en cuenta “cambios de signo” cuando aparecen ceros (0s) en la representación binaria, leyendo estas de izquierda a derecha. Así, para la representación 1111 (del número 15) se obtiene el término 4 (suma de los cuatro 1s); para la representación 1110 (del número 14) se obtiene -3 (suma de tres 1s, más un 0 que cambia el signo); para la representación 1101 (del número 13) se obtiene -1 (suma de dos 1s, luego 2, con el 0 se cambia el signo a -2 y luego se suma el último 1, luego -2 + 1 = -1); para 1010 (número 10), se obtiene 0 (se empieza sumando 1, que cambia de signo con el 0, a -1, se suma 1, luego 0, y el cambio de signo, del último 0, no modifica nada); o para 1001 (número 9), se obtiene 2 (primero 1, que cambia de signo con el primer 0, luego -1, que vuelve a cambiar de signo con el segundo 0, luego 1, al que se le suma el último 1, finalmente 2). Veamos ahora la tabla de dicha construcción.
 Construcción de la sucesión del infinito mediante las representaciones binarias de los números
Construcción de la sucesión del infinito mediante las representaciones binarias de los númerosSucesiones fractales
Vamos a terminar esta entrada viendo las propiedades que hicieron que la sucesión del infinito fuera importante como herramienta de creación musical para el compositor Per Nørgård, propiedades de autosemejanza. Aunque antes recordemos la definición de sucesión fractal o autosemejante.
 Doble página del libro Seeing New Music – Contemporary classical music through the eyes of a graphic designer (2015), de Denise Burt, en el que se recoge la explicación del diseño de la portada del álbum Libra (2012) de Per Nørgård
Doble página del libro Seeing New Music – Contemporary classical music through the eyes of a graphic designer (2015), de Denise Burt, en el que se recoge la explicación del diseño de la portada del álbum Libra (2012) de Per NørgårdUna sucesión (infinita) de números enteros es una sucesión fractal, también llamada sucesión autosemejante, si una parte de la sucesión es igual a toda la sucesión, es decir, si eliminamos algunos miembros de la sucesión infinita los miembros de la sucesión que quedan constituyen de nuevo toda la sucesión.
Veamos un ejemplo. Consideremos la sucesión finita de números 1, 2, 2, 3, 2, 3, 3 y construyamos la sucesión infinita que consiste en repetir la secuencia anterior de forma infinita, es decir, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, 1, 2, 2, 3, 2, 3, 3, … Ahora si eliminamos de la sucesión infinita todos los números que están en posiciones pares, los que nos quedan, que son los que están en las posiciones impares, siguen siendo la sucesión original, como queda de manifiesto en la siguiente imagen.
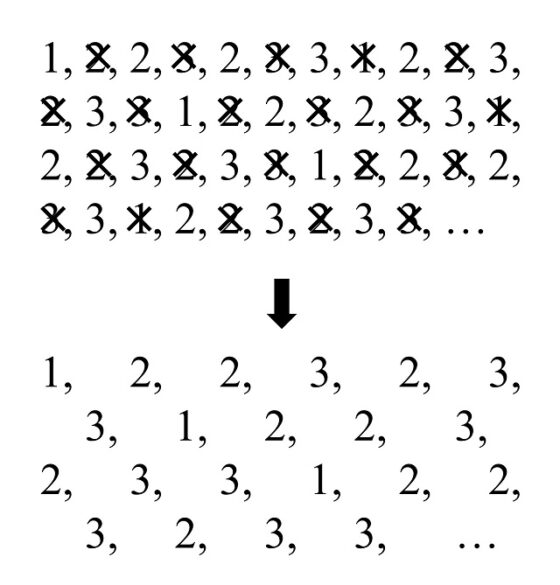
Volvamos a la sucesión inventada, o descubierta, por el compositor danés Per Nørgård. Empecemos recordando los primeros términos de la sucesión, que ya mostramos antes.
0, 1, -1, 2, 1, 0, -2, 3, -1, 2, 0, 1, 2, -1, -3, 4, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, -1, 2, 0, 1, 2, -1, -3, 4, 0, 1, -1, 2, 1, 0, -2, 3, 2, -1, -3, 4, -1, 2, 0, 1, -3, 4, 2, -1, 4, -3, -5, 6, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, 0, 1, -1, 2, 1, 0, …
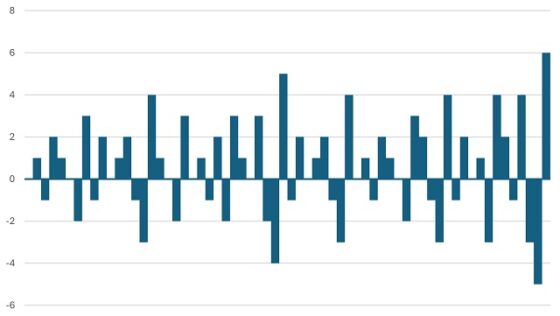 Visualización de la sucesión del infinito mediante un gráfico de barras
Visualización de la sucesión del infinito mediante un gráfico de barras
Ahora, vamos a eliminar los términos que están en posiciones pares, quedarnos con los que están en posiciones impares y veamos qué ocurre.
0, 1, -1, 2, 1, 0, -2, 3, -1, 2, 0, 1, 2, -1, -3, 4, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, -1, 2, 0, 1, 2, -1, -3, 4, 0, 1, -1, 2, 1, 0, -2, 3, 2, -1, -3, 4, -1, 2, 0, 1, -3, 4, 2, -1, 4, -3, -5, 6, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, 0, 1, -1, 2, 1, 0, …
Si nos fijamos bien en el resultado, lo que nos ha quedado es la sucesión del infinito original (0, 1, -1, 2, 1, 0, -2, 3, …) pero invertida, es decir, con el signo opuesto (0, -1, 1, -2, -1, 0, 2, -3, …). Por lo tanto, la sucesión del infinito tiene una cierta propiedad de autosemejanza, pero con inversión del signo. Esta propiedad está reflejada en la fórmula recursiva, a(2n + 1) = – a(n + 1).
Por otra parte, si eliminamos los términos que están en posiciones impares y nos quedamos con los términos de las posiciones pares, ocurre lo siguiente.
0, 1, -1, 2, 1, 0, -2, 3, -1, 2, 0, 1, 2, -1, -3, 4, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, -1, 2, 0, 1, 2, -1, -3, 4, 0, 1, -1, 2, 1, 0, -2, 3, 2, -1, -3, 4, -1, 2, 0, 1, -3, 4, 2, -1, 4, -3, -5, 6, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, 0, 1, -1, 2, 1, 0, …
De nuevo, si nos fijamos en el resultado, lo que queda es la sucesión del infinito original (0, 1, -1, 2, 1, 0, -2, 3, …) pero desplazada en una unidad, es decir, se suma 1 a cada término de la sucesión del infinito (1, 2, 0, 3, 2, 1, -1, 4, …). Otra propiedad del tipo de autosemejanza, pero con traslación de una unidad. También esta propiedad está reflejada en la fórmula recursiva, a(2n) = a(n) + 1.
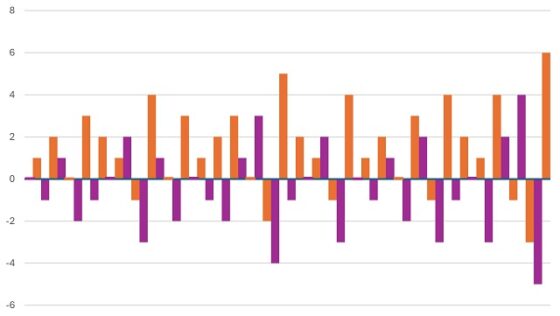 Visualización de los términos pares (naranja) e impares (ciruela) de la sucesión del infinito mediante un gráfico de barras
Visualización de los términos pares (naranja) e impares (ciruela) de la sucesión del infinito mediante un gráfico de barras
Podemos cuestionarnos si la sucesión del infinito es una sucesión fractal en sentido estricto y la respuesta es, claramente, afirmativa. De hecho, es lo que se llama una sucesión fractal de razón d = 4, es decir, el subconjunto de la sucesión que no eliminamos son el primer número de la sucesión y los que van apareciendo cada d posiciones, es decir, los números que están en las posiciones que son múltiplos de d más 1 y de esta forma obtenemos de nuevo la sucesión original. Veamos si es así para la sucesión del infinito.
0, 1, -1, 2, 1, 0, -2, 3, -1, 2, 0, 1, 2, -1, -3, 4, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, -1, 2, 0, 1, 2, -1, -3, 4, 0, 1, -1, 2, 1, 0, -2, 3, 2, -1, -3, 4, -1, 2, 0, 1, -3, 4, 2, -1, 4, -3, -5, 6, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, 0, 1, -1, 2, 1, 0, …
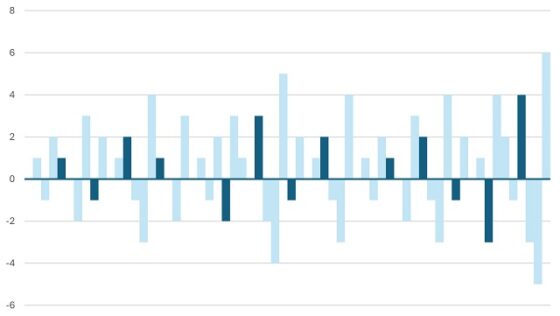 Visualización mediante un gráfico de barras de la propiedad de que la sucesión del infinito es una sucesión fractal de razón 4
Visualización mediante un gráfico de barras de la propiedad de que la sucesión del infinito es una sucesión fractal de razón 4
La propiedad de ser una sucesión fractal de razón 4 también se podía observar en la fórmula recursiva, ya que a(4n + 1) = – a(2n + 1) = a(n + 1).
La sucesión del infinito es una sucesión con muchas más propiedades matemáticas, pero en las que no vamos a entrar ahora. Simplemente terminaremos esta entrada viendo la relación que tiene con la sucesión de Thue-Morse.
La sucesión de Thue-MorseEn la entrada del Cuaderno de Cultura Científica titulada La sucesión fractal de Thue-Morse y la partida infinita de ajedrez [https://culturacientifica.com/2023/04/05/la-sucesion-fractal-de-thue-morse-y-la-partida-infinita-de-ajedrez/] presentamos la sucesión de Thue-Morse, o sucesión de Prouhet-Thue-Morse, que es una curiosa sucesión de números enteros que aparece en diferentes ramas de las matemáticas, desde la combinatoria de palabras a problemas de ajedrez, pasando por la geometría diferencial, la teoría de números, el análisis matemático de funciones, la física matemática, los cuasi-cristales o la teoría de grupos.
Los primeros términos de la sucesión de Thue-Morse (que es la sucesión A010060 en la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS) son los siguientes.
0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, …
Resulta que si consideramos la sucesión del infinito módulo 2, es decir, los números pares serán 0 y los números impares 1, entonces se obtiene la sucesión de Thue-Morse. A continuación, volvemos a mostrar los primeros términos de la sucesión del infinito, para que podáis comprobar que los números pares coinciden con los 0s de la sucesión de Thue-Morse y los impares con los 1s.
0, 1, -1, 2, 1, 0, -2, 3, -1, 2, 0, 1, 2, -1, -3, 4, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, -1, 2, 0, 1, 2, -1, -3, 4, 0, 1, -1, 2, 1, 0, -2, 3, 2, -1, -3, 4, -1, 2, 0, 1, -3, 4, 2, -1, 4, -3, -5, 6, 1, 0, -2, 3, 0, 1, -1, 2, -2, 3, 1, 0, 3, -2, -4, 5, 0, 1, -1, 2, 1, 0, …
 Portada, con una obra del artista Adolf Wölfli, del álbum Per Nørgård, Symphony no. 2 & Symphony no. 4, de la Aarhus Symphony Orchestra, dirigida por Jorma Panula
Portada, con una obra del artista Adolf Wölfli, del álbum Per Nørgård, Symphony no. 2 & Symphony no. 4, de la Aarhus Symphony Orchestra, dirigida por Jorma PanulaBibliografía
1.- Benoît Mandelbrot, Los objetos fractales: forma, azar y dimensión, colección Metatemas, Tusquets, 1984.
2.- Benoît Mandelbrot, La geometría fractal de la naturaleza, colección Metatemas, Tusquets, 1982.
3.- Clifford A. Pickover, La maravilla de los números, MA NON TROPPO, 2002.
4.- Tom Johnson, Self-similar Melodies, Editions 75, 2014.
5.- Tom Johnson, Rational Melodies, Editions 75, 1982.
6.- Página web del compositor Per Nørgård [http://www.pernoergaard.dk/] (enlace roto)
7.- Jørgen Mortensen, Uendelighedsrækken / La serie del infinito
8.- Yu Hin (Gary) Au, Christopher Drexler-Lemire, Jeffrey Shallit, Notes and note pairs in Nørgård’s infinity series, Journal of Mathematics and Music, vol. 11, no. 1, pp. 1-19, 2017.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo La sucesión del infinito del compositor Per Nørgård se ha escrito en Cuaderno de Cultura Científica.
El infanticidio íbero que no fue
Los bebés de la cultura íbera (VIII-I a. C.) que aparecen inhumados en contextos domésticos habrían muerto por causas naturales, como complicaciones en el parto o prematuridad, y no por prácticas rituales.
 Entierro de un individuo con muerte perinatal del yacimiento de la Fortaleza de Els Vilars (Arbeca, Lleida). Fuente: ARQHISTEC-GIP, UdL
Entierro de un individuo con muerte perinatal del yacimiento de la Fortaleza de Els Vilars (Arbeca, Lleida). Fuente: ARQHISTEC-GIP, UdLLa cultura ibérica habitó las regiones costeras orientales y meridionales de la península Ibérica durante la Edad del Hierro (siglos VIII-I a. C.). El ritual funerario más común de los íberos era la cremación de los difuntos y posterior depósito de los restos en urnas que se enterraban en necrópolis. Pero los arqueólogos han descubierto también entierros con restos de recién nacidos, que no habían sido quemados, en áreas destinadas a vivienda o producción. Tres tipos de hipótesis podían explicar este hecho: que fuesen muertes por causas naturales, infanticidio o sacrificios rituales.
Un nuevo estudio aporta ahora evidencias muy precisas a favor de la hipótesis de que estos recién nacidos enterrados en contextos domésticos murieron principalmente por causas naturales y que, por lo tanto, son un reflejo de la elevada mortalidad infantil durante el primer año de vida en el mundo íbero.
Los autores han llegado a esta conclusión después de estudiar 45 esqueletos de bebés de cinco yacimientos arqueológicos de época íbera en Cataluña: Camp de les Lloses (Osona), Olèrdola (Alt Penedès), Puig de San Andreu e Illa d’en Reixac (Baix Empordà) y la Fortaleza de Els Vilars d’ Arbeca (Lleida).
 Reconstrucción digital del aspecto de la Fortaleza de Els Vilars d’ Arbeca (Lleida). Fuente: Universitat de Lleida.
Reconstrucción digital del aspecto de la Fortaleza de Els Vilars d’ Arbeca (Lleida). Fuente: Universitat de Lleida.El equipo de investigación ha aplicado una metodología innovadora, basada en el análisis histológico y elemental (tejido y composición química) de los dientes deciduos o temporales (dientes de leche) presentes en los esqueletos de los bebés. El estudio ha permitido visualizar mediante microscopia óptica las líneas de crecimiento de la corona dental que se generan al formarse los dientes durante la vida intrauterina y hasta poco después del nacimiento, e identificar así la presencia de la línea neonatal que se produce en el momento de nacer. De esta manera los investigadores han podido identificar el momento del nacimiento de los individuos y su supervivencia, así como determinar con mucha precisión la edad cronológica en el momento de la muerte. La edad cronológica se refiere al tiempo transcurrido desde el nacimiento y no el desarrollo biológico del esqueleto.
Muertes perinatales naturalesCasi la mitad de los bebés murieron durante el periodo perinatal, concretamente entre la semana 27 de gestación y la primera semana de vida. La gran mayoría de las muertes perinatales no sobrevivieron al momento del nacimiento, y muchos de estos bebés murieron a causa de nacimientos prematuros. «Estos datos refuerzan la hipótesis de que la mayoría de muertes perinatales fueron causadas por factores naturales, como complicaciones en el parto o problemas de salud asociados a la prematuridad, y no por prácticas culturales como infanticidios o sacrificios rituales, tal como algunas hipótesis habían sugerido», señala Xavier Jordana, profesor de la Unidad de Antropología Biológica del Departamento de Biología Animal, de Biología Vegetal y de Ecología de la UAB.
Los investigadores han observado también que de la veintena de bebés que sobrevivieron más allá de la primera semana de vida, el más longevo solo llegó a los 67 días. «En los yacimientos estudiados no se ha identificado ningún entierro de un bebé más allá de los dos meses de vida. Esto nos hace pensar que probablemente podría obedecer a una práctica cultural, que sería la de enterrar en los espacios domésticos a los bebés que morían en las etapas más tempranas», apunta Assumpció Malgosa, investigadora de la UAB y coautora del estudio.
Una técnica única para precisar el nacimiento y la muerteEl análisis histológico que han aplicado los investigadores es una innovación importante para calcular con mucha precisión la edad a la muerte de los individuos a partir del estudio de la corona de los dientes. Los dientes temporales se empiezan a formar durante la vida intrauterina y acaban de formarse en la etapa postnatal, alrededor del nacimiento, un periodo en el que graban su crecimiento debido a la propiedad singular de formar líneas de crecimiento. Estas líneas pueden formarse diariamente, pero también se pueden formar líneas más gruesas por un hecho puntual y estresante. Una de las líneas puntuales que se pueden visualizar con microscopia óptica en los dientes de los niños que han sobrevivido al nacimiento es la línea neonatal, que se forma por el estrés fisiológico resultante del cambio brusco de la vida intrauterina a la extrauterina.
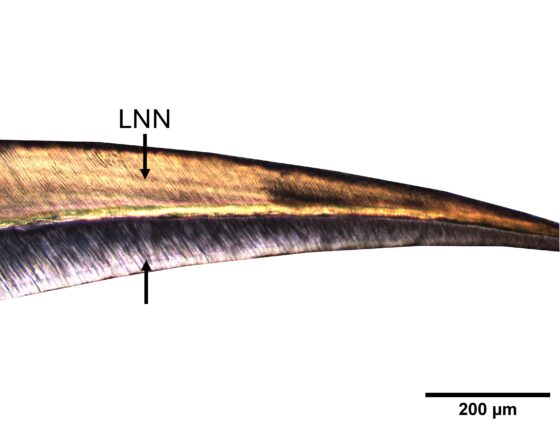 Línea neonatal en el diente incisivo central de un bebé del yacimiento de Olèrdola (Alt Penedès). Fuente: Unidad de Antropología Biológica, UAB.
Línea neonatal en el diente incisivo central de un bebé del yacimiento de Olèrdola (Alt Penedès). Fuente: Unidad de Antropología Biológica, UAB.«La técnica que hemos empleado es única, porque permite identificar el momento del nacimiento y calcular la edad cronológica en restos esqueléticos. Las técnicas convencionales estiman la edad biológica del individuo a partir del crecimiento y desarrollo esquelético, por lo que tienen una gran variabilidad en la determinación de la edad, y no permiten identificar el momento del nacimiento», señala Ani Martirosyan, investigadora predoctoral de la UAB y primera autora del artículo.
La innovación metodológica les ha permitido diferenciar los individuos que murieron en el nacimiento de los que sobrevivieron. De los que murieron al nacer, han identificado los que fueron a término (entre la semana 37 y 42 de gestación) y los que fueron prematuros (antes de la semana 37). También han podido determinar la edad cronológica de los bebés que sobrevivieron.
El papel del zinc y la luz sincrotrónLos investigadores han confirmado la precisión de su técnica en dientes actuales en los que se conoce la edad cronológica de muerte del individuo. Además, han empleado también microfluorescencia de rayos X a partir de luz sincrotrón en el Sincrotrón ALBA (Cerdanyola del Vallès), concretamente en la línea de luz Xaloc, para analizar la composición elemental a la línea neonatal, y en particular la cuantificación de zinc en los casos en los que la visualización histológica de la línea era incierta.
«El zinc es un elemento importante en el momento del nacimiento, relacionado particularmente con el inicio de la lactancia materna, pero por su bajo contenido no se pueden detectar por microscopia electrónica variaciones de concentración en el esmalte y la dentina. La luz sincrotrón nos permite aplicar un haz de rayos X de solo diez micras para analizar diferentes elementos en el esmalte y la dentina en concentraciones extremamente bajas», señala Judit Molera, investigadora de la UVic-UCC y también coautora de la investigación. Los resultados del experimento han mostrado un aumento de la cantidad de zinc y una disminución del calcio, un elemento principal del esmalte dental, coincidiendo con la presencia de la línea neonatal, lo que ha servido a los investigadores para corroborar los resultados histológicos.
«Los datos de nuestro estudio aportan información mucho más detallada y concreta que la que teníamos hasta ahora para establecer el patrón de mortalidad infantil en las poblaciones íberas y contribuyen a descifrar aspectos importantes de su historia de vida y prácticas culturales. Confiamos en que la metodología que hemos aplicado sirva para continuar desvelando otros misterios que todavía quedan por conocer en poblaciones antiguas», concluye Xavier Jordana.
Referencia:
Ani Martirosyan, Carolina Sandoval-Ávila, Javier Irurita, Judith Juanhuix, Nuria Molist, Immaculada Mestres, Montserrat Durán, Natàlia Alonso, Cristina Santos, Assumpció Malgosa, Judit Molera, Xavier Jordana (2024) Reconstructing infant mortality in Iberian Iron Age populations from tooth histology Journal of Archaeological Science doi: 10.1016/j.jas.2024.106088
Edición realizada por César Tomé López a partir de materiales suministrados por la Universitat Autònoma de Barcelona
El artículo El infanticidio íbero que no fue se ha escrito en Cuaderno de Cultura Científica.
Miranda, ¿otro mundo océano?
Miranda es uno de los satélites más misteriosos de nuestro sistema solar, quizás porque todavía sabemos muy poco sobre este -solo ha sido visitado por la Voyager 2- y su aspecto nos evoca una tortuosa historia en la que su superficie nos recuerda al cascarón de un huevo agrietado y reconstruido a partir de remiendos de su propia cáscara. Y sin una misión en el horizonte que nos permita volver a visitarlo y tomar datos más detallados, nuestra única alternativa para conocerlo un poco mejor es la reinterpretación de los datos de nuestra única visita y la confección de modelos numéricos cada vez más avanzados para explicar a lo que vemos.
Este satélite de Urano ostenta el título de ser el más pequeño de los satélites “esféricos” del planeta y uno de los más pequeños -tiene tan solo un radio de 236 kilómetros- de todo el Sistema Solar que probablemente haya alcanzado el equilibrio hidrostático. Algo a lo que probablemente haya ayudado su composición, que se estima podría superar el 60% de hielo de agua.
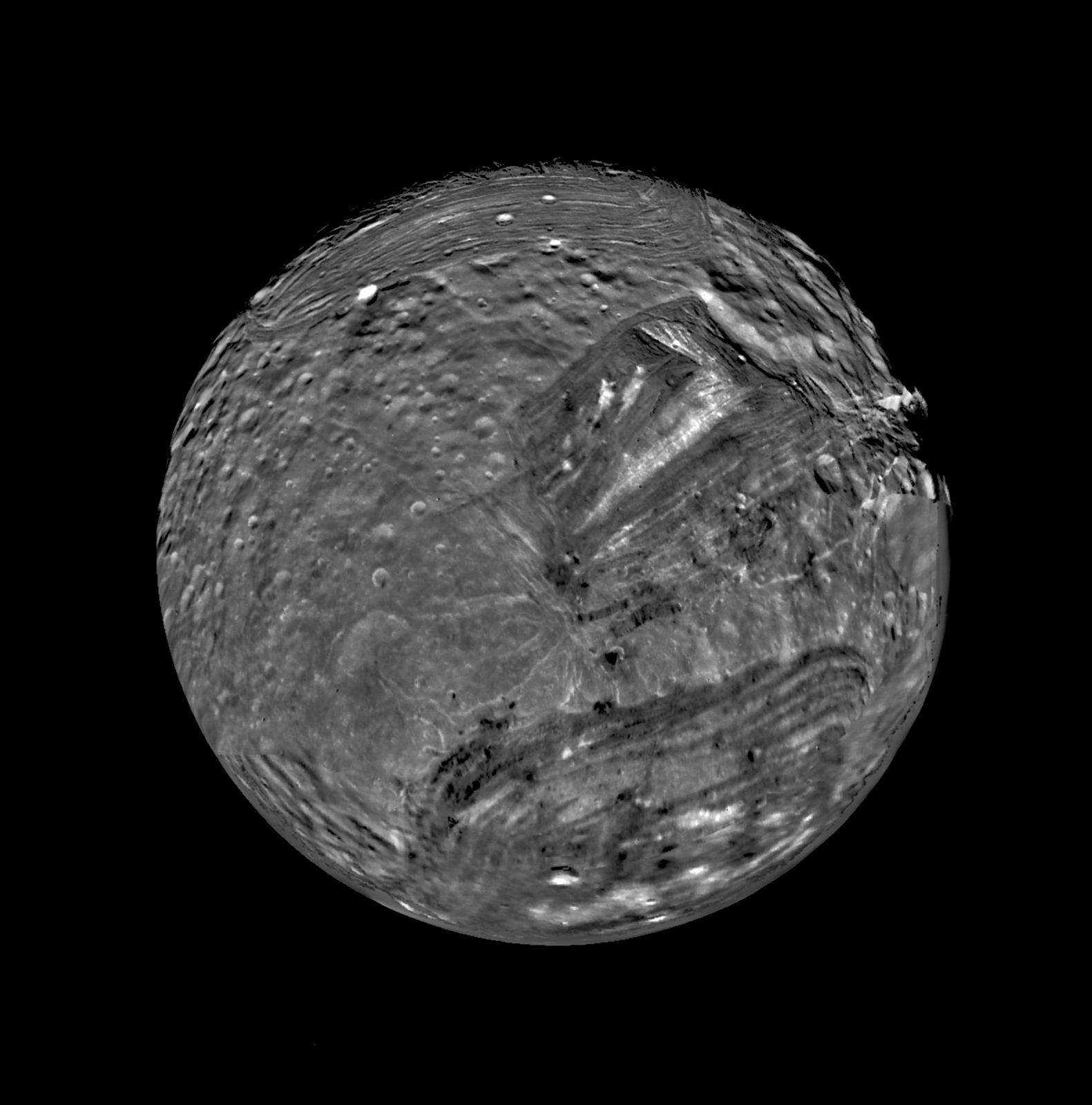 Figura 1. mosaico de imágenes de Miranda en la que podemos apreciar perfectamente la presencia de zonas más antiguas -y cubiertas de cráteres- y otras más recientes, con muchos menos cráteres, indicando procesos de rejuvenecimiento de la superficie del satélite. Cortesía de NASA/JPL/USGS.
Figura 1. mosaico de imágenes de Miranda en la que podemos apreciar perfectamente la presencia de zonas más antiguas -y cubiertas de cráteres- y otras más recientes, con muchos menos cráteres, indicando procesos de rejuvenecimiento de la superficie del satélite. Cortesía de NASA/JPL/USGS.Con toda esta cantidad de hielo de agua cabría preguntarse si Miranda podría albergar -o albergó en el pasado- un océano subterráneo, al igual que otros cuerpos de nuestro Sistema Solar exterior, a pesar de que su tamaño hace muy difícil, al menos en principio, albergar un océano capaz de aguantar sin congelarse una gran cantidad de tiempo. La primera pista de que esta puede ser una posibilidad real es que, si hacemos un esfuerzo y miramos con detalle su superficie, observaremos que hay zonas de su superficie más antiguas y más modernas, algo que reconocemos por el número y tamaño de sus cráteres, entre otras cosas de las que ahora hablaremos.
Este hecho nos indica que Miranda habría sufrido un proceso, o quizás procesos, de rejuvenecimiento activo de su superficie con la capacidad suficiente de cambiar su aspecto desde dentro y borrar o transformar los cráteres y otras formas del relieve, indicándonos la existencia de una cierta dinámica que a su vez apuntaría a la posibilidad de la presencia de un océano subterráneo como correa de transmisión de la energía interna del satélite hacia el exterior.
Aunque vamos a centrarnos en las pistas más puramente geológicas, este año, Hemingway et al. (2024) han propuesto usar las libraciones para comprobar si los satélites de Urano albergan un océano subterráneo. Las libraciones son un movimiento de oscilación y bamboleo que muestran algunos cuerpos celestes, como nuestra Luna, cuando los observamos desde un punto “fijo” como puede ser la superficie de nuestro planeta. Este fenómeno es el que nos permite, desde la Tierra, ver parte de la “cara oculta” de nuestra Luna.
Pues bien, analizando la amplitud de estas oscilaciones, podríamos conocer mejor la distribución de masas en el interior de los satélites de Urano, de tal manera que podríamos inferir detalles como, por ejemplo, si el núcleo está en estado sólido o líquido o si hay un océano subterráneo, entre otros.
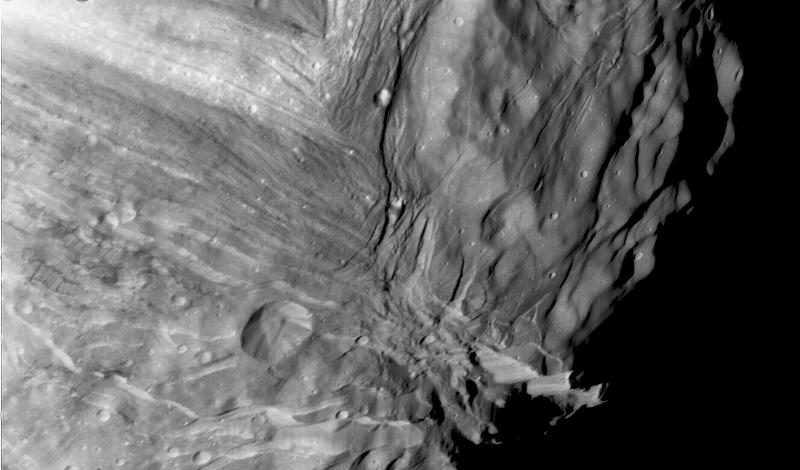 Figura 2. Detalle de la superficie de Miranda en el entorno de Verona Rupes, uno de los acantilados más altos de todo el Sistema Solar. Cortesía de NASA/JPL.
Figura 2. Detalle de la superficie de Miranda en el entorno de Verona Rupes, uno de los acantilados más altos de todo el Sistema Solar. Cortesía de NASA/JPL.En el caso de Miranda (también en el de Ariel y Umbriel), si la capa de hielo que hay por encima del océano subterráneo tiene unos 30 kilómetros de espesor o potencia, la amplitud de las libraciones en el ecuador superarían los 100 metros y cuanto más fina fuese la capa de hielo que sirve como corteza, más precisa podrá ser la detección de un posible océano.
Y cuanto menos “profundo” sea el océano, más difícil será de detectar mediante las libraciones, por lo que habría que usar también datos como las medidas del campo gravitatorio, que permitan complementar los modelos y dar una respuesta fiable a la pregunta de si hay un océano bajo el hielo de la superficie o no. Este caso sería aplicable a los satélites que tengan ya un océano en proceso de congelación. Cabe decir que tanto las libraciones como las medidas del campo gravitatorio habría que hacerlas in situ, desde el propio sistema de Urano.
Pero volvamos a las pruebas geológicas que apuntarían a la existencia de un océano subterráneo: En Miranda se han observado unas formas circulares u ovaladas sobre su superficie que conocemos como coronas -también observadas en planetas como Venus- y que son unas regiones que muestran una intensa actividad geológica marcada por sistemas de fracturas concéntricos.
En Miranda hay al menos tres de estos sistemas: Arden Corona, Inverness Corona y Elsinore Corona, identificados gracias a las imágenes tomadas en 1989 por la Voyager 2 y que muestran algunas diferencias morfológicas entre sí, aunque en el fondo podrían representar un mismo mecanismo de formación.
¿Y qué tienen que ver las coronas con los océanos subterráneos? Los científicos proponen dos posibles orígenes para estas. Por un lado, procesos diapíricos en los cuales materiales más calientes y menos densos -como un hielo a mayor temperatura que el que compone la corteza- asciende a través de la corteza, deformándola y provocando la formación de los sistemas de fracturas. La convección de las aguas dentro del océano podría facilitar este tipo de fenómenos.
Por otro lado, si el océano se congeló -o está en proceso de congelación actualmente- el aumento de volumen que sufriría tendría la capacidad de generar unos importantes esfuerzos en la corteza helada de Miranda y, de nuevo, dando lugar a los sistemas de fracturas que vemos.
 Figura 3. Detalle de la superficie de Miranda donde podemos apreciar tipos de terreno diferentes: Uno más rugoso y antiguo con cráteres en distintos grados de preseveración y otro más reciente y con menos cráteres. Cortesía de NASA/JPL.
Figura 3. Detalle de la superficie de Miranda donde podemos apreciar tipos de terreno diferentes: Uno más rugoso y antiguo con cráteres en distintos grados de preseveración y otro más reciente y con menos cráteres. Cortesía de NASA/JPL.Si echamos un vistazo al artículo publicado por Strom et al. (2024), los resultados de los modelos de estos autores sugieren que la corteza es bastante delgada, de 30 kilómetros o menos de espesor y que ha existido un océano de unos 100 kilómetros -una barbaridad, ya que supondría ocupar casi la mitad del radio del satélite- de potencia en los últimos 100 a 500 millones de años.
Y, si es un cuerpo con esta elevada proporción de hielo en su composición, ¿Cómo es posible que haya estado a una temperatura suficiente para sostener un océano de agua líquida a lo largo del tiempo geológico? Pues esto podría explicarse por las interacciones gravitatorias entre Miranda y el resto de grandes satélites, que podrían generar suficiente fricción en su interior como para elevar la temperatura y fundir parte del hielo de Miranda. Y este proceso podría haberse repetido varias veces desde la formación del Sistema Solar.
Es posible que hoy día ese mecanismo haya dejado de funcionar y el interior de Miranda esté casi totalmente congelado, aunque todavía podría quedar un pequeño océano atrapado entre la corteza y su núcleo algo que, como ocurre en estos casos, eleva mucho el interés astrobiológico de este satélite.
Pero de momento, y hasta que nuevas misiones sean capaces de llegar al sistema de Urano, tendremos que seguir esperando para conocer si Miranda – y quizás alguno de los otros satélites- alberga un océano subterráneo incluso hoy en día.
Referencias:
Hemingway, D. J., & Nimmo, F. (2024). Looking for Subsurface Oceans Within the Moons of Uranus Using Librations and Gravity. Geophysical Research Letters, 51(18), e2024GL110409. doi: 10.1029/2024GL110409
Leonard, E. J., Beddingfield, C. B., Elder, C. M., & Nordheim, T. A. (2023). Unraveling the Geologic History of Miranda’s Inverness Corona. The Planetary Science Journal, 4(12), 235. doi: 10.3847/PSJ/ad0552
Strom, C., Nordheim, T. A., Patthoff, D. A., & Fieber-Beyer, S. K. (2024). Constraining Ocean and Ice Shell Thickness on Miranda from Surface Geological Structures and Stress Modeling. The Planetary Science Journal, 5(10), 226. doi: 10.3847/PSJ/ad77d7
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Miranda, ¿otro mundo océano? se ha escrito en Cuaderno de Cultura Científica.
Una aldea global en Marte, con escala en la Luna
Colonizar nuestro satélite será el primer paso para llegar a Marte y más allá. Cultivar sus propias verduras allí arriba será una de las cosas que harán los astronautas gracias a proyectos como el español Green Moon. Pero ese no será el único reto al que tendrán que enfrentarse.
 Ilustración artística de una posible colonización futura de la Luna. / ESA
Ilustración artística de una posible colonización futura de la Luna. / ESA“Queremos convertir a la especie humana en una especie interplanetaria”, dice Jorge Pla García, investigador en el Centro de Astrobiología (CAB-INTA-CSIC). “El próximo paso es explorar Marte. La idea es usar antes la Luna como entrenamiento y aprendizaje para dar el salto a otros planetas”.
En eso está la misión Artemis, una colaboración de la NASA con la Agencia Espacia Europea (ESA), la japonesa JAXA, la canadiense CSA, la israelita ISA y la australiana ASA, que en su tercera fase propone llevar al polo sur de nuestro satélite a la primera mujer y al próximo hombre en septiembre de 2026. Su objetivo, sentar la bases para que las empresas privadas afiancen una economía lunar y hacer lo mismo en Marte a partir de 2033.
Es un objetivo arraigado en la comunidad astrocientífica, que desde hace un década acaricia el sueño de una aldea lunar global. El concepto de Moon Village, introducido en 2015 por Jan Woerner, director general de la ESA, se centra en la cooperación entre países y actores privados. “No es un único proyecto, ni un plan fijado con un calendario definido. Es una visión para una iniciativa comunitaria internacional. Su naturaleza abierta permitirá que muchas nacionalidades vayan a la luna, dejando atrás, en Tierra, sus diferencias de opiniones”, dijo Woerner.
Irresistible instinto colonizadorPero si tenemos la Tierra, que es cómoda y tiene todo lo que necesitamos, ¿por qué tanto ímpetu –y tantos recursos– en colonizar el espacio? “Queremos seguir expandiendo nuestras fronteras”, recalca Pla. Y las razones son muchas.
Por una parte, en el campo de la exploración y la investigación, “cuanto más conocemos los planetas rocosos del sistema solar, mejor conocemos el nuestro. Por ejemplo, las atmósferas de Venus o Marte parece que son similares a la de la Tierra primitiva, pero los tres se han transformado de formas muy diferentes. Entender esto nos ayuda a comprender cómo evolucionará la Tierra”, apunta Pla. En este sentido, “nuestros robots están muy limitados y no pueden hacer el mismo trabajo que hace un astronauta”, añade.
 Primera pisada del hombre en la Luna, con la misión Apolo. / NASA
Primera pisada del hombre en la Luna, con la misión Apolo. / NASAEn opinión de este experto, “dentro de dos o tres décadas, las sondas que ahora enviamos al espacio más allá de Marte podrán ir tripuladas por humanos. La experiencia nos dice que la ciencia ficción termina convirtiéndose en realidad”.
Por otro lado, está el poderoso tema económico, que mueve montañas y cohetes: “la Luna, Marte, los asteroides y los cometas son fuente de recursos muy valiosos para nuestro avance como sociedad. Poseen metales preciosos, minerales de tierras raras que son escasos en la Tierra”, indica Pla. Nuestro satélite, sin ir más lejos, es rico en helio-3, un isótopo de este elemento que se forma cuando el Sol interacciona con el suelo lunar –algo que no pasa en la Tierra porque nuestra atmósfera actúa como escudo–. Y resulta que el helio 3 que campa por toneladas sobre la superficie de la Luna, promete ser un supercombustible: su reacción en centrales de fusión produciría grandes cantidades de energía; encima, sin emitir radiaciones peligrosas.
“Estos elementos críticos se podrían extraer y traer a la Tierra o empezar a emplearse in situ, en el espacio”, observa este investigador, a quien no le cuesta visualizar asentamientos humanos fuera de nuestro planeta, con sus propias necesidades energéticas y tecnológicas.
Otra necesidad básica de los intrépidos colonos espaciales será comer. No solo los alimentos disecados y empaquetados que vemos en las películas, sino también una ensalada de lechuga recién cortada y cultivada en un huerto extraterrestre. Es la idea que inspira el proyecto español Green Moon, formado en 2016 por tres estudiantes malagueños y hoy integrado por científicos de los campos de la ingeniería espacial, la geología planetaria y la biología vegetal. Algunos de ellos, como Pla, su coordinador técnico y científico, ya han participado en varias misiones de la NASA.
Invernaderos extraterrestresPor el momento, la única planta que ha conseguido crecer en un cuerpo celeste distinto al nuestro es una especie de algodón que germinó en la Luna, como parte de la misión china Chang´e 4, en 2019. “Estaba dentro de una microsfera, pero el instrumento no realizó bien el control térmico y el brote murió en 24 horas. La idea era buena, pero pretenciosa. Proponían que la planta generara el oxígeno que consumían unas larvas de mosca y, a cambio, los desechos producidos por estas proveerían del CO2 a la planta”, nos comenta Pla.
En la cápsula-huerto diseñada por los investigadores de Green Moon, las plantitas estarían a salvo de las inclemencias del tiempo. Han probado diferentes productos hortofrutícolas, “de porte pequeño y ciclos cortos, que germinan en 24-72 horas desde que se humedece la semilla, para ver cuáles pueden germinar en esas condiciones extraterrestres”, explica a SINC Eva Sánchez, coordinadora biológica del proyecto. Entre ellas, distintas variedades de lechugas, pimiento, tomate, rábano o zanahoria.
 Experimento con plantas sobre un simulante del suelo lunar, con condiciones ambientales controladas en la cápsula Green Moon. / Green Moon Project
Experimento con plantas sobre un simulante del suelo lunar, con condiciones ambientales controladas en la cápsula Green Moon. / Green Moon ProjectSalvando las distancias, será como un invernadero. Tendrá regulada la luz que recibe, el suministro de agua y el rango de temperatura (constante entre 15ºC y 28ºC) y estará protegida de las radiaciones solares y cósmicas. La electricidad para mantener en funcionamiento todos esos procesos la lleva incorporada. “Nuestra cápsula es muy adaptable. Se puede incluir en cualquier tipo de misión y, aunque es autosuficiente porque incluye sus propios paneles solares, puede aprovechar cualquier tipo de de fuente de energía”, apunta Pla.
Una cuestión de sueloPor si el reto fuera pequeño, las plantas de Green Moon también tendrán que sobrevivir en el suelo de la Luna, cuya tierra arenosa y estéril recibe el nombre de regolito. Para ensayar, el equipo buscó un suelo parecido a la muestra que trajo a la misión Apolo 14. Lo encontraron en Lanzarote: procesando restos volcánicos, han elaborado un ‘simulante lunar’, que coincide en un 99,5% con el suelo de nuestro satélite.
“Por su composición, tiene unas características muy complicadas para que crezca cualquier planta. Posee gran cantidad de metales pesados y apenas nada de nitrógeno y fósforo, indispensables para la vegetación”, nos explica Eva Sánchez, que también es directora y fundadora, desde hace nueve años, de la empresa granadina de investigación agrícola Innoplant.
Es aquí donde entran en juego ciertas bacterias de suelo extremófilas, capacitadas para sobrevivir en condiciones muy hostiles. Algunas, por ejemplo, fueron aisladas del suelo de las minas de Riotinto, en Huelva. “Colaboramos para eso con la empresa española de fertilizantes Herogra, que nos ha suministrado los microorganismos. Los hemos probado de forma individual y combinados, para ver cómo podían fertilizar la tierra. De la batería inicial de 20 cepas candidatas, hemos detectado tres que, cuando se ponen juntas, tienen un efecto positivo. A través de su metabolismo, digieren esos metales pesados y generan nitrógeno y fósforo”, explica Sánchez.
La siguiente fase sería aportar materia orgánica al suelo, que funcione como una especie de estiércol. “Queremos usar algo que esté presente en las bases lunares. Para eso, tenemos que hacer un estudio sobre las características de los residuos que encontraremos allí”, observa. Además, partiendo de la misma idea de los chinos con sus brotes de algodón, se podría lograr, por qué no, un aprovechamiento circular de los gases vitales para las plantas y los humanos, de forma que el oxígeno que desprenden las primeras en la fotosíntesis fuera desviado a la microatmósfera donde vivan las personas y, al revés, el CO2 que exhalan los astronautas sirviera de sustento a las plantas.
¿Y de dónde van a sacar el agua para regarlas? El proyecto plantea un sistema de hidroponía para necesitar cantidades mínimas. Además, “la propia planta, por su transpiración, permite hacer un mecanismo cerrado de agua, que se puede reaprovechar. Del agua que se aporta a un vegetal, el 95 % lo pierde o lo transpira a la atmósfera”, afirma esta científica.
Otro detalle con el que tendrán que enfrentarse las lechugas y las zanahorias será la microgravedad de la Luna, que es un sexto de la que tenemos en la Tierra. ¿Cómo alterará su metabolismo? Para dar una respuesta, los científicos tienen que simular esas mismas condiciones, algo que puede hacerse con los vuelos parabólicos, cuando sobrepasan las capas altas de la atmósfera. “Lo malo es que es en un tiempo muy corto y son muy caros: uno puede costar 40.000”, nos dice Sánchez. Luego están los ciclostatos, unos aparatos que reproducen la microgravedad. “Necesitamos llegar a un acuerdo con alguno de los centros privados que los tienen para meter ahí dentro las plantitas y ver cómo crecen”.
Por lo pronto, los investigadores tienen sus propias hipótesis y ya hay algo de literatura científica al respecto, con algunos experimentos que se han hecho con una especie no hortícola muy versátil, la Arabidiopsis thaliana. “Creemos que van a crecer más alto, porque no hay gravedad que las retenga. Y más rápido, porque es lo que pasa en situaciones de estrés. Si la lechuga tiene un ciclo de 45 días, igual crece en 28. A nivel metabolico, en cuanto a su sabor color, nutrientes… también cambiarán, aunque no sabemos cómo. Eso es lo que queremos estudiar”, señala.
También aprovechable en la TierraPara Eva Sánchez, los beneficios de implementar cápsulas como la que están desarrollando en Green Moon van más allá del cultivo de hortalizas en la Luna o en Marte. Su invento se podría utilizar para cultivar en zonas extremas donde apenas hay agua, como los desiertos. De igual manera, la misma combinación de bacterias fertilizantes sería una opción interesante para tratar suelos que han sufrido una erupción volcánica, como La Palma. “Se acortaría mucho el tiempo de regeneración”, apunta.
Para pasar de ser un modelo digital en 3D a una realidad, por el momento, lo único que le falta a la cápsula de Green Moon es financiación. En concreto, nada menos que un millón de euros. “La construcción sería por parte de empresas privadas especializadas en instrumentación espacial”.
Buen viaje a MarteCuando el ser humano esté preparado para la aventura de pisar el planeta rojo, tendrá que aprovechar una ventana óptima de lanzamiento que, según Pla, ocurre cada dos años. Será, además, una travesía de casi dos años, si contamos la ida y la vuelta. Los retos más acuciantes serán la radiación procedente del Sol –“habrá que apantallar bien y protegerse con escudos, como el agua o la vegetación”, dice Pla– y la radiación cósmica que proviene de protones cargados energéticamente, expelidos por la muerte de estrellas. “La probabilidad de contraer cáncer debido a esta radiación obliga a reducir el tiempo de las misiones. La solución que tenemos por ahora es la protección pasiva”, añade. Sin embargo, la ciencia no deja de investigar. Por ejemplo, “hemos descubierto que, cuanto mayor es la edad del astronauta, menos es su posibilidad de desarrollar tumores”.
 Esquema del proyecto Green Moon para cultivar plantas en la Luna y planetas fuera de la Tierra. / J.M. Ortega et al / Resources, Environment and Sustainability
Esquema del proyecto Green Moon para cultivar plantas en la Luna y planetas fuera de la Tierra. / J.M. Ortega et al / Resources, Environment and SustainabilitySon escollos que afectarán a las personas, pero también a las plantas. En este sentido, en el invernadero del Centro de Astrobiología (CAB-CSIC), un equipo liderado por el biólogo molecular Eduardo González Pastor está estudiando cómo modificar genéticamente la Arabidiopsis thaliana con genes de microorganismos resistentes a las radiaciones. Por el momento, se está probando su efectividad en simuladores de radiación espacial y de microgravedad, con resultados muy prometedores. Es algo que, en opinión de Pla, quizá podría algún día hacerse con los astronautas.
Mientras, lo que ya se está haciendo es la medición y evaluación del clima marciano, una fase previa importante porque, cuanto mejor conozcamos el entorno al que pensamos enviar humanos en el futuro, mejor podrán minimizarse los riesgos. “El Centro de Astrobiología es líder en meteorología planetaria”, recalca Pla. Y es que, en la actualidad, las únicas estaciones meteorológicas que hay en suelo del planeta rojo, REMS y MEDA, son españolas.
“Nos sirven para entender las temperaturas de Marte, la presión, la humedad atmosférica, la radiación que llega al suelo… Y, sobre todo, para estudiar el actor principal de su atmósfera, el polvo, que tiene un papel clave en los cambios de sus condiciones meteorológicas. Además, es un polvo fino y tóxico, que puede penetrar en los instrumentos y estropearlos, o enfermar a los astronautas”, apunta.
Llegar hasta allí será, sin duda, una epopeya con lucha contra los elementos incluida. Aunque Pla insiste en que, tal vez, la prueba más difícil será la psicológica. “Al final, de una forma u otra puedes generar oxígeno, alimentarte, protegerte de la radiación… pero pasar tanto tiempo en soledad en el espacio es algo a lo que los astronautas les cuesta acostumbrarse”.
El espacio no es un plan BEn opinión de este astrobiólogo, el motivo que subyace a todas estas aventuras conquistadoras del espacio no es encontrar un nuevo hogar para salvarnos de un cataclismo inevitable en el nuestro. “Marte no es un plan B”, recalca. “Hay que proteger lo que tenemos y, al mismo tiempo, seguir explorando”.
No seremos nosotros quienes terminemos con la Tierra, dice, que “estará aquí hasta que el Sol se inflé y acabe engulléndola, dentro de por lo menos 5.000 millones de años. Lo que sí puede pasar si seguimos así, aumentando la temperatura, es que muchas especies desaparezcan. Pero la edad de nuestro planeta será más larga que la de nuestra especie, a no ser que nos convirtamos en una especie interplanetaria”.
¿Y después de Marte? El próximo escalón son las lunas heladas de Júpiter y Saturno: Europa, Encelado, Titán. “Desde el punto de vista biológico, las probabilidades de encontrar actividad biológica allí son mucho más altas que en Marte, que es una roca estéril flotando en el sistema solar en comparación”, apunta. Y es que los satélites de Júpiter tienen agua líquida en sus océanos internos, bajo una gruesa capa de hielo. Además, es agua en movimiento, que tiene actividad, como demuestran los géiseres que fueron captados por primera vez en Europa, en 2013, por el telescopio espacial Hubble.
Y el agua, como sabemos, es un ingrediente fundamental para la vida –aunque no el único–. Por el momento, están a punto de despegar varias misiones no tripuladas: Europa Clipper de la NASA este mes de octubre, Dragon Fly, también de la NASA, partirá hacia Titán en julio de 2028 y la misión Juice de la ESA planea llegar a Júpiter en 2031 para explorar Ganímedes, Calisto y Europa…
Según Pla, es solo el inicio. “Conociendo su capacidad de progreso, el ser humano también llegará hasta allí en persona, seguro. Hemos conseguido explorar todos los rincones del planeta, desde el Polo Norte al Polo Sur, pasando por las Américas y todas las islas de los océanos. No solo se trata de crear nuevas vías comerciales, sino de conocer nuestro entorno mejor”.
Por ahora, como señala Eva Sánchez, antes de soñar con Marte y más allá, “tenemos que pisar bien la Luna, que ya es mucho”.
Sobre la autora: Laura G. De Rivera es periodista especializada en ciencia
Una versión de este artículo apreció originalmente en SINC el 1 de noviembre de 2024
El artículo Una aldea global en Marte, con escala en la Luna se ha escrito en Cuaderno de Cultura Científica.
Naukas Pro 2024: PLASTeMER: microplásticos en compartimentos ambientales incluyendo la biota

Los últimos avances en el ámbito de las energías renovables marinas o la proliferación de los microplásticos fueron algunos de los temas que componen la última edición de NAUKAS PRO. Una cita en la que el personal investigador se sube al escenario del Euskalduna Bilbao para hablar de las investigaciones más destacadas del momento en un ámbito concreto.
En esta ocasión el personal investigador de la Universidad del País Vasco, de la Estación Marina de Plentzia (PiE-UPV/EHU), AZTI, Tecnalia o el CSIC acercaron las últimas investigaciones relacionadas en el ámbito marítimo.
La conferencia PLASTeMER: microplásticos en compartimentos ambientales incluyendo la biota corre a cargo de Nerea-García Velasco, investigadora de la Estación Marina de Plentzia-Plentziako Itsas Estazioa.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Pro 2024: PLASTeMER: microplásticos en compartimentos ambientales incluyendo la biota se ha escrito en Cuaderno de Cultura Científica.
¿Somos una persona distinta cuando hablamos otro idioma?
 Foto: Ling App on Unsplash
Foto: Ling App on Unsplash¿Alguna vez se ha preguntado cómo influye el idioma que hablamos en nuestras emociones y en la forma en que percibimos la realidad? Según diversos estudios en psicolingüística, psicología cognitiva y antropología lingüística, las lenguas que utilizamos no solo nos permiten comunicarnos, sino que también moldean nuestra percepción del mundo y de nosotros mismos.
En la actualidad, más de la mitad de la población mundial utiliza dos o más lenguas en su vida cotidiana. Ya sea por motivos de educación, inmigración o antecedentes familiares, el bilingüismo y el multilingüismo son fenómenos cada vez más comunes en nuestra sociedad globalizada.
¿Cómo afecta conocer dos o más lenguas a la manera en que procesamos las emociones? Investigaciones recientes apuntan a que cada lengua puede hacer a los hablantes percibir la realidad de maneras diferentes. Incluso, estos pueden sentir que ellos mismos cambian al alternar la lengua que emplean.
Otros estudios han demostrado que los individuos bilingües pueden comportarse de manera diferente dependiendo de qué lengua estén usando; también son percibidos de manera diferente por sus interlocutores según la lengua que utilicen.
El peso de las emociones en las lenguasLos hablantes bilingües procesan las palabras que definen o describen emociones de forma diferente en su lengua materna (o aquella que aprende el ser humano desde la infancia y que funciona como su instrumento de pensamiento y comunicación) y en su segunda lengua o meta (lengua que ha sido objetivo de un aprendizaje, en un contexto formal o natural). La lengua materna suele tener una ventaja emocional sobre la segunda lengua: los hablantes bilingües sienten una mayor intensidad emocional cuando usan la lengua materna, especialmente al recordar experiencias vividas en ese idioma.
Por ejemplo, algunos estudios han demostrado que, al revivir recuerdos de la infancia, las personas los describen con más detalle y emoción si lo hacen en su lengua materna, ya que fue la lengua en la que etiquetaron esas experiencias. En contraste, la segunda lengua puede facilitar cierta distancia emocional, lo que permite a los hablantes reducir la ansiedad o el pudor al comunicarse en situaciones complejas, como pueden ser aquellas que impliquen la expresión de enojo o de disculpa.
Dicho de otro modo, perciben la lengua materna como una lengua más rica emocionalmente, mientras que ven la segunda lengua como más práctica, pero menos expresiva. Como consecuencia de ello, la expresión emocional en lengua materna se percibe más intensamente independientemente de que la emoción sea positiva o negativa.
La elección de la lengua en la que se comunican los bilingües no solo afecta a la intensidad emocional, sino también a la forma en que las personas se perciben a sí mismas y a los demás. Usar uno u otro idioma puede influir en la construcción del discurso y revelar aspectos culturales y sociales propios de las comunidades lingüísticas a las que pertenecen.
En un estudio realizado con hablantes bilingües chino-inglés en EE. UU., los participantes indicaron que se sentían más cómodos al expresar sus emociones en inglés (su segunda lengua) debido a las menores restricciones sociales, pero experimentaban una mayor intensidad emocional en mandarín (su lengua materna).
Así, la segunda lengua puede ofrecer algunas ventajas en contextos donde los hablantes prefieren mantener distancia emocional, tanto por cuestiones personales como socioculturales. Al expresar emociones en una lengua menos emocionalmente conectada las personas pueden reducir sentimientos de vergüenza, ansiedad o implicación personal. Especialmente cuando hablamos una lengua materna que pertenece a una cultura en la que se da mayor valor a lo colectivo y hay menos tradición de compartir sentimientos.
Dominio del idioma y entorno en el que lo aprendimosTambién influye mucho el nivel de dominio de la segunda lengua: los progenitores prefieren la lengua materna para expresar emociones cuando hablan con sus hijos –por ejemplo, para una reprimenda– si esta es la lengua que mejor dominan; sin embargo, si tienen una segunda lengua que también dominan, pueden optar por ella para contenido emocional.
Asimismo, el entorno en el que se aprendió la segunda lengua puede ser determinante. En aquellos casos en los que el aprendizaje se ha producido en un contexto formal o académico en lugar de familiar, los hablantes reportan más ansiedad al comunicarse en público, a pesar de ser competentes.
Emoción, identidad y aprendizaje de lenguasNuestras experiencias de vida, la edad de adquisición de los idiomas y el contexto de uso influyen en cómo procesamos y expresamos nuestras emociones en diferentes lenguas. Comprender estas dinámicas no solo enriquece nuestro conocimiento sobre el lenguaje y la mente humana, sino que también nos ayuda a mejorar la comunicación intercultural y la comprensión emocional en un mundo cada vez más diverso y conectado.
Las implicaciones para la enseñanza de segundas lenguas son también importantes. Que los estudiantes se sientan o no felices y satisfechos con la percepción que tienen de sí mismos en la lengua que están aprendiendo, es decir, con la identidad construida en esa lengua, será clave para saber si se sienten extraños o diferentes cuando hablan en esa lengua. El papel del enseñante será, en cualquier caso, contribuir a que el alumnado se sienta menos extraño en la lengua que está aprendiendo.
La actitud hacia el idioma que se aprende es, por lo tanto, determinante: influye en cómo evaluamos nuestras experiencias con el idioma, lo que impacta en cómo afrontamos los retos, cómo nos vemos a nosotros mismos y cómo creemos que nos ven los demás. A mejor actitud, habrá también una mayor satisfacción en el proceso y una mejor conexión emocional con la lengua. El resultado será una identidad más sólida en el nuevo idioma y, por lo tanto, un aprendizaje más profundo y efectivo.![]()
Sobre las autoras: Mari Mar Boillos Pereira, Profesora contratada doctora de la Facultad de Educación de Bilbao, Universidad del País Vasco / Euskal Herriko Unibertsitatea y Ana Blanco Canales, Profesora Titular de Lengua Española, Universidad de Alcalá
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Somos una persona distinta cuando hablamos otro idioma? se ha escrito en Cuaderno de Cultura Científica.
Dinosaurios petroleros
Recientemente he visto en la televisión el anuncio que ha preparado una empresa energética, principalmente enfocada en el procesado de petróleo, para anunciar su cambio de nombre, debido a su futura estrategia de búsqueda de nuevas fuentes de energía. En dicho anuncio, varias personas se despiden de una serie de dinosaurios y un reptil volador, en clara alusión a dejar atrás los combustibles fósiles. De esta manera, se refuerza esa creencia popular de que los hidrocarburos proceden de los restos de reptiles extintos hace millones de años. Pero, como no podía ser de otra manera, aparezco por aquí para acabar con ese bonito mito que nos acompaña desde nuestra infancia.
Los hidrocarburos son unos compuestos que, como su propio nombre indican, están formados por la combinación de átomos de hidrógeno y carbono. Esta composición química es la que les capacita para ser empleados como combustibles, ya que liberan energía térmica (calor) al ser quemados, aunque este proceso también provoca la expulsión de dióxido de carbono (CO2) gaseoso a la atmósfera. Los hidrocarburos más conocidos, y empleados, por el ser humano son el gas natural, el petróleo y, en menor medida, el asfalto natural. Y todos ellos tienen el mismo origen, que es el asunto que nos ocupa en este momento.
Estos materiales proceden de la descomposición de grandes cantidades de materia orgánica, animal y vegetal, que se acumuló en el fondo de ambientes acuáticos como mares, lagos, márgenes de ríos, pantanos y otros humedales hace millones de años. Y aquí es donde viene la confusión, porque estos restos bióticos no proceden de grandes animales como los dinosaurios, sino de organismos microscópicos que forman parte del plancton, es decir, que se encuentran nadando en el agua, y del bentos, que son aquellos que habitan en el fondo acuático, y que tienen nombres tan fáciles de recordar como foraminíferos, cocolitofóridos, diatomeas u ostrácodos, así como de algas, polen, semillas, tallos y otros restos de vegetación, tanto marina como continental.
 Proceso de formación de hidrocarburos. A) Ilustración de un fondo marino en el que se van acumulando los restos orgánicos de los microorganismos acuáticos. B) Tras millones de años, el enterramiento de la materia orgánica ha provocado su transformación química convirtiéndola en petróleo y gas natural, que se encuentran depositados en el subsuelo. Imagen modificada del Proyecto Ciudad Ciencia del IGEO-CSIC.
Proceso de formación de hidrocarburos. A) Ilustración de un fondo marino en el que se van acumulando los restos orgánicos de los microorganismos acuáticos. B) Tras millones de años, el enterramiento de la materia orgánica ha provocado su transformación química convirtiéndola en petróleo y gas natural, que se encuentran depositados en el subsuelo. Imagen modificada del Proyecto Ciudad Ciencia del IGEO-CSIC.Después de que estos restos orgánicos cayeran al fondo acuático, mezclándose con el lodo, se fueron cubriendo poco a poco por nuevas capas de arena y barro que acabaron enterrándolos, cada vez, a mayor profundidad. Según aumentaba el enterramiento, también aumentaba la presión y la temperatura a la que se sometían los materiales, lo que provocó que diese comienzo una transformación química de la materia orgánica que se conoce como maduración. En realidad, es como si se cocinase a fuego lento, perdiendo los gases y la humedad que tuviera durante su enterramiento, transformándose en una sustancia viscosa de color oscuro llamada kerógeno. Si continúa el enterramiento y es sometido a más presión y temperatura, el kerógeno se transforma primero en petróleo líquido y, a mayor profundidad, en gas natural. Pero la materia orgánica no es la única que sufre una transformación al soterrarse, porque el lodo en el que se encontraba inicialmente acabó convirtiéndose en una roca sólida a la que llamamos “roca madre”, ya que es aquella en la que se han originado los hidrocarburos.
Estos hidrocarburos no se van a quedar quietecitos en su roca madre. Se trata de líquidos y gases, por lo que van a tender a migrar hacia la superficie aprovechando la porosidad de las rocas, deteniéndose únicamente cuando encuentren una barrera que frene su avance, tales como capas de rocas impermeables (llamadas “roca sello”), fracturas que corten los materiales o estructuras geológicas como los pliegues y los diapiros. Entonces, el petróleo o el gas natural quedarán contenidos en una “roca almacén” y aprisionados en una “trampa de hidrocarburos” en el interior del terreno. Por eso es necesario tener un conocimiento geológico preciso del subsuelo para poder localizar estas zonas de acumulación de los combustibles fósiles y poder extraerlos mediante sistemas de perforación. Y, una vez sacados a superficie, se llevan a las refinerías para que sean procesados, obteniendo así una serie de materiales sólidos, líquidos y gaseosos que podemos utilizar en nuestros hogares, medios de transporte o como materiales de construcción.
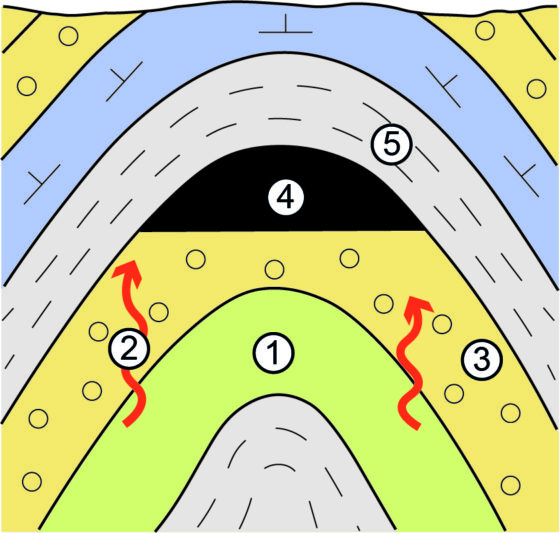 Proceso de migración y acumulación de hidrocarburos. 1) Roca madre en la que se han formado los hidrocarburos. 2) Migración de los hidrocarburos a través de los materiales geológicos. 3) Roca almacén porosa. 4) Depósito del petróleo y el gas natural en una “trampa”. 5) Roca impermeable que hace de tapón o “sello”, impidiendo que los hidrocarburos sigan migrando.
Proceso de migración y acumulación de hidrocarburos. 1) Roca madre en la que se han formado los hidrocarburos. 2) Migración de los hidrocarburos a través de los materiales geológicos. 3) Roca almacén porosa. 4) Depósito del petróleo y el gas natural en una “trampa”. 5) Roca impermeable que hace de tapón o “sello”, impidiendo que los hidrocarburos sigan migrando.Reconozco que el anuncio ha quedado bastante chulo y tiene buenos efectos especiales y que siempre me ha gustado la idea de que mis dinosaurios de juguete están hechos con un plástico que procede de dinosaurios de verdad, pero ya hemos descubierto que esto no es real. Los hidrocarburos tienen su origen en unos pequeños bichitos que no vemos a simple vista pero que, también hoy en día, nos rodean por millones cuando nos damos un bañito en el agua del mar e, incluso, nos los podemos comer sin darnos cuenta si el bocata se nos llena de arena en la playa. En lo que sí estoy de acuerdo es que hay que reducir al máximo posible el uso de los combustibles fósiles, porque la transformación de la materia orgánica en petróleo o gas natural tarda millones de años en producirse y no se trata de recursos infinitos, aparte de que su utilización provoca la contaminación atmosférica por gases de efecto invernadero. Así que dejemos ir de nuestras vidas a los grandes reptiles mesozoicos y, poco a poco también, a los hidrocarburos.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Dinosaurios petroleros se ha escrito en Cuaderno de Cultura Científica.
El problema del puente y la linterna
El problema del puente y la linterna es un rompecabezas de lógica que involucra a cuatro personas, un puente y una linterna.
 Fuente: Freepik
Fuente: Freepik
Pertenece a la familia de los conocidos como puzles de cruce de ríos en los que una serie de objetos deben moverse a través de un río sometidos a determinadas restricciones.
Planteamiento del problemaCuatro personas —Ángela (A), Boris (B), Carmen (C) y Damián (D)— viajan durante la noche. En cierto momento, deben cruzar un río. El puente que cruza el río es muy estrecho y solo puede sostener a dos personas a la vez. Además, el grupo dispone de una única linterna que necesitan utilizar aquellas personas que van a cruzar el puente.
Las personas A, B, C y D pueden cruzar el puente en 1, 2, 5 y 8 minutos, respectivamente. Todas las parejas de cruzan el puente se desplazan al ritmo de la persona más lenta.
Además, la linterna solo tiene pilas para 15 minutos.
¿Podrán Ángela, Boris, Carmen y Damián cruzar el puente?
Solucionando el problemaUna estrategia que parece lógica es que Ángela, la persona más rápida, acompañe a cada uno de sus compañeros a través del puente. Pero esta táctica requiere demasiado tiempo. En efecto:
- Al principio A, B, C y D se sitúan en la entrada del puente.
- A y B cruzan el puente en 2 minutos.
- A regresa en un minuto al lugar de origen (han transcurrido en total 3 minutos).
- A y C cruzan en 5 minutos (han transcurrido en total 8 minutos).
- A regresa en un minuto al lugar de origen (han transcurrido en total 9 minutos).
- A y D cruzan en 8 minutos (han transcurrido en total 17 minutos).
La linterna se agota antes de conseguir terminar de cruzar el puente. Por lo tanto, esta estrategia no es válida.
Una solución correcta es aquella que minimiza el tiempo de recorrido. Reflexionando brevemente por la estrategia fallida se observa que el problema es que las dos personas más lentas han cruzado el puente en distintos viajes.
La realidad es que se ahorra tiempo si las dos personas más lentas atraviesan el puente juntas. En efecto, una solución a este problema pasa por usar esta estrategia:
- Al principio A, B, C y D se sitúan en la entrada del puente.
- A y B cruzan el puente en 2 minutos.
- B regresa en 2 minutos al lugar de origen (han transcurrido en total 4 minutos).
- C y D cruzan en 8 minutos (han transcurrido en total 12 minutos).
- A regresa en un minuto al lugar de origen (han transcurrido en total 13 minutos).
- A y B cruzan en 2 minutos (han transcurrido en total 15 minutos).
Una solución alternativa a la anterior es la siguiente:
- Al principio A, B, C y D se sitúan en la entrada del puente.
- A y B cruzan el puente en 2 minutos.
- A regresa en 1 minuto al lugar de origen (han transcurrido en total 3 minutos).
- C y D cruzan en 8 minutos (han transcurrido en total 11 minutos).
- B regresa en 2 minutos al lugar de origen (han transcurrido en total 13 minutos).
- A y B cruzan en 2 minutos (han transcurrido en total 15 minutos).
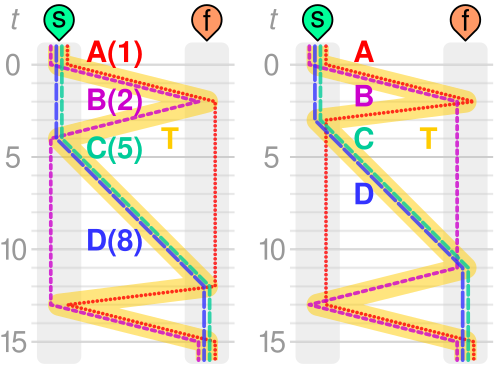 Las dos soluciones al problema del puente y la linterna. El eje vertical indica el tiempo, s el inicio del puente, f el final del puente y T la linterna. Las letras A, B, C y D representan a las personas que cruzan. Fuente: Wikimedia Commons.
Las dos soluciones al problema del puente y la linterna. El eje vertical indica el tiempo, s el inicio del puente, f el final del puente y T la linterna. Las letras A, B, C y D representan a las personas que cruzan. Fuente: Wikimedia Commons.
Nota
Según el matemático Torsten Sillke, el problema del puente y la linterna apareció en 1981, en el libro Super Strategies For Puzzles and Games. En la versión que aparece en esta publicación, las personas que desean cruzar el puente tienen como límite de tiempo 60 minutos, y A, B, C y D tardan en atravesarlo 5, 10, 20 y 25 minutos, respectivamente. La estrategia empleada para encontrar la solución es la misma que en la versión que hemos dado.
Sillke ha investigado la historia de este problema y en su página web ha coleccionado sus hallazgos y referencias sobre el tema hasta 2001. Así, no menciona esta divertida versión de 2022 con unos zombis mutantes que obligan a cuatro personas a cruzar un puente en un tiempo escaso para conseguir escapar…
Existen generalizaciones de este rompecabezas para un número cualquiera de personas con tiempos de cruce arbitrarios. Por ejemplo, en Crossing the Bridge at Night se analiza (suponiendo que la capacidad del puente sigue siendo de dos personas) completamente el problema mediante métodos de teoría de grafos. Como sucede en tantas ocasiones, un sencillo juego de lógica puede dar lugar a interesantes teoremas matemáticos.
Referencias
- Firelight, Futility Closet, 29 octubre 2024
- Bridge and torch problem, Wikipedia
- Saul X. Levmore y Elizabeth Early Cook, Super Strategies For Puzzles and Games, Garden City, N.Y.: Doubleday,1981
- River crossing puzzle, Wikipedia
- Günter Rote, Crossing the Bridge at Night, Bulletin of the European Association for Theoretical Computer Science 78 (2002) 241–246
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
El artículo El problema del puente y la linterna se ha escrito en Cuaderno de Cultura Científica.
¿Cómo pasan el último pársec los agujeros negros supermasivos en fusión?
Los agujeros negros gigantes en los centros de las galaxias no deberían poder fusionarse, pero lo hacen. Los científicos sugieren que una forma inusual de materia oscura puede ser la solución.
Un artículo de Jonathan O’Callaghan. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
https://culturacientifica.com/app/uploads/2024/11/FinalParsecProblemCOMP.mp4 En esta simulación, se ven corrientes de gas de colores brillantes alrededor de un par de agujeros negros supermasivos en órbita. Fuente: Luciano Combi et al. (2022) ApJ 928 187A lo largo de la historia cósmica, las galaxias se han ido fusionando para formar estructuras cada vez más grandes. Cuando las galaxias se fusionan, los agujeros negros supermasivos que se encuentran en sus centros también deben fusionarse, formando un agujero negro aún más gigantesco.
Sin embargo, durante décadas, una pregunta ha desconcertado a los astrofísicos: ¿cómo pueden los agujeros negros supermasivos acercarse lo suficiente para rotar en espiral y fusionarse? Según los cálculos, cuando los agujeros convergentes alcanzan el llamado pársec final (una distancia de aproximadamente un pársec, o 3,26 años luz), su progreso se detiene. En teoría deberían orbitarse indefinidamente.
“Se pensaba que los tiempos de permanencia en espiral podían alcanzar… la edad del universo”, explica Stephen Taylor, astrofísico de la Universidad Vanderbilt. “A la gente le preocupaba que no pudieran obtenerse fusiones de agujeros negros”.
Se han acumulado evidencias de que sí se fusionan. El año pasado, las observaciones de los movimientos sutiles de las estrellas pulsantes, conocidas como matriz de sincronización de púlsares, revelaron un zumbido de fondo de ondas gravitacionales en el universo: ondulaciones en el tejido del espacio-tiempo. Es muy probable que estas ondas gravitacionales provengan de agujeros negros supermasivos que se orbitan muy cerca, a un pársec de distancia entre sí y que están a punto de fusionarse. “Esta fue nuestra primera evidencia de que los sistemas binarios de agujeros negros superan el problema del pársec final”, narra Laura Blecha, astrofísica de la Universidad de Florida.
Entonces, ¿cómo lo hacen?
Los astrofísicos tienen una nueva sugerencia: la materia oscura podría absorber el momento angular de los dos agujeros negros y acercarlos.
 Gonzalo Alonso-Álvarez, físico de la Universidad de Toronto, cree que un tipo viscoso de materia oscura podría ser la solución al problema del parsec final. Foto cortesía de Gonzalo Alonso-Álvarez
Gonzalo Alonso-Álvarez, físico de la Universidad de Toronto, cree que un tipo viscoso de materia oscura podría ser la solución al problema del parsec final. Foto cortesía de Gonzalo Alonso-ÁlvarezMateria oscura es el término que se utiliza para designar el 85% de la materia del universo, aún no descubierta. Podemos ver sus efectos gravitacionales sobre las galaxias y la estructura cósmica, pero por el momento no podemos determinar qué es. Las partículas hipotéticas más simples que podrían componer esta forma invisible de materia no ayudarían a facilitar las fusiones de agujeros negros. Pero este verano, un grupo de físicos en Canadá argumentó que algo más complejo llamado materia oscura autointeractuante sí podría. Estas partículas podrían arrastrar a los agujeros negros supermasivos lo suficiente como para dejarlos a un pársec de distancia entre sí. Si esta explicación es correcta, “te dirá que la materia oscura no es tan simple como pensábamos”, afirma Gonzalo Alonso-Álvarez, físico teórico de la Universidad de Toronto y uno de los autores.
Luego, en septiembre, un grupo independiente de físicos señaló que otro candidata a materia oscura, a veces llamado materia oscura difusa, también podría funcionar.
A lo largo de los años también se han propuesto soluciones más prosaicas al problema. En medio de esta multitud de opciones —algunas mundanas, otras exóticas— los científicos se están planteando formas de poner a prueba unas posibilidades frente a otras.
“A estas alturas, la mayoría de la comunidad prácticamente da por sentado que el problema del pársec final está resuelto”, afirma Sean McWilliams, astrofísico teórico de la Universidad de Virginia Occidental que ha estudiado varias soluciones al problema. “La única pregunta es: ¿cuál es la solución más eficiente?”
Dos para bailar un tangoLos agujeros negros pequeños —objetos del tamaño de una estrella tan densos que su gravedad atrapa todo lo que se acerca demasiado, incluso la luz— están dispersos por todas las galaxias. Se forman a partir del colapso gravitacional de estrellas individuales. Pero los agujeros negros supermasivos que se encuentran en los centros de las galaxias, que pueden ser tan pesados como miles de millones de soles, son más misteriosos e influyentes. De alguna manera dirigen la formación y evolución de la galaxia que los rodea.
Cuando dos galaxias se fusionan, las interacciones gravitacionales con las estrellas, el gas y la materia oscura hacen que los dos agujeros negros supermasivos caigan lentamente uno hacia el otro. Los astrofísicos describieron por primera vez este proceso, llamado fricción dinámica, en 1980. “Se cree que esta es la principal forma en que los agujeros negros se acercan”, explica Dan Hooper, astrofísico de la Universidad de Wisconsin, Madison.
Sin embargo, en un punto determinado (que técnicamente oscila entre una fracción de pársec y unos pocos pársecs, dependiendo de las masas de los agujeros negros), la fricción dinámica “resulta que deja de ser muy efectiva”, explica Hooper. Aquí, en el centro de las galaxias en fusión, los dos agujeros negros comen material y lo arrojan lejos, creando un hueco. Como resultado, la densidad de estrellas y gas cae drásticamente, dejando a los agujeros negros en un espacio relativamente vacío. Sin cosas a su alrededor que los frenen, deberían orbitar uno alrededor del otro casi sin fin.
“La Tierra está orbitando alrededor del Sol y no estamos cayendo la una contra el otro”, dice Alonso-Álvarez, y lo mismo debería ser cierto para dos agujeros negros. “Hay una conservación del momento angular en la órbita que evita que caigan, a menos que haya algo que esté extrayendo esta energía”.
La materia oscura autointeractuante podría desempeñar este papel, como propusieron Alonso-Álvarez y sus colegas en Physical Review Letters en julio. Este tipo difiere de la llamada materia oscura fría, el tipo más simple de partículas hipotéticas de materia oscura, en que serían pesadas, lentas e inertes. La materia oscura fría no interactuaría con nada excepto a través de la gravedad, por lo que la influencia gravitatoria de los agujeros negros debería expulsarla de la vecindad mucho antes de que los agujeros negros alcancen el pársec final.
Sin embargo, la materia oscura que interactúa consigo misma está formada por partículas ligeras que tienen al menos una fuerza actuando entre ellas. Como las partículas de materia oscura autointeractuantes se desplazan unas de otras como bolas de billar sobre una mesa, no se dispersarían tan fácilmente y, en cambio, interactuarían con los agujeros negros, ralentizándolos. “Se quedan ahí y generan fricción”, continúa Alonso-Álvarez. “Tiene algún tipo de viscosidad”. Esa fricción podría entonces dar lugar a una fusión dentro de 100 millones de años, resolviendo el problema del pársec final.
La materia oscura “ultraligera” o “difusa” estaría formada por partículas con masas extremadamente pequeñas que se unirían para formar ondas inmensas. Estas partículas también se concentrarían en el centro galáctico y experimentarían fricción con los agujeros negros, lo que permitiría que la materia oscura difusa “se llevara eficientemente su momento angular y la energía orbital”, explica Jae-Weon Lee, cosmólogo de la Universidad Jungwon en Corea del Sur y coautor de un artículo de septiembre en Physics Letters B que describe la idea. Los agujeros negros harían que esta materia oscura vibrara como una campana en lugar de dispersarse.
La navaja de OccamNo todo el mundo está convencido de que necesitemos recurrir a una física tan exótica para explicar cómo se fusionan los agujeros negros supermasivos. “Yo no diría que necesitamos materia oscura autointeractuante”, afirma Priyamvada Natarajan, astrofísico teórico de la Universidad de Yale.
Otra posibilidad es que las estrellas pasen de largo a los agujeros negros que se están fusionando y extraigan suficiente momento angular para unirlos. Tal vez las estrellas se vean arrojadas aleatoriamente en la dirección de los agujeros negros desde otras partes de la galaxia a través de interacciones con otras estrellas. “Si tienes un montón de estas estrellas que se acercan a los dos agujeros negros supermasivos centrales, entonces puedes extraer cada vez más momento angular”, apunta Fabio Pacucci, astrofísico teórico de la Universidad de Harvard.
 Laura Blecha, astrofísica de la Universidad de Florida, sostiene que un tercer agujero negro podría ser la clave. Foto: John Hames
Laura Blecha, astrofísica de la Universidad de Florida, sostiene que un tercer agujero negro podría ser la clave. Foto: John HamesSin embargo, los modelos han demostrado que es difícil dispersar suficientes estrellas hacia los agujeros negros para resolver el problema del pársec final.
Otra alternativa es que cada agujero negro tenga un pequeño disco de gas a su alrededor, y que estos discos absorban material de un disco más amplio que rodea la región vacía excavada por los agujeros. “Los discos que los rodean se alimentan del disco más amplio”, explica Taylor, y eso significa, a su vez, que su energía orbital puede filtrarse hacia el disco más amplio. “Parece una solución muy eficiente”, afirma Natarajan. “Hay mucho gas disponible”.
En enero, Blecha y sus colegas investigaron la idea de que un tercer agujero negro en el sistema podiese proporcionar una solución. En algunos casos en los que dos agujeros negros se han estancado, otra galaxia podría comenzar a fusionarse con las dos primeras, trayendo consigo un agujero negro adicional. «Puede haber una fuerte interacción de tres cuerpos», explica Blecha. «Puede quitar energía y reducir en gran medida la escala de tiempo de la fusión». En algunas circunstancias, el más ligero de los tres agujeros es expulsado, pero en otras los tres se fusionan.
Pruebas en el horizonteLa tarea ahora es determinar cuál solución es la correcta, o si hay múltiples procesos en juego.
Alonso-Álvarez espera probar su idea buscando una señal de materia oscura autointeractuante en los próximos datos de la matriz de sincronización de púlsares. Una vez que los agujeros negros se acercan más allá del último pársec, pierden momento angular principalmente al emitir ondas gravitacionales. Pero si la materia oscura autointeractuante está en juego, entonces deberíamos ver que absorbe parte de la energía a distancias cercanas al límite del pársec. Esto, a su vez, generaría ondas gravitacionales menos energéticas, explica Alonso-Álvarez.
Hai-Bo Yu, físico de partículas de la Universidad de California en Riverside y defensor de la materia oscura autointeractuante, sostiene que la idea es plausible. “Es una vía para buscar características microscópicas de la materia oscura a partir de la física de ondas gravitacionales”, dice. “Creo que es simplemente fascinante”.
La sonda espacial LISA (Laser Interferometer Space Antenna) de la Agencia Espacial Europea, un observatorio de ondas gravitacionales cuyo lanzamiento está previsto para 2035, podría darnos aún más respuestas. LISA captará las fuertes ondas gravitacionales emitidas por la fusión de agujeros negros supermasivos en sus últimos días. “Con LISA veremos realmente la fusión de agujeros negros supermasivos”, cuenta Pacucci. La naturaleza de esa señal podría revelar “rasgos particulares que muestran el proceso de desaceleración”, resolviendo el problema del pársec final.
El artículo original, How Do Merging Supermassive Black Holes Pass the Final Parsec?, se publicó el 23 de octubre de 2024 en Quanta Magazine.
Traducido por César Tomé López
El artículo ¿Cómo pasan el último pársec los agujeros negros supermasivos en fusión? se ha escrito en Cuaderno de Cultura Científica.
La pitón ajusta el tamaño del corazón a su dieta
Las serpientes pitón practican la estrategia depredadora conocida como “siéntate y espera”. Se trata de permanecer inmóvil y esperar a que una presa se ponga al alcance de sus mandíbulas, algo que sucede muy de tarde en tarde. Esta estrategia requiere que en los largos periodos de ayuno se reduzca drásticamente el metabolismo, y que las presas sean suficientemente grandes para compensar esos periodos.
 Figura 1. Pitón de Birmania (Python bivittatus). Foto: NPSPhoto, R. Cammauf, dominio público
Figura 1. Pitón de Birmania (Python bivittatus). Foto: NPSPhoto, R. Cammauf, dominio públicoLa pitón de Birmania (Python bivittatus) es una serpiente que alcanza los cuatro metros de longitud (Figura 1). Es capaz de permanecer durante meses sin alimentarse, pero cuando captura una presa y comienza a digerirla, su metabolismo se multiplica por diez. En 2005 se descubrió que en las 48 horas posteriores a la ingesta se producía un aumento del 40% en el tamaño del corazón. El crecimiento no se producía por proliferación de las células musculares cardiacas (los cardiomiocitos), sino por un incremento en la síntesis de proteínas, sobre todo las del aparato contráctil, lo que llevaba a un aumento del tamaño de los cardiomiocitos. Se trataba, por tanto, del proceso conocido como hipertrofia cardiaca.
Una vez terminada la digestión, al cabo de 7-10 días, el metabolismo de la pitón vuelve a reducirse al mínimo y el corazón disminuye de tamaño hasta regresar a su volumen inicial. Este rápido proceso de aumento y disminución del tamaño cardiaco en cuestión de días resultaba excepcional, no se había observado nada parecido en otros animales.
En los humanos, una hipertrofia cardiaca reversible puede inducirse por el ejercicio prolongado y también ocurre de forma natural durante el embarazo, pero se trata de fenómenos mucho más lentos. También existe hipertrofia y remodelación cardiaca en respuesta a situaciones patológicas (infarto, hipertensión), pero suele ser irreversible. Por ello, el fenómeno observado en las pitones de Birmania cobraba un potencial interés clínico.
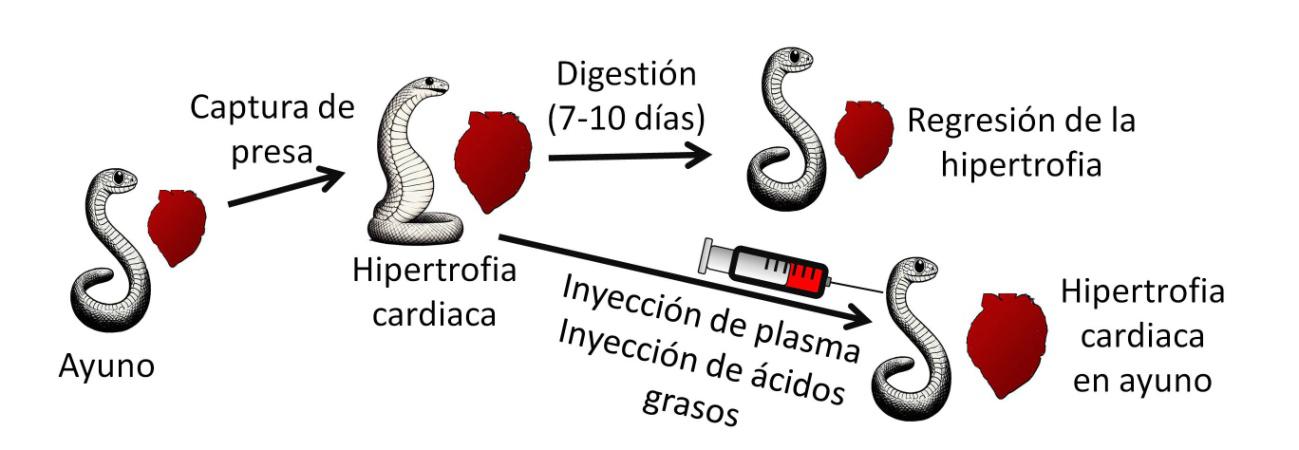 Figura 2. La captura de una presa provoca un rápido crecimiento del corazón (hipertrofia) que responde al fuerte aumento del metabolismo. Finalizada la digestión, el corazón regresa a su tamaño normal en el plazo de 7-10 días tras la ingesta. La hipertrofia cardiaca puede ser inducida en pitones en ayunas mediante la inyección de plasma de pitón recién alimentada o de una combinación de ácidos grasos (mirístico, palmítico y palmitoleico).
Figura 2. La captura de una presa provoca un rápido crecimiento del corazón (hipertrofia) que responde al fuerte aumento del metabolismo. Finalizada la digestión, el corazón regresa a su tamaño normal en el plazo de 7-10 días tras la ingesta. La hipertrofia cardiaca puede ser inducida en pitones en ayunas mediante la inyección de plasma de pitón recién alimentada o de una combinación de ácidos grasos (mirístico, palmítico y palmitoleico).Un equipo de investigación de la Universidad de Colorado (EE.UU.) descubrió en 2011 que la hipertrofia cardiaca era inducida por factores circulantes en la sangre de la pitón. Después de analizar los compuestos del plasma tras la ingesta de alimento, se seleccionaron como candidatos algunos ácidos grasos (mirístico, palmítico, palmitoleico). Bastaba la inyección de estos tres ácidos grasos en la sangre de la pitón para inducir un aumento del tamaño del corazón similar al provocado por la ingesta de una presa (Figura 2). Se observó incluso un aumento en la masa del ventrículo izquierdo de ratones tras la inyección de estos ácidos grasos.
Aclarado este punto, el grupo de investigación se aplicó al estudio de la rápida disminución del tamaño del corazón al volver a la fase de ayuno. Sus resultados acaban de ser publicados en la revista PNAS. Registrando cambios en la expresión génica durante la fase regresiva, se observó la activación de un conjunto de genes regulados por el factor de transcripción FoxO1. Como ya hemos comentado anteriormente en esta serie de artículos, los factores de transcripción se unen al ADN activando o reprimiendo a otros genes.
FoxO1 es bien conocido por su papel en múltiples procesos fisiológicos, como la regulación de la adipogénesis, los niveles de glucosa, el ciclo celular o la respuesta inmune. Más recientemente se ha descrito un papel importante de los factores FoxO en el proceso llamado autofagia, consistente en la degradación controlada de proteínas, orgánulos y otros elementos celulares. La autofagia es necesaria cuando la célula tiene que adaptarse al ayuno, o cuando debe reciclar orgánulos y proteínas deteriorados o que se han vuelto innecesarios. Se trata de un proceso conocido desde hace relativamente poco tiempo. De hecho, el Premio Nobel 2016 en Medicina y Fisiología fue otorgado al japonés Yoshinori Ohsumi por sus estudios pioneros sobre la autofagia.
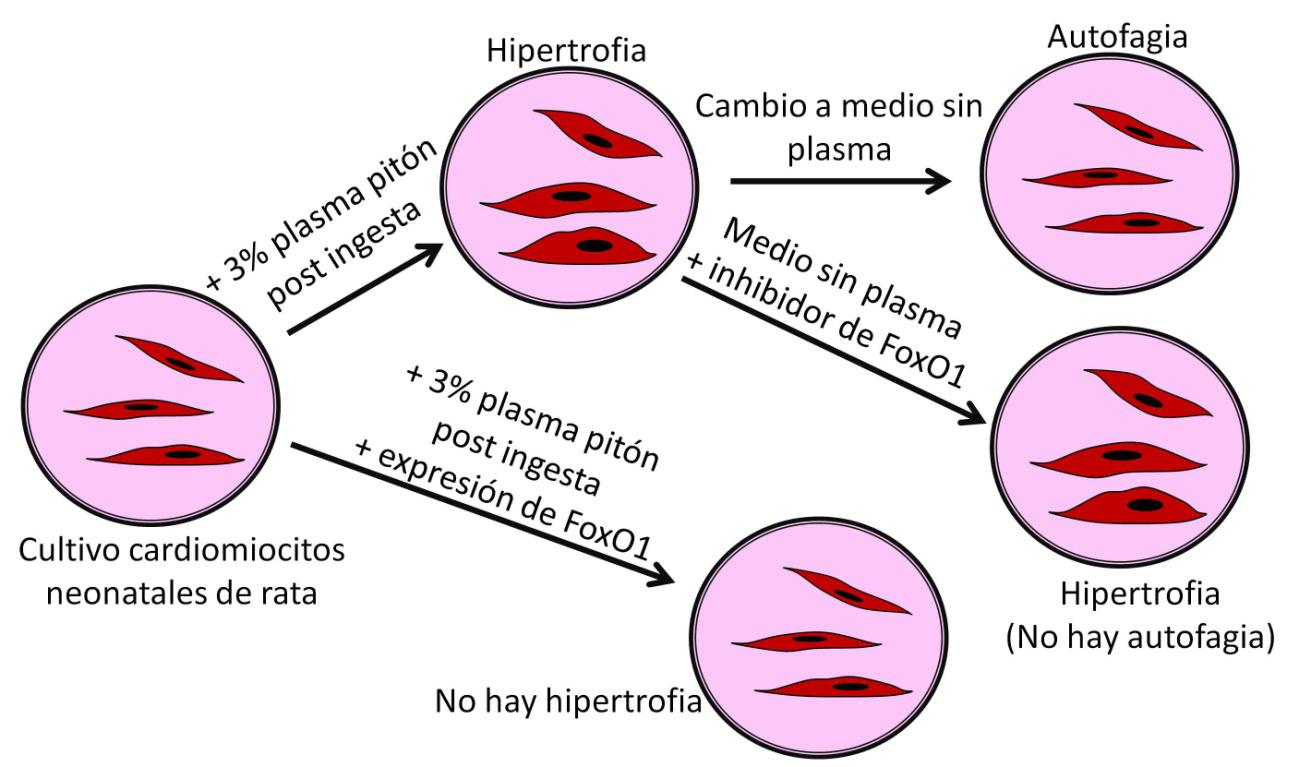 Figura 3. La adición de plasma de pitón recién alimentada al medio de cultivo provoca la hipertrofia de cardiomiocitos de rata recién nacida. Estos cardiomiocitos revierten a su tamaño normal después de un cambio a medio de cultivo sin plasma, debido a un proceso de autofagia (degradación de proteínas y otros componentes celulares). Si este medio contiene un inhibidor farmacológico del factor FoxO1, se evita el proceso de autofagia y los cardiomiocitos mantienen su gran tamaño. Por el contrario, si se fuerza la expresión de FoxO1 mediante vectores adenovirales, se bloquea la hipertrofia en presencia de plasma de pitón
Figura 3. La adición de plasma de pitón recién alimentada al medio de cultivo provoca la hipertrofia de cardiomiocitos de rata recién nacida. Estos cardiomiocitos revierten a su tamaño normal después de un cambio a medio de cultivo sin plasma, debido a un proceso de autofagia (degradación de proteínas y otros componentes celulares). Si este medio contiene un inhibidor farmacológico del factor FoxO1, se evita el proceso de autofagia y los cardiomiocitos mantienen su gran tamaño. Por el contrario, si se fuerza la expresión de FoxO1 mediante vectores adenovirales, se bloquea la hipertrofia en presencia de plasma de pitónEn el caso de la serpiente pitón, el papel de FoxO1 en los cardiomiocitos consistía en desencadenar un proceso de autofagia. A partir del sexto día tras la ingesta, FoxO1 activa la degradación de proteínas y otros elementos celulares en los cardiomiocitos, provocando una drástica reducción de tamaño. Para demostrarlo, se utilizó un modelo de cardiomiocitos neonatales de rata cultivados con un 3% de plasma de pitón recién alimentada (Figura 3). El equipo confirmó que aumentaban de tamaño 24 h después del tratamiento, y regresaban a su tamaño normal 48 h tras el cambio a un medio de cultivo normal. Pero cuando se desactivó FoxO1 en los cardiomiocitos hipertrofiados mediante un inhibidor farmacológico, estos mantuvieron su gran tamaño en condiciones de ayuno. Por otro lado, cardiomiocitos en los que se forzó la expresión de FoxO1 mediante adenovirus no se hipertrofiaron a pesar de ser cultivados con plasma de pitón recién alimentada.
En conclusión, tanto los mecanismos de activación de la hipertrofia cardiaca como los implicados en la rápida reducción del corazón han quedado desvelados en la pitón de Birmania. Será muy importante saber si este nuevo conocimiento ayudará a comprender mejor la inducción y la reversión de la hipertrofia cardiaca humana en condiciones normales (embarazo, ejercicio) o patológicas.
Referencias
Andersen, J.B., Rourke, B.C., Caiozzo, V.J. et al. (2005) Postprandial cardiac hypertrophy in pythons. Nature. doi: 10.1038/434037a.
Martin, T.G., Hunt, D.R., Langer, S.J. et al. (2024) Regression of postprandial cardiac hypertrophy in burmese pythons is mediated by FoxO1. Proc Natl Acad Sci U S A. doi: 10.1073/pnas.2408719121.
Riquelme, C.A., Magida, J.A., Harrison, B.C. et al. (2011) Fatty acids identified in the Burmese python promote beneficial cardiac growth. Science. doi: 10.1126/science.1210558.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga
El artículo La pitón ajusta el tamaño del corazón a su dieta se ha escrito en Cuaderno de Cultura Científica.
Por qué hoy el Titanic no se habría hundido
 El Titanic durante su construcción. Foto:Robert John Welch (1859-1936) / Wikimedia Commons
El Titanic durante su construcción. Foto:Robert John Welch (1859-1936) / Wikimedia Commons
La falta de un conocimiento adecuado en ciencia e ingeniería de materiales, así como priorizar otros intereses, ha contribuido a algunos de los mayores desastres tecnológicos de la historia. Son ejemplos icónicos la tragedia del transbordador espacial Challenger; los dramáticos accidentes del Havilland Comet, el Columbia y los buques Pendleton y Fort Mercer, además de la caída del puente Hasselt Road en Bélgica. Sin olvidarnos del desastre del Titanic.
Todas estas catástrofes se habrían evitado con los avances en materiales que conocemos hoy.
La fragilidad del acero del TitanicEl 1 de septiembre de 1985, Robert Ballard encontró el Titanic a 3 700 m en el fondo del océano Atlántico. El barco se había dividido en dos secciones principales, separadas por unos 600 m. La colisión había creado aberturas en el casco por un total de 1 115 m².
Durante una expedición a los restos del naufragio en el Atlántico Norte el 15 de agosto de 1996, los investigadores trajeron acero del casco del barco para realizar análisis metalúrgicos. El minucioso análisis desveló que el acero tenía una alta temperatura de transición dúctil-frágil, lo que le hacía inadecuado para el servicio a bajas temperaturas. En el momento de la colisión, la temperatura del agua era –2° C.
Hoy, la calidad de estos aceros se ha multiplicado exponencialmente.
El error se mantuvo en los Liberty shipsDurante la Segunda Guerra Mundial, Estados Unidos construyó más de 6 000 buques Liberty ships para apoyar a Gran Bretaña. Una de las peculiaridades en su fabricación fue que la planchas de acero del casco estaban soldadas y no unidas por remaches. Cuando tres de estos buques se partieron literalmente por la mitad, la razón pareció estar clara en un primer momento y se responsabilizó a la soldadura de las planchas. Sin embargo, la verdadera causa estaba relacionada con la fragilidad del acero a bajas temperaturas.
 En 1943 el petrolero SS Schenectady estaba amarrado en el muelle de prueba de Swan Island. El casco se agrietó casi por la mitad.
En 1943 el petrolero SS Schenectady estaba amarrado en el muelle de prueba de Swan Island. El casco se agrietó casi por la mitad.Wikimedia commons
Estos buques, junto con el SS Schenectady y los Pendleton y Fort Mercer, soportaron temperaturas próximas a -2⁰ C , como las que sufrió el Titanic al hundirse en el Atlántico Norte en 1912
A esas temperaturas, el acero utilizado en los cascos se volvía frágil, rompiéndose con facilidad. La clave del problema radica en la temperatura que determina cuándo un material pasa de ser dúctil a frágil (DBTT). Este cambio de comportamiento no se descubrió hasta años después y ha supuesto un reto para la investigación metalúrgica en la última mitad de siglo.
Los avances en metalurgia del siglo XX han permitido modificar la composición del acero para que no ocurra una transición tan brusca y poder reducir este riesgo. Hoy en día sabemos que la relación entre los elementos que forman el acero es clave para optimizar su comportamiento, y también que esto influye en su sensibilidad a las bajas temperaturas y su susceptibilidad a la formación de grietas.
Con algunos cambios en la composición del acero, muchos desastres se habrían evitado. Y no solo el hundimiento de barcos.
Challenger: el efecto de la temperaturaLa tragedia del Challenger en 1986 fue uno de los desastres más impactantes del siglo XX. Este vuelo de la NASA tenía una relevancia especial, ya que a bordo iba Christa McAuliffe, una profesora seleccionada para el programa Teachers in Space, promovido por el gobierno de Ronald Reagan.
Se esperaba que el lanzamiento reavivara el interés en los viajes espaciales, mostrando su creciente seguridad. Sin embargo, 73 segundos después del despegue el Challenger se desintegró a 14,6 kilómetros de altura, causando la muerte de los siete tripulantes.
La investigación reveló que el accidente fue causado por un fallo en las juntas tóricas de los propulsores de combustible sólido. Estas juntas, fabricadas con fluoroelastómeros (FKM), tenían pérdida de elasticidad a bajas temperaturas.
La mañana del lanzamiento, la temperatura era de -3⁰ C, lo que impidió que las juntas se sellaran adecuadamente. Esto permitió la fuga de gases calientes que provocaron la ruptura del propulsor derecho, desatando el desastre.
En 1986 ya sabía que las juntas tóricas eran vulnerables a bajas temperaturas, y varios expertos sugirieron posponer el despegue. Pero la presión por el éxito de la misión prevaleció, ignorando las advertencias sobre el comportamiento del material en condiciones adversas.
Havilland Comet y la fatiga del metalEl Havilland DH.106 Comet fue el primer avión comercial a reacción y marcó un hito en la aviación cuando comenzó a operar en 1949. Propulsado por turbinas, volaba a mayor altitud y con menos turbulencias, lo que mejoraba la comodidad para los pasajeros. Su diseño aerodinámico, con alas en flecha y motores empotrados, lo hacía más eficiente.
Sin embargo, entre 1953 y 1954 el Comet sufrió una serie de accidentes, incluido el vuelo G-ALYV, que se desintegró sobre Calcuta.
Inicialmente, se pensó que las causas eran climáticas. Pero la investigación reveló un problema en el diseño estructural del avión: las ventanas cuadradas.
 Detalle de las ventanas del Havilland DH Comet que provocaban la ruptura del avión.
Detalle de las ventanas del Havilland DH Comet que provocaban la ruptura del avión.Wikimedia commons, CC BY
Estas ventanas actuaban como concentradores de tensiones, lo que generaba grietas debido a los ciclos de presión durante los vuelos. Con cada ciclo, las fisuras aumentaban hasta provocar una descompresión explosiva, causando la desintegración del avión.
Este descubrimiento resultó clave para la industria de la aviación, que adoptó las ventanas ovaladas que ahora vemos en los aviones para evitar la concentración de tensiones y reducir el riesgo de fatiga del metal.
Trasbordador espacial Columbia: la corrosiónEl 1 de febrero de 2003, el transbordador espacial Columbia se desintegró durante su reingreso a la atmósfera, causando la muerte de sus siete tripulantes.
El desastre se debió a un daño en el ala izquierda, causado por una pieza de espuma aislante que se desprendió durante el lanzamiento, afectando las planchas de protección térmica. Este daño expuso la estructura interna del transbordador a los gases calientes de la atmósfera, lo que debilitó la nave y causó su desintegración.
Uno de los factores fue la corrosión de los materiales metálicos, que se agrava en el espacio debido a la exposición al oxígeno elemental altamente reactivo en las capas superiores de la atmósfera. Desde entonces, las inspecciones de seguridad han prestado mayor atención a la corrosión de los materiales, que ya no se pasa por alto, lo que evita futuros accidentes.
La apuesta por la ciencia e ingeniería de materialesLos desastres mencionados resaltan la importancia de la ciencia e ingeniería de materiales en la seguridad y el éxito de las tecnologías modernas.
Entender cómo se comportan los materiales en diferentes condiciones es fundamental para prevenir fallos catastróficos. Figuras como Elon Musk han destacado la importancia de esta disciplina, alentando a estudiar carreras en ciencia e ingeniería, cruciales para el desarrollo de la industria espacial y otros campos. Y, como hemos visto, para evitar terribles accidentes en la historia futura.![]()
Sobre la autora: Paula Alvaredo Olmos, Profesora Titular en Ciencia e Ingeniería de Materiales, Universidad Carlos III
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Por qué hoy el Titanic no se habría hundido se ha escrito en Cuaderno de Cultura Científica.
Naukas Pro 2024: Corrientes oceánicas y submarinos amarillos

Los últimos avances en el ámbito de las energías renovables marinas o la proliferación de los microplásticos fueron algunos de los temas que componen la última edición de NAUKAS PRO. Una cita en la que el personal investigador se sube al escenario del Euskalduna Bilbao para hablar de las investigaciones más destacadas del momento en un ámbito concreto.
En esta ocasión el personal investigador de la Universidad del País Vasco, de la Estación Marina de Plentzia (PiE-UPV/EHU), AZTI, Tecnalia o el CSIC acercaron las últimas investigaciones relacionadas en el ámbito marítimo.
La conferencia Corrientes oceánicas y submarinos amarillos corre a cargo de Anna Rubio Company, investigadora del Centro de Investigación Marina y Alimentaria AZTI.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Pro 2024: Corrientes oceánicas y submarinos amarillos se ha escrito en Cuaderno de Cultura Científica.
Desimetrización enantioselectiva de ciclobutanos
Los sistemas vivos están basados en biomoléculas que son asimétricas. El Grupo de Investigación en Catálisis metálica y Organocatálisis liderado por el catedrático de la Universidad del País Vasco José Luis Vicario ha conseguido, en colaboración con la Universidad Rovira i Virgili, “sintetizar moléculas con una asimetría esquiva utilizando una novedosa metodología que abre una nueva vía a un tipo de estructuras moleculares nunca conseguidas hasta el momento, que potencialmente podrían utilizarse como fármacos, entre otras cosas”.
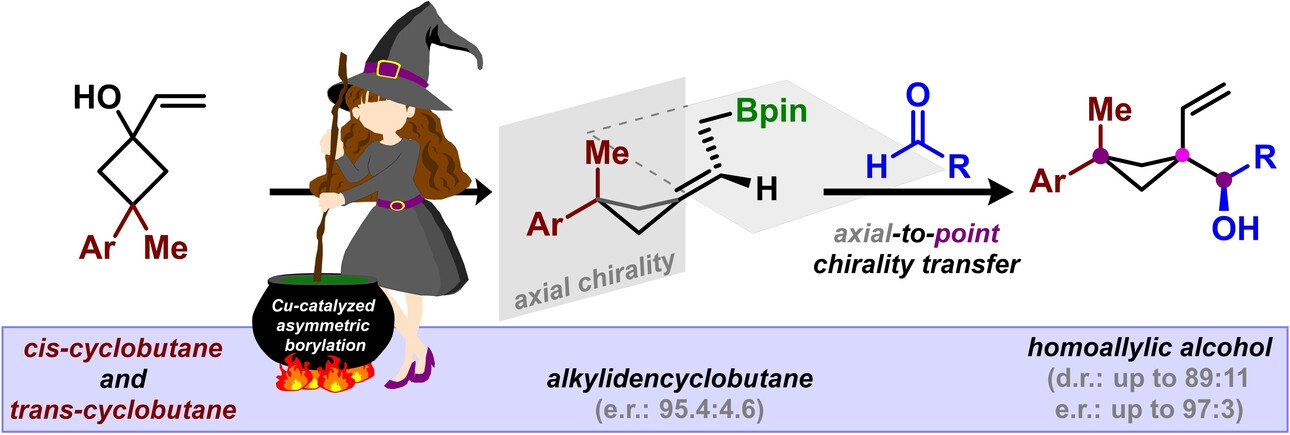
El grupo de la Facultad de Ciencia y Tecnología de la UPV/EHU, que trabaja en síntesis asimétrica de moléculas orgánicas de pequeño tamaño, ha conseguido “sintetizar moléculas cíclicas intrínsecamente asimétricas empleando catálisis. Hemos desarrollado una metodología eficaz y directa, utilizando pequeñas cantidades de un catalizador derivado del cobre, un metal abundante y no nocivo”, señala el Catedrático de Química Orgánica de la UPV/EHU.
La gran mayoría de moléculas orgánicas (basadas en una estructura de carbono) no son planas, tienen geometría tridimensional. Dependiendo de la manera en que los átomos se ordenan dentro de cada molécula se pueden obtener resultados. En algunos casos una molécula y su imagen especular (es decir, dos moléculas simétricas que guardan la misma relación que la que tiene un objeto con su imagen en un espejo) pueden tener propiedades totalmente diferentes.
Utilicemos el símil de las manos para explicarlo: nuestras manos son las imágenes especulares una de la otra; se puede decir que son idénticas. Sin embargo, cuando se dispone una mano sobre la otra (no en disposición de juntar las palmas, sino superponiendo una mano a la otra), la posición de los dedos no es la misma. Ocurre lo mismo con algunas moléculas, la organización de los átomos no coincide. Cada una de las imágenes especulares de una molécula que no son superponibles se llama enantiómero.
Simétricas pero con propiedades muy diferentes“En la naturaleza y en farmacología existen muchísimos ejemplos en los que los dos enantiómeros tienen propiedades dispares. Es el caso de la talidomida (un fármaco administrado como sedante y calmante de las náuseas durante los tres primeros meses de embarazo, que provocó miles de casos de malformaciones congénitas), uno de los enantiómeros tiene propiedades analgésicas y el otro produce malformaciones —explica el doctor de la UPV/EHU Efraim Reyes, uno de los autores principales del trabajo—. Eso ocurre porque las dianas terapéuticas no interaccionan de la misma manera con un enantiómero u otro. Por tanto, es fundamental controlar la síntesis de este tipo de moléculas, para conseguir únicamente uno de los dos enantiómeros”.
La investigadora predoctoral Josebe Hurtado ha sido capaz de construir selectivamente una de las dos moléculas enantioméricas de un grupo de ciclobutanos (moléculas cíclicas que contienen esencialmente átomos de carbono e hidrógeno), “mediante la desimetrización; es decir, rompiendo la simetría planar y convirtiéndolas en bloques sintéticos elementales de moléculas más complejas”, explica su director de tesis Efraim Reyes.
Este logro responde a un gran reto actual y un área de investigación de interés creciente. “Hemos conseguido sintetizar moléculas con una asimetría axial (sustentada en un eje), que no tiene precedente en la naturaleza y que abre una puerta al estudio de un nuevo tipo de moléculas, que pueden servir también para desarrollar nuevas vías terapéuticas”, añade Vicario. Además, a través de un estricto control de las reacciones “hemos roto la simetría planar para convertirla en asimetría axial y a continuación en asimetría puntual (sustentada en un punto)”, explica el profesor catedrático de la UPV/EHU. Esto demuestra “que existe una posibilidad real de que las biomoléculas con asimetría puedan tener también un origen común”.
La desimetrización espontánea, origen de la vidaEste hallazgo recuerda a una de las teorías relacionadas con el origen de la vida, que se basa en que mediante una desimetrización espontánea de la simetría se formaron las moléculas que dieron lugar a la vida. “Una de las teorías del origen de la vida, muy aceptada, dice que originalmente solo había moléculas simétricas y que por un proceso de desimetrización espontánea surgieron moléculas asimétricas, que son evidentemente el origen de la vida, porque todo nuestro organismo y los sistemas vivos están basados en biomoléculas que son asimétricas y solo contienen uno de los dos enantiómeros”, concluye Reyes.
Referencia:
Josebe Hurtado, Nerea Iragorri, Efraim Reyes, Jose L. Vicario, Elena Fernández (2024) Cu-Catalyzed Enantioselective Borylative Desymmetrization of 1-Vinyl Cyclobutanols and Axial-to-Point Chirality Transfer in a Diastereoconvergent/Stereoretentive Allylation Scenery Angewandte Chemie International Edition doi: 10.1002/anie.202411232
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Desimetrización enantioselectiva de ciclobutanos se ha escrito en Cuaderno de Cultura Científica.
Amianto, una historia de terror
Basta pronunciar la palabra amianto, o asbesto, para que a muchos —y, sobre todo, a los propietarios de las casas de los programas de reformas— se nos pongan los pelos de punta. Utilizada desde la Antigüedad en numerosos ámbitos, las propiedades de esta fibra mineral son ampliamente conocidas desde entonces, algunas muy útiles, de ahí su popularidad, y otras muy dañinas. Aun así, no fue hasta 2005 cuando la Unión Europea prohibió completamente su uso —algunos países miembros ya lo habían empezado a eliminar mucho antes—. Pero ¿qué es exactamente el amianto?, ¿para qué se ha utilizado a lo largo de la historia?, ¿por qué es tan peligroso? Para empezar, hasta que se empezaron a estudiar sus nocivos efectos sobre la salud, fue el material del futuro, un compuesto milagroso a prueba de todo… y con aplicaciones para casi todo.
 Fibras de amianto (tremolita, en este caso) sobre un mineral de muscovita. Créditos: Dominio Público/Aram Dulyan
Fibras de amianto (tremolita, en este caso) sobre un mineral de muscovita. Créditos: Dominio Público/Aram Dulyan
El amianto es un grupo de seis minerales fibrosos de origen metamórfico compuestos de silicatos —los de mayor abundancia en la naturaleza—: grunerita (o amosita, para la variante fibrosa), crisotilo, riebeckita (crocidolita), tremolita, bisolita (actinolita) y antofilita. La combinación de este origen mineral y que se presente en forma de fibras largas, flexibles y resistentes es lo que le otorga tanto sus propiedades como su versatilidad. Estamos ante un material ignífugo, con excelentes propiedades aislantes tanto eléctricas como térmicas, una gran durabilidad, resistencia química y mecánica, y, sobre todo, abundante y barato. Su ligereza y que se presente en forma de fibras posibilita, además, manipularlo con facilidad, pero también es lo que lo convierte en un peligro para la salud.
 Microfibras de amianto (amosita), vistas a través de un microscopio electrónico de barrido. El pequeño tamaño que pueden alcanzar hace que puedan inhalarse sin detectarse. Una vez alojadas en los pulmones, el cuerpo tiene mucha dificultad para eliminarlas. Créditos: CC BY-SA 3.0/Ravaka
Microfibras de amianto (amosita), vistas a través de un microscopio electrónico de barrido. El pequeño tamaño que pueden alcanzar hace que puedan inhalarse sin detectarse. Una vez alojadas en los pulmones, el cuerpo tiene mucha dificultad para eliminarlas. Créditos: CC BY-SA 3.0/Ravaka
La inhalación de fibras microscópicas de amianto, que pueden encontrarse flotando en el ambiente en cualquier entorno en el que se esté trabajando con él, puede provocar graves patologías. Estas se quedan alojadas en los pulmones durante largo tiempo, dada la dificultad del cuerpo para eliminarlas, lo que, a largo plazo, acaba produciendo inflamación y daño celular. Aparecen así enfermedades como la asbestosis, que causa fibrosis pulmonar, o ciertos tipos de cáncer como el de pulmón y el mesotelioma, que afecta a la pleura o el peritoneo.
Que las personas que trabajaban con amianto enfermaban se sabe desde casi los orígenes de su uso. Existen testimonios incluso de Plinio el Viejo, que ya habló del padecimiento pulmonar de los esclavos que manipulaban habitualmente amianto, y en 1899, se documentó clínicamente en Londres el primer caso de fibrosis pulmonar de una trabajadora del amianto de 33 años por inhalación de estas fibras. Las primeras regulaciones del trabajo con amianto, dada su alta peligrosidad, se remontan a los años treinta, por eso sorprende que no haya sido hasta hace relativamente poco cuando por fin se han tomado medidas. Y no solo eso: la locura comercial y la mayor expansión de la industria del amianto se produjo, incluso sabiendo esta información, durante la década de los años cuarenta, con su pico durante los cincuenta y los sesenta.
A lo largo de la historia de la ciencia ha sido habitual que, ante la llegada de un nuevo descubrimiento o adelanto tecnológico, este se haya visto como una especie de santo grial o piedra filosofal que iba a solucionar todos nuestros problemas. Sucedió con la electricidad, con la radiactividad —recordemos todos aquellos productos de uso cotidiano que llevaban radio, como pastas de dientes—, e incluso puede que esté sucediendo ahora con la inteligencia artificial. El amianto no se quedó atrás, pero con la diferencia de que, en su momento de mayor auge, como hemos comentado, sí se conocían los riesgos que su uso implicaba.
La mayoría de aplicaciones del amianto son de sobra conocidas. En la construcción se ha usado como aislamiento, revestimiento, para aumentar la durabilidad y resistencia de los suelos… En la industria automotriz, era un material habitual en pastillas de freno y embragues, pero las aplicaciones más espeluznantes fueron, probablemente, en el ámbito textil, para la confección de ropa ignífuga. Se utilizó incluso en electrodomésticos, sobre todo en aquellos que generan calor, como calentadores, hornos y secadores. Lo que tal vez muchos no sepan es que, durante mucho tiempo, se promovió muchísimo su uso en objetos mucho más cotidianos. Y, para muestra, este documento de 1942:
Cortinas, fundas, manteles… también mantas, guantes de cocina, bolsas, cuerdas… incluso el tejido para confeccionarlos uno mismo se anunciaba como maravilloso. Todos estos productos se vendían con total, demasiada, normalidad. Por ejemplo, para los fanáticos de la Navidad que ya estén pensando en la decoración de su árboles y belenes existía incluso nieve artificial hecha de amianto.
 Nieve decorativa de amianto y mica. Créditos: Flickr/Asbestorama fuck you
Nieve decorativa de amianto y mica. Créditos: Flickr/Asbestorama fuck you
Parece que del mismo tipo que la que le cayó a Dorothy, el Espantapájaros y el León de camino a Oz.
 La nieve artificial que se usó en El mago de Oz en 1939 eran fibras de amianto. Créditos: Metro Goldwyn Mayer
La nieve artificial que se usó en El mago de Oz en 1939 eran fibras de amianto. Créditos: Metro Goldwyn Mayer
Solo cabe hacerse una pregunta cuando la historia nos pone en situaciones similares: ¿cuál es nuestra prioridad? ¿El beneficio económico o el beneficio humano? El uso de amianto, a diferencia de lo que sucedió con el radio y sus efectos, no se promovió desde la ignorancia.
Bibliografía
The Mesothelioma Center. (s. f.). History of asbestos. Asbestos.com. https://www.asbestos.com/asbestos/history/
Asbestorama. Perfil de Flickr. https://www.flickr.com/photos/asbestos_pix/asbestos
Rare Historial Photos (s. f.). Vintage photos show how asbestos products were once marketed, 1930s-1970s. Rare Historial Photos. https://rarehistoricalphotos.com/asbestos-vintage-advertisements/
Tweedale, G. (2000). Magic mineral to killer dust. Oxford University Press.
.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo Amianto, una historia de terror se ha escrito en Cuaderno de Cultura Científica.
Fibonacci está en todas partes (y III)
Esta es la última jornada de un paseo por algunos lugares de lo más curiosos e inesperados, en los que aparecen los números de Fibonacci. Durante la primera jornada, recogida en la entrada del Cuaderno de Cultura Científica titulada Fibonacci en todas partes (I), visitamos espacios destacados como el árbol genealógico de un zángano (abeja macho), los paseos de una abeja por un panal de dos filas de celdas o los embaldosados con fichas de dominó, mientras que para la segunda jornada, Fibonacci en todas partes (II), reservamos la visita a lugares de interés como la óptica de la luz, unas escaleras que se suben, o se bajan, de una en una o de dos en dos, y las sumas de números con unos y doses.
 Girasole (en italiano), acrílico sobre lienzo, 60 x 70 cm, del artista suizo Eugen Jost. Obra perteneciente a la exposición Everything is numberPintando un edificio de apartamentos
Girasole (en italiano), acrílico sobre lienzo, 60 x 70 cm, del artista suizo Eugen Jost. Obra perteneciente a la exposición Everything is numberPintando un edificio de apartamentos
Con el problema de pintar un edificio de apartamentos con dos colores distintos iniciamos la tercera jornada de este paseo. El enunciado de este clásico problema dice así.
Problema: Si un edificio de apartamentos de n plantas va a ser pintado de azul y amarillo, de manera que cada planta esté pintada de un color y no haya dos plantas adyacentes pintadas ambas de amarillo, ¿de cuántas formas es posible hacerlo?
Para resolver este problema, podemos empezar de forma experimental, viendo qué ocurre para los edificios con un número pequeño de plantas. Para un edificio de apartamentos con una sola planta, existen solo dos opciones (2), pintar esa única planta de azul o de amarillo. Para dos plantas, hay tres opciones (3), pintar las dos plantas de azul, ambas de amarillo no es posible, o pintar cada planta de un color, lo cual se puede hacer de dos formas distintas, como se observa en la siguiente imagen. Mientras que para un edificio de tres plantas pueden pintarse todas de azul, puede pintarse una de amarillo, que puede ser la primera, la segunda o la tercera planta, o pueden pintarse dos plantas de amarillo, que por la condición de que no haya plantas amarillas contiguas, solo puede hacerse de una manera, en las plantas de los extremos, en total cinco formas distintas (5).
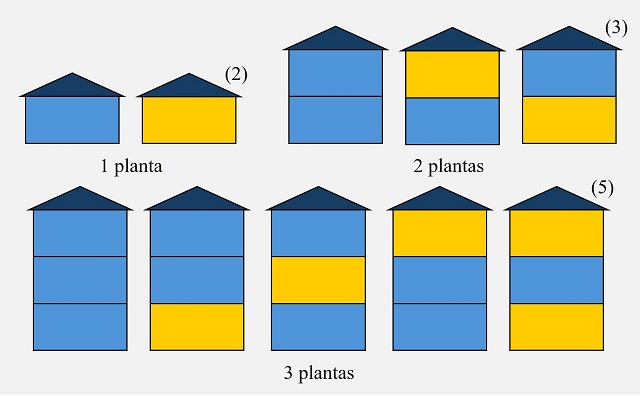 Maneras de pintar un edificio de apartamentos de una, dos o tres plantas de azul y amarillo, si el color amarillo no lo pueden compartir plantas contiguas
Maneras de pintar un edificio de apartamentos de una, dos o tres plantas de azul y amarillo, si el color amarillo no lo pueden compartir plantas contiguas
Si ahora consideramos un edificio de cuatro plantas, puede pintarse todo de azul, con una planta amarilla y hay cuatro plantas, o con dos plantas amarillas, que puede hacerse de tres formas diferentes sin que coincidan de amarillo plantas adyacentes, pero no es posible que tres o cuatro plantas estén pintadas de amarillo. En total, hay ocho (8) maneras de pintar el edificio de apartamentos.
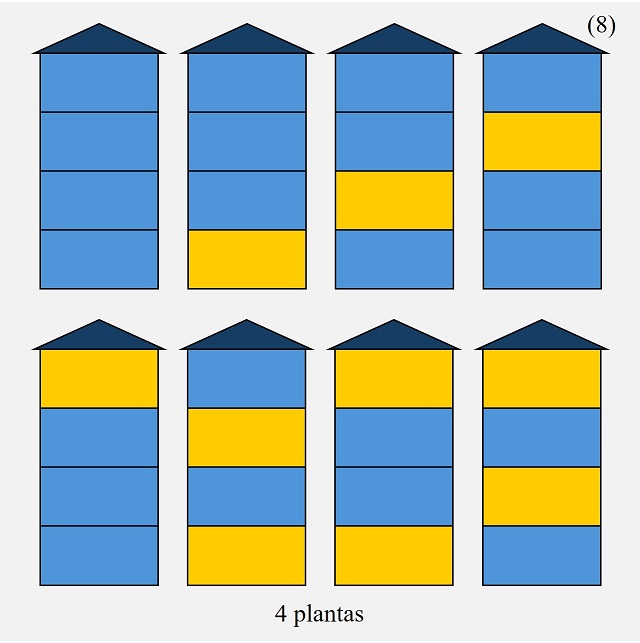 Formas de pintar un edificio de apartamentos de cuatro plantas de azul y amarillo, si el color amarillo no lo pueden compartir plantas contiguas
Formas de pintar un edificio de apartamentos de cuatro plantas de azul y amarillo, si el color amarillo no lo pueden compartir plantas contiguas
Como observamos los números que nos salen son 2, 3, 5 y 8, que son números de la sucesión de Fibonacci. Veamos que es la sucesión de Fibonacci, empezando en 2 y 3, viendo que satisface la condición recursiva, que la cantidad de maneras de pintar un edificio de n plantas se puede obtener a partir de las de n – 1 y n – 2 plantas. Para ello, observemos qué ocurre con el caso de n = 4 (cuatro plantas).
Si tomamos los edificios de 3 plantas (n – 1, en general) y consideramos una planta más, por encima de las otras, pintada de azul, generaremos algunos de los casos posibles para un edificio de 4 plantas (n, en general), tantos como las formas de pintar un edificio de 3 plantas (n – 1 plantas en general), que son 5 maneras distintas. Observemos que no podemos pintar de amarillo en todos los casos puesto que en algunos la última planta está pintada de amarillo, por lo que coincidirían dos plantas amarillas, mientras que los casos en los que la última planta es azul, aunque sí podríamos pintar la siguiente de amarillo, ese caso va a estar considerado en los casos que se derivan del edificio de n – 2 plantas (2 plantas en nuestro ejemplo), que veremos a continuación. Recíprocamente, si tomamos las maneras de pintar un edificio de 4 plantas (n, en general) en las cuales su última planta es azul, son todas las de 3 plantas (n – 1), a las que le añadimos una última planta azul.
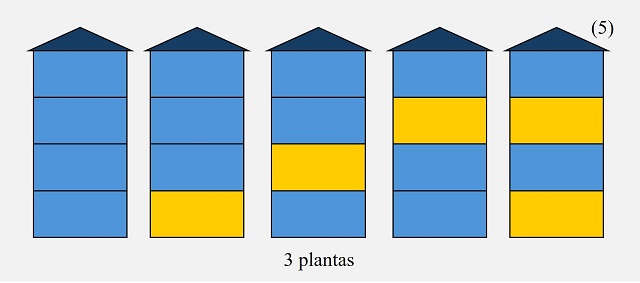 Las distintas maneras de pintar un edificio de 4 plantas, en las cuales su última planta es azul, son todas las posibles para 3 plantas, a las que le añadimos una última planta azul
Las distintas maneras de pintar un edificio de 4 plantas, en las cuales su última planta es azul, son todas las posibles para 3 plantas, a las que le añadimos una última planta azul
Si tomamos los edificios de 2 plantas (n – 2, en general) y consideramos dos plantas más, por encima de las otras, pintadas de amarillo y azul (de arriba a abajo), generaremos algunos de los casos posibles para un edificio de 4 plantas (n, en general), tantos como las formas de pintar un edificio de 2 plantas (n – 2 plantas en general), que son 3 maneras distintas. Observemos que no podríamos pedir pintar esas dos plantas superiores de azul y amarillo, ya que podrían coincidir dos plantas adyacentes amarillas, además los casos en los que sí se pueda, ya que la última planta de las anteriores es azul, ya está considerado en el caso anterior. Más aún, así cubrimos todos los casos de un edificio de 4 plantas (n, en general) en las cuales su última planta es amarilla.
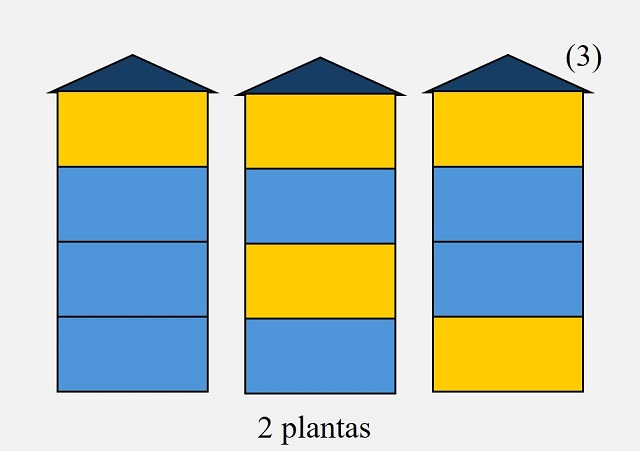 Las distintas maneras de pintar un edificio de 4 plantas, en las cuales su última planta es amarilla, son todas las posibles para 2 plantas, a las que le añadimos dos plantas más, por encima de las otras, pintadas de amarillo y azul (de arriba a abajo)
Las distintas maneras de pintar un edificio de 4 plantas, en las cuales su última planta es amarilla, son todas las posibles para 2 plantas, a las que le añadimos dos plantas más, por encima de las otras, pintadas de amarillo y azul (de arriba a abajo)
En consecuencia, hemos demostrado que se cumple la misma propiedad recursiva que para la sucesión de Fibonacci, Fn = Fn – 1 + Fn – 2. Por lo tanto, el número de formas distintas de pintar un edificio de apartamentos de n plantas, pintado de azul y amarillo, de manera que cada planta esté pintada de un color y no haya dos plantas adyacentes pintadas ambas de amarillo, es Fn + 2.
Palabras de n-bitsEmpecemos por lo elemental. Una palabra de n-bits es una cadena de n bits, donde un bit –acrónimo de bi[nary digi]t / dígito binario– es la unidad mínima de información y se corresponde con un dígito del sistema de numeración binario, 0 ó 1. Así, 1001001 sería una palabra de 7-bits o 1010101110110 una palabra de 13-bits.
Si lo pensamos un momento, resulta que la cuestión anterior de pintar de dos colores (azul y amarillo) un edificio de n plantas es equivalente al siguiente resultado.
Teorema: El número de palabras de n-bits que no contengan dos 1s consecutivos es igual a Fn + 2.
Veamos en la siguiente tabla, las palabras de n-bits para longitudes n pequeñas.
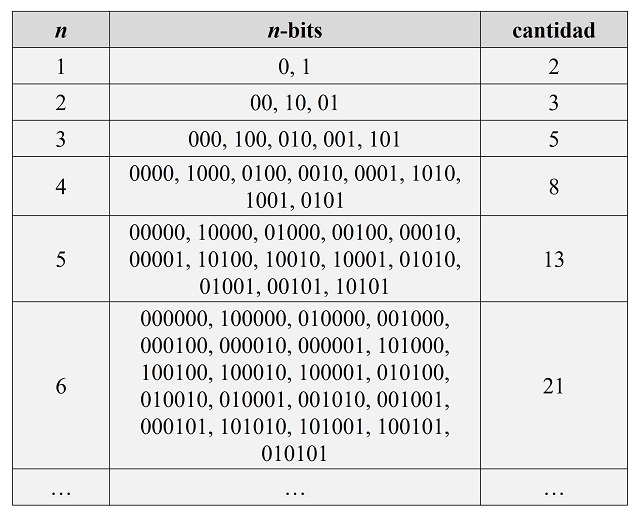 Número de palabras de n-bits que no contengan dos 1s consecutivos
Número de palabras de n-bits que no contengan dos 1s consecutivosLa demostración del teorema anterior es la misma que la de las maneras de pintar un edificio. Si se consideran las palabras de n-bits, las que terminan en 1 (por la derecha) son las palabras de (n – 1)-bits a las que se les añade un 1 por la derecha, mientras que las palabras que terminan en 0 son las palabras de (n – 2)-bits a las que se les añade 10 por la derecha.
Lanzar una monedaLlegados a este punto del paseo, nos podemos plantear una visita extra a un lugar que es un problema de probabilidad.
Problema: Si lanzamos una moneda n veces (sea n la cantidad que queramos), ¿cuál es la probabilidad de que no haya dos lanzamientos adyacentes que sean ambos cara?
Empecemos recordando que la probabilidad de que un evento ocurra se calcula dividiendo “el número de casos favorables” entre “el número de casos posibles” (pueden leerse las entradas relacionadas con la probabilidad, La probabilidad en el banquillo de los acusados o El cuento de la ruleta rusa ). Así, dada una determinada familia con dos “hijos”, si nos preguntamos cuál es la probabilidad de que los dos sean chicas, tendríamos que calcular primero el espacio muestral, es decir, el espacio de todos los casos posibles. En esta ocasión, habrá cuatro posibles casos (chica, chica), (chica, chico), (chico, chica) y (chico, chico), donde el orden en el par expresa el orden cronológico de nacimiento. Como solo uno de los cuatro es favorable, son dos chicas, la probabilidad de que los dos “hijos” sean chicas es 1/4 = 0,25, es decir, una probabilidad del 25%.
 Escena de la película No es país para viejos (2007), dirigida por Joel Coen y Ethan Coen, e interpretada por Tommy Lee Jones, Javier Bardem y Josh Brolin, entre otros, en la cual el personaje interpretado por Javier Bardem, un asesino a sueldo, decide si deja vivir al dependiente de una gasolinera lanzando una moneda al aire
Escena de la película No es país para viejos (2007), dirigida por Joel Coen y Ethan Coen, e interpretada por Tommy Lee Jones, Javier Bardem y Josh Brolin, entre otros, en la cual el personaje interpretado por Javier Bardem, un asesino a sueldo, decide si deja vivir al dependiente de una gasolinera lanzando una moneda al airePara analizar nuestro problema, si lanzamos una moneda al aire puede salir cara (que vamos expresarlo, para simplificar, pero también para disponer de una notación simple, con un 1) o puede salir cruz (que lo expresaremos con un 0). De esta manera, si lanzamos una moneda n veces, la representación de un posible resultado es un n-bit. Por ejemplo, si hablamos de lanzar la moneda 5 veces, entonces 10011 representa la posibilidad de que salga cara / cruz / cruz / cara / cara, mientras que 00101 sería cruz / cruz / cara / cruz / cara.
Por lo tanto, ya estamos en condiciones de calcular la probabilidad de que, si lanzamos una moneda n veces, no haya dos lanzamientos adyacentes que sean ambos cara. En primer lugar, calculemos el número de casos posibles. Estos son, teniendo en cuenta la descripción anterior de los posibles lanzamientos, todas las palabras de n-bits, que son 2n, ya que cada vez que lanzamos la moneda hay dos posibilidades, cara (1) o cruz (0), en un total de n lanzamientos. Y ahora toca calcular el número de los casos posibles, que, por la descripción anterior, son las palabras de n-bits para las que no hay dos 1s consecutivos, que ya hemos calculado y que es igual al número de Fibonacci Fn + 2.
Por lo tanto, la probabilidad de que, si lanzamos una moneda n veces, no haya dos lanzamientos adyacentes que sean ambos cara, es igual a:
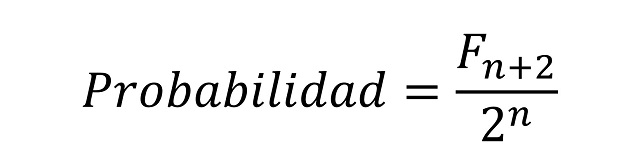
Por ejemplo, si lanzamos una moneda 5 veces, la probabilidad de que no haya dos lanzamientos consecutivos que sean cara es 13 / 32 = 0,40625, es decir, un 40,625 por ciento. Si vamos realizando cada vez más lanzamientos, nos podemos plantear si esa probabilidad aumenta o disminuye. Si lo pensamos un poco, intuitivamente es bastante claro que esa probabilidad irá disminuyendo, ya que con más lanzamientos será más fácil que salgan dos caras seguidas. Veamos qué pasa con las primeras cantidades de lanzamientos.
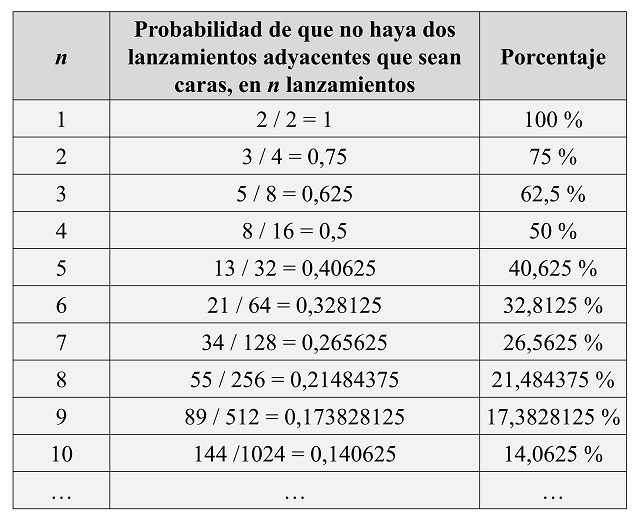
Efectivamente, la probabilidad va disminuyendo, como intuíamos. Esto se debe, matemáticamente, a que la sucesión de las potencias de 2 crece más rápido que la sucesión de los números de Fibonacci.
Subconjuntos alternadosVamos a terminar este paseo con un problema propuesto por el matemático francés Olry Terquem (1782-1862), del que ya hablamos en la entrada La circunferencia de los nueve puntos.
Un subconjunto del conjunto {1, 2, 3, …, n – 1, n} se dice que es alternado si sus elementos, cuando se colocan en orden creciente, siguen el patrón impar, par, impar, par, etcétera. Por ejemplo, los conjuntos {4}, {3, 6} o {1, 2, 5, 6} son subconjuntos alternados de {1, 2, 3, 4, 5, 6}, mientras que {2, 4, 5} o {1, 2, 3, 5} no lo son. El problema que se planteó Terquem fue calcular el número de subconjuntos alternados del conjunto {1, 2, 3, …, n – 1, n}. Veamos qué ocurre para los primeros casos.
 Cantidad de subconjuntos alternados del conjunto {1, 2, 3, …, n}, para n = 1, 2, 3, 4, 5, 6
Cantidad de subconjuntos alternados del conjunto {1, 2, 3, …, n}, para n = 1, 2, 3, 4, 5, 6Por lo tanto, el número de subconjuntos alternados del conjunto {1, 2, 3, …, n – 1. n} es igual al número de Fibonacci Fn + 2.
Podemos llegar a la sucesión de Fibonacci de muchas otras maneras, pero esas os las dejo para quienes os animéis a indagar sobre este tema.
 Coyote Breath / Aliento de coyote (2016), monotipo de la artista estadounidense Holli Marmon
Coyote Breath / Aliento de coyote (2016), monotipo de la artista estadounidense Holli MarmonBibliografía
1.- Alfred S. Posamentier, Ingmar Lehmann, The Fabulous Fibonacci Numbers, Prometheus Books, 2007.
2.- Thomas Koshy, Fibonacci and Lucas Numbers with Applications, John Wiley & Sons, 2001.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Fibonacci está en todas partes (y III) se ha escrito en Cuaderno de Cultura Científica.
Un magnetómetro de tamaño atómico
Si colocas unos cuantos átomos de hierro en fila sus espines magnéticos pueden organizarse en un patrón antiferromagnético alterno. O, mejor dicho, patrones. Debido a su naturaleza cuántica los átomos se encuentran en una superposición de dos estados antiferromagnéticos. Normalmente, la fila de átomos oscila rápidamente entre los dos estados. Pero un equipo de investigadores acaba de demostrar que es posible llevar una cadena corta de átomos de hierro a un punto diabólico, con el efecto de alargar espectacularmente el tiempo que la cadena pasa en un estado u otro. Este efecto podría ser la base sobre la que fabricar un magnetómetro de tamaño atómico.
 A la izquierda diábolo, figura geométrica (véase el texto). Fuente: Elbertse et al. (2024). A la derecha, diábolos, juguetes. Fuente: StoatBringer / Wikimedia Commons
A la izquierda diábolo, figura geométrica (véase el texto). Fuente: Elbertse et al. (2024). A la derecha, diábolos, juguetes. Fuente: StoatBringer / Wikimedia CommonsEl punto diabólico recibe su nombre del diábolo, un yoyó chino cuyas dos mitades cónicas opuestas se unen en un cuello estrecho. Si se representa gráficamente la energía de una cadena de espín antiferromagnética frente a la fuerza del campo magnético aplicado se obtiene una forma similar: un cono que apunta hacia arriba es el estado fundamental, mientras que el cono que apunta hacia abajo es el primer estado excitado. En su unión (el punto diabólico), los dos estados están degenerados.
 Elbertse et al. (2024)
Elbertse et al. (2024)Para crear su punto diabólico los investigadores colocaron cinco átomos de hierro sobre una superficie de nitruro de cobre a baja temperatura y en un vacío ultraalto. Encontraron que un campo magnético aplicado en paralelo a la superficie tenía el valor justo para crear unos estados fundamental y excitado casi degenerados.
Midiendo el giro del átomo central con un microscopio de efecto túnel los investigadores descubrieron que, en el punto diabólico, el patrón antiferromagnético cambiaba de dirección aproximadamente cada 10 segundos. Al variar el campo paralelo y aplicar un campo perpendicular adicional puediron crear un mapa de las condiciones alejadas del punto diabólico. A la distancia más grande, el tiempo de cambio de dirección se redujo en 3 órdenes de magnitud.
Los investigadores afirman que la sensibilidad del tiempo de cambio de dirección al campo magnético local podría aprovecharse para construir un magnetómetro de tamaño atómico.
Referencias:
R. J. G. Elbertse, D. Borodin, J. Oh, T. Ahn, J. Hwang, J. C. Rietveld, A. J. Heinrich, F. Delgado, S. Otte, and Y. Bae (2024) Long-Lived Magnetization in an Atomic Spin Chain Tuned to a Diabolic Point Phys. Rev. Lett. doi: 10.1103/PhysRevLett.133.166703
C. Tomé López (2017) Defeating spin decoherence Mapping Ignorance ISSN 2529-8992
C. Day (2024) Diabolical Nanomagnets Physics 17, s118
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Un magnetómetro de tamaño atómico se ha escrito en Cuaderno de Cultura Científica.

