4.0 Industriako teknologien ondorioak langileen segurtasunean eta laneko osasunean
UPV/EHUko ikerketa-talde batek egindako azterketa batek agerian utzi du 4.0 Industriako teknologien integrazioak eragin positiboa duela langileen laneko segurtasunaren eta osasunaren zenbait alderditan. Arreta bereziz aztertu ditu teknologia horiek ezartzearen ondorioz sortzen diren arrisku berriak ere.
4.0 Industriako teknologiek abantaila ugari eta askotarikoak eskaintzen dituzte: prozesatze-denborak eta beharrezko baliabide eta tresnak murrizten dituzte, eragiketen kudeaketa hobetzen dute, produktibitatea areagotzen dute… Horrek guztiak pertsonen laneko segurtasunean eta osasunean nola eragiten duen aztertzeko, UPV/EHUren Adimen teknologikoa gizartean enpresaren garapen ekonomiko jasangarria lortzeko ikerketa-taldeak inkesta bat diseinatu zuen, eta 4.0 Industriako teknologiak garatzen aitzindariak diren enpresetako 130 zuzendarik eta/edo teknikarik erantzun zuten.
 Irudia: 4.0 Industriako teknologiek abantaila ugari eta askotarikoak eskaintzen dituzte. (Argazkia: Pavel Danilyuk – domeinu publikoko irudia. Iturria: Pexels.com)
Irudia: 4.0 Industriako teknologiek abantaila ugari eta askotarikoak eskaintzen dituzte. (Argazkia: Pavel Danilyuk – domeinu publikoko irudia. Iturria: Pexels.com)Inkestak erantzunda, ikerketa-taldeak integrazio teknologikoaren adibide esanguratsu diren proiektuak aukeratu zituen. Proiektuok sakon aztertzeko zortzi talde teknologikoak kontuak hartu zituzten: fabrikazio aditiboa, adimen artifiziala, ikusmen artifiziala, big data eta/edo analitika aurreratua, zibersegurtasuna, gauzen Internet, robotika eta errealitate birtuala eta areagotua. “37 elkarrizketa egin ondoren, beste informazio-iturri batzuk aztertu genituen, hala nola proiektu-txostenak eta txosten teknikoak” azaldu du Iker Laskurain Iturbek, ikerketa-taldeko kide eta lanaren egileetako bat.
Ikerketan ikusi denez, “oro har, aztertu diren 4.0 Industriako teknologiek eragin positiboa dute edozein enpresatako langileen segurtasunean eta osasunean”. Baina “arazo edo arrisku berriak ere sortzen dira —batez ere psikosozialak—. Azken horiek kontuan hartu behar dituzte enpresek, langileen konfiantza eta osasuna mantenduko badituzte. Sortzen ari diren arrisku berrien eraginak teknologia guztietan hauteman dira, gauzen Interneten kasuan izan ezik”, azpimarratu dute Germán Arana Landínek eta Mikel Iturratek.
Adibidez, “adimen artifizialari esker, bulegoetako kamerek zaintza proaktiboa egiten dute, eta, hala, plantillaren ergonomia hobetzen lagundu dezakete. Izan ere, kamerak in situ jasotzen du informazioa, langileen eta enplegatuen mugimenduak jasotzen ditu une oro. Beraz, jarduerak zuzentzeko gomendioak emateko informazioa atera daiteke”, adierazi du Beñat Landeta Manzanok. Hala ere, UPV/EHUko ikertzaileak erantsi duenez, “langileak zelatatuta senti daitezke ekintza horrekin, bai eta estresatuta ere”.
Antzeko zerbait gertatzen da robotak enpresaren jardueran sartzean. Robotak lan arriskutsuez ardura daitezke, eta, beraz, muntaketa-kate bateko lan errepikakor, estresagarri eta astunak arindu ditzakete langileentzat. Robotikak lanpostu berri asko sortuko ditu, eta, horrenbestez, lanik gabe gelditzen direnek trebetasun berriak ikasi beharko dituzte eta ziurgabetasun-egoera bati aurre egin beharko diote. Eta egoera horrek estresa eta antsietatea sor ditzake.
Ikertzaileek onartzen dute beren lan honek mugak dituela, batetik, enpresa gutxi aztertu dituztelako eta, bestetik, komeni delako 4.0 industriaren teknologiak industria-azpisektore askotarikoetan hedatzen diharduten eragile guztien iritziak biltzea. Beraz, etorkizuneko ikerketa-ildoek muga horiei erantzun beharko diete. Adibidez, teknologia bakoitzaren eragina lagin zabalago batekin aztertu beharko litzateke. Interesgarria litzateke, halaber, ikerketa hori industria-sektore desberdinetan egitea eta alderdi interesdun bakoitzaren ikuspegia izatea (langileak, zuzendariak, hornitzaileak…).
Hala eta guztiz ere, egileak ados daude “4.0 industriako teknologiek askoz aukera gehiago eskaintzen dituztela, eta enpresei eraginkorragoak eta lehiakorragoak izaten laguntzen dietela”. Teknologia horiek ezartzeko prozesuan, nahitaezkoak dira aldez aurreko komunikazioa eta prestakuntza laneko segurtasuna eta osasuna kudeatzeko, hala murriztu egiten baitira sor daitezkeen arrisku berriak. Aldaketa-prozesuan edozein enpresatako langileak inplikatzeko modu bat dira”.
Iturria:UPV/EHU prentsa bulegoa: 4.0 Industriako teknologiek langileen segurtasuna eta laneko osasuna sustatzen dituzte.
Erreferentzia bibliografikoa:Arana-Landín, Germán; Laskurain-Iturbe, Iker; Iturrate, Mikel; Landeta-Manzano, Beñat (2023). Assessing the influence of Industry 4.0 technologies on occupational health and safety. Heliyon, 9, 3. DOI: 10.1016/j.heliyon.2023.e13720
The post 4.0 Industriako teknologien ondorioak langileen segurtasunean eta laneko osasunean appeared first on Zientzia Kaiera.
Virtudes de la nostalgia
 Photo by Jon Tyson on Unsplash
Photo by Jon Tyson on Unsplash
El pasado es la referencia de la nostalgia, pero su ámbito psicológico puede extenderse hacia el futuro. Los sentimientos de nostalgia son universales, y resulta que, por comparación con la evocación de episodios ordinarios, elevan el optimismo o, al menos, generan expresiones de optimismo.
Esa es la conclusión principal de una serie de cuatro estudios en los que, utilizando diferentes procedimientos que no detallaré, se ha analizado la medida en que los sentimientos de nostalgia producen un estado de optimismo, así como los procesos mentales que intermedian en esa relación. Los estudios se han realizado con hombres y mujeres de distintas edades y de tres nacionalidades, estadounidenses, daneses e ingleses.
El primero de los estudios sirvió para identificar la posible existencia de la relación. El segundo ilustró que la inducción experimental de sentimientos de nostalgia hace que aumente el optimismo de las personas. El tercero reprodujo los hallazgos del anterior, utilizando, para ello, la exposición a canciones nostálgicas y, como control, a canciones normales. Este tercer estudio puso de manifiesto el papel mediador de la autoestima en el efecto de la nostalgia sobre el optimismo. Esto es, los sentimientos de nostalgia mejoran la autoestima y es esta última la que, al parecer, eleva el optimismo. Esta observación es coherente con hallazgos anteriores, según los cuales los recuerdos del propio pasado ayudan a mantener los sentimientos de amor propio; pero, además, extiende ese conocimiento hacia el futuro, en el sentido de que los sentimientos de autoestima provocados por la nostalgia pueden ayudarnos a mejorar nuestras perspectivas de futuro. El cuarto estudio ayudó a clarificar en mayor medida estos procesos, exponiendo a las personas que participaron en los experimentos a letras de canciones nostálgicas y, como control, a letras de canciones normales. Mediante este cuarto estudio se estableció una secuencia causal más extensa para la relación entre los sentimientos nostálgicos y la autoestima, al incluir como mediador de dicha relación la sensación de conectividad social.
Así pues, la nostalgia promueve la sensación de conectividad social; ésta, a su vez, eleva la autoestima, y como consecuencia de una mayor autoestima, aumenta el optimismo. O, dicho de otra forma, el aumento en la autoestima que experimentan los participantes es la consecuencia de un más intenso sentimiento de conectividad social que se deriva del ensueño nostálgico; y esa mayor autoestima es, por su parte, la que hace que aumente el optimismo.
Es sabido que el optimismo proporciona bienestar y beneficios en términos de salud. Por ello, y a tenor de los resultados obtenidos en estos experimentos, la nostalgia puede ser una vía muy adecuada hacia el bienestar, favoreciendo comportamientos saludables y éxito en las relaciones. Además, como se da la circunstancia de que el recurso a los recuerdos nostálgicos suele acentuarse en periodos de tristeza, soledad, aburrimiento o dudas existenciales, los resultados obtenidos en este trabajo implican que la nostalgia, al promover el optimismo, podría ayudar a las personas a hacer frente a la adversidad psicológica. La nostalgia, según los autores del trabajo, puede, en definitiva, ser un catalizador para conectar el pasado, presente y futuro de una persona, proporcionándole un sentido de continuidad.
Utilizando palabras casi textuales (pero traducidas) de los autores, la conclusión de este trabajo es que “la nostalgia no es una vieja fotografía en sepia guardada bajo llave en un cajón. Su poder, de largo alcance, puede iluminarnos el camino a seguir.”
Fuente: Wing-Yee Cheung, Tim Wildschut, Constantine Sedikides, Erica G. Hepper, Jamie Arndt y Ad J. J. M. Vingerhoets (2013): “Back to the Future: Nostalgia Increases Optimism” Pers Soc Psychol Bull 39: 1484.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Virtudes de la nostalgia se ha escrito en Cuaderno de Cultura Científica.
Asteon zientzia begi-bistan #445
Asteon zientzia begi-bistan igandeetako gehigarria da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna jaso eta laburbiltzea da gure helburua.

Emakumeek ere ehizatzen zuten gizarte ehiztari-biltzaileetan, ikerketa berri baten arabera. Ondorio horretara heldu dira mundu osoko 63 talde ehiztari-biltzaileren azken ehun urteko datuak aztertuta. Ikertzaileek ikusi dute talde horietatik 50etan emakumeek eta gizonek ehizatzen zutela, eta are gehiago, emakumeek gizonek baino estrategia eta arma-mota gehiago erabiltzen zituztela. Azalpen guztiak Elhuyar aldizkarian.
OsasunaIkerketa-sorta batek ondorioztatu du diabetes-kasuak bikoiztu egingo direla hiru hamarkadatan. Ikertzaileek azaldu dutenez, gehienbat 2. motako diabetesak egingo du gora, eta horren arrazoi nagusia arrazismoa eta desberdintasun geografikoak dira. Izan ere, gaur egun ere eritasun horren ondoriozko heriotza-tasak bi aldiz handiagoak dira diru-sarrera txikiak dituzten herrialdeetan, diru-sarrera handiak dituzten herrialdeekin alderatuta. Kalkuluen arabera, 2050erako 1.300 milioi pertsonek baino gehiagok izango dute diabetesa munduan, 2021ean erregistratutakoaren bikoitza baino gehiago. Datuak Elhuyar aldizkarian.
MedikuntzaIkerketa berri batek ondorioztatu duenez, Y kromosoma galtzeak minbizia oldarkorragoa izatea eragin dezake. Zahartzen garen heinean, zelula batzuek Y kromosoma galtzen dute, eta galera horren ondorioz, minbizi-zelulek organismoaren immunitate-sistema saihesteko gai dira. Dirudienez, Y kromosoma galtzean, T linfozitoak agortu egiten dira, eta ezin diete aurre egin minbizi-zelulei. Alabaina, Y kromosoma galdua dutenengan immunoterapia-tratamendua eraginkorragoa da, tratamenduak bere onera ekartzen baititu T linfozitoak. Informazio gehiago Elhuyar aldizkarian.
PsikologiaUPV/EHUko ikerketa batek erakutsi du adimen emozional handiagoa duten nerabeek ideiagintza suizidak izateko arrisku txikiagoa dutela. Ondorio horretara iristeko, Héctor Galindo eta Daniel Losada UPV/EHUko ikertzaileek aztertu dute zer eragin duten babes-mota ezberdinek ideiagintza suizidetan eta adimen emozionalean. Babes-mota horiek dira bitartekari eta moderatzaile duten berdinen arteko babesa, familiaren babesa eta irakasleen babesa. Azterketan 898 nerabek parte hartu dute, eta ikusi dute adimen emozionalak eragin zuzena duela ideiagintza suizidetan. Ikertzaileen esanetan, inteligentzia emozional handiagoa duten nerabeak gaitasun handiagoa dute babes-mota ezberdinak hautemateko, eta horrek emozionalki indartsuagoak egiten ditu. Azalpenak Zientzia Kaieran.
BotanikaEduardo Angulok mahatsondoaren eboluzioa eta etxekotzea azaldu du Zientzia Kaieran. Datuen arabera, Mediterraneo osoko landare indigena bat da mahatsondoa, baina eztabaida dago landare honen etxekotzea noiz eta nola gertatu zen. Ikerketa baten arabera, Kristo aurreko 5000. urtea baino lehen iritsi zen etxe mahatsondoa Anatoliatik Ekialde Hurbilera, eta duela 6.000 eta 8.000 urte bitartean etxekotu zen. Beste ikerketa berri batek iradoki du etxekotzea aldi berean gertatu zela duela 11.000 urte inguru Asiako Mendebaldean eta Kaukason. Gai honen inguruko informazio gehiago Zientzia Kaieran: Errezeta egiteko osagaiak: mahatsondoa.
Zientzia-dibulgazioaJosu Lopez-Gazpiok zientziaren dibulgazioari artikulu-sorta bat eskaini dio Zientzia Kaieran, eta sorta honetan lehena dibulgazioa kokatzeko erabili du. Definizioz, dibulgatzea da jakintza edo arte bateko ezagutzak horretan aditu ez direnek ulertzeko moduko era errazean azaltzea. Hortaz, komunikazio mota hau zientzian aditu direnei zein ez direnei zuzenduta dago. Hemen, alabaina, beste bereizketa bat egin daitekeela azaldu du Lopez-Gazpiok, zientzia-kazetaritzaren eta zientzia-dibulgazioaren artean. Izatez, bi esparru ezberdin badira ere, estuki loturik daude. Alabaina, kazetariei askotan zientzian formakuntza falta zaie, eta zientzialariei, berriz, komunikazioan. Datuak Zientzia Kaieran: Begirada bat dibulgazioari (I): zientzia-komunikazioan kokatzen.
KimikaAzken urteetan asko areagotu da biomasatik eratorriak diren konposatuen erabilera polimeroak sintetizatzeko. Helburu horretarako, bereziki interesgarriak dira talde aromatikoak eta, bereziki, fenolikoak dituzten monomero naturalak, sortzen dituzten material polimerikoen propietate termiko, kimiko eta mekaniko nabarmenengatik. Konposatu fenolikoen artean, eugenola da material desiragarriena bere propietateengatik. Konposatu hauek, oro har, industria askotan erabili daitezke, eta bereziki interesgarriak dira erregai fosilen kontsumoa ekiditeko. Azalpen guztiak Zientzia Kaieran: Eugenola: polimero jasangarrien biomasatik erauzitako lehengaia.
AstronomiaEsne Bidearen barrutik igorritako neutrinoak detektatu ditu IceCube neutrinoen behatokiak. Behatoki hori izotz antartikoaren sakonean eraikitako partikulen detektagailua bat da, eta 10 urtez bildu dituen datuak aztertuta egin dute aurkikuntza. Orain arte, gure galaxiaz kanpoko lekuetatik igorritako neutrinoak soilik detektatu izan dira. Aurkikuntza berri honekin ordea, frogatu da Esne Bidea energia handiko neutrinoen sorburua dela. Berri honen inguruko informazio gehiago Elhuyar aldizkarian.
Egileaz:Irati Diez Virto Biologian graduatu zen UPV/EHUn eta Plentziako Itsas Estazioan (PiE-UPV/EHU) tesia egiten dabil, euskal kostaldeko zetazeoen inguruan.
The post Asteon zientzia begi-bistan #445 appeared first on Zientzia Kaiera.
Adicción, ¿el hambre de toda la vida?

Cómo influyen los parásitos en el comportamiento de los animales, cómo se modifica la conducta de las madres mamífero o cuáles son las enfermedades que nos afectan y desde cuándo hemos desarrollado comportamientos funerarios ante la muerte son algunos de los aspectos que se analizarán en la V Jornada Nacional sobre Evolución y Neurociencias.
Especialistas en ambas materias se reunirán el 11 y 12 de mayo en una nueva edición conducida por Eva Garnica y Pablo Malo, psiquiatras y miembros de la Red de Salud Mental de Bizkaia, y organizada por esa misma entidad y la Cátedra de Cultura Científica de la UPV/EHU.
La jornada, cuya primera edición se celebró en 2017, se ha convertido en una cita imprescindible para las y los expertos en ámbitos como la psiquiatría, la psicología o la biología. Una jornada que sirve para analizar el comportamiento humano desde un punto de vista evolucionista y divulgar de un modo accesible para todos los públicos.
El fenómeno de la adicción (a lo que sea) se basa en mecanismos que hemos desarrollado a lo largo de la evolución para sobrevivir, pero que entran en funcionamiento para otras cosas. Si lo pensamos un momento, la adicción funciona como el hambre de toooda la vida. Esta es la tesis que expone en esta charla Gerardo Sabio.
Gerardo Sabio es psicólogo clínico y director técnico de la Asociación Ferrolana de Drogodependencias (ASFEDRO).
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Adicción, ¿el hambre de toda la vida? se ha escrito en Cuaderno de Cultura Científica.
Ezjakintasunaren kartogragfia #453
 Irudia: Andrea De Santis / Unsplash
Irudia: Andrea De Santis / UnsplashHizkuntzak gizaki bihurtu gintueneko ideia pellokeria da. Baina, egun adimen artifizial batek egin dezakeena kontuan izanda, inplikazioz josita dagoen baieztapena da. Language makes us human. Or not Egilea: Juan F. Lillo.
Termodinamikaren lehen printzipioaren baliokidea ekonomian eta finantzetan da ezer ez dela doan. Geologiari ere aplikatzen dio: Groundwater pumping alters Earth’s spin
Leku sinesgaitzenetan ere garatzen da bizia, baita oraindik sutan dauden basoetan ere. For some fire-loving insects, wildfires provide the best breeding grounds, Aaron Bell.
Etorkizuneko materialak diseinatzeko, sormen handiko kimika erabili behar da. DIPCko jendea A new way to rationally design anti-Kasha emitters
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartogragfia #453 appeared first on Zientzia Kaiera.
Ondas gravitacionales gigantescas detectadas usando púlsares
Astrofísicos de varias asociaciones internacionales, valiéndose de algunos de los más grandes radiotelescopios en el mundo, han encontrado evidencia de ondas gravitacionales gigantescas, que oscilan con períodos que van de años a décadas. Estos resultados han sido posibles gracias a una precisa observación de un conjunto de púlsares (relojes cósmicos) en nuestra galaxia.
 Imagen desde el telescopio del Chinese Pulsar Timing Array. Fuente: NAOC of CAS
Imagen desde el telescopio del Chinese Pulsar Timing Array. Fuente: NAOC of CAS
La señal de ondas gravitacionales se ha podido observar a través de los datos tomados por el Observatorio Norteamericano de Nanohercios para Ondas Gravitacionales (NANOGrav) del Physics Frontiers Center (PFC) durante 15 años. Esta colaboración, de más de 190 científicos, en su mayoría de EE. UU. y Canadá, financiada por la National Science Foundation (NSF) americana, utiliza los púlsares (una estrella de neutrones que gira muy rápidamente sobre su eje, emitiendo en cada giro un ‘pulso’ de radio) para identificar la presencia de las ondas gravitacionales. Las colaboraciones internacionales que utilizan telescopios en Europa, India, Australia y China han mostrado resultados similares de forma independiente.
Si bien resultados anteriores de NANOGrav descubrieron una misteriosa señal temporal en todos los púlsares que se observaron, esta señal era demasiado débil para revelar su origen. Los datos hechos públicos hoy de los 15 años de observación demuestran que la señal es consistente con la presencia de ondas gravitacionales de ondulación lenta que atraviesan nuestra galaxia. «Esta es una evidencia clave de las ondas gravitacionales a frecuencias muy bajas», según el Dr. Stephen Taylor de la Universidad de Vanderbilt, actual investigador principal de esta colaboración internacional «Después de años de trabajo, NANOGrav está abriendo un camino nuevo en el universo de las ondas gravitacionales».
A diferencia de las fugaces ondas gravitacionales de alta frecuencia observadas por instrumentos terrestres como LIGO (el Observatorio de ondas gravitacionales por interferometría láser), esta señal continua de baja frecuencia solo puede percibirse con un detector mucho más grande que la Tierra. Para ello, los astrónomos convirtieron nuestro sector de la Vía Láctea en una enorme antena de ondas gravitacionales usando estrellas exóticas llamadas púlsares. NANOGrav ha obtenido datos de 68 púlsares durante 15 años lo que le ha permitido formar un tipo de detector llamado “Conjunto de sincronización de púlsares” (Pulsar Timing Array en su descripción en inglés).
Un púlsar es el remanente ultradenso del núcleo de una estrella masiva después de su desaparición en una explosión de supernova. Los púlsares giran rápidamente, emitiendo pulsos de ondas de radio que barren el espacio a su alrededor de manera similar a los pulsos de luz de un faro en la costa. Estas estrellas, por tanto, parecen «latir» cuando se observan desde la Tierra. Los más rápidos de estos objetos, llamados púlsares de milisegundos, giran cientos de veces cada segundo. Sus pulsos son muy estables, lo que los hace útiles como relojes cósmicos precisos.
La teoría de la relatividad General de Einstein predice de manera precisa cómo las ondas gravitacionales deberían afectar las señales de estos púlsares. Al estirar y comprimir la estructura del espaciotiempo a su paso, las ondas gravitacionales afectan al ritmo de cada pulso, de manera leve pero predecible, retrasando algunos de ellos y adelantando a otros. Estos desfases están correlacionados para todos los pares de púlsares de acuerdo a la distancia que separa a las dos estrellas en el cielo. Los datos obtenidos por NANOGrav son perfectamente compatibles con lo que predice la teoría de la relatividad.
Comparando estas predicciones teóricas con los datos presentados hoy podemos asegurar que, el conjunto de datos más reciente de NANOGrav muestra evidencias de la presencia de ondas gravitacionales con períodos que abarcan de años a décadas. Estas ondas podrían surgir de los agujeros negros más masivos de todo el Universo: miles de millones de veces más masivos que el Sol, con tamaños superiores a la distancia entre la Tierra y el Sol. Los estudios futuros de esta señal abrirán un nuevo camino en el universo de ondas gravitacionales, proporcionando información sobre los agujeros negros titánicos que se fusionan en el corazón de galaxias distantes, entre otras fuentes exóticas.
En palabras de Jose Juan Blanco-Pillado, Investigador Ikerbasque en la UPV/EHU y miembro asociado de NANOGrav: “Estos resultados marcan un hito en la historia de la detección de ondas gravitacionales y nos permiten observar el universo desde una nueva perspectiva. En el futuro esperamos que este tipo de observaciones nos ayuden a entender procesos astrofísicos conocidos e identificar o descubrir otros fenómenos que han permanecido ocultos hasta ahora. »
“En particular la investigación que realizamos en la UPV/EHU se centra en identificar nuevos procesos en el universo primordial que puedan dar una señal detectable por este tipo de observatorios de ondas gravitacionales. La detección de este tipo de señales de forma inequívoca nos daría una información muy valiosa de como evolucionó el universo en sus primeros instantes.”
Astrofísicos de todo el mundo han estado persiguiendo esta señal de ondas gravitacionales. Varios documentos publicados hoy por las colaboraciones de Parkes Pulsar Timing Array en Australia, Chinese Pulsar Timing Array y European Pulsar Timing Array/Indian Pulsar Timing Array muestran indicios de la misma señal en sus datos. A través del consorcio International Pulsar Timing Array, las colaboraciones regionales están trabajando juntas para combinar sus datos a fin de caracterizar mejor la señal y buscar nuevos tipos de fuentes, convencidas de la importancia y necesidad de la colaboración internacional.
Para saber más:
Ondas gravitacionales: una nueva era para la humanidad
Cosmología de ondas gravitacionales en 29 órdenes de magnitud
Comprimiendo la luz para detectar mejor ondas gravitacionales
Referencia:
Gabriella Agazie et al (2023) The NANOGrav 15 yr Data Set: Evidence for a Gravitational-wave Background The Astrophisical Journal Letters. doi: 10.3847/2041-8213/acdac6
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Ondas gravitacionales gigantescas detectadas usando púlsares se ha escrito en Cuaderno de Cultura Científica.
Kiñuren begirada: gatza
Mahaiko gatzak, sodio kloruroa (NaCl) izenekoak, gure zentzumenak pizten dituen zapore gazia du. Egunean 2-3 gramoko dosia gomendatzen da, eta 6 gramora iristea ariketa bizia egin ondoko egunean.
Baina mineral honen presentzia ez da gure sukaldeetara mugatzen, neguan ohikoa baita izotz eta elur errepideak garbitzeko erabiltzea. Gaurkoan, gure kirikiñoa, bere ikerketetan sakondu ahala, konturatu da ohitura horrek ondorio kezkagarriak dituela, bai ingurumenerako bai giza osasunerako.
Kiñuk gatzaren garrantzi ekonomiko eta sinbolikoari buruz ere ikasi du, historian zehar arkeologoek eta historialariek zehatz-mehatz aztertutako gaiak eta hamaika datu ekartzen dizkigu.

Hilero, azkenengo ostiralean, Kiñuk bisitatuko du Zientzia Kaiera bloga. Kiñuren begirada gure triku txikiaren tartea izango da eta haren eskutik gure egileek argitaratu duten gai zientifikoren bati buruzko daturik bitxienak ekarriko dizkigu fin.
Egileaz:Maddi Astigarraga Bergara (IG: @xomorro_) Biomedikuntzan graduatua, UPV/EHUko Ilustrazio Zientifikoko masterra egin du eta ilustratzailea da.
The post Kiñuren begirada: gatza appeared first on Zientzia Kaiera.
La catenaria: una introducción a su mantenimiento (2/4)
mantenimiento
Another flaw in the human character is that everybody wants to build and nobody wants to do maintenance. (Otra falta de la condición humana es que todo el mundo quiere construir, pero nadie quiere hacer el mantenimiento.)—Kurt Vonnegut
 Foto: Catherine / Unsplash
Foto: Catherine / UnsplashEl mantenimiento es el conjunto de procesos necesarios para conservar la funcionalidad de cualquier sistema tecnológico en su nivel de diseño. Como todo proceso industrial, el mantenimiento tiene un coste asociado en capital, trabajo y huella medioambiental. Además, el mantenimiento lleva aparejado cierto nivel de indisponibilidad de los sistemas mantenidos. Estos periodos de parada o funcionamiento degradado suponen pérdidas que se pueden contabilizar en el propio proceso de mantenimiento. Reducirlas al mínimo imprescindible es un reto interesante, en el que juegan un papel fundamental las políticas de mantenimiento.
Al igual que los elementos materiales que comprenden toda tecnología, las políticas de mantenimiento también han experimentado una evolución con el tiempo. La primera y elemental es «cuando algo se rompe, se repara», también llamado mantenimiento correctivo. Esta aproximación, por sí sola, es inviable cuando tratamos con sistemas de los que depende la seguridad de las personas. Pronto se percibió que la indisponibilidad del sistema afectado, desde la avería hasta su puesta en funcionamiento, suponía por sí misma una fuente de costes considerable. Esto aparejó la creación de la política «revisamos el sistema a intervalos regulares», o mantenimiento preventivo. El objetivo es «cazar» los fallos antes de que sucedan, algo más fácil de decir que de hacer y que supone de por sí toda una nueva disciplina de la técnica.
Naturalmente, los fallos aún ocurren, ora porque escapen a los mecanismos de detección cuando aún son «prefallos», ora por puro azar. Un intervalo de inspección muy pequeño detectará un número creciente de fallos en desarrollo, y viceversa para tiempos crecientes. El propio acto de la inspección tiene un coste. Esto introduce su frecuencia en la fórmula del objetivo que deseamos optimizar. La práctica totalidad de los mantenimientos son todavía una combinación, ajustada para buscar un coste mínimo a mano o mediante herramientas estadísticas sencillas, de prevención y corrección.
 Una herramienta especializada de mantenimiento ferroviario, el tren esmerilador de carriles de Metro de Madrid, estacionado en una vía de apartado de la estación de Almendrales (línea 3). Foto: Iván RiveraUn mundo ideal
Una herramienta especializada de mantenimiento ferroviario, el tren esmerilador de carriles de Metro de Madrid, estacionado en una vía de apartado de la estación de Almendrales (línea 3). Foto: Iván RiveraUn mundo ideal
Dos tipos de avances tecnológicos han permitido soñar con una política ideal, que podríamos denominar «cambiamos la pieza justo antes de que falle», o mantenimiento predictivo. Si, de algún modo, logramos retrasar las acciones de mantenimiento hasta un momento arbitrariamente cercano al del fallo, pero siempre anticipándolo, habremos eliminado la indisponibilidad por avería a la vez que espaciamos al máximo las intervenciones. El coste teórico de este mantenimiento es, por tanto, el mínimo posible para nuestro nivel de servicio deseado. ¿Cuáles son los avances que habilitan este salto conceptual?
En primer lugar, la disponibilidad masiva y barata de potencia de cálculo. Los ordenadores actuales son capaces de simular sistemas físicos de gran complejidad. Aunque estimar las solicitaciones sobre una catenaria flexible requiere realizar cálculos mecánicos, eléctricos y térmicos de forma simultánea, esto está al alcance de computadoras con un precio razonable.
Pero los cálculos no lo son todo. Cualquier sistema físico más complejo que la proverbial vaca esférica carece de soluciones analíticas. Es decir: no existen ecuaciones sencillas y fáciles de calcular que lo representen. Hay que recurrir a métodos numéricos iterativos: un conjunto de fórmulas más o menos simplificadas que se ejecuta, recurrentemente, para momentos sucesivos de un tiempo en el que consideramos una subdivisión básica. No importa cuál: horas, segundos, milésimas de segundo. Cualquiera de ellas establecerá una contrapartida entre la precisión obtenida y el tiempo real en el que obtendremos respuestas. Disponer de ordenadores más rápidos no evita la existencia de este dilema, solo lo desplaza a un punto de equilibrio diferente. Además, el tipo de matemáticas que suele ser necesario resolver provoca que doblar la potencia de cálculo no suponga, en general, dividir por dos el tiempo de proceso o multiplicar por dos la precisión, sino considerablemente menos. Cada iteración calculada tendrá un error que irá, inevitablemente, a alimentar la entrada de la siguiente. En un número de ciclos que depende de cada sistema simulado, la deriva de las respuestas respecto de la realidad será tan grande como para hacer inútil todo el ejercicio.
Es aquí donde entra en juego el segundo avance: los sensores. Hoy es mucho más sencillo y barato conocer valores para las variables de estado de un sistema real gracias a la miniaturización de la electrónica. Quien mide, sabe (aunque medir también es un arte de la ingeniería, sujeto a sus propios balances entre precisión y exactitud). Si en una simulación introducimos periódicamente correcciones derivadas de lecturas de sensores en un sistema real, podemos controlar el error y, por tanto, la deriva.
 Equipos de alimentación eléctrica y control en una subestación de tracción de Serveis Ferroviaris de Mallorca. Foto: Iván Rivera«Mellizos digitales»
Equipos de alimentación eléctrica y control en una subestación de tracción de Serveis Ferroviaris de Mallorca. Foto: Iván Rivera«Mellizos digitales»
Lo que tenemos entre manos pretende ser un «gemelo digital»: un sistema simulado capaz de ofrecer respuestas concretas ante todo tipo de cuestiones. ¿Qué efecto tendría sobre la catenaria duplicar el tráfico de trenes? Podríamos «copiar y pegar» series de datos registrados en los sensores para hacernos una idea. ¿Y si queremos conocer el efecto de un aumento de la temperatura en un verano particularmente duro? Podríamos simular la dilatación extra sobre el metal.
Ni que decir tiene que un auténtico gemelo digital es una quimera, tanto por las limitaciones de los métodos y la capacidad de cálculo como por las imprecisiones —inevitables— cometidas por los sensores. O por su ausencia, ya que no será económicamente viable llenar de artefactos de medida toda la infraestructura. Medio en broma, podríamos decir que lo que obtendremos de la fusión de simuladores físicos y sensores será un «mellizo digital». Algo razonablemente parecido al sistema real. Lo suficiente como para poder hacer predicciones fiables sobre su rendimiento y sobre las diferentes necesidades del mantenimiento. Esta es la teoría, pero ¿y la práctica?
En una instalación industrial genérica, una vez determinados los puntos de medida necesarios, debemos garantizar tanto la alimentación eléctrica de los sensores como su conectividad. Para lo que podríamos llamar «instalación concentrada», esto no es un problema serio. La alimentación está garantizada por una red de distribución de baja tensión convencional. En lo que respecta a la conectividad, podremos encontrar alternativas de todo tipo, inalámbricas y cableadas.
 Salida sur de la estación de Valladolid Campo Grande. Foto: Iván RiveraEl problema de las instalaciones lineales
Salida sur de la estación de Valladolid Campo Grande. Foto: Iván RiveraEl problema de las instalaciones lineales
Pero la catenaria no es una instalación industrial concentrada: es una instalación lineal distribuida a lo largo de decenas, centenares, miles de kilómetros de red férrea. A pesar de que la catenaria transporta energía eléctrica, lo hace en unas condiciones en las que resulta particularmente oneroso transformarla entre su forma de consumo para el ferrocarril (en España, corriente continua a 3 kilovoltios o alterna a 25 kilovoltios) en una alimentación adecuada para los sensores y su circuitería asociada, generalmente 12 o 24 voltios en continua. Este problema se puede solventar, evitando kilómetros de red de distribución en baja tensión, mediante el uso de placas fotovoltaicas y baterías.
Los problemas de conectividad pueden soslayarse con el uso de la red celular 3G/4G, y si la cobertura resulta ser defectuosa, con agregadores y radioenlaces punto a punto u otras alternativas. Las redes específicas de baja potencia y largo alcance, como LoRaWAN o SigFox, diseñadas específicamente para ofrecer conectividad a sensores son interesantes siempre que la cantidad de datos a transferir por unidad de tiempo sea lo suficientemente pequeña; la experiencia muestra, sin embargo, que esta suposición resulta ser problemática para un buen número de prototipos de sensores asociados a la operación ferroviaria. La solución, el despliegue generalizado de las nuevas redes celulares 5G y sus sucesoras (6G está a la vuelta de la esquina), es cuestión de tiempo. A esto nos referimos los ingenieros de teleco cuando hablamos de «la Internet de las Cosas».
Suele decirse que, sin salir del planeta, los requisitos más estrictos de resistencia y durabilidad frente a los elementos están en el entorno militar, y justo después en la industria del transporte, donde la ferroviaria destaca por méritos propios. El ferrocarril tiene instalaciones extendidas a lo largo de centenares de kilómetros, expuestas a la intemperie, cruzando estepas, desiertos o selva, bajo temperaturas extremas y variables, en ambientes húmedos, salinos o contaminados por partículas en suspensión, con poca o ninguna vigilancia activa. ¿Cómo lograr hacer de una instalación como la catenaria una infraestructura monitorizada del siglo XXI?
Del mismo autor:
Los límites del Hyperloop
El camión solar: ¿una posibilidad real?
Sobre el autor: Iván Rivera es ingeniero especializado en proyectos de innovación de productos y servicios para ferrocarriles.
El artículo La catenaria: una introducción a su mantenimiento (2/4) se ha escrito en Cuaderno de Cultura Científica.
Eugenola: polimero jasangarrien biomasatik erauzitako lehengaia
Gaur egun plastikoen kontsumoa izugarri zabaldu da. Hori dela eta, material horiek birziklatzea eta berrerabiltzea funtsezkoa da plastikoen erabilera eta jatorri fosileko lehengaien kontsumoa murrizteko. Tamalez, aldaketa horiek ez dira nahikoak. 2050. urterako munduko birziklatze-tasa % 14tik % 55era igoko balitz ere, baliabide berriztagarrien kontsumoa bikoiztu egin beharko bailitzateke. Hortaz, erregai fosilak ordezkatzeko eta industria kimikoa garatzeko asmoz, ezinbestekoa da lehengai naturalen kontsumoa areagotzea.
Testuinguru honekin, hiru arrazoik eragin dute komunitate zientifikoak biomasatik datozen konposatu kimikoak erabiltzeko duen interesa nabarmen handitzea. Lehenengoa, karbono-isurietan eta hondakinen sorreran izan den gorakada. Hazkunde horiek jatorri antropogenikoa dute, hau da, batez ere gizakiarekin zerikusia duten jardueren ondorioak dira. Bigarrena gizartearen ingurumen-kontzientziaren handitzea izan da eta, horrekin batera, garatu diren araudi eta legedi zorrotzak. Hirugarren arrazoia, prezio-aldakortasuna eta erregai fosilen hornidura-arazoak eta eskasia da.
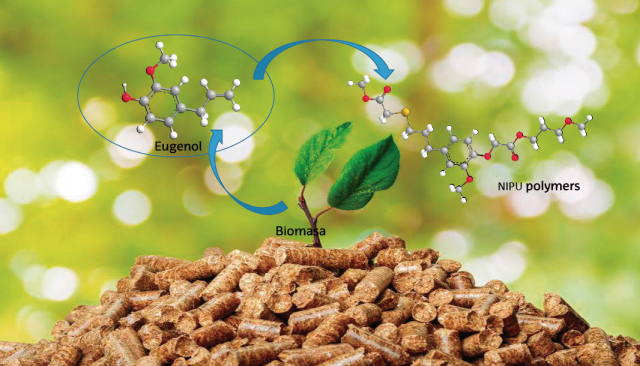 Irudia: talde aromatikoak eta, bereziki, fenolikoak dituzten monomero naturalak oso desiragarriak dira sortzen dituzten material polimerikoen propietate termiko, kimiko eta mekaniko nabarmenengatik. (Iturria: Ekaia aldizkaria)Biomasatik eratorriak diren konposatuen bila
Irudia: talde aromatikoak eta, bereziki, fenolikoak dituzten monomero naturalak oso desiragarriak dira sortzen dituzten material polimerikoen propietate termiko, kimiko eta mekaniko nabarmenengatik. (Iturria: Ekaia aldizkaria)Biomasatik eratorriak diren konposatuen bila
Gizartearen aipatutako ingurumen-kontzientziak aldaketak eragin ditu gaur egun oso erabiliak diren material polimerikoen sintesi-prozesuetan. Alegia, areagotu egin da biomasatik eratorriak diren konposatuen erabilera polimeroak sintetizatzeko. Material polimeriko horiek bereziki interesgarriak dira dituzten propietateak direla eta. Izan ere, hainbat sektoretan aplika daitezke; esate baterako, energiaren sorkuntzan eta biltegiratze-prozesuetan, biomedikuntzan, elikagaien kontserbazioan edota industria kimikoan. Biomasa jatorri biologikoko produktu eta hondakinen frakzio biodegradagarria da; funtsean, energia-iturri gisa erabilitako materia organikoari deritzo. Erregai fosilak ordezkatzeko potentzial handia duen lehengaia da, baina baita hautagai ezin hobea ere mota desberdinetako polimeroak ekoizteko. Gainera, polimero horiek erregai fosiletatik lortutako polimeroekin alderatuz, produkzio energetiko eraginkorragoa dute, karbono-emisioak murrizten baitituzte.
Normalean, biomasatik eratorriak diren konposatu gehienak gantz-azidoak eta karbohidratoak dira. Horrez gain, polimero jasangarriagoak sintetizatzeko, karbohidratoak, gantz-azidoak, furanoak, terpenoak, aminoazidoak edota landare-olioak erabil daitezke. Sor daitezkeen polimero motak askotarikoak dira, hala nola poliesterrak, poliamidak, poliuretanoak (PU) edota polihidroxialkanatoak. Talde aromatikoak eta, bereziki, fenolikoak dituzten monomero naturalak oso desiragarriak dira sortzen dituzten material polimerikoen propietate termiko, kimiko eta mekaniko nabarmenengatik. Beraz, oso aproposak izan daitezke aeronautikan, itsasgarri eta estaldura moduan edota isolatzaile gisa. Horrelako polimeroak sortzeko gehien erabiltzen diren lehengai naturalak, normalean, iltzea, lignina, anakardoak, kanela, albaka, piperrak, oreganoa, ezkaia, intxaur muskatua edota kimuak dira.
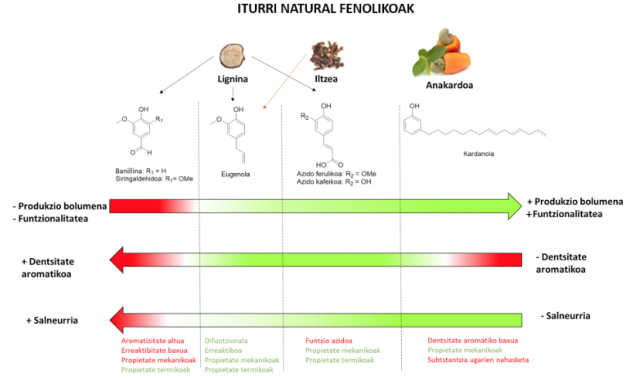 2. irudia: aitzindari natural eta fenoliko batzuen konparaketa zenbait baldintzaren arabera, bolumen-ekoizpena, funtzionalitatea, dentsitate aromatikoa eta kostu ekonomikoa. (Iturria: Ekaia aldizkaria)
2. irudia: aitzindari natural eta fenoliko batzuen konparaketa zenbait baldintzaren arabera, bolumen-ekoizpena, funtzionalitatea, dentsitate aromatikoa eta kostu ekonomikoa. (Iturria: Ekaia aldizkaria)2. irudian zenbait lehengai naturaletatik (lignina, iltzea eta anakardoa) lor daitezkeen konposatu natural fenolikoen (banillina, siringal-dehidoa, eugenola, azido ferulikoa, azido kafeikoa eta kardanola) konparaketa adierazi da zenbait baldintzaren arabera (konposatuen produkzio-bolumena, funtzionalitatea, dentsitate aromatikoa eta salneurriak). Iruditik argi ikus daiteke funtzionalitate, erreaktibitate eta propietate mekaniko-termiko onenak dituen konposatu fenolikoa eugenola dela.
Eugenola hainbat landaretan dagoen konposatu fenoliko naturala da. Bakterioen, onddoen eta parasitoen aurkako propietateak dituen iltze-olio esentzialaren osagai nagusietako bat da. Eugenol lehengai naturalaren potentziala denez, oso baliagarri bihurtu da biomasatik eratorriak diren polimeroak garatzeko. Batez ere, konposatu natural honek dituen propietate fisiko-kimiko eta mekanikoak baliatuz hainbat industria motatan aplika daitezkeen polimeroak sintetiza daitezkeelako, hala nola industria odontologikoan, aeroespazialean, biomedikuntzan eta kimikoan. Gainera, lehengai naturala izanik, erregai fosilen kontsumoa ekiditen da, eta, hala, polimero jasangarriagoak lortzen dira. Hortaz, esan daiteke eugenoletik abiatutako polimerizazio erreakzioen bidez lortutako polimeroek etorkizun oparoa izango dutela.
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: 43
- Artikuluaren izena: Eugenola: polimero jasangarrien biomasatik erauzitako lehengaia
- Laburpena: Azken urteotan, gizartean ingurumenaren kalteaz dagoen kezkak bultzaturik, zientzia -komunitatean baliabide berriztagarrien interesa handitu egin da. Izan ere, karbono-emisioek eta haiek sortzen dituzten hondakinek lehengai jasangarriagoak bilatzera eraman dute. Hortaz, erregai fosilak lehengai naturaletatik ordezkatzea premiazko bihurtu da. Talde aromatikoak eta, bereziki, fenolikoak dituzten monomero naturalak oso desiragarriak dira, sortzen dituzten material polimerikoen propietate termiko, kimiko eta mekaniko nabarmenengatik. Lan honen bidez, eugenola deritzon lehengai naturalaren funtzionalitate bikainaz baliatuz garatu diren polimerizazioak bildu dira. Alde horretatik, erradikal bidezko polimerizazioa eta kationikoa, metatesi olefinikoa, polikondentsazioa, ene erreakzioak eta tiolene erreakzioak erabiliz, eugenol konposatuan oinarritutako polimeroen sintesia aztertu da.
- Egileak: Ane Araiz-Márquez, Julia Sánchez-Bodón, Antonio Veloso-Fernández, Leire Ruiz-Rubio, Isabel Moreno-Benítez eta José Luis Vilas-Vilela
- Argitaletxea: UPV/EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 27-40
- DOI: 10.1387/ekaia.23782
Ane Araiz-Márquez, Julia Sánchez-Bodón, Antonio Veloso-Fernández, Leire Ruiz-Rubio eta José Luis Vilas-Vilela UPV/EHUko Kimika Fisikoa Saileko eta Kimika Makromolekularra ikerketa-taldeko (LABQUIMAC) ikertzaileak dira.
Isabel Moreno-Benítez UPV/EHUko Kimika Organikoa eta Ez-organikoa Saileko eta Kimika Makromolekularra ikerketa-taldeko (LABQUIMAC) ikertzailea da.
Leire Ruiz-Rubio eta José Luis Vilas-Vilela BCMaterials zentroko (Basque Centre for Materials, Applications and Nanostructures) ikertzaileak dira.
Ekaia aldizkariarekin lankidetzan egindako atala.

The post Eugenola: polimero jasangarrien biomasatik erauzitako lehengaia appeared first on Zientzia Kaiera.
El recorrido del caballo de Vandermonde
Me encanta que hoy en día cuando estamos estudiando sobre un tema, por ejemplo, el problema del recorrido del caballo sobre el tablero de ajedrez (tema al que hemos dedicado varias anotaciones en el Cuaderno de Cultura Científica, como El problema del recorrido del caballo en el tablero de ajedrez, El problema del recorrido del caballo en el tablero de ajedrez (II) o ¿Existen recorridos mágicos del caballo en el tablero de ajedrez?), podamos acudir a las fuentes originales y comprobar, por nosotros mismos, lo que está escrito en las ellas, gracias a que muchos textos clásicos ya están digitalizados. Esto es lo que me ha pasado con el método de Vandermonde para construir un recorrido cerrado del caballo. En varios textos nos encontrábamos comentarios sobre el mismo, pero no se explicaba cómo funcionaba.
 Primera página del trabajo Remarques sur les problèmes de situation / Comentarios sobre los problemas de la situación (1771) del matemático francés Alexandre-Théophile VandermondeEl problema del recorrido del caballo
Primera página del trabajo Remarques sur les problèmes de situation / Comentarios sobre los problemas de la situación (1771) del matemático francés Alexandre-Théophile VandermondeEl problema del recorrido del caballo
Empecemos recordando el enunciado del problema del recorrido del caballo.
Problema del recorrido del caballo: Buscar un recorrido de la figura del caballo (con su característico salto en forma de L) sobre el tablero de ajedrez que consista en mover esta pieza del juego, desde una casilla inicial, de forma sucesiva a través de todas las casillas del tablero, pasando una sola vez por cada una de ellas, y terminando en la casilla inicial (recorrido cerrado) o en otra casilla distinta (recorrido abierto).
En las mencionadas entradas, en concreto en la entrada El problema del recorrido del caballo en el tablero de ajedrez (II), se mostraron algunos métodos para construir recorridos como el sencillo método del matemático francés Abraham de Moivre (1667-1754), el ingenioso método del matemático suizo Leonhard Euler (1707-1783), la ingeniosa y elegante técnica del matemático alemán H. C. von Warnsdorff (1780-1858) o la hermosa construcción el médico, matemático, físico, teólogo y lexicólogo británico Peter Mark Roget (1779-1869). En la anotación de hoy vamos a abordar un nuevo método de construcción de recorridos cerrados del caballo sobre el tablero de ajedrez, el método de Vandermonde.
Si buscamos información sobre este método, podremos leer, por ejemplo, en el libro clásico de matemática recreativa Mathematical Recreations and Essays, de W. W. Rouse Ball, H. S. M. Coxeter, lo siguiente:
El siguiente intento de especial interés se debe a Vandermonde, que redujo el problema a la aritmética. Su idea era cubrir el tablero por dos o más rutas independientes tomadas al azar, y luego conectarlas. Definió la posición de una casilla mediante una fracción x/y, cuyo numerador x es el número de la casilla desde un lado del tablero, y cuyo denominador y es su número desde el lado adyacente del tablero; esto equivale a decir que x e y son las coordenadas de una casilla.
Y se explican algunas cuestiones más, por ejemplo, como afecta el movimiento del caballo a la nueva notación, y se muestra el recorrido concreto expresado mediante las fracciones, pero no se explica cómo se obtiene ese recorrido, ni por qué el método es aritmético. Por suerte podemos acudir al texto original y ver qué nos dice el mismo.
El método de VandermondeAlexandre-Theophile Vandermonde (1735-1796), fue un el músico, matemático y químico francés, cuyo nombre a muchos nos hace recordar nuestra época de estudiantes, cuando aprendimos el conocido determinante de Vandermonde. En matemáticas tan solo escribió cuatro trabajos, uno sobre la resolución de ecuaciones, otro sobre el problema del recorrido del caballo, otro sobre combinatoria y el último sobre la teoría de los determinantes. El problema del recorrido del caballo sobre el tablero de ajedrez lo abordó en su segundo trabajo Remarques sur les problèmes de situation / Comentarios sobre los problemas de la situación (1771), que es uno de los textos fundacionales de la rama de las matemáticas denominada Topología (véase la anotación La topología modifica la trayectoria de los peces).
Como el texto está en francés tendremos que traducirlo, o nosotros mismos o con la ayuda de alguien, incluido algún traductor online.
Empecemos por la forma en la que Vandermonde denota las diferentes casillas del tablero de ajedrez. Cada casilla se denota con una fracción de la forma x/y, donde x denota la fila en la que se encuentra esa casilla en el tablero (empezando por el lado inferior) e y la columna en la que se encuentra la casilla (empezando por el lado izquierdo), para x e y con valores entre 1 y 8. Así, como vemos en la siguiente imagen, la casilla de abajo a la izquierda es la casilla 1/1, la de abajo a la derecha 1/8, etcétera.
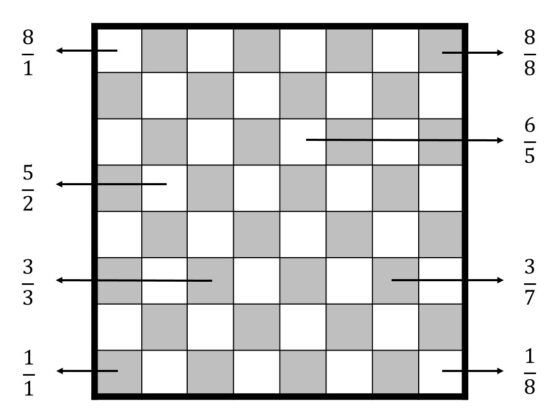
En otras palabras, la notación de las casillas es un sistema para describir la posición de las mismas en el tablero de ajedrez y nada tiene que ver con el número racional x/y.
La siguiente cuestión a analizar es cómo afecta el movimiento del caballo a la notación utilizada. Como el caballo realiza un salto en forma de L, dos casillas “hacia delante” y una “hacia un lado”, entonces si el caballo está en una casilla x/y, puede saltar a alguna de las casillas siguientes x + 2/y + 1, x + 1/y + 2, x – 1/y + 2, x – 2/y + 1, x – 2/y – 1, x – 1/y – 2, x + 1/y – 2, x + 2/y – 1, siempre que sea posible (por ejemplo, de 1/1, que es una casilla de la esquina, solo puede ir a 3/2 y 2/3, o de 5/1, que es una casilla de un lateral, solo puede ir a 7/2, 6/3, 4/3 y 3/2), como se muestra en la siguiente imagen.
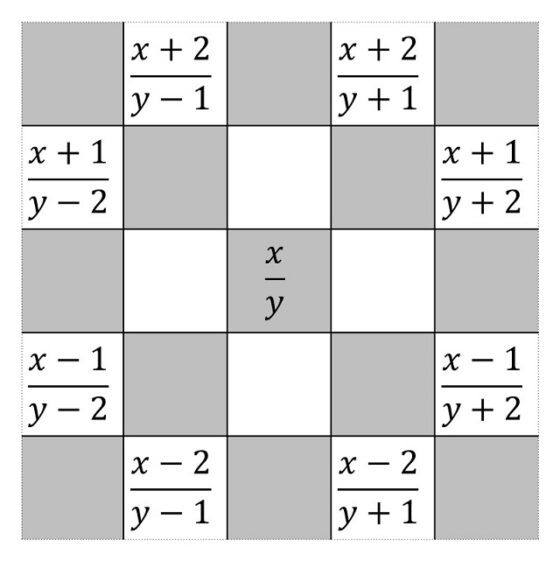
Por lo tanto, encontrar un recorrido del tablero de ajedrez consiste en reordenar los 64 valores de las fracciones que describen las casillas 1/1, 1/2, 1/3, 1/4, …, 2/1, 2/2, 2/3, 2/4, …, 3/1, 3/2, 3/3, 3/4, …, 8/5, 8/6, 8/7, 8/8, de manera que de cada casilla del reordenamiento se pasa a la siguiente mediante alguno de los movimientos anteriores (correspondientes con el salto del caballo), así después de 5/5 puede ir 4/3, pero no 7/2. Además, si el recorrido es cerrado, la última fracción de la reordenación deberá continuarse con la primera, mediante alguno de esos movimientos.
Después, Vandermonde plantea que “la búsqueda de la solución se simplifica tratando de aproximar el recorrido del caballo a una forma simétrica”. Además, “el recorrido del caballo formará una figura simétrica si cuando, en la expresión mediante fracciones del recorrido, se intercambian los números 8 por 1, 7 por 2, 6 por 3, 5 por 4, y viceversa, ya sea solo en los números de los numeradores, solo en los números de los denominadores o en ambos a la vez, no cambia la expresión total (el recorrido)”.
Por lo tanto, si antes se buscaba un recorrido (del caballo) con 64 movimientos (el recorrido es cerrado, y de la última casilla se salta a la primera), ahora basta encontrar 16 movimientos, es decir, 16 términos (casillas) de la sucesión 1/1, 1/2, 1/3, 1/4, …, 2/1, 2/2, 2/3, 2/4, …, 3/1, 3/2, 3/3, 3/4, …, 8/5, 8/6, 8/7, 8/8, de manera que si se intercambian los números 8 y 1, 7 y 2, 6 y 3, 5 y 4, en el numerador, no se consigue ningún término de los 16 anteriores (notemos que al realizar esos cambios en el numerador se obtiene un recorrido que es simétrico al primero –con 16 términos- respecto a la recta horizontal que pasa por el centro del tablero), si se cambian en el denominador tampoco coinciden los nuevos términos con los anteriores (notemos que al realizar esos cambios en el denominador se obtiene un recorrido que es simétrico al primero –con 16 términos- respecto a la recta vertical que pasa por el centro del tablero), ni tampoco si se cambian tanto en el numerador, como en el denominador.
Con el objetivo de obtener esos 16 términos, pero de manera que al intercambiar los números 8 y 1, 7 y 2, 6 y 3, 5 y 4, en el numerador y/o el denominador no se repiten términos se procede de la siguiente manera. Se empieza escribiendo los 64 términos que describen las casillas:
1/1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 2/1, 2/2, 2/3, 2/4, 2/5, 2/6, 2/7, 2/8, 3/1, 3/2, 3/3, 3/4, 3/5, 3/6, 3/7, 3/8, 4/1, 4/2, 4/3, 4/4, 4/5, 4/6, 4/7, 4/8, 5/1, 5/2, 5/3, 5/4, 5/5, 5/6, 5/7, 5/8, 6/1, 6/2, 6/3, 6/4, 6/5, 6/6, 6/7, 6/8, 7/1, 7/2, 7/3, 7/4, 7/5, 7/6, 7/7, 7/8, 8/1, 8/2, 8/3, 8/4, 8/5, 8/6, 8/7, 8/8.
Y se toma, de forma aleatoria, un primer término, por ejemplo, 5/5 (hemos elegido el mismo que Vandermonde para obtener el mismo ejemplo que él obtiene en su trabajo). Para construir los cuatro recorridos simétricos se toman los cinco términos equivalentes (utilizando que podemos intercambiar 4 y 5), que son 5/5, 4/5, 5/4 y 4/4, que serán los primeros términos de los cuatro recorridos simétricos que se van a construir.

Como estos cuatro términos ya los hemos utilizado, los quitamos del conjunto de las fracciones (casillas) a elegir, quedando ahora las restantes:
1/1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 2/1, 2/2, 2/3, 2/4, 2/5, 2/6, 2/7, 2/8, 3/1, 3/2, 3/3, 3/4, 3/5, 3/6, 3/7, 3/8, 4/1, 4/2, 4/3, 4/4, 4/5, 4/6, 4/7, 4/8, 5/1, 5/2, 5/3, 5/4, 5/5, 5/6, 5/7, 5/8, 6/1, 6/2, 6/3, 6/4, 6/5, 6/6, 6/7, 6/8, 7/1, 7/2, 7/3, 7/4, 7/5, 7/6, 7/7, 7/8, 8/1, 8/2, 8/3, 8/4, 8/5, 8/6, 8/7, 8/8.
Ahora, se toma un segundo término para el recorrido, de entre los que nos quedan (arriba), que sea continuación de 5/5. Entre los ocho posibles términos que continuarían a 5/5 (mediante el movimiento del salto del caballo), elegimos el 4/3. Entonces, este nuevo término 4/3, junto con sus transformados 5/3, 4/6 y 5/6, los colocamos a continuación de los anteriores.

Y se eliminan los cuatro nuevos términos de las posibilidades de elección, quedando ahora:
1/1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 2/1, 2/2, 2/3, 2/4, 2/5, 2/6, 2/7, 2/8, 3/1, 3/2, 3/3, 3/4, 3/5, 3/6, 3/7, 3/8, 4/1, 4/2, 4/3, 4/4, 4/5, 4/6, 4/7, 4/8, 5/1, 5/2, 5/3, 5/4, 5/5, 5/6, 5/7, 5/8, 6/1, 6/2, 6/3, 6/4, 6/5, 6/6, 6/7, 6/8, 7/1, 7/2, 7/3, 7/4, 7/5, 7/6, 7/7, 7/8, 8/1, 8/2, 8/3, 8/4, 8/5, 8/6, 8/7, 8/8.
A continuación, elegimos otro término para el recorrido. Nos habíamos quedado en 4/3, que se podría continuar, a priori, con 2/2, 2/4, 3/1, 3/5, 5/1, 5/5, 6/2, 6/4, aunque 5/5 ya no es posible, luego tomamos 2/4, que, junto con sus transformados, 7/4, 2/5 y 7/5, añadimos a continuación de los anteriores.

Eliminando los cuatro nuevos términos del listado de elegibles:
1/1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 2/1, 2/2, 2/3, 2/4, 2/5, 2/6, 2/7, 2/8, 3/1, 3/2, 3/3, 3/4, 3/5, 3/6, 3/7, 3/8, 4/1, 4/2, 4/3, 4/4, 4/5, 4/6, 4/7, 4/8, 5/1, 5/2, 5/3, 5/4, 5/5, 5/6, 5/7, 5/8, 6/1, 6/2, 6/3, 6/4, 6/5, 6/6, 6/7, 6/8, 7/1, 7/2, 7/3, 7/4, 7/5, 7/6, 7/7, 7/8, 8/1, 8/2, 8/3, 8/4, 8/5, 8/6, 8/7, 8/8.
Para continuar debemos de tener en cuenta que nos hemos quedado en el 2/4 y que nos quedan los términos anteriores para continuar (ya se han eliminado 12 términos de los 64 iniciales). El 2/4 se podría continuar, a priori, con una de las seis opciones siguientes 1/2, 1/6, 3/2, 3/6, 4/3 y 4/5, pero de estas ya no son elegibles 4/3 y 4/5, luego podríamos continuar con 1/2. Entonces, se añade 1/2 y sus transformados 8/2, 1/7 y 8/7.

Veamos en la siguiente imagen esos cuatro primeros términos de nuestro recorrido y sus simétricos, cada uno de un color distinto (en azul el primero, que empieza en 5/5; en rojo el segundo, que empieza en 4/5 y, como se ve, es simétrico al azul, respecto a la recta horizontal que pasa por el centro del tablero; el tercero, que empieza en 5/4, en verde, y que es simétrico al azul respecto a la recta vertical que pasa por el centro del tablero; y en amarillo oro el cuarto recorrido, que empieza en 4/4 y que es simétrico horizontalmente al verde y verticalmente al rojo).
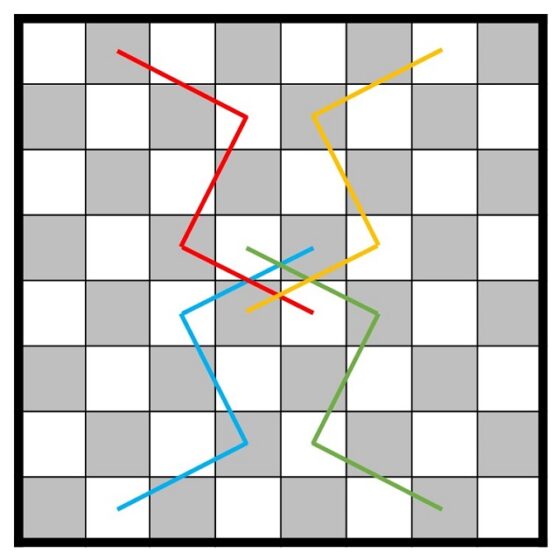
De nuevo, eliminaríamos los cuatro últimos términos del listado de posibles términos:
1/1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 2/1, 2/2, 2/3, 2/4, 2/5, 2/6, 2/7, 2/8, 3/1, 3/2, 3/3, 3/4, 3/5, 3/6, 3/7, 3/8, 4/1, 4/2, 4/3, 4/4, 4/5, 4/6, 4/7, 4/8, 5/1, 5/2, 5/3, 5/4, 5/5, 5/6, 5/7, 5/8, 6/1, 6/2, 6/3, 6/4, 6/5, 6/6, 6/7, 6/8, 7/1, 7/2, 7/3, 7/4, 7/5, 7/6, 7/7, 7/8, 8/1, 8/2, 8/3, 8/4, 8/5, 8/6, 8/7, 8/8.
Ahora, tenemos que seguir desde el término (casilla) 1/2, que solo podría seguir a 2/4, 3/1 y 3/3, pero el 2/4 no es posible, luego elegimos uno de los otros dos, por ejemplo, 3/1, que, junto a sus transformados, 6/1, 3/8 y 6/8, añadimos a los anteriores. De esta forma podríamos continuar hasta terminar los cuatro recorridos simétricos:

Y podemos representar esos cuatro recorridos simétricos (azul, rojo, verde y amarillo oro) que hemos obtenido mediante nuestro procedimiento.
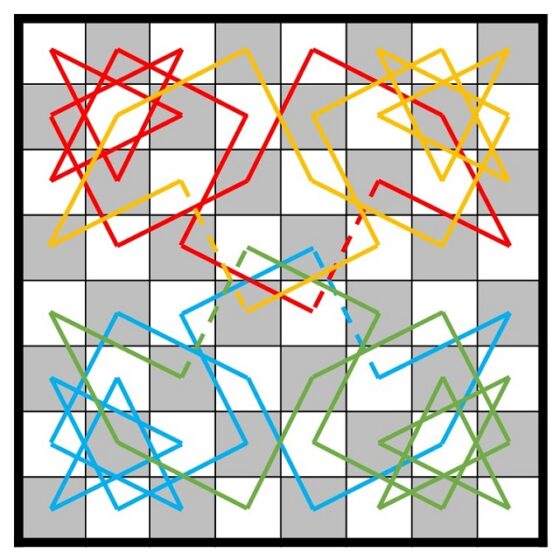
A continuación, tenemos que unir esos cuatro recorridos parciales, que pasan por 16 casillas cada uno, para obtener el recorrido cerrado final, que pase por las 64 casillas del tablero.
Si observamos las cuatro sucesiones de fracciones que hemos creado (véase imagen un poco más arriba), podremos darnos cuenta de que la primera se puede continuar con la cuarta, puesto que la primera termina en 3/6 y la cuarta empieza en 4/4, y es una continuación permitida (ya que se corresponde con el salto del caballo, 3+1/6 – 2 = 4/4). De esta forma creamos un recorrido parcial que es la unión del primero con el cuarto (en el tablero, los recorridos azul y amarillo oro, que dejamos en azul oscuro en la siguiente imagen donde los representamos). Mientras que la segunda sucesión, que termina en 6/6, se puede continuar con la tercera, que empieza por 5/4 (= 6 – 1/6 – 2), creando así otro recorrido parcial fruto de unir los recorridos segundo y tercero (en el tablero, los recorridos rojo y verde, que dejamos en verde oscuro en la siguiente imagen donde los representamos).
Por lo tanto, los dos recorridos parciales son:

Y representados, con colores, sobre el tablero nos quedarían como se muestra en la imagen.
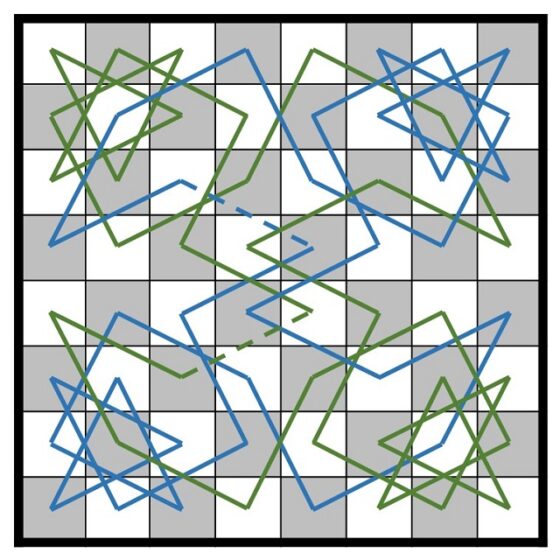
Para finalizar hay que unir esos dos recorridos que nos han quedado. Como no se puede continuar un recorrido con el otro, puesto que el último elemento de uno de los recorridos no se puede conectar con un movimiento válido con el primer elemento del otro (por ejemplo, el 6/3 del primero no se puede conectar con el 4/5 en el segundo, ni el 3/3 del segundo con el 5/5 del primero), esto obliga a romper la simetría y buscar otra forma de unirlos. Si nos fijamos en el primer recorrido parcial, tenemos que entre los elementos 2/4 y 1/2 podemos intercalar el otro recorrido, ya que de 2/4 pasamos a 4/5 y de 3/3 a 1/2. Por lo tanto, el orden final de las 64 fracciones quedaría:

Y sobre el tablero el recorrido cerrado del caballo que se ha construido es el siguiente.
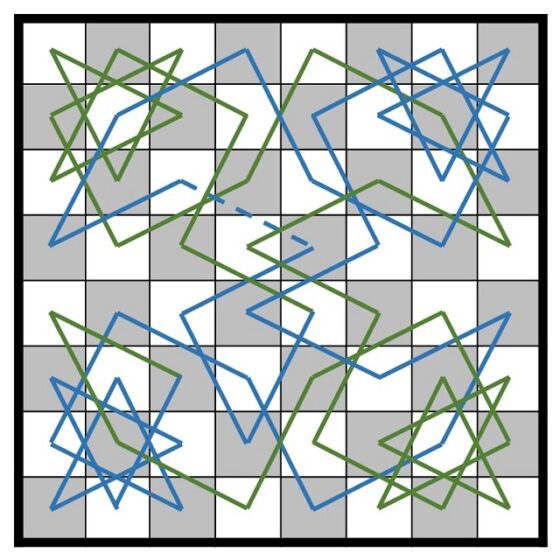
Podemos observar en el trabajo original de Vandermonde, que este es efectivamente el recorrido que construyó con su método.
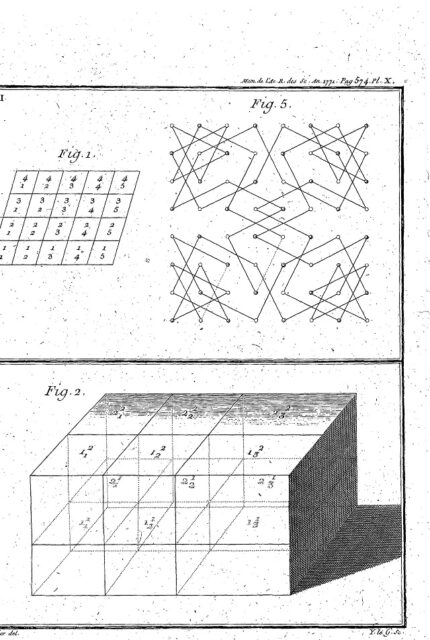 Anteúltima página del trabajo Remarques sur les problèmes de situation / Comentarios sobre los problemas de la situación (1771) del matemático francés Alexandre-Théophile Vandermonde, en la que se muestra el recorrido cerrado del caballo construido con el método descrito en el trabajo
Anteúltima página del trabajo Remarques sur les problèmes de situation / Comentarios sobre los problemas de la situación (1771) del matemático francés Alexandre-Théophile Vandermonde, en la que se muestra el recorrido cerrado del caballo construido con el método descrito en el trabajoPara finalizar os animo a que iniciéis la construcción en otro elemento distinto a 5/5 y construyáis vuestro propio recorrido cerrado.
Bibliografía
1.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, El mundo es matemático, RBA, 2015.
2.- W. W. Rouse Ball, H. S. M. Coxeter, Mathematical Recreations and Essays, Dover Publications, 1987 (originalmente publicada por W. W. R. Ball en 1892 –la versión original puede encontrarse en el Proyecto Gutenberg – y extendida por el geómetra H. S. M. Coxeter en 1974)
3.- Miodrag S. Petrovic, Famous Puzzles of Great Mathematicians, AMS, 2009.
4.- A. T. Vandermonde, Remarques sur les problèmes de situation, Histoire de l’Académie Royale des Sciences, avec les Mémoires de mathématiques et de physique, 1771, pp. 566-574.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El recorrido del caballo de Vandermonde se ha escrito en Cuaderno de Cultura Científica.
Begirada bat dibulgazioari (I): zientzia-komunikazioan kokatzen
Zientziaren komunikazio egokia ezinbestekoa da zientzia bera ulertu ahal izateko. Komunikatzen ez dena ez da existitzen eta, horrexegatik, geroz eta ahalegin handiagoa egiten da zientzia komunikatzeko. Komunikazio horren barruan, dibulgazioa da, agian, atalik interesgarriena; izan ere, gizarte guztiari zuzendutako zientziaz ari gara dibulgazioaz ari garenean. Begirada bat dibulgazioari izeneko artikulu sortan zientzia-dibulgazioari buruzko nire hausnarketak partekatu nahi ditut hedabide honen irakurleekin.
 1. irudia: komunikazioan kontuan hartu behar dira hartzailea, igorlea eta biek ezagutzen duten kodea. Ezagutza komunen arabera, zientzia-komunikazioa bi ataletan bereizten da: difusioa eta dibulgazioa. (Argazkia: Susanne Jutzeler – domeinu publikoko irudia. Iturria: pixabay.com)
1. irudia: komunikazioan kontuan hartu behar dira hartzailea, igorlea eta biek ezagutzen duten kodea. Ezagutza komunen arabera, zientzia-komunikazioa bi ataletan bereizten da: difusioa eta dibulgazioa. (Argazkia: Susanne Jutzeler – domeinu publikoko irudia. Iturria: pixabay.com)Zientzia-dibulgazioa zer den aztertzea da egin beharreko lehendabiziko lana. Esate baterako: Dibulgatzea da Farmakologia Elkartearen Biltzarrean hitzaldi bat ematea? Kazetari bati zure ikergaiari buruzko azalpenak ematea dibulgatzea da? Laborategiko lankideari azken esperimentuari buruzko azalpenak ematea dibulgatzea da? Lagunei edo senitartekoei zure lanaren berri ematea dibulgatzea da? Beno, galdera hauek erantzun ahal izateko, has gaitezen hasieratik.
Harluxet Hiztegi Entziklopedikoaren arabera, dibulgatzea da jakintza edo arte bateko ezagutzak horretan aditu ez direnek ulertzeko moduko era errazean azaltzea. Definizioa oso zehatza eta egokia da, baina badira egin beharreko ñabardura batzuk. Ñabardura horiei esker, bereizi egin daitezke sarritan berdintzat hartzen diren esparru desberdinak. Zehaztasun horien abiapuntu interesgarria da Seguí Simarro, Poza Luján eta Mulet Salort adituek 2015. urtean argitaratutako Estrategias de divulgación científica izeneko liburua. Liburu horrek zientzia-dibulgaziorako hainbat estrategia azaltzen ditu, beti ere modu praktiko eta erabilgarrian. Benetan gomendagarria da dibulgatzen hasi nahi duten ikertzaileentzat.
Dibulgazioaren oinarrian kokatzeko, lehenik eta behin komunikazioa zer den azaldu behar da. Komunikatzea, definizioz, ezagutzaren transmisioarekin lotzen da eta, hortaz, zientzia-komunikazioa zientzia-ezagutzen transmisioa litzateke. Alabaina, zientzia-ezagutzak oso modu desberdinetara komunikatu daitezke eta hartzailearen eta igorlearen arteko ezagutza-desberdintasuna arazoa izan daiteke komunikazio eraginkor baterako. Hain zuzen ere, berriro ere Harluxetera jotzen badugu, kontuan hartu behar dugu komunikazioa igorleak hartzaileari, biek ezagutzen duten kodea erabiliz, mezu bat bidaltzeko ekintza dela.
Biek ezagutzen duten kode horretan jartzen badugu fokua, Seguí Simarro eta bere lankideek zientzia-komunikazioa delako multzo handi hori bitan banatzea proposatzen dute. Alde batetik, zientzia-difusioa legoke, zabalkundea edo hedapena ere deitua, eta, beste alde batetik, zientzia-dibulgazioa. Difusioa espezialisten edo zientzian diharduten profesionalen arteko komunikazioa da. Kasu horretan, jakintza arlo desberdinetako hartzaile eta igorleak izan badaitezke ere, oinarrizko ezagutza komunak dituzte eta, beraz, komunikazioa espezializatuagoa izan daiteke. Dibulgazioa, aldiz, gizarte guztiari zuzendutako zientzia-komunikazioa da. Hortaz, komunikazio mota hau zientzian aditu direnei zein ez direnei zuzendua da. Zientzia-dibulgazioa ulergarria izan behar da gizarteko kide guztientzat.
Zientzia-kazetaritza ere kontuan hartu beharreko beste atal garrantzitsu bat da, sarritan zientzia-komunikaziotik bereiztea zaila den arren. Oro har, esan daiteke zientzia-dibulgazioaren zeregina dela azaltzea nola funtzionatzen duten Naturak edo gizakiak Naturatik eratorritako gauzek eta zientzia-kazetaritzaren esparrua, aldiz, gizarteari gertatzen zaiona azaltzea dela. Hortaz, Seguí Simarro eta haren lankideen arabera, zientzia-dibulgazioa atenporala da eta zientzia-kazetaritza, aldiz, gizartean testuinguratutako zientzia da, bere eragina, egokitasuna, mugak eta abar kontuan hartzen dituena. Adibide bat jartze aldera, maiatz amaieran jakin berri dugu ume bat jaio dela umetokiko transplante bati esker. Bada, dibulgazio-lan batek umetokiko transplantearen nondik norakoak azalduko lituzke: umetokiaren funtzioa, transplante baten gorabeherak, medikuek jarraitzen duten prozesua, eta abar. Zientzia-kazetaritzako lan batek, aldiz, gertatutakoaren ikuspuntu etikoari buruzko eztabaida abiatu dezake, informazio horretaz baliatuz.
Nik neuk ez dut guztiz argi ikusten zientzia-kazetaritzaren eta zientzia-dibulgazioaren arteko muga hori -egileek ere aipatzen dute muga lausoa dela-, baina kazetaritza arloa gaurkotasunean kokatzen dut, albisteetan… eta ez hainbeste kontzeptu zientifikoen azalpenean. Zientzialariaren eta kazetariaren lan egiteko moduak, oro har, zeharo desberdinak dira eta formakuntzan ere desberdintasun nabarmenak dituzte. Zilegi dira bi kritika hauek: kazetariek ez dute (ia) formakuntzarik jasotzen zientzia-ezagutzetan eta zientzialariek ez dute (ia) formakuntzarik jasotzen komunikazioan. Alabaina, bi esparruek beste arloaren beharra dute. Sarritan, zientziaren azalpenak behar ditu gertakari batek, erabaki politiko batek zein arazo ekonomiko batek. Era berean, zientzialari baten eguneroko lana da bere emaitzen berri ematea -aldizkari espezializatu batean zein zientzia-biltzar batean-. Lehena zientzia-kazetariak egiten du eta bigarrena, berriz, zientzialariak. Nork du, beraz, zientzia-ezagutzak gizarteari komunikatzeko, hau da, dibulgatzeko, ardura eta erantzukizuna?
Jarraituko du…
Erreferentzia bibliografikoa:Seguí Simarro, J.M., Poza Luján, J.L., Mulet Salort, J.M. (2015). Estrategias de divulgación científica, Ed. Universitat Politècnica de València.
Egileaz:Josu Lopez-Gazpio (@Josu_lg), Kimikan doktorea, irakaslea eta zientzia dibulgatzailea da. Tolosaldeko Atarian Zientziaren Talaia atalean idazten du eta UEUko Kimika sailburua da.
The post Begirada bat dibulgazioari (I): zientzia-komunikazioan kokatzen appeared first on Zientzia Kaiera.
La clave de la diversidad de especies podría estar en sus similitudes
diversidad
Un nuevo trabajo de modelado sugiere por qué la naturaleza es más diversa de lo que predice la teoría ecológica basada en nichos.
Un artículo de Veronique Greenwood. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Ilustración: Allison Li / Quanta Magazine
Ilustración: Allison Li / Quanta MagazineHace más de cuatro décadas los ecólogos de campo se propusieron cuantificar la diversidad de árboles en una parcela boscosa en la isla de Barro Colorado en Panamá, una de las extensiones de bosque más intensamente estudiadas del planeta. Comenzaron a contar cada árbol con un tronco de más de un centímetro de diámetro. Identificaron las especies, midieron los troncos y calcularon la biomasa de cada individuo. Pusieron escaleras en los árboles, examinaron los árboles jóvenes y lo registraron todo en hojas de cálculo cada vez mayores.
Mientras observaban los datos que se acumulaban año tras año, comenzaron a notar algo extraño en ellos. Con más de 300 especies, la diversidad de árboles en la pequeña isla de 15 kilómetros cuadrados era asombrosa. Pero la distribución de los árboles entre esas especies también estaba muy desequilibrada, ya que la mayoría de los árboles pertenecían a unas pocas especies.
Desde esos primeros estudios, ese patrón sobrecargado y altamente desigual se ha visto repetidamente en los ecosistemas de todo el mundo, particularmente en las selvas tropicales. El ecólogo Stephen Hubbell de la Universidad de California, Los Ángeles, quien formó parte del equipo de las mediciones en Barro Colorado, estima que menos del 2% de las especies de árboles en el Amazonas representan la mitad de todos los árboles individuales, lo que significa que el 98 % de las especies son poco comunes.
Una biodiversidad tan alta va en contra de las predicciones hechas por una importante teoría de la ecología, que dice que en un ecosistema estable cada nicho o rol debe ser ocupado por una especie. La teoría de nichos sugiere que no hay suficientes nichos para permitir que todas las especies que los ecólogos observaron existan de manera estable. La competencia por los nichos entre especies similares debería haber llevado a las poco comunes a la extinción.
Un nuevo artículo sobre modelado ecológico en Nature de James O’Dwyer y Kenneth Jops de la Universidad de Illinois, Urbana-Champaign explica al menos parte de esta discrepancia. Han descubierto que las especies que aparentemente deberían ser competidoras frente a frente pueden compartir un ecosistema si los detalles de sus historias de vida, como cuánto tiempo viven y cuántos descendientes tienen, se alinean de la manera correcta. Su trabajo también ayuda a explicar por qué una de las formas con más exito de modelar ecologías a menudo llega a resultados precisos, aunque pasa por alto casi todo lo que sabemos sobre cómo funcionan los organismos.
 El biólogo de plantas James O’Dwyer de la Universidad de Illinois, Urbana-Champaign quería entender cómo los modelos basados en la teoría neutral de la ecología pueden reproducir tan bien los patrones naturales de la biodiversidad cuando ignoran los detalles de cómo viven e interactúan las especies. Fuente: Universidad de Illinois / Michelle Hassel
El biólogo de plantas James O’Dwyer de la Universidad de Illinois, Urbana-Champaign quería entender cómo los modelos basados en la teoría neutral de la ecología pueden reproducir tan bien los patrones naturales de la biodiversidad cuando ignoran los detalles de cómo viven e interactúan las especies. Fuente: Universidad de Illinois / Michelle HasselEn 2001, la paradójicamente alta biodiversidad en la isla de Barro Colorado inspiró a Hubbell a proponer la revolucionaria teoría neutral de la ecología. La teoría de la ecología tradicional enfatizaba la competencia por los nichos entre las especies. Pero Hubbell señaló que las especies podrían no importar realmente en esa ecuación porque, en efecto, los individuos también compiten por los recursos con miembros de su propia especie. Sugirió que los patrones de diversidad en los ecosistemas podrían ser en gran parte productos de procesos aleatorios.
Para una teoría que se ocupaba de la biodiversidad, la teoría neutral de Hubbell era escasa. Ignoró las variaciones en las esperanzas de vida, las peculiaridades nutricionales y otros detalles que distinguen a una especie de otra. En los modelos basados en la teoría cada individuo en un ecosistema teórico es idéntico. Una vez que se empieza a contar el tiempo el ecosistema evoluciona estocásticamente, con individuos compitiendo y reemplazándose entre sí al azar. La teoría estaba completamente en desacuerdo con los enfoques de la ecología basados en especies, y provocó un apasionado debate entre los ecólogos porque parecía muy contraria a la intuición.
Sin embargo, sorprendentemente, a medida que avanzaban las caminatas aleatorias en los modelos neutrales, se reproducían características clave de lo que Hubbell y sus colegas habían visto en sus datos de la isla de Barro Colorado y lo que otros han visto en otros lugares. En este modelado que casi perversamente no reconoce diferencias, hay destellos del mundo real.
Esa tensión entre los modelos y la realidad ha interesado a O’Dwyer durante mucho tiempo. ¿Por qué la teoría neutral parecía funcionar tan bien? ¿Había alguna manera de incorporar información sobre cómo funcionan las especies para obtener resultados que pudieran parecer aún más realistas?
 Antes de unirse al laboratorio de O’Dwyer como estudiante de posgrado, Kenneth Jops había estudiado formas en las que las historias de vida podrían usarse para predecir la vulnerabilidad de las especies de plantas a la extinción. Foto: Dra. Hannah Scharf
Antes de unirse al laboratorio de O’Dwyer como estudiante de posgrado, Kenneth Jops había estudiado formas en las que las historias de vida podrían usarse para predecir la vulnerabilidad de las especies de plantas a la extinción. Foto: Dra. Hannah ScharfUna de las cosas que hace que los modelos neutrales sean atractivos, afirma O’Dwyer, es que realmente hay profundas universalidades entre muchos seres vivos. Si bien las especies animales no son idénticas, son notablemente similares a nivel de, digamos, el sistema circulatorio. Los mismos números relacionados con la fisiología surgen una y otra vez en animales y plantas, reflejando quizás las limitaciones de su historia evolutiva compartida. De acuerdo con un principio llamado ley de Kleiber, por ejemplo, la tasa metabólica de un animal generalmente aumenta con su tamaño, escalando como una ley de potencias, la misma ley de potencias, sin importar la especie. (Se han ofrecido varias teorías sobre por qué la ley de Kleiber es verdadera, pero la respuesta aún se debate).
Dados esos signos del orden subyacente, O’Dwyer se preguntó si algunos detalles de cómo viven los organismos importan más que otros para determinar el éxito con el que las especies competirán y sobrevivirán durante el tiempo evolutivo. Tomemos nuevamente el metabolismo: si un ecosistema puede verse como una expresión de los metabolismos de sus habitantes, entonces los tamaños de los organismos son números especiales y significativos. El tamaño de un individuo puede ser más útil para modelar su destino a lo largo del tiempo que cualquier otro detalle sobre su dieta o identidad de especie.
O’Dwyer se preguntó si uno de esos factores cruciales y privilegiados podría ser capturado por la historia de vida, un concepto que combina estadísticas de especies como el número promedio de descendientes, el tiempo hasta la madurez sexual y la esperanza de vida. Imagina una parcela de 50 plantas individuales. Cada una tiene su propia esperanza de vida, su propio patrón de reproducción. Después de tres meses, una planta puede producir 100 semillas, mientras que otra similar produce 88. Tal vez el 80% de sus semillas germine, produciendo la próxima generación, que pasará por su propia versión de este ciclo. Incluso dentro de una especie, el número de plantas individuales variará, a veces un poco, a veces mucho, un fenómeno llamado ruido demográfico. Si esta variación es aleatoria, a la manera de la teoría neutral de Hubbell, ¿qué patrones surgirán en las generaciones sucesivas?
O’Dwyer sabía que había encontrado a alguien que podía ayudarlo a explorar esa pregunta cuando Jops se unió a su laboratorio como estudiante de posgrado. Jops había estudiado previamente si los modelos que usaban historias de vida podían predecir si una especie de planta vulnerable sobreviviría o si estaba a punto de desaparecer. Juntos, comenzaron a elaborar las matemáticas que describirían lo que sucede cuando la historia de vida se encuentra con la competencia.
En el modelo de Jops y O’Dwyer, como en los modelos neutrales, la estocasticidad, la influencia de los factores aleatorios en las interacciones deterministas entre las especies, es importante. Las historias de vida de las especies, sin embargo, pueden amplificar o reducir los efectos de esa aleatoriedad. “La historia de vida es una especie de lente a través de la cual funciona el ruido demográfico”, explica O’Dwyer.
Cuando los investigadores permitieron que su modelo progresara a lo largo del tiempo, poniendo a prueba a cada individuo simulado, descubrieron que ciertas especies podían persistir una junto a la otra durante largos períodos a pesar de que competían por los mismos recursos. Al profundizar en los números en busca de una explicación, Jops y O’Dwyer encontraron que un término complejo llamado tamaño efectivo de la población parecía útil para describir un tipo de complementariedad que podría existir entre las especies. Encapsulaba el hecho de que una especie podría tener una mortalidad alta en un punto de su ciclo de vida, luego una mortalidad baja en otro, mientras que una especie complementaria podría tener una mortalidad baja en el primer punto y una mortalidad alta en el segundo. Cuanto más similar era este término para dos especies, más probable era que una pareja pudiera vivir una junto a la otra a pesar de competir por el espacio y la nutrición.
“Experimentan el ruido demográfico con la misma amplitud”, explica O’Dwyer. “Esa es la clave para que vivan juntos mucho tiempo”.
 Estas cuatro especies de plantas herbáceas perennes (en el sentido de las agujas del reloj desde la parte superior izquierda: Eryngium cuneifolium, Polygonella robusta, Lechea deckertii y Lechea cernua) coexisten en las comunidades de Florida en lugar de llevarse unas a otras a la extinción. Como predice la nueva investigación, las cuatro especies tienen historias de vida excepcionalmente similares. Fuentes: South Florida Listed Species USFWS y Bob Peterson (fila de arriba); Jay Horn.
Estas cuatro especies de plantas herbáceas perennes (en el sentido de las agujas del reloj desde la parte superior izquierda: Eryngium cuneifolium, Polygonella robusta, Lechea deckertii y Lechea cernua) coexisten en las comunidades de Florida en lugar de llevarse unas a otras a la extinción. Como predice la nueva investigación, las cuatro especies tienen historias de vida excepcionalmente similares. Fuentes: South Florida Listed Species USFWS y Bob Peterson (fila de arriba); Jay Horn.Los investigadores se preguntaron si prevalecían patrones similares en el mundo real. Se basaron en la base de datos COMPADRE, que alberga detalles sobre miles de especies de plantas, hongos y bacterias tomados de una variedad de estudios y fuentes, y se concentraron en plantas perennes que vivían juntas en las mismas parcelas de investigación. Descubrieron que, como había predicho su modelo, las especies de plantas que vivían juntas tenían historias de vida muy parecidas: los pares de especies que viven en el mismo ecosistema tienden a ser más complementarios que los pares creados al azar.
Los hallazgos sugieren maneras en que las especies que no están necesariamente en competencia directa podrían funcionar bien juntas sin recurrir a nichos distintos, afirma Annette Ostling, profesora de biología en la Universidad de Texas, Austin. “Lo mejor es que señalan que estas ideas… pueden extenderse a especies que son bastante diferentes pero complementarias”, comenta.
Para William Kunin, profesor de ecología en la Universidad de Leeds en Inglaterra, el artículo sugiere una razón por la cual el mundo natural, a pesar de toda su complejidad, puede parecerse a un modelo neutral: los procesos ecológicos pueden tener una forma de anularse entre sí, por lo que que lo que parece una variedad infinita puede tener un resultado simple que describe como «neutralidad emergente». Hubbell, por su parte, agradece la ampliación de su obra inicial. “Ofrece algunas ideas sobre cómo generalizar modelos neutrales, modificarlos para incluir un poco de diferencias específicas, expandirse y contraerse para ver qué sucede con la diversidad en una comunidad local”, dijo.
Sin embargo, este es solo una parte del problema de comprender cómo surge la biodiversidad y por qué persiste. “En ecología, luchamos con la relación entre patrón y proceso. Muchos procesos diferentes pueden producir el mismo patrón”, explicao Ostling. O’Dwyer espera que, en los próximos años, más datos sobre el mundo real puedan ayudar a los investigadores a discernir si el tamaño efectivo de la población es capaz de explicar la coexistencia de manera consistente.
Kunin espera que el artículo inspire a otros a seguir trabajando con ideas de la teoría neutral. En un campo donde las cualidades únicas de los individuos, en lugar de sus puntos en común, han prevalecido durante mucho tiempo, la teoría neutral ha obligado a los ecólogos a ser creativos. “Nos sacó de nuestras rutinas mentales y nos hizo pensar en qué cosas realmente importan”, afirma.
Hubbell, quien planteó la teoría neutral sobre la ecología hace tantos años, se pregunta si conjuntos de datos verdaderamente inmensos sobre bosques reales podrían producir el tipo de detalle necesario para aclarar la relación entre la historia de la vida y la biodiversidad. “Este es el tipo de construcción sobre la teoría neutral que esperaba que sucediera”, comenta sobre el nuevo artículo. “Pero es solo un pequeño paso hacia la comprensión real de la diversidad”.
El artículo original, The Key to Species Diversity May Be in Their Similarities, se publicó el 26 de junio de 2023 en Quanta Magazine.
Traducido por César Tomé López
El artículo La clave de la diversidad de especies podría estar en sus similitudes se ha escrito en Cuaderno de Cultura Científica.
Errezeta egiteko osagaiak: mahatsondoa
Basamahatsak eta haztegiko mahatsak Bibliaren 72 kapitulutan aipatzen dira, eta Koraneko 12 kapitulutan. Noski, Noe gogora ekartzea baino ez dago, bere produktu eratorri ezagunena azaltzen baita, hain zuzen ere, alkohola, mahatsaren azukreak irakin osteko emaitza, eta ardoa (azken helburua). Horregatik, mahatsondoa da testu sakratuetan gehien aipatzen den landarea. Oxfordeko Unibertsitateko Stephen Harrisek ere aipatzen du mundua aldatu zuten 50 landare famatuenen artean.
Basamahatsondoak (Vitis sylvestris) Anatoliakoak eta Kaukasokoak dira. Bertan hasi zen mahastizaintza eta Mediterraneoan zehar zabaldu zen, Estatu Batuetako Purdue Unibertsitateko Jules Janicken arabera. Mahatsaren haziak aurkitu dira Europako historiaurreko aztarnategietan eta, zehazki, Grezian, Balkanetan, Italian, Suitzan, Alemanian eta Frantzian. Basamahatsondoa Portugaletik (mendebaldea) Turkmenistaneraino (ekialdea) eta Alemaniatik (iparraldea) Tunisiaraino (hegoaldea) banatzen da.
 Irudia: basamahatsondoak Mediterraneoko arroan duen hedapena kontuan hartuta, baliteke etxe mahatsondoa eskualdeko toki batean baino gehiagotan sortu izana eta ez Ekialde Ertainean eta Kaukason bakarrik (Argazkia: Laura Stanley – domeinu publikoko argazkia. Iturria: Pexels.com)
Irudia: basamahatsondoak Mediterraneoko arroan duen hedapena kontuan hartuta, baliteke etxe mahatsondoa eskualdeko toki batean baino gehiagotan sortu izana eta ez Ekialde Ertainean eta Kaukason bakarrik (Argazkia: Laura Stanley – domeinu publikoko argazkia. Iturria: Pexels.com)
Beraz, Iberiar Penintsulan dago, iparraldean eta Pirinioetan izan ezik, Neolitikotik aurkitu diren haziek frogatzen dutenez. Pompeu Fabrako Unibertsitateko Ramón Buxóren esanetan, datuek baieztatzen dute mahatsondoa Mediterraneo osoko landare indigena bat dela eta haztegiko mahatsondoaren haziak Brontze Aroaz gero berreskuratu direla.
Eztabaida hau irekita dago oraindik: basamahatsondoak Mediterraneoko arroan duen hedapena kontuan hartuta, baliteke etxe mahatsondoa eskualdeko toki batean baino gehiagotan sortu izana eta ez Ekialde Ertainean eta Kaukason bakarrik. Rosa Arroyo-Garcíak eta Madrilgo Nekazaritza eta Elikaduraren Ikerketa eta Teknologiako Institutu Nazionaleko lankideek banaketa eremu guztiko basamahatsondoaren eta etxe mahatsondoaren 1.201 laginen kloroplastoen DNA aztertu dute. Egileen arabera, emaitzek diote Iberiar Penintsulako laginen % 70etan kloroplastoak basamahatsondoaren mendebaldeko populazioetatik eratorritako materialarekin bakarrik bateragarriak direla.
Valladolideko Unibertsitateko José Carlos Santanaren taldeak egindako beste ikerketa batek barietate basatiei eta etxekoei dagozkien kloroplastoak aztertu ditu Gaztela Zaharreko lautadan, eta 121 genotipo desberdin bereizi ditu. Interesgarria da horietako askok gurutzatuta daudela basamahatsondo autoktonoaren eta Frantziako etxeko mahatsondoen artean. Egileen ustez azkenekoen barietateak Donejakue Bideko merkataritza gauzatzean iritsi ziren.
Etxe mahatsondoak, 8.000 urteKristo aurreko 5000. urtea baino lehen, etxe mahatsondoa (Vitis vinifera) Anatoliatik Ekialde Hurbilera iritsi zen. Kaukasoko hegoaldetik, Itsaso Beltzaren nahiz Karpiar itsasoaren eta Ilgora Emankorraren, Jordan haranaren eta Egiptoren artean, egin zuen. Hala adierazten du Cornell Unibertsitateko (Ithaca) Sean Mylesek eta bere lantaldeak argitaratu basamahatsondoen eta etxe mahatsondoen 1.000 laginen analisi genetikoak.
Etxeko bihurtu zen duela 6.000 eta 8.000 urte bitartean. Brontze Aroko mahats haziak daude Mesopotamian, Israelen, Sirian, Egipton, Egeon eta Suitzako aintziretan. Amerikan ere aurkitu dira. Gogora ekarri behar da Leif Erikson bikingoa Labradorreko kostaldeetara iritsi zenean herrialde hari Vinland (Ardoaren Herrialdea) deitu ziola, Vitis riparia espezieko basamahatsondo asko zeudelako –ohikoak dira Ipar Amerikan–.
Ardoa eta mahaspasak gordetzeko duela 4.000 urteko (Brontze Aroa) ontziak aurkitu dira. Israelgo Tel Kabriko aztarnategian, lokal batean, 40 ontzi berreskuratu ziren eta, horiek ardoaren ohiko osagaien aztarnak zituzten, hala nola azido tartarikoa, erretxinak, eztia eta zedro eta altzifre olioa. Estatu Batuetako Brandeis Unibertsitateko Andrew Kohren eta bere lankideen arabera, ardoz betetako ontziak gordetzeko gela bat zen; hau da, upategi bat, orain arte ezagutzen ditugunetako zaharrenetako bat, hain zuzen ere.
Yunnaneko Nekazaritza Unibertsitateko (Txina) Dongek zuzendu duen ikerketa bat (84 egile ditu) argitaratu berri da orain dela aste batzuk eta, horretan, planeta osoko basamahatsen eta haztegiko mahatsen 3.525 barietateren datu genetikoak aztertu dira. Emaitzek azaltzen dutenez, klimak (zehazki, glaziazioenek) ondorioak izan ditu populazio tamaina historikoetan, eta, ematen duenez, aldi berean etxekotu ziren ardoa eta mahaiko mahatsak eta etxekotzearen ezaugarriekin lotutako aldaerak identifikatzen dituzte, besteak beste, baiaren kolorea eta palatabilitatea.
Pleistozenoan baldintza klimatikoek basamahatsondoen ekotipoak aukeratzera bultzatu zuten; horretan, habitataren zatikatzeak ere lagundu zuen. Etxekotzea aldi berean gertatu zen duela 11.000 urte inguru Asiako Mendebaldean eta Kaukason, mahaiko frutetarako eta ardorako mahatsondoak ekoizteko. Lehenengo nekazariekin, Asiako Mendebaldean etxekotu zirenak Europan sakabanatu ziren, eta mendebaldeko ekotipo basati zaharrekin gurutzatu ziren. Gerora, Neolitikoaren amaieran, gizakien migrazioen laguntzaz, dibertsifikatu egin ziren.
Ordukoak dira Rovira i Virgili Unibertsitateko eta Atapuercako lantaldeko Eudald Carbonellek eta Cinta Bellmuntek, María Ángeles Torresen argazkiekin, aurkezten dizkiguten muskuiluak mahatsekin. Errezeta erraz eta azkar bat da, eta landan bazkari bat egiteko hasierako plater on bat ere.
Muskuiluak kostalde hurbileneko harkaitzetan bilduko ditugu, eta sutzarrean erreko ditugu harri baten gainean. Irekitzen direnean oskol bakoitzean mahats bana ipiniko dugu, eta batera jango ditugu muskuilua eta mahatsa.
Erreferentzia bibliografikoak:- Arroyo-García, R. et al. (2006). Multiple origins of cultivated grapevine (Vitis vinifera L. ssp. sativa) based on chloroplast DNA polymorphisms. Molecular Ecology 15, 3707-3714. DOI: 10.1111/j.1365-294X.2006.03049.x
- Dong, Y. et al. (2023). Dual domestications and origin of traits in grapevine evolution. Science 379, 892-901. DOI: 10.1126/science.add8655
- Janick, J. (2007). Fruits of the Bibles. HortScience 42, 1072-1076. DOI: 10.21273/HORTSCI.42.5.1072
- Koh, A. J. et al. (2014). Characterizing a Middle Bronze palatial wine cellar from Tel Kabri, Israel. PLOS One 9, e106406. DOI: 10.1371/journal.pone.0106406
- Myles, S. et al. (2011). Genetic structure and domestication history of the grape. Proceedings of the National Academy of Sciences USA 108, 3530-3535. DOI: 10.1073/pnas.1009363108
- Santana, J.C. et al. (2010). Genetic structure, origins, and relationships of grapevine cultivars from the Castilian Plateau of Spain. American Journal of Enology and Viticulture 61, 214-224. DOI: 10.5344/ajev.2010.61.2.214
- Zohary, Daniel; Spiegel-Roy, Pinhas (1975). Beginnings of fruit growing in the Old World. Science 187, 319-327. DOI: 10.1126/science.187.4174.319
- Buxó, R. (1997). Arqueología de las plantas. La explotación económica de las semillas y los frutos en el marco mediterráneo de la Península Ibérica. Crítica. Barcelona. 367 pp.
- Carbonell, E. et al. (2016). Recetas paleo. La dieta de nuestros orígenes para una vida saludable. Ed. Planeta. Barcelona. 143 pp.
- Harris, S. (2021). Plantas legendarias: 50 plantas que cambiaron el mundo. Rey Naranjo Eds. Barcelona. 358 pp.
- Payo, A. 2023. Los ciclos glaciares determinaron la domesticación de la uva y la aparición del vino. Boletín SiNC 2023ko martxoaren 2an
- Piqueras Haba, J. (2005). La filoxera en España y su difusión espacial: 1878-1926. Cuadernos de Geografía 77, 101-136.
- Wikipedia. Vino. 2023ko martxoaren 14an
Eduardo Angulo Biologian doktorea da, UPV/EHUko Zelula Biologiako irakasle erretiratua eta zientzia-dibulgatzailea. La biología estupenda blogaren egilea da.
Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2023ko maiatzaren 28an: Ingredientes para la receta: la vid.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Errezeta egiteko osagaiak: mahatsondoa appeared first on Zientzia Kaiera.
La evolución del interior de la luna Europa
Europa, el satélite de Júpiter, es uno de los lugares de nuestro Sistema Solar en los que pensamos hay un mayor potencial astrobiológico debido a la posible existencia de un océano de agua líquida debajo de su corteza helada. Algo que esperamos que en la próxima década confirmen misiones como la europea JUICE, que despegó a mediados del mes de abril de este año, o la norteamericana Europa Clipper, cuya fecha de despegue prevista es octubre de 2024, y cuyo ensamblaje se encuentra en una fase muy avanzada.
Europa es un satélite algo más pequeño que nuestra Luna -unos 3100 kilómetros de diámetro frente a 3474 kilómetros- pero a pesar de eso su superficie atestigua que hay una actividad geológica capaz de rejuvenecerla desde dentro, e incluso, como hablamos en “Una tectónica de placas más allá de la Tierra” en diciembre de 2022, podría tener una tectónica de placas, y esto significa que hay alguna fuente de energía interna capaz de provocar estos procesos.
 Europa observada por la sonda JUNO en septiembre de 2022. Obsérvese la relativa juventud de su superficie por la escasez de cráteres de impacto que se pueden observar. Imagen cortesía de NASA/JPL-Caltech/SwRI/MSSS/Kevin M. Gill.
Europa observada por la sonda JUNO en septiembre de 2022. Obsérvese la relativa juventud de su superficie por la escasez de cráteres de impacto que se pueden observar. Imagen cortesía de NASA/JPL-Caltech/SwRI/MSSS/Kevin M. Gill.Por si esto fuese poco, en 2013 se anunció el descubrimiento de posibles géiseres de agua -capaces de llegar a los cien kilómetros de altura- a partir de datos del Telescopio Espacial Hubble, agua, aunque cuyo origen no sabemos si procede de bolsas de agua existentes en el interior de la corteza o del océano, un fenómeno que sería similar al observado en Encélado, satélite de Saturno, y que añade, si cabe, más interés al estudio de Europa, ya que estudiando el agua que sale despedida en estos fenómenos, podemos intentar averiguar su procedencia, y en el caso de ser del interior de Europa, conocer mejor ese posible océano.
Pero, ¿cómo es Europa por dentro y cómo ha sido su evolución? Un artículo recién publicado en Science Advances aporta un nuevo modelo sobre su estructura interna y la evolución que ha tenido a lo largo del tiempo, algo fundamental de cara a conocer qué fuentes de energía serían las responsables de mantener un océano de agua líquida desde su formación o si el océano en realidad se formó posteriormente.
En las últimas décadas, muchos de los estudios científicos han apuntado a una rápida evolución del interior de Europa tras su formación. Es decir, que los procesos de diferenciación planetaria, aquellos que dan lugar a la estructura por capas de los planetas y otros cuerpos, ocurrieron muy pronto en la historia de Europa, procesos para los que generalmente se necesita mucho calor para fundir total o parcialmente, en este caso Europa, y que los elementos más pesados se hundan hacia el fondo y los más ligeros vayan hacia la superficie.
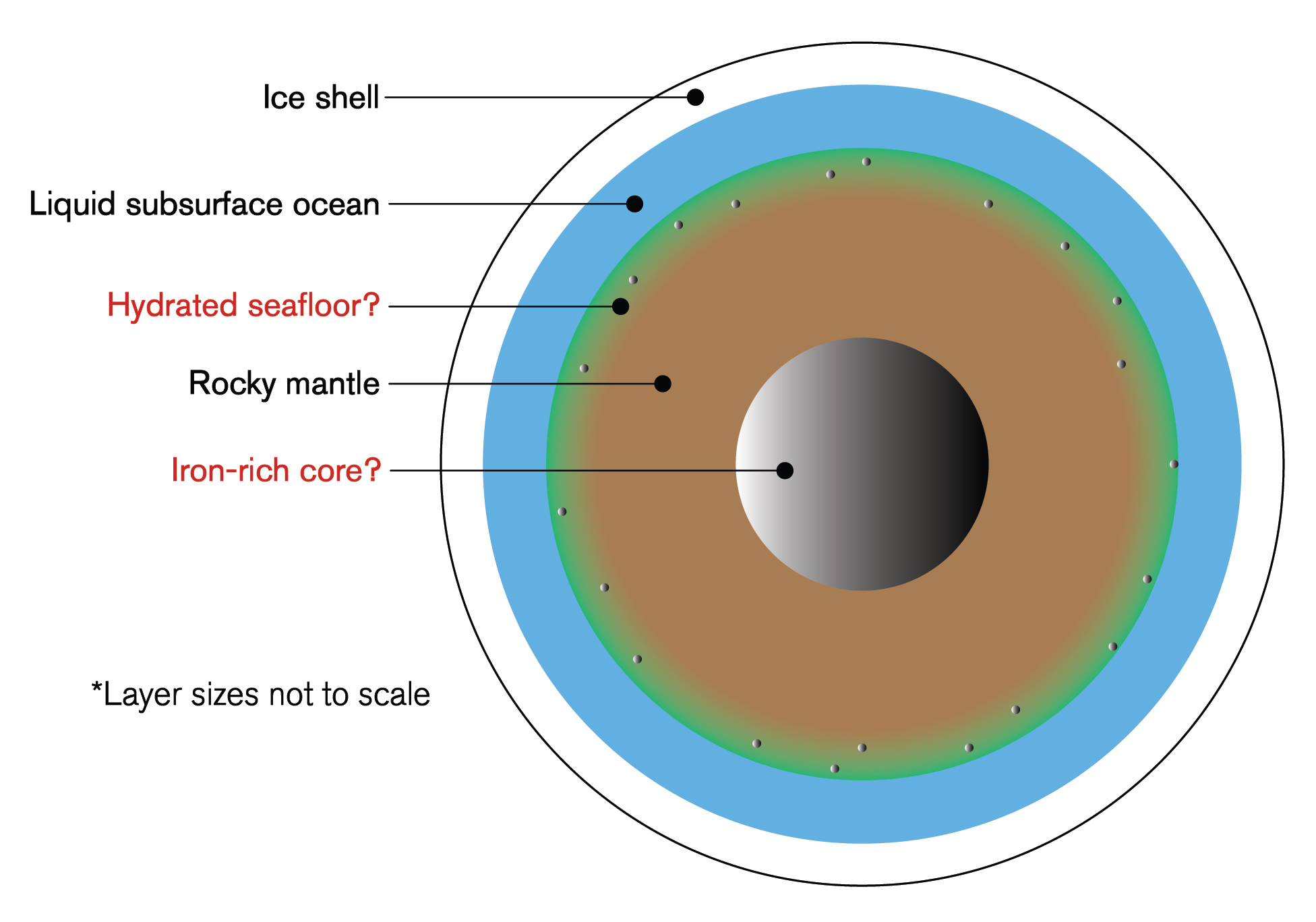 Posible estructura interna de Europa. En rojo y con interrogantes, algunas de las dudas planteadas por el estudio, especialmente sobre un núcleo bien desarrollado. Cortesía de Kevin Trinh/ASU.
Posible estructura interna de Europa. En rojo y con interrogantes, algunas de las dudas planteadas por el estudio, especialmente sobre un núcleo bien desarrollado. Cortesía de Kevin Trinh/ASU.Por los datos que tenemos hasta el momento, la estructura de Europa, a grandes rasgos, estaría formada por una corteza de hielo de unos 15 a 25 kilómetros de potencia, un océano subterráneo de entre 60 y 150 kilómetros de espesor, un manto rocoso y un núcleo metálico.
Este nuevo estudio propone que Europa se formó como una mezcla más o menos homogénea de roca, hielo y elementos metálicos que lentamente fue segregándose en las distintas capas, tardando en formarse el núcleo interno -si está formado completamente- a lo largo de miles de millones de años. La existencia o no de este núcleo y su estado nos podría dar pistas sobre el calor interno que todavía se genera en Europa.
Además, proponen que la deshidratación de los minerales silicatados -fruto del calor procedente de la desintegración radioactiva- presentes en Europa -algunos silicatos pueden contener moléculas de agua o grupos hidroxilo en su estructura cristalina- podría haber sido la responsable de la formación del océano y de la capa de hielo, ya que el agua iría migrando desde zonas más profundas hacia las más superficiales, primero formando la corteza de hielo, y después permitiendo, bajo esta, la existencia de un océano.
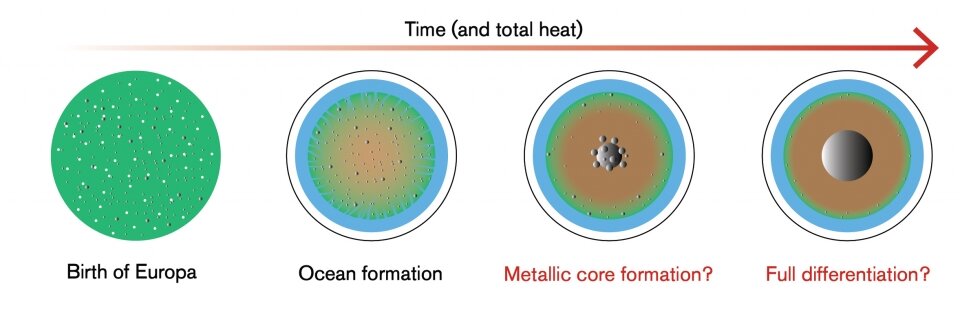 Posibles caminos evolutivos del interior de Europa. Dependiendo de la cantidad de calor disponible para Europa, podría no existir una diferenciación completa de su interior. Imagen cortesía de Kevin Trinh/ASU
Posibles caminos evolutivos del interior de Europa. Dependiendo de la cantidad de calor disponible para Europa, podría no existir una diferenciación completa de su interior. Imagen cortesía de Kevin Trinh/ASUHay algo más. Este modelo es ciertamente desfavorable, ya que predice que la actividad geológica en la interfaz entre el océano y el manto rocoso podría ser muy poca, limitando mucho la existencia de fenómenos hidrotermales o volcánicos en su interior en la actualidad, lo que limitaría de una manera importante el potencial astrobiológico del satélite joviano, algo que también podría explicar la menor actividad que hemos observado con respecto a Encélado.
A pesar de esto, los científicos reconocen que, aunque sus modelos son muy detallados y muestran distintos escenarios evolutivos para Europa, todavía se necesitan más datos para confirmar si realmente están en lo cierto o si incluso pueden estar ocurriendo otro tipo de fenómenos -como el calentamiento por mareas- que mantengan un interior más activo de lo predicho por ellos.
Sea como fuere, probablemente tengamos que esperar todavía hasta la llegada de las misiones JUICE y Europa Clipper en la próxima década para tener más datos que nos permitan conocer un poco mejor el interior de Europa y sentar si es el mundo habitable que todos esperamos o si, por el contrario, las condiciones no son tan favorables como pensábamos anteriormente.
Referencia:
Kevin T. Trinh et al. (2023) Slow evolution of Europa’s interior: metamorphic ocean origin, delayed metallic core formation, and limited seafloor volcanism. Sci. Adv. doi: 10.1126/sciadv.adf3955
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo La evolución del interior de la luna Europa se ha escrito en Cuaderno de Cultura Científica.
Gizarte-babesa eta adimen emozionala gazteen suizidioa prebenitzeko
Adimen emozional handiagoa duten nerabeek neurri handiagoan hautematen dute jasotzen duten gizarte-babesa. Horrek haien ideiagintza suizida murrizten laguntzen du. Kontrara, adimen emozional handia duten nerabeek, familia-babes urria badute, zailtasun handiak izango dituzte beren ideiagintza suizidak murrizteko. Hauek izan dira UPV/EHUko Didaktika eta Eskola Antolaketa Sailak gizarte-babesak adimen emozionalaren eta ideiagintza suizidaren arteko erlazioan duen eraginari buruz egindako azterketaren emaitzak.
Osasunaren Mundu Erakundearen (OME) datuen arabera, 2020an, jokabide suizida izan zen nerabeen arteko munduko hirugarren heriotza-kausa. Kasu horien % 90ean jatorria maila sozioekonomiko apal eta ertaineko herrialdeetan zuten nerabeak ziren. Nerabeen ideiagintza eta jokabide suizida arazo publiko bihurtu dira, eta ahalegin handia eskatzen dute nola eta noiz prebenitu jakiteko. Nerabeen ideiagintza eta jokabide suizidaren aurkako babes-faktoreetako bat adimen emozionala da —pertsonek beren emozioak erabiltzeko eta emozioak hobeto identifikatu, erabili eta kudeatzeko abian jartzen dituzten trebetasunak—. Izan ere, estatistikoki esanguratsua den lotura bat hauteman da adimen emozional baxuaren eta nerabeen ideiagintza suizida altuaren artean.
 Irudia: inteligentzia emozional handiagoa duten nerabeak neurri handiagoan direlako gai irakasleengandik, familiakoengandik eta ikaskideengandik jasotzen duten babesa hautemateko. (Argazkia: Askar Abayev – domeinu publikoko argazkia. Iturria: Pexels.com)
Irudia: inteligentzia emozional handiagoa duten nerabeak neurri handiagoan direlako gai irakasleengandik, familiakoengandik eta ikaskideengandik jasotzen duten babesa hautemateko. (Argazkia: Askar Abayev – domeinu publikoko argazkia. Iturria: Pexels.com)Héctor Galindo eta Daniel Losada UPV/EHUko ikertzaileek aztertu dute zer eragin bitartekari eta moderatzaile duten berdinen arteko babesak, familiaren babesak eta irakasleen babesak adimen emozionalaren eta nerabeen ideiagintza suizidaren arteko erlazioan. 898 neraberekin egindako ikerketak ondorioztatu duenez, “adimen emozionalak eragin zuzena du ideiagintza suizidan. Hori gertatzen da, neurri batean, inteligentzia emozional handiagoa duten nerabeak neurri handiagoan direlako gai irakasleengandik, familiakoengandik eta ikaskideengandik jasotzen duten babesa hautemateko. Eta horrek laguntzen die, hain zuzen ere, ideiagintza suizida murrizten: jasotzen ari diren babes hori behar bezala hautemateak”, azaldu dute.
Gizarte-babesaren garrantziaEra berean, ikerketaren emaitzek agerian uzten dute familiaren babesak eragina duela adimen emozionalaren eta ideiagintza suizidaren arteko erlazioan. Ikertzaileen arabera, harreman hori aldatu egiten da pertsona batek jasotzen duen familiaren babesaren neurriaren arabera: “pertsona batek ez badu etxean familia-babesik, nahiz eta adimen emozional handia izan, horrek ez dio laguntzen bere ideiagintza suizida murrizten. Hala ere, familiaren babes ertaina edo handia izateak gehiago laguntzen dio bere ideiagintza suizida murrizten emozionalki adimentsua den pertsona bati, adimen emozional baxua duen pertsona bati baino”.
Halaber, emaitzek erakusten dute berdinen arteko babesak ideiagintza suizida murrizten laguntzen diola adimen emozionalari soilik babes hori adin handiagoko nerabeen artekoa bada: “nerabe batek 12 urte dituenean, berdinen arteko babesa ez da nerabe batek 15 edo 16 urte dituenean bezain garrantzitsua”. Eta irakasleen babesari dagokionez, azterlanak ondorioztatu duenez, “adimen emozional handia duen nerabe batek bere ideiagintza suizida asko murriztu ahal izango du, irakasleengandik hautemandako babesa edozein dela ere. Adimen emozional baxua duen pertsona batek, berriz, zailtasun handiak izango ditu ideiagintza suizida murrizteko, irakasleengandik hautemandako babesa edozein dela ere”.
Alde horretatik, Galindok eta Losadak azpimarratu dute adimen emozionala ikasgelan lantzea oso garrantzitsua dela, “baina are garrantzitsuagoa pertsona horiek gizarte-babes handia jasotzea. Hori dela eta, garrantzitsua da familiek ikasketa-prozesuetan parte hartzea eta berdinen arteko kalitate-harremanak sustatzea, nerabeen heriotza-kausa nagusietako bat murrizteko, hau da, jokabide suizida. Egiazki, irakasleok kontuan hartu eta sustatu behar dugu, ahal den neurrian, nerabe bat bere ingurunetik jasotzen ari den babes-maila; izan ere, pertsona hori gizarte-babes baxua jasotzen ari bada, gerta liteke, ikasgelan adimen emozionala zeharka edo diziplina gisa landu arren, espero diren ondorioak ez izatea nerabeen jokabide suizida murrizteko.
Iturria:UPV/EHU prentsa bulegoa: Gizarte-babesak adimen emozional handiko gazteen ideagintza suizida moderatzen du.
Erreferentzia bibliografikoa:Galindo Domínguez, Héctor; Losada Iglesias, Daniel (2023). Inteligencia emocional e ideación suicida en adolescentes: el rol mediador y moderador del apoyo social (Emotional intelligence and suicidal ideation in adolescents: The mediating and moderating role of social support). Revista de Psicodidáctica. DOI: 10.1016/j.psicod.2023.02.001
The post Gizarte-babesa eta adimen emozionala gazteen suizidioa prebenitzeko appeared first on Zientzia Kaiera.
La ecuación trascendente de la txalaparta
 Txalaparta en La menor: idiófono basado en tablones tallados sobre caballetes y bastones para interpretación por parejas a cuatro manos
Txalaparta en La menor: idiófono basado en tablones tallados sobre caballetes y bastones para interpretación por parejas a cuatro manosLa txalaparta es un antiguo idiófono original de Vasconia, cuya peculiaridad como instrumento de percusión y su enigmática historia ha despertado mucho interés entre los musicólogos e historiadores. La primera referencia histórica a la txalaparta aparece en 1882 en un libro sobre la producción de sidra en el País Vasco ([1], p. 129), aunque existen menciones anteriores a las toberas (una variante metálica de la txalaparta): la primera de ellas en un documento legal de 1688 ([2], pp. 52-53). Se sabe muy poco sobre la práctica de la txalaparta antes del siglo XX, pero antropólogos, historiadores, músicos y otros científicos han colocado el instrumento en una novedosa vía de crecimiento, utilización y actualización cultural de gran interés internacional:
Las hermanas Sara y Maika Gómez (Ttukunak) en el Festival de Primavera de Budapest, Palacio de las Artes, 2017
La txalaparta ordinaria consta de unos tablones de madera colocados de forma horizontal sobre dos soportes, y golpeados a cuatro manos por bastones también de madera. Debido al origen rural del instrumento, es muy habitual utilizar tablones de maderas de árboles locales como el roble, castaño o aliso, y bastones de fresno, similares a los mangos cortos de las herramientas del campo.
Modelado matemático de la txalapartaLa vibración transversal de los tablones se puede modelar matemáticamente mediante la conocida teoría de vigas o barras de Euler-Bernoulli. Dado que los listones sonoros de la txalaparta están libres sin sujeción a ambos extremos, estas condiciones de contorno restringen las frecuencias permitidas para vibrar. Así, las tablas de la txalaparta solamente pueden sonar según los modos de vibración soluciones de una preciosa ecuación trascendente (no algebraica).
Esta ecuación trascendente se expresa como cosh(kL)cos(kL)=1, donde k es el número de onda de los infinitos modos de vibración y L es la longitud del tablón.
Esta ecuación no puede resolverse de forma analítica sino por medios numéricos o gráficos, y los infinitos modos de vibración de cada tablón siguen una serie inarmónica musical, muy diferente a la serie armónica que resulta en las cuerdas vibrantes de las guitarras, violines o pianos, o en las columnas de aire de las flautas, oboes o clarinetes.
Así pues, si calculamos el modo fundamental de vibración de una tabla golpeada, y resolvemos con métodos numéricos la ecuación trascendente de la txalaparta, resulta que las notas musicales que corresponden a cada tablón siguen una serie de frecuencias sonoras muy poco armónicas: f1, f2=2.76f1, f3=5.40f1, f4=8.94f1, f5=13.35f1,…
Si terminamos los cálculos, podemos también representar la distribución espacial de los primeros modos vibratorios de cada listón sonoro, tal y como se muestra en la figura siguiente. Como el primer modo de vibración es el más importante en cada tabla, la txalaparta apoya sus tablones en las líneas nodales de este primer modo, para dejarlos vibrar con total libertad. Como puede observarse en la figura, el apoyo óptimo del instrumento se encuentra en puntos simétricos cercanos a ¼ de la longitud de cada tabla, si damos preferencia al primer modo de vibración.
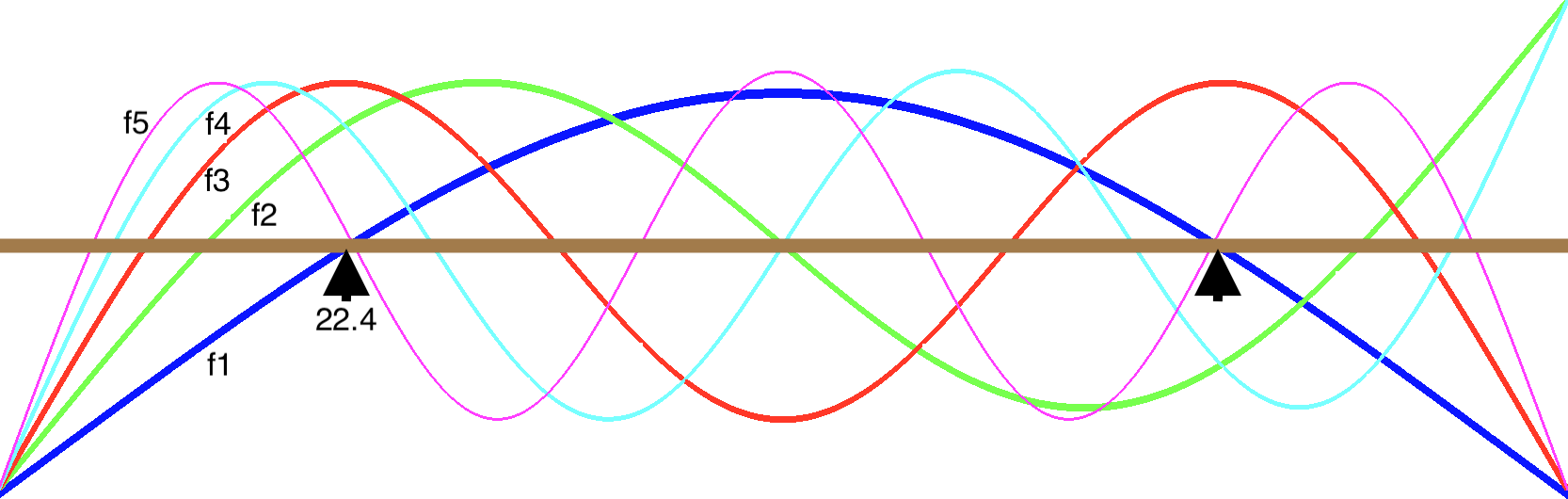 Vibraciones transversales de un tablón golpeado en una txalaparta. Se incluyen los cinco primeros modos de vibración, la tabla horizontal en color marrón y sus dos soportes situados en las dos líneas nodales del primer modo: a 22.4% de la longitud del tablón, desde sus extremos izquierdo y derecho. Fuente: cálculo computacional del autor.
Vibraciones transversales de un tablón golpeado en una txalaparta. Se incluyen los cinco primeros modos de vibración, la tabla horizontal en color marrón y sus dos soportes situados en las dos líneas nodales del primer modo: a 22.4% de la longitud del tablón, desde sus extremos izquierdo y derecho. Fuente: cálculo computacional del autor.
El movimiento oscilatorio de este primer modo de vibración se puede visualizar en la animación mostrada a continuación. Los modos superiores, cada uno a su propia frecuencia fn, efectúan movimientos vibratorios similares. Los n+1 puntos nodales de cada modo se mantienen inmóviles y sus n máximos y mínimos móviles corresponden con puntos ventrales de la vibración. Notemos que en la figura anterior se pueden localizar los nodos de cada modo mediante la intersección de las gráficas con la tabla horizontal trazada en color marrón. Los puntos ventrales de cada modo se encuentran entre sus puntos nodales, y corresponden con zonas de máxima flexión de las tablas.
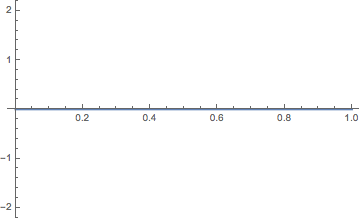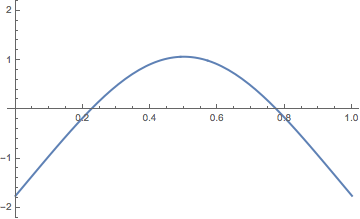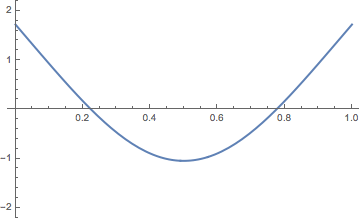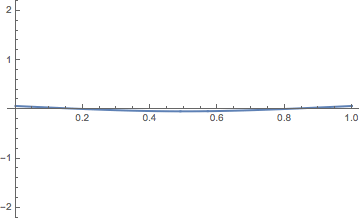 Animación del primer modo de vibración transversal de las tablas golpeadas con condiciones de contorno libres a ambos extremos. Fuente: Wikimedia Commons
Animación del primer modo de vibración transversal de las tablas golpeadas con condiciones de contorno libres a ambos extremos. Fuente: Wikimedia Commons
Observamos que la txalaparta es un instrumento de percusión que incluye una serie inarmónica musical. En instrumentos de percusión cromática como los modernos xilófonos o marimbas, las barras sonoras se afinan tallando las maderas para poder conseguir instrumentos con toda la escala cromática ([3], pp 628-629). Aunque la txalaparta no es de naturaleza cromática, es posible construir un instrumento afinado y mejorar su serie armónica y propiedades musicales.
La txalaparta bien afinadaPara construir una txalaparta bien afinada, basta con tallar las tablas eliminando madera en su parte central-inferior. Existen dos razones para realizar este tallado inferior de los tablones: por un lado, alcanzar la afinación de nota (frecuencia) deseada para el primer modo de cada barra sonora del instrumento, y por otro, conseguir notas cercanas a una serie armónica para los principales modos superiores de cada uno de sus elementos vibrantes. Cada tablón se esculpe para ajustar selectivamente la frecuencia y forma de un modo normal de vibración que se pretende, sintonizando la masa y la rigidez de la madera. La eliminación de madera en una zona de flexión pronunciada reduce la rigidez más que la masa de la tabla, de modo que la frecuencia disminuye. Por otro lado, la supresión de madera en una zona de poca flexión reduce la masa más que la rigidez, de forma que la frecuencia aumenta. Esta técnica escultórica permite perfectamente construir una txalaparta musical y afinada.
 Proceso de eliminación de madera en la parte central-inferior de uno de los tres tablones de roble de la txalaparta fabricada por el autor.
Proceso de eliminación de madera en la parte central-inferior de uno de los tres tablones de roble de la txalaparta fabricada por el autor.Aunque no existe un modelo estándar de txalaparta, dependiendo de los estilos musicales o interés de los intérpretes, es común emplear típicamente entre 1 y 5 tablones. Un ajuste básico para poder emitir acordes tonales requiere al menos tres notas simultáneas, que pueden ejecutarse golpeando tres tablas. Utilizando tres robustos listones de roble de longitud 123cm, anchura 16cm y grosor 5 cm, como el mostrado en la fotografía, es sencillo tallar estas barras como hemos indicado y generar potentes y armónicos elementos sonoros. En este caso concreto los tablones han sido esculpidos de manera que sus modos fundamentales vibren a 110 Hz (La1), 131 Hz (Do2), 165 Hz (Mi2): esto nos permite denominar el instrumento como una txalaparta en La menor. Además, el golpeo de los tablones en zonas intermedias, excitan los modos de vibración superiores, que han sido ajustados en una serie armónica. Por todo ello, una buena pareja ejecutante en esta txalaparta afinada puede extraer del instrumento verdadera recóndita armonía.
Hutsun en las calles de Aviñón (Francia)
Referencias
[1] Severo de Aguirre-Miramon (1882) Fabricación de la sidra en las provincias vascongadas. Hijos de I.R. Baroja, San Sebastian, p. 129.
[2] Manuel de Lekuona (1920) Las toberas. Revista de cultura vasca, Euskalerriaren Alde n. 194, pp: 52-53.
[3] Neville H. Fletcher and Thomas D. Rossing (1998) The Physics of Musical Instruments (2nd Edition), ISBN-9780387983745, Springer, New York, pp: 628-629.
Del mismo autor:
Lutería y acústica (serie)
Sobre el autor: Victor Etxebarria Ecenarro está diplomado como lutier por el Conservatorio Juan Crisóstomo de Arriaga (Bilbao) y es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (UPV/EHU)
El artículo La ecuación trascendente de la txalaparta se ha escrito en Cuaderno de Cultura Científica.
Asteon zientzia begi-bistan #444
Asteon zientzia begi-bistan igandeetako gehigarria da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna jaso eta laburbiltzea da gure helburua.

Eltxoek nahiago dituzte usain zehatz bateko gizakiak, ikerketa berri batek frogatu duenez. Malaria Ikertzeko Institutuko zientzialari talde batek egin du ikerketa, eta egoera ahalik eta errealistena irudikatzeko helburuarekin, esperimentazio eremu zabal batean zortzi kanpin denda jarri zituzten barruan giza akuiluekin. Ondoko kaiola batean Anopheles gambiae eltxoak gorde zituzten, eta kanpin denda bakoitzeko usaina bertara bideratu zuten. Hala ikusi zuten eltxoen erasoak, eta sei gizakietatik, bereziki batek piztu zuela eltxoen gosea. Ondoren aztertu zutenez, pertsona horren azalean, besteak beste, azido karboxiliko lurrunkor gehiago aurkitu zuten, eta baita azetoina gehiago ere. Ikerketa honen inguruko informazio gehiago Zientzia Kaieran: Distantzia handira ere, eltxoek usainduko zaituzte.
Science aldizkarian argitaratutako ikerketa batek frogatu du tundrako biodibertsitatearen galera motelago ari da gertatzen herbiboro handiak dauden lekuetan. Ikertzaileek 15 urtez tundrako biodibertsitatearen jarraipena egin dute, eta ikusi dute 2002 eta 2017 bitartean tundrako biodibertsitateak behera egin duela. Alabaina, alde nabarmena nabaritu dute elur-oreina, idi musketaduna eta bestelako herbiboroak dauden eremuetan. Zehazki, ikusi dute herbibororik ez zegoen eremuetan biodibertsitatea bi aldiz azkarrago galdu zela. Gainera, herbiboroen aniztasuna ere garrantzitsua dela azaldu dute, espezie bakoitzak desberdin kimatzen baititu landareak. Azalpenak Elhuyar aldizkarian.
GenetikaKristobal Kolon nabigatzailearen jatorriari buruzko ikerketa genetikoak egiten ari da Joxe Mari Ertzilla historiazalea. Bere hipotesiaren arabera, nabigatzailea agota eta euskalduna zen. Kristobal Kolonen DNA geografikoari buruzko ikerketa batean bildu ditu bere hipotesia eta ateratako ondorioak, eta bere ikerketaren oinarria HLA-B27 antigenoa da. Agoten eta beste hainbat gizatalderen ohikoa zen antigeno hori, eta Ertzillaren ustez, Kristobal Kolonek HLA-B27 antigenoa izateak azaltzen ditu bizitzan izan zituen hainbat osasun arazo. Oraindik ez da gauzatu Kolon nabigatzailearen jatorria zehazteko azterketa genetikoa, lau hezur zati bakarrik baitaude, almendra baten neurrikoak, eta baldintza eskasean. Ikerketa honen inguruko informazio gehiago Berrian: Antigeno bat Kolonen bidaide.
MedikuntzaEndometriosia bakterio baten eraginez sor daitekeela iradoki du ikerketa berri batek. Zehazki, Fusobacterium generoko bakterio bati egotzi diote gaixotasun horren sorrera. Endometriosiak ugaltze-adinean dauden emakumeen %15ari eragiten dio, eta oso mingarria izan daiteke. Alabaina, oso gutxi ikertu den gaixotasuna da. Argitaratu berri den ikerketa batean, 155 emakume japoniar aztertu dituzte, eta endometriosia zutenen erdietan baino gehiagotan aurkitu dute Fusobacterium bakterioa. Horrez gain, sagu ereduetan ere frogatu dute bakterio hori inokulatuta endometriosiaren sintomak eta lesioak okertu egiten direla. Azalpenak Elhuyar aldizkarian.
BotanikaAlga inbaditzaile batek mahatsondoen defentsa-mekanismoak nabarmen indartzen dituela frogatu berri dute. UPV/EHU eta IFAPA institutua buru dituen SEAWINES proiektuaren barruan egin dute aurkikuntza hori. Mahastietan oso ohikoak dira mildiu eta oidio infekzioak, biak hala biak onddoek sortutakoak. Infekzio horien kontra ohikoena tratamendu kimikoak erabiltzea da. Ikerketa berritzaile horretan alternatiba bat topatzen saiatu dira, eta bi alga erabili dituzte horretarako: Ulva ohnoi eta Rugulopteryx okamurae. Azken hori, gainera, alga inbaditzailea da, eta ehunka tona alga erauzten dira Mediterraneotik urtero. Hala, egin dituzten probetan ikusi dute Rugulopteryx okamurae algatik erauzitako estraktu batekin landarea tratatzean areagotu egin zirela, besteak beste, landareko erresistentzia-geneen espresioa eta entzima antioxidatzaileen jarduera. Informazio gehiago Zientzia Kaieran: Alga inbaditzaileak mahastizaintzarako.
GeologiaAste honetan Zientzia Kaieran Blanca Martinez mapa geologikoen inguruan jardun da. Mota honetako mapa eraikitzeko, mapa topografiko bat hartzen da oinarri, eta hura oinarri hartuta zelaian identifikatzen dira arrokak, egiturak eta prozesu geologikoak. Ondoren, elementu horiek guztiek ikurrekin identifikatzen dira eta duten adinaren arabera kolorez margotzen dira mapan. Ikur eta kolore horiek nazioartean ezarritako kode batzuei jarraiki aukeratzen dira, eta horrela, edozein mapa geologikoren historia berreraiki daiteke. Gainera, informazio hori guztia mapa geologikoaren ondoan jartzen den legenda batean idazten da. Azkenik, maparen eskala ezartzea ere oso garrantzitsua da, eta bi mota daude: zenbakizko eskalak, eta eskala grafikoak. Datu guztiak Zientzia Kaieran: Mapa geologikoa, koloretako mihisea baino askoz gehiago.
Materialen zientziaBanbua aukera interesgarria da eraikuntzaren sektorerako. Material honek hainbat abantaila ditu beste material batzuekin alderatuz. Alde batetik, jasangarria da, hazkuntza azkarra baitu, eta ondorioz, zuhaitzek baino karbono gehiago xurgatzen dute denbora tarte berdinean. Bestetik, bere izaera tubularragatik, banbuak erresistentzia espezifiko eta zurruntasun espezifiko handiak eskaintzen ditu. UPV/EHU eta TECNALIAren arteko lankidetza batek banbuaren erabilera sustatzeko ikerketa bat egin du, eta material horren propietate mekanikoak eta kimikoak ezagutu nahi izan dituzte. Hala ondorioztatu dute, kimikoki ezaugarri oso esanguratsurik ez duen arren, banbuak erresistentzia handiagoa daukala baina zurruntasun txikiagoa, pinu gorriarekin alderatuz. Azalpenak Zientzia Kaieran: Banbuaren karakterizazio mekanikoa eta kimikoa.
ArkeologiaHatzez grabatutako horma-irudi batzuk neandertalek egindakoak direla baieztatu dute. Orain arte datatu diren grabatu zaharrenak dira, eta La Roche-Cotard haitzuloan daude (Erdialdea-Loira harana). Ikertzaileek azaldu dutenez, gutxienez 57000 urte dituzte, baina litekeena da 75000 urte ere izatea. Hatz-marken 3D ereduak erabiliz, frogatu dute, hain zuzen ere, irudiak hatzez eginda daudela, eta espazioa eta kokapena aintzat hartuta, ikertzaileek ondorioztatu dute nahita sortutakoak direla. Ikerketa honek frogatu du neandertalen portaera eta jarduerak sapiensenak bezain konplexuak izan zitezkeela. Informazio gehiago Elhuyar aldizkarian.
Adimen artifizialaIkertzaile batzuk ohartarazi dute adimen artifizial sortzaileko sistemek pertsonen sinesmenak eralda ditzaketela, informazio faltsua eta alborapenak transmitituz. Izan ere, adimen artifizialak segurtasun handia transmititzen du ematen dituen erantzunetan, eta gizakiak berezko joera du aditua dirudien batek emandako informazioa azkarrago eta gehiago barneratzeko. Sistema hauek, gainera, informazio faltsua edo ez-zuzena ematen dute batzuetan, eta ikertzaileek uste dute informazio hori jendearen sinesmenetan hedatzeko arrisku handia dagoela. Datuak Elhuyar aldizkarian: Adimen artifizial sortzaileak sinesmenak eralda ditzake.
Egileaz:Irati Diez Virto Biologian graduatu zen UPV/EHUn eta Plentziako Itsas Estazioan (PiE-UPV/EHU) tesia egiten dabil, euskal kostaldeko zetazeoen inguruan.
The post Asteon zientzia begi-bistan #444 appeared first on Zientzia Kaiera.
Psicodelia y tratamientos psiquiátricos, notas clínicas y evolucionistas

Cómo influyen los parásitos en el comportamiento de los animales, cómo se modifica la conducta de las madres mamífero o cuáles son las enfermedades que nos afectan y desde cuándo hemos desarrollado comportamientos funerarios ante la muerte son algunos de los aspectos que se analizarán en la V Jornada Nacional sobre Evolución y Neurociencias.
Especialistas en ambas materias se reunirán el 11 y 12 de mayo en una nueva edición conducida por Eva Garnica y Pablo Malo, psiquiatras y miembros de la Red de Salud Mental de Bizkaia, y organizada por esa misma entidad y la Cátedra de Cultura Científica de la UPV/EHU.
La jornada, cuya primera edición se celebró en 2017, se ha convertido en una cita imprescindible para las y los expertos en ámbitos como la psiquiatría, la psicología o la biología. Una jornada que sirve para analizar el comportamiento humano desde un punto de vista evolucionista y divulgar de un modo accesible para todos los públicos.
En los años noventa del siglo pasado se produjo el resurgimiento de la investigación en psicodelia, abriendo todo un mundo de tratamientos psiquiátricos y un mejor conocimiento de las bases evolutivas en las que se basa el efecto de estos fármacos, como nos cuenta Luis Caballero en esta charla.
Luis Caballero es psiquiatra, jefe de la Sección de Psiquiatría del Hospital Universitario Puerta de Hierro y Profesor Asociado del Departamento de Psiquiatría de la Universidad Autónoma de Madrid.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Psicodelia y tratamientos psiquiátricos, notas clínicas y evolucionistas se ha escrito en Cuaderno de Cultura Científica.
Ezjakintasunaren kartogragfia #452
 Irudia: ESA/Webb, NASA & CSA, J. Lee and the PHANGS-JWST Team / J. Schmidt
Irudia: ESA/Webb, NASA & CSA, J. Lee and the PHANGS-JWST Team / J. SchmidtGaixotasun mentalak arazoak sortzen ditu, ez bakarrik sortzen den unean eta agertzen den bitartean, baizik eta epe luzean ere. A lifetime of mental illness accelerates ageing Rosa García-Verdugoren eskutik.
Beroarekin zerikusia duen guztiaren azalpena bibrazioak direla ez da erabat egia: Traditional understanding of heat transport, involving phonons, is not applicable to strong heat insulators
Boxer txakurretan aurkitutako parasito bat giza minbizi mota batzuen konponbidea izan daiteke: A dog parasite could help fight incurable cancers Arthur Battistoni eta Françoise Debierre-Grockiego.
Hubbleko irudien eta James Webb-eko irudien konbinazioak objektu astrofisikoen misterio asko argitzen lagunduko du, baina, oraingoz, misterio berriak aurkitzeko balio izan du. DIPC jendea New mysteries in the nuclear star cluster of the Phantom galaxy
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartogragfia #452 appeared first on Zientzia Kaiera.
Una batería biodegradable para móviles
 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsActualmente no seríamos capaces de realizar nuestras tareas diarias sin los teléfonos móviles y otros aparatos electrónicos. Pero, desgraciadamente, la esperanza de vida de estos dispositivos es bastante limitada. En España se desechan anualmente más de 20 millones de dispositivos de telefonía móvil.
Detrás de esta cifra está, por un lado, la obsolescencia programada, tanto por incompatibilidad de hardware como por falta de actualización en el sistema operativo. Otro aspecto clave en este tipo de dispositivos es la batería, normalmente basada en tecnología de iones de litio. Estas baterías cuentan normalmente con una vida útil inferior a las 1 000 cargas.
Así, los teléfonos inteligentes tienen una media de uso de 18 meses, y en muy raras ocasiones se emplean durante más de cuatro o cinco años.
Una de las estrategias para solventar estos problemas sería el desarrollo de baterías transitorias (transient, en inglés), basadas en materiales abundantes que se degraden en subproductos no tóxicos. Todo ello, manteniendo los altos estándares de funcionamiento que poseen las baterías convencionales de iones de litio. Pero ¿es esto realmente posible?
Economía circular, una solución parcialLa solución actualmente más extendida consiste en adoptar patrones circulares que se alejen del sistema de producción lineal. Es decir, transitar desde “producir, consumir, tirar” a nuevos hábitos de manera que puedan volver a reutilizarse los dispositivos móviles, o parte de ellos, en otras aplicaciones.
Si consideramos una perspectiva circular, las alternativas de reutilización o remanufactura deben ser preferentes sobre el reciclaje. Una posible opción son los sistemas de garantía extendida, los sistemas de recogida y los mercados de segunda mano.
Existen empresas que, tras una recogida selectiva, reacondicionan teléfonos móviles para posteriormente venderlos a menor coste. Iniciativas como estas generan grandes beneficios ambientales, sociales y económicos.
Otra opción es el reciclaje de las baterías. Mediante diversos tratamientos químicos y térmicos, es posible extraer los materiales económicamente relevantes de las baterías, que serán utilizados posteriormente para fabricar nuevas baterías. De este modo, se limitan los posibles efectos nocivos de materiales como el litio, el cobalto o el manganeso, y se evita la necesidad de procesos de extracción de metales de la minería tradicional.
Pero ¿qué ocurre con los dispositivos electrónicos que no puedan ser tratados?
Los móviles que no se recogenDebemos tener en cuenta que los teléfonos móviles son los aparatos electrónicos con los índices de recogida más bajos. A pesar de los esfuerzos que desarrollan diversas entidades públicas, como por ejemplo la instalación de puntos limpios móviles no asistidos, existe un altísimo riesgo de que gran cantidad de teléfonos móviles se pierdan en el medio ambiente.
Únicamente el 17,4 % de los residuos electrónicos se recogen, tratan y reciclan adecuadamente. El restante no se documenta, y gran parte acaba en destinos de lo más variados, desde vertederos, a bosques, ríos o mares. Ello implica que gran cantidad de materiales no biodegradables y altamente tóxicos, como son el cobalto, el níquel, el manganeso y los electrolitos orgánicos acaben contaminando los suelos, el aire, el agua y los seres vivos; incluidos los humanos.
Por ejemplo, las sustancias tóxicas que forman parte de las baterías convencionales de iones de litio pueden filtrarse en las aguas subterráneas, donde pueden influir en las especies acuáticas y terrestres. La Organización Mundial de la Salud estima que la exposición a los residuos electrónicos puede provocar alteraciones de las funciones pulmonares y problemas respiratorios, especialmente en niños y adolescentes, entre otros efectos.
Baterías compostables, otra posible soluciónEn un reciente estudio desarrollado por la Universidad del País Vasco/Euskal Herriko Unibertsitatea, la Escuela Politécnica Federal de Zúrich y la Universidad de Nueva Gales del Sur, hemos demostrado que es posible fabricar baterías compostables que además sean competitivas en cuanto a rendimiento.
La tecnología transitoria busca el desarrollo de materiales, dispositivos o sistemas que experimenten procesos de degradación controlada tras un periodo de funcionamiento estable, dejando tras de sí residuos inocuos.
Así, primero identificamos elementos no tóxicos, abundantes y biodegradables, que ofrecieran unas características físicas, mecánicas y electroquímicas mínimas.
Tras una extensa búsqueda, identificamos y aplicamos las siguientes opciones:
- Polímeros de origen natural como la celulosa y la agarosa para el electrolito.
- La polidopamina, un material natural con alta capacidad de reducción-oxidación, para el desarrollo del cátodo.
- Un ánodo de zinc, metal biodegradable y biocompatible que permite fabricar electrolitos basados en agua.
 Fotografías que muestran la degradación de los componentes individuales de la pila transitoria en el tiempo.
Fotografías que muestran la degradación de los componentes individuales de la pila transitoria en el tiempo.Author provided
El trabajo dio como resultado una batería recargable que combina compostabilidad con un rendimiento electroquímico sobresaliente. De hecho, se observó una pérdida de peso del 49,9 ± 2,9 % tras 63 días en condiciones de compostaje industrial.
También se ha demostrado que estas baterías pueden cargarse a lo largo de más de 10 000 ciclos, el equivalente a 27 años continuados considerando una carga diaria. Gracias nuestro prototipo, el sueño de una batería compostable que también cumpla la función completa de un dispositivo de almacenamiento de energía desde el punto de vista electroquímico es una realidad.![]()
Sobre el autor: Erlantz Lizundia, Profesor de Ecodiseño y Economía Circular, Universidad del País Vasco / Euskal Herriko Unibertsitatea
Para saber más:
Por qué la tecnología deja de funcionar
Basura electrónica y economía circular
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Una batería biodegradable para móviles se ha escrito en Cuaderno de Cultura Científica.

