Tutik ere ez dakigu. Unibertso ezezagunerako gida bat

Jorge Cham komikilariak eta Daniel Whiteson partikula-fisikariak elkar harturik Tutik ere ez dakigu. Unibertso ezezagunerako gida bat liburuan (2017) ekin diote unibertsoari buruz ez dakigun hori guztia arakatzeari: kosmosaren ezagueran ditugun zulo itzelak, alegia. Gizadiak mundu fisikoari buruz duen ezagutza hutsunez beterik dago. Ez dira horiek, alabaina, hutsune txikitxo batzuk, hola-hola ez ikusi egitekoak, baizik eta izugarrizko leize hondogabeak munduaren funtzionamenduari buruzko gure ideia oinarri-oinarrizkoetan.
 Irudia: Tutik ere ez dakigu. Unibertso ezezagunerako gida bat liburuaren azala. (Iturria: UPV/EHU argitalpenak)
Irudia: Tutik ere ez dakigu. Unibertso ezezagunerako gida bat liburuaren azala. (Iturria: UPV/EHU argitalpenak)Zientziaren azalpen jostari bezain argien lagungarri harturik infografia bitxi eta bineta umoretsuak, oraingoz eskura dauden erantzunik onenak ematen dizkigute ziurrenik inoiz bururatuko ez zitzaizkizun hainbat galderaren aurrean. Unibertsoa, hara, mukuru beterik dago itxura batean ez hanka ez buru duten gauza xelebrez. Cham eta Whitesonek, haatik, argi erakusten dute erantzuteko gai ez garen galderak ez direla interes gutxiagokoak, inondik inora ere, dagoeneko erantzuna dutenak baino.
Fisikako misteriorik handienetarako gida goitik beheraino irudiz apaindu hau, halaber da baliagarri badakizkigun baina korapilatsu diren hainbat gauzaren katramilak askatu eta argitzeko: hasi quark eta neutrinoetatik, eta uhin grabitazional eta zulo beltz lehergarrietaraino. Umore eta atsegin bizian, hor garamatzate Cham eta Whitesonek bazter jakinik eta mapa zehatzik gabeko lurraldetzat ikustera unibertsoa, oraindik ere esploragai guretzat.
“Zientziak asko daki unibertsoari buruz; benetan kitzikagarri dena, hala ere, ez dakiguna da. Eta nekez irudika liteke ezezaguna esploratzeko modu atseginago bat liburu honen orrietan murgiltzea baino.” (Sean Carroll, kosmologoa)
Jorge Cham (1976) Piled Higher and Deeper online-komiki arrakastatsuaren sortzailea da. Robotikan doktore da Stanford unibertsitatetik.
Daniel Whiteson (1975) Partikulen Fisika Esperimentaleko katedradun da Kaliforniako Unibertsitatean, eta Estatu Batuetako Fisikari Elkarteko kide. CERNeko Hadroi Talkagailu Handia erabiliz dihardu ikerlanean.
Argitalpenaren fitxa:- Izenburua: Tutik ere ez dakigu. Unibertso ezezagunerako gida bat
- Egilea: Jorge Cham eta Daniel Whiteson
- Itzultzailea: Juan Garzia Garmendia
- ISBN: 978-84-1319-347-2
- Hizkuntza: Euskara
- Urtea: 2021
- Orrialdeak: 500 or.
Euskara, Kultura eta Nazioartekotzearen arloko Errektoretza, UPV/EHU argitalpenak, ZIO bilduma: Tutik ere ez dakigu. Unibertso ezezagunerako gida bat
The post Tutik ere ez dakigu. Unibertso ezezagunerako gida bat appeared first on Zientzia Kaiera.
El problema de los calissons
Este verano he pasado unos días visitando la región francesa de la Provenza. Mi visita empezó en la hermosa ciudad de Aix-en-Provence, donde compré una caja de los famosos calissons.
 Fotografía de mi visita a la Fundación Vasarely, en Aix-en-Provence, Francia. Fotografía: Marian Espinosa
Fotografía de mi visita a la Fundación Vasarely, en Aix-en-Provence, Francia. Fotografía: Marian EspinosaCalissons
El calisson es un dulce típico de la región francesa de la Provenza, asociado especialmente con la ciudad de Aix-en-Provence. Está elaborado a partir de una pasta formada por almendras molidas y melón confitado (u otras frutas confitadas), con un glaseado blanco por encima, que se cuece a fuego lento. La forma del calisson es, más o menos, la de un rombo formado por dos triángulos equiláteros (similar a la de la forma de la caja que mostramos en la siguiente imagen).
 Fotografía de una caja de calissons, con forma de rombo (como la forma de los propios calissons), que me compré en la ciudad francesa de Aix-en-Provence. Fotografía: Marian Espinosa
Fotografía de una caja de calissons, con forma de rombo (como la forma de los propios calissons), que me compré en la ciudad francesa de Aix-en-Provence. Fotografía: Marian Espinosa
No está muy claro el origen de este dulce, que parece ser originario de Italia. Como se comenta en la correspondiente entrada de la Wikipedia (en francés), “una de sus primeras referencias se remonta al siglo XII, en un texto medieval italiano en latín que utiliza el término calisone para referirse a un pastel de almendra y harina similar al mazapán moderno”. Y existe otra referencia posterior, el texto Chronique des Vénitiens / Crónica de los venecianos (1275), del italiano Martino Canal, en la que se menciona un dulce, a base de pasta de almendras y nueces a la que se añadían diversas especias (canela y clavo), de nombre “calissons”.
Tampoco está claro cuando llegan estos dulces a la Provenza. Según algunas versiones podría haber sido importado por uno de los cocineros del príncipe francés René d’Anjou / Renato de Anjou (1409-1480), que entre otros títulos fue rey de Nápoles, Sicilia, Aragón y Mallorca. Se cuenta que durante el segundo matrimonio de Renato de Anjou con Jeanne de Laval / Juana de Laval, en 1454, el jefe de la confitería del rey sirvió algunos de estos dulces a la futura reina, que dijo entonces en provenzal “Di calin soun” (que no sé bien cómo traducir, pero para darle cierta gracia me aventuro a traducirlo como “estos son besos”). Por otra parte, en la Wikipedia se cita que el término calisson, con el significado actual, ya aparece en la Provenza en el año 1503. De hecho, la almendra, elemento principal de los calissons, se introdujo en la Provenza en el siglo XVI, por lo que es posible que la introducción del dulce en esta región sea paralela al desarrollo de la producción y comercialización de las almendras.
 Fotografía de los calissons dentro de su caja, que me compré en mi reciente visita a Aix-en-Provence. Aunque como vemos la forma de estos calissons es más bien como una vesica piscis y no como un diamante formado por dos triángulos equiláteros. Fotografía: Marian Espinosa
Fotografía de los calissons dentro de su caja, que me compré en mi reciente visita a Aix-en-Provence. Aunque como vemos la forma de estos calissons es más bien como una vesica piscis y no como un diamante formado por dos triángulos equiláteros. Fotografía: Marian EspinosaPero dejemos las cuestiones históricas aparte y vayamos a la cuestión matemática relacionada con estos dulces provenzales. Aunque si os animáis a prepararlos vosotros mismos, podéis encontrar la receta en muchos blogs de postres, o de recetas de cocina, en general.
 Fotografía de un plato con calissons, cuya forma es la de un rombo o diamante formado por dos triángulos equiláteros, que hemos tomado de una página francesa de recetas, en la que podéis leer cómo se hacen los calissons. La página de recetas es Odelices.Demostraciones sin palabras
Fotografía de un plato con calissons, cuya forma es la de un rombo o diamante formado por dos triángulos equiláteros, que hemos tomado de una página francesa de recetas, en la que podéis leer cómo se hacen los calissons. La página de recetas es Odelices.Demostraciones sin palabras
La primera vez que leí sobre el problema de los calissons fue en el magnífico libro Proofs without words / Demostraciones sin palabras, de Roger B. Nelsen. Este es un tema, el de las demostraciones sin palabras, al que le hemos dedicado varias entradas en el Cuaderno de Cultura Científica, entre ellas:
* Matemáticas para ver y tocar
* Más matemáticas para ver y tocar
* Teoremas geométricos sin palabras: Viviani
* Teoremas geométricos sin palabras: Conway
* Teoremas geométricos sin palabras: Herón
* Teoremas geométricos sin palabras: Snover
Las demostraciones sin palabras, como comenta el matemático Roger B. Nelsen –autor del libro Proofs without words / Demostraciones sin Palabras (publicado por la MAA, Mathematical Association of America, en 1993) –, se fueron haciendo populares en la comunidad matemática a raíz de su publicación en las revistas de la MAA, Mathematics Magazine y The College Mathematical Journal, en las que empezaron a aparecer hacia 1975, primero como imágenes de relleno entre artículos y posteriormente como secciones fijas de las revistas. Las demostraciones sin palabras no son realmente demostraciones matemáticas en sí mismas, son más bien diagramas, esquemas o dibujos que nos ayudan a comprender por qué un teorema es cierto o que encierran la idea de la verdadera demostración matemática. Son sugerentes, atractivas y todo un ejercicio de estímulo del pensamiento.
El origen del problema de los calissons y su demostración visual, tema que nos ocupa en esta entrada del Cuaderno de Cultura Científica, es el artículo The problem of calissons, de los matemáticos Guy David y Carlos Tomei, publicado en 1989 en la revista The American Mathematical Monthly (que también es una revista de la MAA, creada en 1894).
El problema de los calissonsTomando las mismas palabras que utilizaron David y Tomei en su artículo de la revista The American Mathematical Monthly,
“Un calisson es un dulce francés con la forma de dos triángulos rectángulos pegados por uno de sus lados. Los calissons podrían guardarse en una caja con la forma de un hexágono regular, y su empaquetado sugeriría un interesante problema de combinatoria. Supongamos una caja (hexagonal) cuyos lados tienen longitud n que se llena con calissons cuyos lados tienen longitud 1. La diagonal larga de cada calisson en la caja tiene tres posibles orientaciones, como en la imagen.
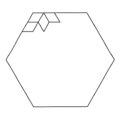 Las tres posibles orientaciones de los calissons en una caja hexagonal
Las tres posibles orientaciones de los calissons en una caja hexagonal
Nuestro resultado principal es que el número de calissons de cada una de las tres orientaciones es un tercio del número de calissons que entran en la caja (hexagonal).”
El problema de los calissons consiste en cómo demostrar esa afirmación, es decir, que el número de calissons de cada orientación es el mismo, un tercio del total de los calissons que entran en la caja hexagonal. Y lo hermoso de la demostración es que consiste en un argumento intuitivo y visual relacionado con el espacio tridimensional.
Los matemáticos David y Tomei, en su artículo The problem of calissons, toman una caja hexagonal cuyo lado tiene longitud 5 (es decir, n = 5), considerando que los lados del calisson son de longitud 1, que es la imagen que mostramos a continuación, con el objetivo de mostrar que hay la misma cantidad de calissons en cada una de las tres direcciones posibles.
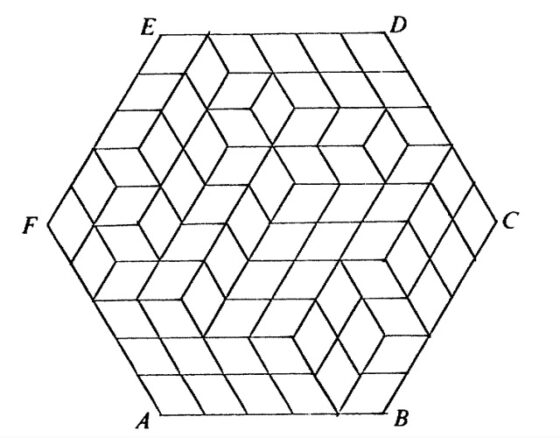 Distribución aleatoria de los 75 calissons que entran en una caja hexagonal cuyo lado tiene longitud 5, considerando que los lados del calisson son de longitud 1, que es la considerada por los matemáticos David y Tomei en su artículo The problem of calissons
Distribución aleatoria de los 75 calissons que entran en una caja hexagonal cuyo lado tiene longitud 5, considerando que los lados del calisson son de longitud 1, que es la considerada por los matemáticos David y Tomei en su artículo The problem of calissonsLa solución consiste en rotar un poco la caja hexagonal para que un vértice quede arriba y colorear cada calisson en función de la orientación que tiene, es decir, los pintamos de tres colores distintos (por ejemplo, en el artículo se utiliza blanco, gris y negro). De esta forma, nuestra imagen de una caja hexagonal rellena con calissons (luego, una imagen esencialmente plana) se convierte en una imagen tridimensional que representa una serie de pequeños cubos apoyados entre tres paredes cuadradas perpendiculares (de tamaño 5 x 5, en el ejemplo de David y Tomei, luego con una superficie de 25 cuadrados, pero en general serán paredes cuadradas con n2 cuadrados), una abajo, otra a la derecha y una tercera a la izquierda. En esta representación tridimensional de pequeños cubos (se verán algunos ejemplos a continuación) puede verse que cada calisson es una cara visible de un pequeño cubo, de manera que todas las caras de un mismo color (que provienen de calissons con la misma orientación) miran en la misma dirección, paralelas a una de las tres paredes sobre las que se apoyan los pequeños cubos. Resulta que todas las caras de pequeños cubos (incluyendo los cuadrados de las paredes de apoyo que no se han cubierto) que miran en una misma dirección son las mismas que todos los cuadrados de la pared de apoyo, por lo tanto, 25 en este caso y n2, en general.
Veámoslo con algunos ejemplos de distribuciones de calissons en una caja hexagonal de tamaño n = 3 (como la que vemos en la siguiente imagen), por lo tanto, que se rellena con 27 dulces con forma de diamante.
 Caja hexagonal, cuyo lado mide 3, siendo la medida de los lados de los calissons 1, y los 27 calissons con los que se rellena la caja
Caja hexagonal, cuyo lado mide 3, siendo la medida de los lados de los calissons 1, y los 27 calissons con los que se rellena la caja
A continuación, vamos a rellenar la caja hexagonal (de lado 3) con los 27 calissons, de tres formas distintas y vamos a utilizar el procedimiento anterior (girar ligeramente y pintar con tres colores distintos los calissons en función de su orientación en la caja) para comprobar que en los tres casos la cantidad de calissons en cada orientación es igual a 9.
Ejemplo 1, con los calissons agrupados
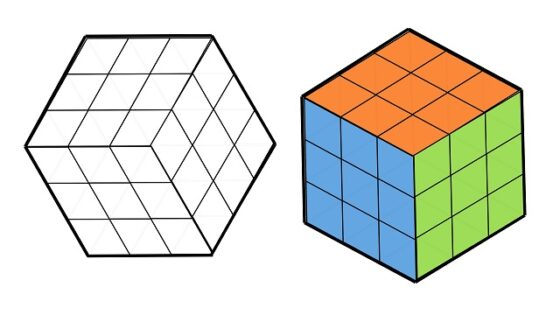
Ejemplo 2
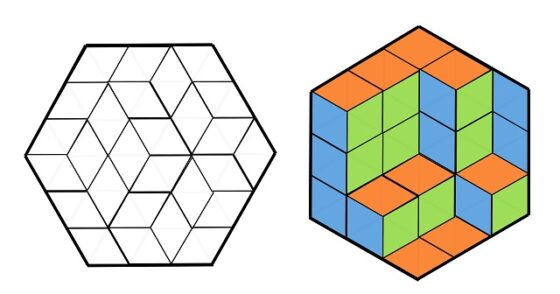
Ejemplo 3
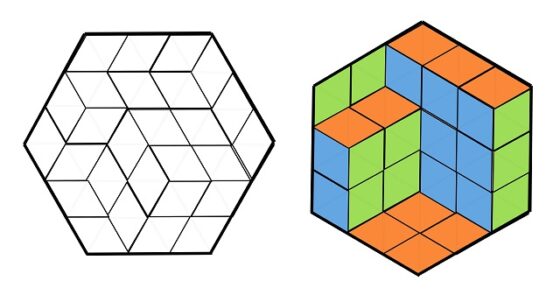
Este argumento visual nos sirve para cualquier tamaño n de la caja hexagonal, en la que introduciremos 3n2 calissons.
En esta misma línea, la imagen que ilustraba la demostración de David y Tomei, con la distribución mostrada arriba, para una caja de tamaño 5, es la siguiente (utilizando blanco, gris y negro).
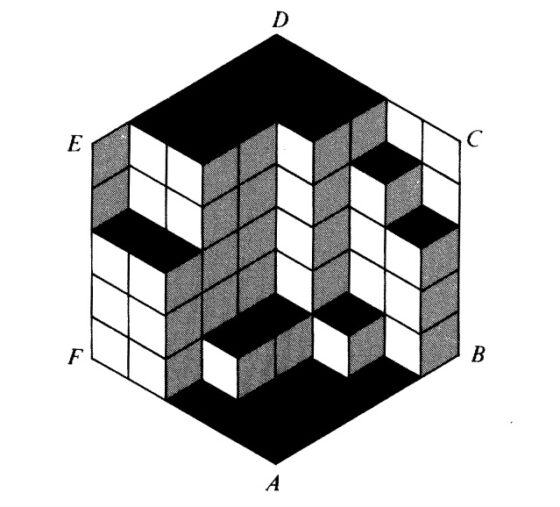
En consecuencia, se ha demostrado el resultado buscado.
Teorema: En todo empaquetamiento de calissons (con forma de diamante) en una caja hexagonal, la cantidad de ellos con una orientación dada es igual a la tercera parte del total de calissons que se incluyen en la caja.
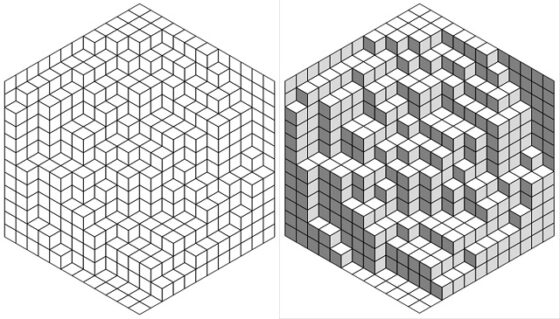 Distribución de 432 calissons en una caja hexagonal de lado igual a 12, junto con su transformación en una imagen tridimensional, mediante el coloreado –blanco, gris claro y gris oscuro- de los calissons en función de su orientación, y en la que se comprueba que hay la misma cantidad de dulces en cada orientación, en concreto, 144. Imagen del blog Possibly wrong
Distribución de 432 calissons en una caja hexagonal de lado igual a 12, junto con su transformación en una imagen tridimensional, mediante el coloreado –blanco, gris claro y gris oscuro- de los calissons en función de su orientación, y en la que se comprueba que hay la misma cantidad de dulces en cada orientación, en concreto, 144. Imagen del blog Possibly wrongLa demostración que aparece en el artículo de David y Tomei, y que después incluye Nelsen en su libro, es una demostración sin palabras, luego visual e intuitiva, pero no una demostración matemáticamente rigurosa. Sin embargo, sí es posible dar demostraciones más matemáticas de este resultado, y de alguna generalización del mismo, para la cual, además, no es válido el razonamiento visual anterior. Para quienes estéis interesados en la misma (solo se necesita un poco de álgebra de vectores) podéis leerla en el blog Symmetry de Gábor Damásdi.
Bibliografía
1.- Roger B. Nelsen, Demostraciones sin palabras (ejercicios de pensamiento visual), Proyecto Sur, 2001.
2.- Guy David, Carlos Tomei, The problem of the Calissons, American Mathematical Monthly, vol. 96, n. 5, pp. 429-430, 1989.
3.- Gábor Damásdi, Symmetry (blog): Problem of calissons
4.- Wikipedia: Calisson
El artículo El problema de los calissons se ha escrito en Cuaderno de Cultura Científica.
Musikak neke fisikoa arintzen du
Pentsatzen dut gutako askok jarduera fisikoren bat egin dugula –lana edo kirola– ekintzaren erritmoari musikarekin lagunduta. Halakorik egin ez duenak ere ikusiko zituen noizbait, ziur aski, filmen batean pertsona taldeak batera lan egiten musika piezaren baten edo kanturen baten erritmoan. Eta maila handiko atletek sarri jotzen dute musika entzutera entrenamenduetan edota proba fisikoetan. Hala egiten dutenean, neke txikiagoa sentitzen dute. Musikari eta kantuari esker, eramangarriagoa da jarduera fisikoa.
 Irudia: musikari eta kantuari esker, eramangarriagoa da jarduera fisikoa. (Argazkia: Andrea Piacquadio – Domeinu publikoko irudia. Iturria: pexels.com)
Irudia: musikari eta kantuari esker, eramangarriagoa da jarduera fisikoa. (Argazkia: Andrea Piacquadio – Domeinu publikoko irudia. Iturria: pexels.com)Galdera da ea neke sentsazio txikiago hori musikak edo kantuak neke seinale propiozeptiboari (norberaren egoeraren hautemate sentsoriala) arreta txikiagoa jartzen laguntzen duelako ote den, edo, distrakzio efektu horretaz gain, beste efekturen bat ote dagoen neke seinale horren gainean. Fenomeno hori esperimentuen bidez aztertu da. Batetik, baldintza normaletan ariketa fisikoren bat egiten ari ziren bitartean musika entzuten ari ziren pertsonen sentsazioak eta, alderatu egin da. Bestetik, musikak neke sentsaziotik aldentzea oso zaila –ezinezkoa ez esatearren– zuten beste batzuen sentsazioak (une oro behartuta baitzeuden egiten zuten jardueraz jabetzera).
Ikertzaileek baldintza esperimental bat sortu zuten –musical agency deitu zioten– eta, horri jarraikiz, parte hartzaileek musika soinuak modulatzen zituzten gorputz mugimenduen bidez. Horretarako, musika soinuen sorrera modulatzeko balio zuten sentsoreak jarri zituzten entrenamendu makinetan. Horrela, baldintza esperimentalean (musika agentzia), parte hartzaileak musikalki mintzatu zitezkeen fitness makinan egiten zituzten mugimenduen bidez. Pertsona horiek une oro jabetzen ziren egiten zuten jardueraz, eta, beraz, suposatzen da lehen aipatutako distrakzio efektua ez zela gertatzen.
Musika agentziako taldean parte hartu zutenek akidura fisiko txikiagoa sentitu zuten musika modu pasiboan entzun zutenek baino. Eta neke sentsazio txikiago hori ez zen bat etorri ez indar txikiagoa egitearekin ez gastu metaboliko txikiagoarekin, nahiz eta azken kasu horretan bi baldintzen arteko aldea esangura estatistikoaren mugan egon. Lehen adierazi dudan bezala, diseinu esperimental horretan pertzepzio propiozeptiboa funtsezkoa da zer musika sortu erabakitzeko. Hau da, fitness makinarekin nola elkarreragin, zer mugimendu maiztasun egin edo zer indar erabili erabakitzeko orduan, neke sentsazioa funtsezko elementua da, eta, beraz, parte hartzaileak ezin dira sentsazio horretatik aldendu. Beraz, musika entzun edo sortzen den bitartean jarduera fisikoren bat egitean izaten den neke sentsaziorik txikiena ere ez da musika horrek ematen duen distrakzioagatik bakarrik gertatzen; aitzitik, efektu horrek berezko garrantzia du.
Ez dirudi erraza denik efektu hori berehalako kausa zehatz batzuei egoztea. Ikerketaren egileek iradoki dutenez, musika agentziak musika egituraren eta mugimenduen arteko sinkronizazio handiagoa ekar dezake, eta horrek mugimenduak egitea erraztu dezake, koordinazio hobeak ahalegin txikiagoa ekar dezakeelako. Halaber, baldintza horretan mugimendu bakoitza egiteko behar diren denborak iragartzeko gaitasuna handiagoa izateko aukera planteatzen dute, eta horrek propiozepzioaren garun azaleko irudikapenean nolabaiteko eragina izateko aukera, neke sentsazioa murrizten lagunduz.
Bestalde, baliteke musikak efektu lasaigarria izatea, eta horrek giharretako tentsioa txikiagoa izatea ekarriko luke, baita oxigenazio eraginkorragoa ahalbidetu ere; azken horrek egoera aktiboaren eta pasiboaren arteko gastu metabolikoaren aldea azalduko luke (eskatutako esangura estatistikoa lortu gabe, dena dela). Era berean, ez dirudi ikusitako efektua muskulu uzkurdura isotonikoen (lana sortzen dutenak) eta isometrikoen (lana sortzen ez dutenak, horma bati bultza egiten diogunean edo altxatu ezin dugun karga bat altxatzen saiatzen garenean esaterako) nekea modu desberdinean hautematen delako ematen denik. Bi uzkurdura modu horiek zeregin fisikoak egitean gertatzen dira eta izan liteke isometrikoek neke txikiagoa eragitea (dena dela gai hori esperimentalki egiaztatu zen ere, eta ez zen hala izan). Azken batean, ez dago argi zergatik sortzen duen musika agentziak neke sentsazio txikiagoa eta zergatik dakarren, agian, gastu metaboliko txikiagoa, indar bera egiten bada ere.
Musika ekoizpena (musika agentzia) erritu gehienen funtsezko alderdi bat da, baita gizakien gizarteetako jarduera neketsu askorena ere. Ez da harritzekoa jendeak, zerbait ospatzeko biltzen denean, musika eta dantza erabiltzea adierazpide gisa. Era berean, ez da harritzekoa talde lanetan aritzean, batez ere fisikoki gogorrak direnean, denek batera abestea eta, batzuetan, are musika tresnez laguntzea ere. Bada, jarduera musikalak nekea edo akidura modulatzeak eta hura murrizteak, gure bilakaeran eta giza zibilizazioaren garapenean, musika ekoizpena dakarten testuinguru batean egiten diren mota horretako jarduerak erraztuko zituen, batik bat gizarte tradizionaletan.
Erreferentzia bibliografikoa:Fritz, Thomas Hans; Hardikar, Samyogita; Demoucron, Matthias; Niessen, Margot; Demey, Michiel; Giot, Olivier; Li, Yongming; Haynes, Jhon-Dylan; Villringer, Arno; Leman, Marc (2013). Musical agency reduces perceived exertion during strenuous physical performance. PNAS 110, 44. DOI: 10.1073/pnas.1217252110
Egileaz:Juan Ignacio Pérez (@JIPerezIglesias) UPV/EHUko Fisiologiako katedraduna da eta Kultura Zientifikoko Katedraren arduraduna.
The post Musikak neke fisikoa arintzen du appeared first on Zientzia Kaiera.
Alan Turing y el poder del pensamiento negativo
Las pruebas matemáticas basadas en una técnica llamada diagonalización pueden ser implacablemente contrarias, pero ayudan a revelar los límites de los algoritmos.
Un artículo de Ben Brubaker. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Ilustración Kristina Armitage / Quanta Magazine
Ilustración Kristina Armitage / Quanta MagazineLos algoritmos se han vuelto omnipresentes. Optimizan nuestros viajes, procesan pagos y coordinan el flujo del tráfico en Internet. Parece que para cada problema que puede articularse en términos matemáticos precisos, hay un algoritmo que puede resolverlo, al menos en principio.
Pero ese no es el caso: algunos problemas aparentemente simples nunca pueden resolverse algorítmicamente. El científico informático pionero Alan Turing demostró la existencia de estos problemas “incomputables” hace casi un siglo, en el mismo artículo en el que formuló el modelo matemático de computación que lanzó la informática moderna.
Turing demostró este resultado innovador utilizando una estrategia contraria a la intuición: definió un problema que simplemente rechaza todo intento de resolverlo.
«Te pregunto qué estás haciendo y luego digo: ‘No, voy a hacer algo diferente'», explica Rahul Ilango, un estudiante de posgrado en el Instituto de Tecnología de Massachusetts que estudia informática teórica.
La estrategia de Turing se basa en una técnica matemática llamada diagonalización que tiene una historia ilustre. He aquí una explicación simplificada de la lógica de su prueba.
Teoría de cadenasLa diagonalización surge de un truco inteligente para resolver un problema rutinario que involucra cadenas de bits, cada uno de los cuales puede ser 0 o 1. Dada una lista de estas cadenas, todas igualmente largas, ¿se puede generar una nueva cadena que no esté en la lista?
La estrategia más sencilla es considerar cada cadena posible por turno. Supongamos que tienes cinco cadenas, cada una de cinco bits de longitud. Comienza repasando la lista en busca de 00000. Si no está, puedes parar; si está, pasa a 00001 y repite el proceso. Esto es bastante simple, pero lento para listas largas de cadenas largas.
La diagonalización es un enfoque alternativo que construye poco a poco una cadena nueva. Comienza con el primer bit de la primera cadena de la lista e inviértelo; ese será el primer bit de tu nueva cadena. Luego invierte el segundo bit de la segunda cadena y utilízalo como el segundo bit de la nueva cadena, y repite hasta llegar al final de la lista. Los bits que inviertes garantizan que la nueva cadena difiera de cada cadena de la lista original en al menos un lugar. (También forman una línea diagonal a través de la lista de cadenas, lo que da nombre a la técnica).
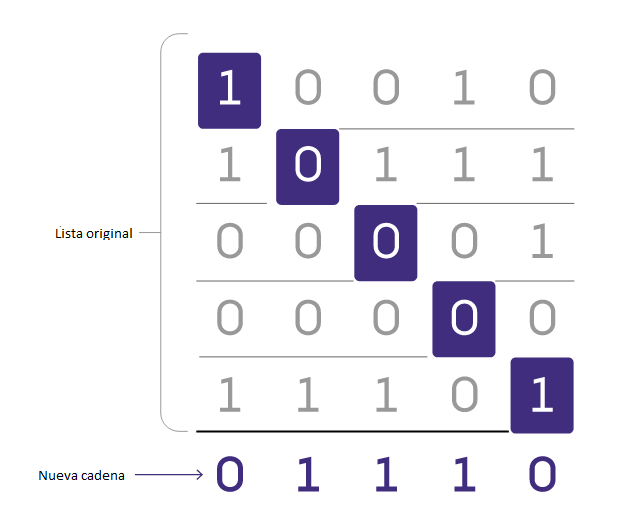 Ilustración: Merrill Sherman / Quanta Magazine
Ilustración: Merrill Sherman / Quanta MagazineLa diagonalización sólo necesita examinar un bit de cada cadena de la lista, por lo que suele ser mucho más rápido que otros métodos. Pero su verdadero poder reside en lo bien que se comporta con el infinito.
“Las cadenas ahora pueden ser infinitas; la lista puede ser infinita; todavía funciona”, afirma Ryan Williams, científico informático teórico del MIT.
La primera persona en aprovechar este poder fue Georg Cantor, el fundador del subcampo matemático de la teoría de conjuntos. En 1873, Cantor utilizó la diagonalización para demostrar que algunos infinitos son más grandes que otros. Seis décadas después, Turing adaptó la versión de Cantor de la diagonalización a la teoría de la computación, dándole un tono claramente a contracorriente.
El juego de la limitación [*]Turing quería demostrar la existencia de problemas matemáticos que ningún algoritmo puede resolver, es decir, problemas con entradas y salidas bien definidas pero sin un procedimiento infalible para pasar de la entrada a la salida. Hizo que esta vaga tarea fuera más manejable al centrarse exclusivamente en problemas de decisión, donde la entrada puede ser cualquier cadena de ceros y unos y la salida es 0 o 1.
Determinar si un número es primo (divisible sólo por 1 y por sí mismo) es un ejemplo de un problema de decisión: dada una cadena de entrada que representa un número, la salida correcta es 1 si el número es primo y 0 si no lo es. Otro ejemplo es comprobar los programas informáticos en busca de errores de sintaxis (el equivalente a errores gramaticales). Aquí, las cadenas de entrada representan código para diferentes programas (todos los programas se pueden representar de esta manera, ya que así es como se almacenan y ejecutan en los ordenadores) y el objetivo es generar 1 si el código contiene un error de sintaxis y 0 si no lo contiene.
Un algoritmo resuelve un problema sólo si produce la salida correcta para cada entrada posible; si falla aunque sea una vez, no es un algoritmo generalista para ese problema. Normalmente, primero especificarías el problema que deseas resolver y luego intentarías encontrar un algoritmo que lo resuelva. Turing, en busca de problemas irresolubles, le dio la vuelta a esta lógica: imaginó una lista infinita de todos los algoritmos posibles y utilizó la diagonalización para construir un problema pertinaz que frustraría todos los algoritmos de la lista.
Imagina un juego amañado de ’20 preguntas’ [**], donde en lugar de comenzar con un objeto particular en mente, quien responde inventa una excusa para decir no a cada pregunta. Al final del juego, han descrito un objeto definido completamente por las cualidades que le faltan.
La prueba de diagonalización de Turing es una versión de este juego en el que las preguntas recorren la lista infinita de algoritmos posibles, preguntando repetidamente: «¿Puede este algoritmo resolver el problema que nos gustaría demostrar que es incomputable?»
«Es una especie de ‘preguntas infinitas'», comenta Williams.
Para ganar el juego Turing necesitaba elaborar un problema en el que la respuesta fuera no para cada algoritmo. Eso significaba identificar una entrada particular que hiciese que el primer algoritmo generase una respuesta incorrecta, otra entrada que hiciese que el segundo fallase, y así sucesivamente. Encontró esas entradas especiales utilizando un truco similar al que Kurt Gödel había utilizado recientemente para demostrar que afirmaciones autorreferenciales como “esta afirmación no es demostrable” significaban problemas para los fundamentos de las matemáticas.
La idea clave fue que cada algoritmo (o programa) se puede representar como una cadena de ceros y unos. Eso significa, como en el ejemplo del programa de comprobación de errores, que un algoritmo puede tomar el código de otro algoritmo como entrada. En principio, un algoritmo puede incluso tomar su propio código como entrada.
Con esta idea, podemos definir un problema no computable como el de la prueba de Turing: “Dada una cadena de entrada que representa el código de un algoritmo, genera 1 si ese algoritmo genera 0 cuando su propio código es la entrada; de lo contrario, la salida es 0”. Cada algoritmo que intente resolver este problema producirá una salida incorrecta en al menos una entrada, es decir, la entrada correspondiente a su propio código. Eso significa que este perverso problema no puede resolverse mediante ningún algoritmo.
Lo que la negación no puede hacerLos informáticos aún no habían terminado con la diagonalización. En 1965, Juris Hartmanis y Richard Stearns adaptaron el argumento de Turing para demostrar que no todos los problemas computables son iguales: algunos son intrínsecamente más difíciles que otros. Este resultado lanzó el campo de la teoría de la complejidad computacional, que estudia la dificultad de los problemas computacionales.
Pero la teoría de la complejidad también reveló los límites del método a la contra de Turing. En 1975, Theodore Baker, John Gill y Robert Solovay demostraron que muchas cuestiones abiertas en la teoría de la complejidad nunca pueden resolverse únicamente mediante la diagonalización. La principal de ellas es el famoso problema de las clases de complejidad P y NP, que pregunta si todos los problemas con soluciones fácilmente comprobables también son fáciles de resolver con el algoritmo adecuado.
Los puntos ciegos de la diagonalización son una consecuencia directa del alto nivel de abstracción que la hace tan poderosa. La demostración de Turing no implicaba ningún problema incomputable que pudiera surgir en la práctica; en cambio, inventó un problema de ese tipo sobre la marcha. Otras pruebas de diagonalización están igualmente alejadas del mundo real, por lo que no pueden resolver cuestiones en las que los detalles del mundo real importan.
«Manejan la computación a distancia», explica Williams. «Me imagino a un tipo que se enfrenta a un virus y accede a él a través de una caja de guantes».
El fracaso de la diagonalización fue una indicación temprana de que resolver el problema de las categorías P y NP iba a ser un largo camino. Pero a pesar de sus limitaciones, la diagonalización sigue siendo una de las herramientas clave en el arsenal de los teóricos de la complejidad. En 2011, Williams lo utilizó junto con una serie de otras técnicas para demostrar que cierto modelo restringido de computación no podía resolver algunos problemas extraordinariamente difíciles, un resultado que había eludido a los investigadores durante 25 años. Estaba muy lejos de resolver el problema de las categorías P y NP, pero aun así representó un avance importante.
Si quieres demostrar que algo no es posible, no subestimes el poder de simplemente decir no.
Notas del traductor:
[*] El original en inglés “The limitation game” es un juego de palabras con el título de la película “The Imitation Game” basada en aspectos de la vida y obra de Alan Turing.
[**] En el juego tradicional de ’20 preguntas’ la persona que responde (la “respondedora”) elige algo que las demás jugadoras, las «interrogadoras», deben adivinar. Se turnan para hacer una pregunta a la que la respondedora debe responder «sí» o «no». Ejemplos de preguntas podrían ser: «¿Es más grande que un móvil?», «¿Está vivo?» y, finalmente, «¿Es este bolígrafo?». No se permite mentir. Si una interrogadora adivina la respuesta correcta, gana y se convierte en la respondedora en la siguiente ronda. Si se hacen 20 preguntas sin una respuesta correcta, entonces la respondedora gana y vuelve a ser la persona que responde en otra ronda.
El artículo original, Alan Turing and the Power of Negative Thinking, se publicó el 5 de septiembre de 2023 en Quanta Magazine.
Traducido por César Tomé López
El artículo Alan Turing y el poder del pensamiento negativo se ha escrito en Cuaderno de Cultura Científica.
Neuronek duten banaketa berezia azaleratu dute
Ugaztunen garunean dauden zelulak banaketa patroi jakin baten araberakoa dela aurkitu du ikertzaile talde batek. Arrazoia argitzeko moduan egon ez badira ere, zelulen biderketa prozesuaren ondorio izan zitekeela iradoki dute.
Sarritan errepikatu izan da kanpo espazioa ez dela, inondik inora, esploratzeke daukagun lurralde bakarra, eta ozeanoena ere badela, hein handi batean, apenas urratu gabe daukagun eremu erraldoi bezain gertukoa. Hala da, zentzu batean. Baina gero eta gehiago dira apustua maila bat igotzen dutenak: hauek azpimarratzen dute gertuago daukagula oraindik ere are ezezagunagoa zaigun espazio zabal eta handi bat: geure garuna bera.
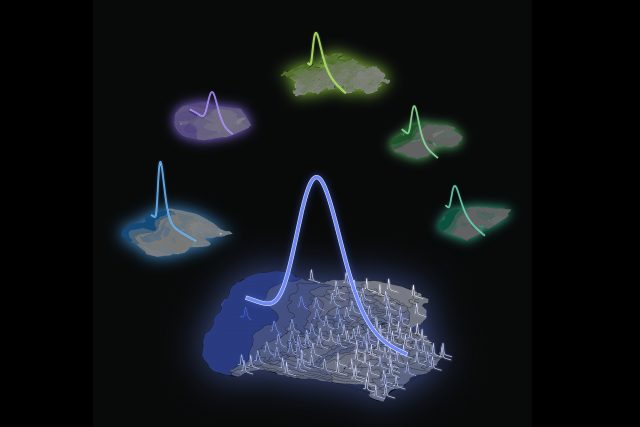 1. irudia: ugaztunen burmuinetako area kortikaletan dauden neuronen dentsitatea patroi jakin baten araberakoa dela aurkitu dute. (Irudia: Aitor Morales-Gregorio)
1. irudia: ugaztunen burmuinetako area kortikaletan dauden neuronen dentsitatea patroi jakin baten araberakoa dela aurkitu dute. (Irudia: Aitor Morales-Gregorio)Behin baino gehiagotan aipatu dugu garunaren mapa bat osatzeak suposatzen duen erronka. Eta, mapa horretara iritsita ere, hori eskura izateak ez du bermatuko, inondik inora, lurralde ezezagun honen barruan gertatzen dena ulertuko dugunik. Gauzak hala izanik, nekez ulertuko dugu gizakia bere benetako arimaren motorra ulertu gabe. Zentzu honetan, beste eremu askotan bezala, arazoa ez da soilik zer ez dakigun, ez dakigula ez dakigun hori baizik.
Azken paradoxa honen adibide xumea dakargu oraingoan. Zientzialari talde batek hainbat ugaztunen garunetan neuronen banaketa nolakoa den ikertzeari ekin dio, eta konturatu da horien banaketa patroi jakin baten araberakoa dela. Zehazki, ugaztunen garunetako eremu kortikaletan neuronen dentsitatearen banaketa nola antolatzen den aurkitu dute: banaketa lognormal baten arabera izaten da. Ikasitakoa Cerebral Cortex aldizkarian argitaratutako zientzia artikulu batean aurkeztu dute.
Ikerketa egiteko, aurretik argitaratutako datuetan oinarritu dira. Garunetako lagin histologikoetan abiatuta, datuek adierazten dute garunaren toki bakoitzean zenbat neurona dauden. Behin hauek jasota eta bateratuta, horien analisi estatistikoa egin dute. Zazpi ugaztun espezieren inguruan publiko diren bederatzi datu basetan abiatu dira azterketa osatzeko. Horietatik gehienak primateak dira: sagua, titia, makakoa, galagoa, tximino hontza (Aotus nancymaae), babuinoa eta gizakia.
Prentsa ohar batean azaldu dutenez, banaketa lognormalek banaketa asimetriko positiboa dute: eskumako errenkada luzeagoa da ezkerreko errenkadaren aldean, banaketa mota honetan aldagaiek balore handiak hartzeko joera dutelako.
“Banaketa estatistiko batean, normalean erdian batez besteko bat dago, eta, inguruan, gehiago edo gutxiago”, azaldu du Forschungszentrum Jülich ikerketa zentroko neurozientzialari konputazional Aitor Morales-Gregoriok. “Alabaina, aztertu ditugun garunen kasuan, ez da horrela izaten: batez besteko bat ematen da, baina balio asko oso altuak dira. Horrek sortzen du buztan luze baten itxura hartzen duen banaketa mota bat”.
Aldagai independente asko batzen direnean banaketa normalak sortzen diren modu berean, aldagai independente asko biderkatzen direnean sortzen dira naturan banaketa lognormalak. Horrek eraman ditu ikertzaileak pentsatzera zelulen biderketan egon daitekeela orain ikusitako banaketa honen abiapuntua. “Jakina denez, organismoak hazten direnean, eta zelula diren heinean, neuronak biderketa prozesu baten bitartez sortzen dira. Prozesu horrek badu, nolabait esateko, zarata apur bat, eta hortik abiatu zitekeen banaketa berezi hau”, iradoki du Morales-Gregoriok.
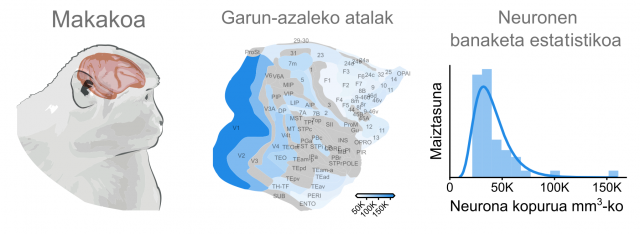 2. irudia: zientzia artikuluan aztertutako datu gehienak primateenak izan dira. Besteak beste, makako baten garun laginez baliatu dira. (Irudia: Aitor Morales-Gregorio)
2. irudia: zientzia artikuluan aztertutako datu gehienak primateenak izan dira. Besteak beste, makako baten garun laginez baliatu dira. (Irudia: Aitor Morales-Gregorio)Banaketa berezi hau unibertsala izan daiteke, ala soilik ugaztunetan gertatzen al da? “Ez dakigu. Guk momentuz soilik ugaztunetako kortexa aztertu dugu; ugaztunetan baino ez dago, hain justu, garunaren zati hau. Ikusteko dago, beraz, bestelako garunetan banaketa hau ere ematen ote den”. Jatorri hau izatekotan, litekeena da animalia guztietan gertatzea. Are gehiago, gerta liteke ere gorputzaren beste toki batzuetako ehunetan ere gertatzea, baina hori etorkizuneko ikerketek argitu beharko dute. Espezie desberdinetan aurkitu dutenez, susmoa dute banaketa honek nolabaiteko “abantaila konputazionala” izan dezakeela.
Zientzialariek babestu dutenez, aurkikuntza honen aplikazioetako bat konektibitateari buruzko ikerketa berrietara bideratu daiteke. Izan ere, neuronen banaketaren araberakoa izan daiteke hau. Kasurako, sinapsia konstantea izatekotan, ezinbestean neurona dentsitate txikiagoa dagoen eremuetan neurona bakoitzak sinapsi gehiago izan beharko lituzke.
Besteak beste, bereziki garrantzitsua izan daiteke hardware neuromorfikoaren garapenerako. Jakina da gaur egun dauden ordenagailuek ez dutela lan egiten gure garunak egiten duen moduan, baina zenbait proiektutan garunaren funtzionamendua imitatzen saiatzen ari dira. Arrazoietako bat garuna beste ezein ordenagailu baino askoz efizienteagoa dela. “Ahalegin horretan, garrantzitsua izango da jakitea zelan konektatu ahal diren nodo desberdinak sarean”, azpimarratu du neurozientzialari konputazionalak.
Gaia ezagutzen ez dugunontzat, eman lezake garunean zehar neuronen banaketa uniformea dela, baina hau ez da horrela, inondik inora, Morales-Gregoriok berak argitu duenez. “Adibide bat jartzearren, atzeko aldean dagoen kortex bisualean milimetro kubo bakoitzeko ehun mila neurona inguru egongo dira. Aldiz, kortex motorrean hogeita hamar mila daude”.
Hortaz, orain eskuratutako ezagutza garuna ulertzeko baliogarria izango dela uste du zientzialariak. Dena dela, norabide horretan oraindik dagoen lana eskerga da.
“Ordenagailuak asmatu zirenean, pentsatzen zen hamarkada baten bueltan erreplikatu ahalko zela garuna ordenagailu baten barruan, baina beti atzeratu izan den kontua da, bidean aurrera egin ahala konplexutasun maila gehiago ateratzen direlako. Adibideetako bat da orain argitu dugun banaketa estatistiko berri hau”, babestu du Morales-Gregoriok. “Baina horrek ez du esan nahi, noski, erronka horretan ahalegindu behar ez garenik”.
Erreferentzia bibliografikoa:
Morales-Gregorio, Aitor; van Meegen, Alexander; van Albada, Sacha J. (2023). Ubiquitous lognormal distribution of neuron densities in mammalian cerebral cortex. Cerebral Cortex, Volume 33, Issue 16, Pages 9439–9449. DOI: 10.1093/cercor/bhad160.
Egileaz:Juanma Gallego (@juanmagallego) zientzia kazetaria da.
The post Neuronek duten banaketa berezia azaleratu dute appeared first on Zientzia Kaiera.
La diversidad mineral en Marte
Nuestro planeta tiene una gran diversidad mineralógica. Tanta que hasta el momento hay reconocidas casi siete mil especies minerales y una de las preguntas que a menudo nos surgen cuando estudiamos otros planetas es: ¿Habrá un número similar en otros planetas o cuerpos del Sistema Solar? ¿O quizás es la Tierra un caso extremo dentro del mundo de los minerales?
Pero antes de continuar, ¿tenemos claro qué es un mineral? Llamamos minerales a sustancias sólidas, que tienen una composición química definida, de origen natural y con una estructura cristalina ordenada. Aunque esta definición nos pueda parecer un poco laxa, lo cierto es que en las últimas dos décadas sigue habiendo algo de debate, ya que se sigue discutiendo si los compuestos orgánicos -los de origen biológico o los que aparecen de manera espontánea- se deben considerar minerales.
 La cámara WATSON del Perseverance toma una imagen de cerca de una roca en Marte de la que posteriormente realizará análisis para conocer su composición. En la imagen se pueden ver distintos minerales, entre ellos uno traslúcido que ha llamado la atención de los científicos. Imagen cortesía de NASA/JPL-Caltech.
La cámara WATSON del Perseverance toma una imagen de cerca de una roca en Marte de la que posteriormente realizará análisis para conocer su composición. En la imagen se pueden ver distintos minerales, entre ellos uno traslúcido que ha llamado la atención de los científicos. Imagen cortesía de NASA/JPL-Caltech.Para los geólogos, los minerales son más que una curiosidad o un elemento de coleccionista, ya que nos pueden ayudar a conocer aquellos procesos que han tenido lugar en los planetas a lo largo de los 4500 millones de historia. Muy probablemente los planetas terrestres, de Mercurio a Marte, tuvieron una evolución mineralógica muy similar durante su infancia, pero que poco a poco fue divergiendo debido a las particularidades de cada uno.
Los planetas interiores partíamos con una serie de elementos y minerales similares por nuestra posición en el disco protoplanetario a partir del cual nos formamos. Una vez acabaron todos los procesos que dieron lugar a la formación de los planetas, muy probablemente los primeros minerales existentes en estos cuatro planetas podrían haber sido muy similares en número y composición, ya que se habrían formado a partir de la cristalización del océano de magma existente en estas primeras etapas de infancia planetaria.
Pero tras esa etapa comenzó un proceso evolutivo que nos ha hecho muy diferentes: la presencia o no de atmósfera, de una tectónica de placas o la aparición de la vida son algunos de los eventos que han podido marcar la mayor o menor diversidad mineral de los planetas.
Y aquí viene el segundo término que quería introducir en el artículo de hoy: los modos paragenéticos. Esta palabra engloba los procesos a partir los minerales se forman, es decir, como un conjunto de átomos en forma sólida o líquida son capaces de reconfigurarse dando lugar a una o más formas minerales. Estos modos son una gran cantidad de procesos naturales que llevan a la formación de nuevos minerales.
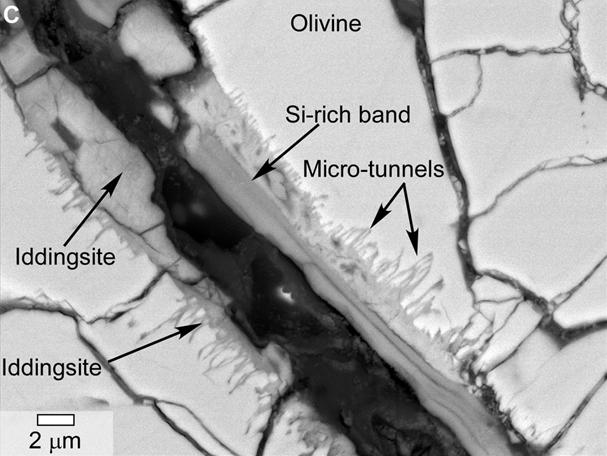 Imagen de microscopio electrónico de un meteorito marciano donde podemos ver algunos de los minerales anotados. Imagen cortesía de la NASA.
Imagen de microscopio electrónico de un meteorito marciano donde podemos ver algunos de los minerales anotados. Imagen cortesía de la NASA.Algunos ejemplos de los modos paragenéticos son la formación a partir de un gas o un líquido -por condensación, precipitación…-, transformaciones físicas a partir de eventos como la caída de rayos, impactos de meteoritos o fenómenos de metamorfismo regional, interacción del agua y las rocas o incluso la formación de minerales por efecto de la vida, como las biomineralizaciones-.
Marte es uno de los planetas que mejor conocemos debido a dos cuestiones principalmente: la primera de ellas son las misiones espaciales con capacidad de observación y análisis que nos han permitido conocer los minerales de su superficie, incluso desde la órbita, sin contacto. La segunda, gracias a los meteoritos que han caído a nuestro planeta y cuyo estudio podemos hacer con mucho detalle en los laboratorios terrestres. A pesar de esto, solo se han podido identificar un total de 161 minerales.
Una nueva investigación (Hazen et al. (2023)) sugiere que esta ausencia de minerales se podría deber a la existencia de un menor número de modos paragenéticos en Marte que los que hay en la Tierra… ¿Por qué? Pues porque nuestro planeta es algo especial con respecto al resto, al menos por lo que sabemos de momento.
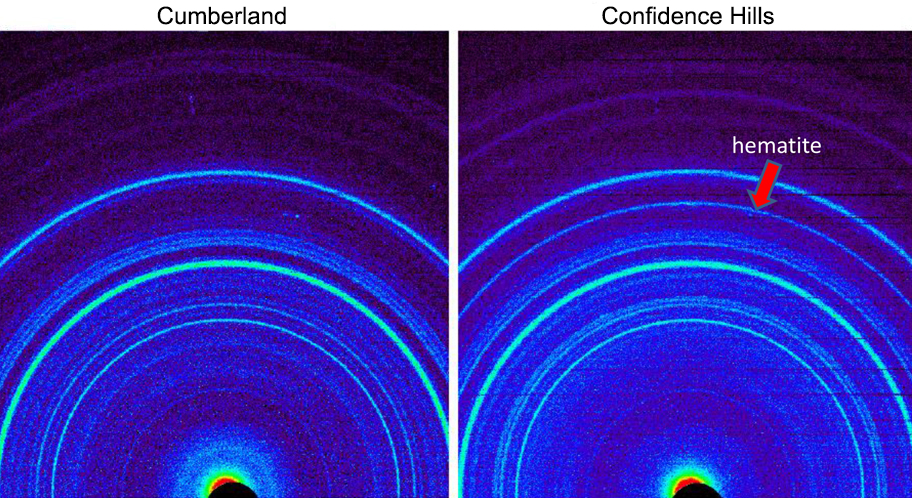 Patrón de difracción de rayos X capturado por el Curiosity en Marte. Gracias a instrumentos como el que permite tomar esta imagen, podemos conocer la composición de las rocas y el suelo de Marte con misiones de superficie. Imagen cortesía de NASA/JPL-Caltech.
Patrón de difracción de rayos X capturado por el Curiosity en Marte. Gracias a instrumentos como el que permite tomar esta imagen, podemos conocer la composición de las rocas y el suelo de Marte con misiones de superficie. Imagen cortesía de NASA/JPL-Caltech.En primer lugar, las interacciones entre los fluidos -como el agua- y las rocas en nuestro planeta tiene una mayor escala que en Marte gracias a la tectónica de placas, que a través de la subducción y de los procesos de fracturación de las rocas hace que nuestro planeta sea más permeable a este tipo de interacciones.
También la existencia de un metamorfismo de altas presiones como el que ocurre durante procesos de colisión continental algo que solo puede ocurrir bajo el régimen de tectónica de placas y, por supuesto, el efecto de la vida en la generación de minerales.
Estos tres procesos de los que hemos hablado podrían ser, según los autores del artículo, los responsables del 80% de la diversidad mineral de nuestro planeta, y precisamente estos modos paragenéticos son de momento exclusivos en la Tierra o podrían tener un ámbito mucho más restringido en el resto de los planetas.
¿Quiere esto decir que en Marte solo existen 161 minerales? No, todavía podrían existir más, ya que apenas hemos podido arañar la superficie y podríamos estar perdiéndonos los minerales existentes en zonas más profundas o inaccesibles debido a procesos hidrotermales o a fenómenos de metamorfismo de contacto, como el que podría haberse dado en las zonas volcánicas, pero a pesar de esto los investigadores sugieren que el número de minerales seguiría siendo un orden de magnitud inferior que en la Tierra.
No cabe la menor duda que los minerales pueden ayudarnos a comprender mejor la historia de los planetas y otros cuerpos, pero todavía nos queda por recorrer un largo camino hasta que podamos estudiar con detalle la composición de estos. Solo entonces podremos decir… ¿realmente somos tan diferentes?
Referencia:
Hazen, R. M., Downs, R. T., Morrison, S. M., Tutolo, B. M., Blake, D. F., Bristow, T. F., Chipera, S. J., McSween, H. Y., Ming, D., Morris, R. V., Rampe, E. B., Thorpe, M. T., Treiman, A. H., Tu, V. M., & Vaniman, D. T. (2023). On the diversity and formation modes of martian minerals. Journal of Geophysical Research: Planets, 128(9). doi: 10.1029/2023je007865
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo La diversidad mineral en Marte se ha escrito en Cuaderno de Cultura Científica.
Espezieen aniztasunaren gakoa haien antzekotasunetan egon liteke
Modelatze lan berri batek iradokitzen du zergatik den natura anitzagoa nitxoetan oinarritutako teoria ekologikoak iragartzen duena baino.
Duela lau hamarkada baino gehiago, landa ekologoek Panamako Barro Colorado uhartean dagoen baso lurzati bateko zuhaitzen aniztasuna kuantifikatzea proposatu zuten. Planetan gehien aztertutako baso eremuetako bat da. Zentimetro batetik gorako diametroa zuen enbor bakoitza hasi ziren kontatzen. Espezieak identifikatu, enborrak neurtu eta ale bakoitzaren biomasa kalkulatu zuten. Zuhaitzetan eskailerak jarri zituzten, zuhaitz gazteak aztertu zituzten, eta dena kalkulu orri gero eta handiagoetan erregistratu zuten.
 1. irudia: modelatze lan berri batek iradokitzen du zergatik den natura anitzagoa nitxoetan oinarritutako teoria ekologikoak iragartzen duena baino. (Iluztrazioa: Allison Li. Iturria: Quanta Magazine)
1. irudia: modelatze lan berri batek iradokitzen du zergatik den natura anitzagoa nitxoetan oinarritutako teoria ekologikoak iragartzen duena baino. (Iluztrazioa: Allison Li. Iturria: Quanta Magazine)Urtez urte metatzen ziren datuak behatzen zituzten bitartean, zerbait arraroa nabaritzen hasi ziren. 300 zuhaitz espezie baino gehiago izanik, harrigarria zen 15 kilometro koadroko uharte txiki hartako zuhaitz dibertsitatea. Baina espezietik espezierako zuhaitz banaketa ere oso desorekatuta zegoen, zuhaitz gehienak espezie gutxi batzuetakoak baitziren.
Lehen azterketa horietatik, gainkargatutako eta desberdintasun handiko eredu hori behin eta berriz ikusi da mundu osoko ekosistemetan, bereziki oihan tropikaletan. Kaliforniako Unibertsitateko (Los Angeles ) Stephen Hubbell ekologoaren arabera (Barro Coloradoko neurketa taldean parte hartu zuen), Amazonaseko zuhaitz espezieen % 2 baino gutxiago zuhaitz ale guztien erdiak dira, hau da, espezieen % 98 ez dira oso ohikoak.
Hain biodibertsitate handia izatea ekologiaren teoria garrantzitsu batek egindako iragarpenen aurka doa; izan ere, teoria horrek dio ekosistema egonkor batean nitxo edo rol bakoitza espezie bakar batek hartu behar duela. Nitxoen teoriak iradokitzen du ez dagoela nahikoa nitxorik ekologoek behatutako espezie guztiak modu egonkorrean existitzeko. Antzeko espezieen arteko nitxoengatiko lehiak ohikoak ez diren espezieak desagertzera eraman beharko zituen.
Nature aldizkariko modelatze ekologikoari buruzko artikulu berri batek, Illinoiseko Unibertsitateko (Urbana-Champaign) James O’Dwyer eta Kenneth Jops-enak, desadostasun horren zati bat behintzat azaltzen du. Ohartu dira itxuraz aurrez aurre lehiakide izan beharko luketen espezieek ekosistema bat parteka dezaketela, baldin eta haien bizi historien xehetasunak, hala nola bizialdia eta ondorengo kopurua, modu egokian lerrokatzen badira. Era berean, haien lanak azaltzen du ekologiak modelatzeko modu arrakastatsuenetako bat zergatik iristen den askotan emaitza zehatzetara, nahiz eta organismoen funtzionamenduari buruz dakigun ia guztia alde batera uzten duen.
 2. irudia: Illinoiseko Unibertsitateko James O’Dwyer landare biologoak (Urbana-Champaign) ulertu nahi zuen ekologiaren teoria neutralean oinarritutako ereduek nola erreproduzitu ditzaketen hain ondo biodibertsitatearen eredu naturalak, espezieak nola bizi diren eta nola elkarreragiten duten kontuan hartu gabe. (Iturria: Illinoiseko Unibertsitatea / Michelle Hassel)
2. irudia: Illinoiseko Unibertsitateko James O’Dwyer landare biologoak (Urbana-Champaign) ulertu nahi zuen ekologiaren teoria neutralean oinarritutako ereduek nola erreproduzitu ditzaketen hain ondo biodibertsitatearen eredu naturalak, espezieak nola bizi diren eta nola elkarreragiten duten kontuan hartu gabe. (Iturria: Illinoiseko Unibertsitatea / Michelle Hassel)2001ean, Barro Colorado uharteko biodibertsitate paradoxikoki handiak inspiratu zuen Hubbell ekologiaren teoria neutral iraultzailea proposatzeko. Ekologia tradizionalaren teoriak espezieen arteko nitxoengatiko lehia azpimarratzen zuen. Baina Hubbellek adierazi zuen posible zela espezieek ekuazio horretan axola ez izatea; izan ere, aleak beren espezieko kideekin ere lehiatzen baitira baliabideak lortzeko. Ekosistemetako dibertsitate ereduak, neurri handi batean, ausazko prozesuen ondorio izan daitezkeela iradoki zuen.
Biodibertsitateaz arduratzen zen teoria baterako, Hubbell-en teoria neutrala ez zen nahikoa. Ez zituen aintzat hartu bizi itxaropenen aldakuntzak, nutrizio berezitasunak eta espezie bat bestetik bereizten dituen beste xehetasun batzuk. Teorian oinarritutako ereduetan, ekosistema teoriko bateko ale guztiak berdin-berdinak dira. Behin denbora zenbatzen hasiz gero, ekosistemak bilakaera estokastikoa izaten du, eta aleak ausaz lehiatzen dira elkarren artean eta ausaz ordezkatzen dute elkar. Teoria ez zetorren bat espezieetan oinarritutako ekologiaren ikuspegiekin inondik inora, eta eztabaida sutsua eragin zuen ekologoen artean, intuizioaren oso kontrakoa zirudielako.
Hala ere, harrigarriki, eredu neutraletan ausazko ibilbideek aurrera egin ahala, Hubbellek eta lankideek Barro Colorado uharteko datuetan ikusi zutenaren eta beste batzuek beste leku batzuetan ikusi dutenaren funtsezko ezaugarriak errepikatzen ziren. Ia era gaiztoan ezberdintasunik antzematen ez duen eredu honetan, mundu errealaren izpiak daude.
Modeloen eta errealitatearen arteko tentsio hori luzaroan interesatu izan zaio O’Dwyerri. Zergatik funtzionatzen zuen hain ondo teoria neutralak? Ba al zegoen espezieek nola funtzionatzen duten jakiteko modurik, are errealistagoak diruditen emaitzak lortzeko?
 3. irudia: O’Dwyerren laborategian graduondoko ikasle gisa sartu aurretik, Kenneth Jopsek honakoa aztertu zuen: zein modutan erabil zitezkeen bizi historiak, landare espezieek desagertzearekiko zuten zaurgarritasuna iragartzeko. (Argazkia: Hannah Scharf doktorea)
3. irudia: O’Dwyerren laborategian graduondoko ikasle gisa sartu aurretik, Kenneth Jopsek honakoa aztertu zuen: zein modutan erabil zitezkeen bizi historiak, landare espezieek desagertzearekiko zuten zaurgarritasuna iragartzeko. (Argazkia: Hannah Scharf doktorea)Eredu neutralak erakargarriak izatea eragiten duen gauzetako bat da, O’Dwyerren arabera, izaki bizidun askoren artean unibertsaltasun handiak daudela. Animalia espezieak berdinak ez badira ere, zirkulazio sistemari dagokionez oso antzekoak dira. Fisiologiari lotutako zenbaki berak sortzen dira behin eta berriz animalietan eta landareetan, eta, agian, haien bilakaeraren historia partekatuaren mugak islatzen dituzte. Kleiber-en legea deritzon printzipioaren arabera, adibidez, animalia baten tasa metabolikoa, eskuarki, bere tamainarekin batera handitzen da, potentzien lege bat bezala eskalatuz; potentzien lege bera, espeziea dena delakoa izanda ere. (Hainbat teoria eskaini dira Kleiberren legearen egiazkotasuna frogatzeko, baina erantzuna eztabaidan dago oraindik).
Azpiko ordenaren ezaugarri horiek kontuan hartuta, O’Dwyerrek aztertu nahi izan zuen ea organismoen bizimoduari buruzko xehetasun batzuek beste batzuek baino garrantzi handiagoa duten, espezieek denbora ebolutiboan lehiatzeko eta bizirauteko izango duten arrakasta zehazteko orduan. Begira diezaiogun berriz metabolismoari: ekosistema bat bere biztanleen metabolismoen adierazpen gisa ikus badaiteke, orduan, organismoen tamainak zenbaki berezi eta esanguratsuak dira. Ale baten tamaina erabilgarriagoa izan daiteke denboran zehar bere patua modelatzeko, bere dietari edo espezie identitateari buruzko beste edozein xehetasun baino.
O’Dwyerrek aztertu nahi izan zuen ea faktore erabakigarri eta pribilegiatu horietako bat bizi historiak bil zezakeen; kontzeptu horrek espezieen estatistikak konbinatzen ditu, hala nola ondorengoen batez besteko kopurua, sexu heldutasunera arteko denbora eta bizi itxaropena. Irudikatu 50 landare aleko lurzati bat. Nork bere bizi itxaropena du, baita bere ugalketa patroia ere. Hiru hilabete igaro ondoren, landare batek 100 hazi ekoitzi ditzake, eta antzeko beste batek 88. Baliteke hazien % 80 ernamuintzea, eta hurrengo belaunaldia sortzea, ziklo horren bertsio propiotik pasatuko dena. Espezie baten barruan ere, landare aleen kopurua aldatu egingo da, batzuetan gutxi, beste batzuetan asko: zarata demografiko deritzo fenomeno horri. Aldakuntza hori ausazkoa bada, Hubbellen teoria neutralaren moduan, zer patroi sortuko dira hurrengo belaunaldietan?
O’Dwyerrek bazekien hori aztertzen lagun ziezaiokeen norbait aurkitu zuela, Jops bere laborategira batu zenean graduondoko ikasle gisa. Jopsek aldez aurretik aztertu zuen ea bizi historiak erabiltzen zituzten ereduek iragarri zezaketen landare zaurgarri batek biziraungo zuen ala desagertzear egongo zen. Elkarrekin hasi ziren matematikak egiten, bizi historiak lehiarekin topo egiten duenean gertatzen dena deskribatzeko.
Jops eta O’Dwyerren ereduan, eredu neutraletan bezala, garrantzitsua da estokastizitatea, hau da, ausazko faktoreek espezieen arteko interakzio deterministetan duten eragina. Espezieen bizi historiek, ordea, ausazkotasun horren ondorioak handitu edo murriztu ditzakete. “Bizi historia lente moduko bat da, eta haren bidez funtzionatzen du zarata demografikoak”, azaldu du O’Dwyerrek.
Ikertzaileek ahalbidetu zutenean beren ereduak denboran aurrera egitea, simulatutako ale bakoitza probatuta, espezie batzuek aldi luzeetan elkarren ondoan jarrai zezaketela ikusi zuten, baliabide berengatik lehiatu arren. Azalpen baten bila zenbakietan sakontzean, Jopsek eta O’Dwyerrek aurkitu zuten populazioaren benetako tamaina izeneko termino konplexu bat baliagarria izan zitekeela espezieen artean egon zitekeen osagarritasun mota bat deskribatzeko. Erakusten zuenez, espezie batek bere bizi zikloaren puntu batean hilkortasun handia izan zezakeen, eta hilkortasun txikia beste batean; aldi berean, espezie osagarri batek hilkortasun txikia izan zezakeen lehen puntuan eta hilkortasun handia bigarrenean. Termino hori bi espezierentzat zenbat eta antzekoagoa izan, orduan eta gertagarriagoa zen bikote bat bata bestearen ondoan bizitzea, nahiz eta eremuaren eta nutrizioarengatik lehiatu.
“Zarata demografikoa anplitude berarekin bizi izaten dute”, azaldu du O’Dwyerrek. “Hori da elkarrekin denbora luzez bizitzeko gakoa”.
 4. irudia: Landare belarkara iraunkorren lau espezie hauek (erlojuaren orratzen noranzkoan, goiko ezkerraldetik: Eryngium cuneifolium, Polygonella robusta, Lechea deckertii eta Lechea cernua) Floridako komunitateetan elkarrekin bizi dira, batak bestea galzorira eraman beharrean. Ikerketa berriak aurreikusten duen bezala, lau espezieek oso antzekoak diren bizi historiak dituzte. (Iturriak: South Florida Listed Species USFWS eta Bob Peterson (goiko lerroa); Jay Horn.)
4. irudia: Landare belarkara iraunkorren lau espezie hauek (erlojuaren orratzen noranzkoan, goiko ezkerraldetik: Eryngium cuneifolium, Polygonella robusta, Lechea deckertii eta Lechea cernua) Floridako komunitateetan elkarrekin bizi dira, batak bestea galzorira eraman beharrean. Ikerketa berriak aurreikusten duen bezala, lau espezieek oso antzekoak diren bizi historiak dituzte. (Iturriak: South Florida Listed Species USFWS eta Bob Peterson (goiko lerroa); Jay Horn.)Ikertzaileek jakin nahi zuten ea antzeko patroiak gailentzen ziren mundu errealean. COMPADRE datu-basean oinarritu ziren. Datu base horretan hainbat azterketa eta iturritatik hartutako milaka landare, onddo eta bakterio espezieri buruzko xehetasunak biltzen dira, eta ikerketarako lurzati berberetan elkarrekin bizi ziren landare iraunkorretan ardaztu ziren. Ikusi zutenez, modeloak aurreikusi zuen bezala, elkarrekin bizi ziren landare espezieek oso antzeko bizi historiak zituzten: ekosistema berean bizi diren espezie bikoteek ausaz sortutakoek baino osagarriagoak izateko joera dute.
Aurkikuntzek iradokitzen dutenez, nahitaez zuzeneko lehian ez dauden espezieek modu egokian funtziona dezakete elkarrekin nitxo desberdinetara jo gabe, dio Annette Ostling-ek, Texaseko Unibertsitateko (Austin) biologiako irakasleak. “Onena da ideia horiek… nahiko desberdinak diren baina osagarriak diren espezieetara zabal daitezkeela adierazten dutela”, esan du.
William Kunin Ingalaterrako Unibertsitateko (Leeds) Ekologiako irakaslearen iritziz, artikuluak arrazoi bat iradokitzen du, mundu naturala, bere konplexutasuna gorabehera, eredu neutral baten antzekoa izan daitekeela azaltzen duena: prozesu ekologikoek elkar deuseztatzeko modu bat izan dezakete, eta, beraz, aldakortasun amaigabea dirudienak emaitza sinple bat izan dezake, «neutraltasun emergente» gisa deskribatzen duena. Hubbellek, bere aldetik, bere hasierako obra handitzea eskertzen du. “Ideia batzuk eskaintzen ditu eredu neutralak nola orokortu, nola aldatu azaltzeko, desberdintasun espezifiko batzuk gehitzeko, nola hedatu eta murriztu tokiko komunitate batean aniztasunarekin zer gertatzen den ikusteko”, esan zuen.
Hala ere, biodibertsitatea nola sortzen den eta zergatik irauten duen ulertzeko arazoaren zati bat baino ez da hau. “Ekologian, patroiaren eta prozesuaren arteko harremanarekin borrokatzen dugu. Prozesu ezberdin askok patroi bera sor dezakete”, dio Oslingek. O’Dwyerrek espero du, datozen urteetan, mundu errealari buruzko datu gehiagok ikertzaileei lagunduko dietela bereizten populazioaren benetako tamaina gai ote den koexistentzia modu sendoan azaltzeko.
Kuninek espero du artikuluak beste batzuk inspiratzea teoria neutralaren ideiekin lan egiten jarraitzeko. Eremu horretan, aleen ezaugarri bereziak luzaroan gailendu zaizkienez komunean dituztenei, teoria neutralak ekologoak sortzaile izatera behartu ditu. “Gure ohitura mentaletatik atera gintuen eta benetan garrantzitsuak diren gauzetan pentsatzera bultzatu gintuen”, adierazi du.
Hubbellek, duela urte asko ekologiari buruzko teoria neutrala planteatu zuenak, jakin nahi luke benetako basoei buruzko datu multzo zinez izugarriek bizi historiaren eta biodibertsitatearen arteko erlazioa argitzeko behar den xehetasun mota sortuko luketen. “Horixe da gertatzea espero nuen teoria neutralari buruzko eraikuntza mota”, azaldu du artikulu berriari buruz. “Baina aniztasuna benetan ulertzeko urrats txiki bat besterik ez da”.
Jatorrizko artikulua:Veronique Greenwood (2023). The Key to Species Diversity May Be in Their Similarities, Quanta Magazine, 2023ko ekainaren 26a. Quanta Magazine aldizkariaren baimenarekin berrinprimatua.
Itzulpena:The post Espezieen aniztasunaren gakoa haien antzekotasunetan egon liteke appeared first on Zientzia Kaiera.
ZientZinema 5: Los herederos del viento
Scopes
Título original: Inherit the Wind. En las adaptaciones se ha titulado como La herencia del viento o Heredarás el viento. 1960, blanco y negro, 128 minutos. Dir.: Stanley Kramer. Guion: Nedrick Young, Harold Jacob Smith, según la obra de teatro de Jerome Lawrence y Robert Edwin Lee. Música: Ernest Gold. Fotografía: Ernest Laszlo. Montaje: Frederic Knudtson. Intérpretes. Spencer Tracy, Fredric March, Gene Kelly, Dick York, Harry Morgan.
El que perturba su propia casa heredará viento, y el necio será esclavo del sabio.
Proverbios, 11: 29.
Llamar a un hombre mamífero, al parecer, era también ignorar una revelación divina. El efecto de esta doctrina sería destruir la moralidad y promover la infidelidad.
H.L. Mencken sobre el juicio Scopes, The Baltimore Evening Sun, 17 julio 1925.
En 1925, John Thomas Scopes fue juzgado por violar la ley del Estado de Tennessee que prohibía enseñar la teoría de la evolución en las escuelas públicas. El darwinismo se enfrentaba al creacionismo en una batalla judicial en la que participaron Spencer Tracy, en el papel de Henry Drummond (nombre supuesto de Clarence Darrow para el film); Fredric March en el papel de Matthew Harrison Brady (nombre supuesto para William Jennings Bryan); Gene Kelly en el papel del periodista progresista E. K. Hornbeck (nombre que en la película a H. L. Mencken); Dick York como Bertram T. Cates (nombre supuesto para John Scopes) y Claude Atkins como el reverendo fundamentalista que denuncia al profesor Cates.
Posteriormente se rodaron para televisión otras tres versiones del juicio Scopes: en 1965 con Melvyn Douglas y Ed Begley, en 1988 con Jason Robards y Kirk Douglas, y en 1999 con Jack Lemmon y George C. Scott.
Cuando Estados Unidos salió de la Primera Guerra Mundial, una nostalgia colectiva recorrió el país por la simplicidad y normalidad anterior a la guerra. En las áreas rurales, particularmente en el sur y el medio oeste, los estadounidenses recurrieron a la fe para recuperar de la estabilidad, y la religión creció en popularidad. Los fundamentalistas, que creían en una interpretación literal de la Biblia, encontraron en Darwin y la teoría de la evolución la amenaza más evidente a la verdad que estaban seguros de que solo ellos poseían. Con la evolución como enemiga, se propusieron erradicarla de su sociedad, comenzando por el sistema educativo.
 Debido al excesivo calor el 20 de julio de 1925 el presidente del tribunal decidió que la sesión se trasladase al exterior del juzgado. En la imagen Bryan (de pie) interroga a Darrow (sentado a la izquierda). Fuente: Wikimedia Commons
Debido al excesivo calor el 20 de julio de 1925 el presidente del tribunal decidió que la sesión se trasladase al exterior del juzgado. En la imagen Bryan (de pie) interroga a Darrow (sentado a la izquierda). Fuente: Wikimedia CommonsPara 1925, varios estados del sur habían aprobado leyes que prohibían la enseñanza de la evolución. Oklahoma, Florida y Mississippi tenían esas leyes, e influían en las de Carolina del Norte y Kentucky. En Tennessee, la Ley Butler se aprobó en 1925, y aunque el gobernador no era fundamentalista, muchos de sus electores lo eran. Y la Unión Estadounidense de Libertades Civiles de Nueva York, cada vez más cautelosa, y declararon la prohibición de la evolución como una infracción de sus derechos constitucionales. Con la vista puesta en Tennessee, la ACLU se dispuso a iniciar un caso judicial para probar si era constitucional la Ley Butler.
A los pocos días de la decisión de la ACLU de poner a prueba la Ley Butler, se publicó un comunicado de prensa en un periódico de Tennessee que ofrecía apoyo legal a cualquier maestro que desafiara la ley. El 5 de mayo, varios líderes locales se reunieron y acordaron los detalles de su plan. Necesitaban un maestro para probar la ley, y lo encontraron en John T. Scopes, un profesor de ciencias y entrenador de fútbol de 24 años. Cuando se le preguntó acerca de su enseñanza de la evolución como parte de la enseñanza de la biología, Scopes respondió que lo mismo haría cualquier otro maestro.
La película se adaptó en Hollywood en 1960, cinco años después del estreno de la obra de teatro en Broadway. Entonces el Movimiento por los Derechos Civiles iniciaba sus acciones, el macartismo había terminado y el país recibía a un nuevo presidente, John F. Kennedy, que pronto sería elegido. El asunto de las leyes contra la teoría de la evolución no parecía interesar. Ese año, el New York Times publicó pocas noticias sobre el juicio de Scopes. En uno de ellos presentaron las declaraciones de un profesor de ciencias adventista del séptimo día que advirtió sobre los peligros de enseñar la evolución a los estudiantes. Sin embargo, el segundo de los dos artículos más largos sugería que la obra de teatro y su contenido ocupaban un lugar importante en la memoria del público.
La versión de Hollywood era muy diferente de la que Lawrence y Lee habían escrito para el teatro. Aunque la película era entretenida y hábil, muchos de debates de Lawrence y Lee se distorsionaron en la película de 1960.
En julio de ese año, en Dayton, Tennessee, donde se celebró el juicio a Scopes en 1925, se declaró el 21 de julio, Día del Juicio Scopes. La ciudad había aprovechado el juicio como una bendición comercial para Dayton, y en 1960 buscaba revivir el legado, trayendo más visitantes a Dayton. Donde antes había carteles que proclamaban «Lea su Biblia«, ahora, treinta y cinco años después, una pancarta decía «Bienvenido a Dayton, día del juicio de Scopes, 21 de julio«. En realidad, la ciudad había cambiado muy poco y el palacio de justicia seguía como siempre, como medio siglo atrás. Para la gente de Dayton, el juicio todavía se vivía no tanto como un conflicto cultural sino como un evento publicitario que honraba a este pequeño pueblo olvidado.
En resumen, el juicio a Scopes se convirtió en un objetivo para la lucha por las libertades civiles y en un exponente del conflicto entre la ciencia y el cristianismo fundamentalista en auge en Estados Unidos. Scopes fue declarado culpable y condenado a pagar la multa mínima de 100$. Pero, aparte del veredicto concreto, en la opinión pública vencieron los proevolucionistas. Sin embargo, como escriben Judith Grabiner y Peter Miller desde California y Ohio en 1974, los partidarios de la teoría de la evolución fallaron en la continuidad de su defensa y, por ello, los debates continúan incluso en la actualidad.
Referencias:
Grabiner, J.V. & P.D. Miller. 1974. Effects of the Scopes Trial. Was it a victory for evolutionists? Science 185: 832- 837.
Martínez-Salanova Sánchez. E. s.f. La herencia del viento. Libertad de pensamiento y tolerancia religiosa en las aulas. Cine y educación. 9 pp.
Mencken, H.L. 2007. El juicio Scopes. La acusación del fundamentalismo cristiano (The Baltimore Evening Sun 17-20 julio 1925). Letras Libres 71: 38-43.
Wikipedia. 2022. Inherit the wind (película). 22 diciembre.
Wikipedia. 2023. Scopes trial. 9 July.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo ZientZinema 5: Los herederos del viento se ha escrito en Cuaderno de Cultura Científica.
Asteon zientzia begi-bistan #452
Asteon zientzia begi-bistan igandeetako gehigarria da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna jaso eta laburbiltzea da gure helburua.

UPV/EHUko ikerketa-talde batek aztertu du Urdaibai Bird Centerreko ingurumen-heziketako jardueren eraginkortasuna gazteek hegaztien inguruko ezagutzan. DBHko 908 ikaslek hartu dute parte azterketan, eta emaitzen arabera, ikasleek ezagutza urria dute biosfera-erreserben, paduren eta hegazti-migrazioaren inguruan, ingurumen-heziketako ekintza egin ostean. Gainera, ikasle askok uste dute ingurumenaren babesa batzuetan gehiegizkoa dela, eta garapen ekonomikoa oztopatzen dutela. Azalpen guztiak Zientzia Kaieran: DBHko ikasleen ingurumen-hezkuntzako programen ebaluazioa.
IPBESek argitaratu berri duen txosten baten arabera, galdu diren izakien % 60 espezie inbaditzaileen ondorioz galdu dira. Gaur egunera arte 37.000 espezie baino gehiago mugitu dira eskualde batetik bestera, eta horietatik 3.500 inbaditzaileak direla argitu dute adituek. Txostenean adierazi denez, espezie inbaditzaileak mehatxu larria dira tokian tokiko ekosistementzat, ekonomiarentzat, elikadura segurtasunarentzat eta giza osasunarentzat. Horregatik, ikertzaileek urrats batzuk proposatu dituzte txostenaren amaieran, espezie inbaditzaileen hedapena kontrolpean izateko. Azalpen guztiak Berrian.
ZientziaEuropar Batasunak zientzia-aldizkarien argitalpen-tasak gaitzetsi ditu. Hau da, adierazi dute diru publikoz finantzatutako ikerketa-lanak sarbide irekikoak izan behar direla. Izan ere, kasu askotan ikerketa-lanak irakurri nahi dituzten zientzialariek ordaindu egin behar dute horretarako. Zientzia-argitaletxeak oso negozio errentagarria dira, zientzia-artikulu bat argitaratzegatik ordaindu egin behar izaten baita, eta gainera, ikerketa-lanak ebaluatzen dituzten adituek ere musu-truk egin ohi dute lan hori. Informazio gehiago Zientzia Kaieran.
PaleontologiaNeandertal kulturaren aztarnak aurkitu ditu Aranzadi Zientzia Elkarteak San Adriango pasabidean. Dozena bat pieza aurkitu dituzte momentuz, eta adituen esanetan, duela 40.000 urte egindakoak dira, eta, zalantzarik gabe, neandertalenak. Gainera, azaldu dute tresna horiek egiteko erabilitako silex harria Trebiñutik eta Urbasatik hartutakoa dela. Orain arte San Adriango pasabidean azaldu izan diren arrasto zaharrenak duela 14.000 bat urte ingurukoak ziren. Aurkikuntza honek galdera asko sortu ditu. Datuak guztiak Alea aldizkarian: Neandertalak ere bertatik igaro ziren.
Hegaztien eboluzioa hobeto ulertzen lagundu du Fujianvenator prodigiosus izeneko fosilak, hegaztien eta dinosauroen ezaugarriak baititu. Ezaugarri horietako bat tibiaren luzera da, femurra baino bi aldiz luzeagoa. Horrek zientzialariei iradoki die korrikalari azkarra izan zitekeela, edo paduran bizi zen limikola bat. Ezaugarri horiengatik guztiengatik, Ikertzaileek ondorioztatu dute hegaztien arbaso zuzena zela, eta tetrapodoetatik eboluzionatu zuela Jurasikoaren amaieran. Azalpenak Elhuyar aldizkarian.
MedikuntzaGaixotasun mikotikoen hilkortasuna % 20-% 50 artekoa da, eta osasun-arazo garrantzitsua bihurtu dira. Gaixotasun horien adibide da Aspergillus generoko onddoek eragindako biriketako infekzioa, baina oraindik ez dago gaixotasuna diagnostikatzeko metodo guztiz fidagarririk. Alabaina, azkeneko urteetan indarra hartzen ari da bigarren mailako metabolitoak gaixotasunaren diagnosirako biomarkatzaile moduan erabiltzea. Metabolito horietako bat da fumagilina izeneko mikotoxina, eta UPV/EHUko ikertzaile talde batek horren determinaziorako metodo analitiko bat garatu du. Informazio gehiago Zientzia Kaieran: Onddoek ekoizten duten mikotoxinen bila.
Denbora azkarrago igarotzen dela iruditzen zaigu urteak bete ahala, eta Esther Samper medikuak horren arrazoiak azaldu ditu Zientzia Kaieran. Hainbat hipotesi daude prozesu hori azaltzen saiatu direnak. Ikertzaile batzuek diote adinarekin informazio bisualaren prozesamendua moteldu egiten dela; hau da, irudi gutxiago hautematen ditugu segundoko, eta horrek denbora azkarrago igaro delako sentsazioa sor dezake. Beste hipotesi batzuek iradokitzen dute denbora kuantifikatzeko orduan egon litezkeen perspektiba desberdintasunagatik dela, edota oroitzapenak finkatzeko joeren ondorio direla denboraren pertzepzioan ditugun desberdintasunak.
Adimen artifizialaIkerketa berri baten arabera, adimen artifizialak gizakiek baino emaitza hobeak lortu ditu pentsamendu dibergentean. 256 boluntariok parte hartu dute azterketan, eta hauen emaitzak alderatu dituzte hiru txatboten emaitzekin: ChatGPT3, ChatGPT4, eta Copy.Ai. Pentsamendu dibergentea kuantifikatzeko objektu arrunt batek izan ditzakeen erabilera desberdinak asmatzeko gaitasuna neurtu dute. Emaitzen arabera, txatboten erantzunak gizakienak baino hobeak izan dira sormenean eta distantzia semantikoan. Datuak Elhuyar aldizkarian.
AstronomiaIndiako Chandrayaan-3 misioak Ilargiaren Hego poloko ionosferaren tenperatura eta dentsitatea neurtu ditu lehen aldiz. Bi aste pasa dira misioa Ilargira iritsi zenetik, eta aurkikuntza esanguratsuak egin dituzte dagoeneko. Zoruaren tenperatura ere neurtu dute 8 cm-ko sakoneran, eta azalekoa baino 60 ºC baxuagoa dela ikusi dute. Azaleko tenperaturari dagokionez, NASAk neurtutakoa baino epelagoa da. Informazio gehiago Elhuyar aldizkarian.
GeologiaAnetoko glaziarrak azaleraren % 64,7 galdu du azken 41 urteetan, IPE-CSIC Pirinioetako Ekologia Institutuaren arabera. Izotz Aro Txikiaren amaiera oinarritzat hartuta, berriz, Piriniotako glaziar-eremuaren %92 galdu da. Garai desberdinetako bereizmen handiko irudi aereoez baliatu dira emaitza horiek lortzeko, eta baita georradar bidezko neurketez, eta bestelako teknikez ere. Egin dituzten iragarpenen arabera, Anetoko glaziarra hiru izotz-gorputz txikiagotan zatituko da. Adibide honek glaziarraren egoera kritikoa islatzen du. Datu guztiak Elhuyar aldizkarian.
Egileaz:Irati Diez Virto Biologian graduatu zen UPV/EHUn eta Plentziako Itsas Estazioan (PiE-UPV/EHU) tesia egiten dabil, euskal kostaldeko zetazeoen inguruan.
The post Asteon zientzia begi-bistan #452 appeared first on Zientzia Kaiera.
Ezjakintasunaren kartogragfia #460
Zer izan zen lehen, arrautza edo oiloa, polipoa edo marmoka? The oldest known jellyfish, Ramón Muñoz-Conpuliren eskutik.
James Webb-en potentziaren adibide bikaina: New structures within iconic supernova 1987A.
Emakumeek gizonek baino insomnio handiagoa jasaten dute, eta loaren osasuna nabarmen okerragoa dute: The gender gap in sleep, José R. Alonsoren eskutik.
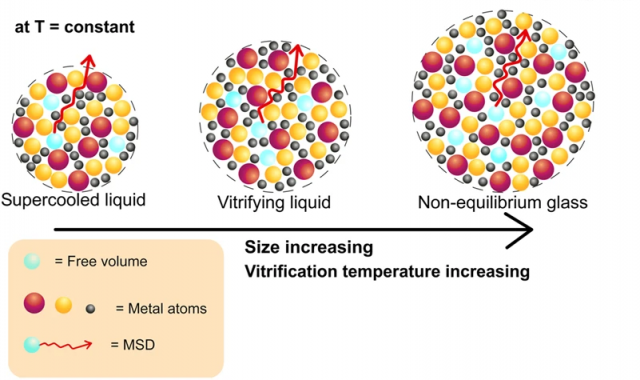
Beira nola sortzen den ulertzearen kontua ez da lortu, baina orain DIPCko jendeak aurrerapauso garrantzitsua eman du metalezko beiren kasuan: Size-dependent glass transition in metallic glasses
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartogragfia #460 appeared first on Zientzia Kaiera.
Konstante kosmologikoa
Ezagutza zientifikoaren testuinguru zabalean, batzuetan, iraultzak pizten dituzten txinpartak dira akatsak. Une historiko horietako bat 1917an izan zen. Garai hartan, unibertsoa estatikotzat jotzen zen. Baina Albert Einsteinen ekuazioek unibertso dinamikoa iragartzen zuten. Hori ezinezkoa zela sinetsita, ekuazioari elementu bat gehitu zion: konstante kosmologikoa.
Urte batzuk geroago, astronomoen zenbait behaketek berretsi egin zuten orain dakigun zerbait: unibertsoa hedatzen da. Beraz, Einsteinek onartu behar izan zuen konstante kosmologikoa akatsa izan zela, nahiz eta, bitxia bada ere, energia ilunak bezala jokatzen duen, unibertsoaren hedapena azkar zabaltzearen benetako eragilea.
UPS! ataleko bideoek gure historia zientifiko eta teknologikoaren akatsak aurkezten dizkigute labur-labur. Bideoak UPV/EHUko Kultura Zientifikoko Katedrak eginak daude eta zientzia jorratzen duen Órbita Laika (@orbitalaika_tve) telebista-programan eman dira gaztelaniaz.
The post Konstante kosmologikoa appeared first on Zientzia Kaiera.
Naukas Bilbao 2023 en directo
El gran evento de divulgación organizado por Naukas y la Cátedra de Cultura Científica vuelve a Bilbao para celebrar su decimotercera edición que tendrá lugar nuevamente en el gran Palacio Euskalduna. Las sesiones del acto central durante los días 15 y 16 de septiembre, Naukas Bilbao 2023, pueden seguirse por streaming aquí o en la web de Naukas.

El programa es el siguiente (horas GMT+2):
Viernes 15 septiembre – Sesión de Mañana10:00 a 10:10 – José Miguel Viñas: ¡Leed a Verne, malditos!
10:10 a 10:30 – Javier S. Burgos y Luisma Escudero: Ciencia ochentera (20 minutos)
10:30 a 10:40 – Juan Francisco Hernández: Recreo Naukas, un nuevo espacio de divulgación
10:40 a 10:50 – Sara Barja: Vamos a mover átomos
10:50 a 11:00 – Teresa Valdés-Solís: Ilustradas y aventureras
11:00 a 11:10 – Iván Rivera: El ancho de banda de la Stasi
11:10 a 11:20 – José A. Prado-Bassas: Series a lo Grandi
11:20 a 11:30 – Juan Ignacio Pérez: Una taxonomía de los saberes
11:30 a 12:00 – Descanso de 30 minutos
12:00 a 12:10 – Raúl Ibáñez: Las matemáticas como herramientas de creación artística
12:10 a 12:20 – Carlos Lobato: Archaea, las pequeñas grandes desconocidas
12:20 a 12:30 – Anabel Forte: Entre datos y lámparas
12:30 a 12:40 – Lorena Pérez Hernández: Anna Wierzbicka y la tabla periódica del pensamiento
12:40 a 12:50 – Laura Morrón: La revolución newtoniana… a pesar de Newton
12:50 a 13:00 – Pablo Rodríguez: Las charlas de mis pesadillas
Viernes 15 septiembre – Sesión de Tarde17:00 a 17:10 – Ignacio López Goñi: Andeuineris
17:10 a 17:20 – Eva Caballero: Nuestras madres nos alteran
17:20 a 17:30 – Ángel López Sánchez: El cielo es tu laboratorio
17:30 a 17:40 – Naiara Barrado: Júpiter ¿Héroe o villano?
17:40 a 17:50 – Miguel A. Delgado: ¿Y si resulta que la revolución científica la inició España?
17:50 a 18:00 – Gaby Jorquera: Sombras largas
18:00 a 18:10 – Isabel Moreno: Que llueva, que llueva
18:10 a 18:20 – Francis Villatoro: Lo que sabemos que no sabemos
18:20 a 18:30 – Sergio P. Acebrón: Explorando los límites de la vida
18:30 a 19:00 – Descanso (30 minutos)
19:00 a 19:20 – Gemma del Caño y Conchi Lillo: Comer con los ojos (20 minutos)
19:20 a 19:30 – Susana Escudero: Granjas de cadáveres
19:30 a 19:40 – Guillermo Peris: La expresión de la muerte
19:40 a 19:50 – José Ramón Alonso: La lección de anatomía
19:50 a 20:00 – Miguel Santander: Dear Doctor,
Sábado 16 septiembre – Sesión de Mañana10:00 a 10:10 – Ambrosio Liceaga: ¿Es Bilbao el mejor lugar para una civilización tecnológica en expansión?
10:10 a 10:20 – Paula Serras : En la cresta de la ola
10:20 a 10:30 – Helena Matute: Experimentos con humanos e IAs
10:30 a 10:40 – Javier Pedreira Wicho: IA: no es inteligencia todo lo que reluce
10:40 a 10:50 – Onintze Salazar: Sobre perturbaciones y no precisamente de la atmósfera
10:50 a 11:00 – Gemma Marfany: Ni tuyo ni mío, de todos
11:00 a 11:10 – Gisela Baños: Cuando la ciencia ficción puso en jaque a Seguridad Nacional
11:10 a 11:20 – Alberto García Salido: Toda su sangre en mis manos
11:20 a 11:30 – Lluís Montoliu: Millones de raras
11:30 a 12:00 – Descanso de 30 minutos
12:00 a 12:10 – Javier Fdez. Panadero: Ilusiones cacharrísticas
12:10 a 12:30 – Luis Martínez Otero: FESTIVAL JA (20 minutos)
12:30 a 12:40 – Julián Estévez: Drones y Ramstein
12:40 a 12:50 – Fernando Frías: Benidorm y la Tierra
12:50 a 13:00 – Laura Toribio: Ese huequito entre Marte y Júpiter
Sábado 16 septiembre – Sesión de Tarde17:00 a 17:10 – Laura Morán: La erótica del fregao
17:10 a 17:20 – César Tomé: La desviación de Einstein
17:20 a 17:30 – Sara Cazzoli: Feo, fuerte y formal
17:30 a 17:40 – Álvaro Bayón: Nuestra vida por unas monedas
17:40 a 17:50 – Ricardo Moure: Seguro dental, Lisa necesita un aparato
17:50 a 18:00 – Txema Campillo: De Guttemberg a Marilyn
18:00 a 18:10 – Pablo José Barrecheguren: La paradoja del sueño lúcido
18:10 a 18:20 – Virginia Arechavala: Los vulgares exploradores del laberinto.
18:20 a 18:30 – Juan Carlos Gil: Vuela, gaviota… ¡Vuela!
18:30 a 19:00 – Descanso (30 minutos)
19:00 a 19:10 – Carlos Briones: Invisible a los ojos
19:10 a 19:20 – Álvaro Carmona: El borde del espejo
19:20 a 19:30 – Elisabete Alberdi: Las matemáticas del glioma
19:30 a 19:40 – Joaquín Sevilla: Una mañana de verano
19:40 a 19:50 – Antonio Martínez Ron: Etiquetar el asombro
19:50 a 20:00 – Oskar González: La última de Vermeer
20:00 a 20:10 – Entrega de los Premios Tesla 2023 y despedida del evento.
El artículo Naukas Bilbao 2023 en directo se ha escrito en Cuaderno de Cultura Científica.
Fantasías de colores microscópicos
En Geología, al igual que en otras disciplinas científicas como la Biología o la Medicina, cuando queremos hacer un estudio detallado de cualquier roca para conocer de manera precisa su composición y sus propiedades internas, debemos utilizar un microscopio de luz transmitida. Pero, en nuestro caso, se trata de un microscopio un poco particular, al que llamamos microscopio petrográfico.
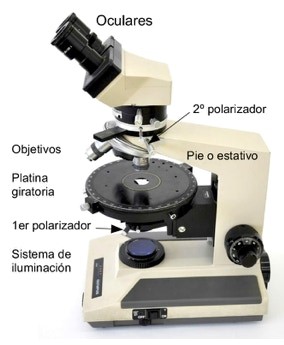 Microscopio petrográfico modelo Olympus BHT utilizado para las prácticas de petrología en el Departamento de Geología de la Universidad del País Vasco (UPV/EHU). Imagen: UPV/EHU
Microscopio petrográfico modelo Olympus BHT utilizado para las prácticas de petrología en el Departamento de Geología de la Universidad del País Vasco (UPV/EHU). Imagen: UPV/EHULa principal diferencia con los microscopios biológicos es que tiene un sistema de luz polarizada formado por dos filtros (o nícoles): el primero se encuentra situado en el foco de luz, por debajo de la muestra, y el segundo está posicionado entre la muestra y el ocular. El primer filtro, que generalmente está fijo, hace que las ondas lumínicas se muevan en una sola dirección para que puedan atravesar la muestra sin desviarse. Pero el segundo filtro, que podemos sacar y meter del microscopio a nuestra voluntad, se coloca de manera perpendicular al primero, de tal manera que, cuando lo activamos, o, para ser más exacta, lo cruzamos, hace de barrera e impide el paso de la luz. Es decir, si miramos por el ocular de un microscopio petrográfico sin colocar ninguna muestra y lo encendemos con el segundo filtro sacado, veremos la luz incidiendo sobre nuestros ojos. Pero si metemos, o cruzamos, el segundo polarizador, lo veremos todo negro.
Seguro que os estaréis preguntando que, entonces, para qué sirve ese segundo polarizador si no nos permite ver nada. Pues la respuesta está en las propiedades ópticas de los minerales. Si ponemos una muestra en el microscopio que sea capaz de cambiar la dirección de la luz polarizada a medida que la atraviesa (esta propiedad se denomina birrefringencia), cuando cruzamos el segundo filtro surgirá la magia, porque entonces la luz no incidirá de manera perpendicular, sino que tendrá un ángulo que se verá reflejado en la aparición de una serie de colores ante nuestros ojos, denominados colores de interferencia. Y esta propiedad óptica es un criterio de identificación de los minerales.
La segunda diferencia más importante con el resto de microscopios es que el petrográfico dispone de una platina, es decir, de una superficie donde se coloca la muestra que puede girarse 360º. Y, aunque parezcamos DJs intentando sacar una buena base musical de la muestra que estamos analizando cuando nos ponemos a girar adelante y atrás la platina, lo que estamos haciendo es comprobar cómo cambian los colores de interferencia de los minerales al modificar el ángulo de incidencia de la luz. En algunos casos, apenas varían y nos encontramos con tonos similares del mismo color. Pero en otras ocasiones parece una imagen psicodélica de los años sesenta del siglo pasado, encontrando variaciones extremas en los colores de interferencia de un mismo mineral. Este rango de variación de los colores de interferencia también es un criterio identificativo de los minerales.
 Aspecto de una roca ígnea (gabro) vista al microscopio petrográfico. La imagen de la izquierda se ha obtenido con el segundo polarizador no activado, mientras que la imagen de la derecha se obtiene al cruzar el segundo polarizador, revelando los colores de interferencia de los minerales que componen la muestra analizada. Imagen: Open University / OpenLearn
Aspecto de una roca ígnea (gabro) vista al microscopio petrográfico. La imagen de la izquierda se ha obtenido con el segundo polarizador no activado, mientras que la imagen de la derecha se obtiene al cruzar el segundo polarizador, revelando los colores de interferencia de los minerales que componen la muestra analizada. Imagen: Open University / OpenLearnPero el estudio de las rocas al microscopio petrográfico no solo nos permite identificar la composición mineral de la misma. También podemos observar estructuras microscópicas de la muestra, como la existencia de fracturas o de poros internos, o la presencia de microfósiles que nos informen sobre la edad de la roca o el ambiente en el que se formó. Características que no podíamos apreciar a simple vista y que son necesarias a la hora de describir el material con el que estamos trabajando.
Vídeo: Variación de los colores de interferencia en varios minerales, principalmente feldespatos, al girar la platina del microscopio petrográfico con los dos polarizadores cruzadosAhora es cuando nos surge otra cuestión: ¿Cómo podemos hacer que la luz atraviese una roca, si estamos trabajando con una sustancia sólida y, por tanto, opaca? Pues exactamente igual que en Biología o Medicina, cortando una rodaja muy fina de nuestra muestra hasta conseguir transformarla en algo transparente. Para ello usamos una cortadora de rocas, que tiene un disco de diamante, con la que preparamos un pequeño taco con forma de prisma de base rectangular, de unos 2,5 cm de ancho por unos 4 cm de largo, que se pega a un portamuestras de vidrio. Este taco de roca se va puliendo con diferentes abrasivos, también de polvo de diamante, hasta que alcanza un grosor de 0,03 mm, tras lo que se tapa con un cubreobjetos de vidrio. Así se transforma en lo que en Geología denominamos una lámina delgada, o sección pulida de roca si queremos usar un término un poco más serio. Ahora ya podemos poner la muestra sobre el microscopio permitiendo que la luz la atraviese sin problemas.
 Proceso de preparación de una lámina delgada desde la muestra de roca hasta que se obtiene la sección pulida que permite el paso de la luz a través de la misma. Imagen: Instituto de Geología de la Universidad Nacional Autónoma de México
Proceso de preparación de una lámina delgada desde la muestra de roca hasta que se obtiene la sección pulida que permite el paso de la luz a través de la misma. Imagen: Instituto de Geología de la Universidad Nacional Autónoma de MéxicoEl microscopio petrográfico lleva usándose más de un siglo para hacer estudios geológicos a lo largo de todo el mundo, pero la técnica se va perfeccionando año tras año. Los aparatos que usé durante la carrera hace un par de décadas están a años luz, nunca mejor dicho, que los que pueden emplear ahora mismo las nuevas hornadas de profesionales de la Geología que se están cocinando a fuego lento en las facultades españolas. Y esto es una buena noticia, porque, aunque las propiedades ópticas de los minerales sigan siendo las mismas, cualquier avance tecnológico va a permitir que sea mucho más fácil determinarlas, pudiendo así afinar cada vez más y mejor en la identificación de los componentes de las rocas que estemos estudiando, lo cual se agradece mucho durante los exámenes. Aunque lo que tampoco va a cambiar será la impresión que sufrirán estas futuras generaciones cuando vean por primera vez una lámina delgada al microscopio y descubran el maravilloso juego de colores que se oculta en el interior de una oscura y simple roca.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Fantasías de colores microscópicos se ha escrito en Cuaderno de Cultura Científica.
Onddoek ekoizten duten mikotoxinen bila
Azken urteotan nabarmen hazi da onddoek eragindako infekzioen intzidentzia. Igoera horren arrazoietako bat diagnostiko-metodoen hobekuntza izan da, baina baita gaixo immunodeprimituen populazioa nabarmen hazi dela ere. Gaixotasun mikotiko horiek kezka larrikoak dira, hilkortasuna % 20 – % 50 artekoa baita. Hortaz, osasun-arazo garrantzitsu bihurtu dira gaur egungo gizartean.
Infekzio horiek sortzen duten onddoen artean Aspergillus generoa dugu. Generoa osatzen duten 200 espezieen artean, 30 baino gehiagok gizakiongan infekzioak eragin ditzakete, aspergilosi inbasiboa deritzona, esaterako. Tuberkulosiaren antzeko sintomak dituen gaixotasun horren erantzule nagusia Aspergillus fumigatus espeziea da, hain zuzen ere.
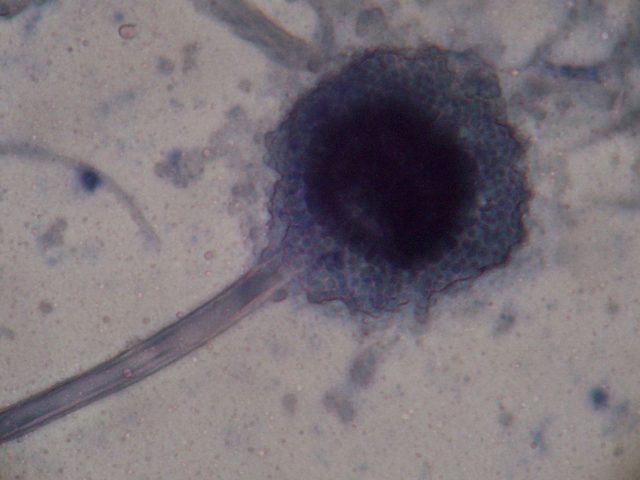 Irudia: Kalkulatu da pertsona bakoitzak egunean ehunka konidio arnasten dituela.(Argazkia: Roberto J. Galindo – CC BY-SA 3.0 lizentziapean. Iturria: Wikimedia Commons)
Irudia: Kalkulatu da pertsona bakoitzak egunean ehunka konidio arnasten dituela.(Argazkia: Roberto J. Galindo – CC BY-SA 3.0 lizentziapean. Iturria: Wikimedia Commons)A. fumigatus erraz hedatzen da, hazteko gaitasunaren eta aireko dispertsio eraginkorraren ondorio. Gainera, ostalariaren ingurunera arin egokitzen da, eta haien konidioak (espora mota batzuk) gure arnasbideetara erraz iritsi daitezke. Kalkulatu da pertsona bakoitzak egunean ehunka konidio arnasten dituela. Etengabeko esposizio hori gorabehera, nabarmentzekoa da gizaki gehienek ez dutela gaixotasunik garatzen, birikietako defentsa mekanismoek konidioak ezabatzen baitituzte. Erantzun immunea ahulduta daukaten pertsonek, ordea, ez dute zorte berbera.
Aspergilosi inbasiboen kasuen %60 inguru birikietako infekzio moduan agertzen da, baina kasu batzuetan infekzioa gorputz osoan zehar hedatu daiteke, horrek dakartzan ondorio latzekin. Gaixotasun honen hilkortasuna handia den arren, ez da erraza datu hori zehaztea. Izan ere, oraindik ez dago gaixotasuna diagnostikatzeko metodo guztiz fidagarririk. Hori dela eta, gaixotasunaren diagnostikorako metodo sentikor eta espezifikoak garatzearen premia larria dago. Ikerketa batzuen arabera, uste da bigarren mailako metabolito deritzen konposatuek eginkizun erabakigarriak izan ditzaketela gaixotasunaren garapenean; beraz, konposatu horiek aspergilosi inbasiboaren diagnosirako biomarkatzaile moduan erabiltzearen ideia indarra hartzen ari da.
Aipatutako metabolito horiek asko dira, baina azken urteotan fumagilina izeneko mikotoxinak piztu du arreta handiena. Hortaz, substantzia hori analizatzeko metodoak garatzea oso erabilgarria izan daiteke gaixotasuna garaiz detektatzeko eta aspergilosi inbasiboaren garapena hobeto ulertzeko.
Bitxia bada ere, bere toxikotasuna dela eta, fumagilina agente antimikrobiar gisa erabili da hainbat aplikaziotan, hala nola, erle arruntak beste onddo batzuek eragindako infekzioetatik babesteko eta arrainetan parasitoekin erlazionaturiko gaixotasunak sendatzeko. Hori dela eta, fumagilinaren analisirako metodo analitikoak existitzen dira, gehienak eztian edo arrain ehunetan aplikatu direnak. Ez dira metodo analitikoak existitzen, berriz, substantzia hori zelula-hazkuntzako ingurunean kuantifikatzeko. Kontuan izanda matrize horretan A. fumigatusek sortzen duen fumagilina aztertu daitekeela, metodo analitiko horiek garatzeak berebiziko garrantzia dauka. Hori dela eta, lan honetan fumagilinaren determinaziorako metodo analitiko bat garatu eta balidatu da RPMI-1640 ingurune zelularrean. Gainera, metodoa A. fumigatusen lau andui analizatzeko aplikatu da, bakoitzak mikotoxina ekoizteko duen gaitasuna ezagutzeko.
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: 43
- Artikuluaren izena: Fumagilina mikotoxinak aspergilosi inbaditzailearen garapenean duen rola aztertzeko SPE-UHPLC-DAD metodo analitikoa
- Laburpena: Aspergillus fumigatus onddoak sortutako aspergilosi inbaditzailea mehatxua da immunoeskasia duten gaixoentzat. Azkeneko ikerketa batzuen arabera, fumagilinak, onddoak sortutako mikotoxinak, gaixotasunaren hedapenarekin zerikusia duela ikusi da. Hori dela eta, konposatu honen determinazioa lagungarria izan daiteke bai gaixotasunaren mekanismoak hobeto ulertzeko eta baita aspergilosi inbaditzailearen biomarkatzaile gisa erabili ahal izateko ere. Ikerketa mikrobiologikoetan fumagilinaren analisiak garrantzia izan arren, oraindik ez da haren determinaziorako metodo kuantitatiborik garatu zelula-hazkuntzako inguruneetan. Beraz, lan honetan fumagilinaren determinazio kuantitatiborako lehenengo metodo analitikoa balidatu da RPMI-1640 zelula-hazkuntzako ingurunean. Laginaren tratamendua fase solidoko erauzketarekin egin da, anioi trukatzaile sendoak diren modu mistoko kartutxoak erabiliz. Horrela, egon daitezkeen interferentziak modu eraginkorrean ezabatu dira, eta % 83 ± 7ko berreskurapena lortu da. Analisia fotodiodo detektagailuari akoplaturiko bereizmen oso altuko likido kromatografia erabiliz egin da 336 nm-ko uhin-luzeran. Horrela, metodoak EMA (Europako Medikamentuen Agentzia) eta FDA (Elikagai eta Sendagaien Administrazioa) agentziek balidazio bioanalitikoetarako zehazten dituzten parametro guztien onartze-irizpideak betetzen dituela egiaztatu da. Gero, metodoa A. fumigatus-en lau andui analizatzeko aplikatu da, eta bakoitzak mikotoxinaren kantitate desberdina ekoizteko gaitasuna daukala ikusi da.
- Egileak: Ane Yaldebere, Oskar González-Mendia, Xabier Guruceaga, Andoni Ramirez-García, Aitor Rementeria eta Rosa Alonso
- Argitaletxea: UPV/EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 41-58
- DOI: 10.1387/ekaia.23368
- Ane Yaldebere eta Rosa Alonso UPV/EHUko Zientzia eta Teknologia Fakultateko Kimika Analitikoa Saileko ikertzaileak dira.
- Oskar González-Mendia UPV/EHUko Arte Ederren Fakultateko Pintura Saileko ikertzailea da.
- Xabier Guruceaga, Andoni Ramirez-García eta Aitor Rementeria UPV/EHUko Zientzia eta Teknologia Fakultateko Immunologia, Mikrobiologia eta Parasitologia Saileko ikertzaileak dira.
Ekaia aldizkariarekin lankidetzan egindako atala.

The post Onddoek ekoizten duten mikotoxinen bila appeared first on Zientzia Kaiera.
Dozena erdi ariketa 2023ko udarako: erantzunak
Erantzun asko eta gehienak zuzenak izan ditugu aurten. Eskerrik asko denoi parte hartzeagatik.
Zenbaki baten zifren biderkadura 18900 da. Zein da propietate hori duen zenbakirik txikiena?
18900 = 2 x 2 x 3 x 3 x 3 x 5 x 5 x 7 denez, faktore horiek guztiak agertu beharko dira gure zenbakiaren zifretan. Eta nahi beste bider jar dezakegu 1 zifra, baina horrela zifra kopurua handituko genuke eta ez genuke eskatzen den zenbakirik txikiena lortuko.
Faktore guztiak dauden moduan idatzita, edo ordena aldatuta, zortzi zifrako zenbakia genuke. Zifra gutxiago erabiltzeko, 2 eta 2 idatzi ordez, 4 jar dezakegu. Era berean, 2 eta 3ren ordez, 6; edo 3 eta 3ren ordez, 9. Horren bitartez, sei zifrako zenbakia lor dezakegu, baina ez zifra gutxiagokoa.
Eskatzen zaigun zenbakirik txikiena lortzeko, 2 zifra mantentzea komeni zaigu. Horrela, 2, 6, 9, 5, 5 eta 7 izango dira gure zenbakiaren zifrak. Txikiena lortzeko, txikitik handira ordenatuko ditugu: 255679.
Denda batean gozoki batek 5 zentimo balio du. Eskaintza bat jarri dute: 35 gozokitik behera erosiz gero, %5eko deskontua egiten dute; 36 eta 55 gozoki artean, %12koa; eta 56 gozokitik gora, %20koa. Lehen erosketan %5eko deskontua egin digute, eta bigarren erosketan, %12koa. Dena batera erosi izan bagenu, %20ko deskontua lortuko genukeen eta 39 zentimo aurreztu. Zenbat gozoki erosi ditugu?
Lehenengo aldian m gozoki erosi baditugu, 5m-ren %95 ordainduko dugu. Bigarren aldian n gozoki erosita, 5n-ren %88. Dena batera erosi izan bagenu, 5(m + n)-ren %80 ordainduko genuen, 39 zentimo gutxiago. Beraz,
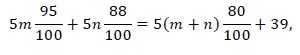
edo 15m + 8n = 780. Hemendik, 8n = 780 -15m = 15 (52 – m) ateratzen dugu. Hortaz, 8n 15en multiploa da, eta horretarako, n izan behar da 15en multiploa. Gainera, 36 eta 55 artean egon behar denez, n = 45 da aukera bakarra. Horrek m = 28 dakar. Denetara, 73 gozoki erosi ditugu.
1, 2, 3, 4, 5, 6 eta 7 digituak errepikatu barik erabiliz idatz daitezkeen zazpi zifrako zenbaki guztiak txikitik handira ordenatu ditugu. Zer tokitan dago 3654712 zenbakia zerrenda horretan?
Aurretik egongo dira 1 edo 2 hasieran duten guztiak. Bakoitzetik 6! = 720 zenbaki, sei zifraren artean aukeratu behar baitugu jarraipena. Aurretik baita ere 31, 32, 34 eta 35 hasierakoak, bakoitzetik 5! = 120. Gero, 361, 362 eta 364 hasierakoak, 4! = 24 bakoitzetik. Ondoren, 3651 eta 3652 hasierakoak, 3! = 6 bakoitzetik. Azkenik, 36541 eta 36542 hasierakoak, 2 bakoitzetik. Denetara,
2 x 720 + 4 x 120 + 3 x 24 + 2 x 6 + 2 x 2 = 2008
dira aurretik dituen zenbakiak. Beraz, 2009. lekuan egongo da.
Maren eta Miren pista zirkular batean korrika hasi dira, bakoitza diametro baten mutur batean. Abiadura konstantea mantentzen dute, nork berea, eta elkarren kontrako noranzkoan doaz. Lehen aldiz gurutzatzen direnean, Marenek 100 metro egin ditu. Une horretatik aurrera, Mirenek 150 metro egin dituenean gurutzatu dira berriro. Zein da pistaren luzera?
Lehen soluziobidea. Pista erdiaren luzera l bada, Marenek 100 metro egin ditu eta Mirenek l – 100 metro. Hurrengoan elkartzen direnerako, Marenek 2l – 150 metro eta Mirenek 150 metro. Abiadura konstantean egiten dutenez, distantziak proportzionalak izan behar dira:
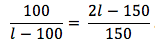
Ekuazio horren soluzioak l = 0 (baliogabea) eta l = 175 dira. Pistaren luzera 350 metrokoa da.
Bigarren soluziobidea. Gehienok ekuazioen bide hori hartuko genuke, seguruenik, baina Joseluk modu erraz eta dotorean ebatzi du problema. Abiadura konstante mantentzen dutenez, pista osoa egiteko bien artean, pista erdia egiteko behar dutenaren bikoitza da. Hortaz, pista osoaren 200 metro egingo ditu Marenek (erdian 100 egin dituelako) eta 150 metro Mirenek. Bien artean, 350 metro. Horixe da pistaren luzera.
ABC triangelu aldeberdina da eta M, BC aldeko puntu bat. M puntutik BC aldearen zuzen perpendikularrak P puntuan ebakitzen du AC aldea eta Q puntuan AB aldearen luzapena. Izan bedi N, MQ zuzenkiaren erdiko puntua. Baldin PC = 2 cm eta BN = 7 cm badira, zenbat da BC aldearen luzera?
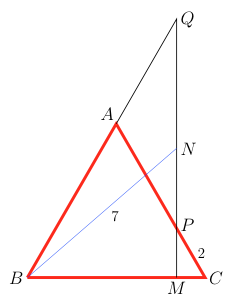
Izan bedi l triangeluko aldearen luzera. Triangelu aldeberdinaren angeluak 60 gradukoak dira. CMP triangeluan CP = 2 denez, MC = 1 da. Orduan, BM = l – 1 izango da eta BMQ triangeluari begiratuz,
MQ = (l – 1) izango da. MN = MQ/2 denez, Pitagorasen teorema erabiliko dugu BMN triangeluan:
![]()
Hortik,
![]()
Eta Gutxi gorabehera, 6.2915 da.
Ehun karta ditugu 1etik 100eraino zenbakituta. Hiru kartako multzoak egin nahi ditugu propietate honekin: hirukoteko karta baten zenbakia beste karta bien zenbakien biderkadura da. Zenbat multzo egin daitezke gehienez? (Ezin dira kartak errepikatu, noski.)
Hirukote bakoitzak derrigorrez behar du 10 baino txikiago den karta bat. Bestela, edozein zenbaki biren biderkadura 100 baino handiagoa izango litzateke, eta ezin izango genuke hirugarren karta aukeratu. Gainera, ezin da 1 zenbakia egon, horrek bi zenbaki berdin beharko lituzkeelako. 2tik 9rainoko zenbaki bakoitza hirukote desberdin batean sartuz gero, zortzi hirukote lortuko genituzke eta hori izango litzateke kopuru handiena. Eta bai, egin daitezke zortzi, modu askotan. Esate baterako,
(9,10,90), (8,11,88), (7,12,84), (6,13,78), (5,14,70), (4,15,60), (3,16,48), (2,17,34).
Beraz, zortzi multzo egin daitezke gehienez.
Iñakiren erantzunaren arabera, esango nuke hirukote posible guztiak hartu dituela, hirukote batetik bestera kartak errepikatu arren. Horiek zenbatu nahi izanez gero, bide hau segi dezakegu. Hirukoteko karta txikiena 2 bada, 48 aukera daude (hurrengo karta 3 eta 50 artean egon daiteke); txikiena 3 bada, 30 aukera (hurrengoa 4 eta 33 artean); txikiena 4 bada, 21 aukera (hurrengoa 5 eta 25 artean); eta horrela, txikiena 9 izan arte, 2 aukera (hurrengoa 10 edo 11). Denetara, 137 hirukote ateratzen dira.
Egileaz:Javier Duoandikoetxea Analisi Matematikoko Katedradun erretiratua da UPV/EHUn.
The post Dozena erdi ariketa 2023ko udarako: erantzunak appeared first on Zientzia Kaiera.
Las matemáticas del bordado sashiko
Las matemáticas definen el sashiko a través de la geometría de los patrones. […] El sashiko y el proceso de coser patrones ejemplifican la relación entre las matemáticas y los textiles.
La palabra sashiko viene del japonés 刺し子, que significa “pequeñas puntadas”. Este nombre alude al acto de ir empujando la aguja verticalmente a través de gruesas capas de tela.
Historia del sashikoDesde el periodo Edo, esta técnica de bordado se utilizaba para reforzar la ropa de trabajo de la población rural japonesa. Las piezas así obtenidas eran más resistentes y aislaban mejor del frío. Gracias al sashiko, los agricultores con escasos recursos podíanhacer durar más tiempo su ropa, remendándola o juntando varias capas de telas viejas con esta técnica.
En esta época, las leyes imperiales imponían a la población los colores, los tejidos y el tipo de vestimenta que podían llevar dependiendo de su clase social. Las clases trabajadoras no podían usar ni colores brillantes, ni grandes estampados, ni tejidos ricos como la seda. Por ello, utilizaban telas de color índigo (había una gran abundancia de telas baratas de este tono) y con motivos pequeños, en particular en sus bordados. Además, como el hilo de algodón blanco era relativamente barato (se retorcía para ser más resistente y para conseguir un acabado mate), el sashiko tiene una apariencia que la caracteriza: el bordado blanco sobre azul.
 Detalle de un kimono de mediados del siglo XIX decorado con sashiko, con hilos de algodón blanco sobre fondo de tejido tafetán teñido de añil. Fuente: Museo Metropolitano de Arte de Nueva York / Wikimedia Commons.
Detalle de un kimono de mediados del siglo XIX decorado con sashiko, con hilos de algodón blanco sobre fondo de tejido tafetán teñido de añil. Fuente: Museo Metropolitano de Arte de Nueva York / Wikimedia Commons.Durante el periodo Meiji el trabajo de bordado sashiko se tornaba una ocupación relevante durante el invierno, especialmente en las comunidades rurales del norte de Japón, en un momento en el que hacía demasiado frío para trabajar en el exterior.
Las jóvenes aprendían las técnicas tradicionales de otras mujeres, “porque el rigor y la paciencia necesarios para el bordado son considerados cualidades esenciales para una esposa”.
Esta última frase me recuerda a aquello que se valoraba de las mujeres calculistas en los observatorios astronómicos, o también de las primeras programadoras. Entre los años 1910 y 1921, el Observatorio del Vaticano colaboraba para completar la Carte du Ciel; su responsable pensaba que el trabajo de calcular posiciones de estrellas a partir de placas fotográficas podía ser realizado por “simples” monjas. En julio de 1909, envió una carta a la madre superiora de la orden de Maria Bambina (cercana al Observatorio) comentándole que “necesitaba dos hermanas con visión normal, paciencia y predisposición al trabajo metódico y mecánico”. ¡La paciencia y la precisión pensadas en tantas actividades como cualidades típicas de mujeres!
Las matemáticas del sashikoLos patrones mayoritariamente utilizados en el bordado sashiko se basan en elementos geométricos (rombos, hexágonos o semicírculos), a veces estilizados en formas de olas, montañas, plantas de bambú o flores.
Algunos diseños tienen un valor simbólico o protector: las estrellas takonomekura de cinco puntas protegerían a los pescadores de los naufragios, los patrones en zigzag ahuyentarían a los espíritus malignos, las puntadas de arroz komezashi (en el caso de los agricultores) o las escamas de pescado urokozashi (en el caso de los pescadores) atraerían la prosperidad.
Los bordados tradicionales se clasifican en dos grandes clases según la manera de coser: los moyōzashi, patrones cuyos puntos no se cruzan, y los hitomezashi (literalmente, sashiko de una sola puntada) trabajados en cuadrícula, con puntos verticales y horizontales, y que pueden cruzarse.
 Muestrario con diferentes patrones de sashiko en una exposición del Museo de Arte Textil de Canadá. Fuente: Daderot / Wikimedia Commons.
Muestrario con diferentes patrones de sashiko en una exposición del Museo de Arte Textil de Canadá. Fuente: Daderot / Wikimedia Commons.En [Seaton and Hayes, 2023] las autoras analizan precisamente dos aspectos matemáticos de la forma de coser hitomezashi: la codificación de diseños mediante palabras de un alfabeto binario y la dualidad.
Para las personas que alguna vez han bordado consultando las instrucciones en alguna revista de costura, las indicaciones para realizar las puntadas consisten en una serie de símbolos concatenados, una especie de diccionario simbólico que “dirige” la manera de mover la aguja sobre la tela. En el caso del hitomezashi, la puntada única permite indicar si la puntada va del derecho (1) o del revés (0) de la tela. Las instrucciones consistirían entonces en una serie de 0s y 1s (debería indicarse, además, la dirección de la puntada).
Cuando se cose del modo hitomezashi, el anverso y el reverso de la tela poseen patrones duales; en algún caso pueden incluso ser auto-duales (cuando el anverso y el reverso reproducen exactamente el mismo patrón).
Usando estos dos conceptos es posible codificar matemáticamente todos los bordados tradicionales del hitomezashi del sashiko japonés.
En [Seaton and Hayes, 2023] las autoras también analizan las formas de los bordados; estudian en particular los hitomezashi que construyen fractales de la palabra de Fibonacci u otrospoliominós basados en los números de Pell.
He descubierto esta técnica de bordado gracias a mi hermana Inés que la ha conocido a su vez a través de un colega japonés. Este vídeo es una estupenda ilustración.
Muchas artes textiles pueden disfrutarse con mirada matemática: patrones, simetrías, codificación de los dibujos o formas geométricas son claves para coser, bordar o tejer un hermoso objeto cotidiano o una pieza decorativa.
Referencias
-
Barbara Setsu Pickett. Sashiko: the stitched geometry of rural Japan. Bridges Conference Proceedings (2006) 211-214.
-
Katherine A. Seaton and Carol Hayes, A two-dimensional introduction to sashiko, arXiv:2003.14235.
-
Katherine A. Seaton and Carol Hayes, Mathematical specification of hitomezashi designs, arXiv:2208.12580v2.
-
Lucy Arai, Sashiko Workshop: Experiential Geometry. Textile Society of America Symposium Proceedings (2006) 211-219.
-
Sashiko, Wikipedia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Las matemáticas del bordado sashiko se ha escrito en Cuaderno de Cultura Científica.
Zergatik iruditzen zaigu denbora motelago doala gu zahartu ahala?
Tik, tak… tik tak… Denbora aurrera doa halabeharrez denontzat. Nahiz eta denborak erritmo berean egiten duen aurrera denontzat, denboraren joanaren pertzepzio subjektiboa oso desberdina izan daiteke pertsona bakoitzarentzat. Horrela, dibertitzen garenean edo jardueraren batez gozatzen dugunean, badirudi denbora hegan igarotzen dela; lan monotono, aspergarri edo desatsegin batean murgilduta bagaude, berriz, minutuak betierekoak egiten zaizkigu. Alde horretatik, bada fenomeno berezi bat, psikologian luze-zabal egiaztatu dena: oro har, denbora azkarrago igarotzen dela iruditzen zaigu urteak bete ahala.
Atzera begiratuz gero, gure haurtzaroko oroitzapenetan arakatuz, iruditzen zaigu egunak luzeagoak zirela eta askoz ere probetxu handiagoa ateratzen geniela: jarduera ugari egin genitzakeen, ia denetarako denbora zegoelako. Gainera, haurtzaroko udek helduaroko udek baino luzeagoak ziruditen, hasperen bat baino azkarrago pasatzen baitira orain, batez ere udako oporrak hartzen ditugunean. Helduaroko une batetik aurrera, denbora «bizkortu» egiten dela eta dena pixkanaka azkarrago igarotzen dela iruditzen zaigu. Zein da denboraren pertzepzio subjektiboaren bilakaera horren arrazoia? Gaur egun, ez dakigu arrazoia zein den, eta asko dira hori azaltzen saiatu diren hipotesiak.
 Irudia: zein da denboraren pertzepzio subjektiboaren bilakaera horren arrazoia? Gaur egun, ez dakigu arrazoia zein den, eta asko dira hori azaltzen saiatu diren hipotesiak. (Argazkia: Mikhail Nilov – domeinu publikoko argazkia. Iturria: Pexels.com)
Irudia: zein da denboraren pertzepzio subjektiboaren bilakaera horren arrazoia? Gaur egun, ez dakigu arrazoia zein den, eta asko dira hori azaltzen saiatu diren hipotesiak. (Argazkia: Mikhail Nilov – domeinu publikoko argazkia. Iturria: Pexels.com)Fenomeno horren atzean dagoen arrazoi posible bat egunero ikusten ditugun irudien prozesamendu zerebralarekin dago lotuta. Adrian Bejan Duke Unibertsitateko Ingeniaritza Mekanikoko irakasleak planteatutako hipotesiaren arabera, badirudi egunak laburragoak direla zahartzen garen heinean, denboran zehar informazio bisualaren prozesamendua moteldu egiten delako. Irudi gutxiago hautematen baditugu segundoko, horrek denbora azkarrago igaro delako sentsazioa sor dezake, eta alderantziz: segundoko irudi gehiago hautematen ditugunean, denbora motelago doala senti dezakegu, bideo bat kamera geldoan ikusten dugunean bezala.
Planteamendu horren oinarria da informazioa garraiatzen duten nerbio seinaleek denbora gehiago behar dutela faktoreen batuketa bat egiteko urteak betetzen ditugun heinean: garuneko neurona sareen tamaina eta konplexutasuna areagotu egiten da, eta, gainera, zahartzeak kalteak eragiten ditu, eta horrek seinale elektriko horien fluxua atzeratu dezake. Horregatik, haurrek helduek baino irudi gehiago prozesatu ahal izango lituzkete segundoko, eta, beraz, denbora motelago doala sumatu.
Baliteke, halaber, irudien prozesamenduaz harago, pertsona bakoitzaren denboraren erritmoa markatzen duen «metronomo neural» bat egotea. Haurrengan, metronomo hori helduengan baino azkarrago joango litzateke (geldi zaudeneko bihotz maiztasunarekin edo arnasketarekin gertatzen den bezala, horiek ere azkarragoak baitira haurrengan), eta horrek denboraren igarotze motelagoa hautematea eragingo luke. Izan ere, Clifford Lazarus psikologoak gai horri buruzko esperimentu bitxi bat kontatzen du: haurrak eserita, begiak itxita eta ezer egin gabe utziz gero, gehienek benetan igaro dena baino denbora gehiago igaro delako sentsazioa dute (askok aipatzen dute minutu bat igaro dela, benetan 40 segundo igaro direnean). Aldiz, baldintza berak helduei aplikatzen bazaizkie, denboraren pertzepzio subjektiboa errealistagoa da edo atzerapen txiki batekin doa: minutu bat igaro dela zehazten dute, baina, benetan, minutu bat edo 70 segundo igaro dira.
Denboraren erritmoak haurren eta helduen artean eragiten duen sentsazio desberdinari buruzko beste azalpen bat denbora kuantifikatzeko orduan biek duten perspektiba desberdinean zentratzen da. 10 urteko haur batentzat, adibidez, urtebete igarotzeak haren bizitza osoaren % 10 igaro dela esan nahi du, eta haren memoria kontzientearen % 15 eta % 20 artean. Aldiz, 65 urteko pertsona batentzat, urte bat haren bizitzaren % 1,5 baino ez da. Bizipenak eta oroitzapenak modu erlatiboan hautemateak haurtzaroan denbora motelago igarotzen zelako sentsazioa sor dezake, denbora unitate berak askoz pisu handiagoa zuelako bizitako esperientzia guztien barruan.
Baliteke, halaber, haurtzaroaren, helduaroaren eta zahartzaroaren arteko denboraren pertzepzio desberdina oroitzapenak finkatzeko joeren ondorio izatea. Gure oroimenean markarik handiena uzten duten bizitzako esperientziak, hain zuzen ere, emozioak eragiten dizkigutenak dira, batez ere emozio biziak badira. Haurrentzako eta nerabeentzako ia dena da berria, eta bizitzako etapa berantiarragoetan baino intentsitate emozional handiagoarekin bizi dira. Errutina eta monotonia nagusi izaten dira gero, eta horiek arrasto txikia uzten dute gure oroitzapenetan.
Horrela, gure iraganeko eta egungo oroitzapenak ebaluatzean, irudipena izan dezakegu askoz esperientzia gehiago bizi genituela denbora berean (eta, beraz, denbora motelago igarotzen zela) azken urteetan baino. Ez ditugu pasarte gogoangarri asko bizitzen eta interesik gabeko oroitzapen asko desagertu egiten dira, aurrekoan zer jan genuen, esaterako. Hipotesi hori egia balitz, gure buruei denbora motelago doala sentiarazteko modu bat monotoniatik ihes egitea eta maiz esperientzia berriak bizitzea litzateke.
Egileaz:Esther Samper (@Shora) medikua da, Ehunen Ingeniaritza Kardiobaskularrean doktorea eta zientzia-dibulgatzailea.
Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2023ko ekainaren 5ean: ¿Por qué nos parece que el tiempo pasa más rápido conforme envejecemos?
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Zergatik iruditzen zaigu denbora motelago doala gu zahartu ahala? appeared first on Zientzia Kaiera.
El origen de las cascadas electrónicas en las bicapas de grafeno rotado con ángulo mágico
Investigadoras del Instituto de Ciencia de Materiales de Madrid (ICMM), CSIC, han descubierto por qué se forman los sistemas de cascadas electrónicas en bicapas de grafeno rotado con ángulo mágico. Este resultado contradice teorías anteriores sobre esta intrigante propiedad de las bicapas de grafeno con ángulo mágico.

Fue hace algo más de cinco años cuando se descubrió que, al girar una capa de grafeno con respecto a la otra solamente 1,1 grados (el llamado ‘ángulo mágico’), este material adquiría nuevas y sorprendentes propiedades por la interacción de sus electrones: se vieron estados aislantes y superconductores que no se esperaban. Posteriormente se encontraron cambios dramáticos en la energía de los electrones en forma de cascadas. Todos estos fenómenos abrieron un nuevo campo de investigación y estos sistemas (simples, a priori, al estar basados solo en carbono) muestran mayor variedad de estados electrónicos que ningún otro.
«En las primeras interpretaciones de las cascadas, se creía que tenían que ver con estados ordenados, tales como estados magnéticos, que se han detectado en el sistema a muy bajas temperaturas, del orden de 5 Kelvin, pero estas cascadas son mucho más resilientes, sobreviven hasta temperaturas de decenas de Kelvin», explica Elena “Leni” Bascones, investigadora en el ICMM y coautora del estudio. Este trabajo apunta a que el origen de este fenómeno es otro.
En concreto, este estudio viene a demostrar que pueden aparecer las cascadas sin necesidad de invocar ningún orden. «No decimos que en las bicapas de ángulo mágico no haya orden, este se ha observado, pero a temperaturas más bajas», señala María José Calderón, investigadora en el ICMM y también coautora del trabajo.
La clave de la nueva investigación radica en la técnica utilizada para su descripción teórica: la teoría de campo medio dinámica combinada con cálculos Hartree. «Es la técnica numérica más avanzada utilizada hasta ahora para estudiar el tipo de efecto que buscamos», explica Bascones. «Es un problema muy complejo, porque en los sólidos hay muchos electrones interaccionando y el comportamiento colectivo es emergente, es decir, no puedes entenderlo trivialmente como la suma del comportamiento de los electrones individuales», añade Calderón.
«Cuando se empezaron a descubrir las propiedades de estas bicapas de grafeno rotadas se quiso ver si podía tener que ver con los superconductores de alta temperatura», explica Bascones.
Aunque en un principio se pensó que la fenomenología detrás de estos materiales no afectaba a las bicapas de grafeno, «lo que nosotras precisamente decimos es que el origen subyacente de estas cascadas está relacionado con el tipo de física que ocurre en otros sistemas correlacionados», como los superconductores a alta temperatura. Esto puede ser clave para lograr comprender cómo funcionan estos superconductores, que a su vez son esenciales para objetivos tecnológicos como la transmisión eficiente de energía o los ordenadores cuánticos.
Referencia:
Datta, A., Calderón, M.J., Camjayi, A. & Bascones, E. (2023) Heavy quasiparticles and cascades without symmetry breaking in twisted bilayer graphene Nat Commun doi: 10.1038/s41467-023-40754-4
Edición realizada por César Tomé López a partir de materiales suministrados por ICMM-CSIC
El artículo El origen de las cascadas electrónicas en las bicapas de grafeno rotado con ángulo mágico se ha escrito en Cuaderno de Cultura Científica.
Europar Batasunak zientzia-aldizkarien argitalpen-tasak gaitzetsi ditu
Udaberrian hedabide honetan bertan aztertu nuen gaur egungo zientziaren atzean dagoen berrikuspen-sistema, peer review edo parekoen berrikuspen-prozesu deritzona. Gaiaz argitaratu genituen bi lanetan, zientzialariek eta argitaletxeek zientziaren jokoan nola hartzen duten parte azaldu nuen. Argiak eta itzalak dituen sistema bada ere, oraingoz ez daukagu aukera hoberik. Bada, ordea, artikulu horietan aipatu gabe gelditu zen puntu garrantzitsu bat eta, maiatzean Europar Batasunak esan zuenarekin lotuz, argitaletxeen atzean dagoen sistema ekonomikoa ekarriko dut gaur plazara.
 Irudia: zientzia-aldizkariak argitaratzen dituzten argitaletxeen irabaziak oparoak dira eta zientziari berari eragiten diote argitalpen-tasa altuek. (Argazkia: Dmitriy – domeinu publikoko irudia. Iturria: pixabay.com)
Irudia: zientzia-aldizkariak argitaratzen dituzten argitaletxeen irabaziak oparoak dira eta zientziari berari eragiten diote argitalpen-tasa altuek. (Argazkia: Dmitriy – domeinu publikoko irudia. Iturria: pixabay.com)Berrikuspen-sistema berrikusteko beharra (I eta II) lanetan, zientziaren oinarrian dagoen berrikuspen-sistemari begiratu sakona eman genion, baita dituen arrisku handienak aztertu ere. Laburtuz, argitalpenak berak ezinbestekoak direla esan daiteke; izan ere, zientziak aurrera egin ahal izateko, ezinbestekoa da zientzialarien arteko nolabaiteko komunikazioa eta, gaur egun, biderik ohikoena zientzia-aldizkariak dira. Publish or perish “argitaratu ala hil” lelopean, geroz eta nabariagoak dira argitaletxeen jokabideak dakartzan hainbat arazo. Ikertzaileek beharra dute kalitatezko aldizkarietan lanak argitaratzeko eta, sarri askotan, ordaindu egin behar izaten da lanak argitaratzeagatik. Ikerketa-lanak irakurri nahi dituzten zientzialariek ere ordaindu egin behar dute, haiek edo unibertsitateek ordaintzen dituzten harpidetzen bidez; beraz, negozio ezin hobea da argitaletxeentzat. Hori gutxi balitz, ikerketa-lanak ebaluatzen dituzten adituek ere musu-truk egin ohi dute lan.
Argitalpen-tasak negozioa direneanArgitaletxeen jokabide hori arriskuan jartzen ari da zientzia, eta diru publikoaren kantitate handiak xahutzen ari dira, bai ikerketa-lanak argitaratu ahal izateko, bai eta aldizkarietara harpidetzak ordaintzeko. Gauzak horrela, oso garrantzitsua da maiatzean Europar Batasuneko Kontseiluaren baitan dagoen Lehiakortasun Kontseiluak adierazitakoa. Gaian kokatzeko, kontuan hartu behar dugu aldizkari entzutetsuenetan lan bat argitaratzeko 10.000 eurora bitarteko tasak ordaindu behar direla. Kontseiluak hartutako erabakiaren arabera (hemen ebazpen osoa), diru publikoz finantzatutako ikerketa lanak sarbide irekikoak, alegia, open access motakoak, izan behar dira. Berehala eta mugarik gabe edonork irakurtzeko moduko ikerketa-lanak izan beharko lirateke, haien aburuz.
Argitaletxeen negozioa oso errentagarria da eta urtean 17.500 milioi euroko diru-sarrerak dituztela jotzen da. Bolumen hori parean kokatzen da industria diskografikoaren edo zinematografikoaren, baina argitaletxeena askoz ere errentagarriagoa da. The Objective hedabideko Lidia Ramírez kazetariak argitaratutako artikuluaren arabera, bi bide daude argitaratzen diren ikerketa-lanen %90 irakurri ahal izateko: irakurri nahi duenak harpidetza ordaintzea edo artikulua argitaratu nahi duenak lana sarbide irekikoa izateko ordaintzea. Esan bezala, lanak sarbide irekikoak izan daitezen, argitaletxeek tasa bat eskatzen diote zientzialariari eta handiak izan daitezke eskatutako kopuruak. Aldizkariaren arabera, 170 eurotik hasi eta ia 10.000 eurora bitarteko tasak izan daitezke. Joko honetan dauden argitaletxerik ezagunenak dira Elsevier, Springer-Nature, Taylor & Francis eta MDPI, besteak beste. Testuinguru egokia izan dezagun, kontuan hartu behar da Elsevierrek, esaterako, 2022. urtean 3.380 mila milioi euroko diru sarrerak izan zituela eta 1.350 milioi euroko irabaziak; ia %40ko errentagarritasuna, hortaz. Errentagarritasun hori Apple, Google edo Amazon enpresena baino handiagoa da, adibidez.
Gauzak horrela, Europar Batasunaren Kontseiluak adierazi du argitalpen akademikoen sistemak kalitatezkoa, gardena, irekia, fidagarria eta bidezkoa izan behar duela. Gainera, zuzen-zuzenean doa argitaletxeen gaur egungo sistemaren aurka; izan ere, Kontseiluak azpimarratu du sarbide irekiko eta irabazi asmorik gabeko argitalpen-ereduen alde egiten duela. Era berean, adierazten du zientzialari batek ez duela mugarik izan behar, ez bere lanak argitaratzeko orduan ezta beste ikertzaileen lanak irakurtzeko orduan. Hain zuzen ere, harpidetza- eta argitalpen-tasa altuen ondorioz, finantzaketa-iturri urriak dituzten zientzialariek ezin dute edozein aldizkaritan argitaratu ezta edozein artikulu irakurri ere. Kontseiluak herrialde guztiei dei egiten die martxan jar ditzaten sarbide irekiaren eta lizentzia libreko zientziaren aldeko politikak. Momentuz itxurakeria hutsa izan badaiteke ere, itxaropentsua da Europar Batasunak iparra horrela adieraztea.
Poliki bada ere, zientzia-komunitatea ohartuz doa arazo horretaz, eta maiatzean albiste garrantzitsua irakurri ahal izan genuen. Neuroimage eta Neuroimage:Reports aldizkari entzutetsuen editoreek –zientzialariak izan ohi dira haiek ere- dimisioa eman zuten Elsevierri argitalpen-tasak murrizteko eskatu eta ezetza jaso ostean. Aldizkariak 3.450 dolar eskatzen zituen lanak argitaratzeko eta editore-taldeak prezio hori 2.000 dolar baino gutxiagokoa izatea eskatzen zuen. Argitaletxearen ezezkoa jaso ostean, 40 editorek dimisioa eman zuten gutun hau argitaratuz eta sarbide irekiko aldizkari baten sorrera sustatu behar dutela adieraziz. Editore ohien ustez, ez da etikoa tasa horiek eskatzea. Albisteak hautsak harrotu ditu zientzia-komunitatean, ez baitago argi kasu puntuala ote den edo etor daitekeen errebolta bat den.
Bide horretan, Europar Batasunaren adierazpenak adierazpen besterik ez diren arren, badirudi zerbait aldatzen hasi daitekeela. Ezinbestez aldatu beharko da; izan ere, argitalpen-sistema bideraezina den puntu batean egon daiteke eta zientzia bera arriskuan jartzen du horrek.
Informazio gehiago:- Lidia Ramírez (2023). La UE exige acabar con el chanchullo millonario de las publicaciones científicas, theobjective.com, 2023ko uztailaren 5a.
- Josu Lopez-Gazpio (2023). Berrikuspen-sistema berrikusteko beharra (I), zientziakaiera.eus, 2023ko martxoaren 28a.
- Josu Lopez-Gazpio (2023). Berrikuspen-sistema berrikusteko beharra (eta II), zientziakaiera.eus, 2023ko apirilaren 26a.
- José Manuel López Nicolás (2023). ¿Cómo se revisa un artículo científico y qué dos problemas provoca el comportamiento de las editoriales?, scientiablog.com, 2023ko otsailaren 19a.
- Koldo Garcia (2013). Artikulu zientifikoak eta argitaratzeko presioa, edonola.net, 2013ko abenduaren 11.
Josu Lopez-Gazpio (@Josu_lg), Kimikan doktorea, irakaslea eta zientzia dibulgatzailea da. Tolosaldeko Atarian Zientziaren Talaia atalean idazten du eta UEUko Kimika sailburua da.
The post Europar Batasunak zientzia-aldizkarien argitalpen-tasak gaitzetsi ditu appeared first on Zientzia Kaiera.
Los esteroides prenatales, arma de doble filo frente a la prematuridad
La prematuridad es, en la actualidad, la principal causa de muerte infantil en el mundo y la Organización Mundial de la Salud (OMS) lo califica de «emergencia silenciosa». Según el informe «Nacidos demasiado pronto: una década de acción sobre la prematuridad», en el que han participado este organismo y la Organización de las Naciones Unidas, cada año nacen alrededor de 15 millones de bebés prematuros (antes de la semana 37 de embarazo). Es decir, más de uno de cada 10 bebes que nace en el mundo es prematuro. De ellos, casi un millón muere por complicaciones desencadenadas por esta razón y algunos de los que sobreviven se enfrentan a una vida con discapacidad (problemas de aprendizaje, visuales y auditivos, entre otros).
 Photo: Janko Ferlič / Unsplash
Photo: Janko Ferlič / UnsplashEn España, según la Sociedad Española de Neonatología (SENEO), cada año nacen en torno a 28.000 prematuros, lo que supone el 7 % de todos los nacimientos. Un millar de ellos son prematuros extremos, al nacer antes de las 28 semanas de embarazo. Varios son los factores que propician la prematuridad, como una mayor edad de la madre, el consumo de tabaco, la contaminación ambiental y niveles altos de estrés durante el embarazo.
Las probabilidades de que un bebé prematuro salga adelante dependen principalmente de dos factores: el grado de prematuridad (cuanto más prematuro es el nacimiento, mayor riesgo hay de muertes y de secuelas) y el acceso a los servicios sanitarios. En los países en desarrollo es precisamente dónde el pronóstico de los bebés con prematuridad es más sombrío porque muchas familias no pueden conseguir la atención médica que necesitan.
Además de otros tejidos y órganos, en los bebés más prematuros los pulmones no se encuentran totalmente desarrollados, en parte por el déficit del surfactante pulmonar. Esta sustancia normalmente recubre el interior de los pulmones (concretamente, los alveolos) para disminuir su tensión superficial y facilitar la expansión de estos órganos. Algunos prematuros, al no tener cantidad suficiente de surfactante, deben realizar un gran esfuerzo en la inspiración, para la entrada de aire en los pulmones, por lo que sufren dificultades respiratorias importantes.
Esteroides contra la prematuridadPara reducir el riesgo de complicaciones (dificultades respiratorias, infecciones, hemorragias cerebrales…) y muertes en los bebés, un tratamiento ampliamente extendido es la administración de esteroides a aquellas madres que tienen altas probabilidades de tener un parto prematuro, antes de las 34 semanas de embarazo.
Estos fármacos aceleran la maduración de los pulmones, la producción de surfactante pulmonar y de los vasos sanguíneos, por lo que mejoran de forma clara el pronóstico de los bebés que nacen antes de tiempo. Sin embargo, apenas se conocen los efectos a largo plazo que podrían tener estos fármacos en la salud de los neonatos. Dos recientes estudios, publicados en la revista The British Medical Journal, advierten de que los esteroides podrían tener consecuencias negativas más tarde en la vida de los prematuros.
Uno de los estudios analizó la frecuencia de aparición de diversas enfermedades en dos grupos de niños, aquellos que se expusieron a corticosteroides durante el embarazo y aquellos que no, con un total de 2 millones de niños que nacieron entre 2008 y 2019 en Taiwán. La información se obtuvo a partir de una base de datos nacional. Los investigadores descubrieron que aquellos niños que estuvieron expuestos a los esteroides tenían un riesgo significativamente mayor de sufrir infecciones graves como neumonía y sepsis en el primer año de vida.
El otro estudio consiste en una revisión sistemática de 7 ensayos clínicos y 10 estudios poblaciones que, en total, reúnen datos de 1,6 millones de niños que nacieron a partir del año 2000. Los bebés expuestos a los esteroides tenían un riesgo incrementado de entrar en cuidados intensivos neonatales, tener una menor circunferencia de la cabeza y padecer más trastornos del comportamiento y del neurodesarrollo a largo plazo. Además, los autores comprobaron que en torno al 40 % de los bebés que recibieron corticosteroides durante el embarazo nacieron finalmente a término, por lo que, en realidad, no hubieran necesitado de estos fármacos.
Los hallazgos de ambas investigaciones invitan a reflexionar sobre el uso de los esteroides y a valorar con más cuidado la necesidad de ellos, considerando los potenciales riesgos que podrían tener. Aún es pronto para afirmar con certeza que estos medicamentos son los responsables directos de los citados problemas de salud, ya que una gran parte de los datos proceden de estudios observacionales que no permiten identificar relaciones de causas y efectos. Por tanto, serán necesarios más ensayos clínicos para poder conocer con más rigor los efectos de los esteroides. Sus beneficios clínicos a corto plazo están ampliamente demostrados, pero sus efectos negativos más tardíos siguen siendo todavía bastante desconocidos.
Sobre la autora: Esther Samper (Shora) es médica, doctora en Ingeniería Tisular Cardiovascular y divulgadora científica
El artículo Los esteroides prenatales, arma de doble filo frente a la prematuridad se ha escrito en Cuaderno de Cultura Científica.

