Madrilgo jatetxearen sutea eta zianuro intoxikazioak
Gaur egun etxebizitza eta eraikuntzetan gertatzen diren suteetan heriotzaren kausarik nagusiena ez da karbono monoxidoa, zianuro-gasak baizik. Horrekin lotuta, apiril amaieran Madrilgo jatetxe baten sutean antzeko zerbait gertatu izana da ziurrena. Sabaiko plastikozko dekorazioak su hartu zuen eta bi lagun hil ziren, antza, gas-intoxikazioaren kausaz. Emandako azalpenetan, zianuroa aipatzen da, baina nola liteke sute baten kean zianuroa egotea?
Apirilaren 21ean Madrilgo jatetxe batean gertatutako sutearen ondorioz hiru lagun hil ziren eta gutxienez beste hamar zauritu ziren. Sutea 23:00ak aldera hasi zen, antza, pizza bat flanbeatzeko erabilitako soplete baten kausaz. Jatetxearen sabaia plastikozko lore eta bestelako apaingarriz beterik zegoen eta, dirudienez, plastikozko dekorazioak su hartu zuen segundo gutxiren barruan. Hedabideetan irakurri ahal izan dugunez, litekeena da bi heriotzen kausa gas toxikoak arnastea izatea, batik bat karbono monoxidoa eta zianuro-gasak. Bertaratutako suhiltzaileen arduradunek aipatu zutenez, zianuroa izan zitekeen arrazoi nagusia. Oraingoz heriotzen arrazoiak argitzeke dauden arren, nola da posible zianuroa askatzea sute batean? Bada, ez da harritzekoa zianuro-gasak askatzea eta badauka azalpen zientifikoa. Instagram-estiloko dekorazioak eztabaidan dauden bitartean, azter dezagun zianuroaren kimika Madrilgo sutearen arriskuak hobeto ulertu ahal izateko.
 1. irudia: sabaiko plastikozko loreen errekuntzak zianuro-gasak aska ditzake. (Argazkia: Yung-pin Pao – domeinu publikoko irudia. Iturria: pixabay.com)
1. irudia: sabaiko plastikozko loreen errekuntzak zianuro-gasak aska ditzake. (Argazkia: Yung-pin Pao – domeinu publikoko irudia. Iturria: pixabay.com)Lehenik eta behin, egin dezagun zuzenketa bat. Oro har, zianuroa aipatu den arren, hidrogeno zianuro (HCN) gasaz hitz egiten ari gara, baina beste zianurodun konposatu batzuk ere aska daitezke sute batean. Zein da desberdintasuna? Zianuroa anioi monobalentea da, karbono atomo baten eta nitrogeno atomo baten loturaz sortzen dena. Modu desberdinetan aurki daiteke; esaterako, konplexu kristalinoetan -potasio zianuroa-, zianogeno kloruroa edo zianogeno bromuroa bezalako konposatu gisa edo hidrogeno zianuro moduan -bai gas-fasean bai ur-fasean-. Hidrogeno zianuroari, ur-fasean disolbatuta dagoenean, azido zianhidriko deritzo. Antzeko zerbait gertatzen da azido klorhidrikoarekin, zeina hidrogeno kloruroaren ur-disoluzioa den. Zianuroari, konposatu organikoen talde funtzional gisa dagoenean, nitrilo talde funtzionala deritzo. Beste modu batera esanda, zianuro taldea duen konposatu organiko bati nitriloa deritzo, horixe baldin bada haren talde funtzionalik garrantzitsuena.
Hidrogeno zianuroa, HCN formula kimikoa duen gasa, oso toxikoa da. Haren eraso-mekanismoa C zitokromo oxidasa konplexua inhibitzea da. Oxidasa horren funtzioa eteten bada, elektroien garraio katea ere eten egiten da eta horixe da, hain zuzen ere, zelula-arnasketaren funtsezko mekanismoa. Zelula-barneko ATPa ekoizten jarraitzea ez denez posible, zelulek ezin dute beren funtzioa eraginkortasunez bete. Zianuroaren eraginik kaltegarrienetakoa globulu gorrien lana oztopatzea da. Zelulek ezin dutenez erabili globulu gorrietan garraiatzen den oxigenoa, zianuro-intoxikazioz hildako gorpu baten zainetan oxigeno-kontzentrazio altuak aurkitu ohi dira.
Madrilgo sutera itzuliz, kontuan hartu behar dugu karbonoa eta nitrogenoa duten plastikoek –eta, oro har, osagai horiek dituzten beste materialek– hidrogeno zianuroa sor dezaketela errekuntza-prozesuetan. Aipatzekoak dira melamina, nylona, nitrozelulosa, poliakrilonitriloa, poliuretanoak eta bestelako poliamida motako plastikoak. Plastiko horiek erretzen direnean, hidrogeno zianuroa sortzen da. Litekeena da Madrilgo jatetxeko sabaiko dekorazioan zeuden plastikozko lore eta bestelakoak mota horretakoak izana. Oro har, sute batean gertatzen diren hildakoen %82 gasak arnasteagatik hiltzen direla jotzen da. Esan bezala, gas horien artean arriskutsuenak karbono monoxidoa eta zianuro-gasak dira. Hidrogeno zianuroaren arriskua handia da; izan ere, bizirauteko oinarrizkoak diren funtzioak nahiko azkar eteten dituen pozoia da. Bi gas horien akzio-mekanismoa antzekoa da: hipoxia zelularra eragiten dute eta horrek heriotza azkarra dakar. Dirudienez, erabiltzen ditugun materialen kausaz, geroz eta arruntagoa da suteetan zianuro-intoxikazioak gertatzea.
Arazoa ez da gaurkoa eta 2008. urtetik eskuragarri daude suteetan zianuro-intoxikazioei aurre egiteko antidotoak. Gaur egun gehiago ere badira, baina, oro har, hidroxokobalamina konposatuan oinarritzen dira. Jada eskuragarri daude zianuroaren eta karbono monoxidoaren aurkako antidoto konbinatuak ere. Ezin dugu ziurtatu, jakina, baina litekeena da Madrilgo intoxikatuei horien antzeko antidotoak eman izana gas toxikoen eragina arintzeko asmoz. Hidroxokobalamina B12 bitaminaren aurrekaria da eta hari esker lotzen da zianuroa hidroxokobalaminak duen kobalto metalarekin. Kobaltoarekin lotzen denean, zianokobalamina sortzen da eta hura gernuarekin batera kanporatzen da inongo arazorik gabe.
Madrilgo jatetxearen sutean zehazki zer gertatu zen ez dakigun arren, hedabideetan agertu diren albisteetan zianuroa zergatik aipatu den badakigu orain eta suteetan egon daitekeen arrisku ezkutuaren berri ere orain badaukagu. Gaitz erdi.
Informazio gehiago:- elDiario.es (2023). Una pizza flambeada y la decoración, detonantes del fuego que convirtió en “una ratonera” el restaurante de Madrid, eldiario.es, 2023ko apirilaren 23a.
- Robert Burke (2008). Hydrogen cyanide: The real killer among fire gases, 2007ko urtarrilaren 1a.
Dugard, Paul H. (1987). Clinical and experimental toxicology of cyanides. Ed. Wright.
Egileaz:Josu Lopez-Gazpio (@Josu_lg), Kimikan doktorea, irakaslea eta zientzia dibulgatzailea da. Tolosaldeko Atarian Zientziaren Talaia atalean idazten du eta UEUko Kimika sailburua da.
The post Madrilgo jatetxearen sutea eta zianuro intoxikazioak appeared first on Zientzia Kaiera.
Cómo cambios en 3D del genoma convirtieron a los tiburones en rayas
Los cambios en la estructura 3D de su genoma dieron a las rayas sus distintivas aletas en forma de alas y su planitud de torta.
Un artículo de Viviane Callier. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
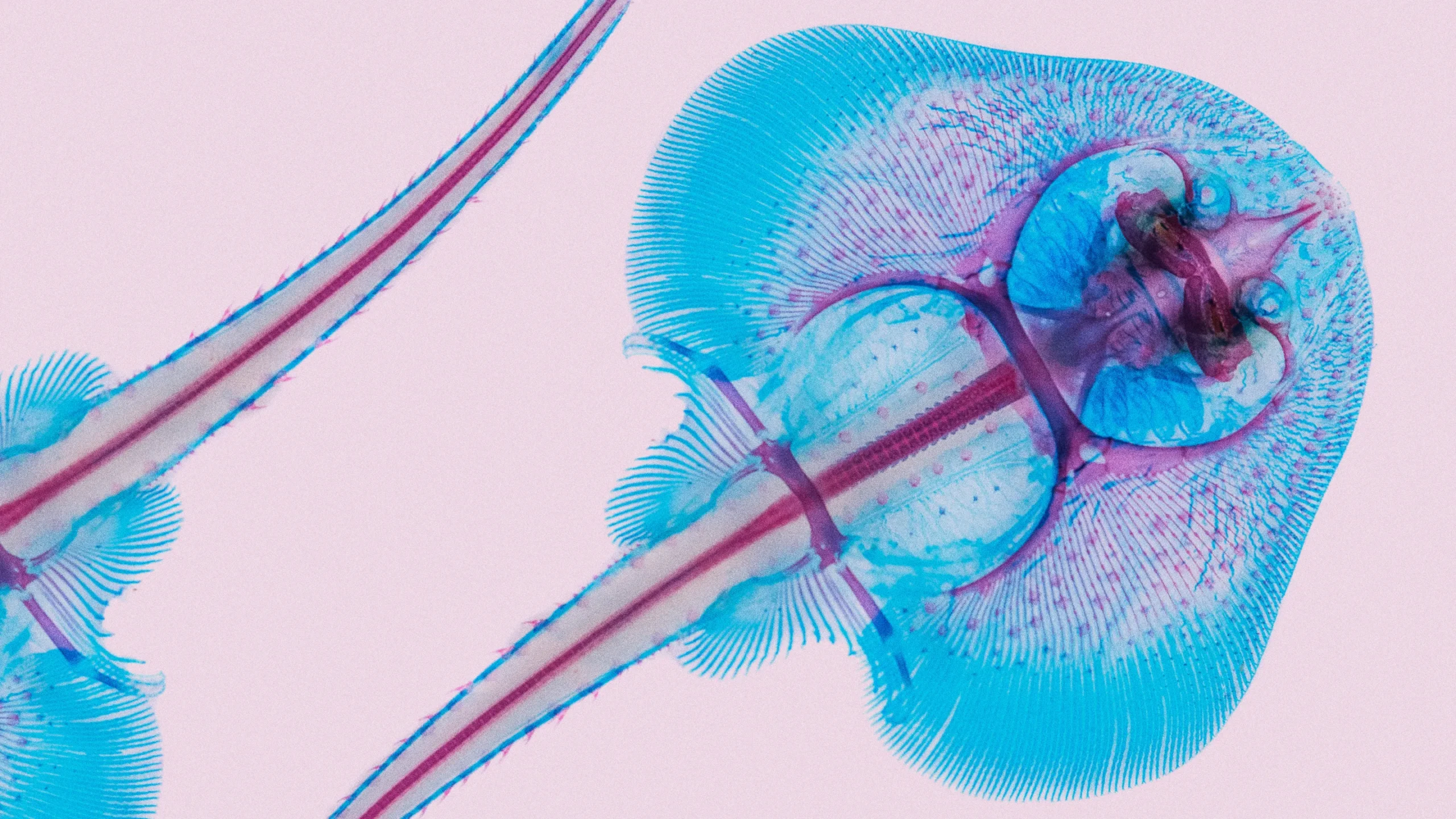 Una raya teñida químicamente revela las características estructurales que contribuyen al diseño corporal inusual de este pez. Fuente: Teresa Zgoda/Science Source
Una raya teñida químicamente revela las características estructurales que contribuyen al diseño corporal inusual de este pez. Fuente: Teresa Zgoda/Science SourceLas criaturas marinas llamadas rayas se deslizan por el fondo del mar, agitando sus aletas pectorales en forma de alas para impulsarse y revolver a las pequeñas criaturas que se esconden en la arena. Su inusual plan corporal aplanado las convierte en una de las familias de peces más extrañas del mar, y parece aún más extraño que hayan evolucionado a partir de carnívoros estilizados parecidos a tiburones que nadaron hace unos 285 millones de años.
Ahora, los investigadores han descubierto cómo las rayas desarrollaron su perfil distintivo: los reordenamientos en la secuencia de ADN de la raya alteraron la estructura 3D de su genoma e interrumpieron las antiguas conexiones entre los genes clave del desarrollo y las secuencias reguladoras que los gobernaban. Esos cambios, a su vez, rediseñaron el plan corporal del animal. Los científicos publicaron sus hallazgos en Nature en abril.
El descubrimiento resuelve el misterio de la transformación evolutiva de las rayas fijándolo en los mecanismos genéticos que dirigen el desarrollo. “El registro fósil te dice que ocurrió este cambio, pero ¿cómo ocurrió realmente?” comenta Chris Amemiya, genetista molecular de la Universidad de California en Merced, que no participó en el nuevo estudio. “Esta es una pregunta clásica de evo-devo [Nota del traductor: nombre informal de la biología evolutiva del desarrollo]”.
Para descubrir los orígenes de la nueva forma del cuerpo de las rayas, hace unos años, el genomicista evolutivo José Luis Gómez-Skarmeta* reunió a un equipo internacional diverso de investigadores en genómica y biólogos del desarrollo evolutivo. Se necesitaba un equipo en parte porque el primer paso sería secuenciar y ensamblar el genoma de una raya, y compilar los genomas de peces cartilaginosos como rayas y tiburones es tremendamente difícil.
“Son realmente difíciles de ensamblar, porque son enormes, a menudo más grandes que el genoma humano”, apunta Mélanie Debiais-Thibaud, genetista del desarrollo evolutivo de la Universidad de Montpellier en Francia, que no participó en el trabajo.
Para su trabajo, el equipo seleccionó la raya pequeña (Leucoraja erinacea), que se captura fácilmente a lo largo de la costa atlántica de América del Norte. También se puede criar en un laboratorio, lo que hizo posible realizar experimentos funcionales y de desarrollo en los animales como parte del proyecto.
Al comparar el genoma de la raya pequeña con los genomas de otros vertebrados, los investigadores determinaron que el genoma de la raya se ha mantenido en general muy similar al de sus ancestros vertebrados a nivel de secuencia. Sin embargo, hubo algunos reordenamientos notables que habrían afectado la plan 3D del genoma. En el ADN de los individuos reordenamientos así pueden causar enfermedades al alterar la regulación genética. El descubrimiento llevó a los investigadores a preguntarse si los reordenamientos en las rayas podrían haber interrumpido de manera similar las instrucciones genéticas originales para su plan corporal.
Rompiendo los límitesSi observas la secuencia de ADN de un cromosoma, los genes que contiene pueden parecer sorprendentemente alejados de las secuencias cortas «potenciadoras» que regulan la actividad de esos genes. Sin embargo, en la práctica, debido a la forma en que el ADN se enrolla, pliega y gira sobre sí mismo en el núcleo de una célula, a menudo no están muy separados en absoluto.
En los vertebrados, los conjuntos de genes funcionalmente relacionados y sus potenciadores se agrupan físicamente en tres dimensiones en unidades denominadas dominios asociados topológicamente o TAD (por sus siglas en inglés). Las regiones límite ayudan a garantizar que los potenciadores solo actúen sobre genes en el mismo TAD.
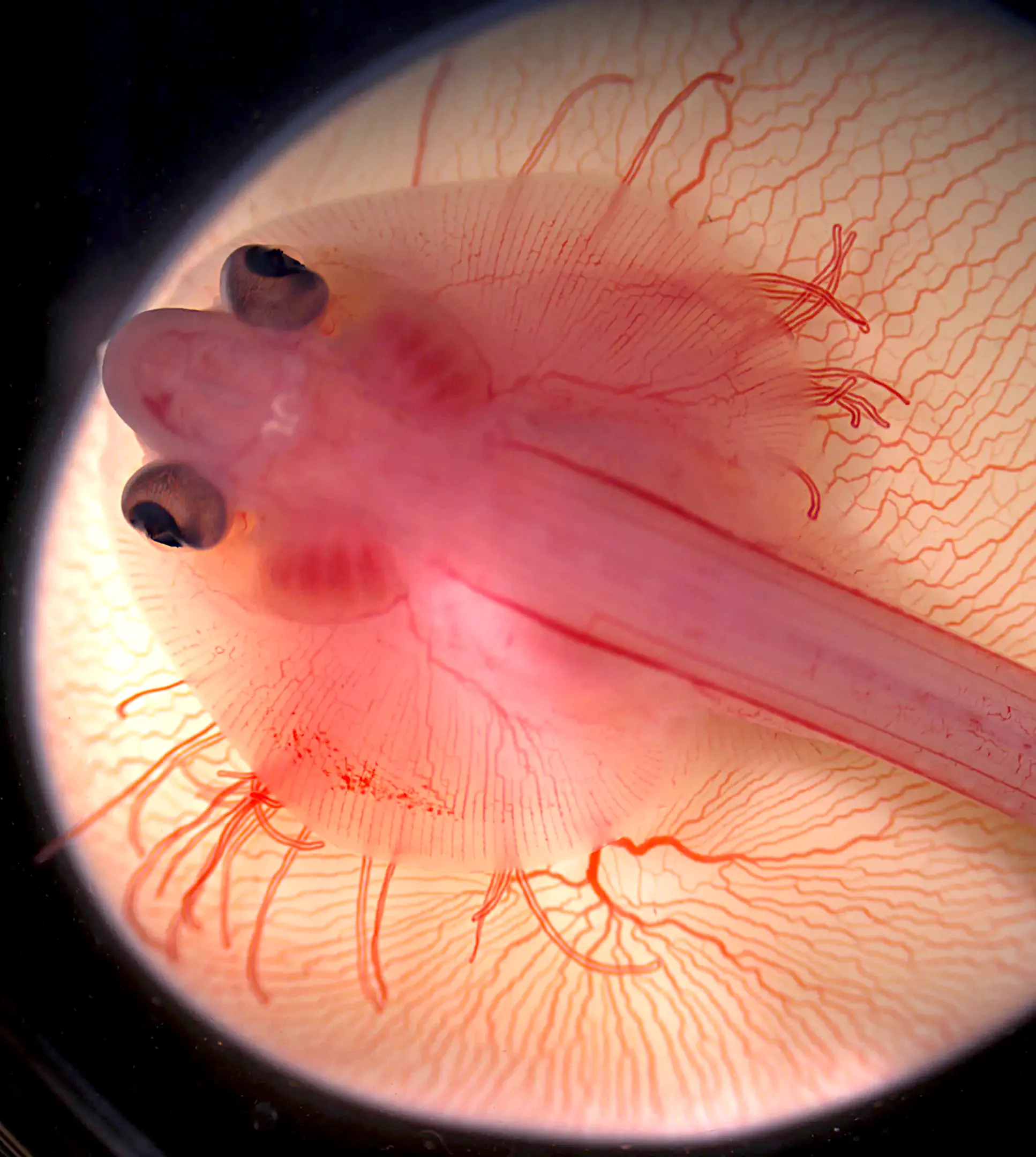 Un embrión de raya en su saco vitelino. Las alteraciones en su programa de desarrollo hacen que el borde frontal de sus aletas pectorales se extienda hacia adelante y se fusione con la cabeza. Fuente: Mary Colasanto & Emily Mis, Embryology Course, Marine Biological Laboratory (MBL)
Un embrión de raya en su saco vitelino. Las alteraciones en su programa de desarrollo hacen que el borde frontal de sus aletas pectorales se extienda hacia adelante y se fusione con la cabeza. Fuente: Mary Colasanto & Emily Mis, Embryology Course, Marine Biological Laboratory (MBL)Sin embargo, cuando ocurren reordenamientos importantes del genoma, como los que el equipo estaba viendo en el ADN de la raya, los límites pueden perderse y las posiciones relativas de los genes en los cromosomas pueden cambiar. Como resultado, “algunos potenciadores pueden proporcionar instrucciones al gen equivocado”, explica Darío Lupiáñez, biólogo evolutivo del Centro Max Delbrück en Berlín y uno de los autores principales del estudio.
Parecía posible que los cambios en la arquitectura 3D del genoma de las rayas pudieran haber interrumpido los antiguos bloques de genes que las rayas heredaron de sus ancestros parecidos a tiburones, afectando a la función de los genes. “Estábamos tratando de ver si algunos reordenamientos del genoma en la raya pequeña realmente rompen estos bloques”, explica Ferdinand Marlétaz, genomicista del University College London y coprimer autor del estudio.
Los investigadores identificaron reordenamientos del genoma en la raya pequeña que no estaban presentes en ningún otro vertebrado. Luego concentraron su atención en los cambios que parecían afectar con mayor probabilidad a la integridad de los TAD, según las secuencias del genoma.
El esfuerzo les llevó a un reordenamiento que predijeron que eliminaría el límite de un TAD que regula un sistema de desarrollo llamado vía de polaridad celular planar (PCP). No lo habían anticipado: nada sobre las funciones conocidas de la vía PCP sugería de entrada que regularía el desarrollo de las aletas. Principalmente, establece la forma y la orientación de las células en los embriones.
Un nuevo vecindario genéticoPara probar el impacto potencial del cambio en el TAD en el desarrollo de las aletas, Tetsuya Nakamura, biólogo del desarrollo evolutivo de la Universidad de Rutgers, expuso pequeños embriones de rayas a un inhibidor de la vía PCP. El borde anterior (delantero) de sus aletas se vio fuertemente alterado y no creció para unirse con la cabeza como lo haría normalmente. Esto sugería que la interrupción del TAD ancestral había producido las aletas distintivas de la raya al activar los genes PCP en una nueva parte del cuerpo.
“Este reordenamiento del TAD básicamente cambia todo el entorno del gen y trae nuevos potenciadores a las inmediaciones del gen”, explica Lupiáñez.
 Las aletas expandidas y la forma aplanada de la raya le permitieron ocupar un nuevo nicho ambiental, cazando cerca del fondo del mar. Fuente: eff Rotman/Science Source
Las aletas expandidas y la forma aplanada de la raya le permitieron ocupar un nuevo nicho ambiental, cazando cerca del fondo del mar. Fuente: eff Rotman/Science SourcePero este no fue el único cambio relevante en el genoma que encontraron los investigadores. También identificaron una mutación en un potenciador que regula la expresión de algunos genes en el grupo hox importante para el desarrollo. Los genes hox especifican el plan corporal general en todos los animales simétricos bilateralmente. Un subconjunto de ellos, el grupo de genes hoxa, generalmente se expresa solo en los bordes posteriores (de atrás) de las aletas en desarrollo y en las extremidades, donde especifica la formación de los dedos.
En la raya pequeña, los genes hoxa estaban activos tanto en la parte posterior como en la anterior de la aleta. Era como si la zona de crecimiento a lo largo de la parte posterior de la aleta se hubiera duplicado a lo largo de la frontal, de modo que el animal creó un nuevo conjunto de estructuras en la parte anterior de la aleta que era simétrica con las estructuras en la parte posterior, explica Debiais-Thibaud.
Nakamura demostró que el potenciador mutado de la raya estaba causando este nuevo patrón de expresión hoxa. Combinó el potenciador de la raya con un gen para una proteína fluorescente y luego insertó esa combinación de genes en embriones de pez cebra. Las aletas pectorales del pez crecieron de manera anormal y apareció fluorescencia a lo largo de los bordes delantero y trasero, lo que demostró que el potenciador de la raya estaba impulsando la expresión hoxa en ambas partes de la aleta. Cuando Nakamura repitió el experimento con un potenciador de tiburón el crecimiento de la aleta no se vio afectado y la fluorescencia se limitó a la parte posterior.
«Así que ahora pensamos que las mutaciones genéticas ocurrieron específicamente en el potenciador de las rayas, y eso puede impulsar la expresión única del gen hox en las aletas de las rayas», explica Nakamura.
Configurado para nuevas formas de vidaEn el cuadro de la evolución de las rayas que los investigadores han reconstruido, en algún momento después de que el linaje de las rayas se separara de los tiburones, adquirieron una mutación en un potenciador que hizo que sus genes hoxa se activaran tanto en la parte delantera como en la trasera de sus aletas pectorales. Y dentro de los nuevos tejidos que crecen a lo largo de la parte anterior de la aleta los reordenamientos del genoma hicieron que la vía PCP fuera activada por potenciadores en un TAD diferente, lo que tuvo el efecto adicional de hacer que la aleta se extendiera hacia adelante y se fusionara con la cabeza del animal.
«Al formar la estructura en forma de ala, [las rayas] ahora pueden habitar un nicho ecológico completamente diferente, el fondo del océano», explica Amemiya.
Las rayas de aguijón, las mantas y otras rayas están estrechamente relacionadas con las rayas pequeñas (todas están clasificadas como peces «batoideos»), y su similar forma de torta probablemente se deba a los mismos reordenamientos del genoma. Las rayas, sin embargo, también han modificado sus aletas en forma de alas de manera que básicamente les permiten volar a través del agua. “Las rayas tienen estas ondulaciones de la aleta y permanecen en el fondo, pero las mantarrayas pueden salir a la superficie y tener una forma de locomoción completamente diferente”, explica Amemiya.
Aunque los biólogos del desarrollo evolutivo habían especulado previamente que estos cambios en la arquitectura 3D de un genoma podrían ser posibles, este es probablemente uno de los primeros artículos que los relaciona claramente con cambios bastante grandes en la forma del cuerpo, afirma Marlétaz.
Lupiáñez también cree que los hallazgos tienen una significancia que va mucho más allá de la comprensión de las rayas. “Esta es una forma completamente nueva de pensar sobre la evolución”, afirma. Los reordenamientos estructurales “pueden hacer que un gen se active en un lugar donde no debería estarlo”. Añade: «Esto puede ser un mecanismo de enfermedad, pero también puede servir como motor de la evolución».
El artículo original, How 3D Changes in the Genome Turned Sharks Into Skates, se publicó el 30 de mayo de 2023 en Quanta Magazine.
Traducido por César Tomé López
* Nota del traductor:
José Luis Gómez-Skarmeta, que firma el artículo como investigador principal, falleció en 2020. El enlace en el texto lleva a su obituario en Nature, en inglés. El enlace en esta nota lleva a la entrada en Wikipedia en español.
El artículo Cómo cambios en 3D del genoma convirtieron a los tiburones en rayas se ha escrito en Cuaderno de Cultura Científica.
Sukarra: ulertu gabea, ospe txarrekoa eta mitoz inguratua
Giza gorputza sistema biologiko oso konplexu bat da eta defentsa mekanismo ugari ditu, helburu nagusi bat betetzen dutenak: gu bizirik mantentzea. Hala ere, ez ditugu gure organismoan gertatzen diren erreakzio fisiologiko guztiak behar bezala ulertzen. Sukarra, esate baterako, duen fama txarragatik nabarmentzen da ia mundu osoan, baita harekin lotzen diren mito anitzengatik ere –horien ondorioz, okerreko osasun praktikak egiten dira hari aurre egiteko–.
Gurasoak dira, bereziki hasi berriak, sukarrarekin gehien izutzen direnak beren haurrei eragiten dienean, haien bizitza arriskuan jartzen duela uste baitute. Arrastoan sartzeko asmoz, guraso askok beren seme-alabei sukarraren kontrako botikak ematen dizkiete, baina horiek ere badute kontrako ondoriorik. Hain zuzen ere, Estatu Batuetan egin berri den inkesta nazional baten arabera, hiru gurasotik batek, arrazoirik gabe, sukarra arintzeko botikak ematen dizkie bere seme-alabei. Hori ez da fenomeno bakana. Beste herrialde askotan ere, besteak beste, Espainian, gurasoek sarritan eskatzen dizkiete sukarraren kontrako tratamenduak pediatrei edo farmazialariei, beldur irrazional batek bultzatuta.
 Irudia: hainbat azterlan zientifikoren bidez sukarraren onurak hobeto ezagutu ahala, gero eta argiago gelditzen ari da hura kosta ahala kosta jaisten saiatzea kalterako izan daitekeela. (Argazkia: Matteo Fusco – Unsplash lizentziapean. Iturria: Unsplash.com)
Irudia: hainbat azterlan zientifikoren bidez sukarraren onurak hobeto ezagutu ahala, gero eta argiago gelditzen ari da hura kosta ahala kosta jaisten saiatzea kalterako izan daitekeela. (Argazkia: Matteo Fusco – Unsplash lizentziapean. Iturria: Unsplash.com)Ia kasu guztietan, sukarra infekzioen (sarritan, birusek eta bakterioek eraginak) aurkako defentsa erreakzio natural bat da. Gorputzaren termostatoari (hipotalamoari) esker, gorputzaren tenperatura zehaztasun handiz igotzen da, immunitate sistemari agente patogenoak suntsitzen laguntzeko eta haiek ugaldu daitezen eragozteko. Bestela esanda, sukarra ez da etsaia, aliatua baizik. Noski, sukarra izatea ez da atsegina, ondoez orokorra eta ahulezia eragin ditzake eta. Infekzio prozesua laburtzeagatik eta mikroorganismo inbaditzaileari aurre egiteko aukera gehiago izateagatik ordaindu beharreko prezioa da.
Hainbat azterlan zientifikoren bidez sukarraren onurak hobeto ezagutu ahala, gero eta argiago gelditzen ari da hura kosta ahala kosta jaisten saiatzea kalterako izan daitekeela. Horregatik, medikuntzan gero eta ohikoagoa da sukarra beharrezkoa denean bakarrik tratatzea, handiegia delako edo pertsonari sufrimendu nabarmena eragiten diolako, adibidez. Bestela esanda, pertsona tratatu behar da, ez termometroa. Horren harira, zenbait osasun erakundek, tartean, Espainiako Pediatria Elkarteak, Mayo Klinikak eta Erresuma Batuko Osasun eta Arreta Bikaintasunerako Institutu Nazionalak kasu puntualetan baino ez dute gomendatzen sukarrari aurre egitea.
Sukarraren inguruko mitorik nabarmenenak1. mitoa: sukarra arriskutsua da, kalte zerebrala ez ezik, heriotza ere eragin baitezake.
Hori ez da horrela sukarra duten ia paziente guztietan. Prozesu horrek garuneko lesio larri eta itzulezinak eragin ahal izateko, gorputzaren tenperatura 42 °C-tik gora igo beharko litzateke (hainbat proteina desnaturalizatzeko). Sukar handia dagoen kasu horietan gomendatzen da sukarraren kontrako botikekin jaistea, baina, normalean, hori ez da gertatzen.
2. mitoa: sukarrak konbultsio larriak eragiten dizkie haurrei, eta tratatu egin behar da horiek ager ez daitezen.
Guraso askok sekulako beldurra diete adingabe batzuek infekzio prozesuetan izan ditzaketen konbultsioei, alarma seinaletzat hartzen baitituzte. Kasu horietan, ordea, konbultsioak ez dira alarma seinaleak: arinak izaten dira eta, gainera, ez dute zerikusirik gorputzaren tenperaturarekin. Are gehiago, konbultsioak ohikoagoak dira sukar baxuekin, eta sukarraren kontrako botikek ez dituzte eragozten.
3. mitoa: sukarra bainuak, oihal hotzak eta bestelako neurri fisikoak erabiliz edo haurrak biluztuz jaitsi behar da.
Erakunde mediko askok baliabide horiek saihestea aholkatzen dute. Ekintza horiek alferrikakoak izaten dira gorputzaren tenperatura jaisteko, eta, batzuetan, igo ere egin dezakete, larruazaleko odol hodiak uzkurtu egiten baitira.
Sukarra alarma seinale badeneanBerez, sukarra prozesu normal bat da gaixotasun infekzioso batean. Dena den, batzuetan, seinale horrek zerbait ondo ez doala adieraz dezake. Ondorengo kasuetan, sukarrak kezkatu egin beharko gintuzke, eta medikuarenera joan beharko genuke haren atzean zer dagoen jakiteko:
Sukarraren jatorria ezagutzen ez dugunean.
Hiru astean baino gehiagoan sukarra izatea, dela etengabe, dela aldizka, gaixotasun infekzioso baten ageriko zantzurik gabe, pisuzko arrazoia da medikuarenera joateko.
Edozein pertsonak 40 °C-tik gorako sukarra duenean edo haur baten sukarrak hiru egun edo gehiago irauten duenean.
Kasu horietan, berehala joan behar dugu kontsultara, medikuak tratamendu egokia ezartzeko.
3 hilabetetik beherako haurtxo batek sukarra duenean.
Berehala joan behar dugu Larrialdietara, hain adin txikiko haur bati sukarra zerk eragin dion jakiteko.
Horiez gain, badira beste alarma seinale batzuk, sukarrarekin batera ager daitezkeenak eta Larrialdietara azkar joatea justifikatzen dutenak. Hauek dira seinale horietako batzuk: garondo zurruntasuna (meningitisaren susmoa), buru nahasmendua, larruazaleko orbanak edo kolore zurbil-grisaxka, arnasa hartzeko zailtasuna, okada etengabeak eta mina pixa egiterakoan edo gernu kantitate murriztua. Bestela esanda, sukarra duen pertsona batek medikuarenera joan behar duen ala ez erabakitzeko orduan, termometroak markatzen duenarekin itsutu ordez, pertsonaren egoeran jarri beharko genuke arreta.
Egileaz:Esther Samper (@Shora) medikua da, Ehunen Ingeniaritza Kardiobaskularrean doktorea eta zientzia-dibulgatzailea.
Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2023ko martxoaren 13an: La fiebre: incomprendida, con mala fama y rodeada de mitos
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Sukarra: ulertu gabea, ospe txarrekoa eta mitoz inguratua appeared first on Zientzia Kaiera.
¿Por qué nos parece que el tiempo pasa más rápido conforme envejecemos?
 Foto: Lucian Alexe / Unsplash
Foto: Lucian Alexe / UnsplashTic, tac… Tic, tac… El tiempo avanza inexorablemente para cada uno de nosotros. Y, aunque el ritmo al que avanza es igual para todos, la percepción subjetiva del transcurso del tiempo puede ser muy distinta entre personas. Así, cuando nos divertimos o disfrutamos de alguna actividad, parece que el tiempo pasa volando, mientras que si estamos inmersos en una tarea monótona, soporífera o desagradable los minutos se nos hacen eternos. En ese sentido, existe un fenómeno peculiar, que se ha constatado ampliamente en psicología: en general, el tiempo nos parece que pasa más rápido conforme vamos cumpliendo años.
Si echamos la vista atrás, rebuscando en los recuerdos de nuestra niñez, tenemos la sensación de que los días eran más largos y los «exprimíamos» mucho más: podíamos realizar multitud de actividades porque había tiempo para casi todo. Además, los veranos en la infancia parecían durar bastante más que aquellos en la vida adulta, que pasan en un suspiro, sobre todo cuando disfrutamos de las vacaciones en esta época. A partir de cierto momento de la vida adulta, tenemos la sensación de que el tiempo se «acelera» y de que todo pasa poco a poco más rápido. ¿Cuál es la razón para esta evolución en la percepción subjetiva del tiempo? En la actualidad, se desconoce cuál es la causa y son múltiples las hipótesis que tratan de darle una explicación.
Una posible razón tras este fenómeno tendría que ver con el procesamiento cerebral de las imágenes que vemos cada día. Según la hipótesis planteada por el profesor de Ingeniería Mecánica de la Universidad de Duke, Adrian Bejan, los días parecen ser más cortos conforme envejecemos porque el procesamiento de la información visual a lo largo del tiempo se enlentece. Si percibimos menos imágenes por segundo, esto puede generar la sensación de que el tiempo ha pasado más rápido y viceversa: cuando captamos más imágenes por segundo, podemos tener la sensación de que el tiempo avanza más lento, como cuando vemos un vídeo a cámara lenta.
La base tras este planteamiento es que las señales nerviosas, que transportan la información, tardan más en llegar por una suma de factores cuando cumplimos años: el tamaño y la complejidad de las redes neuronales cerebrales se incrementa y, además, el envejecimiento provoca daños que pueden retrasar el flujo de dichas señales eléctricas. Por esta razón, los niños podrían procesar más imágenes por segundo que los adultos y percibir que el tiempo pasa más lento.
También podría ser que, más allá del procesamiento de las imágenes, existiera un «metrónomo neural» que marca el ritmo del tiempo en cada persona. En niños, este metrónomo iría más rápido que en los adultos (igual que ocurre con la frecuencia cardíaca en reposo o la respiración que son también más rápidas en los niños), lo que haría percibir el paso del tiempo de forma más lenta. De hecho, el psicólogo Clifford Lazarus narra un curioso experimento sobre esta cuestión: Si se deja a los niños sentados, con los ojos cerrados y sin hacer nada, la gran mayoría de ellos tienen la sensación de que ha transcurrido más del tiempo del que realmente ha pasado (muchos mencionan que ha pasado un minuto, cuando solo han trascurrido 40 segundos, en realidad). En cambio, si las mismas condiciones se aplican a los adultos, su percepción subjetiva del tiempo es más realista o va con un ligero retraso: detallan que ha pasado un minuto cuando, en realidad, ha transcurrido un minuto o 70 segundos.
Otra explicación sobre la dispar sensación del ritmo del tiempo entre los niños y los adultos se centra en la diferente perspectiva de ambos a la hora de cuantificar el tiempo. Para un niño de 10 años, por ejemplo, el transcurso de un año supone nada más y nada menos que el 10 % del total de su vida y entre un 15 y un 20 % de su memoria consciente. En cambio, para una persona de 65 años, un año solo solo es el 1,5 % de su vida. A la hora de percibir, de forma relativa, las vivencias y los recuerdos esto puede generar la sensación de que el tiempo fluía más lento en la infancia, porque una misma unidad de tiempo implicaba mucho más dentro del total de experiencias vividas.
Podría ser también que la desigual percepción del tiempo entre la infancia y la edad adulta y anciana se debiera a sesgos en la consolidación de los recuerdos. Las experiencias de la vida que dejan más marca en nuestra memoria son precisamente aquellas que nos provocan emociones, sobre todo si son intensas. Durante la infancia y la adolescencia casi todo es nuevo y se vive con más intensidad emocional que en etapas más tardías de la vida, donde la rutina y la monotonía suelen imperar y estos dejan poca huella en nuestros recuerdos.
Así, al evaluar nuestros recuerdos pasados y actuales, podemos tener la sensación de que vivíamos muchas más experiencias en el mismo tiempo (y, por tanto, que el tiempo pasaba más lento) que en los últimos años, que no nos dejan muchos episodios memorables y muchos recuerdos anodinos desaparecen (como lo que comimos el otro día). Si esta hipótesis fuera cierta, una forma para hacernos sentir que el tiempo transcurriera más lento sería huir de la monotonía y vivir nuevas experiencias con frecuencia.
Sobre la autora: Esther Samper (Shora) es médica, doctora en Ingeniería Tisular Cardiovascular y divulgadora científica
El artículo ¿Por qué nos parece que el tiempo pasa más rápido conforme envejecemos? se ha escrito en Cuaderno de Cultura Científica.
Dieta azterketa piloto bat heste suminkorraren sindromea duten pazienteekin
Biodonostia Osasun Ikerketa Institutuko eta BCC Innovation Basque Culinaryko Gastronomiako Zentro Teknologikoko ikertzaileen arteko lankidetzan ikerketa pilotu bat egin dute heste suminkorraren sindromea duten pazienteentzako dieta espezifiko baten erabilera euskal herritarrei helarazteko. Luis Bujanda UPV/EHUko Medikuntzako katedradun eta Donostialdeko ESIko Gaixotasun Hepatiko eta Gastrointestinalen Arloko arduraduna, eta Koldo Garcia Etxebarria UPV/EHUko Genetikan doktore eta Biodonostia Osasun Ikerketa Institutuko Genetika Gastrointestinaleko Taldeko arduraduna ikerketaren parte izan dira.
Heste suminkorraren sindromea biztanleriaren %20ak pairatzen duen gaitza da, eta sintoma nagusiak abdomeneko mina eta hesteetako aztura alteratua dira. Patologia horrek gaixoen bizi-kalitatea murrizten du, eta gaur egungo tratamenduak ez dira eraginkorrak.
 Irudia: sakarosa eta almidoi gutxiko dieta bat (modu hoberenean digeritu ez daitezkeen bi nutriente), onuragarria izango litzateke heste suminkorraren sindromea duten pertsonentzat. (Argazkia: Ewa Raymond – Pexels lizentziapean. Iturria: Pexels.com)
Irudia: sakarosa eta almidoi gutxiko dieta bat (modu hoberenean digeritu ez daitezkeen bi nutriente), onuragarria izango litzateke heste suminkorraren sindromea duten pertsonentzat. (Argazkia: Ewa Raymond – Pexels lizentziapean. Iturria: Pexels.com)Suediako Lund University eta Skäne University Hospitaleko ikertzaileek aurretik egindako ikerketa baten arabera, sakarosa eta almidoi gutxiko dieta bat (modu hoberenean digeritu ez daitezkeen bi nutriente), onuragarria izango litzateke gaixotasun hori duten eta askotan beherakoak izaten dituzten pertsonentzat. Ildo horretan, ikerketa pilotu bat egin zen dieta horrek euskal herritarrengan duen eraginkortasuna ikusteko, sukaldaritza-kultura maila handiko gizartea baita. Dieta horren jarraipena errazteko, Zentro Teknologikoko chefek eta ikertzaileek gida bat diseinatu zuten, errezeta bat, menuak eta nutrizio eta sukaldaritza-gomendio egokituak biltzen zituena.
Biodonostia OIIko ikertzaileek aukeratutako 34 pertsonak hartu zuten parte Basque Culinary Centerren instalazioetan egin zen azterketa pilotu honetan, lau asteko iraupenarekin. Prozesuaren amaieran, parte-hartzaileen %85ek erantzun positiboa eman zion dietari, eta 50 puntu baino gehiagoko murrizketa lortu zen heste suminkorraren sindromearen sintomen larritasun-eskalan (horrelako ikerketetan erabilitako neurri estandarra). Bizi-kalitatea nabarmen hobetu zela ikusi zen, eta testeoa amaitu eta bi hilabetera arte iraun zuen hobekuntza hori. Ekimen honen arrakastaren arrazoia, neurri handi batean, parte-hartzaileek erakutsitako interes eta inplikazio-maila handiak izan dira, lau asteetan zehar jasotako dieta eta nutrizio eta sukaldaritza-aholkuak jarraitu baizituzten.
Ikerketaren emaitzak Therapeutic Advances in Gastroenterology aldizkarian argitaratu dira. Azterketa pilotu honen egileek espero dute etorkizun handiko emaitza horiek ikerketa zabalagoa bultzatuko dutela. Dieta hori beste nutrizio-aukera batzuekin alderatzea eta beste paziente-talde batzuetara zabaltzea da helburua.
Iturria:UPV/EHU prentsa bulegoa: Emaitza oparoak lortu dituzte heste suminkorraren sindromea duten pazienteekin egindako azterketa pilotu batean.
Erreferentzia bibliografikoa:Gayoso, Lucia; Garcia-Etxebarria, Koldo; Arzallus, Teresa; Montalvo, Isabel; Lizasoain, Jacobo; D’Amato, Mauro; Etxeberria, Usune; Bujanda, Luis (2023). The effect of starch- and sucrose-reduced diet accompanied by nutritional and culinary recommendations on the symptoms of irritable bowel syndrome patients with diarrhoea. Therapeutic Advances in Gastroenterology, 16, DOI: 10.1177/17562848231156682
The post Dieta azterketa piloto bat heste suminkorraren sindromea duten pazienteekin appeared first on Zientzia Kaiera.
El mundo come cada vez más carne
 Foto: Eiliv Aceron / Unsplash
Foto: Eiliv Aceron / UnsplashEn el mundo se comen cada vez más productos de origen animal (carne, pescado y lácteos) y menos de origen vegetal (plantas, semillas y derivados). El desarrollo económico que han experimentado en las últimas décadas China e India, principalmente, ha venido acompañado por un aumento en el consumo de productos de origen animal. Por el contrario, en otros países, principalmente nórdicos, se está reduciendo el consumo de esos productos por razones de salud e impulsado por iniciativas gubernamentales.
Como a cualquier otra, a la especie humana también se le puede asignar un nivel trófico. A las plantas se les asigna un nivel trófico 1, porque al ser productores primarios, no consumen ningún otro organismo, sino que su producción de energía consiste en el aprovechamiento de la energía solar para sintetizar biomasa propia a partir del CO₂ y H₂O, principalmente. Los animales herbívoros, como el ganado vacuno, por ejemplo, ocupan el segundo nivel. A los animales que solo consumieran carne de vacuno o carne de animales del mismo nivel se les asignaría el nivel 3. Por eso, si en una población humana consumen, a partes iguales, carne de vacuno y pan, por ejemplo, a esa población habría que asignarle un nivel trófico 2,5. A los animales que se encuentran en la cúspide de la cadena trófica, como son las orcas o los osos polares, que consumen animales que, a su vez, consumen otros animales carnívoros, les corresponde el nivel 5, que es el más alto.
Han determinado cómo varió el valor del nivel trófico humano (NTH) en el medio siglo transcurrido desde 1960 hasta 2009 en los 176 países para los que se dispone de información (son la mayoría y en conjunto, incluyen al 98% de la población mundial). Para ello han utilizado los datos de consumo de alimentos en esos países (proporcionados por la FAO), asignando los correspondientes niveles tróficos a cada alimento.
La mediana global mundial fue en 2009 de 2,21. Conviene recordar aquí que la mediana es un estadístico de posición: deja a la mitad de los valores por encima y a la mitad por debajo. Para el cálculo de ese estadístico se tuvo en cuenta la población de cada país, por lo que en su valor pesan mucho los países más poblados. Los dos valores extremos en 2009 fueron los de Burundi, con 2,04 (97% de la comida de origen vegetal) e Islandia, con 2,57 (50% de la comida de origen animal). Aunque hay una gran diversidad de tendencias, los autores de la investigación han agrupado los países en cinco grandes grupos en virtud de los valores absolutos del NTH así como del modo en que han variado durante medio siglo.
En el grupo 1 se encuentran la mayoría de los países subsaharianos y del Sudeste asiático; en esos países se mantiene bajo y estable el NTH. Son países en los que la alimentación se basa, mayoritariamente, en productos de origen vegetal. El 2 agrupa a países sudamericanos, africanos y asiáticos, incluyendo China e India. En esos países los valores de NTH son bajos pero creciente. El grupo 3 incluye a países de América Central, Brasil, Chile, algunos africanos, países del Sur de Europa y Japón. En este grupo también crece el nivel trófico, pero el punto de partida era superior al del grupo 2. Tanto en el grupo 2 como en el 3 la tendencia creciente del NTH revela un aumento en la proporción relativa de productos de origen animal en la dieta. Al grupo 4 pertenecen América del Norte, Europa septentrional y oriental, Australia y Nueva Zelanda. En estos países los valores de NTH eran altos y permanecieron estables hasta 1990, y a partir de ahí empezaron a descender, aunque muy levemente. El grupo 5 incluye a los países con los niveles tróficos más altos, pero decrecientes; en él se incluyen Islandia, países escandinavos, Mongolia y Mauritania. En estos países se consume principalmente carne, pescado y productos lácteos, y muy pocos vegetales.
Como cabía esperar, el nivel trófico de las poblaciones humanas tiene mucho que ver con las características socioeconómicas, ambientales, y culturales de los países. En general, es más alto en países con mayor esperanza de vida, producto interior bruto, emisiones de CO2 y grado de urbanización. Todos esos indicadores se han elevado a lo largo del último medio siglo en casi todo el mundo. Solo en los países del grupo 5 ha disminuido el NTH a pesar de que los indicadores de desarrollo también hayan aumentado.
En el mundo se está produciendo, por tanto, una convergencia nutricional, ya que cada vez se va pareciendo más la composición de la dieta en los diferente países. A la gente le gusta comer carne y cuando mejora la situación económica de un país, los productos cárnicos se consumen en mayor medida. Y a la vez, en los que tienen un alto nivel de consumo de productos de origen animal, se produce la tendencia contraria, por los problemas de salud que conlleva ese alto consumo.
Un elemento a considerar a la hora de valorar estas tendencias es el de las implicaciones ecológicas de los patrones de consumo. La producción animal tiene una eficiencia energética baja. Aunque puede variar entre un 3% y un 20%, dependiendo de diferentes circunstancias, se suele considerar que, en promedio, viene a ser de un 10%. Es decir, solo un 10% de la energía consumida por un animal se convierte en energía propia. Por lo tanto, para producir 1 Kg de C, una especie en el nivel 5 hace uso de 10.000 Kg de C de biomasa vegetal, y una de nivel 3, hace uso de 100 kg de C. La especie humana utiliza un 25% de la producción primaria del planeta y es posible que esa utilización esté alcanzando su límite máximo. Por esa razón, es posible que el aumento en la proporción de alimentos de origen animal se acabe encontrando con una limitación derivada de la dificultad o, incluso, imposibilidad de hacer uso de porcentaje creciente de la producción primaria neta de la Tierra.
Información adicional
Información detallada para cada país y más datos aquí.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El mundo come cada vez más carne se ha escrito en Cuaderno de Cultura Científica.
Asteon zientzia begi-bistan #441
Asteon zientzia begi-bistan igandeetako gehigarria da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna jaso eta laburbiltzea da gure helburua.

Arrate Santaolalla ingurumen-ingeniaria da, eta bere lanean mikroorganismoak erabiltzen ditu solubilizazio-prozesu batean, metalak berreskuratzeko. Bi alderditan aplikatu eta ikertu dute bioprozesu hori. Batetik, biomekanizazioan, eta, bestetik, biolixibiazioan. Santaolallak aitortu du pozik dagoela ikerketa-munduan egiten ari den lanarekin, baina ingurumen arloko ikerketetan finantziazio falta sumatzen duela adierazi du. Bestalde, dibulgazioaren eta hezkuntzaren garrantzia azpimarratu du ikerketan ere, aurkikuntzak gizartera hel daitezen. Ikertzaile honen inguruko informazio gehiago Zientzia Kaieran: Arrate Santaolalla, ingurumen-ingeniaria: “Mundua hobetzeko ikertzen dugu”.
ArgitalpenakMia. Marteko robota (2022) Josu Goiko eta Juan Rolleren liburuak haurrei Marteko istorioak azaltzen die. Denonartean argitaletxearen liburuak zientzia eta abentura uztartzen ditu. Mia izeneko robota da liburuko protagonista, eta pertsonaia horrek bere egunerokoa aurkeztuko du planeta gorrian.
TeknologiaPerovskita mineralaz osatutako eguzki-zelulen efizientzia eta egonkortasuna frogatu du nazioarteko ikerketa batek. Oxfordeko Unibertsitateko Henry Snaith fisikariak eta UPV/EHUko Juan Luis Delgado Ikerbasque ikertzaileak informazioa bildu dute gai honen inguruan, azken urteetako ikerketak aztertuz. Hala ondorioztatu dute gaur egun silizio kristalinozko zelulak izan arren merkaturatzen direnak, perovskitaz eginikoak efizienteagoak direla (% 25etik gorako efizientzia), eta kostu txikiagoa dutela. Izan ere, mineral hori ekonomikoki merkeagoa da eta gutxiago kutsatzen du silizioa araztearen aldean. Emaitza hauek etorkizunean gailu fotovoltaiko egonkorragoen eta efizientzia handiagokoen garapena sustatzea espero da. Datuak Zientzia Kaieran: Efizientzia eta egonkortasun handiko eguzki-zelulak.
IngurumenaBioplastikoek uste baino iraupen luzeagoa dutela ondorioztatu du ikerketa batek. Bioplastiko horiek itsasoan nola degradatzen diren aztertu dute, eta ikusi dute urte bat baino gehiago irauten duela batere degradatu gabe. Bioplastiko erabiliena PLA da, artotik, maniokatik, erremolatxatik eta abarretik abiatuta ekoizten den materiala, eta biodegradagarri eta konpostagarri gisa etiketatzen da. Alabaina, baldintza industrial jakinetan degradagarria den arren, prozesua ez da hain erraz gertatzen ingurumenean. Emaitzok ikusita, ikertzaileek aldarrikatu dute beharrezkoa dela materialak ingurumenean nola degradatzen diren jakiteko azterketak estandarizatzea. Azalpen guztiak Elhuyar aldizkarian: Plastiko biodegradagarriak ez dira hain biodegradagarriak.
Lurra sistema egonkor bat izateko muga berriak proposatu ditu nazioarteko ikerketa batek, mundu osoko pertsonen segurtasuna eta justizia kontuan hartuta, lehenengoz. Lurraren egonkortasuna eta erresilientzia mantentzeko guztira 8 muga seguru eta justu proposatu dituzte. Besteak beste, klimari, biodibertsitateri eta ekosistemei dagozkie, eta pertsonen segurtasuna eta justizia gehitu dituzte ekuazioan. Hala ikusi dute, bi irizpide horiek kontuan hartuta, mugak zorrotzagoak direla. Kalkulatu dutenez, lurrazalaren % 52 hartzen duten eremuetan bi muga edo gehiago gaindituta daude dagoeneko, eta horrek munduko giza populazioaren % 86ri eragiten dio. Datuak Elhuyar aldizkarian: Lur seguru eta justu baten mugak aurrekoak baino estuagoak dira.
FarmaziaBotiken soberakinak eta ontziak dagozkion tokira eramatea oso garrantzitsua dela gogorarazi du Juan del Arco Bizkaiko Farmazeutikoen Elkargoko zuzendari teknikoak, Bizkaiko Medikuen Elkargoak antolatutako Impacto medioambiental de los farmacos jardunaldietan. Juan del Arcok gomendatu du tratamendu bat amaitzen denean sobera dauden medikamentuak farmazietako SIGRE edukiontzietara eramatea, baita kutxa ere, nahiz eta hutsik egon, arrastoak egon baitaitezke. Mota honetako hondakinak ondo kudeatzen ez badira, oso kaltegarriak izan daitezke ingurumenerako. Kudeaketa hau bereziki garrantzitsua da antibiotikoen kasuan, uretara edo zabortegietara botatzen badira, erresistentzia sor baitezakete. Azalpenak Berrian: «Antibiotikoak txarto kudeatzen badira, oso arriskutsuak dira».
BiologiaAnimalien aldean, ahalegin gutxi egiten dira landareen kontserbazio politiketan, Richard T. Corlett ekologo eta biodibertsitatean adituak ohartarazi duenez. Haren esanetan gainera, erreinu begetala babestea animaliak babestea baino merkeagoa eta errazagoa izan daiteke. Ekologoak nabarmendu du, alabaina, jende, espazio, finantziazio eta monitorizazio gehiago behar dela helburu hori lortzeko. Bestalde, dagoen ezagutza optimizatu aldera, online jarritako metaherbario bat osatzea proposatu du, herbario desberdinetako informazioa elkar lotzeko. Artikulu honen inguruko informazio gehiago Zientzia Kaieran: ‘Ikusezinak’ dira landareak, baita zientziarentzat ere.
Juan Ignacio Pérez Iglesiasek baraualdia egitean gertatzen diren prozesu fisiologiko eta biokimikoak azaldu ditu Zientzia Kaierako artikulu berri batean. Pertsona batek barau egiten duenean gertatzen den lehenengo gauza da metabolismoak behera egiten duela. Horren ondorioz, bihotz taupaden maiztasuna murrizten da, gorputzeko tenperatura 37 gradutik 35,5 gradura jaisten da, eta oro har, gorputzak masa galtzen du. Metabolismoa moteldu egiten da nagusiki hormona paratiroideo gutxiago jariatzen delako, eta pentsatzen da hormona horren jariapena gutxitzen dela adipozitoek leptina gutxiago jariatzen dutelako. Kalkulatzen da 70 kg pisatzen duen eta 18 kg gantz erreserba dituen pertsona batek 100 egun iraungo lituzkeela bizirik baraualdian. Azalpen guztiak Zientzia Kaieran: Baraua.
Arrain diadromoen onura ekologiko eta kulturalak handiak direla adierazi dute Europako Diades proiektuaren emaitzek. Diadromoak dira ibairik itsasora migrazioak egiten dituzten espezieak, eta kontrako bidaia egiten dutenak katadromoak dira. Arrain horien adibide dira izokinak, aingirak eta itsas amuarrainak, besteak beste. Euskal Herrian aurkitu daitezkeen arrain diadromoak kolaka, lanproia, aingira, izokina eta itsas amuarraina dira. Arrain espezie horien onurak eta mehatxuak kontuan izanda, AZTIk Europako agintariei eskatu die ardura har dezatela hauen kontserbazioa sustatzeko. Azalpen guztiak Berrian: Joan-etorriko arrainen balioa.
NeurologiaZentzumenek nola engainatzen duten erakutsi dute Urteko Irudipen Onenaren lehiaketan. AEBetako Neural Correlate Society elkarteak antolatzen du lehiaketa hori, eta aurten Harry Potterren geltoki magikoaren inguruko begitazioak irabazi du lehenengo saria. Lehiaketaren helburua pertzepzioaren eta kognizioaren inguruko ikerketa zabaltzea da. Aurtengo hiru irabazleen lanak ikusteko, jo Berriako artikulura: Zentzumenek nola engainatzen duten erakutsi dute Urteko Irudipen Onenaren lehiaketan.
Egileaz:Irati Diez Virto Biologian graduatu zen UPV/EHUn eta Plentziako Itsas Estazioan (PiE-UPV/EHU) tesia egiten dabil, euskal kostaldeko zetazeoen inguruan.
The post Asteon zientzia begi-bistan #441 appeared first on Zientzia Kaiera.
Parásitos y comportamiento animal: de hormigas a humanos

Cómo influyen los parásitos en el comportamiento de los animales, cómo se modifica la conducta de las madres mamífero o cuáles son las enfermedades que nos afectan y desde cuándo hemos desarrollado comportamientos funerarios ante la muerte son algunos de los aspectos que se analizarán en la V Jornada Nacional sobre Evolución y Neurociencias.
Especialistas en ambas materias se reunirán el 11 y 12 de mayo en una nueva edición conducida por Eva Garnica y Pablo Malo, psiquiatras y miembros de la Red de Salud Mental de Bizkaia, y organizada por esa misma entidad y la Cátedra de Cultura Científica de la UPV/EHU.
La jornada, cuya primera edición se celebró en 2017, se ha convertido en una cita imprescindible para las y los expertos en ámbitos como la psiquiatría, la psicología o la biología. Una jornada que sirve para analizar el comportamiento humano desde un punto de vista evolucionista y divulgar de un modo accesible para todos los públicos.

A famosísima sentencia de Dobzhansky «Nada tiene sentido en biología si no es a la luz de la evolución», Antonio J. Osuna le añade «y nada tiene sentido en la evolución si no es a la luz de los parásitos». Los parásitos modifican el comportamiento de los animales de formas extraordinarias, y esos cambios favorecen la evolución.
Antonio J. Osuna Mascaró, es doctor en Paleontología (Universidad de Granada) y está a punto de concluir su segundo doctorado en Cognición Comparada (Universidad de Medicina Veterinaria de Viena) como investigador del Messerli Research Institute; Carmen Mascaró Lazcano es bióloga y catedrática jubilada de Parasitología de la Universidad de Granada.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Parásitos y comportamiento animal: de hormigas a humanos se ha escrito en Cuaderno de Cultura Científica.
Ezjakintasunaren kartogragfia #449

Ama-hizkuntzak, hitzez hitz, garuna zizelkatzen du. Literalki. How our first language shapes brain’s connectivity structure, Juan F. Trillok egina.
Eta atmosferaren berotzean metanoaren eragina uste zena baino txikiagoa balitz? New insights on methane’s effects on climate warming Ruben Sousseren eskutik.
Supernobak “ikusi” egin ohi dira, baina orain arte ez da bat bera ere hauteman irrati-frekuentzietan. Type Ia supernova detected at radio wavelengths
Ezagunak diren arauak aplikatu baino, trebezia kontua dira nanoteknologian interesgarriak diren konposatuen sintesi organikoak. DIPCko jendea Synthesis of thioether polymers on Au(111).
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartogragfia #449 appeared first on Zientzia Kaiera.
El poder del polen
 Foto: Juliana Malta / Unsplash
Foto: Juliana Malta / UnsplashEl comienzo de la primavera, seco y caluroso, ha provocado un aumento significativo de los niveles de polen, uno de los alérgenos más comunes del continente europeo. A pesar de su diminuto tamaño –y de ser una pesadilla para los alérgicos–, los granos de polen cumplen una función ecológica esencial para la supervivencia de la humanidad. Es momento de valorarla como se merece.
La chispa que enciende la vida vegetalHace más de 350 millones de años, un linaje de plantas, las gimnospermas (con semillas desnudas, como los abetos, cedros y pinos), desarrolló granos de polen y semillas, marcando un antes y un después en la reproducción y adaptación al medio terrestre del reino vegetal.
Doscientos millones de años más tarde, en plena revolución terrestre del Cretácico, aparecieron las plantas con flores y con semillas protegidas por frutos: las angiospermas. Gracias al ingenio evolutivo del polen y las flores y su coevolución con los polinizadores, las angiospermas se diversificaron rápidamente, vistiendo el planeta de multitud de colores vibrantes. Son las que hoy por hoy dominan los ecosistemas terrestres y las principales protagonistas de las tierras de cultivo.
Más que un alérgenoEl polen, ese polvillo a menudo dorado que flota en el aire durante la primavera y el verano, es en realidad una estructura reproductiva minúscula pero poderosa.
El grano de polen maduro es el gametofito masculino de las plantas. Contiene tres células, dos espermáticas y una vegetativa, protegidas por una doble envoltura que le confiere resistencia. Se produce en los órganos masculinos de las angiospermas (estambres) y gimnospermas (cono masculino).
El grano de polen funciona como un intermediario que transporta el material genético masculino desde la planta productora hasta los órganos femeninos de otras plantas, o de ella misma, en algunos casos. Así se logra la fertilización y la producción de semillas.
Como las posibilidades de que un grano de polen llegue a una pareja ideal son escasas, las plantas tienden a producir mucho polen. Y como sabemos, e incluso padecemos, esta sobreproducción tiene consecuencias que van más allá de la reproducción vegetal.
 Polen de Orthosiphon stamineus preparado mediante el método de liofilización, imagen SEM.
Polen de Orthosiphon stamineus preparado mediante el método de liofilización, imagen SEM.Wikimedia commonsEl amor está en el aire
La producción de polen está finamente orquestada por las condiciones ambientales como la temperatura, la humedad y la luz, así como por el estado hormonal de la planta. Pero además, la danza de polinizadores alrededor de la planta también puede incentivar la producción de polen.
A medida que el polinizador se mueve de flor en flor en busca de néctar, su cuerpo se va cargando y descargando de granos de polen que se depositan en los pistilos de las flores (concretamente en los estigmas), aumentando la posibilidad de fertilización y la formación de semillas. Efectivamente, en las plantas, el amor está en aire.
Para aumentar el éxito reproductivo, las plantas han ido creando una asombrosa variedad de estructuras, formas y colores para sus granos de polen, que están íntimamente relacionadas con los mecanismos de dispersión y los polinizadores.
Así, los granos de polen más visibles y pesados, y también aquellos provistos de pequeñas espinas y superficie pegajosa, son generalmente transportados a lomos de grandes polinizadores como abejas (entomofilia) y aves (ornitofilia). En cambio, aquellos más pequeños, ligeros, esféricos y alados son transportados por la brisa primaveral (anemofilia).
Pigmentos tales como los flavonoides y/o carotenoides están detrás de la coloración rojiza-azulada y/o amarillo-anaranjada tan frecuente en los granos de polen, que hace que sean aún más atractivos para los polinizadores. Además, no hay que olvidar que, junto con el néctar, el polen también es recolectado por los polinizadores como alimento rico en proteínas, lípidos y carbohidratos.
¿Qué sería del mundo sin polen?El polen desempeña un papel crucial en la agricultura, sobre todo en la producción de frutas, verduras y cereales. Se estima que más del 75 % de los cultivos alimentarios del mundo dependen en cierta medida de la polinización (transferencia de polen). Está en juego, por tanto, gran parte de nuestra dieta. Cada semilla, grano y fruta que comemos es producto directo de la polinización.
Sin polinización, los cultivos no producirían semillas viables, lo que reduciría su rendimiento y conllevaría importantes pérdidas económicas. En un escenario de alta demanda de alimentos por el incremento de la población mundial, no podemos despreciar el polen ni el trabajo de los polinizadores.
Como agentes polinizadores, las abejas, mariposas, pájaros, polillas, escarabajos e incluso los murciélagos influyen en la estabilidad y diversidad vegetal de los ecosistemas y en el rendimiento (cantidad y calidad nutricional) de los cultivos en los agroecosistemas.
Por pequeños que sean los granos de polen y los polinizadores, desempeñan un gran papel en la consecución de varios de los Objetivos de Desarrollo Sostenible (ODS) fijados por la ONU, desde la lucha contra el hambre y la pobreza hasta la creación de empleo y el crecimiento económico.
 Las abejas actúan como polinizadores.
Las abejas actúan como polinizadores..Capiro. / Flickr, CC BY-NC-NDLa tormenta perfecta a escala planetaria
Desafortunadamente, la fragmentación y destrucción de hábitats, el uso de pesticidas y el cambio climático están provocando la tormenta perfecta a escala planetaria: disminución de la diversidad vegetal, reducción de la calidad del polen y declive de las poblaciones de polinizadores.
¿Qué podemos hacer? Restaurar y conservar los hábitats, restringir el uso de pesticidas, potenciar la lucha biológica contra las plagas y diversificar las explotaciones agrícolas para crear un ecosistema equilibrado para las abejas y sus compañeros polinizadores. Nos queda mucho trabajo por delante.![]()
Sobre la autora: María Teresa Gómez Sagasti es profesora adjunta e investigadora en el área Fisiología Vegetal, Dpto. Biología Vegetal y Ecología de la Facultad de Ciencia y Tecnología de la UPV/EHU
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo El poder del polen se ha escrito en Cuaderno de Cultura Científica.
Arrate Santaolalla, ingurumen-ingeniaria: “Mundua hobetzeko ikertzen dugu”
Ukaezina da gaur egun ingurumenaren zaintzak eta leheneratzeak duen garrantzia. Arrate Santaolalla Ramirez horretan ikertzen du, baina ez zen horregatik hasi horretan. Onartu du, hala ere, betitik iruditu zaiola funtsezkoa ingurumena zaintzea, baina, batez ere, gustuko ikasgaiekin eta irakasleekin topo egin izanak eraman dute bide horretatik. Are gehiago; ingurumenarekin lotutako sailetara, bizi-zientzietatik iristen dira asko; Santaolalla, ez: “Industria Kimikoa Ingeniaritza Gradua ikasi nuen EHUn, eta, hor bertan, laugarren mailan, ingurumen-teknologiak izeneko ikasgai bat zegoen, eta konturatu nintzen gustatzen zitzaidala”.
Hala, Ingurumen Ingeniaritza masterra egitea erabaki zuen. Han ezagutu zituen master-amaierako lanaren zuzendariak izango zirenak, eta haiek proposatuta hasi zen ingurumen-ingeniaritzan ikertzen.
 Irudia: Arrate Santaolalla Ramirez ingurumen-ingeniaria.
Irudia: Arrate Santaolalla Ramirez ingurumen-ingeniaria.Santaolallak azaldu duenez, prozesu industrialak aurrera doaz, eta hondakinak sortzen dira. “Hondakin horiek kudeatu behar dira, eta, teknologiak horretan laguntzen du”. Horren adibide da bere lana: “Guk metalak berreskuratzen ditugu. Mikroorganismoak erabiltzen ditugu solubilizazio-prozesu batean, metalak berreskuratzeko”.
Berez, bi alderditan aplikatu eta ikertu dute bioprozesu hori. Batetik, biomekanizazioan, mikroegituren ekoizpenean; eta, bestetik, biolixibiazioan, tresna elektriko eta elektronikoen zirkuitu inprimatuetan dauden metalen berreskuratzeko, adibidez. “Izan ere, gero eta gehiago metatzen dira munduan, eta horien kudeaketa arazo oso larria da. Gu horretan zentratzen gara”, zehaztu du.
Finantzazioa, zailtasun nagusiaSantaolallak aitortu du pozik dagoela ikerketa-munduan egiten ari den lanarekin, bere aletxoa jartzen ari dela iruditzen baitzaio. Baina oztopo handi bat ere aurkitu du: finantzazioa lortzea. “Bekak eta diru-laguntzak, normalean, beste talde batzuei ematen dizkiete; agian, ikerketa oso garrantzitsuak egiten dituztelako. Baina, hori hala izanda ere, ingurumena gure osasunarekin erlazionatuta dago, eta ez dugu ahaztu behar funtsezkoa dela zaintzea”.
Haren iritziz, dibulgazioak lagundu dezake babes handiagoa lortzen, baita irakaskuntzak ere. “Dibulgazioa ikerketaren parte da. Jendeak ikusi behar du zertan egiten dugun lan, zer lortzen dugun, zer ondorio dituen… Nire ustez, horrek lagundu dezake ikerketaren garrantziaz jabetzen eta finantzazioa hobetzen”.
Bestalde, gustuko du irakasle-lana: “Nik ikasitako guztia, gazteei irakasten nabil. Baita ikerketa zein garrantzitsua den; ez bakarrik ingurumen-arloan, baizik eta arlo guztietan, mundua hobetzeko, nolabait. Horretarako egiten dugu ikerketa”.
Etorkizun labur-ertainean, hezkuntzan eta ikertzen jarraitzea gustatuko litzaioke. Izan ere, gustura dago taldean: “Talde txikia gara, eta uste dut guztiok gaudela gustura, eta egiten duguna oso garrantzitsua dela”.
Fitxa biografikoa:Arrate Santaolalla Ramirez 1991n jaio zen, Gasteizen. Industria Kimikaren Ingeniaritzako Graduko titulua lortu ondoren, Ingurumen Ingeniaritza Masterra egin nuen (Euskal Herriko Unibertsitatearen eta Kantabriako Unibertsitatearen artekoa). 2017an doktorego-ikasketak hasi zituen Astrid Barona eta Naiara Rojo doktoreen zuzendaritzapean, 2021eko uztailean, doktorego-tesia defendatu zuen UPV/EHUn: Copper solubilization strategies for mold biomachining and bioleaching from printed circuit boards, eta Ingurumen Ingeniaritzako “Nazioarteko Doktorea”-ren aipamena lortu zuen. Doktoregoan, nazioarteko egonaldi bat egin zuen National University of Ireland Galway-n (NUIG).
Informazio gehiago:EHUko Zientzia eta Gizarte Garapenaren eta Transferentziaren Arloko Errektoreordetza (2023). EHU Ekinean podcasta: Arrate Santaolalla, Campusa aldizkaria, UPV/EHU.
Zuazagoitia, Daniel; Rojo, Ainara; Santaolalla, Arrate eta Zuazagoitia, Iñigo (2018). Gorbeialdeko Hondakinen Partzuergoak kudeatutako hiri-hondakin solidoen errefusaren karakterizazioa. Ekaia, 34, 225-241. DOI: 10.1387/ekaia.19068
Egileaz:Ana Galarraga Aiestaran (@Anagalarraga1) zientzia-komunikatzailea da eta Elhuyar aldizkariko zuzendarikidea.
Elhuyar aldizkariarekin lankidetzan egindako atala.

The post Arrate Santaolalla, ingurumen-ingeniaria: “Mundua hobetzeko ikertzen dugu” appeared first on Zientzia Kaiera.
Los bigotes del delfín
¿Tú sabías que los bebés de delfín tienen bigotes cuando acaban de nacer?
Probablemente no lo habías notado, no es algo que resulte evidente a primera vista. Así que, si te estabas imaginando un pequeño delfín con un frondoso mostacho a lo Groucho Marx, ya puedes eliminar esa imagen de tu cabeza (o quizás no, es ciertamente memorable). Se trata más bien de unos pequeños pelitos, que estos mamíferos marinos lucen nada más nacer alrededor de la boca. Podrían recordar a la pelusilla que empieza a asomar bajo la nariz de algunos cachorros humanos durante la adolescencia. Pero al contrario de lo que sucede en este caso, los incipientes pelitos de los delfines bebé acaban desapareciendo al cabo de unos pocos días.
 Foto: Nathalie Goddard / Marudah Cruises
Foto: Nathalie Goddard / Marudah Cruises¿Pero de dónde salen estos bigotes y por qué su existencia es tan efímera? Bien, se trata de lo que se conoce como una característica vestigial, es decir, un rasgo que se encuentra presente en un organismo, pero que ha perdido su función original en el desarrollo evolutivo de una especie. Podríamos imaginar los vestigios como los souvenirs de la evolución: una cosa inservible pero difícil de desechar, que recuerda distintos momentos de su historia. “Este bicho pasó por aquí, y como prueba se trajo un llavero espantoso” (o un bigote, en este caso).
Precisamente por su capacidad de ejercer como recuerdo y testimonio, las características vestigiales tienen especial importancia para la biología evolutiva. A menudo proporcionan evidencia de la historia compartida entre varias especies o nos muestran cómo ciertas estructuras biológicas han cambiado a lo largo del tiempo en respuesta a la selección natural y otros procesos evolutivos. En el caso del delfín, los bigotes nos hablan de un pasado remoto, cuadrúpedo y mucho más “frondoso”: cuando el pelo cubría todo su cuerpo, y no únicamente los alrededores de su mandíbula.
A fin de cuentas, los delfines son mamíferos, unos que nadan muy bien, eso sí. Hace 50 millones de años, su antepasados evolutivos se paseaban por la tierra y, de cuando en cuando, se adentraban en el mar para refugiarse o para cazar. Entre ellos, el más conocido es el Pakicetus, un bicho que, si me permitís la apreciación, se parecían más a una rata mutante que a un delfín (al menos, de acuerdo con algunas reconstrucciones contemporáneas). Pero esa rata tenía un plot twist (que diría Jaime Altozano) escondido debajo de la manga: su destino era regresar al mar y legar sus genes a los futuros delfines, ballenas y marsopas.
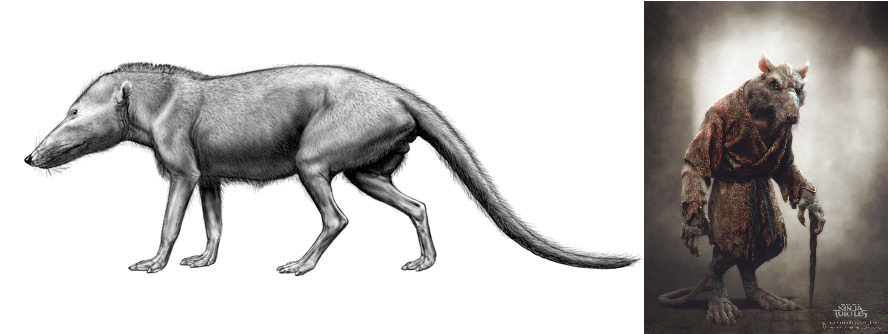 Reconstrucción del Pakicetus de Carl Buell a la izda (Fuente). Ilustración de Mr. Splinter de Tsvetomir Georgiev a la derecha
Reconstrucción del Pakicetus de Carl Buell a la izda (Fuente). Ilustración de Mr. Splinter de Tsvetomir Georgiev a la derecha
Los fósiles de Pakicetus fueron descubiertos por primera vez en la década de 1980 en Pakistán. El nombre de este país sirvió para bautizar a la especie, de hecho. Los Pakicetus mostraban características de mamíferos terrestres, pero también algunas que los emparentan con los cetáceos y que nos dan pistas sobre sus incipientes hábitos acuáticos. Tenían cráneos alargados, y dientes adaptados a una dieta carnívora. Contaban con extremidades posteriores alargadas y una columna vertebral que les permitía moverse tanto en tierra como en el mar. Debieron de vivir en junto a la costa del mar de Tetis durante el período Eoceno temprano. Por todo ello, se cree que eran nadadores hábiles y que probablemente pasaban bastante tiempo en el agua.
Con el tiempo, las generaciones y el lento pero implacable trabajo de la evolución, los Pakicetus fueron adaptándose cada vez más al medio acuático. Sus patas se volvieron más cortas hasta quedar convertidas en aletas. Su orificio nasal se fue desplazando hasta ocupar la posición actual, en lo alto de la coronilla. Hoy, el cuerpo de los delfines (de los cetáceos, en general) se parece mucho más al de un pez, es más hidrodinámico, está mejor preparado para nadar. Además, no queda ni un pelo en su superficie… bueno, siempre que no contemos los primeros días de vida, el tiempo que tarda el bigotillo de los delfines en caer.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Los bigotes del delfín se ha escrito en Cuaderno de Cultura Científica.
Mia. Marteko robota
Mia. Marteko robota (2022) planeta gorrira eramango gaitu bidaia liluragarri batean. Josu Goiko eta Juan Rolleren liburua zientzia eta abentura uztartzen dituen istorio xarmagarria da haurrei Marteko ezaugarriak erakusteko.
Istorio honetan, Mia izeneko robotaren egunerokoa auzoko planetan ikusiko dugu. Irakurleek, beren begien bidez, Marteko paisaia deskubrituko dute: mendi handi-handiak, arroila erraldoaik, zulo beldurgarriak…
 Irudia: Mia. Marteko robota liburuaren azala. (Ilustrazioa: Juan Roller. Iturria: Denonartean)
Irudia: Mia. Marteko robota liburuaren azala. (Ilustrazioa: Juan Roller. Iturria: Denonartean)Jakin, gaur egun badakigu Marten ura egon izan bazela urte luzez, airearen batez besteko tenperatura zero azpitik 55 gradu ingurukoa dela, etab. Ipuin hau umeei informazio hori hurbiltzeko medio bikaina da.
Argitalpenaren fitxa:- Izenburua: Mia. Marteko robota
- Egilea: Josu Goiko
- Ilustratzailea: Juan Roller
- Argitaletxea: Denonartean
- ISBN: 978-84-17940-97-3
- Hizkuntza: Euskara
- Urtea: 2022
- Orrialdeak: 40 or.
The post Mia. Marteko robota appeared first on Zientzia Kaiera.
Los números insólitos
Mi libro La gran familia de los números (2021), de la colección Miradas matemáticas (Catarata, ICMAT, FESPM), está dedicado a algunas importantes familias de números naturales, entre los que están los números figurados, primos, capicúas, cíclicos, perfectos, amigos, intocables, narcisistas, felices o vampiros, entre muchos otros.
 Portadas de mis tres libros de la colección Miradas matemáticas, a saber: Los secretos de la multiplicación (2019), La gran familia de los números (2021) y Las matemáticas como herramienta de creación artística (2023)Por sus dígitos los conoceréis
Portadas de mis tres libros de la colección Miradas matemáticas, a saber: Los secretos de la multiplicación (2019), La gran familia de los números (2021) y Las matemáticas como herramienta de creación artística (2023)Por sus dígitos los conoceréis
En el capítulo 5, titulado “Por sus dígitos los conoceréis”, se muestran familias de números naturales definidas por características de los dígitos de sus representaciones numéricas, como los números narcisistas (sobre los que también podéis leer en la entrada ¿Pueden los números enamorarse de su propia imagen?), que son aquellos números que son iguales a la suma de las potencias de sus dígitos elevados a la cantidad de dígitos que tiene el número. Por ejemplo, el número 153 es un número narcisista, puesto que, teniendo 3 cifras, que son 1, 5 y 3, se cumple que 13 + 53 + 33 = 1 + 125 + 27 = 153; o también, el número 1.634, ya que 14 + 64 + 34 + 44 = 1 + 1.296 + 81 + 256 = 1.634.
 Imagen del episodio Marge, Homer y el deporte en pareja, en la que aparecen tres números curiosos, uno de ellos un número narcisista, 8.208
Imagen del episodio Marge, Homer y el deporte en pareja, en la que aparecen tres números curiosos, uno de ellos un número narcisista, 8.208Otra familia de números relacionada con los números narcisistas es la que podríamos llamar números de Follet, puesto que aparecen mencionados en la novela Doble juego (2000), del escritor Ken Follet, que está formada por aquellos números que son iguales a la suma de las potencias de sus dígitos elevados a la posición que ocupan en el número (empezando por la izquierda), como el número 175, ya que 11 + 72 + 53 = 175 (1 es el primer dígito, 7 el segundo y 5 el tercero).
 Portada de la edición DEBOLSILLO (Penguin Libros) de 2003, del libro Doble juego, de Ken Follet
Portada de la edición DEBOLSILLO (Penguin Libros) de 2003, del libro Doble juego, de Ken FolletOtra familia de números relacionada con los números narcisistas es la formada por los números de Munchausen, aquellos números que son iguales a la suma de sus dígitos elevados a ellos mismos. Por ejemplo, el número 3.435 es un número de Munchausen, ya que 33 + 44 + 33 + 55 = 3.435 (si admitimos que 00 = 1, resulta que el anterior número es el único que existe).
 Imagen de la película El barón de Munchausen (1988), dirigida por Terry Gilliam, que fue uno de los integrantes de los Monty Python, en la que el barón de Munchausen sale volando de las aguas tirando de su coleta hacia arriba
Imagen de la película El barón de Munchausen (1988), dirigida por Terry Gilliam, que fue uno de los integrantes de los Monty Python, en la que el barón de Munchausen sale volando de las aguas tirando de su coleta hacia arribaUna extensión natural de los números narcisistas es considerar que los dígitos están elevados, no a la cantidad de dígitos del número, sino a una cifra fija cualquiera, llamada orden. En este caso, a los números que son iguales a la suma de las potencias de sus dígitos elevados a una cantidad fija cualquiera, no necesariamente la cantidad de dígitos del número, se les llama números potentes o también invariantes digitales perfectos. Por ejemplo, el número 4.150, que puede expresarse como la suma de las potencias quintas de sus dígitos (que son solo cuatro), 45 + 15 + 55 + 05 = 1.024 + 1 + 3.125 = 4.150, es un número potente. Los números insólitos están relacionados con estos últimos.
Los números insólitosEn el artículo On a very thin sequence of integers (Sobre una sucesión de números enteros poco numerosa), sus autores introducen el término de número insólito. Definen un número insólito como aquel número, mayor que 1, para el cual la suma y el producto de las potencias cuadradas de sus dígitos divide al propio número (en particular, no contiene al 0 entre sus dígitos). Por ejemplo, dado el número 122.121.216, la suma de los cuadrados de sus dígitos es
12 + 22 + 22 + 12 + 22 + 12 + 22 + 12 + 62 = 56,
mientras el producto de los cuadrados de sus dígitos es
12 x 22 x 22 x 12 x 22 x 12 x 22 x 12 x 62 = 9.216,
y como ambos dividen a número 122.121.216, por lo tanto, es un número insólito.
El número más pequeño que es insólito es el 111, ya que es divisible por 3 (suma de los cuadrados de sus dígitos) y por 1 (producto de los cuadrados de sus dígitos). Y los diez primeros números insólitos son:
111, 11.112, 1.122.112, 111.111.111, 122.121.216, 1.111.112.112, 1.111.211.136, 1.116.122.112, 1.211.162.112 y 11.111.113.116.
La sucesión de números insólitos es la sucesión A098034 de la Enciclopedia On-line de Sucesiones de Números Enteros – OEIS. Además, existen solo 428 números insólitos más pequeños que 100 trillones, 1020 = 100.000.000.000.000.000.000.
En la siguiente tabla se muestran los primeros números insólitos que contienen una cifra concreta entre sus dígitos, del 1 al 9.
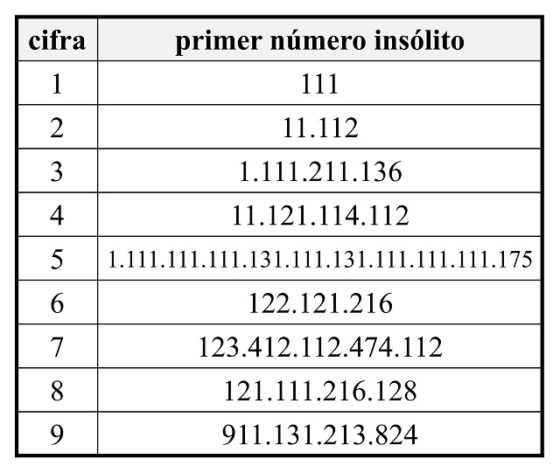
Parece ser que es muy difícil encontrar números insólitos que contengan la cifra 5. Como se muestra en la anterior tabla, el número insólito más pequeño que incluye la cifra 5 tiene 31 dígitos. Además, el siguiente número insólito que contiene a la cifra 5 tiene 37 dígitos:
1.111.111.111.111.111.117.111.111.111.911.111.375.
Por otra parte, el número insólito más pequeño que contiene todas las cifras, con la excepción del 5 teniendo en cuenta lo comentado, tiene 18 dígitos y es el siguiente:
711.813.411.914.121.216.
 Doble página del artículo On a very thin sequence of integers en la que aparecen los 195 números insólitos menores que un trillón, 1018, aunque se saltaron el número insólito 112.264.112.111.616¿Existen infinitos números insólitos?
Doble página del artículo On a very thin sequence of integers en la que aparecen los 195 números insólitos menores que un trillón, 1018, aunque se saltaron el número insólito 112.264.112.111.616¿Existen infinitos números insólitos?
Si miramos a las familias de números naturales definidas por características de los dígitos de sus representaciones numéricas, que hemos comentado al inicio de esta entrada, tenemos que:
A. Existe una cantidad finita de números narcisistas (en el libro La gran familia de los números puede leerse una sencilla demostración de que no existen números narcisistas con más de 60 dígitos), concretamente, hay tan solo 88 números narcisistas;
B. solo existe una cantidad finita de números de Follet (también en el libro La gran familia de los números, puede leerse una sencilla demostración de que no existen números de Follet con más de 22 dígitos), en concreto, hay 19 números en esta familia;
C. tan solo hay un número de Munchausen, el 3.435 (asumiendo que 00 = 1, aunque si se considera que 00 = 0, o en la definición solo se consideran dígitos no nulos, entonces hay otro más, es el número 438.579.088);
D. se desconoce si la familia de invariantes digitales perfectos es finita o infinita.
Por lo tanto, podemos tener nuestras dudas sobre si existirá una cantidad finita o infinita de números insólitos.
 Number structure No. 5 (1983), del artista japonés-canadiense Kazuo Nakamura (1926-2002). Óleo sobre lienzo, 55 x 55 cm. Christopher Cutts Galklery, Toronto. Imagen de la página del Art Canada Institute
Number structure No. 5 (1983), del artista japonés-canadiense Kazuo Nakamura (1926-2002). Óleo sobre lienzo, 55 x 55 cm. Christopher Cutts Galklery, Toronto. Imagen de la página del Art Canada InstituteA continuación, vamos a construir una familia de números insólitos, de lo cual se deducirá que existen infinitos números insólitos. Empecemos considerando los números repitunos (en inglés, repunit numbers), que son aquellos que están formados por la repetición de la cifra 1, es decir, 1, 11, 111, 1.111, 11.111, etc. Si consideramos un número repituno con k dígitos (todos ellos iguales a 1), entonces la suma de los cuadrados de sus dígitos es k y el producto de los cuadrados de sus dígitos es 1. Por lo tanto, un número repituno es un número insólito si el número de dígitos k divide al número. Por ejemplo, 111 es un número repituno que es insólito, puesto que 3 divide a 111 (recordemos la regla de divisibilidad del 3, que dice que un número es divisible por 3 si, y sólo si, la suma de sus dígitos es divisible por 3).
Teorema: Si k = 3n, entonces el número repituno con k dígitos es un número insólito.
Vamos a ver que efectivamente estos números repitunos son insólitos. Para n = 1 tenemos el número 111, que claramente es insólito, ya que 3 divide a 111.
Para n = 2, tenemos el número 111.111.111, que al dividirlo por 111 se obtiene 1.001.001:
![]()
Por lo tanto, el número 111.111.111 es divisible por 9 (que es la cantidad k = 32 de dígitos), ya que 111 es divisible por 3 y 1.001.001 también es divisible por 3 (sus dígitos suman 3).
Para n = 3, tenemos un número repituno formado por 27 unos, 111.111.111.111.111.111.111.111.111, que si lo dividimos por el anterior 111.111.111 (que es divisible por 9) se obtiene 1.000.000.001.000.000.001, es decir, 1 seguido de ocho 0, luego 1, otros ocho 0 y 1, que es divisible por 3. Por lo tanto, el número repituno con 27 = 33 unos es un número insólito.
Y, de forma similar, se puede demostrar, por inducción, que los números repitunos con k = 3n son números insólitos.
Corolario: Existen infinitos números insólitos.
Los números insólitos son una curiosa familia de números naturales, de la que se conocen algunas propiedades matemáticas (algunas de ellas mostradas en esta entrada del Cuaderno de Cultura Científica) y de la que se seguirá investigando en el futuro, como ocurre con las demás familias, al menos para ampliar más nuestro conocimiento sobre la naturaleza de los números.
Bibliografía
1.- R. Ibáñez, La gran familia de los números, Libros de la Catarata – ICMAT – FESPM, 2021.
2.- J. M. De Koninck, N. Doyon, On a very thin sequence of integers, Annales Universitatis Scientiarum Budapestinensis de Rolando Eötvös Nominatae, tomo 20, pp. 157-177 (2001).
3.- Página web: Numbers Aplenty.
4.- Página web: Enciclopedia On-line de Sucesiones de Números Enteros – OEIS
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Los números insólitos se ha escrito en Cuaderno de Cultura Científica.
‘Ikusezinak’ dira landareak, baita zientziarentzat ere
Animalien aldean, ahalegin gutxi egiten dira landareen kontserbazio politiketan, zientzialari batek ohartarazi duenez.
2023ko apirilaren amaieran, Bidebarrieta Zientifikoa hitzaldi sortaren barruan, Landareekiko itsutasuna izenburupeko mintzaldia eskaini zuen Ainara Achurra EHUko biologoak —bideoa, hemen—. Achurrak bizitzaren abenturan bidaide ditugun izaki horien inguruan izan ohi dugun indiferentzia lazgarriaz ohartarazi zuen bertan.
Sinple bezain argia da arazoaren abiapuntua: gure biziraupenerako funtsezkoak izan arren, eta gure eguneroko jardueran edonon egonik ere, ez gara konturatzen beren presentziaz. Haietaz ohartu gabe ematen dugu bizitza gehiena. Landareekiko erabateko itsutasunak jota gaude.
Halere, itsutasun hori ez da soilik gizartera mugatzen. Landare ekologo batek ohartarazi duenez, zientzia jardunean ere ematen da fenomenoa, eta hori, noski, arazo iturri garrantzitsua izan daiteke landareentzat. Baita gizateriarentzat ere.
 1. irudia: landareak edonon gaude egunerokotasunean, baina gehienetan ez gara konturatzen beren presentziaz, eta espezie gutxi batzuen izenak baino ez ditugu ezagutzen. (Argazkia: Juanma Gallego)
1. irudia: landareak edonon gaude egunerokotasunean, baina gehienetan ez gara konturatzen beren presentziaz, eta espezie gutxi batzuen izenak baino ez ditugu ezagutzen. (Argazkia: Juanma Gallego)Trends in Plant Science aldizkarian argitaratutako berrikusketa artikulu batean, Yunnango (Txina) Xishuangbanna Lorategi Botaniko Tropikaleko ikertzaile Richard T. Corlett-ek landareen gaineko ezagutzaren aldeko aldarria egin du. Ez du egin, noski, pertzepzio soilean oinarrituta, gaiaren bueltan egin diren aurreko ikerketetan baizik.
Artikuluan helarazitako mezu nagusia da landareak kontserbatzeko politiketan oso gutxi egiten dela gaur egun, batez ere animalien aldean. Zientzialariaren esanetan, erreinu begetala babestea eskura dagoen zerbait da, eta helburu hori, gainera, merkea eta erraza izan daiteke, beste behin, animalien kontserbazioari bideratutako ahaleginekin konparatuta.
382.000 landare espezie inguru ezagutzen dira. Horiez gain, kalkulatzen da espezieen %10–25 oraindik ez direla deskribatu. Ezagutzak, halere, pixkanaka aurrera egiten du: urte bakoitzeko 2.000 espezie berri deskribatzen dira. Noski, deskribatu gabeko espezie horiek guztiak zientziarentzat eta kontserbazio ekimenenetarako «ikusezinak» dira.
Kalkuluak ez dira oso zehatzak, baina, datuen tarte zabala izanda ere, argi dago kezkatzeko moduko arrazoiak badirela. Landare baskular espezieen %21-48 desagertu daitezkeela kalkulatzen da. Besteak beste, zoruaren erabileran egindako aldaketak eta nekazaritza praktika ez jasangarriak daude arazoaren atzean, egilearen ustez.
Mundu mailako de facto estandarra da IUCN Naturaren Kontserbaziorako Nazioarteko Erakundeak kudeatzen duen mehatxatutako espezieen Zerrenda Gorria, baina, horretan ere, datuak nahiko etsigarriak dira. Ia ornodunen %100 ebaluatu dira zerrenda hori begira, baina, landareak %15 baino ez dira ebaluatu orain arte.
Egoera hala izanik ere, Corlettek dio buelta eman dakiokeela. Ez da mugatu gaiaren bueltan dauden arazoen katalogo bat osatzera. Aitzitik, irtenbideak ere proposatu ditu. Gauza berriak egiteari ekin beharrean, beharrezkotzat jo du dagoeneko martxan diren ekimen eta jardueretan sakontzea. «Jende, espazio, finantziazio eta monitorizazio gehiago, bai eta eraginkorrak diren tokian tokiko esku hartze gehiago», behar direla nabarmendu du egileak.
Adituaren esanetan, gakoetako bat izan daiteke landareetan aditu gehiago trebatzea, jardun horretan nahikoa ez daudela uste duelako. Batez ere eremu tropikaletan omen dira beharrezkoak, bertan ikertu gabeko espezie asko daudelako; horietako batzuk, gainera, oraindik deskribatu gabe daude. Ezaugarritu gabeko landare horiek zientziarentzat «ikusezin» direla dio egileak. Ondorioz, espezie horiek desagertu daitezke gizakiok horren jakitun izan gabe. Egilea sinetsita dago horrelako «iraungipen ilunak» gertatu direla dagoeneko.
 2. irudia: munduko leku askotan hazien bankuak sortu dira, espezie eta barietateen kontserbazioa erraztu aldera. Halere, hazi guztiak ezin daitezke kontserbatu. (Argazkia: Juanma Gallego)
2. irudia: munduko leku askotan hazien bankuak sortu dira, espezie eta barietateen kontserbazioa erraztu aldera. Halere, hazi guztiak ezin daitezke kontserbatu. (Argazkia: Juanma Gallego)Modu berean, landareentzako babesleku txikiak sortzearen alde azaldu da. «Existitzen diren babesleku gehienak paisaia karismatikoak edo eta ornodunak babesteko izendatu ziren“, idatzi du artikuluan. «Ondorioz, askotan ez dute modu egokian babesten arriskuan dauden landare taxonak».
Espeziearen eta arloaren araberako erabakiak hartu beharko direla sinetsita dago. Kasurako, espezie bat babesteko kontserbazio eremu bat ezarri daiteke, baina, aldi berean, beharrezkoa izan daiteke ere espeziearen hazi izoztuak mantentzea, badaezpada ere. Halere, hoberena da landareentzako babeslekuak izatea. Modu horretan, espezieak aukera izango du eboluzionatzeko, aldaketa eta erronka berrietara egokituz; agerikoa denez, klimarena da aldaketa horietako bat.
Hazi biltegiei dagokienez, zientzialariak dio haziak dituzten landare espezieen %17 inguru gordeta daudela hazien bankuetan, baina horiek kontserbatzeak ere erronka bat suposatzen du. Landare motaren arabera, zabaltzen diren aukerak oso mugatuta egon daitezke. Bereziki kontserbatzeko zailak dira tropikoetako landareen haziak. Kalkulatzen da espezieen %10 ezin direla ez lehortu ez izoztu, eta, horrela, kontserbatzeko aukera ezinezkoa bilakatzen da. Prozesu horietan lagungarri diren teknikak garatzen ari diren arren, oraindik erronka tekniko handia da hazi horien kudeaketa.
Nabarmendu du ere informazio baliogarria eskura izatearen garrantzia. Dioenez, uneotan informazio fidagarri gehiena espezieetako aleetatik eskuratzen da, baina egoera horrek ez du errazten distantziatik ikerketa egitea. Dagoen ezagutza optimizatu aldera, online jarritako metaherbario bat osatzea proposatu du, herbario desberdinetako informazioa elkar lotzeko. Halako proiektu batean, noski, are beharrezkoagoa izango da katalogazio eta ikerketa estandarretara jotzea.
Herbarioen arteko informazio trukaketarako estandar batzuk finkatuta dauden arren, egileak dio erreferentzia asko ez daudela digitalizatuta, eta horietako asko denetariko «estilo idiosinkratiko» batzuen bidez jasota daudela; askotan, geoerreferentziak ere falta bide dira. Landareak kokatzeko eta identifikatzeko iNaturalist bezalako proiektuen garrantzia eta potentziala aitortuta ere, hiritar zientziaren baitan aritzen diren halako proiektuek gabeziak dituztela azaldu du. Besteak beste, halako egitasmoek datu base erraldoiak sortzen dituzte, baina gutxitan egiten dira laginketa sistematikoak, eta horrek mugatzen du datu horiekin zer egin daitekeen.
Erronkak erronka, zientzialariak itxaropena agertu du, eta eremu geografiko zehatzetan egitasmoak abiatzeko garrantzia nabarmendu du. «Landare espezieen zero desagertzea helburu global batek urruneko asmoa eman dezake, baina tokiko, eskualdeko eta nazio mailako zenbait helburu potentzialki lorgarriak dira orain».
Erreferentzia bibliografikoa:Corlett, Richard T. (2023). Achieving zero extinction for land plants. Trends in Plant Science. DOI: 10.1016/j.tplants.2023.03.019
Egileaz:Juanma Gallego (@juanmagallego) zientzia kazetaria da.
The post ‘Ikusezinak’ dira landareak, baita zientziarentzat ere appeared first on Zientzia Kaiera.
Cómo la aleatoriedad mejora los algoritmos
La imprevisibilidad puede ayudar a los informáticos a resolver problemas que de otro modo serían intratables.
Un artículo de Ben Brubaker. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Cuando abundan las buenas opciones, adivinar al azar puede ser sorprendentemente fructífero. Ilustración: Kristina Armitage / Quanta Magazine
Cuando abundan las buenas opciones, adivinar al azar puede ser sorprendentemente fructífero. Ilustración: Kristina Armitage / Quanta MagazineDesde los primeros días de la informática, un campo conocido por su enfoque metódico para la resolución de problemas, la aleatoriedad ha jugado un papel importante. El primer programa que se ejecutó en el primer ordenador electrónico de uso general del mundo utilizó la aleatoriedad para simular procesos nucleares. Desde entonces se han utilizado enfoques similares en astrofísica, climatología y economía. En todos estos casos, introducir números aleatorios en ciertos pasos del algoritmo ayuda a los investigadores a tener en cuenta la incertidumbre sobre las muchas formas en que pueden desarrollarse los procesos complejos.
Pero agregar aleatoriedad en un algoritmo también puede ayudarlo a calcular la respuesta correcta a preguntas inequívocas de verdadero o falso. «Simplemente dices ‘Está bien, déjame rendirme, déjame no intentarlo, déjame elegir algo al azar'», explica Eric Blais, científico informático de la Universidad de Waterloo. “Para un montón de problemas, este termina siendo un enfoque ganador”.
Supongamos que quieres determinar si un número dado es primo (divisible solo por 1 y por sí mismo) o compuesto (también divisible por otros números enteros). Simplemente podrías intentar dividirlo entre todos los factores posibles, pero para números grandes este método de «fuerza bruta» y otros algoritmos de factorización son terriblemente lentos. Y si el número resulta ser compuesto, los algoritmos de factorización te dicen los valores de sus divisores, más información de la que pediste. Si solo te importa la «primalidad» de un número, ¿existe un algoritmo más eficiente?
Lo hay si usas la aleatoriedad. La idea básica se remonta a un resultado del matemático francés del siglo XVII Pierre de Fermat, conocido como su “pequeño teorema”. Fermat consideró dos números enteros, llámelos N y x. Demostró que si N es un número primo, entonces xN – x es siempre un múltiplo de N, independientemente del valor de x. De manera equivalente, si xN – x no es un múltiplo de N, entonces N no puede ser un número primo. Pero la afirmación inversa no siempre es cierta: si xN – x es un múltiplo de N, entonces N suele ser primo, aunque no siempre.
Para convertir el pequeño teorema de Fermat en una prueba de primalidad, simplemente toma el N que te interesa, elige x al azar y reemplaza los dos números en xN – x. Si el resultado no es un múltiplo de N, entonces ya está: sabes que N es definitivamente compuesto. Si el resultado es un múltiplo de N, probablemente N sea primo. Ahora elige otra x aleatoria e inténtalo de nuevo. En la mayoría de los casos, después de algunas docenas de intentos, puedes concluir con casi certeza que N es un número primo. “Haces esto una pequeña cantidad de veces”, explica Blais, “y de alguna manera ahora tu probabilidad de tener un error es menor que la probabilidad de que un asteroide golpee la Tierra entre ahora y cuando mires la respuesta”.
Las primeras pruebas de primalidad utilizando algoritmos aleatorios (basados en refinamientos del pequeño teorema de Fermat) marcaron el comienzo de una nueva era. Problema tras problema resultó ser mucho más fácil de resolver con aleatoriedad que con algoritmos no aleatorios o deterministas. La clave era reformular cada problema como uno que pudiera resolverse rápidamente dado un valor apropiado para algún número x, y luego probar que casi cualquier x valdría. La solución funciona a pesar de que los investigadores no tienen idea de cómo determinar si una opción específica es buena. Los matemáticos han bromeado diciendo que este desafío inusual es similar a encontrar paja en un pajar.
Pero estos éxitos hicieron que los investigadores se preguntaran por qué la aleatoriedad debería ayudar con problemas como las pruebas de primalidad, que consisten todos en encontrar patrones ocultos no aleatorios. “Hay algo un poco paradójico al respecto”, afirma Rahul Santhanam, científico informático de la Universidad de Oxford. “La aleatoriedad pura te ayuda a encontrale el truco a la estructura que resuelve el problema”.
En 1994, los informáticos Noam Nisan y Avi Wigderson ayudaron a resolver esta confusión al demostrar que la aleatoriedad, aunque útil, probablemente no sea necesaria. Demostraron que una de dos cosas debe ser cierta: o todos los problemas que se pueden resolver de manera eficiente usando la aleatoriedad también tienen algoritmos deterministas rápidos, o muchos problemas con fama de difíciles son secretamente fáciles. Los informáticos consideran muy improbable la segunda posibilidad.
De hecho, a los científicos informáticos a menudo les resulta más fácil desarrollar un algoritmo determinista comenzando con una versión aleatoria y luego «desaleatoriazarla». “Una vez que la tengo, de repente veo una forma muy obvia de hacerla determinista”, afirma Eli Upfal, científico informático de la Universidad de Brown. “Pero si no hubiese pensado en ella de forma aleatoria como una pregunta probabilística, probablemente no se me habría ocurrido”.
Casi 30 años después de la prueba histórica de Nisan y Wigderson, los algoritmos aleatorios siguen siendo tan populares como siempre, porque la desaleatorización puede ser complicada y los algoritmos deterministas a menudo son eficientes solo en principio. No fue hasta 2002 que tres investigadores encontraron una forma de eliminar la aleatoriedad de las pruebas de primalidad y, en la práctica, su algoritmo es mucho más lento que los mejores algoritmos aleatorios. Para otros problemas es difícil incluso saber por dónde empezar: el algoritmo más conocido tiene un problema del huevo y la gallina del que solo se puede escapar a través de la aleatoriedad.
Ese es el caso de un avance reciente en la teoría de grafos. El año pasado, tres científicos informáticos desarrollaron un algoritmo rápido para encontrar la ruta más corta a través de un grafo, una red de nodos conectados por segmentos lineales, que funciona incluso cuando algunos segmentos se restan de la longitud total de la ruta en lugar de sumarse. Su algoritmo implicaba transformar el grafo en uno más simple eliminando ciertos segmentos, resolver el problema del grafo simplificado y luego tener en cuenta los segmentos eliminados. Pudieron demostrar que el algoritmo se ejecutaría rápidamente si ninguna ruta más corta pasa a través de demasiados segmentos eliminados; de lo contrario, el último paso emplearía demasiado tiempo.
Pero, ¿cómo decidir qué segmentos eliminar en primer lugar? No solo es difícil encontrar el conjunto ideal de segmentos de forma determinista, es imposible. El conjunto depende de qué caminos sean los más cortos, el mismo problema que los tres investigadores estaban tratando de resolver. Pero aunque no pudieron encontrar el mejor conjunto de segmentos para eliminar, pudieron demostrar que la mayoría de las elecciones aleatorias serían lo bastante buenas, y eso fue suficiente para romper el ciclo autorreferencial. En los raros casos en los que el algoritmo toma una decisión desafortunada y se atasca en el último paso, solo hay que pararlo y ejecutarlo nuevamente.
“La aleatoriedad es básicamente una forma de garantizar que algo es cierto sobre la solución óptima sin conocer la solución óptima”, explica Aaron Bernstein, uno de los autores del nuevo algoritmo.
La aleatoriedad ha encontrado innumerables otros usos en la informática, desde la criptografía hasta la teoría de juegos y el aprendizaje automático. Lo más probable es que esté aquí para quedarse.
El artículo original, How Randomness Improves Algorithms, se publicó el 3 de abril de 2023 en Quanta Magazine.
Traducido por César Tomé López
El artículo Cómo la aleatoriedad mejora los algoritmos se ha escrito en Cuaderno de Cultura Científica.
Baraua
Pertsona batek barau egiten duenean gertatzen den lehenengo gauza da metabolismoak behera egiten duela. Baraua egiten dutenek jarduera gutxiago egiten dute, edo are ezinbestekoa ez den edozein jarduera egiteari uzten diote. Baina metabolismoak behera egitea ez da jarduera murriztearen ondorio bakarrik; atsedeneko tasa metabolikoak ere behera egiten du. Bihotz taupaden maiztasuna murriztu egiten da. Gorputzeko tenperatura 37 gradutik 35,5 gradura jaisten da. Muskuluek masa galtzen dute, baita bihotz muskuluak ere. Gibela eta giltzurrunak ere argaldu egiten dira. Entzefaloa da bolumena galtzen ez duen bakarra. Horrek esan nahi du printzipioz organismorako beharrezkoak edo oso komenigarriak diren prozesu jakin batzuk egiteari uzten zaiola edo horiek intentsitate txikiagoarekin egiten direla. Jarduera metabolikoak behera egiten du baraurik egotean halabeharrez gertatu behar den gorputz masaren galera baino neurri handiagoan. Horrela, aurrerago ezinbestekoak izan daitezkeen energia erreserbak aurrezten dira.
 Irudia: Kurt Gödelek barau egin zuen, harik eta ahuleriagatik hil zen arte. (Iturria:)
Irudia: Kurt Gödelek barau egin zuen, harik eta ahuleriagatik hil zen arte. (Iturria:)Metabolismoa moteldu egiten da nagusiki hormona paratiroideo gutxiago jariatzen delako (batik bat T3 edo triiodotironina izeneko forma aktiboa). Oso litekeena da prozesu hori, bere aldetik, adipozitoek leptina gutxiago jariatzearen ondorio izatea. Leptina adipozina bat da; hots, hura sortzen duten zelulen egoeraren berri ematen duen proteina bat. Adipozitoak organismoan gantza gordetzen duten zelulak dira eta, gainera, leptinaren ekoizle nagusiak dira. Lipidoz kargatuta daudenean, odolera askatzen dute, hipotalamora –edo entzefalora– iristen da eta jateko gogoa gutxitzea eragiten dute. Gainera, tiroide guruina estimulatzen duen hormona, hipofisi guruinetik –hipotalamoaren bizilagun eta kidea da–, askatzea eragiten dute. Ondorioz, T3 gehiago askatzen da eta, beraz, metabolismoak gora egiten du eta bero gehiago ekoizten da. Adipozito horietako lipidoen mailek behera egiten badute, horiek leptina gutxiago askatzen dute; beraz, jateko gogoa areagotzen da eta metabolismoak behera egiten du. Barau egiten dutenak hotz dira.
Glukogenoa, animalien karbohidratoen erreserba, 24 orduan agortzen da gibelean –horrek hornitzen du entzefaloa glukosaz–, eta, seguru asko, astebetean, muskuluan. Metabolismo globala murrizteaz gain, proteinetan ere aurrezten da, gutxiago katabolizatzen baitira, karbohidratoen eta gantzen aldean. Ondorioz, gantz deposituak energia hornidura nagusia (eta ia bakarra) izatera igarotzen dira. Hain zuzen ere, barau egiten duten pertsonen biziraupena depositu horien tamainaren araberakoa da. Lipidoak amaitzen direnean, proteinak bakarrik geratzen dira energia lortu ahal izateko; beraz, horiek azkar erabiltzen dira. Askok bizirauteko ezinbesteko funtzioak betetzen dituztenez, heriotza azkar iristen da.
Ezin da erraz aurreikusi zenbat denbora iraungo duen barau egiten ari den pertsona batek bizirik; izan ere, faktore asko daude tartean, batik bat baraualdiaren aurretik zuen osasun egoera eta erreserba lipidikoen bolumena. Demagun 70 kg pisatzen duen eta 18 kg-ko gantz erreserbak (bere pisuaren % 25) dituen pertsona batek barau egitea erabakitzen duela. Hasteko, 700 megajoule inguruko erreserbak dituela (megajoule bat milioi bat joule dira: MJ); bestetik, barau egitean, metabolismoak atsedeneko balio normaletik, hau da, 10 MJ/egun-etik, 7 MJ/egun-era jaitsiko da. Beraz, erreserbek 100 bat egun iraungo lukete. Bobby Sands IRAren militante espetxeratuak gose greba bat egin zuen beste kide batzuekin batera 1981ean, eta baraualdiko 66. egunean hil zen. Litekeena da Sandsek suposizio teorikoan adierazitako 18 kg horiek baino gantz gutxiagorekin hasi izana greba.
Egileaz:Juan Ignacio Pérez (@JIPerezIglesias) UPV/EHUko Fisiologiako katedraduna da eta Kultura Zientifikoko Katedraren arduraduna.
The post Baraua appeared first on Zientzia Kaiera.
LP 791-18d, el planeta cubierto de volcanes
LP 791-18d
Una de las carreras más importantes que se están desarrollando en el campo de la astronomía hoy en día es la búsqueda de un planeta similar en tamaño y características a la Tierra, algo que desde el punto de vista de la geología nos podría ayudar mucho a saber que “ingredientes” son necesarios para la formación de planetas como el nuestro. De momento no hemos encontrado un planeta b, y es posible que tardemos en encontrarlo por dos cuestiones principales: por las dificultades propias de la observación de planetas tan relativamente “pequeños” y porque no sabemos todavía cómo de raros son los planetas como el nuestro -si es que hay más.
Pero el ir completando el catálogo de planetas extrasolares -aquellos que giran en torno a una estrella diferente a nuestro Sol- está aportándonos una visión sobre la enorme diversidad de planetas existentes, muchos de los cuales no tienen una representación directa en nuestro Sistema Solar.
 Figura 1. Reconstrucción artística de LP 791-18d. El punto azul en la lejanía correspondería con el LP 791-18c. Imagen cortesía de NASA’s Goddard Space Flight Center/Chris Smith/KRBwyle.
Figura 1. Reconstrucción artística de LP 791-18d. El punto azul en la lejanía correspondería con el LP 791-18c. Imagen cortesía de NASA’s Goddard Space Flight Center/Chris Smith/KRBwyle.Recientemente, se ha publicado un nuevo estudio en la revista Nature hablándonos de cómo podría ser un planeta de un tamaño similar al de la Tierra (1.03 radios terrestres) llamado LP 791-18d, situado a unos 90 años-luz de nuestro planeta y que gira en torno a una enana roja junto a otros dos planetas, estos dos últimos ya descubiertos en 2019.
Pero, ¿qué tiene de especial este planeta? Los científicos piensan que podría tener una gran actividad volcánica distribuida por toda su superficie, algo similar a lo que ocurre en Ío, un satélite de Júpiter. La actividad volcánica es muy importante en planetas rocosos, ya que puede ayudar a generar una atmósfera -los gases más importantes que emiten los volcanes son el vapor de agua, el dióxido de carbono y el de azufre, entre otros- y a ir rellenándola en el caso de que esta pueda sufrir pérdidas por cualquier motivo, como la carencia de un campo magnético o el propio viento estelar.
Además, las atmósferas de los planetas, si se dan las condiciones adecuadas, pueden permitir la existencia de agua líquida en la superficie, algo que, como sabemos, es de gran importancia para la astrobiología y la búsqueda de la vida más allá de nuestras fronteras.
Al mismo, tiempo, los volcanes son capaces de llevar a la superficie elementos que de otro modo estarían atrapados en su interior, pudiendo crear un ciclo de transferencia y reciclaje entre la corteza y el interior del planeta. También podrían incluso aportar calor a zonas más frías, como el fondo de posibles océanos, permitiendo ambientes menos hostiles.
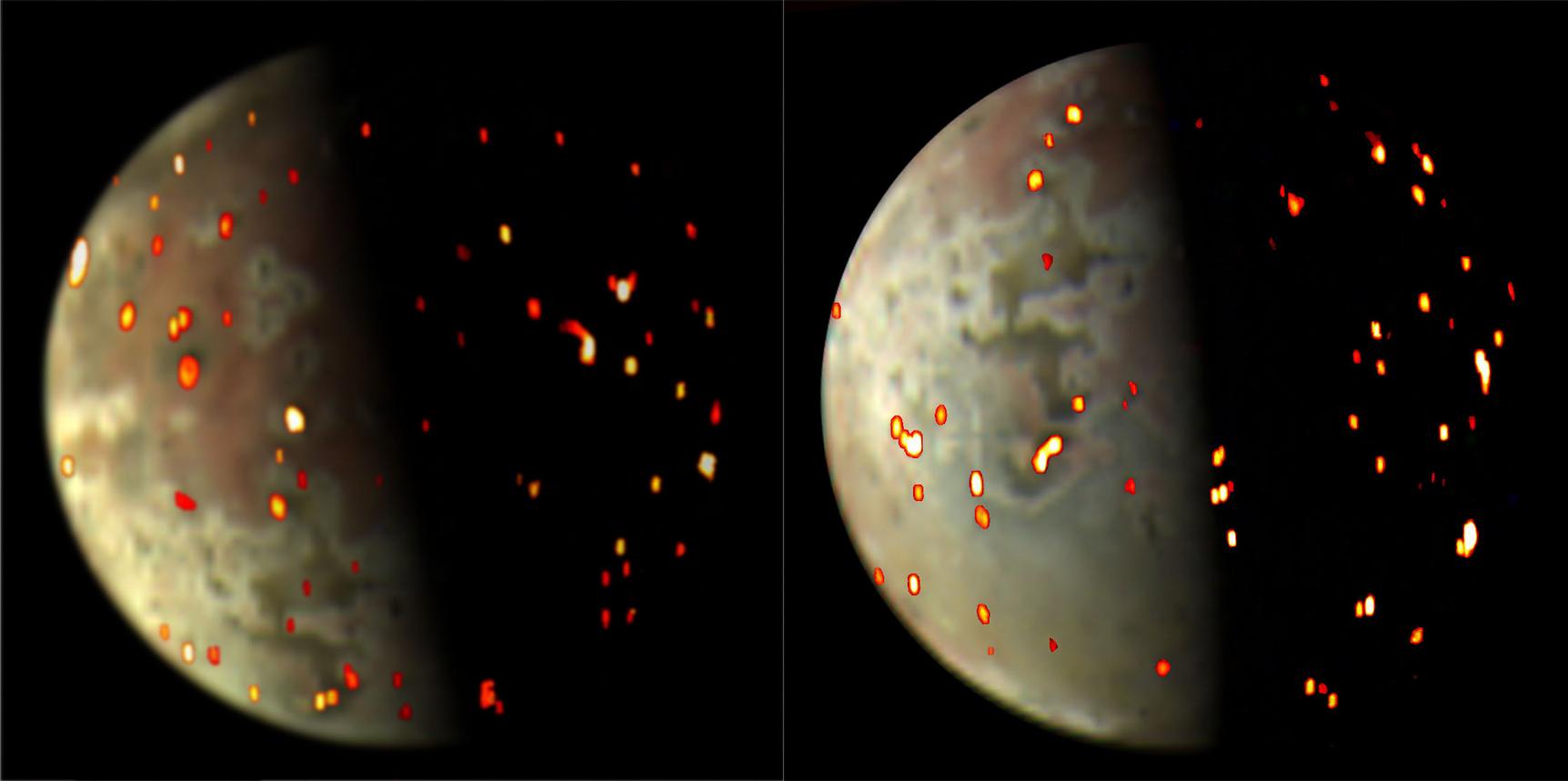 Figura 2. Dos imágenes de Ío tomadas el 14 de diciembre de 2022 y el 1 de marzo de 2023 desde la sonda Juno. En color podemos ver la superficie de Ío, y los puntos rojos, amarillos y blancos corresponden con puntos que tienen una elevada temperatura y que probablemente correspondan con puntos de emisión volcánica recientes o actuales. Cortesía de NASA/JPL-Caltech/SwRI/ASI/INAF/JIRAM.
Figura 2. Dos imágenes de Ío tomadas el 14 de diciembre de 2022 y el 1 de marzo de 2023 desde la sonda Juno. En color podemos ver la superficie de Ío, y los puntos rojos, amarillos y blancos corresponden con puntos que tienen una elevada temperatura y que probablemente correspondan con puntos de emisión volcánica recientes o actuales. Cortesía de NASA/JPL-Caltech/SwRI/ASI/INAF/JIRAM.¿De dónde sacaría este planeta la energía interna suficiente como para poder estar cubierto de volcanes? La respuesta está en la existencia de uno de los otros planetas, el c, que tiene una masa de aproximadamente nueve veces la de la Tierra. Conforme van haciendo órbitas alrededor de su estrella, los planetas c y d pasan cerca el uno del otro, de tal forma que el c es capaz de modificar ligeramente la órbita del d, haciéndola más elíptica.
Esta deformación en la órbita es suficiente como para que el planeta sufra un fenómeno que conocemos como calentamiento de marea, de tal forma que a lo largo de su órbita el planeta sufre una deformación en su superficie y su interior diferente en cada punto de la órbita debido a la atracción gravitatoria de su estrella y de los otros planetas del sistema.
Para que podamos entendernos, imagina que tienes una pelota antiestrés en las manos y que empiezas a comprimirla y a dejar que vuelva a su forma. Después de un rato, verás que esta ha aumentado ligeramente su temperatura y esto se debe en parte a la energía que transfiere el movimiento de tu mano sobre la propia pelota.
De una manera parecida, cuando un cuerpo masivo ejerce una fuerza de atracción gravitatoria sobre otro más pequeño, acaba provocando que el más pequeño sufra un proceso de deformación en el cual se comprime y se estira, parecido a lo que has hecho con la pelota. Esto ocurre normalmente porque la fuerza de atracción de la gravedad en un lado, el que mira al objeto más masivo, es más fuerte, y más débil su efecto sobre el lado opuesto.
 Figura 3. En los planetas con acoplamiento de mareas no hay ciclo día-noche. Solo un lado donde hay oscuridad y otro donde es un día perpetuo. Imagen cortesía de la NASA y el JSC.
Figura 3. En los planetas con acoplamiento de mareas no hay ciclo día-noche. Solo un lado donde hay oscuridad y otro donde es un día perpetuo. Imagen cortesía de la NASA y el JSC.Este proceso, si ocurre en repetidas ocasiones, genera una serie de fricciones que a su vez se traducen en calor, a veces suficiente para generar magmas que pueden dar lugar a erupciones volcánicas, y como decíamos anteriormente, es el mismo proceso que ocurre sobre la luna de Júpiter Ío, y que lo convierte en uno de los objetos con mayor actividad del Sistema Solar.
Otro de los detalles aportados en el estudio sobre este planeta indica que sufre un acoplamiento de mareas con su estrella y que, por lo tanto, siempre tiene la misma cara apuntando a su estrella -algo parecido a lo que ocurre en nuestro planeta con la Luna, en la que el periodo de rotación es igual al orbital- y esto a su vez se traduce en que su cara diurna probablemente tenga una temperatura muy alta, aunque dependiendo de su atmósfera, el agua podría ser estable en su cara nocturna, donde las temperaturas serían menores.
Eso si no ha sufrido un proceso evolutivo como el de Venus, donde los volcanes han sido capaces de generar una atmósfera muy importante, capaz de equilibrar la temperatura en su lado nocturno y diurno, y volviendo totalmente inhabitable cualquier parte del planeta.
Pero precisamente este hecho abre otra cuestión muy importante de cara a entender la habitabilidad de la Tierra. Podríamos suponer que Venus y la Tierra tienen una actividad volcánica similar a grandes rasgos… entonces, ¿por qué Venus ha seguido sumando gases de efecto invernadero? Una de las posibles respuestas a esta pregunta es la existencia de una tectónica de placas capaz de almacenar parte de estos gases -obviamente, no en estado gaseoso sino transformado en otras sustancias químicas- dentro de su corteza o su manto, donde seguirá un ciclo en el que se vaya incorporando al interior del planeta y posteriormente siendo expulsado por los volcanes.
En nuestro planeta este ciclo viene regulado por la tectónica de placas, pero al menos aparentemente no hay una en Venus, y quizás tampoco lo exista en este exoplaneta, por lo que la tectónica de placas podría ser un condicionante para conseguir unas condiciones más habitables en los planetas. O quien sabe si hay algún detalle o mecanismo que todavía desconozcamos por completo a la hora de regular estos ciclos en otros planetas.
Sea como fuere, el estudio de los exoplanetas va a seguir aportándonos una importante visión no solo sobre la diversidad de mundos que pueblan nuestra galaxia, sino también ayudarnos a contestar aquellas preguntas que todavía tenemos sobre nuestro propio Sistema Solar.
Bibliografía:
Crossfield, I.J. et al. (2019) ‘A super-earth and sub-neptune transiting the late-type M dwarf LP 791-18’, The Astrophysical Journal Letters, 883(1). doi: 10.3847/2041-8213/ab3d30.
Peterson, M.S. et al. (2023) ‘A temperate Earth-sized planet with tidal heating transiting an M6 star’, Nature, 617(7962), pp. 701–705. doi: 10.1038/s41586-023-05934-8.
Para saber más:
25 años de planetas extrasolares
El valle de la evaporación de planetas
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo LP 791-18d, el planeta cubierto de volcanes se ha escrito en Cuaderno de Cultura Científica.
Efizientzia eta egonkortasun handiko eguzki-zelulak
Perovskita mineralaz osatutako eguzki-zelulen efizientzia eta egonkortasuna aztertu du nazioarteko ikerketa batek, eguzki-panel eraginkorragoak lortzeko asmoz.
Perovskita minerala ohikoa da lurrazalean eta eroale ona. Izan ere, gaur egun eguzki-zelula organikoen ohiko materiala da eta Juan Luis Delgado kimikariak, Polymat zentroko eta UPV/EHUko Ikerbasque ikertzaileak, perovskita eguzki-zelulen efizientzia eta egonkortasuna hobetzeko zelula hauen aukerak eta funtzionamendua aztertu du nazioarteko ikertalde baten barruan.
Perovskita eguzki-zelulek gaur egun merkaturatzen diren silizio kristalinozko zelulak ordezkatu ditzakete; izan ere, abantailak dituzte ohiko siliziozko panelekin alderatuta, hala nola efizientzia handiagoa -% 25etik gorako efizientzia- eta kostu txikiagoa. Perovskita zelulak «soluzio bidezko prozesamenduaren» bitartez egiten dira. Ekonomikoki merkeagoa da eta gutxiago kutsatzen du silizioa araztearen aldean. Merkaturatzeko eragozpen nagusia egonkortasuna da. Hain zuzen ere arlo horretan zentratzen da ikerketa zientifikoa.
 Irudia: ikertzaileek perovskita eguzki-zelulak eguzkiaren energia modu eraginkorragoan aprobetxatzeko erabili dituzte. (Argazkia: andreas160578 – Pixabay lizentziapean. Iturria: Pixabay.com)
Irudia: ikertzaileek perovskita eguzki-zelulak eguzkiaren energia modu eraginkorragoan aprobetxatzeko erabili dituzte. (Argazkia: andreas160578 – Pixabay lizentziapean. Iturria: Pixabay.com)Oxfordeko Unibertsitateko Henry Snaith fisikariak eta UPV/EHUko Juan Luis Delgado Ikerbasque ikertzaileak zuzendu dute ikerketa-taldea elkarlanean, efizientzia eta egonkortasun handiko eguzki-zelulak lortzeko azken belaunaldiko gehigarrien erabilerari buruzko informazioa eskuratzeko asmoz. 2019aren eta 2022aren artean, zenbait ikerketa-taldek oso efizientzia handiko perovskita eguzki-zelulak deskribatu dituzte gehigarri kopuru txiki bat (metilendiamonio dikloruroa) txertatzearen bidez, horrela momentura arte perovskita eguzki-zeluletarako ziurtatu den efizientziarik handiena lortzeko (% 25,7ko PCE).
Lan honetan, aldiz, aztertu dute gehigarriak perovskita kristalen hazkundean jokatzen duen rola, eta ikusi dute gehigarri hori, denboran zehar, forma kimiko egonkorragoetan deskonposatzen dela. Horrek egonkortasun hobea ematen dio perovskitari (> 1 urte airean).
Emaitza horiek oso garrantzitsuak dira, eta zuzeneko ondorioak izango dituzte etorkizunean, perovskita gailu fotovoltaiko egonkorrak eta efizientzia handikoak garatzeko orduan. Horrek eguzkiaren energia hobeto aprobetxatzea eta beste energia-iturri batzuekiko dagoen mendekotasuna murriztea ekar dezake.
Ikerketaren emaitzak Journal of the American Chemical Society (JACS) aldizkarian argitaratu berri dira eta bertan azaltzen dituzte efizientzia eta egonkortasun hobetuko perovskita eguzki-zelulen funtzionamendua.
Iturria:UPV/EHU prentsa bulegoa: Eguzki zelula eta efizienteenen eta egonkorrenen funtzionamendua argitu du ikerketa batek.
Erreferentzia bibliografikoa:Duijnstee, Elisabeth A.; Gallant, Benjamin M.; Holzhey, Philippe; Kubicki, Dominik J.; Collavini, Silvia; Sturdza, Bernd K.; Sansom, Harry C.; Smith, Joel; Gutmann, Matthias J.; Saha, Santanu; Gedda, Murali; Nugraha, Mohamad I.; Kober-Czerny, Manuel; Xia, Chelsea; Wright, Adam D.; Lin, Yen-Hung; Ramadan, Alexandra J.; Matzen, Andrew; Hung, Esther Y.-H.; Seo, Seongrok; Zhou, Suer; Lim, Jongchul; Anthopoulos, Thomas D.; Filip, Marina R.; Johnston, Michael B.; Nicholas, Robin J.; Delgado, Juan Luis; Snaith, Henry J. (2023). Understanding the Degradation of Methylenediammonium and Its Role in Phase-Stabilizing Formamidinium Lead Triiodide. Journal of the American Chemical Society, 145, 18. DOI: 10.1021/jacs.3c01531
The post Efizientzia eta egonkortasun handiko eguzki-zelulak appeared first on Zientzia Kaiera.
Ingredientes para la receta: la vid
20. Noé se dedicó a la labranza y plantó una viña.
21. Bebió del vino, se embriagó, y quedó desnudo en medio de su tienda.
22. Vio Cam, padre de Canaán, la desnudez de su padre, y avisó a sus dos hermanos.
23. Entonces Sem y Jafet tomaron el manto, se lo echaron al hombro los dos, y andando hacia atrás, vueltas las caras, cubrieron la desnudez de su padre sin verla.
Biblia de Jerusalén, Génesis, 9: 20-23.
… El dios hijo de Zeus
da sin distinción al rico y al miserable
el goce apaciguador del vino.
Eurípides, Las bacantes, 405 a.C.
Porque con ser la vid un árbol tan pequeño, no es pequeño el fruto que da. Porque da uvas casi para todo el año, da vino que mantiene, esfuerza y alegra el corazón del hombre, da vinagre, da arrope, da pasas, que es mantenimiento sabroso y saludable para sanos y enfermos.
Fray Luis de Granada (1504-1588).
 Foto: José Alfonso Sierra / Unsplash
Foto: José Alfonso Sierra / UnsplashTanto las uvas silvestres como las cultivadas se mencionan en la Biblia hasta en 72 capítulos o, también, en 12 del Corán. Por supuesto, solo hay que recordar a Noé, que también aparece su producto derivado más conocido, el alcohol, resultado de la fermentación de los azúcares de la uva, y el vino como objetivo final. Por todo ello, la vid es la planta más citada en los textos sagrados. Y también la cita Stephen Harris, de la Universidad de Oxford, entre las 50 plantas legendarias que cambiaron el mundo.
Las uvas silvestres, Vitis sylvestris, son autóctonas del Asia Menor y el Cáucaso donde se inició la viticultura y se difundió por el Mediterráneo, según Jules Janick, de la Universidad Purdue, en Estados Unidos. Se han encontrado semillas de uva en yacimientos prehistóricos de Europa y, en concreto, en Grecia, los Balcanes, Italia, Suiza, Alemania y Francia. La distribución de la vid silvestre va de Portugal al oeste hasta Turkmenistán al este, y desde Alemania al norte hasta Túnez en el sur.
Por tanto, se encuentra en la Península Ibérica, excepto en el norte y en Pirineos, como lo muestran los hallazgos de sus pepitas desde el Neolítico. Los datos confirman, según Ramón Buxó, de la Universidad Pompeu Fabra, que la vid es una planta indígena en todo el Mediterráneo y las pepitas de vid cultivada se han recuperado a partir de la Edad del Bronce.
Todavía está abierto el debate que propone que, dada la extensión de la vid silvestre por la cuenca mediterránea, es posible que la vid doméstica se originara en más de un lugar de la región y no solo de Oriente Medio y el Cáucaso. Rosa Arroyo-García y sus colegas del Instituto Nacional de Investigación y Tecnología Agraria y Alimentaria de Madrid, han estudiado el ADN de los cloroplastos de 1201 muestras de vid silvestre y doméstica de toda el área de su distribución. Los resultados, según los autores, muestran que el 70% de las muestras de la Península Ibérica llevan cloroplastos que son únicamente compatibles con material derivado de poblaciones occidentales de la vid silvestre.
Otra investigación, centrada en los cloroplastos de las variedades silvestre y doméstica de la meseta de Castilla La Vieja, del grupo de José Carlos Santana, de la Universidad de Valladolid, diferencia hasta 121 genotipos diferentes. Es interesante que muchos de ellos muestran cruces entre la vid silvestre autóctona y vides domésticas de Francia que los autores sitúan en variedades que llegaron por el comercio a través del Camino de Santiago.
8000 años de vid domésticaAntes del 5000 a. C., la uva doméstica, Vitis vinifera , llegó de Anatolia a Oriente Próximo, desde el sur del Cáucaso, entre los mares Negro y Caspio y el Creciente Fértil, el valle del Jordán y Egipto, según el análisis genético de 1000 muestras de vides silvestres y domesticadas publicado por Sean Myles y su grupo, de la Universidad Cornell en Ithaca.
La fecha de la domesticación se sitúa hace entre 6000 y 8000 años atrás. Hay semillas de uva de la Edad del Bronce en Mesopotamia, Israel, Siria, Egipto, el Egeo y en lagos de Suiza, y también se han encontrado en América. Solo hay que recordar que cuando el vikingo Leif Erikson llegó a las costas de Labrador llamó Vinland, País del Vino, a aquel país por la abundancia de vides silvestres de la especie Vitis riparia, habitual en América del Norte.
De hace 4000 años, en la Edad del Bronce, se han encontrado vasijas para almacenar vino y pasas. En el yacimiento de Tel Kabri, en Israel, en un local se recuperaron hasta 40 vasijas con restos de compuestos típicos del vino como ácido tartárico, resinas, miel, aceite de cedro o de ciprés. Es, según Andrew Koh y sus colegas, de la Universidad Brandeis de Estados Unidos, una habitación donde se almacenaban vasijas con vino, es decir, una bodega, una de las más antiguas conocidas hasta ahora.
El estudio, reciente y publicado hace unas semanas, y dirigido por Yang Dong, de la Universidad Agrícola de Yunnan, en China, con 84 autores, se analizan datos genéticos de 3525 variedades de uva silvestre y uva cultivada de todo el planeta. Los resultados revelan los efectos del clima, en concreto de las glaciaciones, en los tamaños de población históricos, sugieren domesticaciones simultáneas de vino y uvas de mesa e identifican variantes asociadas con rasgos de domesticación como el color de la baya y la palatabilidad.
En el Pleistoceno, las condiciones climáticas empujaron a la selección de ecotipos de uva silvestre a lo que ayudó la fragmentación del hábitat. La domesticación ocurrió simultáneamente hace unos 11.000 años en Asia occidental y el Cáucaso para producir vides de frutas de mesa y vino. Las domesticadas de Asia occidental se dispersaron en Europa con los primeros agricultores, y se cruzaron con antiguos ecotipos occidentales salvajes y, posteriormente, se diversificaron ayudados por las migraciones humanas a finales del Neolítico.
Y de por entonces son los Mejillones con uvas que nos presentan Eudald Carbonell y Cinta Bellmunt con las fotografías de María Ángeles Torres desde la Universidad Rovira i Virgili y el grupo de Atapuerca. Es receta sencilla y rápida y un buen entrante para una comida en el campo.
Recolectamos los mejillones en las rocas de la costa más cercana y los tostamos a la hoguera encima de una piedra. Cuando se abran ponemos una uva en cada concha y los comemos a la vez, mejillón y uva.
La vid en AméricaUn ejemplo revelador de la difusión del cultivo de la vid nos llega desde América después de la llegada de Cristóbal Colón. Según lo resume Julio Luelmo, cuando llegaron los europeos encontraron muchas variedades de vid que crecían espontáneamente, sobre todo Vitis riparia, aunque no hay evidencias de que se utilizaran para obtener vino o cualquier otro líquido fermentado a pesar del nombre que los vikingos dieron al Labrador. La viticultura se introdujo en América con la importación de las cepas europeas. Los cultivos de vid resultaron en México, California y, sobre todo, en Sudamérica. En cambio, fracasaron al este de las Montañas Rocosas y en las Antillas donde lo había intentado Colón en 1493.
Hasta el siglo XIX no se conoció que fracasaron por la acción de un insecto de la especie Daktulosphaira vitifoliae, parásito de las especies americanas que ya estaban inmunizadas. Sin embargo, atacaba a las variedades europeas y, cuando llegó al Atlántico europeo, casi acaba con la viticultura en el continente durante el siglo XIX. Su recuperación llegó con injertos de la vid europea en troncos de la vid americana resistente.
Con la domesticación se seleccionan el aumento del tamaño de las uvas y su contenido en azúcar, los varios colores de la piel y la ausencia de semillas, importante para las uvas de mesa y las pasas. Según Stephen Harris, en la actualidad se conocen hasta 10000 cultivares distintos de uva y pocas de ellas llegan hasta el gran comercio. Muchas quedan en exclusiva para pequeños productores. Todo ello influye en la fermentación del mosto de la uva y la obtención del vino. La levadura convierte los azúcares del zumo de uva, glucosa y fructosa, en etanol y dióxido de carbono. Entre la levadura y otras bacterias se sintetizan compuestos aromáticos variados que darán la personalidad típica a cada vino.
Una de las pruebas arqueológicas más antiguas que conocemos de la producción de vino se ha encontrado en una aldea datada en el Neolítico de las montañas Zagros, en el norte de Irán. El grupo de Patrick McGovern, de la Universidad de Pennsylvania, encontró una vasija, fechada hace 7000 años, con residuos de ácido tartárico y de una resina del árbol Pistacia que se utiliza para mezclar con el vino y detener la formación de vinagre.
Las antocianinas son las responsables principales del color rojo en el vino. Se encuentran en la capa exterior de la piel de la uva y se extrae durante la maceración. La mayoría de los mostos, incluso los de uvas negras, son incoloros, y por ello la maceración es un proceso importante para la coloración de los vinos. El color rojo o rosado depende, por tanto, de la extracción de las antocianinas de la piel de la uva durante el proceso de fermentación. También se ha encontrado antocianina en vasijas fechadas hace 8000 años recuperadas de la excavación de Areni, en Armenia, y por tanto, otro de los más antiguos restos que indican la presencia de vino según Hans Barnard y sus colegas, de la Universidad de California en Los Angeles. Confirman la obtención de vino en el Cáucaso ya como ya se conocía de las montañas Zagros de Irán.
 Foto: Jaime Casap / Unsplash
Foto: Jaime Casap / UnsplashEs interesante que nuestro gastrónomo romano de hace más de 15 siglos, Marco Gavio Apicio, destaque qué hacer para cambiar el color del vino y, en concreto, de vino tinto a vino blanco. Su consejo es “Pones en la botella harina de habas o bien tres claras de huevo y lo mezclas durante un buen rato. Al día siguiente, el vino será blanco. Las cenizas blancas de viña también pueden producir esta transformación”. Espero que le sea útil a quien le interese.
Es una receta de Juan Altamiras en su texto Nuevo arte de la cocina española. Así recomienda cocinar la Ternera estofada en vino blanco, que publicó en 1758. Era fraile franciscano y había nacido en 1709 en La Almunia de Doña Godina, Zaragoza. La fecha original de publicación de su libro era 1745 y es importante pues presenta la cocina española de la época anterior a la influencia de la cocina francesa a finales del siglo XVIII y en el siglo XIX. La receta aparece en la reciente edición sobre Altamiras publicada por Vicky Hayward.
De lo magro de la ternera cortarás pedazos como nuezes: freirás tocino, y con su pringue has de freír los trozos de ternera: echarás la carne en la olla, con el pringue que te quedó freirás cebolla menuda, y echarás con la carne, pondrás un poco de vino blanco, dos granos de ajos majados, sal, todas especias; peregil y unas hojas de laurel: después de este recado, la pondrás a fuego manso, con un papel en la boca del puchero, para que no levante el hervor, y con un pucherito, que la tape, con agua. Harás un poco masseta, y la pondrás en la circunferencia de la olla principal, de modo que no se exhale, dexala cocer dos horas: así sacarás poco, pero buen caldo, y muy gustoso.
El cultivo de la vid implica un extenso laboreo y la poda anual de los sarmientos. Es el arte de la poda lo que distingue al buen viñador. Y es la base de un plato típico de La Rioja: Chuletillas de cordero al sarmiento.
Una receta para celebrar en cualquier celebración que tenga lugar en tierras riojanas o en cualquier sitio al aire libre. Se trata básicamente de chuletas de cordero asadas, a las que habremos echado sal gorda. Aunque se pueden hacer, por supuesto, en una chimenea, estas chuletas se suelen asar al aire libre, usando para ello una parrilla puesta al fuego, prendido con sarmientos, es decir, ramas secas de vid. Las chuletas se colocan cuando el fuego ya se ha extinguido y sólo quedan las brasas. Es la temperatura ideal para asar las chuletillas. Hay quien les echa un chorro de vino de Rioja poco antes de sacarlas de la parrilla.
Las uvas se conservan secándolas al sol para producir pasas, o transformando el mosto de la uva en vino. Es la bebida alcohólica de difusión universal y, según Jean-François Revel, lo es por su capacidad de viajar y, también, por su gran variedad y, siendo siempre el zumo fermentado de la uva, mantiene características propias del lugar de origen por su sabor, aroma y color. Es una bebida que depende de la habilidad y perspicacia del viticultor y, en último término, de la capacidad y la memoria del catador. Para Revel, la degustación del vino es una partida de ajedrez de infinitas soluciones jamás agotadas.
Una vez probado el vino, el catador queda hechizado. El vino se asocia al amor y a la falta de amor, a la alegría y a la tristeza, al éxito y al fracaso, a la amistad, a los negocios, a la guerra y a la paz, al reposo y a la violencia, y a tantos otros sentimientos y conductas. Incluso el vino se asocia, inevitablemente, a la templanza, aunque Revel menciona civilizaciones donde dejar de beber vino es casi como renunciar a toda otra actividad, a todo intercambio, incluso supone dejar de pensar. Es lo que el ensayista, escritor y crítico literario Jean-François Revel opina sobre el vino en su historia literaria de la sensibilidad gastronómica.
 Foto: Juan Ugarte / Pixabay
Foto: Juan Ugarte / PixabaySin embargo, después de los elogios al vino llega el debate actual sobre los beneficios y daños que provoca el alcohol en la salud humana. Como ejemplo sirve una publicación reciente de Aitor Hernández y sus colegas de la Universidad de Navarra sobre la relación en la ingesta de alcohol y la hipertensión. Son datos de la encuesta “Seguimiento Universidad de Navarra” que, desde octubre de 2015, hace un seguimiento de 14651 participantes con encuestas bianuales durante 14 años. Según los resultados, si el consumo de alcohol sigue las pautas de la dieta mediterránea se asocia con un menor riesgo cardiovascular, aunque todas las relaciones no son significativas según la estadística. En conclusión, se necesitan más datos.
Hace unos años, Jonathan Silvertown, de la Universidad de Edimburgo, escribía que la afinidad entre los humanos y el alcohol, y la levadura, de la especie Saccharomyces cerevisiae, que lo produce, es muy profunda. El alcohol posee el poder transformador de una droga que altera el estado mental. Eleva o deprime el ánimo, inspira o nubla el razonamiento, enciende la pasión, disminuye la pericia, induce la agresión y la violencia o, también, provoca el sueño.
El alcohol ata a los humanos con nudos difíciles, para muchos imposibles, de deshacer. En resumen, el alcohol es una toxina para la que tenemos una cierta tolerancia. Además, es una toxina sin otro equivalente funcional en el metabolismo humano, como pueden ser las que provocan los opioides que son el producto final de nuestro sistema de recompensa cerebral. Pero nuestra especie ha estado expuesta al alcohol resultado de la fermentación de azúcares, sobre todo en frutas maduras, incluso antes de la aparición de Homo. Nuestros ancestros comunes desde hace cinco millones de años ya comían abundante fruta que, al madurar y por la levadura, ya transformaban los azúcares en alcohol. Donde hay fruta madura hay levadura, y donde hay levadura habrá alcohol.
En Bilbao, a los mejillones se les llama mojojones o, con más precisión, se les llamaba así. Ahora mojojón es, me parece, una palabra moribunda. Ni siquiera aparece en el Diccionario de la Lengua y, en Bilbao, a los antiguos mojojones con tomate antes y ahora se les llama tigres. Sin embargo, aquí va una receta con mojojones. La incluye Íñigo Azpiazu en su libro sobre la cocina tradicional vasca y la titula como Mojojones bilbotarras, o sea, mejillones bilbaínos. Dice así, más o menos:
Necesitamos mojojones, puerros, chacolí, harina, limón, perejil, sal y pimienta. Hay quien le añade mostaza. Lavamos los mojojones y los ponemos al fuego en una cazuela grande para que se abran. Entonces los pasamos a otra cazuela grande, quitamos media concha y los regamos con el caldo de la primera hervida. Rehogamos en aceite los puerros picados muy finos, añadimos una cucharada de harina, y juntamos los mojojones y un vaso de chacolí. Hervimos unos diez minutos y añadimos el zumo de medio limón y un poco de pimienta. Dejar que se enfríen y ponemos una buena cantidad de perejil por encima, y a servir.
ReferenciasApicio, M.G. 2007. De re coquinaria. El arte de la cocina. Recetas de la Roma Imperial. Comunicaciones y Publicaciones. Barcelona. 119 pp.
Arroyo-García, R. et al. 2006. Multiple origins of cultivated grapevine (Vitis vinifera L. ssp. sativa) based on chloroplast DNA polymorphisms. Molecular Ecology 15: 3707-3714.
Azpiazu, I. 1989. La cocina tradicional vasca. Ed. Iru. Barcelona. 64 pp.
Barnard, H. et al. 2010. Chemical evidence for wine production around 4000 BCE in the Late Chalcolithic Near Eastern highlands. Journal of Archaeological Science doi: 10.1016/j.jas.2010.11.012.
Biblia de Jerusalén. 1967. Desclée de Brouwer Eds. Bilbao. 1693 pp.
Brothwell, D. & P. Brothwell. 1998. Food in Antiquity. A survey of the diet of early peoples. Johns Hopkins University Press. Baltimore and London. 283 pp.
Buxó, R. 1997. Arqueología de las plantas. La explotación económica de las semillas y los frutos en el marco mediterráneo de la Península Ibérica. Crítica. Barcelona. 367 pp.
Carbonell, E. et al. 2016. Recetas paleo. La dieta de nuestros orígenes para una vida saludable. Ed. Planeta. Barcelona. 143 pp.
Dong, Y. et al. 2023. Dual domestications and origin of traits in grapevine evolution. Science 379: 892-901.
Granada, Fray Luis de. 1947. Maravillas de las plantas y de los animales. Apostolado de la Prensa. Madrid. 184 pp.
Harris, S. 2021. Plantas legendarias: 50 plantas que cambiaron el mundo. Rey Naranjo Eds. Barcelona. 358 pp.
Hayward, V. 2017. Nuevo arte de la cocina española de Juan Altamiras. Círculo de Lectores. Barcelona. 493 pp.
Hernández-Hernández, A. et al 2023. Mediterranean alcohol-drinking pattern and arterial hypertension in the “Seguimiento Universidad de Navarra” (SUN) prospective cohort study. Nutrients doi: 10.3390/nu15020307.
Janick, J. 2007. Fruits of the Bibles. HortScience 42: 1072-1076.
Koh, A. J. et al. 2014. Characterizing a Middle Bronze palatial wine cellar from Tel Kabri, Isr ael. PLOS One 9: e106406.
Luelmo, J. 1975. Historia de la agricultura en Europa y América. Ed. Istmo. Madrid. 469 pp.
McGovern, P.E. et al. 1996. Neolithic resonated wine. Nature 381: 480-481.
Myles, S. et al. 2011. Genetic structure and domestication history of the grape. Proceedings of the National Academy of Sciences USA 108: 3530-3535.
Payo, A. 2023. Los ciclos glaciares determinaron la domesticación de la uva y la aparición del vino. Boletín SiNC 2 marzo.
Piqueras Haba, J. 2005. La filoxera en España y su difusión espacial: 1878-1926. Cuadernos de Geografía 77: 101-136.
Revel, J.-F. 1996. Un festín de palabras. Historia literaria de la sensibilidad gastronómica desde la Antigüedad hasta nuestros días. Tusquets Eds. Barcelona. 289 pp.
Santana, J.C. et al. 2010. Genetic structure, origins, and relationships of grapevine cultivars from the Castilian Plateau of Spain. American Journal of Enology and Viticulture 61: 214-224.
Silvertown, J. 2019. Cenando con Darwin. Tras las huellas de la evolución en nuestros alimentos. Crítica. Barcelona.285 pp.
Wikipedia. 2023. Vino. 14 marzo.
Zohary, D. & P. Spiegel-Roy. 1975. Beginnings of fruit growing in the Old World. Science 187: 319-327.
Para saber más:El consumo del alcohol no mata a las neuronas, pero sí las trastorna
La podredumbre noble: Cuando una infección mejora un vino
«Una copita de vino es buena para el corazón». Claro que sí, guapi.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Ingredientes para la receta: la vid se ha escrito en Cuaderno de Cultura Científica.

