I, Mammal. The Story of What Makes Us Mammals
Juan Ignacio Pérez Iglesias, lector

Un balonazo en la diana testicular del autor cuando jugaba como portero de fútbol condujo a este a preguntarse acerca de las razones de la ubicación de las gónadas masculinas de un gran número de especies de mamíferos en el exterior del abdomen (advierto a futuros posibles lectores de que el asunto está lejos de haber sido resuelto y de que es materia de controversia). Y a partir de esa indagación y por culpa de otros avatares de la vida, y más concretamente de su paternidad, llegó a interrogarse acerca de la condición mamífera, esa que compartimos los seres humanos con los miembros de otras muchas especies.
A cualquiera que nos preguntasen acerca de tal condición, responderíamos que los mamíferos nos caracterizamos por ser especies vivíparas, por el modo en que las hembras alimentan a sus crías recién nacidas –con leche que producen ellas mismas-, o por el pelaje que cubre nuestro cuerpo. Sin embargo, ninguna de esas características es común a todas las especies del grupo. Por eso no es fácil responder a la pregunta de qué es lo que nos hace mamíferos.
Para responderla, Liam Drew recorre un buen número de aspectos de la biología de los mamíferos. Una parte muy importante del libro lo dedica a cuestiones que tienen que ver, directa o indirectamente, con nuestra reproducción. De especial importancia son los capítulos dedicados a la lactación -no en balde se trata del rasgo que sirve para denominarnos como grupo- y a la placenta –dispositivo del que disfrutamos la mayoría de especies de mamíferos-. Pero Drew repasa muchos más aspectos de nuestra biología: condición endoterma (íntimamente relacionada con la posesión de pelaje), receptores sensoriales, corteza cerebral y otros.
No obstante, lo más notable de este libro no es el repaso de temas de paleontología, biología del desarrollo, fisiología o neurobiología, sino la aproximación evolutiva que impregna todos los aspectos tratados. El autor expresa en todo momento su interés por desentrañar la razón de ser de los rasgos que nos caracterizan a los mamíferos. Se pregunta acerca de las presiones selectivas que pudieron dar lugar a su aparición y a posteriores modificaciones. Y en ese repaso valora las diferentes interpretaciones que se han ido dando a lo largo del tiempo.
El libro es riguroso, muy completo, ameno e instructivo. Es un gran libro de divulgación. No me extrañaría que lo tradujesen al español, aunque vistos los desmanes que se suelen cometer con las traducciones, recomiendo encarecidamente su lectura en inglés. Se lee con facilidad.
Ficha:
Autor: Liam Drew
Título: I, Mammal. The Story of what Makes Us Mammals
Año: 2017
Editorial: Bloomsbury
En Editoralia personas lectoras, autoras o editoras presentan libros que por su atractivo, novedad o impacto (personal o general) pueden ser de interés o utilidad para los lectores del Cuaderno de Cultura Científica.
El artículo I, Mammal. The Story of What Makes Us Mammals se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El ingenio de los pájaros, de Jennifer Ackermann
- La cara más emocionante, humana y filosófica de la ciencia
- El tamaño importa en organismos, empresas, ciudades y economías
Naukas Bilbao 2017 – Teresa Valdés-Solís: Limpia, fija y da esplendor
En #Naukas17 nadie tuvo que hacer cola desde el día anterior para poder conseguir asiento. Ni nadie se quedó fuera… 2017 fue el año de la mudanza al gran Auditorium del Palacio Euskalduna, con más de 2000 plazas. Los días 15 y 16 de septiembre la gente lo llenó para un maratón de ciencia y humor.

Si bien el título de esta charla hace referencia al ideal despótico ilustrado de determinada pomposa institución, a todos los efectos prácticos manifiestamente prescindible, en ella Teresa Valdés-Solís repasa algunas aplicaciones insospechadas de los materiales porosos.
Teresa Valdés-Solís: Limpia, fija y da esplendorEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2017 – Teresa Valdés-Solís: Limpia, fija y da esplendor se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – Guillermo Peris: Los trapecistas del genoma
- Naukas Bilbao 2017- Daniel Torregrosa: ¡Estamos rodeados!
- Naukas Bilbao 2017 – Diana González: Identidad digital y robots
Los efectos climáticos de un calentamiento sin precedentes en el Mediterráneo
Una investigación colaborativa en la que ha participado la UPV/EHU ha descubierto una interacción entre dos fenómenos climáticos que podría ser esencial para la planificación hídrica, agraria y forestal y para evaluar la vulnerabilidad climática de los ecosistemas frente unas condiciones de calentamiento sin precedentes en el Mediterráneo.

Bosque de pino silvestre (Pinus sylvestris), una de las especies investigadas en este trabajo (Asier Herrero / UPV/EHU).
¿Cuáles son las causas de las sequías que se sufren periódicamente en la Península Ibérica? ¿Por qué a veces los inviernos son templados y lluviosos y otros son fríos y secos o fríos y húmedos? ¿Influye el cambio climático de origen antropogénico sobre estos procesos? ¿Cómo actúan estos ciclos sobre la productividad de los ecosistemas terrestres? Y finalmente, ¿se pueden predecir estos ciclos y así adecuar la economía a dichos ciclos? El trabajo, publicado esta semana en Nature Communications, liderado por la Universidad de Alcalá de Henares y llevado a cabo en colaboración con la UPV/EHU, la Universidad Ginebra y la Universidad de Castilla-La Mancha, aporta claves importantes para responder a algunas de estas preguntas.
La oscilación del Atlántico Norte (NAO) es una fluctuación a gran escala en la masa atmosférica situada entre la zona de altas presiones subtropicales y la baja polar en la cuenca del Atlántico Norte, y es, en gran parte, responsable de los períodos de sequía en el continente europeo. Estudios anteriores muestran que la NAO tiene un gran efecto potencial sobre diferentes aspectos, desde la fijación de carbono y el crecimiento de los árboles, a la producción de frutos o los ciclos de plagas forestales. Sin embargo, la conexión entre la productividad forestal a largo plazo y la NAO presentaba algunas inconsistencias, como periodos en los que los ciclos climáticos no se correspondían a lo esperado por el valor de la NAO. En su trabajo, los investigadores muestran justamente que estas inconsistencias pueden tener su origen en anomalías periódicas de la temperatura a nivel superficial del Océano Atlántico, conocidas como Oscilación Multidecadal Atlántica (AMO). Se trata de fenómenos oceánicos que aparecen en el norte del Océano Atlántico y por el cual las temperaturas oceánicas siguen un ciclo de una duración total de unos 70 años. Estos cambios de la temperatura del océano afectan a la atmósfera pero no instantáneamente, sino con un cierto retraso.
Datos del siglo XIX analizados con herramientas modernas
El trabajo, en el que ha participado el investigador posdoctoral del grupo de investigación FisioClimaCO2 de la UPV/EHU Asier Herrero, es el resultado de una línea de investigación exhaustiva que comenzó hace más de cinco años y que integra datos de archivos históricos, climatología, modelos estadísticos y ecología forestal. “Ha sido un trabajo fascinante, desempolvar archivos de finales del siglo XIX para tener estimaciones precisas de cómo ha evolucionado la productividad de los bosques en la Península durante el último siglo y analizarlos con herramientas del siglo XXI para comprender las causas de los ciclos climáticos y sus consecuencias sobre la productividad de los ecosistemas”, explican los investigadores.
La investigación integra datos de pinares de varias localidades en Castilla-La Mancha y en Castilla y León. “Estos pinares eran la base del sustento de muchas zonas rurales desde el siglo XIX, por este motivo se llevaba a cabo una cuantificación exhaustiva de los recursos disponibles, madera, pastos, resina etc.”, apuntan. El problema es que muchos de los trabajos anteriores se basaban en proyecciones de modelos y, además, no consideraban la interacción entre ambos modos climáticos, la NAO y AMO. Gracias a la existencia de esta serie temporal, en el estudio se demuestra por primera vez que es la interacción de ambos modos climáticos la que controla en gran medida la productividad de los ecosistemas.
Así, los resultados del trabajo muestran que las fases AMO+ NAO+ y AMO- NAO- ejercen un elevado control sobre la productividad forestal, debido a la disminución de las precipitaciones y temperaturas invernales. La NAO es como una llave que abre y cierra la entrada de las borrascas pero es necesario el control de la AMO (ligada a la temperatura del Atlántico en latitudes extratropicales y a la formación de borrascas), lo que finalmente determina la temperatura y humedad del aire que llega a la Península.
“El seguimiento de los modos climáticos analizados puede ayudar a predecir los periodos de sequía extrema, aunque no será una tarea fácil, favoreciendo así la aplicación de medidas de adaptación en los bosques de una manera más eficaz”, apunta Asier Herrero. En una situación de sequía como la que está azotando el Mediterráneo en los últimos tiempos, estos hallazgos podrían ser esenciales para la planificación hídrica, agraria y forestal, y en particular para evaluar la vulnerabilidad climática de los ecosistemas.
Referencia:
Jaime Madrigal-González, Juan A. Ballesteros-Cánovas, Asier Herrero, Paloma Ruiz-Benito, Markus Stoffel, Manuel E. Lucas-Borja, Enrique Andivia, Cesar Sancho-García & Miguel A. Zavala (2017) Forest productivity in southwestern Europe is controlled by coupled North Atlantic and Atlantic Multidecadal oscillations Nature Communications, 2017 doi: 10.1038/s41467-017-02319-0
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Los efectos climáticos de un calentamiento sin precedentes en el Mediterráneo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los efectos protectores de la lactancia materna frente a la contamincación atmosférica
- Riesgo de sufrir los efectos de un vertido de petróleo en el mar de las costas europeas
- El calentamiento global y el aceite de oliva
¿Cuántos animales se usan en España para experimentación?
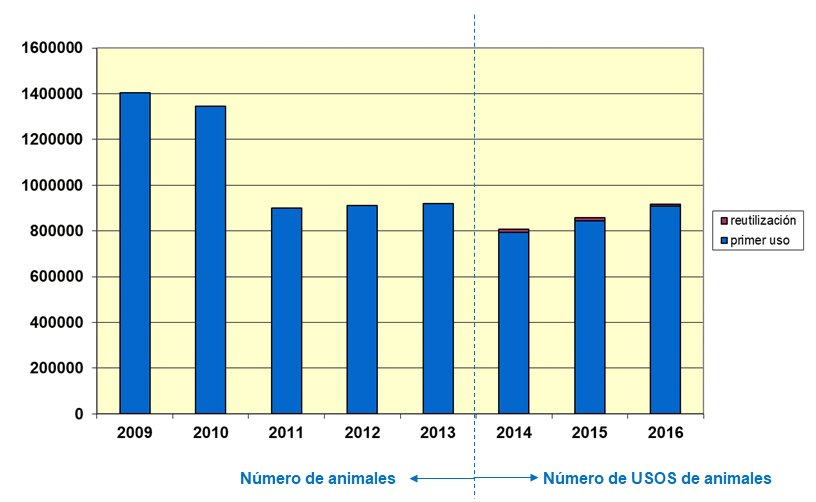
Figura 1: Número de animales/usos de animales en experimentación en España en los últimos 8 años, del 2009 al 2016 (Gráfica preparada a partir de los datos disponibles en el MAPAMA).
Con independencia de que uno esté a favor o en contra del uso de animales para la experimentación estaremos seguramente de acuerdo que algo esencial es saber cuántos animales se destinan cada año a la experimentación en cada país. Para poder opinar es esencial tener la información correcta y actualizada. Es importante conocer las cifras exactas de utilización de animales en experimentación y otros fines científicos, incluyendo la docencia, para poder comprender la dimensión precisa de esta actividad, que sigue siendo esencial en investigación científica, y que está a la par extraordinariamente regulada.
Efectivamente, de acuerdo a la legislación europea (Directiva 2010/63/UE, del Parlamento Europeo y del Consejo, de 22 de septiembre) y española (Real Decreto 53/2013, de 1 de febrero) sobre bienestar animal es obligatorio comunicar a la Comisión Europea y publicar anualmente información estadística sobre la utilización de los animales en procedimientos. En nuestro país esta labor la asume el Ministerio de Agricultura y Pesca, Alimentación y Medio Ambiente (MAPAMA), a través de la Dirección General de Producciones y Mercados Agrarios, quienes publican anualmente los usos de animales en experimentación. Estos datos son aportados inicialmente por los usuarios (centros de investigación, universidades, empresas u otras instituciones) a sus respectivas autoridades competentes (en nuestro país, las Comunidades Autónomas), quienes, a su vez, los remiten al MAPAMA para su contabilización y publicación colectiva. En esta página web del MAPAMA es posible encontrar datos estadísticos de utilización de animales en experimentación desde 2009 hasta el año 2016, último año publicado, a finales de 2017.
A partir de los datos hechos públicos por el MAPAMA he preparado unos gráficos (Figura 1 y siguientes), que ilustran este artículo de divulgación, y que también podéis encontrar en la página web que mantengo sobre la iniciativa de transparencia en experimentación animal en nuestro país. Lo primero que salta a la vista es que el número de animales que se emplearon en 2016 en España para experimentación ha disminuido considerablemente en los últimos ocho años (Figura 1). De los 1.403.290 animales usados en 2009 hemos pasado a 917.896, un 34,6% menos, lo cual representa una reducción significativa (usamos ahora más de un tercio de animales menos que los que usábamos hace 8 años), en la línea de los principios generales de Reemplazo, Reducción y Refinamiento (las comúnmente denominadas 3Rs), que iluminan todas las normativas y recomendaciones actuales en bienestar animal. Por ello es relevante señalar que los usuarios de la experimentación animal en nuestro país han hecho esfuerzos considerables para reducir el número de animales empleados a los estrictamente necesarios, optimizando la gestión de las diferentes colonias de animales y los experimentos llevados a cabo. Es cierto que la cifra fue todavía inferior en 2014 (808.827) y que, desde entonces, parece constatarse un cierto aumento (de un 13% desde 2014), aunque todavía es prematuro analizar estas fluctuaciones menores entre años cercanos y sea más informativo apreciar las variaciones significativas, a la baja, observadas entre 2009 y 2016. De hecho, a la vista de la gráfica, la reducción en el uso de animales empezó en 2011 y desde entonces el número de animales usados en experimentación se ha mantenido en cifras similares, alrededor de 800.000-900.000 usos anuales.
En el cálculo de estos números hay que hacer notar una variación en la forma de contabilizarlos. Hasta 2013 se contaban el número de animales empleados (es decir, el número de individuos). A partir de 2014, a raíz de la actualización legislativa producida por la entrada en vigor de la nueva Directiva Europea y su trasposición a las legislaciones nacionales, se contabilizan el número de usos de animales, que no es exactamente lo mismo (aunque las variaciones sean mínimas). Un animal, en especial los de gran tamaño, como un primate no humano, un perro, una oveja o un cerdo, puede usarse en más de un procedimiento experimental, si el animal ha podido recuperarse adecuadamente de su participación en un procedimiento previo, siempre bajo estricta supervisión veterinaria de las alteraciones de bienestar animal que le supone participar en los mismos. El objetivo es propiciar la reutilización de los animales en experimentación, siempre que sea posible, como una medida adicional en aras de reducir el número global de individuos utilizados en experimentación. Por ejemplo, para 2016, el número anual de usos de animales (917.896) se reparte en 909.475 primeros usos (animales solamente utilizados una vez, un 99,1% del total) y apenas 8.511 reutilizaciones (un 0.9% del total). Como se puede observar en la Figura 1, el impacto de esta nueva manera de contabilizar el uso de animales es todavía muy limitado.
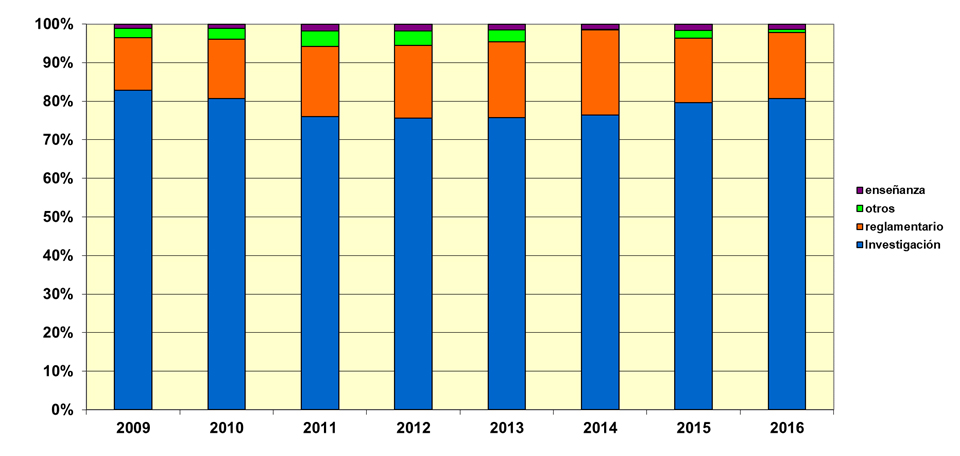
Figura 2: Finalidad del uso de animales en experimentación en España en los últimos 8 años, del 2009 al 2016 (Gráfica preparada a partir de los datos disponibles en el MAPAMA).
Los datos disponibles en el MAPAMA también permiten preguntar cuál es la finalidad o el destino del uso de animales en experimentación en España. Tal y como podemos comprobar en la segunda gráfica (Figura 2) la gran mayoría de usos de animales en nuestro país se destinan a investigación, en un porcentaje, siempre mayoritario, que oscila alrededor del 80% hasta situarse, en 2016, en el 80,7% del total anual de los usos de animales. Y es lógico que así sea, siendo la investigación científica (en particular todas las disciplinas relacionadas con la biomedicina) la principal demandante de animales para acometer los experimentos necesarios para entender cómo funcionan los seres vivos, para investigar sobre las enfermedades que afectan a humanos y al resto de los animales, sobre sus causas y sobre qué hacer para desarrollar terapias que las alivien o curen. Ya en febrero de 2015, la Confederación de Sociedades Científicas de España (COSCE), publicó un informe sobre el uso de animales en investigación científica que explicaba al conjunto de la sociedad por qué la mayoría de animales que se emplean en experimentación se destinan a la investigación científica, qué se investiga con ellos y por qué es tan relevante y sigue siendo necesario su uso, que todavía no puede ser reemplazado en su totalidad por métodos alternativos.
Las finalidades minoritarias que siguen al uso de animales en investigación corresponden a usos reglamentarios (un 17,1% en 2016, como por ejemplo: producción y control de calidad de productos e instrumentos de medicina, odontología y veterinaria; evaluaciones de seguridad toxicológica), y en la enseñanza (un 1,3% en 2016, en universidades, en facultades de veterinaria, medicina, biología y otras relacionadas) así como otros usos diversos (un 0,9% en 2016).
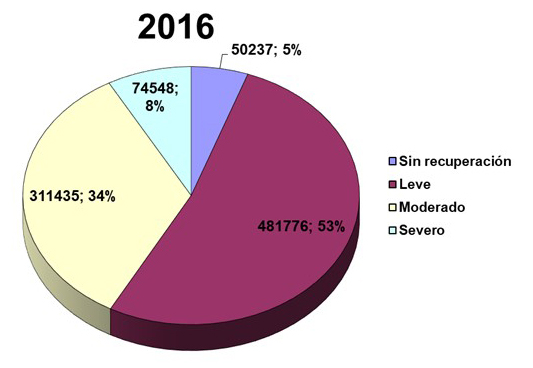
Figura 3: Grado de severidad de los procedimientos empleados con animales en experimentación en España en 2016 (Gráfica preparada a partir de los datos disponibles en el MAPAMA).
Otro de los cambios importantes que aportó la nueva Directiva Europea 2010/63/UE, trasladada luego a las legislaciones nacionales, fue la obligación de asignar un grado de severidad a todo procedimiento (a todo experimento) aplicado sobre animales, usando para ello una escala con cuatro categorías posibles: leve, moderado, severo o sin recuperación. Estos datos no están por lo tanto disponibles antes de 2014. Para 2016 se vuelve a constatar que la gran mayoría (87%) de procedimientos en los que se utilizan animales en España corresponden a un grado de severidad leve (481.776, un 53%) o moderado (311.435, un 34%), en los cuales la alteración del bienestar animal es limitada, y que solamente en un porcentaje limitado (74.548 usos de animales, un 8%) el procedimiento que se aplica tiene la connotación de severo, y en un número menor de casos (50.237, un 5%) se trata de procedimientos sin recuperación (Figura 3). Todos quienes usamos animales de experimentación estamos obligados, por la legislación y por las recomendaciones de bienestar animal, a refinar los métodos para reducir el daño o dolor que directa o indirectamente infligimos a los animales debido a las características del procedimiento experimental usado. Por ejemplo, como en cualquier otra intervención quirúrgica en personas, naturalmente todos los animales operados reciben la anestesia y analgesia necesarias para mitigar el dolor durante y después de la misma.
El RD53/2013 ilustra en su Anexo IX ejemplos de procedimientos considerados como leves (p.e. técnicas no invasivas de diagnóstico por imagen; administración de sustancias por vía subcutánea, intramuscular, intraperitoneal, por sonda gástrica e intravenosa a través de los vasos sanguíneos superficiales), moderados (p.e. cirugía bajo anestesia general y analgesia apropiada; irradiación o quimioterapia con una dosis subletal, o con una dosis que de otro modo sería letal, pero con reconstitución del sistema inmunitario, en estudios de trasplante de médula ósea) o severos (p.e. ensayos de toxicidad en los que la muerte sea el punto final; ensayo de potencia de una vacuna caracterizada por la alteración persistente del estado del animal, enfermedad progresiva que causa la muerte, asociada con dolor, angustia o sufrimiento moderado duradero).
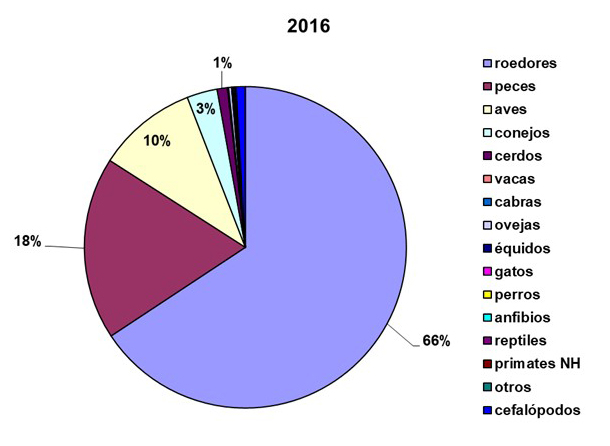
Figura 4: Especies animales empleadas en experimentación en España en 2016 (Gráfica preparada a partir de los datos disponibles en el MAPAMA).
Ya sabemos cuántos animales se usan en España, a qué se destinan y el grado de severidad que conlleva la experimentación realizada sobre ellos. Pero ¿qué tipo de animales se usan en España en experimentación? ¿Cuáles son las especies animales más utilizadas en nuestro país? De nuevo los datos del MAPAMA ofrecen una información pormenorizada de las especies o grupos de animales utilizados en España durante 2016 (Figura 4).
Los roedores, principalmente ratones (539.974), en menor medida ratas (54.895), y en mucha menor medida cobayas (7.223), hámsteres (734) y otros roedores (322), siguen siendo el grupo de animales más utilizado en experimentación con un 65,7% del total (603.148 usos de roedores de un total de 917.896 usos). Tras los roedores encontramos a los peces (168.746, un 18,4%), las aves (92.195, un 10,0%), los conejos (28.035, un 3,1%, que no son roedores sino lagomorfos) y los cerdos (9.434, un 1,0%). El resto de especies y grupos animales están a gran distancia y representan, cada uno de ellos, menos del 1% del total. Por ejemplo, durante 2016 se usaron apenas 888 vacas (bóvidos), 269 cabras, 2.695 ovejas, 91 équidos (caballos, burros y sus cruces), 358 gatos, 1.083 perros y 228 primates no humanos, entre otros.
Adicionalmente se incorpora, desde 2014, también debido a los cambios introducidos por la nueva Directiva Europea 2010/63/UE, al único grupo de animales invertebrados que se considera en las normativas de bienestar animal: los cefalópodos (pulpos, sepias, calamares, …), debido al extraordinario desarrollo de su sistema nervioso y a su capacidad de percibir dolor. En 2016 se usaron 8.444 cefalópodos en España para experimentación (un 0.9% del total).
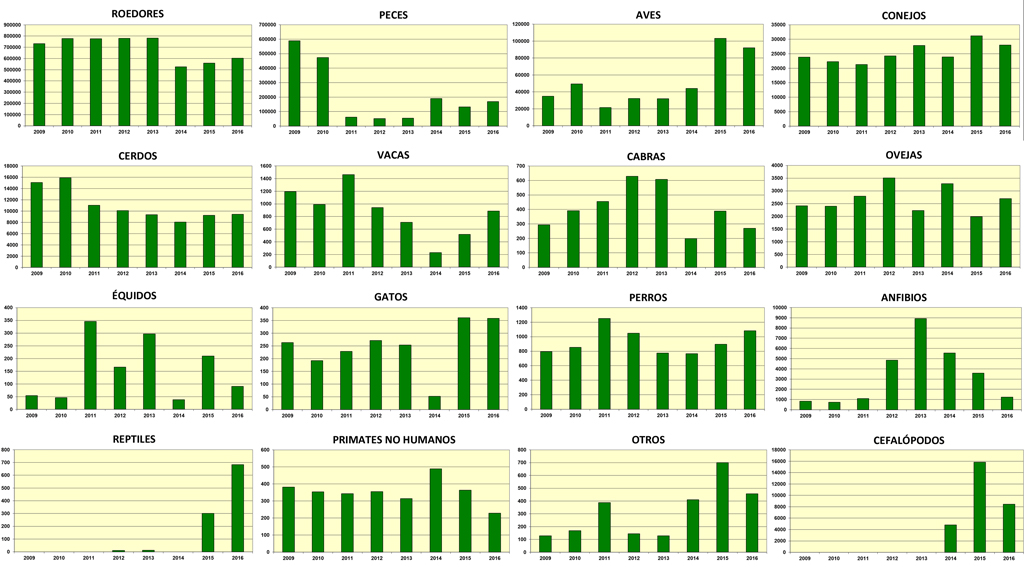
Figura 5: Evolución del número de animales/usos de animales empleados en experimentación en España desde 2009 hasta 2016 analizado por grupos y especies (Gráficas preparadas a partir de los datos disponibles en el MAPAMA).
La evolución del número de animales (o usos de animales, desde 2014) utilizados en experimentación en cada una de las especies o grupos de animales desde 2009 a 2016 ofrece muchos datos interesantes a reseñar (Figura 5). Por ejemplo, el número de roedores empleado en experimentación se redujo considerablemente en 2014 (en un 33%, de 782.200 en 2013 a 526.553 en 2014). El número de primates no humanos (esencialmente macacos cangrejeros y Rhesus) también se han reducido considerablemente desde 2014, pasando de 489 a 228 en 2016. El número de peces se ha reducido considerablemente, mientras que el de aves ha aumentado. Otras especies, como conejos, ovejas, cabras, vacas, cerdos, gatos y perros se han mantenido en cifras similares en los últimos ocho años.
La implementación de la Directiva Europea 2010/63/UE ha podido influir en la manera sobre cómo se realizan estos recuentos estadísticos anuales. Por ejemplo, anteriormente (RD1201/2005, ya derogado) la definición de animal, a los efectos de la legislación de protección del bienestar animal, era la de “cualquier ser vivo vertebrado no humano, incluidas las crías de vida propia o las formas de cría en reproducción, excluidas las formas fetales o embrionarias”, mientras que actualmente la definición actualizada de animal es la de “a) vertebrados no humanos vivos, incluidos: i) las larvas autónomas para su alimentación, y ii) los fetos de mamíferos a partir del último tercio de su desarrollo normal; y b) cefalópodos vivos”. También la definición de procedimiento ha cambiado. Anteriormente (RD1201/2005, ya derogado) se entendía por procedimiento “toda utilización de un animal para los fines establecidos en el artículo 2 que pueda causarle dolor, sufrimiento, angustia o daño prolongados, incluida toda actuación que de manera intencionada o casual pueda dar lugar al nacimiento de un animal en las condiciones anteriormente mencionadas”. Actualmente (RD53/2013) se entiende por procedimiento “la utilización, tanto invasiva como no invasiva, de un animal con fines experimentales u otros fines científicos, cuyos resultados sean predecibles o impredecibles, o con fines educativos siempre que dicha utilización pueda causarle al animal un nivel de dolor, sufrimiento, angustia o daño duradero equivalente o superior al causado por la introducción de una aguja conforme a las buenas prácticas veterinarias”.
El número de animales usados en experimentación puede parecernos normal, excesivo o reducido, según como y con qué lo comparemos. Estos números deben de observarse tanto en sus valores absolutos como relativos. En nuestro informe COSCE de Febrero de 2015 sobre el uso de animales en investigación científica ya alertábamos al respecto. Por ejemplo, usando nuevamente datos del ministerio (MAGRAMA en 2013), si nos fijamos en los cerdos utilizados para experimentación en España en 2013 (9.373 cerdos) y los comparamos con el número de cerdos sacrificados para alimentación (más de 41 millones de cerdos) resulta que por cada cerdo que se destinó a experimentación se consumieron más de 4.400 cerdos para alimentación.
Existen especies animales que suscitan una mayor empatía, como los perros o los primates no humanos, y por ello algunos grupos de nuestra sociedad demandan una mayor protección o la prohibición del uso de perros y primates no humanos en experimentación. Sin embargo, se debe constatar que el uso de perros y de primates no humanos es extremadamente reducido en experimentación (en 2016, 1.083 perros y 228 primates no humanos, sobre un total de 917.896 usos de animales) pero también extraordinariamente relevante y necesario. Por ejemplo, los perros han sido un modelo animal muy útil para el desarrollo de estrategias de terapia génica efectivas para el tratamiento de la diabetes de tipo 1 o para curar enfermedades raras como el síndrome de Sanfilippo. Igualmente, los primates no humanos han sido esenciales para el estudio de muchas alteraciones cerebrales, de la conducta, que nos afectan y para el desarrollo y validación de vacunas como la desarrollada frente al virus Ébola.
La experimentación animal sigue siendo necesaria en biología, biomedicina y veterinaria. No podemos prescindir todavía de ella. Todas las normativas actuales de bienestar animal, de protección de los animales utilizados en experimentación y otros fines científicos, incluyendo la docencia, incorporan un párrafo en la parte introductoria que contiene un deseo o fin último de estas normas. Por ejemplo, el RD53/2013 dice en su introducción “Se marca como objetivo último el total reemplazo de los animales en los procedimientos”. Sin embargo, hoy en día no es posible todavía aplicar métodos alternativos (in silico, mediante simulaciones bioinformáticas, o in vitro, en cultivos celulares) para todos y cada uno de los experimentos e investigaciones científicas (p.e. no es posible investigar sobre un órgano tan complejo como el ojo o la función visual asociada si no es utilizando animales), aunque es obligatorio el uso de estos métodos alternativos cuando existen y han sido validados.
En septiembre de 2016 lanzamos en España, desde la COSCE y con la ayuda de EARA (Asociación Europea de Animales de Experimentación), el Acuerdo de transparencia sobre el uso de animales en experimentación científica. En la actualidad más de 100 instituciones españolas se han adherido a esta propuesta que contiene cuatro compromisos: (1) “Hablar con claridad sobre cuándo, cómo y por qué se usan animales en investigación”; (2) “Proporcionar información adecuada a los medios de comunicación y al público en general sobre las condiciones en las que se realiza la investigación que requiere el uso de modelos animales y los resultados que de ella se obtienen”; (3) “Promover iniciativas que generen un mayor conocimiento y comprensión en la sociedad sobre el uso de animales en investigación científica”; y (4) “«Informar anualmente sobre el progreso y compartir experiencias”. Es en cumplimiento también de este acuerdo por la transparencia en experimentación animal que escribo este artículo, compartiendo y analizando los datos de usos de animales en experimentación en nuestro país, a partir de los datos publicados por el MAPAMA.
El MAPAMA también merece ser destacado en su apuesta por la transparencia en experimentación animal. La publicación del informe sobre usos de animales de experimentación y otros fines científicos, incluyendo la docencia en 2016 mejora muchísimo los informes anteriores, al incorporar los datos presentados de una forma mucho más comprensible e ilustrar el informe con diversas gráficas de producción propia que contribuyen a trasladar información veraz y contrastable al ciudadano interesado.
Sin duda la apuesta por la transparencia empieza por compartir la información disponible. Espero igualmente que tras la lectura de este artículo sea más sencillo responder a la pregunta que lo encabeza: ¿Cuántos animales se usan en España para experimentación?
Este post ha sido realizado por Lluis Montoliu (@LluisMontoliu) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
El artículo ¿Cuántos animales se usan en España para experimentación? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:El mito de Arquímedes, mención especial del jurado “On zientzia”
“El mito de Arquímedes” de Eneko Amezaga Angulo recibió la mención especial del jurado en la 6ª edición de los premios On zientzia. En el siglo XXI, un Arquímedes moderno muy peculiar revivirá uno de los mitos que hizo pasar a la historia al personaje.
¿Tienes una idea genial para explicar un concepto científico en un vídeo? ¿Quieres ver tu trabajo emitido en televisión? La Fundación Elhuyar y el Donostia International Physics Center (DIPC) han organizado la octava edición de On zientzia, un concurso de divulgación científica y tecnológica enmarcado en el programa Teknopolis, de ETB. Este certamen pretende impulsar la producción de vídeos cortos y originales que ayuden a popularizar el conocimiento científico.
On zientzia tendrá tres categorías. El mejor vídeo de divulgación recibirá un premio de 3.000 euros. Para impulsar la producción de piezas en euskera, existe un premio de 2.000 euros reservado a la mejor propuesta realizada en ese idioma. Por último, con el objetivo de impulsar la participación de los estudiantes de ESO y Bachillerato, hay un premio dotado con 1.000 euros para el mejor vídeo realizado por menores de 18 años.
Los vídeos han de tener una duración inferior a los 5 minutos, se pueden realizar en euskera, castellano o inglés y el tema es libre. Deben ser contenidos originales, no comerciales, que no se hayan emitido por televisión y que no hayan resultado premiados en otros concursos. El jurado valorará la capacidad divulgativa y el interés de los vídeos más que la excelencia técnica.
Las bases las encuentras aquí. Puedes participar desde ya hasta el 25 de abril de 2018.
Edición realizada por César Tomé López
El artículo El mito de Arquímedes, mención especial del jurado “On zientzia” se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El frustrante viaje de un átomo de carbono, mención especial del jurado “On zientzia”
- Fallos científicos en el cine, mejor vídeo de divulgación joven “On zientzia”
- Keats vs Feynman, mejor vídeo de divulgación “On zientzia”
La razón del querer saber

Los humanos estamos equipados con un sistema interno de recompensa que nos premia cuando comprendemos algo. Es ese momento de placer que sentimos al entender un chiste, al resolver un problema matemático, al ensamblar un rompecabezas; es la razón de que nos apasionen las narraciones, las historias con sorpresa, los cuentos de terror. A lo largo de nuestra evolución se han reproducido más aquellos de nosotros que disfrutaban conectando causas con consecuencias, resolviendo problemas teóricos o prácticos o buscando nuevos métodos para hacer las cosas; en nuestro cerebro la innovación es recompensada con el mismo tipo de premio biológico con el que se recompensa comer o practicar el sexo. Como demuestran nuestras galerías de juegos, nuestras bibliotecas y nuestras colecciones cinematográficas somos sobre todo monos curiosos, y lo somos porque estamos hechos así; porque descubrir nos proporciona placer interior.
De esta realidad pueden sacarse dos conclusiones interesantes y valiosas para comprendernos mejor a nosotros mismos y para juzgar de modo más eficaz el papel de la ciencia en nuestra vida social. Por una parte la curiosidad sistemática sobre el funcionamiento del cosmos que nos rodea es algo profunda, quintaesencialmente humano; tanto que se podría considerar que menos investigación y menos conocimiento son una afrenta básica a la esencia misma de nuestra Humanidad. Las sociedades que recortan en esto no sólo están perjudicando sus propios intereses económicos y estratégicos a largo plazo, sino que también están deteriorando el espíritu de sus ciudadanos. No es sólo mal negocio: es mala gestión política y un deterioro del alma de la nación.
Quizá más interesante sea el papel del conocimiento en la satisfacción interna de cada uno como justificación para dedicar el tiempo y el esfuerzo necesarios. Es un tópico afirmar que cuando nuestra vida se acaba no podemos llevarnos con nosotros el dinero, ni las fincas, ni los títulos, ni los oropeles; que las riquezas materiales e incluso sociales jamás han conseguido garantizar la permanencia de ningún ser humano. Reyes, faraones, Incas y Emperadores murieron y desaparecieron por muchos monumentos, pirámides o imperios que construyeran sin que sus esfuerzos les proporcionaran ni un sólo día más de vida; a menudo lo contrario. El éxito económico y social no ser puede acarrear al más allá; tan sólo disfrutar en el acá, y a menudo con limitaciones y contraindicaciones.
El conocimiento tampoco se puede transportar allende la muerte, pero en cambio produce un bienestar real y patente gracias a los vericuetos de nuestra evolución; algo palpable y real. Saber más no sólo es vivir mejor en el sentido material, sino en el espiritual, dado que nuestra estructura básica interna nos recompensa por conocer. Dedicarse a aumentar el saber humano puede ofrecer el mismo tipo de recompensas sociales que otras actividades, pero además incluye de fábrica un sentimiento de satisfacción interior que estamos biológicamente determinados a sentir. También, es necesario decirlo, una cierta y exquisita forma de frustración que proviene de la ausencia de explicaciones cuando algo no se comprende, cuando la conexión entre efectos y causas no es clara, cuando el experimento o el instrumental fallan o se revelan insuficientes. La contraparte del placer de conocer es la frustración de fracasar en el conocimiento, y cualquier científico en activo debe familiarizarse en profundidad con esa sensación porque la sentirá a menudo a lo largo de su carrera.
Pero si tiene suerte también sentirá el inenarrable placer del descubrimiento, aunque sea menor; el súbito destello de comprensión, la repentina confirmación de teorías y años de trabajo, ese momento glorioso en el que se convierte en la primera persona de la historia en entender un poco más, en empujar un poco más allá el límite del conocimiento humano. Puede que esto venga acompañado de honores, premios y proyectos, o puede que sea arrinconado, olvidado, considerado secundario; tal vez incluso falseado. Aunque una cosa es real: la verdadera razón por la que se practica ciencia es la caza de esa elusiva sensación. Porque los premios, los proyectos y los honores no pueden competir con esa satisfacción interior: la verdadera razón del querer saber.
Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.
El artículo La razón del querer saber se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El peligro de saber sólo un poco
- Abraham Flexner y el saber por el saber
- Saber que tú no sabes me permite saber
En este núcleo sobra masa

El deuterio es un isótopo del hidrógeno. Eso significa que el número de protones en su núcleo es idéntico, uno, pero el deuterio tiene un neutrón, cosa que el hidrógeno más básico no tiene.
En un núcleo como el del deuterio se ilustra fácilmente el efecto de la equivalencia entre masa y energía que hizo famosa Einstein con su ecuación E = mc2. Las cuentas son muy simples: si la masa de un protón es mp = 1.007276 u (donde u representa la unidad de masa atómica ≈ 1.66053886 x 10-27 kg) y la del neutrón es mn= 1.008665 u, entonces mp + mn = 1.007276 + 1.008665 = 2.015941 u. Pero resulta que la masa medida real del núcleo de deuterio es 2.013553 u, es decir, que existe una diferencia de masa de 2.015941 – 2.013553 = 0.002388 u. = 3.9654 x 10-30 kg. Aplicando la fórmula de Einstein obtenemos que este déficit de masa corresponde a 2,224 MeV de energía, que es lo que se conoce como energía de enlace del núcleo de deuterio. Visto de otra forma, este defecto de masa es la energía que se ha liberado al “construirse” el núcleo.
En pura teoría podríamos seguir así hasta completar todos los isótopos existentes. Y decimos en pura teoría porque en 2015 se midió por primera vez y ahora acaba de confirmarse con mayor precisión que esta forma de proceder falla de forma muy significativa a las primeras de cambio. con el núcleo de helio-3, esto es, con solo dos protones y un neutrón. ¿Qué ocurre? ¿Falla la famosa fórmula?¿Hay algo desconocido que se nos escapa?¿Están mal los experimentos?
En 2015 el equipo liderado por Edmund Myers de la Universidad Estatal de Florida en Tallahassee (Estados Unidos) publicó unas mediciones de las relaciones de masa atómica que dejaron perplejos a los investigadores. Sus datos implicaban que, siguiendo el procedimiento de arriba, la suma de las masas del protón y el deuterón menos la masa del núcleo de helio-3, es decir, (mp + md) – mh, era mucho más pequeña, en más de 4 desviaciones estándar, que el valor deducido al combinar los valores aceptados de las masas individuales. Algo no cuadraba. O las mediciones del equipo de Myers o los valores de masa individuales estaban mal.
Una medición posterior de la masa del protón realizada por otros investigadores, apuntó a que la masa del protón utilizada era un poco demasiado grande. Sin embargo, la discrepancia se mantenía en más de 3 desviaciones estándar. Ahora, en una repetición de su experimento, Myers y colegas confirman su resultado de 2015 con una precisión mejorada.
En los experimentos los investigadores emplean un espectrómetro con una trampa de iones tipo Penning. Este tipo de aparato consigue medir con preción la relación existente entre las frecuencias de resonancia ciclotrón de dos iones atrapados, de la que puede deducirse la relación entre las masas de los iones.
Myers y sus colegas mejoraron significativamente su aparato de 2015, reduciendo tanto la falta de homogeneidad del campo magnético de la trampa como el ruido en el circuito de detección del aparato. Luego rehicieron su medición de la relación de las masas del núcleo de helio-3 (que al no tener un electrón es un ion que se representa como 3He+) y el ion molecular hidrógeno-deuterio (HD+), que se puede convertir fácilmente a la diferencia (mp + md) – mh que mencionamos antes.
Debido a las mejoras en el aparato su resultado difiere de nuevo en más de 4 desviaciones estándar del valor calculado utilizando la masa del protón actualizada (más pequeña) y las masas del deuterón y del núcleo de helio-3.
El hallazgo no solo tiene interés porque es una de esas pequeñas cosas que después pueden llevar a grandes descubrimientos si se descarta el error experimental, sino también porque llega en un momento crítico en el que está en revisión la nueva propuesta del Sistema Internacional de Unidades (SI) en términos de constantes fundamentales.
Referencia:
S. Hamzeloui, J. A. Smith, D. J. Fink, and E. G. Myers (2017) Precision mass ratio of 3He+ to HD+Physical Review A doi: 10.1103/PhysRevA.96.060501
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo En este núcleo sobra masa se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las fluctuaciones del núcleo celular son un reloj
- La suave piel del núcleo
- Nuevo límite superior a la masa de los neutrinos de Majorana
Los cifrados de Feynman
En 1987, Chris Cole publicó en el grupo de Google sci.crypt un mensaje titulado Feynman’s cipher. Se refería a una conversación que había tenido con el físico teórico Richard Feynman (1918-1988), que introducía de la siguiente manera:
“Cuando era estudiante de posgrado en Caltech, el profesor Feynman me mostró tres ejemplos de código con los que había sido retado por un colega científico de Los Álamos, y que no había podido descifrar. También fui incapaz de descifrarlos. Ahora los publico en la red para intentarlo.”

Richard Feynman y los tres códigos.
Cole copiaba después esos tres mensajes cifrados, calificados con diferentes grados de dificultad:
-
El más sencillo:
MEOTAIHSIBRTEWDGLGKNLANEAINOEEPEYST
NPEUOOEHRONLTIROSDHEOTNPHGAAETOHSZO
TTENTKEPADLYPHEODOWCFORRRNLCUEEEEOP
GMRLHNNDFTOENEALKEHHEATTHNMESCNSHIR
AETDAHLHEMTETRFSWEDOEOENEGFHETAEDGH
RLNNGOAAEOCMTURRSLTDIDOREHNHEHNAYVT
IERHEENECTRNVIOUOEHOTRNWSAYIFSNSHOE
MRTRREUAUUHOHOOHCDCHTEEISEVRLSKLIHI
IAPCHRHSIHPSNWTOIISISHHNWEMTIEYAFEL
NRENLEERYIPHBEROTEVPHNTYATIERTIHEEA
WTWVHTASETHHSDNGEIEAYNHHHNNHTW
- El más complicado:
XUKEXWSLZJUAXUNKIGWFSOZRAWURORKXAOS
LHROBXBTKCMUWDVPTFBLMKEFVWMUXTVTWUI
DDJVZKBRMCWOIWYDXMLUFPVSHAGSVWUFWOR
CWUIDUJCNVTTBERTUNOJUZHVTWKORSVRZSV
VFSQXOCMUWPYTRLGBMCYPOJCLRIYTVFCCMU
WUFPOXCNMCIWMSKPXEDLYIQKDJWIWCJUMVR
CJUMVRKXWURKPSEEIWZVXULEIOETOOFWKBI
UXPXUGOWLFPWUSCH
- Nuevo mensaje:
WURVFXGJYTHEIZXSQXOBGSVRUDOOJXATBKT
ARVIXPYTMYABMVUFXPXKUJVPLSDVTGNGOSI
GLWURPKFCVGELLRNNGLPYTFVTPXAJOSCWRO
DORWNWSICLFKEMOTGJYCRRAOJVNTODVMNSQ
IVICRBICRUDCSKXYPDMDROJUZICRVFWXIFP
XIVVIEPYTDOIAVRBOOXWRAKPSZXTZKVROSW
CRCFVEESOLWKTOBXAUXVB
El primero de ellos, de 380 caracteres, el más fácil, fue resuelto al día siguiente por Jack C. Morrison (Laboratorio de Propulsión a Reacción, NASA). Morrison se dio cuenta de que se trataba de un cifrado por transposición de 5 por 76, en el que, comenzando por la última letra “W”, se debía retroceder a lo largo del texto cifrado en 5 posiciones varias veces; al terminar, había que volver a repetir la misma estrategia, comenzando por la anteúltima letra “T”, y así sucesivamente. Tras realizar este descifrado, se obtiene el texto:
WHANTHATAPRILLEWITHHISSHOURESSOOTET
HEDROGHTEOFMARCHHATHPERCEDTOTHEROOT
EANDBATHEDEVERYVEYNEINSWICHLICOUROF
WHICHVERTUENGENDREDISTHEFLOURWHANZE
PHIRUSEEKWITHHISSWEETEBREFTHINSPIRE
DHATHINEVERYHOLTANDHEETHTHETENDRECR
OPPESANDTHEYONGESONNEHATHINTHERAMHI
SHALVECOURSYRONNEANDSMALEFOWELESMAK
ENMELODYETHATSLEPENALTHENYGHTWITHOP
ENYESOPRIKETHHEMNATUREINHIRCORAGEST
HANNELONGENFOLKTOGOONONPILGRIM
que corresponde a las primeras palabras de los Cuentos de Canterbury de Geoffrey Chaucer, como comentaba el propio Morrison en el grupo sci.crypt:
WHAN THAT APRILLE, WITH HIS SHOURES, SOOTE
THE DROGHTE OF MARCH HATH PERCED TO THE ROOTE
AND BATHED EVERY VEYNE IN SWICH LICOUR
OF WHICH VERTU ENGENDRED IS THE FLOUR
WHAN ZEPHIR U SEEK WITH HIS SWEETE BREFTH
INSPIRED HATH IN EVERY HOLT AND HE ETH
THE TENDRE CROPPES AND THEY ONGE SONNE
HATH IN THE RAM HIS HALVE COURSY RONNE
AND SMALE FOWELES MAKE N MELODYE
THAT SLEPEN AL THE NYGHT WITH OPEN.
YES, O PRIKE THHEM, NATURE. IN HIR CORAGES
THANNE LONGEN FOLK TO GO ON. ON PILGRIM!
En la versión del proyecto Gutenberg, estos versos son:
Whan that Aprille with his shoures sote
The droghte of Marche hath perced to the rote,
And bathed every veyne in swich licour,
Of which vertu engendred is the flour;
Whan Zephirus eek with his swete breeth
Inspired hath in every holt and heeth
The tendre croppes, and the yonge sonne
Hath in the Ram his halfe cours y-ronne,
And smale fowles maken melodye,
That slepen al the night with open yë,
(So priketh hem nature in hir corages):
Than longen folk to goon on pilgrimages…

Primera página de los “Cuentos de Canterbury” en el manuscrito Ellesmere. Imagen de Wikipedia.
En [2], Nick Pelling daba algunos detalles y conjeturas sobre los otros dos códigos: el segundo que consta de 261 caracteres y usa las 26 letras del alfabeto inglés, y el tercero de 231 caracteres.
Además, en [4] se comparten algunos datos para intentar identificar a la persona que propuso a Feynman estos complicados códigos aún no resueltos. Parece que Geoffrey Chaucer y alguna de las ediciones de sus Canterbury Tales pueden ser la clave para descubrir a ese ‘colega de Los Álamos’, y quizás poder interpretar los dos cifrados restantes…
Aunque hay muchas personas expertas intentando encontrar la clave de estos códigos, quizás –aprendiendo un poquito de criptografía– te apetezca intentarlo. ¡Suerte!
Nota:
Visto en The Feynman Ciphers, Futility Closet, 5 diciembre 2017
Más información:
[1] Nick Pelling, Feynman Ciphers, Cipher Mysteries, 25 enero 2013
[2] Nick Pelling, A quick look at the Feynman Ciphers, Cipher Mysteries, 24 agosto 2014
[3] Nick Pelling, The British Mission to Los Alamos and the Feynman Ciphers, Cipher Mysteries, 25 enero 2015
[4] Nick Pelling, The Feynman Challenge Ciphers and Geoffrey Chaucer, Cipher Mysteries, 30 abril 2017
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Los cifrados de Feynman se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Interpretando mensajes cifrados
- Feynman en la BBC, y siempre en el recuerdo
- “Richard Feynman, un mago de la Física” por M.A. Vázquez-Mozo
Sistemas respiratorios: distribución de los pigmentos

Gusano de tubo gigante (Riftia pachyptila). Este anélido se aloja en el interior de un gran tubo quitinoso blanco. De su extremo superior, emergiendo del tubo, nace una gran pluma branquial roja por la hemoglobina.
No se han hallado pigmentos respiratorios en ninguna especie de esponjas, cnidarios, ctenóforos, briozoos, quetognatos, hemicordados, tunicados, cefalocordados, onicóforos, tardígrados y gastrotricos.
Los pigmentos más comunes son las hemoglobinas. Hay animales que, además de en la sangre, tienen hemoglobinas en sus músculos, y otros las tienen también en otros tejidos, como el nervioso. Las células musculares de vertebrados contienen una hemoglobina a la que llamamos mioglobina y es especialmente abundante en el citoplasma de las células cardiacas y en el de las fibras oxidativas lentas del músculo esquelético. Por contraste con las hemoglobinas sanguíneas, la mioglobina está formada por una única subunidad (monomérica) de 1.78×104 daltons, cuya globina difiere de las globinas α y β propias de los eritrocitos. Y en algunos anélidos y moluscos, no solo hay hemoglobinas en las células musculares, también las hay en las neuronas, lo que confiere a los ganglios un color rosáceo. Un caso interesantísimo es el de las especies de los géneros Anisops y Buenoa de la familia de insectos Notonectidae (insectos buceadores de agua dulce): en las células grandes de sus tráqueas abdominales hay altas concentraciones de hemoglobina, que hace las veces de una botella de O2 durante la inmersión.
La hemoglobina sanguínea puede encontrarse en el interior de células sanguíneas especializadas, los eritrocitos. En ese caso, puede estar formada por una (monomérica), dos (dimérica) o cuatro (tetramérica) subunidades, y su peso molecular es acorde a su relativamente pequeño tamaño. Lo normal es que varíe de los 1.4×104 daltons característicos de las hemoglobinas monoméricas (como la mioglobina) de menor tamaño a los 7.2×104 de las tetraméricas de mayor peso molecular (la del bivalvo Arca, por ejemplo). Sin embargo, también puede encontrarse en forma disuelta en la sangre, en cuyo caso lo normal es que esté formada por muchas subunidades (cada una con su grupo hemo), por lo que su peso molecular es altísimo: van desde los 2×105 a los 1.2×107 daltons. A las que no se encuentran en el interior de células (sean glóbulos rojos, musculares o de cualquier otro tipo) se las denomina hemoglobinas extracelulares. Un ejemplo ilustrativo es la hemoglobina plasmática del poliqueto Arenicola, formada por 180 subunidades y cuyo peso molecular es de 3×106 daltons.
Tienen hemoglobina representantes de foronídeos (de una y dos subunidades, en la sangre), equinodermos (de dos y cuatro subunidades, en la sangre), vertebrados (de una, dos o cuatro subunidades, en la sangre; y también en otros tejidos), platelmintos (en otros tejidos), nemertinos (en otros tejidos), moluscos (en dos, cuatro y numerosas subunidades en la sangre; y también en otros tejidos), equiuroideos (en otros tejidos), anélidos (una, dos, cuatro o muchas subunidades en la sangre; y también en otros tejidos), artrópodos (una, dos o muchas subunidades en la sangre; y también en otros tejidos), y nemátodos (una y muchas subunidades en la sangre; y también en otros tejidos). La presencia de hemoglobina en muchos grupos es esporádica: puede aparecer en unos clados y no en otros, sean estos del nivel que sean. Es posible que todas las hemoglobinas tengan su origen en un ancestro común y, por lo tanto, surgieran de manera muy temprana. Hay que tener en cuenta que las hemoglobinas son unas formas químicas muy parecidas a los citocromos de la cadena de transporte electrónico, moléculas que tienen una distribución universal y de gran antigüedad.
Los otros pigmentos cuyo metal es el hierro son las clorocruorinas y las hemeritrinas. Solo se han hallado clorocruorinas en cuatro familias de gusanos anélidos, y dada su gran semejanza con las hemoglobinas plasmáticas de los invertebrados, hay quien sostiene que no deberían ser considerados categorías diferentes. Sus pesos moleculares son de unos 3 millones de daltons. Se han hallado hemeritrinas en todos los gusanos sipuncúlidos conocidos, en muchos braquiópodos, en los dos géneros de priapúlidos y en la familia de anélidos Magellonidae. Las hemeritrinas circulantes se encuentran siempre en el interior de células, ya sea en la sangre o el fluido celómico; suele tratarse de octómeros y su peso molecular varía de 4×104 a 1.1×105 daltons. También hay hemeritrinas musculares (miohemeritrinas); son de bajo peso molecular (alrededor de 1.3×104 o 1.4×104 daltons) por tratarse de monómeros.

Cangrejo (Cancer productus ) visto desde abajo. El color púrpura lo proporciona la hemocianina.
Las hemocianinas son los únicos pigmentos cuyo metal no es el hierro, sino el cobre. Son característicos de dos filos, moluscos y artrópodos. Aunque se les da el mismo nombre, hay grandes diferencias entre las de uno y otro grupo por lo que hay quien sostiene que deberían denominarse de forma diferente. Todas las hemocianinas se encuentran en el plasma de forma disuelta, por lo que son moléculas grandes, de entre 4 x106 y 9×106 daltons en los moluscos, y de entre 0,5 x106 y 3×106 daltons en los artrópodos. Todas ellas tienen múltiples sitios de unión de oxígeno. En moluscos, tienen hemocianina los cefalópodos, muchos quitones, gasterópodos y algunos bivalvos. La mayoría de estos últimos, no obstante, carecen de pigmentos respiratorios. Y entre los artrópodos, poseen hemocianinas crustáceos decápodos, limúlidos, arañas y escorpiones. Se da la curiosa circunstancia de que hay moluscos cuya sangre contiene hemocianina, pero que tienen hemoglobina en sus células musculares y neuronas. Toda la hemocianina es plasmática.
Con independencia de la categoría de pigmentos de que se trate, se cumple la norma de que los extracelulares son grandes moléculas formadas por numerosas subunidades, mientras que los intracelulares están formadas por un número relativamente pequeño de subunidades (ocho como mucho). Al parecer, los pigmentos cuyo peso molecular es inferior a 200000 daltons pueden atravesar los filtros renales o estructuras equivalentes, por lo que si se encontrasen en disolución, se perderían con la orina. En las especies en que el pigmento se encuentra en el líquido celómico el problema es similar, pues si fuese de pequeño tamaño se perdería a través del celomoducto o el nefridio.
En el caso de los vertebrados hay razones adicionales para que la hemoglobina se encuentre en el interior de los eritrocitos. Por un lado, si se encontrase en forma disuelta, la presión coloidosmótica que generaría no sería compatible con el equilibrio hídrico entre el plasma y los tejidos. No habría problema osmótico si las moléculas del pigmento fueran de gran tamaño, pero en ese caso, la viscosidad de la sangre sería demasiado alta como para que el corazón la pudiese impulsar a través de todo el sistema circulatorio. Las cosas son diferentes en los invertebrados, porque sus demandas metabólicas son muy inferiores y, por ello, también lo es la necesidad de transportar oxígeno. Eso les permite operar con grandes moléculas (y evitar así su perdida a través de los filtros renales) sin que la presión coloidosmótica ni la viscosidad de la sangre sean demasiada altas.
Fuentes:
Richard W. Hill, Gordon A. Wyse & Margaret Anderson (2004): Animal Physiology. Sinauer Associates, Sunderland
John D. Jones (1972): Comparative physiology of respiration. Edward Arnold, Edinburgh
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Sistemas respiratorios: distribución de los pigmentos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sistemas respiratorios: los pigmentos respiratorios
- Sistemas respiratorios: la emergencia de un doble sistema circulatorio
- Sistemas respiratorios: los límites a la difusión de los gases
La relatividad del tiempo (1)

Veamos qué le ocurre a la medición del tiempo cuando se tiene en cuenta la teoría de la invariancia. Para ello seguiremos el argumento original de Einstein, que es sorprendentemente simple, puesto al día con la tecnología actual. Es tan simple que para llegar a la conclusión que buscamos lo más complejo desde el punto de vista matemático que se usa (nosotros no lo haremos) es el teorema de Pitágoras y álgebra de primaria.
En este experimento, una observadora, Mónica, está en una nave espacial moviéndose a una velocidad uniforme extremadamente rápida y en línea recta en relación con otra nave en la que está Esteban, que permanece estacionario. En la nave espacial de Mónica (es decir, en su marco de referencia) hay un reloj que mide el tiempo en intervalos precisos mediante el uso de un pulso de láser. El pulso viaja directamente desde un láser, golpea un espejo y se refleja. Cuando el pulso regresa al punto inicial, es detectado por un fotosensor, que registra entonces el tiempo transcurrido, al que llamaremos Δtm (que se corresponde con el tiempo de ida y vuelta al espejo, por tanto), y emite otro pulso. Como la velocidad de la luz es constante y la distancia que recorre es fija, el segundo pulso tarda exactamente la misma cantidad de tiempo Δtm para realizar el viaje de ida y vuelta según Mónica. Son estos intervalos de tiempo idénticos los que se usan como un reloj, tic-tac, tic-tac, para medir el tiempo en la nave de Mónica.
Dado que Mónica viaja a una velocidad uniforme, el principio de relatividad de Einstein le dice que el reloj se comporta exactamente como lo haría si estuviera en reposo. De hecho, de acuerdo con este principio, ella no podría decir a partir de este experimento (o de cualquier otro) si su nave está en reposo o en movimiento en relación con Esteban sin mirar hacia fuera de la nave espacial. Pero para Esteban, que no está en marco de referencia de Mónica, sino en el suyo propio, le parece que avanza rápidamente en línea recta con respecto a él. (Por supuesto, podría ser que Esteban fuese quien se mueve hacia atrás, mientras que Mónica está estacionaria, pero la observación y el argumento que sigue serían los mismos).
Al observar el reloj láser de Mónica mientras su nave espacial pasa volando a su lado, ¿qué ve Esteban? Al igual que en el experimento de la relatividad galileana con la pelota que cae al suelo cuando la suelta una persona en movimiento, Esteban ve algo muy diferente de lo que ve Mónica. Debido a que la nave espacial de ella se está moviendo con respecto a la de él, observa que el pulso de luz sigue una trayectoria en diagonal hacia el espejo y otra trayectoria diagonal hacia el detector. Usaremos el símbolo te para el tiempo que mide Esteban.
Aquí es donde entra el segundo postulado de Einstein: la velocidad de la luz, c, medida debe ser la misma independientemente de que la observe Mónica o Esteban. Pero la distancia que recorre el pulso de luz durante un viaje de ida y vuelta tal y como lo ve Mónica es más corta de la que ve Esteban. Si llamamos dm a la distancia total que recorre el pulso desde el emisor hasta el espejo y vuelta para Mónica y de para Esteban, podemos escribir que c = dm/Δtm = de/Δte
Como de es mayor que dm, Δte debe ser mayor que Δtm, para que las proporciones tengan el mismo valor, c. Esto significa que el intervalo de tiempo (Δte ) para el viaje de ida y vuelta del pulso de luz, registrado en el reloj como Esteban lo observa, es más largo que el intervalo de tiempo (Δtm ) registrado en el reloj cuando es Mónica la que lo observa.
La conclusión sorprendente de este experimento mental (que en realidad es una deducción a partir de los postulados de la teoría de la invariancia) es:
Los intervalos de tiempo no son absolutos e invariables, sino relativos. Cualquier fenómeno repetitivo que se mueva con relación a un observador estacionario (como un reloj como el de Mónica), parece para el observador estacionario que transcurre más lentamente de lo que parece hacerlo cuando lo mide el observador que se mueve con el reloj, y tanto más despacio cuanto más rápido se mueva. Esto se conoce como dilatación del tiempo.
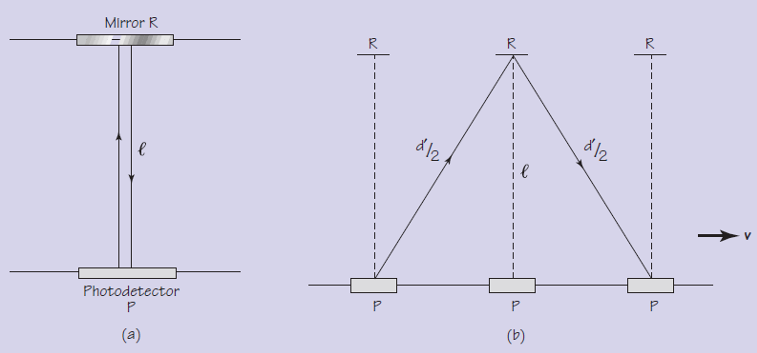
Dispositivo de nuestro experimento mental. Para Mónica (a) su reloj consiste en un espejo (Mirror R) separado una distancia l (por tanto dm = 2l) de un fotodetector (Photodetector P). Cuando Esteban observa (b) este dispositivo que se mueve con una velocidad constante v, el pulso láser viaja una distancia d’ (que en el texto principal llamamos d sub e, de) en dos tramos iguales d’/2. Usando las igualdades que damos en el texto deducir la fórmula final debería ser trivial a partir del teorema de Pitágoras.
Pero, ¿cuánto más lento parece un reloj que se mueve respecto de un observador? Para obtener la respuesta, se puede usar el gráfico de arriba y usar el teorema de Pitágoras. Con un poco de álgebra básica, se obtiene la relación exacta entre el intervalo de tiempo transcurrido registrado por un reloj que está estacionario con respecto al observador (como en el caso de Mónica) y el intervalo de tiempo transcurrido para el mismo fenómeno medido por alguien que observa el reloj en movimiento a una velocidad constante v (como en el caso de Esteban).
El resultado viene dado por una ecuación muy sencilla, Δte = Δtm /√(1-v2/c2), que viene a decir que el intervalo de tiempo que observa Esteban es diferente del intervalo de tiempo que observa Mónica para el mismo reloj, estacionario en el marco de referencia de ella, por el efecto de la velocidad constante v con la que Esteban observa que se mueve el marco de referencia de Mónica, su nave y todo lo que ésta contiene, incluido el reloj. Este efecto lo introduce el denominador √(1-v2/c2).
En la próxima entrega analizaremos en detalle esta ecuación.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La relatividad del tiempo (1) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La simultaneidad de los sucesos
- El principio de relatividad (2): la versión de Galileo
- El principio de relatividad (1): movimiento relativo
Los enigmas que nos cantan desde el fondo del océano

La ballena más solitaria del mundo Fuente: 52thesearch.com
Mientras lees este artículo, en algún lugar del Pacífico Norte, una ballena vaga solitaria por sus aguas. Se la conoce como la ballena de los 52 hercios porque es esa la frecuencia en la que emite su canto, una frecuencia mucho más alta que las otras ballenas (la ballena azul canta a entre 10 y 39 hercios, y la ballena de aleta a 20). Se la detectó por primera vez a finales de los años 80 y desde entonces se la ha captado en distintos puntos del océano. Siempre ella, y siempre sola. Parece que nadie oye ni responde a su canto (puedes escucharlo aquí), y por eso se la conoce como la ballena más solitaria del mundo.
Para un oyente atento, el océano es un lugar de lo más interesantes. Señales humanas y animales cruzan las aguas enviando todo tipo de información a kilómetros de distancia. Solo hay que tener la habilidad (y las herramientas) para interpretarla.
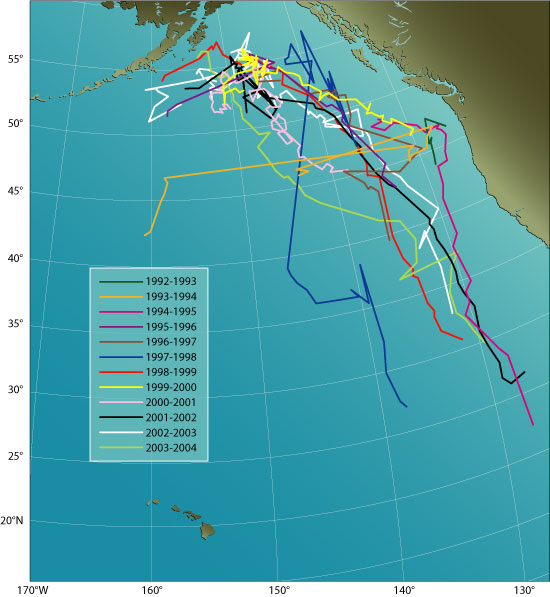
Registro de los movimientos de la ‘ballena más solitaria del mundo’. Fuente: Woods Hole Oceanographic Institution
Claro que a veces eso no es suficiente. El canto de la melancólica ballena solitaria es misterioso por la particular situación del animal, dotado, al parecer, para su desgracia de un sistema vocal único en el mundo. Pero no fue especialmente difícil de interpretar para los científicos que lo captaron.
Otros sonidos fueron más complejos de desentrañar, y algunos no lo han sido todavía.
Upsweep, un barrido de origen desconocido
Cuando en agosto de 1991 el Laboratorio Ambiental Marino del Pacífico, perteneciente a la Administración Nacional Oceánica y Atmosférica comenzó a grabar los sonidos marinos de la zona, uno de estos enigmas por resolver ya estaba allí. Lo llamaron Upsweep (literalmente “barrido arriba”) y se trata de una serie de sonidos de barrido de varios segundos de duración que se repiten durante varios minutos y que son tan potentes que se han registrado de un lado al otro de ese océano (puedes oírlo aquí).
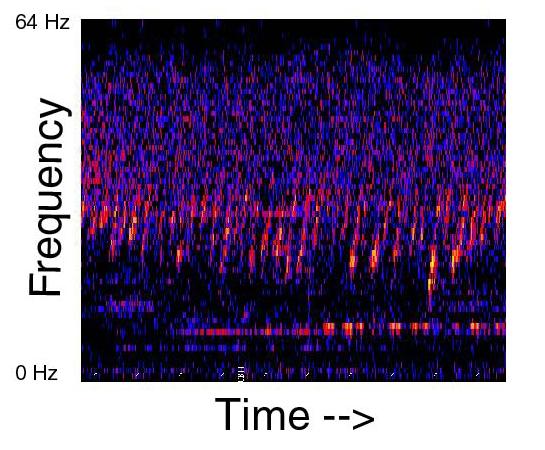
Upsweep. Fuente NOAA
No se sabe qué lo genera, aunque sí se saben otras cosas, como por ejemplo que alcanzó su máxima intensidad en 2004 y que desde entonces se ha ido atenuando aunque sigue siendo claramente audible. También que se escucha mejor en primavera y en otoño, aunque esto podría deberse tanto a la naturaleza de su fuente como a que el sonido viaje mejor con las condiciones ambientales de esas estaciones.
También se han descartado algunas posibilidades. El sonido es bastante uniforme, lo que en principio significaría que no proviene de una fuente animal, como las ballenas, ni de la actividad volcánica, que suele ser cíclica. Sin embargo, según una teoría, aun sin probar, quizá sea un tipo concreto de actividad volcánica submarina constante o con variaciones muy tenues a lo largo del tiempo la responsable del Upsweep.
Otra hipótesis es que el sonido esté causado por el propio movimiento del agua y el rozamiento del viento contra su superficie. Hasta que alguna de esta hipótesis sea descartada o confirmada, la naturaleza de este sonido sigue siendo un enigma.
¿Es un calamar? ¿Una ballena gigante?
Para otros sonidos misteriosos ya creemos tener una respuesta. Uno de ellos es el Bloop (puedes escucharlo aquí). Captado en 1997 en las costas de Chile al reparar los micrófonos submarinos instalados durante la Guerra Fría, se trata de un sonido muy potente que desciende lentamente hasta una frecuencia casi subsónica durante unos 7 minutos y con un volumen tan fuerte que fue captado por tres sensores diferentes distanciados entre sí por miles de kilómetros.
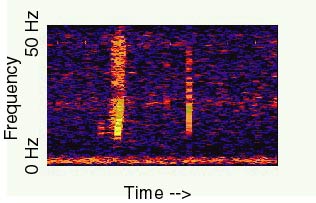
Bloop. Fuente: NOAA
Gracias a la información disponible se consiguió situar el origen de este sonido: un punto distante en el sur del Océano Pacífico, al oeste del extremo sur de América del Sur frente a las costas de Chile.
En cuanto a su causa, se ha especulado con que pudiese ser un animal de gran tamaño, quizá un calamar gigante o una ballena de una especie desconocida mayor que todas las conocidas hasta ahora, aunque las dos posibilidades han sido descartadas. Por un lado, porque los cefalópodos carecen de sistemas que les permitan emitir sonidos, y por otro, porque las ballenas, como mamíferos que son, están obligadas a subir a la superficie en búsqueda de oxígeno, así que se habrían producido avistaciones en algún momento.
Ahora se considera que las características del Bloop coinciden con los sonidos que se producen cuando grandes icebergs se desgajan, produciendo auténticos terremotos, y raspan con su duro hielo contra el fondo marino.
Referencias:
Song of the Sea, a Cappella and Unanswered – The New York Times
Icequakes (Bloop) – NOAA
Upsweep – NOAA
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo Los enigmas que nos cantan desde el fondo del océano se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La importancia del ritmo en la carrera de fondo
- Océano y salud: ¿qué es esto?
- El fondo cósmico de microondas y el espejo de feria
Sangre de dragón

El dragón de Komodo –Varanus komodoensis– no es un dragón sino un lagarto. Es quizás el de mayor tamaño que existe: puede llegar a medir hasta 3 m de largo y pesar 70 kg. Sobreviven hoy unos pocos miles de ejemplares de la especie en algunas islas de Indonesia; la mayor parte, alrededor de mil quinientos, en la de Komodo de donde proviene su nombre.
El dragón de Komodo se alimenta principalmente de carroña, pero también se comporta como depredador sit-and-wait, o sea, “siéntate-y-espera”. Quiere esto decir que no es un cazador al uso, no persigue a sus presas, sino que las espera, agazapado, de manera que cuando una pasa a su lado le lanza un zarpazo y, si puede, le propina un buen mordisco. En algunos casos eso es suficiente para atraparla. En otros, sin embargo, la presa escapa, aunque normalmente acaba muriendo.
La mordedura del dragón de Komodo causa un daño grave a sus presas. Por un lado, y aunque este es un tema controvertido, parece que al morder, el dragón transfiere algo de veneno a la presa. Y por el otro, mantiene en su boca un multicultivo de bacterias que, al penetrar en la sangre de la presa, le producen una infección que acaba dando lugar a su muerte y captura por su asaltante o por otros dragones.
Que se alimente de carroña y que mantenga un cultivo de múltiples bacterias en su cavidad bucal son dos hechos con una interesante implicación: el varano es inmune a buen número de patógenos bacterianos. La carroña es materia orgánica con un alto contenido en microorganismos, bacterias patógenas entre ellos. Y qué decir de sus propios cultivos bacterianos: si son capaces de provocar septicemias en sus presas es porque contienen cepas patógenas. Por lo tanto, si el dragón de Komodo no se infecta cada vez que ingiere una presa, aparte de la barrera que pueda suponer el epitelio de sus tejidos digestivos, ha de tener algún potente sistema defensivo. Y en efecto, así es. La sangre de Varanus contiene medio centenar de péptidos –proteínas de pequeño tamaño- con actividad antibacteriana.
Lo interesante de los péptidos antibacterianos encontrados en la sangre del dragón de Komodo es que parecen ser eficaces contra Pseudomonas aeruginosa y Staphylococcus aureus. Esas dos bacterias se encuentran en la lista de doce declaradas en febrero de este año por la Organización Mundial de la Salud como “patógenos prioritarios”. Son bacterias que han desarrollado resistencia a muchos antibióticos. Pseudomonas, en concreto, es una de las tres de máxima prioridad, y Staphylococcus es de prioridad alta.
En este momento se desarrolla una línea de investigación que busca encontrar nuevos antibióticos a partir de los péptidos antibacterianos de la sangre de los varanos. Pero hay un problema. Hay pocos ejemplares de esta especie, razón por la cual se encuentra en peligro de extinción. Por eso resulta muy caro trabajar con estos animales, además de que al tratarse de una especie protegida no pueden capturarse tantos como sería de desear. Este caso nos recuerda, una vez más, que nos interesa proteger los entornos naturales: no solo por razones de equilibrio ecológico global, sino porque además, esos entornos son y serán fuente de numerosas sustancias con las que ampliar el catálogo de fármacos al servicio de nuestra salud.
Esta historia tiene un cierto aroma a brujería y hechizos. Nos recuerda a las pociones para las que había que utilizar sangre de víbora o similares. Y sin embargo, no tiene nada de medieval; al contrario, es una historia de hoy y esperemos que, también, sea una historia de mañana.
—————————————————————–
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
Una versión anterior de este artículo fue publicada en el diario Deia el 8 de octubre de 2017.
El artículo Sangre de dragón se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La ecología de una enfermedad
- Nanotubos de carbono y regeneración neuronal
- El consumo de alcohol para el corazón y las dificultades de divulgar ciencia
Naukas Bilbao 2017 – Daniel Marín: Algo se muere en el alma cuando una sonda se va
En #Naukas17 nadie tuvo que hacer cola desde el día anterior para poder conseguir asiento. Ni nadie se quedó fuera… 2017 fue el año de la mudanza al gran Auditorium del Palacio Euskalduna, con más de 2000 plazas. Los días 15 y 16 de septiembre la gente lo llenó para un maratón de ciencia y humor.

Daniel Marín, una de las referencias internacionales para la divulgación de la exploración espacial en español, apoyándose en una imponente colección de imágenes reales, nos narra la aventura de la misión Cassini-Huygens, que llegó a Saturno, para quedarse, en 2004.
Daniel Marín: Algo se muere en el alma cuando una sonda se vaEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2017 – Daniel Marín: Algo se muere en el alma cuando una sonda se va se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017- Daniel Torregrosa: ¡Estamos rodeados!
- Naukas Bilbao 2017 – Diana González: Identidad digital y robots
- Naukas Bilbao 2017 – Guillermo Peris: Los trapecistas del genoma
¿Cuánta gente ha vivido en la Tierra?
El pasado noviembre superamos los 7.500 millones de habitantes en la Tierra. Mucho se ha hablado sobre el gran crecimiento de la población de las últimas décadas. El consenso es claro, pese a que la tasa de natalidad mundial está en los niveles más bajos de la historia de la humanidad, la tasa de mortalidad está en niveles aún más bajos. Aquí no queda más que dar las gracias a los grandes avances de la ciencia y la medicina, que ha permitido reducir la mortalidad infantil y alargar la esperanza de vida al nacer hasta más superar los 70 años (de media mundial).
Pero este dulce momento no ha sido siempre así. En tiempos pasados las tasas de natalidad estaban disparados, pero la gran mortalidad infantil a causa de razones de lo más variadas impedía que la población creciese de la forma que lo hace actualmente. Y, con tanta gente naciendo y muriendo a lo largo de milenios, ¿cuánta gente ha poblado la Tierra a lo largo de la historia?[1]

En todo momento hay que dejar claro es que esto es un juego de números para intentar encontrar una cifra más o menos válida. Como siempre que se juega a los grandes cálculos, hay que establecer varias hipótesis que nos limitan tomar estos datos como ciertos, pero sí que nos permiten hacernos a una idea de las cifras que podemos manejar.
Lo primero es establecer el punto de partida. Los registros arqueológicos y paleontológicos nos han permitido conocer una gran cantidad de especies de homínidos que poblaron la Tierra antes que nosotros. Como bien es sabido, algunos de estos homínidos pueden considerarse antepasados directos de nosotros, pero una gran mayoría pertenecen a ramas hoy extintas. Para facilitar los cálculos, nos centraremos únicamente en el Homo sapiens moderno, para lo que podemos poner el punto de partida hace unos 50.000 años, momento en el que se considera que el Homo sapiens sale de África.
Miguelón y Lucy, muy a nuestro pesar, se quedan fuera de la lista.[2]
El segundo paso es determinar la cantidad de población que se estima que existía en la tierra desde el 50.000 B.P. hasta la actualidad. Aquí los registros son nulos, por lo que sólo nos quedan estimaciones de lo más burdas, especialmente para los primeros momentos del Homo sapiens moderno.
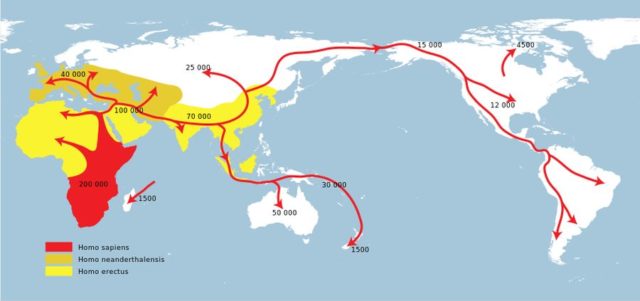
Expansión del Homo sapiens
En torno al año 8.000 B.P., varias fuentes coinciden en situar la población mundial en torno a los 5 millones de habitantes, donde prácticamente la totalidad de la Tierra estaba ya habitada y además existía un poblamiento relativamente estable. Para llegar a esta cifra, lo lógico es establecer un crecimiento sostenido desde un número inicial de 0 ó 2.[3]
En el año 1 ya no existe tanto consenso. El Population Reference Bureau estima una población de 300 millones de habitantes, basándose en la hipótesis de que el Imperio Romano tenía una población de unos 40 ó 50 millones y que Asia era ya entonces la zona más poblada del mundo. Las estimaciones de otras fuentes varían desde los 170 millones de habitantes hasta más de 500 millones.
A partir de este momento, pese a no tener aún registros históricos fiables, sí que tenemos más información que pueden facilitar la estimación de los datos de población mundial, cosa que queda contrastada por la poca diferencia entre las estimaciones de distintas fuentes. Para facilitar los cálculos, nos quedaremos de nuevo con los datos del Population Reference Bureau.
El tercer paso, y seguramente el más determinante de todos, es determinar qué tasa de natalidad[4] hubo desde el momento inicial hasta la actualidad. Para esto tenemos que inventarnos cuál pudo ser la tasa de mortalidad infantil[5] a la que se enfrentaron nuestros antepasados. Sabemos que tenía que ser elevada, así que estimar que la mitad de los niños que nacían morían antes del año no es descabellado. Lo que es difícil es establecer si esta mortalidad infantil no fue mayor en grupos de cazadores recolectores, ya que un niño más sin suficientes recursos para el sustento podría ser un problema de que era necesario deshacerse si no era esencial para mantener el futuro del grupo.
Asumiendo que la mortalidad infantil no fue mayor de 500 por cada 1.000, sabiendo que la esperanza de vida rondaba los 10 – 12 años en la Edad de Bronce y Edad de Hierro, podemos determinar que una tasa de natalidad de 80 por cada 1.000 habitantes era la necesaria para garantizar el reemplazo de población y un leve crecimiento de la misma que permita casar con las estimaciones de población puestas anteriormente.
A partir de la Baja Edad Media, las condiciones fueron poco a poco mejorando, mejorando los datos de mortalidad infantil y requiriendo una menor tasa de natalidad para garantizar el reemplazo poblacional. Sin embargo, no sería hasta la invención de la leche pasteurizada y los grandes avances de la medicina cuando la mortalidad infantil disminuiría de forma acusada, comenzando con la gran explosión de población mundial.
Así que, teniendo en cuenta el punto de partida, las estimaciones de población en momentos concretos del estudio y la tasa de natalidad durante los distintos periodos, nos quedaría una tabla como la siguiente.
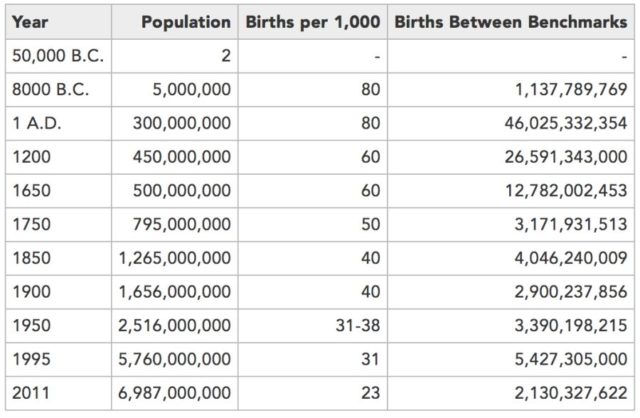
Datos del Population Reference Bureau
Estas estimaciones que os presento fueron realizadas por Carl Haub[6], trabajador del Population Reference Bureau. Según ellas, en el año 2011, en la Tierra ya habían nacido más de 107.000 millones de personas. O lo que es lo mismo: En la actualidad viven en la Tierra un 6% – 7% de las personas que alguna vez han estado vivas.
Para finalizar, recordar algo que ya se ha dicho más arriba: Estos cálculos, si bien se basan en distintos estudios y datos aportados por la ciencia, necesitan de varias suposiciones que a día de hoy no se pueden mostrar como ciertas. Por ello las estimaciones son burdas, pero no absurdas.
Este post ha sido realizado por Miguel García (@Milhaud) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
Notas del autor:
[1] Historia y prehistoria, ya que en este caso la división por aparición de la escritura no procede.
[2] Miguelón es un ejemplar de Homo heidelbergensis hallado en Atapuerca y datado hace 300.000 años. Lucy por su parte es un ejemplar de Australopithecus afarensis hallado en Hadar (Etiopía) y datado hace 3,2 millones de años.
[3] Este número deja semblanzas de Adán y Eva, pero simplemente es necesario desde un punto de vista matemático para poder realizar los cálculos. El número inicial se puede considerar un error de partida necesario.
[4] La tasa de natalidad se calcula como el número total de nacimientos por cada mil habitantes.
[5] La tasa de mortalidad infantil se calcula como el número de muertos por cada mil nacidos a lo largo del primer año de vida.
[6] How Many People Have Ever Lived on Earth?
El artículo ¿Cuánta gente ha vivido en la Tierra? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Escaneando la Tierra con neutrinos solares
- De la edad de la Tierra
- Una nueva investigación muestra que explicar cosas a la gente “normal” puede ayudar a los científicos a ser mejores en su trabajo
El buen turrón tiene su ciencia

Soy más de turrón blando que de turrón duro. Aunque reconozco que con un pedazo tengo más que suficiente, incluso si es de calidad suprema. Realmente no hay grandes diferencias entre uno y otro, ni nutricionales ni de fabricación.
El turrón de Jijona y el turrón de Alicante tienen denominación de origen. Cuando no la tienen se llaman turrón blando y turrón duro respectivamente. Ambos están compuestos exclusivamente por almendras tostadas, miel, azúcar y clara de huevo. Las calidades varían en función de la cantidad de almendra. Así, la calidad suprema contiene un 60% de almendra, la calidad extra un 50%, la calidad estándar un 40% y la calidad popular un 30%.
-
El valor nutricional del turrón
Ambos turrones son ricos en proteínas de alto valor biológico, provenientes del huevo y de las almendras: contienen 7 de los 9 aminoácidos esenciales. También son ricos en ácido fólico y en vitamina E.
Estos turrones contienen mucha grasa: alrededor de 30 g por cada 100 g de turrón. Pero, como la grasa proviene exclusivamente de la almendra, tiene un buen perfil lipídico. Sólo entre 2 y 3 g son grasas saturadas, naturalmente presentes en las almendras. Contiene ácidos grasos insaturados que también encontramos en el aceite de oliva, como el ácido linoleico y linolénico.
La cantidad de azúcar oscila entre los 40 y los 50 g por cada 100g de turrón, por lo que nutricionalmente son alimentos superfluos. Cualquier bondad que pudiésemos atribuir a las almendras queda ensombrecida por el elevado contenido en azúcar que poseen. A estas alturas nadie duda de que los turrones son alimentos que consumimos sólo por placer, nunca por cuestión de salud.
-
La ciencia de la fabricación del turrón
El primer paso para fabricar ambos turrones consiste en tostar las almendras. Esto se hace en hornos rotatorios esféricos durante 45-50 min. Cuando se tuestan las almendras se generan más de 50 compuestos diferentes, entre ellos cetonas, aldehídos, pirazinas, alcoholes, hidrocarburos aromáticos, furanos, pirroles, terpenos e hidrocarburos lineales. Las pirazinas, junto con los furanos y los pirroles, contribuyen significativamente al característico aroma tostado de la almendra. Los procesos químicos que suceden son muy complejos, tanto es así que todavía no se han determinado todos los compuestos volátiles que se producen durante el tueste.
Aparte se prepara el caramelo en una malaxadora, que es como una olla con una pala mezcladora. El caramelo se hace con miel, azúcar y agua. Los turrones de más calidad contienen más miel que azúcar. La mezcla se hace en caliente para aumentar la miscibilidad del azúcar y favorecer las reacciones de caramelización.
La caramelización es un proceso químico complejo mediante el cual se produce la oxidación de los azúcares, la fragmentación de la sacarosa, la condensación y deshidratación de los azúcares, etc. dando como resultado el sabor acaramelado, el color dorado y la formación de varios compuestos volátiles que dan ese olor característico a caramelo caliente. La caramelización sucede en el azúcar y en la miel. No olvidemos que la miel es 80% azúcar.
Cuando la mezcla de la miel y el azúcar es homogénea, se añade la clara de huevo. La clara de huevo tiene varias funciones: blanquea el caramelo, le da textura y volumen, aglutina todos los ingredientes del turrón y evita que se formen cristales de azúcar.
La clara del huevo es traslúcida, sin embargo, cuando la calentamos o la agitamos, las proteínas pierden el orden interno y se convierten en un entramado amorfo. A esto se le llama desnaturalización. Cuando esto sucede, ni siquiera la luz es capaz de atravesar ese caos proteico y por eso se vuelve de color blanco. Si seguimos batiendo, esas proteínas desnaturalizadas comienzan a coagular, a formar agregados de proteínas con una nueva estructura que es capaz de almacenar aire en su interior. Esto es lo que da textura y volumen al caramelo.
La clara de huevo funciona como aglutinante. Esto quiere decir que funciona como un pegamento, haciendo que los diferentes ingredientes se adhieran entre sí. También por esto es anticristalizante, es decir que, aunque haya alta concentración de azúcar, evita que éste forme cristales cuando la mezcla se enfríe.
Esta mezcla se sigue agitando hasta que alcanza el «punto de melero» o «punto de garguirol». Esto significa que cuando coges una pequeña porción de mezcla, ésta se solidifica en segundos y se rompe con un leve golpe; y al morderla se resquebraja sin pegarse a los dientes.
Cuando esta mezcla está en su punto, se le añade la almendra tostada y se mezcla bien con unas palas.

Tras este último paso, el turrón de Alicante y el de Jijona toman caminos diferentes. Por una parte, el turrón de Alicante se divide en bloques, se introduce en moldes cubiertos de oblea para que no se pegue y se prensa a mano hasta que queda con el menor número de imperfecciones. Finalmente, se cortan los bloques en tabletas y se envasan para su distribución.
Para el turrón de Jijona, la pasta caliente formada por las almendras y el caramelo se extiende sobre bandejas y se deja enfriar hasta que endurece. Estas placas se introducen en un molino de piedra, generalmente junto a más cantidad de almendras tostadas ya molidas. Todo esto se muele finamente y se bate hasta que quede una pasta homogénea, sin granos apreciables a simple vista.

Esta mezcla se lleva al boixet. El boixet es como un gran mortero caliente automatizado que permite alcanzar la cremosidad óptima. Una vez alcanzada, la pasta se vierte en unos moldes y se deja reposar durante 24 horas. Estos moldes son porosos, de forma que durante ese tiempo el turrón va exudando parte del aceite de las almendras. Una vez terminado este proceso, se desmolda, se corta en tabletas y se envasa.
Tanto el turrón de Jijona como el de Alicante, a menudo se envasan al vacío para que duren al menos un año.
-
Sí, sí, el turrón caduca
La vida útil del turrón depende sobre todo de la variedad. Según la calidad del envasado, rondará los 12-18 meses tras su fabricación. El turrón de Jijona dura más que el de Alicante, porque el aceite de la almendra impregna toda la tableta y favorece su conservación. Mas allá de la fecha de caducidad podría ser peligroso consumirlo, principalmente porque la grasa se enrancia.
-
Vuelve a casa, vuelve por Navidad
Lo interesante del turrón es su valor gastronómico, cultural y tradicional. Como cualquier alimento propio de una época del año, tiene ese algo de ritual que nos conquista y que lo convierten en parte fundamental de la ceremonia de estas fiestas.
La ciencia que hay tras él también nos hace entender gran parte de su atractivo culinario. Aun así, el turrón es un dulce altamente calórico y atiborrado de azúcar y, como tal, ningún nutricionista te recomendará consumirlo a lo largo de todo el año ni lo incluiría dentro de una dieta saludable.
Así que, tanto por conservar lo especial del ritual gastronómico navideño, como por salud, si el turrón vuelve a casa, que sólo vuelva por Navidad.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo El buen turrón tiene su ciencia se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El mejor lacón con grelos tiene su ciencia
- La pantalla de tu móvil solo tiene tres colores
- Azúcar moreno, ¿mejor que el azúcar blanco?
Del nudo gordiano al nudo de los enamorados, por territorio matemático
Según cuenta la leyenda, mientras Alejandro Magno (356 – 323 a.c.), rey de Macedonia y de los griegos, se encontraba conquistando el Imperio Persa, llegó a Gordion, capital del reino de Frigia, que formaba parte del Imperio Persa. El nombre de la capital se debía a su rey Gordio (padre del rey Midas, el que transformaba en oro todo lo que tocaba). Parece ser que en el templo de Zeus, situado en la acrópolis de Gordion, se encontraba un carro que estaba atado a un yugo mediante un complicadísimo nudo. Según las creencias de Frigia, un antiguo oráculo estableció que aquel que consiguiese deshacer el nudo se convertiría en el Rey de Frigia, y se le abrirían las puertas de toda Asia.
Alejandro Magno se vio atraído por la leyenda e intentó beneficiarse de las creencias locales desatando el nudo gordiano, sin embargo, este era muy intrincado y se le resistía. Por este motivo, el general mecedonio tomó una solución radical, sacó su espada y con ella cortó el nudo. Se cuenta que esa noche hubo una gran tormenta de rayos, lo que se interpretó como que el propio dios Zeus estaba de acuerdo con aquella solución, y Alejandro afirmó que “¡Es lo mismo cortarlo que desatarlo!” Por cierto, en once años Alejandro Magno conquistó todo el oriente… su imperio se extendió desde Grecia y Egipto hasta el valle del rio Indo.

“Alejandro cortando el nudo gordiano”, de Jean-Simon Berthélemy (1743–1811). Wikimedia
El lema de Fernando el Católico “Tanto monta” hace referencia a esta leyenda, “lo mismo da [tanto monta] cortarlo que desatarlo”, por eso está asociado a un yugo y a un nudo cortado, que aparecerán después en el escudo, junto a las flechas.

Yugo y nudo gordiano cortado, con el lema “tanto monta”, como emblema de Fernando II de Aragón en la techumbre de una de las estancias del palacio de los Reyes Católicos de la Aljafería de Zaragoza, 1488-1492. Wikimedia
La expresión “nudo gordiano” acabó incorporándose al lenguaje ordinario como una metáfora de un problema irresoluble, deshacer un nudo “imposible”, y que en ocasiones puede superarse cambiando el marco de pensamiento. En consecuencia, esta expresión también aparece reflejada en la literatura. Un ejemplo es La vida de Enrique V (1600), de William Shakespeare. Hablando Canterbury del rey dirá…
“CANTERBURY:
Basta oírlo razonar en teología para que,
lleno de admiración, uno desee en lo profundo
que el rey se convierta en prelado;
basta oírlo discutir asuntos de bien común
para afirmar que nunca estudió otra cosa;
escucharlo hablar de guerra es como oír
una batalla temible vuelta música;
si pasa a cualquier cuestión política,
desatará el nudo gordiano con tanta facilidad
como su jarretera: porque cuando habla,
el aire, ese libertino leve, permanece inmóvil,
y el mudo asombro acecha en los oídos de los hombres
para captar sus frases dulces e impregnadas de miel…”
O también se menciona en un par de ocasiones en Segunda parte del ingenioso caballero don Quijote de la Mancha (1615), de Miguel de Cervantes.

Portada del disco “Gordian Knot” (1999) del grupo de rock progresivo del mismo nombre
En mi anterior entrada del Cuaderno de Cultura Científica, La artista Anni Albers, The Walking Dead y la teoría de nudos, habíamos explicado qué es la teoría de nudos y que su principal problema es la clasificación topológica de los nudos, el cual incluye el problema de reconocimiento, es decir, determinar cuándo dos nudos son equivalentes (iguales desde el punto de vista topológico), para lo cual se introducen diferentes invariantes de los nudos.
Recordemos que los invariantes son objetos (por ejemplo, un número, un polinomio o un grupo algebraico) o propiedades (como la tricoloreabilidad) de un nudo, que tienen el mismo valor para todos los nudos equivalentes. En consecuencia, si un invariante es distinto para dos nudos, estos no pueden ser equivalentes. En la entrada La artista Anni Albers, The Walking Dead y la teoría de nudos se vieron algunos ejemplos de invariantes de los nudos, como la quiralidad, la tricoloreabilidad y el número mínimo de cruces.
En esta entrada de la sección Matemoción Cuaderno de Cultura Científica se van a analizar otros dos invariantes de la teoría de nudos, el número gordiano y el índice poligonal. El primero tiene que ver con la historia del nudo gordiano que acabamos de contar. El “número gordiano de un nudo” es el mínimo número de cruces que hay que cambiar en un nudo para deshacerlo, para obtener el nudo trivial.
Más concretamente, dado un nudo N, se dice que el número gordiano de N es n, y se denota u(N) = n (la u viene del inglés unknotting number, que es otro de los nombres que recibe), si existe un diagrama D del nudo N tal que si se cambian n cruces del mismo, el nuevo diagrama obtenido es equivalente al trivial, y no existe ningún otro diagrama D’ del nudo N tal que con menos cambios que n se obtenga un diagrama equivalente al trivial. Este es un invariante, es decir, para cualesquiera dos nudos equivalentes N1 y N2, su número gordiano es el mismo, u(N1) = u(N2).
El número gordiano del nudo de trébol es igual a 1, como se muestra en la siguiente imagen, puesto que si se cambia uno de los cruces se obtiene el no-nudo.

Si se cambia el cruce marcado en el nudo de trébol, el nuevo diagrama puede transformarse mediante los movimientos de Reidemeinster en el nudo trivial
De igual forma puede verse que el nudo del ocho también tiene número gordiano igual a 1, y para los demás nudos de la clasificación de los nudos con mínimo número de cruces menor o igual que 7 (más abajo también aparecen), que vimos en la anterior entrada, es:

Veamos una sencilla aplicación de este invariante. Por ejemplo, los dos nudos que existen con número mínimo de cruces igual a 5, son ambos no tricoloreables, como se puede observar fácilmente (véanse las imágenes de abajo), además no son anfiquerales. Sin embargo, el primero, 51, que se conoce con los nombres de nudo de cinco lóbulos, nudo pentagrama o nudo sello de Salomón, tiene número gordiano igual a 2, mientras que el segundo, 52, conocido como nudo con tres retorcimientos, tiene numero gordiano igual a 1. Luego ambos nudos no son equivalentes, no son el mismo desde un punto de vista topológico.

El nudo de cinco lóbulos no es tricoloreable, además, si cambiamos uno de los cruces (por simetría da igual cuál de ellos) queda el nudo de trébol, que necesita cambiar otro cruce para desatarlo, luego u(51) = 2

El nudo de tres retorcimientos es no tricoloreable y si cambiamos el cruce del medio es el nudo trivial, luego u(52) = 1
A continuación, vamos a introducir otro invariante curioso, el “número mínimo de aristas de un nudo” o “índice poligonal”, que en inglés se suele conocer también como “stick number”. Un nudo puede ser representado, en el espacio, por una serie de segmentos rectos (llamados aristas) que se intersecan solo en los extremos de los mismos (llamados vértices). Es lo que se llama una representación poligonal del nudo. En la siguiente imagen vemos una representación poligonal del nudo de trébol, que hemos realizado con “barras y bolas” de la herramienta zome.

Representación poligonal del nudo de trébol, realizada con la herramienta zome, para la que se han necesitado 6 barras, que es el mínimo posible para este nudo
El mínimo número de aristas de un nudo N, que se denota s(N), se define como el mínimo número de segmentos rectos que son necesarios para formar una representación poligonal del nudo N. Por ejemplo, el no-nudo tiene índice poligonal igual a 3, ya que aunque podemos realizar representaciones poligonales del no-nudo con 4 (cuadrado), 5 (pentágono), 6 (hexágono), o más aristas, la que requiere el menor número de aristas es la representación triangular, con tan solo 3 aristas. En la siguiente imagen, una escultura del nudo de trébol realizada por el artista Kevin Caron, puede verse una representación poligonal del nudo de trébol realizada con 12 aristas, sin embargo, de la anterior imagen se deduce que el número mínimo de aristas del nudo de trébol es 6.

Escultura “Luz de luna” (2016), en bronce y acero, del artista estadounidense Kevin Caron, perteneciente a su serie “Enterna”
Podríamos plantearnos cuántos nudos admiten representaciones poligonales realizadas con 8, o menos, aristas. Hay exactamente 12 nudos, que son los que se ven en la siguiente imagen, en la cual se ha dibujado los modelos, realizados con “barras (rígidas) y bolas”, de dichas representaciones poligonales. Los 10 primeros son nudos primos, mientras que los dos últimos son nudos compuestos, el nudo de la abuela y el nudo de rizo, de los que ya hablamos en la entrada La artista Anni Albers, The Walking Dead y la teoría de nudos.

Podríamos tener la impresión de que el nudo 51 que aparece en la imagen realizado con 8 aristas, c(51) = 8, podría ser realizado con tan solo con 5 aristas, mediante su representación como el pentagrama. Sin embargo, hay que tener en cuenta que las aristas de las representaciones poligonales no se pueden intersecar entre sí, salvo en los vértices, donde se intersecan solo dos aristas, mientras que al realizar el pentagrama con 5 aristas, estas se intersecarían entre sí en puntos que no son los extremos, o las barras se doblarían dejando de ser segmentos rectos.

Colgante de oro con el pentagrama
El número mínimo de cruces c(N) de un nudo N nos da información sobre el mínimo número de aristas s(N) del mismo. Aunque el conocimiento de c(N) no nos permite determinar con exactitud el valor de s(N), sí establecer unas cotas, superior e inferior, para el mismo. En concreto, se ha demostrado que
![]()
En 2011 se mejoró la cota superior, demostrándose que
![]()
Para los nudos con mínimo número de cruces c(N) menor o igual a 7, que son los de la clasificación que mostramos en la entrada La artista Anni Albers, The Walking Dead y la teoría de nudos, el índice poligonal s(N) es el mismo para los nudos con el mismo número mínimo de cruces. Como se observa en una imagen anterior, c(51) = c(52) = 8 y c(61) = c(62) = c(63) = 8. Además, se puede probar que c(N) = 9, si N tiene número mínimo de cruces igual a 7. Veamos, por lo tanto, una clasificación más amplia que la que habíamos visto.
En la entrada anterior, habíamos comentado que la primera clasificación de los nudos la realizó Peter G. Tait en 1846, e incluía todos los nudos primos con mínimo número de cruces menor o igual que 7. La siguiente clasificación fue realizada por el matemático e ingeniero civil estadounidense Charles N. Little (1858-1923) en 1885 y contenía los nudos primos con mínimo número de cruces menor o igual que 10 (de nuevo no se distingue entre un nudo y su imagen especular). En ella se refleja que existen 21 nudos primos con mínimo número de cruces igual a 8, 49 con 9 cruces y 165 con 10 cruces.
En la actualidad están clasificados todos los nudos primos hasta mínimo número de cruces igual a 16, para lo cual Jim Hoste, Jeff Weeks, y Morwen Thistlethwaite realizaron búsquedas por ordenador mediante algoritmos diseñados por ellos mismos. La sucesión de la cantidad de nudos primos en función de su número mínimo de cruces, denominada A002863 en la Enciclopedia on-line de números enteros, es:
0, 0, 1, 1, 2, 3, 7, 21, 49, 165, 552, 2.176, 9.988, 46.972, 253.293, 1.388.705.

Clasificación de los nudos con mínimo número de cruces menor o igual que 9
Los nudos primos con mínimo número de cruces igual a 8 ya no tienen todos el mismo índice poligonal, contrariamente a lo que ocurría hasta 7 cruces. Así, los nudos primos del 81 hasta el 815 tienen número mínimo de aristas igual a 10, los nudos 819 y 820 igual a 8 y para los cuatro restantes el valor es 9. Veamos tres ejemplos concretos de nudos con 8 cruces.
El primero de los nudos es el nudo 81. Este pertenece a la familia de los nudos retorcidos, que consisten en coger el nudo trivial e ir dando vueltas (de hecho, medias vueltas) y después “enganchar” los dos extremos desde los que hemos estado girando el nudo trivial. El nudo 81 es el nudo retorcido de 6 medias vueltas (véase la siguiente imagen). Con media vuelta se obtiene el nudo de trébol, con dos medias vueltas el nudo de ocho, con 3 el nudo 52, conocido como el nudo de tres retorcimientos, para cuatro el 61, conocido dentro de los nudos marineros como nudo Stevedore, y para cinco el 72. Una cuestión interesante de los nudos retorcidos es que todos tienen, por su construcción, número gordiano igual a 1. Además, ninguno es anfiquiral, salvo en nudo de ocho. Por otra parte, el nudo 81 tiene número poligonal igual a 10 y es tricoloreable.

El nudo retorcido 81 y su representación poligonal minimal con 10 barras, realizada con Knot Plot
Nuestro siguiente nudo, el nudo 818 es un nudo que deriva de los conocidos nudos de Carrick, que se obtienen anudando dos cuerdas. Se deriva del nudo marinero de Carrick (utilizado en náutica desde la edad media, aunque en la actualidad se utiliza principalmente en escalada; además, también es un nudo heráldico, que aparece en la heráldica de la familia Wake (Inglaterra) y del Condado de Ormond (Ireland)), que es el que vemos en la imagen de abajo realizado por una cuerda roja y otra azul, y después se unen los dos extremos de arriba, respectivamente, de abajo, entre sí, formando el nudo topológico, que se conoce como “estera o tapete de Carrick”. También puede obtenerse a partir del nudo, con una sola cuerda, conocido como nudo de doble moneda, uniendo los extremos.

Nudo marinero de Carrick

Tapete de Carrick, realizado con doble cuerda
El tapete de Carrick ha sido muy utilizado en decoración. Precisamente, el logo de la International Guild of Knot Tyers, es decir, la asociación internacional de personas interesadas en los nudos, es un tapete de Carrick. Este también es el “nudo húngaro” que aparece decorando algunos uniformes militares franceses.

Logo de la “International Guild of Knot Tyers” y el “nudo húngaro” que aparece decorando algunos uniformes militares franceses
El tapete de Carrick, es decir, el nudo 818, tiene número poligonal igual a 9, como se ve en la siguiente imagen de una representación poligonal minimal suya. Además, su número gordiano es 2, no es tricoloreable y es anfiquiral.

El nudo retorcido 818 y su representación poligonal minimal con 9 barras, realizada con Knot Plot
El tercero de los nudos, el nudo 819, se deriva de uno de los nudos más conocidos, el nudo de los enamorados (en inglés, true lover’s knot, el nudo del verdadero amante), y que vemos en la siguiente imagen, en las versiones físicas de una o dos curvas. Muchos nudos han sido asociados desde la antigüedad con la amistad y el amor.

Nudo de los enamorados con dos cuerdas

Nudo de los enamorados con una cuerda, y una variación equivalente
Existen muchos diagramas planos equivalentes del nudo de los enamorados, cada uno de los cuales intenta transmitir una propiedad diferente de este nudo topológico. Abajo vemos cuatro de esos diagramas, el primero derivado del nudo físico a partir del cual se genera, en el que se destacan los dos corazones entrelazados, el segundo expresa que este es un nudo tórico puesto que es equivalente a un nudo que está sobre una superficie de toro (la superficie de un donuts o un flotador), la tercera indica que es un nudo pretzel (familia de nudos cuyo nombre deriva del pretzel, o bretzel, un tipo de galleta o bollo salado retorcido en forma de lazo de origen alemán) y el último es un diagrama normal para expresar cierta disposición espacial del nudo.

Cuatro diagramas planos del nudo de los enamorados, del libro “Knots and Links”
El nudo 819 tiene número poligonal igual a 9, como se vio en la imagen de las representaciones poligonales con 8, o menos, aristas. Además, su número gordiano es 3, no es anfiquiral y es tricoloreable.
Existen muchos más invariantes numéricos, geométricos o algebraicos de los nudos topológicos, como el género de un nudo, el número de puentes, la alternancia, los polinomios de Alexander, Conway, Jones o HOMFLY, los invariantes de Vasiliev, o el grupo fundamental, entre otros, pero esta es otra historia que ya tendrá su momento.
Por cierto, si consideramos el “nudo de Anni” que mostramos en la anterior entrada, ¿cuál es su comportamiento respecto a los invariantes topológicos que hemos visto? ¿Es primo o compuesto? ¿Cuál es su número mínimo de cruces (como mucho es 15)? ¿Es tricoloreable? ¿Cuáles son los valores de su número gordiano y su índice poligonal? Eso queda como problema abierto para aquellas personas que os animéis. No es un problema sencillo.
Terminaremos esta entrada volviendo a lo que fue la motivación del inicio de estas dos entradas dedicadas a la teoría de nudos, el arte. Shinkichi Tajiri (1923-2009) fue un escultor estadounidense-neerlandés, descendiente de japoneses, en cuya obra escultórica tienen mucha importancia los nudos.

La escultura “Nudo de la amistad” (1981), del artista Shinkichi Tajiri, es una de sus esculturas inspiradas en el nudo de rizo

La escultura “Nudo de la abuela” (1992), del artista Shinkichi Tajiri, es una de sus obras inspiradas en el nudo homónimo
Bibliografía
1.- Raúl Ibáñez, La artista Anni Albers, The Walking Dead y la teoría de nudos, Cuaderno de Cultura Científica, 2017.
2.- Raúl Ibáñez, La topología modifica la trayectoria de los peces, Cuaderno de Cultura Científica, 2016.
3.- María Teresa Lozano, La teoría de nudos en el siglo XX, Un Paseo por la Geometría 1998/99, Departamento de Matemáticas, UPV/EHU, 1999. Versión on-line en divulgamat
4.- Martín Gardner, Huevos, nudos y otras mistificaciones matemáticas, Gedisa, 2002.
5.- Colin C. Adams, The Knot Book, An Elementary Introduction to the Mathematical Theory of Knots, AMS, 2001.
6.- Peter Cromwell, Knots and Links, Cambridge, 2004.
7.- Stephan C. Carlson, Topology of Surfaces, Knots, and Manifolds, John Wiley and Sons, 2001.
8.- The Knot Atlas
9.- Página web del artista Kevin Caron
10.- Youngsik Huh, Seungsang Oh, An upper bound on stick number of knots, J. Knot Theory Ramifications 20, no. 5, 2011, pp. 741-747.
11.- Jim Hoste, Morwen Thistlethwaite, Jeff Weeks, “The first 1,701,936 knots”, The Mathematical Intelligencer 20 (4), (1998, pp. 33–48.
12.- J. C. Turner, P. van der Griend, History and Science of Knots, World Scientific, 1996.
13.- Página web del escultor Shinkichi Tajiri
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Del nudo gordiano al nudo de los enamorados, por territorio matemático se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La artista Anni Albers, The Walking Dead y la teoría de nudos
- El problema matemático de las cartas extraviadas
- Un convite matemático ‘de altura’
La simultaneidad de los sucesos
Aplicando los dos postulados de la teoría de la invariancia [1], el principio de relatividad y el principio de constancia de la velocidad de la luz en el vacío, a una situación similar al barco de Galileo, Einstein propuso un experimento mental extremadamente simple y que, sin embargo, proporcionó un primer resultado sorprendente. Descubrió que dos sucesos que ocurren simultáneamente para un observador pueden no ocurrir simultáneamente para otro observador en movimiento relativo con respecto a los sucesos. En otras palabras, la simultaneidad de los sucesos es un concepto relativo [2].

Una linterna LED, como las empleadas en el experimento mental, emite un haz de luz
El experimento mental de Einstein, en una versión actualizada, sería como sigue . Un observador, Esteban, está estático al lado de una vía de ferrocarril perfectamente recta. Está situado en el punto medio entre dos puntos A y B. Imaginemos que sostiene un interruptor eléctrico que conecta cables de exactamente la misma longitud a dos linternas LED colocadas en A y B. Como se encuentra en el punto medio entre A y B, si cierra el interruptor, las linternas se encenderán, y muy poco después de eso Esteban verá la luz de A y de B llegando a sus ojos en el mismo momento. Esto se debe a que la luz de cada linterna, viajando a la velocidad constante de la luz y cubriendo exactamente la misma distancia a Esteban desde cada linterna, empleará exactamente el mismo tiempo para alcanzar sus ojos. Como es lógico, Esteban concluye de todo ello que las dos linternas se encienden simultáneamente.

Esto es a lo que se conoce como un vagón plataforma. Podríamos haber empleado en el experimento mental un tren de alta velocidad, pero el tipo de vagón de este clase de trenes no es el óptimo habida cuenta del tipo de sucesos implicados en el experimento.
Ahora imaginemos a una segunda observadora, Mónica, de pie en un vagón plataforma que viaja por la vía a una velocidad uniforme muy alta desde A hacia B. Mónica y Esteban han acordado que cuando Mónica llegue al punto medio exacto entre A y B, Esteban activará inmediatamente el interruptor y encenderá las linternas [3].
Mónica y Esteban realizan el experimento. En el instante en que Mónica alcanza la posición del punto medio entre A y B, el interruptor se cierra, las linternas se encienden y Esteban ve los haces de luz simultáneamente. Pero Mónica ve algo diferente: para ella los haces no ocurren simultáneamente. De hecho, le parece que la linterna en B se enciende antes que la que está en A.
¿Por qué? Como Mónica se desplaza muy rápidamente hacia B y se aleja igual de rápidamente de A y como la velocidad de la luz es finita y exactamente la misma independientemente del movimiento del observador, Mónica se encontrará con el haz de B antes que el haz de A la alcance. En consecuencia, verá el haz de B antes que el haz de luz de A.
La conclusión: los dos sucesos que Esteban percibe que ocurren simultáneamente no se producen simultáneamente para Mónica. Las razones de esta discrepancia son que la velocidad de la luz es la misma para ambos observadores y que cada observador se mueve de una manera diferente en relación con los sucesos en cuestión.
Sería muy natural pensar que Mónica podría usar una calculadora y que, conociendo su velocidad y la velocidad de la luz, podría averiguar muy fácilmente si las linternas se encendieron tal y como ella las vio o como dice Esteban que las vio él. Sin embargo, si hace esto, y aquí viene la sutileza del experimento, entonces Mónica está afirmando una relación concreta entre los marcos de referencia; en otras palabras, está asumiendo que ella es el observador en movimiento y que Esteban es el observador estacionario. Pero esta asunción de Mónica no es posible ya que, de acuerdo con el principio de relatividad, no hay ningún experimento que se pueda realizar dentro de un marco de referencia inercial [4] que revele si éste está en reposo o moviéndose a una velocidad uniforme. Nada impide por tanto que ella sea el observador estacionario, y Esteban, parado al lado de la vía, ¡podría ser el observador en movimiento!
Si esto es así, entonces Mónica puede afirmar que la linterna en B en realidad se encendió antes que la que está en A y que Esteban percibió que las dos se encendían simultáneamente solo porque, desde el punto de vista de ella, Esteban se estaba moviendo hacia A y alejándose de B. Por supuesto, Esteban podría argumentar exactamente lo contrario, que él está en reposo y que es Mónica quien se está moviendo.
Pero, ¿qué interpretación es la correcta? En contra de nuestro sentido común, resulta que no hay una interpretación “correcta” porque no hay un marco de referencia preferido. Ambos observadores se mueven uno con relación al otro. Pueden ponerse de acuerdo a la hora de describir qué ocurrió realmente, pero solo si están de acuerdo en usar uno solo de los dos marcos de referencia [5], un acuerdo que es puramente arbitrario.
Por consiguiente, el que un observador considere dos sucesos como simultáneos, esto es, que ocurren al mismo tiempo, depende del movimiento del observador. De aquí se sigue que el tiempo mismo también debería ser un concepto relativo al observador cuando se examina a la luz de los postulados de la teoría de la invariancia [1]. Este será el tema de la próxima entrega.
Notas:
[1] Popularmente conocida como teoría de la relatividad.
[2] A pesar de ello, las leyes de la física implicadas en estos sucesos son iguales para ambos obervadores, de ahí que la teoría se llame de la invariancia.
[3] Dado que este es un experimento mental, podemos despreciar el tiempo de reacción de Esteban o el de la alternativa, un interruptor activado electrónicamente así como el implicado en la activación de las linternas.
[4] Un marco de referencia inercial es un marco de referencia que está en reposo o en velocidad uniforme en relación con otro marco de referencia.
[5] Tal y como hemos hecho implícitamente en el planteamiento del experimento, cuando hemos afirmado que es Mónica la que se mueve.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La simultaneidad de los sucesos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El principio de constancia de la velocidad de la luz
- El principio de relatividad (y 4): la versión de Einstein
- El principio de relatividad (2): la versión de Galileo
Conviene que los hijos se parezcan a su padre

El título de esta anotación expresa de forma sintética la conclusión de una investigación hecha en Senegal, en una sociedad en la que está muy extendida la poliginia. En las sociedades poligínicas hay un incentivo muy fuerte para que los varones solteros intenten mantener relaciones con mujeres casadas y para que las mujeres casadas que ocupan una posición inferior o son peor tratadas en la familia mantengan relaciones con otros hombres. De esa forma, y expresado en términos demográfico-evolutivos, esos varones tienen alguna posibilidad de reproducirse y, por lo tanto, de dar continuidad a su linaje; y las mujeres, por su parte, pueden diversificar así su apuesta reproductiva. Ahora bien, bajo esas condiciones, la incertidumbre acerca de la paternidad es relativamente alta, algo que puede condicionar el comportamiento de los padres para con su progenie.
Y efectivamente, utilizando el parecido facial y el olor corporal como criterios de similitud fenotípica, la investigación concluyó que los padres dedican un mayor esfuerzo a los hijos que más se les parecen. Como consecuencia de ese mayor esfuerzo y atención, los hijos más parecidos a sus padres también crecen más y se encuentran en un mejor estado nutricional, con lo que ello implica en términos de adecuación (fitness, en términos darwinianos).
Los resultados obtenidos en el estudio son consistentes con predicciones teóricas basadas en el supuesto de que la inversión de recursos en la progenie actual compromete los recursos que puedan ser utilizados en la progenie futura. Por esa razón, bajo condiciones de incertidumbre acerca de la paternidad, los padres recurrirían a criterios de similitud fenotípica (los únicos a los que tienen acceso) a la hora de canalizar recursos hacia la progenie.
Fuente: Alexandra Alvergne, Charlotte Faurie y Michel Raymond (2009): Father–offspring resemblance predicts paternal investment in humans. Animal Behaviour 78: 61-69.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Conviene que los hijos se parezcan a su padre se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La reacción de las madres al llanto de los bebés es universal
- Los padres mienten a sus hijos… mucho y en todo el mundo
- “Norman Borlaug, padre de la Revolución Verde” por Elías Fereres
Un viaje a Serendipia
“Serendipia. Hallazgo valioso que se produce de manera accidental o casual.”
“Chiripa. 1. Carambola, casualidad favorable. 2. En el juego de billar, suerte favorable que se gana por casualidad.”
Diccionario de la Real Academia
“En el campo de la investigación el azar no favorece más que a los espíritus preparados.”
Louis Pasteur
“La inspiración existe pero tiene que encontrarnos trabajando.”
Pablo Picasso
“Las ideas experimentales frecuentemente nacen a partir de una observación casual, por ello representan la forma más sencilla de comenzar un trabajo científico.”
Claude Bernard
El 28 de enero de 1754, Horace Walpole, cuarto Conde de Orford, hijo de un Primer Ministro y famoso escritor, envió una carta a Sir Horace Mann, amigo y embajador en Florencia, e incluyó en el texto un término recién inventado, serendipity o, en español, serendipia. Walpole construye el término a partir de una antigua fábula asiria titulada “Los tres príncipes de Serendip”, que, en sus viajes, “siempre descubrían, por accidente o por sagacidad, cosas que no estaban buscando”.

Serendip es el antiguo nombre de la isla de Ceilán, hoy conocida como Sri Lanka. Como ejemplo nos sirve aquella aventura en la que los príncipes describen un camello, al que no han visto, y afirman que está ciego del ojo derecho porque en el camino que recorre solo está comida la hierba del margen izquierdo, la única que ve con su ojo sano. O que lleva una carga de mantequilla y miel, cada una en un costado, pues en una cuneta hay hormigas comiendo y en el otro un enjambre de abejas, avispas y moscas. Las hormigas comen la mantequilla y los otros insectos la miel. Estos príncipes más bien me parecen ancestros de Sherlock Holmes que viajeros con suerte que descubren por casualidad.
Así explica Walpole a su amigo Mann lo que significa serendipia. Ahora, en nuestro tiempo, se usa serendipia en ciencia para describir un hallazgo inesperado y afortunado.
La palabra casi se olvidó hasta que, en 1955, Salvador Luria, después Premio Nobel en 1969, iniciaba un artículo sobre los virus llamados fagos, que destruyen bacterias, con este párrafo: “Nuestra historia tiene como episodio crítico una de esas coincidencias que muestran como el descubrimiento depende a menudo del azar o, más bien, de lo que se ha llamado serendipia –la observación casual que llega a un ojo receptivo”.
Para Pablo Capanna, las serendipias son ocasiones irrepetibles que no suponen un conocimiento fácil y listo para captar. Dependen de una mente alerta, entrenada y con los conocimientos suficientes como para entender lo que aparece de improviso. Hay que saber cómo sacar provecho de la serendipia. Solo lo consigue quien es capaz de ver lo que la mayoría deja pasar, eso que está delante de los ojos. A menudo parece un golpe de suerte pero, más bien, es la conclusión de un razonamiento en segundo plano según se está atento a otra cosa.
El camino que sigue la investigación científica no siempre es lineal ni predecible o, si se quiere, no se puede planificar al detalle. Las rutinas metodológicas ordenan la búsqueda, ahorran tiempo, garantizan la objetividad y evitan fantasías, pero no lo son todo ni aseguran los resultados. Es el inconveniente de los proyectos demasiado específicos y con objetivos muy concretos, pues así no se permite captar los imprevistos. Después de todo esos proyectos se preparan a partir de lo que ya conocemos y no es fácil, más bien no es posible, que planifiquen lo desconocido. Por ello es importante, por un lado, que se deje a los científicos elegir lo que investigan y que, además, siempre exista un componente importante de investigación básica. Y, por otra parte, que los que hagan ciencia estén bien provistos de conocimientos básicos y así les será más sencillo detectar lo inesperado.
También Peter Medawar, Premio Nobel en 1960, escribió que cualquier científico que no sea hipócrita reconocerá el papel de la suerte en los descubrimientos. Para Medawar, un descubrimiento científico nunca es premeditado. Un acto de la imaginación, una aventura especulativa, subyace, por tanto, en todo avance del conocimiento.
Veamos algunos ejemplos de serendipia, aunque no trataré a fondo el más famoso de todos: la llegada a América de Cristóbal Colón, que no solo no encontró lo que buscaba, las Indias y sus riquezas, sino que encontró un continente, América, que no buscaba y que, además, nunca aceptó que lo había hecho y que se había equivocado. Murió convencido de haber llegado a las Indias. Esto sí que es una serendipia sin querer, sin buscarla.
Empezaré con otra serendipia famosa como es el descubrimiento de la penicilina por Alexander Fleming, también Premio Nobel en 1945.
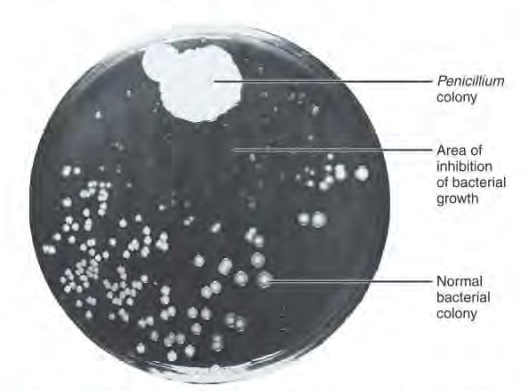
He conocido recientemente un relato del descubrimiento de la penicilina escrito por un testigo directo, el profesor Melvyn Price, colega y amigo de Fleming, y su visitante en el laboratorio en el momento de serendipia de encontrar e interpretar la placa contaminada con el moho Penicillium. Fue en 1928. Fleming estaba haciendo una serie de estudios con estafilococos para incluirlos en un manual de Microbiología de próxima aparición. Price había iniciado los experimentos y luego había marchado del laboratorio sin terminarlos. Fleming los estaba completando. Así que estaba rodeado de placas con cultivos de estafilococos y encontró una de ellas con una contaminación con moho. La observó y, según relata Price, vio donde crecía el moho y que había zonas cercanas de donde habían desaparecido los estafilococos. Comentó para sí mismo “That is funny…”, o sea, “Esto es curioso…”. Tomó una muestra y la guardó para próximos estudios. Fue su primer cultivo con el hongo Penicillium chrysogenum, productor de la penicilina. Fleming guardó toda su vida esa primera placa contaminada.

Otro ejemplo de serendipia es la invención del estetoscopio, el instrumento tan conocido y peculiar que utilizan los médicos para escuchar cómo sonamos por dentro. Antes del estetoscopio, el médico colocaba su oído directamente sobre el pecho del paciente. Pero había dificultades para escuchar con claridad en los obesos y, además, las mujeres no se sentían cómodas pues consideraban que su intimidad se veía invadida.
Fue el médico francés René Laënnec quien encontró la solución en 1816. Observó a unos niños que jugaban en la calle con una tabla de madera. Uno de ellos golpeaba muy suave uno de los extremos y los demás escuchaban los golpes desde el otro extremo. Pensó que el sonido se transmitía bien en un sólido y que, quizá, así conseguiría escuchar mejor los sonidos del interior del cuerpo humano. Primero ensayó con un cilindro de papel y constató que mejoraba el sonido. Entonces encargó que le fabricaran un cilindro de madera, abombado por los dos extremos, de 30 centímetros de longitud, 3 centímetros de diámetro y un conducto interno central de 5 milímetros de ancho. Este fue el primer estetoscopio.

Y ahora, la historia de la droga LSD o dietilamida de ácido lisérgico. Fue, como en toda serendipia, una casualidad que necesitaba de un científico atento y preparado para percibirla. Era Albert Hofmann, investigador de la compañía farmacéutica Sandoz en Basilea, Suiza. Trabajaba con compuestos formados por el ácido lisérgico con varias amidas para conocer sus posibles propiedades estimulantes sobre la circulación y la respiración, el alivio de las migrañas y para detener hemorragias en el parto. El compuesto número 25 era la dietilamida del ácido lisérgico. El día era el viernes 16 de abril de 1943 y así lo relató Hofmann años más tarde a partir de su cuaderno de laboratorio y del informe que preparó para su director.
“El viernes pasado, 16 de abril de 1943, me vi obligado a detener mi trabajo en el laboratorio y regresar a casa, pues sentía una inquietud peculiar asociada con una sensación de leve mareo. Al llegar a casa, me tumbé y caí en una especie de embriaguez que no era desagradable y que se caracterizaba por la extrema actividad de la imaginación. Mientras estaba en un estado aturdido con los ojos cerrados (experimentaba la luz del día como desagradablemente brillante), surgió sobre mi un flujo ininterrumpido de fantásticas imágenes de extraordinaria plasticidad y vivacidad y acompañado por un intenso y caleidoscópico juego de colores. Esta condición pasó gradualmente y terminó después de cerca de dos horas.”
Hofmann quedó impresionado por lo que había provocado aquella molécula que llamaba LSD-25 y comenzó a hacer ensayos cuidadosos consigo mismo. Tres días después, el 19 de abril, se administró una dosis de 0.25 miligramos. En su cuaderno de laboratorio hay una sola nota sobre aquella sesión: “Deseo de reír”. Montó en su bicicleta y se marchó a su casa acompañado por un colega del laboratorio. Tuvo la placentera sensación de que, durante todo el trayecto, permaneció inmóvil. Entre los aficionados al LSD de todo el mundo, ese 19 de abril se conoce como “El Día de la Bicicleta”. Así demostró Hofmann las extraordinarias propiedades del LSD-25.
Después de estos ejemplos, con el primer antibiótico, un instrumento médico como el estetoscopio, y una droga como el LSD, podemos terminar afirmando que la ciencia, vista la contribución de las serendipias, no avanzaría si los investigadores no fueran capaces de responder a lo inesperado y de conectar lo sorprendente con lo rutinario. Además, y como escribió Alexander Fleming años después de su descubrimiento, “La historia de la penicilina tiene un cierto encanto y ayuda a ilustrar la cantidad de azar o fortuna, de fatalidad o destino, llámenlo como quieran, que hay en la carrera de alguien.” Para los científicos, no todo son objetivos a cumplir y planificación, también hay mucho trabajo e intuición y, siempre, muchos conocimientos.

Para terminar y como resumen, ocho puntos sobre la serendipia que ofrece Peter Van Andel, de la Universidad de Groningen. Aquí van:
1.- La serendipia existe.
2.- En las áreas más empíricas (astronomía, química, medicina) los hallazgos por serendipia son habituales.
3.- La serendipia ayuda, es esencial y no debe ser subestimada ni exagerada.
4.- La investigación científica sistemática y la serendipia no se excluyen sino que, más bien, se complementan.
5.- En general, la serendipia tiene a desparecer o a ser disimulada en las narraciones a posteriori cuando se publican los resultados; se racionaliza el método y no hay lugar a la casualidad.
6.- Antes decíamos por suerte o por casualidad, ahora decimos por serendipia.
7.- La mayor parte de los que aceptan y practican la serendipia son de mente abierta, perceptivos, curiosos, intuitivos, ingeniosos, flexibles, artistas, con sentido del humor y laboriosos.
8.- La intuición es una anticipación que no puede ser explícita antes o cuando ocurre y, entonces, la serendipia, por definición, sigue a la intuición.
Referencias:
Bunge, M. 2013. La ciencia: su método y su filosofía. Laetoli. Pamplona. 144 pp.
Capanna, P. 2011. Serendipias. Los descubrimientos que se realizan por “casualidad”. Página 12 Futuro Diciembre 3.
Coppo, J.A. 2012. Serendipia. Revista Veterinaria 23: 71-76.
Darbellay, F. et al. 2014. Interdisciplinary research boosted by serendipity. Creativity Research Journal doi: 10.1080/10400419.2014.873653
Forni, P. 2011. Robert Merton. Miriada 4: 1-4.
Hofmann, A. 1970. The discovery of LSD and subsequent investigations on naturally occurring hallucinogens. En “Discoveries in Biological Psychiatry”, p. 98-109. Ed. por F.J. Ayd, Jr. & B. Blackwell. J.B. Lippincott Co. Philadelphia/Toronto. 254 pp.
Luria, S.E. 1955. The T2 mystery. Scientific American 192: 92-98.
Maurois, A. 1963. La vida de Sir Alexander Fleming. Eds. Cid. Madrid. 318 pp.
Medawar, P.B. 1988. Los límites de la ciencia. Fondo de Cultura Económica. México. 141 pp.
Roberts, R.M. 1992. Serendipia. Descubrimientos accidentales en ciencia. Alianza Ed. Madrid. 443 pp.
Stix, G. 2011. El primer “viaje” alucinógeno. Investigación y Ciencia enero: 7.
Taton, R. 1967. Causalidad y accidentalidad de los descubrimientos científicos. Ed. Labor. Barcelona. 172 pp.
Valer, N.B. 2005. A serendepidade na Medicina e na Anestesiologia. Revista Brasileira de Anestesiologia 55: 224-249.
Van Andel, P. 1994. Anatomy of the unsought finding serendipity: origin, history, domains, traditions, appearances, patterns and programmability. British Journal for the Philosophy of Science 45: 631-648.
Villanueva Meyer, M. 2012. René Laënnec (1781-1826): Inventor del estetoscopio y maestro del examen médico. Galenus 35: 70-71.
Villanueva Meyer, M. 2014. Alexander Fleming: Pionero en el uso de la penicilina. Galenus 47: 68-69.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Un viaje a Serendipia se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Serendipia
- Viaje a la dimensión desconocida
- El frustrante viaje de un átomo de carbono, mención especial del jurado “On zientzia”
Naukas Bilbao 2017 – Diana González: Identidad digital y robots
En #Naukas17 nadie tuvo que hacer cola desde el día anterior para poder conseguir asiento. Ni nadie se quedó fuera… 2017 fue el año de la mudanza al gran Auditorium del Palacio Euskalduna, con más de 2000 plazas. Los días 15 y 16 de septiembre la gente lo llenó para un maratón de ciencia y humor.

Diana González nos plantea una cuestión muy simple: ¿de verdad eres capaz de diferenciar entre un humano y un robot?
Diana González (Pamplonetario): Identidad digital y robotsEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2017 – Diana González: Identidad digital y robots se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – Guillermo Peris: Los trapecistas del genoma
- Naukas Bilbao 2017- Daniel Torregrosa: ¡Estamos rodeados!
- Naukas Pro 2017: Leni Bascones y los superconductores

