Poniéndole cara a una muestra de ADN
Un estudio de la Universidad del País Vasco / Euskal Herriko Unibertsitatea (EHU) ha descubierto una fuerte relación entre diez marcadores genéticos con la morfología de la cara de personas españolas. La investigadora Belén Navarro, autora del trabajo, destaca la importancia de realizar investigaciones en poblaciones específicas, para conseguir modelos de predicción con los que poder reconstruir el rostro de una persona a partir de muestras de ADN.
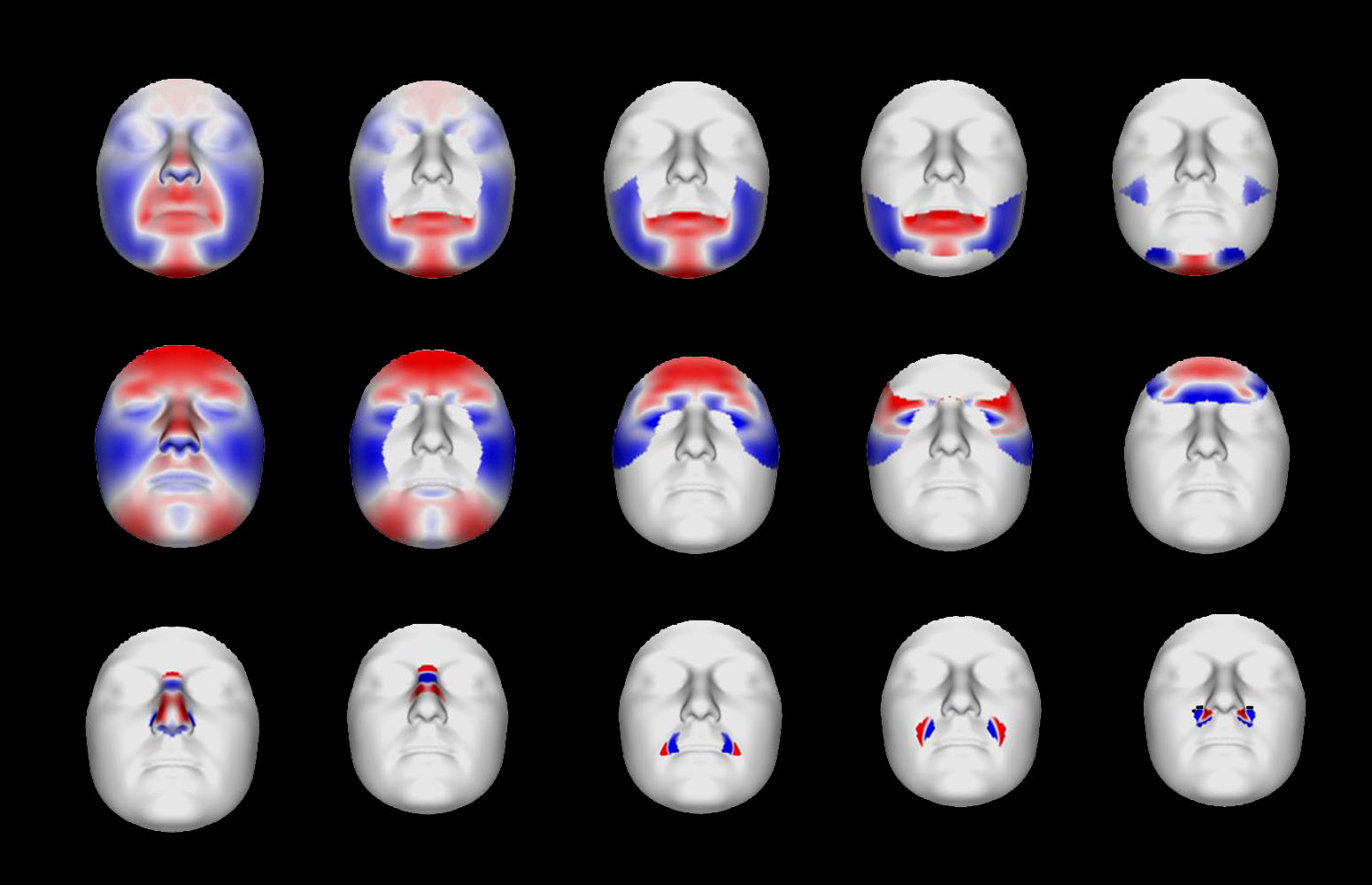 Las zonas marcadas en color señalan aquellas específicas donde se ha encontrado que algún marcador genético tiene asociación. El color muestra el desplazamiento del tejido blando del rostro en función del genotipo. Para un genotipo específico, el azul indica movimiento hacia el interior y el rojo hacia el exterior. Por ejemplo, en las figuras de la nariz, el color rojo señala una nariz que sobresale más hacia fuera, pero con las fosas nasales más recogidas hacia dentro; por tanto, sería una nariz más proyectada hacia fuera y estrecha. Fuente: Belén Navarro / EHU
Las zonas marcadas en color señalan aquellas específicas donde se ha encontrado que algún marcador genético tiene asociación. El color muestra el desplazamiento del tejido blando del rostro en función del genotipo. Para un genotipo específico, el azul indica movimiento hacia el interior y el rojo hacia el exterior. Por ejemplo, en las figuras de la nariz, el color rojo señala una nariz que sobresale más hacia fuera, pero con las fosas nasales más recogidas hacia dentro; por tanto, sería una nariz más proyectada hacia fuera y estrecha. Fuente: Belén Navarro / EHULa obtención de datos de la apariencia física puede ayudar a guiar la búsqueda de sospechosos en casos penales o a la identificación de personas desaparecidas, por lo que es muy interesante poder llegar a predecir las características externas humanas y en particular la forma de la cara mediante análisis de una muestra de ADN.
El análisis de ADN es una herramienta esencial en biología forense, ya que permite la identificación individual mediante la comparación de perfiles genéticos de los vestigios con muestras de referencia. Los últimos avances en el campo de la genética forense buscan determinar las características externamente visibles a partir del ADN que puedan facilitar la identificación. Sin embargo, la morfología de la cara es un rasgo muy complejo.
Ponerle cara al ADNLa investigadora Belén Navarro, del grupo BIOMICs de la EHU, explica que la finalidad “es utilizar ciertos marcadores concretos para poder predecir la forma de la cara de una persona en una escena del crimen o cuando se quiere identificar a alguien y se encuentran solo restos óseos. En las muestras forenses el ADN es muy limitante. No se pueden analizar todos los marcadores que se quieran”. Por ello, es importante “intentar reducir al máximo y quedarse con aquellos marcadores que son más significativos o que tienen más peso”, añade.
Recientes estudios de asociación de todo el genoma han arrojado luz sobre posibles marcadores asociados con los rasgos de la cara. En un trabajo llevado a cabo por el grupo de investigación BIOMICs de la Universidad del País Vasco, que se dedica entre otros ámbitos a la genética forense, han seleccionado un conjunto de 116 posibles marcadores del ADN y han estudiado cómo se asocian con los rasgos faciales en unas 500 personas de diferentes lugares de la península ibérica. “Hemos seleccionado genes y marcadores genéticos que ya se habían asociado con la morfología facial en otras poblaciones a nivel europeo, y lo hemos probado aquí, para ver si había diferencias —explica la investigadora de BIOMICs—. Hemos querido analizar todos y filtrar cuáles de ellos serían los más informativos en nuestra población, para, en caso de tener que utilizar este sistema, centrarnos solamente en ciertos marcadores. Eso es muy útil cuando no se tiene tanto ADN como para poder mirar todos”.
El equipo de investigación de la EHU escaneó el rostro de las personas voluntarias, y así “tomamos una serie de puntos de referencia cefalométricos y estudiamos cómo varían los rasgos del rostro (los ojos, la nariz, caras más anchas, más estrechas, la frente, la barbilla…), llegando a analizar regiones muy concretas de la cara”. A partir de las muestras de saliva estudiaron los citados marcadores genéticos y “luego analizamos si había asociación entre esa variación facial con los marcadores que teníamos”, añade Navarro. El equipo de investigación ha conseguido ver de esta manera, “por ejemplo, que hay una zona de la frente que está un poco más hundida cuanto se tiene un determinado genotipo (o conjunto de genes) para un marcador, o que cuando se tiene otro la frente es más sobresaliente, etc.”, relata la investigadora.
Los resultados han revelado asociaciones significativas dentro de diferentes segmentos faciales: “En particular, diez de los marcadores han presentado una fuerte asociación dentro de esta población local, y algunos de estos han revelado correlaciones con regiones faciales que no habían sido detectadas en investigaciones anteriores”, afirma Navarro.
La importancia de los estudios en poblaciones de referencia pequeñas
Estos hallazgos resaltan “la importancia de analizar marcadores candidatos en diversas poblaciones de referencia para identificar marcadores robustos que a la vez proporcionen información precisa”, dice la investigadora. Si bien gran parte de la investigación realizada hasta ahora se ha centrado en las poblaciones europeas como un grupo homogéneo, “nuestro trabajo muestra que la población que hemos estudiado puede presentar diferencias. Estos resultados sugieren que podría ser valioso no solo realizar estudios europeos a gran escala, sino también considerar estudios específicos de subpoblaciones más pequeñas”, añade. Este enfoque podría ayudar en la consecución de futuros modelos predictivos.
En este camino es fundamental hilar fino: “Ahora habría que validar nuestros resultados con más personas. Habría que probar en otras poblaciones para ver si, por ejemplo, estos resultados se enmarcan a todo el sur europeo o solo a nuestro entorno”. Actualmente el grupo sigue adelante con esta investigación utilizando otros métodos de medida de las características faciales: “Ahora estamos utilizando distintas medidas que están definidas antropológicamente: distancia entre los ojos, entre la nariz y la boca, entre las dos comisuras, etc.”, añade la investigadora. Un siguiente paso sería “intentar conseguir modelos de predicción, que revelen por ejemplo una determinada distancia en el rostro de una persona cuando se detecte ciertos genotipos”. Así sí que se podría “reconstruir más o menos el rostro de una persona. Pero para conseguirlo es necesario seguir validando estos avances en una población mucho más amplia”, concluye Navarro.
Referencia:
Belén Navarro-López, Franziska Wilke, Victoria Suárez-Ulloa, Miriam Baeta, Rubén Martos-Fernández, Olatz Moreno-López, Iñigo Olalde, Begoña Martínez-Jarreta, Susana Jiménez, Susan Walsh, Marian M. de Pancorbo (2025) Exploring the association between SNPs and facial morphology in a Spanish population. Sci Rep doi: 10.1038/s41598-025-98748-9
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Poniéndole cara a una muestra de ADN se ha escrito en Cuaderno de Cultura Científica.
La kriptonita ¡existe!
Vale… tal vez el título de este artículo sea un poco sensacionalista, pero kriptonita es lo que le apareció en 2007 en los resultados de búsqueda a Chris Stanley, mineralogista y geólogo del Museo de Historia Natural de Londres, cuando introdujo la composición de un mineral recientemente descubierto en una mina de Jadar (Serbia). Se trataba de un hidróxido de silicato de boro, litio y sodio —LiNaSiB₃O₇(OH)—, muy similar a un exótico material que aparecía expuesto en el Museo de Historia Natural de Metrópolis en la película Superman Returns, estrenada el año anterior.
 La composición de la kriptonita en Superman Returns es muy similar a la del mineral que Chris Stanley estaba analizando en 2007, salvo porque aquella también contenía flúor. Fuente: Warner Brothers / fair use
La composición de la kriptonita en Superman Returns es muy similar a la del mineral que Chris Stanley estaba analizando en 2007, salvo porque aquella también contenía flúor. Fuente: Warner Brothers / fair use
Los orígenes de la kriptonita se remontan al propio creador de Superman, Jerry Siegel, quien parece ser que ya mencionó algo así en una historia inédita de 1940 titulada «El K-Metal de Kripton», que nunca se llegó a publicar. La primera aparición oficial se produjo algo después: bien en 1943, o bien en 1945 —existen dos capítulos candidatos— en el serial radiofónico Las aventuras de Superman. No fue, sin embargo, hasta 1949 cuando hizo su aparición en el universo de los cómics del superhéroe.
Desde entonces, la kriptonita, el único talón de Aquiles de Superman, ha tomado diversas formas y colores, y ha mostrado diferentes propiedades. Empezó siendo roja, pero también la ha habido azul, negra, rosa, carmesí, dorada, plateada, blanca… y, por supuesto, verde, que es la que primero se nos viene a la cabeza a la mayoría. Sobre su composición nunca se habían dado demasiados detalles, aunque hay quien llegó a especular con que el gas noble kriptón podría estar involucrado en su fórmula…. hasta 2006, cuando apareció descrita en Superman Returns como «hidróxido de silicato de boro y litio y sodio con flúor».
 La kriptonita verde es la variante más popular. Fuente: Canva/whitehoune
La kriptonita verde es la variante más popular. Fuente: Canva/whitehoune
Seguramente, la coincidencia debió de ser una sorpresa para Chris Stanley, pero, lejos de aprovechar la conyuntura para bautizar el nuevo mineral que tenía entre manos como kriptonita —en realidad, hubiera sido confuso, ya que el mineral que tenía entre manos no contenía kriptón— se quedó con el nombre de jadarita, dado su lugar de procedencia.
Hubiera sido fantástico que la jadarita presentara un aspecto similar al de la kriptonita, pero lo cierto es que las similitudes entre ambas acaban en la fórmula. A la jadarita le falta el flúor en su composición —¡a ver si va a ser ese el ingrediente secreto!— y, aunque también tiene estructura cristalina, el tamaño de sus cristales es del orden de micras, por lo que su textura es más bien terrosa. Por otro lado, es blanca mate, en lugar de verde brillante — salvo si la irradiamos con luz ultravioleta, en cuyo caso muestra un suave brillo rosa anaranjado—, y no emite ningún tipo de radiactividad, así que parece que Superman, por el momento, no tendría de qué preocuparse.
 Muestra de jadarita. La jadarita y la kriptonita, a la hora de la verdad, no se parecen demasiado. Foto: Dungodung – Own work, CC BY-SA 4.0 / Wikimedia Commons
Muestra de jadarita. La jadarita y la kriptonita, a la hora de la verdad, no se parecen demasiado. Foto: Dungodung – Own work, CC BY-SA 4.0 / Wikimedia Commons
Sin embargo, y lejos de limitarse a una mera curiosidad geológica, la jadarita, como la kriptonita, tiene un potencial oculto: es muy rica en litio y en boro, dos elementos fundamentales en la transición energética y el desarrollo tecnológico e industrial. La mina de Jadar, donde se encuentra, es uno de los mayores depósitos de litio —y boro— del mundo, lo que la convierte en un posible recurso estratégico sin precedentes para Europa… pero cuya explotación podría conllevar daños medioambientales sin precedentes también. Un conflicto de intereses bastante propio de una película de Superman, por cierto.
El hallazgo de la jadarita, en cualquier caso, fue toda una sorpresa, y apareció en la revista Time como uno de los diez mejores descubrimientos científicos de 2007; la BBC, por su parte, lo reconoció como una de las historias más populares del año. Y nosotros… bueno, es que si hay una historia fantástica —en varias de las acepciones de la palabra— de por medio es imposible resistirse a escribir sobre ella.
Bibliografía
Stanley, Christopher J., Jones, Gary C., Rumsey, Michael S., Blake, Christopher, Roberts, Andrew C., Stirling, John A.R., Carpenter, Graham J.C., Whitfield, Pamela S., Grice, Joel D., Lepage, Yvon (2007) Jadarite, LiNaSiB3O7(OH), a new mineral species from the Jadar Basin, Serbia. European Journal of Mineralogy, 19 (4) 575-580 doi:10.1127/0935-1221/2007/0019-1741
BBC News (24 de abril de 2007). ‘Kryptonite’ discovered in mine. BBC News.
Stanley, C. (s. f.). Dr Chris Stanley. Natural History Museum
Reuters (25 de abril de 2007). Scientists unearth Superman’s “kryptonite”. Reuters.
Paul, A. (14 de julio de 2025). Yes, Superman’s kryptonite is (sort of) real. Popular Science.
Ríos, O. (17 de marzo de 2022). Superman y los diferentes tipos de kriptonita. Comicverso.
Singer, B. (Director). (2006). Superman Returns [Película]. Warner Bros. Pictures.
Stiefel, K. E. (15 de marzo de 2018). Kryptonite in Superman. Science On.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo La kriptonita ¡existe! se ha escrito en Cuaderno de Cultura Científica.
Tiras cómicas de Moebius (I)
En la sección Matemoción del Cuaderno de Cultura Científica somos unos apasionados de la banda de Moebius y de los cómics. Por este motivo, no puede extrañar a ninguna de las personas que habitualmente leéis las entradas de esta sección que nos interesemos por el uso de la banda de Moebius en los cómics.
En la entrada Matemática punk, un homenaje a Calpurnio se mostraba un ejemplo de como la banda de Moebius puede aparecer en el humor gráfico, a través de una de las viñetas de El bueno de Cuttlas titulada La banda de Moebius, del ilustrador, historietista, guionista, animador y videojockey aragonés Calpurnio, seudónimo de Eduardo Pelegrín Martínez de Pisón (1959-2022), publicado en 20 Minutos.
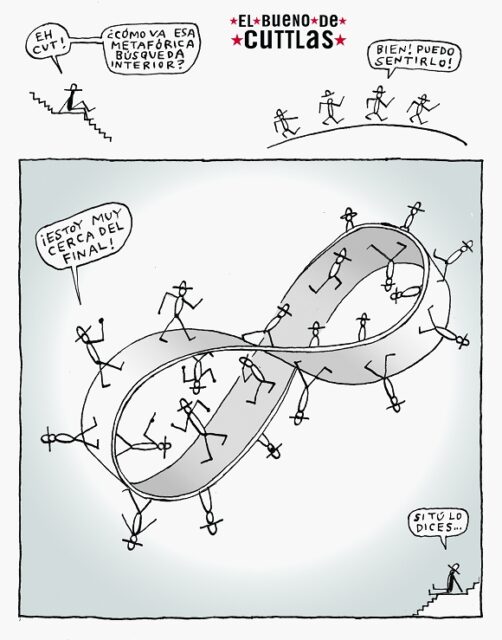 El bueno de Cuttlas (La banda de Moebius), de Calpurnio, publicado en 20 Minutos
El bueno de Cuttlas (La banda de Moebius), de Calpurnio, publicado en 20 Minutos
Una novela gráfica en la que se utiliza la banda de Moebius de una forma metafórica, como símbolo del cambio de fortuna en la vida de su protagonista, de la buena a la mala fortuna, es el cómic El número 73304-23-4153-6-96-8 (La cúpula, 2008), del historietista suizo Thomas Ott, sobre la que podéis leer en la entrada De menú para hoy, dos novelas gráficas negras con salsa matemática.
 Página de la obra El número 73304-23-4153-6-96-8, de Thomas Ott, en la que su protagonista se dirige a una tienda de empeños, pawn shop, en cuyo escaparate, arriba a la izquierda, podemos observar la imagen de la banda de Moebius
Página de la obra El número 73304-23-4153-6-96-8, de Thomas Ott, en la que su protagonista se dirige a una tienda de empeños, pawn shop, en cuyo escaparate, arriba a la izquierda, podemos observar la imagen de la banda de Moebius
Por otra parte, un ejemplo muy bonito de la presencia de la banda de Moebius en un cómic es Promethea (1999-2005), del mítico guionista Alan Moore y el dibujante James H. Williams III, donde la banda de Moebius es un camino infinito de piedra por el que pasean dos de las encarnaciones de Promethea, Sophie y Barbara. Sobre las muchas matemáticas que hay en este cómic podéis leer la entrada Guía matemática para el cómic Promethea.
 Ilustración de doble página que muestra a las dos Prometheas, encarnadas por Sophie y Margaret, paseando por un camino, sin fin, con forma de banda de Moebius
Ilustración de doble página que muestra a las dos Prometheas, encarnadas por Sophie y Margaret, paseando por un camino, sin fin, con forma de banda de Moebius
En esta entrada del Cuaderno de Cultura Científica vamos a hablar de un tipo de uso diferente de la banda de Moebius en el cómic, cuando la estructura del mismo está dada por la propia superficie de Moebius, generando lo que podemos llamar una tira cómica de Moebius.
Tira cómica de Moebius
Preparando mi charla Leyendo cómics con una mirada matemática, que impartí a finales de mayo en la librería Joker de Bilbao, librería especializada en cómic que recibió el Premio Librería Cultural 2023, compartí con el público una interesante tira cómica de Moebius de la artista estadounidense Katherine Myers (@katemyyers.art en instagram).
 Portada de la presentación de la conferencia Leyendo cómics con una mirada matemática (Librería Joker, Bilbao)
Portada de la presentación de la conferencia Leyendo cómics con una mirada matemática (Librería Joker, Bilbao)
Pero antes de la tira cómica, vayamos con lo elemental, qué es una banda de Moebius (aunque muchas de las personas que estáis leyendo esta entrada quizás ya lo conocéis, nunca está de más recordar los conceptos básicos). Una banda de Moebius es una banda retorcida que podemos construir de forma sencilla de la siguiente forma. Si tomamos una tira de papel y pegamos los extremos se obtiene una banda normal, que es una superficie con dos caras (el interior y el exterior) y dos bordes (el de arriba y el de abajo), pero si primero giramos uno de los extremos del papel media vuelta y después juntamos los extremos se obtiene la banda de Moebius, una superficie que solo tiene una cara y un solo borde (como se observa en la siguiente imagen), y propiedades muy curiosas (véase el libro Las matemáticas como herramienta de creación artística (Catarata, 2023) o las entradas Arte Moebius (I) o Arte Moebius (II)).
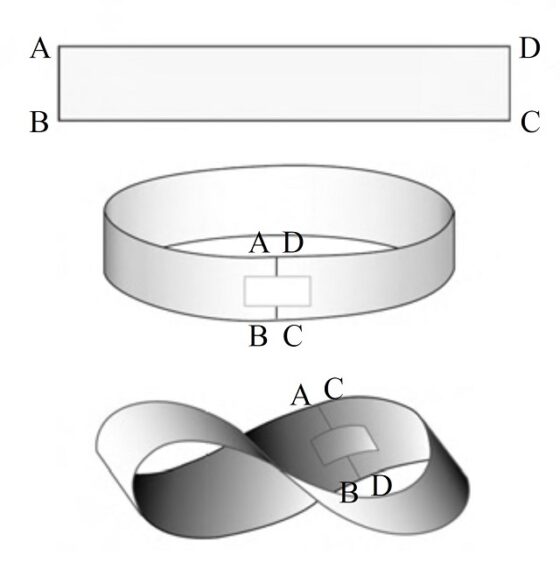
Una de las técnicas habituales para comprobar que la banda de Moebius solo tiene una cara es empezar a pintar la tira de papel longitudinalmente, de manera que cuando lleguemos al punto de partida habremos pintado toda la superficie retorcida, es decir, la única cara de esta superficie. De hecho, si se realiza esta misma operación sobre la banda normal, sin retorcer antes de pegar los extremos, solamente pintaremos una de las caras, la exterior o la interior.
Por otra parte, una tira cómica es una historieta corta, de unas pocas viñetas, e incluso una única viñeta, cuyo formato suele ser rectangular alargado (apaisado), aunque la estructura y longitud es variable, y que se suelen publicar en periódicos y revistas. Algunos conocidos ejemplos de tiras cómicas son Mafalda (del historietista argentino Quino, Joaquín Salvador Lavado Tejón (1932-2020)), como la de la siguiente imagen, Garfield (del autor de cómics estadounidense Jim Davis), Snoopy (del historietista estadounidense Charles Schulz (1922-2000)), las tiras cómicas de Forges (el humorista gráfico madrileño Antonio Fraguas de Pablo (1942-2018)), las distintas tiras cómicas de Max (el artista catalán Francesc Capdevila), como Bardín, el superrealista, El bueno de Cuttlas de Calpurnio o las tiras cómicas, publicadas en diferentes periódicos, de El Perich (el humorista gráfico catalán Jaume Perich Escala (1941-1995)), entre muchos otros.
 Ejemplo de tira cómica de Mafalda, del historietista argentino Quino, Joaquín Salvador Lavado Tejón (1932-2020)
Ejemplo de tira cómica de Mafalda, del historietista argentino Quino, Joaquín Salvador Lavado Tejón (1932-2020)
La tira cómica de Moebius es también una historieta corta, de unas pocas viñetas, pero con algunas diferencias significativas, que funciona de la siguiente manera.
1.- Para empezar, la tira cómica de Moebius se imprime, por las dos caras, en una tira de papel apaisada, pero en la segunda cara la orientación de impresión es la contraria a la de la primera cara, es decir, girada 180 grados.
2.-Cuando se toma la tira de papel apaisada y se juntan los extremos, pero dando primero media vuelta a uno de ellos, entonces la tira de papel sobre la que está impresa la tira cómica se convierte en una banda de Moebius, de manera que solo tiene una cara.
3.-La historieta se ha impreso en las dos caras de la tira de papel apaisada, como hemos dicho, cambiando la orientación de la cara de atrás, de manera que cuando se juntan los extremos formando la banda de Moebius, la historieta que se iniciaba en la primera “cara” se continúa en la segunda “cara” sin necesidad de dar la vuelta a la “tira”.
4.-Por lo tanto, disponemos de una historieta continua que tiene el doble de longitud, pero al llegar a la parte final, como se regresa al inicio de nuevo (no olvidemos que es una superficie de Moebius, de una única cara) se puede continuar leyendo el cómic otra vez, sin interrupción, de manera que si se construye una historia circular (como veremos en la tira cómica de Moebius de la artista estadounidense Katherine Myers) tendremos una historieta infinita.
5.-Por último, mencionar que la tira cómica de Moebius, a diferencia de la tira cómica clásica, tiene una existencia independiente del periódico o revista en la que se pudiera publicar, ya que para poderla leer bien habría que cortarla del periódico y pegar sus extremos formando la tira cómica de Moebius (en la siguiente imagen se muestra la creación de Myers).
 Fotografía de la tira cómica de Moebius, creada por la artista estadounidense Katherine Myers en 2024
Fotografía de la tira cómica de Moebius, creada por la artista estadounidense Katherine Myers en 2024Una tira cómica de Moebius, por Katherine Myers
Aunque lo mejor para entender qué es una tira cómica de Moebius es ver un ejemplo concreto.
Pero antes de mostrar esta historieta infinita creada sobre una estructura tan particular, la superficie de Moebius, presentemos brevemente a la artista que la creó, Katherine Myers. Como ella misma se describe en su página web (Kate Myers), ha estudiado el grado de Animación y Efectos Especiales en la Escuela de Arte de la Universidad Carnegie Mellon (Pittsburgh, Pensilvania, EE.UU.). En su trabajo, se centra en contar historias, utilizando las convenciones de género que se encuentran a menudo en el terror y la ciencia ficción para expresarse de una manera atractiva y visceral. Le fascina la fisicalidad del cuerpo humano y emplea estrategias como los medios basados en el tiempo, el arte secuencial y los efectos prácticos para recrear texturas y formas corporales en contextos anormales e investigar temas como la mortalidad y el yo. Le encanta la accesibilidad que ofrecen tanto el cine como los medios impresos: quiere que su trabajo sea lo más accesible posible. Dirige Full Tilt Comics con su socia Maddie Smoyer y también crea efectos prácticos y de maquillaje para Just a Head Productions.
 Fotografía de Kate Myers en el PIE 2025 – Pittsburgh Indie Expo, del año 2025, en el stand de Full Tilt Comics, donde se observan algunas de sus tiras cómicas de Moebius
Fotografía de Kate Myers en el PIE 2025 – Pittsburgh Indie Expo, del año 2025, en el stand de Full Tilt Comics, donde se observan algunas de sus tiras cómicas de Moebius
Presentemos finalmente la tira cómica de Moebius de la artista Kate Myers. Está formada por seis viñetas, tres que irán impresas en la primera cara (la fila de viñetas de arriba en la siguiente imagen) y las otras tres, pero giradas 180 grados, en la segunda cara (la fila de abajo de la siguiente imagen) de la tira de papel. En la historieta aparecen dos personajes, uno de ellos es una joven que le cuenta a su interlocutora cómo le ha ido en su última cita. Veamos las seis viñetas.
 Las viñetas que van impresas en la “cara” superior y en la “cara” inferior de la tira de papel con la que se forma la tira cómica de Moebius de la artista Kate Myers
Las viñetas que van impresas en la “cara” superior y en la “cara” inferior de la tira de papel con la que se forma la tira cómica de Moebius de la artista Kate Myers
Por lo tanto, cuando la tira cómica de Moebius ya está montada, la lectura de las viñetas es la evidente y que explicamos a continuación. Primero se leen las tres viñetas de la parte de arriba de la anterior imagen. Pero después de la tercera viñeta, en la tira de Moebius, la siguiente es la primera viñeta de la parte de abajo (por el medio giro de la tira antes de pegar los extremos). Por lo tanto, se continúa la lectura con las tres viñetas de abajo. Aunque al llegar a la tercera viñeta de abajo, la siguiente en la tira de Moebius es, de nuevo, la primera viñeta de arriba, por lo que se puede continuar leyendo la historieta de una forma circular e infinita.
A continuación, incluyo una traducción del texto de la tira cómica de Moebius de Kate Myers.
Primera viñeta:
– Recientemente tuve una primera cita muy mala.
– ¿Sí?
Segunda viñeta:
– De lo único que habló fue sobre lo que cree que sucede después de morir.
Tercera viñeta:
– Él piensa que vivimos nuestras vidas una y otra vez como en un circuito cerrado.
Cuarta viñeta:
– Aunque me gusta la idea. Es reconfortante.
– ¿En qué sentido?
Quinta viñeta:
– Ya hemos tenido esta conversación antes, y la volveremos a tener de nuevo. Para siempre.
Sexta viñeta:
– ¡Guau!
– ¡Sí!
 Un montón de tiras cómicas de Moebius de la artista estadounidense Kate Myers
Un montón de tiras cómicas de Moebius de la artista estadounidense Kate MyersSobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Tiras cómicas de Moebius (I) se ha escrito en Cuaderno de Cultura Científica.
Uno de los sólidos más comunes en el universo, el LDA, no es del todo amorfo como se creía
El agua en estado sólido se supone que puede formar un vidrio, lo que se conoce como hielo amorfo de baja densidad (LDA, por sus siglas en inglés). Durante décadas el LDA ha sido considerado un sólido desordenado, casi una “instantánea congelada” del agua líquida. Sin embargo, un nuevo estudio demuestra algo notable: este tipo de hielo no sería completamente amorfo, sino que contendría cristales diminutos en su seno. Las implicaciones de algo aparentemente tan trivial son enormes.
Dos modelos y un experimento muy ingeniosoEl equipo de investigación recurrió a dos modelos computacionales muy utilizados en las simulaciones de las masas de agua para recrear el LDA. Ambos modelos —uno que simula el enfriamiento desde agua líquida y otro que reproduce el proceso de vitrificación desde un estado cristalino— no lograron generar un sólido totalmente caótico, amorfo. En cambio, en los dos casos surgieron nanocristales dispersos en la estructura amorfa.
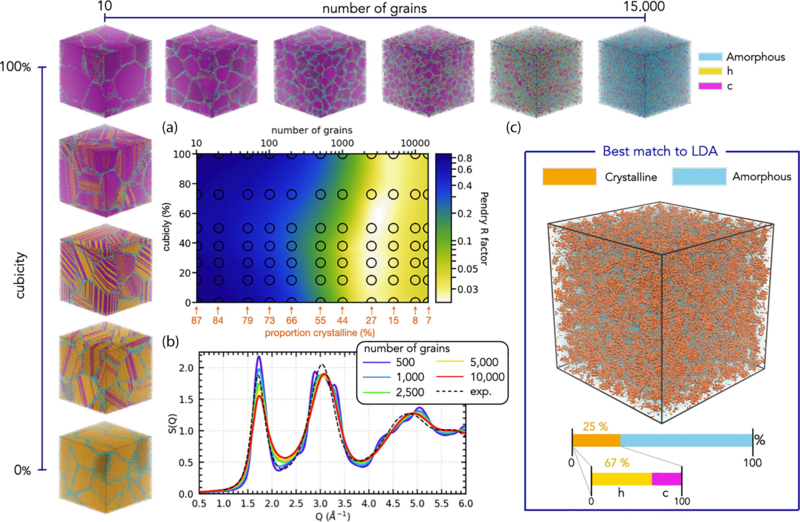 Fuente: M.B. Davies et al (2025) Physical Review B doi: 10.1103/PhysRevB.112.024203
Fuente: M.B. Davies et al (2025) Physical Review B doi: 10.1103/PhysRevB.112.024203Para validar estos resultados, los científicos complementaron las simulaciones con experimentos en el laboratorio muy ingeniosos. Produjeron hielo LDA a partir de dos rutas distintas: como deposición de vapor a muy baja temperatura y como calentamiento de hielo amorfo de alta densidad. Si el LDA fuese verdaderamente amorfo ambas rutas deberían obtener el mismo resultado. Sin embargo, comprobaron que, tras recristalizar, cada muestra mostraba diferencias en la proporción de estructuras cristalinas hexagonales. Esta “memoria” de la ruta de formación solo es posible si existen cristales microscópicos en el material
Este enfoque combinado, datos experimentales y modelado computacional, apunta a que el LDA no es un vidrio puro sino una forma parcialmente cristalina de hielo. Según los autores, la proporción estimada de cristales puede alcanzar hasta un 20 % del volumen total del material.
El LDA es uno de los sólidos más comunes del universo¿Por qué importa este hallazgo? En primer lugar, porque revela la verdadera naturaleza de uno de los sólidos más comunes en el universo. El LDA se encuentra en cometas, nubes moleculares del espacio profundo e incluso en las capas superiores de las atmósferas planetarias. Si su estructura es parcialmente cristalina, esto puede alterar cómo interactúa con la luz, cómo se funde y cómo influye en la química del entorno.
LDA y las anomalías del aguaEn segundo lugar, esta conclusión tiene implicaciones para entender las famosas “anomalías” del agua — fenómenos como su máxima densidad a 4 °C o la existencia de dos posibles estados líquidos en condiciones extremas. El hecho de que el LDA carezca de un equivalente líquido perfectamente correspondiente desafía ciertas teorías sobre el comportamiento del agua superenfriada En otras palabras, la existencia de estos nanocristales pone en entredicho el papel del LDA como referencia estructural para estudiar el agua en condiciones extremas.
Este hallazgo no solo refina nuestra comprensión del agua en condiciones extremas, sino que también invita a reevaluar qué entendemos por estructuras amorfas. Incluso en los sistemas aparentemente más desordenados, la naturaleza parece esconder un grado inesperado de organización.
Referencias:
M.B. Davies et al (2025) Low-density amorphous ice contains crystalline ice grains Physical Review B doi: 10.1103/PhysRevB.112.024203
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Uno de los sólidos más comunes en el universo, el LDA, no es del todo amorfo como se creía se ha escrito en Cuaderno de Cultura Científica.
Las anaranjadas perlas de la Luna
A nuestra escala -la de la humanidad- la Luna ha permanecido en el cielo como un cuerpo gris e inmutable. Su rostro, completamente cubierto de cráteres, nos hace pensar en un mundo geológicamente muerto, casi fósil. Pero no siempre fue así. Nuestra Luna, al igual que la Tierra, también tuvo una juventud fiera y volátil.
Hace unos 3500 millones de años, ocurrieron sobre la superficie lunar fenómenos volcánicos como las fuentes de lava, impulsadas por la expansión de burbujas de gas que procedían del interior del manto lunar. Estas erupciones -que estaban ocurriendo en el casi vacío del espacio- eran muy diferentes a las que ocurren en la Tierra. Gracias a los minúsculos restos de vidrio formados durante estos eventos, los científicos están comenzando a descifrar algunos secretos lunares que hasta ahora habían pasado desapercibidos.
Un nuevo estudio publicado en Icarus por Williams et al. (2025) ofrece una nueva perspectiva sobre este tipo de erupciones gracias al estudio a escala microscópica de unas pequeñas “perlas” de vidrio volcánico que trajeron a nuestro planeta los astronautas de la misión Apolo 17 y que ha permitido reconstruir la presión, la temperatura y la composición de la nube de gases volcánicos fruto de una erupción, abriéndonos la puerta a comprender mejor los mecanismos eruptivos en la Luna.
 Imagen de una de las “trincheras” excavadas para que aflorasen mejor las perlas de color anaranjado. Destaca mucho la diferencia de color entre el regolito de color gris y el anaranjado que hay por debajo de la capa superficial. Imagen cortesía de la NASA.
Imagen de una de las “trincheras” excavadas para que aflorasen mejor las perlas de color anaranjado. Destaca mucho la diferencia de color entre el regolito de color gris y el anaranjado que hay por debajo de la capa superficial. Imagen cortesía de la NASA.La historia del estudio de vidrios lunares comienza en 1972, en el valle de Taurus-Littrow. Los astronautas de la misión Apolo 17 Eugene Cernan y Harrison Schmitt hicieron un descubrimiento asombroso e inesperado en el llamado cráter Shorty: una pequeña zona anaranjada como un oasis entre el infinito gris del regolito lunar.
Schmitt: ¡Oh, hey! ¡Espera un momento!
Cernan: ¿Qué?
Schmitt: ¿… dónde están esos reflejos? Ya me han engañado en otras ocasiones. ¡Hay tierra de color naranja!
Cernan: ¡Bien, no te muevas hasta que no lo vea!
Schmitt: ¡Está por todas partes! ¡Naranja!
Cernan: No te muevas hasta que lo vea.
Schmitt: Lo he removido con mis pies.
Cernan: ¡Hey, aquí está! ¡Puedo verlo desde aquí!
Schmitt: ¡Es naranja!
Cernan: Espera un momento, que subo la visera. ¡Sigue siendo naranja!
Schmitt: ¡Claro que lo es! ¡Que locura! ¡Naranja! Tengo que excavar una trinchera, Houston.
Este suelo naranja al que se refieren en la transcripción de la conversación, junto con el suelo más oscuro de alrededor, estaba formado por incontables pequeñas “perlas” de vidrio anaranjado, restos de un magma enfriado rápidamente y arrojados al cielo durante la erupción mediante fuentes de lava. Los astronautas recogieron estas muestras en tubos de muestras, los sellaron y protegieron de la contaminación de la atmósfera terrestre para su posterior estudio.
Durante décadas, los científicos habían pensado que estas perlas tenían algo de especial. Mientras las gotas de roca fundida viajaban a través del gas expulsado por la erupción, funcionaban como una especie de esponja en miniatura. Conforme estas gotas se alejaban de la parte central de la pluma de gases emitidos por la erupción, mucho más densa y caliente, algunos elementos se condensaron directamente sobre la superficie de estas perlas, recubriéndolas.
Estas coberturas, conocidas como sublimados, son como una especie de “fantasma” de la pluma de gases volcánica, aportándonos un registro directo de su química. Pero hasta ahora, el problema era leer su mensaje, ya que, con menos de 100 nanómetros de espesor, estas capas de minerales son muy frágiles, reactivas con la atmósfera terrestre y, por lo tanto, muy difíciles de analizar.
 El astronauta y geólogo norteamericano Harrison Schmitt es uno de los protagonistas de esta historia. Aquí lo podemos ver con un gigantesco bloque de roca fragmentado que probablemente provenga de la formación de un cráter de impacto. Imagen cortesía de NASA.
El astronauta y geólogo norteamericano Harrison Schmitt es uno de los protagonistas de esta historia. Aquí lo podemos ver con un gigantesco bloque de roca fragmentado que probablemente provenga de la formación de un cráter de impacto. Imagen cortesía de NASA.Es en esta dificultad del estudio de estas muestras donde destaca este nuevo estudio. Los autores han podido trabajar con las muestras de unas perlas de vidrio oscuro que nunca han sido expuestas al aire de la atmósfera terrestre y que aparecen también junto a las anaranjadas.
Mediante unas técnicas de estudio microscópico han podido hacer observaciones tanto a nivel morfológico como químico. No ha sido una tarea fácil, ya que, desde la apertura del tubo donde estaba esta muestra hasta el moverlas entre los distintos instrumentos, se ha tenido que hacer en una atmósfera de nitrógeno puro o en vacío. Algo que no es precisamente pan comido, pero necesario para poder realizar el estudio con las garantías de que al menos no habría alteraciones químicas en la superficie de las perlas.
Este meticuloso análisis ha conseguido descifrar una historia escrita en las distintas capas de las perlas. Una de las cosas que más han llamado la atención de los científicos es la aparición de unos “montículos” microscópicos y con forma semiesférica. Estos están formados por la esfalerita policristalina, un sulfuro de cinc.
Para que se forme la esfalerita, la nube de gas volcánico tiene que contener -obviamente- azufre y cinc. Pero más importante es este otro detalle: su formación apunta directamente a otro elemento, el hidrógeno. Los modelos termodinámicos nos cuentan que en una nube de gas pobre en hidrógeno, el cinc prefiere enlazarse con el cloro para formar cloruro de cinc. La prevalencia del sulfuro de cinc en estas perlas es una fuerte evidencia de que el gas volcánico era rico en hidrógeno en comparación con los elementos halógenos (flúor, cloro, bromo, yodo y astato). Esta prueba sirve como apoyo a la teoría de que el manto lunar no está totalmente seco, sino que contiene grandes cantidades de elementos volátiles que eran capaces de impulsar estas erupciones.
Pero cuando los investigadores pudieron observar más de cerca estos montículos de esfalerita, descubrieron también un gradiente químico muy sutil, pero consistente entre los montículos: en la base, donde se unen a la perla de vidrio, estaban especialmente enriquecidos en hierro con respecto a la cima del montículo. Esta distribución, según interpretan los autores, nos cuenta la historia del viaje de la perla por la nube de gas.
Los modelos muestran que el sulfuro de hierro se condensa a temperaturas más altas y menores presiones que el sulfuro de cinc. Esto significa que conforme la perla sale disparada de la fisura volcánica, pasa primero por una región más densa y caliente donde se enriquecería en el hierro.
Conforme viajara hacia afuera de la nube de gas, hacia las zonas más frías y con menor presión, este cambio en las condiciones favorecería el depósito de las capas ricas en cinc sobre las anteriores. Esto sirve como una especie de registro de las condiciones de presión y temperatura dentro de la misma nube de gas, y del rápido viaje de la perla a través de esta.
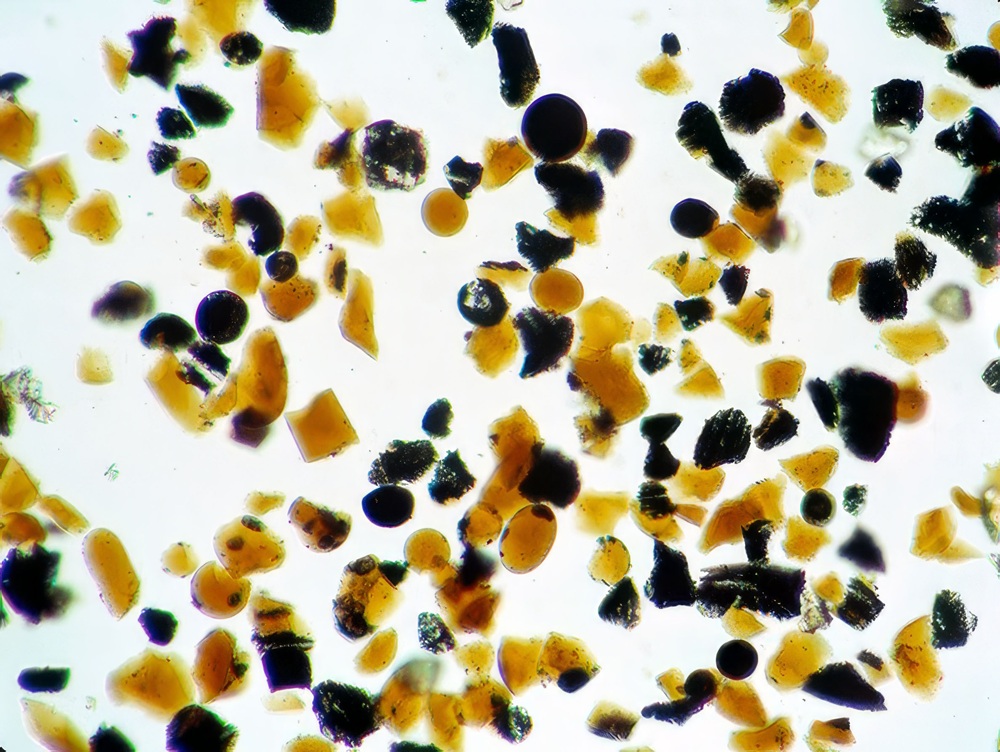 Imagen de las “perlas” de color anaranjado vistas al microscopio. Las más grandes de la imagen están en torno a las 40 micras. Cortesía de NASA/JSC.
Imagen de las “perlas” de color anaranjado vistas al microscopio. Las más grandes de la imagen están en torno a las 40 micras. Cortesía de NASA/JSC.Los investigadores han encontrado otras morfologías sobre la superficie que se habrían superpuesto sobre los montículos, lo que también sugiere que hay un orden en el depósito de otros minerales sobre las perlas. Y este detalle implicaría lo siguiente: No todas las perlas siguieron la misma trayectoria, sino que unas pudieron seguir una más corta antes de caer sobre la superficie y en la que solo dio tiempo a formar los montículos y otras que salieron disparadas mucho más altas y que por lo tanto tuvieron tiempo de quedar recubiertas de una manera más compleja al pasar más tiempo por la pluma de gases de la erupción.
Y, por último, nos falta la interpretación de la propia erupción a partir de estos datos. Los científicos han comparado las perlas de color oscuro con las famosas perlas naranjas. Mientras que las oscuras están recogidas de aproximadamente medio metro de profundidad, las naranjas estaban a muy pocos centímetros de la superficie. Los investigadores piensan que el depósito de estos materiales volcánicos ocurrió en una sola erupción, y por lo tanto su posición estratigráfica es importante: las perlas oscuras se depositaron antes que las naranjas.
Los análisis que se habían realizado anteriormente de las perlas naranjas habían mostrado que los sublimados no estaban compuestos principalmente por sulfuro de cinc, sino por cinc metálico que posteriormente había reaccionado para dar lugar a otros minerales. Los modelos termodinámicos muestran que para que se precipite el cinc nativo en vez de la esfalerita, la presión del gas en la nube tuvo que ser extremadamente baja, órdenes de magnitud por debajo a la presión a la que se forma el sulfuro de cinc.
Esto nos da una pista fundamental sobre la erupción: es posible que comenzase con una presión muy alta, creando una densa nube de gas que provocó el depósito rico en sulfuro de hierro y cinc sobre las primeras perlas de vidrio negro. Con el tiempo, la fuerza de la erupción fue disminuyendo -como ocurre en las erupciones terrestres-, la nube de gas comenzó a ser menos densa y las perlas naranjas se fueron recubriendo del cinc en estado nativo.
Los diferentes recubrimientos de las perlas, separadas por apenas unas decenas de centímetros en el regolito lunar, sirven como un testimonio de la variación en la intensidad de la erupción a lo largo del tiempo, como si pudiésemos ver una película que ha quedado registrada en minúsculos detalles de la geología lunar.
Este trabajo nos abre una ventana para refinar los modelos de funcionamiento del vulcanismo lunar y de la composición de su interior, pero también demuestra que la Luna era un mundo con sistemas volcánicos que evolucionaban y eran químicamente diversos. Y nos debe recordar que, aunque no hayamos vuelto a la Luna -el ser humano, me refiero-, las muestras que se tomaron durante las misiones Apolo todavía tienen mucho que contarnos… ¿Qué secretos aguardarán a ser descubiertos?
Referencias:
Williams, T. A., Parman, S. W., Saal, A. E., Akey, A. J., Gardener, J. A., & Ogliore, R. C. (2025). Lunar volcanic gas cloud chemistry: Constraints from glass bead surface sublimates Icarus, 438, 116607. doi: 10.1016/j.icarus.2025.116607
Fuente de la conversación: N.G. Bai ley and G.E. Ulrich (1975) APOLLO 17 VOICE TRANSCRIPT Pertaining to the geology of the landing site U.S. Geological Survey – Branch of Astrogeology
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Las anaranjadas perlas de la Luna se ha escrito en Cuaderno de Cultura Científica.
Confirmado: El «hombre dragón» es denisovano
 Reconstrucción artística de la apariencia que tendría un denisovano. Ilustración: Chuang Zhao
Reconstrucción artística de la apariencia que tendría un denisovano. Ilustración: Chuang Zhao
Hay quien suele imaginar el camino evolutivo del ser humano como una línea recta que se mueve directa desde nuestros orígenes en África hasta la actualidad, en nuestras ciudades, con ordenadores, coches y teléfonos. Es bastante conocida la viñeta que muestra una ordenada sucesión de figuras, desde el primate encorvado hasta el señor erguido vistiendo orgulloso un traje. A veces se representa la evolución como un árbol, con un tronco común del que nacen diferentes ramas que se extiende de manera independiente creciendo o cortándose abruptamente. La realidad es mucho más compleja y difícil de visualizar, una especie de embrollada madeja con docenas de hilos que no solo se enredan, se anudan o se cruzan, sino que pueden mezclarse dando lugar a nuevos hilos. Homo sapiens, Homo habilis, Homo rudolfensis, Homo heidelbergensis, Homo neanderthalensis, Homo floresiensis, Homo naledi, Homo denisovensis… las hebras son tan variadas y traviesas que se enmarañan con el tiempo y representan un quebradero de cabeza para los científicos que, además, a menudo se ven obligados a trabajar con solo un trocito de ellas.
Uno de los cabos sueltos en ese confuso ovillo de especies del género Homo apareció no hace mucho. En 2008, un equipo de investigadores del Max Planck encabezados por Svante Pääbo, que diez años más tarde ganaría el Premio Nobel de Medicina, analizó un pequeño fragmento de hueso del dedo meñique de una niña, encontrado en las cuevas de Denísova, en los montes Altái de Siberia. Los resultados genéticos fueron sorprendentes. El ADN mitocondrial de aquella niña ofrecía pistas de linajes bien conocidos pero no se podía clasificar claramente como sapiens o como neandertal. La madeja se enredaba aún más. Más adelante, cuando se logró secuenciar su genoma nuclear completo, la conclusión apuntaba a que esa niña estaba más emparentada con los neandertales, con quienes compartió un antecesor común, antes de divergir hace aproximadamente unos 400.000 años. La cueva se convirtió en un buen filón de pistas y, desde entonces, se han encontrado diferentes artefactos y herramientas, así como otros restos humanos. Un molar (bastante grande), varios dientes más, y un puñado de pequeños fragmentos óseos pertenecientes a diferentes estratos y, por tanto a diferentes épocas. Posteriores estudios ayudaron a concluir que nos encontrábamos ante un linaje de humanos diferente al que, en honor a la cueva donde se descubrieron, se bautizó como los denisovanos. La escasez de restos fósiles obligó a aguzar el ingenio de los investigadores y el Homo denisovanis se convirtió en la primera especie humana que se catalogó utilizando ADN y descubriendo que los denisovanos no solo convivieron con sapiens y neandertales, sino llegaron a tener descendencia con ambos.
Lo que no podían sospechar todos los científicos que luchaban por trabajar con esos limitados y escasos restos es que existía un gran cráneo denisovano, oculto desde hace décadas, sin que nadie lo supiera. En 1933, setenta y cinco años antes del primer descubrimiento denisovano, un hombre participaba en la construcción de un puente cerca de la ciudad de Harbin, en China. Por aquel entonces el ejército japonés ocupaba el norte de China y obligaba a un grupo de soldados chinos capturados a trabajar en aquella infraestructura. De entre los escombros, surgió una calavera, incompleta, extraña y diferente. Uno de los soldados chinos la cogió y la escondió de sus enemigos, pensando que tenía en su poder algo valioso. Durante décadas no compartió su hallazgo con nadie, incluso llegó a ocultarla en un pozo cerca de su casa para que no se la quitaran y así pasaron los años. Poco antes de su muerte, aquel hombre reunió a su familia y les habló del pozo y del «precioso tesoro» que guardaba, seguía creyendo que ese insólito cráneo tenía un gran valor. En 2018, sus nietos herederos lo encontraron, lo sacaron del pozo y, lejos de hacerse ricos con él, lo donaron a la Universidad GEO de Hebei.
El soldado había fallecido sin aclarar el lugar exacto donde había encontrado el cráneo y el equipo de paleoantropólogos de Hebei, liderados por Quian Ji, junto a otros expertos en datación y geocronología de la Universidad Griffith, en Australia, tuvieron que esforzarse para confirmar su procedencia. Analizaron isótopos de estroncio incrustados en las fosas nasales del cráneo con una capa específica de sedimentos alrededor del puente y pudieron llegar a una primera aproximación de su edad, entre 138.000 y 309.000 años. Más tarde llegarían estudios de datación por uranio que lo situaban, como mínimo, en 146.000 años.
Realmente era un cráneo extraño, visiblemente más grande que cualquiera que se hubiera encontrado jamás. Realizaron una reconstrucción del cráneo encontrado en Harbin y llegaron a la conclusión de que «pertenecía a un varón de mejillas planas, boca ancha y carente de barbilla. Una imponente frente colgaba sobre sus ojos hundidos y su nariz bulbosa. Y dentro de su enorme cráneo había un cerebro descomunal, que medía un 7 % más que el cerebro medio de un ser humano actual».
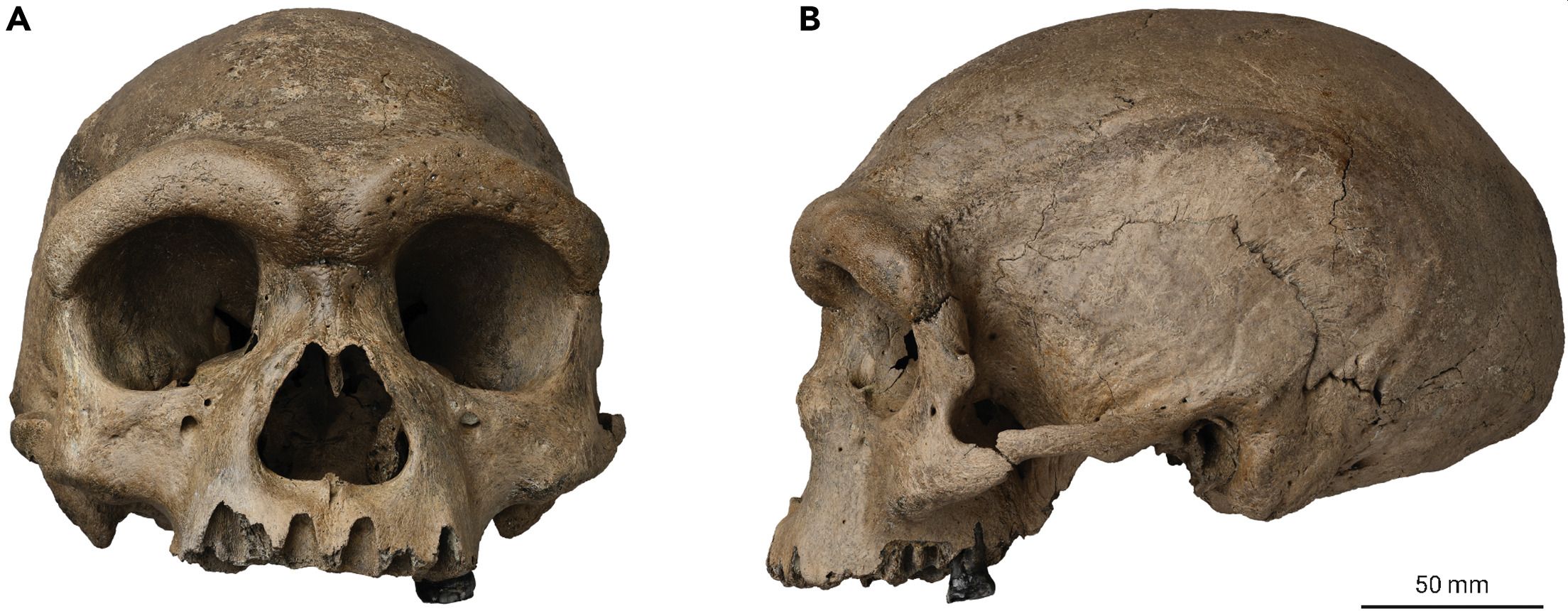 El cráneo encontrado en el puente cerca de Harbin, China en 1933 | Qiang Ji, Wensheng Wu et al. (2021) Cell doi: 10.1016/j.xinn.2021.100132 CC BY-ND 4.0
El cráneo encontrado en el puente cerca de Harbin, China en 1933 | Qiang Ji, Wensheng Wu et al. (2021) Cell doi: 10.1016/j.xinn.2021.100132 CC BY-ND 4.0
En 2021, los investigadores publicaron sus resultados en Cell, describiendo el cráneo e indicando que correspondía a «un homínido extinto masivo en tamaño con una longitud craneal máxima muy grande, tanto en longitud nasiooccipital como en anchura del toro supraorbitario; bóveda craneal larga y baja, con frontal retraído, contorno parietal uniformemente curvado y contorno occipital redondeado; sin quilla sagital; cara superior extremadamente ancha, con órbitas grandes y casi cuadradas; altura facial baja en relación con la anchura facial superior; toro supraorbitario ancho, masivamente desarrollado y suavemente curvado». Estaban entusiasmados y concluyeron que ese cráneo, con todos esos rasgos diferenciados, debía pertenecer a una especie propia. La llamaron Homo longi, en honor a Longjian, la región donde se encontró el cráneo. Longjian significa gran dragón y, consecuentemente, al gran cráneo datado en el Pleistoceno medio tardío se le terminó conociendo como «el hombre dragón», un suculento nombre que abrió muchas portadas por aquellos años.
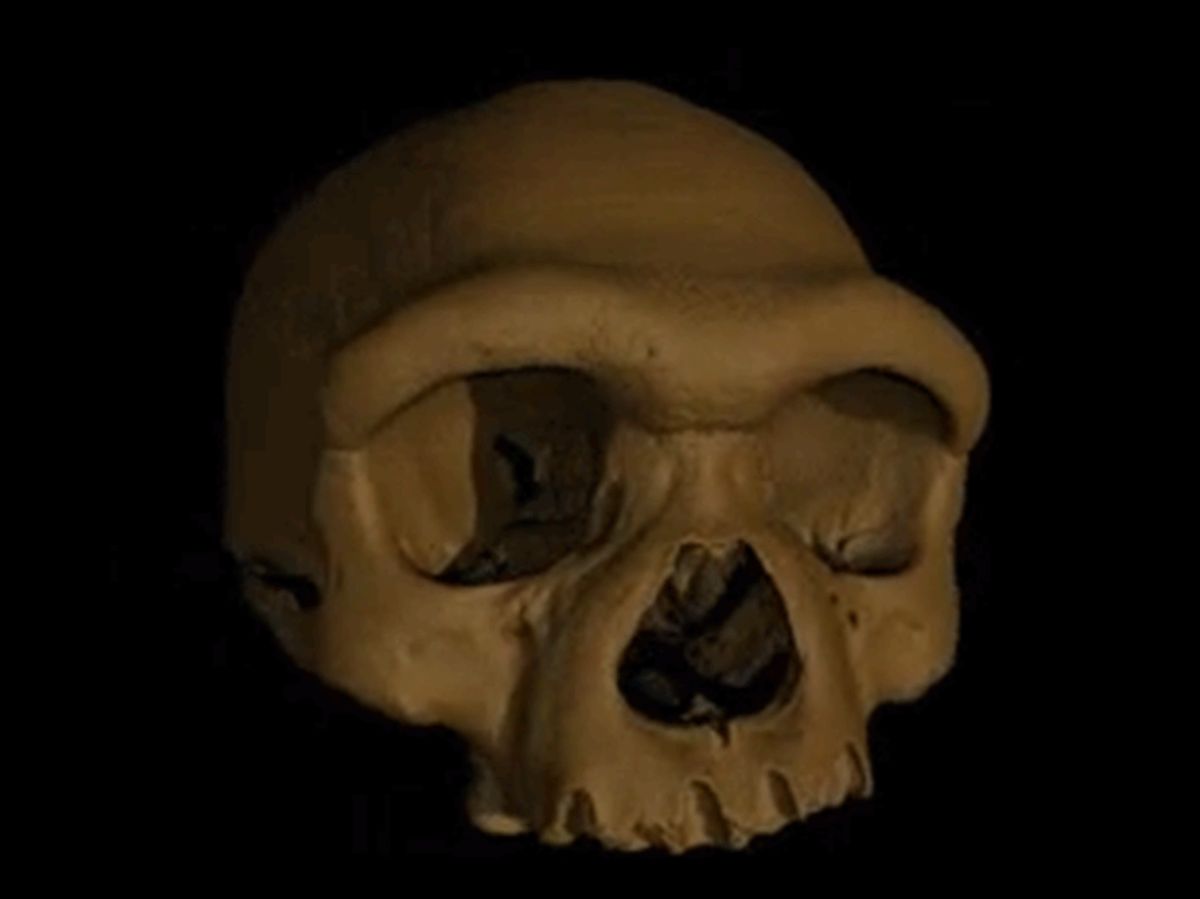 Reconstrucción virtual en 3D del cráneo del «hombre dragón» encontrado en el puente de Harbin, China. Fuente: Xijun Ni et al (2021) The Innovation doi: 10.1016/j.xinn.2021.100130 CC BY-ND 4.0
Reconstrucción virtual en 3D del cráneo del «hombre dragón» encontrado en el puente de Harbin, China. Fuente: Xijun Ni et al (2021) The Innovation doi: 10.1016/j.xinn.2021.100130 CC BY-ND 4.0
El sueño de cualquier paleontólogo es descubrir una nueva especie, ser recordado por encontrar y bautizar un nuevo hilo de la compleja madeja humana, sin embargo ese anhelo puede desembocar, y de hecho así ocurre frecuentemente, en prisas y confusiones. La emoción por el nuevo descubrimiento pronto fue sustituido por críticas en diversos medios especializados y muchos expertos expresaron sus dudas al artículo publicado en Cell. Entre ellos destaca la voz autorizada de María Martinón (CENIEH) que, en un artículo publicado en Science en 2021, afirmaba que «es prematuro nombrar una nueva especie, especialmente un fósil sin contexto y con contradicciones en el conjunto de datos». Cuanto más se analizaba más fuerza tomaba la idea de que el «hombre dragon» podría representar no una nueva especie humana, sino el primer cráneo de un denisovano.
Por supuesto, cada vez que surge una hipótesis en ciencia también aparecen científicos dispuestos a corroborarla o echarla por tierra. La primera en saltar al escenario fue Qiaomei Fu, una genetista china del Instituto de Paleoantropología de Pekin que trabajaba en el primer ADN denisovano procedente del pequeño hueso de Siberia. Comparar ese ADN denisovano de la niña de la cueva de Denísova con el ADN del cráneo del «hombre dragón» despejaría todo el misterio. Intentaron extraer material genético de una parte del cráneo llamada hueso petroso (que suele ser una buena fuente) y también de un diente adherido a la mandíbula superior (la inferior no se ha conservado). No lo consiguieron, pero sí lograron secuenciar fragmentos de 95 proteínas antiguas que compararon con secuencias de humanos modernos, neandertales y, cómo no, sus muestras del hueso denisovano. No encontraron correlación con los dos primeros pero sí descubrieron una secuencia proteica idéntica, tanto en la niña de Denísova como en el cráneo de Harbin… Esto sugería que el «hombre dragón» sí que podría ser denisovano… pero sin ADN que lo confirmase, no era suficiente.
 En rojo la localización de los 0,3 mg de cálculo dental extraídos del cráneo de Harbin, donde se capturó y secuenció el ADNmt. Fuente: Qiaomei Fu, Peng Cao, et al. (2025) Cell doi:10.1016/j.cell.2025.05.040 CC BY-ND 4.0
En rojo la localización de los 0,3 mg de cálculo dental extraídos del cráneo de Harbin, donde se capturó y secuenció el ADNmt. Fuente: Qiaomei Fu, Peng Cao, et al. (2025) Cell doi:10.1016/j.cell.2025.05.040 CC BY-ND 4.0
Qiaomei Fu no se dio por vencida y, unos años más tarde, lo ha conseguido. «En lugar de buscar material genético en el propio cráneo, ella y su equipo rasparon un pequeño fragmento de placa dental fosilizada, o cálculo dental, de la raíz ennegrecida del único molar restante del cráneo». Aunque el cálculo contiene menos ADN antiguo que el que se encuentra habitualmente en huesos o dientes, su estructura mineral permite preservar mejor su contenido. Fue un momento emocionante. El equipo de Fu logró raspar apenas 0,3 miligramos de cálculo de ese diente. Puede parecer muy poco, y mucho menos si tenemos en cuenta que «casi cuatro quintas partes de ese material genético extraído provenían de contaminación moderna», pero con lo que quedó pudieron conseguir el ADN que necesitaban. Sus resultados se han publicado hace unos días en la Revista Cell y confirman que coinciden con el ADN mitocondrial de genomas denisovanos previamente secuenciados, lo que confirma que «el hombre dragón» es de hecho un denisovano.
Referencias científicas y más información:
Qiaomei Fu, Peng Cao, et al. (2025) Denisovan mitochondrial DNA from dental calculus of the >146,000-year-old Harbin cranium Cell doi:10.1016/j.cell.2025.05.040
Marshall, Michael (2025) Who Were the Ancient Denisovans? Fossils Reveal Secrets about the Mysterious Humans Nature doi:10.1038/d41586-025-01549-3.
Lewis, Dyani (2025) First Ever Skull from ‘Denisovan’ Reveals What Ancient People Looked Like Nature DOI:10.1038/d41586-025-01899-y.
Sobre el autor: Javier «Irreductible» Peláez es escritor y comunicador científico multimedia. Es ganador de tres premios Bitácoras, un premio Prisma a la mejor web de divulgación científica y un Premio Ondas al mejor programa de radio digital.
El artículo Confirmado: El «hombre dragón» es denisovano se ha escrito en Cuaderno de Cultura Científica.
Sobrarbe-Pirineos: qué hacemos en un geoparque de montañas

¿Qué tienen en común un paisaje espectacular, un fósil milenario y una cantera abandonada? Todos forman parte del patrimonio geológico, un testimonio de la historia de la Tierra con un gran valor científico, educativo, cultural y estético, y base del patrimonio natural. Sin embargo, su importancia continúa siendo poco apreciada.
Para acercar las distintas aproximaciones del patrimonio geológico a la sociedad, los días 26, 27 y 28 de marzo se celebró la quinta edición de las jornadas divulgativas “Geología para poetas, miopes y despistados. Patrimonio patrimonio”. Organizadas por el grupo de investigación consolidado Procesos Hidro-Ambientales (HGI) de la Facultad de Ciencia y Tecnología de la Universidad del País Vasco (UPV/EHU), estas jornadas contaron con la colaboración del Vicerrectorado del Campus de Bizkaia, la Cátedra de Cultura Científica de la UPV/EHU, el Geoparque de la Costa Vasca / Geoparkea y el Ente Vasco de la Energía (EVE).
Los geoparques no son solo curiosidades científicas, también son motores de desarrollo de las áreas donde se implantan. Los geoparques de montaña son muy particulares. Ánchel Belmonte las describe en esta conferencia.
Ánchel Belmonte Ribas es doctor en Geología y Coordinador de la Comisión Científico Asesora del Geoparque Mundial UNESCO Sobrarbe-Pirineos.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Sobrarbe-Pirineos: qué hacemos en un geoparque de montañas se ha escrito en Cuaderno de Cultura Científica.
PCSK9, sospechoso habitual
La proteína PCSK9 (del inglés Proprotein Convertase Subtilisin/Kexin type 9) es miembro de una familia de proteínas llamadas proproteínas convertasas. Dentro de la familia, PCSK9 fue la última en descubrirse y difiere de las demás por su comportamiento. Aquellas personas que tienen problemas de hipercolesterolemia probablemente tengan conocimiento de su existencia puesto que las personas que no responden a tratamientos clásicos como las estatinas se medican con inhibidores de PCSK9.
¿Qué hace PCSK9?PCSK9 es una enzima que tiene la capacidad de cortar otras proteínas como si fuera una tijera, pero en la mayoría de las ocasiones no hace uso de esa cualidad más que consigo misma. Antes de que se produzca el corte, PCSK9 no es funcional; de ahí la importancia de que se corte a sí misma para que se vuelva activa. La proteína, una vez procesada, funciona principalmente como transportadora. Se une a otras proteínas para llevarlas a orgánulos determinados donde son procesadas.
PCSK9 en la hipercolesterolemia
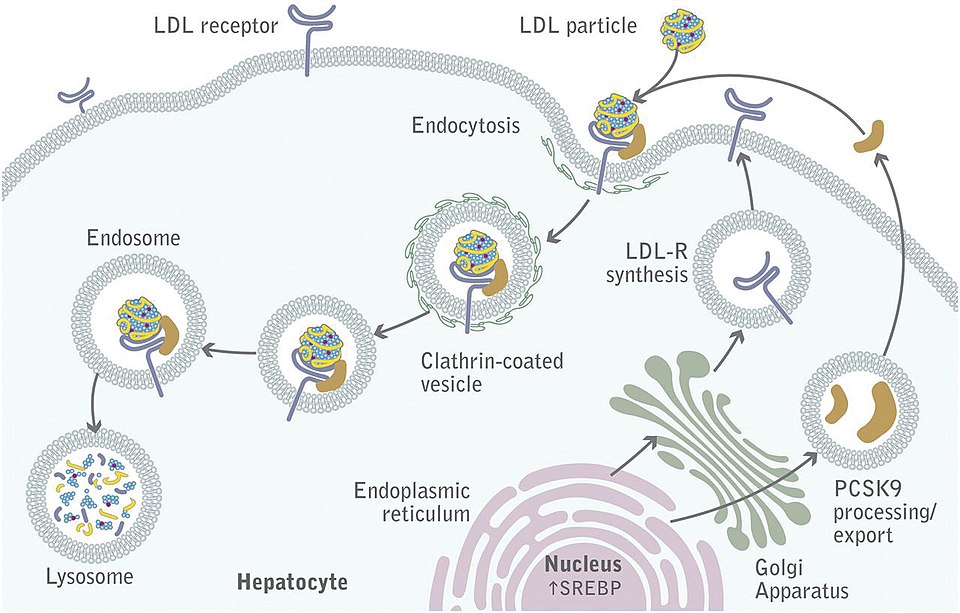 PCSK9 en los hepatocitos. Fuente: Gilles Lambert, Barbara Sjouke, Benjamin Choque, John J.P. Kastelein, G. Kees Hovingh – doi: 10.1194/jlr.R026658 CC BY 4.0 / Wikimedia Commons
PCSK9 en los hepatocitos. Fuente: Gilles Lambert, Barbara Sjouke, Benjamin Choque, John J.P. Kastelein, G. Kees Hovingh – doi: 10.1194/jlr.R026658 CC BY 4.0 / Wikimedia CommonsEn el caso de la hipercolesterolemia se ha visto que PCSK9 se une al receptor del colesterol LDL (lipoproteína de baja densidad, del inglés low density lipoprotein); también llamado coloquialmente colesterol malo por su papel en la ateroesclerosis; en los hepatocitos del hígado. El hígado es el órgano que procesa el colesterol que circula por la sangre. Para ello, los hepatocitos que son las células funcionales del hígado tienen unas proteínas que se llaman receptores, los cuales son específicos para diferentes tipos de moléculas. Uno de estos receptores es el del colesterol LDL. Este receptor capta el colesterol LDL de la sangre y se procesa dentro del hepatocito. La proteína PCSK9 tiene la capacidad de unirse al receptor del colesterol LDL que se encuentra anclado sobre la membrana del hepatocito y lo transporta al lisosoma, orgánulo donde se da la degradación del receptor. De esta manera, un alto contenido de PCSK9 celular provoca la destrucción de los receptores de colesterol LDL de los hepatocitos; el colesterol LDL no se internaliza y se acumula en la sangre.
PCSK9 y cáncer
La hipercolesterolemia no es la única patología en la cual se ha identificado a PCSK9. También se ha observado que algunos tumores poseen grandes cantidades de esta proteína. En algunos tipos de tumores como es el caso del cáncer colorrectal, el cáncer de estómago o el cáncer del cuello del útero, se ha visto que PCSK9 también realiza el papel de transportador. En estos casos transporta la proteína MHC I (del inglés Major Histoconpatibiity Complex type I) o complejo mayor de histocompatibilidad clase I. Este complejo formado por proteínas aparece en todas nuestras células nucleadas y su función es presentar antígenos a las células del sistema inmune. Los antígenos son pequeños trozos de proteínas capaces de producir una reacción inmunitaria. Si nuestro cuerpo detecta un antígeno que no es propio como puede ser un fragmento de la proteína de un virus, las células del sistema inmune lo reconocerán y comenzará la respuesta inmunitaria. De esta manera cuando un tumor se va desarrollando, las células aberrantes expresan antígenos modificados también llamados neoantígenos que son presentados a través del MHC I y las células del sistema inmune los reconocen como extraños y atacan a las células tumorales. Tal y como ocurre con el receptor del colesterol LDL, PCSK9 transporta el complejo MHC I a los lisosomas donde se degrada y las células tumorales no visibilizan sus neoantígenos, de esa manera los tumores se vuelven invisibles para las células del sistema inmune y de ahí su agresividad.
Tratamientos contra PCSK9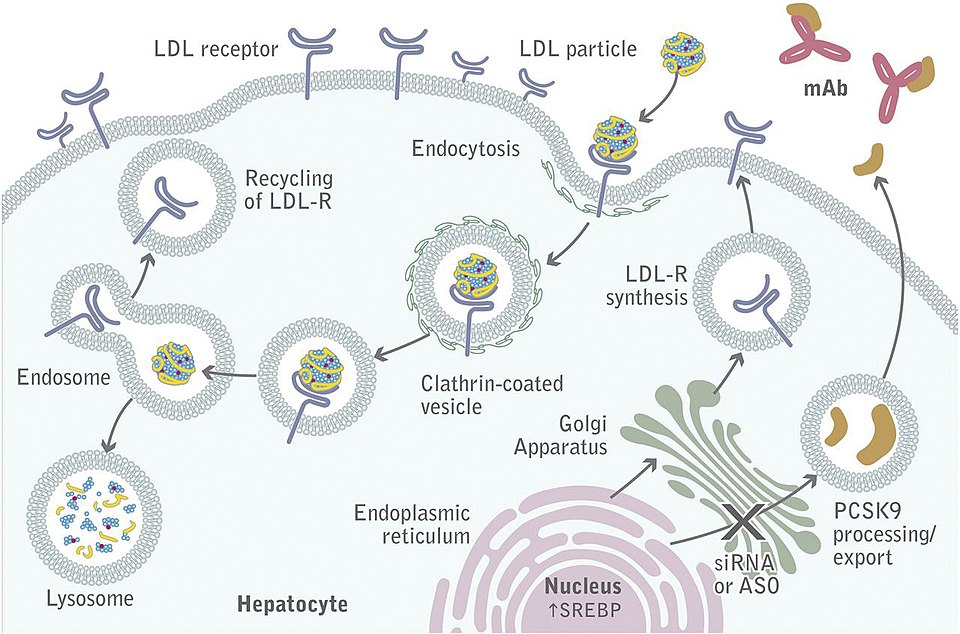 Los anticuerpos monoclonales (mAb) bloquean la acción de PCSK9 permitiendo el reciclado del receptor de LDL. Fuente: Gilles Lambert, Barbara Sjouke, Benjamin Choque, John J.P. Kastelein, G. Kees Hovingh – doi: 10.1194/jlr.R026658 CC BY 4.0 / Wikimedia Commons
Los anticuerpos monoclonales (mAb) bloquean la acción de PCSK9 permitiendo el reciclado del receptor de LDL. Fuente: Gilles Lambert, Barbara Sjouke, Benjamin Choque, John J.P. Kastelein, G. Kees Hovingh – doi: 10.1194/jlr.R026658 CC BY 4.0 / Wikimedia CommonsLos primeros tratamientos que se desarrollaron contra PCSK9 se diseñaron para atajar los problemas de hipercolesterolemia. Se desarrollaron anticuerpos que bloqueaban la acción de PCSK9 impidiendo su unión a los receptores de colesterol LDL o más recientemente se ha usado la tecnología del pequeño ARN interferente, que permite el silenciamiento a nivel de ARN. Es evidente que, visto el papel de PCSK9 en el cáncer, nos puede surgir la pregunta de si estos medicamentos pueden ser también útiles contra esta enfermedad. Por ello, la investigación actual parece ir en la línea de describir nuevas aplicaciones para estos inhibidores de PCSK9 dado que, al haber superado ya todas las medidas de seguridad requeridas por las agencias que regulan la comercialización de los medicamentos, su utilización como terapia antitumoral podría aplicarse de forma segura en mucho menos tiempo que los nuevos medicamentos.
Bibliografía
Xinjian Liu, Xuhui Bao, Mengjie Hu, Hanman Chang, Meng Jiao, Jin Cheng, Liyi Xie, Qian Huang, Fang Li, Chuan-Yuan Li (2020) Inhibition of PCSK9 potentiates immune checkpoint therapy for cancer Nature doi: 10.1038/s41586-020-2911-7
Roth EM, Davidson MH (2018) PCSK9 Inhibitors: Mechanism of Action, Efficacy, and Safety Rev Cardiovasc Med doi: 10.3909/ricm19S1S0002
Melendez QM, Krishnaji ST, Wooten CJ, Lopez D. (2017) Hypercholesterolemia: The role of PCSK9 Arch Biochem Biophys. doi: 10.1016/j.abb.2017.06.001
Sobre los autores: Ander Martín es doctor en biotecnología e investigador en la Facultad de Medicina y Enfermería de la UPV/EHU, e Iker Badiola Etxaburu es doctor en biología, Profesor Pleno en la Facultad de Medicina y Enfermería de la UPV/EHU, y director de la Cátedra de Cultura Científica de la UPV/EHU
El artículo PCSK9, sospechoso habitual se ha escrito en Cuaderno de Cultura Científica.
Un volcán escondido… a la vista de todos
En los últimos cuatro años, el rover Perseverance ha estado investigando la inmensa cuenca formada por el cráter Jezero buscando signos de la existencia de vida en el pasado remoto del planeta Marte, cuando este lugar era muy diferente y albergaba un profundo lago al que llegaban las aguas desde distintos ríos y en el que incluso existía un delta cuya forma todavía se intuye desde el espacio. Pero al comenzar su andadura, el rover descubrió que todas las rocas del fondo no eran sedimentarias -como uno podría esperar del fondo de un lago- sino que también había rocas ígneas, formadas a partir de un magma que se enfría.
Esta primera sorpresa ayudó a los científicos a confirmar la hipótesis de que el cráter Jezero no solo había sido transformado por la actividad del agua, sino que también existían otros procesos activos. Y es que, si el fondo del cráter estaba cubierto por materiales volcánicos, ¿de dónde procedían? Porque tampoco es que hubiese ningún volcán cercano… al menos en apariencia.
Pero en un nuevo estudio publicado por Cuevas-Quiñones et al. (2025) en Communications Earth & Enviroment parece haber encontrado un volcán que habría permanecido escondido a la vista de todos, aunque suene contradictorio. Este, en realidad, estaría en una montaña que aparece en el borde sureste del cráter Jezero y que oficialmente se denomina Jezero Mons.
 En el centro de la imagen podemos ver el cráter que se encuentra sobre la cima de Jezero Mons, con una forma ovalada y una abertura. En la esquina inferior izquierda podemos observar también una parte del perfil del cráter Jezero, notable especialmente por su superficie más llana y suave que el terreno que le rodea. Imagen cortesía de NASA/JPL/ASU.
En el centro de la imagen podemos ver el cráter que se encuentra sobre la cima de Jezero Mons, con una forma ovalada y una abertura. En la esquina inferior izquierda podemos observar también una parte del perfil del cráter Jezero, notable especialmente por su superficie más llana y suave que el terreno que le rodea. Imagen cortesía de NASA/JPL/ASU.Desde el sitio de aterrizaje del Perseverance, Jezero Mons domina una buena parte del horizonte sureste gracias a sus dos kilómetros de altura. Durante años, los mapas creados a partir de los datos orbitales tomados por las distintas sondas clasificaban esta inmensa mole como parte de lo que llamamos basamento, la corteza antigua y completamente cubierta de cráteres que forma el borde del cráter y sobre el que este fue excavado.
Pero la forma y el tamaño de este “monte” ya había levantado anteriormente la suspicacia de algunos científicos, pero se necesitaban más datos para confirmar que podríamos estar ante algo más que un simple relieve. Para ello, en esta investigación se han ayudado de los datos tomados por misiones anteriores para poder comprender mejor a este sospechoso. Pero, ¿qué pistas han encontrado en estos datos? Os las desgrano una a una.
El primer aspecto en el que se fijaron es la morfometría -término bajo el que se esconde el estudio de la forma de la montaña. Jezero Mons es una estructura prácticamente cónica con unos 21 kilómetros de diámetro y con un cráter desfigurado -poco circular en este caso, y con una abertura- en su cima. No solo se quedaron aquí, sino que aprovecharon para medir las pendientes de las laderas, la proporción entre su anchura y la altura y el tamaño del cráter de su cima con relación a la base para poder comparar edificios volcánicos en la Tierra y en Marte.
Los resultados fueron apabullantes. Jezero Mons se ajustaba a la perfección al perfil de otros volcanes compuestos -o estratovolcanes- marcianos como Zephyria Tholus y Apollinarus Tholus y también es muy parecido al del monte Sidley, un gran pico volcánico -bueno, de hecho el volcán más alto- de nuestra Antártida terrestre.
Pero en lo que desde luego no se parece en nada es a los volcanes en escudo, con sus bases muy anchas y sus suaves laderas -como Mauna Loa, en Hawái- y que dominan el espectro volcánico de Marte, ni tampoco se parece a un cráter en pedestal -esos cráteres “formados” sobre una meseta elevada-. Así que parece que su forma dice a gritos la palabra estratovolcán, esos que en nuestro planeta pueden dar lugar a violentas erupciones volcánicas.
 En esta imagen podemos ver perfectamente el perfil de Jezero Mons visto desde la posición del Perseverance en los primeros 100 días de su misión. Es llamativo como ocupa la mayor parte del horizonte, ya que no solo es una forma prominente, sino que se encuentra elevado por estar situado sobre las tierras altas de Marte, mientras que el Perseverance está en el interior de un cráter excavado sobre estas. Imagen cortesía de NASA/JPL/NASA/ASU/MSSS.
En esta imagen podemos ver perfectamente el perfil de Jezero Mons visto desde la posición del Perseverance en los primeros 100 días de su misión. Es llamativo como ocupa la mayor parte del horizonte, ya que no solo es una forma prominente, sino que se encuentra elevado por estar situado sobre las tierras altas de Marte, mientras que el Perseverance está en el interior de un cráter excavado sobre estas. Imagen cortesía de NASA/JPL/NASA/ASU/MSSS.La segunda pista en la que se han fijado los científicos es en sus propiedades “térmicas”. Y me explico: Usando los datos del instrumento THEMIS de la sonda Mars Odyssey han medido lo que conocemos como inercia térmica, la capacidad de los materiales para retener el calor. El basamento rocoso de Marte, sólido y denso, se calienta de día y sigue caliente durante la noche marciana, dando valores de inercia térmica altos. En contraste, los materiales sueltos y de grano fino como pueden ser la arena o la ceniza volcánica no son buenos conductores, de tal forma que se calientan y enfrían muy rápidamente, lo que da como resultado valores bajos de inercia térmica.
La superficie de Jezero Mons tiene una inercia térmica baja muy característica. Esto sugiere que no está formada por coladas de lava sólidas y endurecidas, sino que está cubierta por una potente capa de materiales finos y poco consolidados, un detalle que es una señal perfecta de depósitos de ceniza formados a partir de erupciones explosivas.
La tercera y última pista sobre la que se apoya este descubrimiento es la mineralogía. Gracias al instrumento CRISM de la Mars Reconaissance Orbiter, se pueden distinguir minerales por como reflejan la luz -al fin y al cabo es un espectrómetro- permitiendo a los científicos crear un mapa de la composición química de la montaña. Y han descubierto que sus laderas son ricas en piroxenos, un mineral que es uno de los más habituales en las rocas volcánicas de tonos oscuros que cubren la superficie de Marte.
Y, además, se han encontrado también minerales de alteración alrededor del cráter de la cima. Los investigadores han hallado arcillas e incluso un área con sílice opalino (sílice hidratada). Estos minerales no serían productos volcánicos primarios, sino que se forman cuando los gases volcánicos, el agua y la roca caliente interactúan entre sí.
De hecho, su presencia sugiere la existencia en el pasado de actividad hidrotermal, con quizás aguas termales y fumarolas sobre la cima. Estos ambientes están considerados hoy día como objetivos primordiales en la búsqueda de vida, ya que nos aportan unos ingredientes importantes para el desarrollo de esta: agua, energía, y nutrientes.
Si ya de por sí estas tres pistas parecen apuntar claramente al origen volcánico de Jezero Mons, todavía queda quizás una de las evidencias más fuertes: una relación física entre el fondo del cráter y el volcán. Las imágenes de alta resolución muestran varios depósitos amplios con formas lobuladas que parecen fluir desde el flanco noroeste de la montaña y desparramarse sobre la llanura que forma el fondo del cráter.
 Detalle del cráter de la cima de Jezero Mons. Si nos fijamos, el número de cráteres de impacto que hay sobre este es excepcionalmente bajo si lo comparamos con los terrenos circundantes, lo que quiere decir que probablemente su formación es más reciente o que al menos su superficie ha sido renovada por otros procesos… como puede ser el vulcanismo. Imagen cortesía de NASA/JPL/Universidad de Arizona.
Detalle del cráter de la cima de Jezero Mons. Si nos fijamos, el número de cráteres de impacto que hay sobre este es excepcionalmente bajo si lo comparamos con los terrenos circundantes, lo que quiere decir que probablemente su formación es más reciente o que al menos su superficie ha sido renovada por otros procesos… como puede ser el vulcanismo. Imagen cortesía de NASA/JPL/Universidad de Arizona.Estos depósitos se superponen sobre el terreno fracturado y antiguo del fondo del cráter y tienen un aspecto de debris flows, o flujos de derrubios en castellano. Bajo este nombre se esconden procesos en los que masas de tierra empapadas en agua y fragmentos de roca fluyen ladera abajo, pero también podrían ser la señal de flujos piroclásticos -corrientes de gas y materiales volcánicos a altas temperaturas- que descienden por las laderas de los volcanes durante una erupción explosiva.
Esta conexión física da un sentido a cómo podrían haber llegado los materiales volcánicos al centro del cráter Jezero. Y es que este volcán no sería simplemente una montaña lejana, sino que era un proceso activo capaz de depositar grandes cantidades de ceniza y otros materiales a la cuenca del lago que albergó antaño el cráter.
Identificar Jezero Mons como un volcán no solo nos ayuda a resolver un enigma geológico, sino que aporta una visión totalmente diferente a como era el ambiente en este lugar. No era solo un lago tranquilo, era un paisaje cambiante en el que la actividad volcánica podría enriquecer el agua con minerales y calor, haciéndolo más adecuado para el desarrollo de la vida.
Pero hay todavía una ramificación más para este estudio y que entronca con la misión del Perseverance: El rover está recogiendo muestras que en algún momento vendrán a nuestro planeta -aún no sabemos cuándo-, pero si algunas de estas están directamente relacionadas con Jezero Mons, su valor científico se dispara: Son muestras de un volcán marciano concreto.
Y es que ese detalle nos permitiría datar con precisión cuál es su edad gracias a las técnicas de datación radiométrica, pero, además, también contemporizar mejor los materiales que vemos en el fondo del cráter Jezero y a calibrar nuestras escalas de edad de la superficie de Marte que actualmente dependen de contar cráteres, ya que no hemos podido traer muestras todavía a la Tierra.
¿Qué más sorpresas nos deparará la misión del Perseverance? La verdad es que no lo sabemos, pero, por si acaso, mantengamos los ojos bien abiertos… Marte siempre está dispuesto a sorprendernos incluso a plena luz del día.
Bibliografía:
Cuevas-Quiñones, S. C., Wray, J. J., Rivera-Hernández, F., & Adler, J. B. (2025). Evidence for a composite volcano on the rim of Jezero crater on Mars. Communications Earth & Environment, 6(1), 340. doi: 10.1038/s43247-025-02329-7
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Un volcán escondido… a la vista de todos se ha escrito en Cuaderno de Cultura Científica.
Los árboles pueden ayudarnos a predecir erupciones volcánicas
 Los satélites de NASA podrían detectar cambios en la vegetación desde el espacio antes de la erupción de un volcán. Imagen: Jeff Schmaltz / MODIS / NASA
Los satélites de NASA podrían detectar cambios en la vegetación desde el espacio antes de la erupción de un volcán. Imagen: Jeff Schmaltz / MODIS / NASA
El diez por ciento de la población mundial vive en zonas susceptibles a peligros volcánicos. Sin ir más lejos, yo mismo escribo estas letras a la sombra del gran pico Teide, desde una isla que alberga más de un centenar de conos volcánicos. Aquellos que viven bajo sus laderas se enfrentan a rocas expulsadas, toneladas de polvo y material magmático, gases tóxicos e inflamables, nubes de ceniza, terremotos, deslizamientos de tierra e incluso tsunamis provocados por esa actividad. Afortunadamente, la ciencia ha avanzado de manera notable en las últimas décadas desarrollando conocimiento y tecnologías que hacen posible la detección e interpretación de las señales precursoras que anticipan una erupción. Un buen ejemplo de esta ciencia predictiva lo encontramos en la erupción de la isla de la Palma en 2021 que permitió minimizar el número de víctimas gracias a la alerta temprana de los vulcanólogos. Sin embargo, debemos reconocerlo, es un campo científico que está dando sus primeros pasos, aún estamos en pañales y cualquier ayuda que obtengamos será bienvenida.
Los fenómenos naturales no surgen de la nada, siempre existe un proceso de efectos y consecuencias que desencadenan una reacción. En la mayoría de los volcanes la erupción se produce «cuando el depósito en el que se almacena el magma alcanza una presión determinada y rompe, produciendo cambios de forma y/o terremotos, por lo que su vigilancia, permite en ocasiones, realizar pronósticos a corto plazo sobre una posible erupción». En los centros de investigación y seguimiento los vulcanólogos trabajan atentos a cualquier cambio que apunte al inicio de la actividad y a una posible erupción a corto o medio plazo. Esos indicadores incluyen «actividad sísmica, cambios en la altura del terreno y, especialmente, emisiones de gases como el dióxido de azufre o el dióxido de carbono».
Los compuestos de azufre son algo más fáciles de detectar desde el espacio, utilizando satélites en órbita, mientras que las emisiones de dióxido de carbono son mucho más difíciles de registrar y, a menudo, es necesario desplazarse en persona hasta el volcán con equipos de detección, con el riesgo que esto implica. Poder detectar con precisión emisiones de CO2 sería un paso en la dirección adecuada ya que el dióxido de carbono precede a la emisión de su homólogo sulfúrico y constituye uno de los primeros indicios de que el volcán está activo.
«Los volcanes emiten mucho dióxido de carbono», explica el vulcanólogo Robert Bogue en la web de NASA, «pero la cantidad de dióxido de carbono que ya hay presente en la atmósfera suele ser tan alta que a menudo resulta difícil medir específicamente el dióxido de carbono volcánico. Las grandes erupciones pueden expulsar suficiente dióxido de carbono como para registrarlas desde el espacio, con sensores como el Observatorio Orbital de Carbono 2 de la NASA, pero la detección de estas señales de alerta mucho más tenues resulta muy complicada. Un volcán que emita una modesta cantidad de dióxido de carbono que podrían presagiar una erupción no aparecerá en las imágenes satelitales».
 El magma ascendente calienta una poza de agua en Costa Rica, cerca del volcán rincón de la Vieja y libera dióxido de carbono indicando un aumento de su actividad. Foto: Alessandra Baltodano / Universidad Chapman / NASA
El magma ascendente calienta una poza de agua en Costa Rica, cerca del volcán rincón de la Vieja y libera dióxido de carbono indicando un aumento de su actividad. Foto: Alessandra Baltodano / Universidad Chapman / NASA
Sin embargo, hace solo unos días la agencia espacial NASA ha publicado un artículo en su web oficial en el que descubrimos una ayuda inesperada para registrar esas emisiones de CO2: los árboles se vuelven más verdes, y eso sí que se puede detectar desde el espacio.
Conforme el magma volcánico asciende, liberando dióxido de carbono hacia la superficie, los árboles que absorben ese CO2 adquieren un color verde más intenso. Estos cambios en la tonalidad son visibles en imágenes de satélites, instrumentos meteorológicos y vehículos aerotransportados. «La detección remota del enverdecimiento de la vegetación por dióxido de carbono proporciona a los científicos otra herramienta que, sumada a las ondas sísmicas y los cambios en la altura del suelo, nos ofrecen una idea más clara de lo que está ocurriendo bajo el volcán».
En la actualidad contamos con numerosos satélites que podrían servir para realizar este tipo de análisis, el Landsat 8,el satélite Terra, el Sentinel-2 y otras sondas de observación terrestre y meteorológica a las que se pueden sumar proyectos aerotransportados como el Experimento Unificado de Validación Aérea: Tierra-Océano.
Los proyectos que ya se están llevando a cabo en este sentido cuentan con un añadido extra y sirven como experimentos multidisciplinares en los que, además de en la vulcanología podrían ser de utilidad en ecología y estudio de las consecuencias del calentamiento global. «Será muy interesante estudiar no solo la respuesta de los árboles al dióxido de carbono volcánico como alerta temprana de una erupción, sino también su capacidad de absorción, como una ventana al futuro de la Tierra cuando todos los árboles del planeta estén expuestos a altos niveles de dióxido de carbono».
Por supuesto esta señal natural en el color de los árboles tiene sus limitaciones, por ejemplo en volcanes donde la vegetación a su alrededor es escasa o inexistente. «Ninguna de las señales que utilizamos actualmente es la gran solución y monitorear los efectos del dióxido de carbono volcánico en los árboles tampoco será la panacea. Pero sí podría ser un punto de inflexión».
Referencias científicas y más información:
James Riordon «NASA Satellite Images Could Provide Early Volcano Warnings» NASA’s Earth Science News Team (2025)
Sascha Pare «The closer a volcano is to erupting, the greener the trees around it look from space» Live Science (2025)
Sobre el autor: Javier «Irreductible» Peláez es escritor y comunicador científico multimedia. Es ganador de tres premios Bitácoras, un premio Prisma a la mejor web de divulgación científica y un Premio Ondas al mejor programa de radio digital.
El artículo Los árboles pueden ayudarnos a predecir erupciones volcánicas se ha escrito en Cuaderno de Cultura Científica.
Valle Salado: ¿de dónde viene la sal? ¿De dónde viene el agua?

¿Qué tienen en común un paisaje espectacular, un fósil milenario y una cantera abandonada? Todos forman parte del patrimonio geológico, un testimonio de la historia de la Tierra con un gran valor científico, educativo, cultural y estético, y base del patrimonio natural. Sin embargo, su importancia continúa siendo poco apreciada.
Para acercar las distintas aproximaciones del patrimonio geológico a la sociedad, los días 26, 27 y 28 de marzo se celebró la quinta edición de las jornadas divulgativas “Geología para poetas, miopes y despistados. Patrimonio patrimonio”. Organizadas por el grupo de investigación consolidado Procesos Hidro-Ambientales (HGI) de la Facultad de Ciencia y Tecnología de la Universidad del País Vasco (UPV/EHU), estas jornadas contaron con la colaboración del Vicerrectorado del Campus de Bizkaia, la Cátedra de Cultura Científica de la UPV/EHU, el Geoparque de la Costa Vasca / Geoparkea y el Ente Vasco de la Energía (EVE).
El catedrático de hidrogeología de la UPV/EHU, Iñaki Antigüedad, explica en esta charla cómo se combinan los procesos del agua y la química de las rocas para dar lugar al Valle Salado de Añana, un lugar en el que se extrae sal desde hace 7000 años y que hay que visitar al menos una vez en la vida.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Valle Salado: ¿de dónde viene la sal? ¿De dónde viene el agua? se ha escrito en Cuaderno de Cultura Científica.
Algunas células tumorales roban mitocondrias como estrategia de supervivencia
En 2023, un equipo de investigadores del UT Southwestern Medical Center de Dallas observó que las células tumorales «roban» mitocondrias a los linfocitos T que actúan contra ellas.
 Micrografía de un linfocito T humano (también llamado célula T) del sistema inmune de una persona sana. Fuente: NIAID/NIH – NIAID Flickr’s photostream, Dominio público / Wikimedia Commons
Micrografía de un linfocito T humano (también llamado célula T) del sistema inmune de una persona sana. Fuente: NIAID/NIH – NIAID Flickr’s photostream, Dominio público / Wikimedia CommonsDesarrollar tratamientos contra el cáncer se ha convertido en un reto a nivel mundial, y en cierta medida contagiados por esta necesidad recibimos constantemente información sobre los trabajos que se publican en torno a esta enfermedad. Últimamente, además de estudiar la célula tumoral, se están desarrollando grandes progresos en el campo de conocimiento que estudia las células y moléculas que rodean el tumor, también conocido como microambiente tumoral. Es obvio que la célula tumoral es el actor principal del desarrollo tumoral, pero es de suma importancia conocer los mecanismos por los cuales el tumor manipula su entorno para poder progresar. En el microambiente tumoral encontramos gran cantidad de tipos celulares y moléculas que participan directamente en el avance de la enfermedad y tienen sus propias peculiaridades dependiendo del tipo de tumor, pero hay algunos elementos comunes a todos ellos como son las células que forman los vasos sanguíneos (llamadas células endoteliales), los fibroblastos y diversos tipos de células del sistema inmune, así como moléculas que se encuentran entre las células. En cuanto al sistema inmune se refiere, se trata de un sistema extremadamente complejo que comprende muchos subtipos celulares y una gran variedad de moléculas y la inmunooncología se ha convertido en un subapartado del microambiente tumoral.
El eje PD-L1/PD1Se sabe que algunos tumores desarrollan mecanismos para burlar o reducir el sistema inmune y que nos quedamos sin defensas ante el crecimiento de algunos tipos de cánceres. En este sentido, el estudio de la inmunooncología vivió un hito importante en el año 2018 con la concesión del Premio Nobel de Medicina y Fisiología a James P. Allison y Tasuku Honjo. Estos dos investigadores descubrieron y describieron los puntos de control (en inglés check-points) que tienen las células del sistema inmune para combatir el cáncer. El mecanismo más conocido es el eje PD-L1/PD1, donde la proteína PD-L1 se expresa en la membrana de las células tumorales y la proteína PD1 en la membrana de los linfocitos T, células cruciales para el buen funcionamiento del sistema inmune.
Cuando un tumor está en proceso de crecimiento, se inicia un proceso inflamatorio por el cual los linfocitos T se acercan a la zona tumoral. Las células tumorales son reconocidas como células con aberraciones y los linfocitos T las atacan y anulan directamente. Al asociar el PD-L1 de las células tumorales al PD-1 de los linfocitos T, las células del sistema inmune se inactivan y son incapaces de atacar el tumor, dejando fuera de juego a los linfocitos T. Tras este descubrimiento, se han creado anticuerpos tanto frente a PD-L1 como frente a PD1 para inhibir la unión de ambas moléculas y de esta manera se evita el bloqueo del sistema inmune; se trata de la inmunnoterapia más común que hoy en día se utiliza en la clínica.
Linfocitos T modificadosAdemás de los inhibidores de los puntos de control, también se han desarrollado terapias basadas en linfocitos T modificados. En este tipo de inmunoterapia también conocida como terapia basada en linfocitos CAR-T (en inglés Chimeric Antigen Receptor-T cell), primero se realiza una biopsia del tumor y se identifican fragmentos específicos de proteínas (antígenos) que solo aparecen en las células tumorales del paciente. A continuación, se extraen los linfocitos T del cuerpo del paciente y en el laboratorio se programan para que ataquen exclusivamente los antígenos tumorales que se han identificado previamente. A continuación, se vuelven a introducir los linfocitos T para atacar las células tumorales.
Tanto los fármacos basados en puntos de control como las terapias basadas en linfocitos modificados han sido exitosos en algunos casos, pero han fracasado a menudo por agotamiento de los linfocitos, es decir, los linfocitos T acaban exhaustos en la lucha contra la célula tumoral y quedan incapacitados para realizar su función. Pero dos investigaciones recientes podrían arrojar más luz sobre el concepto linfocitos exhaustos que nos serviría para diseñar terapias más eficaces.
Linfocitos exhaustos y robo de mitocondriasEn 2023, un equipo de investigadores del UT Southwestern Medical Center de Dallas observó que las células tumorales «roban» mitocondrias a los linfocitos T que actúan contra las células tumorales en el interior del tumor. Formando unas finas estructuras con forma de finos tubos llamadas nanotubos, las células tumorales emiten unas prolongaciones que contactan con los linfocitos T que tienen en su entorno más cercano y absorben sus mitocondrias funcionales. Entre las mutaciones que sufren las células tumorales aparecen frecuentemente las relacionadas con las mitocondrias. Aunque estas mutaciones se han relacionado con la progresión del cáncer y los cambios beneficiosos que experimenta metabólicamente la célula tumoral, en algunos casos, dichas mutaciones comprometen la supervivencia de las células tumorales. De esta manera, algunas células tumorales son capaces de utilizar estos nanotubos para “robar” las mitocondrias funcionales de los linfocitos T.
En un principio se pensaba que este tipo de transporte se producía en una sola dirección, pero un grupo de investigación formado por científicos japoneses ha descubierto que es bidireccional. Investigando diferentes tipos de tumores, han descubierto que algunas células tumorales son capaces de transmitir sus mitocondrias defectuosas a los linfocitos T mientras «roban» los sanos de los linfocitos. Esta transferencia se realiza a través de los mencionados nanotubos y también por la emisión de pequeñas vesículas. Así, los linfocitos T pierden sus mitocondrias sanas y, en su lugar, se les transfieren las mitocondrias defectuosas de las células tumorales. De esta manera los linfocitos T pierden su funcionalidad porque la mitocondria es la fuente más importante que posee la célula para obtener energía y el principal orgánulo para canalizar las principales rutas metabólicas.
Estos trabajos nos permiten profundizar en el conocimiento sobre el proceso de agotamiento de los linfocitos y añadir a las terapias existentes nuevos tratamientos que dificultarían los procesos de transferencia de mitocondrias entre los linfocitos y las células tumorales.
Referencias bibliográficas:
Cárdenas-Oyarzo, Areli M.; Bocchieri-Oyarce, Pamela A.; Méndez-Laport, Cristian R.; Zolezzi, Juan M.; Ríos, Juvenal A. (2022) Immune checkpoint inhibitors. A breakthrough in cancer therapy. Rev Med Chil, 150, 1, 93-99. doi: 10.4067/S0034-98872022000100093
Ikeda, Hideki et al. (2025) Immune evasion through mitochondrial transfer in the tumour microenvironment Nature, 638, 225-236. doi: 10.1038/s41586-024-08439-0
Wang, Sheng-Fan; Tseng, Ling-ming; Lee, Hsin-Chen (2023) Role of mitochondrial alterations in human cancer progression and cancer immunity Journal of Biomedical Science, 30, 61. doi: 10.1186/s12929-023-00956-w
Zhang, Hongyi et al. (2023) Systematic investigation of mitochondrial transfer between cancer cells and T cells at single-cell resolution Cancer Cell, 9, 41, 1788-1802. doi: 10.1016/j.ccell.2023.09.003
Sobre el autor: Iker Badiola Etxaburu es doctor en biología, Profesor Pleno en la Facultad de Medicina y Enfermería de la UPV/EHU, y director de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Algunas células tumorales roban mitocondrias como estrategia de supervivencia se ha escrito en Cuaderno de Cultura Científica.
Extrañas faunas que inspiran animes titánicos
Existe una serie de animación japonesa que a mí me encantó cuando la vi, aunque tengo cuidado a la hora de recomendarla porque no es apta para menores de 18 años (por la violencia y la sangre, no penséis mal), que te está bombardeando continuamente con spoilers escondidos desde el opening (es decir, la canción de apertura) del primer episodio. Su título es Shingeki no Kyojin, más conocida por estos lares como Ataque a los Titanes (una traducción mal hecha a propósito para evitar hacer el primer gran spoiler). Sin entrar demasiado en detalles sobre la trama, la historia trata sobre una ciudad amurallada que parece anclada en la edad media, pero con ciertos adelantos modernos (al estilo steam punk), que es atacada por unos gigantes hambrientos de carne humana, a los que llaman titanes, contra los que deben combatir, literalmente, a espadazos en la nuca.
Vale, seguro que os estáis preguntando qué demonios tiene que ver esto con la Geología. Pues para daros una explicación, voy a haceros unos spoilers yo también. Empecemos con el tercer opening de los ocho que hicieron (a cuál más épico y cargado de spoilers, por cierto), donde vemos al final desfilar una serie de animales prehistóricos con los que nos intentan hacer creer que el “gen” que transforma a los seres humanos en titanes ha existido siempre y ha afectado a diferentes seres vivos durante millones de años. Pues uno de los bichos que aparece durante apenas un par de segundos es una especie de gamba que ha tomado demasiados esteroides.
 A) Captura de pantalla del tercer opening del anime de Shingeki no Kyojin, donde aparece un extraño animal acuático. B) Página del tomo 137 del manga, momento en que uno de los personajes habla sobre el origen de la vida, apareciendo más organismos acuáticos con formas muy curiosas. C) Captura de pantalla del tráiler de la cuarta temporada del anime en el que reaparece el gusano acuático de la imagen anterior. Fuentes: A y C, Estudio Mappa / fair use; B, Kodansha / fair use. A, B y C vía Crunchyroll
A) Captura de pantalla del tercer opening del anime de Shingeki no Kyojin, donde aparece un extraño animal acuático. B) Página del tomo 137 del manga, momento en que uno de los personajes habla sobre el origen de la vida, apareciendo más organismos acuáticos con formas muy curiosas. C) Captura de pantalla del tráiler de la cuarta temporada del anime en el que reaparece el gusano acuático de la imagen anterior. Fuentes: A y C, Estudio Mappa / fair use; B, Kodansha / fair use. A, B y C vía CrunchyrollPero esta no es la única vez que aparece este extraño animal en la obra. Si avanzamos hacia el final de la misma, hay un momento en que uno de los personajes intenta darle una explicación a todo lo que está pasando en ese mundo fantástico. Para ello, directamente se retrotrae a los orígenes de la vida en nuestro planeta, volviendo a aparecer esa enorme gamba. Aunque, en este momento, toma protagonismo otro bicho aún más extraño, una especie de gusano con peinado estilo punk, que, al parecer, es el culpable de todo lo que sucede en Shingeki no Kyojin.
Hasta aquí podríamos pensar que estos bichos tan raros han salido, directamente, de la mente artística del autor del manga original, Hajime Isayama. Pero, en realidad, este hombre se basó en hechos reales para inspirarse. En concreto, se fijó en una fauna muy particular y que supone uno de los hitos de la vida en nuestro planeta: la Fauna de Burgess Shale.
 Visita guiada al yacimiento de Burgess Shale, en la Columbia Británica (Canadá), donde se enseñan al público asistente algunos de los ejemplares fósiles encontrados. Foto: Ryan Creary / Parques Nacionales de Canadá, vía IUGS
Visita guiada al yacimiento de Burgess Shale, en la Columbia Británica (Canadá), donde se enseñan al público asistente algunos de los ejemplares fósiles encontrados. Foto: Ryan Creary / Parques Nacionales de Canadá, vía IUGSPara comenzar nuestra historia, debemos viajar hasta la Columbia Británica, en Canadá, a una cantera cercana al monte Burgess. Allí, a comienzos del siglo XX, se encontró un yacimiento con miles de fósiles en los que aparecen preservadas las partes blandas de unos organismos que vivieron en un mar poco profundo a comienzos y mediados del Periodo Cámbrico, hace más de 520 millones de años. Gracias a esta conservación excepcional, se ha podido reconstruir el aspecto de estos seres vivos ancestrales. Y aquí es donde aparecen las sorpresas.
 A la izquierda de la imagen, reconstrucción de un ambiente marino precámbrico con organismos de cuerpo blando; a la derecha, reconstrucción del fondo marino cámbrico con los seres vivos más complejos encontrados en el yacimiento de Burgess Shale. Ilustración: D.W. Miller / Smithsonian Institution / fair use
A la izquierda de la imagen, reconstrucción de un ambiente marino precámbrico con organismos de cuerpo blando; a la derecha, reconstrucción del fondo marino cámbrico con los seres vivos más complejos encontrados en el yacimiento de Burgess Shale. Ilustración: D.W. Miller / Smithsonian Institution / fair useEstos organismos son muy diferentes de los que vivieron durante el Precámbrico. Estos últimos eran seres de cuerpo blando, donde unos pocos parecen que nadaban libres, pero la mayoría posiblemente o bien vivían fijos en el fondo marino, creciendo en la vertical, o bien se desplazaban por encima del barro de ese fondo del mar. Sin embargo, muchos de los ejemplares del Cámbrico tenían un caparazón duro y resistente; desarrollaron cuerpos complejos con grandes mandíbulas, cuerpos segmentados, varias filas de patas o pinchos defensivos; aparecen morfologías que son coherentes con seres nadadores veloces; y hay evidencias que muchos organismos empezaron a enterrarse en el barro del fondo, pudiendo incluso vivir en madrigueras.
Es decir, en el Cámbrico la vida se hizo más compleja, la cadena trófica empezó a gestarse, apareciendo organismos que actuaban como depredadores (los que tenían mandíbulas grandes y fuertes o apéndices para atrapar la comida a distancia) y otros como presas (algunas de las cuales tenían estructuras defensivas, como caparazones duros o espinas afiladas) y los seres vivos empezaron a enterrarse en el sedimento, explorando nuevos nichos ecológicos hasta entonces desconocidos. A todos estos cambios faunísticos se les conoce en Geología como la Explosión del Cámbrico, ya que en apenas unos 10 millones de años se produjo una auténtica revolución biológica que significó el pistoletazo de salida de la evolución biótica gracias a la cual el ser humano está aquí.
A lo largo de todo el siglo XX han aparecido otros yacimientos cámbricos con organismos similares a los encontrados en Canadá en otros lugares del mundo, como Groenlandia o China. Incluso, hoy en día, se siguen encontrando otras localidades fosilíferas que nos permiten ir sumando nuevas formas de esta vida compleja primitiva al listado. Pero en todas las ocasiones nos referimos a estos lugares como yacimientos o fauna tipo Burgess Shale, en honor a este primer afloramiento canadiense.
 Ejemplos de los fósiles encontrados en el yacimiento de Burgess Shale. A) Anomalocaris, Foto: J.B. Caron/ Royal Ontario Museum via IUGS; B) Hallucigenia, Foto: Maura McCarthy / Smithsonian Institution / fair use C) Opabinia, Foto. Han Zeng / Smithsonian National Museum of Natural History
Ejemplos de los fósiles encontrados en el yacimiento de Burgess Shale. A) Anomalocaris, Foto: J.B. Caron/ Royal Ontario Museum via IUGS; B) Hallucigenia, Foto: Maura McCarthy / Smithsonian Institution / fair use C) Opabinia, Foto. Han Zeng / Smithsonian National Museum of Natural HistoryY volviendo un poco a los bichos que aparecen en Shingeki no Kyojin, la gamba dopada es un Anomalocaris, un artrópodo primitivo que podía llegar a medir varios metros de longitud que se convirtió en el mayor depredador marino del Cámbrico, capturando a sus presas con sus enormes mandíbulas, tan poderosas que eran capaces de romper los caparazones defensivos de animales como los trilobites. Pero para bicho anómalo, tenemos el gusano punki. En este caso, se trata de la Hallucigenia, un antepasado lejano de los gusanos, que tenía dos filas de tubos filamentosos que actuaban como patas y una serie de espinas afiladas en la espalda. Aunque si este os ha hecho alucinar, el que a mí me flipa de verdad es la Opabinia, otro artrópodo primitivo que, en este caso, tenía cinco ojos compuestos que sobresalían de su cabeza y un apéndice largo al final del cual aparecían dos pinzas que, supuestamente, eran las mandíbulas.
Muchos de los organismos de la Fauna de Burgess Shale no se han podido clasificar de forma segura en ningún clado, animal o vegetal, actual. Así que podrían ser “pruebas evolutivas” que no tuvieron continuidad más allá del Cámbrico. Sin embargo, todos los grupos faunísticos actuales proceden de estas primeras formas de vida compleja. Así que no me extraña que Isayama escogiese unos de estos animales tan raros para darle una explicación al origen de sus monstruos terribles. Además, me da una excusa para que yo pueda fantasear con que provengo de una de esas gambas con cinco ojos que parece salida de una pesadilla de H. P. Lovecraft.
Para saber más:
IUGS – Burgess Shale Paleontological Record
Wikipedia – Esquisto de Burgess
The Burgess Shale Geoscience Foundation
Royal Ontario Musem (ROM) – The Burgess Shale
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Extrañas faunas que inspiran animes titánicos se ha escrito en Cuaderno de Cultura Científica.
El problema del ascensor
Proponemos un problema de lógica relacionado con un ascensor que asciende trasladando a siete pasajeras.
 Freepik
FreepikEnunciado del problema
Estamos en un edificio de veinte pisos. En un trayecto ascendente, el ascensor ha transportado a siete personas (Alicia, Beatriz, Cecilia, Daniela, Enara, Fátima y Gabriela). Se conocen las siguientes informaciones:
- Cada persona ha subido al menos dos pisos, pero ninguna ha subido la misma cantidad de pisos;
- Como mucho, una persona ha cruzado el umbral (entrando o saliendo) del ascensor en un piso determinado;
- El ascensor no se ha parado en el piso 17;
- Las puertas del ascensor se han abierto (para recoger o dejar a una persona) en más pisos impares que pares;
- Alicia ha sido la última persona en entrar y la segunda en salir del ascensor. Beatriz ha subido justo antes que Cecilia y justo después de Daniela, y ha subido más pisos que Daniela. Enara ha subido exactamente el doble de pisos que Fátima y ha salido antes de que Gabriela haya entrado en el ascensor. Gabriela no ha sido la última en salir.
¿En qué piso han entrado y salido Alicia, Beatriz, Cecilia, Daniela, Enara, Fátima y Gabriela?
Solución del problema
Alicia ha sido la última pasajera en subir y la segunda en bajar, así que nadie ha entrado al ascensor después de ella y solo una persona ha salido antes. Y ha subido al menos dos pisos.
Enara ha salido antes de que Gabriela haya entrado en el ascensor, así que Enara debe ser la pasajera que ha salido del ascensor antes que Alicia. Esto significa que Fátima ha entrado en el ascensor en algún momento antes que Alicia y ha salido en algún momento después de ella, lo que significa que ha subido al menos cuatro pisos. Enara ha subido exactamente el doble de pisos que Fátima, así que Enara ha subido al menos ocho pisos. Supongamos que Fátima ha subido solo cuatro pisos, entonces tenemos como mínimo esta situación:
Piso 1: Enara entra en el ascensor
Piso 9: Enara sale (porque ha subido ocho pisos)
Piso 10: Gabriela entra
Piso 11: Fátima entra
Piso 12: Alicia entra (ya no sube nadie más a partir de este piso; ella es la última en acceder al ascensor. Así, el resto de los pisos, si el ascensor se detiene, solo son de bajada)
Piso 13: Nadie sale (porque Alicia es la segunda en bajar y Enara ya ha salido del ascensor. Es decir, nadie puede salir antes de que Alicia lo haga)
Piso 14: Alicia sale (así, ha subido exactamente dos pisos)
Piso 15: Fátima sale (porque ha subido cuatro pisos)
Piso 17: Nadie sube ni baja del ascensor
Este esquema “mínimo” deja exactamente cuatro pisos (16, 18, 19 y 20) para que bajen cuatro pasajeras (Beatriz, Cecilia, Daniela y Gabriela), por lo que parece ser correcto.
Así, tendríamos ya once paradas (para subida o bajada de pasajeras) conocidas, cinco son impares (1, 9, 11, 15 y 19) y seis son pares (10, 12, 14, 16, 18 y 20). Como el enunciado afirma que el ascensor se ha detenido más veces en pisos impares que en pares más paradas en pisos impares que en pares (y el ascensor abre sus puertas catorce veces), debe de detenerse ocho veces en pisos impares. Por eliminación, solo quedan las plantas 3, 5 y 7.
Es decir, las catorce plantas en las que el ascensor se detiene son:
Piso 1: Enara entra
Piso 3: ¿?
Piso 5: ¿?
Piso 7: ¿?
Piso 9: Enara sale (recorre 8 pisos)
Piso 10: Gabriela entra
Piso 11: Fátima entra
Piso 12: Alicia entra
Piso 14: Alicia sale (recorre 2 pisos)
Piso 15: Fátima sale (recorre 4 pisos)
Piso 16: ¿?
Piso 18: ¿?
Piso 19: ¿?
Piso 20: ¿?
Como Alicia es la última en entrar al ascensor (y lo hace en el piso 12), Daniela, Beatriz y Cecilia (en este orden, según se dice en el enunciado) entran en el ascensor en los pisos 1, 3 y 5, respectivamente:
Piso 1: Enara entra
Piso 3: Daniela entra
Piso 5: Beatriz entra
Piso 7: Cecilia entra
Piso 9: Enara sale (recorre 8 pisos)
Piso 10: Gabriela entra
Piso 11: Fátima entra
Piso 12: Alicia entra
Piso 14: Alicia sale (recorre 2 pisos)
Piso 15: Fátima sale (recorre 4 pisos)
Piso 16: ¿?
Piso 18: ¿?
Piso 19: ¿?
Piso 20: ¿?
Además, como Beatriz sube más pisos que Daniela, Daniela debe bajar en el piso 16 (sube así trece pisos; Daniela no puede bajar en el piso 18 porque recorrería quince pisos y Beatriz no podría subir más que ella) y Beatriz baja entonces en el 19 o el 20 (subiendo catorce o quince pisos).
Como dos personas no pueden subir la misma cantidad de pisos, Gabriela (que ha entrado en el ascensor en el piso 10) no puede bajar en el 18 (porque Enara ha subido ocho alturas). Además, no ha sido la última en salir, así que ha debido salir del ascensor en el piso 19. De este modo, Beatriz sale en el piso 20 y es Cecilia quien baja en el piso 18:
Piso 1: Enara entra
Piso 3: Daniela entra
Piso 5: Beatriz entra
Piso 7: Cecilia entra
Piso 9: Enara sale (recorre 8 pisos)
Piso 10: Gabriela entra
Piso 11: Fátima entra
Piso 12: Alicia entra
Piso 14: Alicia sale (recorre 2 pisos)
Piso 15: Fátima sale (recorre 4 pisos)
Piso 16: Daniela sale (recorre 13 pisos)
Piso 18: Cecilia sale (recorre 11 pisos)
Piso 19: Gabriela sale (recorre 9 pisos)
Piso 20: Beatriz sale (recorre 15 pisos)
Así, finalmente:
- Alicia: entra en el piso 12 y sale en el 14 (sube 2 pisos)
- Beatriz: entra en el piso 5 y sale en el 20 (sube 15 pisos)
- Cecilia: entra en el piso 7 y sale en el 18 (sube 11 pisos)
- Daniela: entra en el piso 3 y sale en el 16 (sube 13 pisos)
- Enara: entra en el piso 1 y sale en el 9 (sube 8 pisos)
- Fátima: entra en el piso 11 y sale en el 15 (sube 4 pisos)
- Gabriela: entra en el piso 10 y sale en el 19 (sube 9 pisos)
Referencias
Going Up, Futility Closet, 20 abril 2025
Virginia McCarthy, Upwardly mobile, Games, abril 1993 (enunciado en la página 62 y solución en la 41)
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
El artículo El problema del ascensor se ha escrito en Cuaderno de Cultura Científica.
¿Cuánta energía se usa en pensar?
Los estudios del metabolismo neuronal revelan el esfuerzo de nuestro encéfalo para mantenernos vivos y las limitaciones evolutivas que esculpieron nuestro órgano más complejo.
Un artículo de Conor Feehly. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Ilustración: Myrian Wares / Quanta Magazine
Ilustración: Myrian Wares / Quanta MagazineAcabas de llegar a casa después de un día agotador. Todo lo que deseas es poner los pies en alto y desconectar viendo lo que sea en la televisión. Aunque esta inactividad pueda parecer un merecido descanso, tu encéfalo no está precisamente relajándose. De hecho, según investigaciones recientes, está consumiendo casi tanta energía como durante tu estresante actividad.
Sharna Jamadar, neurocientífica de la Universidad Monash en Australia, junto con sus colegas, ha revisado investigaciones de su laboratorio y de otros equipos en todo el mundo para estimar el coste metabólico de la cognición —es decir, cuánta energía necesita el encéfalo humano para funcionar. Sorprendentemente, han concluído que las tareas exigentes y dirigidas a un objetivo consumen solo un 5% más de energía que la actividad encefálica en reposo. En otras palabras, usamos el encéfalo solo un poco más cuando estamos concentrados que cuando está en modo de reposo.
A menudo sentimos que gastamos nuestra energía mental en prestar atención y concentrarnos intensamente. Sin embargo, esta nueva investigación se suma a una idea cada vez más aceptada: la mayor parte de la actividad encefálical se dedica al mantenimiento. Aunque muchos neurocientíficos se han centrado históricamente en los procesos cognitivos activos y externos —como la atención, la resolución de problemas, la memoria de trabajo y la toma de decisiones—, cada vez está más claro que bajo esa superficie existe una intensa actividad de procesamiento en segundo plano. Nuestros encéfalos regulan los sistemas fisiológicos clave del cuerpo, distribuyendo recursos donde se necesitan mientras respondemos consciente o inconscientemente a las demandas de un entorno en constante cambio.
 La neurocientífica Sharna Jamadar ha recopilado datos de imágenes por resonancia magnética y tomografía por emisión de positrones simultáneamente para estimar el uso de energía del encéfalo. Foto: Emma Liang
La neurocientífica Sharna Jamadar ha recopilado datos de imágenes por resonancia magnética y tomografía por emisión de positrones simultáneamente para estimar el uso de energía del encéfalo. Foto: Emma Liang“Existe la idea de que el encéfalo sirve para pensar”, comenta Jordan Theriault, neurocientífico de la Universidad de Northeastern que no ha participado en este nuevo análisis. “Pero, desde el punto de vista metabólico, su función principal es gestionar el cuerpo, coordinar y regular los órganos, mantener este sistema tan costoso al que está conectado y enfrentarse a un entorno externo complicado.”
El encéfalo no es una simple máquina de pensar, sino un órgano moldeado por la evolución y, por tanto, sujeto a las estrictas limitaciones energéticas de un sistema biológico. Pensar puede hacernos sentir cansados no porque se nos acabe la energía, sino porque hemos evolucionado para conservar recursos. Este estudio del metabolismo neuronal, combinado con investigaciones sobre la dinámica de los impulsos eléctricos encefálicos, revela las fuerzas evolutivas que compiten entre sí y que explican las limitaciones, el alcance y la eficiencia de nuestras capacidades cognitivas.
El coste de una máquina predictiva
El encéfalo humano es increíblemente costoso de mantener en funcionamiento. Aunque representa solo alrededor del 2% del peso corporal consume el 20% de los recursos energéticos del cuerpo. “Tiene unas demandas metabólicas enormes”, afirma Jamadar. En los bebés, este porcentaje se acerca al 50%.
La energía del encéfalo proviene de una molécula llamada adenosín trifosfato (ATP), que las células producen a partir de glucosa y oxígeno. Una vasta red de finos capilares —se estima que unos 600 kilómetros de vasos sanguíneos— recorre el tejido encefálico para transportar sangre rica en glucosa y oxígeno hacia las neuronas y otras células del encéfalo. Una vez sintetizado dentro de las células, el ATP alimenta la comunicación entre neuronas, que es la base del funcionamiento encefálico. Las neuronas transmiten señales eléctricas hasta sus sinapsis, donde intercambian mensajes moleculares; la intensidad de la señal determina si liberarán esas moléculas (es decir, si “dispararán”). Si lo hacen, esa señal molecular dictará si la siguiente neurona transmitirá el mensaje, y así sucesivamente. Mantener lo que se conoce como potenciales de membrana —voltajes estables a través de la membrana neuronal que mantienen a la célula lista para disparar cuando sea necesario— consume al menos la mitad del presupuesto energético total del encéfalo.
Medir el ATP directamente en el encéfalo humano resulta muy invasivo. Por eso, el equipo de Jamadar revisó estudios, incluidos sus propios resultados, que utilizaron otras formas de estimar el uso de energía – como el consumo de glucosa, medido mediante tomografía por emisión de positrones (PET), y el flujo sanguíneo, evaluado mediante resonancia magnética funcional (fMRI) – para encontrar las diferencias en cómo el encéfalo usa la energía durante las tareas activas y cuando está en reposo. Según Jamadar, cuando se realizan al mismo tiempo, el PET y la fMRI pueden aportar información complementaria sobre cómo el encéfalo consume glucosa. Aunque no se trata de una medida completa del gasto energético encefálico —ya que los tejidos neuronales también pueden convertir ciertos aminoácidos en ATP—, la gran mayoría del ATP del encéfalo proviene del metabolismo de la glucosa.
El análisis de Jamadar muestra que un encéfalo que realiza tareas activas consume apenas un 5% más de energía que uno en reposo. Cuando llevamos a cabo una tarea exigente y orientada a un objetivo —como consultar el horario de autobuses en una ciudad nueva—, aumenta la tasa de activación neuronal en las regiones o redes cerebrales relevantes, como las encargadas del procesamiento visual y del lenguaje. Ese aumento justifica ese 5% adicional; el otro 95% se destina a las funciones metabólicas básicas del encéfalo.
 El neurocientífico Jordan Theriault, de la Universidad Northeastern, cree que el encéfalo es un motor de predicción que siempre está planeando lo que viene después. Foto: Matthew Modoono / Universidad Northeastern
El neurocientífico Jordan Theriault, de la Universidad Northeastern, cree que el encéfalo es un motor de predicción que siempre está planeando lo que viene después. Foto: Matthew Modoono / Universidad NortheasternLos investigadores no saben con exactitud cómo se reparte esa carga energética, pero en las últimas décadas han logrado esclarecer qué hace el encéfalo en segundo plano. “A mediados de los años 90 comenzamos, como disciplina, a darnos cuenta de que en realidad ocurren muchísimas cosas cuando alguien está tumbado en reposo y no está involucrado en ninguna tarea explícita”, explica. “Antes se pensaba que la actividad encefálica en reposo que no estaba relacionada con ninguna tarea era simplemente ruido, pero ahora sabemos que hay mucha información en ese supuesto ruido.”
Gran parte de esa señal procede de la red por defecto del encéfalo, que se activa cuando estamos en reposo o no involucrados en una actividad aparente. Esta red está implicada en la experiencia mental de ir y venir entre escenarios del pasado, presente y futuro —qué vas a preparar para cenar, un recuerdo de la semana pasada, un dolor en la cadera. Además, bajo ese iceberg que es la consciencia, el encéfalo supervisa un mosaico de variables físicas —temperatura corporal, nivel de glucosa en sangre, ritmo cardíaco, respiración, entre otras— que deben mantenerse estables, en un estado conocido como homeostasis, para garantizar nuestra supervivencia. Si alguna de estas variables se desvía demasiado, las consecuencias pueden ser graves en muy poco tiempo.
Theriault plantea que la mayor parte de la carga metabólica básica del encéfalo se dedica a la predicción. Para mantener la homeostasis, el encéfalo necesita estar constantemente anticipando lo que vendrá —construyendo un modelo sofisticado del entorno y de cómo los cambios pueden afectar a los sistemas biológicos del cuerpo. Según él, es la capacidad de predecir —más que de reaccionar— lo que permite al encéfalo distribuir eficazmente los recursos del cuerpo.
Las limitaciones evolutivas del encéfalo
Un aumento del 5% en el consumo de energía durante el pensamiento activo puede no parecer gran cosa, pero si se considera el contexto del cuerpo entero y el enorme apetito energético del encéfalo, la cifra adquiere importancia. Y si además se tienen en cuenta las estrictas limitaciones energéticas con las que vivían nuestros antepasados, el agotamiento que sentimos al final de un día exigente cobra mucho más sentido.
“El motivo por el que te sientes fatigado, al igual que ocurre tras una actividad física, no es porque te falten calorías para costear ese esfuerzo”, afirma Zahid Padamsey, neurocientífico de Weill Cornell Medicine-Qatar, que no ha participado en esta nueva investigación. “Es porque hemos evolucionado como sistemas muy tacaños… Evolucionamos en entornos con escasez de energía, por lo que detestamos gastar energía.”
 El neurocientífico Zahid Padamsey ha estudiado cómo la disponibilidad de energía (o alimentos) ha influido en la evolución del encéfalo. Foto: Dr. Raphael Courjaret
El neurocientífico Zahid Padamsey ha estudiado cómo la disponibilidad de energía (o alimentos) ha influido en la evolución del encéfalo. Foto: Dr. Raphael CourjaretEl mundo moderno, en el que para muchas personas las calorías están disponibles en abundancia, contrasta fuertemente con las condiciones de escasez en las que evolucionó el Homo sapiens. Ese incremento del 5% en la tasa de gasto energético, si se mantiene durante 20 días de concentración activa y constante, puede equivaler a toda una jornada de energía cognitiva. Si el alimento escasea, esto podría suponer la diferencia entre la vida y la muerte.
“Este gasto puede acumularse de forma considerable con el tiempo si no se limita la tasa de consumo energético, por lo que creo que se trata, en gran parte, de un vestigio de nuestra herencia evolutiva”, añade Padamsey. De hecho, el encéfalo cuenta con mecanismos internos para evitar el sobreesfuerzo. “Se activan sistemas de fatiga que impiden que el consumo siga aumentando”, concluye.
Para comprender mejor estas limitaciones energéticas, en 2023 Padamsey revisó investigaciones sobre ciertas peculiaridades de la señalización eléctrica que apuntan a una tendencia evolutiva hacia la eficiencia energética. Por ejemplo, uno podría pensar que cuanto más rápido se transmite la información, mejor. Sin embargo, la velocidad óptima de transmisión del encéfalo es mucho más baja de lo que cabría esperar.
En teoría, la velocidad máxima a la que una neurona puede disparar y enviar información a su vecina es de 500 hercios. No obstante, si las neuronas realmente operaran a esa velocidad, el sistema se saturaría por completo. La tasa óptima de transmisión de información —es decir, la frecuencia máxima a la que las neuronas pueden seguir distinguiendo los mensajes de sus vecinas— es la mitad: unos 250 hercios.
Sin embargo, nuestras neuronas disparan, en promedio, a tan solo 4 hercios, lo que es entre 50 y 60 veces menos que la frecuencia óptima para transmitir información. Y aún más: muchas transmisiones sinápticas fallan. Incluso cuando una señal eléctrica llega a la sinapsis y la prepara para liberar moléculas hacia la siguiente neurona, esto ocurre solo en el 20% de los casos.
Esto se debe a que no hemos evolucionado para maximizar la cantidad total de información transmitida. “Hemos evolucionado para maximizar la información transmitida por cada molécula de ATP consumida”, explica Padamsey. “Y esa es una ecuación muy distinta.” Transmitir la mayor cantidad de información con el menor gasto energético posible (bits por ATP) sitúa la frecuencia de disparo neuronal óptima por debajo de los 10 hercios.
Desde una perspectiva evolutiva, el gran y sofisticado encéfalo humano ofreció un nivel de complejidad conductual sin precedentes —a un altísimo coste energético. Esta negociación constante, entre la flexibilidad e innovación de un encéfalo grande y las limitaciones energéticas de un sistema biológico, define tanto la forma en que nuestro encéfalo transmite información como la fatiga mental que sentimos tras periodos de concentración, y también el trabajo incesante que realiza para mantenernos con vida. Que sea capaz de hacer tanto dentro de sus limitaciones resulta, sencillamente, asombroso.
Nota del traductor: Si bien el texto original inglés emplea la misma palabra «brain» para referirse tanto al conjunto del encéfalo como al cerebro (que es una parte de él), en nuestra versión al castellano se ha distinguido claramente entre encéfalo y cerebro. Afirmar, por ejemplo, que el cerebro controla la homeostasis es equivalente a afirmar que el base de un equipo de baloncesto de primera división también se encarga de las compras de bebidas isotónicas y toallas.
Para saber más: Sistemas nervisos, una serie de Juan Ignacio Pérez Iglesias
El artículo original, How Much Energy Does It Take To Think?, se publicó el 4 de junio de 2025 en Quanta Magazine.
Traducido por César Tomé López
El artículo ¿Cuánta energía se usa en pensar? se ha escrito en Cuaderno de Cultura Científica.
Vórtices, dinámica de fluidos y la alimentación de los flamencos
Alrededor de 20 000 parejas de flamencos se han beneficiado de un invierno especialmente lluvioso y se están reproduciendo en la laguna de Fuente de Piedra, a unos cincuenta kilómetros del lugar en el que escribo estas líneas. Esta laguna salobre es rica en pequeños invertebrados, cianobacterias y otros microorganismos que les sirven de alimento. Es un espectáculo bellísimo contemplar a los flamencos alimentándose en una postura insólita, con la cabeza invertida y la parte distal del pico superior paralela al fondo o a la superficie del agua (Figura 1).
 Figura 1. Flamenco común (Phoenicopterus roseus) filtrando la capa superficial del agua. .Fuente: © Giles Laurent, gileslaurent.com, License CC BY-SA, CC BY-SA 4.0 / Wikimedia Commons
Figura 1. Flamenco común (Phoenicopterus roseus) filtrando la capa superficial del agua. .Fuente: © Giles Laurent, gileslaurent.com, License CC BY-SA, CC BY-SA 4.0 / Wikimedia CommonsSabemos que los flamencos utilizan la lengua como pistón para bombear agua de forma que los organismos que constituyen su alimentación, generalmente entre uno y cinco milímetros de tamaño, queden retenidos por finas láminas córneas localizadas en el borde del pico. Otras aves, por ejemplo los patos, utilizan este sistema de filtración, pero un grupo de investigadores estadounidenses acaba de publicar un artículo en PNAS que nos proporciona una visión diferente de la alimentación de los flamencos. Además, los resultados obtenidos nos explican dos peculiaridades de los flamencos. Por un lado, la insólita forma angulosa de su pico, diferente al de cualquier otro grupo de aves. Por otro, el hecho de que filtren el agua superficial colocando el pico a favor de la corriente, y no a contracorriente, como hace la inmensa mayoría de animales filtradores.
Para este estudio se realizaron observaciones directas de flamencos, modelos biofísicos de dinámica de fluidos y modelos mecánicos elaborados con impresoras 3D. Al final de este artículo se puede acceder a vídeos representativos de todas estas observaciones.
La primera estrategia desvelada por los investigadores es la formación de “mini-tornados” por la retracción súbita de la cabeza (40 cm/s en 400 milisegundos). El flamenco sitúa la porción distal del pico superior, que es bastante plana, cerca del suelo. Al levantarla rápidamente provoca una succión que remueve el sedimento y los organismos próximos, atrapándolos en un vórtice (Figura 2, Vídeo 1).
 Figura 2. Vórtice formado por la retracción rápida de la cabeza. Antes de la retracción la porción distal y superior del pico se dispone paralelamente al sustrato (derecha). Fuente: Ortega-Jiménez et al. (2025), cita completa en referencias, CC BY-SA 4.0.
Figura 2. Vórtice formado por la retracción rápida de la cabeza. Antes de la retracción la porción distal y superior del pico se dispone paralelamente al sustrato (derecha). Fuente: Ortega-Jiménez et al. (2025), cita completa en referencias, CC BY-SA 4.0.Una segunda técnica de los flamencos es el “castañeteo” del pico superior, un rápido movimiento de apertura y cierre (alrededor de 12 veces por segundo). Este movimiento impulsa el agua contenida en la cavidad bucal hacia arriba, no hacia los lados, como se pensaba. Esto genera una aspiración del agua subyacente hacia el pico, mejorando la captura de alimento. Un experimento realizado con un modelo mecánico demostró que el bombeo de agua a través del pico acoplado al castañeteo multiplicaba por siete la captura de artemias[1] respecto al bombeo de agua sin castañeteo (Figura 3, Vídeo 2).
 Figura 3. Flujo de agua generado por el castañeteo del pico superior. El agua situada entre el pico y el sustrato es aspirada, arrastrando partículas de alimento hacia el pico. Fuente: Ortega-Jiménez et al. (2025), cita completa en referencias, CC BY-SA 4.0.
Figura 3. Flujo de agua generado por el castañeteo del pico superior. El agua situada entre el pico y el sustrato es aspirada, arrastrando partículas de alimento hacia el pico. Fuente: Ortega-Jiménez et al. (2025), cita completa en referencias, CC BY-SA 4.0.Las patas palmeadas de los flamencos se mueven arriba y abajo durante su alimentación. Ya se suponía que esto contribuía a desenterrar organismos del sustrato. Los modelos utilizados en esta investigación muestran que los dedos palmeados se pliegan al subir, se despliegan al bajar y originan vórtices verticales que concentran a los organismos, impidiendo que escapen y haciendo más eficiente el filtrado (Figura 4, Vídeo 3).
 Figura 4. Este modelo mecánico del funcionamiento de la pata del flamenco muestra la generación de un vórtice vertical justo en la zona en la que se alimenta el flamenco. El vórtice atrapa pequeños invertebrados que no pueden escapar nadando. Fuente: Ortega-Jiménez et al. (2025), cita completa en referencias, CC BY-SA 4.0.
Figura 4. Este modelo mecánico del funcionamiento de la pata del flamenco muestra la generación de un vórtice vertical justo en la zona en la que se alimenta el flamenco. El vórtice atrapa pequeños invertebrados que no pueden escapar nadando. Fuente: Ortega-Jiménez et al. (2025), cita completa en referencias, CC BY-SA 4.0.Por último, cuando el flamenco filtra la superficie del agua para capturar, por ejemplo, huevos flotantes de invertebrados, sitúa su pico con la punta en la dirección de la corriente de agua. La forma del pico induce la formación de vórtices de Kárman, una serie de remolinos que provocan la recirculación del agua dirigiendo las partículas alimenticias hacia los bordes del pico, (Figura 5, Vídeo 4).
 Figura 5. La filtración en superficie (skimming) se efectúa en la misma dirección de la corriente de agua. Esto provoca la formación de vórtices de Kárman y un área de recirculación que dirige las partículas flotantes hacia el pico. Fuente: Ortega-Jiménez et al. (2025), cita completa en referencias, CC BY-SA 4.0.
Figura 5. La filtración en superficie (skimming) se efectúa en la misma dirección de la corriente de agua. Esto provoca la formación de vórtices de Kárman y un área de recirculación que dirige las partículas flotantes hacia el pico. Fuente: Ortega-Jiménez et al. (2025), cita completa en referencias, CC BY-SA 4.0.En resumen, los flamencos no se limitan a filtrar pasivamente agua y sedimentos, sino que son depredadores que despliegan estrategias sofisticadas para concentrar y capturar los organismos que constituyen su alimento. Estas estrategias implican la generación de distintos tipos de vórtices, y la forma tan peculiar de su pico parece ser una eficiente adaptación morfológica para este propósito.
Notas:
[1] Pequeño crustáceo que constituye un elemento fundamental de la dieta del flamenco, además de proporcionar los carotenoides que dan color rojo a sus plumas.
[2] Los vídeos también están disponibles en esta página web (De Ortega-Jiménez et al., 2025, cita completa en referencias, CC BY-SA 4.0.)
Referencias
Ortega-Jimenez, V.M., Yee, T., Rohilla, P. et al. (2025). Flamingos use their L-shaped beak and morphing feet to induce vortical traps for prey capture. Proc Natl Acad Sci U S A. doi: 10.1073/pnas.2503495122.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga.
El artículo Vórtices, dinámica de fluidos y la alimentación de los flamencos se ha escrito en Cuaderno de Cultura Científica.
Resultados «emocionantes» para el primer ensayo clínico de inmunoterapia en tumores sólidos
 Inmunoterapia de Células T Car frente a tumores sólidos. Fuente: BMS Science / Fair use
Inmunoterapia de Células T Car frente a tumores sólidos. Fuente: BMS Science / Fair use
Los orígenes de la quimioterapia se remontan a la lejana década de los cincuenta del siglo pasado y, durante todo este tiempo, se ha convertido en la herramienta más directa y eficaz frente a algunos tipos de cáncer. Sin embargo, el avance de nuevas terapias en este campo se había ralentizado hasta que, con el nuevo siglo, surgió una alternativa mucho menos invasiva y agresiva: la inmunoterapia. En diciembre de 2013, la célebre revista Science elegía la inmunoterapia como el «descubrimiento científico del año» y, la definía a grandes rasgos como un novedoso tratamiento médico que busca entrenar, fortalecer o dirigir nuestro propio sistema inmunitario y convertirlo en un ejército mejor preparado frente a la amenaza.
Es una idea brillante y, en teoría, bastante simple de entender: la inmunoterapia busca potenciar el propio sistema inmunitario del paciente para luchar contra las células tumorales. El funcionamiento de estas inmunoterapias consiste en extraer las defensas del paciente (ya sean linfocitos T, B o Natural Killer) y modificarlas genéticamente para que produzcan receptores específicos que reconozcan y ataquen a un tumor determinado. Explicado de manera muy visual y sencilla, sería una especie de «gimnasio» para linfocitos. Los investigadores extraen células defensivas de una persona con algún tipo de cáncer y, en el laboratorio, las «ponen en forma y entrenan». Cuando están listas y reforzadas, se las vuelven a inyectar al paciente.
Las inmunoterapias poseen una innegable ventaja frente a la quimioterapia ya que son mucho menos invasivas. Al inocular al paciente sus propias células inmunitarias generan menos rechazo y no resultan tan agresivas con el resto de células. Entre estas terapias se encuentra la denominada CART-T que utiliza linfocitos T, modificados genéticamente en laboratorio, y que han probado ser muy eficaces contra determinados cánceres de origen sanguíneo.
Por supuesto, queda mucho camino por recorrer y las diferentes formas de inmunoterapia poseen dos problemas generales que deben solucionar. En primer lugar, todavía no pueden distinguir con exactitud entre células cancerosas y no cancerosas, algo que los investigadores están buscando desde hace años y que representaría un paso de gigante en este tipo de terapias. Por otro lado, la eficacia de CART-T frente a tumores sólidos sigue estando muy lejos de ser viable y eso es un importante freno ya que estos tumores sólidos «representan aproximadamente el 90% de todos los cánceres, incluidos el cáncer de mama, de pulmón y de páncreas».
Respecto al primer problema, afortunadamente van llegando poco a poco algunos avances, como el estudio presentado en 2021 donde un equipo de investigadores canadienses presentó un estudio con células específicamente diseñadas para destruir los tumores malignos sin atacar al resto de células. Sin embargo, el segundo obstáculo, el de la eficacia de la inmunoterapia frente a tumores sólidos parecía estancado… hasta ahora.
 Infografía del funcionamiento de las inmunoterapias con células T CAR. Fuente: Arnaud M, Bobisse S, Chiffelle J and Harari A (2021) The Promise of Personalized TCR-Based Cellular Immunotherapy for Cancer Patients. Front. Immunol. 12:701636. doi: 10.3389/fimmu.2021.701636 CC BY 4.0
Infografía del funcionamiento de las inmunoterapias con células T CAR. Fuente: Arnaud M, Bobisse S, Chiffelle J and Harari A (2021) The Promise of Personalized TCR-Based Cellular Immunotherapy for Cancer Patients. Front. Immunol. 12:701636. doi: 10.3389/fimmu.2021.701636 CC BY 4.0
Se acaba de publicar en The Lancet un ensayo clínico que los expertos califican como un «hito» en inmunoterapia de células T Car en tumores sólidos. El estudio nos sitúa ante un «avance único y esperanzador» en el que los pacientes con cáncer gástrico avanzado que fueron tratados con inmunoterapia «vivieron en promedio aproximadamente un 40% más que los pacientes que recibieron la atención estándar». Además el ensayo también ha sido presentado en la Conferencia sobre cáncer más importante a nivel mundial, la reunión anual de la Sociedad Americana de Oncología Clínica, celebrada en Chicago hace unos días, donde los investigadores asistentes calificaron los resultados como «emocionantes e innovadores».
Esta nueva inmunoterapia se centra en células T con un receptor quimérico de antígeno (CAR) denominado satricabtagene autoleucel (satri-cel) y los resultados presentados corresponden a un ensayo controlado aleatorizado de fase 2 que involucró a 156 pacientes con cáncer gástrico en una etapa avanzada.
Estos participantes se dividieron aleatoriamente en dos grupos en una proporción de 2:1. Los pacientes del grupo de estudio recibieron la inmunoterapia con T Car satri-cel (n=104) mientras que los del grupo de control (n=52) recibieron el tratamiento actual que incluía Nivolumab, paclitaxel, docetaxel, irinotecán o rivoceranib. Además, para evaluar la eficacia de las diferentes actuaciones, dentro del grupo de inmunoterapia satri-cel, el 85% de los pacientes recibió al menos una infusión de satri-cel, el 31% recibió una segunda infusión y el 6% recibió una tercera infusión. En el grupo de control, el 92% de los pacientes recibió al menos una dosis de su tratamiento.
Los resultados publicados arrojan datos notables: Los pacientes que recibieron terapia con células T Car satri-cel «vivieron un promedio de 7,9 meses tras la aleatorización, en comparación con los 5,5 meses que vivieron con la atención estándar».
Es un pequeño paso, sí, pero hay que entender que se produce en un campo que llevaba estancado más de una década y, según Nature, demuestra que esta inmunoterapia «ofrece beneficios significativos a los pacientes con cáncer gástrico avanzado que han fracasado en al menos dos líneas de tratamiento previas». Además, nos abre la puerta a otras aplicaciones en diferentes tipos de cáncer que no estaban previstos en el estudio inicial. En este sentido, en la misma reunión oncológica de Chicago se presentará un segundo estudio sobre células T Car, dirigido por la Universidad de Pensilvania que apunta a que el enfoque también se puede utilizar para tratar tumores cerebrales, en especial reducir el tamaño de los tumores en el glioblastoma, un cáncer cerebral agresivo y de rápido crecimiento, y ayudar a los pacientes a vivir mucho más tiempo.
En definitiva, y como afirma el oncólogo John Haanen en The Guardian, «para los tumores sólidos, ahora no solo existe un claro interés sino también evidencia de que las inmunoterapias pueden beneficiar a los pacientes. Es posible que estemos presenciando los inicios de una nueva generación de tratamientos que antes no existía para los oncólogos médicos».
Referencias científicas y más información:
Changsong Qi, Chang Liu, et al. (2025) Claudin-18 isoform 2-specific CAR T-cell therapy (satri-cel) versus treatment of physician’s choice for previously treated advanced gastric or gastro-oesophageal junction cancer (CT041-ST-01): a randomised, open-label, phase 2 trial The Lancet doi: 10.1016/S0140-6736(25)00860-8
Fieldhouse, Rachel. «Cancer Fighting CAR-T Cells Show Promising Results for Hard-to-Treat Tumours». Nature News, junio de 2025. DOI:10.1038/d41586-025-01722-8.
Andrew Gregory «Immunotherapy trial helps cancer patients with tumours live 40% longer» The Guardian Science (2025)
Sobre el autor: Javier «Irreductible» Peláez es escritor y comunicador científico multimedia. Es ganador de tres premios Bitácoras, un premio Prisma a la mejor web de divulgación científica y un Premio Ondas al mejor programa de radio digital.
El artículo Resultados «emocionantes» para el primer ensayo clínico de inmunoterapia en tumores sólidos se ha escrito en Cuaderno de Cultura Científica.
Y… ¿cómo se gestiona el patrimonio natural?

¿Qué tienen en común un paisaje espectacular, un fósil milenario y una cantera abandonada? Todos forman parte del patrimonio geológico, un testimonio de la historia de la Tierra con un gran valor científico, educativo, cultural y estético, y base del patrimonio natural. Sin embargo, su importancia continúa siendo poco apreciada.
Para acercar las distintas aproximaciones del patrimonio geológico a la sociedad, los días 26, 27 y 28 de marzo se celebró la quinta edición de las jornadas divulgativas “Geología para poetas, miopes y despistados. Patrimonio patrimonio”. Organizadas por el grupo de investigación consolidado Procesos Hidro-Ambientales (HGI) de la Facultad de Ciencia y Tecnología de la Universidad del País Vasco (UPV/EHU), estas jornadas contaron con la colaboración del Vicerrectorado del Campus de Bizkaia, la Cátedra de Cultura Científica de la UPV/EHU, el Geoparque de la Costa Vasca / Geoparkea y el Ente Vasco de la Energía (EVE).
En esta charla Xabier Arana nos expone como han evolucionado las ideas sobre conservación del patrimonio natural y cómo se ejecuta desde la Diputación Foral de Bizkaia. Xabier Arana fue Director de la Reserva de la Biosfera de Urdaibai entre 1996 y 2007, es miembro de la Comisión Ambiental del Colegio Oficial de Biólogos de Euskadi y, desde el año 2012, es Jefe de Sección de Sostenibilidad y Educación Ambiental de la Diputación Foral de Bizkaia.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Y… ¿cómo se gestiona el patrimonio natural? se ha escrito en Cuaderno de Cultura Científica.
Mejor aprender a escribir con lápiz y papel
El equipo de la investigadora Joana Acha ha analizado las consecuencias que tiene en las competencias de niños y niñas el hecho de escribir a mano o con teclado durante el proceso de aprendizaje de la lectura y la escritura. A un grupo de niños y niñas de 5 años se les ha enseñado un alfabeto artificial mediante diferentes técnicas, y se ha llegado a la conclusión de que quienes se ejercitan con lápiz y papel asimilan mejor las letras y las palabras nuevas.
 Foto: Julia M Cameron / Pexels
Foto: Julia M Cameron / PexelsHoy en día es habitual la presencia de recursos digitales en las aulas infantiles y su utilización como herramienta en distintos procesos de aprendizaje. Por ejemplo, existen programas informáticos dirigidos a alumnos que están aprendiendo a leer y escribir. Como los ejercicios que proponen se realizan en el ordenador, los escolares pulsan teclas y botones, dejando de lado el lápiz y el papel. Para medir el impacto de estos métodos basados en la mecanografía, un estudio de la UPV/EHU ha realizado una comparativa con el fin de analizar las consecuencias que tiene en las capacidades de los niños el hecho de practicar la escritura a mano o con teclado: “Ya que los niños escriben cada vez menos a mano, queríamos investigar la influencia que eso tiene en las competencias alfabéticas y ortográficas. Es decir, queríamos ver si tanto la capacidad de aprender letras como la de interiorizar y recordar la estructura de las palabras se desarrolla de forma diferente a través de la práctica manual o del uso del teclado. Hemos llegado a la conclusión de que los niños que se han ejercitado a mano han obtenido los mejores resultados”, explica la investigadora Joana Acha.
 Las 9 letras empleadas en el estudio. Fuente: Modificado de Gorka Ibaibarriaga, Joana Acha, Manuel Perea (2025) Journal of Experimental Child Psychology doi: 10.1016/j.jecp.2025.106195
Las 9 letras empleadas en el estudio. Fuente: Modificado de Gorka Ibaibarriaga, Joana Acha, Manuel Perea (2025) Journal of Experimental Child Psychology doi: 10.1016/j.jecp.2025.106195Para llegar a esta conclusión, se ha llevado a cabo un experimento con niños de entre 5 y 6 años. Se ha elegido esa edad porque es el momento evolutivo más propicio: es entonces cuando comienzan a adquirir la capacidad lectoescritora. Así, se enseñó a 50 niños y niñas con conocimientos básicos de lectura 9 letras de los alfabetos georgiano y armenio, así como 16 pseudopalabras inventadas por el equipo investigador combinando dichas letras.
 Las 16 pseudopalabras empleadas en el estudio. Fuente: Modificado de Gorka Ibaibarriaga, Joana Acha, Manuel Perea (2025) Journal of Experimental Child Psychology doi: 10.1016/j.jecp.2025.106195
Las 16 pseudopalabras empleadas en el estudio. Fuente: Modificado de Gorka Ibaibarriaga, Joana Acha, Manuel Perea (2025) Journal of Experimental Child Psychology doi: 10.1016/j.jecp.2025.106195“El objetivo es utilizar letras y palabras totalmente nuevas para los participantes, con el fin de asegurarnos de que están aprendiendo desde cero. De hecho, las investigaciones previas han utilizado los alfabetos propios de la cultura de los niños, por lo que no resulta tan fácil saber hasta qué punto conocían los símbolos presentados”, afirma Acha.
A todo el alumnado se le enseñaron las mismas letras y palabras, pero no a todos de la misma manera: a la mitad se les pidió que las copiaran a mano y a la otra mitad, que las escribieran utilizando el teclado. De este modo, el estudio de la Universidad del País Vasco ha podido analizar la importancia de la grafomotricidad, es decir, cómo influye el movimiento de la mano en el proceso de lectura y escritura. De hecho, cuando escribimos con teclado no trazamos la forma de las letras, por lo que la influencia de la grafomotricidad es escasa a la hora de interiorizar su estructura. En cambio, al escribir a mano, esta influencia es significativa.
“Una vez que se les enseñaron las letras y palabras nuevas, y cada grupo practicó con un método distinto, realizamos tres pruebas para evaluar los conocimientos adquiridos. Medimos la capacidad de identificar, escribir y pronunciar letras y pseudopalabras, y los resultados indican claramente que quienes practicaron a mano desarrollaron una mayor destreza. La diferencia se nota, sobre todo, en las pseudopalabras, ya que casi todos los que aprendieron con ordenador realizaron incorrectamente los ejercicios relacionados con las secuencias de letras. Por lo tanto, nuestro trabajo reafirma que la grafomotricidad es fundamental para memorizar las letras y las estructuras de las palabras”, explica Acha.
La variabilidad al usar el lápiz también influyePero no solo se ha estudiado el impacto del grado de movimiento de la mano. Los grupos que trabajaban a mano y con teclado se dividieron, desde el principio, en dos subgrupos. En el caso de quienes utilizaban lápiz, a algunos se les pidió que siguieran las guías marcadas con puntos (técnica de baja variabilidad), mientras que otros practicaron sin ninguna referencia, copiando libremente en una hoja en blanco (alta variabilidad). Lo mismo se aplicó a quienes usaban ordenador: algunos utilizaron siempre la misma tipografía para practicar (por ejemplo, Tahoma), y otros, varias.
Así, además de la grafomotricidad, se ha podido analizar la influencia del factor de variabilidad en la forma.
Lo que se ha observado es que los que practicaron a mano obtuvieron mejores resultados que todos los que utilizaron el teclado, aunque también se encontraron diferencias dentro del grupo que escribió a mano. Aquellos que practicaron de forma libre lograron los mejores resultados. “Por tanto, lo que hemos deducido es que, aunque al principio contar con una guía para practicar resulta de gran ayuda, una vez que los niños son capaces de realizar movimientos pequeños y precisos, conviene pasar a la escritura libre. En cualquier caso, lo que está claro es que debe priorizarse la escritura a mano como práctica en los procesos de aprendizaje. Aprenden mejor a través del movimiento de la mano y, por tanto, los dispositivos tecnológicos deberían utilizarse únicamente como complemento”, concluye Acha.
Referencia:
Gorka Ibaibarriaga, Joana Acha, Manuel Perea (2025) The impact of handwriting and typing practice in children’s letter and word learning: Implications for literacy development Journal of Experimental Child Psychology doi: 10.1016/j.jecp.2025.106195
Para saber más:
La adquisición de la lectura desde la evidencia científica: una hoja de ruta para educadores, conferencia de Joana Acha
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Mejor aprender a escribir con lápiz y papel se ha escrito en Cuaderno de Cultura Científica.
¿Nos llevó la ciencia ficción a la Luna?
La historia de la Luna es, una vez más, la historia del mito que se convirtió en ciencia. La de una humanidad idealista que soñaba con alcanzarla, construyó un cohete y lo hizo. Y es posible que la ciencia ficción tuviera mucho que ver en todo esto, sobre todo por la época que vivíamos cuando empezaron a gestarse los inicios de la carrera espacial.
 Foto: Luca / Unsplash
Foto: Luca / UnsplashNuestro satélite no siempre estuvo, metafóricamente hablando, cerca de nosotros. Durante mucho tiempo, en la Antigüedad, conformó la frontera que separaba dos mundos de naturaleza muy distinta: el sublunar, material y cambiante, y el supralunar, etéreo e inmutable. Hasta que Johannes Kepler la concibió como un lugar —pero un lugar «real»—, en su Somnium[1] y Galileo Galilei nos ayudó a verlo con nuestros propios ojos gracias al telescopio.
Sí, es cierto que se escribieron historias de viajes a la Luna mucho antes que la de Kepler, pero, como bien apunta Jorge Luis Borges en el prólogo que escribió para Crónicas marcianas, de Ray Bradbury: «Para Luciano y para Ariosto, un viaje a la Luna era símbolo o arquetipo de lo imposible; para Kepler ya era una posibilidad, como para nosotros». De hecho, tras conocer las investigaciones de Galileo, así se lo hizo saber en 1610 su Dissertatio cum nuncio sidereo, en una respuesta abierta al Sidereus nuncius:
Ciertamente no faltarán pioneros humanos cuando hayamos dominado el arte del vuelo […]. Construyamos naves y velas adaptadas al éter celestial, y habrá muchas personas sin miedo a los vacíos inmensos. Mientras tanto, prepararemos, para los valientes viajeros del cielo, mapas de los cuerpos celestes; yo lo haré para la Luna, tú, Galileo, para Júpiter.
¿Es posible que estuviera hablando ya de que algún día habría naves espaciales? Dejando esto de lado, este fue, probablemente, el momento en el que comenzó la carrera espacial —al menos en nuestra imaginación—, o el momento en que plantearse algo así empezó a tener sentido desde un punto de vista racional.
 Dissertatio cum nuncio sidereo es la respuesta de Johannes Kepler al Sidereus nuncius de Galileo Galilei. En él, plantea la posibilidad de que algún día la humanidad pueda viajar a las estrellas y la Luna gracias al desarrollo de nueva tecnología. Fuente: Dominio público
Dissertatio cum nuncio sidereo es la respuesta de Johannes Kepler al Sidereus nuncius de Galileo Galilei. En él, plantea la posibilidad de que algún día la humanidad pueda viajar a las estrellas y la Luna gracias al desarrollo de nueva tecnología. Fuente: Dominio público
Pasarían aún algunos siglos para terminar de creérnoslo, y aunque los viajes a la Luna siguieron presentes en la literatura a través de obras medio fantásticas, medio racionales —al menos ya no eran solo fantásticas, sino que intentaban acercar al mundo terrenal lo que en otro momento fue divino—, no fue hasta el siglo XX cuando decidimos que era el momento de intentar, en serio, llegar a nuestro único satélite.
Ya a finales del siglo XIX, cuando ni siquiera existían los aviones, visionarios como Konstantin Tsiolkovsky o Robert Goddard sentaron las bases de la cohetería moderna y soñaron a lo grande con el espacio. El despegue del primer aeroplano de los hermanos Wright, por su parte, empezó a cambiar tecnológicamente, pero, sobre todo, en la imaginación humana, el paradigma de la aeronáutica. Y dos guerras mundiales lo consolidaron —a un precio que la humanidad nunca debería haber pagado, me atrevo a añadir—.
Para entonces la ciencia ficción estadounidense estaba en su mejor momento. Y no es casual. Existen estudios que correlacionan las épocas de mayor desarrollo tecnológico de algunos países con una eclosión de publicaciones de este tipo de literatura. Pero el espacio dejaba de limitarse a las historias fantásticas. En 1946, la revista Life publicó un artículo titulado «Trip to the Moon: artist paints journey by rocket», con ilustraciones de Chesley Bonestell en las que muchos, por primera vez, pudieron observar, de una forma que parecía casi realista, qué había más allá de la Tierra… Vieron por primera vez ese espacio exterior del que todo el mundo empezaba a hablar después de la Segunda Guerra Mundial.
El ilustrador Chesley Bonestell supo reflejar en imágenes la desbordante imaginación de una posguerra en la que cualquier cosa era posible. Y el miedo a un desastre nuclear y la competitividad de la Guerra Fría, alimentaron ese fuego en medio de un tenso tecnooptimismo.
 Habitual de las revistas de ciencia ficción de la época, el ilustrador Chesley Bonestell supo reflejar en sus dibujos los sueños espaciales de toda una generación… o tal vez contribuir a que los tuvieran.
Habitual de las revistas de ciencia ficción de la época, el ilustrador Chesley Bonestell supo reflejar en sus dibujos los sueños espaciales de toda una generación… o tal vez contribuir a que los tuvieran.Fuentes: New Mexico Museum of Space History / Fair use | World Editions, Inc./Chesley Bonestell
El mencionado artículo llegó, en un momento dado, a las manos del productor George Pal, quien decidió que era el momento de rodar una película no de science fiction (‘ficción científica’), sino de science fact (‘hechos científicos’). Estaría basada en una de las recientes novelas juveniles de Robert A. Heinlein: Rocket ship Galileo (1947).
Que el ser humano llegara a la Luna era casi una obsesión para Heinlein. Aunque en su momento se había visto obligado a abandonar el Ejército a causa de una tuberculosis y a retirarse de su labor de ingeniero, siempre se mantuvo actualizado y al día en ese tipo de cuestiones. Estaba suscrito a revistas como Scientific American, Popular Mechanics y estaba en contacto permanentemente con científicos e ingenieros, muchos de los cuales había conocido en su época militar. No es extraño, entonces, que George Pal quisiera contar con él como director técnico. La rigurosidad de Heinlein en ese aspecto, y de la película en general, fue determinante. Destination Moon, estrenada en 1950 —antes del lanzamiento del Sputnik y antes de que Yurin Gagarin se convirtiera en el primer ser humano en orbitar la Tierra— fue capaz de mostrar a todo el mundo, de forma bastante acertada además, cómo serían los viajes espaciales y le hizo sentir, creer y, sobre todo, tener fe en que llegar a la Luna solo era una cuestión de tiempo, que estaba más cerca de lo que pensábamos y solo requería de nosotros un poco de espíritu emprendedor y de aventura. Por supuesto, fue Chesley Bonestell —y Heinlein ni se quiso plantear la posibilidad de que lo hiciera cualquier otro— quien se encargó del diseño y los decorados.
 Basada en la novela Rocket ship Galileo de Robert A. Heinlein, y científicamente rigurosa con los estándares de la época —aunque algo anacrónica para los gustos cinematográficos de hoy—, Destination Moon mostró, en 1950, cómo sería un viaje a la Luna en tecnicolor. Fuente: George Pal Productions / Fair use
Basada en la novela Rocket ship Galileo de Robert A. Heinlein, y científicamente rigurosa con los estándares de la época —aunque algo anacrónica para los gustos cinematográficos de hoy—, Destination Moon mostró, en 1950, cómo sería un viaje a la Luna en tecnicolor. Fuente: George Pal Productions / Fair use
Así que se podría decir, en última instancia, que si Neil Armstrong pisó la Luna aquel 21 de julio de 1969, fue porque, poco a poco y a lo largo de varios siglos, empezamos a creer en que algún día podríamos llevarlo hasta allí.
Bibliografía
Borges, J. L. (2005 [1955]). Prólogo. En R. Bradbury, Crónicas marcianas. Minotauro.
Brake, M. (2018). The science of science fiction. Simon & Schuster.
Heinlein, R. A. (1947). Rocket ship Galileo. Scribner’s.
Newell, C. L. (2014). The greatest adventure awaiting humankind: Destination Moon and faith in the future. Implicit Religion, 17(4), 459-479. https://doi.org/10.1558/imre.v17i4.459
Pichel, I. (Director). (1950). Destination Moon [Película]. Eagle-Lion Classics.
Nota:
[1] Para muchos, entre quienes me incluyo, el Somnium, seu opus posthumum De astronomia lunari, de Johannes Kepler, es la primera novela de ciencia ficción. Empezó a escribirla alrededor de 1608, como apoyo para el desarrollo de sus tres leyes que rigen los movimientos planetarios, aunque se publicó a título póstumo en 1934.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo ¿Nos llevó la ciencia ficción a la Luna? se ha escrito en Cuaderno de Cultura Científica.

