Generalización de la invariancia: principios de covariancia y equivalencia

En la nave “Avalon”, que aparece en la película “Passengers”, la aceleración que produce el giro alrededor del eje central de la nave proporciona un efecto idéntico al de la gravedad para los pasajeros; ese es el principio de equivalencia. A pesar de ello, las leyes de la física siquen siendo las mismas dentro de la nave; ese es el principio de covariancia.
Entre 1907 y 1916 Einstein empleó buena parte de su tiempo y esfuerzos en la generalización de la teoría de la invariancia a marcos de referencia no inerciales [1]. Si bien el resultado de estos trabajos, la que después se conocería como teoría general de la relatividad, es sustancialmente más compleja que la teoría especial, en lo que sigue emplearemos lo que ya hemos aprendido de la teoría especial para comprender algunos aspectos importantes de la teoría general y después explorar algunas de sus implicaciones.
Sabemos que la teoría especial se basa en dos principios básicos, el principio de relatividad y la constancia de la velocidad de la luz. De forma similar, la teoría general también se basa en dos principios: el principio de covariancia [2] y el principio de equivalencia. Vamos a ver que los dos son muy fáciles de plantear y entender, otra cosa mucho más complicada es expresar sus consecuencias matemáticamente, algo en lo que no entraremos.
El principio de covariancia se puede resumir diciendo que las leyes de la física son las mismas en todos los marcos de referencia. Una afirmación que nos retrotrae al principio de relatividad de la teoría especial:
Todas las leyes de la física son exactamente las mismas para cada observador en cada marco de referencia que está en reposo o moviéndose con una velocidad relativa uniforme. Esto significa que no hay ningún experimento que se pueda realizar dentro de un marco de referencia que revele si éste está en reposo o moviéndose a una velocidad uniforme.
El principio de covariancia es pues una generalización del principio de relatividad [3]: mientras que éste se limita a los marcos de referencia inerciales, el principio de covariancia dice que las leyes de la física son las mismas en cualquier marco de referencia, independientemente de cómo se esté moviendo respecto a otro. Es en este sentido cómo las teorías de la relatividad se distinguen en especial y general: mientras que la teoría especial se aplica cuando se dan ciertas circunstancias especiales (siempre que estemos tratando con marcos de referencia inerciales), la teoría general carece de esta restricción.
El otro principio básico de la teoría general es el principio de equivalencia que viene a decir que los efectos debidos a la aceleración y los debidos a la gravedad son indistinguibles. Puede parecer una afirmación huera, porque ya sabíamos que la gravedad provoca una aceleración en física newtoniana y la relación ya la conocía el propio Newton.
¿Qué novedad introduce Einstein entonces? En la física de Newton aceleración y gravedad son tratadas como dos fenómenos separados y la relación entre ellas como una coincidencia. Pero el principio de equivalencia afirma que esencialmente no existe diferencia entre ambos efectos: no podemos distinguir entre ellos.
Esta equivalencia esencial entre aceleración y gravedad se suele ilustrar con el experimento mental del ascensor. Imagina que estás en una caja de ascensor sin ventanas, y que la caja está depositada en la superficie de la Tierra estática, pero tú no lo sabes. Comienzas a hacer experimentos físicos para ver qué puedes averiguar de tu situación. ¿Qué mides? Pues mides que los objetos que dejas libres a la altura de tu hombro se mueven con movimiento uniformemente acelerado hacia el suelo (sabes que es el suelo porque hay una fuerza que te empuja hacia esa superficie y, por eso, la llamas suelo) con una aceleración constante de 9,8 m/s.
Ahora supongamos que, de nuevo sin que tú sepas nada, la caja de ascensor se mueve por el espacio interestelar (y, por tanto, no le influye significativamente ningún campo gravitatorio) con una aceleración uniforme de 9,8 m/s en la dirección perpendicular a lo que tú antes llamabas suelo y sentido “del suelo al techo”. De nuevo, tus experimentos te llevarían en estas circunstancias exactamente a los mismos resultados. Es decir, los efectos prácticos de aceleración y gravedad son idénticos y no puedes distinguir una situación de otra.
Notas:
[1] Los marcos de referencia que están en reposo o se mueven con velocidad uniforme en relación con otro marco de referencia son llamados marcos de referencia inerciales, ya que la ley de inercia de Newton se cumple en ellos. Los marcos de referencia que se aceleran respecto a otros se denominan marcos de referencia no inerciales.
[2] Recibe varios nombres según el texto que consultemos: principio de covariancia, de covariancia general o general de la relatividad. Nosotros preferimos el nombre más eficiente.
[3] Einstein se refería a él como principio general de la relatividad.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Generalización de la invariancia: principios de covariancia y equivalencia se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El principio de relatividad (3): la invariancia de Galileo
- El principio de relatividad (y 4): la versión de Einstein
- ¿La teoría de la invariancia es física o metafísica?
Ingredientes para la receta: El garbanzo
“-Lo que real y verdaderamente tengo son dos uñas de vaca que parecen manos de ternera, o dos manos de ternera que parecen uñas de vaca; están cocidas con sus garbanzos, cebollas y tocino, y la hora de ahora están diciendo: “¡Cómeme! ¡Cómeme!”
-Por mías las marco desde aquí –dijo Sancho-, y nadie las toque, que yo las pagaré mejor que otro, porque para mí ninguna otra cosa pudiera esperar de más gusto, y no se me daría nada que fuesen manos, como fuesen uñas.”
Miguel de Cervantes, Don Quijote de La Mancha, 1605.
Oda al garbanzo
Si a pensar en los males de Castilla
y en su miseria y desnudez me lanzo,
como origen fatal de esta mancilla,
te saludo, ¡Oh garbanzo!
Tú en Burgos, y en Sigüenza, y en Zamora,
y en Guadalajara, capital del hielo,
alimentas la raza comedora,
y así le crece el pelo.
Esa tu masa insípida y caliza,
que de aroma privó naturaleza,
y de jugo y sabor, ¿qué simboliza?
vanidad y pobreza.
En El Practicón, de Ángel Muro, “de un eminente poeta” anónimo, 1894.

Siempre podemos empezar a tratar del garbanzo con una buena receta, esa de las manos de vaca de El Quijote que, como solo él sabe hacer, degustará con entusiasmo Sancho, que para eso se apellida Panza.
Limpiamos, raspamos, cortamos las manos de vaca y las maceramos en vinagre con zumo de limón. Las sacamos, lavamos y al puchero a cocer con cebolla, unos pimientos choriceros, laurel, perejil, pimienta, azafrán, garbanzos que han estado a remojo la noche anterior, y vinagre. Cocer hasta que todo esté tierno y, si se necesita, añadir agua caliente. Y a la mesa.
El garbanzo, de nombre científico Cicer arietinum y perteneciente a la familia Fabaceae, es una planta que crece en climas cálidos, con pluviometría superior a 400 milímetros, aunque tiene problemas de cultivo con exceso de agua. Es una herbácea anual, de unos 50 centímetros de altura, con tres o cuatro granos como máximo en cada pie. Tiene muchas variedades pero destacan dos como origen de otras: el tipo Kabuli, de grano medio o grande, liso, redondeado, de color crema y que se cultiva en el Mediterráneo y Asia occidental, y procedente de Kabul, en Afganistán, llegó a la India en el siglo XVIII; y el tipo Desi, rugoso, más pequeño y de color marrón oscuro, y se siembra entre Irán y la India. El tipo Desi tiene más variabilidad genética que el Kabuli y, por ello, los expertos suponen que este deriva de aquel y que su aparición es relativamente reciente. Además, el Desi se parece más al Cicer reticulatum, el antecesor silvestre del garbanzo domesticado. Sin embargo, algunos de los estudios genéticos parecen indicar que el tipo Kabuli también deriva directamente del Cicer reticulatum, tal como sugiere Deepak Ohri, de la Universidad de Uttar Pradesh, en la India.
Por otra parte, como ocurre en muchas especies domesticadas, el garbanzo doméstico tiene poca variabilidad genética, tal como dijo Vavilov. En varios momentos del proceso de domesticación, ha pasado por cuellos de botella que han reducido su población y su variabilidad. Solo algunas variedades han superado estos cuellos de botella y han llegado a nuestros campos.

Garbanzo kabuli (izquierda) y desi (derecha)
Según Shahal Abbo, han sido cuatro estos cuellos de botella. En primer lugar, partimos de una especie antecesora, Cicer reticulatum, con una distribución geográfica restringida y, por tanto, y, en segundo lugar, con escasa variabilidad genética. En tercer lugar, el garbanzo pasó por un proceso selectivo muy fuerte para convertirse en cultivo de verano. Y, finalmente, se eliminaron muchas variedades locales cuando se seleccionaron, por su eficacia en el cultivo, los dos grandes tipos, Desi y Kabuli.
En España y por hibridación y selección se han obtenido muchas variedades: Fardón, Puchero, Alcazaba, Bujeo, Pedrosillano, Lechoso, Blanco Andaluz, el de Fuentesaúco, el de Pico Pardal, y otras más. Escriben José del Moral y su grupo, del Servicio de Investigación y Desarrollo Tecnológico de la Junta de Extremadura, que, en España, la superficie dedicada al cultivo del garbanzo ha pasado por grandes variaciones en el último siglo. Entre 1919 y 1936, de media eran unas 2400000 hectáreas al año, para subir hasta casi 4000000 de hectáreas durante la Guerra Civil y los diez años siguientes. Desde 1950, la superficie disminuye hasta las 44000 hectáreas en 1993, con un aumento hasta casi 150000 hectáreas en 1996 cuando se empieza aplicar la Política Agraria Común de la Unión Europea. En 2015, la disminución de la superficie dedicada al garbanzo es notable y quedan 38000 hectáreas. Sin embargo, la productividad llega a las dos toneladas de garbanzos por hectárea.
Se ha secuenciado el genoma de 90 genotipos de garbanzo, con más de 28000 genes y ha servido para encontrar hasta 77 variantes que mejoran diversos aspectos de su cultivo.
Es la segunda o tercera especie de legumbre más cultivada, según los años, y se siembra desde la cuenca mediterránea, al oeste, y Etiopía, al sur, hasta la India, en el este. Es la India el primer productor mundial y allí, de media y entre 2000 y 2004, se recogió el 63% de la cosecha. Le siguen Turquía, con el 8%, Pakistán, con el 7%, e Irán, con el 4%. También son zonas de cultivo de garbanzo Australia, el Mediterráneo, Asia occidental, y en las Grandes Llanuras de Estados Unidos. En el año 2013, la cosecha mundial de garbanzos fue de algo más de 13 millones de toneladas, con casi 9 millones recogidas en la India.
Además, la India es también el mayor importador, con 133000 toneladas en 2004. En cuarto lugar está España con 58000 toneladas en 2004. Sin embargo, solo entre el 5% y el 10% de la producción mundial entra en el comercio internacional. El garbanzo es un cultivo muy consumido por las comunidades que lo cultivan. El mayor exportador es Australia, con 150000 toneladas en 2004, seguido de Turquía, con 133000 toneladas, e Irán, con 85000 toneladas.

Presentación de hummus con aceite de oliva
Es un alimento habitual desde Oriente Próximo hasta la India y el ingrediente básico del hummus, del falafel y es habitual en el cuscús. El garbanzo se come asado, cocido, frito y molido para obtener harina.
Destaca, entre otros cultivos domésticos del Oriente Próximo, por ser de verano y no de invierno. Es resistente a la sequía y con pocas necesidades de agua. Shahal Abbo, de la Universidad Hebrea de Jerusalén, indica que le basta con el agua del rocío.
Lo habitual en esas plantas domesticadas del Creciente Fértil es que germinen en otoño, florezcan al final del invierno y principio de la primavera, y maduren al comienzo del verano. Es lo típico en los ancestros del trigo, la cebada, la lenteja, el guisante e, incluso, del garbanzo silvestre, el Cicer reticulatum. En la actualidad, todos mantienen este ciclo excepto el garbanzo. Es una planta que se siembra en primavera y se recoge en verano. Fueron griegos y romanos quienes nos dan las evidencias más antiguas del garbanzo como planta que se siembra en marzo y abril.

Planta en flor
En Oriente Próximo, en el Crecente Fértil, más del 80% de la lluvia anual cae entre diciembre y enero, y el largo verano es cálido y seco. El cultivo que necesite agua en verano solo tiene la que queda en el suelo. Es este ciclo anual de lluvias el que ha seleccionado las plantas a sembrar en otoño y recoger al inicio del verano. Abbo plantea la incógnita que supone cambiar del garbanzo silvestre de invierno y de éxito por el cultivo más arriesgado del garbanzo de verano, doméstico y actual. Durante milenios ha sido, en el entorno de Asia, Oriente y el Mediterráneo uno de los escasos cultivos de verano. Además, con este paso de invierno a verano se evita el daño que produce un hongo, Didymella rabiei, que provoca la llamada rabia del garbanzo. El hongo necesita humedad y en el cálido y seco verano no la tiene.
El garbanzo silvestre, antecesor del cultivado, solo se localiza en el sudeste de Turquía y, en concreto, en solo 18 localidades. Es la especie Cicer reticulatum. Además, el garbanzo es la única especie cultivada del género Cicer.
Con fecha de hace 13000 a 11000 años, el garbanzo se encuentra en yacimientos del Oriente Próximo, en Tell Abu Hureyra, en el norte de la Siria actual. De hace 10500 años ha aparecido en Cayonii, en el sudeste de Turquía, en Jericó, en Israel, y en Tell Ramad, en el sur de Siria, yacimientos situados lejos del área de distribución del garbanzo silvestre y, por ello, quizá cultivados aunque todavía sin seleccionar el garbanzo actual. Se considera que fue domesticado hace entre 7000 y 10000 años en Asia occidental.
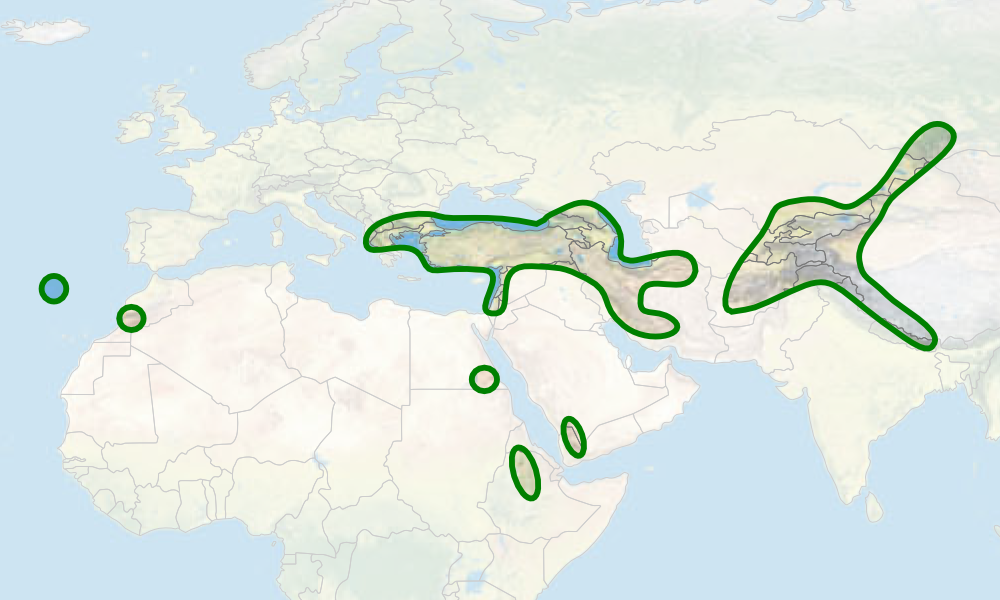
Distribución del garbanzo según Maesen et al (2007): “Taxonomy of the genus Cicer revisited”.
Para Deepak Ohri, la fecha más temprana a la que conocemos con certeza la existencia del garbanzo doméstico es de 10600 a 12250 años en el yacimiento de Tell el-Kerkh, en el noroeste de Siria, donde se encuentra a la vez y se distinguen claramente granos de garbanzo silvestre y de garbanzo domesticado. En esta excavación, Ken-Ichi Tanno y George Willcox, del centro Archeorient del CNRS en Minneapolis, en Francia, recogieron un centenar de granos de garbanzo con una morfología variable y que iba del reticulatum al arietinum, es decir, del silvestre al domesticado. Como este yacimiento está lejos del área de distribución original del garbanzo silvestre, los autores consideran que la domesticación ocurrió mucho tiempo antes de esta fecha de hace 10000 años.
Hace 7500 años aparece en yacimientos en Jericó, en Israel, y en Cayonii y Hacilar, en Turquía. Por su presencia en los yacimientos, hace 6000 años eran alimento habitual en Palestina. Y de hace casi 7000 años aparece en la cueva L’Abenrador, en Francia.
Son los garbanzos de consumo habitual en la Palestina de hace 6000 años, según los restos encontrados en los yacimientos. En la India, los restos más antiguos son de hace 5000 años.
También hace unos 5000 años, en la Edad del Bronce de Grecia, se han encontrado garbanzos en yacimientos del la isla de Creta. En estos años ya se encuentra el garbanzo en la cuenca mediterránea y Oriente Próximo y, en la misma época, ha alcanzado la cultura Harapa, entre los actuales estados de la India y Pakistán. En la Edad del Hierro, con fechas entre 3300 y 2500 años, aparece por primera vez en Etiopía, uno de los mayores cultivadores y consumidores actuales.
Hay un curioso e inexplicable lapso de hallazgos de garbanzo doméstico hace entre 8000 y 11000 años. Algunos autores han propuesto que se debe a que entonces se estaban seleccionando las variedades para el actual cultivo de verano del garbanzo.
También se han encontrado garbanzos nada menos que en la tumba de Tutankamon, faraón que reinó en Egipto hace algo más de 3000 años. Y, también hace casi 3000 años, Homero citaba los garbanzos en La Iliada, ponderando, si lo entiendo bien, su extraordinaria dureza.
Comían garbanzos con gusto los romanos y los cita Petronio en banquetes fastuosos, y hay varias recetas con garbanzos, por cierto, condimentados con cebada y con la famosa salsa romana, el garum, en el Re coquinaria de Marco Gavio Apicio, libro fechado en el siglo I, en la Roma imperial. Sin embargo, eran considerados alimento de pobres, del pueblo.
En aquellos años de la Roma imperial, los garbanzos se vendían por las calles para comer o para picar, tanto cocidos como fritos. Pero maestros y sacerdotes prohibían el consumo de garbanzos a sus discípulos pues, según se creía en aquellos tiempos, inhibían el pensamiento claro y preciso y los elevados principios espirituales que se les exigían. Pitágoras, por ejemplo, no solo prohibía a sus seguidores comer garbanzos sino, también, pasear por un campo sembrado de legumbres. Sin embargo, Dioscórides, Apicio y Plinio recomendaban los garbanzos como alimento saludable.
Según la revisión de Ramón Buxó, aparece en pocos yacimientos arqueológicos en la Península Ibérica, y no se conoce con exactitud cómo y cuándo llegó el garbanzo, quizá con los fenicios y, con certeza, con los romanos. De la época ibérica se ha encontrado en Los Castillejos, en Granada, con un solo ejemplar, y en el Castillo de Doña Blanca, en Cádiz, con nueve ejemplares, todos ellos fechados hace entre 2600 y 2700 años. También se han encontrado garbanzos en varios yacimientos en el sur de Francia de hace entre 2400 y 2500 años. Según los datos de Buxó, el garbanzo aparece en nuestra área geográfica hace de 2400 a 2900 años.
Tito Livio cuenta que los soldados cartagineses de Asdrúbal ya sembraban garbanzos en Cartago Nova, la actual Cartagena, hace unos 2400 años. Y, por supuesto, también los romanos y, como ejemplo, está el único grano de garbanzo que se ha recuperado en las excavaciones de la aldea de Obulco, en Porcuna, provincia de Jaén. Fue Columela, hace unos 2100 años, quien escribió del garbanzo como un cultivo habitual en Iberia.
El Cocinero Mayor de Felipe II y de varios de sus descendientes Austrias, Francisco Martínez Montiño, publicó en 1611 su “Arte de Cocina” e incluye varias recetas con garbanzos. Y no resisto el transcribir una de ellas que, creo, está completamente olvidada y que propongo a los que experimentan en la cocina: son los Garbanzos dulces con membrillo.
“Echarás los garbanzos a cocer, quando estén cocidos, tomarás membrillos, tanta cantidad como los garbanzos; móndalos, quítales las pepitas, y córtalos por medio; luego del medio cortarás rebanadillas delgadas a lo largo, y a lo ancho del membrillo; luego tomarás manteca de vacas fresca, freirás cebolla y los membrillos hasta que estén bien blandos; luego échalos con los garbanzos, sazona con todas especias, canela, y un poco de vinagre, échales dulces de azúcar, que estén bien dulces, y tengan poco caldo; luego harás unos tallarines muy delgados, fríelos, echarás en el plato un lecho de tallarines (aunque se pueden servir sin ellos) y otro de garbanzos, azúcar y canela, y de esta manera hincharás el plato. Y advierte, que este plato ha de servirse bien dulce y bien agrio; y si no hubiere manteca, hágase con un buen aceyte; si no hubiese membrillos, hágase con peros agrios”.
Fue el famoso cocinero y escritor Ángel Muro el que escribió que “yo concedo que con el garbanzo –Sólo el garbanzo- se puede alimentar un hombre, pero a este hombre no hay que pedirle que trabaje material o intelectualmente lo que trabajaría otro hombre que comiera carne”. Pero ya Carlomagno, hace 1200 años, afirmó la utilidad del garbanzo como alimento para el pueblo pues era barato, nutritivo y sencillo de cultivar. El emperador emitió un decreto que obligaba a los campesinos de su imperio a sembrar garbanzos. También tienen propiedades medicinales, son ricos en azúcares y proteínas, vitamina B y hierro, fósforo, zinc y magnesio. Es una fuente barata de proteína y puede cubrir hasta el 20% de la proteína de la dieta.
Para terminar, una receta de garbanzos para el pueblo más pobre, como escribe su recopilador, el Doctor Alfredo Juderías, en su libro “Cocina para pobres”. Además, nos permite aprovechar las sobras, lo que siempre viene bien, antes por falta de recursos y ahora por eso del consumo sostenible. Son los garbanzos “endomingaos”:
Se aliñan los garbanzos sobrantes del cocido, bien secos, con aceite de oliva, ajos cortados en rodajas, perejil muy picado y vinagre y ya está. Al servir se espolvorean con huevos duros picados.
Referencias:
Abbo, S. et al. 2003. The chickpea, summer cropping, and a new model for pulse domestication in the Ancient Near East. Quarterly Review of Biology 78: 435-448.
Abbo, S. et al. 2003. Evolution of cultivated chickpea: four bottlenecks limit diversity and constrain adaptation. Functional Plant Biology 30: 1081-1087.
Abbo, S. et al. 2009. Reconsidering domestication of legumes versus cereals in the Ancient Near East. Quarterly Review of Biology 84: 29-50.
Brothwell, D. & P. Brothwell. 1969. Food in Antiquity. A survey of the diet of early peoples. Johns Hopkins University Press. Baltimore and London. 283 pp.
Buxó, R. 1997. Arqueología de las plantas. Crítica. Barcelona. 367 pp.
del Moral de la Vega, J. et al. 1996. El cultivo del garbanzo. Diseño para una agricultura sostenible. Hojas Divulgadoras 12/94 D. Ministerio de Agricultura, Pesca y Alimentación. Madrid. 24 pp.
Diamond, J. 1998. Armas, gérmenes y acero. La sociedad humana y sus destinos. Ed. Debate. Madrid. 527 pp.
Dusunceli, F. et al. 2007. International trade. En “Chickpea Breeding and Management”, p. 555-575. Ed. por S.S. Yadav. CAB International. Wallingford, UK.
Juderías, Al. 1994. Cocina para pobres. 11ª ed. Ed. SETECO. Madrid. 325 pp.
Khoury, C.K. et al. 2016. Origins of food crops connect countries worldwide. Proceedings of the Royal Society B doi: 10.1098/rspb.2016.0792
Muro, A. 1982 (1894). El Practicón. Tusquets Eds. Barcelona. 774 pp.
Ohry, D. 2016. Genetic resources of chickpea (Cicer arietinum L.) and their utilization. En “Gene Pool Diversity and Crop Improvements”, p. 77-106. Ed. por V.R. Raipal et al. Springer International Publ. Switzerland.
Redden, R.J. & J.D. Berger. 2007. History and origin of chickpea. En “Chickpea Breeding and Management”, p. 1-13. Ed. por S.S. Yadav. CAB International. Wallingford, UK.
Tanno, K. & G. Willcox. 2006. The origins of cultivation of Cicer arietinum L. and Vicia faba L.: early finds from Tell el-Kerkh, north-west Syria, late 10th millenium b.p. Vegetation History and Archaeobotany 15: 197-204.
van der Maesen, L.J.G. 1987. Origin, history and taxonomy of chickpea. En “The Chickpea”, p. 11-34. Ed. por M.C. Saxena & K.B. Singh. CAB International. Wallingford, UK.
Voropaeva, I & H.-P. Stika. 2016. Plant remains from Roman period town of Obulco (today Porcuna) in Andalusia (Spain) – distribution and domestication of olive in the west Mediterranean region. Archaeological and Anthropological Sciences DOI: 10.1007/s12520-016-0405-1.
Weiss, E. & D. Zohary. 2011. The Neolithic Southwest Asia founder crops. Current Anthropology 52, Suppl. 4: S237-S254.
Wikipedia. 2017. Cicer arietinum. 20 septiembre.
Wikipedia. 2017. Chickpea. 15 November.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Ingredientes para la receta: El garbanzo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ingredientes para la receta: el ajo
- Ingredientes para la receta: El arroz
- Ingredientes para la receta: El kiwi
¿Qué factores han impulsado la evolución cognitiva en el linaje humano?
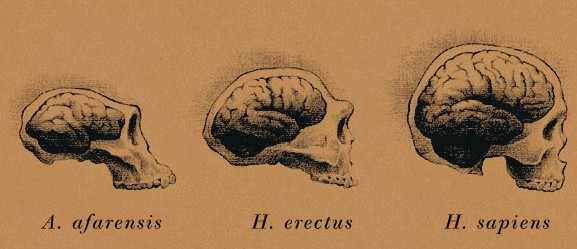
Como vimos en una anotación anterior, se han barajado diferentes hipótesis para dar cuenta de las presiones selectivas que dieron lugar al gran encéfalo que caracteriza a la especie humana. Se asume que ese tamaño permitió el desarrollo de capacidades cognitivas idóneas para hacer frente a aquellas presiones. Un trabajo más reciente, realizado por Suzanne Shultz, Emma Nelson y Robin I. Dunbar ha barajado y valorado varias posibilidades: (1) que gracias a esas habilidades cognitivas los homininos pudieran desenvolverse bajo condiciones climáticas variables e impredecibles, con fuentes de alimento cambiantes e igualmente difíciles de prever; (2) que les permitieran afrontar con éxito la amenaza de diversos y poderosos depredadores al aventurarse por espacios y ecosistemas nuevos; (3) que posibilitasen la vida en grandes grupos de individuos y que favoreciesen la cooperación en el seno de dichos grupos (dentro de esta categoría se consideran de importancia crucial las capacidades para valorar los intereses de los otros miembros del grupo); (4) que dieran lugar al desarrollo del lenguaje, con todas las posibilidades que tal adquisición conllevó.
El grupo de Dunbar estudió un amplio conjunto de cráneos correspondientes a un periodo que va de hace 3.2 millones a hace 10000 años, y analizó su posible relación con los factores que pudieron propiciar sus cambios de tamaño. En el análisis optó por dos procedimientos en paralelo. Por un lado estudió el curso temporal de variación en las dimensiones craneales para todo el conjunto de homininos estudiados. Y por otro lado analizó el cambio en el seno de cuatro grandes categorías taxonómicas: Australopithecus sp., Homo habilis, Homo erectus (incluido H. ergaster) y H. sapiens (incluidos H. heidelbergensis y H. neanderthalensis).
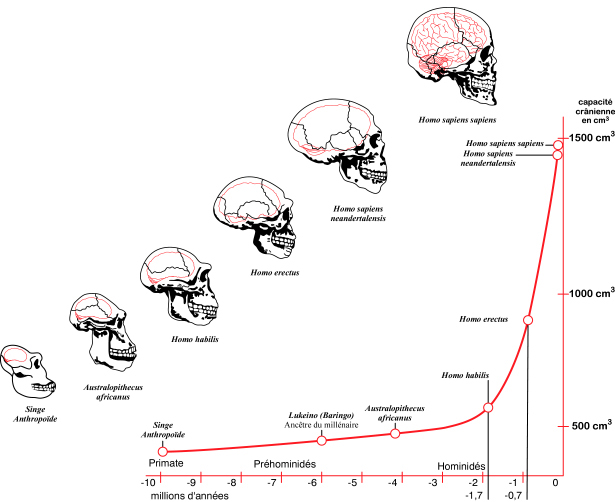
Los resultados indican que el crecimiento del cráneo de los homininos a lo largo de tres millones largos de años no ha sido gradual, sino que se han producido saltos en determinados momentos: los dos primeros saltos coinciden con la aparición de los primeros H. habilis (hace unos dos millones de años) y de H. erectus (hace unos 1.8 millones de años). El tercero ocurrió entre 1.0 y 1.2 millones de años, sin aparente relación con la aparición de ninguna especie. Y los dos últimos han ocurrido, el primero de ellos, hace entre cuatrocientos y doscientos mil años, en el entorno de la aparición de los seres humanos anatómicamente modernos, y hace unos cien mil años el segundo, sin coincidir este tampoco con la aparición de ninguna especie en concreto. Aparte de esos saltos, en algunas de las categorías también se observaron aumentos graduales en el tamaño encefálico a lo largo del tiempo.
Esta investigación no permitió atribuir a un único factor la encefalización observada durante la evolución de los homininos. Los factores climáticos y ambientales ejercieron, muy probablemente, cierta influencia, ya fuese de forma directa o indirecta, al obligarles a modificar su comportamiento, de manera que ocuparon hábitats más periféricos y peligrosos, vivieron en grupos de mayor tamaño o utilizaron nuevos recursos.
Dado que los factores relacionados con el clima no pueden por sí solos dar cuenta de la variación observada en el tamaño encefálico a lo largo del tiempo, han de ser considerados otros posibles efectos, y muy en especial los ejercidos por factores de carácter social y lingüístico. Aunque no se dispone de medidas directas de la estructura de los grupos sociales o de su complejidad, es conocida la gran importancia que la inteligencia social tiene para la condición humana. Las conclusiones a que han llegado los estudios acerca de la evolución del lenguaje, morfología encefálica y la aparición del comportamiento simbólico sugieren que la evolución del lenguaje es una componente clave de la evolución cognitiva humana y que los avances culturales han podido ocurrir en una serie de pasos que habrían tenido su reflejo en cambios en el tamaño y arquitectura del encéfalo. En ese sentido, los autores del trabajo sugieren que el último salto en el tamaño encefálico, el producido a partir de hace unos cien mil años, puede estar asociado a la adquisición del lenguaje complejo, o sea, en la transición de un habla basada en la capacidad para emitir sonidos vocálicos articulados a la producción de proposiciones plenamente gramaticales.
Fuente:
Suzanne Shultz, Emma Nelson & Robin I Dunbar (2012): Hominin cognitive evolution: identifying patterns and processes in the fossil and archaeological record. Phil Trans R Soc B 367: 2130-2140; doi:10.1098/rstb.2012.0115
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo ¿Qué factores han impulsado la evolución cognitiva en el linaje humano? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El gran encéfalo humano es un “encéfalo social”
- Gradualismo o saltacionismo… en evolución lingüística
- Evolución del tamaño animal
‘Entre selfies y whatsapps’: Internet, infancia y adolescencia en Europa y Latinoamérica
Oficina de comunicación de la UPV/EHU

Cada día más niños y niñas utilizan los medios digitales para descargar música, ver vídeos, hacer los deberes, participar en redes sociales y comunicarse. Esta realidad conlleva un mundo de oportunidades que no está exento de problemas y situaciones peligrosas derivadas del mal uso de la red. En este contexto, sus coordinadores destacan que “más allá de tópicos y alarmismo, es necesario formar en la prevención de riesgos y alentar a niños y niñas a que asuman su papel como internautas exigentes y conscientes con autonomía y seguridad”.
El libro es el resultado de la colaboración entre autores de más de una veintena de universidades europeas y latinoamericanas que abordan diferentes cuestiones relacionadas con la vida online de los y las menores. Cada capítulo se centra en un aspecto concreto: el ciberbullying, el sexting, el contacto con desconocidos, el uso excesivo, la perspectiva de género, la gestión del desembarco de internet en la escuela o la labor de mediación de las familias, entre otros. Según afirmó en la presentación Maialen Garmendia, “la clave para mejorar la seguridad en internet está en la educación, entendida en un sentido amplio: desde las familias y la escuela hasta las actividades extraescolares”.
Con la participación de la doctora Honoris Causa de la UPV/EHU e investigadora principal de la red europea EU Kids Online Sonia Livingstone, el libro permite conocer realidades de diferentes países, incluidos varios latinoamericanos. En este sentido, Carmelo Garitaonandia, catedrático de Periodismo de la UPV/EHU y coautor de uno de los capítulos, remarcaba en la presentación la importancia de prestar atención a la vida online de la infancia y adolescencia desde un punto global: “Aunque no es fácil conseguir datos fiables y seriados de todos los países de América Latina, sí es claramente constatable las diferencias de conexión entre los hogares de alto y bajo estatus socioeconómico, así como entre zonas urbanas y rurales, en países que han combinado un acelerado desarrollo económico con la emergencia de profundas desigualdades. En Brasil, por ejemplo, la población de mayores ingresos está conectada casi al 100%, mientras que la de menos ingresos no llega ni a una cuarta parte. Y en Colombia las diferencias de conexión entre hogares urbanos y rurales es de 6 a 1”.
En España y los niños y niñas disponen de su primer móvil a los 8 años. Hace seis años se accedía por primera vez a Internet a los 10 y se tenía móvil por primera vez a los 11. Aunque la presencia de niños y niñas en internet y el uso de teléfonos, tabletas y ordenadores son hábitos cada vez más tempranos, la exposición a los riesgos no ha aumentado en la misma medida. Sin embargo, la incidencia del bullying entre usuarios de 9 a 16 años se ha doblado en menos de una década: en 2010 un 15% declaraba haberlo sufrido en cualquiera de sus variedades, incluido el ciberbullying, y según los hallazgos de investigación recogidos en el libro, este dato se eleva al 31%. Así mismo, el porcentaje de menores que ha recibido mensajes sexuales ha aumentado extraordinariamente en los últimos años: casi uno de cada tres de los menores responden afirmativamente a esa pregunta.
Entre los riesgos detectados para la infancia y la adolescencia aparecen los mensajes sexuales, y el ciberbullying. En este último caso, la implicación del profesorado y la intervención del alumnado son parte esencial para detectar y combatir el ciberacoso. Los programas Ciberprogram 2.0 o Asegúrate son estrategias útiles para revenirlo, junto con los protocolos habituales utilizados en casos de bullying tradicional (el bullying cara a cara), que sigue siendo más frecuente que el online. En cuanto a los mensajes sexuales, la mayoría de jóvenes españoles entre 11 y 16 años (94,5%) opina que el sexting es una práctica peligrosa, el 44,7% admite que es parte del juego erótico y/o sexual y sólo uno de cada cuatro (19,5% de mujeres y 31’4% de hombres) considera que mejora las relaciones de pareja.
Aunque la Organización Mundial de la Salud no reconoce la adicción a internet a nivel clínico, sí existen jóvenes que presentan los síntomas habituales de las adicciones, que están enganchados. De todas maneras, tampoco hay que confundir el uso frecuente o abusivo de las redes con el uso problemático, el cual depende del grado de interferencia que internet pueda suponer en la vida diaria de cada persona.
Los riesgos existen, pero hay un aumento de la concienciación sobre ellos entre padres, madres y menores. Aunque la frecuencia de uso de internet y los dispositivos móviles ha aumentado y en consecuencia lo ha hecho el peligro, la proporción de quienes han sufrido daños tras afrontar riesgos en internet es menor. Así todo, es necesario dotar a los menores de recursos para que aprovechen al máximo las oportunidades que ofrece el entorno digital y minimicen esos riesgos.
El indiscutible acceso cada vez más temprano a internet es una oportunidad para que padres y madres supervisen o acompañen a sus hijos e hijas en el uso de móviles, tabletas e internet. Sin embargo, el apego por su teléfono y el deseo de privacidad dificultan la mediación de padres y madres, especialmente cuando sus progenitores respetan la privacidad y valoran la confianza de los niños y niñas.
En la educación digital la escuela debe jugar un papel activo. Invertir en infraestructura y en equipos es una oportunidad para aprovechar el potencial de las Tecnologías de la Información y la Comunicación (TIC), pero no será suficiente si, al mismo tiempo, el profesorado no juega un papel más activo y hay una revisión de los métodos pedagógicos convencionales. Esta responsabilidad en la educación de los menores también debe ser compartida por madres, padres y el conjunto de la sociedad.
Entre selfies y whatsapps aborda también la situación en Latinoamérica, donde se han detectado diferencias significativas en la capacidad para acceder a internet entre los y las jóvenes de diferentes países. En Uruguay y Chile las posibilidades de acceso son mayores, los hogares están mejor conectados y presentan el mejor ratio de estudiantes por ordenador. En cuanto a porcentaje de colegios conectados a internet también se ubican en los primeros puestos junto con Costa Rica. En todos los países son significativas las diferencias de conexión entre zonas urbanas y rurales, así como entre el estatus socioeconómico alto y bajo.
Ficha:
Autores: Estefanía Jiménez, Maialen Garmendia, Miguel Ángel Casado (coordinadores)
Título: Entre selfies y whatsapps. Oportunidades y riesgos para la infancia y la adolescencias conectadas
Año: 2018
Editorial: Gedisa
En Editoralia personas lectoras, autoras o editoras presentan libros que por su atractivo, novedad o impacto (personal o general) pueden ser de interés o utilidad para los lectores del Cuaderno de Cultura Científica.
El artículo ‘Entre selfies y whatsapps’: Internet, infancia y adolescencia en Europa y Latinoamérica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La menor influencia de las mujeres en Internet
- Marcapasos con conexión a Internet
- Adolescencia, sexismo y publicidad
Naukas Bilbao 2017 – Ricardo Oltra: Que inventen ellos
En #Naukas17 nadie tuvo que hacer cola desde el día anterior para poder conseguir asiento. Ni nadie se quedó fuera… 2017 fue el año de la mudanza al gran Auditorium del Palacio Euskalduna, con más de 2000 plazas. Los días 15 y 16 de septiembre la gente lo llenó para un maratón de ciencia y humor.

Ricardo Oltra, que es ingeniero agrónomo y físico teórico de formación, trabaja en la Oficina Europea de Patentes en La Haya (Holanda) nos introduce en el proceloso mundo de las patentes.
Ricardo Oltra: Que inventen ellosEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2017 – Ricardo Oltra: Que inventen ellos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – Álex Méndez: Luz de luna
- Naukas Bilbao 2017 – Ignacio López-Goñi: Las bacterias también se vacunan
- Naukas Bilbao 2017 – Mónica Lalanda: Una muerte de cómic
Nanopartículas para reducir la metástasis hepática del cáncer de colon
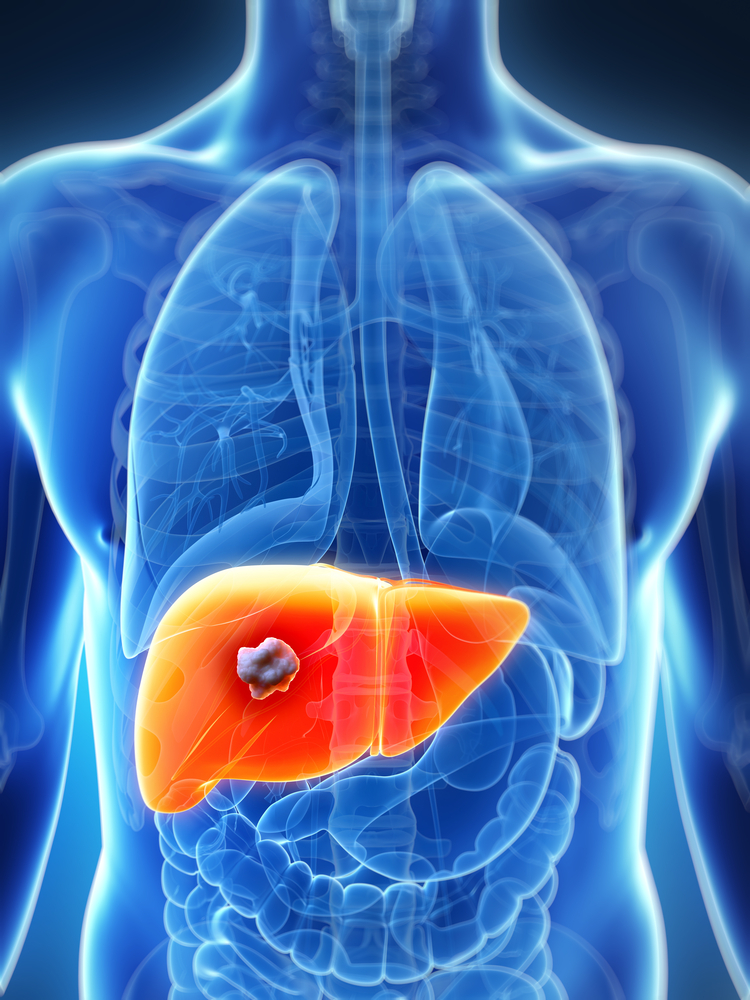
Representación gráfica de una metástasis (blanco/gris) en el hígado (naranja).
La metástasis es el proceso por el cual un tumor que crece en un órgano se desprende de este y viaja a otro órgano y lo coloniza. En el proceso de colonización necesita crear nuevos vasos sanguíneos, a través de los que las células cancerosas obtienen los alimentos y oxígeno necesarios para crecer. Ese proceso de formación de vasos sanguíneos se denomina angiogénesis, y lo llevan a cabo las células endoteliales. “A diferencia de las células endoteliales normales, y como consecuencia de las señales que les llegan de las células tumorales, las células que abastecen a los tumores tienen un crecimiento mayor y tienden a moverse hacia la masa metastásica, para ayudarla a crecer”, comenta Iker Badiola, miembro del grupo de investigación Signaling Lab del Departamento de Biología Celular e Histología la Facultad de Medicina y Farmacia de la UPV/EHU.
Con el fin de revelar qué es lo que provoca ese cambio en las células endoteliales, el grupo de investigación Signaling Lab de la UPV/EHU y el Departamento de Farmacología, Farmacia y Tecnología Farmacéutica de la Universidad de Santiago de Compostela iniciaron una investigación con ratones, en colaboración con otra serie de investigadores. El fin último era, tal como afirma Badiola, “frenar el proceso metastásico incidiendo sobre la angiogénesis, en caso de conseguir restablecer las células endoteliales”. En la investigación, provocaron una metástasis hepática a ratones utilizando células de cáncer de colon, y de esa masa extrajeron células endoteliales. Posteriormente, realizaron una comparación entre esas células endoteliales y otras sanas. La comparativa la hicieron en dos aspectos: a nivel proteico, donde vieron que proteínas aparecían y cuáles no en cada tipo de células, y en qué nivel lo hacían, y de igual manera a nivel de micro-RNA. Los microRNA son unos pequeños elementos, que durante un tiempo se pensó que no tenían ninguna función, pero ahora se sabe que participan en la regulación de proteínas.
Mediante herramientas bioinformáticas, hicieron el cribado y selección de las proteínas y los elementos micro-RNA relevantes, y “en el último paso de esa selección nos quedamos con un micro-RNA concreto, el miR-20a. Se trata de un elemento que aparece en las células endoteliales sanas, pero desaparece en las que están en contacto con el tumor. Vimos que como consecuencia de la desaparición del miR-20a en las células endoteliales aparecían una serie de proteínas, y era entonces cuando comenzaba a cambiar su comportamiento y empezaban a crecer y desplazarse”, aclara Badiola.
Seguidamente, iniciaron los experimentos para demostrar si la inclusión del elemento miR-20a haría restablecer el comportamiento de las células endoteliales que abastecen los tumores. Para ello, desarrollaron unas nanopartículas “diseñadas para ser dirigidas a las células endoteliales hepáticas, y cargadas de miR-20a. Se las suministramos a ratones a los que previamente habíamos provocado la metástasis, para conocer el efecto. El análisis patológico reveló que en los casos tratados se habían formado muchos menos vasos sanguíneos nuevos dentro de los tumores. Asimismo, certificamos que el número y tamaño de las masas de metástasis se habían reducido en un 80 %”, detalla.
Badiola valora positivamente el poder reducir el tamaño de la metástasis en un 80 %, pero tiene claro que “si alguna vez llega a ser utilizado como tratamiento, será un tratamiento complementario. No hay que ignorar que la metástasis sigue creciendo un 20 %, y, además, en ningún momento se destruyen las células tumorales, no se arremete contra ellas directamente. La estrategia de hacer frente a la metástasis que hemos conseguido limita el aporte de alimentos y oxígeno; es decir, le restringimos la ayuda”.
Referencia:
Joana Marquez, Ines Fernandez-Piñeiro, Marcos J. Araúzo-Bravo, Gereon Poschmann, Kai Stühler, Abdel-Majid Khatib, Alejandro Sanchez, Fernando Unda, Gaskon Ibarretxe, Irantzu Bernales, Iker Badiola (2018) Targeting liver sinusoidal endothelial cells with miR-20a-loaded nanoparticles reduces murine colon cancer metastasis to the liver. International Journal of Cancer doi: 10.1002/ijc.31343
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Nanopartículas para reducir la metástasis hepática del cáncer de colon se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Seguridad diagnóstica en el cáncer de colon y tratamiento del de páncreas
- Nanopartículas de oligoquitosano para terapia génica
- Detección precoz del cáncer de colon por métodos no invasivos
Una breve historia del método de la hipótesis

Corazonada, especulación, conjetura son tres palabras válidas para describir lo que es una hipótesis. Una hipótesis no es otra cosa que una corazonada, una especulación o una conjetura que se propone como solución a un problema, pero cuya aceptabilidad necesita de más investigación mediante argumentos, observaciones o experimentos.
La formulación de hipótesis es indispensable en el pensamiento humano: desde el de una niña que aprende a manejar su último regalo tecnológico sin leerse las instrucciones a el de esa misma niña cuando se dedica profesionalmente a la metafísica, pasando por el de los detectives novelescos à la Sherlock Holmes.
Sin embargo, a pesar de ser algo común a cualquier empresa intelectual humana, muchos ven a la hipótesis como parte fundamental de eso que se ha dado en llamar “el” método científico, como si hubiese solo uno y se identificase con el hipotético-deductivo. Muchas de estas personas adoptan, sin saberlo probablemente, una posición filosófica asociada a Popper, según la cual las teorías científicas no serían otra cosa que “hipótesis empíricas”, estatus que mantienen siempre sin importar el éxito que puedan tener a la hora de soportar los repetidos intentos de hacer ver que son falsas (falsarlas).
Curiosamente esta visión de la ciencia y del papel central del método de la hipótesis es muy contemporánea, y las narrativas de la ciencia desde el siglo XVII a nuestros días como manifestaciones de este método son ahistóricas, por presentistas, además de mayoritarias. Para ilustrar este hecho esbocemos la historia del método de la hipótesis en ciencia.

Los “Principios de filosofía” de Descartes en la edición realizada en Amsterdam en 1685
Habitualmente en las narrativas contemporáneas del método de la hipótesis habría sido Francis Bacon el referente a principios del XVII para su origen. Y no es cierto, eso es atribuirle una influencia en su tiempo que no tuvo. Fue René Descartes el que lo hizo objeto de discusión en sus “Principia philosophiae” (1644).
Argumentaba Descartes que el mundo se presenta a sí mismo como el dial de un reloj cuyos mecanismos internos están ocultos. Para hablar de estos mecanismos debemos recurrir a hipótesis o conjeturas. De forma análoga, si queremos hablar de un fenómeno que observamos, como la reflexión o la refracción de la luz, y si queremos explicarlo en términos de corpúsculos hemos de recurrir a hipótesis. Los argumentos de Descartes fueron desarrollados por muchos que se dedicaban a la “filosofía mecánica”, siendo probablemente el más significado de ellos Robert Boyle.
La formación clásica de los eruditos de la época hacía que todos ellos tuviesen unos conocimientos elementales de lógica, más en una época tan cercana al Renacentismo. Hemos de recordar que en esta época Bento Spinoza escribe su obra cumbre, “Ethica more geometrico demonstrata” (Ética demostrada geométricamente) (1677), como un tratado lógico-matemático. Cualquiera con estos conocimientos elementales de lógica sabía que aceptar el método de la hipótesis era aceptar como válida una falacia, la afirmación del consecuente [1]. Incluso si damos una explicación plausible de la refracción como causada por corpúsculos, el éxito de la explicación no demuestra que los corpúsculos existan realmente [2].

Primera edición de los “Principia” de Newton (1687)
Por lo tanto era evidente para los filósofos de la época, mecánicos o no, que el método de la hipótesis no permitía alcanzar lo que Aristóteles llamaba conocimiento cierto. Isaac Newton, horrorizado por lo chapucero del método de la hipótesis (aunque él, como humano que era, recurriese a él informalmente), escribe lo siguiente [3] en el “Escolio general” que añadió a la segunda edición (1713) de los “Philosophiæ Naturalis Principia Mathematica”:
Todavía no he podido descubrir la razón de estas propiedades de la gravedad a partir de los fenómenos, y no compongo una hipótesis [hypotheses non fingo]. Porque lo que no se deduce de los fenómenos debe llamarse una hipótesis; y las hipótesis, ya sean metafísicas o físicas, o basadas en cualidades ocultas, o mecánicas, no tienen cabida en la filosofía experimental. En esta filosofía, las proposiciones particulares se infieren de los fenómenos, y luego se vuelven generales por inducción.
El prestigio de Newton llevó a la condenación del método de la hipótesis durante 150 años. Así se puede encontrar esta condena explícitamente en textos tan influyentes en su época como el “Traité des systèmes” (1741) de Condillac, los “Discours prélimenaires” (1751) de la “Encyclopedie” o el “Inquiry into de Human Mind” (1764) de Thomas Reid. Con el redescubrimiento de Francis Bacon durante la primera mitad del siglo XIX, y en contra de la narrativa presentista del siglo XXI, los métodos alternativos al de la hipótesis como la inducción enumerativa [4]y la inducción eliminativa se hicieron aún más populares.
Con todo, desde la segunda mitad del siglo XVIII existe una minoría de filósofos naturales y, ya, científicos de pleno derecho, que argumentan que la ciencia no puede evitar el método de la hipótesis. Los filósofos que usaban fluidos imponderables para explicar los fenómenos gravitatorios, como George le Sage, neurofisiológicos, como David Hartley, o la propia materia, como Ruder Boscovich, se dieron cuenta de que repudiar el método de la hipótesis era autoengañarse.
El estatus del método de la hipótesis a comienzos del siglo XIX lo ilustra muy bien el debate sobre la naturaleza de la luz. Aquellos que pensaban que el método de la hipótesis era inaceptable, como John Stuart Mill, rechazaban la teoría ondulatoria. Por tanto, el debate sobre la naturaleza de la luz, como muchos en ciencia, era tan científico como filosófico.

Edición de 1847 de “La filosofía de las ciencias inductivas basada en su historia ” de Whewell
El método de la hipótesis fue así ganando predicamento con figuras de la influencia de William Whewell en su “Philosophy of the Inductive Sciences” (1840) y Claude Bernard en su “Introduction à l’étude de la médecine expérimentale” (1865) dándole apoyo.
Los que apoyaban el método de la hipótesis trabajaron para consolidarlo, por ejemplo añadiendo que cuanto más amplio fuese el rango de fenómenos que una hipótesis puede explicar, más probable es que sea verdadera. Whewell fue un paso más allá sugiriendo que las hipótesis aceptables tenían que explicar más que aquello para lo que habían sido creadas, esto es, tenían que ser capaces de predecir nuevos fenómenos.

Ernst Mach en 1900
Sin embargo, los que apoyan el método de la hipótesis si bien crecen en número e influencia durante el siglo XIX aún no son la mayoría. Muchos científicos siguen sospechando de esta forma de proceder y afirman que solo se puede generalizar por inducción. Ernst Mach, un físico y epistemólogo de enorme influencia a finales de siglo (sus ideas se encuentran en los primeros trabajos de Einstein por ejemplo [2]), al igual que muchos positivistas, descarta su uso más allá de una ayuda heurística, reservas que se traducen en que él mismo niegue la existencia de los átomos, muchos hagan la vida imposible a Boltzmann por proponerlos y Wilhelm Ostwald reconociese su existencia [2] solo el año antes de recibir el premio Nobel de química en 1909. La sociología y la historia de la ciencia del XIX y primeros años del XX no se entiende sin una comprensión del papel del rechazo al método de la hipótesis.
Con el siglo XX comienza en serio el conocimiento en profundidad de la estructura de la materia y el universo, lo que favorece el uso de la especulación ante la limitación de observaciones, cuando son posibles, a partir de las que hacer inducciones. Esto lleva a que hoy el método de la hipótesis, conocido como método hipotético-deductivo sea el más popular de los métodos de la ciencia. Algunos historiadores, filósofos y prácticantes de la ciencia deslumbrados por la física del XX lo elevaron a paradigma de lo que es ciencia y lo identificaron con “el” método de la ciencia, cosa que, como hemos visto, no es así.
Notas:
[1] Si la hipótesis A es cierta, entonces debe ocurrir B; como ocurre B, entonces A es cierto. Por ejemplo, si está criado en Inglaterra entonces habla inglés, como habla inglés entonces es inglés; esto, como sabemos, no es necesariamente cierto, puede ser neozelandés, hablar inglés perfectamente y no haber pisado Inglaterra en su vida.
[2] Por eso la existencia de los átomos no se acepta como realidad por la comunidad científica hasta la formulación de Einstein del movimiento browniano comprobada experimentalmente por Perrin en 1908, porque no es del tipo lógico “si A entonces B” sino del “B si, y solo si, A”.
[3] Realmente lo escribe en latín. Proporcionamos una traducción libre.
[4] Se suele denominar inducción a secas: extrapola a partir de sucesos/datos concretos a afirmaciones generales. Si he visto 1000 ovejas y todas las ovejas que he visto son blancas, entonces todas las ovejas son blancas.
[5] A partir de los datos se llega a todas las conclusiones posibles (a estas conclusiones las llamaríamos hoy día hipótesis, pero preferimos conclusiones para evitar la confusión polisémica); la aparición de nuevos datos va eliminando conclusiones hasta, idealmente, quedar solo una.
Para saber más:
Este post ha sido realizado por César Tomé López (@EDocet) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
El artículo Una breve historia del método de la hipótesis se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una breve historia del concepto de trastorno bipolar
- Breve historia del trastorno bipolar (II): neurobiología y tratamiento
- La bombilla de colores (y el método científico)
Las pruebas de la educación 2018: El coloquio

¿Cómo se tratan algunos de los trastornos cognitivos más frecuentes en las aulas? ¿Son efectivos los programas y herramientas del sistema educativo actual? ¿Carecen de eficacia algunas de las prácticas educativas más populares?
Estas son algunas de las cuestiones que se debatieron en la jornada “Las pruebas de la educación”, que se celebró el pasado 2 de febrero de 2018 en el Bizkaia Aretoa de Bilbao. El evento, en su segunda edición, estuvo organizado por la Cátedra de Cultura Científica de la UPV/EHU y el Consejo Escolar de Euskadi, con la colaboración de la Fundación Española para la Ciencia y la Tecnología (FECYT).
Las ponencias de los expertos que expusieron múltiples cuestiones relacionadas con la educación, basándose siempre en las pruebas científicas existentes. Los especialistas hicieron especial hincapié en destacar cuál es la mejor evidencia disponible a día de hoy con el objetivo de abordar las diferentes realidades que coexisten en las aulas y en el sistema educativo en general.
“Las pruebas de la educación” forma parte de una serie de eventos organizados por la Cátedra de Cultura Científica de la UPV/EHU para abordar cuestiones del día a día como la educación o el arte desde diversos ámbitos de la actividad científica. La dirección del seminario corre a cargo de la doctora en psicología Marta Ferrero.
En el coloquio final asistentes y ponentes podudieron compartir sus diferentes puntos de vista e intercambiar dudas y opiniones.
Charla coloquio de la jornada ''Las pruebas de la educación''Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Las pruebas de la educación 2018: El coloquio se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Autismo y educación: problemas y pautas en el aula
- Cómo destruir un buen sistema de educación. El ejemplo sueco
- Las ideas erróneas sobre educación entre el profesorado: prevalencia, causas y soluciones
La ciencia y los errores
En última instancia, y por definición, todo los que creemos saber, avanzar y entender en el campo de la ciencia es incorrecto. Porque está mal, simplemente, o porque es insuficiente e incompleto. Porque una teoría posterior englobará y digerirá cualquier idea, o porque un descubrimiento posterior desmoronará la lógica de cualquier hipótesis. Todo lo que se avanza o descubre en ciencia será sobrepasado; todo lo que creemos saber sobre el universo es menos de lo que el universo es, y posteriores científicos trabajarán con ahínco en demostrarlo así. El sino de cualquier avance, descubrimiento, hipótesis o teoría es acabar en los libros de historia de la ciencia. Porque el avance del conocimiento la habrá dejado arrumbada. Porque nunca, jamás conseguiremos saberlo Todo sobre Todas las cosas, entender Todo sobre Todo lo que hay.
En ese sentido toda la ciencia es un error. Y así es como debe ser, porque lo contrario sería detenerla en seco, parar su avance, impedir su desarrollo. A lo más que puede aspirar quien se dedica a la ciencia es a cometer errores.
Eso sí, si esa persona es ambiciosa sus errores serán interesantes. A lo más que puede aspirar un científico es a cometer errores interesantes.
Errores que dejen puertas abiertas; errores que impulsen el avance de la ciencia. Errores que sean insuficientes, pero apunten en una buena dirección. Errores fecundos, preñados de preguntas que generen nuevas respuestas. Errores que impulsen la mente de nuevos científicos; errores incluso que cabreen e irriten a otros, impulsándoles así a corregirlos. Errores grandes, ricos, plenos, que generen polémica, que empujen la investigación, que supongan un avance. Aunque sea un avance ínfimo, insuficiente, demasiado pequeño; aunque no sea más que otro error más en una cadena de errores que se remonta al conocimiento de los primeros humanos, una saga de errores que comenzó en la prehistoria y se dirige al futuro.
El conocimiento nunca puede ser definitivo, perfecto, cerrado, final. Siempre deja flecos, rincones por explorar, nuevas partes por conocer. En la vieja metáfora sobre el saber de la Humanidad se compara con una esfera, que cuando más aumenta de volumen tiene mayor superficie de contacto con lo desconocido: en realidad cuanto más sabemos tanto más desconocemos, porque cada brizna de nuevo saber abre nuevos campos a la ignorancia. Mucho mejor aportar conocimiento imperfecto pero que abra nuevas puertas que intentar conseguir lo que por definición es imposible.
Al fin y al cabo Todos los Modelos son Erróneos, pero algunos son útiles. Lo mismo ocurre con el trabajo de cualquier científico; siempre será erróneo, pero si la ciencia es buena al menos será interesante, fecundo, útil. ¿Se puede aspirar, acaso, a más?
Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.
El artículo La ciencia y los errores se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Más blanco que un escarabajo blanco

Escarabajo Cyphochilus. Foto: Olimpia Onelli
En 2014 se hacía famoso un pigmento negro, el Vantablack, por su capacidad para absorber el 99,96 % de la luz que recibe. Una sustancia así tiene aplicaciones evidentes en exploración espacial y militares. Su capacidad para absorber la luz no se debe a su composición química como tal, carbono, sino a su estructura, nanotubos de carbono. Y es que es la estructura lo que determina muchas de las propiedades ópticas de los materiales.
Ahora, un equipo de investigadores encabezado por Matti Tiavonen, de la Universidad Aalto (Finlandia), ha desarrollado un recubrimiento extremadamente delgado, ligero y, sobre todo, brillantemente ultrablanco que podría tener aplicación comercial en productos farmacéuticos y alimentarios, además de la evidente en pinturas y barnices.
El material, que es 20 veces más blanco que el papel blanco, está hecho de celulosa comestible no tóxica. Logra esta blancura excepcional, al igual que el pigmento negro, no por su composición como tal sino porque se hace que la celulosa imite la estructura de las escamas ultradelgadas de ciertos tipos de escarabajos.
Los colores brillantes generalmente se producen utilizando pigmentos, que absorben ciertas longitudes de onda de la luz y reflejan otras, que nuestros ojos perciben como el color. Para que nos parezca blanco, sin embargo, todas las longitudes de onda de la luz deben reflejarse con la misma eficacia. La mayoría de los productos blancos disponibles comercialmente, como cremas solares, cosméticos y pinturas, incorporan partículas altamente refractivas (generalmente dióxido de titanio u óxido de zinc) para reflejar la luz de manera eficiente. Estos materiales, si bien se consideran seguros, no son totalmente sostenibles o biocompatibles.
En la naturaleza, el escarabajo Cyphochilus, que es originario del sudeste asiático, produce su coloración ultra blanca no a través de pigmentos, sino explotando la geometría de una densa red de quitina, una molécula que también se encuentra en las conchas de los moluscos, los exoesqueletos de insectos y las paredes celulares de hongos. La quitina tiene una estructura que dispersa la luz de manera extremadamente eficiente, dando como resultado revestimientos ultra blancos que son muy delgados y ligeros.
En los casos de los colores de las mariposas o de los ópalos los colores brillantes también se obtienen estructuralmente. A diferencia de estos colores, que responden a patrones concretos en la estructura, el blanco solo se consigue con estructuras lo más aletorias posible.

Escarabajos Cyphochilus en presencia de una membrana del nuevo pigmento blanco. Foto: Olimpia Onelli
Los investigadores han imitado la estructura de la quitina usando celulosa, que no es tóxica, es abundante, resistente y biocompatible. Utilizando pequeños filamentos de celulosa, o nanofibrillas de celulosa, lograron primero el mismo efecto ultra-blanco en una membrana flexible. Después, mediante el uso de una combinación de nanofibrillas de diferentes diámetros, los químicos pudieron ajustar la opacidad y, por lo tanto, la blancura del material final. Las membranas hechas de las fibras más delgadas eran más transparentes, mientras que la adición de fibras medias y gruesas daba como resultado una membrana más opaca. De esta manera, los investigadores pudieron ajustar la geometría de las nanofibras para que reflejaran la mayor cantidad de luz.
Al igual que las escamas de los escarabajos, las membranas de celulosa son extremadamente delgadas: solo unas pocas micras (millonésimas de metro) de grosor, aunque los investigadores dicen que se podrían producir membranas incluso más delgadas optimizando aún más su proceso de fabricación. Las membranas dispersan la luz de 20 a 30 veces más eficientemente que el papel, y podrían usarse para producir los materiales blancos brillantes, sostenibles y biocompatibles eficientes de la siguiente generación.
Referencia:
Matti S. Toivonen et al (2018) Anomalous-Diffusion-Assisted Brightness in White Cellulose Nanofibril Membranes Advanced Materials doi: 10.1002/adma.201704050
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Más blanco que un escarabajo blanco se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Otra pieza en el puzle de la fotosíntesis
- Un atlas para materiales 2D
- Usando ADN para sintetizar nanoestructuras de oro
La invención matemática
Acaba de publicarse en KRK Ediciones el magnífico texto La invención matemática. Cómo se inventa: el trabajo del inconscientede Henri Poincaré, traducido y prologado por Francisco González Fernández.

L’invention mathématique es el título de una conferencia impartida por Henri Poincaré en el Institut général psychologique de París el 23 de mayo de 1908 y publicada ese mismo año (entre otras, en la revista L’Enseignement Mathématique 10, 357-371). El científico francés publicó Comment on invente. Le travail de l’Inconscienten el periódico Le Matin a finales del año 1908.
En esta edición en castellano publicada en febrero de 2018, Francisco González Fernández, enamorado y estudioso de la obra de Poincaré, traduce los textos originales y los analiza en una magnífica introducción, que en nada desmejora el discurso posterior del científico.
En la contraportada, la editorial presenta esta singular publicación del siguiente modo:
¿Cómo surgen las ideas? ¿Qué caminos conducen a la resolución de un problema? ¿Cuáles son los procesos mentales que intervienen en un acto creativo? En 1908, a petición de la Sociedad Psicológica de París, el gran matemático francés Henri Poincaré (1854-1912) impartió una conferencia en la que quiso responder a estas preguntas contando y elucidando cómo se le había ocurrido una de sus teorías primordiales. Al dar carta de naturaleza a la intuición, a la belleza y al inconsciente en el acto creativo, La invención matemática se convirtió en un modelo explicativo ineludible, no sólo en el ámbito matemático, vigente aún hoy en su esencia y que ha sido refrendado por los datos de la psicología moderna.
«Henri Poincaré se contó entre los primeros en proponer aquello que todavía se considera como los pasos básicos del proceso creativo de solución de problemas».
Daniel Goleman, El espíritu creativo
«Todos los libros sobre creatividad cuentan la manera como Poincaré descubrió las funciones fuchsianas».
José Antonio Marina, Teoría de la inteligencia creadora
«La invención matemática es «una de las más famosas exposiciones nunca escritas por un científico acerca de su propio trabajo creativo».
Peter Galison, Relojes de Einstein, mapas de Poincaré
En su introducción, Francisco González Fernández comienza tendiendo puentes entre el arte y la ciencia a través de la invención, y cita para ello testimonios sobre los procesos creativos del compositor Wolfgang Amadeus Mozart, del poeta Samuel Taylor Coleridge o del químico August Kekulé.
En el caso del matemático Henri Poincaré (1854-1912), la conferencia impartida en 1908 se centraba en la teoría de funciones fuchsianas y en la manera en la que la había “inventado”. Esta teoría forma parte de sus primeras creaciones matemáticas, realizada en los años 1880, poco después de defender su tesis doctoral.
Como comenta en la introducción González Fernández: “Para el matemático francés no se trata de referir el momento en el que se enciende la luz del genio, sino de comprender la naturaleza de esa súbita inspiración”; recordemos que su conferencia estaba dirigida a especialistas en psicología, no a personas entendidas en matemáticas.
Francisco González Fernández compara en su prólogo la creatividad de Edgar Allan Poe al escribir El cuervo –“Poe relataba la elaboración de su poema como si fuera un problema de álgebra”– y la de Poincaré en sus matemáticas –“A la inversa, Poincaré mostraría que la invención matemática no surgía del puro raciocinio, sino merced ante todo a la intuición”–. El álgebra necesaria para encadenar versos y la creatividad al servicio del análisis matemático son dos buenos ejemplos de la naturaleza híbrida de muchos procesos de invención.
Poincaré distingue en su texto entre la invención y el descubrimiento, critica la excesiva axiomatización de las matemáticas, y cita el papel fundamental del inconsciente en su proceso creativo, entre otros. Por cierto, su discurso ha sido avalado posteriormente por numerosos neurocientíficos.
Termino con una cita del discurso del científico francés, que invita a la lectura de la disertación completa de Poincaré… ¡y del magnífico prólogo de González Fernández!
Los hechos matemáticos dignos de ser estudiados son aquellos que, por su analogía con otros hechos, son susceptibles de conducirnos al conocimiento de una ley matemática, al igual que los hechos experimentales nos conducen al conocimiento de una ley física. Son aquellos que nos revelan parentescos insospechados entre distintos hechos, conocidos hace mucho, pero que se creía erróneamente que no tenían nada que ver entre sí.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo La invención matemática se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Lógica vs. intuición en la creación matemática
- Matemática discreta y trasplantes cruzados de riñones
- Los institutos Isaac Newton y Oberwolfach, dos curiosas instituciones de investigación matemática
“Filosofía, Ciencia y Valores”, el máster

Si las sociedades contemporáneas necesitan más cultura científica, el sistema educativo necesita responder a esa demanda formando a personas que sean capaces de crearla y transmitirla lo mejor posible. En esa tarea se afana la Cátedra de Cultura Científica, pero no lo hace sola. Como ya anunciamos el año pasado, en esta aventura colabora con el Máster en Filosofía, Ciencia y Valores, que se imparte en el campus de Gipuzkoa de la Universidad del País Vasco desde hace ya varios años.
Quienes cursan un máster prolongan su periodo de formación, o bien retornan a las aulas universitarias como estudiantes para adquirir conocimientos especializados en las materias que le son propias. En el caso que nos ocupa, esas materias incluyen temas de filosofía e historia de la ciencia (o de las ciencias, como prefieren algunos). Pero también filosofía de la biología, de la física y la matemática, filosofía del lenguaje y de la lógica, éticas aplicadas y bioética, filosofía política y de la cultura, estudios de ciencia y tecnología, etc. Como puede comprobarse hay diversidad disciplinar, pero es una diversidad articulada en torno a un cuerpo común de conocimientos, un cuerpo en el que las ciencias, el conocimiento, son el objeto de estudio, reflexión e investigación, y la filosofía, en varias de sus especialidades (epistemología, lógica, ética, política), constituye la aproximación o, si se quiere, la mirada con la que las ciencias son analizadas.
Quienes cursan este máster adquieren una formación especializada, como se ha dicho, y como ocurre con otros másteres, también pueden, si así lo desean, iniciar una carrera investigadora. Tras completar el Máster en Filosofía, Ciencia y Valores, el o la estudiante tiene garantizado, si así lo desea, el acceso a un doctorado, pero eso no es lo más importante. Lo que al final cuenta es haber adquirido herramientas de trabajo para profundizar e intervenir en algunos de los problemas más acuciantes de nuestro tiempo.
Como señalábamos al principio, la Cátedra de Cultura Científica se ha embarcado en una aventura en relación con este máster. En concreto, colaboramos en actividades de difusión social de la ciencia en internet. Y estamos diseñando nuevas iniciativas de manera conjunta que daremos a conocer próximamente.
El Máster en Filosofía, Ciencia y Valores está organizado por la UPV/EHU en colaboración con la Universidad Nacional Autónoma de México. El alumnado es interdisciplinar: además de Filosofía, se puede acceder desde grados de Humanidades, Ciencias Sociales, Ingeniería, Ciencias Experimentales, Bellas Artes y Ciencias de la Salud. El profesorado es internacional e incluye investigadores e investigadoras de prestigio (Ikerbasque, UNAM, UPV/EHU). Las personas interesadas en el máster pueden acudir a las sesiones informativas que se organizan en los campus. En Donostia será el viernes 16 de marzo a las 17:30 en el Centro Barriola, y en Bilbao el sábado 17 a las 10:30 en Bizkaia Aretoa.
El artículo “Filosofía, Ciencia y Valores”, el máster se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La Cátedra se va de máster
- Ciencia y valores en la sociedad del riesgo
- Por qué la filosofía es tan importante para la educación científica
Regulación de la circulación (2): control de la microcirculación
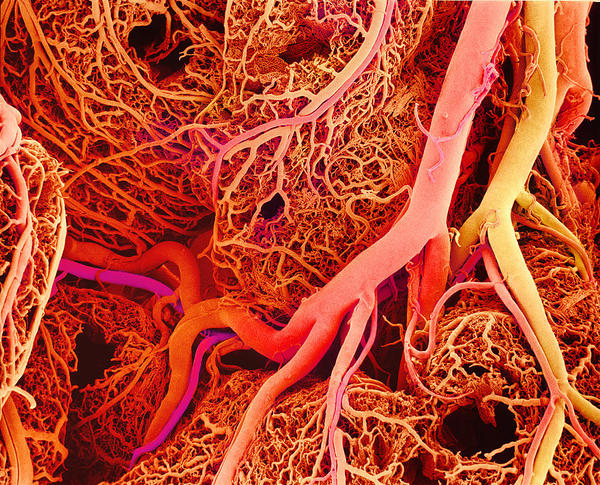
Arteriolas y capilares sanguíneos.
La circulación está sometida a un estricto control al objeto de garantizar, en primer lugar, un suministro de sangre suficiente al encéfalo y al corazón, un suministro suficiente al resto de órganos y tejidos corporales a continuación y, por último, una cierta constancia en el volumen de los tejidos y la composición del fluido intersticial. El flujo sanguíneo a través de los capilares se ajusta en función de las necesidades de irrigación de los tejidos, y ese ajuste se puede producir tanto por la acción del sistema nervioso, como mediante control local. Ya vimos aquí las particularidades del sistema de control nervioso de la circulación. En esta anotación pasaremos a describir el control de la microcirculación en los tejidos y, para ello, conviene no perder de vista los elementos que configuran el sistema circulatorio.
La mayoría de las arteriolas están inervadas por fibras simpáticas que liberan el neurotransmisor noradrenalina. En las arteriolas hay dos tipos de receptores adrenérgicos, α y β. Cuando se une una molécula de noradrenalina a los α-adrenorreceptores de la musculatura lisa de las arteriolas, estas reducen su diámetro (vasoconstricción), por lo que aumenta la resistencia al flujo y sube la presión arterial. Los β-adrenorreceptores, sin embargo, se encuentran en posiciones distantes de las terminaciones nerviosas simpáticas, por lo que lo normal es que se combinen con catecolaminas (adrenalina y noradrenalina) que han sido liberadas por neuronas adrenérgicas del sistema nervioso autónomo (noradrenalina, principalmente) y, sobre todo, por las células del tejido cromafín de la médula adrenal (adrenalina). En otras palabras, se trataría más bien de receptores hormonales. Paradójicamente, su efecto es vasodilatador, por lo que se opone al de la noradrenalina que se une a los -adrenorreceptores.
Las catecolaminas ejercen efectos variados y, como hemos visto, incluso pueden ser contrapuestos. Esos efectos dependen del tipo de receptor con el que se unen pero, además, también varían dependiendo de su concentración sanguínea, debido a la diferente sensibilidad de los receptores a una catecolamina y a la otra. Y para complicar aún más el panorama, otros factores, como el tono del músculo liso o el efecto modulador de sustancias como el neuropéptido Y o el ATP, también inciden en la forma en que las catecolaminas ejercen sus efectos.
Las arteriolas que irrigan el encéfalo y los pulmones son inervadas por fibras parasimpáticas que liberan acetilcolina (fibras colinérgicas). En mamíferos la estimulación de estas fibras provoca vasodilatación.
Sean cuales fueren los mecanismos implicados en la regulación del flujo a través de arteriolas y capilares, el sistema funciona de manera que lo que se tiende a garantizar es la irrigación adecuada del encéfalo y el corazón. Por ello, si se produce una caída en la presión arterial, la respuesta del sistema consiste en limitar al máximo el flujo sanguíneo hacia el resto de órganos y dirigirlo preferentemente hacia los dos prioritarios.
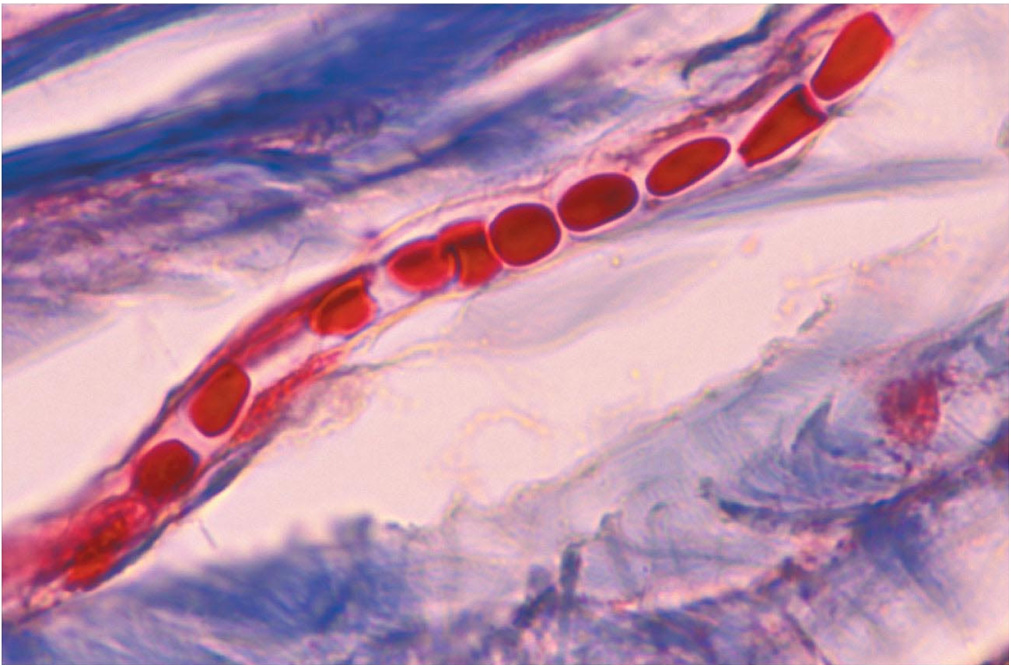
Capilar sanguíneo.
Además del control nervioso, diferentes mecanismos operan a nivel local para regular la circulación en órganos y tejidos. Así, el músculo liso de los vasos se contrae en respuesta a la dilatación provocada por un aumento del flujo a su través. Se opone al aumento del diámetro y contribuye de esa forma a mantener dentro de unos límites relativamente estrechos el flujo a través del sistema capilar. Por otro lado, el calor provoca vasodilatación, y el frío tiene el efecto contrario.
La elevación del metabolismo de un tejido también suele venir acompañada por una disminución de la concentración de O2, y un aumento de la de CO2 y pH. Por ello, no es sorprendente que esas señales provoquen la dilatación de los vasos, permitiendo de ese modo una más rápida renovación de la sangre en esos tejidos y un mayor suministro de O2 y sustratos.
El endotelio vascular y otras células asociadas con la circulación liberan sustancias con actividad sobre los vasos. El endotelio produce y libera óxido nítrico (NO) de forma permanente. Regula el flujo sanguíneo y la presión en mamíferos y otros vertebrados provocando una relajación de la musculatura lisa. Al parecer, el estiramiento del endotelio, debido a un aumento del flujo, podría servir de señal para la síntesis de NO, gracias a la entrada de calcio en sus células y al papel de este en la activación de las enzimas responsables de su síntesis. Por otro lado, la hipoxia y la reducción del pH provocan la liberación de NO, de manera que bajo esas condiciones, su acción conduce a un aumento del diámetro de los vasos y, por lo tanto, del flujo.
Además de NO, el endotelio vascular también libera endotelinas (proteínas vasoconstrictoras) en respuesta al estiramiento (dilatación de la pared endotelial) y prostaciclina, que causa vasodilatación e inhibe la coagulación sanguínea.
En el corazón y los riñones, principalmente, se produce adenosina en respuesta a condiciones de anoxia o hipoxia. Cuando se reduce el suministro de oxígeno la adenosina coordina el suministro y el gasto energético provocando una reducción de la frecuencia de latido del corazón, de manera que disminuye el trabajo que realiza y, simultáneamente, causa vasodilatación coronaria, lo que eleva el suministro de oxígeno y nutrientes al corazón.
En los tejidos hipóxicos se eleva la actividad del denominado HIF-I (factor inducible por hipoxia 1), que reduce la transcripción génica con carácter general, a la vez que estimula la específica de genes asociados con la producción de eritropoietina, factores de crecimiento endotelial vascular, endotelina 1, sintetasa de NO y enzimas glucolítica
En definitiva, además del control que el sistema nervioso ejerce sobre la circulación general (que vimos aquí), también la circulación a través de arteriolas y capilares está sometida a control. En este segundo caso también interviene el sistema nervioso, pero además, hay mecanismos que actúan localmente. El conjunto de controles y mecanismos compensatorios consigue efectuar una regulación muy precisa, tanto del gasto cardiaco total (Q), a través de ajustes de la frecuencia de latido y la fuerza de impulsión, como del volumen preciso que se dirige a cada destino orgánico en función de las necesidades. Salvo condiciones patológicas, todo ello se consigue manteniendo la presión arterial dentro de los límites de referencia.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Regulación de la circulación (2): control de la microcirculación se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Regulación de la circulación (1): control del sistema cardiovascular
- El flujo sanguíneo se reorganiza en respuesta a las necesidades
- Un viaje a través del sistema circulatorio humano
Espaciotiempo

Ya hemos dicho que la teoría de la relatividad especial de Einstein no representó una ruptura traumática con la física clásica, pero que sí acabó con la visión mecánica del mundo introduciendo los campos como entes necesarios. Otra ruptura con la visión mecanicista tiene que ver con los conceptos de espacio y tiempo. La concepción newtoniana del universo considera que el espacio y el tiempo son absolutos, lo que significa que son los mismos para todos los observadores independientemente de su movimiento relativo. Einstein demostró que las mediciones de espacio y tiempo en relatividad especial dependen del movimiento relativo de los observadores. Además, resultó que el espacio y el tiempo están, de hecho, entrelazados.
Una aproximación intuitiva a esta realidad la vimos cuando consideramos el experimento mental en el que hacíamos mediciones de longitud de una plataforma móvil. Los mediciones del metro se deben realizar en los extremos de la plataforma en el mismo instante de tiempo. Debido al postulado de la constancia de la velocidad de la luz, una persona en reposo en la plataforma y una persona que ve la plataforma en movimiento no se pondrán de acuerdo sobre cuándo las mediciones serán simultáneas.
Los sucesos ocurren no solo en el espacio, también en el tiempo. En 1908, el matemático alemán Hermann Minkowski sugirió que en la teoría de la relatividad, el tiempo y el espacio se pueden ver como unificados para formar las cuatro dimensiones de un mundo cuatridimensional llamado espaciotiempo. El espaciotiempo cuatridimensional es universal porque un “intervalo” medido en este mundo resultaría ser el mismo para todos los observadores, independientemente de su movimiento relativo a una velocidad uniforme.
El intervalo de espaciotiempo es una especie de “distancia” entre sucesos. Pero no la distancia que separa a los sucesos en el espacio, ni la distancia que los separa en el tiempo, sino la distancia que los separa usando una medida que incluye tanto al espacio como al tiempo.
Algo más formalmente, en general, el intervalo de espaciotiempo entre dos sucesos en sistemas de coordenadas que están en movimiento relativo uniforme será el mismo. Por lo tanto el intervalo de espacio y el intervalo de tiempo variarán en los distintos sistemas de corrdenadas, pero no así el intervalo de espaiotiempo. Esto no es otra cosa que afirmar que en la teoría de la invariancia el intervalo de espaciotiempo es una propiedad invariante.
En resumen, mientras que para Newton tanto la longitud como el tiempo y la simultaneidad eran invariantes, no lo son para la teoría de la invariancia. En ésta, sin embargo, estas propiedades invariantes se convierten en relativas y lo que era relativo para Newton, la velocidad de la luz (en el vacío), se convierte en una invariante (una constante) y se introduce una nueva propiedad el intervalo de espaciotiempo que también lo es.
La aproximación de Minkowski es una aproximación “geométrica” a la relatividad: se parte de la existencia de un espaciotiempo de cuatro dimensiones y, por lo tanto, de sistemas de coordenadas de cuatro dimensiones también que están en movimiento relativo uniforme, y en el que se pueden emplear las expresiones que hemos visto para la relatividad del tiempo y la longitud, que se conocen habitualmente como transformaciones de Lorentz, para pasar las coordenadas en un sistema a otro.
Esta aproximación geométrica es muy común cuando se estudia la relatividad y se hace la principal cuando se generaliza a sistemas de coordenadas que están en movimiento relativo de cualquier clase, es decir, cuando también existen aceleraciones. Es lo que exploraremos a continuación: las bases de la llamada teoría general de la relatividad.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Espaciotiempo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El principio de relatividad (y 4): la versión de Einstein
- La relatividad de la masa
- La relatividad del tiempo (2)
Tojisha-Kenkyu, la técnica japonesa con la que los pacientes se estudian a sí mismos

Alrededor de los años 70 ocurrió algo en Japón que puso en marcha una cadena de acontecimientos que, a modo de efecto mariposa, está influyendo en cómo hoy se analizan algunas enfermedades discapacitantes, como el autismo. Se trata de una idea llamada Tojisha-Kenkyu, un tipo de autoanálisis en el que son los propios pacientes los que estudian sus síndromes o discapacidades con la colaboración de sus iguales.
Lo que ocurrió, en realidad fue una tragedia. Una madre asesinó a su hija de dos años afectada de parálisis cerebral. Fue condenada por ese asesinato y la noticia fue muy comentada en los medios. El público simpatizaba con la madre, defendiendo que el crimen fue cometido bajo el peso de una responsabilidad que cargaba sola y sin ayudas institucionales de ningún tipo. Se inició un movimiento que pedía una reducción de su condena.
Esto inició a su vez otro movimiento, el de las asociaciones de personas con discapacidad, que protestaban contra la idea de que fuese comprensible que, en determinadas circunstancias, una persona con discapacidad fuese asesinada.
También en 1970 otro acontecimiento vino a sumarse al caldo de cultivo. En 1968 el gobierno municipal de Tokio había puesto en marcha el centro Fuchu, un lugar de internamiento para personas con discapacidades físicas y mentales graves con 400 plazas. El internamiento de estas personas se consideraba algo urgente, una necesidad apremiante. En 1970 muchos internos comenzaron a protestar, denunciando malos tratos y un ambiente opresivo por parte de los responsables del centro público.
Entre ambas cosas, en los años 70 y 80 se formó en Japón un movimiento de personas con discapacidad, muy activa en las protestas de aquellos asuntos que les afectaban directamente, liderado por los afectados por parálisis cerebral. Fueron entre otras cosas muy activos en la protesta contra una enmienda a la Ley de Protección Eugenética que permitiría el aborto intencionado del feto si este presentaba malformaciones o enfermedades discapacitantes de cualquier tipo.
“Sí, me gustaría estudiar”
Aceleramos el paso del tiempo y llegamos a 2001. En la ciudad de Urakawa se encuentra la Casa Bethel, un centro local de actividades para personas con pacientes y expacientes psiquiátricos. Algunos de estos expacientes se reúnen allí para apoyarse mutuamente e incluso se mudan a vivir a la antigua iglesia cercana al centro. Las actividades de la Casa Bethel no se parecen a las de la mayoría de las instituciones mentales japonesas: la estructura es horizontal, con los pacientes y sus cuidadores apoyándose entre sí, algo más parecido a un grupo de autoayuda que a una terapia dirigida por una figura de autoridad.
Entre los pacientes de este centro se encontraba Hiroshi Kawasaki, un paciente que un día perdió los nervios cuando sus padres se negaron a pedir sushi y videojuegos para él. Estaba tan alterado que rompió el teléfono del centro. Su médico, Ikuyoshi Mukaiyachi, sin saber cómo tranquilizarle, le propuso dedicar su tiempo a estudiar. Cuenta Mukaiyachi que la palabra “estudiar” hizo reaccionar la paciente. “Sí, me gustaría estudiar”.
La técnica de estudiarse a uno mismo
Así surgió la idea de Tojisha-Kenkyu, originalmente llamada jiko kenkyu (auto-estudio): los pacientes de Casa Bethel analizaban sus síntomas y sus problemas. Se extendió más allá de sus paredes a otros afectados por enfermedades psiquiátricas, y después también a muchos más con un rango mayor de afecciones mentales: parálisis mental, adicciones, trastornos del desarrollo…

El profesor Kumagaya aplica la técnica Tojisha-Kenkyu al estudio de su discapacidad (Fuente: Centro de Investigación de Tecnología y Ciencia Avanzadas, Universidad de Tokyo).
“En la literatura existen muchos trabajos a través de los cuales uno se pone frente a frente consigo mismo. Las autobiografías o las novelas semiautobiográficas tienen un largo recorrido en la historia. Pero, ¿qué hay de la ciencia? ¿Hay alguna disciplina científica en la que uno pueda concentrarse en sí mismo?”, se pregunta Shin-ichiro Kumagaya, profesor asociado de la Universidad de Tokio, afectado él mismo por una discapacidad física que le impide caminar.
Eso pretende ser esta técnica que mezcla ciencia y autoayuda. “Tojisha-Kenkyu está basado en el hecho de aceptar que no sabemos mucho sobre nosotros mismos. Aquellos que padecen dificultades similares se observan entre sí con cuidado y compasión mientras trabajan para formular hipótesis sobre sí mismos, y luego las ponen a prueba experimentalmente en su día a día”, continúa Kumagaya.
Gracias a este proceso, desarrollan palabras con las que nombrar sus dificultades y necesidades, lógicas que expresen y predigan la regularidad de estos obstáculos, y medidas para compensarlos. “Al trabajar para resolver sus propios desafíos, en vez de confiar ciegamente en un especialista para que lo haga, asumen un papel activo como investigadores y no solo como pacientes, lo que puede ayudar a estos individuos a conseguir una mayor calidad de vida”.
Pero no se trata de que los pacientes se conviertan en investigadores y queden ya limitados a sus propios recursos. En realidad la técnica es una forma de reenfocar la relación entre el tojisha (la persona estudiada) y el especialista, es decir, entre el conocimiento de la experiencia y el conocimiento de la especialización. La idea es que los conceptos y teorías generados mediante Tojisha-Kenkyu se acepten como nuevas hipótesis dentro del conocimiento especializado, y luego sean puestas a prueba siguiendo todos los protocolos científicos experimentales. Mientras, el tojisha aprende del especialista, ya que todo ese conocimiento es una herramienta muy útil para tener en cuenta todos los factores de su afección, especialmente aquellos difíciles de ver a simple vista.
“El respeto mutuo entre el tojisha y el especialista por sus respectivos conocimientos, junto con los esfuerzos colaborativos de ambos lados, ayudará sin duda a restaurar la confianza en el conocimiento académico. Desde mi punto de vista, como paciente receptor de tratamiento médico de niño que luego se convirtió en un investigador médico, Tojisha-Kenkyu tiene un enorme potencial para conectar ambos mundos”, asegura Kumagaya.
El autismo estudiado por una paciente con autismo
Avanzamos de nuevo y llegamos a mayo de 2018. Satsuki Ayaya tiene 43 años y está haciendo un doctorado en historia y filosofía de la ciencia en la Universidad de Kyoto. Uno de los materiales con los que trabaja son sus propios diarios, decenas de cuadernos que llenó de joven cuando, desesperada por entenderse a sí misma durante la adolescencia, comenzó a escribir todo lo que pensaba. “¿Qué me pasa? ¿Quién soy? ¿Qué hay de malo en mí?”. Ayaya, cuenta en este reportaje, siempre había notado que le costaba jugar con otros niños, como si una pantalla invisible la separase de ellos.

Al principio de la treintena, Ayaya fue diagnosticada de autismo y esa sensación de desconexión cobró sentido. Sus cuadernos se convirtieron en una forma de estudiar la enfermedad, que para ella se manifiesta por ejemplo en la desconexión de sus percepciones: siente con infinitos detalles el abanico de sensaciones que llamamos hambre, pero le cuesta un mundo conectarlas: “Me cuesta mucho darme cuenta de que tengo hambre. Me siento irritada, triste, noto que algo va mal… pero todo me llega por separado, no tiene sentido entre sí”, cuenta. Tarda tanto en darse cuenta de que tiene hambre que a menudo llega a sentirse débil y solo come algo después de que otra persona se lo haya sugerido.
También ha podido asociar el origen de algunas de sus dificultades para hablar con normalidad con la diferencia entre cómo escucha su propia voz, y cómo espera escucharla. Es como si justo después de decir algo su voz volviese a ella y pudiese notar la diferencia, como si escuchase un incómodo eco en una conversación telefónica.
¿Cómo decide nuestro cerebro a qué prestar atención?
En un claro ejemplo de Tojisha-Kenkyu, el registro detallado que Ayaya ha hecho durante años de sus experiencias ha servido para proponer una nueva idea sobre el autismo que está relacionada con uno de los mayores desafíos de nuestra forma de percibir las cosas: ¿cómo decide nuestro cerebro a qué debería prestar atención?
En principio, la novedad atrae nuestra atención, pero para decidir qué es una novedad el cerebro necesita tener una expectativa previa que sea alterada de alguna forma. También es necesario alcanzar cierto nivel de confianza en esa expectativa, es decir, tener al menos una seguridad determinada de que eso iba a ser de determinada forma y que luego no lo sea.
De momento, la sugerencia más sólida sobre cómo ocurre esto es que el cerebro sigue un proceso de metaaprendizaje: aprender qué debe aprender y qué no, y según esta teoría, un sesgo en este proceso de metaaprendizaje explicaría lo que consideramos el núcleo del autismo. Es decir, que de acuerdo con esta idea, el autismo es una afección básicamente perceptual y no tanto social: se trataría principalmente de un inusual apego por la rutina como resultado de diferencias en el modo en que el cerebro procesa los estímulos sensoriales.
La sorpresa por encima de los patrones predecibles
Para entenderlo un poco mejor, piensa en lo que ocurre cuando te enfrentas a una situación por primera vez: cada detalle parece significativo, pero a medida que ganas en experiencia, aprendes a distinguir la norma de la excepción, los detalles dejan de llamar tanto la atención y el cerebro pasa a concentrarse en la situación al completo, y así es como logra dominar algo nuevo y pasa a lo siguiente, evitando el aburrimiento y la frustración.

Pues en este panorama, el autismo sería una curva de aprendizaje diferente, una que favorece siempre los detalles (y con ello, la sorpresa) sacrificando para ello el aprendizaje de los patrones generales. En el caso de Ayaya, sus propias sensaciones la sorprenden impidiéndole aprender lo que significan (que tiene hambre), igual que le pilla por sorpresa la diferencia entre las expectativas sobre su voz y su voz en sí misma, dificultándole avanzar en el desarrollo de relaciones sociales normales.
Por ahora se trata de una teoría que resulta demasiado vaga en algunos detalles cruciales, y de hecho hay dudas sobre si un solo modelo puede servir para explicar un trastorno tan heterogéneo como el autismo, pero es precisamente esa diversidad lo que impulsa la búsqueda de un mecanismo básico: si realmente las habilidades de predicción están en la baso de las dificultades que sufren las personas con autismo, una terapia o tratamiento que influya en ese aspecto tendría un gran impacto sobre otras habilidades diferentes.
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo Tojisha-Kenkyu, la técnica japonesa con la que los pacientes se estudian a sí mismos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Programar no es “divertido”, es técnica y éticamente complejo
- Optogenética, la fascinante técnica que apasiona a los neurocientíficos
- #Naukas15 Ficha técnica
¿Cada cuánto tiempo se renuevan las células de nuestro cuerpo?
¿Cuántos años tiene usted? Sea cual sea su edad, no lo es de la mayor parte de las estructuras que conforman su cuerpo. Algunas ni siquiera tienen horas de existencia y solo unas pocas le acompañan desde que nació. Sus tejidos u órganos, así como las células que los forman tienen edades muy diferentes unas de otras. En su gran mayoría las células se van renovando y así lo hacen también los tejidos de los que son sillares.
Las células más efímeras son las que recubren el interior del intestino delgado. El epitelio intestinal es un tejido muy activo, que se ocupa de absorber y digerir infinidad de pequeñas moléculas. Sus células se renuevan entre cada dos y cuatro días. En el aparato digestivo hay otras de vida muy breve: las de las criptas del colon se renuevan cada tres o cuatro días, las del estómago entre cada dos y nueve, y las células de Paneth del intestino delgado –entre cuyas funciones se encuentra la defensa frente a patógenos intestinales- cada veinte.
Perduran mucho más los hepatocitos (células del hígado): entre seis meses y un año. Si bien es parte del aparato digestivo, el hígado es de hecho un órgano diferente y aunque los hepatocitos son las células que producen la bilis (esencial en la digestión intestinal de las grasas), sus principales funciones son metabólicas: tienen su sede en ellas innumerables procesos metabólicos cuyo ámbito de influencia es el conjunto del organismo.
Las células de la sangre tienen tasas de renovación muy diferentes. Las de vida más corta son las del sistema inmunitario: los neutrófilos, que son los leucocitos más abundantes, se renuevan entre cada uno y cinco días, y otros leucocitos, los eosinófilos, entre cada dos y cinco. Las plaquetas, cuya función es facilitar la cicatrización de las heridas, viven unos diez días. Y mucho más longevos son los glóbulos rojos, que se renuevan cada cuatro meses. Las células madre hematopoyéticas, de las que provienen las anteriores, permanecen bajo esa condición durante dos meses antes de convertirse en leucocitos, plaquetas y glóbulos rojos.
Otras células de vida relativamente breve son las del cuello uterino, que duran seis días; de los alveolos pulmonares, ocho días; de la epidermis de la piel, entre diez y treinta días. Más prolongada es la existencia de los osteoclastos, las células que remodelan el hueso: se renuevan cada dos semanas; y más aún la de los osteoblastos, las que lo producen: se recambian cada tres meses. La actividad de esas células da lugar a que un 10% del tejido óseo se renueve cada año. Las células de la tráquea lo hacen cada uno o dos meses. Y los espermatozoides cada dos meses, aunque, por contraste, las mujeres nacen con todos sus óvulos.
Las que menos se renuevan son los adipocitos -células que almacenan reservas de grasa- que lo hacen cada ocho años; las musculares, cada quince; y los cardiomiocitos (células musculares del corazón) experimentan una renovación de entre un 0,5% y un 10% al año. Las neuronas del sistema nervioso central apenas se renuevan; la excepción es el recambio diario de unas setecientas células de un área muy concreta denominada “hipocampo”, lo que implica que esa zona repone un 0,6% de sus neuronas al año. En promedio, el cuerpo se renueva entero cada 15 años.
Si lo pensamos un poco, vivimos en un cierto frenesí de reposición permanente de algunas -casi todas, en realidad- de nuestras estructuras coporales. Podría decirse, incluso, que ya no somos el mismo organismo que éramos hace un par de meses.
—————————————————————–
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
Una versión anterior de este artículo fue publicada en el diario Deia el 3 de diciembre de 2017.
El artículo ¿Cada cuánto tiempo se renuevan las células de nuestro cuerpo? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Cuántas células hay en el cuerpo humano?
- ¡Sincronicemos relojes! Dentro y fuera de nuestro cuerpo
- Cómo ver todas las células en tejido cerebral vivo
Naukas Bilbao 2017 – Joaquín Sevilla: Los instrumentos del capitán Fitzroy
En #Naukas17 nadie tuvo que hacer cola desde el día anterior para poder conseguir asiento. Ni nadie se quedó fuera… 2017 fue el año de la mudanza al gran Auditorium del Palacio Euskalduna, con más de 2000 plazas. Los días 15 y 16 de septiembre la gente lo llenó para un maratón de ciencia y humor.

El capitán Fitzroy, famoso por ser el capitán del Beagle durante el viaje en el que Darwin fue el naturalista, era un usuario de instrumentos científicos de primer nivel. Con la predicción meteorológica, sin embargo, fue un paso más allá porque se involucró emocionalmente y cayó en la fascinación de las evoluciones caóticas. Joaquín Sevilla lo expone magistralmente.
Joaquín Sevilla: Los instrumentos del capitán FitzRoyEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2017 – Joaquín Sevilla: Los instrumentos del capitán Fitzroy se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – Ignacio López-Goñi: Las bacterias también se vacunan
- Naukas Bilbao 2017 – Álex Méndez: Luz de luna
- Naukas Bilbao 2017 – Guillermo Peris: Los trapecistas del genoma
Cómo ver todas las células en tejido cerebral vivo
Un grupo interdisciplinar de físicos y biólogos que trabajan en la investigación de las células cerebrales ha concebido una nueva y revolucionaria técnica de microscopía que, por primera vez, permite obtener imágenes de todas las células dentro de un área determinada del tejido cerebral vivo. Permite obtener imágenes de todas las células vivas no etiquetadas en un área cerebral determinada, cosa que hasta ahora era imposible. Este avance científico es fruto de la colaboración entre grupos de investigación de la Universidad de Burdeos, la UPV/EHU y el Achucarro Basque Center for Neuroscience . Esta nueva técnica permitirá expandir el conocimiento de la biología del cerebro.
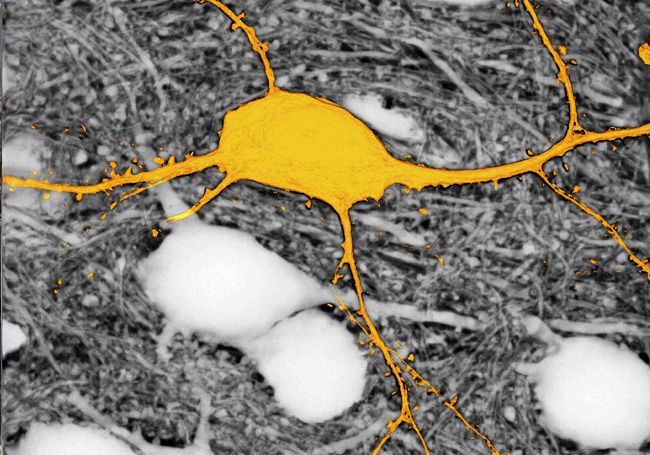
Imagen de la neurona etiquetada en amarillo, rodeada de neuronas no marcadas (aparecen en blanco), utilizando la técnica SUSHI. Sin esta técnica, las neuronas que aparecen en blanco no se verían. © Jan Tønnesen & Valentin Nägerl.
La microscopía es una herramienta básica en la investigación de la biología de cualquier organismo, dado que los elementos que se estudian, las células, tienen un tamaño microscópico y muchas veces, nanoscópico. Hasta el momento, los métodos de microscopía existentes para investigar el tejido cerebral vivo se limitaban a visualizar solo las células previamente marcadas. Sin embargo, por limitaciones técnicas, no todas las células en una región cerebral determinada podían etiquetarse simultáneamente, lo que ha restringido la visión, y por tanto, la comprensión que tenemos sobre cómo las células cerebrales, que están altamente interconectadas, se organizan e interactúan.
El Dr. Jan Tønnesen (Suecia, 1977), investigador del Programa Ramón y Cajal en el Departamento de Neurociencias de la UPV/EHU, y que trabaja en el Achucarro Basque Center for Neuroscience es uno de los autores de un trabajo que acaba de publicar Cell, y en el que describen una nueva técnica de microscopía, denominada “SUSHI”, para mejorar la visualización de las células en tejido cerebral vivo.
La nueva técnica SUSHI (acrónimo de su nombre en inglés “Super-resolution Shadow Imaging”) permite etiquetar de una pasada el minúsculo espacio, lleno de líquido, que rodea las células cerebrales, evitando tener que etiquetar individualmente todas las células que se quieren analizar.
Dado que además esta “etiqueta” permanece fuera de las células, produce una especie de imagen en negativo, que podemos asemejar a la película de las antiguas cámaras de fotos. Así, la imagen negativa contiene la misma información sobre las células cerebrales que la imagen positiva correspondiente, pero gracias a que el procedimiento de etiquetado es más simple, es mucho más fácil de obtener esta imagen y toda la información que contiene.
Según el Dr. Tønnesen “La técnica SUSHI es revolucionaria porque nos permite visualizar simultáneamente todas las células cerebrales en una región determinada del tejido cerebral vivo. Antes encontrábamos espacios en blanco en las imágenes de microscopía, ya que no podíamos etiquetar todas las células al mismo tiempo. Este hecho nos resultaba muy limitante. Desde ahora, con esta técnica podremos ver todas las células del área de estudio que situemos en la lente del microscopio, así como sus interacciones, de manera que podremos avanzar en nuestro conocimiento de las funciones el cerebrales, tanto en el órgano sano, como cuando enferma”.
Referencia:
Tønnesen J, Inavalli VVGK & Nägerl UV (2018) Super-resolution imaging of the extracellular space in living brain tissue Cell doi: 10.1016/j.cell.2018.02.007
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Cómo ver todas las células en tejido cerebral vivo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cómo criopreservar células madre
- El GPS cerebral: cómo nos orientamos en el espacio
- Cómo detectar un defecto en el ADN viendo cómo se retuerce
¿Qué nos puede decir un elefante del cáncer en humanos?

¿Qué nos puede decir un elefante del cáncer en humanos? | imagen Pixabay
A grandes rasgos llamamos cáncer a un amplio abanico de enfermedades provocadas por errores en los mecanismos de replicación celular y cuya característica común es un proceso descontrolado en la división de las células del cuerpo. Todos los seres vivos poseen este mecanismo y por tanto están expuestos al riesgo de padecer cáncer… sin embargo, no todos contraen la enfermedad en iguales proporciones.
Existen factores determinantes, como el tamaño (número de células) o la longevidad, que afectan a la probabilidad de contraer cáncer, sin embargo algo no cuadra en animales como los elefantes. Son grandes, muy grandes, de hecho pueden superar fácilmente los 6000 kilos siendo los mayores mamíferos terrestres del planeta. Son animales longevos, algunas especies como el elefante de selva africano (Loxodonta cyclotis) suelen alcanzar los 70 años, y aún así rara vez contraen cáncer: Solo un 5% de los elefantes fallecen por esta causa.
Para dar respuesta a algunas de estas incógnitas, investigadores de la Universidad de Utah han querido bucear en el genoma de los elefantes, prestando especial atención a esas regiones incomprendidas, que algunos llaman despectivamente “ADN basura” y que para otros, como el genetista Christopher Gregg, responsable del estudio, son más bien “una jungla desconocida que aún hay que explorar”.

P53, mólecula del año para la Revista Science
Pero primero viajemos al año 1979 para hablar un gen, conocido como P53, que tiene mucho que decir en este tema. En ese año, hasta cinco grupos diferentes de investigadores descubrieron simultáneamente esta proteína que cobró protagonismo por sus funciones supresoras de tumores. En 1993 la Revista Science eligió a P53 como “molécula del año” y en su último número ocupaba la portada y el editorial, reuniendo calificativos como “guardián del genoma” o “líder del ejército anti-tumoral”.
En el estudio, publicado hace unos días en Cell, confirman que el genoma del elefante posee hasta veinte copias de P53 que aumentan considerablemente sus defensas frente a procesos tumorales. A esta abundancia de copias de P53 hay que sumar la presencia de otros tres genes reparadores de ADN (llamados ANCL, VRK2 y BCL11A) que se han encontrado tras exponer a las células del elefante a radiación y examinar cómo el ADN respondía al daño.
Todos estos mecanismos de reparación de daño celular se han descubierto en regiones no codificantes del genoma que han tenido una evolución acelerada en elefantes, es decir, partes de su genoma que han evolucionado rápidamente y que les ha llevado a desarrollar rasgos distintos. Explicado metafóricamente, la evolución en el elefante le ha llevado a conseguir de manera natural una efectiva defensa contra los errores celulares que dan lugar al cáncer.
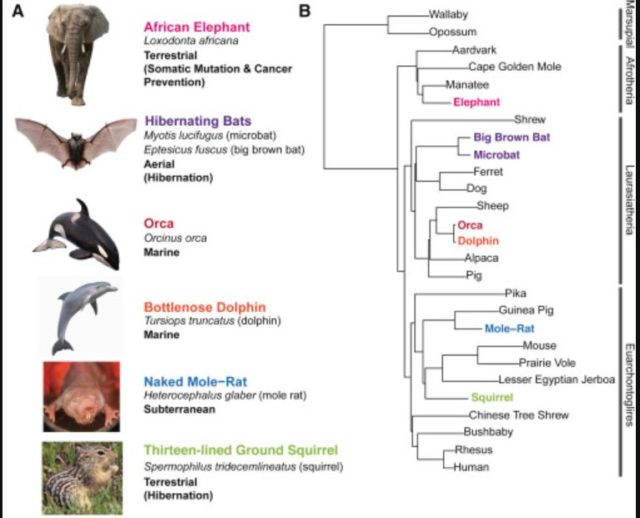
El estudio también estudia el genoma de otros animales como la orca o el murciélago | Gregg et al.
Pero no miren con envidia a los paquidermos, estos descubrimientos en su genoma son buenas noticias también para nosotros porque de hecho el artículo publicado en Cell se titula: “Evolucion acelerada en diferentes especies revela elementos candidatos para relevantes tratamientos clínicos, incluyendo mutación y resistencia al cáncer”. El trabajo ha analizado las mismas regiones del genoma en otros animales como la orca, el murciélago, el delfín, la ardilla y, cómo no, la rata topo) y ha encontrado una gran variedad de rasgos característicos.
Ya hemos visto que el genoma del elefante vinculado a la reparación del ADN podría ayudar en el estudio de la resistencia al cáncer, pero además, el estudio revela que:
- El genoma del murciélago relacionado con el desarrollo del ala podría ayudar en el estudio de las anormalidades en manos y pies.
- Los genomas de delfín y de la orca relacionados con el desarrollo del ojo y podrían ayudar en el estudio del desarrollo de la córnea. También se han detectado elementos relacionados con la adaptación a entornos de alta presión que podrían ayudar a comprender los trastornos de la coagulación sanguínea.
- El genoma de la ardilla terrestre de trece líneas que está relacionado con la coloración y pigmentación podría ser muy útil en el estudio del albinismo y el síndrome de Leopard.
- El genoma de la rata topo desnudo relacionado con el desarrollo del ojo que podría ayudar en el estudio del glaucoma.
Al igual que la ingeniería ha desarrollado trenes más rápidos observando la aerodinámica de pájaros como el martín pescador o mejores adhesivos inspirados en geckos, la medicina también avanza fijándose y aprendiendo de las ideas desarrolladas por la naturaleza. La evolución ha recorrido diferentes caminos en la inmensidad de organismos vivos que existen, es más que probable que otros animales ya hayan conseguido las soluciones a muchos de los problemas a los que nos enfrentamos, ahora solo faltaría descubrir cómo adaptarlas a nosotros.
Este post ha sido realizado por Javier Peláez (@irreductible) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
Referencias científicas y más información:
Elliott Ferris, Lisa M. Abegglen, Joshua D. Schiffman, Christopher Gregg “Accelerated Evolution in Distinctive Species Reveals Candidate Elements for Clinically Relevant Traits, Including Mutation and Cancer Resistance” Cell Reports, DOI: 10.1016/j.celrep.2018.02.008
University of Utah “Mapping the genome jungle: Unique animal traits could offer insight into human disease” Phys.org
El artículo ¿Qué nos puede decir un elefante del cáncer en humanos? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Microbiota y cáncer
- Sobre la predisposición genética a padecer enfermedades
- Todo lo que se puede medir en un río
Cómo destruir un buen sistema de educación. El ejemplo sueco

¿Cómo se tratan algunos de los trastornos cognitivos más frecuentes en las aulas? ¿Son efectivos los programas y herramientas del sistema educativo actual? ¿Carecen de eficacia algunas de las prácticas educativas más populares?
Estas son algunas de las cuestiones que se debatieron en la jornada “Las pruebas de la educación”, que se celebró el pasado 2 de febrero de 2018 en el Bizkaia Aretoa de Bilbao. El evento, en su segunda edición, estuvo organizado por la Cátedra de Cultura Científica de la UPV/EHU y el Consejo Escolar de Euskadi, con la colaboración de la Fundación Española para la Ciencia y la Tecnología (FECYT).
Las ponencias de los expertos que expusieron múltiples cuestiones relacionadas con la educación, basándose siempre en las pruebas científicas existentes. Los especialistas hicieron especial hincapié en destacar cuál es la mejor evidencia disponible a día de hoy con el objetivo de abordar las diferentes realidades que coexisten en las aulas y en el sistema educativo en general.
“Las pruebas de la educación” forma parte de una serie de eventos organizados por la Cátedra de Cultura Científica de la UPV/EHU para abordar cuestiones del día a día como la educación o el arte desde diversos ámbitos de la actividad científica. La dirección del seminario corre a cargo de la doctora en psicología Marta Ferrero.
Inger Enkvist, catedrática de Filología Española de la Universidad de Lund, Suecia, presenta los entresijos del sistema sueco de educación. Entre 1962 y 1985 el país nórdico adoptó una serie de leyes de educación que introdujeron lo que los británicos denominan “comprehensive school”, es decir, una única opción para todos los alumnos desde los 7 hasta los 16 años de edad. No creerás lo que ocurrió.
Cómo destruir un buen sistema de educación. El ejemplo suecoEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Cómo destruir un buen sistema de educación. El ejemplo sueco se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Autismo y educación: problemas y pautas en el aula
- Las ideas erróneas sobre educación entre el profesorado: prevalencia, causas y soluciones
- La evaluación y los deberes escolares

