El Organum Mathematicum: una enciclopedia portátil
Athanasius Kircher (1602-1680) fue uno de los científicos más importantes de la época barroca. Él y sus cinco hermanas y hermanos ingresaron en diversas órdenes religiosas, ya que la familia era demasiado pobre para costearles los estudios. Él fue ordenado sacerdote jesuita en 1628, en cuyas instituciones se formó en humanidades, ciencias naturales y matemáticas, lenguas clásicas y filosofía, entre otras.
Estudió e investigó en campos tan diversos como la vulcanología, el chino, el magnetismo o una posible escritura universal. Tenía reputación como experto en resolver jeroglíficos, en parte por su conocimiento de la lengua copta. Tal era su fama que el alquimista Georgius Barschius, uno de los primeros propietarios del famoso Manuscrito Voynich, le escribió en varias ocasiones para que intentara descifrarlo, aunque no tuvo ningún éxito.
A lo largo de su obra describió diferentes artilugios e inventó varias máquinas, con éxito diverso. El Organum Mathematicum fue precisamente uno de sus inventos: fue descrito completamente en el monumental y póstumo Organum Mathematicum : Libris IX Explicatum (1668) escrito por Gaspar Schott (1608-1666), ayudante del jesuita.
Era un dispositivo diseñado para ayudar a realizar cálculos matemáticos y de otro tipo. Se inspiró en otros instrumentos como el ábaco de Napier, algunos almanaques y su propia Arca Musarithmica. –dispositivo inventado por el jesuita para componer música eclesiástica: a través de simples técnicas combinatorias era capaz de producir millones de piezas de música polifónica en cuatro partes–.

El Organum Mathematicum de Athanasius Kircher ilustrado en el libro Organum Mathematicum de Gaspar Schott (1668). Imagen: Wikimedia Commons.
El Organum Mathematicum era una especie de caja, un cofre de madera divido en nueve o más compartimentos, cada uno de los cuales contenía unas varillas de madera –Kircher las llamaba tariffa– que ayudaban a realizar diferentes cálculos de matemáticas y otras ciencias o artes.
Como hemos comentado, cada compartimento estaba dedicado a un tema: aritmética, geometría, fortificaciones, cronología, orografía, astronomía, astrología, esteganografía y música. Y, a su vez, cada uno de ellos contenía unas veinticuatro varillas de madera –coloreadas en su parte superior y en forma triangular– con definiciones e información sobre el tema correspondiente.
Las varillas aritméticas eran capaces de realizar la multiplicación de números de varios dígitos y divisiones; las geométricas ayudaban a determinar alturas; las de fortificaciones apoyaban el diseño de planos de baluartes; las varillas de la sección de cronología podían usarse para determinar las fechas de festividades eclesiásticas como la Pascua; las correspondientes al compartimento de orografía contenían la información necesaria para construir relojes de sol; las de la sección de astronomía proporcionaban, para cada día del año, información sobre la duración del día y la noche, los horarios de salida y puesta del sol y la duración de los crepúsculos matutino y vespertino –todo ello basado en mediciones tomadas a 48 grados de latitud (Viena) –; las de astrología contenían tablas describiendo los movimientos de los planetas, la constelación Draco y también daba interpretaciones astrológicas de los doces signos del zodiaco; las de esteganografía se usaban para encriptar y descifrar textos –usando un cifrado de transposición cíclica basado en una palabra clave–; finalmente, en el compartimento de música, las varillas ayudaban a personas sin formación a componer música eclesiástica, de la misma manera que en su Arca Musarithmica –contenían conjuntos de frases que podían combinarse aleatoriamente para componer versos acordes a la música y produciendo millones de himnos. En las referencias 4, 5 y 6 se dan ejemplos de composiciones musicales usando esta máquina–.
Para usar el Organum Mathematicum se tomaban los listones correspondientes al tema elegido, y se reordenaban para efectuar la operación requerida. Por ejemplo, en el de aritmética, para multiplicar 74 por 8, se elegía la varilla negra del compartimiento de aritmética y se colocaba junto a los listones numerados 7 y 4. La octava línea de la varilla de punta negra devolvía el producto deseado.

Organum Mathematicum en el Museo Galileo en Florencia (Italia). Imagen ´compuesta a partir de dos extraídas de Wikimedia Commons.
El Organum Mathematicum servía para componer música de manera automática, para efectuar operaciones… era una pequeña enciclopedia portátil, un sistema global de organización del conocimiento, un ancestro de nuestros modernos ordenadores.
Más información:
-
Organum Mathematicum, Museo virtual Galileo
-
The Organum Mathematicum: A 17th Century Computer, Neatorama, 2015
-
Jim Bumgardner, Kircher’s Mechanical Composer: A Software Implementation, Crazy Dad
-
Organum Mathematicum, Crazy Dad, 2006
-
Christophe Robert, A. Kircher : Organum Mathematicum – Mode d’emploi, MusicAlgo, 2017
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo El <i>Organum Mathematicum</i>: una enciclopedia portátil se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un espectrómetro Raman portátil mide el punto óptimo de maduración del tomate
- #Naukas14 La música de las esferas
- El joven Arquímedes
Zeruan badira ibaiak, eta olatu erraldoiak eragiteko gai dira
1768an Britainia Handiko agintariek misterio bat argitzea eskatu zioten Ipar Amerikako kolonietako Posta Zerbitzuko zuzendariordeari. Merkataritza-ontziekin alderatuz, Ingalaterratik Amerikara posta eramaten zuten ontziek bi aste gehiago ematen zituzten ibilbide berdina egiteko. Stan Ulanski irasleak The Gulf Stream liburuan idatzitakoaren arabera, zuzendariordeak misterioa argitzea lortu zuen.
Ez zen, baina, edonolako zuzendariorde. Besteak beste, tximisten inguruko ikerketak burutu zituen, eta Ameriketako Estatu Batuetako sorreran ezinbesteko parte-hartzea izan zuen ere. Bale ehiztariekin hitz egin ondoren, Benjamin Franklin zuzendariordeak argitu zuen itsas postarien akatsa: Golkoko ur-lasterraren aurka ari ziren, eta horrek izugarri moteltzen zuen bidaia.
Gerora, hegazkintza garatu zenenerako, ikasgaia ondo ikasita zeukaten hegazkinen ibilbideak prestatzen zituztenak. Kasu honetan, beste korronte baten abantailak kontuan hartu zituzten: gaur egun, Jet korrontea izeneko haize-lasterra baliatzen dute hegazkinek erregaia eta denbora aurrezteko. Kontrako bidea egiten dute, Ipar Amerikatik Europara.
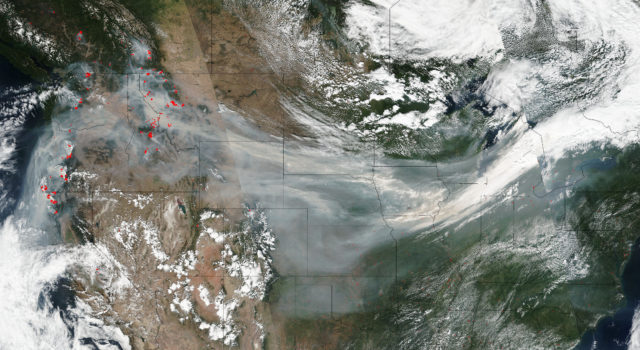
1. irudia: Zaila da haize-lasterrak zuzenean ikustea; baina sute erraldoiak daudenean, satelite bidez posible da igartzea korrontearen eragina kearen ibilbidean. Irudian, Ipar Amerikako suteak, korronterantz. (Argazkia: NASA)
Zeruan eskegitako benetako haize ibaiak dira jet korronteak. Mendebaldetik ekialdera jotzen duten haizete hauek Lurrari bira ematen diote. Bi daude hemisferio bakoitzeko. Gure kasuan, Ipar Atlantikoko jet korrontea da gehien eragiten gaituena. Batez bestean, 10 kilometroko altueran kokatzen den haize-laster hau tenperaturen arteko alde nabarmenen poderioz sortzen da. Bertan dago, hain zuzen, troposferaren eta estratosferaren arteko muga. Atmosferako bi geruza hauen artean tenperatura alde nabarmena dago: zorutik hasita, atmosferan gero eta gorago joanez, orduan eta hotzago izaten da airea. Baina tropopausara heltzean, tenperaturak berriro gora egiten du. Haizete indartsuak daude, 200 kilometro orduko abiadurakoak, baina 400 km/h-ra ere hel daitezke. Udan abiadura txikiagoa eta gorako latitudeetan daude korronteak. Neguan, berriz, hegoalderantz jaisten da eta haizea indartu egiten da.
Aspalditik ezagutzen da haize-laster hauen eragina, bai eguraldian zein patroi klimatikoetan; baina, orain, Nature Communications aldizkarian argitaratutako ikerketa batean eragin hau xehetasun handiarekin zehaztu ahal izan dute.
Paradoxikoa bada ere, ikerketaren protagonistak ez dira izan puntako satelite meteorologikoak, zuhaitzak baizik. Enborren eraztunetan hiru mendetan zehar pilatutako erregistroei esker, ikertzaileak gai izan dira ezagutzeko denbora tarte horretan Ipar hemisferioko klimak izan duen bilakaera. Zehazki, Bretainia Handiko eta Mediterraneoaren ipar-ekialdeko zuhaitz enborren analisia baliatu dute iraganeko klimari buruzko informazioa lortzeko. Bide horretatik, 1725 urtera arte atzera jo ahal izan dute.
Atera duten ondoriorik argiena da jet korronteak eragin zuzena duela Europan gertatzen diren muturreko eguraldiko fenomenoetan. Bestalde, egiaztatu dute haize-lasterrak iparraldera eta hegoaldera izaten duen anplitudea bereziki handitu dela azken mende erdian. Hain zuzen, 1960ko hamarkadatik aurrera egon diren aldaketa hauek bat datoz Europan egon diren muturreko eguraldiko gertaerekin. Besteak beste, beroaldiak, lehortzeak, baso suteak eta uholdeak.

2. irudia: Jet korrontearen eta Europan izaten den muturreko eguraldiaren arteko lotura atzeman dute ikertzaileek; besteak beste, uholdeekin eta lehorteekin lotu dute haize-lasterraren kokapena. (Argazkia: Juanma Gallego)
Lasterra iparraldeen dagoenean, Britaniar Uharteetan eta Europako mendebaldean beroaldiak nozitzen dituzte udan; Europako hego-ekialdean, berriz, eurite gogorrak eta uholdeak jasaten dira. Atmosferako “ibaia” hegoaldeen dagoenean, kontrakoa gertatzen da: Europako mendebaldean ura barra-barra dago, ekialdea “erretzen” den bitartean.
1960ko hamarkadatik aurrera izan den gorabehera hauen handitzeak “aurrekaririk ez duela” esan du ikerketa artikuluaren egile nagusi Valerie Trouet dendrokronologoak. Europan izandako eraginaz gain, noski, Ipar Amerikan sortutakoak ere aztertu dituzte. AEBko erdi-mendebaldean izandako beroaldiak eta 2017-2018ko neguan ipar-ekialdean izandako negu hotza ere lotuta omen daude haize-lasterraren gorabeherei. Kasu honetan, Ozeano Bareko haize-lasterra legoke atzean.
Filma batean bezala, 2012ko udan haren ama Belgikan bisitatzen ari zela bizi izan zuen Trouetek halako “eureka” momentu txiki bat. Amaren etxean egunkaria irakurtzen ari zela, eguraldi mapari erreparatu zion. Europako ipar-mendebaldean euri gogorrak iragartzen ziren bertan, Mediterraneoko ipar-ekialdean muturreko beroa aurreikusten zen bitartean. “Justu mapa berdina ikusita neukan zuhaitz eraztunen maparekin osatutako beste mapa batean”, gogoratu du adituak Arizonako Unibertsitateak (AEB) zabaldutako ohar batean.
1725etik 1978ra arteko neurketak eskuratzeko Erresuma Batuko eta Balkanetako zuhaitzen eraztunak baliatu badituzte ere, 1978. urtetik aurrerako datuak ohiko erregistro meteorologikoei esker eskuratu dituzte. Trouetek azaldu du eztabaida egon dela zientzialarien artean, klima-aldaketa antropogenikoaren eta jet korrontearen gorabeheren handitzearen artean loturarik ote dagoen argitzeko. 1978tik gaurdainoko datuak besterik ez izanda, eztabaida hori herrena izan da. Baina azken hiru mendeetako datuak eskura izateak informazio gehiago jarri ditu mahai gainean. Erabaki garrantzitsuak hartzeko, bada, zeruetako ibaiei ere begiratu beharra dago.
Erreferentzia bibliografikoa:
V. Trouet, F. Babst & M. Meko. Recent enhanced high-summer North Atlantic Jet variability emerges from three-century context. Nature Communications 9, Article number: 180 (2018). DOI:10.1038/s41467-017-02699-3
———————————————————————————-
Egileaz: Juanma Gallego (@juanmagallego) zientzia kazetaria da.
———————————————————————————-
The post Zeruan badira ibaiak, eta olatu erraldoiak eragiteko gai dira appeared first on Zientzia Kaiera.
Sistemas respiratorios: moduladores de la afinidad de los pigmentos
Las características básicas del pigmento respiratorio de un mismo individuo pueden experimentar importantes variaciones como consecuencia de la acción de varios agentes moduladores. La más importante de esas modulaciones es la conocida como efecto Bohr, pero no es la única.
El efecto Bohr

El efecto Bohr se llama así por Christian Bohr, padre de los Bohr más famosos, Niels (físico) y Harald (matemático) Bohr .
El efecto Bohr lo experimentan algunos pigmentos respiratorios y consiste en una reducción de la afinidad por efecto de la concentración de CO2 o de H+ en la sangre. En términos gráficos se puede decir que la elevación de la concentración de protones y de CO2 sanguíneos provoca un desplazamiento de la curva de disociación del pigmento hacia la derecha. El efecto fue dado a conocer en 1904 por un trío encabezado por Christian Bohr del que formaba parte August Krogh, quien posteriormente recibiría el premio Nobel de Fisiología por otros hallazgos muy relevantes en fisiología respiratoria.
Hoy sabemos que el CO2 ejerce un efecto doble sobre la afinidad del pigmento. Hay por un lado un efecto directo, ya que se puede combinar con el pigmento y funcionar como modulador alostérico. Y por otro lado, al disolverse en el plasma sanguíneo una parte del CO2 reacciona con el agua para dar iones bicarbonato, iones carbonato y protones. Y esos protones, al combinarse con el pigmento, actúan también como moduladores alostéricos. En ambos casos aumenta la dificultad para que el pigmento y el O2 se unan, o lo que es lo mismo, se reduce su afinidad. Por otra parte, la concentración de protones en la sangre se puede elevar no sólo al aumentar la de CO2 sino también por otras causas. En los vertebrados, cuando la musculatura esquelética realiza un ejercicio físico intenso no es raro que se produzca lactato, que pasa a la sangre para ser reciclado posteriormente en el hígado; pues bien, ese ácido láctico es también una fuente de protones que puede, a su vez, reducir la afinidad de la hemoglobina.
El efecto Bohr amplía la descarga de oxígeno del pigmento y se cree que esa es la razón por la que se ha seleccionado en ciertas especies. Para entender de dónde viene la ventaja que reporta hay que pensar que la sangre, al salir del órgano respiratorio, va cargada de oxígeno, contiene muy poco CO2 y su pH es relativamente alto. Al llegar a los tejidos el oxígeno pasa de los capilares a las células y, a la vez, el CO2 sale de estas y pasa a la sangre. CO2 y protones se combinan con la hemoglobina y la afinidad de esta por el O2 disminuye. Como consecuencia, se facilita la liberación de más oxígeno, por lo que su transferencia a las células resulta favorecida.

En una ballena jorobada (“Megaptera novaeangliae”), uno de los animales más grandes del planeta, el efecto Bohr tiene una magnitud similar a la que tiene en el conejillo de indias.
El efecto Bohr no se produce en todos los pigmentos y su magnitud es muy variable, seguramente porque las circunstancias de cada especie son también distintas. En mamíferos, el tamaño del animal, por ejemplo, influye: cuanto más pequeño es el animal y, por lo tanto, mayor es su tasa metabólica, el efecto es de mayor intensidad. Tortugas, lagartos y serpientes experimentan un efecto Bohr de menor magnitud que los mamíferos, pero en los cocodrilos es muy intenso. Se cree que ese intenso efecto ayuda a los cocodrilos a ahogar a sus presas bajo el agua: al atraparlas y sumergirlas ha de dejar de respirar, por lo que su única fuente de O2 es la sangre; y su liberación hacia las células se ve favorecida por tal efecto.
El efecto Root
Algunas especies de peces, teleósteos principalmente, tienen más de un tipo de hemoglobina en su sangre; se denominan isoformas. Unas son muy sensibles a la concentración de CO2 y a la de protones, y las otras no. La peculiaridad de las sensibles consiste en que experimentan una pérdida de su capacidad para combinarse con el O2 no solo porque disminuya su afinidad, sino porque se reduce de forma importante su capacidad de oxígeno o capacidad de carga. A ese fenómeno se le denomina efecto Root, por el nombre de su descubridor1.
Gracias al efecto Root las especies que lo experimentan elevan la tensión parcial de oxígeno en el entorno de dos órganos, la vejiga natatoria y los ojos. La acidificación de la sangre en esos entornos provoca que una parte importante del oxígeno pase a estar en forma disuelta. Aumenta así la tO2 en ese entorno y, como consecuencia de ello, el O2 disuelto pasa al interior de la vejiga o de los globos oculares. De ese modo pueden aumentar el contenido gaseoso de la vejiga natatoria y actuar sobre la flotabilidad. Y en lo relativo a los globos oculares, la retina de algunos peces necesita altas tensiones parciales de oxígeno para funcionar correctamente.
Las isoformas insensibles, por su parte, son una especie de seguro anti-asfixia: sin ellas podría ocurrir que un exceso de CO2 y H+ en sangre por efecto de una actividad física muy intensa provocase una pérdida de la capacidad del pigmento para captar O2 del exterior tal que llegase incluso a asfixiarse.
Moduladores orgánicos
La afinidad de la hemoglobina de muchos vertebrados varía en función de la concentración de ciertas sustancias orgánicas fosfatadas. En mamíferos (seres humanos, caballos, perros, o ratas) se trata del 2,3-bifosfoglicerato (2,3-DPG), en aves es el inositol pentafosfato (IIP) y en peces es el adenosina trifosfato (ATP) (predominante en salmónidos, tiburones y rayas) y el guanosina trifosfato (GTP) (predominante en anguilas, carpas y carpas doradas). Esas sustancias se encuentran en el interior de los eritrocitos, puesto que son productos de su metabolismo, y se combinan de forma reversible con el pigmento reduciendo su afinidad. La reducción de la afinidad no se limita, como ocurría con la provocada por la acidificación y el CO2 propios del efecto Bohr, a la sangre que se encuentra en los tejidos, sino que es un efecto permanente, ya que se encuentran en el interior de los glóbulos rojos en todo momento.
Al parecer, la concentración de los moduladores orgánicos citados aumenta en el interior de los eritrocitos en respuesta a condiciones de hipoxia (ya sea de origen ambiental o por razones patológicas), lo que facilita la descarga de O2 a los tejidos; sin embargo, también dificulta su captación desde el órgano respiratorio, aunque el balance neto de estos efectos favorece el suministro de oxígeno a los tejidos en esas condiciones.
Temperatura
La elevación de la temperatura provoca un desplazamiento de la curva de disociación del pigmento hacia la derecha y, por lo tanto, un descenso de su afinidad por el O2. Quiere esto decir que a igualdad de tO2, el pigmento contiene menos oxígeno a altas que a bajas temperaturas. Por lo tanto, un aumento de temperatura facilita la descarga de O2 del pigmento. Las consecuencias prácticas de este efecto térmico son evidentes; los aumentos de temperatura -incluso los que ocurren localmente en tejidos especialmente activos de animales homeotermos- están asociados a una mayor actividad metabólica, de manera que al facilitarse la descarga por efecto térmico, se favorece el suministro de oxígeno a las células que más lo necesitan o cuando lo necesitan en mayor medida.
Fuentes:
Richard W. Hill, Gordon A. Wyse & Margaret Anderson (2004): Animal Physiology. Sinauer Associates, Sunderland
Knut Schmidt-Nielsen (1997): Animal Physiology. Adaptation and Environment. Cambridge University Press; Cambridge
Lauralee Sherwood, Hillar Klandorf & Paul H. Yancey (2005): Animal Physiology: from genes to organisms. Brooks/Cole, Belmont.
Nota:
1 Según algunos autores el efecto Root no es sino un fuerte efecto Bohr.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Sistemas respiratorios: moduladores de la afinidad de los pigmentos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sistemas respiratorios: pigmentos de alta afinidad
- Sistemas respiratorios: pigmentos de baja afinidad
- Sistemas respiratorios: los pigmentos respiratorios
La relatividad de la masa

No existe tecnología que pueda conseguir que un motor genere la fuerza suficiente como para llevar a una nave a velocidades cercanas a la velocidad de la luz, mucho menos igualarla.
La segunda ley de Newton establece que la aceleración de un objeto es inversamente proporcional a la masa del objeto. Cuanto mayor sea la masa de un objeto, menor será su aceleración si se le aplica una fuerza neta dada. A veces se llama masa inercial, para enfatizar que mide la inercia, esto es, la resistencia a alterar el estado de movimiento o reposo del objeto. En otras palabras, la masa es una propiedad de los objetos que se opone a la aceleración cuando se aplica una fuerza. Todo esto se reúne en una expresión tan simple como F = m·a., donde F es la fuerza neta que actúa sobre el objeto, m es la masa (inercial) y a la aceleración resultante.
A partir de la segunda ley de Newton podemos afirmar que una fuerza constante producirá una aceleración constante. Por tanto, si una vez que un objeto se está moviendo, se le continúa empujando con la misma fuerza, seguirá acelerándose, yendo más y más rápido. Y, según la fórmula de Newton, no existe límite a la velocidad que puede alcanzar.
Pero esto es inconsistente con la teoría de la relatividad, que impone un límite de velocidad para objetos en el espacio de c = 299.792.458 m/s, la velocidad de la luz en el vacío. Hay que alterar pues la expresión de la segunda ley de Newton para que tenga en cuenta este hecho.
Einstein lo hizo afirmando que m, la masa inercial, no permanece constante sino que aumenta a medida que aumenta la velocidad, un hecho que se observa experimentalmente, por ejemplo, en partículas elementales a alta velocidad.
Si la masa inercial aumenta con la velocidad eso quiere decir que se requiere cada vez más fuerza para conseguir la misma aceleración, y finalmente haría falta una fuerza infinita para intentar alcanzar la velocidad de la luz. Einstein dedujo de los dos postulados de la teoría de la invariancia que la inercia de un objeto en movimiento aumenta con la velocidad, y lo hace de forma completamente análoga a la que empleó para la dilatación del tiempo. Como cabía esperar, llega a una expresión equivalente a la que encontró para el tiempo: mm = me/√(1-v2/c2), donde mm es la masa del objeto en movimiento relativo, y me es la masa del mismo objeto antes de que empiece a moverse, estático. Muy a menudo a me se la llama masa en reposo.
De forma similar a nuestro análisis de la expresión para los intervalos de tiempo, encontramos que, a medida que aumenta la velocidad de un objeto, la masa observada a partir de un marco de referencia estacionario también aumenta. Alcanzará una masa infinita (o indefinida) si alcanza la velocidad de la luz. Esta es otra razón por la cual no puede hacerse que algo que posea masa alcance la velocidad de la luz; requeriría, como decíamos antes, aplicar una fuerza infinita para acelerarla a esa velocidad.
Por el mismo argumento, los objetos que sí se mueven a la velocidad de la luz, como la luz misma, deben tener masa en reposo cero. Siguiendo el resultado de Einstein de que la masa de un objeto aumenta cuando está en movimiento en relación con un observador estacionario, la ecuación de Newton que relaciona la fuerza y la aceleración puede escribirse como una ley más general de la sigiente forma: F = me·a /√(1-v2/c2).
Démonos cuenta de que para velocidades muy pequeñas en comparación con la velocidad de la luz, como las de nuestro mundo ordinario, esta fórmula se convierte de forma continua en F = m·a. De nuevo vemos que la física de Einstein no es una ruptura con la de Newton, sino una continuación de la misma.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La relatividad de la masa se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La relatividad del tiempo (y 3)
- El principio de relatividad (1): movimiento relativo
- El principio de relatividad (2): la versión de Galileo
Taula periodikoa ez dago bukatuta, oraingoz
Hideto En’yo Japoniako Riken ikerketa zentroko zuzendariak 2017an jakinarazi zuen 119. elementua bilatzeko ikerketak martxan jarriko zirela. 2017ko abenduan hasi ziren lanak eta, bost urteko epean, bi elementu -119 eta 120 zenbaki atomikokoak- sintetizatzeko gai izango direla adierazi zuen ikerketaren zuzendariak. Hortaz, litekeena da hurrengo bost urteetan taula periodikoari 8. lerroa gehitu behar izatea.

1. irudia: Orain arteko taula periodiko berriena hau da, baina, baliteke laster 8. lerroa gehitu behar izatea. (Iturria: zientziakaiera.eus)
UnunennioaRiken ikerketa zentroan sintetizatuko den elementu horren behin behineko izena ununennioa izango da -bat, bat, bederatzi, latineraz- eta, esan behar da, elementu hori ez dela sekula Naturan existitu. Ununennioak taula periodikoaren beste lerro bati hasiera emango dio, 1859an Dmitri Mendeléiev-ek proposatutako elementuen sailkapen periodikoari jarraipena emanez. Kasualitatez, 2019an taula periodikoaren 150. urteurrena beteko da eta IUPAC Kimika Puru eta Aplikatuko Nazioarteko Batasunak urte horixe Taula Periodikoaren Nazioarteko Urtea izendatuko du. Baliteke urte berezi horretan bertan gertatzea 8. lerroaren hasiera, baina, oraingoz, ezer ez da ziurra.
Ununennioa sintetizatzeko ikerketaren zailtasuna ulertzeko, jakin behar da plutonioa –94 protoi ditu bere nukleoan- baino zenbaki atomiko handiagoa duten elementuak ez direla Naturan existitzen eta laborategian sintetizatu behar direla. Elementu arinenak, alegia, hidrogenoa eta helioa Big Bangaren ondoren agertu ziren. Oro har, astunagoak direnak -burdina bitarte, 26 protoi dituena- gero agertzen joan ziren, gehienak izarren nukleoetan sortuta. Zenbaki atomiko horretatik aurrera, jatorria azaltzea zailagoa da eta, esaterako, supernobak edo antzeko prozesu leherkorretan agertu zirela pentsatzen dute zientzialariek. Dena den, plutonioa baino astunagoak direnak ez dira Naturan sortu eta laborategietan sintetizatu dira. Horretarako, laborategian elementu astun bat ioiekin bonbardatzen da, talka horiek bitartez nukleoen fusioa gertatu eta elementu astunagoak lortzeko. Oro har, elementu horiek ezegonkorrak dira eta desintegratzeko joera dute berriz, baina, une batez, elementu horiek existitu egin dira. Une honetan, taula periodikoko azken elementua oganesona da, 118 zenbaki atomikoa duena, blog honetan bertan Gotzone Barandikak azaldu zuen moduan.

2. irudia: Oganesona da une honetan taula periodikoaren azken elementua, 118 zenbaki atomikoa duena. (Argazkia: LJNovaScotia – domeinu publikoko irudia. Iturria: Pixabay.com)
Riken ikerketa zentroko ikertzaileek antzeko prozedura erabiliko dute 119. elementua sintetizatzeko. Erabiliko duten bidea hauxe izango da: banadio-sortekin bonbardatuko dituzte kurio atomoak. Lehenak 26 protoi ditu nukleoan eta bigarrenak, aldiz, 96. Hortaz, nukleoen fusioa gertatzen bada -eta hala izatea espero dute-, ununennioa sintetizatuko dute, sekula existitu ez den elementua. Jakina, prozedura ez da batere erraza eta aurrez egindako saiakuntzetan ez da arrakastarik lortu -Alemanian saiakuntzak egin zituzten 2012an-. Nolanahi ere, esandakoa lortzen badute, zientzian mugarri garrantzitsua jarriko dute ikertzaile japoniarrek.
Taula periodikoaren azken muga, zertarako?Pentsa liteke, agian, azaldutako prozeduren bidez edozein zenbaki atomikoko elementuak lortu ahal izango liratekeela, baina, ziur asko hori ez da bideragarria. Hain zuzen ere, elektrodinamika kuantikoaren kalkuluen arabera 170-210 artean legoke gehienez lor daitekeen zenbaki atomikoa, eta, ziurrenik 173 litzateke gehienezko zenbaki atomiko posiblea -hemen dituzue Francisco R. Villatororen azalpen argiak gai honi buruz-. Eta azken galderak hauexek dira: zertarako bilatu elementu berriak? Ba ote du erabilpenik segundo gutxi batzuetan desegiten diren elementuak sintetizatzen baliabideak xahutzea? Bada, Hideto En’yo berak esan zuenez, elementua bera aurkitzea praktikoa da, taula periodikoari beste lerro bat gehitzeagatik bakarrik izanik ere. Une honetan beste erabilpen praktikorik ez du, eta baliteke ununennioak inoiz ezertarako ez balio izatea, baina, baliteke etorkizunean oso erabilgarria izatea. Batek daki. Horixe da oinarrizko ikerkuntzaren xarma. XVIII. mende bukaeran Martin H. Klaproth kimikari alemaniarrak uranioa aurkitu zuenean pentsatuko ote zuen 220 urte beranduago gizateriaren energia ekoizpenaren %10a zentral nuklearretan lortuko zela bere aurkikuntzari esker?
Informazio osagarria:
- Hunt for element 119 set to begin, Kit Chapman, chemistryworld.com
- La tabla periódica se asoma a una nueva fila por primera vez en la historia, Manuel Ansede, elpais.com
- Where in the periodic table will be put element 119, lynceans.org
—————————————————–
Egileaz: Josu Lopez-Gazpio (@Josu_lg) Kimikan doktorea eta zientzia dibulgatzailea da. Tolosaldeko Atarian Zientziaren Talaia atalean idazten du eta UEUko Kimika sailburua da.
—————————————————–
The post Taula periodikoa ez dago bukatuta, oraingoz appeared first on Zientzia Kaiera.
Es el fin del mundo tal y como lo conocemos

Quedan dos minutos para medianoche en el Reloj del Apocalipsis (Foto: Bulletin of the Atomic Scientists)
“El fracaso de los líderes mundiales para hacer frente a las amenazas para el futuro de la humanidad es lamentable”. Así, sin delicadeza ni paños calientes, comenzaba el comunicado anual del Bulletin of the Atomic Scientists en el que nos avisa de cuánto tiempo falta en el Reloj del Apocalipsis para que llegue la medianoche que simboliza el fin del mundo. Dos minutos, aseguran, lo más cerca que hemos estado nunca de causar nuestra propia destrucción.
Este reloj del Apocalipsis nació en 1947, en plena Guerra Fría, como una metáfora visual de lo cerca que estaba el desastre de la Destrucción Mutua Asegurada. Los autores, miembros del Comité de Seguridad del Bulletin, situaron el minutero a 7 minutos de la medianoche.
Aunque la aguja ha avanzado y retrocedido desde entonces, solamente una vez habíamos estado tan cerca del final: fue en 1953, cuando Estados Unidos desarrolló la bomba de hidrógeno, un arma mucho más poderosa que cualquier otra bomba nuclear creada hasta el momento. En octubre de 1952, EEUU ponía a prueba su primer artefacto termonuclear, borrando completamente del mapa un islote del Pacífico en el proceso, y nueve meses después los soviéticos hacían lo mismo con su propia bomba H. “Las manecillas del reloj del Final se han movido de nuevo. Unas oscilaciones más del péndulo y de Chicago a Moscú, las explosiones nucleares traerán la medianoche a Occidente”.
Han pasado 65 años y volvemos a estar a esas pocas oscilaciones de cargárnoslo todo. Sin la tensión de la Guerra Fría y de sus superpotencias apuntándose directa y mutuamente a la cabeza con misiles nucleares, ¿cómo hemos llegado hasta aquí? La respuesta es compleja, y igual que lo es el mundo en comparación con cómo era hace unas cuantas décadas.
La guerra nuclear está a un error de distancia
Por un lado, sigue existiendo una amenaza nuclear latente en la que ya no hay solamente dos jugadores involucrados. Los autores del reloj señalan el progreso nuclear de Corea del Norte en 2017 como un aumento del riesgo para la propia Corea, los países de la región y Estados Unidos.
Por otro, existe un riesgo nuevo añadido: que las armas nucleares terminen utilizándose por accidente o por un fallo de cálculo. La retórica matona, ostentosa y provocadora de ambos bandos hace temer que un mal movimiento termine desencadenando un ataque no planeado por puro accidente.
Claro que no es solo Corea la que nos pone nuclearmente nerviosos: Estados Unidos y Rusia continúan enfrentados, haciendo ejercicios militares en las fronteras de la OTAN, ignorando los tratados nucleares, aumentando sus arsenales y evitando las negociaciones para el control de armas. Por primera vez en muchos años, no hay actualmente en marcha negociaciones para el control de armas nucleares entre Rusia y Estados Unidos.
Las tensiones en el Mar de China entre China y Estados Unidos han aumentado, las relaciones diplomáticas entre ambos países han demostrado ser insuficientes para restablecer una situación segura; Pakistán e India siguen aumentando el tamaño de sus arsenales nucleares, que ahora son más grandes que nunca, y en Oriente Medio, la incertidumbre sobre el avance nuclear de Irán solo suman más oscuridad a un panorama que pinta negro.
Tan negro que cuando la Campaña Internacional para la Abolición de las Armas Nucleares obtuvo el Nobel de la Paz 2017, para muchos fue interpretado como un gesto de apoyo y también de frustración por los escasos y lentos progresos realizados hasta ahora por tantos países.
Trump desanda lo andado contra el cambio climático
El segundo argumento de los científicos nucleares para declarar inminente el fin del mundo es un guantazo a mano abierta a la administración de Donald Trump: el cambio climático y una respuesta insuficiente. Esta amenaza global avanza imparable y no parecemos saber o querer hacer algo para detenerla.
“El año pasado, el gobierno de EEUU llevó a cabo políticas poco inteligentes e ineficaces en materia del cambio climático, cumpliendo la promesa de descarrilar las políticas climáticas previas. La administración Trump, que incluye negacionistas climáticos declarados en posiciones de mando, ha anunciado su intención de retirarse del Acuerdo de París. En su prisa por desmantelar políticas energéticas y climáticas racionales, el gobierno ha ignorado análisis económicos bien fundamentados en datos científicos”, denuncian los científicos.
Desconfianza en la información, el conocimiento y los datos
El desprecio de la administración Trump por los datos y las evidencias, sumado un clima general de incertidumbre tecnológica, forman el tercer punto del informe, quizá el más importante porque apela al efecto directo sobre todos nosotros del entorno de información/desinformación en el que estamos envueltos: “El Comité de Ciencia y Seguridad está profundamente preocupado por la pérdida de confianza en las instituciones políticas, los medios, la ciencia y los propios datos, una pérdida que la propia tecnología de la información ha alentado”.
La democracia, siguen los autores, depende en definitiva de que un electorado bien informado tome decisiones racionales sobre políticas públicas, incluidas aquellas que afectan al armamento y desarme nuclear, el cambio climático y otras amenazas globales.

Cómo detectar si una noticia es falsa. (Fuente: International Federation of Library Associations and Institutions)
Pero eso está en peligro, amenazado por intentos de interferir en procesos electorales a través de sofisticadas operaciones de hackeo, dispersión de desinformación a través de las redes, descrédito del conocimiento y los datos empíricos… “Mientras, los líderes de las corporaciones que dominan la información, incluidos los medios de comunicación pero también compañías como Facebook o Google, están siendo demasiado lentos en la adopción de protocolos que prevengan el mal uso de sus servicios y así proteger a los ciudadanos de la desinformación”.
“Hacer un mundo más sano, y más cuerdo”
Por todas estas razones, el reloj ha avanzado 30 segundos y si en año 2017 nos encontrábamos a 2 minutos y medio del desastre, ahora son solo 2 minutos. Sin embargo, hay una nota de esperanza en todo esto: ya estuvimos aquí una vez y conseguimos volver atrás.
La humanidad creó los caminos hacia el apocalipsis, así que también puede eliminarlos, nos animan los científicos, que además de leerle la cartilla a los políticos, apelan a nuestra responsabilidad y poder ciudadano para forzar un cambio que ya es urgente.
“El mundo ha visto la amenaza que supone el mal uso de la tecnología de información, y ha sido testigo de lo vulnerable que es la democracia ante la desinformación. Pero hay un lado positivo en el abuso de las redes sociales: los líderes reaccionan cuando los ciudadanos insisten en que lo hagan, así que lo ciudadanos pueden usar ese poder que les da internet para mejorar las perspectivas a largo plazo para sus hijos y nietos. Pueden insistir en los datos y descartar los disparates. Pueden exigir medidas que reduzcan las amenazas para la existencia que son la guerra nuclear y el cambio climático descontrolado. Pueden utilizar esta oportunidad para hacer un mundo más sano, y más cuerdo”.
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo Es el fin del mundo tal y como lo conocemos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La fusión nuclear como fuente de neutrones eficiente
- Sopcawind: cómo optimizar parques eólicos
- Cómo detectar un defecto en el ADN viendo cómo se retuerce
Energia gordetzen duen kontraleihoa

Azterketa horien emaitzetatik ateratako ondorioei esker, isolamendu eta inertzia termikoa duen kontraleiho diseinu berri baterako oinarriak ezarri dira, eraikinaren eskaera energetikoa ahalik eta gehien gutxitzeko kontraleihoa irekita zein itxita dagoenean. Egunez, irekita dagoenean, energia gordetzeko gai da eta gauean eraikinari energia ematen dio. Eraikin bateko eraginkortasun txikiko leihoak oso leiho eraginkorrekin ordezkatuta baino gehiago gutxitzen da energia eskaria diseinatutako kontraleihoekin.
Zenbakizko metodoak erabili dituzte eraikinetako simulazio energetiko tresna gisa. Erregimen geldikorrean (eraikinaren barneko eta kanpoko tenperaturak finkoak direnean) eta erregimen dinamikoan (tenperatura aldaketak daudenean) kontraleihoek duten portaera termikoa aztertzea izan du ardatz ikerketak. Erregimen geldikorra une jakin baten idealizazio bat da, ohikoa eta errealetik hurbilen dagoena erregimen dinamikoa da, kanpoko tenperatura etengabe ari delako aldatzen.
Azterketa ez da kontraleihoan bakarrik egin, ondoko elementuetan, hala nola leihoaren zubi termikoetan, eragiten dituen efektuak ere aztertu dira. Oro har, isolamendu gutxiagoko eremuak izaten dira zubi termikoak, beraz, bero galera handitzen dute; baita kondentsazio zein hezetasun orbanak azaltzeko arriskua handitu. Kontraleihoekin bero galera txikiagoa da, leihoaren zubi termikoak isolatzen baititu, modu honetan kondentsazioak gertatzeko eta hezetasun orbanak azaltzeko arriskua txikitzen.
Energia politikekin batEuropar Batasunaren azken urteotako politiketan energia eraginkortasuna sustatu da eta, ondorioz, eraikinetako inguratzaile termikoa osatzen duten elementuak aztertzeko joera nabarmendu da, energia kontsumoa murriztu ahal izateko eta ia kontsumorik gabeko eraikinak edota energia ekoizle diren eraikinak egitea lortzeko.
Indarrean dagoen araudiak baditu zenbait erreferentzia eta ekuazio analitiko kontraleihoak zer eragin duen kuantifikatu ahal izateko, baina erregimen geldikorrari baino ez dagozkio eta ez dira nahikoak kontraleihoen portaera termikoa zehaztasunez kalkulatu ahal izateko. Erregimen dinamikoarekin lotutako erreferentziarik ez dago ia, aurkitzen diren erreferentziek oso kasu espezifikoak aztertu besterik ez dute egiten eta ezin dira beste irtenbide mota batzuetara estrapolatu.
Ikerketan lortutako emaitza teorikoak baliozkotzeko epe laburrean benetako saiakuntza bat egitea litzateke egokiena ikertzailearen aburuz eta energia eraginkortasuna hobetzeko kontraleihoek izan dezaketen garrantzia eraikuntzaren sektoreari jakinarazi.
Iturria: UPV/EHUko prentsa bulegoa: Energia gordetzeko gai den kontraleiho-modelo berri bat diseinatu dute.
The post Energia gordetzen duen kontraleihoa appeared first on Zientzia Kaiera.
Detectores de mentiras de ayer, hoy y mañana
En 1921 John Augustus Larson, estudiante de medicina y miembro del Departamento de Policía de Berkeley (California, EEUU), inventó el polígrafo, también conocido como detector de mentiras. Se trata de un instrumento que registra variables fisiológicas tales como presión arterial, frecuencia cardiaca, frecuencia respiratoria y conductancia de la piel (relacionada esta última con la sudoración) mientras una persona se encuentra respondiendo a las preguntas que se le hacen para poner a prueba su sinceridad. El recurso a este instrumento se basa en el supuesto de que al mentir, el registro combinado de las variables citadas ofrece un perfil característico, y ello permitiría detectar las mentiras dichas por la persona investigada. En la actualidad los polígrafos son utilizados en más de noventa países por diferentes entidades y con distintos propósitos: servicios de inteligencia y seguridad en investigaciones, tribunales de justicia para obtener pruebas, y empresas para contratar empleados.
Sin embargo, su eficacia no cuenta con pruebas consistentes que respalden su uso. Varios de los supuestos teóricos en que se basa no han podido verificarse experimentalmente o han sido, incluso, refutados. No se ha encontrado ningún patrón común en las respuestas fisiológicas de las personas cuando se inclinan por una u otra opción, mentir o decir la verdad; y ni siquiera se ha podido comprobar que todas las personas respondan de forma diferenciada en uno y otro caso. Por todo ello, el uso del polígrafo ha concitado el rechazo de buena parte de la comunidad científica.
Dada la gran oposición que provoca su uso y la utilidad que podría tener el disponer de una tecnología realmente válida para detectar mentiras, no es extraño que se estén barajando alternativas. Es el caso de la Truthful Brain Corporation, una empresa que se ha propuesto conseguir que el sistema judicial norteamericano incorpore la utilización de imágenes obtenidas por resonancia magnética funcional (IRMf) como técnica para la detección de mentiras en los juicios.
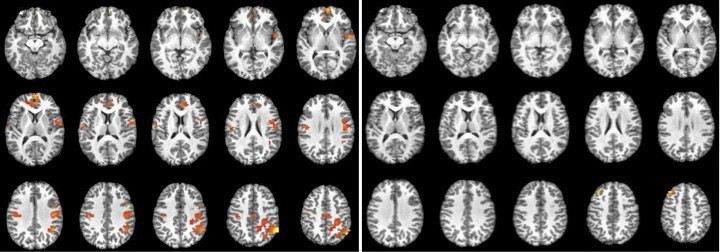
La IRMf se utiliza para obtener imágenes que muestran la actividad de diferentes regiones encefálicas cuando la persona examinada se encuentra realizando una tarea, que puede ser manual o intelectual. Se basa en que la hemoglobina oxigenada y la desoxigenada tienen diferentes características magnéticas (la desoxigenada se comporta como un microimán) y que al activarse una región encefálica se producen cambios en la proporción de las dos formas de hemoglobina como consecuencia de la mayor afluencia de sangre y consumo de oxígeno por las regiones más activas. La técnica permite localizar las zonas que reciben un mayor flujo sanguíneo.
Truthfull Brain Corporation esgrime a favor de sus pretensiones las investigaciones científicas que avalan la hipótesis de que la IRMf sirve para detectar mentiras. El problema es que esas investigaciones se han hecho en un único laboratorio y haría falta que, para tener mayor credibilidad, sus conclusiones fuesen corroboradas por otros equipos de investigación. Y por otro lado, ni siquiera ese requisito sería quizás suficiente. Porque una cosa es mentir en condiciones experimentales acerca de cuestiones relativamente triviales, y otra muy diferente es hacerlo cuando se encuentra uno sometido a juicio acusado de haber cometido un delito grave.
Es demasiado pronto para saber si las imágenes obtenidas mediante resonancia magnética funcional se harán un hueco en los sistemas judiciales. No es descartable que eso llegue a ocurrir, pero si así fuera, seguramente no se tratará de la prueba que determine el resultado de un proceso, sino que servirá para, junto con otros elementos de juicio, llegar a un veredicto mejor fundamentado. No necesitaría demasiados méritos para superar a los “detectores de mentiras” que se usan hoy.
El artículo Detectores de mentiras de ayer, hoy y mañana se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las mentiras allanan su propio camino
- Voy a comprar mentiras
- La entropía de Shannon y las lubinas como detectores de contaminación
Asteon zientzia begi-bistan #187
Primateak klonatu dituzte lehen aldiz. Dolly ardia lortzeko erabili zen teknika berberarekin sortu ditu bi makako Txinako Neurozientzien Institutuak. Orain arte, ez zituzten emaitza onak lortu primateetan baina orain erdietsi dute eta interesgarria da, batez ere, primateak oso antzekoak direlako gure espeziarekin alderatuz gero. Ikertzaileek erabili duten teknika zelula somatikoen nukleo-transferentzia izan da. Ikerketa honen inguruan gehiago jakiteko, jo ezazue artikulura.
MedikuntzaEstatu Batuetako Osasunaren Institutu Nazionalak (NIHk) iragarri du aldatu egingo duela biomedikuntzako ikerketak finantzatzeko politika. Helburua? Ikerketa klinikoetan gardentasuna, zehaztasuna, errepikakortasuna lortzea, eta gizartearekiko konpromisoz jokatzea. Baldintza batzuk jaso dituzte; hala nola, erabiliko diren protokolo klinikoak aurrez erregistratu eta ikerketaren emaitza guztiak argitaratu beharko dira. Hartu nahi dituzten neurriak “entsegu kliniko” gisa definitutako ikerketetan bakarrik hartuko dira. Aldaketa hauen aurrean, zientzialari guztiak ez daude ados.
EkologiaSardako balea edo ‘Euskal balea’ ere deitua desagertzear dago, zalantzan jarri da bere iraupena. Geratzen direnak Ameriketako Estatu Batuen eta Kanadaren arteko kosta atlantikoan daude. Daukaten arriskurik handiena inguru horretako itsas nabigazioari lotuta dago. NOAAren arabera, 450 baleetatik hamazazpi hil ziren iaz. Egun soilik 100 eme ugaltzaile geratzen direla diote. “Larriena” da espeziea ez dela hazten ari, Enrike Francor Ambar itsas fauna ikertu eta babesteko elkarteko kideak azaltzen duen moduan.
Azken urtean beste 1.800 animalia espezie desagertzeko arriskuan daudela dio Naturaren Kontserbaziorako Nazioarteko Erakundeak. 2017an zerrendara horretara gehitu dira, besteak beste, koalak, pangolinak eta itsas-zalditxoak. Habitat galerak eta neurriz kanpoko pestiziden erabilerak eragina izan dute horretan. Badago itxaropenerako tartea, dena dela. Itsas dortoka populazio batzuen egoera hobetu egin da, esaterako.
MeteorologiaNazioarteko Meteorologia Erakundeak (WMO), NOAAk eta beste zenbait erakundek eman dituzte azken datu ofizialak eta ez dira itxaropentsuak: 2017a izan da historiako 2. urterik beroena (El Niño fenomenorik gabe). Historiako urterik beroenak azken hiruak izan dira (2015-2017), eta 5 beroenak 2010etik aurrera gertatu dira.
AntropologiaMalakako penintsulan bizi diren bi herrik usainak izendatzeko trebezia berezia dutela iradoki du esperimentu batek. Guk hizkuntza mugatua dugu usainak izendatzeko. Ez, ordea, Jahai eta Mani herriek. Diotenez, ahalmen paregabe hau sistema ekonomikoari lotuta dago. Herri bakoitzeko hogei bat lagunek parte hartu dute esperimentuan, Semelai eta Semaq Beri izan dira hautatutako giza taldeak. Adibidez, bi herriek erabilitako hizkuntzek usainak izendatzeko hitzak dituzten arren, egileek argitu dute Semelai nekazariek joera dutela jatorriaren arabera usainak deskribatzeko: “platano usaina”, esaterako.
ZoologiaIngurumenean gertatzen dena kontatzeko garrantzitsuak dira narrastiak eta anfibioak. Hala adierazi dute Iñaki Sanz-Azkue eta Egoitz Alkorta herpetologoek. Animalia horien inguruko informazio biltzen hasi ziren Hernanin eta inguruan: espeziea, arra edo emea, adina, GPSaren datu koordenadak, argazkia ahal bada… Duela hamabi urte abian jarri zuten Ziraba proiektua, “Hernaniko eta inguruetako anfibioak eta narrastiak” liburu-gida, hain zuzen. “Ziraba proiektuaren baitan, datu mordoa jaso dugu ikerketa adarrari dagokionez. Proiektuak badu beste adar bat, ahozko ondarearena”, diote.
PaleontologiaEkialde Hurbilean aurkitutako giza aztarna berri batzuek agerian jarri dute gizaki modernoak uste zena baino lehenago atera zirela Afrikatik. 177.000 eta 194.000 urte bitartean dituzten giza hortzak aurkitu dituzte. Orain arte uste zen gizaki modernoak duela 90.000-120.000 urte atera zirela lehenengo aldiz Afrikatik. Joseba Rios Burgosko Giza Eboluzioari buruzko Ikerketa Zentroko ikertzailearentzat oso garrantzitsua da aurkikuntza hori: “Ia 80.000 urte aurreratzen du gizaki modernoaren irteera”.
BiologiaTestu honetan planktona dugu protagonista. AZTIko ikertzaile Ernesto Villarinok dio: “Ozeanoetako elikadura katearen oinarria da. Hortik gora, beste talde guztiak daude”. Adituak azaltzen duenez, Lurrean sortzen den oxigenoaren %50 planktonari zor zaio. Bestalde, atmosferatik CO2 kopuru handiak kentzeko gai da. Hortaz, kliman garrantzi handia du. Tamaina omen da funtsa Villarinoren ustetan: “Organismo planktonikoen tamaina gero eta handiago izan, orduan eta txikiagoa da itsas komunitateen arteko lotura. Planktonaren sakabanaketan eta banaketa globalean, tamaina gakoa dela frogatu dugu”.
Hainbat animalia-taldek estrategia ugari garatu dituzte elikagaiak izateko eta etsaietatik babesteko. Animalia horiek toxinak ekoizten dituzte. Horietako batzuk, gainera, mekanismo sofistikatuak erabiltzen dituzte pozoia txertatzeko. Egileek azaltzen digutenez, badago toxina-talde bat neurotransmisorearen askatze-prozesuan eraginik ez izan arren hurrengo prozesua zapuzten duena. Adibidez, α-bungarotoxina. Sugegorri marradunaren pozoia osatzen duten peptidoetariko bat da toxina hori. Hozka egiten duenean eta pozoia txertatzean, harrapakina paralizatzea lortzen du. Hego Amerikako zenbait indiok erabiltzen duten prozedura oso antzekoa da. Amazoniako tribu batzuetan kurarea erabiltzen dute, gezien puntak bustitzen dituzte eta horrela animalia pozoitsuek bezala jokatzen dute.
KimikaSagar mota bakarrarekin egindako sagardoak aztertu ditu UPV/EHUko ikerketa batek, sagardoari ematen dizkion edo eman ahal dizkion ezaugarriak zehatz-mehatz aztertzeko. Sagarretan dauden polifenolak dira aztertutako molekulak. Sagar mota bakarreko zukuekin sagar-mota horren ezaugarriak nabarmentzen dira eta, askotan, muturreko sagardoak lortzen direla azaltzen du Andoni Zuriarrain ikertzaileak testuan.
Polimerozko-diru paperak XXI. mendeko kontuak diruditen arren plastikozko lehenengo billeteak 80ko hamarkadan garatu ziren. Egun erabiltzen den diru-papera ez dago paper arruntez egina; izan ere, zuretik lortzen den paperak ez dauka bizi-iraupen luzea. Horren ordez kotoizko zuntza erabiltzen da; zenbaitetan beste ehun batzuk ere gehitzen zaizkio esaterako lihoa. Polimeroz egindako diru-paperak zenbait abantaila ditu. Esaterako, bizi-iraupena luzeagoa da, ez dira hain erraz puskatzen eta gainera behin bere bizitza erabilgarria amaituta birziklatu egin daitezke. Polimeroz egindako diru-papera seguruagoa da gainera. Desabantailak ere baditu, hala nola diru-paper arruntak baino ekoizpen-kostua handiagoa dute.
EkonomiaLan honetan, banaketa-katean zehar arrantza prezioen integrazio bertikala aztertu da. Jatorrizko arrantza prezioen indizea 2002-2014 denboraldian harrapatutako 136 espezietatik, 36 espezietarako datuen bitartez eraiki da. Galiziako lonjetan duen arrain fresko eta izoztuaren prezioen indizearekin (API) eta Estatistika Institutu Nazionalak (EIN) argitaratutako kontsumoko prezioen indizearekin (KPI) konparaketa egin da. Irakur itzazue analisiaren ondorioak.
———————————————————————–
Asteon zientzia begi-bistan igandeetako atala da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna erreparatuz, Interneteko “zientzia” antzeman, jaso eta laburbiltzea da gure helburua.
———————————————————————–
Egileaz: Uxue Razkin Deiako kazetaria da.
———————————————————————–
The post Asteon zientzia begi-bistan #187 appeared first on Zientzia Kaiera.
Naukas Bilbao 2017 – María José Calderón y Belén Valenzuela: Esta física es la leche
En #Naukas17 nadie tuvo que hacer cola desde el día anterior para poder conseguir asiento. Ni nadie se quedó fuera… 2017 fue el año de la mudanza al gran Auditorium del Palacio Euskalduna, con más de 2000 plazas. Los días 15 y 16 de septiembre la gente lo llenó para un maratón de ciencia y humor.

Hay muchas ramas de la ciencia que son interesantísimas, pero pocas pueden aspirar al título de ser la leche como la física de la materia condensada. Calderón y Valenzuela, investigadoras del Instituto de Ciencias de Materiales de Madrid-CSIC, lo explican.
María José Calderón y Belén Valenzuela: Esta física es la lecheEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2017 – María José Calderón y Belén Valenzuela: Esta física es la leche se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – Francisco R. Villatoro: El espín para irreductibles
- Naukas Bilbao 2017 – Teresa Valdés-Solís: Limpia, fija y da esplendor
- Naukas Bilbao 2017 – Guillermo Peris: Los trapecistas del genoma
Ezjakintasunaren kartografia #200
Zazpi bizitza dituzte katuek. Eterrak, baina, zazpi aldiz zazpi ditu. Jaume Navarrok azaltzen dizkigu honen inguruko hainbat kontu Æther and Modernity. The recalcitrance of an agonising epistemic object artikuluan.
Giza entzefalo heldua neurona berriak sortzeko gai ez dela uste zen duela zenbait urte. Orain badakigu ez dela hala. Ez hori bakarrik, zenbait kontuk, ariketa fisikoak adibidez, prozesua faboratzen dutela dakigu. JR Alonso Adult neurogenesis and physical activity artikuluan.
Egoera solidoko fisikak oso hizkuntza partikularra du, serie B pelikuletako pertsonai maltzurren izenak dituzten partikulei lotutakoa. Pasa den astean DIPCk fonoia bazekarren, oraingoan polaritoia aurkezten digu: What on earth is a polariton?
–—–
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #200 appeared first on Zientzia Kaiera.
Física de partículas en un simulador cuántico
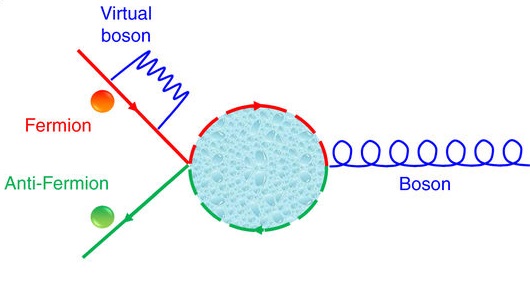
En 2012 el Grupo QUTIS de la UPV/EHU publicó en Physical Review Letters una novedosa propuesta teórica para reproducir colisiones de partículas como las de los grandes aceleradores sin necesidad de utilizar esas impresionantes infraestructuras. Ahora, con la colaboración del laboratorio de del profesor Kihwan Kim de la Universidad de Tsinghua, en Pekín (China), han confirmado la validez de la propuesta en un simulador cuántico de iones atrapados.
En los grandes laboratorios de física de partículas del mundo disponen de imponentes aceleradores de hasta, como es el caso del CERN, 27 kilómetros de circunferencia. En esos aceleradores se llevan a cabo costosísimos experimentos para estudiar la creación y aniquilación de la materia. ¿Sería posible simular esas colisiones en pequeños experimentos encima de la mesa? El Grupo QUTIS que dirige en la UPV/EHU el profesor Ikerbasque Enrique Solano planteó en 2011 una propuesta teórica que siete años después han podido verificar en el laboratorio de iones atrapados del profesor Kihwan Kim, de la Universidad de Tsinghua.
“Pusimos en marcha un teatro cuántico, en el que las partículas se comportan como actores en un simulador cuántico, es decir, unas imitan a otras para diversos fines”, explica el profesor Enrique Solano. Tuvo un aspecto lúdico, pero también muy práctico, ya que estos experimentos conllevarían en un futuro un ahorro de dinero y serían, además, pruebas controladas imposibles de calcular en los ordenadores convencionales. “Hemos conseguido imitar cómo la materia (representada por fermiones, uno de los dos tipos de partículas elementales que existen en la naturaleza) y la antimateria (antifermiones) se crea y se destruye, usando láseres, átomos cargados (iones) y trampas atómicas. Es decir, hemos simulado una física muy similar a la de los grandes aceleradores en un simulador cuántico de iones atrapados”, añade el director del grupo QUTIS.
Referencias:
Casanova, J., Mezzacapo, A., Lamata, L. & Solano, E. Quantum simulation of interacting Fermion lattice models in trapped ions. Phys. Rev. Lett. 108, 190502 (2012)
Xiang Zhang, Kuan Zhang, Yangchao Shen, Shuaining Zhang, Jing-Ning Zhang, Man-Hong Yung, Jorge Casanova, Julen S. Pedernales, Lucas Lamata, Enrique Solano & Kihwan Kim (2018) Experimental quantum simulation of fermion-antifermion scattering via boson exchange in a trapped ion. Nature Communications 9, 195 DOI: 10.1038/s41467-017-02507-y
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Física de partículas en un simulador cuántico se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un simulador cuántico de fenómenos imposibles
- Un observador cuántico de lo más útil
- De los secretos del Universo a la vida cotidiana: aceleradores de partículas.
La nueva forma de enfriar que lo cambiará todo

Los sistemas de refrigeración no solo sirven para tomar las bebidas bien frescas, sino que nos permiten conservar alimentos, transportar medicamentos y vacunas, y vivir cómodamente en ambientes cálidos gracias al aire acondicionado. La refrigeración es fundamental para nuestra salud y bienestar. A lo largo de la historia hemos utilizado diferentes sustancias y métodos para tal fin. Desde el agua, el amoníaco, el dióxido de carbono, los CFCs (clorofluorocarbonados) hasta los modernos HFCs (hidrogenofluorocarbonados). Todos ellos, en mayor o menor medida, producen diferentes efectos negativos en el medioambiente. El principal problema es que los refrigerantes son fluidos (gases o líquidos) que se fugan a la atmósfera, contribuyendo al calentamiento global y a la destrucción de la capa de ozono. Por ello la mayoría se han prohibido y los más modernos ya tienen fecha de caducidad. Ha llegado la hora de implicarse a fondo y apostar por alternativas ecológicas. En la Universidad de A Coruña han encontrado un material revolucionario que lo cambiará todo. Lo han llamado perovskiña.
- Por qué usamos fluidos para refrigerar
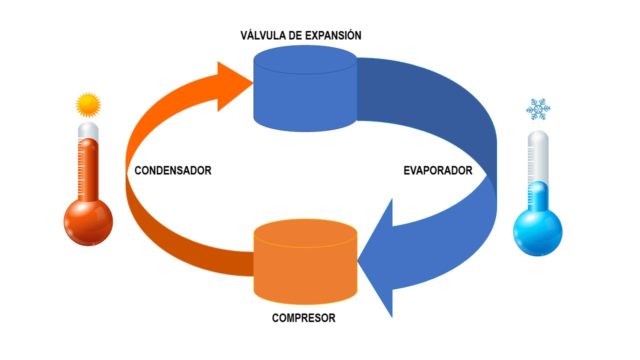
Los fluidos resultan interesantes para refrigerar por la sencilla razón de que los podemos comprimir con facilidad. Su funcionamiento es bastante intuitivo. Cuando comprimimos un fluido (le aplicamos presión) éste se calienta. Cuando lo expandimos se enfría (o absorbe calor, que viene a ser lo mismo). Así es cómo funciona el sistema de refrigeración de nuestra nevera, por expansión y compresión de un fluido.
- Cómo afectan al medioambiente los fluidos refrigerantes
En los años 80 descubrimos que los CFCs (también denominados freones) estaban destruyendo la capa de ozono. El mecanismo a través del cual atacan la capa de ozono es una reacción fotoquímica: al incidir la luz sobre la molécula de CFC, se libera un radical de cloro, muy reactivo y con gran afinidad por el ozono, hasta tal punto que rompe la molécula de ozono e inicia una reacción en cadena altamente destructiva.
El ozono es fundamental para la supervivencia. Protege la vida en el planeta mediante la absorción de la radiación ultravioleta, potencialmente cancerígena, que afecta a nuestro sistema inmunológico y daña la vida de las plantas.
Después de varios años de negociaciones, se llevó a cabo un acuerdo internacional en 1987 en la ciudad de Montreal, Canadá, que se conoce como el Protocolo de Montreal. Este protocolo es un esfuerzo unido de gobiernos, científicos, industrias y grupos ecologistas coordinados por la UNEP (Programa Ambiental de las Naciones Unidas). Este acuerdo consistió en regular la producción y uso de los CFCs hasta su desaparición gradual. En la Unión Europea se prohibieron totalmente en 1996.
La aplicación del Protocolo de Montreal ya ha dado sus frutos. Investigadores de la NASA demostraron a principios de 2018 que la disminución de CFCs ha provocado la reducción en un 20% del agujero de la capa de ozono.
El impacto medioambiental de los fluidos refrigerantes también se mide a partir de su potencial de calentamiento global, es decir, cuánto calor pueden atrapar en comparación con un compuesto de referencia y cómo esto afecta al calentamiento global. El dióxido de carbono es el gas de referencia, al que se le asigna un potencial de calentamiento global de 1.
Los CFCs y HFCs tienen un potencial de calentamiento global entre 1.000 y 15.000 veces mayor que el del CO2. Una vez prohibidos los CFCs, su sustituto inmediato fueron los HFCs, compuestos análogos que carecen de cloro y, por tanto, sin capacidad de destruir la capa de ozono. Sin embargo, el HFC que más se utiliza en la actualidad tiene un potencial de calentamiento global de unos 1.400, que sigue siendo muy elevado.
El conocimiento de los potenciales de calentamiento global nos llevó en 2014 a aprobar una normativa europea a partir de la cual el uso de los HFCs también se tendrá que minimizar. Antes del 2020, todos aquellos fluidos con un potencial mayor de 2.500, estarán prohibidos. En 2022, estarán prohibidos los que tengan un potencial superior a 150.
Esta normativa ha puesto en jaque a la industria de la refrigeración. Algunos han previsto volver a usar refrigerantes anticuados, como el amoníaco, el isobutano, el propano, o el mismo CO2. La razón es que tienen potenciales de calentamiento global muy bajos. El problema de volver a ellos es el mismo que nos hizo decidir prescindir de ellos en su momento: son tóxicos y/o inflamables. Producen un menor impacto medioambiental, sin embargo comprometen la seguridad de nuestros hogares.
- El problema de los fluidos refrigerantes es que son fluidos, ¿y si usamos sólidos?
Los problemas medioambientales y de seguridad de los refrigerantes que hemos utilizado hasta ahora radica en que son fluidos, es decir, se fugan. Por ese motivo desde hace poco tiempo hemos empezado a investigar la posibilidad de utilizar sólidos. Eso sí, han de ser sólidos que se puedan comprimir con facilidad, aplicando una presión baja. Las neveras actuales funcionan con presiones de hasta 50-70 bar, así que lo ideal sería usar refrigerantes sólidos eficientes en ese rango de presiones. El mecanismo por el que se enfrían y calientan los sólidos es el mismo por el que lo hacen los fluidos, por ciclos de compresión y expansión (procesos barocalóricos), o también por ciclos de tensión y relajación (procesos elastocalóricos).
Al deformar un sólido elastocalórico, por ejemplo estirándolo, sus componentes se alinean en la dirección de la fuerza aplicada, aumentando de esta manera el grado de ordenación interna (lo que conocemos como entropía), de forma que el sólido se calienta. Una vez que el sólido recupera su temperatura inicial, si dejamos de estirarlo, se enfriará notablemente. En ese momento podemos usarlo para enfriar otro objeto. Este fenómeno de calentamiento-enfriamiento de un sólido lo podemos observar con una goma elástica (ver vídeo). Cuando la estiramos, ésta se calienta. Lo podemos comprobar acercándola a los labios. Una vez recupere la temperatura ambiente, dejamos de estirar la goma. Cuando recupera su forma inicial, comprobaremos sobre nuestros labios que se enfría. Esto se ve claramente utilizando una cámara de infrarrojos.
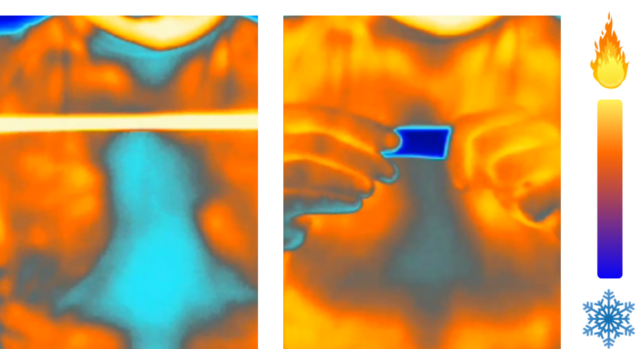
Sólido elastocalórico cuando se calienta al estirarlo (izquierda), y cuando se enfría al eliminar esa fuerza de deformación (derecha).
En junio de 2017, un equipo de investigadores de la Universidad de A Coruña publicaba en Nature un gran hallazgo. Un nuevo material sólido respondía a la aplicación de bajas presiones enfriándose con facilidad. Con solo 70 bar, presión que pueden alcanzar las neveras actuales, muestra una capacidad de refrigeración sobresaliente.
Este hallazgo fue fruto de la tesis doctoral de Juan Manuel Bermúdez-García. El equipo multidisciplinar con el que trabaja, formado por María Antonia Señarís, Manuel Sánchez, Socorro Castro, Jorge José López y Ramón Pedro Artiaga, integra a químicos e ingenieros de la UDC procedentes del Centro de Investigaciones Científicas Avanzadas (CICA) y de los Departamentos de Química y de Ingeniería Naval e Industrial. El pasado 24 de enero de 2018 fueron galardonados con el Premio de Investigación Ernesto Viéitez, concedido por la Real Academia Galega de Ciencias.

Premios de la Real Academia Galega de Ciencias. 24 de enero de 2018, Santiago de Compostela.
Se trata de un sólido híbrido, con una parte inorgánica (metales como hierro, níquel o manganeso) y otra orgánica (basada en carbono, nitrógeno e hidrógeno), dispuestos en una estructura tridimensional denominada perovskita y a la que debe el nombre que han decidido ponerle: perovskiña, en honor a su origen galego.
La perovskiña es fácil de sintetizar, sus componentes son económicos, ninguno es tóxico, y además es ligero y compacto, lo que implica que podremos fabricar neveras que también sean ligeras. La parte orgánica del sólido es la que le confiere flexibilidad a la estructura y por tanto es la responsable que de que sea fácilmente comprimible.
La investigación en perovskitas iba dirigida a encontrar mejores materiales para celdas solares, capaces de transformar eficientemente la energía solar en energía eléctrica. Afortunadamente, algunas de estas perovskitas resultaron ser comprimibles y útiles para refrigerar (tienen propiedades barocalóricas). En vista de los magníficos resultados, a estos investigadores les han concedido un proyecto de investigación de cuatro años. En ese tiempo cuentan con optimizar las propiedades de la perovskiña, perfeccionar su síntesis y adaptarla a los sistemas de refrigeración actuales.
Hay que tener en cuenta que sólo quedan cuatro años para que los refrigerantes actuales se prohíban, y las subvenciones para que las industrias de la refrigeración se adapten a la normativa son escasas y tardías. El futuro próximo de la industria de la refrigeración sufrirá un cambio espectacular. Y ese cambio pasará por incluir refrigerantes sólidos. Con toda probabilidad, en cuatro años nuestras neveras contendrán perovskiña, el material híbrido que lo cambiará todo.
Este post ha sido realizado por Deborah García Bello (@Deborahciencia) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
Nota de la autora: Agradezco a Juan Manuel Bermúdez-García y Socorro Castro de la Universidad de A Coruña la ayuda que me han brindado para escribir este artículo.
El artículo La nueva forma de enfriar que lo cambiará todo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Cambiará algún día la imagen del científico?
- La forma de las hojas
- Abonar el mar para enfriar el planeta
Javier Aizpurua: “Mikroskopia azken mugara eramatea posible da nanofotonikari esker” #Zientzialari (87)
Nanofotonika materia eta argiaren arteko elkarrekintza ikertzen duen zientziaren arlo bat da. Besteak beste, argia nanoegituren kontra jotzean sortzen dituen interakzioak eta eraginak aztertzeaz arduratzen da nanofotonika.
Argia, uhina den heinean, ezin da bere uhin-luzera baino neurri txikiagoetan lokalizatu eta manipulatu. Hala ere, CFM eta DIPC ikerketa zentroetan metalezko nanoegiturak osatuz eta diseinatuz argia eskala nanometrikoan lokalizatzea eta manipulatzea lortu dute. Azken urte hauetan, metalezko nanoegitura hauei esker, nanoantenak deritzonak, argia nanoeskalara eraman dute ikertzaileek.
Baina, zeintzuk dira nanofotonikaren erabilera zehatzak? Nola osatzen dira nanofotonikan erabiltzen diren nanoegiturak? Honen inguruan hitz egiteko CFM eta DIPC zentroetako nanofotonika taldeetako arduraduna den Javier Aizpuruarekin izan gara. Bere esanetan, nanofotonikaren erabilerak mota askotakoak dira. Medikuntzan, adibidez, nanopartikulek argia lokalizatzean posible dute berotzea eta bero horrekin inguruneko tumore-zelulak akabatzea.
‘Zientzialari’ izeneko atal honen bitartez zientziaren oinarrizko kontzeptuak azaldu nahi ditugu euskal ikertzaileen laguntzarekin.
The post Javier Aizpurua: “Mikroskopia azken mugara eramatea posible da nanofotonikari esker” #Zientzialari (87) appeared first on Zientzia Kaiera.
La pubertad está comenzando antes para muchos niños; la educación sexual debería afrontar esta realidad
Celia Roberts
![]()
 

Noñas de tan solo seis o siete años comienzan a mostrar los primeros signos de la pubertad. Imagen: Shutterstock
El gobierno británico está haciendo una consulta sobre un nuevo plan de estudios para la educación sexual y en relaciones [1] en los colegios ingleses. Este cambio brinda una ocasión oportuna para actualizar cómo, cuándo y qué se enseña a los niños sobre la pubertad.
Sorprendentemente, las orientaciones del Departamento de Educación (DdE) [2] sobre la educación sexual no han cambiado en casi dos décadas. Pero tras la presión concertada, la investigación y las recomendaciones de múltiples comités de miembros del parlamento, en 2017, la Ley de niños y trabajo social finalmente reconoció la necesidad de proporcionar “educación sexual para el siglo XXI”.
Se publicarán nuevas directrices legales para los colegios tras la consulta pública, que se cierra a mediados de febrero. A partir de 2019, los colegios de secundaria estarán obligados a ofrecer educación sexual y en relaciones, y los de primaria ofrecerán educación en relaciones. Los padres mantendrán el derecho a decidir que sus hijos no reciban educación sexual, aparte de la que se trata en el plan de estudios de ciencias, pero no se les permitirá que decidan sobre la educación en relaciones.
Estos cambios se basan en la preocupación generalizada por los efectos negativos que las tecnologías digitales tienen en la vida sexual de los jóvenes, en particular el “sexting”[3], el abuso y la explotación sexual infantil y los “extraños en línea”. El nuevo plan de estudios, al parecer, enseñará a los niños y jóvenes cómo son las relaciones sanas en el tenso contexto de teléfonos inteligentes, porno online e Instagram.
La nueva pubertad
Pero el nuevo plan de estudios también debería tener en cuenta lo que está sucediendo en los cuerpos de los jóvenes en el siglo XXI. No solo los niños parecen crecer mucho más rápido hoy, muchos de ellos en realidad están comenzando a desarrollarse físicamente antes que nunca.
Según con muchos científicos y médicos, estamos viviendo en la era de la “nueva pubertad” en la que un número creciente de niñas comienza a desarrollarse sexualmente a la edad de siete u ocho años. En la década de los sesenta, solo el 1% de las chicas entraban en la pubertad antes de cumplir los nueve años. En la actualidad, hasta el 40% de algunas poblaciones tanto en países ricos y como pobres lo están haciendo.
El desarrollo sexual también se está ampliando en el tiempo, y a muchas niñas comienzan a crecerles los senos y el vello púbico dos o tres años antes de que tengan su primera mentruación. Si bien hay menos pruebas de que el desarrollo de los niños esté cambiando tan rápidamente, algunos estudios también indican que una entrada más temprana en las etapas iniciales de la pubertad se está haciendo cada vez más común.
Las causas de estos cambios siguen sin estar claras. Muchos científicos apuntan al aumento simultáneo de la obesidad infantil, mientras que otros estudian los efectos de los compuestos químicos ambientales, como el Bisfenol A o BPA (que se encuentra en algunos plásticos), en el cuerpo. Otra investigación ha explorado los efectos de los factores sociales, incluidas las estructuras familiares, las experiencias traumáticas en la primera infancia y las desventajas socioeconómicas. Esta variedad de explicaciones evidencia lo complejo que es el fenómeno de la pubertad.
La guía del DdE en vigor establece que:
Todos los niños, incluidos aquellos que se desarrollan antes que el promedio, necesitan saber sobre la pubertad antes de experimentar la aparición de cambios físicos.
Pero deja que los colegios decidan, en consulta con los padres, “la edad apropiada” para hablar a los niños sobre la pubertad. En 2017, la Asociación de Educación Personal, Social y de la Salud [4] argumentó que esto debería ocurrir cuando tengan siete años. Pero hablar con niños de siete años sobre los senos, el vello púbico, el olor corporal y los cambios genitales puede no ser fácil para muchos maestros o para muchos padres. Tener siete años se supone que es una época de libertad, juego e inocencia.

Preparándose para la pubertad. Imagen: Shutterstock
Actualización de la educación sexual
Los niños que se desarrollan pronto presentan un desafío tanto para el pensamiento cultural sobre el sexo como para la política de educación sexual. Si bien muchos padres y jóvenes desean una educación sexual actualizada, esto generalmente viene con la condición de que dicha educación sea “apropiada para su edad”. Aunque es muy importante, esta frase es dolorosamente vaga, y no está claro si se refiere a la edad cronológica, la edad emocional o la etapa de desarrollo físico.
Hoy en día, algunas niñas de siete años pueden ser emocionalmente jóvenes, pero también les comienzan a crecer los senos y el vello púbico. Otros que se han desarrollado pronto porque han experimentado estrés en la primera etapa de la vida, por abandono o abuso, pueden sentirse más maduros que sus iguales y estar listos antes para aprender sobre la pubertad y la sexualidad. La creciente brecha en el momento del desarrollo sexual de niños y niñas también plantea un desafío. Enseñar a las niñas por separado o antes que a los niños, la estrategia en la escuela primaria de mi propio hijo, corre el riesgo de reforzar nocivas normas de género yfomentar el secretismo en torno a cuestiones como la menstruación.
En cambio, tal vez podríamos tratar de desenredar la pubertad de la sexualidad adolescente y desarrollar relatos de la pubertad que no la enmarquen como el comienzo de la adolescencia. Una niña de siete años con senos no se está “convirtiendo en mujer”, y una niña de nueve años que está menstruando probablemente no va a querer tener relaciones sexuales pronto.
En última instancia, esto significa ir más allá de las representaciones tradicionales de los cuerpos femeninos que se centran en la capacidad reproductiva con la idea de explorar significados y experiencias más amplias de lo que es ser una chica. Crecer también se trata de nuevos horizontes, como la fuerza, la salud e incluso el placer. La educación sexual y en relaciones incluso podría incluir la pubertad como algo que debe esperarse, notarse e incluso celebrarse, y no como un riesgo más.
Notas del traductor:
[1] Clases que el currículo británico hace obligatorias desde el 2000 bajo la denominación PSHE education y que incluye temas de salud y bienestar (higiene personal, alcohol y drogas, sexo), relaciones (entre iguales, con los adultos, con la familia) y vivir en el mundo (economía personal, mundo del trabajo).
[2] El Deparment of Education es el equivalente al Ministerio de Educación español.
[3] “Sexting” es un anglicismo para referirise al envío de contenidos eróticos o pornográficos por medio de teléfonos móviles u otros dispositivos conectados a Internet.
[4] Esta asociación agrupa a profesores y profesionales que imparten las clases de PSHE education (véase nota [1])
Sobre la autora:
Celia Roberts es catedrática de estudios de ciencia y género y codirectora del departamento de sociología de la Universidad de Lancaster (Reino Unido)
Texto traducido y adaptado por César Tomé López a partir del original publicado por The Conversation el 18 de enero de 2018 bajo una licencia Creative Commons (CC BY-ND 4.0)![]()
El artículo La pubertad está comenzando antes para muchos niños; la educación sexual debería afrontar esta realidad se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Realidad conexa, porque todo está conectado.
- Por qué la filosofía es tan importante para la educación científica
- De cómo la ludificación del aula prepara a los niños para vivir en un estado policial
Arrantza prezioen bilakaera: merkaturatze-katearen analisia

Jatorrizko arrantza prezioen indizea 2002-2014 denboraldian harrapatutako 136 espezietatik, 36 espezietarako datuen bitartez eraiki da, izan ere, 36 horiek harrapaketa guztien eta zenbateko osoaren %90 baino gehiago dira. Ondoren, jatorria Galiziako lonjetan duen arrain fresko eta izoztuaren prezioen indizearekin (API) eta Estatistika Institutu Nazionalak (EIN) argitaratutako kontsumoko prezioen indizearekin (KPI) konparaketa egin da.
Aztertutako aldia 2002 eta 2014 artekoa da eta, batez ere, 2008 baino lehenagoko urteetan eta krisiaren osteko aldian indize horiek izandako jokabidea hartu da kontuan. Izan ere, lortutako emaitzek, arrainaren merkatu horretako maila guztietan, eskaintzaren eta eskariaren jokaeren arteko bereizte argia egiteko bidea eman dute 2008ko krisia piztu aurreko urteetan eta beraren ondorengo aldian 2014ra arte.
Krisiaren aurreko analisiaren lehenengo fasean, 2002 eta 2008 artean, ikus daiteke ekonomia multzorako kontsumoko prezioen indizea txikiagoa izaten ari zela eta azkeneko kontsumoari zegokion arrantza produktuen prezioen indizearen azpitik zegoela. Hori dela eta, ulertu behar da arrantza produktuen eskaria aski handia zela APIa KPI orokorraren gainetik manten zedin.
Halaber, nabarmen daiteke arrain eskariak balio erantsiaren funtsezko zati bat eskuratzeko aukera eman diola merkaturatze-kateari. Baina 2008az geroztik, erabateko aldaketa gertatu da eta kontrako joera dago. Kontsumo orokorreko prezioen indizearen eta beste bi arrantza adierazleen arteko arraila nabarmena jazo da. Krisiaren aurreko aldian ez bezala, non arrain eskariak kontsumo orokorreko prezioen indizearen gainetik arrainaren prezioen adierazleari eutsi zion, KPIak arrantza produktuen kontsumoko prezioen indizeari, analisiak 2008az geroztik hartzen duen denbora guztian zehar atzean geratzen denari, aldea atera dio.
Hortaz, 2008 eta 2014 bitartean, arrainaren azkeneko kontsumoarekin lotutako prezioen indizea (API) sistematikoki KPIaren azpitik kokatu da, baita ez-ohiko distantzian ere, krisiaren aurreko denboraldian nagusia zen ereduarekin erkatzen bada. Beraz, beste mota bateko elikagaiek arraina ordeztu egin dutela ondoriozta daiteke. Ildo berean, analizatutako denboraldi osoan zehar, lehenengo salmentako prezioen indizea (JPI) parte hartzea galduz joan da beste indizeei dagokienez.
Modu honetan, KPIaren eta JPIaren artean gero eta handiagoa den aldeak erakutsi du arrantzaleek, beren inputak erosteko, ordaintzen dituzten prezioak gora egiten ari direla eta beraien jardueraren prezioak, aldiz, behera; horren ondorioz, arrantzaleen erosteko ahalmena jaitsi da. Hortaz, krisiak merkatu horretako esku-hartzaileen posizio erlatiboak aldatu ditu eta, ondorioz, guztiek okerrera egin dute krisia hasi baino lehenagoko aldiaren aldean. Emaitza horiek hainbat politika-estrategia iradoki dituzte; bereziki ekoizleen eta merkatarien arteko itun estrategikoak eratzea, arrantzaleek eta erauzketa-sektoreak truke desorekatu baten ondorioak saihestu ditzaten, azken finean, arrantza-sektoreko oinarri dira eta.
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: Ekaia 30
- Artikuluaren izena: Arrantza prezioen bilakaera: merkaturatze-katearen analisia.
- Laburpena: Lan honen helburu nagusia banaketa-katean zehar arrantza prezioen integrazio bertikala aztertzea da eta horretarako agregazio-ikuspegi bat du oinarri. Ikuspegi hori jatorriko arrantza prezioen agregazio-indize sintetiko bat (JPI) eraikitzean oinarritua dago eta ondoren arrantza prezioen indizearekin (API) eta Estatistika Institutu Nazionaleko (EIN) kontsumoko prezioen indizearekin (KPI) konparaketa egingo da.
- Egileak: Eneko Martin, Ikerne del Valle eta Kepa Astorkiza
- Argitaletxea: UPV/EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- Orrialdeak: 7-18
- DOI: 10.1387/ekaia.16316
—————————————————–
Egileez:
Eneko Martin, Ikerne del Valle eta Kepa Astorkiza UPV/EHUko Ekonomia Aplikatua V Sailekoak (Ekonomia eta Enpresa Fakultatea) dira.
—————————————————–
Ekaia aldizkariarekin lankidetzan egindako atala.

The post Arrantza prezioen bilakaera: merkaturatze-katearen analisia appeared first on Zientzia Kaiera.
En The Big Bang Theory no hay químicos, sin embargo…

En la serie The Big Bang Theory hay físicos, biólogos, ingenieros… pero no hay ningún personaje protagonista que sea químico. Sheldon Cooper es físico teórico, Leonard Hofstadter es físico experimental, Raj Ramayan Koothrappali es astrofísico, Howard Wolowitz es ingeniero mecánico, Bernardette Rostenkowski es microbióloga, Amy Farrah Fowler es neurobióloga y Penny es una aspirante a actriz que, siendo la única protagonista sin formación científica, acaba trabajando como visitadora médica.
En el último capítulo emitido, el episodio 13 de la temporada 11, Leonard y Amy juegan en casa a reproducir algunos de los experimentos que hicieron en sus años de colegio. El primero de ellos es un experimento de química. Ninguno de los dos es químico, sin embargo, deciden hacer un experimento de química para obtener «hielo caliente».
-We’re making «hot ice».
-It’s very cool!
El «hielo caliente»no es realmente hielo, es decir, no se trata de agua sólida a una temperatura diferente a los cero grados Celsius, sino que se trata de otro sólido que, a simple vista, se parece mucho al hielo.
Lo sorprendente de este experimento es que, al introducir la mano u otro objeto en un vaso que parece contener agua, éste se recubre instantáneamente con algo similar a cristales hielo. Es muy bonito y aparente, por eso es un experimento al que se recurre con frecuencia en las clases de química del instituto.

No son cristales de hielo, sino que son cristales de acetato de sodio. Podemos comprar el acetato de sodio, en cambio, también podemos sintetizarlo en casa con dos sustancias que habitualmente todos tenemos en nuestra cocina: vinagre blanco, el mismo que usamos para las ensaladas, y bicarbonato, lo que utilizamos para que los bizcochos luzcan esponjosos —y para un montón de cosas más—.
El vinagre es una disolución de ácido acético en agua. El bicarbonato es una sal, el hidrogenocarbonato de sodio. Si echamos un par de cucharadas de bicarbonato sobre medio litro de vinagre estaremos dando el primer paso para producir acetato de sodio. Lo que observaremos es una reacción química muy efervescente. Se forman cientos de pequeñísimas burbujas, como cuando agitamos enérgicamente una bebida gaseosa. Lo que está ocurriendo es que los átomos de ambos compuestos se reordenan para dar lugar a nuevos compuestos más estables. Esta es la definición de reacción química. En este caso forman acetato de sodio, agua y dióxido de carbono. El dióxido de carbono es el gas que observamos como burbujas.
 Lo que nos interesa para hacer «hielo caliente» es el acetato de sodio. Tenemos que reducir la cantidad de agua y de dióxido de carbono producidos y forzar a que todo el ácido acético reaccione efectivamente con el bicarbonato. El dióxido de carbono es el menor de nuestros problemas, ya que el ser un gas, se escapa por sí solo. Para el resto, lo más efectivo es calentar la mezcla hasta que hierva. Al hervirla estamos evaporando gran parte del agua que se produjo, de modo que, por un lado, forzamos a que todo reaccione y, por otro lado, cuanta menos agua más saturada estará la disolución de acetato resultante.
Lo que nos interesa para hacer «hielo caliente» es el acetato de sodio. Tenemos que reducir la cantidad de agua y de dióxido de carbono producidos y forzar a que todo el ácido acético reaccione efectivamente con el bicarbonato. El dióxido de carbono es el menor de nuestros problemas, ya que el ser un gas, se escapa por sí solo. Para el resto, lo más efectivo es calentar la mezcla hasta que hierva. Al hervirla estamos evaporando gran parte del agua que se produjo, de modo que, por un lado, forzamos a que todo reaccione y, por otro lado, cuanta menos agua más saturada estará la disolución de acetato resultante.
Si lo dejamos hervir el tiempo suficiente, veremos cómo se empieza a formar una película superficial. Esto nos indica que la disolución está suficientemente concentrada (estará sobresaturada), así que la apartamos del fuego y la dejamos enfriar. Una vez fría, la dejamos refrigerar media hora en la nevera.
Si a continuación introducimos cualquier objeto o nuestra mano en esa disolución, ¡sorpresa!, empezarán a crecer cristales a su alrededor inmediatamente. Esto es lo que hacen Leonard y Amy, introducir una varilla metálica en la disolución. Ésta se empieza a cubrir de cristales. En la serie hacen un primer plano del suceso, así que en este capítulo se observa muy bien la cristalización.

Lo que está ocurriendo es que el acetato de sodio está sobreenfriado. Se mantiene en estado líquido aunque esté por debajo de su temperatura de fusión (54oC). Este estado es inestable, por lo que cualquier perturbación —como introducir un objeto— desencadena que las moléculas de acetato comiencen a organizarse formando cristales, que es su estado estable a temperatura ambiente. Al ser un proceso tan favorable, sucede desprendiendo calor. A esto se le denomina proceso exotérmico. Es decir, la disolución se calienta a medida que se produce la cristalización. Por eso al meter la mano no solo sentimos cómo se forman cristales, sino que también sentiremos cómo estos se calientan, de ahí el nombre de «hielo caliente».
Por el momento no hay químicos en la serie The Big Bang Theory, como tampoco están representados científicos de otras muchas áreas de la ciencia. Sin embargo, han sido el físico experimental y la neurobióloga los que se han puesto a jugar a las cocinitas y a darle un poco a esa maravillosa ciencia llamada química.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo En The Big Bang Theory no hay químicos, sin embargo… se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Animalien beste zenbait pozoi
 Juan Ignacio Pérez eta Miren Bego Urrutia Defentsak eta erasoak
Juan Ignacio Pérez eta Miren Bego Urrutia Defentsak eta erasoak ———————————————————————————————————–
Eboluzioan zehar hainbat animalia-taldek askotariko estrategiak garatu dituzte, bai elikagaiak izango dituztela bermatzeko, bai etsaietatik babesteko. Estrategia horien artean animaliek ekoizten dituzten toxinak daude. Pozoiak erabiltzen dituzten animaliak talde askotakoak dira: ekinodermoak, zelenteratuak, anelidoak, moluskuak, artropodoak, arrainak, narrastiak, anfibioak… eta horietako batzuek oso egitura eta mekanismo sofistikatuak erabiltzen dituzte pozoia txertatzeko.
Sinapsietan gertatzen den neurotransmisore-askapenean eragiten duten toxinak eta toxina horien ekintzen ondorioak ikusi ditugu aurreko atal batean. Baina badago beste toxina-talde bat neurotransmisorearen askatze-prozesuan eraginik ez izan arren hurrengo prozesua zapuzten duena.
Toxina horien artean dugu, esaterako, α-bungarotoxina. Bungarus multicinctus krait sugegorri marradunaren pozoia osatzen duten peptidoetariko bat da toxina hori. α-bungarotoxina modu itzulezinean lotzen zaio azetilkolinaren hartzaile mota bati (hartzaile nikotinikoei), eta, horren ondorioz, azetilkolinak ezin ditu kanalak ireki. Sugegorriak, koska egitean eta pozoia txertatzean, toxinak daukan eragin horri esker paralizatzen ditu harrapakinak. Eragin bera dute kobra sugearen α-neurotoxina peptidoak eta itsas sugegorriaren erabutoxina peptidoak.

1. irudia: ‘Bungarus multicinctus’ krait sugegorri marradunaren pozoia osatzen duten peptidoetariko bat da α-bungarotoxina, azetilkolinaren hartzaile nikotinikoei modu itzulezinean lotu eta, ondorioz, azetilkolinak ezin ditu kanalak ireki.
Harrigarria gerta badakiguke ere, oso antzekoa da Hego Amerikako zenbait indiok erabiltzen duten prozedura. Amazoniako tribu batzuetan kurarea erabiltzen dute gezi-puntak bustitzeko; kurareak lehen aurkeztutako toxinen eragin bera du. Egia da kurareak ez daukala animalietan jatorria, Chondrodendron tomentosum landarearen toxinen nahastea den aldetik, baina horrek ez ditu kontuak gehiegi aldatzen: animalia bat (gizakia) dugu landare jatorriko pozoi bat (kurarea) erabiltzen harrapakina errazago ehizatzeko. Azken batean, Amazoniako indioek naturak eskainitako produktu bat baliatzen dute animalia pozoitsuek bezala jokatu ahal izateko.
Kontu honi dagokionez, ez dira salbuespen itsasoko ornogabeak. Hor dugu esaterako itsasoko barraskilo konikoen pozoia, konotoxinaz osatuta dagoena. Hainbat peptidoren nahastea da konotoxina (batzuk kanalak blokeatzen dituztenak) eta horien artean azetilkolinaren hartzaileak blokeatzen dituztenak ere aurkitu daitezke. Sinapsi neuromuskularraren kasuan uzkurketa inhibitzen da blokeatze horren ondorioz. Hau da, harrapakinaren nerbio-sistemak giharrei mugitzeko agindua eman arren, hauek ezin dute erantzun, agindua atariraino baino ez baita iristen. Egoera horretan harrapariarengandik ihes egiteko aukerak oso urriak dira, eta barraskiloak erraz asko irentsi dezake ehizakia.
Clostridium generoko bakterioek ekoitzitako toxinak aurkeztu ditugunean, toxina botulinikoak medikuntzan eta estetikan duen erabilera ikusi dugu. Hemen aipatutako pozoi batzuk ere zenbait gaixotasuni aurre egiteko erabiltzen dira edo erabili ote daitezkeen ikertzen da. Kurarea, esaterako, erlaxatzaile muskular modura erabili izan da. Itsas jatorriko konotoxinak ere ikertzen hasi dira; morfina bera baino askoz eraginkorragoa da, eta opiazeoa ez izaki adikziorik eragiten ez duenez, dagoeneko konotoxinak dituen farmakoren bat atera da merkatura min muskularrak arintzeko. Beraz, pozoiak berak ere, neurri egokian eta ongi erabilita, onuragarri!
—————————————————–
Egileez: Juan Ignacio Pérez Iglesias (@Uhandrea) eta Miren Bego Urrutia Biologian doktoreak dira eta UPV/EHUko Animalien Fisiologiako irakasleak.
—————————————————–
Artikulua UPV/EHUren ZIO (Zientzia irakurle ororentzat) bildumako Animalien aferak liburutik jaso du.
The post Animalien beste zenbait pozoi appeared first on Zientzia Kaiera.
La atmósfera de CoRoT-2b lleva la contraria

Concepción artística del gigante gaseoso CoRoT-2b, con un punto caliente hacia el oeste, orbitando su estrella. Fuente: NASA/JPL-Caltech/T. Pyle (IPAC)
Los escritores de ciencia ficción y algunos científicos especulan con cómo podían ser algunas cosas en el universo a partir de una muestra muy limitada de objetos conocidos de nuestro entorno. Un ejemplo típico de esas cosas es la vida extraterrestre, en la que unos hacen hincapié más en sistemas sociales asumiendo que en lo básico serán iguales (como en el caso de Star Wars o Star Trek), o en una combinación de características de especies animales o vegetales terrestres. Otro son los posibles planetas en otros sistemas solares, sospechosamente parecidos a la Tierra o Marte. Sin embargo, el hecho cierto es que conforme avanza la exploración, aún muy limitada, de los planetas extrasolares nos encontramos con tantas sorpresas que cualquier parecido con la realidad de lo que imaginamos será pura coincidencia.
Si nos planteamos una pregunta aparentemente muy simple como “¿cuál es el punto más caliente de un planeta gaseoso cercano a una estrella?” nos parece que los físicos y planetólogos no deberían tener demasiada dificultad en responderla correctamente desde un punto de vista teórico. Y, sin embargo, el escritor de ciencia ficción dura o el científico que asuma que la respuesta teórica es la correcta se puede llevar una sorpresa mayúscula. El punto más caliente en al menos un planeta gaseoso real cerca de una estrella distante real no está donde los físicos esperaban que estuviese, un descubrimiento que desafía la comprensión de los científicos de los muchos planetas de este tipo que se encuentran en sistemas solares fuera del nuestro.
A diferencia de nuestro conocido planeta Júpiter, los llamados Júpiter calientes orbitan asombrosamente cerca de su estrella anfitriona, tan cerca que normalmente necesitan menos de tres días para completar una órbita. Además un hemisferio de estos planetas siempre se enfrenta a su estrella anfitriona, mientras que el otro está en la oscuridad permanentemente.
Como era de esperar, el lado “día” de los planetas se calienta mucho más que el lado nocturno, y el punto más caliente de todos tiende a ser el punto más cercano a la estrella. Los astrofísicos elaboran modelos que predicen que estos planetas también experimentan fuertes vientos que soplan hacia el este cerca de sus ecuadores, lo que a veces pueden desplazar el punto caliente hacia el este, algo que también ha sido observado. Sin embargo, en el misterioso caso del exoplaneta CoRoT-2b, el punto caliente se encuentra en la dirección opuesta: al oeste del centro. Un descubrimiento realizado por Lisa Dang, de la Universidad McGill (Canadá), y sus colegas usando el Telescopio Espacial Spitzer de la NASA.
CoRoT-2b, descubierto hace una década, está a 930 años luz de la Tierra. Si bien se han detectado muchos otros Júpiter calientes en los últimos años, CoRoT-2b ha seguido intrigando a los astrónomos debido a dos factores: su enorme tamaño y el desconcertante espectro de las emisiones luminosas de su superficie. Ambos factores combinados sugieren que algo raro sucede en la atmósfera de este Júpiter caliente.
Los investigadores ofrecen tres posibles explicaciones para este descubrimiento inesperado, cada una de las cuales plantea nuevos interrogantes. La primera es que el planeta podría estar girando tan lentamente que una rotación lleva más tiempo que una órbita completa a su estrella; esto podría crear vientos que soplan hacia el oeste en lugar de hacia el este, pero también supondría un problema para las teorías sobre la interacción gravitacional planeta-estrella en órbitas tan próximas.
Otra posibilidad es que la atmósfera del planeta podría interactuar con el campo magnético del propio planeta para modificar su patrón de vientos; si esto fuera así podríamos estar ante una oportunidad única de estudiar el campo magnético de un exoplaneta.
Finalmente, una tercera sería que grandes nubes estuviesen cubriendo el lado oriental del planeta, lo que podría hacer que parezca más oscuro de lo que sería realmente; pero esto socavaría los modelos actuales de circulación atmosférica en tales planetas.
Serán necesarios muchos más y mejores datos para ver si alguna de estas hipótesis es correcta o es necesario recurrir a otra. El telescipio espacial James Webb, que se supone será lanzado al espacio el próximo año y que tiene 100 veces la potencia del Spitzer, podrá proporcionarlos. En cualquier caso, preparémonos para ser sorprendidos con lo que hay ahí fuera.
Referencia:
Lisa Dang et al (2018) Detection of a westward hotspot offset in the atmosphere of hot gas giant CoRoT-2b Nature Astronomy doi: 10.1038/s41550-017-0351-6
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo La atmósfera de CoRoT-2b lleva la contraria se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Algo raro pasa alrededor de Gliese 436
- De guijarro a asteroide en una trampa de polvo
- La presencia de sales podría hacer que exista una tectónica de placas en Europa
Variaciones artísticas del teorema de Napoleón
Si hace unas semanas iniciaba mi entrada en el Cuaderno de Cultura Científica con la magnífica exposición Anni Albers: tocar la vista (Museo Guggenheim, Bilbao) de la artista alemana Anni Albers (1899-1994), hoy lo voy a hacer con otras dos excelentes exposiciones, en esta ocasión de la artista donostiarra Esther Ferrer, una que está teniendo lugar en estos momentos en el Palacio Velázquez de Madrid, organizada por el Museo Nacional Centro de Arte Reina Sofía, con el título Esther Ferrer. Todas las variaciones son válidas, incluida esta (26 de octubre de 2017 – 25 de febrero de 2018) y la otra la que se celebrará en el Museo Guggenheim de Bilbao, con el título Esther Ferrer. Espacios entrelazados (16 de marzo – 10 de junio, 2018).

Esther Ferrer durante la performance “Performance Art: Theory and Practice”, en 2012, en Ljubljana (Eslovenia). Foto de Dalila Ingold
Esther Ferrer (Donostia/San Sebastián, 1937) es una pionera del arte de la performance y una de sus máximas representantes en España. En 1963 crea en Donostia el Taller de libre expresión, junto con el artista donostiarra José Antonio Sistiaga y una Escuela experimental en Elorrio (Bizkaia). En el año 1967 se incorpora al grupo musical vanguardista ZAJ, fundado por los compositores Walter Marchetti, Ramón Barce y Juan Hidalgo, que tenían como referencia al compositor norteamericano y teórico de la música John Cage (1912-1992) y al movimiento artístico Fluxus. Fueron famosos sus performances conceptuales y radicales. En la década de 1970, Esther Ferrer retoma su actividad plástica con fotografías trabajadas, instalaciones, objetos, videos y cuadros. Su obra se suele relacionar con la corriente minimalista y conceptual, iniciada en la década de los sesenta del siglo XX, que tiene al poeta francés Stéphane Mallarmé (1842-1898), el escritor francés Georges Perec (1936-1982), al compositor John Cage o al movimiento Fluxus, como referentes, así como en los feminismos de aquel momento.

“Permutaciones. En el marco del arte matemático” (década años 1980), de Esther Ferrer
Esther Ferrer ha recibido muchos premios, entre ellos, el Premio Nacional de Artes Plásticas, en 2008, el Premio Gure Artea, en 2012, o los siguientes premios en 2014, Premio MAV (Mujeres en las Artes Visuales), Premio Marie Claire de l’Art Contemporain y Premio Velázquez de las Artes Plásticas. Y ha expuesto y realizado performances a lo largo de todo el mundo. En sus obras podemos encontrar muchos elementos relacionados con las matemáticas, desde los números primos con los que trabaja desde la década de los años 1970, hasta el infinito en el número pi, pasando por la combinatoria, el azar, la medición, las ilusiones ópticas o la geometría.
En esta entrada me gustaría traer su serie de obras titulada Triángulo de Napoleón, realizadas por Esther en la década de 1980, como las dos siguientes.

Serie “Triángulo de Napoleón” (1987), de Esther Ferrer. Técnica mixta en papel. Galería Àngels Barcelona

Serie “Triángulo de Napoleón” (1988), de Esther Ferrer. Técnica mixta en papel. Galería Àngels Barcelona
Esta serie de obras de la artista Esther Ferrer titulada Triángulo de Napoleón, está relacionada con el conocido teorema de Napoleón, un resultado clásico de la geometría.
Este resultado clásico sobre la geometría del triángulo dice lo siguiente.
Teorema de Napoleón: Si sobre los tres lados de un triángulo cualquiera ABC se construyen tres triángulos equiláteros exteriores (respectivamente, interiores), los centros de estos tres triángulos equiláteros forman un nuevo triángulo XYZ, que es equilátero, al que se denomina triángulo exterior (respectivamente, interior) de Napoleón.
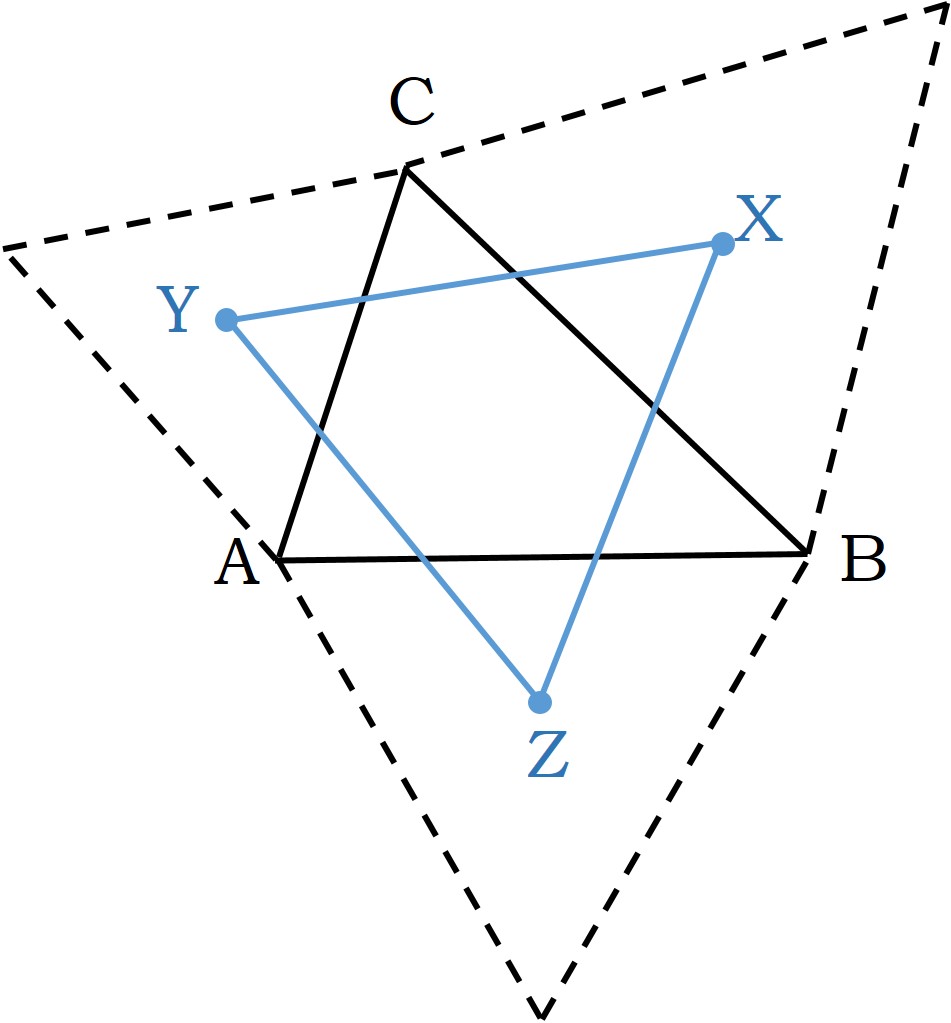
En esta imagen se ve la construcción del triángulo exterior de Napoleón (en azul en la imagen) del triángulo ABC (en negro). El punto X es el centro del triángulo equilátero apoyado en el lado BC, el punto Y el centro del triángulo equilátero apoyado en el lado AC y Z lo es del triángulo apoyado en AB. El teorema de Napoleón nos dice que el triángulo XYZ, construido de esta forma, es equilátero, tiene todos sus lados iguales. La anterior obra de Esther Ferrer de la serie Triángulo de Napoleón, de 1987, es un ejemplo de triángulo exterior de Napoleón.
Antes de continuar, una pequeña aclaración sobre el punto que es el centro de un triángulo equilátero. Dado un triángulo cualquiera se pueden definir varios puntos que son de alguna forma el centro del triángulo, a saber, el baricentro (el punto de intersección de las tres medianas del triángulo, siendo una mediana la recta que pasa por un vértice del triángulo y el punto medio del lado opuesto; también se llama centroide o centro de masas), el incentro (el punto de intersección de las tres bisectrices, rectas que dividen a un ángulo en dos partes iguales, de un triángulo, y que es el centro de la circunferencia inscrita en el triángulo), el circuncentro (el punto de intersección de las tres mediatrices –recta perpendicular a un segmento que pasa por el medio del mismo- de los lados del triángulo, y que es el centro de la circunferencia circunscrita al triángulo) y el ortocentro (el punto de intersección de las tres alturas del triángulo, donde recordemos que una altura pasa por un vértice y es perpendicular al lado opuesto del mismo).
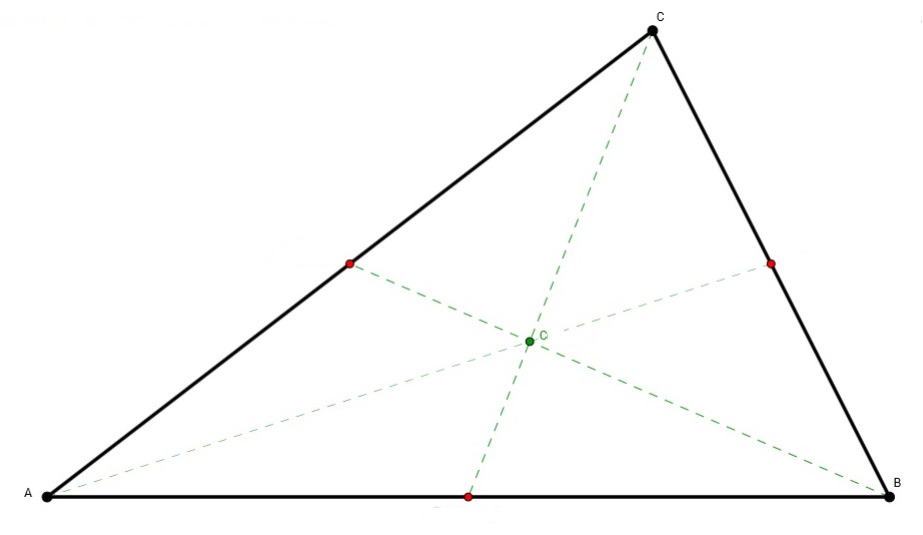
Baricentro, o centroide, de un triángulo, realizado con GeoGebra
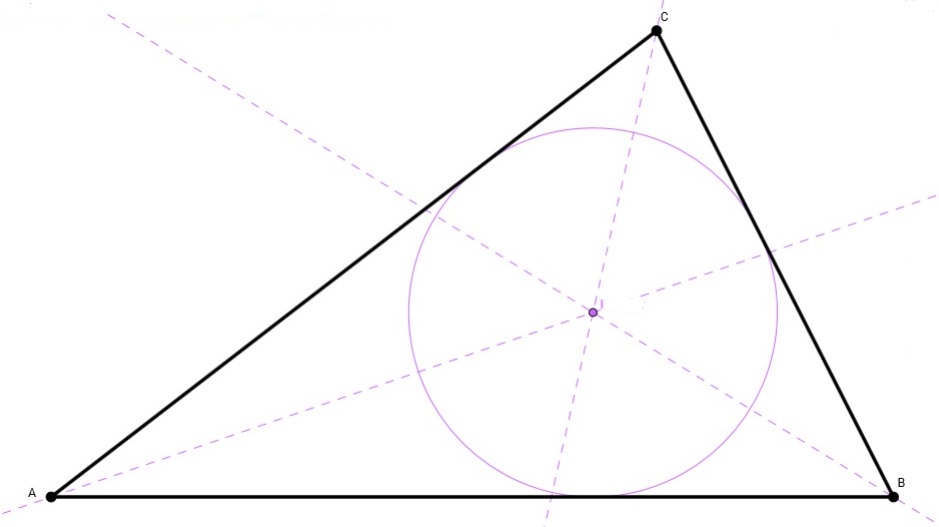
Incentro de un triángulo, realizado con GeoGebra
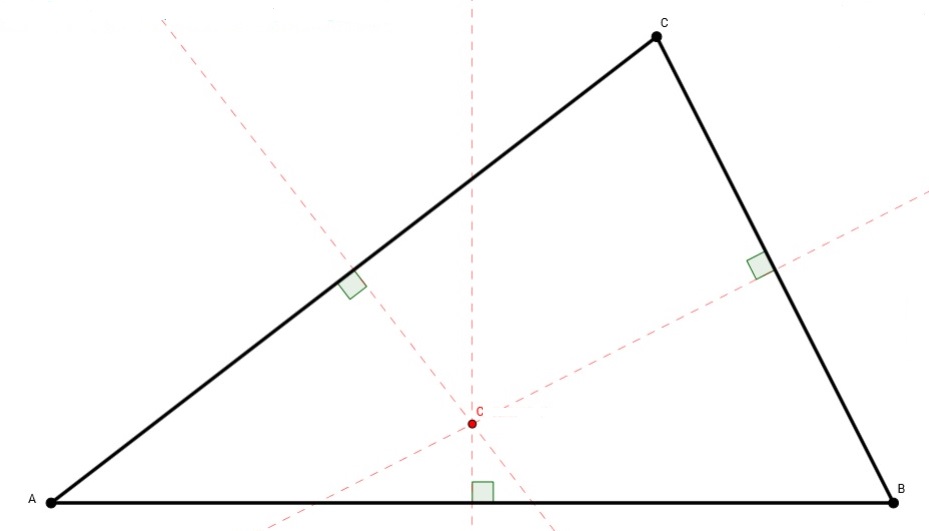
Circuncentro de un triángulo, realizado con GeoGebra
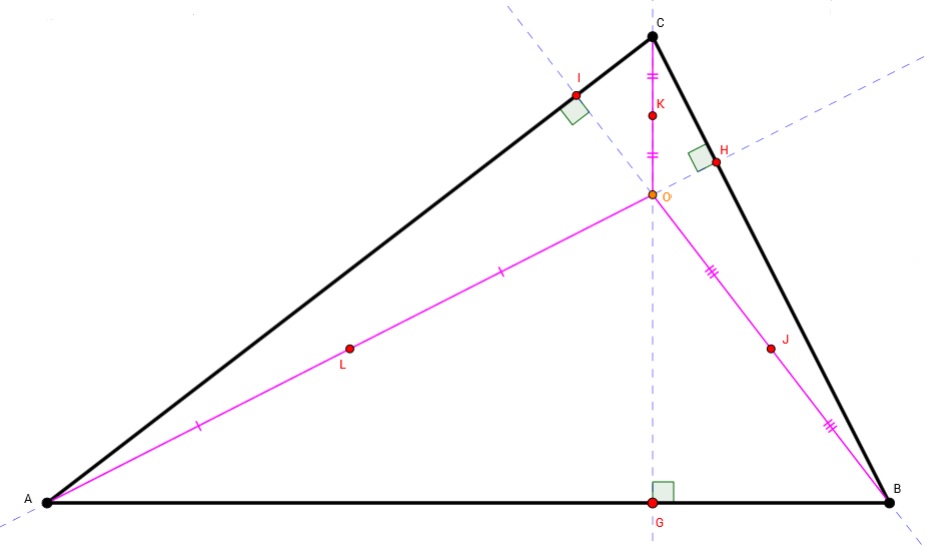
Ortocentro de un triángulo, realizado con GeoGebra
Aunque en el caso de un triángulo equilátero esos cuatro puntos son el mismo, por eso en el teorema de Napoleón hablamos simplemente del centro de un triángulo equilátero, sin especificar cuál de ellos es, puesto los cuatro son el mismo.
Continuemos con el teorema de Napoleón. A continuación, se muestra un ejemplo de construcción de un triángulo interior de Napoleón (en azul en la imagen) del triángulo ABC (en negro).
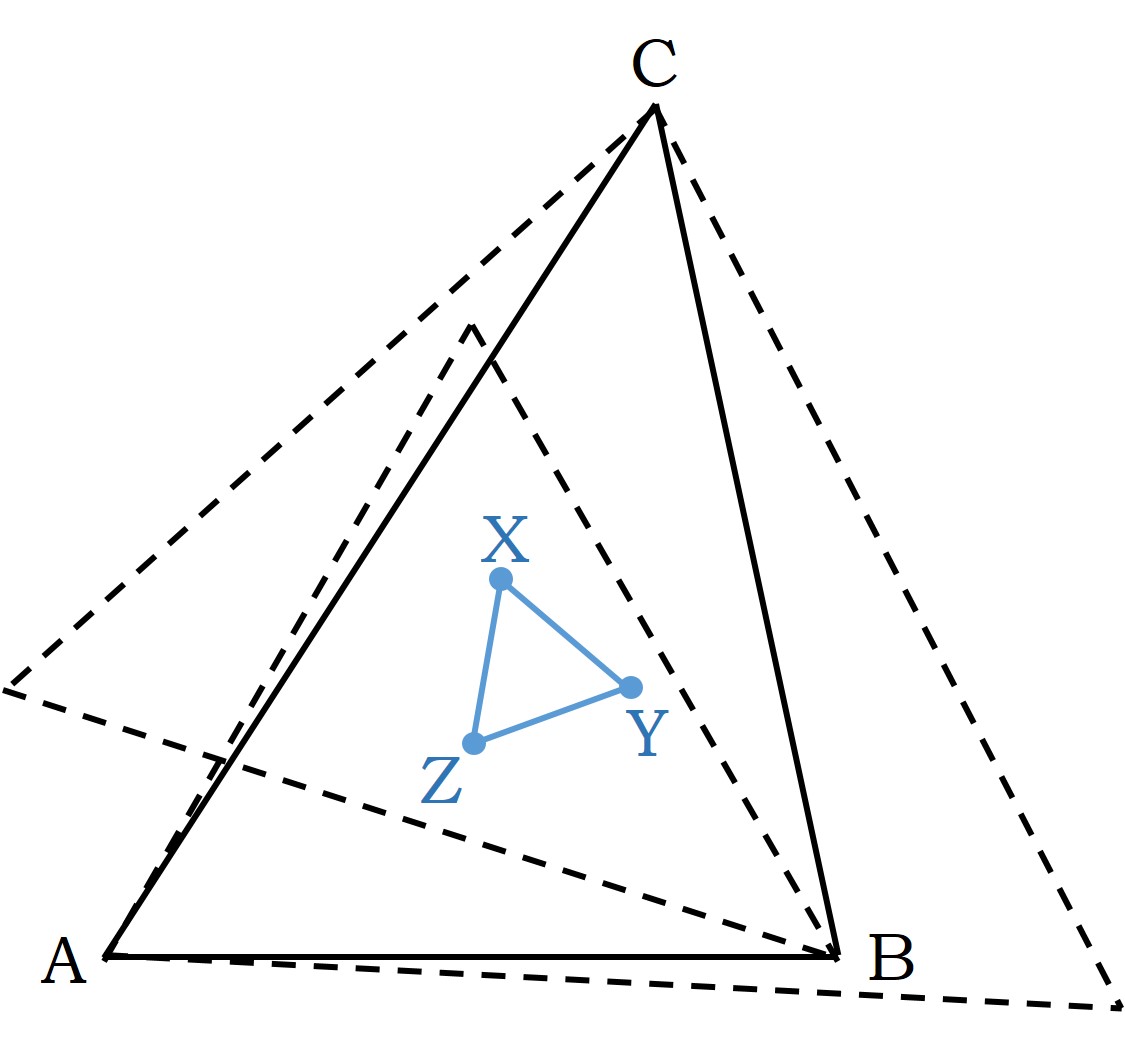
Precisamente, la obra de 1988 de la serie Triángulo de Napoleón, de Esther Ferrer, que hemos mostrado más arriba, es un ejemplo de triángulo interior de Napoleón.
Pero el resultado geométrico sobre los triángulos de Napoleón, exterior e interior, de un triángulo dado va más allá aún. También se cumplen las siguientes propiedades.
Propiedad 1: El centro del triángulo exterior (respectivamente, interior) de Napoleón y el baricentro, o centroide, del triángulo original coinciden.
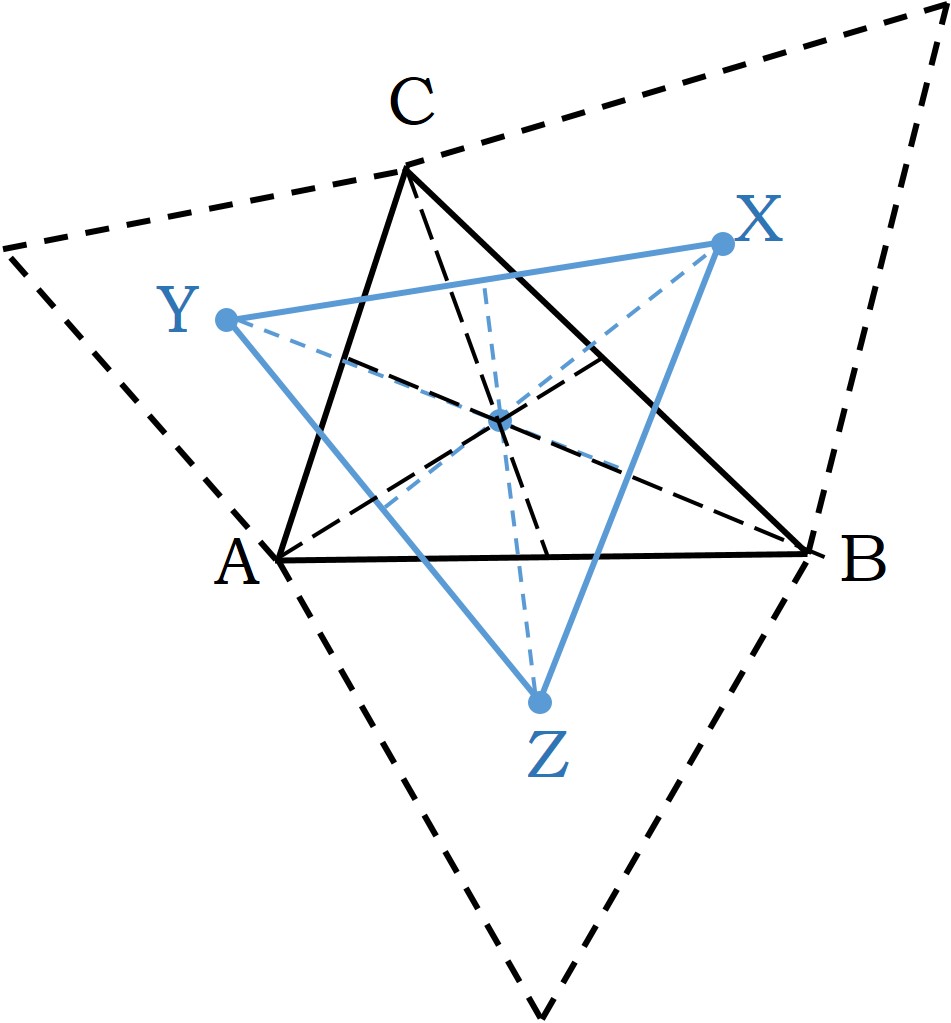
Propiedad 2: La diferencia entre las áreas de los triángulos exterior e interior de Napoleón es igual al área del triángulo original.

El área del triángulo azul, que es el triángulo exterior de Napoleón, menos el área del triángulo verde, triángulo interior de Napoleón, es igual al área del triángulo gris, el triángulo original ABC
Existen varias demostraciones distintas del teorema de Napoleón que utilizan diferentes herramientas de las matemáticas, desde la geometría analítica a los números complejos, pasando por la trigonometría o la simetría, que se pueden encontrar en la literatura matemática. Para quien esté interesado, varias de estas demostraciones se pueden encontrar en la página cut-the-knot de Alexander Bogomolny.
El nombre de este interesante teorema geométrico, teorema de Napoleón, tiene un gran atractivo, puesto que lleva el nombre del general y emperador francés Napoleón Bonaparte (1769-1821). Pero, una cuestión interesante es si este resultado es realmente de Napoleón.
La verdad es que Napoleón Bonaparte siempre estuvo interesado en la ciencia, y muy especialmente en las matemáticas. Era un matemático aficionado, al que apasionaba la geometría. Hacer ejercicios matemáticos solía relajarle y causarle gran placer. Su biógrafo J. S. C. Abbott escribió “Cuando tenía un momento para la diversión, no era infrecuente que lo utilizara en un libro de logaritmos, en el cual siempre encontraba entretenimiento”.
Se sentía orgulloso de ser miembro del Instituto de Francia. Entre sus amistades se contaban muchos científicos y matemáticos, entre los que estaban los matemáticos Jean-Baptiste Joseph Fourier (1768-1830), Gaspard Monge (1746-1818), Joseph-Louis Lagrange (1736-1813), Pierre-Simon Laplace (1749-1827), o los químicos Jean-Antoine Chaptal (1756-1832) y Claude Louis Berthollet (1748-1822). Monge y Fourier, con quienes Napoleón acabaría teniendo una fuerte amistad, le acompañaron en su campaña en Egipto. Se cuenta que por las noches solían resolver problemas juntos en su tienda de campaña.

Grabado “El general Bonaparte a borde del buque L’Orient discute con los científicos de la expedición a Egipto”, en el que podemos ver a Gaspard Monge en el centro de la imagen
Napoleón Bonaparte era consciente de la importancia de la educación, por eso fundó las dos grandes instituciones educativas de Francia, la Escuela Normal Superior y la Escuela Politécnica. La siguiente cita nos da una idea de la importancia que Napoleón le daba a las matemáticas: “El avance y perfección de las matemáticas está íntimamente ligado a la prosperidad del Estado”.
Por otra parte, Napoleón era muy amigo del poeta y matemático italiano Lorenzo Mascheroni (1750-1800). Este le dedicó su libro Geometria del Compasso (1797) a Napoleón. Incluso existe un problema que recibe el nombre de Problema de Napoleón, por haber sido propuesto por el general, y que resolvió Mascheroni. Es el problema de dividir la circunferencia en cuatro partes iguales utilizando únicamente el compás. Se dice que en cierta ocasión estaba Napoleón explicando este resultado de geometría a Lagrange y Laplace, y este último le contestó “Lo último que esperábamos de usted General, era una lección de geometría”.
“Napoleón en Fontainebleau”, 31 de Marzo de 1814, por Paul Hippolyte Delaroche (1797-1856)
Sin embargo, no hay ninguna constancia de que el teorema de Napoleón fuera realmente de Napoleón Bonaparte. Coxeter y Greitzer en su libro Geometry revisited, afirman que “la posibilidad de que [Napoleón] supiese suficiente geometría para realizar este logro es tan cuestionable como que supiese suficiente inglés como para componer el famoso palíndromo ABLE WAS I ERE I SAW ELBA (Hábil fui antes de ver Elba)”.
La primera vez que se publica algo relacionado con el teorema de Napoleón, fue en forma de problema en la revista The Ladies’ Diary, en 1825, propuesto por el matemático inglés William Rutherford (1798–1871):
Trácense triángulos equiláteros (los vértices apuntando todos hacia fuera o todos hacia dentro) sobre los tres lados de un triángulo ABC: entonces las líneas que unen los centros de gravedad de estos tres triángulos rectángulos forman un triángulo equilátero. Se requiere demostración.
Al año siguiente se publicaron en The Ladies’ Diary dos demostraciones del problema de los triángulos, una geométrica y otra analítica, aunque la revista recibió muchas más.

Extracto de la revista The Ladies’ Diary, de 1826, que contiene las dos soluciones, geométrica y analítica, del problema planteado por W. Rutherford
Aunque el teorema de Napoleón ya había apareció, con anterioridad, en forma de tres ejercicios de un examen para obtener la Medalla de Oro de la Universidad de Dublín, en 1820.
Muchos estudiosos son de la opinión de que este resultado ya era conocido con anterioridad, pero no se ha conservado ninguna publicación del mismo. Hay quienes citan a los matemáticos italianos Evangelista Torricelli (1608-1647), Bonaventura Cavalieri (1598-1647) o Vincenzo Viviani (1622-1703), puesto que habían estudiado figuras en las que se disponían triángulos equiláteros en los lados de un triángulo y podrían haber obtenido el resultado, o hay quien cita también al francés Pierre de Fermat (1601-1665), aunque no hay ninguna prueba documental de ello.
Por otra parte, después de ser publicado en The Ladies’ Diary este resultado ha sido redescubierto independientemente por muchas personas, lo cual nos da una pista de que quizás ya había sido enunciado y demostrado con anterioridad.
Según Branko Grünbaum, en su artículo Is Napoleon’s Theorem Really Napoleon’s Theorem?, la primera publicación conocida en la que se menciona a Napoleón en relación a este resultado es de 1911, en la edición decimoséptima del libro Elementi di Geometria, del matemático italiano Aureliano Faifofer (1843-1909). Faifofer menciona que es un “teorema propuesto para la demostración por Napoleón a Lagrange”.
Sin embargo, en el artículo de la wikipedia sobre el teorema de Napoleón se menciona que en la Enciclopedia Chambers, en el volumen IX, de 1867, ya se citaba a Napoleón en relación a esta cuestión.
Lo cierto es que no se sabe quién descubrió originalmente este teorema de triángulos, ni si realmente Napoleón se lo propuso a Lagrange para su demostración y este fue el motivo de que lleve su nombre. Lo único que sí es cierto es que este resultado se conoce hoy en día con este nombre, el teorema de Napoleón. Seguramente, será un ejemplo más de la ley de la eponimia de Stigler (por cierto, que el propio Stephen Stigler mencionó que esta ley ya había sido formulada por Robert K. Merton con anterioridad, cumpliéndose de nuevo la propia ley), que dice que “ningún descubrimiento científico recibe el nombre de quien lo descubrió en primer lugar”, como la regla de L´Hôpital, que realmente es de Johann Bernoulli, la ley de Benford, que la descubrió el astrónomo Simon Newcomb o los sistemas triples de Steiner, que estudió primero el matemático Thomas P. Kirkman.
Pero terminemos con algunas otras obras de la serie Triángulo de Napoleón de la artista donostiarra Esther Ferrer.

Obra de la serie “Triángulo de Napoleón” (finales años 1980), collage, de Esther Ferrer

“Triángulo interno de Napoleón”, Esther Ferrer, presentada en ARCO 2013

Maqueta de Esther Ferrer para la instalación “Triángulo interno de Napoleón” (finales años 1980), es la proyección del triángulo interno de Napoleón mediante hilo o cable

Dibujo para la instalación “Triángulo interior de Napoleón” (finales años 1980), de Esther Ferrer)
Bibliografía
1.- Esther Ferrer. Todas las variaciones son válidas, incluida esta (Palacio Velázquez, 26 de octubre de 2017 – 25 de febrero de 2018), Museo Reina Sofia
2.- Página web de Esther Ferrer
3.- Galería Àngels Barcelona, Esther Ferrer
4.- H. S. M. Coxeter and S. L. Greitzer, Geometry Revisited, Mathematical Association of America, 1967.
5.- GeoGebra
6.- Howard W. Eves, Mathematical Circles (volume I), MAA, 2003.
7.- Branko Grünbaum, Is Napoleon’s Theorem Really Napoleon’s Theorem?, The American Mathematical Monthly, vol. 119, n. 6, p. 495 – 501, 2012.
8.- Wikipedia: Napoleon’s theorem
9.- M. R. F. Smyth, MacCool’s Proof of Napoleon’s Theorem, Irish Math. Soc. Bulletin 59, p. 71 – 77, 2007.
10.- Alexander Bogomolny, Cut-the-knot, Napoleon’s Theorem
11.- Esther Ferrer, Maquetas y dibujos de instalaciones 1970/2011, EXIT, 2011.
12.- Esther Ferrer, Entre líneas y cosas, CEART, 2016.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Variaciones artísticas del teorema de Napoleón se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El teorema de Marion (Walter)
- El teorema de los cuatro colores (2): el error de Kempe y la clave de la prueba
- El teorema de los cuatro colores (1): una historia que comienza en 1852

