La intervención en la dislexia: de la evidencia científica a la práctica educativa

¿Cómo se tratan algunos de los trastornos cognitivos más frecuentes en las aulas? ¿Son efectivos los programas y herramientas del sistema educativo actual? ¿Carecen de eficacia algunas de las prácticas educativas más populares?
Estas son algunas de las cuestiones que se debatieron en la jornada “Las pruebas de la educación”, que se celebró el pasado 2 de febrero de 2018 en el Bizkaia Aretoa de Bilbao. El evento, en su segunda edición, estuvo organizado por la Cátedra de Cultura Científica de la UPV/EHU y el Consejo Escolar de Euskadi, con la colaboración de la Fundación Española para la Ciencia y la Tecnología (FECYT).
Las ponencias de los expertos que expusieron múltiples cuestiones relacionadas con la educación, basándose siempre en las pruebas científicas existentes. Los especialistas hicieron especial hincapié en destacar cuál es la mejor evidencia disponible a día de hoy con el objetivo de abordar las diferentes realidades que coexisten en las aulas y en el sistema educativo en general.
“Las pruebas de la educación” forma parte de una serie de eventos organizados por la Cátedra de Cultura Científica de la UPV/EHU para abordar cuestiones del día a día como la educación o el arte desde diversos ámbitos de la actividad científica. La dirección del seminario corre a cargo de la doctora en psicología Marta Ferrero.
Joana Acha, profesora en el departamento de Procesos Psicológicos Básicos y su Desarrollo de la UPV/EHU, revisa los métodos de prevención e intervención más efectivos para el desarrollo de las habilidades básicas implicadas en la dislexia. La especialista en procesos cognitivos infantiles aporta evidencias de los cambios cerebrales que acompañan a la adquisición de dichas habilidades.
Joana Acha: ''La intervención en la dislexia''Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo La intervención en la dislexia: de la evidencia científica a la práctica educativa se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Autismo y educación: problemas y pautas en el aula
- Prohibir los herbicidas con glifosato es anteponer la ideología a la evidencia científica
- La evaluación y los deberes escolares
Funtzio anitzeko polimero metal-organiko porotsuak (MOF): etorkizuneko material adimendunei begira
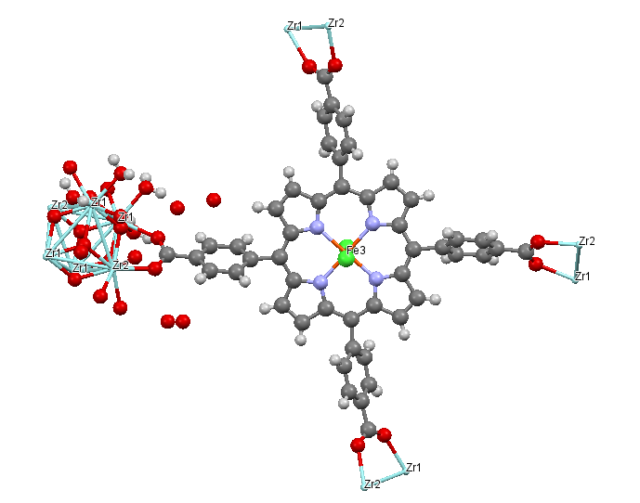
MOF (ingelesez Metal-Organic Frameworks) deritzen polimero metal-organikoek, azken bi hamarkadetan, material porotsuen munduan iraultza sorrarazi dute. Porositate itzelak (bolumen hutsak: % 90 arte) eta ikaragarrizko barne-azalerak (gaur egungo marka 7000 m2/g-tan kokatzen da) dauzkaten konposatu kristalinoak dira. Hain zuzen ere, MOF-ak estekatzaileen eta nodoen arteko loturen (koordinazio-loturen) ondorioz eratzen diren egitura molekularrak dira. Estekatzaileak atomo emaileak dituzten molekula organikoak dira, eta nodoak ioi metaliko edo kluster metalikoak. Egituraren barruan eratutako poroak molekula ostalariak harrapatzeko, eta kasu batzuetan, erreakzio kimikoetan parte hartzeko oso egokiak dira.
Bere natura hibridoak propietate anitzak jorratzeko aukera ematen die, porositatearekin erlazionatuta daudenez gain (gasen bilketa eta banaketa) katalizatzaile heterogeneo, sentsore magnetiko edota lumineszente bezala jokatzekoak ere bermatuz. Halaber, energia berriztagarrien arloari begira, hidrogeno eta metano gasen biltegi molekular gisa erabil daitezke, hala nola gas kutsatzaileen adsorbatzaile selektibo gisa.
Gainera, material hauek beste material porotsuekin (zeolitak, karboi aktiboak) konparatuta abantaila nagusia daukate: beraien egitura zehaztasun osoz diseinatzeko erraztasuna. Izan ere, gaur egun material hauen 20.000 ale baino gehiago ezagutzen dira. Bereziki, egitura hauek topologia anitzetan sailka daitezke, eta asko naturan sorturiko mineraletan oinarrituta daude. Era horretan, propietate eta funtzio zehatzak dituzten egiturak diseinatzea ahalbidetzen dute konposatu hauek, eta materialak ikertzen dituzten zientzialarien ametsari edo xedeari eusten diete.
Hasiera batean, MOF-ak ahulegiak zirelako sinesmena hedatu zen zientzia mailan, maiz, aurretik harrapatutako molekulak askatzean egitura orokorra suntsitzen baitzen. Horregatik, zientzialari batzuen ustez, produktu hauek inoiz ez zuketen erakutsiko zeolitek industria mailan iragazteko eta katalizatzeko erakusten duten ahalmena. Hala ere, urte batzuk geroago, eta milaka laborategietan gauzatu den lanaren ondorioz, MOF materialak aplikazio komertzialetan debuta egin dute, eta zientzialari horien ustea suntsitu dute.
Bere aplikazioei esker, hainbat kimika-enpresek, BASF multinazionala barne, material hauek jadanik merkaturatu dituzte. Horregatik, diseinatu beharreko material berrien propietateak hobetzeaz gain, merkeak eta ingurumena zaintzen duten sintesi-bide berriak aurkitzea ere helburu nagusia bihurtu da.
Material hauen izenetan unibertsitate edo laborategi bakoitzak bere zigilua utzi dezake. Orain arte ospetsuenen artean MIL-101 (Materials of Institut Lavoisier), HKUST-1 (Hong Kong University of Science and Technology), UiO-66 (Universitetet i Oslo), eta NU-110E (Northwestern University) aipa ditzakegu, besteak beste. EHU izena daukan batek ere argia ikusi du. Betiko iraungo duen zigilua… Lortuko al dugu kopurua handitzea? Gure ahaleginak horretan dabiltza. MOF konposatu berriak lortu nahi ditugu, gasen bilketan eta banaketan erabilgarriak direnak, baina propietate magnetikoak eta lumineszenteak erakusten dutenak ere. Prozedura merke eta jasangarrian bada, are hobeto.
MOF konposatuek dituzten propietate anitzak hainbat aplikazioetan arrastoa utzi dezaketela kontutan hartuz, haien gaineko ikerkuntzak etorkizuneko material adimendunekiko begirada islatzen du.
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: Ekaia 31
- Artikuluaren izena: Funtzio anitzeko polimero metal-organiko porotsuak (MOF): etorkizuneko material adimendunei begira.
- Laburpena: MOF deritzen polimero metal-organikoak ioi metalikoz eta estekatzaile organikoz osatutako koordinazio-sare porotsuak dira. Azken urteotan beste material porotsuen artean gailentzen ari dira. Bere natura hibridoak propietate anitzak jorratzeko aukera ematen die, porositatearekin erlazionatuta daudenez gain (gasen bilketa eta banaketa) katalisia, sentsore magnetiko edota lumineszente bezala jokatzekoak ere bermatuz. Material hauek egitura eta funtzionalitatea aldatzeko erraztasun handia dutenez, aldi berean ikatz aktibatuaren eta zeoliten barne-azaleren mugak gainditzen dituzte. Hori dela eta, MOFen arloak garapen sakona sustatu du eta kimikaren barnean hazkunde azkarrenetariko esparrua izatea lortu du.
- Egileak: Javier Cepeda, Sonia Pérez-Yáñez
- Argitaletxea: UPV/EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- Orrialdeak: 105-116
- DOI: 10.1387/ekaia.16220
—————————————————–
Egileez:
Javier Cepeda, UPV/EHUko Kimika Fakultateko Polimeroen Zientzia eta Teknologia Sailean eta Kimika aplikatua Sailean dabil eta Sonia Pérez-Yáñez Zientzia eta Teknologia Fakultateko Kimika Ez-organikoa Sailekoa da.
————————————————–
Ekaia aldizkariarekin lankidetzan egindako atala.
The post Funtzio anitzeko polimero metal-organiko porotsuak (MOF): etorkizuneko material adimendunei begira appeared first on Zientzia Kaiera.
Aunque tengas colesterol, podrás desayunar huevos

Las enfermedades cardiovasculares son la principal causa de muerte en el mundo. Cada año mueren más personas por enfermedades cardiovasculares que por cualquier otra causa. Por eso cuando el médico nos alerta de que tenemos el colesterol alto, nos entra el miedo.
¿Recuerdas aquello de que no debemos tomar más de tres huevos a la semana? Pues olvídalo. La culpa de tu colesterol no la tienen los huevos.
¿Qué es el colesterol?
El colesterol es un tipo de lípido denominado esterol. Lo encontramos en los tejidos y en la sangre. Pese a su mala fama en cuestiones de salud, el colesterol es esencial para la vida. Forma parte de las membranas de nuestras células y ayuda a controlar qué entra y qué sale de ellas, es un precursor de la vitamina D, por tanto, es fundamental para el metabolismo del calcio, es precursor de las hormonas sexuales, etc.
Colesterol bueno y colesterol malo
El colesterol no se disuelve ni se mezcla con la sangre. El modo que tiene de permanecer en el torrente sanguíneo es formando parte de una especie de cápsulas denominadas lipoproteínas. Cuando estas cápsulas tienen más proteínas que lípidos, son más densas. Esta propiedad es la que se utiliza para clasificarlas: HDL (lipoproteína de alta densidad) y LDL (lipoproteína de baja densidad). El HDL lo conocemos como colesterol bueno y el LDL como colesterol malo.
Que uno sea el bueno y el otro sea el malo tiene que ver con la ateroesclerosis. La ateroesclerosis se caracteriza por la acumulación de placa en el interior de las arterias, haciéndolas más rígidas y pudiendo llegar a taponarlas (produciendo una isquemia o infarto). Cuando analizamos esta placa solo encontramos LDL. Es decir, solo el LDL es capaz de adentrarse en nuestras arterias y causarnos problemas cardiovasculares, por eso le hemos llamado colesterol malo.
Estudios recientes han ido todavía más allá. Lo más relevante con respecto al riesgo cardiovascular no es tanto la cantidad de colesterol que contengan esas lipoproteínas, sino la cantidad de lipoproteínas LDL que haya, independientemente de si contienen más o menos colesterol en su interior. Esto no implica que deberíamos dejar de preocuparnos por el colesterol, al menos no en todos los casos. La evidencia nos dice el colesterol malo aumenta el riesgo cardiovascular si además va unido a otros factores como la obesidad, niveles altos de triglicéridos, hipertensión, niveles altos de glucosa, estrés o bajo nivel de colesterol bueno.
Los alimentos que contienen colesterol no hacen subir el colesterol
Además del huevo y los quesos, los alimentos que más colesterol contienen en su composición son los que tienen más grasas saturadas: las mantecas, la nata, algunos mariscos, los patés, el hígado, etc.
Numerosos estudios han demostrado que el colesterol que consumimos apenas repercute en los niveles de colesterol en sangre. De hecho, el colesterol que ingerimos es un factor poco relevante, ya que nuestro cuerpo sintetiza por sí solo la mayor parte del colesterol que utiliza. Si no comiésemos nada de colesterol, nuestro cuerpo lo fabricaría por sí mismo.
A esto hay que sumarle que la mayor parte del colesterol que ingerimos ni se absorbe ni se metaboliza, sino que se expulsa directamente. Esto es debido a que el colesterol de la mayoría de los alimentos está esterificado (es químicamente diferente al colesterol libre) y eso afecta a su biodisponibilidad. Solo podríamos absorber el colesterol libre (no esterificado) y éste es difícil de encontrar en los alimentos. Por lo tanto, en la mayor parte de las personas la cantidad de colesterol ingerido tiene poca relación con el nivel de colesterol que se queda en su cuerpo.
Es un mito que consumir huevos suba el colesterol
En los años 70 se empezó la lucha contra las grasas, especialmente contra los alimentos con colesterol, en gran medida a causa de una interpretación un tanto alarmista de este estudio. Para más inri, en 1973 la Asociación Americana del Corazónpropuso limitar la ingesta de huevos a un máximo de tres por semana.
Actualmente sabemos que aquella recomendación era innecesaria, y que por su culpa este mito se ha perpetuado hasta nuestros días. La realidad es que consumir un huevo al día no aumenta el riesgo cardiovascular en comparación con tres huevos semanales.
En enero de 2014 la Fundación Española del Corazón publicó una nota de prensa en la que decía que no es necesario restringir la ingesta de huevosen la dieta de las personas sanas.
Hay indicios de que el huevo, además de colesterol, contiene unas sustancias que bloquean su entrada en el organismo. Por eso, a la luz de la evidencia científica, ninguna organización nutricional desaconseja su consumo por miedo a que nos suba el colesterol.
Alimentos funcionales para bajar el colesterol

Los alimentos funcionales formulados para bajar el colesterol contienen esteroles y estanoles añadidos. Estas dos sustancias forman parte de las plantas, donde desarrollan funciones análogas a las de nuestro colesterol. Cuando consumimos esteroles y estanoles, estos bloquean la absorción intestinal del colesterol, impidiendo que más adelante lleguen a la sangre.
Estas sustancias las encontramos en frutas, verduras, aceites vegetales, legumbres, frutos secos, etc. Pero están presentes en cantidades tan pequeñas que no afectan al nivel de colesterol. Sin embargo, los alimentos funcionales multiplican por 10 o más la cantidad de esteroles y estanoles. Contienen una media de 3 g por cada 100 g de producto.
Una de las funciones de la Agencia Europea de Seguridad Alimentaria (EFSA) es verificar si las alegaciones saludables publicitadas de un alimento son válidas. A la luz de los estudios presentados, la EFSA ha confirmado que «los alimentos funcionales que contienen esteroles o estanoles contribuyen a mantener los niveles normales de colesterol sanguíneo». Tanto es así, que estos productos van exclusivamente dirigidos a personas con problemas de colesterol, no se debe consumir más de 3 g al día de esteroles y estanoles, no lo pueden tomar los menores de 5 años, ni las embarazadas, por lo que es aconsejable que sea el médico el que paute su consumo.
Según publica la EFSA, tomar entre 1,5 y 3 g de esteroles o estanoles al día durante 2-3 semanas puede reducir el colesterol malo en un 11,3 u 11,4 % respectivamente. Todavía queda por analizar si esta reducción de los niveles de colesterol malo es tan relevante como se cree con respecto a la salud cardiovascular.
Qué dice la ciencia para bajar el colesterol
Lo que sí sabemos que disminuye el riesgo cardiovascular, mantiene a raya nuestro nivel de colesterol y la cantidad de lipoproteínas portadoras de colesterol malo, es seguir una dieta basada en unas sencillas recomendaciones: tomar frutas y verduras, suficientes proteínas y grasas saludables, apostar por las harinas integrales y evitar las harinas refinadas. También deberíamos evitar los alimentos procesados de alto índice glucémico como los dulces y la bollería, especialmente el azúcar y los siropes.
Además de seguir una dieta saludable, los estudios confirman que la actividad física es fundamental para controlar el colesterol malo y la cantidad de lipoproteínas portadoras.
Conclusión
Si tenemos que lidiar con el colesterol, lo primero es seguir las indicaciones de nuestro médico. Como hay otros factores que regulan la síntesis de colesterol, no siempre es posible controlarlo a través de la dieta. Si esto sucede, será el médico quien nos pondrá un tratamiento.
Si éste no es nuestro caso, la solución a nuestro colesterol no será emprender una batalla contra los huevos, sino en apostar por una dieta saludable. La batalla, como casi siempre, la deberíamos mantener con los alimentos procesados, aquellos que contienen harinas refinadas, azúcares y grasas saturadas. Si a esto le sumamos actividad física, no sólo estaremos combatiendo el colesterol, sino que ganaremos en muchos otros frentes.
Si eres de los que desayunan huevos revueltos o cenan tortilla francesa, no cambies esos hábitos por miedo al colesterol. Ya lo estás haciendo bien.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Aunque tengas colesterol, podrás desayunar huevos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Atunen berogailua
 Juan Ignacio Pérez eta Miren Bego Urrutia Igeri egiten, lasterka egiten, hegan egiten
Juan Ignacio Pérez eta Miren Bego Urrutia Igeri egiten, lasterka egiten, hegan egiten ———————————————————————————————————–
Eskonbridoak etengabe igeri egiteko ahalmen handiena duten arrain teleosteoak dira. Beste zenbaiten artean, atunak eta berdelak dira talde horretako kideak. Iraupen laburreko ahalegin handiak egiteko gai dira, giharreria zuri[1] indartsuari esker. Baina beste teleosteoekin erkatzen baditugu, haien gihar gorriak[2] ere oso ahaltsuak dira. Gihar gorriei esker egin dezakete igeri horren distantzia luzeetan.
Eskonbridoen artean tunidoak dira, alde handiarekin gainera, fisikoki ahaltsuenak. Igerilari apartak, oso distantzia luzeak egiten dituzte lastertasun handiz. Harrigarria bada ere, atunen giharreria eta gainerako eskonbridoena ez da oso desberdina. Izan ere, ezin liteke alde handiegirik izan eskonbrido desberdinen gihar-ahalmenen artean. Adituen iritziz arrain multzo horren giharren ezaugarri metabolikoak nekez hobetu litezke, oso egokiak baitira lan handia eta eraginkorra garatzeko. Kasik ez dago, beraz, hobetzeko tarterik. Baina muskuluen metabolismoari dagokionez batzuk eta besteak antzeko samar badira ere, oso berezia da tunidoek erakusten duten ezaugarri bat, eskonbridoek eta gainerako arrainek erakusten ez dutena. Ezaugarri bereizgarri hori ez da metabolikoa, fisiologikoa baino; hau da, ez dagokio zelulen organuluen funtzionamenduari, sistemaren funtzionamenduari baino.
Gihar gorrien tenperatura inguruko itsas urarena baino 10 °C altuago mantentzen dute tunidoek. Horixe da ezaugarri gakoa. Beste eskonbrido guztiek baino jarduera-maila altuagoa garatu dezakete giharraren tenperatura horri esker. Esan bezala, gihar gorriak dira beroago daudenak, ez beste gihar- edo gorputz-atalak. Azken batean, tunidoek egiten dutena eta animalia homeotermoek egiten duguna, nonbait, ez da oso desberdina, baina tunidoak noski, ez dira homeotermoak.
Gihar-jarduerak sortzen duen beroa gordetzeko edo ez galtzeko ahalmena dute, eta horri zor zaio, hain zuzen ere, tenperatura altuagoa mantendu ahal izatea. Rete mirabile (sare miragarria) latinezko izena duen zirkulazio-sistemaren gailu berezi bati dagokio atunen ahalmen hori. Gailu horri esker, brankietatik datorren odol hotza berotu egiten da giharretara heldu baino lehen. Ibilbide horretan arteria-odolak irabazten duen beroa kontrako noranzkoan doan beste odol batek galtzen du. Giharretatik igaro berria den zain-odola da beste odol hori; zain-odola bero dago, muskuluaren metabolismo-jarduerak sortu duen beroaren eraginez, eta gihar gorrietatik irteten denean arteria txikietatik datorren odolari ematen dio berotasuna. Odol-hodiak, zainak eta arteriak, elkarren ondoan daude, eta kontrako noranzkoan mugitzen dira barruan daramaten zain- eta arteria-odolak. Odolak (edo beste edozein fluidok) zirkulatzeko era horri “korrontearen kontra” deitzen zaio, eta horri esker lortzen da bi azpisistemen arteko bero-transferentzia ahalik eta handiena izatea.
Korrontearen kontrako trukatzailea dugu rete mirabile. Bera bezalako zenbait trukatzaile fisiologiko daude animalietan, eta beroa, ioiak edo arnas gasak eta abar trukatzeko erabiltzen dira. Korrontearen kontrako trukatzaileak oso erabiliak dira instalazioetan eta lokaletan tenperatura konstante mantendu ahal izateko, eta ingeniariek giza adimenak sortuak direla uste duten arren, naturak sortu zituen duela milioika urte.
Orain arte emandako azalpenetatik ondoriozta daiteke tunidoek badutela endotermiarako ahalmena; hau da, barne-jatorria duen beroa gordetzeko gai dira eta bero horri esker igo dezakete gorputz-atal baten tenperatura. Oso antzekoa da animalia endotermook egiten duguna, geure metabolismoaren emaitza den beroari esker egon baikaitezke bero. Antzekoa da, bai, homeotermook egiten duguna eta atunek egiten dutena, baina ez berdina: homeotermook konstante[3] mantentzen dugu barne-tenperatura eta atunek euren gihar gorriak kanpo-medioa baino apur bat beroago mantentzea lortzen dute. Lorpen txikia dirudi, baina lorpen horri esker dira igeri egiteko makina ahaltsuak atunak. Eta lorpen hori bi ezaugarriri esker da posible: gihar-metabolismoaren berogailua bata, eta berogailu horrek sortzen duen beroa ez galtzeko sare miragarria bestea.
[1] Gihar zurien ezaugarriak: uzkurtze azkarrekoak, anaerobikoak, berehala nekatzen dira.
[2] Gihar gorrien ezaugarriak: astiro uzkurtzen dira, aerobikoak, mitokondrio askokoak, ondo odololeztatuak, ez dira erraz nekatzen.
[3] Ez beti eta ez guztiz konstante, eskualde-heterotermia deritzon gertaera oso arrunta baita animalia homeotermoetan.
—————————————————–
Egileez: Juan Ignacio Pérez Iglesias (@Uhandrea) eta Miren Bego Urrutia Biologian doktoreak dira eta UPV/EHUko Animalien Fisiologiako irakasleak.
—————————————————–
Artikulua UPV/EHUren ZIO (Zientzia irakurle ororentzat) bildumako Animalien aferak liburutik jaso du.
The post Atunen berogailua appeared first on Zientzia Kaiera.
Colores vivientes: nanoestructuras que se cultivan, no se fabrican.
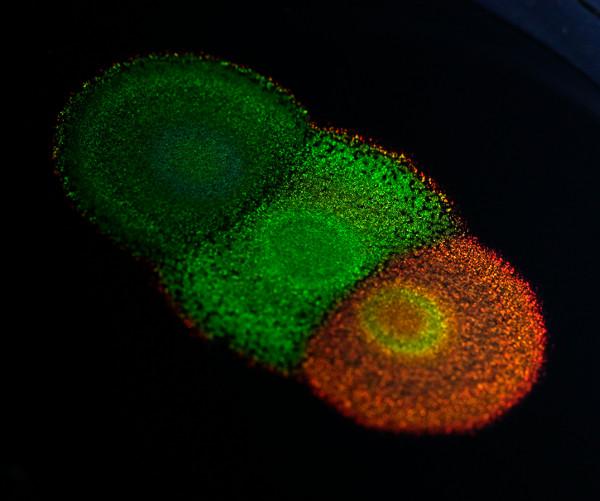
Fuente: University of Cambridge
Una nueva investigación muestra cómo la genética puede cambiar el color y la apariencia de ciertos tipos de bacterias que crecen en colonias de colores llamativos. Este sería uno de los primeros estudios, si no el primero, de la genética del color estructural, ese que se manifiesta espectacularmente en las alas de las mariposas o en las plumas de los pavos reales. Los resultados abren la vía para la investigación genética de toda una variedad de organismos coloreados estructuralmente. Desde un punto de vista práctico cosechar estas bacterias para la fabricación a gran escala de materiales nanoestructurados se convierte ahora en una posibilidad; es decir, que las pinturas biodegradables y no tóxicas podrían “cultivarse” y no fabricarse, por ejemplo.
Flavobacterium es un tipo de bacteria que se agrupa en colonias que producen llamativos colores metálicos. Estos colores no provienen de la existencia de pigmentos, sino de su estructura interna, que refleja la luz a ciertas longitudes de onda. Sin embargo, la ciencia aún no tiene muy claro cómo la genética afecta a estas estructuras. De ahí el interés de este trabajo, que estudia por primera vez los genes que provocan estas estructuras de color en un sistema vivo.
Los investigadores, encabezados por Villads Egede Johansen, de la Universidad de Cambridge (Reino Unido), compararon la información genética con las propiedades ópticas y la anatomía de colonias bacterianas sin mutar y mutadas para comprender cómo regulan los genes el color de la colonia.
Al mutar genéticamente la bacteria, los investigadores cambiaron sus dimensiones o su capacidad de movimiento, lo que alteró la geometría de las colonias. Al cambiar la geometría, cambiaron el color: cambiaron el color verde metálico original de la colonia en todo el rango visible de azul a rojo. También fueron capaces de crear una coloración más opaca o hacer que el color desapareciese por completo.
Desde el punto de vista práctico, y usando el lenguaje no de la biología genética sino de la nanotecnología, esto significa que se pueden diseñar estructuras fotónicas del color deseado y que estas estructuras se pueden autorreproducir en abundancia, todo ello evitando los laboriosos métodos tradicionales de la nanofabricación.
Para darnos cuenta de lo que esto significa, pensemos que estamos hablando de la posibilidad de usar colonias bacterianas como pigmentos fotónicos que pueden optimizarse fácilmente para cambiar la coloración bajo estímulos externos y que pueden interactuar con otros tejidos vivos, adaptándose así a entornos variables. La potencialidad de aplicaciones es tan amplia como la imaginación.
Referencia:
Villads Egede Johansen el al. (2018) Living colors: Genetic manipulation of structural color in bacterial colonies, PNAS doi: 10.1073/pnas.1716214115
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Colores vivientes: nanoestructuras que se cultivan, no se fabrican. se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Usando ADN para sintetizar nanoestructuras de oro
- Descubierto el proceso por el que las bacterias fabrican nanoimanes
- Paneles solares orgánicos…y de colores
Teselaciones rítmicas perfectas
En mi anterior entrada del Cuaderno de Cultura Científica, titulada Las vacas de Narayana, la versión hindú de los conejos de Fibonacci , estuvimos hablando de una curiosa sucesión de números, la sucesión de las vacas de Narayana, y de cómo el compositor minimalista estadounidense Tom Johnson (Greeley, Colorado, EE.UU., 1939), la había utilizado para componer una obra musical de título homónimo.

Portada del disco “Rational Music”, de Tom Johnson, interpretado por Dedalus, New World Records, 2010
En el proceso creativo de su música, Tom Johnson busca encontrar la belleza de una forma objetiva, alejándose de la subjetividad de la música romántica y expresionista, que lo hace a través de los sentimientos. El compositor minimalista utiliza las matemáticas, es decir, la simetría, la combinatoria, las sucesiones numéricas, los números binarios, las funciones matemáticas, los fractales o la geometría, en su búsqueda de una belleza musical objetiva.
Un ejemplo ilustrativo podría ser la pieza musical Tango, que Tom Johnson compuso en 1984 para el virtuoso pianista estadounidense Yvar Mikhashoff, y para la cual utilizó el concepto matemático de las permutaciones. Si se toman cinco objetos cualesquiera, ya sean cinco números o cinco notas, existen 120 formas diferentes de colocarlos en orden, es decir, 120 permutaciones de los mismos. En concreto, el factorial de 5, 5! = 5 × 4 × 3 × 2 × 1 = 120, como ya explicamos en las entradas Cuadrados latinos, matemáticas y arte abstracto y El problema matemático de las cartas extraviadas o en el video La combinatoria, de la sección Una de Mates, en el programa de TV2 Órbita Laika.
Por lo tanto, si se toman cinco notas, hay 120 permutaciones distintas de esas cinco notas. Como puede apreciarse en la imagen de la partitura que mostramos más abajo, las cinco notas de partida son [Re, Fa, Sol(#), La, Si(Ь)], y estas se van permutando [Re, Fa, Sol(#), Si(Ь), La], [Re, Fa, La, Sol(#), Si(Ь)], [Re, Fa, La, Si(Ь), Sol(#)], [Re, Fa, Si(Ь), Sol(#), La], [Re, Fa, Si(Ь), La, Sol(#)], y así hasta las 120 permutaciones que utiliza el compositor Tom Johnson para crear esta hermosa pieza, cuyo título es Tango, y que tiene un acompañamiento con ritmo argentino.

Primera parte de la partitura de la obra “Tango” (1984), de Tom Johnson. La partitura la podéis encontrar gratis en la página del compositor Tom Johnson.
Pero lo mejor es que escuchéis el resultado. A continuación, dos versiones de la obra Tango. La primera es la interpretada por el pianista argentino Alberto Neuman
mientras que la segunda está interpretada con la estación de trabajo de audio digital Renoise,
Pero vayamos al tema de esta entrada del Cuaderno de Cultura Científica, las “teselaciones rítmicas perfectas”, un concepto matemático que ha sido introducido por el compositor Tom Johnson, mientras estudiaba algunos conceptos matemáticos para utilizarlos en la creación de nuevas piezas musicales.
Durante los años 2002 y 2003, Tom Johnson estuvo trabajando en lo que se conoce como teselaciones rítmicas, que son una traslación a dimensión uno, a la línea de tiempos musicales, del concepto clásico de teselación del plano o del espacio. Este trabajo dio lugar a su disco Tilework: 14 Pieces for 14 Solo Instruments (2003).
Pero el concepto de teselaciones rítmicas perfectas se le ocurrió a Tom Johnson intentando formular un equivalente en dimensión uno a lo que en matemáticas se conoce como las teselaciones perfectas del cuadrado o el problema de la cuadratura del cuadrado. Una teselación perfecta de un cuadrado es una teselación del cuadrado mediante cuadrados más pequeños, luego los cuadrados pequeños cubren el cuadrado original sin superponerse unos con otros, pero además con la condición de que todos los cuadrados de la teselación tengan diferentes tamaños.
La primera teselación perfecta de un cuadrado se obtuvo en 1938 por Cedric Smith, Arthur Stone, Leonard Brooks y William Tutte, conocidos como “Los cuatro de Trinity” (puede verse la historia de estos en la entrada Blanche Descartes y la cuadratura del cuadrado), utilizando para ello 69 cuadrados de diferentes tamaños. La teselación perfecta del cuadrado con menos cuadrados posibles, neceisita 21, y fue obtenida por A. J. Duijvestijn en 1978.
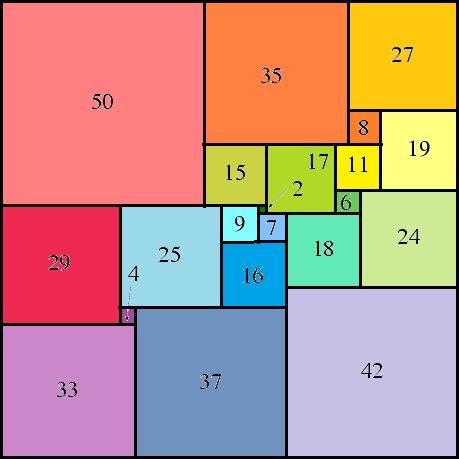
Teselación del cuadrado con 21 cuadrados, dada por A. J. Duijvestijn en 1978, cuyos lados tienen longitud igual a 50, 35, 27, 8, 19, 15, 17, 11, 6, 24, 29, 25, 9, 2, 7, 18, 16, 42, 4, 37, 33
Tom Johnson propuso teselar, o rellenar, la línea de los números {0, 1, 2, … , m – 1, m} (pensemos en los tiempos musicales) con tríos de números que formen progresiones aritméticas (cada trío de números en progresión aritmética, es decir, de la forma a, a + r, a + 2r, como por ejemplo, 5, 7 y 9, son las baldosas de la teselación), de forma que entre todas esas progresiones aritméticas de tres números (las baldosas) llenen el espacio de la línea de los números, que no se superpongan, es decir, no haya números que estén en más de una progresión, y que cada progresión aritmética tenga una diferencia r, llamada “tempo” por Tom Johnson, diferente. El orden n de la teselación rítmica perfecta es el número de baldosas, esto es, progresiones aritméticas. Aquí el número de términos de cada progresión es tres, pero más adelante extenderemos la noción a progresiones aritméticas con más elementos, el índice.
Claramente, la cantidad de números que abarca una teselación rítmica perfecta de orden n (con índice 3) es 3n, desde 0 al 3n – 1.
La mejor manera de entender el concepto es mediante un ejemplo. Aquí mostramos el ejemplo que utiliza Tom Johnson, que es de orden 5 y que tesela los quince primeros números {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15} mediante las siguientes teselas: (2, 3, 4), (8, 10, 12), (5, 9, 13), (1, 6, 11) y (0, 7, 14), cuyas diferencias son 1, 2, 4, 5 y 7, todas ellas distintas.
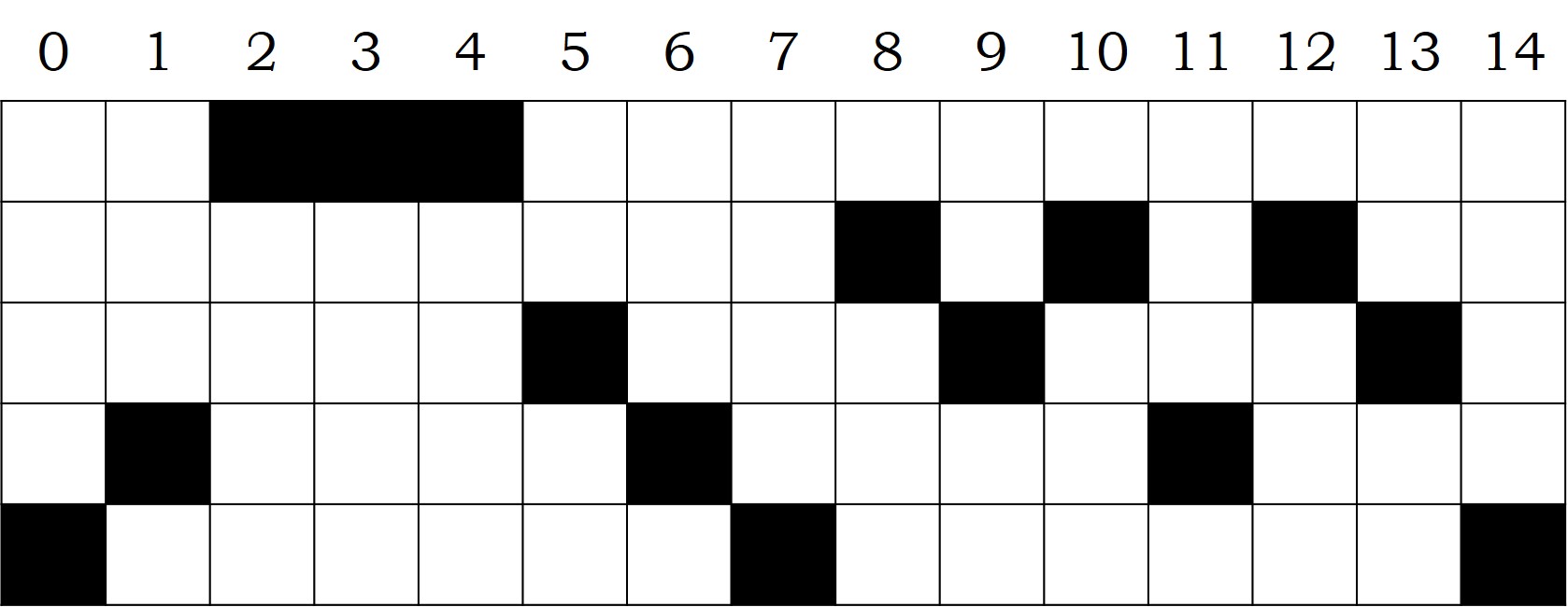
Teselación rítmica perfecta introducida por Tom Johnson y utilizada para su composición “Tileworks for Piano” (2003)
Utilizando esta teselación rítmica perfecta, con 5 teselas (tríos) diferentes y cuyos tempos (diferencias), de graves a agudos, son 7, 5, 4, 2 y 1, Tom Johnson compuso la pieza Tileworks for Piano (2003). La siguiente imagen que se ha extraído del libro Mathemusical Conversations, Mathematics and Computation in Music Performance and Composition (2016) explica, con la partitura original, el uso de esta teselación rítmica perfecta en la pieza.
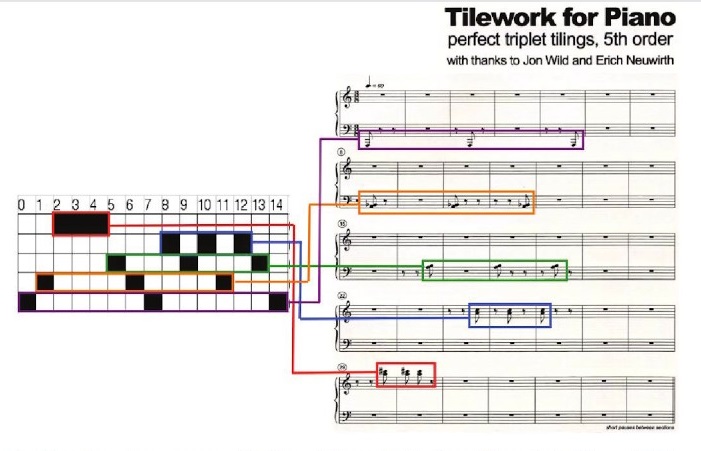
Pero escuchemos la pieza Tileworks for Piano compuesta por Tom Johnson, y que podemos encontrar en la página del compositor: Tileworks for Piano.
Como el propio compositor puso de manifiesto en el texto de la conferencia que impartió en 2004 en el Seminario MaMuX (Matemáticas, Música y relaciones con otras disciplinas), del IRCAM (Institut de Recherche et Coordination Acoustique/Musique), con el título Perfect Rhythmic Tilings, no existen teselaciones rítmicas perfectas de orden 2 (es decir, dos tríos que llenen seis tiempos, seis números), ni 3 (tres tríos que llenen 9 tiempos), ni 4 (cuatro tríos que teselen la línea de 12 números). Solo hay una de orden 5, que es la dada por Johnson, y su simétrica. Tampoco hay teselaciones rítmicas perfectas de orden 6. De orden 7, hay 9 soluciones, con sus simétricas, luego 18. Una de ellas la siguiente, cuyas diferencias son 1, 2, 4, 5, 7, 8 y 10.

En la Enciclopedia On-line se Sucesiones de Enteros aparece la sucesión A261516 del número de teselaciones rítmicas perfectas de {0, …, 3n – 1} con tríos (sucesiones aritméticas de tres números), en función del orden n, la cual empieza así
1, 0, 0, 0, 2, 0, 18, 66, 382, 1.104, 4.138, 15.324, 61.644, etc
Por ejemplo, hay 61.644 teselaciones rítmicas perfectas de orden 13 (sobre los primeros 39 números). Y se conoce hasta el orden 19.
De forma obvia, el concepto de teselaciones rítmicas perfectas se puede extender a progresiones aritméticas (baldosas) con cualquier número de elementos, no necesariamente tres. Por lo tanto, una teselación rítmica perfecta de orden n e índice k estaría dada por n progresiones aritméticas con k números cada una de ellas, a, a + d, a + 2d, …, a + kd, que cubren toda la línea de números {0, 1, 2, …, nk – 1}, que no se solapan, y tal que las diferencias d de las progresiones aritméticas son todas distintas.
En su texto Perfect Rhythmic Tilings, Tom Johnson estudió las teselaciones rítmicas perfectas con índices k = 2 y 3, es decir, con 2 y 3 números por progresión aritmética, pero dejó abierto el problema de la existencia de teselaciones rítmicas perfectas para k = 4. Afirmó que no existían tales teselaciones para órdenes menores, o iguales, que 7, pero quedaba abierto el problema para órdenes mayores.
Shalosh B. Ekhad (de quien ya hablamos en la entrada El extraño caso del matemático Shalosh B. Ekhad ) y Lara Pudwell resolvieron el problema planteado por Tom Johnson construyendo una teselación rítmica perfecta de índice 4 y orden 15, que es el orden más bajo posible para el índice 4, sobre los 60 primeros números. Es la siguiente…
[0, 16, 32, 48], [1, 3, 5, 7], [2, 13, 24, 35], [4, 22, 40, 58], [6, 21, 36, 51], [8, 14, 20, 26], [9, 10, 11, 12], [15, 29, 43, 57], [17, 25, 33, 41], [18, 30, 42, 54], [19, 23, 27, 31], [28, 37, 46, 55], [34, 39, 44, 49], [38, 45, 52, 59], [47, 50, 53, 56],
cuyas diferencias son 16, 2, 11, 18, 15, 6, 1, 14, 8, 12, 4, 9, 5, 7, 3.

Siguiendo los pasos de Tom Johnson, el compositor estadounidense Dean Rosenthal (Concord, Massachusetts, EE. UU., 1974) utiliza esta teselación rítmica perfecta, pero reordenando las diferencias de mayor a menor, para componer la pieza Perfecto para… violín (2011), que podéis escuchar, interpretada por la violinista y compositora Morgan Gerstmar, en la página de Dean Rosenthal.
Tras el ejemplo de Ekhad y Pudwell de teselación rítmica perfecta de índice 4, se han estudiado más en profundidad este tipo de teselaciones. Así, en la página Enciclopedia On-line se Sucesiones de Enteros aparece la sucesión A261517 del número de teselaciones rítmicas perfectas de {0, …, 4n – 1} con cuartetos (sucesiones aritméticas de cuatro números), en función del orden n, que es la siguiente (se conoce hasta el orden 23)
1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 2, 24, 38, 96, 444, 1.414, 5.134, 19.490
Para terminar esta entrada de la sección Matemoción del Cuaderno de Cultura Científica vamos a considerar un tipo especial de teselaciones rítmicas perfectas.
Dado el concepto de teselación rítmica perfecta de orden n e índice k, nos podríamos plantear si existen ejemplos de estas teselaciones pero con la propiedad de que las diferencias no solo sean diferentes, sino que sean todos los números entre 1 y n. A estas se las llama teselaciones rítmicas super perfectas.
Ninguno de los ejemplos de teselaciones rítmicas perfectas que hemos presentado hasta el momento son super perfectas. Por ejemplo, las diferencias del ejemplo de Tom Johnson son 1, 2, 4, 5 y 7, mientras que para que fuesen super perfectas deberían ser 1, 2, 3, 4 y 5.
Veamos un par de ejemplos. Una teselación rítmica super perfecta de índice 2, es decir, mediante pares de números, de orden 4, es (0, 4), (1, 3), (2, 5) y (6, 7).

Y un ejemplo, que encontramos en el artículo Perfect Rhythmic Tailings de Jean-Paul Davalan, con orden 9 e índice 3 (es decir mediante tríos de números) es (0, 6, 12), (1, 8, 15), (2, 11, 20), (3, 5, 7), (4, 9, 14), (10, 18, 26), (13, 16, 19), (17, 21, 25) y (22, 23, 24).

Las teselaciones rítmicas super perfectas ya existían en la literatura matemática, pero descritas desde otro punto de vista, bajo el nombre de sucesiones de Skolem (relacionadas también con las sucesiones de Langford).
Para explicar las sucesiones de Skolem, empecemos con el problema de los emparejamientos de Langford (para más información sobre el mismo puede consultarse el libro Del ajedrez a los grafos, La seriedad matemática de los juegos, que aparece en la bibliografía).
El origen de este juego se remonta a 1958, cuando el matemático escocés C. Dudley Langford publicó en la revista Mathematical Gazette el que es conocido como problema de los emparejamientos de Langford, o simplemente problema de Langford. En este artículo explicaba que viendo a su hijo pequeño jugar con un juguete de cubos de colores, dos de cada color, observó que había formado una torre de cubos, de tal forma que los dos cubos rojos estaban separados por un único cubo, los dos azules por dos cubos y había tres cubos entre los dos amarillos. Entonces se planteó si, añadiendo los dos cubos verdes podía mantener la propiedad anterior y que además hubiese una separación de cuatro cubos entre los dos verdes.
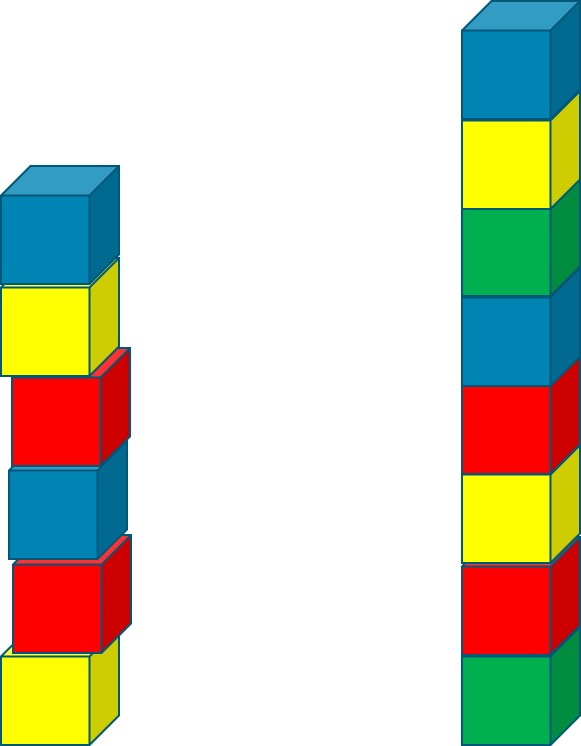
Torre de cubos rojos, azules y amarillos similar a la formada por el hijo de Langford, así como la compuesta por el matemático escocés al añadir dos cubos verdes
En su artículo, Langford reemplazó los cubos de colores por números y formuló el problema que lleva su nombre, en el que se plantea si es posible, y cómo, distribuir parejas de los números del 1 hasta n, de forma que entre los dos 1 haya un único número, entre los dos 2 haya dos, entre los dos 3 haya tres, así hasta los dos números n, entre los que habrá n números, es decir, si denotamos como ad la primera posición en la que aparece el número d (por ejemplo, contando desde la izquierda) y como bd la segunda, entonces
bd – ad = d + 1, para d = 1, 2, …, n.
A una tal distribución de los 2n números 1, 1, 2, 2, …, n, n se le llama sucesión de Langford. Por ejemplo, para n = 4 una solución es:
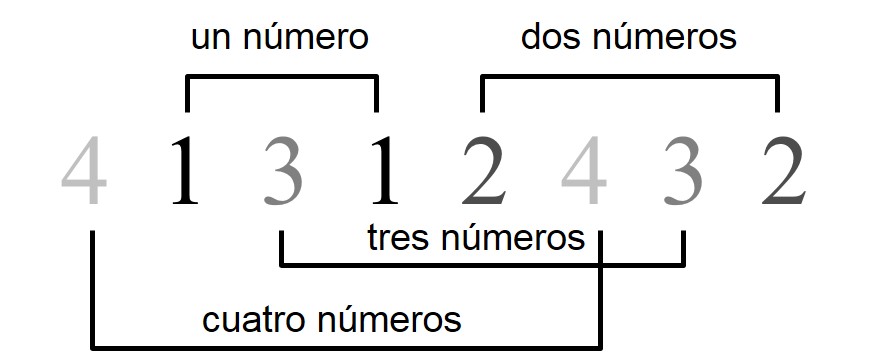
El problema de Langford, ya se formule con cubos de colores o con números, se puede extender a cualquier cantidad de cubos de colores o copias de cada número de 1 a n, así como el concepto de sucesión de Langford asociado, de tipo (k, n), es decir, con k copias de los números 1, 2, …, n. Por ejemplo, a continuación se muestra una sucesión de Langford de tipo (3, 9):
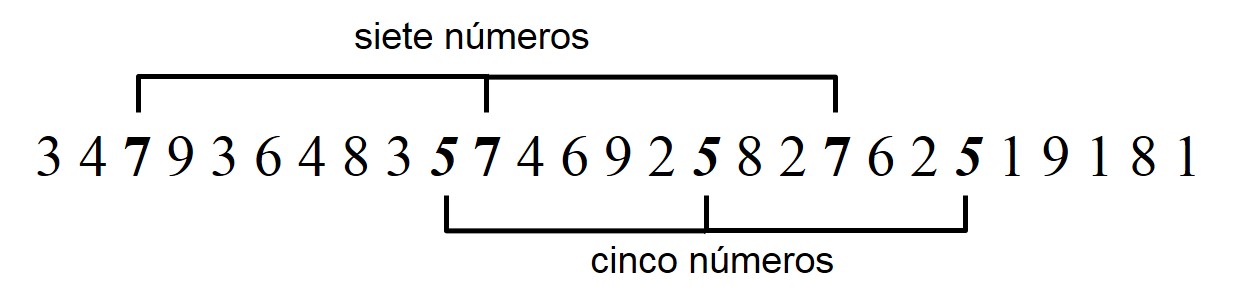
Mientras que C. Dudley Langford planteó este problema sobre la existencia de estas sucesiones numéricas en el contexto de la matemática recreativa, un problema similar surgió en 1957 en la investigación del matemático noruego T. H. Skolem sobre sistemas triples de Steiner, que son unos objetos matemáticos que pertenecen a la teoría del diseño combinatorio. Aunque en su investigación la condición matemática era que
bd – ad = d, para d = 1, 2, …, n,
es decir, los dos números 1 están juntos, los dos 2 tienen un número entre ellos, hay dos posiciones entre los 3, y así para el resto.
Así un ejemplo de sucesión de Skolem para parejas de números, para n = 4, sería
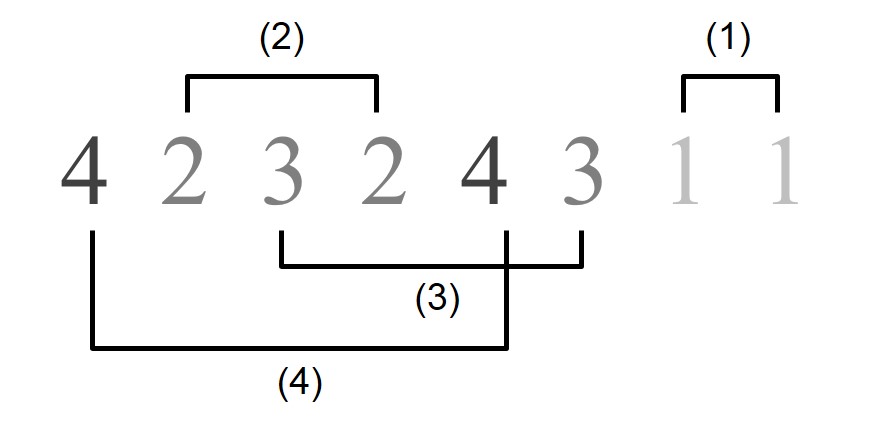
Y un ejemplo para tríos, esto es, de sucesiones de Skolem de tipo (3, 9) sería:
6, 7, 9, 2, 5, 2, 6, 2, 7, 5, 8, 9, 6, 3, 5, 7, 3, 4, 8, 3, 9, 4, 1, 1, 1, 4, 8.
La condición de la sucesión de Skolem es realmente la misma que la de teselación rítmica super perfecta. Si tenemos una sucesión de Skolem de tipo (k, n), es decir, con n números distintos que se repiten k veces cada uno, tendremos una teselación rítmica super perfecta de la siguiente forma.
La línea de números que vamos a teselar son las nk posiciones de la sucesión de Skolem, empezando a contar desde la posición 0, es decir, desde 0 hasta nk – 1. Ahora, cada número de la sucesión de Skolem, que se repite k veces, va a ser una de las progresiones aritméticas de k números (nuestras baldosas), ya que la diferencia de los elementos de la progresión aritmética es d, la diferencia de las posiciones de cada dos números iguales (que además toma valores de 1 a n). Así, la sucesión de Skolem para pares de números anterior, 42324311, dará lugar a la teselación rítmica superperfecta (0, 4) –que son las posiciones del 4–, (1, 3) –que son las posiciones del 2–, (2, 5) –que son las posiciones del 3– y (6, 7) –que son las posiciones del 1–. De la misma forma, la sucesión de Skolem de tipo (3,9) anterior, no es más que la teselación rítmica super perfecta de orden 9 e índice 3, que hemos visto anteriormente.
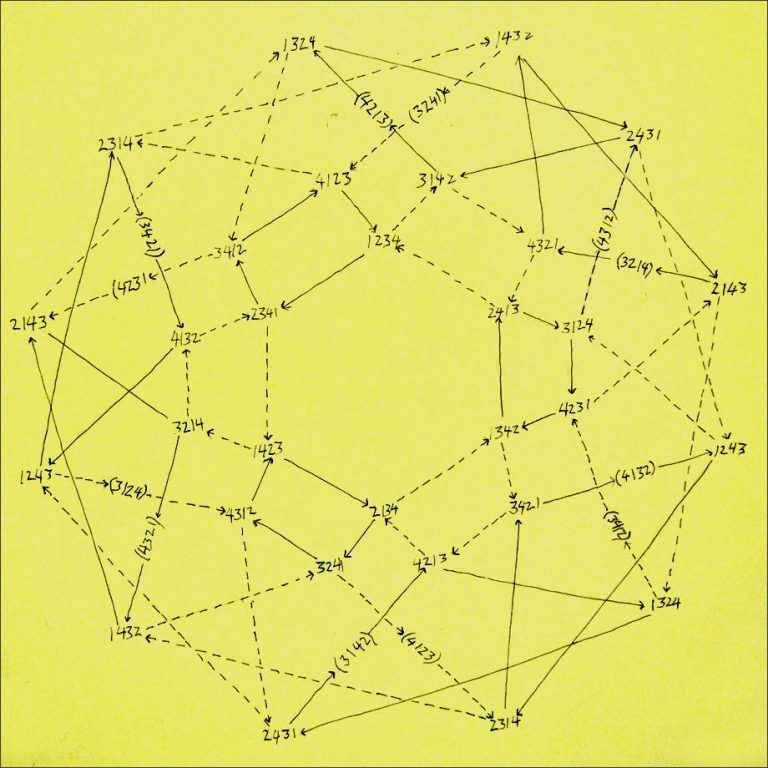
“Las 24 permutaciones de 1, 2, 3, 4 permutadas por (1234) con líneas sólidas y por (1342) por líneas interrumpidas” (2011), de Tom Johnson. Diseño en papel
Bibliografía
2.- Tom Johnson, Perfect Rhythmic Tilings, Lecture delivered at MaMuX meeting, IRCAM, 2004. Versión on-line en Editions75
3.- Tom Johnson, Tiling the Line in Theory and Practice, Lecture delivered at MaMuX meeting, IRCAM, 2002. Versión on-line en Editions75
4.- Tom Johnson, Tiling in my music, Perspectives in New Music 49, n. 2, p. 23-31, 2011.
5.- Jordan B L Smith, Elaine Chew, Gérard Assayag (editors), Mathemusical Conversations, Mathematics and Computation in Music Performance and Composition, (Lecture Notes Series, Institute for Mathematical Sciences, National University of Singapore 32), World Scientific, 2016.
6.- Jean-Paul Davalan, Perfect Rhythmic Tilings, Perspectives of New Music, vol. 49, n. 2, p. 144-197, 2011.
7.- Shaloh B. Ekhad, Lara Pudwell, A Perfect Rhythmic Tiling of Quadruplets, The Personal Journal of Shalosh B. Ekhad and Doron Zeilberger, 2004.
8.- Raúl Ibáñez, Del ajedrez a los grafos, La seriedad matemática de los juegos, colección El mundo es matemático, National Geographic, 2015.
9.- Tom Johnson, Looking at numbers, Birkhäuser, 2014.
10.- Exposición “Tom Johnson”, en Bains-Douches (d’Alençon, Francia), Febrero, 2018
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Teselaciones rítmicas perfectas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las vacas de Narayana, la versión hindú de los conejos de Fibonacci
- Uno, dos, muchos
- La magia del teorema de Zeckendorf
Zeruko keinukari erraldoien misterioa goitik behera azaltzea lortu dute
Ohiko esperimentua da ikasgeletan, eta, aurreneko aldiz ikusten denean, harrigarria izaten da: paper baten gainean burdin txirbilak zabaldu, eta behean iman bat jarri. Imanak sorraraziko eremu magnetiko ikusezinei jarraituz, bat-batean, txirbilek estruktura zehatza osatzen dute paperaren gainean. Natura moldatzen duten indarrak irudikatzeko esperimentu sinple bezain eraginkorra da.
Zientzialariek ere antzeko amarruak erabili behar dituzte paper baten gainean kabitzen ez diren eremu magnetiko handiagoak azalarazteko. Munduan zehar sakabanatuta dauden magnetometroen bitartez, noski, posible da horiek ikertzea, eta zenbait satelitetan ere magnetismoa neurtzeko halako gailuak daude. Bestetik, argi polarizatua erabil daiteke; adibidez, eguzkiaren magnetismoa aztertzeko.

1. irudia: Ohiko auroren aldaera bereziak dira aurora taupakariak. Hauek ere poloetan ikusten dira, baina euren jatorria ekuatore magnetikoan dago. (Argazkia: Joshua Earle/Unsplash)
Baina, batzuetan, paisaia hutsak ikustea nahikoa izan daiteke begi hutsez ikusezinak diren indar harrigarri horiek atzemateko. Kasurako, poloen inguruetan ikusten diren aurorak. Horiek ikusteko pribilegioa dutenek zientzia eta edertasuna biltzen dituen ikuskizunaz gozatzen dute.
Ezaguna da fenomenoaren atzean dagoen zientzia azalpena. Eguzki haizeak bidalitako partikulak Lurraren eremu magnetikoaren poderioz planetara inguratzen dira, eta “autobide” magnetiko horren bitartez atmosferara heltzen dira. Bertan dauden molekulen aurka jotzen dutenean sortzen dira argi zoragarriak. Elementu kimiko nagusiaren arabera (oxigenoa eta nitrogenoa, batez ere) eta altueraren arabera kolore bat ala bestea margotuko da zeruan.
Aurora horiek, ordea, ez dira mota bakarrekoak. Aurora taupakariak poloen inguruan izan ohi den fenomeno ezagunaren aldaera bereziak dira. Ohiko aurorek ez bezala, aldizkako pultsu edo taupada ikusgarriak “marrazten” dituzte zeruetan, batez ere goizaldean (NASAren Eguneko irudi astronomikoa zerbitzu ezagunean, adibide ikusgarri bat dago hemen) Kasu honetan, prozesua ez da abiarazten goiko atmosferan, magnetosfera urrunean baizik: 30.000 kilometro ingurura. Argiak poloetan ikusten badira ere, fenomenoak planetaren ekuatore magnetikoan du abiapuntua. Behin elektroi horiek “erorita”, poloen inguruan pultsu ikusgarriak agertzen dira: zeruetan jarritako keinukari erraldoiak balira bezala azaltzen dira ortzian.
Orain arte ez zegoen argi aurora berezi horiek nola sortzen diren. Eredu teorikoek eskema bat irudikatzen bazuten ere, behin betiko azalpena falta zen. Behaketan oinarritutako berrespena 2018an iritsi da. Nature aldizkarian argitaratutako artikulu batean, Japoniako, Taiwango eta Ameriketako Estatu Batuetako ikertzaileek lehenengo aldiz aurora taupakariak nola sortzen diren deskribatu ahal izan dute.
Eremu magnetikoan dauden elektroien eta eguzkitik datorren plasma uhinen arteko elkarrekintzaz abiatzen da fenomenoa, magnetosferan. Plasma uhin hauek “koru” uhin gisa ere ezagunak dira. Aurretik, jakina zen koru uhinek elektroiak garraiatzen dituztela atmosferara, eta argia isurtzeko gai zirela, baina orain arte ez zegoen argi elektroi horiek aurorak sortzeko bezain indartsuak ote ziren. Aurkeztutako datuek hipotesi hori berretsi dute.
Sentsore berezia
Gakoa erabilitako sentsoreetan datza. Orain arte erabilitako gailuak ez ei ziren gai bereizteko ohiko elektroiak eta atmosferara jauzitako elektroiak. Tokioko Unibertsitateko (Japonia) ikertzaile Satoshi Kasahara-ren taldeak, berriz, elektroi hauek bereizteko moduko gailua eratu eta ERG izeneko satelitean jarri zuen.

2. irudia: JAXA Japoniako Espazio Agentziaren ERG satelitearen bitartez egin dute aurkikuntza. (Argazkia: ISAS/JAXA)
JAXA Japoniako Espazio Agentziaren satelite hau berariaz prestatuta dago energia eta erradiazioa neurtzeko. Satelitearen bitartez, ikertzaileek magnetosferan dauden plasma uhinak zein elektroiak neurtu dituzte. Bestetik, Lurrean kokatutako neurketak egin dituzte, Kanadako erdialdean (The Pas izeneko hiritik gertu, Manitoban). 2017ko martxoan burutu dituzte behaketak. Zehazki, ortzi osoko irudiak eskuratzeko gai den kamera bat erabili dute, all-sky motakoa. Bi behatokietako datuak baliatuta, eureka aldarrikatzeko unea heldu zaien ikertzaileei: komunitate zientifikoari prozesu osoaren azalpena emateko garaia, hain zuzen.
Bideoa: Aurora taupakariak. ERG satelitearen behaketak.
Nature aldizkariaren ale berean egindako iruzkin batean, Iowako Unibertsitateko (AEB) Allison N. Jaynes fisikariak aurkikuntzaren garrantzia azpimarratu du. “Kasaharari eta haren kideei esker, aurrenekoz, aurora taupakarien sorreraren prozesua bere osotasunean ikusteko aukera izan dugu: kanpo espazioan dauden elektroien gorabeherak, gorabehera hauen erantzule diren koru uhinak, eta Lurretik ikusten diren auroren argiaren indarrean izaten diren aldaketak”.
Adituak etorkizunari begira irekitzen diren aukerak azpimarratu ditu. “Ereduetan azaldutako aztarnen kokapena eta behatutako kokapena alderatuta, teknika honek izugarrizko potentziala dauka orain ditugun eredu magnetikoen ereduak frogatzeko eta txukuntzeko”.
Erreferentzia bibliografikoa:
Kasahara, S. et al. Pulsating aurora from electron scattering by chorus waves. Nature volume 554, pages 337–340 (15 February 2018) DOI:10.1038/nature25505
———————————————————————————-
Egileaz: Juanma Gallego (@juanmagallego) zientzia kazetaria da.
———————————————————————————-
The post Zeruko keinukari erraldoien misterioa goitik behera azaltzea lortu dute appeared first on Zientzia Kaiera.
El control nervioso de la respiración
La mayor parte de los animales necesitan respirar continuamente. Por esa razón, los movimientos que proporcionan o permiten el flujo de medio respiratorio al órgano correspondiente son generados por programas rítmicos innatos que corren a cargo de estructuras neuronales específicas y pueden operar independientemente de los centros encefálicos superiores. Esos centros procesan señales procedentes de quimiorreceptores que reciben información relativa a la concentración de los gases respiratorios en el fluido interno que los transporta. Y como consecuencia de la valoración de esa información emiten señales que regulan la concentración de esos gases mediante un sistema de retroalimentación negativa. La ventilación traqueal de insectos terrestres parece estar regulada mediante señales enviadas por los ganglios metatorácicos. Y en los vertebrados el ritmo respiratorio viene marcado por el centro respiratorio ubicado en el tronco encefálico.
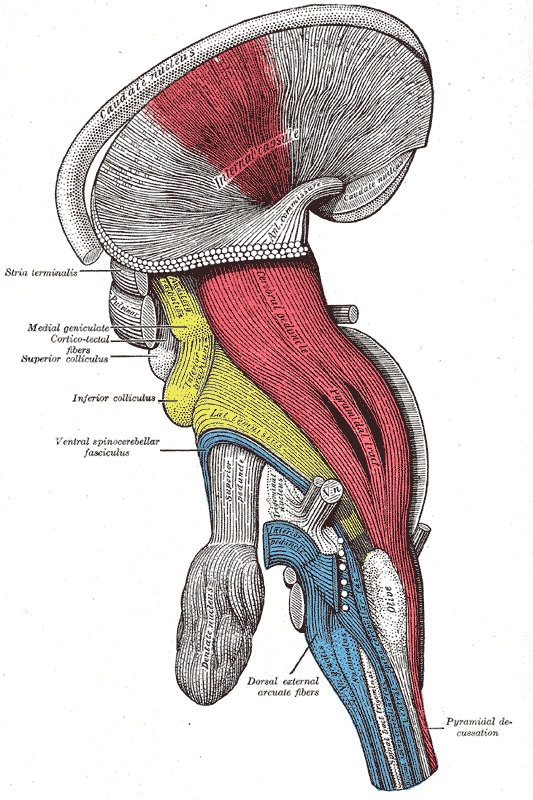
Tronco del encéfalo humano. Ilustración de “Anatomía” de Gray (1918)
En los vertebrados, el control nervioso de la respiración tiene tres componentes: (1) el programa generador de patrones, para el ritmo alternante de inspiración/espiración; (2) los factores que regulan la intensidad de la ventilación (frecuencia y profundidad de la respiración) para ajustarla a las necesidades; y (3) los factores que modifican la actividad respiratoria para que sirva a otros propósitos (como hablar, por ejemplo); en este último caso, los centros superiores pueden tomar parte en el control.
En mamíferos, con independencia de cuál sea el nivel de consumo de oxígeno o de la producción de dióxido de carbono por parte de los tejidos, las tensiones parciales de oxígeno (tO2) y de dióxido de carbono (tCO2) de la sangre arterial que abandona los pulmones presentan una considerable constancia, lo que indica que ambas magnitudes están sometidas a un estricto control.
En los mamíferos, el principal centro de control respiratorio es el centro respiratorio medular, que consta de dos grupos o agregaciones de cuerpos celulares neuronales en el interior de la médula: el grupo respiratorio dorsal y el grupo respiratorio ventral. Pero además de ese centro principal, hay otro grupo respiratorio en el puente troncoencefálico (puente de Varolio), formado a su vez por dos áreas: el centro neumotáxico y el centro apnéustico.
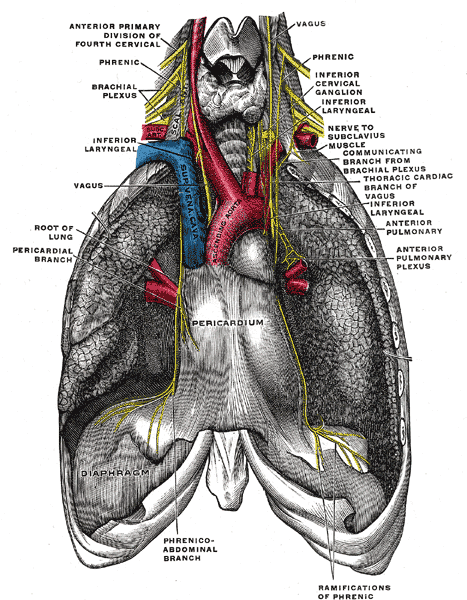
Inervación de los pulmones humanos. Ilustración de “Anatomía” de Gray (1918)
El nervio frénico y los nervios intercostales son los que transmiten las órdenes motoras al diafragma y músculos intercostales que provocan los movimientos rítmicos de contracción y relajación de la caja torácica. Los cuerpos celulares de esos nervios se encuentran en la médula espinal (espina dorsal) y reciben señales del centro respiratorio medular. Cuando esas neuronas motoras estimulan los músculos inspiratorios, provocan el movimiento de inspiración; la espiración se produce cuando esas neuronas no transmiten impulsos. El grupo dorsal del centro respiratorio medular consta principalmente de neuronas inspiratorias, cuyas fibras descendentes establecen sinapsis con las motoneuronas de la médula espinal citadas. El grupo ventral se encuentra interconectado con el dorsal, y está compuesto tanto por fibras inspiratorias como espiratorias. Pero este grupo se encuentra inactivo durante la respiración normal; solo interviene cuando debe elevarse la ventilación y es especialmente importante para intensificar la espiración. Durante la respiración normal (tranquila) no se envían señales a través de las vías descendentes de las neuronas espiratorias. Las motoneuronas que inervan los músculos espiratorios (abdominal e intercostales internos) solo son estimuladas cuando se requiere una espiración activa. Además, las neuronas inspiratorias del grupo ventral, cuando son estimuladas por el grupo dorsal, aceleran la actividad inspiratoria cuando las demandas ventilatorias aumentan.
La generación del ritmo respiratorio parece descansar en un área denominada médula rostral ventromedial, que se encuentra en la zona superior del grupo respiratorio ventral, en la que se han localizado redes neuronales que generan una actividad marcapasos. No obstante, no se conoce muy bien el mecanismo que da lugar a los movimientos respiratorios rítmicos.
Por su parte, los centros neumotáxico y apnéustico del puente de Varolio ejercen un control fino sobre el centro respiratorio medular que ayuda a suavizar los movimientos respiratorios. El centro neumotáxico envía señales al grupo respiratorio dorsal que ayudan a desconectar las neuronas inspiratorias, limitando así la duración de las inspiraciones. Por el contrario, el centro apneústico impide la desconexión de esas mismas neuronas, las inspiratorias. En ese sistema de contrapesos domina el centro neumotáxico, lo que contribuye a poner límites a la inspiración, permitiendo que la espiración curse con normalidad. Sin la acción del centro apnéustico el ciclo respiratorio consistiría en prolongadas espiraciones interrumpidas por inspiraciones rápidas y muy bruscas.
Como es lógico, la tasa ventilatoria se ajusta para satisfacer las demandas metabólicas de cada momento. Y en ese ajuste se valoran tres indicadores diferentes, la tO2, la tCO2 y el pH, aunque como veremos al final, hay circunstancias en que intervienen otras señales.
En mamíferos, la tO2 arterial es monitorizada mediante unos quimiorreceptores conocidos como cuerpos carótidos y cuerpos aórticos, que se localizan en las bifurcaciones de las arterias carótidas y en el arco de la aorta, respectivamente. En los peces hay quimiorreceptores similares a los de mamíferos pero se localizan en las branquias de forma difusa, y cuando esos receptores detectan una reducción en la tO2 se produce un aumento de la ventilación branquial. Sin embargo, en los vertebrados que respiran en aire las cosas son diferentes. Tiene que caer la tO2 hasta valores tan bajos como 60 mmHg (¡un 40%!) para que se produzca una respuesta por parte de los sistemas de control. La razón de que no haya respuesta a valores superiores de tO2 es que aunque estos sean relativamente bajos, el porcentaje de saturación de la hemoglobina es todavía alto (alrededor del 90% se encuentra combinada con O2). Sin embargo, por debajo de 60 mmHg la saturación del pigmento se reduce muy rápidamente, por lo que la situación se puede volver muy peligrosa y conducir a la asfixia. El pigmento amortigua los efectos de variaciones no demasiado grandes en la tO2 arterial, por lo que funciona, de hecho, como un reservorio de oxígeno que asegura el suministro a los tejidos siempre que la tensión arterial de oxígeno no se reduzca en exceso.
Un aspecto ciertamente llamativo de este sistema receptor es que al responder a la tO2, cualquier factor que reduzca la fracción de O2 combinado con el pigmento pero que no provoque una bajada en aquella, puede resultar fatal, ya que puede darse la circunstancia de que se produzca una caída muy fuerte en el contenido total de O2 en la sangre y ello no dé lugar a una respuesta respiratoria. Es lo que ocurre, por ejemplo, cuando altas cantidades de monóxido de carbono (CO) se unen con la hemoglobina desplazando al O2 de sus sitios de unión. Quienes se intoxican con CO no experimentan una elevación de la tasa ventilatoria en respuesta a la intoxicación porque el CO no provoca una reducción en la tO2 pero sí en el contenido total de oxígeno en la sangre.
Bajo condiciones de reposo, la tCO2 es el parámetro que más importancia tiene en el ajuste de la tasa ventilatoria en mamíferos. Al contrario de lo que ocurre con la tO2, pequeños cambios en la tCO2 dan lugar a una respuesta en la ventilación pulmonar. Un exceso de CO2 en la sangre genera una respuesta refleja a cargo de los centros respiratorios que provocan un aumento en la ventilación y, como consecuencia, la eliminación de tal exceso y la restauración de su nivel normal. Lo contrario ocurre cuando la tCO2 se reduce por debajo del nivel de referencia. La mayoría de los peces también ajustan su tasa ventilatoria en respuesta a las variaciones sanguíneas en la tCO2; se cree que los centros respiratorios reciben las señales de quimiorreceptores branquiales.
En la mayor parte de los animales que respiran en aire no se monitoriza la tCO2 arterial; de hecho, los cuerpos carótidos y aórticos responden muy levemente a los cambios en el nivel arterial de CO2. De mucha mayor importancia son los quimiorreceptores centrales, que se encuentran en la médula, en una posición muy próxima al centro respiratorio. Aunque en realidad, esos quimiorreceptores no monitorizan la concentración de CO2 directamente, sino la de protones –que depende de la anterior- en el líquido extracelular del encéfalo. Los peces sin embargo, parecen carecer de receptores centrales de ese tipo. De hecho, lo más probable es que los receptores centrales aparecieran en los sarcopterigios (peces pulmonados).
Se da la circunstancia de que el CO2 atraviesa la barrera hematoencefálica con gran facilidad, al contrario de lo que ocurre con los H+. Por ello, cuando se produce una elevación de la concentración de estos últimos en el líquido extracelular encefálico ello es señal de que se ha producido un aumento en la concentración de CO2 en el encéfalo.
El gran efecto que ejercen los quimiorreceptores centrales sobre el centro respiratorio es el responsable de que no podamos dejar de respirar a voluntad durante más de un minuto (las personas normales, claro). Cuando dejamos de respirar, la concentración de CO2 no deja de aumentar, porque el metabolismo no cesa y, en paralelo, también aumenta la concentración de protones. Ese aumento acaba ejerciendo un efecto tal sobre el centro respiratorio, que este supera las órdenes provenientes de los centros superiores y provoca la ejecución de los movimientos de los correspondientes músculos.
Dependiendo de las demandas de oxígeno del organismo y de la correspondiente necesidad de eliminar dióxido de carbono, la ventilación alveolar puede llegar a multiplicarse hasta por veinte. Lo curioso es que esa elevación no parece ser provocada por los cambios en las concentraciones de O2, CO2 y H+. De hecho, la concentración arterial de ninguna de esas sustancias experimenta cambios significativos al elevarse la tasa de ventilación pulmonar. Y por otro lado, el aumento de esa tasa se produce en el mismo instante en que se intensifica la actividad que da lugar a la elevación de las demandas metabólicas, pero mucho antes de que haya dado tiempo a que varíen las concentraciones de los gases respiratorios y de los protones en una medida suficiente como para provocar una respuesta regulatoria. Para eso habría hecho falta que transcurriera al menos un minuto, pero la respiración se acelera enseguida.
Son otros los mecanismos que determinan la aceleración de los movimientos respiratorios al iniciarse una actividad física. Y se han sugerido los siguientes: (1) Reflejos cuya génesis se encontraría en los propios movimientos musculares cuya actividad ha de sostenerse y que vendrían activados por señales procedentes de músculos y articulaciones; (2) elevación de la temperatura corporal; (3) liberación de adrenalina; y (4) control anticipatorio a cargo de la corteza cerebral. Como se ha señalado, se trata de posibles mecanismos; todos son verosímiles, pero ninguno de ellos o combinación de varios resultan satisfactorios para explicar el efecto tan marcado e intenso que ejerce el inicio de la actividad sobre la tasa ventilatoria.
Fuentes:
David Randall, Warren Burggren & Kathleen French (2002): Eckert Animal Physiology: Mechanisms and Adaptations 5th ed.; Freeman & Co, New York
Lauralee Sherwood, Hillar Klandorf & Paul H. Yancey (2005): Animal Physiology: from genes to organisms. Brooks/Cole, Belmont.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El control nervioso de la respiración se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El pulmón de los mamíferos
- La curva de disociación de un pigmento respiratorio
- Los animales que respiran en agua
Confirmación experimental de la teoría de la relatividad especial (1)
La teoría de la invariancia es una de las más comprobadas experimentalmente en física. Por lo tanto experimentos hay muchos, como debe ser, ya que la idea un solo experimento crucial es novelesca. No obstante recogemos en esta entrega y en la próxima algunos ilustrativos de las conclusiones de la teoría. Empezamos por el primer postulado de Einstein, que también debe probarse.
La velocidad de la luz en el vacío es constante.

Se ha obtenido una confirmación directa de la constancia de la velocidad de la luz a partir del estudio de las estrellas dobles, que son estrellas que orbitan una alrededor de la otra. Si la órbita de una estrella está en la línea de visión desde la Tierra, entonces en un lado de la órbita se está moviendo hacia la Tierra, en el otro lado se está alejando. Los estudios precisos de la velocidad de la luz emitida por estas estrellas cuando se acercan o alejan de nosotros a alta velocidad no muestran diferencia en la velocidad de la luz, lo que confirma que la velocidad de la luz es independiente de la velocidad de la fuente. Estos experimentos los propuso Willem de Sitter en 1913, y después se han comrpobado reiteradamente cada vez con mayor precisión.

Aún más espectacular es otro experimento que tiene que ver con una partícula a muy alta velocidad en un acelerador. Mientras la partícula se mueve cerca de la velocidad de la luz, emite radiación electromagnética en direcciones opuestas, hacia adelante y hacia atrás. Hay instrumentos sensibles que detectan la radiación y miden su velocidad. Por asombroso que pueda parecer para los no iniciados, la velocidad de la radiación emitida en ambas direcciones resulta ser exactamente la velocidad de la luz, a pesar de que la propia partícula se mueve cerca de la velocidad de la luz, una confirmación del postulado de la constancia de la velocidad de la luz.
Las pruebas experimentales son de tal calibre que la constancia universal de la velocidad de la luz es una ley física fundamental.
La relatividad del tiempo
La teoría de la relatividad predice que un reloj en movimiento, tal y como lo ve un observador estacionario, funcionará más lentamente que un reloj estacionario. Ya hemos mencionado que este efecto ha sido probado y confirmado utilizando relojes atómicos dentro de aviones y satélites.
Una confirmación de la relatividad del tiempo se encontró con la solución a un curioso rompecabezas. Los rayos cósmicos son protones, núcleos y otras partículas de alta velocidad que fluyen a través del espacio desde el Sol y la galaxia en su conjunto. Cuando chocan con las moléculas de la atmósfera de la Tierra su energía y su masa se convierten en otras partículas elementales, una confirmación en sí misma de la equivalencia energía-masa. Una de las partículas que se producen en la atmósfera es el llamado mesón mu, o simplemente el muón. Cuando se producen en el laboratorio, los muones lentos tienen una vida corta. En promedio, solo duran alrededor de 2,2·10-6 s, momento en el cual hay una probabilidad del 50 % de que cada uno se descomponga en otras partículas elementales.
El enigma está en que los muones que se crean en la atmósfera superior y que se mueven a gran velocidad se ha medido que “viven” más tiempo antes de desintegrarse que aquellos generados en el laboratorio. Duran tanto que sobreviven al largo viaje hasta los detectores en el suelo muchos más lo que debería ser posible. Teniendo en cuenta la velocidad con la que viajan y la distancia que deben recorrer desde la atmósfera superior hasta el nivel del mar (unos 30 km), su vida media de 2,2·10-6 s medida para muones lentos no debería ser suficiente para que sobrevivan al viaje. La mayoría de ellos debería desintegrarse antes de tocar el suelo; pero, el hecho cierto es que la mayoría llega al suelo. ¿Cómo es esto posible?
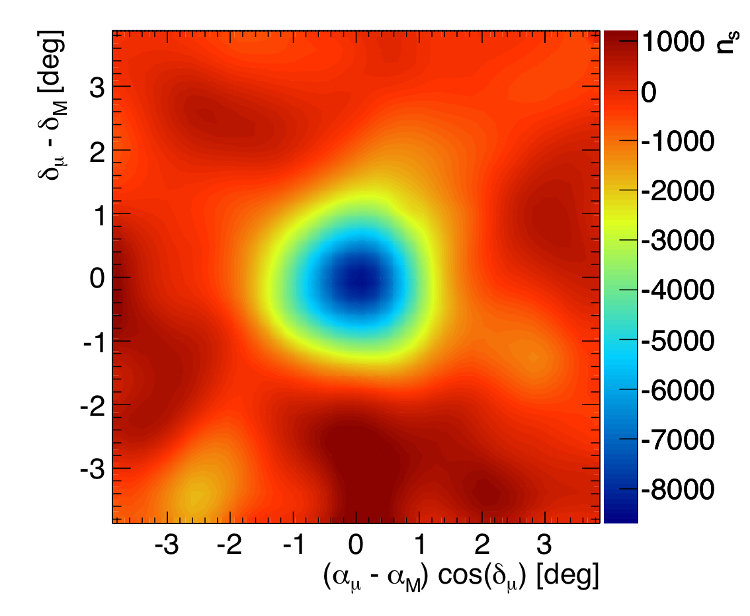
Déficit de muones observados por Ice Cube y que revelan la presencia de la Luna. Esto se debe a que los muones generados por los rayos cósmicos en las capas altas de la atmósfera llegan hasta el detector desde todas las direcciones del espacio, pero la Luna hace que disminuya el número que llegan desde su dirección.
La respuesta es la dilatación temporal predicha por la teoría de la relatividad. En relación con los detectores en el suelo, los muones se mueven a una velocidad tan alta que su “reloj” parece ralentizado, lo que les permite sobrevivir el tiempo suficiente para alcanzar el suelo. La cantidad de ralentización, según lo indicado por el número de muones que llegan al suelo, se encuentra que es exactamente la cantidad predicha por la teoría de la invariancia.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Confirmación experimental de la teoría de la relatividad especial (1) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La primera confirmación experimental de la teoría de Maxwell
- El principio de relatividad (3): la invariancia de Galileo
- La relatividad de la masa
Zer dakigu minbiziaz? Minbiziaren markak

1. irudia: Egun, minbizia gaixotasun hedatuenetariko bat da herrialde garatuetan.
Minbiziaren markakMinbizia da herrialde garatuetan gaixotasunek eragindako heriotzen bigarren kausa. Adierazle demografiko guztiek aditzera ematen dute gero eta zaharrago bilakatzen ari dela gure gizartea, eta minbizia zahartze prozesuari estuki lotuta dagoenez, urtero kasu berri gehiago diagnostikatzen dira. Hala ere, intzidentziak gora egin arren, minbizidun gaixoen biziraupena bakoitzean luzeagoa da. Honek esan nahi du aurrerapauso garrantzitsuak egiten ari direla gaixotasunaren ezagutzan. Baina, era berean, ikerketek eta tratamendu berrien agerpenak ageri-agerian jartzen dute minbiziaren konplexutasuna.
Ugariak eta anitzak dira ehun talde edo zelula talde normal batetik minbizi zelulak sortu eta tumore txar honen garapenean zehar emandako prozesu biologiko eta molekularrak. Minbizia oso gaixotasun heterogeneoa da, ez baitaude minbizi berdin bi. Baina hau horrela izanda ere, badira minbiziek bere bilakaeran zehar eskuratzen dituzten ezaugarri komun batzuk, Douglas Hanahan eta Robert Weinberg-ek Cell aldizkari ospetsuan “Minbiziaren Markak” (“Hallmarks of Cancer”) bezala definitu zituztenak (2. Irudia).
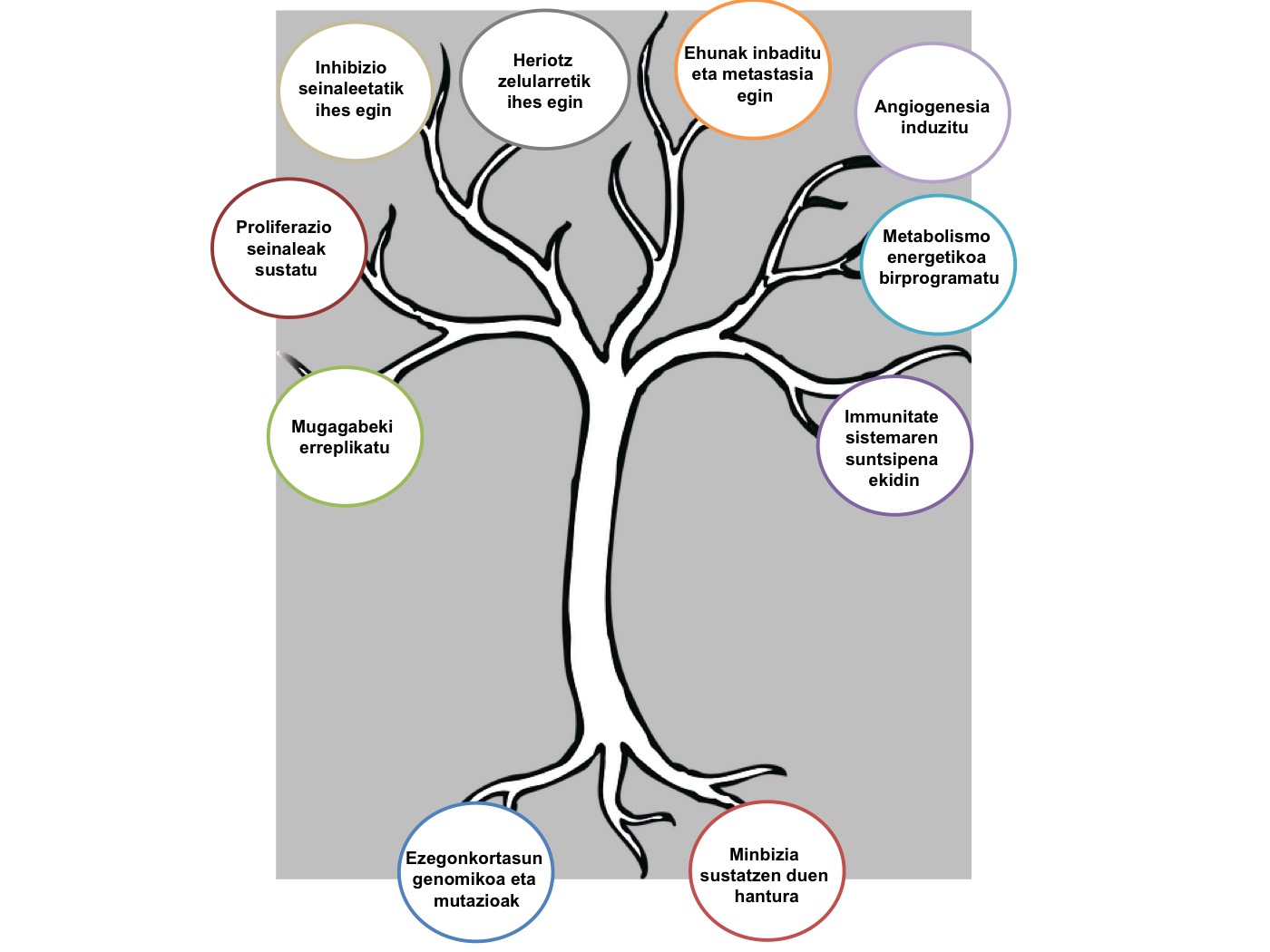
2. irudia: Minbiziaren Markak. Adarretan minbizi zelulek eskuratzen dituzten ezaugarriak edo markak ditugu. Sustraietan marka edo ezaugarri hauek ahalbidetzen dituzten fenomeno biologikoak. (Argazkia: Gorka Larrinaga, Iker Badiola eta José Ignacio López)
Gure ehunetako zelulen hazkundeak eta garapenak hainbat kontrol fisiologiko ditu prozesuak era egokian gerta daitezen. Zelulak maila edo intentsitate ezberdinetan banatzen dira mitosia izeneko prozesu batean, baina banaketa hauen kopurua mugatua da, belaunaldiz belaunaldi zelulen egitura eta funtzioa asaldatu egiten baita, seneszentzia izeneko prozesuan. Zahartzen doazen zelula hauek banatzeari uzten diote eta hil egiten dira. Gainera, zelulen hazkunde eta garapen anormala ekiditeko, gure zeluletan badago apoptosi izeneko programa antzeko bat, buru-hiltzea eragiteko prozesuak abian jartzen dituena.
Zelulen banatze eta hazkunde honen kontrola gure geneek ez ezik zelularen inguruan jariatutako substantzia ezberdinek ere egiten dute, hazkundea eta banaketa estimulatu edo inhibitzen dituzten mezulari kimiko ezberdinak daudelarik.
Minbizi-zelulek kontrol mekanismo hauek galdu edo eten egiten dituzte. Alde batetik, mugagabeki erreplikatzeko gaitasuna eskuratzen dute, eta hilezinak bilakatzen dira. Bestetik, zelula-heriotza programatutik, hau da, apoptositik ihes egin dezakete. Honez gain, euren hazkundea estimulatuko duten seinaleak sustatu eta, era berean, seinale inhibitzaileetatik ihes egiteko gaitasuna daukate.
Tumorea hazi ahala, mantenugai ezberdinen eskaria handitu egiten da, baita hondakin metabolikoak kanporatzeko beharrizana ere. Horretarako, ezinbestez sortu behar dira mantenugaiak eta metabolitoak garraiatuko dituzten odol-hodi berriak. Gure ehun helduetan, baldintza fisiologiko arruntetan, angiogenesia egoera gutxitan aktibatzen da, zaurien sendatze prozesuetan. Ordea, tumore zelulak angiogenesia induzitzeko gaitasuna daukate, eta horrela odol-hodi berrien ekoizpena tumorearen hazkundera egokitzen dute. Minbizi-zelulek prozesu hau estimulatzen duten seinaleak sustatu eta seinale inhibitzaileak mugatzeko gaitasuna eskuratzen dute.
Baina gaixoaren pronostikoa nabarmen baldintzatzen duen minbiziaren marka inguruko ehunak inbaditu eta metastasia aktibatzeko gaitasuna da. Minbizi-zelulek plastikotasun handia daukate, euren egituran aldaketa nabarmenak izan ditzaketelarik. Epitelio-mesenkima trantsizioa (EMT) izeneko prozesu konplexu bati esker, zelula hauek lehen mailako tumoreari (euren “sorterriari”) lotuta mantentzen dituzten “aingurak” jaso eta mugikortasuna eskuratzen dute. Horrela, inguruko ehunak inbaditu eta odol-hodi eta hodi-linfatikoetara sartzeko gai dira, bidai luzea eginez eta gorputzeko beste organo eta ehunetara helduz. Organo berri hauetan kolonizazioa gauzatzeko hainbat prozesu gertatu behar dira eta urteak luza daiteke kontua. Hauen artean bat mesenkima-epitelio trantsizioa da (MET), alegia EMT-aren alderantzizko prozesua. Fenomeno honen bitartez, minbizi-zelulek mugikortasuna galtzen dute, berriro aingurak botatzen dituzte, eta inguru berri batean sustraitu eta hazi egiten dira.
3. irudia: Minbizia gaixotasun konplexua eta heterogeneoa da. Horren adierazle dira azken urteotan ikerketek hartutako ikerlerro anitzak.
Mugagabeki erreplikatu eta ehunak inbaditzen doazen minbizi-zelulen energia-beharrizanak handiak dira. Beharrizan hauek asetzeko, angiogenesia sustatzeaz gain, metabolismo energetikoa birprogramatzen dute tumore-zelulek. Adibidez, tumore txar askotan glukosaren harmena nabarmenki handitzen da, energia lortzeko bere metabolismoa (glukolisia) eta hartzidura gailentzen baitira beste bide metabolikoekiko. Glukosaren harmena hobetzeko, minbizi-zelulen mintzetan zelula normaletan baino askoz garraiatzaile gehiago aurki daitezke mantenugai honen barneratzea errazteko. Fenomeno hau tumore batzuetan hain garrantzitsua delarik, gaur egun, tomografiaren bitartez irudizko diagnostikoa egiteko glukosaren antzeko molekula sintetikoak (erradioaktiboki markatuak) erabiltzen dira. Bai lehen mailako tumorean, bai metastasietan zelulek markatzaile erradioaktibo hau kantitate handiagotan hartzen dute eta, ondorioz, ondo ikus daitezke.
Etengabe banatzen doazen minbizi-zelulen ezegonkortasun genomikoa eta mutazio kopurua zelula normalena baino askoz handiagoa da. Honela, tumorearen garapenean zehar minbizi zelula talde edo klon ezberdinak bereizten doaz eta euren artean konpetentzia bat eratzen da, batzuk besteak baino hobeto egokitzen direlarik ingurune horretara. Mutazioen ondorioz klon batzuek banan-banan eskuratzen dituzte goian azaldu ditugun ezaugarri edo marka ezberdinak.
Gainera, mutazio batzuek minbiziaren tratamendu askorekiko erresistente bilakatzen dituzte zelula hauek. Beraz ezegonkortasun genomikoa eta mutazioak minbiziaren ezaugarrien oinarrian egoteaz gain, bere agresibitatearen eragile ere badira.
Baina tumore batean bakarrik dira protagonistak minbizi-zelulak? Zalantzarik gabe ez. Tumorearen mikroinguruan hainbat zelula ezberdin daude eta tumore-zelulekin izandako elkarrekintzak nabarmen baldintzatzen du minbiziaren bilakaera. Horregatik, azkeneko urteotan tumorearen mikroinguruaren ikerketa hainbat ikertalderentzako lerro estrategikoa bilakatu da.
Adibidez, minbiziaren diagnostikoa egiten duten patologoek aspaldidanik ikusi dute tumoreetan gure babes-zelula ezberdinak aurki daitezkeela. Horrela, esan izan da mikroinguru horretan tumore zelulei erasotzea dela leukozito, makrofago eta linfozitoen betebeharra. Baina, paradoxikoa dirudien arren, gaur egun badakigu tumorean sorturiko hanturak ekintza protumoralak ere izan ditzakeela eta onartu da ezegonkortasun genomikoa bezala, hantura ere minbiziaren ezaugarrien eragilea dela. Handitutako ehunean angiogenesia, hazkuntza zelularra, mutazio genikoak eta abarreko fenomenoak eragin ditzaketen mezulari kimikoak askatzen dira eta tumore-zelulek euren alde erabil dezakete askapen hau. Gainera, mutazio genetikoei esker, minbizi-zelulek immunitate-sistemaren suntsitzeari ihes egiteko gaitasuna ere eskuratzen dute (hurrengo artikulu batean azalduko dugun bezala).
Beraz, minbiziaren ikerketek aurrera egin ahala, gaixotasun oso konplexu bat dugula berretsi baino ez dugu egiten. Aurrerantzean ere, seguruenik, ezaugarri berriak aurkituko dira. Marka hauek ondo definitzea oso garrantzitsua izango da diagnostiko eta tratamendu bide berriak zabaltzeko. Bere ezaugarri ezberdinetan oinarritutako tratamenduak sortuz, eta baita ere hain heterogeneoa den gaixotasun honen aurrean ahalik eta tratamendu espezifiko edo zuzenenak lortuz, minbizia alderdi ezberdinetatik erasotzea erraztuko da.
Erreferentzia bibliografikoak:
– Hanahan D, Weinberg RA. The hallmarks of cancer. Cell, 2000; 100: 57-60.
– Hanahan D, Weinberg RA. The hallmarks of cancer: The next generation. Cell, 2011; 144: 646-674.
– Fouad YA, Aanei C. Revisiting the hallmarks of cancer. Am J Cancer Res 2017; 7:1016-36.
———————————————————————————-
Egileez:Gorka Larrinaga, UPV/EHUko Medikuntza eta Erizaintza Fakultateko ikertzailea eta Erizaintza Saileko irakaslea da.
Iker Badiola, UPV/EHUko Medikuntza eta Erizaintza Fakultateko irakaslea eta Zelulen Biologia eta Histologia Saileko ikertzailea da.
José Ignacio López, UPV/EHUko Medikuntza eta Erizaintza Fakultateko irakaslea eta Gurutzetako Unibertsitate Ospitaleko Anatomia Patologikoko Zerbitzu burua eta ikertzailea da.
———————————————————————————-
The post Zer dakigu minbiziaz? Minbiziaren markak appeared first on Zientzia Kaiera.
Asesinos en serie
Este capítulo, así como el que se refiere a la utilización política de la violencia que vendrá más adelante, no me dan para escribir mucho. Es un tema poco estudiado con enfoque científico y, a la vez, es muy popular. Una pequeña introducción, aclarar algunos conceptos y dejar hablar a los asesinos, ellos lo dicen todo y, espero, nos quedarán pocas dudas sobre lo que son. Y es difícil encontrar una explicación evolutiva a su existencia. Por ahora sigo en la duda.

Uno de los más famosos asesinos en serie, Jack “el destripador”, representado en una caricatura de “Punch” de 1888 como el fantasma de la muerte que recorre Whitechapel.
Los asesinos en serie, que forman parte de la humanidad desde siempre, y solo hay que recordar los 28 cadáveres de la Sima de los Huesos en Atapuerca, quizá más crimen en masa que asesinatos en serie, son el 1% del total en Estados Unidos, el país donde más abundan las investigaciones y las estadísticas sobre este asunto. Se define al asesino en serie como el que comete tres o más asesinatos en lugares y tiempos diferentes, con fases temporales de recuperación y con fallos emocionales o psicopatológicos. Pueden ser organizados o desorganizados, localizados o itinerantes, visionarios o controladores, y otros tipos.
Peter Kurten: La verdadera historia de Peter Lorre

“Tenía un pequeño cuchillo de bolsillo con el cual corté su garganta. Oí los chorros y el goteo de la sangre en la estera al lado de la cama. Salió a borbotones en un arco. La cosa entera duró cerca de tres minutos. Entonces salí, cerré la puerta otra vez y regresé a mi casa en Düsseldorf.”
Siempre recordaré a El Vampiro de Düsseldorf, con el rostro atormentado y los ojos saltones de Peter Lorre en la película, dirigida por Fritz Lang, estrenada en 1931, el mismo año en que el verdadero Vampiro fue ejecutado. Se llamaba Peter Kurten y había nacido el 26 de mayo de 1893 en Mülheim, que hoy forma parte de Colonia. Era el tercero de 13 hermanos de una familia pobre sometida a un padre alcohólico y violento que los maltrataba y llegó a violar a alguna de las hermanas de Peter; es probable que el mismo Peter también fuera violado. A los ocho años huyó de casa y cometió diversos delitos y eran frecuentes sus entradas y salidas de la cárcel. A los nueve años, y según propia confesión, asesinó a dos amigos ahogándolos en el Rhin. Fueron sus primeros asesinatos. También violaba, torturaba y mataba animales, sobre todo perros, e incluso llegó a trabajar en una perrera. Entre 1902 y 1913, es acusado de estafa, robo con fractura, pirómano y desertor.
En 1913 estranguló y degolló a Kristine Klein, de trece años, que se encontraba en una casa en la que entró a robar. Kurten se casó en 1921 y se trasladó a Altenburg donde encontró trabajo de camionero. Su boda, una condena en la cárcel y la Primera Guerra Mundial interrumpieron los asesinatos. Pero en 1925 volvió a Düsseldorf y volvió a matar.
Su año más sangriento fue 1929. El 8 de febrero, atacó a una joven y violó y mató a Rosa Ohliger, una niña de ocho años; el 13, apuñala veinte veces a un inválido borracho, mecánico de oficio, y cuando es descubierto el cadáver, Kurten aparece por allí y charla sobre el caso con la policía; el 11 de agosto, estrangula y apuñala a una criada llamada Marie Hahn; el 21, ataca con su navaja a tres personas; el 23, dos hermanas de cinco y catorce años; el 24, mata a un hombre; en septiembre, comete dos violaciones y dos asesinatos, y en uno de ellos mata a una mujer con un martillo; y el 7 de noviembre, otra niña de cinco años. De este último asesinato, envió a la prensa un mapa para que pudieran localizar el cadáver. La policía, ante la cantidad de ataques y la diversidad de armas y víctimas, empieza a creer que hay más de un loco suelto. En febrero y marzo de 1930, ataca a varias personas con el martillo pero ninguna muere.
Düsseldorf enloqueció de terror. Nadie se atrevía a salir solo a la calle. La recompensa por la captura del asesino alcanzó cifras fabulosas y la policía recibió denuncias de hasta 900000 personas. Se siguieron 12000 pistas y hasta 200 personas se acusaron de ser los autores de los crímenes del Vampiro.
Maria Budlick era criada. Conoció a Kurten el 14 de mayo de 1930. La convenció para ir a un bosque y allí la estranguló y violó. Pero Maria sobrevivió al ataque. Acudió a la policía y describió a Kurten y pronto su retrato robot circulaba por toda Alemania. Era cuestión de tiempo.
Kurten, con su habitual y extraña conducta, le confesó a su esposa quien era y, para no perder el dinero de la recompensa por su captura, le pidió que le delatara a la policía. El 24 de mayo de 1930, el Vampiro de Düsseldorf se entregó a la policía. Confesó sus crímenes, aunque en el juicio que se celebró un año después, en mayo de 1931, cambió varias veces su declaración. Con un acuerdo muy amplio entre los conocedores de la historia de Kurten, se le atribuyen nueve asesinatos, siete intentos frustrados y unas ochenta agresiones sexuales. Los expertos psiquiatras lo declararon responsable de sus actos y fue condenado a muerte.
Peter Kurten murió guillotinado en el patio de la prisión de Klügelputts el 2 de julio de 1931, a los 48 años. Según cuentan, quizá es una leyenda, una de las últimas frases de Kurten, raro como era, fue preguntar si “una vez guillotinado, aunque sea por poco tiempo, ¿podré oír la sangre saliendo de mi cuello?”
El 11 de mayo de 1931, durante el juicio de Kurten y mes y medio antes de su ejecución, Fritz Lang había estrenado en Berlín M, El Vampiro de Düsseldorf. Sólo dirigió una película más en Alemania; pronto marcharía, primero a Francia y después a Estados Unidos. El fantasma del nazismo cubría Alemania. Hasta 1959 no volvería a dirigir películas en su país.
Saber por qué un asesino mata a menudo es una incógnita de difícil respuesta. Kurten, en el juicio, habló de su pasión por beber la sangre de sus víctimas, en un síndrome llamado hematodipsia, del placer sexual en el momento de matar y, también, de matar para “aleccionar a una sociedad opresiva”. También declaró que llegaba al orgasmo cuando mataba y que variaba el número de puñaladas según el tiempo que tardaba en eyacular. Además, estaba su vampirismo, su afán de beber sangre, con implicaciones sexuales. El vampirismo se define, en términos psiquiátricos, como el acto de extraer sangre de un objeto, normalmente un objeto de amor, y recibir excitación sexual y placer. La sangre se puede obtener de varias maneras, aunque las usuales son la puñalada y el mordisco. El momento de extraer o sorber la sangre de la herida es una parte importante de la acción del vampiro. Como ven, todo coincide con las declaraciones de Peter Kurten.
El Vampiro de Düsseldorf fue la cristalización del miedo de todo un pueblo. Como ocurre con nuestro Sacamantecas, al que tanto se parece, el Vampiro sigue dando miedo en la actualidad. Un vampiro siempre ejerce una cierta fascinación, tiene poder sobre otras personas y produce terror. Hablar del Vampiro es hablar de un ser maléfico difícil de encarnar en una persona concreta, en el ciudadano llamado Peter Kurten (o en el rostro de Peter Lorre). El Vampiro es, al final, un mito cuyas apariciones traen, y a la vez predicen, los malos tiempos que se viven. Hay que recordar que estamos en la torturada Alemania de entreguerras, y pronto llegará el nazismo, que ya era entonces una realidad palpable en las calles de Alemania.
Arnold Edelstein, del Sistema de Prisiones de Israel, publicó hace unos años una revisión de los tipos de asesinos en serie. Para el autor está el asesino en serie en sentido estricto, con una víctima en cada crimen y repitiendo después de un intervalo de tiempo, hasta llegar a las tres víctimas y convertirse, oficialmente, en asesino en serie. En cambio, el asesino de masas llega a las tres víctimas en un solo episodio. Y también define Edelstein al asesino de masas en serie como el que coloca bombas, con muchas víctimas, en varias ocasiones. Finalmente, el autor comenta la orgía de asesinatos de quien mata a tres o más víctimas en varios episodios separados por horas o por pocos días.
Cuesta encontrar un motivo o, si se quiere, un móvil, para estos crímenes. O. por lo menos, un motivo que entendamos los demás. Ya veremos más adelante que, viendo sus antecedentes y la historia de su vida, sobre todo en la infancia, quizá podamos llegar a las causas de su conducta pero es difícil captar la justificación de sus actos. Como ocurre a menudo en este libro, podemos explicar pero eso no justifica en absoluto el comportamiento de los asesinos desde nuestra cultura y sociedad.
En general, se afirma que, para los asesinos de un solo crimen, la violencia quizá sea un experimento sin control. Sin embargo, para el asesino en serie, la violencia es el equivalente de un programa de intenciones, incluso de un programa de investigación, con diferentes experimentos para mejorar lo que busca el autor, sea lo que sea.
El asesino en serie se enfrenta al caos o al disparate que para él es su vida e intenta, con sus crímenes, ponerle un orden y encontrarle un sentido. Como escribió hace unos años un asesino en serie “se convierte la vida en un cómic en el que cualquier cosa es posible”. Por ejemplo, es, en el fondo, lo que intentan conseguir los profesionales de la medicina que matan deliberadamente a sus pacientes con la excusa de liberarles de su sufrimiento.
Sylvestre Matuska: El amante de los trenes

Austríaco, de origen húngaro, era un ingeniero de ferrocarriles que, por lo que cuentan, solo alcanzaba el orgasmo ante una catástrofe ferroviaria con descarrilamiento incluido. Quizá, en psiquiatría, esta obsesión hasta tiene un nombre específico; lo ignoro, pero la obsesión es fascinante.
Nació Sylvestre Matuska, o Szilveszter Matuschka, el 29 de enero de 1892 en Csantaver, en la Vojvodina, pueblo que ahora se llama Cantavir y pertenece a Serbia. Hijo de un zapatero, fue movilizado en 1914 por el ejército austro-húngaro durante la Primera Guerra Mundial. En 1915 pertenece a un regimiento de zapadores que cubre la retirada ante el avance de los rusos en Galitza, hoy Polonia. Su regimiento vuela puentes, carreteras, vías de tren y esclusas y Matuska, ya ingeniero, destaca por su habilidad y sangre fría. Ingeniero mecánico especializado en trenes, inventó un sistema de frenos para locomotoras y tenía otras 92 patentes depositadas.
Aunque incluso es condecorado, cuando la guerra termina, la vida en Hungría derrotada es difícil. Prueba varios oficios y fracasa; es comerciante, tendero, albañil, transportista y, por fin, prospera con la explotación de una cantera. Excelente marido y padre, se instala en Viena como un buen burgués y un católico practicante
En Austria, en diciembre de 1930 y enero de 1931, hizo sus dos primeros intentos, uno en Viena y otro en Berlín, ambos fallidos, para descarrilar un tren y provocar un desastre. Tuvo éxito el 8 de agosto de 1931 al conseguir que descarrilara el tren expreso Berlín- Basilea. No hubo víctimas. Entre los restos se encontró un medio destrozado periódico nazi y, por ello, se supuso que había sido un atentado con trasfondo político. Se ofreció una fuerte suma como recompensa por la captura de los culpables.
Un mes más tarde, el 13 de septiembre, a las 12.20 horas, el expreso de Viena descarriló y cayó del viaducto de Biatorbagy, cerca de Budapest. Matuska voló parte del puente y la locomotora y nueve de los once vagones cayeron unos 30 metros al barranco. Murieron 22 personas y 120 resultaron heridas, 17 de ellas de gravedad. Entre los pasajeros que se salvaron estaba la cantante y actriz Josephine Baker, que entretuvo a los heridos y a los viajeros ilesos con sus canciones.
Matuska, que, por supuesto, estaba en la escena del crimen observando, y supongo que disfrutando, todo lo que veía, se hizo pasar por un pasajero del tren que no había resultado herido y le dejaron marchar.
Sin embargo, ya en ese momento, la policía de varios países perseguía al autor de los cuatro descarrilamientos o intentos de descarrilamientos. Sospechaban de Matuska y le detuvieron en Viena un mes más tarde, el 10 de octubre de 1931, y pronto confesó.
En Austria le juzgaron y le condenaron por los atentados fallidos pero, a continuación, fue extraditado a Hungría, con la condición de que no fuera ejecutado. Así ocurrió: fue condenado a muerte y su pena conmutada por cadena perpetua.
Escapó de la cárcel en 1944, en la confusión del final de la Segunda Guerra Mundial, cuando el ejército soviético invadió Hungría, todavía aliada de los alemanes. Matuska desapareció, aunque hay quien asegura que se convirtió en un experto en explosivos en el Ejército Rojo y que, incluso, participó en la guerra de Corea.
Los motivos de Matuska para descarrilar trenes son, por supuesto, o desconocidos o estrambóticos. En el juicio declaró que se lo había ordenado Dios. Además se explayó afirmando que “destrozo trenes porque me gusta ver a la gente morir, me gusta escuchar como gritan”. También se afirmó en el juicio que Matuska solo alcanzaba el orgasmo cuando veía los trenes que había descarrilado.
Un personaje así parecía fuera de lugar en nuestra época pero, en 1990, la banda Lard, de heavy metal, lo recuperó y compuso una canción con su nombre y su historia (se puede escuchar en YouTube). Es obvio que es un tema heavy metal y, por lo tanto, feroz y ruidoso. Una de las estrofas dice así:
“Es un mensaje de Dios
Dinamita
Fin de la línea
Rechina el metal
Gritan los heridos
Explotan las bombas”.
Cuenta Juan Antonio Cebrián que hay tres características en los niños que les hacen candidatos a asesinos en serie: micción nocturna, hacer daño a animales o amiguitos, y atracción por el fuego. Por supuesto, no todos los que llevan estas conductas serán, al crecer, asesinos. Sería terrible porque esas conductas se dan en muchos niños. Vienen de la incompetencia de los padres, a menudo delictiva, con un entorno social poco eficaz y con fantasías ligadas al sexo y a la violencia.
Los asesinos en serie no sienten que sean malos sino, más bien, que las humillaciones y las provocaciones les obligan a cometer todo tipo de actos terribles. Eran, muchos de ellos, psicópatas, pero no enfermos mentales y distinguían con claridad el bien y el mal.
Todas estas características de los asesinos en serie las comenzó a organizar a finales de los ochenta Robert Ressler, entonces en el FBI. Fue el primero en utilizar el término de asesino en serie después de que, en una conferencia, uno de los asistentes hiciera una referencia a “crímenes en serie”. A Ressler le gustó el término y, a su vuelta al cuartel del FBI, comenzó a utilizar el concepto de asesinos en serie para aquel que “comete un crimen, y otro y otro de manera repetitiva”.
Definió asesino en serie y enumeró las conductas y comportamientos que lo caracterizaban. También afirmó que un asesino en serie es un don nadie que quiere ser alguien, y no a través de una fama positiva, sino de la infamia y la crueldad. Cualquier tipo de reconocimiento es bueno para él. Muchos comienzan a matar porque son tan inadecuados para otra cosa que se sienten incapaces de sentir reconocimiento por lo que hacen. Fantasean con ser asesinos, con matar, con ser famosos,… Son el centro de atención, se sienten bien, aunque la atención sea positiva o negativa, les da igual.
Pittsburgh Phil Strauss: El mejor trabajador de la empresa

Es el más profesional de los asesinos de la Mafia y fascina por su sangre fría y su indiferencia ante el dolor de los demás. Declaró en una ocasión que, como un jugador de fútbol, “me preparé para hacer este trabajo; los jefes se fijaron en mí, y acabé jugando en primera división”. Es cierto, personas con tanta experiencia y criterio como Lucky Luciano, Joe Adonis o Albert Anastasia se fijaron en Pittsburgh Phil Strauss y terminó siendo el asesino más eficaz de la Murder, Inc., la empresa de crímenes por encargo con sede en Nueva York y contratos por todo Estados Unidos. De Brooklyn al cielo, si lo deseabas, y los expertos de Murder, Inc., te facilitaban el tránsito al otro mundo.
Nacido en Brooklyn como Harry Strauss en 1908, adoptó el alias de Pittsburgh Phil aunque no tenía nada que ver con la ciudad del mismo nombre, pero le sonaba bien. De todas formas, sus amigos de confianza le llamaban “Pep”.
Era todo un experto en mil maneras de matar, como el buen profesional y artesano que aspiraba a ser. Cuando tenía que cumplir un contrato en cualquier lugar del país, ponía en su maleta una camisa, unos calcetines, unos calzoncillos, una pistola, un cuchillo, un trozo de cuerda bueno para estrangular y un pico de hielo, herramienta que le gustaba especialmente. Iba en tren o en avión, hacía su trabajo y cogía el siguiente enlace a Nueva York. A menudo, Pittsburgh Phil no sabía quién era el muerto, es más, no le importaba en absoluto no saberlo.
Cuando en 1940 la fiscalía de Brooklyn, dirigida por William O’Dwyer, desmanteló Murder, Inc., encontraron pruebas suficientes como para acusar a Pittsburgh Phil de 28 asesinatos. Son los probados; hay quien afirma que el total se acercaría a los 500. Quizá es exagerado, pero es muy probable que superen en mucho los 100.
Era y se sentía un dandi, elegante y mujeriego, y ocupaba la habitación de hotel más cara y lucía la ropa más fina de la ciudad. Un comisario de policía que le interrogó dijo que era el tío más elegante del lugar y, sin embargo, no había tenido un trabajo honrado en su vida. Es obvio que el bribón, alto, esbelto y elegante Pittsburgh Phil tuvo gran éxito con las mujeres. En Brooklyn, donde le conocían bien, le perseguían y su romance con Evelyn Mittelman, incluido el asesinato de un rival, contribuyó a que la chica fuera conocida como “Miss Beso Mortal”.
En su trabajo, Pittsburgh Phil era eficaz y salvaje. Uno de los asesinatos que se le atribuyen es el de George Rudnick, que tenía la mala fama de ser confidente de la policía. Cuando se encontró su cuerpo, la descripción del forense es fría y directa: “Es un varón adulto, algo desnutrido, con un peso aproximado de 140 libras y 6 pies de altura. Presenta 63 heridas de puñales en el cuerpo. En el cuello tiene 13 puñaladas. En la parte derecha del tórax tiene 50 heridas circulares. Tiene una laceración en la región frontal de la cabeza; la herida es abierta y el hueso está hundido. El rostro está azul. La lengua sobresale de la boca. A la altura de la laringe se observa un surco, blanco y hundido, más o menos de la anchura de una cuerda de colgar la ropa (de tendedero). En la disección del corazón se observó que su pared estaba completamente atravesada por puñaladas. Mi conclusión es que la causa de la muerte fueron múltiples puñaladas y asfixia debida a estrangulamiento.”
Todo un profesional Pittsburgh Phil Strauss. Si le encargan un asesinato, se asegura a conciencia de que el “contrato” está muerto y bien muerto. Vamos, ni siquiera el forense sabe de qué ha muerto al haber tantas causas probables.
En otra ocasión, en un contrato en Detroit no encontraba manera de cumplirlo pues el condenado, Harry Millman, siempre se mantenía a cubierto o entre multitudes o comía en restaurantes repletos de comensales. Es igual, nuestro asesino se harto de esperar y, cuando Millman estaba comiendo, apareció armado con dos revólveres y lo mató y, de paso, hirió a otros cinco clientes del establecimiento. O como cuando mató a un tipo al que se acusaba de quedarse el dinero de las tragaperras. Se lo cargó con 32 golpes de un pico para el hielo, lo ató a una tragaperras y lo tiró a un lago en las montañas Catskills. Una semana más tarde, el cadáver subió a la superficie del agua, hinchado por los gases de la descomposición. Pittsburgh Phil comentó a sus colegas que para conseguir que este tipo no flotara había que ser doctor en medicina. Así, nuestro experto asesino aprendió algo más sobre el caprichoso comportamiento de los cadáveres.
Que se sepa, Pittsburgh Phil solo falló en el cumplimiento de un contrato. Fue a Florida a matar a un mafioso. Lo siguió, entró en un cine y se sentó en la última fila. Pittsburgh Phil llevaba una pistola pero pensó, con razón, que usarla sería muy ruidoso. Vio un hacha en un armario contraincendios. La cogió y, cuando se acercaba a su víctima, esta se levantó y se volvió a sentar unas filas más adelante, en el centro del patio de butacas. Nuestro asesino se hartó y dejó el hacha, salió del cine y volvió a Brooklyn. Allí contó a sus amigos que el tipo era “un maldito culo inquieto”.
A veces, un experto, si no encuentra las circunstancias apropiadas, las crea. También fue en Florida donde Pittsburgh Phil Strauss tenía que asesinar a un mafioso ya entrado en años y que no hablaba ni palabra en inglés. Nuestro experto no encontraba forma de llevarle a algún lugar discreto donde asesinarlo sin testigos. Se le ocurrió una solución ingeniosa pero, también complicada. Visitó al mafioso, le enseñó una maleta llena de armas y, por señas, le pidió ayuda para cumplir un contrato. El viejo mafioso, feliz de volver a ser útil, cogió una cuerda de la maleta y llevó a Phil a un callejón oscuro muy apropiado para cumplir un contrato. Y se cumplió el contrato. Phil le quitó la cuerda de las manos y le estranguló allí mismo.
Fue Abe Reles, su compañero de negocios en Murder, Inc., quien comenzó a cantar para la policía y la fiscalía de O’Dwyer y no paró y acabó por enviar a todos sus colegas a la silla eléctrica. Así pasó hasta que el mismo Reles fue objeto de contrato y saltó desde la ventana de la habitación del hotel, la 623 del Half Moon Hotel de Coney Island, en el que vivía protegido por las fuerzas del orden.
Mientras Abe Reles volaba, Pittsburgh Phil Strauss iba a juicio el 4 de septiembre de 1939, junto a su compañero en Murder, Inc., Martin “Buggsy” Goldstein, por el asesinato por estrangulamiento del corredor de apuestas Irving “Puggy” Feinstein, cuyo cadáver apareció quemado en un solar. Phil, para salvarse en el juicio, se hizo el loco y él, tan elegante, dejó de afeitarse y lavarse, iba con la ropa sucia y sus declaraciones eran un balbuceo incoherente a la vez que mascaba sin parar la correa de un maletín. No convenció a nadie y el 12 de junio de 1941, en una calurosa noche de verano, Pittsburgh Phil Strauss, a los 31 años de edad, se sentó en la maldita silla eléctrica del penal de Sing Sing.
Referencias:
Abeijón, s.f. Peter Kürten: El Vampiro de Dusseldorf. http://www.asesinos-en-serie.com/Peter_Kurten/El_Vampiro_de_Dusseldorf.php
Cebrián, J.A. 2007. Psicokillers. Perfiles de los asesinos en serie más famosos de la historia. Ed. Nowtilus. Madrid.
Cuquerella Fuentes, A. 2004. Asesinos en serie. Clasificación y aspectos médico-forenses. Estudios Jurídicos 4135-4160.
Edelstein, A. 2014. Re-thinking typologies of multiple murders: The missing category of serial-mass murder and its theoretical and practical implications. International Journal of Emergency Mental Health and Human Resilience 16: 122-126.
Garrido Genovés, V. et al. 2015. Asesinos múltiples en un solo acto. Mente y Cerebro 72: 64-69.
Kinnell, H.G. 2000. Serial homicide by doctors: Shipman in perspective. British Medical Journal 321: 1594-1597.
Olmos, M. 2010. El vampiro de Düsseldorf. El Correo 11 septiembre.
Reouven, R. 1976. Diccionario de los asesinos. DOPESA. Barcelona. 386 pp.
Ressler, R.K. & T. Shachtman. 2005. Asesinos en serie. Ariel/Centro Reina Sofía para el Estudio de la Violencia. Barcelona. 382 pp.
Schroeder, B. 2007. Strange and Terrible!: Serial Killers. Number 1: Why did they do it? Zem Books. Marion, Indiana. 84 pp.
Sifakis, C. 2005. The Mafia Encyclopedia. Facts On File, Inc. New York. 510 pp.
Turkus, B.B. & S. Fidler. 1966. Crímen, S.A. Ed. Bruguera. Barcelona. 671 pp.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Asesinos en serie se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los asesinos
- Nuestros ancestros asesinos
- Apilando bloques: de los Lemmings a la serie armónica cruzando el Guadalquivir
On Zientzia: Zer da entropia?
- Energia lan bat egiteko gaitasuna da.
- Termodinamikaren lehenengo legea: energia ez da ez sortzen ezta suntsitzen, kontserbatu egiten da.
- Termodinamikaren bigarren legea: unibertsoaren entropia maila beti hazten ari da.
Deabrutxo bat baliatuta entropiaren ingurukoak azaldu dizkigu Jonas Casado Etxebarriak “Zer da entropia?” bideoan, On Zientzia lehiaketaren VII. edizioan euskarazko epaimahaiaren azken errondaren parte izan zena.
—–—–
Elhuyar Fundazioak eta Donostia International Physics Center-ek (DIPC) zientzia eta teknologiaren dibulgaziorako lehiaketa da On Zientzia, jakintza zientifikoa ezagutzera emango duten bideo labur eta originalen ekoizpena bultzatzeko helburuarekin.
Lehiaketaren oinarriek ezarri bezala, bideoek 5 minutu baino gutxiago iraun behar dute eta euskaraz, gaztelaniaz edo ingelesez izan daitezke, gaia librea delarik. Edukiak jatorrizkoak izan behar dira, telebistan inoiz atera ez direnak, eta beste lehiaketaren bat irabazi ez dutenak.
Hiru sari kategoria ditu On Zientzia lehiaketak:
- Gazte saria (18 urtetik beherakoentzat). 1000 €
- Euskarazko bideo onena. 2000 €
- Dibulgazio bideorik onena. 3000 €
2017-2018koa VIII. edizioa da eta parte hartzeko epea zabalik dago jada 2018ko apirilaren 25era arte.
The post On Zientzia: Zer da entropia? appeared first on Zientzia Kaiera.
El gran encéfalo humano es un “encéfalo social”

Los seres humanos actuales tenemos encéfalos muy grandes, más grandes que casi todos nuestros antecesores. De hecho, el volumen de nuestro cráneo es tres veces mayor (corregido el efecto del tamaño corporal) que el de nuestros antecesores austraolopitecinos. Las excepciones son los primeros seres humanos de nuestra especie y los neandertales, que tenían cerebros algo más grandes que nosotros. Probablemente, gracias a esos encéfalos más grandes exhibimos habilidades cognitivas valiosas, aunque no está muy claro cuál es el elemento -si es que pudiese atribuirse a uno único- que habiendo resultado de esas habilidades, ha constituido factor de éxito en términos evolutivos.
Los científicos de este campo han venido considerando tres razones posibles por las que resultan ventajosas las habilidades cognitivas de que son capaces encéfalos más grandes. Una es que esos encéfalos proporcionan a sus poseedores la capacidad para hacer frente a cambios climáticos y meteorológicos haciendo uso de tecnologías adecuadas para ello; gracias a esa capacidad se habrían podido superar los obstáculos que se derivan de variaciones temporales y geográficas del clima y que hubiesen podido limitar la continuidad de la especie en el tiempo o su distribución geográfica. De ser correcta esta hipótesis, los aumentos en el volumen encefálico se habrían producido bajo la presión selectiva de la variabilidad e impredecibilidad climática.
Otra posible razón es que las mayores capacidades cognitivas hicieron a los miembros de nuestra especie más capaces para hacer uso de diferentes fuentes de recursos alimenticios, principalmente mediante la caza, y búsqueda y recolección de alimentos; en particular, el desarrollo de variadas técnicas de caza pudo resultar clave a la hora de capturar animales de todo tipo. Esta idea se basa en la observación de que las especies con comportamientos alimenticios complejos o de intensa actividad depredadora tienden a tener volúmenes encefálicos comparativamente grandes.
Y la tercera razón es que esas habilidades cognitivas permitieron un mejor desenvolvimiento en las relaciones que se establecen con los otros en las cada vez más complejas sociedades humanas. Según sus defensores, nuestros antecesores homínidos desarrollaron adaptaciones que les permitieron un uso muy eficiente de los recursos biológicos y un mayor control de sus propias condiciones de vida. Esas capacidades propiciaron menores tasas de mortalidad y, en consecuencia, aumentos en el tamaño de las poblaciones. Un mayor número de individuos habían de competir por los recursos disponibles y, de esa forma, se dieron las condiciones que facilitaron el desarrollo de habilidades que mejoraron la cooperación dentro de unos grupos que eran cada vez de mayor tamaño. A esta tercera se la denomina “hipótesis del encéfalo social”.
Pues bien, según las conclusiones de un estudio realizado por Drew H. Bailey y David C. Geary, de la Universidad de Missouri en Columbia, es este tercer elemento el que resultó determinante. Lo sostienen basándose en un análisis del tamaño de 175 cráneos de diferentes especies de homínidos, correspondientes a variadas localizaciones geográficas y a un periodo comprendido entre 1’9 millones y 10.000 años de antigüedad. Entre las diferentes variables con las que correlacionaron el tamaño de los cráneos, fue el tamaño poblacional el que resultó ser el mejor predictor de aquél, aunque a la vista del efecto de otros predictores, las variables de carácter climático, también han podido ejercer una cierta influencia.
Referencia:
Drew H. Bailey y David C. Geary (2009): “Hominid Brain Evolution. Testing Climatic, Ecological and Social Competition Models”. Human Nature, vol. 20, p. 67-79.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El gran encéfalo humano es un “encéfalo social” se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Familia ingurunea, umeen garapen kognitiboaren iragarle

Haurren garapenaren lehen urteen garapen kognitibo, pertsonal, emozional eta sozioafektiboan gehien eragiten duen alderdietako bat familia da. Familiaren eragina hainbat urtean luzatzen da, baina lehenbiziko urte horietan funtsezkoa da. Familia taldea da haurrari maitasun, aintzatespen, onarpen edo gutxiespen, arrakasta edo porrot seinale guztiak ematen dizkiona.
Lortutako emaitzek agerian utzi dute gurasoen eta seme-alaben artean kalitate handiko elkarrekintza sozioemozionala duten familiak direla aldi berean garapen kognitibo eta linguistikoa estimulatzeko gaitasun handiena dutenak.
Gurasoek seme-alaben garapena bultzatzeko asmoarekin lotutako prozesua da aldamiatzea, haurren gaitasunen zertxobait gainetik dauden jarduera edo eginkizunak ezartzen dizkiete gurasoek, betiere haurrari frustraziorik eragin gabe. Gidari bihurtzen dira gurasoak jarduera egiten lagunduta eta haurraren jakintza osatuz eta barneratuz doan neurrian, gurasoak urrundu egiten dira. Neuronen arteko konexioak estimulatzea lortzen dute gurasoek modu honetan eta, horrenbestez, haurraren garapen kognitiboa aktibatzea.
Garapen kognitiboa behar bezala sustatzeko ez da nahikoa prozesua abian jartzea, baizik eta prozesuak kalitate oneko interakzio sozioemozionalarekin lotuta egon behar du nahitaez: autonomia eta autoestimuaren sustapenarekin, giro afektibo positiboarekin eta atxikimendu seguru bat ezartzearekin.
Lehensemeak/lehenalabak gurasoen baliabide ekonomikoen eta gurasoek haiekin pasatzen duten denboraren esklusibitatea balia ditzaketeela egiaztatu da, betiere familia-ingurunea kalitatekoa bada garapena estimulatzeko. Horretaz gain, familia horietan guztietan etxean bertan bigarren hizkuntza bat erabiltzearekin osatzen da estimulazioaren aberastasuna.
Ikerketa luzeaBi urteko haurren familia ingurunearen kalitatea eta faktore soziodemografikoak ebaluatu ditu ikerketa honek eta aztertu du nola eragiten duten garapen kognitiboan lau urte dituztenean. INMA proiektuko Gipuzkoako 295 haurren populazio kohorte bat eta haien familiak hartu dute parte ikerketan.
Familia ingurunea ebaluatzeko eta informazioa eskuratzeko etxez etxeko bisitak egin ziren: zuzenean behatu ziren seme-alabekiko elkarrekintzak eta ingurunearen kalitatea. Horretaz gain, gurasoek galdetegiak bete zituzten eta elkarrizketa bana egin zitzaien. Ingurune fisikoaren kalitatearen eta estimulazio kognitiboaren inguruko informazioa ere batu zen: zenbat ipuin eta puzzle zegoen etxean, afektibitate adierazpenen kalitatea, gaizki ahoskatutako hitzak zuzentzen ziren, eta abar.
Ondoren, umeek lau urte bete zituztenean garapen kognitiboa bakarka ebaluatu zitzaien. Haurraren zenbait gaitasun neurtu dira: hitzezko gaitasuna, pertzepzio eta manipulazio gaitasuna, zenbakizko gaitasuna, memoria-gaitasuna eta gaitasun orokor kognitiboa. Horretarako, garapen kognitiboa zenbait azpieskalaren batura gisa ebaluatzen duen tresna bat erabili zen.
Lortutako emaitzak gidari izan daitezke haurren garapen kognitiboaren sustapena sendotzen duten hazkuntza-programak sortzeko. Gainera, familien populazio orokorrari informazio hau helarazteak lagungarria izan daiteke seme-alaben garapen intelektualean familiek duten eragin aukeraren kontzientzia har dezaten.
Iturria: UPV/EHU prentsa bulegoa: Familia-ingurunea, lehen urteetako garapen kognitiboaren iragarle.
Erreferentzia bibliografikoa: Florencia Belén Barreto, Manuel Sánchez de Miguel, Jesús Ibarluzea, Ainara Andiarena, Enrique Arranz “Family context and cognitive development in early childhood: A longitudinal studyIntelligence”. Vol. 65. November-December 2017. Pages 11-22DOI: https://doi.org/10.1016/j.intell.2017.09.006
The post Familia ingurunea, umeen garapen kognitiboaren iragarle appeared first on Zientzia Kaiera.
Insectos agrícolas
Jorge Poveda Arias
La primera imagen que nos viene a la cabeza cuando pensamos en insectos son las típicas moscas molestas y avispas peligrosas que nos llegan a margar las tardes de verano, pero, ya lo dijo el microbiólogo descubridor de la primera vacuna contra la polio, Jonas Salk: “Si desaparecieran todos los insectos de la tierra, en menos de 50 años desaparecería toda la vida. Si todos los seres humanos desaparecieran de la tierra, en menos de 50 años todas las formas de vida florecerían”.
Los insectos son una clase de animales invertebrados de seis patas incluidos dentro del Phylum de los artrópodos. Estos últimos se caracterizan por tener el cuerpo dividido en segmentos a los cuales se les unen diferentes apéndices (patas, antenas, alas), además de tenerlo recubierto de quitina, de la cual necesitan desprenderse para crecer mediante mudas sucesivas. Las principales clases dentro de este grupo son los crustáceos, los arácnidos, los miriápodos y los insectos, diferenciándose estos últimos del resto por tener el cuerpo dividido en tres regiones (cabeza, torax y abdomen), y poseer un par de antenas, un par de alas y tres pares de patas.
La denominada como “entomología agrícola” se describe como la ciencia que estudia todos aquellos insectos capaces de relacionarse directamente con el sistema agrícola y modificarlo. Por lo tanto, dentro de esta definición se incluyen los insectos polinizadores, los fitófagos (que se alimentan de material vegetal) y los que desarrollan una simbiosis mutualista (ambos individuos obtienen un beneficio), por ejemplo, al vivir en el interior de las plantas, como es el caso de varias especies de hormigas que viven en estructuras formadas en las ramas de las acacias y la protegen si algún herbívoro pretende consumir sus hojas. Además, todos aquellos insectos que interaccionen con ellos directamente, también podrán ser objeto de estudio de esta ciencia.

Hormigas en simbiosis mutualista con acacia. Wikimedia Commons
Por lo que se refiere a la polinización de los cultivos, se calcula que el 80% la llevan a cabo insectos polinizadores como las abejas de la miel (Apis mellifera), de ahí la enorme importancia de los insectos en la productividad agrícola de alimentos. Pero no solo las abejas (melitofilia) son capaces de transportar el polen de una flor a otra provocando su fecundación, también otros insectos visitan las flores con el fin de alimentarse de su néctar, como los escarabajos (cantarofilia), las moscas (miofilia), las avispas (esfecofilia), las hormigas (mirmecofilia) o las mariposas (faenofilia y psicofilia). Por otro lado, las hormigas también pueden dispersar activamente las semillas de diferentes plantas, al perderlas en el camino de vuelta al hormiguero.
En lo concerniente a los insectos fitófagos, destacar que la mitad de ellos consumen materia vegetal en algún momento de sus vidas, clasificándose en defoliadores (comen hojas), minadores o barrenadores (forman galerías en los tallos), xilófagos (consumen madera) o chupadores (succionan los fluidos vegetales). Para que una población de insectos pase de estar simplemente presente en un cultivo agrícola a conformar una plaga es necesario que ocurran cambios en la presión que el medioambiente ejerce sobre ellos. Los insectos siguen la denominada como estrategia biológica de la “r”, basada en tener gran cantidad de descendientes de los cuales muy pocos llegarán a la edad adulta para reproducirse. Esto es debido a la presión del medio, que incluye, la temperatura, la humedad, el viento, los depredadores etc. Si el ser humano disminuye la presión que estos factores externos ejercen sobre los insectos fitófagos, por ejemplo, aumentando la temperatura debido al cambio climático o esparciendo por el cultivo insecticidas que acaben con todos sus enemigos naturales, la población de insectos perjudiciales no dejará de aumentar y su daño sobre las plantas será tan elevado que conformarán una plaga.
Myzus persicae es el nombre científico con el que se le conoce al pulgón verde del melocotonero. Este pequeño insecto se incluye dentro del grupo de los hemípteros y se alimenta introduciendo un pico en el interior de las plantas y absorbiendo sus fluidos nutritivos. Su ciclo de vida comienza en árboles del género Prunus (ciruelos, cerezos, melocotoneros, almendros) donde las hembras pusieron sus huevos el otoño anterior. Estos huevos eclosionan justo antes de empezar la primavera y surgen pequeños pulgones verdes sin alas que se alimentan sobre estos árboles. Tras un par de generaciones, los individuos que nacen de los nuevos huevos ya presentan alas y se dispersan, atacando a prácticamente cualquier planta que encuentren a su paso, incluyendo cultivos hortícolas. Sobre estos nuevos hospedadores desarrollan varias generaciones, volviendo a los árboles Prunus en septiembre. Esta plaga es capaz de provocar graves daños a los cultivos, al atacar hojas, flores y frutos, produciendo su secado o manchas que dificultan su venta. Además, al alimentarse de gran cantidad de plantas diferentes es transmisor de más de 100 virus vegetales distintos.
La mosca de la fruta (Ceratitis capitata) es un díptero algo más pequeño que la mosca doméstica (Musca domestica) con colores muy llamativos. El verdadero problema en la agricultura lo causan sus larvas, al alimentarse de los frutos de cítricos y frutales de pepita y hueso. En primavera surgen las moscas adultas que, tras reproducirse, pondrán sus huevos en los frutos que encuentren. Entonces la larva nacerá e irá alimentándose de la pulpa del fruto hasta que alcance su máximo tamaño y se transforme en mosca adulta. Los frutos atacados muestran graves daños, caracterizados por una pulpa semilíquida en la cual se desarrollan diferentes hongos.

Mosca de la fruta (Ceratitis capitata). Wikimedia Commons
El escarabajo de la patata (Leptinotarsa decemlineata) es un coleóptero cuyo adulto es redondeado y listado en amarillo y negro. Por otro lado, las larvas son de color rojo-amarillo, muy blandas y gibosas. Aunque es un insecto que puede alimentarse de las hojas de cualquier solanácea (tomate, berenjena) prefiere la patata sobre cualquier otra planta. Son animales muy voraces, que consumen el tejido vegetal hasta dejar a las plantas totalmente defoliadas, disminuyendo enormemente la formación de los tubérculos, tanto en número como en tamaño. Como curiosidad, destacar que estos escarabajos se encontraban aislados en la zona de las Montañas Rocosas, alimentándose únicamente de una especie silvestre de solanácea, pero con la expansión del cultivo de la patata por todo el territorio americano estos insectos salieron de su aislamiento, aumentando enormemente su población y estando presentes, en la actualidad, en todo el hemisferio norte.

Larva del escarabajo de la patata comiendo hoja. Wikimedia Commons
El control biológico se define como la utilización de organismos vivos con el fin de disminuir la población de alguna especie que cause perjuicios al hombre. En este sentido, contra los insectos plaga de los cultivos agrícola existen diferentes estrategias, como son la utilización de microorganismos entomopatógenos (hongos, bacterias, virus y nematodos) o la utilización de otros insectos. Las estrategias seguidas en la utilización de insectos que acaben con otros insectos plaga se basan en conservar a los enemigos naturales presentes en el propio cultivo, incrementar el número de estos enemigos por liberación de nuevos individuos, o introducir nuevos enemigos exóticos.

Larva de mariquita cazando pulgones. Wikimedia Commons
Existen muchos ejemplos de éxito dentro de esta forma sostenible de reducir las plagas agrícolas, muchos de los cuales pueden ser adquiridos de forma comercial por los agricultores. Por ejemplo, contra los pulgones existen depredadores muy efectivos como las mariquitas (Coccinellidae), cuyas larvas y adultos atacan activamente a todos los pulgones que encuentran a su paso, consumiéndolos por completo. También contra los pulgones, existen los denominados como insectos parasitoides, los cuales ponen sus huevos en el pulgón y la larva que nazca lo irá devorando internamente, dejando únicamente su cutícula externa. Dentro de este grupo destacan pequeñas avispas, como Lysiphlebus testaceipes.

Avispilla introduciendo su huevo en pulgón. Wikimedia Commons
La importancia que los insectos tienen sobre el sistema agrícola es de elevada relevancia, no sólo vistos como un problema, sino también como medios para aumentar su productividad, al favorecer la polinización o atacar directamente a otros insectos perjudiciales.
“La ciencia que no es divulgada hacia la sociedad es como si no existiera”
Referencias y más información:
Avilla, J. (2005). El control biológico de plagas y enfermedades. La sostenibilidad de la agricultura mediterránea. Universitat Jaume I de Castellón.
Barrientos, J. A. (Ed.). (2004). Curso práctico de entomología (Vol. 41). Univ. Autònoma de Barcelona.
Dajoz, R. (2001). Entomología forestal: los insectos y el bosque: papel y diversidad de los insectos en el medio forestal. Mundi-prensa.
Gillott, C. (2005). Entomology. Springer Science & Business Media.
Jacas, J. A., & Urbaneja, A. (Eds.). (2008). Control biológico de plagas agrícolas. Phytoma.
Moreno, A. A. & Álvarez, C. S. (2005). Entomología agraria: los parásitos animales de las plantas cultivadas. Diputación Provincial de Soria.
Planelló M.R., Rueda M.J., Escaso F., Narváez I. (2015). Manual de entomología aplicada. Sanz & Torres.
Sobre el autor: Jorge Poveda Arias está realizando su tesis doctoral sobre la interacción planta-microorganismo en el grupo de investigación ‘Fitopatología y control biológico’ del Centro Hispano-Luso de Investigaciones Agrarias (CIALE) – Universidad de Salamanca
El artículo Insectos agrícolas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- “Las plantas transgénicas y los retos agrícolas del siglo XXI” por F. García Olmedo
- Subproductos agrícolas para mantener la calidad nutricional de los lácteos
- Una hiperlente que permite ver un virus en la superficie de una célula viva
Asteon zientzia begi-bistan #190

NanoBioCel taldeko Haritz Gurrutxagaren ikerketaren arabera, zelula ama mesenkimalen ezaugarri onuragarriak babes daitezke tenperatura baxuetan gordeta. Zelulak biomaterialetan babesteko zenbait metodo daude eta ikerketa honetan kriobabeste geldoa izan da funtsa. Lan honek ate berria ireki dio zelula ama mesenkimalen babesteari, prozedura berri eta erraz bat proposatuta, bai prozesuen kostua zein konplexutasuna gutxituz. Asko areagotu da zelula ama mesenkimalen erabilera hainbat izaerako gaixotasunak tratatzeko.
Arrainen haragiaren itxura oso desberdina da espezieen arabera. Alde batetik, atunak ez dira zuriak, eta hezurraren inguruan dagoen haragia odol-hodiz beterik dago. Odol asko galtzen dute arraina ebakitzean. Bestalde, Arrain zapalen haragia, berriz, zuri-zuria da, eta ez du odolik botatzen ez eta xerrak egitean ere. Haragi odoleztatuagoa duten arrainak oso aktiboak dira. Mihi-arrainak, aldiz, eseri-eta-itxaron harrapariak dira. Harrapakin bat ikusten dutenean, mugimendu azkar eta indartsua egiten dute. Harrapakinarenganaino iristeko egin behar duten mugimendurako erabiltzen dituzten giharrek ez dute oxigenorik behar. Bereziak dira muskulu horiek. Mugimendua egiteko behar duten energia (ATP) glukolisiaren bitartez lortzen dute. Zer da glukolisia? bide metaboliko azkarra da, denbora laburrean energia asko ematen duena.
Planetako eremurik hotzenetako bakterioek sortutako molekula tentsioaktiboak industrian erabiltzeko modukoak izan daitezkeela proposatu dute Alemaniako ikertzaileek. Erabilpen potentzial mordoa omen dute molekula tentsioaktiboek. Hala nola detergenteak, garbitzaileak, kosmetikoak, botikak, elikadura osagarriak eta emultsionatzaileak sortzeko erabili daitezkeela diote. Gainera, horien erabilpenak ingurumen abantailak izango lituzke. Molekula hori sortzeko gai diren organismoen artean, ikertzaileek legamia bat nabarmendu dute, Moesziomyces antartcticus izena duena.
Emakumeak zientzianNazio Batuek sustatzen duten Zientziaren arloko Emakume eta neskatoen Nazioarteko Egunarekin batera, Euskal Herrian ‘Ez da pertzepzio bat’ ekimena abiatu zuten aurreko igandean. Honen helburua da emakumeek zientzian pairatzen duten diskriminazioa salatzea eta era berean, zientzian murgildu nahi duten neskak animatzea. Ekimen honek bat egiten du orain dela gutxi Pew Research Center-ek argitaraturiko azterlan batekin. Ikerketak argitara eman zituen ondorioen arabera, zientziarekin, teknologiarekin, ingeniaritzarekin edo matematikarekin lotutako ogibideak dituzten emakumeen lantokia euren lankide gizonena ez bezalako ingurune bat izan ohi da, batzuetan deserosoagoa. Maizago jasaten dute sexu diskriminazioa eta jazarpena eta uste dute emakume izatea abantaila baino gehiago desabantaila dela euren karreran arrakasta izateko. Adibidez, emakume ikertzaileak mendebaldeko herrialde guztietako (Mendebaldeko Europa eta Ipar Amerika) ikertzaile guztien % 32 dira; Espainian, % 39ra iristen dira. Txosten horietan agertzen diren datuak ulertzeko, Nobel saridunen zerrenda ikusi besterik ez da egin behar: historian zehar, sarien %3 baino ez zaizkie eman emakumeei. Zientziaren munduan dagoen desoreka nabarmena da, ez da pertzepzio bat.
Wangari Muta Maathair biologo, ekologista eta aktibista politikoa aurkeztu digute artikulu interesgarri honetan. Kikuyu etniako nekazarien alabak, Wangari barne, landa-eremuan lan egin, egurra pilatu eta ura ekartzera kondenatuta zeuden. Baina Wangarik zortea izan zuen; ikasketak egiteko aukera izan zuen. 1960an, Estatu Batuetan ikasteko beka bat lortu zuen. Biologiako Gradua eta Biologia Zientzietako Masterra egin zituen. Horren ondotik, Kenyara itzuli zen eta lanpostu bat lortu zuen Nairobiko Unibertsitateko Albaitaritza Anatomiako Sailean mikroanatoniako ikerketako laguntzaile gisa. Doktorego bat eskuratu zuen Afrika Erdialde eta Ekialdeko lehen emakumea izan zen. Horretaz gain, Saileko lehen emakumezko Burua (Albaitaritza Anatomian, 1975) izan zen eta Nairobiko Unibertsitateko Irakasle Elkartu (1977) ere bai. 2004an, Bakearen Nobel Saria lortu zuen.
Emakume eta Neska Zientzialarien Nazioarteko Eguna izan zen pasa den igandean. Argi dago oraindik berdintasun teorikoak ez duela bermatzen parekidetasun erreala. Artikulu honetan zenbait emakume zientzialariren ahotsak izango dira irakurgai. Adibidez, Naiara Barrado Izagirre astrofisikariarena: “Lehen uste nuen genero berdintasun nahikotxo bazegoela, eta orain hasia naiz konturatzen gauzak ez direla uste nuen bezain politak”. Beste kontakizun bat: Inmaculada Delage arkeologoarena, bokazioz hasi zen alor horretan. 2014. urtetik Egipton induskatzen ari da Delage, Myriam Seco egiptologoaren gidaritzapean. Emakumezkoek zientziaren eta ikerkuntzaren alorreko goi mailako postuetara heltzea denbora kontua dela dio. Halere, bidean oztopo ugari daudela ohartarazi du. Emakume hauen (eta beste batzuen) ibilbide zientifikoak topatuko ditu irakurleak, baita berauen pentsamendu eta iritziak ere. Ez galdu!
FisikaErloju atomiko eramangarri batekin, Frantziako Alpetako puntu baten altuera neurtu ahal izan dute. Laborategitik kanpo egiten den lehen neurketa izan da. Ikertzaileek aitortu dute erlojuak ezin izan zuela kondizio onenetan lan egin, eta lortutako emaitzaren zehaztasuna ez dela gaur egungo beste metodoekin lortu daitekeena baino hobea; baina, azpimarratu dute, oraindik erronka tekniko batzuk gainditu behar diren arren, pausu garrantzitsua izan dela erloju atomikoen aplikazio geofisikoetarako.
Ingeniaritza, teknologiaAurpegi-ezagutzaren teknologiak zure sexualitatea antzeman lezake. Bai, ondo irakurri duzu. Stanford Unibertsitateko ikertzaileek jakinarazi dute algoritmo bat sortu dutela, bereizteko pertsona gay eta heterosexualak, argazkiak erabilita. Aurpegiaren irudia eskaneatzean, hainbat gauza hartzen ditu kontuan: zer distantzia dagoen begietatik belarrietara, adibidez. Datu horiek gero konparatzen ditu milaka pertsonaren datu-base batekin. Nick Rule Psikologia irakaslea da Torontoko Unibertsitatean, Kanadan, eta bere iritziz, gizon heterosexualek aurpegi nasaiagoak dituzte, testosterona maila altuagoak dituztelako.
Fulsion Smart Systems enpresak sortu du Irudikon aplikazioa, arreta-defizitaren nahasmendua duten haurrengan pentsatutakoa. Aplikazio honek bestelako joko-estrategia dakar. Umeak tarte labur batez egon behar du kontzentratuta oinarrizko mailetan, baina, aurrera egin ahala, joko- eta kontzentrazio-denbora luzeagoa eskatuko dio haurrari.
Betaurreko adimendunak erabiltzen hasi da polizia txinatarra, herritarrak automatikoki identifikatzeko. Nola funtzionatzen du? Betaurrekoek herritarren argazkiak ateratzen dituzte; zuzenean datu-base batekin alderatzen dute; poliziak une horretan jakin dezake parean daukan hori nor den eta ea poliziak bilatzen ote duen. Orain dela astebete jarri zuten martxan metodo berri hau eta dagoeneko zazpi pertsona atxilotu dituztela esan dute agintariek.
Garraio publikoan aldaketa handia gertatzen ari da. KERS sistema (kinetic energy recovery system) jarri diote Euskotrenek utzitako autobus diesel bati. Garatu duten sistema ideala da hiri barneko garraio publikorako. David Arredondo Zumaiako eMotion Dynamics enpresako zuzendari teknikoak azaltzen du “sorturiko indarra, bero gisa degradatu beharrean, argindar bihurtzen du sistemak”. Sistemak superkondentsadoreetan biltzen du argindarra, ez baterietan; beraz, askoz arinagoa da, eta merkeagoa. Ibilgailu elektrikoei buruz, hau da bere iritzia: “Garraioaren iraultza elektrikoak arazo bat du, Arredondoren aburuz: “Ibilgailu elektrikoak errealitatea dira dagoeneko, baina garesti samarrak asko zabaltzeko”. Badaude, baina, beste konpainia batzuk horien alde egiten dutenak. Irakur ezazue artikulua!
Ibilgailuekin jarraituz, Didi enpresa txinatarra ere gidaririk gabeko ibilgailuen lehian sartu da bete-betean, dagoeneko trafiko errealarekin probak egiten hasia da Shangain.
Bertso-doinuz osatutako bilduma batetik abiatuta, doinu berriak automatikoki sortzeko metodo bat garatu du Izaro Goienetxea Urkizu ikertzaileak. EHUko Robotika eta Sistema Autonomoen taldean (RSAIT) egiten du lan eta euren proiektu nagusietako bat da BertsoBot-a. Helburua roboten arteko elkarrekintzan aurrera egitea da eta horretarako, robotak bertsotan jartzen dituzte. Musika automatikoki sortzeko eta sailkatzeko bi metodo berri sortu dituzte. Jo ezazue artikulura horiek ezagutzeko!
MedikuntzaZelula amak minbiziaren aurkako txerto modura erabili ahalko liratekeela adierazi dute Stanford Unibertsitateko ikertzaileek. Zelula amen eta minbizi zelulen artean antzekotasunak daudela azpimarratu dute: batzuek zein besteek ez dute mugatua hazteko eta ugaltzeko gaitasuna. Gainera, bien mintzetan antzeko antigenoak azaltzen direla ikusi dutenez, tratatutako zelula amak gorputzean txertatu, eta immunitate-sistema minbiziaren aurka entrenatzeko erabili daitezkeela iradoki dute. Elhuyarrek eman dizkigu ikerketa horren xehetasunak.
OsasunaDuela bi urte inguru, MOE Munduko Osasun Erakundeak minbizia eragiten zuten gaien zerrendan haragi prozesatuak sartu zituen. Albiste andana bat publikatu zen horren inguruan; gehienetan sentsazionalismoa izan zen nagusi. Haragi prozesatua janez gero, minbizi tasa %18 igotzen zela esan zuten prentsan. MOEren menpekoa den IARC Minbizia Ikertzeko Nazioarteko agentziak nahiko ebidentzia zeudela iragarri zuen eta horregatik minbizi eragileen 1 taldean sailkatu zituen haragi prozesatuak eta 2A taldean haragi gorria. Josu Lopez-Gazpiok azaltzen digu tabakoa, plutonioa edo haragi prozesatua talde berean egoteak ez duela esan nahi modu berean minbizia eragiten dutenik. Datuak ematen ditu: Mundu mailan haragiaren kontsumoarekin lotutako minbiziak 34.000-50.000 dira urteko, baina tabakoarekin, alkoholaren kontsumoarekin edo aire-kutsadurarekin lotutakoak 1.000.000, 600.000 eta 200.000 dira, hurrenez hurren. Halaber, ohartarazi digu substantzia oro toxikoa izan daitekeela, baita fruta ugari ere! Ez galdu!
———————————————————————–
Asteon zientzia begi-bistan igandeetako atala da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna erreparatuz, Interneteko “zientzia” antzeman, jaso eta laburbiltzea da gure helburua.
———————————————————————–
Egileaz: Uxue Razkin Deiako kazetaria da.
———————————————————————–
The post Asteon zientzia begi-bistan #190 appeared first on Zientzia Kaiera.
Naukas Bilbao 2017 – Álex Méndez: Luz de luna
En #Naukas17 nadie tuvo que hacer cola desde el día anterior para poder conseguir asiento. Ni nadie se quedó fuera… 2017 fue el año de la mudanza al gran Auditorium del Palacio Euskalduna, con más de 2000 plazas. Los días 15 y 16 de septiembre la gente lo llenó para un maratón de ciencia y humor.

Alex Méndez se dedica profesionalmente a simular la luz y sus efectos. En esta charla aplica sus conocimientos para desmontar las bases de dos de las conspiranoias que afirman que el hombre no llegó a la Luna.
Alex Méndez: Luz de LunaEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2017 – Álex Méndez: Luz de luna se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – José Miguel Viñas: Me río yo del cambio climático
- Naukas Bilbao 2017 – Francisco R. Villatoro: El espín para irreductibles
- Naukas Bilbao 2017 – Teresa Valdés-Solís: Limpia, fija y da esplendor
Ezjakintasunaren kartografia #203

Disruptore endokrinoa, oreka hormonalean eragiteko gai den substantzia da bisfenol-A (BPA). Haurdunaldian zehar esposizioak diabetesaren antzeko sintomatologia eragin lezake, bai amarengan bai umearengan. NuRCaMein-en BPA and pregnancy: diabetes for you and your kids artikulua.
Gaixotasun neuroendekatazile lazgarria da adrenoleukodistrofia. Terapia genikoa baliatuta sendabidea iragarri zen pasa den urtean lehen aldiz. Terapia horren nondik-norakoak azaltzen dizkigu Pablo Raneak: Gene therapy is back: The X-ALD case.
Mundu guztiak entzun du grafenoari buruz. Gutxiago nanografenoei buruz, pluralean, hainbat molekula baitira. Metodo lehorren bidez (egoera solidoan) nanografeno egiturak lortzea oso garrantzitsua da espintronikan, elektronikan eta etorkizuneko eguzki-biltzaileetan erabiltzeko. DIPCko jendea Mechanochemistry of nanographenes artikuluan.
–—–
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #203 appeared first on Zientzia Kaiera.
BertsoBot, el robot versolari

BertsoBot. Imagen: Nagore Iraola. UPV/EHU
Una de las líneas de trabajo del grupo de investigación Robótica y Sistemas Autónomos (RSAIT) de la Facultad de Informática de la UPV/EHU consiste en progresar en la interacción entre humanos y máquinas o robots. Uno de sus principales proyectos es el denominado BertsoBot, “en el que ponemos a los robots a cantar bertsos”, comenta el líder del grupo, Basilio Sierra. El grupo de investigación trabaja en múltiples aspectos de ese proceso: la comprensión de la señal de voz, la visión a través del ordenador, la navegación, la generación de nuevas melodías musicales, etc.
La investigadora y doctoranda Izaro Goienetxea trabaja en dos de estos temas: la generación automática de música y la clasificación automática de la música. La investigadora señala que ya hay numerosos métodos de generación automática de música, basados en modelos gramaticales o estadísticos; pero en ellas “habría que tener en cuenta la coherencia de las melodías, para generar melodías fáciles de comprender. Habría que tener la seguridad de que dentro de la melodía se repite algún segmento, tanto en lo que respecta a las notas como en otros niveles más complejos de la melodía”.
La labor de esta investigadora comenzó en la generación musical, pero los resultados la llevaron a estudiar las formas de clasificarla. Goienetxea destaca el interés que tiene la clasificación, ya que “en Internet cada vez hay más música al alcance, y cada vez está adquiriendo más importancia el poder realizar la clasificación de la música de forma automática, y poder organizar grandes recopilaciones musicales”.
En un artículo publicado por la revista PLOS ONE, el grupo de investigación ha presentado dos métodos fruto de este trabajon. Por un lado, un método para clasificar la música en función del género, basado en una forma nueva de representar la música lograda a través de la agrupación de melodías de bertsos semejantes. Con este método, “analizamos una melodía, y determinamos a qué se parece, es decir, en qué género podemos clasificarla”, explica Goienetxea. Esos agrupamientos son utilizados, asimismo, para generar de forma automática nuevas melodías del estilo de las que forman ese conjunto. “Las nuevas melodías son parecidas a las originales”, concreta la investigadora. “Y si se incluye en el sistema más de un modelo musical, creará otra melodía nueva, una nueva versión, que será una mezcla de los diferentes géneros”, añade Sierra.
En el desarrollo de su trabajo, la investigadora se ha servido de un corpus o conjunto de melodías de bertsos. “Proponemos la forma en la que se pueden representar los bertsos, y, posteriormente, cómo clasificar esas melodías. En nuestro grupo hemos conseguido el método, que puede ser aplicado en cualquier otro tipo de corpus, o de música”, declara Goienetxea.
Según la investigadora, han conseguido generar de forma automática melodías de bertsos, “pero este método puede servir para aplicaciones de musicoterapia, el aprendizaje de composición musical, o también en los programas de composición, entre otros”.
Referencia:
I. Goienetxea, J. M. Martínez-Otzeta, B. Sierra, I. Mendialdua Towards the Use of Similarity Distances to Music Genre Classification: a Comparative Study (2017) PLoS ONE doi: 10.1371/journal.pone.0191417
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo BertsoBot, el robot versolari se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Traducción automática neuronal sin supervisión
- Estroncio en la leche
- Fotovoltaicos siempre a máxima potencia
La movilidad contraintuitiva
El 30 de marzo del pasado año un incendio presuntamente provocado provocó el colapso de un viaducto en la Interestatal 85 a su paso por Atlanta. Cuatro kilómetros de uno de los sentidos permanecieron cortados al tráfico hasta el verano mientras se reparaba. La I-85 es la vía que más tráfico desplaza en la ciudad de la Coca-Cola y se preveía un auténtico caos circulatorio y de atascos. La realidad es que no pasó nada incluso el tráfico se redujo en las vías alternativas. ¿Qué estaba pasando?
Para los que trabajamos en cuestiones de movilidad (la de mover personas, no la de los teléfonos) existen algunos conceptos que cuesta hacer entender a los gestores, pero sobre todo al gran público, y que son fundamentales para comprender por qué esta disciplina es tan compleja de gestionar. Estos conceptos son totalmente contraintuitivos y hace falta mucha pedagogía y buena comunicación para tomar la decisión correcta.*
El error de acabar con los atascos con más infraestructuras
Cuando tenemos un atasco recurrente en una vía, la solución más sencilla suele ser pensar en su posible ampliación. Cuando esta ampliación se ejecuta, a los pocos meses se vuelven a producir los mismos atascos y no hemos solucionado nada.
Al ampliar una vía con más carriles, mucho de los usuarios que no se planteaban usar el coche por los continuos atascos, ahora si se lo plantean porque perciben el tráfico fluido. Pero los atascos no se debían a que la infraestructura estuviera mal dimensionada sino a otros factores como, por ejemplo, acabar en el cuello de botella de una ciudad. Como más usuarios se plantean coger el coche al final tenemos un vía con más coches pero nuevamente atascada. Es lo que se llama demanda inducida y es un error que hemos estado cometiendo desde los años 50 del siglo pasado.

23 carriles para el mayor atasco del mundo | Wikipedia
Pero si la demanda se puede inducir, ¿se podrá también disipar? Sí, y eso fue exactamente lo que ocurrió en la I-85. Al preverse más tráfico con menos espacio, las personas no solo tomaron rutas alternativas sino que lo hicieron fuera de sus horarios habituales. Incluso se plantearon si ir en coche era necesario. Solo cogían el coche aquellos que lo necesitaban. Y tenemos otro ejemplo más cercano en el famoso cierre de la Gran Vía al tráfico por Navidad que causó menos tráfico y no más en las vías no afectadas por los cortes como la M-30, por ejemplo.
Esto no funciona siempre, si reduces carriles o cortas tráfico en las vía diseñadas precisamente para ser alternativas a las congestionadas solo vas a conseguir aumentar los atascos, como se ha podido comprobar en Murcia al quitar un carril por sentido en sus rondas exteriores.
Si queréis saber más sobre el tráfico disipado os recomiendo leer el documento «Reclamando las calles de la ciudad para las personas» de la Comisión Europea.
En la cantidad está la seguridad
¿Qué ocurre si paulatinamente fuéramos aumentando el número de ciclistas en una ciudad? ¿Aumentarían los accidentes de forma proporcional? Eso es lo que nos diría la lógica pero los accidentes ni siquiera se mantienen estables sino que disminuyen. Y todo esto no es achacable por completo a la creación de vías segregadas y seguras sino que hay otro factor implicado.
Este factor se llama “seguridad por número” y va relacionado con nuestro comportamiento al volante y la costumbre que tengamos de encontrarnos imprevistos. En una ciudad donde los ciclistas sean algo testimonial, los conductores se comportarán como si estos no existieran, no tomarán las precauciones necesarias para evitar accidentes. Sin embargo, conforme el número de ciclistas va aumentando los conductores interiorizarán una serie de hábitos para evitar los accidentes: frenarán en las intersecciones, abrirán las puertas mirando si no viene nadie (el caso extremo es la “apertura a la holandesa”, con la manos contraria), reducirán su velocidad…
El caso de Sevilla con la ampliación de sus carriles bicis es un buen ejemplo. En el año 2006 la ciudad contaba con 12 km de carril bici, 3 millones de desplazamiento y se producían 16 accidentes coche-bici cada millón de viajes. Siete años después la red se había ampliado hasta llegar a los 152 km, los desplazamientos se habían multiplicado por 5,4, 16 millones de desplazamientos fluían por sus calles y los accidentes habían disminuido hasta los 6 por millón (1).
Otro ejemplo de ello es la ciudad de Nueva York, que va camino de los 140 millones de viajes y ha reducido su accidentalidad ciclista un 71 % en 20 años. Y esto es algo que se mantienen más o menos por todo el mundo: donde hay más ciclistas hay menos accidentes (2).
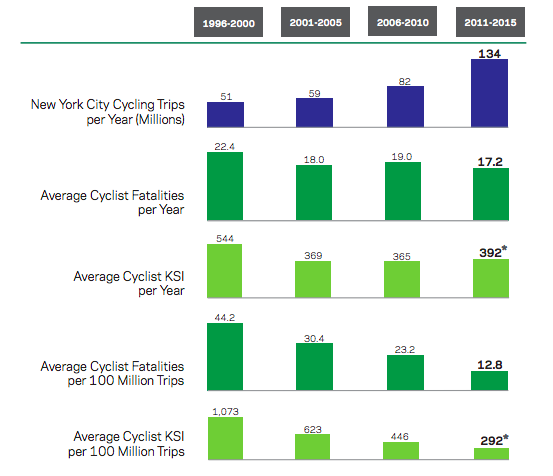
Fuente: Departamento de Transporte de Nueva York
Menos carriles para mover a más personas
Cuando pensamos en vehículo motorizados, nos movemos de forma muy ineficiente. La cantidad de área que necesita un coche para moverse en una ciudad es desorbitada si tenemos en cuenta que la media de ocupación es 1,2 personas por vehículo. Quitarle carriles a los coches hace que más personas puedan circular por esa calle.
Volvamos al ejemplo de la Gran Vía. En una situación ideal de tráfico, los dos carriles dedicados a los coches moverían unos 1200 vehículos/hora, unos 1500 pasajeros/hora. Si destinamos ese espacio a peatones en una situación de flujo peatonal denso como el que se vive en Navidad estaríamos hablando de 13.000 peatones/hora (si nos vamos a las situaciones previas al colapso tenemos 25.000 peatones/hora). Destinar esos dos carriles a peatones multiplica por 10 el número de personas que circulan por ellos.

La imagen de la izquierda fue tomada originalmente por @ClaraCarlille; la imagen derecha está extraída de la cuenta de @hcjulio
Queda mucho más claro en la siguiente gráfica que la NACTO incluyó en su «Guía global para el diseño de calles» usando los datos de circulación de Estados Unidos y Canadá. Cuando destinamos más espacios a medios de desplazamientos que mueven a más personas por área, el tránsito que puede soportar una calle se dispara.
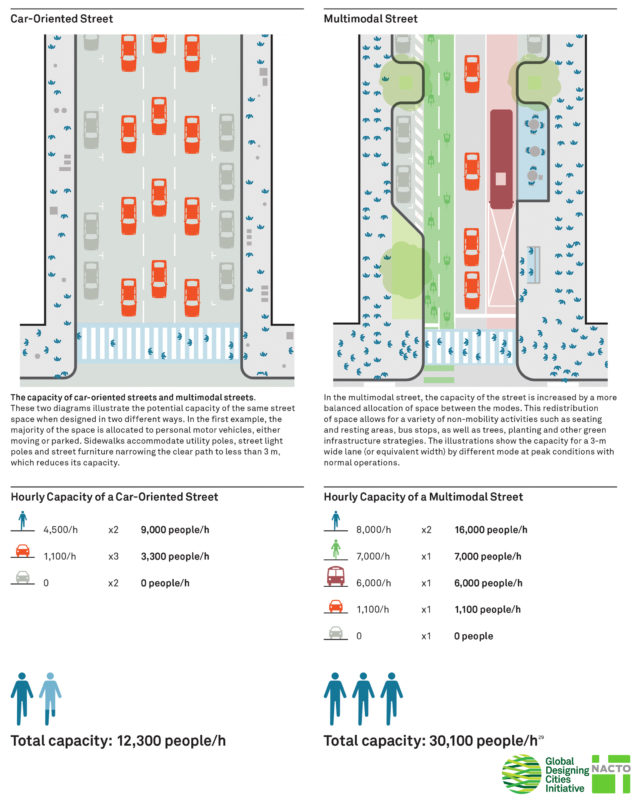
Fuente: NACTO
En resumen: ampliar o disminuir la autopistas puede tener el efecto contrario al deseado; cuantos más ciclista haya en una ciudad menor será el número de accidentes y quitar carriles de coches en una calle hace que aumente el número de personas que pueden circular por ella.
Cuando leas que tu ayuntamiento va a realizar esta o aquella actuación y creas que va a suponer caos, colapso, víctimas mortales, apocalipsis y atascos de tráfico párate a pensar si en realidad la situación no será la contraria y te están haciendo un favor tanto si vas a pie como si vas en coche.
Este post ha sido realizado por Txema Campillo (@Txemacg) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
Nota del autor: *Luego existen otros mitos contraintuitivos como que los vehículos privados no están subvencionados o que ocupar el espacio público no cuesta dinero pero entran más en el terreno de la economía y no los trataré aquí.
Referencias y más información:
(1) On the effect of networks of cycle-tracks on the risk of cycling. The case of Seville. Marqués y Hernández-Herrador, Accidents; analysis and prevention. 2017 May;102:181-190 https://www.ncbi.nlm.nih.gov/pubmed/28319756
(2) Safety in numbers: more walkers and bicyclists, safer walking and bicycling. Jacobsen, P. L., Injury Prevention. 2003;9:205–209 https://ecf.com/sites/ecf.com/files/Safety_in_Numbers_JacobsenPaper.pdf
El artículo La movilidad contraintuitiva se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Por qué no nos basta con el viento
- Del zumo de naranja a la selva, un ejemplo de reciclaje extremo
- La carrera hacia la supremacía cuántica

