El futuro es inescrutable, sus amenazas también lo son
 Foto: Louis Reed / Unsplash
Foto: Louis Reed / UnsplashEn 1971, dos años después de haber sido elegido presidente de los Estados Unidos, Richard Nixon firmó la denominada National Cancer Act, una ley mediante la que se proponía acabar con el cáncer. Aunque la ley en cuestión no la recogía en su tenor literal, la expresión “guerra al cáncer” fue profusamente utilizada para referirse al plan federal de actuaciones. Junto con otras medidas, se destinaron al plan 1.500 millones de dólares y Nixon prometió que lo “derrotarían”.
Otros gobiernos, el español incluido, declaran ahora la “guerra” a otra enfermedad, la provocada por el coronavirus SARS-CoV-2. Además de las medidas implantadas para contener la expansión de la pandemia, los planes contienen actuaciones de política científica, con una importante inyección de recursos económicos para investigar sobre el coronavirus y posibles tratamientos para “vencerlo”.
En medio de tanta zozobra, dolor e incertidumbre como está causando la pandemia, gobernantes y prescriptores de opinión parecen depositar su confianza en la ciencia como instrumento para resolver el reto más formidable que afrontan generaciones. Porque parece haber calado la idea de que, como decíamos hace dos semanas, solo el conocimiento permitirá superarlo.
Conviene, no obstante, ser cautos. El pasado lunes 23 la revista Science publicó un editorial en el que advertía del riesgo de que se le pida demasiado a la ciencia o de que, incluso, la propia comunidad científica genere más expectativas de las debidas. El editorial utilizaba, a tal efecto, el caso del VIH: fueron necesarias décadas de esfuerzo en virología, epidemiología y desarrollo de nuevos fármacos para empezar a obtener resultados. Y si bien es cierto que desde hace tiempo el SIDA se ha convertido en una enfermedad crónica, tan solo ahora, cuatro décadas después, están empezando a curarse algunos enfermos.
Algo parecido cabe decir de las investigaciones sobre el cáncer y sus resultados. Hoy sabemos más sobre los procesos implicados en las diferentes enfermedades que se engloban bajo esa denominación, y desde 1971 se han hecho progresos en el conocimiento de cuestiones tales como los factores de riesgo, los tratamientos y la prognosis de algunos tipos. Pero muchos siguen siendo incurables y la mortalidad se ha reducido solo levemente desde entonces. Recuperando la metáfora bélica, el cáncer sigue sin haber sido “derrotado”.
El contraejemplo de esas “guerras” es el proyecto Manhattan -este sí, de carácter bélico-, que se saldó con la producción de la bomba atómica. La comunidad científica contaba con suficiente conocimiento acerca de la estructura del átomo y la naturaleza de la materia. Y eso permitió a los norteamericanos disponer, en tiempo récord, del arma más mortífera que ha creado la humanidad.
Es importante, por supuesto, que se destinen recursos a la investigación sobre coronavirus y sobre epidemias en general. Pero la conclusión que cabe extraer de lo anterior debe llevarnos más allá.
No sabemos qué nos deparará el futuro. Si bien es cierto que algunos peligros posibles son demasiado probables como para ignorarlos, también lo es que otros son completamente impredecibles, de la misma forma que desconocemos en qué materias o en qué campos necesitaremos generar conocimiento en el futuro próximo. También ignoramos aspectos fundamentales que subyacen a algunos de los problemas del presente, como pone de manifiesto la historia del cáncer. Por eso, la estrategia más útil consiste en aumentar y diversificar el esfuerzo, sembrando en terrenos diferentes, porque desconocemos hoy lo que necesitaremos mañana. Es importante atesorar conocimiento en materias diversas porque cuanto más sepamos, mejor pertrechados estaremos para hacer frente a los retos que, en forma de pandemias o de cualquier otra naturaleza, esperan a la humanidad.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El futuro es inescrutable, sus amenazas también lo son se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:¡Leamos poesía astronómica en las rocas!
Los fósiles, los minerales o las rocas son, entre otras cosas, en lo primero que pensamos al hablar de geología, pero lo cierto es que la física es un ámbito científico que difícilmente se puede desvincular de la geología. Y es que el fundamento físico resulta clave a la hora de explicar algunos procesos geológicos que suceden tanto en el océano como en la superficie terrestre.
Con el fin de poner sobre la mesa la estrecha relación entre la geología y la física, los días 27 y 28 de noviembre de 2019 se celebró la jornada divulgativa “Geología para poetas, miopes y despistados: La Geología también tiene su Física”. El evento tuvo lugar en la Sala Baroja del Bizkaia Aretoa de la UPV/EHU en Bilbao.
La segunda edición de esta iniciativa estuvo organizada por miembros del grupo de investigación de Procesos Hidro-Ambientales (HGI) de la Facultad de Ciencia y Tecnología de la Universidad del País Vasco, en colaboración con el Vicerrectorado del Campus de Bizkaia, el Geoparque de la Costa Vasca y la Cátedra de Cultura Científica de la UPV/EHU.

En las rocas se puede leer la historia climática de la Tierra. Pero si se hace con los ojos de un poeta y se busca inspiración en la astronomía te encuentras con que puedes leer poesía en las rocas, como los que explica Aitor Payros, profesor del departamento de estratigrafía y paleontología de la Universidad del País Vasco.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo ¡Leamos poesía astronómica en las rocas! se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las mareas del pasado leídas en las rocas del presente
- Terremotos en la gran pantalla: algunas verdades y diversas mentiras
- La eternidad en un grano de arena
La supervivencia siempre tiene un coste: la prevalencia del haplogrupo H en Europa
 Esqueleto de uno de los individuos enterrados en la necrópolis de la ermita de San Miguel de Ereñozar. Foto: Mikel Neira.
Esqueleto de uno de los individuos enterrados en la necrópolis de la ermita de San Miguel de Ereñozar. Foto: Mikel Neira.Entre el siglo XIV y el XIX se produjo un período de inestabilidad climática conocido como la Pequeña Edad de Hielo que afectó principalmente al hemisferio norte. Durante este período se produjo un incremento de la actividad tormentosa y un descenso de la temperatura, que, aunque no fue muy severo, entre 1º y 2ºC, tuvo consecuencias devastadoras. El clima benigno de siglos anteriores, que había provocado un aumento notable de la población, se transformó en otro más duro y conllevó la destrucción de cosechas, la muerte de animales y, en definitiva, hambre. Y con las hambrunas, la salud de las poblaciones se debilitó y se propagaron las enfermedades. Basta recordar la pandemia de peste negra que asoló Europa en el siglo XIV, acabando con aproximadamente un tercio de su población.
¿Influyeron ese cambio climático y las consiguientes enfermedades en la genética humana? En la población europea actual el linaje del ADN mitocondrial, es decir, el material genético que se transmite por vía materna, más frecuente es el H. ¿Por qué?
 Reconstrucción del Castillo-Ermita de San Miguel de Ereñozar en época medieval. Fuente: Urdailife. Abajo, vídeo con el estado actual y la ubicación de la ermita.
Reconstrucción del Castillo-Ermita de San Miguel de Ereñozar en época medieval. Fuente: Urdailife. Abajo, vídeo con el estado actual y la ubicación de la ermita.
En el yacimiento medieval de San Miguel de Ereñozar el grupo de Biología Evolutiva Humana de la Facultad de Ciencia y Tecnología de la UPV/EHU, ha encontrado elementos que podrían servir para esclarecerlo. En esa necrópolis de la comarca vizcaína de Busturialdea-Urdaibai, en uso del siglo XIII al XVI, hay enterrados 163 individuos, de los que un 73% pertenecen al haplogrupo H, una frecuencia más alta que la que se da hoy en día en Europa.
“En la bibliografía ya se había postulado que algunos linajes mitocondriales podrían tener una relación con diferentes tipos de enfermedades y además, presentar un comportamiento diferencial con respecto al desarrollo de las mismas”, explica Imanol Martín, quien ha desarrollado la investigación como parte de su tesis. Así, los haplogrupos J y T protegerían frente al desarrollo de la osteoartritis, mientras que el haplogrupo H incrementaría el riesgo a desarrollar enfermedades reumáticas.
Así, que los investigadores de la UPV/EHU buscaron manifestaciones reumáticas en los esqueletos de los 163 individuos enterrados en Ereñozar, y los encontraron en 47. Y, puesto que para que las enfermedades reumáticas dejen signos óseos es necesario que pase el tiempo, se eligieron los restos de otras 43 personas de más de 45 años de edad de la misma necrópolis como grupo de control. En ambos grupos se llevaron a cabo análisis de los distintos linajes mitocondriales. “El haplogrupo H fue más frecuente entre los individuos con manifestaciones reumáticas que en el grupo control y, a su vez, fue este haplogrupo mitocondrial el más frecuente entre los individuos afectados con espondiloartritis (grupo de enfermedades reumáticas e inflamatorias de las articulaciones)”, añade Martín.
En definitiva, el estudio confirma la relación entre las enfermedades reumáticas y el haplogrupo H, y también da pistas sobre la elevada frecuencia de este haplogupo en la población europea: “En esa época de déficit de alimentos los individuos del haplogrupo H tenían una ventaja selectiva frente a los que tuvieran otros haplogrupos, ya que el H es más eficiente a la hora de obtener energía de la dieta”. Sin embargo, ese metabolismo altamente eficiente también genera las llamadas especies reactivas de oxígeno (radicales libres, iones de oxígeno…), que desencadenan la disfunción y apoptosis celular y provocan, a la larga, la degradación del cartílago y el desarrollo de enfermedades de carácter reumático. La supervivencia siempre tiene un coste.
Referencia:
I.M. Laza, M. Hervella, M. Neira Zubieta & C. de-la-Rúa (2019) Environmental factors modulated ancient mitochondrial DNA variability and the prevalence of rheumatic diseases in the Basque Country Scientific Reports doi: 10.1038/s41598-019-56921-x
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La supervivencia siempre tiene un coste: la prevalencia del haplogrupo H en Europa se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Fotovoltaicos siempre a máxima potencia
- El planeta enano Haumea tiene anillo
- La selección positiva de la piel clara en el sur de Europa
Lienzos y partituras para crear nuevas vacunas
![]()
José de la Fuente, Juan José Pastor Comin y Sara Artigas Jerónimo
 “El beso”, de Israel León Viera, que representa la nueva e inexplorada interacción de AKR con AKR o de SUB con SUB.
“El beso”, de Israel León Viera, que representa la nueva e inexplorada interacción de AKR con AKR o de SUB con SUB.KGJ Colección, Author provided
¡Que suene la música! La trucha alpina al oboe. Una rana al clarinete. El fagot para la mosca del vinagre. La única persona de esta peculiar banda toca el violín, mientras que una garrapata se encarga de la viola. Completa el sexteto de viento y cuerda un Caenorhabditis elegans, un pequeño gusano de un milímetro que hará que suene un imponente chelo.
¿Puede un compositor procurar una banda sonora que transcriba los datos que emergen de la rutina experimental de tubos de ensayo y probetas? Todos los componentes de la banda tienen algo en común: una proteína en su ADN. ¿Puede la información genética trasladarse a una partitura?
 Secuencias de AKR/SUB dispuestas polifónicamente. Recurrencias y motivos.
Secuencias de AKR/SUB dispuestas polifónicamente. Recurrencias y motivos.Juan José Pastor., Author provided
La ciencia consiste en plantear nuevos interrogantes. Innovar es romper con lo establecido ¿Pueden el arte y la música ayudarnos a comprender la respuesta de nuestro organismo a una infección? ¿Y si los diseños de los artistas plásticos pudieran recoger sobre un lienzo los caminos que la ciencia debe abordar en el diseño de nuevos experimentos? ¿Podría una composición musical ayudar a entender con el comportamiento de sus voces, sus líneas melódicas, su forma y su estructura, las interacciones de las proteínas cuando estas responden ante la amenaza de un nuevo patógeno?
Para responder a esto tenemos que abrir nuestra mente. Y experimentar.
Científicos y artistas
Investigadores del área de Genómica, Proteómica y Biotecnología del grupo SaBio en el Instituto de Investigación de Recursos Cinegéticos, centro mixto de la Universidad de Castilla-La Mancha y el CSIC, hemos desarrollado a través de un equipo interdisciplinar de científicos, artistas y músicos una nueva metodología. Esta nueva aproximación, publicada en el último número de la revista Vaccines, reúne el enfoque artístico y científico en la caracterización de la akirina (AKR), una proteína también conocida como subolesina (SUB) en garrapatas, para avanzar en el estudio del papel que juegan estas moléculas en la regulación de la respuesta inmune.
De esta forma, se identifican los mecanismos y genes que son expresados en nuestras células y se convierten en proteínas con un papel funcional en respuesta a la infección. Estas proteínas están muy conservadas a través de la evolución en distintas especies y han sido eficaces en el desarrollo de vacunas. Este conjunto de proteínas interactúa física y funcionalmente entre ellas en respuesta a algún estímulo, como podría ser su comportamiento ante una infección en células humanas.
La colaboración entre científicos y artistas proporcionó dos resultados:
- Un algoritmo que utiliza conjuntos musicales, basados en la akirina y secuencias de proteínas que interactúan, como un nuevo método para caracterizar la evolución y las interacciones entre proteínas.
- La sugerencia de artistas visuales de propiedades previamente inexploradas.
Este planteamiento proporciona un enfoque combinado para comprender algunas de las preguntas desafiantes de la biología molecular.
Del ADN a la partitura
Tradujimos las secuencias del ADN de la akirina de distintas especies animales a motivos musicales. Para ello utilizamos un primer algoritmo modificado que atendía a la altura y el ritmo. Esto permitió generar el patrón melódico de cada especie animal y su configuración motívica, y también observar las similitudes presentes entre las secuencias en distintas especies y la identificación de los motivos repetidos.
La representación musical no solo permitió una comprensión lineal –-melódica-– de la singularidad de cada especie estudiada, sino que permitió su visión polifónica –conjunta y simultánea-–, como una composición compleja y lógica. El análisis del contrapunto –cómo unas voces o especies se imitan unas a otras-– aportó una textura musical llena de correspondencias, que se mostraba viva a través del sonido.
Ciencia sobre lienzo
En el caso de la pintura, trasladamos al artista una hipótesis científica de partida que sirvió al pintor para expresar un problema biológico sobre los materiales artísticos elegidos y que este tratara de resolverlo a través de formas, composición, trazos y color sobre la tela y el bastidor.
Esta contribución creativa nos ayudó a representar su propia teoría de una forma original y desde un punto de vista completamente diferente, no conceptual, lejos de la organización estadística de los datos recogidos.
La nueva representación visual constituye un nuevo contexto de referencias aperturista que estimula la imaginación y la creatividad y que permite establecer nuevas hipótesis que, a la única luz de los datos experimentales obtenidos, tal vez no hubieran surgido. La representación artístico-visual sirvió no solo para identificar problemas conocidos en las formas de expresión de un lenguaje artístico, sino también para suscitar nuevas ideas divergentes.
 KGJ Colección, Ciudad Real, España., Author provided
KGJ Colección, Ciudad Real, España., Author providedLos resultados mostraron de un modo plural e interdisciplinar que la interacción entre varías moléculas de AKR y SUB y las interacciones físicas con diferentes proteínas simultáneamente están involucradas en la regulación de varios procesos biológicos. Además, ayudaron a entender, a través de estas nuevas formas de representación artística y musical, el papel de las interacciones estudiadas en la regulación positiva y negativa de respuesta inmune. Así entendimos cómo se activa o suprime la expresión de algunos genes concretos.
¿Qué implicaciones alcanza esta colaboración? No solo contribuye a la investigación, sino que puede lograr el desarrollo de vacunas para el control de infestaciones por garrapatas, así como para el estudio de patógenos transmitidos por estas.
Este puede ser un avance esencial en contextos de exclusión social en un mundo que cuenta con un importante índice poblacional situado bajo el umbral de pobreza. Ahí es donde científicos y artistas pueden avanzar juntos y de la mano, iluminando el avance de la investigación ante los nuevos desafíos científicos que permitan construir un mundo mejor.![]()
Sobre los autores: José de la Fuente es profesor de investigación en el Instituto de Investigación en Recursos Cinegéticos (CSIC – Universidad de Castilla-La Mancha) y profesor adjunto en el departamente de patobiología veterinaria de la Universidad Estatal de Oklahoma (Estados Unidos); Juan José Pastor Comin es es profesor titular del área de Música en la Universidad de Castilla-La Mancha y co-director del Centro de Investigación y Documentación Musical (CIDoM); Sara Artigas Jerónimo es investigadora predoctoral en el Instituto de Investigación en Recursos Cinegéticos.
Este artículo fue publicado originalmente en The Conversation. Artículo original
El artículo Lienzos y partituras para crear nuevas vacunas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Dudas sobre las vacunas: problemas y soluciones
- Nuevas tecnologías para el estudio del cerebro: Desde Cajal a nuestros días
- Desmitificando: Vacunas peligrosas
La cuadratura del cuadrado: las redes eléctricas de Kirchhoff
En mi anterior entrada del Cuaderno de Cultura Científica La cuadratura del cuadrado: en busca del santo grial estuvimos hablando de un hermoso rompecabezas matemático, el problema de la cuadratura perfecta del cuadrado, que recuerdo a continuación:
Problema de la cuadratura perfecta del cuadrado (o rectángulo): Dividir un cuadrado (o rectángulo) en un número finito de cuadrados más pequeños, todos de distintos tamaños.
Este problema, que durante mucho tiempo se pensó que no tenía solución para cuadrados, lo que se conoció como la conjetura de Luzin, fue finalmente resuelto en positivo, alrededor del año 1939, por dos grupos de matemáticos. Por una parte, el matemático alemán Roland P. Sprague (1894-1967) construyó un cuadrado con una cuadratura perfecta, pero compuesta (recordemos que eso significa que contiene la cuadratura de algún sub-rectángulo), de orden 55. Mientras que los cuatro estudiantes del Trinity College de la Universidad de Cambridge (Reino Unido), Rowland L. Brooks (1916-1993), Cedric A. B. Smith (1917-2002), Arthur H. Stone (1916-2000) y William Th. Tutte (1917-2002), consiguieron construir el primer cuadrado perfecto simple (no compuesto), también de orden 55. Para ello, los cuatro de Trinity (puede leerse más sobre ellos en la entrada Blanche Descartes y la cuadratura del cuadrado) relacionaron el problema de las disecciones cuadradas de los rectángulos, en particular, de los cuadrados, con la teoría de las redes eléctricas de Kirchhoff, que es de lo que vamos a hablar en esta entrada.
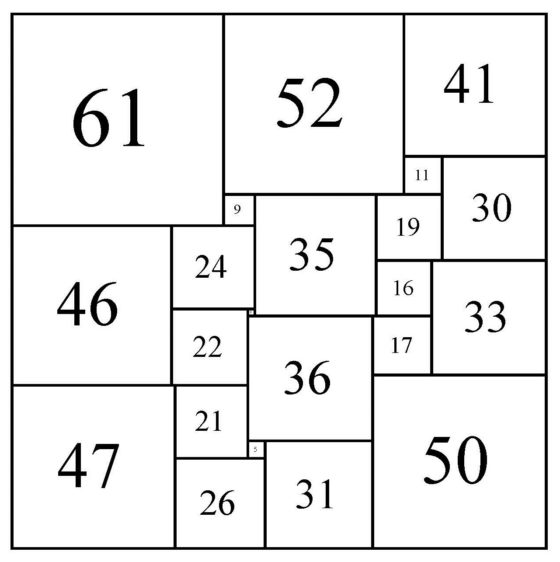 Una de las ocho cuadraturas perfectas simples del cuadrado de orden 22 que existen. Imagen de la página Tiling by squares, de Stuart Anderson
Una de las ocho cuadraturas perfectas simples del cuadrado de orden 22 que existen. Imagen de la página Tiling by squares, de Stuart AndersonComo explicamos en la anterior entrada, La cuadratura del cuadrado: en busca del santo grial, el primer acercamiento de los jóvenes estudiantes de Cambridge, Brooks, Smith, Stone y Tutte, fue experimental. Intentaron construir mediante una sencilla técnica algebraica algún ejemplo de disección de un cuadrado en cuadrados más pequeños de diferentes tamaños. Con esta técnica sí consiguieron construir algunos ejemplos de cuadraturas perfectas de rectángulos, pero no de cuadrados. Este método experimental dependía demasiado de la suerte y podrían no encontrar nunca el ansiado grial, una cuadratura perfecta del cuadrado. Era como encontrar una aguja en un pajar, sin saber además si había aguja. Por este motivo, abandonaron el camino experimental a favor de un enfoque más teórico, que además les permitiera conocer más sobre el problema.
Entonces, empezaron a asociar diferentes tipos de diagramas a las cuadraturas de los rectángulos. Hasta que llegaron a un diagrama propuesto por Cedric Smith, que sus compañeros no dudaron en llamar el “diagrama de Smith”, que asociaba cada cuadratura de un rectángulo con el grafo de una red eléctrica.
Para ilustrar la construcción de la red eléctrica asociada a una cuadratura, consideraremos el ejemplo de la división de un rectángulo de dimensiones 32 x 33 en 9 cuadrados de distintos tamaños, de lados 1, 4, 7, 8, 9, 10, 14, 15 y 18, luego de orden 9, obtenida por el matemático polaco Zbigniew Moron en 1925, que aparece en la siguiente imagen. Cada segmento horizontal se representará como un vértice del grafo y dos vértices estarán unidos mediante una arista si existe un cuadrado que tiene su lado superior apoyado en el segmento horizontal correspondiente a uno de los vértices y su lado inferior apoyado en el segmento horizontal del otro vértice. Además, el grafo está dirigido, como se muestra mediante las fechas de las aristas, de arriba hacia abajo, que es el orden de la corriente eléctrica, del polo positivo (que consideramos el vértice del lado horizontal superior) al polo negativo (el vértice del lado horizontal inferior). Más aún, es un grafo etiquetado, ya que asociamos a cada arista el valor del lado del cuadrado correspondiente, que será el valor de la corriente eléctrica.
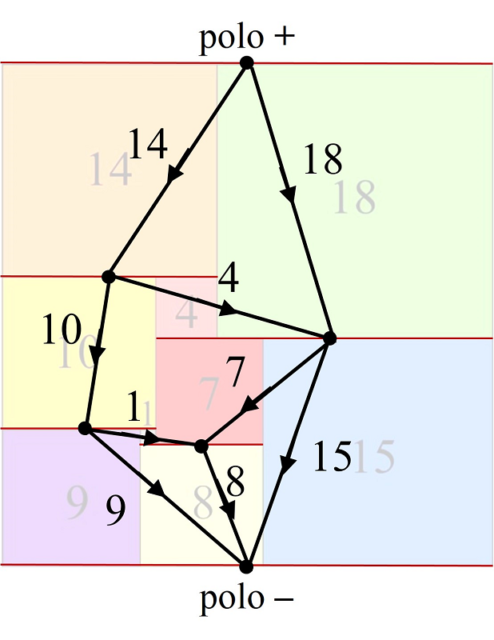 Diagrama de Smith de la cuadratura perfecta del rectángulo de dimensiones 32 x 33 en 9 cuadrados de distintos tamaños, de lados 1, 4, 7, 8, 9, 10, 14, 15 y 18
Diagrama de Smith de la cuadratura perfecta del rectángulo de dimensiones 32 x 33 en 9 cuadrados de distintos tamaños, de lados 1, 4, 7, 8, 9, 10, 14, 15 y 18
Lo curioso es que el diagrama de Smith cumple las leyes de Kirchhoff para las redes eléctricas, asumiendo que la resistencia de cada arista es igual a 1. La primera ley de Kirchhoff establece que en cada nodo (vértice) del circuito eléctrico, con excepción de los polos, la suma de las corrientes debe ser cero, es decir, la suma de las corrientes que entran en el nodo es igual a la suma de las corrientes que salen del mismo. Por ejemplo, si miramos a la red eléctrica anterior, en el primer vértice después del polo positivo, entra una corriente de 14 y salen dos de 10 y 4, o en el siguiente entran dos corrientes de 4 y 18, mientras que salen dos corrientes de 7 y 15. Esto es debido a que, en un segmento horizontal (vértice) cualquiera de la cuadratura del rectángulo, la suma de los lados de los cuadrados que se apoyan en el segmento desde arriba (la suma de las corrientes que entran) es igual a la suma de los lados de los cuadrados que se apoyan en el segmento desde abajo (la suma de las corrientes que salen), que en ambos casos es la longitud del segmento horizontal.
Teniendo en cuenta que, por la ley de Ohm de los circuitos eléctricos, la diferencia de potencial de cada arista del circuito es igual al producto de la resistencia, que en este caso hemos asumido que es 1, por la corriente, ambas –diferencia de potencia y corriente- son iguales. Por lo tanto, la segunda ley de Kirchhoff establece que la suma algebraica de las corrientes –diferencias de potencial- de cualquier circuito cerrado es cero. En el ejemplo de arriba, en el primer circuito cerrado tenemos que 14 + 4 – 18 = 0 o en el segundo 10 + 1 – 7 – 4 = 0. Esto es debido a que cada segmento vertical de la cuadratura del rectángulo se corresponde con un circuito cerrado, y la suma de las longitudes de los lados de los cuadrados a izquierda y derecha del segmento valen lo mismo, la longitud del segmento vertical.
La corriente que entra en el circuito eléctrico por el polo positivo, que es igual a la que sale por el polo negativo, es la longitud de los lados horizontales del rectángulo. En el ejemplo de arriba, 14 + 18 = 9 + 8 + 15 = 32. Por otra parte, la diferencia de potencial entre los dos polos es igual a la longitud de los lados verticales del rectángulo. De nuevo, en el ejemplo la diferencia de potencial la podemos calcular a través de cualquiera de los recorridos entre el polo positivo y el negativo, 14 + 10 + 9 = 14 + 4 + 7 + 8 = 18 + 15 = 33, entre otros. Por lo tanto, si la corriente que entra por el polo positivo, y sale por el negativo, es igual a la diferencia de potencial, estaríamos ante un circuito eléctrico que se corresponde con la cuadratura del cuadrado.
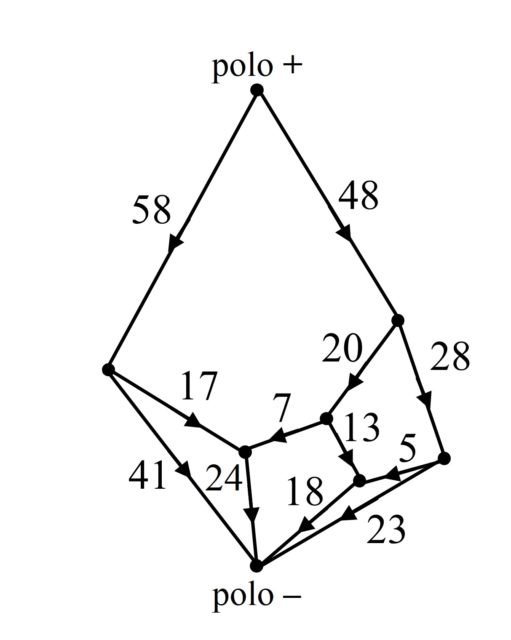 Diagrama de Smith asociado a una cuadratura perfecta de un rectángulo
Diagrama de Smith asociado a una cuadratura perfecta de un rectángulo
En conclusión, cada cuadratura de un rectángulo se corresponde con una red eléctrica, lo cual les permitió utilizar los conocimientos de la teoría de redes eléctricas para estudiar el problema de la cuadratura de los rectángulos, y del cuadrado. Por ejemplo, en la imagen anterior tenemos una red eléctrica, os dejo como divertimento el construir la cuadratura del rectángulo asociada (solución al final de la entrada).
En particular, esto simplificó el problema de construir y clasificar las cuadraturas perfectas simples de rectángulos. Por ejemplo, analizaron todos los circuitos eléctricos con hasta 11 aristas y construyeron las cuadraturas de rectángulos asociadas. Así probaron que no existen cuadraturas perfectas simples de rectángulos de orden menor que 9, que solo hay dos de orden 9 (mostradas en la anterior entrada La cuadratura del cuadrado: en busca del santo grial, una de ellas es la asociada al primer circuito eléctrico que hemos mostrado más arriba), seis de orden 10 y veintidós de orden 11. Y siguieron clasificando las cuadraturas de orden 12, que hay sesenta y siete, y después de orden 13. Este fue el inicio de una fructífera investigación sobre las cuadraturas perfectas de rectángulos. Pero como veremos, también del cuadrado.
Uno de los estudios que realizaron fue el análisis de redes eléctricas con ciertas simetrías. Por ejemplo, consideraron el circuito eléctrico asociado a un cubo, vértices y aristas, que no proporcionaba cuadraturas perfectas de rectángulos, pero cuando se añadía una de las diagonales de una de las caras del cubo, se obtenía el diagrama de Smith de la siguiente imagen y la correspondiente cuadratura perfecta simple del rectángulo, que se muestra después.
 Red eléctrica definida sobre un cubo, junto con una diagonal de una de sus caras, introducida por Brooks, Smith, Stone y Tutte, para construir cuadraturas perfectas simples de rectángulos
Red eléctrica definida sobre un cubo, junto con una diagonal de una de sus caras, introducida por Brooks, Smith, Stone y Tutte, para construir cuadraturas perfectas simples de rectángulos
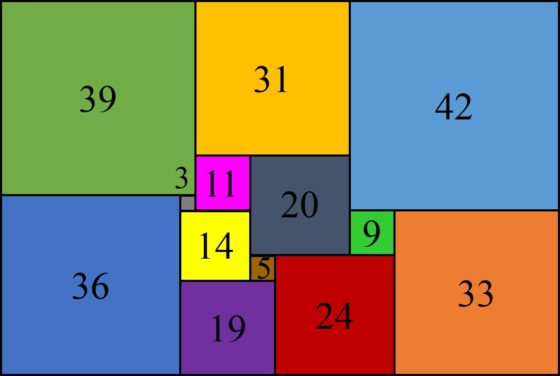 Cuadratura perfecta simple de un rectángulo de dimensiones 112 x 75 obtenida a través del circuito eléctrico anterior
Cuadratura perfecta simple de un rectángulo de dimensiones 112 x 75 obtenida a través del circuito eléctrico anterior
Una bonita historia relacionada con esta cuadratura del rectángulo es la siguiente. Leonhard Brooks estaba tan satisfecho con este ejemplo que decidió construirse un rompecabezas geométrico cuyas piezas eran los cuadrados de la cuadratura del rectángulo anterior, es decir, de lados 3, 5, 9, 11, 14, 19, 20, 24, 31, 33, 36, 39 y 42, con el que jugar a realizar el rectángulo original. Entonces su madre cogió el rompecabezas para jugar con él y consiguió formar el rectángulo con ellas, pero resultó que no era la misma solución anterior, las piezas estaban colocadas de forma diferente. Con la ayuda de la madre de Brooks, habían encontrado dos disecciones perfectas simples del rectángulo 112 x 75 realizadas con los mismos cuadrados.
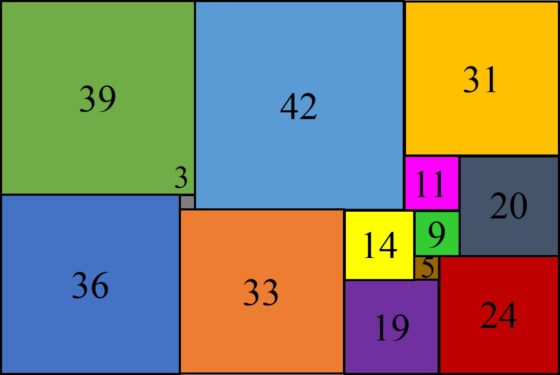 Segunda cuadratura perfecta simple del rectángulo de dimensiones 112 x 75 realizada con los mismos cuadrados que la anterior
Segunda cuadratura perfecta simple del rectángulo de dimensiones 112 x 75 realizada con los mismos cuadrados que la anterior
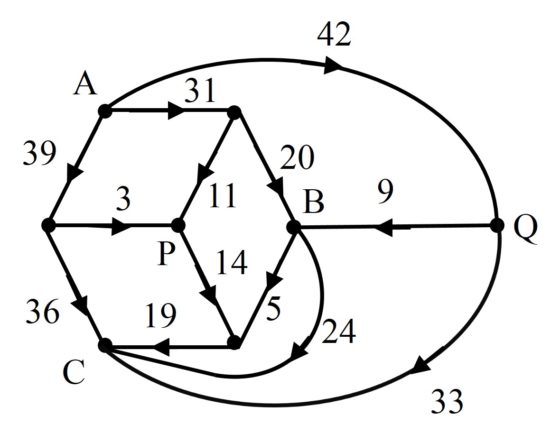
La red eléctrica asociada a esta nueva descomposición perfecta y simple del rectángulo 112 x 75 se puede obtener a partir del primer circuito eléctrico (que está representado arriba) identificando los vértices P y Q, lo cual es posible ya que tienen la misma diferencia de potencial, en concreto, 42.
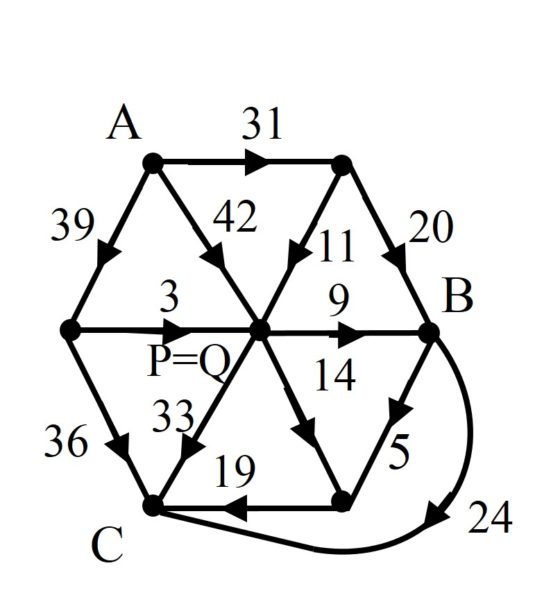 Red eléctrica asociada a la anterior descomposición perfecta simple del rectángulo 112 x 75, que se puede obtener a partir de la anterior identificando P y Q
Red eléctrica asociada a la anterior descomposición perfecta simple del rectángulo 112 x 75, que se puede obtener a partir de la anterior identificando P y Q
Analizaron el motivo por el cual se producía este fenómeno y tenía que ver con la simetría de algunas redes eléctricas, aunque no entraremos en los detalles técnicos en esta entrada, por este motivo empezaron a analizar circuitos eléctricos en los cuales cogían la red eléctrica anterior, que habían obtenido a partir del cubo, y sustituyeron la parte simétrica central (el hexágono plano que contiene a los vértices A, B, C y centro P) por otras estructuras simétricas. Así consiguieron obtener más ejemplos de dobles cuadraturas perfectas simples de un mismo rectángulo con los mismos cuadrados.
Esta técnica, después de seguir investigando y obtener otros ejemplos, les llevó a encontrar su primer ejemplo de cuadratura perfecta de un cuadrado. La pieza central simétrica tenía la siguiente forma.
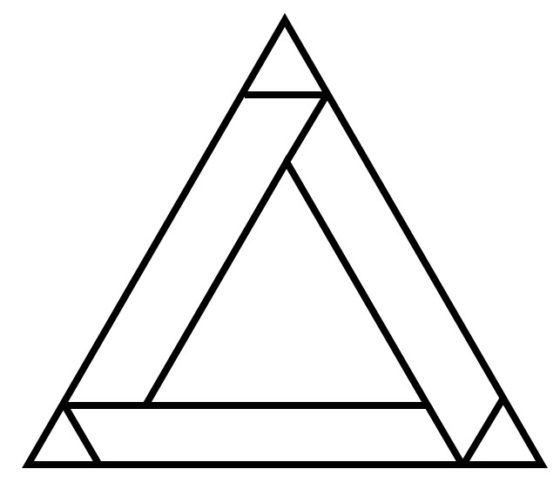
La cuadratura perfecta, que era compuesta, que obtuvieron era de orden 39, es decir, formada por 39 cuadrados de diferentes tamaños, que componían un cuadrado de lado 4.639. Utilizando el código de Bouwkamp que explicamos en la anterior entrada, esta era la cuadratura [2.378, 1.163, 1.098], [65, 1.033], [737, 491], [249, 242], [7, 235], [478, 259], [256], [324, 944], [219, 296], [1.030, 829, 519, 697], [620], [341, 178], [163, 712, 1.564], [201, 440, 157, 31], [126, 409], [283], [1231], [992, 140], [852]. Como cada corchete del código de Bouwkamp nos dice qué cuadrados, su lado, están debajo de cada segmento horizontal, de arriba abajo, podemos ver qué cuadratura prefecta del cuadrado, de lado 4.639, habían construido.
 Cuadratura perfecta, compuesta, de un cuadrado de lado 4.639, de orden 39, construida por Brooks, Smith, Stone y Tutte utilizando la teoría de las redes eléctricas
Cuadratura perfecta, compuesta, de un cuadrado de lado 4.639, de orden 39, construida por Brooks, Smith, Stone y Tutte utilizando la teoría de las redes eléctricas
Poco después, encontrarían el primer ejemplo de cuadratura perfecta simple de un cuadrado de orden 55, utilizando las mismas técnicas.
Como hemos podido ver, relacionar las cuadraturas perfectas de los rectángulos con redes eléctricas se demostró una técnica muy fructífera en la resolución del problema de la cuadratura del cuadrado, y del rectángulo, y en el estudio general de estas cuestiones.
Y, por cierto, la solución a la cuestión planteada arriba sobre cuál es la cuadratura perfecta asociada a la red eléctrica que habíamos mostrado, es la siguiente.
 Cuadratura perfecta simple de un rectángulo de tamaño 106 x 99 de orden 12, que es la solución al divertimento que os he dejado arriba de encontrar la cuadratura asociada a la red eléctrica mostrada
Cuadratura perfecta simple de un rectángulo de tamaño 106 x 99 de orden 12, que es la solución al divertimento que os he dejado arriba de encontrar la cuadratura asociada a la red eléctrica mostrada
Bibliografía
1.- Wolfram MathWorld: Perfect Square Dissection.
2.- Stuart Anderson, Tiling by squares.
3.- Martin Gardner, The 2nd Scientific American Book of Mathematical Puzzles and Diversions, University of Chicago Press, 1987. Contiene el capítulo de W. Th. Tutte Squaring the square.
4.- Wikipedia: Kirchhoff’s circuit laws
5.- Arkadiusz Maciuk, Antoni Smoluk, Tiling by squares, Kirchhoff’s Laws and a Flow Problem in the Economy, Didactics of Mathematics, n. 14 (18), 2017.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo La cuadratura del cuadrado: las redes eléctricas de Kirchhoff se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La cuadratura del cuadrado: en busca del santo grial
- Blanche Descartes y la cuadratura del cuadrado
- ¿Sueñan los babilonios con multiplicaciones eléctricas?
Sólidos cuánticos
 Foto: Pixabay
Foto: PixabayUno de los primeros grandes éxitos de la hipótesis cuántica de Planck surgió, no del estudio de la radiación, sino de la teoría de los sólidos. Una vez más, Albert Einstein fue la vanguardia.
Después de presentar la hipótesis de los cuantos de luz que explicaba el efecto fotoeléctrico en 1905, Einstein demostró en 1906 que los resultados anteriores de Planck sobre la distribución de energía en la radiación electromagnética podrían derivarse utilizando dos supuestos. El primero, ya presente en su artículo de 1905, fue que la luz se compone de cuantos de luz; el segundo fue que los cuantos de luz son emitidos y absorbidos por cargas oscilantes dentro de la materia que vibran solo con ciertas energías cuantificadas. Esto significa que la luz es emitida por cargas oscilantes dentro de la materia, como podría esperarse de la teoría de Maxwell, pero las energías tanto de la luz emitida como de los osciladores están restringidas a ciertos valores permitidos, lo que contradice la teoría clásica. Los osciladores se comportaron como cargas unidas a resortes, oscilando de un lado a otro solo con ciertas frecuencias correspondientes a ciertas energías cuánticas.
En 1904, Paul Drude había propuesto un modelo de sólido cristalino en el que los átomos están dispuestos en una red tridimensional de tal manera que cada átomo está unido a sus átomos vecinos por enlaces que pueden actuar como pequeños muelles (osciladores). Drude demostró, utilizando la física clásica, que la oscilación tridimensional de los átomos de la red puede explicar la absorción observada de la radiación infrarroja por algunos sólidos, si se supone que los átomos están ionizados. Una oscilación similar de los electrones, unidos a los átomos o iones, explicaba la absorción observada de la radiación ultravioleta en estos sólidos.
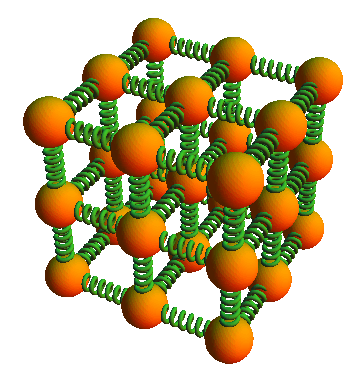 Figura 1. Modelo de Drude de átomos y muelles. Fuente: Wikimedia Commons
Figura 1. Modelo de Drude de átomos y muelles. Fuente: Wikimedia CommonsEn 1907, Einstein aplicó la hipótesis cuántica a los osciladores clásicos de Drude. Incluso antes del modelo de Drude, Einstein había especulado desde 1901 con la idea de que la energía cinética interna de los sólidos y líquidos podría considerarse como la energía de los «resonadores eléctricos». Un enigma considerable en ese momento era el comportamiento del calor específico, c, de los sólidos a medida que la temperatura disminuía. Normalmente se supone que el calor específico es una constante en la relación entre la transferencia de calor y el cambio de temperatura de una sustancia ΔQ = m·c·ΔT [2]. Y la aplicación de la física clásica al modelo de red de átomos y muelles de Drude llega a la conclusión de que, efectivamente, el calor específico c debe ser una constante para los sólidos a todas las temperaturas.
Sin embargo, cuando Einstein aplicó la hipótesis cuántica a los osciladores en el modelo de Drude obtuvo una expresión para el calor específico que afirmaba que el valor del calor específico debería cambiar con la temperatura. Para ser precisos, decía que debería ser constante a temperatura ambiente o algo menos, pero que el calor específico debería caer rápidamente a cero conforme la temperatura se va a cero (absoluto), como se muestra en la figura 2. Visto de otra forma: partiendo desde 0 K, el valor de Einstein para el calor específico de una sustancia cristalina en función de su temperatura debe acercarse a un valor constante que se alcanza más o menos a temperatura ambiente.
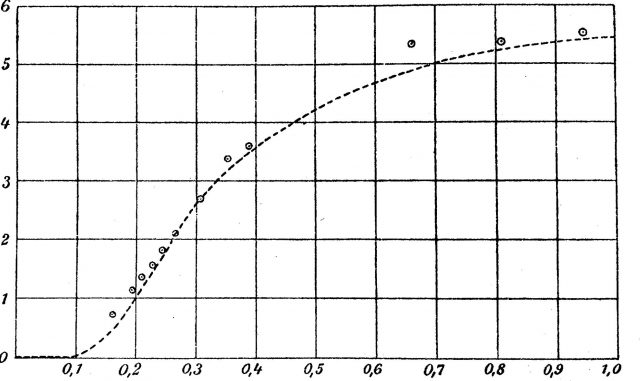 Figura 2. Gráfica original del artículo de Einstein de 1907
Figura 2. Gráfica original del artículo de Einstein de 1907Es importante recalcar esto: las predicciones de Einstein para el comportamiento del calor específico de los sólidos en función de la temperatura se basaron en una aplicación de la hipótesis cuántica a un modelo de un sólido cristalino en el que los átomos de la red se comportan como osciladores tridimensionales que vibran con energías cuantificadas. Los físicos Walther Nernst y Frederick A. Lindemann, que trabajan en un laboratorio de bajas temperaturas en Berlín, asombraron a la comunidad científica con una confirmación completa de la predicción de Einstein sobre la forma en la que el calor específico de un sólido cristalino cambia con la temperatura. Fue la primera confirmación de la hipótesis cuántica fuera del campo de radiación, y demostraba inequívocamente que los sólidos cristalinos pueden considerarse como una red tridimensional de átomos oscilantes sujetos a los requisitos de la hipótesis cuántica y, más tarde, de la mecánica cuántica.
Este modelo ha servido como modelo básico de sólido cristalino desde entonces. Como escribieron Nernst y Lindemann:
«[…] que las observaciones en su totalidad suponen una confirmación brillante de la teoría cuántica de Planck y Einstein es obvio».
Notas:
[1] Este artículo es una adaptación de nuestro Einstein and quantum solids
[2] Nosotros lo asumimos en El misterio de la temperatura constante, por ejemplo. En el ejemplo que usamos en ese texto es suficientemente cierto.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Sólidos cuánticos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los experimentos de Joule
- La teoría cinética y la segunda ley de la termodinámica
- La ley del gas ideal a partir del modelo cinético
La ciencia al servicio de la guerra
 Lois Cook-Leurgan examinando la unidad aritmética principal del MANIAC ( Mathematical Analyzer, Numerical Integrator And Computer). El ordenador jugó un papel importante en los cálculos termonucleares que se llevaron a cabo en el Los Alamos Scientific Laboratory de la Universidad de California dentro del Proyecto Manhattan. Klara Dan von Neumann fue la autora de los primeros programas.
Lois Cook-Leurgan examinando la unidad aritmética principal del MANIAC ( Mathematical Analyzer, Numerical Integrator And Computer). El ordenador jugó un papel importante en los cálculos termonucleares que se llevaron a cabo en el Los Alamos Scientific Laboratory de la Universidad de California dentro del Proyecto Manhattan. Klara Dan von Neumann fue la autora de los primeros programas.En las guerras siempre se ha utilizado el conocimiento del que se disponía en la época. Por tanto, la ciencia y la tecnología, en tanto que formas de conocimiento, no han sido ajenas a los conflictos bélicos. Más bien habría que decir que las guerras han incentivado la generación de conocimiento científico y tecnológico, y lo siguen haciendo en la actualidad.
A Arquímedes (s III aec) se le atribuye haber inventado un dispositivo basado en espejos ustorios para concentrar rayos de luz solar y producir suficiente calor como para dar fuego a las naves que transportaban las tropas romanas que pretendían ocupar la ciudad de Siracusa. Aunque en realidad, no sabemos si esa atribución es correcta.
Si nos limitamos al siglo XX y lo que llevamos del XXI, está claro que laboratorios y despachos de científicos han tenido un protagonismo determinante en los conflictos bélicos.
Fritz Haber fue galardonado con el premio Nobel por su descubrimiento del proceso llamado de Haber-Bosch, para la síntesis catalítica de amoniaco a partir de hidrógeno y nitrógeno atmosférico bajo condiciones de alta presión y temperatura. Ese proceso abrió la era de la producción industrial de fertilizantes y, en general, de la industria química. Pues bien, él fue el químico al frente del programa de producción de gases letales que utilizó Alemania en la I Guerra Mundial. F Haber puso sus conocimientos al servicio del esfuerzo bélico alemán por su forma de entender el patriotismo; llegó a decir que «en tiempo de paz, un científico pertenece al mundo, pero en tiempo de guerra pertenece a su país».
No solo él, James Franck, Gustav Hertz y Otto Hahn, futuros premios Nobel, también formaron parte de la unidad de Haber. Y en el bando galo, otro galardonado con el Nobel, Victor Grignard, participó en el esfuerzo francés para producir gases venenosos.
El radar, invención basada en la patente obtenida por Robert Watson-Watt (descendiente de James Watt), fue seguramente determinante del curso que siguió la II Guerra mundial. El invento, de 1935, de Watson-Watt se basaba en el uso de ondas de radio para detectar y alertar de movimientos de objetos invisibles con la vista. En este caso se trató de una invención de carácter defensivo (sirvió, entre otras cosas, para poder anticipar los bombardeos alemanes sobre la población civil británica), pero en lo relativo a su influencia sobre el curso de la guerra, a largo plazo no es posible diferenciar la función defensiva de la ofensiva.
El ejemplo más evidente de contribución científica a la guerra es el proyecto Manhattan, nombre clave con el que se conocía el proyecto que desarrolló Estados Unidos para fabricar la bomba atómica durante la II Guerra Mundial. El objetivo del proyecto era producir la bomba antes de que los nazis lo consiguieran. Lo lograron, como es bien sabido. Y como consecuencia de ello, lanzaron sendas bombas sobre las ciudades japonesas de Hirosima y Nagasaki, provocando de esa forma la rendición del Japón. El proyecto, en su parte científica, fue dirigido por el físico Julius Robert Oppenheimer y de una u otra forma, participaren numerosos científicos e ingenieros. También estos científicos tomaron parte en el proyecto por una causa. Todos ellos quisieron colaborar en la derrota de las potencias del Eje.
En las guerras del siglo XXI los científicos e ingenieros siguen teniendo una función determinante en el perfeccionamiento del armamento clásico y en las innovaciones. Drones, robots, inteligencia artificial, sistemas de telecomunicaciones, invisibilidad a los sistemas de detección son áreas en las que los ejércitos más poderosos del mundo invierten enormes cantidades de recursos. Muchos científicos e ingenieros participan en el desarrollo de nuevas ideas con fines militares.
Tanto Haber como Oppenheimer ejemplifican bien el tipo de dilemas éticos al que se han de enfrentar los científicos que toman parte activa en el desarrollo de armas de gran potencial para segar vidas humanas. Ambos actuaron motivados por su compromiso con el destino de los conflictos bélicos en que se vieron involucrados. Haber por patriotismo y Oppenheimer para frenar el avance del fascismo. Sus casos son especiales porque el resultado de su trabajo científico tuvo como consecuencia la pérdida de miles de vidas humanas, pero en rigor, nada los diferencia de la actuación de otros científicos que han desarrollado y desarrollan su actividad al servicio del ejército de sus países.
Este artículo se publicó originalmente en el blog de Jakiunde. Artículo original.
Sobre los autores: Juan Ignacio Perez Iglesias es Director de la Cátedra de Cultura Científica de la UPV/EHU y Joaquín Sevilla Moroder es Director de Cultura y Divulgación de la UPNA.
El artículo La ciencia al servicio de la guerra se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:El límite entre la vida y la muerte en las neuronas
![]()
Jorge Valero Gómez-Lobo y Amanda Sierra
 La apoptosis de la neurona es un tipo de muerte autoinducida.
La apoptosis de la neurona es un tipo de muerte autoinducida.Kateryna Kon / Shutterstock
“Hasta que la muerte nos separe”. Esa es la fecha de caducidad que tienen la mayoría de nuestras neuronas. Estas células, encargadas de transmitir el impulso nervioso en el cerebro, son de las más longevas de nuestro organismo. Nacen prácticamente a la vez que nosotros y, por lo general, no se renuevan.
Pero existe una excepción a toda regla, y esta no iba a ser menos. No hace mucho que sabemos que en el cerebro de la mayoría de los mamíferos se producen nuevas neuronas a lo largo de toda la vida. Este fenómeno, que conocemos como neurogénesis adulta, sólo ocurre en unas pocas regiones del cerebro. Entre ellas el hipocampo, una región especializada en procesos de memoria y aprendizaje.
Las conexiones que establecen las neuronas dan forma a nuestros pensamientos y manera de ser, haciéndolas únicas e insustituibles. De ahí que la pérdida de neuronas que sufrimos al envejecer, o cuando caemos en las garras de una enfermedad neurodegenerativa, suela ser irreparable.
Lo normal es morir
Las neuronas mueren cuando envejecemos debido a que acumulan residuos y defectos que hacen que pierdan su función y degeneren. Este proceso natural se limita a unas pocas neuronas pero se ve agravado en enfermedades neurodegenerativas como las enfermedades de Parkinson o Alzheimer. Sin embargo, también hay mucha muerte neuronal al inicio de la vida.
De hecho, antes del nacimiento se producen muchas más neuronas de las necesarias. Tantas que la mayoría no sobreviven al no establecer las conexiones adecuadas. No solo eso, sino que gran parte de las neuronas que se generan en la vida adulta y sus precursores mueren sin llegar a incorporarse a los circuitos cerebrales. Esta muerte temprana no es patológica: todo lo contrario. Estos procesos de muerte neuronal se producen de forma normal y están destinados a mantener el buen funcionamiento del cerebro.
Una muerte limpia
La muerte temprana de las neuronas se produce de manera controlada a través de un proceso que llamamos apoptosis. Para entendernos, la apoptosis es una tipo de muerte autoinducida y limpia, que no genera desechos tóxicos dispersos y evita daños mayores. Solo deja atrás un residuo: los restos de las células que acaban de morir. Estos “cadáveres neuronales” son eliminados por unas células del cerebro llamadas microglía.
 Microglía (cian) fagocitando una célula muerta, apoptótica. Arriba a la derecha una imagen de los núcleos celulares. La flecha morada señala a la célula muerta, apoptótica. La célula apoptótica tiene un tamaño menor que el resto de núcleos debido a que su contenido se ha compactado. En la imagen inferior derecha se ve la microglía, la flecha blanca señala la prolongación que la microglía extiende hasta la célula muerta.
Microglía (cian) fagocitando una célula muerta, apoptótica. Arriba a la derecha una imagen de los núcleos celulares. La flecha morada señala a la célula muerta, apoptótica. La célula apoptótica tiene un tamaño menor que el resto de núcleos debido a que su contenido se ha compactado. En la imagen inferior derecha se ve la microglía, la flecha blanca señala la prolongación que la microglía extiende hasta la célula muerta.Author provided
Las células de la microglía son células muy dinámicas cuyos cuerpos tiene prolongaciones finas que escanean continuamente el cerebro. Su misión es contener cualquier tipo de daño. Y como parte de esta función se encargan de detectar, englobar y destruir los restos de células muertas.
A este proceso por el que la microglía “se come” a las células muertas y “las digiere” lo llamamos fagocitosis. La fagocitosis es necesaria para evitar que los restos celulares degeneren y produzcan residuos tóxicos. La fagocitosis, por tanto, constituye el último paso en la gestión de la muerte de las neuronas: su eliminación definitiva. Pero, ¿qué ocurre después de la fagocitosis? ¿Acaba ahí, con la eliminación de los residuos?
Microglía en movimiento. Imagen “en vivo” del cultivo de una rodaja de hipocampo. El punto rojo representa la zona en la que se generó daño con un láser.La microglía regula la producción de nuevas neuronas
Los resultados de nuestra investigación muestran que la microglía no se limita a retirar los residuos del sistema sin más. Por el contrario, cuando la microglía se “come” a las células muertas comienza un proceso de auto-reprogramación que cambia la expresión de sus genes. Este cambio en la expresión génica se da, entre otros, en genes que codifican para sustancias que pueden regular la propia neurogénesis. Es decir, que las células de microglía fagocítica liberan factores que limitan la formación de nuevas neuronas. Pero, ¿cuál puede ser el sentido de todo esto?
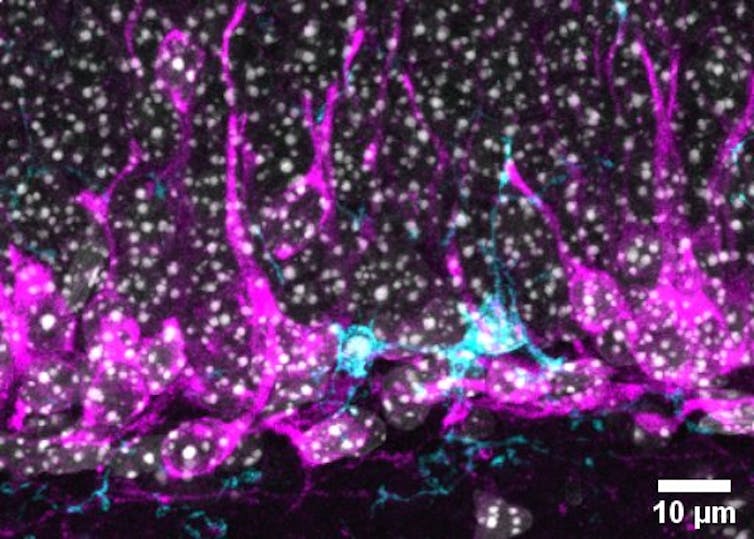 Microglía (cian) fagocitando una célula muerta y rodeada de nuevas neuronas (magenta).
Microglía (cian) fagocitando una célula muerta y rodeada de nuevas neuronas (magenta).Author provided
La formación de nuevas neuronas en el cerebro adulto tiene un coste. Estas neuronas se generan a partir de células madre que se activan y se agotan en el proceso. Producir un exceso de nuevas neuronas cuando no son necesarias agotaría la reserva de células madre rápidamente y la capacidad de formar neuronas cuando realmente se necesite.
La microglía detecta un exceso en la producción de neuronas al fagocitar a aquellas que mueren y, mediante las moléculas que secreta, le indica al hipocampo que frene la producción porque está gastando recursos sin sentido. De esta manera, podemos especular que la microglía fagocítica regula el equilibrio entre la oferta y la demanda, y ajusta la tasa de producción de nuevas neuronas en función de cuántas se mueren y cuántas se pueden incorporar al circuito neuronal.
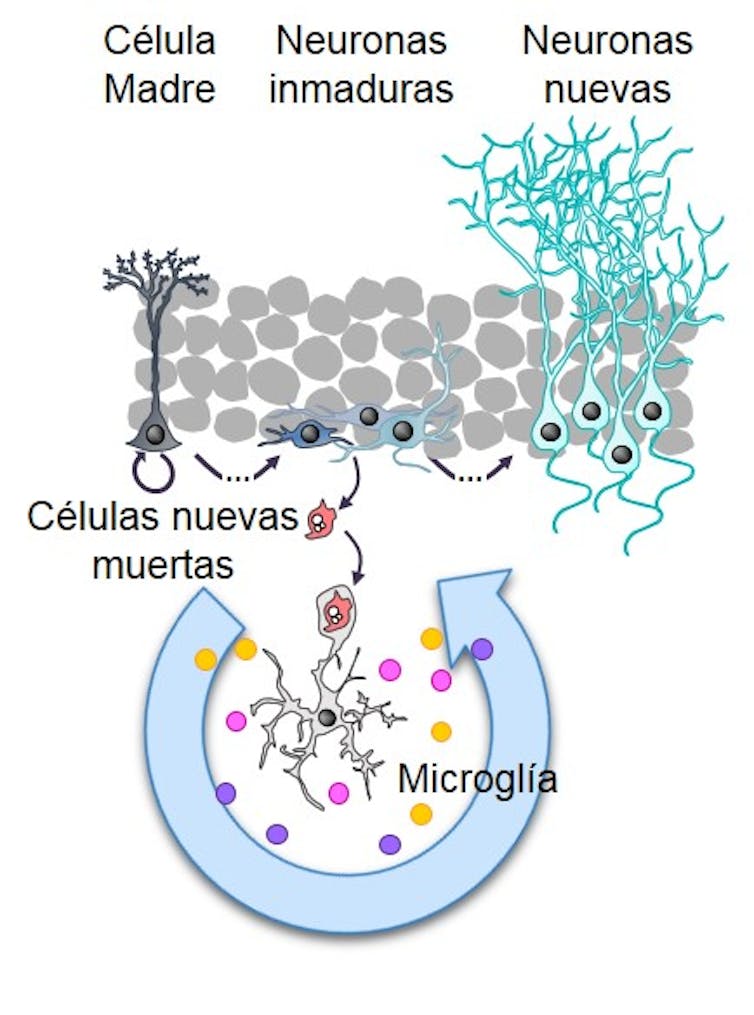 La microglía tras fagocitar libera sustancias que regulan la producción de nuevas neuronas.
La microglía tras fagocitar libera sustancias que regulan la producción de nuevas neuronas.Author provided
Estos hallazgos tienen implicaciones en el campo de las enfermedades neurodegenerativas. En estas patologías, las neuronas mueren y la microglía es la encargada de retirarlas del tejido cerebral. En ocasiones, como hemos observado en anteriores estudios sobre la epilepsia, la naturaleza de la enfermedad impide a la microglía ejercer su función fagocítica y retirar los residuos celulares. Estos resultados nos llevan a plantear lo siguiente: incrementar la actividad fagocítica de la microglía
puede constituir una nueva vía terapéutica.
En los próximos años determinaremos si potenciar los mecanismos de auto-reparación devuelve al cerebro el adecuado equilibrio entre la vida y la muerte en las enfermedades neurodegenerativas.![]()
Sobre los autores: Jorge Valero Gómez-Lobo y Amanda Sierra son investigadores del Achúcarro Basque Center for Neuroscience
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo El límite entre la vida y la muerte en las neuronas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Más allá de las neuronas
- La microglía es un sensor de mortalidad neuronal
- Muerte entre las ecuaciones (Historias de muerte y matemáticas 1)
Las mareas del pasado leídas en las rocas del presente
Los fósiles, los minerales o las rocas son, entre otras cosas, en lo primero que pensamos al hablar de geología, pero lo cierto es que la física es un ámbito científico que difícilmente se puede desvincular de la geología. Y es que el fundamento físico resulta clave a la hora de explicar algunos procesos geológicos que suceden tanto en el océano como en la superficie terrestre.
Con el fin de poner sobre la mesa la estrecha relación entre la geología y la física, los días 27 y 28 de noviembre de 2019 se celebró la jornada divulgativa “Geología para poetas, miopes y despistados: La Geología también tiene su Física”. El evento tuvo lugar en la Sala Baroja del Bizkaia Aretoa de la UPV/EHU en Bilbao.
La segunda edición de esta iniciativa estuvo organizada por miembros del grupo de investigación de Procesos Hidro-Ambientales (HGI) de la Facultad de Ciencia y Tecnología de la Universidad del País Vasco, en colaboración con el Vicerrectorado del Campus de Bizkaia, el Geoparque de la Costa Vasca y la Cátedra de Cultura Científica de la UPV/EHU.

Las mareas, esos movimientos de mares y océanos provocados por la Luna, dejan su marca en el proceso de formación de las rocas sedimentarias. Estas marcas las podemos leer hoy para saber que ocurrió hace millones de años. Lo explica en esta conferencia Isabel Emma Quijada, profesora del departamento de geología de la Universidad de Oviedo.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Las mareas del pasado leídas en las rocas del presente se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La eternidad en un grano de arena
- Geotermia urbana
- Los ecos del fondo submarino: imágenes de las estructuras geológicas.
Estimación de la edad en obras de arte contemporáneas
 Obra de Jesús Mari Lazkano empleada en la investigación. Fuente: UPV/EHU
Obra de Jesús Mari Lazkano empleada en la investigación. Fuente: UPV/EHUEl comercio ilícito de arte se ha convertido en el tercer mercado ilegal a escala mundial después de las drogas y las armas. Una investigación de la UPV/EHU ha desarrollado un novedoso método para la datación de obras de arte contemporáneo, hasta la fecha no existía ninguno, a través del estudio del proceso de envejecimiento de las pinturas acrílicas.
El objetivo era conseguir una correcta identificación y datación precisa de los materiales utilizados en las obras que pudiese ayudar en la detección de trabajos falsificados o mal atribuidos. “El punto de partida del estudio es conocer cómo envejecen las pinturas acrílicas en el arte contemporáneo, y determinar que llevan depositadas el mismo tiempo que el que se supone que tiene la obra, para poder así decir si esa obra tiene 20 años por ejemplo o está hecha antes de ayer”, cuenta Itxaso Maguregi, profesora de Bellas Artes y coautora del trabajo.
“El principal problema del arte contemporáneos es que los materiales utilizados para las obras se pueden encontrar a día de hoy fácilmente, por tanto, las falsificaciones son más sencillas, de ahí la importancia de este estudio”, explica Luis Bartolomé, otro de los coautores.
Para ello, las pinturas fueron sometidas a ensayos de envejecimiento acelerado, mediante el uso de cámaras con condiciones de luz, temperatura y humedad controladas que permiten recrear el paso del tiempo en las pinturas. “50 horas en la cámara equivaldría a un año de envejecimiento natural, y se monitorizó su evolución química a fin de desarrollar modelos matemáticos de predicción de edad. Básicamente lo que se ha realizado ha sido un estudio controlado del envejecimiento de una pintura acrílica, mediante un time lapse de la pintura”, señala Luis Bartolomé.
Tras la realización del ‘envejecimiento artificial’ se logra una serie de patrones, de muestras, que sirven para comparar con la obra original. “Una vez que creamos nuestra ‘serie patrón de muestras artificiales’, incorporamos muestras reales para compararlas. Así, hemos visto que nuestro modelo funcionaba correctamente porque estimaba justamente la edad que tenían las obras reales. Por ejemplo, se pudo ratificar que un cuadro cedido por el pintor vasco Jesús Mari Lazkano y realizado en el año 2015 tenía 4 años de antigüedad”, asegura Bartolomé.
Esta correlación ha podido utilizarse para fechar obras de hasta 22 años, conservadas en condiciones comparables y creadas con el mismo tipo de pintura. “Esta metodología podría ser un primer paso para fechar obras pictóricas contemporáneas. Asimismo, este trabajo puede resultar de ayuda en el desarrollo de otras metodologías apropiadas de conservación y restauración en pintura contemporánea”, exponen las investigadoras Laura Ortiz-Herrero e Irene Cardaba.
Referencia:
L.Ortiz-Herrero, I.Cardaba, S.Setien, L.Bartolomé, M.L.Alonso, M.I.Maguregui (2019) OPLS multivariate regression of FTIR-ATR spectra of acrylic paints for age estimation in contemporary artworks Talanta doi: 10.1016/j.talanta.2019.120114
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Estimación de la edad en obras de arte contemporáneas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Arte & Ciencia: Cómo descubrir secretos que esconden las obras de arte
- Arte & Ciencia: Conservación de obras con componentes tecnológicos
- Técnicas «low cost» para el estudio de obras de arte
Tomanowos: el meteorito que sobrevivió a las megainundaciones y a la insensatez humana
 Tomanowos en el Museo de Historia Natural de Nueva York.
Tomanowos en el Museo de Historia Natural de Nueva York.Daniel García-Castellanos, Author provided
La roca con la historia más fascinante que conozco tiene un nombre milenario: Tomanowos. Significa el visitante del cielo en el extinto idioma de los indios clacamas, para quienes Tomanowos vino para unir el cielo, la tierra y el agua.
Hoy yace en el Museo de Historia Natural de Nueva York. Sin embargo, cuando los colonos europeos la encontraron hace más de cien años junto a Portland (Oregón), protagonizó una de las historias más hilarantes en geología, fruto de la atracción fatal que una roca rara como esta produce en los humanos.
¿Qué sabemos sobre sus orígenes?
Tomanowos es un raro meteorito de 15 toneladas compuesto de hierro y níquel (Fe 91 %, Ni 7,6 %). Estos átomos de Fe y Ni se formaron mediante fusión nuclear en el núcleo de estrellas. Convertidas en supernovas, sufrieron gigantescas explosiones que los esparcieron por el espacio.
 Las explosiones de supernovas esparcen por el espacio el hierro producido en las estrellas más pesadas. Este hierro termina en nebulosas de partículas que eventualmente producen nuevas estrellas y protoplanetas como el que formó Tomanowos.
Las explosiones de supernovas esparcen por el espacio el hierro producido en las estrellas más pesadas. Este hierro termina en nebulosas de partículas que eventualmente producen nuevas estrellas y protoplanetas como el que formó Tomanowos.X-ray: NASA/CXC/Rutgers/J.Hughes; Optical: NASA/STScI
Hace unos 4 500 millones de años, estos átomos pululaban en una nebulosa de detritos cósmicos que comenzaba a agregarse para formar protoplanetas en el sistema solar. Tomanowos fue parte del núcleo de uno de estos protoplanetas, en cuyo centro se acumulan siempre los metales más pesados.
Más tarde, hace unos 4 000 millones de años, una colisión entre dos de esos protoplanetas devolvió nuestra pieza de museo a la soledad espacial. Lo sabemos porque un choque es la única manera conocida de extraer una masa de 15 toneladas del centro de un protoplaneta.
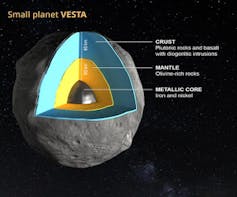 Vesta, un protoplaneta superviviente del sistema solar primigenio. Debido a su gran tamaño, los protoplanetas desarrollan una estructura de capas por densidades con elementos más pesados como el hierro concentrados en el núcleo. Tomanowos es un pedazo del núcleo expulsado por una colisión de un protoplaneta similar.
Vesta, un protoplaneta superviviente del sistema solar primigenio. Debido a su gran tamaño, los protoplanetas desarrollan una estructura de capas por densidades con elementos más pesados como el hierro concentrados en el núcleo. Tomanowos es un pedazo del núcleo expulsado por una colisión de un protoplaneta similar.EPFL/Jamani Caillet, Harold Clenet
Hace apenas 17 000 años, la órbita de Tomanowos finalmente se cruzó con la terrestre. Como resultado de este billar cósmico, el meteorito entró en nuestra atmósfera, con la suerte de aterrizar plácidamente en un casquete glaciar en Canadá. El hielo glaciar suele ser una importante fuente de meteoritos bien preservados.
La acción del agua y el hielo
Durante las siguientes décadas, el glaciar transportó lentamente a Tomanowos hacia una lengua glaciar que en ese momento bloqueaba el río Fork en Montana (EE. UU.).
El hielo obstruía el valle fluvial formando una barrera de 600 m de altura que dio lugar aguas arriba el enorme lago Missoula. Aunque ya no quedan restos de esa barrera, conocemos su existencia porque Joseph Pardee encontró en la década de 1920 los sedimentos del enorme lago que ocupó el valle.
Arrastrada por el glaciar, la roca llegó a la presa de hielo justo el año en que esta colapsó por la presión del agua. Provocó una de las mayores inundaciones jamás documentadas: las inundaciones de Missoula, que dieron forma a los Scablands y transformaron el paisaje del estado de Washington. El fenómeno alcanzó una intensidad equivalente a varios miles de cataratas del Niágara.
Al caer el dique glaciar, el meteorito quedó atrapado en un bloque de hielo y fue arrastrado flotando en la inundación. Cruzó los estados de Idaho, Washington y Oregón siguiendo el cauce del desbordado río Columbia a velocidades de más de 20 m/s, según simulaciones numéricas del evento. Cuando flotaba ya a la altura de la actual Portland, la carcasa de hielo se rompió y la roca se hundió bajo las aguas.
Tras la inundación, Tomanowos quedó expuesto a la atmósfera. Durante miles de años, la lluvia reaccionó con un mineral raro en la Tierra pero común en los meteoritos, la troilita (FeS). El agua disolvió lentamente el hierro, formando las cavidades de la roca.
La llegada del hombre
Los clacamas llegaron a Oregón probablemente poco después de la inundación. ¿Sabían que las rocas de níquel provienen del cielo? ¿Les intrigaba la ausencia de un cráter en el lugar del meteorito? ¿Vislumbraron la posibilidad de que una inundación lo llevara al lugar, una teoría que tardaría miles de años en ser desarrollada por la geología? En cualquier caso, el nombre que le dieron al meteorito nos recuerda que las culturas precientíficas no eran tontas. O al menos no lo eran más que las posteriores.
La historia que sigue confirma de alguna manera esta hipótesis. En 1902 un colono llamado Ellis Hughes decidió apropiarse en secreto de la roca de hierro trasladándola a sus tierras. Pero no es fácil mover 15 toneladas más de un kilómetro sin despertar sospechas, ni siquiera en Oregón. Durante los tres meses de penoso transporte nocturno, el meteorito sufrió severas mutilaciones.
 Después de acabar con la mudanza de Tomanowos, Hughes construyó una cabaña alrededor del meteorito, anunció que lo había encontrado en su propiedad y comenzó a cobrar veinticinco centavos por verlo.
Después de acabar con la mudanza de Tomanowos, Hughes construyó una cabaña alrededor del meteorito, anunció que lo había encontrado en su propiedad y comenzó a cobrar veinticinco centavos por verlo.En otro despliegue de insensatez, un vecino demandó a Hughes alegando que la roca había aterrizado en su propiedad. Y para respaldar su reclamación mostró a los investigadores un enorme cráter en su terreno. El caso hubo de ser desestimado cuando un tercer vecino de la zona informó de una gran explosión escuchada unos días antes.
Irónicamente, el propietario legítimo del lugar del meteorito resultó ser la Compañía de Hierro de Oregón. La empresa desconocía su existencia hasta el momento, pero pronto contrató a un guardia que se sentó encima de la roca con un arma hasta que la vendió al museo de Nueva York.
Las autoridades, que ya habían decidido relocalizar a los Clacamas en una reserva, decidieron también reubicar a Tomanowos en la otra costa de los EE. UU. Hoy, los descendientes de los clacamas conservan aún el derecho a visitar al visitante que reunió al cielo, el agua y la tierra en la última parada de su billar cósmico.![]()
Sobre el autor: Daniel Garcia-Castellanos es investigador del Instituto de Ciencias de la Tierra Jaume Almera (ICTJA – CSIC)
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Tomanowos: el meteorito que sobrevivió a las megainundaciones y a la insensatez humana se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:La extraordinaria capacidad poética de las matemáticas
Las matemáticas también son un mundo de imaginación, no sólo los caminos de letras. […] Las matemáticas me han hecho más consciente de la importancia de la estructura y por otro me han educado en la síntesis. En mis obras existen ciertas simetrías, repeticiones que se dan en un mismo texto que de algún modo se puede decir que son una matemática oculta.
Juan Mayorga en [2]
En la entrada Personas famosas que estudiaron matemáticas: literatura y cine, Raúl Ibáñez citaba al premiado dramaturgo Juan Mayorga, licenciado en matemáticas y doctor en filosofía, que también ejerció como profesor de matemáticas durante cinco años. En 2010, cuando la revista Matematicalia aún se publicaba, tuvimos la suerte de poder concertar una entrevista con Mayorga; el título de esta entrada alude precisamente a una frase de la conversación mantenida con la periodista Leticia Fernández Abejón (Divulga). La reportera preguntaba al dramaturgo sobre la relación entre las matemáticas y el teatro:
A mi modo de ver, primero las matemáticas son una escritura de precisión, y así ha de ser también la del teatro: una escritura sin un gramo de grasa. Segundo, porque las matemáticas y el teatro coinciden en su búsqueda de síntesis significativas: igual que para un matemático una fórmula define toda una clase de objetos, para un dramaturgo una frase puede definir un personaje o incluso una época, así como un objeto puede definir un espacio, por ejemplo, un banco puede ser todo un parque.
 Portada del libreto de El chico de la última fila.
Portada del libreto de El chico de la última fila.
Mayorga comentaba en la entrevista que su El chico de la última fila era una obra en la que «las matemáticas sirven como elemento dramático e hilo conductor. Se establece una relación entre dos alumnos; uno ofrece al otro enseñar matemáticas y el segundo le enseña al primero filosofía. […] Un motivo poético de la obra es el mundo de los números imaginarios. En ese sentido, creo que las matemáticas tienen una capacidad poética extraordinaria: la noción de matriz, elipse, tienen una poesía propia y un mundo.».
Los personajes de El chico de la última fila pertenecen a tres familias distintas: Claudio García –el chico de la última fila– y su padre; el profesor de Lengua y Literatura Germán y su esposa Juana y “Los Rafa”, familia burguesa formada Rafael Artola padre, Ester –ama de casa– y Rafa hijo, compañero de Claudio.
Claudio es uno de los alumnos de Germán. Se sienta en la última fila de clase. Desde allí observa lo que sucede dentro y fuera del aula. No es un mal estudiante, excepto en la asignatura de filosofía. Rafa también es alumno de Germán. No se le dan bien las matemáticas, pero si la filosofía. Claudio encuentra en esta situación la ocasión para colarse en casa de Rafa: propone a su compañero ayuda en matemáticas a cambio del apoyo de Rafa en filosofía. Se trata solo de una estratagema de Claudio para espiar a esta familia perfecta: él no tiene madre y su padre es un extraño personaje al que ni siquiera se le da nombre en la obra.
Germán es profesor de Lengua y Literatura. Propone a su alumnado una redacción sobre Mi pasado fin de semana. Entre las simplezas escritas por sus estudiantes, Germán descubre un texto distinto, el de Claudio, que explica en su escrito cómo su deseo de entrar en casa de Rafa le llevó a vivir su primer día con la familia de su compañero:
A las once toqué el timbre y la casa se abrió ante mí.
Su atracción por la vivienda –que esconde los secretos, las miserias, las alegrías y los anhelos de sus habitantes– se muestra también al final de la obra:
Algo necesitarán. Siempre habrá un modo de entrar. Siempre hay un modo de entrar a cualquier casa.
Intrigado, Germán decide hablar con Claudio para saber si ese relato es real o ficticio. Claudio le confirma que no inventa, que solo expone lo que está viviendo. Germán no puede –¿o quizás no desea?– frenar a Claudio, que prosigue redactando sus vivencias en la casa de “los Rafa”, finalizando cada nuevo episodio con un desafiante Continuará.
Claudio pasa de ser un simple cronista a desencadenar voluntariamente situaciones para escrutar, analizar, embaucar, burlarse y escribir para Germán todo lo que observa. Los escritos de Claudio van mostrando su gradual injerencia en la vida de “los Rafa” ante la progresiva incomodidad de Germán. Entre el profesor y el alumno prospera un ambiguo juego de seducción, disgusto, arrogancia, recelo, apego y rivalidad. Claudio se hace con la victoria final en un sorprendente desenlace.
Mientras que a Germán y Claudio les une el amor por la literatura, la conexión entre Claudio y Rafa se realiza a través de las matemáticas y la filosofía. A Claudio le gustan las matemáticas, mientras que Germán está obsesionado por Tolstoi y Dostoievski:
– Claudio: El de Filosofía está empeñado en convencernos de que su asignatura es útil. Siempre empieza planteándonos un caso, él lo llama “dilema moral”, y luego nos explica el filósofo, Platón, Hegel, lo que toque. Todos quieren convencernos de que enseñan cosas útiles. Todos menos el de Matemáticas. Ése ya nos advirtió el primer día que las Matemáticas no sirven para nada.
– Germán: Las Matemáticas son importantes. También la Filosofía. Aunque ni las Matemáticas ni la Filosofía tengan respuesta para la gran pregunta.
– Claudio: ¿La gran pregunta?
– Germán: ¿Tolstoi o Dostoievski? Ésa es la gran pregunta, la que resume todas las demás.
 Cartel de una representación de El chico de la última fila.
Cartel de una representación de El chico de la última fila.
Claudio explica a su amigo ejercicios sobre cónicas –Rafa debe aprender a distinguirlas a través de sus ecuaciones– o sobre números imaginarios:
– Rafa: Raíz cuadrada de menos uno. Por más que lo pienso, no le veo el sentido.
– Claudio: No es un número real. Por eso se les llama números imaginarios: raíz de menos cinco, raíz de menos siete… Sólo existen en la cabeza. Pero se les puede sumar, multiplicar… ¡dibujar! Se puede hacer cosas con ellos, aunque no existan.
– Rafa: No consigo memorizar las fórmulas. Las aprendo y se me van.
– Claudio: No tienes que memorizarlas, tienes que comprenderlas. (Le pone tres ejercicios.) Le pongo tres ejercicios: uno fácil, para animarlo; otro no tan fácil; y otro difícil, para que se atasque. Mientras él combate con los números imaginarios, yo doy una vuelta por la casa.
Los números imaginarios, ¿permiten al protagonista deambular por la casa de Rafa con completa libertad o quizás aluden a esa delgada línea entre lo auténtico y lo inventado?
– Germán: Hay algo de lo que todavía no hemos hablado. Hasta ahora hemos evitado hablar de ello, pero no podemos postergarlo más tiempo. El título. El título compromete. El título establece un pacto con el lector. El título le orienta acerca de qué ha de valorar, en qué ha de fijarse: “Guerra y paz”, “Los hermanos Karamazov”… ¿Qué tal “El chico de la última fila”?
(Silencio.)
– Claudio: Yo he pensado“Los números imaginarios”.
Cuando Rafa descubre que Claudio ha enviado una poesía a su madre, corta radicalmente con él. El joven escritor encuentra refugio en las matemáticas:
Ahora estudio solo. Matemáticas. Las Matemáticas nunca defraudan.
Más información:
[1] Juan Mayorga, El chico de la última fila, Ed. Ñaque, 2006
[2] Leticia Fernández Abejón, Las matemáticas tienen una capacidad poética extraordinaria, Entrevista a Juan Mayorga, Matematicalia, Cultura, Vol. 6, no. 1, 2010
[3] Marta Macho Stadler, El chico de la última fila de Juan Mayorga, DivulgaMat, julio 2010
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo La extraordinaria capacidad poética de las matemáticas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las dos culturas de las matemáticas: construir teorías o resolver problemas
- FUN WITH MATHS, diversión con matemáticas
- Artistas que miran a las matemáticas
Tipos de materia sólida
 Foto: Wolfgang Hasselmann / Unsplash
Foto: Wolfgang Hasselmann / UnsplashA medida que se forma un sólido a partir de un líquido, el tipo de disposición ordenada que se crea depende de los tipos de constituyentes (moléculas, átomos o iones) y de la naturaleza de la atracción eléctrica entre ellos.
Los estados de entropía más bajos implicarían el mayor número posible de enlaces (conexiones) entre los constituyentes. Esto ocurre en la formación de cristales, disposiciones muy ordenadas de miles y miles de millones de constituyentes [1]. En los cristales una estructura básica que involucra solo un pequeño número de constituyentes se repite muchas veces. El agua, la sal y muchos metales forman estructuras cristalinas. Muchas aleaciones metálicas, que implican una mezcla de diferentes metales, forman lo que se llama sólidos «policristalinos» («muchos cristales»). [2]
Los cristales se suelen clasificar según el tipo de constituyente. Así, los cristales iónicos están formados por iones positivos y negativos que se mantienen unidos por la atracción eléctrica entre ellos. La sal común es un ejemplo típico. En los cristales metálicos los electrones de los átomos que forman la red cristalina están deslocalizados, manteniendo el metal unido. Las redes no-metálicos, o cristales covalentes, son redes de átomos que se mantienen unidos por enlaces covalentes (que pueden ser polares) no existiendo moléculas individuales. El diamante, el grafito (ambos carbono puro), el silicio (Si) o la sílice (SiO2) son ejemplos de cristales covalentes.
En cristales iónicos, metálicos o covalentes no es posible hablar de moléculas individuales. El cristal completo es una única molécula gigante. En los llamados cristales moleculares, sí se puede hablar de moléculas individuales. Los átomos de las moléculas se mantienen unidos por enlaces covalentes, y las moléculas entre sí por fuerzas intermoleculares relativamente débiles [3]. El ejemplo prototípico para hablar de cambios de estado, el agua, resulta ser un cristal molecular.
Sin embargo, no todos los sólidos son cristales. Hay otros tres tipos importantes de materia sólida: cuasicristalina, amorfa y compuesta. El tipo de constituyente involucrado, e incluso cómo se forma el sólido, determinan el tipo de estructura resultante.
Si el enfriamiento del líquido ocurre demasiado rápido, los constituyentes que normalmente podrían formar un cristal perfecto no tienen tiempo para organizarse en una estructura cristalina de baja entropía. Podríamos decir que se congelan donde estaban mientras aun formaban un líquido [4]. En este caso, solo se observa un orden local de corto alcance y no una matriz repetitiva de largo alcance. Estos son los llamados sólidos amorfos (sin forma). Algunos sólidos son intrínsecamente amorfos, incluso cuando se enfrían lentamente. Son amorfos el caucho, el vidrio [5] y la mayoría de los plásticos [6]. El carbono en forma de carbón es amorfo, pero en forma de grafito o diamante es altamente cristalino.
Los cuasicristales se descubrieron en 1983. Las moléculas están dispuestas en un patrón tridimensional muy ordenado, pero el patrón no se repite en todo el cristal como lo hace en una estructura completamente cristalina. [7]
Finalmente, tenemos los sólidos compuestos, que implican la unión de diferentes materiales con diferentes estructuras. Los ejemplos son abundantísimos: la madera, el cemento, la fibra de vidrio, y muchos materiales biológicos como el hueso, la carne o el músculo. La investigación en los últimos años para desarrollar materiales que puedan actuar como «repuestos» biológicos ha experimentado una revolución debido al descubrimiento de la posibilidad de fabricar sólidos compuestos artificiales (composites).
Notas:
[1] Para explorar el mundo de los cristales puede verse nuestra serie Introducción histórica a la mineralogía, especialmente las entregas de la 9 a la 23 dedicadas específicamente a la cristalografía.
[2] Los aficionados al programa de televisión “Forjado a fuego” están muy familiarizados con este concepto, pues es la estructura policristalina del acero templado la que da sus características de dureza, flexibilidad y fragilidad a las hojas. De hecho, en ocasiones, cuando se rompe alguna durante las pruebas, los jueces suelen mostrar a cámara las estructuras policristalinas que han provocado el “fallo catastrófico”.
[3] Fuerzas de van der Waals (por ejemplo, hielo de CO2) o enlaces de hidrógeno (por ejemplo, hielo de agua).
[4] Esta afirmación es tan matizable que debe considerarse solo como una imagen útil para visualizar qué ocurre.
[5] El vidrio es sílice y otros materilaes enfriados rápidamente. La sílice enfriada lentamente forma un cristal covalente.
[6] Algunos polímeros, como el polietieleno, pueden considerarse cristales covalentes en una red monodimensional. Estos polímeros tienen en común que son de cadena larga. Hay casos es los que se puede establecer una red tridimensional de polímeros por un fenómeno llamado entrecruzamiento, y seguiría siendo un cristal covalente, pero esto ya se sale del ámbito de esta serie.
[7] La definición estricta de cuasicristal implica conocimientos matemáticos que se escapan de nuestro objetivo. Bástenos saber que en los cuasicristales existen simetrías centrales (respecto a un punto), como ocurre en dos dimensiones con el pentágono, por ejemplo, cosa que no existe en los cristales.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Tipos de materia sólida se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un modelo simple de gas
- El demonio de Maxwell
- Otras predicciones del modelo cinético. Movimiento browniano
Mala ciencia de consecuencias catastróficas
 Cartel británico de promoción de la eugenesia de los años 20. El texto dice: » ¡Solo la semilla sana debe plantarse! Compruebe que las semillas [están libres de ] enfermedades hereditarias e incapacidad mediante la eugenesia». Fuente.En algunas ocasiones nociones erróneas, por carecer de suficiente respaldo científico o por ser claramente anticientíficas, han conducido a la adopción de medidas que han causado gran sufrimiento humano. Lo más sangrante, además, es que quienes las han aplicado lo han hecho con el objeto de promover un nuevo (y supuestamente mejor) orden social y convencidos de que contaban con suficiente sustento científico a su favor. Nos ocuparemos aquí de dos de esos casos, el de la eugenesia y el del lysenkoismo.
Cartel británico de promoción de la eugenesia de los años 20. El texto dice: » ¡Solo la semilla sana debe plantarse! Compruebe que las semillas [están libres de ] enfermedades hereditarias e incapacidad mediante la eugenesia». Fuente.En algunas ocasiones nociones erróneas, por carecer de suficiente respaldo científico o por ser claramente anticientíficas, han conducido a la adopción de medidas que han causado gran sufrimiento humano. Lo más sangrante, además, es que quienes las han aplicado lo han hecho con el objeto de promover un nuevo (y supuestamente mejor) orden social y convencidos de que contaban con suficiente sustento científico a su favor. Nos ocuparemos aquí de dos de esos casos, el de la eugenesia y el del lysenkoismo.
Francis Galton fue un polímata británico (primo de Charles Darwin) que, abogó en 1883 por apoyar a las personas más favorecidas para que tuvieran más hijos, en detrimento de las menos favorecidas. A este proceder lo denominó eugenesia, y se basaba en una interpretación errónea de la teoría de la evolución por selección natural. La eugenesia que proponía Galton era una eugenesia positiva, pues no pretendía actuar de forma directa para evitar que los menos favorecidos tuvieran descendencia (eugenesia negativa). Pero mucho de lo que vino después no lo era.
Las propuestas eugenésicas llegaron a ser aceptadas en varios países y se llegó incluso a practicar mediante esterilizaciones masivas de personas que, supuestamente, tenían rasgos genéticos considerados indeseables. En el conjunto de estados que aprobaron leyes eugenésicas en los Estados Unidos llegaron a esterilizarse a más de sesenta mil personas a lo largo de varias décadas en pleno siglo XX. Todavía en la década de 1960, el endocrinólogo D. J. Ingle, miembro de la Academia de Ciencias, director del Departamento de Fisiología de la Universidad de Chicago y fundador de la revista Perspectives in Biology and Medicine, reivindicó la esterilización masiva de la población afroamericana para “evitar el debilitamiento de la cepa caucásica”.
En Alemania, el gobierno del III Reich, a imitación del modelo estadounidense y al servicio de las doctrinas raciales nacionalsocialistas, llegaron a esterilizar a más de 400.000 personas. En el programa, iniciado a partir del ascenso de Hitler al poder, era conocido y apoyado por buena parte de los médicos y científicos que permanecieron en Alemania. Tres de los científicos que más responsabilidad tuvieron en las esterilizaciones fueron Ernst Rüdin, director del Instituto de Psiquiatría, y Ernst Fischer y Otmar von Verschuer, directores del Instituto de Antropología. Los tres asesoraron a las autoridades alemanas. Rüdin en concreto fue uno de los autores de las leyes de pureza racial y presidió el comité para “la higiene y la política raciales” que fijó los criterios para la castración de criminales y la esterilización forzosa de mujeres consideradas inferiores.
Además de los Estados Unidos y Alemania, Canadá llevó a cabo miles de esterilizaciones forzosas hasta la década de los años setenta y otros países como Australia, Reino Unido, Noruega, Francia, Finlandia, Dinamarca, Estonia, Islandia y Suiza también desarrollaron programas de esterilización de personas que habían sido declaradas deficientes mentales.
Durante los mismos años en que se practicaban esterilizaciones forzosas masivas en Norteamérica y Europa Occidental, en la Unión Soviética se inició un proceso de eliminación de la ciencia de la genética por razones puramente ideológicas. Al frente del proceso se encontraba Trofim Denisovich Lysenko, un ingeniero agrónomo ucraniano cuyo objetivo era obtener variedades de plantas que ofreciesen un mayor rendimiento. Lysenko rechazaba los principios de la genética basada en los descubrimientos de Mendel porque pensaba que eran una construcción burguesa. Defendía, además, la visión lamarckiana de la transmisión a la descendencia de caracteres que, supuestamente, se adquieren como mecanismo de adaptación a las condiciones ambientales. Esa adaptación era según Jean-Baptiste Lamarck, padre de esa teoría, el origen de las diferencias que presentan diferentes individuos de una misma especie y que, eventualmente, pueden conducir a la aparición de especies diferentes.
Lysenko adoptó las ideas de Lamarck, que resultaron ser del agrado de las autoridades comunistas. Postuló que las condiciones ambientales podían alterar la constitución genética del trigo y llego a proponer que el trigo, cultivado en un entorno especial, podía convertirse de esa forma en centeno. El gobierno lo respaldó y le permitió dirigir los destinos de la agricultura soviética durante décadas, a pesar de los sonoros fracasos que cosechó. En 1945 llegó a presidir el Instituto de genética de la Academia Soviética de Ciencias, puesto en el que se mantuvo hasta 1965. Muchos de quienes se opusieron a su doctrina fueron eliminados o deportados a Siberia.
Los dos casos analizados tienen algo en común: al objeto de defender o promover unas ideas, o construir un nuevo orden social, hay científicos que, consciente o inconscientemente, vulneran los principios básicos del funcionamiento de la ciencia. En muchos casos ni siquiera es necesario “actuar” conscientemente de forma incorrecta. Basta con dejar actuar a algunos de los sesgos que se han visto en una anotación anterior sin tomar las medidas necesarias para impedirlo. Cuando de esa forma de proceder se derivan actuaciones que afectan a numerosas personas, las consecuencias pueden llegar a ser catastróficas.
Fuente:
Agin, D (2007): Ciencia basura. Starbooks, Barcelona.
Este artículo se publicó originalmente en el blog de Jakiunde. Artículo original.
Sobre los autores: Juan Ignacio Perez Iglesias es Director de la Cátedra de Cultura Científica de la UPV/EHU y Joaquín Sevilla Moroder es Director de Cultura y Divulgación de la UPNA.
El artículo Mala ciencia de consecuencias catastróficas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sobre la percepción social de la ciencia y sus consecuencias
- Sesgos ideológicos que aquejan a la ciencia
- Sesgos cognitivos que aquejan a la ciencia
No habrá solución sin más conocimiento
 Foto: Claudio Schwarz / Unsplash
Foto: Claudio Schwarz / UnsplashSegún todos los indicios nos enfrentamos a la mayor crisis de salud pública que ha conocido la población occidental actual. Su causante, la pandemia COVID-19 no solo va a tener efectos directos sobre la salud y la vida de miles de personas. Los tendrá también de otra naturaleza, más difusos pero de más largo alcance.
La llamada gripe española de 1918 no nos sirve para anticipar cuáles pueden ser las consecuencias de orden social de la pandemia actual. Hay, por un lado, una gran incertidumbre con relación a la incidencia y letalidad de ambas, aquella gripe y esta pandemia. Habrá de pasar más tiempo para tener datos fiables de COVID-19. Por otro lado, hoy sabemos mucho más que hace un siglo y contamos con medios muy superiores para combatir la enfermedad. Y por último, en muchos países la pandemia de gripe española no dejó la huella social que podría haber dejado de no haber coincidido con la Gran Guerra.
En una época en la que las guerras ocurren ya lejos de nuestras fronteras y en una zona geográfica en la que no se producen grandes catástrofes naturales, COVID-19 revela un flanco vulnerable de nuestras sociedades. Por primera vez para muchas generaciones de europeos, una amenaza real se cierne sobre nuestro modo de vida. Incluso aunque la letalidad del virus SARS-CoV-2 sea inferior al 1% de los contagiados, se transmite con tal facilidad que puede acabar infectando a millones de personas (las autoridades alemanas barajan cifras del 70% de la población). Y como sabemos, un porcentaje nada desdeñable de los infectados enferman de gravedad y requieren cuidados intensivos. Por eso, los sistemas de salud se encuentran en riesgo y su eventual insuficiencia podría provocar problemas adicionales y una gran crisis de confianza en el modelo. A lo anterior hay que añadir los efectos económicos que ya se están produciendo sobre sectores que, como el turístico en España, crean riqueza y mantienen muchos puestos de trabajo.
Es difícil evaluar las consecuencias que tendría un trauma sociosanitario en sociedades habituadas a la tranquilidad que proporciona el contar con un buen sistema de salud, pero sus efectos no serán inocuos en términos sociopolíticos. Por ello, los países que no acierten a la hora de contener la extensión rápida del virus y mitigar los efectos sobre la salud pública experimentarán, seguramente, inestabilidad política.
Por otro lado, las epidemias son caldo de cultivo de la xenofobia. Las restricciones al movimiento de personas entre diferentes países o zonas geográficas quizás sean útiles para contener la expansión de la enfermedad, pero también influyen en la percepción que tiene la gente de los extranjeros. Así ha sido durante milenios y no hay razones para pensar que ahora será diferente.
Y a la par que afrontamos serias amenazas, también hay datos para el optimismo. El esfuerzo que están haciendo las potencias científicas del mundo para conocer el virus y la forma de combatirlo no tiene parangón. Nunca se había compartido tanta información entre equipos de diferentes países. Probablemente no se había hecho antes un esfuerzo colectivo de tal magnitud. Esta es una buena noticia para la humanidad porque la solución a largo plazo solo puede venir del conocimiento. Estamos mejor que hace un siglo porque hoy sabemos más que entonces. Y para resolver el problema, deberemos aprender más aún. En el futuro nos esperan otras pandemias, quizás de nuevos virus o de superbacterias. Y otros desafíos nos aguardan, unos de orden sanitario y otros de diferente índole. No bastará con la ciencia y la tecnología para resolverlos, pero sin ciencia y tecnología no serán resolubles.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo No habrá solución sin más conocimiento se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Terremotos en la gran pantalla: algunas verdades y diversas mentiras
Los fósiles, los minerales o las rocas son, entre otras cosas, en lo primero que pensamos al hablar de geología, pero lo cierto es que la física es un ámbito científico que difícilmente se puede desvincular de la geología. Y es que el fundamento físico resulta clave a la hora de explicar algunos procesos geológicos que suceden tanto en el océano como en la superficie terrestre.
Con el fin de poner sobre la mesa la estrecha relación entre la geología y la física, los días 27 y 28 de noviembre de 2019 se celebró la jornada divulgativa “Geología para poetas, miopes y despistados: La Geología también tiene su Física”. El evento tuvo lugar en la Sala Baroja del Bizkaia Aretoa de la UPV/EHU en Bilbao.
La segunda edición de esta iniciativa estuvo organizada por miembros del grupo de investigación de Procesos Hidro-Ambientales (HGI) de la Facultad de Ciencia y Tecnología de la Universidad del País Vasco, en colaboración con el Vicerrectorado del Campus de Bizkaia, el Geoparque de la Costa Vasca y la Cátedra de Cultura Científica de la UPV/EHU.

Volver a ver una película con un especialista al lado puede ser una experiencia de lo más enriquecedora. En este caso la película es San Andreas (2015) y el especialista Arturo Apraiz, profesor del departamento de geodinámica de la Universidad del País Vasco, UPV/EHU. En esta charla se repasan escenas y diálogos de la película, con sus aciertos y errores geológicos, y Apraiz aprovecha para aclarar conceptos y profundizar en algunos aspectos más desconocidos de los terremotos.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Terremotos en la gran pantalla: algunas verdades y diversas mentiras se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La eternidad en un grano de arena
- Geotermia urbana
- Los ecos del fondo submarino: imágenes de las estructuras geológicas.
El efecto de los microplásticos en los ríos
 Foto: Landsil / Unsplash
Foto: Landsil / UnsplashLa preocupación por la contaminación producida por los microplásticos es cada vez mayor; debido a su abundancia, ubicuidad y persistencia en el tiempo, los microplásticos representan un riesgo potencial para los organismos y los ecosistemas. Sin embargo, los estudios sobre su distribución en sistemas de agua dulce, tanto en lagos como en ríos, y sus efectos sobre los organismos de estas aguas son escasos, y hay muy poca información sobre su potencial influencia en el funcionamiento de estos ecosistemas.
En este contexto, el grupo de investigación Stream Ecology de la UPV/EHU, en colaboración con el Museo Nacional de Ciencias Naturales (CSIC) de Madrid, ha estudiado “los efectos de los microplásticos en los ecosistemas de agua dulce y en dos de los grupos más importantes de organismos que viven en ellos: los anfibios y los invertebrados”, explica Naiara López Rojo, investigadora del grupo de la UPV/EHU. Para ello han realizado experimentos de laboratorio, en los que han replicado las condiciones de los ríos y lagunas donde viven estos animales, y los han expuesto a diferentes concentraciones de microplásticos fluorescentes: “Réplicas sin microplásticos (control), a baja concentración, a concentración intermedia y a alta, siendo el resto de características idénticas (iluminación, temperatura, etc)”.

De esta manera, el grupo ha estudiado, por una parte, el efecto de los microplásticos en la supervivencia, alimentación y el crecimiento de los renacuajos, así como la ingestión y la egestión de los mismos. Además, “hemos analizado si los microplásticos se adhieren al perifiton (conjunto de organismos microscópicos que crece sobre las rocas del lecho y principal fuente de alimentación de estos renacuajos) y si alteran su productividad, pues eso demostraría una alteración del funcionamiento de los ecosistemas de agua dulce”, afirma la investigadora. Por otra parte, han examinado los efectos de los microplásticos en la descomposición de la hojarasca (uno de los procesos más importantes de los ecosistemas fluviales) y en la supervivencia y crecimiento de los organismos que se alimentan de ella (invertebrados detritívoros); asimismo, han estudiado el grado de adhesión de los microplásticos a la hojarasca y el grado de ingestión y egestión de los detritívoros, evaluando así los mecanismos de la transferencia trófica de los microplásticos.
Los resultados demuestran que “los microplásticos causan mortalidad a los detritívoros en todas las concentraciones (en la concentración más alta la mortalidad es nueve veces mayor), pero no afectan a su crecimiento. En el caso de los renacuajos, hemos visto que mueren en la concentración más alta de microplásticos; en las otras concentraciones, no hemos observado letalidad, pero sí un descenso en el crecimiento de los anfibios”, añade López-Rojo.
Los estudios de fluorescencia realizados a los renacuajos indican, según la investigadora, “una presencia de microplásticos en los organismos, en sus heces y en el perifiton. Y esto sugiere que los microplásticos pueden ser estresores importantes para los anfibios, al igual que otros contaminantes, el cambio climático, la pérdida de hábitat, etc. Además, los anfibios pueden ser una importante vía de transmisión de los microplásticos del agua dulce a los ecosistemas terrestres”. En el caso de los invertebrados, los análisis sugieren que los microplásticos también fueron ingeridos (muy probablemente a través de la ingestión de partículas adheridas a la hojarasca) y parte de ellos, excretados. La descomposición de la hojarasca se redujo en función del incremento de la concentración de los microplásticos. “Estos resultados aportan nuevas evidencias de los efectos perjudiciales de este contaminante en los insectos acuáticos y en el funcionamiento de los ecosistemas fluviales, y pone en evidencia la necesidad de estandarizar los métodos a utilizar en futuros experimentos con microplásticos, para poder hacer comparaciones”, concluye la investigadora del Departamento de Biología Vegetal y Ecología de la UPV/EHU.
López Rojo remarca la necesidad de seguir investigando el efecto de este tipo de contaminante en los ecosistemas de agua dulce: “Estamos viendo que la respuesta depende del tipo de organismo que analices, del tiempo de exposición, etc. Se tendría que estudiar una exposición más prolongada, porque precisamente los plásticos persisten mucho más que 15 días. Sería interesante, también, estudiar el efecto de este contaminante junto con otro tipo de estresores, a los que también están sujetos tanto los ríos como las lagunas. Porque, probablemente, la interacción entre varios estresores puede resultar más perjudicial todavía”.
Referencias:
Naiara López-Rojo, Javier Pérez, Alberto Alonso, Francisco Correa-Araneda, Luz Boyero (2020) Microplastics have lethal and sublethal effects on stream invertebrates and affect stream ecosystem functioning Environmental Pollution doi: 10.1016/j.envpol.2019.113898
Luz Boyero, Naiara López-Rojo, Jaime Bosch, Alberto Alonso, Francisco Correa-Araneda, Javier Pérez (2020) Microplastics impair amphibian survival, body condition and function Chemosphere DOI: 10.1016/j.chemosphere.2019.125500
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo El efecto de los microplásticos en los ríos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La contribución global de los ríos intermitentes al ciclo del carbono
- Verdín, eucaliptos y cambio climático
- Todo lo que se puede medir en un río
La emoción de las escalas musicales
 Foto: Darya Tryfanava / Unsplash
Foto: Darya Tryfanava / UnsplashNo hace falta ser un experto en música. Si alguna vez has oído hablar de “el modo menor”, probablemente haya sido asociado a su poder para evocar tristeza. En cambio, su luminoso hermano “el Modo Mayor”, suele llegar anunciando la alegría.
Esto es así… en general, hasta cierto y siempre dentro del contexto de la música occidental. A fin de cuentas, para componer la tristeza no existe una receta fácil, ni ingredientes mágicos. Pero incluso en algo tan aparentemente convencional como el uso de una escala musical y su asociación emocional, podemos encontrar las huellas de la voz humana.
La aparente bipolaridad de la música Mayor-menor, es relativamente reciente, para empezar. Incluso dentro de la tradición occidental, existen siete modos distintos que se vienen utilizando desde tiempos de la Antigua Grecia —y puede que incluso antes: existen indicios de que la música sumeria ya utilizaba un sistema similar basado en escalas de siete notas. Cada uno de estos modos, tradicionalmente, se ha asociado a distintos usos con sus propias connotaciones emocionales. Y, si nos alejamos un poquito de Europa y su legado, el abanico se amplía aún más: encontramos escalas pentatónicas, octatónicas, escalas con microtonos o escalas que dividen el rango sonoro en más o menos unidades iguales (como la escala cromática occidental, de 12 semitonos).
Sólo hay una cosa común dentro de toda esta diversidad: allá donde uno vaya, los sistemas musicales utilizan escalas. Y allá donde se utilizan escalas, estas suelen asociarse a distintas emociones. Esto no es un detalle menor. A priori, el espectro sonoro es un continuo: existen sonidos de 440 Hz, de 441 Hz… y también los infinitos sonidos cuyas frecuencias se pueden definir entre estas dos. El hecho de que para cantar, decidamos quedarnos sólo con “algunos” de estos sonidos posibles es una de las características más universales de la música. Y, también, una de las características que más fácilmente nos ayudan a distinguirla del habla humana (al hablar normalmente, nuestro uso del sonido no está discretizado… a menos que estemos queriendo imitar a un robot).
 Espectrogramas de sonidos musicales (izquierda) y habla (derecha). Fuente: Speech detection on broadcast audio
Espectrogramas de sonidos musicales (izquierda) y habla (derecha). Fuente: Speech detection on broadcast audio
Podemos pensar en las notas de una escala como una limitación deliberada de los sonidos disponibles para hacer música. En esa misma línea, el ritmo podría entenderse como una limitación de los cuándos posibles disponibles. Quizás, ambas restricciones sean simplificaciones necesarias para poder cantar coordinadamente con otros seres humanos y para poder recordar esas melodías1. Ritmo y escalas forman una especie de matriz, como la cuadrícula de un papel pautado, que nos sirve de plantilla. Si los sonidos musicales y los momentos fuesen infinitos, la probabilidad de cantar las mismas frecuencias, al mismo tiempo, con otras personas, sería despreciable. Sin notas y figuras rítmicas, todas las melodías se emborronarían en una gaussiana de probabilidad en torno a alguna frecuencia siempre variable y mal definida. Todos los coros disonarían, todos los auditorios se llenarían de desconciertos…
Si bien la utilización de escalas puede obedecer a cuestiones adaptativas, su asociación emocional resulta más difícil de desentrañar. Pero parece claro que las escalas son unos de los ingredientes que, sin saberlo, utilizamos para interpretar una pieza musical. Su sonido define el molde sobre el que se construye cada canción y esto, a su vez, nos permite generar ciertas expectativas. Bastan unos pocos compases de música para hacernos a una idea de qué sonidos vamos a escuchar, en qué orden, con qué frecuencia… durante toda la pieza. Estas expectativas pueden cumplirse, o no, lo que a su vez nos mantiene involucrados en la escucha, en un constante devenir de sorpresas, sospechas y deseos cumplidos.
Los sonidos de un modo o una escala, por su parte, le dan su propia sonoridad característica. Se podría decir que la escala es a la música lo que la paleta de color es a un cuadro ─curiosamente, raga, la palabra que designa los modos melódicos de la música indica, significa literalmente “lo que colorea la mente”. Pero establecer qué colecciones de colores son “los alegres” o “los tristes” depende de muchos factores, algunos de ellos puramente culturales. La escala menor, por ejemplo, con su innegable fama de triste, se utiliza en la tradición folklórica búlgara asociada a otro tipo de emociones.
O, sin irse tan lejos: ¿os acordáis de Despacito? La canción del verano más bailada en las discotecas de medio mundo está escrita en modo menor. En este caso, muchos otros aspectos de la canción ─especialmente, su ritmo─ son capaces de eliminar la posible tristeza que habitualmente asociamos a su modo. Aún así… basta cambiarla a modo mayor para que el carácter cambie por completo. Os presento a Luis Fonsi, el éxito del tíovivo:
Otras alegrías célebres escritas en modo menor incluyen Aserejé, It’s raining men y hasta el tema de El Hormiguero. Happy de Pharrell Williams, una canción que lleva la alegría hasta en el título, literalmente, no está escrita en modo menor sino en modo dórico pero podría argumentarse que los dos se parecen bastante.
Por otra parte, haciendo melancólico al modo Mayor, encontramos el precioso Adagio del concierto para piano de Ravel, el tema principal de la banda sonora de Memorias de África de John Barry, o Wish you were here de Pink Floyd.
Si bien la asociación del modo menor con la tristeza es culturalmente dependiente y matizable de muchas maneras, esto no significa que sea una asociación arbitraria. Existen motivos por los probablemente, percibimos el modo menor como más triste que su contraparte, el modo Mayor. Y todo podría radicar, precisamente, en la comparación inconsciente que hacemos entre ambos y en su paralelismo con ciertos aspectos de la prosodia humana. Pero este asunto tiene su propia enjundia y merece su propio post.
Nota:
1The Origins of Musicality. Edited by Henkjan Honing
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo La emoción de las escalas musicales se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:La cuadratura del cuadrado: en busca del santo grial
Una de mis pasiones dentro de las matemáticas es el estudio de aquellos pequeños problemas matemáticos o de ingenio que surgieron dentro de la matemática recreativa como sencillos divertimentos matemáticos, pero que fueron creciendo con el interés de muchos matemáticos que dedicaron su tiempo a pensar sobre ellos y que se acabaron convirtiendo en hermosos diamantes, con una interesante investigación matemática a su alrededor.
Sobre algunos de estos problemas matemáticos clásicos hemos hablado en el Cuaderno de Cultura Científica, como El problema de las estudiantes de Kirkman, El problema de los sellos de Sylvester, El problema de la plantación de árboles en fila, El problema de las cartas extraviadas, El teorema de los cuatro colores, El problema de Malfatti, o El problema de pesas de Bachet de Méziriac, entre otros.
En esta entrada de la sección Matemoción vamos a hablar de otro de estos problemas clásicos, el conocido como problema de la cuadratura del cuadrado, del que ya hemos hablado brevemente en otras dos entradas, Blanche Descartes y la cuadratura del cuadrado y Teselaciones rítmicas perfectas.
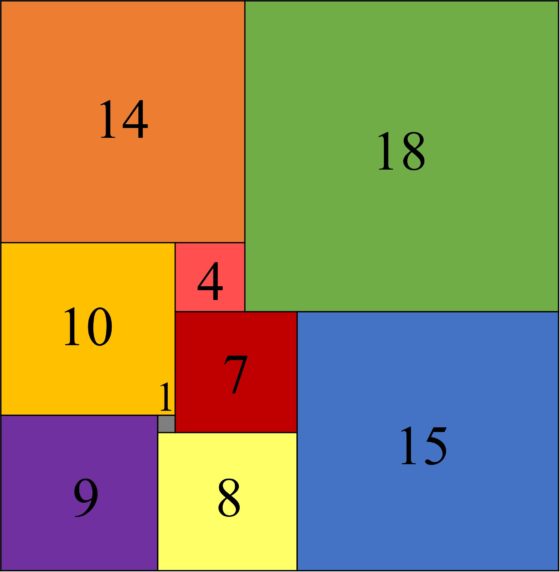 División de un rectángulo de dimensiones 32 x 33 en 9 cuadrados de distintos tamaños, de lados 1, 4, 7, 8, 9, 10, 14, 15 y 18. Construcción de Zbigniew Moron (1925)
División de un rectángulo de dimensiones 32 x 33 en 9 cuadrados de distintos tamaños, de lados 1, 4, 7, 8, 9, 10, 14, 15 y 18. Construcción de Zbigniew Moron (1925)El problema, enunciado de forma sencilla, sería el siguiente:
Problema de la cuadratura del cuadrado (o rectángulo): Dividir un cuadrado (o rectángulo) en un número finito de cuadrados más pequeños, todos de distintos tamaños.
Vayamos con algunos conceptos que vamos a utilizar a lo largo de esta entrada. La cuadratura, o disección, de un rectángulo (en particular, de un cuadrado) en cuadrados más pequeños, todos de distintas dimensiones, como se plantea en el problema, se denomina perfecta. A la cuadratura de un rectángulo que contiene la cuadratura de algún sub-rectángulo se le llama compuesta, mientras que si no existe un sub-rectángulo tal, diremos que es simple. Se llama orden de la cuadratura al número de cuadrados que se han utilizado en la cuadratura del rectángulo. La cuadratura del rectángulo de la imagen anterior es perfecta y simple.
Por otra parte, los lados de los cuadrados pequeños tienen que ser múltiplos racionales de los lados del cuadrado (o del rectángulo) grande, por lo tanto, podemos trabajar con cuadrados tales que sus lados tengan longitud entera, así como los lados del rectángulo grande.
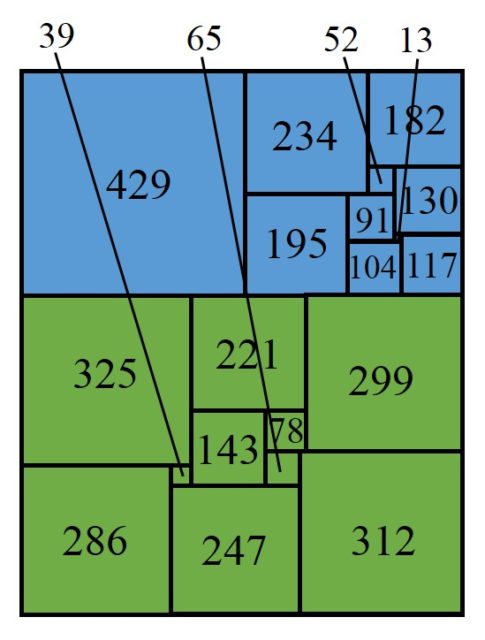 Cuadratura perfecta, pero compuesta, de un rectángulo de dimensiones 845 x 1.040 en 20 cuadrados de distintos tamaños. Esta cuadratura de un rectángulo forma parte de la construcción de Roland Sprague de 1939, que se verá más adelante. Obsérvese que esa descomposición contiene cuadraturas de dos sub-rectángulos, el azul y el verde en la imagen
Cuadratura perfecta, pero compuesta, de un rectángulo de dimensiones 845 x 1.040 en 20 cuadrados de distintos tamaños. Esta cuadratura de un rectángulo forma parte de la construcción de Roland Sprague de 1939, que se verá más adelante. Obsérvese que esa descomposición contiene cuadraturas de dos sub-rectángulos, el azul y el verde en la imagen
En la página Sources in recreational mathematics, an annotated bibliography, el matemático estadounidense David Singmaster menciona que la primera persona que publica, que se tenga constancia de ello, sobre algún problema relacionado con la cuadratura del cuadrado es el matemático recreativo inglés Henry E. Dudeney (1857-1930). En su conocido libro Los acertijos de Canterbury, publicado en 1907, publica el problema El joyero de Lady Isabel, que decía lo siguiente.
El joyero de Lady Isabel: La joven prima y pupila de Sir Hugh, Lady Isabel de Fitzarnulph, era conocida por todo el mundo como “Isabel la Bella”. Entre sus tesoros había un joyero, cuya tapa superior tenía la forma de un perfecto cuadrado. La tapa del joyero estaba incrustada con trozos de madera y una franja de oro de 10 pulgadas* de largo por un cuarto de pulgada de ancho.
Cuando los jóvenes empezaron a pedir la mano de Lady Isabel, Sir Hugh prometió que daría su consentimiento a aquel que consiguiese decirle las dimensiones de la tapa del joyero con solo los siguientes datos: que había una franja rectangular de oro de 10 pulgadas de largo por 1/4 de pulgada de ancho; y el resto de la tapa estaba incrustado exactamente con trozos de madera, cada uno de los cuales era un cuadrado perfecto y no había dos piezas del mismo tamaño. Muchos jóvenes fracasaron, pero uno de ellos finalmente tuvo éxito. El rompecabezas no es uno de los fáciles, pero las dimensiones del rectángulo de oro, junto con las otras condiciones, determinan completamente el tamaño de la tapa del joyero.
[* Recordemos que una pulgada es una medida de longitud inglesa equivalente a 25,4 milímetros]
 Ilustración que acompaña el problema El joyero de Lady Isabel, que aparece en el libro Los acertijos de Canterbury, de Henry Dudeney
Ilustración que acompaña el problema El joyero de Lady Isabel, que aparece en el libro Los acertijos de Canterbury, de Henry Dudeney
El propio Henry Dudeney decía en la solución al problema que este no era precisamente un rompecabezas sencillo. La solución, única, era que la tapa del joyero era un cuadrado de 20 pulgadas de lado, como se muestra en la imagen.
 Ilustración con la solución al problema El joyero de Lady Isabel, que aparece en el libro Los acertijos de Canterbury, de Henry Dudeney
Ilustración con la solución al problema El joyero de Lady Isabel, que aparece en el libro Los acertijos de Canterbury, de Henry Dudeney
Aunque este rompecabezas ya había sido publicado, como comenta David Singmaster, por Henry Dudeney en enero de 1902, en el número 584 de la revista The London Magazine. En cualquier caso, el problema de Dudeney no era realmente una cuadratura del cuadrado, ya que incluía un rectángulo en la disección del mismo, aunque se le aproximaba mucho y sugería un interés en el problema de la cuadratura del cuadrado.
El problema de la cuadratura del cuadrado (o del rectángulo) debía de interesar ya desde tiempo atrás, puesto que en 1903 el matemático alemán Max Dehn (1878-1952), que era estudiante del matemático alemán David Hilbert (1862-1943) y que en su habilitación de 1900 había resuelto el tercer problema de los famosos problemas del milenio del propio Hilbert, publicó el primer trabajo matemático sobre la “disección de un rectángulo en cuadrados más pequeños”. Demostró que un rectángulo podía ser diseccionado en cuadrados más pequeños si y sólo si la proporción entre su altura y su anchura era un número racional.
En la obra póstuma del jugador de ajedrez y matemático recreativo estadounidense Sam Loyd (1841-1911) Cyclopedia of 5000 Puzzles (Los acertijos de Sam Loyd), publicada en 1914, se incluía el rompecabezas de la colcha de retazos (the patch quilt puzzle), que planteaba dividir una colcha cuadrada con 13 x 13 cuadraditos pequeños en retales cuadrados de una, o más piezas. Es decir, el problema de diseccionar un cuadrado en cuadrados más pequeños, aunque sin importar que se repitan los tamaños de estos.
 Ilustración que acompaña el problema El rompecabezas de la colcha de retazos, que aparece en el libro Los acertijos de Sam Loyd
Ilustración que acompaña el problema El rompecabezas de la colcha de retazos, que aparece en el libro Los acertijos de Sam Loyd
 Ilustración con la solución al problema El rompecabezas de la colcha de retazos, que aparece en el libro Los acertijos de Sam Loyd. Esta formada por retales cuadrados cuyos lados son 7, 6 (dos retales cuadrados), 4, 3 (dos retales), 2 (tres retales) y 1 (dos cuadrados)
Ilustración con la solución al problema El rompecabezas de la colcha de retazos, que aparece en el libro Los acertijos de Sam Loyd. Esta formada por retales cuadrados cuyos lados son 7, 6 (dos retales cuadrados), 4, 3 (dos retales), 2 (tres retales) y 1 (dos cuadrados)
David Singmaster menciona que este rompecabezas había sido publicado previamente, en 1907, por Sam Loyd en la revista Our Puzzle Magazine. Además, también aparecería en el libro de Henry Dudeney Amusements in Mathematics (1917), con el nombre La colcha de la señora Perkins. Por este motivo el problema de diseccionar un cuadrado en cuadrados más pequeños, permitiendo que estos tengan el mismo tamaño se conoce como el problema de la colcha de la señora Perkins.
Aunque recordemos que en esta entrada estamos interesados en el problema de la cuadratura perfecta del cuadrado, es decir, la disección de un cuadrado, o rectángulo, en cuadrados más pequeños todos de distintos tamaños, y no en el problema de la colcha de la señora Perkins.
Los primeros ejemplos de rectángulos con cuadraturas perfectas y, además, simples, fueron publicados en 1925 por el matemático polaco Zbigniew Moron (1904-1974), en el artículo O Rozkladach Prostokatow Na Kwadraty (Sobre la disección de un rectángulo en cuadrados). Eran el rectángulo de tamaño 33 x 32 dividido en 9 cuadrados distintos (orden 9), cuyos lados eran 1, 4, 7, 8, 9, 10, 14, 15 y 18, que aparece en la primera imagen de esta entrada y el rectángulo de tamaño 65 x 47, dividido en 10 cuadrados distintos (orden 10), con lados 3, 5, 6, 11, 17, 19, 22, 23, 24 y 25, que mostramos a continuación.
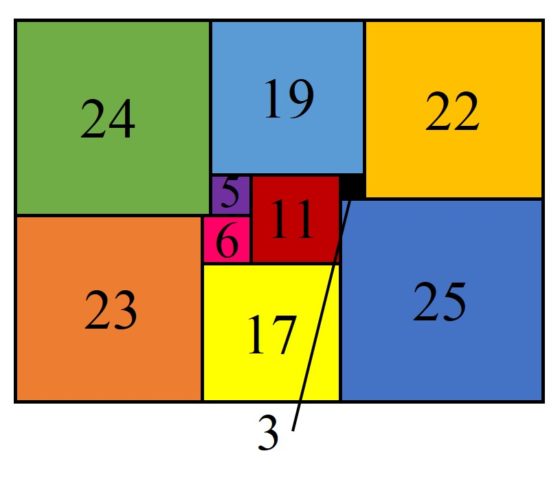 Cuadratura perfecta y simple de un rectángulo de dimensiones 65 x 47 en 10 cuadrados de distintos tamaños, de lados 3, 5, 6, 11, 17, 19, 22, 23, 24 y 25. Construcción de Zbigniew Moron (1925)
Cuadratura perfecta y simple de un rectángulo de dimensiones 65 x 47 en 10 cuadrados de distintos tamaños, de lados 3, 5, 6, 11, 17, 19, 22, 23, 24 y 25. Construcción de Zbigniew Moron (1925)
En los años 1930 el problema de descomponer un cuadrado en un número finito de cuadrados de distintos tamaños fue añadido, por el matemático polaco Stanislaw Ruziewicz -que era quien le había hablado a Zbigniew Moron del problema de la cuadratura del rectángulo- al Cuaderno escocés, como el problema número 59. Un grupo de matemáticos polacos, conocidos como La escuela matemática de Lwow (entre los matemáticos relacionados con esta escuela estaban Stephan Banach, Marek Mac, Kazimierz Kuratowski, Stanisław Mazur, Hugo Steinhaus o Stanislaw Ulam, entre otros), se reunían en el Café Escocés de Lwow para hablar de problemas matemáticos. Solían escribir con lápiz sobre el mármol de las mesas, pero al final del día las mesas se limpiaban y se perdían los problemas y discusiones que habían tenido. Por este motivo, a partir de 1935 decidieron recoger los problemas y soluciones en un cuaderno que sería conocido como Cuaderno Escocés. El último problema, número 193, es de 1941.
 Postal de la Plaza Academia, en Lwow, Polonia, antes de la Segunda Guerra Mundial (en la actualidad la ciudad pertenece a Ucrania). En el edificio de la derecha estaba el Café Escocés, donde se reunían los matemáticos de La escuela matemática de Lwow
Postal de la Plaza Academia, en Lwow, Polonia, antes de la Segunda Guerra Mundial (en la actualidad la ciudad pertenece a Ucrania). En el edificio de la derecha estaba el Café Escocés, donde se reunían los matemáticos de La escuela matemática de Lwow
Poco tiempo después, el matemático japonés Michio Abe construyó más de 600 rectángulos perfectos simples, que recogió en el artículo Covering the square by squares without overlapping (Recubriendo un cuadrado con cuadrados que no se solapan) publicado en 1930 en la revista Journal of Japan Mathematical Physics. Además, en un segundo artículo publicado en 1931 mostró la construcción de una serie infinita de rectángulos perfectos compuestos, construidos a partir de un rectángulo perfecto simple de tamaño 195 x 191.
¿Y qué ocurría con la cuadratura perfecta del cuadrado? Por un lado, sabemos que alrededor del año 1930, el gran matemático húngaro Paul Erdös (1913-1996) había conjeturado que cualquier disección de un cuadrado en cuadrados más pequeños tenía que contener, al menos, dos cuadrados del mismo tamaño, luego no podía ser perfecta. Por otra parte, existía en ese tiempo una conjetura del matemático ruso Nikolai N. Luzin (1883-1950), la conjetura de Luzin, según la cual era imposible diseccionar un cuadrado en un número finito de cuadrados distintos. El matemático belga Maurice Kraitchik (1882-1957), en su libro La mathématique des jeux ou Récréations mathématiques (1930), afirmaba que en una comunicación personal el matemático Luzin le había hablado de esa conjetura. Quizás la conjetura de Luzin llegó a oídos de Erdös o ambos conjeturaron lo mismo de forma independiente, pero lo cierto es que en los años 1930 se creía que la cuadratura (perfecta) del cuadrado era imposible.
 Los cuatro del Trinity -Leonard Brooks, Cedric Smith, Arthur Stone y William Tutte- en Cambridge, en 1938
Los cuatro del Trinity -Leonard Brooks, Cedric Smith, Arthur Stone y William Tutte- en Cambridge, en 1938
Pero la historia continúa. Como cuenta el matemático británico William Th. Tutte (1917 – 2002) en su artículo Squaring the square (Cuadrando el cuadrado), publicado por Martin Gardner en su columna de juegos matemáticos de la revista Scientific American, su colega Arthur H. Stone (1916-2000), cuando aún eran estudiantes en la Universidad de Cambridge (Gran Bretaña), quedó intrigado por la supuesta imposibilidad de descomponer un cuadrado en cuadrados más pequeños distintos, relacionada con el problema planteado por Dudeney en Los acertijos de Canterbury. Entonces intentó probar, sin éxito, dicha imposibilidad, aunque acabó construyendo una disección perfecta de un rectángulo de dimensiones casi cuadradas, 177 x 176, en 11 cuadrados más pequeños.
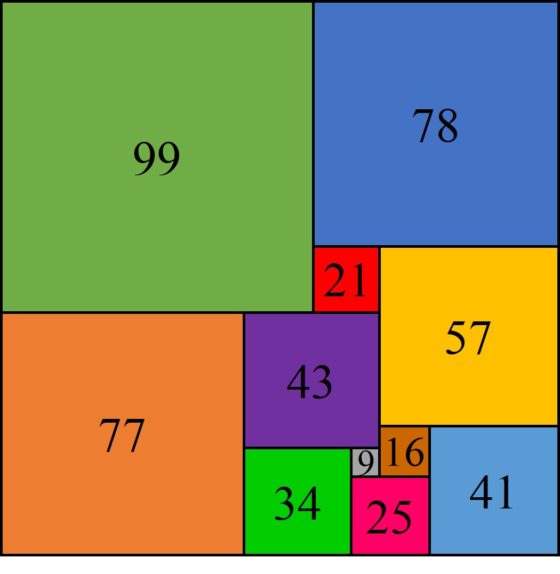 Disección perfecta de un rectángulo, de tamaño 177 x176, en 11 cuadrados distintos, de lados 9, 16, 21, 25, 34, 41, 43, 57, 77, 78 y 99
Disección perfecta de un rectángulo, de tamaño 177 x176, en 11 cuadrados distintos, de lados 9, 16, 21, 25, 34, 41, 43, 57, 77, 78 y 99
El método empleado para construir este rectángulo es sencillo. Se parte de un rectángulo que se divide en rectángulos más pequeños, por ejemplo, como aparece en la siguiente imagen que contiene 11 rectángulos. Se asume que ese diagrama nos da realmente una descomposición en cuadrados de un rectángulo, pero asumiendo que hemos dibujado mal la descomposición cuadrada del rectángulo, es decir, el rectángulo grande sí es un rectángulo, aunque quizás de dimensiones distintas a las que aparece en el dibujo, y los rectángulos pequeños son realmente cuadrados mal dibujados. Se empieza dando valor a los lados de dos de los pequeños cuadrados (en la imagen rectángulos) que estén juntos, de valores x e y, y se van calculando los valores de los lados de los demás cuadrados pequeños, en relación a estos, con sencillas expresiones algebraicas. Por ejemplo, el cuadrado debajo de los cuadrados de lados x e y, sería un cuadrado de lado x + y, el pequeño cuadrado a la derecha de los de dimensiones x y x + y tendrá lado 2 x + y, y así con el resto de cuadrados. De esta manera, todos los cuadrados encajan bien, unos con otros, salvo quizás los que están a ambos lados de la línea AB de la imagen, por lo que hay que elegir valores de x e y para que ahí también encajen, es decir, 14 y – 3 x = (3 x – 3 y) + (3 x + y). Despejando, 16 y = 9 x. Y tomando x = 16 e y = 9 se obtiene la cuadratura perfecta de un rectángulo de dimensiones 177 x 176, encontrada por Stone.
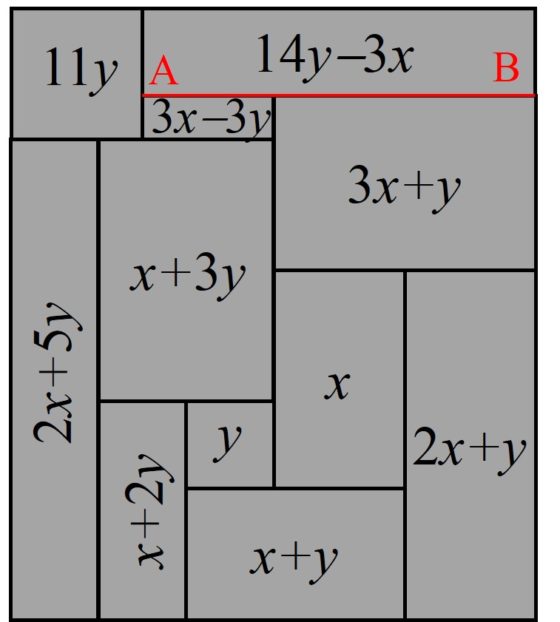 Método algebraico para construir una cuadratura perfecta de un rectángulo
Método algebraico para construir una cuadratura perfecta de un rectángulo
Entonces, el joven Arthur Stone y sus tres compañeros, también estudiantes del Trinity College de la Universidad de Cambridge, Rowland L. Brooks (1916-1993), Cedric A. B. Smith (1917-2002) y William Th. Tutte, los cuatro de Trinity, empezaron a construir rectángulos con disecciones perfectas mediante cuadrados utilizando el anterior método algebraico y a discutir sobre el problema de la cuadratura del cuadrado y el rectángulo. Entonces, relacionaron el problema de las disecciones cuadradas de los rectángulos con la teoría de las redes eléctricas de Kirchhoff (de lo que hablaremos en mi siguiente entrada en la sección Matemoción del Cuaderno de Cultura Científica), lo que les llevó finalmente a poder construir ejemplos de cuadraturas perfectas de cuadrados, tanto compuestas (es decir, con su-rectángulos perfectos), como simples.
En el artículo The Dissection of Rectangles into Squares (La disección de rectángulos en cuadrados), publicado en Duke Math. J. en 1940 se recoge toda esta investigación sobre las redes eléctricas, algunos de los ejemplos obtenidos y, en particular, el primer ejemplo de cuadratura perfecta y simple de un cuadrado de lado 5.468, de orden 55. Así mismo, se demuestra que el menor orden posible para la cuadratura perfecta de un rectángulo es 9 y que existen dos rectángulos con disecciones perfectas de orden 9.
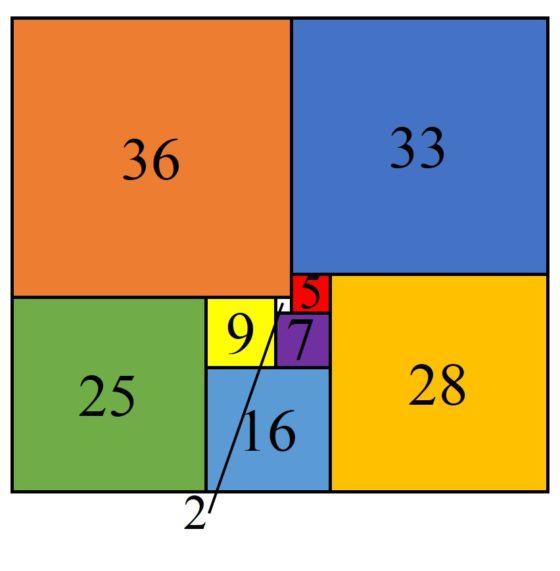 : Una de las dos cuadraturas perfectas simples de orden 9 de un rectángulo que existen, la otra es la que hemos mostrado al principio de esta entrada
: Una de las dos cuadraturas perfectas simples de orden 9 de un rectángulo que existen, la otra es la que hemos mostrado al principio de esta entrada
David Singmaster recoge en Sources in recreational mathematics, an annotated bibliography que en las actas del Encuentro 203 de la Sociedad Matemática del Trinity (Cambridge) de marzo de 1939, Arthur Stone anunció, en el artículo de su conferencia Squaring the square, que Rowland Brooks había obtenido un ejemplo de cuadratura perfecta del cuadrado, de orden 39, que sería el primer ejemplo que demostraba que la conjetura de Luzin era errónea. Y en las actas del encuentro número 204, abril de 1939, Cedric Smith anunciaba que William Tutte había encontrado el primer cuadrado perfecto simple, de orden 55. Estos ejemplos se recogían en el artículo de 1940 de los cuatro de Trinity.
Aunque el primer artículo publicado con un contraejemplo a la conjetura de Luzin fue anterior al artículo de Brooks, Smith, Stone y Tutte de 1940, ya que fue publicado en la revista Mathematische Zeitschrift en 1939, por el matemático alemán Roland P. Sprague (1894-1967). Sprague construyó, a partir de los ejemplos de Zbigniew Moron, un rectángulo perfecto simple de orden 12 y otros cinco cuadrados, un cuadrado con una cuadratura perfecta, pero compuesta, de orden 55.
 Cuadratura perfecta, compuesta, de orden 55 de un cuadrado de lado 5.205, obtenida por Roland Sprague en 1939. Imagen de Wikimedia Commons, cedida por Cmglee
Cuadratura perfecta, compuesta, de orden 55 de un cuadrado de lado 5.205, obtenida por Roland Sprague en 1939. Imagen de Wikimedia Commons, cedida por Cmglee
Poco a poco se fueron construyendo más ejemplos de cuadraturas perfectas de cuadrados, tanto compuestas, como simples. Por ejemplo, en 1948 el matemático británico Theophilus H. Willcocks (1912-2014) construyó una cuadratura perfecta de un cuadrado de orden 24, es decir, con tan solo 24 cuadrados, aunque era compuesta (véase la siguiente imagen). Durante mucho tiempo fue el orden más pequeño encontrado de una cuadratura perfecta de un cuadrado, de hecho, el orden 24 es el más pequeño posible para el caso de las cuadraturas compuestas.
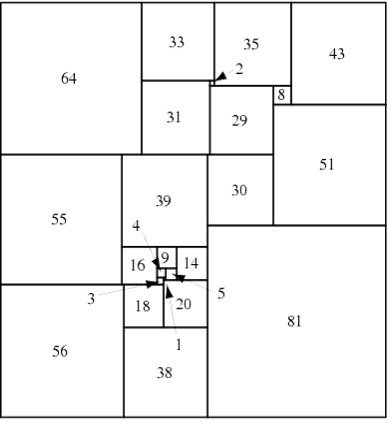 Cuadratura perfecta, compuesta, de orden 24 de un cuadrado de lado 175, obtenida por Theo Willcocks en 1948. Imagen de Wolfram MathWorld
Cuadratura perfecta, compuesta, de orden 24 de un cuadrado de lado 175, obtenida por Theo Willcocks en 1948. Imagen de Wolfram MathWorld
La llegada de los ordenadores cambió la investigación del problema de la cuadratura del cuadrado, permitiendo búsquedas más exhaustivas y la clasificación de todas las cuadraturas en función del orden. Es de destacar en esta nueva etapa la investigación de los matemáticos neerlandeses Christoffel J. Bouwkamp (1915 – 2003) y Adrianus J. W. Duijvestijn (1927-1998). En 1978, Duijvestijn descubrió la única cuadratura perfecta simple del cuadrado del orden más bajo posible, 21.
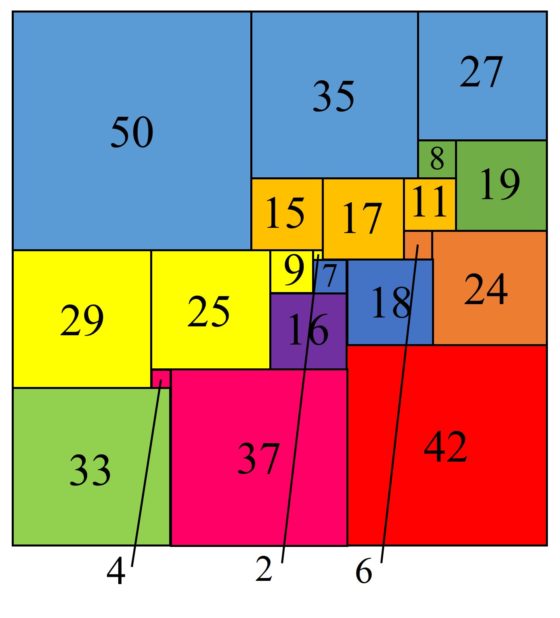 Cuadratura perfecta simple de orden 21 de un cuadrado de lado 112, obtenida por Arie Duijvestijn en 1978. Hemos coloreado los cuadrados para observar los cuadrados que van juntos en el código de Bouwkamp que se describe a continuación
Cuadratura perfecta simple de orden 21 de un cuadrado de lado 112, obtenida por Arie Duijvestijn en 1978. Hemos coloreado los cuadrados para observar los cuadrados que van juntos en el código de Bouwkamp que se describe a continuación
Antes de terminar esta entrada, expliquemos una notación sencilla, llamada código de Bouwkamp, que existe para describir las cuadraturas mediante cuadrados. En esta notación, se utilizan corchetes para incluir los cuadrados adyacentes que tienen el lado superior a la misma altura (horizontal) y los grupos de corchetes se van escribiendo desde el lado superior del cuadrado (o rectángulo) grande hacia abajo. Por ejemplo, la cuadratura perfecta simple del cuadrado de orden 21 descrita en la imagen anterior tiene el código de Bouwkamp [50, 35, 27], [8, 19], [15, 17, 11], [6, 24], [29, 25, 9, 2], [7, 18], [16], [42], [4, 37], [33].
Además, el número de cuadraturas perfectas del cuadrado de orden n, para n mayor o igual que 21, es la sucesión 1, 8, 12, 26, 160, 441, 1.152, 3.001, 7.901, … que en la Enciclopedia on-line de sucesiones de números enteros es la sucesión OEIS A006983.
Para terminar esta entrada del Cuaderno de Cultura Científica sobre el problema de la cuadratura (perfecta) del cuadrado, vamos a pensar en una disección muy particular, aquella en la que los lados de los cuadrados pequeños recorren todos los números naturales desde 1 hasta uno dado m. ¿Existirá una cuadratura como esta?
Si existiese esa cuadratura, el área del cuadrado grande, que será un número cuadrado N2, sería la suma de las áreas de los cuadrados pequeños, que como están todos los lados desde 1 hasta m, sería la suma de los cuadrados de los cuadrados de los primeros m números naturales, es decir,
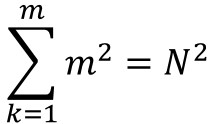
La suma de los cuadrados de los primeros números naturales es la sucesión de números que se conoce como números piramidales cuadrados (la sucesión OEIS A000330, de la Enciclopedia on-line de sucesiones de números enteros), pero solo hay un número piramidal cuadrado que sea el cuadrado de un número natural,´distinto de 1, el número 4.900 = 702, que es la suma de los cuadrados de los 24 primeros números naturales. Sin embargo, en 1974 se demostró, realizando una búsqueda exhaustiva por ordenador, que es imposible colocar los 24 cuadrados con lados de todos los tamaños entre 1 y 24 de manera que formen un cuadrado de lado 70.
Bibliografía
1.- Wolfram MathWorld: Perfect Square Dissection.
2.- Stuart Anderson, Tiling by squares
3.- David Singmaster, Sources in recreational mathematics, an annotated bibliography
4.- Henry Dudeney, Los acertijos de Canterbury, RBA, 2011.
5.- Sam Lyod, Los acertijos de Sam Loyd, RBA, 2011.
6.- Wikipedia: Scottish book
7.- Slanislaw Ulam, tradución al inglés del Scottish book
8.- Martin Gardner, The 2nd Scientific American Book of Mathematical Puzzles and Diversions, University of Chicago Press, 1987. Contiene el capítulo de W. Th. Tutte Squaring the square.
9.- Hallard T. Croft, Kenneth J. Falconer, Richard K. Guy, Unsolved Problems in Geometry, Springer-Verlag, 1991.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo La cuadratura del cuadrado: en busca del santo grial se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Blanche Descartes y la cuadratura del cuadrado
- Motivar a los alumnos: el «santo grial» de la educación
- Un cuadrado mágico ‘papal’
El misterio de la temperatura constante
 Foto: Aaron Burden / Unsplash
Foto: Aaron Burden / UnsplashDe forma tradicional se dice que la materia aparece en uno de tres estados o fases: sólido, líquido o gaseoso (vapor) [1]. De acuerdo con la teoría cinético-molecular [2], un factor que distingue cada uno de estos estados es la cantidad de energía distribuida entre las moléculas que componen el material. En el estado gaseoso las moléculas tienen la mayor cantidad de energía y en el estado sólido la menor. Las transiciones de un estado a otro se pueden conseguir agregando o extrayendo energía en forma de calor.
Pero no es tan fácil. Existe un hecho misterioso que puede comprobarse con un recipiente con agua y un termómetro. El hecho es que, a pesar de aportar energía, por ejemplo, para evaporar el agua, la temperatura de ésta no cambia en absoluto mientras se produce el cambio de fase. Dicho de otra manera, en cada transición de un estado a otro, ¡la cantidad de energía térmica parece desaparecer (si vamos a estados de temperatura más alta) o aparece sin que haya pérdida de energía en otro lugar (si vamos a estados de temperatura más baja)!
Nos vemos obligados, pues, a incluir un concepto adicional [3], el concepto de entropía, que da una idea del nivel de desorden [4].
Para ver el proceso básico que conduce a la formación de un sólido tomemos el agua como sustancia ejemplo. Comenzamos con agua líquida, que enfriaremos extrayendo energía como calor. A medida que el agua se enfría, la variación de su temperatura, ΔT, está relacionada con la cantidad de la energía neta transferida como calor, ΔQ, por la relación ΔQ = m·c·ΔT , donde m es la masa de agua y c es el calor específico del agua líquida, que en este caso es 1 caloría por gramo y por grado centígrados. A medida que continuamos enfriando el agua, alcanzamos una temperatura a la cual el líquido experimenta un cambio de fase de líquido a sólido. Todos los líquidos terminan transformándose en sólidos, pero lo hacen a temperaturas muy diferentes. El agua a presión atmosférica comenzará a congelarse a 0 °C (273 K), pero el helio líquido no se congela hasta que alcanza los 4 K, muy cerca del cero absoluto.
En este punto, observamos el hecho misterioso: a medida que “extraemos calor”, el líquido continúa congelándose formando hielo, pero la temperatura se mantiene igual. ¿De dónde sale la energía que estamos extrayendo? La energía extraída parece haber estado «oculta» en el líquido y estar asociada con la formación del sólido, el hielo. Este “calor oculto» se llama calor latente [5]. Para el agua, tiene un valor de aproximadamente 80 calorías por gramo de agua.
Pero ¿qué es este calor latente y qué tiene que ver con la transformación de un líquido en un sólido? Dado que el proceso de enfriamiento implica la extracción de energía del material, las moléculas comienzan a organizarse en un estado de energía mínima. Esto se logra a medida que las moléculas se agrupan en una disposición lo más ordenada y estructurada posible. El estado de energía mínima tendrá el orden más alto, lo que significa que tiene la entropía más baja. El cambio en la entropía, ΔS, se define como la energía neta transferida como calor, ΔQ, ganada o perdida por el sistema, dividida por la temperatura absoluta (en kelvin) del sistema: ΔS = ΔQ/T .
Vemos pues que el calor latente que se extrae del agua a medida que se congela, ΔQ, está directamente asociado con la disminución de la entropía de las moléculas de agua a medida que forman la estructura ordenada del hielo sólido.
Por supuesto, si la energía térmica se introduce nuevamente en el sistema la entropía comenzará a aumentar a medida que las moléculas comiencen a vibrar más y más rápido. Finalmente podrán romper los enlaces que la convierten en un sólido. Esto es lo que llamamos fusión. Nuevamente, la temperatura permanece constante mientras el sólido se derrite mientras se aporta energía térmica. Durante este proceso, la energía térmica entrante se vuelve latente una vez más, ya que la temperatura no cambia, pero la entropía aumenta y la disposición ordenada dentro del sólido se rompe, formando un charco de agua donde una vez tuvimos un cubo de hielo ordenado.
Notas:
[1] Existen varios más, pero ese conocimiento no nos aporta nada ahora.
[2] Para repasar algunos conceptos básicos de esta teoría pueden consultarse las entregas 18 y siguientes de nuestra serie La dinámica del calor.
[3] Lo mismo pasa con la energía o materia oscuras, con la diferencia de que en este caso sabemos explicar el origen del mismo, mientras que en estas cosas oscuras no tenemos las ideas muy claras todavía (discúlpese el mal juego de palabras).
[4] Quizás sea conveniente señalar en este punto que gran parte de la comprensión básica de las transiciones de fase y la formación de la materia sólida se desarrolló alrededor del año 1900, pero fue necesaria la mecánica cuántica en las décadas posteriores para una comprensión completa, y algunos aspectos de estos complicados procesos son aun objeto de intensa investigación.
[5] “Latente” es una forma culta de decir “escondido, oculto”, culta por aquello de que latente es oculto en latín (discúlpese el mal juego de palabras).
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El misterio de la temperatura constante se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los experimentos de Joule
- La primera ley de la termodinámica
- Se intuye la conservación de la energía (1)

