Montañeros, espeleólogos y mineros

Ilustración del libro XII de “De re metallica” (1556) de Georg Bauer “Agricola”
Desde el Renacimiento has el siglo XVIII produjeron clasificaciones de minerales y rocas una tras otra. Entre las más importantes cabe mencionar la del ingeniero de minas y alquimista alemán Georg Pawer (también Bauer), más conocido como Agricola, la del químico sueco Johan G. Wallerius (considerado el padre de la química agrícola, por cierto) o la del geólogo alemán Abraham Gottlob Werner (otro padre, en este caso del neptunismo, algo de lo que nos ocuparemos más adelante).
Todas estas clasificaciones tenían un trasfondo alquímico y todas tenían en común la clasificación general en cuatro grupos en función de sus “químicas”, más concretamente en su relación con el calor y los fluidos: tierras, metales, sales y combustibles. Así, las tierras resistían el calor y el agua, los metales se volvían fluidos al calentarse, las sales se disolvían en los fluidos y los combustibles (como el carbón, por ejemplo) generaban calor al arder.
Como la química era la base de la clasificación de las rocas y minerales, los aprendices y estudiantes pasaban más tiempo en talleres, fundiciones, gabinetes y laboratorios trabajando con sustancias y aparataje químicos que sobre el terreno.

La Calzada del Gigante (Irlanda) está formada por duras columnas de basalto.
Después de siglos de clasificaciones minerales, Werner sería el primero en expresar la frustración que producía el estudio de minerales y rocas desde el punto de vista científico a principios del siglo XIX, concluyendo que no existían y, por tanto, no podían encontrarse, principios teóricos consistentes para la clasificación de los minerales. Una consecuencia de este convencimiento es que Werner empieza a dar instrucciones a sus estudiantes de clasificar las rocas en función del tiempo de su formación (lo que se enmarca en lo que se conoce como estratigrafía, que también veremos más avanzada la serie) y los minerales aparte de la clasificación general se asocian al tipo y antigüedad de las rocas en las que aparecen, algo que estrá relacionado con el origen mismo de esas rocas.
La creciente industrialización junto a la aparición de estados nacionales ilustrados lleva a que los gobiernos comiencen a contratar inspectores de minas, especialistas en sondeos mineros y mineralogistas para que estudien el territorio nacional concienzudamente en busca de riquezas y recursos. Los mineralogistas abandonan sus cubículos para convertirse en montañeros, espeleólogos y mineros.

La blanda piedra arenisca del Cañón del Antílope (Arizona, Estados Unidos) está formada por arena (cuarzo, blanco); los colores los porporcionan mayoritariamente los minerales hematites (rojo), goetita (pardo / amarillo ocre) y limonita (pardo / amarillento claro).
En la segunda mitad del siglo XVIII, estos mineralogistas de aire libre, entre ellos, Lazzaro Moro y Giovanni Arduino en Italia, Johann Lehmann en Alemania o Guillaume-François Rouelle en Francia, encuentran conveniente clasificar las rocas en dos tipos fundamentales: primarias y secundarias.
Las rocas primarias eran duras, a menudo cristalinas, y la matriz en la que se encontraban los metales y minerales preciosos; constituían el núcleo de las cadenas montañosas.
Las rocas secundarias eran relativamente blandas y granulares, a menudo formaban capas o estratos en las laderas de las montañas cuyos núcleos eran las rocas primarias. A menudo, las rocas secundarias contenían fósiles, que ya entonces los mineralogistas consideraban restos endurecidos de animales y plantas.
Esta clasificación tenía que ver con la cosmogonía: el estudio del desarrollo del planeta.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Montañeros, espeleólogos y mineros se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Clasificación y origen, los dos problemas de la mineralogía
- Esa pesadilla científica llamada mineralogía
- Potencia y eficiencia de una máquina
La polilla que se parecía a Donald Trump: más allá del chascarrillo

La polilla bautizada en honor a Donald Trump. Imagen: Wikimedia Commons
Con todos ustedes, bajo estas líneas, el escarabajo acuático Grouvellinus leonardodicaprioi, bautizado como habrán podido deducir mis avezados lectores, en honor del actor Leonardo DiCaprio como homenaje a su activismo en favor de la conservación del medio ambiente y para conmemorar el 20 aniversario de la Leonardo DiCaprio Foundation, creada por el actor con este fin.

Leonardo DiCaprio junto al escarabajo que lleva su nombre. Imagen: Wikimedia Commons
Este recién descubierto escarabajo fue encontrado en la cascada en la remota zona de Maliau Basin, en el Borneo Malasio, y su descubrimiento es un logro de la llamada ciencia ciudadana: fue un grupo de excursionistas aficionados el que encontró el espécimen nunca antes descrito. En total descubrieron tres nuevas especies de escarabajos acuáticos, y uno de ellos quisieron dedicarlo a DiCaprio, que ha dedicado sus esfuerzos a proteger el medio ambiente, y en concreto los hábitats vírgenes e inexplorados, como el propio lugar donde su escarabajo vive. “Pequeño y negro, este nuevo escarabajo nunca ganará un Oscar por su carisma, pero en la conservación de la biodiversidad, todas las criaturas cuentan”, ha dicho la entomóloga Iva Njunjic.
Permítanme que les presente a otra amiga. Pueden verla al comienzo de este texto y si se fijan bien en su aspecto quizá puedan adivinar su nombre. Presten atención sobre todo a esas escamas pálidas sobre su cabeza y a su parecido con el proceloso flequillo del hombre a su lado: están ustedes ante un ejemplar de Neopalpa donaldtrumpi bautizada, como no podía ser de otra manera, en recuerdo del actual presidente de Estados Unidos, Donald Trump.

Shakira y sus movimientos de cadera dan nombre a esta avispa. Imagen: Wikimedia Commons
Pero esperen, que traigo más amigos a esta pequeña reunión nuestra. Esta curiosa avispa se llama Aleiodes shakirae en honor a la cantante colombiana Shakira. No es porque se le parezca, o porque Shakira haya hecho nada concreto por ella y su entorno. No, en este caso el homenaje se debe a que “el parasitismo por esta especie causa que la oruga anfitriona doble y retuerza su abdomen de forma muy particular, y Shakira también es famosa por su habilidad en la danza del vientre”, explicaban los bautizadores del insecto.

La tarántula bautizada en honor a Johnny Cash. Imagen: Wikimedia Commons
Y aquí está la araña Aphonopelma johnnycashi. Dado que se puede encontrar en los alrededores de la prisión Folsom, en California, y que los machos a partir de determinada edad son de color negro completamente, sus descubridores decidieron que no había nombre más apropiado para esta especie que un homenaje al cantante Johnny Cash. Y yo coincido en ese juicio.

Jonh Cleese y ‘su’ lemur. Imagen: Wikimedia Commons
En 2005 este simpático lemur fue descrito por primera vez y bautizado como Avahi cleesei en honor al actor inglés John Cleese, que en la película Criaturas feroces interpretaba a un cuidador de lemures y que después dio voz y presentó a un afamado documental sobre estos animales.
Para no extenderme, pero no queriendo dejar a nadie atrás, dejad simplemente que mencione a los trilobites Avalanchurus simoni y Avalanchurus garfunkeli (en homenaje a Simon y Garfunkel), al escarabajo Cheguevaria (que recuerda al Che Guevara), al pterosaurio Coloborhynchus spielbergi (bautizada en honor al director Steven Spielbergh), la araña Filistata maguirei (para recordar a Tobey Maguire, actor en tres películas de Spiderman), el mamífero extinto Gagadón (que homenajea a Lady Gaga), la polilla Hellinsia pizarroi (que recuerda al conquistador Francisco Pizarro) o la rana Hyloscirtus princecharlesi (en honor al príncipe Carlos de Inglaterra).
¿Cómo se bautiza a una especie?
Imaginarse a una polilla con un pelucón a lo Donald Trump tiene su gracia. ¿Cómo se convierte eso en el nombre oficial de una nueva especie?
Lo primero que hace falta es asegurarse de que lo que tenemos entre manos es efectivamente una nueva especie lista para ser bautizada. Para eso hace falta designar un holotipo, esto es, un ejemplar que sirva como identificación de esa nueva especie descubierta. También son de ayuda los paratipos, ejemplares complementarios, por ejemplo un macho si el holotipo es una hembra, o una cría de la misma especie, de forma que se puedan reunir y observar todas las características distintivas de la especie descubierta.

Esta rana recibe su nombre del Príncipe Carlos, ya que este siempre utiliza una rana como símbolo en sus campañas para la conservación tropical. Imagen: Wikimedia Commons
Normalmente estos especímenes se conservan en un lugar donde puedan ser examinados por otros científicos, a fin de determinar con seguridad si se trata de una especie nueva o no. La taxonomía es una disciplina en constante discusión y reexaminación, y no son pocas las veces que un ejemplar ha obtenido y perdido después el estatus de especie independiente.
También hace falta una descripción: una recolección de las características que dan forma a una nueva especie. Y aquí las cosas pueden empezar a ponerse delicadas porque el ojo y las palabras son muchas veces subjetivos y por tanto dificultan la diferenciación ente dos animales lo suficientemente parecidos. Características contables, como el número de vértebras o de crías en cada camada, por ejemplo, son aquí más útiles que la descripción de colores o de cantos.
Una vez seguros de que lo descubierto es una especie nueva, entonces llega el momento de nombrarla, puesto que lo que no se nombra no existe. El nombre de una especie (por ejemplo, Homo sapiens) está compuesto por el género al que pertenece (Homo) y después por el apelativo concreto que la identifica (sapiens), ambos latinizados. El proceso de bautizar una nueva especie se completa cuando el nombre y descripción se publica de forma que quede internacionalmente accesible y sea consultable. Esto antes implicaba a revistas científicas de renombre, pero ahora internet ha hecho las cosas más fáciles. Curiosamente el proceso por el que se otorga nombre a nuevas especies es uno de los pocos relacionados con la ciencia que no depende del peer-review, lo que en ocasiones causa confusión si dos nombres se parecen demasiado o si algún nombre no se clasifica correctamente dentro de su género.
Bautizar una especie con el nombre de un famoso: más allá del chascarrillo
Los científicos llevan bautizando animales con nombres de famosos desde el siglo XVIII. Carl Linnaeus, científico suizo que sentó las bases de la taxonomía actual, lo hacía ya para ganarse el favor, y con ello el dinero, de los patrones ricos que así podían ayudarle a continuar con sus investigaciones.

La abeja nombrada en honor a Beyoncé. Imagen: Wikimedia Commons
Algo parecido ocurre hoy: el descubridor de la abeja Scaptia beyonceae sabía perfectamente que relacionando el trasero redondeado y dorado de este animal con el de la cantante Beyoncé se asegura la atención del público, aunque sea solo durante unos pocos pero valiosos segundos. Se trata por tanto de llamar la atención para que, junto con el chistecito del nombre y la gracia que nos hace latinizar el nombre de Shakira hablemos también de algunas de las características de la avispa que ahora lleva su nombre, del hábitat en el que vive el animal en cuestión, de los riesgos que la amenazan, de los esfuerzos de conservación que se realizan pero aun más de los que todavía tenemos que hacer.
Así que se trata de marketing: una estrategia para conseguir que se hable de sus animales, su trabajo (lo que puede a su vez convertirse en más fondos para su investigación) y la conservación del medio ambiente. Hace unas semanas hablábamos aquí mismo de cómo el marketing es una buena opción para la supervivencia de especies que no son majestuosas como un águila o imponentes como un gorila. Los animales feos, sosos o desagradables pueden beneficiarse de una buena campaña de comunicación. Y si eso incluye ser bautizado en honor a Donald Trump, habrá que hacer de tripas corazón y llevar el nombre con dignidad. O con toda la dignidad posible.
Referencias:
Three new species of Grouvellinus Champion, 1923 from Maliau Basin, Sabah, Borneo, discovered by citizen scientists during the first Taxon Expedition – Hendrik Freitag, Clister V. Pangantihon, Iva Njunjić.ZooKeys, 2018; 754: 1 DOI: 10.3897/zookeys.754.24276
How a new species is named – Dr. David Hone, The Guardian
List of organisms named after famous people – Wikipedia
It’s funny to name species after celebrities, but there’s a serious side too – Kevin Thiele, The Conversation
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo La polilla que se parecía a Donald Trump: más allá del chascarrillo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Kim Jong-un, Donald Trump y la geología de la aniquilación
- Naukas Bilbao 2017 – Aitor Sánchez: Si Donald Trump fuese nutricionista
- Colonialismo científico: los investigadores africanos se rebelan contra el expolio de datos genéticos
Las aves de Prometeo

Milanos negros sobrevolando un fuego que podrían haber iniciado ellos mismos. Imagen: Bob Gosdorf
Las aves tienen capacidades asombrosas. Los pájaros cantores, por ejemplo, tienen excelentes habilidades vocálicas, algunos extraordinarias. El caso más espectacular es el de una especie cuyos machos, para cortejar a la hembra, aprenden un canto nuevo cada año. Los pergoleros macho fabrican pérgolas muy complejas y de gran cromatismo; también lo hacen para conquistar a su pareja. Otras aves fabrican instrumentos, como ganchos para extraer lo que les interesa de lugares de difícil acceso. Hay cuervos que reconocen personas y son capaces de recordarlas durante largo tiempo, sobre todo si, por lo que fuese, las temen. También hay aves que juegan. Como es bien sabido, muchas migran, y algunas de sus migraciones son verdaderas heroicidades, tanto desde el punto de vista físico como cognitivo. Y de algunos pájaros sabemos que son capaces de posponer las gratificaciones a una tarea bien completada a la espera de una recompensa mejor.
Desde hace tiempo los indígenas de las sabanas del norte de Australia sostienen que hay aves que ayudan a propagar fuegos. Algunos bomberos también afirman haber visto a ciertas aves de presa reavivar incendios ya controlados. Algunas de esas observaciones datan de los ochenta del pasado siglo. Pero casi nadie las creía. Hace dos años el ornitólogo Robert Gosford sugirió que esos testimonios podían ser correctos, pero la mayoría de sus colegas manifestaron serias dudas al respecto. Como mucho pensaban que podía tratarse de hechos fortuitos. Sin embargo, las dudas parecen estar disipándose. Un grupo formado por ornitólogos y bomberos han recogido veinte testimonios -considerados fidedignos- de observaciones de aves de presa que propagaban incendios de manera intencionada, y han dado a conocer su investigación en la revista científica Journal of Ethnobiology.
Las observaciones se refieren a las especies Milvus migrans (milano negro), Haliastur sphenurus (milano silbador) y Falco berigora (halcón berigora) y se han realizado en las sabanas septentrionales australianas, aunque los autores del trabajo afirman haber recibido informaciones en el mismo sentido de otras zonas del país. El comportamiento observado consiste en el traslado de pequeñas ramas encendidas de zonas ya quemadas a zonas a las que no ha llegado el fuego. Llevan las ramas de un sitio a otro en el pico o las patas. A veces son actos individuales y en ocasiones son varios los individuos que actúan de forma cooperativa. Aunque no siempre lo consiguen, con frecuencia logran extender el fuego hacia zonas que no habían ardido. Al parecer, solo se comportan así cuando un fuego se ha detenido al llegar a una barrera o por haber sido apagado por los servicios contra incendios. Y solo unos pocos individuos aprenden a hacerlo.
Que hay aves que se valen de los incendios para atrapar presas que huyen de zonas en llamas era algo ya sabido. La novedad que aportan los testimonios recogidos consiste en la participación activa de milanos y halcones en la extensión del fuego. Se trata de un comportamiento de importantes requerimientos cognitivos.
Solemos pensar que los pájaros son animales estúpidos, de escasa inteligencia, entre otras cosas porque nos parece que tienen la cabeza pequeña. Pero eso no es cierto; en la evolución su encéfalo se redujo mucho menos que el resto del cuerpo en relación con el de sus antecesores, los dinosaurios. Además, sabemos muy poco del funcionamientos de ese encéfalo. Y quizás seamos incapaces de valorar de forma adecuada la capacidad cognitiva de las aves, simplemente porque utilizamos la nuestra como referencia y modelo. Prometeo robó el fuego a los dioses y se lo entregó a los mortales. Pero es posible que entre los mortales también incluyera aves de presa.
—————————————————————–
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
Una versión anterior de este artículo fue publicada en el diario Deia el 28 de enero de 2018.
El artículo Las aves de Prometeo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Naukas Bilbao 2017 – Sergio Palacios: Precausión, amigo conduztó
En #Naukas17 nadie tuvo que hacer cola desde el día anterior para poder conseguir asiento. Ni nadie se quedó fuera… 2017 fue el año de la mudanza al gran Auditorium del Palacio Euskalduna, con más de 2000 plazas. Los días 15 y 16 de septiembre la gente lo llenó para un maratón de ciencia y humor.

Dolor, aceleraciones y extraterrestres de la mano del inefable Sergio Palacios.
Sergio L. Palacios: Precausión, amigo conduztóEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2017 – Sergio Palacios: Precausión, amigo conduztó se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – José Miguel Viñas: Me río yo del cambio climático
- Naukas Bilbao 2017 – Mónica Lalanda: Una muerte de cómic
- Naukas Bilbao 2017 – Laura Morrón: La gran divulgadora
Entrelazamiento cuántico entre dos nubes de átomos ultrafríos
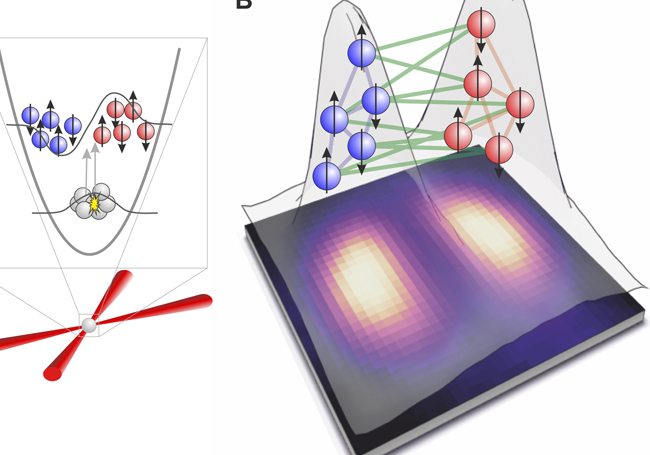
Science publica los resultados de un experimento en el que han colaborado varios miembros del grupo de investigación Quantum Information Theory and Quantum Metrology del Departamento de Física Teórica e Historia de la Ciencia de la Facultad de Ciencia y Tecnología de la UPV/EHU, liderados por Géza Tóth, Ikerbasque Research Professor, y llevado a cabo en la Universidad de Hannover. En el experimento, han conseguido el entrelazamiento cuántico entre dos nubes de átomos ultrafríos, conocidos como condensados de Bose-Einstein, donde los dos conjuntos de átomos estaban espacialmente separados entre sí.
El entrelazamiento cuántico es un fenómeno que no tiene análogo en la física clásica. Los conjuntos de partículas que están entrelazadas pierden su individualidad y se comportan como una sola entidad. Cualquier cambio en una de las partículas conduce a una respuesta inmediata en la otra, incluso si están espacialmente separadas. “El entrelazamiento cuántico es indispensable en aplicaciones como la computación cuántica, ya que permite la resolución de ciertas tareas de forma mucho más rápida que en computación clásica”, explica Géza Toth.
A diferencia de la forma en que se ha creado hasta ahora el entrelazamiento cuántico entre nubes de partículas, utilizando conjuntos de partículas incoherentes y térmicas, en este experimento utilizaron conjuntos de átomos en estado de condensado de Bose-Einstein. Tal como explica Toth, “los condensados de Bose-Einstein se consiguen al enfriar los átomos utilizados a temperaturas muy bajas, cercanas al cero absoluto. A esa temperatura, todos los átomos comparten el mismo estado cuántico, con gran coherencia; se podría decir que todos ocupan la misma posición en el espacio. En ese estado se da el entrelazamiento cuántico entre los átomos del conjunto”. Posteriormente, lo que hicieron fue separar en dos nubes de átomos ese conjunto. “Dejamos una distancia entre las dos nubes de átomos, y pudimos demostrar que seguía habiendo entrelazamiento cuántico entre ellas”, continúa.
La demostración de que se puede crear el entrelazamiento entre dos nubes en estado de condensado de Bose-Einstein puede dar lugar a una mejora en muchos campos en los que se utiliza la tecnología cuántica, como la computación cuántica, la simulación cuántica y metrología cuántica, dado que estas requieren de la creación y el control de un gran número de conjuntos de partículas entrelazadas. “La ventaja que ofrecen los átomos ultra fríos es que se pueden conseguir estados fuertemente entrelazados que contienen cantidades de partículas superiores en varios órdenes de magnitud a otros sistemas físicos, lo cual podrá ser la base para la computación cuántica a gran escala”, relata el investigador.
Referencia:
Karsten Lange, Jan Peise, Bernd Lücke, Ilka Kruse, Giuseppe Vitagliano, Iagoba Apellaniz, Matthias Kleinmann, Geza Toth, Carsten Klempt (2018) Entanglement between two spatially separated atomic modes Science (2018) DOI: 10.1126/science.aao2035
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Entrelazamiento cuántico entre dos nubes de átomos ultrafríos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Física de partículas en un simulador cuántico
- Materia oscura entre nubes intergalácticas
- Un observador cuántico de lo más útil
¡Cuidado! Publicación depredadora a la vista

La historia la contaba Kelly Cobey en una pasada columna para Nature: un colega investigador, ya con tablas y algunas canas, había caído en uno de los más extraños, peligrosos y agresivos timos del mundo científico. Aunque esta estafa lleva bebiendo de las sangres del “publica o muere” muchos años ya, parece que es capaz de atrapar hasta al más experimentado de los investigadores.
Hablamos, nada menos, que de las “revistas depredadoras”, más conocidas como Predatory Journals o, en casos concretos, Open Access Predatory Journals (OAPJ). Esta peligrosa práctica puede bloquear nuestra investigación o hacernos perder una cantidad ingente de dinero. ¿En qué consiste esta engañifa? ¿Cómo podemos reconocer una publicación de este tipo?. Entender cómo operan y qué consecuencias trae el caer en sus garras es crucial para poder defender nuestro paper en el peor de los casos.
¿Qué son los ‘Predatory Journals’?
El nombre de “revista depredadora” fue acuñado por Jeffrey Beall para describir una serie de journals científicos (publicaciones) que se hacen pasar por revistas típicas del ámbito especializado pero que en realidad esconden prácticas abusivas y que en muchos casos rozan la pura estafa. El término “depredador” refleja la naturaleza intencionalmente engañosa de estas revistas, que “cazan” a los investigadores y sus estudios con artimañas diversas.
Entre las estratagemas, y haciéndonos eco de las investigaciones realizadas por el propio Beall o Cobey (et al), estas entidades afirman, por ejemplo, realizar una exhaustiva revisión por pares, cosa que no hacen. También ofrecen un servicio de acceso Open Access, pero más adelante, cuando ya es demasiado tarde para los autores, no cumplen con la conocida como Declaración de Bethesda a la hora de darle acceso gratuito a los investigadores y lectores, faltando en varios puntos a los derechos de autor.
Como guinda de este pastel, los Predatory Journals utilizan tácticas agresivas y trucos sucios para obligar a los autores a enviarles el manuscrito, incluso si estos se han dado cuenta del lío en el que se estaban metiendo. De esta manera, los investigadores se encuentran en una tesitura muy difícil. Para muestra un botón: el encontronazo del que hablábamos resultó ocurrir como sigue.
De investigador a “presa”
Parafraseando a la Dra. Cobey, en 2017 recibió un correo de un colega explicándole su problema con cierta publicación. Al parecer, meses antes había llegado una “invitación” para que publicara el material de cierto estudio en forma de artículo. Unos meses antes, este investigador había hecho una presentación oral mostrando parte de sus resultados. Esta “invitación” parecía la oportunidad perfecta para convertir este esfuerzo en un paper que contara en su currículum.
Tanto el título de la revista como el tema al que se refería el correo que recibió encajaban a la perfección con su especialización. “Qué diablos”, pensaría nuestro desdichado científico. Poco después, tras algunas correcciones menores, el investigador recibió un email explicando que el artículo había sido aceptado para su publicación. “¡Albricias!”. Pero no, no había motivo para alegrarse. Un poco más abajo, en ese mismo mensaje, se incluía un albarán de casi mil dólares por la publicación del artículo en el dichoso journal. “Un momento, a mi nadie me había avisado de esto”.
Así que, molesto por la argucia, el investigador decidió pasar de la publicación y, ya que el trabajo estaba hecho, enviarlo a una publicación legítima y que no tratara de timarle. Durante los siguientes meses le siguieron llegando mensajes de la anterior publicación, claramente depredadora, donde se le seguía solicitando el dinero de la publicación. Cuando su paper fue admitido en la otra editorial (esta vez sí, con una correcta revisión por pares), se alegró. “Albricias, ahora de verdad”. Pero el problema estaba lejos de acabar.
Así son las tácticas depredadoras
Resulta que una vez aceptado y todo preparado para la publicación, los investigadores (y la nueva publicación) se encontraron con que el paper ya había sido expuesto en la web del Predatory Journal de marras. Esto, como cualquiera familiarizado con la publicación científica, la revisión por pares y los embargos sabe, es un problema muy gordo.
Porque una vez publicada la información ya no es susceptible de ser publicada de nuevo en otra revista científica. La única manera posible de hacerlo es eliminando dicho documento. Al solicitarlo formalmente, explicaba Cobey en su artículo, los editores (mal eufemismo para estos estafadores), indicaron que el coste de la retirada del artículo era de unos 300 dólares, aproximadamente.
De esta manera, habían puesto al investigador y a su equipo en jaque: “¿Quiere que lo publiquemos? Bien, son mil dólares. ¿No quiere que lo publiquemos? Bien, son 300 dólares”. Y ante la tesitura, ¿qué haría cualquiera? Este investigador, aconsejado por la Dra. Cobey, contactó con los supuestos miembros editores del Journal y, para su sorpresa, estos indicaron que poco o nada tenían que ver con él, una muestra más de la estafa.
Finalmente, y para alivio del investigador (y a pesar de las semanas de esfuerzo y sufrimiento causadas) la publicación legítima decidió publicar el artículo sin que existiera “perjuicio” para los investigadores, reconociendo las prácticas del Predatory Journal como una vulgar estafa alejada de la ética editorial de cualquier publicación real.
¿Cómo se si mi ‘paper’ está en manos de un ‘Predatory Journal’?
Existen pocas universidades que cuenten con unidades y especialistas dedicados, casi exclusivamente, a la publicación. Esto, explican algunos expertos como Beall o la propia Cobey, es un problema muy serio ya que muchos (muchísimos investigadores) carecen de la experiencia (o incluso formación) sobre cómo funciona el mundo de las editoriales científicas. En otras ocasiones es la presión por publicar la culpable de una mala decisión.
En cualquier caso, los datos indican que no importa la formación o la carrera del investigador, cualquiera es susceptible a caer en las garras de un Predatory Journal. Hablamos de miles de investigaciones que son extorsionadas por estas mal llamadas publicaciones. Según los datos recogidos por Cobey, tras analizar unos 2.000 papers dispuestos en este tipo de revistas, ni tan siquiera el tipo de subvención, la procedencia de la investigación o el origen del equipo investigador libra a nadie de ser objeto de este tipo de prácticas. Por cierto, los países con más presencia de publicaciones depredadoras, con diferencia, son la India y Estados Unidos, aunque también se encuentran en Nigeria, Egipto, Turquía o incluso Japón y Reino Unido.
¿Cómo podemos esquivar a estos depredadores de la información? Para identificar este tipo de publicaciones varios hechos deberían hacer sonar nuestras alarmas alarmas. En primer lugar, la afiliación editorial. Una afiliación editorial dudosa, o la falta de información sobre la empresa que la maneja, son buenas razones para dudar. En segundo, una publicación legítima jamás pondrá tasas absurdas. Por ejemplo, el recargo por “retirar” un artículo no aparecerá en ninguna publicación que cumpla con una buena ética editorial.
Según el criterio de Jeffrey Beall para identificar a este tipo de Predatory Journals, estos se caracterizan por no seguir, o simplemente violar, el “Código de conducta de los editores de publicaciones científicas” o los “Principios de transparencia y buenas prácticas de las publicaciones académicas“. En ellas, por ejemplo, se recogen asuntos tan variados como la información que se intercambia entre autores y editores, la cuestión de las tasas o los derechos de autor.
Las razones son muchas y muy variadas, demasiadas para recogerlas aquí. Por otro lado, estos criterios están bien recapitulados y arduamente resumidos en el documento preparado por el propio Beall, el cual podría servir como código genérico para detectar este tipo de publicaciones. Este documento, de hecho, surge a la par que una lista de publicaciones listadas en su web, con lo que revisar si el journal en cuestión entra dentro de estos criterios puede ser tan sencillo como comprobar que no haya sido mencionado en la “Lista Beall de Predatory Journals“. i
Una piedra más en esto de “hacer ciencia”
Si algo queda cada vez más claro es que la ciencia y el proceso para generar conocimiento científico está viviendo una profunda crisis. Desde cuestiones socioeconómicas a políticas, pasando por técnicas o humanas, el proceso de revisión por pares y la publicación en revistas científicas se encuentra ahora mismo con graves problemas.
Cada año son más los papers retirados debido a un sinfín de razones (en el peor de los casos porque sus investigaciones no se sustentan); los investigadores se ven envueltos en condiciones inasumibles de trabajo, cobrando poco y trabajando demasiado. Y lo peor es que en la mayoría de los casos se ven envueltos en una especie de “carrera de la reina roja” en los que han de publicar cada vez más para mantener su financiación o el apoyo institucional.
Al final, dentro de este círculo vicioso, se busca la publicación con el mayor índice de impacto para poder optar a la financiación y, mientras tanto, los artículos que no cumplen con las expectativas de los editores de grande publicaciones o, sencillamente, los resultados negativos se pierden el el frenesí del “publica o muere”.
Volviendo al tema de las grandes editoriales, y aunque a muchos no les gusta escucharlo, los investigadores viven regidos por un índice de impacto que ha sido decidido de forma interna y cuasi secreta por las mismas compañías que deciden qué papers son mejores o peores. Al final, todo el mundo científico danza al son de unas pocas marcas que contienen el 90% del haber científico del mundo.
Y en todo este maremagnum, los predatory journals acechan para hacerse con la carroña que puedan desgarrar de este tejido intelectual científico. Pero las víctimas no son solo los incautos investigadores que caen en sus artimañas. También lo son, y probablemente de forma más amarga, las pequeñas publicaciones. Esos journal que, sin tratar de acercarse a la sombra de los titanes editoriales, pretenden hacerse un hueco en la literatura científica especializada.
Estos son los primeros en sufrir las consecuencias en forma de rechazo y suspicacia, probablemente inmerecida, por culpa de otros estafadores sin escrúpulos. Por desgracia, los Predatory Journals han aumentado su número en las últimas décadas, lo que complica muchísimo más el trabajo a la hora de publicar, tanto para los científicos como para las pequeñas editoriales. Pero admitiremos una cosa: no hay mal que por bien no venga. Si al menos, tras el mal trago de gente como la que ha llegado a conocer Cobey el resto de la comunidad científica se pone las pilas, algo bueno sacaremos de esto. Y es que nos hace falta ser más conscientes de cómo funciona el mundo de la publicación científica si queremos mejorar la manera que tenemos de “hacer ciencia”.
Este post ha sido realizado por Santiago Campillo (@ScruzCampillo) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
El artículo ¡Cuidado! Publicación depredadora a la vista se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La contradicción de la publicación
- ¿Puede ser culto alguien de Letras?
- La estrella individual más lejana jamás vista
Las absurdas declaraciones saludables de algunos alimentos están amparadas por las autoridades

Cada vez hay más alimentos que muestran en su etiquetado alguna declaración saludable. Desde postres lácteos que «contribuyen al normal funcionamiento del sistema inmunitario» a bollería industrial que «aumenta la capacidad de atención y memoria». Este tipo de declaraciones hacen que algunos alimentos de bajo interés nutricional aparenten ser saludables. Ante esta vorágine de caretas saludables, da la impresión de que todo está permitido y que no hay ninguna autoridad al mando que lo regule.
-
Las declaraciones saludables se regulan
En los años 90 se pusieron de moda los anuncios de patés ricos en hierro y zumos ultravitaminados que nos harían crecer fuertes y sanos. El reglamento que prevalecía en aquel momento permitía alegar casi cualquier cosa con tal de que una porción de alimento (100 g o 100 ml) contuviese al menos el 15% de la cantidad diaria recomendada de vitaminas o minerales.
Para poner un poco de orden, en 2006 se publicó un nuevo reglamento en el que se decía que para incluir una alegación saludable en un alimento, primero había que probar que alguno de sus ingredientes ayudaba de alguna manera a mantener nuestra salud. Eso propició una avalancha de peticiones que la Autoridad Europea de Seguridad Alimentaria (EFSA) se encargaba de revisar para dar el visto o bueno o no. Esto sigue funcionando así. Cada vez que se descubre alguna propiedad saludable de un ingrediente, se envían los informes pertinentes a la EFSA y desde aquí revisan la evidencia científica aportada para aceptar o rechazar una nueva declaración saludable.
Como consecuencia de todo esto, las declaraciones saludables relativas a cada ingrediente se recogen periódicamente en el Diario Oficial de la EFSA y se detallan en los anexos de los reglamentos específicos que se han ido publicando a continuación (como en éste de 2012).
Si todo esto está regulado, ¿cómo es posible que un alimento atiborrado de azúcares y harinas refinadas pueda mostrar alguna declaración saludable?
-
Las declaraciones saludables se regulan, pero se regulan mal
Por ejemplo, para poder declarar que un alimento «contribuye a la formación normal de colágeno para el funcionamiento normal de la piel» tiene que poder ser considerado «fuente de vitamina C» según el reglamento de 2006. A su vez, este reglamento hace referencia al reglamento de 1990, en el que se recoge el dichoso mínimo del 15% de la cantidad diaria recomendada (CDR).
La cantidad diaria recomendada de vitamina C según el reglamento de 1990 era de 60 mg. En el Real Decreto 1669/2009 fue modificada estableciéndose una cantidad diaria recomendada de vitamina C de 80 mg. Por tanto, si un alimento contiene 12 mg de vitamina C (el 15% de 80 mg), ya sea añadida o formando parte de alguno de sus componentes, está permitido que muestre cualquier declaración referida a las bondades de la vitamina C, incluida la formación normal de colágeno.
Lo mismo ocurre con una larga lista de declaraciones saludables autorizadas para vitaminas, minerales y otros nutrientes cuyas propiedades individuales han sido avaladas por la EFSA.
Así que lejos de la intención inicial de poner orden en la publicidad de los alimentos, el reglamento sirve de coladero para incluir legalmente casi cualquier declaración saludable. Añadiendo una cantidad irrisoria de vitaminas o minerales a un alimento, se permite decir casi de todo. No estamos mucho mejor que en los años 90.

-
El reglamento se fundamenta en el maldito nutricionismo
Una de las consecuencias de todo esto es que es legal que un alimento sin interés nutricional, como puede ser la bollería industrial o un refresco cargado de azúcar, puede publicitarse de forma que parezca saludable. La razón es que el reglamento no tiene en consideración el alimento en su conjunto, sino sus ingredientes individuales. La única excepción son las bebidas alcohólicas de más de 1,2 % en volumen de alcohol. Estas no pueden contener declaraciones saludables en su etiqueta ni en su publicidad. Aun así, algunos medios de comunicación publicitan indirectamente las bondades del consumo de alcohol, a pesar de ser siempre falsas.
Un alimento no se debe considerar más o menos saludable atendiendo a sus ingredientes individuales. Hay que tener en cuenta el alimento en su conjunto. La matriz del alimento puede disminuir, potenciar o anular completamente las bondades de sus ingredientes. Ese es el principal motivo por el que el reglamento actual y, por tanto, la evaluación que hace la EFSA aprobando o rechazando declaraciones saludables es absurda.
Valorar un alimento en función de sus ingredientes individuales, y no como conjunto, se llama nutricionismo. El nutricionismo es un error. Entre otras cosas alienta el consumo exagerado e innecesario de suplementos alimenticios y la elección de alimentos insanos creyendo que son beneficiosos solo porque contengan tal o cual ingrediente.
Otra consecuencia no menos importante es que en el reglamento no se contempla la posibilidad de declarar las virtudes de un alimento en su conjunto, o de declarar las virtudes de la suma de una serie de ingredientes que interactúan entre sí. Por esa razón, aunque un alimento estuviese perfectamente formulado y demostrase su eficacia, solo podría mostrar la declaración de salud que el reglamento le permita. Por ese motivo algunos suplementos alimenticios contienen ingredientes con virtudes previamente aprobadas por la EFSA, a pesar de que las bondades del suplemento sean propiciadas por otros. O lo que es lo mismo, un suplemento alimenticio mediocre puede alegar las mismas bondades que uno bien formulado si contiene la misma cantidad de ingrediente avalado por la EFSA.
Para publicitar la efectividad de un suplemento alimenticio, da igual si haces ciencia o no, el reglamento te permite decir lo que quieras si incluyes el dichoso 15% de la cantidad diaria recomendada de alguna vitamina o mineral.
El maldito nutricionismo nos ha llevado a repetir durante años mentiras como que los frutos secos son insanos o engordan, atendiendo exclusivamente a la cantidad de grasas que contienen. Los estudios confirman que no podemos juzgar a un alimento por sus ingredientes individuales, sino en su conjunto. Siguiendo con el ejemplo, a pesar de las calorías de los frutos secos y su elevado aporte de grasas, la evidencia científica nos dice lo contrario, que el consumo de frutos secos es saludable y que se relaciona con menores tasas de obesidad.
Lo mismo ocurre con algunos productos lácteos que contienen grasas saturadas y que por ello creíamos que afectaban al aumento del colesterol. La evidencia científica nos dice lo contrario, que algunos ayudan a prevenir enfermedades cardiovasculares.
-
Conclusiones
El reglamento de 2006 (incluidas sus modificaciones posteriores) pretendía poner orden en las declaraciones saludables que se publicitan en los alimentos, sin embargo, ha incurrido en el grave error del nutricionismo. Esa es la razón por la que alimentos insanos y de bajo interés nutricional pueden disfrazarse de alimentos saludables. La legislación les ampara.
Esa también es la razón por la que se permite anunciar las bondades de los suplementos alimenticios o de los alimentos funcionales, porque no tienen que probar su eficacia, sino contener una cantidad irrisoria de tal o cual ingrediente previamente avalado por la EFSA. De nada sirve formular un buen suplemento, porque las autoridades no contemplan las virtudes del alimento completo, sino de sus ingredientes individuales. Aunque los resultados de unos y otros deberían condicionar las ventas a largo plazo, la realidad es que buenos y malos pueden lanzarse legalmente al mercado publicitando lo mismo. Los que invierten en I+D para desarrollar sus productos y los que no, pueden alegar las mismas bondades. El coste de la declaración saludable es tan pequeño como unos cuantos gramos de vitaminas añadidas.
La consecuencia de todo esto es que, si no replanteamos el reglamento, su aplicación y la forma en la que la EFSA avala las declaraciones saludables, será posible publicitar cualquier virtud del alimento, sea cierta o no. Hoy en día es legal vender refrescos azucarados y bollería industrial como si fuesen saludables. O esto cambia, o al final acabaremos por creer que cualquier alegación saludable es una farsa legitimada por las autoridades.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Las absurdas declaraciones saludables de algunos alimentos están amparadas por las autoridades se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El azúcar oculto en los alimentos
- Dani y Fiti sobre los alimentos
- #Naukas14 Algunos curiosos experimentos
Una explicación a la existencia de películas de carbono tipo diamante (DLC)
Las películas muy densas de carbono amorfo pueden presentar unas propiedades, como una dureza excepcional, la ausencia de reactividad química o ser ópticamente transparentes que habitualmente se asocian al carbono pero con una estructura cristalina muy concreta, esa que llamamos diamante. Pensemos esto un segundo, ¿películas de diamante? Pues sí, aunque parezca sacado de una película de ciencia ficción de serie B de los sesenta. Precisamente explicar cómo es posible que algo tan extraordinario ocurra es lo que ha conseguido un equipo de investigadores encabezado por el español Miguel A. Caro, que trabaja en la Universidad de Aalto (Finlandia).

Diamante, grafito y sus estructuras.
La alotropía es la capacidad que tienen algunos elementos de poseer estructuras atómicas o moleculares diferentes. Cada una de estas formas se llama alótropo. El carbono es capaz de formar muchos alótropos diferentes debido a su capacidad de formar distintos tipos de enlaces químicos. Las formas más conocidas de carbono incluyen el diamante y el grafito (la mina de los lápices). En las últimas décadas se han descubierto e investigado muchos más alótropos y formas de carbono, incluidas formas esféricas como el buckminsterfullereno, láminas como el grafeno o las nanocintas y tubulares como los nanotubos. Se estima que existen del orden de 500 alótropos del carbono.

Lámina de carbono tipo diamante (DLC) sobre silicio
El carbono amorfo es el alótropo del carbono que no tiene una estructura cristalina. Como con todos los materiales vítreos (los llamados vidrios), puede presentarse algún orden de corto alcance, pero no hay patrones de largo alcance de las posiciones atómicas. Una variedad de carbono amorfo es el llamado carbono tipo diamante, más comúnmente conocido en la industria por sus siglas en inglés, DLC (diamond-like carbon)
Los químicos e ingenieros han aprendido mediante ensayo y error a crear películas de DLC a base de depositar átomos de carbono en un sustrato de carbono. El uso del ensayo y error se debe precisamente a que no se entiende teóricamente cómo se forman estas películas. Ahora, combinando un algoritmo de aprendizaje automático con simulaciones de dinámica molecular, Caro y sus colegas han demostrado que las películas de DLC se forman a través de un mecanismo de “granallado”.
Si en el granallado de un taller de chapa y pintura, se trata la carrocería de un automóvil con un “chorro de granalla” (o “de arena”) para dejar la superficie completamente limpia y lista para recibir la imprimación previa a la pintura, en el caso del DLC el impacto de un átomo de carbono sobre la superficie induce ondas de presión que cambian localmente la densidad de la película y, a su vez, la hibridación orbital, es decir, el tipo de enlaces químicos que pueden formar los átomos en la película.
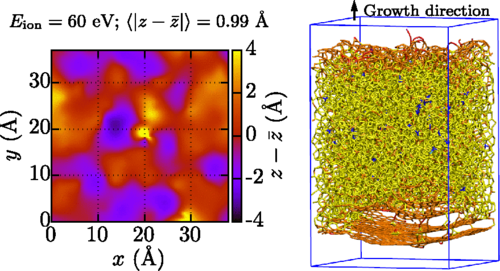
Rugosidad de la superficie (izquierda) y estructura atómoca de la película de DLC (derecha)
El equipo simuló la deposición secuencial de átomos de carbono individuales en un sustrato de carbono. Utilizando un algoritmo de aprendizaje automático desarrollado previamente calcularon los potenciales interatómicos entre los átomos e introdujeron esa información en las simulaciones de dinámica molecular. Este procedimiento les permitió mapear la densidad de las películas después de cada impacto. Descubrieron que los átomos entrantes creaban una onda de presión que alejaba los átomos del sitio de impacto, de modo que cada impacto disminuía la densidad de los átomos en la superficie de la película y la aumentaba en el interior de la película. En el interior de la película, el cambio de densidad causó que una alta fracción de átomos de carbono adquiriese una hibridación tetraédrica: exactamente el mismo estado que tienen los átomos de carbono en el diamante. Los perfiles de densidad simulados concuerdan con los que se derivan experimentalmente.
La películas de DLC ya se emplean industrialmente como recubrimientos de piezas expuestas a alto rozamiento. Lo que estos resultados pueden hacer es ayudar a los químicos a optimizar el crecimiento de películas DLC, lo que puede ser extremadamente interesante para la construcción de dispositivos electrónicos implantables en el cuerpo humano. Y es que el DLC, al ser químicamente inerte, es biocompatible.
Referencia:
Mguel A. Caro et al (2018) Growth Mechanism and Origin of High sp3 Content in Tetrahedral Amorphous Carbon Physical Review Letters doi: 10.1103/PhysRevLett.120.166101
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Una explicación a la existencia de películas de carbono tipo diamante (DLC) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un diamante ultraduro a partir de cebollas de carbono
- Nanotubos de carbono y regeneración neuronal
- Combustibles solares por un tubo
Crímenes áureos
Me gusta leer. Me gusta todo tipo de literatura, pero, en especial, leo muchas novelas. De todos los estilos. En estos momentos estoy terminando de leer la magnífica, aunque dura, novela Manual para mujeres de la limpieza (Alfaguara, 2016) de Lucia Berlin, antes de este libro he leído la excelente novela gráfica de Paco Roca, Las calles de arena (Astiberri, 2015) y Las normas de la casa (Temas de Hoy, 2012), de Jodi Picoult, y mis dos siguientes lecturas, salvo que se cruce alguna otra en el camino, serán Solenoide (Impedimenta, 2017), de Mircea Catarescu, cuyas primeras páginas te enganchan y es difícil dejar de leer (aunque antes tenía que terminar el magnífico libro de Lucia Berlin), y La torre de Babel (Alfaguara, 2011), de A. S. Byatt, un interesante descubrimiento que hice mientras preparaba una conferencia sobre la sucesión de Fibonacci.

Portada del libro “Manual para mujeres de la limpieza” (Alfaguara, 2016), de Lucia Berlin
Pero, en especial, me gusta la novela policiaca. Desde las clásicas novelas de raciocinio, como los relatos de Edgar Allan Poe, las historias de Sherlock Holmes, de Arthur Conan Doyle, o las sencillas novelas de Agatha Christie, hasta la novela negra actual, que es mucho más realista y social. Y si estas novelas tienen alguna referencia matemática, entonces mi interés y disfrute es mucho mayor aún.
En esta entrada del Cuaderno de Cultura Científica vamos a ver un pequeño ejemplo de presencia de las matemáticas en una novela negra. No es un caso aislado, existen muchos ejemplos, como la novela La chica que soñaba con una cerilla y un bidón de gasolina, del escritor sueco Stieg Larsson (Destino, 2008), de la que ya hablamos en la entrada La chica que soñaba con una cerilla y un bidón de gasolina. En esta ocasión, se trata de la novela La mano del diablo (Plaza & Janés, 2005), de los escritores Douglas Preston y Lincoln Child.

Portada de la novela “La mano del diablo” de Douglas Preston y Lincoln Child, publicada por Plaza & Janés en 2005, un año después de su publicación en inglés
Los escritores estadounidenses Douglas Preston y Lincoln Child suelen escribir juntos, a cuatro manos, novelas policiacas, de misterio y de aventuras. Son dos escritores de éxito, aunque tengo que confesar que no están entre mis escritores preferidos. Su primer éxito fue El ídolo perdido (1995), novela en la cual se inspiró la película The Relic (Peter Hyams, 1997). Esta novela, como muchas de las que han escrito juntos, está protagonizada por el agente del FBI, Aloysius Pendergast, acompañado del teniente de la policía, Vicent D’Agosta.
La novela La mano del diablo es la primera novela de la trilogía de Diogenes, el hermano de Aloysius. En esta historia, el agente del FBI Aloysius Pendergast y el teniente de la policía Vicent D’Agosta investigan una serie de asesinatos que parecen implicar al propio Lucifer.
En la novela aparece un periodista del Post, Bryce Harriman, que investiga también estas misteriosas muertes. El periodista decide entrevistar, para recabar información sobre esta serie de asesinatos relacionados con el diablo, al profesor Friedrich Von Menck, doctor en filosofía por la Universidad de Heidelberg (Alemania), en medicina por la Universidad de Harvard (EE.UU.) y en teología por la Universidad de Canterbury (Nueva Zelanda), pero que siempre se había interesado por el misticismo, lo paranormal y lo inexplicable, lo cual le hace un candidato ideal, según el periodista, para hablar de los “asesinatos del diablo”. Una mezcla de científico y apasionado de los temas esotéricos.
Leamos la parte de la novela en la que el periodista Harriman está en casa de Von Menck preguntándole por los “asesinatos del diablo”.
“—Lo de menos son las personas y la manera. Lo decisivo es el momento.
Von Menck se levantó para abrir una de las vitrinas y sacar algo, Lo trajo y lo dejó sobre la mesa, delante de Harriman. Era una sección de concha de nautilo, con sus celdas de crecimiento formando una espiral de hermosa regularidad.
—Señor Harriman, ¿sabe qué hay en común entre esta cocha, el Partenón, los pétalos de una flor y las pinturas de Leonardo da Vinci?
Harriman negó con la cabeza.
—Que encarna la proporción más perfecta de la naturaleza, la proporción áurea.
—No sé si le entiendo.
—Es la proporción que se obtiene al dividir una línea de modo que el segmento más corto sea al segmento más largo, lo mismo que el segmento más largo a la línea entera.
Harriman lo anotó con la esperanza de entenderlo más tarde.
—El segmento más largo es 1,618054 veces más largo que el segmento más corto. El segmento más corto representa el 0,618054 por ciento del más largo. Son dos números exactamente recíprocos, que solo se diferencian en el primer dígito. Se trata de los dos únicos números que presentan esta propiedad.
—Ah, claro.
Las matemáticas nunca habían sido su fuerte.
—Y tienen otras propiedades muy notables. Se considera que un rectángulo construido con lados de estas longitudes es la forma más agradable a la vista. Recibe el nombre de rectángulo áureo. La planta del Partenón se construyó según esta figura. Y en ella se basan catedrales y pinturas. Estos rectángulos tienen otra propiedad destacable: si se recorta un cuadrado en cada lado se obtiene un rectángulo áureo de menor tamaño, pero con las mismas proporciones. Se pueden recortar cuadrados y obtener rectángulos dorados más pequeños hasta el infinito.
—Comprendo.
—Bueno, pues si parte de un rectángulo grande y lo reduce a una serie infinita de rectángulos áureos más pequeños, y si después conecta todos los centros de los rectángulos, obtendrá una espiral logarítmica natural perfecta. Es la espiral que está viendo en la cocha del nautilo, la misma que forman las semillas en la cabeza del girasol, y de la armonía musical. La proporción áurea es una característica básica del mundo natural.
—Ajá.
—Es una proporción que forma parte de la estructura del universo.”
Paremos un momento en este punto, en el cual el periodista Harriman piensa que ha perdido el tiempo al ir a entrevistar al profesor Von Menck. No entiende nada y no cree que las personas que van a leer el Post entiendan tampoco nada. Paremos un momento para recordar algunos de los conceptos matemáticos que aparecen citados.
Para empezar, recordemos que es el número áureo, que ya hemos introducido en el Cuaderno de Cultura Científica, por ejemplo, en la entrada Visitad los museos, también en clave matemática y en la entrada ¿Es áureo el Aston Martin de James Bond?. La proporción áurea es un concepto matemático muy antiguo, que ya fue estudiado por los griegos, en particular, por los pitagóricos. La definición de esta proporción aparece recogida en el gran texto matemático, Los Elementos de Euclides (aprox. 325-265 a.c.). Y dice así:
“Se dice que un segmento está dividido en media y extrema razón cuando la longitud del segmento total es a la parte mayor, como la de esta parte mayor es a la menor”.
Es decir, si tenemos un segmento como el que aparece en la siguiente imagen, buscamos el punto del mismo que divide al segmento en dos partes, de longitudes a y b, de forma que la proporción o razón (división) entre la parte mayor y la menor, a/b es igual a la proporción entre la longitud del segmento y la parte mayor (a + b)/a.
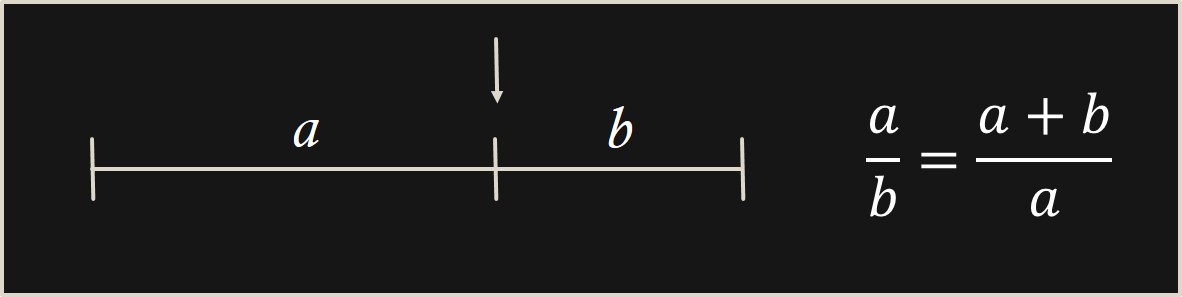
Ahora, si llamamos Φ al cociente a/b, la condición anterior se puede escribir como la ecuación algebraica siguiente:

Esta es una ecuación algebraica de segundo grado, cuyas soluciones, sin más que utilizar la conocida fórmula de resolución de la ecuación de segundo grado que estudiamos en el instituto, son:

Si tenemos en cuenta que la inversa de Φ, es decir, Φ-1, es b/a, entonces la propia expresión de la definición nos dice que
Φ = 1 + Φ-1,
es decir, que ambas soluciones se diferencian en 1, como se comenta en la novela. Aunque el número que aparece citado en la misma, “1,618054”, no es exactamente el número áureo, que más bien, por aproximación sería “1,618034”, ahí se ha colado un 5, en lugar de un 3.
Un pequeño error. Cuando se dice que “El segmento más corto representa el 0,618054 por ciento del más largo”, lo correcto sería que “El segmento más corto representa el 0,618054 del más largo”, sin la expresión “por ciento”.
Sigamos. Un rectángulo áureo es un rectángulo de dimensiones a (alto) y b (ancho), tal que la proporción entre ambas, a/b, es el número áureo, Φ = 1,618033…, como aparece en la siguiente imagen y no como está escrito en la novela, es decir, que los lados del rectángulo sean “1,618034” (Φ) y “0,618034” (Φ-1),… “Se considera que un rectángulo construido con lados de estas longitudes es la forma más agradable a la vista. Recibe el nombre de rectángulo áureo”. En cuanto a que sea el rectángulo más bello que existe, esa es una creencia basada en la supuesta demostración estadística del sicólogo alemán Gustav Fechner (1801-1887).

Una interesante reflexión sobre las supuestas relaciones del rectángulo áureo con la belleza, el Partenón, el arte de Leonardo da Vinci y algunas otras cuestiones, la encontramos en el artículo Misconceptions about the Golden Ratio (Ideas erróneas sobre la proporción áurea), del matemático, de la Universidad de Harvard, George Markowsky.
Una propiedad interesante de los rectángulos áureos es que se pueden construir fácilmente a partir de un cuadrado, como se muestra en la siguiente imagen. Se parte de un cuadrado ABDE (en la imagen se ha considerado de lado 1) y se traza un arco de circunferencia, con centro el medio M del lado del cuadrado AB y de radio igual al segmento ME, determinando así el punto C (la intersección de la recta que pasa por A y B, con el arco de circunferencia), de forma que el rectángulo generado ACDF resulta ser un rectángulo áureo.
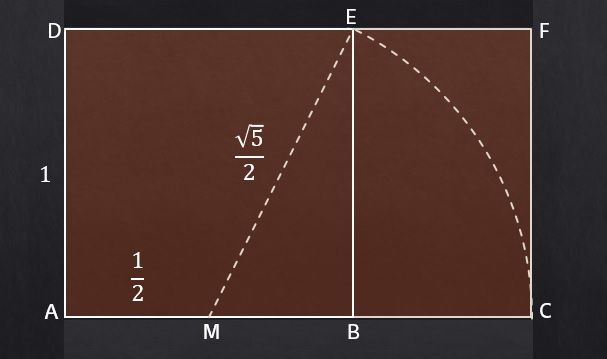
Esta es una forma sencilla de construir rectángulos áureos, que puede ser desarrollada por personas dedicadas, por ejemplo, al arte o la jardinería.
Pero esta propiedad pone de manifiesto, como se expresa en la cita anterior (aunque de una forma un poco confusa), que un rectángulo áureo puede descomponerse en un cuadrado y un rectángulo más pequeño, con la sorprendente propiedad de que resulta ser también un rectángulo áureo. Ahora, con este rectángulo áureo más pequeño podríamos, a su vez, descomponerlo en un cuadrado y un rectángulo áureo, así hasta el infinito.
Si se considera un trozo de circunferencia en cada uno de los cuadrados de la descomposición, como aparece en la siguiente imagen, se construye lo que se conoce como “espiral áurea”.
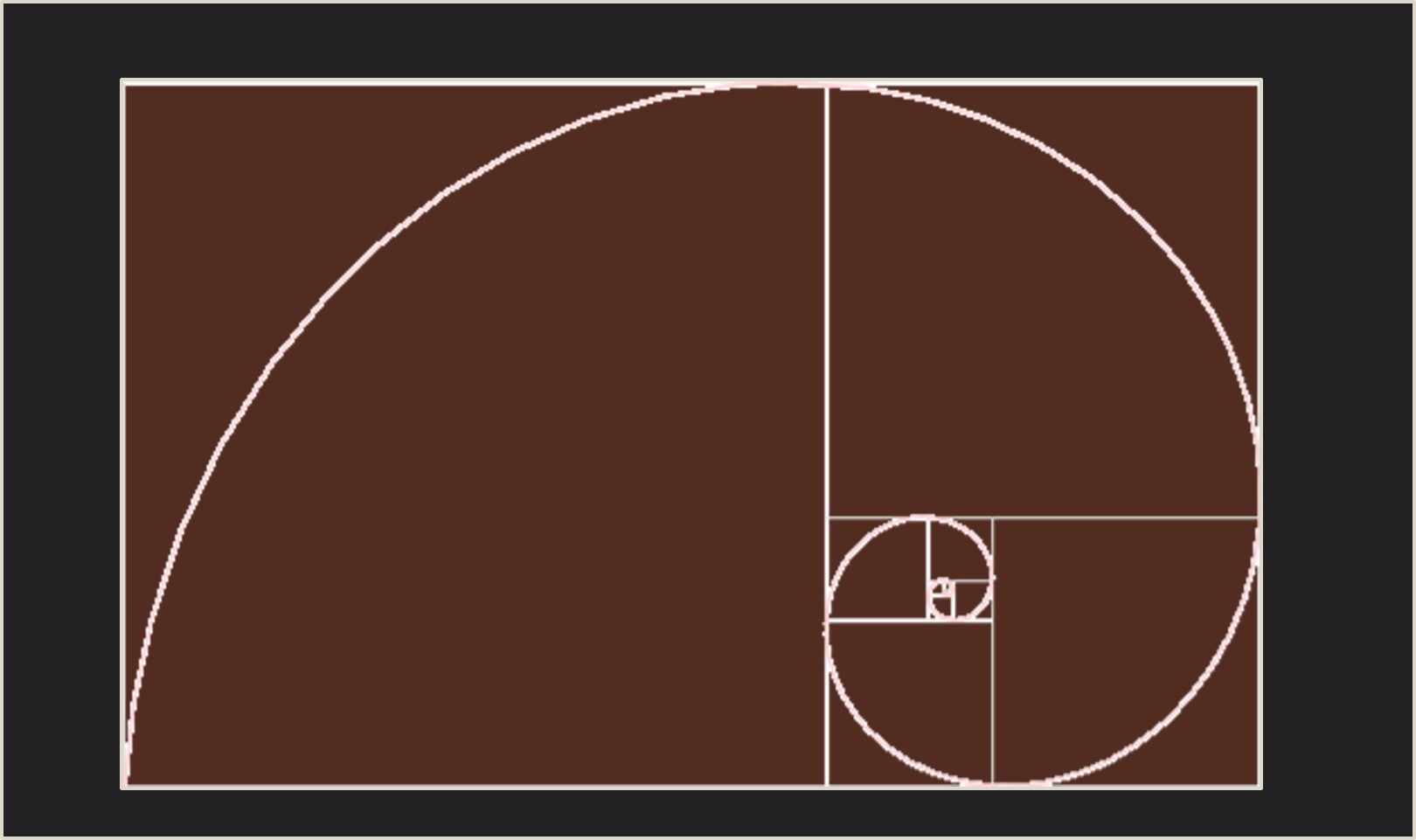
A pesar de lo que se suele leer en muchos sitios, ni esta espiral, ni la construida con segmentos rectos, al unir los centros de los cuadrados, según la novela, son la espiral logarítmica o espiral del crecimiento que aparece en el nautilus.
La espiral logarítmica, que aparece en la siguiente imagen, se define como aquella espiral cuyo radio aumenta de forma exponencial según va creciendo el ángulo de giro (θ en la imagen), es decir, matemáticamente la longitud del radio es igual a r(θ) = a ebθ.
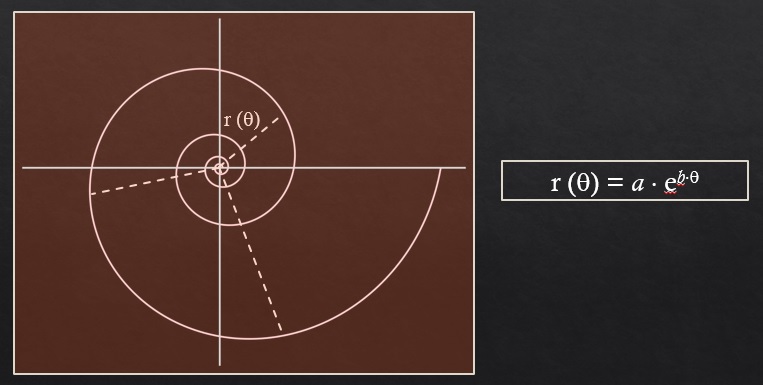
Y esta espiral sí modeliza la sección de la concha del nautilus.

Disculpad que me haya entretenido un poco con estos conceptos iniciales y algunas cuestiones relacionadas. Volvamos a la novela La mano del diablo, de la pareja de escritores Preston y Child. La persona que este leyendo la novela se preguntará en el punto en el que habíamos dejado la cita, al igual que el periodista del Post, … ¿todo esto para qué? ¿qué tiene que ver con los “asesinatos del diablo”? Para dar respuesta a esta cuestión volvamos a la novela, puesto que toda la cita anterior es una introducción a lo que es el asunto principal, que explica el profesor Von Meck a continuación.
“—Se lo voy a explicar. He dedicado toda mi vida a estudiar lo misterioso y lo inexplicable. En muchos casos, la solución del misterio me ha satisfecho del todo. Otros misterios, casi siempre los de mayor importancia, se me siguen resistiendo.
Von Menck cogió un papel de la mesa, hizo unas anotaciones y se lo puso delante de Harriman: 3243, 1239. Dio un golpecito en la hoja.
—Para mí, estos números siempre han representado el mayor de los misterios. ¿Los reconoce?
Harriman negó con la cabeza.
—Identifican los dos mayores cataclismos que ha sufrido la civilización humana. En 3243 a.C., la explosión de la isla Santorini produjo un maremoto que barrió la gran civilización minoica de Creta y devastó todo el Mediterráneo. Es la fuente tanto de la leyenda de la Atlántida como de la del Diluvio Universal. En 1239 a.C., las ciudades gemelas de Sodoma y Gomorra fueron reducidas a cenizas por una lluvia de fuego.
—¿La Atlántida? ¿Sodoma y Gomorra?
La cosa empeoraba.”
Tras una larga explicación sobre la Atlántida y Sodoma y Gomorra, el profesor Von Menck continúa con su teoría, para lo cual es necesario saber que la novela transcurre en el año 2004, luego ese es el año de los “asesinatos del diablo”.
“Von Menck cogió la hoja de papel y escribió otro número debajo de los dos primeros: 3243, 1239, 2004
—2004 d.C., señor Harriman. Constituye el término de la proporción áurea. Han pasado exactamente 5246 años desde 3243 a.C.: la proporción áurea. La siguiente fecha de la serie es 2004 d.C. Resulta que también es el número exacto de años que separan los desastres anteriores. ¿Una coincidencia?
Harriman se quedó mirando el papel. “¿Está diciendo lo que creo?”, pensó. Parecía increíble, una locura.”
Lo que está diciendo Von Menck, entre otras cosas, es que si se toma el segmento de tiempo que va desde el año 3243 a.C. hasta el año 2004 d.C., el punto que está en “media y extrema razón”, es decir, el que produce la proporción áurea, es el año 1239 a.C., como se muestra en la siguiente imagen.

Continuemos leyendo.
“Se acercó a otra vitrina y sacó una cartulina blanca que tenía dibujada una espiral de grandes dimensiones, como la concha de un nautilo. En la parte inferior había una anotación en lápiz rojo: “3243 a.C. – Santorini/Atlántida”. A dos tercios de la curva, otra anotación en rojo: “1239 a.C. – Sodoma/Gomorra”. En otros puntos de la espiral, una serie de marcas en negro componían una lista de decenas de fechas y lugares:
79 d.C. – La erupción del Vesuvio destruye Pompeya/Herculano.
426 d.C. – Caída de Roma, saqueada y destruida por los bárbaros.
1321 d.C. – La peste azota Venecia. Mueren dos tercios de la población.
1665 d.C. – Gran incendio de Londres.
Y justo en el centro, donde la espiral se cerraba sobre si misma y terminaba en un gran punto negro, había otra anotación en rojo, la tercera: 2004 d.C. ¿…?
Von Menck dejó la cartulina en equilibrio sobre la mesa.
Como ve, he levantado acta de muchos desastres y todos coinciden con puntos exactos de la espiral logarítmica natural. Todos están perfectamente alineados en proporciones áureas.”
Lo importante del anterior comentario es que las fechas de los desastres “están perfectamente alineados en proporciones áureas” y la continua mención a la “espiral logarítmica natural” es más bien metafórica, salvo por la idea de que esas fechas de desastres van aproximándose a la fecha límite, la fecha final, el año 2004, que es cuando se desarrolla la historia de la novela.
Mientras que las tres primeras fechas mencionadas por el profesor 3243 a.C., 1239 a.C. y 2004 d.C. efectivamente están situadas en proporción áurea, en el sentido explicado arriba, no sucede lo mismo cuando se consideran las nuevas fechas de desastres presentadas por Von Menck. Contrariamente a lo expresado por el profesor, las cuentas no salen, no están en proporción áurea.
Los autores de la novela, Preston y Child, son conscientes de ello, solamente quieren darle un aire de misterio satánico a los acontecimientos que se desarrollan en la novela, a los “asesinatos del diablo”. Y que los autores son conscientes de que las cuentas no salen para las demás fechas lo sabemos leyendo los agradecimientos, en los que han escrito:
“Para acabar, queremos pedir disculpas […] de la aplicación incorrecta de la proporción áurea del profesor Von Menck.”
La razón áurea, divina proporción o número de oro aparece en muchas novelas policiacas y de misterio, como la famosa El código Da Vinci (Umbriel, 2004), de Dan Brown.

“Canto de espigas” (1929), de Maruja Mallo. Toda la estructura de esta obra está realizada mediante la razón áurea
Bibliografía
1.- Douglas Preston, Lincold Child, La mano del diablo, Plaza & Janés, 2005.
2.- Mario Livio, La proporción áurea, La historia de phi, el número más sorprendente del mundo, Ariel, 2006.
3.- George Markowsky, Misconceptions about the Golden Ratio, The College Mathematical Journal 23, n. 1, 1992.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Crímenes áureos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El diablo y Simon Flagg, una lectura ligera para el verano
- Las vacas de Narayana, la versión hindú de los conejos de Fibonacci
- ¿Es normal el número pi?
Animales eurihalinos

Tiburón toro (“Carcharius taurus”). Foto: Jeff Kubina / Wikimedia Commons
La mayor parte de los animales acuáticos son estenohalinos, no toleran cambios en la concentración de sales del medio externo y están, por lo tanto, obligados a vivir en un medio osmóticamente estable, ya sea el mar o las aguas dulces. En ese grupo se encuentran tanto animales osmoconcordantes (u osmoconformadores) como osmorreguladores. De los primeros ya nos ocupamos aquí; baste recordar que se encuentran en equilibrio hídrico y osmótico con el medio externo; son, de hecho, isosmóticos con el agua de mar. Pero han de realizar una cierta regulación iónica, porque las concentraciones de solutos inorgánicos no son las mismas dentro y fuera del organismo. Y de los segundos hemos tratado aquí (de agua dulce) y aquí (de agua de mar).
Pero aunque son una minoría, también hay animales acuáticos eurihalinos. Algunos son peces elasmobranquios, como el tiburón toro y otros de su mismo grupo, de los que nos ocupamos aquí. Pero también hay invertebrados y teleósteos eurihalinos. Y los mecanismos que ponen en juego para poder hacer frente a los cambios ambientales de salinidad o para poder vivir en medios de concentración muy diferente (aunque en la práctica esa concentración no varíe) son muy distintos dependiendo, principalmente, de si son osmoconcordantes (poiquilosmóticos) u osmorreguladores (homeosmóticos).
Aunque la mayor parte de los invertebrados marinos osmoconcordantes son estenohalinos, hay unas pocas especies que toleran cambios en la salinidad ambiental. Los mejor estudiados son, quizás, los bivalvos. Numerosos miembros de este grupo viven en zonas costeras sometidas a la influencia de los ríos (bahías, ensenadas, lagunas costeras) o penetran, incluso, en los estuarios. Muchas especies de mejillones, berberechos, almejas u ostras, se encuentran en ese grupo. Estos animales permiten que su medio interno se diluya cuando lo hace el externo, y por ello, también el medio intracelular se diluye en la misma medida. Pero esa dilución no es pasiva; no es consecuencia de una invasión de agua de sus células, ya que si ello ocurriera podrían llegar a estallar o, cuando menos, a ver alterados gravemente todos los procesos que dependen de la estructura de la membrana celular. Además, también la concentración intracelular de potasio se reduciría, con los consiguientes daños al funcionamiento de las proteínas celulares, cuya integridad funcional depende precisamente de la concentración del principal catión intracelular. La dilución del medio intracelular se produce mediante una reducción activa de la concentración de solutos orgánicos como aminoácidos, taurina y otros, los denominados efectores osmóticos, sustancias gracias a las cuales las células de los invertebrados marinos pueden mantenerse isosmóticas con el medio interno, sin que el K+ tenga por qué alcanzar concentraciones intracelulares inconvenientes.
Y luego tenemos animales eurihalinos que regulan activamente la concentración osmótica de su medio interno, aunque lo suelen hacer en rangos limitados de salinidad. Estos suelen asignarse, a su vez, a dos grandes categorías, los reguladores hiper-isosmóticos y los reguladores hiper-hiposmóticos.
Los del primer grupo mantienen su concentración interna por encima de la ambiental, aunque la diferencia se reduce conforme aumenta la concentración osmótica exterior. A este grupo pertenecen especies predominantemente dulceacuícolas que tienen la capacidad para adentrarse en aguas salobres, como algunos peces de la familia Cyprinidae, y otras propias de zonas costeras y estuarinas, como algunos anfípodos y crustáceos. La adaptación a aguas de diferente concentración, pero siempre igual o inferior a la interna, se basa en la capacidad para modificar la intensidad con que funcionan los mecanismos propios de la regulación hiperosmótica (grado de dilución y tasa de producción de orina, así como tasas de recuperación de solutos a través de las branquias).
Los reguladores hiper-hiposmóticos son animales que mantienen su concentración interna constante en condiciones tanto hiper como hiposmóticas. En otras palabras, a bajas concentraciones ambientales, su concentración interna se encuentra por encima de la externa, y lo contrario ocurre a altas concentraciones ambientales. Esta forma de regulación es característica de ciertos crustáceos que habitan zonas intermareales, como algunos cangrejos violinistas y especies próximas.
Por último tenemos a los peces diádromos, pero de esos nos ocuparemos en una próxima anotación, porque es dudoso que deban ser considerados eurihalinos.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Animales eurihalinos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Animales en equilibrio osmótico: invertebrados marinos y peces bruja
- La regulación osmótica de los animales de agua dulce
- Relaciones hídricas y salinas de los animales
Clasificación y origen, los dos problemas de la mineralogía

Fluorita. Fluoruro cálcico, CaF2; sistema cúbico; color violeta; raya blanca; dureza de Mohs 4; peso específico 3,1; brillo vítreo; opaco; fractura lisa a concoidea; exfoliación perfecta; en macla; fluorescente.
A pesar de los cambios en estatus como disciplina desde el siglo XVIII hasta la actualidad la mineralogía se ha concentrado en dos problemas principales: la clasificación y el origen de los minerales.
El primero, la clasificación, aunque pueda parecer un tecnicismo, es fundamental tanto para la teoría geológica como para los aspectos más prácticos y económicamente relevantes de la ingeniería de minas: encontrar vetas rentables.
Por su importancia se han dedicado a lo largo de los siglos importantes esfuerzos a desarrollar clasificaciones coherentes, relevantes y útiles, lo que ha probado ser de todo menos fácil. Digámoslo claramente, las clasificaciones minerales han sido tan numerosas como arbitrarias.
Clasificar algo depende de la capacidad de hacer distinciones claras a distintos niveles de organización. En el caso de los animales y plantas distinguir entre especies no es tan difícil y siempre existe un criterio último que dirime la cuestión de si un especimen es de la especie A o B: la capacidad de reproducirse con A o B.
En el siglo XVIII Carl Nilsson Linnæus (castellanizado, Linneo) se atrevió osadamente a aplicar los principios de clasificación que con tanto éxito había aplicado a animales y plantas a los minerales. Todo ese esfuerzo para fracasar estrepitosamente: aparecían tantas categorías casi como minerales conocidos, tantas excepciones había.

Isomorfismo. tanto la halita (NaCl) a la izquierda y la galena (PbS) a la derecha cristalizan en el sistema cúbico, sin embargo, a pesar de compartir sistema cristalino sus composciones difieren completamente.
Tras ese escarmiento los mineralogistas han oscilado principalmente entre el uso de la composición química y la forma cristalográfica. Para complicar la cosa hay que decir que estos dos tipos de clasificaciones no casan entre sí, ya que dos minerales con la misma composición pueden tener distinta forma cristalina y al revés, dos minerales con la misma forma cristalina pueden tener composiciones completamente dispares. Para añadir más dificultad, la composición química de un mineral no corresponde necesariamente a una fórmula exacta. De hecho, la mayoría de los minerales tienen un rango de variación en la composición.

Polimorfismo. Calcita (izquierda) y aragonito (derecha) tienen la misma composición, carbonato cálcico (CaCO3), sin embargo, la primera cristaliza en el sistema trigonal y el segundo en el ortorrómbico.
Esto ha llevado a ingenieros, geólogos y aficionados ha desarrollar suplementos a la clasificacón que se esté usando en forma de características macroscópicas para poder decidir más o menos rápidamente y con cierta seguridad ante que se está. Así en una guía moderna siguen apareciendo criteros de identificación como el color (aunque no sirva de mucho), la raya [1], la dureza de Mohs [2], el peso específico, el brillo [3], la brillantez (que no es lo mismo que el brillo), irisaciones (que tampoco hay que confundir con el brillo ni con la brillantez) [4], transparencia, fractura [5], exfoliación (si el mineral se rompe en hojas planas) y muchas más.

Sistema portátil para determinar la dureza en la escala de Mohs [2].
El segundo problema mineralógico clave es cómo se originaron los minerales y las rocas. Como aparecen mezclados unos con otros, desde el siglo XVII lo mineralogistas asumieron que se originaban a partir de fluidos y que se endurecían en las posiciones y localizaciones en las que se encontraban. El estado de de fluidez podía deberse al calor, al agua o a alguna combinación de ambos.Los mineralogistas han librado batallas recurrentes en lo que parece una guerra interminable sobre la importancia relativa de todos estos factores. En cualquier caso, siempre han mantenido la esperanza de que serían capaces de usar sus conocimientos de química para reconstruir una narración de la génesis histórica de las rocas: una geogonía basada en una invariable secuencia de reacciones químicas a partir de un estado inicial. Buena parte de esos relatos están más próximos a la leyenda que a la realidad, que se ha mostrado exasperantemente tozuda.
Notas:
[1] La raya es el color “propio” de mineral que aparece al rayar una porcelana sin vidriar
[2] La escala de Mohs es una relación de diez minerales ordenados por su dureza, de menor a mayor. Se utiliza como referencia de la dureza de un material dado. Es necesario, por tanto, poseer una caja con minerales de referencia para poder determinar el valor de dureza.
[3] El ojo entrenado distingue entre vítreo, sedoso, nacarado, adamantino, graso y metálico
[4] Hay expertos que a simple vista disciernen entre ojo de gato, adularescencia, irisación propiamente dicha, labradorescencia y opalescencia
[5] O cómo se rompe un mineral; la fractura puede ser concoidea, astillosa, fibrosa, desigual y terrosa
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Clasificación y origen, los dos problemas de la mineralogía se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Esa pesadilla científica llamada mineralogía
- ¿Y si la Gran Oxidación tuvo un origen geológico?
- Los amiloides y el origen de la vida
El nivel socioeconómico familiar influye en el desarrollo del encéfalo infantil

El entorno familiar influye de forma marcada en el desarrollo del encéfalo infantil. Los bebés tienen similares volúmenes de materia gris al nacer y en su más temprana infancia, pero al cabo de unos pocos meses de vida los que pertenecen a familias de bajo estatus socio-económico tienen menos que los de nivel medio o alto. Las diferencias no tienen relación con el peso al nacer, con la salud en las primeras semanas de vida o con diferencias en el tamaño de la cabeza en el momento del nacimiento. Y sabemos, por otro lado, que las diferencias en la cantidad de materia gris están relacionadas con problemas de comportamiento en los años anteriores a la escolarización.
Esas son las principales conclusiones de un estudio en el que se compararon los volúmenes de materia gris en varias áreas encefálicas de bebés y niños y niñas de edades preescolares procedentes de diferentes familias de los Estados Unidos. En el estudio se utilizaron imágenes obtenidas por resonancia magnética de encéfalos de bebés a los que se les siguió a lo largo de su desarrollo hasta los tres años edad, aproximadamente. Los análisis de imagen se hicieron con niños y niñas de los que se conocía su historial médico, no habían sido adoptados, no habían estado expuestos a sustancias nocivas durante el embarazo de la madre, el parto había sido normal, habían tenido un desarrollo normal y en la familia no había antecedentes psiquiátricos.
Las diferencias observadas se localizaron específicamente en las áreas frontal y parietal del cerebro, con menores volúmenes de estas áreas en los niños de familias de menores recursos. El lóbulo frontal está implicado en funciones ejecutivas, tales como planificación, control de impulsos y atención. El lóbulo parietal participa en la integración de señales sensoriales y aspectos relativos a la atención visual. Además, el desarrollo del lóbulo parietal parece ser importante para la conectividad entre diferentes áreas encefálicas.
No son los primeros resultados que ponen de manifiesto la relación entre las condiciones en que se desenvuelve el desarrollo temprano ligadas al nivel socioeconómico familiar y la posterior salud y capacidad de adaptación de los niños. Y al parecer, que el volumen de determinadas áreas dependa de las circunstancias ambientales experimentadas por los individuos tiene que ver con el establecimiento en ellas de diferente número de conexiones sinápticas, así como con diferencias en la producción de tejido de soporte (capilares sanguíneos y glía).
La variable de referencia utilizada para determinar el estatus socioeconómico fue el volumen de ingresos con relación al “nivel de pobreza federal”, que varió desde un 4% de dicho nivel hasta valores que lo cuadriplicaban. En los Estados Unidos, un 19% de las personas viven por debajo de esa línea. Los autores del trabajo descartan establecer relaciones causales concretas, porque el estatus socioeconómico lleva emparejado muchas otras condiciones ambientales, como el nivel cultural o educativo de los padres, el estilo de vida, la calidad de la alimentación, el ruido, la incidencia de enfermedades infecciosas, el ambiente familiar u otros. Y es muy posible que sea alguno de esos factores o determinada combinación de ellos lo que dé lugar a los efectos observados.
Conviene tener en cuenta que los criterios utilizados para seleccionar a los niños y niñas incluidos en los análisis conducen, de hecho, a atenuar las diferencias que cabría esperar encontrar, pues es sabido que los factores de exclusión (del estudio) están sobrerrepresentados en las personas de bajos recursos económicos. Por lo tanto, las conclusiones obtenidas en este trabajo deben considerarse conservadoras. Las diferencias reales son, con toda seguridad, de una magnitud muy superior.
Los resultados obtenidos en este y otros trabajos son importantes por lo que aportan al conocimiento de la naturaleza humana y, más concretamente, a la forma en que el desarrollo neurocognitivo se puede ver condicionado por factores ambientales. Pero a nadie se le escapa que pueden, también, tener implicaciones en términos de políticas públicas, principalmente con las iniciativas orientadas a mejorar el capital humano.
Fuente:
Jamie L. Hanson, Nicole Hair, Dinggang G. Shen, Feng Shi, John H. Gilmore, Barbara L. Wolfe, Seth D. Pollak (2013): Family Poverty Affects the Rate of Human Infant Brain Growth. PLoS ONE 8(12): e80954. doi:10.1371/journal.pone.0080954
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El nivel socioeconómico familiar influye en el desarrollo del encéfalo infantil se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El gran encéfalo humano es un “encéfalo social”
- La sensibilidad medioambiental se desarrolla a nivel inconsciente
- Juguetes y hormonas sexuales
Los 40 Radikales
Oficina de comunicación de la UPV/EHU

David Mota Zurdo (Barakaldo, 1985), doctor internacional en Historia Contemporánea por la IPV/EHU, ha publicado recientemente el libro ‘Los 40 Radikales. La música contestataria vasca y otras escenas musicales: origen, estabilización y dificultades (1980-2015)’. La obra analiza la evolución de la música contestataria vasca desde 1980 hasta la actualidad, centrándose fundamentalmente en los géneros del punk, hardcore y hip-hop.
Siguiendo las corrientes historiográficas que están en plena batalla por el relato, en ‘Los 40 Radikales’ se analiza, por un lado, la estrategia de instrumentalización de la música underground que llevó a cabo la izquierda nacionalista vasca para transmitir y expandir su ideario entre la juventud durante las décadas de 1980 y 1990; y, por otro, se estudian los cambios, las sinergias y las dificultades que desde entonces ha padecido ese tipo de música contestataria. Se trata, sin duda, de una interpretación novedosa sobre la música política de nuestro país, donde se recopilan diferentes trabajos inéditos y artículos ya publicados en revistas especializadas de difícil acceso, que han sido actualizados y ampliados.
El libro se divide en dos grandes partes. En la primera, se analiza el origen y evolución del movimiento musical underground vasco. En la segunda se presta atención a la situación de este género en la actualidad, atendiendo a sus problemas legales, y se cruza a fin de establecer comparativas entre la situación de la música underground durante la Transición y la actualidad, haciendo especial hincapié en las obstaculizaciones que sufrió este género contestatario. “He examinado las divergencias existentes entre los grupos, sus problemas, sus lugares de sociabilidad y su imagen durante las tres grandes etapas de nuestra historia reciente: la Transición, la consolidación de la democracia y la actualidad”, explica el autor.
Además, se dedica un amplio espacio para la historia de ese movimiento, atendiendo a su inspiración filosófico-política, sus dificultades de expansión, sus críticas y sus obstáculos. Para concluir con los problemas judiciales que han tenido algunos de los protagonistas. “Los últimos acontecimientos en torno al 15-M y la Ley Mordaza están produciendo un repunte de la politización de la música. Este contexto de ultraderechización de la sociedad y el constreñimiento de la libertad de expresión está provocando de manera generalizada un repunte de la música antisistema”, llega a comentar David Mota en su libro.
Para el periplo de presentaciones de su nueva obra, Mota ha contado con la colaboración de un importante elenco de historiadores y representantes de la cultura que, además, han vivido en primera persona muchos de los acontecimientos que en ella se relatan.
Para Santiago Burutxaga, promotor cultural y presidente de Cultura Abierta, no es frecuente que, para investigar una época, un historiador ponga la música en su punto de mira y que, además, se fije en las bandas que al comienzo de ese tiempo eran poco menos que subterráneas y malditas para el establishment cultural. “Lo interesante y singular del libro es que va más allá de hacer un recorrido por los temas y los grupos de lo que el autor llama la escena underground vasca: el punk, heavy metal y otras corrientes musicales que en los años 80 se englobaron bajo la etiqueta de Rock Radical Vasco. David Mota se detiene a estudiar los lazos que se tejieron entre los grupos políticos radicales y aquellos chavales de garaje, tugurio y barriada que escupían sus frustraciones y mala leche en sus canciones y que estaban, quizás sin saberlo, abriendo nuevos caminos a la música vasca de la época. En definitiva, es un libro tanto para rockeros como para los que no siéndolo especialmente, quieran conocer o recordar sin nostalgia, -como es mi caso-, aquellos años “alegres y combativos”, pero también violentos y oscuros”.
Mikel Toral, exdirector de Cultura del Gobierno Vasco y miembro del Consejo Vasco de la Cultura, que prologa el libro, cree que es una buena oportunidad para repasar de manera solvente y amena la difícil relación entre la música contestataria y los poderes establecidos y los contrapoderes que aspiran a sustituir a estos. “En un mundo de autocomplacencia y aduladores, sorprende gratamente la valentía con la que David Mota se enfrenta al periodo más reciente de nuestra historia musical desde la objetividad del historiador y desde la crítica “sin paños calientes”, ya sea a la IA o al PP. Creo que la mayoría de los lectores que se acerquen al libro confirmarán sus sospechas y vivencias de la maldad del poder respecto a la música contestataria. Es así en un 90%, y más en los últimos tiempos. Pero también pienso que es un libro que sirve para que los más jóvenes desarrollen su espíritu crítico y reflexionen, tal y como constantemente se invita a lo largo de la obra”.
En la presentación del libro en Bilbao también participó Joseba Martín, doctor en Periodismo, profesor de la UPV/EHU y director del programa ‘La Jungla Sonora’ de Radio Euskadi, a quien le ha llamado la atención la cantidad y la calidad de las fuentes consultadas a la hora de dar contexto al conjunto, sobre todo desde una visión sociopolítica. “Si bien es cierto que en los años 80 y en los primeros 90 la escena vasca más contestataria estaba fagocitada por la izquierda abertzale, no es menos cierto que en la actualidad la música que se hace en Euskal Herria, salvo contadas excepciones, es mucho más acomodaticia, con un perfil más mainstream que busca un éxito que se pueda convertir en numerosos conciertos”, comenta. Para Joseba Martín, el acierto del libro, además de esa revisión del contexto histórico de los 80, reside en la constatación de que la libertad de expresión está, en los últimos años, bajo sospecha. “En el caso vasco se ha traducido en una cierta persecución (algunas denuncias, suspensión de conciertos…), lejos aún del ensañamiento actual de la derecha y su caverna mediática, capaz de calentar el ambiente para que, leyes restrictivas mediante, un rockero, un rapero o un grupo acabe con penas de cárcel por esta o aquella letra”, afirma.
Para Antonio Rivera, catedrático de Historia Contemporánea de la UPV/EHU, el libro proporciona gran cantidad de información sobre la relación que mantuvo la múltiple variante vasca del punk-rock, sobre todo de los ochenta y noventa, con culturas políticas como la de la izquierda abertzale. “Da muchos datos y analiza con inteligencia la doble influencia e instrumentalización que se produjo entre esos dos ámbitos y cómo uno y otro se vieron modificados con esa relación. Un sector de la izquierda abertzale se modernizó haciendo propios mensajes y formas que en origen le resultaban ajenas, y el llamado RRV se contagió de discurso nacionalista, aunque siguiera primando en él unas letras contra el sistema democrático que se instalaba en nuestro país en los ochenta, muchas veces justificando la violencia política y el terrorismo, y denunciando situaciones de injusticia producidas en una sociedad muy crispada y crítica como fue la vasca de los ochenta”, destaca.
En ese sentido, como se expone en la obra, el RRV fue más político y reivindicativo que la Movida madrileña (o viguesa) porque respondían a dos sociedades distintas. “En la vasca de los ochenta –explica Rivera-, la ciudadanía no había abandonado las calles para dejar que las instituciones condujeran la política cotidiana. La calle estuvo agitada todavía durante algunos años por reivindicaciones de diverso género: sociolaboral (son los años de la reconversión industrial), antirrepresivo, antisistémico, nacionalista, en el combate por “liberar” espacios respecto de las nuevas instituciones que se iban asentando… Aunque la Transición tuvo los mismos efectos que en el resto de España, la consolidación institucional estuvo cuestionada hasta más tarde. En el resto del país ese proceso no se produjo y sí el del llamado “desencanto”, una vuelta al territorio de lo privado después de la intensa politización de las vidas de las gentes que se produjo durante el tardofranquismo y la Transición. Unas letras menos precisamente políticas, más preocupadas por la vida privada, más lúdicas que sacrificadas, algo desencantadas o, lo que el autor llama, “metafísicas” son expresión de “esa radical diferencia entre esos dos territorios en ese tiempo”.

David Mota. Foto: Nuria González. UPV/EHU.
Otro joven doctor en Historia y profesor en la UPV/EHU, Aritza Sáenz del Castillo, también ha intervenido en las presentaciones del libro. “A diferencia de otras publicaciones que han tratado el tema, que podríamos catalogar como crónicas o anecdotarios de tinte autobiográfico de una época, el autor se suma a la corriente de las Ciencias Sociales –New Popular Music Studies- que ha analizado esta época y esta materia con el rigor científico que merece”, opina.
Para este historiador, el autor consigue despertar el interés del lector al introducirse y analizar de forma exhaustiva las relaciones existentes entre los diferentes movimientos musicales underground y el poder hegemónico y no tan hegemónico a lo largo de estos casi cuarenta años. “Muchas de sus reflexiones coinciden con ideas que ya manifestaron los protagonistas de aquella primigenia escena punk que eclosionó a finales de los 70 y primeros 80, y que puso el País Vasco patas arriba. Otros, por la juventud que poseemos y asumiendo muy a nuestro pesar aquello que coreaba La Polla Records – “no soy joven, yo soy muy viejo, ríete de mí que soy tu espejo”- no contemplamos aquellos primeros acordes y desacuerdos, pero sí fuimos testigos del eco o, mejor dicho, reflujo de aquello que llamaron Rock Radical Vasco y que dejó su impronta en la cultura musical vasca décadas después, para bien y para mal”, destaca.
En Logroño o Lleida también se han realizado presentaciones de ‘Los 40 Radikales’, actos en los que han intervenido académicos como Sergio Cañas, doctor en Historia Contemporánea e investigador de la Universidad de La Rioja. Para este historiador, el libro es necesario para comprender una parte importante de la historia reciente del País Vasco y está escrito con habilidad para analizar la parte más salvaje, rompedora e internacional de la cultura popular desde las ciencias sociales, pero carente de la inocencia de quien simplemente ve en el rock radical surgido en los años 80 una representación marginal de una tribu urbana. “Su mayor aportación –incide-, es explicar los mecanismos de instrumentalización que la izquierda nacionalista vasca hizo de una contracultura que vino para quedarse, y su relación con los dispositivos de censura y marginación que sufrió por parte del resto del espectro político más interesados en promocionar la Movida Madrileña o el folclore vasco tradicional”.
Sergio Cañas, además, ha formado parte de diversos grupos musicales, si bien al margen de su instrumentalización nacionalista y desde un prisma anarcopunk. “Al entrar en la universidad, me sumergí de lleno en su vertiente intelectual y comencé a utilizarla como fuente para la historia, releyendo lo anterior y descubriendo nuevos autores y estilos diferentes, al tiempo en que continuaba siendo miembro de nuevas bandas musicales. Pero ya era tarde para cambiar y sólo podía evolucionar. Tal vez por eso cada capítulo que he ido leyendo del libro me ha obligado a buscar mis cintas, vinilos y cedés para volverlos a escuchar”, relata.
En Lleida participó en la presentación Carles Feixa, catedrático de Antropología Social de la Universidad Pompeu Fabra, que tuvo un personal acercamiento a ese movimiento musical y destaca de la obra que va mucho más allá de la superficie política en la que se le ha querido encasillar. “Mi encuentro con la música rock-punk/hardcore vasca tuvo lugar en la ciudad de México en 1991. Al haber paseado por el mercado callejero de El Chopo (un tianguis que cada sábado reúne desde los 80s a todas las tribus urbanas de una de las mayores metrópolis del planeta), conocía a la banda de los Mierdas Punks, que se sabían de memoria las letras de Kortatu y Eskorbuto (además de las de LPR, claro), cuyos discos se vendían en casetes autograbados en varios puestos del mercado. De todos ellos destacaba el de un vasco transterrado en el que también se podían comprar camisetas, gadgets y literatura contracultural. Mis cuates punks de ciudad Nezahualcóyotl me contaron las míticas visitas de esos grupos al DF. Cuando regresé a Cataluña me interesé por esa historia subterránea. Luego estuve en la tesis doctoral de Huan Porrah, un andaluz pionero en bucear en ella, pero hasta que leí el libro de David Mota no acabé de entender lo sumergido, lo emergente y lo visible de uno de los movimientos músico-culturales más interesantes que durante el último medio siglo ha surgido al sur de los Pirineos”.
Ficha:
Autor: David Mota Zurdo
Título: Los 40 Radikales. La música contestataria vasca y otras escenas musicales: origen, estabilización y dificultades (1980-2015)
Año: 2017
Editorial: Ediciones Beta
En Editoralia personas lectoras, autoras o editoras presentan libros que por su atractivo, novedad o impacto (personal o general) pueden ser de interés o utilidad para los lectores del Cuaderno de Cultura Científica.
El artículo Los 40 Radikales se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- I, Mammal. The Story of What Makes Us Mammals
- Cálculo y geometría analítica, de George F. Simmons
- El filósofo que baila con las sepias
Naukas Bilbao 2017 – Clara Grima & Enrique F. Borja: Matemáticas, epidemias y vacunas
En #Naukas17 nadie tuvo que hacer cola desde el día anterior para poder conseguir asiento. Ni nadie se quedó fuera… 2017 fue el año de la mudanza al gran Auditorium del Palacio Euskalduna, con más de 2000 plazas. Los días 15 y 16 de septiembre la gente lo llenó para un maratón de ciencia y humor.

Cuando aplicamos las matemáticas a la salud se obtienen datos muy interesantes. En el caso de las vacunaciones deberían hacer reflexionar a más de una persona; más que nada para evitar la tercera variable de la ecuación: las epidemias.
Clara Grima y Enrique Borja: Matemáticas, epidemias y vacunasEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2017 – Clara Grima & Enrique F. Borja: Matemáticas, epidemias y vacunas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – Francisco R. Villatoro: El espín para irreductibles
- Naukas Bilbao 2017 – Álex Méndez: Luz de luna
- Naukas Bilbao 2017 – Ignacio López-Goñi: Las bacterias también se vacunan
La gran infraestructura europea de investigación en biotecnologías azules es ya una realidad
La gran infraestructura europea de investigación European Marine Biological Resource Centre (EMBRC-ERIC) es ya una realidad, y la Estación Marina de Plentzia (PiE) de la UPV/EHU es uno de los dos centros seleccionados por el Estado español para participar en la misma. El EMBRC-ERIC es el resultado de unión de 24 centros de investigación de 9 países, que aunando sus recursos y know-how y ofertando servicios de investigación trabajarán para resolver cuestiones fundamentales sobre la salud de los ecosistemas marinos en un medioambiente cambiante, promover nuevas tecnologías científicas en esta área, impulsar descubrimientos en el campo de la salud mediante el uso de modelos biológicos marinos y mantener a largo plazo la monitorización del estado de los mares.
Como indican las siglas ERIC (European Research Infrastructure Consortium), esta infraestructura se ha constituido legalmente como un Consorcio Europeo Infraestructuras de Investigación, siendo la decimoctava infraestructura europea de este tipo. Según Ibon Cancio, profesor de Biología Celular de la UPV/EHU y responsable de la adscripción de la Estación Marina de Plentzia al EMBRC-ERIC. “Es muy importante participar en una organización de este nivel y dimensión. ¿Quién no conoce el CERN? Nuestra infraestructura será del mismo nivel. Ellos se dedican al campo de la física, mientras que nosotros trabajaremos en el área de la salud y alimentación (‘Health and Food‘). El CERN tiene una única sede. Nosotros tenemos 24 sedes en 9 países, si bien tenemos un presupuesto mucho más modesto y mucho para demostrar”.
Los estatutos de la infraestructura de investigación paneuropea EMBRC acaban de publicarse en el Diario Oficial de la Unión Europea. “Somos oficialmente uno de los centro de investigación que conforman EMBRC-ERIC, y la única infraestructura de este tipo en el País Vasco”, señala Cancio. Los nueve países en los que se encuentran los 24 centros de investigación que constituyen el EMBRC-ERIC son Bélgica, Francia, Grecia, Israel, Italia, Noruega, Reino Unido, Portugal y España. En el nodo español participa, además de la Estación Marina de Plentzia de la UPV/EHU, la Estación de Ciencias Marinas de Toralla (ECIMAT) de la Universidad de Vigo.
Biotecnología azulEl EMBRC-ERIC proporcionará acceso a información y recursos los ecosistemas de todos los mares de Europa. “El objetivo es que cualquier investigador o investigadora o empresa tenga a su disposición los recursos biológicos marinos necesarios para su labor de investigación, y asimismo tenga acceso a todo el know-how en biología molecular y genómica, de manera que puedan explotarlos de un modo sostenible”.
Los primeros trabajos para constituir el EMBRC empezaron en 2008, una vez que la Comisión Europea introdujo esta iniciativa en su segunda hoja de ruta. En 2011 los promotores del EMBRC pusieron en marcha su primer proyecto, y para 2014 todos los países participantes habían suscrito un memorandum de entendimiento para iniciar el proceso de formalización legal de la infraestructura. A mediados de noviembre se aprobaron los estatutos y el presupuesto de lo que será el EMBRC-ERIC, que en el caso del nodo español contará con financiación del Gobierno Vasco y la Xunta de Galicia. Posteriormente todos los países han ratificado su compromiso con el EMBRC-ERIC, que en el caso de España se produjo en el Consejo de Ministros el 15 de diciembre de 2017. La sede principal del EMBRC-ERIC se encuentra en París.
El EMBRC es, además, una de las grandes infraestructuras promovidas por la Comisión Europea dentro del foro estratégico ESFRI (European Strategy Forum on Research Infrastructures- ESFRI) para impulsar la investigación de calidad en la Unión Europea. En total cuenta con 50 infraestructuras o proyectos de infraestructuras.
Estación Marina de PlentziaLa Estación Marina de Plentzia (PIE) es un centro de investigación y enseñanza de alto nivel de la UPV/EHU. Situada en el antiguo sanatorio de Plentzia, estudia la salud del medio ambiente marino y su influencia en la salud humana. En concreto, promueve la investigación y formación en materias relacionadas con la salud de los ecosistemas marinos, los efectos de las alteraciones medioambientales sobre la salud humana y los biorrecursos marinos. La Estación Marina imparte tres másteres, dos de los cuales cuentan con la máxima distinción de calidad que otorga la Unión Europea, el sello Erasmus Mundus: Erasmus Mundus Master in Marine Environment and Resources (MER); Erasmus Mundus Master in Marine Biological Resources (IMBRSEa) y Environmental Contamination and Toxicology, Asimismo, cuenta con programas de doctorado. Una veintena de científicos y científicas y una treintena de doctorandos y doctorandas trabajan en el centro.
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La gran infraestructura europea de investigación en biotecnologías azules es ya una realidad se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Lado oscuro del genoma y leucemia: aspectos éticos y legales de una investigación
- La pubertad está comenzando antes para muchos niños; la educación sexual debería afrontar esta realidad
- Equilibrio tautomérico en un sistema modelo de gran interés biológico
Científicos, animalistas y el uso de animales para investigación
Mucho se ha hablado de los animales utilizados en investigación. Valga como ejemplo esta estupenda revisión sobre el tema realizada por el investigador Lluís Montoliu o el informe Confederación de Sociedades Científicas de España (COSCE). El tema del uso de animales para fines científicos salta a la palestra periódicamente por presiones del lobby animalista, el cual, sin lugar a dudas, ha influido en las leyes y normas vigentes. Por parte de la razón, es decir, de la ciencia, existe una defensa férrea del uso de animales para investigación, ya que, sin su utilización, no podríamos acometer las nuevas aproximaciones terapéuticas y diagnósticas que necesitamos para poder combatir las enfermedades que todavía hoy no tienen solución y que necesitamos para mejorar la vida de los enfermos. Así que existe un enconado desencuentro entre científicos y animalistas sobre el uso de animales para fines científicos. Sin embargo, hay una entidad, o grupo de entidades, en los que no cabe debate alguno.

Anuncio de PACMA contra la experimentación animal
La talidomida fue prescrita y utilizada entre los años 1957 y 1963 en Europa. Hasta ese momento ningún país europeo contaba con regulación alguna sobre el uso de medicamentos, por lo que la tragedia de este fármaco produjo un verdadero terremoto en el desarrollo de medicamentos en el viejo continente. Alemania, un país particularmente afectado por el caso de la talidomida, tuvo que aprobar con urgencia en el año 1961 la primera ley que regulaba el uso de medicamentos.
Hasta ese momento la responsabilidad de evaluar los medicamentos recaía sobre los propios fabricantes. Aunque su distribuidor, Grünenthal, realizó algunos experimentos de seguridad, estos no fueron suficientes para detectar los efectos secundarios del fármaco, y en ninguno de los casos se evaluó el fármaco en animales gestantes. En aquellos años tampoco era obligatorio evaluar los medicamentos en animales en periodo de gestación en el Reino Unido, pero de nuevo la catástrofe de la talidomida propició que se formara en 1964 el Comité de Seguridad de Medicamentos y que, cuatro años más tarde, se promulgara la primera Ley del Medicamento británica.

Niña afectada por la talidomida
Hoy en día todos los países de primer orden cuentan con agencias para el control del desarrollo, liberación y evaluación de nuevos medicamentos. Es el caso de la European Medicines Agency (EMA) en Europa o la Food and Drug Administration (FDA) en los Estados Unidos. Dichas organizaciones se encargan de velar por la seguridad de los fármacos que se prueban en humanos. La única obsesión de dichas agencias es que no se vuelva a dar un “caso talidomida”. Así que solicitan que se realice un estudio completo y pormenorizado de la toxicidad de los fármacos bajo estudio, y siempre antes de autorizarlos para su uso en humanos. La eficacia del medicamento se supone; de lo que se encargan las correspondientes agencias es de que los fármacos sean suficientemente inocuos.

Sede de la EMA en Londres, que será trasladada a Amsterdam y no a Barcelona.
Las agencias reguladoras obligan a la industria farmacéutica a realizar una exhaustiva batería de estudios para conocer cómo los fármacos afectan a diferentes sistemas del organismo y a procesos patológicos críticos, determinando sus rangos de su seguridad en el mejor de los casos (en el peor y más habitual el desarrollo de los nuevos fármacos es interrumpido por estas cuestiones).
Veamos un ejemplo concreto de los estudios requeridos por las autoridades:
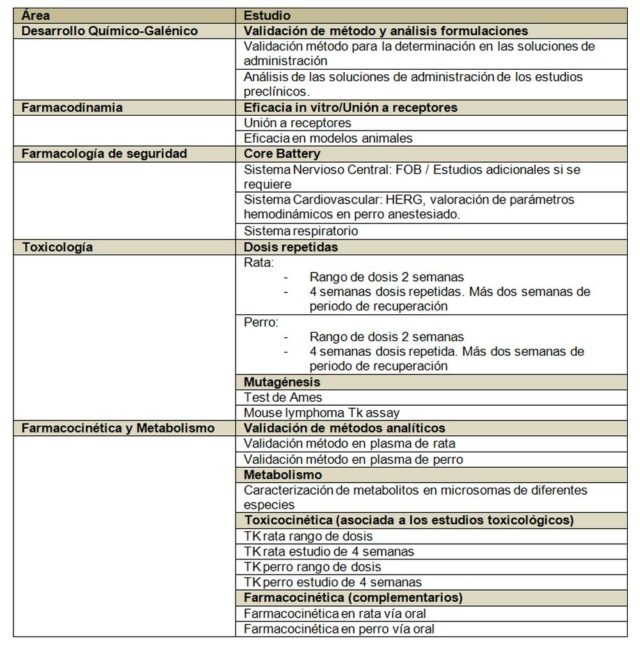
Podemos observar en la tabla anterior, grosso modo, los estudios que las agencias exigen. Hagamos algunas apreciaciones al respecto:
- La tabla refleja los estudios mínimos necesarios, los cuales pueden no ser suficientes si se encuentra algún hallazgo patológico inesperado, cosa que suele ocurrir ya que se fuerzan las dosis hasta encontrar efectos secundarios, lo cual permite definir las dosis de trabajo. Aquí es necesario recordar a Paracelso, que ya explicó la importancia de las dosis hace casi 500 años.
- El paquete básico de estudio está por encima del medio millón de euros en prácticamente todos los casos y los estudios tienen una duración de un año al menos. Esto si las cosas van bien, claro. En muchas ocasiones los tiempos y los costes se incrementan.
- Los laboratorios que realizan este tipo de estudios deben estar certificados en Buenas Prácticas de Laboratorio (BPL; o GLP en inglés), por lo que lo realizan exclusivamente empresas especializadas llamadas Contract Research Organizations (CRO). Todos los protocolos de estudios están normalizados y acordados, y hay que seguirlos estrictamente, registrando cualquier desviación detectada.
- Se estudian los principales sistemas del organismo, tales como el sistema respiratorio, cardíaco o nervioso, así como procesos que puedan afectar a la seguridad, tales como la mutagénesis o los estudios de interacción con receptores.
- Se estudian dos especies animales siempre; una de roedores y otra de no roedores. Por cuestiones históricas la especie de roedor mayoritaria es la rata (el ratón no se usa para estudios regulatorios normalmente). Las agencias tienen un amplio recorrido de estudios realizados en rata y pueden comparar expedientes. La especie no roedora suele ser el perro, aunque se pueden utilizar otros no roedores con su justificación pertinente. Sólo en contadas ocasiones las agencias autorizan el uso de primates. El perro habitualmente usado para estos estudios es de la variedad Beagle; los monos suelen ser macacos.
- Toda la información extraída de los estudios regulatorios preclínicos es utilizada para diseñar los estudios en humanos First-in-human, y las primeras dosis de estudio vienen definidas por la dosis anterior a la más baja que produce algún efecto en cualquiera de las dos especies animales utilizadas en los estudios. A esta dosis se le conoce como NOAEL (de non-observed adverse effect level).
- Previamente a los estudios en humanos se aplicará un factor de dilución a la dosis elegida como medida adicional de seguridad. La dosis final que será utilizada para iniciar los estudios en humanos es lo que se conoce como MRSD (del inglés máximum recommended starting dose).

A grandes rasgos, para todo lo anteriormente expuesto, es necesario el uso de animales. Y en este caso el factor limitante no son los comités de ética, que los hay, si no la cuantía económica de los estudios y la duración de los mismos (para la empresa farmacéutica, tiempo y dinero son parámetros esencialmente equivalentes).
La pregunta ahora es: ¿Cuántos animales se usan para este tipo de estudios en nuestro país? Si analizamos el último informe oficial publicado por el Ministerio de Agricultura, Pesca, Alimentación y Medio Ambiente (MAPAMA), el número de animales utilizados en 2016 para fines científicos fueron los siguientes:
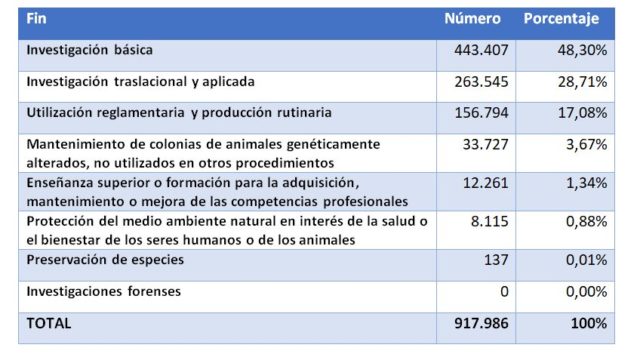
Es decir, que la mayoría de animales fueron usados para investigación (básica o traslacional/aplicada, en un 77%). La siguiente partida en importancia es la utilización reglamentaria y producción rutinaria. Si atendemos sólo al uso reglamentario los datos indican que se utilizaron 49.640 animales para este fin repartidos de la siguiente forma:
Es decir, de cada 100 animales utilizados para fines científicos aproximadamente 5 fueron sacrificados por cuestiones regulatorias, por los 75 que fueron usados en las diferentes fases de investigación. Tal vez 50.000 animales al año para estudiar la seguridad de los fármacos pueda parecer mucho, tal vez no parezca tanto si lo comparamos con las incontables personas que sufrieron el efecto de la talidomida en nuestro país.
Si salimos de nuestra zona de confort y atendemos, por ejemplo, al uso de animales para la alimentación, según Eurostat sólo en 2015 se sacrificaron más de 46 millones de cerdos en España. O lo que es lo mismo, un cerdo por español. Por el contrario, en 2015 por cada español tan sólo se usaron 0,018 animales con fines regulatorios. Juzguen ustedes mismos.
Este post ha sido realizado por Javier Burgos (@Javisburgos) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
Referencias y más información
- Lluís Montoliu (2018) ¿Cuántos animales se usan en España para experimentación? Cuaderno de Cultura Científica
- Informe COSCE sobre el uso de animales de investigación.
- Informe 2016 de uso de animales para investigación del MAPAMA. [PDF]
- Guía de desarrollos preclínicos. Genoma España. [PDF]
El artículo Científicos, animalistas y el uso de animales para investigación se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Cuántos animales se usan en España para experimentación?
- #Naukas15 ¿Es necesario usar animales en investigación?
- Una nueva investigación muestra que explicar cosas a la gente “normal” puede ayudar a los científicos a ser mejores en su trabajo
La neurociencia está desentrañando los misterios del encéfalo adolescente
Lucy Foulkes
![]()
 

¿Cómo describirías al adolescente medio? A la mayoría las siguientes características pueden venirnos a la mente: temperamental, impulsivo, arriesgado, propenso a sucumbir a la presión de grupo.
Si bien está claro que la adolescencia es un período de la vida que está plagado de estereotipos, hay algo de verdad en los clichés. Muchos estudios neurocientíficos han establecido que ocurren cambios significativos en el encéfalo durante la adolescencia. Y las cosas por las que a menudo se ridiculiza a los adolescentes, como su asunción de riesgos y la vulnerabilidad a la presión de los compañeros, en realidad están enraizadas en los cambios que ocurren en sus encéfalos. Solo hay un problema con esto: muchos adolescentes no se ajustan a los estereotipos.
Todos sabemos por experiencia personal que la forma en la que los adolescentes piensan y actúan puede variar ampliamente según el adolescente del que se trate. Pero, a pesar de esto, la gran mayoría de los estudios hasta la fecha se han centrado en las medias: ¿qué ocurre de media con el encéfalo durante la adolescencia o cómo se comportan y sienten los adolescentes de media?
Depender de las medias de esta manera tiene un beneficio estadístico importante, ya que es más probable que los investigadores sean capaces de detectar un efecto genuino si promedian sus hallazgos entre muchos participantes. Pero el coste obvio es que estos hallazgos generales no se aplican a todos y cada uno.
Comprender las diferencias individuales
En un artículo reciente, mis colegas y yo argumentamos que esto debe cambiar. A partir de ahora, la investigación del encéfalo de los adolescentes necesita prestar más atención a estas importantes variaciones entre adolescentes, lo que se conoce en el campo como “diferencias individuales”.
Además de documentar que todos los adolescentes son diferentes, también debemos comenzar a entender por qué esto es así. Los estudios que ya están investigando esto han demostrado que tanto la genética, como la nutrición, la crianza de los hijos o las enfermedades mentales afectan a la forma en la que se desarrolla nuestro encéfalo y la manera en la que nos comportamos durante la adolescencia. Y en nuestro último artículo, analizamos otros tres factores que podrían afectar el desarrollo del encéfalo: el estatus socioeconómico, las relaciones con los compañeros y la cultura.
No útil para retrato robot. Imagen: Shutterstock
El estatus socioeconómico es una medida de la posición social y financiera de una persona en la sociedad, y a menudo se mide por el nivel de educación de sus padres y por los ingresos familiares totales. La investigación ya ha descubierto que tu encéfalo se desarrolla de manera diferente en la adolescencia dependiendo de tu nivel socioeconómico. Pero lo que aún no entendemos del todo es por qué. Podría ser, por ejemplo, que criarse en un ambiente de bajos ingresos es más estresante o que esté relacionado con diferentes tipos de nutrición, y que esto a su vez afecte el desarrollo del encéfalo, pero se necesitan más estudios sobre este tema.
Compañeros de clase y cultura
El tipo de relación que los adolescentes tienen con sus compañeros también afecta la actividad encefálica. Los adolescentes con una historia de acoso, por ejemplo, muestran diferentes patrones de activación encefálica ante ciertas informaciones sociales: sus encéfalos parecen ser más sensibles a la experiencia de ser excluidos. Por la misma razón, tener muchos amigos y un historial de ser querido por los compañeros de clase también afecta a la activación encefálica, y puede hacerte más resistente al desarrollo de problemas de salud mental.
En todo el mundo, los adolescentes también crecen en culturas muy diferentes, lo que afecta muchos aspectos de sus vidas: desde cuántos años pasan estudiando hasta cuándo se casan e incluso cuánto tiempo pasan con sus familias.
Recientemente, los científicos se han interesado en cómo esto se podría reflejar en las diferencias en los encéfalos adolescentes. Ya sabemos que los adultos de diferentes culturas muestran diferencias interesantes en su actividad y estructura encefálicas, y esto ahora está empezando a investigarse en adolescentes.
Solo tu adolescente medio
La razón por la que la mayoría de las investigaciones sobre el encéfalo de adolescentes aún no consideran las diferencias individuales se debe en parte a que el campo tiene solo 20 años de edad, y las nuevas áreas de investigación deben comenzar con lo básico, las medias, antes de intentar comprender los matices.
La investigación del encéfalo adolescente es un campo relativamente nuevo. Imagen: Shutterstock
También hay razones prácticas. La tecnología de imágenes encefálicas hasta la fecha no ha sido lo suficientemente buena como para cartografiar exactamente cómo los factores específicos, como las relaciones entre iguales, podrían afectar el desarrollo del encéfalo. Luego también está el hecho de que para tener suficiente capacidad para detectar hallazgos fiables, se necesitan grandes tamaños de muestra.
Esto significa cientos, a veces miles, de adolescentes. Por el momento, un escáner cerebral cuesta alrededor de 600 € por hora, por lo que el tamaño de las muestras a menudo está limitado por el coste. Una forma de resolver este problema es que los científicos compartan sus datos entre ellos, y esto ya está comenzando a suceder .
Todos los encéfalos son diferentes
Reconocer que todos los adolescentes son diferentes tiene implicaciones realmente importantes para cosas como la educación o la publicidad. Si, por ejemplo, la forma en que los adolescentes aprenden depende de su patrón específico de desarrollo encefálico, entonces las estrategias educativas basadas en medias solo tendrán una utilidad limitada.
Del mismo modo, las campañas publicitarias para temas como la salud sexual, si se basan en los estudios que promedian entre los participantes, funcionarán para algunos adolescentes, pero no para otros.
Cuanto antes entendamos la diferencia entre los adolescentes, más pronto podremos integrar esta información en las escuelas y las políticas. Esto es importante porque, después de todo, no existe un adolescente medio, y debemos recordar esto a medida que continuamos refinando nuestra comprensión del encéfalo adolescente.
Nota del traductor sobre las referencias bibliográficas: Todos los artículos científicos están enlazados en el texto en sus contextos apropiados, basta pulsar en las palabras azules.
Sobre el autor:
Lucy Foulkes es profesora de de psicología de la educación en la Universidad de York (Reino Unido)
Texto traducido y adaptado por César Tomé López a partir del original publicado por The Conversation el 23 de abril de 2018 bajo una licencia Creative Commons (CC BY-ND 4.0)
El artículo La neurociencia está desentrañando los misterios del encéfalo adolescente se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El gran encéfalo humano es un “encéfalo social”
- La pubertad está comenzando antes para muchos niños; la educación sexual debería afrontar esta realidad
- El encéfalo bilingüe: por qué no existe un modelo único
La humildad como virtud científica

Linus Pauling (1901-1994). Ganador de dos premios Nobel. Uno de los padres de la química cuántica y de la biología molecular. Pacifista y activista. Pero también padre de la medicina ortomolecular (sin base científica; una teoría inventada en un sillón, como el psicoanálisis de Freud o la homeopatía de Hahnemann) y perseguidor arrogante, hostil e incansable de Dan Shechtman, los cuasicristales y de cualquiera que trabajase en ellos desde su descubrimiento en 1984 hasta su muerte en 1994 (Shechtman recibiría el Nobel en 2011 por el descubrimiento de los cuasicristales).
Gente que practica ciencia desde la arrogancia hay, ya lo creo; incluso en según qué disciplinas o instituciones abundan. Personas de teoría única que acertaron una vez en algo importante y desde entonces mantienen su hipótesis favorita como única aceptable; científicos que sólo se relacionan con discípulos de su secta, que rechazan a quien tiene ideas diferentes, que son incapaces de imaginar que sus ideas puedan ser insuficientes o mucho menos erróneas. Abundan los jefes de laboratorio, directores de centro, catedráticos eminentes, editores de revistas u organizadores de congresos que en cualquier disciplina, de cualquier sexo (aunque más a menudo, ay, varones), con variado acierto y casi siempre con temibles consecuencias practicas la ciencia desde la más absoluta arrogancia intelectual y a menudo social. Todos los que practica ciencia los conocen o los sufren, tratando siempre de sobrevivirlos.
Porque un científico arrogante, especialmente cuando esa arrogancia se manifiesta en su producción intelectual, es un mal científico. No porque su trato sea muy desagradable, que lo es; no porque suponga un obstáculo al avance del conocimiento al dificultar la adopción de nuevas ideas, que lo hace; sino porque su ciencia es mala por definición.
La buena ciencia sólo puede ser humilde, porque errar es humano y porque al universo le importan poco nuestros sentimientos y aunque no hace trampas para engañarnos tampoco nos pone las cosa fáciles: comprender como funciona es complicado y está lleno de trampas. Malinterpretar, crear hipótesis bellas (pero erradas), teorizar en ausencia de datos o con datos equivocados o desconocer factores relevantes son certezas con las que tenemos que lidiar a la hora de establecer nuestras hipótesis y explicaciones. Y cuando esas hipótesis bellas pero erróneas se enfrentan a la comparación con el cosmos real éste es inmisericorde, y las tumba sin remedio.
Cuando esto ocurre podemos refugiarnos en la ceguera desde la arrogancia: ese factor no es relevante porque YO no lo considero así, porque MI experimento no lo tiene en cuenta, porque NUESTRA hipótesis no lo incluye. Al hacer esto estamos intentando imponer nuestras formas de pensar y nuestros límites al universo, forzando sobre el funcionamiento de cosmos nuestra interpretación limitada. Si tenemos bastante poder terrenal conseguiremos que esto funcione, durante un tiempo; si controlamos las carreras de los científicos que vienen después mediante tribunales o consejos editoriales de revistas, si somos determinantes al escribir los libros de texto, si empujamos y apartamos a las voces discrepantes e impedimos que se les escuche. Con arrogancia y poder es posible mentir a todo el mundo, durante algún tiempo.
Pero no hay arrogancia capaz de forzar la mano del universo, así que a la larga todos nuestros esfuerzos serán en vano. Quizá tengamos una larga y poderosa carrera, quizá incluso muramos pensando que lo hemos logrado, pero tarde o temprano (y será temprano) la realidad se impondrá y nuestras teorías e hipótesis pasarán al basurero de la historia. No será siquiera recicladas como parte de teorías mejores, como ocurre con los avances correctos pero siempre (ay) insuficientes, sino que serán descartadas y quedarán como notas a pie de página en la historia de la ciencia, asociando para siempre nuestro nombre con el fracaso.
Los mejores científicos son humildes, no por vocación propia, sino por experiencia duramente ganada. Por errores cometidos, hipótesis rechazadas, experimentos fallidos, dificultades no superadas; por meteduras de pata risibles, confusiones involuntarias, complejidades experimentales o de campo no tenidas en cuenta. Es cierto que la naturaleza no nos miente de modo malicioso, pero a veces puede ser puñeteramente sutil y esconder fuentes de error en los rincones más inverosímiles; uno puede estar al borde del Nobel y descubrir de repente que sus datos están contaminados y no dicen lo que uno pensaba que decían, perdiendo cualquier posibilidad de alcanzar la gloria.
Y eso duele, pero sólo se convierte en una catástrofe si se le suma una buena dosis de arrogancia. En presencia de humildad el error se desarrolla y se acaba convirtiendo en el germen de nuevas ideas, nuevas hipótesis, nuevos avances. Por eso los buenos practicantes de ciencia comparten como rasgo común la humildad intelectual; no porque eso les haga mejores personas o les convierta en practicantes de la filosofía Zen, sino porque eso les hace mejores científicos. Ante el maravilloso, complejo y sutil universo que hay ahí fuera pensar que una mente humana pueda contener toda la verdad no sólo es arrogante: es estúpido. La humildad, pues, es una virtud científica, porque nos ayuda a entender mejor.
Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.
El artículo La humildad como virtud científica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cómo leer una noticia científica
- Las matemáticas como herramienta (II): La Revolución Científica y el cálculo
- Ellen Richards: la economía doméstica como cultura científica
Grietas de desecación marcianas

Imagen que Curiosity tomó de “Old Soaker” durante el sol 1555. La losa tiene unos 80 cm de longitud. Foto: NASA.
A principios de 2017, y a partir de imágenes recopiladas por el róver Curiosity, los científicos anunciaron el descubrimiento de posibles grietas de desecación en el cráter Gale, que habría estado lleno de lagos hace 3.500 millones de años. Ahora, un nuevo estudio ha confirmado que son realmente grietas de desecación, lo que revela nuevos detalles sobre el antiguo clima de Marte.
Dado que las grietas de desecación se forman solo cuando el sedimento húmedo está expuesto a la atmósfera, su posición más cercana al centro del antiguo lecho del lago que al borde también sugiere que los niveles del lago aumentaron y disminuyeron drásticamente con el tiempo. Esto es, los lagos del cráter Gale habrían pasado por el mismo tipo de ciclos que vemos en la Tierra
Los investigadores se centraron en una losa de roca del tamaño de una mesa de café apodada “Old Soaker”. Old Soaker está atravesado por polígonos idénticos en apariencia a los característicos de los procesos de desecación terráqueos. El equipo analizó los aspectos físicos y químicos de los polígonos utilizando todo el despliegue de medios de análisis de Curiosity. Hay que recordar en este punto que Curiosity es un potentísimo laboratorio geoquímico autopropulsado.
Este escrutinio puso de manifiesto que los polígonos, confinados a una sola capa de roca y con sedimentos llenando las grietas entre ellos, se formaron por la exposición a la atmósfera, y no por otros mecanismos como la fracturación térmica o hidráulica. Y si bien los científicos sabían casi desde el momento en que Curiosity aterrizó en 2012 que el cráter Gale alguna vez contuvo lagos, la confirmación de la existencia de grietas de desecación añade un contexto a nuestra comprensión de este antiguo sistema lacustre.
Hallazgo tras hallazgo, Curiosity está transformando continua y completamente nuestra visión del presente y del pasado de Marte.
Referencia:
N. Stein et al (2018) Desiccation cracks provide evidence of lake drying on Mars, Sutton Island member, Murray formation, Gale Crater Geology doi: 10.1130/G40005.1
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Grietas de desecación marcianas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- En Marte el viento crea montañas
- Cómo se formaron las columnas hexagonales de la Calzada del Gigante
- Ox Bel Ha, un ecosistema tropical alimentado por metano
Muriel Bristol, la gran catadora de té

Estamos en Rothamsted (Harpenden, Reino Unido). Son las cuatro de la tarde, la ‘sagrada’ hora del té. Un grupo de personas hace una pausa en su trabajo para tomarse su infusión. Entre ellas están Muriel y Ronald. Ronald ofrece a su amiga una taza de té. Ella, tras tomar un sorbo, la rechaza. A Muriel le gusta el té, pero solo si la leche se ha servido en la taza en primer lugar. Ronald cree que se trata de una broma, e insiste con vehemencia; piensa que es lo mismo el orden en el que se vierten los líquidos, y se burla de su colega. Pero Muriel, enfadada, la rechaza de nuevo… no le gusta el sabor. William, otro de los miembros del grupo, intenta mediar y pide a Ronald que deje demostrar a Muriel que efectivamente es capaz de distinguir el momento en el que se ha servido la leche en la taza. Rápidamente, se organiza el experimento: Muriel debe distinguir entre ocho tazas de té, cuatro de cada tipo (leche antes del té o té antes de la leche) colocadas de manera aleatoria ante ella. Tras una pausada cata –en la que se permite a Muriel comparar el sabor de dos tazas–, y ante el asombro de sus compañeros, Muriel distingue con precisión el orden en el que se ha servido la leche de cada taza. ¿Ha sido pura suerte? ¿O quizás Muriel es una experta catadora capaz de distinguir esos detalles? Ronald tuvo que admitir la “victoria” de Muriel y se puso a reflexionar mucho sobre el tema…
Por cierto, Muriel y William se casaron poco tiempo después.
La anterior historia –me he permitido alguna pequeña licencia– es una historia real. Sus protagonistas son la bióloga Muriel Bristol (1888-1950) –que trabajó en la estación experimental de Rothamsted (Harpenden, Reino Unido) desde 1919 y era especialista en algas–, el biólogo y estadístico Ronald Fisher (1890-1962) y William Roach –con el que es cierto que Muriel se casó–.

Muriel Bristol y Ronald Fisher.
El experimento se realizó realmente, fue diseñado por el propio Fisher y dio lugar a un experimento aleatorizado que el estadístico presentó en su libro The Design of Experiments (1935) –llamado The lady tasting tea, la catadora de té–, en el que la prueba de significación estadística usada fue el test exacto de Fisher.
En este experimento, Fisher introdujo el concepto de hipótesis nula, unaafirmación que no se demuestra o establece, y no se rechaza excepto si durante el curso de la prueba parece demostrarse su falsedad. En el caso de la catadora de té la hipótesis nula suponía que Muriel no tenía la capacidad de distinguir las tazas.
Fisher eligió ocho tazas porque le pareció una cantidad suficiente para que la suerte no fuera un factor determinante. Observar que, efectivamente, existen 70 maneras de colocar las ocho tazas, con cuatro de cada tipo, y parece difícil acertar solo por azar.
Muriel aclaró –una explicación muy científica, desde su condición de bióloga– que, si se añadía leche fría al té caliente, las proteínas de la leche coagulaban y cambiaba el sabor, y ella lo percibía como desagradable.
Por cierto, el escritor George Orwell (1903-1950) no coincide con Muriel… en 1946 publicó el texto A nice cup of tea en el que describía con detalle el procedimiento a seguir para preparar una taza de té perfecta. Entre las instrucciones decía (traducción extraída de [3]):
En décimo lugar se debe verter el té en la taza antes que la leche. Este es uno de los puntos más polémicos, de hecho en todas las familias de Gran Bretaña probablemente hay dos escuelas de pensamiento sobre el tema. La escuela que echa primero la leche (que puede tener argumentos contundentes) y la escuela que la echa después. Yo sostengo que mi teoría es irrefutable. Al poner el té primero se puede regular exactamente la cantidad de leche, mientras que si se hace al revés se puede poner demasiada leche y no tendrá arreglo.
A lo mejor, para saber quién lleva la razón, es mejor leer lo que dice la norma ISO 3103 respecto al método estándar de preparar el té…
Referencias
[1] Sturdivant, Lt. Col. Rod., Lady Tasting Tea, 2004
[2] Jesús Ortiz, La ciencia y el té de las cinco, El Diario, 23 noviembre 2016
[3] Las onces reglas de George Orwell para ‘Una buena taza de té’, Territorio gastronómico
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Muriel Bristol, la gran catadora de té se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El gran cuatro, o los números siguen estando locos
- Artistas que miran a las matemáticas
- ¡Es la Aritmética!

