Cuaderno de Cultura Científica

En #Naukas17 nadie tuvo que hacer cola desde el día anterior para poder conseguir asiento. Ni nadie se quedó fuera… 2017 fue el año de la mudanza al gran Auditorium del Palacio Euskalduna, con más de 2000 plazas. Los días 15 y 16 de septiembre la gente lo llenó para un maratón de ciencia y humor.

Alex Méndez se dedica profesionalmente a simular la luz y sus efectos. En esta charla aplica sus conocimientos para desmontar las bases de dos de las conspiranoias que afirman que el hombre no llegó a la Luna.

Alex Méndez: Luz de Luna

Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Naukas Bilbao 2017 – Álex Méndez: Luz de luna se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Naukas Bilbao 2017 – José Miguel Viñas: Me río yo del cambio climático
2. Naukas Bilbao 2017 – Francisco R. Villatoro: El espín para irreductibles
3. Naukas Bilbao 2017 – Teresa Valdés-Solís: Limpia, fija y da esplendor

BertsoBot. Imagen: Nagore Iraola. UPV/EHU

Una de las líneas de trabajo del grupo de investigación Robótica y Sistemas Autónomos (RSAIT) de la Facultad de Informática de la UPV/EHU consiste en progresar en la interacción entre humanos y máquinas o robots. Uno de sus principales proyectos es el denominado BertsoBot, “en el que ponemos a los robots a cantar bertsos”, comenta el líder del grupo, Basilio Sierra. El grupo de investigación trabaja en múltiples aspectos de ese proceso: la comprensión de la señal de voz, la visión a través del ordenador, la navegación, la generación de nuevas melodías musicales, etc.

La investigadora y doctoranda Izaro Goienetxea trabaja en dos de estos temas: la generación automática de música y la clasificación automática de la música. La investigadora señala que ya hay numerosos métodos de generación automática de música, basados en modelos gramaticales o estadísticos; pero en ellas “habría que tener en cuenta la coherencia de las melodías, para generar melodías fáciles de comprender. Habría que tener la seguridad de que dentro de la melodía se repite algún segmento, tanto en lo que respecta a las notas como en otros niveles más complejos de la melodía”.

La labor de esta investigadora comenzó en la generación musical, pero los resultados la llevaron a estudiar las formas de clasificarla. Goienetxea destaca el interés que tiene la clasificación, ya que “en Internet cada vez hay más música al alcance, y cada vez está adquiriendo más importancia el poder realizar la clasificación de la música de forma automática, y poder organizar grandes recopilaciones musicales”.

En un artículo publicado por la revista PLOS ONE, el grupo de investigación ha presentado dos métodos fruto de este trabajon. Por un lado, un método para clasificar la música en función del género, basado en una forma nueva de representar la música lograda a través de la agrupación de melodías de bertsos semejantes. Con este método, “analizamos una melodía, y determinamos a qué se parece, es decir, en qué género podemos clasificarla”, explica Goienetxea. Esos agrupamientos son utilizados, asimismo, para generar de forma automática nuevas melodías del estilo de las que forman ese conjunto. “Las nuevas melodías son parecidas a las originales”, concreta la investigadora. “Y si se incluye en el sistema más de un modelo musical, creará otra melodía nueva, una nueva versión, que será una mezcla de los diferentes géneros”, añade Sierra.

En el desarrollo de su trabajo, la investigadora se ha servido de un corpus o conjunto de melodías de bertsos. “Proponemos la forma en la que se pueden representar los bertsos, y, posteriormente, cómo clasificar esas melodías. En nuestro grupo hemos conseguido el método, que puede ser aplicado en cualquier otro tipo de corpus, o de música”, declara Goienetxea.

Según la investigadora, han conseguido generar de forma automática melodías de bertsos, “pero este método puede servir para aplicaciones de musicoterapia, el aprendizaje de composición musical, o también en los programas de composición, entre otros”.

Referencia:

I. Goienetxea, J. M. Martínez-Otzeta, B. Sierra, I. Mendialdua Towards the Use of Similarity Distances to Music Genre Classification: a Comparative Study (2017) PLoS ONE doi: 10.1371/journal.pone.0191417

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo BertsoBot, el robot versolari se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Traducción automática neuronal sin supervisión
2. Estroncio en la leche
3. Fotovoltaicos siempre a máxima potencia

El 30 de marzo del pasado año un incendio presuntamente provocado provocó el colapso de un viaducto en la Interestatal 85 a su paso por Atlanta. Cuatro kilómetros de uno de los sentidos permanecieron cortados al tráfico hasta el verano mientras se reparaba. La I-85 es la vía que más tráfico desplaza en la ciudad de la Coca-Cola y se preveía un auténtico caos circulatorio y de atascos. La realidad es que no pasó nada incluso el tráfico se redujo en las vías alternativas. ¿Qué estaba pasando?

Para los que trabajamos en cuestiones de movilidad (la de mover personas, no la de los teléfonos) existen algunos conceptos que cuesta hacer entender a los gestores, pero sobre todo al gran público, y que son fundamentales para comprender por qué esta disciplina es tan compleja de gestionar. Estos conceptos son totalmente contraintuitivos y hace falta mucha pedagogía y buena comunicación para tomar la decisión correcta.*

El error de acabar con los atascos con más infraestructuras

Cuando tenemos un atasco recurrente en una vía, la solución más sencilla suele ser pensar en su posible ampliación. Cuando esta ampliación se ejecuta, a los pocos meses se vuelven a producir los mismos atascos y no hemos solucionado nada.

Al ampliar una vía con más carriles, mucho de los usuarios que no se planteaban usar el coche por los continuos atascos, ahora si se lo plantean porque perciben el tráfico fluido. Pero los atascos no se debían a que la infraestructura estuviera mal dimensionada sino a otros factores como, por ejemplo, acabar en el cuello de botella de una ciudad. Como más usuarios se plantean coger el coche al final tenemos un vía con más coches pero nuevamente atascada. Es lo que se llama demanda inducida y es un error que hemos estado cometiendo desde los años 50 del siglo pasado.

23 carriles para el mayor atasco del mundo | Wikipedia

Pero si la demanda se puede inducir, ¿se podrá también disipar? Sí, y eso fue exactamente lo que ocurrió en la I-85. Al preverse más tráfico con menos espacio, las personas no solo tomaron rutas alternativas sino que lo hicieron fuera de sus horarios habituales. Incluso se plantearon si ir en coche era necesario. Solo cogían el coche aquellos que lo necesitaban. Y tenemos otro ejemplo más cercano en el famoso cierre de la Gran Vía al tráfico por Navidad que causó menos tráfico y no más en las vías no afectadas por los cortes como la M-30, por ejemplo.

Esto no funciona siempre, si reduces carriles o cortas tráfico en las vía diseñadas precisamente para ser alternativas a las congestionadas solo vas a conseguir aumentar los atascos, como se ha podido comprobar en Murcia al quitar un carril por sentido en sus rondas exteriores.

Si queréis saber más sobre el tráfico disipado os recomiendo leer el documento «Reclamando las calles de la ciudad para las personas» de la Comisión Europea.

En la cantidad está la seguridad

¿Qué ocurre si paulatinamente fuéramos aumentando el número de ciclistas en una ciudad? ¿Aumentarían los accidentes de forma proporcional? Eso es lo que nos diría la lógica pero los accidentes ni siquiera se mantienen estables sino que disminuyen. Y todo esto no es achacable por completo a la creación de vías segregadas y seguras sino que hay otro factor implicado.

Este factor se llama “seguridad por número” y va relacionado con nuestro comportamiento al volante y la costumbre que tengamos de encontrarnos imprevistos. En una ciudad donde los ciclistas sean algo testimonial, los conductores se comportarán como si estos no existieran, no tomarán las precauciones necesarias para evitar accidentes. Sin embargo, conforme el número de ciclistas va aumentando los conductores interiorizarán una serie de hábitos para evitar los accidentes: frenarán en las intersecciones, abrirán las puertas mirando si no viene nadie (el caso extremo es la “apertura a la holandesa”, con la manos contraria), reducirán su velocidad…

El caso de Sevilla con la ampliación de sus carriles bicis es un buen ejemplo. En el año 2006 la ciudad contaba con 12 km de carril bici, 3 millones de desplazamiento y se producían 16 accidentes coche-bici cada millón de viajes. Siete años después la red se había ampliado hasta llegar a los 152 km, los desplazamientos se habían multiplicado por 5,4, 16 millones de desplazamientos fluían por sus calles y los accidentes habían disminuido hasta los 6 por millón (1).

Otro ejemplo de ello es la ciudad de Nueva York, que va camino de los 140 millones de viajes y ha reducido su accidentalidad ciclista un 71 % en 20 años. Y esto es algo que se mantienen más o menos por todo el mundo: donde hay más ciclistas hay menos accidentes (2).

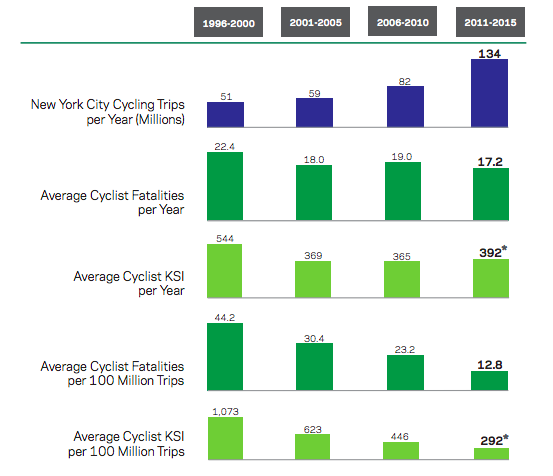
Fuente: Departamento de Transporte de Nueva York

Menos carriles para mover a más personas

Cuando pensamos en vehículo motorizados, nos movemos de forma muy ineficiente. La cantidad de área que necesita un coche para moverse en una ciudad es desorbitada si tenemos en cuenta que la media de ocupación es 1,2 personas por vehículo. Quitarle carriles a los coches hace que más personas puedan circular por esa calle.

Volvamos al ejemplo de la Gran Vía. En una situación ideal de tráfico, los dos carriles dedicados a los coches moverían unos 1200 vehículos/hora, unos 1500 pasajeros/hora. Si destinamos ese espacio a peatones en una situación de flujo peatonal denso como el que se vive en Navidad estaríamos hablando de 13.000 peatones/hora (si nos vamos a las situaciones previas al colapso tenemos 25.000 peatones/hora). Destinar esos dos carriles a peatones multiplica por 10 el número de personas que circulan por ellos.

La imagen de la izquierda fue tomada originalmente por @ClaraCarlille; la imagen derecha está extraída de la cuenta de @hcjulio

Queda mucho más claro en la siguiente gráfica que la NACTO incluyó en su «Guía global para el diseño de calles» usando los datos de circulación de Estados Unidos y Canadá. Cuando destinamos más espacios a medios de desplazamientos que mueven a más personas por área, el tránsito que puede soportar una calle se dispara.

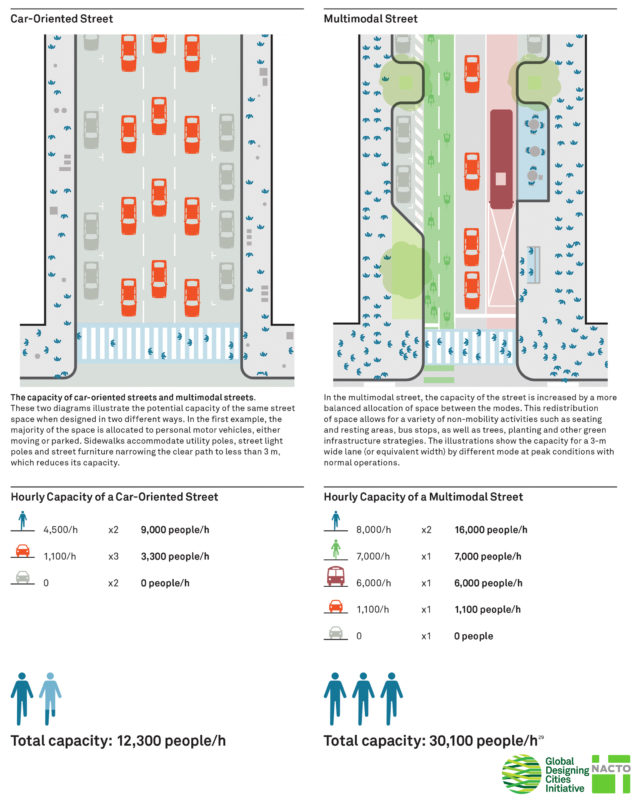
Fuente: NACTO

En resumen: ampliar o disminuir la autopistas puede tener el efecto contrario al deseado; cuantos más ciclista haya en una ciudad menor será el número de accidentes y quitar carriles de coches en una calle hace que aumente el número de personas que pueden circular por ella.

Cuando leas que tu ayuntamiento va a realizar esta o aquella actuación y creas que va a suponer caos, colapso, víctimas mortales, apocalipsis y atascos de tráfico párate a pensar si en realidad la situación no será la contraria y te están haciendo un favor tanto si vas a pie como si vas en coche.

Este post ha sido realizado por Txema Campillo (@Txemacg) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.

Nota del autor: *Luego existen otros mitos contraintuitivos como que los vehículos privados no están subvencionados o que ocupar el espacio público no cuesta dinero pero entran más en el terreno de la economía y no los trataré aquí.

Referencias y más información:

(1) On the effect of networks of cycle-tracks on the risk of cycling. The case of Seville. Marqués y Hernández-Herrador, Accidents; analysis and prevention. 2017 May;102:181-190 https://www.ncbi.nlm.nih.gov/pubmed/28319756

(2) Safety in numbers: more walkers and bicyclists, safer walking and bicycling. Jacobsen, P. L., Injury Prevention. 2003;9:205–209 https://ecf.com/sites/ecf.com/files/Safety_in_Numbers_JacobsenPaper.pdf

El artículo La movilidad contraintuitiva se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Por qué no nos basta con el viento
2. Del zumo de naranja a la selva, un ejemplo de reciclaje extremo
3. La carrera hacia la supremacía cuántica

¿Cómo se tratan algunos de los trastornos cognitivos más frecuentes en las aulas? ¿Son efectivos los programas y herramientas del sistema educativo actual? ¿Carecen de eficacia algunas de las prácticas educativas más populares?

Estas son algunas de las cuestiones que se debatieron en la jornada “Las pruebas de la educación”, que se celebró el pasado 2 de febrero de 2018 en el Bizkaia Aretoa de Bilbao. El evento, en su segunda edición, estuvo organizado por la Cátedra de Cultura Científica de la UPV/EHU y el Consejo Escolar de Euskadi, con la colaboración de la Fundación Española para la Ciencia y la Tecnología (FECYT).

Las ponencias de los expertos que expusieron múltiples cuestiones relacionadas con la educación, basándose siempre en las pruebas científicas existentes. Los especialistas hicieron especial hincapié en destacar cuál es la mejor evidencia disponible a día de hoy con el objetivo de abordar las diferentes realidades que coexisten en las aulas y en el sistema educativo en general.

“Las pruebas de la educación” forma parte de una serie de eventos organizados por la Cátedra de Cultura Científica de la UPV/EHU para abordar cuestiones del día a día como la educación o el arte desde diversos ámbitos de la actividad científica. La dirección del seminario corre a cargo de la doctora en psicología Marta Ferrero.

Partiendo de la premisa de que en educación existe una brecha profunda entre la investigación y la práctica educativa, la doctora en psicología Marta Ferrero aborda los pormenores de estrategias que se han convertido en la actualidad en “enemigos públicos” del sistema: la evaluación y los deberes escolares. Ferrero explica, desde la evidencia, cómo estas prácticas educativas, utilizadas correctamente, pueden constituir una auténtica herramienta aliada para el profesorado.

La evaluación y los deberes escolares: ¿Enemigos públicos o fieles aliados?

Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo La evaluación y los deberes escolares se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. A favor de la evaluación escolar objetiva
2. Autismo y educación: problemas y pautas en el aula
3. Las ideas erróneas sobre educación entre el profesorado: prevalencia, causas y soluciones

Muchas personas creen en algún tipo de magia, probablemente incluso usted, que se considera superescéptico pero aprieta varias veces el botón del ascensor porque así llegará antes, o ‘toca madera’ golpeándose la cabeza on los nudillos cuando habla de algo que desea ocurra. Nuestro cerebro es una enloquecida máquina de establecer conexiones causa-efecto entre distintos aspectos de lo que ocurre a nuestro alrededor, igual que una parte de ese cerebro es una enajenada máquina de encontrar caras en cada agrupación de dos puntos con una raya o hueco debajo que nos entre por la vista. Si una vez hicimos el pino aburridos porque el autobús no llegaba y el autobús llegó ya nada podrá quitarnos la profunda convicción de que hacer el pino atrae a los autobuses por mucho Martin Gardner y Carl Sagan que hayamos leído y aunque jamás lo digamos en voz alta. Es un defecto de fábrica de la Humanidad y sólo podemos saberlo y tratar de limitar sus efectos deletéreos en lo posible.

Para lo cual hay una reflexión que nos puede ser útil, una herramienta para ayudarnos a luchar contra esa desaforada tendencia que tenemos a asignar causas a cualquier efecto, que consiste en recordar que la magia esconde una desmesurada, una increíblemente desmedida arrogancia, por no citar chulería, y un egocentrismo inconmensurable con cualquier sistema de medida.

Porque en el fondo todos los tipos de magia se reducen a esta afirmación: el Universo entero, el Cosmos todo, está dispuesto a suspender las reglas que se aplican a todo el resto de lo existente para favorecer MIS intereses personales. ¿Qué es un hechizo al estilo Harry Potter? Es el Universo obedeciendo a MIS palabras. ¿Qué es un milagro? Es el Cosmos suspendiendo sus leyes para MÍ por intervención de MI divinidad o santón favorito. ¿Qué es el Karma? Es Todo lo que Es ocupándose de compensar alguna maldad que alguien me ha hecho a MÍ con un castigo conmensurado con su ofensa. El horóscopo son los planetas gobernando MI vida; la homeopatía es el agua cambiando las propiedades que caracterizan a esta sustancia en todo el resto del espacio conocido cuando se aplica a MÍ. La magia no es más que el cosmos a MI servicio particular.

Y no hablemos de las religiones, esas que postulan que existen seres lo bastante poderosos como para crear Todo lo que Existe que no tienen otra cosa que hacer que preocuparse de que cumplamos con el número de genuflexiones correcto, la dieta adecuada y el empleo inocente de las manos debajo de las cobijas de nuestras camas. Tanto la religión como la magia asumen que todos y cada uno de nosotros somos tan importantes en el devenir cósmico que todo lo demás, literalmente, gira alrededor de nuestras necesidades, pasiones, intereses y acciones; hasta tal punto que las entidades más poderosas o las leyes más universales sólo se preocupan de cada uno de nosotros.

Ante tamaño empeño la palabra arrogancia se queda corta; quizá pueda emplearse el término yiddish ‘chutzpah’, que designa una desvergüenza de tan exagerado calibre que no queda por menos que admirarla incluso cuando se rechaza. De manera que cuando alguien le sugiera que rezar a determinado santo, realizar determinado ritual, alinear algunos cristales concretos o esquivar a un gato de determinado color su suerte va a cambiar, pregúntese: ¿Soy YO lo bastante importante como para que el Cosmos suspenda sus reglas de funcionamiento por mí? ¿No sería el colmo de la arrogancia pensarlo?

Y si la respuesta es sí, recuerde: eso es lo que hay debajo de la magia. Un egocentrismo que no cabe en el Sistema Solar.

Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.

El artículo Lo que la magia esconde se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. #Naukas14: Magia y neurociencia
2. La magia y el nacimiento de la ciencia moderna
3. Una de mates: Magia matemática

Efectos del tsunami de Tokohu, Japón, en 2011.

¿Cómo prevenir el efecto de los tsunamis? Aparte de dar la alarma cuando se detecta un terremoto, otra forma de hacerlo sería conseguir lo mismo que se tiene en las montañas nevadas en invierno: conocer qué zonas y en qué condiciones hay riesgo de aludes. Increíblemente para conseguirlo hay que estudiar el clima del Jurásico. Y es que na reciente investigación puede que haya encontrado qué indicios buscar en el fondo del mar.

Los mayores corrimientos de tierra del planeta no ocurren en tierra firme, sino en el fondo marino. Estos mega-corrimientos pueden mover miles de kilómetros cúbicos de material y, a veces, provocar tsunamis. Sin embargo, sorprendentemente, ocurren en pendientes casi planas, de menos de tres grados de inclinación. ¿Cómo es esto posible? Morelia Urlaub, del Centro de Investigación Oceánica Geomar Helmholtz (Alemania)y sus colegas puede que hayan descubierto la respuesta: una capa de microfósiles silíceos de unas algas unicelulares llamadas diatomeas que aparecieron en el Jurásico.

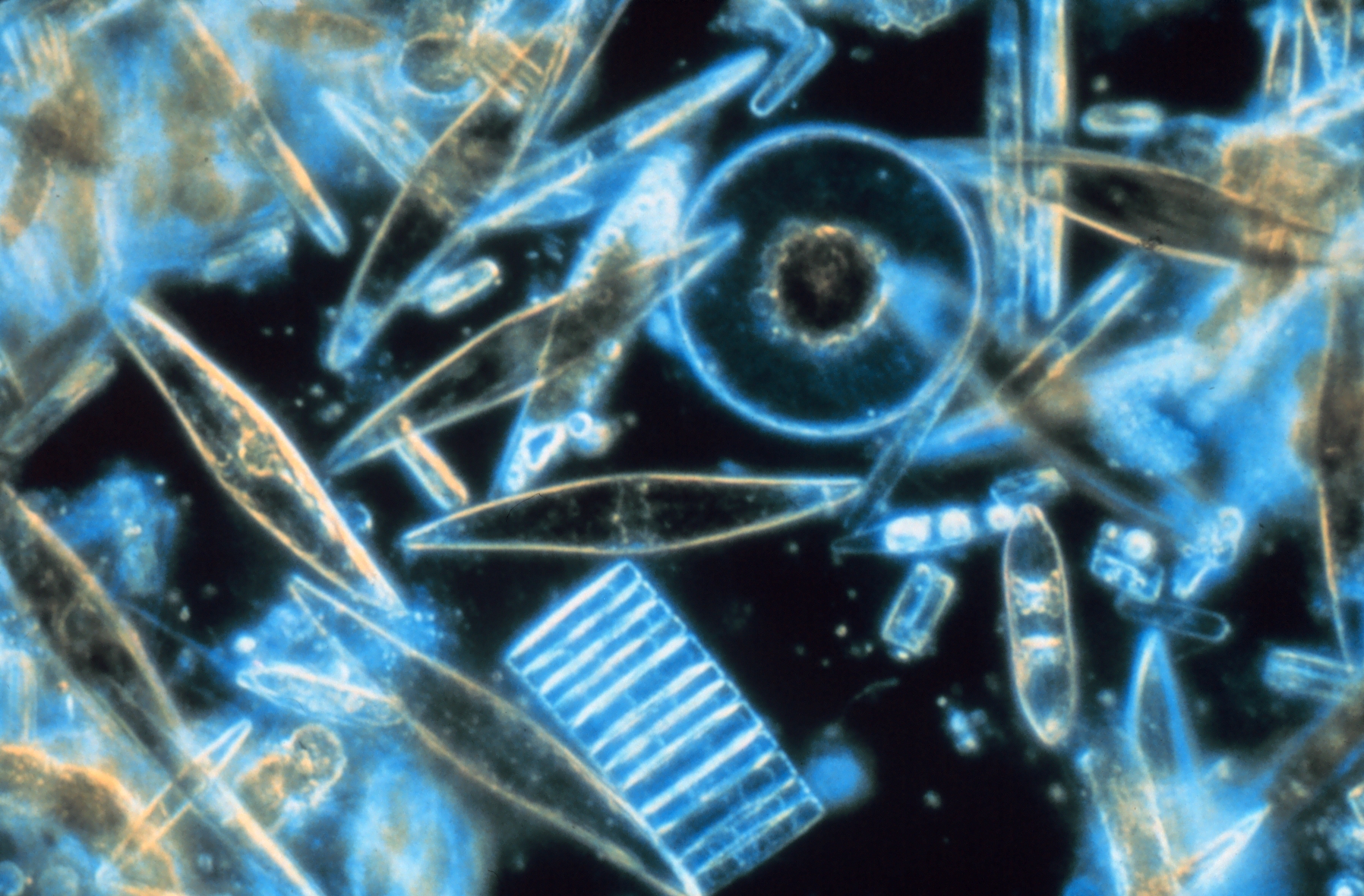
Diatomeas al microscopio

Este trabajo es el primero en identificar la capa débil responsable de un mega-corrimiento submarino. Aunque la naturaleza de estas capas débiles críticas ha sido muy debatida, su estudio ha sido casi imposible porque, en general, se destruyen durante los corrimientos de tierra.

Urlaub estaba compilando datos de perforaciones oceánicas desde 1980 del Ocean Drilling Program cuando se dio cuenta de que la mayoría de sus datos muestreaba el lecho marino justo en el borde del corrimiento Cap Blanc, un mega-corrimiento de 149,000 años de antigüedad frente a la costa del noroeste de África. Correlacionó esos datos con datos de reflexión sísmica de alta resolución registrados en la misma área en 2009. Juntos estos datos indicaban la presencia capas ricas en diatomeas, de hasta diez metros de grosor, que iban directamente desde la zona muestreada hasta la base de las capas de corrimiento en el Cap Blanc.

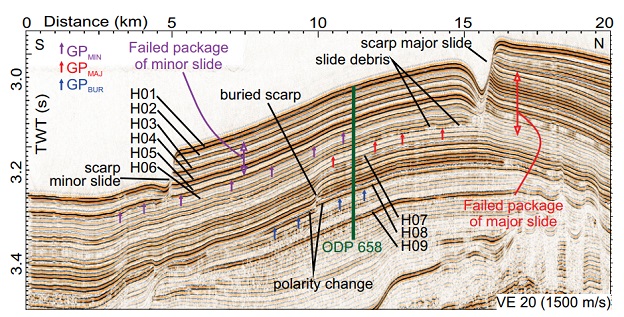
Además, cada capa de diatomeas tenía encima una capa de sedimentos ricos en arcilla. La presencia de esta arcilla es la clave que llevó al equipo a una solución del problema. Las capas de diatomeas son muy compresibles y ricas en agua, a medida que aumenta la presión el agua sería “exprimida” desde la capa de diatomeas hacia la arcilla. En última instancia, la arcilla o la interfaz entre la arcilla y las diatomeas falla, lo que hace que los sedimentos que están encima se deslicen aunque la pendiente sea muy pequeña.

En el corrimiento de Cap Blanc el fondo marino tiene una inclinación de solo 2,8 grados. Sin embargo, cuando se desprendió, el corrimiento movió más de 30 kilómetros cúbicos de material (el equivalente a 30.000 veces el volumen interior del estadio Santiago Bernabéu) y se extendió al menos 35 kilómetros. Otro mega-corrimiento submarino hace 8.500 años frente a Noruega movió uns impresionantes 3.000 kilómetros cúbicos, causando un tsunami terrible. Y algunos científicos especulan que el tsunami de Tohoku (Japón) de 2011, el que causó el desastre de Fukushima, pudo haber sido amplificado por un mega-corrimiento submarino.

Aunque corrimientos de esta magnitud no ocurren muy a menudo, su tamaño los hace bastante significativos. Se cree que una quinta parte de todos los tsunamis puede tener su origen en mega-corrimientos submarinos. Si las capas de diatomeas son un factor importante, conocer en qué lugares las condiciones paleoclimáticas en el Jurásico pudieron favorecer el crecimiento de estas algas podría ayudar a crear un mapa de riesgos de mega-corrimientos submarinos y poder vigilarlos para así poder dar las alarmas de tsunami lo antes posible.

Referencia:

M. Urlaub, Jacob Geersen, Sebastian Krastel, and Tilmann Schwenk. (2018) Diatom ooze: Crucial for the generation of submarine megaslides? Geology: 10.1130/G39892.1.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

Este texto es una colaboración del Cuaderno de Cultura Científica con Next

El artículo Corrimientos, diatomeas y tsunamis se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. La presencia de sales podría hacer que exista una tectónica de placas en Europa
2. Escaneando la Tierra con neutrinos solares
3. Ox Bel Ha, un ecosistema tropical alimentado por metano

Sí, no hay duda, nos encanta Fibonacci… bueno, mejor dicho, nos encanta la sucesión de Fibonacci…

Mi compañero Raúl cambió los conejos por las vacas en su entrada Las vacas de Narayana, la versión hindú de los conejos de Fibonacci, y en Cronología porcina hablé de la sucesión de Vauban que modeliza la reproducción de cerdos y cerdas en lugar de la de los mamíferos de largas orejas.

En esta entrada, cambiamos la reproducción por la poesía, sin abandonar la sucesión de Fibonacci…

Las relaciones numéricas existen en la naturaleza: la forma en la que un puerro se envuelve sobre sí mismo desde el interior, y la parte superior de un girasol, ambas están basadas en estas series.

Inger Christensen

Una de las obras más conocidas de la escritora y poeta danesa Inger Christensen (1935-2009) es Alfabet (1981), un poemario traducido al castellano por Francisco J. Uriz en Alfabeto (Ed. Sexto Piso, edición bilingüe danés-español, 2014).

La editorial presenta el libro del siguiente modo:

‘Alfabeto’ es uno de los libros esenciales de la poesía europea del siglo XX. Hasta hoy era, de forma incomprensible, inédito en nuestra lengua. Es un largo poema cuya forma sigue dos principios de composición. El primero es la secuencia de Fibonacci. Es decir, cada verso es la suma de los dos precedentes: 0, 1, 1, 2, 3, 5, 8, 13… El segundo es el alfabeto. Cada poema, y las palabras que utiliza, sigue el orden de las letras: a, b, c, d, e. Sin embargo, bajo esta forma aparentemente estricta, hay lugar para el azar.

En efecto, el poemario está basado en el alfabeto –cada una de sus catorce series comienza y está dominada por una letra, de la A [albaricoquero] a la N [noche]– y la sucesión de Fibonacci –cada poema posee tantos versos como el término correspondiente de esta sucesión, prescindiendo de los dos primeros–. Además, la división de las estrofas muestra también algunos de los términos de la sucesión de Fibonacci.

Dominan en el poemario los conceptos de existencia y destrucción. La autora enumera, confronta, describe y analiza. Las continuas repeticiones, como si de un eco se tratara, inciden en el encanto de la naturaleza y en los estragos producidos sobre ella por la acción del ser humano.

Estos son los primeros versos de Alfabeto:

1-A
los albaricoqueros existen, los albaricoqueros existen

2-B
los helechos existen; y zarzamoras, zarzamoras
y bromo existen; y el hidrógeno, el hidrógeno

3-C
las cigarras existen; chicoria, cromo
y limoneros existen; las cigarras existen;
cigarras, cedros, cipreses, cerebelo

Las razones del agua (Adeshoras, 2017) es un poemario del escritor Francisco Javier Guerrero (1976), dividido en tres partes –Valle en V, Vega y Estuario– y cuyos versos se estructuran siguiendo los quince primeros términos de la sucesión de Fibonacci.

La editorial presenta el libro del siguiente modo:

‘Las razones del agua’ es un único poema, escrito sin puntuación y sin mayúsculas, dividido en tres partes que aluden al curso de un río: valle, vega y estuario. La unidad, la aspiración totalizadora, ese anhelo por decirlo todo, está presente desde el principio del volumen: “voy a escribir la vida / que yace con nosotros o el lenguaje la ciencia / hoy me voy a morir escribiendo la historia”. Con ese propósito, Francisco Javier Guerrero articula quince secuencias que coinciden con los primeros términos de la sucesión de Fibonacci. Así, la matemática es uno de los ejes vertebradores de esta obra, que gravita también alrededor de reflexiones metapoéticas, el compromiso comunitario y la memoria personal.

La primera parte –Valle– se organiza a partir de los once primeros números de la sucesión, es decir, sus estrofas contienen 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 y 55 versos respectivamente. La segunda parte –Vega– continúa con los tres números 89, 144 y 233 de esta sucesión; ellos dictan la cantidad de versos que constituyen los tres poemas de Vega. Los 377 versos de Estuario son los que cierran el poemario, y nos transportan a una página desplegable que revela una bellísima ilustración de la bióloga y artista Lola Castillo (1971).

La sucesión de Fibonacci no sólo está presente en la estructura del texto. El poeta alude a la manera de construirla, y menciona algunos términos relacionados con ella, como las espirales, los caracoles logarítmicos, la divina proporción, el número phi, los girasoles, etc.

El séptimo poema de Las razones del agua dice así:

8

qué será de nosotros si nos acomodamos

al silencio ovalado de las tumbas abiertas

al dolor de la infancia a la lluvia de otoño

al lapso horizontal que equilibra un presente

convulso y lapidario con su abrasador péndulo

cómo se puede ser siendo solo uno mismo

si somos la delgada nervadura en las hojas

de los espinos blancos su olor y su reflejo

¿Conoces más poemarios en los que la sucesión de Fibonacci sea su ‘hilo conductor’?

Más información:

• Marta Macho Stadler, Inger Christensen: letras abrazando a Fibonacci, Mujeres con ciencia, Ciencia y más, 8 enero 2016

• Marta Macho Stadler, Las razones del agua, de Francisco Javier Guerrero, DivulgaMAT, Literatura y matemáticas, enero 2018

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.

El artículo ¡Nos encanta Fibonacci! se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Los números (y los inversos) de Fibonacci
2. Las vacas de Narayana, la versión hindú de los conejos de Fibonacci
3. La magia del teorema de Zeckendorf

El dióxido de carbono es un producto terminal del metabolismo energético aerobio. Su presencia en los fluidos internos a altas concentraciones altera el pH, por lo que ha de ser eliminado. El CO2 sigue la misma ruta que el O2, aunque en sentido contrario. Pasa de las células a la sangre u otros fluidos internos y de ahí al exterior a través de la pared corporal o del órgano respiratorio.

Sin embargo, el transporte de dióxido de carbono se produce de forma muy diferente a como ocurre el del oxígeno. El CO2 puede hallarse en la sangre (1) en forma disuelta, (2) combinado con proteínas sanguíneas en forma de compuestos carbamino, y (3) combinado químicamente con el agua en forma de ión carbonato o bicarbonato.

Cuando el CO2 se disuelve en disoluciones acuosas experimenta una serie de reacciones:

CO2 + H2O ⇌ H2CO3

H2CO3⇌ H+ + HCO3–

HCO3–⇌ CO32- + H+

En condiciones fisiológicas, el ión carbonato se encuentra en los fluidos de la mayoría de animales en concentraciones muy bajas, por lo que a los efectos que nos interesan aquí podemos limitarnos a la siguiente reacción:

CO2 + H2O ⇌ H+ + HCO3–

La concentración de dióxido de carbono disuelto en una disolución acuosa dependerá, como ocurre con el oxígeno, de su tensión parcial y vendrá determinada por los principios de la solubilidad de los gases. Sin embargo, la concentración de bicarbonato va a depender de la presencia de sustancias tamponadoras (amortiguadoras) del pH.

Aplicando la ley de acción de masas a la ecuación anterior tenemos que [HCO3–] [H+]/[CO2] = K, siendo K una constante.

Dado que [CO2] se mantiene constante, también lo es el producto [CO2] K, por lo que la expresión anterior indica que la concentración del ión bicarbonato ([HCO3–]) dependerá de la concentración de protones ([H+]), de manera que cuanto menor sea esta, mayor será aquella. Por lo tanto, si la concentración de protones se mantiene baja, el bicarbonato podrá alcanzar una concentración relativamente alta. Por esa razón, si en la disolución hay sustancias tamponadoras efectivas, la concentración de protones podrá mantenerse relativamente baja y, en consecuencia, podrá alcanzarse una alta concentración de bicarbonato.

Las reacciones de amortiguación pueden representarse de la siguiente forma: HX ⇌ H+ + X– , donde X– representa a los compuestos o grupos químicos que se combinan con los protones, amortiguando el pH de ese modo. Así, cuando se añaden protones a una solución tamponada, la reacción se desplaza a la izquierda, lo que ayuda a mantener a bajas concentraciones la concentración de H+. Y por otro lado, si se retiran protones de la disolución, la reacción se desplazará hacia la derecha, liberándose aquellos del compuesto HX. Como en el caso anterior, de acuerdo con la ley de acción de masas tenemos que [H+] [X–]/[HX] = K’, siendo K’ otra constante.

Se da la circunstancia de que la efectividad de una reacción amortiguadora es máxima cuando la mitad de los grupos X– están combinados con los H+ y la otra mitad no lo están; en otras palabras, el cambio que sufre el pH al añadir o retirar protones de la disolución es mínimo cuando [HX] = [X–]. Bajo esas condiciones [H+] = K’, por lo que la máxima capacidad tamponadora se produce cuando pH = pK’1. Así pues, si se aplica este principio a una sangre cualquiera, las reacciones de amortiguación relevantes son aquellas cuyos valores de pK’ se encuentran próximos al pH de la sangre.

La sangre de los mamíferos y de la mayor parte de los demás vertebrados es muy eficaz amortiguando el pH porque contiene abundantes grupos tampón, la mayor parte en la hemoglobina. Los grupos con valores adecuados de pK’ son los amino terminales de las proteínas sanguíneas y, sobre todo, los grupos imidazol, que se encuentran allí donde en una estructura proteica haya histidina. Son estos últimos los principales grupos amortiguadores, y son tan efectivos que retiran de la disolución el 99.999% de los protones que se producen. Gracias a ello, la sangre tiene capacidad para captar importantes cantidades de dióxido de carbono, ya que la mayor parte del mismo se encuentra en forma de ión bicarbonato.

También en el caso del CO2, como en el del O2, cabe hablar de curvas de disociación o curvas de equilibrio, aunque la forma y el significado de estas difiere de forma notable de las correspondientes para el oxígeno. Como se ha señalado más arriba, además de la fracción que se combina con el agua para dar iones bicarbonato y protones, la sangre contiene CO2 en forma disuelta y también en forma de compuestos carbamino. A las tensiones parciales de CO2 propias de la sangre arterial y de la sangre venosa, su concentración total (disuelto o en forma de otra especie química) no se aproxima a un valor asintótico máximo como lo hace el O2, sino que mantiene una tendencia creciente.

En las especies cuya sangre experimenta el efecto Bohr, la curva de disociación del CO2 es dependiente del grado de oxigenación de la sangre. A este fenómeno se le denomina efecto Haldane y consiste en una menor afinidad para con el CO2 de la sangre oxigenada que de la desoxigenada. Esto quiere decir que cuando la sangre llega al órgano respiratorio y empieza a captar oxígeno, cede el CO2 con mayor facilidad. Se debe a que la sangre oxigenada tiene menos capacidad amortiguadora que la desoxigenada, razón por la cual, también tiene menos capacidad para contener iones bicarbonato. Como ocurría con la descarga de O2 en los tejidos a causa del efecto Bohr, el efecto Haldane facilita la descarga de CO2 en la sangre que llega a los pulmones, con lo que eleva la capacidad de la sangre para transportarlo.

La conversión de CO2 en bicarbonato en el plasma sanguíneo de los vertebrados es un proceso relativamente lento: se necesita un minuto para alcanzar el equilibrio. Sin embargo, las cosas son muy diferentes en el interior de los eritrocitos, ya que en estos se encuentra la anhidrasa carbónica, enzima que acelera el proceso de forma muy notable.

Así pues, cuando entra el CO2 en la sangre, una pequeña parte se disuelve y otra, mucho más importante, difunde rápidamente al interior de los glóbulos rojos. Allí una fracción se combina con los grupos amino de la hemoglobina para formar carbaminohemoglobina (o carbohemoglobina) y otra fracción se convierte rápidamente en bicarbonato gracias a la acción de la anhidrasa carbónica. Ambos procesos dan lugar a la aparición de protones, que se unen, principalmente, a los grupos imidazol de la misma hemoglobina y de esa forma se amortigua el pH del interior de los glóbulos rojos. El bicarbonato formado en los eritrocitos, por su parte, no se acumula en su interior, ya que es intercambiado por iones cloruro gracias a la acción de una transportador antiporte de membrana. De no producirse tal intercambio, el aumento de su concentración dentro de los glóbulos rojos provocaría una disminución de la velocidad de la reacción catalizada por la anhidrasa carbónica.

Aparte de en los eritrocitos, también hay anhidrasa carbónica en las membranas de las células endoteliales que forman las paredes de los capilares pulmonares y en las membranas de las células musculares esqueléticas en algunos vertebrados. Los protones que resultan de la reacción del CO2 con el agua para dar bicarbonato se combinan con proteínas plasmáticas, lo que permite amortiguar el pH también en el plasma.

Un aspecto muy importante del transporte de CO2 en la sangre es que cada una de las formas en que este se produce contribuye en una medida muy diferente al total. Veamos esto con cierto detalle en la sangre humana2, la más estudiada y, por ello, mejor conocida a estos efectos.

La concentración total de CO2 en la sangre venosa es de 23.21 mmol·l-1 y en la arterial, de 21.53 mmol·l-1, por lo que la descarga total es de 1.68 mmol·l-1. La fracción que se descarga, como puede verse, es muy pequeña, de algo más de un 7% del dióxido de carbono que hay en la sangre venosa.

En el plasma venoso hay 16.99 mmol·l-1, de los que 0.8 se encuentran en forma disuelta y 16.19 en forma de ión bicarbonato; en el plasma arterial, por su parte, la concentración total es de 15.94 mmol·l-1, del que 0.71 se encuentra disuelto y 15.23 como ión bicarbonato. La descarga total es de 1.05 mmol·l-1 (0.09 en forma disuelta y 0.96 en forma de iones bicarbonato), por lo que esta es la principal contribución al transporte de dióxido de carbono, ya que representa el 62.5% de la total. Hay que tener en cuenta, no obstante, que la mayoría de iones bicarbonato se forman en el interior de los eritrocitos por lo que, en última instancia, los glóbulos rojos juegan un papel determinante y muy principal en el proceso.

Los eritrocitos contienen 6.22 mmol·l-1 de CO2 en la sangre venosa y 5.59 mmol·l-1 en la arterial. La descarga de esa fracción es de 0.63 mmol·l-1, un 37.5% del total. Y en lo relativo a las diferentes formas de transporte, se puede precisar que en forma disuelta se transporta una fracción mínima (las concentraciones venosa y arterial son, respectivamente, de 0.39 y 0.34 mmol· l-1), en forma de bicarbonato la descarga es de 0.13 mmol· l-1 (4.41 y 4.28 mmol·l-1 en sangre venosa y arterial, respectivamente), y 0,45 mmol· l-1 en forma de carbohemoglobina, aunque las concentraciones de CO2 en esta forma son realmente bajas (1.42 y 0.97 mmol· l-1). Como puede apreciarse, aunque la concentración de dióxido de carbono en forma de carbaminos es relativamente baja, su contribución al transporte no lo es tanto.

En conclusión cabe señalar que la mayor parte del CO2 se transporta en forma de CO3H–, ya que considerada en conjunto la descarga de esa forma es de 1.09 mmol·l-1, un 65% de la total. En forma de compuestos carbamino se descargan los 0.45 mmol· l-1, un 27% del total. El resto, 0.14 mmol·l-1, se descarga de forma disuelta, pero tan solo representa un 7%. En todo caso, conviene resaltar que el pigmento respiratorio es protagonista principal, tanto de forma directa –por su contribución gracias a la combinación del CO2 con grupos amino y grupos imidazol- como de forma indirecta, por su efecto amortiguador del pH- del transporte del dióxido de carbono.

Fuentes:

Richard W. Hill, Gordon A. Wyse & Margaret Anderson (2004): Animal Physiology. Sinauer Associates, Sunderland.

John D. Jones (1972): Comparative physiology of respiration. Edward Arnold, Edinburgh.

Lauralee Sherwood, Hillar Klandorf & Paul H. Yancey (2005): Animal Physiology: from genes to organisms. Brooks/Cole, Belmont.

Notas:

1pK’ = -log K’

2Las cifras no son muy diferentes para el resto de mamíferos, aves y reptiles. Sin embargo, en peces y anfibios no se forman grupos carbamino porque su hemoglobina se encuentra acetilada y eso impide la combinación con el CO2.

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo Sistemas respiratorios: transporte de dióxido de carbono se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Sistemas respiratorios: los pigmentos respiratorios
2. Sistemas respiratorios: el pulmón de los mamíferos
3. Sistemas respiratorios: la emergencia de un doble sistema circulatorio

La hipótesis que plantea Einstein en sus artículos de 1905 no es solo elegante y simple, es de consecuencias enormes, aunque estas consecuencias fueron tan sorprendentes en su momento como aún lo son hoy cuando se las aborda por primera vez. Tan contraintuitivas son, que todavía hoy son legión los que afirman que Einstein estaba equivocado (el que ello esté relacionado con el antisemitismo de la llamada “física alemana” nazi, es un factor menor, aunque no marginal).

Recopilemos algunos aspectos importantes de lo que hemos visto hasta ahora antes de seguir y veremos que nos falta por tratar algo importantísimo.

Einstein se da cuenta de que existe una inconsistencia en la interpretación habitual de la teoría de Maxwell, y al generalizar las ideas de Galileo sobre el movimiento relativo establece dos postulados generales. De estos dos postulados extrae consecuencias que afectan al estudio de los procedimientos para medir los conceptos más fundamentales de la física (tiempo, longitud, masa, energía); estas consecuencias se extraen de la misma forma en la que se obtienen resultados geométricos a partir de postulados: solo se usa la lógica.

Usando la lógica, pues, llega a la conclusión general de que las mediciones de estas variables pueden ser diferentes para diferentes observadores en movimiento relativo entre sí. Concluye que, mientras que las leyes de la física [1] y la velocidad de la luz son las mismas para todos los observadores, de ahí que Einstein hablase de teoría de la invariancia, los valores de conceptos básicos que entran en las leyes de la física, como el tiempo o la masa, no son los mismos para todos, son relativos con respecto al marco de medición. Es por esto que popularmente se llama teoría de la relatividad; en concreto teoría de la relatividad especial, ya que en esta teoría las velocidades relativas de los observadores deben ser uniformes (sin aceleración), por lo tanto, se aplican únicamente a un caso especial, el de sistemas inerciales.

Pero alguien podría objetar que esto es indiscernible de las discusiones metafísicas sobre el sexo de los ángeles. Cualquiera puede inventar un par de postulados y, siguiendo la lógica, llegar a las conclusiones más absurdas, pero perfectamente consistentes, y afirmar que tiene una teoría revolucionaria [2]. ¿Por qué aceptamos la teoría de Einstein como ciencia? Por tres razones: la primera y principal es por la confirmación experimental; la segunda por su consistencia interna y la tercera porque es coherente con otras teorías bien establecidas.

Esta última frase merece que nos detengamos en ella un poco más, habida cuenta de la cantidad de personas que parecen tener dificultad para distinguir lo que es ciencia de lo que son patrañas evidentes [3], como las “teorías” que niegan a Einstein sin fundamento.

Cada hipótesis científica, ya sea deducida a partir de unos pocos postulados o inducida experimentalmente, debe pasar la prueba rigurosa del examen experimental por varios investigadores, habitualmente de forma reiterada e independiente y a lo largo de un período de tiempo que puede ser largo. De hecho, cuanto más implicaciones tenga la nueva hipótesis, más extensa será la evidencia experimental requerida antes de que pueda ser aceptada.

Debería parecer obvio que, además, la derivación de una nueva hipótesis no puede contener ningún error lógico o violación infundada de leyes y principios aceptados. Y que debe ser compatible con las teorías existentes, o bien debe mostrar convincentemente cómo y por qué estas teorías deben ser revisadas. De hecho, se necesitó más de una década para comprobar la consistencia interna, la coherencia y confirmar experimentalmente las ideas de Einstein.

Lejos de ser “dogmáticos”, como algunos prejuzgan, los científicos siempre son escépticos hasta que la evidencia sea abrumadora. Dicho de otra forma, la falsabilidad bien entendida afirma que toda hipótesis es falsa hasta que se demuestra más allá de toda duda razonable lo contrario [4].

Hemos visto cómo y por qué la física clásica de Newton y Maxwell tuvo que revisarse para su aplicación a fenómenos a altas velocidades relativas. Pero no olvidemos que, a medida que la velocidad relativa disminuye, todos los resultados “extras” de la teoría de la relatividad se desvanecen suavemente hasta dejarnos con la familiar física clásica del mundo cotidiano. La teoría de la relatividad está tan probada que ahora se usa como una herramienta para estudiar teorías relacionadas y para construir nuevos experimentos. La mayoría de estos experimentos involucran partículas subatómicas que se mueven a velocidades extremadamente altas, como los aceleradores de partículas, aunque algunos también son realizables en condiciones más ordinarias. Estos resultados experimentales serán lo próximo que veamos.

Notas:

[1] En puridad, las leyes de la física generalizadas para todos los rangos de energía posibles; las leyes newtonianas son casos particulares de esta generalización.

[2] Esto es mucho más común de lo que se cree. Hay dos grandes tipos de “teorías de esta especie”, la de los revolucionarios incomprendidos (habitualmente de la física), con teorías del todo y grandes soluciones, pero que desarrollan en foros, blogs y webs, y curiosamente nunca en artículos con revisión por pares, y las pseudociencias. Un ejemplo magnífico es la homeoptía: de dos postulados falsos, uno de ellos incompatible con una verdad científica incuestionable, la existencia de los átomos, se desarrolla todo un cuerpo de doctrina que permite que algunos ganen mucho dinero a costa de la salud de otros.

[3] No hablamos aquí del problema de la demarcación, algo mucho más sutil y peliagudo, sino de distinguir lo que es ciencia real de mentiras que deberían ser evidentes.

[4] A este respecto quizás sea interesante leer Provisional y perfectible

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo ¿La teoría de la invariancia es física o metafísica? se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. La teoría de la invariancia
2. Incompletitud y medida en física cuántica (I): la teoría superpositiva
3. El principio de relatividad (y 4): la versión de Einstein

Un ejemplar de “Leucoraja erinacea”, la raya que camina en el fondo del océano

Parece el comienzo de un chiste, ¿verdad? Pero no lo es. Se trata de una pregunta que se han hecho científicos genetistas de la Universidad de Nueva York. ¿En qué se parecen un ratón y un tipo de raya conocida como Leucoraja erinacea?

La primera respuesta que nos viene a la mente es que nada, no se parecen en nada. Uno es un mamífero de sangre caliente, con pelo y bigotes que vive en un laboratorio o como polizón inadvertido en una casa, mientras que el otro es un pez que respira a través de agallas, que repta por el fondo del océano, de un acuario o de la piscina también de un laboratorio.

Y sin embargo, algo tienen en común: la habilidad de caminar, y esto podría cambiar nuestra idea sobre cómo evolucionó esa habilidad en los animales terrestres, un momento considerado como el de cambios adaptativos más radicales en la evolución de los animales terrestres.

Por qué unos nadan y otros caminan

Pero vayamos por partes. Resulta que la capacidad locomotora de la mayoría de los peces se basa en movimientos ondulatorios, mientras que la habilidad de caminar en los animales cuadrúpedos se basa en un patrón locomotor que alterna los lados derecho e izquierdo. Es fácil de entender porque nuestro propio caminar se basa en ese patrón. Ese patrón se corresponde con una huella genética que predispone a los animales a desarrollar esa capacidad.

Siempre se ha considerado que el paso de los movimientos ondulatorios al movimiento alternante derecha-izquierda fue algo lineal y que ocurrió después de que los primeros animales saliesen del océano.

Bien, pues los científicos de la Universidad de Nueva York han descubierto que la Leucoraja erinacea, a diferencia de la mayoría de los peces, posee esa huella genética que le predispone a ese movimiento alternante derecha-izquierda y, según sus conclusiones, esos genes provienen de un ancestro común de las rayas con los primeros tetrápodos y que vivió hace 420 millones de años, mucho antes de que los vertebrados saliesen del mar y caminasen por la tierra.

Es decir, que algunos animales pudieron tener la configuración neurológica necesaria para caminar mucho antes de que saliesen del mar.

Un pez que camina, ¿cómo lo hace?

La investigación comenzó con una pregunta sencilla: ¿cómo ha evolucionado con el tiempo la forma de moverse de distintas especies? El autor del estudio, Jeremy Dasen, profesor asociado del Intituto de Neurociencia de la Universidad de Nueva York, ya había trabajado antes estudiando el movimiento de las serpientes, pero en este caso no sabía por dónde empezar.

Así que hizo lo que haríamos todos: buscar en Google. Buscó vídeos de rayas, y encontró uno en el que una de ellas parecía estar caminando por el fondo del océano. Le pareció muy interesante, y de ahí surgió la primera pregunta: ¿cómo lo hace?

Con ayuda del Laboratorio Biológico Marino de Woods Hole, de la Universidad de Chicago, recogieron unos cuantos ejemplares y comenzaron a observarlos. Comenzaron por lo básico: estas rayas son habitantes del fondo marino que no tienen patas, y por tanto, su caminar no se parece en nada a lo que estamos acostumbrados. Lo que utilizan son unas aletas situadas en la parte anterior de su pelvis, situadas debajo de su gran aleta en forma de rombo, que compone todo el cuerpo y que se ondula cuando nadan.

Normalmente se desplazan nadando, pero cuando comen o quieren moverse más despacio es cuando ponen en marcha ese movimiento aleatorio derecha-izquierda en el que parece, visto desde debajo, que unos diminutos pies impulsan al animal.

Los mecanismos neuronales que nos hacen caminar

Pero a Dasen y su equipo no les interesaba solo la biomecánica del pez, también los genes que controlan los mecanismos neuronales de ese movimiento. Comenzaron estudiando los genes Hox, un grupo de genes con un papel esencial en el desarrollo embrionario y por tanto en que el organismo en cuestión tenga la forma y las partes correctas. Cuando estos genes se silencian o están desordenados, el organismo puede terminar siendo deforme o no salir adelante.

Vistas desde abajo se distinguen las dos aletas pélvicas con las que caminan las rayas

Los científicos analizaron también la transcripción genética del gen FOXP1 que se encuentra en la espina dorsal de los cuadrúpedos y que interviene en la formación de las neuronas motoras que dan pie al movimiento de caminar. Cuando el factor FOXP1 es silenciado en ratones, los animales pierden la habilidad de coordinar los músculos de las piernas y sufren una descoordinación motora severa: no es que no tengan las patas para caminar, es que su cerebro no sabe cómo hacerlo.

Ambos están presentes en las rayas, igual que lo están en los ratones, y se cree que se remontan hasta hace más de 420 millones de años lo cual es sorprendente porque se creía que la habilidad para caminar después de que la vida saliese de los océanos o ocupase firme, y no antes.

“No hay fósiles de neuronas”

“Hay mucha literatura científica sobre la evolución de las extremidades, pero muy poca tiene en cuenta el aspecto neuronal porque es mucho más difícil de estudiar: no hay fósiles de los nervios o las neuronas. Pero hay formas mejores de estudiar la evolución que simplemente mirando estructuras óseas”, explica Dasen a The Smithsonian Magazine.

Efectivamente, otros investigadores han analizado fósiles para aprender más sobre los primeros animales que se arrastraron por la tierra. Uno de ellos fue el Elginerpeton pancheri, uno de los primeros tetrápodos que vivieron fuera del océano hace unos 375 millones de años, o el Acanthostega, otro vertebrado primitivo cuyos fósiles han sido estudiados par aprender sobre el desarrollo de sus extremidades.

Mientras, algunos biólogos han ido uniendo piezas analizando algunos de los peces más extraños que aún viven hoy, la mayoría con líneas ancestrales que se remontan millones de años, como los celacantos, los sarcopterigios o los peces pulmonados (estos también mueven sus aletas pélvicas de forma parecida a caminar).

Los poliptéridos son peces con pulmones además de agallas capaces de caminar cuando se encuentran fuera del agua

Por último, un protagonista en esta búsqueda del eslabón que falta en la cadena de acontecimientos que nos llevó a caminar fuera del agua ha sido el poliptérido, o bichir, una especie de pez africano que tiene pulmones además de agallas y que puede sobrevivir fuera del agua, donde se mueve de forma similar al caminar.

La flexibilidad del sistema nervioso

Ahora, los científicos saben cómo son las rutas neuronales de ese caminar, y lo parecidas que son a las de los animales terrestres, algo que, indican los científicos, es una señal de la flexibilidad del sistema nervioso, de su desarrollo y sus funcionales.

Una flexibilidad que ha sido clave a lo largo de la historia evolutiva de todas las especies: gracias a ese ancestro común que vivió hace 420 millones de años, ahora hay en la Tierra peces que nadan, serpientes que reptan, ratones que caminan y mantas raya que utilizan una combinación única de todos esos movimientos.

Y quizá, ahora que sabemos todo esto, podamos aprender un poco más el bipedismo en nosotros, los humanos.

Referencias:

Heekyung Jung et al (2018) The Ancient Origins of Neural Substrates for Land Walking Cell doi: 10.1016/j.cell.2018.01.013

Lorraine Boissoneault What a walking fish can teach us about human evolution Smithsonian Magazine 08/02/2018
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista

El artículo ¿En qué se parecen un ratón y una manta raya? se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Antes de que el león se hiciese con el trono de rey de la selva
2. Adiós al yeti: las desventuras y tribulaciones de un criptozoólogo
3. Los enigmas que nos cantan desde el fondo del océano

De acuerdo con las conclusiones de un estudio recién publicado por el Pew Research Center [1], el lugar de trabajo de las mujeres que desempeñan profesiones relacionadas con ciencia, tecnología, ingeniería o matemáticas (agrupadas bajo el acrónimo STEM) es un entorno diferente, en ocasiones más hostil, que el de sus compañeros masculinos. Perciben con más frecuencia discriminación y acoso sexual [2], y piensan que el ser mujer representa más una desventaja que una ventaja para el éxito de sus carreras.

Entre todas las que trabajan en estas áreas, la probabilidad de que declaren haber sido tratadas peor es mayor en tres grupos de mujeres: las que trabajan en entornos en los que la mayoría de compañeros son hombres, las que trabajan en tareas relacionadas con ordenadores y las que tienen estudios de posgrado.

El estudio aporta información adicional acerca de la distribución de hombres y mujeres en las 74 ocupaciones clasificadas dentro de la categoría STEM, con un desequilibrio a favor de las mujeres en el campo de la salud (75% mujeres) y a favor de los hombres en física (39% mujeres), informática y ordenadores (25%) e ingeniería (14%). Hay un cierto equilibrio en matemáticas (47%) y ciencias de la vida (48%); en conjunto, el 50% de los puestos de trabajo está ocupado por mujeres. Estos y los anteriores datos corresponden a los Estados Unidos aunque lo más probable es que sus principales conclusiones sean válidas para el conjunto de países occidentales.

Si nos limitamos al mundo de la investigación y la academia, las investigadoras representan el 32 % del total en los países occidentales (Europa Occidental y Norteamérica), aunque en España ese porcentaje llega al 39 %. En nuestro entorno el porcentaje de mujeres en los estudios de grado y entre quienes completan el doctorado es algo superior al de hombres, y en algunos casos, como ocurre en la UPV/EHU, acceden al doctorado más mujeres (58%) que hombres (42%) en disciplinas STEM. Sin embargo, tal y como han mostrado diversos estudios, conforme se asciende en el escalafón y, sobre todo, en los niveles de máxima responsabilidad, autoridad y reconocimiento, las proporciones de mujeres se desploman hasta valores de entre el 10% y el 25%, dependiendo de la instancia y sector de que se trate. Los informes al respecto del CSIC, MICINN y Comisión Europea (She Figures 2015) aportan abundante y pormenorizada información.

Las tendencias que apuntan esos informes tienen su reflejo más depurado en la proporción de mujeres a las que se conceden los máximos galardones en sus respectivas disciplinas y, muy en especial, a las que se ha concedido el premio Nobel. Desde su creación, solo el 3% de estos premios ha sido otorgado a mujeres. Suele argumentarse, para justificar ese bajo porcentaje, que refleja la presencia de las mujeres en el mundo de la investigación científica desde que existen esos galardones. Es indudable que cuanto menos son los miembros de un colectivo a segmento de la población que desempeñan una actividad, menos son quienes alcanzan los niveles más altos. Pero si nos fijamos en la última década, se han concedido a mujeres el 6,5 % de los galardones. Y si bien es cierto que los méritos que se reconocen pueden datar de décadas atrás, es más que dudoso que las mujeres solo hayan representado el 6,5 % de quienes se dedicaron a la ciencia al más alto nivel durante el último cuarto del siglo XX. Y de haber sido así, tal desequilibrio sería, en buena medida, consecuencia de otros desequilibrios relacionados con las diferentes oportunidades de hombres y mujeres para acceder a los recursos y las posiciones que facultan para desempeñar una carrera científica al más alto nivel [3].

Los límites a la presencia de las mujeres en las posiciones de más alto rango en las carreras científica y profesional son, de suyo, injustos y tienen, además, dos consecuencias perniciosas. Por un lado, privan al sistema científico y a la sociedad en general de la aportación de las mujeres más capacitadas al bien común. Y por la otra, contribuyen a alimentar los estereotipos que muestran a las profesiones científicas y tecnológicas como inadecuadas o impropias de las mujeres, con las consecuencias amplificadoras que tales estereotipos tienen (el círculo vicioso).

La Universidad del País Vasco está comprometida con el objetivo de una sociedad en la que hombres y mujeres tengan los mismos derechos y gocen de las mismas oportunidades. La Cátedra de Cultura Científica de la UPV/EHU comparte ese compromiso y se ha propuesto, en la medida de sus modestas posibilidades, contribuir a cambiar ese estado de cosas. Por esa razón publica desde el 8 de mayo de 2014 Mujeres con ciencia.

Pero hoy, 11 de Febrero, no hemos querido quedar al margen de la celebración internacional, promovida por Naciones Unidas del Día Internacional de la Mujer y la Niña en la Ciencia. Con ese propósito hemos producido “No es una percepción“, el vídeo que acompaña este texto. Quiere ser un gesto de denuncia y, en consecuencia, una llamada a la acción y, sobre todo, al trabajo. Por eso, para la Cátedra de Cultura Científica de la UPV/EHU mañana, como ayer, también será día de la mujer y la niña en la ciencia.

“No es una percepción” es una producción dirigida por Jose A. Pérez Ledo y grabada en la Universidad del País Vasco gracias a la colaboración de cinco científicas e investigadoras de la propia universidad:

• Itziar Alkorta, bioquímica.
• Arantza Aranburu, geóloga.
• Gotzone Barandika, química.
• Txelo Ruiz, ingeniera informática.
• Ana Zubiaga, genetista.

Notas:

[1] Pew Research Center es un prestigioso think tank estadounidense especializado en el estudio de tendencias sociales y demográficas.

[2] Aunque los resultados del trabajo se publicaron el pasado 9 de enero, el trabajo de campo se realizó en el verano de 2017, antes de que se produjese la ola de denuncias por acoso sexual contra personajes masculinos prominentes de diferentes sectores profesionales.

[3] El caso de Jennifer y John es un ejemplo ilustrativo de los desequilibrios mencionados.

—————————————————————–

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

————————

El artículo No es una percepción se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Presentación del estudio “Percepción social de la ciencia y la tecnología en el País Vasco”
2. Hoy es el día de la mujer y la niña en la ciencia, todos lo son
3. La percepción del propio peso es peor en las chicas que en los chicos

En #Naukas17 nadie tuvo que hacer cola desde el día anterior para poder conseguir asiento. Ni nadie se quedó fuera… 2017 fue el año de la mudanza al gran Auditorium del Palacio Euskalduna, con más de 2000 plazas. Los días 15 y 16 de septiembre la gente lo llenó para un maratón de ciencia y humor.

Raúl Gay habla de discapacidad desde una perspectiva muy diferente a la habitual: llamando a las cosas por su nombre. Posiblemente, una de las charlas más memorables de esta edición de Naukas Bilbao.

Raúl Gay: Todo sobre mi órtesis

Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Naukas Bilbao 2017 – Raúl Gay: Todo sobre mi órtesis se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Naukas Bilbao 2017 – José Miguel Viñas: Me río yo del cambio climático
2. Naukas Bilbao 2017 – Mónica Lalanda: Una muerte de cómic
3. Naukas Bilbao 2017 – Diana González: Identidad digital y robots

La mayoría de los sistemas de aprendizaje automático requieren supervisión humana, y la traducción automática no es una excepción: el ordenador utiliza millones de traducciones hechas por personas para extraer patrones y, de esta forma, aprender a traducir cualquier texto. Este método funciona bien con pares de idiomas como el inglés y el francés, pues existen muchas traducciones entre ambos. Sin embargo, no es tan efectivo para la gran mayoría de pares de idiomas con recursos limitados, como es el caso del alemán-ruso o el euskera-inglés, por ejemplo.

En este contexto, Mikel Artetxe, Eneko Agirre y Gorka Labaka, investigadores del grupo IXA de la Facultad de Informática de la UPV/EHU, han desarrollado un método de traducción automática basado en el aprendizaje sin supervisión, es decir, sin necesidad de diccionarios o traducciones humanas.

“Imagina que le das a una persona una gran cantidad de libros escritos en chino y otros tantos, distintos, en árabe, con el objetivo de que aprenda a traducir del chino al árabe. A priori parece una tarea imposible para un ser humano. Pero nosotros hemos demostrado que un ordenador es capaz de hacerlo”, afirma Mikel Artetxe, que está realizando su tesis doctoral sobre el procesamiento del lenguaje natural y el aprendizaje automático.

Este nuevo método que proponen los investigadores de la UPV/EHU supone un gran avance en el campo de la traducción automática, ya que abre una nueva línea de trabajo que muestra que las redes neuronales, algoritmos informáticos que se inspiran en el cerebro humano, pueden aprender a traducir sin necesidad de traducciones preexistentes.

Se da la casualidad que otro estudio, desarrollado por un equipo de investigadores de Facebook y la Universidad de la Sorbona de París, ha propuesto un método similar. “Es sorprendente -subraya Artetxe- que nuestros métodos sean tan parecidos. Pero al mismo tiempo es positivo, pues significa que esta nueva aproximación va por el buen camino”.

Los dos estudios, de los que se ha hecho eco la revista científica Science en su sección digital de noticias, fueron publicados en el repositorio virtual arXiv con un día de diferencia, y serán presentados en uno de los congresos más relevantes del área, el sexto encuentro internacional sobre el aprendizaje de representaciones (International Conference on Learning Representations – ICLR), que se celebrará en el mes de abril en Vancouver, Canadá.

En los únicos resultados comparables entre ambos estudios, el método del grupo IXA de la UPV/EHU obtuvo resultados ligeramente superiores, con una puntuación BLEU del 15% entre el francés y el inglés. A modo de comparativa, la máxima puntuación la obtienen métodos supervisados como Google Translate con cerca del 40%, si bien una persona supera el 50%. “Estamos en los inicios -aclara Mikel Artetxe- por lo que no sabemos hasta dónde puede llegar esta nueva línea de investigación”.

Referencia:

Mikel Artetxe, Gorka Labaka, Eneko Agirre, Kyunghyun Cho (2017) Unsupervised Neural Machine Translation arXiv:1710.11041

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo Traducción automática neuronal sin supervisión se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Buscando la traducción automática perfecta
2. Chatbots de traducción automática profunda
3. La hiperactividad neuronal impide que las microglías realicen su trabajo

Mary Temple Grandin

En los años sesenta, Leo Kanner (uno de los dos primeros descubridores del autismo) defendía su teoría de las “madres nevera/refrigerador”. En ella argumentaba que el autismo de los hijos era consecuencia de la falta de contacto materno adecuado: afirmaba que estas madres de hijos autistas eran distantes, poco afectivas con sus hijos y llegó incluso a decir que esas mujeres se habían “descongelado” lo justo para dar a luz a un hijo. Según Kanner, si una mujer tenía un hijo autista era porque ella había hecho algo mal. Esta idea falsa que directamente culpabilizaba a las madres tuvo un importante calado e incluso hoy en día es posible encontrar personas que argumentan que el origen de los trastornos del espectro autista (TDA) se deben a la educación, traumas, etc. Lo cual significa que hay gente que cree que los TDA son algo adquirido. Mientras que el enfoque opuesto es pensar que los TDA son trastornos del desarrollo: es decir, que su origen está en alteraciones internas producidas durante el propio desarrollo del individuo.

Antes de ver cuál de estos dos planteamientos es el correcto, creo que es importante aclarar qué es exactamente el autismo. Lo primero que debemos saber es que no existe “el autismo” sino los trastornos del espectro autista (TDA), dentro de los cuales hay una gran diversidad. Esto ya se ve en los dos primeros estudios donde se documentan estos trastornos: el trabajo de Leo Kanner (1943) describe niños que mayoritariamente tienen muchas dificultades para hablar y discapacidad intelectual, mientras que en el estudio de Hans Asperger (1944) los niños tienen un uso preciso del lenguaje y no presentan discapacidad intelectual. Hablo de niños porque los TDA afectan principalmente a varones en una proporción que va desde 4 a 1, hasta 8 niños por cada niña según el tipo de TDA. Independientemente del género, algunas de las características principales de los trastornos del espectro autista son problemas en el uso del lenguaje o habilidades sociales. Además, junto con el propio trastorno los pacientes suelen padecer algún tipo de discapacidad intelectual en más de la mitad de los casos o epilepsia (alrededor del 30% de los casos); entre otros problemas.

La primera pista sobre el origen de estos trastornos la tenemos en el incremento de los casos en las últimas décadas, que ahora se sitúa en cerca del 1% de la población y es un porcentaje superior al documentado con anterioridad. Esta subida se debe principalmente a tres motivos: el primero es una mejora de las técnicas diagnósticas que permiten detectar más casos, el segundo es un cambio en lo que entendemos por TDA hacia una definición clínica más amplia que recoge casos que antes no se consideraban TDA, y el tercer motivo es un incremento de la edad a la que las parejas conciben hijos. Aquí está la pista. Muchos estudios están documentando que cuanto más mayores son los progenitores a la hora de concebir un hijo (y en muchos de ellos se señala que es especialmente importante la edad del padre), más probable es que su descendencia tenga un TDA. ¿Por qué? Porque conforme envejecemos nuestra capacidad de generar células reproductoras es peor y los genes que trasmitimos a través de ellas contienen más fallos. Esto indica que los problemas genéticos tienen un papel importante en el desarrollo del TDA, y eso es algo que también se ve si uno estudia árboles genealógicos o trabajos donde se ha documentado casos de gemelos. En ellos se ha visto que si uno de ellos desarrolla un TDA, en el 60-90% de los casos el otro hermano también desarrollará un TDA.

Que la genética tenga un factor decisivo en la aparición de TDA no es suficiente para definirlo como un trastorno que se produce durante el desarrollo del organismo: para ello es esencial ver cuándo aparece el TDA. Los seres humanos nacemos extremadamente poco desarrollados, siendo además el cerebro el tejido más inmaduro y tarda unas dos décadas en acabar de formarse. Trastornos neurológicos que se manifiesten dentro de este espacio de tiempo pueden deberse en parte a anomalías del desarrollo, y cuanto más pronto aparezcan pues es más probable que el desarrollo nervioso esté implicado en su aparición. En el caso de los TDA, los diagnósticos tempranos se sitúan entorno a los dos/tres años de edad. Lo cual ya es muy temprano pero es que además, en estudios con bebés de seis meses ha sido posible analizar el funcionamiento de sus redes neuronales a los seis, doce y veinticuatro meses; encontrándose que aquellos pequeños que a los veinticuatro meses eran diagnosticados con un TDA, a los seis meses ya presentaban alteraciones en el funcionamiento de sus redes neuronales. Y además, se ha hallado una correlación entre la severidad de estas anomalías a los seis meses y la gravedad de los síntomas a los veinticuatro meses.

En resumen, todo esto nos dice que los TDA son intrínsecos a la propia formación del sistema nervioso del paciente y por lo tanto es parte de ellos mismos. No es algo que se adquiera después de nacer sino que se manifiesta después de nacer. Se nace siendo autista. Esto es importante por dos aspectos: en primer lugar para no culpar al entorno, la familia, el calendario de las vacunas infantiles, etc. de los casos que aparezcan. Y en segundo lugar es vital para el tratamiento: actualmente la única posibilidad para intentar mitigar los síntomas del TDA es diagnosticar y tratar a los pacientes cuanto antes, porque los procesos del desarrollo son mayoritariamente irreversibles pero durante las fases iniciales a veces hay un cierto margen para dirigirlos parcialmente en otra dirección.

Este post ha sido realizado por Pablo Barrecheguren (@pjbarrecheguren) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.

Referencias:

• Constantino, J. N., & Marrus, N. (2017). The Early Origins of Autism. Child and Adolescent Psychiatric Clinics of North America, 26(3), 555–570.
• John D. Lewis*, Alan C. Evans, John R. Pruett Jr, Kelly N. Botteron, Robert C. McKinstry, Lonnie Zwaigenbaum, Annette Estes, Louis Collins, Penelope Kostopoulos, Guido Gerig, Stephen Dager, Sarah Paterson, Robert T. Schultz, Martin Styner, Heather Hazlett, and Joseph Piven, for the IBIS network. (2017). The emergence of network inefficiencies in infants with autism spectrum disorder. Biol Psychiatry. 2017 August 01; 82(3): 176–185.
• Principles of Neural Science, Fifth Edition (2012). Editorial McGraw-Hill Education.
• Swaab D. We are our brains (2014). Penguin Books.

El artículo Nacido para ser autista se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El universo recién nacido
2. Luminoterapia para el cambio de estación
3. ¿Cuántos animales se usan en España para experimentación?

¿Cómo se tratan algunos de los trastornos cognitivos más frecuentes en las aulas? ¿Son efectivos los programas y herramientas del sistema educativo actual? ¿Carecen de eficacia algunas de las prácticas educativas más populares?

Estas son algunas de las cuestiones que se debatieron en la jornada “Las pruebas de la educación”, que se celebró el pasado 2 de febrero de 2018 en el Bizkaia Aretoa de Bilbao. El evento, en su segunda edición, estuvo organizado por la Cátedra de Cultura Científica de la UPV/EHU y el Consejo Escolar de Euskadi, con la colaboración de la Fundación Española para la Ciencia y la Tecnología (FECYT).

Las ponencias de los expertos que expusieron múltiples cuestiones relacionadas con la educación, basándose siempre en las pruebas científicas existentes. Los especialistas hicieron especial hincapié en destacar cuál es la mejor evidencia disponible a día de hoy con el objetivo de abordar las diferentes realidades que coexisten en las aulas y en el sistema educativo en general.

“Las pruebas de la educación” forma parte de una serie de eventos organizados por la Cátedra de Cultura Científica de la UPV/EHU para abordar cuestiones del día a día como la educación o el arte desde diversos ámbitos de la actividad científica. La dirección del seminario corre a cargo de la doctora en psicología Marta Ferrero.

En “Autismo y educación: Problemas y pautas en el aula”, José Ramón Alonso, neurobiólogo y catedrático de biología celular en la Universidad de Salamanca, nos acerca al concepto del autismo, sus posibles causas y los tratamientos más empleados, con el objetivo de identificar las pautas concretas que pueden ayudar a maestros y profesores a tratar en el aula este trastorno cognitivo.

José Ramón Alonso: ''Autismo y educación: Problemas y pautas en el aula''

Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Autismo y educación: problemas y pautas en el aula se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Las ideas erróneas sobre educación entre el profesorado: prevalencia, causas y soluciones
2. La ciencia perdida: los curiosos casos de los protocolos de TDAH y de leer.es
3. Del mito al hecho: hemisferios, gimnasia cerebral y estilos de aprendizaje

Muchos de los fármacos que conocemos son compuestos muy complejos. Esto quiere decir que están formados por muchos átomos unidos entre sí de una manera concreta. Hacer que estos átomos se unan de una forma y no de otra es una tarea complicada. Al estudio de estos procesos de ensamblaje de átomos se le llama «síntesis química».

Los átomos no se comportan como piezas de Lego. No siempre podemos ensamblarlos y desensamblarlos a nuestro antojo, ya que unos átomos tienen más afinidad por unos que por otros, tienen tendencia a colocarse en unas posiciones y no en otras, a girarse, etc. Por eso es tan importante diseñar una buena ruta de síntesis, en la que cada átomo acabe ocupando la posición deseada.

Uno de los átomos más famosos de los fármacos es el carbono. El carbono está presente en casi todos los fármacos que conocemos. Es capaz de unirse a otros átomos de forma muy diferente. El carbono es como una pieza de Lego con cuatro posiciones de ensamblaje. Desgraciadamente es muy difícil conseguir una pieza solitaria de este carbono. En la naturaleza siempre está unido a más piezas y, en el caso de tener alguna posición libre (formando lo que denominamos radicales libres) son muy inestables y enseguida encuentran a quién unirse.

Esto ha sido un quebradero de cabeza para los químicos que trabajan en síntesis. Al menos hasta ahora. Recientemente, un grupo de investigadores del Instituto Catalán de Investigación Química (ICIQ), liderado por el joven químico Marcos García Suero, acaba de encontrar un método revolucionario que permite conseguir la ansiada pieza solitaria de carbono. Esta pieza sólo tiene una de sus posiciones ocupadas por hidrógeno, el resto están listas para ensamblarse a los átomos que deseemos. Esta pieza se denomina carbino.

El carbino fue una de las primeras moléculas halladas en el espacio interestelar. Los astrofísicos lo detectaron en los años 30 del siglo pasado. Estos carbinos se detectan en eventos astonómicos muy energéticos y violentos, como en la formación de estrellas. Duran muy poco como carbinos porque tienen esa tendencia a unirse rápidamente a otros átomos. Esto es lo que los hace tan escurridizos.

Lo que han hecho los investigadores del ICIQ es sintetizar un equivalente de los carbinos. Este equivalente se llama radical diazometilo. Si seguimos con la analogía de las piezas de Lego, el radical diazometilo sería como una pieza de carbino con sus posiciones ocupadas por piezas de quita y pon, fáciles de intercambiar por piezas definitivas.

Tanto el hallazgo de este carbino equivalente, como la forma de sintetizarlo, ha llevado a estos investigadores a publicar su descubrimiento en la prestigiosa revista científica Nature. Su artículo lleva por título «Generación de carbinos equivalentes por medio de catálisis fotorredox». Para obtener carbino en el laboratorio no se pueden emular los violentos eventos astronómicos. Lo que han hecho estos investigadores es darle un empujón a la reacción de obtención de estos carbinos ayudándose de catalizadores. Los catalizadores que utilizaron son unos compuestos con rutenio sensibles a la luz, de ahí el prefijo foto de catálisis fotorredox. El catalizador, al recibir un fotón de luz LED, da el pistoletazo de salida para que se forme el carbino. Los procesos de fotocatálisis son, de hecho, una de las líneas de investigación más importantes del ICIQ.

Estos investigadores han probado la eficacia del carbino para modificar a antojo algunos medicamentos ya existentes. Así, han modificado con éxito el principio activo del ibuprofeno, del antidepresivo duloxetina, del antitumoral taxol, y del fingolimod, el primer tratamiento oral que existe para la esclerosis múltiple.

Este carbino no solo se podrá usar para mejorar los fármacos que ya conocemos, sino que podrá ayudar a acelerar el diseño y desarrollo de nuevos medicamentos. Si la química del desarrollo de fármacos fuese como jugar a Lego, la pieza más guay se llamaría carbino.

Agradezco a Fernando Gomollón Bel su ayuda con este artículo.

Sobre la autora: Déborah García Bello es química y divulgadora científica

El artículo Si hacer fármacos fuese como jugar a Lego, la pieza más guay se llamaría carbino se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Cómo mecanizar una pieza de cobre usando bacterias
2. Otra pieza en el puzle de la fotosíntesis
3. Cómo hacer más eficiente un mini aerogenerador

Nanoestrellas de óxido de vanadio (IV)

Primero vino el interruptor. Luego el transistor. Ahora otra innovación puede revolucionar la forma en que controlamos el flujo de electrones a través de un circuito: el óxido de vanadio (IV), de fórmula VO2. Una característica clave de este compuesto es que se comporta como un aislante a temperatura ambiente, pero como un conductor a temperaturas superiores a 68 °C. Este comportamiento, también conocido como transición de aislante de metal, podría ser muy útil para una variedad de aplicaciones nuevas y emocionantes.

Los científicos conocen desde hace mucho tiempo las propiedades electrónicas del VO2, pero no han podido explicarlas hasta ahora. Resulta que su estructura atómica cambia de fase a medida que aumenta la temperatura, pasando de una estructura cristalina a temperatura ambiente a una metálica, a temperaturas superiores a 68 ° C.

Lo verdaderamente interesante es que esta transición ocurre en menos de un nanosegundo, algo que lo hace muy útil para aplicaciones electrónicas. No solo eso, además de a la temperatura, resulta que el VO2 también es sensible a otros factores que podrían hacer que cambie de fase, como la inyección de energía eléctrica, determinadas iluminaciones, o la aplicación de un pulso de radiación de terahercios (en el límite entre microondas e infrarrojo). Todo ello implica que el consumo energético del interruptor es minúsculo.

Contrariamente a lo que podamos suponer, 68ºC es una temperatura de transición demasiado baja para la electrónica de los dispositivos actuales, donde los circuitos funcionan sin problemas a unos 100 ºC. Una solución a este problema la propusieron investigadores de la Escuela Politécnica Federal de Lausana (Suiza) en julio de 2017 que consistía en añadir germanio a una lamina de VO2. Simplemnete con esto la transición pasaba a ocurrir a 100 ºC.

Un chip basado en dióxido de vanadio (IV) fabricado en la Escuela Politécnica Federal de Lausana. Imagen: EPFL / Jamani Caillet

Solucionado este problema, investigadores del mismo grupo suizo, que incluye a la ingeniera española Montserrat Fernández-Bolaños, han sido capaces de fabricar por primera vez filtros de frecuencia modulables ultracompactos. Esta tecnología hace uso de las características de interruptor por cambio de fase del VO2 y es especialmente eficaz en un rango de frecuencias que es crucial para las comunicaciones espaciales, la llamada banda Ka. Esta banda es la que se emplea, por ejemplo, para la descarga de datos científicos del telescopio espacial Kepler y es la que se usará en telescopio espacial James Webb. Los filtros pueden programarse para modular entre los 28,2 y los 35 GHz.

Estos primeros resultados es muy posible que estimulen la investigación de las aplicaciones del VO2 en dispositivos electrónicos de potencia ultrabaja. Además de las comunicaciones espaciales que mencionábamos, otras posibilidades podrían ser la computación neuromórfica (computación basada en circuitos analógicos que simulan estructuras neurobiológicas) y los radares de alta frecuencia para automóviles autónomos.

Referencia:

E. A. Casu , A. A. Müller, M. Fernández-Bolaños et al (2018) Vanadium Oxide bandstop tunable filter for Ka frequency bands based on a novel reconfigurable spiral shape defected ground plane CPW IEEE Access doi: 10.1109/ACCESS.2018.2795463

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

Este texto es una colaboración del Cuaderno de Cultura Científica con Next

El artículo Óxido de vanadio (IV), un material para una revolución de ciencia ficción se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Siligrafeno, ¿el material para la revolución optoelectrónica?
2. Un equipo de alta fidelidad de ciencia ficción
3. Ciencia para todos a través del cine y la literatura de ciencia ficción

En octubre de 2002, el compositor minimalista norteamericano Tom Johnson visitó la Universidad del País Vasco/Euskal Herriko Unibertsitatea. Durante dicha visita Tom Johnson ofreció dos interesantes seminarios sobre su forma de componer utilizando las matemáticas y se organizaron algunos conciertos. Una de las composiciones musicales que tuve el placer de escuchar entonces fue Las vacas de Narayana (1989), interpretada por los miembros del grupo Kuraia Ensemble (Asociación de Música Contemporánea del País Vasco), Andrea Cazzaniga (violín), Rafael Climent (clarinete) e Iñigo Ibaibarriaga (saxofón).

El compositor minimalista norteamericano Tom Johnson preparando el instrumento para ejecutar la obra “Galileo” (2001), que estrenó en la Facultad de BBAA de la UPV/EHU en 2002

Para componer la obra Las vacas de Narayama, Tom Johnson se basó en el problema homónimo propuesto por el matemático indio Narayana Pandita (1340-1400) en su tratado de aritmética Ganita Kaumudi (1356). Una de las cuestiones estudiadas por Narayana Pandita en esta obra fueron las sucesiones que él llamó “aditivas”, entre las que se encuentra la que nosotros conocemos como sucesión de Fibonacci.

El problema de las vacas de Narayana dice lo siguiente:

Si las vacas tienen una cría cada año, y cada ternera, después de los tres años que necesita para convertirse en una vaca madura, tiene una cría a principio de cada año, ¿cuántas vacas habrá después de 20 años a partir de una primera ternera?

El proyecto artístico “CowParade” es un proyecto internacional que se ha desarrollado en muchas ciudades del mundo, entre ellas Bilbao, Barcelona o Madrid. La vaca “cowculus” fue exhibida en Kansas city (EE.UU.)

Si empezamos con una ternera recién nacida, a principios de año, durante los tres primeros años solamente tendremos una (1) vaca, esa primera ternera. El cuarto año empezará realmente a crecer la población bovina, con la vaca inicial y su primera ternera, luego dos (2) vacas en total. Habrá una ternera más al principio de cada uno de los dos siguientes años, luego tres (3) el quinto año y cuatro (4) el sexto. Al inicio del séptimo, la primera ternera nacida de la vaca original ya puede tener también terneras, por lo que ese año habrá dos vacas adultas y cuatro terneras, en total, seis (6) vacas. El siguiente año una nueva ternera pasa a la madurez y tres vacas tienen una ternera cada una, luego en total hay tres vacas maduras y seis terneras, luego nueve (9) vacas. Al inicio del noveno año, habrá trece (13) vacas, cuatro adultas y nueve terneras. En el siguiente gráfico hemos representado la evolución de vacas en esos nueve primeros años.

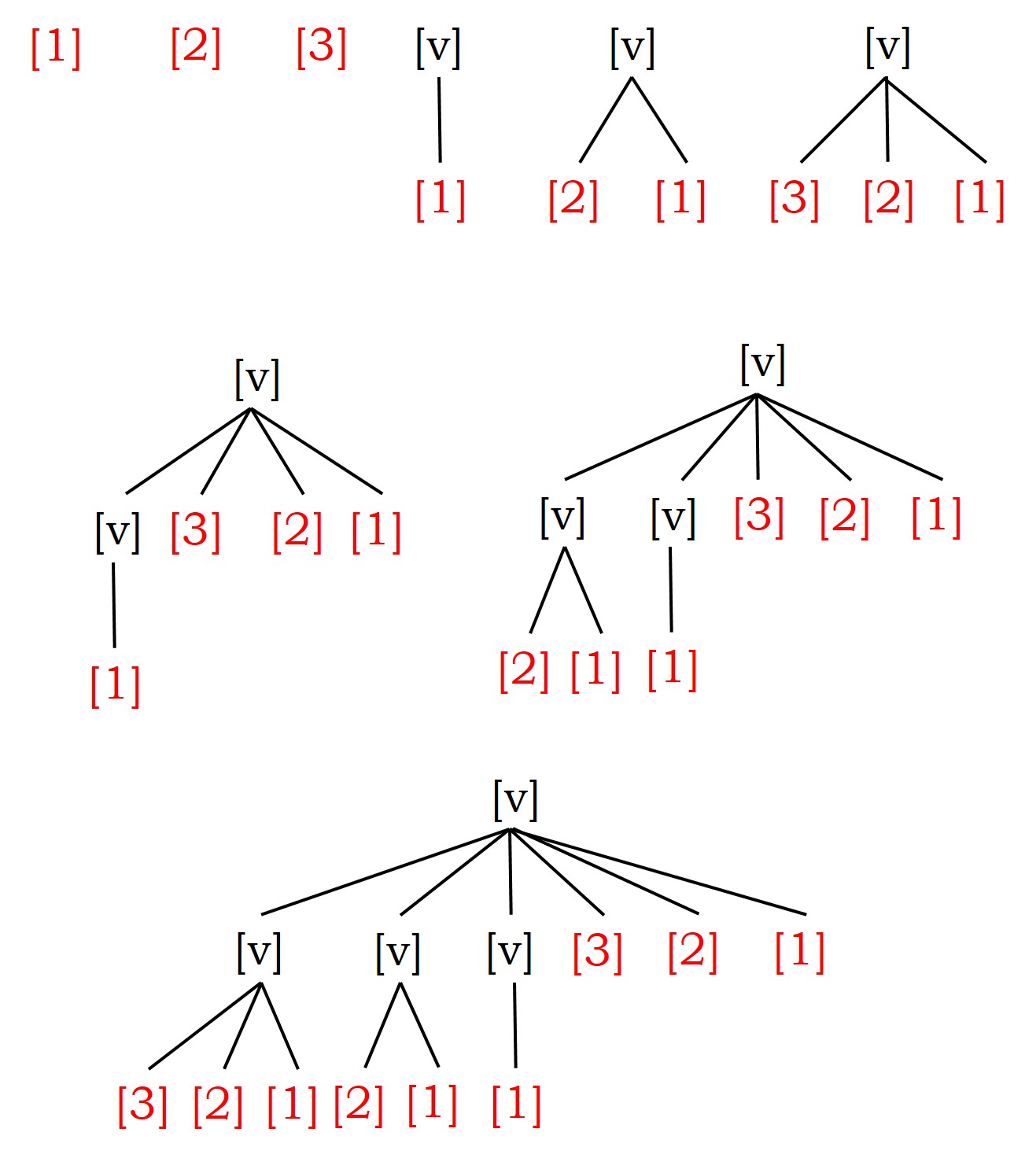
Gráfico del problema de las vacas de Narayana en los nueve primeros años

Pero continuemos… ¿cuántas vacas habrá el décimo año? Estarán las que ya estaban el año anterior, es decir, trece (13) vacas, más las terneras de las vacas que ese año pueden tener crías, que son exactamente las vacas que había hace tres años, seis (6) vacas, en total, diecinueve (13 + 6 = 19) vacas. Como se ve en el siguiente gráfico, seis son vacas maduras y trece son terneras, pero también podemos numerarlas por generaciones, la vaca original es la primera generación, hay siete vacas de la segunda generación, diez de la tercera y una de la cuarta.

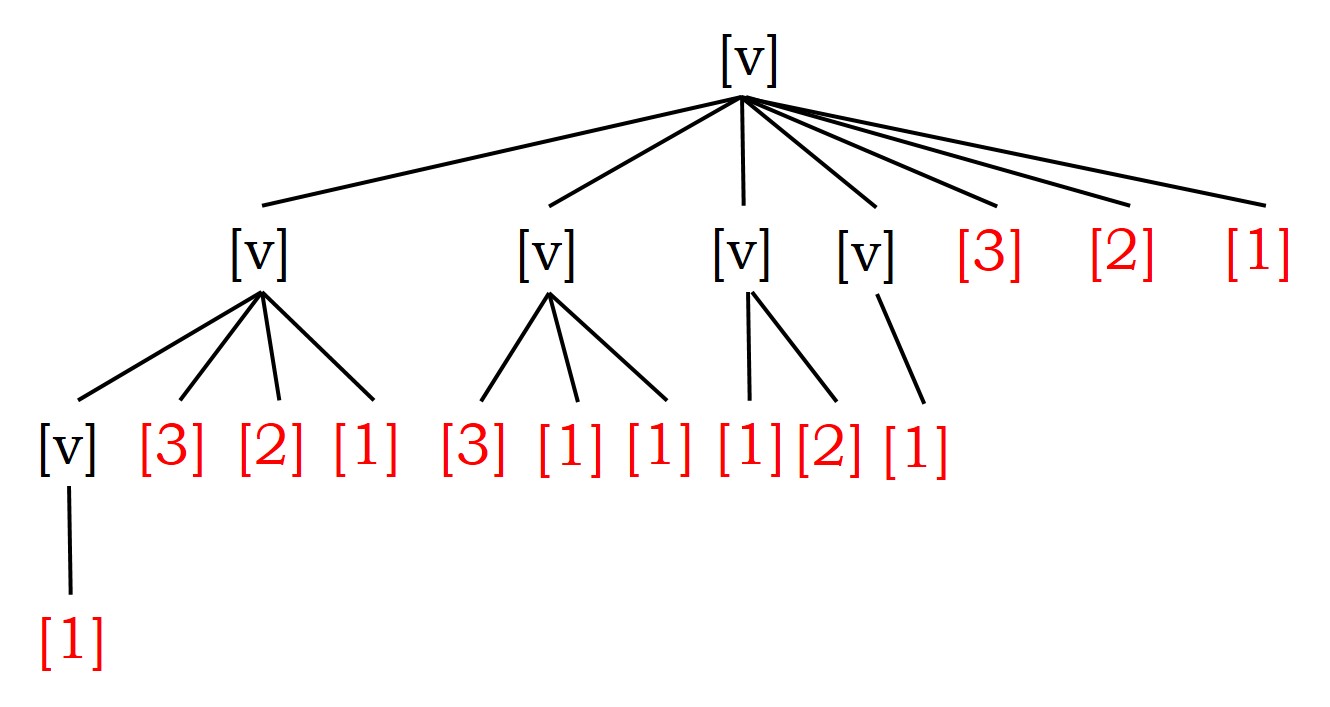
Gráfico del problema de las vacas de Narayana en el décimo año

El razonamiento que hemos realizado para obtener el número de vacas al inicio del décimo año es, de hecho, general y realmente nos da una fórmula recursiva para resolver el problema de las vacas de Narayana. Si se denota por v(n) el número de vacas que habrá en el año n, entonces

v(n) = v(n – 1) + v(n – 3),

siendo además, v(1) = v(2) = v(3) = 1.

Por lo tanto, se pueden obtener fácilmente los primeros veinte números de la sucesión de vacas de Narayana,

1, 1, 1, 2, 3, 4, 6, 9, 13, 19, 28, 41, 60, 88, 129, 189, 277, 406, 595, 872, …

Luego, después de veinte años, es decir, al inicio del año veintiuno, habrá 406 + 872 =1.278 vacas.

Incluso, podemos hacer una tabla de la sucesión de vacas de Narayana, viendo las vacas que hay de cada generación.

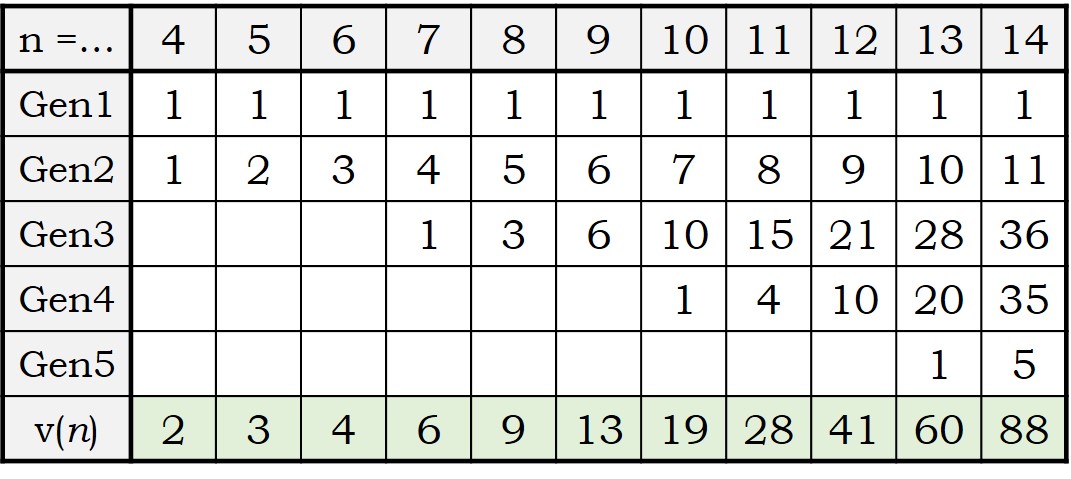
Observando esta tabla con los primeros años ya podemos extraer algunas curiosas conclusiones. Por ejemplo, el número de vacas de la segunda generación son los números naturales, puesto que son las vacas que van naciendo de la vaca original, y cada año tiene una nueva ternera, luego cada año una más, 1, 2, 3, 4, 5, …

En la tercera generación se obtienen los números triangulares, ya que son las sumas de los primeros números naturales, puesto que son las vacas descendientes de las de la generación anterior. Por ejemplo, en el décimo año hemos visto que el número de vacas de la segunda generación eran 1 + 2 + 3 + 4 = 10. Recordemos que los números triangulares T(n), que se llaman así puesto que son los que se obtienen al colocar piedras o discos circulares formando un triángulo equilátero (como se ve en la imagen siguiente), son aquellos que son la suma de los primeros números naturales, T(n) = 1 + 2 + 3 + … + (n – 1) + n.

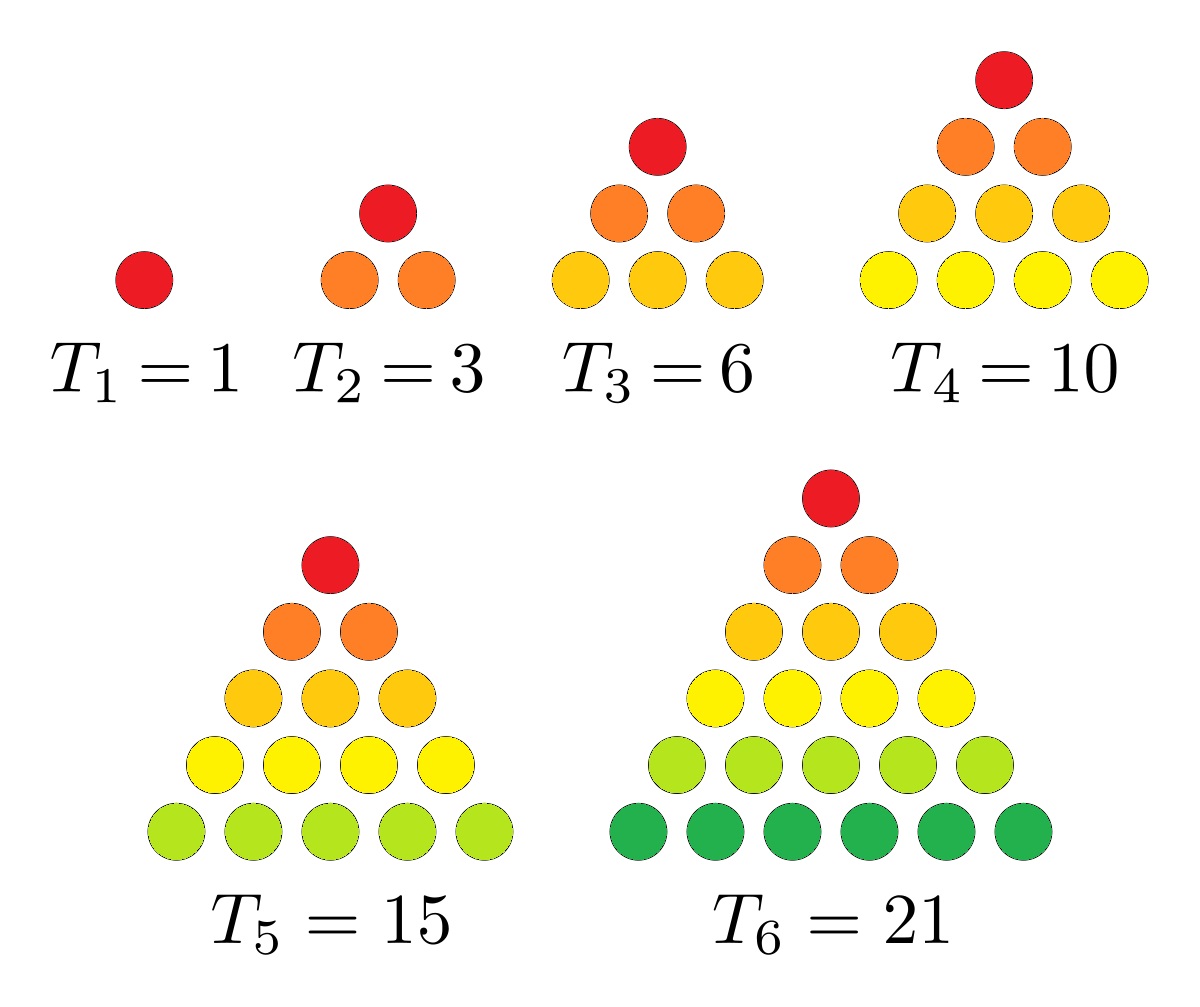
: Los números triangulares son aquellos que son la suma de los primeros números naturales, 1, 1 + 2 = 3, 1 + 2 + 3 = 6, 1 + 2 + 3 + 4 = 10, 1 + 2 + 3 + 4 + 5 = 15, 1 + 2 + 3 + 4 + 5 + 6 = 21,…

Por el mismo motivo, las vacas de la cuarta generación serán los llamados números tetraédricos, 1, 4, 10, 20, 35, … ya que serán las sumas de los primeros números triangulares, los que aparecen en la tercera generación. Recordemos que los números tetraédricos son el número de bolas que hay en una pirámide triangular (como la de la imagen), es decir, un tetraedro, y que es igual a la suma de los primeros números triangulares, TT(n) = T(1) + T(2) + … + T(n).

Los números tetraédricos son aquellos que son la suma de los primeros números triangulares, 1, 1 + 3 = 4, 1 + 3 + 6 = 10, 1 + 3 + 6 + 10 = 20, 1 + 3 + 6 + 10 + 15 = 35, … Imagen de cults3d.com

Dejemos por un momento la sucesión de las vacas de Narayana y volvamos a la composición musical basada en este problema. Pero antes presentemos brevemente a su autor, el compositor Tom Johnson.

El compositor norteamericano Tom Johnson

Tom Johnson (Greeley, Colorado, EE.UU.), es un compositor minimalista y teórico de la música estadounidense. Se graduó en la Universidad de Yale, donde obtuvo además su grado avanzado en música. Fue alumno del compositor Morton Feldman (1926-1987), uno de los artífices, junto con John Cage (1912-1992), de la música aleatoria.

Es un compositor minimalista, ya que trabaja con formas simples, escalas limitadas y de manera general, con material reducido. Y dentro del minimalismo destaca por el uso de las matemáticas en el proceso creativo. Fórmulas matemáticas, trigonometría, simetrías, teselaciones, combinatoria, sucesiones de números enteros, teoría de números o fractales, son algunas de las teorías matemáticas que utiliza en sus composiciones.

Tom Johnson ha escrito de su música: “quiero encontrar la música, no componerla”, o como decía su maestro Morton Feldman “Deja a la música hacer lo que quiere hacer”. Mientras John Cage, o Morton Feldman, realizan esta búsqueda mediante el azar, Tom Johnson lo hace mediante las matemáticas.

Entre sus obras encontramos óperas como Riemannoper (1988), Trigonometría (1997) o la más famosa La ópera de las cuatro notas (1972), que fue representada en España en 2015 por Vania Produccions bajo la dirección de Paco Mir (que muchos conoceréis por ser uno de los miembros del trío Tricicle) o composiciones musicales muy creativas e interesantes, como Nueve campanas (1973), Simetrías (1981), Melodías Racionales (1982), Melodías infinitas (1986), Música para 88 (1988), Las vacas de Narayana (1889), Galileo (2001), Mosaicos (2002), o Ritmos de Vermont (2008), entre muchas otras.

Ha escrito libros como la colección de artículos de crítica musical The voice of the new music (Apollohuis, 1989), Self-similar Melodies (Editions 75, 1996) o Looking at numbers (Birkhauser, 2014).

En la composición musical Las vacas de Narayana, Tom Johnson realiza en esta obra una demostración musical del problema matemático. Para ello, divide la pieza en diferentes partes, cada una de las cuales se corresponde con un año del problema de las vacas, y en cada una de esas piezas hay tantas notas como el número de vacas que hay ese año, siendo una nota larga para cada vaca madura y una nota corta para cada ternera.

Aunque antes de seguir hablando de esta composición, lo que debemos hacer es escucharla. Esta pieza está incluida en el álbum Kentzy plays Johnson (2004), con el saxofonista Daniel Kientzy y en el álbum Cows, Chords and Combinations (2011), del grupo Ensemble Klang. Os traemos aquí dos conciertos que están en youtube. Uno es un concierto en Toronto en 2010, organizado por Continuum Contemporary Music.

mientras que el otro es un concierto en 2014, en el Switchboard Music Festival

Como hemos podido observar los conciertos empiezan en el cuarto año, cuando la vaca original tiene su primera ternera. Además, Tom Johnson distribuye las notas largas y cortas, que se corresponden con vacas maduras y terneras en la composición, siguiendo unas estructuras de árbol similares a los que hemos incluido más arriba para los diez primeros años del problema, y leyendo las vacas que hay, de arriba hacia abajo y de derecha a izquierda en esos diagramas de tipo árbol.

Por ejemplo, si escuchamos (o leemos la partitura, cuya primera página hemos incluido más abajo) la sucesión de notas que se corresponde con el quinto año del concierto (el octavo en el problema entero de las vacas de Narayana, o también en la partitura escrita) y miramos al diagrama de árbol de ese año, observaremos que las notas serán

larga – corta – corta – corta – larga – corta – larga – corta – corta

Primera página de la partitura de “Las vacas de Narayana” (1989), de Tom Johnson

Cuando se escucha la obra de Tom Johnson, los primeros años de la composición musical sirven para entender el problema de las vacas de Narayana y la forma en la que el compositor asocia las notas musicales con las vacas maduras y crías, mientras que según van pasando los años vamos percibiendo la estructura, que surge a partir del problema matemático, de la composición musical.

Regresemos de nuevo a las matemáticas de la sucesión numérica de las vacas de Narayana. Es un hecho muy conocido, tanto en la literatura matemática, como por las personas interesadas en la sucesión de Fibonacci (véase alguno de los libros titulados La proporción áurea, de Mario Livio o Fernando Corbalán), que si se toma el cociente entre dos miembros consecutivos de la sucesión de Fibonacci F(n + 1) / F(n), esta sucesión de cocientes, converge (al ir aumentando n) a la proporción áurea, phi = 1,6180339…

1/1 = 1; 2/1 = 2; 3/2 = 1,5; 5/3 = 1,666…; 8/5 = 1,6; 13/8 = 1,625; 21/13 = 1,615…; 34/21 = 1,619…; 55/33 = 1,617…; etc…

¿Ocurrirá algo similar si tomamos la sucesión de los cocientes de números consecutivos de la sucesión de las vacas de Narayana? La respuesta es afirmativa, como vamos a ver a continuación.

Empezamos en la fórmula recursiva de la sucesión de vacas de Narayana

v(n + 1) = v(n) + v(n – 2),

a la que le dividimos por v(n) y además, en el último sumando, multiplicamos y dividimos por v(n – 1), para obtener la expresión

v(n + 1) / v(n) = 1 + v(n – 2) / v(n – 1) × v(n – 1) / v(n).

Si llamamos κ al límite, cuando n tiene de infinito, del cociente v(n + 1) / v(n), la anterior expresión nos dice que κ satisface la ecuación de tercer grado κ 3 – κ 2 – 1 = 0, que podemos llamar la ecuación de Narayana. Esta ecuación tiene tres soluciones, dos de ellas imaginarias, y la solución real que buscamos es (calculada con WolframAlfa)

Aproximadamente, κ = 1,46557123187676802665673… que podríamos llamar la proporción de Narayana.

Kodhai. Vaca rescatada del Santuario Dakshin Vrindavan, de la artista Charlotte Gerrard

Vamos a terminar esta entrada del Cuaderno de Cultura Científica mostrando algunas caracterizaciones interesantes de la sucesión de vacas de Narayana.

A. Número de embaldosados con triominós rectos de rectángulos 3 × (n – 1).

Consideremos un rectángulo de tamaño 3 × (n – 1), como el que aparece en la imagen de abajo (ese en particular es de tamaño 3 × 5), entonces el número v(n) de la sucesión de vacas de Narayana para el año n, es igual a la cantidad de embaldosados posibles con triominós rectos, fichas de tamaño 1 × 3, también llamados I-triominós (véase la entrada Embaldosados con L-triominós (un ejemplo de demostración por inducción) [https://culturacientifica.com/2014/07/16/embaldosando-con-l-triominos-un-ejemplo-de-demostracion-por-induccion/]), es decir, el número de diferentes maneras que hay de colocar triominós rectos en el rectángulo 3 × (n – 1).

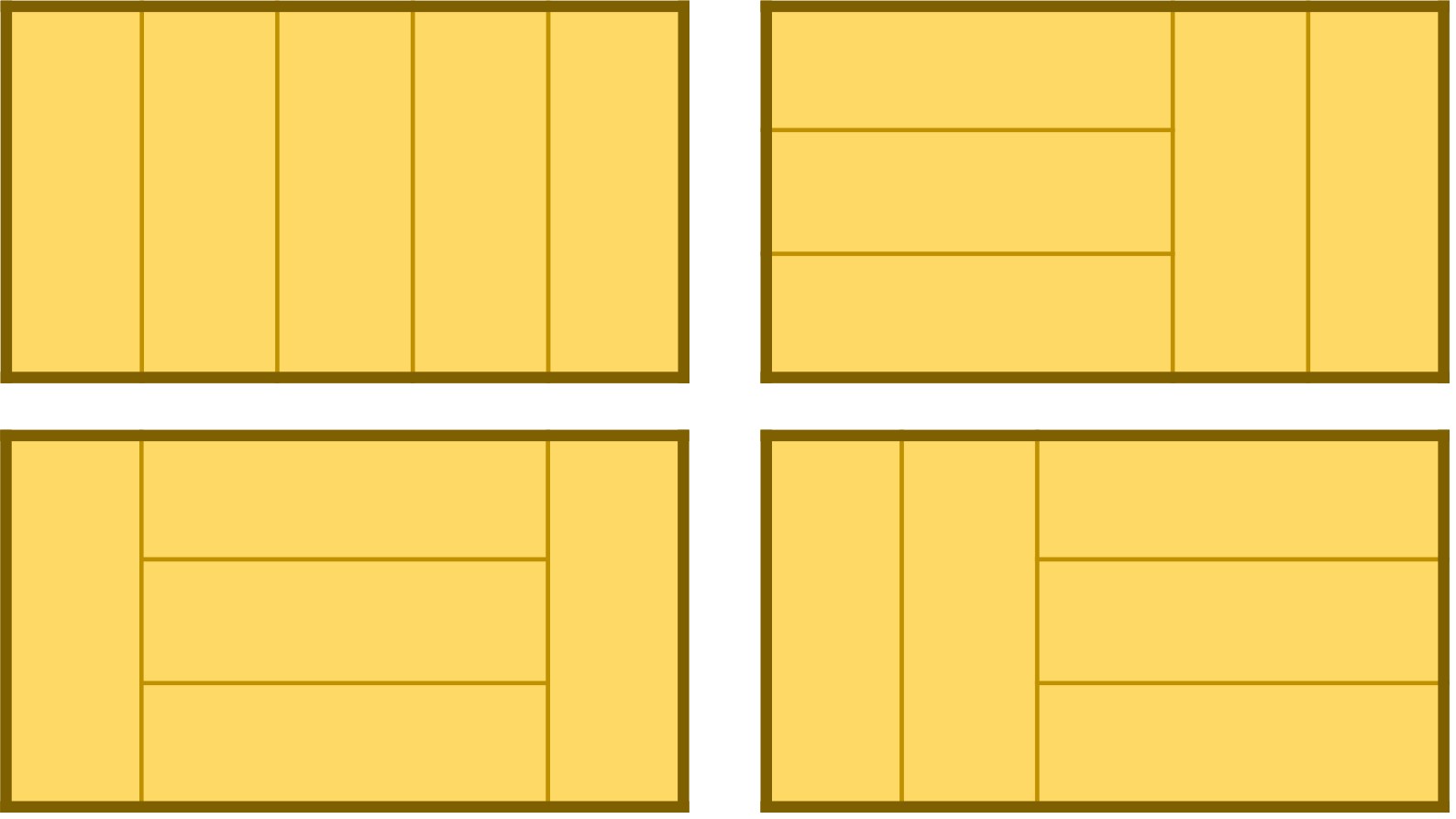
El número de vacas del sexto año, v(6), es 4, al igual que el número de embaldosados con triominós rectos del rectángulo 3 × 5

Esta caracterización es una versión geométrica del siguiente resultado de la Teoría de números relacionado con las particiones de los números.

B. Número de composiciones del número n – 1, con el 1 y el 3.

Recordemos primero dos conceptos básicos de la Teoría de números, como son las particiones y las composiciones. Una partición de un número entero positivo es una forma de expresarlo como suma de números enteros positivos, donde el orden no es relevante. Por ejemplo, el número 3 puede expresarse como suma de tres formas distintas {1 + 1 + 1, 2 + 1, 3}, mientras que existen cinco particiones del número 4 {1 + 1 + 1 + 1, 2 + 1 + 1, 2 + 2, 3 + 1, 4}. Si se denota por p(n) el número de particiones de n, entonces p(3) = 3 y p(4) = 5.

Si en las particiones se tuviera en cuenta el orden, se obtendrían las composiciones, o particiones ordenadas, que se denotan c(n). Así, las particiones ordenadas de 4 son: {1 + 1 + 1 + 1, 2 + 1 + 1, 1 + 2+ 1, 1 + 1 + 2, 2 + 2, 3 + 1, 1 + 3, 4}. Luego, c(4) = 8, mientras que p(4) = 5.

La sucesión de números de Narayama, al igual que la de Fibonacci (véase, por ejemplo, el libro Cayley, el origen del álgebra moderna), se puede relacionar con ciertos tipos de composiciones de números. En particular, la anterior caracterización geométrica es equivalente a que el número v(n) de la sucesión de vacas de Narayana para el año n, es igual al número de composiciones del número n – 1 con únicamente los números 1 y 3. Así, como las composiciones, con 1 y 3, de 6 son {1+1+1+1+1+1, 1+1+1+3, 1+1+3+1, 1+3+1+1, 3+1+1+1, 3+3}, entonces v(7) = 6.

C. Número de formas de colocar n – 2 alfombras tatami en una habitación de tamaño 2 × (n – 2), sin que los vértices de 4 alfombras coincidan.

Recordemos que las alfombras tatami de las casas tradicionales japonesas tienen una relación de tamaño de 1 × 2.

Una distribución de alfombras tatami en una habitación de tamaño 2 × 7

Una distribución no válida de alfombras tatami, ya que los vértices de cuatro alfombras coinciden, en una habitación de tamaño 2 × 7

Existen 13 formas de cubrir una habitación de tamaño 2 × 7 con alfombras tatami, sin que coincidan las esquinas de cuatro de ellas, que es exactamente el número v(9). De hecho, esas 13 maneras pueden describirse de la forma 1111111, 111112, 111121, 111211, 112111, 121111, 211111, 11212, 12112, 21112, 12121, 21121, 21211.

Si lo pensamos un momento, la descripción con 1 y 2 de colocar las alfombras tatami (1 para las verticales, 2 para las horizontales) nos está diciendo realmente que podemos describir el número de la sucesión de vacas de Narayana v(n) como las composiciones de n – 2 con tan solo los números 1 y 2, pero sin que haya dos 2 juntos.

D. Número de composiciones del número n – 2, con el 1 y el 2, sin que haya dos 2 juntos.

Como despedida de esta entrada otra pieza del compositor minimalista norteamericano Tom Johnson, la primera de sus melodías racionales, en mi opinión una hermosa pieza, interpretada por el Gruppo di Musica Contemporanea Steffani, en el Conservatorio Steffani, de Castelfranco Veneto (Italia), en 2009.

Portada del disco Rational Melodies/Bedtime stories, de Tom Johnson, con Roger Heaton al clarinete. El diseño de la portada es la obra de Esther Ferrer, “Project Drawing With Prime Number Series, Spiraling Out From 19.000.041”

Bibliografía

1.- Página web de Editions 75

2.- Tom Johnson, Kientzy plays Johnson (álbum), 2004.

3.- Jean-Paul Allouche, Tom Johnson, Narayana’s Cows and Delayed Morphisms, Cahiers du GREYC Troisiemes Journées d’Informatique Musicale (JIM 96) 4, p. 2-7, 1996.

4.- Parmanand Singh, The so-called Fibonacci Numbers in Ancient and Medieval India, Historia Mathematica 12, p. 229-244, 1985.

5.- Krishnamurthy Kirthi, Subhash Kak, The Narayana Universal Code, ArXiv, 2016.

6.- Tom Johnson, Self-Similar Melodies, Editions 75, 1996.

7.- Tom Johnson, Looking at numbers, Birkhäuser, 2014.

8.- Fernando Corbalán, La proporción áurea, El lenguaje matemático de la belleza, RBA, 2010.

9.- Mario Livio, La proporción áurea, La historia de phi, el número más sorprendente del mundo, Ariel, 2006.

10.- Página web de la artista Charlotte Gerrard

11.- N. J. A. Sloane, La sucesión de vacas de Narayana, A000930 [https://oeis.org/A000930], Enciclopedia on-line de sucesiones de números enteros.

12.- Raúl Ibáñez, Cayley, el origen del álgebra moderna, colección Genios de las matemáticas, RBA, 2017.

13.- Frank Ruskey, Jennifer Woodcock, Counting Fixed-Height Tatami Tilings, The Electronic Journal of Combinatorics 16, 2009.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El artículo Las vacas de Narayana, la versión hindú de los conejos de Fibonacci se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Un rebaño de vacas pastando como sistema complejo
2. Los números (y los inversos) de Fibonacci
3. #Naukas14 ¿Por qué explota una granja de vacas?

En diferentes especies animales y bajo diversas circunstancias, la transferencia de oxígeno desde el medio externo hasta su destino final en las mitocondrias se produce a través de dos pigmentos respiratorios diferentes. En tales casos, los pigmentos suelen mostrar diferente afinidad por el oxígeno y esa diferencia constituye un elemento clave de su funcionamiento. Repasaremos aquí algunos de esos sistemas pigmentarios sin ánimo de exhaustividad.

Sangre fetal y sangre materna

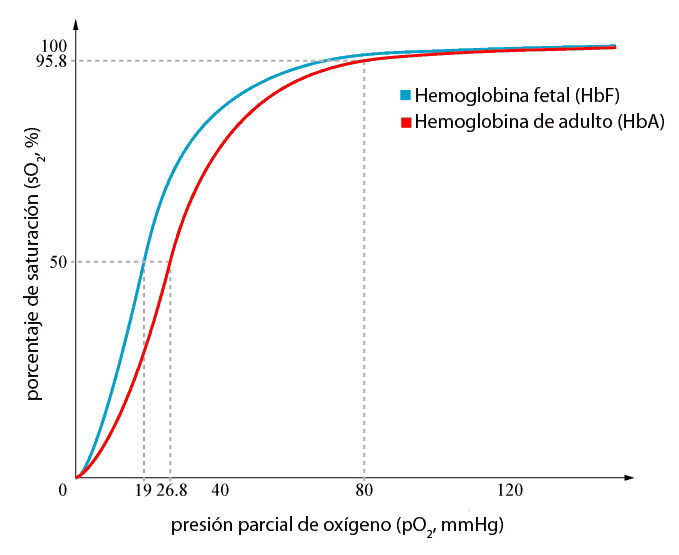
Cuando se comparan las curvas de disociación de la sangre fetal y la sangre materna en mamíferos placentarios, se observa que la curva de la sangre fetal se halla desplazada hacia la izquierda en relación con la de la sangre materna. Quiere decir que la sangre fetal tiene una mayor afinidad por el oxígeno que la materna o, lo que es lo mismo, que para una tensión parcial de oxígeno dada, la fetal se encuentra saturada en un porcentaje mayor que la sangre materna.

Esa diferencia en la afinidad obedece a dos razones. Por un lado, la hemoglobina fetal es algo diferente de la hemoglobina de los adultos, y esa diferencia determina una mayor afinidad. Y además, la concentración de fosfatos orgánicos en los eritrocitos de la sangre fetal es menor que en los de sangre de adultos, por lo que en estos el efecto de esas sustancias moduladoras es mayor. Tras el nacimiento, la hemoglobina fetal es sustituida de forma gradual por hemoglobina de adultos y en los eritrocitos tiende a elevarse la concentración de los fosfatos orgánicos.

La diferente afinidad de las dos hemoglobinas tiene una utilidad evidente para el feto, puesto que de otro modo, la transferencia de oxígeno de la sangre materna a la sangre fetal en la placenta se vería limitada en cierto grado. Y debe tenerse en cuenta que el feto, por su pequeño tamaño y por estar formado por tejidos en pleno desarrollo, tienen una alta demanda de oxígeno.

Función de las mioglobinas

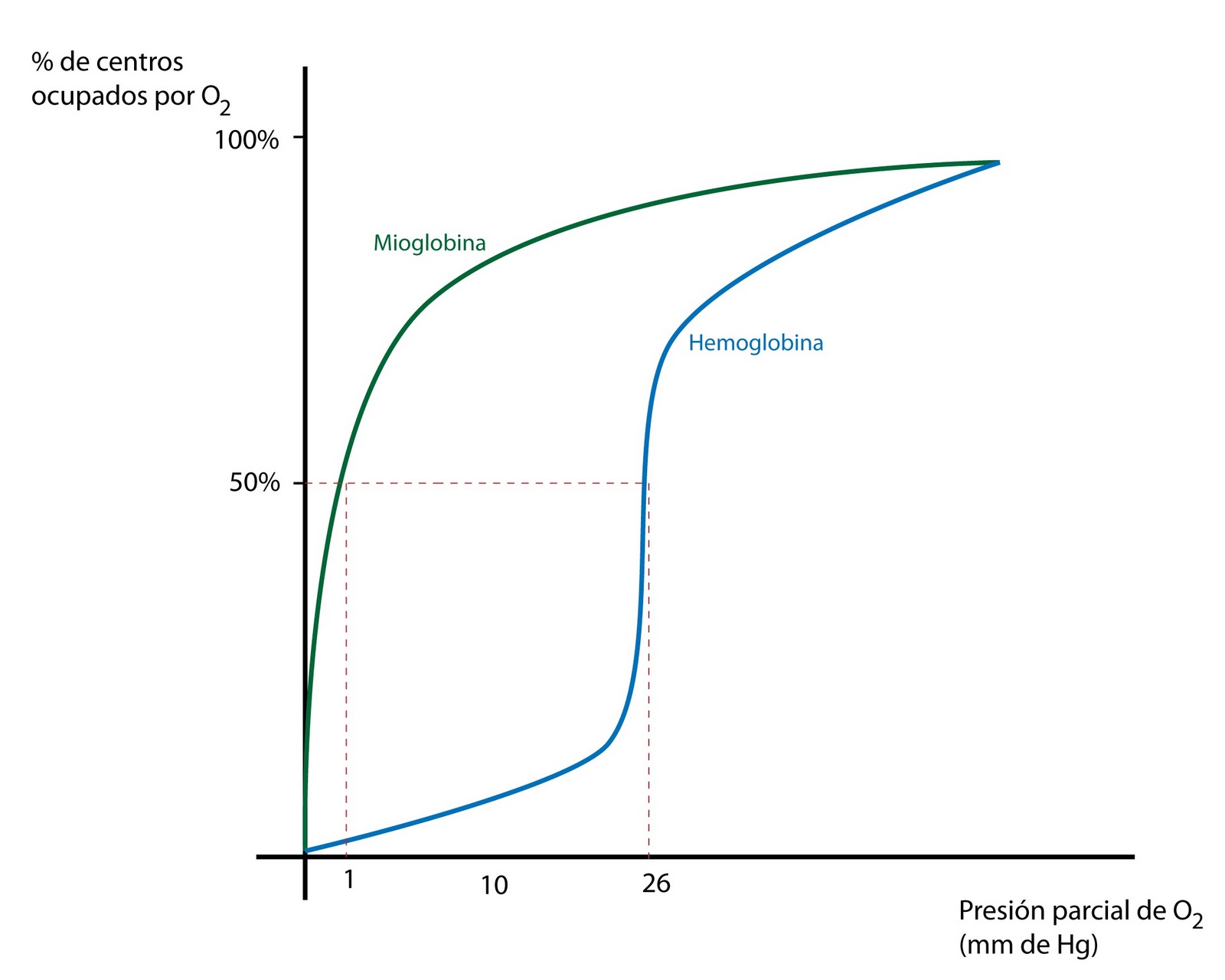
Las mioglobinas son pigmentos musculares muy similares a las hemoglobinas sanguíneas. La diferencia es que son de pequeño tamaño puesto que están formadas por una única cadena de aminoácidos. La mioglobina tiene mayor afinidad por el oxígeno que la hemoglobina.

Gracias a esa diferencia de afinidad capta el O2 sanguíneo y facilita su difusión a las mitocondrias musculares. Se ha comprobado experimentalmente la importancia de esta función con ratones a los que se les privó de la posibilidad de sintetizar mioglobina; aunque los ratones pudieron desarrollar una vida normal, hubieron de compensar la falta de mioglobina elevando de forma significativa la densidad de capilares sanguíneos en los músculos. De otra forma no habrían podido suministrar a los músculos el oxígeno necesario para mantener niveles adecuados de metabolismo aerobio.

La mioglobina sirve, además, de almacén de oxígeno. En especies que respiran con normalidad en medios con suficiente disponibilidad de oxígeno, ese almacén garantiza el suministro de O2 a las mitocondrias durante los breves periodos de tiempo (segundos o fracciones de segundo) que, tras iniciarse una actividad muscular intensa, el sistema cardiovascular necesita para hacer llegar a los músculos el oxígeno necesario. Y también cuando los capilares se ocluyen transitoriamente por efecto de las contracciones musculares. La función de almacén es mucho más importante en las especies –como los mamíferos marinos- que dejan de respirar durante periodos de tiempo relativamente prolongados al sumergirse para ir en busca de alimento. De estas especies, no obstante, nos ocuparemos con más detalle en otra ocasión.

La mioglobina no solo se encuentra en la musculatura de vertebrados. El músculo radular del molusco Cryptochiton también tiene mioglobina, y lo llamativo de este caso es que su pigmento vascular no es hemoglobina, sino hemocianina. Es muy probable que este no sea el único caso en que esto ocurre.

Pigmento vascular y pigmento celómico

Se conocen varios sistemas pigmentarios en invertebrados aunque, quizás, el mejor conocido es el del sipuncúlido Dendrostomum. Este sipuncúlido tiene hemeritrina, tanto en su sangre como en el fluido celómico. Los tentáculos rodean la boca y se encuentran bien irrigados de sangre; el gusano vive dentro de la arena y los tentáculos se proyectan hacia el exterior –hacia la masa de agua circundante- y cumplen una función respiratoria. La hemeritrina celómica de Dendrostomum tiene una mayor afinidad por el oxígeno que la sanguínea, lo que quiere decir que el oxígeno captado por la sangre de los tentáculos es transferido con facilidad al fluido celómico. Y del fluido celómico pasa a las células.

———————————————–

Como se ha podido ver aquí, existen en el mundo animal diversas disposiciones anatómicas y funcionales en las que es necesario el concurso de más de un pigmento para que el O2 pueda ser transferido desde el exterior hasta su destino final (feto, músculos, u otros tejidos) y en todas esas disposiciones el juego de afinidades es clave para que tal transferencia pueda cursar con suficiencia y normalidad. En algunos casos, además, uno de los pigmentos cumple funciones de almacenamiento de oxígeno, lo que constituye una garantía de provisión constante ante la existencia de fluctuaciones de diferente intensidad y duración en el suministro al animal (su órgano respiratorio) o a los músculos.

Fuentes:

John D. Jones (1972): Comparative physiology of respiration. Edward Arnold, Edinburgh

Knut Schmidt-Nielsen (1997): Animal Physiology. Adaptation and Environment. Cambridge University Press; Cambridge

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo Sistemas respiratorios: almacenamiento y transferencia de oxígeno se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Sistemas respiratorios: los pigmentos respiratorios
2. Sistemas respiratorios: pigmentos de alta afinidad
3. Sistemas respiratorios: pigmentos de baja afinidad

El USS Enterprise en 1964 durante la operación “Sea Orbit” en la que dio la vuelta al mundo en 65 días sin repostar, demostrando la capacidad de la tecnología basada en la equivalencia entre masa y energía.

Después de que Einstein completara su artículo sobre la teoría especial de la relatividad en 1905 descubrió una consecuencia más de los postulados de la relatividad que presentó, como una idea de último momento, en un artículo de solo tres páginas posterior ese mismo año. Desde el punto de vista del efecto de la física en la historia mundial, resultó ser el más significativo de todos sus hallazgos: la quivalencia entre masa y energía.

Sabemos que cuando se realiza trabajo sobre un objeto, como golpear una pelota de tenis con una raqueta, el objeto adquiere energía. En la teoría de la relatividad, el aumento de la velocidad y, por lo tanto, el aumento de la energía cinética de una pelota de tenis o de cualquier otro objeto, da como resultado un aumento de la masa (o inercia), aunque en el día a día suele ser solo un aumento infinitesimal.

Al examinar esta relación entre velocidad relativa y masa efectiva con más detenimiento Einstein descubrió que cualquier aumento en la energía de un objeto debería producir un aumento de la masa medida; este incremento de energía daría igual si se hace acelerando el objeto, o calentándolo, o cargándolo con electricidad, o simplemente realizando trabajo elevándolo en el campo gravitacional de la Tierra. En resumen, Einstein descubrió que un cambio en la energía es equivalente a un cambio en la masa.

No solo eso. Descubrió además que la equivalencia funciona en ambos sentidos: un aumento o disminución de la energía en un sistema aumenta o disminuye correspondientemente su masa, y un aumento o disminución de la masa corresponde a un aumento o disminución de la energía. En otras palabras, la masa en sí misma es una medida de una cantidad equivalente de energía.

Dicho de otra manera, un cambio (recordemos que los cambio se expresan con la letra griega delta mayúscula, Δ) en la cantidad de energía, E, de un objeto es directamente proporcional a un cambio en su masa, m. Lo que Einstein hizo en su articulito de tres páginas es demostrar que esa constante de proporcionalidad es el cuadrado de la velocidad de la luz en el vacío, c2. En símbolos, ΔE = Δm·c2, o de forma más genérica, E = m·c2, probablemente la ecuación más famosa de todos los tiempos.

Significa que un cambio de masa observado es equivalente a un cambio de energía, y viceversa. Pero también significa que la propia masa de un objeto, incluso si no cambia, es equivalente a una enorme cantidad de energía, ya que la constante de proporcionalidad, c2, el cuadrado de la velocidad de la luz en el vacío, es un número enorme.

Por ejemplo, la energía contenida en un solo gramo de materia es de E = 0,001 kg · (299792485 m/s)2 = 8,988·1013 kg·m2/s2≈ 9·1013 J. Esta enorme cantidad de energía es aproximadamente la misma que libera la explosión de 20 toneladas de TNT.

La transformación de masa en energía es Es la fuente de las energías liberadas por las sustancias radiactivas, por nuestro Sol y otras estrellas, por las armas nucleares y por los reactores nucleares que producen energía eléctrica.

No solo masa y energía son “equivalentes”, podemos afirmar que la masa es energía. Esto es exactamente lo que concluyó Einstein en 1905: “La masa de un cuerpo es una medida de su contenido energético”. Nada impide que consideremos la masa como “energía congelada”, congelada en el momento en que el Universo se enfrió poco después del Big Bang y la energía se agrupó formando “bolas” de materia, las partículas elementales de las que se compone la materia ordinaria.

Por lo tanto, cualquier energía adicional que se añada a una masa aumentará su masa aún más. Por ejemplo, a medida que aceleramos los protones en el laboratorio a casi la velocidad de la luz, su masa aumenta de acuerdo con la fórmula relativista para mm. Este aumento también se puede interpretar como un aumento en el contenido de energía de los protones.

Estas dos deducciones diferentes de la teoría de la relatividad -aumento de masa y equivalencia de masa de energía- son consistentes entre sí. Esta equivalencia tiene un significado muy importante. Primero, dos grandes leyes de conservación se convierten en dos formas alternativas de una sola ley. En cualquier sistema cuya masa total se conserve, la energía total también se conserva. En segundo lugar, surge la idea de que parte de la energía en reposo podría transformarse en una forma de energía más familiar. Dado que el equivalente energético de la masa es tan grande, una reducción muy pequeña en la masa en reposo liberaría una enorme cantidad de energía, por ejemplo, energía cinética o energía electromagnética.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo Equivalencia entre masa y energía se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. La relatividad de la masa
2. Se intuye la conservación de la energía (1)
3. Se establece el principio de conservación de la energía