Agrégateur de flux

David Brizuela eta Iñaki Garay Fisika teorikoaren ikuspuntutik zulo beltzak unibertsoko objektu bitxienetarikoak direla esan liteke. Haatik, horiek ere betetzen dituzte termodinamikaren legeak. Artikulu honetan, saiatuko gara termodinamikaren legeak zulo beltzei nola aplika diezazkiekegun azaltzen.

Termodinamika, bere izenak dioen moduan, beroaren dinamika aztertzen duen fisikaren adarra da. Bere oinarriak lau lege edo printzipio oso bakunetan labur daitezke. Lege hauek zenbakiturik izendatzen ohi dira, zerotik hasita. Zero printzipioak bi gorputzen arteko oreka termikoa definitzen du: tenperatura desberdinetara dauden bi gorputz kontaktuan jarriz gero, euren artean beroa trukatuko dute, biek tenperatura berdina izan arte.

1. irudia: Termodinamikak beroaren transferentzia aztertzen du. Unibertsala denez, edozein sistemari aplika diezaiokegu: bai irakiten
dagoen ur lapiko bati, bai zulo beltzei. (Argazkia: Stanford University)

Lehenengo legea energiaren kontserbazioari dagokio. Beroa, izatez, energia transferitzeko modu bat da. Aurreko adibideko bi gorputz horiek energia trukatuko dute, baina energia osoa konstante mantenduko da prozesu osoan zehar.

Bigarren legea formulatzeko modu ugari daude, baina horretarako entropia (desordena neurtzen duen magnitude fisikoa) erabiltzen da askotan. Bere esanahi fisikoa sistema isolatu batean desordena (entropia) beti handiagotzen doala da. Horrela, aditzera ematen digu espontaneoki zer prozesu gertatzen diren eta zeintzuk ez. Esate baterako, kontaktu termikoa ezarri ondoren, gorputz berotik gorputz hotzera igaroko da beroa beti, eta ez alderantziz. Bestalde, kafeari azukrea botatzen diogunean, pixka bat irabiatu ondoren, disoluzio homogeneo bat eratzen da; nahiz eta denbora asko itxaron, bat batean azukrea ez da kristalduko eta hasierako egoerara itzuliko.

Azkenik, hirugarren printzipioa dugu eta, horren arabera, ezinezkoa da prozesu finituen bidez 0 Kelvin graduko (-273,15 Celsius graduko) tenperaturara iristea.

Lege horiek era enpirikoan garatu ziren batez ere XIX. mendean zehar. Zentzu batean ez dira oinarrizko legeak, ezin baitzaizkie banakako partikula bati aplikatu. Hala ere, fisikaren legeen artean termodinamikaren printzipioek estatus berezia dute, oinarrizkoak ez badira ere. Portaera estatistiko baten ondorioz betetzen direnez, ez dute oinarrizko elkarrekintza partikularrekiko menpekotasunik eta, beraz, euren formulazioa ez da aldatu (eta ustez ez da aldatuko), nahiz eta fisikaren oinarrizko teoriak zeharo aldatu diren azken mendean zehar.

Horrez gain, printzipio horiek unibertsalak direla esaten da oso aplikazio zabalekoa direlako eta izatez, edozein sistema makroskopikoren portaera deskribatzen dutelako. Sistema makroskopiko bat, osagai askoz osaturik dago: banakako elementuak oinarrizko partikulak, atomoak edo molekulak izan ohi dira. Adibidez, lege horiek betetzen dituzte laborategian prestatzen den edozein disoluziok, eguzkiaren barneak edo argiak berak (fotoi askoz osaturiko sistema bezala).

Hala ere, joan den mendeko 70. hamarkadan zulo beltzen termodinamika aztertzen saiatzen ari zirela, zailtasun larriak aurkitu ziren. Zulo beltzak deritzen gorputz astrofisikoak, izarrak kolapsatzean eratzen dira. Bi indarrek eragiten diote izar bati. Alde batetik, bere masak eragindako grabitateak barneranzko indar bat sortzen du, eta bestalde, izarraren barneko presio hidrostatikoak kanporanzko indar bat eragiten du.

2. irudia: Zulo beltz baten irudikapen artistiko bat. (Argazkia: NASA / Goddard Space Flight Center)

Orekan dagoen bitartean, gaur egun gure eguzkiaren moduan, izarraren barnean erreakzio nuklearrak gertatzen dira, barneko tenperatura oso altu mantentzen da eta ondorioz oso presio handia ekoizten da. Presio horrek grabitatearen indarra deuseztatzen duelarik, izarra egonkor mantentzen da.

Izarren barneko erreakzio nuklear horietan hidrogenoa edo helioa bezalako elementu arinak, astunagoak bihurtzen dira eta soberan dagoen energia argi moduan igortzen dute. Elementu arin horiek agortzen direnean ordea, erreakzio nuklearrak amaitu egiten dira eta izarraren barneko tenperatura eta presioa murriztu egiten dira. Hori gertatzen denean, presioak ezin dio izarraren pisuari eutsi eta izarrak kolapsatu egiten du, eta kanpoko geruza guztiak zentrorantz erortzen dira.

Izarraren masaren arabera, kolapso horretan zehar presio berriak ager litezke (elektroien edo neutroien degenerazioak sortuta). Presio horiek aurka egingo liokete grabitateari, eta ondorioz, kolapsoa gelditu eta izar berri bat (nano zuri edo neutroi-izar izenekoak) eratzen dira.

Izarraren masa oso handia bada ordea, ez dago kolapso hori geldi dezakeen presio ezagunik eta materia guztia zentrora iristen delarik, dentsitate infinituko puntu bat sortzen da. Objektu astrofisiko berri hau zulo beltz bat da. “Zulo” deitzen zaio, zentroko dentsitate infinitu horrek espazio-denbora jarraia zulatzen duelako. “Beltza” esaten zaio bestetik, bere barnean dagoen ezerk ezin duelako ihes egin, ezta argiak ere.

Bere inguruan horizontea deitzen den geruza irudikari bat dago, eta ezinezkoa da kanpotik geruza horren barnean dagoen ezer ikustea. Izatez, geruza hori zeharkatuz gero, ezin izango ginateke kanpora itzuli eta, nahi eta nahi ez, zentroko singularitatean amaituko genuke.

Duela 50 bat urte, Einsteinen erlatibitate orokorraren teoriaren arabera, objektu astrofisiko horiek termodinamikaren legeen pareko legeak betetzen dituztela ondorioztatu zen. Lege horietan grabitatearen azelerazioak tenperaturaren funtzio bera betetzen du, zulo beltzaren masak energiarena eta horizontearen azalerak entropiarena.

Beraz, honela labur ditzakegu zulo beltzek betetzen dituzten printzipioak:

• 0. printzipioa: Grabitatearen azelerazioa horizontean zehar konstantea da.
• 1. printzipioa: Energia kontserbatzen da. Hau da, zulo beltzera zerbait erortzen bada, bere masa eta azalera handituko dira.
• 2. printzipioa: Edozein prozesutan zehar horizontearen azalera handitzen joango da. Adibidez bi zulo beltzek talka egin eta beste zulo beltz berri bat eratzen badute, amaierako zulo beltzaren azalera hasierako bien azaleren batura baino handiagoa izango da.
• 3. printzipioa: Ezinezkoa da horizonteko grabitatearen azelerazioa zero izateraino murriztea. Alegia, ez dago modurik zulo beltza desagerrarazteko.

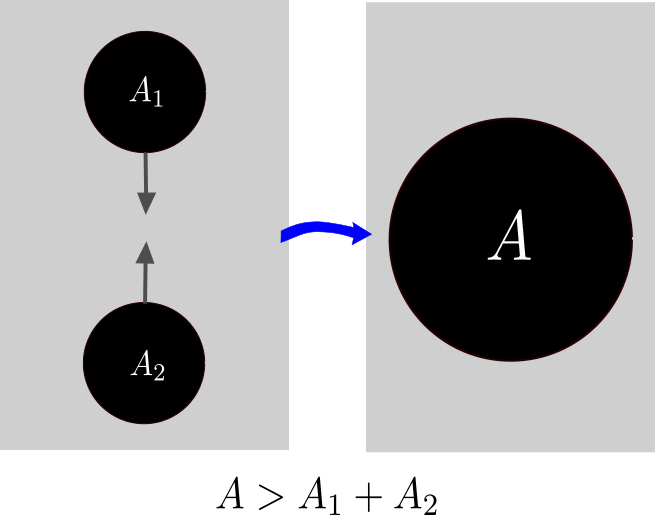
3. irudia: Termodinamikaren bigarren printzipioaren arabera, bi zulo beltz elkartzen direnean eratzen duten zulo beltz berriaren azalera hasierako bien azaleren batura baino handiagoa da. (Grafikoa: David Brizuela eta Iñaki Garay)

Orain arte esandakoa analogia bat baino ez da: lege multzo batetik beste batera igaro gaitezke objektuak berrizendatuz. Hurrengo galdera beraz zuzena da: analogia hori soilik matematikoa da edo zentzu fisiko sakonagoa dauka? Hau da, horizonteko grabitatearen azelerazioa eta bere azalera, hurrenez hurren, benetako tenperatura eta entropia bezala uler ditzakegu? Hala balitz, zulo beltzek, erradiazio elektromagnetikoa igorri beharko lukete tenperatura jakin batean dagoen edozein gorputzen moduan.

Izatez, 1974. urtean Hawkingek argudio teoriko bat plazaratu zuen zulo beltzen erradiazioa kalkulatzeko. Hawkingen kalkuluak zentzu fisikoa ematen dio aurreko analogiari. Alegia, jadanik ez da analogia matematiko bat, erlazio fisiko erreala baizik.

Hawkingen erradiazioa kalkulatzeko prozesu zehatza nahiko korapilatsua da eta teoria kuantikoaren oinarriak erabili behar dira. Haatik, era intuitibo batean uler daiteke nola izan daitekeen zulo beltzek erradiatzea. Lehenengo eta behin, esan behar da erradiazioa ez dela zulo beltzetik irteten, espero genuen bezala. Baina zulo beltzak eragiten dio erradiazio prozesu horri. Teoria kuantikoaren arabera hutsa ez dago guztiz hutsik. Heisenbergen ziurgabetasunaren printzipioaren arabera (oinarrizko printzipio kuantiko bat) energiaren kontserbazioaren legea urra daiteke denbora tarte labur batean zehar. Horren ondorioz, partikula bikoteak sortzen eta azkar elkar deuseztatzen ari dira hutsean eten gabe. Prozesu hori zulo beltz baten horizontearen aldean gertatzen bada, partikula bat zulo beltzera eror liteke eta besteak ihes egin lezake. Hori dela eta, zulo beltzaren kanpoan partikula berriak agertuko dira eta, hain zuzen ere, partikula horiek Hawkingen erradiazioa sortuko dute.

Hawkingen erradiazioa azaltzeko, kontuan hartu behar izan ditugu, bai teoria kuantikoa bai teoria grabitatorioa. Beraz, zulo beltz bat ondo ulertzeko bi teoria horiek bateratu beharko genituzke, ondorioz grabitate kuantikoaren teoriari bide emanda. Teoria hori gauzatzea ordea, arazo itzela da. Izan ere, erlatibitate orokorra eta teoria kuantikoa oso formalismo matematiko desberdinekin formulaturik daude eta gainera, euren oinarri fisikoen artean kontraesanak daude. Horren ondorioz, oraindik ez daukagu eskura grabitate kuantikoaren teoria osorik. Azken 50 urteotan proposamen batzuk jorratu dira elkarrekintza grabitatorioa eskala kuantikoan deskribatzeko; esate baterako, soken teoria (string theory) edo kiribilen grabitate kuantikoa (loop quantum gravity). Dena dela, teoria horiek ez daude osorik gauzatuta eta egungo ezagutzaren mugak topatzen ditugu arlo honetan.

———————————————————————————-

Egileez: David Brizuela eta Iñaki Garay UPV/EHUko Zientzia eta Teknologia Fakultateko Fisika Teorikoa eta Zientziaren Historia Saileko ikertzaileak dira.

———————————————————————————-

The post Zulo beltzen termodinamika appeared first on Zientzia Kaiera.

El pasado mes de mayo, aprovechando la exposición de la artista Esther Ferrer en Tabakalera (Donostia), Esther Ferrer, 2, 3, 5, 7, 11, 13, 17, 19, 23…, dedicamos dos entradas del Cuaderno de Cultura Científica a su serie de obras Poema de los números primos, en la cual utiliza los números primos como herramienta en el proceso de creación artística:

i) Poema de los números primos

ii) Poema de los números primos (2)

En la entrada de hoy vamos a hablar de otro artista que también ha utilizado los números primos en la creación de una de sus obras de arte, es el artista británico Anthony Hill.

Relief construction (1960-62), de Anthony Hill, obra realizada en aluminio y plástico sobre un tablero de madera, de dimensiones 110 x 91 x 5 cm. Obra e imagen de la Tate Gallery 

Anthony Hill nació en Londres en 1930, formó parte del movimiento artístico de los constructivistas británicos y estuvo relacionado con el Grupo Sistemas. Heredero del arte concreto, Anthony Hill utiliza las matemáticas en el proceso creativo artístico. Tiene un profundo conocimiento de esta ciencia, publicando incluso algunos artículos de investigación matemática, como el artículo On the number of crossings in a complete graph (Proceedings of the Edinburgh Mathematical Society 13, n. 4, p. 333-338, 1963), junto al matemático Frank Harary, o siendo elegido Honorary Research Fellow en el Departamento de Matemáticas del University College de Londres.

La obra que vamos a analizar en esta entrada es Prime Rhythms / Ritmos primos (1959 -1962).

Rhythms / Ritmos primos (1959 -1962), de Anthony Hill, realizada en plástico laminado y de unas dimensiones de 91.5 x 91.5 x 1.9 cm. Imagen del artículo del artista A View of Non-Figurative Art and Mathematics and an Analysis of a Structural Relief

Esta obra está inspirada en los números primos y, más concretamente, en los números primos gemelos. Recordemos que los números primos son aquellos números que solamente se pueden dividir por 1 y por ellos mismos. Así, por ejemplo, el número 30 no es un número primo ya que se puede dividir por 2, 3, 5, 6, 10 y 15, además de por 1 y 30, o tampoco el 33, divisible por 3 y 11, mientras que el número 13 sí es primo, ya que solamente es divisible por el 1 y él mismo, al igual que los números 2, 3, 5, 7, 11, 17 o 19. Por motivos formales el número 1 es considerado no primo en matemáticas, aunque en esta obra Anthony Hill lo va a incluir el en grupo de los números primos.

Lo primero que hace el artista británico es considerar todos los números impares menores que 100 (tengamos en cuenta que los números pares, con la excepción del 2, son siempre compuestos, es decir, no primos) y dividir este grupo en dos subgrupos, los primos y los compuestos. Resulta que hay exactamente la misma cantidad de elementos en cada subgrupo, en concreto, veinticinco.

Números primos impares menores que 100:

1, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.

Números compuestos impares menores que 100:

9, 15, 21, 25, 27, 33, 35, 39, 45, 49, 51, 55, 57, 63, 65, 69, 75, 77, 81, 85, 87, 91, 93, 95.

A continuación, Anthony Hill toma un cuadrado, considera la línea intermedia y marca 50 líneas horizontales, igualmente espaciadas, de forma que cada una de ellas es un número impar menor que 100, desde el 1 hasta el 99. Aunque cada línea es un número impar, los números impares primos los considera a la izquierda y los números impares no primos a la derecha, como se muestra en la siguiente imagen esquemática de los primeros números.

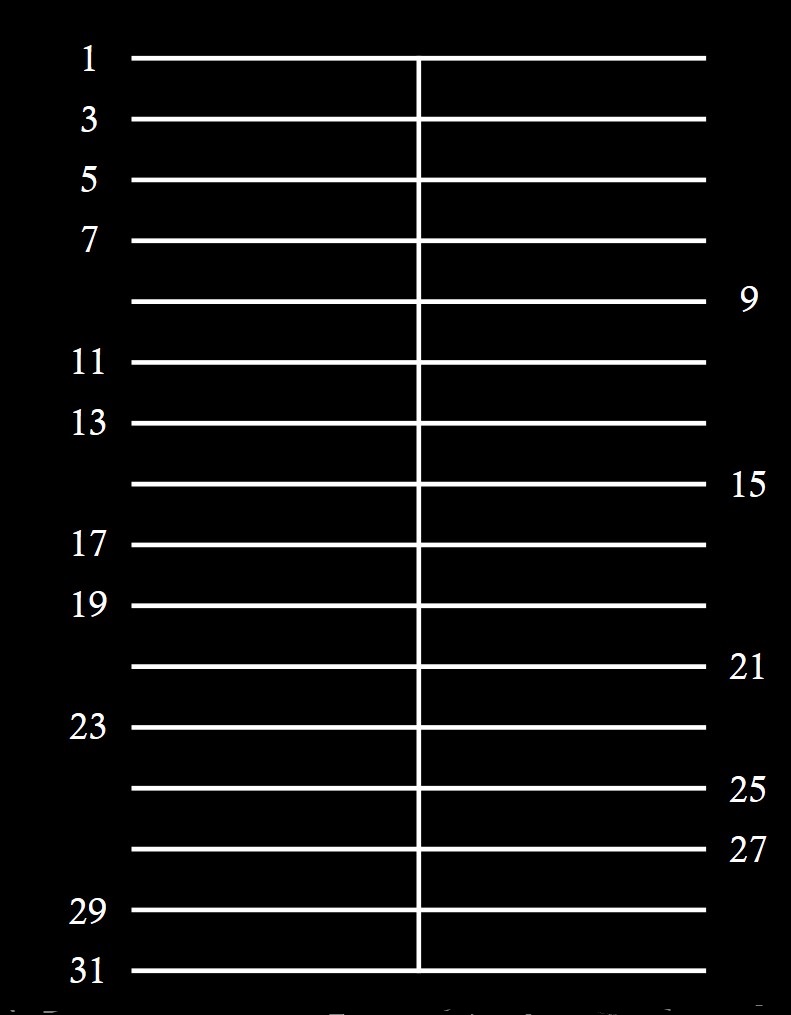
El siguiente paso fue considerar los números primos gemelos, que son aquellos números primos que están lo más cerca posible (con la excepción del 2 y el 3), es decir, con tan solo un número par entre ellos, como las parejas 11 y 13, 17 y 19, 41 y 43, 59 y 61, 71 y 73. Anthony Hill considera los números primos (impares) gemelos, que además son menores de 100, como se ve en la siguiente imagen, en la parte de la izquierda. Observemos que, al considerar solo números impares, los números primos gemelos son números consecutivos, 1 y 3, 3 y 5, 5 y 7, 11 y 13, 17 y 19, y 29 y 31, en la siguiente imagen.

Por otra parte, Anthony Hill considera los números no primos impares consecutivos, que podríamos denominar ahora “números compuestos impares gemelos”. Como por ejemplo el par 25 y 27, que se puede ver en la parte de la derecha de la imagen, aunque hay más, como 33 y 35.

La siguiente acción es pintar de negro las zonas, o bandas entre líneas paralelas, que se corresponden a números gemelos, para los números primos, a la izquierda, y para los números impares no primos, a la derecha, y las demás bandas de color blanco. Podemos apreciar la construcción en la siguiente imagen.

Por lo tanto, sin marcar la separación entre las zonas que hemos realizado en el anterior esquema explicativo, podemos realizar la siguiente recreación de la obra Prime Rhythms / Ritmos primos de Anthony Hill.

Recreación de la obra Prime Rhythms / Ritmos primos (1959 – 1962), de Anthony Hill, realizada por mí mismo, Raúl Ibáñez

Terminamos la entrada mostrando una obra de Anthony Hill relacionada con los grafos, The Nine – Hommage à Khlebnikov / El nueve, homenaje a Khlebnikov (1976).

The Nine – Hommage à Khlebnikov / El nueve, homenaje a Khlebnikov (1976), de Anthony Hill, realizada en plástico laminado, con un tamaño de 91.5 x 91.5 x 1.9 cm. Imagen del artículo del artista A View of Non-Figurative Art and Mathematics and an Analysis of a Structural Relief

Bibliografía

1.- Anthony Hill, A View of Non-Figurative Art and Mathematics and an Analysis of a Structural Relief, Leonardo, Vol. 10, No. 1, pp. 7-12, 1977.

2.- Alan Fowler, A Rational Aesthetic. The Systems group and associated artists, Southampton City Art Gallery, 2008.

3.- Michael Holt, Mathematics in Art, Littlehampton Book Services, 1971.

4.- Raúl Ibáñez, Las Matemáticas como herramienta en la creación artística (conferencia), Curso de verano de la UPV/EHU, “Cultura con M de matemáticas, una visión matemática del arte y la cultura”, 2019.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El artículo Los ritmos primos de Anthony Hill se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Buscando lagunas de números no primos
2. Criptografía con matrices, el cifrado de Hill
3. El poema de los números primos (2)

Juanma Gallego Ostruka bat baino hiru handiz handiagoa zen hegazti bat ezagutzera eman du paleontologo talde batek. Duela 1,5 eta 1,8 milioi urte bitartean kokatu dute fosila, Krimean, eta Europara sartu ziren Homo erectus espezieko lehen hominidoak iritsi zirenean hegazti hori kontinentean zegoela iradoki dute.

Europara iritsi zirenean, baliteke lehen hominidoek tona erdiko hegaztiekin topo egin izana. Egia esanda, momentuz ez dago ziurtatzea hala izan zenik, baina aukera hori planteatu du ikertzaile talde batek, Krimean (Ukraina) aurkitu berri duten fosil baten datazioa jakinda. Teorian bederen, eta epe luzeko datazioak nahiko malguak direla kontuan izanda, bai hominidoek zein hegazti erraldoiek denboran eta espazioan bat egiteko aukera bazegoelako. Dena dela, batera agon ziren ala zen gutxienekoa da. Deigarriena da ipar hemisferioan horrelakorik aurkitzen den lehenengo aldia dela honakoa.

1. irudia: Krimeako aztarnategian aurkitutako hegaztiaren berreraikitze artistikoa. (Ilustrazioa: Andrey Atuchin)

Aurkitutakoa ez da edonolako fosila. Zinez, hezur puska bat da: 40 zentimetroko luzera duen izterreko hezurra, hain zuzen. Lehen aldiz fosila eskutan izan zuenean, elefante-hegazti baten fosila zelakoan zegoen Errusiako Zientzien Akademiko ikertzaile Nikita Zelenkov, artean Europako erregistro fosilean tamaina horretako hegaztiren aztarnarik ez zegoelako. Orain arte uste zen horrelako hegazti erraldoiak soilik Madagaskarren, Australian eta Zeelanda Berrian bizi izan zirela, beti ere, uharteei lotuta.

Ez da izan Taurida izeneko leize sare batean aurkitutako fosil bakarra, baina bai esanguratsuena. Ezaguna da paleontologoak ederki moldatzen direla hezur bakar batean abiatuta animalia osoa “eraikitzen”, baina badira hainbat hezur mota bereziki aproposak direnak horretarako. Tamaina kalkulatzeko, bereziki femurra edo humeroa dira oso egokiak. Animalia pisutsuenek hezur indartsuagoak behar dituzte euren gorputzaren pisuari eusteko, eta ia animalia guztietan aurkitu da hezur horien eta pisuaren arteko korrelazioa badagoela.

Hortaz, aurkitutako fosilean oinarrituta, hegaztia nolakoa izan zen irudikatzeko modua izan dute. 3,5 metroko altuera eta 450 kilo inguruko pisua kalkulatu dute; ostruka bat baino hiru aldiz handiagoa, gutxi gorabehera. Pachystruthio dmanisensis espeziekoa dela uste dute, baina bere katalogazioa ez dago guztiz argi oraindik. Ikerketa hau ahalbidetu duen Errusiako Zientzien Fundazioaren txostenaren arabera, aurretik espezie horretako aztarnak aurkituak izan dira Georgian eta Hungarian, baina “ostruka erraldoienak” zirela zehazterik baino ez dute izan, haien tamaina kalkulatu ahal izan gabe. Orain Krimean aurkitutako hezurrarekin tamaina fintzeko modua izan dute. Journal of Vertebrate Paleontology aldizkarian argitaratutako zientzia-artikulu batean egin dute fosilaren deskribapen osoa.

Hezurra luzea eta nahiko mehea izateagatik, uste dute abiadura handia hartzeko gaitasuna zuela, hegal egiteko ahalmena galduta izan arren. Hori izan zen, ikertzaileen arabera, espezieari bizirik irautea ahalbidetu zion estrategia. Beharko zuen, seguruenera, aztarnategi berean aurkitu dituztelako hegazti horren harrapakari izan zitezkeen bestelako animalia beldurgarrien aztarnak: sable horzdun tigrea, gepardo erraldoia edota hiena erraldoia, besteak beste. Horiez gain, mamut baten eta bisoi baten aztarnak aurkitu dituzte. Azaldu dutenez, aztarna hauek erabakigarriak izan dira hegaztiaren datazioa egiteko.

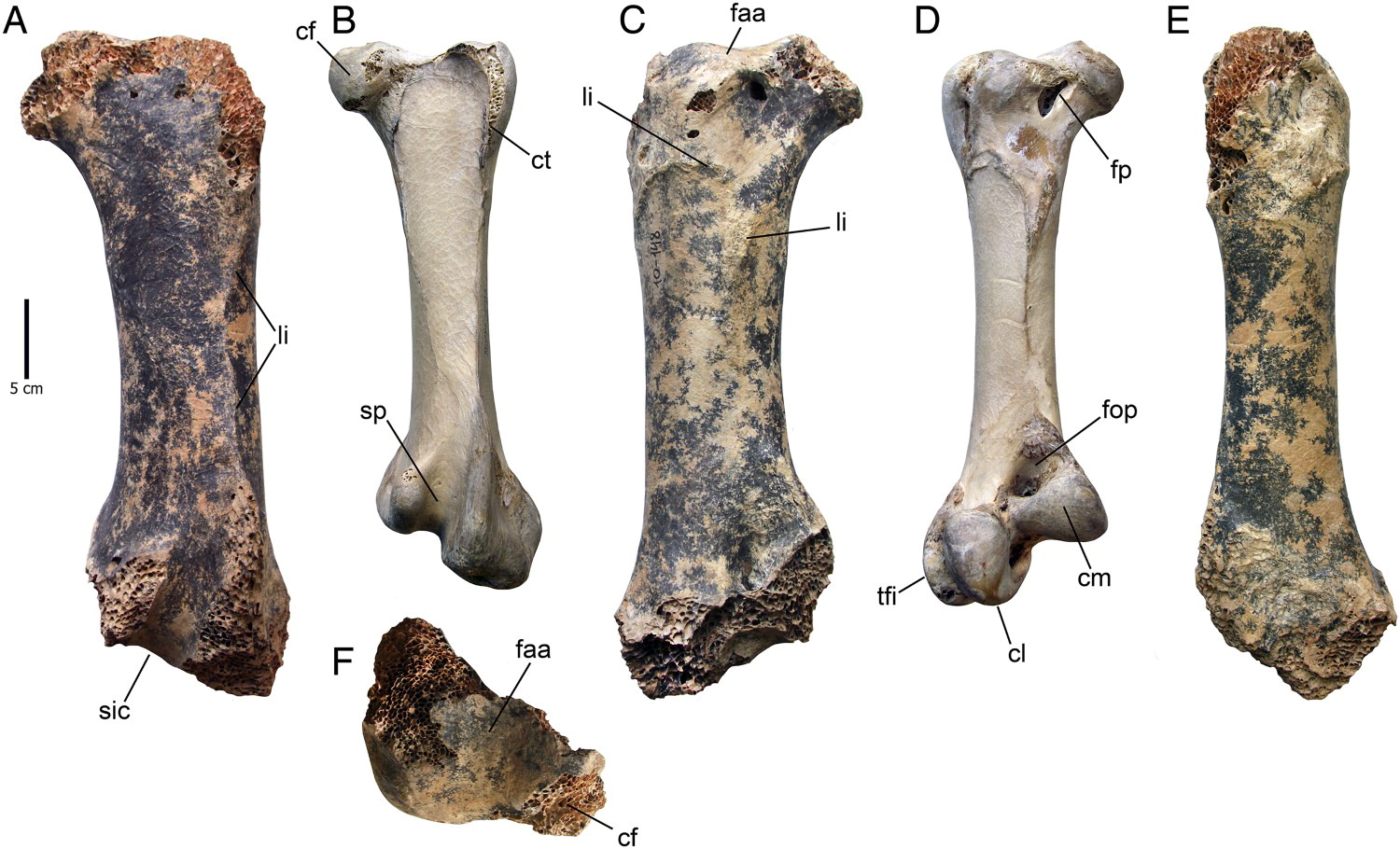
2. irudia: Aurkitu berri duten hegaztiaren hezurrak (ezkerrean, erdian eta eskuman), ostruka baten hezurrekin alderatuta. (Argazkia: Nikita Zelenkov/Society of Vertebrate Paleontology)

Hegazti horren fosila duela 1,5 eta 1,8 milioi urte bitartean bizi izan zela uste dute, eta, Homo erectus hominidoa duela 1,2 milioi urte iritsi izan zela kontuan hartuta, biak aldi berean kontinentean egoteko aukera planteatu dute. Zelenkovek aitortu du ez dakitela ziur noiz desagertu zen hegazti erraldoi hori, eta balitekeela 1,2 baino milioi urte inguru desagerrarazita egotea. Halere, “Homo erectus espezieko kideek horiek ikusteko aukera” izan zezaketela erantsi du, prentsa ohar batean, eta hegazti handi hori haragiaren, hezurren edota arrautzen iturria izan zitekeela planteatu dute. Esan beharrik ez dago, hegazti horiek gure espeziekoak ez ziren baina gizakitzat hartzen ditugun hominido horien alboan irudikatzeak joko gehiago ematen du hedabideetan, eta bide hori jarraitu dute haien ikerketa zabaltzeko. Baina, kasu honetan, ez da hedabideei begira diseinatutako estrategia hutsa izan: zientzia-artikuluaren tituluan bertan ere azaldu dute ideia.

Dena dela, datarena ez da erabili dute argudio bakarra ustezko lotura hori proposatzeko. Georgiako Dmanisi aztarnategian hegazti hori ez baina bai hegaztiarekin batera aurkitu diren antzeko fosilak aurkitu dituzte, eta ezaguna da Dmanisin ere Homo erectus izan zela. Zientzialariek beraiek aitortu dutenez, oraingo erronka da espeziea Europako beste lekuren batean aurkitzea, baina iragarri dute Krimeako aztarnategian bertan beste kanpaina bat aurrera eramateko aukera dutela.

Simferopol eta Kertx hirien artean eraikitzen ari diren autobiderako lanetan aurkitu dute aztarnategia. 2014an Krimea okupatu zuenetik, Errusiar Federakundeak martxan jarri nahi izan dituen azpiegituretako bat da hori, penintsularen erdian dagoen Simferopol hiriburu administratiboa eta Errusiarako sarbidea den Kertx hiriak lotzeko.

Gigantismo mota honen arrazoi ebolutiboa orduko klima-aldaketei egokitzeko beharrarekin lotu dute. Estepa irekietan zailagoa da nutritiboak diren elikagaiak eskuratzea, eta animalia handiek behar metaboliko txikiagoak dituztela azaldu dute egileek. Ez dago argi zein izan den Lurraren historian zehar planetan inoiz izan den hegaztirik handiena, baina ikertzaileek uste dute marka hori Vorombe titan deritzonari eman behar zaiola. Hiru metroko altuera zuela kalkulatu da, eta 800 kilo inguruko pisua.

Erreferentzia bibliografikoa:

Zelenkov, Nikita V. et al., (2019). A giant early Pleistocene bird from eastern Europe: unexpected component of terrestrial faunas at the time of early Homo arrival. Journal of Vertebrate Paleontology, e1605521. DOI: 10.1080/02724634.2019.1605521

———————————————————————————-

Egileaz: Juanma Gallego (@juanmagallego) zientzia kazetaria da.

———————————————————————————-

The post Europan inoiz aurkitutako hegazti fosilik handienaren berri eman dute appeared first on Zientzia Kaiera.

¿Clásica o moderna? He ahí la cuestión. Imagen: Wikimedia Commons

Hemos visto que la explicación de Einstein del efecto fotoeléctrico cuadra muy bien con las observaciones experimentales. Pero cuadra muy bien cualitativamente, es decir, explica lo que ocurre de forma genérica. Otra cosa muy distinta es que el modelo fotónico de Einstein explique cuantitativamente la observaciones. Solo entonces cabe hablar de un modelo realmente bueno.

Era necesario pues comprobar experimental y cuantitativamente el modelo de Einstein, en concreto dos afirmaciones claves:

a) La energía cinética máxima de los electrones es directamente proporcional a la frecuencia de la luz incidente; y

b) El factor de proporcionalidad h que relaciona la energía del fotón E con la frecuencia f (E = hf )es realmente el mismo para todas las sustancias.

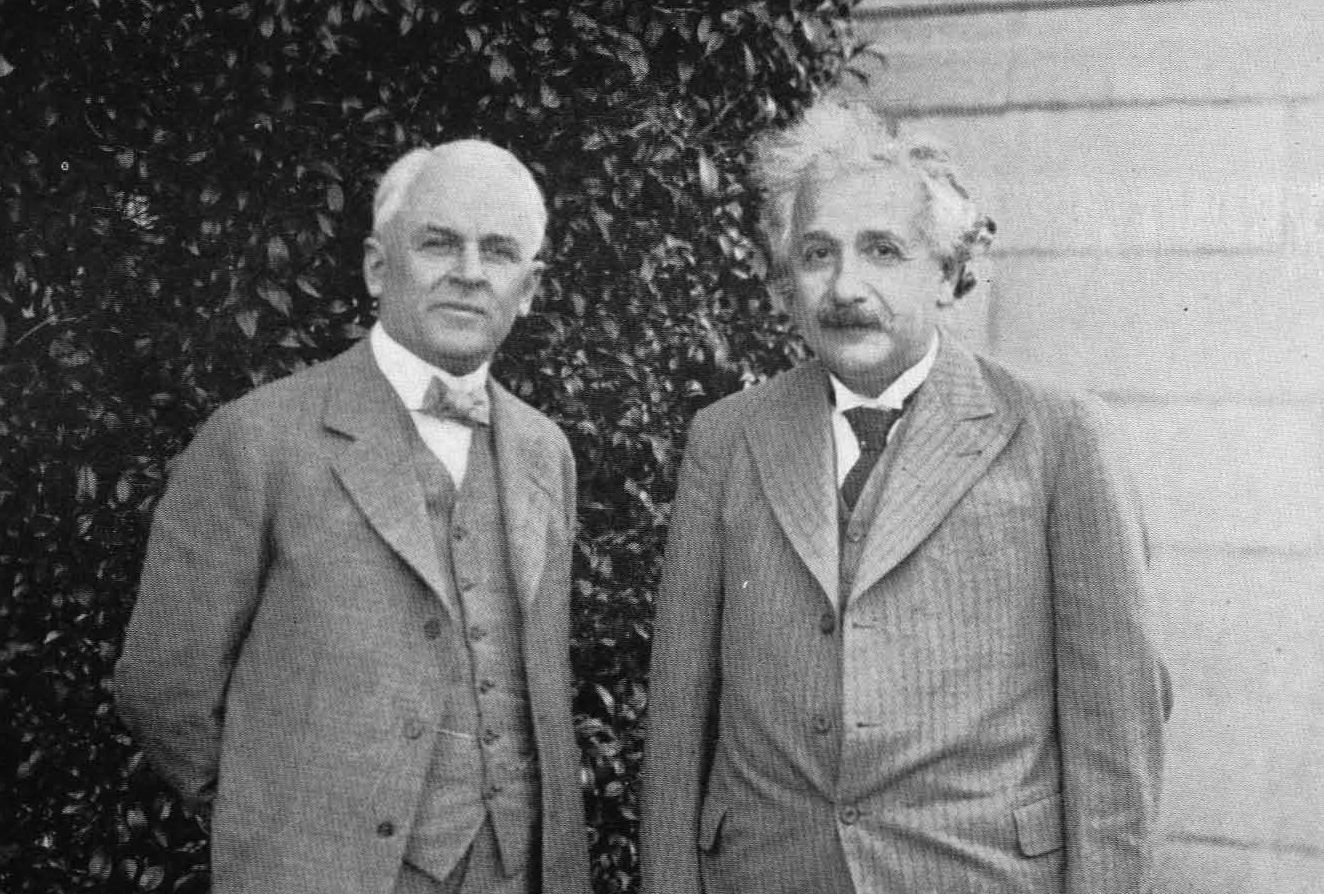Millikan y Einstein en 1932. Fuente: Wikimedia Commons

Durante 10 años, los físicos experimentales intentaron realizar las pruebas cuantitativas necesarias. Una dificultad experimental era que el valor de la función de trabajo W para un metal cambia mucho si hay impurezas (por ejemplo, una capa de óxido del metal) en la superficie. Finalmente, en 1916, Robert A. Millikan estableció que existe una relación en forma de línea recta entre la frecuencia de la luz absorbida y la energía cinética máxima de los fotoelectrones, como lo exige la ecuación de Einstein.

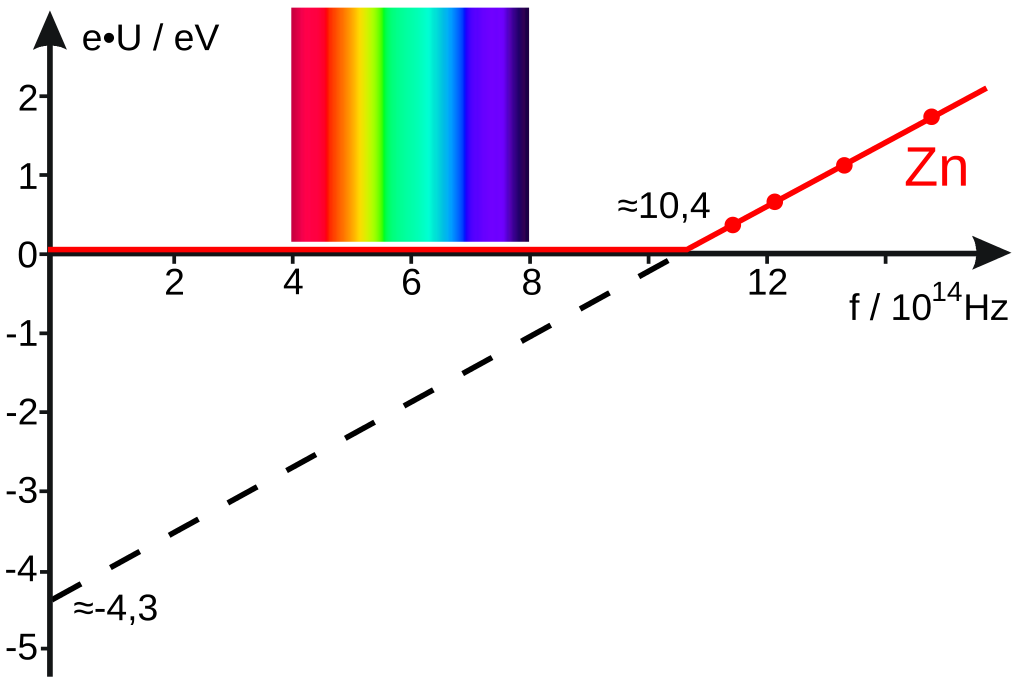
Si Ecmax se representa en el eje y y f a lo largo del eje x, entonces la ecuación de Einstein (Ecmax = hf – W) tiene la forma familiar de la ecuación para una línea recta y = mx + b. En una gráfica de la ecuación de Einstein, la pendiente debe ser igual a h, y la intersección con el eje y (f = 0) debe ser igual a -W. Esto es exactamente lo que encontró Millikan. Vemos en la imagen los datos para el zinc. La imagen es de Wikimedia Commons.

Para obtener sus datos, Millikan diseñó un aparato en el que la superficie fotoeléctrica del metal se obtenía por un corte en vacío. Un electroimán situado fuera de la cámara de vacío manipulaba una cuchilla dentro de la cámara para realizar los cortes. Este dispositivo, bastante complejo, era imprescindible para garantizar que se obtenía una superficie reproducible de metal puro.

Las líneas rectas que obtuvo Millikan para diferentes metales tenían la misma pendiente, h, aunque las frecuencias umbral (relacionadas con W) fuesen diferentes.

El valor de h obtenido a partir de los experimentos de Millikan eran, como hemos dicho, igual para distintos metales. De hecho también era el mismo encontrado por otros experimentos independientes. Este resultado sorprendió antes que ha nadie al propio Millikan, firme partidario de la teoría clásica de la luz. Su experimento demostró convincentemente que el modelo fotónico de la luz era correcto hasta donde se podía comprobar. El efecto fotoeléctrico dio como fruto dos premios Nobel, uno para Einstein por la teoría y otro para Millikan, por el experimento.

Albert Einstein recibe la Medalla Max Planck de manos de…Max Planck (1929). Era la primera vez que se entregaba la distinción creada por la Sociedad Alemana de Física; se otorgó en esta primera edición a los dos teóricos. El primero en recibirla fue Max Planck, quien, a continuación hizo entrega de la suya a Einstein. Fuente: Institute for Advanced Study.

Pero, ¿qué era esta h?

Históricamente, la primera sugerencia de que la energía en la radiación electromagnética está «cuantificada» (viene en cantidades, cuantos, definidas) no aparece en el modelo fotónico del efecto fotoeléctrico. Lo hizo en estudios sobre el calor y la luz irradiados por los sólidos calientes. Max Planck introdujo el concepto de cuanto de energía (aunque en un contexto diferente) a finales de 1899, 5 años antes de la teoría de Einstein. Es por esto que a la constante h se la conoce como constante de Planck.

Planck trataba de explicar cómo la energía térmica (y la luz) irradiada por un cuerpo caliente está relacionada con la frecuencia de la radiación. La física clásica (termodinámica y electromagnetismo del siglo XIX) no podía explicar los hechos experimentales. Planck descubrió que los hechos solo podían interpretarse suponiendo que los átomos, al irradiar, cambian su energía no en cantidades variables continuas, sino en cantidades discretas, en paquetes. El modelo fotónico del efecto fotoeléctrico de Einstein puede considerarse como una extensión y aplicación de la teoría cuántica de Planck de la radiación térmica. La gran diferencia y punto esencial es que Einstein postuló que el cambio en la energía del átomo E que se transporta está localizada en un fotón de energía E = hf, donde f es la frecuencia de la luz emitida por el átomo, como si el fotón fuese una partícula, en lugar de estar repartida por toda la onda de luz.

El éxito del modelo fotónico del efecto fotoelectrico ponía a toda la comunidad científica ante un verdadero dilema. Según la teoría ondulatoria clásica, la luz consiste en ondas electromagnéticas que se extienden continuamente a lo largo del espacio. Esta teoría tuvo mucho éxito en la explicación de los fenómenos ópticos (reflexión, refracción, polarización, interferencia). La luz se comporta como una onda experimentalmente, y la teoría de Maxwell da buena cuenta de este comportamiento ondulatorio. Pero la teoría de Maxwell no puede explicar el efecto fotoeléctrico. La teoría de Einstein, que postula la existencia de cantidades discretas de energía luminosa, sí explica el efecto fotoeléctrico, pero no otras propiedades de la luz, como la interferencia.

O sea, que había dos modelos de luz cuyos conceptos básicos parecían contradecirse entre sí. Según uno la luz es un fenómeno ondulatorio; según el otro la luz tiene propiedades similares a las partículas. Cada modelo tenía sus éxitos y sus limitaciones. La solución de este problema tendría consecuencias enormes para toda la física y tecnologías modernas en general y para nuestra comprensión de los átomos en concreto.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo El dilema del efecto fotoeléctrico se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. La explicación de Einstein del efecto fotoeléctrico
2. La incompatibilidad del efecto fotoeléctrico con la física clásica
3. El desconcertante efecto fotoeléctrico

Naiara Barrado, Itziar Garate eta Peio Iñurrigarro Azken asteotan Jupiterren orban ikusgarriena materia galtzen eta, ondorioz, tamainaz txikitzen ari da. Eguzki-sisteman ezagutzen den ekaitzik handiena eta luzaroena da Orban Gorri Handia, baina litekeena da laster desagertzea.

Jupiterrera begiratzean edota planetaren irudi bat ikuskatzean, marra horizontalez osatutako planeta ikusten dugu. Zuri-marroi tonalitate ezberdinetako marrak dira izatez (ilunak bandak eta argiak zonak deiturikoak). Hego-hemisferioan, 22º-ra ordea, elipse gorri handi bat azaltzen da (ikus 1. irudiaren ezkerraldea), Orban Gorri Handia modura ezaguna dena.

1. irudi-elkarketa: Ezkerrean, Jupiterren ohiko itxura, Orban Gorri Handia argi eta garbi identifikatzen delarik hego hemisferioan. Eskuinean, orbanaren behe-ezker aldean kanporanzko beso espiral gorri bat antzematen da. Bi irudiak behatzaile amateurrek Lurretik hartuak dira, bata 2018ko apirilean eta bestea 2019ko maiatzean. (Irudien elkarketa: Peio Iñurrigarro)

Oraindik ez dago argi kolore gorri berezi horren jatorria. Orbana inguruko hodeietatik 8 km gorago hedatzen da eta bertan atmosferako baldintzak ezberdinak direnez, pentsatzen da atmosferako konposatuen eta eguzki erradiazioaren arteko erreakzio kimikoak ezberdinak izan daitezkeelarik, horrek kolore gorria eragin dezakeela.

Kontua da orban hau oso ondo bereizita dagoela bere ingurutik, eta beraz, bere koloreari esker oso ondo identifika daitekeela orbanaren muga. Horregatik, orbanak materia galtzen duenean ere, askatutako materia argi eta garbi azaldu ohi da irudietan. Adibidez, maiatzaren 19an orbanetik kanporantz beso espiral gorri moduko bat ateratzen zela ikusi zen (ikus 1. irudiaren eskuinaldea). Astebete geroago, orbanak materia zati handi bat galdu zuela ere ikusi genuen.

Orbana oso gune dinamikoan dago. Jupiterren bandak eta zonak korronte atmosferikoen mugak dira, ia denak ekialderanzkoak. Bada ordea bat mendebalderanzkoa, ekuatoretik hegoaldera 20º-ra dagoen korronte estu baina indartsu bat. Orban Gorri Handiaren goi muga ezartzen du korronte honek. Izatez, orbana bi korronteen artean kokatuta dago, goitik (iparraldetik) mendebalderanzko korronte indartsua du eta behetik (hegoaldetik) ekialderanzko korronte bat.

Konfigurazio honek eragiten du orbanak erlojuaren orratzen aurkako noranzkoan biziki biratzea (430km/h abiadurako haizeak izan ditzakeelarik), baina tarteka ezegonkortasunak ere eragiten ditu. Hauen ondorioz, orbana eta bere ingurunearekin materia-trukaketak gerta daitezke. Zurrunbilo txikiak (zikloiak eta antizikloiak) orbanera hurbiltzean, orbanak irentsi egin ohi ditu, eta materia berria barrura sartzen da. 2017ko maiatzean ordea, aurkako fenomenoa gertatu zen, orbanak materia galdu zuen kanporanzko beso espiral baten ondorioz. Beso honek egun batzuk iraun zituen ikusgai, azkenean inguruko atmosferarekin nahastu eta desagertu zen arte.

Beraz, duela aste pare bat ikusitako besoa ez da fenomeno berria. Izan ere, urtarriletik hona behin baino gehiagotan ikusi da. Azken beso horrek orbanean eragin duena ordea, ezberdina da; izan ere, orbana mugatzen duen elipsea nabarmen txikitu da. Horrela dirudi baina baliteke beste zerbait izatea: orbana uzkurtu ez baina kanpoaldeak kolorez aldatu izana.

2. irudi-elkarketa: Jupiter metanozko filtroarekin behatuta. Horrela, Orban Gorri Handia elipse distiratsu baten moduan ikusten da eta jasaten dituen eraldaketak errazago iker daitezke. Lehenengo irudia maiatzaren 19koa da, eta bertan 1. irudiko eskuinaldean ikusitako beso espirala argi identifika daiteke. Irudi guztiak behatzaile amateurrek Lurretik hartuak dira. (Irudien elkarketa: Peio Iñurrigarro)

Bestalde, badirudi inguruko atmosferak orbana “erasotzen” jarraitzen duela, eta materia zatiak behin eta berriz kanporatzen direla (ikus 2. irudia). Oraindik ez dago erabat argi orban inguruko korronteak edota korronteei esker orbanera hurbiltzen diren zurrunbiloak diren materia kanporatze honen erantzule, baina egoerak honela jarraituz gero, Jupiterren Orban Gorri Handia desagertu egin daiteke.

Edo agian ez. Orbanaren nukleoak indartsu darrai eta ez dirudi ahuldu egin denik. Agian orbanak nukleo inguruko materia guztia gal lezake, baina bihotza tinko mantenduz. Beharbada, ondoren, berriz indartu eta hazi liteke.

Ekaitzak etengabe sortzen eta desagertzen dira Lurrean, bai eta Jupiterren ere. Izatez, ezin dugu baieztatu egun ikusten dugun Orban Gorri Handia 1665ean ikusitakoaren berdina denik. Hooke eta Cassiniren lehen behaketa haien ondoren, 1713. urtera arte, orbanaren erregistro gehiago egin ziren. Ondoren ordea, 1830. urtera arte ez dago datu gehiagorik. 115 urteko hutsunea dago behaketetan. Beraz, baliteke hasierako orban gorri hura desegin eta birsortzea, guk berriz behatu aurretik.

Edozein kasutan, egungo orbana ahuldu eta indartuz gero, edota guztiz desagertuz gero, edota desegin eta berriz sortuz gero, zientziaren une garrantzitsu baten aurrean gaude, eta adi adi jarraituko dugu Jupiterrerantz begira.

Izatez, aspaldi gaude erne: iaz The Astronomial Journal aldizkariko artikulu batean orbana hurrengo 20 urteetan desager zitekeela azaldu zutenetik. Egia da bere tamaina (XIX. mendean) lehenengo aldiz neurtu zenetik asko txikitu dela. Garai hartan orbanaren diametroa Lurrarenaren hirukoitza zen, eta iaz 1.3 aldiz handiagoa soilik. Artikulu horretan esaten zen, txikitze erritmo horri eutsiz gero 20 urte beharko zirela orbana guztiz desegiteko. Edonola, zenbat eta txikiagoa izan, orduan eta ahulagoak izaten dira ekaitzak, eta beraz, hauskorragoak. Agian, ez ditugu 20 urte beharko orbanaren amaiera ikusteko. Apika, 20 egunean gerta daiteke.

—————————————————–

Egileez: Naiara Barrado Izagirre (@naierromo) eta Itziar Garate Lopez (@galoitz) UPV/EHUko Fisika Aplikatua I Saileko irakasleak dira eta Zientzia Planetarioen Taldeko kideak, Peio Iñurrigarro fisikaria da eta Zientzia Planetarioen Taldeko
kidea.

—————————————————–

The post Jupiterren Orban Gorri Handia, desagertzear? appeared first on Zientzia Kaiera.

 

Los que tenemos la suerte de no haber tenido un encontronazo serio con la justicia (y que así siga muchos años…) solo conocemos una sala de interrogatorios por haberla visto en las películas así que nuestro conocimiento sobre el tema debería ser puesto en cuarentena. Sin embargo, gracias a la abundante oferta de documentales sobre crímenes reales que incluyen escenas reales de interrogatorios, confesiones y juicios, no es difícil hacerse una idea, al menos aproximada, de cómo funciona el asunto.

Un sospechoso, más o menos atolondrado por el impacto del crimen sucedido, responde a una serie de preguntas más o menos amables o agresivas según avanza la investigación y, como resultado de la astucia del que pregunta y la suya propia, termina confesando el crimen. Y ante la confesión, ¡ajá, crimen resuelto!

¿Verdad? ¿Acaso no es una confesión la prueba definitiva? Solamente evidencias físicas muy contundentes pueden revertir una confesión, rastros de ADN que inequívocamente sitúen a otro sospechoso en el lugar de los hechos o al dueño de la confesión en otro lugar diferente. Excepto eso, una confesión es todo lo que parecería necesario para resolver un delito. Al fin y al cabo, ¿quién reconocería haber hecho algo grave, un asesinato, una violación, si no lo hubiese hecho? ¿Y por qué?

 

¿Son fiables todas las confesiones?

Saul Kassin es psicólogo en la universidad de justicia criminal John Jay de Nueva York y uno de los principales expertos mundiales en interrogatorios y falsas confesiones. La revista Science ha dedicado recientemente un reportaje a su trabajo, en el que cuenta por qué algo aparentemente tan contraintuitivo como que un sospechoso se autoinculpe de un crimen que no cometió no solo es algo más común de lo que podríamos pensar, sino que tiene una causa que la psicología puede explicar.

Las confesiones siempre se han considerado el indicador máximo de la culpabilidad, incluso aunque se conocen casos históricos de falsas autoacusaciones. Científicamente la primera alerta al respecto está fechada en 1908, cuando Hugo Müsterberg, reputado psicólogo de la Universidad de Harvard de la fecha ya alertó de “confesiones inciertas bajo el efecto de poderosas influencias”. Sin embargo, fue a finales de los años 80 con la introducción en los juzgados de las evidencias basadas en técnicas de reconocimiento de ADN para exonerar a condenados que en realidad eran inocentes cuando se empezó a vislumbrar cómo de frecuente podía ser el problema.

Kassin ha dedicado su carrera a este tema. Estudió y se doctoró en psicología, y cómo investigador postdoctoral, analizando la forma en que los jurados toman decisiones, quedó sorprendido con el poder que tiene una confesión para prácticamente garantizar un veredicto de culpabilidad.

Al mismo tiempo empezó a preguntarse si era posible analizar cuántas de esas confesiones eran reales. Comenzó a estudiar una técnica de interrogatorio llamada Reid, por uno de sus autores, John Reid, basada en un método publicado en 1962 y que es una forma habitual de entrenar a los agentes que se dedican a este área del trabajo policial. “Me quedé horrorizado. Era como los estudios sobre la obediencia de Milgram, pero peor”.

Bajo presión de la autoridad, hacemos lo que no haríamos

Echemos un paso atrás. Stanley Milgram, psicólogo de la Universidad de Yale, llevó a cabo una serie de estudios sobre la conducta en la década de los 60 en los que se animaba a los participantes a aplicar descargas eléctricas sobre otros sujetos si consideraban que éstos no estaban aprendiendo lo suficientemente deprisa. Los voluntarios, que no sabían que esas descargas en realidad eran falsas y creían estar causando dolor real a sus compañeros, resultaron estar sorprendentemente dispuestos a hacerlo si una persona a la que consideraban con autoridad sobre ellos se lo pedía.

El manual para interrogar de Reid parece diferente al principio. La técnica comienza con una evaluación previa en la que el interrogador hace una serie de preguntas, algunas irrelevantes y otras más sustanciosas, mientras busca en el interrogado determinadas señales de que esté mintiendo, como evitar el contacto visual o cruzarse de bazos. Después va la fase dos, considerada el interrogatorio formal. Aquí el que pregunta sube el tono, acusando al sospechoso repetidamente, pidiendo detalles concretos e ignorando los momentos en que niega su implicación. Al mismo tiempo ofrece su simpatía y comprensión, minimizando las implicaciones morales del crimen, pero no las legales, facilitando el momento de la confesión. “Esto no habría pasado si ella no te hubiese faltado al respeto” y cosas así.

Foto: nihon graphy / Unsplash

“¿He pulsado yo esa tecla?”

Esta es la fase que Kassim relacionaba con el experimento de Milgram: una figura de autoridad presionando para causar un daño, solo que en vez de a un tercero, aquí sería a uno mismo al admitir una culpabilidad que no es propia. Kassim sospechaba que esa presión autoritaria podía llevar a veces a realizar confesiones falsas.

Para averiguarlo, en los años 90 decidió modelar en el laboratorio la técnica Reid con estudiantes voluntarios, creando lo que llamó el experimento del bloqueo informático: hacía a los estudiantes seguir órdenes rápidas ante un ordenador, avisándoles de que tenía un fallo y que si pulsaban la tecla Alt, el ordenador se bloquearía. Esto era falso en parte: el ordenador estaba programado para bloquearse en todas las pruebas. Cuando ocurría, el investigador acusaba al estudiante que estuviese haciendo la prueba en ese momento de haber apretado la tecla Alt.

Al principio, ninguno de los estudiantes confesaba. Luego fue introduciendo distintas variaciones basadas en esas técnicas de interrogatorios policiales. A veces, por ejemplo, un policía le decía falsamente a un sospechoso que tenían un testigo del crimen, haciéndole dudar de su versión de los hechos. Funcionó en el caso de Marty Tankleff, adolescente estadounidense que en 1988 llegó a casa y se encontró a sus padres apuñalados en la cocina, su madre muerta y su padre en coma. La policía le consideró el principal sospechoso y tras horas interrogándole sin éxito le dijeron que su padre había despertado en el hospital y había dicho que fue él quién lo hizo (aunque no era verdad, su padre murió sin despertar del coma). Completamente en shock y dudando de sus propios recuerdos, Tankleff confesó y pasó 20 años en la cárcel antes de que nuevas evidencias sirviesen para exonerarle.

Ante un testigo o en espera de más pruebas

Un impacto de ese tipo no se podía generar en el laboratorio, pero Kassin sí podía aliarse con un “testigo” que asegurase haber visto al estudiante apretar la tecla en cuestión, y resultó que esos estudiantes confesaban el doble de veces que aquellos que hacían la prueba en presencia de un testigo que aseguraba no haber visto nada. En determinadas circunstancias, prácticamente todos los estudiantes que trabajaban ante un testigo acusatorio falso terminaban confesando.

Algunos estudiantes terminaban tan convencidos de haber causado el bloque que sin querer inventaban explicaciones y justificaciones, y algunos internalizaban tanto su fallo que se negaban a creer al investigador cuando este les contaba la verdad sobre la prueba.

Otro truco policial puede ser, no mentir sobre las evidencias disponibles, pero si advertir de que se están esperando más pruebas, por ejemplo, un análisis de rastros de ADN encontrados en la escena del crimen. Ante esa situación, que intuitivamente daría al acusado inocente más razones para defenderse y resistir, muchos se derrumban y confiesan, precisamente para liberarse de la presión en ese momento y confiando en que la posterior llegada de nuevas pruebas servirá para exonerarles.

Kassin creó una variante de la prueba del ordenador para testar estas situaciones: además de acusar al estudiante de haber apretado la tecla Alt, les decía que el registro de las teclas pulsadas estaba grabado y que podrían consultarlo muy pronto. El número de estudiantes que confesaba se disparó, precisamente porque querían salir de allí en ese momento y esperaban que la posterior consulta del registro les liberase de culpa. En ese sentido, la confianza en el correcto funcionamiento del sistema y en la propia inocencia pueden ser factores de riesgo de terminar realizando una confesión falsa.

Otros experimentos: jóvenes, adictos o enfermos mentales, los más vulnerables

Existen algunas críticas obvias a estos experimentos. Por ejemplo, que en este contexto de pruebas universitarias difícilmente se temen las mismas consecuencias, o estas son tan obvias ante una falsa confesión que en el entorno de una investigación criminal, o que pulsar una tecla sin querer es relativamente común y eso puede hacer que alguien dude de su propia versión de los hechos, algo que no parece igual de probable cuando hablamos de cometer el asesinato, por ejemplo, de tus propios padres.

Por eso otros investigadores han buscado cómo complementarlos. Es el caso de Melissa Russano, psicóloga social en la Universidad Roger Williams en Rhode Island. Ella diseñó un experimento en el que se pedía a una serie de voluntarios que resolviesen un conjunto de problemas de lógica, algunos en grupo y otro de manera individual. Ante de empezar se dejó bien claro que bajo ningún concepto era aceptable ayudar a los estudiantes que debían trabajar solos, a algunos de los cuales se les había instruido previamente para mostrar muchas dificultades y disgusto ante las pruebas. Esto llevó a algunos de sus compañeros a echarles una mano, lo cuál suponía una clara violación de las reglas.

En esos experimentos los que ayudaban sabían que estaban saltándose las reglas, y confesar conllevaba ciertas consecuencias ya que se había roto el código de conducta de las sesiones. Pero, igual que Kassin, Russano observó que un interrogatorio acusatorio podía provocar falsas confesiones. Ella y sus colegas probaron otro truco habitual en los interrogatorios policiales: el de la minimización de la carga emocional o moral de la falta cometida, diciendo cosas como que “seguro que no te has dado cuenta de cómo de serio era lo que estabas haciendo”, y con eso consiguieron que la tasa de falsas confesiones subiese un 35%.

Otros investigadores, como Gísli Gudjónsson, detective islandés y psicólogo en el King’s College de Londres, han explicado que determinados factores hacen a algunos individuos más susceptibles que a otros a este tipo de presión. Por ejemplo, enfermedades mentales, ser muy jóvenes o la adicción a sustancias hacen que algunas personas estén más dispuestas a dudar de su propia memoria y a confesar bajo presión cosas que no han cometido.

Richard Leo, profesor de derecho de la Universidad de San Francisco en California, y Rochard Ofshe, por entonces en la Universidad de California Berkeley, describieron en varios informes una “persuasión” hacia la confesión: confesiones que eran resultado de situaciones en las que un sospechoso, destrozado tras horas de interrogatorio, entra en un camino mental en el que empieza a creer en su propia culpa aunque sea falsa. Es un fenómeno especialmente pronunciado entre adolescentes que son impresionables y fácilmente intimidables por una figura autoritaria.

Las confesiones quizá no sean lo más importante

Entre todos consiguieron crear un cuerpo de evidencias suficientes que hicieron que en torno al año 2010 Kassin y varios colegas americanos y británicos escribieron un documento para la Asociación Americana de Psicología advirtiendo del riesgo de coacción en estos interrogatorios y sugiriendo algunas reformas, como por ejemplo prohibiendo las mentiras por parte de los investigadores, limitando el tiempo que podían durar esos interrogatorios y exigiendo la grabación de éstos de principio a fin.

De hecho, cuestionaban el valor de las confesiones como tal y ponían en duda lo idóneo de que eso sea lo que busquen principalmente los investigadores, señalando que ante el peso de otro tipo de pruebas forenses o de otro tipo, quizá seguir utilizando las confesiones como la principal medida de la culpabilidad no solo sea un riesgo, sino que además no sea lo más inteligente.

Para la espectacularidad de un asesino que por fin confiesa siempre nos quedarán las series policiales.

Referencias

This psychologist explains why people confess to crimes they didn’t commit – Science

Migram Experiment – Simple Psychology

Inside interrogation: The lie, the bluff, and false confessions – American Psychology Association

Marty Tankleff – Wikipedia

Investigating True and False Confessions Within a Novel Experimental Paradigm – Psychological Science

The Psychology of False Confessions: Forty Years of Science and Practice – Wiley Online Library

The Social Psychology of Police Interrogation: The Theory and Classification of True and False Confessions – Studies in Law, Politics, and Society

Police-Induced Confessions: Risk Factors and Recommendations – Law and Human Behaviour

Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista

El artículo Por qué a veces confesamos cosas que, en realidad, nunca hicimos se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. ¿Por qué si nunca hemos vivido mejor que ahora el mundo nos parece cada vez peor?
2. Realidad conexa, porque todo está conectado.
3. Nunca es tarde

Bidaian zoaz hegazkin komertzial batean, 35.000 oineko altueran zaude hau da, lurretik 10.668 metrora. Hegazkina diseinatuta dago kabina barruan 2.438,4 metrora (8.000 oin) dagoen presio bera izateko. Baina ba al dakizu zergatik? Lurreko presioa mantenduko balu esfortzu ikaragarria eragingo liokeelako hegazkinaren egiturari eta… ez zenuke nahi izango horrelakorik.

Maiz egiten diren galderak ataleko bideoek labur eta modu entretenigarrian aurkeztu nahi dituzte, agian, noizbait egin ditugun galderak eta hauen erantzunak. Bideoak UPV/EHUko Kultura Zientifikoko Katedrak eginak daude eta zientzia jorratzen duen Órbita Laika (@orbitalaika_tve) telebista-programan eman dira gaztelaniaz.

The post Zer gertatzen da hegazkinak presioa galtzen badu kabinan? appeared first on Zientzia Kaiera.

Los grandes dioses, propios de religiones moralizantes, aparecieron mucho después de que se desarrollasen entidades políticas de gran complejidad social. Esta es la principal conclusión de un estudio publicado hace unos meses en la revista Nature por un amplio equipo de investigadores. Sus resultados refutan la conocida tesis de que fue la adopción de divinidades moralizantes lo que facilitó el desarrollo de grandes entidades políticas. La tesis rechazada sostenía que los códigos morales de inspiración religiosa habían servido para promover la convivencia y cooperación dentro de sociedades heterogéneas y que sin ellos, esas sociedades habrían sido inviables.

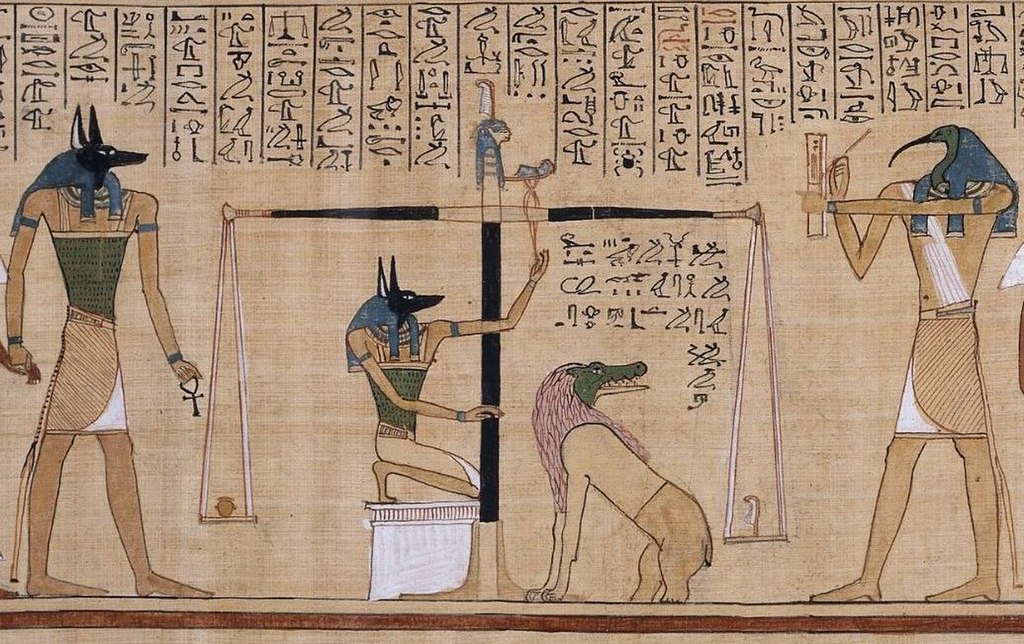El Juicio de Osiris representado en el Papiro de Hunefer (ca. 1275 a. C.). Anubis, con cabeza de chacal, compara el peso del corazón del escriba Hunefer con el de la pluma de la verdad en la balanza de Ma’at. Tot, con cabeza de ibis, escriba de los dioses, anota el resultado. Si el corazón es más ligero que la pluma, a Hunefer se le permitirá pasar a la otra vida. Si no es así, será devorado por la quimera Ammyt, compuesta por partes de cocodrilo, león e hipopótamo, que espera expectante. Fuente British Musem / Wikimedia Commons

La primera aparición de deidades moralizantes se produjo en Egipto, alrededor de 2.800 aC (II Dinastía), donde Ma’at era venerada como la diosa de la verdad, la justicia, la moralidad y el equilibrio. A esta siguieron apariciones esporádicas de cultos locales a lo largo y ancho de Eurasia (Mesopotamia, 2.200 aC; Anatolia, 1500 aC; China, 1000 aC), antes de que comenzase la expansión de importantes religiones durante el primer milenio aC con el Zoroastrismo y el Budismo, seguidos más tarde por el Cristianismo y el Islam. Aunque estos dos credos acabarían siendo adoptados por numerosas sociedades, ya existían en muchas de ellas dioses moralizantes como es el caso de los romanos desde 500 aC.

Utilizaron información sobre 414 unidades políticas independientes de 30 regiones geográficas, para un periodo que va del comienzo del Neolítico a la época industrial o colonial. Caracterizaron cada una de las sociedades mediante un índice de complejidad social (establecido a partir del registro arqueológico y escrito) y en virtud de la existencia (o no) de divinidades moralizantes (como el Dios de Abraham) o de sistemas equivalentes de creencias que inspiraron alguna forma de castigo, de origen sobrenatural, de las transgresiones morales (como el karma en el Budismo). Esta segunda posibilidad la basaron en la existencia de normas, basadas en la creencia en entes sobrenaturales, que promovían la reciprocidad, la justicia y la lealtad intragrupal.

Encontraron que la complejidad social antecedía a las divinidades moralizantes y que predecía su adopción. De hecho, la complejidad crecía mucho más rápido antes de la aparición de los dioses que después. Observaron también que la deidad moralizante era adoptada dentro del siglo siguiente a la superación de un cierto umbral de complejidad social (60% del máximo), que corresponde a lo que los autores denominan una megasociedad (aproximadamente un millón de habitantes). Y de entre las sociedades de las 10 regiones que no adoptaron dioses moralizantes solo el imperio Inca (61% de la complejidad máxima) superó el umbral de megasociedad.

La adopción de deidades moralizantes tampoco fue –como a veces se ha propuesto- consecuencia de la bonanza económica que trajeron una agricultura y ganadería cada vez más eficientes durante la llamada Era Axial (primer milenio aC), ya que en Egipto, Mesopotamia y Anatolia fueron adoptados antes de 1500 aC.

Los autores del estudio conceden mucha importancia a los rituales. Su celebración frecuente, así como la vigilancia institucionalizada de su cumplimiento, propia de religiones con varios niveles jerárquicos, antecedió a las grandes religiones unos 1.100 años en promedio. Creen que fueron esos rituales y su reforzamiento por las autoridades religiosas el elemento que permitió unificar numerosas poblaciones por primera vez en la Historia, al favorecer la aparición de identidades comunes en el interior de grandes estados. Los dioses moralizantes llegaron después y aunque no fuesen ellos la causa de la evolución de megasociedades, fueron una adaptación cultural clave para favorecer la cooperación en su seno, algo de especial importancia en sociedades multiétnicas.

Fuente: H. Whitehouse et al (2019): Complex societies precede moralizing gods throughout world history. Nature 568: 226-229.

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

 

 

 

 

El artículo Los dioses moralizantes no crearon los grandes estados se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. ¿Cinco o seis grandes?
2. Retrospectiva de un cuadro: El festín de los dioses
3. ¿Por qué son tan grandes las ballenas?

Uxue Razkin

Musika

Josu Lopez-Gazpiok azaldu digun moduan, soinuaren eta musikaren atzean zientzia asko dago. Asteon, kulturak soinuen pertzepzioan duen eragina eta armonia zer den aztertu du. Ideia honi jarraiki, zergatik ditugu gustuko musika mota batzuk? Zergatik dira sinfonia batzuk hain erakargarriak?, galdetzen du egileak. Badu erantzuna ere: kulturak musikan duen eragina omen da gakoa. Armoniak, esaterako, abesti bat bere osotasunean egonkorra izatea egiten du eta, neurri batean, matematikan dago armoniaren azalpena. Ez galdu testuan eman dituen xehetasunak!

Emakumeak zientzian

Judit Muñoz Matute matematikaria elkarrizketatu du Ana Galarragak. Txikitatik gustuko izan ditu, bereziki problemak ebaztea. Orain, ingeniaritzan dabil doktoretza egiten, Matematika aplikatuetan, eta aipatzen duenez, oso emakume gutxi dira: “Irudipena dut Matematika ikasi duten emakume gehienak joaten direla Biologia, Medikuntza edo Estatistika arloetara, baina Ingeniaritzan ez da ohikoa”. Esklerosi anizkoitza diagnostikatu zioten duela sei urte, Matematika karrerako azken urtean, baina horrek ez du geldiarazi.

Psikologia

Joana Jauregizar psikologoa elkarrizketatu dute Berrian. Bertan dio edozein adin eta maila sozioekonomikotako pertsonek izan dezaketela depresioa. Bere taldeak –berarekin batera aritu dira Maite Garaigordobil eta Elena Bernaras irakasleak–haurren depresioari aurre egiteko azterlan bate gin du UPV/EHUn. “Pozik bizi” deitu diote sortu duten programari, irakasleei eta eskolei zuzenduta dagoena, 8-10 urteko haurretan emozioak eta depresio sintomak hobetzeko martxan jarri dutena.

Mikrobiologia

Krisi klimatikoan mikroorganismoek duten papera oso garrantzitsua da zientzialari talde batek azaldu duenez eta horiek alboratzearen arriskuaz mintzatu dira. Gales Berriko Unibertsitateko (Australia) ikertzaile Ricardo Cavicchioli gidatzen ari da ekimena eta berarekin batera, bederatzi herrialdetako beste 32 mikrobiologok sinatu dute agiria. Adituek argudiatu dutenez, goiko mailako bizidun guztiek mikroorganismoen beharra dute. Juanma Gallegok azaltzen du testuan.

Dibulgazioa

50 urte hauetan zehar Zientzia eta Teknologia Fakultatea osatzen duten langileek jarduera ugari egin dituzte, hala nola Olinpiada Zientifikoak, fakultatean ikasi dezaketen Batxilergoko ikasleen artean, hainbat diziplina zientifikori buruzko jakin-nahia pizteko asmoz antolatzen direnak, hain zuzen. Horiei buruzko informazioa artikulu honetan topatuko duzue.

———————————————————————–
Egileaz: Uxue Razkin kazetaria da.

——————————————————————

The post Asteon zientzia begi-bistan #262 appeared first on Zientzia Kaiera.

La invisibilidad, los metamateriales y la capa de Harry Potter tienen en común… exacto, las matemáticas. El Ikerbasque Research Fellow Pedro Caro, del BCAM, lo explica.



Quizás sea el número más famoso de la historia. Lo cierto es que el número Pi, representado por la letra griega π, es una de las constantes matemáticas más importantes que existen en el mundo, estudiada por el ser humano desde hace más de 4.000 años. La fascinación que ha suscitado durante siglos es tal que el popular número cuenta con su propio día en el calendario, así el mes de marzo se celebra el Día de Pi en todo el planeta.

Este evento internacional vino de la mano del físico estadounidense Larry Shaw, quien lanzó en 1988 la propuesta de celebrar esta efeméride. La forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos de la famosa constante matemática. (3-14 martxoaren 14 en euskara / 3-14 march, 14th en inglés) y además, la celebración coincide con la fecha del nacimiento de Albert Einstein. En 2009, el congreso de EEUU declaró oficialmente el 14 de marzo como el Día Nacional de Pi.

Actualmente, el Día de Pi es una celebración mundialmente conocida que sobrepasa el ámbito de las matemáticas. Este número irracional, que determina la relación entre la longitud de una circunferencia y su diámetro, concierne a múltiples disciplinas científicas como la física, la ingeniería y la geología, y tiene aplicaciones prácticas sorprendentes en nuestro día a día.

Este 2019 nos unimos de nuevo al festejo con el evento BCAM–NAUKAS, que se desarrolló a lo largo del 13 de marzo en el Bizkaia Aretoa de UPV/EHU. BCAM-NAUKAS contó durante la mañana con talleres matemáticos para estudiantes de primaria y secundaria y durante la tarde con una serie de conferencias cortas dirigidas al público en general.

Este evento es una iniciativa del Basque Center for Applied Mathematics -BCAM, enmarcada en la celebración de su décimo aniversario, y de la Cátedra de Cultura Científica de la Universidad el País Vasco.

Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Metamateriales, invisibilidad y la capa de Harry Potter se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Palo seco
2. E-pi-logo (después de esto, mi carrera ha muerto)
3. Matemáticas modernas

Zerbaiterako balio du sare sozialetan haserratzea? Martha Villabonaren The effects of online outrage

Amaren sabeleko konforta eta soinuak atzean utzi eta inkubagailuko aspesia eta makina zaratara pasatzen da ume goiztiarra. Musikak ondo letorke garapen neurologikorako? José Ramón Alonsok aztertu du Music and preterm babies

Material bat isolatzailea den ala ez dioen teoria makroskopikoa izan da orain arte. Beste modu batera ikusita, bere osotasunean kontsideratuta baino ezin du esan teoriak material jakin bat isolatzailea izango den ala ez. Ezin du aurreikusi multzo horren bolumen jakin bat isolatzaile izango den ala ez. Orain arte. DIPCkoek: A local theory of insulators

–—–

Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.

The post Ezjakintasunaren kartografia #269 appeared first on Zientzia Kaiera.

La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebra dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Publicamos en el Cuaderno de Cultura Científica y en Zientzia Kaiera una serie de artículos que narran algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas.

 

Los neandertales fueron cazadores recolectores que habitaron Europa, Oriente Medio y parte de Asia durante más de 150 mil años, hasta que desaparecieron hace unos 30-40 mil años. Físicamente eran de estatura media, con un promedio de 166 cm los hombres y 154 cm las mujeres, pero más robustos y con los cuerpos más anchos. Tenían una gran capacidad craneal, la frente huidiza, dos grandes arcos óseos por encima de los ojos, entre otros numerosos rasgos anatómicos que nos permiten diferenciarlos de nuestra especie. El uso de nuevas tecnologías, nos está permitiendo conocer con mayor detalle la anatomía de estos humanos (Figura 1).

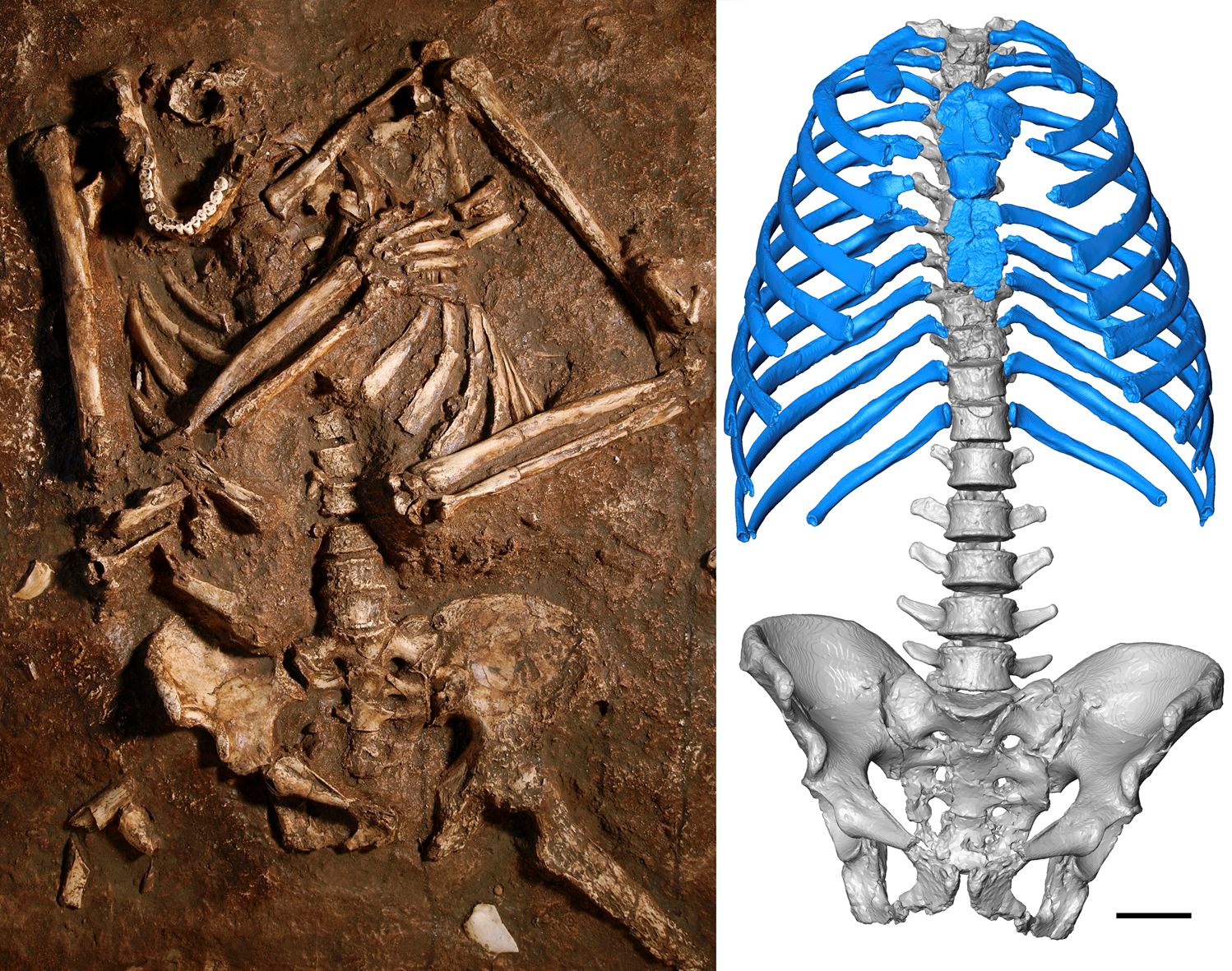Figura 1. Izquierda: Fotografía del molde del esqueleto de Kebara 2 (Madrid Scientific films). Derecha: Reconstrucción virtual del tórax de Kebara 2 (escala = 5 cm). Figura originalmente publicada por Gómez-Olivencia et al. (2018). Licencia Creative Commons 4.0.

Los neandertales soportaron cambios climáticos muy severos: momentos glaciares, y momentos interglaciares (como el actual), pero en general habitaron una Europa algo más fría que la actual. A pesar de eso, y en contra de la creencia tradicional, no estaban especialmente adaptados al frío, y de hecho la mayor parte de los descubrimientos se localizan en latitudes templadas, especialmente en la península ibérica, el sudoeste de Francia, la península itálica y el levante mediterráneo. Los neandertales habitaron gran cantidad de ecosistemas: cazaban gamos y gacelas en zonas de bosque mediterráneo de Oriente medio, mamuts, renos y caballos en las llanuras de Bélgica o cabras montesas en la cordillera cantábrica. Conocemos muy bien los animales que consumían ya que se han encontrado muchos restos de huesos con marcas de corte junto con herramientas de piedra (industria lítica) en muchos yacimientos, especialmente en las cuevas que usaron como refugio. De hecho, los análisis de estos restos de fauna y el análisis de los isótopos estables del colágeno de sus huesos indican que los neandertales, junto con los leones, leopardos y hienas, eran grandes depredadores. Es más, en algunas ocasiones, también se alimentaban de sus congéneres, y por tanto, practicaban el canibalismo (Figura 2).

Figura 2. Fémur neandertal (Fémur III) del yacimiento de Goyet (Bélgica) que presenta marcas de corte (c1,c2) y marcas de haber sido usado como retocador de hueso (b1,b2). Figura originalmente publicada por Rougier et al. (2016) Licencia Creative Commons 4.0.

Los neandertales también se alimentaban de vegetales y usaban la madera para hacer herramientas (ver más abajo). Como, en general, la materia vegetal se descompone más fácilmente que los huesos, no tenemos mucha información de qué plantas consumían. El estudio al microscopio del sarro de varios dientes fósiles neandertales ha permitido saber que consumían dátiles, semillas de hierbas y plantas acuáticas, y además se ha visto que cocinaban estos vegetales. Esto no debería sorprendernos, ya que existen numerosas evidencias del uso del fuego por parte de los neandertales. En ciertos yacimientos excepcionales, como Abric Romaní en Barcelona, se han conservado hogares de distintos tamaños y se ha podido hacer estudios más precisos de su situación espacial. Estos estudios ponen en evidencia distintos usos del espacio de este yacimiento durante las distintas ocupaciones que se produjeron durante miles de años, con la presencia de fuegos más grandes como zonas centrales de los campamentos o de fuegos tipo brasero en zonas de dormitorio.

Los animales cazados, además de alimento proporcionaban pieles para vestirse así como huesos que después eran usados como herramientas para tallar, como percutores blandos. Los neandertales tallaban distintos tipos de rocas que podían conseguir directamente o mediante intercambio con otros grupos. El estudio de la industria lítica ha aportado evidencias de diferencias culturales entre distintos grupos neandertales que habitaban Europa en un mismo momento, así como evolución cultural de estos grupos a lo largo del tiempo. Todo esto nos habla de comportamientos flexibles, que por un lado se amoldarían a los distintos ecosistemas que habitaban y a sus recursos, pero también de nos habla de transmisión cultural independiente del entorno que habitaban. Por ello, más de que cultura neandertal, en singular, deberíamos hablar de culturas neandertales, en plural.

Los neandertales en Pirineos occidentales

En esta región se han encontrado evidencias de ocupaciones de estas poblaciones en distintos yacimientos, tanto en cueva como al aire libre. Solamente en tres de estos yacimientos se han encontrado restos humanos: Axlor (Bizkaia), Lezetxiki (Gipuzkoa) y Arrillor (Araba/Álava), en su mayoría restos de dientes. El yacimiento de Aranbaltza III, además de proporcionar evidencia de distintas ocupaciones neandertales ha preservado la presencia de un palo cavador de más de 70 mil años (Figura 3).

Figura 3. a) Fotografía mostrando la punta del palo cavador inmediatamente después de haber sido desenterrada. b) conservación actual. Figura originalmente publicada por Rios-Garaizar et al. (2018). Licencia Creative Commons 4.0

Este es un descubrimiento excepcional porque, tal y como apuntábamos anteriormente, los objetos de madera no fosilizan frecuentemente. Además, el yacimiento de Axlor ha proporcionado ejemplos de explotación y consumo de un águila real (Figura 4), un cuervo, un lince y un lobo, indicando que además de animales herbívoros los Neandertales también podían cazar aves y carnívoros por su carne o su piel.

Figura 4. Fragmento proximal de fémur de águila real (Aquila chrysaetos) del nivel IV de Axlor, donde se pueden ver dos zonas (A1,A2) con marcas de corte. Figura originalmente publicada por Gómez-Olivencia et al. (2018). Licencia Creative Commons 4.0.

Origen y desaparición

El origen de los Neandertales se encuentra en poblaciones que habitaron Europa en el Pleistoceno Medio hace medio millón de años. De hecho, en el yacimiento de la Sima de los Huesos, en la Sierra de Atapuerca, con una cronología de 430 mil años, encontramos la primera población con características neandertales claras, especialmente en la cara, la mandíbula y los dientes y en algunos rasgos del esqueleto postcraneal. En cambio, la causa de la extinción de los neandertales es todavía desconocida. Se han planteado varias hipótesis para la misma, incluyendo competencia por parte de nuestra especie (incluyendo razones demográficas), o altas tasas de endogamia en los Neandertales. Hoy en día sabemos que los Neandertales interactuaron y se cruzaron con otros grupos humanos. Sabemos que se mezclaron con los enigmáticos Denisovanos, un grupo humano que sólo es conocido por su ADN, así como con nuestra especie, ya que ciertas poblaciones de nuestra especie conservamos un pequeño porcentaje de ADN neandertal. Aunque se ha avanzado mucho en el conocimiento de estos humanos fósiles desde la primera vez que se describieron sus restos, hace más de 150 años, todavía queda mucho más por conocer.

Para saber más:

A. Galarraga (2018) “…eta neandertalek sua piztu zuten”. https://aldizkaria.elhuyar.eus/erreportajeak/eta-neandertalek-sua-piztu-zuten/

A. Gómez-Olivencia, et al. (2018) “3D virtual reconstruction of the Kebara 2 Neandertal thorax”. Nature communications 9(1), 4387. DOI: 10.1038/s41467-018-06803-z

A. Gómez-Olivencia, et al. (2018) “First data of Neandertal bird and carnivore exploitation in the Cantabrian Region (Axlor; Barandiaran excavations; Dima, Biscay, Northern Iberian Peninsula)”. Scientific Reports. 8, 10551. DOI: 10.1038/s41598-018-28377-y

J. Rios-Garaizar (2018) Arqueobasque

J. Rios-Garaizar et al. (2018) “A Middle Palaeolithic wooden digging stick from Aranbaltza III, Spain” PLOS ONE. 13, e0195044. DOI:10.1371/journal.pone.0195044

H. Rougier et al. 2016. Neandertal cannibalism and Neandertal bones used as tools in Northern Europe. Scientific Reports. 6, 29005. DOI: 10.1038/srep29005

Sobre el autor: Asier Gómez es investigador Ramón y Cajal en el Departamento de Estratigrafía y Paleontología de la Facultad de Ciencia y Tecnología de la UPV/EHU.

El artículo Neandertales se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Por qué nos fascinan los neandertales
2. La cronología de la desaparición de los neandertales
3. Neandertales ¿crónica de una muerte anunciada?, por María Martinón-Torres

Ana Galarraga /Elhuyar Zientzia Matematikak betidanik izan ditu gustuko Judit Muñoz Matutek. Dioenez, txikitatik zen ona zenbakiekin, eta ez hainbeste Historian, Euskaran eta Gaztelanian: “Asko gustatzen zitzaidan problemak ebaztea, eta Batxilergoan, Durangon, matematika-irakasle oso ona izan nuen, eta horrek ere bultzatu ninduen Matematikak aukeratzera unibertsitatean”, gogoratu du Muñozek.

Onartu du, hori bai, oso desberdinak direla unibertsitatera iritsi aurretik ikasten diren Matematikak eta gero han landu dituenak: “Institutuan ekuazioak ebazten ikasten dugu, baina unibertsitatean da oso abstraktua eta oso zaila. Egia esan, aldaketa erronka bat izan zen niretzat, baina guztiz positiboa izan zen, asko gustatu zitzaidan. Hala ere, etsitzeko arriskua ere badago: nire ikasturtean, karrera hasi genuenotatik erdiak edo bukatu genuen, besteek utzi egin zuten”.

Muñozen ikaskideen generoari erreparatuta, bada datu esanguratsu bat: karreran, bi izan ezik, gainerako guztiak neskak ziren; orain, ordea, Ingeniaritzan dabil doktoretza egiten, Matematika aplikatuetan, eta oso emakume gutxi dira. “Irudipena dut Matematika ikasi duten emakume gehienak joaten direla Biologia, Medikuntza edo Estatistika arloetara, baina Ingeniaritzan ez da ohikoa. Kongresuetan eta gertatzen zait emakumeak, guztira, bizpahiru izaten garela, eta da oso arraroa”.

Irudia: Judit Muñoz Matute, matematikaria eta UPV/EHUko Matematika Aplikatua, Estatistika eta Ikerkuntza Operatiboa saileko ikertzailea.

Haren iritziz, onuragarria izango litzateke emakume gehiago egotea bere arloan: “Dibertsitatea beti da aberasgarria, bestelako ikuspuntuak azaltzen baitira. Nire taldean ere ni izan naiz lehen emakumea, baina, geroztik, emakume gehiago sartzen joan dira, eta orain, 9tik 4 emakumeak gara. Eta nabaritzen da”.

Bere taldean, Matematika Aplikatuan lan egiten dute, batez ere geofisikan, uhin-hedapen problemetan. “Elkarlanerako aukera asko ematen ditu. Nik UPV/EHUn egiten dut lan, baina lankide batzuk BCAMen aritzen dira, eta Europako proiektu batean gaude, beste unibertsitate batzuekin elkarlanean, nazioarteko mailan. Eta enpresekin ere baditugu lankidetzak. Oso motibagarria da”.

Horrekin batera, asko baloratzen du kongresuetara joateko eta atzerrian egonaldiak egiteko aukera izatea ere. Besteak beste, Australian izan zen zortzi hilabetez lanean, eta aurten Txilen izan da hilabetez. Orain, berriz, Texasera doa.

Esklerosi anizkoitzarekin bizi eta ikertu

Esklerosi anizkoitza diagnostikatu zioten duela sei urte, Matematika karrerako azken urtean, baina, bistan denez, horregatik ez da geldirik geratu. Horrek ez du esan nahi, ordea, ez dionik eragin: “Hasieran, ikusmena galdu nuen begi batean, eta azterketetan nengoen. Izugarrizko mina nuen, oso gogorra izan zen. Ospitalean egon behar izan nuen… Hala ere, azterketak egin nituen eta guztiak gainditu nituen”, gogoratu du.

Aurrerago agerraldi bat izan zuen, eta orduan bizi osorako tratamendu bat jarri zioten. 2014tik ez du beste agerraldirik izan. Bere egoeran daudenak edo bestelako diagnostiko batzuk dituztenak ikerketa-taldeetan parte-hartzeak onurarik ekartzen ote duen galdetuta, baietz erantzun du: “Problemak ebazteko bestelako ikuspuntuak eman ditzakegula iruditzen zait. Besteen egoeraz jabetzeko eta enpatia lantzeko ere lagungarria da“.

Ez da erraza, dena den. Bidaiatzeko, adibidez, izan ditu oztopoak: “Australiara ezin nuen hiru hilabete baino gehiagorako tratamendua eraman, debekatuta dago. Bestela, bertan erosi behar da, baina oso garestia da, eta ezin da bidali. Hortaz, asmoa lau hilabeterako joatea bazen ere, hiru hilabetez baino ez nuen egoterik izan. Baina, tira, gero beste bi aldiz joan naiz”.

Ez da hori bidegabekeria bakarra: Espainian, aseguruek ez dituzte gaixotasun kronikoa duten pertsonen larrialdiak estaltzen. Horrenbestez, Danimarkako aseguru bat kontratatu behar izan du.

Hala ere, itxaropenez begiratzen dio etorkizunari. Ezin du jakin agerraldi gehiago izango dituen ala ez, eta orain duen tratamendua ez da sendagarria, baina aurrera egiteko asmoa du: “Oraintxe baieztatu didate nik nahi nuen lekuan egingo dudala lan uda honetan: Oden Institutua. Leszek F. Demkowicz da zuzendaria, munduko matematikaririk onenetakoa. Aurtengo Abel sariaren irabazlea ere, Karen Uhlenbeck, institutu horretakoa da, eta lehenengo aldia izan da emakume bati eman diotela!”, dio, poza ezkutatu ezinik.

Fitxa biografikoa:

Judit Muñoz Matute Bilbon jaioa da, 1991ean. Matematikako gradua egin zuen UPV/EHUn, eta jarraian Modelizazio eta Ikerkuntza Matematikoa, Estatistika eta Konputazioko masterra. orain, tesia egiten ari da. Tartean, BCAMen (Basque Center for Applied Mathematics) aritu da lanean, baita atzerriko zentroetan ere: Polonia, AEBak, TXile, Australia eta Britainia Handia.

———————————————————————————-

Egileaz: Ana Galarraga Aiestaran (@Anagalarraga1) zientzia-komunikatzailea da eta Elhuyar Zientzia eta Teknologia aldizkariko erredaktorea.

———————————————————————————-

Elhuyar Zientzia eta Teknologia aldizkariarekin lankidetzan egindako atala.

The post Judit Muñoz, matematikaria: “Dibertsitateak problemak ebazteko beste ikuspuntu batzuk ematen ditu” appeared first on Zientzia Kaiera.

En 1993 se publicó en Nature uno de los artículos científicos que más impacto social ha tenido de las últimas décadas. Tres investigadores de la Universidad de California habían reclutado a un grupo de 36 estudiantes universitarios para resolver una serie de tests que involucraban razonamiento espacial. Tras escuchar durante 10 minutos una sonata de Mozart, los estudiantes parecían ver incrementada ligeramente su habilidad (8-9 puntos más de CI) en comparación con otros dos grupos de control: estudiantes que habían escuchado un disco de relajación o que habían permanecido en silencio durante el mismo tiempo1.

Poco importó que el estudio no se realizase en ningún momento con bebés, que el efecto de mejora no durase más de 15 minutos o que, de hecho, no hablase de inteligencia. Tras cientos de titulares en prensa y aún más malentendidos, la idea popular que caló era muy distinta a la del artículo original y mucho más vendible: escuchar a Mozart te hace más listo, sobre todo si lo escuchas siendo un niño pequeño. A mediados de la década de los 90, cientos de CDs, libros interactivos y cascos adaptables para vientres de embarazadas invadían ya los escaparates de todo el mundo bajo un sello común: el “efecto Mozart”.

Antes de que os lo sigáis preguntando, dejadme despejar cualquier remanente de duda: el efecto Mozart no existe, no tiene fundamento científico, ni siquiera en su limitada versión publicada en 1993. Estudios posteriores han intentado replicar el resultado original con un éxito más bien variable2. En 1999, un meta-análisis basado en 16 de dichos estudios3 concluyó que el efecto, de haberlo, resultaba despreciable. En 2010 un nuevo meta-análisis4 llegó a una conclusión parecida basándose, esta vez, en 40 estudios previos.

Algunos psicólogos han apuntado que el “efecto Mozart” podría tratarse, más bien, de una especie de “efecto buen rollo”5 (“enjoyment arousal” en la literatura científica): al estar de buen humor (por haber escuchado, por ejemplo, una música que nos gusta) somos capaces de resolver ciertas tareas con mayor facilidad. Esto podría explicar los resultados variables a la hora de replicar el estudio de Nature de 1993: quizás, solo los sujetos que disfrutaban de la música de Mozart veían mejorada su habilidad espacial.

En esta línea, otros estudios han mostrado que el efecto Mozart tiene, de hecho, poco que ver con Mozart: los mismos resultados pueden obtenerse escuchando cualquier otro tipo de música6 o, incluso, leyendo historias de Stephen King. Esto último se ha probado tal cual7: en un estudio de 2001, se medían las habilidades espaciales de los sujetos tras permanecer 10 minutos en silencio o tras escuchar 10 minutos de Mozart, de Schubert o un relato de Stephen King. Los resultados variaban, sí, pero lo hacían en función de las preferencias del sujeto. Es decir, lo único importante es que la actividad resultase agradable, que los participantes en el test se pudiesen de buen humor.

Por supuesto, hoy en día todo el mundo habla del “efecto Mozart” y no del “efecto Stephen King” y a estas alturas de la película, con tantos estudios realizados y tantos meta-análisis descartando el mito, cabe preguntarse por qué siguen vendiéndose CDs con carátulas tan feas: ¿por qué caló tanto y aún hoy sigue calando el efecto Mozart?

Existen varias posibles explicaciones y todas ellas explotan algún tipo de sesgo o prejuicio, de esos que tanto nos gusta utilizar para no pensar. Para empezar, el efecto Mozart encaja muy bien con otros mitos muy arraigados, como el determinismo infantil8: la idea de que lo que nos sucede en etapas tempranas del desarrollo tiene consecuencias irreversibles durante el resto de la vida (este mito es probablemente anterior a Freud pero qué duda cabe de que él ayudó a popularizarlo). También resuena con una creencia mucho más antigua que atribuye poderes mágicos a la música: si es capaz de “amansar a las fieras”, ¿por qué no iba a hacer más listos a los bebés? Para colmo, el efecto Mozart promete efectos espectaculares a cambio de ningún esfuerzo y sin consecuencias negativas posibles. Curar lo incurable sin efectos secundarios, ¿os suena de algo?

Pero entre todos los motivos por los que el efecto Mozart es hoy conocido por todos, la figura del propio compositor juega un papel muy importante. Para empezar porque, debido a nuestra herencia romántica, seguimos creyendo en los artistas genio, verdaderos héroes de la historia cuyo legado es irrepetible e inconfundible. Cuando la realidad es que cualquier sonata de Mozart no es muy distinta a las de otros compositores de su tiempo. Con melodías preciosas, no me malinterpretéis, Mozart era un compositor estupendo… y un hijo del Clasicismo como lo fueron antes que él Haydn o Salieri (podéis probar, si no, a resolver este test9). El hecho de que popularmente se atribuyan semejantes poderes a su música no deja de ejemplificar la creencia de que los genios tienen habilidades mágicas (y no sólo los que salen de una lámpara).

Para colmo, Mozart fue un niño prodigio. Y por el mismo razonamiento erróneo que lleva a los seguidores de la homeopatía a creer que lo similar cura lo similar, otros pueden pensar que quizás el genio se contagia. Después de todo, fue el puro azar lo que llevó a unos investigadores de California a elegir una sonata de Mozart y no, pongamos, un tango de Gardel, para realizar sus experimentos sobre razonamiento espacial. De no haber sido así, quizás los titulares no hubiesen resonado tanto ni se hubiesen vendido tantos CDs. Quizás entonces, la gente seguiría escuchado a Mozart por el único motivo sensato que sigue habiendo para hacerlo: no porque nos haga más listos, sino porque afortunadamente nos hace más felices.

Referencias:

1 Music and Spatial Task Performance. Frances H. Rauscher, Gordon L. Shaw & Catherine N. Ky. Nature, 1993.

2 The mystery of the Mozart effect: Failure to replicate. K.M. Steele, K. E. Bass, & M. D. Crook. Psychological Science, 1999.

3 Prelude or requiem for the ‘Mozart effect’? Christopher F. Chabris. Kenneth M. Stelle, Simone Dalla Bella, Isabelle Peretz. Nature, 1999

4 Mozart effect–Shmozart effect: A meta-analysis. Jakob Pietschnig, Martin Voracek & Anton K. Formann. Intelligence 2010

5 Arousal, mood, and the Mozart effect. William Forde Thompson, E. Glenn Schellenberg, Gabriela Husain. Psychological Science, 2001.

6 Music Listening and Cognitive Abilities in 10‐ and 11‐Year‐Olds: The Blur Effect. E. Glenn Schellenberg & Susan Hallam. Annals of the New York Academy of Sciences, 2005

7 The Mozat effect: an artifact of preference. Kristin M. Nantais & E. Glenn Schellengerg.

8 Three seductive ideas. Kagan, J. (1998). Cambridge, MA: Harvard University Press.

9 Scientific comparison of Mozart and Salieri. M. V. Simkin

Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica

El artículo Escuchar Mozart no te hará más listo se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El caso de Wolfgang Amadeus Mozart
2. Lo que la magia esconde
3. Los parabenos usados en cosmética son seguros

Ana Puente, Sergio Seoane eta Beñat Zaldibar
Ez dugu zalantzan jartzen 50 urte hauetan zehar Zientzia eta Teknologia Fakultatea osatzen (eta bizitzen) duten langileek jarduera ugari egin dituztela Fakultatean garatzen diren ekitaldiak eta gertatzen diren berriak zabaltzeko eta jakinarazteko. Horrela, ahalegin hauen guztien hauen zati bat behintzat etorkizuneko ikasleek Fakultatearekiko duten harrera onean islatzen da.

Fakultatea gizarteari hurbiltzeko egiten diren jardueren artean Olinpiada Zientifikoak ditugu. Olinpiadak, Fakultatean ikasi dezaketen Batxilergoko ikasleen artean, hainbat diziplina zientifikori buruzko jakin-nahia pizteko asmoz antolatzen dira.

1. irudia: 2014. urtean UPV/EHUko Zientzia eta Teknologia Fakultatean egin ziren Olinpiadetako irabazleak. Kimika, Fisika, Matematika, Biologia eta Geologia arloetako irabazleak. (Argazkia: UPV/EHU)

Gure lankide (eta oraindik lagun) diren matematikariek aurten beraien tradizio handiko LV Olinpiada egiten duten bitartean, Euskal Autonomi Erkidegoko Biologiako Olinpiadak XII. edizioa betetzen du aurten. Fakultatearen L. urteurrenaz baliatuz, guk uste dugu une egokia izan dezakegula hausnarketa txiki bat egiteko gure jatorriari buruz, egin den ibilbideari buruz eta gutxienez etorkizun hurbil batean izango ditugun erronkei buruz.

2007-2008. ikasturtean eta garaiko dekanoa zen Ester Dominguezen proposamenari esker, Alberto Vicario, Isabel Smith eta Manu Soto irakasleek lehendabiziko Euskal Autonomi Erkidegoko Biologiako Olinpiada antolatu zuten Euskal Herriko Unibertsitatean. Esan beharra dago aurreko ikasturtean Nafarroako Unibertsitateak antolatu zuela Euskal Autonomia Erkidegoko zein Nafarroako Erkidegoko Biologiako Olinpiada bateratua. Hala ere, 2007-2008 ikasturteaz geroztik Euskal Autonomi Erkidegoko eta Nafarroako Biologiako Olinpiadak beregain funtzionatu dute eta Erkidegoari dagokionez Zientzia eta Teknologia Fakultatean antolatu izan da betidanik. Ez gaitu beraz ustekabean harrapatu behar Olinpiada garai horretan abian jarri behar horrek. Izan ere, Goi Mailako Europar Hezkuntza baterako konbergentziak bultzatuta, zientzia esperimentalen inguruko gogoeta sakon bat egitera behartuta geunden, beren indarrak eta ziurgabetasunak agerian uzteko.

Biologiako Olinpiadak hiru helburu nagusi dituztela esan dezakegu:

• batetik, Biozientziek erakarritako ikasleen maila ebaluatzea;
• bestetik, Batxilergoko irakaslegoa erakartzea iritzien elkartruke bultzatuz eta hobetzerako ekintzak garatuz;
• azkenik, parte hartzen duten ikasleen beraien estimulazioa bultzatzea Biozientzien garapenean, beraien aurrerapen eta zabalkundea sustatuz.

Gainera, gehienentzat, Fakultatearekin izango duten lehenengo harremana izango da Olinpiadetan parte hartzea eta bide batez Fakultatera gerturatzeko baliagarria gertatuko zaie, “bolizko dorrea” delako hori alde batera utzita.

Egitura

Olinpiadaren probaren egitura gutxi aldatu da edizio guztietan zehar. Abiapuntu gisa Nazio Mailako Faseak erakusten duen egitura geureganatuz, bi ariketetan banatzen dugu proba hau. Alde batetik, teoria mailako ariketa bat dago, eta bertan aukera anitzeko galdera sorta bat dago biologiaren atal desberdinei buruz galdetzen delarik. Horrela, parte-hartzaileek teoria mailan eskuratutako ezagutzak ebaluatuko dira. Ondoren, teoria mailako proba teorikoan emaitza onenak eskuratu dituzten parte-hartzaileek praktika mailako bigarren ariketa bat egin beharko dute. Ariketa hau askoz bideratuago dago lortutako ezagueren aplikazioetara.

Biologiako Olinpiada, Zientzia eta Teknologia Fakultatetik haratago eramateko esfortzu eta konpromisoa hartuta, UPV/EHUk, Zientzia eta Teknologia Fakultateak eta Zubia-Santillana argitaletxeak “Olinpiada de Biologia: preguntas y respuestas” liburua plazaratu zuten 2010. urtean.

2. irudia: Biologiako Olinpiadako parte-hartzaileak burutu behar dizuten ariketak jasotzen. (Argazkia: UPV/EHU)

Zenbait datu

Biologiako Olinpiadak izan dituen 12 edizio hauetan, hiru eskualdeetako 40 ikastetxe baino gehiagotik etorritako 450 ikasle baino gehiagok hartu dute parte.

Bizkaia da Euskal Herrian biztanle gehien duen eskualdea, eta gainera, gure Fakultatea Bizkaian dago, Leioan alegia. Hori guztia dela eta, ulergarria da eskualde honetakoa izatea parte-hartzaileen %69a.

Gipuzkoako ikastetxeak parte-hartzaileen % 18a dira eta Arabako ikastetxeak % 13. Zientzia eta teknologiaren arloa nagusiki gizonezkoen parte hartzearekin lotuta egon da historian zehar, baina egoera hau ez da Biologia Olinpiadan gertatzen, bertan emakumeak ia parte-hartzaileen %60a baitira. Azkenik, ezin dugu ahaztu euskararen garrantzia Biologiako Olinpiadetan.

Izan ere, lehenengo urteetan, %30ekoa izan zen proba euskaraz egiten zuten parte-hartzaileen portzentajea. Azkeneko bi urteotan (2018 eta 2019) aldiz, %48koa izan da proba euskaraz egin duten parte-hartzaileen portzentajea.

3. irudia: 2019ko martxoaren 21etik 24ra, Espainiako 55. Matematika Olinpiadaren azken fasea jokatu zen eta bertan Leioako Inés Borchers Arias ikasle euskaldunak zilarrezko domina lortu zuen. (Argazkia: UPV/EHU)

Eta hemendik aurrera zer?

12 urteko esperientzia jarduera baten egonkortasun eta finkatzearen seinale izan daitekeen arren, etorkizun hurbilean gainditu behar ditugun erronka eta ziurgabetasun ugari daude. 2020. urtean, besteak beste Biologia Olinpiadetako Fase Nazionalaren antolakuntza UPV/EHUren ardura pean egongo da. Espero da 60 ikasle eta horrenbeste irakasle eta ordezkari bertaratzea. Ideia-trukerako aukera paregabea baina baita erantzukizun handiko erronka bat ere. Bestalde, Olinpiaden parte-hartzaile kopurua nahiko egonkor mantendu da azken urteotan eta, horrek proiektuaren harrera ona adierazten duen arren, bestetik, nolabaiteko geldialdiaren seinale ere izan liteke, azkenean jarduera honen inguruko interes-galera eta/edo motibazio-gabezia egon litekeelako tartean. Bizkaitik kanpoko ikastetxeen portzentaje txikia ere hausnarketara bultzatu behar gaituen beste gai bat da.

——————————————-
Egileez: Ana Puente eta Beñat Zaldibar UPV/EHUko Zoologia eta Animalia Zelulen Biologia saileko kideak dira eta Sergio Seoane Landare Biologia eta Ekologia Saileko kidea.

——————————————-

The post Biologiako Olinpiadak appeared first on Zientzia Kaiera.

 

El teorema de los infinitos monos
de Borel-Cantelli
enuncia esta posibilidad:
si un infinito número de monos mecanografiaran
por un intervalo infinito de tiempo
podrían escribir cualquier texto posible.
Todo lo que incluye este poema.
Todas las palabras que alguna vez me has dicho.

José Manuel Gallardo

Este bello poema se titula Infinitos monos. Variación III. Pertenece al poemario Infinitos monos (El Desvelo, 2016) de José Manuel Gallardo, que la editorial presenta del siguiente modo:

Infinitos monos es un poemario sobre la comunicación y sus (im)posibilidades: «Las palabras que forman el poema,/ estas palabras, sacadas de contexto / en cualquier otro lugar podrían salvar vidas / quizá, o condenarlas.», pero también una visión sobre la vida como viaje, sobre la importancia de la mirada sobre los otros y sobre nosotros mismos. Era inevitable, por lo tanto, que en este poemario del autor madrileño hiciera acto de presencia una reflexión sobre el amor, incursión en la que alcanza gran profundidad, sirviéndose para ello de versos tranquilos y doblemente libres: libres por su composición técnica y libres por el espíritu que los insufla vida.

El libro comienza con el poema-prólogo titulado Infinitos monos, que va acompañado de cuatro variaciones. En este preámbulo el autor deja claro que, en número, las posibilidades de comunicación –combinando palabras– son inconcebibles, aunque no infinitas. Explica así la esencia del teorema de los infinitos monos y los objetivos de su poemario.

Imagen: Wikimedia Commons

El teorema de los infinitos monos afirma que con “suficiente” tiempo –tiempo infinito– un chimpancé pulsando al azar las teclas de una máquina de escribir podría redactar –con probabilidad 1– cualquier texto, por ejemplo, El Quijote de Miguel de Cervantes.

Esta idea fue planteada por Émile Borel en 1913 (ver 1., página 194) que intentaba ilustrar con esta metáfora la cabida de un suceso altamente improbable:

Concevons qu’on ait dressé un million de singes à frapper au hasard sur les touches d’une machine à écrire et que, sous la surveillance de contremaîtres illettrés, ces singes dactylographes travaillent avec ardeur dix heures par jour avec un million de machines à écrire de types variés. Les contremaîtres illettrés rassembleraient les feuilles noircies et les relieraient en volumes. Et au bout d’un an, ces volumes se trouveraient renfermer la copie exacte des livres de toute nature et de toutes langues conservés dans les plus riches bibliothèques du monde. Telle est la probabilité pour qu’il se produise pendant un instant très court, dans un espace de quelque étendue, un écart notable de ce que la mécanique statistique considère comme le phénomène le plus probable. Supposer que cet écart ainsi produit subsistera pendant quelques secondes revient à admettre que, pendant plusieurs années, notre armée de singes dactylographes, travaillant toujours dans les mêmes conditions, fournira chaque jour la copie exacte de tous les imprimés, livres et journaux, qui paraîtront la semaine suivante sur toute la surface du globe. Il est plus simple de dire que ces écarts improbables sont purement impossibles.

[Imaginemos que se ha adiestrado a un millón de monos para pulsar al azar las teclas de una máquina de escribir y que, bajo la supervisión de capataces analfabetos, estos monos mecanógrafos trabajan con diligencia diez horas al día con un millón de máquinas de escribir de varios tipos Los capataces analfabetos recogerían las hojas ennegrecidas y las encuadernarían en volúmenes. Y al cabo de un año, estos volúmenes conseguirían contener la copia exacta de libros de todo tipo e idiomas conservados en las bibliotecas más ricas del mundo. Tal es la probabilidad de que se produzca durante un instante muy corto, en un espacio de cierta extensión, una diferencia notable de lo que la mecánica estadística considera el fenómeno más probable. Suponer que la desviación así producida subsistirá durante unos segundos equivale a admitir que, durante varios años, nuestro ejército de monos mecanógrafos, trabajando siempre en las mismas condiciones, proporcionará todos los días la copia exacta de todos los papeles impresos, libros y periódicos, que aparecerán la siguiente semana en todo el mundo. Es más simple decir que estas diferencias improbables son puramente imposibles.]

Más adelante esta idea sufrió varias reformulaciones conduciendo a la noción de infinito. Desde una cantidad infinita de monos tecleando durante un tiempo infinito hasta un único chimpancé inmortal –que podríamos llamar Tristam… ¿por qué no?–, mecanografiando sin tregua, este trabajo generaría cualquier texto imaginable y, además, infinitas veces.

Volviendo al poemario Infinitos monos, tras el prólogo, el texto de Gallardo prosigue en tres partes: Elementos de la comunicación –una reflexión sobre la comunicación, con algún guiño a la química, al caos, al determinismo o a la lógica–, En el camino –que incluye poemas en los que se habla de la vida como un viaje: la familia, el desarraigo, la soledad, etc.– y Escápate conmigo –sobre el amor y desamor–. El autor incluye algunas referencias a las matemáticas –teoría del caos, teoría de cuerdas, procesos estocásticos, etc.–, la física –principio de incertidumbre de Heisenberg, el gato de Schrödinger, difracción, etc.– o la química –por ejemplo, uno de los poemas se titula Alótropos de carbón e incluye una ‘pequeña lección’ de química del carbono–.

¿Quizás es el mono Tristam, el inmortal, el autor de Infinitos monos?

Referencias

1. Émile Borel. La mécanique statique et l’irréversibilité. J. Phys. Theor. Appl., 1913, 3 (1), 189-196

2. Teorema del mono infinito, Wikipedia (consultado el 29 de junio de 2019)

3. Marta Macho Stadler, Infinitos monos, de José Manuel Gallardo, DivulgaMAT, 2016

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.

El artículo Infinitos monos se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Los monos mecanógrafos contra la evolución
2. El libro de las caras de los monos
3. Apeirofobia

Juanma Gallego Krisi klimatikoari erantzuna ematerakoan mikroorganismoek duten garrantzia kontuan hartzeko deia egin du zientzialari talde batek. Aditu taldeak ohartarazi duenez, gaiari buruzko eztabaidan mikrobioak alde batera uzteak ondorio garrantzitsuak izan ditzake.

Mikrobiologoek aspalditik dakite, eta mikrobiologo ez direnak ere pixkanaka ari dira konturatzen mikrokosmosaren garrantziaz: ia gai gehienetan, mikroorganismoak transbertsalak dira, eta argi dago bereziki ingurumenari zein osasunari lotutako arloetan oraindik asko dagoela heiei buruz ikasteko.

Baina, antza, horiek ez dira behar bezala kontuan hartzen ari klima aldaketari buruzko zientzia ikerketetan, eta hori krisi klimatikoari aurre egiteko oztopo izan daiteke. Hala uste du bederen ikertzaile talde batek; agiri batean jaso dute haien kezka. Hegoaldeko Gales Berriko Unibertsitateko (Australia) ikertzaile Ricardo Cavicchiolik hartu du ekimenaren gidaritza. Berarekin batera, bederatzi herrialdetako beste 32 mikrobiologok sinatu dute agiria. Deia luzatu diete mundu osoko mikrobiologoei agiriarekin bat egin dezaten.

1. irudia: Munduko landare biomasaren %1 baino ez izanda, fitoplanktonak sortzen du arnasten dugun oxigenoaren erdia, eta fotosintesiaren bidez egiten den CO2 gasaren finkapenaren erdia egiten du ere. (Argazkia: NOAA)

Bioaniztasunaren “gehiengo ikusezintzat” jo dituzte, eta bizidun ñimiño horiek kontutan hartzeko eskatu dute. Zientzialarien ohartarazpena gizateriari: mikroorganismoak eta klima aldaketa izena eman diote adierazpen honi, eta Nature Reviews Microbiology aldizkarian zabaldu dute. Zientzian egin behar den moduan, ez dira mugatu manifestu bat sinatzera, eta argudioak jarri dituzte mahai gainean, bibliografia sendo batez babestuta.

“Modu sinple batean esanda, mikrobioen mundua biosferaren bizitzarako euskarri sistema da”, laburbildu dute artikuluan. Adituek argudiatu dutenez, goiko mailako bizidun guztiek mikroorganismoen beharra dute. Gainera, mikrobioak leku guztietan daude: bai organismo handiak dauden lekuetan zein horiek ez dauden inguruenetan, lurraren azpian edo muturreko inguruetan. Duela 3.800 milioi urtetik Lurrean daude, eta etorkizunean beste iraungipen masibo bat dagoenean ere, seguruenera bizirik aterako direla aipatu dute.

Dena dela, eta klima aldaketan garrantzi handia duten arren, gaiari buruzko ikerketetan “gutxitan” kontuan hartuak direla diote adituek, eta ez dira ere kontuan hartzen klima aldaketa arintzeko politiketan. Nabarmendu dutenez, bi norabidetako harremana da. Batetik, mikroorganismoek klima aldaketan eragina dute, eta, bestetik, klima aldaketak mikroorganismoetan ere eragiten du. Bereziki bigarren norabide hori aztertu gabe dagoela diote.

Adibide zehatz ugari jarri dituzte. Itsas inguruneei dagokienez, ozeanoetako biomasaren %90 osatzen dute mikrobioek. Bertan garrantzia berezia du fitoplanktonak: fotosintesia egiten du, eta atmosferako karbono dioxidoa xurgatzen du. Modu berean, itsasoko kate trofikoaren oinarria da. Fotosintesiaren bitartez munduan egiten den CO2 finkapenaren erdia fitoplanktonak egiten du, eta oxigenoaren erdia ere sortzen du. Hori guztia, munduko landare biomasaren %1 baino ez izanda. Hala izanik ere, fitoplanktonak azkar erantzuten die klimaren bariazioei.

Oso garrantzitsua izan arren, zientzia-artikuluan ohartarazi dute gaur egun zientziak ez dakiela ziur fitoplanktonaren kopurua handitzen ala txikitzen ari ote den. “Horrek handitzen du ikertzeko beharra: epe luzerako datuak eskuratu behar dira, bai fitoplanktonaren ekoizpenari zein mikrobio komunitateei buruzkoak”. Era berean, itsas hondoetan metanoa kontsumitzen eta isurtzen duten mikrobioen ekarpenari buruzko datu gutxi dagoela ohartarazi dute.

2. irudia: Luze eta zabal daude barreiatuta mikroorganismoak munduan zehar. Irudian, izotzari atxikitako algak, Antartidan. (Argazkia: Rick Cavicchioli)

Itsasoan, uraren tenperaturaren arabera banatzen dira itsas komunitateak, estratifikazio baten bidez. Mikroorganismoak ozeanoetako sare trofikoen oinarria dira, eta, beraz, karbonoen eta nutrienteen ziklo globalen oinarria ere badira. Aurrean aipatu bezala, hau egiten dute bereziki karbonoaren eta nitrogenoaren finkapena egiten dutelako, baina baita ere materia organikoa deskonposatzen eta oinarrizko elementu kimikoetara bueltatzen dituztelako.

Lurrean ere, gasen igorle

Lur eremuetan, berriz, negutegi efektuko gasak isurtzen dituztela gogoratu dute: karbono dioxidoa, metanoa eta oxido nitrosoa. Eta, giza jardunaren ondorioz abereak asko ugaritu direlako, bereziki hausnarkarien hesteetan bizi diren mikroorganismoak kontuan hartu behar dira. Ezin izan dute ahaztu, noski, patogenoen arazoa, eta berotze globalak horien hedapenean duen eragina, azken faktore hau zientzia ikerketetan dezente jorratuta dagoen arren.

Egin duten deialdiaren bitartez, harreman horiei buruzko kontzientziazioa handitzea espero dute. Mikroorganismoak “kontserbazioari bideratutako webguneetan ikusten ez diren bizidunak” direla adierazi du Cavicchiolik, kexu. Mikrokosmosa ez bada modu egokian kontuan hartzen, egiten ari diren eredu klimatikoak ez direla zuzenak izango argudiatu du, eta horrek “zehaztasun gabeko aurreikuspenak” ekar litzake. Izan ere, uncertain hitza sarri errepikatzen da artikuluan, arloz arlo gaiari buruzko gaur egungo ezagutzaren errepasoa egin dutenean.

Besteak beste, eskatu dute teknologia berritzaileak erabiltzen dituzten ikerketak sustatzeko, eta gaiari buruzko hezkuntza hobetzeko. Modu horretan, Cavicchioliren hitzetan, “pertsonek gaitasun handiagoa izango dute mikrobiologiari buruzko gaiekin konpromisoa erakusteko, eta baita mikrobioen garrantzia eta gaiak dituen adarrak ulertzeko ere”.

Erreferentzia bibliografikoa:

Cavicchioli Ricardo et al., (2019). Scientists’ warning to humanity: microorganisms and climate change. Nature Reviews Microbiology. DOI: https://doi.org/10.1038/s41579-019-0222-5

———————————————————————————-

Egileaz: Juanma Gallego (@juanmagallego) zientzia kazetaria da.

———————————————————————————-

The post Bizidun txikienek ere badute zeresana krisi klimatikoan appeared first on Zientzia Kaiera.

En un rincón del litoral donostiarra donde los estratos de la corteza terrestre descienden y se ocultan bajo el mar Cantábrico, para emerger de nuevo sobre la isla Santa Clara, se narra una historia de tierra, mar y viento. “El Origen”, fascinación del escultor Eduardo Chillida Juantegui.

El “Peine del Viento”, es la XV obra de un dilatado proceso creativo fruto de la reflexión, ensayos con formas y materiales, y aquel “Origen” como lugar condicionante. Su trabajo evolucionó, desde diseños rígidos y estáticos hacia figuras más orgánicas, y su posterior simplificación.

Influenciado tanto por movimientos artísticos, como por los avances científicos en el campo de la metalurgia, el artista se valió de las propiedades del acero Cor-ten, que contiene aditivos mejorando así su tenacidad y resistencia a la corrosión. El material genera una barrera protectora de herrumbre en la superficie, optimizándolo ante la corrosión atmosférica. Su característico color rojizo y meteorización paulatina visibiliza el inevitable “bagaje del tiempo” en su piel. Idea que el artista plasmó integrando el proceso de degradación material en el conjunto, realzado por manchas en las bases rocosas.

Imagen: Arte y ciencia. Interacción entre el proceso creativo del escultor Eduardo Chillida Juantegui y los avances científicos en el acero al cobre, aplicados en la creación del conjunto escultórico “Peine del viento XV”. Se justifica la elección del acero Cor-Ten por sus propiedades materiales y el modo en el que se degrada a causa de las condiciones atmosféricas adversas de su ubicación. (Ilustración: Amaia Torres Piñeiro)

El arte y la ciencia convergen en este lugar donostiarra, donde la historia y la naturaleza son protagonistas.

Referencias consultadas:

• Díaz Ocaña, Iván (2013). Corrosión atmosférica de aceros patinables de nueva generación. Tesis doctoral. Universidad Complutense de Madrid, Facultad de Ciencias Químicas, Departamento de Ciencia de los Materiales e Ingeniería Metalúrgica.
• Elósegui Itxaso, José María (1977). El Peine del Viento de Eduardo Chillida en San Sebastián. Ingeniería de su colocación. Donostia – San Sebastián. Fundación Kutxa.

Autora: Amaia Torres Piñeiro (@amaia_torres), alumna del Postgrado de Ilustración Científica de la UPV/EHU – curso 2018/19

Artículo original: El Peine del Viento de Chillida: materia, forma y lugar. Déborah García,  Cuaderno de Cultura Científica, 28 de octubre de 2016.

“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión con un eje central, la ilustración.

El artículo ¿Es posible el arte sin ciencia? se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. #Naukas16 La cultura
2. Arte & Ciencia: Cómo descubrir secretos que esconden las obras de arte
3. Arte & Ciencia: Química y Arte, reacciones creativas

Si conocemos la función de trabajo de los materiales y las frecuencias de la luz incidente podríamos determinar qué materiales emiten electrones al ser expuestos a la luz, como el titanio de colores de las cubiertas del Hotel Marqués de Riscal. Foto: Wikimedia Commons

La explicación del efecto fotoeléctrico fue el trabajo principal citado en cuando se le concedió el premio Nobel de Física en 1921 a Albert Einstein. La explicación de Einstein, propuesta en 1905, desempeñó un papel importante en el desarrollo de la física atómica. Basó su teoría en una hipótesis muy atrevida, ya que pocos de los detalles experimentales se conocían en 1905. Además, el punto clave de la explicación de Einstein contradecía las ideas clásicas de la época.

Einstein asumió que la energía de la luz no estaba distribuida uniformemente en todo el frente de onda en expansión (como suponía la teoría clásica). En cambio, la energía de la luz se concentraría en «paquetes» separados. Además, la cantidad de energía en cada una de estas regiones no sería una cantidad cualquiera, sino una cantidad definida de energía que es proporcional a la frecuencia f de la onda luminosa. El factor de proporcionalidad sería una constante (símbolo h); se llama constante de Planck por razones que veremos más adelante.

Por lo tanto, en el modelo que propone Einstein, la energía luminosa en un haz de frecuencia viene en paquetes, cada uno cona energía E = hf, donde h = 6,626·10-34 J / s. La cantidad de energía radiante de cada paquete se llama cuanto de luz o cuanto de energía luminosa. Como cuanto de energía luminosa es muy largo, más tarde se le daría un nombre, fotón.

No hay una explicación más clara o más directa que la del propio Einstein en al artículo original de 1905 [1]. Presentamos a continuación una cita del mismo, en traducción libre y con la notación adaptada a la que venimos utilizando:

[…]De acuerdo con la idea de que la luz incidente se compone de cuantos con energía hf, la expulsión de los rayos catódicos [fotoelectrones] por luz se puede entender de la siguiente manera. Los cuantos de energía penetran en la capa superficial del cuerpo y su energía se convierte, al menos en parte, en energía cinética de electrones. La imagen más simple es que un cuanto de luz cede toda su energía a un solo electrón; Asumiremos que esto sucede[…]. Un electrón provisto de energía cinética dentro del cuerpo puede haber perdido parte de su energía cinética en el momento en que llega a la superficie. Además, se debe suponer que cada electrón, al abandonar el cuerpo, tiene que realizar una cantidad de trabajo W (que es característica del cuerpo). Los electrones expulsados directamente desde la superficie y en ángulos rectos tendrán las mayores velocidades perpendiculares a la superficie. La energía cinética máxima de uno de estos electrones es

Ecmax = hf – W

Si la placa C se carga a un potencial positivo, Vp , lo suficientemente grande para evitar que el cuerpo pierda carga eléctrica, debemos tener que

Ecmax = hf – W = eVp ,

donde e es la magnitud de la carga electrónica[…]

Si la fórmula derivada es correcta, entonces Vp , cuando se representa gráficamente en función de la frecuencia de la luz incidente, debe producir una línea recta cuya pendiente debe ser independiente de la naturaleza de la sustancia iluminada. […]

A la primera ecuación en la cita anterior se la suele conocer como ecuación fotoeléctrica de Einstein. Veamos si esta ecuación y el modelo fotónico de Einstein pueden explicar los resultados experimentales que la física clásica no puede:

1. De acuerdo con la ecuación fotoeléctrica, la energía cinética de los fotoelectrones es mayor que cero solo cuando la energía del fotón hf es mayor que el trabajo W, que es el trabajo que debe realizar el electrón contra las fuerzas de atracción del material del cátodo en el que se encuentra para escapar de él. La energía requerida para escapar del metal se conoce como la función de trabajo. Por lo tanto, solo se puede emitir un electrón cuando la frecuencia de la luz incidente es mayor que un cierto valor mínimo que corresponde al trabajo requerido para escapar del metal. Usando símbolos, la frecuencia mínima o umbral f0 viene definida para cada material por la igualdad h f0 = W.

2. Según el modelo fotónico de la luz de Einstein, es un fotón individual de frecuencia f el que expulsa a un electrón si f > f0 . Como la intensidad de la luz es proporcional al número de fotones en el haz de luz y el número de fotoelectrones expulsados es proporcional al número de fotones incidentes en la superficie, la cantidad de electrones expulsados (y con ella la corriente fotoeléctrica) es proporcional a la intensidad de la luz incidente. [2]

3. En el modelo de Einstein, la energía luminosa se concentra en una serie de cuantos de luz (fotones). Por tanto no se necesita tiempo para que el electrón acumule energía luminosa. En efecto, los cuantos transfieren su energía inmediatamente a los fotoelectrones, que escapan de la superficie casi inmediatamente.

4. Finalmente, la ecuación fotoeléctrica predice que cuanto mayor sea la frecuencia de la luz incidente mayor será la energía cinética máxima de los electrones expulsados. Esto es así porque la energía del fotón es directamente proporcional a la frecuencia de la luz. La energía mínima necesaria para expulsar un electrón es la energía requerida para que el electrón escape de la superficie del metal. Esto explica por qué la luz de una frecuencia menor que la frecuencia f0 no puede expulsar ningún electrón. La energía cinética del electrón que se escapa es la diferencia entre la energía del fotón absorbido y la energía perdida por el electrón al escapar de la superficie: si la priemera no compensa a la segunda el electrón se queda donde está

Notas:

[1] Einstein, A. (1905) Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt Annalen der Physik 17, 132-149

[2] Ojo, no todos los fotones en un haz de luz incidente golpean un electrón haciendo así que se emita desde el metal. Solo del orden de 1 de cada 50 fotones lo consigue. Esto es muy importante para la ingeniería y el diseño de experimentos, pero para lo que a nosotros nos interesa no es necesario que pase de nota a pie de página.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo La explicación de Einstein del efecto fotoeléctrico se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. La incompatibilidad del efecto fotoeléctrico con la física clásica
2. El desconcertante efecto fotoeléctrico
3. El principio de relatividad (y 4): la versión de Einstein

Josu Lopez-Gazpio Zientzia Kaieran musika izan dugu hizpide eta, azaldu bezala, musikaren eta soinuen atzean zientzia asko dago. Soinuei eta notei buruz aritu gara eta guzti horrek uhinen fisikarekin duen lotura aztertu dugu. Artikulu-sortari amaiera emateko, kulturak soinuen pertzepzioan duen eragina eta armonia zer den aztertuko dugu.

Irudia: Musikaren oinarrian zientzia asko dagoen arren, musikan badaude momentuz erantzun ezin diren zalantzak. (Argazkia: Maret Hosemann – domeinu publikoko irudia. Iturria: pixabay.com)

Soinua uhin mekanikoen hedapena eragiten duen edozein fenomeno da, entzungarria edo entzunezina izan. Soinuak dituen ezaugarrien artean, tonuak soinu jakin baten uhinak eskala batean duen posizioa adierazten du -behe-soinuetatik goi-soinuetara doan eskala-. Eskala horretan, 20 eta 20.000 Hz tartean dauden uhinak entzuteko gai gara eta hori oinarri hartuta antolatu da noten eskala.

Do batetik hurrengo do-ra bibrazioaren maiztasuna bikoizten dela jakinda, zortzidunetan antolatutako zazpi notaz osaturiko eskala erabiltzen da Mendebaldeko herrialdeetan. Soinuaren propietate fisikoak direla-eta, maiztasun bikoitza duten notak aldi berean jotzen direnean sortzen den soinua gustuko dugu, alegia, soinuek kontsonantzia dutela esaten da. Soinuak gustuko izatea edo ez, halere, ez da bakarrik maiztasunetan oinarritzen eta kulturak ere badu eragina.

Musika eta armonia: kulturaren eragina

Sarri askotan musika unibertsala dela pentsatu izan da. Modu batera edo bestera kultura guztietan agertzen da musika eta, modu batera edo bestera, musikak eragina du guregan. Musikari buruzko artikulu-sorta honetan ikusi den bezala, musikak lotura estua du zientziarekin. Musika formalizatu daiteke, arrazionalizatu daiteke eta fisikaren arauen bidez azal daiteke. Musika hainbat osagai fisiko eta neurgarrien bidez deskriba daiteke -soinuaren intentsitatea, tonua, tinbrea eta iraupena-. Uhinen maiztasunaren bidez soinua antolatu dugu notak sortzeko, baina, era berean, musikak badu azaldu ezin den alde irrazionala. Zergatik ditugu gustuko musika mota batzuk? Zergatik dira sinfonia batzuk hain erakargarriak?

Horrela galderen erantzuna kulturak musikan duen eragina da, baina, kulturak musikan duen eragina azaltzea ez da erraza. Soinu edo soinu-konbinaketa batzuk gustuko izatea eta beste batzuk ez kulturala edo biologikoa den erantzuten saiatu dira hainbat ikertzaile. Lehen zailtasuna zer da: ez dago musikaren efektuetatik at dagoen gizarterik, hortaz, ez dago kontrol elementurik. Horren adibide bakarrenetakoa da, halere, Amazonaseko oihanean bizi diren Tsimane indigenak. Musika izan badute, baina, berezitasun garrantzitsua du haien kulturak erabiltzen duen musikak: ez du armoniarik.

Armoniak tonuan jarri gabeko instrumentuek soinu desatseginak sortzea eragiten du eta armoniari esker, era berean, gustuko dugu orkestra baten kontzertua. Armoniak abesti bat bere osotasunean egonkorra izatea egiten du eta, neurri batean, matematikan dago armoniaren azalpena. Azaldu den bezala, soinuak uhinen bibrazio-maiztasunekin lotzen dira. Bi soinu edo gehiago batera entzuten ditugunean, alegia, bibrazio desberdin asko elkartzen direnean, haien elkarrekintza kontsonantea edo disonantea izan daiteke.

Horretarako jakin behar dena zera da: zortzidunen eskala hamabi tonuerditan banatuta dagoenez, zenbait kasutan nota desberdinen -zortzidun berekoak edo ez- arteko maitasunak antzekoak dira edo erlazio sinpleak betetzen dituzte -1/2, 2/3, 3/4 -. Bi noten maiztasunen arteko erlazioa zenbaki sinplea denean, biak batera entzuten direnean gustuko izaten dugu –ikusi honako taula-. Esan behar da, hala ere, kontsonantziaren ideia hori oso sinplista dela eta kasu askotan ez dela baliagarria, esate baterako Blues musika ez genuke gustuko izango teoria honen arabera.

Zentzu horretan, musikaren zati handi bat kultura-eraikuntza da eta guztia ezin da maiztasunen arteko erlazioarekin azaldu. Horrexegatik, armoniaren printzipioak ez dira guztiz unibertsalak Tsimane herriak erakutsi duen moduan. Haien musika monofonikoa da, alegia, tonu bakarraz osatutako abestiak egiten dituzte, abeslari edo instrumentu bakarrarekin interpretatzen direnak. Ondorioz, ez dute armoniarik. Mendebaldeko musikarekin harreman minimoa izan dutenez, haiekin egindako esperimentuek balio handia dute musikaren unibertsaltasuna aztertzeko. Ikerketek erakutsi dutenez, Tsimaneek ez dute ez dute desatsegintzat hartzen disonantzia. Era berean, Mendebaldeko musika entzuteko zenbat eta ohitura gehiago izan kontsonantzia atseginagoa dela adierazten dute hainbat populaziok. Nature aldizkarian argitaratutako ikerketaren ondorioen arabera, emaitzek adierazten dute kontsonantzia atsegina izatearen lotura kulturalagoa dela biologikoagoa baino. Horrexegatik, musika azaldu daiteke fisikaren eta uhinen higiduraren arauak erabiliz, baina, musika bere osotasunean ulertzeko ezinbestekoak da gizarte bakoitzaren kulturak duen ekarpena kontuan hartzea. Zenbaitetan, zientziak dio dena ez dela zientzia.

—————————————————–
Egileaz: Josu Lopez-Gazpio (@Josu_lg) Kimikan doktorea, irakaslea eta zientzia dibulgatzailea da. Tolosaldeko Atarian Zientziaren Talaia atalean idazten du eta UEUko Kimika sailburua da.
—————————————————–

Musikaren zientziari buruzko artikulu-sorta:

1. Musikaren zientzia (I): Soinua
2. Musikaren zientzia (II): Musika notak eta bibrazio maiztasunak
3. Musikaren zientzia (eta III): Kultura eta zientzia

The post Musikaren zientzia (eta III): Kultura eta zientzia appeared first on Zientzia Kaiera.