La ciencia quizás tenga valores… pero no sabemos cuáles son

A lo largo de las anotaciones anteriores hemos visto como, desde una tradición anterior al siglo XX en la que no cabían cuestiones de orden axiológico, durante el primer tercio de ese siglo se pasó, no sin resistencia, a incorporar la noción de los valores al acervo de los estudios de sociología y filosofía de la ciencia. Ello tuvo mucho que ver con las cada vez mayores implicaciones sociales, económicas e ideológicas de la ciencia y sus productos. Fueron sobre todo consideraciones relativas a los efectos de la tecnología que se derivaba del desarrollo de la ciencia y a la contraposición de determinados valores muy extendidos socialmente con valores y principios propios de la empresa científica lo que llevó a Merton (1942) a enunciar el conocido como ethos de la ciencia, ethos al que iban asociados una serie de valores.
Como vimos en la anotación anterior, no obstante, este asunto sigue siendo controvertido en el marco de la filosofía de la ciencia. Por esa razón, y al objeto de disponer de una perspectiva más amplia, y dado que el tema tratado ha concitado el interés no sólo de sociólogos y filósofos de la ciencia, sino también de científicos y divulgadores, he considerado de interés incluir de forma sumaria, lo que algunos de esos científicos y divulgadores han afirmado en relación con el tema. No pretendo que este repaso mínimo sirva para elaborar una reflexión meditada sobre la noción de los valores de la ciencia y sus implicaciones. Mi intención se limita a ilustrar la gran diversidad de rasgos, cualidades, actitudes y virtudes que son consideradas al tratarlo.
Santiago Ramón y Cajal (1898), en su “Reglas y consejos sobre investigación científica. Los tónicos de la voluntad”, incluye un capítulo, el tercero, titulado “Cualidades de orden moral que debe poseer el investigador”. Si bien es cierto que, en sentido estricto, quizás estas cualidades no sean del todo asimilables a la noción de valores utilizada por Merton (1942), no lo es menos que pueden considerarse perfectamente homologables a muchas otras cualidades que han venido siendo consideradas como valores. Por esa razón se han incluido aquí, y porque al fin y al cabo, no deja de ser una de las primeras referencias a estos temas escritas por un científico español. Para Ramón y Cajal, el científico ha de tener independencia de juicio, perseverancia, pasión por la gloria, patriotismo y gusto por la originalidad.
En un libro muy conocido del físico y divulgador científico norteamericano Carl Sagan (1995), “El mundo y sus demonios”, en el capítulo II, “Ciencia y esperanza”, hace una reflexión acerca de la ciencia, de su relación con la sociedad y de lo que cree que significa para la humanidad. En ese contexto, va desgranando una serie de ideas y atribuyendo a la ciencia una serie de cualidades. He recopilado la siguiente lista: cautela (escepticismo), racionalidad, autocrítica, apertura, independencia de juicio, humildad, imaginación, disciplina, coherencia, espíritu crítico, honestidad, y libre intercambio de ideas.
He incluido en esta breve relación a Ramón Núñez (2010), creador de los museos científicos coruñeses y a quien se considera padre de la museología científica española. Núñez, en una intervención en el Senado, enunció lo que su autor denomina “valores culturales de la ciencia”. Son los siguientes: curiosidad, escepticismo, racionalidad, universalidad, provisionalidad, relatividad, autocrítica, iniciativa, apertura y creatividad.
Por último, me ha parecido de interés incluir aquí los resultados de una encuesta en la que unas pocas personas, dedicadas a la investigación, a la docencia de materias de ciencia y a la divulgación científica respondían a la pregunta de cuáles son a su juicio los tres principales valores de la ciencia. No pretendo que los resultados de esta encuesta sean extrapolables, por supuesto. He reformulado algunas respuestas para agrupar las que tenían contenidos muy similares, y he puesto entre paréntesis el número de veces en que se daba la respuesta en cuestión. Comprobé que las respuestas dadas eran clasificables en dos grandes categorías: funciones que cumple la ciencia, una, y sus cualidades (o virtudes), la otra. Y cada una de esas dos categorías podía subdividirse, a su vez, en otras dos, atendiendo a si eran rasgos de carácter general o de carácter epistémico. Así pues, relaciono a continuación las respuestas dadas, agrupadas en las cuatro subcategorías indicadas.
Funciones
Proporciona progreso y bienestar (8); es fuente de criterio (5); promueve la educación y la cultura (1); proporciona placer y asombro (1).
Funciones epistémicas
Proporciona conocimiento objetivo (4); hace uso de y promueve el pensamiento crítico (4); busca respuestas (2); ofrece certezas (2); proporciona experiencia vital (2); atrae la inteligencia (1); desmitifica (1); permite comparar (1); facilita el intercambio de ideas (1).
Cualidades
Humildad (5); cooperatividad (3); honradez (2); belleza (1); generosidad (1); transparencia (1); valentía (1); resiliencia frente a sus demonios (1).
Cualidades epistémicas
Universalidad (7); curiosidad (7); objetividad (3); revisable/provisional (3); creatividad (3); escepticismo (2); racionalidad (2); realismo (1); rigor (1).
Conclusión
Si nos fijamos hoy en lo que diferentes filósofos, científicos y divulgadores de la ciencia han escrito al respecto (la relación contenida en este texto no es, ni de lejos, exhaustiva), vemos fácilmente que las dificultades a las que se refería Menéndez Viso (2005) son reales. Los resultados de la encuesta, aunque carentes de rigor estadístico, dan cuenta de una gran diversidad de visiones que no hace sino confirmar esas dificultades. En definitiva, no puedo sino concluir que la noción “valores de la ciencia” se encuentra sumida en una gran confusión.
Y sin embargo, si pretendemos que esa noción resulte de alguna utilidad, más allá de formular un desiderátum acerca de cómo nos gustaría a cada uno que fuese la ciencia o qué requisitos éticos deberían cumplir la práctica científica, y sus bienes y productos, debería clarificarse esta noción, precisar su significado. Menéndez Viso (2005) propone recuperar la noción aristotélica de la prudencia. Es una idea sugerente, pero creo que es una noción útil sobre todo en relación con la aplicación práctica de los resultados de la ciencia. Dudo que lo sea si de lo que se trata es de caracterizar a la empresa científica en sí.
Me parece una tarea necesaria. La ciencia se sigue encontrando en el punto de mira de ideologías que le son adversas. Me refiero a las ideologías políticas totalitarias y a las corrientes de pensamiento que niegan a la ciencia su valor epistémico atribuyéndole la condición de mera construcción social. Por esa razón, y dado que la ciencia, como cualquier otra empresa humana, requiere de un grado suficiente de legitimación y apoyo social, es necesario clarificar el dominio de los valores de la ciencia de manera que sirvan para proporcionárselos. Para ello, es importante determinar con precisión a qué nos referimos cuando hablamos de valores de la ciencia, si a principios, cualidades, virtudes, actitudes, normas o bienes, por citar algunas de las nociones potencialmente válidas. Sin esa clarificación, la de los valores de la ciencia será una noción inútil, por confusa. Y es que también en este dominio vale el aserto baconiano: “se aprende más del error que de la confusión”.
FuentesMenéndez Viso, Armando (2005): Las ciencias y el origen de los valores Siglo XXI, Madrid
Merton, Robert K (1942): “Science and Technology in a Democratic Order” Journal of Legal and Political Sociology 1: 115-126. [Traducción al español como “La estructura normativa de la ciencia” en el volumen II de “La Sociología de la Ciencia” Alianza Editorial 1977, traducción de The Sociology of Science – Theoretical and Empirical Investigations, 1973]
Núñez Centella, Ramón (2010): “La cultura científica” (Intervención en la Reunión de Presidentes de Comisiones de Ciencia e Innovación de los Parlamentos Nacionales de los Estados miembros de la Unión Europea y del Parlamento Europeo; 25 de marzo de 2010).
Ramón y Cajal, Santiago (1898): Reglas y consejos sobre investigación científica. Los tónicos de la voluntad. Espasa Calpe, Madrid, 1941.
Sagan, Carl (1995): The Demon haunted World, Random House, New York [Traducción al español: El Mundo y sus demonios, Planeta, Barcelona (2006)]
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La ciencia quizás tenga valores… pero no sabemos cuáles son se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La ciencia no tiene valores… ¿o sí los tiene?
- “Filosofía, Ciencia y Valores”, el máster
- Ciencia y valores en la sociedad del riesgo
Algunas visiones en filosofía de la ciencia sobre sus valores

Una vez que Merton (1942) abrió la puerta a los valores como un elemento fundamental para caracterizar la empresa científica y para sustentar la legitimación social de la misma, otros autores han aportado su propia visión. Paso a continuación a hacer un breve repaso, recurriendo, para ello, a referencias recogidas por Javier Echeverría en sendos trabajos de 1995 y de 2002.
De acuerdo con la teoría de los objetivos de la ciencia de Karl Popper: “la ciencia busca la verdad y la resolución de problemas de explicación, es decir, que busca teorías de mayor capacidad explicativa, mayor contenido y mayor contrastabilidad.” Según Popper, la objetividad científica exige que las conjeturas sean sometidas a prueba; por eso, la falsación y la crítica no son sólo preceptos metodológicos, son también reglas propias del ethos de la ciencia. Por otra parte, la comunicabilidad del conocimiento científico (y en concreto la escritura) son condiciones sine qua non para que esa objetividad sea factible. Popper formuló una nueva característica universal para todo tipo de ciencias (formales, naturales, sociales), a saber, su carácter público. “[..] decimos que una experiencia es pública, cuando todo aquel que quiera tomarse el trabajo de hacerlo puede repetirla,” para remachar a continuación: “Esto es lo que constituye la objetividad científica. Todo aquel que haya aprendido el procedimiento para comprender y verificar las teorías científicas puede repetir el experimento y juzgar por sí mismo.” Y por lo mismo, la universalidad de la ciencia es otro valor continuamente subrayado por él. La investigación científica se lleva a cabo en un marco social, cultural, institucional e histórico determinado. Sin embargo, ello no implica que no podamos sobrepasar dicho marco, conduciendo nuestra indagación hacia una mayor universalidad.
“En último término, el progreso depende en gran medida de factores políticos, de instituciones políticas que salvaguarden la libertad de pensamiento: de la democracia.” […] La axiología subyacente a la teoría popperiana del objetivo de la ciencia nos muestra nuevos valores, que él considera fundamentales para el desarrollo de la actividad científica: por ejemplo la libertad de pensamiento y la libertad de crítica.
Mario Bunge negó la dicotomía entre hechos y valores en la ciencia y mantuvo al respecto una postura matizada: “el contenido del conocimiento científico es axiológica y éticamente neutral”, pero “algunos de los criterios que se emplean en ciencia son claramente normativos”. Para Bunge, “los valores son propiedades relacionales que adjudicamos en ciertas ocasiones a cosas, actos o ideas, en relación con ciertos desiderata“. Hay valores que la ciencia moderna ha promovido siempre, como la verdad, la novedad, el progreso, la libertad y la utilidad. Bunge afirmó incluso que “la actividad científica es una escuela de moral” y que “la ciencia es una fuerza moral a la vez que una fuerza productiva”, para terminar diciendo que “en conclusión, la ciencia, en su conjunto, no es éticamente neutral”.
En una conferencia dictada en 1973, Thomas Kuhn planteó una nueva pregunta en filosofía de la ciencia: ¿cuándo una teoría científica es buena (o mala)? En lugar de preguntar sobre la verdad, falsedad, verosimilitud, falsabilidad, contrastabilidad, etc., de las teorías científicas, como era habitual entre los filósofos de la ciencia, Kuhn suscitó una cuestión que es previa a la de la verdad, falsedad o verosimilitud de las teorías. Según Kuhn, los científicos criban previamente las propuestas y para ello recurren a una serie de requisitos y valores a los que hay que prestar gran atención.
Respondiendo a su propia pregunta, Kuhn indicó al menos cinco características para admitir que una teoría científica es buena: precisión, coherencia, amplitud, simplicidad y fecundidad. Posteriormente sugirió un sexto valor, la utilidad, de índole mayormente técnica, por lo que Kuhn no lo incluyó en su lista inicial de “valores de la ciencia”. También subrayó que ninguno de esos criterios basta por sí mismo para dilucidar si una teoría es buena o no y, por supuesto, tampoco para decidir si es verdadera o falsa. Sin embargo, los cinco son requisitos axiológicos exigibles a toda teoría científica, es decir, condiciones necesarias, pero no suficientes.
Según Kuhn, “[,,,] una teoría debe ser precisa: esto es, dentro de su dominio, las consecuencias deducibles de ella deben estar en acuerdo demostrado con los resultados de los experimentos y las observaciones existentes. En segundo lugar, una teoría debe ser coherente, no sólo de manera interna o consigo misma, sino también con otras teorías aceptadas y aplicables a aspectos relacionables de la naturaleza. Tercero, debe ser amplia: en particular las consecuencias de una teoría deben extenderse más allá de las observaciones, leyes o subteorías particulares para las que se destinó en un principio. Cuarto, e íntimamente relacionado con lo anterior, debe ser simple, ordenar fenómenos que, sin ella, y tomados uno por uno, estarían aislados y, en conjunto, serían confusos. Quinto -aspecto algo menos frecuente, pero de importancia especial para las decisiones científicas reales-, una teoría debe ser fecunda, esto es, debe dar lugar a nuevos resultados de investigación: debe revelar fenómenos nuevos o relaciones no observadas antes entre las cosas que ya se saben.” […] “toda elección individual entre teorías rivales depende de una mezcla de factores objetivos y subjetivos, o de criterios compartidos y criterios individuales. Como esos últimos no han figurado en la filosofía de la ciencia, mi insistencia en ellos ha hecho que mis críticos no vean mi creencia en los factores objetivos.”
En su libro Reason, Truth and History (1981), Hilary Putnam no sólo negó la dicotomía positivista entre hechos y valores, sino que afirmó tajantemente que no hay hechos científicos ni mundo sin valores. Según Putnam, “sin los valores cognitivos de coherencia, simplicidad y eficacia instrumental no tenemos ni mundo ni hechos”
En 1984 Larry Laudan publicó un libro con el sugestivo título Science andValues, pero desde las primeras páginas anunciaba que no iba a ocuparse de las relaciones entre la ciencia y la ética, sino que se centraría exclusivamente en los valores epistémicos:
“No tengo nada que decir sobre los valores éticos como tales, puesto que manifiestamente no son los valores predominantes en la empresa científica. Ello no equivale a decir que la ética juegue papel alguno en la ciencia; por el contrario, los valores éticos siempre están presentes en las decisiones de los científicos y, de manera muy ocasional, su influencia es de gran importancia. Pero dicha importancia se convierte en insignificancia cuando se compara con el papel omnipresente (ubiquitous)de los valores cognitivos. Una de las funciones de este libro consiste en corregir el desequilibrio que ha llevado a tantos escritores recientes sobre la ciencia a estar preocupados por la moralidad científica más que por la racionalidad científica, que será mi tema central.”
En relación a los criterios axiológicos que se utilizan para evaluar las teorías y los problemas, Laudan sólo se ocupa de los valores epistémicos (verdad, coherencia, simplicidad y fecundidad predictiva) o, como también dice, de la «evaluación cognoscitivamente racional». Puede haber problemas muy importantes desde un punto de vista político o económico, pero éstos pertenecen a «las dimensiones no racionales de la evaluación de problemas».
FuentesEcheverría, Javier (1995): El pluralismo axiológico de la ciencia. Isegoria 12: 44-79
Echeverría, Javier (2002): Ciencia y Valores; Barcelona, Ediciones Destino.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Algunas visiones en filosofía de la ciencia sobre sus valores se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- “Filosofía, Ciencia y Valores”, el máster
- La ciencia no tiene valores… ¿o sí los tiene?
- Ciencia y valores en la sociedad del riesgo
El ethos de la ciencia y las normas de Merton

Como hemos visto en la anotación anterior (Merton, 1938), la ciencia dejó de ser inmune al ataque, las restricciones y la represión. Antaño la fe de la cultura occidental en la ciencia había sido ilimitada, indiscutida y sin rival. Hace 350 años, cuando la institución de la ciencia poseía escasos títulos propios para reclamar apoyo social, también los filósofos de la naturaleza tuvieron que justificar la ciencia como un medio para lograr los fines culturalmente convalidados de la utilidad económica y la glorificación de Dios. La actividad científica, pues, no era un valor evidente por sí mismo. Pero con la interminable serie de éxitos, lo instrumental se transformó en lo final, el medio en el objetivo. Así fortalecido, el científico llegó a considerarse independiente de la sociedad, y a la ciencia como una empresa que se validaba a sí misma, que estaba en la sociedad pero que no le pertenecía. La revuelta contra la ciencia, sin embargo, obligó a que científicos y legos, por igual, le prestasen su atención.
Los ataques incipientes y manifiestos contra la integridad de la ciencia condujeron a los científicos a reconocer su dependencia de tipos particulares de estructura social. Las asociaciones de científicos han venido dedicado manifiestos y declaraciones a las relaciones entre la ciencia y la sociedad. La crisis invitó a una autoevaluación. Al tener que enfrentarse a los desafíos a su modo de vida, los científicos se vieron obligados a tomar conciencia de sí mismos, como elementos que forman parte de la sociedad y que tienen obligaciones e intereses. Los científicos se vieron obligados a justificar ante la sociedad los modos de obrar de la ciencia.
Así pues, tras indagar acerca de los motivos por los que la empresa científica empezó a ser cuestionada, Merton (1942) pasó a analizar la estructura normativa de la ciencia. Intentó, de esta forma, identificar los valores y las normas que guían la acción de los científicos, porque entendía que debían reexaminarse sus fundamentos, reformular sus objetivos y buscar una nueva justificación. La legitimación que alcanzó en el siglo XVII y que mantuvo durante los dos siglos siguientes, ya no era suficiente para garantizar la continuidad de la empresa científica.
La palabra “ciencia”, según Merton (1942) se refiere a una variedad de cosas distintas, aunque relacionadas entre sí. Normalmente se utiliza para denotar: (1) un conjunto de métodos característicos mediante los cuales se certifica eI conocimiento; (2) un acervo de conocimiento acumulado que surge de la aplicación de estos métodos; (3) un conjunto de valores y normas culturales que gobiernan las actividades científicas; (4) cualquier combinación de los elementos anteriores. Aquí nos ocuparemos, de manera preliminar, de la estructura cultural de la ciencia, esto es, de un aspecto limitado de la ciencia como institución.
Es a esas normas a las que se referirá Merton (1942) a continuación, normas que dejará formuladas y que desde entonces se han considerado una referencia fundamental en todos los estudios que han abordado el asunto de los valores de la ciencia. Se las denomina, de hecho, “normas mertonianas”.
En expresión de quien acuñó la fórmula, “el ethos de la ciencia es ese complejo, con resonancias afectivas, de valores y normas que se consideran obligatorios para el hombre de ciencia. Las normas se expresan en forma de prescripciones, proscripciones, preferencias y permisos. Se las legitima en base a valores institucionales. Estos imperativos, trasmitidos por el precepto y el ejemplo, y reforzados por sanciones, son internalizados en grados diversos por el científico, moldeando su conciencia científica. Aunque el ethos de la ciencia no ha sido codificado, se lo puede inferir del consenso moral de los científicos tal como se expresa en el uso y la costumbre, en innumerables escritos sobre el espíritu científico y en la indignación moral dirigida contra las violaciones del ethos”.
Para Merton (1942), el fin institucional de la ciencia es el crecimiento del conocimiento certificado. Y los métodos empleados para alcanzar ese fin proporcionan la definición de conocimiento apropiada: enunciados de regularidades empíricamente confirmados y lógicamente coherentes (que son, en efecto, predicciones). Los imperativos institucionales (normas) derivan del objetivo y los métodos. Toda la estructura de normas técnicas y morales conducen al objetivo final. La norma técnica de la prueba empírica adecuada y confiable es un requisito para la constante predicción verdadera; la norma técnica de la coherencia lógica es un requisito para la predicción sistemática y válida. Las normas de la ciencia poseen una justificación metodológica, pero son obligatorias, no sólo porque constituyen un procedimiento eficiente, sino también porque se las cree correctas y buenas. Son prescripciones morales tanto como técnicas.
Si la comunidad científica comparte un proyecto común –la construcción de un cuerpo de conocimiento certificado o fiable acerca del mundo y de cómo funciona-, las normas que Merton (1942) identificó son algo parecido a los valores compartidos por esa comunidad, valores que son considerados esenciales. Una interpretación actualizada de las normas mertonianas, es la que propone el físico John Ziman (2000), y que se presenta a continuación.
- Universalismo.Lo importante en la ciencia no es quién la practica, sino su contenido, los conocimientos que adquirimos acerca del mundo y de los fenómenos que ocurren en él.Todos pueden contribuir a la ciencia con independencia de su raza, nacionalidad, cultura o género. Y por lo tanto, todos han de ser tratados como potenciales contribuyentes a la ciencia.
- Comunismo. No se trata del comunismo al que se refiere la ideología marxista-leninista, sino de un punto de vista según el cuál, el conocimiento científico debería ser compartido por el conjunto de la comunidad científica, con independencia de qué parte de los descubrimientos han sido hechos por unos u otros científicos. Así pues, todos los científicos deberían tener el mismo acceso a los bienes científicos y debería haber un sentido de propiedad común al objeto de promover la colaboración. El secretismo es lo opuesto a esta norma, puesto que el conocimiento que se oculta, que no se hace público no es de ninguna ayuda en el cumplimiento del objetivo de la comunidad, que el conocimiento certificado crezca.
- Desinterés.Se supone que los científicos actúan en beneficio de una empresa científica común, más que por ganancia personal. No obstante, no debe confundirse este “desinterés” con altruismo. De lo que se trata es de que los beneficios que puedan proporcionar los descubrimientos científicos, sin dejar de favorecer a quien los realice, no deben entorpecer o dificultar la consecución del objetivo institucional de la ciencia: la extensión del conocimiento cretificado.
- Escepticismo organizado. El escepticismo quiere decir que las declaraciones o pretensiones científicas deben ser expuestas al escrutinio crítico antes de ser aceptadas. Este es el valor que compensa el universalismo. Todos los miembros de la comunidad científica pueden formular hipótesis o teorías científicas, pero cada una de ellas debe ser evaluada, sometida al filtro de la prueba o la refutación para comprobar si se sostiene. Las propuestas que superan esa prueba con éxito pasan a formar parte del bagaje universal de conocimiento científico. El escepticismo es el valor que permite que funciones el del desinterés, porque sin escepticismo es más fácil caer en la tentación de anteponer el interés personal al del conjunto de la comunidad científica.
Las normas mertonianas son las que los científicos creen que deberían seguir, lo que creen que les es permitido hacer, y lo que sería bueno para ellos que hicieran. En otras palabras, por normas no se identifica lo que los científicos hacen normalmente, no necesariamente al menos; a veces lo que hacen no satisface lo que piensan que deberían hacer. Pero eso no quiere decir que a los científicos se les dé un manual que incluye las normas de Merton. Ellos las adquieren prestando atención a lo que hacen otros científicos en su comunidad, qué comportamientos castigan y cuáles premian.
FuentesMerton, Robert K (1938): “Science and the Social Order” Philosophy of Science 5 (3): 321-337. [Traducción al español como “La ciencia y el orden social” en el volumen II de “La Sociología de la Ciencia” Alianza Editorial 1977, traducción de The Sociology of Science – Theoretical and Empirical Investigations, 1973]
Merton, Robert K (1942): “Science and Technology in a Democratic Order” Journal of Legal and Political Sociology 1: 115-126. [Traducción al español como “La estructura normativa de la ciencia” en el volumen II de “La Sociología de la Ciencia” Alianza Editorial 1977, traducción de The Sociology of Science – Theoretical and Empirical Investigations, 1973]
Ziman, John (2000). Real Science: What It Is and What It Means. Cambridge University Press.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El ethos de la ciencia y las normas de Merton se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La hostilidad a la ciencia
- Ciencia a presión: Ciencia abierta vs. ciencia cerrada
- La ciencia no tiene valores… ¿o sí los tiene?
Berpiztuko al ditugu dinosauroak?

1. irudia: Zientzia-fikziozko filmei esker dinosauroekiko interesa piztu zuen. (Argazkia: AzDude – domeinu publikoko irudia. Iturria: pixabay.com)
Egun badakigu Jurassic Park filmak zientzia hauspotu duela eta, nolabait, modan jarri zuela antzinako DNAren ikerketa. Pelikulak dinosauroekiko interesa handitu zuen eta horrek alor horretan ikerketa gehiago egitera eraman zuen. Zenbait kasutan kalterako ere bai, izan ere, itxaropen faltsuak eragin zituen zenbait kasutan. Litekeena da filmean proposatutakoa ezinezkoa izatea orain arte zientziaz dakiguna aldatzen ez den bitartean. Dinosauroei buruzko akatsak ere ugariak dira filmean –esaterako, Tyranosaurus rex-aren inguruko egokitasun falta nabaria da-, baina, ingeniaritza genetikoari dagozkion akatsak ere ez dira gutxi.
Emandako azalpenakJurassic Park filmaren hasiera aldera “Mr DNA” delako sekuentzian azaltzen dute zer teknologia erabiliz egin diren parkean ikus daitezkeen dinosauroak. Bide batez, esan behar da sekuentzia hori –fikzioa sinesteko beharrezkoa diren akatsak alde batera utzita–, zientzia-komunikazioaren lan aparta dela duela 25 urte gizarteak DNAri buruz zekiena kontuan hartzen bada. Azaltzen dutenez, fosilizatutako dinosauroen garaiko eltxoetatik dinosauroen DNA erauztea posible da. DNA hori erauzita eta falta diren hutsuneak igelen DNArekin betez, dinosauroen enbrioiak ostruken arrautzetan txertatzen dituzte eta, hortik, dinosauroak. Istorioa polita da, sinesgarria ere izan daitekeena, baina zientzia fikzioa besterik ez da.
Errealitatetik urrunLehenik eta behin, odola xurgatzen zuten intsektuetan dinosauroen DNA bere horretan gordeta egon daitekeela pentsatzea ez da zuzena -anbarrean fosilizatuta egonik ere-. Eltxo prehistorikoak aurkitu dira, bai, eta dinosauroen DNA dutenak ere bai, baina, eltxo horietan dagoen DNA hondatuta dago. Ez dauka izan zenaren arrastorik ere eta eltxoaren beraren DNA ere guztiz hondatuta dago. Neandertalgo gizakien eta mamuten DNA isolatzea lortu da, baina, dinosauroena zaharregia da. Aurkitu den DNArik antzinakoenak milioi bat urte inguru ditu. Dinosauroak duela 66 milioi urte desagertu ziren, beraz, salto handiegia dago, besterik gabe. Duela gutxi frogatu denez, dinosauroen garaiko zenbait zelula eta zelula-egitura mantendu daitezkeela ikusi da, baina ez genoma osoak.

2. irudia: Stegosaurus-aren hezurdura. (Argazkia: OpenClipart Vectors – domeinu publikoko irudia. Iturria: commons.wikimedia.org)
Dinosauroen DNA erauztea posible izango balitz ere, milioika zati txikitan puskatuta egongo litzateke. Zati horiek elkartzeko gidarik ez legoke eta ia ezinezkoa litzateke DNA zatiak berezko ordena jarraituz berriro elkartzea. Puzzle erraldoi bat osatzearen parekoa da piezarik falta den jakin gabe eta zer irudi lortu behar den jakin gabe. Jurassic Park filmean zientzialariek falta diren piezak osatzeko igelen DNA erabiltzen dute, baina, hori urruti samar dago zientziaren prozeduretatik. Hasteko, igel-dinosauro hibrido bat lortuko litzateke eta, gainera, enbrioiaren bideragarritasuna zalantzan jartzekoa da. Izan ere, dinosauroak hegaztietatik askoz gertuago daude ebolutiboki igeletatik baino eta, hortaz, ez du zentzu zientifiko gehiegirik filmean proposatzen denak.
Genomaren osaketari dagokionez, 2010ean genoma sintetikodun lehen zelula sortu zuten, Mycoplasma mycoides-en laborategiko bertsioa, baina milioi bat base besterik ez dituen genoma bati dagokio. Dinosauro baten genoma eraikitzea lan izugarria litzateke horren aldean, gainera, ez legoke erreferentziarik eraiki behar den hori nolakoa den jakiteko. Kontuan izan behar da DNA katea prest izatea ez dela nahikoa desagertu den izaki bizidun bat berpizteko. DNA hasiera puntua da, bai, baina enbrioiaren garapenerako dinosauroen arrautza ere beharko litzateke. Oilo baten enbrioia ostruka baten arrautzan sartzen bada ez da txitarik jaiotzen -frogak egin dira-. Hortaz, are nekezagoa izango litzateke Velociraptor baten DNA ostruka baten arrautzan jarrita dinosauro bat jaiotzea.
Dinosauroek bizirik dirauteEgia esan, dinosauroak ez dira desagertu eta gure artean jarraitzen dute. Hegaztiek ez dute dinosauroetatik eboluzionatu. Hegaztiak ez daude dinosauroekin lotuta. Hegaztiak dinosauroak dira. Dinosauroak -hegaztiak barne-, lau desagertze masiboren ondorioa dira. Desagertze bakoitzaren ondoren espezie berriak agertu ziren eta guzti horren ondorioa dira egun ikus ditzakegun txoriak. Hortaz, dinosauroak ez dira desagertu: ingurune berrira moldatzeko eboluzionatu dute. Hori jakinik, hegaztietatik dinosauroak lortzeko modua ere proposatu da. Antza, atabismo genetikoak aktibatuz aspaldiko arbasoen ezaugarriak berreskuratu daitezke eta, horrela, posible litzateke hegaztien eboluzioan atzera egitea. Jack Horner irakasle eta paleontologo estatubatuarra alderantzizko eboluzioa eta adierazi zuenez, modu horretan posible izango da dinosauroen zenbait ezaugarri dituzten hegaztiak lortzea. Ez dira dinosauroak izango, baina, hor ere aurrerapausoak eman ahal izango dira.
Bien bitartean, zientzia-fikziozko filmetan bakarrik ikusi ahal izango ditugu dinosauroa- eta haiekin istorio zirraragarriak amestuko ditugu, baina, nekez ikusiko dugu noizbait dinosauro bat bizirik. Une honetan dugun jakintzaren arabera, ezinezkoa da. Agian desagertu diren espezieak berpiztu ahal izango dira –mamuta, esaterako-, baina, hori ere zalantzan jartzekoa da. Edozein kasutan amets edo kimera horiez gain, ikuspuntu etikotik ere aztertu beharko da desagertutako espezieak berpiztu daitezkeen edo ez. Ez dira gutxi horrek sor ditzakeen arazo etikoak, eta horiek argitu beharko ditugu, baina, oraingoz azkarregi goaz kontu etikoez aritzeko. Biologiari dagokionez, oraingoz ezinezkoa da dinosauroak berpiztea eta ez dago pisuzko arrazoi zientifikorik pentsatzeko noizbait egin ahal izango dela. Pelikulak ikusten jarraitu beharko dugu.
Erreferentzia bibliografikoak:
Kruger R.P., (2011). Jurassic Park Revisited. Cell, 153(2), 277-279. DOI: https://doi.org/10.1016/j.cell.2013.03.041
Informazio osagarria:
- Sci-fi and Jurassic Park have driven research, scientists say, E. Jones, theconversation.com, 2018.
- Does Jurassic Park make scientific sense? M. Halton, bbc.com, 2019.
—————————————————–
Egileaz: Josu Lopez-Gazpio (@Josu_lg) Kimikan doktorea eta zientzia dibulgatzailea da. Tolosaldeko Atarian Zientziaren Talaia atalean idazten du eta UEUko Kimika sailburua da.
—————————————————–
The post Berpiztuko al ditugu dinosauroak? appeared first on Zientzia Kaiera.
La hostilidad a la ciencia
En el mismo año que se había publicado el ensayo relativo a la relación entre la ciencia moderna y el protestantismo glosado en la anotación previa, Merton (1938) publicó una conferencia que había pronunciado en diciembre del año anterior ante la American Sociological Society. En dicha conferencia se refirió a los ataques que había venido recibiendo la ciencia en los años anteriores y expuso una serie de ideas acerca de los motivos por los que, a su entender, se estaban produciendo esos ataques. Sintetizo a continuación los puntos más significativos de su trabajo.
Parte de la base de que hace falta que haya personas interesadas en dedicarse a la investigación científica para que haya ciencia. Pero como eso es algo que requiere una serie de condiciones culturales, es importante conocer qué es lo que motiva que se inicie una carrera científica y cuáles son los factores que la pueden obstaculizar o impedir.
Por otro lado, cree que la hostilidad hacia la ciencia tiene un origen doble. El primero sería que los resultados o métodos de la ciencia sean contrarios a determinados valores sociales. O sea, si hay ciertos valores que son mayoritariamente compartidos en la sociedad y la ciencia se percibe como contraria a esos valores, ello sería una fuente de hostilidad. Y el segundo descansa en la sensación de incompatibilidad entre los sentimientos que encarna el ethos científico y los que se encuentran en otras instituciones. De la misma forma, también puede ocurrir lo contrario; por esa razón, la posición de la ciencia puede ser analizada como la resultante de dos conjuntos de factores en conflicto, que apoyan o son contrarias a la ciencia como actividad social a gran escala.
Merton (1938) pone como ejemplo la situación que se produjo en la Alemania nazi a partir de 1933, donde las trabas a la ciencia fueron un subproducto de la ideología nacionalsocialista1. Además, en las instituciones –universidades incluidas- de la Alemania del III Reich había un tono general antiintelectual, por su desprecio del teórico y su glorificación del hombre de acción. Y ese tono, no exclusivo de Alemania además, podía tener consecuencias de largo alcance.
Por otra parte, en los estados totalitarios se exige máxima lealtad al propio Estado, lo que implica, en el caso de los científicos, tener que renunciar a las normas institucionales que entran en conflicto con las de aquél. Las normas del ethos científico deben ser sacrificadas, en tanto exigen repudiar los criterios de validez científica o mérito científico impuestos políticamente. En un orden liberal, sin embargo, la limitación de la ciencia no se produce de esa forma, ya que las instituciones que no son políticas gozan de una considerable autonomía.
Pero la situación que se produjo en Alemania no es la única que pudo dar lugar a actitudes de hostilidad hacia la ciencia. Merton (1938) señala que a menudo los científicos defienden el carácter “puro” de la ciencia, y lo hacen al objeto de preservar su autonomía de elementos extraños como las doctrinas religiosas, la utilidad económica, o la conveniencia política. Por lo tanto, se defiende la pureza de la ciencia para evitar que se limiten las direcciones de su potencial avance y amenacen la estabilidad y continuidad de la investigación científica valorada socialmente. El criterio tecnológico del logro científico también tiene una función social para la ciencia, pues los bienes y productos que ofrece la tecnología -y, en última instancia, también la ciencia- promueven el apoyo social a la misma. La razón es clara: el público difícilmente está en condiciones de comprender el trabajo científico y sus resultados, por lo que la gente no puede evaluarlos directamente; lo que sí puede hacer, sin embargo, es valorar los productos que genera. Esa es, en definitiva, una forma de hacer intelectualmente comprensible una práctica que, de otra forma, sería inaccesible.
Pero ocurre que el énfasis en la pureza de la ciencia ha tenido también efectos negativos para ella. Como consecuencia de esa actitud los científicos, al no poder controlar su posterior desarrollo, se desentienden y no se hacen responsables de los usos posteriores que pueda hacerse de sus descubrimientos. Y si esos usos tecnológicos generan rechazo en la población, el rechazo alcanzará finalmente también a la ciencia. Los motivos pueden ser muy variados, desde la oposición a los usos bélicos hasta el efecto de la tecnología sobre el medio ambiente o el mercado de trabajo. Pero el caso es que sean cuales sean esos motivos o lo justificados que estén, la oposición a la ciencia es su consecuencia. Así pues, la preocupación por el objetivo primario –la promoción del conocimiento por su valor intrínseco, preservando la pureza de la ciencia- está asociada a una desatención hacia las consecuencias que están al margen del interés inmediato, pero los resultados sociales reaccionan de tal modo que obstaculizan las metas originales. Ese comportamiento anula valores que no son fundamentales para la ciencia, pero son parte integrante de la escala social de valores. Por lo tanto, los efectos de la investigación científica, dado que no se realiza en un vacío social, se ramifican en otras esferas de valores e intereses. En expresión de Merton “el principio de la ciencia pura y desinteresada ha contribuido a elaborar su propio epitafio”.
Otro mecanismo potencialmente generador de hostilidad hacia la ciencia, según Merton (1938), es la enorme distancia que hay entre los científicos y los legos en cuanto al grado de comprensión de los asuntos de naturaleza científica. Hay toda una panoplia de conceptos –los que son propios de la Teoría de la Relatividad o de la Mecánica Cuántica, por ejemplo- que resultan completamente ajenos a la experiencia cotidiana de la gente. Es cierto que en la medida en que esos conceptos científicos estén vinculados a la consecución de determinados logros tecnológicos, el público está dispuesto a darlos por buenos. Pero esa distancia implica que para la mayor parte de la gente la ciencia está unida a una terminología esotérica. Y una vez que se dan por buenos conceptos expresados mediante esa terminología, otras ideas que carecen realmente de sentido o de fundamentación científica pueden encontrar una cierta aceptación si se expresan mediante una terminología más sencilla o de similar nivel esotérico, sobre todo si están más cerca de la experiencia cotidiana o de los prejuicios culturales. Por esa razón, el avance científico facilita que la población se adhiera a un nuevo misticismo si va envuelto en una jerga aparentemente científica. De ese modo, la autoridad que la ciencia otorga a sus logros puede acabar al servicio de la doctrinas no científicas si son capaces de apropiarse de su prestigio.
Y por último, un tercer mecanismo susceptible de alimentar actitudes anticientíficas tiene su origen en otro rasgo de la ciencia, el ser un sistema de escepticismo organizado que, en muchas ocasiones, se convierte en iconoclastia. El escepticismo organizado cuestiona de manera latente ciertas bases de la rutina establecida, la autoridad, los procedimientos establecidos y lo sagrado en general. Aunque indagar acerca de la génesis de creencias y valores no significa que se niegue su validez, lo cierto es que es así como se interpreta en muchas ocasiones. De esa forma, la ciencia entra en conflicto psicológico –no necesariamente lógico- con otras actitudes y formas de aprehender la realidad. Ese fenómeno explicaría la oposición a lo que se interpreta como intrusión de la ciencia en otras esferas, ya sean de orden político, económico, religioso o de cualquier otra naturaleza. En otras palabras, el escepticismo es considerado como una amenaza al status quo y frente a esa amenaza se produce una reacción de hostilidad.
Note el lector que prácticamente todos los aspectos de esta cuestión que trató Merton hace ochenta años, están plenamente vigentes en la actualidad, aunque la hostilidad a la ciencia proceda hoy de entornos (quizás) diferentes.
FuenteMerton, Robert K (1938): “Science and the Social Order” Philosophy of Science 5 (3): 321-337. [Traducción al español como “La ciencia y el orden social” en el volumen II de “La Sociología de la Ciencia” Alianza Editorial 1977, traducción de The Sociology of Science – Theoretical and Empirical Investigations, 1973]
Nota:
1Por ejemplo, todas las personas que no cumplían los criterios raciales de ascendencia aria fueron expulsadas de universidades e institutos; fueron muchos los científicos que no los cumplían.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La hostilidad a la ciencia se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ciencia a presión: Ciencia abierta vs. ciencia cerrada
- Curso de verano “La ciencia de nuestras vidas”: Arte, literatura y ciencia, por Gustavo A. Schwartz
- Ciencia de culto
Dozena erdi ariketa 2018ko udarako (3): 11ren multiploa den zenbakia lortu nahian
Gogoan izan ahalegina bera –bidea bilatzea– badela ariketa. Horrez gain tontorra (emaitza) lortzen baduzu, poz handiagoa. Ahalegina egin eta emaitza gurekin partekatzera gonbidatzen zaitugu. Ariketaren emaitza –eta jarraitu duzun ebazpidea, nahi baduzu– idatzi iruzkinen atalean (artikuluaren behealdean daukazu) eta irailean emaitza zuzenaren berri emango dizugu.
Hona hemen gure hirugarren ariketa: 11ren multiploa den bost zifrako zenbakia lortu nahian.
———————————————————————————-
Ariketak Frantziako CNRSren blogeko Défis du Calendrier Mathématique ataletik daude hartuta.
———————————————————————————-
The post Dozena erdi ariketa 2018ko udarako (3): 11ren multiploa den zenbakia lortu nahian appeared first on Zientzia Kaiera.
El nacimiento de la ciencia moderna y la ética protestante

Como señalé en la anotación anterior, fue R K Merton quien introdujo de forma explícita la noción de los valores en la esfera de la ciencia. Antes de formular la teoría de que existe un ethos de la ciencia, que es en relación con la cuál se hace referencia a expresa a un conjunto de valores, Merton (1938) desarrolló una tesis que tuvo en su día una gran influencia en relación con el contexto social, político y, sobre todo, religioso en que se produce la aparición de la ciencia moderna, en Inglaterra durante el siglo XVII. Como se verá, un elemento importante de esa teoría se refiere a la legitimación social que alcanzó la ciencia entonces y que después mantuvo hasta las primeras décadas del siglo XX. Y esa es la razón por la que me parece pertinente hacer aquí una breve incursión en ese terreno. Presento a continuación una síntesis de las ideas desarrolladas por el sociólogo norteamericano.
Durante el siglo XVII la religión era la fuente principal del sistema de valores dominantes. Por ello, se vieron favorecidas aquellas actividades que, por las razones que fuesen, se caracterizaban por unos valores que también eran los de la religión. Ese fue el caso, según Merton (1938), de la ciencia, por lo que las convicciones religiosas de la época contribuyeron a su emergencia o, al menos, constituyeron una suerte de estímulo para ella; dicho de otra forma, fueron las implicaciones psicológicas del sistema puritano de valores las que habrían promovido la adhesión social a la ciencia en la Inglaterra del siglo XVII.
Los sentimientos y creencias puritanas que promovían un trabajo infatigable y una aproximación racional a los problemas fueron factores de éxito económico. Y esa misma relación puede aplicarse a la relación entre el puritanismo y la ciencia, puesto que esos mismos factores son determinantes del éxito de la empresa científica. Probablemente debido a ello también, los protestantes experimentaron un profundo y consistente interés en el progreso de la ciencia.
Por otro lado, el puritanismo había atribuido una utilidad triple a la ciencia. Servía, en primer lugar, para disponer de pruebas prácticas del estado de gracia del científico1. En segundo lugar, la ciencia permitía ampliar el control humano sobre la naturaleza. Y por último, la ciencia se veía como un medio adecuado para glorificar a Dios.
La exaltación de la facultad de la razón en el ethos puritano –por considerar que la racionalidad atenúa las pasiones- condujo inevitablemente a una actitud de simpatía hacia aquellas actividades que demandan la aplicación constante del razonamiento riguroso. Por otra parte, la insistencia puritana en el empirismo, basado en la aproximación experimental, tenía mucho que ver con el rechazo de la contemplación, ya que se identificaba ésta con la ociosidad. Y por lo mismo, también tenía que ver con la relación estrecha que se establecía entre el gasto de energía física y el manejo de objetos materiales, por un lado, y el trabajo por el otro.
Además de lo anterior, hay otro factor que explicaría la relación entre el puritanismo y la ciencia, quizás de la misma importancia que el anterior, aunque más sutil y más difícil de apreciar. En cada época hay un sistema de ciencia que descansa sobre un conjunto de supuestos, normalmente implícitos y muy raramente cuestionados por la mayor parte de los científicos de ese tiempo. El supuesto básico en la ciencia moderna es una convicción muy extendida en la existencia de un Orden de las Cosas y, en particular, un Orden en la Naturaleza, aunque esa creencia, en realidad, es eso, una fe, y en tanto que tal, del todo inmune a la demanda de examen racional.
Paradójicamente, esa fe en la capacidad de la ciencia, muy anterior al desarrollo de la ciencia moderna, es una derivada inconsciente de la teología medieval. Esa condición era un prerrequisito para que surgiera la ciencia moderna, pues sin la creencia en ese Orden de la Naturaleza y lo que es lo mismo, en la existencia de Leyes de la Naturaleza, no hubiera habido un estímulo intelectual suficiente para que los filósofos naturales emprendiesen la tarea científica. Pero siendo necesario el prerrequisito, no era suficiente para provocar su desarrollo. Se necesitaba, además, un interés constante en buscar ese orden de la naturaleza de una forma empírica y racional, esto es, un interés activo en este mundo y sus fenómenos además de una aproximación específicamente empírica al mismo. Con el protestantismo la religión proporcionó ese interés; impuso obligaciones de concentración intensa en la actividad secular con un énfasis en la experiencia y la razón como bases para la acción y la creencia.
FuenteMerton, Robert K (1938): “Motive Forces of the New Science” in Science, Technology and Society in Seventeenth-Century England, pp.: 80-102, 104-110. [Traducción al español: “El estímulo puritano a la ciencia” en el volumen II de “La Sociología de la Ciencia”, Alianza Editorial 1977, traducción de The Sociology of Science – Theoretical and Empirical Investigations, 1973]
Nota:
1Se ve aquí la conexión con el papel que juega la ética del trabajo en el protestantismo, ya que la dedicación al trabajo y el esfuerzo son considerados en el credo de Lutero como manifestaciones del estado de gracia.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El nacimiento de la ciencia moderna y la ética protestante se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La magia y el nacimiento de la ciencia moderna
- La ciencia moderna y la Ilustración
- Platonismo alambicado: el neoplatonismo y la ciencia moderna
La ciencia no tiene valores… ¿o sí los tiene?

A finales de siglo XIX y comienzos del siglo XX los valores no desempeñaban ningún papel en el desarrollo de la ciencia. La noción de ciencia neutra, carente de valores se remonta al siglo XVII, a la creación de la Royal Society londinense. Según el Royalist Compromise, el acuerdo con la corona británica, recogió el compromiso de ésta de permitir a los miembros de la Sociedad investigar en libertad siempre que no se involucrasen en asuntos religiosos, políticos y morales.
Hume, el más importante filósofo empirista, diferenciaba tres tipos de filosofía, Filosofía natural (Ciencia), Filosofía práctica (Ética) y Semiótica (o Lógica), y sostuvo que son completamente diferentes unas de las otras. Para las posiciones empiristas la falacia naturalista sigue siendo un criterio de evaluación filosófica: a partir de aserciones factuales no se pueden implicar aserciones morales. Los científicos pueden conjugar el verbo ser, pero no deben usar la expresión deber ser.
Ya en el siglo XIX, en su Catecismo positivista, Auguste Comte afirmó que la ciencia tiene que ver con los hechos, no con los valores. Max Weber trasladó ese postulado a las ciencias sociales. Según él, también los economistas y los sociólogos deben adoptar una postura neutral cuando investigan. La ciencia ha de buscar la objetividad y por eso ha de describir, comprender y explicar los hechos, pero sin emitir juicios de valor. En la tradición empirista y positivista, esos juicios son subjetivos, por eso caen fuera del discurso científico. En su Tractatus logico-philosophicus (1921), Wittgenstein mantuvo tesis más radicales: «En el mundo todo es como es y sucede como sucede, en él no hay ningún valor, y aunque lo hubiese no tendría ningún valor». Los valores no existen en el mundo objetivo, los aportan los sujetos, sean individuales o colectivos. En su libro Religión y Ciencia, Russell afirmó tajantemente que “cuestiones como los “valores” se encuentran fuera del dominio de la ciencia”, e incluso que “están enteramente fuera del dominio del conocimiento; es decir, cuando afirmamos que esto o aquello tiene “valor”, estamos dando expresión a nuestras propias emociones, no a un hecho que seguiría siendo cierto aunque nuestros sentimientos personales fueran diferentes”. Concluyó que “si es cierto que la ciencia no decide cuestiones de valor, es porque escapan en absoluto a la decisión intelectual y se encuentran fuera del reino de la verdad y la falsedad. Todo conocimiento accesible debe ser alcanzado por métodos científicos, y lo que la ciencia no alcanza a descubrir, la humanidad no logra conocerlo”. Científicos tan prestigiosos como Poincaré, Einstein y otros muchos sostuvieron tesis similares, al igual que los filósofos de la ciencia de la corriente positivista. Y todavía en 1974, Quine recordaba que “la teoría científica se mantiene orgullosa y manifiestamente alejada de juicios de valor”.
Pero tal y como mostró Hilary Putnam (2002), esa dicotomía entre hechos y valores se derrumbó a lo largo del siglo XX. Hay dos causas principales de este giro. Por un lado, la noción de valor ha ampliado su significado. Por otro, la propia ciencia se ha transformado radicalmente, sobre todo a partir de la II Guerra Mundial. La primera gran grieta en el muro conceptual que habían levantado los filósofos empiristas y los propios científicos la abrió Robert K. Merton, a quien se atribuye la condición de fundador de la sociología de la ciencia. Merton, a partir de un análisis histórico del contexto social, político y religioso en que se produjo la llamada “revolución científica”, llegó a la conclusión de que la actividad científica y, más concretamente, su legitimación social, tenía mucho que ver con un conjunto de normas y valores que guían la labor de los científicos y al que denominó “ethos de la ciencia”. Volveremos más adelante sobre este asunto.
Llegados a este punto conviene hacer una petición de principio. Porque en este texto se ha manejado la noción de valores cuando en ningún momento se ha ofrecido una definición de la misma. En efecto, antes de seguir adelante es importante tratar de aclarar la cuestión de qué se entiende por valores y, como veremos, no va a ser tarea fácil. Nos enfrentamos a un término ciertamente elusivo. Es, de hecho, difícil definir qué es un valor, puesto que al respecto hay definiciones muy heterogéneas; y también es difícil clasificar los valores.
Según Echeverría (2002), los valores de la ciencia son considerados como funciones que guían y orientan las acciones científicas. Los valores son utilizados como ideal regulativo de las acciones, incluso como fundamento de la ética; parece que los valores son el motor, y no sólo la guardia o la inspiración, de cualquier empresa (Menéndez Viso, 2002). Pero el mismo Menéndez Viso (2005) señala que no es posible contar con una definición precisa del término, y añade que si los valores han de servir como principio explicativo, han de estar bien definidos, no pueden ser ellos mismos términos confusos. Pero lo son. No está claro si son principios, entidades, cualidades, funciones, o bienes, por ejemplo. En realidad, con un pequeño esfuerzo, el análisis de la literatura permite identificar los siguientes sinónimos de valores: virtudes, bienes, normas, fines, derechos, o dogmas.
Según ese mismo autor (Menéndez Viso, 2005), el término valores se utiliza porque hay ciertas nociones, como la virtud, la verdad, el bien o la belleza, que no resulta cómodo enunciar: hacerlo produce una cierta vergüenza. Y sin embargo, como las nociones en cuestión son básicas y todos nos referimos a ellas en infinidad de contextos, se recurre a un eufemismo que es el de los valores. La proliferación del uso de la noción de los valores se da gracias a un curioso giro semántico del término que, además de a su número, afecta al verbo que lo acompaña. Hasta finales del s. XIX las cosas tenían valor; a partir de entonces, y cada vez más, las cosas son valores.
Comparto la perplejidad que manifiesta Menéndez Viso en relación con este asunto y, como se verá en anotaciones posteriores, no creo que se trate de una perplejidad injustificada. No obstante, y puesto que, con propiedad o sin ella, la noción de los valores tiene amplísimo uso, seguiremos adelante, si bien es importante no perder de vista estas observaciones.
FuentesEcheverría, Javier (1995): El pluralismo axiológico de la ciencia. Isegoria 12: 44-79
Echeverría, Javier (2002): Ciencia y Valores; Barcelona, Ediciones Destino.
Echeverría, Javier (2014): Los valores de las ciencias: Del ideal de neutralidad del siglo XIX a la supremacía actual de la innovación. Investigación y Ciencia nº 452, mayo, pp.: 2-3
Menéndez Viso, Armando (2002): Valores ¿ser o tener? Argumentos de Razón Técnica nº 5: 223-238
Menéndez Viso, Armando (2005): Las ciencias y el origen de los valores Siglo XXI, Madrid
Putnam, Hilary (2002): The Collapse of the Fact/Value Dichotomy and Other Essays. Harvard University Press, Cambridge, Mass. [Traducción al español: El desplome de la dicotomía hecho/ valor y otros ensayos, Paidós Ibérica, Barcelona (2004)]
El artículo La ciencia no tiene valores… ¿o sí los tiene? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- “Filosofía, Ciencia y Valores”, el máster
- El buen turrón tiene su ciencia
- Ciencia y valores en la sociedad del riesgo
Klorhexidinak eraginkortasun mugatua du aho interbentzioetan infekzioak saihesteko

Irudia. Nahiz eta aho interbentzioetan infekzioak saihesteko eraginkortasun mugatua izan, kostu txikia denez eta kontrako erreakziorik eta konplikaziorik ez dakarrenez, klorhexidina irakuzketak erabiltzea gomendatzen dute. (Irudia: John Loo)
Klorhexidinarekin irakuzteak mikrobioen aurkako efektu ahaltsua du, baina aho interbentzioetan erabiltzeko gomendioetan elkarren kontrako iritziak daude. Ikerketak erakutsi du hura erabiltzean % 12 saihestuko liratekeela bakteriemia kasuak.
Gizakiaren aho barrunbean askotariko bakteria daude. Prozedura kirurgikoak egiten direnean, besteak beste, hortzen bat ateratzean, odol zirkulaziora igaro daitezke eta iragankorra izaten den bakteriemia eragin.
Ez dago argi odolean bakterio hauen presentziak zenbait prozesu infekziosoren jatorrian eta bilakaeran duen garrantzia, besteak beste, bihotz balbulen endokarditisaren bilakaeran, balbula protesienean, artikulazioen protesienean (normalean hanka eta belaunekoa), eta infekzio lokalean duen garrantzia.
Hainbat azterlanek erakutsi dute klorhexidinarekin ahoa garbitzeak mikrobioen aurkako efektu ahaltsua duela listu mikrofloran eta plaka bakterianoan.
Hipotesi hori oinarri hartuta, ondorioztatu daiteke aho irakuzketa antimikrobiarrek, hortzen prozedura baten aurretik erabiliz gero, pazientearen odol zirkulazioan sartutako mikroorganismo kopurua murriztu beharko litzatekeela; hala ere, desadostasun handiak daude alderdi horretan.
American Heart Association-ek (AHA), 1997an, iradoki zuen endokarditis infekziosoa duten pazienteek aho irakuzketa antimikrobiarra egin beharko luketela, aho tratamendua egin aurretik. 2006an, Kimioterapia Antimikrobiarraren Sozietate Britainiarrak (BSAC) klorhexidinarekin aho irakuzketa bakarra gomendatu zuen, % 0,2an (CHX) (10 ml 1 minutuz), arriskua duten pazienteetan bakteriemiarekin lotutako hortz prozedurak egin aurretik. Hala ere, 2007an, AHAk gomendatu zuen profilaxi antiseptikoko protokolorik ez erabiltzea.
Ausazko saiakera kontrolatuen berrikuspen sistematikoa eta metaanalisia egin dute, PRISMA Adierazpenari jarraituta. Klorhexidinak hortzen bat atera ondoren bakteriemia prebenitzeko duen eraginkortasuna ebaluatzea izan da helburua.
Azterlanean 8 saiakera kliniko jaso dira, 523 pazienterekin. 267 klorhexidinarekin tratatutako taldean, non bakteriemiako 145 kasu erregistratu diren eta 256 kontrol taldean, non bakteriemiako 156 kasu erregistratu diren.
Ikerketaren emaitzek adierazten dute, beraz, klorhexidinarekin prebentzioa eginez gero saihestu daitekeen bakteriemia kasuen ehunekoa %12koa dela. NNTa, bakteriemia prebenitzeko tratatu beharreko gutxieneko paziente kopurua 16 da.
Eraginkortasun erlatiboa eta esangura gutxikoa erakusten dute emaitzek, klorhexidinaren erabilerari dagokionez, hortzen bat ateratzean ahoan dauden bakteriak odol zirkulazioan sartzeko saihesteko orduan. Hala ere, kostu gutxikoa denez eta kontrako erreakziorik eta konplikaziorik ez dakarrenez, gomendagarria da klorhexidinarekin irakuzketa egitea, horrelako interbentzioren bat egin aurretik.
Iturria: UPV/EHU prentsa bulegoa: Klorhexidinak eraginkortasun mugatua du aho interbentzioetan infekzioak saihesteko.
Erreferentzia bibliografikoa:
Arteagoitia, Iciar, Rodriguez Andrés, Carlos, Ramos, Eva (2018) Does chlorhexidine reduce bacteremia following tooth extraction? A systematic review and meta-analysis. Plos One 13 (4): e0195592. DOI https://doi.org/10.1371/journal.pone.0195592
The post Klorhexidinak eraginkortasun mugatua du aho interbentzioetan infekzioak saihesteko appeared first on Zientzia Kaiera.
Una población mejor formada es una población más sana
La esperanza de vida tiende a ser mayor en los países más ricos -o sea, en los que la gente tiene mayores ingresos- que en los más pobres. Esa correspondencia suele atribuirse a una relación que parece obvia: a más ingresos, mejor alimentación, mejor vivienda, mejor ropa, etc. y, por todo ello, mejor estado de salud.

Sin embargo, hace ya más de cuatro décadas, Samuel Preston se percató de que la relación entre esas variables no era tan sencilla como se pensaba. Aparte de constatar que había bastantes países para los que la esperanza de vida de sus habitantes no se correspondía con el esquema anterior, comprobó que a lo largo del siglo XX la longevidad se había elevado más de lo que cabía esperar del efecto del aumento de la riqueza. Y pensó que no todo dependía del nivel de ingresos. Propuso que habían sido las mejoras en las condiciones sanitarias y los avances médicos no dependientes estrictamente de factores económicos los responsables principales de las mayores esperanzas de vida. Una década después, James Caldwell observó que en regiones pobres (Kerala en la India, Sri Lanka y Costa Rica) la esperanza de vida mejoraba sensiblemente allí donde, además de una mejora en los servicios de salud, las mujeres accedían a la educación.
Teniendo en cuenta esas observaciones y las conclusiones obtenidas en otros estudios, Wolfgang Lutz y Endale Kebede han tratado de identificar el condicionante principal de la salud y la esperanza de vida utilizando para ello datos correspondientes a 174 países de niveles muy dispares de riqueza a lo largo del periodo 1970-2010 en intervalos de cinco años. En su estudio han considerado el efecto que ejercen sobre la esperanza de vida al nacer y la mortalidad infantil dos posibles factores causales: el nivel medio de riqueza de los países (producto interior bruto por persona), y el nivel educativo de la población (años de escolarización de las personas mayores de 15 años de edad, en uno de los análisis, y años de escolarización en las mujeres de edades comprendidas entre 20 y 39 años, en el otro).
La conclusión del análisis estadístico de los datos fue que el nivel educativo explica mucho mejor que el nivel de ingresos el estado de salud de la población. Otra forma de expresar esa conclusión es que el nivel educativo de la gente es un condicionante más importante de la mortalidad infantil y de la esperanza de vida que el nivel de riqueza del país. Los investigadores proponen que el nivel educativo proporciona a las personas mejor criterio a la hora de tomar decisiones que tienen consecuencias en materia de salud, ya sea en relación con la alimentación o con hábitos de vida en general. El efecto del nivel de riqueza no sería real, sino que se trataría, en palabras de los autores, de una relación espuria: la relación observada entre el nivel de ingresos y el estado de salud obedecería a que en los países más ricos la gente suele estar mejor formada.
El estudio no considera la incidencia en la esperanza de vida del esfuerzo que se dedica al sistema de salud. Pero, como ya se ha señalado, cuanto mayor es el nivel de formación de la población mayor es la riqueza del país y, por ello, mayor es también el esfuerzo que se dedica a sanidad. Se constata, una vez más, lo rentable que es el esfuerzo que se dedica a la formación. No solo mejora la vida de las personas bien formadas, también la del conjunto de la población.
—————————————————————–
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
Una versión anterior de este artículo fue publicada en el diario Deia el 20 de mayo de 2018.
El artículo Una población mejor formada es una población más sana se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Salud desigual
- FINGER: estratificar a la población para optimizar el funcionamiento de los servicios sanitarios
- Cuantas menos ecuaciones…. ¿mejor?
Asteon zientzia begi-bistan #215
 Botanika
Botanika Mahats uztan hezetasunak duen eragin kaltegarria irakur daiteke Berrian. Hezetasunak sortu duen mildiu onddoaren eraginez uzta %20-%30 inguru jaits daitekeela espero dute euskal ardogile batzuek. Euria egin eta hurrengo egunean, eguzkia atera eta tenperatura igotzen zen. Onddoa hedatzeko baldintzarik onenak direla horiek azaltzen dute.
BiologiaZenbat zelula daude giza gorputzean? Juan Ignacio Pérez Iglesiasek ematen du erantzuna, nahiz eta erraza ez izan. Kalkuluen arabera, gutxi gorabehera 30 bilioi zelula daude 70 kg-ko eta 170 cm-ko gizon gazte baten gorputzean. Antzeko ezaugarriak dituzten emakumeetan, antzeko kopuruak egon litezke.
——————————————————————–
Asteon zientzia begi-bistan igandeetako atala da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna erreparatuz, Interneteko “zientzia” antzeman, jaso eta laburbiltzea da gure helburua.
———————————————————————–
———————————————————————–
Egileaz: Ziortza Guezuraga (@zguer) kazetaria da eta Euskampus Fundazioko Kultura Zientifikoko eta Berrikuntza Unitateko zabalkunde digitaleko teknikaria.
——————————————————————
The post Asteon zientzia begi-bistan #215 appeared first on Zientzia Kaiera.
Matemáticas a pesar de todo
La profesión matemática, en contra del estreotipo popular, es la profesión más deseada según estudios recientes y, además de los muchos campos en los que puede ejercerse, dedicarse a una de sus facetas, la investigación, pude llegar a ser una pasión que dé sentido a una vida. Ágata Timón (ICMAT) nos presenta dos casos en los que esta pasión supuso poner en riesgo la propia integridad física.
Ágata Timón: ''Matemáticas a pesar de todo''
El número π es una de las constantes matemáticas más importantes que existen. π es un número fascinante que goza de una gran popularidad e, incluso, de un día propio. Desde el año 1988, cada 14 de marzo se celebra el Día de Pi. Este evento fue idea del físico Larry Shaw, quien lanzó la propuesta añadiendo a su favor que la celebración coincidía con la fecha del nacimiento de Albert Einstein. Además, la forma en la que se escribe el 14 de marzo en inglés y euskera coincide con los tres primeros dígitos del número. (3-14 martxoaren 14 en euskara / 3-14 march, 14th en inglés)
En los últimos años la conmemoración del Día de Pi se ha ido extendiendo hasta convertirse hoy en día en una celebración que sobrepasa el ámbito de las matemáticas. π está presente en física, en el principio de incertidumbre de Heisenberg, la teoría de la relatividad o la ley de Coulomb. En geología hace su aparición a la hora de estimar la longitud de los ríos; en bioquímica, en el estudio de la estructura de una molécula de ADN; en astronomía, en el estudio de la forma del universo y en otras muchísimas aplicaciones de nuestro día a día.
Este 2018 nos unimos de manera especial a la celebración del Día de Pi con el evento BCAM-NAUKAS, que se desarrolló el miércoles 14 de marzo en el Bizkaia Aretoa de UPV/EHU. Este evento fue una iniciativa del Basque Center for applied Mathematics (BCAM) y la Cátedra de Cultura Científica de la Universidad el País Vasco.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Matemáticas a pesar de todo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El número de taxis de Bilbao y el espionaje en la 2ª guerra mundial
- π, así en el cielo como en la Tierra
- Diagnóstico de enfermedades: una cuestión de probabilidades
El aprendizaje continuo mejora la interacción de robots con humanos en lenguaje natural
Los sistemas de diálogo son esenciales para que los robots interactúen con las personas en lenguaje natural. Para mejorar estas interacciones con el paso del tiempo, el sistema debe de ser capaz de aprender de sus experiencias, de sus errores y del feedback con la persona usuaria. Este proceso de aprendizaje continuo es la base del proyecto europeo LIHLITH, que lideran los grupos de investigación IXA y RSAIT de la UPV/EHU y financia el programa europeo CHIST-ERA.
La inteligencia artificial es un campo que progresa rápidamente en múltiples áreas, incluyendo los diálogos con máquinas y robots. Ejemplo de ello es que en la actualidad es posible hablar a un dispositivo para solicitarle tareas tan simples como apagar la radio o preguntarle por el tiempo; pero también se ha conseguido que hagan tareas más complejas, como que la máquina llame a un restaurante para hacer una reserva o que un robot atienda a los clientes de una tienda.
El proyecto europeo LIHLITH (Learning to Interact with Humans by Lifelong Interaction with Humans) “es un proyecto orientado a avanzar en los diálogos entre personas y máquinas, cuyo objetivo es mejorar las capacidades de autoaprendizaje de la inteligencia artificial”, explica Eneko Agirre, investigador de la UPV/EHU. Concretamente, en el proyecto LIHLITH se van a tratar sistemas de diálogo que aprenden y mejoran en función de sus interacciones con los humanos. Se trata de un proyecto europeo de tres años, que fue puesto en marcha en enero del 2018, financiado por el programa europeo CHIST-ERA y dirigido por los grupos de investigación IXA y RSAIT de la Facultad de Informática de la UPV/EHU. El proyecto cuenta con la participación de la UPV/EHU, del Laboratorio de Informática para la Mecánica y la Ingeniería (LIMSI, Francia), de la UNED, de la Universidad de Ciencias Aplicadas de Zurich (ZHAW) y de Synapse Développement (Francia).
Los chatbots o los bots conversacionales son programas informáticos que siguen una conversación utilizando métodos textuales o auditivos. Los chatbots industriales actuales se basan en reglas que deben elaborarse de forma manual y minuciosa para cada dominio de aplicación. Por otra parte, los sistemas basados en el aprendizaje automático utilizan datos del dominio anotados manualmente, que permiten entrenar el sistema de diálogo. Tanto para elaborar las reglas como para los datos de entrenamiento de cada dominio de diálogo se necesita mucho tiempo, por lo que limitan la calidad y la difusión de los chatbots. Además, las empresas necesitan monitorizar el rendimiento del sistema de diálogo antes de implementarlo, así como rediseñarlo para que responda a las necesidades de la persona usuaria. “En el proyecto LIHLITH se va a explorar el paradigma del aprendizaje continuo en sistemas de diálogo entre personas y máquinas, con el objetivo de mejorar su calidad, de reducir los costes de mantenimiento y de disminuir los esfuerzos para utilizarlos en nuevos dominios”, añade Agirre, principal investigador del proyecto.
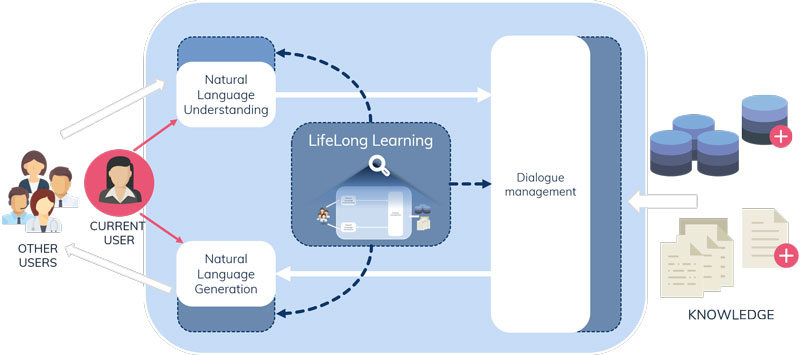
Los sistemas de dialogo estándar utilizan la comprensión de lenguaje natural para procesar la entrada del usuario, la gestión del diálogo para acceder al conocimiento del dominio y decidir qué respuesta va a dar, y la generación del lenguaje natural para emitir la respuesta del sistema. El principal objetivo de los sistemas de aprendizaje continuo es que sigan aprendiendo incluso después de ser implementados. En el caso de LIHLITH, “el sistema de diálogo se desarrollará como de costumbre, pero se incluirá un mecanismo que le permitirá continuar mejorando sus capacidades en función de su interacción con las personas usuarias —apunta Agirre—. La clave es que los diálogos estarán diseñados para recibir el feedback de las personas usuarias, y el sistema aprenderá de este feedback continuo. Esto permitirá al sistema mejorar continuamente a lo largo de su vida, adaptándose rápidamente a los cambios de dominio que ocurren después de ser implementado”.
LIHLITH estará orientado a “diálogos de preguntas y respuestas enfocados a lograr un objetivo, en los que la persona usuaria necesita una información y el sistema intentará satisfacer dicha necesidad mientras conversa con ella”, añade. Para ello, el proyecto trabajará en tres áreas de investigación: el aprendizaje continuo para el diálogo; el aprendizaje continuo para la inducción del conocimiento y la respuesta a preguntas; y la evaluación de la mejora del diálogo. “Todos los módulos serán diseñados para aprender del feedback disponible mediante técnicas de aprendizaje profundo. La clave innovadora del proyecto LIHLITH está en el módulo de aprendizaje continuo, que mejorará todos los módulos a medida que el sistema interactúa con las personas, actualizando el conocimiento del dominio”, comenta. El proyecto explorará la reconfiguración autónoma de estrategias de diálogo y las capacidades proactivas para solicitar a la persona usuaria nuevos conocimientos.
Para llevar a cabo esta investigación, LIHLITH combina el aprendizaje automático, la representación del conocimiento y la experiencia lingüística. El proyecto contará con avances obtenidos recientemente en numerosas disciplinas, incluyendo el procesamiento del lenguaje natural, el aprendizaje profundo, la inducción de conocimiento, el aprendizaje reforzado y la evaluación de diálogo, con los que se explorará su aplicabilidad en el aprendizaje permanente.
Referencia:
Eneko Agirre, Sarah Marchand, Sophie Rosset, Anselmo Peñas, Mark Cieliebak (2018) LIHLITH: Improving Communication Skills of Robots through Lifelong Learning. ERCIM News No. 114, Special theme: Human-Robot Interaction.
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo El aprendizaje continuo mejora la interacción de robots con humanos en lenguaje natural se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La evaluación mejora el aprendizaje
- El aprendizaje del inglés es mejor si se usa para aprender otra cosa
- Estimación del umbral de lactato usando ‘machine learning’
La ciencia que deberías saber antes de comprar tu protector solar (y 4)

Este artículo será, por el momento, el último de la serie. Hemos reunido toda la evidencia científica existente y actual sobre protección solar para que puedas tomar decisiones con criterio. La concienciación con respecto a la protección solar no ha dejado de aumentar. Es el momento de hacerlo bien, además de con conciencia.
A continuación os dejo con las últimas preguntas recibidas que más se han repetido sobre ciencia y protección solar: si la ropa nos protege del sol, si puedo utilizar la crema solar del año pasado o cuál es el orden correcto para utilizar protección solar además de otros cosméticos.
12. ¿Puedo protegerme del sol usando ropa adecuada, gorra, sombrilla, etc?
No todos los tejidos ofrecen la misma protección frente al sol. La radiación ultravioleta puede atravesar el tejido si éste tiene un entramado muy abierto, es fino o esta desgastado. Para medir la capacidad de un tejido para obstaculizar el paso de la radiación ultravioleta usamos el UPF (Ultraviolet Protection Factor). Así, el tejido de un pantalón vaquero oscuro clásico, ofrece el mayor UPF posible, mientras que unas medias de verano, con un denier 15 o menor, serían el tejido que menos protege del sol.
Para certificar cuánto nos protege un tejido del sol, se hacen medidas de absorción de la radiación ultravioleta para cuantificar el UPF. Un tejido con UPF 50+ equivale a una protección del 95% de la radiación UVA y un 98% de la UVB. Es lo más parecido a utilizar un cosmético con protección SPF 50+. A partir de un UPF de 40, la protección que nos ofrece un tejido es muy aceptable.
Esto se consigue gracias al tipo de tejido, cuanto más tupido, mayor UPF. Algunos fabricantes incorporan materiales cerámicos entretejidos que aumentan el UPF, similares a los filtros físicos que se utilizan en cosmética. Los tintes también influyen; para un mismo tejido, presenta mayor UPF un color oscuro que uno claro. Los tejidos de poliéster, como los que se utilizan en las prendas deportivas técnicas, pueden llegar hasta UPF de 30. Mientras que los tejidos más calados, como el algodón o el lino, presentan un UPF de 12 o menor. Así que cuidado con usar ropa para protegernos, si no está debidamente certificada, casi ninguna prenda de ropa ofrece tanta seguridad frente al sol como un cosmético.
Una camiseta clásica de algodón tiene un UPF bajo, de 12. Si además está mojada, el UPF baja a 8, comparativamente sería como llevar puesta una crema solar de tan solo SPF 15. Esto es así porque el agua que entra a formar parte del entramado del tejido puede reducir el efecto de dispersión y aumentar la permeabilidad de la radiación. Además, los lavados, el uso y el sudor las desgastan, dañando su capacidad fotoprotectora, por lo que se recomienda renovar la prenda cada año.
Como todo suma, lo mejor que podemos hacer es combinar: además de fotoevitación, usar fotoprotección. Si no podemos evitar estar expuestos al sol, lo ideal es que además de cosméticos con protección solar usemos ropa adecuada, gorras, sombreros y gafas de sol con la certificación de protección frente a la radiación ultravioleta. La American Academy of Ophthalmology (AAO) recomienda aquellas que bloqueen el 99% de la radiación UVA y B. La protección se relaciona con el color o la oscuridad de las lentes.
Otro método de fotoevitación es el uso de sombrillas o iglús. La mayoría se fabrican con poliéster tupido que ofrece un UPF de 30 o superior. No obstante, hay que tener en cuenta que la radiación ultravioleta se refleja: el césped refleja el 5% de la radiación, el agua un 10%, la arena, un 25% y la nieve un 80%.
La principal ventaja del uso de ropa para protegernos del sol es que la protección no se gasta. Los filtros de las cremas se agotan, y el producto se pierde por sudoración, roce y el baño. Esto no ocurre con la ropa. A excepción de la ropa mojada, ya que el UPF baja considerablemente.
Hay que tener en cuenta que la regulación del UPF varía de un país a otro y no en todas partes se mide de acuerdo con un mismo protocolo. Así como en cosmética el método empleado más extendido para verificar el SPF es el COLIPA, en el caso del UPF se utiliza Test Method 183 tanto en Australia como en EEUU. Por este motivo es muy importante adquirir prendas con UPF certificado de marcas y tiendas de confianza.
13. ¿Puedo usar el protector solar del año pasado?
No, no podemos usar el protector solar del año pasado. Todos los productos cosméticos cuentan o bien con una fecha de caducidad o bien con un PAO. La fecha de caducidad funciona de forma similar a los alimentos. Una vez pasada la fecha de caducidad no podemos garantizar que el producto sea seguro ni efectivo.
EL PAO es el periodo tras la apertura. Lo vemos en el envase con un pictograma que es como un bote abierto en el que dentro hay inscrito un número seguido de la letra M. Normalmente las cremas solares son 12M. Las brumas suelen tener fecha de caducidad, pero no PAO, ya que no hay mucha variación entre el producto usado y sin usar, porque no entra en contacto con el aire ni el consumidor lo puede contaminar por el uso.
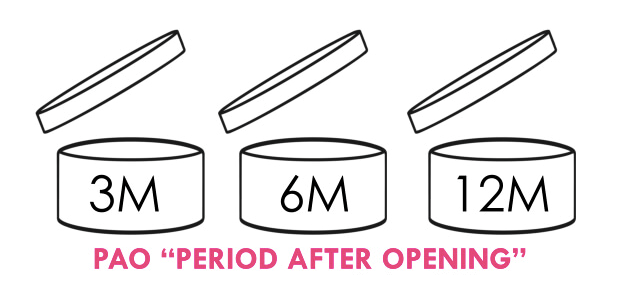
El PAO se mide, es decir, no es un valor arbitrario que los laboratorios fijan para que cada año o cada seis meses renueves tu crema. Para medir el PAO se evalúa la evolución del producto, cómo le afecta el uso, el contacto con el consumidor, cómo se degradan los filtros con el tiempo, con variaciones de temperatura, etc. Y se hace una medida conservadora del tiempo máximo que pueden garantizar que el producto mantiene las propiedades originales. Hay que tener en cuenta que estos productos son muy ricos en agua y nutrientes, un caldo de cultivo ideal para que proliferen todo tipo de microorganismos. Además, los filtros químicos tienen un tiempo de vida estimado. No se mantienen intactos. Por otro lado, muchos de estos productos son emulsiones, y con el paso del tiempo y las variaciones de temperatura terminan por separarse en fases, perdiendo completamente su efectividad y convirtiéndolos en productos insalubres.
Con un tema tan sensible como la protección solar, no seas cutre y recicla tus productos al menos cada año.
14. ¿En qué orden aplico la crema hidratante, la protección solar, el maquillaje, etc?
Hay cremas de uso diario como hidratantes o productos con tratamiento para el acné, la rosácea, antiedad, etc., que cuentan con factor de protección solar. Para los días normales puede ser más que suficiente, y además están formulados para que ningún ingrediente anule a ningún principio activo. Sin embargo, en situaciones de alta exposición solar, como estar en la playa, la piscina o haciendo deporte bajo el sol, estos productos pueden resultar insuficientes. Por eso es importante utilizar protección solar con un SPF adecuado.

La protección solar no tiene por qué impedirnos utilizar otros productos conjuntamente que también son necesarios para la salud de nuestra piel. En el caso de tener que usar varios productos a la vez, el orden adecuado sería el siguiente:
– El primer producto será el que cumpla la función que más nos interese: específico para el acné, las manchas, la rosácea, las arrugas, etc. Si tiene versión sérum, mejor. Los cosméticos tipo sérum son lo que se aplicarán en primer lugar porque presentan mayor concentración de principios activos de interés y mayor capacidad de absorción.
-A continuación se aplican los productos que cumplan una función que para nosotros sea menos relevante. Por ejemplo, si tienes un problema de acné, primero utilizarás el producto para el acné, y encima la hidratante o la antiedad de día. Si tu preocupación son las manchas, primero aplicarás el despigmentante o inhibidor de melanina, y encima el resto de los productos. El contorno de ojos también se pone en este punto.
-Tras aplicar los productos de rutina, encima es donde aplicamos la protección solar.
-Si usamos maquillaje, éste se aplicará encima de la protección solar.
Si queremos reaplicar protección solar por encima del maquillaje a lo largo del día, y no podemos repetir todo el proceso, optaremos por productos tipo bruma. Como tienen formato aerosol, se rocían sobre la piel, sin necesidad de extenderlos con la mano. Matifican la piel y no arruinan el maquillaje, incluso si llevamos sombras de ojos, delineador, colorete o máscara de pestañas.
A modo de cierre
Éste ha sido el último artículo de la serie sobre protección solar. Posiblemente ha sido la serie más extensa publicada sobre toda la evidencia científica que conocemos hasta la fecha sobre protección solar. Si todavía ha quedado alguna duda por resolver, échale un ojo a los otros artículos por si ya se ha resuelto con anterioridad. Si la duda persiste, puedes hacérnosla llegar a través de los comentarios o usando la etiqueta #cienciaprotectorsolar en las redes sociales y te contestaremos. Si alguna duda de envergadura se pudiese haber quedado en el tintero, no descartamos seguir aumentando la serie en el futuro con nuevos contenidos y nuevas evidencias.
Según Academia Española de Dermatología y Venereología (AEDV), cada año se diagnostican en España 4.000 casos más de melanoma, el más grave y letal de todos los tipos de cáncer de piel. En el último año se produjeron 600 muertes asociadas a un cáncer cutáneo. No hagas el tonto y protégete. Protégete bien.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo La ciencia que deberías saber antes de comprar tu protector solar (y 4) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La ciencia que deberías saber antes de comprar tu protector solar (2)
- La ciencia que deberías saber antes de comprar tu protector solar (1)
- Saber y saber que se sabe
Zenbat zelula ote daude giza gorputzean?
Irudia: Orotara, gizakiok 200 zelula tipo baino gehiago ditugu. (Ilustrazioa: Gerd Altmann / Creative Commons lizentziapean)
Globulu gorriak dira argi eta garbi zelula ugarienak. Gutxi gora behera 26 bilioi daude gizonezkoetan eta balio horretatik behera daude andrazkoen kopuruak. Zelula guztien %84a dira. Plaketak ez dira hainbeste, baina ugariak dira edonola: %4.9a. Kontuan hartzen badugu leukozitoak ere badaudela, berehala jakin daiteke gorputzeko zelulen %90a direla odoleko zelulak. Azpimarratzekoa da plaketak nukleogabeak direla, eta beraz gorputzeko zelulen %90a (26 milioi) nukleogabea da.
Hezur-muinekoak ere garrantzitsuak dira kopuruari dagokionez: histologia-metodoak erabilita, ondorioztatu da 750.000 milioi zelula daudela muinean (%2.5). Oso ugariak dira era berean endotelio baskularreko zelulak, odol-zainak barrutik estaltzen dituztenak. Ez da erraza bere kopurua finkatzen, baina saio bat egin dute odolaren osoko bolumenetik abiatuta. Arteria, bena eta kapilarretatik dabil odola, eta tutu mota horietako bakoitzaren luzera finkatu dute bere lodiera ertainean oinarrituta. Ondoren, tutu horien barne azalera zehaztu dute, gero zenbaki hori endotelio-zelulen azalera ertainaz zatikatzeko. Horrela, badakigu 600.000 miloi direla (%2.1).
Immunitate-sistemako linfozitoak, gorputzeko zelulen %1.5a dira eta gibeleko hepatozitoak, %0.8a. Neuronak eta Glia zelulak nerbio-sisteman; azken horiek neuronen euskarri modura jokatzen dute neuronentzat. Garai batean pentsatu izan zen 10 aldiz Glia zelula gehiago zeudela, baina badirudi ez daudela hainbeste eta parean daudela Glia zelulak eta neuronak. Azken estimazioek diote gutxi gorabehera 85.000 milioi neurona daudela eta beste hainbeste Glia zelula. Guztira, gorputz osoaren %6 dira. Gainerako zelula motak are ehuneko txikiagoetan daude giza gorputzean.
Oso ikuspegi desberdina lor daiteke, baldin eta masa hartzen badugu kontuan, kopurua hartu beharrean. Gorputz-pisuaren %25a dira zelulaz kanpoko likidoak (odol-plasma eta likido interstiziala), eta %7a dira zelulaz kanpoko solidoak. Beraz, 46 kg zelula-masa dute, honela bananduta: 20 kg muskulu-zelula, 14 kg adipozito (gantz-deposituak), eta 3 kg globulu gorri. Gainerakoa 10 kg dira. Horrela bada, masen ehunekoak oso desberdinak dira, zeren eta zelula batzuek eta besteek oso bolumen desberdinak baitituzte.
Zer esanik ez, bakterioak ere baditugu batez ere kolonean, baina uste baino askoz ere gutxiago: gutxi gorabehera 38 bilioi, baina 200 g-ko pisua dute.
Erreferentzia bibliografikoa:
Sender R, Fuchs S, Milo R (2016). Revised Estimates for the Number of Human and Bacteria Cells in the Body. PLOS Biology, 14(8), e1002533. DOI: https://doi.org/10.1371/journal.pbio.1002533
Oharra: Nacho López Goñi mikrobiologoak bakterio kopuruari buruzko artikulu argigarri bat idatzi zuen.
Post scriptum: Zelula moten enbrioi-iturriari buruz gehiago jakiteko “Los tipos celulares humanos y origen embrionario” artikulua ikus daiteke eta berriztatze-frekuentziari buruz ¿Cada cuánto tiempo se renuevan las células de nuestro cuerpo? artikulua.
———————————————————————————-
Egileaz: Juan Ignacio Pérez Iglesias (@Uhandrea) UPV/EHUko Fisiologiako katedraduna da eta Kultura Zientifikoko Katedraren arduraduna.
———————————————————————————
—————————————————–
Hizkuntza-begiralea: Juan Carlos Odriozola
——————————————–
Oharra: Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2018ko otsailaren 25ean: ¿Cuántas células hay en el cuerpo humano?
The post Zenbat zelula ote daude giza gorputzean? appeared first on Zientzia Kaiera.
Los números poéticos (y 3)
Cuando esta mañana me he decidido a escribir una tercera entrega de esta serie de entradas del Cuaderno de Cultura Científica, Los números poéticos, sobre poemas con contenido o referencias matemáticas, tenía dos ideas en la cabeza. La primera era empezar esta entrada con la poeta estadounidense Emily Dickinson (1830-1886), de la que confieso que no había leído nada hasta hace poco tiempo, pero que es uno de los nombres claves de la historia de la poesía y de la literatura universal. La segunda era terminar con uno de los grandes poetas vascos, Gabriel Celaya (1911-1991), del cual sí había leído bastantes poemas, algunos de ellos relacionados con las matemáticas.

Fotografía de Emily Dickinson en la Academia Amherts, entre 1846 y 1847. Fuente: Wikimedia Commons
Si buscamos en cualquiera de las biografías publicadas sobre la escritora estadounidense Emily Dickinson, que son muchas, alguna relación de ella con las matemáticas, lo primero que llama la atención es que estudió durante 7 años, entre 1840 y 1847, en la Academia Amherst, de Massachusetts. La amplia educación que recibió en dicha institución incluía, en particular, una buena formación en matemáticas. Entre los textos que se utilizaban en las clases se mencionan la edición de John Playfair (1748-1819) de Los Elementos de Euclides, La introducción al álgebra de Jeremiah Day y “la Aritmética de Adam”, pero también textos de astronomía y lógica.
Por otra parte, su cuñada fue la escritora y poeta Susan H. Gilbert Dickinson (1830-1913), buena amiga desde la adolescencia y con quien mantuvo una importante relación epistolar. Susan Gilbert fue “matemática y profesora de matemáticas en Baltimore en 1851-52”. Y se encuentran referencias a las matemáticas en algunas de sus cartas, como en una de Emily a Susan de 1851 que dice “Te imagino muchas veces bajando al aula con un rollizo Teorema Binomial luchando en tus manos”.
Quizás las matemáticas no fueran la materia que más interesaba a la escritora, o incluso no se le dieran muy bien, pero lo cierto es que sí parece que a lo largo de su vida las matemáticas sí provocaron cierto interés y fascinación en ella, que motivaron la utilización de algunos términos e ideas matemáticas en sus poemas.
Empecemos con una sencilla aritmética de la mano de Dickinson, la negación de la más simple evidencia matemática, que uno más uno es dos. El poema clasificado con el número 769 según la clasificación de Thomas H. Johnson, en su obra The Complete Poems of Emily Dickinson (1960), y que aparece, por ejemplo, publicado en castellano en el libro Emily Dickinson. Poemas a la muerte (Selección, traducción y prólogo de Rubén Martín. Bartleby, Madrid, 2010), dice así:
Uno más Uno — es Uno —
El Dos — es una fórmula gastada —
Buena para enseñarla en las Escuelas —
pero Inferior como Elección —
La propia – Vida — o la Muerte —
o más aún la Eternidad —
serían — demasiado vastas
para que las comprenda nuestro Espíritu —
Otro de los conceptos matemáticos que utiliza en su poesía es el álgebra. Por ejemplo, en el poema 600 (de 1862), que podemos leer en el libro Emily Dickinson. Poemas (Selección y traducción de Silvina Ocampo y prólogo de J.L. Borges. Tusquets editores, Barcelona, 1985), y que dice así…
Antes me perturbaba —
pues yo fui una vez una niña —
conjeturar cómo un átomo — caía —
y sin embargo los cielos — no —
los cielos pesaban mucho más —
azules — y sólidos — permanecían —
sin un perno — que yo pudiera comprobar —
¿podrían los gigantes — comprender?
La vida presentó más grandes — problemas —
algunos guardaré — para resolver
hasta que el álgebra sea más fácil —
o más simplemente probado — arriba —
y luego también — ser comprendida —
qué dolor — me confundía —
por qué el cielo no se rompía —
y caía — azul — sobre mí —
El término “álgebra” también aparece en el poema 269 (que se recoge también en el libro Emily Dickinson. Poemas), escrito en 1861, y que incluye los versos “Tantas — gotas — de vital escarlata — / lidian con el alma/ lo mismo con el álgebra!”. Otro término matemático que aparece en algunos poemas es “logaritmo”, como en el poema 433 (también en el poemario anterior), que dice así “aunque yo fui a la escuela/ no me volví muy sabia/ nada me enseñó el globo/ tampoco el logaritmo”. O en el poema 728 que podría traducirse como algo así “Saciando mi hambre/ con mi diccionario/ el logaritmo –lo tenía yo- para la sed/ como un vino muy seco”.
En tres poemas menciona a las matemáticas. En el poema 1668, que podemos encontrar traducido en el libro Emily Dickinson. Poemas (Edición bilingüe de Margarita Ardanaz, Cátedra, 1987), se incluyen los versos “sé que es un signo/ de que el nuevo dilema esté/ más alejado de las matemáticas/ que de la eternidad”. En otro poema, el 88, se habla de “matemáticas quebradas”. En opinión de Thomas Johnson la poeta puede referirse a las matemáticas como “un sistema ‘quebrado’ en su incapacidad para demostrar sus [de Emily Dickinson] especulaciones”. La profesora de literatura de la Universidad de Harvard, Seo-Young Chu, en su artículo Dickinson and Mathematics, relaciona la expresión “matemáticas quebradas” con las fracciones.
Otros términos matemáticos aparecen en los poemas de Dickinson, “infinito”, “cifra”, “decimales”, … o “geometría”, como en el poema 359, que está recogido en el libro Emily Dickinson. Crónica de Plata (Selección y traducción de Manuel Villar Raso, Hiperión, 2001), que dice así…
La mejor brujería es Geometría
Para la muerte del mago —
Sus actos corrientes son proezas
Para el pensar humano.
Pero el concepto matemático que más menciona Emily Dickinson en su poesía es la “circunferencia”. En una carta al escritor y pastor de la Iglesia Unitaria Thomas Wentworth Higginson (1823-1911) le llega a escribir que “mi asunto [business] es la circunferencia”. Finalicemos con uno de esos “poemas de circunferencias”, el poema 802, que aparece en la selección de Margarita Ardanaz para Cátedra.
Da sensación de ser vasto el Tiempo, que si no fuera
Por una eternidad —
Temo que esta Circunferencia
Mi Finitud absorba —
De Su exclusión, quien se prepare
Por los Procesos del Tamaño
Para la Gran Visión
De Sus Diámetros —
En este poema, Emily Dickinson establece un cierto paralelismo entre la relación que existe entre la temporalidad “finitud” y la eternidad, y la relación de la circunferencia con “sus diámetros”. Esta relación, el cociente entre la circunferencia y el diámetro de la misma, es el importante número π, independientemente del tamaño de la circunferencia, “por los Procesos del Tamaño”.
Estos poemas relacionados con la circunferencia me han recordado dos poemas de la poeta extremeña Ada Salas (Cáceres, 1965), relacionados con el círculo y la esfera. El primero de ellos pertenece a su libro Lugar de la derrota (Hiperión, 2003), y describe la perfección del círculo, de su simétrica construcción.
Exactitud del círculo.
Perfecta equidistancia
en torno a un centro.
Aguja del compás que se desliza
y traza
la forma inexorable de la espera.

Fotografía de la poeta Ada Salas con motivo de su presencia en el Pabellón Madrid de la Feria Internacional del Libro de Guadalajara
Por otra parte, en su libro Arte y memoria del inocente (Universidad de Extremadura, 1988), que obtuvo el Premio Juan Manuel Rozas, aparece este bello poema: “Vivir/ para limar los ángulos/ a las esferas”.
Y seguimos un poco más con poemas geométricos. El siguiente poema es de otra de las grandes poetas en lengua española, la poeta modernista argentina Alfonsina Storni (1892-1938). Es el poema Cuadrados y ángulos, perteneciente a su libro El dulce daño (1918), pero que yo he leído en el libro Alfonsina Storni. Antología mayor (Hiperion, 2005).
Casas enfiladas, casas enfiladas,
casas enfiladas.
Cuadrados, cuadrados, cuadrados.
Casas enfiladas.
Las gentes ya tienen el alma cuadrada,
ideas en fila
y ángulo en la espalda.
Yo misma he vertido ayer una lágrima,
Dios mío, cuadrada.

Alfonsina Storni caminando por la rambla de Mar del Plata, en 1936, imagen del Archivo General de la Nación Argentina. Y retrato de la poeta, más o menos de la misma época. Fuente: Wikimedia Commons
De una poeta modernista argentina pasamos a una poeta modernista estadounidense, Marianne Moore (1887-1972), que entre otras distinciones recibió el Premio Pulitzer de Poesía en 1952. El siguiente poema La icosaesfera está recogido en el libro Marianne Moore. Poesía completa (Lumen, 2010).
“En los setos vivos de Buckinghamshire
los pájaros anidan en la verde espesura sumergida,
tejen trocitos de cuerda, polilla, plumas y vilanos,
en parabólicas curvas concéntricas” y,
buscando la concavidad, dejan proezas esféricas de rara eficacia;]
mientras que, por falta de integración,
ávidos de la fortuna ajena,
tres fueron asesinados y diez cometieron perjurio,
seis murieron, dos se suicidaron y dos pagaron multas por los riesgos que corrieron.]
Pero entonces aparece la icosaesfera
donde por fin se consigue cortar acero con mínimo desperdicio,]
ya que veinte triángulos unidos envuelven una
pelota o una doble concha esférica
sin apenas recortes, tal es la limpieza geométrica
de un icosaedro. ¿Quieren explicarnos los ingenieros que la construyeron,]
o Mr. J. O. Jackson
cómo pudieron los egipcios levantar verticalmente setenta y ocho pies cúbicos de granito?]
Nos gustaría saber cómo lo hicieron.

Portada del libro “Marianne Moore. Poesía completa” (Lumen, 2010)
Una poeta que también cuenta con algunos poemas relacionados, de alguna forma, con las matemáticas, es la poeta y filósofa española Chantal Maillard (Bruselas, 1951), quien, entre otros galardones, ha recibido el Premio Nacional de Poesía, en 2004, por la obra Matar a Platón. Con la intención de cambiar de tema, de volver a los números poéticos que han dado lugar a esta pequeña serie de entradas del cuaderno de Cultura Científica, he elegido un poema de Chantal Maillard, perteneciente al libro La herida en la lengua (Tusquets, 2015), que nos habla de la desconexión entre el número matemático, el número en abstracto, y su significado al contabilizar objetos, como puedan ser las victimas de una guerra o las casas destruidas en la misma.
Diez millones.
Un número.
Un número tan sólo
para diez
millones
de casas incendiadas
de cuerpos mutilados
de gritos
silenciados
uno
a
uno
en boca que arde y
no entiende.
1
0
0
0
0
0
0
0
siete
veces
el signo de la nada sobre
diez
millones
de historias
que nunca contará
la lengua de los otros.
Dos palabras.
Cuatro sílabas.
Un globo que soltamos
Al final de la fiesta.
La piñata que espera
el golpe de una mano
nunca
inocente.

Escenificación poético musical de Matar a Platón, con la interpretación de su autora, Chantal Maillard, y la música de Chefa Alonso (saxo soprano, percusión, kechapi) y Jorge Frías (contrabajo), en Cosmopoética (Córdoba, España), 2016. Fotografía de la página de facebook de Chantal Maillard
Antes de terminar esta entrada con algunos poemas del poeta guipuzcoano Gabriel Celaya, me ha parecido interesante incluir el poema Aritmética (traducción libre que yo mismo he realizado), del escritor y poeta estadounidense Carl Sandburg (1878-1967), quien ganó tres premios Pulitzer, uno por su biografía de Abraham Lincoln y dos por su obra poética.
La aritmética es donde los números vuelan como palomas dentro y fuera de tu cabeza.
La aritmética te dice cuánto pierdes o ganas si sabes cuánto tenías antes de perder o ganar.
La aritmética es nueve cinco llueve con ahínco – o siete ocho chocolate en el bizcocho.
La aritmética es exprimir números de tu cabeza a tu mano, a tu lápiz, a tu papel hasta encontrar la respuesta.
La aritmética es donde la respuesta es correcta y todo es agradable y puedes mirar por la ventana y ver el cielo azul – o la respuesta es incorrecta y tienes que empezar todo de nuevo y volver a intentarlo y ver cómo sale bien esta vez.
Si tomas un número y lo duplicas y lo duplicas de nuevo y entonces lo duplicas unas pocas veces más, el número se hace cada vez más grande y es cada vez más elevado y sólo la aritmética puede decirte qué número se obtiene cuando decides parar de duplicar.
La aritmética es donde tienes que multiplicar – y llevas la tabla de multiplicar en la cabeza y esperemos que no la pierdas.
Si tienes dos galletas de animales, una buena y una mala, y te comes una y una cebra toda llena de rayas se come la otra, ¿cuántas galletas de animales tendrás si alguien te ofrece cinco seis siete y tú dices No no no y tú dices nes nes nes y tú dices neis neis neis?
Si le pides a tu madre un huevo frito para el desayuno y ella te da dos huevos fritos y tú te comes ambos, ¿quién es mejor en aritmética, tú o tu madre?

Fotografía del escritor Carl Sandburg en 1955. Fuente: World Telegram / Al Ravenna
Como ya habíamos anunciado, vamos a terminar con Gabriel Celaya, uno de los representantes de la conocida como poesía social, fundador de la colección de poesía Norte, junto a la poeta Amparo Gastón (su Amparitxu), y Premio Nacional de Poesía en 1986. Si se realiza un repaso sobre el conjunto de su obra, por ejemplo, a través de los tres tomos de Gabriel Celaya. Poesías Completas (Visor, 2001), se observa un profundo interés por los temas científicos, no en vano Gabriel Celaya estudió Ingeniería Industrial. Por ejemplo, la física de partículas es el tema central del poemario Lírica de cámara (1969) o utiliza las funciones matemáticas como metáfora en su libro Función de Uno, Equis, Ene (1973), donde “Uno” es el individuo, “Ene” es el colectivo y “Equis”el universo que se rige por leyes no humanas. En estos libros Gabriel Celaya transmite su idea de que el mundo, el universo, funciona con leyes que nada tienen que ver con la subjetividad humana, con el individualismo, son leyes universales, más allá del “hombre”.
Además, en su libro Exploración de la poesía (Seix Barral, 1964) el poeta de Hernani compara la poesía con las matemáticas, “el poeta se parece al matemático, que ha creado una notación peculiar y ha derivado de ésta un idioma propio” y también, “el poeta da palabras combinadas, como el matemático, ecuaciones, que ni uno ni otro pueden explicar o decir mejor que con esas mismas palabras o ecuaciones”.

Fotografía de Gabriel Celaya, cuyo nombre completo era Rafael Gabriel Juan Múgica Celaya Leceta
La poesía de este poeta comprometido está plagada de referencias matemáticas. Los números y operaciones aritméticas son frecuentes, como en uno de sus poemas de la época inicial en la que firmaba como Rafael Múgica, que dice así “Debajo del pino verde me niego a multiplicar. Y a sumar”, en el poema Apus o el ave del paraíso, de Objetos poéticos (1948), escribe “Verá que dos y dos/ en vez de sumarse,/ se abrazan (se matan)/ o cambian sus nombres”, en el poema La Rosa, de Movimientos elementales (1947), escribe de “un torrente loco de cifras arbitrarias: mil millones, cien ceros”, en Telegrama urgente, de Avisos de Juan de Leceta (1961), nombre con el que también firmó algunos de sus poemas, puede leerse “Las máquinas tiritan/ dando diente con diente, seca cifra con cifra./ Nueve, diez, mil millones/ de ceros con ombligo y con sombrero”, en El amor multiplicado, de Lo que faltaba (1967), la suma y la multiplicación están presentes en todo el poema, que empieza con la estrofa “Yo pregunté: «¿Dos y dos? »/ Me explicaron: «No son cuatro./ Es decir, en cierto modo,/ porque bien considerado…»”, que sigue con “Insistí: «¿Dos y dos, cuatro?»/ Respondieron «¿Dice seis?»/ –«Yo decía lo que digo»./ –«Podemos seguir sumando».”, y sigue con tres estrofas más hasta la última “–«Digo dos»./ –«Yo digo Dios»./ Dos por Dios, ¡qué confusión!/ Este amor, de aguante usted,/ es la multiplicación.”, en su poema Biografía, de La higa de Arbigorriya (1975), que está escrito en forma de normas que nos imponen a lo largo de la vida, en la estrofa de su etapa escolar escribe “Extraiga la raíz cuadrada de tres mil trescientos trece” o en el poema Total, cero, de Buenos días, Buenas noches (1978), menciona el número pi, “Y pensar/ que uno va, y luego se enfada/ con su chica por diez, doce,/ tres coma catorce dieciséis minutos de retraso/ a la hora de la cita”, por citar algunos ejemplos.
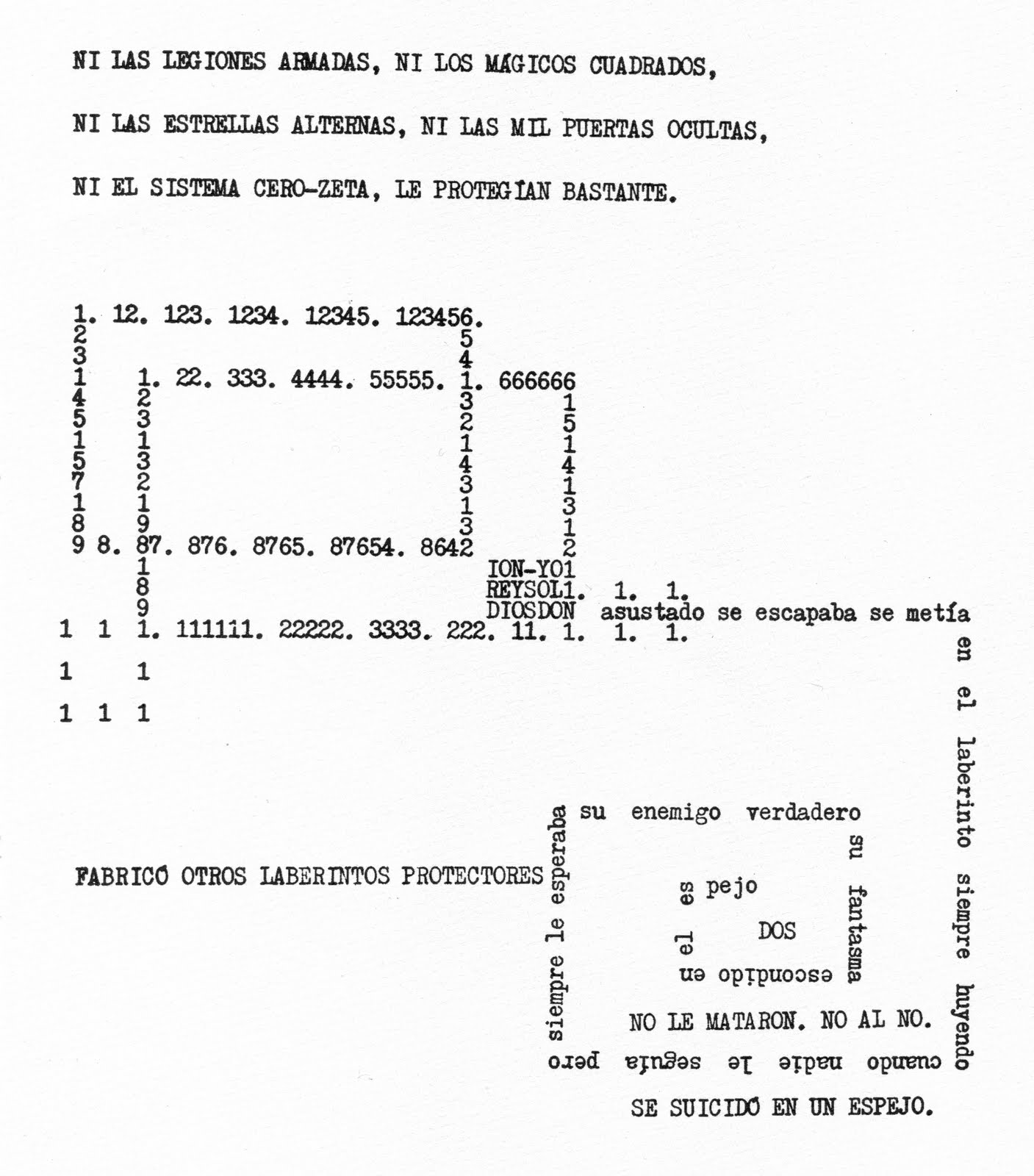
Poema visual “La muerte de Hoang-Ti”, del poemario “Campos Semánticos” (1971)
Aunque quizás el poema más conocido en este sentido sea el que vamos a mostrar a continuación, titulado Tablas de Multiplicar, perteneciente al poemario Ciento volando (1953), en el cual también se incluye el poema La máquina de calcular.
UNO por otro es el hombre
cualquiera como Dios manda
y ese salvar las distancias
que –mala cuenta– se cantan.
Dos por uno es la evidencia
que en un dos por tres tendrás.
Dos por cuatro, buen compás.
Dos por cinco, la sorpresa
del diez redondo y total.
¡Qué divino es, por humano,
el sistema decimal!
Cero por cero es la luz.
Cero por uno, el problema
(pues con el yo creo el tú).
Cero por dos, el amor.
También cero, mas en ¡oh!
(¡Oh!, que es un eco de yo).
Cero por tres… ¡Atención!
Debe haber algún error,
pues cuanto más multiplico
más repito: yo, yo, yo.
En varios poemas se alude a la “matemática Urania”. Recordemos que Urania era la musa de la astronomía, y también se la suele considerar la musa de las matemáticas.

Dibujos de Gabriel Celaya, “Autorretrato” y “Peces”
También nos encontramos con algunos conceptos geométricos en los poemas de Gabriel Celaya, y como ejemplo su poema Así se escribe la ciencia (Homenaje a Kepler), de su poemario Espejos Transparentes (1968).
KEPLER miró llorando los cinco poliedros
encajados uno en otro, sistemáticos, perfectos,
en orden musical hasta la gran esfera.
Amó al dodecaedro, lloró al icosaedro
por sus inconsecuencias y sus complicaciones
adorables y raras, pero, ¡ay!, tan necesarias,
pues no cabe idear más sólidos perfectos
que los cinco sabidos, cuando hay tres dimensiones.
Pensó, mirando el cielo matemático, lejos,
que quizá le faltara una lágrima al miedo.
La lloró cristalina: depositó el silencio,
y aquel metapoliedro, geometría del sueño,
no pensable y a un tiempo normalmente correcto,
restableció sin ruido la paz del gran sistema.
No cabía, es sabido, según lo que decían,
más orden que el dictado. Mas él soñó: pensaba.
Eran más que razones: las razones ardían.
Estaba equivocado, mas los astros giraban.
Su sistema era sólo, según lo presentido,
el orden no pensado de un mundo enloquecido,
y él buscaba el defecto del bello teorema.
Lo claro coincidía de hecho con el espanto
y en la nada, la nada le besaba a lo exacto.
Y para terminar desearos… ¡¡Mucha matemática y poesía!!
Bibliografía
1.- Raúl Ibáñez, Los números poéticos, Cuaderno de Cultura Científica, 2018.
2.- Raúl Ibáñez, Los números poéticos (2), Cuaderno de Cultura Científica, 2018.
3.- Cynthia Griffin Wolff, Emily Dickinson, Knopf, 1986.
4.- Seo-Young Jennie Chu, Dickinson and Mathematics, The Emily Dickinson Journal, Volume 15, Number 1, p. 35-55, 2006.
5.- Lista de poemas (en inglés) de Emily Dickinson en Wikipedia
6.- Blog de poemas de Emily Dickinson
7.- Página web de Chantal Maillard
8.- Página web sobre Gabriel Celaya, de la Diputación Foral de Gipuzkoa
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Los números poéticos (y 3) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Dozena erdi ariketa 2018ko udarako (2): Osatu karratua
Gogoan izan ahalegina bera –bidea bilatzea– badela ariketa. Horrez gain tontorra (emaitza) lortzen baduzu, poz handiagoa. Ahalegina egin eta emaitza gurekin partekatzera gonbidatzen zaitugu. Ariketaren emaitza –eta jarraitu duzun ebazpidea, nahi baduzu– idatzi iruzkinen atalean (artikuluaren behealdean daukazu) eta irailean emaitza zuzenaren berri emango dizugu.
Hona hemen gure bigarren ariketa: Osatu karratua.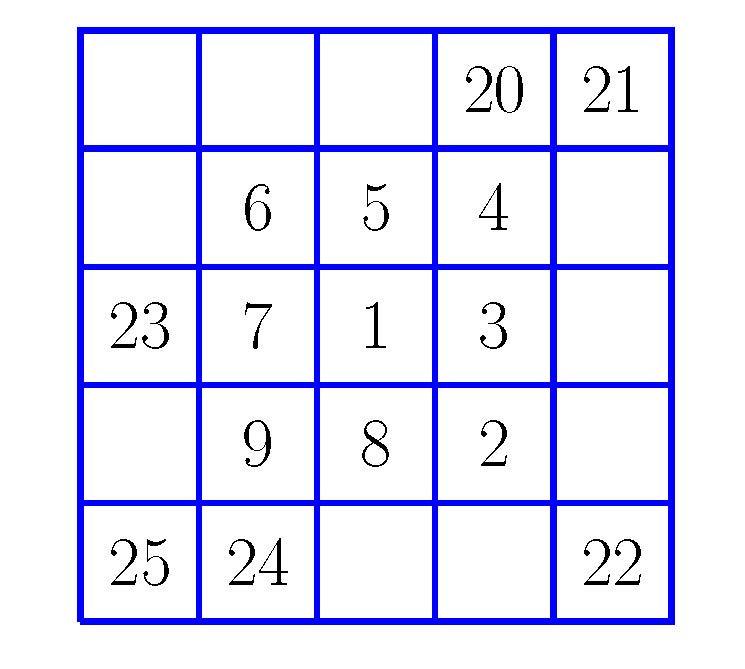
———————————————————————————-
Ariketak Frantziako CNRSren blogeko Défis du Calendrier Mathématique ataletik daude hartuta.
———————————————————————————-
The post Dozena erdi ariketa 2018ko udarako (2): Osatu karratua appeared first on Zientzia Kaiera.
Cristalografía (8): Morfismos químicos

A finales del siglo XVIII Martin Heinrich Klaproth continuó el trabajo donde Dolomieu lo había dejado. Klaproth identificó tres formas cristalográficas diferentes de carbonato cálcico: calcita, aragonito y vaterita. Publicó las diferencias detalladas entre estos tres minerales en su Beiträge zur chemischen Kenntniss der Mineralkörper, obra en cinco volúmenes publicada entre 1795 y 1810. Haüy se mostró muy interesado en este descubrimiento, pero le desconcertaba el aragonito: a diferencia de la calcita, no se rompía en romboedros.


Klaproth, que había sido catedrático en Berlín, dejó su puesto vacante a su muerte en 1817. En 1819, a propuesta de Jöns Jakob Berzelius, fue nombrado para sucederle Eilhard Mitscherlich. Mitscherlich, químico, había comenzado a estudiar en profundidad la cristalografía en 1818 y pronto se dio cuenta de que los cristales que tienen la misma composición pero distinta morfología, como la calcita y el aragonito, no son tan extraños. También se dio cuenta de que había cristales que tienen la misma morfología pero diferente composición química. Así, la dolomita, un mineral descrito por Dolomieu, es muy similar a la calcita, pero contiene calcio y magnesio [CaMg(CO3)2 ]en vez de sólo calcio [CaCO3]. Mediciones precisas realizadas por Wollaston mostraban que las diferencias entre los cristales de dolomita, calcita y la siderita (carbonato de hierro) eran mínimas: el ángulo romboédrico era respectivamente de 105º5′, 106º15′, y 107º0′.
Pero, ¿nadie se había dado cuenta de esto antes? Claro que sí. Sin ir más lejos Romé de l’Isle lo había hecho notar en alumbres cúbicos que forman cristales mixtos. Alrededor de 1812 el propio Wollaston describió más ejemplos de cristales similares con diferente composición química en los que había medido diferencias angulares mínimas. Por ejemplo, en la serie de sulfatos alcalinos [K2SO4, Rb2SO4, Cs2SO4, (NH4)2SO4] los ángulos interfaciales difieren sólo unos pocos minutos, y en un compuesto similar, el Ti2SO4, la variación con respecto a la media es de sólo medio grado. Resultados similares se encuentran en series de fosfatos y arseniatos.
Por tanto, estamos ante dos fenómenos aparentemente opuestos: sustancias de la misma composición química que forman cristales de diferente morfología y sustancias de diferente composición química que forman cristales de morfología muy similar. Mitscherlich les puso nombre; llamó isomorfos a los que tenían diferente composición y (casi) igual forma y polimorfos a los que tenían la misma composición y diferente forma. Y dio el paso definitivo estableciendo la ley del isomorfismo: los compuestos que cristalizan juntos probablemente tengan estructuras y composiciones similares. Lo que implicaría que las sustancias de composición similar es probable que den lugar a cristales isomorfos.

Incluso las sustancias elementales pueden cristalizar de diferentes maneras como observó el propio Mitscherlich en el azufre, que produce cristales diferentes (esto es, con diferentes ángulos interfaciales) dependiendo de las condiciones de cristalización. Incidentalmente, haciendo estos experimentos fue como Mitscherlich descubrió el azufre monoclínico, que cristaliza por encima de los 96ºC. Su razonamiento fue que los átomos de un mismo elemento se organizan en distintas “moléculas” porque se unen entre sí de distintas maneras, lo que resulta en las distintas formas de los cristales. Un ejemplo muy conocido es el diamante, el grafito y el hollín que son prácticamente carbono puro. Este polimorfismo merecía un nombre especial, por lo que Berzelius creó el término alotropía en 1841.
El descubrimiento y caracterización del isomorfismo tuvo una influencia muy importante en el desarrollo de la química, mucho más allá del puramente teórico. Las diferentes propiedades de los compuestos isomorfos permitieron a Berzelius la confección la primera tabla relativamente precisa de pesos atómicos. Hasta ese momento se fijaba el peso atómico del hidrógeno arbitrariamente en 1, por lo que resultaba que el carbono tenía peso atómico 6 (en vez de 12) y el oxígeno 8 (en vez de 16), y el agua era HO en vez de H2O; Berzelius cambió todo esto.
No sólo los pesos atómicos, que son sólo la punta del iceberg; el descubrimiento de Mitscherlich propició el desarrollo muy poco después de multitud de conceptos químicos, relacionados sólo parcialmente con la cristalografía. El ejemplo más importante sea quizás el descubrimiento de la isomería.
Referencias generales sobre historia de la cristalografía:
Referencias generales de la serie:
[1] Wikipedia (enlazada en el texto)
[3] Molčanov K. & Stilinović V. (2013). Chemical Crystallography before X-ray Diffraction., Angewandte Chemie (International ed. in English), PMID: 24065378
[4] Lalena J.N. (2006). From quartz to quasicrystals: probing nature’s geometric patterns in crystalline substances, Crystallography Reviews, 12 (2) 125-180. DOI:10.1080/08893110600838528
[5] Kubbinga H. (2012). Crystallography from Haüy to Laue: controversies on the molecular and atomistic nature of solids, Zeitschrift für Kristallographie, 227 (1) 1-26. DOI: 10.1524/zkri.2012.1459
[6] Schwarzenbach D. (2012). The success story of crystallography, Zeitschrift für Kristallographie, 227 (1) 52-62. DOI: 10.1524/zkri.2012.1453
Este texto es una revisión del publicado en Experientia docet el 2 de enero de 2014
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Cristalografía (8): Morfismos químicos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cristalografía (3): Goniómetros y óxidos dulces
- Cristalografía (6): El cura rompecristales
- Cristalografía (7): Moléculas, superfluidades y contaminaciones
La función renal en vertebrados
La mayor parte de lo que sabemos sobre el funcionamiento de los riñones de vertebrados procede de estudios hechos con anfibios y con mamíferos. Los anfibios resultan ser un modelo animal muy útil a estos efectos, y lo que sabemos del funcionamiento de su riñón es generalizable a la mayoría de vertebrados y, en concreto, a los peces de agua dulce y a los reptiles, exceptuando en parte a las aves.
En la nefrona de la mayor parte de grupos de vertebrados se diferencian los siguientes elementos: (1) cápsula de Bowman, (2) túbulo contorneado proximal, (3) segmento intermedio, (4) túbulo contorneado distal, y (5) túbulo colector. Los segmentos llamados “túbulo contorneado” se caracterizan por que describen múltiples curvas en su trayectoria; a eso se refiere el término “contorneado”. En inglés se dice convoluted, que puede traducirse también como enmarañado, retorcido o complicado; el término “contorneado” es claramente más compasivo. El segmento intermedio es bastante recto y de muy pequeño diámetro, y el túbulo colector es también relativamente recto, pero de mayor grosor que el intermedio. Los segmentos desempeñan diferentes funciones, aunque también pueden cambiar dentro de cada segmento. La longitud de la nefrona viene a ser de 1 cm aproximadamente, aunque el grosor es microscópico en todo su recorrido. El túbulo colector desemboca, junto con muchos otros túbulos, en el ducto o tubo colector, y los ductos colectores desembocan en el uréter, que es el canal que conduce la orina a la vejiga.
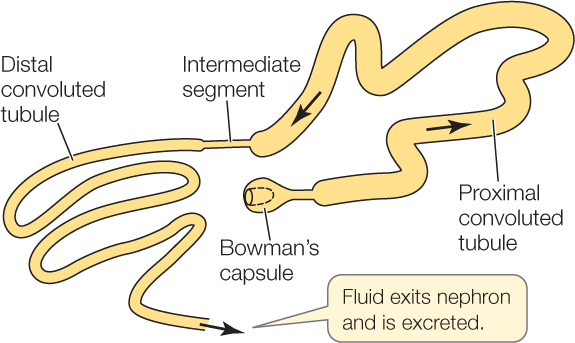
Nefrona de un anfibio
Como vimos en la anotación anterior, lo normal es que una parte muy importante de la orina primaria no sea expulsada al exterior, sino que sea reabsorbida a lo largo de la nefrona, y esa reabsorción afecta tanto al agua como a las sales y otras sustancias que conviene retener. En el caso de los anfibios también es ese el caso, aunque no suele ser agua lo que les falta. De hecho, para la mayor parte de los animales que viven en agua dulce el problema consiste en retener las sales a la vez que expulsan la máxima cantidad de agua posible.
A lo largo del túbulo contorneado proximal se reabsorbe activamente Na+, y lo normal es que el Cl– lo acompañe al moverse a favor del gradiente eléctrico generado por el transporte del catión. La concentración osmótica a lo largo de ese segmento apenas varía, porque su epitelio es permeable al agua, de manera que la reabsorción de NaCl se ve acompañada por una reabsorción de agua de similar magnitud. En los anfibios estudiados, entre un 20% y un 40% de la orina primaria es reabsorbida en este primer segmento de la nefrona. Además de NaCl y agua, en el túbulo proximal se reabsorbe glucosa y aminoácidos.
La reabsorción de NaCl prosigue en el túbulo contorneado distal, aunque en este caso, la recuperación de sal puede ir acompañada de reabsorción de agua, o no, dependiendo de las necesidades que impone el mantenimiento del balance hídrico. En otras palabras, el volumen final de orina que se expulsa depende de la medida en que el agua acompaña al NaCl cuando es reabsorbido este en el túbulo distal; cuanto menor es la reabsorción de agua, mayor es la producción de orina final (mayor es la diuresis) y cuanto mayor es el volumen que se reabsorbe, menor es la diuresis. En algunas especies de anfibios la vejiga también interviene en la formación de orina de forma similar a como lo hace el túbulo contorneado distal.
La permeabilidad para con el agua del epitelio del túbulo contorneado distal está controlada por la hormona antidiurética (ADH) o vasotocina1, una hormona peptídica producida por la neurohipófisis; y ese control se ejerce a través de la inserción de más o menos aquaporinas en la membrana apical de las células epiteliales. Cuando los niveles circulantes de esta neurohormona son bajos, la permeabilidad del epitelio es baja (menor inserción de aquaporinas), de manera que la reabsorción de NaCl por las células epiteliales del túbulo distal no es acompañada por una reabsorción equivalente de agua. Como consecuencia, se recupera poca agua, la orina producida es abundante y además muy diluida, esto es, su concentración de sales es muy baja. Lo contrario ocurre cuando la concentración circulante de vasotocina es alta: hay una intensa reabsorción de agua en el túbulo distal (en su parte más próxima al túbulo colector, principalmente) y, en consecuencia, la orina es escasa y su concentración salina es más alta. Estos son, precisamente, los procesos mediante los que se efectúa la regulación del volumen de los líquidos coporales y de la concentración osmótica y salina que realizan muchos animales y que vimos en algunas anotaciones de esta serie.
En anfibios, lagartos, aves y otros reptiles la hormona antidiurética no solo aumenta la permeabilidad al agua de ciertas zonas del túbulo contorneado distal, sino que también disminuye la tasa de filtración glomerular, mediante una reducción en el número de nefronas que filtran plasma sanguíneo. Esa reducción se produce provocando vasoconstricción en los vasos que llevan sangre al glomérulo (aferentes). Este mecanismo complementa el descrito anteriormente y ambos contribuyen a retener agua y limitar el volumen de orina que es expulsada al exterior. Y en algunas especies de anfibios la ADH eleva, además, la reabsorción activa de NaCl, favoreciendo también de este modo la reabsorción de agua.
En el mecanismo que desencadena la elevación de la concentración sanguínea de vasotocina intervienen osmorreceptores hipotalámicos (que detectan una subida de la concentración osmótica) y barorreceptores o receptores de estiramiento localizados en ciertos vasos sanguíneos (que detectan cambios en la presión sanguínea). Así, ante un aumento en la concentración osmótica o una reducción en la presión sanguínea, la neurohipófisis responde secretando ADH y elevando así su concentración sanguínea para surtir los efectos descritos y restaurar el volumen de sangre y la concentración osmótica adecuada.
Los riñones de los teleósteos marinos presentan algunas características que los diferencian de los de agua dulce y de los anfibios. Lo normal es que las nefronas de los peces marinos carezcan del túbulo contorneado distal. Puesto que estos peces proceden, de hecho, de antecesores dulceacuícolas, se cree que esa ausencia es secundaria y se atribuye al hecho de no necesitar producir grandes volúmenes de orina diluida. Los peces marinos son reguladores hiposmóticos y el riesgo principal que afrontan es el de la desecación. Además, y por la misma razón, estos peces tienden a tener pocas nefronas y glomérulos pequeños, pues de esa forma limitan la formación de orina primaria, reduciendo significativamente la pérdida de agua por esa vía. En coherencia con esas características renales, no toda la orina primaria la producen por ultrafiltración. De hecho, parte de la orina la generan por secreción activa de iones (Na+, Cl–, Mg2+ y SO42-), a los que acompaña el agua, a la luz del túbulo contorneado proximal.
La reducción de la contribución de la ultrafiltración a la formación de orina primaria alcanza su máxima expresión en un conjunto de especies (se conocen una treintena) de peces marinos cuyas nefronas carecen de glomérulo, son aglomerulares. Se trata de un rasgo que ha aparecido en tres ocasiones diferentes en el curso de la evolución.
Las aves, a diferencia del resto de reptiles, tienen dos tipos de nefronas. Unas son similares a las descritas en esta anotación, pero las otras se asemejan a las de los mamíferos (que veremos más adelante). Entre un 10% y un 30% de las nefronas aviares son de este segundo tipo y se caracterizan por tener lo que se conoce como “asa de Henle”, un segmento que en mamíferos cumple un papel de importancia crucial. En el riñón de las aves las nefronas de tipo anfibio (o reptiliano) se disponen en la corteza renal (parte más exterior), mientras que las de tipo mamífero se disponen en la médula, la zona más interior y más próxima al uréter. Lógicamente, las características funcionales de las nefronas de tipo mamífero se asemejan a las de los mamíferos, por lo que pueden producir una orina de mayor concentración osmótica que la sangre, aunque no en una medida equivalente a la de aquéllas.
Por último, cabe señalar que el uréter de las aves no descarga en una vejiga o directamente al exterior, sino que lo hace en la cloaca, de forma similar a como vimos con los túbulos de Malpigio y el recto en insectos. Y esta no es la única semejanza entre aves e insectos, ya que las aves también eliminan sus restos nitrogenados en forma de ácido úrico, que aparece en la nefrona por filtración o, incluso, por secreción activa. También las aves eliminan sus restos nitrogenados en forma semisólida, lo que ayuda de forma importante al ahorro de agua. En próximas anotaciones presentaremos la nefrona de mamíferos.
1 La arginina vasotocina (AVT) es la equivalente en vertebrados no mamíferos a la arginina vasopresina (AVP) de mamíferos.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La función renal en vertebrados se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Características básicas de los riñones de vertebrados
- Así forman la orina los animales
- Túbulos de Malpigio y recto, el sistema excretor de los insectos
Zarata ez da oztopo atzerriko hizkuntzetako soinuak ikasteko
Irudia: Giro zaratatsuak ez dira oztopo hizkuntzak ikasteko.
Posible da atzerriko hizkuntza bat ikastea nahiz eta ikasketa hori inguru zaratarekin egin, ama hizkuntzak ikasterakoan dauzkagun baldintza berdinak errepikatzen baitira. Hala frogatu du ikerketa batek.
Atzerriko hizkuntza bat ikasi duten ikasle gehienek zailtasun handiak sentitu dituzte, sarritan, aipatu hizkuntza ikasgelatik at ulertzeko. Eguneroko bizitzan, solasaldiak zarata iturri asko eta aldi berean hizketan dauden hiztun ugari dituzten tabernak edo jatetxeak, tren geltokiak edo trafiko handia duten kaleak bezalako leku zaratatsuetan garatzen ohi dira. Testuinguru horietan, hizkuntza ikasleek zailtasun handiagoak dituzte atzerriko hizkuntza ulertzeko.
Ume txikiek ama hizkuntza ikasten dutenean hiztun askorekin eta egoera eta ingurune oso ezberdinetan egiten dute, zarata eta beste nahaste batzuekin, hori baita ohikoa mundu errealean. Ondorioz, hizkuntza egoera horietan ulertu ahal izateko beharrezkoak dituzten estrategiak garatzen dituzte.
Atzerriko soinuen entrenamenduan inguru zarata txertatzea hizkuntzaren ulermenerako erabilgarria izan zitekeela planteatu dute ikerketan. Beste aukera ere bazegoen: inguru zarata txertatzea kaltegarria izatea, gehitutako zailtasunaren ondorioz.
Egindako ikerketak, ordea, zalantzak uxatu ditu: atzerriko soinuak inguru zaratarekin irakastea ez da inolaz ere kaltegarria, ingurune isil batean ikasten diren bezalaxe ikasten baitira. Eta, gainera, atzerriko hizkuntza hobeto ulertzen da zarata duten egoera eta lekuetan.
Ikerketak euskara eta gaztelania hitz egiten duten 88 lagun elebidun aztertu ditu. Ingelesaren kontsonanteak ikasteko 10 saioko entrenamendua egin dira bi talderekin: inguru zaratarekin bata, inolako zaratarik gabe bestea. Bost astez, ingelesaren kontsonante bakoitzaren 200 adibide landu dituzte; 4.800 itemetik gora, guztira. Alderaketa egiteko, hiru kontrol talde erabili dira: bokalak zaratarekin eta zaratarik gabe ikasi dituzten talde bana eta ingelesera ama hizkuntza duen hirugarren taldea.
Emaitzek frogatzen dutenez, zaratarekin eginiko entrenamendua eraginkorra da, zaratak ez du kalterik egiten. Are gehiago, zaratarekin lan egin zutenek emaitza zertxobait hobeak lortu dituzte kontsonanteak identifikatzerakoan.
Ikerketak frogatu du garrantzitsua dela baldintza naturalak erreproduzitzea atzerriko hizkuntz bat ikasterakoan, hiztun anitzak eta era ezberdineko inguru zaratak txertatuz, laborategi baldintza aseptikoetan eginiko irakaskuntzaren aurrean. Zaratarekin eginiko ikaskuntzak nola funtzionatzen duen jakitea da hurrengo pausoa. Ikerketa taldeak esku artean dituen hipotesietako bat da soinuak zaratarekin entzuten dituzten entzuleek arreta handiagoa eskaintzen dietela, zarata bakoitzaren ezaugarri ezberdinen artean, nahasteen aurrean sendoago agertzen zaizkigun horiei.
Iturria: UPV/EHU prentsa bulegoa: Zarata ez da oztopo atzerriko hizkuntzetako soinuak ikasteko.
Erreferentzia bibliografikoa:
Cooke, Martin, García, Maria Luisa, (2018). Effects of exposure to noise during perceptual training of non-native language sounds, The Journal of the Acoustical Society of America 143:5, 2602-2610. DOI: 10.1121/1.5035080
The post Zarata ez da oztopo atzerriko hizkuntzetako soinuak ikasteko appeared first on Zientzia Kaiera.

