Thomson gazelaren beroaldia
 Juan Ignacio Pérez eta Miren Bego Urrutia Igeri egiten, lasterka egiten, hegan egiten
Juan Ignacio Pérez eta Miren Bego Urrutia Igeri egiten, lasterka egiten, hegan egiten ———————————————————————————————————–
Ezaguna denez, jarduera fisiko altuak energia-eskari altuagoak sortzen ditu. Giharrek lan gehiago egitean, uzkurketa-zikloak gauzatzeko beharrezkoa den gainerako energia (ATPa) sortzeko oxigeno gehiago garraiatu behar da gihar-zeluletako mitokondrioetaraino.
Irudia: Ohiko 39 °C-ko tenperaturatik 44 °C-raino hel daiteke odol arterialaren tenperatura Thomson gazelaren kasuan.
Bai zirkulazio-sistemak eta bai arnas aparatuak hartzen dute parte oxigeno gehigarri hori helarazten, lankidetzan: batetik, arnas hartzea azkartu egiten da oxigeno gehiago hel dadin difusioz arnas organoa irrigatzen duen odolerantz, eta bestetik, bihotzaren taupada-maiztasuna emendatu egiten da; sarriago uzkurtuz, denbora-unitateko odol gehiago ponpatzen da beharrizan metaboliko altuagoa duten ehunetarantz.
Beraz, animalia asko hatsankatu egiten dira ariketaren ondorioz. Hatsankatzea, baina, xede anitzeko jokabidea dugu. Goraxeago esan denez, arnasketa-zikloa azkartzeko mekanismoa da, baina ariketak eragindako beroa barreiatzeko ere erabiltzen da zenbait animaliaren kasuan, batez ere izerdirik botatzen ez dutenetan (ikus «Munduko gauza hotzenetako bat» izenburuko atala). Hala ere, batzuetan ariketak sortutako beroa xahutzeko zailtasunak daudenean, hatsankatzeak ba omen du hirugarren betebehar garrantzitsu bat: garuneko tenperaturari balio seguruetan eustea.
Azter dezagun aukera hori adibide baten bidez: Thomson gazela izenaz ezaguna den Afrikako ekialdeko gazela txikiak 15-20 kg inguru pisatzen du. Harrapari baten presiopean, 40 km/h-ko abiaduran 5 minutuz korrika aritu ondoren, jarduera metaboliko emendatuak eragindako ezohiko bero-ekoizpenak animaliaren gorputz guztia berotzen du. Ohiko 39 °C-ko tenperaturatik aldenduz, 44 °C-raino heltzen da odol arterialaren tenperatura. Ariketa gogorraren ondorioz, beraz, animalia homeotermo honek, aldi baterako bada ere, galdu egiten du gorputzeko tenperaturari konstante eusteko gaitasuna.
Zergatik gertatzen da tenperatura-emendio hori? Harrapariaren mehatxupean korrika bizian doala, 40 aldiz emendatzen da gazelaren gastu metabolikoa. Aipatu behar da gainera, lasterketa hori ingurune-tenperatura altuetan burutzen dela. Beraz, Thomson gazelak ariketaren ondorioz ekoitzitako beroa galtzeko zailtasun handiak ditu. Ondorioz, odolaren tenperatura nabarmen igotzen da, beroa galtzeko aukerak mugatuta baitaude. Izan ere, tenperatura-emendio horrek baliteke animaliaren gihar sistemaren funtzionamendua azkartzen laguntzea, eta ondorioz korrikaldiaren etekina hobetzea.
Gazelaren gorputzeko tenperaturaren emendioa ez da gertatzen beroa barreiatzeko mekanismoek huts egiten dutelako, animaliak maiztasun altuko hatsankatzera jotzen baitu, bai freskatzeko, eta baita oxigeno gehiago lortu ahal izateko ere. «Munduko bi gauza hotzenetako bat» izenburuko atalean txakurretarako azaldu dugunez, izerdirik botatzen ez duten animalia askok erabiltzen dute hatsankatzea beroa xahutzeko. Arnas sisteman oinarritutako mekanismo horiek oso eraginkorrak badira ere, ohiko egoeran behintzat, hain da handia gazelaren ihesaldia bezalako larrialdi-egoeretan gertatutako bero-ekoizpenaren zama, ezen tenperaturak gora egiten baitu, ezin baitaiteke sortzen den bezainbeste bero barreiatu.
Baina ariketak eragindako tenperatura-igoera ez da gorputz osoan modu berean gertatzen, hatsankatzeari esker Thomson gazelaren garuna gainerako gorputz guztia baino hotzago mantzentzea lortzen baita. Gorputzeko tenperatura 44 °C-ra dagoen artean, garuneko tenperatura ez da 41 °C-ra heltzen. Balio seguruetan mantentzen da, beraz; jakina denez, garuna osatzen duten zelulentzat oso kaltegarriak dira 41-42 °C-tik gorako tenperaturak.
Nola lor daiteke baina hatsankatzearen bitartez horrelako hozte-prozesu selektiboa? Arteria karotideotik garunerantz bideratzen den odola kaskezurreraino iritsi orduko ehunka arteria txikitan banatzen da; gero, garunera heldu baino lehen, batu egiten dira berriro, bero-trukatzaile modura jokatzen duen rete mirabile bat osatuz. Sare miragarria osatzen duten arteria txiki horiek, zain-odolak osaturiko sinu bat zeharkatzen dute. Zainetako odol hori hotzago dago, hatsankatzen ari den gazelaren sudurretik igaro ondoren heltzen baita sinu horretara. Horrela, hoztu egiten da arteriatxoetan zehar doan odol arteriala, beroaren zati bat zain-odolerantz galtzen baitu, eta garunera heltzen denerako odol hau arteria karotideoko odola baino 2-3 °C freskoago dago. «Atunen berogailua eta sare miragarria» izenburuko artikuluan ikusi dugu sare miragarriaren bero-trukerako sistema hau, justu kontrara jokatzen: atunen giharraren kasuan, odola muskulura heldu orduko berotzeko erabiltzen zen sistema bera.
Hortaz, oro har, bero-galerarako mekanismoa izateaz gain, hatsankatzeak ingelesez «selective brain cooling» deritzon prozesuan ere hartzen du parte. Thomson gazela adibidetzat hartu badugu ere, artiodaktilo hori ez da hozte selektibo hau baliatzen duen animalia bakarra, etxe-abere ungulatu askok ere mekanismo bera erabiltzen baitute. Animalia hauei buruz esan daiteke, bai, «burua hotz» mantentzen dutela!
—————————————————–
Egileez: Juan Ignacio Pérez Iglesias (@Uhandrea) eta Miren Bego Urrutia Biologian doktoreak dira eta UPV/EHUko Animalien Fisiologiako irakasleak.
—————————————————–
Artikulua UPV/EHUren ZIO (Zientzia irakurle ororentzat) bildumako Animalien aferak liburutik jaso du.
The post Thomson gazelaren beroaldia appeared first on Zientzia Kaiera.
Grietas de desecación marcianas

Imagen que Curiosity tomó de “Old Soaker” durante el sol 1555. La losa tiene unos 80 cm de longitud. Foto: NASA.
A principios de 2017, y a partir de imágenes recopiladas por el róver Curiosity, los científicos anunciaron el descubrimiento de posibles grietas de desecación en el cráter Gale, que habría estado lleno de lagos hace 3.500 millones de años. Ahora, un nuevo estudio ha confirmado que son realmente grietas de desecación, lo que revela nuevos detalles sobre el antiguo clima de Marte.
Dado que las grietas de desecación se forman solo cuando el sedimento húmedo está expuesto a la atmósfera, su posición más cercana al centro del antiguo lecho del lago que al borde también sugiere que los niveles del lago aumentaron y disminuyeron drásticamente con el tiempo. Esto es, los lagos del cráter Gale habrían pasado por el mismo tipo de ciclos que vemos en la Tierra
Los investigadores se centraron en una losa de roca del tamaño de una mesa de café apodada “Old Soaker”. Old Soaker está atravesado por polígonos idénticos en apariencia a los característicos de los procesos de desecación terráqueos. El equipo analizó los aspectos físicos y químicos de los polígonos utilizando todo el despliegue de medios de análisis de Curiosity. Hay que recordar en este punto que Curiosity es un potentísimo laboratorio geoquímico autopropulsado.
Este escrutinio puso de manifiesto que los polígonos, confinados a una sola capa de roca y con sedimentos llenando las grietas entre ellos, se formaron por la exposición a la atmósfera, y no por otros mecanismos como la fracturación térmica o hidráulica. Y si bien los científicos sabían casi desde el momento en que Curiosity aterrizó en 2012 que el cráter Gale alguna vez contuvo lagos, la confirmación de la existencia de grietas de desecación añade un contexto a nuestra comprensión de este antiguo sistema lacustre.
Hallazgo tras hallazgo, Curiosity está transformando continua y completamente nuestra visión del presente y del pasado de Marte.
Referencia:
N. Stein et al (2018) Desiccation cracks provide evidence of lake drying on Mars, Sutton Island member, Murray formation, Gale Crater Geology doi: 10.1130/G40005.1
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Grietas de desecación marcianas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- En Marte el viento crea montañas
- Cómo se formaron las columnas hexagonales de la Calzada del Gigante
- Ox Bel Ha, un ecosistema tropical alimentado por metano
Muriel Bristol, la gran catadora de té

Estamos en Rothamsted (Harpenden, Reino Unido). Son las cuatro de la tarde, la ‘sagrada’ hora del té. Un grupo de personas hace una pausa en su trabajo para tomarse su infusión. Entre ellas están Muriel y Ronald. Ronald ofrece a su amiga una taza de té. Ella, tras tomar un sorbo, la rechaza. A Muriel le gusta el té, pero solo si la leche se ha servido en la taza en primer lugar. Ronald cree que se trata de una broma, e insiste con vehemencia; piensa que es lo mismo el orden en el que se vierten los líquidos, y se burla de su colega. Pero Muriel, enfadada, la rechaza de nuevo… no le gusta el sabor. William, otro de los miembros del grupo, intenta mediar y pide a Ronald que deje demostrar a Muriel que efectivamente es capaz de distinguir el momento en el que se ha servido la leche en la taza. Rápidamente, se organiza el experimento: Muriel debe distinguir entre ocho tazas de té, cuatro de cada tipo (leche antes del té o té antes de la leche) colocadas de manera aleatoria ante ella. Tras una pausada cata –en la que se permite a Muriel comparar el sabor de dos tazas–, y ante el asombro de sus compañeros, Muriel distingue con precisión el orden en el que se ha servido la leche de cada taza. ¿Ha sido pura suerte? ¿O quizás Muriel es una experta catadora capaz de distinguir esos detalles? Ronald tuvo que admitir la “victoria” de Muriel y se puso a reflexionar mucho sobre el tema…
Por cierto, Muriel y William se casaron poco tiempo después.
La anterior historia –me he permitido alguna pequeña licencia– es una historia real. Sus protagonistas son la bióloga Muriel Bristol (1888-1950) –que trabajó en la estación experimental de Rothamsted (Harpenden, Reino Unido) desde 1919 y era especialista en algas–, el biólogo y estadístico Ronald Fisher (1890-1962) y William Roach –con el que es cierto que Muriel se casó–.

Muriel Bristol y Ronald Fisher.
El experimento se realizó realmente, fue diseñado por el propio Fisher y dio lugar a un experimento aleatorizado que el estadístico presentó en su libro The Design of Experiments (1935) –llamado The lady tasting tea, la catadora de té–, en el que la prueba de significación estadística usada fue el test exacto de Fisher.
En este experimento, Fisher introdujo el concepto de hipótesis nula, unaafirmación que no se demuestra o establece, y no se rechaza excepto si durante el curso de la prueba parece demostrarse su falsedad. En el caso de la catadora de té la hipótesis nula suponía que Muriel no tenía la capacidad de distinguir las tazas.
Fisher eligió ocho tazas porque le pareció una cantidad suficiente para que la suerte no fuera un factor determinante. Observar que, efectivamente, existen 70 maneras de colocar las ocho tazas, con cuatro de cada tipo, y parece difícil acertar solo por azar.
Muriel aclaró –una explicación muy científica, desde su condición de bióloga– que, si se añadía leche fría al té caliente, las proteínas de la leche coagulaban y cambiaba el sabor, y ella lo percibía como desagradable.
Por cierto, el escritor George Orwell (1903-1950) no coincide con Muriel… en 1946 publicó el texto A nice cup of tea en el que describía con detalle el procedimiento a seguir para preparar una taza de té perfecta. Entre las instrucciones decía (traducción extraída de [3]):
En décimo lugar se debe verter el té en la taza antes que la leche. Este es uno de los puntos más polémicos, de hecho en todas las familias de Gran Bretaña probablemente hay dos escuelas de pensamiento sobre el tema. La escuela que echa primero la leche (que puede tener argumentos contundentes) y la escuela que la echa después. Yo sostengo que mi teoría es irrefutable. Al poner el té primero se puede regular exactamente la cantidad de leche, mientras que si se hace al revés se puede poner demasiada leche y no tendrá arreglo.
A lo mejor, para saber quién lleva la razón, es mejor leer lo que dice la norma ISO 3103 respecto al método estándar de preparar el té…
Referencias
[1] Sturdivant, Lt. Col. Rod., Lady Tasting Tea, 2004
[2] Jesús Ortiz, La ciencia y el té de las cinco, El Diario, 23 noviembre 2016
[3] Las onces reglas de George Orwell para ‘Una buena taza de té’, Territorio gastronómico
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Muriel Bristol, la gran catadora de té se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El gran cuatro, o los números siguen estando locos
- Artistas que miran a las matemáticas
- ¡Es la Aritmética!
Urpekaritzarako egokitzapen genetikoa identifikatu dute, aurrenekoz
Klasiko bat da. Gizakiak genetikaren inguruan gero eta ezagutza gehiago izan, orduan eta argiago geratzen da geneek, hein handi batean, gizakia baldintzatzen dutela. Determinismoa barra-barra dabil, honezkero. Kontua ez da, baina, hain sinplea. Izan ere, azken urteetan, gero eta argiago dago oharkabean gizakia ere geneak baldintzatzeko gai dela. Ez gaude, bada, transgenikoei buruz hizketan, kulturak kode genetikoan eragindako aldaketei buruz baizik.

1. irudia: Modu tradizionalean egiten dute urpekaritza bajauarrek, eta mila urte inguru eman dute horrela. (Argazkia: Melissa Ilardo /University of Cambridge)
Adibide asko daude: altuera handira bizitzera egokitu diren populazioak, omega-3 azidoen kontsumoa errazteko entzima zehatz bat garatu duten herriak edo laktosa onartzeko Neolitoaren geroztik Europan eta mendebaldeko populazioetan garatu den egokitzapena. Horietan guztietan, gizakiek egindako hautespen kulturalek norabidea “erakutsi” diote eboluzioari, eta baldintza berrietara hoberen egokitutako aldaerak nagusitu dira.
Hemendik aurrera, beste adibide bat gehitu ahal izango da pixkanaka hazten den zerrenda horri: uraren barruan eusteko gaitasuna, alegia. Gizakiak lurraren gainean bizi behar badu ere, itsasoarekiko kontaktua gero eta handiagoa da, eta bereziki zenbait kulturatan garrantzitsuagoa izan da lotura hori. Oraingoan, berariaz itsaspean denbora gehiago ematera bideratutako egokitzapen bat azaleratu dute zientzialariek.
Cell aldizkarian argitaratutako ikerketa batean ezagutzera eman dute: Indonesian bizi den Bajau herriko kideek ohi baino bare handiagoak dituzte, eta horrek aukera ematen die itsasoaren azpian 70 metroko sakonerara iristeko.
Aurretik ere zientzialariek susmatzen zuten bare handia edukitzeak eta urpekaritzan hain ondo moldatzeak lotuta egon behar zutela, baina harreman hori ikerketa genetiko baten bitartez berresten den lehenengo aldia da oraingoa.
Tradizionalki, Bajau herria nomada izan da. Azken milurtekoan leku batetik bestera ibili da, Asiako hego-ekialdeko itsasoetan zehar; baina, gehienbat, Indonesian bizi dira bajauarrak. Bertan, nahiko ezagunak dira urpekaritza egiteko daukaten abilezia dela eta. Arrantza da haien ogibide nagusia, batez ere itsas luzokerrak eskuratzen dituztelarik. Holothuroidea familiako animalia hauek itsas hondoan bizi dira. Asiarrek estimu handian duten jakia da, eta, horregatik, bajauarrek baliabide hori ustiatu dute mendeetan zehar, erraztasun handiz saltzen dutelako. Lantokitik gertu bizi dira bajauar asko, etxe flotagarrietan, hain zuzen.

2. irudia: Gizakiek egindako hautespen kulturalek norabidea “erakutsi” diote eboluzioari. Oraingoan, urpekaritzara egokitzeko gaitasuna da azaleratu dutena. (Argazkia: Melissa Ilardo /University of Cambridge)
Horregatik, orain ikerketa aurkeztu duten zientzialariek susmoa zuten uraren azpian hain ondo moldatu izanaren atzean abiapuntu genetiko bat egon ote zitekeen. Izan ere, gizakien kasuan halako gaiaren inguruan informazio gutxi bazegoen ere, animalietan horrelako kasuak ezagunak ziren. Bereziki, sakonera handian arrantza egiten duten fokak aipatu dituzte; horien artean, Weddellgo fokak omen dira uraren pean ederki moldatzeko bare oso handia duten animaliak.
Hipotesia berresteko, hainbat hilabete eman ditu Jaya Bakti (Brunei) izeneko herrian artikuluaren egile nagusi Melissa Ilardok. Ikerketa genetikoa burutzeko laginak hartzeaz gain, urpekarien bareetako tamainak ere neurtu ditu, ekografien bitartez.
Laginketa berdina egin du bajauarren auzokide diren Saluan herrikoekin. Horrek aukera eman die ikertzaileei alderatzeko antzeko ingurunean bizi diren baina praktika kultural desberdinak dituzten populazioak alderatzeko.
Emaitzen arabera, barearen tamainari dagokionean, batez bestean, bajauarren barearen tamaina saluandarrena baino %50 handiagoa da. Arlo genetikoari dagokionez, desberdintasuna PDE10A izeneko genean aurkitu dute. Gene honek T4 hormona tiroideoa arautzen du.
Emaitzek hipotesia oinarritzeko nahikoa froga eman dutela diote. “Uste dugu bajauarrek egokitzapen bat garatu dutela. Horren bidez, hormona tiroidearen mailak handitu dira, eta horrek haien barearen tamaina handitu du”, adierazi du Ilardok, prentsa ohar batean.
Bajau arrantzale bat, 20 metroko sakoneran arrantza egiten. (Bideoa: BBC One)
Globulu gorrien askatzeaOrganismoa urpean dagoenean, bihotzeko taupadak mantsotu egiten dira, eta, ondorioz, barea uzkurtzen da. Horri esker, oxigenoa daramaten globulu gorriak isurtzen dira odol-fluxura, eta horrek urpean denbora gehiago egotea ahalbidetzen du.
Ez da ondo ezagutzen urpekari hauek uraren azpian mantentzeko gaitasuna noraino iristen den, baina, prentsa oharrean diotenez, hauetako batek behin esan zion Melissa Ilardori 13 minutuz egondakoa dela uraren azpian.
Bestalde, nabaritu dute ere medikuntzaren arloan irakaspenak atera daitezkeela ikerketatik. Hipoxia aipatu dute. Organismoa oxigenorik gabe geratzen denean gertatzen da hori. Izan ere, urpekaritza egiten denean hipoxia akutua suertatzean izaten diren antzeko baldintzetan dago organismoa, oxigenorik gabe.
Erreferentzia bibliografikoa:
Ilardo et al. Physiological and Genetic Adaptations to Diving in Sea Nomads. Cell 173, 1–12 April 19, 2018. DOI: doi.org/10.1016/j.cell.2018.03.054
———————————————————————————-
Egileaz: Juanma Gallego (@juanmagallego) zientzia kazetaria da.
———————————————————————————-
The post Urpekaritzarako egokitzapen genetikoa identifikatu dute, aurrenekoz appeared first on Zientzia Kaiera.
Las relaciones hídricas, osmóticas y salinas de los condrictios

Los condrictios (tiburones y rayas, principalmente) son una clase de vertebrados mandibulados a los que se les suele llamar peces cartilaginosos. La mayoría pertenecen a la subclase de los elasmobranquios1, aunque en la misma clase se encuentran también las quimeras, únicos representantes vivos de la subclase de los holocéfalos. Hay menos especies de condrictios que de osteíctios, o peces óseos (la mayoría de cuyas especies son teleósteos).
Los condrictios son muy interesantes pues algunos rasgos de su biología los diferencian claramente de los osteíctios. En concreto, la forma de resolver los problemas hídricos y osmóticos es radicalmente diferente en ambos grupos. De hecho, tal y como adelantamos aquí, en el medio interno de elasmobranquios y celacantos (Latimeria) determinadas sustancias orgánicas alcanzan concentraciones muy elevadas, pudiendo representar hasta un 40% de la concentración total de solutos. Ningún otro grupo tiene representantes con ese extraño rasgo.
La concentración de iones inorgánicos en la sangre de los elasmobranquios marinos es muy similar a la de los teleósteos, pero la concentración osmótica de la sangre de aquellos es ligeramente superior a la del agua de mar. La diferencia obedece a la presencia de urea y, en menor medida, de óxido de trimetilamina (TMAO). Aunque similares, la concentración osmótica del medio interno es lo suficientemente más alta que la del externo como para generar un pequeño flujo de agua hacia el interior del organismo.
Los condrictios son capaces de sintetizar urea y esta es la molécula que utilizan para eliminar los restos nitrogenados del catabolismo de proteínas y otras sustancias2. Pero aunque es la molécula de excreción del nitrógeno, también la retienen en la sangre, lo que consiguen reabsorbiéndola de la orina recién formada en los riñones y evitando su pérdida a través de los epitelios branquiales, que son muy impermeables para con esta sustancia.
La razón por la que, además de urea, la sangre de los elasmobranquios contiene también TMAO es que esta ejerce una función protectora frente a los efectos potencialmente tóxicos de aquella. En efecto, aunque menos que el amonio, la urea también es una sustancia tóxica pues ejerce efectos desestabilizadores sobre proteínas y otras macromoléculas, como consecuencia de lo cual inhibe la acción de las enzimas. Pero hay otras sustancias, como TMAO, glicín betaína y sarcosina, que tienen el efecto contrario, estabilizan macromoléculas y, por lo tanto, activan enzimas. Por esa razón, esas sustancias contrarrestan los efectos de la urea y suelen estar presentes cuando la urea también lo está a altas concentraciones. En humanos, por ejemplo, la concentración de urea se mantiene en el intervalo 2-7 mM, pero en los elasmobranquios marinos esa concentración se encuentra entre 300 y 400 mM. En la sangre del tiburón Squalus acanthias la urea una concentración 351 mM y el TMAO 71 mM (la concentración osmótica total es de 1018 mOsm y la del agua de mar en que vive, de 930 mOsm).
Una consecuencia interesante del hecho de que los elasmobranquios sean ligeramente hiperosmóticos con relación al agua de mar es que el flujo de agua hacia el interior les proporciona toda el agua que necesitan para eliminar las sustancias nitrogenadas de deshecho. No necesitan beber. Por esa razón, no adquieren una cantidad excesiva de sales inorgánicas, como les ocurre a los teleósteos. No obstante, las sales que se introducen con el agua de mar las eliminan a través de la glándula salina rectal, agrupación de miles de túbulos secretores que evacua al recto una solución isosmótica con la sangre aunque sin apenas urea. Por ello, la concentración de Na+ y de Cl– en la secreción salina rectal duplica la concentración sanguínea de esos iones.

Modelo del celacanto “Latimeria chalumnae” que muestra sus colores reales cuando está vivo que se conserva en el Oxford University Museum of Natural History. Foto: Ballista / Wikimedia Commons
Como se ha dicho antes, además de condrictios (elasmobranquios y quimeras), los celacantos también tienen una elevada concentración de urea y TMAO en su medio interno. La concentración de urea en Latimeria chalumnae es de 377 mM y la de TMAO, de 122 mM. El dato es interesante, porque los celacantos son los únicos representantes vivos del grupo de los sarcopterigios, del que suponemos que proceden todos los tetrápodos, muchos de los cuales también recurren a la urea como molécula de excreción de restos nitrogenados.
Hay elasmobranquios que son capaces de penetrar en aguas salobres de estuarios y otros ecosistemas costeros y algunos también han llegado a colonizar los ríos. El tiburón Carcharhinus leucas, tristemente conocido por sus ataques a bañistas, es una de esas especies eurihalinas. En estas especies la concentración sanguínea de urea y TMAO se reduce de forma significativa cuando se encuentran en aguas más diluidas. El citado C. leucas, por ejemplo, pasa de 293 mM (urea) y 47 mM (TMAO) en la sangre cuando está en agua de mar, a 151 mM (urea) y 19 mM (TMAO) en agua dulce. Esa reducción se produce dejando de reabsorber urea en los riñones. No obstante, esa reducción no es suficiente para evitar una intensa entrada de agua en el organismo a favor de gradiente osmótico. Por ello, han de aumentar la producción de orina y, por otro lado, la reabsorción renal y branquial de sales.

Rayas de río “Potamotrygon motoro” en el zoo de Duisburg (Alemania). Foto: Raimond Spekking / Wikimedia Commons
Las rayas de la familia Potamotrygonidae (menos una que es marina) y algunas especies de la familia Dasyatidae son de agua dulce. Al menos algunas de esas especies han llegado a perder incluso la capacidad para sintetizar y retener urea y TMAO, por lo que eliminan sus restos nitrogenados en forma de amonio. Y como no podía ser menos, producen orina abundante y diluida. La fisiología de estas rayas es, de hecho, muy similar a la de los teleósteos de agua dulce en lo que a la regulación hídrica, osmótica y salina se refiere.
Aunque los de agua dulce recurren a mecanismos muy similares, la forma en que los condrictios marinos resuelven sus problemas hídricos y salinos reviste, como hemos visto, características muy diferentes a la de los osteíctios. Esas diferencias son interesantes, porque ponen de manifiesto que la historia evolutiva de unos y otros linajes da lugar a diferentes adaptaciones fisiológicas. En otras palabras, en el funcionamiento de los animales no hay soluciones obligadas para resolver los problemas que plantean los medios a los que se adaptan. Es el azar el que decanta la adopción de una u otra estrategia de entre las disponibles.
Notas:
1 Aunque, como se ha visto, no todos los condrictios son elasmobranquios, en este texto utilizaremos indistintamente ambas denominaciones para referirnos a los peces cartilaginosos. Igualmente, utilizaremos indistintamente las denominaciones osteíctios y teleósteos para referirnos a los llamados peces óseos, aunque no todos los osteíctios sean teleósteos.
2 La inmensa mayoría de las especies de teleósteos eliminan amonio. No llegan a diez las especies que recurren a la urea con ese propósito.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Las relaciones hídricas, osmóticas y salinas de los condrictios se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Relaciones hídricas y salinas de los animales
- La distribución del agua animal y el curioso caso del potasio
- Efectores osmóticos
Esa pesadilla científica llamada mineralogía

Muestra de aragonito procedente de Pantoja (Toledo, España). Imagen: Quebul Fine Minerals
La mineralogía es la ciencia que estudia la estructura y propiedades químicas y físicas de los minerales y cuerpos mineralizados. En lo que sigue la consideraremos como una ciencia en sí misma, aunque es posible que haya quien se apresure a decir que es una rama de las geociencias, lo que, como veremos en su momento, es una apropiación moderna y, aunque cómoda, no deja de ser discutible.
Hay quien describe la mineralogía como una pesadilla científica y, si bien realmente esta podría ser su etiqueta más adecuada, intentaremos en lo que sigue exponer por qué es una ciencia; es posible que se entienda también el por qué lo de llamarla pesadilla. Nuestro objetivo es introducir algunas de las ideas fundamentales de la mineralogía de la forma más intuitiva: estudiando su historia.

Fotografía de la muestra 10003 recogida de la superficie lunar por la misión Apolo XI. Aunque tiene toda la pinta de un basalto con presencia de ilmenita, olivino y otros minerales, según el DRAE no lo son. El informe completo de análisis puede obtenerse aquí [PDF] como separata del Lunar Sample Compendium.
Pero empecemos por lo más básico: ¿qué es un mineral?Si hubiera que hacer caso de eso que la Real Academia Española llama diccionario, podríamos entender por mineral una “Sustancia inorgánica que se halla en la superficie o en las diversas capas de la corteza terrestre”. Si esta definición fuese válida las sustancias inorgánicas en la superficie de la Luna, Mercurio, Venus, Marte o cualquier otro cuerpo del universo distinto de la Tierra no serían minerales; el agua líquida sería un mineral si está en la Tierra pero no en cualquier exoplaneta; y los silicatos, siendo inorgánicos y terrestres no serían minerales si están en el manto terrestre y no en la corteza. Es manifiesto que se impone, pues, dar una definición formal de mineral.

Las columnas coloreadas son erbaita, una forma de turmalina. La fórmula genérica de las turmalinas dista mucho de ser una fórmula química al uso: (Na,Ca)(Mg,Li,Al,Fe2+,Fe3+)3(Al,Mg)6(BO3)3Si6O18(OH,O,F)4. Los otros minerales presentes en la imagen son cuarzo, lepidolita y cleavelandita (una variedad de albita). Imagen: Rob Labinsky / Wikimedia Commons
Un mineral es una sustancia que:
a) existe en la naturaleza (esto incluye cualquier parte del universo) naturalmente, esto es, sin intervención humana;
b) tiene una composición química característica, aunque no tiene por qué tener una fórmula química exacta;
c) posee una estructura generalmente cristalina. Esta afirmación implica que los minerales son, en principio, sólidos, que la estructura cristalina puede tener alteraciones debido a impurezas, y que además se usa la definición actualizada de cristal (sólido con un patrón de difracción definido) lo que incluye a los cuasicristales.
Si nos fijamos no hemos incluido esa distinción arbitraria tan del siglo pasado: inorgánico/orgánico. Cualquier sustancia que cumpla lo anterior es un mineral. A las mezclas estables de minerales las llamaremos rocas.

Roca basáltica con fenocristales de olivino. Un fenocristal es un cristal de tamaño considerable respecto al resto de los componentes de una roca; es el resultado de un enfriamiento lento en el proceso de cristalización del magma. La muestra de la imagen procede de la isla de La Palma (Canarias, España y, a efectos del DRAE, planeta Tierra) y pertenece a la Universidad de Tartu (Estonia). Fuente: Wikimedia Commons
Probablemente no exista rama del conocimiento con más cambios de estatus que el estudio de los minerales, pero podemos reducirlos a tres principales. Desde el siglo XVI hasta comienzos del XIX fue un nexo entre la química y lo que se conocía como historia natural. Empleaba las técnicas de laboratorio de la primera y los principios de clasificación de la segunda para estudiar la totalidad del “reino mineral”. En esta época la mineralogía era una disciplina a la que los eruditos dedican buena parte de su tiempo habida cuenta de su trascendencia económica y alquímica.
Durante el siglo XIX la mineralogía dejó de tener esta posición de privilegio intelectual para convertirse en una subdisciplina de la geología. Es de esta época la definición de mineral como “sustancia química que ocurre naturalmente en la corteza terrestre” y su estudio se separa del de las rocas, “agrupaciones definidas de minerales”, lo que lleva a finales de sigloa distinguir entre mineralogía y petrología.
Tras la Segunda Guerra Mundial la geología pasa a formar parte de las geociencias, y las sub-sub-ramas de la mineralogía y la petrología se ven transformadas por la teoría de la tectónica de placas y por la nueva instrumentación disponible.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Esa pesadilla científica llamada mineralogía se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ellen Richards: la economía doméstica como cultura científica
- De cañones, cátedras y espías
- Una ventana llamada Rosetta
Patata frijituak akrilamida pixka batekin, mesedez
Hedabideetan akrilamida pil-pilean dago egunotan; izan ere, apirilaren 11n elikagaien akrilamida edukia kontrolatzea helburu duen Europar Batasuneko araudia indarrean sartu zen. Albistea horixe izan behar zen, alegia, toxikoa den konposatu bat kontrolatzeko araudi berri bat indarrean sartu dela, baina, akrilamidaren toxikotasuna ez da albiste. Hortaz, ezer berririk ez dago udaberriko eguzkiaren azpian, baina, momentu aproposa da akrilamidari buruz hitz egiteko eta akrilamidak kezkatu behar gaituen hausnartzeko.

1. irudia: Patata frijituek akrilamida konposatu minbizi-sortzailea dute. (Argazkia: 31 images. Iturria: pixabay.com)
Lehenik eta behin, esan behar da indarrean jarri berri den Europar Batasuneko araudiak ez dituela gehienezko mugak ezartzen, erreferentziako mailak gomendatu baizik. Izan ere, ezinezkoa -edo ia ezinezkoa- da akrilamida guztiz kentzea elikagaietatik eta, bestalde, akrilamida prozesaketa unean bertan eratzen denez, zaila da akrilamida kontzentrazioa kontrolatzea. Alabaina, araudiak akrilamida kontzentrazioa murrizteko gomendioak ematen ditu eta patata frijituak, ogia, gosarirako zerealak, kafea, gailetak eta opilak dira ikusmiran dauden elikagaietako batzuk. Oraingoz ez gara iritsi Kaliforniako arauen kasura: kafea saltzen duten saltokiek akrilamida minbizi eragilea dela ohartarazi beharko dute
Zer da akrilamida eta nola iritsi da patata frijituetara?Akrilamida C3H5NO formula duen konposatua da eta almidoia duten eta beroketa prozesuak jasan dituzten elikagaietan aurki daiteke. Oro har, 120 ºC-tik gorako tenperaturan berotu behar dira jakiak -frijitu, egosi edo erre ondoren, adibidez-. Industria aplikazioak ere baditu eta akrilamida poliakrilamidazko kopolimeroak egiteko erabiltzen da, esaterako. Toxikotasunari dagokionez, ezaguna da akrilamidak minbizia eragin dezakeela. MOE Mundiko Osasun Erakundearen menpekoa den IARC Minbizia Ikertzeko Nazioarteko Agentziaren arabera, arriskuaren eskalaren 2A mailan dago akrilamida, alegia, gizakiontzat minbizi-sortzaile probablea da eta animalietan frogatuta dago minbizia eragin dezakeela.
Etxean patatak frijitzen direnean Maillard erreakzioen kausaz eratzen da akrilamida. Maillard erreakzioak erreakzio-multzo izugarria dira, elikagaien arretze-prozesuetan gertatzen direnak. Louis Camille Maillard kimikari eta fisikari frantziarrak ikertu zituen lehen aldiz, 1912an, eta hortik erreakzio-multzoaren izena. Aminoazidoak eta azukreak -horien artean, almidoia- dira akrilamidaren aitzindariak, eta arretzearekin batera areagotzen da akrilamida edukia. Zenbat eta tenperatura altuagoan eta zenbat eta denbora luzeagoan berotu, orduan eta akrilamida gehiago metatzen da. Hala ere, Maillard erreakzioek ez dute arretzean bakarrik eragiten; izan ere, jakien zaporean eta usainean ere funtsezko garrantzia dute. Akrilamida kontzentraziorik altuenak lortzeko, azukreen eta asparagina aminoazidoaren arteko Maillard erreakzioa gertatu behar da eta 160 ºC – 180 ºC artean mantendu behar dira elikagaiak. Patataren kasuan, hain justu, hori da normalean erabiltzen den frijitze tenperatura eta, gainera, patatak duen aminoazidorik ugariena asparagina da. Horregatik, patata frijituak dira akrilamidaren toxikotasunagatik ikusmiran gehien jarri diren jakiak.
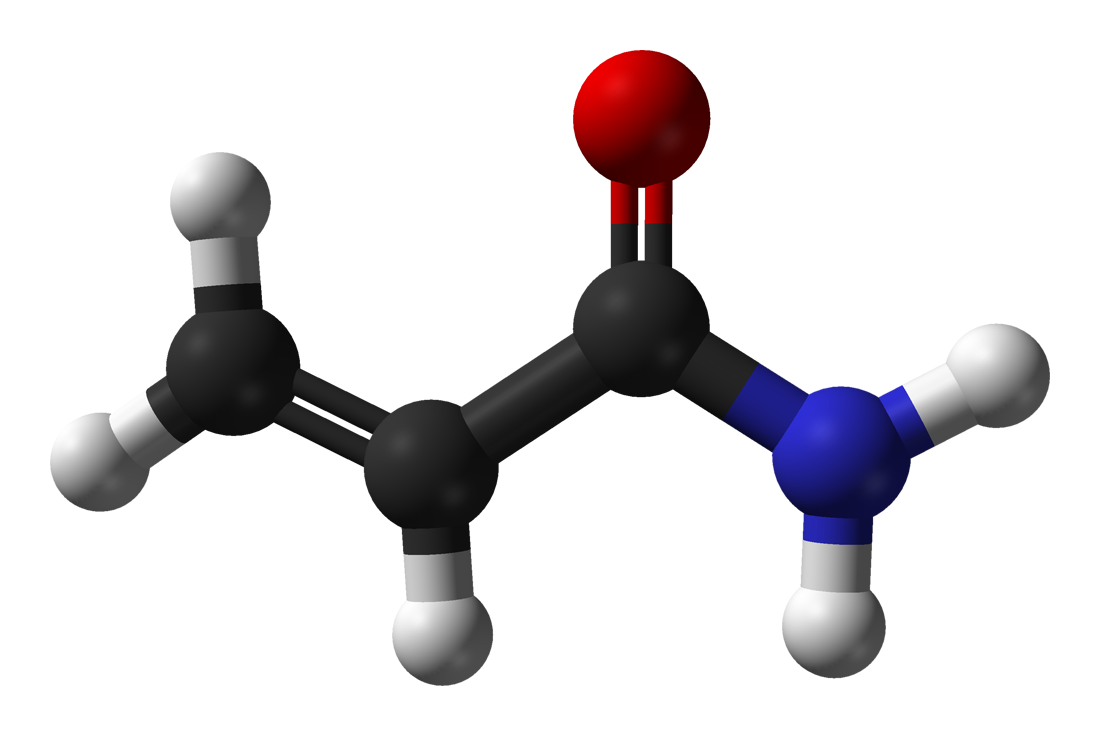
2. irudia: Akrilamida molekula. (Argazkia: Ben Mills – domeinu publikoko irudia. Iturria: wikipedia.org)
Akrilamida gutxiagoEuropar Batasuneko araudian erreferentziako kontzentrazioak ematen dira elikagaien arabera sailkatuta, baina, oro har, zaila da egunean jan daitekeen akrilamida kantitate segurua finkatzea. Kontua da minbizi-sortzaileak diren substantzien kasuan nekeza dela determinatzea zenbateko esposizioak eragin ditzakeen arazo genotoxikoak. Hala ere, ikertzaileak gai izan dira erreferentziako dosiaren konfiantzazko gutxieneko muga ezartzea -BMDL deritzona-, eta horren arabera, gutxi gorabehera egunean 150 g patata frijitu nahikoak dira egunean har daitekeen akrilamida-kantitate segurua gainditzeko. Gainera, kontuan hartu behar da helduen akrilamida-esposizioaren %49 patata eta patataren deribatuak jatearen ondorio dela, %34 kafearen ondorioa eta %23 ogiarena. Hortaz, elikagai horietan egin beharko litzateke akrilamida murrizteko saiakerarik handiena. Zentzu horretan, Europar Batasunaren araudi berriaren saiakera nagusia akrilamida kantitatea murrizteko prozesaketa moduak gomendatzea da.
Pataten kasuan, Europar Batasunak gomendatzen du fruktosa, glukosa eta asparagina eduki baxuko patata motak erabiltzea, horiek baitira akrilamida sortzen dutenak. Patatak modu egokian mantendu behar dira -patatak tenperatura altutxoagoan gordetzen badira akrilamida kontzentrazio handiagoak lortzen dira frijitu ondoren-, eta frijitzeko erabili den olioaren tenperatura kontrolatzea garrantzitsua da. Hortaz, prozesaketa termikoak birplanteatzea eskatzen du araudiak, eta baita lehengaiak aztertzea ere. Askotarikoak dira araudian zerrendatzen diren gomendioak eta betebeharrak eta elikagai motaren arabera desberdinak dira. Gaileta eta opilen kasuan, gasifikatzaile moduan amonio bikarbonatoa ez erabiltzea gomendatzen da, eta fruktosa eta eztia saihestea ere gomendatzen da.

3. irudia: Patata frijituen ondoren, kafea da helduen akrilamida esposizio handienaren erantzulea. (Argazkia: cocoparisienne – domeinu publikoko irudia. Iturria: pixabay.com)
Nolanahi ere, eta lehenago esan bezala, zenbait elikagaik akrilamida dutela ezaguna zen duela urte asko, alegia, hedabideetan argitaratu diren albisteetan ez dago ezer berria akrilamidaren edukiari edo toxikotasunari dagokionez. Bestalde, garrantzitsua da azpimarratzea jakiek akrilamida izatea ez dela prozesatze desegoki baten ondorioa; izan ere, akrilamida berez agertzen da almidoia duten elikagaiak tenperatura altuan kozinatzen direnean. Hortaz, argi izan behar dugu etxean frijitutako patatek ere akrilamida kontzentrazio altuak izan ditzaketela, agian patata komertzialena baino altuagoa izan daitekeena.
OCU kontsumitzaileen elkartearen arabera indarrean jarri berri den araudia ez da nahikoa eta, diotenez, gehiegizko mugak ezarri beharko lirateke. Araudiaren arabera, erreferentziazko kontzentrazioak gainditzen badira elikagaia ez da merkaturik atera behar, prozesaketa berraztertu baizik. Hortaz, ezarritako muga horiek gainditzea posible da akrilamida kantitatea murrizteko balizko modurik ez badago. Nolanahi ere, gehiegizko alarma eragin daiteke horrelako neurriekin; izan ere, patata frijituen gehiegizko kontsumoa arriskutsua da, bai, baina ez bakarrik akrilamida edukiarengatik. Gehiegizko erregulazioak eta mugen ezarpenak zentzurik gabeko beldurra eragin dezake eta eragingo lukeen kaltea handiagoa da ekarriko dituen onurak baino. Izan ere, ia edozein elikagaitan aurkitu daitezke minbizi-sortzaileak diren substantziak -kontzentrazio oso txikitan izanik ere-. Gainera, jakina da patatak moztu ondoren giro tenperaturan dagoen uretan murgiltzen badira 2 orduz, akrilamida kontzentrazioa erdira jaitsi daitekeela, baina, nork ez ditu nahiago txigortutako patata frijitu kurruskariak?
Informazio osagarria:
- Europar Batasuneko 2017/2158 Araudia, eur-lex.europa.eu
- Egunero jaten dituzun pozoiak (I). J. Lopez-Gazpio, Tolosaldeko Ataria, 2015
- El cuadrilátero de la acrilamida. Juan J. Iruin, Naukas.com, 2013
- Acrylamide french fries. Juan J. Iruin, elblogdebuhogris.blogspot.com, 2008
- Acrilamida, AECOSAN, aecosan.msssi.gob.es, 2018
- Acrilamida, NIH, cancer.gov, 2018
—————————————————–
Egileaz: Josu Lopez-Gazpio (@Josu_lg) Kimikan doktorea eta zientzia dibulgatzailea da. Tolosaldeko Atarian Zientziaren Talaia atalean idazten du eta UEUko Kimika sailburua da.
—————————————————–
The post Patata frijituak akrilamida pixka batekin, mesedez appeared first on Zientzia Kaiera.
Colonialismo científico: los investigadores africanos se rebelan contra el expolio de datos genéticos

Fuente: Universidad de Boston. Centro de Estudios Africanos
Desde que en el año 2001 se descodificó el primer genoma humano, miles de ellos han pasado por el mismo proceso y poco a poco estamos creando una enorme base de datos mundial que refleja nuestra diversidad como especie. El continente africano está siendo escenario de gran parte de esa recolección de datos: en África, el lugar donde aparecieron los primeros de nuestros antepasados, los distintos grupos de población contienen interesantes variaciones para entender los cruces genéticos que nos dieron forma, cómo nos movemos y alimentamos y las enfermedades que todavía hoy sufrimos.
Hay grandes beneficios en juego para la población africana a cambio de aportar esta valiosa información al campo de la genómica a nivel global. Conocer las variaciones genéticas de un grupo puede ayudar a mejorar su atención médica. En muchas regiones de África eso puede significar una mejora de la calidad de vida incalculable.
El expolio de los datos
Pero a medida que la genómica avanza y despega, los científicos africanos temen (y están observando ya) como las viejas dinámicas del colonialismo vuelven a hacer de las suyas y las grandes potencias mundiales se dedican a explotar sus recursos y ofrecer nada a cambio. A causa de la falta de recursos, hay pocas instituciones científicas en África que puedan llevar a cabo en solitario investigaciones de este tipo, que en muchos casos requieren complejos equipos informáticos capaces de procesar miles de datos con velocidad. Por eso, los equipos que tienen interés en investigar en este campo a menudo tienen que asociarse y aceptar las condiciones de grupos de otros países. Y esas condiciones muchas veces dejan muy poco margen y resultado para los científicos locales.

Investigación alimentaria en África. Fuente: Wikipedia Commons
Lo llaman ‘investigación helicóptero’, una práctica por la que los investigadores de países desarrollados acuden a los países en desarrollo, recogen sus datos y se marchan de allí sin contar con los científicos locales. A veces incluso pueden compartir a posteriori esos datos con otros grupos que no estuvieron involucrados en su recogida, lo cual crea una indignante contradicción en la que la información recabada y los resultados derivados de ella benefician a todo el mundo excepto a la población de la que se extrajo.
Una guía de buenas prácticas
Conocedores de cómo puede terminar esta historia (los países del continente expoliados de sus datos genéticos, que estarán dando réditos a miles de kilómetros donde sus habitantes apenas llegarán a olerlos, ¿no les suena esto de algo?), los científicos africanos han decidido tomar cartas en el asunto y han publicado una guía de buenas prácticas a exigir para desarrollar investigaciones genéticas en África. Detrás del documento está la Human Heredity and Health in Africa (H3Africa) Initiative, un consorcio que apoya y promueve investigaciones biomédicas en el continente.
“El hecho de compartir [datos] para contribuir al bienestar de otros sería algo ampliamente respaldado en África. Pero eso siempre debe ir unido a la reciprocidad, debe hacerse de una forma responsable, con la aportación de todos los involucrados y con mecanismos que obliguen a los equipos de investigación a hacerse responsables y a dar explicaciones de sus actos”, explican los autores del documento, que aseguran que así los africanos podrán participar y contribuir al avance en este campo de innovación, “algo que, aunque caro por el momento, tiene un enorme potencial para retornar en forma de menores costes sanitarios cuando conozcamos los determinantes genómicos de muchas enfermedades”.

Fuente: Wellcome UK
El documento establece algunos principios básicos. Para empezar, las investigaciones genómicas que se lleven a cabo en África deben ser sensibles y respetuosas con las culturas y valores de los africanos, así como establecer los beneficios para ellos como uno de sus objetivos primordiales. Además, estos proyectos y la publicación y publicitación de sus resultados deben contar con la aportación y participación de científicos africanos. “Teniendo en cuenta que el objetivo principal de la investigación genómica en África debería ser el beneficio de los africanos, la contribución de los científicos que trabajan en instituciones africanas debería ser significativa y sustanciosa, incluyendo el liderazgo o coliderazgo intelectual efectivo”.
La ciencia que reduzca desigualdades y no las aumente
La idea es que esta guía dé ideas y estrategias a los científicos africanos a la hora de negociar con sus socios extranjeros. Los marcos temporales son especialmente críticos debido al desequilibrio en capacidad de computación de unos y de otros, así que una forma de evitar el saqueo de datos podría ser, por ejemplo, exigir periodos de embargo durante los cuales investigadores que no hayan participado en la recogida de datos no puedan publicar resultados basándose en ellos.
A nadie se le escapa que no será fácil conseguir que estas reglas sean respetadas. Los científicos africanos juegan en desventaja económica, lo cual puede mermar su capacidad para imponer condiciones a la hora de pactar las condiciones de futuras colaboraciones científicas.
Pero si hemos aprendido algo de nuestra propia historia, si tenemos claro qué actitudes e injusticias del pasado terminaron conformando el mundo desigual en el que vivimos hoy, si de verdad el avance de la ciencia tiene como objetivo mejorar el bienestar de toda la humanidad… Entonces no dejaremos que la investigación se convierta en otra palanca para seguir ampliando la brecha que separa a ricos y pobres hasta desgajarnos.
Referencias
Ethics and Governance Framework for Best Practice in Genomic Research and Biobanking in Africa – Human Heredity and Health in Africa (H3Africa) Initiative
African scientists call for more control of their continent’s genomic data – Nature
How the genomics revolution could finally help Africa – Nature
‘Helicopter’ researchers – issues with research being conducted on mining impact in North Western Province Zambia – Australian National University
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo Colonialismo científico: los investigadores africanos se rebelan contra el expolio de datos genéticos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Pena de muerte contra el fraude científico
- Contra el furtivismo, genética molecular
- Ciencia aplicada (1): Quibim, los datos ocultos tras una imagen
Angelman sindromearen sintoma konplexuen zergatia aurkitu dute

Irudia: Angelman sindromea duten pertsonen ezaugarririk deigarriena beraien izaera alai eta irribarretsua da (Argazkia: Porsche Brosseau).
Diseinu esperimental berritzaile bati esker eta azken belaunaldiko azpiegiturari esker, UBE3A entzimak eraldatutako proteinetan sortzen diren aldaketak identifikatu dituzte. Emaitzen arabera, proteosomaren funtzioa doitzeaz arduratzen da UBE3A eta proteosomak zeluletan gainerako proteinen oreka erregulatzen du. Hortaz, zeharka, zelulen barruan garatzen diren hainbat eta hainbat prozesuren egonkortasunaren erantzukizuna du UBE3A entzimak.
Angelman sindromearen kasuan, UBE3Aren hutsegitea dela eta, prozesu horiek ez dira behar bezala garatzen eta entzimak bere funtzioa behar bezala betetzen ez duenean sortzen den sindromearen konplexutasuna azaltzen du. Aurretik ere ikertu izan da gaixotasun horren sorburu genetikoa, sintomak eta zelan aurre egin ere, baina orain arte ezin izan da azaldu gene bakar batek zelan sor dezakeen hainbeste alterazio garunaren funtzioan.
Angelman Sindromea15.000 jaioberritik bati eragiten dio Angelman sindromeak. Adimenaren garapenean arazo konplexuak sorrarazteaz gain, epilepsia eta komunikaziorako zailtasunak eragiten ditu; baita mugimenduaren koordinazio gabezia, oreka eta mugimendu arazoak eta ordu gutxi lo egitea. Sindromea duten pertsonen ezaugarririk deigarriena, dena den, izaera alai eta irribarretsua da. Horren guztiaren eragilea garunean huts egiten duen gen bakar bat da: UBE3A. Hala, entzimak garunean ondo funtzionatzen ez badu gaixotasuna sorrarazten du.
Angelman Sindromearen Elkarteak eskainitako funtsak giltzarria izan dira ikerlana gauzatu ahal izateko, une kritiko batean, Mayor doktorearen laborategiak inolako laguntzarik ez zuenean, funts horiek oinarri-oinarrizkoak izan dira proiektua gauzatu ahal izateko.
Iturria: UPV/EHU prentsa bulegoa: Angelman-en sindromearen sintoma konplexuen zergatia aurkitu dute UPV/EHUko ikertzaileek.
Erreferentzia bibliografikoa
Mayor, Ugo et. al : Quantitative proteomics reveals neuronal ubiquitination of Rngo/Ddi1 and several proteasomal subunits by Ube3a, accounting for the complexity of Angelman syndrome, Human Molecular Genetics, , ddy103, https://doi.org/10.1093/hmg/ddy103
The post Angelman sindromearen sintoma konplexuen zergatia aurkitu dute appeared first on Zientzia Kaiera.
El organismo humano es una estufa de unos pocos vatios

El organismo humano es un agregado de millones de células en las que tienen lugar innumerables reacciones químicas de forma permanente, y en su interior se llevan de un lado para otro sustancias de lo más diverso. Gracias a ello se mantiene vivo. Además, suele dedicar parte de su tiempo a desarrollar algunas actividades físicas. Todo ello da lugar a una cierta producción de calor que acaba por disiparse. El calor disipado constituye una pérdida de energía y lo llamamos gasto metabólico porque, en última instancia, tiene su origen en el metabolismo del organismo, que es el conjunto de procesos que intermedian en las actividades citadas.
En promedio, un kilogramo de ser humano en reposo gasta 22 kilocalorías al día (valor promediado para hombres y mujeres adultas de diferentes edades). Pero no todos los kilogramos gastan lo mismo. Corazón y riñones gastan 440 kilocalorías por kilo y día. No está nada mal; aunque la masa de cada uno representa el 0,4% de la del organismo, dan cuenta del 8% (corazón) y 8,5% (riñones) del gasto total. Del corazón sabemos que late unas ochenta veces por minuto sin descanso, noche y día, y como vemos, a un alto coste relativo. No imaginábamos, sin embargo, que los riñones se esforzasen tanto, pero lo hacen. Trasiegan con brío agua y otras sustancias, y gracias a ese gran trabajo llevándolas de aquí para allá, fabrican una orina llena de productos de deshecho pero a la que le han quitado las sustancias que necesita el organismo, para que no se pierdan.
Sin llegar al nivel de los anteriores, el hígado y el encéfalo son también verdaderos campeones metabólicos. La masa de cada uno de ellos no supera el 2% de la de todo el organismo, pero con un gasto de 200 (hígado) y 240 (encéfalo) kilocalorías por kilo y día, su actividad da cuenta de una producción de calor que representa, respectivamente, el 17% y el 20% de la producción total del organismo. Tampoco está mal.
Mucho menos activa es la musculatura (recordemos que el organismo del que hablamos está en reposo), que representa el 36% de la masa total pero solo gasta el 21% de la energía. Y muy parecido es el nivel metabólico del resto de órganos (excluido el tejido graso) que suponen el 19% de la masa y el 34% del gasto energético. La tasa metabólica de músculos y otros tejidos es, respectivamente, de 13 y 12 kilocalorías por kilo y día. Finalmente nos queda la grasa corporal. Un kilo de tejido adiposo gasta unas ridículas 4,5 kilocalorías diarias; por eso, aunque la grasa representa una cuarta parte de la masa corporal, solo gasta el 5,5%. O sea, cuando el organismo acumula grasa, no solo engorda, sino que, además, produce un tejido que prácticamente no gasta energía.
Aunque lo hacen en diferente grado, todos los órganos contribuyen al gasto energético total del organismo en reposo, que se acerca a las 1600 kilocalorías diarias. Esa cifra representa aproximadamente el 75% del gasto diario total de individuos poco o nada activos. Habría que añadirle las 160 kilocalorías que se gastan en la digestión y absorción del alimento. Y si el sujeto en cuestión desarrolla una gran actividad física, el gasto energético diario podría llegar a ser un 50% mayor. Para que nos hagamos una idea, en reposo y sin comer, gastaríamos a diario una cantidad de energía equivalente al calor que produce una estufita de 75 vatios, pero si hiciésemos una actividad física relativamente intensa de forma cotidiana, la estufita podría llegar a ser de casi 150 vatios.
Fuente: Zi Mian Wang, Zhiliang Ying, Ania Bosy-Westphal, Junvi Zhang, Britta Schautz, Wiebke Later, Steven B Heymsfield & Manfred J Müller (2010): Specific metabolic rates of major organs and tissues across adulthood: evaluation by mechanistic model of resting energy expenditure. Am J Clin Nutr 92 (6): 1369-1377 doi: 10.3945/ajcn.2010.29885
—————————————————————–
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
Una versión anterior de este artículo fue publicada en el diario Deia el 31 de diciembre de 2017.
El artículo El organismo humano es una estufa de unos pocos vatios se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El neerlandés que subirá unos pocos metros pero bajará una montaña
- ¿Cuántas células hay en el cuerpo humano?
- El encéfalo humano
Asteon zientzia begi-bistan #199

Bioteknologiaren bitartez bihotz muskuluak sortzea lortu du Columbiako Unibertsitateko (AEB) ikertzaile talde batek. Zelula ama pluripotente induzituetatik eratorritako kardiomiozitoak baliatu dituzte karga elektrikoak jasotzean bihotz muskulu baten antzera funtzionatzen duen ehuna lortzeko. Egokitze elektromekanikoa baliatu dute bihotza “entrenatzeko” eta elektrizitatearen bitartez uzkurdurak eragin dituzte. Aurrerapen honek bide berriak ireki ditzake bihotz ehun artifizialak sortzeko eta kardiologiari buruzko ikerketak egiteko.
Ikerketa baten arabera, kolon distaleko minbizia izateko arrisku txikiagoa dute haragi gorririk gabeko dieta egiten duten emakumeek. Iragarpenen arabera, 2030. urterako 2,2 milioi kolon eta ondesteko edo hesteetako minbizi kasu baino gehiago diagnostikatuko dira munduan. Erresuma Batuko Emakumeen Kohorte Azterketaren datuak baliatu dituzte eta lau dieta alderatu dira ikerketan: erregulartasunez haragi gorria, hegaztiak, arraina kontsumitzen dutenak eta dieta begetarianoak. Dieta bakoitzak zer eragin duen ikertu dute eta ikusi dute haragi gorria sarri jaten dutenek kolon distaleko minbizi tasa handiagoa dute haragi gorririk jaten ez dutenek baino.
Leuzemia tratatzeko bizkarrezur-muinaren transplante bat jaso ondoren, GIBa detektaezin bihurtu zaie zenbait pazienteri. Ondorio horren atzean dauden mekanismoak argitzea da Jon Badiola Gonzálezen helburua. Berlingo paziente bati (leuzemia eta hiesa zituen) bizkarrezur-muinaren transplante bat egin ondoren, leuzemia sendatzeaz gain, GIBa desagerraraztea lortu zuten. Orain bi paziente ari da ikertzen Virgen de las Nieves Unibertsitate Ospitalean (Granada) baina aldea dago lehenengoarekin konparatuta: Berlingoaren kasuan, sendatuta dagoela esan daiteke, ez baitu botikarik hartzen eta ezin zaio birusa detektatu. Granadako pazienteei ere ezin diegu detektatu, baina, oraingoz, erretrobiralak hartzen jarraitzen dute”.
Zainketa intentsiboko unitateko pazienteen familiek dituzten beharren berrikusketa plazaratu dute ikerketa batean. Ospitaleratzea etsigarria izaten da bai pazientearentzat bai bere familiarentzat. Aztertuta dago ospitalizazioa zainketa intentsiboko unitatean izaten bada, are larriagoa suertatzen dela egoera. Familiak pazientearen eboluzioaren informazio falta sentitzen du. Ildo honi jarraiki, lan honen helburua izan da ingresoa irauten duen bitartean familiak pairatu dezakeen estres egoera eta azalarazten dituzten beharrak identifikatu eta deskribatzea. Ondorioak ezagutzeko, jo ezazue artikulura.
PaleontologiaEHUko, Zaragozako Unibertsitateko eta Nova Lisboa Unibertsitateko ikertzaileek 300 sirenio-hezur fosil aurkitu dituzte, eta orain arte ezagutu gabeko sirenio-espezie bati dagozkiola frogatu dute. Aurkitutako espezieari Sobrarbesiren cardieli deitu diote. Duela 42 milioi urteko sirenio-espeziea da eta Piriniotan topatu dute.
Saudi Arabian, Al Wusta izeneko aztarnategian, Homo Sapiens espeziearen hatz fosilizatu bat aurkitu dute. Max Planck Giza Historiaren Zientzia Institutuak 88.000 urtetan datatu du. Hatz baten erdiko falangea da; Arabiako penintsulan aurkitutako gure espezieko lehen arrastoa da eta Afrika nahiz Mediterraneo ekialdetik kanpo aurkitu den Homo Sapiens hezurrik zaharrena.
Emakumeak zientzianBadira emakumeek egindako lanak sarean ikusarazten dituzten pertsonak eta webguneak. Marta Macho Stadler, EHUko Zientzia eta Teknologia Fakultatean irakaslea eta ikerlaria da horietako bat. Mujeres con Ciencia blogean egunero hainbat emakumeri buruzko artikuluak argitaratzen ditu. Machok ohartarazi duenez, emakume “gutxi” daude karrera zientifiko eta teknologikoetan: “Ez badaukazu erreferenterik erakutsiko dizunik zientzia eta teknologia zure kolektiboari ere badagozkiela, pentsa dezakezu —neska gazte askok pentsatzen duten bezala— eremu horiek ez dagozkizula”. Wikipediaren bitartez ere topa ditzakegu emakume zientzialariei buruzko testuak. Baina arazoa da “biografia oso txikiak izaten direla, informazio gutxikoak, eta argazkirik gabe asko”. Horri aurre egiteko, emakumeak euren artean antolatu dira Wikiemakumeok-en moduko proiektuetan.
Curie familiaren inguruan erretratu interesgarri bat egin dute Berrian, Helene Langevin-Joliot Fisikako doktorea Bilbon izan baita asteon, bere familiari buruzko jardunaldietan. Marie eta Pierre Curie senar-emazteek Nobel saria irabazi zuten erradioaktibitateari lotutako lehen ikerketak egiteagatik, Henri Becquerelekin. Marie Curie izan zen Nobel bat jaso duen lehen emakumea. Haien alaba Irene Joliot-Curiek eta haren senar Jean Frederic Joliotek ere Kimika arloko Nobela irabazi zuten, erradioaktibitate artifiziala aurkitzeagatik. Marie Curieren lana, testu honetan aztergai.
2009. urtean bi emakume zientzialarik lortu zuten Medikuntza eta Fisiologiako Nobel saria: Carol Greider eta Elizabeth Blackburnek Jack W. Szostakekin partekatu zutena. Telomeroek kromosomak babesteko funtzioa zutela ikusi, eta Telomerasa entzima aurkitu eta identifikatu zutelako, hain zuzen. Telomeroak kromosomen muturretan dauden egiturak dira eta kromosomak babesteaz arduratzen dira. “Erloju biologikoak” direla esaten da, zehazten baitute zelula batek bere bizitza osoan zehar izan dezakeen zatiketa kopurua. Hortaz, zelulen zahartzeaz arduratzen dira. Telomerasa, aldiz, telomeroak luzatzeaz arduratzen den entzima da.
InformatikaZer dira Txatbotak? Funtsean, software robotiko osagai bateri deritzo, berau, gizakien elkarrizketa bat testu txat edo ahots aginteak erreproduzitzeko balio duena, Sirik egiten duen antzera. Dagoeneko industria eta negozio anitzetan erabiltzen dira, informazioa entregatzeko edo oinarrizko eginbeharrak egiteko, hotel erreserbak egiteko edo eguraldiari buruz informatzeko, adibidez. Txatbot-ak beharrezkoa duten informazioa itzul dezakete, datuak beraien testuinguruan analiza ditzakete eta emaitzak hitz egiten edo idatzian eman ditzakete.
FisikaZer da Coriolis efektua? Testuan adibide garbi batekin azaltzen digute afera: Hegazkin bat A puntutik B puntura doa. Lurrak ez balu bere ardatzaren inguruan birarik emango, hegazkinak lerro zuzen bat egingo luke baina Lurra etengabe errotatzen ari da eta beraz desbideratu egingo litzateke eta C puntura iritsiko litzateke. Desbideraketa hori Coriolis efektuaren ondorioa da. Hegaldietan, jakina, hori kontuan hartu behar dute. Coriolis fisikari frantsesaren izena darama efektu hori, izan ere 1835ean plazaratu zuen efektu hau azaltzen zuen adierazpide matematikoa. Eta nola eragiten du harraskako uraren biraketaren noranzkoan? Etxe harraskan zaila da ikustea efektua. Baldintza arruntetan, hau da, gure etxeko harraskan ez du erabakitzen uraren mugimenduaren noranzkoa.
BiologiaAnimaliek bi aukera dituzte oxigenoa garraitzeko. Alde batetik, odolean arnas pigmentuaren (hemoglobina, adibidez) kontzentrazioa igotzea. Baina hemoglobinaren kontzentrazioak badu muga ere, zeren eta altuegia bada (globulu gorri gehiegi badaude) odola dentsoegi geratzen baita eta kapilarretatik mugitzeko arazoak izan baititzake. Beste aukera da, hemoglobina kontzentrazioa igo gabe. Biriketan oxigeno-kantitate bera hartuta, bada gehiago garraiatzeko modurik baldin eta ehunetara heltzean hemoglobinaren funtsezko ezaugarri bat aldatzen bada. Hau da, biriketatik igarotzen denean, hemoglobinaren oxigenoarekiko kidetasuna altua da, baina jaitsi egiten da ehunetara heltzean. Oxigenoarekiko kidetasunaren kontzeptua da hori eta horren harira, albiste bat aurkezten digute: hemoglobinaren oxigenoarekiko kidetasuna neurri handian jaisten duen gai kimiko bat aurkitu dute eta kidetasunaren jaiste horri esker nabarmen handitzen da pigmentuak zelulei ematen dien oxigeno kantitatea. Jean-Marie Lehn Nobel saridunak zuzendu du ikerketa hori abiatu duen taldea.
GenetikaAste honetan, EGFR genea daukagu mintzagai. Koldok azaltzen digun moduan, zelularen funtzio askotan parte hartzen du. Horretaz gain, minbizi mota batzuetan paper garrantzitsua jokatzen du. EGFR genearen mutazioak ikertzen dira gaixotasun batzuetan edo tumoreetan duten papera zehazteko, izan ere gene horrek prozesu ugaritan parte hartzen du.
———————————————————————–
Asteon zientzia begi-bistan igandeetako atala da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna erreparatuz, Interneteko “zientzia” antzeman, jaso eta laburbiltzea da gure helburua.
———————————————————————–
Egileaz: Uxue Razkin Deiako kazetaria da.
———————————————————————–
The post Asteon zientzia begi-bistan #199 appeared first on Zientzia Kaiera.
Naukas Bilbao 2017 – Pepe Cervera: Despegue: cuando la Inteligencia Artificial supera a la humana
En #Naukas17 nadie tuvo que hacer cola desde el día anterior para poder conseguir asiento. Ni nadie se quedó fuera… 2017 fue el año de la mudanza al gran Auditorium del Palacio Euskalduna, con más de 2000 plazas. Los días 15 y 16 de septiembre la gente lo llenó para un maratón de ciencia y humor.

Si no sabemos definir adecuadamente la inteligencia en humanos, ¿sabremos reconocer una inteligencia artificial? Pepe Cervera tiene claro que sí.
Pepe Cervera: Despegue:cuando la Inteligencia Artificial supera a la humanaEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2017 – Pepe Cervera: Despegue: cuando la Inteligencia Artificial supera a la humana se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – Daniel Marín: Algo se muere en el alma cuando una sonda se va
- Naukas Bilbao 2017 – Guillermo Peris: Los trapecistas del genoma
- Naukas Bilbao 2017 – José Miguel Viñas: Me río yo del cambio climático
Ezjakintasunaren kartografia #212

Pinker/Garcés eztabaidan zein den objektiboago analizatu ostean, filosofikoago jartzen da Jesús Zamora Bonilla, pentsalariek egiten dituzten interpretazioen atzetik zer dagoen bilatzeko The Enlightenment wars (& 3): but…what kind of humanism do we need? artikuluan.
Zelan lortu esfortzua egitea? Guraso, irakasle eta enplegatzaileek beti egin duten galdera da. José Luis Ferrerirak gaiari buruz: What motivates effort?
Ohiko lotura kimikoak ez diren mekanismoei esker eusten dio molekulez osatutako solido batek solido izateari. DIPCkoek What bounds a molecular solid together?
–—–
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #212 appeared first on Zientzia Kaiera.
Consumo de carnes rojas y ubicación del cáncer en mujeres
Al comparar el efecto que tienen cuatro tipos de dieta —que incluyen regularmente carnes rojas, aves, pescado o las dietas vegetarianas— en el desarrollo de cáncer en secciones específicas del colon, se ha encontrado que quienes comen carne roja con regularidad, en comparación con quien sigue una dieta sin carne roja, tenían mayores tasas de cáncer de colon distal, un tipo de cáncer situado en la sección descendente del colon, donde se almacenan las heces.

“El impacto de los diferentes tipos de carne roja y de los patrones dietéticos en la ubicación del cáncer es uno de los mayores desafíos en el estudio de la dieta y el cáncer colorrectal. Nuestra investigación es uno de los pocos estudios que analizan esta relación y, si bien se necesitan análisis adicionales en un estudio más amplio, podría proporcionar información valiosa para aquellas personas que tienen antecedentes familiares de cáncer colorrectal y quienes trabajan en el ámbito de la prevención y la salud pública”, señala Diego Rada Fernández de Jáuregui, miembro del Departamento de Medicina Preventiva y Salud Pública de la Facultad de Farmacia de la UPV/EHU y del Grupo de Epidemiología Nutricional (NEG) en la Universidad de Leeds (Reino Unido) y autor principal de este trabajo.
Se espera que para el año 2030 se diagnostiquen más de 2,2 millones de nuevos casos de cáncer colorrectal, también conocido como cáncer de intestino, en todo el mundo. Es el tercer tipo de cáncer más frecuentemente diagnosticado en las mujeres del Reino Unido. Estudios previos han sugerido que comer mucha carne roja y procesada aumenta el riesgo de desarrollar cáncer colorrectal y se estima que alrededor de 1 de cada 5 cánceres intestinales en el Reino Unido están relacionados con el consumo de este tipo de carne. Sin embargo, hay información limitada disponible sobre los patrones dietéticos específicos y el lugar de aparición del cáncer en el intestino.
En el estudio, utilizaron datos del Estudio de Cohortes de Mujeres del Reino Unido (UKWCS). Esta cohorte incluyó un total de 32.147 mujeres de Inglaterra, Gales y Escocia. Fueron reclutadas y encuestadas por el Fondo Mundial de Investigación del Cáncer entre 1995 y 1998 y fueron monitorizadas durante 17 años de promedio.
Además de registrar sus hábitos dietéticos, se documentaron un total de 462 casos de cáncer colorrectal, y de los 335 cánceres de colon, 119 casos fueron casos de cáncer de colon distal. El análisis del estudio, publicado recientemente en la revista International Journal of Cancer, exploró la relación entre los cuatro patrones dietéticos y el cáncer colorrectal; un análisis exploratorio posterior examinó, asimismo, la asociación entre la dieta y las subsecciones del colon donde apareció el cáncer.
Janet Cade, coautora del trabajo y jefa del NEG, y profesora de Epidemiología Nutricional y Salud Pública en la Facultad de Ciencias de la Alimentación y Nutrición de Leeds, comenta que “nuestro estudio no solo ayuda a arrojar luz sobre cómo el consumo de carne puede afectar de manera diferente a las secciones del colon y recto; pone de manifiesto la importancia de contar con información dietética fiable de grandes grupos de personas. El contar con acceso al Estudio de Cohorte de Mujeres del Reino Unido nos permite descubrir tendencias en la salud pública y analizar cómo la dieta puede influir en la prevención del cáncer. Los informes dietéticos precisos ofrecen al personal investigador la información necesaria para vincular estos dos aspectos”.
Referencia:
Diego Rada Fernández de Jáuregui, Charlotte E. L. Evans, Petra Jones, Darren C. Greenwood, Neil Hancock, Janet E. Cade (2018) Common dietary patterns and risk of cancers of the colon and rectum: Analysis from the United Kingdom Women’s Cohort Study (UKWCS) International Journal of Cancer doi: 10.1002/ijc.31362
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Consumo de carnes rojas y ubicación del cáncer en mujeres se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Seguridad diagnóstica en el cáncer de colon y tratamiento del de páncreas
- Nanopartículas para reducir la metástasis hepática del cáncer de colon
- Detección precoz del cáncer de colon por métodos no invasivos
Antonio de Ulloa, el marino que leía a Newton
El 25 de marzo de 1726 se publica en Londres la tercera edición de Philosophiæ naturalis principia mathematica (los Principia), de Isaac Newton, una de las obras más importantes, revolucionarias e influyentes de la historia de la ciencia. Se imprimieron 1250 copias cuidadosamente encuadernadas en piel de Marruecos. Una de ellas llegó veinte años después a las manos de un joven marino español, apresado por corsarios ingleses cuando participaba en una expedición científica, y que acabó siendo nombrado miembro de pleno derecho de la Real Sociedad de Londres para el Avance de la Ciencia Natural, la Royal Society.
Tercera edición de los Principia
Antonio de Ulloa y de la Torre-Giralt (Sevilla, 1716 – San Fernando, 1795) fue una de las figuras más destacadas de la Ilustración española como escritor, científico y naturalista. Hijo del aristócrata Bernardo de Ulloa, con solo catorce años se embarcó en el galeón San Luis hacia las Antillas para regresar dos años más tarde al puerto de Cádiz. Ingresa unos meses después en la recién creada Real Academia de Guardias Marinas y en 1735 fue destinado, con diecinueve años y el rango de teniente de fragata, como representante de la corona española junto a Jorge Juan y Santacilia en la Misión geodésica francesa, una ambiciosa expedición científica que pretendía medir un grado del arco de meridiano en el ecuador terrestre.

Antonio de Ulloa
El fin último de esta expedición era zanjar la discusión por la forma de la Tierra que enfrentaba a la comunidad científica entre los newtonianos, que sostenían la forma achatada por los polos, y los cartesianos (como los franceses Piccard, La Hire y Cassini), que decían que lo estaba por el ecuador. ¿Tenía la Tierra forma de calabaza o de melón? En paralelo, se envió otra expedición a Laponia encabezada por el astrónomo Pierre Louis Maupertuis y en la que participó activamente el sueco Anders Celsius, creador de la escala de temperatura centígrada que lleva su nombre. Y fue esta segunda expedición en las frías regiones del Ártico la que demostró que la Tierra está achatada en los polos, dando la razón a los newtonianos. El filósofo francés Voltaire, que estuvo muy atento al desarrollo de estas misiones por el alcance científico y político, escribió: «Han confirmado con mucha transpiración lo que Newton descubrió sin salir de su habitación».
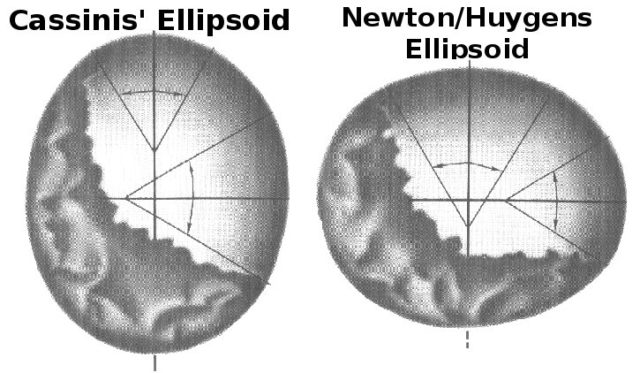
Cassini vs Newton
Durante la expedición francesa en Perú de 1735, un marinero galo descubrió casualmente unos nódulos de arcilla grisácea mientras caminaba por un estuario y se lo entregó a Ulloa. En la arcilla se encontraban unos trozos de un extraño metal plateado que ya era conocido desde tiempo atrás en América del Sur. Ulloa se dio cuenta inmediatamente de que se encontraba delante de un nuevo elemento metálico, el platino, y se le considera su descubridor, pero no sin cierta polémica porque no llegó a aislarlo o a estudiar sus propiedades. El joven teniente de fragata bautizó al metal como platina del Pinto («plata pequeña del río Pinto»), o simplemente platina, y fue posteriormente el insigne químico británico Humphrey Davy el que le dio el nombre definitivo con el que lo conocemos en la actualidad.
Pese al adelanto y el éxito de la misión en Laponia, los resultados científicos de la expedición en Perú y Ecuador fueron muy importantes y productivos para la ciencia del siglo XVIII. Se midió con más exactitud el arco del meridiano, se hicieron medidas de la gravedad a varias altitudes y se realizaron valiosas medidas de la velocidad del sonido.
Como curiosidad añadida, podemos destacar las observaciones y cartografía de la Luna, que con la ayuda de un pequeño telescopio, Ulloa y Jorge Juan recogieron en la obra Observaciones astronómicas y físicas hechas de orden de Su Majestad en los Reinos de Perú.
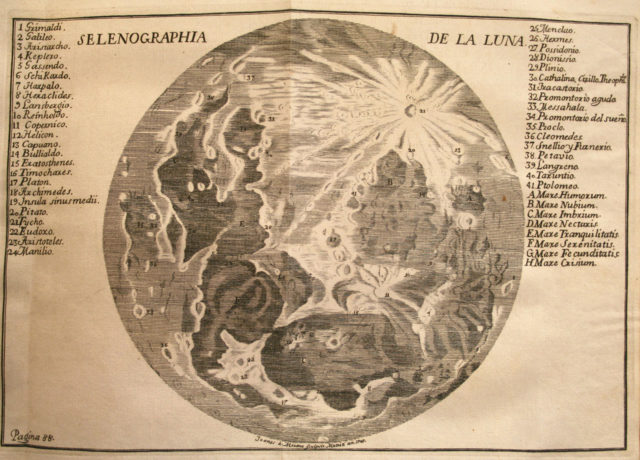
Selenographia de la luna
En agosto de 1745, durante el viaje de regreso a España a bordo de la fragata Délivrance, Antonio de Ulloa fue capturado por un navío británico y enviado preso a Inglaterra. Se le incautó toda la documentación científica que traía de su expedición y se la remitió a la Royal Society. Varios miembros se interesaron por el trabajo de Ulloa, entre ellos se encontraba el entonces presidente Martin Folkes, un brillante matemático que fue nombrado vicepresidente por el mismísimo Isaac Newton en 1923. Folkes entabló amistad con Ulloa en el proceso de recuperación de su trabajo requisado y quedó asombrado con la recopilación de datos científicos en su década de investigación en las Américas. Tanto es así, que Ulloa fue nombrado miembro de la Royal Society en diciembre de 1746 en justicia con su trabajo y sus descubrimientos. Un poco antes, a mitad de ese año de 1746, Martin Folkes le regaló a su amigo sevillano un ejemplar de los Principia de Newton, en su tercera edición, con la siguiente dedicatoria en un latín poco ortodoxo: «Viro doctrina simul et moribus spectabili Dº Antonio de Ulloa, Hispalensi, auspicatum in patriam reditum omniaque dein felicia ex animo precatur. Martinus Folker, Regalis Societatis Londini Praeses, et Regia Scientiarum Academiae Parisiensis Socies. 3º Eid. May Anno salutis reparatae M.DCCC.XLVI».
Ese ejemplar de los Principia se encuentra en la actualidad en la Biblioteca de la Universidad de Sevilla y era uno de los seis libros de Isaac Newton de la fabulosa biblioteca personal del gran Antonio de Ulloa y de la Torre-Giralt, el marino que leía a Newton.
Este post ha sido realizado por Daniel Torregrosa (@DaniEpap) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
Referencias y más información:
- Antonio de Ulloa. La biblioteca de un ilustrado, AA., 2015.
- El secreto de Prometeo y otras historias sobre la tabla periódica de los elementos, Alejandro Navarro Yañez, 2015.
- Observaciones astronomicas y phisicas hechas de orden de S. M. en los Reynos del Perú, Jorge Juan y Antonio de Ulloa, 1748.
- La misión geodésica francesa, Bernard Francou, 2015.
- El mapa lunar de Jorge Juan y Antonio de Ulloa, Paco Bellido, 2010.
El artículo Antonio de Ulloa, el marino que leía a Newton se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los institutos Isaac Newton y Oberwolfach, dos curiosas instituciones de investigación matemática
- “Comunicar la ciencia, menuda historia” por Xurxo Mariño
- Arte & Ciencia: Imaginario marino
Elizabeth Blackburn eta Carol Greider: Gure “erloju biologikoaren” funtzionamendua zehaztu zuten zientzialariak
1. irudia: Elizabeth Blackburn eta Carol Greider zientzialariak. (Argazkia: media.npr.org)
Telomeroak kromosomen muturretan dauden egiturak dira. Horien helburua da kromosomen egituraren osotasuna bermatzea eta jakina, horiek babestea, kalterik sufri ez dezaten. Blackburnek berak irudi polit bat jarri zuen adibide gisa horien lana zein zen zehazteko asmotan: lokarrietako muturretan kokatzen diren plastikozko “txanoak” bezalakoak dira, horrela lokarrien ertzak ez dira inoiz zirpiltzen.
Zelula banaketa gertatzen denean, hau da, jatorrizkoa beste bi zelula alabetan banatzen denean, kromosometako telomeroak laburtu egiten dira eta zatiketa bakoitzarekin are laburragoak bilakatzen dira. Neurri minimora iristen diren arte, jakina. Une horretan, zelula hil egiten da. Telomeroak “erloju biologikoak” direla esaten da, zehazten baitute zelula batek bere bizitza osoan zehar izan dezakeen zatiketa kopurua. Hortaz, zelulen zahartzeaz eta ugaltze egokiaz arduratzen dira.

2. irudia: Elizabeth H. Blackburn, Jack W. Szostak eta Carol W. Greider Nobel saria jaso zuten telomeroek kromosomak babesteko funtzioa zutela ikusteagatik eta Telomerasa entzima aurkitu eta identifikatzeagatik (Argazkia: The Nobel Foundation 2009, Torbjörn Zadig)
Horrez gain, minbiziaren garapenarekin lotuta daude. Izan ere, sufritzen duten laburtze prozesu hori ez da zelula guztietan gertatzen. Adibidez, zelula germinaletan, tumore-zeluletan eta enbrioizko zeluletan. Azken hauetan, Telomerasa entzima dago, zelulen heriotza saihesteko telomeroak luzatzea helburu duena. Hasiera batean, Blackburn eta Szostakek telomeroek DNA berezi bat zeukatela aurkitu zuten eta ondoren Carol Greiderrek, Blackburnekin batera Telomerasa aurkitu zuen 1984an, telomeroen DNA sortzen duen eta hortaz, “txanoa” luzatzeaz arduratzen den entzima, alegia. Tumore-zelulen kasuan, Telomerasa aktibo baldin badago, zelulak ez dira inoiz hilko eta gainera, etengabe ugalduko dira.
Telomeroen erreginakElizabeth Blackburn 1948an Hobarten (Tasmania) jaio zen eta Biokimika ikasi zuen Melbourneko Unibertsitatean. Biologia Molekularrean doktoratu zen, Cambridgen, 1975ean. Bere tesia azido nukleikoen sekuentziazioaren ingurukoa izan zen. Horren ondotik, beka bat lortu zuen bere doktoretza ondokoa egiteko Yaleko Unibertsitatean. Bertan, John Gallekin batera hasi zen Tetrahymena thermophila protozooaren DNAren telomeroak aztertzen. 1980an, azido nukleikoen inguruko bilera batean, Jack Szostack biologo molekularra ezagutu zuen eta bion artean erabaki zuten telomeroen inguruko ikerketa sakon bat abian jarri nahi zutela. Ikerketa talde honetan Carol Greider sartu zen beranduago, 1984ko maiatzean.

3. Irudia: Elizabeth Blackburn biologia molekularrean doktoratu zen eta tesia azido nukleikoen sekuentziazioaren ingurukoa izan zen (Argazkia: Kim Kulish/Corbis)
Greider, bere aldetik, Biologian lizentziatu zen 1983an, Santa Barbaran dagoen Kaliforniako Unibertsitatean. UC Berkeleyn onartu zuten graduondokoa egiteko. Hain zuzen ere bertan ezagutu zuen lehenengo aldiz Blackburn eta berehala konturatu zen harekin lan egin nahi zuela. Elkarrizketa bat eskatu zion eta Greiderrek berak kontatzen du bulego horretan gertatu zena. Bilerak minutu bat iraun omen zuen: “Lehenik, bere laborategian lan egiterik banuen galdetu nion eta berak baietz esan zidan. Ondoren, galdetu nion ea aukera banuen telomeroen proiektuan lan egiteko. Horri ere baietz erantzun zidan. Asko emozionatu ninduen horrek. Telomeroak nola luzatzen ziren jakiteko irrikaz nengoen”.
Irrika horrek eraman zuen Greider Tetrahymena telomeroen luzatze prozesu horren atzean zebilen entzima identifikatzera: telomerasa. Zientzialariak 23 urte zituen hori gertatu zenean, 1984ko abenduan jazo zen eureka momentua. Aurkikuntza Cell aldizkarian publikatu zuten urtebete beranduago.

4. irudia: Hogeita hiru urte zituela topatu zuen telomerasa entzima Carol Greiderek.
Horren ondotik, Cold Spring Harbor (New York) laborategira joan egin zen lau urte geroago. Han ARN telomerasaren genea klonatzeko saiakerak egin zituen. Era berean, Calvin Harley biokimikariarekin kolaboratzen hasi zen, zelula banaketa eta “erloju biologikoa” oinarri zuen ikerketa batean. 1997an John Hopkins Unibertsitatera (Baltimore) aldatu zen. Bertan, bi ildo nagusi zehaztu zituen helburu gisa: alde batetik, telomerasaren identifikazioarekin jarraitzea eta bestetik, tumoreen hazkundean, telomeroek duten papera ikertzea. Egun, Biologia Molekularra eta Genetika Saileko zuzendaria da. Telomeroak, ugaztunetan telomerasak duen papera, eta horrek eragin ditzakeen endekapenezko gaixotasunak ikertzen ari da.
Blackburnek, bere aldetik, Biologia Molekularra sailean jarraitu zuen lanean, Berkeleyn. Ondoren, San Franciskon dagoen Kaliforniako Unibertsitateko Mikrobiologia eta Immunologia departamentura aldatu zen 1990ean. Hiru urte geroago, sail horretako zuzendari izendatu zuten, kargu hori lortzen lehendabiziko emakumea izan zen. Egun, sail honetako zein Biokimika eta Biofisika departamentuko katedraduna da.
Sariei dagokienez, nabarmentzekoa da biek ala biek hainbat lortu dituztela. Esanguratsuenak honakoak izan dira: Albert Lasker Saria (2006), Greiderrek, Blackburnek eta Szostakek jaso zutena; Gall eta Blakburni Louisa Gross Horwitz Saria (2007) eman zioten eta azken honek Greiderrekin batera, Paul-Ehrlich eta Ludwig-Darmstaedter jaso zuen 2009. urtean.
Iturriak:
- Mujeres con Ciencia: Elizabeth Blackburn y Carol Greider: la excelente colaboración de dos biólogas que mereció el Nobel de 2009
- Nobel Prize: Carol W. Greider
- Nobel Prize: Elizabeth H. Blackburn
———————————————————————–
Egileaz: Uxue Razkin Deiako kazetaria da.
———————————————————————–
The post Elizabeth Blackburn eta Carol Greider: Gure “erloju biologikoaren” funtzionamendua zehaztu zuten zientzialariak appeared first on Zientzia Kaiera.
Zainketa intentsiboko unitateko pazienteen familiek dituzten beharren berrikusketa
Irudia: Zainketa intentsiboko unitatean bisitak mugatutak izatea da familiak okerren daramaten araua.
Zainketa intentsiboko unitatea, beste unitateekin alderatuz, ezberdintasun garrantzitsuena eta paziente zein familiarentzat txundigarriena barneratzen dituen arau bereziak dira, horien artean, bisitak mugatutak izatea da familiak okerren daraman araua. Familiak ingresoaren bitartean maitatuaren egoera eta eboluzioaren informazio falta sentitzen dute eta hauxe da zehazki azalarazten duten behar garrantzitsuena.
Zainketa intentsiboetako erizainek, gainontzekoak bezala, era holistiko batean jardun behar dute, beraz, familia pazientearen zainketa planean barneratzea beharrezkoa litzateke. Horrela izanik, ezinbestekoa da unitate honetan lan egiten duen edozein erizainek ingresatuta dagoen pazientearen senideek aurkezten dituzten beharrak ezagutzea, aurrera eramaten dituzten zainketak familiaren behar horietara zuzentzeko.
Beraz, lanaren helburua zainketa intentsiboetan ingresatuta dagoen paziente baten senideek ingresoaren bitartean pairatu ditzaketen estres egoera eta azalarazten dituzten beharrak identifikatu eta deskribatzea da.
Horretarako literaturaren berrikusketa bibliografioa egin da. Zehazki ondorengo datu baseak aztertu egin ziren: Embase, Cinhal, Medline, Psycinfo, Up to Date eta Cochrane Plus. Hauetan gako hitz ezberdinak erabiliz, eta AND eta OR konbinazioak erabilita, artikulu ezberdinak aukeratu egin ziren. Beraz, zainketa intentsiboetako unitateari eta pazienteei dagokionez “intensive care unit”, “intensive care” eta “ critically ill” gako hitzak erabili ziren. Unitate honetan ingresatuta dagoen pazienteen senideak bizitzen dituzten esperientzien eta beharren inguruan aritzen diren artikuluak bilatzeko “experience”, “personal experience”, “life change events”, “Personal experience”, “psychological assessment” eta “life experience” gako hitzak erabili ziren. Familiari erreferentzia egiteko, ordea, “family”, “family member”, “relative” eta “visitors to patients” gako hitzak erabili ziren. Hala ere, datu base hauetaz aparte, beste aldizkari zientifiko batzuk behatu ziren.
Behin artikuluak aukeratuta, hain zuzen zortzi izan ziren aukeratutakoak, hauen irakurketa kritikoa eta analisia burutu egin zen, emaitza, eztabaida eta ondorio ezberdinak lortuz.
Laburbilduz, lortutako emaitzek ondorengoa adierazten zuten batik bat: zainketa intentsiboko unitatean lan egiten duten erizainek familiak aurkezten dituen beharren identifikazio azkarra egitea, ahalik eta azkarren eta era pertsonalago eta familiari zuzendutako artatzea eskaintzeko. Bestetik, familiak informazio ulergarri eta zabala, beraien kexkak argitzen dituena eskatzen dute. Izan ere, familiaren ilusio edo itxaropena pazientearen errekuperazioa da. Gaixotasunaren pronostikorik ez edukitzea, hau da, maitatuaren gaixotasun prozesua zelan garatuko den ez jakiteak, emozio nahaste ugari pairatzea suposatzen du, ziurgabetasuna eta inpotentzia areagotuz. Honen aurrean, baliabide eragingarriena euskarri emozionala ematea komenigarria dela frogatu dute. Beraz, artikulu honen bitartez, zainketa intensiboetako unitatean familia artatuago sentitzeko jarduera ezberdinak eguneroko praktikan barneratu ahal direla berrikusi egin da.
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: Ekaia 31
- Artikuluaren izena: Zainketa intentsiboko unitateko pazienteen familiek dituzten beharren berrikusketa.
- Laburpena: Zainketa intentsiboetan ingresatzea bai ospitaleratutakoek bai familiek egoera estresagarri moduan hautematen dute. Egoera horrek shock egoera, antsietatea eta sinesgaiztasuna eragin ditzake. Beraz, artikuluaren helburua izango da ospitalera- tzeak irauten duen bitartean familiaren eta pazientearen beharrak ezagutzea.
- Egileak: Erik Aostri, Joseba Pineda, Aitziber Mendiguren.
- Argitaletxea: UPV/EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- Orrialdeak: 7-20
- DOI: 10.1387/ekaia.14764
—————————————————–
Egileez: Ekhiñe Unzalu Lerma Gasteizko Erizaintza Eskolakoa da.
————————————————–
Ekaia aldizkariarekin lankidetzan egindako atala.
The post Zainketa intentsiboko unitateko pazienteen familiek dituzten beharren berrikusketa appeared first on Zientzia Kaiera.
No dejarás de comer pescado por culpa del mercurio

Una duda frecuente es si el pescado que consumimos tiene mercurio y si éste supone un riesgo para la salud.
El mercurio entra dentro de la categoría de metal pesado. Aunque desde la comunidad científica no hay un consenso sobre esta denominación, comúnmente se emplea para referirnos a los metales que se bioacumulan, es decir, que se introducen en los organismos vivos de forma casi permanente y pueden llegar a producir efectos tóxicos. Además del mercurio se consideran metales pesados el cadmio, el plomo y el cobalto, entre otros.
La forma más peligrosa del mercurio se llama metilmercurio
El mercurio lo encontramos principalmente en dos formas químicas, como mercurio inorgánico y como metilmercurio, siendo ésta la forma que presenta mayor toxicidad. Esto es así porque el metilmercurio es liposoluble, es decir, tiene la capacidad de acumularse en la grasa de los animales. Afecta especialmente al sistema nervioso central y a los riñones, por eso se considera neurotóxico y nefrotóxico.
El proceso de transformación del mercurio inorgánico en metilmercurio no se conoce con total exactitud, pero sí sabemos que se necesita la participación de determinadas bacterias una vez el mercurio ha llegado al agua. Los pescados y los mariscos son capaces de acumularlo en sus tejidos.

Mercurio metal (inorgánico)
Los depredadores acumulan el mercurio de sus presas
Si un animal ingiere mercurio, éste permanece indefinidamente en su organismo. Si un segundo animal se alimenta de este primero, el mercurio pasará automáticamente al depredador. Esa es la manera que tiene el mercurio de introducirse y permanecer en la cadena alimentaria. Esta cadena se inicia en el momento en que un animal ingiere mercurio.
En el océano, el metilmercurio es ingerido tanto por los succionadores de los fondos como por las formas del plancton que se alimentan de las bacterias. El plancton sirve de alimento a numerosas especies de peces y crustáceos, de modo que el metilmercurio pasa al siguiente nivel de la cadena alimentaria.
En el siguiente escalón de la cadena hay peces como la merluza, que se alimentan de los peces pequeños y crustáceos y, por tanto, acumulan el metilmercurio que estos contenían. Lo mismo sucede con los atunes, que también son carnívoros. Sin embargo, a diferencia de la merluza, algunas especies de túnidos alcanzan gran tamaño y peso, con lo que su tasa de alimento necesaria diaria es mucho mayor, por lo que van acumulando cantidades cada vez más significativas de metilmercurio.

Como el metilmercurio es soluble en la grasa, se acumula principalmente en los peces más grasos, es decir, en el pescado azul. La mayor concentración la encontraremos en las vísceras, las partes más grasas de estos pescados.
Dado que los peces son menos eficientes en la depuración que en la acumulación de metilmercurio, la concentración en los tejidos aumenta con el tiempo. Así, las especies que ocupan un nivel superior en la cadena alimentaria acumulan una carga corporal de mercurio que puede ser diez veces mayor que la de las especies que consumen. Este proceso se denomina biomagnificación.
Por estos motivos, la lista de pescados con más probabilidad de contener mercurio la encabezan los grandes túnidos: pez espada y ciertas variedades de atún, como el atún rojo. Le siguen el cazón, el marrajo, la tintorera y otros tiburones pequeños. El pescado que más quebraderos informativos nos ha traído es el salmón, sin embargo, no hay que preocuparse demasiado por él. Si procede de acuicultura o de aguas vírgenes como las de Alaska, el riesgo de contaminación por mercurio del salmón es muy bajo.
El bonito del norte y el atún claro, al no ser tan grandes como el atún rojo, entrañan menos riesgo. Ambos son los más frecuentes en las conservas y por tanto en el consumo cotidiano. No hay razón para preocuparse por ellos.
Con respecto al marisco, las recomendaciones de AECOSAN se limitan a advertir que no ingiramos las cabezas de las cigalas, gambas o langostinos, cuyo principal contaminante podría ser el cadmio, más que el mercurio. Del mismo modo, convendría no abusar de bivalvos como mejillones, almejas o berberechos. Estas recomendaciones hay que tomarlas con cierta cautela, ya que se refieren a una advertencia sobre el consumo excesivo de marisco y lo cierto es que solemos consumirlos de forma ocasional, con lo que no acarrean un verdadero problema.
La Autoridad Europea de Seguridad Alimentaria (EFSA) recomienda limitar la ingesta de atún rojo, emperador, tiburones o lucio, aunque dictamina que la limitación debe ir en función de la procedencia de la carne, ya que hay aguas más contaminadas que otras. Por ejemplo, el mediterráneo se considera altamente contaminado, pero no así el atlántico, que incluye zonas del cantábrico alejadas de la costa.
Cómo se produce la contaminación por mercurio
Los animales entran en contacto con el mercurio por varios motivos. Uno de ellos es de forma natural. El mercurio forma parte de ciertos minerales como el cinabrio, y estos pueden acabar arrastrados por corrientes de agua en la que habiten animales acuáticos y plantas, y también como consecuencia de la actividad volcánica.
No obstante, la principal vía de contaminación acuática por mercurio es de origen industrial. Puede darse como consecuencia de la actividad minera, por vertidos industriales con alto contenido en mercurio o como resultado de procesos industriales de combustión. Si las chimeneas de las incineradoras, las centrales térmicas que usan carbón con altos niveles de metales pesados o las industrias del cloro, no cuentan con filtros eficientes, las partículas contaminadas con mercurio pueden liberarse al aire. La lluvia se encargará de introducirlas en el subsuelo, donde contaminarán los acuíferos iniciando su camino hacia el mar.
Los niveles de mercurio del pescado se controlan
En la sección 3 del anexo del Reglamento (CE) Nº 1881/2006 (UE, 2006) se toma como contenido máximo para el mercurio en productos de la pesca entre 0,5 y 1 mg/kg de pescado fresco, dependiendo de la especie. Esta cantidad se ha fijado en función de los límites de ingesta que se ha comprobado que son tolerables, es decir, que no suponen un riesgo para nuestra salud, habida cuenta del consumo prolongado en el tiempo y siguiendo una dieta normal.
Para garantizar que los niveles se encuentran dentro de los límites permitidos, se hacen controles periódicos del pescado que llega al mercado, así que, salvo pautas de consumo fuera de lo habitual, no hay que preocuparse del mercurio que contiene el pescado.
La recomendación de AESAN para grupos especialmente sensibles, como niños menores de doce años, mujeres embarazadas o en período de lactancia, es que no consuman más de 50 g de grandes túnidos a la semana, o más de 100 g cada dos semanas. Desaconsejan el consumo de estos pescados a menores de tres años.

No dejes de comer pescado, hay más beneficios que riesgos
Aunque las autoridades sanitarias recomiendan limitar el consumo de determinados pescados en grupos de riesgo, animan al resto a consumirlo con frecuencia para mantener una dieta saludable. Esto es así porque el pescado azul contiene una proporción de grasas beneficiosas muy superior al pescado blanco, en especial los ácidos grasos omega-3. Hay abundante evidencia científica sobre los beneficios de estos ácidos grasos en el buen funcionamiento del sistema cardiovascular y el mantenimiento de los niveles de colesterol.
Lo ideal sería consumir solo un par de veces al mes los pescados que entrañan mayor riesgo y acudir cada semana a alternativas como el atún claro, el bonito, la caballa o el salmón, con el mismo aporte de ácidos omega-3 pero con menor concentración de metilmercurio.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo No dejarás de comer pescado por culpa del mercurio se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Vas a freir pescado? Usa aceite de oliva virgen extra
- Esperma de pescado para extraer tierras raras
- Cómo los olores nos incitan a comer
Oxigeno gehiago garraiatu ahal izateko
 Juan Ignacio Pérez eta Miren Bego Urrutia Igeri egiten, lasterka egiten, hegan egiten
Juan Ignacio Pérez eta Miren Bego Urrutia Igeri egiten, lasterka egiten, hegan egiten ———————————————————————————————————–

Irudia: Hemoglobina da oxigenoa garraiatzeaz arduratzen dena.
Oxigeno gehiago garraiatu behar denean bi aukera dituzte animaliek. Odolean arnas pigmentuaren (hemoglobina, hemozianina edo beste baten) kontzentrazioa igotzea da aukera horietako bat. Oxigenoarekin konbinatzen dira arnas pigmentuak eta horri esker izugarri handitzen da oxigenoa hartzeko eta ehunetara eramateko odolak duen ahalmena. Animalia batzuek hemoglobina asko dute; horixe da, esaterako, zetazeoen kasua. Aurreko atal batean ikusi dugun bezala, horri esker egon daitezke oso denbora luzez urpean. Muga bateraino, bestalde, odolaren hemoglobinaren kontzentrazioa handitu egin daiteke epe ez oso luzean; horixe da, hain zuzen ere, kirolari batzuek egiten dutena goialdeetan entrenatzen direnean, ganbera hipobarikoetan lo egiten dutenean edo eritropoietina (EPO) txertatzen dutenean. Baina hemoglobinaren kontzentrazioak badu gainditu beharko ez lukeen mugarik ere, zeren eta altuegia bada (globulu gorri gehiegi badaude) odola dentsoegi geratzen baita eta kapilarretatik mugitzeko arazoak izan baititzake.
Bada oxigeno gehiago garraiatzeko beste bide bat, hemoglobinaren kontzentrazioa igotzeko beharrik gabe. Biriketan oxigeno-kantitate bera hartuta, bada gehiago garraiatzeko modurik baldin eta ehunetara heltzean hemoglobinaren funtsezko ezaugarri bat aldatzen bada. Hemoglobinak oxigenoarekin duen kidetasunaz ari gara. Oxigenoarekiko kidetasuna jaisten bada zeluletara heltzean, pigmentuak zelulei oxigeno gehiago emango die nahiz biriketan kopuru bera hartu. Hau da, biriketatik igarotzen denean, hemoglobinaren oxigenoarekiko kidetasuna altua da, baina jaitsi egiten da ehunetara heltzean. Animalia askoren ezaugarria da hori, eta «Bohr efektua» deitzen zaio.
Oxigenoarekiko kidetasunaren kontzeptua azaldu ondoren, Jean-Marie Lehn Nobel saridunak zuzentzen duen ikerketa-taldeak egin duen aurkikuntzaren berri emango dugu, oso aurkikuntza interesgarria eta seguru asko erabilgarria baita. Hemoglobinaren oxigenoarekiko kidetasuna neurri handian jaisten duen gai kimiko bat aurkitu du Lehnen taldeak, eta kidetasunaren jaiste horri esker nabarmen handitzen da pigmentuak zelulei ematen dien oxigeno kantitatea; hau da, neurri handian handitzen da oxigenoa garraiatzeko odolak duen ahalmena sustantzia horren eraginez. Gai kimiko horrek myoinositol trispirofosfato (ITPP) du izena; duen eragina izateko, hemoglobinarekin konbinatzen da. Uretan disolbatuta edanez har daiteke eta, beraz, edonork erabil dezake.
Bihotzean kalteren bat edukitzeagatik ahalegin fisikoak egiteko mugak dituen jendearengan pentsatuz garatu dute ikerketa hau. Izan ere, bihotza kaltetuta izan arren, ariketa fisiko normala egin daiteke botika honi esker, ITPParekin konbinatuta dagoen hemoglobinak oxigeno gehiago askatzen baitu ehunetara heltzean. Bistan da, bestalde, botika hau oso erabilgarria izango litzatekeela erresistentzia-kirolen arloan, baina oso erraz hauteman daiteke eta, beraz, ez du inolako erabilgarritasunik izango kirolarien errendimendua hobetzeko.
—————————————————–
Egileez: Juan Ignacio Pérez Iglesias (@Uhandrea) eta Miren Bego Urrutia Biologian doktoreak dira eta UPV/EHUko Animalien Fisiologiako irakasleak.
—————————————————–
Artikulua UPV/EHUren ZIO (Zientzia irakurle ororentzat) bildumako Animalien aferak liburutik jaso du.
The post Oxigeno gehiago garraiatu ahal izateko appeared first on Zientzia Kaiera.
Lo que la tensión puede hacer en dos capas de grafeno

El grafeno, una lámina de un átomo de grosor de átomos de carbono, no deja de sorprendernos. Si el mes pasado el equipo de Pablo Jarillo-Herrero sorprendía a la comunidad científica que trabaja en física de la materia condensada con su descubrimiento de que si las láminas forman determinado ángulo se vuelven superconductoras, lo que puede revolucionar nuestro conocimiento de este fenómeno, ahora un equipo encabezado por Loïc Huder, de la Univesité Grenoble Alpes (Francia) ha encontrado que si las láminas del par están sometidas a tensiones ligeramente diferentes las propiedades eléctricas cambian completamente.
Los investigadores crearon sus bicapas haciendo crecer una lámina de grafeno encima de otra. Este proceso introdujo de forma natural diferentes tensiones en las dos láminas y una determinada rotación de una lámina respecto a la otra. Como resultado, en posiciones periódicas a través de la bicapa, las láminas se alinean, con sus patrones de átomos hexagonales perfectamente superpuestos. Entre estas posiciones los patrones de las láminas se desplazan una distancia equivalente a la mitad de un hexágono. El equipo utilizó un microscopio de efecto túnel (STM) para analizar cómo se comportan los electrones en las áreas alineadas y en las no alineadas.
En las áreas alineadas el equipo observó grandes picos en la cantidad de estados electrónicos disponibles. Estos picos eran significativamente más pequeños en las no alineadas. Las regiones con un gran número de estados electrónicos tienen acumulaciones de electrones atrapados, lo que puede llevar a comportamientos superconductores o magnéticos en la bicapa.
Si bien este hallazgo es sorprendente, lo que en ciencia ya es importante de por sí, también es cierto que ajustar las propiedades eléctricas del grafeno estirando y rotando las láminas aún no ofrece ventajas prácticas concretas frente a otros enfoques, pero tampoco el tren de alta velocidad ofrecía en su momento ventajas frente al avión.
Referencia:
Loïc Huder, Alexandre Artaud, Toai Le Quang, Guy Trambly de Laissardière, Aloysius G. M. Jansen, Gérard Lapertot, Claude Chapelier, and Vincent T. Renard (2018) Electronic Spectrum of Twisted Graphene Layers under Heterostrain Physical Review Letters doi: 10.1103/PhysRevLett.120.156405
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Lo que la tensión puede hacer en dos capas de grafeno se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ajustando la adsorción sobre grafeno
- El estaño beta es como el grafeno pero en 3D
- La esponja de grafeno como propulsor espacial

