Zientzia

Ehunen ingeniaritza, ehunen funtzioa birsortzea, moldatzea edo hobetzea helburu duen disziplina anitzeko teknika da. Ingeniaritza honek, batez ere, ehunak (hezur-ehunak, kartilagoa, bihotz-balbula, maskuria, etab.) konpondu edo ordezteko aplikazioak ditu eta horretarako oso erabilgarriak dira polimero naturalak.

Polimero naturalak edo biodegradagarriak garatu ziren, besteak beste, metalezko inplanteek sor ditzaketen errefusatze eta sentinkortasun arazoei aurre egiteko. Gainera, polimero naturalen propietate kimiko, fisiko eta mekanikoak doitzea nahiko erraza da, honek egoera bakoitzera hobeto egokitzen diren ehun berriak sortzeko aukera ematen du.

Ehunen ingeniaritza eta polimero biodegradagarriei buruz gehiago ezagutzeko Jone Muñozekin, UPV/EHUko Meatze eta Metalurgia Ingeniaritza eta Materialen Zientzia saileko ikertzailearekin bildu gara.

“Zientzialari” izeneko atal honen bitartez zientziaren oinarrizko kontzeptuak azaldu nahi ditugu euskal ikertzaileen laguntzarekin.

The post Jone Muñoz: “Polimero naturalez egindako inplanteek bigarren ebakuntza bat ekidin dezakete” #Zientzialari (149) appeared first on Zientzia Kaiera.

Ilustración: María Lezana

Melville escribió en Moby Dick que “el cachalote solo respira la séptima parte, el domingo de su tiempo”. Hacía referencia así a la gran capacidad del gran cetáceo odontoceto de permanecer bajo el agua. Y es que los cachalotes, como el resto de cetáceos son excelentes buceadores. Algunos se sumergen a grandes profundidades, a pesar de que bajo el agua no puedan respirar.

En efecto, los cetáceos son mamíferos, por lo que no pueden hacer uso del oxígeno disuelto en el agua, como hacen los peces y numerosos invertebrados. El oxígeno que respiran ha de ser atmosférico y han de salir fuera del agua a respirar. Los cachalotes, como la gran ballena blanca que obsesionase al capitán Ahab, por ejemplo, llegan a bajar hasta los 1.000 m y más en busca de presas; otros, como los calderones, no llegan tan abajo, pero se sumergen también a grandes profundidades.

El calderón tropical, cuyo nombre científico es Globicephala macrorhynchus, pertenece a la familia Delphinidae. Es, por lo tanto, un delfín, aunque de gran tamaño: pueden llegar a alcanzar 4 m de longitud y más de 4.000 kg de masa. Aunque su nombre vulgar indica que se trata de una especie propia de mares tropicales, su límite de distribución septentrional se halla al norte del Cantábrico, por lo que puede encontrarse en la zona sur del Golfo de Vizcaya.

Hace unos pocos años, en el curso de una investigación realizada en aguas de Tenerife utilizando marcas digitales (DTAG), el equipo de Natacha Aguilar, de la Universidad de La Laguna (Tenerife), registró los movimientos de 23 de estos calderones, así como los “clics” de ecolocación que producían. Gracias a esos registros conocemos algunas características de la estrategia de caza de Globicephala.

De acuerdo con los registros obtenidos se ha podido saber que cuando van de caza, descienden a profundidades de entre 500 y 1.000 m y permanecen, en promedio, unos 20 min bajo el agua. Cuando bajan en busca de una presa emiten largas secuencias de clics (ondas sonoras de ecolocalización), y en ocasiones, entre las secuencias de clics, emiten zumbidos. Los zumbidos, al parecer, están relacionados con los intentos de atrapar a la presa.

Cuando realizan inmersiones profundas, llegan al punto de máxima profundidad tras realizar un rápido esprint, y en ese momento emiten un zumbido. Esa es la secuencia propia de un episodio de caza. Cuando empiezan la inmersión, se mueven con lentitud, pero cuando realizan el esprint llegan a alcanzar una velocidad de 9 m s-1, una velocidad impresionante para un mamífero que se mueve bajo el agua. Los esprints duran entre 20 y 80 s y les salen, en términos energéticos, muy caros a los calderones. De hecho, aunque el esprint representa entre un 2 y un 8% del total del tiempo de inmersión hasta aguas profundas, se estima que supone entre un 10 y un 36% de su gasto energético total.

Es un comportamiento arriesgado. Tan sólo la mitad de los intentos acaban teniendo éxito; en la otra mitad no aciertan. Si tenemos en cuenta que el coste de la caza es muy elevado, las presas han de ser de cierto tamaño, pues de lo contrario no resultaría rentable y no la practicarían de esa forma. Hasta que se realizó la investigación citada, no se conocía esa modalidad de caza de “alto riesgo-alto rendimiento” entre cetáceos, aunque sí era conocida entre depredadores terrestres. Entre los mamíferos terrestres, es quizás el guepardo el que mejor ejemplifica esa táctica.

Otros cetáceos, como los zifios, utilizan estrategias diferentes. Estos pertenecen a la familia Ziphiidae. Su característica más distintiva es el morro largo y delgado; parecen delfines. Los zifios que han sido estudiados en aguas de El Hierro se sumergen durante mucho más tiempo, hasta una hora y media. Por esa razón no se encuentran en condiciones de realizar esprints intensos, puesto que el oxígeno que albergan en sangre y músculos no da para inmersiones que, a la vez, sean prolongadas y acaben con un esprint. Claro que el comportamiento alimenticio de los zifios no es de “alto riesgo-alto rendimiento”, puesto que actúan de un modo mucho más conservador. En cada inmersión se cobran del orden de 30 piezas, aunque se trata de presas pequeñas cada una de las cuales aporta una pequeña cantidad de alimento. Aunque como sus costes de locomoción son reducidos, pueden permanecer largo tiempo bajo el agua en busca de presas y al final, unos y otros obtienen lo que necesitan.

Fuente: N. Aguilar, M. P. Johnson, P. T. Madsen, F. Díaz, I. Domínguez, A. Brito y P. Tyack (2008): “Cheetahs of the deep sea: deep foraging sprints in short-finned pilot whales off Tenerife (Canary Islands)” Journal of Animal Ecology vol. 77 (5): 936-947

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo Guepardos de aguas profundas se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Un lujo asiático cultivado en aguas del Mediterráneo
2. La regulación osmótica e iónica en los teleósteos marinos
3. La regulación osmótica de los peces diádromos

Yosu Yurramendi Mendizabal

Moritz Abraham Stern (1807-1894) lehenengo lerroko matematikari alemaniar bat izan zen ([1]),eta bere doktorego tesiaren zuzendaria Carl Friedrich Gauss (1777-1855) matematikari aski ezaguna izan zen. Stern-en lan ezagunen artean Stern-en segida izena duena dago ([2], ikus 1 Taula).

 

Modu bakun errekurtsibo honen bitartez defini daiteke:

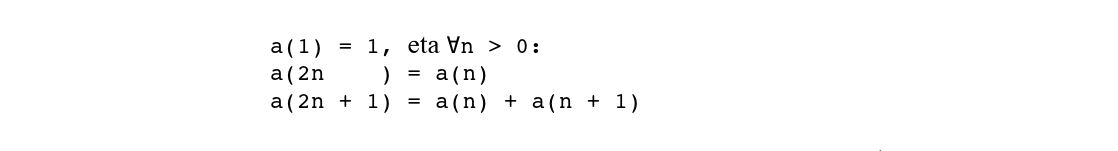
Segida honek garrantzia du, besteak beste, zenbaki arrazional positiboen (ℚ+) hainbat zenbakitze sistemaren oinarrian dagoelako. Esate baterako, Calkin-Wilf-en zenbakitze sistemaren oinarrian [3]: a(n) bada Stern-en segidaren n. gaia, a(n)/a(n+1) (n > 0) zatiki-segidak zenbaki arrazional positibo guztien segida osatzen du, bat ere errepikatu gabe.

Stern-en segida The On-Line Encyclopedia of Integer Sequences (OEIS)-en A002487 etiketaduna da [4]. Bertan ikus daitezke hainbat ikerlarik aurkitu dizkioten hainbat propietate, formula, konputazio-programa, eta beste zenbait segidarekin dituen loturak eta erreferentziak, bai eta beste zenbait problema matematikoei buruzko iruzkinak ere. Webgunea etengabe ari da berritzen eta
hazten.

Problema matematiko bat da segidaren n. gaiaren balioa (a(n), n > 0) ahalik eta azkarren kalkulatzea; hau da, definizio-formularen errekurtsibitatea arintzea. Propietate berri bat burutu da, bai eta horretan oinarrituta problemari soluzio bat ematen dion algoritmo bat ere. Propietate berria enuntziatu aurretik n zenbaki arruntaren adierazpide mota bat aurkeztu behar da:

 

∀n > 0, ∃1m ≥ 0, eta ∃1k 0 ≤ k

Horrela, segidaren a(n) balioak a(2m+k)-ren bitartez azalduko dira. Adierazpide honen arabera definizio-formula hauxe da:

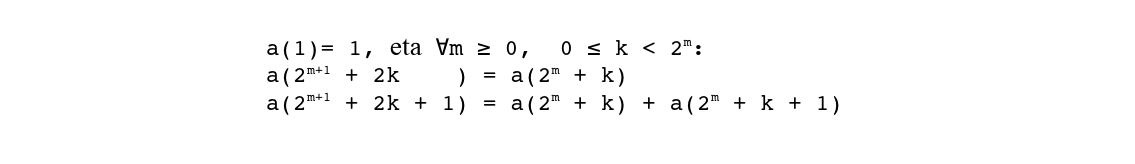
1 Taulako segidan a(n) balioak 2m gaika (m ≥ 0) pilatzen badira ezkerraldean, egitura triangeluar bat osatzen da (ikus 2 Taula).

Modu honetan azalduta, segidaren propietate batzuk nabarmenak dira. Lerroka begiratuta:

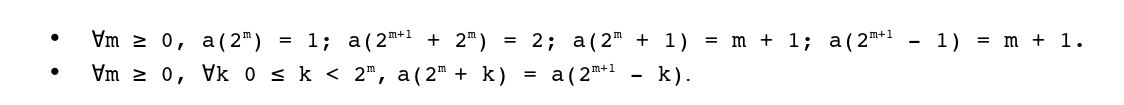
Zutabeka begiratuta, zutabe bakoitzean segida aritmetiko bat ikusten da, eta diferentzien segida Stern-en segida bera da (ikus 3 Taula).

Aurkitutako erlazio hau honela zehaztu daiteke:

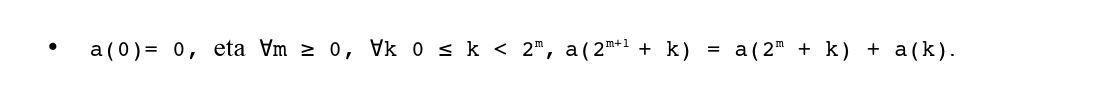
Ohar daitekeenez, segidari beste gai bat gehitu behar izan zaio: a(0)= 0, 2 Taulan agertzen ez dena.

Propietate berria ez da hain nabarmena, baina 3 Taularen zutabekako segida aritmetikoetan oinarritzen da ere.

Adibidez, k = 27:

Orokorrean honela enuntzia daiteke:

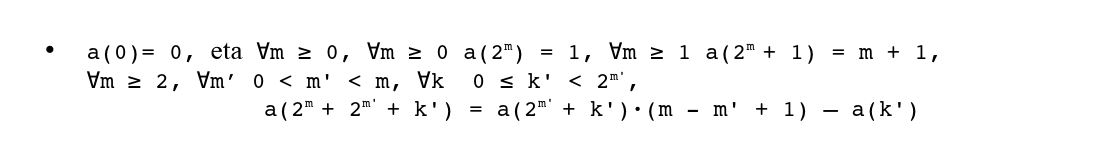
Stern-en segidaren propietate errekurtsibo berria esperimentalki induzitu egin da, bai eta matematikoki bere egiazkotasuna frogatu ere.

Bi formula errekurtsiboak alderatzean ikusten da definizio-formularen errekurtsibitatea datzala 2 Taularen maila batetik ondoz ondoko mailara igarotzean ((m+1)-tik m-ra), eta propietate berriarenean, aldiz, maila batetik aurreko beste maila batetara igarotzean (m-tik m’-ra, m’

Formula edo propietate berri hori garatuz gero, errekurtsiboki (goitik behera, top-down, m handitik txikira), n-ren adierazpide bitarrean oinarritzen den algoritmo bat lortzen da, eta segidaren
hasierako a(0) = 0 eta a(1) = 1 balioak nahikoak dira algoritmoa abiatzeko.

Adibidez:Beraz, 91-ren adierazpide bitarrean oinarritzen diren cj (1 ≤ j

Orokorrean:

Ondorengo biderkagaiek n-ren adierazpide bitarra jartzen dute jokoan. b = 1 baldin bada (‘1’-eko bakarra), orduan bedi c1 = 1 (∀m ≥ 0, a(2m) = 1 delako), eta bestela:

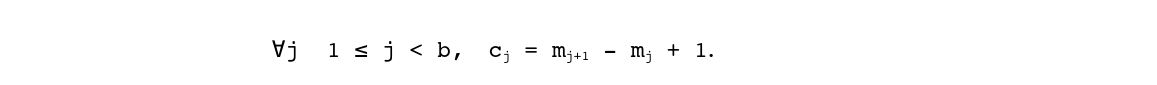
Biderkagai hauek ‘1’-ekoen artean dauden jauziak adierazten dituzte.

Bedi f burututako formula errekurtsibo berria islatzen duen funtzio errekurtsiboa:

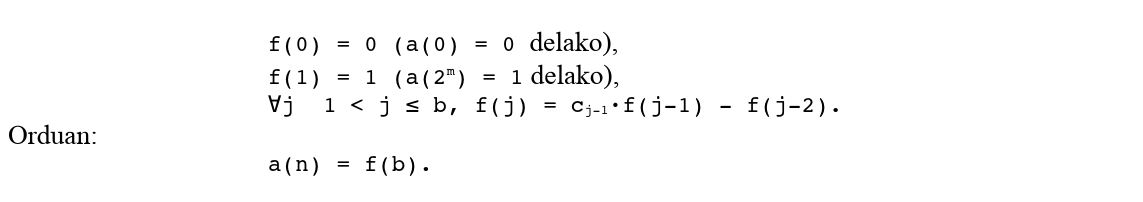
Adibidean:

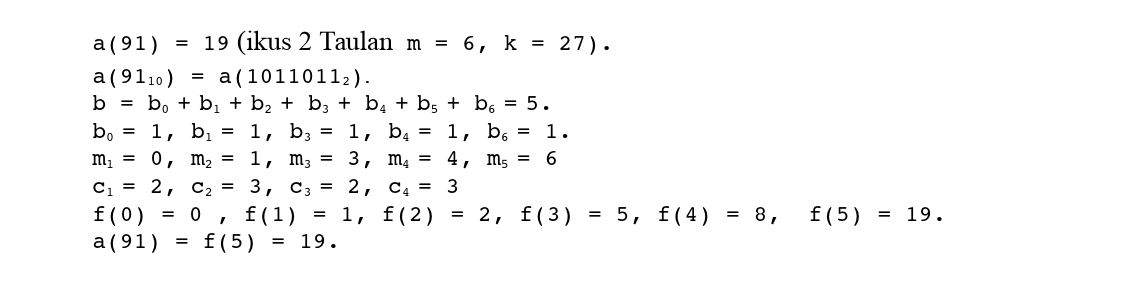
Ondorioz, eraikitako algoritmoa konputazionalki askoz ere azkarragoa da definizio-formulan oinarritutakoa baino.

Stern-en segidaren propietate berri bat esperimentalki induzitu da, eta matematikoki haren egiazkotasuna frogatu. Formula horretan oinarrituz segidaren edozein tokitako balioa kalkulatu daiteke eta eraikitako algoritmoa konputazionalki azkarragoa da definizio-formulan oinarritutakoa baino. Algoritmo hori n-ren adierazpide bitarrean oinarritzen da.

Erreferentzia bibliografikoak:

[1] O’Connor, J. J., Robertson, E. F., (2018). MacTutor History of Mathematics archive, School of Mathematics and Statistics. University of St Andrews, Scotland.

[2] Stern M. A., (1858). Über eine zahlentheoretische Funktion. Journal fur die reine und angewandte Mathematik, 55, 193-220.

[3] Calkin, N., Wilf, H., (2000). Recounting the Rationals. American Mathematical Monthly, 107 (4), 360-363. DOI: https://www.math.upenn.edu/~wilf/website/recounting.pdf.

[4] SLOANE N. J. A. 2018. The On-Line Encyclopedia of Integer Sequences (OEIS) (founded in 1964). https://oeis.org/A002487.

Iturria: Yurramendi Mendizabal, Yosu (2019). Stern-en segidaren propietate berri bat eta segidaren n. gaia azkar kalkulatzeko algoritmo bat. Ekaia, 35, 325-339. DOI: https://doi.org/10.1387/ekaia.19513 Artikuluaren fitxa:

• Aldizkaria: Ekaia
• Zenbakia: Ekaia 35
• Artikuluaren izena: Stern-en segidaren propietate berri bat eta segidaren n. gaia azkar kalkulatzeko algoritmo bat
• Laburpena: Stern-en segida zenbaki arruntez osatuta dago, eta propietate asko ditu. Segidaren propietate berri bat azaltzen da lan honetan, hain zuzen segidaren n. gaia zein den azkar kalkulatzeko balio duena. Azkartasun hori n-k sistema bitarrean duen adierazpidean oinarritzen da. Propietatea nondik nora sortu den azaltzen da, baita haren egiazkotasunaren froga matematikoa ere.
• Egileak: Yosu Yurramendi Mendizabal
• Argitaletxea: UPV/EHUko argitalpen zerbitzua.
• ISSN: 0214-9001
• eISSN: 2444-3255
• Orrialdeak: 325-339
• DOI: 10.1387/ekaia.19513

————————————————–
Egileez:

Yosu Yurramendi Mendizabal UPV/EHUko Informatika fakultateko Konputazio Zientziak eta Adimen Artifiziala sailean dabil.

———————————————–
Ekaia aldizkariarekin lankidetzan egindako atala.

The post Stern-en segidaren propietate berri bat eta segidaren n. gaia azkar kalkulatzeko algoritmo bat appeared first on Zientzia Kaiera.

 

Cuando esta mañana me he sentado frente al ordenador y he empezado a pensar sobre qué iba a escribir en mi entrada del Cuaderno de Cultura Científica, no podía quitarme de la cabeza las diferentes actividades que estamos organizando dentro del proyecto Marzo, mes de las matemáticas.

Cartel del proyecto Marzo, mes de las matemáticas, diseñado por Carla Garrido

 

Finalmente, después de un buen rato dándole vueltas a los diferentes temas matemáticos sobre los que podría escribir, me he rendido a la evidencia, tenía que escribir sobre alguna de las actividades del proyecto Marzo, mes de las matemáticas. Además, lo he tenido claro desde ese momento, el tema de las dos siguientes entradas debería ser la pareja de magníficas exposiciones matemáticas que hemos organizado con Metro Bilbao para colocar en sus estaciones, Geometría Natural y Matemáticas para un mundo mejor.

Imagen general de la exposición Geometría Natural colocada en la estación de Abando del metro bilbaíno el pasado 1 de marzo de 2021. Fotografía de Metro Bilbao

 

Pero vayamos al principio. El 26 de noviembre de 2019, la UNESCO proclamó el 14 de marzo como el Día Internacional de las Matemáticas a propuesta de la Unión Matemática Internacional (IMU). Cada año se dedicará a una temática especial, tratando de despertar la creatividad y mostrando las conexiones entre las matemáticas y todo tipo de campos, conceptos e ideas. Siguiendo este eje temático tendrán lugar numerosos eventos en todo el mundo. El lema de este año 2021 es “Matemáticas para un mundo mejor”. El motivo de elegir la fecha del 14 de marzo fue que ese día ya contaba con una cierta popularidad, por ser el día conocido como Día de pi y ser un día de celebración de las matemáticas.

El número π (pi) es una de las constantes matemáticas, y científicas, más importantes que existen, pero además es un número fascinante que goza de una gran popularidad entre el público, matemático y no matemático. Por este motivo, el 14 de marzo, es decir, 3/14 en inglés o euskera, se celebra el Día de pi, debido a la sencilla aproximación a π que nos enseñaron en la escuela, 3,14. El día de pi se celebra desde el año 1988 a partir de la idea propuesta por el físico Larry Shaw, y apoyado por el hecho de coincidir con la fecha del cumpleaños de Albert Einstein. Fecha que también era el cumpleaños del matemático polaco Waclaw Sierpinski (1882-1969).

Etida number pi, de la artista croata Luka Hatvalić. Imagen de Saatchi Art

 

En el otoño de 2019, la Red de divulgación de las matemáticas DIMA [http://dima.icmat.es/], constituida en mayo de 2018 y cuya presidenta es la profesora de la Universidad de La Laguna Edith Padrón, en colaboración con toda la comunidad matemática española (en particular, la Red Estratégica en Matemáticas (REM), la Real Sociedad Matemática Española (RSME), la Sociedad Española de Matemática Aplicada (SEMA), la Societat Catalana de Matemàtiques (SCM), la Sociedad de Estadística e Investigación Operativa (SEIO), la Federación Española de Profesores de Matemáticas (FEPM), la Federació d’Entitats per a l’Ensenyament de les Matemàtiques a Catalunya (FEEMC), la Conferencia de Decanos de Matemáticas, la Red de Institutos Universitarios de Matemáticas, el Centre de Recerca Matemática (CRM), el Basque Center for Applied Mathematics (BCAM), el Instituto de Ciencias Matemáticas (ICMAT), la Asociación Nacional de Estudiantes de Matemáticas (ANEM), el Museo de Matemàtiques de Catalunya (MMACA), o el Museo de Matemáticas de Aragón y el Comité Español de Matemáticas), diseñaron el proyecto Marzo, mes de las matemáticas, que tiene como objetivo extender la celebración del Día internacional de las matemáticas (14 de marzo), a todo el mes de marzo. El proyecto cuenta con la colaboración de la Fundación Española para la Ciencia y la Tecnología – Ministerio de Ciencia e Innovación (FECYT).

El proyecto Marzo, mes de las matemáticas, cuya web es https://marzomates.webs.ull.es/ , se ha convertido en el mayor evento de divulgación de las matemáticas en España. El proyecto incluye un amplio programa de actividades con diferentes formatos: i) Exposiciones: una exposición temática con paneles interactivos, así como otras exposiciones con formatos y/o temáticas variadas (fotografía matemática, aplicaciones, etc); ii) Conferencias, monólogos y diálogos divulgativos; iii) Tarjetas y carteles matemáticos con contenido diverso y formatos variados (de tres tipos: pasatiempos matemáticos; literatura + matemáticas; sabías que…); iv) Concurso de fotografía escolar “Matemáticas con un clic” a nivel nacional y exposición sobre fotografías matemáticas; v) Escape rooms virtuales, talleres, etc. Además, incluye a diez nodos de trabajo, que son las siguientes autonomías: Andalucía, Aragón, Canarias, Castilla-León, Cataluña, Galicia, La Rioja, Madrid, País Vasco, Valencia.

Logo del proyecto Marzo, mes de las matemáticas

 

Pero vayamos al tema de esta entrada, las exposiciones que hemos organizado en el metro de Bilbao. En particular, en esta entrada empezaremos con la exposición Geometría Natural, y dejaremos para una próxima entrada la exposición Matemáticas para un mundo mejor.

Desde el principio me vi muy implicado en este proyecto. De hecho, en noviembre de 2019, mientras visitaba la Universidad de La Laguna para impartir algunas conferencias, invitado por mi amiga Edith Padrón, dimos forma al actual proyecto, para presentarlo a la convocatoria de la Fundación Española para la Ciencia y la Tecnología – Ministerio de Ciencia e Innovación (FECYT). Dentro de la estructura organizativa que creamos, mi compañero y amigo Pedro Alegría y yo asumimos la responsabilidad de la organización de las actividades del País Vasco (contando con el apoyo y colaboración de la Universidad del País Vasco/Euskal Herriko Unibertsitatea y el Basque Center for Applied Mathematics-BCAM), así como de la organización de la actividad de las tarjetas matemáticas.

Además, dentro de un proyecto como este no podía faltar la fotografía matemática. Inmediatamente me puse en contacto con la persona idónea para este tema, mi amiga Pilar Moreno, matemática jubilada (ha sido profesora de matemáticas durante 38 años) y fotógrafa valenciana. A quien quiero agradecerle aquí su colaboración, su trabajo y su generosidad.

Pilar Moreno es una de las personas con una mayor trayectoria en España dentro de la fotografía matemática, es la responsable de la sección de fotografía matemática en la página DivulgaMAT con un centenar de pequeñas exposiciones virtuales, ha realizado muchas exposiciones (físicas), tanto individuales (como la que organizamos en 2005 desde la RSME, Anda con ojo, la exposición didáctica Veo, veo … geometría cotidiana, o también las exposiciones Geometría en los puertos y Geometría en la sombra), como colectivas (por ejemplo, las realizadas en los últimos años junto al grupo Enfoque geométrico, como Amor a la línea o Geometría natural). Es autora del libro Anda con ojo, Faktoría K de libros (2006), coautora de los libros Ritmos. Matemáticas e imágenes, Nivola (2002) y de Contemplar, conocer, UPV (2005).

Catenaria blanca, Paraboloide rojo y Rojo sobre rojo, fotografías incluidas en la exposición Anda con ojo, de Pilar Moreno

 

Portada del libro Anda con ojo, de Pilar Moreno

 

Pilar Moreno, junto con otros miembros del grupo Enfoque geométrico (como Lucía Morales, Inmaculada Gutierrez, Olga Martín, Leopoldo Martínez, Elia Añón y Amparo Fuentes), aportaron al proyecto Marzo, mes de las matemáticas, dos magníficas colecciones de fotografías para que pudieran organizarse exposiciones en los diferentes nodos del proyecto, una sobre la geometría de la naturaleza (Geometría natural) y otra sobre la geometría de nuestras ciudades (Geometría urbana). A todas ellas quiero agradecerles su colaboración con el proyecto, su generosidad y su arte.

Líneas de fuga, fotografía de Pilar Moreno dentro de la exposición Geometría Urbana. En esta página de GeoGebra podéis disfrutar de una excelente animación matemática sobre esta fotografía realizada por el matemático Jose Antonio Mora

 

Simetría roja, fotografía de Pilar Moreno dentro de la exposición Geometría Urbana. En esta página de GeoGebra podéis disfrutar de una excelente animación matemática sobre esta fotografía realizada por el matemático Jose Antonio Mora

 

Queda curvo el firmamento, fotografía de Amparo Fuentes dentro de la exposición Geometría Urbana

 

La siguiente etapa en el proyecto, relacionada con las fotografías matemáticas, era la realización de las exposiciones físicas con el magnífico material aportado por Pilar Moreno y las fotógrafas del grupo Enfoque geométrico. Un lugar ideal para realizar exposiciones dirigidas al público general en Bilbao era el metro de nuestra villa. Ya en 2007 habíamos colaborado con Metro Bilbao para la organización de la exposición Arte fractal, que tuvo lugar en la estación de metro de Sarriko y que fue todo un éxito.

Por este motivo, Pedro Alegría, Marta Macho y yo mismo nos reunimos, en las instalaciones de Metro Bilbao, con Susana Palomino (directora de comunicación y marketing de Metro Bilbao) y Lide Bidaguren (administrativa de comunicación y marketing de Metro Bilbao), quienes desde el primer momento expresaron su interés, y el de Metro Bilbao, por colaborar con nuestro proyecto de divulgación de las matemáticas. En esa reunión acordamos la organización de las dos exposiciones Geometría Natural y Matemáticas para un mundo mejor (sobre las que hablaremos en estas dos entradas de la sección Matemoción del Cuaderno de Cultura Científica) en diferentes estaciones del metro bilbaíno. Quiero expresar aquí mi más sincero agradecimiento a Susana Palomino, a Lide Bidaguren y a Metro Bilbao por su apoyo y colaboración en la organización de estas exposiciones. El metro de Bilbao es un lugar ideal para acercar las matemáticas, a través de elementos visuales, al público general.

Vista general de la exposición Arte fractal (2007), en la estación de Sarriko de Metro Bilbao. Foto : E. Moreno Esquibel

 

Para la primera de las exposiciones, Geometría Natural, seleccionamos doce de las fotografías enviadas por Pilar Moreno y el grupo Enfoque geométrico, cuyos títulos y autoras son: i) Cardioide. Brunnera Macrophylla (Lucía Morales); ii) Arquitectura móvil (Inmaculada Gutierrez); iii) Giros. Dalia (Lucía Morales); iv) Códigos de barras (Pilar Moreno); v) Estrellas pentagonales. Scabiosa Stellata (Lucía Morales); vi) Mosaico poligonal. Fromia Monilis (Leopoldo Martínez); vii) Fractales sobre círculos (Pilar Moreno); viii) Simetría. Asimetría (Pilar Moreno); ix) Ángulos, giros, hélice. Lupinus Nootkatensis (Pilar Moreno); x) Geometría tejida (Pilar Moreno); xi) Lupa natural (Pilar Moreno); xii) Silencio Azul (Pilar Moreno).

El siguiente paso fue escribir unos pequeños textos para acompañar a cada una de las fotografías matemáticas, destacando algún aspecto matemático relacionado con la imagen de la fotografía, labor que realizamos Pedro Alegría, Marta Macho y yo mismo. Además, tuvimos que traducir los textos al euskera y para ello contamos con la colaboración de los matemáticos y amigos Goyo Lekuona y José Ignacio Royo.

Finalmente, el diseño de los paneles de la exposición corrió a cargo de la diseñadora Carla Garrido, que ha realizado un magnífico trabajo.

Dos fotografías generales de la exposición Geometría Natural, en la estación de Abando de Metro Bilbao. Fotografías de Marian Espinosa

 

En lo que resta de entrada daremos un pequeño paseo por la exposición, mostrando algunos de los paneles, con sus fotografías y sus textos.

Empezaremos por el panel de presentación de la exposición, que podéis ver en la siguiente imagen del día que se colocó la exposición para el público (1 de marzo).

Panel de presentación de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa

 

El texto de ese panel de presentación es el siguiente:

“El libro de la naturaleza está escrito en lenguaje matemático”

(Galileo Galilei)

Dirige tu mirada a una flor, una planta, un animal o un paisaje, y sorpréndete con la geometría presente en la naturaleza. Las matemáticas nos ayudan a comprender el mundo en el que vivimos, pero también a crear un mundo mejor. Ojalá esta exposición provoque tu deseo de saber más, de conocer, de investigar y de descubrir las respuestas a los enigmas que la naturaleza nos propone.

Fotografías del grupo Enfoque Geométrico.

Empecemos nuestro recorrido por el panel de la exposición Geometría Natural correspondiente a la hermosa fotografía de Lucía Morales Giros. Dalia.

Panel de la fotografía Giros. Dahlia, de Lucía Morales, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa

 

El texto que acompaña a dicha fotografía llama la atención sobre el sorprendente hecho de que la belleza de una flor pueda estar relacionada con la sucesión de Fibonacci o el número áureo.

Es sorprendente que detrás de la belleza de esta flor esté la sucesión de Fibonacci (1, 1, 2, 3, 5, 8, 13, …) o el ángulo áureo (137,51º), como explica la filotaxis, la parte de la botánica que se ocupa del estudio de la disposición de hojas, semillas y flores en las plantas.

Otra de las imágenes de la exposición, ahora relacionada con el mundo animal, es la fotografía Arquitectura móvil, de Inmaculada Gutiérrez, que vemos en la siguiente imagen.

Panel de la fotografía Arquitectura móvil, de Inmaculada Gutiérrez, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa

 

El texto que nos acerca a las matemáticas relacionadas con esta hermosa fotografía es:

Las espirales son curvas geométricas muy frecuentes en la naturaleza. En procesos naturales de crecimiento, como en la concha del caracol, aparece la conocida espiral logarítmica. Es una curva autosemejante, al crecer el caracol cambia de tamaño, pero no de forma.

Otra imagen que llama la atención es la fotografía Lupa natural, de Pilar Moreno, cuyo texto es el siguiente:

La forma esférica que adoptan de manera natural las gotas de lluvia es consecuencia de la tensión superficial y las matemáticas demuestran que esta es la forma óptima, la que tiene menor superficie para un volumen dado.

Panel de la fotografía Lupa natural, de Pilar Moreno, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa

 

Panel de la fotografía Códigos de barras, de Pilar Moreno, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa

 

El texto escrito para acompañar a la fotografía Códigos de barras, de Pilar Moreno, que vemos en la anterior imagen, es el siguiente:

¿Por qué algunos animales tienen manchas, como el leopardo y la jirafa, y otros, rayas, como la cebra o el pez cirujano payaso? Las ecuaciones matemáticas llamadas “de reacción-difusión” han sido utilizadas para explicar los patrones de las pieles de los animales.

Otra de las fotografías del mundo vegetal que llama la atención es Cardioide. Brunnera Macrophylla, de Lucía Morales.

Panel de la fotografía Cardioide. Brunnera Macrophylla, de Lucía Morales, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa. En esta página de GeoGebra podéis disfrutar de una excelente animación matemática sobre esta fotografía realizada por la matemática Débora Pereiro

 

El texto que hemos escrito para la misma es:

Son necesarias fórmulas matemáticas complejas para representar el contorno natural de algunas plantas. La figura en forma de corazón invertido de la Brunnera Macrophylla presenta además una casi perfecta simetría axial.

Aunque realmente todas las fotografías son impactantes, como lo es también la titulada Geometría tejida, de Pilar Moreno, cuyo texto hace referencia a la teoría de grafos, una teoría matemática con muchas aplicaciones.

Las telas de araña recuerdan a una estructura matemática llamada grafo. Están formadas por hilos (aristas) y nudos (vértices) uniendo esas fibras. Las redes sociales se comportan del mismo modo: cada arista envía información entre nodos conectados.

Panel de la fotografía Geometría tejida, de Pilar Moreno, dentro de la exposición Geometría Natural, en Metro Bilbao. Fotografía de Marian Espinosa

 

Vamos a terminar con una fotografía para la que la matemática Débora Pereiro ha realizado una bella animación con GeoGebra, es Ángulos, giros, hélice. Lupinus Nootkatensis, de Pilar Moreno. Y me gustaría aprovechar para agradecerle a ella y a Juan Antonio Mora su trabajo con GeoGebra animando matemáticamente algunas de las fotografías.

Panel de la fotografía Ángulos, giros, hélice. Lupinus Nootkatensis, de Pilar Moreno, dentro de la exposición Geometría Natural, en Metro Bilbao. En esta página de GeoGebra podéis disfrutar de una excelente animación matemática sobre esta fotografía realizada por la matemática Débora Pereiro

 

Estos son algunos de los paneles de la exposición Geometría Natural expuesta en Metro Bilbao, durante el mes de marzo en la estación de Abando y en abril en la estación de Basauri.

Me gustaría terminar expresando mi agradecimiento a todas las instituciones y a todas las personas, que han sido muchas, que han hecho posible la realización de esta exposición, y de todo el proyecto Marzo, mes de las matemáticas.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El artículo Exposiciones matemáticas en el metro de Bilbao (I) se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Poesía métrica, ¿de metro?
2. Las dos culturas de las matemáticas: construir teorías o resolver problemas
3. Fractus, arte y matemáticas

Javier Duoandikoetxea

Martxoaren 14a Matematikaren Nazioarteko Eguna da. Bigarren urtez ospatuko da eta bigarrenez eragingo dio pandemia egoerak. 2020an, dena prest zegoenean, bertan behera geratu ziren hainbat ekitaldi, Parisen egitekoa zen hasiera-ekitaldi nagusia barne. Aurten, egoera aurreikusita, online egiteko antolatu dira ekitaldi asko. “Matematika mundu hobe baterako” goiburua du 2021eko ospakizunak, matematika Covid-19ari aurre egiteko erabil daitekeela iradokiz, besteak beste.

1. irudia: Matematikaren Nazioarteko Egunaren logo ofiziala euskaraz. Iturria: idm314.org.

Ospakizunaren jatorria Pi eguna da. 1988an Larry Shaw fisikaria egun seinalatu hori ospatzen hasi zen San Frantzisko hiriko Exploratorium museoan. Pi zenbakiaren dezimal biko adierazpen ezaguna —3.14— data bihurtuz, martxoaren 14a da, hirugarren hilabeteko 14. eguna, alegia. Denborarekin ospakizuna zabalduz joan zen eta azken hamarkadan mundu guztira egin zuen salto. Gure artean ere izan dira ekitaldiak Pi egunaren aitzakiarekin. Dataren arrakasta ikusita, Matematikaren Nazioarteko Eguna izenda zezala eskatu zioten UNESCOri eta hark 2019ko azaroan onartu zuen. Horregatik, duela urtebete egin zen lehen ospakizuna izen berriarekin, “matematika nonahi” goiburu hartuta.

Artikulu honen helburua ospakizunari baino jatorrian duen pi zenbakiari buruzko zenbait kontu jakingarri azaltzea da.

Zer da pi?

Hori bera gertatu zitzaidan Satorrari, Matematiketako irakasleari, pi zer zen galdetu nionean, eta berak «hiru, hamalau, hamasei» zela erantzun zidanean, hori erantzun bat balitz bezala.

Miguel Delibes, Kastila zaharreko kontu zaharrak (Patxi Apalategik euskaratua)

Argi zebilen Delibesen ipuineko mutikoa, pi delako horrek fama badu, ez baita izango “3-14-16” izateagatik, zerbait sakonago beharko du atzean. Eta hala da, noski. Zirkunferentzia baten luzeraren eta haren diametroaren arteko erlazioa (zatidura) bera da edozein delarik horretarako erabiltzen dugun zirkunferentzia. Zenbaki berezi hori π letra grekoaz adierazten dugu, eta, horregatik, pi du izena.

Era berean, zirkulu baten azalera eta haren erradioaren karratuaren arteko erlazioa ere zenbaki bera da. Zenbaki hau eta aurrekoa bat datozela, hots, hau ere π dela, frogatu egin behar da. Arkimedesen emaitza batetik, esaterako, ondorioztatzen da hori, beherago erakutsiko dugunez.

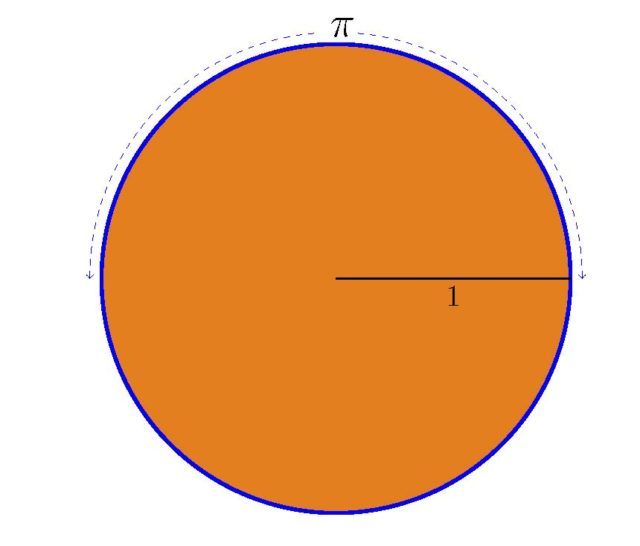2. irudia. Erradioa 1 bada, zirkunferentzia erdiaren luzera π da eta baita zirkuluaren azalera ere. (Irudia: Javier Duoandikoetxea)Zergatik π?

Aipaturiko erlazio horrek ez zeukan izen berezirik. William Oughtred (1574-1660) ingelesa izan omen zen lehena π letra erabiltzen hura adierazteko. Geroago, William Jones galestarrak 1706ko liburu batean erabili zuen. Letra greko hori alfabeto latinoaren p letrari dagokio eta periferia (περιφέρεια) hitzaren lehen letra delako aukeratu zuten. Leonhard Euler matematikari handiak bere egin zuen proposamena eta haren lanek eragin nabarmena izan zutenez XVIII. mendetik aurrera, laster onartu eta orokortu zen erabilera. Handik aurrera π da matematikako notaziorik ospetsuena.

π = 3 izan zenekoa

Urthuz egin zuen halaber itsaso bat, hamar besokoa bazter batetik bertzera, inguruz biribila: haren goratasuna bortz besokoa zen, eta hogoi eta hamar besoko sokhatto batek birundatzen zuen inguruan.

Erregeak III, 7:23 (Jean Pierre Duvoisinek euskaratua)

Bibliako testu horren arabera diametroa 10 besokoa izanik, 30 besoko zirkunferentzia dugu. Hortaz, π = 3 izango genuke. Biblia hitzez hitz hartzen dutenek agian arazoa izango dute matematikako klasean…

Testua K. a. VI. mendekoa omen da eta ordurako hori baino hobeto ezagutzen zen zirkunferentziaren eta diametroaren arteko erlazioa. Batzuen iritziz, testu literario moduan irakurri behar da eta ez zaio inolako asmo zehatzik bilatu behar.

Honen harira, komeni da ohar bat paratzea: matematikako objektu abstraktuak idealak dira eta mundu errealean aurki ditzakegunak haien antzekoak izango dira, baina ez perfektuak. Horrela, praktikan zirkunferentzia baten eta diametroaren arteko zatidurak ezin digu inoiz π-ren balio zehatzik eman (π = 3 baino hobea bai, seguruenik).

Rhind papiroa

Oso zaharra da ezagutzen dugun π-ren lehen hurbilketa. K. a. XVI. mendeko Egipton agertzen da, zehazki Rhind papiroa izeneko dokumentuan. Zirkulu baten azalera bera duen karratu bat eraikitzeko bidea azaltzen da bertan, zilindro baten bolumena ematen duen formula baten barruan. Zirkuluaren diametroa bederatzi zati egin, bat kendu, eta beste zortzien luzerako aldea duen karratua da zirkuluaren azalera bera duena. Ez da zehatza, jakina.

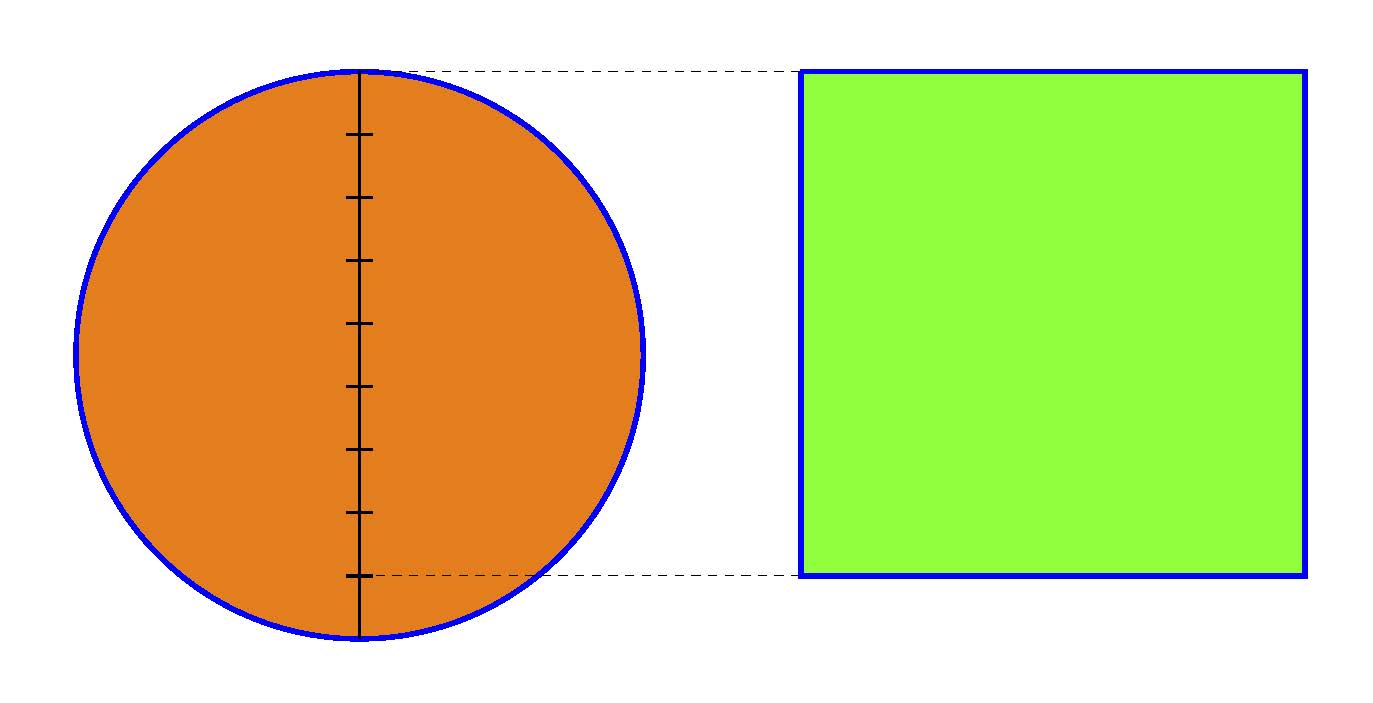3. irudia. Rhind papiroaren arabera zirkulua eta karratua azalera berekoak dira. (Irudia: Javier Duoandikoetxea)

Ez da testuan inon aipatzen guk π deitzen dugun zenbakia, antzinako matematikan irudien arteko erlazioak agertzen baitziren. Baina guk, emandako informazioarekin, lor dezakegu: zirkuluaren erradioa 9/2 izanda, hau dugu:

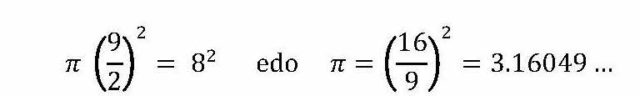
Noizkoa den kontuan hartuta, ez da batere hurbilketa txarra. 

Arkimedes 

K. a. III. mendean Sirakusan bizi zen antzinateko zientzialaririk handiena, Arkimedes. Haren lan ugarien artean bada Zirkuluaren neurketa izeneko eskutitz bat. Bertan, zirkuluaren azalera triangelu zuzen batenaren berdina dela frogatzen du. Triangelu zuzenaren kateto bat erradioa da eta bestea zirkunferentziaren luzera. Horren ondorioz, “zirkunferentziaren π” eta “zirkuluaren π” berdinak dira.

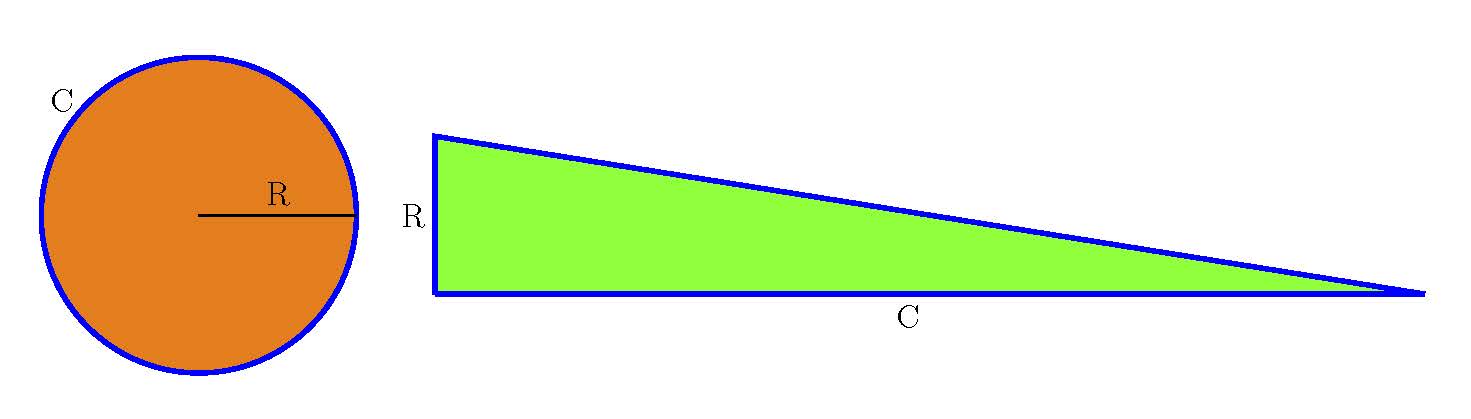4. irudia: Arkimedesen emaitza: zirkuluak eta triangeluak azalera bera dute. R erradioa da eta C, zirkunferentziaren luzera. (Irudia: Javier Duoandikoetxea)

Gainera, zirkulua kanpotik eta barrutik poligonoen bitartez hurbilduta, π goitik eta behetik bornatu zuen. Hau lortu zuen:

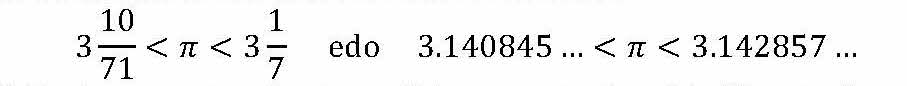
Oso hurbilketa ona da eta, bereziki, π-ren balioa bi zifra dezimalekin 3.14 dela erakusten du.

π-ren dezimalen kalkulua historia amaigabea da eta hobe dugu beste baterako uztea.

Zirkuluaren koadratura

Zirkulu baten erradioa emanda, eraiki erregela eta konpasa erabiliz zirkuluaren azalera bera duen karratuaren aldea. Antzinako Grezian hasi eta mendez mende erantzunik gabe bidaiatu zuen problema bat da hori. Erradioa unitate gisa hartuta, π-ren erro karratuaren luzerako zuzenkia egitea eskatzen da, beraz. Problema baliokidea da π luzerako zuzenkia eraikitzea.

Erabateko erantzuna ez zen XIX. mendera arte heldu:

• Johann Heinrich Lambert, 1761: π irrazionala da, hots, ez da zenbaki oso biren zatidura.
• Ferdinand von Lindemann, 1882: π traszendentea da, hots, ez da koefiziente osoak dituen ezein polinomioren erroa.

Irrazionala izatea lehen urrats modura uler daiteke, baina ez du eragozten eskatzen den eraiketa. Traszendentea izateak bai, ordea. Beraz, erregela eta konpasarekin zirkuluaren koadratura egitea ezinezkoa da, oraindik ere zeregin horretan gogoz saiatzen direnak badauden arren.

π = 3.2 izateko zorian egon zenekoa

Indianako mediku batek, Edward J. Goodwin jaunak, zirkuluaren koadratura egiteko modu “berri” bat asmatu uste zuen XIX. mendearen amaieran. Estatuari oparitu nahi izan zion bere metodoa, hango irakaskuntzan dohainik (sic) erabiltzeko. Horrela, 1897an lege-proiektu bat prestatu zuten, zegokion ibilbide legala egin zezan. Ez zen bertan π aipatzen, baina π = 3.2 ateratzen zen, zirkunferentziaren luzerari begiratuz gero. Hortaz, lege-proiektua onartuz gero, balio hori izango zuen π-k Indianako eskoletan.

Ordezkarien Ganbaran eztabaidatu behar zuten hasteko. Goodwin jaunak lortu zuen zenbait ordezkariren oniritzia proiektuak aurrera egiteko. Handik Senaturako bidea egin behar zuen. Zorionez, Purdue unibertsitateko irakasle batek jakin zuen zertan ari ziren eta astakeria galanta egiten ari zirela jakinarazi zien senatari batzuei. Azkenean ez zuten bozkatu, senatari batek ohartarazi baitzuen Ganbarak ez zuela eskumenik egia matematikoen gainean erabakiak hartzeko. Horrek ez zuen eragotzi ordezkari politikoak barregarri geratzea, garaiko prentsak erakusten duenez.

5. irudia: 1897ko bineta bat, Indianako politikariei barre eginez. (Argazkia: Wikipedia)

 

2021eko Matematikaren Nazioarteko Eguna

Utz dezagun π eta itzul gaitezen martxoaren 14ko ospakizunera. “Matematika mundu hobe baterako” goiburua garatzeko web gune berezi bat prestatu dute eta bertan ikus daiteke matematikak hainbat arlotan duen erabilera. Era berean, iazko “matematika nonahi” ere beste web gune batean gordetzen da. Bietan informazio ugarirako sarbide interesgarriak aurkituko dituzue. Hemen inguruan ere ekitaldi eta dokumentu ugari aurki daitezke Martxoa, matematikaren hilabetea izenburupean (EHU eta BCAM daude babesleen artean). Gehiena gaztelaniaz dago, baina badaude material batzuk euskaraz ere.

Egileaz:

Javier Duoandikoetxea Analisi Matematikoko Katedradun erretiratua da UPV/EHUn.

The post PI = martxoak 14 (3/14) appeared first on Zientzia Kaiera.

Foto: NASA/JPL-Caltech/GSFC

Las reacciones de fusión nuclear son bastante comunes en la naturaleza, aunque no en la Tierra. Son la fuente de la energía generada por el Sol y los miles de millones de estrellas en todo el Universo. En cierto sentido se puede decir que la energía de fusión es la principal fuente de energía de la naturaleza [1]. En las estrellas el confinamiento del plasma lo logra la atracción gravitacional.

Uno de los aspectos más fascinantes de la física nuclear es el estudio de las reacciones de fusión en los diferentes tipos de estrellas. Estas reacciones son las que terminarán formando muchos de los elementos químicos [2]. El Sol es un buen ejemplo.

En el Sol, el proceso de fusión da como resultado la producción de un núcleo de helio a partir de cuatro protones. El resultado neto de las reacciones que tienen lugar se puede escribir como

donde +10e es un «anti-electrón», también conocido como positrón. Esta reacción neta no tiene lugar en un solo paso, sino que se puede llegar a ella a través de diferentes conjuntos de reacciones cuyos resultados netos se resumen en esta ecuación. En cualquier caso la cantidad total de energía liberada es siempre la misma: 26 MeV. La fusión de cuatro protones para formar un núcleo de helio es la principal fuente de energía del Sol.

El hidrógeno y el helio juntos constituyen alrededor del 99% de la masa del Sol, con aproximadamente el doble de H que de He. Afortunadamente, hay suficiente hidrógeno como para que el Sol siga suministrando energía durante varios miles de millones de años más.

¿Mediante cuál de los varios conjuntos posibles de reacciones tiene lugar la transformación del hidrógeno en helio? Tenemos que descartar el proceso directo de colisión de cuatro protones para formar un núcleo de helio no porque sea imposible, sino porque la probabilidad de una reacción así en las condiciones del interior del Sol es demasiado baja. Es decir, puede suceder, pero no con la suficiente frecuencia para generar la cantidad de energía liberada que se observa.

Un conjunto de reacciones más probable es el siguiente: cuando la temperatura es de aproximadamente 107 K, las energías cinéticas son lo suficientemente grandes como para superar la repulsión eléctrica entre los protones y se produce la fusión de dos protones. La reacción nuclear da como resultado un deuterón (hidrógeno-2), un positrón y un neutrino. Tan pronto como se forma el deuterón, reacciona con otro protón, dando como resultado helio-3 y un rayo gamma. Los núcleos de helio-3 se fusionan entre sí, formando partículas alfa y dos protones. En cada una de estas reacciones, se libera energía, lo que da como resultado 26 MeV para el ciclo completo de cuatro protones que dan lugar a un núcleo de helio.

La velocidad de la reacción depende del número de núcleos por unidad de volumen y de la temperatura. Cuanto mayor sea la temperatura, más rápido será el movimiento térmico de las partículas y más frecuentes y enérgicas serán las colisiones. A la temperatura del interior del Sol, que se ha estimado que está entre 10 y 20 millones de grados, las energías cinéticas resultantes del movimiento térmico están en entorno de 1 keV.

Notas:

[1] Decimos en cierto sentido porque existen otras formas de energía, como la energía oscura o, incluso, la atracción gravitatoria de los agujeros negros. Pero no las consideramos.

[2] De aquí viene la expresión “somos polvo de estrellas”, porque los elementos que nos componen se crearon en su mayoría por procesos de fusión en las distintas fases de la vida y muerte de diferentes tipos de estrellas.

[3] Quizás convenga comentar que las reacciones químicas no pueden proporcionar energía a velocidades lo suficientemente grandes (o durante un tiempo lo suficientemente largo) como para explicar la producción de energía en el Sol. Las reacciones de fusión nuclear sí lo logran fácilmente.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo Fusión nuclear en el Sol se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Fusión nuclear
2. Energía de enlace nuclear y estabilidad
3. La fusión nuclear como fuente de neutrones eficiente

Juan Ignacio Pérez Iglesias

The Lancet aldizkariak Dementia prevention, intervention and care (“Dementziaren prebentzioa, esku hartzea eta zaintza”) izeneko txostena argitaratu zuen 2017an. Dementziei dagokienez, honako bederatzi arrisku faktore hauek identifikatzen ziren bertan: hezkuntza eskasa, hipertentsioa, entzumenaren galera, tabakoaren kontsumoa, obesitatea, depresioa, jarduera fisikorik eza, diabetesa eta gizarte harreman gutxi.

Izenburu berarekin aurten argitaratu den txostenean, beste hiru arrisku faktore gehitu dira: alkoholaren gehiegizko kontsumoa, lesio entzefaliko traumatikoak eta kutsadura atmosferikoa. Hamabi arrisku faktore horiek, oro har, munduan diagnostikatutako dementzien % 40 ingururen kausa dira, eta dementzia horiek, teorian, prebenitu edo atzeratu egin litezke. Egileen arabera, aukera handia dago dementziak prebenitzeko; batez ere, maila ekonomiko ertain eta baxuko herrialdeetan, hots, dementzia gehien dagoen herrialdeetan.

Irudia: Edadeko pertsonen kopurua, dementziaz bizi direnak barne, hazten ari da, heriotza-tasa goiztiarrak jaitsi egin baitira. (Argazkia:  Gerd Altmann – Pixabay lizentziapean. Iturria: pixabay.com)

Txostenak denboraren dimentsio guztiz interesgarria jasotzen du, denborarena, arrisku faktoreek bizitzan zehar modu sekuentzialean eragiten dutela erakusteko. Eta alderdi garrantzitsua da; izan ere, faktore bakoitzak sekuentzia horretan duen posizioaren arabera, prebentzio neurriak bizitzako etapa jakinetan hartu beharko lirateke.

Hezkuntzaren defizitari aurre egiteko –dementzien % 7 daude faktore horrekin lotuta–, lehen urteetan jardun behar da, pertsonen erreserba kognitiboari eragiten diolako; hau da, nolabait esatearren, pertsonen gaitasun kognitiboan eta erabil dezaketen ezagutzan inbertitzean datza. Erreserba hori zenbat eta handiagoa izan, orduan eta denbora gehiago iraungo du pertsonak dementzien ondorioetatik salbu.

Tarteko adinetan, garrantzia hartzen dute gerora dementzia eragin dezaketen patologia neuronalen jatorrian dauden arrisku faktoreek. Hori dela eta, audiofonoak erabiltzea gomendatu behar da, halakoen beharra dutenek entzumen maila onargarria izan dezaten, entzumen defizitari % 8ko arriskua egozten baitzaio. Halaber, neurriak hartu behar dira lesio entzefalikoak minimizatzeko (arriskuaren % 3), arteria presioa gomendatutako balioetatik behera mantentzen laguntzeko (% 2), alkoholaren kontsumoa murrizteko (% 1) eta obesitatea prebenitzeko edo hari aurre egiteko (% 1).

Beste faktore batzuek, lehenago sortuak izan arren, eragin handiagoa dute bizitzaren azken etapetan. Tabakismoa (arriskuaren % 5) ez da adin aurreratuetan hartzen, baina orduan eragiten du kalte gehien, eta, beraz, orduan saihestu behar da haren intzidentzia; horrenbestez, inoiz ez da berandu erretzeari uzteko. Dementzien % 2 jarduera fisikorik ezarekin lotzen dira. Faktore hori ere bizitzaren lehenagoko etapetan sortu ohi da, baina areagotu egiten da adinarekin. Hori dela eta, ariketa fisikoa sustatzea komeni da, ondorio babesgarriak baititu, ziurrenik obesitatea, diabetesa (arriskuaren % 1) eta hipertentsioa prebenitzen dituelako. Kutsadura atmosferikoak ere (% 2) lehenagoko etapetan eragiten ditu ondorio negatiboak, baina batez ere bizitzako azken urteetan izaten du dementziak eragiteko aukera.

Depresioa, dementzien % 4ri lotua, faktore konplexua da, ez baitago argi kausazko harremanaren norabidea; nolanahi ere, izan ditzakeen ondorio negatiboak zahartzaroan agertzen direnez, komeni da hura tratatzea, baita aurreko etapa batean sortu bada ere. Bakartze soziala ere adin aurreratuekin lotutako faktore bereizgarria da, eta hari egozten zaio arriskuaren beste % 4.

Prebenitzea sendatzea baino hobea dela esaten dugu, ez dagoelako prebentzioa baino erremedio hoberik. Baina kontuan izanik dementziak ezin direla sendatu, ez dago prebentzioaren ordezko beste aukerarik dementzien kasuan.

Erreferentzia bibliografikoa:

Livingston, G., et. al (2020). Dementia prevention, intervention, and care: 2020 report of the Lancet Commission. The Lancet Commissions, 396 (10248), 413-446. DOI: https://doi.org/10.1016/S0140-6736(20)30367-6

Egileaz:

Juan Ignacio Pérez Iglesias (@Uhandrea) UPV/EHUko Fisiologiako katedraduna da eta Kultura Zientifikoko Katedraren arduraduna.

The post Dementziak prebenitzea hobe, ezin baitira sendatu appeared first on Zientzia Kaiera.

Paula Oliver Vara

Shutterstock / BonNontawat

 

Cuando pensamos en el tejido adiposo, inevitablemente nos vienen a la mente los impopulares “michelines”, que a día de hoy percibimos como un problema. Sin embargo, debemos tener en cuenta que la capacidad de almacenar como depósitos de grasa el excedente de energía ingerida ha permitido la supervivencia de nuestra especie. Osea, que hay mucho que agradecerle.

El principal reservorio de grasa en nuestro cuerpo es el tejido adiposo blanco, pero existe también un tejido adiposo marrón. Este último tiene una función opuesta, ya que nos permite “quemar” la grasa almacenada, disipando la energía como calor. Eso lo convierte en una interesante diana en la lucha contra la obesidad y sus complicaciones.

El tejido adiposo blanco: una reserva de energía para momentos de necesidad

Los alimentos contienen nutrientes que nos proporcionan la energía (calorías) que nuestro cuerpo necesita para funcionar. Si ingerimos más calorías de las que gastamos no las desaprovechamos, sino que las convertimos muy eficientemente en grasa (triacilglicéridos) que almacenamos en unas células, los adipocitos, que forman el tejido adiposo blanco.

Este reservorio de grasa queda disponible para hacer frente a situaciones de escasez de alimentos, en las que podemos movilizar los triacilglicéridos almacenados para obtener la energía que necesitamos. Por eso la grasa aporta una ventaja evolutiva. O más bien la aportaba hasta hace poco. Porque en la época actual, y a diferencia de lo que ha venido ocurriendo a lo largo de miles de años de evolución, nos encontramos frente a una situación bastante diferente.

En estos momentos, la mayoría de individuos de nuestra especie tiene a su disposición una amplia oferta de alimentos, algunos excesivamente calóricos. Si a los frigoríficos y despensas a rebosar le sumamos que nuestro estilo de vida es cada vez más sedentario, la consecuencia inmediata es que acumulamos grasa en exceso y engordamos.

La grasa subcutánea –esto es, la de los michelines– más característica de las mujeres, es la menos problemática. El mayor riesgo para la salud se asocia a la grasa visceral, que es la que se deposita rodeando a órganos como el hígado, corazón o los intestinos.

Es importante resaltar también que el tejido adiposo no solo sirve como reservorio de energía. Los adipocitos blancos son capaces de producir y liberar a la sangre sustancias bioactivas conocidas como adipocitoquinas, con una importante función reguladora del metabolismo. El problema viene cuando acumulamos demasiada grasa en nuestros adipocitos, porque en ese momento la producción de adipocitoquinas se desregula. Como consecuencia, aumentan los procesos inflamatorios y la resistencia a la insulina, que son el detonante de diversas patologías.

Resumiendo, el acúmulo de grasa corporal en forma de sobrepeso u obesidad ha alcanzado a día de hoy dimensiones de pandemia, y van asociado a enfermedades cardiovasculares y a una larga lista de patologías, incluyendo diferentes tipos de cáncer e, incluso, un mayor riesgo de daño cognitivo.

El tejido adiposo marrón: el tejido capaz de quemar la grasa

Si bien el tejido adiposo blanco es el más abundante, existe otro tipo de tejido adiposo, el marrón. Se distingue porque, en respuesta al frío y otros estímulos, moviliza las reservas grasas y libera energía en forma de calor. El proceso se conoce como termogénesis adaptativa, y resulta muy útil para mantener la temperatura corporal en animales, incluidos los hibernantes. Además, en pequeños mamíferos, la termogénesis adaptativa se pone en marcha también frente a la ingesta de dietas ricas en calorías, lo cual les ayuda a mantener el peso corporal.

En el caso de los humanos, durante muchos años se pensó que el tejido adiposo marrón era importante en recién nacidos para regular la temperatura corporal, pero que desaparecía en adultos. La sorpresa surgió hace poco más de una década, cuando se describió que los humanos mantenemos tejido adiposo marrón en edad adulta que es capaz de activarse para generar calor, utilizando ácidos grasos y glucosa.

Este descubrimiento potenció la aparición de proyectos encaminados a identificar diferentes formas de activar la termogénesis en el tejido adiposo marrón para perder peso, mejorar la salud cardiovascular y pararle los pies a la diabetes. Uno de ellos fue el proyecto europeo DIABAT, que se desarrolló entre el 2011 y el 2015, en el que participaron centros de investigación de 12 países europeos, incluido nuestro grupo de Nutrigenómica y Obesidad de la Universidad de las Islas Baleares.

Las investigaciones continúan avanzando, y son múltiples las evidencias que apuntan a los beneficios de la grasa marrón. Por ejemplo, recientemente se ha publicado que la presencia de tejido adiposo marrón está relacionada con un menor riesgo cardiovascular. Y que podría mitigar las complicaciones asociadas a la obesidad, como la diabetes, hipertensión o niveles de lípidos elevados en sangre.

¿Y si pudiéramos convertir la grasa blanca en marrón?

Aunque lo ideal es no acumular grasa en exceso, la buena noticia es que los depósitos de grasa blanca pueden convertirse en lo que ha venido a considerar un tercer tipo de grasa, la grasa beige.

La transformación forma parte de un proceso conocido como marronización. Resulta interesante porque los adipocitos beige son un tipo de células similares a los adipocitos marrones. Como ellos, expresan la proteína UCP1 o termogenina, y por lo tanto pueden realizar termogénesis. Eso sí, están localizados dentro del tejido adiposo blanco.

La marronización del tejido adiposo blanco se puede inducir con estímulos adecuados, como la exposición al frío. Pero también con fármacos, con determinados nutrientes, e incluso con el ejercicio físico. Esta posibilidad es interesante porque con la conversión de grasa blanca en grasa beige se potenciaría la eliminación de los lípidos y glucosa circulantes. Y al incrementar de esta forma el gasto energético contribuiríamos a mantener el peso corporal y la salud metabólica.

Parece indiscutible que estamos ante un arma muy poderosa para combatir la epidemia mundial de obesidad y de diabetes.

Sobre la autora: Paula Oliver Vara es catedrática de bioquímica y biología molecular en la Universitat de les Illes Balears y co-investigadora principal del grupo de “Nutrigenómica y Obesidad” del CIBER de Fisiopatología de la Obesidad y Nutrición (CIBEROBN)

Este artículo fue publicado originalmente en The Conversation. Artículo original.

El artículo ¿Blanca, beige o marrón? No toda la grasa corporal es mala se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Resveratrol y pteroestilbeno en el control epigenético de la acumulación de grasa corporal
2. La combinación de dos moléculas marroniza la grasa
3. Grasa parda

Leire Sangroniz, Ainara Sangroniz

Martxoaren 8an Emakumearen Nazioarteko Eguna ospatzen da eta kolore morea izango dugu nagusi kaleetan. Emakumearen borrokaren ikur den kolore honen atzean kimika asko dago. Hain zuzen ere, sintetizatu zen lehenengo koloratzailea kolore morea izan zen. Morea, bioleta, malba, purpura… izen ugari daude antzekoak diren koloreak adierazteko. Bakoitzak bere berezitasunak baditu ere, artikulu honetan, kolore moreaz mintzatuko gara oro har.

Zergatik da kolore morea emakumeen berdintasunaren adierazle? Zenbait hipotesi daude, tartean ezagunena 1908. urtean Ingalaterrako sufragisten mugimenduak morea aukeratu zuela da, zuriarekin eta berdearekin batera errebindikazio-koloreak bezala. Hala ere, moreak besterik ez zuen aurrera egin eta bera gailendu zen emakumeen borrokaren ikur gisa.

1. irudia: 1909ko intsignia, Emmeline Pankhurst mugimendu sufragistaren buru eta ekintzaile politiko britainiarraren erretratuarekin. Paparrekoan ikus daitezke errebindikazio sufragistaren koloreak. (Argazkia: Museum of London – Domeinu publikoko argazkia- Iturria: Wikimedia Commons)

Kolore morea: ustekabeko aurkikuntza

XIX. mende erdira arte, koloratzaileak iturri naturaletatik lortzen ziren, landareetatik zein animalietatik. Koloratzaile gehienak oso garestiak ziren eta gizartean gehiengoak ezin zituen eskuratu kolore horiek zituzten jantziak.

Koloratzaile garestienetariko bat kolore morea ematen zuena zen. Ordura arte koloratzaile hau Mediterraneoko kostaldeko hainbat barraskilo-maskorretatik lortzen zen. Ehunka barraskilo-maskor behar ziren koloratzaile kantitate txiki bat lortzeko.

Hala ere, 1856an koloratzaileen iraultza eragingo zuen ezusteko aurkikuntza egin zuen William Henry Perkin kimikariak. Perkin oso azkarra zen eta 15 urte besterik ez zuelarik Royal College of Chemistry eskola ospetsuan sartu zen.

Garai hartan kinina zen malariaren aurkako tratamendu bakarra. Substantzia hau garestia zen, Hego Ameriketako kina zuhaitzetatik bakarrik lortu baitzitekeen. Ondorioz, beharrezkoa zen kinina modu merkeago batean lortzea. August Wilhelm von Hofmann kimikari ospetsuak konposatu hori laborategian sintetizatzea zuen helburu, eta zeregin horixe jarri zion bere laborategian laguntzaile gisa lan egiten zuen Perkin gazteari.

2. irudia: XX. mendearen hasierako banderatxoa, emakumeen boto-eskubidea aldarrikatzen duena. (Argazkia: The Children’s Museum of Indianapolis – CC BY-SA 3.0 lizentziapean. Iturria: Wikimedia Commons)

1856ko Aste Santuko oporretan, Hofmann irakaslea kanpoan zegoela, Perkin kinina sintetizatzen saiatzen ari zen bere etxeko laborategian. Horretarako, anilina deritzon konposatua erabili zuen eta potasio dikromatoarekin oxidatzen saiatu zen. Erreakzio hau burutzean lortutako produktua ez zen kinina. Horren ordez, solido beltz bat lortu zuen eta, garbitzen saiatu zenean, disoluzioak kolore morea zeukala konturatu zen. Koloratzailea anilinan zegoen ezpurutasun bati esker, toluidina, lortu zuen. Koloratzaile honek zenbait izen zituen: anilina morea, malba edo Perkinen purpura.

Zenbait erreakzio gehiago burutu zituen eta urte berean produktua patentatu zuen, soilik 18 urte zituela. Bere aita eta anaiekin batera lantegi bat eraiki zuen koloratzailea ekoizteko. Kolore morea modan jarri zen eta horri esker Perkinek etekin ekonomiko handia lortu zuen.

Modu honetan eman zitzaion hasiera koloratzaile sintetikoen iraultzari eta kolore berriak ekoizteari ekin zioten Erresuma Batuan, Alemanian eta Frantzian. Hurrengo 5 urteetan guztira 28 lantegi hasi ziren koloratzaileak sintetizatzen.

Aipatzekoa da, gainera, koloratzaile sintetiko honi esker medikuntzan aurrerapauso handiak egin zirela; esaterako, Walther Flemmingek zelulak koloreztatu ahal izan zituen eta mikroskopian aztertu.

Perkin 36 urterekin erretiratu zen kimikan ikertzen jarraitzeko helburuarekin, lantegiaren ardurekin ez baitzuen denborarik. Koloratzaile berriak sintetizatu eta merkaturatu zituen. Horretaz gain, kumarina (lurringintzan erabiltzen den konposatua) eta azido zinamikoa (sendagaiak, gozagarriak edo anil tindagaia lortzeko erabiltzen den konposatua) lortzeko sintesi bide berriak aurkitu zituen.

Esker onak

Egileek eskerrak eman nahi dizkiote Juan José Iruin irakasleari bere laguntzarengatik.

Iturriak:

• García Visos, Bibiana (2018). Mauve: the History of the Colour that Revolutionized the World. OpenMind BBVA, argitaratze-data: 2018ko uztailaren 13a.
• Hicks, Jan (2017). William Henry Perkin and the first synthetic dye. Science+Industry Museum, argitaratze data: 2017ko abuztuaren 25a.
• Freemantle, Michael (2016). Mauveine. Chemistry World, argitaratzen-data: 2016ko martxoaren 29a.
• Iruin, Juan José (2013). El Sr. Perkin y las cuentas de la vieja. El Blog del Búho, argitaratze-data: 2013ko abenduaren 31a.
• Science Museum. The colourful chemistry of artificial dyes. Argitaratze-data: 2019ko apirilaren 9a.

Egileez:

Leire Sangroniz eta Ainara Sangroniz Kimikan doktoreak dira eta UPV/EHUko Kimika Fakultatearen, Polimeroen Zientzia eta Teknologia Saileko ikertzaileak Polymat Institutuan.

The post Kolore morea eta koloratzaile sintetikoen iraultza appeared first on Zientzia Kaiera.

Pablo Rodríguez Sánchez

Este no es mi primer artículo de divulgación. De hecho, si las cuentas no me fallan, es mi centésimo décimo quinto. Sin embargo, es el primer artículo de divulgación en el que hablo de mi propia investigación. Para alguien con una verborrea como la mía, semejante timidez y silencio respecto a mi propio trabajo son, cuanto menos, llamativos. Sospechosos incluso. Pero todo tiene una explicación: he pasado tanto tiempo embarrado ocho horas diarias con estos problemas que para cuando les puse las guinda y fueron publicados… ya hacía meses que habían dejado de divertirme.

Un artículo científico, peor aún si trata sobre matemáticas, se acerca mucho a la antítesis de la diversión. Especialmente para el que lo lee. Hace falta mucha habilidad para hacerlo entretenido, habilidad que yo no tengo. Sin embargo, escribir un artículo científico es una actividad humana llena de altibajos, frustraciones y curiosidades. Ingredientes estos no muy diferentes de los que uno puede encontrar en algunas novelas, películas e incluso chistes.

Permítanme que les cuente aquí la intrahistoria de mi artículo, pues esta, al contrario que el frío y técnico contenido, es completamente inédita.

Ascendiendo y descendiendo. M.C. Escher (1960). Litografía. Fuente: Wikimedia Commons

El arte, las matemáticas y yo

Lo reconozco. Hubo un tiempo en el que cada vez que escuchaba juntas las palabras “arte” y “matemáticas” me ponía en guardia. Será que he visto demasiadas películas infumables, demasiadas obras de arte pretenciosas (y a menudo feas), o simplemente que estoy hecho un gruñón.

Digo «hubo un tiempo», en pasado, porque actualmente veo la combinación “arte y matemáticas” con ojos más benévolos. Esto se debe a que este dueto me ha proporcionado muchos buenos momentos en los últimos años. Algunos ejemplos son mi colaboración con el videoartista Johan Rijpma, mis charlas en Naukas, o la historia que hoy les traigo.

Como pez fuera del agua

Permítanme que les ponga en antecedentes. En 2015 comencé un doctorado en matemáticas aplicadas en un departamento de ecología. Esto significaba, entre otras cosas, que tenía que escribir artículos sobre matemáticas que fuesen interesantes para la comunidad ecológica.

La mayoría de ecólogos se pueden clasificar en tres categorías: ecólogos de campo, ecólogos de laboratorio y ecólogos computacionales. O si lo prefieren, ecólogos de bota, de bata y de byte. Los ecólogos suelen tener formación en biología, y cualquier suposición sobre su interés por las matemáticas está abocada al fracaso: este puede ir desde casi nulo a altísimo.

Todo esto plantea una dificultad enorme desde el punto de vista de la comunicación: ¿cómo abordar los problemas matemáticos de la ecología sin perder ni aburrir a nadie? En este otro artículo, publicado en esta misma casa, ofrezco algunos consejos generales. Pero permítanme ir de lo general a lo particular, y explicar cómo el arte me echó una mano en cierta ocasión.

La estabilidad como paisaje

Uno de estos problemas de comunicación interdisciplinar es el siguiente: en ecología aparecen de forma bastante natural conceptos procedentes de la teoría de sistemas dinámicos. Hablo de conceptos como ecuación dinámica, clasificación de equilibrios o teoría de bifurcaciones.

Para los matemáticos, los sistemas dinámicos no son nada más (ni nada menos) que unas reglas, normalmente en forma de ecuaciones, que dictan cómo debe moverse un punto. Ese punto puede representar muchas cosas. Una temperatura a lo largo del año, los ahorros presentes en una cuenta bancaria, la cantidad de peces que viven en un lago, etcétera. En definitiva, cualquier cosa que pueda medirse y cambie en el tiempo. Si las reglas están bien fundadas, podemos usarlas nada menos que para predecir la evolución futura de la variable bajo estudio. Un buen ejemplo son los problemas de mecánica, donde conociendo las fuerzas que actúan sobre un objeto podemos calcular cómo se moverá este.

Estos puntos, según cual sea el problema, pueden moverse por una línea recta, por un plano, por el espacio tridimensional, o por inimaginables hiperespacios de cuatro o más dimensiones. Todo depende del número de variables que estemos estudiando (una temperatura, las poblaciones de dos especies de peces, las tres dimensiones de un objeto en movimiento, etc).

Una manera muy habitual de introducir estos conceptos, que ha demostrado su eficacia en innumerables ocasiones, es usando algo que la comunidad ecológica llama stability landscape o ball-in-a-cup diagram (lo que podríamos traducir libremente como «paisaje de estabilidad» o “diagrama de la bolita en el vaso»; no me miren así, yo no les he puesto esos nombres). La idea consiste en construir una curva sobre la cual una bolita se deja rodar, de modo que la forma de la curva, la forma del «paisaje», nos indica cómo ha de moverse1. Al fin y al cabo la teoría de sistemas dinámicos, recordemos, trata de describir cómo se mueve un punto… y dejar rodar una bolita es, en principio, una manera como otra cualquiera de mover un punto de acá para allá. La idea es muy gráfica y explota nuestra natural intuición respecto al movimiento. Ahí radica su fuerza.

Si, además, permitimos que la forma de los «paisajes» cambie en respuesta a condiciones externas (como temperatura, pH, salinidad, …), estas metáforas gráficas pueden usarse para ilustrar conceptos bastante avanzados, como los de estabilidad, bifurcación, o histéresis (ver ejemplo en la figura, y más aquí).

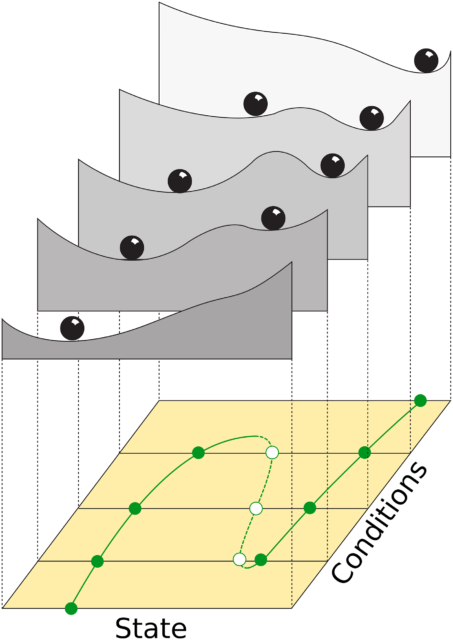
La parte superior de la figura muestra el «paisaje» correspondiente a un sistema dinámico para 5 valores diferentes de las condiciones externas. La parte de abajo muestra, en verde, el diagrama de bifurcación correspondiente, donde los puntos sólidos representan equilibrios estables (correspondientes al fondo de un «valle») y los vacíos equilibrios inestables (correspondientes a una «cresta»). Obsérvese como no sólo la posición, sino también el número de puntos de equilibrio varía con las condiciones externas. Una de las consecuencias de esto es que, para ciertas condiciones externas, el comportamiento del sistema puede cambiar de manera drástica.

Es posible que el lector se haya dado cuenta de que estos «paisajes» se parecen mucho al concepto de potencial en mecánica clásica. De hecho, son casi lo mismo2.

Pedir peras al olmo

Utilizar aproximaciones y analogías gráficas tiene sus ventajas y sus peligros. Algunos, incluso, son ventaja y peligro a la vez. El hecho de que las cosas parezcan más sencillas de lo que realmente son es una de estas ventajas peligrosas.

Muchos biólogos trabajan con sistemas dinámicos de dos variables. Por ejemplo, una coordenada x describiendo una especie de pez, y la coordenada y describiendo a otra. A menudo los peces x se comen a los peces y. ¿Y si usamos estos “paisajes de estabilidad” en modelos con dos (o más) variables? Si una bola rodando sobre curva nos sirve representar la dinámica de una variable, una bola rodando sobre una superficie nos servirá para representar la dinámica de dos variables, ¿no?

En principio no parece mala idea, pero cualquiera que lo intente no tardará en encontrarse en un callejón sin salida. Lo que funciona de maravilla para una variable se convierte en una pesadilla cuando se intenta aplicar a dos o más. En el mejor de los casos, el «paisaje» puede calcularse para algún subcaso muy concreto. En el peor, alguien propondrá un método nuevo, cada cual más complicado y difícil de interpretar que el anterior.

Y es que, aunque en principio usar superficies como “paisajes de estabilidad” puede parecer una buena idea, resulta no serlo. Los motivos últimos son sutiles, y requieren de herramientas con nombres tan poco atractivos como campo irrotacional o teorema del gradiente. Meterme en ese barrizal en un artículo de ecología hubiera sido de un mal gusto intolerable. Pero entonces, ¿cómo abordar el problema?

Aquí es dónde, por fin, el arte vino en mi ayuda. Imaginemos, me dije, un sistema dinámico con estas dos características:

• Tiene dos variables: nuestro punto (x,y) se mueve por un plano.
• Describe una oscilación: el punto describe una trayectoria cerrada, una y otra vez.

Tratemos ahora de imaginar una superficie tal que la bolita, en su constante descenso, dé vueltas y vueltas eternamente en una curva cerrada, sin dejar de rodar hacia abajo. ¿Qué aspecto tendría esa superficie? Intentemos imaginarla. A ojo, sin teoremas ni campos ni derivadas, ¡imaginación al poder! Y hete aquí que, por poder, podemos imaginarla. Y en gran medida, gracias a las extrañas superficies popularizadas por el artista M.C. Escher.

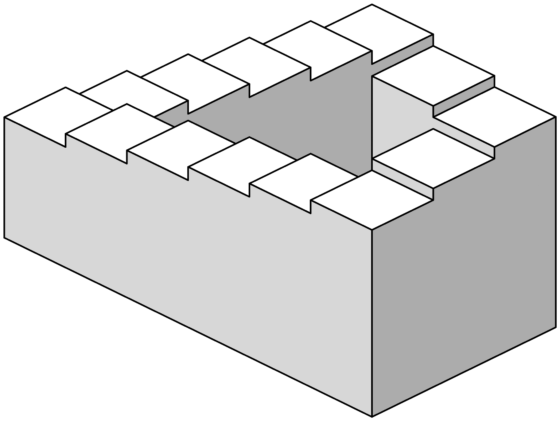
Podemos imaginarla, pero es una superficie que hace saltar todas nuestras alarmas. Algo tiene, algo le pasa, algo no cuadra, es una superficie… imposible. Y lo es, vaya si lo es. Resulta que desde el principio estábamos intentando pedirle peras al olmo. O subir las escaleras de Escher. ¡Con razón la cosa se ponía difícil!

¿Nada más?

Es posible que al lector más acostumbrado a la literatura científica el contenido de este post se le antoje corto para un artículo de investigación. Y llevará razón. El artículo original va más allá de lo que esta pequeña pieza de divulgación pretende (y debe) cubrir. Concretamente, añade un algoritmo para evaluar cuándo y dónde podemos usar estos paisajes de estabilidad en sistemas multidimensionales.

¿Algoritmo has dicho?, o sea, ¡que al final sí que te metiste en berenjenales matemáticos! En efecto… no me quedó más remedio. Diré en mi defensa que, esta parte, la de métodos, intenté hacerla lo más digerible posible. En este caso no fue el arte, sino la ingeniería de software quien vino en mi ayuda. Me explico: además de detallar cómo funciona el algoritmo, lo programé lo mejor que pude, lo empaqueté y lo puse pública y abiertamente a disposición de quien quiera usarlo, mejorarlo o incluso poner a prueba que lo que digo en mi artículo es correcto.

En mi opinión esto es una buena idea por muchos motivos. Además de los obvios (reproducibilidad, comodidad, …) también aporta una ventaja desde el punto de vista de la comunicación: permite a los lectores menos afines a las matemáticas utilizar el algoritmo sin necesidad de bucear demasiado en los detalles.

Para acabar, una reflexión suelta

Escribiendo este artículo tuve el raro honor de citar una publicación antiquísima, concretamente del año 1777. Cuando pensamos en investigación multidisciplinar, tendemos a dar por sentado que los «puentes» que quedan por tender entre disciplinas serán pocos y seguramente muy recientes. Sin embargo, queda claro que aún quedan puentes por tender, incluso, desde los fundamentos.

Y esta es la historia de mi artículo. La parte interesante. Creo. Es, en fin, lo que ningún editor de una revista académica aceptaría. Es también lo que le contaría a un amigo si me insistiese en que hablase del tema durante una cena o tomando unas cervezas.

Notas:

1 En esta otra entrada mostramos algunos ejemplos.

2 ¿Por qué casi?, pues porque el potencial mecánico se relaciona con la derivada segunda del estado, mientras que aquí estamos vinculando los “potenciales” a la derivada primera. Aún así, existe otra analogía mecánica, esta sí, impecable: el movimiento de una bolita en un potencial mecánico al sumergida en un medio viscoso.

Sobre el autor: Pablo Rodríguez Sánchez es doctor en matemáticas aplicadas e ingeniero de software de investigación en el Netherlands eScience Center (Amsterdam, Países Bajos)

El artículo El día que el arte me ayudó a escribir un artículo de matemáticas se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Historia de cómo el VIH ayudó a derribar el dogma central de la biología molecular
2. Cómo leer un artículo científico
3. Cuadrados latinos, matemáticas y arte abstracto

Uxue Razkin

Osasuna

Sendagaien Europako Agentzia Errusiako Sputnik V txertoa aztertzen hasi da, Berriak jakinarazi duenez. The Lancet aldizkariaren artikulu batek dio txerto honek %92ko eraginkortasuna duela.

Txertoak nolakoak diren eta horien inguruko informazio baliagarria eman digu Ana Galarragak testu honen bitartez. Oraindik zalantzak badituzue gai honen inguruan, ezin duzue galdu bere oinarrizko azalpena.

Ia urtebete igaro da COVID-19aren amesgaiztoa hasi zenetik. Hein handi batean horri erreparatu diogu. Baina zer gertatu da gripearekin? Ia ez da kasurik izan Euskal Herrian. Artikulu honen bidez, horretan eragina izan duten aldagaiak aztertu dituzte.

Felix Zubia medikuak pandemiaren zenbakiak aurkeztu dizkigu testu honetan. Horietatik gogorrena: “4.812, Hego Euskal Herrian koronabirusagatik hildakoak. Eskoriatza, Ibarra, Berriz, Plentzia, Agurain, Senpere edo Zangozako herritar guztiak kolpetik hiltzea litzateke, adibidez, neurria”. Irakurri beharrekoa.

Astronomia

Perseverance ibilgailuari begira gaude denok, Marten bizitzarik egon ote den jakiteko gogoz. Ildo horri jarraiki, Uxune Martinezek azaldu digu Giovanni Virginio Schiaparelli astronomoa ospetsu bihurtu zuen lana: antza, XIX. mendean behatu zituen Marten kanal batzuk. Baina… Schiaparelliren behaketak ez ziren oso zehatzak eta finak izan. Ez galdu!

Eboluzioa

Neandertalen mintzatzeko gaitasuna gurearen parekoa zela ondorioztatu dute, Elhuyar aldizkariak kontatu digunez. Entzumen-egiturak eta haiei eboluzioa ikertu dute Mercedes Conde Valverdek gidatu duen azterlanean. Horri buruzko xehetasunak artikulu honetan topatuko dituzue.

Biologia

Birusen hautespen naturala eta horien aurrean antibiralek eta txertoek nola jokatzen duten azaldu digute artikulu honetan. Horretaz gain, nabarmentzen da garrantzitsua dela patogeno baten transmisioa saihestea, horrela ugaltzeko aukerak gutxitzen zaizkiolako.

Baztangaren birusaren errepaso historikoa egin du Ziortza Guezuragak testu honetan. Edward Jennerek aurkitu zuen baztangaren aurkako txertoa 1796an baina aurretik gertatukoari so egin dio ere. Ez galdu!

Kimika

Pisu atomikoaz idatzi du Cesar Tomék artikulu honetan, hori zehazten lan egin zuten zientzialarien eta eurek emandako urratsen kontakizun argia eginez.

Emakumeak zientzian

Ana Ruiz Ilundain ingeniariak leku itxietan, airearen kalitatea neurtzen duen gailu bat egokitu eta hobetu du. Ikasketen Amaierako Lanetarako Rural Kutxa Sarietako sari berezia eman diote lan horregatik. Bere ibilbide zientifikoari buruz irakurtzeko aukera paregabea duzue hau.

Biomaterialak

CIC Biomaguneko ikerketa talde batek tumoreak hazten ditu hiru dimentsioko aldamioetan, eta haien barne funtzionamendua aztertzen du, Berriak azaldu digunez. Tumorea sakon-sakonean ulertzea dute helburu. Clara Garcia Astrain eta Javier Plou ikertzaileen hitzak bildu dituzte honetan.

Asteon zientzia begi-bistan igandeetako atala da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna erreparatuz, Interneteko “zientzia” antzeman, jaso eta laburbiltzea da gure helburua.

Egileaz:

Uxue Razkin (@UxueRazkin) kazetaria da.

The post Asteon zientzia begi-bistan #340 appeared first on Zientzia Kaiera.

Foto: Alex Knight / Unsplash

La mente humana es una gran caja negra. La mente robótica, de hecho, lo es y hasta más oscura. Esta es la tesis que defiende Helena Matute en esta inquietante charla.

Helena Matute es catedrática de psicología experimental de la Universidad de Deusto.



Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Helena Matute – Naukas Bilbao 2019: Mente humana, mente robótica se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Helena Matute – Naukas P4K 2019: Vulnerable-mente
2. Helena Matute: «Los algoritmos nos ganan en cualquier partida que juguemos contra ellos»
3. Francisco Villatoro – Naukas Bilbao 2019: El abrazo de la plata

Denbora zentzu batean eta ez bestean doala azaltzen duten narrazio termodinamikoek zenbait galdera eragiten dizkio gure filosofoari: A paradox in the thermodynamic arrow of time? Jesús Zamora Bonillaren eskutik.

Oso txikia diren gauzen ikerketak, partikula elementalen ikerketak, dagoen gauzarik handienarekin du harremana: unibertsoa bere osotasunean. Jakina da hau. Teknologia kuantikoak erabilera astrofisikoa izatea ez da hain jakina: The search for dark matter gets a speed boost from quantum technology Benjamin Brubakeren eskutik.

Badira molekula aromatikoak eta aromatikoak ez direnak. Eta badira ez direnak baina egoera kitzikatuan badirenak. Eta erdibideko gauzak ere badira. Optoelektronikan erabilera izan dezakeen aromatizidadearen doiketa lortu dute DIPCn: Tuning the excited-state Hückel‐Baird hybrid aromaticity.

Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.

The post Ezjakintasunaren kartografia #343 appeared first on Zientzia Kaiera.

Foto: Tom Eames

Un equipo de investigadores españoles y holandeses ha estimado que el área afectada por incendios forestales en África es un 80 % máyor de lo que se pensaba. Dado que África representa la mayoría del área quemada a nivel global este nuevo hallazgo modifica sustancialmente las estimaciones de emisiones globales de gases a la atmósfera.

Los incendios forestales suelen aparecer en los medios de comunicación cuando las que se queman son regiones boscosas cercanas a asentamientos humanos, pero la mayor parte de la superficie que arde cada año corresponde a sabanas tropicales donde los incendios son parte integral del ecosistema. El área total que se quema en esos ecosistemas es aproximadamente el equivalente al tamaño de la Unión Europea. Hasta ahora, la evaluación a gran escala del área quemada se ha basado en imágenes de satélites con un tamaño de píxel relativamente grande. Esto es un problema ya que, para que un incendio pueda detectarse de esta manera, es necesario que todo un píxel de la imagen aparezca como incendiado.

Los investigadores Rubén Ramo y Emilio Chuvieco, de la Universidad de Alcalá, y Ekhi Roteta y Aitor Bastarrika de la UPV/EHU han estudiado las imágenes de áreas quemadas aportadas por el satélite europeo Sentinel-2 y han comparado estos datos con los empleados habitualmente, de menor resolución. El Sentinel-2 es capaz de distinguir cuadrados de 20 metros de lado, frente a los 500 m de lado de los cuadrados habituales.

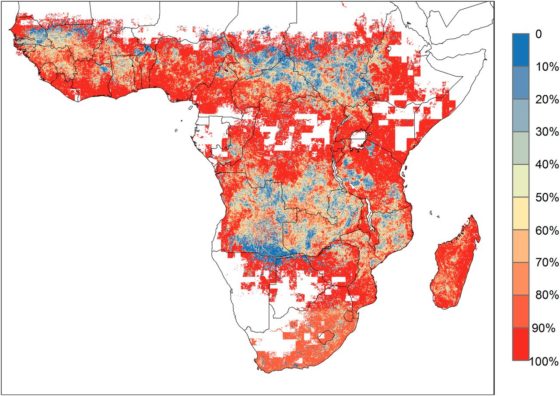Incendios forestales menores detectados en África. Fuente: PNAS

Los investigadores han encontrado que incendios relativamente pequeños, que no pueden ser detectados por los satélites de menor resolución, contribuyen casi tanto al área total quemada como los incendios más grandes. Los incendios pequeños tienen un impacto mucho mayor de lo que se creía.

Por su parte, los investigadores de la Vrije Universiteit Amsterdam, Dave van Wees y Guido van der Werf, han calculado las emisiones de gases correspondientes a dichos incendios menores y encontrado que estas emisiones adicionales son mayores que las emisiones totales producidas por incendios forestales en toda América del Sur.

Se estima que las emisiones totales por incendios forestales en África equivalen al 13 % de las emisiones mundiales por el uso de combustibles fósiles. Sin embargo, dado que las emisiones de dióxido de carbono de esos incendios menores de la sabana africana se compensan con el recrecimiento de la vegetación de la zona afectada, la estimación del aumento del área quemada total no contribuye proporcionalmente a la acumulación de dióxido de carbono en la atmósfera, como lo hacen los combustibles fósiles, pero sí aumenta la contribución de los incendios a las cantidades de otros gases de efecto invernadero como el metano y el óxido nitroso.

Referencia:

Ruben Ramo, Ekhi Roteta, Ioannis Bistinas, Dave van Wees, Aitor Bastarrika, Emilio Chuvieco, and Guido R. van der Werf (2021) African burned area and fire carbon emissions are strongly impacted by small fires undetected by coarse resolution satellite data PNAS March 2, 2021 118 (9) e2011160118 DOI: 10.1073/pnas.2011160118

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo África arde más de lo que se pensaba se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Los ecosistemas acuáticos de África y el cambio climático
2. Hubo una migración de vuelta a África en el Paleolítico
3. La energía de las olas ha aumentado un 40 % en el último siglo.

Ana Galarraga / Elhuyar Zientzia

Ana Ruiz Ilundain Nafarroako Unibertsitate Publikoko Industria Ingeniaritzako Unibertsitate Masterra egin berri du, eta, leku itxietan, airearen kalitatea neurtzen duen gailu bat egokitu eta hobetu du. Gailua baliagarria da inguruneko kondizioak automatikoki ebaluatzeko eta airea berritzeko; beraz, oso baliagarria da COVID-19aren transmisioa eragozteko. Lan horri esker, Ikasketen Amaierako Lanetarako Rural Kutxa Sarietako sari berezia eman diote.

Aitortu duenez, batxilergoan ez zuen ikasketa teknikorik egiteko asmorik. “Adibidez, ez nuen marrazketa teknikoa hartu. Argi nuen, hori bai, zientzietatik joko nuela, historia, hizkuntza eta halakoak ez baitziren nire gustukoak; bai, ordea, matematika, biologia, fisika, kimika…”

Irudia: Ana Ruiz Ilundain ingeniaria. (Argazkia: Nafarroako Unibertsitate Publikoa – NUP)

Farmazia ikastea zen lehen asmoa, baina fisika ikaragarri gustatu zitzaion, eta, fisika teorikoa baino zerbait aplikatuagoa nahi zuenez, orduan hasi zen pentsatzen ingeniaritza ikas zezakeela: “Egia esan, txikitan ere asko gustatzen zitzaizkidan eraikuntza-jolasak, eta Iruñean bertan ingeniaritza industriala baneukanez, eta gainera, etxean banituen erreferenteak, aita ingeniaria baita, eta anaia, arkitektoa”.

Hala, ingeniaritza industriala ikasten hasi zen, Nafarroako Unibertsitate Publikoan. Gutxi gorabehera zer topatuko zuen bazekien arren, lehen urtea gogorra egin zitzaion: “Azken finean, ikasteko modua aldatu behar duzu. Eskolan, ikasitakoa galdetzen dizute; ingeniaritzan, arazoak konpontzen ikasi behar duzu. Arazo horiek edozein arlotakoak izan daitezke; hala, ingeniaritzak irtenbide pila bat ditu, imajinatzen nituenak baino askoz ere gehiago, hasi produktu bat diseinatzetik, eta lantalde bat zuzentzera edo erosketak planifikatzera, edozein eremutan”.

Bestalde, ingeniaritzako ikasketetan gizonek gehiengoa izaten jarraitzen dute, baina Ruizek argi du guztiok balio dugula guztirako, eta, irakasle batzuek oraindik ere iraganeko jarrerak dituzten arren, leku askotan gauzak dagoeneko aldatzen ari direla. Orain, adibidez, Inbiot enpresan dago, eta lankideen erdiak emakumeak direla nabarmendu du: enpresa txiki bat da, ia denok ingeniari teknikoak gara, eta ez dago bereizketarik. “Aurrerago agian topatuko dut baten bat goitik begiratu beharko diodana, kasu egin nazan, baina oraingoz ez dut izan arazorik”.

Lanaren emaitza

Gainerakoan, asko asebetetzen du egiten duen lanak. Adibidez, airearen kalitatea hobetu ahal izatea diseinatu duen gailu bati esker, eta merkatura ateratzea, oso pozgarria zaio. “Horrez gain, lankideak antolatzeaz ere arduratzen naiz. Ez dauka zerikusirik produktuen diseinuarekin, baina lan hori ere asko gustatzen zait. Polita da ikustea lantaldeak ondo funtzionatzen duela eta lana aurrera doala”.

Gaztea da eta denbora gutxi darama lanean, baina, oraingoz, gustura dago hartu duen bidearekin. Oso kritikoa da doktoretza egiteagatik eta ikertzeagatik ematen diren laguntzekiko: “Ingeniari batek, lanean hasten denean, agian irakasle batek edo beste arlo bateko langile batek baino gutxiago kobratzen du hasieran, baina tesia egiten ari direnen eta, oro har, ikertzaileen egoera are okerragoa da. Eta ez da bidezkoa”.

Etorkizunera begira, jendearen bizimodua hobetzen lagunduko duten gailu, produktu edo irtenbideak diseinatzen egin nahiko luke lana, edo erregai berriztagarrietan: “Horretarako lan egiteak asko asebeteko ninduke”.

Fitxa biografikoa:

Ana Ruiz Ilundain Iruñean jaioa da, 1995ean. Ingeniaritza ikasi du NUPen, eta, jarraian, Industria Ingeniaritzako Unibertsitate Masterra egin du. Orain, Inbiot start up enpresan dabil. Airearen kalitatea neurtzeko gailu bat egokitu eta hobetu du, eta, horri esker, Ikasketen Amaierako Lanetarako Rural Kutxa Sarietako sari berezia eman diote.

Egileaz:

Ana Galarraga Aiestaran (@Anagalarraga1) zientzia-komunikatzailea da eta Elhuyar Zientzia eta Teknologia aldizkariko erredaktorea.

Elhuyar Zientzia eta Teknologia aldizkariarekin lankidetzan egindako atala.

The post Ana Ruiz, ingeniaria: “Jendearen onurarako lan egiteak asko asebeteko ninduke” appeared first on Zientzia Kaiera.

María Retuerto Millán, Miguel Antonio Peña y Sergio Rojas Muñoz

Petrmalinak/Shutterstock

 

Es una verdad universalmente admitida que las fuentes energéticas de la humanidad deben ser de carácter renovable. Lo que nos conduce a un uso creciente de las energías eólica y solar fotovoltaica. Estas últimas son actualmente las más desarrolladas y las más competitivas respecto a otras alternativas no sostenibles.

La forma práctica de usar estas fuentes de energía es su transformación en electricidad. Por ello, cualquier país suficientemente avanzado tenderá a la electrificación del sistema energético en los próximos años.

Sin embargo, la gestión de una red eléctrica basada en energías renovables no es sencilla, dado su carácter intermitente. No solo hay que gestionar el ciclo día-noche de la solar fotovoltaica, sino también los ciclos estacionales verano-invierno.

Es necesario almacenar la energía en periodos en los que existan excedentes. De esta forma, se podrán usar en momentos en los que la disponibilidad de energía es menor (menos viento o menos radiación solar en invierno).

Existen diferentes métodos de almacenamiento de energía eléctrica, como las baterías o el bombeo hidráulico. La mayor parte de ellos no permiten cubrir la demanda necesaria o no permiten el almacenamiento a largo plazo de grandes cantidades de energía. Pero existe un vector energético que sí permite ser almacenado y distribuido cumpliendo estos requisitos: el hidrógeno.

Producción y almacenamiento del hidrógeno

El proceso de producción de hidrógeno a partir de la energía eléctrica es conocido como electrolisis. Se realiza aplicando corriente eléctrica al agua, separando así sus elementos: hidrógeno y oxígeno. De esta forma, la electricidad renovable producida se almacena en forma de hidrógeno.

Cuando es necesario disponer de nuevo de electricidad, es posible realizar el proceso inverso: alimentando una pila de combustible con el hidrógeno almacenado se obtiene la electricidad que requerimos, produciéndose también agua.

Existen diversas formas de almacenar hidrógeno, pero la más utilizada actualmente son los depósitos a alta presión. La presión estándar de almacenamiento es 700 bar (unas 700 veces la presión atmosférica). Su uso es seguro gracias a los avances de los últimos años en tecnología de materiales. Podemos almacenar grandes cantidades de energía durante largos periodos de tiempo y, por tanto, gestionar la red eléctrica.

Más allá de la electricidad

Existen otros usos de este hidrógeno renovable diferentes de la electricidad, como los de empresas que requieren calor industrial de calidad. Incluso es posible usar la red de distribución de gas natural inyectando en ella gas de origen renovable.

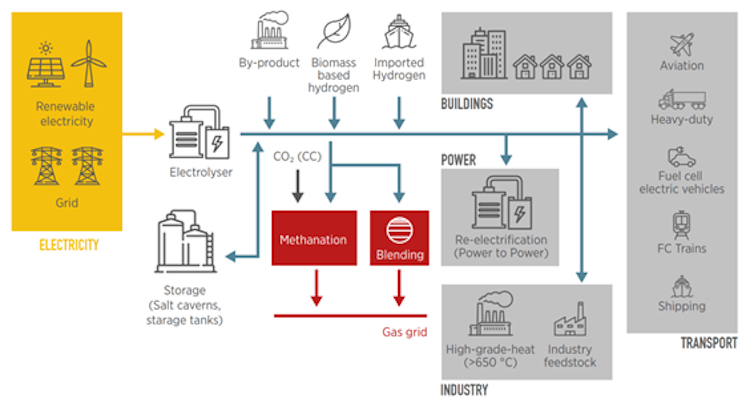Esquema de almacenaje y distribución directa (línea azul) o a través de la red de gas natural (línea roja) de hidrógeno renovable. Fuente: International Renewable Energy Agency (IRENA)

La eficiencia de los electrolizadores y las pilas de combustible suele ser alta, entre el 70 y 90 %, dependiendo de la tecnología usada. El uso directo de la electricidad renovable no tendría ninguna pérdida. Pero, si es necesario almacenarla, la tecnología del hidrógeno resulta ser la más efectiva.

Aplicaciones en transporte

Las primeras aplicaciones del hidrógeno como vector energético se están produciendo en el sector del transporte. Desde 2015 existen en el mercado vehículos eléctricos, como el Toyota Mirai o el Hyundai Nexo.

En los coches, la electricidad se produce en una pila de combustible alimentada por un depósito de hidrógeno. El repostaje del hidrógeno se realiza en una estación se servicio de forma muy similar a como se realiza con otros combustibles. Un tiempo de repostaje de entre 3 y 5 minutos permite una autonomía cercana a los 700 km.

Países como Japón (con más de 100 estaciones de servicio de hidrógeno) o Alemania (con 50 estaciones de servicio) se encuentran a la vanguardia de la tecnología.

Recarga del depósito de un Hyundai NEXO. Fuente: Hyundai

Aunque en Europa se considera una tecnología prioritaria desde hace unos años, en España no existe aún ninguna estación de servicio de hidrógeno abierta al público de forma similar a como existen en otros países europeos. Desde la Asociación Española del Hidrógeno estamos trabajando para que esta situación cambie.

¿El futuro ya está aquí?

La tecnología ha llegado a su desarrollo comercial en esta última década. Pero los próximos años traerán las mejoras necesarias para que su expansión sea posible.

El precio actual de la producción de hidrógeno se sitúa en unos 8 €/kg y el depósito de los vehículos comerciales contiene unos 6 kg de hidrógeno. Esto supone que el precio de llenar un depósito es similar al de la gasolina o el diésel. Sin embargo, el coste del hidrógeno disminuirá aún más en los próximos años.

En los Juegos Olímpicos de 2020 en Tokyo, la organización ha apostado por un transporte eléctrico basado en el hidrógeno. Será un gran impulso para esta tecnología y un incentivo para que los costes sean aún más bajos.

También se esperan mejoras en la tecnología de la electrolisis del agua y en la aplicación práctica de otros procesos nuevos, como la fotólisis directa del agua con luz solar.

En busca de materiales alternativos

Las nuevas tecnologías suelen generar un problema de aumento de la demanda de materiales estratégicos. Éstos son materiales escasos o que se producen en pocos lugares en el mundo. En el caso de los coches eléctricos de baterías, el litio y el cobalto son los materiales estratégicos. Para los electrolizadores y las pilas de combustible, es el platino. Aun así, la cantidad necesaria de platino no es muy superior a la de metales nobles de los tubos de escape de los vehículos de combustión interna.

Los grupos de investigación que trabajamos en estas tecnologías tenemos en cuenta este problema. Estamos empezando a tener éxito en el desarrollo de materiales alternativos al platino que sean abundantes y sostenibles. Muy probablemente, los sistemas electroquímicos de los vehículos eléctricos del futuro serán muy diferentes a los actuales.

Una última consideración: la mayor parte del hidrógeno producido actualmente se obtiene a partir de combustibles fósiles. Esto no encaja en el esquema de sostenibilidad descrito en este artículo. Pero en los próximos años veremos cómo se usarán cada vez más las fuentes de energía renovables. El hidrógeno tendrá un papel fundamental en esta transición.

Sobre los autores: María Retuerto Millán es investigadora contratada, y Miguel Antonio Peña y Sergio Rojas Muñoz investigadores científicos, en el Instituto de Catálisis y Petroleoquímica (ICP-CSIC)

Este artículo fue publicado originalmente en The Conversation. Artículo original.

El artículo El hidrógeno, clave para gestionar las redes eléctricas del futuro se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Generada en plataformas eólicas marinas, desembarcada como hidrógeno
2. Un microrreactor para producir hidrógeno 100 veces más pequeño
3. El modelo de Bohr explica las regularidades en el espectro del hidrógeno

César Tomé

XVIII. mendeko 70eko eta 80ko urteetan burututako lanetan, Antoine-Laurent Lavoisier kimikariak pisua hartu zuen materia-kopuruaren neurri nagusitzat. Elementu kimikoa definitu zuenean kimikoki deskonposa ezin daitekeen substantzia gisa, pisu-galera hartu zuen irizpidetzat deskonposatze bat zegoen ala ez zehazteko.

Lavoisier hil eta geroko kimikarien belaunaldiak kontzeptu eta hipotesi berriak garatu zituen propietate neurgarri bakar pisua zuten atomoei buruz. Baina ezin zenez neurtu atomoa bezain txikia zen zerbaiten pisu absolutua, pisu atomikoak beti adierazi izan dira eredu konbentzional batekiko unitate erlatiboetan.

Irudia: Elementuen taula periodikoa. (Argazkia: Elchinator – Pixabay lizentziapean. Iturria: pixabay.com)

Elementu bakoitzaren atomo-pisu erlatiboa zehazteak hiru kontu praktiko zekartzan: lehenik, eredua aukeratzea; bigarrenik, konposatuen formulak zehaztea, horietatik ondorioztatuko baitziren pisuak; eta hirugarrenik, neurketan ahalik eta zehaztasun handiena lortzea.

Atomista kimikarien lehen belaunaldiaren baitan (gogora dezagun atomista filosofoak ere egon zirela, eta kimikari guztiak ez zirela atomistak, are XX. mende hasieran ere), John Dalton zientzialariak, Humphry Davy kimikariak eta William Prout kimikari eta sendagileak erabaki zuten hidrogeno atomoa hartzea eredutzat, eta balio zehatz bat esleitu zioten arbitrarioki: H = 1. Bestalde, Thomas Thomson kimikariak nahiago izan zuen oxigenoa O = 1 balioa esleitzeko; William Wollaston ere oxigenoaren alde agertu zen, baina O = 10 balioa eman zion; baita Jöns Jacob Berzelius ere, baina azken honek nahiago izan zuen O = 100. Guztiaz ere, XIX. mendearen erdialdean ia kimikari guztiek hidrogenoa hartua zuten eredutzat (horixe da, hain zuzen, gaur egun erabiltzen dena, aldatuta, 12C = 12 eran, eta horrek protioa 1etik oso hurbil uzten du).

XIX. mendean, kimikariek zehaztu behar zituzten (edo onartu, enpirikoki zehaztea ezinezkoa gertatuz gero) pisu atomikoak kalkulatzeko erabilitako konposatu kimikoen formulak. Horrela, adibidez, Daltonen datuek (1810) erakusten zuten ura oxigenoaren % 87,5ek eta hidrogenoaren % 12,5ek osatzen zutela. Aintzat hartzen zuen uraren molekula hidrogeno atomo batek eta oxigeno atomo batek osatzen zutela (HO); hortaz, H = 1 hartuz gero, orduan O = 7. Davyk (1812) eta Berzeliusek (1814), aldiz, H2O hartzen zuten uraren formulatzat; horregatik, Davyk ondorioztatu zuen O = 14 zela. Berzelius, bestalde, prozesu analitikoan askoz zehatzagoa izan zen eta zehaztu zuen oxigenoa % 88,8 zela, eta horrek esan nahi zuen H = 1 baldin bazen, orduan O ≈ 16 zela. Hori dela eta, tirabirak izan zituen Daltonekin.

XIX. mendearen hasieran ez zegoenez metodo fisikorik konposatuen formulak zehazteko, nork bere formula hautatzeak pisu atomikoen elkarren kontrako sistemak erabiltzea ekarri zuen; sistema haietako askotan elementu baten atomoei esleitzen zizkieten pisuek zenbaki arrunt txiki baten aldea zuten (esate baterako, O = 8 eta O = 16). Ia mende erdia behar izan zen poliki-poliki adostasunera heltzea ahalbidetuko zuten metodoak lortzeko. XIX. mendeko hirurogeiko urteen hasierarako, kimikari europar gehienek lortua zuten pisu atomikoen eta formulen sistema bakar bat adostea, gaur egun erabiltzen denaren ia berdina. Hala ere, galiar menderaezin batzuek bereari eutsi zioten, mendearen azken hamarkadara arte esanez uraren formula HO zela.

Daltonen eta Berzeliusen arteko liskarrak ―oxigenoaren, hidrogenoaren eta uraren ingurukoa― agerian uzten du zehaztasunaren eta doitasunaren garrantzia konposatuen analisi grabimetrikoetan, pisu atomikoak zuzen zehaztea lortu ahal izateko. Neurketen aldakortasunak bide ematen zien hainbat hipotesi “dotoreri”. Horrela, pisu atomikoetako asko zenbaki arruntetatik hurbil zeudela zirudienez, H = 1 baldin bazen, Proutek eta Thomsonek uste zuten zenbaki atomiko guztiek zenbaki arruntak izan behar zutela. Hori egia izatera, atomo guztien osagai izan behar zuten pisu-unitateak adierazten zituzten partikula subatomikoek; beharbada partikula horiek hidrogeno atomoak berak ziren. “Prouten hipotesia” 1815ean proposatu zen lehen aldiz.

Berzeliusek hipotesi hori errefusatu zuen, datu esperimentaletan oinarrituta. Beraren ustez Thomson eta beste batzuen gustu eta lehentasunek mugatu egiten zien  objektibotasuna. Hori gorabehera, 1838 eta 1849 urteen artean Berzelius, Justus von Liebig, Jean Baptiste André Dumas, Charles Marignac eta beste batzuen artean emandako datu-truke eta eztabaidetatik ―hidrogenoa, karbonoa eta oxigenoa bezalako elementu erabakigarriei zegokienez― ondorioztatu zen Berzeliusen datu esperimentalek karbonoari izan beharko lukeena baino pisu handiagoa esleitzen ziotela, %2 handiagoa hain zuzen. Berrikusitako pisuak 1, 12 eta 16 ziren, ia zehazki, eta horrek indar berria eman zion Prouten hipotesiari. Jean Servais Stas kimikariaren geroagoko lanek (O = 16 patroia erabilita) frogatu zuten, arrazoizko zalantzetatik harago, pisu atomikoak ez zirela zenbaki arruntak ―horrek Prouten hipotesiari behin betiko kolpea ematen ziola zirudien― eta finkatuta utzi zituzten gerora elementuen taula periodikoa eraikitzeko erabiliko ziren balioak.

Pisu atomikoen zehaztapen kimiko doienak  Edward Morley kimikari eta fisikariak (oxigenoa, 1895) eta, batez ere, Theodore W. Richards kimikariak burutuko zituzten; azken honek 55 elementuren pisu atomikoa zehaztu zuen, hain zehatz ezen lehena izan baitzen isotopoen existentziaren zantzuak aurkitzen metodo kimikoen bidez, mea-berunaren eta fisio nuklearraren bidez lortutako berunaren laginak konparatzean. Lan horiengatik Richardsek Nobel saria jaso zuen 1914an.

Masen espektrometroa garatu ondoren, pisu atomikoak zehaztasun handiz eta askoz errazago zehaztu ahal izan ziren.

Egileaz:

Cesár Tomé López (@EDocet) zientzia dibulgatzailea da eta Mapping Ignorance eta Cuaderno de Cultura Cientifica blogen editorea.

Itzulpena:

Leire Martinez de Marigorta

Hizkuntza-begiralea:

Xabier Bilbao

The post Pisu atomikoaz appeared first on Zientzia Kaiera.

 

La matemática me brinda herramientas, es un camino que tengo más transitado y por lo tanto me sale más naturalmente diseñar espacial y corporalmente en estos términos.

Edgardo Mercado

Edgardo Mercado es coreógrafo, bailarín y docente. Antes de volcarse en el mundo de la danza, estudió ciencias físicas e impartió clases de matemáticas de nivel superior. Esta formación científica es la que, sin duda, le ha llevado a plantear sus coreografías con una especial inspiración matemática y científica: «En mis obras, siempre afloran, desde el diseño y el concepto, temas relacionados a la física o a las matemáticas».

En esta breve reseña destaco cuatro de sus coreografías en las que las matemáticas se incluyen de diferentes maneras.

Tierra de Mandelbrot

Edgardo MercadodescribeTierra de Mandelbrot (2004) de la siguiente manera: «En esta obra no hay narrativa, no hay causa-efecto; solo tres sujetos fractales transformando nuestro modo de mirar, percibir y valorar la realidad dentro del marco del paradigma complejo, regido por el orden-desorden, la recursividad y la autosimilitud».

Tierra de Mandelbrot alude al concepto de conjunto fractal en su contenido y a través del matemático que nombró y estudió este tipo de conjuntos: Benoît Mandelbrot. La obra comienza con dos luces que aparecen en medio de la oscuridad. Apenas se perciben trozos de los cuerpos de dos personas que se dejan ver, reptan, giran y desaparecen. Dos bailarinas, desnudas, se visten con ropas blancas ordenadas de manera geométrica sobre el suelo. Comienzan a proyectarse luces e imágenes: números, códigos de barras y recortes de luz estrían, fraccionan y recomponen los cuerpos de las protagonistas. Aparece un violinista que a veces toca unos acordes que se mezclan con el sonido electrónico grabado, a veces permanece inmóvil en el escenario. Los pequeños cuadrados proyectados sobre los cuerpos provocan un efecto multiplicativo al moverse: las ideas fractales de recursividad y autosimilitud se dejan ver de manera insistente.

 

Rotonda

Estrenada en 2009, Rotonda se presenta del siguiente modo: «Dos obsesiones que encierran el concepto de infinito se funden en una sola para dar origen a esta obra, la primera de Edgardo Mercado para el Ballet Contemporáneo: la agobiante perfección del círculo y la dificultad a la hora de representar el tiempo.

La imagen del “eterno retorno” habilita un camino tomando esta imagen como un avance infinito, recorriendo la circunferencia finita para volver al estado inicial.

Rotonda intenta reflejar en esta visión la angustia por el envolvente flujo del tiempo, que aniquila o redime. Rotonda es el espacio que habla del tiempo. La música fue compuesta especialmente para la pieza por Gabriel Gendín y tanto ésta como la escenografía de Ariel Vaccaro son de carácter minimalista. El diseño de luces de José Luis Fiorruccio completa la puesta superponiendo otro nivel en el orden geométrico propuesto por el diseño coreográfico».

En Rotonda ocho bailarines y siete bailarinas evolucionan, con diferentes ritmos y velocidades, sobre una rotonda, una figura formada por varias circunferencias concéntricas, donde aparecen además marcadas algunas diagonales. Estas curvas estampadas en el suelo aparecen o desaparecen, dependiendo de la iluminación aplicada en cada momento.

Los movimientos son a veces rápidos y enérgicos, a veces pausados y pronunciados, en ocasiones se observa pura danza, en otras complejas acrobacias. Rotonda analiza la circularidad en veinte minutos de danza.

 

Topologías para cuerpos infinitamente inconquistables

Estrenada en 2014, esta obra se presenta así: «¿Qué forma tiene el espacio propio hoy? ¿Cómo se extiende, deforma, hincha o repliega nuestra superficie surcada por diferentes flujos de información? Topologías para cuerpos infinitamente inconquistables es una instalación performativa que trae consigo una atención diferente de nuestras percepciones, para sumergirnos en una experiencia que transforma el espacio en un paisaje dinámico a través de los cuerpos del público y de veinte performers. Así nos permite cuestionarnos acerca de la conectividad, ubicuidad, y límites del cuerpo en movimiento hoy».

Realmente, es pura topología.

 

Apuntes

Augusto Zanela es arquitecto, un verdadero mago de la anamorfosis. Apunte es una de sus propuestas; fue transformada en una video-instalación en el Festival Théâvida 2012. Sin duda esta anamorfosis (que como Rotonda juega con círculos concéntricos) se ha enriquecido con las bellas coreografías de Edgardo Mercado.

 

Más información:

• Edgardo Mercado

• Marta Macho Stadler, Edgardo Mercado: acercando la danza y las matemáticas, DivulgaMAT, mayo 2008

• Marta Macho Stadler, Rotonda, DivulgaMAT, julio 2011

• Marta Macho Stadler, Topologías para cuerpos infinitamente inconquistables, DivulgaMAT, febrero 2017

• Marta Macho Stadler, Anamorfosis danzadas, ZTFNews, abril 2012

 

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad

El artículo Edgardo Mercado: matemáticas en “danza” se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. FUN WITH MATHS, diversión con matemáticas
2. Fractus, arte y matemáticas
3. Más FUN WITH MATHS, diversión con matemáticas

Ziortza Guezuraga

Ume diren txertoak edo txerto diren umeak, nazioarteko espedizioa, emakume aristokrata bat zientziari aurre hartzen eta zaldiek kutsatutako behiak dira protagonistetako batzuk baztangaren historian.

1. irudia: Txertoak eta behiak betirako lotuta geratu dira XVIII. mendetik. (Argazkia: Wilfredor).

1803. urtean 22 ume A Coruñako portutik atera ziren María Pita itsasontzian. Haien gorputzetan munduko historia aldatuko zuen substantzia zeramaten: baztangaren aurkako txertoa. Historiako lehen txertoa. Desagerrarazitako lehen gaixotasunaren aurkako txertoa.

Edward Jennerek aurkitu zuen baztangaren aurkako txertoa 1796an. Baina gaixotasunaren aurkako borroka eta txertoari bidea ireki zion praktika milaka urte lehenago hasi zen.

Zaharra zara Variola

Variola virusak sortzen du baztanga eta gizakiei esklusiboki eragiten dien patogenoa da. Milaka urtez gizakiarekin izan da baztanga, Egiptoko faraoien momietan ere ikusgarriak dira gaixotasunaren markak; Ramses V.aren momian, esaterako.

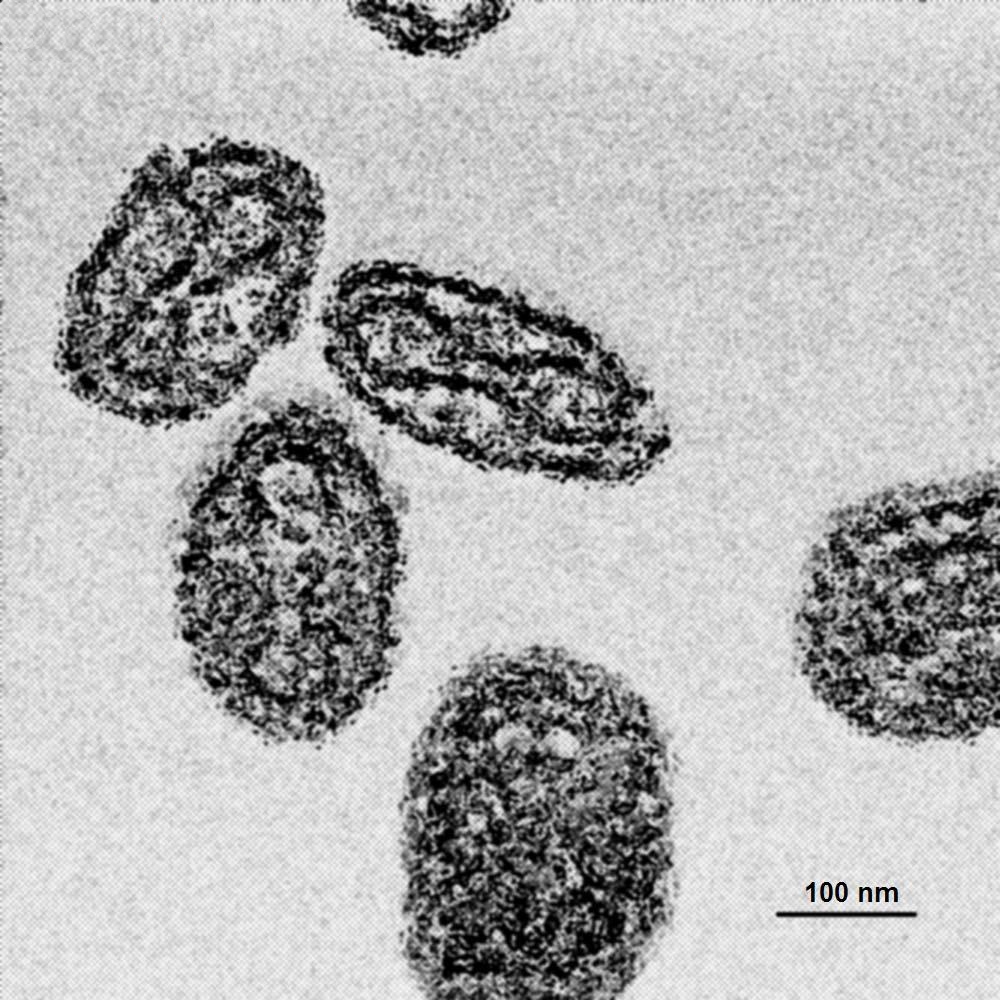2. irudia: Baztangaren birusa. (Argazkia: PhD Dre).

Jatorria K.a. 10.000 urte inguruan kokatzen dute ikertzaileek, Afrikako lehen nekazarien kokalekuetan. Gaixotasunaren aurkako borroka ere zaharra da.

Aspaldi jakin zen gaixotasuna pasatzen zutenek immunitatea lortzen zutela eta, honetan oinarrituta, bariolizazioa sortu zen. Bariolizazioa/inokulazioa da gaixotasunari aurre egiteko dokumentatutako metodorik zaharrena: gaixo baten pustula heldu batetik lantzeta batekin substantzia hartu eta immunizatu gabeko pertsona bati inokulatzean datza.

Metodoa ez zen beti arrakastatsua, batzuetan pertsona hil egiten zen, bai baztanga dela eta bai bestelako infekzioengatik. Ikerketen arabera, Txinan, Indian eta Afrikan aspaldi egiten zen bariolizazioa eta XVII. mendean Otomandar Inperiora heldu zen praktika. Momentu hau inflexio puntua izan zen baztangaren aurkako txertoaren garapenerako.

Izan ere, bertan ezagutu zuen metodoa Ingalaterrara, eta geroago Europara, zabalduko zuen aristokratak: Lady Montaguk.

Senarra Estanbulen enbaxadore izendatu eta hara bidaiatzean izan zuen Lady Mary Wortley Montaguek bariolizazioaren berri. Bere umeekin praktikatu ez ezik, praktika Ingalaterrara eramateko ahaleginak egin zituen XVII. Mende hasieran. Hala ere, garaiko zientzialariek ez zuten konfiantzarik metodoan. Eta bariolizazioa zabaldu bazen ere, ez zuen arrakasta izan.

Bariolizaziotik txertora

XVII. mende amaieran Edward Jenner medikua baztangaren inguruan hausnartzen ibili zen. Behien baztanga (cowpox), pairatu ostean esneketariek ez zutela baztangarik izaten aspaldi zuen entzuna eta ondorioztatu zuen behien baztangak (variolae vaccinae izena eman zion, eta hortik datoz vaccine eta vacuna hitzak) baztangatik babesten zuela. Ez hori bakarrik, babes metodo gisa pertsona batetik bestera pasa zitekeeneko hipotesia garatu zuen.

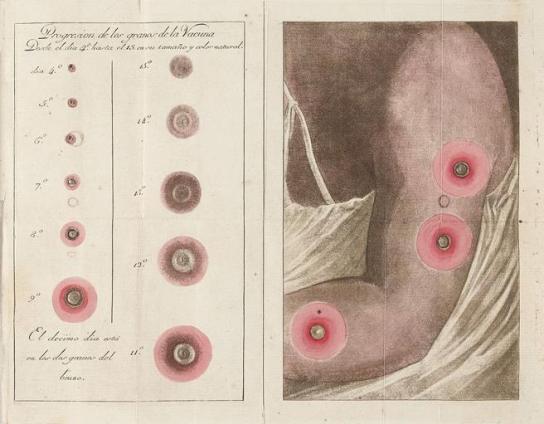3. irudia: Baztangaren pustulen eboluzioaren ilustrazioak. Francisco Javier Balmisek itzulitako “Tratado histórico y práctico de la vacuna”.(Argazkia: Wellcome Library).

Eta bere hipotesia frogatzeko Sarah Nelms izeneko esneketariaren behi baztangaren zauri freskoetatik hartutako materia 8 urteko James Phipps umeari inokulatu zion 1796ko maiatzaren 14an. Sintoma arinekin gaixo egon zen umea hamar egun inguru, baina osatu egin zen. 1796ko uztailean umea baztangarekin inokulatu zuen. Ez zuen gaixotasunik garatu.

Aurkikuntza dokumentatzeko kasu gehiagorekin egin zituen ikerketak Jennerek, baina ez zuen behi-baztanga kasurik eskura. 1798ra arte. Behor batek zaldi baztanga garatu eta, jarraian, abeletxe horretako behiek izan zuten arte[1]

Esperimentuak egin eta An Inquiry into the Causes and Effects of the Variolae Vaccinae, a disease discovered in some of the western counties of England, particularly Gloucestershire and Known by the Name of Cow Pox liburuxka argitaratu zuen.

Akatsak eta polemikak izan ziren, baina 1800 urterako Britaina Handian zehar eta baita Europako herri gehienetan ere zabalduta zegoen txertoaren erabilera.

Europatik mundura

Alacanteko Francisco Javier Balmis doktore eta zirujauak Jenneren txertoaren jakitun izan zenean Carlos IV.a erregearen babesa eta diru laguntza lortu zituen Espainiar Inperioan txertaketa egiteko, nahiz eta txertoaren aurkako jarrerak egon, baita medikuen artean ere. Agian erregearen alabak baztangak jota hil zelako 1794an. Edozein dela arrazoia, erregearen babesa lortu zuen inperioko umeak txertatzeko.

Hartara, baztangaren aurkako txertoa Amerikara eta Filipinetara eramango zuen espedizioa prestatzen hasi zen Balmis. Espainiako itsasoaz haragoko lurraldeetara txertoa eramateko jarri zen abian “Txertoaren Errege Espedizio Filantropikoa” Balmis espedizioa izenez ere ezaguna.

Arazo bat zegoen, baina: garai hartan txertoaren seruma kontserbatzeko mediorik ez zegoen eta Amerikaraino eta Filipinetaraino bidaiak luzeegiak ziren txertoa egoera onean iristeko.

Balmisek berak proposatu zuen irtenbidea: in vivo giza garraioa. Txertatuta ez zegoen jende taldea baliatuko zuen txertoa batetik bestera pasatzeko portura iritsi arte. Pertsonak izango ziren txertoa, giza katea osatuz batetik bestera pasatuta.  

Hartara, hiru eta bederatzi urte bitarteko 22 umezurtz aukeratu zituen Balmisek. Umeak binaka inokulatzen zituzten behi baztangarekin eta gainerako umeengandik aldendu. Hamar egun pasata, agertutako garauetako likidoa hartu eta hurrengo bi umeak inokulatzen zituzten.

A Coruñatik atera eta Kanariar Uharteetara joan zen lehenengo eta behin 37 pertsonak osatutako espedizioa, haien artean 22 ume, Isabel Zendal umeen zaintzailea eta Francisco Javier Balmis medikua. Handik Puerto Ricora joan ziren, 1804an heldu zirelarik. Behin Amerikan ume gehiago bildu zituzten txerto-giza-katearekin jarraitu ahal izateko.

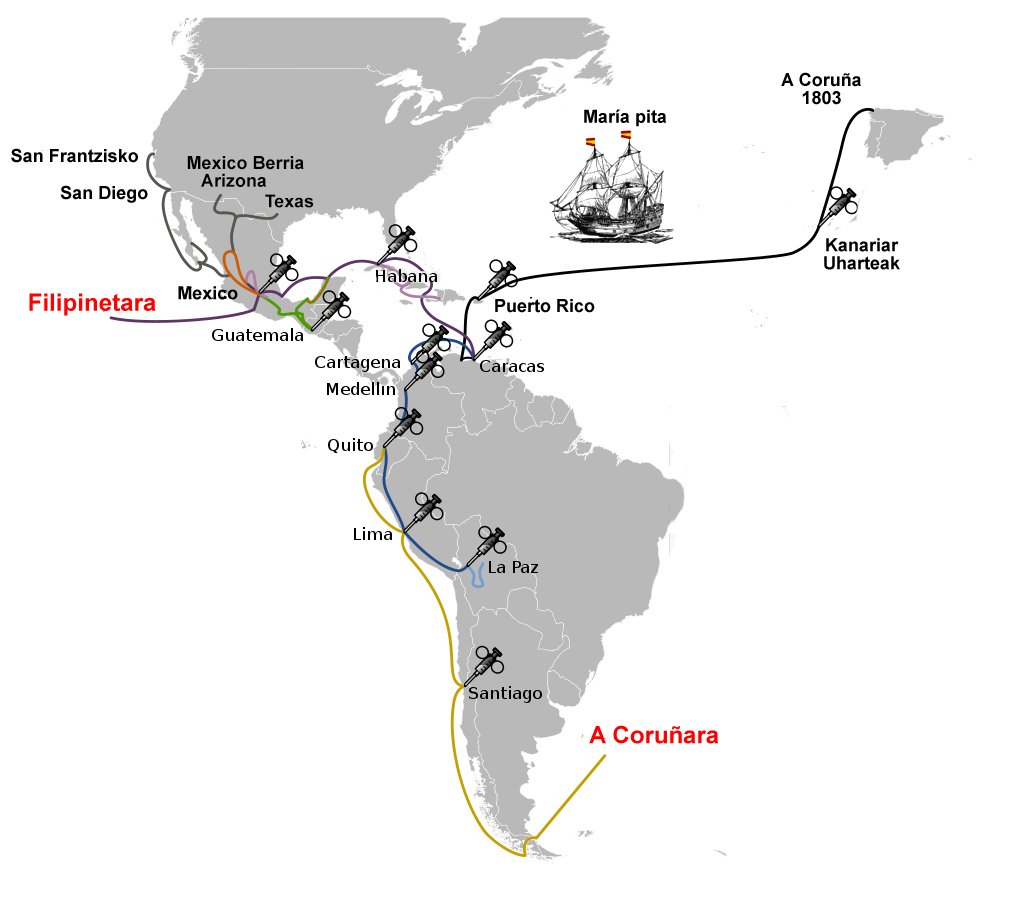4. irudia: Balmis espedizioak egindako ibilbidea. (Argazkia: Ecelan-en iruditik eraldatua).

Baztangarik gabeko munduan jaio eta bizitakoentzat zaila izan daiteke gaixotasuna eta bere ondorioak dimentsionatzea. Antzina-antzinatik dago gizakien artean eta XX. mendean bakarrik 50 milioi hildako baino gehiago eragin zituen. Gaixotasuna pasa eta bizirik irauten zutenek marka izugarriak izaten zituzten, aurpegi eta besoetan, bereziki.

Covid-19ren aurkako txertoarekin gora eta behera gabiltzan honetan, txertoen aurkako mugimenduak dauden honetan, ez dago gaizki gogoratzea 1796ra arte txertoak ez zirela existitu ere egiten. Eta lehenengo txertoa asmatu eta zazpi urtera munduan zabaltzeko ahalegina egin zela.

[1] Egun, ez dago argi txertoa behi baztangatik ala zaldi baztangatik garatu zen, zenbait ikerketen arabera, txertoetako espeziea, vaccinia, eta behi baztangarena ezberdinak dira. Are gehiago, sekuentziazio genetikoak erakutsi du vacciniak eta zaldi baztangak %99.7an berdinak direla eta behi baztanga ahaide hurbila. Jennerek berak ere zalantzak izan zituen.

*Eta norbaitek jakin-mina balu: A Coruñatik abiatutako 22 umeetatik bat ere ez zen itzuli penintsulara: bat bidaian zehar hil zen eta gainerako 21ak hospizioan sartu eta adoptatuak izan ziren Mexikon, Susana Ramírezen arabera. Beste iturrien arabera, ezin da ziur jakin zer gertatu zen haiekin.

Bibliografia:

En el nombre de los Niños. Real Expedición Filantrópica de la Vacuna 1803-1806. AEP. 2003

History of vaccine development. Stanley A. Plotkin. 2011. Springer.

Abbas m. Behbehani. (1983). The Smallpox Story: Life and Death of an Old Disease. Microbiological reviews, dec. 1983, p. 455-509 vol. 47. no. 4 0146-0749/83/040455-55$02.00/0

Riedel S. (2005). Edward Jenner and the history of smallpox and vaccination. Proc (Bayl Univ Med Cent). 18(1):21-25. doi:10.1080/08998280.2005.11928028

Brinkmann, A., Souza, A.R.V., Esparza, J. et al. (2020) Re-assembly of nineteenth-century smallpox vaccine genomes reveals the contemporaneous use of horsepox and horsepox-related viruses in the USA. Genome Biol 21, 286. https://doi.org/10.1186/s13059-020-02202-0

Egileaz:

Ziortza Guezuraga (@zguer) kazetaria da eta Euskampus Fundazioko Kultura Zientifikoko eta Berrikuntza Unitateko zabalkunde digitaleko teknikaria.

The post Behietatik mundura appeared first on Zientzia Kaiera.

Joint European Torus. Fuente: EUROfusion

Una reacción de fusión nuclear consiste en la unión de dos núcleos ligeros para formar un núcleo más pesado. La reacción da como resultado energías de enlace por nucleón más altas cuando se combinan núcleos ligeros. Como consecuencia, se libera una gran cantidad de energía.

Las reacciones de fusión se han producido en el laboratorio mediante el bombardeo de dianas de materiales ligeros apropiados con, por ejemplo, deuterones de alta energía de un acelerador de partículas. En estas reacciones resultan núcleos que son más pesados que los núcleos de los «proyectiles» o de la diana; generalmente también se liberan partículas adicionales, así como energía. Algunos ejemplos típicos de estas reacciones de fusión, junto con la energía liberada en cada reacción, son los siguientes:

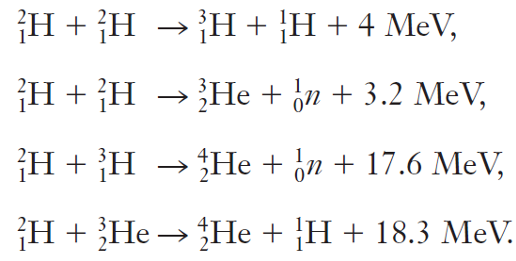
En la primera de las ecuaciones anteriores, el núcleo producto más pesado es un isótopo de hidrógeno, llamado tritio, con número de masa A=3. Se ha encontrado en pequeñas trazas en la naturaleza, es radiactivo, con un periodo de semidesintegración de aproximadamente 12 años, y se desintegra por emisión beta en helio-3, un isótopo de helio. Cuando se bombardea una diana de tritio con deuterones, se puede formar helio-4, como en la tercera ecuación anterior, liberando 17,6 MeV de energía. De esta energía, 14,1 MeV aparecen como energía cinética del neutrón y 3,5 MeV como energía cinética del núcleo producto.

Si bien la energía liberada en una sola fusión es menor que en una sola fisión, la energía liberada por unidad de masa es mucho mayor. Un simple cálculo lo ilustra: la masa de unos 50 átomos de helio es aproximadamente igual a la masa de un átomo de uranio; usando la tercera ecuación tenemos 50 x 17,6 MeV = 1040 MeV, en comparación con los 200 MeV de un fisión típica. De aquí que la fusión de tritio y deuterio ofrece la posibilidad de proporcionar grandes fuentes de energía, por ejemplo, en centrales eléctricas.

El deuterio se encuentra en el agua con una abundancia de aproximadamente una parte en siete mil átomos de hidrógeno y puede separarse del isótopo más ligero. Cuatro litros de agua contienen aproximadamente 0,13 g de deuterio. Si esta pequeña cantidad de deuterio pudiera reaccionar en condiciones apropiadas con tritio la producción de energía sería equivalente a la de aproximadamente 1.140 litros de gasolina. Se estima que la cantidad total de deuterio en los océanos es de aproximadamente 1017 kg, y su contenido energético sería de aproximadamente 1020 kW-año. Si el deuterio y el tritio pudieran usarse para producir energía, proporcionarían una enorme fuente de energía.

Por supuesto, existen algunos problemas no precisamente triviales que deben resolverse antes de que las reacciones de fusión puedan ser útiles como fuentes estables de energía. Los núcleos que reaccionan en los procesos de fusión están cargados positivamente y se repelen entre sí debido a la fuerza eléctrica repulsiva. Por lo tanto, es necesario hacer que los núcleos choquen con una velocidad relativa alta para vencer la fuerza repulsiva que tiende a mantenerlos separados. La interacción nuclear que mantiene unidos a los neutrones y protones en el núcleo es mucho más fuerte que la eléctrica, y a menudo se la llama fuerza nuclear fuerte, pero tiene un alcance muy corto. Su efecto se extiende solo unos 10-14 m, aproximadamente el tamaño de un núcleo. Por lo tanto, los núcleos que se pretende fusionar deben poder situarse a una distancia de ese orden de magnitud para que la fuerza nuclear atractiva supere a la repulsión eléctrica.

Los núcleos también deben estar confinados en una región del espacio donde puedan sufrir muchas colisiones sin que puedan escapar o ser absorbidos por las paredes que limitan la región, o perder energía por colisiones con demasiadas moléculas “más frías” (menos energéticas). Debe haber suficientes colisiones por unidad de tiempo para que la fusión pueda ocurrir a una velocidad que produzca más energía de la necesaria para provocar las colisiones. La combinación de estos requisitos significa que los núcleos deben estar contenidos a una temperatura del orden de 100 millones de grados.

A la temperatura requerida para la fusión, los átomos han perdido sus electrones, este estado de la materia en el que núcleos y los electrones están separados se llama plasma. Un plasma es un gas ionizado en el que las partículas cargadas positiva y negativamente se mueven libremente. Ninguna pared hecha de ningún material conocido puede contener un plasma caliente a 108K (¡la pared se vaporizaría instantáneamente! [1]). Pero la teoría nos dice que las partículas cargadas, y eso es lo que es un plasma, pueden contenerses en un campo magnético diseñado apropiadamente. El primer problema a resolver, por tanto, es contener el plasma de núcleos de deuterio y tritio en un campo magnético, mientras se aceleran los núcleos mediante un campo eléctrico hasta la energía cinética (o temperatura) requerida. El comportamiento de las partículas cargadas en un plasma es, digamos, complicado; hay muchos tipos de inestabilidades que hacen que el plasma sea difícil de contener adecuadamente y durante el tiempo suficiente.

Con todo hay proyectos de fusión muy avanzados. En diciembre de 2020 se iniciaron las pruebas con deuterio y tritio en el Joint European Torus, que es una réplica 1:10 de lo que será el primer reactor de fusión del mundo, el ITER.

Nota:

[1] Para los seguidores de Star Trek: eso es ficción. Por ejemplo, los reactores de fusión de Deep Space 9 usan deuterio como partículas de bombardeo, sí, pero las paredes están hechas de carbono, como que no. No parece ingenierilmente muy trabajado.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo Fusión nuclear se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Energía de enlace nuclear y estabilidad
2. Control de la reacción nuclear en cadena (2): moderadores
3. La energía de enlace nuclear