Feed aggregator

Eder Amayuelas en plena cristalización

Eder Amayuelas se ha doctorado hace unos meses en la Universidad del País Vasco. Estudia materiales utilizando para ello técnicas cristalográficas. Además de la investigación, a Eder le interesa la divulgación. Recientemente ha puesto en marcha, junto con Alessandra Campo, la asociación Logos Elkartea, con la que se proponen desarrollar nuevos proyectos de divulgación científica. Próximamente los daremos a conocer a través de los medios de difusión de la Cátedra.

Entre tanto, Eder se ha animado a participar en el certamen de monólogos científicos FameLab, y ha sido seleccionado para participar en la final que tendrá lugar el próximo 17 de mayo. El vídeo del monólogo con el que se ganó el pase a la final es este:

Desde aquí queremos dar a Eder la enhorabuena y desearle que el 17 de mayo tenga un gran día.

El artículo El monólogo cristalino de Eder Amayuelas se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Keats vs Feynman, mejor vídeo de divulgación “On zientzia”
2. Fallos científicos en el cine, mejor vídeo de divulgación joven “On zientzia”
3. El mecanismo de la vida, mejor vídeo de divulgación joven “On zientzia”

Organismoaren punturen batean kontrolik gabeko zelulen hazkundea dela eta sortzen dira tumoreak. Bularren kasuan, estrogenoek eta estrogeno errezeptoreek hazkunde zelularrean duten kontrolaren akatsengatik gertatzen dira, ama zelulen diferentziazioan eragiten dutenak. Hori dela eta, ama zelula tumoralak diana terapeutiko bihurtu dira bularretako minbizi kasuan. NuRCaMein Cut the stem off to fight breast cancer arikuluan.

Zelan liteke zonalde natural bat babesteak berau andeatzea ekartzea? Manuel San Martínen When protection leads to degradation

Aldi berean transistore moduan eta galbahe molekular moduan aritzen den grafenoa lortzea ez da kontu xumea, baina erabilera anitz izan ditzake. DIPCko jendea How to synthesize a nanoporous graphene that is both transistor and molecular sieve artikuluan.

–—–

Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.

The post Ezjakintasunaren kartografia #211 appeared first on Zientzia Kaiera.

En los últimos años, ha avanzado mucho la investigación sobre la gramática histórica del euskera, la rama de la lingüística encargada de estudiar los cambios de la lengua. En esa área, la lingüista polaca Dorota Krajewska trabaja en ampliar el conocimiento sobre la sintaxis histórica del euskera en el grupo de investigación Monumenta Linguae Vasconum de la UPV/EHU. Para la investigadora, este tipo de trabajos sirven para “comprender por qué el euskera actual es como es”.

‘Doctrina Christiana’ de Esteve Materra, un libro que encontró la propia Dorota Krajewska en la Biblioteca Real de Dinamarca.

Hasta la fecha, no se ha investigado mucho acerca de la evolución histórica de la sintaxis, y mucho menos sobre la transformación de las oraciones subordinadas. El objetivo principal de la investigación de Krajewska ha sido estudiar la manera en la que se emplean esas estructuras complejas en los textos antiguos. Para ello ha analizado en textos de los siglos XVI-XIX de todos los dialectos de la lengua vasca dos temas generales: la secuencia del sustantivo y sus modificadores, y las estrategias de creación de oraciones subordinadas. Es decir, tal como ha reseñado Krajewska, por un lado, “cómo, cuándo y cuánto se utilizaban los modificadores que actualmente se posicionan después del sustantivo; y qué secuencia es más antigua: la que sitúa el modificador antes o después del sustantivo”, y, por otro, “cómo ha cambiado el uso de diferentes oraciones de relativo a lo largo de la historia del euskera”.

En la investigación histórica, “es muy importante contar con una muestra de textos representativa. Esto se traduce, hasta cierto punto, en tener en cuenta toda la extensión geográfica y los dialectos —comenta la investigadora—. El hecho de tener datos insuficientes es uno de los mayores inconvenientes: podría pasar que nos faltaran datos de algún dialecto o de alguna época”. La investigadora añade que estos corpus no están completamente digitalizados y centralizados, por lo que “no existe un corpus digital donde poder hacer la observación fácilmente”. Ha tenido que recopilar textos de numerosas fuentes, y realizar las búsquedas de forma manual o semiautomática. Esta tarea de búsqueda de ejemplos en los textos le ha llevado alrededor de dos años.

La investigación de la historia del euskera dispone de un número menor de datos que la investigación de las lenguas indoeuropeas vecinas, “ya que el corpus del euskera es relativamente pequeño y tardío —explica Krajewska—. En cualquier caso, mi investigación ha revelado que el material existente para estudiar la sintaxis histórica es suficiente. Hay una serie de aspectos de la sintaxis que no han cambiado desde el s. XVI, pero la forma y el uso de numerosas estructuras no es igual ahora que hace unos siglos”. Según la investigadora, “en comparación con otras lenguas minoritarias del mundo, el euskera se ha investigado mucho más, aunque todavía queda mucho por estudiar. A pesar de ser un corpus reducido, no lo conocemos bien todavía, y se puede seguir investigando”.

Referencia:

D. Krajwska (2017) Euskararen sintaxi diakronikorantz: egitura konplexuak / Towards a historical syntax of Basque: complex constructions UPV/EHU Tesis doctoral (Joseba A. Lakarra & Javier Ormazabal, supervisors) doi: 10.13140/RG.2.2.18154.62405

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo La sintaxis histórica del euskera en los últimos quinientos años se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Curso de verano “Las dos culturas y más allá”: Las promesas de la ciencia. Una perspectiva histórica
2. Relaciones a distancia desde hace 16.000 años
3. Técnicas artísticas de hace 40.000 años

La joven de la perla

Hay obras de arte que dibujan un rostro en nuestra imaginación con tan sólo escuchar su nombre. Entre ellas está La joven de la perla, pintada hacia 1665 por Johannes Vermeer. No hay duda de que, a día de hoy, la joven sigue siendo una influencer en toda regla que ha inspirado libros y películas. Por eso, todo tema relacionado con este cuadro despierta un gran interés y el radar de KimikArte no podía pasar por alto el estudio técnico realizado en el Mauritshuis, el museo donde se aloja la obra. Un equipo internacional liderado por Abbie Vandivere ha examinado cada detalle del óleo y ella misma se ha encargado de elaborar un fabuloso blog que reúne toda la información recogida. Como quizás no tengáis tiempo para leer las 20 entradas que ha escrito, a continuación os hago un resumen de los hallazgos más interesantes, no sin antes agradecer a su autora y al museo el permiso para emplear este material*.

La vida de la joven

Se ha especulado mucho sobre quién era La joven de la perla, pero en este artículo no intentaremos despejar esa incógnita. Tampoco nos centraremos en la figura del padre de la criatura, envuelta asimismo en un halo de misterio. Vermeer, uno de los pintores más admirados del siglo XVII, no tuvo tal reputación en su época y fue un pintor poco prolífico. Por lo menos eso es lo que indica el escaso número de obras (34 reconocidas) que han llegado a nuestros días. En las siguientes líneas nos centraremos exclusivamente en su más célebre creación, de ahí que nos interese conocer qué pasó con ella una vez que el neerlandés le dio la última pincelada.

Por mucho que su nombre indique lo contrario, nuestra protagonista tiene ya más de 350 años y ha tenido tiempo de vivir unas cuantas desventuras. No se sabe nada sobre su paradero hasta 1881 cuando un tal Arnoldus Andries des Tombe le echó el ojo en una subasta de La Haya. Como experto en arte enseguida reconoció la calidad de la obra, y debió ser el único, ya que se la llevó por lo que hoy equivaldría a unos 30 euros. Una auténtica ganga, vamos. El afortunado comprador hizo entelar la obra en Amberes y la mantuvo en su poder durante toda su vida. Cuando murió, en 1902, legó el cuadro al Mauritshuis, donde todavía hoy se puede disfrutar.

Imagen 1. La joven de la perla (44×39 cm) de Vermeer (ca. 1665) en una fotografía de catálogo de 1924. Fuente: Imagen cedida por el Mauritshuis.

Durante el s. XX la obra fue sometida a unos cuantos tratamientos de limpieza y a otros tantos barnizados, entre los que cabe destacar los procesos de restauración y conservación llevados a cabo en los años sesenta. La obra se volvió a reentelar, se eliminaron retoques previos y barnices y se le aplicó un nuevo barniz coloreado. En este momento tenemos que puntualizar que, pese a que a día de hoy este último paso sería impensable, los criterios de conservación y restauración han ido cambiado con el tiempo y en aquella época algunos consideraban que los barnices amarillentos dignificaban la obra. En cualquier caso, y con motivo de una exposición dedicada a Vermeer, dicho barniz se eliminó en 1994. Ésta es la última restauración a la que se ha sometido la pieza y en dicho proceso se realizaron dos interesantes hallazgos: el barniz había ocultado el brillo de los labios de la joven y uno de los brillos de la archiconocida perla no era tal. Concretamente, lo que se pensaba que era una pincelada de Vermeer para resaltar la perla no era más que un trocito de pintura que accidentalmente se había dado la vuelta engañando a los expertos durante años (Imagen 2). Así que la obra perdió un detalle, pero, a cambio, ganó otro.

Imagen 2. En la fotografía de la derecha se señala el brillo “falso” descubierto en la perla.

Lo que el ojo no ve

Como ya hemos visto en entradas anteriores, hay diferentes técnicas que nos permiten explorar detalles que a simple vista no podemos percibir. Me refiero a las radiografías, la fotografía infrarroja, la fluorescencia ultravioleta o la luz rasante. En la Imagen 3 podéis ver qué diferentes son las imágenes logradas con algunas de estas técnicas.

Imagen 3. Radiografía (A), fotografía de fluorescencia ultravioleta (B) y fotografía de luz rasante (C) (René Gerritsen). Fuente: Imágenes cedidas por el Mauritshuis.

En la radiografía (Imagen 3A) se puede ver que algunas zonas son más claras. Esto se debe a la presencia de compuestos con átomos que absorben más los rayos X (al igual que nuestros huesos se ven blancos en una radiografía médica debido al calcio). Gracias a ello podemos observar los clavos del marco o las zonas pintadas con pigmentos que contienen átomos pesados como puede ser el blanco de plomo (lo entenderéis mejor si observáis los ojos y la perla). La radiografía también nos permite apreciar mejor el entramado del lienzo, lo que el equipo científico ha empleado para calcular el número de hilos de lino y comparar los resultados con el de otras obras de Vermeer.

La luz ultravioleta (Imagen 3B) nos permite ver la fluorescencia de ciertos materiales. Podéis observar que toda la obra tiene cierta fluorescencia y eso se debe al barniz que la cubre. Los barnices tradicionales, al envejecer, se vuelven fluorescentes lo que permite identificar intervenciones posteriores a su aplicación. Por ejemplo, la mancha oscura en el ojo corresponde a un retoque realizado en 1994. También cabe destacar la fluorescencia acentuada en los labios, que nos indica que Vermeer empleó alguna laca orgánica fluorescente para lograr ese espectacular efecto.

Por último, y aunque en este caso no se necesite ninguna tecnología especial, el empleo de la luz rasante nos ayuda a apreciar la tridimensionalidad del cuadro (Imagen 3C). Así se aprecia mejor la pincelada de Vermeer y, sobre todo, las craqueladuras, esas grietas surgidas a lo largo de los años por el envejecimiento de los materiales y las tensiones provocadas por los cambios de condiciones ambientales.

Los materiales

Puede que Vermeer no fuese un pintor de éxito, pero el hecho de vivir en una ciudad como Delft le facilitó el acceso a materiales de primerísima calidad. Recordemos que las Provincias Unidas eran el centro comercial por excelencia de Europa, además de una referencia en la manufactura de numerosos productos, entre ellos los lienzos. Ya hemos mencionado que el artista empleó un lienzo de lino, pero no hemos dicho que ese soporte no es adecuado para pintar directamente y por eso es necesario cubrirlo con una capa preparatoria que ofrezca una superficie regular: la imprimatura. La imprimatura la podía realizar el propio pintor, pero en aquella época era habitual comprar los soportes ya preparados. Las estratigrafías de la obra han permitido cuantificar que la imprimatura de La joven tiene un grosor de unos 0,2 mm y está compuesta por blanco de plomo, pigmentos ocres y creta. La creta es una roca blanquecina de carbonato cálcico y origen orgánico formada por fósiles de ciertas algas. De hecho, en la Imagen 4 se pueden apreciar algunos de estos fósiles “durmiendo” bajo capas de pinturas.

Imagen 4. Estratigrafía con la preparación y capas de pintura (Rod Erdmann). A la izquierda se distinguen unos cocolitos. La mitad derecha de la imagen corresponde a fotografía de fluorescencia ultravioleta y la de la izquierda a fotografía de luz visible. En este enlace se puede observar la imagen interactiva. Fuente: Imagen cedida por el Mauritshuis.

Otro de los materiales indispensables en un óleo es el aceite empleado como aglutinante. Los análisis de cromatografía de gases han confirmado que el aceite empleado por Vermeer era de linaza, el más habitual en esta técnica pictórica, y que se obtiene de las semillas de la misma planta con la que se elabora el lienzo. Estos análisis también han desvelado que el artista empleó un aceite previamente tratado para contralar su secado, un factor crítico a la hora de pintar al óleo. Curiosamente también se ha detectado aceite de colza, pero lo más probable es que su presencia se deba a una contaminación en el molino en el que se elaboraban los aceites. Lógicamente una sección dedicada a los materiales artísticos no estaría completa sin hablar de los pigmentos que, debido a su relevancia, trataremos en un apartado diferenciado.

Los pigmentos de Vermeer

Empezaremos por uno de los pigmentos que menos destaca en la composición, pero que no por ello es menos importante: el rojo. A priori sólo lo observamos en los labios que, como ya hemos dicho, están realizados con una laca orgánica. Los análisis mediante cromatografía líquida han confirmado que se trata de carmín, un colorante obtenido de las cochinillas y que también se emplea en la industria alimentaria y, paradójicamente, en productos cosméticos como los pintalabios. Pero no es este el único rojo del óleo. Empleando fluorescencia de rayos X se realizó un mapeo de la presencia de ciertos elementos químicos, entre ellos el mercurio, y se observó que era muy abundante en los labios y, en menor medida, en la piel (Imagen 5). La explicación es que Vermeer empleó cinabrio (HgS) entre sus pigmentos rojos. Probablemente pintó los labios con este pigmento y luego lo cubrió con la laca roja para obtener el efecto deseado. Por otra parte, la presencia de mercurio en el rostro de la chica (en la que también se ha detectado carmín) es debida a que Vermeer añadió este pigmento a la pintura para lograr el color deseado para realizar la piel.

Imagen 5. Mapeo de mercurio obtenido mediante fluorescencia de rayos X (detalle). Fuente: Imagen cedida por el Mauritshuis.

Al hablar de la radiografía hemos mencionado un pigmento blanco: el blanco de plomo (o albayalde). Este compuesto destaca, obviamente, en todos aquellas partes del retrato pintadas de dicho color: la blusa, los ojos, la perla, etc. Pero si volvemos la vista a la radiografía de la Imagen 2 veremos que hay una zona de la cara que es mucho más blanquecina de la otra. Eso quiere decir que en esas áreas Vermeer añadió más pigmento blanco a su pintura como recurso para lograr una mayor claridad. Así, uno de los culpables de los fabulosos juegos de luz de la obra es el albayalde.

Y del blanco pasemos al negro. En este caso los análisis químicos han revelado la presencia de dos pigmentos diferentes: el negro de carbón y el negro de hueso. El primero ofrece un tono más azulado y el segundo un tono más marrón, de ahí que Vermeer los combinase y mezclase para lograr las tonalidades deseadas. En cualquier caso, el negro que más llama la atención es el del propio fondo. Pero, ¡oh sorpresa!, esta zona no estaba pintada de tal color originalmente. Es cierto que el neerlandés aplicó una capa de pintura negra sobre la imprimatura, pero encima depositó una veladura de color verde formada por dos lacas de origen vegetal: índigo (azul) y gualda (amarillo). Estas lacas se degradan bajo la exposición lumínica y son sensibles a otros factores ambientales, por lo que el paso del tiempo ha hecho mella en ellas y nos han dejado un fondo más oscuro que el que pintó Vermeer.

Dejemos el fondo a un lado y volvamos a la ropa de nuestra protagonista. ¿De qué color es la chaqueta que viste? ¿Amarilla? ¿Marrón? De hecho no hay una única respuesta, ya que Vermeer usó diferentes pigmentos amarillentos, rojizos y marrones. La fluorescencia de rayos X ha revelado que las ropas contienen una gran cantidad de hierro, lo que indica la presencia de una familia de pigmentos conocida como tierras: ocre amarillo (FeO(OH)·nH2O), ocre rojo (Fe2O3), siena, etc. Estos compuestos son muy habituales en la naturaleza y dibujan, a su manera, paisajes tan espectaculares como los del Roussillon francés.

Y si hablamos de los ropajes, no podemos pasar por alto la prenda más llamativa: el turbante. A los ya mencionados colores amarillos se les une aquí el azul. Un azul que es, incluso, más exótico que el turbante al que le da el color: el azul ultramar. Ya hemos explicado en otra ocasión que este pigmento se traía desde Afganistán y que era increíblemente caro. En La joven de la perla, Vermeer no sólo lo usa en el turbante, sino que lo emplea mezclado con otros pigmentos (por ejemplo en la chaqueta). Resulta sorprendente que, sin ser un pintor de primerísimo orden en su época, tuviese acceso a un producto tan exclusivo. Pero son muchas las cosas que desconocemos de este genio que, además de esta obra maestra, nos ha regalado joyas como Vista de Delft o La lechera.

La firma

Como si se tratase de un cuadro, acabaremos este artículo con la firma. La de Vermeer, por supuesto. Hoy en día es un rastro apenas invisible en la esquina superior izquierda que se confunde con el fondo degradado. Pero, una vez más, la fluorescencia de rayos X (en este caso la de calcio) nos permite ver con mayor claridad, y distinguir así el llamativo monograma que dejó el artista (Imagen 6). Si os apetece curiosear, aquí podéis ver las diferentes firmas que empleó a lo largo de su carrera, que son casi tantas como las obras que pintó.

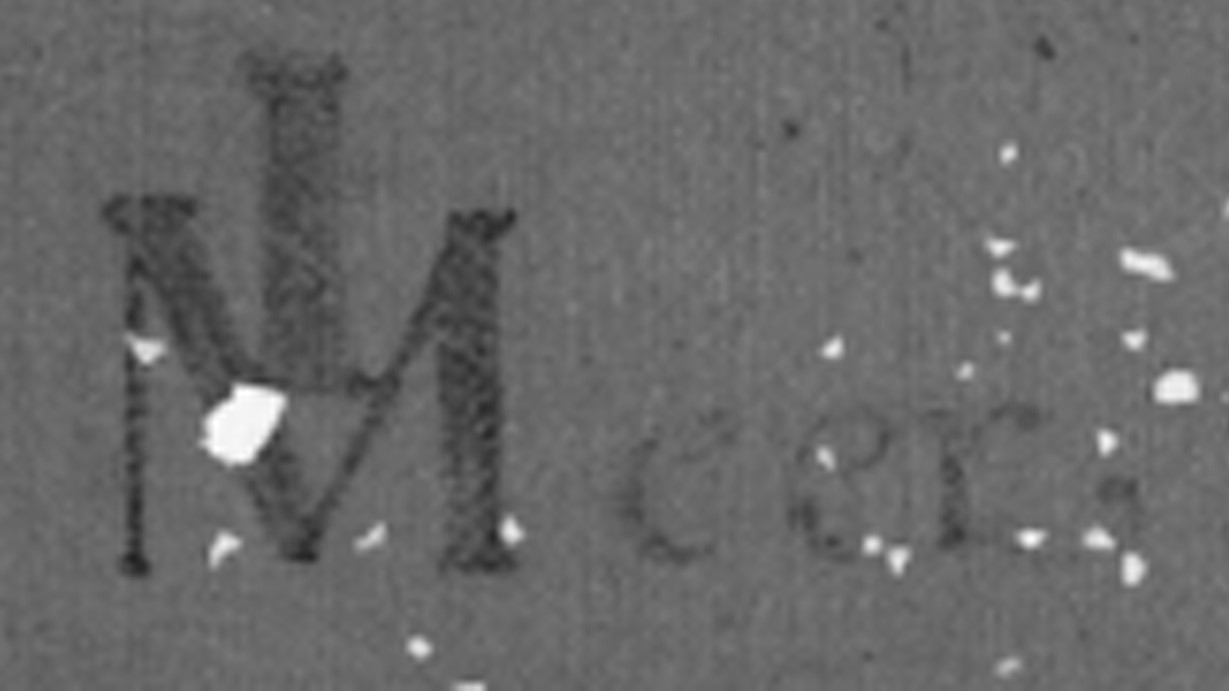
Imagen 6. El monograma de Vermeer identificado gracias al mapeo de calcio con fluorescencia de rayos X (Annelies van Loon). Fuente: Imagen cedida por el Mauritshuis.

*N. del A. Me gustaría expresar mi más sentido agradecimiento al museo Mauritshuis por facilitarme el acceso a las imágenes obtenidas durante el proyecto The girl in the spotlight

Para saber más

Girl with a blog de Abbie Vandivere.

Sobre el autor: Oskar González es profesor en la facultad de Ciencia y Tecnología y en la facultad de Bellas Artes de la UPV/EHU.

El artículo Los secretos de ‘La joven de la perla’ se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Códigos secretos en la primera guerra mundial
2. “Los siete mares de la divulgación” por Pilar Perla
3. Secretos

Jakintza-arlo desberdinetako profesionalen ikerketak ezinbestekoak izan dira azken mendean ehun-ingeniaritzaren arloan eman diren aurrerakuntzak errealitate bihurtzeko. Zientzia honen helburu nagusia ehunen eta organoen funtzioa berreskuratu, mantendu edo hobetzeko erabiltzen diren egitura biologikoak garatzea da.

Ehun-ingeniaritzan erabiltzen diren biomaterialak gorputzarekin elkarrekintzan jartzen dira ehun edo organoen eta inplanteen arteko interakzio egokia bermatzeko. Diseinatu nahi den inplantearen aplikazioaren arabera, propietate ezberdinetako biomaterial mota anitz ekoizten dira gaur egun.

Baina, zer nolako ezaugarriak dituzte biomaterialek? Zeintzuk dira etorkizuneko erronka nagusiak ehun-ingeniaritzaren arloan? Galdera hauei erantzuna bilatzeko UPV/EHUko Bilboko Ingeniaritza Eskolako Ester Zuza irakaslearekin izan gara.

‘Zientzialari’ izeneko atal honen bitartez zientziaren oinarrizko kontzeptuak azaldu nahi ditugu euskal ikertzaileen laguntzarekin.

The post Ester Zuza: “Biomaterialak gorputzean sartzen ditugu ehunen birsortze prozesuan laguntzeko” #Zientzialari (92) appeared first on Zientzia Kaiera.

Juan C. Ripoll

Una curva de la atención es una representación gráfica de cómo evoluciona la atención a lo largo del tiempo que dura una actividad. Pero con “la curva de la atención” me estoy refiriendo a algo más concreto: un modelo que indica que la atención de los alumnos a lo largo de una clase disminuye rápidamente, de tal forma que entre 10 y 20 minutos después de que el profesor comience una explicación, la atención del alumnado es mínima y, consecuentemente, también su aprovechamiento.

Recientemente me llegó una lista de consejos para enseñar a leer de una manera respetuosa con la forma de aprender del cerebro. En esa lista encontré una tabla con indicaciones acerca del tiempo que se podía dedicar a la instrucción directa según el curso de los alumnos, desde los 5 a 8 minutos de 1º y 2º de primaria hasta los 12 a 15 minutos para los alumnos de últimos cursos de la secundaria y el bachillerato. Esta tabla iba acompañada por una referencia a Jensen (2005). El libro de Jensen incluye una tabla con estas recomendaciones pero, a diferencia de lo que hace con otras propuestas, no va acompañada por ninguna referencia.

Podría ser algo anecdótico, pero este modelo de la evolución de la atención se está utilizando como base para proponer modificaciones en la forma de enseñar. Por ejemplo, tenemos esta entrevista a Francisco Mora publicada en el diario El País (Torres, 2017), en la que declara:

“nos estamos dando cuenta, por ejemplo, de que la atención no puede mantenerse durante 50 minutos, por eso hay que romper con el formato actual de las clases. Más vale asistir a 50 clases de 10 minutos que a 10 clases de 50 minutos. En la práctica, puesto que esos formatos no se van a modificar de forma inminente, los profesores deben romper cada 15 minutos con un elemento disruptor: una anécdota sobre un investigador, una pregunta, un vídeo que plantee un tema distinto… Hace unas semanas la Universidad de Harvard me encargó diseñar un MOOC (curso online masivo y abierto) sobre Neurociencia. Tengo que concentrarlo todo en 10 minutos para que los alumnos absorban el 100% del contenido. Por ahí van a ir los tiros en el futuro.”

En otro ejemplo, del blog Escuela con cerebro (Guillén, 2012) encontramos esto:

“existen ciclos clave de nuestro cerebro que oscilan entre 90 y 110 minutos y nos permiten mantener la atención. Diversos estudios demuestran que la atención sostenida sólo puede mantenerse durante cortos períodos de tiempo que no superan los 15 minutos. Aparece el factor temporal como una variable decisiva en el aprendizaje y es que, además, a nivel neuronal, se requiere tiempo para fortalecer las sinapsis y no tener que responder a otros estímulos generados. Como el aprendizaje de nuevos conceptos o destrezas requiere un tiempo de procesamiento y asimilación, los docentes deberíamos organizar nuestros contenidos en bloques que no superaran los 20 minutos. Después de cada bloque, para facilitar el aprendizaje y optimizar los ciclos de atención, deberíamos invertir unos minutos en reflexionar sobre lo explicado o en descansar.”

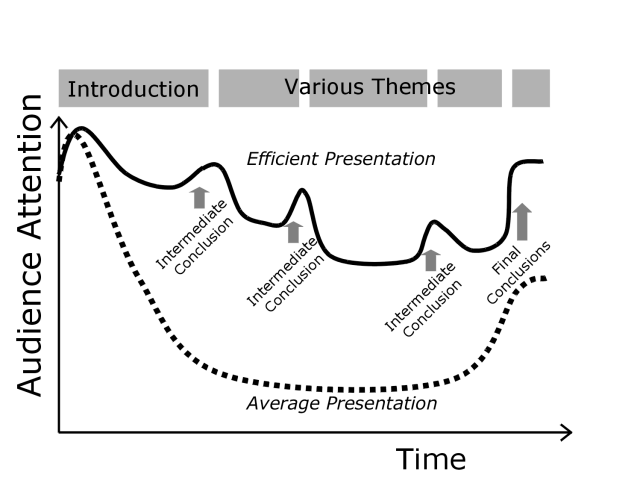
Curvas de atención promedio (discontinua) y presuntamente optimizada (continua).

¿Una leyenda urbana?

Personalmente, cuando me encuentro con este tipo de propuestas, me surgen bastantes dudas. La primera es si no se han considerado las influencias del contexto al medir la evolución de la atención durante una exposición del profesor. ¿Influyen en la la concentración del alumnado el contenido de la exposición, su dificultad, o los recursos retóricos que emplea el profesor para explicarlo? ¿Influye el momento del día o la cantidad de clases que haya habido previamente? Pero la mayor duda que se me plantea es ¿cómo han medido la atención del alumnado a lo largo de la clase y cómo hicieron para que esas medidas no afectaran a la atención, que era el objeto de estudio?

Aparentemente, el modelo de la curva de la atención tiene varios elementos en común con las leyendas urbanas: nos llega de fuentes que no lo han comprobado directamente, pero aseguran conocer datos fiables. Sin embargo, cuando comenzamos a analizar esos datos, la cuestión se enreda y empezamos a encontrar más referencias indirectas y distintas formas de contar la historia. Basta con hacer una búsqueda de imágenes referentes a la “curva de la atención” o “attention curve” para empezar a encontrar diferentes representaciones. La mayoría de ellas comienzan con un aumento rápido de la atención, seguido por una brusca caída, una fase baja (estable o ligeramente decreciente) y un repunte posterior. Sin embargo, las alturas relativas, y las pendientes que se muestran pueden ser bastante diferentes. Algunas van acompañadas por referencias de tiempo y otras no. Las que incluyen estas referencias suelen representar intervalos de 40 a 60 minutos y suelen situar el declive de la atención entre los 15 y los 30 minutos.

Durante esta búsqueda superficial encontré que algunas de las imágenes proporcionaban referencias a manuales dirigidos a mejorar la eficacia de las clases, por ejemplo Gibbs (1992) o Bligh (1998; la primera edición de este manual es de 1971).

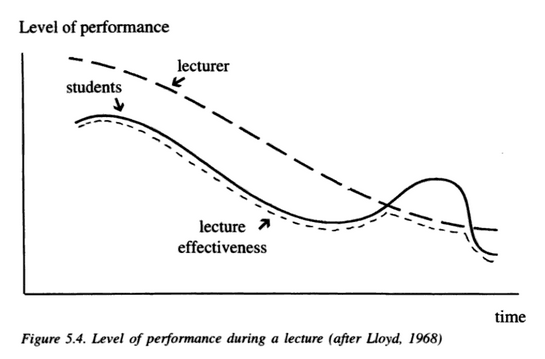
Figura de la página 56 de Bligh (1998)

Se puede acceder parcialmente al manual de Bligh a través de Google Books y es muy ilustrativo ver la imagen que incluye en la página 56. Lo primero que me chocó es que la curva que se representa es mucho más plana que las curvas de Bligh que había encontrado buscando imágenes en internet y, también, que la representación se plantea como una interacción entre la receptividad de los alumnos y la actuación del profesor. Esta segunda parte no la había visto en ninguna de las representaciones que había estado consultando.

Y ahora, otro salto en el tiempo. Bligh referencia la representación que incluye en su manual a Lloyd (1968). Cuanto más retrocedemos en el tiempo (y ya van 50 años) más difícil me resulta consultar las fuentes, y no he podido acceder a este artículo de Lloyd. Sin embargo, en el intento, he encontrado una revisión que describe su contenido y que ofrece información interesante sobre la curva de la atención.

Pero antes de continuar con esa revisión, sí que me gustaría indicar que hay intentos de representar la fluctuación de la atención del alumnado bastante más antiguos, por ejemplo el de Philpott (1934). En realidad, este modelo no tomaba datos sobre la atención de los alumnos durante las explicaciones, sino en la realización de actividades como cálculos aritméticos. Lo curioso es que trata de representarla mediante una curva que representa la evolución de la atención a lo largo de 15 minutos. El propio Philpott menciona otros intentos anteriores de representar los cambios en la atención, así que no parece que sea el modelo más antiguo.

Una revisión

Ahora sí, me centro en la revisión que he presentado en la sección anterior, publicada por Wilson y Korn (2007). Es muy breve y se puede encontrar en internet, así que recomiendo su lectura directa, pero también me gustaría destacar algunos puntos.

Wilson y Korn también encontraron que existe una especie de acuerdo tácito que indica que la atención de los alumnos durante una explicación solo se mantiene durante unos 10 o 15 minutos. Para ver qué respaldo tiene esa idea, examinaron las referencias que daban algunos manuales de pedagogía en los que la encontraron.

En esta búsqueda encontraron que varias de las fuentes que se citaban no eran estudios empíricos, sino que se basaban en otras fuentes o en observaciones e impresiones personales. En ese tirar del hilo localizaron unos pocos estudios empíricos, en los que la atención de los alumnos se medía según la cantidad de apuntes que tomaban durante la clase, a partir de la observación de su comportamiento, el recuerdo de los contenidos explicados, medidas de autoinforme y medidas fisiológicas (tasa cardíaca).

Varios de estos estudios tienen problemas metodológicos como que no se haya evaluado la fiabilidad de los observadores o que no quede clara la relación entre la variable medida y la atención (por ejemplo, los alumnos pueden dejar de tomar apuntes porque se distraen, pero también por otros motivos, como que perciban que el profesor repite ideas, que las consideren poco importantes o algo ya sabido). Además, en algunas ocasiones no hay consistencia entre las medidas de observación y las medidas de aprendizaje o entre los resultados de distintos estudios.

No olvido que esta revisión hablaba de la curva de la atención de Lloyd (1968), la más antigua que he localizado sobre atención a una explicación. Wilson y Korn (2007) indican que el modelo que propone Lloyd no se construyó a partir de datos empíricos, sino de sus experiencias y observaciones como profesor.

Algo más reciente, por favor

Esta revisión de Wilson y Korn ya tiene unos cuantos años, de modo que es posible que en ese tiempo la investigación haya aportado datos a favor de las miniclases de 10 o 15 minutos, o quizá no…

Bradbury (2016) también ha realizado una revisión, ahora más reciente sobre este tema. Sus conclusiones son muy similares a las de Wilson y Korn (2007), pero realiza algunas aportaciones interesantes. Bradbury sitúa el origen del mito de los 15 minutos de atención en un informe sobre la toma de apuntes, publicado en 1978, aunque ya hemos visto cómo Lloyd (1968) ya había expuesto la idea del declive de la atención tras los primeros minutos de clase. Entre los estudios que revisa Bradbury hay uno posterior a 2007, en el que se empleó una medida de autorregistro con pulsadores inalámbricos y en el que se vio como la atención de los alumnos (universitarios que hacían un curso de química) fluctuaba a lo largo de la clase, pero sin seguir una pauta.

Su conclusión es que el límite de 10 a 15 minutos para la duración de las explicaciones no está respaldado por evidencias. También indica que, según los estudios revisados, parece que la mayor fuente de variabilidad en la atención de los alumnos es el profesor, no el formato de la clase. Me imagino que no se trata del profesor en sí, sino de sus habilidades para comunicar los contenidos y mantener el interés de la clase.

Para intentar mantener el rigor, habría que tener en cuenta que las dos revisiones que he presentado no son sistemáticas y, por ejemplo, esta de Bradbury omite estudios como el de Risko, Anderson, Sarwal, Engelhardt y Kingstone (2012) o el de Farley, Risko y Kingstone (2013), sin que sepamos si se trata de una omisión accidental o de algo intencionado porque los participantes no seguían clases presenciales sino grabadas en vídeo.

Concluyendo

La idea de que el funcionamiento de la atención humana hace recomendable no prolongar las explicaciones más allá de un intervalo entre 10 y 20 minutos está bastante extendida. A veces se presenta como una aportación de la “neurodidáctica”, pero no se trata de una novedad ya que se puede encontrar como algo ya establecido a partir de la segunda mitad del siglo XX. Sin embargo, resulta difícil identificar su origen y también localizar un conjunto de evidencias que respalden esta creencia.

Los datos que he aportado aquí para cuestionarla no son especialmente rigurosos: algunas apreciaciones sobre las distintas formas en que se presenta y la facilidad con la que se da por cierta basándose en referencias a fuentes no empíricas. No obstante, no olvidemos que es responsabilidad de quienes plantean modificaciones en la forma de estructurar las clases el aportar las evidencias que respalden sus propuestas. Mi objetivo era, sencillamente, poner de manifiesto que quizá no existan esas evidencias.

La atención del alumnado a las lecciones o explicaciones es un asunto complejo en el que probablemente influyen el nivel de desarrollo, la motivación, los recursos del profesor, el contenido de la explicación, la fatiga, la presencia o ausencia de distractores y otras variables. Explicar esa atención a las explicaciones únicamente en función de su duración es, quizá, demasiado simplista. Buena parte de los estudios sobre el tema se han realizado con alumnado universitario, no de etapas escolares. Esto merecería una exploración más profunda ya que no es extraño que el profesorado de educación primaria y secundaria combine a lo largo de una sesión lectiva explicaciones, intervenciones del alumnado, actividades y corrección de las actividades, de manera que podríamos estar tratando de solucionar un problema poco habitual (largas explicaciones que el alumnado no es capaz de aprovechar).

Sería un exceso de confianza realizar modificaciones generales de la estructura o duración de las clases dando por supuesto que este modelo es válido, sin comprobar que realmente lo es y comunicar claramente a los implicados (alumnado, familias, profesorado y responsables del sistema educativo) la evidencia disponible para promover estos cambios.

Referencias:

Bligh, D. (1998). What’s the use of lectures (5ª ed.). Exeter: Intellect.

Bradbury, N. A. (2016). Attention span during lectures: 8 seconds, 10 minutes, or more? Advances in Physiology Education, 40(4), 509-513.

Gibbs, G. (1992). Improving the quality of student learning. Bristol: Technical & Educational Services Ltd.

Farley, J., Risko, E. F. y Kingstone, A. (2013). Everyday attention and lecture retention: the effects of time, fidgeting, and mind wandering. Frontiers in Psychology, 4, 619.

Guillén, J. C. (2012). La atención: un recurso limitado. Disponible en https://escuelaconcerebro.wordpress.com/2012/03/04/la-atencion-un-recurso-limitado/

Jensen, E. (2005). Teaching with the mind in brain (2ª ed.). Alexandria (EEUU): ASCD.

Lloyd, D. H. (1968). A concept of improvement of learning response in taught lesson. Visual Education, 23-25.

Philpott, S. J. F. (1934). A theoretical curve of fluctuations of attention. British Journal of Psychology, 25(2), 221-255.

Risko, E. F., Anderson, N., Sarwal, A., Engelhardt, M. y Kingstone, A. (2012). Everyday attention: Variation in mind wandering and memory in a lecture. Applied Cognitive Psychology, 26(2), 234-242.

Torres, A. (2017). Hay que acabar con el formato de clases de 50 minutos. Disponible en https://elpais.com/economia/2017/02/17/actualidad/1487331225_284546.html

Wilson, K. y Korn, J. H. (2007). Attention during lectures: Beyond ten minutes. Teaching and Psychology, 34(2), 85-89.

Sobre el autor: Juan Cruz Ripoll es maestro de primaria y doctor en educación.

El artículo La curva de la atención, ¿una leyenda urbana? se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Un chip de ADN para el diagnóstico de TDAH (trastorno por déficit de atención e hiperactividad)
2. La leyenda del cuervo y el búho
3. La curva de disociación de un pigmento respiratorio

Erik Aostri, Joseba Pineda, Aitziber Mendiguren Gizakiak antzinatik naturan aurkitu izan ditu bere gaixotasunen sendabidea. Beraz, ez da harritzekoa printzipio aktibo ezagunenak iturri naturaletan aurkitu izana, gehienak landaretan. Cannabis sativa landarean kannabinoide izeneko konposatuak daude, eta horiek propietate terapeutiko desberdinak aurkezten dituzte.

Irudia: Orain arte dauden ikerlanen arabera, kannabiseko CBDa erabilgarria izan liteke gaixotasun neuropsikiatrikoak tratatzeko. THCVa, obesitatea tratatzeko proposatu da eta CBGa, berriz, endekapenezko gaixotasunetarako.

Dena dela, kannabinoideak medikamentu gisa garatzeko oztopoetako bat dituzten propietate psikotropikoak dira, hau da, hartzaile kannabinoideak (CB) aktibatuz pertzepzioaren aldaketa eragitea. Hori dela eta, egungo terapeutikan kannabinoideen erabilera gaixotasun batzuetara mugatu izan da. Azken urteotan, eragin psikotropikorik ez duten kannabinoideek ikertzaileen arreta piztu dute. Izan ere, konposatu horiek esparru klinikoan erabiltzeko interesgarriagoak izango lirateke, oro har, hartzaile kannabinoideak zuzenean ez aktibatzeagatik segurtasun-profil hobea aurkezten dutelako. Gaur egun, kannabinoide ez-psikoaktibo ugari ikertzeko bidean badaude ere, ezagunenak honakoak dira: kannabidiola (CBD), Δ9-tetrahidrokannabibarina (THCV) eta kannabigerola (CBG). Kannabinoide horiek nerbio-sistemako itu desberdinetan eragiten dute.

CBDa kannabinoide ez-psikoaktiboen artean ikertuena da. In vitro ereduetan zein animalietan egindako ikerketek kannabinoide honek sistema serotonergikoa, sistema endokannabinoidea eta hanturan parte hartzen duen sistema erregulatzen dituela frogatu dute. Animalia-ereduei esker, posiblea izan da kannabinoide horrek dituen efektu antipsikotikoak, antidepresiboak, antsiolitikoak, antiepileptikoak, motoreak eta goitikaren kontrakoak frogatzea. Aipaturiko eragin horiek neurotransmisio-sistema desberdinen modulazioarekin erlazionatzen badira ere, ebidentzia gehien bildu dituena sistema serotonergikoa izan da eta, bereziki, 5-HT1A hartzailea. Gizakietan, bi dira CBDari egotzi zaizkion propietate nagusienak: eragin antiepileptikoa eta antsiolitikoa. Espainian 2010. urtetik aurrera osagai moduan CBDa duen eta esklerosi anizkoitzaren tratamendurako aproposa den medikamentu bat merkaturatuta dago, Sativex (CBD eta Δ9-THC konbinaketa) izenez ezagutzen dena.

Bestalde, THCVaren eta CBGaren efektuak oraindik ez dira ondo karakterizatu. Animalietan egindako ikerketek THCVak gosea inhibitzen duela frogatu dute. Bestetik, 5-HT1A hartzailearen aktibazioaren bidezko eragin antipsikotikoak ere deskribatu dira eta baita eragin antidepresiboak ere. Pertsona osasuntsuengan egindako saio klinikoren batek ere THCVa obesitatearen aurka erabilgarria izan daitekeela frogatu du eta gainera depresiorik eragiten ez duela. Izan ere, aurretik indikazio horretarako merkaturatu zen kannabinoide bat, Acomplia®, obesitatea tratatzeko erabilgarria zen baina egoera emozionalaren asaldura eragiten zuen. Azkenik, CBGaren ituak oraindik deskribatu gabe daude, eta are gutxiago haren efektu farmakologikoak. Ikerketaren batek eragin antidepresiboa duela iradoki badu ere, ebidentzia gehienek hanturaren inhibizioa frogatu dute. Eragin horri esker CBGak efektu neurobabesgarria izan dezakeela proposatu da, adibidez, Huntington gaixotasunean baina oraindik ez da eragin hori saio klinikoetan frogatu.

Laburbilduz, kannabinoide ez-psikoaktiboei buruz dauden ebidentziak itxaropentsuak izan arren, horien ituak, ezaugarri farmakologikoak eta eraginak sakonago ikertu behar dira. Orain arte dauden ikerlanen arabera, CBDa erabilgarria izan liteke gaixotasun neuropsikiatrikoak tratatzeko. THCVa, obesitatea tratatzeko proposatu da eta CBGa, berriz, endekapenezko gaixotasunetarako. Badirudi kannabinoide horien segurtasun-profil hobearen arrazoia, sistema kannabinoidea zeharka erregulatzea edota beste itu desberdinak modulatzea (adibidez, sistema serotonergikoa) dela. Beraz, hurrengo urteetan baliteke kannabinoide horien erabilera klinikoa hedatzea.

Artikuluaren fitxa:

• Aldizkaria: Ekaia
• Zenbakia: Ekaia 31
• Artikuluaren izena: Kannabinoide berriak: segurtasun eta eraginkortasun terapeutikoaren bila.
• Laburpena: Cannabis sativa landarean kannabidiola, kannabigerola edo Δ9-tetrahidrokannabibarina bezalako kannabinoide ez-psikoaktiboak aurki daitezke. Oro har, kannabinoide horiek kannabinoideen hartzaileekiko (CB) afinitate txikia dutenez, ez daukate kannabinoide klasikoek (bereziki Δ9-THCak) duten aktibitate psikoaktiboa. Gizakietan eta animalietan kannabinoide ez-psikoaktiboekin egindako lehenengo ikerketek horien propietate terapeutikoak frogatu dituzte. Efektu horiek azaltzeko itu eta mekanismo desberdinak proposatu dira, besteak beste, hartzaile serotonergikoen aktibazioa edota entzima desberdinen modulazioa.
• Egileak: Erik Aostri, Joseba Pineda, Aitziber Mendiguren.
• Argitaletxea: UPV/EHUko argitalpen zerbitzua
• ISSN: 0214-9001
• Orrialdeak: 7-20
• DOI: 10.1387/ekaia.16320

—————————————————–
Egileez: Erik Aostri, Joseba Pineda eta Aitziber Mendiguren UPVEHUko Medikuntza eta Erizaintza Fakultateko Farmakologia Sailekoak dira.

————————————————–
Ekaia aldizkariarekin lankidetzan egindako atala.

The post Kannabinoide berriak: segurtasun eta eraginkortasun terapeutikoaren bila appeared first on Zientzia Kaiera.

Una fracción de los investigadores y técnicos que trabajan con el detector CMS del CERN.

En los últimos tiempos está de moda la ciencia grande. Los organismos de investigación y quienes financian la ciencia favorecen los proyectos macro, con participación internacional, objetivos enormes y plantillas ingentes. Grandes coaliciones de múltiples laboratorios o centros de investigación, grandes problemas a resolver y grandes ambiciones, a ser posible con grandes instrumentos en proyectos que cuestan grandes cantidades y se alargan en grandes periodos temporales. En algunos casos, como cuando se trata de obtener financiación europea, es obligatorio buscar la cooperación de equipos de investigación externos porque el objetivo no es sólo fomentar la ciencia, sino forzar la cooperación paneuropea. En otros disponer de un socio, incluso extracomunitario, aumenta las posibilidades de conseguir dinero por razones de política internacional.

En otras ocasiones es forzoso que el proyecto sea de gran tamaño, porque el instrumental necesario lo es: si tu trabajo implica usar un macrotelescopio, o un acelerador de partículas, o diseñar e integrar un instrumento en un satélite necesariamente tendrás que integrarte en un gran equipo internacional. Lo cual tiene dos inconvenientes graves, en lo que se refiere a la práctica científica desde el punto de vista personal; dos cuestiones que demasiadas veces no se tienen en cuenta a la hora de pensar en una carrera profesional, o en la ciencia en su conjunto.

Por una parte nadie entrena de modo formal a los científicos para formar parte de, y mucho menos para dirigir, grandes equipos. Las habilidades y capacidades necesarias para integrarse en (o liderar) un gran consorcio internacional, o para gestionar desde el punto de vista práctico un laboratorio, no están en el temario de las carreras de ciencias. Coordinar equipos internacionales, gestionar el suministro de consumibles, pedir permisos de excavación o solicitar becas o financiación de proyectos no es algo que se aprenda durante una carrera de ciencias físicas, biológicas o matemáticas. No hablemos ya de la gestión de personal, una tarea que en las empresas tiene departamentos especializados y que en un entorno científico se ve complicada por el hecho de que no siempre es posible ‘fichar’ a la persona que se desea; a la hora de contratar un técnico de laboratorio, supongamos, es posible que haya que convocar un concurso público que nos traerá a una persona cualificada, sí, pero a la que quizá no conocemos. Y teniendo en cuenta que además la tarea del líder del equipo incluirá definir líneas de investigación para sus becarios y postdoc pensando en las necesidades del equipo propio, pero también en sus carreras profesionales futuras, y la plasmación de todo esto en publicaciones y tesis; otra tarea compleja y que no se enseña de modo reglado sino que se aprende (con suerte) en el ejercicio profesional.

En lo que se refiere a la ciencia esta querencia, o moda, de los estamentos financiadores por los megaproyectos fuerza a los científicos a buscar determinado tipo de problemas como objetivo de sus investigaciones, dejando de lado otros más pequeños, pero no por ello menos interesantes. Es por eso que resulta mucho más sencillo obtener fondos para proyectos de Big Data que para caracterizar la flora y fauna de una región, por ejemplo; o para realizar grandes campañas de geomorfología a gran escala que para caracterizar la geoquímica local. Se organizan consorcios internacionales de miles de investigadores y cientos de laboratorios para luchar contra el cáncer o para crear y operar el Gran Colisionador de Hadrones, pero es mucho más difícil encontrar financiación para otro tipo de ciencia más pequeña, con menos necesidad de grandes equipos o instrumentos y con resultados menos llamativos, aunque no por ello de menor importancia. Y con ello perdemos datos que son también importantes pero que no se capturan, porque iniciar un proyecto para hacerlo es un suicidio a la hora de conseguir un respaldo a tu investigación.

Como en cualquier área los científicos deben escoger entre erigir catedrales y pintar cuadros. El constructor de catedrales necesita grandes equipos de gente, mucho tiempo, capacidades de gestión y paciencia, pero a cambio puede construir enormes edificios que desafiarán a los siglos. Para ello debe tener todas esas cualidades y además debe renunciar a controlar hasta el último detalle de su creación; necesariamente tendrá que delegar en el maestro cantero para que talle los capiteles o en el ebanista para que se ocupe del coro, por lo que la obra final no será tan personal; sólo un Justo Gallego puede construir una catedral él solo (y así le ha salido). En cambio el pintor tiene que renunciar a las obras inmensas más allá de la Capilla Sixtina o los grandes frescos, ya que la capacidad de trabajo de un humano tiene sus límites. Pero a cambio hasta el último detalle del resultado estará bajo su control; si lo desea cada brillo, cada sombra y cada color del cuadro resultante serán su obra. Son dos modos diferentes de enfocar el acto creativo y dos maneras de enfrentarse al trabajo necesario.

El peligro es que concentrándonos demasiado en las catedrales nos olvidemos de pintar cuadros. No sólo no estamos formando a los científicos para el tipo de trabajo que hoy se les exige, sino que además estamos abandonando otro tipo de ciencia más callada, solitaria y de alcance quizá más limitado en principio, pero sin la cual los macroproyectos tampoco pueden llegar muy lejos. Ayudemos a los constructores de catedrales, pero apoyemos también los proyectos menos ambiciosos, más personales y también necesarios. Porque de lo contrario la ciencia grande se comerá a la pequeña, y saldremos todos perdiendo.

Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.

El artículo Ciencia grande, ciencia pequeña se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Ciencia, política y hechos
2. La ciencia y los errores
3. El libro que inspiró al más grande

Juan Ignacio Pérez eta Miren Bego Urrutia Igeri egiten, lasterka egiten, hegan egiten

———————————————————————————————————–

Ospe handiko narra-lasterketak egiten dira Alaskan. «The Copper Basin 300» da horietako bat, horri buruz aritu gara aurreko atalean. Beste bat Iditarod izenekoa dugu; lasterketa ezagunena da eta; seguru asko, gogorrena ere bai.

Irudia: Iditarod lasterketa da, ziur aski, narra-txakurren lasterketarik gogorrena eta ezagunena. (Irudia: Frank Kovalchek)

Parte hartzaileek 1.161 milia (1.868 km) egin behar dituzte Willow-etik (Anchorage hiritik gertu) Nome-raino eta 9-15 egun ematen dituzte horretan. Hamasei txakurrek osatzen dute lasterketa-taldea: narratik tiratzen dutenak eta «musher» izeneko giza gidariak.

Aurreko ataletan esan dugun bezala, lasterketa horietan parte hartzen duten txakurrak oso gogorrak dira, ugaztunen artean erresistentzia fisiko altuena dutenetakoak seguru asko. Azken urteotan, gainera, zenbait musherrek egiaztatu dute uste zena baino erresistentzia eta ahalmen handiagoa dutela txakurrok. Izan ere, lehen 6 orduko lasterketa-aldiak eta beste 6 orduko atsedenaldiak txandakatzen zituzten, baina azken urteotan lasterketa aldi luzeagoak egiten hasi dira, eta emaitza hobeak lortu dituzte horrela. Lasterketaren azken egunetan astiroago badoaz ere, denbora luzeago egon daitezke gelditu gabe (bai eta 14 ordu ere).

Narra-txakurren ahalmen horrek Estatu Batuetako armadan interesa piztu du, soldaduentzat nahi lukete-eta txakurrek duten erresistentzia fisiko hori. Begi-bistakoa da interes horren arrazoia, ezta? Hori dela eta, Defentsarako Ikerketa Aurreratuko Egitasmoetarako Agentziak 1’4 M$-ko diru-laguntza eman dio Oklahoma Estatuko Unibertsitateko ikertzaile bati. Michael Davis doktorea da ikertzailea eta animalien ariketa fisikoa da haren lan-esparrua.

Narra-txakurrek metabolismo altuenaren %50ean manten dezakete jarduera-maila egunetan zehar. Ez hori bakarrik, musherrek diotenaren arabera, nekatu beharrean, erresistentzia gehiago erakusten dute lasterketa egunak igaro ahala. Davis doktoreak, bestalde, lasterketan zehar giharraren energia-erreserbak ez dituztela agortzen aurkitu du. Lasterketaren hasierako orduetan bai, jaitsi egiten dira, baina denbora igaro ahala lasterka hasi aurretik zuten mailara hurbiltzen dira erreserba-mailak berriro, batez ere glukogenoarenak. Azken egunetan bai, jaitsi egiten dira, baina oso astiro. Noski, txakurrak oso ondo elikatuta daude, proteinetan eta batez ere gantzetan oso aberatsa den janaria ematen baitzaie. Beraz, argi dago ariketa egiteko erabiltzen duten erregai gehiena janaritik ateratakoa dela edo giharrak ez diren beste organoetatik, proportzioan oso neurri txikian erabiltzen baitute giharretan gordeta dagoena.

Esan bezala, txakurrek oso neurri mugatuan erabiltzen dituzte giharraren glukogeno-erreserbak. Dirudienez, muskuluko triglizeridoak eta gorputzaren beste organoetan gordeta dauden lipidoak ere erabiltzen dituzte, baina gantzetan aberatsa den janaria emanez, janariaren gantz hori da erabiltzen duten energia-iturri nagusia, erreserbak gehiegi erabili beharrik gabe. Animalia gehienek, eta batez ere ahalegin luzeak egiten dituztenek, gantzak erabiltzen dituzte energia-emari nagusi gisa, baldin eta nahikoa bada eskuragarri dutena; eta eskuragarri egoteak esan nahi du muskuluan edo lipido-biltegietan egotea edo janariaren bitartez lortu ahal izatea.

Narra-txakurrek beste txakur-arrazek baino gihar-zuntz gorri gehiago dute. Ezaguna denez, mioglobinan eta mitokondrioetan aberatsak dira zuntz gorriak, oso ondo odoleztatuta daude eta lipidoak dira haien metabolismoaren substratu nagusiak. Ezaugarri horiei esker astiro uzkurtzen dira eta nekearekiko erresistentzia altua erakusten dute. Entrenamenduaren ondorioz, gainera, areagotu egiten dira ezaugarri horiek, ezaguna baita entrenamenduak katabolismo aerobikoaren etekina eta eraginkortasuna areagotu egiten dituela eta lipidoen erabilera ere handitu egiten duela. Hori dela eta, ariketa fisikoaren eta metabolismoaren mutur batean daude narra-txakurrak, erresistentzia fisiko altuenetakoa duten ugaztunak baitira.

Ezin esan nekaezinak direnik, baina sinesgaitza dirudi egiten duten ahalegina; oso handia da, metabolismo gorenaren erdiari baitagokio, eta luze irauten du, zortzi egunetik gorako lasterketak egiten baitituzte. Ez dakigu gizakiari aplikatzeko moduko kontuak diren ala ez, baina beharbada ez legoke gaizki gero eta lipido gehiago sartzea erresistentzia handiko kirolarien jakian, lipidoak baitira muskulu geldo nekagaitzek erabiltzen dituzten erregai nagusiak eta gihar horiek baitira narra-txakurrek gehien erabiltzen dituztenak.

—————————————————–

Egileez: Juan Ignacio Pérez Iglesias (@Uhandrea) eta Miren Bego Urrutia Biologian doktoreak dira eta UPV/EHUko Animalien Fisiologiako irakasleak.

—————————————————–

Artikulua UPV/EHUren ZIO (Zientzia irakurle ororentzat) bildumako Animalien aferak liburutik jaso du.

The post «Iditarod» lasterketako txakurrak appeared first on Zientzia Kaiera.

A veces, para crear un modelo de algún fenómeno natural aparentemente complejo bastan tan solo dos parámetros. Un ejemplo típico es el movimiento de una bandada de estorninos. Otro ha resultado ser la forma de las charcas de agua marina formadas al derretirse el hielo del Ártico. Y esto puede ser muy importante para conocer nuestro futuro a medio plazo.

El cambio climático ha alterado drásticamente el Ártico, con el hielo marino derritiéndose más rápido de lo que predecían los modelos a gran escala. En parte esta subestimación se debe a la falta de una comprensión completa de las charcas que aparecen a partir del hielo que se derrite. Un nuevo modelo geométrico de charcas árticas puede reproducir las distribuciones observadas tanto de los tamaños como de las formas de las charcas. Debido a su simplicidad, el modelo puede resultar práctico para predecir cómo un mayor calentamiento podría afectar a los casquetes polares.

Cuando el hielo marino del Ártico se derrite, se forman charcas de agua de varias formas y tamaños en la superficie del hielo. Las charcas tienen un impacto enorme en el transporte de energía, ya que el agua es menos reflectante y absorbe más la energía solar que el hielo o la nieve. Esta propiedad conduce a un mecanismo de retroalimentación positiva: cuantos más charcas se forman, más luz solar se absorbe y mayor cantidad de hielo se funde. Es por esto que los investigadores se esfuerzan en formular modelos de charcas que les permitan incorporar estos efectos de retroalimentación de pequeña escala en modelos climáticos a gran escala. Pero, para que esta incorporación sea posible, los modelos de charcas deben ser simples además de eficaces.

Un equipo de investigadores encabezado por Predrag Popović, de la Universidad de Chicago (EE.UU.), ha ideado un modelo de charca simple que se basa en dibujar círculos aleatoriamente en un plano y suponer que se forman charcas de hielo derretido en los huecos entre los círculos. El modelo tiene solo dos parámetros de entrada: el radio medio del círculo y la fracción del área superficial cubierta por huecos (la conectividad).

El equipo afinó estos parámetros para que los huecos exhiban las mismas correlaciones espaciales que las observadas en las charcas de hielo derretido. Utilizando esta parametrización, los autores demuestran que el modelo reproduce con precisión otras características de las charcas, como la caracterización fractal de sus formas y la abundancia de charcas como función de la superficie.

Adicionalmente se analizaron las funciones de correlación de las charcas en varias fechas. Sorprendentemente resulta que la escala de las charcas y su conectividad son constantes en diferentes años y tipos de hielo.

Estos resultados demuestran que la geometría y la abundancia de las charcas de hielo derretido árticas se pueden describir de forma sencilla, lo que puede aprovecharse en futuros modelos que mejorarían las predicciones de la respuesta del hielo marino al calentamiento del Ártico.

Predrag Popović, B. B. Cael, Mary Silber, and Dorian S. Abbot (2018) Simple Rules Govern the Patterns of Arctic Sea Ice Melt Ponds Physical Review Letters doi: 10.1103/PhysRevLett.120.148701

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

Este texto es una colaboración del Cuaderno de Cultura Científica con Next

El artículo La forma de las charcas árticas se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. La presencia de sales podría hacer que exista una tectónica de placas en Europa
2. ¿Y si el Sol estuviese cambiando de forma fundamental?
3. Cómo dejar de usar petróleo y seguir consumiendo sus derivados de forma barata

Quizás la mejor manera de describir mi experiencia haciendo matemáticas sea comparándola con entrar en una mansión oscura. Entras en la primera habitación, y está oscura, completamente a oscuras. Vas dando tumbos, tropezando con los muebles. Poco a poco aprendes donde está cada mueble, y finalmente, después de más o menos seis meses, encuentras el interruptor de la luz y lo conectas. De repente todo se ilumina, y puedes ver exactamente dónde estás. Entonces entras en la siguiente habitación oscura…

Andrew Wilesi

Andrew Wiles en 1995. Fuente: Wikimedia Commons.

El matemático británico Andrew Wiles nació el 11 de abril de 1953. En su 65 cumpleaños quería recordarle a través de dos propuestas teatrales, una didáctica y otra musical.

Pero empecemos por el principio. En 1993, Andrew Wiles deslumbró a la comunidad matemática al revelar que había demostrado del Último Teorema de Fermat, el famoso problema matemático enunciado por Pierre de Fermat en 1637. Recordemos que Fermat escribió en el margen de su copia de la Arithmetica de Diofanto, en el problema que trata sobre la división de un cuadrado como suma de dos cuadrados, lo siguiente:

Es imposible dividir un cubo en suma de dos cubos, o un bicuadrado en suma de dos bicuadrados, o en general, cualquier potencia superior a dos en dos potencias del mismo grado; he descubierto una demostración maravillosa de esta afirmación. Pero este margen es demasiado angosto para contenerla.

Durante siglos, nadie consiguió demostrar este enunciado, hasta que en 1993, durante unos cursos de verano en la Universidad de Cambridge, Wiles anunció que la conjetura había pasado a teorema: después de siete años de afanosa entrega, había probado la conjetura de Taniyama-Shimura, de la que se seguía la conjetura de Fermat según un trabajo previo del matemático Kenneth A. Ribet. A finales del verano de 1993, uno de los especialistas que estaban comprobando el documento con la demostración de Wiles encontró un error en una parte del razonamiento. Wiles repasó la demostración con la ayuda de su entonces alumno Richard Taylor, hasta concluir la prueba definitiva en otoño de 1994.

Las dos propuestas escénicas que recuerdo en estas líneas tratan sobre Wiles y la demostración del teorema de Fermat. La primera de ellas, la más reciente, El misterio de Fermat (2017), es una obra de teatro de la compañía Teatre de l’Enjòlit con texto y dirección de Albert Alemany.

Cartel de “El misterio de Fermat”.

La obra persigue acercar las matemáticas al público más joven a través de este misterio que permaneció sin solución durante más de trescientos cincuenta años: en su resolución participaron numerosas mentes brillantes, que solventaron algunos casos particulares y desarrollaron herramientas matemáticas complejas antes de que Andrew Wiles publicara su demostración.

El misterio de Fermat lleva a escena una apasionante historia de descubrimientos, pasiones, errores y logros por medio de escenas cortas y de continuos saltos en el tiempo involucrando veinticinco personajes históricos. Algunos de ellos son Pierre de Fermat (1601-1665) –que no aparece representado por ningún actor, pero es nombrado continuamente, reforzando el misterio al que alude el título de la obra–, Marin Mersenne (1588-1648) –que tuvo una nutrida correspondencia con Fermat–, René Descartes (1596-1650), Blaise Pascal (1623-1662) –que intercambió con Fermat numerosas cartas analizando los juegos de dados, debido a su común interés por la teoría de la probabilidad–, Leonhard Euler (1707-1783) –que demostró el último teorema de Fermat en el caso n=3. Además, gran parte de los primeros trabajos de Euler en teoría de números se basan en estudios de Fermat: probó el pequeño teorema de Fermat, el teorema de Fermat sobre la suma de dos cuadrados y también comprobó la falsedad de algunas de las conjeturas de Fermat–, Sophie Germain (1776-1831) –cuyas importantes aportaciones en teoría de números permitieron avanzar en la prueba del último teorema de Fermat–, Carl Friedrich Gauss (1777-1855), Ernst Kummer (1810-1893) –que probó el último teorema de Fermat para una clase considerable de exponentes primos–, los matemáticos Yutaka Taniyama (1927-1958) y Goro Shimura (1930) –que enunciaron la conjetura de Taniyama-Shimura, un caso especial de la cual fue demostrada en 1995 por Wiles y Richard Taylor (1962), suficiente para demostrar el último teorema de Fermat– y, por supuesto, Andrew Wiles.

El misterio de Fermat pretende entretener, mostrar una parte esencial de la historia de las matemáticas, enseñar algunos conceptos matemáticos sencillos, hablar de la manera en la que ‘se fraguan’ las matemáticas y de la pasión que se siente al recorrer este camino. A través de los personajes que atraviesan la obra, se intenta transmitir el amor por la ciencia, la belleza de las matemáticas, y el valor del esfuerzo y la pasión personalizados en la figura de Andrew Wiles.

La segunda propuesta es el musical Fermat’s last tango (2001) de Joshua Rosenblum y Joanne Sydney Lessner

Cartel de “Fermat’s last tango”.

Este musical –que mezcla estilos variados como rocanrol, jazz o tango– transcurre en la época en que se ha descubierto un error en la demostración del Wiles del teorema de Fermat.

Andrew Wiles está encarnado por un personaje ficticio, el profesor Daniel Keane. La obra comienza con una conferencia de prensa en la que se anuncia la conclusión de la prueba del Teorema de Fermat. Pronto aparece el fantasma de Fermat afirmando que él ya había demostrado su famoso teorema, y mofándose de la complicada demostración de Keane. Como aliados de Fermat para burlarse de Keane aparecen Pitágoras (c. 569 a. C.–c. 475 a. C.), Euclides (ca. 325 a. C.-ca. 265 a. C.), Carl Friedrich Gauss e Isaac Newton (1643-1727), que llegan desde el Aftermath, el lugar en el que viven los matemáticos inmortales. Menosprecian al joven matemático que, en su opinión, usa métodos oscuros y complicados.

Fermat anuncia a Keane que su prueba contiene un error, en una sarcástica canción:

But your proof contains a flaw, Profesor Keane. It destroys the whole fundation of your finely tunned machine. I hate to be a spoilsport. I know it was your Goal. But your proof contains a big fat hole.ii

Keane, aterrado, comprueba que el error efectivamente existe y comienza, ofuscado, a repasar su prueba. Se origina un complicado triángulo entre Anna, la esposa de Keane, que desea que su marido deje de obsesionarse, el propio Keane y Fermat, que sigue burlándose del joven matemático. El resto de la obra es una lucha entre lo viejo y lo nuevo: Fermat desea mantener a toda costa su fama y desanima a Keane en cada uno de sus progresos. En un socarrón concurso en el que se nombra a muchos famosos matemáticos, Fermat y los miembros del Aftermath presionan implacablemente a Keane para que intente encontrar la demostración. Anna, a su vez, sigue intentando que Daniel – que se pasa la vida encerrado en el ático trabajando– reaccione. En un dramático tango –en el que se canta el tema que da título a la obraiii–, el matemático francés y Anna se disputan a Keane como pareja de baile.

Finalmente, los Aftermath se dan cuenta del valor y la dificultad del trabajo de Keane, de la brillantez de los métodos modernos por él utilizados y terminan apoyándole y dándole la bienvenida a su selecto grupo. Tras un arduo trabajo, Keane encuentra finalmente la demostración del teorema, recibiendo la aprobación de su admirado Fermat…

Debajo dejamos el video de una de las representaciones.

Referencias:

• Teatre de l’Enjòlit

• Dossier sobre la obra El misterio de Fermat, Teatre de l’Enjòlit

• Marta Macho Stadler, El misterio de Fermat, Teatre de l’Enjòlit, DivulgaMAT, Teatro y matemáticas, abril 2018

• R. Osserman, Fermat’s Last Tango, Notices of the AMS, vol. 48, núm. 11, 1330-1332, 2001

• Marta Macho Stadler, Fermat’s Last Tango, DivulgaMAT, Teatro y matemáticas, noviembre 2008

Notas:

iExtraída del documental de S. Singh y John Lynch “Fermat’s Last Theorem” Programa Horizon, BBC, 1997. La traducción es de Capi Corrales Rodrigáñez de su “Un paseo por el siglo XX de la mano de Fermat y Picasso”.

ii Minuto 32:20 del video que acompaña a esta entrada.

iiiMinuto 59:45 del video que acompaña a esta entrada.

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.

El artículo Andrew Wiles: de conjetura a teorema se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El teorema de los cuatro colores (y 4): ¿Podemos creer la prueba de la conjetura?
2. El teorema de Marion (Walter)
3. Euler y el último teorema de Fermat

Juanma Gallego Hamabi zulo beltz bitar antzemateko gai izan dira astrofisikariak, estruktura horiek sortzen dituzten X izpien analisiari esker. Ondorioztatu dutenez, gure galaxiaren erdialdetik gertu milaka zulo beltz egon daitezke.

X izpien bidezko astronomiak izugarrizko aurrerapena egin du azken urteetan. Duela lauzpabost hamarkada, diziplina hori martxan jarri zenean, astrofisikariek izugarrizko trikimailuak egin behar zituzten espaziotik datorren argi espektroaren eremu hori behatu ahal izateko. Ikerketa arlo berriaren hastapenetan, batez ere globo estratosferikoak erabiltzen zituzten. Atmosferak (zorionez) X izpiak xurgatzen dituenez, ezinbestekoa da atmosferaren eraginetik kanpo egotea behaketak egin ahal izateko.

1. irudia: Chandra behatokiak eskuratutako datuei esker egin dute aurkikuntza. Irudian, galaxiaren erdialdeko Sagitarius A* eremua. (Argazkia: NASA/Chandra)

Gaiaren inguruan Walter Lewinek For the love of physics liburuan kontatutakoa zeharo argigarria da. Globoak oso garestiak ziren, eta Esne Bidearen erdialdean sortzen ziren X izpien isuriak antzemateko Hego Hemisferiora jo behar zuten -Lewinen kasuan, AEBetatik Australiara-. Globoei jarraipen etengabea egin behar zieten, batzuetan hegazkinez, eta gero lurrean onik berreskuratu behar zituzten. Ahalegin hauek guztiak egin ostean, gainera, batzuetan datuak betiko galtzen ziren.

Satelite artifizialen garapenak teknika izugarri erraztu zuen, eta denborarekin, gainera, X izpien jarraipena egiteko beren-beregi prestatutako behatoki bat martxan jarri zen: Chandra espazio behatokiari esker, X izpien isuriak zehaztasun handiarekin ikertzeko aukera dago orain.

Behatoki horren bitartez eskuratutako datuak erabili dituzte orain aurkikuntza nabarmena egiteko. Ikertzaile talde batek Nature aldizkarian proposatutakoaren arabera, Esne Bidearen erdialdean milaka zulo beltz egon daitezke. Aurkikuntza hori egiteko, X izpien ikerketa funtsezkoa izan da.

Modu teorikoan bada ere, aurretik ere zientzialariek aurreikusia zuten galaxia handien erdian dauden zulo beltz supermasiboen inguruan beste zulo beltz txikiagoak egon behar direla. Hala ere, orain arte ezinezkoa izan da horien antzematea.

Gure galaxiaren kasuan, erdialdeko zulo beltzak Sagittarius A* izena du. Berez, Esne Bidearen erdian kokatuta dagoen irrati iturria da hori, baina zientzialariek uste dute estruktura horren barruan zulo beltz supermasiboa dagoela. Orain, zulo horren inguruan beste hamabi zulo beltz bitar daudela ikusi dute, eta horrek bidea eman die ikertzaileei pentsatzeko 10.000 zulo beltz baino gehiago egon daitezkeela galaxiaren erdialdetik parsec bateko erradio batean (3,3 argi urte inguru).

Berez, zulo beltzek dentsitate infinitua duen puntu batean –singularitate batean, fisikarien esanetan- bilduta dute materia. Singularitate horren inguruan grabitatea hain da handia ezen argia ere ezin baitaiteke atera. Horregatik, inguruan duten materiaren arabera identifikatu ohi dira berez “ikusezinak” diren estruktura horiek. Normalean gasez eta hautsez osatutako diskoak dituzte inguruan biraka, eta materia hori zuloan erortzen den aldiro materia beroa edota erradiazioa ateratzen dira zulo beltzetik.

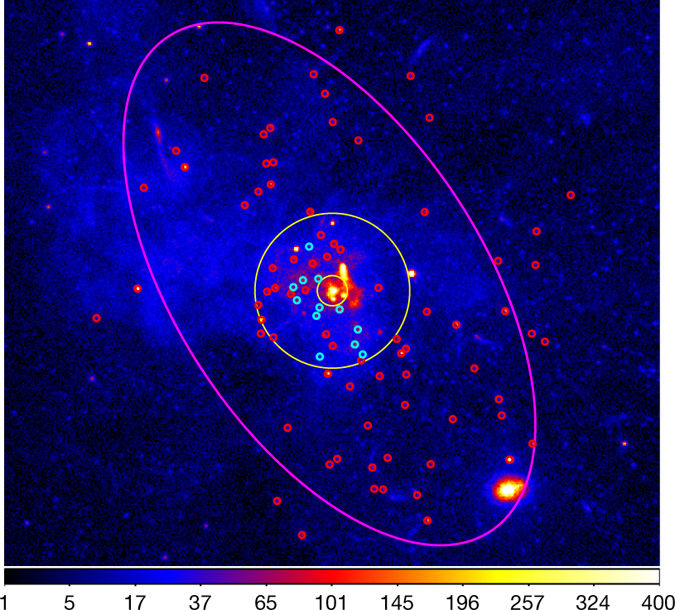
2. irudia: Galaxiaren erdialdea, X izpien bidezko behaketan. Gorriz, iturri termikoak agertzen dira; urdinez, iturri ez-termikoak. Azken hauek zulo beltzei dagozkienak dira. (Argazkia: Nature)

Zulo beltz bitarrak zulo beltz batek eta izar batek osatutako estrukturak dira. Zuloek izarren gasa xurgatzen dute, eta prozesuan izarrek X izpiak isurtzen dituzte. Zulo beltz bitarren eta ohiko zulo beltzen arteko balizko proportzio bat kontuan hartuta, astrofisikariek kalkulatu dute galaxiaren erdialdean egon daitekeen zulo beltzen kopurua.

Hamabi zulo beltz antzematea lortu badute ere, euren banaketa aztertuta 300-500 zulo beltz bitar egon zitezkeela kalkulatu dute. 100 zulotatik 5 zulo bitar direla kalkulatuz gero, orotara 6.000-10.000 zuloko kopurua ateratzen da.

Galaxien osaketari buruz zabalduen dagoen teoria berresteko aukera eman die aurkikuntzak. Teoria horren arabera, gure galaxia sortu zenetik, Sagittarius A* zulo supermasiboaren inguruan dagoen gasezko eta hautsezko haloak izar erraldoi ugari “elikatu” zituen, eta, behin haien erregaia bukatuta, izar horiek zulo beltz bihurtu ziren.

Ikerketaren erronka handienetako bat izan da bereiztea zulo beltzetatik datozen X izpiak eta beste iturrietatik datozenak; kasurako, izar nano zurietatik edo neutroi izarretatik. Kontuan izanda, gainera, galaxiaren erdiko aldea dentsitate handiko eremua dela, eta Lurretik distantzia itzeletara dagoela.

Columbiako Unibertsitateko (AEB) Charles Hailey astrofisikariak gidatu du ikerketa. Hala azaldu du lanaren ekarpena. “Zulo beltz supermasiboak zulo beltz txikiekin nola elkar eragiten duten ikertzeko Esne Bidea baino ez daukagu eskura. Izan ere, beste galaxietan elkarrekintza horiek ikusteko biderik ez dugu. Nolabait esateko, hau da fenomenoa ikertzeko daukagun laborategi bakarra”, azaldu du astrofisikariak ohar batean.

Etorkizunari begira, Haileyk berak aldarrikatu du orain egindako kalkulua baliagarria izan daitekeela urte gutxi barru gero eta modu finagoan garatzea espero den teknika bat hobetzeko: grabitazio uhinen bitartezko astronomia fintzeko, hain zuzen. “Ohiko galaxia batean dauden zulo beltzen kopurua jakinda, errazagoa izango da jakitea zenbat grabitazio uhin lotuta egon daitezke zulo beltzei”.

Erreferentzia bibliografikoa:

Charles J. Hailey et al. A density cusp of quiescent X-ray binaries in the central parsec of the Galaxy. Nature 556, 70–73 (2018). DOI:10.1038/nature25029

———————————————————————————-

Egileaz: Juanma Gallego (@juanmagallego) zientzia kazetaria da.

———————————————————————————-

The post Galaxiaren erdialdean milaka zulo beltz daudela kalkulatu dute appeared first on Zientzia Kaiera.

Carassius auratus

Como vimos aquí, solo los invertebrados marinos y, entre los vertebrados, los peces bruja tienen ancestros exclusivamente marinos. Por esa razón sus medios internos tienen la misma concentración osmótica que el agua de mar –no necesitan regularla- y una composición iónica que no difiere demasiado de la de aquél, aunque esta sí la deben regular. Todos los demás vertebrados tienen en sus linajes ancestros dulceacuícolas. En la actualidad, un buen número de invertebrados viven en aguas dulces, al igual que numerosas especies de peces teleósteos, algunas de peces elasmobranquios y otros vertebrados (anfibios y reptiles, principalmente). Pues bien, todos los animales que viven en aguas dulces regulan la concentración osmótica de su medio interno, manteniéndola muy por encima de la del medio externo. Son, por lo tanto, reguladores hiperosmóticos.

Estos animales han de hacer frente a dos posibles problemas para mantener constante la concentración interna. Por un lado el agua tiende a entrar en sus organismos a favor de gradiente osmótico. Si no consiguiesen contrarrestar fisiológicamente esa tendencia, el organismo se llenaría de agua, el medio interno (plasma y fluido intersticial) en primera instancia y, como consecuencia, el medio intracelular también, lo que provocaría la deformación de las células y, eventualmente, su ruptura. El segundo problema sería la pérdida de los solutos internos a favor de gradiente electroquímico.

Una característica común de los animales de agua dulce es que la concentración osmótica de su medio interno (y, por lo tanto, también intracelular) es muy inferior a la de los animales marinos osmoconformadores (u osomoconcordantes). Así pues, la adaptación a un medio muy diluido conllevó una reducción en la concentración osmótica de su medio interno, de manera que el gradiente que habían de mantener los miembros de los linajes que protagonizaron la transición del mar a los ríos es muy inferior al que habría sido de no haberse producido tal reducción. Ha de entenderse que esa reducción no constituye la respuesta de un individuo a un cambio de salinidad del medio, sino que consistió en un cambio de base genética que requirió de plazos de tiempo muy prolongados. Para que nos hagamos una idea de la magnitud de la reducción, sirvan los siguientes valores de osmolaridad (mOsm) del medio interno de diferentes géneros:

Dulceacuícolas (concentración osmótica del agua dulce: 0,5-10): Spongilla (Porifera): 55; Chlorohydra (Cnidaria): 45; Asplachna (Rotifera): 81; Anodonta (Mollusca): 66; Viviparus (Mollusca): 80; Hirudo (Annelida): 200; Astacus (Arthropoda, Crustacea): 477; Potamotrygon (Chordata, Chondrichthyes): 308; Carassius (Chordata, Actinopterygii): 392; Rana (Chordata, Amphibia): 234.

Marinas (concentración osmótica del agua de mar: 1000): Aurelia (Cnidaria): 1050; Asterias (Echinodermata): 1015; Loligo (Mollusca): 1003; Arenicola (Annelida): 1020; Homarus (Arthropoda, Crustacea): 1035; Myxine (Chordata, Cyclostomi): 1152; Squalus (Chordata, Chondrichthyes): 1000; Latimeria (Chordata, Sarcopterygii): 954; Opsanus (Chordata; Actinopterygii): 392; Fejervarya (Chordata, Amphibia): 830.

Pero incluso habiendo reducido considerablemente el gradiente de concentraciones osmóticas entre el medio interno y el externo, sigue habiendo una fuerte tendencia del agua a entrar en el organismo y de las sales a salir. Por esa razón, el tegumento de estos animales suele ser poco permeable, aunque el grado de permeabilidad es muy diferente en unos grupos y en otros. Esa baja permeabilidad del tegumento es considerada la primera barrera frente a la dilución.

La baja permeabilidad general del tegumento, no obstante, no evita los movimientos de agua y de sales. Hay epitelios que no se pueden impermeabilizar. Las superficies respiratorias son el enclave que mejor ilustra esa imposibilidad. Un epitelio impermeable no permitiría el intercambio de gases. Y con el digestivo pasa algo parecido; no obstante, hay que decir que los reguladores hiperosmóticos evitan beber, por lo que el agua que pueda introducirse a través de los epitelios digestivos es solo la que se incorpora con el alimento. Por las razones dadas, los animales de agua dulce han de contar con mecanismos que contrarresten esos flujos pasivos. Y aquí entra en juego la segunda barrera frente a la dilución, que se explica a continuación.

Rana clamitans

Evitan la invasión de agua produciendo grandes volúmenes de orina. El cangrejo de río Astacus fluviatilis elimina un 8% de su masa corporal en forma de orina; en el anfibio Rana clamitans y el pez Carassius auratus ese porcentaje es del 33%, en el sapo Xenopus laevis es del 58% y en el caracol dulceacuícola Viviparus viviparus, puede variar entre el 36% y el 131%. Esa tarea corre a cargo del órgano excretor.

Y además de eliminar una gran cantidad de agua en forma de orina, los animales de agua dulce deben reducir en la medida de lo posible la concentración de sales en la orina. La concentración osmótica de la orina representa, con respecto a la del medio interno, un 20% en Viviparus, un 16% en Xenopus, un 14% en Carassius y un 10% en Astacus. De no proceder de ese modo, la orina tendría la misma concentración osmótica que el medio interno (sería isosmótica) por lo que el trasiego constante de agua dulce hacia el interior y su eliminación como orina isosmótica con el medio interno, provocaría una fuerte pérdida de sales. Sería como si se produjese un lavado permanente del medio interno, lo que anularía la posibilidad de mantener una concentración osmótica constante y diferente de la del medio externo. El órgano excretor debe hacer, por lo tanto, una doble tarea, producir orina abundante, por un lado, y por el otro reabsorber la mayor cantidad posible de iones de esa orina antes de su evacuación. Ese trabajo, no obstante, requiere gastar energía, pues los iones que se reabsorben han de transportarse gastando ATP en el proceso. Nada es gratis.

Pues bien, para los reguladores hiperosmóticos no es suficiente con producir orina abundante y diluida. Porque por baja que sea su concentración osmótica, nunca lo es tanto como el medio externo. Así pues, la eliminación del agua que entra a favor de gradiente osmótico siempre conlleva una cierta pérdida de sales. Parte de las sales que se pierden pueden recuperarse a través del sistema digestivo, porque se absorben junto con el alimento. Y la otra parte ha de incorporarse a través de otras vías extrarrenales, como son la piel en anfibios, la vejiga urinaria en tortugas o las branquias en peces y crustáceos. La incorporación extrarrenal de sales es la tercera barrera frente a la dilución. Los enclaves en los que tiene lugar pueden ser diferentes dependiendo de la especie, pero los mecanismos básicos son similares, ya que conllevan el transporte activo de las sales que tienden a perderse -Na+ y Cl– en mayor medida- y, por lo tanto, de nuevo con importante gasto de energía en forma de ATP.

Así pues, un buen número de grupos animales se han adaptado a vivir en aguas dulces. Esa adaptación ha conllevado una reducción importante en la concentración osmótica del medio interno, un alto grado de impermeabilización de los tegumentos, la producción de altos volúmenes de orina de la que se recupera la mayor cantidad de sales posible, y la incorporación extrarrenal de las sales necesarias para mantener constante su concentración en el medio interno. Para estos procesos se requieren dispositivos tales como eficaces órganos excretores, así como transportadores de sales en determinados enclaves. La osmorregulación conlleva un importante coste de energía, porque transportar iones contra gradiente electroquímico es caro. Pero está claro que ese coste es compensados por las ventajas que comporta ocupar los nichos que ofrecen las aguas dulces. De otra forma no habría habido linajes que, desde los océanos, “se aventurasen” a colonizar esos nuevos medios.

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo La regulación osmótica de los animales de agua dulce se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Animales en equilibrio osmótico: invertebrados marinos y peces bruja
2. Relaciones hídricas y salinas de los animales
3. La distribución del agua animal y el curioso caso del potasio

Nanoteknologia gazteei hurbiltzea da nanoKOMIK egitasmoaren helburura. NanoKOMIK bi erakunderen eskutik sortzen da, CIC nanoGUNE eta Donostia International Phyiscis Center (DIPC), Zientzia eta Teknologiarako Espainiako Fundazioaren (FECYT) laguntzarekin. NanoKOMIK nanozientzia eta nanoteknologia alorrean ematen diren aurrerapenak ezagutarazteko tresna da, nanofikziozko komiki partehartzaile baten bidez.

2017an egitasmoaren bigarren edizioa gauzatu izan da eta bertan 240 partaidek nanobotereen mundura jauzia eman dute hainbat pertsonai aurkeztuz. Emaitzaren zati bat Nanokomik#2 komikian plazaratu da, non 2017ko helduen kategoriako erronkaren irabazleekin elkarlanean sortutako hiru komiki istorio berri jasotzen diren. Komikia euskaraz, gaztelaniaz, frantsesez eta ingelesez eskura daiteke www.nanokomik.com webgunean.

Irudia: NanoKOMIK#2 komikiaren azala.

Dibulgazio-komikiek erronkara aurkeztutako ideiarik originalenak bilduz, Aśka, Rubén Molina eta Jöse Sénder marrazkilariek, Amaia Arregi (DIPC) eta Itziar Otegui (nanoGUNE) proiektuaren koordinatzaileek eta komikietako egileek istorioak borobildu dituzte hiru hari berri sortuz: Munduaren domi(nano)zioa, Sugarra eta Landare Artean. Komikian zenbait pertsonaiaren gorabeherak kontatzen dira: politikari ustel bati nonahi aldi berean egoteko boterea ematen dion neuro-nano-zientzialariarena, zapuztear dagoen misio espazial bat salbatu nahi duen pertsona anonimoarena eta landareen fotosintesi-prozesua artifizialki erreproduzitzeko nanohibridoekin lanean ari den zientzialariarena.

Obra osoa creative commons lizentziapean eskura daiteke, euskaraz, gaztelaniaz, frantsesez eta ingelesez, paperean zein formatu digitalean www.nanokomik.com webgunean.

The post Nanokomik#2, nanofikziozko komiki partehartzailea appeared first on Zientzia Kaiera.

Titulares de The New York Times del 10 de noviembre de 1919 (izquierda) e infografía del Illustrated London News del 22 de noviembre de 1919 (derecha), que recogen el resultado de Eddington.

Sin duda la predicción que hizo famosa la teoría general de la relatividad y cuya comprobación lanzó al estrellato a la teoría y, con ella, a Einstein fue que el espaciotiempo se curva. La famosa medición de la “desviación de la luz” en las proximidades de un objeto masivo como el Sol por parte de Arthur Eddington en forma de cambio de la posición aparente de una estrella ocupó las portadas de la prensa mundial en 1919. Sn embargo, el concepto de que la luz se “desvía” es erróneo, porque asume un espacio absoluto, newtoniano. Para comprender la magnitud de la predicción de Einstein y el mérito del experimento de eddington, tendremos que hacer un poco de historia.

Ya en otra parte hemos explicado que la predicción de que la luz sufre una desviación al pasar cerca de un objeto masivo está presente en la mecánica newtoniana. Tanto es así que tanto Henry Cavendish en 1784 (en un manuscrito que, fiel a su costumbre, no publicó) como Johan Georg von Soldner [1] realizaron cálculos de la magnitud de esa desviación. El manuscrito de von Soldner, titulado “Sobre la desviación de un rayo de luz de su movimiento rectilíneo por la atracción de un cuerpo celeste del que pasa cerca”, escrito en 1801 y publicado en 1804, contenía los resultados de éste.

En 1911 Einstein publicaba el artículo “Sobre la influencia de la gravedad en la propagación de la luz” [2], ampliación de uno de 1908, en el que obtenía, atención, los valores de von Soldner pero, eso sí, basándose únicamente en el principio de equivalencia. Tal era la coincidencia numérica que Philipp Lénárd tuvo base para acusar después a Einstein de plagio.

Avanzada la teoría general de la relatividad, Einstein se dio cuenta de algunos errores, y corrigió sus cálculos en 1915 obteniendo los datos (la suma de los efectos clásicos y de la dilatación temporal gravitacional) que después Eddington daría por confirmados en 1919.

Diferencias de modelo

Sin embargo, lo importante es la diferencia de modelo. Mientras que Cavendish y Soldner asumen que la luz es una partícula con masa y, por tanto, debe ser atraída por el Sol según la ley gravitatoria de Newton, lo que Einstein afirma es que el espaciotiempo se curva por la presencia de la masa del Sol y que la luz, que viaja en “línea recta”, nos “da la impresión” de que se desvía. Pero hemos de ser conscientes de lo que línea “recta” significa en un espaciotiempo: si el espaciotiempo se curva, la luz se curva.

Quizás un ejemplo de algo aparentemente no relacionado pero que es fácil que hayamos visto alguna vez nos puede servir para aprehender lo que decía Einstein. Está relacionado con los conceptos de campo, en concreto con el de campo magnético. Gilbert describió la acción de la piedra imán diciendo que tenía una “esfera de influencia” alrededor de ella. Con esto quería decir que cualquier otro objeto magnético que entrase en esta “esfera” sería atraído por la piedra imán. Además, la intensidad de la fuerza atractiva sería mayor cuanto más cercano estuviese del imán. En términos actuales diríamos que la piedra imán está rodeada por un campo magnético.

Experimentalmente podemos visualizar fácilmente un campo magnético o, más precisamente, la parte del mismo que intersecta el plano de un papel, colocando debajo de éste un imán (idealmente con una forma regular) y esparciendo limaduras de hierro alrededor, como en la imagen que sigue:

El campo magnético se suele representar en forma de líneas que representan la fuerza y dirección del campo, como en esta otra imagen:

Así es como solemos pensar cuando hablamos de campos, a saber, como líneas de fuerza que existen en el espacio y en el tiempo.

Tengamos en mente que las imágenes anteriores corresponden a un campo magnético en dos dimensiones (la parte del campo que intersecta el plano del papel) porque asumimos que vivimos en un espacio absoluto de 3 dimensiones. Una región del espaciotiempo (que, recordemos, tiene cuatro dimensiones) donde existe un objeto masivo, podemos representarla con una dimensión menos para poder visualizarla de la siguiente forma (asumiendo la perspectiva como una dimensión) según la teoría general de la relatividad:

Las líneas nos pueden parecer las de un campo como las del campo magnético, pero hay una diferencia crucial: estas líneas no representa un campo en el espacio y en el tiempo, estas líneas representan el espaciotiempo mismo y su curvatura. De hecho lo que ves en la imagen es, estrictamente hablando (descartando la perspectiva), bidimensional y representa un “corte” del espaciotiempo cuatridimensional.

Por tanto, en un diagrama de este tipo si un objeto, o la luz, viaja por el espaciotiempo en una región en la que hay un objeto masivo, el camino más corto entre dos puntos será una línea curva. En geometría diferencial estas líneas se llaman geodésicas y no son más que la generalización del concepto de línea recta a espacios curvos.

La observación de Eddington

Decíamos más arriba que tanto la vieja teoría de la gravedad de Newton como la nueva de Einstein predecían que la luz no viaja necesariamente en líneas rectas, sino que puede ser desviada cuando pasa cerca de algo tan pesado como el Sol. Sin embargo Einstein predecía que la desviación aparente sería mayor: lo suficiente como para que las posiciones aparentes de las estrellas detrás del Sol se desplazasen de forma detectable con respecto a las posiciones conocidas y verdaderas.

Un eclipse solar total ocurre cada par de años, pero son solamente visibles desde las regiones ecuatoriales. El eclipse solar del 29 de mayo de 1919 tendría lugar por suerte frente a una brillante constelación de estrellas y daba la oportunidad perfecta para comprobar experimentalmente la nueva teoría Einstein.

Desde Oxford, Arthur Eddington observó cuidadosamente la posición de las estrellas en enero y febrero de 1919. El eclipse sería visible desde ambos lados del Atlántico por lo que, para asegurarse buen tiempo en al menos en un punto de observación, Frank Dyson, el Astrónomo Real, mandó un equipo de observación a Sobral (Brasil) y a Eddington a Príncipe (São Tomé e Príncipe). Los cielos estuvieron despejados en ambas localizaciones y, durante cinco minutos en total, ambos equipos se las arreglaron para tomar varía fotografías nítidas de las estrellas.

Cuando Eddington volvió a casa y comparó las posiciones aparentes de las estrellas detrás del Sol con las reales, ambos conjuntos de datos eran consistentes con la teoría de Einstein. El descubrimiento fue publicado oficialmente en Philosophical Transactions of the Royal Society [3]. Para entonces Einstein ya era una celebridad mundial.

Notas:

[1] J. G. von Soldner (1804) “Über die Ablenkung eines Lichtstrals von seiner geradlinigen Bewegung, durch die Attraktion eines Weltkörpers, an welchem er nahe vorbei geht”, Berliner Astronomisches Jahrbuch, pp. 161-172

[2] A. Einstein (1911) “Einfluss der Schwerkraft auf die Ausbreitung des Lichtes”, Annalen der Physik 35: 898–908.

[3] Dyson, F., Eddington, A., & Davidson, C. (1920). A Determination of the Deflection of Light by the Sun’s Gravitational Field, from Observations Made at the Total Eclipse of May 29, 1919 Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character (1896-1934), 220 (1), 291-333 DOI: 10.1098/rsta.1920.0009

El atento lector se habrá fijado que en el título de este artículo de Eddington et al. se habla de “gravitational field” un concepto que aún es newtoniano, como no puede ser de otra manera ya que esa es la teoría (paradigma, diría alguno) imperante en ese momento.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo Comprobaciones experimentales de la relatividad general (y 2) se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Comprobaciones experimentales de la relatividad general (1)
2. Las ecuaciones de campo de la relatividad general
3. El principio de relatividad (y 4): la versión de Einstein

Josu Lopez-Gazpio Urtero bezala, gaurko egunez Homeopatiaren Eguna ospatzen dute homeopatia zaleek, Samuel Hahnemannen jaiotzaren 263. urteurrenean. Hahnemann kimikari eta mediku alemaniarra izan zen, hain zuzen ere, homeopatiaren asmatzailea. Aurten, gainera, ospakizuna egun aproposa da homeopatiari buruzko azken datuak eta berriak eguneratzeko; izan ere, CIS Espainiako Ikerketa Soziologikoen Zentroak otsaileko barometroan osasunari eta terapiei eskaini zien galdera-sorta bat eta horrek homeopatia zaleak aztoratu ditu.

CISen datuen arabera, homeopatiaren salmentak ere beherantz doaz eta, oro har, geroz eta argiago dago kontsumitzaileak homeopatian zuten fedea galtzen ari direla. Homeopatia diluitzen ari da, bai, baina oraindik badago lanik egiteko.

1. irudia: Apirilaren 10ean Homeopatiaren Eguna ospatzen dute homeopatiaren jarraitzaileek. (Argazkia: Bru-nO – domeinu publikoko irudia. Iturria: pixabay.com)

Homeopatia zertan den

Esan bezala, homeopatia Hahnemannek sortu zuen 1810ean eta bere ateraldietan oinarritzen da bakarrik. Besterik ez. Ez dago beste azalpenik homeopatiaren oinarriak azaltzen saiatzeko. Gainera, arau horiek Kimikaren, Fisikaren, Biologiaren eta Medikuntzaren oinarrizko printzipioak urratzen eta ukatzen dituzte. Alde batetik, antzekotasunaren legean oinarritzen da –similia similibus curantur delakoa- eta horren arabera, antzekoak antzekoa sendatzen du. Homeopaten ustez, substantzia toxiko batek pertsona osasuntsu bati eragiten dizkion sintomak substantzia horrekin berarekin senda daitezke. Bestetik, homeopatiaren gakoa dosi minimoen legea da. Lege horren arabera, sendagaiaren efektua bere kontzentrazioarekiko alderantziz proportzionala da, hau da, sendagai bat dosi txikiagoan hartzen bada, haren sendatzeko ahalmena handiagoa da. Bi printzipio xelebre horiek asmatu ondoren, eta bestelako inolako oinarririk gabe, Hahnemanek Organon der Rationellen Heilkunde liburua argitaratu zuen bere sinesmena fedea bailitzan zabaltzeko. Nolanahi ere, eta aski frogatuta dagoen moduan, homeopatia ez da plazebo efektua baino eraginkorragoa.

Ikerketa sakonak eta zorrotzak egin diren kasu guztietan frogatu da hori eta, hortaz, ondorioa ez da berria zientzia-komunitatean. Hainbat berrikuspen sakonek frogatu dute homeopatia ez dela eraginkorra aztertutako gaixotasun guztietan. Zientziaren arabera, eta orain arte ezagutzen denaren arabera, bi sendagai homeopatiko mota daude bakarrik: eraginkortasuna frogatu ez dutenak eta eraginkortasunik ez dutela frogatu dutenak. Nola liteke orduan homeopatia diotena bezain arrakastatsua izatea?

2. irudia: Pilula homeopatikoek ez dute printzipio aktiborik. (Argazkia: detcos – domeinu publikoko irudia. Iturria: pixabay.com)

Puztutako datuak

2011n esaten zenaren arabera, 10 milioi espainiarrek baino gehiagok erabiltzen zuten homeopatia. Alabaina, 2017ko datuen arabera, 2 milioira jaitsi da homeopatia kontsumitzen dutenen kopurua. Jaitsiera nabarmena da, baina, baliteke duela 7 urteko datuak adierazgarriak ez izatea. Homeopatia zaleek askotan errepikatu izan dute 15.000 farmazietan saltzen dela, 10.000 mediku homeopata daudela, 15 milioi pertsonek kontsumitzen dutela eta kontsumitzaileen %82 pozik gelditzen dela homeopatia erabili ondoren. Hala ere, duela gutxi El Mundo-k jakinarazi duenez, datu horiek ez dira egokiak edo iturriak ez daude kontrastatuta, datu horiek lortzeko erabilitako laginak ez direlako adierazgarriak. Adibide modura aipatzen da 2011n homeopatiaren inguruko industriak egindako txostenean espainiarren %27k homeopatia maiz erabiltzen zuela esaten zen. 2014rako kopuru hori %18,3ra jaitsi zen, baina, orain CISen inkestaren arabera -interes sektorialik gabea- %5ak besterik ez du erabiltzen -sektoreko industriaren txostenak esaten zuena baino %70 gutxiago-. Aipatzekoa da, bestalde, CISen azken barometroaren arabera Espainiako populazioaren %51k badakiela homeopatiaren oinarria zein den, baina, sasi-zientzia guztien artean okerren baloratzen dena dela. Hain zuzen ere, homeopatia erabili dutenen artean 6,86 puntuko asebetetze maila lortzen du -akupunturak 7,03 eta terapia ayurvedikoek 8,89, esaterako-. Hortaz, sasi-zientzien artean ere homeopatiak ez du famarik onena.

Homeopatiaren arloko hiru enpresa nagusienen fakturazio datuak ere asko murriztu dira. 2014tik 2016ra 53 milioi euro fakturatzetik 43 milioi fakturatzera pasa dira. 15.000 farmaziak homeopatia saltzen dutela ez da datu fidagarria eta inork ez daki nola kalkulatu den. 10.000 mediku homeopata daudela errepikatzen dute homeopatia zaleek, baina, kopuru horren jatorria ere ez da ezagutzen. Ez dago iturri fidagarririk edo kontrastaturik hainbestetan errepikatzen diren mantra horien jatorria argitzeko. Horixe izan da homeopatiak oso ondo ezkutatu duen sekretua: datuak puztuz fidagarria eta arrakastatsua dela sinestaraztea.

Informazio osagarria:

• Homeopatiaren astea (I): zer da homeopatia? J. Lopez-Gazpio, guaixe.eus, 2016
• Homeopatiaren astea (II): homeopatiaren eraginkortasuna. J. Lopez-Gazpio, anboto.org, 2016
• Homeopatiaren astea (III): homeopatiaren aldeko argudioen gainbehera. J. Lopez-Gazpio, alea.eus, 2016
• Homeopatiaren astea (eta IV): eztabaida homeopatikoa. J. Lopez-Gazpio, ataria.eus, 2016
• Homeopatia bai ala ez? J. Lopez-Gazpiori elkarrizketa, Norteko Ferrokarrila, 2016
• Homeopatia: uraren memoria txarra. J. Lopez-Gazpio eta J.J. Iruin, Elhuyar Aldizkaria, 2016
• El 30% de las personas que usan homeopatía lo hace semanalmente, elplural.com, 2018
• La otra gran mentira de la homeopatía, elmundo.es, 2018
• Barómetro de febrero 2018, Centro de Investigaciones Sociológicas, 2018

—————————————————–
Egileaz: Josu Lopez-Gazpio (@Josu_lg) Kimikan doktorea eta zientzia dibulgatzailea da. Tolosaldeko Atarian Zientziaren Talaia atalean idazten du eta UEUko Kimika sailburua da.
—————————————————–

The post Homeopatiak alfonbra azpian ezkutatzen zuena appeared first on Zientzia Kaiera.

Acercar la nanotecnología en un formato atractivo para los jóvenes es el objetivo del proyecto nanoKOMIK, desarrollado por los centros de investigación CIC nanoGUNE y Donostia International Phyisics Center (DIPC) y que ha contado con la ayuda de Fundación Española para la Ciencia y la Tecnología (FECYT). NanoKOMIK es una herramienta para dar a conocer los avances que se dan en el campo de la nanociencia y la nanotecnología, a través de un cómic participativo de nanoficción.

En 2017 se ha llevado a cabo la segunda edición del proyecto. En esta segunda edición han participado 240 personas que se han adentrado en el mundo de los nanopoderes de personajes diversos. Parte de los resultados de esta edición se han publicado en el cómic Nanokomik#2, donde se recogen tres historietas en las que han participado los ganadores de la categoría adulta del desafío nanoKOMIK 2017. El cómic está disponible en euskera, castellano, francés e inglés en la página: www.nanokomik.com.

Imagen: Portada del cómic NanoKOMIK#2.

Tomando como referencia las mejores ideas de los cómics presentados al desafío y en colaboración con los ganadores de la categoría adulta, se ha dado forma a las nuevas historietas: Domi(nano)ción del mundo, Míster Llamas y Entre Plantas. En estas divertidas historias se cuentan las aventuras de una ingeniosa neuro-nano-científica que otorga el poder de la ubicuidad a una política corrupta, de un amante de los viajes espaciales que salva una misión a punto de estallar y del científico inmerso en la creación de un nanohíbrido capaz de reproducir el proceso fotosintético de las plantas de manera artificial.

Las historietas del cómic divulgativo recogen las ideas más originales presentadas al desafío. En la recreación han participado los dibujantes Aśka, Rubén Molina y Jöse Sénder, y las coordinadoras del proyecto Amaia Arregi (DIPC) e Itziar Otegui (nanoGUNE). La obra completa está disponible bajo licencia creative commons en euskera, castellano, francés e inglés, tanto en papel como en su versión digital en la web www.nanokomik.com.

El artículo Nanokomik#2, cómic participativo de nanoficción se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Naukas Bilbao 2017 – Mónica Lalanda: Una muerte de cómic
2. Las matemáticas en el cómic Ken Games
3. Un cómic de hace dos mil años a todo color

Historian zehar zibilizazioek astroak begiratzeari eta ikertzeari ekin diote. Gizakia zeruko hainbat gertaeraz ohartu izan da: eguzki eta ilargi eklipseak, besteak beste. Teleskopioak baliatu izan dira horretarako.

1590an asmatu zuen teleskopioa Hans Lippershey-k. Hemeretzi urte geroago, 1609an, Galileo Galileik lehenengo teleskopio astronomikoa egin zuen eta horri esker lau satelite behatu zituen Jupiterren inguruan:

1. Kalisto
2. Ganimede
3. Europa
4. Io

XVII. mendearen hasieratik, teleskopioa gizakiari unibertsoa ekarri dion tresna izan da. “Teleskopioak” bideoan Mikel Ramirezek teleskopioaren funtzionamendua laburki azaltzen digu , On Zientzia lehiaketaren VI. edizioan euskarazko irabazlea izan zena.

—–—–

Elhuyar Fundazioak eta Donostia International Physics Center-ek (DIPC) zientzia eta teknologiaren dibulgaziorako lehiaketa da On Zientzia, jakintza zientifikoa ezagutzera emango duten bideo labur eta originalen ekoizpena bultzatzeko helburuarekin.

Lehiaketaren oinarriek ezarri bezala, bideoek 5 minutu baino gutxiago iraun behar dute eta euskaraz, gaztelaniaz edo ingelesez izan daitezke, gaia librea delarik. Edukiak jatorrizkoak izan behar dira, telebistan inoiz atera ez direnak, eta beste lehiaketaren bat irabazi ez dutenak.

Hiru sari kategoria ditu On Zientzia lehiaketak:

• Gazte saria (18 urtetik beherakoentzat). 1000 €
• Euskarazko bideo onena. 2000 €
• Dibulgazio bideorik onena. 3000 €

2017-2018koa VIII. edizioa da eta parte hartzeko epea zabalik dago jada 2018ko apirilaren 25era arte.

The post On Zientzia: Teleskopioak appeared first on Zientzia Kaiera.

Un inuit (o esquimal) otea el horizonte en busca de ballenas. Fotograma de la película “Arctic Currents. A year in the life of the bowhead whale” del Museo del Norte de la Universidad de Alaska.

Arqueólogos y antropólogos no tienen muy claro en qué momento el ser humano desarrolló la tecnología necesaria para cazar ballenas, pero en general está aceptado que en el Ártico esta actividad comenzó en las costas de Canadá entre el año 600 y el 800. Durante miles de años antes los pobladores del Ártico sobrevivieron cazando focas, caribús y morsas en las orillas del mar helado.

Cuenta Krista Langois en este reportaje de la revista Hakai, que uno de esos grupos, conocidos como los Dorset, o los Tunit en la tradición oral Inuit, son legendarios por el gran tamaño y la fuerza de sus miembros, a los que se consideraban gigantes, además de estar perfectamente adaptados a su entorno. Pero a pesar de sus míticas capacidades de supervivencia, los Tunit desaparecieron hace unos mil años.

Esquimales arponeando una ballena en 1939. Wikimedia Commons

Una teoría sobre su desaparición es que apareció otro grupo de población, los Inuit (que nosotros llamamos esquimales), proveniente de Alaska, que supo adaptarse mejor que ellos y que creó tecnología conveniente y eficaz, comiéndoles el terreno. Parte de esa tecnología pudieron ser sus barcas hechas con piel de foca, que les permitieron alejarse de la costa mar adentro para cazar ballenas: cada primavera, ballenas boreales de más de 54.000 kilos se adentraban en ese mar de hielo y los nuevos pobladores conseguían cazar alguna con habilidad, talento, y mucha suerte.

Las ballenas articulan la vida social

Cazar ballenas cambió para siempre el modo de vida en el Ártico. Por primera vez, era posible conseguir carne de una sola vez suficiente alimento para dar de comer a un pueblo entero, así que empezaron a surgir asentamientos permanentes aquellos lugares a los que las ballenas volvían con regularidad. Con ello evolucionaron también las organizaciones sociales: los cazadores de éxito hicieron fortuna y se situaron en la cima de las nuevas jerarquías. Muy pronto la caza de ballenas se convirtió en el centro de la vida cotidiana pero también de la vida cultural y espiritual.

Familia esquimal en torno a 1900. Wikipedia Commons

Una vida que fascinaba a los europeos. En la literatura medieval se representaba el Ártico como una tierra de peces monstruosos y personas que podían convocarlos en la costa utilizando magia y murmurando hechizos. Incluso cuando siglos después los primeros exploradores volvieron contando en qué consistía realmente la caza, despiece y cocinado de una ballena, nada muy diferente de cazar un esturión excepto por la escala del animal, el misticismo seguía presente. En 1938, la antropóloga Margaret Lantis describió a los Inuit y otros pueblos emparentados, como los Inupiat, como parte de un “culto a las ballenas”.

Lantis se basaba en tabús muy extendidos y en rituales diseñados para fortalecer la relación entre los humanos y las ballenas: en muchos sitios, a una ballena recién cazada se le dejaba agua fresca, comida e incluso bolsas de viaje para asegurarle una vuelta segura al hogar de su espíritu. Cada cazador tenía su propia canción para atraer a las ballenas hacia él, los chamanes realizaban ceremonias en el interior de círculos hechos con huesos de ballena y amuletos hechos con reliquias de ballena pasaban de padres a hijos dentro de las familias de cazadores.

Para cualquier observador externo, todo resultaba misterioso y desconocido, especialmente para arqueólogos y biólogos, para los que toda esta actitud chocaba frontalmente con los valores científicos occidentales, que evitaban cualquier aspecto que se acercase al antropomorfismo, es decir, a dar a los animales cualidades y emociones humanas.

Un sonajero esquimal con forma de ballena fabricado en torno a 1900. Wikimedia Commons

Unos valores que, según cuenta Erica Hill, zooaequeóloga de la Universidad del Sudeste de Alaska, en el mencionado reportaje de la revista Hakai, han limitado el conocimiento que los arqueólogos tienen hoy de la prehistoria en el Ártico: los amuletos y esos círculos de huesos se han descrito como parte de un ritual sin explorar o explicar apenas qué querían decir en realidad para las personas que los hicieron. En vez de eso, los científicos que los han estudiado se han centrado en la información tangible que ofrecían: qué comían esas personas, cuántas calorías consumían y cómo sobrevivían.

¿Puede ser útil mirar a las ballenas como las miraban los inuit?

Ahora, un grupo creciente de arqueólogos están utilizando información etnográfica e historias orales para reexaminar esos artefactos bajo una luz nueva y reinterpretarlos de un modo menos occidental para conocer algo más sobre la historia de sus antepasados.

Pero hay otro motivo por el que este enfoque arqueológico puede ser interesante: porque permite acometer desde otro punto de vista, y por tanto completar, las investigaciones que tratan de determinar si algunos animales, entre ellos los cetáceos, tienen sistemas comunicativos que se acercan en complejidad al de los humanos. Algunas de esas investigaciones están ayudando a confirmar algunos de esos rasgos y habilidades que los habitantes del Ártico atribuían a las ballenas hace más de mil años.

Uno de esos biólogos es Hal Whitehead, profesor de la Universidad Dalhousie de Nueva Escocia, y él argumenta que los cetáceos tienen su propia cultura, algo que siempre ha quedado reservado para las sociedades humanas.

Según su definición, una cultura es un conocimiento social que va pasando de una generación a la siguiente. Bien, pues algo así ha sido señalado en varios estudios recientes, incluido uno que las ballenas boreales que viven en el Norte del Pacífico, cerca de la costa de Alaska, y las que viven en el Atlántico, cerca de Groenlandia, cantan canciones diferentes igual que los humanos hablamos distintos idiomas o tenemos distintos estilos musicales. Igualmente, manadas de orcas que habitan al sur de la isla de Vancouver, y otras que viven hacia el norte de la misma isla, se saludan entre sí mostrando comportamientos diferentes, a pesar de que genéticamente son grupos casi idénticos y viven en territorios que se solapan.

Además, sabemos que las crías pasan años con sus madres, desarrollando fuertes relaciones materno-filiales que sirven precisamente para la transmisión de esa información cultural, y que las ballenas boreales viven suficiente tiempo como para acumular una información y conocimiento que merece la pena transmitir a las generaciones siguientes.

Por otro lado, otros mitos están demostrando ser menos fantasiosos de lo que una vez parecieron. Durante años, los biólogos pensaron que las ballenas no poseían sentido del olfato, a pesar de que los cazadores Inupiat aseguraban que el olor del humo las ahuyentaba, hasta que en 2010 el científico Hans Thewissen descubrió el sistema olfativo perfectamente funcional al analizar el cráneo y cerebro de varias ballenas. También la vieja creencia de los Yupik de que las beluga una vez caminaron por la tierra ha resultado ser cierta: hace 50 millones de años, un ancestro de las ballenas modernas caminó por la tierra, y por eso los fetos de ballena desarrollan patas durante un breve periodo de tiempo antes de perderlas de nuevo.

Imitar sonidos no es hablar… pero ¿nos acerca un paso?

Nada de todo esto quiere decir que las ballenas conversasen con los cazadores o que se entregasen a ellos cuando eran convocadas. Pero sí que es verdad que una vez que terminemos de descubrir en qué consiste el complejo sistema cultural de las ballenas y cómo lo utilizan, será más fácil entender sus señales y aprender hasta qué punto sería posible una comunicación entre especies.

Estamos aún lejos de esa comunicación, pero algunos estudios recientes permiten vislumbrar de qué estamos hablando. Por ejemplo, el caso de Wikie, una orca que vive en el acuario Marineland en Antibes, Francia, y que demostró cómo estos animales son capaces de imitar el habla humana cuando aprendió a decir con su chirriante voz las palabras “hello”, “goodbye”, “one”, “two”, “three” y “Amy”, el nombre de su entrenadora. Las grabaciones de audio demuestran que sin un aparato fonador como el nuestro algunos sonidos no son sencillos, pero que sin duda Wikie era capaz de imitar y repetir dichas palabras. Como curiosidad, Wikie no solo aprendió a imitar palabras, también otros sonidos poco familiares para las orcas, como una pedorreta.

Este avance sirve para entender mejor cómo unos grupos de ballenas se comunican con canciones diferentes a las de otros grupos: el origen estaría precisamente en sus habilidades de imitación, que habrían ido causando poco a poco que cada grupo evolucione su habla en direcciones diferentes. Otro ejemplo de esa cultura de los cetáceos que nos fascina a todos, científicos o no, y que quizá podamos entender mejor si tomamos nota de lo que sabían aquellos primeros hombres que susurraban a las ballenas.

Referencias:

When men and whales talk – Krista Langlois. Hakai Magazine.

Cultura Dorset – Wikipedia.

Alaskan Eskimo Ceremonialism – Margaret Lantis. Univerisdad de Michigan.

Cultural lifes of whales and dolphins – Hal Whitehead y Luke Rendell.

Olfaction and brain size in the bowhead whale (Balaena mysticetus) – J. G. M. Thewissen, John George, Cheryl Rosa, Takushi Kishida. Marine Mammal Science.

Imitation of novel conspecific and human speech sounds in the killer whale (Orcinus orca) – José Z. Abramson, Mª Victoria Hernández-Lloreda, Lino García, et al. Proceedings of the Royal Society B: Biological Sciences.

Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista

El artículo El pueblo que hablaba con las ballenas, ¿podría enseñarnos su idioma a los demás? se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Eran nuestras ballenas
2. Cómo usar a las ballenas como detectores de radiación
3. Los enigmas que nos cantan desde el fondo del océano

Distantzia errekor berria ezarri dute inoiz ikusi den banakako izarrik urrunenaren aurkikuntzaz eta, gainera, bertan behera geratu da materia ilunari buruzko teorietako bat.

Irudia: Eguzkitik gertuegi hegan egin eta lumaz eta argizariz egindako hegoak urtu zitzaizkion pertsonaia mitologiko grekoaren oroimenez eman diote Ikaro izena izarrari.

Hubble teleskopioa erabilita, nazioarteko lantalde batek inoiz ikusi den banakako izarrik urrunena identifikatu du: izar urdin erraldoia. “Ikaro” izena eman diote izarrari, Eguzkitik gertuen hegan egin eta lumaz eta argizariz egindako hegoak urtu zitzaizkion pertsonaia mitologiko grekoaren oroimenez. Izarraren izen ofiziala MACS J1149+2223 Lensed Star1 da.

Egoera normalean, teleskopiorik handienak erabilita ere, ezinezkoa litzateke fenomeno hau hautematea, baina izarraren distira ahula izugarri biderkatzea ahalbidetu duen naturaren fenomeno bati esker, NASAren Hubble teleskopio espaziala erabiltzen duten astronomoek izarra aurkitu eta distantzia errekor berri bat ezartzea lortu dute. Era berean, Ikaroren identifikazioarekin bertan behera geratu da materia ilunari buruzko teorietako bat.

Ikerketa honen emaitzek bazterrean utzi dute materia iluna unibertsoaren hasieran sortutako hainbat zulo beltzek osatutakoa dela dioen teoria, izan ere, 13 urtez Hubble-ren laguntzaz monitorizatu diren hondoko izarren fluktuazio arinak beste era batera ikusiko ziratekeen tarteko hainbat zulo beltz baleude.

“Lente grabitazionala” deritzon fenomeno kosmikoa izan da izar hau bistaratzea ahalbidetu duena. Galaxia-kluster masibo baten grabitateak espazioan dagoen lente natural baten antzera funtzionatzen du, argia bikoiztuz eta areagotuz. Batzuetan, hondoko objektu bakar baten argia hainbat iruditan islatuta ager daiteke. Argia asko magnifika daiteke, distira arin-arina duten urruneko objektuei bistaratzeko moduko distira emanez.

Kasu honetan, Lurraren eta Ikaro finkatuta dagoen galaxiaren artean kokatutako MACS J1149 + 2223 izeneko galaxia-klusterrak “lupa” naturala sortu du. Lente grabitazional honen indarraren eta Hubble teleskopioaren bereizmen eta sentiberatasun apartaren kobinazioari esker, astronomoek Ikaro ikusi eta aztertzeko aukera izan dute, Lurretik ikusita, egiazko distira 2.000 aldiz biderkatu zaionean.

UPV/EHUri atxikitako Tom Broadhurst Ikerbasqueko ikertzailea partaide duen taldea Hubble teleskopioa erabiltzen ari zen urruneko galaxia espiral bateko supernoba bat monitorizatzeko eta 2016an, ustekabean, argi puntu berri bat aurkitu zuten magnifikatutako supernobatik hurbil. Berotu edo lehertzen ez zenez gero, berehala konturatu ziren ez zela beste supernoba bat.

Objektu horretatik iritsitako argiaren koloreak aztertzean, izar urdin superrerraldoia dela konturatu dira. Honelako izarrak Eguzkia baino askoz handiagoak, askoz ere masa handiagokoak, beroagoak eta, seguruenik, ehunka mila aldiz distiratsuagoak dira, baina distantzia horretan urrunegi daude lente grabitazionalen laguntzarik gabe behatu ahal izateko.

Izarra galaxia espiral urrun-urrun batean kokatuta dago, eta horren argiak 9 mila milioi urte behar izan ditu Lurrera iristeko. Hortaz, galaxia hori unibertsoak oraingo adinaren %30 inguru zuenean sortu zela ondorioztatu dute.

Ikaro lente grabitazionalen bitartez aurkitu izanak bide berri bat ireki du astronomoek urruneko galaxietan dauden banakako izarrak iker ditzaten. Metodo honek egundo ez bezalako ikupegi zehatza eskaintzen du izarren bilakaera eta bereziki izarrik distiratsuenen bilakaera ulertzeko.

Iturria: UPV/EHU prentsa bulegoa: Hubble-k inoiz ikusi den izarrik urrunena aurkitu du

Erreferentzia bibliografikoa:

Kelly, Patrick L. et al. Extreme magnification of an individual star at redshift 1.5 by a galaxy-cluster lens. Nature Astronomy, volume 2, pages 334–342 (2018). DOI: 10.1038/s41550-018-0430-3

The post Inoiz ikusi den izarrik urrunena aurkitu du Hubble teleskopioak appeared first on Zientzia Kaiera.