La carrera de obstáculos para el diagnóstico de la endometriosis
La endometriosis es una dolencia crónica muy frecuente en las mujeres. Se estima que una de cada diez está afectada por ella, lo que supone un total de más de 2 millones de casos en España. En todo el mundo, se estiman alrededor de 190 millones de mujeres afectadas. No obstante, su causa es desconocida: ¿por qué el tejido endometrial, que normalmente recubre el interior de la superficie del útero, empieza a crecer en lugares tan extraños como la vejiga, el ovario o el recto? A día de hoy, la respuesta es todo un misterio y la limitada investigación científica que se ha realizado sobre esta dolencia no ayuda a resolverlo.
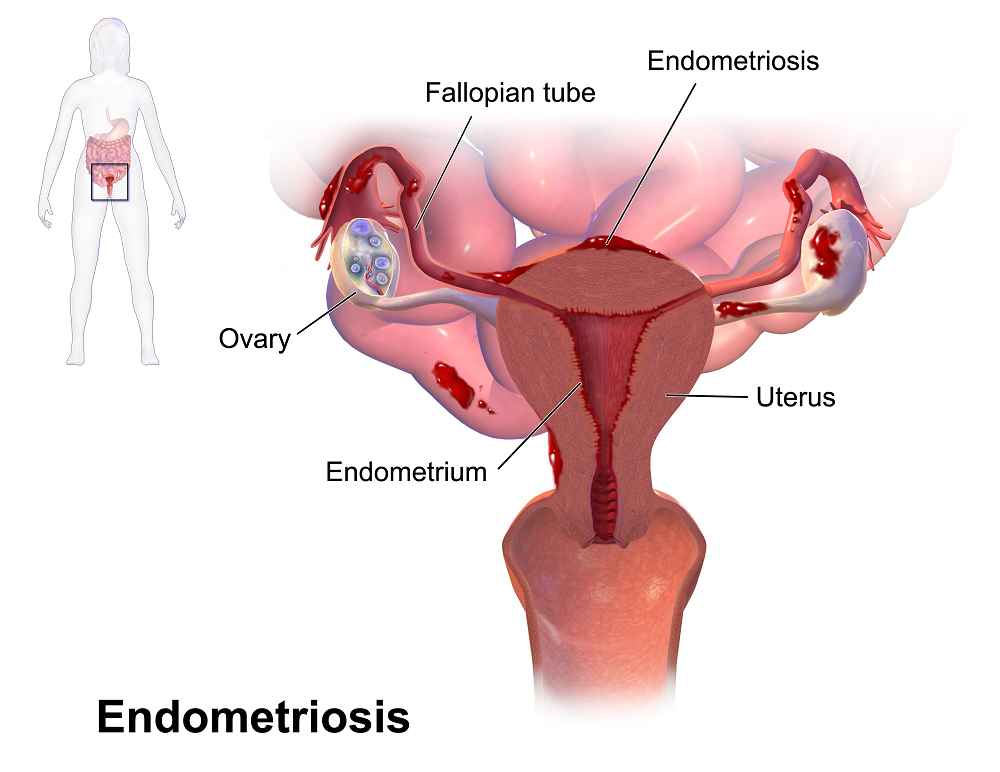 Fuente: Wikimedia Commons8 años para el diagnóstico
Fuente: Wikimedia Commons8 años para el diagnóstico
A pesar de que la endometriosis es muy frecuente, se puede tardar más años en diagnosticar esta dolencia que una enfermedad rara. Tanto es así que las pacientes que sufren endometriosis tienen que esperar una media de 7- 8 años para la identificación de su enfermedad, según datos del Ministerio de Sanidad . Este gran retraso en el diagnóstico no es un fenómeno aislado en nuestro país, sino generalizado a lo largo del mundo.
La larga espera para recibir un diagnóstico implica consecuencias para las mujeres, que pueden sufrir incomprensión y estigmatización durante años por una afectación sin etiqueta médica. Durante todo ese tiempo, aquellas que no reciben tratamiento deben soportar diversos síntomas (especialmente dolor, fatiga y dificultades para conseguir un embarazo) que, en los casos más graves, pueden afectar de forma importante a su calidad de vida, al trabajo y a las relaciones sociales. Además, la enfermedad puede progresar a lo largo de dicho periodo. Las causas que están detrás de este retraso diagnóstico son múltiples y no se comprende bien en qué medida contribuyen a ello. Recientemente, científicos de la Universidad de Aston (Inglaterra) han publicado en la revista Obstetrics & Gynaecology los resultados de su investigación sobre cómo diferentes factores contribuyen en retrasar el diagnóstico de la endometriosis.
El estudio, que consiste en una revisión sistemática y un análisis cualitativo del asunto, examinó un total de 13 artículos científicos realizados en los últimos 20 años en países ricos (con asistencia sanitaria universal en su mayoría). Los factores que contribuyen al retraso del diagnóstico de la endometriosis se relacionan con las características del sistema sanitario y de la endometriosis, así como también por las influencias interpersonales y los rasgos individuales. Los autores clasificaron en 4 grupos las barreras que impiden un diagnóstico temprano de dicha dolencia:
- La dificultad para distinguir los síntomas patológicos de la menstruación normal y el uso de técnicas de autocuidado.
- El estigma de la menstruación y la normalización del dolor menstrual.
- Ciertas actitudes y falta de conocimiento de los profesionales sanitarios, retraso en la derivación a los especialistas y explicaciones deficientes sobre el uso de las pastillas anticonceptivas orales en el proceso diagnóstico.
- Variabilidad en la presentación de los síntomas, que se solapan con otras dolencias, la ausencia de un método no invasivo de diagnóstico de la endometriosis y preocupaciones sobre la importancia del diagnóstico.
Un hallazgo llamativo fue que muchos médicos de familia, en varios de los estudios analizados, reconocían saber poco sobre la endometriosis. Esto, unido a los síntomas variables, poco específicos, que pueden aparecer por esta dolencia (diarrea, estreñimiento, reglas intensas, fatiga crónica, dolor durante el sexo, urgencia para orinar…) complica su diagnóstico. Por otro lado, muchas mujeres que padecían endometriosis y un porcentaje importante de los médicos de familia normalizaban el dolor por esta enfermedad, achacándolo a la regla y no a un problema de salud, lo que impedía investigar en profundidad el origen de este. En su lugar, las mujeres recurrían a medidas de autocuidado para aliviar el dolor, asumiendo que este sufrimiento era inherente a la regla y algo que debían soportar.
Identificar los diferentes factores que contribuyen al retraso diagnóstico de la endometriosis es un primer paso para tomar medidas al respecto. Además, difundir información sobre la endometriosis, derribando sus mitos, al público general puede contribuir a minimizar dicho retraso por una mejor comprensión del problema. En ese sentido, Sophie Davenport, responsable principal del estudio, explica que «la sociedad ha normalizado tradicionalmente el dolor menstrual, así que tenemos que repensar qué significan menstruaciones anormales. Si los síntomas afectan a la vida diaria, y la mujer no acude al trabajo o a la escuela, o es incapaz de continuar con su vida social, eso es un claro signo de que se necesita intervención médica». La experta espera que el artículo científico «anime a las pacientes a buscar ayuda si sienten que sus reglas son anormales o que les provocan un dolor o un sufrimiento importante, y que anime a los clínicos a tomar en serio sus preocupaciones y a derivar al especialista de forma temprana».
Sobre la autora: Esther Samper (Shora) es médica, doctora en Ingeniería Tisular Cardiovascular y divulgadora científica
El artículo La carrera de obstáculos para el diagnóstico de la endometriosis se ha escrito en Cuaderno de Cultura Científica.
Salud Global
Las enfermedades tienen su ecología. El de la borreliosis de Lyme es un ejemplo magnífico. El aumento de la temperatura hace las delicias de las garrapatas, ya que su supervivencia y velocidad de desarrollo son más altas a temperaturas elevadas. A estos ácaros hematófagos se les da bien parasitar ratones de campo; al alimentarse de su sangre les inoculan bacterias del género Borrelia. Además, las bellotas también abundan más en años de inviernos suaves y primaveras benignas, de manera que las poblaciones de roedores también progresan; ambos fenómenos –crecimiento rápido de garrapatas y mayor abundancia de bellotas– facilitan que las garrapatas se multipliquen y expandan. Y, con ellas, las bacterias.
De esa forma, los años de bonanza para los ratones, también lo son para las garrapatas y para las bacterias. Pero son años malos para las personas que frecuentan los bosques y campos de las zonas templadas. A las garrapatas no solo les gusta la sangre de los ratones, también les gusta la sangre de otros mamíferos, incluida la humana, por lo que en los años de invierno suave y primavera benigna, al haber más ratones (porque han comido más bellotas) y más garrapatas (porque han sobrevivido al invierno en mayor número), es más probable que les pique uno de esos detestables ácaros y les transmita la bacteria que provoca una enfermedad –borreliosis de Lyme– que puede revestir cierta gravedad.

Otro magnífico ejemplo de ecología de una enfermedad es el de la cadena que forman cinco especies pertenecientes a taxones de lo más diversos. El hongo Batrachochytrium dendrobatidis provoca a los anfibios una quitridiomicosis que diezma sus poblaciones. Como consecuencia de la menor abundancia de anfibios, disminuye la presión sobre los mosquitos del género Anopheles. Estos son el vector que transmite el protozoo del género Plasmodium a los seres humanos y les provocan la malaria. Por tanto, cualquier factor que favorezca la expansión del hongo en una zona donde la malaria sea endémica, provocará, automáticamente, una aumento de la prevalencia de esta enfermedad. Hay condiciones ambientales sobre las que no se puede actuar, pero sobre otras si es posible. Por ejemplo, cualquier medida que se revele eficaz para dificultar la expansión del hongo, redundará en una menor incidencia de la malaria.
Estos no son más que dos casos que ejemplifican la forma en que interactúan diferentes organismos de manera que dan lugar a que exista una relación íntima entre la salud de los ecosistemas, la de los seres vivos que los pueblan y la de los seres humanos. Y es por esa imbricación por lo que durante los últimos años ha venido ganando peso la noción “Salud Global” (“One Health”).
Salud GlobalMediante la expresión “One Health” se quiere expresar, precisamente, que no es posible tratar de resolver de manera duradera algunos de los más importantes problemas de salud cuya resolución afronta la humanidad sin tener en cuenta la intrincada red de relaciones que hay entre los seres vivos y el modo en que la salud humana depende de la de aquellos y de un normal y saludable funcionamiento de los ecosistemas.
Y ese es, precisamente el tema que han decidido desarrollar el microbiólogo Ignacio López-Goñi, la viróloga veterinaria Elisa Pérez-Ramírez y el farmacólogo Gorka Orive en su libro “Salud Global”.
Tras presentar el tema en su primer capítulo, los autores abordan, en el segundo, la relación entre el clima y la salud humana a través, principalmente, de los efectos de aquel sobre las posibilidades de expansión de las enfermedades infecciosas. Al fin y al cabo, la humedad y la temperatura tienen claros efectos sobre los seres vivos, por lo que el clima, a través de esas dos variables, ejerce una influencia intensa sobre la biología de las especies y las relaciones entre ellas.
Por otro lado, es muy significativo –y de importancia crucial– que un 60% de las enfermedades infecciosas humanas que se conocen tengan origen animal; y ese porcentaje se eleva a un 75% en el caso de las enfermedades emergentes. Por esa razón es importante no perder de vista que las actuaciones humanas que modifican el patrón de comportamiento de otras especies –cambios en las rutas migratorias de aves, alteraciones en la densidad de poblaciones de roedores, reducción de la distancia de los seres humanos a otros animales, salvajes o domésticos, y otras– también cambian las condiciones para que se produzca la transmisión de patógenos entre ellas.
Amenaza para la salud humanaEn los capítulos que siguen, los autores repasan la situación de las enfermedades infecciosas y los patógenos que las provocan que suponen una mayor amenaza para la salud humana: el VIH, la malaria, la viruela del mono, las que se transmiten a través del agua o el aire, la gripe aviar y las que provocan los coronavirus. De cada una de ellas se ofrece información muy actual acerca de su extensión de su forma de transmisión, de su prevención y de su tratamiento.
También se analiza el papel de los vectores que transmiten y propagan enfermedades; el papel de otras especies animales como fuente de los patógenos que amenazan nuestra salud (roedores, insectos y otros), así como la forma en que nosotros mismos –los seres humanos– podemos transmitir patógenos a otras especies. Finalmente, se aborda la espinosa cuestión de la resistencia a los antibióticos, así como el papel de las vacunas –cuando se dispone de ellas– como mecanismo efectivo para prevenir las enfermedades infecciosas.
En resumen, el lector o lectora de este libro se encontrará con un repaso muy completo de la compleja relación entre el medio ambiente, los microorganismos patógenos y la salud humana. El libro expone con claridad y profusión de datos la gran importancia de abordar estas relaciones de forma holística, porque no es realista pensar que la solución a los grandes retos de salud que se nos presentan pueden ser abordados fuera de su contexto ambiental global.
Nota final: Si tiene usted interés en información adicional, la puede encontrar en este artículo firmado por los tres coautores del libro.
Título: Salud Global. La nueva estrategia frente a la amenaza medioambiental.
Autores: Ignacio López-Goñi, Elisa Pérez-Ramírez y Gorka Orive
Ed. B, Penguin Random House, 2023.
En Editoralia personas lectoras, autoras o editoras presentan libros que por su atractivo, novedad o impacto (personal o general) pueden ser de interés o utilidad para los lectores del Cuaderno de Cultura Científica.
Una versión de este texto de Juan Ignacio Pérez Iglesias apareció anteriormente en Lecturas y Conjeturas (Substack).
El artículo Salud Global se ha escrito en Cuaderno de Cultura Científica.
La evaluación de competencias en el marco de la LOMLOE

La jornada Las Pruebas de la Educación tuvo lugar con el objetivo de analizar la validez de las estrategias educativas puestas en marcha durante los últimos años. El enfoque STEAM o las clases virtuales fueron analizados desde la evidencia científica por un grupo de expertos y expertas que se reunió en la Facultad de Educación de Bilbao de la Universidad del País Vasco. La jornada, fruto de la colaboración entre la Cátedra de Cultura Científica de la Universidad del País Vasco y la facultad de Educación de Bilbao, tuvo lugar el 27 de octubre pasado.
Esta sexta edición volvió a estar dirigida a profesionales del ámbito de la educación y a quienes, en un futuro, formarán parte de este colectivo. Su objetivo ha sido reflexionar, desde la evidencia científica, sobre la validez de las estrategias utilizadas hoy en día. El seminario ha contado, una vez más, con la dirección académica de la vicedecana de Investigación y Transferencia de la Universidad Autónoma de Madrid, Marta Ferrero González.
Javier Cortés de las Heras, doctor en Educación y profesor asociado de la Universidad de Valencia, explica en esta charla cómo se supone que han de evaluarse las competencias según la Ley Orgánica por la que se modifica la LOE de 2006 (LOMLOE).
Edición realizada por César Tomé López
El artículo La evaluación de competencias en el marco de la LOMLOE se ha escrito en Cuaderno de Cultura Científica.
La historia genómica del primer milenio de la península balcánica
Los Balcanes fueron una región fronteriza de la antigua Roma tan cosmopolita como el centro imperial; la migración eslava que llegó a los Balcanes a partir del siglo VI representa entre el 30 % y el 60 % de la ascendencia de los pueblos balcánicos en la actualidad. Estas son dos de las conclusiones de la primera reconstrucción de la historia genómica del primer milenio de la península balcánica.
 Cráneo de un individuo de origen subsahariano encontrado en Viminacium. La lámpara legionaria fue encontrada en su tumba. Foto: Miodrag Grbic
Cráneo de un individuo de origen subsahariano encontrado en Viminacium. La lámpara legionaria fue encontrada en su tumba. Foto: Miodrag GrbicIñigo Olalde, investigador Ikerbasque y Ramón y Cajal de la Universidad del País Vasco, ha liderado junto con el Instituto de Biología Evolutiva (IBE: CSIC-UPF) y la Universidad de Harvard, un estudio en el que han reconstruido por primera vez la historia genómica del primer milenio de la península balcánica. Para ello, el equipo ha recuperado y analizado el genoma antiguo de 146 personas que habitaron las actuales Croacia y Serbia durante ese período. El trabajo, publicado en la prestigiosa revista Cell, desvela los Balcanes como una frontera global y cosmopolita del Imperio Romano y reconstruye la llegada de los pueblos eslavos a esta región.
Por primera vez, el equipo ha identificado tres individuos de origen africano que vivieron en los Balcanes bajo el dominio imperial de Roma. Por otro lado, la investigación corrobora que la migración de los pueblos eslavos a partir del siglo VI representó uno de los mayores cambios demográficos permanentes en toda Europa, cuya influencia cultural perdura hasta nuestros días.
El Imperio Romano transformó los Balcanes en una región globalLa República Romana primero y el Imperio Romano después incorporaron los Balcanes y convirtieron esta región fronteriza en una encrucijada de comunicaciones y un crisol de culturas. Así lo confirma el estudio, que desvela que la vitalidad económica del imperio atrajo a inmigrantes de lugares lejanos hasta esta región.
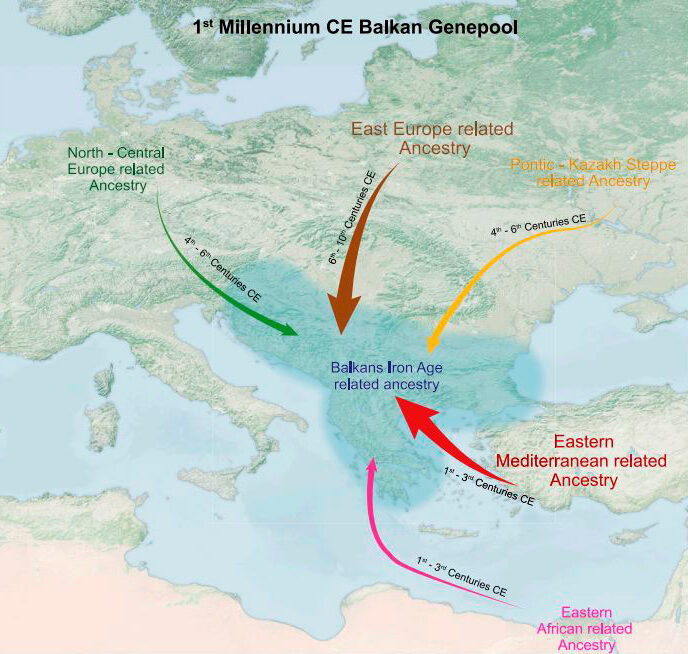 Grupos genéticos de la península balcánica durante el primer milenio de la era común. Imagen: Pablo Carrión e Íñigo Olalde
Grupos genéticos de la península balcánica durante el primer milenio de la era común. Imagen: Pablo Carrión e Íñigo OlaldeA través del análisis de ADN antiguo, el equipo ha podido identificar que, durante el dominio romano de la región, hubo un gran aporte demográfico proveniente de la península anatólica (localizada en la actual Turquía) que dejó huella genética en las poblaciones balcánicas. Sin embargo, no se observa rastro de ascendencia itálica en los genomas analizados. “Estas poblaciones venidas del este se integraron totalmente en la sociedad local de los Balcanes. En Viminacium, por ejemplo (una de las principales ciudades de los romanos, localizada en la actual Serbia), encontramos un sarcófago excepcionalmente rico en el que fueron enterrados un hombre de ascendencia local y una mujer de ascendencia anatólica”, comenta Olalde.
 Sarcófago de Viminacium. Foto: Ilija Mikić
Sarcófago de Viminacium. Foto: Ilija MikićEl equipo también ha revelado la movilidad esporádica de larga distancia de tres individuos de ascendencia africana a la península balcánica durante su dominio imperial. Uno de ellos era un adolescente cuyo origen genético radica en la región del actual Sudán, fuera de los límites del antiguo Imperio. “De acuerdo con el análisis isotópico de las raíces de sus dientes, en su niñez tuvo una dieta marina muy distinta a la del resto de individuos analizados”, comenta Carles Lalueza-Fox, investigador principal del Instituto de Biología Evolutiva (IBE) y director del Museo de Ciencias Naturales de Barcelona (MCNB).
Además, fue enterrado con una lámpara de aceite que representa una iconografía del águila relacionada con Júpiter, uno de los dioses más importantes para los romanos. “El análisis arqueológico de su entierro revela que pudo formar parte de las fuerzas militares romanas, por lo que estaríamos hablando de un inmigrante que viajó desde muy lejos a los Balcanes del siglo II d.C.”, apunta Lalueza-Fox. “Esto nos muestra un Imperio Romano diverso y cosmopolita, que acogía poblaciones mucho más allá del continente europeo”.
El Imperio Romano acogió a poblaciones bárbaras mucho antes de su caídaEl estudio ha identificado algunos individuos de ascendencia del Norte de Europa y de las estepas que habitaron la península balcánica durante el siglo III, en plena ocupación romana. El análisis antropológico de sus cráneos revela que algunos de ellos fueron artificialmente deformados, una costumbre propia de algunas poblaciones de las estepas y de los hunos, a menudo denominados como “bárbaros”.
 Cráneo deformado del siglo IV de la era común, atribuido a un individuo de las estepas. Posible gépido o godo, si bien los hunos también practicaban la deformación craneal. Foto: Carles Lalueza-Fox
Cráneo deformado del siglo IV de la era común, atribuido a un individuo de las estepas. Posible gépido o godo, si bien los hunos también practicaban la deformación craneal. Foto: Carles Lalueza-FoxEstos resultados apoyan las investigaciones históricas y arqueológicas y muestran la presencia de individuos provenientes de fuera de las fronteras del Imperio, más allá del Danubio, mucho tiempo antes de la caída del Imperio occidental. “Las fronteras del Imperio eran mucho más difusas que las fronteras de los estados nación actuales. El Danubio servía como límite geográfico del Imperio, pero actuaba como vía de comunicación y era muy permeable al movimiento de personas”, comenta Pablo Carrión, investigador del IBE y co-primer autor del estudio.
Las poblaciones eslavas cambiaron la demografía de la península balcánicaTras la caída del Imperio Romano de Occidente, y especialmente a partir del siglo VI, el estudio revela la llegada a gran escala a los Balcanes de individuos genéticamente similares a las poblaciones modernas de habla eslava de Europa del Este. Su huella genética representa entre el 30 y el 60 % de la ascendencia de los pueblos balcánicos actuales, lo que supone uno de los mayores cambios demográficos permanentes en cualquier lugar de Europa durante el período de las Grandes Migraciones.
Aunque el estudio detecta la llegada esporádica de individuos procedentes del Este de Europa en periodos anteriores, es a partir del siglo VI cuando se observa una fuerte oleada migratoria. “Según nuestros análisis de ADN antiguo, esta llegada de poblaciones de habla eslava a los Balcanes tuvo lugar a lo largo de varias generaciones e involucró a grupos familiares completos que incluían hombres y mujeres”, explica Carrión.
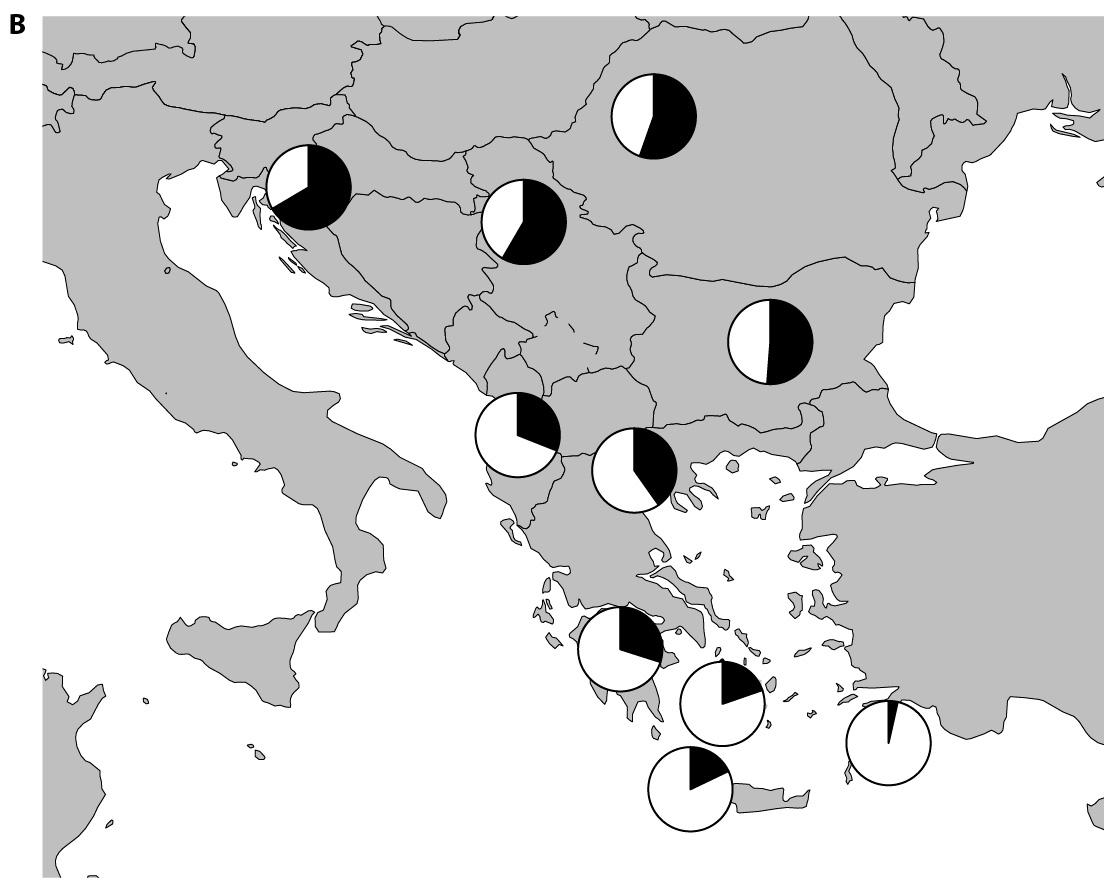 Proporciones de poblaciones de ascendencia eslava, en negro, en los países actuales de la península balcánica y el Egeo. Imagen: Íñigo Olalde y Pablo Carrión
Proporciones de poblaciones de ascendencia eslava, en negro, en los países actuales de la península balcánica y el Egeo. Imagen: Íñigo Olalde y Pablo CarriónEl estudio también identifica que el establecimiento de las poblaciones eslavas en los Balcanes fue mayor en el norte, con una contribución genética de entre el 50 % y el 60 % en la actual Serbia, y gradualmente menor hacia el sur, con entre un 30 y un 40 % de representación genética en la Grecia continental y hasta un 20 % en las islas del Egeo. “Su legado genético es visible no solo en poblaciones balcánicas actuales de habla eslava, sino también en otros grupos que incluyen regiones donde actualmente no se habla lenguas eslavas, como Rumanía y Grecia», puntualiza David Reich, investigador de la Universidad de Harvard en cuyo laboratorio se llevó a cabo la recuperación y secuenciación del ADN antiguo.
Coordinación y cooperación para reescribir la historia de los BalcanesLa guerra de Yugoslavia en 1991 provocó la separación de los pueblos balcánicos en los distintos países que conforman la región hoy en día y sus consecuencias perduran en la actualidad. Sin embargo, investigadores de toda la región han colaborado en el estudio. «En el estudio han estado colaborando investigadores croatas y serbios. Se trata de un gran ejemplo de cooperación, teniendo en cuenta la historia reciente de la península balcánica. Al mismo tiempo, este tipo de trabajos son un ejemplo de cómo datos genómicos objetivos pueden contribuir a dejar atrás problemas sociales y políticos ligados a identidades colectivas que han estado basadas en narraciones épicas del pasado», comenta Lalueza-Fox.
El equipo elaboró una base de datos genética de la población Serbia de novo, con el fin de poder reconstruir la historia de los Balcanes. «Nos encontramos con la situación de que no existía una base de datos genómica de la población serbia actual. Para construirla y utilizarla como referencia comparativa en este estudio, tuvimos que buscar a personas que se autodenominaban como serbias en base a determinados rasgos culturales compartidos, aunque vivieran en otros países como Montenegro o Macedonia del Norte”, comenta Miodrag Grbic, profesor de la Universidad de Western Ontario y profesor visitante en la Universidad de La Rioja.
Pese a la cuestión identitaria, marcada por la historia más reciente de los Balcanes, los genomas de los croatas y serbios analizados hablan de una herencia compartida en igual medida entre las poblaciones eslavas y las poblaciones del mediterráneo.
“Creemos que el análisis del ADN antiguo puede contribuir, junto con los datos arqueológicos y los registros históricos, a la reconstrucción de la historia de los pueblos balcánicos y la formación de los denominados pueblos eslavos del sur de Europa”, apunta Lalueza-Fox.
«La imagen que surge no es de división, sino de historia compartida. Las personas que en la Edad del Hierro habitaban la región de los Balcanes se vieron afectadas de manera similar por las migraciones durante la época del Imperio Romano y por las migraciones eslavas más tarde. Juntas, estas influencias dieron como resultado el perfil genético de los Balcanes modernos, independientemente de las fronteras nacionales», concluye Grbic.
Referencia:
Olalde, I., Carrión, P., Mikić. I. et al. (2023) A genetic history of the Balkans from Roman frontier to Slavic migrations Cell doi: 10.1016/j.cell.2023.10.018
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La historia genómica del primer milenio de la península balcánica se ha escrito en Cuaderno de Cultura Científica.
Estrellas de mar: de no tener cabeza a tener solo cabeza
Las estrellas y los erizos de mar forman parte de uno de los grupos más enigmáticos de seres vivos: los equinodermos. Un estudio publicado recientemente los convierte en criaturas todavía más enigmáticas. Al menos, si las contemplamos con nuestros ojos humanos.
 Foto: Adrian Pingstone / Wikimedia Commons
Foto: Adrian Pingstone / Wikimedia CommonsLa inmensa mayoría de los animales, nosotros incluidos, somos bilaterales: nuestra simetría divide el cuerpo en dos mitades casi idénticas. En otras palabras, estamos organizados sobre la base de un eje anteroposterior y otro dorsoventral. Hacia finales del siglo pasado se descubrió que los genes que controlan la formación de estos ejes durante el desarrollo son los mismos en todos los animales bilaterales. Es decir, el mecanismo que determina qué región va a ser anterior, media o posterior es el mismo en una mosca y en un ser humano.
Una organización bilateral parece la más lógica en animales que tienen un tubo digestivo y se desplazan en una dirección determinada. Lo razonable es que alrededor del extremo anterior, donde está la boca, se concentren los órganos de los sentidos y los centros nerviosos. En pocas palabras, que se desarrolle una cabeza.
Esta es la razón por la que nos resultan fascinantes los equinodermos. Sus ancestros eran bilaterales con todas sus ventajas, cabeza incluida. Sin embargo, en algún momento de su evolución perdieron esta característica y desarrollaron una organización pentámera. Dejaron de tener un único plano de simetría para contar con nada menos que cinco, dispuestos alrededor de un eje oral-aboral, el eje que pasa por la boca y por el lado opuesto del cuerpo.
Esta innovación evolutiva se refleja en el desarrollo de los equinodermos: su larva es bilateral, pero tras una metamorfosis compleja adquiere la simetría pentámera.
La organización pentámera, sin eje anteroposterior ni centros nerviosos, implica la ausencia de una cabeza. O, al menos, esto se creía hasta ahora. Un artículo recientemente publicado en la revista Nature sugiere lo contrario de lo que se pensaba. Los equinodermos no solo tienen cabeza, sino que no tienen nada más. Son cabezas sin cuerpo.
Cuatro hipótesis, todas inválidasHasta ahora se habían formulado cuatro hipótesis para explicar cómo el eje presente en todos los animales bilaterales pudo transformarse en los cinco planos de simetría de los equinodermos. Estos modelos eran la bifurcación, circularización, duplicación y el apilamiento.
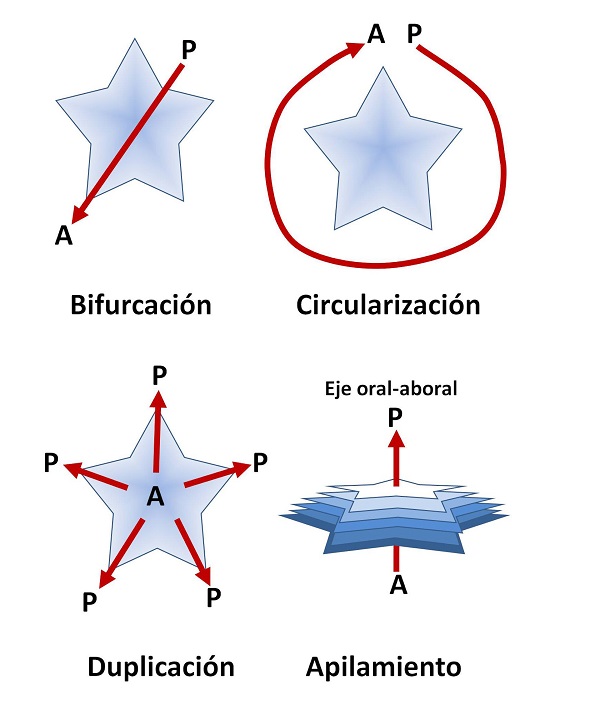 Las cuatro hipótesis formuladas sobre la transición de un eje anteroposterior (A-P) a una simetría pentámera en los Equinodermos.
Las cuatro hipótesis formuladas sobre la transición de un eje anteroposterior (A-P) a una simetría pentámera en los Equinodermos.Un equipo de biólogos de la Universidad de Stanford (EE UU) propone en su artículo un modelo nuevo y diferente, que supone una nueva concepción de cómo evolucionaron los equinodermos.
Su estrategia consistió en seleccionar una serie de marcadores genéticos típicos del eje anteroposterior de los bilaterales. Estos han sido conservados a lo largo de la evolución, por lo que es interesante saber dónde se expresan en un animal pentámero. Entre los 36 marcadores seleccionados los había de la región más anterior del cuerpo, de la media y de la posterior. También se incluyeron los genes del complejo Hox, que son fundamentales en la organización del eje de todos los animales bilaterales.
La técnica utilizada fue la tomografía de ARN aplicada a los pequeños estados juveniles de una estrella de mar abundante en la costa de California, Patiria miniata. Esta avanzada técnica molecular consiste en seccionar brazos de la estrella en tres planos diferentes: a lo largo del eje del brazo, en un plano horizontal y de forma transversal. En las distintas secciones fue detectada la expresión de los diferentes marcadores.
El sorprendente resultado obtenido fue que los genes más anteriores se expresaban en la línea media de los brazos, y los más posteriores en sus márgenes laterales. Como la línea media de los brazos está ocupada por los surcos ambulacrales, en los que se localizan los pequeños pies con los que las estrellas de mar se desplazan, este nuevo modelo de organización se ha denominado ambulacral-anterior.
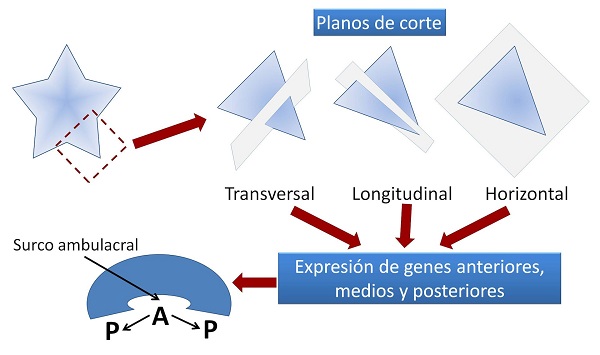 La estrategia consistió en seccionar los brazos de la estrella en tres planos y comprobar la expresión de genes anteriores, medios y posteriores en animales bilaterales. Los más anteriores se expresaban en la línea media de los brazos y los posteriores en sus márgenes.Un resultado inesperado
La estrategia consistió en seccionar los brazos de la estrella en tres planos y comprobar la expresión de genes anteriores, medios y posteriores en animales bilaterales. Los más anteriores se expresaban en la línea media de los brazos y los posteriores en sus márgenes.Un resultado inesperado
Que el centro de los brazos corresponda a la parte anterior de los demás animales y los márgenes a la posterior, no era un resultado esperado. Pero menos todavía lo fue la ausencia de marcadores típicos del tronco de los animales bilaterales.
En el ectodermo de la estrella de mar solo se expresa uno de los trece genes del complejo Hox, Hox1, y lo hace en el margen de los brazos, lo que corresponde a la zona posterior de su cuerpo. Dicho de otra forma, lo más posterior que encontramos en el cuerpo de la estrella corresponde al límite posterior de la cabeza de los vertebrados. El cuerpo de la estrella de mar se corresponde con nuestra cabeza, pero no hay evidencia molecular de que haya nada semejante a un tronco.
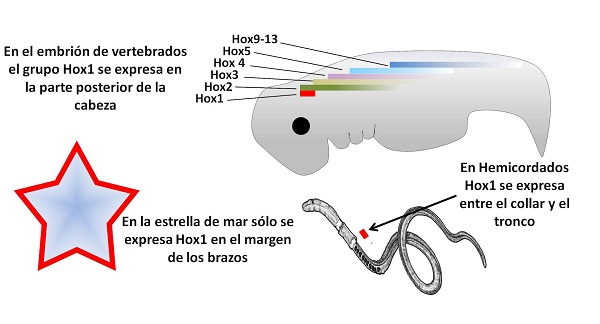 Los genes Hox se expresan ordenadamente a lo largo del cuerpo de los animales bilaterales. En el ectodermo de la estrella de mar sólo se expresa el más anterior, Hox1, y lo hace en el margen de los brazos. Vertebrados y hemicordados sirven como comparación.
Los genes Hox se expresan ordenadamente a lo largo del cuerpo de los animales bilaterales. En el ectodermo de la estrella de mar sólo se expresa el más anterior, Hox1, y lo hace en el margen de los brazos. Vertebrados y hemicordados sirven como comparación.Queda por comprobar si estos resultados son exclusivos de las estrellas de mar o, como parece muy probable, son aplicables a todos los equinodermos. Si se confirma esto, se trataría de una concepción completamente novedosa de la forma en que los equinodermos reorganizaron su eje bilateral y construyeron su cuerpo. Una constatación final que nos confirma este estudio: la biología, y en particular la evolución, mantiene intacta su capacidad de asombrarnos.![]()
Sobre el autor: Ramón Muñoz-Chápuli Oriol, Catedrático de Biología Animal (jubilado), Universidad de Málaga
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Estrellas de mar: de no tener cabeza a tener solo cabeza se ha escrito en Cuaderno de Cultura Científica.
El cuento de la ruleta rusa
Cuando presento alguno de mis libros en una librería, aunque la verdad es que esto no ocurre tantas veces como uno desearía, me gusta pedir a las personas que trabajan en la misma que me recomienden algunos libros, principalmente, novelas. En octubre (de 2023) presenté mi último libro “Las matemáticas como herramienta de creación artística” (Catarata / FESPM, 2023) en la librería Zubieta-TROA, de Donostia/San Sebastián. El responsable de esta librería, Adolfo López Chocarro, me recomendó varios libros, entre los cuales estaba el cuento El Ruletista (Impedimenta), del escritor rumano Mircea Cartarescu (Bucarest, 1956), en el cual se menciona, de pasada, la probabilidad de morir jugando a la ruleta rusa, en su versión en solitario. Y es de esto precisamente de lo que vamos a hablar en esta entrada del Cuaderno de Cultura Científica.
 Portada del cuento El Ruletista (Impedimenta, 2010), del escritor rumano Mircea CartarescuMircea Cartarescu
Portada del cuento El Ruletista (Impedimenta, 2010), del escritor rumano Mircea CartarescuMircea Cartarescu
El escritor y crítico literario Mircea Cartarescu está considerado el mejor escritor rumano de la actualidad y uno de los grandes escritores de la literatura europea contemporánea. La editorial Impedimenta ha traducido al español y publicado muchos de sus libros, como El Levante (Impedimenta, 2015), una epopeya heroico-cómica, que es también una aventura a través de la historia de la literatura rumana; el libro de relatos Nostalgia (Impedimenta, 2012), que se habría precisamente con el cuento El ruletista, y que consagró a Cartarescu como uno de los grandes escritores actuales de Rumanía; la novela Solenoide (Impedimenta, 2017), incluida en el listado de los mejores libros de ese año por la prensa cultural española e iberoamericana (que es parte de mi “tsundoku”, es decir, descansa en mi mesilla a la espera de ser leída); o Poesía esencial (Impedimental 2021), una recopilación de poemas escritos durante sus primeros años creativos. Para describir su filosofía como escritor, podemos acudir a una de sus citas, “Escribo porque quiero entender mi situación en el mundo”.
 Fotografía del escritor rumano Mircea Cartarescu, en la editorial ImpedimentaEl Ruletista, un cuento de Cartarescu
Fotografía del escritor rumano Mircea Cartarescu, en la editorial ImpedimentaEl Ruletista, un cuento de Cartarescu
Aprovechemos la contraportada de la publicación en español, por parte de la editorial Impedimenta, para introducir brevemente el cuento del que vamos a escribir en esta entrada del Cuaderno de Cultura Científica.
Prohibido durante años en Rumanía por lo explícito de su argumento, El Ruletista constituye uno de los más brillantes hitos narrativos de la reciente literatura europea. Esta pieza, tan breve como intensa, narra la improbable historia de un hombre al que nunca le ha sonreído la suerte, un desarraigado que sorprendentemente hace fortuna participando en letales sesiones de ruleta rusa. Multitudes enfervorecidas, presas del morbo, guardan cola para participar en las ceremonias de muerte y redención en que se convierten sus apariciones, y que dan paso a la histeria colectiva. Un escritor moribundo que conoció al Ruletista en su juventud intenta explicar cómo ese hombre insulso termina convirtiéndose en alguien inmortal y aparentemente inexpugnable, cuando en realidad en él solo anida el más desesperado espíritu de la autodestrucción.
Expliquemos en primer lugar en qué consiste el macabro juego de la ruleta rusa que es un elemento principal de este cuento. Mientras que en la ruleta rusa que hemos visto en duras películas como El cazador (1978), dirigida por Michael Cimino e interpretada por Robert de Niro, Christopher Walken, Meryl Streep, John Savage y John Cazale, se juega entre dos, o más jugadores, en el cuento El ruletista es una ruleta rusa solitaria, de un solo jugador.
 Cartel de la película El cazador (1978), dirigida por el director estadounidense Michael Cimino
Cartel de la película El cazador (1978), dirigida por el director estadounidense Michael CiminoLos principales protagonistas de la ruleta rusa de este relato son los siguientes. Por un lado, la persona que se juega la vida en la ruleta rusa, el ruletista, que en el cuento se explica que suele ser alguna persona que por diferentes circunstancias vitales no le importa jugarse la vida a cambio de dinero, normalmente, algún borracho, vagabundo o expresidiario, como se menciona más arriba “un desarraigado”. Luego está el patrón, que es quien contrata, o convence, al ruletista y que va a apostar a su favor, es decir, va a apostar a que esa persona que se juega la vida a la ruleta rusa va a sobrevivir a la misma. Y finalmente están los accionistas que son quienes apuestan en contra del patrón, esto es, ganan si muere el ruletista.

El juego consiste en lo siguiente. Primero se introduce una bala en el tambor de un revólver, que tiene capacidad para alojar seis balas (aunque hay revólveres que admiten otra cantidad de balas, cinco, seis, siete, ocho o diez balas), luego se gira el tambor y se cierra rápidamente para que la bala quede colocada en una posición al azar, entonces el ruletista coge el revólver, se apunta a la sien y dispara. Si tiene la suerte de que no salga la bala (lo cual ocurre en 5 de las 6 posiciones posibles del tambor, es decir, la probabilidad de que sea un disparo fallido es de 5 de cada 6 veces, el 83,33 %) el patrón gana, se queda con el dinero de los accionistas y le da al ruletista un diez por ciento de las ganancias. Por otra parte, si se dispara la bala (lo cual ocurre 1 de cada 6 veces, esto es, una probabilidad del 16,66 %), el ruletista muere y el patrón debe pagar a los accionistas entre diez y veinte veces la cantidad apostada por ellos, según hayan acordado. Es cierto, que el peso de la bala modifica algo estas probabilidades, pero no vamos a tenerlo en cuenta en esta entrada.
En el cuento hay dos protagonistas, el viejo escritor que escribe la historia del Ruletista y este, que se ha ganado el derecho a ser nombrado con la inicial mayúscula, ya que, como escribe el viejo escritor, “ha sido el único hombre al que fue concedido vislumbrar al infinito Dios matemático y luchar cuerpo a cuerpo con él”, refiriéndose a que este hombre ha jugado muchísimas veces a la ruleta rusa solitaria y siempre ha salido indemne, saltándose la “alta” probabilidad de morir. Como escribe el viejo escritor, referente a esto último:
“… el ruletista solo tenía cinco posibilidades entre seis de salvarse en la primera partida. Según el cálculo de probabilidades, si volvía a llevarse la pistola a la sien, sus posibilidades disminuían. En el sexto intento, esas posibilidades se reducían a cero. De hecho, hasta que mi amigo entró en el mundo de la ruleta, en el que llegaría a convertirse en el Ruletista con mayúscula, no se conocían casos de supervivencia ni siquiera tras cuatro intentos. La mayoría de los ruletistas lo eran, por supuesto, de forma ocasional, y no volverían a repetir esa terrible experiencia por nada del mundo…”
Y continuaba:
“… supongo que los accionistas apenas se fijaron en él cuando escapó con vida la primera o la segunda vez, puede que incluso la tercera. Fue considerado, como mucho, un ruletista afortunado. Pero después de la cuarta y de la quinta, se convirtió en la figura central del juego, un verdadero mito llamado a alcanzar proporciones gigantescas en los años posteriores. Durante dos años, hasta nuestro reencuentro en el restaurante, el Ruletista se había llevado el revólver a la sien en ocho ocasiones…”

Antes de entrar en el tema de las probabilidades, al que dedicaremos la siguiente sección de esta entrada, presentemos brevemente al Ruletista, a quien el viejo escritor conocía desde que eran niños. Desde siempre este perdía a todos los juegos, de pequeño a las canicas o el lanzamiento de herradura, cuando estuvo en la cárcel siempre perdía al póquer y cuando al salir de la misma se dedicó a la bebida e iba mendigando un trago de cerveza de mesa en mesa por las tabernas, los parroquianos de las mismas se lo jugaban con él al palillo más largo y, de nuevo, siempre perdía. El Ruletista era un candidato ideal para ser jugador de la ruleta rusa, pero, además, su malísima suerte en todo tipo de juegos hacía que en el caso de la ruleta rusa jugase a su favor, ya que podríamos decir que nunca “acertaba” con la bala en la posición de disparo y salía ileso del juego.
Un poco de probabilidadRealmente hay diferentes cuestiones de probabilidad que se pueden analizar relacionadas con la ruleta rusa, pero vayamos exactamente a la situación descrita en este cuento. Empecemos por lo que ya sabemos y es evidente. Si un ruletista solo juega una vez a la ruleta rusa de un solo jugador, la probabilidad de sobrevivir es del 83,33 %, esto es, 5 de cada 6, mientras que la probabilidad de morir durante el juego es, la complementaria de la anterior, es decir, el 16,67 %, solo 1 de cada 6.
 La probabilidad de que el ruletista viva o muera si juega solo una vez a la ruleta rusa
La probabilidad de que el ruletista viva o muera si juega solo una vez a la ruleta rusa
La siguiente cuestión que nos planteamos, siguiendo lo escrito en este pequeño relato, en extensión, no en calidad literaria, es la siguiente. Si el ruletista juega dos veces a la ruleta rusa, ¿cuál será la probabilidad de que muera o viva?
Pero cuidado, cada vez que se juega a la ruleta rusa la probabilidad es la misma que hemos comentado arriba, no cambia, ya que el juego, o el revólver, no tiene memoria. Lo que queremos conocer es la probabilidad de salir indemne, o respectivamente, morir, si se arriesga a jugar dos veces. Aunque no es necesario, podéis pensar en que ha decidido previamente jugarse la vida a la ruleta rusa solitaria en dos ocasiones. Calculemos esta probabilidad.
Recordemos brevemente, aunque realmente ya lo hemos utilizado, que la probabilidad de un evento es igual al número de casos favorables (del evento) dividido el número de casos posibles (del evento). Por ejemplo, si queremos conocer cual es la probabilidad de que salga un múltiplo de 3 si tiramos un dado, el número de casos favorables sería dos -que salga 3 o 6-, mientras que hay seis casos posibles -los seis valores del dado 1, 2, 3, 4, 5, 6-. Por lo tanto, la probabilidad de que salga un múltiplo de tres (3 o 6) al tirar el dado es 2 / 6 = 0,3333…, esto es, una probabilidad del 33,33 %.
Volvamos a la probabilidad de que el ruletista viva o muera si juega dos veces a la ruleta rusa. Primero veamos los casos posibles. Como en el primer disparo tenemos seis posibles posiciones del tambor del revólver o, dicho de otra forma, seis agujeros para disparar (que en la siguiente imagen hemos numerado como 1, 2, 3, 4, 5, 6) y en el segundo disparo tenemos otros seis posibles agujeros (de nuevo del 1 al 6 en la imagen), entonces el número de posiciones posibles de los tambores en los dos disparos o, mejor dicho, parejas de agujeros sobre los que disparamos son 6 x 6 = 36 (que podemos pensarlos como parejas de números, desde el (1, 1), (1, 2), (1, 3), hasta el (6,6)).
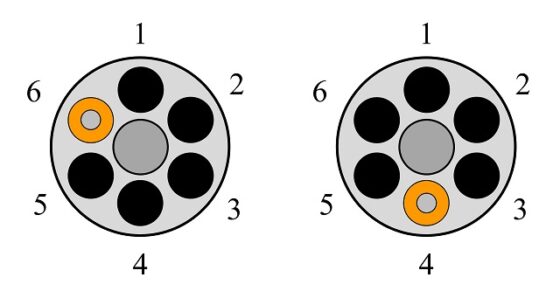
Ahora contemos cuántas parejas de agujeros serían favorables, si queremos calcular la probabilidad de que el ruletista salga indemne de las dos sesiones de la ruleta rusa. Como en el primer revolver hay 5 agujeros para los que el jugador vive, serán estos los que hay que tener en cuenta en la primera posición de la pareja de agujeros (en el ejemplo de la anterior imagen son los agujeros 1, 2, 3, 4, 5) y para cada uno de esos 5 agujeros, tenemos otros 5 agujeros en la segunda pistola que no contienen la bala de la muerte. Por lo tanto, el número de casos favorables, es decir, parejas de agujeros para los que el ruletista no muere, son 5 x 5 = 25. Por lo tanto, la probabilidad de que el ruletista quede con vida si juega dos veces a la ruleta rusa es 25/36 = 0,6944, es decir, una probabilidad del 69,44 %, mientras que la probabilidad de que muera es su complementario, 11/36 = 0,3056, esto es, el 30,56%.
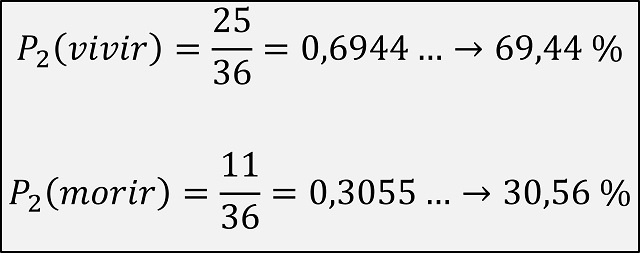 La probabilidad de que el ruletista viva o muera si juega dos veces a la ruleta rusa
La probabilidad de que el ruletista viva o muera si juega dos veces a la ruleta rusa
Aunque, si lo pensamos un poco, la probabilidad de salir indemne de las dos partidas de la ruleta rusa es la probabilidad de vivir en la primera partida (5/6) por la probabilidad de vivir en la segunda partida (5/6), es decir, (5/6)2 = 25 / 36.
Esta forma de entenderlo nos permite obtener fácilmente la respuesta a la cuestión de qué probabilidades tiene el ruletista de vivir, o morir, si juega k veces a la ruleta rusa (para k = 1, 2, 3, 4, 5, …). De hecho, podemos obtener una fórmula en función del número k de partidas jugadas a la ruleta rusa por el ruletista.
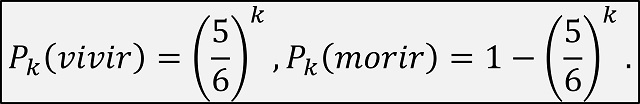 La probabilidad de que el ruletista viva o muera si juega un número k de veces a la ruleta rusa
La probabilidad de que el ruletista viva o muera si juega un número k de veces a la ruleta rusaAhora es fácil ir calculando la probabilidad de vivir o morir en función de cuantas veces juegue el ruletista a la ruleta rusa solitaria, que precisamente es de lo que habla, sin calcular probabilidades, el viejo profesor en los párrafos que hemos incluido más arriba. A continuación, incluimos una tabla con estas probabilidades para los casos en los que el ruletista juega entre una y diez veces, en la cual podemos apreciar la velocidad a la que la probabilidad de que el ruletista salga vivo va disminuyendo, y creciendo la probabilidad de morir.
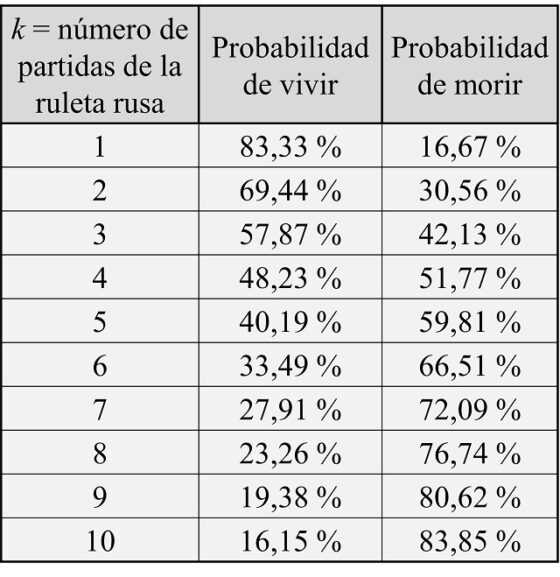 Tabla con las probabilidades de que el ruletista viva o muera si juega k veces a la ruleta rusa, para k = 1, 2, 3, …, 9, 10
Tabla con las probabilidades de que el ruletista viva o muera si juega k veces a la ruleta rusa, para k = 1, 2, 3, …, 9, 10Podemos sacar entonces algunas conclusiones. Para empezar la probabilidad de morir es menor que el 50 % para los casos de una sola partida de la ruleta rusa (16,67 %), dos partidas (30,56 %) e incluso tres partidas (42,13 %). Luego en esos casos hay más probabilidades de ganar que de perder. El problema es que, si el jugador pierde, ha perdido algo tan importante e irrecuperable como es su propia vida. Además, cuando se dice que después de la tercera partida era considerado un ruletista afortunado, aun estando de acuerdo -ya que se está jugando la vida- podemos decir que no era tan excepcional, ya que la probabilidad de salir con vida seguía siendo, como hemos comentado, menor que el 50 %.
Justo se supera la probabilidad del 50 %, es decir, la misma que de sacar cara, o cruz, al tirar una moneda al aire, cuando se juegan cuatro partidas a la ruleta rusa. En concreto, hay una probabilidad del 51,77 % de morir y una probabilidad del 48,23 % de vivir. De hecho, cuando en el relato se escribe que “no se conocían casos de supervivencia ni siquiera tras cuatro intentos”, esto podríamos explicarlo como que los ruletistas no se atrevían a arriesgarse con la cuarta partida, porque lo que nos dicen los fríos números es que, a la larga, entre todos los jugadores que jugasen cuatro partidas, más o menos la mitad de los mismos vivirían y la otra mitad moriría.
Si continuamos, cuando se juegan seis partidas, la probabilidad de vivir no es cero, de hecho, es todavía relativamente alta, ya que es, más o menos, uno de cada tres casos. Aunque, como hemos dicho antes, el jugador no se juega dinero, sino su propia vida, por lo que la apuesta es demasiado arriesgada para él.
Por otra parte, el viejo escritor cuenta que cuando él se encontró con el Ruletista ya había superado 8 partidas de la ruleta rusa solitaria. Salir con vida de ocho partidas, como se ve en la anterior tabla es, más o menos, del 25 %, es decir, uno de cada cuatro casos. Luego, aun siendo algo excepcional, no es tan raro. Dicho de otra forma, si jugasen muchas personas a la ruleta rusa solitaria en ocho ocasiones, de media, una de cada cuatro viviría, aunque eso sí, tres de cada cuatro, moriría. A partir de ahí la probabilidad continúa cayendo cada vez más y más.
Por otra parte, en cierto momento del relato, el Ruletista empieza a incluir más balas en el revólver, aunque el cálculo de las probabilidades, para una cantidad de balas entre 1 y 6, es similar al realizado previamente, lo dejamos como diversión para las personas que están leyendo esto, si así lo desean.
Para terminar, me gustaría comentar que el objetivo de escribir esta entrada del Cuaderno de Cultura Científica no es corregir el cuento de Mircea Cartarescu, que es un cuento de una calidad excepcional, sino de aprovechar la mención a la probabilidad para hablar de la misma y calcular con exactitud cuál es esa probabilidad mencionada. De hecho, mi recomendación es que, si no lo habéis hecho ya, leáis este magnífico cuento.
Terminaremos con un poco de humor negro de la mano de El Mundo Today y la noticia en clave de humor cuyo titular es: Uno de cada ocho jugadores de la ruleta rusa no llega a fin de mes; así como con el cortometraje, también en clave de humor, Ruleta (2015), de Álvaro Carmona, que podéis ver aquí.
 Fotograma del corto Ruleta (2015), dirigido por Álvaro Carmona
Fotograma del corto Ruleta (2015), dirigido por Álvaro CarmonaBibliografía
1.- Mircea Cartarescu, El ruletista, Impedimenta, 2010.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El cuento de la ruleta rusa se ha escrito en Cuaderno de Cultura Científica.
La comprobación experimental de la teoría postcuántica de la gravedad clásica
El pasado 4 de diciembre se publicaron un par de artículos científicos en los que se introducía el concepto de teoría postcuántica para referirse a la gravedad clásica. Un titular típico en la prensa para recoger estas publicaciones podría ser el de Xataka: Esta teoría reconcilia la relatividad general y la mecánica cuántica. Y lo que propone es revolucionario. Los científicos proponen un experimento para comprobar la nueva teoría consistente en “medir la masa de un objeto con muchísima precisión para determinar si su peso fluctúa con el tiempo.” Pero esa no es la única posibilidad, hay una más radical.
 Pesando una masa. Ilustración: Isaac Young
Pesando una masa. Ilustración: Isaac YoungLa mejor teoría de la materia que tenemos es la mecánica cuántica, que describe el comportamiento discreto (cuantizado) de las partículas microscópicas mediante ecuaciones de ondas. La mejor teoría de la gravedad es la relatividad general, que describe el movimiento continuo (clásico) de los cuerpos con masa a través de la curvatura del espaciotiempo. Estas dos teorías de gran éxito chocan a la hora de describir la naturaleza del espacio-tiempo: las ecuaciones de ondas cuánticas se definen en un espacio-tiempo fijo, pero la relatividad general dice que el espacio-tiempo es dinámico y se curva en respuesta a la distribución de la materia.
La mayoría de los intentos de resolver este conflicto se han centrado en la cuantificación de la gravedad, siendo las dos propuestas principales la teoría de cuerdas y la gravedad cuántica de bucles. El nuevo trabajo teórico de Jonathan Oppenheim y sus colaboradores lo que hace es dejar la gravedad como una teoría clásica y acoplarla a la teoría cuántica mediante un mecanismo probabilístico. Esta estrategia híbrida ha sido considera tradicionalmente como estéril, ya que llevaría a inconsistencias. Oppenheim las evita a costa de tener que insertar la probabilidad –una “tirada de dados”– en la evolución del espacio-tiempo.
Comprobando la teoría postcuánticaUna forma de ir delimitando qué modelo es más adecuado es lo que proponen los investigadores, medir las fluctuaciones de la masa de un objeto. Esto supone en realidad medir el tiempo de coherencia de un objeto masivo en una superposición cuántica, ya que el tiempo de coherencia puede relacionarse con la evolución de la métrica del espacio-tiempo. Los datos de tiempo de coherencia existentes ya se han utilizado para descartar ciertos rangos de parámetros para modelos híbridos clásico-cuánticos como el de Oppenheim. Pero, como decimos, estos experimentos no descartarían, solo limitarían.
Es mucho más radical y, por tanto, mucho más interesante, contestar a la pregunta fundamental: ¿la gravedad es cuántica o no? Una forma de hacerlo es detectando gravitones directamente, otra sería entrelazar dos objetos masivos solo con su interacción gravitacional. Esto que se resume así de fácil en una frase, tiene una complejidad enorme.
 Ilustración: G. W. Morley/University of Warwick and APS/Alan Stonebraker
Ilustración: G. W. Morley/University of Warwick and APS/Alan StonebrakerSin embargo, ha habido avances significativos en la segunda idea. En 2017 se hicieron dos propuestas en este sentido que, si bien difieren en los detalles, se basan en el mismo concepto: dos masas (microesferas, por ejemplo) interactúan solo a través de su atracción gravitacional mutua. Si estas masas se entrelazan mecanocuánticamente, entonces la gravedad debe ser la culpable. Para quedar entrelazadas por la gravedad, las masas deben estar en una superposición de estados cuánticos.
Si cada masa se coloca en uno de dos interferómetros próximos, que crearían la superposición. Si las masas están entrelazadas cuando salen de los interferómetros, esto implicaría que la gravedad es inherentemente cuántica, ya que solo un campo cuántico puede inducir el entrelazamiento.
Los experimentos están plagados de obstáculos técnicos, entre ellos cómo garantizar que la gravedad sea la única forma en que las masas interactúen. Pero están más cerca de realizarse que otros métodos propuestos, como la detección directa de gravitones. Para que estos experimentos se realicen, los investigadores deben descubrir cómo crear y mantener superposiciones cuánticas de objetos relativamente masivos y cómo reducir los efectos de fuerzas distintas a la gravedad.
Referencias:
Oppenheim, J. (2023) A Postquantum Theory of Classical Gravity? Physical Review X doi: 10.1103/PhysRevX.13.041040
Oppenheim, J., Sparaciari, C., Šoda, B. et al. (2023) Gravitationally induced decoherence vs space-time diffusion: testing the quantum nature of gravity. Nat Commun doi: 10.1038/s41467-023-43348-2
Marletto, C. and Vedral, V. (2017) Gravitationally Induced Entanglement between Two Massive Particles is Sufficient Evidence of Quantum Effects in Gravity Phys. Rev. Lett. doi: 10.1103/PhysRevLett.119.240402
Bose, S. et al. (2017) Spin Entanglement Witness for Quantum Gravity Phys. Rev. Lett. doi: 10.1103/PhysRevLett.119.240401
Galley, T. (2023) Might There Be No Quantum Gravity After All? Physics 16, 203
Para saber más:
Teoría de la invariancia (serie)
Incompletitud y medida en física cuántica (serie)
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La comprobación experimental de la teoría postcuántica de la gravedad clásica se ha escrito en Cuaderno de Cultura Científica.
Eris, de planeta enano a planeta “blandito”
Aunque un gran desconocido para el público, Eris es el segundo planeta enano más grande de nuestro Sistema Solar, solo por detrás de Plutón. Fue descubierto en 2005, trayendo la discordia y un fuerte debate al mundo de la astronomía que obligó a repensar a que llamábamos planeta.
Esta disputa concluiría con la aparición de una nueva categoría -la de planeta enano- que nos devolvió a un Sistema Solar de ocho planetas… pero en el que ya hay nueve planetas enanos de los cuales -salvo en los casos de Ceres y Plutón- hemos podido ver muy poco debido a las enormes distancias que nos separan y el exiguo número de misiones dedicadas a estos cuerpos.
A pesar de las dificultades que impone la distancia y el tamaño de estos cuerpos, las observaciones de Eris realizadas desde los mejores telescopios nos permiten conocer algunos detalles interesantes que nos dan una idea sobre como podía ser este planeta enano.
 Secuencia de imágenes donde se descubrió Eris en 2005 tomadas desde el observatorio del Monte Palomar, en California. Imagen Cortesía de NASA/JPL/Caltech.
Secuencia de imágenes donde se descubrió Eris en 2005 tomadas desde el observatorio del Monte Palomar, en California. Imagen Cortesía de NASA/JPL/Caltech.Estos datos apuntan a una superficie muy blanca y reflectante -refleja el 96% de la luz solar- algo que contrasta con la de Plutón, que refleja mucha menos luz y que -a grandes rasgos-es de un color bastante rojizo, algo que podría indicar que el hielo que cubre Eris se renueva -ahora mismo sería difícil de saber si por procesos internos o externos- y que, por lo tanto, existe cierta dinámica activa en el planeta.
Eris tiene un satélite llamado Disnomia, con un diámetro aproximado de 615 kilómetros, lo que viene a ser una cuarta parte del de Eris, y que orbita a una distancia de este de unos 37.000 kilómetros. La existencia de este satélite fue la que permitió a los científicos calcular la masa de Eris con gran precisión y empezar a hacer asunciones sobre su composición y estructura interna.
Pues bien, un nuevo estudio publicado en la revista Science Advances ha analizado la relación orbital entre Eris y Disnomia para arrojar algo de luz sobre la estructura interna de Eris o, al menos, para construir una serie de modelos muy interesantes que nos permitan conocer más detalles sobre su interior y evolución, algo que a su vez nos daría pistas sobre una posible dinámica interna.
Para hablar de las conclusiones de este estudio, tenemos que remontarnos prácticamente a la formación del Sistema Solar, hace unos 4500 millones de años. En esta infancia de nuestro sistema planetario, Eris habría sufrido un gran impacto, bien arrebatándole una gran cantidad de materia de su manto -en torno a un 15%- o bien, debido al enorme calor generado por el impacto, se podría haber perdido un porcentaje importante de los elementos volátiles que lo componían. Este impacto resultaría en la formación de Disnomia.
 Imagen tomada por el telescopio espacial Hubble donde se puede apreciar a Eris y a Disnomia, junto con una escala para hacernos a la idea de la distancia. Cortesía de NASA, ESA y M. Brown.
Imagen tomada por el telescopio espacial Hubble donde se puede apreciar a Eris y a Disnomia, junto con una escala para hacernos a la idea de la distancia. Cortesía de NASA, ESA y M. Brown.La consecuencia más inmediata para Eris sería el haberse convertido en un planeta enano más denso y que destaca tanto con respecto a Plutón, por ejemplo, y otros objetos, ya que ese calor habría sublimado o evaporado un gran volumen de elementos volátiles y alterado la proporción hielo/roca del planeta.
Pero hay más: Disnomia se habría formado mucho más cerca de Eris de lo que lo está ahora, provocando importantes mareas sobre Eris (y viceversa). Esta energía generada por las mareas se transformaría, en primer lugar, en calor, pudiendo alimentar fenómenos criovolcánicos y el rejuvenecimiento de la superficie e incluso, quién sabe, si la formación de un océano de agua líquida debajo de su corteza al poder mantener unas temperaturas más elevadas que las que podría haber hoy en día.
Pero esta disipación de la energía generada por las mareas también tendría un componente digamos que… astronómico, capaz de alterar, por un lado, la órbita de Disnomia, que progresivamente se ha ido alejando de Eris y, por otro, provocando el acoplamiento de mareas entre ambos cuerpos.
Este acoplamiento provoca que Eris y Disnomia siempre se “vean” la misma cara, ya que el periodo de rotación de ambos cuerpos y el de traslación de Disnomia están sincronizados, como ocurre con nuestra Tierra y la Luna. Aunque nos parezca algo extraño, es bastante común en nuestro sistema planetario.
 Impresión artística del sistema Eris-Disnomia. Cortesía de NASA/JPL-Caltech.
Impresión artística del sistema Eris-Disnomia. Cortesía de NASA/JPL-Caltech.Este detalle sugiere que el sistema ha alcanzado una configuración estable a lo largo de millones -probablemente miles de millones- de años y que Eris es un cuerpo que es capaz de disipar una gran cantidad de energía generada por su interacción con Disnomia, lo que hace pensar a los científicos que no es un cuerpo totalmente rígido, sino que todavía podría sufrir cierta convección en su capa intermedia de hielo gracias al calor de generado por la disipación de la energía de mareas y también de la desintegración de elementos radioactivos que todavía podrían quedar en su núcleo rocoso, que transferiría ese calor hacia la superficie. De aquí la broma del título de planeta “blandito”.
Precisamente, esta mayor disipación también apuntaría a que Eris sería un cuerpo totalmente diferenciado, es decir, formado por distintas capas -en este caso probablemente una corteza más rígida de hielo en la superficie, un manto de hielo en estado viscoso y en convección y por último un núcleo rocoso- como ocurre en nuestro planeta, en vez de ser una mezcla más o menos homogénea de roca y de hielo como se piensa que podrían ser otros planetas enanos.
Conocer la estructura de estos cuerpos podría ayudarnos en el futuro a estudiar detalles sobre su habitabilidad -presente y pasada- o a reconstruir su historia, algo muy valioso de cara a comprender la compleja dinámica de nuestro Sistema Solar, especialmente durante sus primeras etapas.
Referencias:
Nimmo, F. and Brown, M.E. (2023) The internal structure of Eris inferred from its spin and Orbit Evolution Science Advances doi: 10.1126/sciadv.adi9201
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Eris, de planeta enano a planeta “blandito” se ha escrito en Cuaderno de Cultura Científica.
Comunismo originario en la prehistoria ibérica
Al leer el libro que les traigo hoy, he tenido la impresión de estar ante un (breve y muy bien escrito) tratado de arqueología de la Prehistoria Reciente.

El tratado comienza con unas consideraciones acerca de la naturaleza de la historia como disciplina. El autor quiere indagar acerca del origen de las desigualdades y las relaciones de dominación. Le interesan las sociedades en las que no habían surgido estados y en las que las relaciones entre sus miembros no eran de dominación. Y se remite –para glosar brevemente sus obras– a los autores de los siglos XVII, XVIII y XIX, aunque sus aportaciones no sean hoy consideradas fuentes fidedignas, sino que han de ser valoradas por las preguntas que se hicieron, las ideas que empezaron a hacer circular y por seguir siendo fuente de inspiración.
Dominación y desigualdadEn una de sus primeras aseveraciones, el autor, Rodrigo Villalobos García, sostiene que la dominación y la desigualdad no son relaciones sociales necesarias, eternas o inevitables, sino consecuencia de circunstancias históricas concretas. La afirmación me llamó la atención porque hacía unos pocos años había leído Against the grain: A Deep History of the Earlier States, de James C. Scott, y hace unos meses, The Dawn of Everything: A New History of Humanity, de David Graeber y David Wengrow. En ambos libros se sostienen, expresadas de forma diferente, tesis similares.
Si se me permite un inciso, la obra de Scott, aunque menos conocida en España que la de Graeber y Wengrow, y no tan extensa, me pareció más profunda y mejor documentada. Creo que no está traducida al español (la de los dos David, sí lo está). Scott estudia los albores del sedentarismo y las primeras aldeas en el Creciente Fértil, sobre todo en Mesopotamia.
Su conclusión es que lo que conocemos como neolitización no fue algo lineal, que hubiese obedecido a una trayectoria preestablecida (como se nos enseñó en la escuela), sino que fue un proceso irregular, con idas y vueltas, en el que las sociedades cambiaron de unas formas de vida a otras. Los cereales, su cultivo y las posibilidades de ser almacenados, generando excedentes, fue lo que, según el autor, acabó conduciendo a la aparición de las desigualdades estructurales y los estados.
Graeber y Wengrow no difieren demasiado –al menos para las entendederas de un humilde fisiólogo de animales– de lo que sostiene Scott, pero basan su análisis, sobre todo, en los pueblos originarios de Norteamérica y, en especial, de la costa Oeste. Me pareció que incurrieron en un cierto cherry picking. Sea como fuere, todos ellos, Scott, Graeber y Wengrow, y Villalobos García, vienen a coincidir en esa idea fundamental. Hasta aquí el inciso.
Comunismo originario en la PrehistoriaTras la introducción de las nociones fundamentales, Villalobos García aborda la noción del comunismo originario (que califica de esquiva) y caracteriza los diferentes tipos de sociedades sin gobierno: igualitarias, de rango y estratificadas, que no deben entenderse como peldaños en una escalera que conduce a sociedades con estados. A continuación se ocupa de los orígenes de la familia (el patriarcado), la propiedad privada y el estado. Sostiene que los estados arcaicos han sido menos poderosos, jerarquizados, desiguales y patriarcales que muchos otros estados desarrollados con posterioridad, aunque las semillas de esas desigualdades ya se encontraban en aquellos.
En ciertas sociedades sin estado los recursos se gestionan de forma colectiva, el trabajo se desempeña mediante asociación libre, hay democracia directa y aplican el principio «de cada uno según sus capacidades y a cada cual según sus necesidades»; esto es, se cumplen los requisitos para ser consideradas sociedades comunistas, aunque haya gran diversidad entre ellas. Pero, por otro lado, otras sociedades sin estado son patriarcales, explotan a parte de sus integrantes y practican la conquista. En otras palabras, la ausencia del estado no conlleva ausencia de opresión.
No hay sociedades naturalesConcluye el autor el capítulo dedicado al comunismo originario con una idea muy poderosa: no hay sociedades naturales. Añade: «Nunca las ha habido. Si acaso habrá una base de instintos biológicos que se pueden manifestar de distintas maneras en distintas personas de una sociedad y que, según el caso, pueden ser fomentados o desincentivados por condicionantes medioambientales varios, así como, también, por la propia cultura o subcultura en cada caso.»
Este aspecto me interesa especialmente porque, en efecto, los seres humanos no estamos dotados de serie con unos rasgos que nos hacen comportarnos de una u otra forma. Y, por lo tanto, las sociedades que conformamos no son consecuencia de decisiones o actuaciones condicionadas por esos rasgos. La falacia naturalista, también en aspectos como este, ha sido fuente de inspiración para estudiosos (y para muchos amateurs). No hay una sociedad natural. Y si la hubiera, no tendría por qué ser la buena.
Bipolos como generosidad/egoísmo, belicosidad/pacifismo, individualismo/colectivismo, y cualesquiera otros que se nos puedan ocurrir se encuentran en diferente grado en todas o casi todas las personas. Y si bien es cierto que hay personas más inclinadas a la compasión que a la indiferencia, por ejemplo, también lo es que la situación en que nos encontramos es el factor que más suele influir en nuestro comportamiento y, por tanto, el que inclina el bipolo hacia uno de los componentes. Las sociedades son, en consecuencia, una amalgama diversa de las interacciones entre personas entre las que suele haber bastante diversidad.
No hay una sociedad natural. Aunque también podría decirse que todas las sociedades humanas lo son. En otras palabras, la naturaleza no aboca a un único modelo social.
La observación manchada de teoríaLa arqueología, durante las últimas décadas, ha actualizado su arsenal metodológico, incorporando técnicas propias de las ciencias naturales. Esa transición, no obstante, no ha modificado el carácter básico de la disciplina. Sus practicantes, en función de su particular visión de la realidad, formulan modelos explicativos que pretenden dar cuenta de las observaciones (hallazgos) poniéndolas en un contexto narrativo coherente. En otras palabras, en arqueología hacen algo muy parecido a lo que hacemos en ciencias experimentales y naturales.
En estas disciplinas, en muchas ocasiones, hacemos experimentos en los que controlamos las condiciones y fijamos potenciales fuentes de variación para determinar la existencia e intensidad de los efectos cuya existencia pretendemos establecer, pero en otras ocasiones trabajamos como la haría un historiador. De hecho, hay disciplinas –en geología y biología, principalmente–que son intrínsecamente históricas.
Por otro lado, en determinadas ciencias experimentales y naturales, la visión de la realidad, las teorías en que se enmarcan los estudios, las hipótesis de las que parten las investigaciones, también influyen en los modelos que proponemos para explicar las observaciones. Esto extrañará a más de uno de mis colegas, pero es así. La observación (prácticamente) siempre está manchada de teoría.
Interpretando la PrehistoriaEn el cuarto capítulo se describen las principales líneas de pensamiento que durante el siglo XX han interpretado la Prehistoria reciente –en especial la de Occidente–, a cargo de autores como Childe, Renfrew, Gimbutas y Sherratt. Me ha alegrado ver el nombre de Colin Renfrew entre los autores de referencia, porque siendo estudiante universitario (a caballo entre los setenta y los ochenta del pasado siglo) leí un artículo suyo en Investigación y Ciencia que no he olvidado: trataba de la expansión simultánea, de carácter démico, de las lenguas indoeuropeas y el Neolítico por Europa.
Por fin en el último capítulo, cuyo título es el del libro, se presentan y discuten los hallazgos arqueológicos más relevantes y lo que de ellos cabe inferir sobre las relaciones de poder entre hombres y mujeres, entre clases sociales y entre grupos humanos, en la península Ibérica durante la Prehistoria Reciente.
Finaliza el autor remarcando la idea de que no hay trayectorias históricas prefijadas, y que, dado que en el pasado el futuro estuvo abierto, igualmente abierto lo está en la actualidad. En otras palabras, las sociedades no están condenadas a transitar por cauces preestablecidos. El autor deja clara su posición ideológica –lo que es de agradecer–, sin que esa posición sesgue el contenido de un texto que me ha parecido muy interesante.
Ficha:
Título: Comunismo originario y lucha de clases en la Iberia prehistórica. Arqueología social del neolítico, Calcolítico y Bronce Antiguo
Autor: Rodrigo Villalobos García
Ed. Sabotabby Press, 2022.
En Editoralia personas lectoras, autoras o editoras presentan libros que por su atractivo, novedad o impacto (personal o general) pueden ser de interés o utilidad para los lectores del Cuaderno de Cultura Científica.
Una versión de este texto apareció anteriormente en Lecturas y Conjeturas (Substack).
El artículo Comunismo originario en la prehistoria ibérica se ha escrito en Cuaderno de Cultura Científica.
Aulas virtuales o LMS en la educación presencial

La jornada Las Pruebas de la Educación tuvo lugar con el objetivo de analizar la validez de las estrategias educativas puestas en marcha durante los últimos años. El enfoque STEAM o las clases virtuales fueron analizados desde la evidencia científica por un grupo de expertos y expertas que se reunió en la Facultad de Educación de Bilbao de la Universidad del País Vasco. La jornada, fruto de la colaboración entre la Cátedra de Cultura Científica de la Universidad del País Vasco y la facultad de Educación de Bilbao, tuvo lugar el 27 de octubre pasado.
Esta sexta edición volvió a estar dirigida a profesionales del ámbito de la educación y a quienes, en un futuro, formarán parte de este colectivo. Su objetivo ha sido reflexionar, desde la evidencia científica, sobre la validez de las estrategias utilizadas hoy en día. El seminario ha contado, una vez más, con la dirección académica de la vicedecana de Investigación y Transferencia de la Universidad Autónoma de Madrid, Marta Ferrero González.
La decana de la facultad de Educación de Bilbao de la UPV/EHU, Urtza Garay Ruiz, doctora en psicodidáctica e investigadora en tecnología educativa, habla en esta charla de cómo usar de forma responsable y eficaz las aulas virtuales cuando la educación es presencial.
Edición realizada por César Tomé López
El artículo Aulas virtuales o LMS en la educación presencial se ha escrito en Cuaderno de Cultura Científica.
¿Las tecnologías digitales están corrompiendo la educación obligatoria?
Desde que el mundo es mundo, la tecnología ha estado presente en nuestro día a día. En el paleolítico inferior el Homo habilis empezó a utilizar herramientas de piedra: a partir de ahí, la humanidad no ha parado de generar nuevos objetos a base de los elementos que iba encontrando en su entorno más cercano. No debemos olvidar que la tecnología es todo aquello creado por el hombre, que no se puede encontrar por sí mismo en la naturaleza.
Esos elementos han supuesto un cambio en la manera en que hacemos las cosas, mejorando notablemente nuestra calidad de vida. Pero no todo ha sido de color de rosa. Toda innovación tecnológica ha tenido detractores. La época actual no iba a ser diferente y existe una corriente, cada vez más generalizada, dispuesta a achacar a los avances tecnológicos todos los males de esta sociedad. En el terreno educativo, el foco del debate se ha puesto en la siguiente pregunta dicotómica, a mi juicio, tendenciosa: ¿debemos usar los ordenadores en el aula?
Toda tecnología tiene implícitas unas ventajas y unos inconvenientes. En Educación, se traducen en ayudas y en riesgos para enseñar, para aprender y para la salud. No existe estudio que niegue rotundamente esa cuestión, ni lo habrá. Por lo tanto, la pregunta inicial no debiera ser esa. El debate no gira en usar o no usar tecnología digital en las aulas.
 Foto: Tianyi Ma / UnsplashLas tecnologías no van a desaparecer
Foto: Tianyi Ma / UnsplashLas tecnologías no van a desaparecer
Los avances tecnológicos vienen para quedarse y posicionarnos a favor o en contra no aporta nada a la educación. Además, algunas personas lo plantean como un versus entre lo digital y lo analógico, una pelea en la que debe ganar una de las dos tecnologías. Olvidan que el libro de texto impreso también es una tecnología, sujeta a ventajas e inconvenientes, igual que esos ordenadores, pantallas, móviles y demás aparatos digitales que demonizan.
Vivimos tiempos convulsos, un periodo de grandes transformaciones sociales que influyen constantemente en las nuevas políticas educativas. Eso genera confusión, tanto en los docentes como en los estudiantes y las familias, respecto a la formación del ciudadano del siglo XXI que deseamos fomentar en nuestras escuelas. Sin embargo, la importancia de desarrollar la competencia digital en nuestro alumnado sigue siendo una constante inalterable.
En España, desde la promulgación de la Ley Orgánica de Educación en 2006 hasta la más reciente Ley Orgánica de Mejora de la Ley Orgánica de Educación en 2020, el foco de la formación en la etapa obligatoria ha sido promover un alumnado “multialfabetizado”.
Esa visión implica que, además de adquirir habilidades en lectoescritura, matemáticas y un conocimiento básico en áreas como idiomas, ciencias sociales, naturales, artísticas y culturales, los estudiantes deben ser capaces de enfrentarse a los retos de la sociedad de la información y la comunicación.
Cinco áreas claveLa iniciativa DigComp (Digital Competence Framework), impulsada por la Comisión Europea en 2013 y actualizada de forma continua desde entonces, ha obligado a los sistemas educativos a nivel nacional y autonómico a tomar diversas medidas para asegurar, entre su alumnado, múltiples competencias en cinco áreas clave.
Se busca que el ciudadano que salga de la escuela sea capaz de:
- Buscar, evaluar y organizar información.
- Comunicarse, colaborar y participar en entornos digitales.
- Crear, editar y publicar contenido digital.
- Protegerse de los riesgos asociados al uso de la tecnología y garantizar su privacidad.
- Identificar, analizar y resolver problemas típicos relacionados con el uso de las herramientas tecnológicas.
Lamentablemente, la práctica común de algunos sistemas educativos ha sido tomar medidas para la consecución de la multialfabetización de su alumnado mediante una implementación irreflexiva e indiscriminada de tecnología en las escuelas. En ese modo de actuar subyace una idea errónea basada en las bondades per se de la tecnología digital en los procesos educativos, no respaldada por evidencia alguna.
La literatura científica no ha aceptado la hipótesis de que a más tecnología en el aula se produzcan mejores resultados académicos. Por lo tanto, no se puede afirmar que exista una relación directa, lineal y automática entre esas dos variables, más allá del efecto causal hacia la mejora de la competencia digital del alumnado.
En el campo de la tecnología educativa destinada a estudiar el uso de diferentes herramientas y recursos tecnológicos para mejorar los procesos de enseñanza-aprendizaje existe una máxima que todos los investigadores asumen: la cuestión no es tecnológica, sino pedagógica. Cualquier herramienta o recurso que integrar en educación debe ser analizado desde el prisma del objetivo a lograr. Por lo tanto, la pregunta que nos tenemos que hacer es qué queremos conseguir.
El discente medio no existeSi hablamos de la educación obligatoria, debemos tener en cuenta la necesidad de responder a la diversidad del alumnado existente en nuestras aulas. Los últimos avances en neurociencias derivados por estudios científicos nos informan de esa variabilidad en la manera de aprender.
No obstante, se puede simplificar el aprendizaje a través de un modelo denominado Diseño Universal para el Aprendizaje basado en tres redes neuronales interdependientes:
- Una red afectiva que regula la implicación del alumnado en su aprendizaje.
- Una red de reconocimiento que permite procesar la información que se requiere.
- Una red estratégica que garantiza la acción y la expresión de lo aprendido.
Ese modelo propugna la utilización de diferentes opciones, estrategias y recursos. Y es en esa diversidad de soportes donde podemos encontrar la respuesta a nuestro dilema. Las pantallas, los ordenadores e internet tienen cabida junto a una gran diversidad de otras herramientas sobre la base de una reflexión previa y un diseño que acepte la variabilidad de nuestro alumnado y no intente buscar lo imposible, una planificación para un discente medio que no existe.
Lo importante en nuestras escuelas de educación obligatoria es programar actividades que utilicen una selección variada de herramientas, incluidas las digitales, que garantice a todo el alumnado, sin excepción e independientemente de sus características individuales, su motivación y compromiso, un procesamiento propio de la información y una puesta en práctica de lo aprendido.
A modo de conclusión, es importante subrayar que las tecnologías digitales no están corrompiendo la educación, pero tampoco podemos decir que la estén mejorando por el simple hecho de que se hayan naturalizado en nuestras aulas. Solo con una planificación sosegada hacia una escuela para todos nos puede llevar a un desenlace positivo en su integración.
Sobre el autor : Daniel Losada es Profesor Titular de Universidad en el Departamento de Didáctica y Organización Escolar. Facultad de Educación, Filosofía y Antropología, UPV/EHU
Una versión de este texto apareció originalmente en campusa.
El artículo ¿Las tecnologías digitales están corrompiendo la educación obligatoria? se ha escrito en Cuaderno de Cultura Científica.
I lava (que no magma) you
 Foto: Martin Sanchez / Unsplash
Foto: Martin Sanchez / UnsplashAunque parece que, de momento, no vamos a tener una nueva erupción en Islandia, voy a aprovechar que sigue siendo noticia para traer, una semana más, algunas curiosidades volcánicas.
Una de las cosas que más nos llama la atención de los volcanes, hasta quedarnos mirándolos de manera hipnótica, es ver salir la lava del cráter y deslizarse como si fuese un enorme río de fuego por el terreno, arrasando todo lo que se pone en su camino. Pero, ¿qué es la lava?
Para responder a esta pregunta tenemos que viajar al interior de la Tierra. En concreto, al manto superior y la base de la corteza. Es ahí donde se forma el magma, un material compuesto por rocas fundidas muy calientes y gases. Pero, al contrario de lo que podemos pensar, el magma de nuestro planeta es muy escaso, menos de un 6% de las rocas del manto están fundidas, ya que para que pierdan su componente sólida y los minerales que las forman alcancen el punto de fusión tiene o bien que aumentar la temperatura, o que bajar la presión a la que están sometidas o hay que incorporar agua y/o gases disueltos a la ecuación, y esto solo sucede en contextos geológicos muy concretos, como los límites de las placas tectónicas.
De acuerdo a su composición, los magmas se pueden clasificar en dos grandes grupos. Los magmas ácidos, que son muy ricos en sílice (SiO2) y pobres en ferromagnesianos (minerales que incluyen hierro y magnesio en su composición), tienen una temperatura relativamente baja que permite que cristalicen algunos minerales y son muy viscosos. Y los magmas básicos, pobres en sílice y ricos en ferromagnesianos, de temperatura más elevada y menos viscosidad, por lo que son más fluidos.
¿Y qué tiene que ver todo esto con la lava? Pues muy sencillo. Cuando el magma asciende hacia la superficie y consigue salir al exterior a través de un volcán, pierde los gases. A ese material fundido desgasificado es a lo que denominamos lava y sus propiedades van a depender de las características del magma del que procede.
Cuando la lava discurre por el terreno forma lo que se conoce como colada de lava, una acumulación de materiales volcánicos que cubren la superficie como una especie de costra que ha crecido sobre el suelo. Y, de acuerdo al aspecto exterior y la morfología que adquieren, podemos diferenciar tres tipos de coladas de lava, cuyos nombres son una chuleta que nos permiten acordarnos fácilmente de sus características y propiedades:
Por una lado tenemos las coladas de tipo aa (del hawaiano ‘A’ā, que significa áspero), que tienen una superficie irregular, rugosa y afilada. Se forman a partir de lavas viscosas y de temperaturas no demasiado elevadas (inferiores a 900-1000°C) que avanzan lentamente (a escalas de metros por minuto) formando frentes de coladas que alcanzan decenas y cientos de metros de altura. Es habitual que la parte externa de estas coladas se enfríe rápidamente y empiece a solidificarse, lo que provoca que el avance de la lava aún fundida de su interior genere la caída de bloques volcánicos en el frente, dando lugar a un característico sonido de cristales rotos. Por este motivo también se las denomina coladas en bloques. Y en Canarias se las conoce con el nombre de malpaís porque es difícil caminar sobre ellas una vez enfriadas, además de que es muy costoso trabajar estos terrenos.
 Lavas aa o en bloques del volcán Kilauea, en la isla de Hawaii. Fotografía del Servicio Geológico de Estados Unidos (USGS) / Wikimedia Commons
Lavas aa o en bloques del volcán Kilauea, en la isla de Hawaii. Fotografía del Servicio Geológico de Estados Unidos (USGS) / Wikimedia CommonsPor el otro lado nos encontramos las lavas pahoehoe (también procedente del hawaiano, pāhoehoe, y que significa suave), que son todo lo contrario a las anteriores, ya que adquieren una superficie exterior mucho más lisa. En este caso son producidas por lavas más fluidas y calientes (con temperaturas por encima de los 1000°C) que avanzan con rapidez (en velocidades de metros por segundo). Incluso pueden adoptar unas morfologías similares a cuerdas o cordones entrelazados a las que se llama lavas cordadas.
 Lavas pahoehoe del volcán Kilauea, en la isla de Hawaii. Fotografía de J.D. Griggs (Servicio Geológico de Estados Unidos, USGS) / Wikimedia Commons
Lavas pahoehoe del volcán Kilauea, en la isla de Hawaii. Fotografía de J.D. Griggs (Servicio Geológico de Estados Unidos, USGS) / Wikimedia CommonsY el tercer tipo son las lavas almohadilladas, o pillow lavas en inglés. Estas son particulares, ya que se forman en erupciones submarinas donde la lava se enfría rápidamente al entrar en contacto con el agua dando lugar a formas redondeadas ligeramente cilíndricas que recuerdan a las almohadas.
 Lavas almohadilladas (pillow lavas) recogidas en Enekuri (Bizkaia) y expuestas en el paseo geológico del Arboretum del Campus de Leioa de la Universidad del País Vasco (UPV-EHU). Se formaron a finales del Cretácico Inferior (hace unos 100 millones de años) debido al vulcanismo submarino provocado durante la apertura del Golfo de Bizkaia. Fotografía de Ane García Artola (Departamento de Geología, Facultad de Ciencia y Tecnología, Universidad del País Vasco UPV-EHU).
Lavas almohadilladas (pillow lavas) recogidas en Enekuri (Bizkaia) y expuestas en el paseo geológico del Arboretum del Campus de Leioa de la Universidad del País Vasco (UPV-EHU). Se formaron a finales del Cretácico Inferior (hace unos 100 millones de años) debido al vulcanismo submarino provocado durante la apertura del Golfo de Bizkaia. Fotografía de Ane García Artola (Departamento de Geología, Facultad de Ciencia y Tecnología, Universidad del País Vasco UPV-EHU).Ya veis que, en Geología, no nos comemos mucho la cabeza a la hora de darle nombre a las cosas y siempre buscamos denominaciones muy sencillas, directas, gráficas y, sobre todo, fáciles de recordar, que bastantes cosas tenemos ya en la cabeza como para aprender nombres raros de más. Pero lo que tampoco espero que olvidéis es la diferencia entre magma, un fundido gaseoso depositado en el interior de la Tierra, y lava, el fundido que ha perdido los gases al salir a superficie. Por eso, por mucho que estudiemos las rocas volcánicas y cojamos muestras de lava tras una erupción, nunca podremos reconstruir por completo las características originales del magma del que procede, ya que hemos perdido los gases. Aunque lo que nunca perderemos será la infantil admiración ante una erupción volcánica.
Para saber más:
Montañas y mitos
La Geología según Heracles
Los volcanes submarinos de Bizkaia y Gipuzkoa
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo I lava (que no magma) you se ha escrito en Cuaderno de Cultura Científica.
Herta Taussig Freitag: «Quiero convertirme en una buena profesora de matemáticas»
Por fin he encontrado una materia en la que no necesito memorizar, sino que puedo pensar por mí misma: las matemáticas. (1921).
Quiero ser profesora de matemáticas. No sé si seré suficientemente buena (Poco tiempo más tarde).
No quiero ser simplemente profesora de matemáticas. Quiero convertirme en una buena profesora de matemáticas. (Seis años más tarde).
Diario de Herta Taussig
 Herta Taussig Freitag. Fuente: Hollins Digital Commons.
Herta Taussig Freitag. Fuente: Hollins Digital Commons.Herta Taussig nació el 6 de diciembre de 1908 en Viena, Austria. Era hija de Paula Caroline Sara Taussig y Josef Heinrich Israel Taussig. Herta tenía un hermano mayor, Walter Adolf Taussig, nacido también en 1908, el 9 de febrero. La pasión de Walter era la música; se dedicó a ella profesionalmente llegando a ser director de varias orquestas, al principio en Europa y posteriormente en Canadá y Estados Unidos.
Persiguiendo su sueño de convertirse en profesora de matemáticas (que plasmó en varias ocasiones en su diario), Herta ingresó en la Universidad de Viena con la intención de recibir formación para dedicarse después a la docencia en un gymnasium (centro de enseñanza secundaria).
Recibió el título de Magister Rerum Naturalium en matemáticas y física en la Universidad de Viena en 1934. Allí se cruzó con Kurt Gödel (1906-1978), quien había defendido su tesis en 1930 y trabajaba como Privatdozent desde 1933.
Taussig consiguió enseñar en la Universidad de Viena como Gymnasium Professor entre 1934 y 1938.
Huyendo a Reino UnidoSu vida cambió drásticamente a principios de marzo de 1938, cuando las tropas de la Alemania nazi invadieron Austria. Su padre era el editor del periódico Die Neue Frei Presse y había escrito varios artículos advirtiendo sobre los peligros del nazismo. Perdió su trabajo. Walter estaba de gira por Estados Unidos, allí no corría peligro. El resto de la familia se refugió en una casa de verano en las montañas intentando planificar sus desplazamientos posteriores para huir de la amenaza nazi.
Solicitaron refugio en Reino Unido. Pero este país no deseaba una inmigración a gran escala de profesionales que podían poner en peligro los empleos de los ciudadanos británicos. Aunque necesitaban empleadas domésticas, así que Herta solicitó uno de esos empleos para atender a dos mujeres mayores en Sussex. Unos meses más tarde, sus padres se pudieron reunir con ella. Herta pasó seis años en Inglaterra esperando poder emigrar con sus padres a Estados Unidos; trabajó como empleada doméstica, institutriz, camarera y finalmente como profesora de matemáticas. Su padre falleció en 1943. Herta y su madre obtuvieron finalmente un visado para entrar en Estados Unidos; en abril de 1944 se reunieron finalmente con Walter.
Estados Unidos como destino finalHerta consiguió trabajo en el Greer School, una escuela privada en el norte del estado de Nueva York. Allí enseño entre 1944 y 1948 y conoció al profesor de matemáticas Arthur Henry Freitag (1898-1978) con quien se casó en 1950.
En 1948 Herta comenzó a enseñar en una universidad privada para mujeres, el Hollins College en Roanoke, Virginia. Consiguió crear un Departamento de Matemáticas, alternando la docencia en el centro con su trabajo preparando su tesis doctoral en la Universidad de Columbia. Allí estuvo particularmente influenciada por los matemáticos Edward Kasner (1878-1956) y Howard Eves (1911-2004). Defendió su tesis doctoral en 1953 con la memoria titulada The Use of the History of Mathematics in its Teaching and Learning on the Secondary Level (El uso de la historia de las matemáticas en su enseñanza y aprendizaje en secundaria).
Junto a su marido, Arthur Freitag, escribió varios artículos conjuntos y la monografía The Number Story (National Council of Teachers of Mathematics, 1960).
Herta se jubiló anticipadamente en 1971 para cuidar de Arthur que había caído enfermo; él falleció siete años más tarde. Y, al quedarse sola, volvió a dar clases, a impartir conferencias en escuelas locales y a publicar numerosos artículos en revistas de educación matemática. De hecho, la mayor parte de su trabajo sobre los números de Fibonacci lo realizó tras su jubilación.
Publicó más de treinta artículos en Fibonacci Quarterly a partir de 1985. Esta revista matemática le dedicó su número de noviembre de 1996, cuando Herta cumplía 89 años, “en reconocimiento a sus años de destacado servicio y logros en la comunidad matemática a través de la excelencia en la enseñanza, la resolución de problemas, la docencia y la investigación”. La elección de la fecha no se decidió al azar: recordemos que 89 es el decimosegundo elemento de la sucesión de Fibonacci (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …).
Uno de sus colegas, recordando las palabras de Carl Friedrich Gauss (“Las matemáticas son la reina de las ciencias y la teoría de números es la reina de las matemáticas”), proclamó a Herta Freitag como la “reina de The Fibonacci Association”. Este “nombramiento” agradecía la constancia de esta matemática, que había presentado una ponencia en todas las conferencias internacionales de la Asociación desde la primera realizada en 1984, y había contribuido con numerosos artículos en la revista Fibonacci Quarterly.
Herta Taussig Freitag falleció el 25 de enero de 2000, tenía 91 años. Consiguió, sin duda, cumplir esos deseos que, de niña, anotó reiteradamente en su diario.
Referencias
-
Caren Diefenderfer, Herta Taussig Freitag. A personal reflection, Biographies of Women Mathematicians
-
John J. O’Connor and Edmund F. Robertson, Herta Taussig Freitag, MacTutor History of Mathematics Archive, University of St Andrews
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Herta Taussig Freitag: «Quiero convertirme en una buena profesora de matemáticas» se ha escrito en Cuaderno de Cultura Científica.
La nueva búsqueda para controlar la evolución
Los científicos modernos no se contentan con predecir la evolución de la vida. Quieren darle forma.
Un artículo de C. Brandon Ogbunu. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 James O’Brien para Quanta Magazine
James O’Brien para Quanta MagazineLa evolución es algo complicado. Gran parte de la biología evolutiva moderna busca reconciliar la aparente aleatoriedad de las fuerzas tras el proceso (cómo ocurren las mutaciones, por ejemplo) con los principios fundamentales que aplican a toda la biosfera. Generaciones de biólogos han albergado la esperanza de comprender lo suficiente la lógica de la evolución como para poder predecir cómo sucede.
Pero si bien la predicción sigue siendo un objetivo relevante, los científicos ahora se están centrando en otro mucho más ambicioso: el control sobre cómo sucede.
Esto puede parecer ciencia ficción, pero los mejores ejemplos de este esfuerzo están en nuestro pasado. Consideremos el proceso de selección artificial, término acuñado por Charles Darwin: hace miles de años, los humanos comenzaron a identificar plantas y animales con rasgos preferibles y a criarlos selectivamente, lo que amplificó esos rasgos en su descendencia. Este enfoque nos dio la agricultura, uno de los inventos culturales más transformadores de la historia de la humanidad. Posteriormente, la selección artificial en animales y plantas nos ayudó a comprender la genética y cómo evolucionan los genes en las poblaciones. Pero a pesar de lo eficaz que ha sido, la selección artificial sigue estando bastante limitada.
Esto es diferente de la selección natural, la fuerza que impulsa la evolución adaptativa en la Tierra, donde no hay ningún actor intencional que realice la selección. El actor seleccionador no es un criador humano, sino la naturaleza misma, que selecciona las variantes con mayor “aptitud”: aquellas con mayor probabilidad de sobrevivir y producir descendencia sana. Y cuando la naturaleza es la que selecciona, los resultados pueden ser difíciles de predecir.
Ahora los biólogos esperan establecer cómo ocurre la evolución a nivel molecular y ejercer tanto control directo sobre el proceso reproductivo como el que tenemos en los cultivos agrícolas. ¿Podemos orquestar la evolución, mutación a mutación, hacia el resultado que prefiramos?
Sorprendentemente, ya estamos a mitad de camino. El Premio Nobel de Química de 2018 reconoció el trabajo sobre un método llamado evolución dirigida, que permite a los científicos diseñar nuevas biomoléculas. Una de las ganadoras, Frances Arnold, fue pionera en una forma de mutar proteínas en el laboratorio y luego medir su funcionalidad (por ejemplo, lo bien que una enzima metaboliza el azúcar). Es entonces posible aislar las proteínas candidatas de interés, mutarlas y seleccionarlas más, hasta que generemos una proteína con función mejorada (en este caso, una enzima que metabolice el azúcar de manera muy eficiente). En este sentido, los químicos actúan como los criadores de perros, pero sin depender de la reproducción sexual para generar la descendencia proteica. Más bien, generan una población diversa de proteínas y miden sus propiedades en cuestión de horas. Y al seleccionar lo que quieren, controlan cómo ocurre la evolución.
A partir de este ejemplo queda claro que controlar la evolución (dirigirla hacia ciertos resultados) requiere el conocimiento de cómo ocurrirá la evolución junto con la tecnología para intervenir. Así que podemos pensar en el problema a través de la lente de una ecuación simple: Control = predicción + ingeniería.
Este control puede ser más sutil que el enfoque de Arnold. Un estudio de 2015 sugirió el uso de antibióticos en un orden determinado para evitar que la evolución cree patógenos resistentes a los antibióticos. Y algo similar está sucediendo con el tratamiento del cáncer: los oncólogos están tratando de aprovechar nuestra comprensión molecular del cáncer para dirigir las células cancerosas hacia la susceptibilidad a ciertos medicamentos. Esto es posible porque sabemos que cuando una célula cancerosa desarrolla resistencia a un fármaco puede volverse más susceptible a otros. Este concepto de “sensibilidad colateral” se basa en los principios fundamentales de las compensaciones en los sistemas biológicos: en general, no hay “almuerzos gratis” en la evolución, y la adaptación a menudo conlleva costes.
En trabajos más recientes, los científicos han generalizado estos enfoques. Utilizando ideas de la física cuántica, un equipo multidisciplinar (que incluye médicos, informáticos y físicos) ha aplicado un método llamado conducción contradiabática para llevar a una población hacia objetivos predeterminados. Por ejemplo, las infecciones causadas por algunas cepas de parásitos de la malaria son más fáciles de tratar que otras. Los investigadores podrían intentar «dirigir» las poblaciones de parásitos hacia cepas más fáciles de tratar.

Se están aplicando ideas similares a otros sistemas, como el microbioma, donde los biólogos evolutivos ahora utilizan la evolución dirigida para controlar comunidades microbianas como las que viven en nuestra piel y en nuestro intestino. Para ello, están utilizando el conocimiento de cómo ciertos microbios interactúan entre sí junto con nuevas técnicas microbianas que nos permiten introducir ciertos microbios en una población de otros microbios. La esperanza es que podamos utilizar este conocimiento para algún día dirigir la composición del microbioma hacia una que se asocie con mejores resultados de salud.
Estos avances demuestran que, de alguna forma, el control evolutivo es una cosa del presente, no del futuro. Pero los ejemplos de más éxito han tenido lugar en un pequeño número de entornos: microbios, comunidades microbianas y proteínas. Y lo que es más, los esfuerzos existentes se centran en el control durante períodos de tiempo cortos: ningún científico razonable pretende ser capaz de controlar la evolución molecular que actuando durante décadas o siglos (aparte de la selección artificial que ha tenido lugar durante milenios). El verdadero control sobre el proceso evolutivo sigue estando estrictamente limitado por nuestro conocimiento y herramientas actuales.
Si bien los desafíos técnicos del control evolutivo siguen siendo sustanciales, las barreras éticas también son notables. Los problemas se superponen con los relacionados con los organismos genéticamente modificados. Cuando diseñamos una mutación en una variedad de maíz que le confiere la capacidad de crecer incluso en ambientes estresantes, influimos en las generaciones futuras de esa variedad de maíz. Además, la selección de embriones en humanos puede parecerse a la selección artificial, dándonos la capacidad de controlar la aparición de rasgos humanos en poblaciones futuras. En general, las aplicaciones demasiado entusiastas de estas tecnologías pueden estar impulsadas por una especie de determinismo genético: la visión ingenua de que las diferencias significativas entre organismos dentro de una población pueden explicarse (principalmente) por su composición genética.
Si alguna vez intentáramos ingenuamente dirigir la evolución de los humanos y otros organismos en una escala temporal más larga, seríamos víctimas de una especie de determinismo evolutivo, que sostiene que podemos y debemos tener control total sobre cómo evoluciona la vida en el futuro. En última instancia, estas ambiciones están fuera de lugar. Subestiman el capricho de la evolución biológica: la dificultad de considerar todas las fuerzas que dan forma a cómo funciona y florece de la vida. Algunos podrían concebir que la inteligencia artificial puede ayudar a resolver estas incertidumbres. Pero la IA no es una panacea para la ignorancia. Es más eficaz cuando ya comprendemos las sutilezas del sistema que intentamos modelar y predecir. La biología evolutiva no cumple del todo con este estándar, al menos no todavía.
Podemos (y debemos) al mismo tiempo entusiasmarnos con la ambición de la biología moderna y tener la presencia de ánimo para reconocer nuestros límites. Por ejemplo, el movimiento eugenésico sugirió que la raza humana podría mejorarse utilizando el tipo de métodos que nos dieron animales y cultivos domesticados. Ahora entendemos que fue intolerante y se basó en una mala biología. Ejemplos como estos son advertencias y deberían enseñarnos que los intentos descuidados de controlar fuerzas tempestuosas como la evolución están destinados a fracasar.
El artículo original, The New Quest to Control Evolution, se publicó el 29 de noviembre de 2023 en Quanta Magazine.
Traducido por César Tomé López
El artículo La nueva búsqueda para controlar la evolución se ha escrito en Cuaderno de Cultura Científica.
El microbioma da pistas sobre el riesgo de sufrir cáncer anal
El virus del papiloma humano (VPH) es un patógeno muy común en el ser humano que se transmite principalmente por contacto sexual o piel con piel. Tan frecuente es que se calcula que entre el 80 y el 90 % de la población sexualmente activa se infecta por el VPH alguna vez en su vida. En muchos casos, esta infección desaparece por sí misma y pasa desapercibida. Sin embargo, en otras ocasiones esta puede provocar verrugas y, en el peor de los casos, cáncer.
 Imagen: Ally White / Pixabay
Imagen: Ally White / PixabayAlgunos tipos del VPH (hay más de 200 identificados) tienen la capacidad de transformar las células que infectan, que comienzan a proliferar de forma descontrolada originando, con el tiempo, tumores. El principal cáncer que provoca este conjunto de virus es el de cuello uterino, pero también puede causar cáncer genital, de boca, garganta o anal, entre otros. Para prevenir este desenlace, en España se incluye desde 2007 la vacuna contra el VPH en el calendario vacunal. Primero su administración se dirigió a niñas y ciertos grupos de riesgo y, con el tiempo, se ha extendido su aplicación a niños.
El colectivo de hombres que tienen sexo con hombres con el virus de la inmunodeficiencia humana (VIH) son un colectivo con especial riesgo de sufrir cáncer anal desencadenado por el VPH, pues tienen hasta 300 veces más riesgo de padecerlo que la población general. En la actualidad, la detección temprana de las lesiones en la región anal, provocadas por el virus del papiloma, que tienen una elevada probabilidad de convertirse en cáncer (conocidas como lesiones escamosas intraepiteliales de alto grado o HSIL) resulta un desafío. Normalmente, este tipo de neoplasia se detecta en una etapa tardía, tanto por su localización, como por sus síntomas y signos poco claros y específicos, lo que lleva a un peor pronóstico. Además, el método actual que se utiliza para el cribado de este tipo de lesiones, la citología anal, es poco específica (50 %): da con frecuencia muchos falsos positivos (casos detectados como de alto riesgo de cáncer que realmente no tienen este riesgo).
Detectar mejor el cáncer analHace unos meses, un equipo internacional de investigadores, entre los que se incluyen científicos españoles, mostraron al mundo un enfoque innovador para detectar el cáncer anal de forma temprana y con más precisión que con la citología actual: la detección de dos biomarcadores asociados al microbioma de la región anal: la cobalamina (vitamina B12) y el succinil-CoA. Este hallazgo se ha publicado en la revista Nature Medicine.
Para el estudio, se seleccionaron a 213 participantes con VIH, principalmente (94 %) hombres cis que tenían sexo con hombres, a los que se les realizaron endoscopias anales y biopsias (toma de muestras de las lesiones sospechosas de poder convertirse en tumores). Los voluntarios se dividieron, a su vez, en dos grupos: 167 pacientes para investigar qué biomarcadores asociados al microbioma podían indicar alto riesgo de cáncer (HSIL) y 46 pacientes para validar los resultados.
Los investigadores comprobaron que no había ninguna composición particular del microbioma que se asociara claramente con un elevado riesgo de cáncer. Sin embargo, sí que detectaron que aquellos pacientes con HSIL tenían en la región anal bacterias que producían más cobalamina y succinil-CoA que en circunstancias normales. Es decir, existía algún tipo de interacción entre las células precancerosas, con alto riesgo de provocar cáncer y las bacterias, que modificaban su nivel de síntesis de ambas moléculas. De hecho, cuanto mayor era el riesgo de que la lesión se convirtiera en un tumor maligno, más altas eran las concentraciones de ambos biomarcadores. Otras investigaciones han encontrado también interrelaciones entre ciertos tipos de cáncer y cambios en la microbiota, como la asociación de cierta composición de la microbiota vaginal con un mayor riesgo de cáncer de cérvix uterino o con una mayor probabilidad de detectar la presencia del VPH.
El paso siguiente de la investigación fue comprobar cuál era la capacidad para detectar HSIL si se consideraban los niveles de dichas moléculas en los 46 pacientes del grupo de validación. Los científicos descubrieron que el cribado mediante el análisis de la cobalamina y el succinil-CoA ofrecía resultados mucho mejores que la citología convencional. En concreto, la sensibilidad (la probabilidad para detectar como positivo un caso de HSIL) de este método era de un 96,6 % frente al 91,2 % que aportaba la citología. Además, la mejora era mucho más notoria en la especificidad: la detección de los niveles de ambas moléculas arrojaba una especificidad (la probabilidad de que una persona sin HSIL arroje un valor negativo en la prueba) del 81,8 %, en comparación con el 34,1 % de la citología.
En otras palabras, el análisis de la cobalamina y el succinil-CoA en muestras anales ofrecía muchos menos falsos positivos de pacientes con lesiones anales con un alto riesgo de transformarse en cáncer. Ante estos resultados, los autores proponen usar ambos biomarcadores derivados del microbioma para mejorar la actual estrategia de screening de cáncer anal mediante citología (un método que podría hacerse sin problemas en muchos entornos clínicos). Con este enfoque habría muchos menos falsos positivos y, por tanto, una menor necesidad de biopsias para descartarlos, lo que supondría menos riesgos para los pacientes y un uso más racional de los recursos sanitarios. En todo caso, serán necesarios más estudios para validar este enfoque de cribado y confirmar su utilidad. De ser así, el screening actual solo mediante citología anal podría combinarse o sustituirse con este método en los próximos años.
Sobre la autora: Esther Samper (Shora) es médica, doctora en Ingeniería Tisular Cardiovascular y divulgadora científica
El artículo El microbioma da pistas sobre el riesgo de sufrir cáncer anal se ha escrito en Cuaderno de Cultura Científica.
Cómo decidir la mejor opción ante un dilema moral
Quizás haya oído hablar o haya leído acerca del dilema del tranvía. Este es un dilema moral en el que se plantean dos alternativas: provocar la muerte de una persona para salvar la vida de varias o no hacerlo. Hasta ahora se ha asumido que quienes renuncian a provocar la muerte de una persona, aunque ello conlleve la pérdida de más vidas humanas, actúan guiados por el principio deontológico de no hacer daño de forma deliberada. Y que quienes, por el contrario, optan por sacrificar una vida para que se salven más, actúan en virtud de principios utilitaristas, pues buscan maximizar el número de vidas salvadas.
 Source: Bethesda Game Studios / Fallout 4
Source: Bethesda Game Studios / Fallout 4Las respuestas al dilema del tranvía se han interpretado en virtud del denominado “modelo de procesamiento dual”. De acuerdo con tal modelo, en la decisión participan dos sistemas cognitivos. El sistema 1 se compone de emociones, heurísticos e inferencias que producen intuiciones morales, mientras que el sistema 2 realiza un razonamiento deliberativo. La mayoría de especialistas asume que los cálculos del sistema 1 son automáticos, no conscientes, sin esfuerzo y rápidos, mientras que los cálculos del sistema 2 son controlados, conscientes, requieren esfuerzo y son lentos.
Joshua Greene –uno de los autores más influyentes en el campo de la psicología de las opciones morales y proponente destacado del sistema de procesamiento dual– ha propuesto, además, que las emociones producen respuestas inflexibles, que la flexibilidad (responder al contexto considerando múltiples factores) requiere razonamiento deliberativo, y que los juicios utilitarios se producen mediante el razonamiento, mientras que los juicios deónticos se producen mediante las emociones.
No todo es blanco o negroHay, sin embargo, quienes no comparten ese punto de vista. Cuando las intuiciones morales chocan, generalmente son posibles soluciones que logren un equilibrio entre valores morales en conflicto. Pero los estudios anteriores no pueden encontrar esas soluciones porque utilizan dilemas morales que obligan a realizar juicios extremos: aquellos que satisfacen plenamente un valor moral mientras descartan otros por completo.
Consideremos, por el contrario, un dilema que, aunque comparte muchas propiedades con los dilemas del tranvía, no conduce necesariamente a formular un juicio extremo. Es el siguiente:
Dos países, A y B, han estado en guerra durante años. La guerra la empezaron los gobernantes de B contra la voluntad de su población civil. Recientemente, el equilibrio militar se ha roto y es seguro que A ganará. La pregunta es cómo, cuándo y con qué costes.
El país A dispone de dos estrategias: (1) atacar al ejército contrario con armas convencionales o (2) bombardear a la población civil. Podrían usar una, la otra o una combinación de ambas. Los bombardeos desmoralizarían al país B: cuantos más civiles mueran, antes se rendirá B y menos soldados morirán: aproximadamente la mitad de ambos lados, todos reclutados por la fuerza. Los combates convencionales minimizarán las bajas. Es más, si el país A decide no bombardear al país B, entonces morirán 6 millones de soldados, pero casi ningún civil. Si 4 millones de civiles son sacrificados en los bombardeos, B se rendirá inmediatamente y casi ningún soldado morirá. Y, si A elige una solución intermedia, por cada cuatro civiles sacrificados, morirán aproximadamente seis soldados menos.
¿Cómo debería A poner fin a la guerra? ¿Qué cree que es moralmente correcto?
El modelo de procesamiento dual no le sería de aplicación a este dilema y, por tanto, no solo a este, sino al conjunto de los dilemas morales.
Un modelo alternativo, el sistema de compensación moralUn grupo de investigación liderado por Leda Cosmides, de la Universidad de California en Santa Barbara, ha formulado un modelo alternativo. Lo denominan modelo de sistema de compensación moral (moral trade-off system) y debería poder producir todo el espectro de juicios posibles: extremos y consistentes en soluciones intermedias, de compromiso.
En ese modelo, los sistemas cognitivos implicados en la vida social que son activados por un dilema determinan qué variables son moralmente relevantes para su resolución. El sistema de compensación debe poder sopesar los valores morales en conflicto y elegir la solución más correcta, presentándola como un juicio moral intuitivo. Además, el sistema de compensación moral debe cumplir varios requisitos. Así, los juicios deben poder cambiar en función de incentivos y de variables moralmente relevantes, como la voluntad, la justicia, la reciprocidad, el derecho, el mérito y la honradez.
Los autores proponen que el sistema (mental) de compensación moral está compuesto por tres subsistemas: el de los “valores morales”, el del “conjunto factible” y el que “maximiza la bondad” (o corrección o adecuación) de la opción.
El subsistema de los valores morales evalúa diferentes soluciones al dilema y establece cuál es la mejor o más correcta. Este subsistema y los sistemas cognitivos que le proporcionan la información son universales, pero están calibrados por las experiencias del individuo. De ahí que, ante una misma situación, diferentes personas asignen valoraciones morales diferentes y, en consecuencia, sus juicios morales pueden diferir.
Por otro lado, hay ciertas variables o condiciones que determinan qué soluciones al dilema son factibles y, por lo tanto, de qué soluciones dispone el sistema para elegir. La representación mental de esas posibles soluciones es el “conjunto factible”. El correspondiente subsistema trabaja en paralelo al de valores morales.
Finalmente, está el subsistema que determina cuál es la solución más correcta a partir de las soluciones disponibles. Es el que establece que “la solución X es la mejor” (por ser, de entre las disponibles, la más correcta).
Esos tres subsistemas operan de manera inconsciente: sus cálculos no se realizan mediante razonamiento deliberativo. El sistema de compensación moral opera como el sistema visual: sus productos finales son objetos de la consciencia, pero la computación para producirlos no lo es. Del mismo modo que “vemos” objetos, “sentimos” que algunas opciones son más correctas que otras. Al igual que la visión de un objeto, la sensación de que “la solución X es la mejor” es una representación que pueden leer otros sistemas mentales, incluidos aquellos que han de decidir cómo comportarse. Además, aunque el sistema de compensación moral opera de manera inconsciente, las deliberaciones conscientes pueden desempeñar un papel en el juicio.
Juicios de compromisoUn sistema cognitivo con esta arquitectura puede producir juicios de compromiso; responde a incentivos y variables moralmente relevantes; y asigna ponderaciones a bienes morales en conflicto, lo que le permite elegir la solución factible que sea más correcta.
El equipo de investigación sometió a contraste su modelo testando el cumplimiento de una serie de predicciones emanadas de aquel. Para ello, plantearon a más de 1700 personas un dilema semejante al del tranvía, que oponía las vidas de los civiles a las vidas de los soldados en un supuesto de conflicto bélico similar al descrito antes. El dilema se les planteaba en diferentes escenarios, caracterizados por incentivos tales como el número de soldados salvados por cada civil sacrificado y por variables relevantes en términos morales, como si la población civil había sido partidaria de la guerra o no, o si los soldados habían sido reclutados de forma voluntaria o forzosa. En este caso, y a diferencia de otros dilemas, los sujetos podían elegir opciones intermedias, que sacrifican a algunos (pero no a todos) los civiles para salvar a más (pero no a la mayoría) de los soldados.
Los resultados respaldaron las predicciones del modelo ensayado. Pero, a juicio de los autores, la evidencia más decisiva es que la gran mayoría de los sujetos actuaron de forma racional. Lo hicieron con independencia de cuál era la combinación de juicios extremos y de compromiso que hicieran, y se mantuvieron racionales en todos los escenarios, incluso cuando sus juicios cambiaron con la voluntad (de participar o apoyar la guerra) de los soldados o civiles. Según los autores eso es una prueba muy sólida de que el proceso maximiza la corrección.
En conclusión, el razonamiento deliberativo, sin más, no puede explicar los resultados obtenidos en este trabajo, ni tampoco una competición entre emoción y razón. Los resultados fueron los que cabe esperar de un sistema cognitivo que sopesa consideraciones morales en competencia y elige la solución que maximiza la corrección, la mejor solución.
Fuente:
Guzmán R.A., Barbato M.T., Sznycer D., Cosmides L., A moral trade-off system produces intuitive judgments that are rational and coherent and strike a balance between conflicting moral values. Proc Natl Acad Sci U S A. 2022 Oct 18; 119 (42): e2214005119. doi: 10.1073/pnas.2214005119.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Cómo decidir la mejor opción ante un dilema moral se ha escrito en Cuaderno de Cultura Científica.
STEAM e indagación en el aprendizaje de Ciencias Experimentales

La jornada Las Pruebas de la Educación tuvo lugar con el objetivo de analizar la validez de las estrategias educativas puestas en marcha durante los últimos años. El enfoque STEAM o las clases virtuales fueron analizados desde la evidencia científica por un grupo de expertos y expertas que se reunió en la Facultad de Educación de Bilbao de la Universidad del País Vasco. La jornada, fruto de la colaboración entre la Cátedra de Cultura Científica de la Universidad del País Vasco y la facultad de Educación de Bilbao, tuvo lugar el 27 de octubre pasado.
Esta sexta edición volvió a estar dirigida a profesionales del ámbito de la educación y a quienes, en un futuro, formarán parte de este colectivo. Su objetivo ha sido reflexionar, desde la evidencia científica, sobre la validez de las estrategias utilizadas hoy en día. El seminario ha contado, una vez más, con la dirección académica de la vicedecana de Investigación y Transferencia de la Universidad Autónoma de Madrid, Marta Ferrero González.
Beatriz Baro Torija es doctora en Didáctica de las Ciencias Experimentales y licenciada en Biología por la Universidad de Santiago de Compostela. Actualmente es Profesora Titular de Universidad del Departamento de Didácticas Específicas (área de Didáctica de las Ciencias Experimentales) en la Universidad Autónoma de Madrid. Ella es la encargada de analizar en esta charla los resultados del enfoque STEAM implantado durante los últimos años.
Edición realizada por César Tomé López
El artículo STEAM e indagación en el aprendizaje de Ciencias Experimentales se ha escrito en Cuaderno de Cultura Científica.
Los robotaxis hacen trampas: la conducción autónoma podría no serlo tanto
Los vehículos autónomos han sufrido un verano muy intenso, particularmente las empresas Waymo y Cruise, propiedades de los gigantes Google y General Motors, respectivamente. Se trata de dos de las startups más adelantadas en la carrera por dominar esta tecnología que, sin embargo, han tenido que frenar en seco en los últimos meses.

El 11 de agosto de 2023 ambas compañías obtuvieron la aprobación del estado de California para comenzar a ofrecer servicios de taxis autónomos 24 horas al día, los 7 días a la semana, y cobrando (hasta entonces, su actividad estaba restringida a unos horarios de poca densidad de tráfico). La ciudad de San Francisco se abría por primera vez a estos servicios.
(Comenzar el vídeo en 1:40.)Poco les duró la alegría. Unos días más tarde, el 19 de agosto, las autoridades estatales penalizaron a Cruise por varios fallos graves ocurridos la noche anterior. Primero, un robotaxi se empotró contra un camión de bomberos que acudía una emergencia. En otro incidente, unas horas más tarde, fue un coche normal, pilotado por un humano, el que se saltó un semáforo y arrolló a uno de estos robotaxis.
En total, Cruise tuvo que reducir los 300 vehículos que tenía circulando por la ciudad a la mitad. Sin embargo, aún le faltaba la puntilla a la startup de General Motors, y ésta llegó hace unos días, cuando saltó la noticia de que el estado de California le retiraba la licencia de vehículos autónomos después de que uno de sus modelos no detectara que tenía a una persona atropellada debajo. Tras ello, Cruise anunció que cancelaba todas sus operaciones en Estados Unidos. Waymo ha optado por frenar su ritmo de expansión.
La cruda realidad es que una startup que no circula es una startup que no genera beneficios. Esto es un problema cuando estás inmerso en una carrera empresarial y tecnológica por quemar dinero, demostrar resultados, y seguir quemando dinero de inversores, todo ello hasta que a estos se les agote la paciencia o una de las empresas se erija vencedora.
¿Cuál es la situación de los robotaxis ahora?Tecnológicamente, el hecho de que hayan estado circulando por ciudad cientos de vehículos autónomos es una gran hazaña. Waymo y Cruise han recorrido un total de casi 13 millones de kilómetros sin conductor, incluidos más de 6,4 millones de kilómetros en San Francisco desde principios de 2023. Debido a que la ley de California exige que las empresas de vehículos autónomos informen de cada accidente importante de forma pública, sabemos mucho sobre su desempeño.
En total, las dos empresas han informado de algo más de 100 accidentes con vehículos sin conductor. Puede parecer mucho, pero ocurrieron en unos 10 millones de kilómetros de conducción. Eso equivale a un accidente cada 100 000 kilómetros, unos cinco años de conducción para un automovilista habitual.
Sin embargo, en estas estadísticas no se cuentan otros incidentes también importantes, como atropellos a perros, golpes de chapa en los que el robotaxi huye, o que el vehículo autónomo arda espontáneamente.
Si echamos la vista atrás, lo que las grandes tecnológicas nos prometían eran transportes en ciudad más baratos, rápidos y seguros. Uno de los mayores críticos de esta tecnología es el investigador Filip Piekniewski, quien ya advirtió que, después de 100 000 millones de dólares invertidos en esta tecnología, seis empresas han quebrado, tres están intentando sobrevivir y solo a dos parece irles bien.
Probablemente, la actitud de Piekniewski sea demasiado radical. En mi caso, estoy convencido de que la conducción autónoma se logrará, aunque quizás necesitemos cambios más profundos.
En muchos medios se puede encontrar el dato de que entre el 90 y 94 % de los accidentes en carretera se deben a errores humanos. La historia de esta cifra se remonta nada menos que a 1979. Posteriormente, la autoridad en seguridad vial de EE UU, la NHTSA, publicó en 2015 un documento de dos páginas que decía que “la razón crítica, que es el último evento en la cadena causal del accidente, fue asignada al conductor en el 94 % de los accidentes”. Un poco más adelante, el organismo subrayaba que, “aunque la razón crítica es una parte importante de la descripción de los eventos que condujeron al accidente, no debe interpretarse como la causa del accidente”.
El argumento de sustituir al conductor por un algoritmo para reducir ese 94 % de causas humanas es, por lo tanto, falso. Numerosas voces autorizadas en seguridad vial han levantado la voz sobre este uso tramposo de las estadísticas.
Quizás, por lo tanto, los vehículos autónomos no deban reflejar como métrica principal el número de accidentes, sino que debieran tener sus propias métricas. Y probablemente también sea importante recordar que cada vehículo autónomo en la vía pública tiene un conductor humano de seguridad a bordo o en algún lugar observando y controlando de forma remota.
Los vehículos autónomos podrían no serlo tantoPrecisamente hace unos días, el New York Times publicó un artículo que saca los colores a Cruise y a estos conductores de seguridad.
Según los periodistas del New York Times, la empresa de vehículos autónomos empleaba una media de 1,5 conductores de seguridad por vehículo, y tenían que intervenir en la conducción muy frecuentemente. Si esto fuera cierto, sería lógico cuestionarse si el resto de startup de robotaxis están haciendo las mismas trampas. Siendo así, estaríamos aún muy lejos de la conducción autónoma del imaginario popular.
Quizás la conducción autónoma no sea la solución a nuestros problemas de tráfico. Tal vez haya que pensar en una conducción tecnológicamente asistida, que complemente al humano y que le ayude a no fallar. Al fin y al cabo, puede que la viabilidad técnica de vehículos tan complejos que rocen la inteligencia e intuición humana sea imposible en los marcos de movilidad urbana de nuestras ciudades.
Probablemente, también sea importante entender que los robotaxis no son solo un invento tecnológico, sino uno en gran medida socioeconómico.![]()
Sobre el autor: Julián Estévez Sanz, Profesor e investigador en Robótica e Inteligencia Artificial, Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Los robotaxis hacen trampas: la conducción autónoma podría no serlo tanto se ha escrito en Cuaderno de Cultura Científica.
Al borde de la extinción en el Pleistoceno
José María Bermúdez de Castro, codirector de los yacimientos de Atapuerca, reflexiona en este texto sobre la repercusión de un inquietante estudio sobre lo cerca que estuvo la humanidad de la extinción durante el Pleistoceno.
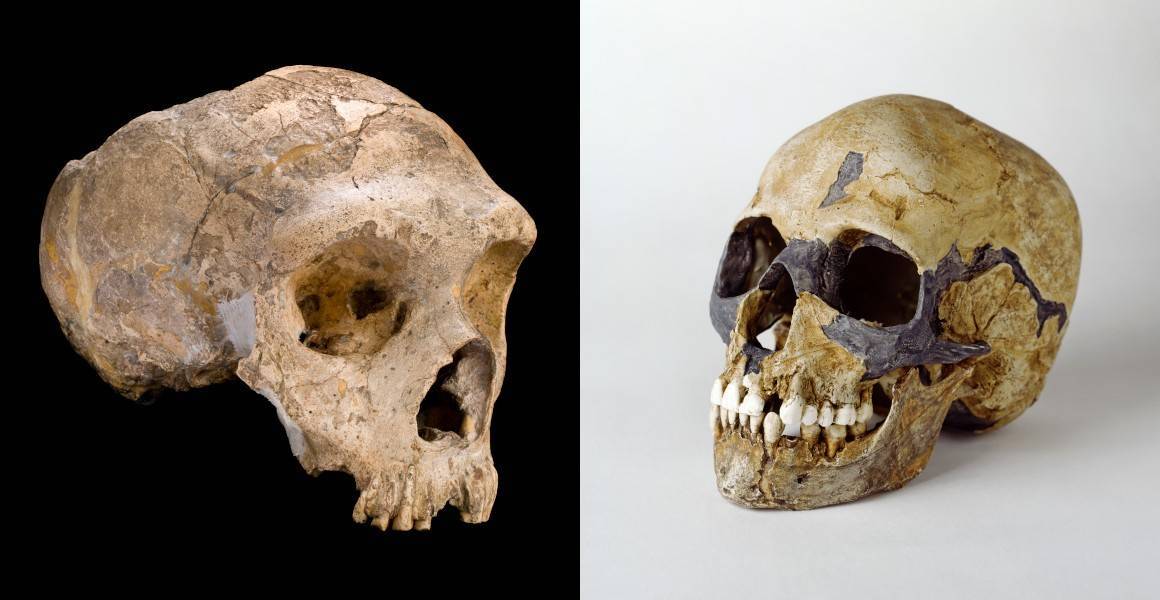 Cráneo de neandertal (a la izquierda) y de Homo sapiens (a la derecha). Fuente: The Trustees of the Natural History Museum
Cráneo de neandertal (a la izquierda) y de Homo sapiens (a la derecha). Fuente: The Trustees of the Natural History MuseumUn prestigioso equipo de investigadores de varias instituciones científicas de China, formado, entre otros, por Hu Wangjie, Ha Zigian, Pan Y-Huan y Li Haipeng, publicó hace poco un trabajo en la revista Science, cuyas conclusiones resultan inquietantes. Estos científicos han estudiado el ADN de una muestra de más de 3.000 individuos actuales procedentes de diferentes regiones del planeta y han desarrollado un nuevo modelo genético (FitCoal), extremadamente complejo para la comprensión de quienes no somos genetistas y matemáticos.
Este modelo posibilita proyectar la variación genética actual hacia el pasado y estimar el tamaño de las poblaciones pretéritas. Los resultados del estudio sugieren que hace entre 813.000 y 930.000 años la humanidad experimentó un cuello de botella y quedó reducida a poco menos de 1.300 individuos reproductores. Ese cuello de botella, quizá causado por las severas condiciones climáticas de finales del Pleistoceno inferior, duró nada menos que 117.000 años y habría dejado al linaje humano al borde de su desaparición.
Esta conclusión nos deja con un nudo en el estómago, pero también con algo de escepticismo en relación con los titulares que el propio editorial de la revista Science ha propiciado. Sabemos que en aquella época existían varias especies del género Homo distribuidas por África y Eurasia: Homo antecessor, Homo erectus, Homo ergaster, Homo floresiensis y tal vez alguna más. Con esta diversidad, parece seguro que nuestra genealogía habría tenido, en conjunto, una respuesta adaptativa suficiente como para salir del cualquier atolladero.
Tras meditar sobre las conclusiones del artículo de nuestros colegas, hemos intentado poner un poco de orden en nuestra mente, sin dejarnos llevar por la autoridad de los trabajos de investigación publicados por una revista de tanto prestigio como Science y por un modelo tan complejo, cuya comprensión está al alcance de pocos.
Un “agujero negro” en la evolución humanaEs cierto que el registro fósil de hace aproximadamente un millón de años es limitado. Tanto es así que desde siempre se ha comentado entre los expertos la existencia de un verdadero “agujero negro” en la evolución de los homininos. Esa falta de yacimientos con fósiles humanos podría explicarse por causas geológicas. Además, el territorio inexplorado por arqueólogos y paleontólogos hasta la fecha por razones económicas, políticas y sociales es inmenso.
Poco a poco, ese agujero negro se ha ido llenando de contenido y ya han empezado a contabilizarse un cierto número de yacimientos de esa época tanto en África como en Eurasia. No olvidemos, por ejemplo, que el nivel TD6 del yacimiento de la cueva de la Gran Dolina, en la sierra de Atapuerca (Burgos), se ha datado en aproximadamente 850.000 años, precisamente en los límites temporales de ese cuello de botella sugerido por los resultados del modelo de los científicos chinos.
El yacimiento de la Gran Dolina y otros yacimientos europeos de la misma época sugieren que el sur de Europa estuvo habitado hacia finales del Pleistoceno inferior por una población humana relativamente numerosa y viable. Ciertamente, cada vez tenemos mayor constancia de la existencia de homininos de esa época en el este de África o China. ¿Entonces?, ¿qué significado tienen los resultados del equipo de científicos chinos?, ¿se trata solo de un modelo, que puede estar equivocado? No necesariamente.
Pienso que el propio resumen realizado por el editorial de la revista Science nos ha confundido a todos. Los medios de comunicación de todo el mundo han publicado titulares llamativos acordes con ese resumen, que no se ajustan a la realidad de lo que pudo haber sucedido hace 900.000 años.
En ese tiempo, una de las poblaciones de homininos, todavía por determinar, pudo ser el origen de los neandertales, los denisovanos y los humanos modernos. Hasta el momento, nadie ha sido capaz de identificar con seguridad esa población enigmática que, en mi opinión, vivió en Oriente Próximo. Mientras tanto, en varias de regiones de África y Eurasia prosperaban otras poblaciones de diferentes especies: Homo antecessor, Homo erectus, Homo ergaster, Homo floresiensis…
¿Cómo lograron sobrevivir tan pocos tanto tiempo?Mi interpretación de los resultados de los científicos chinos es que el modelo FitCoal conduce únicamente a esa población misteriosa de la que surgió finalmente la humanidad actual, junto a los neandertales y los denisovanos.
Si lo que pienso es correcto, no sería de extrañar que esa población enigmática se hubiera originado como resultado de ese cuello de botella que sugiere el modelo FitCoal. Siendo una población de tamaño tan exiguo, es normal que las excavaciones arqueológicas y paleontológicas no hayan dado todavía con algún yacimiento de esa población. Pero todavía quedaría una pregunta por responder: ¿cómo es posible que una población tan pequeña pudiera sobrevivir durante más de 100.000 años?
Si el cuello de botella hubiera persistido durante tanto tiempo, las posibilidades de supervivencia de la población habrían sido casi nulas. Los autores de la investigación son plenamente conscientes de ese problema y plantean la misma pregunta en el último párrafo de su artículo en Science.
Los modelos son eso precisamente: modelos, que no tienen por qué ajustarse necesariamente a la realidad. La hipótesis de que sapiens, neandertales y denisovanos comparten un mismo ancestro común, cuyo origen puede situarse en algún lugar de África o Eurasia hace unos 900.000 años, es ampliamente aceptada por la comunidad científica. El modelo FitCoal seguramente ha podido llegar en sus estimaciones hasta esa población “misteriosa”, pero habría obviado esas otras poblaciones que medraban por buena parte de África y Eurasia a finales del Pleistoceno inferior.
Si esta interpretación es correcta, la población originaria del linaje que condujo finalmente hasta nosotros estuvo pendiente de un hilo. Caso de que esa población enigmática hubiera fracasado por falta de efectivos, otras especies humanas habrían prosperado. ¿Imaginan los lectores un planeta habitado por los descendientes de Homo erectus?
Para saber más:
La humanidad ante su propia extinción
Quince virus que han cambiado la historia de la Humanidad
Sobre el autor: José María Bermúdez de Castro. Investigador ad Honorem. Centro Nacional de Investigación sobre la Evolución Humana (CENIEH), Burgos.
Este texto apareció originalmente en SINC.
El artículo Al borde de la extinción en el Pleistoceno se ha escrito en Cuaderno de Cultura Científica.
El toro, la botella de Klein y el plano proyectivo real (III)
Con esta entrada del Cuaderno de Cultura Científica cerramos una serie dedicada a tres curiosas superficies relacionadas con la banda de Moebius, a saber, el toro, la botella de Klein y el plano proyectivo real, y a cómo algunos artistas contemporáneos han representado estas superficies en sus obras de arte. La primera entrada, titulada El toro, la botella de Klein y el plano proyectivo real (I), estaba dedicada a la superficie del toro y se mostraban esculturas del artista japonés Keizo Ushio, del escultor minimalista estadounidense Richard Serra o del artista británico Jack Eagan, entre otros. Mientras que la segunda entrada, titulada El toro, la botella de Klein y el plano proyectivo real (II), se centraba en la superficie conocida con el nombre de botella de Klein y en obras de artistas como el mexicano Pedro Reyes, la parisina Bettina Samson o la matemática y artista argentina Moira Chas. Y la serie se cierra, en esta entrada, con el plano proyectivo real.
 Down Force / Fuerza hacia abajo (2015), del escultor estadounidense Harry Pollitt, es una escultura en madera de una larga banda de MoebiusTodo empieza con una superficie rectangular
Down Force / Fuerza hacia abajo (2015), del escultor estadounidense Harry Pollitt, es una escultura en madera de una larga banda de MoebiusTodo empieza con una superficie rectangular
Antes de introducir la extraña superficie conocida con el nombre de plano proyectivo real, vamos a repasar cómo se construían el toro y la botella de Klein. Se empieza con una tira de papel rectangular ABCD (véase la siguiente imagen), en general, una superficie “topológica” rectangular, es decir, que nos permitiremos estirarla si fuese necesario, ya que estamos interesados en la creación de superficies topológicas, en este caso, el toro, la botella de Klein y el plano proyectivo real.
 Tira de papel ABCD
Tira de papel ABCD
Dada esa superficie rectangular ABCD, si se pegan los lados AB con DC se obtiene un cilindro, pero en función de cómo se junten los otros dos lados se generan dos nuevas e interesantes superficies. Si lo hacen de forma directa (AD con BC, como indican las flechas de la siguiente imagen) será la superficie cerrada con dos caras, denominada en matemáticas “toro”, que tiene forma de rosquilla o flotador.
 Construcción de la superficie del toro
Construcción de la superficie del toroSi los otros dos lados se pegan en el sentido contrario (AD con CB), girando media vuelta antes de pegarse, entonces se construye la superficie topológica llamada “botella de Klein”, que es una superficie cerrada que solo tiene una cara. Como se explicaba en la anterior entrada y se muestra en la siguiente imagen, los extremos del cilindro no se pegan de forma directa, sino en sentido contrario, luego sería como si se pegaran “por detrás”. El problema es que para hacer esto tenemos que cruzar la propia superficie para poder unir esos dos extremos en la forma descrita. De esta manera, lo que se genera es una “representación” de la botella de Klein que se autointerseca, como se muestra en la imagen.
 Construcción de la botella de Klein con autointersección
Construcción de la botella de Klein con autointersecciónTambién explicábamos en la anterior entrada, que la botella de Klein, tal cual la hemos definido, no debiera de tener autointersecciones. El problema está en que esta construcción geométrica “ideal” no genera una superficie que esté dentro de nuestro espacio tridimensional, sino que su espacio natural es el espacio de dimensión cuatro, y aquí nos encontramos con un gran problema, ya que no somos capaces de visualizar la cuarta dimensión. Por este motivo, nos quedábamos en la anterior entrada con esta representación, que al menos habita en el espacio visual, el espacio de dimensión tres.
Un material muy interesante para observar y entender bien la botella de Klein, en particular, su realización en el espacio tridimensional, es el cristal. En la siguiente imagen podéis disfrutar de una botella de Klein realizada en cristal. Aquí os presento mi botella de Klein construida en cristal, que me ha regalado la junta directiva de la Sociedad Madrileña de Profesores de Matemáticas (SMPM) Emma Castelnuovo, por mi participación en las jornadas formativas de enseñanza y aprendizaje de las matemáticas, de este año 2023. ¡Muchísimas gracias por tan hermoso presente!
 Botella de Klein construida en cristal
Botella de Klein construida en cristal
Por otra parte, mi amiga Mariel García, la conocida “Mariel Mates”, que tiene hermosas creaciones textiles relacionadas con las matemáticas, como las geniales y coloridas bufandas “pi-bufanda” y “fibo-bufanda”, ha tejido recientemente una interesante y hermosa botella de Klein, que podéis ver en la siguiente imagen.
 Fibobufanda (2023), de la matemática y artista Mariel MatesEl plano proyectivo real
Fibobufanda (2023), de la matemática y artista Mariel MatesEl plano proyectivo real
La superficie que nos ocupa para cerrar esta serie, el plano proyectivo real, es una interesante superficie desde el punto de vista matemático, pero también complicada de entender, aunque vamos a intentar definirla siguiendo la línea constructiva que hemos trazado en esta serie.
Volviendo a nuestra tira rectangular ABCD, si se pegan los dos extremos opuestos, pero girando media vuelta uno de los extremos, por ejemplo, en el rectángulo de la siguiente imagen se pega AD con CB, se forma la banda de Moebius, como ya hemos explicado en muchas entradas anteriores y mostramos en la siguiente imagen.
 Construcción de la banda de Moebius, pegando los extremos AD con CB de una tira rectangular ABCD
Construcción de la banda de Moebius, pegando los extremos AD con CB de una tira rectangular ABCDPero, si ahora, dada esa banda de Moebius, pegamos los otros dos extremos del rectángulo, girando media vuelta de nuevo a uno de ellos, es decir, se pega AB con CD, se obtiene la conocida superficie denominada “el plano proyectivo real”, que resulta ser otra superficie cerrada (sin borde) con una sola cara. Para intentar realizar una “imagen” de esta superficie, tenemos que darnos cuenta de que las dos parejas de lados opuestos del rectángulo ABCD se pegan en sentido contrario, DA con BC y AB con CD. Esta forma de pegar los lados opuestos es como si pegáramos DAB con BCD, como se muestra en la siguiente imagen. El problema está, de nuevo, que no hay forma de pegar DAB con BCD sin pasar a través de la propia superficie, por lo que la imagen que se muestra a continuación es una realización tridimensional, con autointersecciones, del plano proyectivo real (que se conoce con el nombre de “gorra cruzada”, del inglés “cross cap”). Al igual que ocurría con la botella de Klein, el plano proyectivo real tampoco está, de forma natural, en el espacio tridimensional, sino que habita de forma natural en el espacio de dimensión cuatro. Por lo tanto, lo que nosotros podemos ver son proyecciones del plano proyectivo real, que existe en el espacio de dimensión cuatro, sobre el espacio tridimensional. Luego no vemos toda su realidad, sino proyecciones del mismo.
 Representación tridimensional, luego con auto-intersecciones, de la construcción del plano proyectivo real, a partir de una tira rectangular ABCD, pegando los extremos DA con BC y AB con CD, o lo que es lo mismo, pegando DAB con BCD. A esta representación del plano proyectivo real se la conoce con el nombre gorra cruzada
Representación tridimensional, luego con auto-intersecciones, de la construcción del plano proyectivo real, a partir de una tira rectangular ABCD, pegando los extremos DA con BC y AB con CD, o lo que es lo mismo, pegando DAB con BCD. A esta representación del plano proyectivo real se la conoce con el nombre gorra cruzadaComo acabamos de comentar, el plano proyectivo real es una superficie que, por su construcción, no se puede representar en el espacio tridimensional (nuestro espacio visual y mental), sino que vive en el espacio de dimensión cuatro. Por este motivo, al proyectarlo en el espacio tridimensional se producen auto-intersecciones, como en la representación anterior. Aunque no vamos a explicar su origen, existen otras formas de representar/proyectar el plano proyectivo real en el espacio tridimensional. Tres representaciones clásicas del plano proyectivo real son el sombrero cruzado, que ya hemos mostrado, la superficie de Boy (que recibe su nombre del matemático alemán Werner Boy (1879-1914), quien descubrió esta superficie en 1901, cuando su director de tesis, el matemático alemán David Hilbert (1862-1943) le pidió que demostrase que era imposible realizar una “inmersión” del plano proyectivo real en el espacio tridimensional) y la superficie romana de Steiner (que recibe su nombre del matemático suizo Jakob Steiner (1896-1963), quien la descubrió en 1844, en un viaje a Roma), que se muestran, con dos puntos de vista distintos de cada una de ellas, en la siguiente imagen.
 El sombrero cruzado, la superficie romana de Steiner y la superficie de Boy, tres proyecciones del plano proyectivo real en el espacio tridimensional
El sombrero cruzado, la superficie romana de Steiner y la superficie de Boy, tres proyecciones del plano proyectivo real en el espacio tridimensionalEsculpiendo el plano proyectivo real
Nos encontramos ante una superficie geométrica compleja y crear una escultura con alguna de sus realizaciones tridimensionales no es una tarea sencilla, por lo que algunos de los trabajos artísticos sobre las mismas los desarrollan artistas con formación matemática o que colaboran con personas del ámbito de las matemáticas.
El primer artista que traemos a esta entrada es el escultor y matemático estadounidense Helaman Ferguson (1940), de quien ya explicamos su obra Toro umbilical (1988) en la entrada Arte Moebius (II). Ferguson es uno de esos artistas cuyo arte podríamos denominar “arte matemático”, ya que sus esculturas tienen una fuerte componente matemática. En particular, trabaja mucho con superficies topológicas, como las que nos ocupan en esta serie. Sobre la relación entre escultura y matemáticas Helaman Ferguson dice lo siguiente: “creo que la escultura es una forma muy poderosa de transmitir las matemáticas, y estas son un lenguaje de creación muy poderoso para la escultura”.
La escultura Torus with cross cap and vector field / Toro con gorra cruzada y campo de vectores (1989), realizada en bronce, no es una escultura de la realización tridimensional del plano proyectivo real denominada gorra cruzada, que acabamos de explicar más arriba, sino de una nueva superficie que está formada por la unión de la gorra cruzada con la superficie del toro.
 Escultura Torus with cross cap and vector field / Toro con gorra cruzada y campo de vectores (1989), del artista y matemático Helaman Ferguson, realizada en bronce
Escultura Torus with cross cap and vector field / Toro con gorra cruzada y campo de vectores (1989), del artista y matemático Helaman Ferguson, realizada en bronceAdemás, realizó una segunda versión en mármol blanco, que mostramos en la siguiente imagen.
 Escultura Torus with cross cap and vector field / Toro con gorra cruzada y campo de vectores (1988), del artista y matemático Helaman Ferguson, realizada en mármol blanco
Escultura Torus with cross cap and vector field / Toro con gorra cruzada y campo de vectores (1988), del artista y matemático Helaman Ferguson, realizada en mármol blancoNuestra siguiente artista también se ha formado en matemáticas, de hecho, tiene formación tanto en matemáticas, como en bellas artes. Se trata de la matemática y artista estadounidense Camila Friedman-Gerlicz. Ella ha realizado una curiosa instalación de la superficie de la gorra cruzada, titulada Cross Cap Surface Parametrization / Parametrización de la gorra cruzada (2018), que consiste en una escultura de madera muy especial, con la forma de la gorra cruzada, un dispositivo rectangular táctil en la base de la escultura, como se muestra en la siguiente imagen, y un sistema de luces dentro de la gorra cruzada de madera.
 Cross Cap Surface Parametrization / Parametrización de la gorra cruzada (2018), de la matemática y artista estadounidense Camila Friedman-Gerlicz
Cross Cap Surface Parametrization / Parametrización de la gorra cruzada (2018), de la matemática y artista estadounidense Camila Friedman-Gerlicz¿Cómo funciona la instalación? Es lo que en matemáticas llamamos una parametrización de la superficie de la gorra cruzada, es decir, cada punto del rectángulo de la base se corresponde con un punto de la superficie. De hecho, en esta instalación cuando se coloca un dedo en un punto del rectángulo táctil de la base se ilumina el correspondiente punto de la superficie, y si vamos moviendo nuestro dedo por el rectángulo se va moviendo la luz por la superficie de madera, visualizando así la relación entre el rectángulo generador y la realización, denominada gorra cruzada, del plano proyectivo real.
 Luces en la instalación Cross Cap Surface Parametrization / Parametrización de la gorra cruzada (2018), de la matemática y artista Camila Friedman-Gerlicz, que se mueven en función de la posición del dedo en la zona rectangular
Luces en la instalación Cross Cap Surface Parametrization / Parametrización de la gorra cruzada (2018), de la matemática y artista Camila Friedman-Gerlicz, que se mueven en función de la posición del dedo en la zona rectangularEsta artista, cuyo arte está muy conectado con las matemáticas, también ha realizado una superficie de la gorra cruzada en cerámica, que es uno de los materiales con los que más trabaja. También en cerámica ha realizado otra de las realizaciones tridimensionales del plano proyectivo real, la superficie de Boy, que hemos mostrado más arriba.
 Cerámica Projective layers / Capas proyectivas (2022), de la matemática y artista estadounidense Camila Friedman-Gerlicz
Cerámica Projective layers / Capas proyectivas (2022), de la matemática y artista estadounidense Camila Friedman-GerliczAdemás, ha creado una escultura colgante en papel, que consiste en una triangulación de la superficie de Boy, es decir, ha representado una superficie poliédrica creada por triángulos, los cuales forman la superficie topológica descubierta por Werner Boy.
 Escultura colgante Project(ive) / Proyect(iv)o (2020), de la matemática y artista estadounidense Camila Friedman-Gerlicz
Escultura colgante Project(ive) / Proyect(iv)o (2020), de la matemática y artista estadounidense Camila Friedman-GerliczEsta artista matemática también tiene hermosas botellas de Klein realizadas en cerámica, que podéis encontrar en su cuenta de instagram.
 Botella de Klein realizada en cerámica, de la matemática y artista estadounidense Camila Friedman-Gerlicz
Botella de Klein realizada en cerámica, de la matemática y artista estadounidense Camila Friedman-Gerlicz
Continuando con la superficie de Boy, una de las esculturas más conocidas de la misma dentro de la comunidad matemática, es la escultura que se encuentra en el exterior del Instituto de Investigación Matemática Oberwolfach, ubicado en la Selva Negra alemana (sobre el mismo escribí en la entrada Los institutos Isaac Newton y Oberwolfach, dos curiosas instituciones de investigación matemática). Esta escultura fue un regalo al instituto IMO de la empresa alemana Mercedes-Benz, que fue realizada en 1991 a partir de las computaciones realizadas por los matemáticos Hermann Karcher, Ulrich Pinkall e Ivan Sterling del Max Planck Institut für Mathematik en Bonn (Alemania).
 Escultura de la superficie de Boy, de 1991, en el exterior del Instituto de Investigación Matemática Oberwolfach (Alemania)
Escultura de la superficie de Boy, de 1991, en el exterior del Instituto de Investigación Matemática Oberwolfach (Alemania)
El desarrollo de las impresoras 3D está permitiendo realizar hermosas esculturas de superficies matemáticas complejas de forma bastante sencilla. En particular, algunos artistas y artesanos están trabajando en esta línea y podemos encontrar, y comprar, curiosos y hermosos diseños en internet. Por ejemplo, el arquitecto, diseñador y matemático Rick Russell entre sus “Mathematical Creations” podemos encontrar esta Boy’ Surface Mesh / Malla de la superficie de Boy, cuyo tamaño es 6.25 x 6.38 x 4.72 cm, y está impresa en plástico metálico y acero bañado en oro.
 Boy’ Surface Mesh / Malla de la superficie de Boy, fabricado por Mathematical Creations, es decir, Rick Russell
Boy’ Surface Mesh / Malla de la superficie de Boy, fabricado por Mathematical Creations, es decir, Rick RussellO esta otra pieza que representa también la superficie de Boy, pero con color y agujeros, realizada por el artista y fabricante Benjamin Berger, que es la persona que está detrás de Implicit Art.
 Color Boy’s surface weave / Entramado de la superficie de Boy en color, fabricado por Implicit Art, es decir, Benjamin Berger
Color Boy’s surface weave / Entramado de la superficie de Boy en color, fabricado por Implicit Art, es decir, Benjamin BergerSi seguimos con objetos realizados con impresión 3D, también nos encontramos a la superficie romana de Steiner. Por ejemplo, el diseñador y fabricante Paul Summers, que es quien está detrás de los diseños de FluidDesigner, ha realizado el diseño de unos pendientes con forma de corazón, que realmente es la superficie de Steiner, que podéis admirar en la siguiente imagen.
 Roman Surface Heart Earring / Pendientes corazón superficie romana, realizados por FluidDesigner, es decir, Paul Summers
Roman Surface Heart Earring / Pendientes corazón superficie romana, realizados por FluidDesigner, es decir, Paul SummersVamos a concluir esta entrada del Cuaderno de Cultura Científica con una escultura de la artista minimalista alemana-estadounidense Ruth Vollmer (1903-1982), relacionada con la escuela de la Bauhaus, con el título de Superficie de Steiner (1979), realizada en metacrilato, de la que también realizaría una versión con colores.
 Superficie de Steiner (1979), de la artista alemana-estadounidense Ruth Vollmer
Superficie de Steiner (1979), de la artista alemana-estadounidense Ruth VollmerBibliografía
1.- Raúl Ibáñez, Las matemáticas como herramienta de creación artística, colección Miradas matemáticas, Catarata, 2023.
2.- Clifford A. Pickover, La banda de Möbius, Almuzara, 2009.
3.- Martin Gardner, Festival mágico-matemático, Alianza editorial, 1984.
4.- Stephen Barr, Experiments in Topology, Dover, 1989.
5.- Martin Gardner, The Sixth Scientific American Book of Mathematical Puzzles and Diversions, Simon & Schuster, 1971.
6.- Raúl Ibáñez, La cuarta dimensión, RBA, 2010.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El toro, la botella de Klein y el plano proyectivo real (III) se ha escrito en Cuaderno de Cultura Científica.

