La realidad resulta enigmática porque es no lineal
no lineal
Aunque el origen de la Dinámica se fundó a partir de los experimentos de Mecánica efectuados por Galileo Galilei, el cálculo infinitesimal -inventado por Isaac Newton y Gottfried Leibniz- permitió describir matemáticamente la evolución general de algunas de las más relevantes magnitudes de todas las ciencias. Las maravillosas ecuaciones diferenciales nos permiten describir, predecir e incluso controlar la dinámica de sistemas no sólo basados en las leyes de la mecánica clásica o relativista, el electromagnetismo o la mecánica cuántica, sino en todas las ciencias naturales y sociales, así como en todas las ingenierías.
El gran Henri Poincaré estableció a finales del siglo XIX las propiedades cualitativas de la teoría de ecuaciones diferenciales, con la Mecánica Celeste [1] como ejemplo de aplicación, pero más allá de esto, estableció su teoría matemática generalizada para fundar la Ciencia General de la Dinámica de Sistemas, aplicable a modelar, predecir su evolución en el tiempo y caracterizar las propiedades esenciales de cualquier efecto medible en cualquier tipo de realidad científica.
 El mundo a nuestro alrededor es mayormente no lineal. Foto: Jorge Fernández Salas / UnsplashEl principio de superposición
El mundo a nuestro alrededor es mayormente no lineal. Foto: Jorge Fernández Salas / UnsplashEl principio de superposición
La mayoría de los científicos naturales o sociales, muy a menudo consideramos verdadera la hipótesis de que la respuesta neta causada en un sistema por dos o más estímulos es la suma de las respuestas que habría causado cada estímulo por separado. Esto es el Principio de Superposición, que parece ser una cuestión casi de sentido común, y que muchas veces la asumimos sin demasiadas cautelas.
Una función matemática que satisface el principio de superposición se denomina función lineal. Estas funciones lineales, muy utilizadas con gran generalidad en todas las ciencias, incorporan dos propiedades matemáticas muy útiles como la aditividad y la homogeneidad, y nos permiten un análisis e interpretación muy profunda -y bastante sencilla- de leyes que establezcamos, experimentos que realicemos, generalizaciones que propongamos o conclusiones que extraigamos de una investigación.
El principio de superposición se aplica a cualquier sistema lineal, descrito mediante ecuaciones algebraicas o ecuaciones diferenciales lineales. Los estímulos sobre un sistema y las respuestas de éste pueden ser números, funciones, vectores, campos vectoriales, señales variables en el tiempo o cualquier otro objeto que cumpla ciertos axiomas muy comunes. Los Sistemas Lineales son una de las maneras más utilizadas para describir la realidad, aún estudiando situaciones complejas, como aquellas basadas en las leyes de Newton, las ecuaciones de Maxwell, la ecuación de Schrödinger o modelos en econometría, ecología, o cualquier tipo de ciencia para la que tratamos de expresar matemáticamente su funcionamiento. Una ventaja que tenemos es que, cuando escribimos un estímulo muy general en un sistema lineal como la superposición de estímulos de una forma específica y simple, a menudo la respuesta global resulta más fácil de calcular y predecir.
Modelos lineales ordinarios o extraordinariosMuchos sistemas dinámicos, basados en algunas de las leyes más valiosas de la historia de la ciencia, se pueden expresar mediante ecuaciones diferenciales ordinarias lineales con coeficientes constantes. Los matemáticos han suministrado para este tipo de sistemas -llamados autónomos- un verdadero arsenal de medios para resolverlos analíticamente, por muy complejos éstos sean. Por ejemplo, la conocida Transformada de Laplace reduce un complejo sistema de ecuaciones diferenciales ordinarias lineales en un sistema de ecuaciones algebraicas, mucho más fácil de solucionar. Ello además nos permite nos solo conocer al dedillo la evolución en el tiempo del sistema dinámico que hemos resuelto, sino también descubrir sus sorprendentes propiedades en el dominio de la frecuencia, extrayendo nuevo conocimiento que no pensábamos obtener de la mera integración de una sencilla ecuación diferencial.
Las ecuaciones diferenciales ordinarias son un caso particular de las ecuaciones en derivadas parciales, muy comunes también para describir la dinámica en todas las ciencias, y que, en contraposición con las anteriores más sencillas descripciones ordinarias, podemos denominar modelos extraordinarios. Aunque su resolución en este caso es algo más compleja, las ecuaciones diferenciales lineales, sean ordinarias o no, permitieron a los físicos expresar asuntos clave como la dinámica de los planetas, todo el electromagnetismo o la dualidad onda-corpúsculo, entre muchas otras cuestiones. Hoy día científicos e ingenieros de toda especie establecen modelos dinámicos para explicar por qué ocurre la realidad experimentada en su propio ámbito.
La realidad es no linealMuy pocos científicos utilizan ecuaciones diferenciales no lineales. Sentimos una cierta reacción alérgica a su empleo, quizás por la dificultad de resolver la matemática de estas ecuaciones o quizás por abandonar el principio de superposición que tanto apreciamos. En la teoría general de relatividad de Albert Einstein, las ecuaciones son no lineales, y su resolución casi siempre implican métodos matemáticos de linealización o de perturbaciones. Incluso para sistemas mucho más sencillos, descritos en simples ecuaciones diferenciales ordinarias no lineales, nuestra tendencia es linealizar el sistema en torno a unas ciertas condiciones y resolver ecuaciones lineales, para tratar de extraer información -al menos parcial- de la realidad que hemos modelado.
La cuestión es que la realidad es no lineal, y nuestras ecuaciones lineales pueden modelar bastante bien las cosas, pero en ocasiones ocurren fenómenos muy imprevisibles y no intuitivos, tanto en las ciencias naturales como en las ciencias sociales o en las ingenierías. Estos fenómenos no se producen en los modelos lineales, y son por tanto exclusivos de los sistemas no lineales.
Múltiples puntos de equilibrioLos puntos de equilibrio son las soluciones constantes en una ecuación diferencial. En sistemas lineales autónomos, el modelo tiende a un único punto de equilibrio. Uno de los ejemplos más sencillos podemos encontrarlo en la aproximada ley de enfriamiento de Newton: una simple ecuación diferencial lineal de primer orden que explica la transferencia de calor entre dos cuerpos partiendo de diferentes temperaturas. El punto de equilibrio es único y establece igualdad de temperaturas entre ambos cuerpos.
Si a esta sencilla ecuación diferencial añadimos un simple término cuadrático nos encontramos con un básico sistema no lineal, cuya resolución numérica puede observarse en la Figura 1.
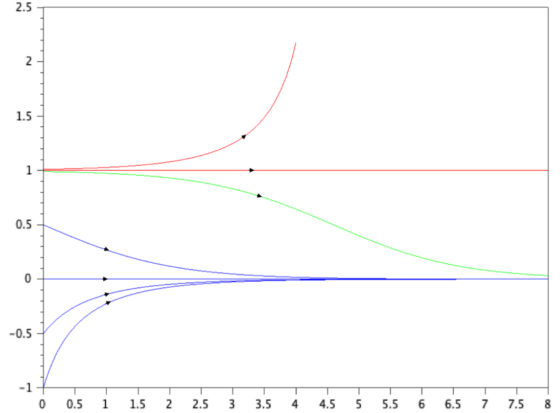 Figura 1: Dos puntos de equilibrio en una simple ecuación diferencial ordinaria autónoma no lineal de primer orden: punto de equilibrio estable en 0 y punto de equilibrio inestable en 1. Ecuación =-x+x2 . Fuente: [2] Cap. 1, pp.: 5-6.
Figura 1: Dos puntos de equilibrio en una simple ecuación diferencial ordinaria autónoma no lineal de primer orden: punto de equilibrio estable en 0 y punto de equilibrio inestable en 1. Ecuación =-x+x2 . Fuente: [2] Cap. 1, pp.: 5-6.Vemos que linealizando el sistema en torno a la temperatura 0, la solución (trayectorias azules) tienden al punto de equilibrio previsto por la ley de enfriamiento de Newton, si partimos de las inmediaciones en torno a la cual hemos linealizado. Pero si resolvemos el sistema no lineal completo, descubrimos que partir de otras condiciones iniciales nos puede dar lugar a otras soluciones radicalmente diferentes causadas por un segundo punto de equilibrio en 1. Cualquier perturbación partiendo de esta segunda temperatura hace que el sistema abandone la situación y, o bien tienda al anterior equilibrio 0 (trayectoria verde), o bien la temperatura crezca sin límite (trayectoria roja).
Ciclos límiteLos sistemas no lineales pueden oscilar sin excitación externa, con amplitud y frecuencia fijas. Las oscilaciones lineales como por ejemplo las de un péndulo linealizado en torno a la vertical, puede cambiar la amplitud de sus oscilaciones (por ejemplo, empujando más o menos un columpio). Balthasar Van der Pol, hacia 1920, añadió un término no lineal a la ecuación diferencial lineal del péndulo, haciendo depender su coeficiente de amortiguamiento con su posición. Se trata entonces de una sencilla ecuación diferencial ordinaria no lineal de segundo orden.
En sistemas dinámicos de orden dos o superior, se emplea muchas veces el espacio de fases para representar los grados de libertad del sistema. En la Figura 2 se muestra la solución de la ecuación de Van der Pol con dos condiciones iniciales diferentes.
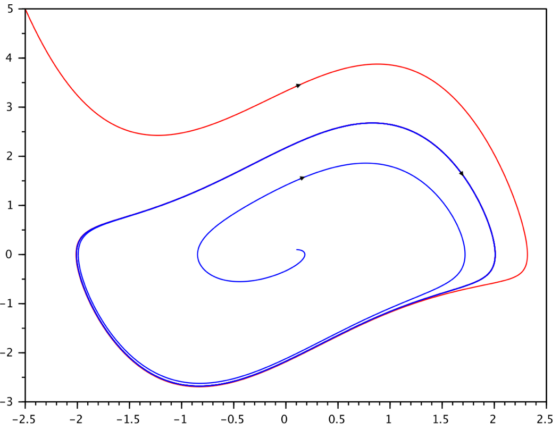 Figura 2: Ciclo límite estable en la ecuación de Van der Pol: solución representada en el plano de fase (posición-velocidad). Ecuación +(x2-1)+x=0 . Fuente [2] Cap 5, pp: 95-99.
Figura 2: Ciclo límite estable en la ecuación de Van der Pol: solución representada en el plano de fase (posición-velocidad). Ecuación +(x2-1)+x=0 . Fuente [2] Cap 5, pp: 95-99.Partiendo de posición y velocidad pequeñas (trayectoria azul inicialmente cerca de cero en la Figura 2), el sistema amplifica su oscilación sin excitación externa y tiende a cierta frecuencia y amplitud fijas (ciclo cerrado azul). Partiendo de posición y velocidad amplias (trayectoria roja) el sistema pierde energía y al final tiende a oscilar exactamente igual. En el plano fásico observamos el ciclo cerrado, llamado ciclo límite, efecto causado por la no linealidad añadida por Van der Pol. Ante cualquier perturbación creciente o decreciente que sufra la posición o velocidad de este especial péndulo no lineal, el dispositivo corregirá la situación y volverá a oscilar a la misma frecuencia y amplitud propias. Se trata de un sorprendente ciclo límite estable, exclusivo de los sistemas no lineales, y que nos lleva a un nuevo concepto de región de equilibrio estable, generalización del concepto de punto de equilibrio estable que hemos descrito arriba.
CaosEn sistemas dinámicos lineales estables, la ligera modificación de sus condiciones iniciales da lugar a ligeros cambios en su respuesta. Sin embargo, en sencillos sistemas no lineales se puede observar una extrema sensibilidad a las condiciones iniciales, propiedad exclusiva de la no linealidad, y que se denomina caos.
En la Figura 3 se muestran las soluciones de una ecuación diferencial ordinaria no lineal de segundo orden que modela un sistema mecánico con deflexiones elásticas no lineales y forzado con un coeficiente no constante ([2] p.7).
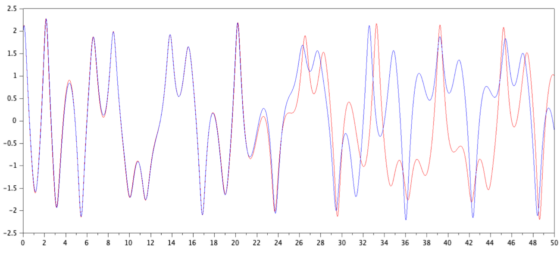 Figura 3: Evolución imprevisible de dos trayectorias en un simple sistema no lineal de segundo orden con dos condiciones iniciales casi idénticas. Ecuación +0,1+x5=6sen t. Fuente: [2] Cap. 1, pp.: 7-8.
Figura 3: Evolución imprevisible de dos trayectorias en un simple sistema no lineal de segundo orden con dos condiciones iniciales casi idénticas. Ecuación +0,1+x5=6sen t. Fuente: [2] Cap. 1, pp.: 7-8.Puede observarse que, ante condiciones iniciales casi idénticas, las dos trayectorias del sistema (azul y roja) son al principio iguales, pero en pocos instantes se produce una bifurcación radical en el comportamiento del sistema. Nuestro modelo es totalmente determinista, su ecuación puede ser exacta, pero su comportamiento es imprevisible: muy parecido a la imposible previsión del tiempo atmosférico que conocemos. Este ejemplo es aún más sencillo que el famoso modelo de dinámica atmosférica que presentó el conocido matemático y meteorólogo Edward Lorenz. En la Figura 4 se muestra una implementación física del atractor de Lorenz y su medida caótica en el laboratorio.
 Figura 4: Circuito electrónico que satisface el modelo del famoso atractor de Lorenz y medida de su respuesta caótica en el plano fásico. Fuente: Dept. de Electricidad y Electrónica UPV/EHU
Figura 4: Circuito electrónico que satisface el modelo del famoso atractor de Lorenz y medida de su respuesta caótica en el plano fásico. Fuente: Dept. de Electricidad y Electrónica UPV/EHU
La dinámica de la naturaleza y las sociedades es inherentemente no lineal. Los sistemas lineales deben entenderse como caso particular de los más generales sistemas no lineales. Los fenómenos impredecibles, anti-intuitivos o sorprendentes los podemos modelar, explicar, predecir, experimentar y controlar en el laboratorio, así como tratar de contribuir a descubrir o solucionar los enigmas de lo que llamamos realidad.
Referencias
[1] Henri Poincaré (1892-1893-1899) Les méthodes nouvelles de la mécanique céleste TOME I, II et III (PDF). Gauthier-Villars et fils, Paris
[2] Victor Etxebarria (1999) Sistemas de control no lineal y robótica. Servicio Editorial de la UPV/EHU, ISBN 8483731924 – 9788483731925, Bilbao
Sobre el autor: Victor Etxebarria Ecenarro es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (UPV/EHU)
El artículo La realidad resulta enigmática porque es no lineal se ha escrito en Cuaderno de Cultura Científica.
El rompecabezas de los cuatro cubos de Nelson
En una reciente entrada de la sección Matemoción del Cuaderno de Cultura Científica, titulada Los cuadrados de MacMahon, estuvimos hablando de un interesante rompecabezas geométrico, cuyo nombre es precisamente el título de la misma. En esta entrada vamos a ir un poco más allá y con los cuadrados de ese juego de ingenio construiremos cubos que nos permitirán crear un nuevo rompecabezas, conocido primero con el nombre de “el rompecabezas de Nelson”, y después como “el rompecabezas de los cuatro cubos”.
 El rompecabezas de Nelson, con la firma de su creador Scott Nelson, comercializado en Japón por el inventor, coleccionista y comunicador de rompecabezas matemáticos y juegos de ingenio japonés Nob Yoshigahara (1936-2004). Imagen de la colección online de rompecabezas mecánicos de Jerry Slocum, cortesía de la Biblioteca Lilly de la Universidad de Indiana.Los cuadrados de MacMahon
El rompecabezas de Nelson, con la firma de su creador Scott Nelson, comercializado en Japón por el inventor, coleccionista y comunicador de rompecabezas matemáticos y juegos de ingenio japonés Nob Yoshigahara (1936-2004). Imagen de la colección online de rompecabezas mecánicos de Jerry Slocum, cortesía de la Biblioteca Lilly de la Universidad de Indiana.Los cuadrados de MacMahon
En primer lugar, recordemos el rompecabezas de los cuadrados de MacMahon, y más concretamente, las piezas con las que se juega al mismo. Percy Alexander MacMahon (1854–1929), que fue un militar y matemático británico, se planteó de cuántas formas distintas, salvo rotaciones, se puede colorear el cuadrado dividido en cuatro partes iguales por sus dos diagonales utilizando tres colores distintos y observó que es posible hacerlo de 24 maneras distintas. A partir de esta información, creó el rompecabezas que lleva su nombre, cuyas piezas, que vemos en la siguiente imagen (con los colores verde, azul y amarillo), son la realización de las 24 formas de colorear el cuadrado dividido en cuatro partes iguales por sus dos diagonales utilizando tres colores distintos.
 Las 24 fichas que componen el rompecabezas de “los cuadrados de MacMahon”
Las 24 fichas que componen el rompecabezas de “los cuadrados de MacMahon”
El rompecabezas consiste en construir un rectángulo de 4 filas y 6 columnas con las 24 fichas del mismo (si deseas imprimirlas te dejamos aquí el PDF con las 24 fichas), de manera que cuando dos fichas tienen un lado en común el color de las regiones triangulares que comparten ese lado, en los dos cuadrados, tienen que tener el mismo color y, además, todo el perímetro, es decir, todas las regiones triangulares que forman el perímetro del rectángulo, tiene que ser de un mismo color, ya sea este, verde, azul o amarillo (para más información sobre este juego de ingenio puede leerse la entrada Los cuadrados de MacMahon).
Con las 24 fichas se puede jugar al rompecabezas de MacMahon, pero también se pueden plantear otros juegos relacionados con el mismo. Por ejemplo, los miembros del Grupo Alquerque de Sevilla, los matemáticos Juan Antonio Hans Martín, José Muñoz Santonja y Antonio Fernández-Aliseda Redondo, plantearon diferentes retos, con diferentes niveles de dificultad, aunque más sencillos que el original (en los mismos solo se pide que se cumpla la primera condición, esto es, cuando dos fichas son adyacentes tienen el mismo color en las regiones de contacto) en su artículo «MacMahon y las matemáticas en colores», publicado en la revista SUMA. Estos problemas serían los siguientes:
A) de las 24 fichas del rompecabezas, separar las 9 que tienen los tres colores y con ellas formar un cuadrado de lado 3, es decir, con tres filas y tres columnas;
 Ejemplo de cuadrado de lado 3 formado por las 9 fichas que tienen los tres colores
Ejemplo de cuadrado de lado 3 formado por las 9 fichas que tienen los tres colores
B) con las 12 fichas que tienen sólo 2 colores construir un rectángulo 3 x 4, tres filas y cuatro columnas;
C) con las 12 fichas complementarias de las anteriores, luego las que tienen 1 o 3 colores, componer también un rectángulo 3 x 4;
D) con las 15 fichas que tienen 1 o 2 colores, construir un rectángulo 3 x 5;
E) con las 15 fichas anteriores (que tienen 1 o 2 colores) y otra cualquiera de las que tienen 3 colores, formar un rectángulo de lado 4, luego con cuatro filas y cuatro columnas;
F) dividiendo primero las 24 fichas en dos grupos de 12 fichas, componer dos rectángulos 3 x 4;
G) con todas las 24 fichas construir rectángulos de tamaños 2 x 12, 3 x 8 y 4 x 6 (si a estos últimos les añadimos la condición del perímetro tenemos el rompecabezas de MacMahon, aunque en los dos tamaños anteriores esta condición nos lleva a que no existan soluciones);
H) con todas las 24 fichas construir rectángulos huecos de tamaños 3 x 11, 4 x 10, 5 x 9, 6 x 8 y 7 x 7 (todos ellos de perímetro igual a 24, que son las piezas que tenemos para construirlos).
 Ejemplo de cuadrado hueco de lado 7 formado por las 24 fichas
Ejemplo de cuadrado hueco de lado 7 formado por las 24 fichasLos cubos de Nelson
El matemático, programador informático y diseñador de juegos de ingenio estadounidense Harry Lewis Nelson (1932), quien diseñó un juego basado en los cuadrados de MacMahon denominado Pohaku (véanse las siguientes imágenes), planteó la cuestión de si sería posible utilizar las 24 piezas cuadradas de MacMahon como las caras de cuatro cubos (como hay 6 caras por cubo, son 24 caras en total) de manera que, si dos caras comparten una arista, el color de las regiones triangulares de contacto sean del mismo color.
 Portada del juego Pohaku, inventado por el matemático estadounidense Harry L. Nelson y comercializado por Penny Norman, que consistía en 5 juegos, para jugar entre dos personas, que utilizaban los 24 cuadrados de MacMahon, denominados Domino Pohaku, Standard Pohaku, 5 x 5 Pohaku y Toroidal Pohaku. Imagen de eBay
Portada del juego Pohaku, inventado por el matemático estadounidense Harry L. Nelson y comercializado por Penny Norman, que consistía en 5 juegos, para jugar entre dos personas, que utilizaban los 24 cuadrados de MacMahon, denominados Domino Pohaku, Standard Pohaku, 5 x 5 Pohaku y Toroidal Pohaku. Imagen de eBay
 Reglas de los juegos Domino Pohaku, Standard Pohaku, 5 x 5 Pohaku y Toroidal Pohaku. Imagen de eBay
Reglas de los juegos Domino Pohaku, Standard Pohaku, 5 x 5 Pohaku y Toroidal Pohaku. Imagen de eBay
La cuestión planteada por el matemático fue resuelta por su hijo Scott Nelson en 1970, cuando tenía tan solo 9 años y fue el nacimiento de un nuevo rompecabezas. En la siguiente imagen se muestran los cuatro cubos, cumpliendo las condiciones de Harry Nelson, al desplegar en el plano las seis caras de los mismos.
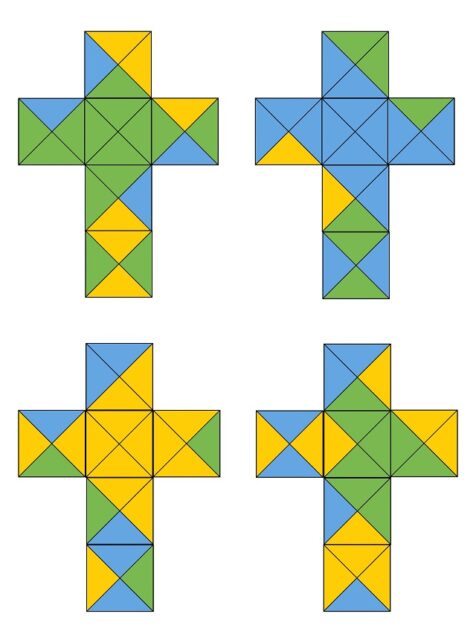
¿En qué consiste el rompecabezas de Nelson? Se trata de crear formas tridimensionales con los cuatro cubos, como una fila de cuatro cubos o los cuatro cubos juntos formando una estructura cuadrada (véase la siguiente imagen), de manera que en las caras visibles se cumpla la condición de que las caras adyacentes tengan el mismo color en las regiones de contacto.
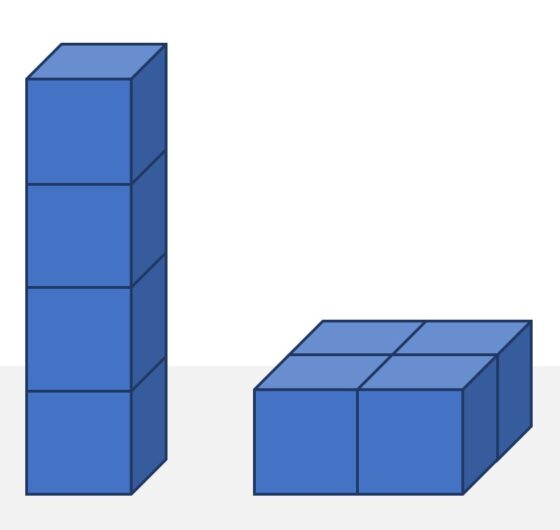
Por ejemplo, las soluciones a las dos figuras anteriores son las siguientes.

Las formas tridimensionales que aparecían en el juego comercial, divididas por nivel de dificultad, eran las siguientes. Nivel para principiantes:
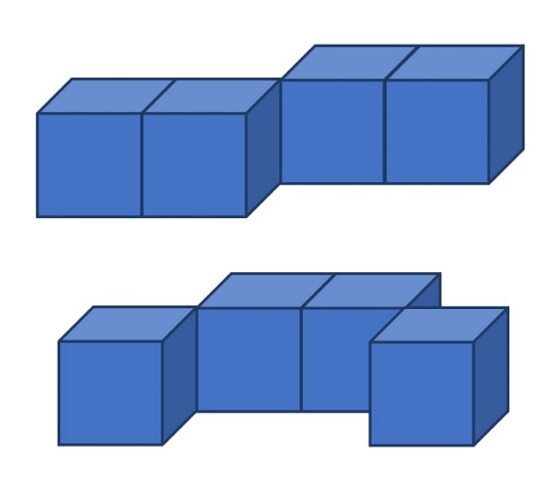
Nivel intermedio:
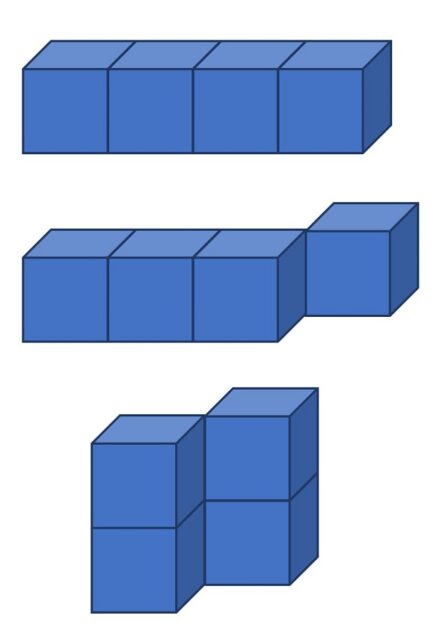
Nivel experto:
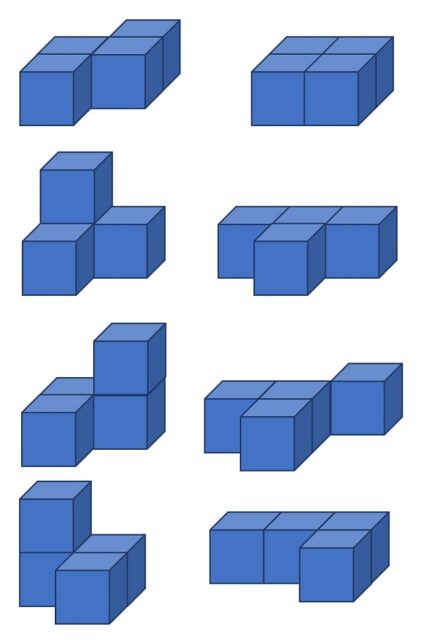
Como cada vez que hablamos de rompecabezas, mi consejo es que construyáis los cuatro cubos de Nelson, cuyas caras son los 24 cuadrados de MacMahon, y disfrutéis del juego.
 El rompecabezas de Nelson fue comercializado como el rompecabezas de los cuatro cubos por la empresa Binary Arts, que hoy es ThinkFun. Imagen de la colección online de rompecabezas mecánicos de Jerry Slocum, cortesía de la Biblioteca Lilly de la Universidad de Indiana
El rompecabezas de Nelson fue comercializado como el rompecabezas de los cuatro cubos por la empresa Binary Arts, que hoy es ThinkFun. Imagen de la colección online de rompecabezas mecánicos de Jerry Slocum, cortesía de la Biblioteca Lilly de la Universidad de IndianaBibliografía
1.- Percy A. MacMahon, New Mathematical Pastimes, Cambridge University Press, 1921 (puede obtenerse una copia en pdf a través de la biblioteca digital Internet Archive [archive.org]).
2.- Martin Gardner, Nuevos pasatiempos matemáticos, Alianza editorial, 2018.
3.- Juan Antonio Hans Martín, José Muñoz Santonja y Antonio Fernández-Aliseda Redondo, MacMahon y las matemáticas en colores, SUMA 63, pp. 51-57, 2010.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El rompecabezas de los cuatro cubos de Nelson se ha escrito en Cuaderno de Cultura Científica.
Primera observación de la rotación de un agujero negro supermasivo
 Ilustración del modelo de disco de acreción inclinado. El eje de giro del agujero negro se alinea verticalmente y la dirección del chorro es casi perpendicular al disco. La desalineación entre el eje de giro del agujero negro y el eje de rotación del disco provocará la precesión (balanceo) del disco y del chorro. Fuente: Yuzhu Cui et al. 2023 / Intouchable Lab@Openverse / Zhejiang Lab
Ilustración del modelo de disco de acreción inclinado. El eje de giro del agujero negro se alinea verticalmente y la dirección del chorro es casi perpendicular al disco. La desalineación entre el eje de giro del agujero negro y el eje de rotación del disco provocará la precesión (balanceo) del disco y del chorro. Fuente: Yuzhu Cui et al. 2023 / Intouchable Lab@Openverse / Zhejiang LabUn equipo científico internacional, con participación del Instituto de Astrofísica de Andalucía (IAA-CSIC), ha analizado datos de 23 años del centro de la galaxia Messier 87 (M87), que alberga un agujero negro supermasivo (6.500 millones de veces más masivo que el Sol), el primero del que se obtuvo una imagen.
Los resultados revelan que el chorro que emerge del agujero negro a altísima velocidad oscila hacia arriba y hacia abajo con una amplitud de unos 10 grados, lo que a su vez confirma que el agujero negro se halla en rotación.
Los agujeros negros absorben grandes cantidades de material debido a su fuerza de gravedad, tan potente que ni siquiera la luz escapa de ellos, e impulsan un flujo de plasma en forma de chorro que se mueve casi a la velocidad de la luz y abarca enormes distancias. La galaxia M87, por ejemplo, presenta un chorro que emerge de sus regiones centrales y se extiende mucho más allá del tamaño de la propia galaxia.
Sin embargo, el mecanismo de transferencia de energía entre los agujeros negros supermasivos, los discos de acreción y los chorros aún se desconoce. La teoría predominante sugiere que se puede extraer energía de un agujero negro en rotación, permitiendo que parte del material que rodea el agujero negro sea expulsado a gran velocidad. A pesar de ello, la rotación de los agujeros negros supermasivos, un factor crucial en este proceso y el parámetro fundamental, además de la masa del agujero negro, nunca se ha observado directamente.
Un chorro en precesiónEl análisis del equipo de investigación, que incluye una comparación con una simulación teórica, indica que el eje de rotación del disco de acreción se desalinea con el eje de giro del agujero negro, lo que genera un chorro en precesión (como el balanceo de una peonza).
La detección de esta precesión constituye una evidencia inequívoca de que el agujero negro supermasivo de M87 se halla, en efecto, girando, lo que abre nuevas dimensiones en nuestra comprensión de la naturaleza de estos objetos.
La desalineación entre el agujero negro y el disco es relativamente pequeña y el período de precesión es de alrededor de once años, por lo que un análisis exhaustivo de los datos de alta resolución de la estructura de M87 acumulados durante dos décadas han sido suficientes para poder detectarla
Pero, ¿qué fuerza puede alterar la dirección de un chorro tan poderoso? La respuesta podría hallarse en el comportamiento del disco de acreción: a medida que los materiales que caen orbitan alrededor del agujero negro, forman una estructura de disco antes de girar gradualmente en espiral hasta que son absorbidos por el agujero negro. Pero si el agujero negro gira, ello ejerce un impacto significativo en el espacio-tiempo circundante, provocando que los objetos cercanos sean arrastrados a lo largo de su eje de rotación, es decir, produciendo el “arrastre de marco” (frame dragging) predicho por la Relatividad General de Einstein.
Si bien este estudio arroja luz sobre cómo funciona un agujero negro supermasivo, también abre grandes incógnitas. La estructura del disco y el valor exacto del giro del agujero negro supermasivo M87* son aún inciertos, y este trabajo predice que existen más factores que intervienen en esta configuración, lo que añade nuevos desafíos a la investigación.
Referencia:
Cui, Y., Hada, K., Kawashima, T. et al. (2023) Precessing jet nozzle connecting to a spinning black hole in M87 Nature doi: 10.1038/s41586-023-06479-6
Edición realizada por César Tomé López a partir de materiales suministrados por IAA-CSIC
El artículo Primera observación de la rotación de un agujero negro supermasivo se ha escrito en Cuaderno de Cultura Científica.
La importancia del dióxido de carbono en la dinámica geológica de Europa
En al menos tres ocasiones, en Planeta B hemos hablado sobre Europa, uno de los satélites más interesantes de Júpiter: “La evolución del interior de la luna Europa”, “Una tectónica de placas más allá de la Tierra” y “¿Y si pudiésemos llegar al océano de Europa sin necesidad de atravesar toda la corteza?”.
Y es que cuando lo miramos de cerca, su superficie atestigua una historia reciente de actividad geológica, quizás no solo pretérita, sino también en la actualidad, con la posible existencia de procesos que siguen rejuveneciendo el aspecto de este satélite. Además de esa juventud que aparenta en términos geológicos, el Hubble descubrió hace una década la posible existencia de penachos de agua que surgen de su superficie, lo que sería otra prueba a favor de ser un mundo activo, aunque estos serían bastante elusivos.
 Los penachos de vapor de agua en Europa tal y como los detectó el telescopio espacial Hubble, abajo a la izquierda, anotados por la palabra “Plumes”. Imagen cortesía de la NASA, ESA, W. Sparks (STScI) y USGS Astrogeology Science Center.
Los penachos de vapor de agua en Europa tal y como los detectó el telescopio espacial Hubble, abajo a la izquierda, anotados por la palabra “Plumes”. Imagen cortesía de la NASA, ESA, W. Sparks (STScI) y USGS Astrogeology Science Center.¿De dónde procede toda esta actividad geológica que observamos? Lo más probable es que el responsable directo sea un océano de agua líquida bastante salado -valga la redundancia- que a su vez está en contacto también con el núcleo rocoso del satélite, de donde procedería la energía para mantener líquido el océano. Este último serviría como una cinta transportadora de materia y energía desde el interior de Europa hacia el exterior, provocando esos cambios que observamos en su superficie.
Una manera indirecta de conocer con mayor grado de detalle la composición química del agua de ese posible océano sería si estuviese de algún modo conectado al exterior, ya que, de momento, carecemos de la tecnología para poder llegar hasta este, que requeriría una sonda capaz de atravesar varios kilómetros de hielo hasta llegar al agua.
Saber qué elementos y compuestos existen en el océano nos abre una puerta a saber si es un océano habitable -habitable para nuestros estándares- puesto que la existencia y abundancia de determinados elementos y compuestos puede ser crucial para el desarrollo de la vida. Por supuesto, esto no quiere decir que haya vida o se pueda haber desarrollado, pero si nos puede indicar si es un lugar hospitalario.
Los lugares más prometedores para “saborear” -me van a permitir que me tome una licencia literaria- este océano serían los penachos de vapor de agua (muestreándolos desde la órbita, por ejemplo- y por supuesto las zonas donde pueda existir actividad geológica reciente en Europa, ya que a través de las fisuras generadas como resultado de la dinámica del satélite podría haberse transportado material desde el océano hasta el exterior. Sería una manera indirecta, pero válida mientras no tengamos una tecnología capaz de llegar al océano.
Pero bueno, ¿qué se ha descubierto ahora que ha generado tanto revuelo? Lo cierto es que descubrir -gracias a Jesús Martínez-Frías por su corrección- no se ha descubierto nada en el sentido más estricto de la palabra, sino que se ha podido identificar mejor en que regiones de la superficie de Europa podemos encontrar dióxido de carbono, algo que ya contaba con detecciones previas como podemos leer en Hansen et al. (2008) y McCord et al. (1998).
El dióxido de carbono no es un compuesto que pueda ser estable a lo largo del tiempo geológico en las condiciones de presión y temperatura existentes en la superficie de Europa, por lo que cualquier cantidad de este que quede expuesta, debería de sublimarse y formar parte de la tenue atmósfera del satélite o escaparse al espacio, sin embargo, tanto las observaciones realizadas por la misión Galileo como con el telescopio espacial James Webb han sido capaces de detectar este compuesto en la superficie.
La diferencia entre el descubrimiento original del dióxido de carbono y los datos aportados en el reciente estudio publicado en Science por Trumbo et al. (2023) es principalmente una mejor localización espacial, así como aportar un contexto para su origen, ya que los datos de la Galileo tenían muy poca resolución en comparación con los del James Webb, que ha permitido adscribir la presencia de este compuesto en regiones muy concretas del satélite de Júpiter.
Lo cierto es que el dióxido de carbono no es un compuesto muy raro, y se había detectado previamente en otros lugares del sistema joviano así como en los satélites de Saturno, pero no con una asociación directa a zonas jóvenes de su superficie. Se sospecha que en algunos de estos casos la presencia de este dióxido de carbono podría deberse a factores externos como, por ejemplo, la aportación de compuestos orgánicos por parte de meteoritos o zonas ya ricas en compuestos orgánicos que sufren procesos de degradación a causa de la intensa radiación.
El caso de Europa es diferente, y las concentraciones de dióxido de carbono se encuentran fuertemente asociadas a regiones jóvenes con terreno de tipo chaos -los chaos, explicado de una manera sencilla, son zonas de la superficie de los planetas donde el terreno parece estar agrietado y desordenado- como son Tara Regio y Powys Regio. En el resto de satélites donde se ha detectado, el dióxido de carbono estaba asociado a zonas más oscuras ricas en compuestos orgánicos, cráteres de impacto o las zonas más afectadas por la radiación.
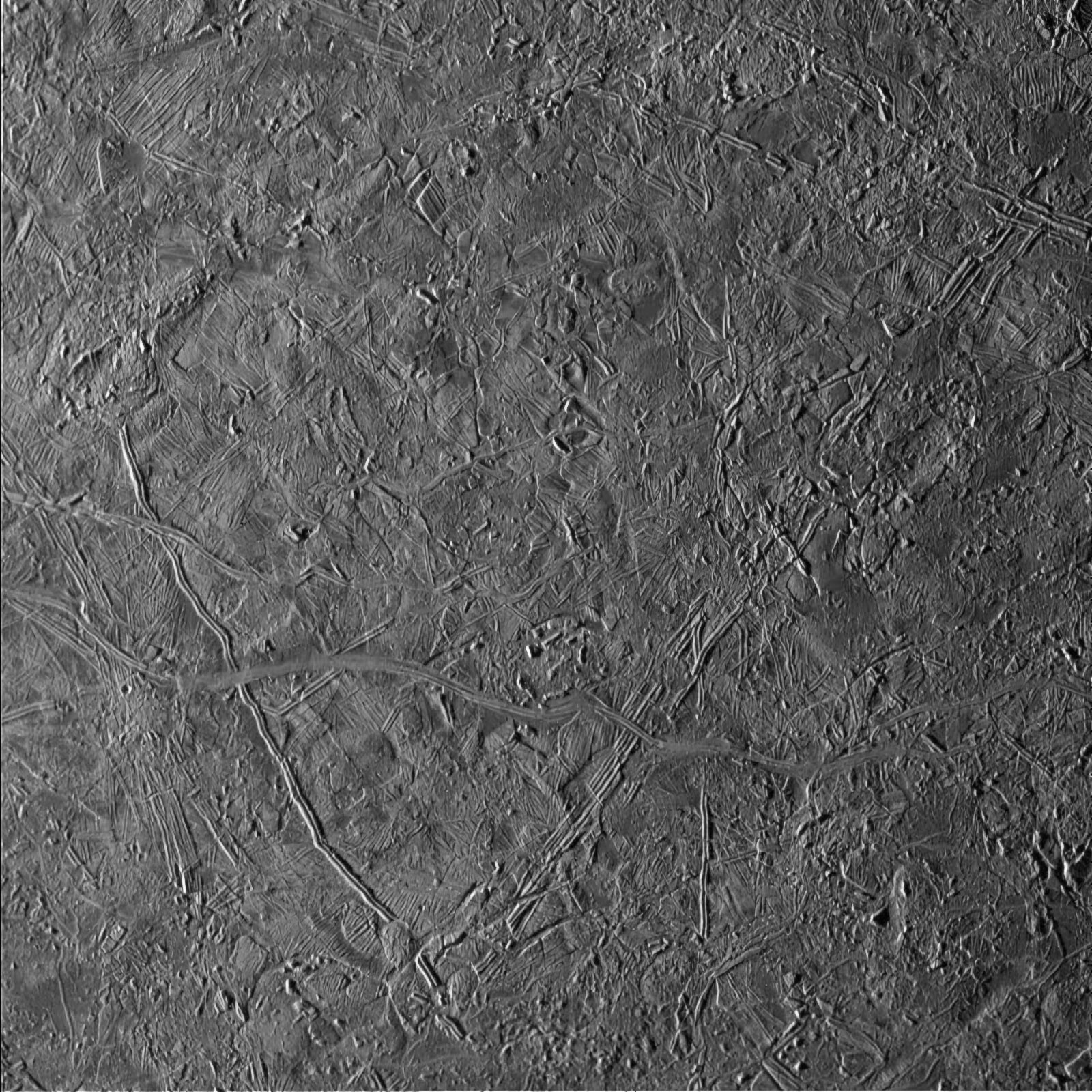 Un detalle de la zona de Tara Regio capturado por la sonda Galileo en septiembre de 1998 a una resolución de 220 metros por píxel. Se aprecia perfectamente la existencia de juegos de grietas, crestas y una forma como de puzle desordenado. Cortesía de NASA/JPL/USGS.
Un detalle de la zona de Tara Regio capturado por la sonda Galileo en septiembre de 1998 a una resolución de 220 metros por píxel. Se aprecia perfectamente la existencia de juegos de grietas, crestas y una forma como de puzle desordenado. Cortesía de NASA/JPL/USGS.Esto nos lleva a la siguiente cuestión. Entonces, ¿de dónde sale el dióxido de carbono? Si en los párrafos anteriores hablábamos del posible origen exógeno -impactos de meteoritos y la degradación de los compuestos orgánicos-, ahora nos toca hablar del origen endógeno de este compuesto. Lo normal es que para que sea estable bajo las condiciones actuales, debe de encontrarse atrapado en el hielo.
Los científicos han estudiado otras posibilidades, como que el dióxido de carbono observado procediese de compuestos orgánicos o de minerales del grupo de los carbonatos, pero no se observan en los espectros señales que hagan pensar en estas dos últimas fuentes -sumada a la radiación- podrían ser una forma plausible de formar las concentraciones de dióxido de carbono encontrados tanto en la asociación a estas regiones jóvenes como en sus proporciones.
Así que solo nos queda una posibilidad, y es que el dióxido de carbono proceda directamente del interior de Europa como dióxido de carbono o como alguna otra molécula precursora de este compuesto desde el océano que hay bajo su superficie. Llegaría a la superficie durante la formación de estas zonas más jóvenes a través del ascenso de materiales del océano -ya sea en estado líquido o como masas de hielo con un comportamiento plástico-, por el colapso del hielo sobre zonas donde exista agua líquida bajo la superficie o por el ascenso de líquidos a través de grietas en la corteza.
Pero todavía hay más: y es que para que observemos las concentraciones de dióxido de carbono que vemos en la superficie, debe de haber un mecanismo continuo que vaya reponiendo este dióxido de carbono que se escapa a la atmósfera o bien la llegada de este compuesto a la superficie ha debido ocurrir en un lapso de tiempo muy reciente a escala geológica.
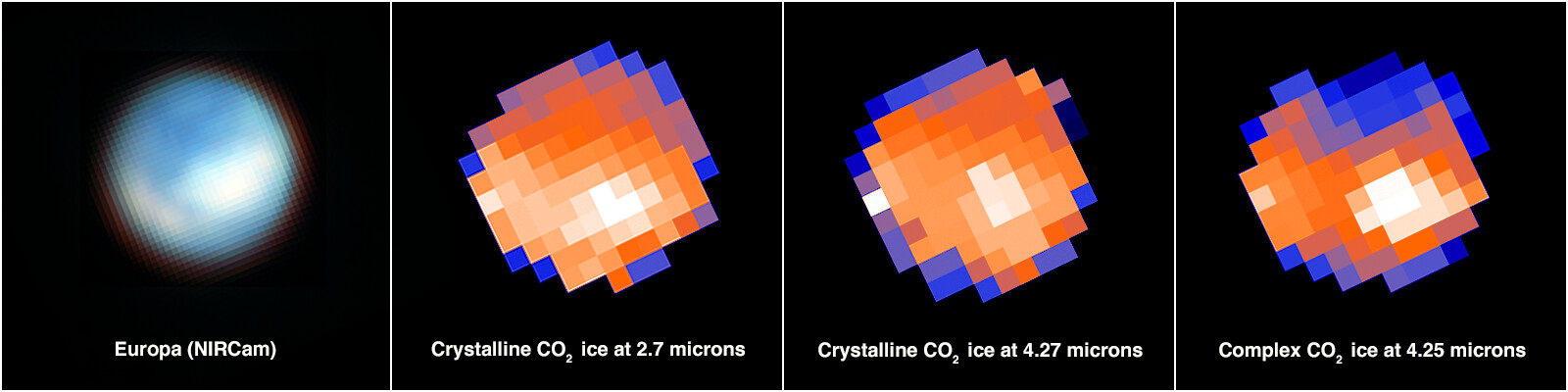 A la izquierda, una imagen de Europa tomada por el JWST. A la derecha, los mapas de concentración de CO2. Cortesía de NASA, ESA, CSA, G. Villanueva (NASA/GSFC), S. Trumbo (Cornell Univ.) y A. Pagan (STScI).
A la izquierda, una imagen de Europa tomada por el JWST. A la derecha, los mapas de concentración de CO2. Cortesía de NASA, ESA, CSA, G. Villanueva (NASA/GSFC), S. Trumbo (Cornell Univ.) y A. Pagan (STScI).Las implicaciones de estos resultados de cara a la astrobiología son muy importantes: el primero, que el carbono, que es un elemento que es necesario para la vida tal y como la conocemos, se encuentra presente en el océano de Europa, y también que este océano tendría unas condiciones ligeramente oxidantes, lo que coincidiría con una entrada al océano de compuestos oxidantes que se producen en la superficie a causa de la intensa radiación, completando también la cinta transportadora de materia desde la superficie hacia el océano y no solo desde dentro hacia afuera.
Un océano reductor, desde nuestro punto de vista, podría ser menos hospitalario para la vida, porque aunque haya organismos como los anaeróbicos que, capaces de realizar la respiración anaeróbica usando moléculas diferentes al oxígeno, o los quimioautótrofos, capaces de extraer su energía de compuestos inorgánicos, en nuestro planeta sabemos que la falta de oxígeno reduce las posibilidades de formas de vida más complejas.
Todos estos estudios son muy interesantes, ya que podrán servir de base a las futuras investigaciones de la sonda europea JUICE, que ya se dirige al sistema joviano, y la Europa Clipper de la NASA que, si todo va bien, despegará en octubre de 2024, desde donde poder verificar estas observaciones eso sí, desde mucho más cerca y aportarnos nuevos detalles de este cuerpo tan interesante.
Bibliografía:
Hansen, G. B., & McCord, T. B. (2008). Widespread CO2 and other non-ice compounds on the anti-Jovian and trailing sides of Europa from Galileo/NIMS observations. Geophysical Research Letters, 35(1), L01202. doi: 10.1029/2007GL031748
McCord, T. B., Hansen, G. B., Clark, R. N., Martin, P. D., Hibbitts, C. A., Fanale, F. P., Granahan, J. C., Segura, M., Matson, D. L., Johnson, T. V., Carlson, R. W., Smythe, W. D., & Danielson, G. E. (1998). Non‐water‐ice constituents in the surface material of the icy Galilean satellites from the Galileo near‐infrared mapping spectrometer investigation. Journal of Geophysical Research: Planets, 103(E4), 8603-8626. doi: 10.1029/98JE00788
Trumbo, S. K., & Brown, M. E. (2023). The distribution of CO 2 on Europa indicates an internal source of carbon. Science, 381(6664), 1308-1311. doi: 10.1126/science.adg4155
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo La importancia del dióxido de carbono en la dinámica geológica de Europa se ha escrito en Cuaderno de Cultura Científica.
Aburrimiento musical
José Manuel González Gamarro
La música, ese hecho cultural transversal a lo largo del planeta, esa gran invención humana que casi empuja a caer irremediablemente en lo interdisciplinar, ha sido estudiada de forma poliédrica. La extensísima literatura que aborda la investigación sobre música tiene casi tantos enfoques como disciplinas del conocimiento existen. Uno de los puntos que más consenso encuentra la investigación es el beneficio que aporta escucharla, estudiarla y/o practicarla. Hay quien, interesadamente sesgado, no duda en atribuirle propiedades casi mágicas con discursos grandilocuentes y atractivos titulares de prensa: «Quítele la pantalla y dele un instrumento musical a su hija o hijo», «La música te hace más inteligente», «¿Quiere envejecer mejor? Practique música», etc. Incluso el refranero popular nos dice que quien canta su mal espanta, pero, como todo en la vida, cabe un gran «depende» en todas estas afirmaciones.
 Foto: Manuel Nägeli / UnsplashEfectos negativos de la música
Foto: Manuel Nägeli / UnsplashEfectos negativos de la música
Todos los estudios en pos de los beneficios causados por la música o cómo ésta mejora la sociedad, tienen una consecuencia evidente: el número de estudios de los efectos negativos de la música es mucho menor y solo han suscitado interés en los últimos años. Uno de estos efectos “negativos” puede ser el aburrimiento. Este aburrimiento no siempre se puede considerar negativo ya que algunos autores1 lo consideran como una retroalimentación que provoca un cambio de tarea, por lo que cumple una función importante. Este estado emocional puede ocurrir cuando se interactúa con el arte. De hecho, ocurre con más frecuencia de la que se puede imaginar en un primer momento. Es por esto que un reciente estudio2 dirigido por la investigadora del Instituo Max Planck de Estética Empírica, Julia Merrill ha abordado esta cuestión, poniendo el foco de atención en investigar la prevalencia y las situaciones de aburrimiento al interactuar con la música. Aunque el estudio no es concluyente, aborda cuestiones poco exploradas, como qué características puede tener una música aburrida (por más que esto dependa del juicio del oyente), qué emociones se asocian a esta supuesta música aburrida, la importancia del contexto en la escucha musical, los rasgos de la personalidad del oyente o un constructo que se denomina “sofisticación musical” medida con una escala llamada Gold-MSI3 donde se autoevalúa el compromiso activo con la música, habilidades de percepción musical y la percepción de emociones al oír música.
Para arrojar luz sobre todas estas cuestiones, en el Instituto Max Planck se llevaron a cabo dos estudios diferentes y complementarios, atendiendo a métodos cualitativos y cuantitativos. Para el estudio cualitativo se formularon preguntas abiertas a 266 participantes sobre las situaciones en las que experimentaron aburrimiento al escuchar música atendiendo a la ubicación, el entorno, si estaban solos o acompañados, el tipo de música o la duración de ésta. También se formularon preguntas relativas a los sentimientos y emociones evocados al aburrirse y cómo reaccionaron ante esto. Otra de esas preguntas abiertas abordaba la cuestión de la definición de la música aburrida, es decir, qué características tiene la música con la que la gente se aburre. Para el estudio cuantitativo se usaron 719 participantes donde respondieron a una encuesta con tres preguntas: ¿Con qué frecuencia te aburres cuando escuchas música?, ¿con qué intensidad te aburres cuando escuchas música? y ¿Con qué frecuencia utilizas música para afrontar el aburrimiento? Usando en las respuestas una escala del 1 al 7, siendo el 1 nunca y el 7 siempre. Además, se realizó una lista con 14 estilos musicales que también fueron calificados desde el 1 (muy interesante) hasta el 7 (muy aburrido). A partir de estos datos se escogió el estilo más aburrido y uno ligeramente aburrido y se volvió a pedir a los participantes que valoraran estos dos estilos en la escala de 1 a 7, para a continuación presentar 16 razones por las que la música es aburrida con una escala de 5 puntos. A todos estos datos se le añaden los recopilados por la escala, anteriormente mencionada, Gold-MSI que mide la sofisticación musical de cada participante.
Aburrimiento musicalLos resultados del estudio cualitativo aportaron datos que revelan que, además de experimentar aburrimiento musical en situaciones con cierta monotonía como viajar en coche, en bus, etc. o no tener el control sobre qué música escuchar (bares, radio, etc.), también se experimenta aburrimiento cuando se está solo y la escucha es concentrada. El juicio estético influye de manera determinante cuando no se ajusta a las expectativas del oyente o bien la música no encaja con el estado de ánimo durante la escucha. Las estrategias para evitar el aburrimiento causado por la música dependen de las posibilidades del contexto de la escucha, dependiendo si se puede evitar la situación (salirse de un concierto o cambiar de música) o eso no es posible (ignorar la música o distraerse con otro estímulo). Uno de los resultados que arroja el estudio cuantitativo es el porcentaje de personas que experimentan aburrimiento al escuchar música. Aunque hay un porcentaje muy elevado (76,5 %) de personas que nunca o rara vez experimenta aburrimiento en la escucha, el porcentaje de personas que se aburren en diferentes grados de intensidad y frecuencia no es nada desdeñable.
En cuanto a las características musicales, el aburrimiento ocurre cuando existen ciertos aspectos generales de la música, como la repetición, la monotonía o las letras de las canciones, con una interesante relación entre aburrimiento y significado. Sin embargo, no solo la baja excitación y la subestimulación lo provocan, sino también la sobreestimualción y la alta excitación. La música con un mayor índice de complejidad, con mayor número de disonancias o caótica resulta aburrida por una sobreabundancia de características musicales muy intensa que provocan disgusto. Otra cuestión es que la música que no nos gusta la etiquetemos como aburrida y la identifiquemos como tal antes de su escucha. El gusto musical tiene mucho de vínculo y no tanto de observación y análisis, donde las cuestiones identitarias son un punto clave.
Experiencia estética fracasadaLa finalidad de la escucha musical, en numerosas ocasiones, es, precisamente, la de acabar con el aburrimiento o provocar en nosotros mismos emociones satisfactorias. Por lo tanto, según los autores del estudio se puede afirmar que, si la música nos provoca aburrimiento, es una experiencia estética fracasada con respecto al éxito de esta experiencia, que se produciría cuando hay un equilibrio entre el agrado, el placer, la excitación, la complejidad y la familiaridad. Sin embargo, este “fracaso” también puede significar éxito, puesto que existe el arte (y por lo tanto la música) deliberadamente aburrido4, es decir, algo creado con la firme intención de aburrir y motivado por diferentes razones.
Por otro lado, juzgar cualquier música como aburrida es controvertido, puesto que puede ser contraproducente tanto para el autor de la música como para la persona que la juzga. Se puede entender que una música es aburrida porque la compositora o compositor no ha sido capaz de crear algo emocionalmente satisfactorio, pero también puede ser negativo para quien juzga, por entenderse que no tiene la suficiente formación o sofisticación para comprender cierta música o sentir emociones satisfactorias al escucharla.
Es de suponer que la música con menos índice de aburrimiento, por decirlo de alguna manera, tendrá un mayor éxito en la sociedad. Sin embargo, como ya se ha advertido, el aburrimiento puede ser una consecuencia de escuchar música con unas ciertas características como una predisposición guiada por nuestro prejuicio y preferencia. Es por ello que también existen investigaciones5 que van más allá, buscando la sincronía neuronal en diferentes individuos al someterse a la escucha, con resultados que indican que a mayor sincronía, mayor éxito musical. Sea como fuere el aburrimiento musical y el fracaso de la escucha para evitarlo dependen en gran medida del concepto (filosófico) de belleza, que se podría establecer en la música como una relación compleja entre uniformidad y variedad. La investigación deberá seguir avanzando para tener una mayor comprensión de todos los factores que componen esta relación adversa con la música. Veremos.
Referencias:
1 Fahlman S. A., Mercer-Lynn K. B., Flora D. B., Eastwood J. D. (2013). Development and validation of the multidimensional state boredom scale. Assessment, 20(1), 68–85. https://doi.org/10.1177/1073191111421303
2 Merrill, J., & Niedecken, T. (2023). Music and Boredom: A First Insight Into an Unexplored Relationship. Music & Science, 6. https://doi.org/10.1177/20592043231181215
3 Müllensiefen D., Gingras B., Musil J., Stewart L. (2014). The musicality of non-musicians: An index for assessing musical sophistication in the general population. PLoS ONE, 9(2), 1–23. https://doi.org/10.1371/journal.pone.0089642
4 Elpidorou A., Gibson J. (2022). Really boring art. Ergo an Open Access Journal of Philosophy, 8(0). https://doi.org/10.3998/ergo.2231
5 Leeuwis, N., Pistone, D., Flick, N., & van Bommel, T. (2021). A sound prediction: EEG-based neural synchrony predicts online music streams. Frontiers in psychology, 12, 672980. https://doi.org/10.3389/fpsyg.2021.672980
Sobre el autor: José Manuel González Gamarro es profesor de guitarra e investigador para la Asociación para el Estudio de la Guitarra del Real Conservatorio Superior de Música “Victoria Eugenia” de Granada.
El artículo Aburrimiento musical se ha escrito en Cuaderno de Cultura Científica.
¡Ups! La fiebre amarilla

Aunque a día de hoy sabemos que la fiebre amarilla es una enfermedad vírica aguda y hemorrágica, ocasionada por arbovirus del género Flavivirus y transmitida por mosquitos infectados de los géneros Aedes y Haemogogus, no siempre ha sido así. Esta enfermedad acabó con el 10% de la población de Filadelfia en 1793. Tras aquello, el médico Stubbins Ffirth empezó a buscar la causa de la fiebre amarilla. Imprudentemente experimentó consigo mismo y después de restregarse los vómitos de enfermos e incluso bebérselos y no contagiarse, publicó en una tesis titulada ‘A Treatise on Malignant Fever’ en la que expuso que definitivamente la enfermedad no era contagiosa, un dato erróneo como sabemos actualmente.
Los vídeos de ¡UPS¡ presentan de forma breve y amena errores de la nuestra historia científica y tecnológica. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se han emitido en el programa de ciencia Órbita Laika (@orbitalaika_tve), en la 2 de RTVE.
Producción ejecutiva: Blanca Baena
Guion: José Antonio Pérez Ledo
Grafismo: Cristina Serrano
Música: Israel Santamaría
Producción: Olatz Vitorica
Doblaje: K 2000
Locución: José Antonio Pérez Ledo
Edición realizada por César Tomé López
El artículo ¡Ups! La fiebre amarilla se ha escrito en Cuaderno de Cultura Científica.
CartoCell o cómo detectar patrones ocultos en tejidos celulares
Una reciente colaboración entre el Instituto de Biomedicina de Sevilla con la Universidad del País Vasco, el Instituto Biofisika, el Donostia International Physics Center y otros prestigiosos centros nacionales e internacionales, han dado como resultado CartoCell, una herramienta de análisis de imágenes en 3D de alto contenido que revela patrones de morfología celular escondidos. Este software, de código abierto, tiene un gran potencial de aplicación tanto en ciencia básica, con la que ya ha sido probado, como para el desarrollo clínico y médico.
 CartoCell es una red neuronal artificial que procesa de forma automática epitelios en 3D, esto es, permite la reconstrucción automática en 3D de imágenes obtenidas por microscopía.En busca de patrones ocultos
CartoCell es una red neuronal artificial que procesa de forma automática epitelios en 3D, esto es, permite la reconstrucción automática en 3D de imágenes obtenidas por microscopía.En busca de patrones ocultos
Los animales y plantas, además de otras estructuras de la naturaleza, presentan patrones que podemos detectar fácilmente: las rayas de las cebras, los polígonos de la jirafa o en las conchas de las tortugas, por ejemplo. Todos estos patrones tienen en común que son macroscópicos. Sin embargo, este mismo fenómeno se da a nivel microscópico, en los tejidos. “Estos patrones también aparecen durante el desarrollo embrionario”, explica Luis M. Escudero, uno de los autores e investigador del Instituto de Biomedicina de Sevilla (IBiS) y profesor de la Universidad de Sevilla. “Por ejemplo, hay genes que se expresan en patrones alternos de rayas y que son fundamentales para establecer los segmentos de los insectos”. Muchos de dichos patrones son ya conocidos y muy estudiados, sin embargo, queda mucho por descubrir.
“En nuestro trabajo hemos encontrado patrones que aún estaban escondidos…. Y que solo han podido ser desvelados al usar herramientas de inteligencia artificial para el análisis de imágenes microscópicas de tejidos. Vemos que, incluso en estructuras muy simples, ya hay asimetrías en la morfología de las células. Esta es la forma en que comienza la morfogénesis”. La morfogénesis se refiere al proceso biológico que causa que un organismo desarrolle su forma y estructura. Es una de las etapas fundamentales durante el desarrollo embrionario y se refiere a la organización y distribución espacial de las células diferenciadas para formar estructuras específicas y eventualmente órganos completos.
CartoCell, una herramienta para cartografiar los tejidos epiteliales“CartoCell es una herramienta software que permite procesar de manera rápida y automática una gran cantidad de imágenes 3D obtenidas en el microscopio para la reconstrucción y el análisis de tejidos epiteliales a nivel celular”, prosigue el Dr. Escudero. En otras palabras, esta herramienta digital es capaz de trabajar de forma automática muchísima información, especializándose en buscar patrones, formas, distribuciones y estructuras en los tejidos a partir de imágenes.
Según aclara, CartoCell utiliza la potencia de las redes neuronales, específicamente una red neuronal artificial diseñada para optimizar la identificación de células tridimensionales en imágenes de microscopía. La principal ventaja de CartoCell es que puede identificar y estudiar la forma y distribución espacial de cada célula en el tejido epitelial, permitiendo descubrir patrones asociados a diferentes tipos de tejidos.
“Cada célula del tejido es reconstruida con una gran fidelidad, gracias a lo cual podemos estudiar tanto su forma como su distribución espacial. De este modo, CartoCell nos permite descubrir patrones asociados a los diferentes tipos de tejidos y células, así como estudiar sus reglas de empaquetamiento”. De momento, el software ha sido usado para estudios de ciencia básica, permitiendo cartografiar la morfología de las células con imágenes de diferentes tipos de tejidos. “De este modo, hemos podido encontrar patrones ocultos de una manera sencilla y muy visual”, continúa el investigador, “lo que es fundamental para estudiar la organización de tejidos epiteliales donde las células presentan un contacto estrecho”.
Pero, además de los patrones ocultos, y de la investigación biológica de tejidos, CartoCell también muestra un gran potencial de aplicación clínica. “En el ámbito biomédico, la posibilidad de analizar una gran cantidad de muestras de manera rápida y fiable, como hace CartoCell, es ideal para evaluar la reproducibilidad de cultivos de organoides [pequeños tejidos creados para simular un pequeño órgano] epiteliales y realizar comparativas detalladas entre condiciones normales y patológicas. Por poner un ejemplo sencillo”, continúa el investigador, “el testeo del efecto de fármacos en tejidos animales o humanos podría beneficiarse de nuestro método. Nuestro avanzado análisis de imágenes podría detectar cambios sutiles a nivel celular, que a la larga pueden ser importantes, del efecto de cada fármaco contra una determinada enfermedad”.
Redes neuronales y código abierto en su núcleoEl corazón de CartoCell es una red neuronal artificial. La arquitectura de la red fue diseñada partiendo de otros modelos desarrollados anteriormente por el grupo de investigación en visión artificial para bioimagen del Instituto Biofisika y el Donostia International Physics Center (DIPC), en el País Vasco, que participa en el proyecto. “Estos modelos ya habían demostrado gran versatilidad y robustez para problemas similares en imagen de microscopía de diferentes modalidades (microscopía electrónica y microscopía confocal, entre otras)”, explica el doctor Ignacio Arganda, líder de dicho grupo e investigador Ikerbasque afiliado también a la Facultad de Informática de la Universidad del País Vasco (UPV/EHU). “En concreto, la arquitectura y las imágenes de salida que genera fueron adaptadas para optimizar la identificación de células tridimensionales adquiridas mediante técnicas de microscopía”.
“Como toda red neuronal artificial”, continúa, “la nuestra necesita del conocido como conjunto de entrenamiento para aprender a realizar la tarea que le propongamos. En nuestro caso, dicha tarea se trata de la identificación (o “segmentación”) de células epiteliales en imágenes tridimensionales”. Normalmente, para que una red neuronal sea capaz de generalizar y realizar esta tarea con precisión, necesita un conjunto de datos muy grande y heterogéneo. Construir dicho conjunto requiere muchísimo trabajo manual, ya que habría que “pintar” una a una todas las células de las imágenes 3D de entrenamiento.
“Sin embargo”, aclara el experto, “CartoCell utiliza un conjunto de entrenamiento inicial de epitelios pintados muy pequeño. Con ese conjunto, entrenamos nuestra red neuronal una primera vez, e intentamos que prediga las identidades celulares en muchas otras imágenes de epitelios. Como es esperado, el resultado no es el ideal, pues muchas identidades no están completas, y quedan huecos entre las células. Para solucionarlo, empleamos un algoritmo de Voronoi que rellena los espacios vacíos entre las células identificadas, consiguiendo así que contacten entre ellas».
“Estas etiquetas celulares transformadas son las que llamamos weak labels [etiquetas débiles], y las utilizamos como nuestro nuevo conjunto de entrenamiento. Aunque estas etiquetas no son totalmente perfectas, capturan de una forma bastante realista la morfología celular (dado que las células epiteliales comparten algunas características de organización con los patrones de Voronoi). Además, al ser muchas y muy heterogéneas, ayudan a mejorar el proceso de re-entrenamiento de la red. Este paso es clave en CartoCell, ya que nos permite conseguir muy buenos resultados en segmentación sin tener que emplear un tiempo excesivo en etiquetar manualmente un conjunto de entrenamiento grande”, completa el investigador.
Una de las características de CartoCell es su versatilidad, según defiende el Dr. Pedro Gómez-Gálvez, autor también del trabajo y actualmente en el Departamento de Fisiología, Desarrollo y Neurociencia de la Universidad de Cambridge (Reino Unido). En concreto, su red neuronal se podría sustituir por cualquier modelo de segmentación del estado del arte (redes neuronales convolucionales 3D o cualquiera de sus variantes), siempre y cuando se utilice el concepto de etiquetado ligero o “weak labels” anteriormente descrito para mejorar el conjunto de entrenamiento. “De hecho, en nuestro artículo probamos con varias arquitecturas de red modernas y, con todas, los resultados fueron muy buenos tras el etiquetado ligero siguiendo el algoritmo de Voronoi”, confirma Gómez-Galvez.
Además, CartoCell es una herramienta de código abierto, lo que brinda la oportunidad a otros expertos de utilizar, mejorar o adaptar libremente su uso. “Todas las personas que hemos participado en la creación de CartoCell creemos firmemente en la idea de ciencia abierta. Consecuentemente, CartoCell ha sido implementado desde el primer día como código abierto, y siempre ha estado disponible para la comunidad. En ese sentido, nuestra intención ha sido crear una herramienta accesible, fácil de instalar y utilizar por personas no expertas, pero también adaptable y ampliable para quien quiera desarrollar nuevas soluciones sobre ella”, concluye.
Referencia:
Jesus A. Andres-San Roman, Carmen Gordillo-Vazquez, Daniel Franco-Barranco, Laura Morato, Cecilia H. Fernández-Espartero, Gabriel Baonza, Antonio Tagua, Pablo Vicente-Munuera, Ana M. Palacios, María P. Gavilán, Fernando Martín-Belmonte, Valentina Annese, Pedro Gómez-Gálvez, Ignacio Arganda-Carreras, Luis M. Escudero (2023) CartoCell, a high-content pipeline for 3D image analysis, unveils cell morphology patterns in epithelia Cell Reports Methods doi: 10.1016/j.crmeth.2023.100597
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo CartoCell o cómo detectar patrones ocultos en tejidos celulares se ha escrito en Cuaderno de Cultura Científica.
Minerales con brillo
brillo
Los minerales, esas sustancias sólidas naturales formadas por elementos químicos ordenados en estructuras cristalinas, presentan una serie de propiedades físicas y químicas que les son únicas y características, lo que nos permite utilizarlas como criterios identificativos y clasificatorios.
Dicho de otro modo y un poco más sencillo. Debido a la composición química de los minerales y la estructura interna que presentan esos elementos químicos, cada mineral tiene unas características concretas que se pueden observar a simple vista y que son propias de cada uno de ellos, lo que nos permite identificarlos rápidamente diferenciándolos de los demás. Si lo asimilamos a los seres humanos, serían esos caracteres heredados que sirven para describir a una persona sin confundirla con otra, como el color del pelo y de los ojos, el tono de la piel, la altura, la presencia de pecas y lunares o el rango de nuestra voz.
Esto nos da mucho juego cuando organizamos actividades de divulgación geológicas, ya que podemos plantear talleres de identificación de minerales de manera muy sencilla y utilizando artilugios de andar por casa, como un trozo de loza, una navaja o un vidrio, que suelen llamar mucho la atención del público asistente. Y, aunque la mayoría de las propiedades físicas y químicas a las que hacemos alusión son muy fáciles tanto de explicar cómo de entender, hay una que se le suele atragantar a la gente. Me estoy refiriendo al brillo.
 A) Ejemplar de galena, mineral con brillo metálico. B) Cristales de cuarzo, mineral con brillo no metálico.
A) Ejemplar de galena, mineral con brillo metálico. B) Cristales de cuarzo, mineral con brillo no metálico.En una definición rápida, el brillo es el aspecto que adquiere la superficie de un mineral cuando refleja la luz. Y de aquí viene la confusión. Cuando hablamos de reflejar la luz, nos imaginamos a las ondas luminosas rebotando con fuerza contra la cara del mineral y volviendo a la fuente de emisión como un nuevo haz de luz, casi como si ese mineral se convirtiese por sí mismo en emisor y produjese un destello luminoso. Esto es lo que vemos, por ejemplo, cuando el Sol incide en un objeto de metal en la calle, cuyo reflejo se convierte en un resplandor que nos marca exactamente su posición y nos molesta si lo miramos fijamente. Esto nos lleva a pensar que existen minerales que brillan, que serían aquellos que generan este efecto luminoso, y minerales que no brillan, entre los que incluiríamos todos aquellos que no provocan ese destello.
Pues este es el error que comentemos todas las personas la primera vez que nos enfrentamos a tener que describir esta propiedad óptica de los minerales, porque, en realidad, todos y cada uno de los minerales del planeta tienen brillo. Precisamente, esa apreciación visual que os he comentado en el párrafo anterior y que es totalmente intuitiva es la que nos permite clasificar el tipo de brillo de los minerales, diferenciando dos grandes grupos. Por un lado, aquellos minerales que tienen el aspecto brillante de un metal cuando les incide la luz decimos que tienen brillo metálico. Se trata de minerales de colores oscuros y opacos, es decir, que no dejan que les atraviese la luz, como la pirita (sulfuro de hierro, FeS2) o la galena (sulfuro de plomo, PbS). Y, por otro lado, tenemos los minerales de brillo no metálico, que son todos aquellos de colores claros y que se comportan como transparentes o translúcidos, por lo que transmiten la luz bien en parte o bien en su totalidad.
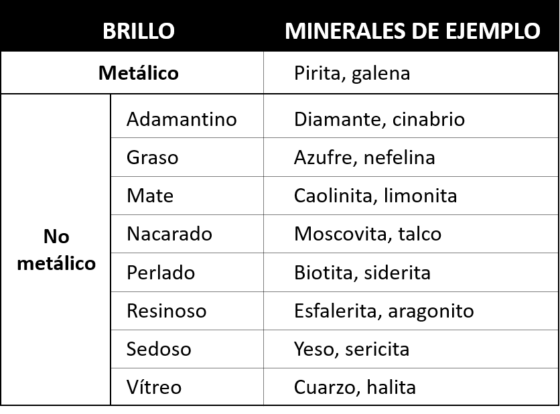 Tabla con la clasificación de los tipos (metálico y no metálico) y subtipos (adamantino, graso, mate, nacarado, perlado, resinoso, sedoso y vítreo) de brillo más comunes en los minerales, con algunos ejemplos característicos. Imagen modificada del original de Minerales de Visu / Universidad de Alicante
Tabla con la clasificación de los tipos (metálico y no metálico) y subtipos (adamantino, graso, mate, nacarado, perlado, resinoso, sedoso y vítreo) de brillo más comunes en los minerales, con algunos ejemplos característicos. Imagen modificada del original de Minerales de Visu / Universidad de AlicantePodemos encontrar diferentes subdivisiones o agrupaciones dentro de los minerales con brillo no metálico, como los de brillo vítreo porque nos recuerdan al brillo que presenta el vidrio de una ventana, que es lo que le ocurre al cuarzo (dióxido de silicio, SiO2), o los de brillo nacarado, que en este caso se asemeja a las irisaciones que se producen en las perlas y es característico del talco (silicato de magnesio hidratado, Mg3Si4O10(OH)2). Pero, por lo general, no entramos en tanto detalle a la hora de clasificar los minerales de acuerdo a su brillo, decimos simplemente que tienen brillo metálico o brillo no metálico.
Sé que he repetido la palabra clave brillo en demasiadas ocasiones a lo largo del texto, pero ha sido totalmente a posta para dejar las ideas bien claras de que todos los minerales tienen esta propiedad y que es una de las características físicas básicas para clasificarlos. Así, cuando os enfrentéis a un apasionante taller divulgativo de identificación de minerales, sabréis la diferencia entre brillo metálico y brillo no metálico y podréis seguir jugando con sus propiedades hasta que acertéis el nombre correcto del ejemplar que tengáis en la mano.
Agradecimiento:
Quiero dar las gracias a Ana Rodrigo, Directora del Museo Geominero del Instituto Geológico y Minero de España (IGME-CSIC), por darme la idea de escribir este artículo tras una interesante conversación sobre cómo mejorar nuestras actividades de divulgación geológicas, resaltando la problemática del público en general a la hora de entender algunas de las propiedades características de los minerales.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Minerales con brillo se ha escrito en Cuaderno de Cultura Científica.
Svetlana Jitomirskaya, la matemática que ganó la mitad de diez martinis
Ella era tan brillante que yo sabía que yo no lo era tanto.
Svetlana Jitomirskaya en [4].
En la anterior cita, la matemática Svetlana Jitomirskaya se refiere a Valentina Borok, su madre, que fue una destacada matemática ucraniana. De ella ya hablamos en este Cuaderno de Cultura Científica.
A pesar de lo brillante que era su madre, Svetlana Jitomirskaya no se queda atrás. Especialista en sistemas dinámicos y física matemática, en 2005 obtuvo el Premio Ruth Lyttle Satter en matemáticas por su trabajo pionero en su especialidad. Y, junto a Artur Ávila, resolvió en 2009 el conocido como problema de los diez martinis en el área de los sistemas dinámicos.
 Svetlana Jitomirskaya. Fuente: Springer.
Svetlana Jitomirskaya. Fuente: Springer.Una familia matemática
Svetlana Yakovlevna Jitomirskaya es la hija pequeña de los matemáticos Valentina Mikhailovna Borok y Yakov Yitomirski, que realizaron conjuntamente una parte importante de su investigación.
Su hermano mayor, Michail Zhitomirski (1958) también ha dedicado su vida profesional a las matemáticas. En este momento trabaja en teoría de variedades diferenciables en el Instituto Tecnológico de Israel en Haifa.
Svetlana Yakovlevna Jitomirskaya nació el 4 de junio de 1966 en Járkov (Ucrania). Comentaba sobre sus primeros años (ver [3]):
Cuando yo nací, mis padres ya eran catedráticos (en una sociedad en la que este título inspiraba mucho respeto). Mi madre era sin duda la matemática más destacada del país. Después de haber criado a mi hermano mayor, que estaba claramente dotado para las matemáticas, mis padres pensaron que un matemático más en nuestra familia sería demasiado. Me animaron a interesarme por cosas variadas, y empecé a inclinarme seriamente por las humanidades. Escribí poesía (premiada) y gané algunos concursos nacionales de bachillerato en literatura rusa. Planeé un futuro estudiando (si no escribiendo) poesía rusa.
A pesar de que ni ella ni su familia pensaban que se iba a dedicar a las matemáticas, Svetlana, a sus 14 años, se enamoró durante unas vacaciones de un chico que vivía en Moscú. Sabía que era difícil mantener una relación a distancia y, ya con 16 años, vio que la única manera que tenía de estar cerca de su amado era ingresando en la Universidad Estatal de Moscú. En aquella época esta institución limitaba el número de estudiantes judíos que podían acceder a sus enseñanzas. Para mantener esas cuotas limitantes los aspirantes judíos eran sometidos a preguntas exageradamente difíciles durante los exámenes orales de ingreso. De esta manera intentaban asegurar que el alumnado judío no constituyera más del 0,5 % del estudiantado total. Svetlana sabía que tenía muy pocas posibilidades de aprobar en cualquier disciplina, pero las matemáticas aparecieron como una opción mejor que las humanidades al haber una competencia mucho menor y una mayor objetividad.
Las matemáticas llegan de manera inesperadaCon esta idea en la cabeza dedicó su último año de instituto a preparar el examen oral de matemáticas. En sus propias palabras (ver [3]):
Creo que durante ese año resolví todos los problemas elementales complicados que había, y algunos más. Me tomaba cada problema como algo personal y lo atacaba como si mi felicidad futura dependiera de si lo resolvía o no. Me aceptaron en la Universidad Estatal de Moscú; sin embargo, no puedo considerarlo una victoria personal como me hubiera gustado. No llegué a mostrar ni una fracción de mis habilidades en aquel examen oral, ya que no me sometieron a ese trato «judío» (quizá, debido a las conexiones de mis padres). Sin embargo, algo me ocurrió durante esa extensa preparación, ya que empecé a amar el proceso.
Y de este modo consiguió acercarse a Moscú para no separarse de Vladimir A. Mandelshtam, quien posteriormente se dedicó a la química, con quien se casó en cuanto alcanzó su mayoría de edad.
Jitomirskaya terminó sus estudios universitarios en 1987, graduándose con matrícula de honor. Continuó con su formación doctoral en la Universidad Estatal de Moscú, bajo la supervisión de Yákov Grigórevich Sinái (1935), que también la había asesorado durante sus estudios universitarios. Sinái es un reconocido especialista en teoría de sistemas dinámicos, física matemática y teoría de la probabilidad. Reconocido con el Premio Abel en 2014, fue el principal artífice de la mayoría de los puentes que conectan el mundo de sistemas deterministas (dinámicos) con el mundo de los sistemas probabilísticos (estocásticos).
Svetlana presentó su tesis doctoral en 1991: Spectral and Statistical Properties of Lattice Hamiltonians. Ese mismo año, Vladimir finalizó también su trabajo doctoral.
Antes de finalizar su tesis, en 1990, comenzó a trabajar como investigadora en el Instituto Internacional de Teoría de la Predicción de Terremotos y Geofísica Matemática de Moscú, centro en el que ya trabajaba su marido.
Un año más tarde ofrecieron a Svetlana un puesto postdoctoral en la Universidad de California en Irvine y a Vladimir otro en la Universidad del Sur de California. Aceptaron ambas ofertas de trabajo porque estarían cerca, aunque no fuera en el mismo centro. Lo que pensaron que iba a ser una estancia de un año se convirtió en su lugar de trabajo y residencia definitivos.
Una matemática reconocidaJitomirskaya recibió el Premio Ruth Lyttle Satter 2005 de la American Mathematical Society. Este premio se concede cada dos años en reconocimiento a una contribución destacada a la investigación matemática realizada por una mujer en los cinco años anteriores. El comité de selección destacó (ver [1]):
El Premio Ruth Lyttle Satter de Matemáticas se concede a Svetlana Jitomirskaya por su trabajo pionero sobre la localización cuasiperiódica no perturbativa, en particular por los resultados de sus artículos (1) «Metal-insulator transition for the almost Mathieu operator«, Ann. of Math. (2) 150 (1999), no. 3, 1159-1175, y (2) con J. Bourgain, «Absolutely continuous spectrum for 1D quasiperiodic operators«, Invent. Math. 148 (2002), no. 3, 453-463. En su artículo de los Annals, desarrolló un enfoque no perturbativo de la localización cuasiperiódica y resolvió la vieja conjetura de Aubry-Andre sobre el operador casi Mathieu. Su artículo con Bourgain contiene el primer resultado general no perturbativo sobre el espectro absolutamente continuo.
Además, entre otros reconocimientos, Jitomirskaya ganó en 2020 del Premio Dannie Heineman de Física Matemática que se otorga cada año desde 1959 conjuntamente por la American Physical Society y el American Institute of Physics. Svetlana recibió este galardón:
Por su trabajo en la teoría espectral de operadores de Schrödinger casi periódicos y cuestiones relacionadas en sistemas dinámicos. En particular, por su papel en la solución del problema de los diez martinis, relativo a la naturaleza de conjunto de Cantor del espectro de todos los operadores casi Mathieu y en el desarrollo de los aspectos matemáticos fundamentales de los fenómenos de localización y transición metal-aislante.
El problema de los diez martinis lleva este nombre porque el especialista en teoría de la probabilidad Mark Kac (1914-1984) ofreció diez martinis a quien lo solucionara. Jitomirskaya lo resolvió junto al matemático Artur Avila (1979) en el artículo The Ten Martini Problem publicado en 2009.
A Svetlana Jitomirskaya aún le quedan muchos éxitos matemáticos por conseguir. Su madre fue un modelo extraordinario para ella. Al recibir el premio Ruth Lyttle Satter, comentó lo siguiente en su discurso de agradecimiento (ver [1]):
Debo decir que nunca me he sentido en desventaja por ser una mujer matemática; de hecho, hasta cierto punto ocurre lo contrario. Sin embargo, en comparación con la mayoría de las demás, tuve una ventaja única: un modelo fantástico desde muy pronto: mi madre, Valentina Borok, que habría sido mucho más merecedora de un premio así que yo ahora, si hubiera existido en su época. Para mí, recibir este premio es un homenaje especial a su memoria. Es un placer aprovechar esta oportunidad para darle las gracias.
Referencias
[1] AMS; 2005 Satter Prize, Notices of the AMS 52 (4) 447-448, 2005.
[2] Svetlana Jitomirskaya, Valentina Mikhailovna Borok, MacTutor History of Mathematics archive, University of St Andrews.
[3] John O’Connor and Edmund Robertson, Svetlana Yakovlevna Jitomirskaya, MacTutor History of Mathematics archive, University of St Andrews.
[4] Margarita Rodríguez, Svetlana Jitomirskaya, la matemática detrás de la solución a “el problema de los diez martinis” de la mecánica cuántica, BBC News, 10 de diciembre de 2022.
[5] Valentina Borok, Wikipedia.
[6] Svetlana Jitomirskaya, Wikipedia.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Svetlana Jitomirskaya, la matemática que ganó la mitad de diez martinis se ha escrito en Cuaderno de Cultura Científica.
La ‘repulsión de la especie’ permite una alta biodiversidad en los árboles tropicales
repulsión
Debido a que las plántulas de los árboles no crecen tan bien cuando están cerca de sus progenitores, se pueden concentrar más especies de árboles en los bosques tropicales.
Un artículo de Veronique Greenwood. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons
 Vista aérea del bosque tropical en la Isla de Barro Colorado. Fuente: Christian Ziegler / Wikimedia Commons / Gewin V, PLoS Biology Vol. 4/8/2006, e278 doi: 10.1371/journal.pbio.0040278
Vista aérea del bosque tropical en la Isla de Barro Colorado. Fuente: Christian Ziegler / Wikimedia Commons / Gewin V, PLoS Biology Vol. 4/8/2006, e278 doi: 10.1371/journal.pbio.0040278Para los ecólogos, las selvas tropicales encierran muchos enigmas. Una sola hectárea puede contener cientos de especies de árboles, muchas más que en los bosques más cercanos a los polos. De alguna manera estas especies coexisten en una abundancia tan vertiginosa que, como han señalado a veces los naturalistas y ecólogos, los bosques tropicales pueden parecer jardines botánicos, donde cada planta es algo nuevo.
Para que tal multitud de especies esté tan densamente agrupada deben coexistir en un equilibrio muy particular. La evolución parece no favorecer situaciones en las que una sola especie prospera de manera demasiado agresiva, sino que favorece aquellas en las que los organismos están rodeados de especies distintas a la suya. Conciliar estos hechos con lo que se sabe sobre cómo las especies se distribuyen, compiten e influyen entre sí es un desafío.
Para estudiar esta extraordinaria diversidad hace años los científicos comenzaron a establecer parcelas de bosque donde podían registrar y rastrear la ubicación y el estado de cada árbol durante décadas. Una de las primeras parcelas de este tipo, en la isla de Barro Colorado (IBC) en Panamá, tiene 500 metros de ancho por 1.000 metros de largo (el área de unos 70 campos de fútbol) y contiene más de 300 especies. Desde 1980, investigadores de todo el mundo han estudiado minuciosamente los registros detallados de sus habitantes.
En un artículo publicado recientemente en Science, investigadores de la Universidad de Texas en Austin modelaron varios escenarios de distribución y los compararon con datos de IBC. Descubrieron que los patrones en la dispersión de semillas por el viento o por las aves y otros animales salvajes, así como procesos más aleatorios, no eran suficientes para explicar la distribución de los árboles adultos en el bosque. Sugieren que esto es evidencia de una “repulsión específica de la especie”, una teoría de larga data de que los árboles de la misma especie se espacian naturalmente porque el ambiente que rodea inmediatamente a un árbol padre es específicamente hostil a la propia descendencia del árbol.
Distanciamiento social en árbolesEsta idea de repulsión, formalmente conocida como dependencia negativa de la densidad conespecífica, o CNDD (por sus siglas en inglés), se remonta a la década de 1970, cuando los ecólogos Daniel Janzen y Joseph Connell sugirieron de forma independiente que los insectos, herbívoros y patógenos que se alimentan selectivamente de una especie podrían hacer que el área alrededor de un árbol adulto fuese peligrosa para sus semillas. No se impediría con la misma eficacia que otras especies creciesen en la zona, aunque seguirían estando limitadas por problemas no específicos, como la falta de luz solar bajo la copa de un árbol adulto. El resultado sería que los árboles adultos de una especie tenderían a mantener una especie de “distancia social” mínima entre sí.
Los ensayos realizados en las últimas décadas, principalmente con plántulas, apoyan la CNDD, afirma Michael Kalyuzhny, autor principal del nuevo artículo, cuyo trabajo como investigador postdoctoral en la Universidad de Texas en Austin le ha llevado a abrir un laboratorio en la Universidad Hebrea de Jerusalén. Las semillas a menudo no crecen tan bien en el suelo tomado de lugares cercanos a sus árboles progenitores como en el suelo de lugares cercanos a árboles no relacionados.
Sin embargo, incluso una mirada superficial a los datos del IBC muestra que los árboles adultos en ese bosque no parecen repelerse entre sí. En cambio, los árboles se agrupan, formando grupos sueltos de la misma especie en toda la parcela.
Kalyuzhny y Annette Ostling, la ecóloga comunitaria que dirige el laboratorio donde trabaja Kalyuzhny, se propusieron modelar diferentes escenarios que podrían explicar las distribuciones de árboles observadas, para saber si algo podría estar dificultando el papel de la CNDD en el bosque.
El azar por sí solo no es la respuesta: cuando ejecutaron un modelo nulo, en el que los árboles estaban espaciados aleatoriamente, los árboles adultos de una especie se dispersaban demasiado.
Entonces los investigadores introdujeron el efecto de la dispersión de semillas en sus modelos, que podría ser por el viento, las aves y otros animales. Helene Muller-Landau y sus colaboradores de IBC han hecho estimaciones de lo lejos que puede viajar una semilla desde su fuente dentro de una parcela de 50 hectáreas, utilizando redes que capturan las semillas a medida que van a la deriva hacia el suelo del bosque. Las semillas se recolectan periódicamente y se calcula la distancia a sus progenitores. Kalyuzhny y sus colegas se han basado en estos datos para modelar disposiciones de los árboles determinadas únicamente por la limitación de la dispersión.
 Adult trees in tropical forests produce seeds and seed pods that have wildly diverse shapes, which allows them to be spread by wind or by animals in different ways. Foto: Christian Ziegler
Adult trees in tropical forests produce seeds and seed pods that have wildly diverse shapes, which allows them to be spread by wind or by animals in different ways. Foto: Christian ZieglerPero este modelo produjo árboles demasiado agrupados. Algo parecía estar actuando sobre la distribución producida por la limitación de la dispersión, dispersando los árboles. “Algo está creando esta repulsión. Y no podemos pensar en otra cosa que en la CNDD”, explica Kalyuzhny.
Cuando los investigadores calcularon lo específica que era la repulsión (cuánto peor era para un árbol estar cerca de su propia especie que de otra), descubrieron que habría tenido que ser bastante fuerte para producir el patrón observado. Esto confirmó un punto esencial de las ideas de Janzen y Connell: «Lo que sea que cree la CNDD tiene que ser específico de cada especie», añade Kalyuzhny.
La importancia de los eventos rarosRyan Chisholm, ecólogo teórico y profesor de la Universidad Nacional de Singapur que estudia la distribución de los árboles tropicales, está de acuerdo en que los hallazgos de Kalyuzhny encajan con trabajos anteriores sobre la CNDD. Sugiere, sin embargo, que los modelos podrían estar subestimando hasta qué punto los mecanismos de dispersión pueden propagar las semillas. Si los eventos de gran dispersión son raros, por ejemplo, podrían ser difíciles de ver en los datos de las trampas de semillas. Y si las semillas son transportadas más lejos de lo que los investigadores creen, eso podría explicar los grupos de árboles más dispersos en los bosques sin necesidad de repulsión.
«Lo que están diciendo aquí es que según su modelo de limitación de dispersión, los patrones que observan son imposibles», dijo Chisholm. «Yo diría que todavía no sabemos lo suficiente para decir eso».
Los eventos raros han sido importantes en la dispersión de especies de todo tipo: se cree que los monos, por ejemplo, llegaron a América desde África en balsas de vegetación, un evento tremendamente improbable que, sin embargo, tuvo consecuencias significativas. «Ocasionalmente, encontrarás ese pájaro que lleva la semilla muy lejos, o que queda atrapado por el viento y se lanza a la aventura», comenta Chisholm.
Señala que todavía no conocemos suficientemente bien la forma de la curva de distribución de semillas; no es una simple curva de campana, como podrían pensar los no expertos, porque parece tener una “cola muy gruesa” al final.
Si los ecólogos tuvieran datos a una escala mucho mayor que 50 hectáreas, algo que prometen las nuevas técnicas de estudio mediante las cuales los científicos pueden contar árboles desde el aire, podría surgir una nueva visión. Podría ser posible ver patrones que no se ven actualmente, lo que podría cambiar la comprensión del papel que desempeñan la CNDD y la limitación de la dispersión de semillas en la disposición de los bosques. «Esta era de simplemente contemplar una parcela de 50 hectáreas parecerá extremadamente pintoresca, como un telescopio portátil en comparación con el Hubble», predice Chisholm.
Por ahora, Kalyuzhny y sus colegas planean realizar análisis similares en otras parcelas de estudio en todo el mundo para ver qué patrones emergen: ahora hay más de 70 sitios en todo el mundo con parcelas de hasta 50 hectáreas de tamaño, todas monitoreadas como la parcela en IBC. También han realizado simulaciones en las que ajustan el alcance de la CNDD y han descubierto que incluso la repulsión en distancias relativamente cortas puede provocar grandes efectos a escala del bosque.
“Yo repelo a mis vecinos, y ellos repelen a sus vecinos, y ellos repelen a sus vecinos”, explica Kalyuzhny, describiendo cómo pueden surgir patrones a gran escala a partir de acciones a pequeña escala. «El bosque es un cristal desordenado».
El artículo original, ‘Species Repulsion’ Enables High Biodiversity in Tropical Trees, se publicó el 13 de septiembre de 2023 en Quanta Magazine.
Traducido por César Tomé López
El artículo La ‘repulsión de la especie’ permite una alta biodiversidad en los árboles tropicales se ha escrito en Cuaderno de Cultura Científica.
¿Qué salió mal en el primer trasplante de un corazón de cerdo a un humano?
 Foto: Ben Mater / Unsplash
Foto: Ben Mater / UnsplashCada año se realizan en el mundo más de 120.000 trasplantes que dan otra oportunidad a decenas de miles de personas para seguir viviendo. Sin embargo, muchas otras mueren en las listas de espera porque la demanda de órganos es muy superior al número de donaciones. Este problema se está acentuando con los años, debido al envejecimiento progresivo de las poblaciones de multitud de países, que incrementa aún más la necesidad de órganos.
Con el objetivo de solucionar este grave problema sanitario, los científicos están investigando otras opciones alternativas a la donación de órganos humanos. En la última década, el campo de los xenotrasplantes (trasplante de células, tejidos u órganos entre diferentes especies) ha experimentado grandes avances gracias a la ingeniería genética y a los avances en el conocimiento y uso de las células madre. En enero de 2022 se dio un hito histórico en ese sentido: por primera vez, se trasplantó con éxito el corazón de un cerdo a una persona y esta siguió viviendo. El animal había sido modificado genéticamente para que no produjera ciertas moléculas en sus células que se consideran extrañas por el sistema inmunitario humano, lo que minimizó el rechazo.
El paciente, David Bennet, recibió el preciado órgano procedente de un cerdo en el Centro Médico de la Universidad de Maryland. Era su única opción, pues no cumplía los requisitos para acceder a la lista de espera de un corazón humano. Parecía que todo iba bien: la función cardíaca era normal y no había signos de rechazo inmunitario agudo. No obstante, a los 47 días del trasplante, Bennet falleció de forma fulminante debido a un fallo cardíaco (el corazón dejó de bombear la sangre necesaria para mantenerle con vida). Antes de ese fatídico día, los estudios de ecocardiografía y otras pruebas mostraban que el corazón funcionaba sin problemas.
En un primer momento, los investigadores no fueron capaces identificar la causa que llevó al trágico desenlace, pero pusieron en marcha diferentes estudios para analizar cada paso tras el trasplante y conocer qué factores estaban involucrados, ya que estos podrían ser obstáculos también en futuros xenotrasplantes. Se espera que en los próximos años aparezcan ensayos clínicos en los que se trasplanten órganos de animales a personas y toda la información que se pueda obtener de casos como el de Bennet resulta esencial.
En ese sentido, un artículo publicado hace unos meses en la revista médica The Lancet aclara con detalle qué pasó para que el paciente falleciera por un fallo cardíaco. Lejos de ser una única causa la responsable del evento, los datos indican que múltiples factores contribuyeron a un deterioro funcional del corazón porcino trasplantado.
Una de las razones que se barajaban inicialmente como causa del fallo cardíaco era el rechazo hiperagudo. Este suele suceder dentro de los primeros días tras el trasplante por la acción de los anticuerpos contra el órgano donado, lo que lleva a la formación de coágulos que llegan a bloquear a vasos sanguíneos pequeños y, como consecuencia, provocan el infarto del tejido por la falta de oxígeno y nutrientes. No obstante, este tipo de rechazo inmunitario no llegó a aparecer. Los investigadores creen que el delicado estado de salud de Bennet, ya antes del trasplante, fue el desencadenante inicial de una serie de eventos que terminó por provocar su fallecimiento.
El paciente tenía una inmunodepresión muy grave, por lo que el uso estándar de inmunosupresores tuvo que restringirse bastante para que no sufriera infecciones fatales. Sin embargo, esto tenía un precio: también aumentaba el riesgo de rechazo inmunitario hacia el órgano recibido, que fue lo que terminó ocurriendo. Otro factor que pudo haber contribuido a la muerte de Bennet fueron las dos veces que se le administró por vía intravenosa inmunoglobulinas (anticuerpos) durante el segundo mes para prevenir infecciones y el intercambio de plasma sanguíneo. Se cree que esto terminó por desencadenar la respuesta inmunitaria de rechazo frente al corazón recibido, porque se detectó un aumento de anticuerpos (sobre todo de IgG) contra moléculas porcinas tras la administración de las inmunoglobulinas y, además, se observó también la unión de estas moléculas a la superficie interna (endotelio) de los vasos sanguíneos del corazón de cerdo.
Los científicos encontraron pruebas indirectas del ataque de anticuerpos hacia células y tejidos del corazón porcino mediante su análisis a través de diferentes técnicas de laboratorio. Por ejemplo, detectaron lesiones generalizadas en el endotelio de los vasos de dicho órgano. Por otro lado, también se identificó la reactivación y la replicación de virus porcinos (en concreto, de citomegalovirus y roseolovirus porcinos) que habían estado sin mostrar señales de actividad hasta ese momento y que probablemente desencadenaron una respuesta inflamatoria que también contribuyó a dañar al órgano donado. Es posible que la atenuación del tratamiento antiviral del paciente como consecuencia de su estado de salud terminase por activar estos virus.
Como resultado de todo lo anterior, el músculo cardíaco fue desarrollando cicatrices (fibrosis) que terminaron por incapacitar al corazón para contraerse con normalidad y bombear la sangre necesaria para mantener a Bennet con vida. Una trágica cadena de desafortunados eventos biológicos que los científicos tratarán de evitar en los próximos pacientes que reciban corazones de cerdo. Ahora están más preparados: cuentan con técnicas novedosas para monitorizar con más detalle a aquellos que reciban un xenotrasplante y así detectar de forma temprana las primeras señales de rechazo inmunitario. Los próximos ensayos clínicos determinarán si los problemas que sufrió Bennet se debieron principalmente a su delicado estado de salud o si, por el contrario, estos aparecerán también en otros pacientes y si será posible evitarlos.
Sobre la autora: Esther Samper (Shora) es médica, doctora en Ingeniería Tisular Cardiovascular y divulgadora científica
El artículo ¿Qué salió mal en el primer trasplante de un corazón de cerdo a un humano? se ha escrito en Cuaderno de Cultura Científica.
Más que la genética, es la cultura la que configura los grupos humanos
cultura
 Foto: Eddi Aguirre / Unsplash
Foto: Eddi Aguirre / UnsplashLos cantos populares son verdaderos registros del pasado de las poblaciones humanas. Sus diferencias reflejan las distintas trayectorias que han seguido aquellas a lo largo del tiempo. Junto con la lengua y otros elementos culturales, pueden aportar un complemento valioso a los estudios genéticos como herramienta para conocer el pasado.
Conforme los seres humanos nos dispersamos por el planeta, no sólo se diferenciaron nuestros genomas, también se diversificaron las lenguas y otros rasgos culturales. De hecho, es posible, y no demasiado difícil, establecer correspondencias entre grupos genéticos y familias o variedades lingüísticas. No obstante, en numerosas ocasiones, y por varios posibles motivos, los grupos humanos han perdido la que era su lengua para adquirir otra diferente. Por ello, la correspondencia original entre grupos genéticos y grupos lingüísticos se difumina, lo que dificulta el análisis conjunto de esos rasgos de cara, por ejemplo, a caracterizar la historia y relaciones entre unos grupos humanos y otros.
Además de la lengua, la música tradicional se ha diferenciado también entre grupos humanos conforme éstos se han desgajado unos de otros y se han diversificado genéticamente. El genetista de poblaciones Floyd Reed presentó, en la reunión anual de 2007 de la American Anthropological Association, un estudio realizado con 39 grupos humanos de África que mostraba una estrecha conexión entre su genética y las canciones que cantaban. Esos resultados venían a apoyar la idea de que la música puede ayudar a identificar las profundas relaciones entre diferentes poblaciones humanas. Al parecer, la música es mucho más resistente al cambio que otros rasgos culturales; puede serlo más incluso que la lengua.
El procedimiento utilizado para caracterizar las canciones que sirvieron de base al estudio de Floyd fue desarrollado por los musicólogos y etnógrafos Alan Lomax y Victor Grauer. Lomax, quien había dado a conocer a Woodie Guthrie y Lead Belly al gran público, creó un archivo de unas 5.500 canciones tomadas de 857 culturas. El sistema, denominado “Cantométrica”, diseñado por los dos etnomusicólogos clasifica las canciones basándose en una escala de 37 rasgos relacionados con ciertas características de la melodía.
Floyd desarrolló un método que permitía determinar la distancia entre pares de culturas musicales, y comprobó que, efectivamente, existía una correlación significativa entre las distancias musicales y las genéticas. Observó que los pueblos que se agrupaban musicalmente, tendían a compartir marcadores genéticos. El método empleado suscitó alguna reserva, ya que la cuantificación de los rasgos utilizados en la clasificación es subjetiva, y eso limita su aplicabilidad universal. No obstante, sus defensores señalan que los resultados avalan su validez.
En esa misma línea, en 2014 se publicaron los resultados de una investigación en Taiwán en la que se estudiaron nueve poblaciones indígenas, cuya genética era conocida, y de las que se contaba con abundantes registros de canciones populares de géneros diversos, principalmente de carácter ritual. Los autores de la investigación trabajaron con una muestra de 220 canciones. Las codificaron combinando Cantométrica (para reflejar estilo vocal, ornamentación y dinámica) y un método desarrollado por ellos mismos, CantoCore (para reflejar ritmo, tono, texto, textura y forma). En total trabajaron con 41 caracteres (15 de Cantométrica y 26 de CantoCore) que han servido para codificar los rasgos de cada canción.
Calcularon la distancia, dos a dos, entre las nueve poblaciones, tanto para la genética (ADN mitocondrial) como para los cantos. Estimaron también las distancias entre las lenguas, a partir de cognados lexicales del vocabulario básico de las culturas incluidas en el estudio. Dado que se analizaron nueve poblaciones, contaron con 36 pares, por lo que obtuvieron 36 distancias para cada aspecto estudiado (genética, lengua y canciones). El análisis estadístico consistió, en lo esencial, en análisis de la varianza –para valorar la variabilidad en y entre culturas– y en correlaciones entre las distancias estimadas a partir de cada uno de los tres rasgos –para establecer el grado de correspondencia entre rasgos genéticos y culturales.
La correlación entre distancias musicales y distancias genéticas fue significativa (r = 0,417; p = 0,015), y lo siguió siendo (r = 0,385; p = 0,032) incluso después de descontar el efecto de la distancia geográfica entre las poblaciones. También era significativa la correlación entre distancias genéticas y lingüísticas (r = 0,492; p = 0,006), pero en este caso la significación se esfumó (r = 0,321; p = 0,071) al introducir las distancias geográficas en el análisis. Eso indica que probablemente las distancias entre las canciones están más firmemente relacionadas con las distancias genéticas que éstas con las lingüísticas. Los autores de la investigación concluyeron que es muy probable que se haya producido una covariación de la música y del genoma mitocondrial de los taiwaneses mediante una ramificación a partir de un ancestro común, de manera que las diferencias, genéticas y musicales no serían mera consecuencia de una separación geográfica relativamente reciente de esas poblaciones.
Los valores de correlación que obtuvieron fueron similares, lo que indica, a mi entender, que tanto las distancias lingüísticas como la musicales reflejan, en una medida similar, el grado de diferenciación de los grupos humanos. Es muy interesante, sin embargo, que la correlación entre las distancias musicales y las lingüísticas sea relativamente débil (r = 0,411; p = 0,085), lo que sugiere que la diferenciación de uno y otro elemento cultural no ha seguido el mismo proceso. Así pues, música, por un lado, y lengua, por el otro, retienen aspectos diferentes de la historia de los grupos humanos analizados.
De todos los elementos contemplados en el estudio, el que más me ha llamado la atención es el de la magnitud relativa de las diferencias entre unos elementos y otros. Porque resulta que, utilizando la misma metodología para analizar distancias, las existentes entre las canciones populares y las lenguas son mayores que las genéticas. En todos los casos –lengua, canciones populares y genoma– la variación dentro de cada población es mayor que la variación entre poblaciones, pero, en términos relativos, hay más variación entre poblaciones en canciones populares y lengua que en los genomas mitocondriales.
En conclusión, los grupos humanos se diferencian en mayor medida en los rasgos culturales que en los rasgos genéticos. Y de aquí se extrae una interesante consecuencia: los grupos humanos se constituyen y diferencian unos de otros sobre la base de elementos culturales. O lo que es lo mismo, a los efectos de la configuración de los pueblos, la cultura es lo que nos hace miembros de uno u otro grupo, no los genes que codifican las proteínas que dan forma y función a nuestro organismo.
Fuente: S Brown S, P E Savage, AM-S Ko, M Stoneking, Y-C Ko, J-H Loo, J A Trejaut (2014): Correlations in the population structure of music, genes and language. Proc. R. Soc. B 281.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Más que la genética, es la cultura la que configura los grupos humanos se ha escrito en Cuaderno de Cultura Científica.
La ceguera a las plantas

A pesar de la importancia que tienen las plantas en nuestro entorno, el conocimiento sobre ellas es escaso, convirtiéndolas en elementos que muchas veces pasan inadvertidos o que, como mucho, quedan como telón de fondo. ¿Por qué generan tan poco interés las plantas? ¿Es el color de las plantas y los paisajes casi monocromáticos los elementos que provocan esa reacción?
En el año 1999 los botánicos James H. Wandersee y Elisabeth Schussler bautizaron este fenómeno como “ceguera a las plantas” o «ceguera vegetal» y, desde entonces, varias investigaciones han intentado entender las razones del mismo.
Entre los motivos que explicarían la ceguera a las plantas se mencionan los factores biológicos y socioculturales. El ser humano cuenta con un sistema visual que no se siente cómodo al no poder fijar la mirada en un punto concreto de un paisaje que, a primera vista, puede parecer monótono. Además, el sistema visual y el cerebro humano habrían evolucionado para detectar con más facilidad a los animales que a las plantas.
La ceguera a las plantas tiene consecuencias y por ejemplo, como muestra el estudio realizado por la Universidad del País Vasco y Aranzadi, mientras hoy en día los y las jóvenes son capaces de nombrar 10 animales, solo el 7% es capaz de nombrar 10 plantas.
La investigadora Ainara Achurra habló sobre este fenómeno en la charla “La ceguera a las plantas: un fenómeno que sufrimos la mayoría” dentro del ciclo Bidebarrieta Científica organizado por la Cátedra de Cultura Científica de la Universidad del País Vasco y la Biblioteca Bidebarrieta.
Ainara Achurra es doctora en Biología y profesora en la Facultad de Educación y Deporte de la Universidad del País Vasco en Vitoria-Gasteiz.
Edición realizada por César Tomé López
El artículo La ceguera a las plantas se ha escrito en Cuaderno de Cultura Científica.
Los cambios en el glaciar de Aneto
El glaciar de Aneto, aunque se considera un glaciar muy pequeño, es el glaciar más grande de los Pirineos y también el más grande del sur de Europa. Sin embargo, el cambio climático ha acelerado su desaparición, al igual que en el resto de los glaciares de la cordillera. La evolución de las técnicas de teledetección de corto alcance posibilita observar la superficie del glaciar con un nivel de detalle muy alto, lo que permite la comparación entre la superficie del glaciar de diferentes años y la evaluación de sus cambios.
 Glaciar del Aneto y vista de la Cresta de los Portillones desde la cima en 2007. Fuente: Faras / Wikimedia Commons
Glaciar del Aneto y vista de la Cresta de los Portillones desde la cima en 2007. Fuente: Faras / Wikimedia CommonsLos glaciares de montaña son excelentes indicadores de la variabilidad y el cambio climático porque su evolución depende del equilibrio entre la acumulación de nieve durante el período frío y la fusión de hielo y nieve durante la estación más cálida. El glaciar del Aneto es uno de los glaciares más meridionales de Europa y, a pesar de ser un glaciar muy pequeño (<0,5 km2), es el más grande de los Pirineos.
Un reciente estudio liderado por el Instituto Pirenaico de Ecología (IPE-CSIC) ha encontrado que, para el periodo 1981-2022, la superficie del glaciar de Aneto ha disminuido un 64,7 % (de 135,7 ha (1,36 km2) a 48,1 ha (0,48 km2)), y su frente ha pasado de 2.828 a 3.026 metros.
El objetivo del estudio era analizar la evolución reciente del glaciar más grande y alto de los Pirineos utilizando el conjunto de datos temporales más largo de pérdida de espesor de los glaciares en los Pirineos. Además, el trabajo ha permitido evaluar el impacto de una única temporada extremadamente cálida y seca (2022) en la evolución de los glaciares. “Hemos realizado el estudio del glaciar de Aneto más detallado (modelos tridimensionales del glaciar de muy alta resolución) y longevo (41 años) hasta el momento. Para ello, hemos reconstruido las superficies del glaciar entre 1981 y 2022 a partir del uso de imágenes aéreas de muy alta resolución que han sido obtenidas, por un lado, por el Instituto Geográfico Nacional para el año 1981 y mediante vuelos LIDAR para el año 2011 y, por otro, por vehículos aéreos no tripulados (drones) para los años 2020, 2021 y 2022 -explica Eñaut Izagirre Estibaritz, profesor del Departamento de Geografía, Prehistoria y Arqueología de la Universidad del País Vasco y participante en la investigación-. Todo ello se complementó con una amplia campaña de georadar en el año 2020, donde a partir de la realización de diferentes transectos (más de 7 km recorridos sobre el glaciar), pudimos conocer el grosor que tenía el glaciar en ese año”.
Desaparición de los glaciaresLa pérdida de superficie glaciar en los Pirineos es notable: había más de 100 glaciares en 1850, 39 en 1984, 21 en 2020 y 18 en 2022, correspondientes a una superficie de 2.060 ha (20,6 km2) en 1850, 810 ha (8,1 km2) en 1984, 232 ha (2,3 km2) en 2020 y 170 ha (1,7 km2) en 2022, lo que representa una pérdida del 92 % del área glaciar desde el final de la Pequeña Edad de Hielo.
 Los investigadores midiendo el grosor del glaciar. Fuente: campusa
Los investigadores midiendo el grosor del glaciar. Fuente: campusaEn el Aneto, durante los últimos 41 años, la superficie glaciar se ha reducido un 64,7 % y el espesor del hielo ha disminuido, en promedio, 30,5 m. “El espesor medio del hielo restante en el otoño de 2022 fue de 11,9 m, frente al espesor medio de 32,9, 19,2 y 15,0 m reconstruido para 1981 y 2011 y observado en 2020, respectivamente. Los resultados demuestran la crítica situación del glaciar, con una inminente segmentación en tres cuerpos de hielo más pequeños y sin evidencia de una zona de acumulación. También encontramos que la influencia de un año extremadamente caluroso y seco, como se observó en la temporada 2021-2022, conduce a una degradación drástica del glaciar, lo que representa un alto riesgo para la persistencia del glaciar de Aneto, situación que podría extenderse al resto de glaciares pirenaicos en un tiempo relativamente corto”, detallan los investigadores.
Los datos de la investigación señalan que la distribución del espesor del hielo muestra zonas alrededor de los glaciares con muy poco espesor (<2 m), por lo que esas zonas están muy cerca de desglaciarse durante los próximos veranos. Las pérdidas de superficie y espesor del glaciar de Aneto indican la situación crítica de esa masa de hielo. Se encuentra en su etapa terminal, mostrando fragmentación en cuerpos de hielo más pequeños y presencia de cubierta de derrubios en algunas áreas. “Las tasas de adelgazamiento del glaciar, que estaban en torno a 1 m por año, se han triplicado en el último año de estudio (entre 2021 y 2022), lo cual demuestra la afección de un año bastante seco y, sobre todo, extremadamente cálido como 2022 sobre la fusión de la nieve y el hielo en el glaciar de Aneto”, concluye el profesor de la UPV/EHU.
Referencia:
Vidaller, I., Izagirre, E., del Rio, L. M., Alonso-González, E., Rojas-Heredia, F., Serrano, E., Moreno, A., López-Moreno, J. I., Revuelto, J. (2023) The Aneto glacier’s (Central Pyrenees) evolution from 1981 to 2022: ice loss observed from historic aerial image photogrammetry and remote sensing techniques The Cryosphere doi: 10.5194/tc-17-3177-2023
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Los cambios en el glaciar de Aneto se ha escrito en Cuaderno de Cultura Científica.
Cómo editar una imagen con matemáticas
En Coordenadas polares os hablé de mi afición por las fotografías con simetría circular. Pero no os conté toda la historia. No solo saco “fotos redondas”. Además, las “despolarizo”, por así decirlo. O, dicho de manera más precisa: utilizo un programa para mapear los píxeles de sus coordenadas polares, sobre los ejes cartesianos de una segunda imagen. Y además de eso, aplico una transformación exponencial sobre el radio, de manera que se conservan las proporciones de cada región en toda la imagen.
Pero… dicho así, creo que suena más complicado de lo que realmente es. Se entiende mucho más fácilmente con un par de imágenes. La idea es convertir la foto de la izquierda en la imagen de la derecha:


O, lo que es lo mismo (quizás con un esquema se entienda mejor):
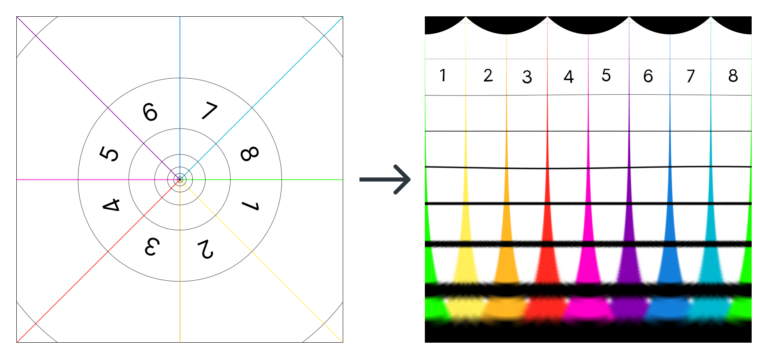
La transformación no se logra con un truco de Photoshop, ni con un filtro de ningún tipo. Es una aplicación de código abierto llamada depolarizer.
¿Qué es depolarizer?Depolarizer es una aplicación de R creada por Iñaki Úcar y una servidora. El proyecto nació como un pequeño código de java que escribí para poder ejecutarlo desde FIJI. Pero Iñaki lo mejoró infinitamente y añadió una interfaz gráfica para que cualquier persona lo pueda instalar, y jugar con él fácilmente. Si queréis probarlo, solo tenéis que ir al repositorio de GitHub, descargar el código, y abrir la aplicación con RStudio. Una vez la ejecutéis, deberíais ver en vuestro navegador aparece una interfaz parecida a esta:
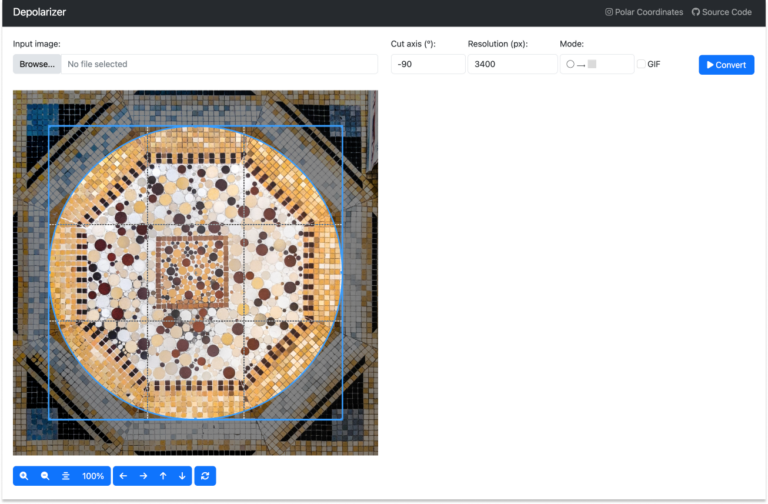
La interfaz está construida con ayuda de la librería shiny de R. Pero el alma de la aplicación vive en este archivito de Python, depolarizer.py. Es ahí donde se puede donde la imagen de entrada se transforma en su versión “despolarizada”. En concreto, en la función “to_polar”.
Voy a intentar a explicar cómo funciona. Pero no te preocupes: no hace falta saber programar para interpretar su código. Y si se te hace bola, siempre puedes saltar hasta la siguiente sección.
¿Cómo funciona el código?La idea es más o menos como sigue:
1- Generamos una imagen de salida (pix0), con la resolución la elegida (res0).

Una imagen, en este contexto, no es más que una matriz, una estructura donde vamos a guardar los valores RGB de los pixeles de la nueva imagen. Las coordenadas de la imagen son los índices de cada elemento de la matriz.
En adelante utilizaremos los subíndices “i” de “input” y “o” de “output” para identificar las variables referidas a la imagen de entrada y de salida respectivamente.
2- Definimos algunas variables auxiliares de utilidad.
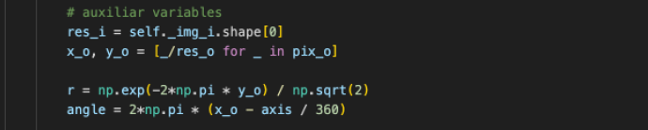
- La resolución de la imagen de entrada es resi.
- Las variables x0 e y0 son las coordenadas de la imagen de salida normalizadas (dividimos sus valores entre la resolución de la imagen, para que vayan de 0 a 1).
Y aquí viene lo más interesante:
- Las coordenadas polares, r y Θ (angle), están definidas directamente sobre las coordenadas cartesianas de la imagen de salida, x0 e y0 . Es decir, cuando el programa “pinte” la imagen de salida (pix0), en la dirección horizontal (x0) veremos el ángulo (angle), y en la vertical (y0), veremos el radio (r).
- En el caso de r, utilizamos una transformación exponencial. Y eso por qué, os preguntaréis, pues eso se merece su propio apartado, más abajo.
3- Definimos la función de mapeo, que es una transformación de coordenadas polares a cartesianas.
Lo que hará este mapeo es lo siguiente: el programa intentará rellenar los píxeles de la imagen de salida de uno en uno. Para saber “qué pintar” en cada pixel, buscará las coordenadas del pixel correspondiente en la imagen de entrada según diga el mapa.

¿Y qué es el mapa? ¡No es más que una función! La entrada de esa función son las coordenadas del pixel que queremos rellenar en la imagen final (x0 , y0) y la salida son las coordenadas correspondientes de la imagen inicial (xi , yi).
Si escribimos este código de manera más matemática, y obviamos la resolución (resi = 1) quedaría algo así:

Pongamos, por ejemplo, que queremos rellenar el pixel situado en (x0 , y0) = (1/8, 0) . El programa utilizará estas coordenadas como input de las funciones mapx y mapy y encontrará las coordenadas del pixel correspondiente en la imagen de entrada. En este caso serían:
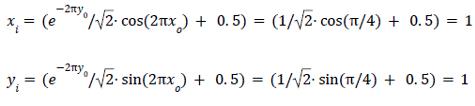
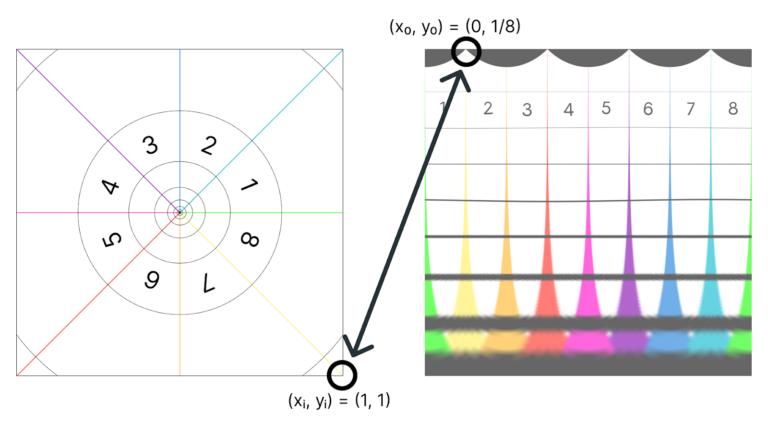
La idea de “desenroscar” las imágenes mediante un cambio de coordenadas resulta más o menos intuitiva después de ver unos cuantos ejemplos. Pero puede que sea más difícil ver qué es lo que hace esa función exponencial sobre el radio. Quizás se entiende mejor si usamos el esquema anterior y representamos el cambio de coordenadas sin la función exponencial. El resultado sería este:
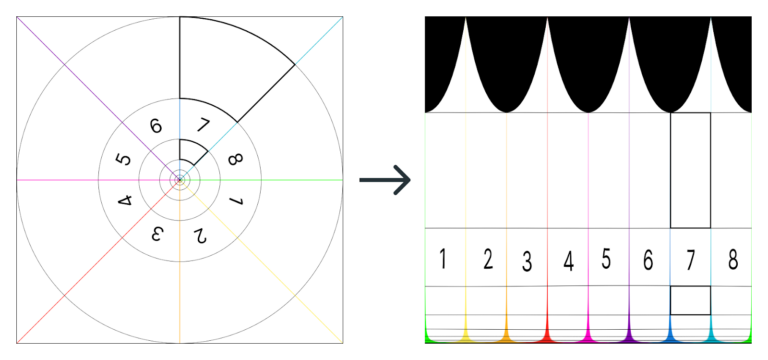
Fíjate en que todas las circunferencias de la imagen de entrada pasan a medir lo mismo en la de salida (son las líneas negras que van de izquierda a derecha). Pero, por eso mismo, el área entre las dos circunferencias más pequeñas queda mucho más “alargada” que la de la circunferencia mayor.
Mira lo que sucede, por ejemplo, con los dos “quesitos” subrayados en color negro. En la imagen de la izquierda los dos son muy parecidos: salvo por un factor de escala, tienen la misma forma. En la imagen de la derecha, en cambio, son muy distintos entre sí. La única manera de preservar las proporciones de todos los quesitos y evitar que distintos puntos de la superficie se deformen es utilizar una función exponencial, la misma que se oculta tras los sucesivos giros de la espiral maravillosa de Bernoulli.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Cómo editar una imagen con matemáticas se ha escrito en Cuaderno de Cultura Científica.
El problema de los calissons
Este verano he pasado unos días visitando la región francesa de la Provenza. Mi visita empezó en la hermosa ciudad de Aix-en-Provence, donde compré una caja de los famosos calissons.
 Fotografía de mi visita a la Fundación Vasarely, en Aix-en-Provence, Francia. Fotografía: Marian Espinosa
Fotografía de mi visita a la Fundación Vasarely, en Aix-en-Provence, Francia. Fotografía: Marian EspinosaCalissons
El calisson es un dulce típico de la región francesa de la Provenza, asociado especialmente con la ciudad de Aix-en-Provence. Está elaborado a partir de una pasta formada por almendras molidas y melón confitado (u otras frutas confitadas), con un glaseado blanco por encima, que se cuece a fuego lento. La forma del calisson es, más o menos, la de un rombo formado por dos triángulos equiláteros (similar a la de la forma de la caja que mostramos en la siguiente imagen).
 Fotografía de una caja de calissons, con forma de rombo (como la forma de los propios calissons), que me compré en la ciudad francesa de Aix-en-Provence. Fotografía: Marian Espinosa
Fotografía de una caja de calissons, con forma de rombo (como la forma de los propios calissons), que me compré en la ciudad francesa de Aix-en-Provence. Fotografía: Marian Espinosa
No está muy claro el origen de este dulce, que parece ser originario de Italia. Como se comenta en la correspondiente entrada de la Wikipedia (en francés), “una de sus primeras referencias se remonta al siglo XII, en un texto medieval italiano en latín que utiliza el término calisone para referirse a un pastel de almendra y harina similar al mazapán moderno”. Y existe otra referencia posterior, el texto Chronique des Vénitiens / Crónica de los venecianos (1275), del italiano Martino Canal, en la que se menciona un dulce, a base de pasta de almendras y nueces a la que se añadían diversas especias (canela y clavo), de nombre “calissons”.
Tampoco está claro cuando llegan estos dulces a la Provenza. Según algunas versiones podría haber sido importado por uno de los cocineros del príncipe francés René d’Anjou / Renato de Anjou (1409-1480), que entre otros títulos fue rey de Nápoles, Sicilia, Aragón y Mallorca. Se cuenta que durante el segundo matrimonio de Renato de Anjou con Jeanne de Laval / Juana de Laval, en 1454, el jefe de la confitería del rey sirvió algunos de estos dulces a la futura reina, que dijo entonces en provenzal “Di calin soun” (que no sé bien cómo traducir, pero para darle cierta gracia me aventuro a traducirlo como “estos son besos”). Por otra parte, en la Wikipedia se cita que el término calisson, con el significado actual, ya aparece en la Provenza en el año 1503. De hecho, la almendra, elemento principal de los calissons, se introdujo en la Provenza en el siglo XVI, por lo que es posible que la introducción del dulce en esta región sea paralela al desarrollo de la producción y comercialización de las almendras.
 Fotografía de los calissons dentro de su caja, que me compré en mi reciente visita a Aix-en-Provence. Aunque como vemos la forma de estos calissons es más bien como una vesica piscis y no como un diamante formado por dos triángulos equiláteros. Fotografía: Marian Espinosa
Fotografía de los calissons dentro de su caja, que me compré en mi reciente visita a Aix-en-Provence. Aunque como vemos la forma de estos calissons es más bien como una vesica piscis y no como un diamante formado por dos triángulos equiláteros. Fotografía: Marian EspinosaPero dejemos las cuestiones históricas aparte y vayamos a la cuestión matemática relacionada con estos dulces provenzales. Aunque si os animáis a prepararlos vosotros mismos, podéis encontrar la receta en muchos blogs de postres, o de recetas de cocina, en general.
 Fotografía de un plato con calissons, cuya forma es la de un rombo o diamante formado por dos triángulos equiláteros, que hemos tomado de una página francesa de recetas, en la que podéis leer cómo se hacen los calissons. La página de recetas es Odelices.Demostraciones sin palabras
Fotografía de un plato con calissons, cuya forma es la de un rombo o diamante formado por dos triángulos equiláteros, que hemos tomado de una página francesa de recetas, en la que podéis leer cómo se hacen los calissons. La página de recetas es Odelices.Demostraciones sin palabras
La primera vez que leí sobre el problema de los calissons fue en el magnífico libro Proofs without words / Demostraciones sin palabras, de Roger B. Nelsen. Este es un tema, el de las demostraciones sin palabras, al que le hemos dedicado varias entradas en el Cuaderno de Cultura Científica, entre ellas:
* Matemáticas para ver y tocar
* Más matemáticas para ver y tocar
* Teoremas geométricos sin palabras: Viviani
* Teoremas geométricos sin palabras: Conway
* Teoremas geométricos sin palabras: Herón
* Teoremas geométricos sin palabras: Snover
Las demostraciones sin palabras, como comenta el matemático Roger B. Nelsen –autor del libro Proofs without words / Demostraciones sin Palabras (publicado por la MAA, Mathematical Association of America, en 1993) –, se fueron haciendo populares en la comunidad matemática a raíz de su publicación en las revistas de la MAA, Mathematics Magazine y The College Mathematical Journal, en las que empezaron a aparecer hacia 1975, primero como imágenes de relleno entre artículos y posteriormente como secciones fijas de las revistas. Las demostraciones sin palabras no son realmente demostraciones matemáticas en sí mismas, son más bien diagramas, esquemas o dibujos que nos ayudan a comprender por qué un teorema es cierto o que encierran la idea de la verdadera demostración matemática. Son sugerentes, atractivas y todo un ejercicio de estímulo del pensamiento.
El origen del problema de los calissons y su demostración visual, tema que nos ocupa en esta entrada del Cuaderno de Cultura Científica, es el artículo The problem of calissons, de los matemáticos Guy David y Carlos Tomei, publicado en 1989 en la revista The American Mathematical Monthly (que también es una revista de la MAA, creada en 1894).
El problema de los calissonsTomando las mismas palabras que utilizaron David y Tomei en su artículo de la revista The American Mathematical Monthly,
“Un calisson es un dulce francés con la forma de dos triángulos rectángulos pegados por uno de sus lados. Los calissons podrían guardarse en una caja con la forma de un hexágono regular, y su empaquetado sugeriría un interesante problema de combinatoria. Supongamos una caja (hexagonal) cuyos lados tienen longitud n que se llena con calissons cuyos lados tienen longitud 1. La diagonal larga de cada calisson en la caja tiene tres posibles orientaciones, como en la imagen.
 Las tres posibles orientaciones de los calissons en una caja hexagonal
Las tres posibles orientaciones de los calissons en una caja hexagonal
Nuestro resultado principal es que el número de calissons de cada una de las tres orientaciones es un tercio del número de calissons que entran en la caja (hexagonal).”
El problema de los calissons consiste en cómo demostrar esa afirmación, es decir, que el número de calissons de cada orientación es el mismo, un tercio del total de los calissons que entran en la caja hexagonal. Y lo hermoso de la demostración es que consiste en un argumento intuitivo y visual relacionado con el espacio tridimensional.
Los matemáticos David y Tomei, en su artículo The problem of calissons, toman una caja hexagonal cuyo lado tiene longitud 5 (es decir, n = 5), considerando que los lados del calisson son de longitud 1, que es la imagen que mostramos a continuación, con el objetivo de mostrar que hay la misma cantidad de calissons en cada una de las tres direcciones posibles.
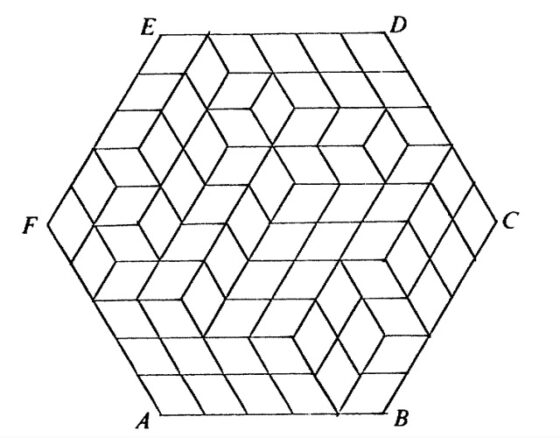 Distribución aleatoria de los 75 calissons que entran en una caja hexagonal cuyo lado tiene longitud 5, considerando que los lados del calisson son de longitud 1, que es la considerada por los matemáticos David y Tomei en su artículo The problem of calissons
Distribución aleatoria de los 75 calissons que entran en una caja hexagonal cuyo lado tiene longitud 5, considerando que los lados del calisson son de longitud 1, que es la considerada por los matemáticos David y Tomei en su artículo The problem of calissonsLa solución consiste en rotar un poco la caja hexagonal para que un vértice quede arriba y colorear cada calisson en función de la orientación que tiene, es decir, los pintamos de tres colores distintos (por ejemplo, en el artículo se utiliza blanco, gris y negro). De esta forma, nuestra imagen de una caja hexagonal rellena con calissons (luego, una imagen esencialmente plana) se convierte en una imagen tridimensional que representa una serie de pequeños cubos apoyados entre tres paredes cuadradas perpendiculares (de tamaño 5 x 5, en el ejemplo de David y Tomei, luego con una superficie de 25 cuadrados, pero en general serán paredes cuadradas con n2 cuadrados), una abajo, otra a la derecha y una tercera a la izquierda. En esta representación tridimensional de pequeños cubos (se verán algunos ejemplos a continuación) puede verse que cada calisson es una cara visible de un pequeño cubo, de manera que todas las caras de un mismo color (que provienen de calissons con la misma orientación) miran en la misma dirección, paralelas a una de las tres paredes sobre las que se apoyan los pequeños cubos. Resulta que todas las caras de pequeños cubos (incluyendo los cuadrados de las paredes de apoyo que no se han cubierto) que miran en una misma dirección son las mismas que todos los cuadrados de la pared de apoyo, por lo tanto, 25 en este caso y n2, en general.
Veámoslo con algunos ejemplos de distribuciones de calissons en una caja hexagonal de tamaño n = 3 (como la que vemos en la siguiente imagen), por lo tanto, que se rellena con 27 dulces con forma de diamante.
 Caja hexagonal, cuyo lado mide 3, siendo la medida de los lados de los calissons 1, y los 27 calissons con los que se rellena la caja
Caja hexagonal, cuyo lado mide 3, siendo la medida de los lados de los calissons 1, y los 27 calissons con los que se rellena la caja
A continuación, vamos a rellenar la caja hexagonal (de lado 3) con los 27 calissons, de tres formas distintas y vamos a utilizar el procedimiento anterior (girar ligeramente y pintar con tres colores distintos los calissons en función de su orientación en la caja) para comprobar que en los tres casos la cantidad de calissons en cada orientación es igual a 9.
Ejemplo 1, con los calissons agrupados
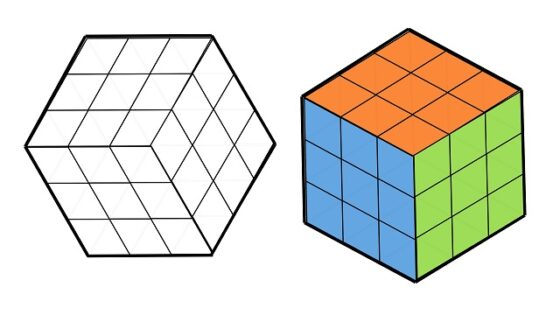
Ejemplo 2
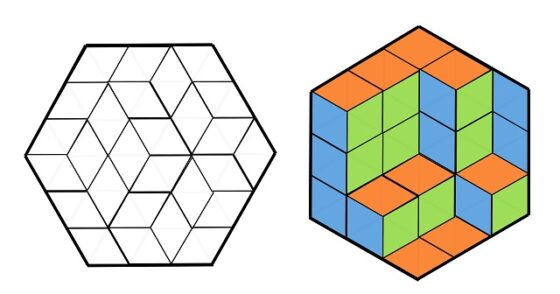
Ejemplo 3
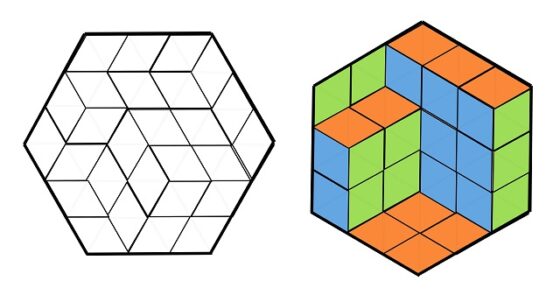
Este argumento visual nos sirve para cualquier tamaño n de la caja hexagonal, en la que introduciremos 3n2 calissons.
En esta misma línea, la imagen que ilustraba la demostración de David y Tomei, con la distribución mostrada arriba, para una caja de tamaño 5, es la siguiente (utilizando blanco, gris y negro).
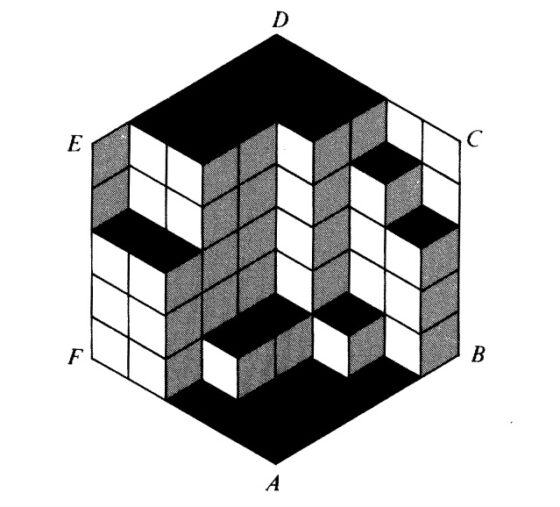
En consecuencia, se ha demostrado el resultado buscado.
Teorema: En todo empaquetamiento de calissons (con forma de diamante) en una caja hexagonal, la cantidad de ellos con una orientación dada es igual a la tercera parte del total de calissons que se incluyen en la caja.
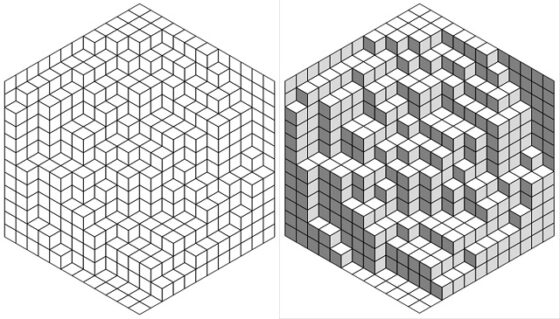 Distribución de 432 calissons en una caja hexagonal de lado igual a 12, junto con su transformación en una imagen tridimensional, mediante el coloreado –blanco, gris claro y gris oscuro- de los calissons en función de su orientación, y en la que se comprueba que hay la misma cantidad de dulces en cada orientación, en concreto, 144. Imagen del blog Possibly wrong
Distribución de 432 calissons en una caja hexagonal de lado igual a 12, junto con su transformación en una imagen tridimensional, mediante el coloreado –blanco, gris claro y gris oscuro- de los calissons en función de su orientación, y en la que se comprueba que hay la misma cantidad de dulces en cada orientación, en concreto, 144. Imagen del blog Possibly wrongLa demostración que aparece en el artículo de David y Tomei, y que después incluye Nelsen en su libro, es una demostración sin palabras, luego visual e intuitiva, pero no una demostración matemáticamente rigurosa. Sin embargo, sí es posible dar demostraciones más matemáticas de este resultado, y de alguna generalización del mismo, para la cual, además, no es válido el razonamiento visual anterior. Para quienes estéis interesados en la misma (solo se necesita un poco de álgebra de vectores) podéis leerla en el blog Symmetry de Gábor Damásdi.
Bibliografía
1.- Roger B. Nelsen, Demostraciones sin palabras (ejercicios de pensamiento visual), Proyecto Sur, 2001.
2.- Guy David, Carlos Tomei, The problem of the Calissons, American Mathematical Monthly, vol. 96, n. 5, pp. 429-430, 1989.
3.- Gábor Damásdi, Symmetry (blog): Problem of calissons
4.- Wikipedia: Calisson
El artículo El problema de los calissons se ha escrito en Cuaderno de Cultura Científica.
Alan Turing y el poder del pensamiento negativo
Las pruebas matemáticas basadas en una técnica llamada diagonalización pueden ser implacablemente contrarias, pero ayudan a revelar los límites de los algoritmos.
Un artículo de Ben Brubaker. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Ilustración Kristina Armitage / Quanta Magazine
Ilustración Kristina Armitage / Quanta MagazineLos algoritmos se han vuelto omnipresentes. Optimizan nuestros viajes, procesan pagos y coordinan el flujo del tráfico en Internet. Parece que para cada problema que puede articularse en términos matemáticos precisos, hay un algoritmo que puede resolverlo, al menos en principio.
Pero ese no es el caso: algunos problemas aparentemente simples nunca pueden resolverse algorítmicamente. El científico informático pionero Alan Turing demostró la existencia de estos problemas “incomputables” hace casi un siglo, en el mismo artículo en el que formuló el modelo matemático de computación que lanzó la informática moderna.
Turing demostró este resultado innovador utilizando una estrategia contraria a la intuición: definió un problema que simplemente rechaza todo intento de resolverlo.
«Te pregunto qué estás haciendo y luego digo: ‘No, voy a hacer algo diferente'», explica Rahul Ilango, un estudiante de posgrado en el Instituto de Tecnología de Massachusetts que estudia informática teórica.
La estrategia de Turing se basa en una técnica matemática llamada diagonalización que tiene una historia ilustre. He aquí una explicación simplificada de la lógica de su prueba.
Teoría de cadenasLa diagonalización surge de un truco inteligente para resolver un problema rutinario que involucra cadenas de bits, cada uno de los cuales puede ser 0 o 1. Dada una lista de estas cadenas, todas igualmente largas, ¿se puede generar una nueva cadena que no esté en la lista?
La estrategia más sencilla es considerar cada cadena posible por turno. Supongamos que tienes cinco cadenas, cada una de cinco bits de longitud. Comienza repasando la lista en busca de 00000. Si no está, puedes parar; si está, pasa a 00001 y repite el proceso. Esto es bastante simple, pero lento para listas largas de cadenas largas.
La diagonalización es un enfoque alternativo que construye poco a poco una cadena nueva. Comienza con el primer bit de la primera cadena de la lista e inviértelo; ese será el primer bit de tu nueva cadena. Luego invierte el segundo bit de la segunda cadena y utilízalo como el segundo bit de la nueva cadena, y repite hasta llegar al final de la lista. Los bits que inviertes garantizan que la nueva cadena difiera de cada cadena de la lista original en al menos un lugar. (También forman una línea diagonal a través de la lista de cadenas, lo que da nombre a la técnica).
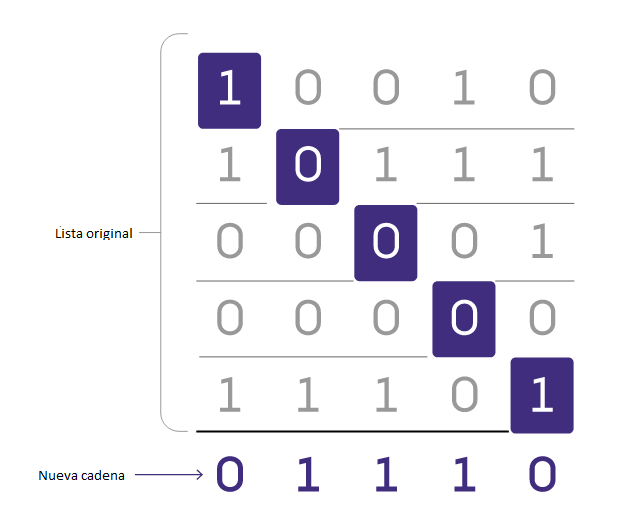 Ilustración: Merrill Sherman / Quanta Magazine
Ilustración: Merrill Sherman / Quanta MagazineLa diagonalización sólo necesita examinar un bit de cada cadena de la lista, por lo que suele ser mucho más rápido que otros métodos. Pero su verdadero poder reside en lo bien que se comporta con el infinito.
“Las cadenas ahora pueden ser infinitas; la lista puede ser infinita; todavía funciona”, afirma Ryan Williams, científico informático teórico del MIT.
La primera persona en aprovechar este poder fue Georg Cantor, el fundador del subcampo matemático de la teoría de conjuntos. En 1873, Cantor utilizó la diagonalización para demostrar que algunos infinitos son más grandes que otros. Seis décadas después, Turing adaptó la versión de Cantor de la diagonalización a la teoría de la computación, dándole un tono claramente a contracorriente.
El juego de la limitación [*]Turing quería demostrar la existencia de problemas matemáticos que ningún algoritmo puede resolver, es decir, problemas con entradas y salidas bien definidas pero sin un procedimiento infalible para pasar de la entrada a la salida. Hizo que esta vaga tarea fuera más manejable al centrarse exclusivamente en problemas de decisión, donde la entrada puede ser cualquier cadena de ceros y unos y la salida es 0 o 1.
Determinar si un número es primo (divisible sólo por 1 y por sí mismo) es un ejemplo de un problema de decisión: dada una cadena de entrada que representa un número, la salida correcta es 1 si el número es primo y 0 si no lo es. Otro ejemplo es comprobar los programas informáticos en busca de errores de sintaxis (el equivalente a errores gramaticales). Aquí, las cadenas de entrada representan código para diferentes programas (todos los programas se pueden representar de esta manera, ya que así es como se almacenan y ejecutan en los ordenadores) y el objetivo es generar 1 si el código contiene un error de sintaxis y 0 si no lo contiene.
Un algoritmo resuelve un problema sólo si produce la salida correcta para cada entrada posible; si falla aunque sea una vez, no es un algoritmo generalista para ese problema. Normalmente, primero especificarías el problema que deseas resolver y luego intentarías encontrar un algoritmo que lo resuelva. Turing, en busca de problemas irresolubles, le dio la vuelta a esta lógica: imaginó una lista infinita de todos los algoritmos posibles y utilizó la diagonalización para construir un problema pertinaz que frustraría todos los algoritmos de la lista.
Imagina un juego amañado de ’20 preguntas’ [**], donde en lugar de comenzar con un objeto particular en mente, quien responde inventa una excusa para decir no a cada pregunta. Al final del juego, han descrito un objeto definido completamente por las cualidades que le faltan.
La prueba de diagonalización de Turing es una versión de este juego en el que las preguntas recorren la lista infinita de algoritmos posibles, preguntando repetidamente: «¿Puede este algoritmo resolver el problema que nos gustaría demostrar que es incomputable?»
«Es una especie de ‘preguntas infinitas'», comenta Williams.
Para ganar el juego Turing necesitaba elaborar un problema en el que la respuesta fuera no para cada algoritmo. Eso significaba identificar una entrada particular que hiciese que el primer algoritmo generase una respuesta incorrecta, otra entrada que hiciese que el segundo fallase, y así sucesivamente. Encontró esas entradas especiales utilizando un truco similar al que Kurt Gödel había utilizado recientemente para demostrar que afirmaciones autorreferenciales como “esta afirmación no es demostrable” significaban problemas para los fundamentos de las matemáticas.
La idea clave fue que cada algoritmo (o programa) se puede representar como una cadena de ceros y unos. Eso significa, como en el ejemplo del programa de comprobación de errores, que un algoritmo puede tomar el código de otro algoritmo como entrada. En principio, un algoritmo puede incluso tomar su propio código como entrada.
Con esta idea, podemos definir un problema no computable como el de la prueba de Turing: “Dada una cadena de entrada que representa el código de un algoritmo, genera 1 si ese algoritmo genera 0 cuando su propio código es la entrada; de lo contrario, la salida es 0”. Cada algoritmo que intente resolver este problema producirá una salida incorrecta en al menos una entrada, es decir, la entrada correspondiente a su propio código. Eso significa que este perverso problema no puede resolverse mediante ningún algoritmo.
Lo que la negación no puede hacerLos informáticos aún no habían terminado con la diagonalización. En 1965, Juris Hartmanis y Richard Stearns adaptaron el argumento de Turing para demostrar que no todos los problemas computables son iguales: algunos son intrínsecamente más difíciles que otros. Este resultado lanzó el campo de la teoría de la complejidad computacional, que estudia la dificultad de los problemas computacionales.
Pero la teoría de la complejidad también reveló los límites del método a la contra de Turing. En 1975, Theodore Baker, John Gill y Robert Solovay demostraron que muchas cuestiones abiertas en la teoría de la complejidad nunca pueden resolverse únicamente mediante la diagonalización. La principal de ellas es el famoso problema de las clases de complejidad P y NP, que pregunta si todos los problemas con soluciones fácilmente comprobables también son fáciles de resolver con el algoritmo adecuado.
Los puntos ciegos de la diagonalización son una consecuencia directa del alto nivel de abstracción que la hace tan poderosa. La demostración de Turing no implicaba ningún problema incomputable que pudiera surgir en la práctica; en cambio, inventó un problema de ese tipo sobre la marcha. Otras pruebas de diagonalización están igualmente alejadas del mundo real, por lo que no pueden resolver cuestiones en las que los detalles del mundo real importan.
«Manejan la computación a distancia», explica Williams. «Me imagino a un tipo que se enfrenta a un virus y accede a él a través de una caja de guantes».
El fracaso de la diagonalización fue una indicación temprana de que resolver el problema de las categorías P y NP iba a ser un largo camino. Pero a pesar de sus limitaciones, la diagonalización sigue siendo una de las herramientas clave en el arsenal de los teóricos de la complejidad. En 2011, Williams lo utilizó junto con una serie de otras técnicas para demostrar que cierto modelo restringido de computación no podía resolver algunos problemas extraordinariamente difíciles, un resultado que había eludido a los investigadores durante 25 años. Estaba muy lejos de resolver el problema de las categorías P y NP, pero aun así representó un avance importante.
Si quieres demostrar que algo no es posible, no subestimes el poder de simplemente decir no.
Notas del traductor:
[*] El original en inglés “The limitation game” es un juego de palabras con el título de la película “The Imitation Game” basada en aspectos de la vida y obra de Alan Turing.
[**] En el juego tradicional de ’20 preguntas’ la persona que responde (la “respondedora”) elige algo que las demás jugadoras, las «interrogadoras», deben adivinar. Se turnan para hacer una pregunta a la que la respondedora debe responder «sí» o «no». Ejemplos de preguntas podrían ser: «¿Es más grande que un móvil?», «¿Está vivo?» y, finalmente, «¿Es este bolígrafo?». No se permite mentir. Si una interrogadora adivina la respuesta correcta, gana y se convierte en la respondedora en la siguiente ronda. Si se hacen 20 preguntas sin una respuesta correcta, entonces la respondedora gana y vuelve a ser la persona que responde en otra ronda.
El artículo original, Alan Turing and the Power of Negative Thinking, se publicó el 5 de septiembre de 2023 en Quanta Magazine.
Traducido por César Tomé López
El artículo Alan Turing y el poder del pensamiento negativo se ha escrito en Cuaderno de Cultura Científica.
La diversidad mineral en Marte
Nuestro planeta tiene una gran diversidad mineralógica. Tanta que hasta el momento hay reconocidas casi siete mil especies minerales y una de las preguntas que a menudo nos surgen cuando estudiamos otros planetas es: ¿Habrá un número similar en otros planetas o cuerpos del Sistema Solar? ¿O quizás es la Tierra un caso extremo dentro del mundo de los minerales?
Pero antes de continuar, ¿tenemos claro qué es un mineral? Llamamos minerales a sustancias sólidas, que tienen una composición química definida, de origen natural y con una estructura cristalina ordenada. Aunque esta definición nos pueda parecer un poco laxa, lo cierto es que en las últimas dos décadas sigue habiendo algo de debate, ya que se sigue discutiendo si los compuestos orgánicos -los de origen biológico o los que aparecen de manera espontánea- se deben considerar minerales.
 La cámara WATSON del Perseverance toma una imagen de cerca de una roca en Marte de la que posteriormente realizará análisis para conocer su composición. En la imagen se pueden ver distintos minerales, entre ellos uno traslúcido que ha llamado la atención de los científicos. Imagen cortesía de NASA/JPL-Caltech.
La cámara WATSON del Perseverance toma una imagen de cerca de una roca en Marte de la que posteriormente realizará análisis para conocer su composición. En la imagen se pueden ver distintos minerales, entre ellos uno traslúcido que ha llamado la atención de los científicos. Imagen cortesía de NASA/JPL-Caltech.Para los geólogos, los minerales son más que una curiosidad o un elemento de coleccionista, ya que nos pueden ayudar a conocer aquellos procesos que han tenido lugar en los planetas a lo largo de los 4500 millones de historia. Muy probablemente los planetas terrestres, de Mercurio a Marte, tuvieron una evolución mineralógica muy similar durante su infancia, pero que poco a poco fue divergiendo debido a las particularidades de cada uno.
Los planetas interiores partíamos con una serie de elementos y minerales similares por nuestra posición en el disco protoplanetario a partir del cual nos formamos. Una vez acabaron todos los procesos que dieron lugar a la formación de los planetas, muy probablemente los primeros minerales existentes en estos cuatro planetas podrían haber sido muy similares en número y composición, ya que se habrían formado a partir de la cristalización del océano de magma existente en estas primeras etapas de infancia planetaria.
Pero tras esa etapa comenzó un proceso evolutivo que nos ha hecho muy diferentes: la presencia o no de atmósfera, de una tectónica de placas o la aparición de la vida son algunos de los eventos que han podido marcar la mayor o menor diversidad mineral de los planetas.
Y aquí viene el segundo término que quería introducir en el artículo de hoy: los modos paragenéticos. Esta palabra engloba los procesos a partir los minerales se forman, es decir, como un conjunto de átomos en forma sólida o líquida son capaces de reconfigurarse dando lugar a una o más formas minerales. Estos modos son una gran cantidad de procesos naturales que llevan a la formación de nuevos minerales.
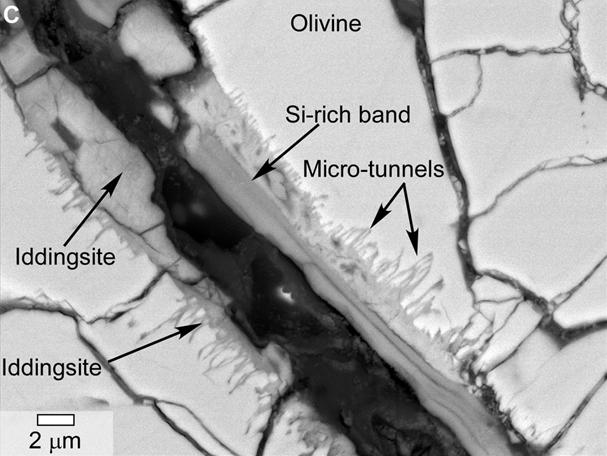 Imagen de microscopio electrónico de un meteorito marciano donde podemos ver algunos de los minerales anotados. Imagen cortesía de la NASA.
Imagen de microscopio electrónico de un meteorito marciano donde podemos ver algunos de los minerales anotados. Imagen cortesía de la NASA.Algunos ejemplos de los modos paragenéticos son la formación a partir de un gas o un líquido -por condensación, precipitación…-, transformaciones físicas a partir de eventos como la caída de rayos, impactos de meteoritos o fenómenos de metamorfismo regional, interacción del agua y las rocas o incluso la formación de minerales por efecto de la vida, como las biomineralizaciones-.
Marte es uno de los planetas que mejor conocemos debido a dos cuestiones principalmente: la primera de ellas son las misiones espaciales con capacidad de observación y análisis que nos han permitido conocer los minerales de su superficie, incluso desde la órbita, sin contacto. La segunda, gracias a los meteoritos que han caído a nuestro planeta y cuyo estudio podemos hacer con mucho detalle en los laboratorios terrestres. A pesar de esto, solo se han podido identificar un total de 161 minerales.
Una nueva investigación (Hazen et al. (2023)) sugiere que esta ausencia de minerales se podría deber a la existencia de un menor número de modos paragenéticos en Marte que los que hay en la Tierra… ¿Por qué? Pues porque nuestro planeta es algo especial con respecto al resto, al menos por lo que sabemos de momento.
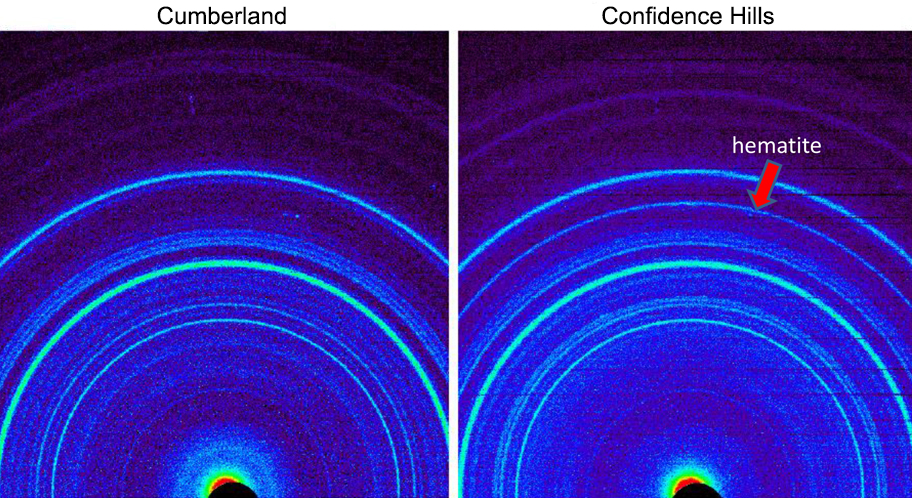 Patrón de difracción de rayos X capturado por el Curiosity en Marte. Gracias a instrumentos como el que permite tomar esta imagen, podemos conocer la composición de las rocas y el suelo de Marte con misiones de superficie. Imagen cortesía de NASA/JPL-Caltech.
Patrón de difracción de rayos X capturado por el Curiosity en Marte. Gracias a instrumentos como el que permite tomar esta imagen, podemos conocer la composición de las rocas y el suelo de Marte con misiones de superficie. Imagen cortesía de NASA/JPL-Caltech.En primer lugar, las interacciones entre los fluidos -como el agua- y las rocas en nuestro planeta tiene una mayor escala que en Marte gracias a la tectónica de placas, que a través de la subducción y de los procesos de fracturación de las rocas hace que nuestro planeta sea más permeable a este tipo de interacciones.
También la existencia de un metamorfismo de altas presiones como el que ocurre durante procesos de colisión continental algo que solo puede ocurrir bajo el régimen de tectónica de placas y, por supuesto, el efecto de la vida en la generación de minerales.
Estos tres procesos de los que hemos hablado podrían ser, según los autores del artículo, los responsables del 80% de la diversidad mineral de nuestro planeta, y precisamente estos modos paragenéticos son de momento exclusivos en la Tierra o podrían tener un ámbito mucho más restringido en el resto de los planetas.
¿Quiere esto decir que en Marte solo existen 161 minerales? No, todavía podrían existir más, ya que apenas hemos podido arañar la superficie y podríamos estar perdiéndonos los minerales existentes en zonas más profundas o inaccesibles debido a procesos hidrotermales o a fenómenos de metamorfismo de contacto, como el que podría haberse dado en las zonas volcánicas, pero a pesar de esto los investigadores sugieren que el número de minerales seguiría siendo un orden de magnitud inferior que en la Tierra.
No cabe la menor duda que los minerales pueden ayudarnos a comprender mejor la historia de los planetas y otros cuerpos, pero todavía nos queda por recorrer un largo camino hasta que podamos estudiar con detalle la composición de estos. Solo entonces podremos decir… ¿realmente somos tan diferentes?
Referencia:
Hazen, R. M., Downs, R. T., Morrison, S. M., Tutolo, B. M., Blake, D. F., Bristow, T. F., Chipera, S. J., McSween, H. Y., Ming, D., Morris, R. V., Rampe, E. B., Thorpe, M. T., Treiman, A. H., Tu, V. M., & Vaniman, D. T. (2023). On the diversity and formation modes of martian minerals. Journal of Geophysical Research: Planets, 128(9). doi: 10.1029/2023je007865
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo La diversidad mineral en Marte se ha escrito en Cuaderno de Cultura Científica.
ZientZinema 5: Los herederos del viento
Scopes
Título original: Inherit the Wind. En las adaptaciones se ha titulado como La herencia del viento o Heredarás el viento. 1960, blanco y negro, 128 minutos. Dir.: Stanley Kramer. Guion: Nedrick Young, Harold Jacob Smith, según la obra de teatro de Jerome Lawrence y Robert Edwin Lee. Música: Ernest Gold. Fotografía: Ernest Laszlo. Montaje: Frederic Knudtson. Intérpretes. Spencer Tracy, Fredric March, Gene Kelly, Dick York, Harry Morgan.
El que perturba su propia casa heredará viento, y el necio será esclavo del sabio.
Proverbios, 11: 29.
Llamar a un hombre mamífero, al parecer, era también ignorar una revelación divina. El efecto de esta doctrina sería destruir la moralidad y promover la infidelidad.
H.L. Mencken sobre el juicio Scopes, The Baltimore Evening Sun, 17 julio 1925.
En 1925, John Thomas Scopes fue juzgado por violar la ley del Estado de Tennessee que prohibía enseñar la teoría de la evolución en las escuelas públicas. El darwinismo se enfrentaba al creacionismo en una batalla judicial en la que participaron Spencer Tracy, en el papel de Henry Drummond (nombre supuesto de Clarence Darrow para el film); Fredric March en el papel de Matthew Harrison Brady (nombre supuesto para William Jennings Bryan); Gene Kelly en el papel del periodista progresista E. K. Hornbeck (nombre que en la película a H. L. Mencken); Dick York como Bertram T. Cates (nombre supuesto para John Scopes) y Claude Atkins como el reverendo fundamentalista que denuncia al profesor Cates.
Posteriormente se rodaron para televisión otras tres versiones del juicio Scopes: en 1965 con Melvyn Douglas y Ed Begley, en 1988 con Jason Robards y Kirk Douglas, y en 1999 con Jack Lemmon y George C. Scott.
Cuando Estados Unidos salió de la Primera Guerra Mundial, una nostalgia colectiva recorrió el país por la simplicidad y normalidad anterior a la guerra. En las áreas rurales, particularmente en el sur y el medio oeste, los estadounidenses recurrieron a la fe para recuperar de la estabilidad, y la religión creció en popularidad. Los fundamentalistas, que creían en una interpretación literal de la Biblia, encontraron en Darwin y la teoría de la evolución la amenaza más evidente a la verdad que estaban seguros de que solo ellos poseían. Con la evolución como enemiga, se propusieron erradicarla de su sociedad, comenzando por el sistema educativo.
 Debido al excesivo calor el 20 de julio de 1925 el presidente del tribunal decidió que la sesión se trasladase al exterior del juzgado. En la imagen Bryan (de pie) interroga a Darrow (sentado a la izquierda). Fuente: Wikimedia Commons
Debido al excesivo calor el 20 de julio de 1925 el presidente del tribunal decidió que la sesión se trasladase al exterior del juzgado. En la imagen Bryan (de pie) interroga a Darrow (sentado a la izquierda). Fuente: Wikimedia CommonsPara 1925, varios estados del sur habían aprobado leyes que prohibían la enseñanza de la evolución. Oklahoma, Florida y Mississippi tenían esas leyes, e influían en las de Carolina del Norte y Kentucky. En Tennessee, la Ley Butler se aprobó en 1925, y aunque el gobernador no era fundamentalista, muchos de sus electores lo eran. Y la Unión Estadounidense de Libertades Civiles de Nueva York, cada vez más cautelosa, y declararon la prohibición de la evolución como una infracción de sus derechos constitucionales. Con la vista puesta en Tennessee, la ACLU se dispuso a iniciar un caso judicial para probar si era constitucional la Ley Butler.
A los pocos días de la decisión de la ACLU de poner a prueba la Ley Butler, se publicó un comunicado de prensa en un periódico de Tennessee que ofrecía apoyo legal a cualquier maestro que desafiara la ley. El 5 de mayo, varios líderes locales se reunieron y acordaron los detalles de su plan. Necesitaban un maestro para probar la ley, y lo encontraron en John T. Scopes, un profesor de ciencias y entrenador de fútbol de 24 años. Cuando se le preguntó acerca de su enseñanza de la evolución como parte de la enseñanza de la biología, Scopes respondió que lo mismo haría cualquier otro maestro.
La película se adaptó en Hollywood en 1960, cinco años después del estreno de la obra de teatro en Broadway. Entonces el Movimiento por los Derechos Civiles iniciaba sus acciones, el macartismo había terminado y el país recibía a un nuevo presidente, John F. Kennedy, que pronto sería elegido. El asunto de las leyes contra la teoría de la evolución no parecía interesar. Ese año, el New York Times publicó pocas noticias sobre el juicio de Scopes. En uno de ellos presentaron las declaraciones de un profesor de ciencias adventista del séptimo día que advirtió sobre los peligros de enseñar la evolución a los estudiantes. Sin embargo, el segundo de los dos artículos más largos sugería que la obra de teatro y su contenido ocupaban un lugar importante en la memoria del público.
La versión de Hollywood era muy diferente de la que Lawrence y Lee habían escrito para el teatro. Aunque la película era entretenida y hábil, muchos de debates de Lawrence y Lee se distorsionaron en la película de 1960.
En julio de ese año, en Dayton, Tennessee, donde se celebró el juicio a Scopes en 1925, se declaró el 21 de julio, Día del Juicio Scopes. La ciudad había aprovechado el juicio como una bendición comercial para Dayton, y en 1960 buscaba revivir el legado, trayendo más visitantes a Dayton. Donde antes había carteles que proclamaban «Lea su Biblia«, ahora, treinta y cinco años después, una pancarta decía «Bienvenido a Dayton, día del juicio de Scopes, 21 de julio«. En realidad, la ciudad había cambiado muy poco y el palacio de justicia seguía como siempre, como medio siglo atrás. Para la gente de Dayton, el juicio todavía se vivía no tanto como un conflicto cultural sino como un evento publicitario que honraba a este pequeño pueblo olvidado.
En resumen, el juicio a Scopes se convirtió en un objetivo para la lucha por las libertades civiles y en un exponente del conflicto entre la ciencia y el cristianismo fundamentalista en auge en Estados Unidos. Scopes fue declarado culpable y condenado a pagar la multa mínima de 100$. Pero, aparte del veredicto concreto, en la opinión pública vencieron los proevolucionistas. Sin embargo, como escriben Judith Grabiner y Peter Miller desde California y Ohio en 1974, los partidarios de la teoría de la evolución fallaron en la continuidad de su defensa y, por ello, los debates continúan incluso en la actualidad.
Referencias:
Grabiner, J.V. & P.D. Miller. 1974. Effects of the Scopes Trial. Was it a victory for evolutionists? Science 185: 832- 837.
Martínez-Salanova Sánchez. E. s.f. La herencia del viento. Libertad de pensamiento y tolerancia religiosa en las aulas. Cine y educación. 9 pp.
Mencken, H.L. 2007. El juicio Scopes. La acusación del fundamentalismo cristiano (The Baltimore Evening Sun 17-20 julio 1925). Letras Libres 71: 38-43.
Wikipedia. 2022. Inherit the wind (película). 22 diciembre.
Wikipedia. 2023. Scopes trial. 9 July.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo ZientZinema 5: Los herederos del viento se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2023 en directo
El gran evento de divulgación organizado por Naukas y la Cátedra de Cultura Científica vuelve a Bilbao para celebrar su decimotercera edición que tendrá lugar nuevamente en el gran Palacio Euskalduna. Las sesiones del acto central durante los días 15 y 16 de septiembre, Naukas Bilbao 2023, pueden seguirse por streaming aquí o en la web de Naukas.

El programa es el siguiente (horas GMT+2):
Viernes 15 septiembre – Sesión de Mañana10:00 a 10:10 – José Miguel Viñas: ¡Leed a Verne, malditos!
10:10 a 10:30 – Javier S. Burgos y Luisma Escudero: Ciencia ochentera (20 minutos)
10:30 a 10:40 – Juan Francisco Hernández: Recreo Naukas, un nuevo espacio de divulgación
10:40 a 10:50 – Sara Barja: Vamos a mover átomos
10:50 a 11:00 – Teresa Valdés-Solís: Ilustradas y aventureras
11:00 a 11:10 – Iván Rivera: El ancho de banda de la Stasi
11:10 a 11:20 – José A. Prado-Bassas: Series a lo Grandi
11:20 a 11:30 – Juan Ignacio Pérez: Una taxonomía de los saberes
11:30 a 12:00 – Descanso de 30 minutos
12:00 a 12:10 – Raúl Ibáñez: Las matemáticas como herramientas de creación artística
12:10 a 12:20 – Carlos Lobato: Archaea, las pequeñas grandes desconocidas
12:20 a 12:30 – Anabel Forte: Entre datos y lámparas
12:30 a 12:40 – Lorena Pérez Hernández: Anna Wierzbicka y la tabla periódica del pensamiento
12:40 a 12:50 – Laura Morrón: La revolución newtoniana… a pesar de Newton
12:50 a 13:00 – Pablo Rodríguez: Las charlas de mis pesadillas
Viernes 15 septiembre – Sesión de Tarde17:00 a 17:10 – Ignacio López Goñi: Andeuineris
17:10 a 17:20 – Eva Caballero: Nuestras madres nos alteran
17:20 a 17:30 – Ángel López Sánchez: El cielo es tu laboratorio
17:30 a 17:40 – Naiara Barrado: Júpiter ¿Héroe o villano?
17:40 a 17:50 – Miguel A. Delgado: ¿Y si resulta que la revolución científica la inició España?
17:50 a 18:00 – Gaby Jorquera: Sombras largas
18:00 a 18:10 – Isabel Moreno: Que llueva, que llueva
18:10 a 18:20 – Francis Villatoro: Lo que sabemos que no sabemos
18:20 a 18:30 – Sergio P. Acebrón: Explorando los límites de la vida
18:30 a 19:00 – Descanso (30 minutos)
19:00 a 19:20 – Gemma del Caño y Conchi Lillo: Comer con los ojos (20 minutos)
19:20 a 19:30 – Susana Escudero: Granjas de cadáveres
19:30 a 19:40 – Guillermo Peris: La expresión de la muerte
19:40 a 19:50 – José Ramón Alonso: La lección de anatomía
19:50 a 20:00 – Miguel Santander: Dear Doctor,
Sábado 16 septiembre – Sesión de Mañana10:00 a 10:10 – Ambrosio Liceaga: ¿Es Bilbao el mejor lugar para una civilización tecnológica en expansión?
10:10 a 10:20 – Paula Serras : En la cresta de la ola
10:20 a 10:30 – Helena Matute: Experimentos con humanos e IAs
10:30 a 10:40 – Javier Pedreira Wicho: IA: no es inteligencia todo lo que reluce
10:40 a 10:50 – Onintze Salazar: Sobre perturbaciones y no precisamente de la atmósfera
10:50 a 11:00 – Gemma Marfany: Ni tuyo ni mío, de todos
11:00 a 11:10 – Gisela Baños: Cuando la ciencia ficción puso en jaque a Seguridad Nacional
11:10 a 11:20 – Alberto García Salido: Toda su sangre en mis manos
11:20 a 11:30 – Lluís Montoliu: Millones de raras
11:30 a 12:00 – Descanso de 30 minutos
12:00 a 12:10 – Javier Fdez. Panadero: Ilusiones cacharrísticas
12:10 a 12:30 – Luis Martínez Otero: FESTIVAL JA (20 minutos)
12:30 a 12:40 – Julián Estévez: Drones y Ramstein
12:40 a 12:50 – Fernando Frías: Benidorm y la Tierra
12:50 a 13:00 – Laura Toribio: Ese huequito entre Marte y Júpiter
Sábado 16 septiembre – Sesión de Tarde17:00 a 17:10 – Laura Morán: La erótica del fregao
17:10 a 17:20 – César Tomé: La desviación de Einstein
17:20 a 17:30 – Sara Cazzoli: Feo, fuerte y formal
17:30 a 17:40 – Álvaro Bayón: Nuestra vida por unas monedas
17:40 a 17:50 – Ricardo Moure: Seguro dental, Lisa necesita un aparato
17:50 a 18:00 – Txema Campillo: De Guttemberg a Marilyn
18:00 a 18:10 – Pablo José Barrecheguren: La paradoja del sueño lúcido
18:10 a 18:20 – Virginia Arechavala: Los vulgares exploradores del laberinto.
18:20 a 18:30 – Juan Carlos Gil: Vuela, gaviota… ¡Vuela!
18:30 a 19:00 – Descanso (30 minutos)
19:00 a 19:10 – Carlos Briones: Invisible a los ojos
19:10 a 19:20 – Álvaro Carmona: El borde del espejo
19:20 a 19:30 – Elisabete Alberdi: Las matemáticas del glioma
19:30 a 19:40 – Joaquín Sevilla: Una mañana de verano
19:40 a 19:50 – Antonio Martínez Ron: Etiquetar el asombro
19:50 a 20:00 – Oskar González: La última de Vermeer
20:00 a 20:10 – Entrega de los Premios Tesla 2023 y despedida del evento.
El artículo Naukas Bilbao 2023 en directo se ha escrito en Cuaderno de Cultura Científica.

