Naukas Bilbao 2021: Oskar Gonzalez – No venderás cuadros a los nazis
El gran evento de divulgación Naukas regresó a Bilbao para celebrar su décima edición en el magnífico Palacio Euskalduna durante los pasados 23, 24, 25 y 26 de septiembre.
Un juicio por alta traición termina desvelando uno de los grandes engaños de la historia del arte. Oskar Gonzalez nos cuenta el papel pionero de la ciencia en la constatación de la falsedad de la que pasaba por ser la gran obra maestra de Vermeer.
El propio Oskar escribió sobre esta historia en su sección del Cuaderno, kimikArte: El pintor que engañó a los nazis, pero no a la química
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2021: Oskar Gonzalez – No venderás cuadros a los nazis se ha escrito en Cuaderno de Cultura Científica.
Un termómetro óptico para entornos industriales extremos
El grupo de investigación Applied Photonics Group de la UPV/EHU ha desarrollado un termómetro óptico para el sector industrial basado en una fibra óptica capaz de medir la temperatura en un amplio rango térmico con una alta sensibilidad sin interacción con el entorno.

La temperatura siempre ha sido una variable muy importante en muchos sectores industriales. Ciertas aplicaciones industriales requieren además una alta sensibilidad ya que existen procesos críticos en los que la medición precisa de la temperatura en tiempo real es esencial para la calidad del producto o para evitar accidentes o averías. Además, habitualmente, los entornos en los que se llevan a cabo estas mediciones provocan que los dispositivos estén sometidos a altos niveles de estrés que pueden reducir su vida útil. Así, por ejemplo, las altas temperaturas en el interior de las turbinas de los motores de aviación; la producción de productos petroquímicos, muchos de ellos inflamables o directamente explosivos, que hay mantener dentro de estrictos rangos de temperatura; o la industria alimentaria donde algunos productos deben conservarse a temperaturas bajo cero.
Existe pues una demanda de termómetros altamente sensibles y robustos capaces de operar en amplios rangos térmicos. Hoy en día, los termómetros electrónicos son los dispositivos más extendidos para la detección de la temperatura en la industria. Entre ellos, los termopares son una tecnología fiable y barata. Pero pueden no ser los mejores candidatos cuando hay que utilizarlos en entornos con gases inflamables, por ejemplo, porque pueden interactuar de forma indeseada con esos gases. En las últimas décadas han aparecido varios sensores basados en fibra óptica como alternativa para superar dicha limitación gracias a su pasividad y su sensibilidad intrínseca a la temperatura.
Por ello, “en este trabajo hemos desarrollado un termómetro basado en una fibra óptica muy especial capaz de soportar condiciones de trabajo extremadamente exigentes. Se trata de la fibra óptica multinúcleo que obtenemos gracias a un acuerdo de colaboración con la Universidad Central de Florida. La fibra óptica común, por ejemplo, es la fibra que nos llega a casa. Se trata de una carretera convencional con un solo carril por sentido de marcha. La fibra óptica multinúcleo sería equivalente a una autopista en la que hay múltiples carriles en cada sentido por los que puede ir la luz. De ahí que las propiedades tanto de transferencia de datos como de cantidad de luz que puede transmitirse se multiplican”, explica Josu Amorebieta investigador del grupo de investigación Applied Photonics Group de la UPV/EHU.
“Para desarrollar el termómetro hemos analizado teóricamente y en detalle cómo afecta la temperatura a las fibras multinúcleo para predecir de esta forma la geometría más sensible a la temperatura. El diseño del termómetro le permite funcionar en un amplio rango térmico (desde los -25 hasta los 900 grados Celsius) y su construcción es lo suficientemente compacta y robusta como para soportar entornos adversos”, añade Josu Amorebieta.
Según el personal investigador del grupo Applied Photonics Group de la UPV/EHU, “los resultados sugieren que el nuevo termómetro óptico es tan preciso como cualquier termómetro electrónico con la ventaja de ser inerte, compacto y fácil de fabricar”. Este prototipo es un importante paso en el camino hacia los termómetros ópticos comercialmente viables.
Referencia:
Josu Amorebieta, Angel Ortega-Gomez, Rubén Fernández, Enrique Antonio-Lopez, Axel Schülzgen, Joseba Zubia, Amezcua-Correa, Gaizka Durana & Joel Villatoro (2021) Sensitivity-optimized strongly coupled multicore fiber-based thermometer Optics and Laser Technology DOI: 10.1016/j.optlastec.2021.107532
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Un termómetro óptico para entornos industriales extremos se ha escrito en Cuaderno de Cultura Científica.
En las entrañas de nuestro planeta
En 1864 Julio Verne publicó su novela “Viaje al centro de la Tierra”, en la que imaginaba nuestro planeta como una especie de queso gruyère en donde era posible encontrar pasadizos que nos conducían, directamente, al interior hueco de nuestro planeta. Sin embargo, y gracias a siglo y medio de avances en las técnicas de estudio geológicas, hoy sabemos que esta fantástica idea no era muy acertada.
Aunque solemos representar a la Tierra como una esfera casi perfecta, en realidad, debido a la rotación que realiza sobre sí misma, se asemeja más a un elipsoide de revolución que se encuentra parcialmente achatado por los polos, por lo que tiene un diámetro máximo de 12.756 km y un diámetro mínimo de 12.714 km, con un radio promedio de unos 6370 km. Y en cuanto a su estructura interna, que es el tema que nos ocupa hoy, podríamos definir nuestro planeta como una cebolla, ya que está formado por diversas capas concéntricas superpuestas una encima de la otra. Pero a la hora de nombrar y describir cada una de esas capas, nos encontramos con dos divisiones diferentes de acuerdo a qué propiedades físicas de los materiales queramos hacer alusión.
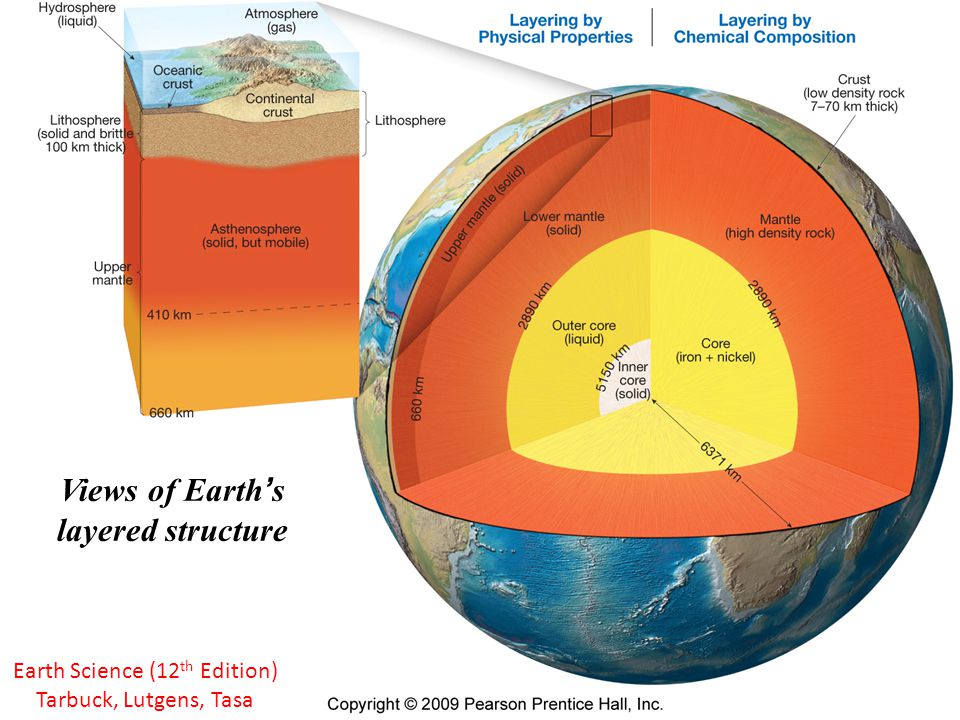 Divisiones internas de la Tierra de acuerdo a la composición química y a las propiedades físicas de los materiales. Autoría: Tarbuck, E.J., Lutgens, F.K. y Tasa, D.G. (2009). Earth Science, 12th Edition. Ed. Pearson Prentice Hall, Estados Unidos. Fair use.
Divisiones internas de la Tierra de acuerdo a la composición química y a las propiedades físicas de los materiales. Autoría: Tarbuck, E.J., Lutgens, F.K. y Tasa, D.G. (2009). Earth Science, 12th Edition. Ed. Pearson Prentice Hall, Estados Unidos. Fair use.La primera división interna que hacemos de nuestro planeta responde a la composición química de los materiales que lo conforman, que tiene que ver directamente con la densidad de los elementos químicos. Cuando nuestro planeta estaba comenzando a formarse, los elementos más densos, es decir, los más pesados, se quedaron en el interior de la Tierra, mientras que los menos densos y, por tanto, más ligeros, migraron hacia la parte más externa. Por este motivo, tenemos composiciones químicas diferentes según aumentamos en profundidad, lo que nos permite definir tres grandes capas en nuestro planeta:
La corteza, que es la capa más externa o superficial de la Tierra y está formada principalmente por silicatos de aluminio y magnesio. Podemos dividirla en corteza oceánica, que se encuentra por debajo de la columna de agua de los océanos y tiene un espesor de entre 7 y 12 km, y corteza continental, que posee un espesor promedio de unos 30 km, aunque llega hasta profundidades de 70 km por debajo de las grandes cordilleras, como el Himalaya. Al límite inferior de la corteza, cuya profundidad oscila entre los 7 y los 70 km, se le denomina discontinuidad de Mohorovicic, o “la Moho”, como la conocemos de manera cariñosa en geología.
Justo por debajo de la corteza y hasta los 2900 km de profundidad nos encontramos con el manto, que está compuesto mayoritariamente por silicatos de hierro y magnesio. También aquí podemos hacer una diferenciación en dos partes, el manto superior y el manto inferior, cuyo límite se encuentra aproximadamente a 660 km de profundidad y se conoce como discontinuidad de Repetti.
Finalmente tenemos el núcleo, formado por hierro y níquel y que está separado del manto por la discontinuidad de Gutenberg. El núcleo también se divide en dos subcapas, el núcleo externo y el núcleo interno, cuyo límite aparece a unos 5150 km de profundidad en la discontinuidad de Lehmann.
La otra división que hacemos de la estructura interna de nuestro planeta se corresponde con las propiedades mecánicas de los materiales que lo componen. En este caso, los principales parámetros físicos a tener en cuenta son la presión y la temperatura. Resulta que, según aumentamos en profundidad hacia el interior de la Tierra, tanto la presión como la temperatura son cada vez más altas, por lo que la acción combinada de ambos parámetros físicos provoca un cambio en el comportamiento mecánico de los materiales que nos vamos encontrando. De esta manera, se puede subdividir nuestro planeta en cuatro capas:
La litosfera, que es la capa sólida y rígida exterior y abarca toda la corteza y parte del manto superior. También se divide en litosfera oceánica y litosfera continental, por lo que su espesor oscila entre los 70 km y los 150 km.
A continuación tenemos la astenosfera, que es un semisólido plástico y viscoso que comprende el resto del manto superior.
Por debajo aparece la mesosfera, algo más sólida que la astenosfera pero cuyos materiales mantienen un comportamiento plástico. Se corresponde con el manto inferior.
Y, por último, encontramos la endosfera, en la que podemos diferenciar el núcleo externo que es líquido y el núcleo interno que es sólido.
De esta manera, utilizaremos una nomenclatura u otra para las capas internas de la Tierra dependiendo de a qué propiedades de los materiales nos queramos referir. Si hacemos alusión a la composición química, usaremos los términos corteza, manto y núcleo para dividir nuestro planeta. Sin embargo, si queremos referirnos al comportamiento mecánico, emplearemos los conceptos de litosfera, astenosfera, mesosfera y endosfera. Incluso, podemos mezclar ambas divisiones y usar términos compuestos tales como manto astenosférico si queremos reseñar tanto la composición como las propiedades mecánicas de los materiales. Pero recordad que estos términos ni son sinónimos ni son intercambiables, por lo que no es lo mismo hablar de la corteza que hablar de la litosfera.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo En las entrañas de nuestro planeta se ha escrito en Cuaderno de Cultura Científica.
Tomás Rodríguez Bachiller: matemático, ingeniero y traductor de textos científicos
En su habitual sonrisa, aparentemente ingenua, casi infantil, destellaba, en efecto, suavemente, esa lumbre de benévola ironía que hemos visto lucir en otras nobles y selectas personalidades, y que revela, junto a ese fondo de milenario saber humano que no se hace ilusiones, la más amplia y exquisita tolerancia.
Fragmento de la necrológica de Tomás Rodríguez Bachiller por Antonio Rodríguez Huéscar, El País, 30/10/1980
 Tomás Rodríguez Bachiller. Imagen extraída de la Gaceta de la RSME.
Tomás Rodríguez Bachiller. Imagen extraída de la Gaceta de la RSME.
Tomás Rodríguez Bachiller nació en Hong Kong el 10 de noviembre de 1899. Su padre, Tomás Rodríguez, era vicecónsul de España en la entonces colonia británica. Su madre era Julia Bachiller. Era el tercero de dos hermanas (Julia y Pilar, nacidas del primer matrimonio de su padre) y tres hermanos (él, Ángel y Jesús). Su madre falleció al dar a luz a Jesús.
Estudió en el Instituto Cardenal Cisneros de Madrid, graduándose en 1916. Se matriculó después en la Universidad Central de Madrid: deseaba estudiar matemáticas. Pero su padre pensaba que estos estudios no le proporcionarían una carrera exitosa. Así, en 1918, Rodríguez Bachiller comenzó sus estudios en la Escuela de Ingenieros de Caminos, Canales y Puertos de Madrid, sin abandonar por ello sus estudios de matemáticas. Algunos de sus profesores fueron Luis Octavio de Toledo (1857-1934), Julio Rey Pastor (1888-1962) y José Ruiz Castizo (1857-1929) que le enseñaron Análisis Matemático, y Cecilio Jiménez Rueda (1858-1950), Miguel Vegas (1865-1943) y José Gabriel Álvarez Ude (1876-1958) fueron sus profesores docentes de Geometría. También estudió Mecánica Celeste con José María Plans (1878-1934).
En enero de 1921, Tullio Levi-Civita (1873-1941) visitó Madrid para dictar un curso sobre Mecánica clásica y relativista. Rodríguez Bachiller, que tenía conocimientos de alemán, francés, inglés e italiano, tomó notas durante las lecciones del matemático italiano y las tradujo al castellano, aunque nunca llegaron a publicarse.
En 1923, el físico Albert Einstein (1879-1955) visitó España para impartir una serie de conferencias públicas sobre relatividad. Rodríguez Bachiller fue uno de los invitados a asistir; debía tomar notas y preparar unos resúmenes de las conferencias. En aquel momento había terminado sus estudios de matemáticas, aunque continuaba con los de ingeniería. Los resúmenes preparados por el matemático español se publicaron en el periódico El Debate, con la satisfacción del físico, que le confesó que«en ningún otro país del mundo se había hecho tan bien».
Gracias a una beca de la Facultad de Ciencias de Madrid, Rodríguez Bachiller pasó el curso académico 1923-1924 en Francia. Allí asistió a los cursos de Émile Borel (1871-1956) sobre elasticidad, de Jules Drach (1871-1949) sobre transformaciones de contacto, de Charles Émile Picard (1856-1941) sobre curvas y superficies algebraicas, de Élie Cartan (1869-1951) sobre mecánica de fluidos, de Jacques Hadamard (1865-1963) sobre ecuaciones diferenciales, de Claude Guichard (1861-1924) sobre geometría diferencial y transformaciones de Laplace, de Henri Lebesgue (1875-1941) sobre topología y de Ernest Vessiot (1865-1952) sobre ecuaciones diferenciales parciales y teoría de grupos.
Al regresar a Madrid en 1924, Rodríguez Bachiller dictó el primer curso de topología impartido en España.
En octubre de 1925 fue nombrado profesor ayudante en la Facultad de Ciencias de Madrid. Además, fue un activo colaborador de la Revista de la Sociedad Matemática Española. Su conocimiento de idiomas le permitió revisar varios trabajos de matemáticos europeos, en particular los artículos sobre topología de Maurice Fréchet (1878-1973), las tesis doctorales de Luigi Fantappié (1901-1956) sobre geometría algebraica y de Louis Antoine (1888-1971) sobre topología, o la monografía L’Analysis situs et la Géométrie algébrique de Solomon Lefschetz (1884-1972). También se ocupaba de la correspondencia con matemáticos extranjeros que publicaron en los primeros números de la Revista de la Sociedad Matemática Española, además de traducir algunos de sus artículos a castellano.
En octubre de 1932, Rodríguez Bachiller se convirtió en profesor interino de la Facultad de Ciencias de Madrid al quedar vacante la Cátedra de Ecuaciones Diferenciales. En 1935, tras pasar las pruebas correspondientes, fue nombrado profesor de Teoría de Funciones, aunque al carecer de un doctorado, le informaron de que debía presentar una tesis antes de poder ocupar la Cátedra. Presentó su tesis Axiomática de la dimensión y la defendió el 27 de agosto de 1935, aunque nunca fue publicada.
Al final de la Guerra Civil, debido a su simpatía por el bando republicano, fue tratado con recelo por el régimen franquista y descalificado para ocupar cargos de dirección y confianza. Aunque pudo volver a ocupar su Cátedra en diciembre de 1939.
En 1941 escribió Comentarios sobre álgebra y topología y, al año siguiente, Sulle superficie del quarto ordine contenenti una conica. Fueron sus últimos trabajos de investigación, aunque mantuvo su interés por la topología e impartió docencia sobre esta disciplina en muchas ocasiones.
En 1947 realizó una visita de cinco meses a Estados Unidos gracias a una beca de Junta de Relaciones Culturales del Ministerio de Relaciones Exteriores. En la Universidad de Illinois en Urbana trabajó con Oscar Zariski (1899-1986), y en Princeton con Solomon Lefschetz (1884-1972), Emil Artin (1898-1962) y Claude Chevalley (1909-1984).
En 1954 comenzó una serie de estancias en la Universidad de Puerto Rico, un lugar especial para el matemático ya que allí había nacido su hermano Jesús y estaba enterrada su madre.
En 1969 se retiró, falleciendo con 80 años, el 9 de julio de 1980.
Referencias
-
Luis Español González y María Ángeles Martínez García, Hacia la matemática abstracta: Tomás Rodríguez Bachiller (1899–1980), Gaceta de la Real Sociedad Matemática Española 13 (4) (2010) 769–795
-
J J O’Connor and E F Robertson, Tomás Rodríguez Bachiller, MacTutor History of Mathematics archive, University of St Andrews
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Tomás Rodríguez Bachiller: matemático, ingeniero y traductor de textos científicos se ha escrito en Cuaderno de Cultura Científica.
Alfred Werner, químico hasta la extenuación
 Imagen oficial de Werner que se conserva en la Biblioteca del Politécnico de Zúrich (ETH Zürich)
Imagen oficial de Werner que se conserva en la Biblioteca del Politécnico de Zúrich (ETH Zürich)Alfred Werner nació en 1866 en uno de esos lugares marcados por la guerra en la vieja Europa, una de esas ciudades en la frontera entre imperios que cambiaba de manos según soplase el viento. Mulhouse tenía tendencia a ser francesa, la mayoría de sus habitantes se sentían franceses, a pesar de que sus apellidos eran una mezcolanza de prusianos y galos. Siendo Alfred niño, la guerra franco-prusiana de 1870 hizo que la ciudad cambiase de nuevo de manos, siendo anexada al recién formado Reich Alemán diseñado por Otto von Bismarck para mayor gloria del káiser Wilhelm.
Muchos ciudadanos con lazos franceses abandonaron la ciudad, no así los padres de Alfred, que prefirieron quedarse y resistir, hablando francés en casa aunque estuviese expresamente prohibido. Ya adulto, Alfred recordaría cómo disparaba su fusil de juguete contra los soldados alemanes y su mesa de despacho en Zúrich estaba presidida por un trozo de bomba que recogió cerca de su casa siendo niño.
Alfred no fue precisamente un alumno ejemplar y, como precaución, solía llevar trozos de cartón dentro de sus pantalones con la idea de aliviar el castigo físico que suponía saltarse clases. Los biógrafos de Werner hablan de rebeldía frente a la extrema rigidez del sistema de enseñanza alemán, la misma que años después mostraría Einstein. Sin embargo, Alfred era muy experimental a la par que teórico: sus escapadas las empleaba en hacer experimentos químicos detrás de un granero cercano y está documentada al menos una explosión en su habitación.
Entre 1885 y 1886 Alfred tuvo que hacer el servicio militar en Karlsruhe, donde aprovechó para asistir a las conferencias que Engler daba en el Politécnico local. En 1886 toma la decisión de alejarse de conflictos y se matricula en el Politécnico de Zúrich. En 1889 se diploma en química técnica y, a pesar de suspender varios exámenes de matemáticas en su primer intento, consigue su doctorado en 1892, tras una estancia de casi dos años en París, con una tesis sobre la disposición espacial de moléculas que contienen nitrógeno, con Arthur Hanztsch como director y Marcellin Berthelot como codirector. Al igual que Einstein, si bien realizó su trabajo en el Politécnico el doctorado se lo otorgó la Universidad de Zúrich.
Los años 1892 y 1893 fueron de subsistencia para Alfred, trabajando como privat dozent, profesor sin sueldo (lo que sus alumnos le pagasen), en la Universidad de Zúrich. En 1893 se convirtió e profesor asociado de la Universidad con un modesto salario, sucediendo a Victor Merz como profesor de química orgánica. En 1895 adquiriría la nacionalidad suiza y, a pesar de tener ofertas de Viena, Basilea o Wurzburg, decide quedarse en la Universidad de Zúrich aceptando la plaza de catedrático con sólo 29 años. Pero, ¿qué había hecho Alfred en este tiempo para escalar así de rápido?
Alfred hizo su primera investigación química independiente con 18 años y su interés siempre había estado en la frontera entre la química orgánica y la inorgánica, alrededor del problema de la valencia y la estructura de los compuestos químicos. Un par de años después de su doctorado, obsesionado como estaba con el problema, cuenta la leyenda que una noche se despertó sobresaltado a las dos de la madrugada, saltó de la cama y se puso a escribir. A las cinco había terminado “Contribución a la constitución de los compuestos inorgánicos”, el artículo que sentaba las bases de la teoría actualmente aceptada sobre los compuestos de coordinación, también llamados complejos.
Alfred proponía flexibilizar las ideas de Kekulé, de una valencia rígida en una dirección, a una esfera de fuerza con el centro en el átomo. Sugería la existencia de un número de coordinación, que sería el número de ligandos que un determinado átomo metálico buscaría adquirir. Estas ideas eran controvertidas pero lo suficientemente interesantes como para asegurarle un puesto en la universidad.
Con el futuro asegurado, se dejó barba y bigote para intentar conseguir un poco de respeto por parte de los alumnos y colegas, se casó con una chica suiza y se dispuso a fundar una familia y a probar su teoría. La familia estuvo completa 8 años después. Probar la teoría le costaría 20 años de trabajo incansable.
La rutina era siempre la misma: sugería una estructura para un compuesto y predecía sus propiedades a partir de ella. Después una laboriosísima serie de síntesis muy meticulosas hasta conseguir el compuesto. Finalmente caracterizar el compuesto, asegurarse de que era el que se quería obtener y comprobar que sus propiedades correspondían a las predichas. Por ejemplo, proponía que los compuestos octaédricos tenían átomos en posiciones fijas alrededor de un centro, lo que significaba que tenían quiralidad y, por tanto, podían rotar la luz polarizada. Si se encontraban los compuestos mediante síntesis, su actividad óptica vendría a confirmar las ideas de Alfred.
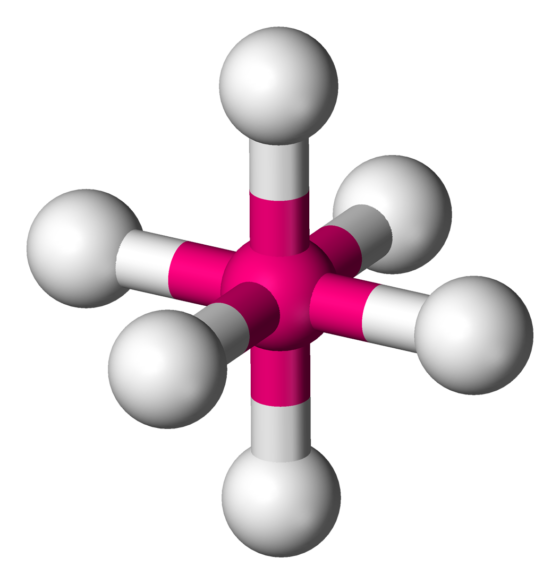 En química, se llama geometría molecular octaédrica a la forma de los compuestos en los que seis ligandos (átomos, moléculas o iones) se disponen alrededor de un átomo o ion central, definiendo los vértices de un octaedro.
En química, se llama geometría molecular octaédrica a la forma de los compuestos en los que seis ligandos (átomos, moléculas o iones) se disponen alrededor de un átomo o ion central, definiendo los vértices de un octaedro.A diferencia de los compuestos que usó Pasteur, las moléculas ópticamente activas de Alfred no formaban cristales que se pudiesen separar con pinzas. Empleó 18 años en perfeccionar el método para conseguir separarlas con la ayuda inestimable de su alumno de doctorado Victor King.
Pero siempre hay críticos, y eso no es necesariamente malo. Se pensaba que la quiralidad era algo propio de los átomos de carbono y, como en los compuestos de Alfred había carbono, sugerían que la actividad óptica era consecuencia de la presencia de estos. En 1914, un año después de recibir el Nobel por sus logros, con la ayuda de otra estudiante de doctorado, Sophie Matissen, Alfred consiguió preparar un compuesto ópticamente activo en el que solo había nitrógeno, hidrógeno y oxígeno, despojando al carbono de sus derechos exclusivos en lo que a quiralidad se refiere.
Werner, maestro
Todos los avances químicos de Alfred Werner están disponibles en múltiples recursos en la red (por ejemplo). Sin embargo, en pocos lugares encontraréis su otra gran contribución a la ciencia. Su labor como enseñante y director de personas, en lo que fue un avanzado a su tiempo.
Alfred era un orador magnífico y profesor vocacional. El aula en el que daba clases Alfred solía contener de forma rutinaria del orden del doble de personas de las que se suponía que era su capacidad: se sentaban en los pasillos, se aglomeraban alrededor del banco de demostraciones. En verano había desmayos y los rectores de la institución mostraban su preocupación por los riesgos de incendio o explosión. Un chascarrillo de la época era “¿cuándo ocupa un estudiante de química el volumen mínimo? En una clase de Nunwiegeht’s”. Ni que decir tiene que Nunwiegeht’s era uno de los motes de Alfred, por su costumbre de saludar con un ¿cómo te va?.
Alfred dirigió más de 200 tesis doctorales y, siendo la Universidad de Zúrich pionera en admitir mujeres para el doctorado, él fue pionero en admitirlas en ciencia, aplicando una meritocracia estricta. Buena parte de sus más 200 tesis dirigidas fueron escritas por mujeres. No es de extrañar que personas de toda Europa y Estados Unidos fuesen a Zúrich a estudiar con él.
El laboratorio de Alfred en Zúrich era extraoficialmente conocido como “las catacumbas”, celdas semisubterráneas donde siempre era necesaria la iluminación artificial. Según una revista humorística de la universidad, una muestra del aire de las catacumbas contenía de forma típica “un 50% de ácidos evaporados, 30% de olores nauseabundos de preparados, 10% de humo de cigarrillo, 5% de alcohol y 5% de gas de iluminación mal quemado, lo suficiente para enviar al más resistente de los individuos al gran más allá”. La universidad, consciente de la necesidad de un nuevo edificio para albergar los laboratorios, lo acabó concediendo, con lo que Alfred trabajó incansablemente en su diseño y construcción mientras seguía dirigiendo elementos fundamentales de su investigación. Alfred empezó a dormir muchos días en su despacho de la universidad y a buscar en el alcohol una manera rápida de relajarse.
El precio que Alfred pagó fue muy alto. El estrés, el exceso de trabajo, su consumo excesivo de tabaco y alcohol le llevaron al colapso nervioso. No mucho después de recibir su nuevo edificio fue obligado a dimitir.
Alfred Werner murió en un hospital psiquiátrico de Zúrich poco después de cumplir los 53 años.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Alfred Werner, químico hasta la extenuación se ha escrito en Cuaderno de Cultura Científica.
¿Por qué la carne de los atunes es roja y la de los lenguados, blanca?
 Cola de atún y cabeza de lenguado.
Cola de atún y cabeza de lenguado.Shutterstock / Natasha Breen
El color de los atunes tiene importancia económica: existen casos de fraude en los que se enrojece la carne de ejemplares de otras especies para hacerlas pasar por atún rojo (Thunnus thynnus) o para que las piezas parezcan frescas y no deterioradas por una conservación deficiente. Pero ¿por qué la carne de estos animales es roja?
El color de la carne de los túnidos (género Thunnus) varía entre especies, pero tiende a ser más oscuro que el del resto de peces. Por un lado, es una carne con un alto contenido en mioglobina, un pigmento que se encuentra en las células musculares de muchos vertebrados y que hace las veces de depósito celular de oxígeno para cuando se necesita.
Por otro lado, es una musculatura con alta densidad de vasos sanguíneos, en especial la del atún rojo. Como norma general, cuando un animal tiene músculos muy irrigados es que es muy activo. Así son los atunes, fuertes, capaces de nadar a velocidades asombrosas y hacerlo de forma sostenida. Recorren por ello grandes distancias. Además, la sangre de los túnidos –la del atún rojo en especial– tiene un contenido muy alto en hemoglobina.
La razón de todos estos rasgos –alto contenido muscular de mioglobina, musculatura muy irrigada, alto contenido de hemoglobina en la sangre– es que la gran actividad que desarrollan exige un suministro permanente e intenso de nutrientes y, sobre todo, de oxígeno. Lo cierto es que la musculatura de los atunes alcanza prestaciones metabólicas difícilmente superables.
Pero hay más. Hay una zona en el tronco de los túnidos que es más oscura, tiene más vasos sanguíneos y una consistencia casi esponjosa. De hecho, los atunes pierden mucha sangre por esa zona cuando sufren un corte. Esa zona oscura, sanguinolenta incluso, es lo que se conoce como rete mirabile.
La red maravillosa —su nombre en español– es un dispositivo que permite que la sangre (arterial) fría procedente de las branquias se caliente antes de llegar a los músculos. Recibe el calor de la sangre (venosa) procedente de la musculatura, donde se ha calentado por efecto del metabolismo. Ese intercambio de calor se produce entre vasos sanguíneos dispuestos en íntima proximidad unos con otros, pero en cuyo interior la sangre circula en sentidos opuestos. Esa forma de circular –contracorriente– permite una transferencia óptima de calor entre los dos subsistemas circulatorios. Es un ejemplo fisiológico de lo que se denomina un “intercambiador contracorriente”. En el mundo animal no son raros intercambiadores así, de calor, de gases o de iones.
Nosotros utilizamos intercambiadores contracorriente –no biológicos, por supuesto– para termostatizar instalaciones, por su gran eficiencia. Aunque hay ingenieros que creen que son una creación de la mente humana, en realidad fueron diseñados por la naturaleza hace millones de años, gracias a la selección natural.
Así pues, el calor generado por la potente actividad muscular de los atunes no se pierde por las branquias cuando la sangre llega a ellas. Se ha transferido a la sangre arterial. Se podría decir que ha quedado preso en una jaula fisiológica. Y gracias a ello, el interior de los atunes –parte de su musculatura, los ojos y el encéfalo– se encuentra, en aguas frías, hasta diez grados más caliente que el agua en que nadan. Desarrollan así niveles metabólicos muy altos, acordes con los de la actividad física que despliegan.
 Atún fresco.
Atún fresco.Shutterstock / Mark Watts
Llegados a este punto se habrán acordado de los lenguados o peces similares cuya carne es blanca. En efecto, esos peces no dan un palo al agua, son lo que en inglés se denomina depredadores sit and wait, porque se “sientan” a esperar.
Durante la mayor parte del tiempo permanecen sobre el sustrato, quietos, mimetizados con el fondo o semicubiertos con partículas de arena o fango. Pasan así inadvertidos por sus posibles presas. Los ojos de los peces planos se encuentran en uno de los lados de la cabeza mirando hacia arriba. Cuando ven que pasa alguna posible presa por encima, realizan un movimiento veloz, como un latigazo, se lanzan hacia ella. Si tienen suerte, la capturan.
Lo interesante es que los músculos que ejecutan ese movimiento no utilizan oxígeno, son anaerobios, músculos que obtienen su energía (el ATP) únicamente de la glucolisis, sin completarse, por lo tanto, la ruta estándar del metabolismo aerobio –a través del ciclo de Krebs y la cadena respiratoria en el interior de las mitocondrias– característico de otros tejidos.
 Lenguado fresco.
Lenguado fresco.Shutterstock / seeshooteatrepeat
La glucolisis es una vía muy rápida aunque ineficiente. Proporciona energía a gran velocidad, que es de lo que se trata en este caso. Surte de ATP a músculos rápidos y por eso la utiliza el lenguado para atrapar a sus presas. Así pues, como no es necesario un aporte permanente de oxígeno, no hace falta que llegue mucha sangre a esa musculatura. A ello se debe que los peces planos y especies con un modo de vida similar tengan la carne tan blanca.
La carne de los atunes es roja; la de los peces planos, blanca, apenas sangra al cortarla. Esas diferencias obedecen al modo de vida de las especies. No son caprichosas, como no lo son gran parte de los fenómenos de la naturaleza, aunque creamos lo contrario.![]()
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Por qué la carne de los atunes es roja y la de los lenguados, blanca? se ha escrito en Cuaderno de Cultura Científica.
Introducción a Bitcoin
Mikel Lezaun Iturralde
Bitcoin es la primera moneda nativa digital. Como moneda digital, Bitcoin no tiene ninguna componente física, simplificando mucho, se puede afirmar que los bitcoin son registros informáticos y claves para realizar transacciones. Bitcoin opera en una extensa red de ordenadores abierta a quien lo desee, descentralizada (todos los nodos son iguales, no hay un nodo central que gestiona la red) y en la que los nodos tienen una copia de la gran base de datos de todas las transacciones. La red Bitcoin funciona con la tecnología blockchain, que garantiza por sí misma la seguridad de su gran base de datos. Bitcoin emite su propia moneda sin ningún respaldo de una entidad financiera o banco central. La emisión de moneda la hace Bitcoin en tiempo, número y destino siguiendo unas reglas fijas, independientemente del valor de cambio de bitcoin y de la coyuntura económica. En este artículo se describe los principales procesos del sistema blockchain, o cadena de bloques, y Bitcoin.
 Foto: Executium / Unsplash
Foto: Executium / Unsplash-
Introducción
En el sistema bancario tradicional, para hacer una transferencia de una cuenta de un banco a otro banco, se cursa la orden, el banco comprueba si la cuenta del ordenante tiene fondos, resta del saldo de su cuenta el dinero de la transferencia y comunica al otro banco que debe sumar esa cantidad al saldo de la cuenta del destinatario. Esta gestión no mueve billetes de un lado a otro, simplemente es un cambio en los saldos de las cuentas. En realidad, todo esto lo hace un programa informático. Los bancos son los intermediarios y garantes de las transacciones, son quienes mantienen de forma segura toda la información en sus bases de datos y por ello cobran sus comisiones.
Ya en 1996, el Premio Nobel de economía Milton Friedman apuntó la necesidad de que se creara un protocolo específico para transferir valor por Internet, para trasferir dinero electrónico de un usuario A a uno B, sin que A tenga por qué saber la identidad de B o B quien es A.
En 2008, Satoshi Nakamoto, del que hasta la fecha no se sabe nada, ni quien, quienes o qué es, publicó un artículo en la lista de correo Cryptography de Internet, en el que definía un protocolo de comunicaciones para transmitir valor, basado en una red en la que todos los nodos se comportan como iguales, sin jerarquías. El año siguiente, él mismo publicó la primera versión del software Bitcoin, creó la red del mismo nombre y las primeras unidades de moneda, que también denominó bitcoin. En 2010, una vez puesto en marcha el sistema Bitcoin, Nakamoto se apartó y desapareció del mapa.
Características de la red Bitcoin
Las características más destacables de las monedas digitales, en particular de la red blockchain (cadena de bloques) de Bitcoin son las siguientes.
-
La red blockchain de Bitcoin es abierta, todo el que quiera puede participar, no se necesita autorización ni identificación.
-
La red es transfronteriza, se puede transferir de un punto a cualquier otro punto del mundo. En realidad, los bitcoin no residen en ningún sitio, no son algo físico.
-
La red es neutral, no hay que dar ninguna explicación a una transferencia. La red procesa cualquier transacción independientemente del ordenante, destinatario y cantidad.
-
La red es resistente a la censura, nadie puede evitar que se realice una transacción.
-
La red es pública, todo es verificable por todos, la red es totalmente transparente.
-
La red por sí misma gestiona las transacciones y garantiza la seguridad tanto de las transacciones como de la base de datos. No necesita de intermediarios ni de bancos.
-
Las transacciones son seudónimas, no se sabe directamente quien es el emisor ni quien el receptor.
-
Las transacciones son muy fáciles de realizar. El único coste es la tasa por transferencia que se abona a los denominados mineros, que además es voluntaria. Ahora bien, hace tiempo que se prioriza las transacciones con las comisiones más altas.
-
Preliminares
Digitalización
Al hablar de Bitcoin se dice que es una moneda digital. Digitalizar no es otra cosa que convertir un texto, un documento en números. Todos los símbolos tipográficos tienen un equivalente numérico. Cualquier número, entendido como el valor que representa, se puede escribir de distintas formas. En el sistema decimal se utilizan los diez caracteres 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9; en el hexadecimal los dieciséis caracteres 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, f y en el binario solamente los caracteres 0 y 1. En particular, cualquier documento se puede convertir en una lista de 0 y 1. Lo mismo que en el sistema decimal, las operaciones matemáticas se pueden realizar en los otros sistemas. En un sistema electrónico el 0 se corresponde con un circuito abierto y el 1 con uno cerrado. Así, la información trasladada a números binarios se puede almacenar y tratar matemáticamente en dispositivos electrónicos.
A modo de ejemplo, la expresión binaria de la palabra covid-19 es
0110001101101111011101100110100101100100001011010011000100111001
y la de Covid-19
0100001101101111011101100110100101100100001011010011000100111001
Notemos que solo se diferencian en el tercer carácter, en el primer caso es 1 y en el segundo 0.
Funciones resumen
Dado un documento, en muchos casos interesa tener un resumen representativo que lo identifique de forma única y que sirva para verificar su correcta trasmisión y almacenamiento en redes y sistemas digitales. Para obtener estos resúmenes, en Bitcoin se utilizan las funciones resumen (hash en inglés) criptográficas. Las principales características de estas funciones son las siguientes.
-
Una función resumen no es aleatoria, en general es fácil de calcular y aplicada a un mismo documento siempre da el mismo resultado. Por contra, de un resumen criptográfico no es posible recuperar computacionalmente el documento del que proviene.
-
Las funciones resumen son muy sensibles, una levísima modificación de la entrada produce un resumen completamente diferente.
-
Sea cual sea el tamaño de la entrada, que en general suele ser grande, la longitud del resumen es la misma. Así, del resumen no se puede deducir si proviene de un documento extenso o de uno breve.
Las funciones resumen se calculan a partir de la expresión binaria del documento, esto es, de su expresión en 0 y 1. Para ello, se expande la lista original de 0 y 1 a una más amplia, se descompone esta nueva lista en bloques, en cada bloque se cambia varias veces de sitio los 0 y 1 y se realizan distintas operaciones matemáticas. Esto es relativamente fácil de hacer, siempre se siguen las mismas reglas. Así, validar el resumen de un texto es prácticamente instantáneo.
En Internet se encuentran muchas páginas web que calculan el resumen de un documento con distintas funciones resumen. En Bitcoin, de todas las transacciones y bloques se calcula el correspondiente resumen identificativo. Para ello utiliza la función resumen SHA-256, que proporciona resúmenes formados por 256 ceros o unos, que se traducen en 64 caracteres hexadecimales 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, f. Por ejemplo, el resumen de la palabra covid-19 es
88529c3ac8ebd2dcb21a432c4ea0190c8370850b73ef95a527d150d4d424bc62
y el de la palabra Covid-19
993ab4dd1fb517c10afcd32c007ec64c3d76bac264104bf44c57f5667f609da7
Como se ve, una simple diferencia de un carácter 0 y 1 da un resumen completamente diferente.
El resumen de los tres párrafos de la introducción de este mismo documento es
aedd1bb22c321638f1155e3611bed6e677b73de5c428a9ed956d35f54d47a3e6
que también tiene 64 caracteres hexadecimales.
Árbol de Merkle
Supongamos que tenemos un bloque de documentos, cada uno con su resumen criptográfico y que, para reforzar la seguridad del contenido del bloque, se quiere obtener un resumen de todos los resúmenes. Para ello se construye un árbol de Merkle, que consiste en lo siguiente. Se ordenan los resúmenes de los documentos del bloque (no hay que olvidar que los resúmenes no dejan de ser números) y se van juntando de dos en dos en un mismo texto. De cada uno de los nuevos textos formados por un par de resúmenes, se obtiene su resumen. Con los resúmenes obtenidos se vuelve a repetir la operación, esto es, se forman los textos de pares de resúmenes y de cada uno se obtiene su resumen. Se sigue el proceso hasta llegar a un solo resumen, que se denomina raíz de Merkle. Así, cualquier modificación en una transacción almacenada, para que sea coherente, implica la modificación de su resumen, lo cual conlleva la modificación de la raíz de Merkle.
Firma digital
Una firma digital es un mecanismo criptográfico que garantiza que la firma de un documento es auténtica, esto es, que no ha sido suplantada; que el documento no ha sido alterado y, además, que quien lo firma no lo puede repudiar. Bitcoin, para la autentificación de las transacciones, para la firma digital, utiliza un sistema criptográfico de clave pública y clave privada. Las claves pública y privada de una firma digital son dos números muy grandes, dependientes entre sí y que se generan simultáneamente mediante un algoritmo matemático. Generar los dos números es relativamente fácil, pero el camino inverso, obtener de uno de ellos el otro, es computacionalmente imposible.
La clave privada se debe guardar de forma muy segura para que nadie tenga acceso a ella. Por contra, como indica su nombre, la clave pública es pública. La firma se realiza con la clave privada. El proceso de firma digital es como sigue. En primer lugar, la aplicación informática de la firma digital obtiene el resumen del documento. Luego, este resumen, mediante un algoritmo matemático basado en la clave privada del firmante, se encripta. Junto con el documento se graba su resumen, el resumen encriptado y la clave pública. Todo esto es público, de acceso libre. Para verificar la autenticidad de la firma se utiliza la clave pública del firmante. Primero se comprueba que el resumen es el del documento. A continuación, se aplica al resumen encriptado un algoritmo matemático basado en la clave pública y el resultado tiene que ser exactamente igual que el resumen del documento firmado. Si ocurre así, el documento firmado es auténtico. Si no, se rechaza, ya que haciendo lo que se indica, solo se recupera el texto del resumen del documento si se utiliza la clave pública de quien lo ha firmado. Esta comprobación la puede hacer quien quiera.
-
Monedero o wallet
Crear una cuenta bitcoin es muy fácil. Basta con registrarse en alguna de las múltiples páginas web dedicadas a ello e introducir una serie de datos personales. Una vez registrado, para operar se necesita instalar un monedero o wallet, que no es más que una simple aplicación informática que permite transferir y recibir moneda digital. Instalado el monedero, él mismo crea los pares de claves pública y privada para la firma digital de las transacciones. A partir de la clave pública, el monedero genera de forma determinista la dirección. Los monederos guardan la identificación de las transacciones dirigidas a sus claves públicas y direcciones y su contenido es de acceso público. Ahora bien, las correspondientes claves privadas se deben mantener bien guardadas, ya que, como se verá, con ellas se hacen las transferencias de las transacciones registradas en el monedero. Una misma persona puede tener varios monederos. También, conforme va recibiendo transacciones, se puede ir cambiando las claves privada y pública y por tanto la dirección de recepción. Así, no se sabe si distintas direcciones en realidad corresponden a un mismo usuario.
Un ejemplo de clave pública es
020766fd4ffbbfa2086a96b335ba6eff24b58e4819936f8dc9d4002dabc9b11405
que genera mediante cálculos matemáticos la dirección
1FVRX63gUDxkQ25C7ivMa27C9nT1DUafmD
-
Transacciones
Las transacciones son el vehículo para transferir bitcoin de un usuario A a uno B. Las transacciones son públicas, están identificadas por su resumen y se guardan agrupadas en bloques, que van conformado una cadena. Una transacción contiene una entrada (input) en la que consta la procedencia de los bitcoin a transferir y una salida (output) que indica a donde van esos bitcoin. Si A quiere hacer una transferencia a B, en la salida de la transacción A incluirá la dirección y clave pública que le habrá proporcionado B. La correspondiente clave privada B la mantendrá oculta y segura, ya que la tendrá que utilizar cuando quiera transferir los bitcoin que reciba en esta transacción. En la entrada de la transacción A incluirá la identificación de una transacción con suficientes bitcoin que tiene por salida una transacción que un usuario C envió a una dirección y clave pública de A. La transacción de la entrada tiene que estar sin gastar, A no la ha tenido que haber utilizado en anteriores transacciones. Esta transacción la tendrá registrada A en su monedero. La validez de la transacción, la seguridad de que A tiene los bitcoin que pretende transferir a B, la realiza A con la firma digital. Para ello A firma la transacción con la clave privada asociada a la clave pública de la salida de la transacción que realizó C dirigida a la dirección y clave pública de A. Con la clave pública se puede verificar que esta transacción solo la ha podido firmar A, lo cual asegura que A es el propietario de los bitcoin que transfiere a B. En realidad los usuarios no tienen en propiedad bitcoin, lo que tienen son claves privadas de salidas de transacciones no gastadas (en inglés UTXO de Unspent Transaction Output) para con ellas hacer transacciones. Si A pierde la clave privada, nadie puede utilizar los bitcoin de la transacción y desaparecen. Y si alguien se apodera de la clave privada, el dinero de la salida de la transacción es suyo, lo puede utilizar sin ninguna cortapisa.
La salida de una transacción solo se puede utilizar una vez y siempre se transfiere completa. Ahora bien, ¿cómo se hace una transferencia de 3,9 bitcoin, cuando se quiere utilizar una salida de transacción no gastada con 5,3 bitcoin, sin perder los 1,4 bitcoin restantes? El procedimiento ideado para solventar esta dificultad es que, en estas situaciones, efectivamente la entrada de la transacción es la salida con 5,3 bitcoin que se quiere transferir, pero se crean dos salidas, una de 3,9 bitcoin a la dirección que se quiere enviar y otra de 1,4 bitcoin a una dirección y clave pública propia. De esta forma, la salida no gastada de la auto transacción con 1,4 bitcoin vuelve al emisor y solo él la puede utilizar firmándola con su clave privada. De esta forma no pierde los 1,4 bitcoin.
Veamos como ejemplo una de transacción incluida en el bloque 672431 que se describirá más adelante. El resumen que identifica a esta transacción es
57ff5d1af48c6687f1500e5acfe9a2297d5091a62e5e8da72ae31967282bdd22
y la dirección del ordenante
1KbnB9GTmUDn9Kjebm9w7aC9s5WxjSMcR5
La entrada de la transacción, es la salida de la transacción con 3,61216838 bitcoin contenida en el bloque 672424, cuyo resumen es
d42f3804872d1b4fe466aa156bfe92e430564f445d6ac5cf172e7e1630b2560e
y dirección la del ordenante
1KbnB9GTmUDn9Kjebm9w7aC9s5WxjSMcR5
La transacción tiene dos salidas. Una con 3,54120686 bitcoin a la dirección
12hy9qkZTiBcN9kCMKvQ62YDj3D7d2Ay3H
y otra con 0,07059952 bitcoin a la dirección
3JmgHw6rjUHgkptYmKX5SmekScxjFzHve9
La tarifa que fija la transacción es 0,00036200 bitcoin
El gasto total de la transacción es 0 bitcoin, que es igual a la cantidad de la entrada.
Este sistema público de transacciones es anónimo. Aunque se puede seguir el recorrido de las transacciones, de los usuarios solo se conoce claves públicas y direcciones obtenidas de ellas.
Para facilitar las transacciones un bitcoin está fraccionado en satoshi. Un bitcoin son cien millones de satoshi.
-
Nodos de la red
La red Bitcoin es una red descentralizada, no hay un nodo central que gestiona la red, y abierta, quien quiera puede unirse libremente a la red con solo descargar e instalar en su ordenador el software adecuado. En la red Bitcoin existen varios tipos de nodo, cada uno con sus funciones específicas.
Los nodos completos son los nodos que almacenan una copia exacta y actualizada de la cadena de bloques. Son los que verifican la validez de las transacciones y bloques de transacciones y los propagan por la red a otros nodos. Los nodos completos son los encargados de verificar que se cumplen todas las reglas del protocolo Bitcoin y, por tanto, son los que verdaderamente otorgan robustez, seguridad y estabilidad a la red. Entre los nodos completos se destacan los nodos públicos. Estos nodos ejercen de forma continua e ininterrumpida como un punto de comunicación e interconexión con otros nodos de la red para transmitir datos e información. Cualquier nodo que desee conectarse con un nodo público lo puede hacer libremente cuando quiera.
Los nodos de minería o mineros son los nodos completos que agrupan las transacciones en bloques y los confirman realizando lo que se denomina minado y que se explica más adelante.
Por último, están los nodos ligeros. Son nodos que no mantienen una copia de la cadena de bloques y no participan en el proceso de verificación y validación de las transacciones. Los nodos ligeros pueden solicitar y recibir de los nodos completos públicos el estado de una transacción concreta. En particular pueden obtener información de sus propias transacciones, si están incluidas o no en un bloque. Los nodos ligeros trabajan únicamente como puntos finales de comunicación y son ejecutables en dispositivos móviles como teléfonos y tablet.
Hay que destacar que toda transacción también debe incluir el pago voluntario de una comisión para quienes realizan las verificaciones, agrupan las transacciones en bloques y confirman los bloques, esto es, para los mineros.
-
Bloques de la cadena
Una ver realizadas, las transacciones se trasmiten entre los nodos mediante el protocolo de comunicación de la red Bitcoin y los nodos completos verifican su validez. Una vez verificada su validez, las transacciones quedan a la espera de que los nodos mineros las agrupen en un bloque y lo confirmen. Cada minero construye su propio bloque seleccionando las transacciones que más le beneficien y no estén incluidas en bloques ya confirmados. Estos bloques son los bloques candidato y su tamaño tiene que ser inferior a un megabyte. Como se verá más adelante, para que un bloque sea confirmado, y en consecuencia también todas sus transacciones, se tiene que minar. Como minar un bloque está recompensado, hay muchos mineros construyendo su bloque candidato y todos ellos contendrán más o menos las mismas transacciones. Además, junto con las transacciones verificadas, en los bloques se introduce una primera transacción denominada coinbase, que no tiene entrada y la salida está dirigida a una clave pública y dirección del minero. Esta salida de transacción contiene los bitcoin que recibirá el minero por el minado y las comisiones de las transacciones. También, de los resúmenes de las transacciones de cada bloque se calcula su raíz de Merkle.
Todos los bloques confirmados tienen su propio resumen. Para encadenar un bloque con los anteriores, se introduce en los bloques candidato el resumen del último bloque confirmado. Así confirmado un bloque candidato con su correspondiente resumen, queda encadenado al anterior. Cualquier modificación en una transacción almacenada en un bloque requerirá cambiar el resumen de su bloque y, como este resumen está contenido en el bloque siguiente, también se deberá cambiar su resumen, y así sucesivamente. En definitiva, modificar una transacción almacenada en un bloque requiere modificar el resumen de su bloque y el de todos los bloques siguientes, lo cual resulta técnicamente irrealizable. Ésta es la gran garantía de seguridad de la base de datos Bitcoin.
Para su identificación e información, en el encabezado de cada bloque se incluye su resumen, la raíz de Merkle, una marca de tiempo, timestamp en inglés, y los datos del minado.
-
Minado de un bloque. Prueba de trabajo
En Bitcoin, una vez conformado un bloque de transacciones, para confirmarlo hay que minarlo realizando una prueba de trabajo (PoW del inglés Proof-of-Work). La prueba de trabajo consiste en obtener un resumen del bloque que sea menor que un número fijado, denominado target, que en hexadecimal es un número de 64 cifras que comienza por unos cuantos ceros. Recordemos que los resúmenes son números y se pueden comparar con el target. Esta prueba de trabajo es muy difícil de realizar, pero muy fácil de verificar.
En Bitcoin, cada bloque se conforma y mina más o menos cada diez minutos y el primer minero que supera la prueba de trabajo recibe una recompensa en bitcoin de nueva creación. Se consigue mantener un ritmo de más o menos diez minutos en la creación de los bloques, controlando la dificultad del minado. La dificultad del minado es una medida de la cantidad de recursos necesarios para minar Bitcoin, que sube o baja dependiendo de la cantidad de potencia computacional disponible en la red. La dificultad se actualiza automáticamente cada 2016 bloques, más o menos cada dos semanas. Se calcula mediante una fórmula matemática a partir de lo que se ha tardado en minar los 2016 bloques precedentes.
Una vez obtenida la nueva dificultad, a partir de ella, inmediatamente se actualiza y fija un nuevo target para los 2016 bloque venideros. Éste será menor, y por tanto será más difícil minar el bloque, cuanto menor haya sido la dificultad del minado de los 2016 bloques precedentes. Así, conforme más fácil sea el minado debido a la mejora computacional, se aumenta la dificultad del minado imponiendo un target más pequeño. De esta forma, aunque varíe la capacidad computacional de la red, se consigue mantener el tiempo de unos 10 minutos entre cada bloque.
El procedimiento para superar la prueba de trabajo consiste en añadir al bloque un número arbitrario, que sólo se puede usar una vez, con el fin de que el resumen resultante cumpla la condición de ser menor que el target. Este número se denomina nonce o número de un solo uso y normalmente consta de 8 cifras hexadecimales. La única forma de obtener el número de un solo uso requerido es probando por fuerza bruta. Este proceso requiere un intensivo trabajo computacional con hardware especializado (ASIC) y consume gran cantidad de energía eléctrica. A esto se debe la creación de pools de mineros en países como China, en los que la energía es barata y el minado resulta rentable.
Una cuestión a solucionar es cómo resolver el problema del doble gasto, que una misma moneda no se pueda gastar dos veces. Esta dificultad es propia de las monedas descentralizadas, ya que al no haber un centro que controle la llegada de las transacciones, ante dos iguales, no siempre es posible decidir cual se ha producido la primera y darle a ésa la validez. En Bitcoin, con frecuencia se da el caso en que, a partir de un mismo bloque, dos mineros minen casi simultáneamente su bloque y lo distribuyen a la red por caminos distintos. Como son los propios mineros quienes conforman los bloques, los dos bloques serán parecidos, contendrán casi las mismas transacciones, pero no serán idénticos, tendrán distinto resumen. En estos casos, unos mineros trabajarán con de uno de los bloques para conformar y minar un nuevo bloque, y otros lo harán con el otro bloque. Detectada esta situación, aunque los dos bloques sean válidos, los mineros confirmarán el bloque que tenga mayor prueba de trabajo, el que tenga mayor resumen. El bloque descartado se denomina bloque huérfano. El bloque huérfano se invalida; el minero que realizó la prueba de trabajo se queda sin recompensa y las transacciones que no estén incluidas en el bloque confirmado quedan a la espera de ser incluidas en un nuevo bloque. De esta forma se evita que una transacción se utilice dos veces, que haya doble gasto, y el resultado es una única versión de la cadena de bloques. Una vez que un minero encuentra el número de un solo uso, lo anuncia inmediatamente a los otros mineros, éstos verifican la prueba de trabajo y las transacciones y deshacen su bloque candidato. La comprobación de que el minado es correcto por parte de los mineros es fácil e inmediata y el bloque junto con todas las transacciones que contiene queda confirmado e incluido en la cadena de bloques.
Como ejemplo volvemos al resumen de los tres párrafos de la introducción de este artículo. Hemos mostrado que es
aedd1bb22c321638f1155e3611bed6e677b73de5c428a9ed956d35f54d47a3e6
Fijamos como target el número
00000000000000000fffffffffffffffffffffffffffffffffffffffffffffff
Este número es el mayor escrito con 64 cifras hexadecimales que tiene 47 cifras significativas (las 17 primeras son 0). La prueba de trabajo, el minado, consiste en añadir al texto del resumen un número de un solo uso para forzar que el resumen sea menor que este número, es decir, que tenga 46 cifras significativas (las 18 primeras 0) o 47 significativas (las 17 primeras 0) seguidas de alguna que no sea la f. Esto solo se puede hacer probando, probando y probando. Como se ha indicado, esto requiere de hardware específico que consume mucha energía. Como hay muchos mineros intentando superar la prueba trabajo y como esto hay que hacerlo prácticamente de forma continua para todos los bloques, el consumo global de energía en el minado es altísimo.
-
Recompensa por minar
Una de las claves de la superveniencia de Bitcoin se debe a que, por cada bloque minado, quien lo consigue en primer lugar recibe una recompensa en nuevos bitcoin. En concreto, todos los bitcoin que se van acuñando son para los mineros que consiguen en primer lugar el minado. También, estos son quienes reciben las comisiones de las transacciones. Está programado que cada 210.000 bloques, unos 4 años a diez minutos por bloque, la emisión de bitcoin se reduzca a la mitad. En consecuencia, la remuneración del minado por bloque también se reduce a la mitad. En los cuatro primeros años, de 2009 a 2012, se pusieron en circulación 10.500.000 bitcoin y por el minado de cada bloque se pagaron 50 bitcoin (210.000×50=10.500.000). A partir de mayo de 2020 y hasta 2024, el pago por minado se ha reducido a 6,250 bitcoin, por lo que en esos cuatro años se acuñarán en total 1.312.500 bitcoin. La producción total de bitcoin está limitada a 21 millones y a este ritmo finalizará en el año 2140. A partir de esa fecha, los mineros solo recibirán por el minado las comisiones de las transacciones. Otra cuestión muy distinta es por cuantos euros o dólares se cambie un bitcoin.
Veamos como ejemplo el bloque número 672431 de fecha 2021-02-27 13:28.
-
Bloque: 672431
-
Resumen:
00000000000000000003120e9aa5b6f1247a730c4b0dfc6716db4b855c978da5
-
Raíz de Merkle:
6b44315f7b2621d8a21554e1dc96178bd935d042e23cb77e75bf4b1f4fd78ff1
-
Número de transacciones: 2096
-
Volumen de la transacción: 1446,34840523 bitcoin
-
Recompensa por minado: 6,250 bitcoin
-
Remuneración por comisiones: 0,41695539 bitcoin
-
Target:
0000000000000000000cf4e30000000000000000000000000000000000000000
-
Nonce: 04e9a917
Es inmediato comprobar que, como números hexadecimales, el resumen es menor que el target.
-
Comentario final
Bitcoin es una moneda totalmente digital, no se sustenta en nada físico, ni en bancos centrales, ni en organizaciones financieras. El propio Bitcoin es quien crea y emite su moneda. Bitcoin opera en una red de ordenadores abierta, descentralizada y distribuida. Esto es, quien quiera se puede integrar en la red Bitcoin, todos los nodos son iguales, no hay jerarquías, y tienen una copia de la gran base de datos de todas las transacciones. Las transacciones se realizan directamente entre origen y destino y son públicas. Su fiabilidad y seguridad reposa en la firma digital. Para almacenar de forma segura los datos, las transacciones se agrupan en bloques que se van encadenando uno detrás de otro, de forma que un bloque contiene el resumen del anterior. Una modificación de una transacción de un bloque requiere modificar su resumen, al estar este resumen incluido en el siguiente bloque, se tendrá que modificar su resumen y así uno a uno el resumen de todos los bloques siguientes, lo cual no es realizable computacionalmente. Además, como la base de datos está replicada en los nodos, habría que cambiar la de todos los nodos. Los bloques los confirman los mineros mediante una prueba de trabajo. El primer minero que supera la prueba de trabajo transmite el bloque al resto de mineros, éstos verifican la validez de las transacciones y de la prueba de trabajo, el bloque queda confirmado e incluido en la base de datos y el minero recibe una recompensa en bitcoin de nueva creación.
La emisión de moneda bitcoin está totalmente regulada, tanto en sus tiempos como en su número y destino, por unas reglas fijas. La emisión es totalmente independiente del valor de los bitcoin, de que haya una mayor o menor demanda de bitcoin y de la coyuntura económica del momento. Ninguno de los bitcoin que se emiten van al mercado, todos se adjudican a los mineros que superan la prueba de trabajo. La retribución en bitcoin por minado también está fijada por el propio sistema. Cada cuatro años la emisión de bitcoin se reduce a la mitad. Como en total se emitirán 21 millones de bitcoin, se alcanzarán los 21 millones en el año 2140. En 2020 ya han sido acuñados alrededor de 18.593.000 bitcoin. Se estima que alrededor de tres o cuatro millones de bitcoin han desaparecido por pérdida de las claves privadas, errores en las direcciones, etc.
Realizar la prueba de trabajo requiere hardware especializado de elevado consumo energético. Como le retribución por minado resulta al cambio alta, hay muchos mineros y pools de mineros que se dedican al minado. Como el minado de los bloques es prácticamente continuo, ya que en cuanto se mina un bloque se comienza a conformar el siguiente, el consumo global de energía por minado es muy elevado, lo cual suscita mucha controversia.
Para terminar, unas observaciones sobre Bitcoin.
Las monedas al uso tienen que cumplir tres funciones: permitir almacenar valor, realizar intercambios y transacciones, y servir como unidad de cuenta. Esto último significa servir de referencia de valor como, por ejemplo, basta con leer el precio en euros de un teléfono móvil para hacerse una idea de su valor. Según estos criterios, no se puede decir que las criptomonedas sean monedas de verdad, ya que no cumplen estas tres propiedades. La que más se cumple es la de almacenamiento de valor. Pero como medio de intercambio no se acepta en demasiados sitios, y debido a su constante cambio de valor, tampoco sirve como referencia. Las criptomonedas no serán monedas de verdad hasta que no se cumplan estas tres propiedades, en particular hasta que no se generalice cambiar bitcoin por, por ejemplo, un coche, un billete de avión o la realización de un trabajo.
Existen en el mercado casas de cambio que permiten cambiar bitcoin por dólares o euros y viceversa. Así, quienquiera puede adquirir bitcoin e ingresar en la red Bitcoin. En sus dos primeros años, 2009 y 2010, el valor del bitcoin era prácticamente cero y el 2-01-2011 valía 5 dólares. En enero de 2015 se cambiaba por alrededor de 300 dólares y desde entonces, con grandes altibajos, no ha dejado de acumular valor. ¿Hasta cuanto podrá alcanzar su valor? ¿Se está ante una burbuja?
Bibliografía
Para un estudio más detallado
Mikel Lezaun. Blockchain. Bitcoin, La Gaceta de la RSME, Vol. 24 (2021), Núm. 3, Págs. 533-558.
Sobre el autor: Mikel Lezaun Iturralde es catedrático de matemáticas aplicadas en el Departamento de Matemáticas de la UPV/EHU
El artículo Introducción a Bitcoin se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2021: Daniel Torregrosa – La química al servicio del mal
El gran evento de divulgación Naukas regresó a Bilbao para celebrar su décima edición en el magnífico Palacio Euskalduna durante los pasados 23, 24, 25 y 26 de septiembre.

Daniel Torregrosa, famoso popularmente entre otras cosas por su libro del Mito al laboratorio (Ed. Cálamo), se hizo muy conocido en la blogosfera por sus textos sobre venenos. Estaba tardando que diese una charla sobre su historia.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2021: Daniel Torregrosa – La química al servicio del mal se ha escrito en Cuaderno de Cultura Científica.
Observación experimental del fraccionamiento del espín en un material orgánico
 Una cadena con siete nanografenos triangulares (triangulenos) depositada en una superficie de oro es sondeada con un microscopio de efecto túnel. Mientras que cada trianguleno tiene espín 1, las correlaciones cuánticas a lo largo de la cadena dan lugar a la emergencia de dos espines ½, representados de color azul y rojo en los bordes de la cadena. (Imagen: EMPA)
Una cadena con siete nanografenos triangulares (triangulenos) depositada en una superficie de oro es sondeada con un microscopio de efecto túnel. Mientras que cada trianguleno tiene espín 1, las correlaciones cuánticas a lo largo de la cadena dan lugar a la emergencia de dos espines ½, representados de color azul y rojo en los bordes de la cadena. (Imagen: EMPA)Nos resulta de sentido común el que unidades sencillas se unan para formar estructuras más complicadas. Así, los átomos se unen para formar moléculas, que a su vez se combinan formando células y estas forman tejidos, dando lugar por último a seres vivos. En el mundo cuántico, este proceso puede ocurrir en dirección contraria, de forma que la interacción entre cosas “complejas” da lugar a cosas más “sencillas”. Así, en ciertas circunstancias, como el efecto Hall cuántico fraccionario, la interacción entre electrones, partículas indivisibles con carga eléctrica e, puede dar lugar a la emergencia de partículas con carga e/3. Este fenómeno se conoce como fraccionamiento.
Todas las partículas elementales poseen propiedades intrínsecas como masa o carga, que nos resultan intuitivas, y otras que nos lo son menos, como el espín, pero que podemos visualizar como una brújula. A diferencia de las brújulas normales, que pueden apuntar en cualquier dirección, el espín de los sistemas cuánticos está cuantizado, valga la redundancia, y únicamente puede tomar un conjunto discreto de valores. Por ejemplo, decimos que el espín del electrón es 1/2 y puede tomar únicamente dos valores, +1/2 y -1/2. Partículas con espín 1 pueden tomar tres valores, +1, 0 y -1.
En los años 80 el físico inglés Duncan Haldane construyó un modelo matemático para partículas de espín 1 en el que se producía el fraccionamiento de los espines. Así, una cadena unidimensional de partículas indivisibles de espín 1, interactuando con sus vecinas, daba lugar a la aparición de partículas de espín 1/2 en los bordes de la cadena. Igual que el truco de magia en el que el mago que corta en dos mitades a una persona y las separa, el modelo de Haldane permite fraccionar espines 1 y separarlos. Se trata de uno de los modelos centrales del magnetismo cuántico, un trabajo que le valió el premio Nobel en 2016.
La verificación experimental de esta predicción era complicada por varios motivos, empezando por el hecho de que no existen materiales unidimensionales. Había evidencia indirecta del fenómeno de fraccionamiento del espín en materiales orgánicos que contienen cadenas de átomos magnéticos, pero faltaba una observación directa. Ahora esa observación se ha llevado a cabo por un equipo internacional de investigadores, entre los que se encuentra el investigador Ikerbasque David Jacob, del Departamento de Polímeros y Materiales Avanzados: Física, Química y Tecnología de la Facultad de Química de la UPV/EHU, que ha colaborado en este trabajo con el INL, la Universidad de Alicante, el EMPA en Zurich y la Universidad de Dresde.
Para conseguirlo los investigadores han combinado técnicas de química orgánica con ciencia de superficies en ultraalto vacío para sintetizar moléculas de grafeno con espín 1 que forman cadenas unidimensionales. Usando un microscopio de efecto túnel los investigadores han podido estudiar los estados cuánticos de la cadena depositada en una superficie de oro, con resolución atómica, compararlos con los predichos por la teoría, y establecer que en efecto el sistema se comporta como el modelo de Haldane. En particular, en cadenas con un número suficientemente alto de moléculas magnéticas, los investigadores encontraron en los extremos de la cadena resonancias Kondo, un fenómeno que ocurre cuando partículas de espín ½ interactúan con los electrones de un conductor como el oro.
Los investigadores afirman que este trabajo “muestra el potencial para usar nanografenos para formar redes bidimensionales de nanoimanes que permitan comprobar predicciones análogas a las de Haldane, como por ejemplo la existencia de estados cuánticos que permitirían realizar la computación cuántica”.
Referencia:
Shantanu Mishra, Gonçalo Catarina, Fupeng Wu, Ricardo Ortiz, David Jacob, Kristjan Eimre, Ji Ma, Carlo A. Pignedoli, Xinliang Feng, Pascal Ruffieux, Joaquín Fernández-Rossier, Roman Fasel (2021) Observation of fractional edge excitations in nanographene spin chains Nature doi: 10.1038/s41586-021-03842-3
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Observación experimental del fraccionamiento del espín en un material orgánico se ha escrito en Cuaderno de Cultura Científica.
Nuestro cerebro no piensa (y el de usted, tampoco)
José Manuel Muñoz y Javier Bernácer
 Shutterstock / Mopic
Shutterstock / Mopic
“Los seres humanos solo utilizamos el 10 % de nuestro cerebro”. “El cerebro de los adultos no cambia”. “El cerebro reptiliano es el que gobierna la conducta de los niños”. “Una persona es más inteligente cuantas más neuronas tenga”. ¿Quién de nosotros no ha escuchado estas afirmaciones alguna vez? Y, sin embargo, son falsas.
Se trata de malas interpretaciones acerca del cerebro (“neuromitos”) que calan a menudo en la población a través de ciertas formas de divulgación científica. También llegan incluso al ámbito de la educación. Así lo demuestra un estudio publicado en 2014, en el que se comprobó que los profesores de diversos países, tanto occidentales como orientales, tendían a creer en esta clase de afirmaciones.
La difusión de estas ideas erróneas no es banal, sino que puede llevar a estrategias educativas sin sustento científico y dañinas. Por ejemplo, el enriquecimiento excesivo del entorno de los niños y la obsesión por enseñarles cuantas más cosas mejor antes de los seis años.
Confundir la parte con el todo
Otro error que se presenta con frecuencia en la comunicación de la neurociencia consiste en perpetuar la llamada “falacia mereológica”: adjudicar a la parte (el cerebro) atributos psicológicos que, en realidad, pertenecen al todo (el ser humano en su conjunto).
Mediante una rápida búsqueda en internet podemos toparnos con expresiones como “el cerebro piensa”, “el cerebro recuerda”, “tu cerebro ve”, o hasta “tu cerebro odia”.
Este tipo de expresiones no solo se emplean por parte de los divulgadores científicos, sino también en ámbitos como la enseñanza e, incluso, la ciencia profesional. Sirva como muestra de esto último uno de los objetivos perseguidos por la iniciativa australiana para la investigación del cerebro (Australian Brain Initiative), que sus promotores plantean como “entender y optimizar cómo el cerebro aprende en la infancia”.
Esta falacia mereológica constituye la base conceptual de lo que el filósofo Carlos Moya califica como un nuevo (y paradójico) “dualismo materialista”. Una vez superada la concepción dualista alma-cuerpo (al modo cartesiano), se tiende ahora a pensar en un cerebro independiente o aislado del cuerpo. Este último parece, en cierto modo, prescindible. Esto no se ajusta a la realidad: el cerebro es solo una parte del sistema nervioso, que a su vez es solo una parte del cuerpo. Dicho cuerpo, además, se enmarca en un contexto social (no es un “cerebro en una cubeta”) que afecta decisivamente al desarrollo y la historia vital del individuo.
Ni los pies caminan, ni el cerebro piensa
El lector estará de acuerdo en que sus pies no caminan, sino que es usted quien camina empleando sus pies. De igual forma, no es su cerebro el que piensa, recuerda, odia o ama, sino que es usted quien hace todo esto utilizando su cerebro.
Podría pensarse que la comparación entre cerebro y pies no resulta adecuada, pues el cerebro, a diferencia de aquellos, goza de una gran capacidad de control sobre las demás partes del organismo. Sin embargo, no debe olvidarse que el cerebro depende, a su vez, de otros órganos para su subsistencia y funcionamiento, en especial (aunque no solo) del corazón.
De ningún modo el cerebro es independiente y gobernador del resto del cuerpo, como demuestra la dinámica de su desarrollo: no es hasta la vigesimotercera semana de vida prenatal cuando aparecen las primeras sinapsis en el embrión humano, y no es hasta pasados los veinte años cuando el cerebro termina de desarrollarse por completo. De hecho, el cerebro sigue cambiando hasta el día de nuestra muerte. Sencillamente, sin cuerpo no puede haber cerebro, tanto funcional como cronológicamente.
Hasta cierto punto, resulta comprensible que científicos o divulgadores formados en neurociencia tiendan a transmitir, consciente o inconscientemente, la falacia mereológica. Después de todo, su conocimiento especializado puede conducir a sobredimensionar la importancia de una parte de la realidad.
Por eso, y al igual que se ha normalizado el hecho de que una “ciencia de la parte”, como es la neurociencia, impregne decisivamente la comprensión de las ciencias sociales y las humanidades que estudian al ser humano en su conjunto, debería normalizarse también el camino complementario: que estas “ciencias del todo” contribuyan a un entendimiento más completo (y realista) del sistema nervioso.
Para lograrlo, la neurociencia debería ser más receptiva al estudio y el diálogo genuino con otras disciplinas (psicología, educación, comunicación, derecho, filosofía). La colaboración interdisciplinar podría, así, contribuir a frenar la proliferación de neuromitos y visiones reduccionistas de lo humano que entorpecen incluso el avance de la propia neurociencia. El rigor metodológico no debería asociarse a una falta de rigor argumentativo. Comunicar el cerebro, después de todo, no implica limitarse al cerebro.![]()
Sobre los autores: José Manuel Muñoz es investigador en el Centro Internacional de Neurociencia y Ética (CINET) de la Fundación Tatiana Pérez de Guzmán el Bueno, y en el Grupo Mente-Cerebro, Instituto Cultura y Sociedad (ICS) de la Universidad de Navarra y Javier Bernácer es investigador en el Grupo Mente-Cerebro del ICS.
Este artículo fue publicado originalmente en The Conversation. Artículol original.
El artículo Nuestro cerebro no piensa (y el de usted, tampoco) se ha escrito en Cuaderno de Cultura Científica.
La disección de Dudeney, de rompecabezas matemático a creación artística
La historia que está detrás de esta entrada del Cuaderno de Cultura Científica empieza cuando hace unos meses descubro la existencia de varias obras de la artista constructivista británica Natalie Dower (1931, Londres) relacionadas con la conocida disección de Dudeney, una disección geométrica de un triángulo equilátero cuyas piezas se pueden reordenar formando un cuadrado, o viceversa.
 Red flyer (1989), de la artista británica Natalie Dower, quien toma la disección de Dudeney como herramienta de creación artística. El cuadro pertenece a la colección artística de la Universidad de Warwick
Red flyer (1989), de la artista británica Natalie Dower, quien toma la disección de Dudeney como herramienta de creación artística. El cuadro pertenece a la colección artística de la Universidad de Warwick
De hecho, esta entrada podría tener de subtítulo “Sobre la importancia de la divulgación de las matemáticas”, ya que en una entrevista realizada por el artista Patrick Morrisey a la artista Natalie Dower, para Saturation point, esta ponía de relieve cómo había llegado a la disección de Dudeney a través de un texto del gran divulgador de las matemáticas Martin Gardner (1914-2010):
La exploración es el uso que yo hago de cualquier sistema con el que estoy trabajando. El más importante ha sido la disección de Dudeney, que encontré en “Mathematical Puzzles and Diversions” de Martin Gardner. Se trata de la disección de un cuadrado en cuatro piezas diferentes que, incluso articuladas, pueden ensamblarse formando un triángulo equilátero. Recuerdo dónde estaba y la emoción del momento exacto en que me di cuenta del enorme abanico de posibilidades que ofrecía. Durante la década siguiente, todos los dibujos, relieves, esculturas y pinturas, variando en escala de centímetros a metros, se generaron a partir de esta […].
 Tetraedro (1985), de la artista británica Natalie Dower, escultura realizada en aluminio y esmalte cocido, cuyo tamaño es 43 x 40,5 x 28 cm. Imagen de la Eagle Gallery EMH Arts
Tetraedro (1985), de la artista británica Natalie Dower, escultura realizada en aluminio y esmalte cocido, cuyo tamaño es 43 x 40,5 x 28 cm. Imagen de la Eagle Gallery EMH Arts
Pero vayamos con la disección de Dudeney. En general, una disección geométrica consiste en cortar una figura geométrica dada, como un triángulo, un cuadrado u otra figura más compleja, en una serie de piezas que reordenadas dan lugar a otra figura geométrica.
Como ejemplo de disección geométrica podemos mostrar la solución a uno de los problemas que el matemático recreativo británico Henry E. Dudeney (1857-1930) comenta en su libro Amusements in mathematics (1917). El problema consiste en saber cómo dividir un cuadrado en cuatro partes para generar una cruz griega, es decir, una cruz con los cuatro brazos iguales. Las soluciones mostradas en el libro, que podían realizarse con dos cortes, eran:
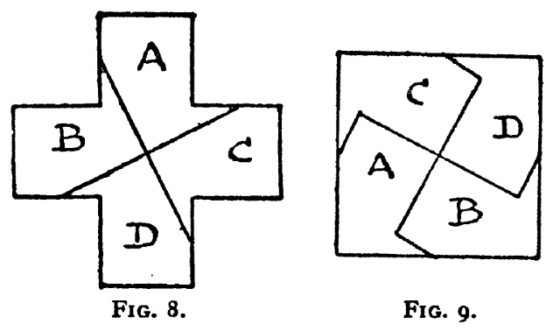
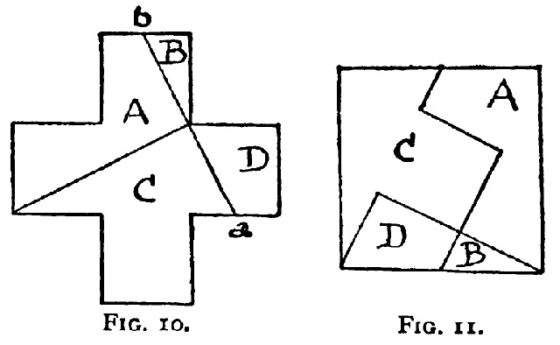
Estas disecciones geométricas, como muchas otras, son utilizadas a menudo como rompecabezas geométricos. El rompecabezas consistiría en las cuatro piezas –las cuatro iguales en el primer caso o todas distintas en el segundo– para construir con ellas tanto el cuadrado como la cruz griega. De hecho, este es uno de los cuatro rompecabezas que utilizamos en la Real Sociedad Matemática Española para darle publicidad a la página DivulgaMAT y que se muestran a continuación.

Pero hay muchos rompecabezas geométricos relacionados, de diferentes formas, con las disecciones, como los clásicos Tangram (véanse las entradas Tangram, El arte contemporáneo que mira al Tangram y Un teorema sobre el Tangram) y Stomachion (véanse las entradas El puzle Stomachion y el palimpsesto de Arquímedes (1) y El puzle Stomachion y el palimpsesto de Arquímedes (2)).
 Las siete piezas del Tangram formando la figura básica del cuadrado
Las siete piezas del Tangram formando la figura básica del cuadrado
Las disecciones geométricas tienen una historia muy larga y rica, ya que nos las podemos encontrar hace dos milenios en la matemática griega o hace mil años en la matemática árabe. Dentro de la matemática recreativa tiene una historia más reciente. En la revisión del libro Récréations mathématiques et physiques (1694) del matemático francés Jacques Ozanam que realiza Jean Montucla (1778), ya aparecen problemas con disecciones geométricas. También se incluyen disecciones geométricas en el libro Rational Amusement for Winter Evenings (1821), del matemático John Jackson.
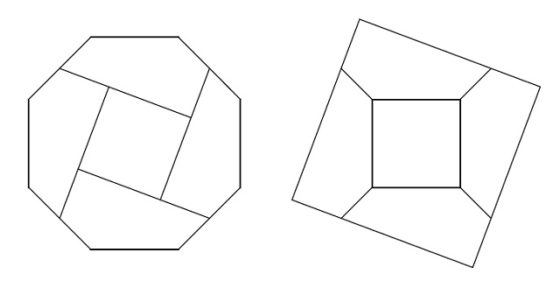 Disección de un octógono en un cuadrado que aparece en el manuscrito persa Compendio de figuras entrelazadas similares y complementarias (escrito entre los siglos XIII-XV), redescubierto, según Henry Dudeney, por el matemático británico Geoffrey Th. Bennett (1868-1943)
Disección de un octógono en un cuadrado que aparece en el manuscrito persa Compendio de figuras entrelazadas similares y complementarias (escrito entre los siglos XIII-XV), redescubierto, según Henry Dudeney, por el matemático británico Geoffrey Th. Bennett (1868-1943)
El problema de las disecciones geométricas cautivó a la comunidad matemática en el siglo XIX. Entre otras cuestiones estudiadas, varios matemáticos demostraron, de forma independiente, que para cualesquiera dos polígonos simples (es decir, cuyos lados no contiguos no se intersecan) con la misma área, se puede cortar cualquiera de ellos en una cantidad finita de piezas que reordenadas nos permiten obtener el otro. Fueron el matemático británico John Lowry (1769-1850) en 1814, el matemático británico William Wallace (1768-1843) en 1831 (según Greg Frederickson, aunque según Ian Stewart fue en 1807), el matemático húngaro Farkas Bolyai (1775-1856), padre de uno de los protagonistas del nacimiento de las geometrías no euclídeas, Janos Bolyai (1802-1860), en 1832, y el matemático alemán Paul Gerwien (1799-1858) en 1833. La idea de la prueba es cortar cada polígono simple en triángulos y luego estos en piezas de forma que con las mismas se pueda generar un cuadrado, después superponiendo las dos disecciones sobre el cuadrado se obtienen las nuevas piezas que nos dan la disección geométrica entre los dos polígonos simples.
El resultado anterior nos asegura la existencia de una disección entre dos polígonos simples con la misma área, sin embargo, el método genera una disección compleja (podríamos decir fea) con muchísimas piezas. Por otra parte, desde la matemática recreativa se preocuparon de disecciones más atractivas y con pocas piezas. Entre los autores que estudiaron las disecciones geométricas encontramos al matemático francés Edouard Lucas (1842-1891), autor del texto Recreaciones matemáticas (1894), al corredor de bolsa y matemático amateur británico Henry Perigal (1801-1898), conocido por su demostración del teorema de Pitágoras mediante disecciones que aparece en su texto Geometric Dissections and Transpositions (1891), el matemático y abogado británico Henry M. Taylor (1842-1927) o el matemático e ingeniero británico William H. Macaulay (1853-1936).
 Página 1 del texto Geometric Dissections and Transpositions (1891), de Henry Perigal, con la demostración del teorema de Pitágoras por medio de una disección geométrica
Página 1 del texto Geometric Dissections and Transpositions (1891), de Henry Perigal, con la demostración del teorema de Pitágoras por medio de una disección geométrica
Aunque debemos destacar a dos de los más grandes creadores de juegos lógicos y rompecabezas matemáticos, el matemático británico Henry E. Dudeney y el matemático recreativo y ajedrecista estadounidense Sam Loyd (1841-1911). Estos dos matemáticos, que colaboraron por correspondencia durante algún tiempo hasta que el inglés acusó al norteamericano de robarle sus rompecabezas y publicarlos con su nombre, se preocuparon de encontrar disecciones geométricas con el menor número de piezas posibles. Pueden encontrarse sus rompecabezas y problemas matemáticos relacionados con las disecciones en sus libros, entre ellos, Cyclopedia of 5000 Puzzles, Tricks and Conundrums with Answers (1914), de Sam Loyd, The Canterbury Puzzles (1907) y Amusements in Mathematics (1917), de Henry E. Dudeney.
La conocida como disección de Dudeney, de un triángulo equilátero en un cuadrado, aparece como “el acertijo del mercero” en el libro de Henry E. Dudeney The Canterbury Puzzles.
El acertijo del mercero: […] Enseñó [el mercero] un trozo de tela con forma de triángulo equilátero perfecto, como se ve en la ilustración y dijo: “¿Es alguno de vosotros diestro en el corte de género? Estimo que no. Cada hombre a su oficio, y el estudioso puede aprender del lacayo, y el sabio del necio. Mostradme, pues, si podéis, de qué manera puede cortarse este trozo de género en cuatro piezas, para que puedan reunirse y formar un cuadrado perfecto”.

La solución al acertijo del mercero que incluye Dudeney en su libro The Canterbury Puzzles es la que aparece en la siguiente imagen.
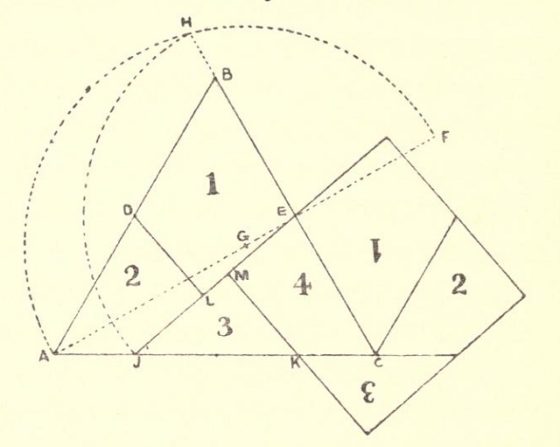
Dado el triángulo ABC la construcción que propone Dudeney, mostrada en la anterior imagen, es la siguiente:
a. marcar los puntos medios D y E de los lados AB y BC, respectivamente;
b. extender el segmento AE hasta un punto F tal que EF = EB;
c. marcar el punto medio G del segmento AF y trazar el arco de circunferencia de centro G y radio GF = AG;
d. extender el segmento CB hasta que corte el arco de circunferencia en el punto H;
e. trazar un arco de circunferencia con centro E y radio EH hasta que corte el lado AC en el punto J;
f. determinar el punto K tal que JK = AD (= DB = BE = EC);
g. trazar el segmento JE;
h. trazar desde D y K los segmentos perpendiculares al segmento JE, dando lugar a los puntos L y M (los segmentos serían DL y KM).
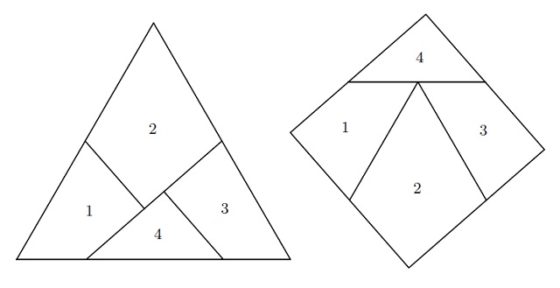
El problema del mercero fue propuesto por primera vez por Dudeney en 1902 en el periódico británico Weekly Dispatch. Dos semanas después de publicarse el acertijo el matemático realizó una pequeña discusión sobre el problema y finalmente, otras dos semanas después, Dudeney publicó la solución y la explicación.
Pero la disección de Dudeney del triángulo equilátero en el cuadrado tiene una propiedad muy especial –es lo que se conoce como una disección con bisagras, pero incluso estas direcciones han tomado el nombre de disecciones de Dudeney–, ya que todas las piezas pueden conectarse a través de una serie de puntos “bisagra” que permiten transformar una figura en la otra (en este caso el triángulo en el cuadrado, o viceversa) girando las piezas alrededor de las bisagras. En el caso de la disección de Dudeney se pueden colocar tres bisagras en los puntos D, E y K de la imagen anterior, aunque esos puntos no son únicos, también podrían ponerse las bisagras en los puntos J, K y E.
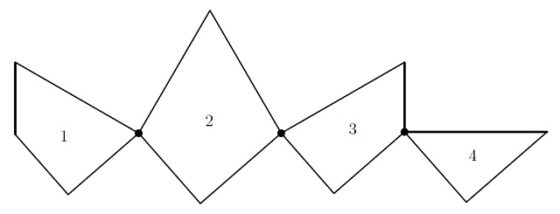 Piezas con bisagras que permiten transformar el triángulo equilátero en el cuadrado, o viceversa, de forma cinética
Piezas con bisagras que permiten transformar el triángulo equilátero en el cuadrado, o viceversa, de forma cinética
Utilizando la anterior propiedad se puede construir un juguete cinético como el siguiente.
 Juguete de geometría de cuadrado a triángulo – Disección de Dudney, construido por Steven Mattern Design y vendido en etsy.com
Juguete de geometría de cuadrado a triángulo – Disección de Dudney, construido por Steven Mattern Design y vendido en etsy.com
Más aún, se podría diseñar una mesa que en algunas ocasiones se puede utilizar con forma cuadrada y en otras con forma triangular, como aparece en el siguiente diseño de Mackenzie Kovaka (véase su página web Mackenzie Kovaka).



La disección de Dudeney del triángulo equilátero en el cuadrado, al igual que otras disecciones con bisagras, puede obtenerse con el “método de la tira en T” introducido por el ingeniero y matemático aficionado británico-australiano Harry Lindgren (1912-1992) en su libro Geometric Dissections (1964). Expliquemos en qué consiste este método geométrico (véase Recreational Problems in Geometric Dissections and How to Solve Them de Lindgren o Dissections: Plane & Fancy de Frederikson).
El método para obtener la disección del triángulo equilátero y el cuadrado empieza construyendo dos tiras, una de cuadrados y otra de triángulos (ambas figuras con la misma área) y luego marcando los puntos de ancla de las dos tiras, es decir, aquellos puntos tales que si se hace una rotación de 180 grados alrededor de ellos se obtiene de nuevo la tira inicial (es decir, los puntos ancla son los centros de las simetrías rotacionales, de 180 grados, de las tiras).
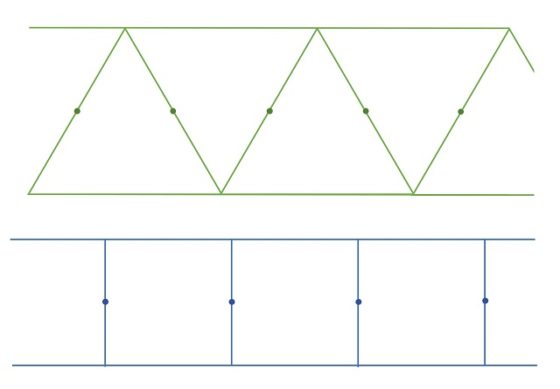
El siguiente paso es cruzar las dos tiras de manera que los puntos ancla de una tira estén sobre los bordes o los puntos ancla de la otra tira, como se puede observar en la siguiente imagen para el caso que estamos analizando.
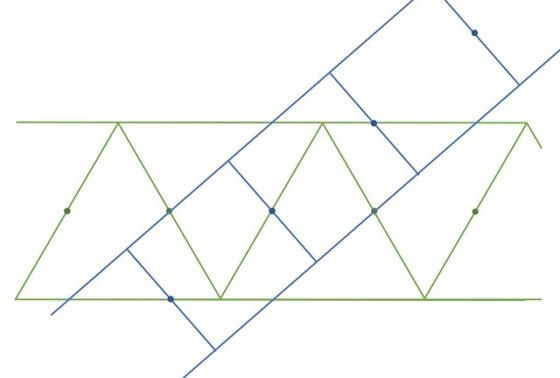
Y se obtiene así la disección con bisagras (que están en los puntos ancla) del triángulo equilátero en el cuadrado, o viceversa.
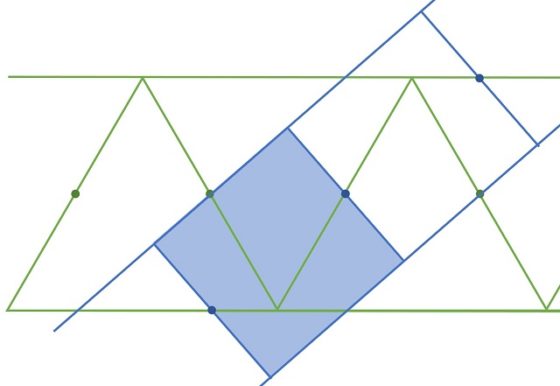
El método de la tira en T nos permite obtener más ejemplos, como se muestra, por ejemplo, en los libros Recreational Problems in Geometric Dissections and How to Solve Them de H. Lindgren o Dissections: Plane & Fancy de Frederikson. En la siguiente imagen, del segundo de los libros, tenemos una disección geométrica de un triángulo en una cruz griega, que no es de Dudeney, es decir, no pueden unirse las piezas con bisagras.
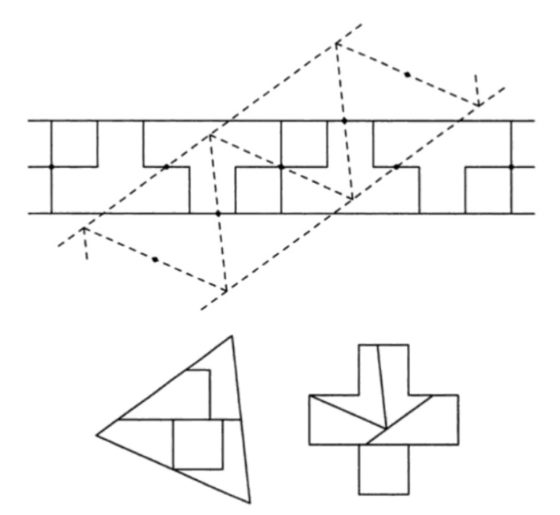
En relación a las disecciones geométricas con bisagras también se planteó el problema de la existencia, es decir, el problema de si dadas dos figuras geométricas cualesquiera con la misma área y cuyos bordes son polígonos simples, siempre era posible encontrar una disección con bisagras entre ellas. La respuesta llegó en 2008 de la mano de los matemáticos Timothy G. Abbott, Zachary Abel, David Charlton, Erik D. Demaine, Martin L. Demaine y Scott D. Kominers, que publicaron (en 2012) su resultado en el artículo Hinged Dissections Exist.
Pero finalicemos esta entrada del Cuaderno de Cultura Científica volviendo a la artista constructivista británica Natalie Dower y a algunos ejemplos más que ponen de manifiesto su profundo interés en este resultado matemático y en su uso como herramienta de creación artística.
Empecemos con una versión en madera de la anterior escultura Tetraedro (1985), en cuya base se puede apreciar la disección de Dudeney que da lugar a las dos esculturas.
 Tetraedro de Dudeney – Área 3 (1985), de Natalie Dower. Madera pintada al óleo, de tamaño 33,5 x 36,8 x 24 cm. Imagen de la página de Natalie Dower
Tetraedro de Dudeney – Área 3 (1985), de Natalie Dower. Madera pintada al óleo, de tamaño 33,5 x 36,8 x 24 cm. Imagen de la página de Natalie Dower
A continuación, mostramos dos pasteles al óleo de Dower cuyo motivo central es el cuadrado, respectivamente el triángulo, con la disección de Dudeney, mientras que alrededor hay una composición con las piezas de la misma, que son sus herramientas en toda esta serie de obras constructivistas.
 Dudeney Stencil n. 1 / Plantilla de Dudeney no. 1 (1987), de Natalie Dower. Pastel al óleo de tamaño 58 x 48 cm. Imagen de la página de Natalie Dower
Dudeney Stencil n. 1 / Plantilla de Dudeney no. 1 (1987), de Natalie Dower. Pastel al óleo de tamaño 58 x 48 cm. Imagen de la página de Natalie Dower Dudeney Stencil n. 2 / Plantilla de Dudeney no. 2 (1987), de Natalie Dower. Pastel al óleo de tamaño 58 x 48 cm. Imagen de la página de Natalie Dower
Dudeney Stencil n. 2 / Plantilla de Dudeney no. 2 (1987), de Natalie Dower. Pastel al óleo de tamaño 58 x 48 cm. Imagen de la página de Natalie Dower
La siguiente obra, Círculo de Dudeney (1989), está creada a partir de las piezas de la disección de Dudeney. En la parte central de la misma pueden verse dos copias, complementarias, del triángulo diseccionado.
 Dudeney’s circle / círculo de Dudeney (1989), de Natalie Dower. Imagen de la Eagle Gallery EMH Arts
Dudeney’s circle / círculo de Dudeney (1989), de Natalie Dower. Imagen de la Eagle Gallery EMH Arts
 Detalle de la obra Dudeney’s circle (1989), de Natalie Dower
Detalle de la obra Dudeney’s circle (1989), de Natalie Dower
Terminamos con otra obra donde se intuye, por su título Dudeney codificado (1987), que su diseño está inspirado también en la disección de Dudeney.
 Dudeney encoded / Dudeney codificado (1987). De Natalie Dower. Imagen de Saturation point
Dudeney encoded / Dudeney codificado (1987). De Natalie Dower. Imagen de Saturation point
Bibliografía
1. Greg N. Frederickson, Dissections: Plane & Fancy, Cambridge University Press, 1997.
2. Ian Stewart, From Here To Infinity, Oxford University Press, 1996.
3. Greg N. Frederickson, Ernest Irving Freese’s Geometric transformations: the man, the manuscript, the magnificent dissections!, World Scientific, 2018.
4. Harry Lindgren, Recreational Problems in Geometric Dissections and How to Solve Them, Dover, 1972 (versión revisada por Greg Frederickson del libro Geometric Dissections de 1964).
5. Timothy G. Abbott, Zachary Abel, David Charlton, Erik D. Demaine, Martin L. Demaine, and Scott D. Kominers, Hinged Dissections Exist, Discrete & Computational Geometry volume 47, pp. 150–186, 2012.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo La disección de Dudeney, de rompecabezas matemático a creación artística se ha escrito en Cuaderno de Cultura Científica.
Tres modelos atómicos de los que no has oído hablar
En 2013 se cumplió el centenario del modelo atómico de Bohr. Es el que todavía hoy, a pesar de ser incompatible con principios básicos de la física cuántica, como el de incertidumbre, se sigue explicando para introducir a los estudiantes en el mundo cuántico. Curiosamente, en los libros de texto tan sólo se mencionan dos modelos atómicos anteriores al de Bohr: el de Thomson y el de Rutherford. Parece como si los átmos modernos apareciesen con Dalton en 1804 y lo siguiente fuese el modelo de Thomson.
Leyendo la descripción habitual, a saber,
modelo de Dalton => descubrimiento del electrón => modelo de Thomson => experimentos de Geiger y Marsden => modelo de Rutherford => física cuántica v 1.0 => modelo de Bohr
a uno le queda la sensación de que el desarrollo del modelo de Bohr es algo lineal y que todo se deduce de lo anterior de manera lógica, sólo con esperar el experimento crucial o la idea genial adecuada. Y esto no es así. Para ilustrarlo vamos a conocer solo tres de los modelos atómicos clásicos sugeridos antes del modelo de Bohr.
Cada uno tiene su lógica y su fundamento; todos o bien pasaron desapercibidos o tuvieron vidas breves, habida cuenta de la rapidez con la que descubrían nuevas leyes y se realizaban más experimentos.
 Imagen: NASA / JPL-Caltech / Space Science Institute
Imagen: NASA / JPL-Caltech / Space Science InstituteLas mónadas físicas de Lomonósov
Empecemos por el principio. Se suele recoger en los libros de texto que la teoría atómica moderna empieza con John Dalton. Y a efectos prácticos, efectivamente es así, porque fueron sus ideas las que se propagaron por la comunidad científica y fructificaron casi 80 años después de haber sido formuladas, eso sí. Pero la primera teoría atómica moderna no se formuló ni en Inglaterra ni en Francia, sino en Rusia 60 años antes de que lo hiciese Dalton.
Su autor fue Fue Mijail Vasílievich Lomonósov quien escribió una serie de artículos entre 1743 y 1744, el primero de los cuales deja claro su visión atomista de la materia ya en el título: “Sobre las partículas físicas intangibles que constituyen las sustancias naturales”. A este artículo le seguiría otro sobre lo que hoy entendemos como enlace químico “Sobre la adhesión de los corpúsculos”. En el tercero de la serie, ante la necesidad de referirse a las partículas o corpúsculos de materia de una manera diferenciada, aparece el nombre elegido: “Sobre la adhesión y la posición de las mónadas físicas”. Lomonósov obviamente había leído a Leibniz, y le tomó prestada la palabra mónada con el apellido física para diferenciarla.
Las mónadas de Lomonósov tenían forma, peso y volumen y las empleó para explicar la naturaleza del calor y la elasticidad de los gases en función del movimiento de partículas, anticipando la teoría cinética de los gases de Krönig de 1856 en ciento once años, y descartando la existencia del flogisto 30 años antes que Lavoisier. Nadie le hizo caso en Occidente (salvo Euler).
El oscilador electrónico de Lorentz
En muchos textos se suele citar a J.J. Thomson como descubridor del electrón. Y es cierto, sus experimentos de 1897 con Townsend y Wilson no dejan lugar a dudas, el fue el descubridor experimental. Sin embargo, la teoría electrónica venía dando sus frutos ya desde 1892. En esa fecha Hendrik Lorentz comenzaba una serie de artículos en los que utilizando un átomo ideal pudo explicar una propiedad de la materia tras otra: la conducción de la electricidad o del calor, el comportamiento dieléctrico, la reflexión y la refracción de la luz, etc. Para ello en su modelo atómico sólo necesitó cuatro ecuaciones que gobernaban cómo responden los campos eléctricos y magnéticos a la carga eléctrica y su movimiento, y una adicional que especificaba la fuerza que esos campos ejercen sobre la carga. Este conjunto de ecuaciones se conocen por el nombre de su autor, Maxwell.
Y, ¿en qué consistía el modelo atómico de Lorentz? Pues en algo muy simple: el átomo sería una masa dada, llamémosla núcleo, aunque no tenemos que postular que tenga carga alguna, unida a otra menor (el electrón) por un muelle (suena raro, pero es solo para que te hagas una imagen). El muelle se pondría en movimiento cuando un campo eléctrico interactuase con la carga del electrón. El campo atrae o repele al electrón lo que resulta en que el muelle se estira o comprime.
Lorentz, como es lógico, no suponía que hubiese ningún muelle físico conectando electrón y núcleo; sin embargo sí postuló que la fuerza que unía a los dos podría ser descrita por la ley de Hooke, que es la misma que describe a los muelles (y a los dinamómetros). Una aproximación que es válida hasta en algunas consideraciones de la mecánica cuántica.
Por cierto, la conferencia que Lorentz dio cuando recibió el Nobel de física en 1902 iba sobre, efectivamente, la teoría del electrón, aunque el premio se lo hubiesen dado con Zeeman por la explicación de los efectos del magnetismo sobre la radiación.

El modelo planetario de Nagaoka
Tras el descubrimiento experimental del electrón era lógico pensar que la existencia de átomos neutros implicaba la existencia de una parte positiva en ellos. En 1904 Thomson propuso el modelo del pudin de pasas, esto es, que el átomo era una esfera de electricidad positiva uniforme con los electrones incrustados como las pasas en el pudin.
Hantaro Nagaoka consideró el modelo de Thomson inviable en cuanto terminó de leer el artículo en el que se lo describía: las cargas opuestas eran impenetrables desde su punto de vista. Él propuso un modelo alternativo ese mismo año en el que el centro cargado positivamente es muy masivo y está rodeado por electrones que lo orbitan a una distancia y unidos a él por fuerzas electrostáticas. En su mente estaban Saturno y sus anillos.
Los experimentos de Geiger y Marsden de 1909 con el pan de oro dieron una primera confirmación experimental al modelo de Nagaoka. En el artículo de 1911 en el que Rutherford presentaría su famoso modelo en el que se propone la existencia del núcleo atómico cita a Nagaoka. Pero en 1908 el propio Nagaoka había renunciado a su modelo al darse cuenta de que los anillos se repelerían entre sí, haciendo el modelo inestable.
Basten estos tres ejemplos para ilustrar lo que decíamos al principio, que el desarrollo de la ciencia no es tan lineal como los libros de texto nos hacen creer. Hay algunos modelos interesantes más, algunos de ellos cuánticos, que preceden al de Bohr. Sobre algunos de ellos hablé aquí: Bohr no fue el primero.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Esta una versión revisada de este texto publicado en Naukas.
El artículo Tres modelos atómicos de los que no has oído hablar se ha escrito en Cuaderno de Cultura Científica.
La aparente paradoja del polimorfismo de color
Juan Gefaell
Uno de los fenómenos biológicos más extendidos en la naturaleza es el del polimorfismo de color, esto es, la coexistencia de individuos de más de un color en las poblaciones naturales de las distintas especies. Consideremos los siguientes lagartos, todos ellos de la especie Podarcis erhardii:
 Figura 1. Polimorfismo de color en Podarcis erhardii. Tomada de Brock et al. (2020) PeerJ, 8:e10284. doi: 10.7717/peerj.10284
Figura 1. Polimorfismo de color en Podarcis erhardii. Tomada de Brock et al. (2020) PeerJ, 8:e10284. doi: 10.7717/peerj.10284
Tal y como se observa en la Figura 1, los distintos individuos de esta especie pueden mostrar tres colores bien diferenciados en la zona de la garganta.
A pesar de su extensión a lo largo y ancho del reino animal (y vegetal), las causas evolutivas del polimorfismo de color todavía no se conocen con exactitud.
Es más, desde cierto punto de vista, su existencia misma es paradójica, puesto que los principales mecanismos que los biólogos emplean para dar cuenta de la evolución de las especies predicen que las poblaciones, más que polimórficas, deberían tender en realidad hacia el monomorfismo, esto es, a la prevalencia de individuos de un único color. Así, los modelos clásicos de selección natural y deriva genética establecen que la variabilidad genética (en última instancia responsable de la variación fenotípica) mengua a medida que estos dos mecanismos operan sobre las poblaciones de organismos.
Por este motivo, el polimorfismo de color es un tema de investigación que atrae especialmente a los biólogos evolutivos.
La selección negativa dependiente de las frecuencias (NFDS)
Uno de los mecanismos evolutivos que se han formulado para explicar el paradójico origen del polimorfismo de color es la selección negativa dependiente de las frecuencias (NFDS por sus siglas en inglés). A pesar de su enrevesado nombre, la idea clave de la NFDS es sencilla: cuanto más frecuente es un fenotipo en una población, menor es su eficacia biológica o capacidad para reproducirse. O lo que es lo mismo: cuanto más raro es un fenotipo, mayor es su eficacia. Esto queda claro con el siguiente gráfico:
 Representación gráfica de la NFDS.
Representación gráfica de la NFDS.
La hipótesis de la NFDS ya ha mostrado su capacidad para explicar el polimorfismo de color en algunas especies. Quizás el ejemplo más clásico en este sentido sea el de los caracoles del género Cepaea, estudiados por Bryan Clarke en los años 60 del siglo pasado. En sus investigaciones, Clarke mostró que la NFDS era en gran parte responsable del polimorfismo de color presente en dichas especies.
 Cepaea nemoralis. Tomada de Silvertown et al. (2011) PLoS ONE, 6(4):e18927. doi: 10.1371/journal.pone.0018927
Cepaea nemoralis. Tomada de Silvertown et al. (2011) PLoS ONE, 6(4):e18927. doi: 10.1371/journal.pone.0018927
Resulta que los depredadores de Cepaea, principalmente aves, tienden a formarse imágenes de los colores más habituales en estas especies, de manera tal que, a la hora de depredar, buscan preferentemente a aquellos individuos que coinciden con dichos colores. De este modo, aquellos ejemplares que se alejan significativamente de los colores más frecuentes tienden a dejar más descendencia, pues son ignorados por los depredadores, convirtiéndose así con el paso de las generaciones en el fenotipo más frecuente de la población.
Una vez esto sucede, se invierte la ecuación: las aves depredadoras pasan a formarse imágenes de este nuevo color más frecuente, por lo que lo cazan en mayor medida que a aquellos colores se presentan en menor frecuencia (que en el pasado eran los predominantes). Esto, a la larga, favorece que las poblaciones mantengan el polimorfismo de color.
El género Littorina
Otro grupo de caracoles (en este caso marinos) en el cual el polimorfismo de color está también extendido es el género Littorina. Así, las diversas especies de este género a menudo muestran poblaciones diversas en lo que a su color de concha se refiere, tal y como se puede apreciar, por ejemplo, en la siguiente imagen de L. saxatilis.
 Algunos colores y patrones de concha que puede mostrar L. saxatilis. Fotos: Juan Gefaell.
Algunos colores y patrones de concha que puede mostrar L. saxatilis. Fotos: Juan Gefaell.Las especies del género Littorina han sido ampliamente estudiadas por los biólogos evolutivos, y especialmente por nuestro grupo de investigación, debido a diversos rasgos que las convierten en organismos modelo ideales (Rolán-Alvarez et al. 2015a). Para nuestros propósitos, cabe destacar uno de estos rasgos: la abundancia de cópulas en la naturaleza, lo cual permite estudiar fácilmente los procesos evolutivos relacionados con el sexo y la reproducción.
La NFDS y los patrones reproductivos
En ciertos estudios, se ha relacionado el patrón de reproducción de una especie con el mantenimiento del polimorfismo de color a través de NFDS. Para entender por qué, es necesario en primer lugar explicar brevemente dos conceptos: el apareamiento asociativo negativo y la elección de pareja.
Empecemos por este último: la elección de pareja a menudo se define como la propensión conductual a aparearse con aquellos individuos que tienen unos rasgos determinados. Es decir, se trata de un mecanismo de comportamiento por el cual los individuos de algún modo prefieren aparearse con ejemplares que poseen unas determinadas características físicas. Por ejemplo, en el caso de los pavos reales, se dice que las hembras tienen una propensión conductual a aparearse con aquellos machos que presentan una cola vistosa y de gran tamaño.
Por otro lado, los biólogos definen el apareamiento asociativo negativo como la correlación negativa que se da entre los fenotipos homólogos de los individuos involucrados en un apareamiento. O, en otras palabras, el fenómeno por el cual los individuos que se aparean son distintos entre sí en algún rasgo fenotípico determinado. Por ejemplo, puede ser que los individuos involucrados en una cópula tengan un color de piel distinto, o un tamaño diferente de pico, etc.
El apareamiento negativo asociativo y la elección de pareja están íntimamente relacionados. Así, por ejemplo, en muchas ocasiones el primero (apareamiento asociativo negativo) está causado por el segundo (elección de pareja).
Además de eso, el apareamiento asociativo negativo ha sido relacionado con la NFDS tanto a nivel teórico como empírico. La idea clave es que, al aparearse con aquellos individuos que son distintos a uno mismo, los caracoles pueden premiar a aquellos ejemplares que están en menor frecuencia en la población, haciendo que esta frecuencia suba a lo largo de las generaciones y que los distintos colores no desaparezcan de la población.
En la práctica, los anteriores vínculos indican que, si se encuentra apareamiento asociativo negativo en las cópulas de una especie polimórfica, entonces se podría pensar que el polimorfismo de dicha especie está causado por NFDS. Así, el apareamiento asociativo negativo puede ser empleado como indicador tanto de la elección de pareja como de la NFDS.
 Esquema de las relaciones entre el apareamiento asociativo, la elección de pareja y la NFDS
Esquema de las relaciones entre el apareamiento asociativo, la elección de pareja y la NFDSEn efecto, esto es lo que nuestro grupo ha encontrado en estudios previos con la especie L. fabalis. En L. fabalis, el polimorfismo de color parece estar mantenido por NFDS a través de un mecanismo conductual de elección de pareja. Nuestro grupo determinó esta relación, entre otras cosas, detectando la existencia de apareamiento asociativo negativo.
En cualquier caso, el alcance filogenético de esta asociación no se conoce; es decir, no se sabe si otras especies del género Littorina, que habitan en un entorno similar, también pueden estar manteniendo sus respectivos polimorfismos de color a través de NFDS.
Por este motivo, nuestro grupo ha realizado un nuevo estudio, de reciente publicación en la revista Marine Biology (Gefaell et al. 2021), en el cual tratamos de responder exactamente a ese interrogante estudiando si en las cópulas de varias especies del género Littorina puede existir algún tipo de NFDS mediado por apareamiento asociativo negativo.
Averiguar si el polimorfismo de color de otras especies del género Littorina se mantiene a través de NFDS puede contribuir a averiguar el alcance explicativo de este mecanismo evolutivo tanto en el género Littorina como en otros gasterópodos marinos, avanzando así nuestro conocimiento de la evolución y la conservación de estas especies en sus entornos naturales.
Metodología seguida en nuestro estudio
Para llevar a cabo nuestro estudio, tomamos datos de cópulas en el campo de las especies L. obtusata y L. saxatilis, además de nuevas poblaciones de L. fabalis. Dichos datos provenían de poblaciones del interior de las distintas Rías Baixas, así como de dos localidades bien estudiadas del Mar Blanco (Rusia). El motivo de la elección de las anteriores especies es que todas ellas comparten un patrón similar de polimorfismo, en el cual los colores más frecuentes son el marrón oscuro, el naranja y el amarillo, distinguiéndose únicamente en el color oliva (L. fabalis y L. obtusata) y el blanco (presente solo en L. saxatilis).
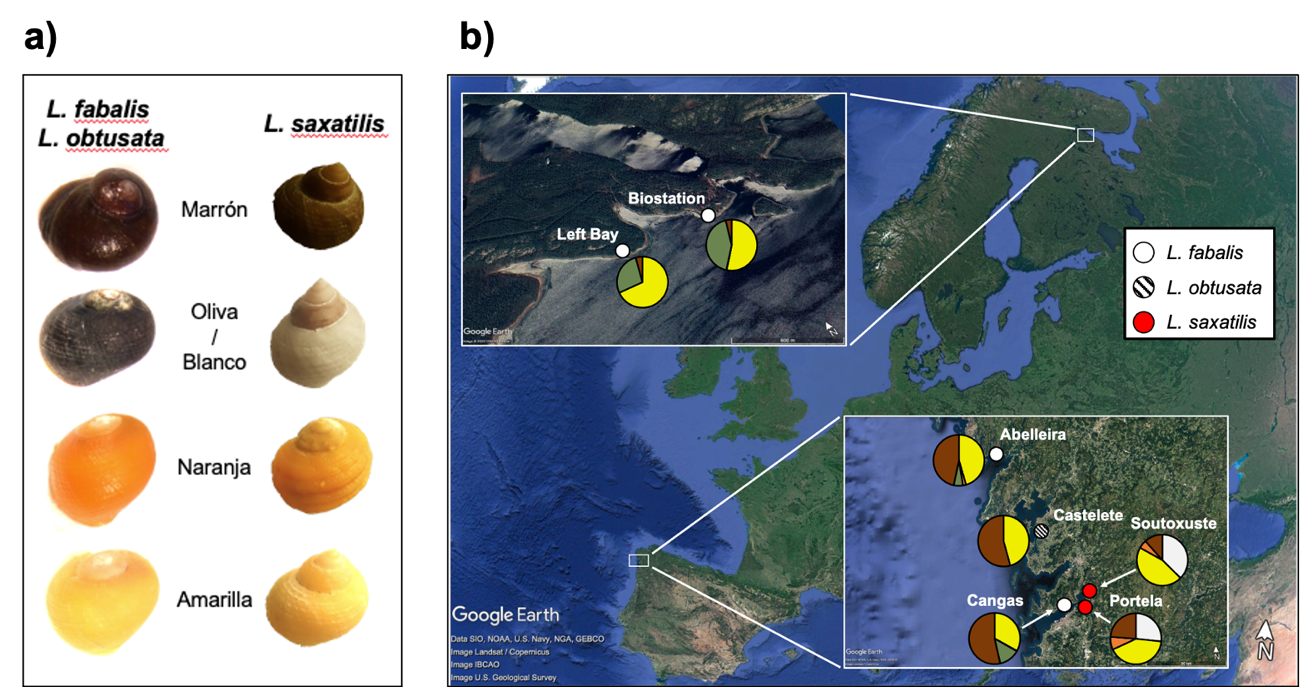 a) Colores de las distintas especies de Littorina. b) Localidades analizadas para cada especie junto con las correspondientes frecuencias de colores. La localidad de Castelete incluye también, además de L. obtusata, L. fabalis
a) Colores de las distintas especies de Littorina. b) Localidades analizadas para cada especie junto con las correspondientes frecuencias de colores. La localidad de Castelete incluye también, además de L. obtusata, L. fabalis
El protocolo de recogida de cópulas en el campo para estudiar el apareamiento asociativo no causó problemas, pues está bien establecido. De hecho, nuestro grupo ha diseñado un método que permite evitar sesgos en la recogida y análisis de datos relativos a las cópulas, lo cual nos permite concluir que la información obtenida es fiable.
Lo mismo sucede con la estimación del apareamiento asociativo negativo: nuestro equipo ha diseñado un programa de ordenador que permite estimar este parámetro de una manera rápida y robusta. Dicho programa mide el apareamiento asociativo a través del índice conocido como IPSI. En pocas palabras, el IPSI cuantifica entre -1 y 1 en qué medida los apareamientos observados se desvían de un patrón de apareamiento aleatorio. Así, un apareamiento asociativo negativo perfecto obtendría un valor de -1 y un apareamiento asociativo positivo perfecto equivaldría a 1. Por último, un apareamiento completamente aleatorio rondaría el 0.
Resultados principales
Pues bien, una vez analizado el IPSI, ¿qué resultados obtuvimos?
Si agrupamos los distintos colores de las tres especies en dos grandes categorías, correspondientes a los colores “claros” y los “oscuros” (algo que está justificado en base a análisis previos de espectrometría de reflectancia), lo que observamos es un patrón claro: todas estas especies muestran una clara tendencia hacia el apareamiento asociativo negativo. Así, los valores de IPSI están comprendidos entre -0.59 y -0.33, tal y como se puede ver en la siguiente tabla.
 Resultados de IPSI obtenidos tras los análisis.
Resultados de IPSI obtenidos tras los análisis.En este sentido, pensamos que está suficientemente justificado asumir la existencia de apareamiento asociativo negativo en las tres especies estudiadas. Ahora bien, cuando se analizan más en detalle los resultados, desglosándolos por colores y localidades, se advierte una excepción a esta pauta que puede darnos pistas acerca de las presiones selectivas a las que puede estar sometido el color.
En una población de L. fabalis de Cangas, el apareamiento asociativo es de naturaleza positiva (si bien no significativa), al contrario de lo que sucede con el resto de especies y poblaciones.
 Valores de IPSI para L. fabalis en las distintas localidades. En ella se ve el valor discordante de una de la población de Cangas
Valores de IPSI para L. fabalis en las distintas localidades. En ella se ve el valor discordante de una de la población de CangasTal y como discutimos en nuestro artículo, este resultado discordante sugiere que el verdadero objeto de la selección en esta especie (aquello que favorece la reproducción) no es el color de la concha en sí, sino algún otro rasgo correlacionado con este a nivel genético.
Conclusiones
En definitiva, a partir de nuestro artículo se pueden extraer dos conclusiones: (1) el apareamiento asociativo negativo es un hecho en las tres especies de Littorina analizadas. Esto sugiere que la NFDS y la elección de pareja pueden jugar un papel clave en el mantenimiento del polimorfismo de color de la concha y que la elección de pareja puede ser un rasgo conductual ancestral en el género Littorina.
Y (2), que el color de la concha puede estar relacionado genéticamente con algún otro carácter fenotípico que sea el verdadero objeto de la selección y la elección de pareja.
Como sucede habitualmente en la ciencia, estas dos conclusiones abren futuras vías de investigación, que nuestro grupo tratará de abordar en los próximos meses. Una de estas vías tiene que ver con el diseño y ejecución de un experimento que permita corroborar la existencia de elección de pareja en estas especies. De ese modo, se podrá evaluar más directamente la importancia de la NFDS en el mantenimiento del polimorfismo de color de Littorina. Por otro lado, una segunda vía está relacionada con el estudio de las bases moleculares del color de la concha, para tratar de determinar si en efecto este rasgo está asociado a otros caracteres potencialmente adaptativos.
¡Os mantendremos informados de futuros progresos en ambas líneas de investigación!
Agradecimientos
El presente estudio ha sido financiado gracias al proyecto de investigación CGL2016-75482-P del Ministerio de Economía, Industria y Competitividad (IP, Emilio Rolán-Alvarez), así como gracias a dos ayudas predoctorales de la Universidad de Vigo (PREUVIGO/00VI 131H 641.02) y de la Xunta de Galicia (ED481A-2021/274).
Referencias
Gefaell J, Galindo J, Malvido C, Nuñez V, Estévez D, Blanco S, González-Conde M, Martínez-Domínguez S, Pérez-Fernández G, Rus B, Mosconi I, Rolán-Alvarez E (2021) Negative assortative mating and maintenance of shell colour polymorphism in Littorina (Neritrema) species. Marine Biology, 168:151. doi: 10.21203/rs.3.rs-242300/v1
Rolán-Alvarez E, Austin CJ, Boulding EG (2015a) The contribution of the genus Littorina to the field of evolutionary ecology. En: Hughes RN, Hughes DJ, Smith IP, Dale AC (eds). Oceanogr Mar Biol, vol. 53. CRC Press, Boca Ratón, 157-214
Sobre el autor: Juan Gefaell se graduó en psicología en la Universidad Pontificia de Salamanca y en biología en la Universidad de Vigo; tras cursar un máster en lógica, historia y filosofía de la ciencia en la UNED, en la actualidad realiza su doctorado en biología evolutiva en el departamento de Bioquímica, Genética e Inmunología de la Facultad de Biología de la Universidad de Vigo.
El artículo La aparente paradoja del polimorfismo de color se ha escrito en Cuaderno de Cultura Científica.
El tercer ángel
“Tocó el tercer ángel… Entonces cayó del cielo una estrella grande, ardiendo como una antorcha. Cayó sobre la tercera parte de los ríos y sobre las manantiales de agua. La estrella se llama Ajenjo. La tercera parte de las aguas se convirtió en ajenjo, y mucha gente murió por las aguas, que se habían vuelto amargas.”
Juan de Patmos (siglo I e.c.) Apocalipsis 8: 10-11.
 Meteoro del 1 de agosto de 2017 desde Pensacola Beach (Florida, Estados Unidos). Foto: Austin Houser / Wikimedia Commons
Meteoro del 1 de agosto de 2017 desde Pensacola Beach (Florida, Estados Unidos). Foto: Austin Houser / Wikimedia CommonsHace 66 millones de años un asteroide de más de 10 km de diámetro (unos tres billones de toneladas) alcanzó la superficie de nuestro planeta a una velocidad de unos 20 km/s (72000 km/h). Impactó en la península de Yucatán, México, cerca de la actual población de Chicxulub, con una energía de 400 zettajulios (4 x 1023 julios), equivalente a 100 teratones (1014 toneladas) de TNT. Para hacernos una idea cabal, si es que tal cosa es posible, de su magnitud, la explosión fue dos millones de veces más potente que la que provoca la llamada Bomba del Zar -la mayor jamás detonada-, de 50 megatones. La mayor erupción volcánica de la que se tiene constancia, la de la Caldera de la Garita, en Colorado, EEUU, liberó del orden de 10 zettajulios, cuarenta veces menos que la del asteroide que impactó en Chicxulub.
Produjo un cráter en la corteza terrestre de 20-30 km de profundidad y 150-180 km de diámetro. En 1000 km a la redonda, todos los seres vivos murieron por efecto del calor de la bola de fuego que se formó. Un tsunami gigantesco -de unos 100 m de altura- devastó miles de kilómetros de áreas costeras. Otros tsunamis siguieron al primero, aunque de menor altura, provocados por las alteraciones geológicas en la zona del cráter.
El impacto provocó un movimiento sísmico equivalente a un terremoto de magnitud 12 en la zona en que se produjo, y sucesivas ondas de choque provocaron terremotos de magnitud 8 y la erupción de volcanes a miles de kilómetros del cráter. Billones de toneladas de rocas y polvo fueron lanzadas a la atmósfera. Parte de esos materiales, ardiendo, llovió sobre millones de kilómetros cuadrados, abrasando plantas y animales, y prendiendo fuegos que extendieron la devastación más lejos aún. En la zona próxima al impacto, los vientos llegaron a superar los 1000 km/h.
El polvo y las cenizas ascendieron hasta niveles muy altos de la atmósfera, de donde, al estar por encima de las nubes, no pueden ser arrastradas por la lluvia. Tras ascender, se extendieron por todo el planeta. La luz solar fue reflejada al espacio por la neblina de aerosoles de sulfatos, o absorbida por las partículas de ceniza. Las sombras provocaron un enfriamiento global que duró varios años. El frío y la oscuridad acabó con muchísimas especies de plantas y animales, que murieron ateridas o de inanición. Entre esas especies se encontrarían los dinosaurios no aviares.
Lógicamente no todos los impactos que pueden ocurrir son de esa magnitud. De hecho, de forma permanente entran objetos sólidos a la atmósfera. Muchos se volatilizan por efecto de la alta temperatura que toman al entrar en contacto con los gases atmosféricos. Otros caen sobre la superficie. Pero la gran mayoría no causa daño alguno.
La probabilidad de que en los próximos 100 años se produzca un impacto de un cometa o asteroide peligroso de menos de 10 km de diámetro es de una en 120000. Y con los mayores de 10 km, el riesgo es aún menor, inferior a una en 150 millones. Este es uno de los riesgos existenciales mejor evaluado, porque el espacio próximo está sometido a escrutinio de forma permanente. Tampoco los asteroides me quitan el sueño.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El tercer ángel se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2021: Javier Fernández Panadero – Busco un centro de gravedad permanente
El gran evento de divulgación Naukas regresó a Bilbao para celebrar su décima edición en el magnífico Palacio Euskalduna durante los pasados 23, 24, 25 y 26 de septiembre.

Cantaba Franco Battiato:
Busco un centro de gravedad permanente
Que no varíe lo que ahora pienso de las cosas de la gente
De las cosas de la gente, no, pero de las cosas a secas lo encuentra Javier Fernández Panadero.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
N. del E.: Una crónica de esta charla puede leerse aquí
El artículo Naukas Bilbao 2021: Javier Fernández Panadero – Busco un centro de gravedad permanente se ha escrito en Cuaderno de Cultura Científica.
Las consecuencias de la crisis de biodiversidad para los ecosistemas y los humanos
Luz Boyero
 Foto: Nina Lishchuk / Shutterstock
Foto: Nina Lishchuk / Shutterstock
El término biodiversidad, hasta hace poco utilizado casi exclusivamente en un ámbito científico, hoy en día está de moda. Todos sabemos que la biodiversidad es, a grandes rasgos, la variedad de especies que habitan nuestro planeta (aunque técnicamente el término engloba también la variedad de genes y de ecosistemas).
El hecho de que la biodiversidad esté de moda es, sin embargo, una mala noticia, ya que el origen de esta fama es precisamente la gran velocidad a la cual las especies están desapareciendo. Lamentablemente, la actual tasa de extinción de especies no tiene precedente histórico, e incluso podría estar superando a la de la última extinción masiva que ocurrió durante la transición Cretácico-Terciario, cuando los dinosaurios desaparecieron.
De la evolución a la mano del hombre
La biodiversidad es el resultado de varios miles de millones de años de evolución, desde el aún incierto origen de la vida hasta nuestros días. Así, el registro fósil y el material genético de las especies actuales nos dan pistas sobre el número y las características de las especies que han habitado la Tierra en los distintos periodos.
Las extinciones, junto con la especiación, forman parte del proceso de evolución y han ocurrido siempre por causas naturales. En el caso de las extinciones masivas han sido presumiblemente fenómenos catastróficos tales como el vulcanismo o los impactos de asteroides.
Sin embargo, sabemos que el ser humano es responsable de gran parte de las extinciones actuales. Ha contribuido bien de manera directa (por ejemplo, a través de la caza) o indirecta (a causa de la destrucción de hábitat, los cambios climáticos o la introducción de especies exóticas que desplazan a las autóctonas).
El papel que desempeña el ser humano en los cambios ambientales actuales es clave. Esto ha llevado a denominar Antropoceno al periodo que transcurre desde la revolución industrial. Pero los humanos, además de ser los principales responsables de los cambios que sufre nuestro planeta, nos vemos seriamente afectados por dichos cambios ambientales y por la pérdida de biodiversidad.
La biodiversidad no solo tiene un valor intrínseco que debe ser valorado y respetado en sí mismo. Además, las especies son valiosas para nosotros porque nos proporcionan servicios que son básicos para nuestra surpervivencia, y que están relacionados con los ecosistemas de los que forman parte: son los llamados servicios ecosistémicos.
 Zona deforestada de la selva amazónica brasileña. Foto: Tarcisio Schnaider / Shutterstock
Zona deforestada de la selva amazónica brasileña. Foto: Tarcisio Schnaider / ShutterstockConsecuencias para los ecosistemas
Los seres vivos interaccionan unos con otros mediante distintos tipos de relaciones (tróficas, competitivas, sociales, etc.), así como con su ambiente (del cual obtienen recursos para mantenerse vivos), formando ecosistemas que están en continuo funcionamiento. Dicho funcionamiento se define por una serie de procesos, como son la producción de biomasa, la descomposición o los ciclos de nutrientes.
Hoy en día sabemos que la biodiversidad afecta directamente al funcionamiento de los ecosistemas, es decir: el número de especies presentes en un ecosistema, así como la identidad de dichas especies y sus características, pueden acelerar o decelerar las tasas de los distintos procesos. Este hecho, que ha sido demostrado en los últimos 30 años gracias a una rama específica de la ciencia denominada BEF, del inglés biodiversity-ecosystem funcioning, ha despertado conciencia sobre el papel fundamental que desempeñan las especies para mantener el equilibrio dinámico en el que se encuentra nuestro planeta. Así, todas las especies son piezas de una maquinaria cuyo funcionamiento depende del conjunto, y las consecuencias de su pérdida son difíciles de predecir debido a la complejidad de los ecosistemas.
Por ejemplo, los ríos de cabecera son ecosistemas heterotróficos cuya principal fuente de energía y materia radica en la hojarasca que proviene de la cuenca. Esta hojarasca es procesada por organismos y microorganismos acuáticos, que son capaces de incorporar el carbono y los nutrientes de origen terrestre en la red trófica acuática y así abastecer al ecosistema fluvial.
La disminución de especies vegetales en las cuencas puede ocurrir como consecuencia de la sustitución de especies autóctonas por otras de interés comercial o por la aparición de enfermedades infecciosas. Nuestras investigaciones indican que esta pérdida de especies altera los procesos fundamentales que conforman el funcionamiento del ecosistema fluvial: por lo general, se favorecen las vías microbianas en detrimento de los procesos mediados por organismos acuáticos y disminuye la eficiencia del ecosistema para utilizar los recursos de origen terrestre.
Aunque todavía no se ha cuantificado la repercusión que esto tiene a nivel de servicios ecosistémicos, los efectos negativos sobre la calidad del agua, la producción de recursos alimentarios o el valor paisajístico y recreativo son más que probables.
Es también importante recalcar que distintas zonas del planeta pueden verse afectadas de forma diferente por la pérdida de biodiversidad. En primer lugar, las tasas de extinción no son homogéneas. En la actualidad afectan principalmente a los países en vías de desarrollo, con algunos puntos calientes (del inglés hotspots) en Sudamérica y el sureste asiático.
En segundo lugar, un mismo tipo de ecosistema en ocasiones puede funcionar de manera diferente en distintas zonas climáticas. Así, en los ríos de cabecera, las comunidades de invertebrados que procesan la hojarasca en zonas templadas y tropicales utilizan diferentes estrategias en el uso de este recurso.
En las zonas tropicales, la pérdida de biodiversidad vegetal acarrea mayores consecuencias funcionales que en las templadas. Por eso en estos países la protección de la biodiversidad debería ser aún más prioritaria, y esto es justamente lo contrario a lo que ocurre en realidad.![]()
Sobre la autora: Luz Boyero es Profesora de Investigación Ikerbasque en Ecología, UPV/EHU
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Las consecuencias de la crisis de biodiversidad para los ecosistemas y los humanos se ha escrito en Cuaderno de Cultura Científica.
Geólogos en la Luna
 Fotografía de la Tierra conocida como “La Canica Azul” tomada por la tripulación de la misión Apolo 17 (de la que formaba parte Harrison Schmitt) de camino hacia la Luna. Autoría: NASA/ Tripulación del Apolo 17.
Fotografía de la Tierra conocida como “La Canica Azul” tomada por la tripulación de la misión Apolo 17 (de la que formaba parte Harrison Schmitt) de camino hacia la Luna. Autoría: NASA/ Tripulación del Apolo 17.El 21 de julio de 1969, el astronauta estadounidense Neil Armstrong se convirtió en el primer hombre en pisar la Luna. Pero este hito histórico de la humanidad no habría sido posible sin la geología.
 Mareta N. West. Fuente
Mareta N. West. FuenteVamos a viajar al principio de esta historia. Corría el año 1915 cuando, en el estado de Oklahoma (Estados Unidos), nació una niña a la que pusieron por nombre Mareta Nelle West. Mareta estudió en la Universidad de Oklahoma, en la que se graduó en geología con 22 años. Tras varias décadas trabajando en la industria del petróleo, se convirtió en la primera geóloga contratada por el Servicio Geológico de Estados Unidos en el año 1964. Nos encontrábamos en plena carrera espacial, lo que provocó que Mareta entrara a formar parte del Equipo Experimental de Geología de la NASA encargado del entrenamiento de los astronautas de las misiones Apolo, siendo así considerada como la primera astrogeóloga.
Su trabajo fue determinante para el desarrollo favorable de la misión Apolo 11 que llevó a los primeros seres humanos hasta la Luna, ya que fue Mareta la encargada de realizar la cartografía de nuestro satélite y decidir el punto exacto en el que se produciría el primer alunizaje de la historia. Es decir, fue una geóloga la que eligió el lugar en el que quedaría marcada la primera huella humana de la Luna. Y no fue el único, ya que tras revisar los mapas lunares realizados por la tripulación de la Apolo 11, Mareta seleccionó los puntos de alunizaje de otras misiones tripuladas de la NASA. Tras su muerte en 1988, sus cenizas fueron enviadas a ese espacio que tanto estudió.
 Eugene M. Shoemaker. Fuente: Wikimedia Commons
Eugene M. Shoemaker. Fuente: Wikimedia CommonsHay otro nombre propio que debemos mencionar en esta carrera espacial geológica, el de Eugene Merle Shoemaker. Eugene nació en 1928 en el estado de California (Estados Unidos) y se le puede considerar como un auténtico geólogo vocacional, ya que de niño se dedicaba a buscar y coleccionar rocas y minerales que despertaron su interés por esta ciencia. Su carrera profesional siempre estuvo ligada al Servicio Geológico de Estados Unidos, donde se especializó en el estudio de cráteres de impacto de cuerpos extraterrestres en nuestro planeta relacionándolos con ciertos eventos críticos de nuestra historia geológica. Y trasladó este conocimiento al estudio de los cráteres de impacto de la Luna, colaborando estrechamente con la NASA. Así, en 1961 pondría en marcha el plan de astrogeología del Servicio Geológico de Estados Unidos, que culminaría en 1965 con la creación del Centro de Astrogeología asociado a esta institución.
Por todo este trabajo, Eugene es considerado como uno de los padres de la Geología Planetaria. En la NASA, al igual que Mareta, se dedicó a entrenar a los astronautas del programa Apolo e, incluso, intentó convertirse él mismo en uno de los elegidos para viajar a la Luna. Pero unos problemas de salud le impidieron conseguirlo. Sin embargo, tras su muerte en 1987 pudo cumplir su sueño, ya que sus cenizas fueron transportadas por una sonda lunar hasta nuestro satélite, convirtiéndose en la primera y única persona cuyos restos descansan en la Luna, al menos hasta la fecha.
 Harrison H. Schmitt. Fuente: Wikimedia Commons
Harrison H. Schmitt. Fuente: Wikimedia CommonsVamos a terminar este pequeño paseo espacial recordando a un tercer geólogo. En 1935, en el estado de Nuevo México (Estados Unidos), nació Harrison Hagan Schmitt. Después de formarse como geólogo tanto en Estados Unidos como en Noruega, Harrison trabajó en el Centro de Astrogeología del Servicio Geológico de Estados Unidos creado por Eugene justo antes de unirse a la NASA en 1965, donde, además de estudiar las muestras de polvo y rocas traídas de la Luna, también colaboró en los entrenamientos para astronautas.
Él mismo se preparó para ser uno de los elegidos para viajar a nuestro satélite, cosa que consiguió gracias a la recomendación de Eugene. De esta manera, Harrison formó parte de la tripulación de la misión Apolo 17, que alunizó en nuestro satélite a finales de 1972. Así, se convirtió en el primer y único científico que ha pisado la Luna. Y, para dejar constancia de que un geólogo ha estado dando un paseo por su superficie, antes de abandonar nuestro satélite lanzó su martillo geológico lejos del módulo lunar, no sin dejar de hacer bromas sobre la posibilidad de que se lo descontasen del sueldo (se puede ver el lanzamiento en el vídeo de abajo).
Sin duda, estos tres pioneros de la Geología Planetaria dejaron su propia huella en la Luna, aunque cada uno a su manera.
Más información sobre Mareta West:
Más información sobre Eugene Shoemaker:
Más información sobre Harrison Schmitt:
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Geólogos en la Luna se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Poniéndose bien dos pares de calcetines
El otoño avanza y empieza a hacer frío. A Pedro se le quedan los pies helados en la cama, así que decide ponerse los dos únicos pares de calcetines que tiene (uno rojo y otro negro). Tiene metidos esos calcetines en un cajón, tirados de cualquier manera. Para que su gata no crea que ya es de día y empiece a pedir de comer, Pedro decide no encender la luz. Así que abre el cajón y se coloca los calcetines sin poder ver su color. Al volver a la cama, ya desvelado, empieza a pensar en la siguiente cuestión: ¿Cuál es la probabilidad de que me haya puesto los calcetines de manera que los visibles (los de fuera) sean del mismo color?

Intentemos ayudar a Pedro, razonando de varias maneras.
Razonamiento 1
Pedro coge un calcetín al azar y se lo pone en el pie derecho. Toma un segundo calcetín y lo coloca sobre el primero. Para conseguir su objetivo (que los calcetines visibles tengan el mismo color) necesita que el segundo calcetín tomado (entre los tres que quedaban en el cajón) no sea la pareja del primero. Esto sucederá en dos de cada tres ocasiones.
Se pone después el tercer calcetín (en el pie izquierdo) elegido al azar entre los dos que quedan. Para cumplir su propósito, el tercero debe ser la pareja del primer calcetín. Esto sucederá una de cada dos veces.
Así, la probabilidad de éxito es de: P1 = 2/3 x 1/2 = 1/3.
Razonamiento 2
Pedro coge dos calcetines a ciegas y los coloca en su pie derecho. Necesita que sean diferentes. Como las posibles parejas son (R es rojo y N negro) (R-R), (N-N), (R-N) y (N-R), Pedro tiene una oportunidad sobre dos de atrapar bien esos dos calcetines. Después (si su pie derecho tiene calcetines de diferentes tonos) debe ponerse los dos calcetines que quedan (que son, por lo tanto, de colores diferentes) en el orden adecuado: conseguirá hacerlo una de cada dos veces.
Así, la probabilidad de éxito es de P2 = 1/2 x 1/2 = 1/4.
Razonamiento 3
Pedro coge dos calcetines del cajón y se coloca uno en el pie izquierdo y otro en el derecho. Para intentar conseguir su objetivo (que los calcetines visibles sean del mismo tono) necesita que los dos calcetines colocados sean del mismo color. Como las posibles parejas son (R-R), (N-N), (R-N) y (N-R), se conseguirá éxito en la disposición una vez de cada dos. En este caso, los dos calcetines que quedan son del mismo color.
Por lo tanto, la probabilidad de éxito es de P3 = 1/2.
¡Esto es bastante raro! Tres razonamientos totalmente convincentes han proporcionado probabilidades diferentes de conseguir el objetivo de Pedro. ¿Puede ser que la probabilidad de tener éxito dependa del procedimiento seguido? ¿O, por el contrario, de los tres anteriores razonamientos (al menos) dos son falsos? Debajo aparece la solución, pero (si os apetece) pensad en la respuesta, quizás razonando de diferente manera para intentar entender que sucede…
Solución
No hay ninguna razón para que diferentes procedimientos de colocación de los calcetines proporcionen distintas soluciones, ya que se trata únicamente de elegir cuatro calcetines y ponérselos, sin utilizar ninguna información adicional. Así que (al menos) dos de los razonamientos anteriores son falsos.
Denotemos R1, R2, N1 y N2 los cuatro calcetines. Cuando se cogen dos calcetines entre los cuatro, estamos eligiendo dos elementos en un conjunto de cuatro, y esto puede hacerse de seis maneras:
{R1,R2}, {R1,N1}, {R1,N2}, {R2,N1}, {R2,N2} y {N1,N2}.
Los anteriores son conjuntos de calcetines, el orden no se tiene en cuenta. Es decir, son las combinaciones de cuatro elementos tomados de dos en dos, C(4,2)=4!/2!.2!=6.
Así, la probabilidad de tomar dos calcetines del mismo color cuando se cogen dos entre los cuatro que hay en el cajón es de 2/3, y no de 1/2 como se afirma en los razonamientos 2 y 3.
Por lo tanto, en el razonamiento 2 debe reemplazarse el primer 1/2 por 2/3 y la probabilidad es entonces de P2 = 2/3 x 1/2 = 1/3.
El razonamiento 3 falla por el mismo motivo; por ello debe sustituirse 1/2 por 1/3, con lo que P3 = 1/3.
Esto es tranquilizador, los tres razonamientos dan lugar al mismo resultado. ¿Y si las tres se han argumentado mal? Podría suceder… Veamos un método exhaustivo para comprobar que la probabilidad buscada es, efectivamente, de 1/3.
Hay 24 modos posibles de colocar los calcetines; son las maneras de ordenar un conjunto de cuatro elementos (variaciones sin repetición de cuatro elementos tomados de cuatro en cuatro), como se muestra en la siguiente tabla:

Si convenimos que el orden de colocación de los calcetines es: pie derecho, pie derecho, pie izquierdo y pie izquierdo, entonces las configuraciones que consiguen el objetivo de Pedro son (N-R-N-R) o (R-N-R-N), que marcamos en la tabla:
Como se observa, son cuatro de cada tipo, es decir 8 entre las 24 configuraciones posibles; luego la probabilidad buscada es, efectivamente, de 1/3.
De cualquier modo, si Pedro fuera más ordenado y emparejara sus calcetines en vez de meterlos de cualquier manera en el cajón, lo tendría más fácil. Solo se desvelaría intentando adivinar el color visible de sus calcetines una vez colocados…
Nota
Este problema fue propuesto por el profesor Jean-Paul Delahaye en la sección de paradojas del número 16.1 de la revista Accromath (invierno-primavera 2021). La solución apareció en la sección de paradojas del número 16.2 (verano-otoño 2021).
Este texto es una traducción (adaptada) del problema y de la solución planteada por Delahaye.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Poniéndose bien dos pares de calcetines se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿No es la vida misma una paradoja?
- Un juego con un premio colosal
- El jugador: una lección de teoría de la probabilidad
Alcohol y sandía
Daniel Arias Ramirez

Los mitos urbanos son expresiones típicas de la sociedad con una gran influencia sobre la población y por lo tanto definitivos en la toma de decisiones. Esto lo pudimos apreciar con gran preocupación durante la pandemia, en especial con las vacunas. Estas fueron objeto de discusión dando lugar a diferentes mitos: “chips implantados por el gobierno”, “reacciones adversas y fatales”, “modificación del ADN”, etc.
Ahora bien, desde mi perspectiva puedo afirmar con seguridad que esto es doblemente cierto para los latinos, somos muy susceptibles a este tipo de creencias, después de todo, nuestra región es el lugar donde lo mágico y lo real se combinan. Por ejemplo, de acuerdo a nuestras mamas y abuelas el piso es una fuente inagotable de temibles enfermedades y por eso podría asegurar que un latino jamás se atrevería a salir descalzo. Por otro lado, otro rasgo de identidad cultural que es común en muchas partes del mundo es el consumo de alcohol. Un evento social sin una bebida alcohólica es inconcebible para muchas personas (lo cual he experimentado de primera mano en el gremio de los que nos dedicamos a la química). De hecho, el consumo promedio de alcohol en Latinoamérica y el Caribe supera por 2,2 litros el consumo promedio mundial (Moreno, 2015) y en el caso de Europa, los países con mayor consumo de alcohol en promedio (en orden creciente) son: Francia, España, Alemania y Republica Checa con un promedio de 13.10 litros per cápita (Hannah Ritchie, 2018).
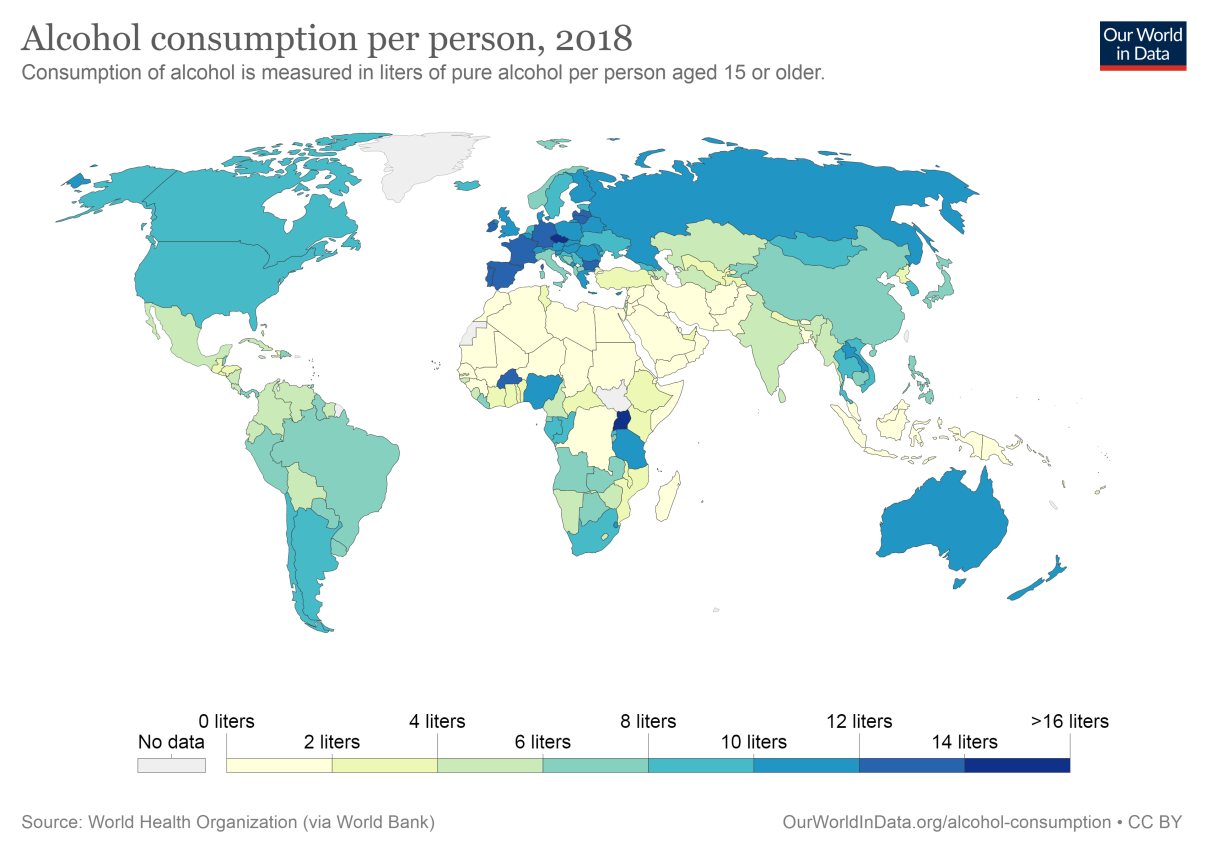
Así pues, el punto en el cual los mitos urbanos y el consumo de alcohol coinciden se da en un fruto: la sandía (patilla o melón de agua como se le conoce en Colombia, Venezuela y algunos países antillanos). Existen muchos mitos asociados al consumo de alcohol, estos van desde soluciones extrañas para la resaca hasta supuestos efectos específicos para determinadas bebidas alcohólicas (en Colombia, por ejemplo, se dice que el consumo de ron aumenta la libido en las mujeres) y el caso de la sandía es un mito ampliamente conocido.
Este mito reza que el consumo alcohol y sandía al mismo tiempo puede tener consecuencias fatales (Soho, 2021) algunas de estas versiones mencionan que lo realmente fatal es comer sandia poco tiempo después de haber bebido (Riera, 2014). Con esto en mente, el primer paso para desmentir o confirmar este mito sería establecer las sustancias presentes en este fruto y su posible toxicidad.

Para empezar, la sustancia que se encuentra en mayor cantidad en la sandía (en lo que a la pulpa respecta) es el agua (94.47 %), seguido por los carbohidratos (4.23 %) y por ultimo las proteínas, fibras y minerales (1.1 %) (Olayinka & Etejere, 2018). Lo cual en principio no da ninguna pista sobre las posibles sustancias toxicas en la sandía, así pues, habría que analizar las sustancias que se encuentran en menor cantidad.
Por ejemplo, las sustancias responsables del color de la pulpa en la sandía: los carotenoides, en especial el licopeno, el cual es el carotenoide más abundante en promedio para la sandía (Nkoana et al., 2021). Del mismo modo, debemos recordar que los carotenoides son sustancias en cuya estructura encontramos dobles enlaces conjugados y largas cadenas de carbono obtenidas por la unión de muchas unidades de isopreno (Murillo et al., 2013).
Esta sustancia no solamente es la responsable del color de la sandía, también le da el rojo al tomate, el color naranja a la papaya y el rosado a la toronja y la guayaba. El licopeno no ha demostrado ser toxico, de hecho, tiene una alta capacidad antioxidante, lo cual es un indicador (que en primera instancia) es bueno para la salud (Bojórquez et al., 2013). Por otro lado, hay que tener en cuenta que las bebidas alcohólicas son mezclas de etanol y agua principalmente, es decir, es una mezcla de sustancias con alta polaridad, así pues, para que este mito sea cierto es necesario que la sustancia mortal sea soluble en esta mezcla, es decir, que tenga una polaridad relativamente elevada. Así pues, en el caso del licopeno tenemos una sustancia que no podría ser soluble (la cadena larga de carbonos hace que sea una molécula lipofílica) y por lo tanto, se puede descartar el licopeno de las posibles sustancias toxicas.
Por otro lado, se tienen los ácidos: grasos y orgánicos. Debemos recordar que la principal diferencia entre los ácidos grasos y los orgánicos se dan en la estructura. Los primeros tienen una cadena larga de carbonos y los segundos son estructuras pequeñas.
Dentro del primer grupo los más representativos en la sandía son el ácido linolenico (63.37%), oleico (16.42 %) y palmítico (10.60%) (Nkoana et al., 2021) teniendo en cuenta que ninguno de ellos es polar, no podrían ser solubles en un delicioso, vodka, tequila o ron, por lo tanto, pueden ser descartados. En cuanto a los ácidos orgánicos, los que se encuentran en mayor cantidad son el ácido cítrico y el ácido málico (no se preocupe, el nombre del ácido málico deriva del latín “malum” que significa manzana, no está relacionado con la maldad) y estas dos sustancias son polares, es decir, podrían ser disueltas en una bebida alcohólica con facilidad, pero ninguna es toxica, de hecho estos ácidos están presentes en albaricoques, moras, arándanos, cerezas, uvas, melocotones, peras y ciruelas. Por lo tanto, dentro este tipo de ácidos tampoco se encuentra la sustancia toxica.
Otro grupo de sustancias interesantes en la pulpa de la sandía se conocen como “curcubacitinas”, este nombre digno de un trabalenguas se debe a la familia de frutos Cucurbitaceae, a la cual pertenecen la calabaza, el pepino, el zucchini y la fruta en cuestión, la sandía.
Al igual que las vitaminas, existen varias versiones de esta molécula dependiendo de las diferencias estructurales. Así pues, podemos encontrar Curcurbacitina A, Curcurbacitina B, E, I, etc. Inicialmente, estas moléculas tienen un rol defensivo, por lo tanto, estas sustancias tienen una acción toxica contra los insectos. La pregunta entonces será: ¿Las curcubacitinas son toxicas para los seres humanos? El en 2017 se reportaron en Francia dos casos por intoxicación (los primeros y únicos hasta al momento). Estos casos estuvieron muy lejos de ser fatales, los síntomas reportados fueron náuseas y problemas estomacales (Assouly, 2018). Por otro lado, la fruta en cuestión para este reporte fue la calabaza no la sandía y no se debió al consumo directo, la calabaza fue procesada y luego consumida. Por otro lado, una gran cantidad de estudios han demostrado que muchos tipos de curcubacitinas en la sandía tienen la capacidad de inhibir líneas de células cancerosas, es decir, en principio son beneficias para la salud (Duangmano et al., 2012; El-Senduny et al., 2016;Touihri-Barakati et al., 2017; Alsayari et al., 2018) (esto no quiere decir que curen el cáncer, solamente indica el potencial de estas sustancias para iniciar estudios que permitan establecer a futuro una probable actividad anticancerígena). Así pues, es muy poco probable que dentro de las curcubacitinas se encuentre la posible molécula toxica. La sustancia en cuestión debe generar sin lugar a dudas un efecto nocivo en el cuerpo y en el caso de estas moléculas la probabilidad es increíblemente baja.
Ahora bien, otra parte interesante y por la que es muy conocida la Sandia son las semillas, en esta parte del fruto podemos encontrar una gran cantidad de sustancias llamadas “anti-nutrientes” (de nuevo, no se preocupe, el nombre hace referencia a un concepto totalmente distinto, el consumo de sandía no va a generar “anti-nutrición” en el sentido literal de la palabra). La función de esta familia de compuestos está asociada a la absorción de nutrientes (Akande et al., 2010). Por ejemplo, el Ácido Fítico mejora la bioabsorción de minerales dado que puede interactuar con estos mediante los grupos fosfato presentes en esta molécula (Zitterman, 2003).

Dada la capacidad de esta molécula para “quelar” (unirse a) los metales, se le considera como un antioxidante, dado que los metales son conocidos por ser iniciadores de reacciones de oxidación, así pues, si se remueven los metales (en especial el hierro) del medio la probabilidad de una oxidación disminuye, en otra palabras el Ácido Fítico es una sustancia que puede ayudar a la salud (Watson et al., 2014). Hay que mencionar niveles muy altos de este Acido en el organismo pueden generar deficiencias de minerales a largo plazo (Petry et al., 2010), pero es definitivamente claro que no puede tener consecuencias fatales. Por lo tanto, esta sustancia tampoco podría generar un efecto toxico si es combinada con una bebida alcohólica.
Por otro lado, dentro de este gran grupo de anti-nutrientes también se tienen los “oxalatos” y las “saponinas”. Los primeros están relacionados con la bioabsorción del calcio y el magnesio ya que los oxalatos pueden unirse a los metales en su forma iónica mediante los grupos carboxilatos y de esta manera ser transportado con mayor facilidad (Akande et al., 2010). Los segundos son los responsables de los sabores astringentes de muchas frutas y semillas y se ha demostrado que estas sustancias tiene una actividad “hipocolesterolémica”, es decir, ayudan a controlar los niveles de colesterol (Mohan et al., 2015), por lo tanto, las saponinas están muy lejos de ser toxicas. Por otro lado, la saponegina (la estructura base de todas las saponinas) podría ser soluble en una bebida alcohólica, dada su unión varias unidades de azucares (que son muy solubles en agua) hacen que esta molécula sea hidrofilica (es decir, soluble en agua o en este caso soluble en un delicioso vodka), pero a pesar es que soluble, no hay reportes de efectos adversos a la salud. Así pues, se pueden descartar tanto a las saponinas como a los oxalatos como potenciales moléculas nocivas.
En lo discutido hasta el momento, no hay en principio ninguna sustancia en la sandía que al mezclarse con alcohol puede generar algún efecto nocivo. Pero, es en este punto que hay que mencionar unas sustancias que si han demostrado ser peligrosas por su capacidad de producir una sustancia muy toxica: el ácido cianhídrico.
Los glucósidos cianogénicos son sustancias que se dan por la unión entre un grupo nitrilo y un carbohidrato (generalmente un monosacárido) (Akande et al., 2010). Estas sustancias no son en sí mismas toxicas, la toxicidad se puede generar al romperse la pared celular (este rompimiento puede favorecerse cuando se tritura o se fermenta la semilla) de tal manera que los glucósidos cianogénicos se pongan en contacto con enzimas que puedan generar una hidrolización (rompimiento) produciendo ácido cianhídrico (Bolarinwa et al., 2016).
Entonces en principio este es un buen candidato para el mito. Habría entonces que revisar si estas sustancias se pueden disolver en una bebida alcohólica. Debemos recordar que estamos en búsqueda de una sustancia toxica con una polaridad elevada y los grupos “OH” en los carbohidratos de estas sustancias son puntos polares que favorecen la interacción con el agua, de tal manera que los glucósidos cianogénicos son solubles en una bebida alcohólica.
Entonces, ¿Este mito es verdadero?, un pequeño cálculo podría confirmar esta hipótesis. Así pues habría que partir de varias consideraciones: un ser humano de un peso promedio (80 Kg), la dosis letal de cianuro para un humano promedio (0.5 mg/Kg) (Burns et al., 2012) y la concentración de glucósidos cianogénicos en las semillas de sandía (0.79 mg/100 g de semilla) (Egbuonu, 2015).
El primer paso sería calcular la cantidad de cianuro que necesitamos para matar una persona de 80 Kg. Con esto en mente, habría que calcular la cantidad de semillas (si se tiene en cuenta que una semilla tiene un peso promedio de 0.2 g) que necesitan para obtener esta cantidad de cianuro. El último paso entonces será calcular la cantidad de sandias que se necesitan para matar una persona teniendo que la cantidad máxima de semillas en una sandía promedio es 150. Así, se tiene que, para que este mito fuese cierto, usted debería tomar las semillas de 169 sandias, molerlas y/o fermentarlas y luego comerse toda esta masa con un buen trago de tequila, ron, vodka, etc.
De manera, se puede concluir que este mito es sin lugar a dudas falso. La sandía es de hecho un perfecto acompañante del alcohol y se puede usar para preparar gran variedad de cocteles (Graham, 2021). Así pues y dado el componente experimental de la química y la sana curiosidad científica cabe plantearse probar cada uno de estos cocteles sin preocuparse por ningún efecto nocivo (exceptuando tal vez una fuerte resaca) a corto o medio plazo*.
Sobre el autor: Daniel Arias Ramírez es investigador en química en el Instituto de Investigaciones Científicas INICIEN de la Fundación Universitaria Juan de Castellanos (Tunja, Boyacá, Colombia)
Referencias
Akande, K. E., Doma, U. D., Agu, H. O., & Adamu, H. M. (2010). Major antinutrients found in plant protein sources: Their effect on nutrition. Pakistan Journal of Nutrition. https://doi.org/10.3923/pjn.2010.827.832
Alsayari, A., Kopel, L., Ahmed, M. S., Soliman, H. S. M., Annadurai, S., & Halaweish, F. T. (2018). Isolation of anticancer constituents from Cucumis prophetarum var. prophetarum through bioassay-guided fractionation. BMC Complementary and Alternative Medicine. https://doi.org/10.1186/s12906-018-2295-5
Assouly, P. (2018). Hair loss associated with cucurbit poisoning. In JAMA Dermatology. https://doi.org/10.1001/jamadermatol.2017.6128
Bojórquez, R. M. C., Gallego, J. G., & Collado, P. S. (2013). Functional properties and health benefits of Lycopene. Nutrición Hospitalaria. https://doi.org/10.3305/nh.2013.28.1.6302
Bolarinwa, I. F., Oke, M. O., Olaniyan, S. A., & Ajala, A. S. (2016). A Review of Cyanogenic Glycosides in Edible Plants. In Toxicology – New Aspects to This Scientific Conundrum. https://doi.org/10.5772/64886
Burns, A. E., Bradbury, J. H., Cavagnaro, T. R., & Gleadow, R. M. (2012). Total cyanide content of cassava food products in Australia. Journal of Food Composition and Analysis. https://doi.org/10.1016/j.jfca.2011.06.005
Duangmano, S., Sae-lim, P., Suksamrarn, A., Domann, F. E., & Patmasiriwat, P. (2012). Cucurbitacin B inhibits human breast cancer cell proliferation through disruption of microtubule polymerization and nucleophosmin/B23 translocation. BMC Complementary and Alternative Medicine. https://doi.org/10.1186/1472-6882-12-185
Egbuonu, A. C. C. (2015). Assessment of some Antinutrient Properties of the Watermelon (Citrullus lanatus) Rind and Seed. Research Journal of Environmental Sciences. https://doi.org/10.3923/rjes.2015.225.232
El-Senduny, F. F., Badria, F. A., EL-Waseef, A. M., Chauhan, S. C., & Halaweish, F. (2016). Approach for chemosensitization of cisplatin-resistant ovarian cancer by cucurbitacin B. Tumor Biology. https://doi.org/10.1007/s13277-015-3773-8
Graham, C. (2021). 15 Watermelon Cocktails and Mocktails for Summer. https://www.thespruceeats.com/tasty-watermelon-cocktail-recipes-4156892
Hannah Ritchie, M. R. (2018). Alcohol Consumption. https://ourworldindata.org/alcohol-consumption
Mohan, V. R., Tresina, P. S., & Daffodil, E. D. (2015). Antinutritional Factors in Legume Seeds: Characteristics and Determination. In Encyclopedia of Food and Health. https://doi.org/10.1016/B978-0-12-384947-2.00036-2
Moreno, J. (2015). Los países que más beben en América Latina: la dramática radiografía del consumo de alcohol en la región. 23 Julio. https://www.bbc.com/mundo/noticias/2015/07/150723_consumo_alcohol_latinoamerica_muertes_paises_jm
Murillo, E., Giuffrida, D., Menchaca, D., Dugo, P., Torre, G., Meléndez-Martinez, A. J., & Mondello, L. (2013). Native carotenoids composition of some tropical fruits. Food Chemistry. https://doi.org/10.1016/j.foodchem.2012.11.014
Nkoana, D. K., Mashilo, J., Shimelis, H., & Ngwepe, R. M. (2021). Nutritional, phytochemical compositions and natural therapeutic values of citron watermelon (Citrullus lanatus var. citroides): A Review. In South African Journal of Botany. https://doi.org/10.1016/j.sajb.2020.12.008
Olayinka, B. U., & Etejere, E. O. (2018). Proximate and chemical compositions of watermelon (Citrullus lanatus (Thunb.) Matsum and Nakai cv red and cucumber (Cucumis sativus L. cv Pipino). International Food Research Journal.
Petry, N., Egli, I., Zeder, C., Walczyk, T., & Hurrell, R. (2010). Polyphenols and phytic acid contribute to the low iron bioavailability from common beans in young women. Journal of Nutrition. https://doi.org/10.3945/jn.110.125369
Riera, A. (2014). ¿Mezclar vino con sandía te mata? https://chequeado.com/mitos-y-enganos/imezclar-vino-con-sandia-te-mata/
Soho. (2021). ¿Se intoxica uno si toma trago después de comer patilla?? Soho. https://www.soho.co/entretenimiento-/articulo/se-intoxica-uno-si-toma-trago-despues-de-comer-patilla/9920#
Touihri-Barakati, I., Kallech-Ziri, O., Ayadi, W., Kovacic, H., Hanchi, B., Hosni, K., & Luis, J. (2017). Cucurbitacin B purified from Ecballium elaterium (L.) A. Rich from Tunisia inhibits α5β1 integrin-mediated adhesion, migration, proliferation of human glioblastoma cell line and angiogenesis. European Journal of Pharmacology. https://doi.org/10.1016/j.ejphar.2017.01.006
Watson, R. R., Preedy, V., & Zibadi, S. (2014). Wheat and Rice in Disease Prevention and Health. In Wheat and Rice in Disease Prevention and Health. https://doi.org/10.1016/C2012-0-00472-3
Zitterman, A. (2003). DIETARY FIBER | Bran. In B. Caballero (Ed.), Encyclopedia of Food Sciences and Nutrition (Second Edition) (Second Edi, pp. 1844–1850). Academic Press. https://doi.org/https://doi.org/10.1016/B0-12-227055-X/00346-1
* N. del E.: Todos los tipos de bebidas alcohólicas, como los vinos tintos y blancos, la cerveza, los cócteles y licores, están asociados al cáncer. Cuanto más beba, mayor será su riesgo de cáncer. Véase El alcohol y el cáncer
El artículo Alcohol y sandía se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El consumo de alcohol para el corazón y las dificultades de divulgar ciencia
- Alcohol, aqua vitae
- Sobre los orígenes de la quimifobia
Granda, Villareal y Losada: Una estampa de los inicios de la matemática en Perú
Alberto Mercado Saucedo
En buena parte de los países de Latinoamérica, la investigación en matemática comenzó a desarrollarse durante el siglo XX, con el nacimiento y desarrollo de universidades y centros de educación, donde la investigación fue convirtiéndose gradualmente en una actividad permanente. Una historia especial es la de la Universidad Nacional Mayor de San Marcos -UNMSM- la más antigua de todo el continente americano, fundada en 1551 por el imperio español y la iglesia católica. Inició funciones en 1553 y durante algunos periodos fue conocida como la Universidad de Lima. Notablemente, es la única del continente que nació en el siglo XVI y que ha funcionado interrumpidamente hasta nuestros días.
Durante la época colonial, la función mas importante de la Universidad de San Marcos era la enseñanza de filosofía, artes y latín. La docencia estaba organizada en distintas cátedras, relacionadas en su mayoría con la existencia de órdenes religiosas. En 1657 se inaugura la Cátedra de Matemáticas, donde principalmente enseñaron astrónomos, y en 1850, ya en la época del Perú independiente, nace la Facultad de Ciencias Naturales y Matemáticas, con lo que se puede considerar que dio inicio la actividad académica en la disciplina de Pitágoras. En esta facultad se otorgaban los grados de Bachiller, Licenciado y Doctor. Para obtener este último grado se debía realizar un trabajo individual, la tesis, usualmente de un año de duración y realizada después de obtener el grado de licenciado.
 Ilustración de Constanza Rojas-Molina. Todos los derechos reservados; cesión en exclusiva para su publicación en el Cuaderno de Cultura Científica.
Ilustración de Constanza Rojas-Molina. Todos los derechos reservados; cesión en exclusiva para su publicación en el Cuaderno de Cultura Científica.En 1866 se otorga por primera vez el grado de doctor en matemáticas en la UNMSM: se gradúa José Granda, quien anteriormente había sido enviado a estudiar a Paris para obtener el título de ingeniero de minas, pero sobre todo aprovechó su estadía para estudiar matemáticas, en las que se interesó cada vez más. José Granda tendría un importante papel en el desarrollo de la disciplina en Perú, y por cierto que también tendría una nieta que se dedicaría a la música y que se convertiría en una compositora mundialmente conocida: Chabuca Granda.
 Juan José de la Granda y Esquivel más conocido como José Granda
Juan José de la Granda y Esquivel más conocido como José GrandaDespués de obtener el grado de doctor, José Granda trabaja como profesor en la Facultad de Ciencias, llamada así desde 1876. El país atraviesa entonces por un complicado conflicto: en 1879 da inicio la Guerra del Pacífico, lo que en particular ocasiona a la vida universitaria innumerables dificultades. En 1881 Lima es ocupada por las tropas chilenas, lo que provoca destrozos y pillaje en la universidad. Tristemente, la Facultad de Ciencias se queda sin lugar físico dónde funcionar, ante lo cual José Granda tiene la generosidad de poner a disposición de la facultad la casa familiar durante el tiempo que sea necesario.
Podemos imaginar que las tesis doctorales realizadas en ese contexto consistían en desarrollos matemáticos paralelos a la investigación que se llevaba a cabo en Europa, dadas las dificultades en la comunicación durante esos tiempos. Quizá en ocasiones se redescubrían teoremas que ya se conocían en otras latitudes, pero también sucedía que se llegaba a resultados científicos realmente originales que no eran adecuadamente apreciados por la comunidad y que no se difundían mayormente.
 Federico Villarreal
Federico VillarrealTal fue el caso de Federico Villarreal, singular e importante personaje de la matemática peruana de fin de siglo XIX. Nació en 1850 e ingresó a la Facultad de Ciencia de la UNMSM en 1877, cuando era profesor de escuela primaria. Obtuvo los grados que otorgaba la institución: bachiller, licenciado y doctor, este último tras realizar su tesis en 1881: Clasificación de las curvas de tercer grado, realizada durante la ocupación de Lima por el ejército invasor chileno. Podemos imaginar a Villarreal trabajando en la casa de Granda, en donde funcionaba la facultad durante ese triste periodo de guerra. De hecho, Villarreal tuvo otras preocupaciones inmediatas además de las curvas cúbicas: se enlistó en el ejército y llegó a combatir en alguna batalla contra el ejército invasor, periodo durante el cual probablemente debió interrumpir su trabajo matemático.
Los trabajos de Villarreal han sido puestos en valor por varias personas dedicadas a las matemáticas y a la historia de Perú. Uno de sus resultados es particularmente destacado: a los 23 años, cuando trabajaba como profesor y aún no ingresaba a la Facultad de Ciencias, encontró una fórmula para elevar un polinomio a cualquier potencia entera, una suerte de generalización del Binomio de Newton (un binomio es un polinomio de dos términos, y la fórmula de Villarreal funciona para cualquier número de términos). Sus resultados originales, pero quizá principalmente esta fórmula, llevaron a la expresión Newton del Perú, que no es raro encontrar en la literatura sobre Villareal. A lo largo de su carrera, tuvo una gran influencia en la vida académica de su país: Después de obtener el grado de doctor, también se convirtió en ingeniero, fue profesor y luego llegó a ser decano de la facultad, rector de la universidad e incluso senador del país. Una universidad nacional lleva su nombre, lo mismo que revistas académicas y varias cátedras. Podemos mencionar algunos nombres de la descendencia académica de Villarreal: Godofredo García fue uno de sus alumnos, se graduó como doctor en 1912 y realizó investigación junto con Alfred Rosenblatt, matemático polaco que llegó a Perú en 1936, y que a su vez tuvo como alumno a José Tola, que también realizó importantes aportes a la matemática del país.
 Cristóbal de Losada y Puga
Cristóbal de Losada y PugaPero aquí quiero detenerme en otro matemático peruano que destacó especialmente la obra de Villareal y que quizá es menos conocido: Cristóbal de Losada y Puga. Acuñó el nombre de polinomio de Villarreal para la fórmula que generaliza el binomio de Newton: es tan perfecto, que aun para el caso de un binomio resulta más fácil y seguro y rápido que el método del binomio de Newton, escribió Losada. Él mismo llegó, por su parte, a realizar investigación en matemáticas de gran nivel y quizá fue el matemático peruano más reconocido por sus pares en el mundo durante aquel tiempo.
Losada nació el 14 de abril de 1894 en New York, de madre y padre peruanos. Tras la muerte de su padre, a sus dos años de vida, se trasladó con su madre a Cajamarca, región andina de Perú de donde ella era originaria. Cristóbal pasó allí toda su infancia y adolescencia. Después de sus estudios medios se tituló como Ingeniero de Minas en la Escuela de Ingenieros de Lima, algo frecuente entre quienes se sentían atraídos por la ciencia. Posteriormente obtuvo el grado de bachiller en ciencias y el de doctor en matemáticas en 1923 en la Universidad Nacional Mayor de San Marcos, con la tesis Sobre las curvas de rodadura. El catálogo de la Biblioteca Nacional de Perú registra la existencia de una copia de su tesis.
Losada trabajó en distintas universidades del Perú, realizó docencia de matemáticas avanzadas, elaboró libros de texto e hizo investigación en matemáticas. Me parece destacable su participación en el Congreso Internacional de Matemáticos de 1924 en Toronto Canadá, donde expuso la charla A short contribution to the kinetic theory of gases en la sección de Mecánica, Física, Astronomía y Geofísica, lo que nos da una idea que la investigación que realizaba estaba conectada con la comunidad internacional. Losada trabajaba en problemas relacionados con Análisis, ecuaciones diferenciales, física-matemática y otros temas.
 Cicloide
CicloideEl término que aparece en el título de su tesis, curvas de rodadura, se refiere a curvas trazadas por un punto en movimiento. Por ejemplo, un punto fijo en una circunferencia que avanza rodando, sin deslizarse, sobre una línea recta o sobre otra figura. Si nos imaginamos la trayectoria que recorre el punto cuando la circunferencia avanza rodando, se formará una curva conocida como la cicloide, quizá la más famosa curva de rodadura. Se pueden obtener otras curvas si el punto no está en el borde de la rueda sino al interior, o incluso fuera de ella: se obtiene una hipocicloide o una epicicloide, respectivamente. Podrá pensarse en un espirógrafo, ese entretenido juguete que consta de distintas figuras que se mueven de manera conjunta y con las que es fácil hacer bonitos dibujos geométricos.
Estas curvas, además de ser llamativas figuras, están relacionadas con propiedades de la física-matemática, razón por la cual aparecen en la tesis de Losada. En efecto, un concepto común a varios fenómenos físicos es el principio de mínima acción: la naturaleza invierte la menor energía posible en realizar una tarea dada. Por ejemplo, una burbuja toma la forma de una esfera, pues así encierra el mayor volumen de aire con una película de área mínima. Un haz de luz se propaga en línea recta, pues es la forma más rápida de ir de un punto al otro; bueno, esto es lo que percibimos a escalas humanas, pues sabemos que la gravedad afecta la luz, cuyo haz se curva de acuerdo con la teoría de la relatividad, lo que de hecho propone otra geometría para el universo donde, de nuevo, el trayecto de luz sigue el camino más rápido.
 Braquistócrona
BraquistócronaUn problema clásico es el de la curva braquistócrona. Lo podemos plantear así: imaginemos que tenemos dos puntos A y B en el espacio, B más abajo que A, y nos preguntamos cuál es la superficie por la que un objeto que se desliza sobre ella bajo solamente el efecto de la gravedad llega desde A hasta B en el menor tiempo posible. Esta pregunta fue planteada desde hace siglos, y fue resuelta a finales del siglo XVII usando las herramientas que proporcionó el cálculo diferencial. En efecto, sucede que el camino más rápido no es una recta, sino una curva: podemos pensar que una forma de aprovechar la gravedad es curvarse al inicio más que al final, para ganar aceleración rápidamente. Esta curva es justamente un arco de cicloide, la curva de rodamiento que mencionamos arriba. Algunas pistas con rampas para patineta (o skate) tienen justamente esa forma, para que el skater pueda tomar la mayor velocidad posible al deslizarse.
Pero regresemos a la historia de Losada: después de exponer en el Congreso Internacional de Matemáticos continuó su trabajo en investigación y escribió textos de análisis matemático que fueron publicados por la Universidad Católica del Perú y que se convirtieron en importantes referencias de Cálculo y Análisis Matemático para las siguientes generaciones de estudiantes del país. En nuestros días, la Pontificia Universidad Católica de Perú otorga la medalla CRISTÓBAL DE LOSADA Y PUGA como parte del Premio Southern-Perú (por la compañía minera que lo patrocina), en su categoría ciencias, que se entrega cada dos años, en memoria de la obra que realizó Losada en las matemáticas. Por cierto, al igual que Federico Villarreal, Losada tuvo a su cargo diversas responsabilidades en la vida pública de su país. Dirigió la revista Fénix e inauguró la Sala de Física Nuclear y Energía Atómica en 1955, luego fue director de la Biblioteca Nacional y ministro de Educación. Una frase que mencionaba frecuentemente: «Los maestros tienen en sus manos el porvenir de los pueblos«. Falleció en la ciudad de Lima el 30 de agosto de 1961.
Hoy, una búsqueda en las bases de datos de revistas internacionales de investigación en matemáticas nos permite encontrar, además de las mencionadas Universidad Nacional Mayor de San Marcos y Universidad Católica de Perú, a la Universidad Nacional de Trujillo, a la Universidad Nacional de Ingeniería y a la Universidad del Pacífico, entre otras instituciones. Granda fue el primer matemático, Villarreal una excepción notable y Losada fue parte de la incursión del Perú en la investigación matemática de nivel mundial. La historia en cuyos inicios participaron ellos tres hoy es protagonizada por todas las personas que se dedican a la disciplina en los centros de investigación y universidades del país, que trabajan en contacto con redes científicas del mundo y hacen crecer cada día a la matemática en el Perú.
Referencias
- Historia de la matemática en el Perú. Moisés Toledo Julián.
- Historia de la matemática peruana. César Carranza.
- Premio Southern-Perú (1996 – 2015) 20 años, 20 peruanos notables. Editor: Salomón Lerner Febres. Equis Equis S.A. 2016.
- Entre la docencia y la academia. La modernización de la Universidad de San Marcos 1860-1928. Alex Loayza. Investigaciones Sociales XII N 20, 2008.
Sobre el autor: Alberto Mercado Saucedo es profesor de matemáticas en la Universidad Técnica Federico Santa María (Valparaíso, Chile)
Sobre la ilustradora: Constanza Rojas Molina es profesora del departamento de matemáticas de la CY Cergy Paris Université (Cergy-Pontoise, Francia)
El artículo Granda, Villareal y Losada: Una estampa de los inicios de la matemática en Perú se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:
