Un retrato alfabético de Srinivasa Ramanujan
El matemático Srinivasa Ramanujan (1887-1920) nació un 22 de diciembre. En el 134 aniversario de su nacimiento le dedico este modesto retrato alfabético.
 Srinivasa Ramanujan. Fuente: Wikimedia Commons.
Srinivasa Ramanujan. Fuente: Wikimedia Commons.
AUTODIDACTA
Con una escasa educación académica en matemáticas, de manera autodidacta, consiguió investigar y contribuir de manera sorprendente y significativa a las matemáticas.
BRAHMANES
Descendía de una familia de brahmanes, una de las castas tradicionales de la India.
Cuaderno perdido de Ramanujan
Anotó gran parte de sus resultados, la mayoría de ellos sin demostraciones, en cuatro cuadernos. El matemático Bruce C. Berndt (1939), autor de Ramanujan’s Notebooks, sostiene que Ramanujan era capaz de demostrar la mayor parte de sus enunciados matemáticos, aunque decidió no hacerlo (debido quizás a la carestía del papel, a que eran apuntes considerados meramente personales o a un estilo de trabajo aprendido). El cuarto cuaderno, el llamado perdido, fue encontrado en 1976: contenía 600 fórmulas escritas durante su último año de vida.
Diario de la Sociedad Matemática de la India
Su primer resultado formal fue publicado en el Diario de la Sociedad Matemática de la India. Trataba sobre las propiedades de los números de Bernoulli: Ramanujan descubrió que los denominadores de las fracciones de números de Bernoulli eran siempre divisibles por seis.
EJEMPLOS
Prefería concentrarse en ejemplos relevantes antes que en construcciones teóricas y pruebas rigurosas.
FRACCIONES CONTINUAS
Realizó aportaciones relevantes en análisis matemático, teoría de números, series y fracciones continuas.
GRAFO DE RAMANUJAN
Un grafo de Ramanujan es un tipo de grafo regular. Lleva este nombre en alusión a la llamada conjetura de Ramanujan-Petersson que se usó en la construcción de algunos de estos grafos.
HARDY
El 8 de febrero de 1913, el matemático británico Godfrey Harold Hardy (1877-1947) escribió una carta a Ramanujan expresando su interés por su trabajo. Comenzó una fructífera colaboración entre ambos científicos, a pesar de sus métodos de trabajo tan distantes.
INDIA
La India fue el país de origen de Ramanujan.
Janakiammal
El 14 de julio de 1909, se casó con Janakiammal (1899-1994), una niña de diez años que su madre había elegido para él un año antes.
Kumbakonam
Aunque nació en Madrás, pasó gran parte de su infancia en Kumbakonam (distrito de Thanjavur, estado de Tamil Nadu) y allí fue donde falleció.
Littlewood
El matemático británico John Edensor Littlewood (1885-1977) decía de Ramanujan: Creo que es al menos un nuevo Jacobi. Junto a Hardy, Littlewood colaboró con el matemático indio durante los años que pasó en Inglaterra.
Método del círculo de Hardy-Littlewood
El trabajo de Ramanujan y de Hardy en teoría de particiones (ver la letra P) dio lugar a un método para la búsqueda de fórmulas asintóticas, denominado el método del círculo de Hardy-Littlewood.
NÚMERO PRIMO DE RAMANUJAN
Es un número primo que satisface cierto resultado demostrado por Ramanujan relativo a la función contador de números primos.
OBRA
La obra matemática de Ramanujan es inmensa. Entre otras llevan su nombre la constante de Landau-Ramanujan, la función theta de Ramanujan, las identidades de Rogers-Ramanujan, la constante de Ramanujan-Soldner, la suma de Ramanujan, la ecuación de Ramanujan–Nagell, laconjetura de Ramanujan–Petersson, elgrafo de Ramanujanola función tau de Ramanujan.
PARTICIONES
Las particiones de un número entero n son el número de sus posibles descomposiciones en sumas de enteros positivos. Por ejemplo, las particiones de 4 son 5, ya que 4 = 1+1+1+1 = 2+1+1 = 3+1 = 2+2 = 4. n aumenta el número de particiones crece rápidamente: si n=200, las particiones de n son ¡3 972 999 029 388! Hardy y Ramanujan lograron hallar una fórmula asintótica para calcular las particiones de cualquier número.
 Cartel de una de las representaciones de Partition. Imagen: University of California, Berkeley.
Cartel de una de las representaciones de Partition. Imagen: University of California, Berkeley.
La obra de teatro Partition del dramaturgo Ira Hauptman tiene a Hardy y Ramanujan como protagonistas: el título se refiere tanto a la teoría matemática de las particiones de números como a las particiones (en el sentido de antagonismo) de temperamento, de cultura y de método matemático que los distanciaron.
QUÍNTICA
Ramanujan aprendió a resolver ecuaciones cúbicas en 1902 y encontró su propio método para resolver las cuárticas. Al año siguiente, sin saber que las quínticas no podían resolverse por radicales, trató de hacerlo, por supuesto, sin conseguirlo.
Royal Society
Propuesto por trece matemáticos, entre los que estaban Hardy y Littlewood, el 2 de mayo de 1918 fue aceptado como miembro de la Royal Society.
SERIE DE RAMANUJAN-SATO
Las series de Ramanujan-Sato generalizan las fórmulas sobre pi de Ramanujan.
TAXICAB
El n-ésimo número taxicab es el menor número que puede expresarse como una suma de dos cubos positivos no nulos de n maneras distintas (sin contar el orden). El nombre de estos números proviene de una anécdota entre Hardy y Ramanujan: el matemático indio estaba ingresado en un hospital cerca de Londres y recibió la visita de Hardy que le contó que había llegado allí en un taxi (taxicab, en inglés) cuya matrícula era un número poco interesante, el 1 729. Ramanujan le replicó: No diga usted eso. El número 1 729 es muy interesante, pues es el número más pequeño expresable como suma de dos cubos de dos maneras diferentes, ya que 1 729 = 13+123 y también 1729 = 93+103. Es decir, 1 729 es el número taxicab correspondiente a n=2.
UNIVERSIDAD DE CAMBRIDGE
Ramanujan redactó cartas dirigidas a los principales matemáticos de la Universidad de Cambridge, y consiguió investigar allí a partir de 1914.
VEGETARIANO
Era un Brahmán ortodoxo y, por ello, un vegetariano estricto.
WILL HUNTING
La películaEl indomable Will Huntingmenciona a Ramanujan en una escena en la que el profesor Gerald Lambeau habla de la genialidad de Will Hunting comparándolo con el matemático indio.
XX
Ramanujan nació el 22 de diciembre de 1887 y falleció el 26 de abril de 1920. Es probablemente uno de los más fructíferos matemáticos del siglo XX.
YO
Hardy, tras ver unos resultados de Ramanujan sobre fracciones continuas, comentó: … yo nunca había visto antes nada parecido en absoluto.
ZETA
Hardy escribió sobre Ramanujan: Era un hombre capaz de resolver ecuaciones modulares y teoremas de un modo jamás visto antes, su dominio de las fracciones continuas era superior a la de todo otro matemático del mundo; ha encontrado por sí solo la ecuación funcional de la función zeta y los términos más importantes de la teoría analítica de los números…
Referencias
-
J J O’Connor and E F Robertson, Srinivasa Ramanujan, MacTutor History of Mathematics archive, University of St Andrews
-
Antonio Córdoba y Ágata Timón G. Longoria, La intuición matemática de Ramanujan, Café y teoremas, El País, 2 junio 2016
-
Srinivasa Ramanujan, Wikipedia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Un retrato alfabético de Srinivasa Ramanujan se ha escrito en Cuaderno de Cultura Científica.
Cómo usar uranio para saber si un neandertal pintó en una cueva
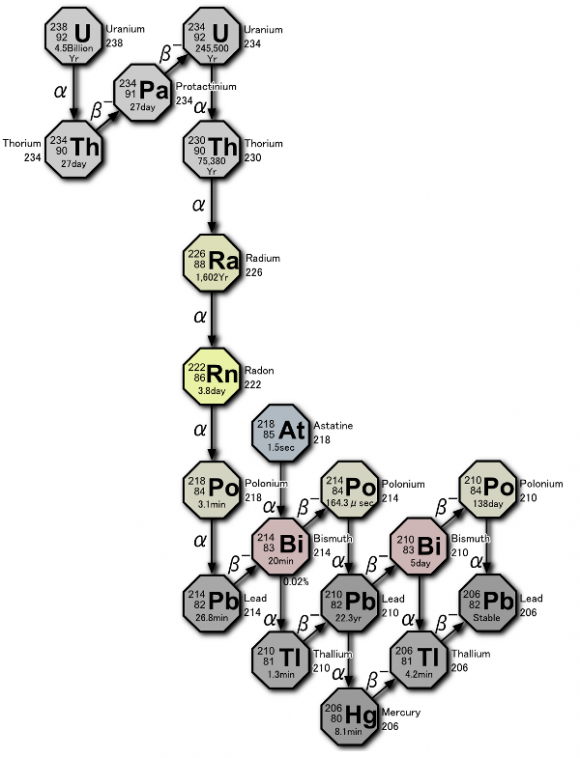 Serie de desintegración del uranio. Fuente: Wikimedia Commons
Serie de desintegración del uranio. Fuente: Wikimedia CommonsEn la última década ha habido mucho revuelo mediático con la posibilidad de que los neandertales hubiesen tenido la oportunidad de ser los pintores de Altamira y otras 10 cuevas del norte de España. Pero, ¿cómo podemos fechar la antigüedad de una puntura en la pared de una cueva? Un método que se emplea mucho es la datación por serie U.
Vamos a explorar la base teórica (incluidas las matemáticas) del mismo, que es muchísimo más sencilla que la experimental, porque si bien no hay nada más práctico que una buena teoría, también es cierto que aún no debiendo haber teóricamente diferencia entre teoría y práctica, en la práctica, la hay. [*]
Las investigadoras emplean los ratios entre los isótopos uranio-234 y torio-230 para datar los depósitos de calcita sobrepuestos a las pinturas para calcular la edad mínima de las mismas. Los resultados, con edades mínimas en el entorno de los 40.000 años de antigüedad, abren distintas posibilidades. Como se supone que Homo sapiens sapiens no migró a Europa hasta hace poco más de 40.000 años es probable que trajese sus habilidades artísticas africanas con él y decorase las cuevas poco después de llegar o, quizás, las pinturas más sencillas y antiguas fuesen de hecho la obra de neandertales.
La datación uranio-torio es especialmente interesante en el análisis de carbonatos cálcicos, como la calcita, ya que ninguno de los elementos puede escapar del mineral, ni otros átomos de ellos pueden entrar, una vez se ha formado. En las condiciones de formación de las calcitas el uranio es soluble mientras que el torio no lo es, por lo que cuando se forma el depósito mineral contendrá uranio pero no torio. La cantidad del isótopo U-234, que es el isótopo que por desintegración alfa se convierte en torio 230, que podemos esperar tener en una calcita recién formada es del orden de partes por millón o inferiores. Suponiendo que sepamos la cantidad original de uranio presente en la muestra, necesitamos poder calcular cuánto Th-230 tendremos pasado un tiempo a partir de una determinada cantidad de U-234 para tener un método para determinar el tiempo transcurrido.
Imaginemos que el isótopo A se desintegra para dar B, por el proceso que sea: A → B. La desintegración de un núcleo inestable es algo completamente aleatorio y es imposible predecir cuándo un átomo en concreto se va a desintegrar. Sin embargo, la probabilidad es igual en cualquier tiempo t. Si tenemos un número N de núcleos de un isótopo concreto, transcurrido un tiempo infinitesimal, que llamaremos dt, se habrán desintegrado un número infinitesimal de núcleos, dN, quedando N-dN. Por otra parte, el número de desintegraciones que se produce en la unidad de tiempo, -dN/dt (con signo negativo porque son núcleos de ese isótopo que desaparecen), debe ser proporcional al número de nucleones presente, igual que en una sala en silencio el número de toses es proporcional al número de personas presentes, como bien saben los músicos de clásica. Así, si llamamos a la constante de proporcionalidad característica de ese isótopo λ, podemos escribir:
-dN/dt = λN
Esto es una ecuación diferencial muy sencillita que no es más que escribir en forma matemática la frase “la desaparición de nucleones con el tiempo es proporcional al número de nucleones”. Esta ecuación tiene como solución [**]:
N = N0e-λt , donde N0 es el número de átomos pata t = 0. [1]
Sin embargo, el sistema U-234 – Th-230 no es tan sencillo, puesto que el Th-230 también se desintegra. Estamos entonces ante esta situación: A → B → C. El razonamiento es análogo: si tengo N núcleos, pasado un tiempo infinitesimal dt, tendré N+dN núcleos.
En este caso escribo +dN, porque dN puede ser positivo o negativo, dependiendo de si se forman más núcleos de los que se desintegran o al revés. En cualquier caso, la variación en el número de núcleos será los que se forman menos lo que se desintegran, por tanto, usando [1]:
dNB/dt = λANA– λBNB = λAN0Ae -λAt – λBNB
Esto sigue siendo una ecuación diferencial nada complicada, que se puede comprobar que tiene como solución:
NB = (NA0 λA) / (λB – λA) · (e -λAt – e -λBt) [2]
En pura teoría ya tenemos la ecuación que buscábamos. Si conocemos las constantes de los isótopos U-234 (que ocupa el lugar de A) y del Th-230 (B), que las conocemos, tendríamos un método para medir la antigüedad de los depósitos de calcita.
La inteligente lectora que haya llegado hasta aquí se habrá dado cuenta de que venimos arrastrando un problema no menor desde el principio: ¿cómo sabemos qué cantidad había al comienzo del isótopo A, lo que hemos llamado NA0? Simplemente, no lo sabemos, ni lo podemos saber con suficiente precisión. Por eso un método de datación que se base en una serie radioactiva sólo es válido si uno de los núcleos es estable (λB = 0) o, como el caso de U-234 y Th-230, que se cumpla que λA es distinto de cero pero mucho menor que λB.
Entonces [2] queda reducida a
NB / NA ≈ λA / λB (1 – e -λBt) [3]
Ya que también en este caso, NA ≈ NA0.
Vemos pues que si medimos por espectrometría de masas el ratio Th-230/U-234 tenemos una forma directa de medir el tiempo desde que se formó la calcita con un error más que razonable. Sólo nos quedará corregir por la cantidad de U-238 que se convierta en U-234, pero eso es más de lo mismo (se deja como ejercicio).
Observando la ecuación [3] vemos una de las limitaciones del método: para tiempos suficientemente grandes NB / NA tiende a un valor constante λA / λB, es lo que se denomina equilibrio secular (se forma tanto Th-230 como se destruye). De aquí que el método uranio-torio no puede datar más allá de 500.000 años, aproximadamente.
Nota:
[*] Los conceptos empleados en este texto pueden encontrarse desarrollados sin matemáticas y de forma muy sencilla en nuestra serie El núcleo
[**] La comprobación de que esto es cierto debería estar al alcance de cualquier persona que haya cursado matemáticas de bachillerato.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este texto se publicó en Naukas el 22 de junio de 2012.
El artículo Cómo usar uranio para saber si un neandertal pintó en una cueva se ha escrito en Cuaderno de Cultura Científica.
Un viejo matrimonio: música y algoritmo
José Manuel González Gamarro
 Foto: Jesus Hilario H. / Unsplash
Foto: Jesus Hilario H. / UnsplashDesde que vivimos en primera persona la era digital hemos ido asumiendo nuevas (o viejas) palabras que se han hecho habituales en nuestro día a día, ya sea porque las hemos empezado a usar de manera más frecuente o porque las personas de nuestro entorno o las que habitualmente leemos las han subido a la categoría de lo cotidiano. Una de esas palabras es «algoritmo». Una palabra que, hasta hace relativamente poco, solo usaban matemáticos o informáticos y que ahora redescubrimos y la leemos con frecuencia gracias a cosas como las redes sociales. Gracias al desarrollo de las tecnologías y a ciertos cambios de paradigmas en el ámbito artístico, también la música se ha visto afectada por esta corriente de innovación, muy ligada, obviamente, a la inteligencia artificial. Todo esto que nos suena a pura innovación científica y tecnológica no es más que una actualización constante de ideas antiquísimas. La unión entre algoritmo y música es antigua y su relación ha ido evolucionando, ganando en profundidad y repertorio.
Simplificando mucho, un algoritmo es, en esencia, un conjunto prescrito de instrucciones. Estas instrucciones son reglas bien definidas, ordenadas y finitas que hacen posible llevar a cabo una actividad mediante pasos sucesivos. Escrito así no parece tan innovador ni revolucionario. De hecho, esta forma de pensar algorítmica es bastante antigua, que ya podemos localizar en los trabajos del astrónomo persa conocido como al-Juarismi, nombre del que deriva la propia palabra actual «algoritmo». Pero no solo los persas tenían mentes privilegiadas, ya que, en la Europa más cercana, en Italia concretamente, tenemos al monje benedictino Guido D’Arezzo (ca.991-1033). Los músicos profesionales lo conocen por su aportación a la escritura musical y el famosísimo nombre de nuestras notas musicales. Sin embargo, Guido también es una referencia fundamental en la creación del viejo matrimonio entre música y algoritmo. Diseñó un sistema de generación automática de melodías en base a textos. Se mapeaban las vocales a diferentes notas de la escala, creando un método de composición melódica. Investigaciones actuales han desarrollado este método.1
Si avanzamos un poco más en la historia, nos encontramos a dos compositores del s. XIV, Philippe de Vitry y Guillaume de Machaut, dos reconocidos autores franceses. Ellos practicaron un tipo de composición llamada motete isorrítmico, basado en dos ideas básicas: el color y la talea. El color es el conjunto de los sonidos (únicamente las alturas) que van a intervenir en la pieza. La talea es un patrón rítmico que no coincide en extensión con el color. La pauta rítmica solía ser más corta que la melódica, interfiriendo una con otra. El resultado es azaroso, pero dentro de un entorno controlado. No está nada mal para los años en torno a 1300. Un par de siglos hacia adelante, nos encontramos al autor Ghiselin Danckerts (c. 1510-1567), que usó para la composición los movimientos de las piezas del tablero de ajedrez. Como se puede ver en la imagen, cada casilla poseía un motivo melódico y una letra para cantarlo.
 Ajedrez musical. Ghiselin Danckerts. Fuente: Wikimedia Commons
Ajedrez musical. Ghiselin Danckerts. Fuente: Wikimedia Commons
El propio autor dejó escrito que eran posibles 20 cánones a 4 voces, pero al morir la información para descifrarlos no se conservó y no fueron descubiertas todas las soluciones hasta 1986.
Ya en el siglo XVII, el gran Atanasius Kircher creo una máquina fascinante capaz de crear canciones sin que fueran necesarios conocimientos musicales. Todo un invento revolucionario para ayudar a los misioneros a inventar canciones en función de la ocasión y las necesidades del momento. La máquina tenía 10 parámetros, como el ritmo, número de sílabas, sonidos, etc. Mediante tablas se programaba para satisfacer la carga emocional adecuada para el texto. Todo un artilugio de ingeniería, como se puede apreciar en la imagen, que funcionaba de manera parecida a un ordenador.
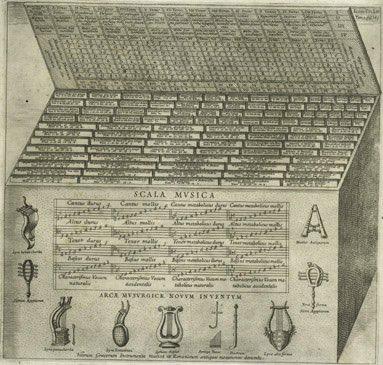 Arca Musarithmica. Atanasius Kircher. Fuente: Wikimedia Commons
Arca Musarithmica. Atanasius Kircher. Fuente: Wikimedia Commons
Los resultados del algoritmo de Kircher tienen muchísimas similitudes a lo que se obtiene modernamente con los modelos matemáticos de Markov.2 A medida que la historia sigue avanzando y nos adentramos en el s. XVIII nos damos de lleno con el conocido compositor W. A. Mozart. El gran compositor austriaco, junto con otros compositores, se sumaron a una especie de moda que surgió, creando un juego para crear música con unos dados sin necesidad de tener conocimientos musicales. Este juego editado como partitura y con unas instrucciones para poder realizar la composición se titula Instrucciones para componer tantos valses como desee mediante dos dados sin entender nada de música o composición. Tanto Mozart como sus colegas sabían que en las tiradas de los dados todos los resultados no eran igualmente probables. Resulta llamativo el hecho de que no fue hasta años después que Poisson formuló su teoría de la distribución de la probabilidad. El juego consistía en escribir compases sueltos, en el caso de Mozart 176, y asignarlos a los resultados de las tiradas mediante una tabla, tal como se ve en la imagen.
 Op. K516f. Wolfgang Amadeus Mozart. Fuente: Wikimedia Commons
Op. K516f. Wolfgang Amadeus Mozart. Fuente: Wikimedia Commons
Todos los posibles valses (214.358.881 combinaciones posibles tan solo en el primer cuadro) se parecen, pero todos son diferentes, lo cual era la intención de Mozart porque así lo que estaba creando era el estilo, es decir, se podían componer valses al estilo de Mozart sin tener conocimientos, solo tirando dos dados. Este algoritmo en base a la aleatoriedad y la distribución de probabilidad se puede probar aquí haciendo tiradas de dados y escuchando el resultado.
A medida que el tiempo transcurre y llegamos a la Revolución Industrial el concepto «máquina» y su necesidad para la sociedad se hace patente. Una de las consecuencias de este momento histórico es la creación de la máquina analítica, que también tuvo su aplicación teórica en la música. Esta máquina analítica fue creada por Charles Babbage (1791-1871), y pretendía que fuese programable para realizar cualquier tipo de cálculo. La idea está basada en un telar programable de un comerciante francés conocido como el telar de Jacquard. La relación de todo esto con la música proviene de las sinergias entre Charles Babbage y la matemática y escritora Ada Lovelace (1815-1852). Esta ilustre matemática hizo un estudio teórico sobre la máquina llegando a mencionar una aplicación en la música del algoritmo creado. Pensó que si se sometían las relaciones de los sonidos y sus reglas a las normas prescritas del algoritmo podrían crearse obras musicales con una extensión y complejidad programables. Además, se crearían de manera automática.
En el s. XX se empezaron a estudiar los procesos de funcionamiento de la inteligencia humana para poder elaborar sistemas que la imitasen. De esta manera se establecerían modelos de aprendizaje. Este hecho también tuvo su relación con la música, haciendo que los ordenadores se emplearan en la ardua tarea de componer música a partir de algoritmos. En 1957 encontramos la primera obra compuesta íntegramente por un ordenador titulada Illiac Suite, un cuarteto de cuerda con cuatro movimientos.3 Dos profesores de la universidad de Illinois (Lejaren Hiller y Leonard Issacson) desarrollaron varios algoritmos para que el ordenador fuera capaz de semejante empresa. Por estos años, ya había empezado también el compositor e ingeniero Iannis Xenakis a desarrollar programas de cálculo probabilístico para aplicar en sus obras musicales. En 1977 terminó de crear UPIC, que en esencia era una mesa de arquitecto convertida en tablet. Mediante un bolígrafo electrónico convertía el dibujo en música mediante algoritmos. Toda esta época vivió un auge de la relación entre música y algoritmos o bien de la sinergia entre matemáticas y música. A esto también contribuyó el matemático polaco Benoît Mandelbrot con el concepto de fractal. Las dos propiedades básicas de este concepto matemático son la autorreferencia y la autosimilitud, que han sido fundamentales para la creación de obras más recientes, como por ejemplo Liturgia fractal, del compositor Alberto Posadas.
Los algoritmos empleados en la música son de diferente índole, llegando incluso a la biomimética, imitando modelos de la naturaleza. Tal es el caso de los algoritmos genéticos, que fueron empleados en la universidad de Málaga para que el ordenador Iamus compusiera música sin intervención humana. Se denominó el proyecto Melomics. Existen otros algoritmos que no están relacionados con la composición de música, sino con su análisis. Con esto se pueden obtener una cantidad ingente de datos de un gran número de partituras a la vez. Es posible obtener la matriz serial de obras dodecafónicas (que utilizan una serie de doce sonidos como materia prima musical) o bien análisis armónicos de grandes corpus de obras. Además, estos análisis se pueden usar para saber la autoría de alguna obra anónima de la que se tengan dudas de quién es el compositor. Estos algoritmos identifican multitud de variables relacionadas con cada compositor, calculando estadísticamente cual sería la probabilidad de que fuera un autor u otro. Huelga decir que aciertan casi en el 100% de los casos. Sin embargo, las sinergias entre ingenieros, matemáticos, físicos, etc. y músicos no se quedan en la composición y el análisis, sino que la relación con los algoritmos va más allá, llegando al mundo de la interpretación.
¿Es posible que una máquina pueda interpretar la música de manera expresiva y «humana»? Se pueden determinar los criterios que distinguen una interpretación expresiva de una automatizada4, mediante software que analiza interpretaciones de concertistas. Cualquier músico profesional sabe que hay criterios interpretativos que no aparecen en las partituras de forma exacta. Lo invisible pero audible de la partitura. Los simuladores informáticos optimizan y definen códigos emocionales. El ordenador no copia lo que hace un intérprete, sino que realiza su propia interpretación a partir de algoritmos. Esto puede causar revuelo o controversia en el mundo de los músicos profesionales, pero si se escucha aquí esta interpretación de una sonata de Beethoven, nos queda claro que una interpretación mecánica queda bastante lejos y nos costaría saber si es un humano o una máquina si no fuéramos advertidos de ello.
Los algoritmos y la música son inseparables si queremos entender en profundidad la historia de la música occidental. La inteligencia artificial desarrollada en los últimos años hace que se replanteen nuevos paradigmas en el entendimiento filosófico del arte, traspasando los límites de lo humano. El hijo de este viejo matrimonio podría ser una distopía artística sin precedente o bien un escalón más en el avance de la humanidad con respecto a su arte más temporal. Hagan sus apuestas.
Referencias:
1 Trufó, Francisco. Algorithmic composition using an extension of Guido D’Arezzo Method, 2009.
2 McLean, Alex, and Roger T. Dean, eds. The Oxford handbook of algorithmic music. Oxford University Press, 2018. 3 Sandred, Orjan; Laurson, Mikael; Kuuskankare, Mika. “Revisiting the Illiac Suite-a rule-based approach to stochastic processes.”Sonic Ideas/Ideas Sonicas 2 (2009): 42-46. 4 Cancino-Chacón, Carlos E., et al. “Computational models of expressive music performance: A comprehensive and critical review.” Frontiers in Digital Humanities 5 (2018): 25. 
Sobre el autor: José Manuel González Gamarro es profesor de guitarra e investigador para la Asociación para el Estudio de la Guitarra del Real Conservatorio Superior de Música “Victoria Eugenia” de Granada.
El artículo Un viejo matrimonio: música y algoritmo se ha escrito en Cuaderno de Cultura Científica.
Pirocúmulos, los temibles aliados de los incendios forestales
Onintze Salazar Pérez
17 de junio de 2017. Una carretera rural del centro de Portugal, la EN 236-1 en Pedrògão Grande, en el departamento de Leiria. Son las 14:30 y en el exterior el termómetro se acerca a los 42°C a la sombra. La carretera atraviesa un bosque de pinos y eucaliptos que arrastra un importante déficit de lluvia. La sequía es palpable a ambos lados. Y hace calor, mucho calor.
Avanza la tarde y en el cielo empiezan a verse las primeras nubes de tormenta. Nubes que nacen, se desarrollan y mueren en una misma zona y que reciben el nombre de cumulonimbos. A priori, no es mala noticia. Estas tormentas podrán traer la tan necesaria lluvia y harán que la temperatura descienda.
Comienza el juego de luces. Relámpagos que iluminan en fracciones de segundo el sediento bosque. Pero no llueve y los relámpagos se hacen cada vez más numerosos. Un rayo que impacta en el bosque, no muy lejos de la carretera de Pedrògão Grande, hace sobresaltar a los ocupantes de los coches que por allí circulan. Al rato, comienzan a verse los primeros focos de fuego. El bosque comienza a arder. Arde mientras los habitantes de la zona y los que por allí pasaban comienzan a huir. Y lo hacen por esa misma carretera por la que, según los indicios, el fuego no va a propagarse.
Sin embargo, esa tarde de junio, el incendio forestal se llevó por delante 67 vidas, la mayoría ocupantes de los coches que trataban de huir del infierno por esa carretera del centro de Portugal. El fuego les cerró las vías de escape en pocos minutos y murieron calcinados. Un incendio forestal originado por una tormenta seca que se volvió absolutamente imprevisible y voraz.
 Foto: Lucilia Monteiro / Expresso
Foto: Lucilia Monteiro / ExpressoTormentas secas
Seguramente pocos habían oído hablar de las tormentas secas o tormentas eléctricas secas. Se trata del mismo fenómeno de las tormentas “habituales”, con sus cumulonimbos y sus descargas eléctricas, pero en este caso, la diferencia se encuentra en la precipitación. Sí se produce, pero no llega a tierra. En determinadas situaciones, si la temperatura del aire que se sitúa debajo de los cumulonimbos es muy alta y la humedad muy baja, la precipitación, en su camino a tierra, se evapora.
A pesar de que la lluvia no llegue a tocar tierra, las descargas eléctricas, fruto de la separación de las cargas eléctricas dentro de la nube, sí se producen. Y son las que se dirigen a la superficie las que presentan peligro, en especial si la vegetación contra la que impactan está muy seca. Es así como, con mayor probabilidad y según los estudios realizados, se originó el incendio de Portugal esa sofocante tarde de junio. Las tormentas secas aportaron la chispa necesaria, mientras que la seca vegetación se convirtió en el combustible ideal.
Pirocúmulos y pirocumulonimbos
Pero la tormenta seca no fue la única causa del mortal desenlace. Y es que los incendios forestales cuentan con más armas, que las utilizan si sus dimensiones y las condiciones atmosféricas reinantes son las idóneas. Hablamos de los pirocumulos y los pirocumulonimbos. Nubes bautizadas como flammagenitus por la Organización Mundial de Meteorología desde que en 2017 actualizó su Atlas Internacional de Nubes.
Así, se denominan cumulus flammagenitus o cumulunonimbus flammagenitus a las nubes convectivas de tipo cúmulo o cumulonimbo cuyo origen se encuentra en los incendios forestales y en las erupciones volcánicas. Sin embargo, es más habitual referirse a ellas como pirocúmulos y pirocumulonimbos.
 Foto: NASA
Foto: NASAEsa tarde de junio en Pedrògão Grande la formación de pirocumulonimbos resultó ser un factor clave en el desencadenamiento trágico de los hechos. Contra todo pronóstico, el incendio se volvió, no solo mucho más virulento, sino que, además, imprevisible en su desplazamiento. Así, surgieron nuevos focos y un gran frente de fuego de unos 4 km de longitud, originados lejos del foco inicial. Este frente se propagó hacia la carretera por la que tantos vecinos intentaban huir y que, en principio, se encontraba fuera de la ruta del avance de las llamas.
Más rayos y fuertes vientos
El calor originado por el foco inicial en su ascenso por la atmósfera, se encontró con el suficiente aire frío para que el vapor de agua, principalmente resultante de la combustión, permitiera la formación de nubes. Nubes que crecieron en la vertical convirtiéndose en cúmulos primero, y cumulonimbos posteriormente. Cuando estas nubes se encuentran con la tropopausa (límite entre la troposfera y la estratosfera), generalmente no pueden crecer más hacia arriba y comienzan a crecer en la horizontal, de manera que se extienden sobre zonas lejanas al foco inicial.
Es precisamente lo que se concluye que ocurrió en Pedrògão Grande. El pirocumulonimbo que se formó generó nuevos focos lejos del origen del incendio, provocados tanto por la posible caída de nuevos rayos como por los desplomes de aire que se producen al descargar precipitación.
Otro elemento fundamental en la propagación de los incendios forestales, el viento, también tienen su origen en estas tormentas. La precipitación que parte de la base de la nube, llegue o no a tocar suelo, se evapora en su descenso al encontrarse con aire más cálido. Para evaporarse, las gotas de agua roban calor al ambiente, por lo que el aire bajo la nube se enfría muy rápidamente. Ese aire frío, al ser más denso y, por tanto, pesar más, tiende a descender, en este caso, de manera muy rápida. Estos vientos fuertes que se originan en las tormentas y reciben el nombre de downburst, pueden tomar cualquier dirección tras llegar a la superficie y dificultan enormemente las tareas de extinción.
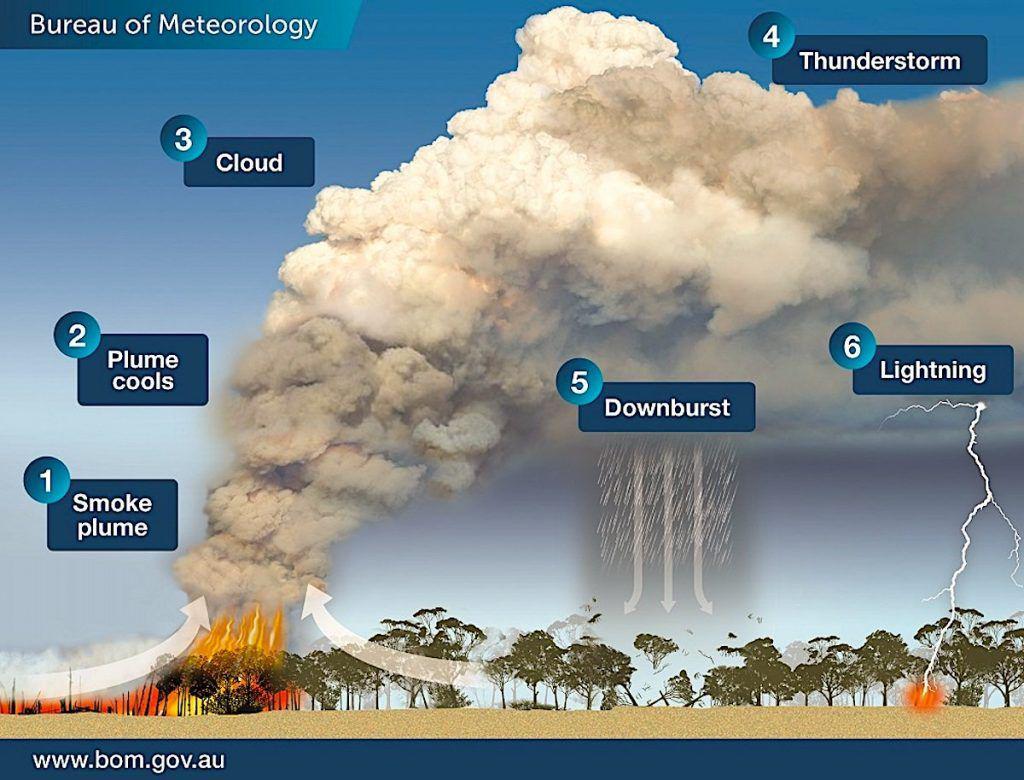 Bureau of Meteorology, Australian Government
Bureau of Meteorology, Australian Government
Además de servir como elemento de propagación, el viento también aviva el fuego, ya que le inyecta oxígeno. Los downburst son más fuertes cuánto más desarrollo tenga el cumulonimbo, pero tanto el lugar donde se van a producir, como la dirección que estas corrientes vayan a tomar una vez llegan a tocar suelo, son altamente imprevisibles. Así, el desarrollo de pirocumulonimbos en los incendios forestales los convierte en muy peligrosos y su control y extinción se complica enormemente.
El incendio de Australia
El incendio de Portugal no es el único ejemplo que sobrecoge por sus dimensiones y sus graves consecuencias. En los últimos años han sido numerosos los incendios forestales que han afectado a grandes extensiones en diferentes partes del planeta. Uno de los más llamativos, por su extensión, virulencia y duración fue el que mantuvo en máxima alerta a buena parte del oeste de Australia entre octubre de 2019 y enero de 2020. Más de 90 días en los que las llamas quemaron millones de hectáreas y obligaron a desplazarse o directamente acabaron con la vida de aproximadamente 3 millones de animales.
A lo largo de todos esos días se formaron diversos pirocúmulos y pirocumulonimbos que llamaron la atención de los medios de comunicación. Pero, al margen de la belleza de estas nubes, su aparición elevó el riesgo del ya de por sí peligroso incendio.
 Foto: Meganesia / Wikimedia Commons
Foto: Meganesia / Wikimedia CommonsAustralia y, en especial, el oeste de Australia estaba sufriendo una larga y prolongada sequía, además de temperaturas inusualmente altas. 2019 resultó ser el año más seco y más cálido en el país, llegando incluso a batir récords de temperaturas máximas más altas en verano (49,9°C en Nullarbor, en diciembre de 2019).
El cambio climático
Sequías y olas de calor como las que sufría el centro de Portugal en la primavera de 2017 o Australia en el verano de 2019-2020, conforman el marco perfecto para el origen de importantes incendios forestales. Sequías y olas de calor cada vez más severas, más duraderas y más frecuentes. Es el nuevo escenario en el que vivimos como consecuencia del calentamiento global, sin esperanza ya de que pueda mejorar. Según el último informe del IPCC, si se supera en más de 2°C la temperatura media global en superficie con respecto a los niveles de la época preindustrial, y no estamos muy lejos, en la región mediterránea aumentará más del 50% la superficie quemada como consecuencia de los incendios forestales. Más incendios forestales, con mayor probabilidad de que formen pirocúmulos y, por tanto, con una mayor dificultad para su control y extinción.
Seguramente el único responsable de la gran mortalidad del incendio de Portugal no fuera el cambio climático (la gestión de los suelos, los planes de prevención y extinción de incendios forestales, entre otros, parecen haber tenido su peso en las fatales consecuencias). En cualquier caso, en el futuro vamos a tener que enfrentarnos a este tipo de incendios forestales con mayor frecuencia. Y será clave poder predecir la formación, el desarrollo y el comportamiento de estos temibles aliados de los incendios forestales, los pirocúmulos.
Referencias:
- Taking the pulse of pyrocumulus clouds.
- Estudio sobre el comportamiento explosivo del fuego en incendios forestales. (pág. 26-28)
- Fire growth patterns in the 2017 mega fire episode of October 15, central Portugal.
- California’s Creek Fire Creates Its Own Pyrocumulonimbus Cloud
- Las posibles causas de los incendios pavorosos en Portugal.
- Wildfires and global change.
- Relatório condições meteorológicas associadas ao incêndio de Pedrógão Grande de 17 junho 2017. Instituto Português do Mar e da Atmosfera
- El cambio climático y la tierra. Resumen para responsables de políticas.
- El incendio de Sierra Bermeja es el primero de sexta generación en España: por qué y cómo se clasifican los grandes fuegos forestales
Sobre la autora: Onintze Salazar Pérez es física y meteoróloga en Euskalmet, Agencia Vasca de Meteorología
El artículo Pirocúmulos, los temibles aliados de los incendios forestales se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2021: José Antonio Prado Bassas – Dando vueltas al compás
El gran evento de divulgación Naukas regresó a Bilbao para celebrar su décima edición en el magnífico Palacio Euskalduna durante los pasados 23, 24, 25 y 26 de septiembre.
En matemáticas, un número construible es aquel que puede representarse mediante finitas operaciones de sumas, restas, multiplicaciones, divisiones y raíz cuadrada de enteros. Tales números corresponden a los segmentos que se pueden construir con regla y compás, son la ligazón entre álgebra y geometría. Cuando no existía el álgebra y los matemáticos eran geómetras empeñados en usar solo una regla sin marcar y un compás, tres problemas sobresalieron por imposibles: duplicación del cubo, trisección del ángulo y cuadratura del círculo. Andando el tiempo la construcción del heptágono regular se uniría al grupo. El concepto de número construible nos da el porqué y José Antonio Prado Bassas nos lo explica.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2021: José Antonio Prado Bassas – Dando vueltas al compás se ha escrito en Cuaderno de Cultura Científica.
Los volcanes submarinos de Bizkaia y Gipuzkoa
Fernando Sarrionandia-Ibarra Eguidazu
 Vistas desde las Peñas de Aya (Aiako Harria), con parte del Golfo de Bizkaia arriba a la derecha. Como referencia puede distinguirse la isla de Santa Clara en la bahía de La Concha (San Sebastián / Donosti). Las rocas en primer término son de origen magmático.
Vistas desde las Peñas de Aya (Aiako Harria), con parte del Golfo de Bizkaia arriba a la derecha. Como referencia puede distinguirse la isla de Santa Clara en la bahía de La Concha (San Sebastián / Donosti). Las rocas en primer término son de origen magmático.La erupción en el volcán Cumbre Vieja (La Palma) ha despertado un inusitado, pero a la vez comprensible, interés por el vulcanismo. Las impactantes imágenes que ofrecen los volcanes se hacen noticia cada vez que entran en erupción. Sin embargo, la mayor parte de la actividad volcánica terrestre se desarrolla en los fondos oceánicos, donde son casi diarias las erupciones. Esa importante actividad volcánica submarina, que genera una inmensa cantidad de depósitos volcánicos al año (3 km3/año), pasa generalmente inadvertida debido a la enorme presión hidrostática ejercida por las aguas oceánicas sobre los centros de emisión de las lavas. Es más, aunque parezca paradójico, muchos de los depósitos volcánicos preservados en áreas emergidas también se formaron en erupciones submarinas. Un excelente ejemplo de esa situación podemos encontrarlo en Bizkaia y Gipuzkoa. En algunos taludes de las carreteras de esos dos territorios, cauces de ríos y cimas, aflora una potente sucesión volcánica, cuya formación estuvo estrechamente relacionada con la apertura del Golfo de Bizkaia. Por tanto, aunque actualmente en Euskadi no hay volcanes activos ni síntomas de actividad volcánica (emisión de gases volcánicos, gradientes geotérmicos elevados, sismicidad volcánica, etc.), se puede afirmar con rotundidad que en este territorio hubo en algún momento una actividad volcánica submarina importante.
¿Dónde están esos volcanes submarinos?
Esas formaciones volcánicas submarinas, que alcanzan en algunos puntos hasta 2.500 m. de espesor, se extienden actualmente decenas de kilómetros por Bizkaia y Gipuzkoa, definiendo un alineamiento cartográfico con dirección general N120E. Así, es posible observar interesantes depósitos volcánicos en zonas de Getxo, Sopelana, Lemoiz, Arrieta, Fruiz, Errigoiti, Gernika, Markina, Elgoibar, Eibar, Soraluze, Bergara, Azkoitia y Zumarraga. También son observables pequeñas cámaras magmáticas y diques de alimentación de esos volcanes en Zierbena, Santurtzi, Abadiño, Elorrio y Elgeta, además de en los municipios anteriormente indicados.
El volcanismo submarino terrestre
Los fondos oceánicos están formados por rocas volcánicas, parcialmente cubiertas por una capa de sedimentos. La formación de la mayor parte de esas rocas, y por tanto el volcanismo, se localizan en los márgenes divergentes de las placas litosféricas. La litosfera es la capa externa rígida de la Tierra. Está fragmentada en una serie de placas que se desplazan unas con respecto a otras generando importantes interferencias (sismicidad, volcanismo y deformaciones) en sus bordes. Las rocas situadas bajo esas placas conforman la región denominada astenosfera, donde las rocas están a más de 1200ºC. En los entornos oceánicos donde las placas litosféricas se separan (“márgenes divergentes”) las rocas de la astenosfera se descomprimen adiabáticamente (sin perder energía calorífica) y se funden generando magmas que, tras ascender, originan el volcanismo de las dorsales centro-oceánicas. Precisamente, la mayor actividad volcánica de la Tierra se concentra a lo largo de las dorsales centro-oceánicas, donde se estima que puede haber del orden de 1.000 erupciones volcánicas al año.
El registro volcánico de Bizkaia y Gipuzkoa
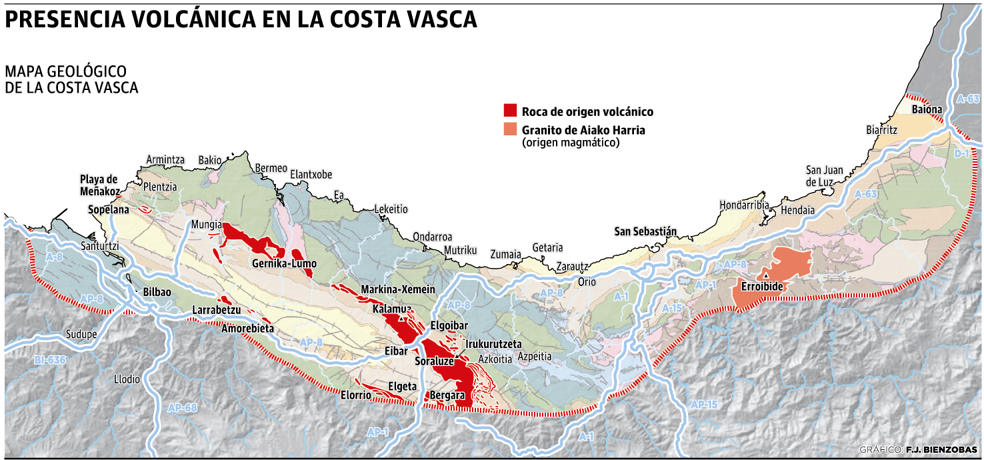 Fuente: El Diario Vasco
Fuente: El Diario VascoLas rocas volcánicas de esos territorios afloran intercaladas entre los depósitos sedimentarios cretácicos que conforman la Cordillera Cantábrica. Los materiales volcánicos se corresponden con coladas de lava (pillow lavas y lavas tabulares), tobas de cenizas y lapillis, y aglomerados de bombas y bloques. En esos afloramientos también se puede reconocer una compleja red de cuerpos intrusivos (diques, sills y lopolitos) que representan los conductos (“sistema de alimentación”) por los que ascendían los magmas que alimentaban esas erupciones. Ese volcanismo dio lugar sobre todo a la erupción de basaltos, aunque no son raras rocas subordinadas de otras composiciones (p.ej. traquitas). Las erupciones volcánicas se desarrollaron durante el Cretácico Superior (de 110 Ma a 85 Ma -Ma: millones de años-) a profundidades batiales (de 900 a 1.400 m.), un tiempo durante el cual se fue abriendo el Golfo de Bizkaia con la formación de nueva corteza oceánica en su eje central. La gran variedad de rocas y estructuras volcánicas de esa sucesión, actualmente en estudio, sugiere que la actividad eruptiva fue cambiante y diversa, con estilos eruptivos efusivos y explosivos hawaiianos y estrombolianos, pero también surtseyanos (freatomagmáticos), como consecuencia de la violenta expansión del agua al contactar con las lavas.
¿Cuáles fueron las causas de ese volcanismo?
En el Pérmico (299 Ma) la práctica totalidad de la litosfera continental estaba unida formando un supercontinente denominado Pangea. En el Pérmico superior (259 Ma) se inició el desmembramiento de Pangea. El estiramiento y la fracturación de la litosfera continental de ese supercontinente, trajo consigo la separación de la microplaca Ibérica de la placa Euroasiática. La separación de ambas placas se estaba desarrollando en el marco de la apertura del Atlántico Norte, en el que también se integraría el origen del Golfo de Bizkaia. Entre ambas placas se generó una cuenca marina, instalada sobre una corteza continental hiperextendida, en la que podría haberse acumulado una secuencia sedimentaria de hasta 17 km. de espesor. La hiperextensión de la litosfera continental también trajo consigo la fusión parcial del manto, como consecuencia de su descompresión adiabática. La fusión del manto generó magmas basálticos alcalinos que ascendieron a través de la litosfera continental a favor de fracturas, formando diques. Muchos de esos diques alcanzaron el fondo marino, alimentando las erupciones volcánicas submarinas. En cambio, otros magmas no llegaron a la superficie, formando pequeñas cámaras magmáticas en el interior de la corteza que actualmente están representados por los sills y los lopolitos. En esas pequeñas cámaras magmáticas, algunos magmas basálticos experimentaron procesos de cristalización fraccionada, alcanzando las composiciones traquíticas anteriormente citadas.
¿Cómo emergieron los volcanes submarinos de Bizkaia y Gipuzkoa?
Tras la extinción del vulcanismo submarino, la sedimentación en la cuenca marina comprendida entre la microplaca Ibérica y la placa Euroasiática continuó. Los volcanes y sus depósitos quedaron cubiertos por una potente pila sedimentaria. Durante el Santoniense (86 Ma) la placa Africana empezó a desplazarse hacia el norte como consecuencia de la expansión del océano Índico. El acercamiento entre las placas Africana y Euroasiática empujó la microplaca Ibérica hacia el norte, provocando su colisión contra la placa Euroasiática. Ese proceso de convergencia e imbricación litosférica, y que trajo consigo la formación de la cordillera Pirenaica, tuvo lugar entre 70 y 40 Ma. La deformación y emersión de los materiales rocosos de la cuenca marina que separaba ambas placas puso en exposición los afloramientos volcánicos que hoy podemos visitar en Bizkaia y Gipuzkoa.
¿Por qué son interesantes esos depósitos volcánicos?
A pesar de la cotidianidad de las erupciones submarinas, ese proceso geológico continúa siendo enigmático, ya que son testimoniales el número de observaciones directas realizadas hasta hoy. En contra de lo que inicialmente se creía, las observaciones realizadas desde batiscafos tripulados, las imágenes obtenidas con sumergibles no tripulados y las muestras de rocas extraídas con dragas y sondeos mecánicos, evidencian que la actividad volcánica submarina no es muy distinta a la que se desarrolla en condiciones subaéreas. Es cierto que la investigación del desarrollo de las erupciones submarinas sigue presentando importantes limitaciones tecnológicas, pero existe un itinerario alternativo: el estudio de los depósitos volcánicos submarinos que afloran en áreas emergidas. Por ese motivo, las formaciones volcánicas de Bizkaia y Gipuzkoa son un extraordinario laboratorio en el que se pueden inferir, a partir del estudio de los productos volcánicos, cómo se desarrollan las erupciones submarinas. Sus excelentes afloramientos han sido visitados por geólogos de distintas universidades y centros de investigación. La calidad de esos afloramientos ha sido incluso reconocida por varios investigadores de prestigio internacional. Sin duda alguna, la investigación geológica de los fondos oceánicos actuales y la de las sucesiones volcánicas submarinas en áreas emergidas deben considerarse complementarias. En ambos casos están aportando información crítica que permite entender mejor las unas gracias a las otras. De ahí la necesidad de seguir progresando en la senda del conocimiento, en este caso geológico.
Sobre el autor: Fernando Sarrionandia-Ibarra Eguidazu es profesor agregado del Departamento de Geología y miembro del Grupo de Investigación GIU20/010 de la UPV/EHU
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Los volcanes submarinos de Bizkaia y Gipuzkoa se ha escrito en Cuaderno de Cultura Científica.
Un mensaje en una bombilla
En la década de 1660, un brote de peste bubónica asoló Inglaterra y obligó a sus ciudadanos a aislarse para evitar los contagios. Entre ellos se encontraba un joven de 22 años llamado Isaac Newton. En 1665 abandonó la Universidad de Cambridge y se recluyó en su casa de campo. Fue allí donde tuvo lugar uno de los frenesís creativos más locos de la historia de la ciencia, un periodo que hoy conocemos como “el año maravilloso de Newton”.
La leyenda de este año está adornada, sin duda, por las exageraciones que acompañan a los relatos cuando viajan a través de los siglos. Para empezar, porque el año maravilloso no duró, precisamente, “un año”. Pero, además, porque parece que el propio Newton contribuyó a inflar, de manera interesada, lo prodigioso de su productividad durante todo este periodo. De un modo u otro, sabemos que fue en esta época cuando el genio inglés comenzó a explorar con sus primeras teorías ópticas, y cuando diseñó el experimento del arcoíris por el que hoy le recordamos. Newton utilizó un prisma para dividir un rayo de luz blanca en sus distintos colores. Por si fuese poco, demostró también que todos estos colores podían volver a sumarse en un único haz, restituyendo así el tono blanco original. Los colores, por tanto, no procedían del cristal, ni eran una ilusión generada por el experimento: aquellos eran los ingredientes que formaban la luz del sol.
 Ilustración de Jean-Léon Huens
Ilustración de Jean-Léon HuensCada rayo que llega a nuestros ojos contiene información más allá de aquella que nosotros percibimos. Es un mensaje encerrado en una botella, que durante siglos no supimos leer. Nuestro ojo pondera las frecuencias y crea una sensación unificada, que en cada punto identificamos con un único color. Pero ese color es, en la mayoría de los casos, una suma, un agregado de frecuencias, del que podemos extraer muchísima información. Gracias al prisma de Newton y a otras herramientas ópticas que vendrían después es posible destejer la luz y analizar sus distintos componentes en lo que se conoce como el espectro electromagnético. Este es el mensaje que encerraba la luz de las estrellas para los astrónomos. Cada receta de colores nos indica qué frecuencias componen la luz, en qué proporción, y conforma una verdadera “factura” capaz de desvelarnos su historia.
Pero volvamos al náufrago de nuestra analogía. Al abrir las botellas de su playa, acaba de acceder a un montón de datos nuevos. Ahora tiene ante sí una enorme cantidad de papeles llenos de números y cuentas pendientes, el tipo de correspondencia que uno preferiría no tener que leer. Pero esos números describen en detalle las transacciones económicas de los distintos países que desea conocer, así que el náufrago se dispone a estudiarlos meticulosamente. Como, además de curioso, es un tipo muy metódico, después de unas cuantas facturas acaba encontrando ciertos patrones que se repiten. Para empezar, descubre que las transacciones se encuentran “cuantizadas”. En todas las facturas, encuentra una serie de valores discretos, indivisibles, que representan las monedas propias de cada país: la base de su economía.
El espectro electromagnético de las estrellas es parecido en ese sentido. Si uno mira la recetas de colores de la luz con atención, puede observar ciertas líneas oscuras que se repiten a distancias discretas, bien definidas. Aunque, en un primer momento, los astrofísicos no podían saber qué causaba estas grietas en el arcoíris que conforma la luz de las estrellas, terminaron encontrando patrones parecidos en la luz emitida por distintos gases aquí en la Tierra. Así dedujeron que el universo debía estar compuesto por los mismos elementos químicos que se encuentran en nuestro planeta. Es difícil sobreestimar la importancia que tuvo este descubrimiento. Richard Feynman lo señaló como “el más notable de toda la astronomía”1.
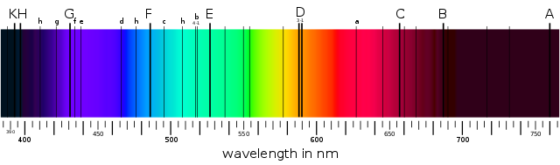 Espectro solar en el que se pueden ver las “grietas” del arcoíris. Fuente: Wikimedia Commons
Espectro solar en el que se pueden ver las “grietas” del arcoíris. Fuente: Wikimedia CommonsDe hecho, cada una de estas líneas oscuras representa un intercambio energético, discreto e indivisible, del mismo modo que una moneda representa un intercambio económico básico. En este caso, los compradores son átomos, que pagan o cobran energía a cambio de poder mover sus electrones. Para que electrón salte de un nivel energético a otro superior, dentro de un átomo, debe absorber un fotón de una energía muy determinada2 (de un color muy determinado): aquella correspondiente al salto que quiere dar. Sucede lo contrario si salta a un nivel inferior, en tal caso emite un fotón. Así, las frecuencias correspondientes a estos intercambios energéticos aparecen reflejadas en el espectro de la luz, separadas en el espacio, en forma de líneas de emisión o de absorción, dependiendo de si la energía ha sido “pagada” (emitida) o “cobrada” (absorbida).
Como los niveles energéticos de un átomo son siempre los mismos (son, por así decirlo, la moneda propia de su país), cada elemento químico tiene un espectro de absorción característico. Gracias a ello, podemos averiguar cuál es el gas que rodea a una estrella y deja sobre su luz su huella dactilar3. Podemos averiguar cuál es su composición química: la base de su economía… digo, de su energía.
Referencias:
1Richard Feynman. Seis piezas fáciles. Critica, 2017.
2D. Maoz. Astrophysics in a Nutshell. 2007.
3J. B. Hearnshaw. The analysis of starlight. Cambridge: Cambridge University Press. 1986.
Para saber más:
El espectro electromagnético, capítulo de la serie Electromagnetismo
Los espectros de absorción de los gases, capítulo de la serie Átomos
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Un mensaje en una bombilla se ha escrito en Cuaderno de Cultura Científica.
Geometría en los pavimentos romanos cosmatescos
El mundo está lleno de casualidades. Mi anterior entrada del Cuaderno de Cultura Científica titulada Paseando entre árboles de Pitágoras terminaba con una construcción similar al árbol de Pitágoras, pero tomando como base un triángulo equilátero, en lugar de un triángulo rectángulo, junto a los tres cuadrados apoyados en los lados del triángulo. Esta construcción da lugar, no a un árbol fractal, sino al mosaico rhombitrihexagonal.
Las dos siguientes imágenes son las que cerraban la anterior entrada. La primera es la estructura generada utilizando el triángulo equilátero y los tres cuadrados laterales, después de cuatro pasos, aunque representando solo los cuadrados.
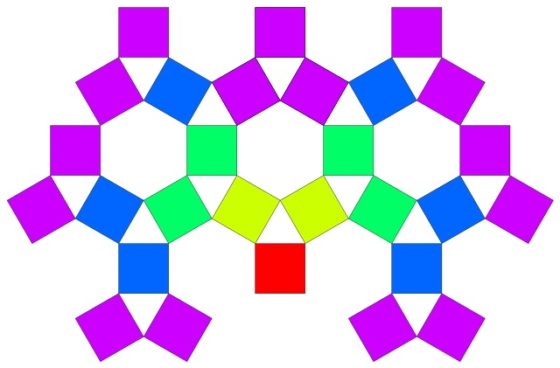 Fuente: Wikimedia Commons
Fuente: Wikimedia Commons
Mientras que la segunda es el mosaico rhombitrihexagonal que, como comentábamos, se puede generar con esta construcción.
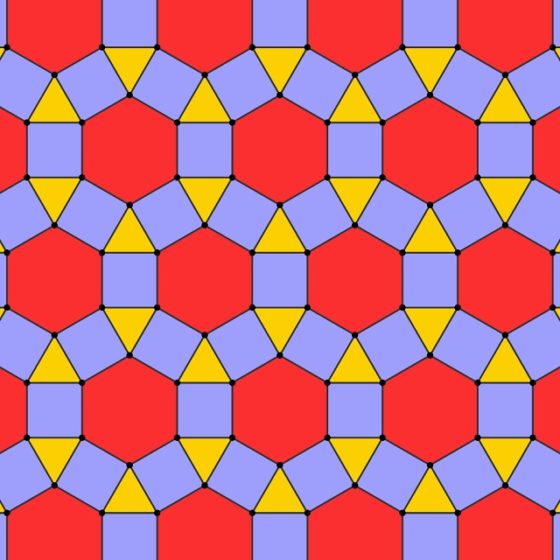 Fuente: Wikimedia Commons
Fuente: Wikimedia Commons
Lo curioso es que unos días después de publicarse esa entrada me fui de viaje a Roma, esa monumental y hermosa ciudad italiana que muchos hemos conocido a través del cine, de la mano de Gregory Peck y Audrey Hepburn subidos a una moto Vespa en la película Vacaciones en Roma (1953) de William Wyler o junto a Anita Ekberg y Marcelo Mastroianni en la Dolce Vita (1960) de Federico Fellini, con la mítica escena de sus personajes bañándose en la Fontana de Trevi, entre otras películas.
Mi primera sorpresa llegó nada más aterrizar en el Aeropuerto de Roma-Fuimicino, mientras salía del mismo. Uno de los carteles publicitarios del aeropuerto mostraba la siguiente imagen.

 Foto: Marian Espinosa
Foto: Marian EspinosaEsta imagen, que pertenecía a la publicidad del pabellón italiano en la Expo Dubai 2020, que debido al covid 19 se está celebrando entre octubre de 2021 y marzo de 2022, no era otra que la de la construcción geométrica anterior. ¡Qué bonita casualidad!
La siguiente casualidad no lo era tanto si tenemos en cuenta que la ciudad de Roma está llena de hermosos mosaicos geométricos muy bien conservados. Con la intención de visitar la Boca de la Verdad, para emular a Gregory Peck y Audrey Hepburn, entré en la Basílica de Santa María en Cosmedin. Allí se encuentra esta antigua máscara de mármol pavonazzetto, que según cuenta la leyenda quién miente se queda sin mano al meterla en el hueco de la boca de la misma. La Basílica de Santa María en Cosmedin fue construida en el siglo VIII sobre los restos romanos del Templum Herculis Pompeiani, templo de la Antigua Roma dedicado a Hércules, y destaca por su decoración en estilo cosmatesco. Este estilo de decoración debe su nombre a la familia Cosmati, una familia de artesanos, de alrededor del siglo XII, que cogían mármol de antiguas ruinas romanas y utilizaban sus fragmentos para crear nuevas decoraciones geométricas, como las que podemos ver en la Basílica de Santa María en Cosmedin.
 Vista general del interior y el pavimento de la Basílica de Santa María en Cosmedin. Foto: Dnalor01 / Wikimedia Commons
Vista general del interior y el pavimento de la Basílica de Santa María en Cosmedin. Foto: Dnalor01 / Wikimedia Commons
Observando este hermoso pavimento me llevé algunas sorpresas. Una de ellas fue una parte del pavimento en el que aparecía el mosaico rhombitrihexagonal anteriormente mencionado, que está formado por triángulos equiláteros (aunque en este mosaico cosmatesco estos están divididos a su vez en cuatro pequeños triángulos equiláteros), cuadrados y hexágonos regulares, con mármoles blancos veteados, rojos y verdes. ¡Qué bella realización del mosaico rhombitrihexagonal!
 Parte del pavimento de la Basílica de Santa María en Cosmedin con el mosaico rhombitrihexagonal, formado por triángulos equiláteros, cuadrados y hexágonos. Foto: Marian Espinosa
Parte del pavimento de la Basílica de Santa María en Cosmedin con el mosaico rhombitrihexagonal, formado por triángulos equiláteros, cuadrados y hexágonos. Foto: Marian Espinosa
Llegados a este punto podríamos pensar un poco en los mosaicos desde el punto de vista de las matemáticas, de la geometría.
Para empezar, imaginemos que queremos embaldosar un suelo con baldosas que tengan la misma forma y tamaño. En concreto queremos que las baldosas sean sencillas, que sean polígonos regulares, que son aquellos polígonos cuyos lados –y también ángulos interiores- son iguales entre sí, como en el triángulo rectángulo, el cuadrado o polígonos con más lados como el pentágono, el hexágono, el heptágono o el octógono regulares. Además, queremos embaldosar el suelo de forma regular, es decir, no solo que las baldosas sean polígonos regulares, sino que estén pegadas lado con lado. Si pensamos en mosaicos de este tipo, llamados embaldosados o teselaciones regulares, se nos ocurrirán tres sencillos ejemplos que están muy presentes en nuestro día a día, con triángulos equiláteros, con cuadrados y con hexágonos, como se muestra en la siguiente imagen.
 Embaldosados regulares con triángulos, cuadrados y hexágonos. Composición a partir de imágenes de R. A. Nonenmacher en Wikimedia Commons
Embaldosados regulares con triángulos, cuadrados y hexágonos. Composición a partir de imágenes de R. A. Nonenmacher en Wikimedia Commons
El siguiente mosaico del pavimento de la Basílica de Santa María en Cosmedin toma como base el embaldosado regular con cuadrados, aunque algunos cuadrados no son lisos, sino que tienen su propio diseño geométrico (con pequeños cuadrados y triángulos).
 Mosaico del pavimento de la Basílica de Santa María en Cosmedin que toma como base el embaldosado regular con cuadrados. Foto: Marian Espinosa
Mosaico del pavimento de la Basílica de Santa María en Cosmedin que toma como base el embaldosado regular con cuadrados. Foto: Marian Espinosa
Mientras que este otro mosaico del mismo lugar, toma como base el mosaico regular hexagonal. Aunque en este ejemplo los propios lados de los hexágonos están muy marcados al ser pequeñas baldosas –es lo que se llama un teselado hexagonal achaflanado- y además el interior de los hexágonos está a su vez decorado a base de rombos.
 Mosaico del pavimento de la Basílica de Santa María en Cosmedin que toma como base el embaldosado regular con hexágonos. Fuente: Wikimedia Commons
Mosaico del pavimento de la Basílica de Santa María en Cosmedin que toma como base el embaldosado regular con hexágonos. Fuente: Wikimedia Commons
Pero volviendo a la geometría, la cuestión importante es si hay más embaldosados regulares. Ya en la entrada Diseños geométricos con chocolate abordábamos esta cuestión, que recuperamos en esta entrada.
Si nos fijamos en un vértice cualquiera de alguno de los tres embaldosados anteriores, formados por triángulos equiláteros, cuadrados o hexágonos regulares, en él confluyen un cierto número de baldosas (triangulares, cuadradas o hexagonales). En el caso del mosaico triangular, en cada vértice se juntan 6 triángulos equiláteros, puesto que el ángulo interior del triángulo equilátero es de 60 grados, y seis veces 60 grados son 360 grados (6 x 60 = 360), que es la vuelta completa alrededor del vértice. En la teselación por cuadrados se juntan 4 de estos polígonos, cada uno de ellos con un ángulo interior de 90 grados en el vértice, y de nuevo, 4 veces 90 grados son 360 grados (4 x 90 = 360). Finalmente, los ángulos interiores de los hexágonos son de 120 grados, lo cual es coherente con el hecho de que alrededor de cada vértice del embaldosado por hexágonos, hay exactamente tres hexágonos en la configuración alrededor del vértice (es decir, 120 x 3 = 360).
La pregunta, llegados a este momento, es si es posible que existan más embaldosados mediante polígonos regulares. La respuesta viene de la mano de la configuración alrededor de cualquier vértice del mosaico. Dada una teselación, alrededor de cada vértice hay un cierto número n de baldosas, luego los ángulos del polígono medirán 360 / n grados, por lo que podemos ver qué posibilidades existen: i) 360 / 2 = 180 grados (que no nos da ningún polígono); ii) 360 / 3 = 120 grados (hexágonos); iii) 360 / 4 = 90 grados (cuadrados); iv) 360 / 5 = 72 grados (pero no hay ningún polígono regular con un ángulo interior de 72 grados); v) 360 / 6 = 60 grados (triángulos); y no hay más posibilidades que nos den un polígono. En consecuencia, acabamos de demostrar el siguiente teorema:
Los únicos embaldosados regulares lado a lado son los formados con triángulos equiláteros, con cuadrados o con hexágonos regulares.
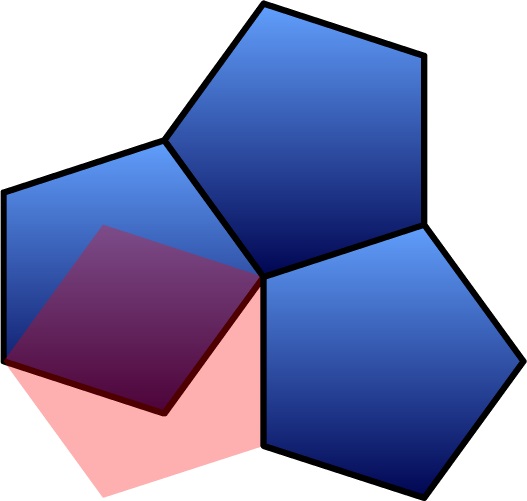 No es posible embaldosar el pavimento con losetas pentagonales regulares. Los ángulos interiores de un pentágono valen 108 grados, luego con tres baldosas pentagonales no acabamos de completar los 360 grados alrededor de un vértice, pero con cuatro baldosas nos pasamos
No es posible embaldosar el pavimento con losetas pentagonales regulares. Los ángulos interiores de un pentágono valen 108 grados, luego con tres baldosas pentagonales no acabamos de completar los 360 grados alrededor de un vértice, pero con cuatro baldosas nos pasamos
Por cierto, que los ángulos interiores de un pentágono miden 108 grados, de un heptágono 128,6 grados, y en general, para un polígono regular de n lados, no es difícil de probar que el ángulo interior vale (n – 2) x 180 / n grados.
Este tipo de embaldosado regular –con triángulos equiláteros, cuadrados o hexágonos regulares- es muy frecuente en la decoración de nuestra vida. Sin embargo, consideremos embaldosados un poco más complejos. Imaginemos que ahora en lugar de considerar únicamente baldosas con la forma de un único polígono regular, se construyen mosaicos utilizando varios polígonos regulares distintos como baldosas. El número de lados de las baldosas puede variar, pero no la longitud de cada lado, ya que las baldosas se seguirán pegando lado con lado. Por ejemplo, en el mosaico rhombitrihexagonal se utilizan baldosas triangulares, cuadradas y hexagonales, con lados de la misma longitud. Otro ejemplo aparece en la siguiente imagen, que es un mosaico formado por hexágonos y triángulos equiláteros cuyos lados son iguales (aunque de nuevo, en este pavimento, los triángulos equiláteros están divididos a su vez en cuatro pequeños triángulos equiláteros, para darle más riqueza geométrica al pavimento), que se llama mosaico trihexagonal.
 Parte del pavimento de la Basílica de Santa María en Cosmedin con un mosaico formado con triángulos equiláteros y hexágonos. Foto: Marian Espinosa
Parte del pavimento de la Basílica de Santa María en Cosmedin con un mosaico formado con triángulos equiláteros y hexágonos. Foto: Marian Espinosa
Estos dos ejemplos de mosaicos se llaman embaldosados o teselaciones uniformes, o semiregulares, ya que alrededor de cualquiera de sus vértices se tiene la misma configuración de polígonos regulares, en el primer caso en cada vértice vemos cuadrado, triángulo, cuadrado y hexágono, mientras que en el segundo es triángulo, hexágono, triángulo, hexágono. Si queremos estudiar qué tipos de teselaciones uniformes existen, el procedimiento es similar al anterior para las regulares.
Para empezar, el número de polígonos regulares –denotémoslo k– alrededor de cada vértice del embaldosado semiregular es menor o igual que 6, ya que el polígono regular con menor ángulo interior es el triángulo, con un ángulo de 60 grados, y solo puede haber 6 triángulos en un vértice. Por lo tanto, tomando los posibles valores de k como 3, 4, 5 o 6, y realizando un pequeño razonamiento sobre los ángulos interiores de los polígonos regulares se puede deducir que las únicas posibilidades son las siguientes:
i) Para k = 6 (seis polígonos en cada vértice), solo puede haber 6 triángulos equiláteros alrededor de cada vértice. A esta configuración la denotamos (3, 3, 3, 3, 3, 3) y da lugar a la teselación regular triangular.
ii) Para k = 5 (cinco polígonos en cada vértice), hay tres configuraciones posibles (3, 3, 3, 3, 6) –cuatro triángulos y un hexágono-, (3, 3, 3, 4, 4) –tres triángulos y dos cuadrados- y (3, 3, 4, 3, 4) –de nuevo, tres triángulos y dos cuadrados, pero en otro orden-.
iii) Para k = 4, hay siete configuraciones posibles, a saber (3, 3, 6, 6) –dos triángulos y dos hexágonos-, (3, 6, 3, 6) –dos triángulos y dos hexágonos, con otro orden-, (3, 4, 4, 6) –un triángulo, dos cuadrados y un hexágono-, (3, 4, 6, 4) –un triángulo, dos cuadrados y un hexágono, con otro orden-, (3, 3, 4, 12) –dos triángulos, un cuadrado y un dodecágono-, (3, 4, 3, 12) –dos triángulos, un cuadrado y un dodecágono, en otro orden- y (4, 4, 4, 4) –cuatro cuadrados-.
iv) Y para k = 3, hay diez configuraciones posibles, que son (3, 7, 42), (3, 8, 24), (3, 9, 18), (3, 10, 15), (3, 12, 12), (4, 5, 20), (4, 6, 12), (4, 8, 8), (5, 5, 10) y (6, 6, 6).
En la siguiente imagen vemos todas las 21 posibles configuraciones en los vértices de una teselación uniforme.
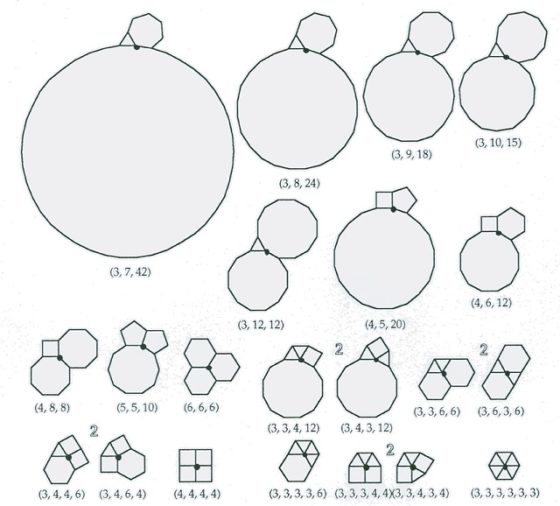 Lista de las 21 configuraciones posibles de vértices para mosaicos uniformes. Imagen del artículo k-uniform tilings by regular polygons, de Nils Lenngren
Lista de las 21 configuraciones posibles de vértices para mosaicos uniformes. Imagen del artículo k-uniform tilings by regular polygons, de Nils Lenngren
Por lo tanto, no puede haber embaldosados uniformes tal que los vértices tengan configuraciones diferentes a estas 21 que acabamos de mostrar. Sin embargo, esto no quiere decir que todas estas configuraciones den lugar a mosaicos semiregulares. De hecho, trabajando configuración a configuración se puede obtener que solamente existen 8 embaldosados uniformes, obviando los 3 regulares ya conocidos (luego 11 en total), que se muestran en la siguiente imagen.
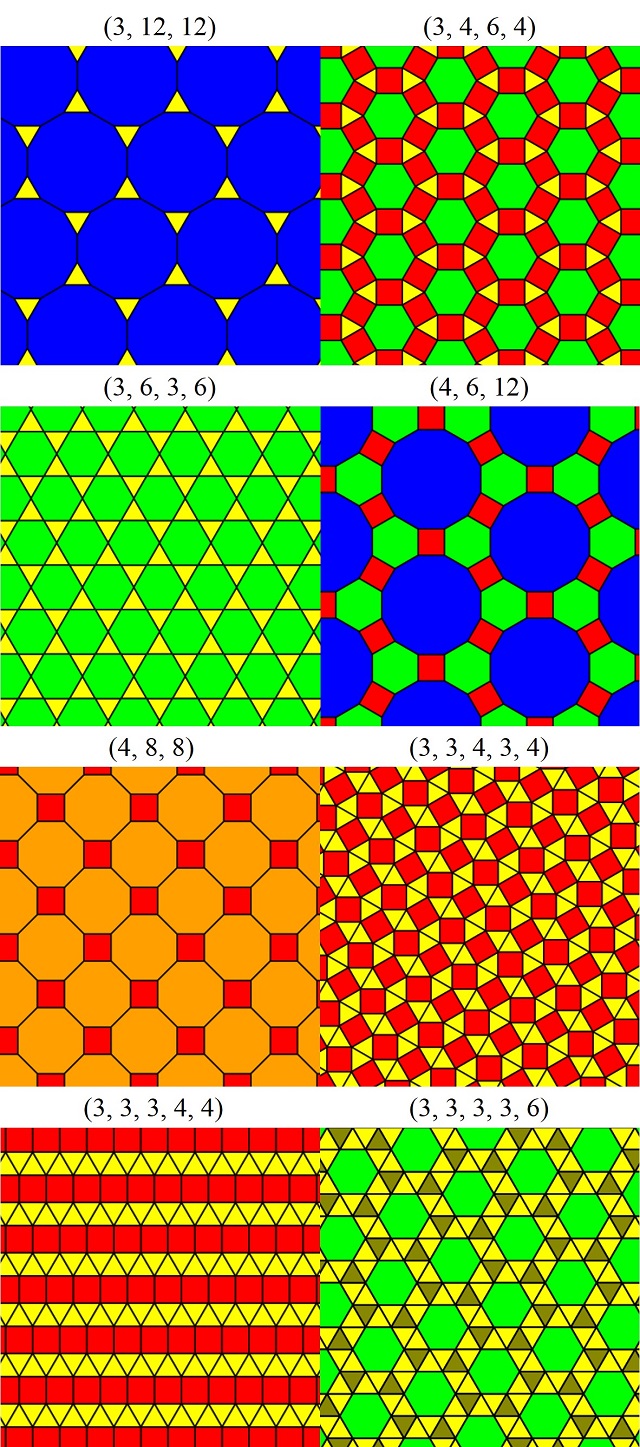 Ilustraciones de los 8 embaldosados uniformes no regulares. Composición a partir de imágenes de Tomruen en Wikimedia Commons
Ilustraciones de los 8 embaldosados uniformes no regulares. Composición a partir de imágenes de Tomruen en Wikimedia Commons
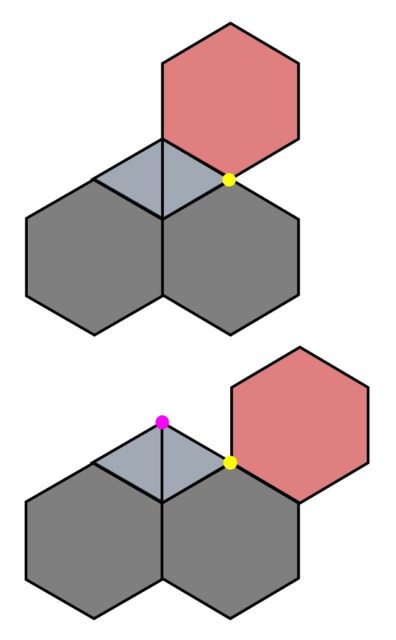
Por ejemplo, si se hacen “baldosas” de cartón (o de cualquier otro material) de triángulos equiláteros (3) y hexágonos (6) se puede ver que la configuración (3, 3, 6, 6) no da lugar a ningún embaldosado, aunque la configuración (3, 6, 3, 6) sí, como se muestra en la anterior imagen. Veamos el razonamiento. Dada la configuración (3, 3, 6, 6) en un vértice (como se muestra en la siguiente imagen, en gris las dos baldosas hexagonales y en azul las dos triangulares) e intentamos completar el vértice marcado en amarillo con un hexágono solo hay dos opciones. En la primera (imagen superior) en el vértice amarillo quedaría la configuración (3, 6, 3, 6), que no es la buscada, mientras que en la segunda (imagen inferior) nos provocaría que en el vértice marcado en rosa aparecieran ya tres triángulos, lo que tampoco es la configuración buscada (3, 3, 6, 6). Luego esta configuración es imposible.
Volviendo a la Basílica de Santa María en Cosmedin, los dos mosaicos mostrados arriba se corresponden con las configuraciones (3, 4, 6, 4), el rhombitrihexagonal, y (3, 6, 3, 6), el trihexagonal. Pero veamos que aún hay algún otro embaldosado uniforme en esta hermosa iglesia. En la siguiente imagen podemos apreciar el mosaico (3, 6, 3, 6) anteriormente comentado y el (4, 8, 8), llamado embaldosado cuadrado truncado, formado por cuadrados y octógonos.
 Embaldosados (3, 6, 3, 6) y (4, 8, 8) de la Basílica de Santa María en Cosmedin. Foto: Sailko / Wikimedia Commons
Embaldosados (3, 6, 3, 6) y (4, 8, 8) de la Basílica de Santa María en Cosmedin. Foto: Sailko / Wikimedia Commons
Si a la teselación (3, 3, 3, 3, 6), que se conoce con el nombre de teselado hexagonal romo, se le juntan los dos triángulos de cada vértice del hexágono para formar un rombo, como se muestra en esta imagen
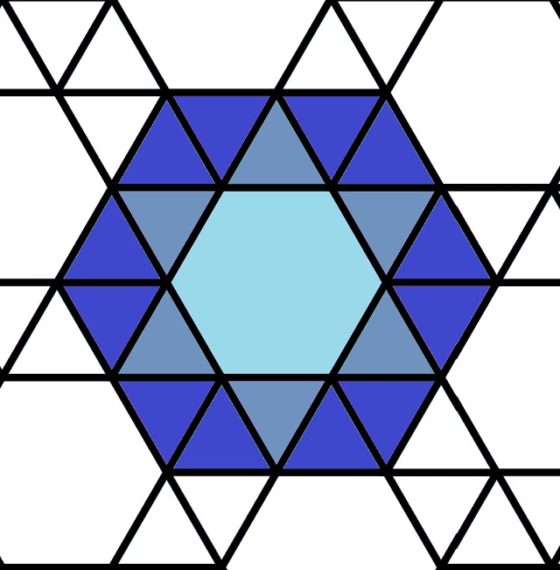
se obtiene el siguiente pavimento de esta basílica romana.
 Mosaico construido a partir del embaldosado uniforme (3, 3, 3, 3, 6) en Basílica de Santa María en Cosmedin. Foto: Denhgiu / Wikimedia Commons
Mosaico construido a partir del embaldosado uniforme (3, 3, 3, 3, 6) en Basílica de Santa María en Cosmedin. Foto: Denhgiu / Wikimedia Commons
Llegados a este punto de la escritura de esta entrada, me puse a buscar algún ejemplo más de pavimento cosmatesco con alguno de los mosaicos uniformes que me faltaban, entonces me encontré con esta imagen (aunque como la descarté en un inicio no tengo la referencia de la misma, ¡perdón!).

En la misma teníamos triángulos, cuadrados y octógonos, luego no podía ser uno de los once embaldosados uniformes. Entonces me fijé en los vértices y observé que había dos tipos de vértices, aquellos con una configuración (3, 8, 3, 8) y otros con (3, 4, 3, 8). Como el ángulo interior de un octógono es de 135 grados, en la primera configuración los ángulos alrededor del vértice sumarían 60 + 135 + 60 + 135 = 390 grados, lo cual supera la vuelta entera, mientras que en el otro caso, la suma de los ángulos alrededor del vértice sería 60 + 90 + 60 + 135 = 345, que no llega a una vuelta entera. Por lo tanto, en este mosaico hay una pequeña trampa y las baldosas no son polígonos regulares, por ejemplo, el triángulo puede no ser equilátero o el cuadrado ser realmente cualquier otro cuadrilátero, ya sea un paralelogramo, un trapecio o un trapezoide.
Aunque podíamos haber tenido un mosaico con polígonos regulares y dos tipos de vértices con configuraciones distintas, es lo que se llama teselaciones 2-uniformes. Por ejemplo, en la siguiente imagen podemos ver un mosaico de la Catedral de Santa María de la Asunción en Sutri.

Si nos fijamos bien en la parte posterior de la imagen y consideramos el rombo formado por dos triángulos equiláteros, entonces la estructura del mosaico sería la siguiente.

Es un mosaico que tiene dos tipos de vértices, con configuraciones (3, 3, 6, 6) y (3, 6, 3, 6), es decir, es un embaldosado 2-uniforme. Pero dejemos este tipo de embaldosados para otra ocasión.
Aunque como decía al principio de esta entrada del Cuaderno de Cultura Científica, la Basílica de Santa María en Cosmedin me deparó alguna sorpresa más, pero de eso hablaremos en una siguiente entrada.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Geometría en los pavimentos romanos cosmatescos se ha escrito en Cuaderno de Cultura Científica.
Una escala de pH para el mundo real
 Algas en el río Tinto. Foto: Paco Naranjo / Wikimedia Commons
Algas en el río Tinto. Foto: Paco Naranjo / Wikimedia CommonsEl pH es un índice omnipresente: desde la publicidad cosmética hasta el estado de la piscina. Es una escala sencilla, y cualquiera puede determinar el valor de una muestra fácilmente en caso de necesidad. Incluso el concepto no es demasiado complicado, bastan las matemáticas y la química de secundaria para tener una idea bastante precisa.
Pero lo que está bien para un ciudadano medio puede no estarlo para un científico. Hace unos años un divulgador de fama mundial publicaba un artículo sobre organismos extremófilos en entornos de acidez extrema, con valores de ph negativos. Una microbióloga de fama también mundial en los comentarios llamó la atención sobre lo que ella consideraba un error, los pHs negativos.
Increíble, pero cierto. Porque los pHs negativos existen, por definición de pH.
Hechos como este hacen que uno se cuestione sobre el nivel de formación química elemental de algunos personas con títulos universitarios: desde graduadas en medicina que prescriben homeopatía (cuyo mero concepto es incompatible con la existencia de los átomos), por ejemplo, a microbiólogas de renombre, como hemos visto. Como, a fin de cuentas, esto es algo que no podemos remediar en su conjunto, vamos a intentar explicar el concepto de pH que debería conocer, no ya un científico, sino un ciudadano informado, y más que nada por si alguien lo busca en Internet, siguiendo la filosofía educativa de según qué ministres. Para ello haremos un repaso más o menos formal sobre el concepto habitualmente admitido, luego nos iremos al fútbol y finalmente veremos como nos queda la definición de pH.
Un poco de historia
Svante Arrhenius fue un químico sueco al que habitualmente se le atribuye la idea de que las moléculas en disolución acuosa se disocian en sus iones (esto es discutible; Max Planck, de fama cuántica, tendría algo que decir, pero esta es otra historia). Una parte muy interesante de este concepto es que se encuentran similitudes y, por tanto, se pueden pueden aplicar las ecuaciones termodinámicas, entre una disolución en la que el soluto está parcialmente ionizado con un gas parcialmente disociado. Siguiendo esta línea de razonamiento Wilhelm Ostwald llegó a su “ley de la dilución” en 1887, posteriormente confirmada experimentalmente, en la que afirma que existe una relación constante entre el grado de disociación (α) de una molécula y el volumen de la disolución (v) que contiene un mol del electrolito, en concreto
α2/(1- α)v = k
donde k , como se demostraría más tarde, es la constante de equilibrio. Esta relación proporciona un modo de medir la fortaleza de ácidos y bases. Veámoslo.
Consideremos el agua, que se disocia como:
2H2O ↔ H3O+ + OH–
Como a partir de medidas de conductividad sabemos que α para el agua es del orden de 10-8, la ley de Ostwald podemos aproximarla a
k = α2/v, ya que (1- α) es prácticamente 1.
Por otro lado, la constante de equilibrio de la disociación, es decir,
k = [H3O+][OH–]/[H2O]
donde los corchetes indican concentración de la especie moles por litro (o dm3), se puede reducir a
k’ = [H3O+][OH–]
Lo que es cierto porque la cantidad de agua es muy grande y, por tanto, [H2O], prácticamente constante.
Este producto, llamado producto iónico del agua, es constante a ciertas temperaturas en las que, en la práctica, toma un valor de 10-14 mol2/dm6. Esto es lo mismo que afirmar que para el agua pura a determinadas temperaturas
[H3O+] = [OH–] = 10-7 mol/dm3.
Si bien varios investigadores ya habían sugerido que la concentración de ion hidronio (H3O+) podía usarse como una referencia para comparar la fortaleza de los ácidos y bases, no fue hasta 1909 que el bioquímico sueco Søren Peder Lauritz Sørensen sugirió eliminar el uso de un número exponencial, con exponente negativo además, y sustituirlo por el logaritmo en base 10 cambiado de signo de [H3O+] , formando de esta forma una escala que iba convenientemente de 1 a 14, con el 7 para “neutro”. Como Sørensen, que se expresaba en alemán, abrevió la “potencia de la concentración de ion hidronio” a potenz-H, o pH, esto es,
pH = -log10[H3O+]
La escala de pH tuvo una aceptación inmediata entre la comunidad biológica/bioquímica. Los químicos no empezaron a usarla hasta unos años después, con la aparición del libro de 1914 de Leonor Michaelis sobre las concentraciones de ion hidronio. La emigración de Michaelis a Estados Unidos en 1926, propagó la escala a aquel país, y la aparición del pehachímetro portátil de Arnold Beckam en 1935 terminó de convertir a los indecisos.
 Escala del pH de andar por casa.
Escala del pH de andar por casa.Una definición conveniente para sistemas biológicos (terráqueos)
Hoy día esta definición de pH es la que aparece en la mayoría de libros de texto de química general, y es la que la inmensa mayoría de personas asume. Pero démonos cuenta de que se hacen muchas suposiciones en esta definición, entre otras que las especies no interaccionan entre sí, esto es, que el ácido o la base se disocian en agua y esta disociación no se ve afectada por otras especies presentes. Además que los efectos de la temperatura son despreciables y que la cantidad de agua es mucho mayor que las especies disueltas en ella.
Si nos fijamos esas suposiciones encajan bastante bien con los sistemas biológicos que conocemos y el rango de la escala definida se adapta convenientemente. A título de ejemplo señalemos que el pH más bajo que tiene nuestro cuerpo se mide en el estómago, corresponde al ácido gástrico y vale 1; nuestra piel tiene un pH de 5,5, la sangre del orden de 7,4 (como comparación el agua a 37ºC tiene 6,8; 7 solamente en condiciones normalizadas) y las secreciones del páncreas, que son las más básicas, 8,1.
El problema surge cuando se tratan sistemas químicos alejados de las condiciones idealizadas de esta definición de pH o cuando tratamos sistemas biológicos en condiciones extremas: alta salinidad, temperaturas muy bajas o muy altas, cantidades mínimas de agua líquida presente, etc. De hecho, el artículo al que nos referíamos al comienzo trata de la búsqueda de vida extremófila en un entorno en el que el pH es de -3,6 (menos tres coma seis). Un simple cálculo nos indica que, con la definición de pH que tenemos, la concentración de ion hidronio es de ¡3981 moles por litro de disolución! ¡No tiene sentido!. ¿Se han equivocado los autores? No, es que la definición de pH que hemos visto no es válida en términos estrictos para ningún sistema real. Como el concepto nuevo que necesitamos puede ser un poco complicado de entender al principio, vámonos al fútbol primero.
Bienvenidos al Estadio Olímpico de Páramos de Hiendelaencina
Consideremos [esto a los españoles les costará menos] que en Páramos de Hiendelaencina, que tiene 1000 habitantes pero está cerca de una parada de tren de alta velocidad y también está próximo al nuevo aeropuerto intercontinental, hace unos pocos años se construyó un estadio olímpico con capacidad para 150.000 personas, todas sentadas. Mientras llegan o no las olimpiadas y aviones al aeropuerto, el estadio lo usa el equipo de fútbol del pueblo que, gracias al patrocinio del constructor local y presidente, milita en la segunda división B.
Un aficionado al fútbol de Páramos, con algún conocimiento de matemáticas y química, decide crear una escala de popularidad/fortaleza de los equipos de fútbol que visitan el estadio en función del número de espectadores que acuden a verlo. Su fórmula es muy sencilla: es el logaritmo cambiado de signo del número resultante de dividir los espectadores que acuden a un partido por el número de asientos que tiene el estadio. Ha llamado a su escala PdH, y en ella cuanto más bajo es el número más fuerte es el equipo visitante.
Estos son algunos resultados obtenidos, incluyendo partidos de la Copa del Rey:
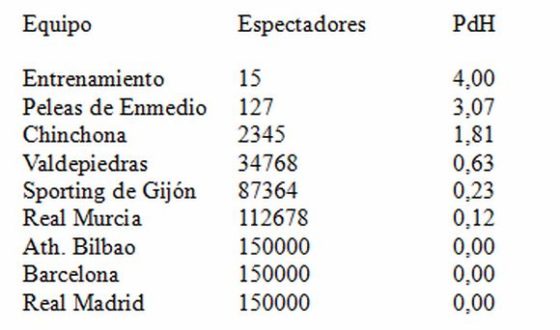
Observando la tabla vemos las limitaciones de la escala en aquel año histórico en el que el Páramos jugó la final de la Copa del Rey. La escala otorga la misma fuerza a un Atleti que a un Barcelona o un Real Madrid y, aunque en justicia ello es así, la realidad es que la capacidad de atracción de los dos últimos equipos es mucho mayor.
¿Cómo tendríamos que reformar la escala para que siguiese siendo válida? Tendríamos que tener en cuenta la misma unidad de medida básica, espectadores, aunque existen otras posibilidades además de los que van al estadio como los espectadores por televisión, u otras variables más rebuscadas como el precio de la reventa. A efectos de nuestra exposición vamos a considerar además de los espectadores en el estadio solo a los espectadores presentes en Páramos, esto es, a los que acuden a las pantallas habilitadas en la era del tío Eufrasio, antiguo Campo Municipal de fútbol. Fijémonos que, al incluir a estos espectadores, la PdH se hace negativa.
Sin embargo, el creador de la escala, queriendo prepararla para el futuro, se da cuenta de que su definición no sirve para captar la fortaleza de un equipo si no considera otros factores además de los espectadores del estadio y de las pantallas. Entre ellos están el tiempo meteorológico, el morbo del partido (como el clásico con el Valdepiedras) y la competición que se juega. Así que crea una nueva variable a la que llama actividad y que incluye de alguna forma todo lo anterior y define la nueva escala PdH+ en función del logaritmo cambiado de signo de esa actividad.
Una escala de pH para el mundo real
En una disolución real nos ocurre exactamente igual. Tenemos que tener en cuenta la temperatura de la disolución y el entorno en el que se van a encontrar los iones. De la misma forma que no es lo mismo un amistoso para recaudar fondos para el asilo con el Valdepiedras que el partido decisivo de la liguilla de ascenso con el mismo equipo, o ir a ver el partido con tu abuelo que con los setenta de la peña, la acidez de una sustancia depende de qué otras cosas haya en juego en la disolución.
Al igual que nuestro amigo de Páramos, también se define una actividad química en términos de lo una variable termodinámica que se llama potencial químico, que tiene en cuenta todos los factores que hemos mencionado y algunos más. Pero, ¿tanto afecta el entorno realmente? Veamos un ejemplo. El cloruro magnésico es una sal que se disuelve bien en agua. En un mundo ideal el pH de una disolución de un ácido no debería verse afectado por la presencia de cloruro magnésico. Sin embargo, esto no es así. Cuando una disolución muy ácida (pH = 1) que contiene el indicador verde de metilo se añade [él (ácido) sobre ella (agua), siempre] a una disolución 5 M de cloruro de magnesio, el color del indicador vira de verde a amarillo, señalando que la acidez ¡ha aumentado!
Es por ello que las constantes de equilibrio se definen en términos de actividad, no de concentraciones, aunque se usen éstas como aproximaciones. Como las constantes de equilibrio están en la base de la definición de pH, éste se define como el logaritmo cambiado de signo de la actividad del ion hidronio.
Con esto en mente ya sabemos que si vamos a estudiar, por ejemplo, la vida en sitios como el río Tinto, que el pH medido variará significativamente de un día de invierno a bajo cero a uno de verano a 40 ºC a la sombra; que variará además si el agua está muy turbia o cristalina (la has podido enturbiar tú al coger la muestra) y que variará por el lugar donde tomes la muestra, no sólo por la posible dilución sino por el aporte iónico del suelo por el que haya pasado.
Por tanto, a la hora de interpretar un dato de pH debemos tener en cuenta la temperatura a la que se midió y la composición exacta de la muestra. Pero esto sólo cuando necesitamos un poquito de precisión; para la piscina puedes seguir usando papelitos de colores.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este texto se publicó en Naukas el 9 de mayo de 2012.
El artículo Una escala de pH para el mundo real se ha escrito en Cuaderno de Cultura Científica.
El caso de la dieta de los esquimales
Esta historia comienza en la década de los setenta del siglo pasado, cuando dos estudiantes de medicina daneses, Jan Dyerberg y Hans Olaf Bang, entonces en el Hospital del Norte de Aalborg, en Dinamarca, viajaron en trineo hasta 500 kilómetros al norte del Círculo Polar Ártico, en la costa occidental de Groenlandia, a la ciudad de Uummannaq, con 900 habitantes más siete asentamientos cercanos, con 1350 habitantes en total. Allí tomaron muestras de sangre de 130 esquimales, con 69 mujeres. Conservaron las muestras a 20ºC bajo cero, las transportaron a su centro e hicieron los análisis de sangre habituales.
 Uummannaq. Fuente: Wikimedia Commons
Uummannaq. Fuente: Wikimedia CommonsUn par de años antes, en 1968, un editorial anónimo en el noticiario semanal de la Sociedad Médica de Dinamarca mencionaba la tasa muy baja y poco habitual de enfermedades cardiovasculares entre los esquimales de Groenlandia, entonces región autónoma danesa. El autor del editorial animaba a los investigadores a profundizar en este hecho y, añadía, “antes de que sea demasiado tarde”. Un joven estudiante y científico en ciernes, Jan Dyerberg, leyó el editorial con interés y se propuso profundizar en el asunto que mencionaba el autor anónimo. Dos años después, en 1970, junto a su colega Hans Olaf Bang, iniciaban la primera de cinco expediciones a Groenlandia, al norte del Círculo Polar Ártico.
Dyerberg y Bang viajaron para comprobar el rumor que era, también, una creencia popular: los esquimales de Groenlandia tenían una incidencia muy baja de enfermedades cardiovasculares, que se situaba entonces entre el 8.5% y el 11.8% del total de muertes. Su hipótesis inicial era que esta baja incidencia estaba relacionada con la dieta de los esquimales y, en concreto, con su ingesta de ácidos grasos polinsaturados, los llamados Omega-3, abundantes en el pescado que era la base de su alimentación. Los dos médicos querían probar la relación según la concentración de lípidos en la sangre.
Los primeros datos de Dyerberg y Bang se publicaron en 1971 en la revista The Lancet. Los resultados del análisis de las muestras de sangre muestran concentraciones menores en lípidos totales, colesterol y triglicéridos que en daneses sanos. Según la hipótesis de los autores estos datos pueden explicar la baja incidencia de enfermedades cardiovasculares entre los esquimales.
Años después, Dyerberg y Bang confirmaron la dieta de los esquimales con la toma de muestras de los alimentos de 50 inuits, la mitad mujeres, de la costa occidental de Groenlandia, durante 3 a 7 días y analizando 178 muestras. Focas y pescado eran los alimentos principales, con una concentración alta de ácidos grasos y, sobre todo, de Omega-3. De nuevo, en su publicación, relacionan la dieta con la baja incidencia de enfermedades cardiovasculares.
Sin embargo, en los 2000 se han publicado varios meta-análisis que dudan de la metodología de la investigación de Dyerberg y Bang, de la relación entre la dieta de los esquimales y la baja incidencia de enfermedades cardiovasculares y, además, en la eficacia de las grasas Omega-3 en la prevención de esas enfermedades. Vayamos por partes y en orden.
En 2012, se publicó un meta-análisis en el Journal of American Medical Association, firmado por Evangelinos Rizos y sus colegas, de la Universidad de Ioannina, en Grecia, que, después de revisar 20 estudios con 68680 pacientes, no encuentran que los suplementos nutricionales de grasas de pescado, con Omega-3, tengan relación con las enfermedades cardiovasculares, los ataques al corazón o los derrames cerebrales. Otro estudio, publicado un año después, en 2013, confirmó las conclusiones de Rizo. Venía de Italia, del Grupo de Estudio de Riesgo y Prevención. Incluía el seguimiento de 12513 pacientes que tomaban suplementos con Omega-3 o un placebo durante cinco años. Los autores no encuentran reducción en las enfermedades cardiovasculares ni en la mortalidad que provocan.
Dos años más tarde, en 2014, George Fodor y su equipo, de la Universidad de Ottawa, en Canadá, publicaron una revisión sobre la incidencia de las enfermedades cardiovasculares entre los esquimales, punto central de los trabajos de Dyerberg y Bang. Cuando estudiaron en detalle la incidencia de estas enfermedades, para su sorpresa, encontraron que era parecida a la encontrada en poblaciones no esquimales.
Afirman que Dyerberg y Bang no investigaron directamente la tasa de enfermedades cardiovasculares entre los esquimales y tomaron sus datos de las listas del Oficial Médico de Dinamarca que, a su vez, se basaban en certificados de defunción e ingresos en hospitales. Pero, para una población tan dispersa como la de los esquimales en Groenlandia, las cifras finales no son muy fiables. Hasta un 30% de los inuits vivía en lugares remotos, a los que no llegaba la sanidad oficial, lo que, a su vez, implica que solo el 20% de los fallecimientos tenía un certificado de defunción.
De hecho, los datos revisados por Fodor demuestran que, por ejemplo, los infartos son una enfermedad común entre los inuit de Groenlandia o que la mortalidad por derrame cerebral es alta. Su esperanza de vida es 10 años menor y su tasa de mortalidad el doble que la de los daneses que le sirven a Fodor para comparar. Afirma Fodor que Dyerberg y Bang investigaron únicamente la dieta de los esquimales y, en cambio, no lo hicieron directamente con su tasa de enfermedades vasculares.
Fodor concluye que, con estos datos de enfermedades cardiovasculares más ajustados, su dieta, más que recomendable, debería ser considerada un riesgo para la salud. Sin embargo, las conclusiones de Dyerberg y Bang todavía se citan con frecuencia para recomendar la toma de suplementos nutricionales, muy publicitados, con grasas de pescado, con Omega-3, para prevenir las enfermedades cardiovasculares.
Hasta la fecha de la publicación de Fodor, en 2014, más de 5000 trabajos se habían publicado sobre los beneficios de los ácidos grasos Omega-3 con la cita del estudio de los esquimales. Por cierto, las citas actuales del artículo de Dyerberg y Bang de 1971 son, según Google Académico, de 1059. En Estados Unidos, Europa y Canadá, los nutricionistas recomiendan el consumo de pescado, sobre todo de pescado azul, como el salmón, rico en Omega-3, para prevenir estas enfermedades. Y, por otra parte, son, para 2016, 32000 millones de dólares los que se movieron con la comercialización de los suplementos nutricionales con Omega-3 y, todo ello, según Fodor, basado en una hipótesis cuestionable desde que se publicó en los setenta.
Además, otro estudio, esta vez dirigido por Matteo Fumagalli, del Colegio Universitario de Londres, añade otro aspecto, muy diferente, a la polémica sobre la dieta de los esquimales. Después de un análisis genético de 191 esquimales, han encontrado que tienen varias mutaciones que implican cambios en el metabolismo de las grasas, sobre todo de las Omega-3. Aparecen en el 100% de los esquimales estudiados, en el 2% de los europeos o en el 15% de los chinos de la etnia han. Son cambios aparecidos hace unos 20000 años y permiten la adaptación a dietas ricas en grasas. Metabolizan grasas Omega-6 y Omega-3 a lípidos menos saturados y con un riesgo más bajo respecto a las enfermedades cardiovasculares. Por tanto, suponen menos grasas peligrosas en el organismo y una mejor adaptación a la dieta habitual de los inuit.
Sin embargo y para terminar, los estudios de Dyerberg y Bang y, ahora, las publicaciones de Rizos, Fodor y Fumagalli, llevan a muchos investigadores a revisar el papel de las grasas del pescado en la prevención de las enfermedades cardiovasculares que, a pesar de todo, parecen recomendables para una dieta saludable. Quizá, como a menudo ha ocurrido en ciencia, un error o, más bien, una conclusión sin suficientes evidencias, ha llevado a muchos científicos a investigar hechos que, en último término, son verídicos y recomendables.
Así, en una revisión reciente de Richard Kones y U. Rumana, del Instituto de Investigación Cardiometabólica de Houston, relatan que la controversia a favor y en contra de los Omega-3 continua muy activa. Revisan 19 estudios de 16 países, con el seguimiento durante varios años de 45637 pacientes, un 37% son mujeres, con una media de 59 años de edad y un rango de 18 a 97 años.
El resultado final es que los Omega-3 disminuyen modestamente el riesgo de enfermedad cardiovascular, aunque los datos no tienen relación con la toma de suplementos nutricionales y su recomendación a la población. Añaden que poco pueden decir pues no conocen con exactitud la pureza de los suplementos, ni lo aclara su etiquetado y tampoco las razones de los propios consumidores para tomarlos.
Con unos días de diferencia, Evangelinos Rizos y Moses Elisaf, de la Universidad de Ioannina, en Grecia, publican otro meta-análisis centrado en los suplementos con Omega-3. Repasan 21 estudios y la conclusión es que no suponen ninguna mejora consistente para la protección respecto a las enfermedades cardiovasculares.
Referencias:
Bang, H.O. et al. 1971. Plasma lipid and lipoprotein pattern in Greenlandic west-coast Eskimos. The Lancet 297: 1143-1146.
Bang, H.O. et al. 1980. The composition of the Eskimo food in north western Greenland. American Journal of Clinical Nutrition 33: 2657-2661.
Fodor, G. et al. 2014. “Fishing” for the origins of the “Eskimos and Heart Disease” story: Facts or wishful thinking? Canadian Journal of Cardiology 30: 864-868.
Fumagalli, M. et al. 2015. Greenlandic Inuit show genetic signatures of diet and climate adaptation. Science 349: 1343-1347.
Kones, R. & U. Rumana. 2017. Omega-3 polyinsaturated fatty acids: new evidence supports cardiovascular benefits. Journal of Public Health and Emergency doi: 10.21037/jphe.2017.03.04
McCoy, T. 2014. Fish oil may not prevent heart disease. The Washington Post May 16.
Rizos, E.C. et al. 2012. Association between Omega-3 fatty acid supplementation and risk of major cardiovascular disease events. A systematic review and meta-analysis. Journal of American Medical Association 308: 1024-1033.
Rizos, E.C. & M.S. Eliaf. 2017. Does supplementation with Omega-3 PUFAs add to the prevention of cardiovascular disease? Current Cardiology Reports DOI: 10.1007/s11886-017-0856-8
The Risk and Prevention Study Collaborative Group. 2013. n-3 fatty acids in patients with multiple cardiovascular risk factors. New England Journal of Medicine 368: 1800-1808.
Wikipedia. 2020. Dieta Inuit. 20 diciembre.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo El caso de la dieta de los esquimales se ha escrito en Cuaderno de Cultura Científica.
El sexto ángel
Tocó el sexto ángel… Entonces oí una voz que salía de los cuatro cuernos del altar de oro que está delante de Dios; y decía al sexto ángel que tenía la trompeta: «Suelta a los cuatro ángeles atados junto al gran río Éufrates.» Y fueron soltados los cuatro ángeles que estaban preparados para la hora, el día, el mes y el año, para matar a la tercera parte de los hombres. El número de su tropa de caballería era de 200.000.000; pude oír su número. Así vi en la visión los caballos y a los que los montaban: tenían corazas de color de fuego, de jacinto y de azufre; las cabezas de los caballos como cabezas de león y de sus bocas salía fuego y humo y azufre. Y fue exterminada la tercera parte de los hombres por estas tres plagas: por el fuego, el humo y el azufre que salían de sus bocas.
Juan de Patmos (siglo I e.c.) Apocalipsis 9: 13-18.
 Foto: Pixabay
Foto: PixabayLa llamada guerra fría, con la amenaza latente de las armas nucleares, dejó episodios en los que, por momentos, pareció que todo podía irse al garete. El de máximo peligro, quizás, fue el de la crisis de los misiles en Cuba. Los máximos mandatarios de las dos superpotencias en conflicto reconocieron después que hubo momentos en los que ni siquiera tuvieron el control de sus propias fuerzas.
Una guerra nuclear tendría efectos a varias escalas y causaría muertes por causas diferentes. En primer lugar, por los efectos directos de las explosiones. Serían efectos térmicos -por el calor liberado y el fuego-, mecánicos -por la onda expansiva-, y químicos -por la radiactividad liberada-. Matarían a decenas o centenares de millones de personas, aunque los efectos serían locales. Las bombas de Hiroshima y Nagasaki fueron el antecedente de lo que, a mucha mayor escala, podría ocurrir.
Se producirían también efectos globales en plazos de tiempo más largos -meses-, debidos a los efectos del polvo radiactivo. Es difícil calibrar cuál sería su alcance, pues dependería, sobre todo, de la magnitud del enfrentamiento. No obstante, aunque provocase la pérdida de millones de vidas y una destrucción enorme, no sería suficiente para acabar con nuestra especie, según los datos que aporta Toby Ord en “Precipice”, harían falta diez veces más bombas atómicas que las existentes en la actualidad para acabar con gran parte de la humanidad a causa de los efectos de la radioactividad.
La mayor pérdida de vidas humanas provendría, sin embargo, de otro fenómeno, también de carácter global: el invierno nuclear. Como consecuencia de las explosiones y los incendios, finísimas partículas y el humo ascenderían hasta la estratosfera, por encima de la altura a la que se forman las nubes y, por tanto, sin poder ser retirados por la lluvia en plazos de tiempo no demasiado largos. Esas finísimas partículas y gases liberados por la combustión generada por los incendios se extenderían por todo el globo e impedirían la llegada de la luz a la superficie de la Tierra. El efecto sería similar al provocado por el impacto de un gran asteroide contra nuestro planeta o la explosión de un supervolcán de magnitud muy grande. Las temperaturas caerían en todo el planeta unos 7 °C, provocando heladas en amplias zonas del planeta. El descenso térmico se prolongaría durante no menos de cinco años, y harían falta diez más para su recuperación. Entre tanto, sobrevendrían hambrunas, graves conflictos, destrucción y muertes.
Bajo las peores condiciones que pudieran darse, una catástrofe como esa podría acabar con la humanidad o dejarla en una postración total. Pero no parece que tal eventualidad nos deba quitar el sueño. Las opciones de que eso ocurra se estiman de una entre mil en el próximo siglo. Hay amenazas peores.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El sexto ángel se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2021: Clara Grima – Maryam y sus colores
El gran evento de divulgación Naukas regresó a Bilbao para celebrar su décima edición en el magnífico Palacio Euskalduna durante los pasados 23, 24, 25 y 26 de septiembre.

Si a una persona aficionada a las matemáticas le piden que complete el nombre y le dicen «Maryam», probablemente lo pronuncie mal (algo como «mirza’kani»), pero se referirá sin duda a Maryam Mirzajaní (transliteración al castellano del persa مریم میرزاخانی ). Clara Grima nos habla de ella como solo Clara sabe hacer.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2021: Clara Grima – Maryam y sus colores se ha escrito en Cuaderno de Cultura Científica.
Resistencia bacteriana y consumo de antibióticos: el caso de Helicobacter pylori
 Helicobacter pylori. Imagen: drmicrobe / 123rf.com
Helicobacter pylori. Imagen: drmicrobe / 123rf.comHelicobacter pylori (H. pylori) es una de las infecciones bacterianas más comunes en todo el mundo que afecta a más del 40 % de la población y es una de las causas de los síntomas digestivos como el malestar epigástrico, la pesadez o la hinchazón del estómago, o de otras enfermedades más graves como el desarrollo de úlceras gástricas y duodenales, el linfoma gástrico o el cáncer gástrico. Así, por ejemplo, se debería investigar y descartar su presencia en personas sanas que han tenido un progenitor o un hermano con cáncer gástrico.
La resistencia a los antibióticos es la principal causa del fracaso del tratamiento de las enfermedades infecciosas como ocurre con la infección por H. pylori. En 2017 la Organización Mundial de la Salud (OMS) ya publico una lista de patógenos, en el que incluía a la infección por H. pylori, en el que alertaba de la necesidad de investigar y promover nuevas alternativas terapéuticas por el impacto que tenían estas bacterias en la salud pública por la resistencia a los antibióticos y la falta de opciones terapéuticas. La resistencia bacteriana a los antibióticos cambia con el tiempo en función de múltiples factores; por tanto, es esencial conocer la tendencia de los patrones de resistencia a los medicamentos para diseñar estrategias para disminuir el desarrollo de la resistencia y mejorar las pautas de tratamiento.
“Desgraciadamente —comenta Luis Bujanda Fernández de Piérola, catedrático de Medicina de la UPV/EHU— conocemos que en los últimos años la eficacia de los tratamientos contra la bacteria H. pylori es baja, está por debajo del 80 % muchas veces a pesar de utilizar conjuntamente dos antibióticos durante 7 a 10 días. Por ello, es muy importante obtener una visión o fotografía general de lo que está ocurriendo en la actualidad para investigar los motivos por los que esta bacteria es resistente a los antibióticos”.
Por ello, “este estudio elaborado a lo largo en el periodo de 2013-2020, en el estado español y otros países europeos como Italia, Francia o Noruega pretendía conocer y analizar cuál es la resistencia de esta bacteria a los antibióticos que habitualmente utilizamos para tratar la infección y dar con el tratamiento eficaz y apropiado”, señala Luis Bujanda. Para ello, “hemos recogido alrededor de 4.000 cultivos de personas afectadas por dicha bacteria; no es una tarea fácil, puesto que para aislarla hay que extraer el tejido del estómago a través de una biopsia para su análisis en los laboratorios de microbiología. La muestra para la biopsia se extrae gracias a una gastroscopia”, explica el catedrático de la UPV/EHU.
“La claritromicina, el levofloxacino y el metronidazol son los tres antibióticos que habitualmente se utilizan para tratar la infección. Sin embargo, hemos visto que al mismo tiempo son los que mayor resistencia generan. Muestran unas resistencias de un 25 %, 20 % y 30 %, respectivamente, y se trata de cifras muy elevadas”, comenta Luis Bujanda. Por tanto, “es fundamental cambiar las estrategias de tratamiento. No es suficiente utilizar solo dos antibióticos para erradicar la infección porque la tasa de éxito se sitúa por debajo del 80 %, sino que hay que utilizar al menos tres antibióticos entre 10 y 14 días con los posibles efectos secundarios que puede generar el mayor uso de antibióticos. Nuestro objetivo con la infección de H. pylori es llegar a alcanzar un éxito de mas del 90 %”, dice Luis Bujanda.
Según Bujanda, “a pesar de que las resistencias a los antibióticos que utilizamos habitualmente son altas, este estudio demuestra que existe una tendencia a disminución a lo largo del tiempo. Es decir, por un lado, tenemos una noticia mala, pero, por otro lado, una noticia buena porque esa tendencia va a menos”. “Probablemente —añade— eso sea porque hay una concienciación por la población y por los médicos a una mejor utilización de los antibióticos, puesto que las resistencias a esta bacteria están muy unidas al consumo y al mal uso de los antibióticos. Las resistencias, en este caso, van paralelas al consumo de estos antibióticos por otras infecciones en los 10-15 años previos”.
En un futuro, “deseamos que las resistencias a estos antibióticos bajen del 15 % y que podamos utilizar menos antibióticos para erradicar la infección con tasas de éxito mayores al 90 %, y todo esto pasa por racionalizar el uso de los antibióticos para evitar que las resistencias sigan aumentando”, concluye Luis Bujanda.
Referencia:
Luis Bujanda, Olga P. Nyssen, Dino Vaira, Ilaria M. Saracino, Giulia Fiorini, Frode Lerang , Sotirios Georgopoulos, Bojan Tepes, Frederic Heluwaert, Antonio Gasbarrini, Theodore Rokkas, Dmitry Bordin, Sinead Smith, Vincent Lamy, María Caldas, Elena Resina, Raquel Muñoz, Ángel Cosme, Ignasi Puig, Francis Megraud, Colm O’Morain, Javier P. Gisbert and on behalf of the Hp-EuReg Investigators (2021) Antibiotic Resistance Prevalence and Trends in Patients Infected with Helicobacter pylori in the Period 2013–2020: Results of the European Registry on H. pylori Management (Hp-EuReg) Antibiotics doi: 10.3390/antibiotics10091058
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Resistencia bacteriana y consumo de antibióticos: el caso de Helicobacter pylori se ha escrito en Cuaderno de Cultura Científica.
¿De qué está hecha la arena?
 Aspecto en lupa binocular de la arena de Islandia, con fragmentos de rocas volcánicas de color negro y algunos cristales del mineral olivino de color verde. Foto: Julio Rodríguez Lázaro / Dpto. de Geología de la UPV/EHU.
Aspecto en lupa binocular de la arena de Islandia, con fragmentos de rocas volcánicas de color negro y algunos cristales del mineral olivino de color verde. Foto: Julio Rodríguez Lázaro / Dpto. de Geología de la UPV/EHU.
Esta es una de las preguntas más habituales que el público asistente a un evento de divulgación científica nos hace a los geólogos. Y la respuesta es siempre la misma: depende.
Aunque parezca que estamos intentando disimular que no somos capaces de dar una explicación, en realidad es la respuesta correcta, porque la composición de la arena depende del lugar en donde la hayamos recogido. Y es que, en Geología, el término arena define un tamaño de grano del sedimento muy concreto y no hace referencia a la naturaleza del mismo.
Los sedimentos son las partículas o materiales sólidos que están sin consolidar y que pueden ser transportados por la acción del agua o del viento hasta su acumulación en la superficie terrestre o en el fondo de los mares y océanos. Cuando queremos hacer una clasificación de los sedimentos, tenemos dos opciones: o bien considerar su composición, o bien referirnos a su tamaño. Y es en este último caso donde encontramos el término arena.
 Aspecto en lupa binocular de la arena del desierto de Uadi Rum (Jordania), con granos de cuarzo cubiertos por una pátina de óxidos de hierro que les da una coloración rojiza. Foto: Julio Rodríguez Lázaro / Dpto. de Geología de la UPV/EHU.
Aspecto en lupa binocular de la arena del desierto de Uadi Rum (Jordania), con granos de cuarzo cubiertos por una pátina de óxidos de hierro que les da una coloración rojiza. Foto: Julio Rodríguez Lázaro / Dpto. de Geología de la UPV/EHU.De acuerdo a la actual escala estandarizada y universal empleada para la clasificación por tamaño de grano del sedimento, se define como arena a todas aquellas partículas cuyas dimensiones están comprendidas entre 0,063 mm y 2 mm, independientemente de su composición. Si queréis un truco más fácil para identificar si el sedimento es arena o no, coged un poco en la mano y rozadlo con los dedos; si notáis que os pincha o araña la piel, habéis encontrado arena.
Además, podemos hacer subdivisiones dentro de la clasificación arena de acuerdo al diámetro de las partículas que la componen. De esta manera, diferenciamos arena muy fina (0,063-0,125 mm), arena fina (0,125-0,25 mm), arena media (0,25-0,5 mm), arena gruesa (0,5-1 mm) y arena muy gruesa (1-2 mm).
Y respondiendo a la pregunta relativa a su composición, pues realmente depende del tipo de materiales geológicos que se encuentran en su área fuente, es decir, en la zona de la que procede el sedimento, por lo que podemos encontrarnos con arenas de naturaleza muy diversa. Os voy a poner algunos ejemplos.
 Aspecto en lupa binocular de la arena de la playa de Trengandín (Noja, Cantabria), con granos de cuarzo de colores transparentes y grisáceos y fragmentos de organismos marinos con colores amarillentos y pardos. Foto: Julio Rodríguez Lázaro / Dpto. de Geología de la UPV/EHU.
Aspecto en lupa binocular de la arena de la playa de Trengandín (Noja, Cantabria), con granos de cuarzo de colores transparentes y grisáceos y fragmentos de organismos marinos con colores amarillentos y pardos. Foto: Julio Rodríguez Lázaro / Dpto. de Geología de la UPV/EHU.La arena de las playas del margen Cantábrico está formada, principalmente, por granos de cuarzo acompañados por otros minerales, como feldespatos y carbonatos, y algunos fragmentos de conchas y caparazones de organismos marinos. Esta composición mixta es la que provoca que tenga esas tonalidades cromáticas pardas que todos reconocemos. Por el contrario, en las playas bañadas por el Mar Caribe, la arena está compuesta casi en su totalidad por fragmentos de organismos marinos carbonatados, sobre todo de corales, adoptando un color muy blanquecino. Sin embargo, en las playas de las Islas Canarias encontramos arena constituida por fragmentos de diferentes tipos de rocas volcánicas, que le dan una coloración en tonos negros, grises o pardos.
Aunque el ejemplo más curioso lo encontramos en las playas de Tunelboka y Gorrondatxe, ambas situadas en la localidad de Getxo (Bizkaia), ya que aparece una arena muy particular. En esta zona del litoral, las corrientes marinas han ido acumulando todos los vertidos realizados por las empresas metalúrgicas de los márgenes del río Nervión al mar Cantábrico durante el siglo pasado, incluidas las escorias de fundición. Así que estas playas están cubiertas por una arena negra brillante formada por fragmentos de escorias de fundición que, además, tienen una componente magnética, por lo que resultan atraídas si les acercas un imán.
Pero no solo encontramos arena en las playas. Las partículas sedimentarias acumuladas en grandes desiertos, como el Sahara, y que son transportadas por el viento, también tienen tamaño arena. Y su composición, de nuevo, varía de acuerdo a las rocas previas de las que provienen estos granos sedimentarios.
Ya lo decía el poeta William Blake, “para ver un mundo en un grano de arena”. Y es cierto, cada grano de arena es un mundo en sí mismo que nos cuenta una historia apasionante, sólo hay que saber escucharla con oídos geológicos.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo ¿De qué está hecha la arena? se ha escrito en Cuaderno de Cultura Científica.
Conozco tu número, y ahora sé que tú también sabes el mío
Andrés, Beatriz, César y Dafne se aburren en una tarde de lluvia. Andrés les propone un juego: escribe un número en un papel y se lo pasa a Beatriz (sin que César y Dafne lo vean) y escribe otro y se lo pasa a César (sin que Beatriz y Dafne lo vean). Además, dice a sus amigos:
Estoy pensando en un conjunto (con al menos dos elementos) de números enteros positivos distintos, cada uno de ellos inferior a 7. A Beatriz le he dado el resultado de la suma de los elementos del conjunto y a César el de su producto. ¿Sabéis qué números he pensado?

Dubitativa, Beatriz le dice a César: «No sé si tú sabes mi número».
Por su lado, César reflexiona un momento y responde a su amiga: «Conozco tu número, y ahora sé que tú también sabes el mío».
¿Cómo han averiguado Beatriz y César el número? Dafne es la única que no ha visto ninguno de los números, aunque ha escuchado las dos afirmaciones de Beatriz y César. Andrés se dirige a Dafne en estos términos:
Confío en tus capacidades de razonamiento. Creo que eres capaz de resolver el enigma.
Tenemos la misma información que Dafne, así que deberíamos poder responder a la pregunta de Andrés. Pensemos en las afirmaciones de Beatriz y de César; es importante comprender cómo sus preguntas y respuestas (lo que no saben y lo que saben en cada momento) les han ayudado a encontrar la solución.
Beatriz no está segura de que César conozca su número, aunque cree que puede conocerlo: «No sé si tú sabes mi número». Por otro lado, César comenta a Beatriz: «Conozco tu número», y solo puede conocerlo si hay una única manera de factorizar el número que Andrés le ha pasado. Por ejemplo, el producto no puede ser el 6 (o un número con dos factores primos distintos) porque habría distintas factorizaciones posibles: 1×6 o 1x2x3.
El número de César solo puede ser un primo p (1xp) o el cuadrado de un número primo p2 (1xp2). En ambos casos hay exactamente una suma posible (1+py 1+p2, respectivamente). ¿Por qué? Recordemos que los números del conjunto de César son todos distintos, es decir, una factorización de la forma 1xpxp no es posible. Tampoco es posible que el producto sea un número como el 8, porque hay diferentes maneras de factorizarlo (2×4 o 1x2x4) y, por lo tanto, diferentes opciones para la suma.
Como los números del conjunto de Andrés son inferiores a 7, teniendo en cuenta la anterior observación, se concluye que el producto de César tiene que ser uno de los cuatro siguientes: 1×2, 1×3, 1×4 o 1×5, o lo que es lo mismo, las sumas de Beatriz son 1+2=3, 1+3=4, 1+4=5 o 1+5=6. Recordemos que Beatriz duda sobre si César conoce su número. Así, podemos eliminar de la anterior lista las sumas 3 y 4, ya que los productos en esos casos son 2 y 3, y Beatriz no dudaría sobre si César conoce o no su número. Sin embargo, una suma de 5 puede obtenerse como 1+4 o 2+3. Del mismo modo, una suma de 6 puede conseguirse como 1+5, 1+2+3 o 2+4.
Es decir, en el momento en el que Beatriz dice a César: «No sé si tú sabes mi número», se deduce que ella solo puede tener un 5 o un 6. Y eso también lo sabe César. De hecho, en ese momento, incluso Dafne conoce esa información. Aunque César es el único que tiene información sobre el producto.
César comienza diciendo a Beatriz: «Conozco tu número…». Razonemos sobre los posibles números de Beatriz. ¿Qué pasaría si el número de ella fuera el 5? Como hemos comentado antes, esa suma solo es posible como 1+4 o 2+3, con lo que César tendría un 4 o un 6. El 4 le diría a César lo que tiene Beatriz, porque solo hay una manera de tener 4 como producto: 1×4. ¿Y qué pasaría si el número de Beatriz fuera 6? El 6 puede descomponerse de tres maneras: 1+5, 1+2+3 o 2+4. Y entonces César no sabría si el número de Beatriz es 5 (1×5) o 6 (1x2x3).
Así, la suma de 5 y el producto de 4 son soluciones al enigma de Andrés. Pero, ¿son las únicas soluciones posibles? Para responder a esta pregunta es necesario recordar la última parte de la afirmación de César: «…, y ahora sé que tú también sabes el mío».
Si el número de Beatriz fuera el 6 (1+5, 1+2+3 o 2+4), César tendría un producto de 5, 6 u 8, respectivamente. Si César tuviera un 5, sabría que Beatriz tiene un 6. Y si el producto fuera 8, las posibilidades de Beatriz serían 2+4 o 1+2+4. Solo el 6 (2+4) sería posible, así que César sabría, de nuevo, que Beatriz tiene un 6. En resumen, si Beatriz tuviese un 6, ella no sabría si César tiene un 5 o un 8. Eso contradice la segunda mitad de lo que dice César y, por lo tanto, los números correctos tienen que ser 5 en el caso de Beatriz y 4 en el caso de César. O lo que es lo mismo, el conjunto de números en el que ha pensado Andrés es {1,4}.
Nota:
Este problema se ha extraído de ¿Puedes resolver el acertijo del submarino rebelde?
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Conozco tu número, y ahora sé que tú también sabes el mío se ha escrito en Cuaderno de Cultura Científica.
La madre de todos los prejuicios

La evolución de la visión del mundo de un adolescente es un tema apasionante. En mi caso, atribuyo a la idealización de la figura del médico que tenía mi madre el querer ser médico desde que tenía uso de razón (existen fotografías y restos de libros que demuestran la seriedad de mi compromiso). Entonces, con 14 años ocurrió Cosmos de Carl Sagan, la serie primero y el libro para Reyes después. Y quise ser físico/astrónomo/científico.
Un efecto colateral de Cosmos fue mi descubrimiento de la figura de Einstein. La fascinación, común a muchos, fue inmediata. Leía todo lo que encontraba en bibliotecas sobre él. De entre todo lo que leía había un punto, sin embargo, que solía pasar sin pena ni gloria, como un dato más, que a mí me llamó poderosamente la atención: su admiración por Baruch Spinoza. Dispuesto a explorar por mi mismo el origen de esa admiración, a los 16 compraba mi primera Ética (una no demasiado buena edición de Bachiller, como me hizo notar mi primo Pedro, estudiante por aquel entonces de filosofía en Salamanca). A esta primera copia han seguido otras cuantas.
¿Imagináis ese momento en que la lectura y meditación de solo un párrafo supone una revolución en tu forma de ver el mundo? ¿Algo que hace que todo encaje de cierta forma? ¿Una idea que hará que digieras la información de determinada manera el resto de tu vida? A mí me ocurrió con 16 años con el Apéndice del libro I de la Ética. Si solamente tuvieses que leer en tu vida unas páginas de filosofía yo te recomendaría ese apéndice que se lee en menos de 10 minutos. Una de las ideas principales de ese apéndice y la revolucionaria, según mi punto de vista, cuando se medita, es esta:
[…]Todos los prejuicios que intento indicar aquí dependen de uno solo, a saber: el hecho de que los hombres supongan, comúnmente, que todas las cosas de la naturaleza actúan, al igual que ellos mismos, por razón de un fin […]
Spinoza, escribiendo este texto en la soledad de su habitación en los primeros años 70 del siglo XVII describe lo que la psicología y la sociología constatan hoy día. De hecho si se lee el Apéndice completo comprobaremos que, salvo la sintaxis y el léxico, estamos ante un texto de una actualidad manifiesta. El ser conscientes de la existencia de este prejuicio de forma activa cambia tu visión del universo. Ahora podía empezar a comprender la admiración de Einstein.
Para una persona con cultura científica pensar que el universo no tiene fin ni propósito alguno es algo que debería darse por descontado si solo se atiene a los hechos; algo que no es así para la inmensa mayoría de los humanos. Y, sin embargo, el prejuicio sigue ahí, acechante, incluso entre los científicos de primer nivel.
Un estudio realizado por un equipo de investigadores encabezado por Deborah Kelemen, de la Universidad de Boston (EE. UU.), ilustra perfectamente este hecho. Han encontrado que, a pesar de años de formación científica, químicos, geólogos y físicos de universidades de primer nivel mundial (Harvard, MIT, Yale entre otras) también sucumben al prejuicio de creer que los fenómenos naturales tienen un propósito. Veamos el resultado con un poco más de detalle.
Cuando los científicos tienen tiempo de reflexionar acerca de por qué pasan las cosas rechazan explícitamente las explicaciones teleológicas, que es como se llama a las explicaciones que se basan en asumir la existencia de un fin o propósito y que son las que permean todas las religiones de una u otra forma. Sin embargo, según el estudio que nos ocupa, cuando se pide a los científicos que piensen muy rápido, aparece una tendencia subyacente a encontrar un propósito en la naturaleza. Estos resultados serían una prueba bastante sólida de que la mente humana tiene una posición por defecto, bien implantada, para favorecer las explicaciones basadas en fines.
Para comprobar la hipótesis de que existe una preferencia natural a las explicaciones teleológicas los investigadores pidieron a un grupo de científicos de universidades estadounidenses de alto nivel que juzgasen afirmaciones del tipo “Los árboles producen oxígeno para que los animales puedan respirar” o “La Tierra tiene una capa de ozono para protegerla de la radiación ultravioleta” presentadas de tal manera que no tenían prácticamente tiempo para pensar sus respuestas. Otro grupo de científicos, equivalente al anterior, pudo dar sus respuestas sin límites de tiempo. Los investigadores encontraron que, a pesar de tener una gran precisión en los ítems de control (expresiones falsas más allá de la componente teleológica), los científicos bajo presión mostraban una mayor aceptación de las explicaciones finalistas sin base científica que sus colegas sin presión de tiempo, que consistentemente las rechazaban.
La misma pauta de mayor orientación al fin se presentó en dos grupos de control, estudiantes (que en psicología viene a ser equivalente a población en general) y graduados universitarios de la zona de la misma edad que los científicos, si bien los científicos aceptaban menos las explicaciones teleológicas comparativamente. ¿Sería esto así por la formación científica, o por la capacidad intelectual de estos últimos?
En un segundo ensayo los investigadores encontraron que, a pesar de los años de formación científica, los químicos, geólogos y físicos no tenían un prejuicio cognitivo menor que profesores de historia o de literatura de las mismas universidades. Esto es, la actividad intelectual de alto nivel aminora el sesgo teleológico (posiblemente por la capacidad intelectiva asociada), pero no así la formación en ciencias físicas y naturales. Un resultado sorprendente. E ilustrativo de la fortaleza de los sesgos cognitivos.
Parece, por tanto, que nuestras mentes tienen una disposición natural hacia la religión más que a la ciencia. Y que conseguir comprender las cosas como son en vez de como aparentan ser lleva un esfuerzo asociado que no todo el mundo está dispuesto a hacer. Pero de esto ya se dio cuenta Spinoza hace 344 años de la misma forma que Feynman arreglaba radios: pensando.
Referencia:
Kelemen, D., Rottman, J., Seston, R. (2013) Professional Physical Scientists Display Tenacious Teleological Tendencies: Purpose-Based Reasoning as a Cognitive Default. Journal of Experimental Psychology: General doi: 10.1037/a0030399
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este texto se publicó en Naukas el 22 de octubre de 2012.
El artículo La madre de todos los prejuicios se ha escrito en Cuaderno de Cultura Científica.
Envejecer sanamente gracias al ejercicio físico
María Larumbe / GUK

La Organización Mundial de la Salud (OMS) define la salud como un estado de completo bienestar físico, mental y social y no solamente a la ausencia de afecciones o enfermedades. Y en este peregrinaje vital hacia el bienestar en las tres esferas, el ejercicio físico tiene un peso considerable, tanto en la física -da fuerza, estabilidad, ayuda a mantener el equilibrio-, como en la social -aumenta la sensación de pertenencia a un grupo- y en la mental -reduce el nivel de ansiedad y depresión-, entre otros efectos beneficiosos.
Asimismo, la actividad física regular y constante tiene efectos positivos a lo largo de todas las etapas del ciclo vital, incluida la vejez, y puede contribuir a disminuir los efectos negativos del envejecimiento, como la fragilidad física, un síndrome multifactorial que afecta principalmente a las personas mayores y hace que tengan una mayor vulnerabilidad para sufrir eventos adversos -caídas, hospitalizaciones, dependencia o, incluso, mortalidad-.
En este sentido, el grupo de investigación AgeingOn del departamento de Fisiología de la Facultad de Medicina y Enfermería de la UPV/EHU trabaja desde hace años en el desarrollo de distintas herramientas y estrategias para hacer frente a la fragilidad de las personas mayores, promoviendo un envejecimiento saludable y estimulante que permita a las personas mayores mejorar su calidad de vida a nivel físico, social y mental mediante el ejercicio y la actividad física.
Programa para mejorar la calidad de vida de las personas que viven en residencias de mayores
En 2015, y con el fin de mejorar la calidad de vida de las personas mayores vulnerables, en el grupo AgeingOn se preguntaron si las personas mayores que viven en residencias de mayores tenían capacidad para revertir la fragilidad. “La mayoría de los estudios y programas de ejercicio físico planteados hasta la fecha se habían realizado en personas que vivían en comunidad y que no habían alcanzado un nivel de dependencia como aquellas que viven en geriátricos”, explica Ana Rodríguez Larrad, miembro del grupo y profesora de Fisioterapia del departamento de Fisiología de la UPV/EHU.
“Nuestra hipótesis era que podríamos frenar el deterioro que sufren estas personas, e incluso mejorar su condición física, mental y social, y, por lo tanto, revertir la fragilidad, a través de un programa de ejercicio”.
Partiendo de esa premisa, el grupo diseñó un novedoso programa de ejercicio físico individualizado y progresivo dirigido a las personas mayores que viven en residencias. Tal y como explica Rodríguez Larrad, este trabajo consistió en la validación de dicho programa, que ha demostrado considerables beneficios a nivel físico, mental y social para estas personas, reduciendo las caídas y el nivel de fragilidad”.
Como se puede ver en el vídeo, se trata de un programa de ejercicio multicomponente, es decir, que trabaja de manera combinada el equilibrio, la fuerza y la capacidad aeróbica y que cuenta con tres características principales: individualización, progresividad y trabajo a intensidades moderadas.
La primera característica es que consiste en un programa de ejercicio individualizado. “Todas las personas participantes tenían unas características muy variadas, pero nos interesaba que los realizaran en grupo por el componente social, aunque de manera individualizada adaptando los ejercicios, intensidad, y gustos a cada participante”.
La segunda es que este programa contempla el ejercicio físico de manera progresiva, “de menor a mayor intensidad, respetando la evolución de cada uno de los participantes”, apunta Rodríguez Larrad. Y, por último, la tercera característica es que se trabaja a intensidades moderadas. “Hasta ese momento, los programas que se habían dirigido a las personas mayores que viven en residencias eran siempre de muy baja intensidad”.
“Hemos observado cómo aquellas personas que participaron en el programa han conseguido mejorar su capacidad funcional, no solo a nivel físico sino también a nivel cognitivo y, lo que es aún más importante, mejorando su calidad de vida y bienestar con respecto a las personas del grupo control que no realizaron el ejercicio físico. Asimismo, también hemos podido observar una reducción en el número de caídas y en el nivel de fragilidad de estas personas”, explica Rodríguez Larrad.
En resumen, los y las participantes en el estudio obtuvieron efectos beneficiosos en mejoras de fuerza, reducciones de prevalencia de fragilidad, mejora de parámetros cognitivos -memoria, agilidad mental, resolución de problemas-, reducción de niveles de ansiedad y depresión, mejora de la percepción de la soledad, etc. Curiosamente, incluso el grupo control, que no hizo ejercicio, redujo también esta sensación de soledad, aunque de manera más discreta. “Esto puede explicarse por la participación en el estudio y el contacto con el personal de investigación, que les realizaba valoraciones periódicas”.
Este programa se implantó en más de 10 residencias de Gipuzkoa con un acogimiento “espectacular” por parte de los participantes y personal de las residencias. Asimismo, contó con la participación de más de 100 personas mayores de 70 años residentes en estos centros y sus familiares. Las sesiones se realizaban dos días a la semana y consistían en una hora de ejercicio, entre el calentamiento, la sesión propiamente dicha y la vuelta a la calma.
En cuanto a la tipología de ejercicios, como se ha señalado antes, las personas participantes trabajaron principalmente el equilibrio, la fuerza y la capacidad aeróbica. “La fuerza la trabajaron mediante pesas, mancuernas y tobilleras lastradas; la capacidad aeróbica, mediante paseos; y el equilibrio, con el uso de otros materiales e interactuando con otros participantes, creando esa sensación de grupo”.
Modalidades en remoto
Como es de suponer, la pandemia provocada por la COVID-19 ha supuesto grandes retos para la implementación de este tipo de programas. “La mayoría de proyectos en los que estábamos trabajando desde el grupo AgeingOn estaban ya en fase de seguimiento, pero el no poder acceder a las residencias nos ha puesto de manifiesto la necesidad de desarrollar programas que se puedan realizar en modalidad remota”.
A este respecto en la actualidad el grupo trabaja en el diseño y puesta en marcha de distintos proyectos en modalidad online, entre ellos, planes de ejercicio en remoto dirigidos a auxiliares de geriatría. “Hemos visto que en este grupo hay una alta prevalencia de dolor músculo-esquelético y que las modalidades online tienen buena acogida y seguimiento en este colectivo. Por ahora se trata de una experiencia piloto pero el feedback es muy prometedor”. A posteriori, la idea es conseguir adaptar este tipo de programas a modalidad remota también para las personas que viven en residencias.
Bien sea en modalidad online o presencial, este tipo de estrategias preventivas, que ponen el foco en trabajar las capacidades más que en reducir los efectos producidos por las enfermedades, ayudan a las personas mayores a continuar su proyecto de vida de manera normalizada, mejorando su autoestima, calidad de vida y sensación de bienestar en esta etapa tan importante de la vida que es la vejez.
Ana Rodríguez Larrad es fisioterapeuta, profesora de Fisioterapia del departamento de Fisiología de la Facultad de Medicina y Enfermería de la UPV/EHU y miembro del grupo AgeingOn.
 Grupo AgeingON, Donostia (izquierda) y Leioa (derecha)
Grupo AgeingON, Donostia (izquierda) y Leioa (derecha)Agradecimientos
Matia Fundazioa (Bermingham, Rezola, Fraisoro, Otezuri, Lamourous, Txara I), Fundación Caser (Lurreamendi, Uzturre), DomusVi (Berra, Villa Sacramento, Fundación Zorroaga).
A las y los participantes de todas las residencias y a sus familiares por su cooperación, disponibilidad y entusiasmo.
El artículo Envejecer sanamente gracias al ejercicio físico se ha escrito en Cuaderno de Cultura Científica.
La física cuántica no es tan extraña como temíamos
Patricia Contreras Tejada y Giannicola Scarpa
 Shutterstock / Yellow duck
Shutterstock / Yellow duck
Dicen que todas las buenas historias tienen un conflicto, y en este equipo había conflicto para rato. Los dos economistas estaban convencidos de que el “teorema del acuerdo”, un resultado central en economía, tenía que cumplirse también en el mundo cuántico. Pero para sus tres colegas de tecnologías cuánticas era imposible que se cumpliera. No querían involucrarse en un proyecto destinado al fracaso.
El teorema del acuerdo, que demostró Robert Aumann (Premio Nobel de Economía en 2005), dicta que, si dos personas racionales parten de los mismos conocimientos previos, no pueden estar de acuerdo sobre su desacuerdo.
Más precisamente: cada persona puede estimar la probabilidad de un evento basándose en la información que conozca. Esta información siempre será parcial, por tanto las estimaciones pueden ser diferentes. Es decir, las personas pueden estar en desacuerdo. Pero si las estimaciones se convierten en conocimiento común, este desacuerdo no se puede mantener. Juntando toda la información, las personas necesariamente alcanzan la misma conclusión. Es decir, se ponen de acuerdo.
Este resultado vertebra la coherencia de los mercados económicos, de ahí que los economistas estuvieran tan convencidos de que la teoría cuántica tenía que respetarlo. Pero, según les recordaban sus colegas de la cuántica, en esta teoría es imposible conocer dos propiedades incompatibles sobre un mismo objeto con la máxima precisión. Si conoces una, la otra se te escapa. Lo dice el principio de incertidumbre de Heisenberg (otro Premio Nobel, esta vez de Física en 1932).
La economía, en peligro por culpa del mundo cuántico
Parecía que el teorema del acuerdo estaba en conflicto directo con el principio de incertidumbre. Dos personas podrían intentar estimar la probabilidad de un evento según la información que ya conocían. Pero incluso juntando toda la información, la única conclusión posible sería que ese evento no se podía conocer. Ambas estimaciones serían válidas, y el desacuerdo se mantendría.
Más allá del optimismo, sin embargo, los economistas tenían un buen argumento para comenzar esta investigación. Si el teorema del acuerdo también se aplicaba al mundo cuántico, estarían demostrando que la teoría que mejor describe el mundo tiene una coherencia interna hasta ahora desconocida.
Si, por el contrario, resultaba que la teoría cuántica no cumplía el teorema, las implicaciones podrían ser dramáticas. No sería raro que las tecnologías cuánticas se utilizaran para hacer finanzas en un futuro cercano. En este caso, podría volverse imposible acordar el precio de las cosas. La economía mundial podría estar en peligro.
Tanto si la teoría cuántica cumplía el teorema del acuerdo como si no, las repercusiones irían mucho más allá de la física. Los economistas habían convencido a sus colegas de la cuántica: había que conocer la respuesta. Otra prueba de que cuanto más hay en juego, mejor funcionan los conflictos.
El camino no fue fácil. El lenguaje de la teoría cuántica y el de la economía no tenían nada que ver. Traducir entre ellos era muy complicado. Pero, poco a poco, comenzaban a surgir ejemplos de situaciones donde no se cumplía el teorema del acuerdo.
Eso sí, ninguna parecía tener una representación en la teoría cuántica.
Rescatando la coherencia
Hasta que, de repente, descubrieron por qué. Ninguno de los ejemplos podía tener representación cuántica, y la clave estaba en un teorema fundamental en esta teoría física. El teorema de Tsirelson, simple pero profundo. Parecía que simplificaba los cálculos. El equipo al completo se puso manos a la obra a atar los cabos que faltaban. Por fin, las matemáticas lo confirmaron: la teoría cuántica respetaba el teorema del acuerdo.
El conflicto se había resuelto. Efectivamente, la teoría cuántica es coherente. La economía mundial puede respirar tranquila y, a pesar de que a veces se resista a nuestra intuición, la teoría cuántica no es tan rara como pensábamos.
Nuestro equipo protagonista, ya reconciliado, ha publicado esta semana sus resultados en Nature Communications.
Una buena historia acabaría aquí. Conflicto resuelto, final feliz, misión cumplida. Pero la realidad no siempre se atiene a las normas de la narración, y nuestra historia tiene un epílogo sorprendente.
¿Nuevas teorías físicas?
Que la teoría cuántica cumpla el teorema del acuerdo tiene implicaciones que van más allá de la propia teoría. Podría ocurrir que, en un futuro, desarrolláramos una nueva teoría que superara a la cuántica en cuanto a capacidad de explicar el mundo en el que vivimos. Si esta teoría no cumpliera el teorema del acuerdo, ¿qué deberíamos pensar?
Según el equipo investigador, deberíamos descartarla. Plantean considerar el teorema del acuerdo como un principio físico. Es más, proponen una prueba para nuevas teorías: solo la superan las que cumplan el teorema del acuerdo. Así, es sencillo asegurarse de que cualquier nueva teoría tiene coherencia interna.
El teorema del acuerdo se añade a la larga lista de principios físicos que ya se han propuesto. El objetivo es descartar cualquier teoría que no los respete. Conforme crezca la lista, iremos rechazando cada vez más teorías y, quizá, nos encontremos con que la cuántica es la única teoría que cumple todos los principios. Solo así podremos dejar de buscar, porque sabremos que la teoría cuántica es la mejor descripción posible de la naturaleza.![]()
Sobre las autoras: Patricia Contreras Tejada es investigadora en matemáticas e información cuántica en el Instituto de Ciencias Matemáticas (ICMAT-CSIC) y Giannicola Scarpa es profesor ayudante doctor en la Escuela Técnica Superior de Ingeniería de Sistemas Informáticos de la Universidad Politécnica de Madrid (UPM)
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo La física cuántica no es tan extraña como temíamos se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2021: Isabel Moreno y José Miguel Viñas – Milibares en los bares, el tiempo entre costuras climáticas
El gran evento de divulgación Naukas regresó a Bilbao para celebrar su décima edición en el magnífico Palacio Euskalduna durante los pasados 23, 24, 25 y 26 de septiembre.

En los bares se habla de muchas cosas: de política, de fútbol, cotilleos varios. Pero algo que nunca falla es hablar del tiempo: del calor cuando hace calor, del frío cuando hace frío, de si llueve porque llueve, de si no llueve porque no llueve. Ahora, eso sí la conversación de bar de dos meteorólogos tiene que ser para no perdérsela, y eso es lo que son Isabel Moreno y José Miguel Viñas.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2021: Isabel Moreno y José Miguel Viñas – Milibares en los bares, el tiempo entre costuras climáticas se ha escrito en Cuaderno de Cultura Científica.
Rusia contra Estados Unidos: por qué la exploración espacial debe contar con todos
Santiago Pérez Hoyos y Jorge Hernández Bernal
 La Estación Espacial Internacional fotografiada desde una nave espacial Soyuz el 30 de octubre de 2018.
La Estación Espacial Internacional fotografiada desde una nave espacial Soyuz el 30 de octubre de 2018.NASA / Roscosmos
“El espacio no es un lugar remoto. Está a una hora en coche, si puedes conducir hacia arriba”. Esta frase del siempre brillante y polémico astrofísico Fred Hoyle tiene muchas lecturas. Ante el reciente incidente espacial entre Rusia y Estados Unidos nos ofrece una nueva interpretación. Apenas cien kilómetros sobre nuestras cabezas se desarrolla la misma estrategia geopolítica que en la superficie del planeta, con los mismos defectos y los mismos peligros para la humanidad.
Comencemos por los hechos: Rusia realiza una prueba de un misil tierra-espacio, destruye un satélite inoperativo y genera una gran cantidad de fragmentos con diferentes trayectorias.
Estados Unidos denuncia que este evento ha puesto en peligro a los astronautas de la Estación Espacial Internacional y ha contribuido a aumentar la ya inquietante cantidad de basura espacial en órbitas bajas.
Rusia resta importancia al evento y apunta en cambio a la negativa estadounidense a suscribir un tratado contra la proliferación de armas espaciales.
Denunciemos en primer lugar y con claridad cualquier acción que ponga en riesgo vidas humanas y que contribuya a degradar aún más el entorno espacial. Pero, más allá de su pobreza argumental, es importante señalar que Rusia no carece de razón. Los Estados Unidos también han participado anteriormente en este tipo de pruebas balísticas y no han querido poner control a nuevos tipos de armas.
Esto, bajo la perversa lógica en la que vivimos inmersos, ha empujado a otros países a seguir los mismos pasos y repetir las mismas acciones que la potencia americana. Parece bastante obvio que en este caso, así como en los relativos a las armas nucleares, los Estados Unidos carecen, no ya de capacidad coercitiva para controlar a sus oponentes, sino de autoridad moral para reclamar responsabilidades.
¿Quién lleva la razón en este conflicto? Todas las partes tienen una porción de ella y ninguna la tiene por completo. Sorprende por ello la sobrerreacción mediática comparada con otros eventos que han puesto en riesgo a los astronautas o con decisiones políticas y militares de Estados Unidos con respecto al espacio que han sido aceptadas sin más por la opinión pública.
Añadamos a las ya citadas pruebas militares, por ejemplo, la proliferación de satélites de telecomunicaciones de empresas privadas o los planes de explotación de recursos espaciales que, aunque parezcan lejanos en el tiempo, adquieren mayor importancia ante la evidente escasez de recursos en nuestro planeta para mantener de forma indefinida el crecimiento económico.
La administración Obama otorgó una auténtica patente de corso a las grandes corporaciones estadounidenses para la explotación de unos recursos que, aunque los tratados internacionales son ambiguos al respecto, deberían ser aprovechados por toda la humanidad.
Una exploración espacial alejada del colonialismo
Somos muchos los que queremos una exploración civil y pacífica del espacio. También los que pensamos que, si en algún momento decidimos explotar los recursos que nos ofrece, no pueden ser propiedad del primero que llegue a ellos. La carrera tecnológica que nos lleva al espacio no se desarrolla en igualdad de condiciones para todos los países: la larga historia mundial de colonialismo y guerras deja a buena parte de la humanidad fuera del reparto de beneficios de una forma que muchos consideramos injusta.
En todo caso, sería positivo que estas decisiones se discutieran abiertamente en la esfera pública, con la participación de diferentes puntos de vista e intereses en un debate que nos permita tomar decisiones sensatas y sostenibles.
El espacio no es un lugar remoto. Apenas a una hora en coche, o incluso a cuatro días de viaje espacial, estamos proyectando muy eficientemente los mismos problemas que oscurecen nuestro futuro en la Tierra. La misma incapacidad de establecer acuerdos entre potencias que hemos visto en la reciente cumbre del clima, la misma preponderancia de intereses económicos explotados por unos pocos, como en el conflicto sobre el Ártico. Es hora de terminar esta película de vaqueros y comenzar a escribir el futuro guión de la humanidad. No está tan lejos.![]()
Sobre los autores: Santiago Pérez Hoyos es profesor titular y Jorge Hernández Bernal investigador en el Grupo de Ciencias Planetarias de la UPV/EHU.
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Rusia contra Estados Unidos: por qué la exploración espacial debe contar con todos se ha escrito en Cuaderno de Cultura Científica.

