Las ideas erróneas sobre educación entre el profesorado: prevalencia, causas y soluciones

¿Son eficaces los programas y sistemas educativos actuales? Durante los últimos años, es cada vez mayor el debate generado en torno a este tema. Muchos expertos argumentan que las teorías y prácticas educativas implementadas en los centros carecen de evidencia científica. El esfuerzo y los medios empleados en estas prácticas de dudosa utilidad obligan, además, a dejar de lado aquellas otras teorías cuya eficacia está probada.
Con el objetivo de abordar esta situación, el Bizkaia Aretoa de Bilbao acogió el pasado 17 de marzo la jornada titulada “Las pruebas de la educación”, donde varios expertos abordaron cuestiones relacionadas con la educación desde un punto de vista científico.
“Las pruebas de la educación” forma parte de una serie de eventos organizados por la Cátedra de Cultura Científica de la UPV/EHU para abordar cuestiones del día a día como la educación o el arte desde una perspectiva científica. La dirección del seminario corrió a cargo de la doctora en psicología Marta Ferrero.
La propia Marta Ferrero trató en la cuarta ponencia sobre las ideas erróneas sobre educación más extendidas entre el profesorado. En ella identificó los factores que facilitan o provocan la creciente aparición de ideas pseudocientíficas en el ámbito escolar y propuso algunas soluciones a diferentes niveles.
Las ideas erróneas sobre educación entre el profesoradoEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Las ideas erróneas sobre educación entre el profesorado: prevalencia, causas y soluciones se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La ciencia perdida: los curiosos casos de los protocolos de TDAH y de leer.es
- Estudio de eficacia escolar en el País Vasco
- Mestizajes: La ciencia en “La educación de Henri Adams”, por José Manuel Sánchez Ron
Del mito al hecho: hemisferios, gimnasia cerebral y estilos de aprendizaje

¿Son eficaces los programas y sistemas educativos actuales? Durante los últimos años, es cada vez mayor el debate generado en torno a este tema. Muchos expertos argumentan que las teorías y prácticas educativas implementadas en los centros carecen de evidencia científica. El esfuerzo y los medios empleados en estas prácticas de dudosa utilidad obligan, además, a dejar de lado aquellas otras teorías cuya eficacia está probada.
Con el objetivo de abordar esta situación, el Bizkaia Aretoa de Bilbao acogió el pasado 17 de marzo la jornada titulada “Las pruebas de la educación”, donde varios expertos abordaron cuestiones relacionadas con la educación desde un punto de vista científico.
“Las pruebas de la educación” forma parte de una serie de eventos organizados por la Cátedra de Cultura Científica de la UPV/EHU para abordar cuestiones del día a día como la educación o el arte desde una perspectiva científica. La dirección del seminario corrió a cargo de la doctora en psicología Marta Ferrero.
En esta tercera conferencia el El maestro y divulgador Albert Reverter abordó diversas cuestiones pseudocientíficas en materia educativa como la teoría según la cual las personas aprendemos mejor si se nos enseña en nuestro estilo de aprendizaje preferido. También se ocupó de la llamada “gimnasia cerebral” que consiste en una serie de ejercicios dirigidos a activar el cerebro, promover la reestructuración neurológica y facilitar la capacidad de aprender. A pesar de su gran popularidad, no hay estudios científicos que avalen su eficacia.
Del mito al hechoEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Del mito al hecho: hemisferios, gimnasia cerebral y estilos de aprendizaje se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Dejad de propagar el mito de los estilos de aprendizaje
- La ciencia perdida: los curiosos casos de los protocolos de TDAH y de leer.es
- Estudio de eficacia escolar en el País Vasco
Prosopagnosia, la incapacidad de reconocer los rostros

Prosopagnosia o ceguera al rostro (Imagen vía pexels)
Diariamente, por norma general, nos cruzamos y tenemos trato con un gran número de personas. Algunos son individuos a los que tan solo hemos visto en una ocasión pero que reconocemos gracias a que nuestro cerebro almacenó información sobre ellos (normalmente reteniendo alguna peculiaridad o un rasgo físico característico).
El área específica del reconocimiento facial en nuestro cerebro se encuentra en el giro fusiforme desde donde se empieza a procesar toda la información que entra por nuestros ojos, por lo que cualquier persona (que no padezca de un trastorno visual, evidentemente) cuando se cruza con otro individuo es capaz de reconocerlo si ya lo había visto con anterioridad e incluso, si es la primera vez, retiene información sobre los rasgos del mismo que en un futuro servirá para recordar de quién se trata (nuestra memoria es capaz de identificarlo en aproximadamente cien milisegundos).
Pero al igual que la inmensa mayoría de nosotros logra reconocer a alguien (obviamente, algunas veces con ciertas dificultades para terminar de ubicar y recordar su nombre, de qué o dónde lo conocimos) en el planeta se estima que hay un dos por ciento de la población que padece un curioso trastorno de agnosia visual llamado ‘Prosopagnosia’ y por el cual es incapaz de reconocer cualquier rostro.
La prosopagnosia o ceguera al rostro consiste en ver a alguien y no saber quién es, a pesar de que ese ‘alguien’ se trate de un familiar muy allegado y que convive con quien padece este curioso trastorno.
Existen diversos grados dentro de esta patología y, dependiendo del nivel de afectación del mismo, el prosopagnósico puede incluso llegar a no reconocerse a si mismo cuando se ve en una fotografía en la que aparece e incluso, en casos extremos, cuando pasa frente a un espejo.
La mayoría de ellos pueden distinguir los ojos, nariz o boca dentro de una cara, son capaces de señalar a qué parte del rostro corresponden y ubicarlo en él, pero les es imposible que su cerebro los ordene visualmente para reconocerlos en su conjunto dentro del rostro de alguien.
También son capaces de distinguir entre los rostros de varias personas diferentes, saber que cada una de ellas no son el mismo individuo, pero se sienten totalmente incapaces de averiguar quién es quién e identificarlas.
Una simple sonrisa, la forma de guiñar un ojo o de ladear la cabeza puede ser clave para que el prosopagnósico pueda tener una referencia clara sobre a quién pertenece y poder así reconocer fácilmente cuando se encuentran de nuevo.
El retener y memorizar esos rasgos y peculiaridades faciales, como tics, una cicatriz, si lleva bigote, forma de la nariz e incluso el modo de reír, caminar, si lleva gafas o tiene el pelo ondulado o recogido con una coleta, se convierte en algo fundamental para las personas que padecen la ceguera al rostro, por lo que cualquier cambio físico, por sutil que este sea (afeitarse, teñirse el pelo, cambiar de montura de gafas o de peinado…), puede provocar que el prosopagnósico no reconozca a quien tiene frente a él.
Actualmente no existe tratamiento farmacológico para curar esta patología, por lo que los enfermos que sufren esta agnosia visual se apoyan en terapias en las que les enseñan a memorizar el mayor número de datos sobre los rasgos faciales de las personas que les rodean, lo cual les ayuda a salir airosos para reconocer a determinadas personas y así evitar cualquier situación social embarazosa.

Prosopagnosia, la incapacidad de reconocer los rostros (Imagen vía Hubert Figuière-Flickr)
Entre las pruebas y terapias a las que son sometidos se encuentran algunas pruebas basadas en el famoso ‘test de Reconocimiento Facial de Benton’ (creado en 1946 por el profesor en neuropsicología, de la Universidad de Iowa, Arthur Lester Benton) diseñado para evaluar la percepción y memoria visual y en el que en lugar de presentar una serie de figuras o dibujos abstractos (que posteriormente el paciente debe reproducir) se realiza con imágenes de personas en las que debe señalarse las características de la cara de estas y emparejar las fotografías con la que corresponde (rostros de frente, perfil, iluminados y vistos desde diferentes ángulos, que hacen que el cambio de perspectiva pueda hacer que varíen sustancialmente los rasgos).
Aunque en un principio se asoció esta patología únicamente a una lesión en el hemisferio derecho del cerebro, posteriormente se estableció que era necesaria una lesión bilateral y simétrica en ambos hemisferios para padecer tal desorden. Durante largo tiempo se tuvo el convencimiento que la prosopagnosia era una de las consecuencias tras haber sufrido algún accidente cerebrovascular, tumor cerebral e incluso, aunque con menor frecuencia, un traumatismo craneoencefálico o infecciones del Sistema Nervioso Central, siendo denominada ‘prosopagnosia adquirida’, pero, gracias a los avances e investigaciones que se han desarrollando en el campo de la neurología, se ha logrado identificar que también existe un vínculo genético y que esta agnosia puede tener un origen congénito (‘prosopagnosia evolutivas o de desarrollo’) desarrollándose desde la infancia sin que tenga asociada una lesión específica.
Varios son los grados de incidencia de la ceguera al rostro y cada individuo puede padecerla en mayor o menor medida pero si tuviéramos que diferenciarla en dos bloques estos serían la ‘prosopagnosia asociativa’, en la que el paciente puede llegar a reconocer algún rostro gracias a aquellos rasgos faciales que ha memorizado y la ‘prosopagnosia aperceptiva’, por la cual se es incapaz de analizar la estructura facial, distinguir y memorizar las peculiaridades de cualquier individuo e incluso no tener la capacidad de percibir la sensación de familiaridad que se tiene al reconocer un rostro.
Para encontrar la etimología del término debemos buscar en la composición de los vocablos griegos prosopon (cara) y agnosia (ausencia de conocimiento). Fue el neurólogo alemán Joachim Bodamer quien, en 1947, acuñó dicho término el cual incluyó en un ensayo que escribió sobre la prosopagnosia, diferenciándola de la agnosia general y de la alexia y describiéndola como […]la interrupción selectiva de la percepción de rostros, tanto del propio como del de los demás, los que pueden ser vistos pero no reconocidos como los que son propios de determinada persona[…].
A pesar de ser una patología englobada dentro de las catalogadas como ‘enfermedades raras’ y que afecta a una de cada cincuenta personas, varios son los personajes populares a los que se les ha diagnosticado, entre ellos el famoso neurólogo Oliver Sacks, quien escribió sobre la prosopagnosia en 1985, en el libro ‘El hombre que confundió a su mujer con un sombrero’, incluso antes de saber que la padecía; la primatóloga Jane Goodall; la princesa Victoria de Suecia; la periodista de The Times Mary Ann Sieghart (su hija Evie también la padece) o el conocidísimo actor hollywoodiense Brad Pitt (según declaró en una entrevista realizada en 2013, aunque reconoció no estar diagnosticado por un especialista).
Este post ha sido realizado por Alfred López (@Yelqtls) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
Fuentes de consulta y más info:
http://www.jpsychores.com/article/S0022-3999(08)00157-8/abstract
http://www.visionlab.harvard.edu/Members/Ken/Papers/130NeurologyDuchaine04.pdf
https://pdfs.semanticscholar.org/3c99/7a718e53a5d5363b631a7d9116498fcd3069.pdf
http://www.tandfonline.com/doi/abs/10.1080/17470218.2016.1173076
http://dx.doi.org/10.1080/02643299008253437
http://www.sciencedirect.com/science/article/pii/0022510X72900044
http://biorxiv.org/content/early/2017/01/15/100479
http://dx.doi.org/10.1016/j.tics.2005.02.011
http://www.uninet.edu/neurocon/congreso-1/conferencias/neuropsicologia-2-2.html
https://www.wired.com/2006/11/blind/
Fuentes de las imágenes:
https://www.pexels.com/photo/apples-blurryface-dress-moonlight-80864/
https://www.flickr.com/photos/hfiguiere/10199319943
El artículo Prosopagnosia, la incapacidad de reconocer los rostros se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El sesgo a la izquierda al reconocer un rostro
- Los volcanes de Venus
- ¿Por qué el Rover Curiosity es más lento que un caracol?
Por qué los colegios no deberían enseñar habilidades de pensamiento crítico generales
Carl Hendrick

Foto cortesía de la Armada de los Estados Unidos / Flickr
Ser controlador de tráfico aéreo no es fácil. Parte fundamental del trabajo es una capacidad cognitiva llamada “conciencia situacional” que implica “la extracción continua de información ambiental [y la] integración de esta información con conocimiento previo para formar una imagen mental coherente”. Grandes cantidades de información fluida deben mantenerse en la mente y, bajo extrema presión, se toman decisiones de vida o muerte a lo largo de turnos rotatorios de 24 horas. El trabajo es tan estresante y exigente mentalmente que, en la mayoría de los países, los controladores de tráfico aéreo cumplen los requisitos para una jubilación anticipada. En los Estados Unidos, deben retirarse a los 56 sin excepciones.
En los años sesenta se realizaron una interesante serie de experimentos sobre las capacidades mentales de los controladores de tráfico aéreo. Los investigadores querían explorar si poseían una capacidad aumentada general para “seguir varias cosas a la vez” y si esa habilidad podía aplicarse a otras situaciones. Tras observarlos en su trabajo, los investigadores asignaron a los controladores de tráfico aéreo un conjunto de tareas genéricas con formas y colores basadas en la memoria. Lo extraordinario fue que, cuando se les evaluaba en estas tareas alejadas de su área de conocimiento, los controladores de tráfico aéreo no eran mejores que cualquier otro. Sus extraordinariamente sofisticadas capacidades cognitivas no se aplican fuera de su ámbito profesional.
Desde comienzos de los años ochenta, sin embargo, los colegios se han visto cada vez más cautivados por la idea de que los estudiantes deben aprender un conjunto de destrezas de razonamiento generalizadas para prosperar en el mundo contemporáneo; y especialmente en el mercado de trabajo contemporáneo. Llámense “habilidades de aprendizaje del siglo XXI” o “pensamiento crítico”, el objetivo es equipar a los estudiantes con un conjunto de métodos generales de resolución de problemas que pueden aplicarse a cualquier campo; los líderes empresariales los aplauden como parte esencial de la preparación para el siglo XXI. Naturalmente, queremos que niños y graduados tengan un conjunto de herramientas cognitivas multipropósito que les permitan manejarse en el mundo. Es una vergüenza, entonces, que hayamos fallado a la hora de aplicar un mínimo de pensamiento crítico a la cuestión de si una cosa así se puede enseñar.
Tal y como sugerían los estudios de los años sesenta sobre los controladores aéreos, para ser bueno en un campo concreto tienes que saber un montón de él: no es fácil trasladar esas habilidades a otros ámbitos. Esto es aún más cierto con el tipo de conocimiento complejo y especializado que conlleva la pericia profesional: estudios posteriores encontraron que cuanto más complejo es el campo, más importante es el conocimiento específico de ese campo. Esta no traslabilidad de la habilidad cognitiva está bien establecida en la investigación psicológica y ha sido replicada muchas veces. Otros estudios, por ejemplo, han demostrado que la capacidad de recordar largas series de dígitos no se transfiere a la capacidad de recordar largas series de letras. Sin duda esto no es sorprendente, ya que todos conocemos personas que son muy “inteligentes” en sus vidas profesionales y que, sin embargo, parece que toman decisiones estúpidas en sus vidas personales.
En casi cualquier campo, cuanto mayor es el nivel de habilidad, más probable es que la pericia se haga más concreta. En un equipo de fútbol, por ejemplo, ha diferentes “campos” o posiciones: portero, defensa, delantero. Dentro de éstas, hay todavía más categorías: defensa central, lateral, mediocentro atacante, mediocentro defensivo, delantero centro. Bueno, podría estar bien para un grupo de aficionados, jugando un partido amistoso, cambiar de posiciones. Pero, a nivel profesional, si pones un lateral izquierdo en la posición del delantero centro o a un centrocampista en la de portero, los jugadores estarían perdidos. Para que puedan tomar decisiones excelentes en fracciones de segundo y ejecutar estrategias robustas y eficaces necesitan miles de modelos mentales concretos, y miles de horas de práctica para crear esos modelos, todos los cuales son concretos y exclusivos de una posición.
Por supuesto, el pensamiento crítico es una parte esencial del equipamiento mental de un estudiante. Sin embargo, no puede separarse del contexto. Enseñar a los estudiantes “destrezas de razonamiento” separadas del resto de su currículo no tiene sentido y es ineficaz. Como dice el pedagogo estadounidense Daniel Willingham:
Si recuerdas a un estudiante suficientemente a menudo que “mire un problema desde múltiples perspectivas”, aprenderá que debe hacer eso, pero si no sabe mucho de un problema, no puede pensar sobre él desde múltiples perspectivas…el pensamiento crítico (así como el pensamiento científico y cualquier otro pensamiento basado en un campo) no es una habilidad. No hay un conjunto de destrezas de pensamiento críticas que pueden adquirirse y usarse sin tener en cuenta el contexto.
Esta separación de los ideales cognitivos del conocimiento contextual no se circunscribe al aprendizaje del pensamiento crítico. Algunos colegios se precian de colocar las “destrezas de aprendizaje para el siglo XXI” como parte fundamental de su misión. Se ha llegado incluso a sugerir que algunas de estas nebulosas habilidades son ahora tan importantes como la alfabetización y que debería otorgárseles el mismo estatus. Un ejemplo de esto son los juegos de entrenamiento mental que afirman que ayudan a los niños a ser más inteligentes, estar más alerta y ser capaces de aprender más rápido. Sin embargo, investigaciones recientes ha demostrado que los juegos de entrenamiento mental son solo buenos para una cosa: ser bueno en los juegos de entrenamiento mental. La afirmación de que ofrecen a los estudiantes un conjunto general de habilidades de resolución de problemas fue recientemente rebatida por un estudio que revisó más de 130 artículos de investigación, que concluía:
No conocemos prueba alguna de mejora general en cognición, rendimiento académico, desempeño profesional, y/o competencias sociales que se derive de una práctica descontextualizada de habilidades cognitivas carentes de contenido de un campo concreto.
Lo mismo aplica para la enseñanza de “predisposiciones” como la “mentalidad de crecimiento” (centrada en la voluntad y el esfuerzo en oposición al talento innato) o la “firmeza” (la determinación para superar obstáculos). No está claro que estas disposiciones se puedan enseñar, y no hay pruebas de que enseñarlas aparte de un tema concreto tenga efecto alguno.
En vez de enseñar habilidades de pensamiento crítico genéricas, deberíamos centrarnos en habilidades de pensamiento crítico concretas para un tema que busquen ampliar el conocimiento individual del estudiante del tema y desentrañar los complicados misterios propios de cada tema. Por ejemplo, si un estudiante de literatura sabe que la madre de Mary Shelley murió poco después del nacimiento de Mary y que la misma Shelley perdió varios hijos al poco de nacer, la comprensión del estudiante de la obsesión de Victor Frankenstein con crear vida a partir de la muerte, y del lenguaje empleado para describirla, será mejor que si se aproxima al texto sin este conocimiento. Un estudiante de física que investiga por qué dos aviones se comportan de forma diferente durante el vuelo puede saber cómo “pensar críticamente” gracias al método científico pero, sin un sólido conocimiento de factores contingentes como la temperatura del aire exterior y un repertorio de casos de estudio previos en los que fijarse, el estudiante tendrá dificultades para saber en qué hipótesis centrarse y qué variables descartar.
Como escribe Willingham: “Los procesos del pensamiento están entrelazados con aquello en lo que se piensa”. Los estudiantes necesitan que se les den cosas reales y significativas del mundo con las que y sobre las que pensar, si los profesores quieren influir en cómo hacen ese pensar.
Sobre el autor: Carl Hendrick es responsable de aprendizaje e investigación en el Wellington College (Berkshire, Reino Unido) y está terminando su doctorado en educación en el King’s College de Londres.
Texto traducido y adaptado por César Tomé López a partir del original publicado por Aeon el 5 de diciembre de 2016 bajo una licencia Creative Commons (CC BY-ND 4.0)
![]()
El artículo Por qué los colegios no deberían enseñar habilidades de pensamiento crítico generales se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El encéfalo bilingüe: por qué no existe un modelo único
- La ciencia perdida: los curiosos casos de los protocolos de TDAH y de leer.es
- El corpus de confusión consistente del inglés oral
La ciencia y la duda
Lo más complicado y duro de practicar ciencia es mantener la permanente capacidad de hacerse preguntas: sobrevivir mentalmente en un entorno de duda continua. Porque la esencia del conocimiento científico es su volubilidad: cualquier teoría, hipótesis o hecho puede ser descartado debido a un nuevo avance, a un nuevo descubrimiento. Todo el andamiaje de lo que creemos saber es volátil; nada es permanente ni debe ser considerado fijo e inmutable. La obligación de cualquier científico es poner constantemente en duda todo lo que cree que sabe.
Y sí; es cierto que a veces y por razones diversas se cuelan en el corpus del conocimiento científico cosas que no son ciertas. La tradición, los intereses comerciales, los errores y la simple mala praxis contribuyen a engrosar el listado de errores de la ciencia. Hay múltiples razones por las que hechos, datos o interpretaciones falsas se pueden perpetuar, muchas de ellas derivadas de los intereses personales de alguien. Y no hablamos sólo de intereses económicos: en la ciencia a menudo el dinero no es la divisa más importante superada con mucho por el prestigio y la reputación. La resistencia a admitir errores o malas interpretaciones que puedan dañar el estátus de un científico o de una escuela o instituto puede ser un importante obstáculo para aceptar correcciones.
También es verdad que la desconfianza radical es poco práctica, y que nunca se replican los experimentos ajenos con ánimo de comprobar sus resultados. Si cada científico tuviese que demostrar todos los presupuestos de su disciplina desde cero para poder avanzar un paso más no sólo se repetiría sin necesidad una enorme cantidad de trabajo, sino que los avances serían muy lentos. De hecho el uso del trabajo anterior como peldaño para avanzar sirve en la práctica como sistema de comprobación: un resultado falso dura poco no porque nadie se dedique a comprobarlo, sino porque otros lo usarán como etapa intermedia en sus propios experimentos. Si no funciona, se sabrá: este no es el principal problema.
Para algunas personas, sin embargo, esta característica inestabilidad de la ciencia es inaceptable. Hay quien necesita sentir que conoce cuáles son los hechos básicos y permanentes sobre el cosmos y se siente inseguro cuando las respuestas a las preguntas cambian. Algunas personas sienten una especie de inestabilidad filosófica cuando las explicaciones sobre el mundo real varían, como si el universo mismo fuese tan poco inamovible como las teorías con las que lo explicamos. En el fondo todos nos sentimos más cómodos con las historias que conocemos y con las teorías con las que nos criamos y educamos; todo cambio de paradigma científico conlleva una cierta incomodidad, un esfuerzo mental de readaptación contra el que la inercia de nuestra mente se rebela.
Pero esta es la esencia del conocimiento científico: su capacidad de avanzar, de sobrepasar las teorías precedentes, de buscar nuevas y mejores explicaciones. Un científico debe estar dispuesto a aceptar que las ideas y teorías que aprendió en la carrera serán superadas por nuevos descubrimientos y nuevas hipótesis, incluso algunas suyas si tiene suerte. Aceptar que lo que antaño sabías ya no sirve no es fácil, pero si se quiere hacer ciencia es necesario. No es este un campo en el que se vayan a sentir cómodos quienes necesitan un cimiento firme e inamovible en el que asentar su concepción del universo. Porque a diferencia de otros sistemas de conocimiento que aspiran a ser equiparables la ciencia, cuando se equivoca, cambia de teoría. Y aunque para sus practicantes no sea fácil la duda constante como método de conocimiento es, sin duda, mucho más potente.
Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.
El artículo La ciencia y la duda se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ciencia, poder y comercio
- De los héroes de la ciencia y sus frágiles teorías
- Pozos de conocimiento: el problema de la profundidad
Los castillos de arena en Titán no necesitan agua

Imagen compuesta de Titan formada a partir de 4 imágenes tomadas por la sonda Cassini en 2004.
Los vientos predominantes en Titán, la luna de Saturno, van de Este a Oeste sobre la superficie del satélite, pero las dunas de algo que podemos llamar arena (aunque no lo sea) de casi 100 m de alto se forman en la dirección contraria. Varias teorías se han propuesto para explicar este fenómeno, pero ninguna es completamente satisfactoria.
Ahora un grupo de investigadores encabezado por Joshua Méndez Harper, del Georgia Institute of Technology (EE.UU.), ha realizado una serie de experimentos que sugieren que las partículas que cubren la superficie de Titán están cargadas eléctricamente.

Arriba dunas de arena en el desierto de namibia (Tierra); abajo, dunas en la región de Belet (Titán)
Cuando el viento sopla con velocidad suficiente (unos 25 km/h; lo que representa la fuerza de un viento de unos 100 km/h en la Tierra, ya que la atmósfera de Titán tiene 4 veces la densidad de la de nuestro planeta) los gránulos “salen volando” y rebotando en un movimiento que los geólogos llaman saltación. Estos gránulos no son silicatos (como la arena de la Tierra) sino probablemente algún tipo de hidrocarburo oscuro (como si fuese hollín); recordemos que en Titán hay lagos y mares de metano y etano líquidos.
Durante la saltación los choques de los gránulos entre sí y con los componentes de la atmósfera rica en nitrógeno provocan que adquieran carga eléctrica por fricción, y terminan formando agrupaciones unidas electrostáticamente que adquieren tamaño suficiente como para que sean difíciles de mover. Mantendrían la carga durante días, si no meses, uniéndose a otras sustancias hidrocarbonadas presentes en el medio. Como resultado, los vientos predominantes, muy suaves, serían incapaces de mover las dunas.
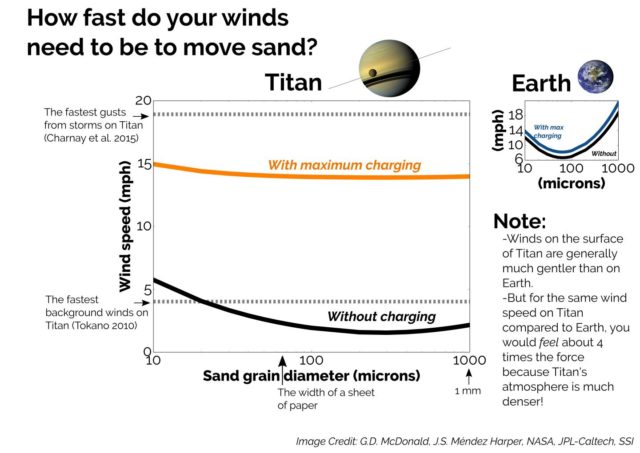
El experimento se llevó a cabo en unas condiciones como las de Titán en un recipiente cilíndrico a presión. Se introdujeron granos de naftaleno y bifenilo, dos compuestos que se cree que existen en la superficie de Titán, en una atmósfera de nitrógeno puro. Tras 20 minutos de hacer girar el cilindro los investigadores midieron las características eléctricas de cada grano conforme salía del tubo.
Todas las partículas estaban cargadas y aproximadamente el 5 % no salía del tubo. Los experimentos se repitieron con arena y con ceniza volcánica; en estos casos todo el contenido salía del tubo. Ello se debe a que los silicatos de arena y cenizas adquieren carga, pero es pequeña y se disipa pronto. Por eso hace falta agua para construir castillos de arena en la playa. En Titán, simplemente, no hace falta.
Referencia:
J.S. Méndez Harper et al (2017) Electrification of sand on Titan and its influence on sediment transport Nature Geoscience doi: 10.1038/ngeo2921
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Los castillos de arena en Titán no necesitan agua se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una proteína humana para potabilizar agua
- El agua lunar creada por el Sol
- La fragmentación del agua al congelarse
Un convite matemático ‘de altura’
Hace casi cuatro años, en la entrada Guateque en el Aftermath del blog de la Facultad de Ciencia y Tecnología de la UPV/EHU, adaptaba una propuesta vista en el libro [1].
En esa anotación, y en una supuesta fiesta que iba a tener lugar en el Aftermath –el universo en el que viven los matemáticos ‘inmortales’ tras su fallecimiento (ver [2])–, los invitados reaccionaban tras recibir la invitación al convite. En tono de humor, las respuestas de cada científico se relacionaban de alguna manera con las aportaciones matemáticas que habían realizado.
Entre los veintiún científicos que aparecían no había ninguna mujer… Hoy realizo en esta entrada el mismo ejercicio, pero eligiendo a cinco de los veintiún ‘ilustres’ matemáticos de Guateque en el Aftermath, introduciendo las respuestas de otras cinco no menos ilustres científicas, y proponiendo, para finalizar, un juego.
Empecemos con el listado de las reacciones ante esta invitación de estas diez insignes personalidades de la ciencia. Cada concepto matemático aparece en negrita y se explica en una nota final.

De arriba abajo y de izquierda a derecha: David Hilbert, Emmy Noether, Paul Erdös, Émilie du Châtelet, Georg Cantor, Ada Lovelace, Felix Klein, Sophie Germain, Kurt Gödel y Sofía Kovalevskaya. Imágenes extraídas de la Wikipedia.
Las reacciones ante la invitación
-
David Hilbert cerrará su hotel (ver [3]) por esta noche, y espera que nadie se aproxime demasiado a su espacio vital durante la fiesta.
-
Emmy Noether dice que solo asistirá si August Möbius lleva unos anillos de chocolate que él mismo prepara –él los llama ‘cintas’– que le han dicho que le salen ‘ideales’ (ver [4]).
-
Paul Erdös ha invitado a sus amigos, a los amigos de sus amigos, a los amigos de los amigos de sus amigos… (ver [5]).
-
Émilie du Châtelet espera encontrar a Isaac Newton desde el principio… tiene mucho que discutir con él sobre su forma de redactar (ver [6]).
-
Georg Cantor no es capaz de contar todas las invitaciones que ha recibido (ver [7]).
-
Ada Lovelace tiene muy bien programada su agenda, y acudirá sin dudarlo (ver [8]).
-
Felix Klein dice que él se ocupará de las botellas (ver [9]).
-
Sophie Germain sólo irá a la fiesta si le garantizan que el número de asistentes es primo, y además un primo de su familia… (ver [10]).
-
.Kurt Gödelinsiste en que la invitación no es completa y no lo será nunca. Pero él estará allí aunque nunca podrá probarlo (ver [11]).
-
Sofia Kovalevskaya llevará unas peonzas para jugar: en la última fiesta, los rompecabezas que llevó Martin Gardner no le gustaron nada… (ver [12]).
El juego final
El juego final consiste en proponer otras posibles respuestas a esta supuesta invitación a esta selecta fiesta… esas frases deben proceder de mujeres matemáticas (ya fallecidas, y se puede elegir a las cinco anteriores también), y en ellas debe de estar incluida, de alguna manera, una alusión a sus aportaciones matemáticas (explicándolas).
Podéis enviar las propuestas a esta dirección de correo electrónico. Si hay suficientes, haremos una entrada (citando a sus autoras o autores) en el blog Mujeres con ciencia de la Cátedra de Cultura Científica de la UPV/EHU. ¡Animaos!
Notas
[1] Bruno Winckler, Recueil de blagues mathématiques et autres curiosités, Ellipses, 2011.
[2] En inglés aftermath significa secuela. Aquí se trata de un juego de palabras ‘After math’, es decir, ‘después de las matemáticas’. Se usa en este sentido, por ejemplo, en el musical Fermat’s last tango de Joshua Rosenblum y Joanne Sydney Lessner.
[3] El ejemplo del hotel infinito es una construcción abstracta debida a David Hilbert para explicar alguna de las ‘paradojas’ que envuelve el concepto de infinito. La introdujo durante la conferencia Über das Unendliche impartida en 1924. Raúl Ibáñez lo explicaba en Una de mates: El hotel infinito.
[4] Emmy Noether, la madre del álgebra abstracta, trabajo en teoría de anillos y de ideales. La cinta se refiere, por supuesto, a la cinta de Möbius.
[5] Se está hablando del número de Erdös, al que también nos referimos en la entrada El número de Erdős-Bacon-Sabbath.
[6] Émilie du Châtelet tradujo los Principia de Newton al francés.
[7] Georg Cantor formalizó el concepto de infinito a través de los llamados números transfinitos.
[8] Ada Lovelace pasa por ser la primera persona programadora de la historia.
[9] La botella de Klein es una superficie, de la que hemos hablado en las entradas La botella de Klein: geometría ‘palindrómica’ y Una visión topológica de la Odisea.
[10] Se está hablando de los números primos de Germain.
[11] Se refiere a los teoremas de incompletitud de Gödel y a la indecibilidad, ambos enmarcados en la teoría de lógica matemática.
[12] Sofía Kovalevskaya recibió en 1888 el Premio Bordin de la Academia de Ciencias de París por su trabajo Sobre la rotación de un cuerpo sólido alrededor de un punto fijo, es decir, un trabajo sobre el movimiento de una peonza.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Un convite matemático ‘de altura’ se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:A mayor tamaño, mayor complejidad
A partir del modelo animal básico consistente en una estructura procedente de tres capas embrionarias (ectodermo, mesodermo y endodermo), una simetría bilateral y la aparición de una cavidad interna, la división del trabajo biológico se acentúa considerablemente, con lo que la complejidad aumenta cada vez más.
Recordemos ahora que en el curso de la evolución de los animales se ha producido un aumento global del tamaño corporal. Pues bien, ese aumento del tamaño no habría sido posible sin el proceso paralelo del aumento de la complejidad organizativa y funcional. Por expresarlo de forma muy simple: no sería posible que un animal del tamaño y forma de un tortuga estuviese constituido por un bloque de células ameboides todas iguales.
Podemos considerar que el número de tipos celulares distintos que hay en un organismo constituye un indicador de su complejidad. Al fin y al cabo, cada uno de los tipos celulares realiza alguna tarea diferenciada del resto y es habitual que forme parte de algún tejido u órgano en concreto. Y cuantos más tejidos diferentes y órganos tiene un animal, más compleja es su organización y funcionamiento1.
Los representantes de los grupos más antiguos que aún perviven (Porifera) tienen alrededor de diez tipos celulares y algunos de esos tipos ni siquiera se organizan en tejidos, menos aún en órganos. Los animales con simetría bilateral más antiguos dotados de celoma tienen treinta tipos celulares. Los artrópodos tienen alrededor de cincuenta y los cefalópodos del orden de setenta y cinco. Los anfibios tienen cerca de ciento cincuenta. Las aves alrededor de ciento ochenta. Y los homínidos doscientos diez. Si el filo Porifera surgió hace aproximadamente unos quinientos ochenta millones de años y los primeros animales de simetría bilateral –con un número estimado de treinta tipos celulares distintos- aparecieron hace unos quinientos setenta millones de años, el ritmo de aparición de nuevos tipos celulares ha sido, aproximadamente, de uno cada tres millones de años. En resumen, conforme han ido apareciendo nuevos grupos animales, el número de funciones diferentes que es desempeñado por tipos celulares distintos no ha dejado de aumentar. De acuerdo con ese criterio, la complejidad organizativa y funcional ha sido cada vez mayor.
La especialización celular, como se ha dicho, refleja en gran medida un funcionamiento basado en órganos y sistemas y es la consecuencia, y a la vez reflejo, de una forma de división del trabajo de la que muy probablemente se deriva una mayor eficacia biológica. Así pues, en el curso de la evolución de los animales la división del trabajo no ha dejado de acentuarse. Creemos, además, que ese proceso es el que ha permitido el aumento del tamaño de los linajes de metazoos, aunque no lo ha hecho obligatorio. Por esa razón la mayor parte de los animales están organizados como un conjunto de sistemas que funcionan de forma armónica.
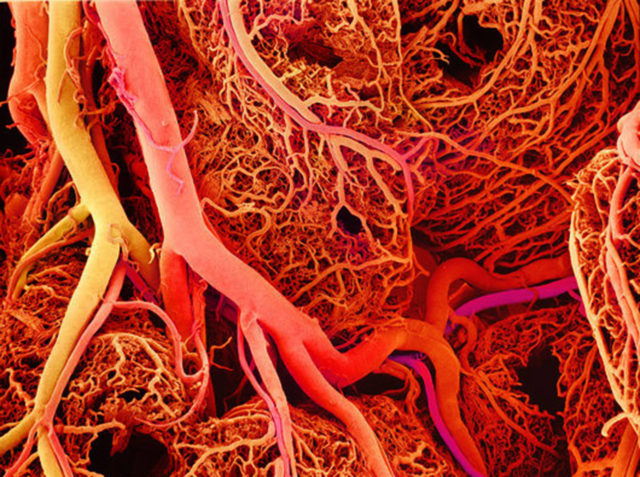
Para ilustrar los principios a los que me he referido en el párrafo anterior, fijémonos en la respiración. En los animales que carecen de sistema circulatorio (poríferos, cnidarios, gusanos planos, por ejemplo) el oxígeno no puede penetrar más de 1 mm desde el exterior del organismo, por lo que las mitocondrias más alejadas de la superficie corporal no pueden estar más alejadas del medio respiratorio que esa distancia. Eso, obviamente, limita mucho el tamaño total que puede alcanzarse. Sin embargo, una vez los animales cuentan con un medio líquido que circula por el interior del organismo y que pone en contacto unos sistemas con otros y el conjunto de ellos con el exterior, las limitaciones al tamaño motivadas por la difusión de los gases respiratorios se relajan considerablemente. Por otra parte, si, por las razones que fuese, los animales necesitan que la mayor parte de su superficie corporal sea impermeable al paso de diferentes sustancias, se requiere de un enclave especial en el que realizar el intercambio de gases: el sistema respiratorio. Éste, a su vez, si está asociado al sistema vascular, ya se encuentra en disposición de captar el oxígeno necesario, y transferirlo al plasma o sangre y, a través de ella, enviarlo a todos los tejidos. Hay una notabilísima excepción a ese esquema que es la de los insectos, que respiran a través de un sistema traqueal, pero precisamente por eso, el tamaño máximo que puede alcanzar un insecto está muy limitado. Una mosca no podría alcanzar el tamaño de un cerdo, por ejemplo, porque su sistema traqueal no se lo permitiría.
El ejemplo que he utilizado (sistema circulatorio y sistema respiratorio) ilustra bien a las claras la forma en que la especialización basada en tipos celulares distintos organizados en órganos y sistemas conlleva una mayor eficacia en el desempeño de una función y cómo esa mayor eficacia permite -en este caso de forma palmaria, no tanto en otros- mayores tamaños corporales.
Todas estas cosas pueden parecer obvias. Pero no lo son.
Referencias:
John Tyler Bonner (2006): Why Size Matters. Princeton University Press, Princeton.
James W Valentine, Allen G. Colins & C. Porter Meyer (1994): Morphological Complexity Increase in Metazoans. Palebiology 20 (2): 131-142
Nota:
1 Esto es, obviamente, muy discutible, pues depende de cómo definamos la complejidad. A los efectos que aquí interesan, sin embargo, me parece que el número de tipos celulares diferentes es un buen indicador. La idea la he tomado de Valentine et al (1994).
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo A mayor tamaño, mayor complejidad se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Historia mínima de la complejidad animal
- Evolución del tamaño animal
- De la edad y tamaño del universo
De la reforma a la revolución

Thomas Wijck (1640-1677), “El Alquimista”. Óleo sobre madera, 43 x 37,5 cm. Ámsterdam, Rijksmuseum.
En los siglos XIV y XV las artes químicas, como tales, avanzaron poco, salvo en lo que se refiere a los trucos del alquimista estafador. Las avances técnicos del siglo XVI tampoco fueron espectaculares. De hecho, este periodo no fue otra cosa que una pausa en la investigación que se empleó en la reforma de la propia consideración de la química.
El objetivo de la química fue redefinido y reajustado. La minería, la medicina y la parte noble de la alquimia pasaron a estar interrelacionadas. Se pusieron en su sitio a las autoridades del pasado y surgieron nuevas basadas en nuevos libros cuyas afirmaciones podían comprobase en la práctica por mineros, metalúrgicos, farmacéuticos y médicos. Se puso un énfasis especial en los preparados químicos de uso en medicina y en la forma de prepararlos por parte de los farmacéuticos, que ahora debían ser también alquimistas, lo que tuvo un efecto muy estimulante en las investigaciones de los siglos posteriores.
Si bien no se avanzó mucho teóricamente, sí se pusieron las bases durante la Reforma para lo que después se llamaría la Revolución Química. Pero con la reforma también llegó la reacción, y en el siglo XVII habría casi tantos pasos para atrás como pasos hacia adelante.
La Europa del siglo XVII estaba en una etapa de grandes cambios, de ambigüedades y al frente del inicio de la globalización. Un ejemplo en lo político es Inglaterra donde, en la primera mitad de siglo, el rey Carlos I era descabezado (literalmente) durante la Guerra Civil Inglesa, para, en la segunda mitad, sustituir al católico Jacobo II por su protestante hija María II, tras una votación en el Parlamento que incluyó la Declaración de Derechos (1689), limitando los poderes del monarca.

Diego Velázquez, “La rendición de Breda” (1634-35). Óleo sobre lienzo, 307 x 367 cm. Madrid, Museo del Prado. La obra representa el momento en que Justino de Nassau rindió la ciudad de Breda, en 1625, a las tropas españolas al mando del general Ambrosio Spínola, que aparece recibiendo las llaves de la ciudad de manos de su enemigo.
Mientras, la Guerra de los Treinta Años (1618-1648) es la última gran guerra de religión pero la primera gran lucha nacionalista por la hegemonía continental, barriendo prácticamente las últimas trazas de feudalismo.
La exploración y colonización del mundo (África, Asia, América, Australia) supuso la aparición de un flujo continuo de nuevos productos (azúcar, café, tabaco, tomates, patatas, maíz, por nombrar algunos), que cambiaron muchos usos y costumbres. También un torrente de nueva información que forzaron a muchos a cambiar su cosmovisión. La creencia en la superioridad europea también llevó al restablecimiento de una práctica perdida con el Imperio Romano, la esclavitud.
La higiene brillaba por su ausencia y las grandes ciudades de Europa eran básicamente un pestilente foco de basuras y enfermedades. Los ricos comienzan con la costumbre de huir de ellas en verano, hacia mansiones que construyen en el campo.
El siglo XVII será el de la Revolución Científica pero, y esto se subraya poco, para las ciencias macroscópicas, física y astronomía, no así para la química.
Efectivamente, cuando a Richard Feynman le pidieron que resumiera en una frase el conocimiento científico más importante que tenemos, tras reflexionar un momento, dijo: “Todo está hecho de átomos”. Esto, que hoy damos por sentado y como algo poco menos que evidente, fue una suposición que ganó peso en el siglo XIX y que sólo se pudo confirmar más allá de toda duda razonable cuando Jean Perrin demostró en 1908 que la teoría del movimiento browniano formulada por Albert Einstein en 1905 era correcta.
En el siglo XVII, por tanto, para los químicos los principios fundamentales de su arte les eran desconocidos. Se intuía que la materia estaba compuesta por algún número indeterminado de los llamados “elementos” (que no hay que confundir con los actuales) y que éstos estaban presentes en todas las clases de materia. Esta hipótesis, muy vaga, era de poca utilidad práctica. Sin embargo, a finales de siglo se producirán aproximaciones a una definición alternativa.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo De la reforma a la revolución se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La Reforma química
- Las matemáticas como herramienta (II): La Revolución Científica y el cálculo
- Biringuccio, la química práctica y rentable del XVI
Las razones del asesino
Las razones para matar son muchas y variadas, según el interesado en este asunto que nos lo cuente. Aquí van varios ejemplos. Agatha Christie dice que la causa puede ser pasional, el dinero o una idea. Erle Stanley Gardner habla del poder y el dinero, y añade que es inevitable en una sociedad tan competitiva como era Estados Unidos en la época de Perry Mason, en los cincuenta del pasado siglo. Y John Verdon, escritor de este siglo, repite el sexo, el dinero, el poder, la venganza y los delirios o misiones sagradas. Arthur Koestler, filósofo y ensayista, se acerca a algunas de las propuestas más actuales de la neurociencia cuando afirma que matamos por una coordinación insuficiente entre el neocórtex racional y el hipotálamo emocional que nos lleva a ”esa veta única, alucinatoria, asesina, que lo ha impulsado a matar, torturar y hacer la guerra.” Es más, para Peter Morrall, el crimen fascina, intriga y repugna a la vez.
Cayetano Galeote: El honor de un cura

Narciso Martínez Izquierdo
El obispo Narciso Martínez Izquierdo había nacido 1830 en Pineda de la Sierra, Guadalajara. El cura Cayetano Galeote Cotilla había nacido en 1841 en Vélez Málaga. Sus caminos se encontraron el 18 de abril de 1886, Domingo de Ramos, en la escalinata de entrada a la Catedral de San Isidoro de Madrid. De esta manera, una vida disoluta, un obispo estricto, un asunto de política eclesiástica y una cuestión de honor acabaron en un asesinato. En esa fecha y en ese lugar, el cura Galeote disparó tres veces contra el Obispo Martínez Izquierdo que, atendido en el sitio, fue llevado al hospital y falleció al día siguiente.
Narciso Martínez Izquierdo venía de una familia de labradores que, como era habitual en la época, mandaba a uno de sus hijos al seminario pues era la mejor manera de alimentarlo y educarlo sin muchos gastos. Pero el joven Narciso hizo una brillante carrera en la Iglesia y llegó a Obispo de Salamanca en 1874 y a Obispo de Madrid en 1885. Además, participó en política y fue diputado carlista en 1871 y 1873, y senador en 1876 y 1881. Dadas sus opiniones fuertemente conservadoras, se opuso a la libertad de cultos en la Constitución de 1886 y a la instauración del matrimonio civil en los debates en las Cortes en 1881. Era muy estricto en cuanto al comportamiento del clero, lo que no le hizo muy popular entre algunos de sus administrados. Cuenta Benito Pérez Galdós que, nada más ser nombrado Obispo de Madrid, inició una campaña contra la corrupción en el clero y, entre otras cosas, obligó a los sacerdotes a inscribirse en una sola iglesia y, así, terminar con el sistema de misas diarias dobles, triples o cuádruples que seguían muchos curas para aumentar sus ingresos pues se cobraba por misa celebrada. Los que no cumplían veían como el Obispo les retiraba la licencia para celebrar la misa.
Cayetano Galeote Cotilla, natural de Vélez Málaga, provenía también de familia pobre que con dificultad alimentaba a sus seis hijos. El niño Cayetano, con pocos años, enfermó de otitis bilateral y de ello le quedó la sordera de un oído para toda su vida. Al acabar sus estudios de sacerdocio, fue destinado un tiempo en Madrid, luego en Puerto Rico durante cinco años y, además, fue capellán castrense en Fernando Poo. En 1880 regresó a Madrid y se inició el drama que aquí contamos.
El cura Galeote era un sacerdote inestable que cambiaba a menudo de parroquia en busca de mayores ingresos. Era lo que denominaba un “cura suelto, sin oficio ni beneficio”, iba donde más y mejor pagaban una misa. Sordo desde niño, de mal carácter, violento e irascible, fue descrito por un compañero de colegio como “un verdadero epiléptico”. Finalmente, era notorio y público que, en sus numerosos cambios de domicilio le seguía siempre su ama de llaves, su “sobrina”, Doña Tránsito Durdal, de 33 años y natural de Marbella, con quien parece ser vivía amancebado. En el juicio se utilizó, en este sentido, el hecho demostrado de que en la casa del cura sólo había una cama.
Esta mujer es, quizá, la figura misteriosa de este drama. Según Pérez Galdós, “no es una mujer vulgar”. De figura esbelta, fisonomía inteligente y modales corteses, los que la vieron la describen como de unos treinta años, “guapetona, alta, ojos negros, boca grande y conjunto agradable.” Acompañaba al cura Galeote cuando en 1880 regresó a Madrid desde Fernando Poo. Cómo se encontraron e iniciaron su vida en común y de qué tipo de era esa vida, todos son misterios cuya respuesta sólo se vislumbró en el juicio y en las crónicas de la prensa.
Según su declaración, el cura Galeote disparó contra el Obispo como reparación de su honra mancillada y para hacerse justicia. Todo comenzó con una disputa con el cura Vizcaíno, Rector de la Capilla del Cristo de la Salud. Galeote consideró, quisquilloso a más no poder como era, que Vizcaíno le había retirado el saludo y no le trataba con la educación debida. Además, prohibió a Galeote cantar misa en la Capilla, prohibición que Galeote ignoró. La Junta de la Capilla le destituyó y Galeote se sintió insultado, además de perder unos buenos ingresos. Indignado, Galeote se entrevistó o escribió al Obispo, a su secretario, a su confesor, al Nuncio y a algún que otro político. Cada vez más insolente y amenazador, más tarde confesó que había acechado, con el revólver cargado, al cura Vizcaíno y al Obispo. Y el 18 de abril, Domingo de Ramos, cumplió sus amenazas.
En el juicio no se debatió en absoluto sobre la culpabilidad del cura Galeote pues medio Madrid le había visto disparar al Obispo y, además, él mismo se apresuró a confesar el crimen. Lo que se discutió fue su responsabilidad, o sea, si en el momento de los hechos era dueño de sus actos o era un loco rematado y, por lo tanto, irresponsable. Uno de los psiquiatras que le examinó le describe como “un hombre de carácter violento, poco humilde, tenaz, de imaginación excitable, cargante, iracundo, acalorado, pronunciadamente nervioso, receloso, acusador, insultador, raro, extravagante; es decir, un sacerdote imposible y que no atendía a razones.” Y este mismo psiquiatra, partidario de las teorías degeneracionistas del delincuente promovidas por Cesare Lombroso en las que el aspecto físico revela las cualidades mentales, hace una descripción de Galeote realmente impactante: “es un hombre de complexión recia, seco de carnes, enjuto de rostro, de cráneo chico, cara larga, frente cuadrada, estrecha y oblicua, quijadas pronunciadas, cuyos dientes salen unos hacia el paladar, y otros divergen empujando el belfo lo que le impide cerrar bien los labios, por entre los cuales despide espumarajos de saliva cuando se excita.” Y así sigue el psiquiatra durante varios párrafos de los que aquí nos vamos a librar.
Más sencillo es Pérez Galdós al describir al cura Galeote. Es “de nariz pequeña y corva, la boca muy grande y muy separada de la nariz, los ojos negros y vivos, la frente despejada.”
En resumen, para los psiquiatras de la defensa, Galeote es un paranoide con delirio persecutorio. Realmente, en el juicio tuvo una conducta sorprendente. Uno de los psiquiatras que leyó su informe al tribunal fue un joven médico llamado Jaime Vera, con un trabajo profundo, directo, preciso y, se agradece, comprensible para cualquiera. Según el corresponsal de El Socialista, una vez leyó el informe, Galeote, entusiasmado, “le alzó en sus robustos brazos, como quien alza una pluma, y le paseó triunfalmente alrededor de la sala, en medio de la estupefacción de todos.” En realidad, Galeote no quería que le declarasen loco; aseguraba que su crimen era por su honor, que el Obispo le “trató como a un perro” y que “matose a sí mismo” y, así, su honra quedó reparada.
Cada vez que su abogado defensor hablaba de su locura, el cura protestaba enérgicamente. Pero nadie le hacía caso. Benito Pérez Galdós, que asistió al juicio como periodista y corresponsal, vio en el acusado, como el resto de la prensa, a una persona extraña, enérgica y de rara conducta. Así lo describe: “el reo se ha permitido las mayores extravagancias, ya desconociendo la autoridad del presidente, ya interrumpiendo a cada instante las declaraciones de los testigos; pasando bruscamente del llanto a la ira, siempre agitado y nervioso, sus palabras, sus apóstrofes, ora epigramáticos, ora terribles, han excitado vivamente el interés público”. Galdós, finalmente, se pregunta, “y en resumidas cuentas, ¿está loco o no?”
El cura Galeote fue condenado a muerte el 9 de octubre de 1886. Sin embargo, su rara conducta en la cárcel llevó al tribunal ordenar un nuevo reconocimiento a una comisión formada por seis médicos, que dictaminó delirio persecutorio. Este informe fue ratificado por la Real Academia de Medicina el 3 de diciembre de 1887. El reo fue encerrado en el manicomio de Leganés donde murió en 1922.
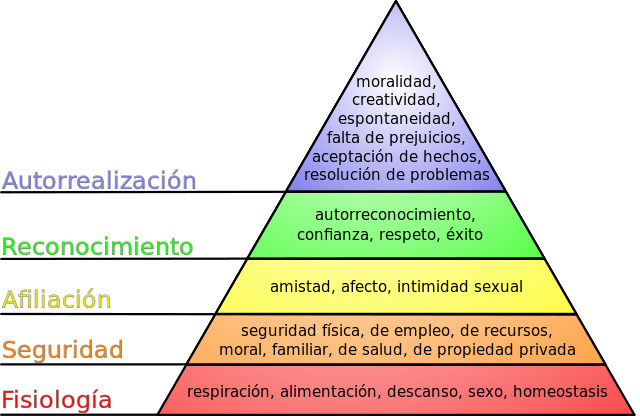
Pirámide de Manslow
Cuando son los asesinos los que hablan de justificación casi siempre comienzan afirmando que no querían matar, pero han matado y, en el fondo, ha sido sin querer, un accidente, no sé cómo ocurrió,… Por el contrario, la mayoría de las personas en nuestra sociedad occidental, en un momento u otro de su vida, querrían matar, pero no lo hacen. Veamos lo que dicen los expertos de las razones para matar. Podemos empezar con lo que Abraham Maslow escribió en 1943 sobre la motivación humana. Se puede suponer que lo que nos motiva en nuestra vida es, también, lo que nos impulsa a matar. La motivación, según Maslow, comienza con la fisiología, es decir, con las necesidades fisiológicas básicas como la comida, la respiración o el descanso. Después, o más arriba en esta pirámide que estamos construyendo, están las necesidades de seguridad que incluyen nuestra protección, la casa o el territorio. Y por encima está la pertenencia a algo o a alguien y el amor, con el afecto, la amistad y el grupo. También necesitamos la autoestima y la confianza en nosotros mismos cuando buscamos el respeto, el éxito y el estatus. Finalmente, queremos la autorrealización con la moralidad y la creatividad.
Para cubrir estas necesidades es por lo que, en las circunstancias adecuadas, nuestra especie mata a un semejante, o a muchos. Philip Zimbardo fue el que ensayó cómo es que personas normales, como usted y como yo, si se me permite personalizar, acaban cometiendo actos crueles y atroces. Es lo que nos enseñó Hannah Arendt cuando asistió en Jerusalén al juicio de Adolf Eichmann, responsable de la organización del exterminio de judíos en la Segunda Guerra Mundial. No era un asesino cruel y sanguinario, era, simplemente, un funcionario obediente y eficaz que cumplía órdenes. Y sus órdenes eran exterminar a los judíos, y millones murieron bajo la responsabilidad del funcionario Eichmann.
August Hirt: Por la ciencia y el nazismo
El 23 de noviembre de 1944, la 2ª División Blindada de la Francia Libre bajo el mando del general Leclerc, adscrita al 2º Ejército de Estados Unidos de George Patton, entró en Estrasburgo, expulsó al ejército alemán y liberó la ciudad. De inmediato y tal como establecía el protocolo habitual, varios grupos del ejército francés entraron en diferentes instituciones de la ciudad en busca de pruebas y testimonios sobre la ocupación. Entre otros, entraron en el Instituto de Anatomía de la Universidad de Estrasburgo y, en el sótano, encontraron decenas de cadáveres, completos o desmembrados, cuidadosamente conservados en alcohol.
No había pasado un mes desde la llegada de Leclerc cuando, el 17 de diciembre, comenzaba sus averiguaciones una comisión de oficiales médicos cuyas órdenes eran investigar posibles crímenes de guerra en relación con los cuerpos humanos encontrados en el sótano del Instituto. Pronto descubrieron que la colección pertenecía a August Hirt, profesor de Anatomía y director del Instituto.

Monolito con los nombres de las víctimas de Hirt
August Hirt había nacido en Mannheim el 28 de abril de 1898. Fue voluntario en el ejército alemán durante la Primera Guerra Mundial, herido gravemente en 1916 y condecorado. Inició sus estudios de Medicina en la Universidad de Heidelberg y se doctoró en 1922 con una tesis sobre el sistema nervioso simpático en reptiles. Fue profesor de Anatomía en la Universidad de Greifswald en 1936. En los años siguientes contribuyó con hallazgos significativos al desarrollo de la microscopía de fluorescencia y fue el autor del concepto de epifluorescencia. Tiene, hasta 1940, un buen curriculum de investigación, con 27 artículos publicados sobre el sistema nervioso y la microscopía de fluorescencia . Siguió investigando, a su manera como veremos más adelante, pero a partir de 1940 no volvió a publicar ningún trabajo. Por esta época, se afilia al Partido Nazi y en la Segunda Guerra Mundial alcanza el grado de Obertsturmführer en las SS y, en 1941, el de Sturmbannführer. En 1942 ingresa en la sociedad Ahnenerbe.
También en 1941 es nombrado director del Instituto de Anatomía de la entonces llamada Reichsuniversitat de Estrasburgo. En los años de guerra, Hirt, junto a Wolfram Sievers, de la Ahnenerbe, y Sigmund Rascher, médico en el campo de concentración de Dachau y colaborador de Mengele, y con la coordinación con Adolf Eischmann, planeó y realizó experimentos con los prisioneros del campo de concentración de Struthof-Natzweiler, situado cerca de Estrasburgo. En particular, su labor principal fue organizar la recogida de cuerpos para la colección del Instituto de Anatomía. En el sótano en el que entraron los hombres de Leclerc había 86 cadáveres.
En 1933, la manía de Himmler por las pseudociencias y por las investigaciones raciales le había llevado a fundar Ahnenerbe o “Herencia de los Antepasados” (¿recuerdan las películas de Indiana Jones y lo que buscaban los nazis?) que, desde 1935, se dedicó a estudiar todo lo relacionado con la “raza nórdica indo-germánica”. Da una idea de sus objetivos el nombre completo de la institución: “Herencia de los Antepasados – Sociedad de Estudios para una Prehistoria Espiritual”. Es evidente por qué Hirt solicitaba fondos y prisioneros a través de la Ahnenerbe y de su director, Wolfram Sievers.
Hirt pretendía crear una colección de cuerpos de judíos para las generaciones futuras, cuando aquella raza hubiera sido exterminada por completo. En concreto, y en carta fechada en febrero de 1942, Hirt quiere cráneos de comisarios soviéticos judíos con el “propósito de dedicarlos a investigaciones científicas”, y además solicita fondos para construir un nuevo microscopio con el que hacer observaciones en vivo. La carta llevaba dos notas adjuntas. En la primera, que se ha perdido, detallaba la nueva técnica microscópica, derivada de la que había desarrollado en sus investigaciones antes de la guerra. En la segunda nota, que se conserva, da instrucciones detalladas a la Wehrmacht y a la Policía Militar de cómo localizar, identificar, tomar datos antropólogicos, ejecutar a los comisarios (lo que llama, con cínico eufemismo, “muerte inducida”) , separar su cabeza y enviarla a Estrasburgo en un recipiente con líquido conservante.
Para Hirt, la colección de Estrasburgo estaba bien provista, pero le faltaban judíos y la guerra en el Este le da la oportunidad que buscaba. Considera los cráneos de los comisarios soviéticos judíos como el no va más de la degradación humana, incluso los considera infrahumanos. Su sueño era desarrollar una nueva disciplina, la Anatomía de la Razas. Quiere reunir en su museo muestras de la especie humana y su ausencia total de respeto hacia los hombres que considera inferiores le ofrece, en medio de la guerra, la oportunidad de conseguirlo. Hirt propone y la Ahnenerbe, Sievers y Himmler, con la ayuda de Rascher y la organización de Eichmann, disponen. El fantasma de la ciencia se convierte en cruel realidad.
Además de las instrucciones para conseguir los cráneos de los comisarios, y en coordinación con Rascher y Eichmann, Hirt organizó el traslado de reclusos, elegidos por ser judíos, desde otros campos de concentración hasta el de Struthof-Natzweiler, donde eran ejecutados por el jefe del campo, Josef Kramer. Este, que fue capturado por los aliados, lo cuenta así en los interrogatorios: “A principios de 1943, recibo los 80 internados destinados a ser suprimidos con la ayuda del gas que me había enviado Hirt. Comencé por llevar a la cámara de gas, una tarde hacia las 4, y con la ayuda de una camioneta, un primer grupo de unas 15 mujeres. Les dije que debían pasar por la cámara de desinfección, y les oculté que iban a ser asfixiadas. Ayudado por algunos SS, les hice desnudarse y entrar en la cámara de gas. Cuando cerraba la puerta, comenzaron a gritar… Di la luz del interior de la cámara con un conmutador externo… y observé lo que ocurría en el interior, medio minuto, y después se derrumbaron.”
Los cuerpos se conservaban en Estrasburgo hasta que Hirt procedía a separar la cabeza y obtener el cráneo; siempre ordenaba destruir lo que quedaba de los cadáveres. Es posible que estos cadáveres, o quizá otros ejecutados de la misma manera, fueron los encontrados en el sótano del Instituto de Anatomía. Hirt también ordenaba destruir los tatuajes que identificaban a los prisioneros de los campos de concentración. El único cadáver con tatuaje fue rápidamente identificado por la comisión médica de los aliados como el de Menahem Taffel. El médico francés Henri Henripierre, ayudante a la fuerza de Hirt, fue quien destruyó los tatuajes, pero los memorizó, los apuntó y guardó los datos durante años.
Unas semanas antes de entrar Leclerc en Estrasburgo, Hirt huyó. Meses después se entregó al alcalde de Schönenbach, cerca de Friburgo, en Alemania. Y el 2 de junio de 1945 volvió a desaparecer; hay quien asegura que se suicidó y otros, en cambio, creen que se esfumó entre los miles de refugiados que entonces recorrían Europa. Como tenía doble nacionalidad, alemana y suiza, en este último país estuvo en busca y captura hasta 1959. En Metz, Francia, fue juzgado en rebeldía en 1953 y condenado a muerte.
Los cargos contra Hirt procedían de tres hallazgos: la carta que he mencionado con las instrucciones para ejecutar comisarios soviéticos judíos; los 86 cadáveres encontrados en el sótano del Instituto de Anatomía; y, en tercer lugar, las preparaciones histológicas encontradas en la Facultad de Medicina de la Universidad de Estrasburgo, descubiertas también al entrar las tropas de Leclerc en la ciudad. Sobre las 54 preparaciones encontradas, el profesor Christian Champy, uno de los mejores histólogos franceses de la época, hizo un informe que trastornó el mundo de la Medicina, incapaz de creer que hubiera médicos que cometieran semejantes atrocidades.
Tras la liberación, el doctor Reisler, junto con la policía francesa, registró las dependencias a cargo de Hirt en la Facultad de Medicina y encontró una serie de preparaciones de testículo humano así como varios cadáveres en los que faltaba un testículo. El doctor Henry Henrypierre, ayudante de Hirt, contó que le habían ordenado hacer las preparaciones histológicas del testículo izquierdo de los cadáveres. Cuando las preparaciones fueron encontradas estaban hechas hacía poco tiempo y los materiales utilizados todavía estaban frescos. Champy y Reisler redactaron un informe que se leyó en la sesión de la Academia de Medicina celebrada el 1 de mayo de 1945 (el 7 de mayo, Alemania se rindió a los aliados y terminó la guerra en Europa).
Son 54 preparaciones que provienen de, al menos, siete individuos. Las lesiones que se observan indican que son consecuencia de inyecciones en el testículo de sustancias tóxicas o irritantes. Por el estado de las lesiones, las inyecciones se han hecho entre ocho días y varias semanas antes de la muerte del sujeto. En la hipótesis más favorable, es decir, suponiendo que las inyecciones se han puesto con anestesia, las lesiones producidas han tenido que ser muy dolorosas. El resto de los tejidos están en buen estado, lo que implica que la persona fue asesinada para tomar la muestra en el momento que se consideró oportuno. Dos de los testículos provienen de dos adolescentes de entre 13 y 15 años. No se consigue averiguar la finalidad de los experimentos. Otra vez el fantasma de la ciencia se hace cruel realidad.

Núrenberg, 1938
Para Zimbardo, la línea que separa el bien del mal es muy tenue, tal como explica Antonio Crego en su blog en Investigación y Ciencia. El paso que hay que dar, a menudo suave e imperceptible, depende de circunstancias externas y de factores como el sistema legal, económico, social, político y cultural.
Se da el primer paso sin más, sin pensarlo mucho. Hay que recordar las declaraciones de muchos acusados de corrupción en política cuando explican y tratan de justificar su conducta. Volvamos a Zimbardo.
Una vez dado el primer paso, se impone deshumanizar al contrario, a las futuras víctimas. Así es más sencillo no sentir repugnancia o arrepentimiento por el mal que se hará. Después, es aconsejable perderse en la multitud, no ser un individuo sino alguien entre muchos. Ayudan los uniformes, las máscaras, los grupos, y hasta la música, y así se llega a los linchamientos. Ya hemos difuminado y repartido entre muchos la responsabilidad personal. También es interesante como excusa la obediencia debida, la obediencia ciega, la obediencia de Eichmann; otro lo ordenó y no hubo más remedio que obedecer. Es obvio que el grupo y la obediencia no permiten en absoluto la crítica a los comportamientos violentos. Todo lleva, en último término, a la tolerancia neutra del mal, a la banalidad que definía Hannah Arendt.
Kandido Azpiazu Beristain: Uno de los nuestros
Era el 21 de septiembre de 1962 en Azkoitia, Gipuzkoa, después de comer, hacia las cuatro de la tarde. Una mujer, con un niño de la mano y otro en brazos paseaba. Al chaval se le escapó el balón con el que jugaba y salió a la calle. El niño no lo dudó y salió de inmediato a recogerlo y su madre le siguió. Venía un camión. Un hombre, sentado en una silla a la puerta de una tienda de muebles, cogió al bebé de brazos de su madre mientras esta saltaba a la calzada. Ambos, madre e hijo murieron atropellados por el camión. El hombre que salvó al bebé se llamaba Ramón Baglietto y el niño, de 11 meses, era Kandido Azpiazu Beristain.

Ramón Baglietto
Han pasado 18 años. Estamos a 18 de mayo de 1980. En la carretera entre Elgoibar y Azkoitia, un Seat 131 robado, con el conductor y un pasajero, se sitúa en paralelo a un Seat 124 blanco y disparan con una metralleta Steiner y con pistolas Browning. El 124 se sale de la calzada y se estrella contra un árbol. El pasajero del 131 sale del coche, se acerca al 124 y con la pistola le dispara el tiro de gracia. No quiere errores, solo muertos. El militante de ETA se llama Kandido Azpiazu Beristain y el asesinado es Ramón Baglietto.
Ahora pasamos otros 25 años y llegamos al 16 de marzo de 2005. Ese día, un etarra salido de la cárcel 10 años antes, se instala como cristalero en una lonja del número 14 de la calle Ibai Ondo de Azkoitia. En ese portal, dos pisos más arriba, vive la viuda de un asesinado por ETA, ahora concejala del PP en el ayuntamiento de su pueblo por donde se mueve siempre acompañada de sus dos guardaespaldas. La viuda se llama Pilar Elías, su marido era Ramón Baglietto, y el cristalero es Kandido Azpiazu Beristain.
Ramón Baglietto, apodado El Pintor, había nacido en Bilbao en 1936 y, en 1962, cuando el accidente con el camión, tenía una tienda de muebles en Azkoitia y estaba prometido a Pilar Elías, la hija del viejo Elías, propietario de la única gasolinera en la carretera de Elgoibar. Fue teniente de alcalde y militante de UCD. Cuando fue asesinado tenía dos hijos, de 9 y 13 años. Su tienda de muebles estaba en la Avenida de Calvo Sotelo, hoy Xabier Munibe Kalea.
María Pilar Elías era de Azkoitia e hija, como ya he dicho, del dueño de la gasolinera de la carretera de Elgoibar. Nació en 1942 en la casa en que todavía vive, en la calle Ibai Ondo, frente al río Urola. En los bajos está la cristalería de Kandido Azpiazu. Tiene, en 2006, dos hijos y tres nietos. Después del asesinato de su marido, años más tarde, fue concejala del PP en el Ayuntamiento de su pueblo durante mucho tiempo, hasta 2011.
Kandido Azpiazu Beristain, de Azkoitia, donde nació el 20 de octubre de 1961, hijo de José Azpiazu, carpintero, y María Nieves Beristain, sus labores, que murió con su hijo mayor, de dos años, José Manuel, atropellados por un camión. Desde los 14 años, Kandido se movió por ambientes de la izquierda abertzale y a los 16 ya quiso entrar en ETA. Empezó a trabajar de carpintero, como su padre, aunque en otra empresa, pero a los 18 años cometió sus primeros atentados y acabó en la cárcel. Se casó con Milagros y tuvo, por lo menos, una hija. Su padre se volvió a casar y nunca le contó a su hijo que Ramón Baglietto le había salvado la vida cuando era un bebé. No se lo relató pero, después del asesinato, nunca pudo aceptar que su hijo había matado al que le salvó la vida.
Todos vecinos del mismo pueblo, todos se conocen desde niños, todos son uno de los nuestros. Por lo menos, eso parece. Pero Kandido Azpiazu nos aclaró algunas dudas en una entrevista que se publicó en 2001. Por ejemplo,
“-Yo no soy un asesino.
-Pero usted ha matado.
-Porque tenía que hacerse.”
…
“-¿Cómo te convertiste en asesino?
-Yo no soy un asesino.
-Has matado.
-Por necesidad histórica.”
…
“Y era bonita esa sensación de ser vasco. Desde que tengo uso de razón he luchado por la independencia de los vascos.”
…
“-Uno siempre era consciente -dice Azpiazu- de que algún día haríamos lo que después realmente hicimos. Era un largo proceso. Uno no se dice de repente: ‘Hoy me convierto en autor de atentados’, ¿entiendes?, ¿entiendes? Uno madura hasta que…”
…
“-¿Te asustaste?
-Nosotros no sentimos el deseo de matar.
-¿No te pudiste negar?
-No quise.
-Ese momento… Ese momento fue duro.
-¿Tuviste miedo?
-No. Uno estaba preparado para entregar su vida.
-¿Conocías a la persona?
-Sí.”
…
“-Tuvo que ser así.
-¿Por qué?
-Ese hombre formaba parte del aparato opresor, era conocido de Marcelino Oreja, el entonces ministro de Asuntos Exteriores del Estado español.
-¿Y eso bastaba?
-La decisión vino de arriba.”
La decisión vino de Eugenio Etxebeste, Anton, entonces número dos de ETA y además, no hay que olvidarlo, primo del asesinado Ramón Baglietto.
“-¿Cómo le mataste?
-Una acción armada no se hace con globos. Lo que ocurrió fue la acción de un miembro consecuente… Nada más.
-¿Te arrepientes?
-Tuvo que ser así. Uno no se sentía orgulloso de ello, no se sentía ni odio ni alegría.”
O, también, al hábito humano primario, como afirmó Alfred Hitchcock. Para el cineasta, nuestra especie mata porque le da la gana, e, incluso, si no hay costumbre de hacerlo, por la cultura del entorno, para experimentar lo que se siente al matar. O, según Robert Mitchum en “La batalla de Anzio”, “el hombre mata porque le gusta matar”. Es más, como propone Peter Morrall, detrás de muchos crímenes está el Schadenfreude, la alegría que provoca la desgracia ajena.
En fin, a nuestra especie le fascina matar, aunque sea, a veces, una banalidad, como decía Hannah Arendt, y, si no podemos matar, nos fascina cómo lo hacen otros.
Referencias:
Arendt, H. 1967. Eichmann en Jerusalén: un estudio sobre la banalidad del mal. Ed. Lumen. Barcelona. 440 pp.
Aumüller, G. & K. Grundmann. 2002. Anatomy during the Third Reich – The Institute of Anatomy at the University of Marburg, as an example. Annals of Anatomy 184: 295-303.
Bernadac, C. 1979. Los médicos malditos. Luis de Caralt Ed. Barcelona. 243 pp.
Boo, M.I. 1977. La perspectiva de Galdós en el asesinato del obispo Martínez Izquierdo. Anales galdosianos 12: 141-145.
Campos Marín, R. 2003. Criminalidad y locura en la Restauración. El proceso del cura Galeote (1886-1888). Frenia 3: 111-145.
Champy, C. & Risler. 1945. Sur une série de préparations histologiques trouvées dans le laboratoire d’un professeur allemand. Expériences faites sur l’homme au champ de Struthof. Bulletin de l’Académie de Médecine 129: 263-266.
Delarue, J. 1963. La Gestapo. Ed. Bruguera. Barcelona. 444 pp.
Hildebrandt, S. 2009. Anatomy in the Third Reich: An outline, Part 1. National Socialist politics, anatomical institutions, and anatomists. Clinical Anatomy 22: 883-893.
Koch, E. 2001. Confesiones de un asesino. El País 14 agosto.
Malvar, A. 2006. El cristalero de hierro. El Mundo 8 enero.
Maslow, A.H. 1943. A theory of human motivation. Psychological Review 50: 370-396.
Morrall, P. 2006. Murder and society. John Wiley & Sons. Chichester. 214 pp.
Ordaz, P. 2005. Víctima y verdugo, puerta con puerta. El País 4 diciembre.
Ricard, R. 1966. El asesinato del Obispo Martínez Izquierdo (1886) y el clero madrileño en la época de Galdós. Anales galdosianos 1: 125-129.
Ternon, I. & S. Helman. 1971. Historia de la Medicina SS o El mito del racismo biológico. Fomento de Cultura Ed. Valencia. 408 pp.
Wechsler, P. 2005 (1991). La Faculté de Medecine de la “Reichsuniversität Strassburg” (1941-1945) à l’heure nationale-socialiste. These Doctorat en Medecine, Université Louis Pasteur Strasbourg.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Las razones del asesino se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- 8 razones para que los niños estudien ciencias… o cualquier otra cosa
- Ingredientes para la receta: El arroz
- Historias de la malaria: El árbol de la quina
¿Son las ‘beachrocks’ una prueba del Antropoceno?
Nikole Arrieta, del Departamento de Química Analítica de la UPV/EHU, encabeza el equipo autor de un estudio en el que se analizan las beachrocks, formaciones de arena cementada en las que han quedado atrapados desechos industriales derivados de las actividades metalúrgicas. Estas peculiares rocas atestiguan el impacto del desarrollo industrial y su influencia en el entorno costero.
“El estudio de ciertos fenómenos geológicos ayuda a reconstruir el pasado ambiental y a determinar la influencia que ha tenido el ser humano en el medio, puesto que lo registran todo. Incluso podrán ofrecer información valiosa para afrontar posibles efectos del cambio climático”, afirma Arrieta.

Formación de arena cementada situada en Tunelboka. Foto: Nikole Arrieta. UPV/EHU.
Se trata de formaciones rocosas que se producen en zonas intermareales, normalmente en zonas tropicales y subtropicales. A pesar de ello, también es posible encontrarlas en la costa vizcaína. Las beachrocks estudiados son formaciones recientes situadas en la margen derecha del estuario Nerbioi-Ibaizabal, donde han sufrido una gran influencia de la actividad humana.
“Su presencia en latitudes templadas como la nuestra es rara, hay 8-10 casos en todo el mundo” añade Arrieta. Estas formaciones sedimentarias son derivadas de la precipitación intergranular de cementos carbonatados (CaCO3). “Entre los diferentes sedimentos se ha formado un cemento. Así, la arena, en vez de estar suelta, como en las playas normales, forma estas rocas”, explica Arrieta.
Sin embargo, aunque normalmente los cementos de los que están compuestos las beachrocks son carbonatados, las formaciones geológicas de la costa vasca presentan además cementos ferruginosos. Las escorias atrapadas en los cuerpos cementados han sufrido procesos de disolución por fenómenos de meteorización o atmosféricos, como la lluvia ácida, llegando a reprecipitar en los poros como sales insolubles de hierro.
La investigación se ha centrado en la caracterización de dichos cementos. Por una parte, para estudiar los tipos de cementos se han aplicado innovadoras técnicas espectroscópicas que han permitido analizar exhaustivamente las distintas fases minerales. “A escala microscópica, aparecen distintas capas de cemento, y cada una aporta una información sobre el momento en que han precipitado, las condiciones que había, etc.”.
Por otro lado, han analizado los materiales atrapados en esos cementos, donde “hemos encontrado escorias de fundición de la revolución industrial, incluso residuos con sellos de empresas europeas que al venir con sus barcos echaban sus escorias. Por ello, en las playas encontramos los llamados tecnofósiles o vestigios de la actividad humana, en este caso desechos industriales de empresas internacionales que ayudan a estimar la edad de la beachrock”.
Todo ello constituiría un ejemplo del registro geológico de la época del Antropoceno, actualmente discutida entre especialistas de todo el mundo. Y es que, según los científicos partidarios de esta denominación, la Tierra se encuentra en una nueva época geológica, “la era del ser humano”, ya que la acción humana genera grandes cambios que dejan su huella en los estratos geológicos de la Tierra. Sus detractores, en cambio, argumentan que se trata de una cuestión más política que científica.
Esta edad geológica abarcaría el periodo más reciente del Cuaternario, y actualmente está siendo de gran interés para especialistas de todo el mundo. “Los estratos de Tunelboka, una cala situada en la margen derecha del estuario donde se centra la investigación, han sido discutidos a nivel mundial de cara a ser evidencias del Antropoceno”, señala Arrieta. Y es que, además de haber muy pocos emplazamientos en el mundo en latitudes templadas que presenten este fenómeno, “aún son menos los que presentan las características de los nuestros; la cantidad de escorias que contienen es desorbitada. He colaborado con distintos investigadores de reconocido prestigio de universidades de Estados Unidos y Australia, y todos quedan prendados al ver las fotos o materiales del emplazamiento”.
Según Nikole Arrieta, autora del estudio, “es indispensable mantener activa la investigación de este fenómeno geológico tan especial y único que tenemos en nuestras costas, por el interés geoquímico, ambiental e histórico que tienen estas formaciones, sus aplicaciones en ámbitos de ingeniería y restauración, su importancia para la definición de la reciente época del Antropoceno y por qué no, el interés arqueológico industrial de los materiales que engloban”.
Referencia:
Arrieta, N., Iturregui, A., Martínez-Arkarazo, I., Murelaga, X., Baceta, J.I., de Diego, A., Olazabal, M.A., Madariaga, J.M.. Characterization of ferruginous cements related with weathering of slag in a temperate anthropogenic beachrock. Science of The Total Environment, 581-582, 49-65 (2017). DOI: 10.1016/j.scitotenv.2016.12.132.
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo ¿Son las ‘beachrocks’ una prueba del Antropoceno? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Comenzó el Antropoceno con la era nuclear?
- Activa tu neurona – Antropoceno. El comienzo de “la era de los hombres”
- Sobre el alzhéimer y la prueba del cacahuete
Moluscos en el Arte
Intercambiar información y comunicar ciencia son los objetivos esenciales de la divulgación científica. Hay que llegar a la ciudadanía y unir ciencia y cultura que, sin remedio, son y han sido siempre lo mismo. Por ello, me parece interesante repasar el arte de épocas pasadas para aprender qué ciencia conocían y cómo la utilizaban en su vida cotidiana. Y encontraremos conchas y, en general, moluscos en la pintura, y nos ayudarán a interpretar lo que eran y significaban en culturas anteriores.
El arte sirve para conocer la historia y, ahora, si unimos arte y ciencia, y como en este texto, arte y moluscos, podemos deducir cómo los utilizaban y, también, su distribución y su ecología. Podemos reconstruir, sea con aproximación, las poblaciones originales de estos animales a partir de las especies representadas en el arte. Y, también, su valor y manipulación como alimentos. Plantearemos hipótesis sobre cómo se relacionaban aquellas culturas con su entorno.

Adriaen van Stalbent, “Las Ciencias y las Artes”, óleo sobre tabla, 89,9 x 117 cm, Madrid, Museo del Prado.
Ya en aquellos siglos era evidente para muchos pintores la unión de ciencia y arte e, incluso, hubo cuadros que los representaron en conjunto pues esa era la idea de algunos de los mecenas que los patrocinaban. Así, Adriaen van Stalbent, pintor holandés del siglo XVII, ofreció una obra con ese título, “Las Ciencias y las Artes”, cuadro que se expone en el Museo del Prado. Representa un gabinete, habitual en esa época, con conchas y otros animales encima de una mesa junto a la que aparecen unos caballeros que las estudian y consultan varios voluminosos libros para ello. Mientras, en el otro lado de la habitación, hay varios cuadros en la pared, y algunos son bodegones con plantas y animales. Es evidente que no hay separación entre ciencia y arte.

Salvador Dalí, “La Madonna de Port Lligat”, óleo sobre lienzo, 144 × 96 cm, Tokio, Fukuoka Art Museum.
Hay muchos ejemplos de moluscos en el arte, desde las cuevas del Paleolítico a los mosaicos romanos, con la Venus de Botticelli en el siglo XV, con la diosa saliendo de una vieira, quizá del bivalvo de la especie Pecten maximus, hasta Murillo en el siglo XVII con los Niños de la concha, de nuevo el Pecten maximus, el Bodegón de peces y tortugas del italiano Giuseppe Recco, con un par de calamares, y pintado a finales del XVII, o, más cercanos en el tiempo, Picasso en 1911 con su bodegón con un plato de ostras, o El caracol, abstracto y polihédrico, de Matisse, de 1953, con La tierra labrada de Joan Miró en 1923, o La Madonna de Port Lligat con su gasterópodo marino bien visible, de Dalí, de 1950.

Conchas marinas encontradas en distintas cuevas marroquíes con asentamientos paleolíticos. Del 1 al 19 las correspondientes a la “Grotte des Pigeons”. Compárese con las conchas de moluscos actuales: 28, “Nassarius gibbosulus”; 29 y 30, “Nassarius circumcinctus”; 31, “Columbella rustica”
Fue hace miles de años cuando hemos fechado uno de los usos más antiguos que conocemos de conchas de moluscos como arte. El estudio lo lideró Abdeljalil Bouzouggar, del Instituto Nacional de Ciencias de la Arqueología y del Patrimonio de Rabat, que fechó hace 82000 años las conchas de caracol marino, de Nassarius, que encontró en la Grotte des Pigeons, en Taforalt, Marruecos. Eran 13 conchas en total y las habían utilizado como adorno, con orificios para convertirlas en cuentas de collar. Además, algunas estaban pintadas con un pigmento rojo del tipo de la hematita, con mucho hierro. Y estaban a unos 40 kilómetros del Mediterráneo, a gran distancia del hábitat natural del Nassarius.
En Europa se conoce el uso de conchas como adorno con fechas de hace unos 40000 años y, además, tanto en yacimientos de nuestra especie como en los de neandertales.
Entre los romanos, las imágenes de moluscos en frescos y mosaicos son numerosas y están bien documentadas. Steve Wilkinson relata las que aparecen en las ruinas de Pompeya, ciudad destruida por la erupción del Vesubio en el año 79, y excavada a partir del siglo XVIII. En algunos de los mosaicos hay gasterópodos como el Murex, bivalvos, pulpos y calamares. También aparecen algunos caracoles terrestres como Eobania y Marmorana, especies que todavía se encuentran vivas en los alrededores de las ruinas.
Desde el siglo XII, la concha de vieira es el símbolo de la peregrinación a Santiago de Compostela. Los expertos aseguran que es la concha del bivalvo Pecten maximus, típico del Atlántico, más que el Pecten jacobeus, a pesar de su nombre científico, que es especie del Mediterráneo.
En Holanda, en los siglos XVI al XVIII, los gabinetes naturalistas, todos ellos colecciones privadas, son extraordinarios y con muestras de todo el mundo que llegaban al país a través del puerto de Amsterdam, como hemos visto en la obra de van Stalbent. En algunas de esas colecciones, los moluscos estaban representados con miles de ejemplares.
En otros países europeos ocurrió algo parecido, como en Francia, Italia o España. Llegaban muchos ejemplares de plantas y animales de las exploraciones de América, Asia y África y las colecciones crecían. Años más tarde, algunas de esas colecciones, en principio privadas o de aristócratas y reyes, fueron la base de museos e instituciones públicas.

Giuseppe Arcimboldo, “L’Acqua”, óleo sobre tabla, 66,5 x 50,5 cm, Viena, Kunsthistorisches Museum
Y también se basaban en estas colecciones los abundantes cuadros, de los géneros naturaleza muerta y bodegón, que se pintaron en esos países y en la misma época. Por ejemplo, en Holanda, el pintor Adriaen Coorte pintó varias composiciones solo con conchas. O en España, los bodegones de Luis Egidio Meléndez, que están depositados en el Museo del Prado. En Italia, en el siglo XVI, vivió, quizá, uno de los pintores más originales en la representación de bodegones. Era Giuseppe Arcimboldo, con sus reconstrucciones de rostros y cabezas con diferentes, y numerosas, especies de plantas y animales y, entre ellas, cinco especies de moluscos en el cuadro titulado Acqua.
Pero también hay conchas en entornos populares, sobre todo en cuadros de autores holandeses y belgas. Las ostras hasta el siglo XVII habían sido un alimento para pobres pero, a partir de entonces, aparecen en las mesas de los burgueses, de nobles y de ricos, sobre todo en Holanda, y, a la vez, llenaron las despensas de los pudientes y los bodegones que encargaban a sus pintores favoritos.

David Teniers “el joven”, “La cocina”, óleo sobre cobre, 75 x 77,8 cm, La Haya, Mauritshuis
Autores como David Teniers el Joven, en el siglo XVII, representa cocinas y posadas en las que las conchas de los mejillones, que seguían siendo para pobres, aparecen ya comidos y por el suelo, como en su cuadro La cocina. Todavía los mejillones son plato nacional en la cocina belga. Y es delicioso. Y, además, considero que también es un arte.
Mejillones como los ponen en Bélgica
Ingredientes:
1 kg de mejillones
1-2 cebollas
1-2 tallos de apio
mantequilla, tomillo, laurel, (vino blanco)
patatas para las patatas fritas
Preparación:
Raspar y limpiar los mejillones.
Preparar una cazuelita por comensal.
Pelar tres cebollas grandes y cortarlas en rodajas que ya se soltarán solas durante la cocción.
Cortar en trozos como de centímetro y medio, tres tallos de apio en la parte verde.
Derretir la mantequilla (mejor mucha que poca), calientar un poco para que se funda, aunque no mucho, y vierta las cebollas y el apio y rehogue hasta que la cebolla quede transparente y el apio crujiente.
Añada los mejillones. Revuelva y los mejillones empezarán a soltar líquido.
Después de dos a tres minutos, añada dos o tres vasos de agua o dos o tres vasos de vino, según el líquido que le apetezca y que necesiten. También agregue tres o cuatro ramitas de tomillo y dos hojas de laurel. Sal y pimienta al gusto (yo no le pondría sal).
Revolverlo todo hasta que los mejillones se abran.
Servir con patatas fritas y pan con mantequilla para mojar en el jugo, y, además, cerveza.
Por cierto, las patatas también se deben freír al estilo belga: una primera vez a fuego lento para que se hagan por dentro, sacar y dejar enfriar, y una segunda vez a fuego fuerte para que queden doradas por fuera. Otra delicia para acompañar a los mejillones.

Maestro de Hartford, “Una mesa puesta con flores y frutas”, óleo sobre lienzo, 74 x 100 cm, Hartford, Wadsworth Atheneum
También aparecen caracoles terrestres, aunque con una presencia más escasa, como ocurría en los mosaicos de Pompeya. Por ejemplo, el holandés Abraham Mignon representa a una especie del género Cepaea, nuestro “navarrico” que, por cierto, aparece en varios cuadros de los pintores holandeses de los siglos XVII y XVIII. O nuestro caracol comestible, el Cornu aspersum, que pintó en alguno de sus bodegones el llamado Maestro de Hartford, que algunos expertos sospechan era el alias de Caravaggio cuando era joven. Y el Helix pomatia, el caracol comestible francés, que pintó el italiano Evaristo Baschenis en un cuadro dedicado a la despensa. Allí aparece con el típico opérculo calcáreo que tapa la abertura y que fabrica cuando el entorno no le es propicio.
En muchos de los cuadros, la aparición de una o de otra especie tenía un significado místico, moral o religioso. Así, el caracol terrestre indicaba apego a la tierra y, además, pereza por la lentitud de sus movimientos. La ostra era afrodisiaca y, por tanto, representaba al pecado de la lujuria. Las conchas de gasterópodos marinos, como rarezas que eran en aquellos años, son a menudo símbolos de salud.
Visto lo anterior y demostrada la presencia de abundantes moluscos en el arte, desde las conchas de adorno coloreadas de hace 80000 años hasta los pintores más actuales, nos podemos preguntar, como hacen Brian Wansink y sus colaboradores, de la Universidad Cornell de Ithaca, en Nueva York, si esos moluscos, como alimento o simplemente como arte, son un vistazo a tiempos pasados que nos permitirán captar la relación de aquellas gentes con su entorno.
Algo así hicieron con su estudio sobre la presencia del mero (Epinephelus marginatus) en 23 mosaicos romanos fechados entre los siglos I y V, Paolo Guidetti y Fiorenza Micheli, de las universidades de Salerno, en Italia, y Stanford, en Estados Unidos. Sus resultados describen la presencia, distribución y pesca del mero en el Mediterráneo romano.
Wansink y su equipo analizan 750 cuadros con alimentos y seleccionan 140, fechadoss del siglo XVI a la actualidad, que representan comidas familiares. No utilizan la representación de banquetes ni los bodegones y naturalezas muertas. Su objetivo es estudiar si los alimentos que aparecen en estos cuadros reflejan lo que las familias comían en su vida diaria. Cuantifican los alimentos de las pinturas y comparan los resultados con lo que sabemos por otras fuentes históricas.
Los alimentos más habituales en las comidas diarias de las familias, como el pollo o los huevos, son los menos representados en las pinturas. Los que más aparecen son los alimentos escasos y caros como el marisco, incluso en países con poca costa, o frutas difíciles de encontrar en el norte de Europa como, por ejemplo, los limones en más de la mitad de los cuadros con alimentos de Holanda. Hay casos, como el pan, que aparece un 75% menos de lo esperado, o las manzanas que están tres veces más, y que, sin embargo, son alimentos siempre disponibles en las comidas familiares.
Por cierto, los moluscos aparecen en el 22% de los cuadros estudiados, con el máximo en Holanda con el 57% y Alemania con el 20% y, sobre todo, en las pinturas de los siglos XVI y XVII.
En general, se prefieren representar alimentos que desean las familias, que son estéticamente bellos para los pintores, o que son difíciles de trasladar al lienzo, o, también, como ya hemos visto, que tienen algún significado cultural, religioso o político. Como conclusión, Wansink apunta que los cuadros con comidas familiares no sirven para conocer lo que las familias comían de manera habitual.
Sin embargo y para terminar, también es Brian Wansink nos demuestra que la comida en los cuadros también tiene su utilidad para obtener conclusiones quizá no esperadas. Estudia 52 representaciones pictóricas de la Última Cena y cuantifica el pan que hay sobre la mesa, el tamaño de los platos y la cantidad de comida que hay en cada plato que, por cierto, es pescado, cordero o cerdo. La comida en el plato principal aumenta un 27% desde el año 1000 hasta la actualidad, con el máximo crecimiento en los siglos XVI y XVII. También el pan es un 9% mayor, con el máximo en los últimos cuatro siglos. Y, además, en muy pocos cuadros hay vino.
Referencias:
Alcázar Álvarez, J.L. et al. 1982. Moluscos marinos de los pueblos hispanos. Cuadernos del CRINAS 4: 1-63.
Begossi, A. & R. Caires. 2015. Art, fisheries and ethnobiology. Journal of Ethnobiology and Ethnomedicine 11: 7.
Berger, J. et al. 2000. El bodegón. Fundación Amigos del Museo del Prado. Galaxia Gutenbertg/Círculo de Lectores. Barcelona. 210 pp.
Bouzouggar, A. et al. 2007. 82000-year-old Shell beads from North Africa and implications for the origins of modern human behavior. Proceedings of the National Academy of Sciences USA 104: 9964-9969.
Cheney, L.G. 1987. The oyster in Dutch genre paintings: Moral or erotic symbolism. Artibus et Historiae 15: 135-158.
Dretz, B. 2006. Mobile objects: the space of shells in eighteenth-century France. British Journal of History of Science 39: 363-382.
Grieco, A.J. 1992. Themes in Art: The meal. Scala Books. London. 64 pp.
Grootenboer, H. 2016. Sublime still lifes on Adriaen Coorte, Elias van der Broeck, and the “je ne sais quoi” of painting. Journal of Historians of Netherlandish Art DOI: 10.5092/jhna.2016.8.2.10
Guidetti, P. & F. Micheli. 2011. Ancient art serving marine conservation. Frontiers in Ecology and Environment 9: 374-375.
Nebot, J. 2016. Los caracoles y el hombre. En “Caracoles y babosas de la Península Ibérica y Baleares”, p. 20-24. Ed. por J. Cadevall & A. Orozco. Ed. Omega. Barcelona.
van de Roemer, B. 2004. Neat nature: The relations between nature and art in a Dutch cabinet of curiosities from the early eighteenth century. History of Sciences 13: 47-84.
Speaking, J. 1974. Los animales en el Arte. Ed. Argos. Barcelona. 331 pp.
Veca, A. 1990. La natura morta. Giunti Gruppo. Firenze. 50 pp.
Wansink, B. & C.S. Wansink. 2010. The largest Last Supper: depictions of food portions and plate size increased over the millenium. International Journal of Obesity 34: 943-944.
Wansink, B. et al. 2016. Food art does not reflect reality: A quantitative content analysis of meals in popular paintings. SAGE Open DOI: 10.1177/2158244016654950
Wilkinson, S.e2012. Shell ornaments provide group identity in the Palaeolithic. Mollusc World 14: 3p.
Wilkinson, S. 2012. Molluscs in Roman art: the archeological sites of the Naples área, Italy. Mollusc World 16: 3 p.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Moluscos en el Arte se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La creatividad científica y el arte: La muerte de Sócrates
- Arte cartográfico, arte con mapas
- Ciencia, arte, religión
La ciencia perdida: los curiosos casos de los protocolos de TDAH y de leer.es

¿Son eficaces los programas y sistemas educativos actuales? Durante los últimos años, es cada vez mayor el debate generado en torno a este tema. Muchos expertos argumentan que las teorías y prácticas educativas implementadas en los centros carecen de evidencia científica. El esfuerzo y los medios empleados en estas prácticas de dudosa utilidad obligan, además, a dejar de lado aquellas otras teorías cuya eficacia está probada.
Con el objetivo de abordar esta situación, el Bizkaia Aretoa de Bilbao acogió el pasado 17 de marzo la jornada titulada “Las pruebas de la educación”, donde varios expertos abordaron cuestiones relacionadas con la educación desde un punto de vista científico.
“Las pruebas de la educación” forma parte de una serie de eventos organizados por la Cátedra de Cultura Científica de la UPV/EHU para abordar cuestiones del día a día como la educación o el arte desde una perspectiva científica. La dirección del seminario corrió a cargo de la doctora en psicología Marta Ferrero.
En esta segunda conferencia el doctor en Educación Juan Cruz Ripoll puso en entredicho los protocolos oficiales para la atención al Trastorno por Déficit de Atención e Hiperactividad (TDAH) así como las orientaciones presentes en portales de Internet como leer.es, una iniciativa del Ministerio de Educación, Cultura y Deporte que busca fomentar la lectura. A pesar del respaldo oficial con el que cuentan ambos, Ripoll argumenta que carecen de base científica y relega otras prácticas mejor fundamentadas desde la investigación.
La ciencia perdida: los curiosos casos de los protocolos de TDAHEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo La ciencia perdida: los curiosos casos de los protocolos de TDAH y de leer.es se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #Naukas14 Algunos curiosos experimentos
- Sobre la percepción social de la ciencia y sus consecuencias
- Curso de verano “La ciencia de nuestras vidas”: Arte, literatura y ciencia, por Gustavo A. Schwartz
Estudio de eficacia escolar en el País Vasco

¿Son eficaces los programas y sistemas educativos actuales? Durante los últimos años, es cada vez mayor el debate generado en torno a este tema. Muchos expertos argumentan que las teorías y prácticas educativas implementadas en los centros carecen de evidencia científica. El esfuerzo y los medios empleados en estas prácticas de dudosa utilidad obligan, además, a dejar de lado aquellas otras teorías cuya eficacia está probada.
Con el objetivo de abordar esta situación, el Bizkaia Aretoa de Bilbao acogió el pasado 17 de marzo la jornada titulada “Las pruebas de la educación”, donde varios expertos abordaron cuestiones relacionadas con la educación desde un punto de vista científico.
“Las pruebas de la educación” forma parte de una serie de eventos organizados por la Cátedra de Cultura Científica de la UPV/EHU para abordar cuestiones del día a día como la educación o el arte desde una perspectiva científica. La dirección del seminario corrió a cargo de la doctora en psicología Marta Ferrero.
En la primera conferencia “Estudio de eficacia escolar en el País Vasco”, Beronika Azpillaga y Luis Lizasoain, profesores e investigadores de la UPV/EHU, y colaboradores del Instituto Vasco de Evaluación e Investigación Educativa, presentaron los resultados de un estudio realizado con el objeto de identificar las buenas prácticas pedagógicas empleadas en las escuelas de alta eficacia del País Vasco.
Estudio de eficacia escolar en el País VascoEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Estudio de eficacia escolar en el País Vasco se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Presentación del estudio “Percepción social de la ciencia y la tecnología en el País Vasco”
- LocosxCiencia llega al País Vasco
- La ciencia al rescate del país
Las cartas de Darwin: ¿Dejamos que el chaval se vaya de viaje?
Las cartas de Darwin, una serie para conocer aspectos sorprendentes de la vida del naturalista
Tal y como vimos en el artículo anterior de esta serie, el 13 de agosto de 1831, el matemático George Peacock enviaba una carta a John Stevens Henslow informándole de la posibilidad de embarcar en un viaje alrededor del mundo, patrocinado por el Almirantazgo y capitaneado por Robert Fitzroy. Consciente de la importancia de este proyecto y de que representa una oportunidad única para formarse, Henslow recomienda al joven Charles Darwin para aprovechar ese pasaje en el HMS Beagle.
Carta de John Stevens Henslow a Charles Darwin [24 de agosto de 1831]
“Afirmé que te consideraba como la persona más calificada que conozco y que estuviera en condiciones de emprender una situación de este tipo. Afirmé tal cosa sin dar por sentado que tú fueras un naturalista recibido, sino que simplemente calificabas para recolectar, observar y anotar cualquier cosa que valiera la pena en historia natural. […] El capitán FitzRoy quiere a alguien (según entiendo) más como compañero que como mero recolector y no tomará a nadie por buen naturalista que sea que no se le haya recomendado por lo demás como un caballero”.
De esta carta se extraen diversas conclusiones fundamentales: Darwin sería una especie de acompañante de FitzRoy y no sería el naturalista oficial del Beagle (ese cargo correspondía a Robert McCormick, de quien ya conté su increíble vida de viajes en este artículo), de hecho ni siquiera poseía un salario asignado y tendría que pagar el pasaje en el barco y el resto de gastos de su propio bolsillo, o para ser más exactos del bolsillo de su padre.
El ofrecimiento de Henslow a Darwin para embarcar en este viaje llegaba tras una serie de negativas por parte de otros personajes como Harry Chester, Georges Peacock o Leonard Jennings, quienes rechazaron la posibilidad de embarcarse en el Beagle.
Lo que poca gente sabe es que Charles Darwin también rechazó la invitación.

Reverendo John Stevens Henslow
Henslow en esa misma carta de 24 de agosto animaba a Charles Darwin a embarcarse en el viaje y sobreponerse a las dudas sobre si estaba suficientemente preparado.
“No pongas por delante dudas o temores por modestia acerca de no estar calificado, ya que te aseguro que considero que eres el hombre adecuado que buscan”
Por supuesto la decisión de iniciar un viaje alrededor del mundo, con los peligros que esto conlleva y sin una duración realmente definida, no estaba totalmente en manos de Darwin quien debería consultarlo con su padre, el doctor Robert Waring Darwin.
Al fin y al cabo, el joven apenas tenía veintidós años y no contaba con el dinero necesario para sufragar los gastos de ese viaje; la opinión de su padre era muy importante para Darwin, y resultó que su padre desaconsejaba firmemente aquel proyecto…
Carta de Charles Darwin a John Stevens Henslow [30 de agosto de 1831]
“En cuanto a mí concierne, tal y como lo pienso, desde luego que con gran gusto aceptaría la oportunidad que con tanta generosidad me ofrece. Pero mi padre, aunque no me lo rechazó con absoluta decisión, aconseja con determinación que no vaya, por lo que no me sentiría cómodo si no sigo su consejo”.

El doctor Robert Waring Darwin, padre de Charles
La cuestión podría haber quedado zanjada ahí mismo: Un padre que niega a su hijo un caro y caprichoso viaje, y un hijo que se queda en tierra. La historia de Darwin hubiera sido totalmente diferente a la que conocemos y seguramente el joven Charles, sin el viaje que le abrió la mente, no habría pasado de ser un naturalista más de los cientos que poblaban aquellos tiempos.
El giro inesperado llegó gracias a la intervención de su tío Josiah Wedgwood, a quien el doctor Darwin tenía en alta estima y cuyas opiniones influenciaron la decisión original de impedir el viaje de Charles.
Carta del doctor Robert Darwin a Josiah Wedgwood [30 de agosto de 1831]
“Estoy seguro de que Charles te contará la oferta que se le ha hecho de participar en un viaje de descubrimiento por dos años. Yo la objeto firmemente por varias razones, pero no las detallaré porque él podrá tener su opinión imparcial sobre el tema, y si usted piensa distinto de mí, desearía que él siguiera su consejo”
PD [31 agosto]: “Charles ya ha desechado la idea del viaje”.

Josiah Wedgwood, tío de Charles Darwin
Este 31 de agosto sería una fecha clave en la vida epistolar de Darwin. Aquel día la correspondencia sobre el tema del viaje en el Beagle se cruzó entre los tres máximos implicados: el joven Charles, su padre Robert y su tío Josiah Wedgwood II.
Carta de Charles Darwin a su padre Robert Darwin [31 de agosto de 1831]
“Querido padre: Me temo que voy de nuevo a hacer que se sienta incómodo. Pero considerándolo todo, creo que me perdonará una vez más por dar mis opiniones sobre la oferta del viaje. Tengo una disculpa, y la razón es la forma distinta con la que todos los Wedgwood consideran el tema respecto de la suya y de mis hermanas.
Le proporcioné a mi tío Jos lo que considero de todo corazón como una lista cuidada y completa de sus objeciones, y ha sido tan amable como para darme su opinión sobre ellas. Incluyo la lista y sus respuestas. De todos modos, le pido solo un favor: sería de todo punto una gran amabilidad suya que me enviara una respuesta decidida: sí o no”.
Efectivamente, en esta carta de Darwin se enumeran las ocho objeciones principales que su padre esgrimía para oponerse a su viaje, las cuales serían respondidas una por una por su tío Josiah.
Carta de Charles Darwin a su padre Robert Darwin [31 de agosto de 1831]
Lista de objeciones:
- Poco respetable respecto de mi carácter como clérigo.
- Un plan alocado.
- Que seguramente ofrecieron a mucha otra gente antes que a mí este viaje
- Que si no fue aceptado por todos ellos es que debe haber objeciones serias respecto del barco o de la expedición.
- Que nunca sentaré cabeza ante mi futura vida.
- Que mis alojamientos serían incómodos con toda seguridad.
- Que usted debe considerar que, de nuevo, estoy cambiando de profesión.
- Que será una empresa sin utilidad alguna.
Esta es la lista que el joven realizó resumiendo las razones de su padre. En la misma carta, Charles Darwin incluyó las respuestas de su tío para convencer al doctor.
Carta de Josiah Wedgwood al doctor Robert Darwin [31 de agosto de 1831]
“Querido doctor: Siento gran responsabilidad ante su solicitud acerca de la oferta que se le hizo a Charles, pero como usted deseó que Charles me consultara, no puedo rehusar a darle el resultado de mis reflexiones. Charles me ha dado la lista de lo que cree que son sus principales objeciones, y creo que lo mejor que puedo hacer es afirmar lo que pienso acerca de cada una de ellas:
- No creo que fuera de ninguna manera poco respetable para su carácter como clérigo. Por el contrario, pienso que la oferta lo honra y que la incursión en la historia natural, aunque ciertamente no profesional, es muy conveniente para un clérigo.
- No veo cómo enfrentarme a esta objeción, pero habrá conocimientos bien definidos en los que ocuparse y seguramente adquirirá y reforzará su disciplina de trabajo, y quiero pensar que puede lograrlo tanto de esta manera como quedándose en casa durante los próximos dos años.
- Ante la lectura de las cartas, no veo el problema, y al leerlas de nuevo con el tema en mente no le veo fundamento.
- No puedo concebir que el Almirantazgo mande un barco en malas condiciones para un servicio como éste. En cuanto a objetar la expedición, dependerá del individuo, pero nada puede inferirse en el caso de Charles si se llega a saber que otros han rechazado la oferta.
- Usted es un juez mucho más adecuado acerca del carácter de Charles de lo que puedo serlo yo. Si usted piensa que con toda probabilidad el viaje lo hará inestable e incapaz de establecerse, cuando compare la forma en que transcurrirán estos dos años con la forma en que transcurrirán si no acepta la oferta, desde luego que es una objeción a considerar. No es el caso que los marinos propendan a adquirir costumbres domésticas y tranquilas.
- No puedo dar mi opinión más allá de lo que ya he expresado, pues si la proporciona el Almirantazgo podrá reclamar el mejor acomodo posible según lo permita el barco.
- Si viera a Charles absorbido en sus estudios profesionales, probablemente pensaría que no es aconsejable interrumpirlos, pero no es así, y creo que no será el caso en cuanto a él. Su interés en busca de conocimientos lleva la misma ruta que podrá seguir con la expedición.
- Seguramente que la empresa no concuerda con su profesión, pero si lo consideramos como un hombre que muestra gran curiosidad, ésta es una oportunidad tal de ver gente y otras cosas como a pocos puede dárseles.
Piense usted que tuve poco tiempo para considerar las objeciones, y que usted y Charles son las personas que deben decidir.
Soy, estimado doctor, suyo con afecto: Josiah Wedgwood”.
He querido reproducir íntegramente la carta de Josiah al doctor Robert Darwin porque, probablemente, es el documento que más ha influido en la vida del naturalista. Sin esta lista de argumentos rebatiendo las objeciones de su padre, Darwin jamás hubiera subido al Beagle. La prueba de la influencia de su tío Jos la tenemos en que, al día siguiente, el doctor Robert Darwin contestaba a esta carta del siguiente modo:
Carta del doctor Robert Darwin a Josiah Wedgwood [01 de septiembre de 1831]
“Querido Wedgwood: Charles le agradece grandemente por tomarse tantas molestias, así como por su interés por sus planes. Me decidí a dejar de lado mis objeciones, ya que usted no lo ve con el mismo ángulo que yo. Charles expuso mis objeciones clara y plenamente y si sigue con la misma idea después de informarse con más amplitud, le daré toda la ayuda que esté en mi poder”.
Charles Darwin tenía el visto bueno de su padre para embarcar en el Beagle… pero aún había un obstáculo que superar. Unos días antes el joven había escrito a George Peacock rechando el ofrecimiento, por lo que en estos momentos los responsables de la expedición no contaban con la presencia de Darwin y posiblemente habrían empezado a buscar sustituto.

Sir Francis Beaufort
Raudo y veloz, ese mismo día en que obtuvo el beneplácito de su padre, Charles Darwin se puso en contacto directamente con el Almirantazgo (saltándose a los intermediarios Peacock y Henslow) y escribió esta carta a sir Francis Beaufort.
Carta de Charles Darwin a Francis Beaufort [01 de septiembre de 1831]
“Señor: Me tomo la libertad de escribirle de acuerdo con el deseo del señor Peacock de darle a conocer mi aceptación de la oferta de viajar con el capitán FitzRoy.
Seguramente habrá recibido una carta del señor Peacock anunciándole mi rechazo, lo cual se debió a que mi padre no aprobaba en principio el plan; desde entonces ha reconsiderado el tema y ha dado su consentimiento. Por lo tanto, si no se ha ocupado el puesto, sería un honor para mí aceptarlo”.
El resto de la historia es fácilmente imaginable: El Almirantazgo aceptó finalmente a Charles y el joven pudo embarcarse en el Beagle para dar la vuelta al mundo en la expedición que cambiaría totalmente su vida.
Este post ha sido realizado por Javier Peláez (@irreductible) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
El artículo Las cartas de Darwin: ¿Dejamos que el chaval se vaya de viaje? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las Cartas de Darwin: El sueño truncado de Canarias
- Las cartas de Darwin: 50 años para un proyecto titánico
- Bilbao celebrará el día de Darwin
Por qué los niños preguntan “por qué” y qué constituye una buena explicación
Matteo Colombo

Cuando tenía alrededor de cuatro años formulé a mi madre una de mis primeras preguntas “¿por qué?”: “Mamá, ¿por qué vive Pippo debajo del agua?” Mamá me explicó que Pippo, nuestro pez de colores, era un pez, y que los peces viven debajo del agua. Esta respuesta me dejó insatisfecho, por lo que seguí preguntando: “¿Por qué viven los peces debajo del agua? ¿¿Podemos nosotros vivir debajo del agua?” Mamá respondió que los peces respirar extrayendo oxígeno del agua que los rodea; las personas no pueden vivir debajo del agua. Pregunté entonces algo aparentemente sin relación: “¿De qué está hecho el hielo?””El hielo está hecho de agua, Matteo”. Dos días después se encontró a Pippo en nuestro congelador.
Como la mayoría de los niños de cuatro años, me sorprendía con las cosas que ocurrían a mi alrededor. Tan pronto como comencé a hablar empecé a preguntar por qué suceden las cosas. Esto molestaba a los adultos frecuentemente. Pero cuando querían responder a mis preguntas, sus explicaciones me ayudaban a imaginar qué ocurría si las cosas fuesen diferentes. Mis conclusiones eran completamente erróneas algunas veces (como el pobre Pippo comprobó en carne propia). En cualquier caso, errores y explicaciones guiaron mi descubrimiento del mundo: estaba haciendo ciencia antes de empezar a ir al colegio, y lo estaba disfrutando también.
¿Qué es una buena explicación? ¿Y cómo lo podemos saber? Los filósofos de la ciencia han respondido a estas cuestiones tradicionalmente concentrándose en las normas que rigen la práctica explicativa de los científicos, evaluando estas normas sobre la base de sus intuiciones en una serie de casos que implican supuestas explicaciones.
Comenzando con el trabajo de Carl G Hempel en los años sesenta, los filósofos de la ciencia han desarrollado tres modelos de explicación principales. Según el modelo de cobertura legal de Hempel, las explicaciones son argumentos que demostrarían que lo que se está explicando se sigue lógicamente de una ley general. Por el modelo de cobertura legal si un pregunta “¿Por qué un determinado mástil de bandera arroja una sombra de 10 metros de largo?”, una buena respuesta debería citar las leyes de la óptica, la altura del mástil, y la posición del Sol. Esta explicación es buena porque “demuestra que, dadas las circunstancias concretas y las leyes en cuestión, el que el fenómeno ocurriese era algo esperable”.
Otra aproximación es el modelo unificacionista, que dice que las buenas explicaciones aportan un relato unificado que puede aplicarse exhaustivamente a muchos fenómenos diferentes. La teoría de la gravedad de Newton y la teoría de la evolución de Darwin son explicaciones maravillosas porque poseen un enorme poder unificador. Estas teorías apelan una y otra vez a unos pocos principios básicos que pueden dar cuenta de una gran cantidad de fenómenos. Así, las teorías unificadoras reducen a un mínimo el número de lo que el biólogo Thomas Huxley llamó en 1896 “incomprensibilidades fundamentales”.
El modelo mecánico causal es quizás el más popular entre los filósofos. Dice que las explicaciones buenas ponen de manifiesto piezas componentes y actividades que hacen que las cosas pasen. Si uno pregunta:¿Por qué se rompió la ventana?”, una buena respuesta es: “Porque alguien le tiró una piedra”. O si uno pregunta: “¿Cómo llega la sangre a todas las partes del cuerpo?”, una buena respuesta debería incluir información acerca del corazón, los vasos sanguíneos y el sistema circulatorio y sus funciones.
Estos modelos capturan la forma de muchas buenas explicaciones. Sin embargo, los filósofos no deberían asumir que exista un solo modelo verdadero de explicación y que se deba tomar una decisión sobre qué modelo nos dice qué es realmente una buena explicación. Es decir, muchos asumen que un modelo explicativo “talla única” se ajusta a todas las áreas de investigación. Esta asunción significa que los filósofos han ignorado a menudo la psicología del razonamiento explicativo.
Dar una buena respuesta a una pregunta “¿por qué?” no es solo una abstracción filosófica. Una explicación tinene funciones cognitivas en el mundo real. Fomenta el aprendizaje y el descubrimiento y las buenas teorías explicativas son vitales para navegar por el entorno sin problemas. En este sentido, una explicación es lo que se conoce como un acto de habla, que es una unidad de emisión que realiza una cierta función en la comunicación. Evaluar cuando alguien realiza este acto de habla con éxito debería tener en cuenta la psicología del razonamiento explicativo y su sutil sensibilidad al contexto. Una labor estupenda en la psicología de la explicación demuestra que tanto las leyes, como la unificación y los mecanismos causales tienen un lugar en la psicología humana, trazando distintos conceptos que se activan dependiendo de la audiencia, intereses, creencias previas y el entorno social.
Los resultados de la psicología también ponen de manifiesto una sorprendente similitud entre los razonamientos explicativos de niños y científicos. Tanto niños como científicos observan el mundo intentando encontrar patrones, buscando violaciones sorprendentes de esos patrones e intentando comprenderlas basándose en consideraciones explicativas y probabilísticas. Las prácticas explicativas de los niños sugieren un conocimiento único de la naturaleza de una buena explicación.
Los modelos de explicación deberían calibrarse con datos acerca de la práctica explicativa real desde la psicología, pero también desde la historia y sociología de la ciencia. La misma conclusión aplica a otros temas tradicionales estudiados por los filósofos de la ciencia como la confirmación, los cambios de teorías y el descubrimiento científico, donde demasiado a menudo la especulación filosófica abstracta ofusca los fundamentos cognitivos de la ciencia. Los estudios de base experimental de la explicación nos dicen claramente algo importante acerca de cómo la gente explica, qué encuentra explicativamente valioso, y cómo las prácticas explicativas cambian a lo largo de la vida. Si todo niño es un científico nato los filósofos de la ciencia harían bien en prestar más atención a la psicología de la explicación, y en concreto a las preguntas “¿por qué?” y al razonamiento explicativo de los niños. Conseguirán una comprensión más matizada de qué constituye una buena explicación.
Sobre el autor: Matteo Colombo es profesor ayudante en el Tilburg Center for Logic, Ethics, and Philosophy of Science y en el departamento de filosofía de la Universidad de Tilburg en los Países Bajos.
Texto traducido y adaptado por César Tomé López a partir del original publicado por Aeon el 1 de febrero de 2017 bajo una licencia Creative Commons (CC BY-ND 4.0)
El artículo Por qué los niños preguntan “por qué” y qué constituye una buena explicación se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una buena colección de historias maravillosas
- ¡Esta mierda es buena!
- Aprender un idioma: esa cosa de niños que ayuda a los ancianos
La pantalla de tu móvil solo tiene tres colores
De las pantallas de plasma al OLED, la tecnología se adapta a nuestra visión.
Es posible que tu primer móvil fuese el Alcatel One Touch Easy -también conocido como el ‘one tochazo’- uno de los que encabezó las listas de ventas desde 1997 hasta 2000, cuando fue desbancado por el indestructible Nokia 3310. Sus diseños guardan más parecido con una calculadora que con un móvil actual: carcasa de colores y una minúscula pantalla rectangular LCD monocroma.
Actualmente, las pantallas de nuestros móviles, ordenadores y televisores, ya sea a través de LCD o sistemas de plasma, nos permiten ver en color. Si pusiésemos la pantalla de nuestro móvil en blanco y la observásemos ampliada a través de una lente o un microscopio, veríamos lo siguiente:

Cada uno de esos grupos rojo-verde-azul es un píxel. La manera de organizarlos en la pantalla varía entre los dispositivos. Se suelen organizar en líneas verticales, aunque algunas pantallas los organizan en triángulos o diagonales con el fin de optimizar la sensación de movimiento.
En el caso de una pantalla de plasma, ésta está formada por dos cristales que encierran gases (neón y xenón). Entre estos dos cristales hay unas celdas (píxeles) con 3 compartimentos (uno por cada color) que contienen una sustancia fosforescente distinta que reacciona generando luz en alguno de los 3 colores (rojo, azul y verde).
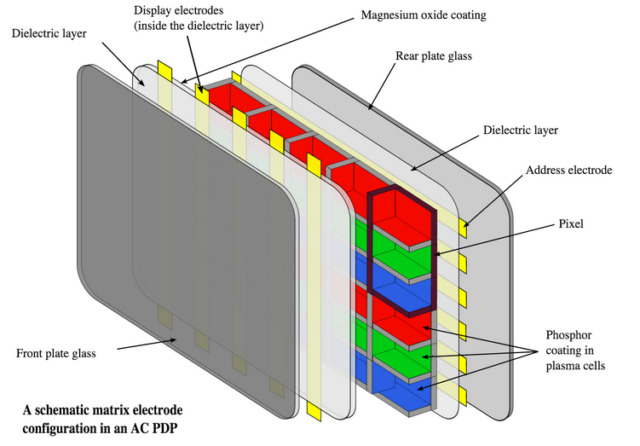
Esquema de una pantalla de plasma.
Al aplicar electricidad al gas, éste se transforma en plasma y, a su vez, el plasma provoca que la sustancia fosforescente reaccione y genere luz, iluminando así cada píxel de la pantalla.
Cuando se dejan imágenes estáticas mucho tiempo se llega a perder color en ciertas zonas de la pantalla, ya que se va gastando el material fosforescente. Esta tecnología nunca llegó a utilizarse en teléfonos móviles por dos razones: el tamaño mínimo de las pantallas de plasma es 42 pulgadas y el consumo es tan elevado que sería imposible fabricar una batería ligera que le diese suficiente autonomía.
La tecnología LCD se apoya en una fuente de iluminación que, desde atrás, proyecta luz sobre una pantalla formada por píxeles (cada píxel, a su vez, lleva los 3 colores básicos).
Esta luz pasa por unos filtros polarizados y por unos filtros de color que la tiñen de rojo, verde o azul. Esta luz coloreada pasa por otro filtro polarizado para dejar pasar la luz que finalmente se proyecta sobre la pantalla.
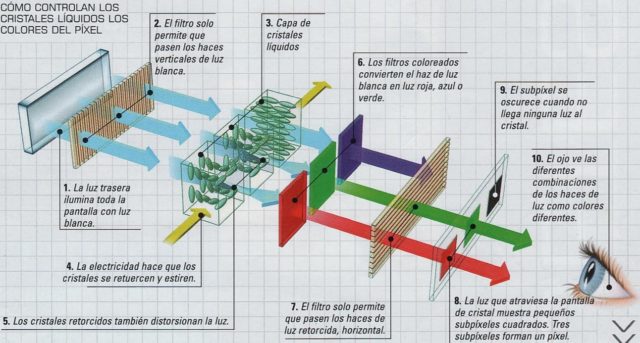
Esquema de pantalla LCD.
Durante un tiempo se libró una batalla mercantil entre la tecnología LCD y el plasma. La gran ventaja del plasma es que ofrecía negros más intensos que el LCD.
Finalmente, la tecnología LCD triunfó, y uno de los motivos es que ofrecía una mayor vida útil que las pantallas de plasma y, además, un consumo energético mucho menor (consumían hasta un 30% menos y emitiendo mucho menos calor), sobre todo cuando la iluminación de estas pantallas LCD comenzó a hacerse con tecnología LED (diodo emisor de luz). El LED puso fin a la guerra contra el plasma y terminó casi expulsando del mercado a esta tecnología.
Sin embargo, la última revolución que estamos viviendo es, sin duda alguna, la de la tecnología OLED. Más allá del 3D y el 4K, la gran revolución está en la calidad de la imagen y, sobre todo, en lo realista de los colores. Si en el paso de LCD a LED el cambio estaba en el uso de iluminación trasera LED, ahora el gran salto se produce en eliminar la iluminación trasera.
El OLED es un diodo orgánico que genera luz por sí mismo, es decir, que está formado por píxeles que se iluminan de manera autónoma.
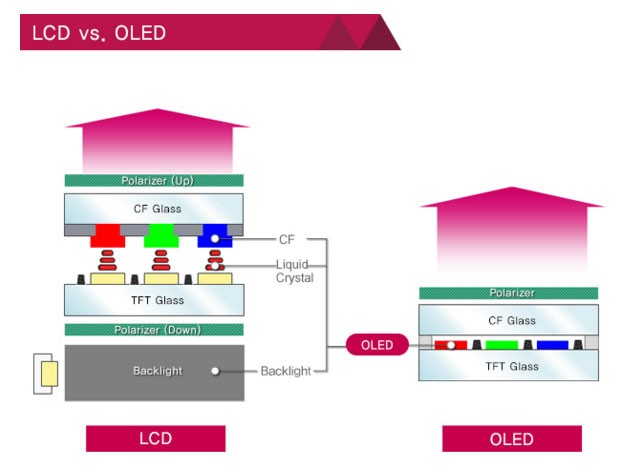
Sea cual sea la tecnología de nuestro dispositivo, todos ellos se basan en tres colores. ¿Cómo es posible que veamos muchísimos más?
La respuesta empieza por el método de obtención de colores de la luz: la síntesis aditiva del color. Los colores rojo, verde y azul son los denominados colores primarios luz, ya que a partir de su mezcla podemos obtener cualquier otro color. Si tenemos tres fuentes de luz, de los colores rojo, verde y azul, y las superponemos, observaremos luz blanca. Si superponemos luz roja y luz verde, observaremos luz amarilla; si superponemos verde y azul, observaremos luz cian; si superponemos luz roja y luz azul, observaremos luz magenta.

Síntesis aditiva del color.
A esta forma de componer colores en las pantallas de nuestros dispositivos se le llama modelo RGB, por las siglas en inglés de rojo, verde y azul.
Para indicar con qué proporción mezclamos cada color, se asigna un valor a cada uno de los colores primarios, de manera que el valor 0 significa que no interviene en la mezcla y, a medida que ese valor aumenta, se entiende que aporta más intensidad a la mezcla. Aunque el intervalo de valores podría ser cualquiera, es frecuente que la intensidad de cada una de las componentes se mida según una escala que va del 0 al 255. La mayor parte de los dispositivos trabajan de esta manera con lo cual pueden representar aproximadamente 16,6 millones de colores distintos. El color blanco se forma con los tres colores primarios a su máximo nivel (255,255,255). La ausencia de color —lo que conocemos como color negro— se obtiene cuando las tres componentes son 0 (0,0,0).
Según la intensidad de cada parte del pixel, se forma una sensación de color diferente.
El modelo de color RGB no define por sí mismo lo que significa exactamente rojo, verde o azul, por lo que los mismos valores RGB pueden mostrar colores notablemente distintos en diferentes dispositivos que usen este modelo. Aunque utilicen un mismo modelo de color, sus espacios de color pueden variar considerablemente, por eso hay tanta diferencia entre el realismo de colores que ofrece un dispositivo y otro (incluso asumiendo que estos estuviesen perfectamente calibrados por el usuario).
Una de las cosas que resultan más interesantes de este modelo RGB es la razón última por la que es un modelo tan eficaz. Esa razón está en nuestros ojos.
Resulta que el modelo RGB está diseñado a semejanza de nuestros ojos. Aunque parezca contraintuitivo, también están limitados a tres colores, es decir, a efectos prácticos los receptores de nuestros ojos también se comportan como píxeles del modelo RGB.
Los ojos tienen sus propios sensores de luz, los bastones y los conos. Los bastones contienen rodopsina y son los responsables de la visión en condiciones de baja luminosidad, presentando un pico de mayor sensibilidad hacia la longitud de onda de 500 nm (luz verde azulada), se saturan en condiciones de mucha luminosidad y no detectan los colores.
Los conos contienen tres tipos diferentes de pigmentos visuales y son los responsables de la visión en color. Cada pigmento visual está formado por una proteína llamada yodopsina y una molécula derivada de la vitamina A, el retinal, que puede adoptar dos formas diferentes que denominamos cis y trans.
Los tres tipos de pigmentos visuales de los conos son: la eritropsina, con mayor sensibilidad para las longitudes de onda largas (luz roja); la cloropsina, que es sensible a las longitudes de onda media (luz verde); y la cianopsina, con mayor sensibilidad a las longitudes de onda cortas (luz azul). Es decir, nuestros ojos son sensibles a los colores del modelo RGB.
La respuesta al color azul es una veinteava parte de la respuesta a los otros dos colores. Este hecho lo aprovechan algunos sistemas de codificación de imagen reduciendo información de la componente azul, ya que el ser humano no percibe esta pérdida.
Que un pigmento visual sea sensible a una longitud de onda quiere decir que cuando la luz de determinado color impacta con el pigmento se produce un cambio en su forma. Este cambio lo sufre el retinal, que pasa de su forma cis a su forma trans. Es como si el impacto de la luz le provocase un cambio de postura. Este cambio de postura es enviado como señal por el nervio óptico hacia el cerebro, quien sí lo interpreta como color.
Nuestra mente es la que ve el rosa, el amarillo, el cian y toda la inmensidad de colores que conocemos, a pesar de que la señal que recibimos y emitimos esté limitada a tres. El color es biológico, es un lugar de encuentro de nuestra mente con el resto del universo.
La ciencia del color debe ser considerada, en esencia, como una ciencia de la mente.
James Clerk Maxwell
Fuentes:
Fundamentos de fisiología. E. Martín Cuenca. Ed. Thomson, 2006.
El ojo desnudo. Antonio Martínez Ron. Ed. Crítica, 2016.
Todo es cuestión de química. Deborah García Bello. Ed. Paidós, 2016.
Especial de Xataka: Inventando el OLED. 2016.
Agradecimientos: Agradezco a Manuel Muñoz Iglesias, apasionado de la tecnología audiovisual, su ayuda en la investigación y revisión de este artículo.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo La pantalla de tu móvil solo tiene tres colores se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El mejor lacón con grelos tiene su ciencia
- La bombilla de colores (y el método científico)
- El problema de los tres caballeros y los tres criados
El helio superfluido y los agujeros negros

Aspecto que podría tener un agujero negro como el que hay en el centro de la Vía Láctea
En los años setenta los físicos Stephen Hawking y Jacob Bekenstein descubrieron algo extraño en los agujeros negros. Calcularon que, cuando la materia cae en uno de estos agujeros sin fondo espaciales, la cantidad de información que engullen, lo que los científicos llaman entropía, se incrementa en proporción a lo que se incrementa el área del agujero negro, no de su volumen. Dicho de otra manera, si el agujero negro fuese un armario archivador, la cantidad de archivos que puede contener dependería solo y exclusivamente de la superficie de la puerta y no de la profundidad del armario. Esta es una de esas cosas aparentemente absurdas de la física que cuadran bien con las matemáticas y las observaciones, pero poco con el sentido común.
Ahora un grupo de investigadores encabezado por Christopher Herdman, de la Universidad de Waterloo (Canadá), ha encontrado que el mismo tipo de ley aplica a la información cuántica en el helio superfluido. Lo que podría ser solo una coincidencia o un indicio de que existe una relación entre lo muy pequeño y lo muy grande que permitiría ayudar a formular una teoría cuántica de la gravedad.

Una esfera de átomos de helio superenfriados (en verde) inteacciona con un contenedor formado por átomos de helio (en azul).
Los científicos emplearon dos superordenadores para explorar las interacciones de 64 átomos de helio en un superfluido formando una esfera. Encontraron que la cantidad de información cuántica entrelazada compartida entre dos regiones del contenedor (la esfera y el resto) estaba determinada por la superficie de la esfera y no por su volumen. Al igual que ocurre con las holografías, un volumen tridimensional de espacio está completamente codificado en su superficie bidimensional. Como un agujero negro.
Las simulaciones realizadas recogen todos los atributos conocidos del helio, lo que demostraría por primera vez la existencia de una ley del área de la entropía de entrelazamiento en un líquido cuántico real.
De momento, el estudio de la gravedad aún no ha permitido cuadrarla adecuadamente en el marco de la teoría cuántica. Una pieza en el puente entre las dos grandes teorías de la física, la relatividad general y a mecánica cuántica, podría ser la contribución de este estudio al “principio holográfico”: ¿y si todo el universo tridimensional pudiese entenderse como información bidimensional? Daría igual lo que fuese, un agujero negro inimaginablemente enorme o una gota ultramicroscópica de helio líquido, todo se regiría por el mismo principio fundamental.
Referencia:
C.M. Herdman et al (2017) Entanglement area law in superfluid 4He Nature Physics doi: 10.1038/nphys4075
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo El helio superfluido y los agujeros negros se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los agujeros negros binarios en cúmulos globulares y Advanced-LIGO
- Una hipernova en los confines del Universo apuntala el modelo de formación de los agujeros negros
- Ciencia express: Que son los agujeros negros
666, el número de la Bestia (y 2)
En mi anterior entrada de la sección Matemoción del Cuaderno de Cultura Científica, 666, el número de la Bestia (1), estuvimos hablando del origen del número de la Bestia, el 666, que no es otro que el Apocalipsis de San Juan, o Libro de las revelaciones, del Nuevo Testamento (aunque tal vez el verdadero número de la Bestia bíblico fuese el 616 y la creencia en el 666 se deba simplemente a un error al copiar el texto original del Apocalipsis de San Juan, y se mantuviese en las siguientes copias), así como de algunas propiedades matemáticas de este número, el 666.
En dicha entrada vimos 13 sorprendentes relaciones numéricas relacionadas con el 666, algunas bestiales, y en esta entrada empezamos con un par de ellas más, para quienes disfrutaron de aquellas.
14.- La suma de los cubos de los dígitos de 6662 más la suma de los dígitos de 6663, es el número de la Bestia, 666. Veámoslo…
6662 = 443.556; 6663 = 295.408.296;
y entonces,
[43 + 43 + 33 + 53 + 53 + 63]
+ [2 + 9 + 5 + 4 + 0 + 8 + 2 + 9 + 6]
= 666.
15.- El número de la Bestia también se puede relacionar con el número de oro, o divina proporción, Φ, mediante la siguiente relación que implica a las funciones trigonométricas seno y coseno,
Φ = – [ sen (666) + cos (6 × 6 × 6)].

Excelente fotografía de Tomas Eriksson Fotography del número de la Bestia, 666
Pero dejemos estas propiedades matemáticas curiosas a un lado y centrémonos en el tema de esta entrada, la numerología relacionada con el número de la Bestia, el 666.
Una de las prácticas numerológicas actuales, pero que tienen un origen antiguo, consiste en asignar a las letras valores numéricos de forma que a cada palabra, nombre o frase se le asocia un valor numérico en función del cual se realizan interpretaciones sobre la palabra o frase en cuestión. Un ejemplo se vio en la entrada anterior, donde se mostraba una cita de la novela Guerra y Paz en la cual se realizaba una determinada asignación de valores numéricos a las letras de nuestro abecedario, a partir de dicha asignación se asociaba al Emperador Napoleón con el valor numérico 666. Pero puesto que el 666 es el número de la Bestia y está relacionado con el diablo o el anticristo, se está echando mano de la numerología para explicar el carácter maléfico de Napoleón.
Esta práctica numerológica es muy antigua y tiene su origen en la existencia de sistemas de numeración alfabéticos en la antigüedad. Nuestro sistema de numeración, que es posicional, utiliza diez cifras básicas para expresar, utilizando la posición, todos los números. Estas diez cifras básicas, 0, 1, 2, …, 9, están “destinadas únicamente para este fin”. Sin embargo, en la antigüedad existían sistemas de numeración que eran alfabéticos, es decir, que las letras del alfabeto, con las que se formaban las palabras, también eran las cifras del alfabeto numérico, con las que se construían, se representaban, los números.
Sistemas de numeración alfabéticos eran, por ejemplo, los sistemas fenicios, armenio, egipcio, hebraico, griego o árabe, entre otros. Para más información sobre estos sistemas de numeración se puede leer el magnífico texto Historia universal de las cifras, de Georges Ifrah. A continuación, mostramos los sistemas de numeración alfabéticos hebraico, árabe y griego.
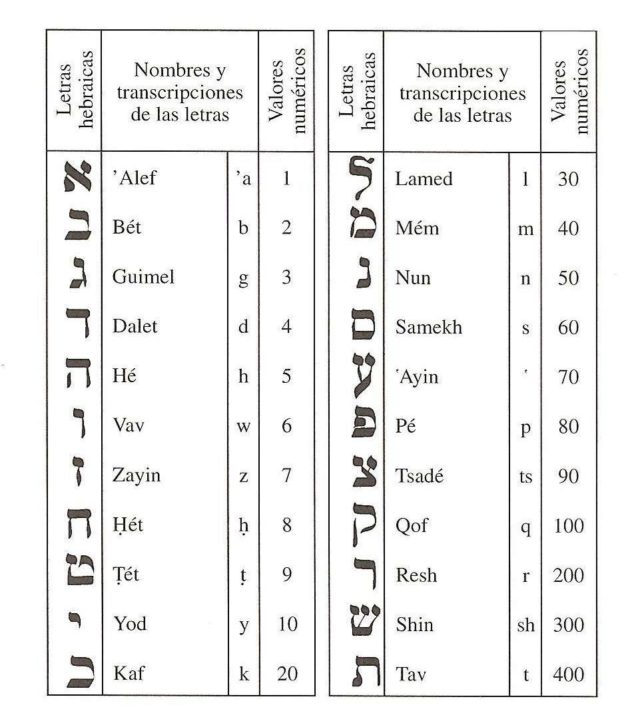
Numeración alfabética hebrea
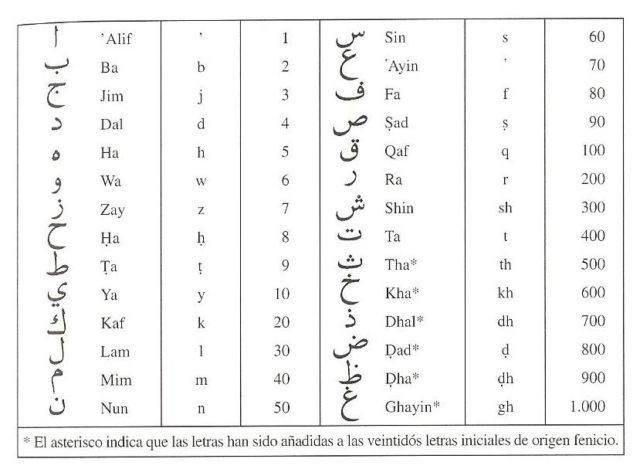
Numeración alfabética árabe

Numeración alfabética griega
Al existir sistemas de numeración alfabéticos era normal que se utilizase el doble significado, literal y numérico, de palabras o frases, no solo para cuestiones relacionadas con las creencias, sino también en el contexto social y cultural. Así, uno de los usos de esta doble lectura, que nos comenta el historiador de la ciencia Georges Ifrah, es la composición de “cronogramas”, la expresión de algunas fechas mediante alguna frase escrita que estaba relacionada con el hecho que se quería datar.
Uno de los ejemplos que se muestran en la Historia universal de las cifras es la utilización de “cronogramas” en inscripciones funerarias para expresar la fecha en la que ha fallecido la persona que está enterrada allí. El siguiente ejemplo pertenece a una inscripción funeraria judía de la ciudad de Toledo. Está escrito, en hebreo, “año gota de rocío sobre cinco mil” (véase la imagen más abajo, teniendo en cuenta que la escritura hebrea es de derecha a izquierda), que como frase no tiene mucho sentido, salvo que se tenga en cuenta que la expresión “gota de rocío”, escrita en el alfabeto hebraico, está formada por seis letras cuyo valor como números es 1, 3, 30, 10, 9, 30, y la suma de estos alcanza el valor 83. Por lo tanto, el año en el que murió la persona de la inscripción funeraria era el año 5.083, 83 sobre 5.000, del calendario judío, que se corresponde con el año 1.322-1.323 del calendario actual, el gregoriano.

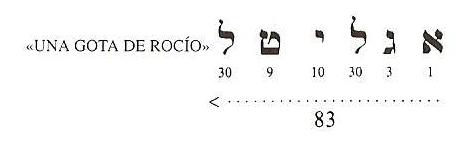
Mientras que en otra lápida de Toledo se encuentra escrito, de nuevo en hebreo, “año nos hemos quedado sin padre” y la frase, en hebreo, “nos hemos quedado sin padre”, que aparece en la siguiente imagen, tiene el valor 144, por lo que en la inscripción funeraria se refiere al año 5.144, es decir, el año 1.373-1.374 de nuestro calendario.
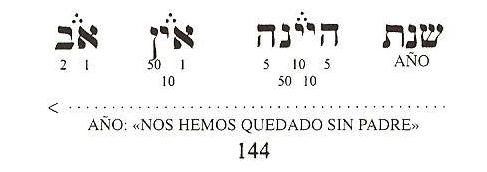
Otro ejemplo que recoge Ifrah es el “cronograma” que se utilizó para representar el año de la muerte del rey Sher Shah Suri, también conocido como Sher Khan (“Rey Tigre” en pastún), fundador del imperio Suri, en una parte del subcontinente indio, y que murió de una explosión accidental de pólvora en el año 952 de la Hégira (año 1.545 de nuestro calendario). El cronograma, que se ve en la imagen siguiente, dice así “muerto de quemaduras” y su valor numérico es precisamente 952.
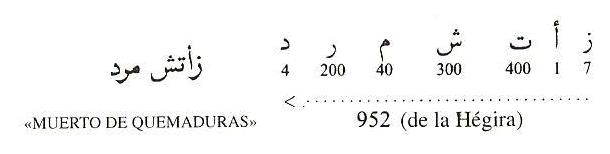
O también, la inscripción en un edificio de la Kasba de Tanger que dice “año la luna llena de mi belleza se ha instalado en la habitación de la felicidad”, de donde deducimos que el año en el que se ha construido el edificio es el 1.145, que es el valor numérico de la frase, de la Hégira (año que en el calendario gregoriano empezó el 24 de junio de 1.732).

La asignación de valores numéricos a las letras de un alfabeto ha dado lugar a que se desarrollen diferentes procedimientos para obtener valores numéricos de palabras o frases, y realizar interpretaciones más o menos místicas o esotéricas a partir de esos valores y las relaciones entre ellos. Este procedimiento lo aplicaron los judíos con el nombre de gematría (palabra que significa literalmente “cálculo alfabético” o “cálculo numérico de la palabra”), que es una de las herramientas de la kábala, los griegos con el nombre de isopsefia y los musulmanes con el nombre de “hisab al jumal” (“cálculo de la suma, de la totalidad”).
La kábala es una de las principales corrientes del esoterismo judío, que tiene como base estructural el árbol de la vida y que fundamentalmente es una tradición oral que ayuda a leer, descifrar e interpretar los textos sagrados (la Torah o Pentateuco del Antiguo Testamento), buscando conocer el mundo, el universo, la “verdad”. Y también tiene una parte más práctica, que ayuda a las personas a orientarse, a buscar respuestas, a vivir en armonía con las leyes espirituales del universo, a alcanzar la paz.

La gematría es una de las partes de la Kábala. Es una de las herramientas que utiliza esta para interpretar los textos sagrados [el universo]. A partir de la obtención de los valores numéricos de palabras y textos, se inicia un “movimiento” de relaciones, interpretaciones,… Recogiendo la explicación de uno de los textos sobre la gematría, esta “es el punto de partida para el pensamiento, no es el pensamiento en sí”.
Veamos algunos sencillos, pero ilustrativos, ejemplos. Algunos rabinos relacionan las palabras hebreas yayin (“vino”) y sod (“secreto”), pues se dice que “del vino provendrá el secreto” (Nikhnas Yayin Yatsa Sod, de donde deriva, en latín, “in Vino Veritas”). Estas dos palabras tienen exactamente el mismo valor numérico en el sistema hebraico usual:
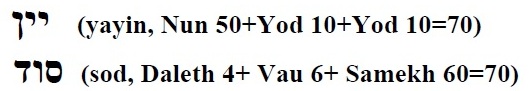
También hay quienes relacionan las palabras Ahavah (“Amor”) con Ehad (“Uno”),
![]()
que se relaciona con el concepto de Dios-amor que aparece en la Biblia. Por otra parte, la suma de los valores de ambas palabras nos da 26, que es el número asignado al nombre mismo de Yahveh:
![]()
Hay quienes se apoyan en la gematría para demostrar que el mundo fue creado cuando comenzó el año civil hebraico (en el equinoccio de otoño), ya que las dos primeras palabras de la Torá (Bereshit Bara “al comienzo [Dios] ha creado”) tienen el mismo valor numérico que Berosh Hashanah Nibrah (“Él ha sido creado al comienzo del año”):
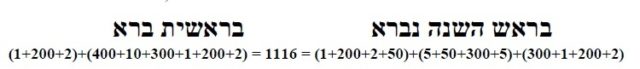
Veamos a continuación tres ejemplos de isopsefia. En estos ejemplos hemos utilizado las letras griegas mayúsculas. Suetonio (Nerón, pag. 39), evocando la muerte de Agripina, relaciona el nombre de Nerón, escrito en griego, con la frase Idian Metera apekteine (“Él mata a su propia madre”). Los dos grupos tienen el mismo valor numérico:
N E P Ω N
(50+5+100+800+50= 1.005)
I Δ I A N M H T E P A A Π E K T E I N E
([10+4+10+1+50] + [40+8+300+5+100+1] + [1+80+5+20+300+5+10+50+5 = 1.005] )
El padre Theófanes Kérameus (s. XII) en una de sus homilías cita la equivalencia numérica de las palabras Theos (“Dios”), Aguios (“Santo”) y Agathos (“Bueno”):
ΘΕΟΣ (9 + 5 + 70 + 200)
ΑΓΙΟΣ (1 + 3 + 10 + 70 + 200)
ΑΓΑΘΟΣ (1 + 3 + 1 + 9 + 70 + 200)
Una forma mística de afirmar la santísima trinidad recurre a la isopsefia. En el Nuevo Testamento (Apocalipsis, Juan, XXII, 13) se dice que Dios es el Alfa y el Omega (esto es, el principio y fin de todas las cosas), además el espíritu santo se manifestó a Jesús bajo la forma de una paloma (peristera), pero
Α y Ω (1 + 800 = 801)
ΠΕΡΙΣΤΕΡΑ (80 + 5 +100 + 10 + 200 + 300 + 5 + 100 + 1 = 801)
Pero dejémonos de ejemplos y vayamos al tema que hemos planteado en la presente entrada del Cuaderno de Cultura Científica, el 666, la numerología del número de la bestia.
Los místicos cristianos se dedicaron a descifrar quién, quiénes o qué era el anticristo, utilizando para ello cualquier sistema numérico que fuera oportuno, viniese o no de un sistema de numeración alfabético, así como cualquier procedimiento que les sirviese para sus fines. Por ejemplo, Nerón, el primer emperador romano que persiguió a los cristianos, fue identificado por algunos intérpretes como la bestia del Apocalipsis, ya que el valor numérico de su nombre al acompañarle del título de “César” es 666 en el sistema hebraico, nos da 666.
![]()
Nun (50) Resh (200) Waw (6) Nun (50)
Qoph (100) Samech (60) Resh (200)

Busto de Nerón, que se encuentra en los Museos Capitolinos, en Roma
Por otra parte, hubo quienes interpretaron que la bestia era el emperador Diocleciano, cuya política religiosa se acompañó de violentas persecuciones contra los cristianos, para ello consideraron el sistema que consiste en considerar únicamente las letras de su nombre latino que se corresponden con cifras romanas:
D I O C L E S A V G V S T V S
(500 + 1 + 100 + 50) + (5 + 5 + 5) = 666
Para otros el número de la bestia podría ser no una persona sino un grupo de personas. Por ejemplo, en el libro El misterio de las cifras de Marc-Alain Ouaknin, se menciona que el obispo Ireneo de Lyon (siglo II) relaciona el número de la Bestia con el término griego “Lateinos”, que significa latino, y que aludiría a la procedencia del anticristo. Efectivamente,
Λ 30 A 1 T 300 E 5 I 10 N 50 O 70 Σ 200,
suma 666, el número de la Bestia.
Más tarde, en la época de las convulsiones religiosas, un católico de nombre Petrus Bungus, publicó en 1585 un libro titulado “Numerum mysteria” (Los misterios de los números) en el que consideraba el siguiente sistema:
A = 1, B = 2, C = 3, D = 4, E = 5, F = 6,
G = 7, H = 8, I,J = 9, K = 10, L = 20, M = 30,
N = 40, O = 50, P = 60, Q = 70, R = 80, S = 90,
T = 100, U,V = 200, X = 300, Y = 400, Z = 500
e intenta demostrar que el nombre de Martín Lutero sumaba 666, con lo que, en su opinión, demostraba que este era el anticristo. Según I. B. Cohen, si Bungus considera su nombre, es decir, en alemán, se tiene MARTIN (260) y LUTHER (413), luego en total 673. Entonces, lo que hace es latinizar su apellido Luther (Lutera), pero no su nombre Martín, ya que LUTHERA suma 406, y en total sería 666. Otra forma de llegar al deseado 666 con Lutero era considerar la forma hebraica de Lutero, Lultr, y calcula su valor obteniendo de nuevo 666,
לולתר(ר= Raish = 200, ת= Tav = 400, ל= Lamed = 30, ו= Wav = 6, ל= Lamed = 30).

Cuadro de Ferdinand Pauwels (1830-1904) en el que aparece Martin Lutero haciendo públicas “las 95 tesis”, la carta de Lutero a la Iglesia de Roma, en las puertas de la Iglesia del Palacio de Wittenberg el 31 de octubre de 1517
Por su parte, los discípulos de Matin Lutero, que consideraban a la Iglesia romana heredera directa del Imperio Romano, no tardaron en replicar a la provocación. Tomaron las cifras romanas contenidas en la frase VICARIVS FILII DEI (“Vicario del Hijo de Cristo”) que lleva la tiara papal obtuvieron la conclusión que buscaban.
VICARIVS FILII DEI
(5+1+100+1+5) +(1+50+1+1+500+1) = 666
Así a lo largo de la historia ha habido una gran cantidad de interpretaciones del número 666, lo cual no es tan difícil ya que con tantas posibilidades a la hora de elegir el método de numeración y en la elección de las palabras y combinaciones entre ellas, da una infinidad de posibilidades. Un ejemplo literario lo habíamos incluido en la anterior entrada sobre el número de la Bestia, el libro “Guerra y Paz” de Tolstoi, en el que con una nueva interpretación numérica se asociaba el anticristo con Napoleón.
Esta práctica numerológica se ha seguido utilizando con diferentes personajes históricos. Por ejemplo, no podía faltar la asociación de Hitler con el número de la Bestia. Para ello se considera la siguiente relación entre números y letras
A = 100, B = 101, C = 102, D = 103, …
(sin tener en cuenta la Ñ) para la cual se tiene que
H (107) + I (108) + T (119) + L (111) + E (104) + R (117) = 666.
También hay quienes han relacionado a Bill Gates, cofundador de la empresa Microsoft, con el número de la Bestia. Para ello han considerado el código ASCII (American Standard Code for Information Interchange), que vemos en la siguiente imagen.
El código ASCII, American Standard Code for Information Interchange, completo
Si se toman todas las letras del nombre “Bill Gates III”, cuyo nombre completo es William Henry Gates III, incluido el ordinal III para poder sumar el valor 3, y se suman los valores de los números en el código ascii correspondientes con las letras de su nombre, según se ha mostrado en la imagen anterior, se obtiene 666.
B = 66, I = 73, L = 76, L = 76
G = 71, A = 65, T = 84, E = 69, S = 83
I = 1, I = 1, I = 1.
Pero todo vale en la numerología. Por ejemplo, un argumento sencillo relacionaba al presidente de EE.UU. Ronald Wilson Reagan con el anticristo, según algunos miembros de la extrema derecha de su país, que las tres palabras de su nombre tenían 6 letras.
La verdad es que la numerología acaba convirtiéndose en un juego, en el que cada persona puede acabar consiguiendo lo que desea encontrar. Podríamos plantear el siguiente juego/reto: buscar una asignación de valores a las letras del alfabeto para que su nombre, o si se prefiere el mío, esté relacionado con el número de la Bestia.
Terminemos con algunas anécdotas más sobre el número 666, que ha tenido más atención de la que realmente se merece.
a. El primer ordenador de Apple, el Apple 1, fue lanzado al mercado en julio de 1976 con un valor de 666,66 dólares.

Ordenador Apple 1 expuesto en el museo del Instituto Smithsoniano
b. El “sevendust 666” fue un virus que afectó a los ordenadores Macintosh en 1998. Fue un virus de los más destructivos que han afectado a los ordenadores de Apple anteriores al sistema Mac OS X.
c. El Edificio Tishman, que ahora pertenece a la compañía Kushner Cos, situado en el número 666 de la Quinta Avenida de Manhattan en Nueva York, que tiene 41 plantas y una altura de 147 metros, posee tres grandes seises en su parte superior.

El edificio del 666 de la Quinta Avenida de Nueva York
d. El número 666 se escribe en el sistema de numeración binario, en base 2, como 1010011010, pero si ahora se sustituyen los 0s por los 1s, y al revés, y se invierte el orden del resultado, se obtiene de nuevo es número 1010011010, es decir, 666.
Bibliografía
1.- Raúl Ibáñez, Numerología, cábala y otros enigmas, Geometrian barrenako ibilaldia / Un paseo por la geometría 2007/08, UPV-EHU, 2008.
2.- Martin Gardner, Juegos y enigmas de otros mundos, Gedisa, 2000.
3.- Georges Ifrah, Historia universal de las cifras, Ensayo y pensamiento, Espasa, 2002.
4.- Marc-Alain Ouaknin, El misterio de las cifras, Ma Non Troppo, Ediciones Robinbook, 2006.
5.- I. B. Cohen, El triunfo de los números, Alianza Editorial, 2007.
6.- Lamberto García del Cid, Números notables, el 0, el 666 y otras bestias numéricas, RBA, 2010.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo 666, el número de la Bestia (y 2) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Historia mínima de la complejidad animal

Los primeros animales eran probablemente formas coloniales muy sencillas y surgieron, quizás, hace algo más de 600 millones de años. Los metazoos actuales más parecidos a esas colonias son seguramente las esponjas, filo Porifera. Tienen la peculiaridad de que carecen de tejidos, por lo que hay muy escasa diferenciación funcional en ellos. Sí hay, sin embargo, diferentes tipos celulares, pero muy pocos: no más de diez. Esa diferenciación de tipos celulares se produce porque empieza a producirse lo que podemos considerar, sin temor a equivocarnos, una verdadera división del trabajo. Cada tipo celular se ocupará a partir de entonces de una o varias tareas especializadas.
Otro filo de animales muy sencillos es Placozoa, cuya única especie Trichoplax adhaerens es como una bolsa cuya cavidad interna se encuentra a cierta presión. Carece de órganos y solo tiene dos tipos celulares. Se asemejan a minúsculas tortas (0,5 mm). Su posición filogenética no está nada clara; y es posible que procedan de animales más complejos, con órganos incluso.
Algo más complejos son los cnidarios, aunque son diblásticos: sólo tienen dos capas celulares. La ectodermis es la capa que da hacia el exterior, y la gastrodermis da hacia el interior o cavidad gastrodérmica (verdadero sistema digestivo de estos animales). Las dos capas pueden ser consideradas como tejidos y desempeñan funciones diferentes. Tienen también muy pocos tipos celulares, pero son ya los primeros animales con células nerviosas (tienen un plexo nervioso circular, ya que son de simetría radial) y cuentan con células receptoras de estímulos. Es por ello el primer grupo animal del que sabemos que realiza una cierta integración nerviosa: a la recepción de señales sigue un procesamiento nervioso muy básico que da lugar a una respuesta motora. Es posible que los cnidarios surgieran hace 600 millones de años o algo menos, junto con la llamada fauna de Ediacara, que es el conjunto de organismos multicelulares complejos más antiguos del que se tiene conocimiento; la mayoría de ellos desapareció antes de la denominada explosión cámbrica.
Los ctenóforos son otro filo de simetría bilateral, también diblásticos y de complejidad algo mayor que la de los cnidarios, aunque se conocen bastantes menos especies de este grupo.
Al surgir los primeros animales de simetría bilateral crece la complejidad estructural y aparece un número significativamente mayor de tipos celulares. A pesar de que el aumento de la complejidad es bastante general, también hay organismos con ese tipo de simetría, como los gusanos planos o platelmintos, que carecen de una cavidad interna (celoma) y de los sistemas circulatorio y respiratorio. Su sistema digestivo es extraordinariamente simple, con un único orificio. La ausencia de un sistema circulatorio que pueda transportar el oxígeno del medio externo a todas las células es el condicionante que determina la estructura plana y el escasísimo grosor de estos gusanos. Solo con un grosor mínimo puede acceder tanto el oxígeno –procedente del exterior-, como los nutrientes –procedentes del tubo digestivo- a todas las células. El oxígeno, en concreto, no penetra más de 1 mm al difundir desde el exterior.
La organización de los animales se hace cada vez más compleja conforme van apareciendo cavidades internas (celoma u otras). Además, la simetría bilateral da lugar a la definición de un eje anteroposterior (según el sentido de la macha) que propicia la progresiva concentración de estructuras sensoriales en la parte anterior del cuerpo y de la consiguiente coalescencia de ganglios nerviosos, como consecuencia de la cual aparecen los primeros cerebros o protocerebros.
A partir de la aparición de la simetría bilateral y una cavidad interna, el modelo corporal básico de la mayoría de los metazoos mantiene esos dos rasgos básicos, aunque hay grupos que posteriormente lo han modificado desarrollando una simetría radial, como los equinodermos, o reduciendo al máximo la cavidad celómica. En los metazoos más complejos varios tipos celulares pueden asociarse en un tejido, varios tejidos en un órgano y varios órganos en un sistema. La organización y funcionamiento sobre la base de órganos y sistemas que funcionan de forma armónica es lo que caracteriza a la gran mayoría de los animales. Y buenos ejemplos de ello son el grupo más exitoso de los metazoos –el de los insectos– y los cordados, el filo de mayor complejidad estructural y funcional.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Historia mínima de la complejidad animal se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:
