Los árboles pueden ayudarnos a predecir erupciones volcánicas
 Los satélites de NASA podrían detectar cambios en la vegetación desde el espacio antes de la erupción de un volcán. Imagen: Jeff Schmaltz / MODIS / NASA
Los satélites de NASA podrían detectar cambios en la vegetación desde el espacio antes de la erupción de un volcán. Imagen: Jeff Schmaltz / MODIS / NASA
El diez por ciento de la población mundial vive en zonas susceptibles a peligros volcánicos. Sin ir más lejos, yo mismo escribo estas letras a la sombra del gran pico Teide, desde una isla que alberga más de un centenar de conos volcánicos. Aquellos que viven bajo sus laderas se enfrentan a rocas expulsadas, toneladas de polvo y material magmático, gases tóxicos e inflamables, nubes de ceniza, terremotos, deslizamientos de tierra e incluso tsunamis provocados por esa actividad. Afortunadamente, la ciencia ha avanzado de manera notable en las últimas décadas desarrollando conocimiento y tecnologías que hacen posible la detección e interpretación de las señales precursoras que anticipan una erupción. Un buen ejemplo de esta ciencia predictiva lo encontramos en la erupción de la isla de la Palma en 2021 que permitió minimizar el número de víctimas gracias a la alerta temprana de los vulcanólogos. Sin embargo, debemos reconocerlo, es un campo científico que está dando sus primeros pasos, aún estamos en pañales y cualquier ayuda que obtengamos será bienvenida.
Los fenómenos naturales no surgen de la nada, siempre existe un proceso de efectos y consecuencias que desencadenan una reacción. En la mayoría de los volcanes la erupción se produce «cuando el depósito en el que se almacena el magma alcanza una presión determinada y rompe, produciendo cambios de forma y/o terremotos, por lo que su vigilancia, permite en ocasiones, realizar pronósticos a corto plazo sobre una posible erupción». En los centros de investigación y seguimiento los vulcanólogos trabajan atentos a cualquier cambio que apunte al inicio de la actividad y a una posible erupción a corto o medio plazo. Esos indicadores incluyen «actividad sísmica, cambios en la altura del terreno y, especialmente, emisiones de gases como el dióxido de azufre o el dióxido de carbono».
Los compuestos de azufre son algo más fáciles de detectar desde el espacio, utilizando satélites en órbita, mientras que las emisiones de dióxido de carbono son mucho más difíciles de registrar y, a menudo, es necesario desplazarse en persona hasta el volcán con equipos de detección, con el riesgo que esto implica. Poder detectar con precisión emisiones de CO2 sería un paso en la dirección adecuada ya que el dióxido de carbono precede a la emisión de su homólogo sulfúrico y constituye uno de los primeros indicios de que el volcán está activo.
«Los volcanes emiten mucho dióxido de carbono», explica el vulcanólogo Robert Bogue en la web de NASA, «pero la cantidad de dióxido de carbono que ya hay presente en la atmósfera suele ser tan alta que a menudo resulta difícil medir específicamente el dióxido de carbono volcánico. Las grandes erupciones pueden expulsar suficiente dióxido de carbono como para registrarlas desde el espacio, con sensores como el Observatorio Orbital de Carbono 2 de la NASA, pero la detección de estas señales de alerta mucho más tenues resulta muy complicada. Un volcán que emita una modesta cantidad de dióxido de carbono que podrían presagiar una erupción no aparecerá en las imágenes satelitales».
 El magma ascendente calienta una poza de agua en Costa Rica, cerca del volcán rincón de la Vieja y libera dióxido de carbono indicando un aumento de su actividad. Foto: Alessandra Baltodano / Universidad Chapman / NASA
El magma ascendente calienta una poza de agua en Costa Rica, cerca del volcán rincón de la Vieja y libera dióxido de carbono indicando un aumento de su actividad. Foto: Alessandra Baltodano / Universidad Chapman / NASA
Sin embargo, hace solo unos días la agencia espacial NASA ha publicado un artículo en su web oficial en el que descubrimos una ayuda inesperada para registrar esas emisiones de CO2: los árboles se vuelven más verdes, y eso sí que se puede detectar desde el espacio.
Conforme el magma volcánico asciende, liberando dióxido de carbono hacia la superficie, los árboles que absorben ese CO2 adquieren un color verde más intenso. Estos cambios en la tonalidad son visibles en imágenes de satélites, instrumentos meteorológicos y vehículos aerotransportados. «La detección remota del enverdecimiento de la vegetación por dióxido de carbono proporciona a los científicos otra herramienta que, sumada a las ondas sísmicas y los cambios en la altura del suelo, nos ofrecen una idea más clara de lo que está ocurriendo bajo el volcán».
En la actualidad contamos con numerosos satélites que podrían servir para realizar este tipo de análisis, el Landsat 8,el satélite Terra, el Sentinel-2 y otras sondas de observación terrestre y meteorológica a las que se pueden sumar proyectos aerotransportados como el Experimento Unificado de Validación Aérea: Tierra-Océano.
Los proyectos que ya se están llevando a cabo en este sentido cuentan con un añadido extra y sirven como experimentos multidisciplinares en los que, además de en la vulcanología podrían ser de utilidad en ecología y estudio de las consecuencias del calentamiento global. «Será muy interesante estudiar no solo la respuesta de los árboles al dióxido de carbono volcánico como alerta temprana de una erupción, sino también su capacidad de absorción, como una ventana al futuro de la Tierra cuando todos los árboles del planeta estén expuestos a altos niveles de dióxido de carbono».
Por supuesto esta señal natural en el color de los árboles tiene sus limitaciones, por ejemplo en volcanes donde la vegetación a su alrededor es escasa o inexistente. «Ninguna de las señales que utilizamos actualmente es la gran solución y monitorear los efectos del dióxido de carbono volcánico en los árboles tampoco será la panacea. Pero sí podría ser un punto de inflexión».
Referencias científicas y más información:
James Riordon «NASA Satellite Images Could Provide Early Volcano Warnings» NASA’s Earth Science News Team (2025)
Sascha Pare «The closer a volcano is to erupting, the greener the trees around it look from space» Live Science (2025)
Sobre el autor: Javier «Irreductible» Peláez es escritor y comunicador científico multimedia. Es ganador de tres premios Bitácoras, un premio Prisma a la mejor web de divulgación científica y un Premio Ondas al mejor programa de radio digital.
El artículo Los árboles pueden ayudarnos a predecir erupciones volcánicas se ha escrito en Cuaderno de Cultura Científica.
Valle Salado: ¿de dónde viene la sal? ¿De dónde viene el agua?

¿Qué tienen en común un paisaje espectacular, un fósil milenario y una cantera abandonada? Todos forman parte del patrimonio geológico, un testimonio de la historia de la Tierra con un gran valor científico, educativo, cultural y estético, y base del patrimonio natural. Sin embargo, su importancia continúa siendo poco apreciada.
Para acercar las distintas aproximaciones del patrimonio geológico a la sociedad, los días 26, 27 y 28 de marzo se celebró la quinta edición de las jornadas divulgativas “Geología para poetas, miopes y despistados. Patrimonio patrimonio”. Organizadas por el grupo de investigación consolidado Procesos Hidro-Ambientales (HGI) de la Facultad de Ciencia y Tecnología de la Universidad del País Vasco (UPV/EHU), estas jornadas contaron con la colaboración del Vicerrectorado del Campus de Bizkaia, la Cátedra de Cultura Científica de la UPV/EHU, el Geoparque de la Costa Vasca / Geoparkea y el Ente Vasco de la Energía (EVE).
El catedrático de hidrogeología de la UPV/EHU, Iñaki Antigüedad, explica en esta charla cómo se combinan los procesos del agua y la química de las rocas para dar lugar al Valle Salado de Añana, un lugar en el que se extrae sal desde hace 7000 años y que hay que visitar al menos una vez en la vida.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Valle Salado: ¿de dónde viene la sal? ¿De dónde viene el agua? se ha escrito en Cuaderno de Cultura Científica.
Algunas células tumorales roban mitocondrias como estrategia de supervivencia
En 2023, un equipo de investigadores del UT Southwestern Medical Center de Dallas observó que las células tumorales «roban» mitocondrias a los linfocitos T que actúan contra ellas.
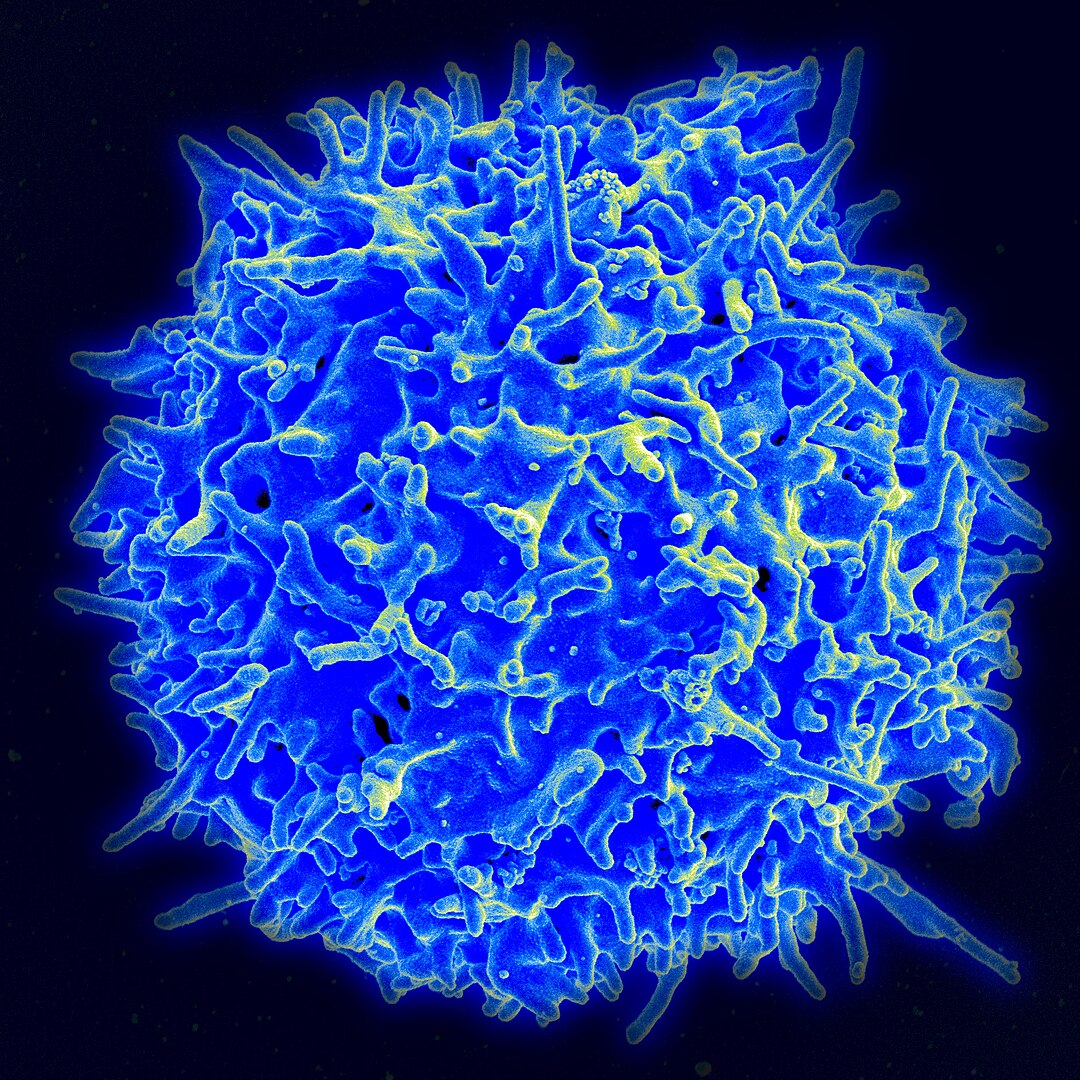 Micrografía de un linfocito T humano (también llamado célula T) del sistema inmune de una persona sana. Fuente: NIAID/NIH – NIAID Flickr’s photostream, Dominio público / Wikimedia Commons
Micrografía de un linfocito T humano (también llamado célula T) del sistema inmune de una persona sana. Fuente: NIAID/NIH – NIAID Flickr’s photostream, Dominio público / Wikimedia CommonsDesarrollar tratamientos contra el cáncer se ha convertido en un reto a nivel mundial, y en cierta medida contagiados por esta necesidad recibimos constantemente información sobre los trabajos que se publican en torno a esta enfermedad. Últimamente, además de estudiar la célula tumoral, se están desarrollando grandes progresos en el campo de conocimiento que estudia las células y moléculas que rodean el tumor, también conocido como microambiente tumoral. Es obvio que la célula tumoral es el actor principal del desarrollo tumoral, pero es de suma importancia conocer los mecanismos por los cuales el tumor manipula su entorno para poder progresar. En el microambiente tumoral encontramos gran cantidad de tipos celulares y moléculas que participan directamente en el avance de la enfermedad y tienen sus propias peculiaridades dependiendo del tipo de tumor, pero hay algunos elementos comunes a todos ellos como son las células que forman los vasos sanguíneos (llamadas células endoteliales), los fibroblastos y diversos tipos de células del sistema inmune, así como moléculas que se encuentran entre las células. En cuanto al sistema inmune se refiere, se trata de un sistema extremadamente complejo que comprende muchos subtipos celulares y una gran variedad de moléculas y la inmunooncología se ha convertido en un subapartado del microambiente tumoral.
El eje PD-L1/PD1Se sabe que algunos tumores desarrollan mecanismos para burlar o reducir el sistema inmune y que nos quedamos sin defensas ante el crecimiento de algunos tipos de cánceres. En este sentido, el estudio de la inmunooncología vivió un hito importante en el año 2018 con la concesión del Premio Nobel de Medicina y Fisiología a James P. Allison y Tasuku Honjo. Estos dos investigadores descubrieron y describieron los puntos de control (en inglés check-points) que tienen las células del sistema inmune para combatir el cáncer. El mecanismo más conocido es el eje PD-L1/PD1, donde la proteína PD-L1 se expresa en la membrana de las células tumorales y la proteína PD1 en la membrana de los linfocitos T, células cruciales para el buen funcionamiento del sistema inmune.
Cuando un tumor está en proceso de crecimiento, se inicia un proceso inflamatorio por el cual los linfocitos T se acercan a la zona tumoral. Las células tumorales son reconocidas como células con aberraciones y los linfocitos T las atacan y anulan directamente. Al asociar el PD-L1 de las células tumorales al PD-1 de los linfocitos T, las células del sistema inmune se inactivan y son incapaces de atacar el tumor, dejando fuera de juego a los linfocitos T. Tras este descubrimiento, se han creado anticuerpos tanto frente a PD-L1 como frente a PD1 para inhibir la unión de ambas moléculas y de esta manera se evita el bloqueo del sistema inmune; se trata de la inmunnoterapia más común que hoy en día se utiliza en la clínica.
Linfocitos T modificadosAdemás de los inhibidores de los puntos de control, también se han desarrollado terapias basadas en linfocitos T modificados. En este tipo de inmunoterapia también conocida como terapia basada en linfocitos CAR-T (en inglés Chimeric Antigen Receptor-T cell), primero se realiza una biopsia del tumor y se identifican fragmentos específicos de proteínas (antígenos) que solo aparecen en las células tumorales del paciente. A continuación, se extraen los linfocitos T del cuerpo del paciente y en el laboratorio se programan para que ataquen exclusivamente los antígenos tumorales que se han identificado previamente. A continuación, se vuelven a introducir los linfocitos T para atacar las células tumorales.
Tanto los fármacos basados en puntos de control como las terapias basadas en linfocitos modificados han sido exitosos en algunos casos, pero han fracasado a menudo por agotamiento de los linfocitos, es decir, los linfocitos T acaban exhaustos en la lucha contra la célula tumoral y quedan incapacitados para realizar su función. Pero dos investigaciones recientes podrían arrojar más luz sobre el concepto linfocitos exhaustos que nos serviría para diseñar terapias más eficaces.
Linfocitos exhaustos y robo de mitocondriasEn 2023, un equipo de investigadores del UT Southwestern Medical Center de Dallas observó que las células tumorales «roban» mitocondrias a los linfocitos T que actúan contra las células tumorales en el interior del tumor. Formando unas finas estructuras con forma de finos tubos llamadas nanotubos, las células tumorales emiten unas prolongaciones que contactan con los linfocitos T que tienen en su entorno más cercano y absorben sus mitocondrias funcionales. Entre las mutaciones que sufren las células tumorales aparecen frecuentemente las relacionadas con las mitocondrias. Aunque estas mutaciones se han relacionado con la progresión del cáncer y los cambios beneficiosos que experimenta metabólicamente la célula tumoral, en algunos casos, dichas mutaciones comprometen la supervivencia de las células tumorales. De esta manera, algunas células tumorales son capaces de utilizar estos nanotubos para “robar” las mitocondrias funcionales de los linfocitos T.
En un principio se pensaba que este tipo de transporte se producía en una sola dirección, pero un grupo de investigación formado por científicos japoneses ha descubierto que es bidireccional. Investigando diferentes tipos de tumores, han descubierto que algunas células tumorales son capaces de transmitir sus mitocondrias defectuosas a los linfocitos T mientras «roban» los sanos de los linfocitos. Esta transferencia se realiza a través de los mencionados nanotubos y también por la emisión de pequeñas vesículas. Así, los linfocitos T pierden sus mitocondrias sanas y, en su lugar, se les transfieren las mitocondrias defectuosas de las células tumorales. De esta manera los linfocitos T pierden su funcionalidad porque la mitocondria es la fuente más importante que posee la célula para obtener energía y el principal orgánulo para canalizar las principales rutas metabólicas.
Estos trabajos nos permiten profundizar en el conocimiento sobre el proceso de agotamiento de los linfocitos y añadir a las terapias existentes nuevos tratamientos que dificultarían los procesos de transferencia de mitocondrias entre los linfocitos y las células tumorales.
Referencias bibliográficas:
Cárdenas-Oyarzo, Areli M.; Bocchieri-Oyarce, Pamela A.; Méndez-Laport, Cristian R.; Zolezzi, Juan M.; Ríos, Juvenal A. (2022) Immune checkpoint inhibitors. A breakthrough in cancer therapy. Rev Med Chil, 150, 1, 93-99. doi: 10.4067/S0034-98872022000100093
Ikeda, Hideki et al. (2025) Immune evasion through mitochondrial transfer in the tumour microenvironment Nature, 638, 225-236. doi: 10.1038/s41586-024-08439-0
Wang, Sheng-Fan; Tseng, Ling-ming; Lee, Hsin-Chen (2023) Role of mitochondrial alterations in human cancer progression and cancer immunity Journal of Biomedical Science, 30, 61. doi: 10.1186/s12929-023-00956-w
Zhang, Hongyi et al. (2023) Systematic investigation of mitochondrial transfer between cancer cells and T cells at single-cell resolution Cancer Cell, 9, 41, 1788-1802. doi: 10.1016/j.ccell.2023.09.003
Sobre el autor: Iker Badiola Etxaburu es doctor en biología, Profesor Pleno en la Facultad de Medicina y Enfermería de la UPV/EHU, y director de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Algunas células tumorales roban mitocondrias como estrategia de supervivencia se ha escrito en Cuaderno de Cultura Científica.
Extrañas faunas que inspiran animes titánicos
Existe una serie de animación japonesa que a mí me encantó cuando la vi, aunque tengo cuidado a la hora de recomendarla porque no es apta para menores de 18 años (por la violencia y la sangre, no penséis mal), que te está bombardeando continuamente con spoilers escondidos desde el opening (es decir, la canción de apertura) del primer episodio. Su título es Shingeki no Kyojin, más conocida por estos lares como Ataque a los Titanes (una traducción mal hecha a propósito para evitar hacer el primer gran spoiler). Sin entrar demasiado en detalles sobre la trama, la historia trata sobre una ciudad amurallada que parece anclada en la edad media, pero con ciertos adelantos modernos (al estilo steam punk), que es atacada por unos gigantes hambrientos de carne humana, a los que llaman titanes, contra los que deben combatir, literalmente, a espadazos en la nuca.
Vale, seguro que os estáis preguntando qué demonios tiene que ver esto con la Geología. Pues para daros una explicación, voy a haceros unos spoilers yo también. Empecemos con el tercer opening de los ocho que hicieron (a cuál más épico y cargado de spoilers, por cierto), donde vemos al final desfilar una serie de animales prehistóricos con los que nos intentan hacer creer que el “gen” que transforma a los seres humanos en titanes ha existido siempre y ha afectado a diferentes seres vivos durante millones de años. Pues uno de los bichos que aparece durante apenas un par de segundos es una especie de gamba que ha tomado demasiados esteroides.
 A) Captura de pantalla del tercer opening del anime de Shingeki no Kyojin, donde aparece un extraño animal acuático. B) Página del tomo 137 del manga, momento en que uno de los personajes habla sobre el origen de la vida, apareciendo más organismos acuáticos con formas muy curiosas. C) Captura de pantalla del tráiler de la cuarta temporada del anime en el que reaparece el gusano acuático de la imagen anterior. Fuentes: A y C, Estudio Mappa / fair use; B, Kodansha / fair use. A, B y C vía Crunchyroll
A) Captura de pantalla del tercer opening del anime de Shingeki no Kyojin, donde aparece un extraño animal acuático. B) Página del tomo 137 del manga, momento en que uno de los personajes habla sobre el origen de la vida, apareciendo más organismos acuáticos con formas muy curiosas. C) Captura de pantalla del tráiler de la cuarta temporada del anime en el que reaparece el gusano acuático de la imagen anterior. Fuentes: A y C, Estudio Mappa / fair use; B, Kodansha / fair use. A, B y C vía CrunchyrollPero esta no es la única vez que aparece este extraño animal en la obra. Si avanzamos hacia el final de la misma, hay un momento en que uno de los personajes intenta darle una explicación a todo lo que está pasando en ese mundo fantástico. Para ello, directamente se retrotrae a los orígenes de la vida en nuestro planeta, volviendo a aparecer esa enorme gamba. Aunque, en este momento, toma protagonismo otro bicho aún más extraño, una especie de gusano con peinado estilo punk, que, al parecer, es el culpable de todo lo que sucede en Shingeki no Kyojin.
Hasta aquí podríamos pensar que estos bichos tan raros han salido, directamente, de la mente artística del autor del manga original, Hajime Isayama. Pero, en realidad, este hombre se basó en hechos reales para inspirarse. En concreto, se fijó en una fauna muy particular y que supone uno de los hitos de la vida en nuestro planeta: la Fauna de Burgess Shale.
 Visita guiada al yacimiento de Burgess Shale, en la Columbia Británica (Canadá), donde se enseñan al público asistente algunos de los ejemplares fósiles encontrados. Foto: Ryan Creary / Parques Nacionales de Canadá, vía IUGS
Visita guiada al yacimiento de Burgess Shale, en la Columbia Británica (Canadá), donde se enseñan al público asistente algunos de los ejemplares fósiles encontrados. Foto: Ryan Creary / Parques Nacionales de Canadá, vía IUGSPara comenzar nuestra historia, debemos viajar hasta la Columbia Británica, en Canadá, a una cantera cercana al monte Burgess. Allí, a comienzos del siglo XX, se encontró un yacimiento con miles de fósiles en los que aparecen preservadas las partes blandas de unos organismos que vivieron en un mar poco profundo a comienzos y mediados del Periodo Cámbrico, hace más de 520 millones de años. Gracias a esta conservación excepcional, se ha podido reconstruir el aspecto de estos seres vivos ancestrales. Y aquí es donde aparecen las sorpresas.
 A la izquierda de la imagen, reconstrucción de un ambiente marino precámbrico con organismos de cuerpo blando; a la derecha, reconstrucción del fondo marino cámbrico con los seres vivos más complejos encontrados en el yacimiento de Burgess Shale. Ilustración: D.W. Miller / Smithsonian Institution / fair use
A la izquierda de la imagen, reconstrucción de un ambiente marino precámbrico con organismos de cuerpo blando; a la derecha, reconstrucción del fondo marino cámbrico con los seres vivos más complejos encontrados en el yacimiento de Burgess Shale. Ilustración: D.W. Miller / Smithsonian Institution / fair useEstos organismos son muy diferentes de los que vivieron durante el Precámbrico. Estos últimos eran seres de cuerpo blando, donde unos pocos parecen que nadaban libres, pero la mayoría posiblemente o bien vivían fijos en el fondo marino, creciendo en la vertical, o bien se desplazaban por encima del barro de ese fondo del mar. Sin embargo, muchos de los ejemplares del Cámbrico tenían un caparazón duro y resistente; desarrollaron cuerpos complejos con grandes mandíbulas, cuerpos segmentados, varias filas de patas o pinchos defensivos; aparecen morfologías que son coherentes con seres nadadores veloces; y hay evidencias que muchos organismos empezaron a enterrarse en el barro del fondo, pudiendo incluso vivir en madrigueras.
Es decir, en el Cámbrico la vida se hizo más compleja, la cadena trófica empezó a gestarse, apareciendo organismos que actuaban como depredadores (los que tenían mandíbulas grandes y fuertes o apéndices para atrapar la comida a distancia) y otros como presas (algunas de las cuales tenían estructuras defensivas, como caparazones duros o espinas afiladas) y los seres vivos empezaron a enterrarse en el sedimento, explorando nuevos nichos ecológicos hasta entonces desconocidos. A todos estos cambios faunísticos se les conoce en Geología como la Explosión del Cámbrico, ya que en apenas unos 10 millones de años se produjo una auténtica revolución biológica que significó el pistoletazo de salida de la evolución biótica gracias a la cual el ser humano está aquí.
A lo largo de todo el siglo XX han aparecido otros yacimientos cámbricos con organismos similares a los encontrados en Canadá en otros lugares del mundo, como Groenlandia o China. Incluso, hoy en día, se siguen encontrando otras localidades fosilíferas que nos permiten ir sumando nuevas formas de esta vida compleja primitiva al listado. Pero en todas las ocasiones nos referimos a estos lugares como yacimientos o fauna tipo Burgess Shale, en honor a este primer afloramiento canadiense.
 Ejemplos de los fósiles encontrados en el yacimiento de Burgess Shale. A) Anomalocaris, Foto: J.B. Caron/ Royal Ontario Museum via IUGS; B) Hallucigenia, Foto: Maura McCarthy / Smithsonian Institution / fair use C) Opabinia, Foto. Han Zeng / Smithsonian National Museum of Natural History
Ejemplos de los fósiles encontrados en el yacimiento de Burgess Shale. A) Anomalocaris, Foto: J.B. Caron/ Royal Ontario Museum via IUGS; B) Hallucigenia, Foto: Maura McCarthy / Smithsonian Institution / fair use C) Opabinia, Foto. Han Zeng / Smithsonian National Museum of Natural HistoryY volviendo un poco a los bichos que aparecen en Shingeki no Kyojin, la gamba dopada es un Anomalocaris, un artrópodo primitivo que podía llegar a medir varios metros de longitud que se convirtió en el mayor depredador marino del Cámbrico, capturando a sus presas con sus enormes mandíbulas, tan poderosas que eran capaces de romper los caparazones defensivos de animales como los trilobites. Pero para bicho anómalo, tenemos el gusano punki. En este caso, se trata de la Hallucigenia, un antepasado lejano de los gusanos, que tenía dos filas de tubos filamentosos que actuaban como patas y una serie de espinas afiladas en la espalda. Aunque si este os ha hecho alucinar, el que a mí me flipa de verdad es la Opabinia, otro artrópodo primitivo que, en este caso, tenía cinco ojos compuestos que sobresalían de su cabeza y un apéndice largo al final del cual aparecían dos pinzas que, supuestamente, eran las mandíbulas.
Muchos de los organismos de la Fauna de Burgess Shale no se han podido clasificar de forma segura en ningún clado, animal o vegetal, actual. Así que podrían ser “pruebas evolutivas” que no tuvieron continuidad más allá del Cámbrico. Sin embargo, todos los grupos faunísticos actuales proceden de estas primeras formas de vida compleja. Así que no me extraña que Isayama escogiese unos de estos animales tan raros para darle una explicación al origen de sus monstruos terribles. Además, me da una excusa para que yo pueda fantasear con que provengo de una de esas gambas con cinco ojos que parece salida de una pesadilla de H. P. Lovecraft.
Para saber más:
IUGS – Burgess Shale Paleontological Record
Wikipedia – Esquisto de Burgess
The Burgess Shale Geoscience Foundation
Royal Ontario Musem (ROM) – The Burgess Shale
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Extrañas faunas que inspiran animes titánicos se ha escrito en Cuaderno de Cultura Científica.
El problema del ascensor
Proponemos un problema de lógica relacionado con un ascensor que asciende trasladando a siete pasajeras.
 Freepik
FreepikEnunciado del problema
Estamos en un edificio de veinte pisos. En un trayecto ascendente, el ascensor ha transportado a siete personas (Alicia, Beatriz, Cecilia, Daniela, Enara, Fátima y Gabriela). Se conocen las siguientes informaciones:
- Cada persona ha subido al menos dos pisos, pero ninguna ha subido la misma cantidad de pisos;
- Como mucho, una persona ha cruzado el umbral (entrando o saliendo) del ascensor en un piso determinado;
- El ascensor no se ha parado en el piso 17;
- Las puertas del ascensor se han abierto (para recoger o dejar a una persona) en más pisos impares que pares;
- Alicia ha sido la última persona en entrar y la segunda en salir del ascensor. Beatriz ha subido justo antes que Cecilia y justo después de Daniela, y ha subido más pisos que Daniela. Enara ha subido exactamente el doble de pisos que Fátima y ha salido antes de que Gabriela haya entrado en el ascensor. Gabriela no ha sido la última en salir.
¿En qué piso han entrado y salido Alicia, Beatriz, Cecilia, Daniela, Enara, Fátima y Gabriela?
Solución del problema
Alicia ha sido la última pasajera en subir y la segunda en bajar, así que nadie ha entrado al ascensor después de ella y solo una persona ha salido antes. Y ha subido al menos dos pisos.
Enara ha salido antes de que Gabriela haya entrado en el ascensor, así que Enara debe ser la pasajera que ha salido del ascensor antes que Alicia. Esto significa que Fátima ha entrado en el ascensor en algún momento antes que Alicia y ha salido en algún momento después de ella, lo que significa que ha subido al menos cuatro pisos. Enara ha subido exactamente el doble de pisos que Fátima, así que Enara ha subido al menos ocho pisos. Supongamos que Fátima ha subido solo cuatro pisos, entonces tenemos como mínimo esta situación:
Piso 1: Enara entra en el ascensor
Piso 9: Enara sale (porque ha subido ocho pisos)
Piso 10: Gabriela entra
Piso 11: Fátima entra
Piso 12: Alicia entra (ya no sube nadie más a partir de este piso; ella es la última en acceder al ascensor. Así, el resto de los pisos, si el ascensor se detiene, solo son de bajada)
Piso 13: Nadie sale (porque Alicia es la segunda en bajar y Enara ya ha salido del ascensor. Es decir, nadie puede salir antes de que Alicia lo haga)
Piso 14: Alicia sale (así, ha subido exactamente dos pisos)
Piso 15: Fátima sale (porque ha subido cuatro pisos)
Piso 17: Nadie sube ni baja del ascensor
Este esquema “mínimo” deja exactamente cuatro pisos (16, 18, 19 y 20) para que bajen cuatro pasajeras (Beatriz, Cecilia, Daniela y Gabriela), por lo que parece ser correcto.
Así, tendríamos ya once paradas (para subida o bajada de pasajeras) conocidas, cinco son impares (1, 9, 11, 15 y 19) y seis son pares (10, 12, 14, 16, 18 y 20). Como el enunciado afirma que el ascensor se ha detenido más veces en pisos impares que en pares más paradas en pisos impares que en pares (y el ascensor abre sus puertas catorce veces), debe de detenerse ocho veces en pisos impares. Por eliminación, solo quedan las plantas 3, 5 y 7.
Es decir, las catorce plantas en las que el ascensor se detiene son:
Piso 1: Enara entra
Piso 3: ¿?
Piso 5: ¿?
Piso 7: ¿?
Piso 9: Enara sale (recorre 8 pisos)
Piso 10: Gabriela entra
Piso 11: Fátima entra
Piso 12: Alicia entra
Piso 14: Alicia sale (recorre 2 pisos)
Piso 15: Fátima sale (recorre 4 pisos)
Piso 16: ¿?
Piso 18: ¿?
Piso 19: ¿?
Piso 20: ¿?
Como Alicia es la última en entrar al ascensor (y lo hace en el piso 12), Daniela, Beatriz y Cecilia (en este orden, según se dice en el enunciado) entran en el ascensor en los pisos 1, 3 y 5, respectivamente:
Piso 1: Enara entra
Piso 3: Daniela entra
Piso 5: Beatriz entra
Piso 7: Cecilia entra
Piso 9: Enara sale (recorre 8 pisos)
Piso 10: Gabriela entra
Piso 11: Fátima entra
Piso 12: Alicia entra
Piso 14: Alicia sale (recorre 2 pisos)
Piso 15: Fátima sale (recorre 4 pisos)
Piso 16: ¿?
Piso 18: ¿?
Piso 19: ¿?
Piso 20: ¿?
Además, como Beatriz sube más pisos que Daniela, Daniela debe bajar en el piso 16 (sube así trece pisos; Daniela no puede bajar en el piso 18 porque recorrería quince pisos y Beatriz no podría subir más que ella) y Beatriz baja entonces en el 19 o el 20 (subiendo catorce o quince pisos).
Como dos personas no pueden subir la misma cantidad de pisos, Gabriela (que ha entrado en el ascensor en el piso 10) no puede bajar en el 18 (porque Enara ha subido ocho alturas). Además, no ha sido la última en salir, así que ha debido salir del ascensor en el piso 19. De este modo, Beatriz sale en el piso 20 y es Cecilia quien baja en el piso 18:
Piso 1: Enara entra
Piso 3: Daniela entra
Piso 5: Beatriz entra
Piso 7: Cecilia entra
Piso 9: Enara sale (recorre 8 pisos)
Piso 10: Gabriela entra
Piso 11: Fátima entra
Piso 12: Alicia entra
Piso 14: Alicia sale (recorre 2 pisos)
Piso 15: Fátima sale (recorre 4 pisos)
Piso 16: Daniela sale (recorre 13 pisos)
Piso 18: Cecilia sale (recorre 11 pisos)
Piso 19: Gabriela sale (recorre 9 pisos)
Piso 20: Beatriz sale (recorre 15 pisos)
Así, finalmente:
- Alicia: entra en el piso 12 y sale en el 14 (sube 2 pisos)
- Beatriz: entra en el piso 5 y sale en el 20 (sube 15 pisos)
- Cecilia: entra en el piso 7 y sale en el 18 (sube 11 pisos)
- Daniela: entra en el piso 3 y sale en el 16 (sube 13 pisos)
- Enara: entra en el piso 1 y sale en el 9 (sube 8 pisos)
- Fátima: entra en el piso 11 y sale en el 15 (sube 4 pisos)
- Gabriela: entra en el piso 10 y sale en el 19 (sube 9 pisos)
Referencias
Going Up, Futility Closet, 20 abril 2025
Virginia McCarthy, Upwardly mobile, Games, abril 1993 (enunciado en la página 62 y solución en la 41)
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
El artículo El problema del ascensor se ha escrito en Cuaderno de Cultura Científica.
¿Cuánta energía se usa en pensar?
Los estudios del metabolismo neuronal revelan el esfuerzo de nuestro encéfalo para mantenernos vivos y las limitaciones evolutivas que esculpieron nuestro órgano más complejo.
Un artículo de Conor Feehly. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Ilustración: Myrian Wares / Quanta Magazine
Ilustración: Myrian Wares / Quanta MagazineAcabas de llegar a casa después de un día agotador. Todo lo que deseas es poner los pies en alto y desconectar viendo lo que sea en la televisión. Aunque esta inactividad pueda parecer un merecido descanso, tu encéfalo no está precisamente relajándose. De hecho, según investigaciones recientes, está consumiendo casi tanta energía como durante tu estresante actividad.
Sharna Jamadar, neurocientífica de la Universidad Monash en Australia, junto con sus colegas, ha revisado investigaciones de su laboratorio y de otros equipos en todo el mundo para estimar el coste metabólico de la cognición —es decir, cuánta energía necesita el encéfalo humano para funcionar. Sorprendentemente, han concluído que las tareas exigentes y dirigidas a un objetivo consumen solo un 5% más de energía que la actividad encefálica en reposo. En otras palabras, usamos el encéfalo solo un poco más cuando estamos concentrados que cuando está en modo de reposo.
A menudo sentimos que gastamos nuestra energía mental en prestar atención y concentrarnos intensamente. Sin embargo, esta nueva investigación se suma a una idea cada vez más aceptada: la mayor parte de la actividad encefálical se dedica al mantenimiento. Aunque muchos neurocientíficos se han centrado históricamente en los procesos cognitivos activos y externos —como la atención, la resolución de problemas, la memoria de trabajo y la toma de decisiones—, cada vez está más claro que bajo esa superficie existe una intensa actividad de procesamiento en segundo plano. Nuestros encéfalos regulan los sistemas fisiológicos clave del cuerpo, distribuyendo recursos donde se necesitan mientras respondemos consciente o inconscientemente a las demandas de un entorno en constante cambio.
 La neurocientífica Sharna Jamadar ha recopilado datos de imágenes por resonancia magnética y tomografía por emisión de positrones simultáneamente para estimar el uso de energía del encéfalo. Foto: Emma Liang
La neurocientífica Sharna Jamadar ha recopilado datos de imágenes por resonancia magnética y tomografía por emisión de positrones simultáneamente para estimar el uso de energía del encéfalo. Foto: Emma Liang“Existe la idea de que el encéfalo sirve para pensar”, comenta Jordan Theriault, neurocientífico de la Universidad de Northeastern que no ha participado en este nuevo análisis. “Pero, desde el punto de vista metabólico, su función principal es gestionar el cuerpo, coordinar y regular los órganos, mantener este sistema tan costoso al que está conectado y enfrentarse a un entorno externo complicado.”
El encéfalo no es una simple máquina de pensar, sino un órgano moldeado por la evolución y, por tanto, sujeto a las estrictas limitaciones energéticas de un sistema biológico. Pensar puede hacernos sentir cansados no porque se nos acabe la energía, sino porque hemos evolucionado para conservar recursos. Este estudio del metabolismo neuronal, combinado con investigaciones sobre la dinámica de los impulsos eléctricos encefálicos, revela las fuerzas evolutivas que compiten entre sí y que explican las limitaciones, el alcance y la eficiencia de nuestras capacidades cognitivas.
El coste de una máquina predictiva
El encéfalo humano es increíblemente costoso de mantener en funcionamiento. Aunque representa solo alrededor del 2% del peso corporal consume el 20% de los recursos energéticos del cuerpo. “Tiene unas demandas metabólicas enormes”, afirma Jamadar. En los bebés, este porcentaje se acerca al 50%.
La energía del encéfalo proviene de una molécula llamada adenosín trifosfato (ATP), que las células producen a partir de glucosa y oxígeno. Una vasta red de finos capilares —se estima que unos 600 kilómetros de vasos sanguíneos— recorre el tejido encefálico para transportar sangre rica en glucosa y oxígeno hacia las neuronas y otras células del encéfalo. Una vez sintetizado dentro de las células, el ATP alimenta la comunicación entre neuronas, que es la base del funcionamiento encefálico. Las neuronas transmiten señales eléctricas hasta sus sinapsis, donde intercambian mensajes moleculares; la intensidad de la señal determina si liberarán esas moléculas (es decir, si “dispararán”). Si lo hacen, esa señal molecular dictará si la siguiente neurona transmitirá el mensaje, y así sucesivamente. Mantener lo que se conoce como potenciales de membrana —voltajes estables a través de la membrana neuronal que mantienen a la célula lista para disparar cuando sea necesario— consume al menos la mitad del presupuesto energético total del encéfalo.
Medir el ATP directamente en el encéfalo humano resulta muy invasivo. Por eso, el equipo de Jamadar revisó estudios, incluidos sus propios resultados, que utilizaron otras formas de estimar el uso de energía – como el consumo de glucosa, medido mediante tomografía por emisión de positrones (PET), y el flujo sanguíneo, evaluado mediante resonancia magnética funcional (fMRI) – para encontrar las diferencias en cómo el encéfalo usa la energía durante las tareas activas y cuando está en reposo. Según Jamadar, cuando se realizan al mismo tiempo, el PET y la fMRI pueden aportar información complementaria sobre cómo el encéfalo consume glucosa. Aunque no se trata de una medida completa del gasto energético encefálico —ya que los tejidos neuronales también pueden convertir ciertos aminoácidos en ATP—, la gran mayoría del ATP del encéfalo proviene del metabolismo de la glucosa.
El análisis de Jamadar muestra que un encéfalo que realiza tareas activas consume apenas un 5% más de energía que uno en reposo. Cuando llevamos a cabo una tarea exigente y orientada a un objetivo —como consultar el horario de autobuses en una ciudad nueva—, aumenta la tasa de activación neuronal en las regiones o redes cerebrales relevantes, como las encargadas del procesamiento visual y del lenguaje. Ese aumento justifica ese 5% adicional; el otro 95% se destina a las funciones metabólicas básicas del encéfalo.
 El neurocientífico Jordan Theriault, de la Universidad Northeastern, cree que el encéfalo es un motor de predicción que siempre está planeando lo que viene después. Foto: Matthew Modoono / Universidad Northeastern
El neurocientífico Jordan Theriault, de la Universidad Northeastern, cree que el encéfalo es un motor de predicción que siempre está planeando lo que viene después. Foto: Matthew Modoono / Universidad NortheasternLos investigadores no saben con exactitud cómo se reparte esa carga energética, pero en las últimas décadas han logrado esclarecer qué hace el encéfalo en segundo plano. “A mediados de los años 90 comenzamos, como disciplina, a darnos cuenta de que en realidad ocurren muchísimas cosas cuando alguien está tumbado en reposo y no está involucrado en ninguna tarea explícita”, explica. “Antes se pensaba que la actividad encefálica en reposo que no estaba relacionada con ninguna tarea era simplemente ruido, pero ahora sabemos que hay mucha información en ese supuesto ruido.”
Gran parte de esa señal procede de la red por defecto del encéfalo, que se activa cuando estamos en reposo o no involucrados en una actividad aparente. Esta red está implicada en la experiencia mental de ir y venir entre escenarios del pasado, presente y futuro —qué vas a preparar para cenar, un recuerdo de la semana pasada, un dolor en la cadera. Además, bajo ese iceberg que es la consciencia, el encéfalo supervisa un mosaico de variables físicas —temperatura corporal, nivel de glucosa en sangre, ritmo cardíaco, respiración, entre otras— que deben mantenerse estables, en un estado conocido como homeostasis, para garantizar nuestra supervivencia. Si alguna de estas variables se desvía demasiado, las consecuencias pueden ser graves en muy poco tiempo.
Theriault plantea que la mayor parte de la carga metabólica básica del encéfalo se dedica a la predicción. Para mantener la homeostasis, el encéfalo necesita estar constantemente anticipando lo que vendrá —construyendo un modelo sofisticado del entorno y de cómo los cambios pueden afectar a los sistemas biológicos del cuerpo. Según él, es la capacidad de predecir —más que de reaccionar— lo que permite al encéfalo distribuir eficazmente los recursos del cuerpo.
Las limitaciones evolutivas del encéfalo
Un aumento del 5% en el consumo de energía durante el pensamiento activo puede no parecer gran cosa, pero si se considera el contexto del cuerpo entero y el enorme apetito energético del encéfalo, la cifra adquiere importancia. Y si además se tienen en cuenta las estrictas limitaciones energéticas con las que vivían nuestros antepasados, el agotamiento que sentimos al final de un día exigente cobra mucho más sentido.
“El motivo por el que te sientes fatigado, al igual que ocurre tras una actividad física, no es porque te falten calorías para costear ese esfuerzo”, afirma Zahid Padamsey, neurocientífico de Weill Cornell Medicine-Qatar, que no ha participado en esta nueva investigación. “Es porque hemos evolucionado como sistemas muy tacaños… Evolucionamos en entornos con escasez de energía, por lo que detestamos gastar energía.”
 El neurocientífico Zahid Padamsey ha estudiado cómo la disponibilidad de energía (o alimentos) ha influido en la evolución del encéfalo. Foto: Dr. Raphael Courjaret
El neurocientífico Zahid Padamsey ha estudiado cómo la disponibilidad de energía (o alimentos) ha influido en la evolución del encéfalo. Foto: Dr. Raphael CourjaretEl mundo moderno, en el que para muchas personas las calorías están disponibles en abundancia, contrasta fuertemente con las condiciones de escasez en las que evolucionó el Homo sapiens. Ese incremento del 5% en la tasa de gasto energético, si se mantiene durante 20 días de concentración activa y constante, puede equivaler a toda una jornada de energía cognitiva. Si el alimento escasea, esto podría suponer la diferencia entre la vida y la muerte.
“Este gasto puede acumularse de forma considerable con el tiempo si no se limita la tasa de consumo energético, por lo que creo que se trata, en gran parte, de un vestigio de nuestra herencia evolutiva”, añade Padamsey. De hecho, el encéfalo cuenta con mecanismos internos para evitar el sobreesfuerzo. “Se activan sistemas de fatiga que impiden que el consumo siga aumentando”, concluye.
Para comprender mejor estas limitaciones energéticas, en 2023 Padamsey revisó investigaciones sobre ciertas peculiaridades de la señalización eléctrica que apuntan a una tendencia evolutiva hacia la eficiencia energética. Por ejemplo, uno podría pensar que cuanto más rápido se transmite la información, mejor. Sin embargo, la velocidad óptima de transmisión del encéfalo es mucho más baja de lo que cabría esperar.
En teoría, la velocidad máxima a la que una neurona puede disparar y enviar información a su vecina es de 500 hercios. No obstante, si las neuronas realmente operaran a esa velocidad, el sistema se saturaría por completo. La tasa óptima de transmisión de información —es decir, la frecuencia máxima a la que las neuronas pueden seguir distinguiendo los mensajes de sus vecinas— es la mitad: unos 250 hercios.
Sin embargo, nuestras neuronas disparan, en promedio, a tan solo 4 hercios, lo que es entre 50 y 60 veces menos que la frecuencia óptima para transmitir información. Y aún más: muchas transmisiones sinápticas fallan. Incluso cuando una señal eléctrica llega a la sinapsis y la prepara para liberar moléculas hacia la siguiente neurona, esto ocurre solo en el 20% de los casos.
Esto se debe a que no hemos evolucionado para maximizar la cantidad total de información transmitida. “Hemos evolucionado para maximizar la información transmitida por cada molécula de ATP consumida”, explica Padamsey. “Y esa es una ecuación muy distinta.” Transmitir la mayor cantidad de información con el menor gasto energético posible (bits por ATP) sitúa la frecuencia de disparo neuronal óptima por debajo de los 10 hercios.
Desde una perspectiva evolutiva, el gran y sofisticado encéfalo humano ofreció un nivel de complejidad conductual sin precedentes —a un altísimo coste energético. Esta negociación constante, entre la flexibilidad e innovación de un encéfalo grande y las limitaciones energéticas de un sistema biológico, define tanto la forma en que nuestro encéfalo transmite información como la fatiga mental que sentimos tras periodos de concentración, y también el trabajo incesante que realiza para mantenernos con vida. Que sea capaz de hacer tanto dentro de sus limitaciones resulta, sencillamente, asombroso.
Nota del traductor: Si bien el texto original inglés emplea la misma palabra «brain» para referirse tanto al conjunto del encéfalo como al cerebro (que es una parte de él), en nuestra versión al castellano se ha distinguido claramente entre encéfalo y cerebro. Afirmar, por ejemplo, que el cerebro controla la homeostasis es equivalente a afirmar que el base de un equipo de baloncesto de primera división también se encarga de las compras de bebidas isotónicas y toallas.
Para saber más: Sistemas nervisos, una serie de Juan Ignacio Pérez Iglesias
El artículo original, How Much Energy Does It Take To Think?, se publicó el 4 de junio de 2025 en Quanta Magazine.
Traducido por César Tomé López
El artículo ¿Cuánta energía se usa en pensar? se ha escrito en Cuaderno de Cultura Científica.
Vórtices, dinámica de fluidos y la alimentación de los flamencos
Alrededor de 20 000 parejas de flamencos se han beneficiado de un invierno especialmente lluvioso y se están reproduciendo en la laguna de Fuente de Piedra, a unos cincuenta kilómetros del lugar en el que escribo estas líneas. Esta laguna salobre es rica en pequeños invertebrados, cianobacterias y otros microorganismos que les sirven de alimento. Es un espectáculo bellísimo contemplar a los flamencos alimentándose en una postura insólita, con la cabeza invertida y la parte distal del pico superior paralela al fondo o a la superficie del agua (Figura 1).
 Figura 1. Flamenco común (Phoenicopterus roseus) filtrando la capa superficial del agua. .Fuente: © Giles Laurent, gileslaurent.com, License CC BY-SA, CC BY-SA 4.0 / Wikimedia Commons
Figura 1. Flamenco común (Phoenicopterus roseus) filtrando la capa superficial del agua. .Fuente: © Giles Laurent, gileslaurent.com, License CC BY-SA, CC BY-SA 4.0 / Wikimedia CommonsSabemos que los flamencos utilizan la lengua como pistón para bombear agua de forma que los organismos que constituyen su alimentación, generalmente entre uno y cinco milímetros de tamaño, queden retenidos por finas láminas córneas localizadas en el borde del pico. Otras aves, por ejemplo los patos, utilizan este sistema de filtración, pero un grupo de investigadores estadounidenses acaba de publicar un artículo en PNAS que nos proporciona una visión diferente de la alimentación de los flamencos. Además, los resultados obtenidos nos explican dos peculiaridades de los flamencos. Por un lado, la insólita forma angulosa de su pico, diferente al de cualquier otro grupo de aves. Por otro, el hecho de que filtren el agua superficial colocando el pico a favor de la corriente, y no a contracorriente, como hace la inmensa mayoría de animales filtradores.
Para este estudio se realizaron observaciones directas de flamencos, modelos biofísicos de dinámica de fluidos y modelos mecánicos elaborados con impresoras 3D. Al final de este artículo se puede acceder a vídeos representativos de todas estas observaciones.
La primera estrategia desvelada por los investigadores es la formación de “mini-tornados” por la retracción súbita de la cabeza (40 cm/s en 400 milisegundos). El flamenco sitúa la porción distal del pico superior, que es bastante plana, cerca del suelo. Al levantarla rápidamente provoca una succión que remueve el sedimento y los organismos próximos, atrapándolos en un vórtice (Figura 2, Vídeo 1).
 Figura 2. Vórtice formado por la retracción rápida de la cabeza. Antes de la retracción la porción distal y superior del pico se dispone paralelamente al sustrato (derecha). Fuente: Ortega-Jiménez et al. (2025), cita completa en referencias, CC BY-SA 4.0.
Figura 2. Vórtice formado por la retracción rápida de la cabeza. Antes de la retracción la porción distal y superior del pico se dispone paralelamente al sustrato (derecha). Fuente: Ortega-Jiménez et al. (2025), cita completa en referencias, CC BY-SA 4.0.Una segunda técnica de los flamencos es el “castañeteo” del pico superior, un rápido movimiento de apertura y cierre (alrededor de 12 veces por segundo). Este movimiento impulsa el agua contenida en la cavidad bucal hacia arriba, no hacia los lados, como se pensaba. Esto genera una aspiración del agua subyacente hacia el pico, mejorando la captura de alimento. Un experimento realizado con un modelo mecánico demostró que el bombeo de agua a través del pico acoplado al castañeteo multiplicaba por siete la captura de artemias[1] respecto al bombeo de agua sin castañeteo (Figura 3, Vídeo 2).
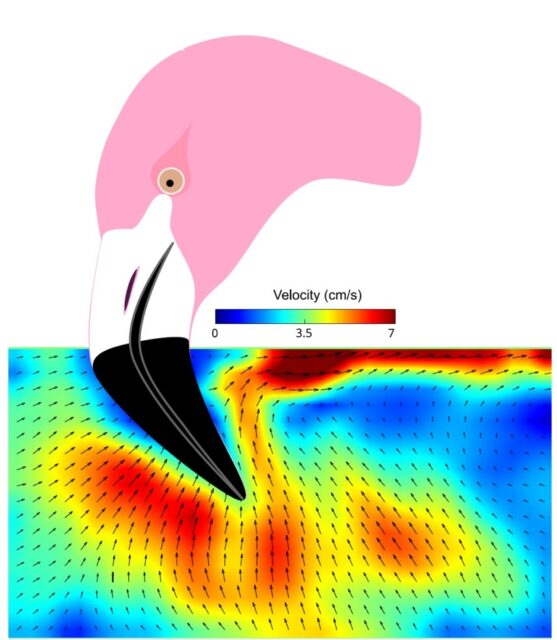 Figura 3. Flujo de agua generado por el castañeteo del pico superior. El agua situada entre el pico y el sustrato es aspirada, arrastrando partículas de alimento hacia el pico. Fuente: Ortega-Jiménez et al. (2025), cita completa en referencias, CC BY-SA 4.0.
Figura 3. Flujo de agua generado por el castañeteo del pico superior. El agua situada entre el pico y el sustrato es aspirada, arrastrando partículas de alimento hacia el pico. Fuente: Ortega-Jiménez et al. (2025), cita completa en referencias, CC BY-SA 4.0.Las patas palmeadas de los flamencos se mueven arriba y abajo durante su alimentación. Ya se suponía que esto contribuía a desenterrar organismos del sustrato. Los modelos utilizados en esta investigación muestran que los dedos palmeados se pliegan al subir, se despliegan al bajar y originan vórtices verticales que concentran a los organismos, impidiendo que escapen y haciendo más eficiente el filtrado (Figura 4, Vídeo 3).
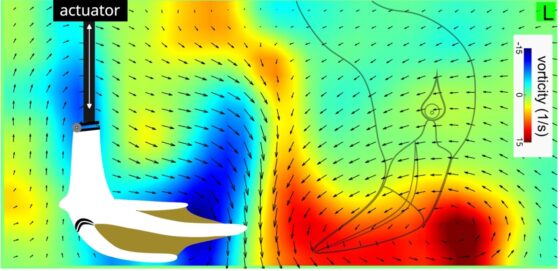 Figura 4. Este modelo mecánico del funcionamiento de la pata del flamenco muestra la generación de un vórtice vertical justo en la zona en la que se alimenta el flamenco. El vórtice atrapa pequeños invertebrados que no pueden escapar nadando. Fuente: Ortega-Jiménez et al. (2025), cita completa en referencias, CC BY-SA 4.0.
Figura 4. Este modelo mecánico del funcionamiento de la pata del flamenco muestra la generación de un vórtice vertical justo en la zona en la que se alimenta el flamenco. El vórtice atrapa pequeños invertebrados que no pueden escapar nadando. Fuente: Ortega-Jiménez et al. (2025), cita completa en referencias, CC BY-SA 4.0.Por último, cuando el flamenco filtra la superficie del agua para capturar, por ejemplo, huevos flotantes de invertebrados, sitúa su pico con la punta en la dirección de la corriente de agua. La forma del pico induce la formación de vórtices de Kárman, una serie de remolinos que provocan la recirculación del agua dirigiendo las partículas alimenticias hacia los bordes del pico, (Figura 5, Vídeo 4).
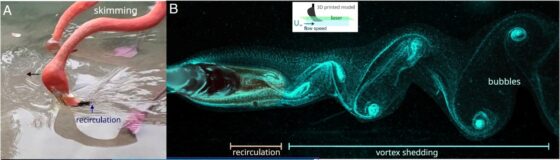 Figura 5. La filtración en superficie (skimming) se efectúa en la misma dirección de la corriente de agua. Esto provoca la formación de vórtices de Kárman y un área de recirculación que dirige las partículas flotantes hacia el pico. Fuente: Ortega-Jiménez et al. (2025), cita completa en referencias, CC BY-SA 4.0.
Figura 5. La filtración en superficie (skimming) se efectúa en la misma dirección de la corriente de agua. Esto provoca la formación de vórtices de Kárman y un área de recirculación que dirige las partículas flotantes hacia el pico. Fuente: Ortega-Jiménez et al. (2025), cita completa en referencias, CC BY-SA 4.0.En resumen, los flamencos no se limitan a filtrar pasivamente agua y sedimentos, sino que son depredadores que despliegan estrategias sofisticadas para concentrar y capturar los organismos que constituyen su alimento. Estas estrategias implican la generación de distintos tipos de vórtices, y la forma tan peculiar de su pico parece ser una eficiente adaptación morfológica para este propósito.
Notas:
[1] Pequeño crustáceo que constituye un elemento fundamental de la dieta del flamenco, además de proporcionar los carotenoides que dan color rojo a sus plumas.
[2] Los vídeos también están disponibles en esta página web (De Ortega-Jiménez et al., 2025, cita completa en referencias, CC BY-SA 4.0.)
Referencias
Ortega-Jimenez, V.M., Yee, T., Rohilla, P. et al. (2025). Flamingos use their L-shaped beak and morphing feet to induce vortical traps for prey capture. Proc Natl Acad Sci U S A. doi: 10.1073/pnas.2503495122.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga.
El artículo Vórtices, dinámica de fluidos y la alimentación de los flamencos se ha escrito en Cuaderno de Cultura Científica.
Resultados «emocionantes» para el primer ensayo clínico de inmunoterapia en tumores sólidos
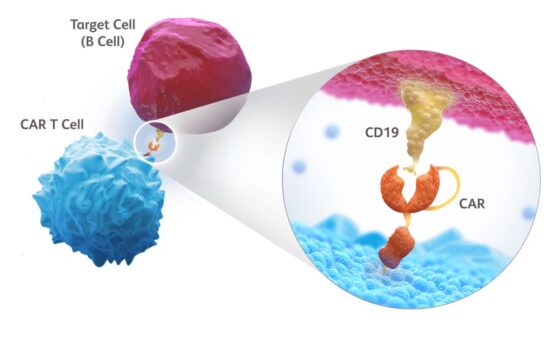 Inmunoterapia de Células T Car frente a tumores sólidos. Fuente: BMS Science / Fair use
Inmunoterapia de Células T Car frente a tumores sólidos. Fuente: BMS Science / Fair use
Los orígenes de la quimioterapia se remontan a la lejana década de los cincuenta del siglo pasado y, durante todo este tiempo, se ha convertido en la herramienta más directa y eficaz frente a algunos tipos de cáncer. Sin embargo, el avance de nuevas terapias en este campo se había ralentizado hasta que, con el nuevo siglo, surgió una alternativa mucho menos invasiva y agresiva: la inmunoterapia. En diciembre de 2013, la célebre revista Science elegía la inmunoterapia como el «descubrimiento científico del año» y, la definía a grandes rasgos como un novedoso tratamiento médico que busca entrenar, fortalecer o dirigir nuestro propio sistema inmunitario y convertirlo en un ejército mejor preparado frente a la amenaza.
Es una idea brillante y, en teoría, bastante simple de entender: la inmunoterapia busca potenciar el propio sistema inmunitario del paciente para luchar contra las células tumorales. El funcionamiento de estas inmunoterapias consiste en extraer las defensas del paciente (ya sean linfocitos T, B o Natural Killer) y modificarlas genéticamente para que produzcan receptores específicos que reconozcan y ataquen a un tumor determinado. Explicado de manera muy visual y sencilla, sería una especie de «gimnasio» para linfocitos. Los investigadores extraen células defensivas de una persona con algún tipo de cáncer y, en el laboratorio, las «ponen en forma y entrenan». Cuando están listas y reforzadas, se las vuelven a inyectar al paciente.
Las inmunoterapias poseen una innegable ventaja frente a la quimioterapia ya que son mucho menos invasivas. Al inocular al paciente sus propias células inmunitarias generan menos rechazo y no resultan tan agresivas con el resto de células. Entre estas terapias se encuentra la denominada CART-T que utiliza linfocitos T, modificados genéticamente en laboratorio, y que han probado ser muy eficaces contra determinados cánceres de origen sanguíneo.
Por supuesto, queda mucho camino por recorrer y las diferentes formas de inmunoterapia poseen dos problemas generales que deben solucionar. En primer lugar, todavía no pueden distinguir con exactitud entre células cancerosas y no cancerosas, algo que los investigadores están buscando desde hace años y que representaría un paso de gigante en este tipo de terapias. Por otro lado, la eficacia de CART-T frente a tumores sólidos sigue estando muy lejos de ser viable y eso es un importante freno ya que estos tumores sólidos «representan aproximadamente el 90% de todos los cánceres, incluidos el cáncer de mama, de pulmón y de páncreas».
Respecto al primer problema, afortunadamente van llegando poco a poco algunos avances, como el estudio presentado en 2021 donde un equipo de investigadores canadienses presentó un estudio con células específicamente diseñadas para destruir los tumores malignos sin atacar al resto de células. Sin embargo, el segundo obstáculo, el de la eficacia de la inmunoterapia frente a tumores sólidos parecía estancado… hasta ahora.
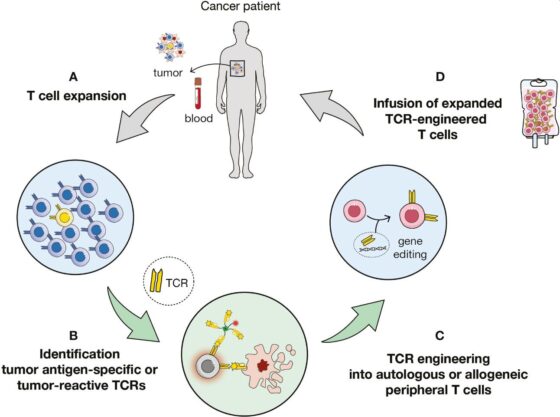 Infografía del funcionamiento de las inmunoterapias con células T CAR. Fuente: Arnaud M, Bobisse S, Chiffelle J and Harari A (2021) The Promise of Personalized TCR-Based Cellular Immunotherapy for Cancer Patients. Front. Immunol. 12:701636. doi: 10.3389/fimmu.2021.701636 CC BY 4.0
Infografía del funcionamiento de las inmunoterapias con células T CAR. Fuente: Arnaud M, Bobisse S, Chiffelle J and Harari A (2021) The Promise of Personalized TCR-Based Cellular Immunotherapy for Cancer Patients. Front. Immunol. 12:701636. doi: 10.3389/fimmu.2021.701636 CC BY 4.0
Se acaba de publicar en The Lancet un ensayo clínico que los expertos califican como un «hito» en inmunoterapia de células T Car en tumores sólidos. El estudio nos sitúa ante un «avance único y esperanzador» en el que los pacientes con cáncer gástrico avanzado que fueron tratados con inmunoterapia «vivieron en promedio aproximadamente un 40% más que los pacientes que recibieron la atención estándar». Además el ensayo también ha sido presentado en la Conferencia sobre cáncer más importante a nivel mundial, la reunión anual de la Sociedad Americana de Oncología Clínica, celebrada en Chicago hace unos días, donde los investigadores asistentes calificaron los resultados como «emocionantes e innovadores».
Esta nueva inmunoterapia se centra en células T con un receptor quimérico de antígeno (CAR) denominado satricabtagene autoleucel (satri-cel) y los resultados presentados corresponden a un ensayo controlado aleatorizado de fase 2 que involucró a 156 pacientes con cáncer gástrico en una etapa avanzada.
Estos participantes se dividieron aleatoriamente en dos grupos en una proporción de 2:1. Los pacientes del grupo de estudio recibieron la inmunoterapia con T Car satri-cel (n=104) mientras que los del grupo de control (n=52) recibieron el tratamiento actual que incluía Nivolumab, paclitaxel, docetaxel, irinotecán o rivoceranib. Además, para evaluar la eficacia de las diferentes actuaciones, dentro del grupo de inmunoterapia satri-cel, el 85% de los pacientes recibió al menos una infusión de satri-cel, el 31% recibió una segunda infusión y el 6% recibió una tercera infusión. En el grupo de control, el 92% de los pacientes recibió al menos una dosis de su tratamiento.
Los resultados publicados arrojan datos notables: Los pacientes que recibieron terapia con células T Car satri-cel «vivieron un promedio de 7,9 meses tras la aleatorización, en comparación con los 5,5 meses que vivieron con la atención estándar».
Es un pequeño paso, sí, pero hay que entender que se produce en un campo que llevaba estancado más de una década y, según Nature, demuestra que esta inmunoterapia «ofrece beneficios significativos a los pacientes con cáncer gástrico avanzado que han fracasado en al menos dos líneas de tratamiento previas». Además, nos abre la puerta a otras aplicaciones en diferentes tipos de cáncer que no estaban previstos en el estudio inicial. En este sentido, en la misma reunión oncológica de Chicago se presentará un segundo estudio sobre células T Car, dirigido por la Universidad de Pensilvania que apunta a que el enfoque también se puede utilizar para tratar tumores cerebrales, en especial reducir el tamaño de los tumores en el glioblastoma, un cáncer cerebral agresivo y de rápido crecimiento, y ayudar a los pacientes a vivir mucho más tiempo.
En definitiva, y como afirma el oncólogo John Haanen en The Guardian, «para los tumores sólidos, ahora no solo existe un claro interés sino también evidencia de que las inmunoterapias pueden beneficiar a los pacientes. Es posible que estemos presenciando los inicios de una nueva generación de tratamientos que antes no existía para los oncólogos médicos».
Referencias científicas y más información:
Changsong Qi, Chang Liu, et al. (2025) Claudin-18 isoform 2-specific CAR T-cell therapy (satri-cel) versus treatment of physician’s choice for previously treated advanced gastric or gastro-oesophageal junction cancer (CT041-ST-01): a randomised, open-label, phase 2 trial The Lancet doi: 10.1016/S0140-6736(25)00860-8
Fieldhouse, Rachel. «Cancer Fighting CAR-T Cells Show Promising Results for Hard-to-Treat Tumours». Nature News, junio de 2025. DOI:10.1038/d41586-025-01722-8.
Andrew Gregory «Immunotherapy trial helps cancer patients with tumours live 40% longer» The Guardian Science (2025)
Sobre el autor: Javier «Irreductible» Peláez es escritor y comunicador científico multimedia. Es ganador de tres premios Bitácoras, un premio Prisma a la mejor web de divulgación científica y un Premio Ondas al mejor programa de radio digital.
El artículo Resultados «emocionantes» para el primer ensayo clínico de inmunoterapia en tumores sólidos se ha escrito en Cuaderno de Cultura Científica.
Y… ¿cómo se gestiona el patrimonio natural?

¿Qué tienen en común un paisaje espectacular, un fósil milenario y una cantera abandonada? Todos forman parte del patrimonio geológico, un testimonio de la historia de la Tierra con un gran valor científico, educativo, cultural y estético, y base del patrimonio natural. Sin embargo, su importancia continúa siendo poco apreciada.
Para acercar las distintas aproximaciones del patrimonio geológico a la sociedad, los días 26, 27 y 28 de marzo se celebró la quinta edición de las jornadas divulgativas “Geología para poetas, miopes y despistados. Patrimonio patrimonio”. Organizadas por el grupo de investigación consolidado Procesos Hidro-Ambientales (HGI) de la Facultad de Ciencia y Tecnología de la Universidad del País Vasco (UPV/EHU), estas jornadas contaron con la colaboración del Vicerrectorado del Campus de Bizkaia, la Cátedra de Cultura Científica de la UPV/EHU, el Geoparque de la Costa Vasca / Geoparkea y el Ente Vasco de la Energía (EVE).
En esta charla Xabier Arana nos expone como han evolucionado las ideas sobre conservación del patrimonio natural y cómo se ejecuta desde la Diputación Foral de Bizkaia. Xabier Arana fue Director de la Reserva de la Biosfera de Urdaibai entre 1996 y 2007, es miembro de la Comisión Ambiental del Colegio Oficial de Biólogos de Euskadi y, desde el año 2012, es Jefe de Sección de Sostenibilidad y Educación Ambiental de la Diputación Foral de Bizkaia.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Y… ¿cómo se gestiona el patrimonio natural? se ha escrito en Cuaderno de Cultura Científica.
Mejor aprender a escribir con lápiz y papel
El equipo de la investigadora Joana Acha ha analizado las consecuencias que tiene en las competencias de niños y niñas el hecho de escribir a mano o con teclado durante el proceso de aprendizaje de la lectura y la escritura. A un grupo de niños y niñas de 5 años se les ha enseñado un alfabeto artificial mediante diferentes técnicas, y se ha llegado a la conclusión de que quienes se ejercitan con lápiz y papel asimilan mejor las letras y las palabras nuevas.
 Foto: Julia M Cameron / Pexels
Foto: Julia M Cameron / PexelsHoy en día es habitual la presencia de recursos digitales en las aulas infantiles y su utilización como herramienta en distintos procesos de aprendizaje. Por ejemplo, existen programas informáticos dirigidos a alumnos que están aprendiendo a leer y escribir. Como los ejercicios que proponen se realizan en el ordenador, los escolares pulsan teclas y botones, dejando de lado el lápiz y el papel. Para medir el impacto de estos métodos basados en la mecanografía, un estudio de la UPV/EHU ha realizado una comparativa con el fin de analizar las consecuencias que tiene en las capacidades de los niños el hecho de practicar la escritura a mano o con teclado: “Ya que los niños escriben cada vez menos a mano, queríamos investigar la influencia que eso tiene en las competencias alfabéticas y ortográficas. Es decir, queríamos ver si tanto la capacidad de aprender letras como la de interiorizar y recordar la estructura de las palabras se desarrolla de forma diferente a través de la práctica manual o del uso del teclado. Hemos llegado a la conclusión de que los niños que se han ejercitado a mano han obtenido los mejores resultados”, explica la investigadora Joana Acha.
 Las 9 letras empleadas en el estudio. Fuente: Modificado de Gorka Ibaibarriaga, Joana Acha, Manuel Perea (2025) Journal of Experimental Child Psychology doi: 10.1016/j.jecp.2025.106195
Las 9 letras empleadas en el estudio. Fuente: Modificado de Gorka Ibaibarriaga, Joana Acha, Manuel Perea (2025) Journal of Experimental Child Psychology doi: 10.1016/j.jecp.2025.106195Para llegar a esta conclusión, se ha llevado a cabo un experimento con niños de entre 5 y 6 años. Se ha elegido esa edad porque es el momento evolutivo más propicio: es entonces cuando comienzan a adquirir la capacidad lectoescritora. Así, se enseñó a 50 niños y niñas con conocimientos básicos de lectura 9 letras de los alfabetos georgiano y armenio, así como 16 pseudopalabras inventadas por el equipo investigador combinando dichas letras.
 Las 16 pseudopalabras empleadas en el estudio. Fuente: Modificado de Gorka Ibaibarriaga, Joana Acha, Manuel Perea (2025) Journal of Experimental Child Psychology doi: 10.1016/j.jecp.2025.106195
Las 16 pseudopalabras empleadas en el estudio. Fuente: Modificado de Gorka Ibaibarriaga, Joana Acha, Manuel Perea (2025) Journal of Experimental Child Psychology doi: 10.1016/j.jecp.2025.106195“El objetivo es utilizar letras y palabras totalmente nuevas para los participantes, con el fin de asegurarnos de que están aprendiendo desde cero. De hecho, las investigaciones previas han utilizado los alfabetos propios de la cultura de los niños, por lo que no resulta tan fácil saber hasta qué punto conocían los símbolos presentados”, afirma Acha.
A todo el alumnado se le enseñaron las mismas letras y palabras, pero no a todos de la misma manera: a la mitad se les pidió que las copiaran a mano y a la otra mitad, que las escribieran utilizando el teclado. De este modo, el estudio de la Universidad del País Vasco ha podido analizar la importancia de la grafomotricidad, es decir, cómo influye el movimiento de la mano en el proceso de lectura y escritura. De hecho, cuando escribimos con teclado no trazamos la forma de las letras, por lo que la influencia de la grafomotricidad es escasa a la hora de interiorizar su estructura. En cambio, al escribir a mano, esta influencia es significativa.
“Una vez que se les enseñaron las letras y palabras nuevas, y cada grupo practicó con un método distinto, realizamos tres pruebas para evaluar los conocimientos adquiridos. Medimos la capacidad de identificar, escribir y pronunciar letras y pseudopalabras, y los resultados indican claramente que quienes practicaron a mano desarrollaron una mayor destreza. La diferencia se nota, sobre todo, en las pseudopalabras, ya que casi todos los que aprendieron con ordenador realizaron incorrectamente los ejercicios relacionados con las secuencias de letras. Por lo tanto, nuestro trabajo reafirma que la grafomotricidad es fundamental para memorizar las letras y las estructuras de las palabras”, explica Acha.
La variabilidad al usar el lápiz también influyePero no solo se ha estudiado el impacto del grado de movimiento de la mano. Los grupos que trabajaban a mano y con teclado se dividieron, desde el principio, en dos subgrupos. En el caso de quienes utilizaban lápiz, a algunos se les pidió que siguieran las guías marcadas con puntos (técnica de baja variabilidad), mientras que otros practicaron sin ninguna referencia, copiando libremente en una hoja en blanco (alta variabilidad). Lo mismo se aplicó a quienes usaban ordenador: algunos utilizaron siempre la misma tipografía para practicar (por ejemplo, Tahoma), y otros, varias.
Así, además de la grafomotricidad, se ha podido analizar la influencia del factor de variabilidad en la forma.
Lo que se ha observado es que los que practicaron a mano obtuvieron mejores resultados que todos los que utilizaron el teclado, aunque también se encontraron diferencias dentro del grupo que escribió a mano. Aquellos que practicaron de forma libre lograron los mejores resultados. “Por tanto, lo que hemos deducido es que, aunque al principio contar con una guía para practicar resulta de gran ayuda, una vez que los niños son capaces de realizar movimientos pequeños y precisos, conviene pasar a la escritura libre. En cualquier caso, lo que está claro es que debe priorizarse la escritura a mano como práctica en los procesos de aprendizaje. Aprenden mejor a través del movimiento de la mano y, por tanto, los dispositivos tecnológicos deberían utilizarse únicamente como complemento”, concluye Acha.
Referencia:
Gorka Ibaibarriaga, Joana Acha, Manuel Perea (2025) The impact of handwriting and typing practice in children’s letter and word learning: Implications for literacy development Journal of Experimental Child Psychology doi: 10.1016/j.jecp.2025.106195
Para saber más:
La adquisición de la lectura desde la evidencia científica: una hoja de ruta para educadores, conferencia de Joana Acha
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Mejor aprender a escribir con lápiz y papel se ha escrito en Cuaderno de Cultura Científica.
¿Nos llevó la ciencia ficción a la Luna?
La historia de la Luna es, una vez más, la historia del mito que se convirtió en ciencia. La de una humanidad idealista que soñaba con alcanzarla, construyó un cohete y lo hizo. Y es posible que la ciencia ficción tuviera mucho que ver en todo esto, sobre todo por la época que vivíamos cuando empezaron a gestarse los inicios de la carrera espacial.
 Foto: Luca / Unsplash
Foto: Luca / UnsplashNuestro satélite no siempre estuvo, metafóricamente hablando, cerca de nosotros. Durante mucho tiempo, en la Antigüedad, conformó la frontera que separaba dos mundos de naturaleza muy distinta: el sublunar, material y cambiante, y el supralunar, etéreo e inmutable. Hasta que Johannes Kepler la concibió como un lugar —pero un lugar «real»—, en su Somnium[1] y Galileo Galilei nos ayudó a verlo con nuestros propios ojos gracias al telescopio.
Sí, es cierto que se escribieron historias de viajes a la Luna mucho antes que la de Kepler, pero, como bien apunta Jorge Luis Borges en el prólogo que escribió para Crónicas marcianas, de Ray Bradbury: «Para Luciano y para Ariosto, un viaje a la Luna era símbolo o arquetipo de lo imposible; para Kepler ya era una posibilidad, como para nosotros». De hecho, tras conocer las investigaciones de Galileo, así se lo hizo saber en 1610 su Dissertatio cum nuncio sidereo, en una respuesta abierta al Sidereus nuncius:
Ciertamente no faltarán pioneros humanos cuando hayamos dominado el arte del vuelo […]. Construyamos naves y velas adaptadas al éter celestial, y habrá muchas personas sin miedo a los vacíos inmensos. Mientras tanto, prepararemos, para los valientes viajeros del cielo, mapas de los cuerpos celestes; yo lo haré para la Luna, tú, Galileo, para Júpiter.
¿Es posible que estuviera hablando ya de que algún día habría naves espaciales? Dejando esto de lado, este fue, probablemente, el momento en el que comenzó la carrera espacial —al menos en nuestra imaginación—, o el momento en que plantearse algo así empezó a tener sentido desde un punto de vista racional.
 Dissertatio cum nuncio sidereo es la respuesta de Johannes Kepler al Sidereus nuncius de Galileo Galilei. En él, plantea la posibilidad de que algún día la humanidad pueda viajar a las estrellas y la Luna gracias al desarrollo de nueva tecnología. Fuente: Dominio público
Dissertatio cum nuncio sidereo es la respuesta de Johannes Kepler al Sidereus nuncius de Galileo Galilei. En él, plantea la posibilidad de que algún día la humanidad pueda viajar a las estrellas y la Luna gracias al desarrollo de nueva tecnología. Fuente: Dominio público
Pasarían aún algunos siglos para terminar de creérnoslo, y aunque los viajes a la Luna siguieron presentes en la literatura a través de obras medio fantásticas, medio racionales —al menos ya no eran solo fantásticas, sino que intentaban acercar al mundo terrenal lo que en otro momento fue divino—, no fue hasta el siglo XX cuando decidimos que era el momento de intentar, en serio, llegar a nuestro único satélite.
Ya a finales del siglo XIX, cuando ni siquiera existían los aviones, visionarios como Konstantin Tsiolkovsky o Robert Goddard sentaron las bases de la cohetería moderna y soñaron a lo grande con el espacio. El despegue del primer aeroplano de los hermanos Wright, por su parte, empezó a cambiar tecnológicamente, pero, sobre todo, en la imaginación humana, el paradigma de la aeronáutica. Y dos guerras mundiales lo consolidaron —a un precio que la humanidad nunca debería haber pagado, me atrevo a añadir—.
Para entonces la ciencia ficción estadounidense estaba en su mejor momento. Y no es casual. Existen estudios que correlacionan las épocas de mayor desarrollo tecnológico de algunos países con una eclosión de publicaciones de este tipo de literatura. Pero el espacio dejaba de limitarse a las historias fantásticas. En 1946, la revista Life publicó un artículo titulado «Trip to the Moon: artist paints journey by rocket», con ilustraciones de Chesley Bonestell en las que muchos, por primera vez, pudieron observar, de una forma que parecía casi realista, qué había más allá de la Tierra… Vieron por primera vez ese espacio exterior del que todo el mundo empezaba a hablar después de la Segunda Guerra Mundial.
El ilustrador Chesley Bonestell supo reflejar en imágenes la desbordante imaginación de una posguerra en la que cualquier cosa era posible. Y el miedo a un desastre nuclear y la competitividad de la Guerra Fría, alimentaron ese fuego en medio de un tenso tecnooptimismo.
 Habitual de las revistas de ciencia ficción de la época, el ilustrador Chesley Bonestell supo reflejar en sus dibujos los sueños espaciales de toda una generación… o tal vez contribuir a que los tuvieran.
Habitual de las revistas de ciencia ficción de la época, el ilustrador Chesley Bonestell supo reflejar en sus dibujos los sueños espaciales de toda una generación… o tal vez contribuir a que los tuvieran.Fuentes: New Mexico Museum of Space History / Fair use | World Editions, Inc./Chesley Bonestell
El mencionado artículo llegó, en un momento dado, a las manos del productor George Pal, quien decidió que era el momento de rodar una película no de science fiction (‘ficción científica’), sino de science fact (‘hechos científicos’). Estaría basada en una de las recientes novelas juveniles de Robert A. Heinlein: Rocket ship Galileo (1947).
Que el ser humano llegara a la Luna era casi una obsesión para Heinlein. Aunque en su momento se había visto obligado a abandonar el Ejército a causa de una tuberculosis y a retirarse de su labor de ingeniero, siempre se mantuvo actualizado y al día en ese tipo de cuestiones. Estaba suscrito a revistas como Scientific American, Popular Mechanics y estaba en contacto permanentemente con científicos e ingenieros, muchos de los cuales había conocido en su época militar. No es extraño, entonces, que George Pal quisiera contar con él como director técnico. La rigurosidad de Heinlein en ese aspecto, y de la película en general, fue determinante. Destination Moon, estrenada en 1950 —antes del lanzamiento del Sputnik y antes de que Yurin Gagarin se convirtiera en el primer ser humano en orbitar la Tierra— fue capaz de mostrar a todo el mundo, de forma bastante acertada además, cómo serían los viajes espaciales y le hizo sentir, creer y, sobre todo, tener fe en que llegar a la Luna solo era una cuestión de tiempo, que estaba más cerca de lo que pensábamos y solo requería de nosotros un poco de espíritu emprendedor y de aventura. Por supuesto, fue Chesley Bonestell —y Heinlein ni se quiso plantear la posibilidad de que lo hiciera cualquier otro— quien se encargó del diseño y los decorados.
 Basada en la novela Rocket ship Galileo de Robert A. Heinlein, y científicamente rigurosa con los estándares de la época —aunque algo anacrónica para los gustos cinematográficos de hoy—, Destination Moon mostró, en 1950, cómo sería un viaje a la Luna en tecnicolor. Fuente: George Pal Productions / Fair use
Basada en la novela Rocket ship Galileo de Robert A. Heinlein, y científicamente rigurosa con los estándares de la época —aunque algo anacrónica para los gustos cinematográficos de hoy—, Destination Moon mostró, en 1950, cómo sería un viaje a la Luna en tecnicolor. Fuente: George Pal Productions / Fair use
Así que se podría decir, en última instancia, que si Neil Armstrong pisó la Luna aquel 21 de julio de 1969, fue porque, poco a poco y a lo largo de varios siglos, empezamos a creer en que algún día podríamos llevarlo hasta allí.
Bibliografía
Borges, J. L. (2005 [1955]). Prólogo. En R. Bradbury, Crónicas marcianas. Minotauro.
Brake, M. (2018). The science of science fiction. Simon & Schuster.
Heinlein, R. A. (1947). Rocket ship Galileo. Scribner’s.
Newell, C. L. (2014). The greatest adventure awaiting humankind: Destination Moon and faith in the future. Implicit Religion, 17(4), 459-479. https://doi.org/10.1558/imre.v17i4.459
Pichel, I. (Director). (1950). Destination Moon [Película]. Eagle-Lion Classics.
Nota:
[1] Para muchos, entre quienes me incluyo, el Somnium, seu opus posthumum De astronomia lunari, de Johannes Kepler, es la primera novela de ciencia ficción. Empezó a escribirla alrededor de 1608, como apoyo para el desarrollo de sus tres leyes que rigen los movimientos planetarios, aunque se publicó a título póstumo en 1934.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo ¿Nos llevó la ciencia ficción a la Luna? se ha escrito en Cuaderno de Cultura Científica.
Los números primos de las ciudades oscuras
En esta nueva entrada del Cuaderno de Cultura Científica regresamos a una maravillosa serie de novelas gráficas, Las ciudades oscuras, publicadas originalmente en francés, del dibujante belga François Schuiten (1956) y el guionista francés Benoît Peeters (1956), cuyo primer álbum Las murallas de Samaris fue publicado en 1983. A día de hoy se han publicado los siguientes álbumes: Las murallas de Samaris, La fiebre de Urbicande, La Torre, El Archivista (extra), La ruta de Armilia, Brüsel, La chica inclinada, La sombra de un hombre, La Frontera Invisible (doble), La teoría del grano de arena (doble), Recuerdos del eterno presente, El eco de las ciudades (extra) y El regreso del Capitán Nemo.
En la entrada titulada La ecuación de las ciudades oscuras centramos nuestra atención en el álbum La fiebre de Urbicande (1985), en la red de cubos con forma de un octaedro (es decir, una doble pirámide, hacia arriba y hacia abajo), que protagoniza esta novela gráfica, y las fórmulas matemáticas que aparecen en el cómic y que describen la cantidad de cubos de la red. Mientras que en esta entrada vamos mirar ál álbum La teoría del grano de arena (2007/08).
 Portada de la edición en español, de Norma Editorial, del cómic La teoría del grano de arena (2010), de Francois Schuiten (dibujante) y Benoit Peeters (guionista), perteneciente a su serie Las ciudades oscuras
Portada de la edición en español, de Norma Editorial, del cómic La teoría del grano de arena (2010), de Francois Schuiten (dibujante) y Benoit Peeters (guionista), perteneciente a su serie Las ciudades oscuras
Como comentábamos en la anterior entrada, en Las ciudades oscuras nos encontramos ante una serie de historias entre fantásticas y surrealistas que transcurren en diferentes ciudades de un continente imaginario que se encuentra situado en el planeta Antichton, o Anti-Tierra. Este hipotético planeta fue inventado por el filósofo y matemático pitagórico Filolao (aprox. 470 – 380 a.n.e.) cuando describió un sistema cosmológico, no geocéntrico, en el que había un fuego central distinto del Sol y un planeta situado en la posición diametralmente opuesta a la Tierra, respecto a dicho fuego central, la anti-Tierra.
La teoría del grano de arena
La historia de La teoría del grano de arena transcurre en la ciudad de Brüsel (en el año 784, de Antichton), ciudad que ya aparecía en el álbum homónimo de la serie.
Con la llegada a Brüsel de un misterioso y extraño sujeto, Gholam Mortiza Khan, jefe de la tribu de los Bugtis que viven en la desértica y alejada zona de Boulachistan, con la intención de vender algunas joyas de su tribu para comprar armas, empiezan a ocurrir extraños sucesos, como la aparición de forma misteriosa y continua de una gran cantidad de arena en un piso en el que vive una madre con sus dos hijos, la materialización de misteriosas piedras, de diferentes formas, pero tamaños similares, en el piso del florista Constant Abeels, protagonista del álbum Brüsel, la pérdida de peso, pero sin adelgazar, del propietario y chef de la famosa brasserie Maurice, o los extraños ruidos de la casa en la que vive Elsa Autrique, la experta en arte tribal a la que acude el guerrero Bugti.
 Contraportada de la edición en español, de Norma Editorial, del cómic La teoría del grano de arena (2010), de Francois Schuiten (dibujante) y Benoit Peeters (guionista), perteneciente a su serie Las ciudades oscuras
Contraportada de la edición en español, de Norma Editorial, del cómic La teoría del grano de arena (2010), de Francois Schuiten (dibujante) y Benoit Peeters (guionista), perteneciente a su serie Las ciudades oscuras
Con el paso de los días los sucesos son cada vez más graves y preocupantes, por lo que se contrata a una mujer “coleccionista de fenómenos sin explicación” para que investigue el origen de los extraños fenómenos que están ocurriendo en la ciudad. Se trata de Mary Von Rathen, protagonista del álbum La chica inclinada. La investigación de los extraños sucesos le llevan a deducir que todos están relacionados con una persona, el jefe de los Bugtis, Gholam Mortiza Khan. Pero como el guerrero Bugti falleció poco después de su llegada a la ciudad, atropellado por un tranvía, resulta complicado averiguar el origen de los desastres. Aunque el lector sabe que está relacionado con una joya muy especial que llevaba el jefe Bugti, el Nawaby (que aparece en la imagen anterior, en el centro, así como en la imagen siguiente, la página de la novela gráfica en la que el guerrero Bugti le deja la joya a Elsa Autrique), que fue un botín de guerra que le quitó al jefe de los Moktars, con los que están en perpetuo conflicto.
 Página de la novela gráfica La teoría del grano de arena, en la que se muestra a la experta en arte tribal Elsa Autrique admirando el Nawaby, una joya muy especial, que le ha dejado el jefe de los Bugtis
Página de la novela gráfica La teoría del grano de arena, en la que se muestra a la experta en arte tribal Elsa Autrique admirando el Nawaby, una joya muy especial, que le ha dejado el jefe de los Bugtis
Cuando los dos hijos del jefe Bugti, Gholam Mortiza Khan, viajan a Brüsel en busca de su padre, se descubre que el motivo de los extraños fenómenos que están ocurriendo es la joya Nawaby, que deberá ser devuelta a su lugar de origen para restablecer el orden que había sido roto por el robo del objeto más sagrado de los Moktars, el Nawaby. Entonces, la investigadora Mary Von Rathen, el florista Constant Abeels y los hijos de Gholam Mortiza Khan realizarán un viaje a Boulachistan a devolver el Nawaby a los Moktars.
Los números primos oscuros
En esta historia de las ciudades oscuras nos encontramos con una sencilla mención a los números primos, que explicaremos a continuación.
Como hemos comentado más arriba, en el apartamento del florista Constant Abeels empiezan a aparecer piedras, una a una, que el protagonista de Brüsel empieza a catalogarlas (número en la serie de apariciones, fecha, hora y lugar de la aparición) y medirlas. Entonces descubre que todas las piedras, que tienen formas distintas y dimensiones parecidas, pesan exactamentre lo mismo, 6.793 gramos. Entonces, Constant le menciona a Maurice, que es quien le ha dejado la báscula, que “6.793 … es un número primo”, a lo que el chef le contesta “un número primo … ¡lo que faltaba!”.
 Página de la novela gráfica La teoría del grano de arena, en la que se muestra al florista Constant Abeels catalogando las primeras piedras que aparecen en su apartamento
Página de la novela gráfica La teoría del grano de arena, en la que se muestra al florista Constant Abeels catalogando las primeras piedras que aparecen en su apartamento
Aunque los números primos son muy conocidos, recordemos que son aquellos números naturales que solamente se pueden dividir por 1 y por ellos mismos. Así, por ejemplo, el número 25 no es primo ya que se puede dividir por 5 (además de por 1 y 25), o tampoco el 27 (divisible por 3 y 9), mientras que el número 19 sí es primo, ya que solamente es divisible por el 1 y él mismo, al igual que lo son los números 2, 3, 5, 7, 11 y 13, entre otros. Para quien quiera profundizar más en el significado de los números primos puede leer la entrada Buscando lagunas de números no primos, o algunas de las otras entradas que hemos escrito en el Cuaderno de Cultura Científica sobre esta importante familia de números.
La mención a que el número 6.793 es un número primo podría haberse limitado al anterior pasaje y ser algo puramente anecdótico, pero los números primos volverán a mencionarse más adelante en la historia.
Cuando Maurice está ayudando a Constant a sacar las piedras de su piso, ya que existe el peligro de que el suelo acabe rompiéndose por el peso de las piedras, el chef, que recordemos que está perdiendo peso pero sin adelgazar, le dice al florista “me estoy enamorando de tus números primos”. Es una metáfora para referirse a las piedras, por lo que sigue siendo anecdótico, pero mantiene viva la referencia a los números primos.
Pero es cuando la investigadora Mary Von Rathen, el florista Constant Abeels y los hijos de Gholam Mortiza Khan van de viaje hacia Boulachistan cuando volverán a aparecer con un poco más de protagonismo. Los cuatro van en un coche cuando se podruce el siguiente diálogo:
– [Constant]: Una de las cosas que no entiendo es el peso siempre idéntico de mis piedras, 6.793 gramos… De cuerdo, es un número primo, ¿pero por qué ese?
– [Mary]: Ni que fuera lo único que ignoramos…
– [Constant]: ¡Increíble! ¡Miren lo que acabo de descubrir! 6.971 también es un número primo … 6.971 y 6.973 son números primos gemelos, ¡igual que ustedes!
[Se refiere a los hijos de Gholam Mortiza Khan que son hermanos gemelos]
Recordemos el concepto de números primos gemelos. Como todos los números pares, a excepción del 2, son números no primos, entonces lo más cerca que pueden estar dos números primos, salvo el 2 y el 3 que están pegados, es con solo un número par entre ellos. Y precisamente, a las parejas de números primos que están tan cerca, es decir, con solo un número par entre ellos, o dicho de otra forma, que la diferencia entre ellos es 2, se les llama números primos gemelos, como las parejas 11 y 13, 17 y 19, o los que aparecen en la novela gráfica, 6.971 y 6.973.
 Página de la novela gráfica La teoría del grano de arena, en la que se muestra a Mary Von Rathen, Constant Abeels y los hijos de Gholam Mortiza Khan en su viaje a Boulachistan
Página de la novela gráfica La teoría del grano de arena, en la que se muestra a Mary Von Rathen, Constant Abeels y los hijos de Gholam Mortiza Khan en su viaje a Boulachistan
Al llegar a Boulachistan, los cuatro personajes de esta historia se dirigirán a la antigua fortaleza de los Moktars, para dejar al Nawaby en su sitio. La fortaleza tiene una gran cúpula en su parte superior, pero está medio derruida, como consecuencia del desorden causado por el robo de la joya moktar. Esa cúpula esférica posee una especie de decoración en forma de laberinto en su interior. Al entrar los viajeros en su interior se podrá observar muchos números en las paredes del laberinto. Esos números son números primos (entre los que se ven están 3, 5, 11, 83, 89, 97, 563, 599, 607, 701, 719) que están distribuidos alrededor del centro del laberinto. Al verlos dentro del laberiento, se produce el siguiente diálogo.
– [Constant]: Mire, ¡es increible! ¡Series de números primos! Estudiar todo esto llevará días…
– [Mary]: Quizás más tarde … lo que hace falta ahora es saber dónde colocar el Nawaby.
– [Constant]: Los números primos nos podrán ayudar sin duda… habría que explorar esas cavidades…
– [Mary]: Hum, no creo que sea la pista correcta… Yo seguiría más bien a nuestros amigos…
[Y mira a los hijos de Gholam Mortiza Khan que están en el centro del laberinto, donde efectivamente irá la joya, aunque ese centro donde están los hermanos gemelos está justo al lado de la primera pareja de números primos gemelos, 3 y 5]
 Página de la novela gráfica La teoría del grano de arena, en la que se muestra a Mary Von Rathen, Constant Abeels y los hijos de Gholam Mortiza Khan en la cúpula de la fortaleza de los Moktars
Página de la novela gráfica La teoría del grano de arena, en la que se muestra a Mary Von Rathen, Constant Abeels y los hijos de Gholam Mortiza Khan en la cúpula de la fortaleza de los Moktars
Y ya no sabemos más sobre el significado de los números primos que se encuentran en la cúpula laberíntica de la torre de los Moktars. Puesto que el Nawaby es muy importante para los Mokstar y se encuentra colocado en el centro de un laberinto de números primos, estos deben ser muy importantes, al menos para los Moktars, pero la historia no nos cuenta nada más. Quizás haya que buscarlos en las publicaciones extra, como en El Archivista o El eco de las ciudades.
Para concluir simplemente recomendaros esta interesante serie de novelas gráficas, Las ciudades oscuras, de uno de los grandes del cómic europeo, François Schuiten (dibujo), acompañado en esta serie por el escritor Benoit Peeters.
 Portadas de las dos publicaciones extra, publicadas en español por Norma Editorial, de la serie de novelas gráficas Las ciudades oscuras
Portadas de las dos publicaciones extra, publicadas en español por Norma Editorial, de la serie de novelas gráficas Las ciudades oscurasSobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Los números primos de las ciudades oscuras se ha escrito en Cuaderno de Cultura Científica.
Aprendizaje por refuerzo basado en modelos de máxima entropía
El problema de la toma de secuencias de decisiones que sean globalmente óptimas, a menudo en relación con la disponibilidad de una capacidad de previsión, es relevante para la aplicación de técnicas y modelos de Inteligencia Artificial en ámbitos tan diversos cómo la robótica y las finanzas (Sargent and Stachurski 2024).
Aunque las tomas de decisiones se refieran típicamente al presente, la posibilidad de retrasar la toma de una decisión específica, reservándonos el derecho de tomarla (o de no hacerlo) en un momento futuro bien determinado, es en sí una posible acción, cuyo valor cabe entender y cuantificar (Roman 2004). Cabe preguntarnos: ¿En qué sentidos la opcionalidad es un elemento significativo para la toma de decisiones (o, mejor dicho, en la definición de secuencias óptimas de decisiones)? ¿Como medir la opcionalidad? ¿Cómo utilizarla?
 Foto: Pietro Jeng / UnsplashAprendizaje por refuerzo
Foto: Pietro Jeng / UnsplashAprendizaje por refuerzo
En ciencias de la computación e inteligencia artificial, el aprendizaje automático por refuerzo es un conjunto de metodologías que tiene por objetivo la formulación de secuencias óptimas de decisiones (“políticas”) frente a un entorno (por ejemplo, un videojuego) cuyas reacciones a acciones definidas (cuyas probabilidades de transición) son en principio desconocidas. Usando estas técnicas, un agente automático inteligente aprende a optimizar una recompensa (Malone 1975) que recibe de un entorno simulado o real a las acciones que decide tomar según su observación (potencialmente lagunosa) del estado pasado y actual, determinista y completo o estocástico e incompleto/probabilista del entorno mismo (Sutton and Barto 2018).
La estructura recursiva permite al agente equilibrar recompensas inmediatas con recompensas futuras descontadas.
La limitación fundamental del enfoque de aprendizaje por refuerzo en aplicaciones reales, y especialmente en entornos con espacios de estados y de acciones de alta dimensionalidad y cardinalidad, y potencialmente de limitada observabilidad, se encuentra en su limitada eficiencia en muestreo: llevarlos a la práctica requiere tiempos largos de interacción entre el agente que va aprendiendo y el entorno que observa y sobre en el que acciona, y grandes cantidades de capacidad de cálculo.
Reducir esos costes es valioso, por ejemplo, para poder llevar de forma eficaz herramientas basadas en esas capacidades de gestión óptima a los complejos problemas puestos por las transiciones climático-energética, digital y demográfica.
Esa reducción de costes de entrenamiento puede apoyarse en una extensión de los procedimientos lógicos en base a los cuales se definen los procesos de aprendizaje hacia contextos de incertidumbre como esos entornos desconocidos.
Pero, ¿como juntar probabilidad e incertidumbre, por un lado, y lógica rigurosa por el otro?
La teoría de la probabilidad como lógica extendidaJaynes (1957) redefine la mecánica estadística, que describe las propiedades y la evolución de sistemas físicos conocidos de forma incompleta, a partir de la propuesta que Shannon (1948) formula para la medición del contenido de la información de un mensaje por ejemplo transmitido por una estación radio. Esa medición se basa en la entropía , un valor (esperado) de la probabilidad del propio mensaje (en bits si el logaritmo es en base 2): mensajes “inevitables”, que ya sabemos que vamos a recibir (“lluvia en Donostia”) conllevan información nula, mientras que mensajes más improbables (“has ganado la lotería”) conllevan información progresivamente más significativa.
Jaynes parece proponer sacar la información/entropía de Shannon del ámbito de la comunicación para darle el rol de una (de la) cantidad física fundamental. La cosecha de esa resemantización: es posible llegar de la entropía a cualquier elemento de la mecánica estadística en pocos elegantes pasos.
Un problema es por un lado, según las observaciones del propio Shannon (1956), la dificultad de verificar empíricamente el carácter “primario” de la entropía/información en las ciencias físicas. Un otro problema (Lairez 2024) es puesto por la necesaria extensión de la interpretación de probabilidad frecuentista clásica bien basada en axiomas (Kolmogorov 1933) en la dirección de una interpretación bayesiana: de la frecuencia de un evento en el limite de infinitas repeticiones de un experimento hacia un “grado de creencia” que es a menudo percibido como inherentemente subjetivo (por ejemplo: quien es el “creyente” respecto a quien se define la medición de probabilidad?) y por consecuencia menos científico.
Por otro lado, si un axioma es un punto de partida completamente arbitrario para un desarrollo formal, cabe observar como los “axiomas” de la teoría de la probabilidad en 1957 ya no son definibles como tales: casi una década antes de Jaynes, Cox (1946) ya se pone el problema de definir una extensión de la lógica binaria de Boole (2003 [1854]) a situaciones y enunciados “grises” con valores de verdad asociados intermedios entre el seguramente falso y el absolutamente cierto a partir de pocos requerimientos básicos (Terenin and Draper 2015).
A partir de esos requerimientos básicos, Cox (1946) consigue llegar a los “axiomas” arriba: cualquier medición consistente (cualquier álgebra) de niveles de certidumbre tiene que seguir las reglas de la teoría de la probabilidad. Los “axiomas” de la teoría de la probabilidad por consecuencia ya no son propiamente axiomas, es decir puntos de apoyo arbitrarios para un desarrollo matemático, sino consecuencias directas de unos requerimientos lógicos. Como propone posteriormente Jaynes (2003): la teoría de la probabilidad, interpretada como una extensión de la lógica, puede representar el marco general para el razonamiento y la inferencia en condiciones de incertidumbre — una base directamente relevante para la Inteligencia Artificial. En esa teoría de la probabilidad reinterpretada como una lógica formal para enunciados inciertos, un rol central es asumido por el teorema de Bayes (Bolstad and Curran 2016), que describe las reglas para actualizar, potencialmente de forma recursiva, unos grados de creencia frente a nuevas observaciones, o, para decirlo mejor, una (distribución de valores de grados de) creencia/certidumbre/credibilidad de un enunciado en base a nuevas evidencias (por ejemplo datos numéricos) .
En esa cadena de actualizaciones recursivas, un problema abierto es evidentemente como definir el punto cero, es decir el punto de partida de esa cadena de creencias progresivamente actualizadas: la distribución a priori, que describe asunciones (y potencialmente prejuicios) antes de la adquisición de cualquier dato.
Una posible superación del carácter subjetivo de la interpretación bayesiana de la teoría de la probabilidad pasa nuevamente por el mismo Jaynes (1957), y por su definición, inspirada en Jeffreys (1946), de los métodos de máxima entropía, que derivan formas funcionales y parámetros de una distribución de probabilidad a priori a través de una maximización de la entropía. La distribución a priori de máxima entropía se obtiene maximizando la expresión de la información de Shannon sujeta a condicionantes que expresan todo lo que es noto o asumido sobre . Diferentes asunciones y prejuicios pueden legítimamente corresponder a distribuciones de máxima entropía diferentes, pero convergerán rápidamente a la misma distribución a posteriori en consecuencia de la misma cadena de observaciones.
Aprendizaje por refuerzo basado en modelosEl aprendizaje por refuerzo basado en modelos intenta definir la información a priori disponible sobre un nuevo entorno a explorar/explotar, para reducir los costes del aprendizaje por refuerzo mediante procedimientos para esbozar mapas de su espacio de fases y configuraciones antes de la fase de experimentación/entrenamiento.
Hasta antes de empezar a interaccionar con el entorno, simplemente observándolo desde fuera, los agentes que maximicen (valores esperados, descontados) recompensas correspondientes con la información según Shannon están aprendiendo de forma implícita a aproximar la distribución que describe las transiciones del entorno. Cestero (2024), por ejemplo, muestra como recompensas basadas en la información de Shannon resultan ser ideales para las fases tempranas y de meta-aprendizaje, de forma independiente de la estructura y del sentido de las recompensas a utilizar para las fases de explotación. En este sentido, maximizar la información disponible en fases tempranas parece ser una buena estrategia de meta-aprendizaje y de observación del entorno mediante una interacción no orientada a una explotación específica. Por ejemplo: la Figura 1 describe como mejoran las capacidades de exploración de un agente que hayan sido inicializados con la experiencia de otro agente (su versión “estudiante”) cuya recompensa “abstracta” y no orientada a resultados aplicativos era una medición de la información según Shannon.
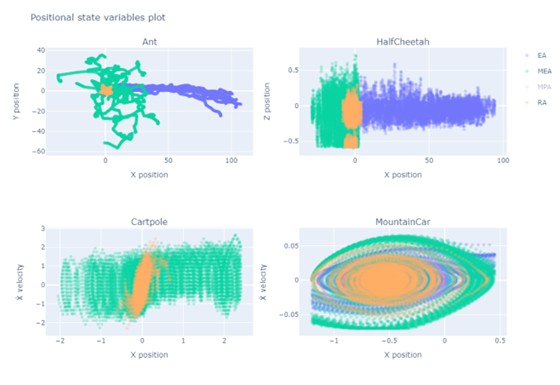 Figura 1: Las capacidades de exploración de un agente inicializado con la experiencia cobrada maximizando la información recolectada (en morado) superan significativamente las alternativas
Figura 1: Las capacidades de exploración de un agente inicializado con la experiencia cobrada maximizando la información recolectada (en morado) superan significativamente las alternativasUna manera de hacer concretas estas capacidades adquiridas mediante una interacción no orientada a resultado es, por ejemplo, el algoritmo SMILE (Mutti, Pratissoli, and Restelli 2021), que busca las configuraciones en el espacio de las fases que maximizan una medición de utilidad futura, por ejemplo, para asociarlas a nuevas acciones secundarias, o compuestas o de más alto nivel, en términos de las cuales definir las políticas óptimas a aprender. Se trata, esencialmente, del aprendizaje de un nuevo vocabulario de acciones, máximamente esparzo e informacional, en el que basar la optimización de Bellman. Para ello, son especialmente valiosos mapas del nivel de opcionalidad que conlleva cada posición en el espacio de las fases. Usando el mapa, el agente puede privilegiar esas posiciones.
Lo que resulta de la experimentación con respecto a la búsqueda de nuevas capacidades (skills), y al definir e incluir automáticamente entre las acciones disponibles nuevas secuencias de decisiones que buscan los estados “más interesantes”, es que es exactamente una medición de información de Shannon, que es capaz de identificar configuraciones en las que es difícil entrar y a partir de las cuales es fácil llegar a numerosas nuevas configuraciones (por ejemplo, una puerta difícil de encontrar que en un laberinto dé acceso a una nueva parte del mismo).
El ejemplo en la Figura 2 abajo representa un entorno de juego de agentes de aprendizaje por refuerzo de tipo taxi (Towers et al. 2024), en el que un agente toma el rol de un conductor que recibe recompensas por recoger y llevar a un pasajero a un destino concreto, extendiendo sus características con una gestión energética de una “gasolina” y teniendo en cuenta los costes de movimiento. El problema del entorno es resuelto por ejemplo mediante optimización de política proximal (Schulman et al. 2017), integrado con el aprendizaje a priori y basado en métodos SMILE de nuevas acciones que directamente llevan el taxi hacia localizaciones en el mapa especialmente valiosas en términos informacionales, entrópicos y de opcionalidad.
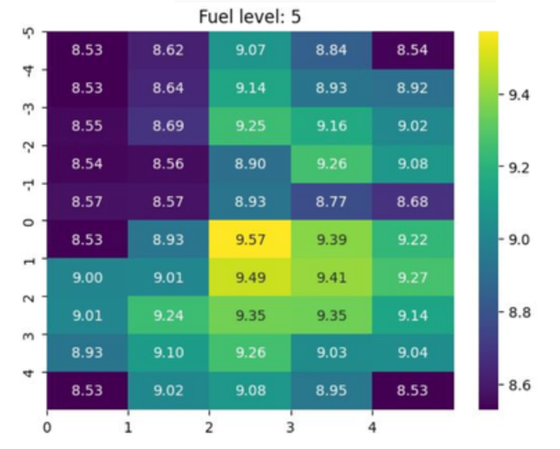 Figura 2: Mapa de opcionalidad en un entorno Taxi Fuel para métodos SMILE
Figura 2: Mapa de opcionalidad en un entorno Taxi Fuel para métodos SMILEA nivel de resultados, el algoritmo de búsqueda a priori de capacidades y estrategias muestra mejoras claras en la exploración y en la identificación de estados de alta opcionalidad, aunque todavía enfrenta dificultades para aprender de manera eficiente ciertas políticas complejas o altamente especializadas. El resultado de ese análisis a priori del entorno a explorar/explotar es en cualquier caso una significativa mejora en la política óptima identificada por el aprendizaje.
Opcionalidad e informaciónLos resultados de Cox indican como la entropía de Shannon representa una medición útil para la toma de decisiones del nivel de opcionalidad de un agente en fase de meta-aprendizaje, es decir, con independencia de la recompensa a definir para la fases “prácticas” sucesivas de exploración/explotación. En este sentido, para contestar a las preguntas iniciales, el valor de la opcionalidad, medida en bits, parece ser evidente sobre todo en fases (¿tempranas?) de meta-aprendizaje, en las cuales (¿todavía?) no estén bien definidos los objetivos a perseguir.
Referencias:
Bolstad, William M, and James M Curran (2016) Introduction to Bayesian Statistics. John Wiley & Sons.
Boole, G. (2003 [1854]) An Investigation of the Laws of Thought: On Which Are Founded the Mathematical Theories of Logic and Probabilities. Edited by John Walton and George Maberly. Cambridge University Press.
Cestero, J., Quartulli, M., Restelli, M. (2024) Building Surrogate Models Using Trajectories of Agents Trained by Reinforcement Learning. In: Wand, M., Malinovská, K., Schmidhuber, J., Tetko, I.V. (eds) Artificial Neural Networks and Machine Learning – ICANN 2024 Lecture Notes in Computer Science, vol 15019. Springer, Cham. doi: 10.1007/978-3-031-72341-4_23
Cox, R. T. (1946) Probability, Frequency, and Reasonable Expectation American Journal of Physics 14 (1): 1–13. doi: 10.1119/1.1990764.
Jaynes, E. T. (1957) Information Theory and Statistical Mechanics The Physical Review 106 (4): 620–30. doi: 10.1103/PhysRev.106.620
Jaynes, E. T. (2003) Probability Theory: The Logic of Science. 1st ed. Cambridge University Press. PDF
Jeffreys, H. (1946) An Invariant Form for the Prior Probability in Estimation Problems Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences 186 (1007): 453–61 JSTOR: http://www.jstor.org/stable/97883.
Kolmogorov, A. N. (1933) Grundbegriffe Der Wahrscheinlichkeitsrechnung. Springer Nature Ergebnisse Der Mathematik 3 (2): 3–47.
Lairez, Didier (2024) Thermostatistics, Information, Subjectivity: Why Is This Association so Disturbing? Mathematics 12 (10). doi: 10.3390/math12101498.
Malone, John C. (1975) William James and BF Skinner: Behaviorism, Reinforcement, and Interest Behaviorism 3 (2): 140–51. JSTOR: https://www.jstor.org/stable/27758839
Mutti, M., L. Pratissoli, and M. Restelli (2021) Task-Agnostic Exploration via Policy Gradient of a Non-Parametric State Entropy Estimate. arXiv arXiv:2007.04640v2 [cs.LG]
Roman, Steven (2004) Introduction to the Mathematics of Finance: From Risk Management to Options Pricing. Springer Science & Business Media.
Sargent, Thomas J, and John Stachurski (2024) Dynamic Programming: Finite States arXiv arXiv:2401.10473v1 [econ.GN]
Schulman, John, Filip Wolski, Prafulla Dhariwal, Alec Radford, and Oleg Klimov (2017) Proximal Policy Optimization Algorithms arXiv arXiv:1707.06347v2 [cs.LG]
Shannon, C. E. (1948) A Mathematical Theory of Communication The Bell System Technical Journal 27: 379–423. doi: 10.1002/j.1538-7305.1948.tb01338.x
Shannon, C. E. (1956) “The Bandwagon (Editorial).” IRE Transactions on Information Theory. Collected Papers Of Claude E. Shannon PDF
Sutton, Richard S., and Andrew G. Barto (2018) Reinforcement Learning: An Introduction. Second Edition. The MIT Press.
Terenin, A., and D. Draper (2015) Cox’s Theorem and the Jaynesian Interpretation of Probability.” arXiv arXiv:1507.06597v3[math.ST]
Towers, Mark, Ariel Kwiatkowski, Jordan Terry, John U. Balis, Gianluca De Cola, Tristan Deleu, Manuel Goulão, et al. (2024) Gymnasium: A Standard Interface for Reinforcement Learning Environments arXiv arXiv:2407.17032v3 [cs.LG]
Sobre el autor: Marco Quartulli es doctor en Electrónica e Informática y responsable del área de Energía y Medio Ambiente de Vicomtech
Sobre Vicomtech: Centro tecnológico espacializado en tecnologías digitales relacionadas con Artificial Intelligence y Visual Computing & Interaction. Transfiere tecnología para que las empresas sean más competitivas y para conseguir un impacto positivo en la sociedad, en coherencia con su compromiso social.

Basque Research & Technology Alliance (BRTA) es una alianza que se anticipa a los retos socioeconómicos futuros globales y de Euskadi y que responde a los mismos mediante la investigación y el desarrollo tecnológico, proyectándose internacionalmente. Los centros de BRTA colaboran en la generación de conocimiento y su transferencia a la sociedad e industria vascas para que sean más innovadoras y competitivas. BRTA es una alianza de 17 centros tecnológicos y centros de investigación cooperativa y cuenta con el apoyo del Gobierno Vasco, SPRI y las Diputaciones Forales de Araba, Bizkaia y Gipuzkoa.
El artículo Aprendizaje por refuerzo basado en modelos de máxima entropía se ha escrito en Cuaderno de Cultura Científica.
Cómo se forman los “pancake domes” de Venus
A menudo decimos que Venus es el planeta gemelo de la Tierra, pero esta comparación solo se sostiene si nos referimos exclusivamente al tamaño y a la composición de ambos. Las distintas misiones espaciales que han viajado al planeta han demostrado que es un mundo tremendamente hostil para los seres humanos y nuestra tecnología en todos los sentidos de la palabra: temperaturas en la superficie que superan los 450ºC, una densa atmósfera compuesta principalmente por dióxido de carbono y una presión aplastante que en su superficie alcanza a ser 92 veces superior a la de la Tierra.
Y no solo hay estas diferencias. Su relieve nos recuerda muy poco al de la Tierra, quizás por la ausencia de una tectónica de placas y una hidrosfera que sean los principales protagonistas de su modelado. Lo que nos sugiere que planetas que pudieron ser muy similares en sus orígenes pueden tener una evolución totalmente diferente.
Algunos autores llegan a segerir que el funcionamiento a nivel geológico hoy podría ser similar al de la Tierra durante el eón Arcaico -entre hace 4000 y 2500 millones de años. Si esto es así podríamos estar ante un análogo perfecto para comprender como era nuestro planeta en esas primeras etapas tras su formación y poder ver que procesos dinámicos existían tanto en la superficie como en su interior.
Hoy vamos a detenernos en unas formas del relieve que aparecen en Venus y que no tienen un equivalente terrestre: Son los pancake domes o, en castellano, los domos tortita. Aunque su nombre nos recuerde más a una dulce delicia culinaria, son una expresión del intenso vulcanismo venusiano.
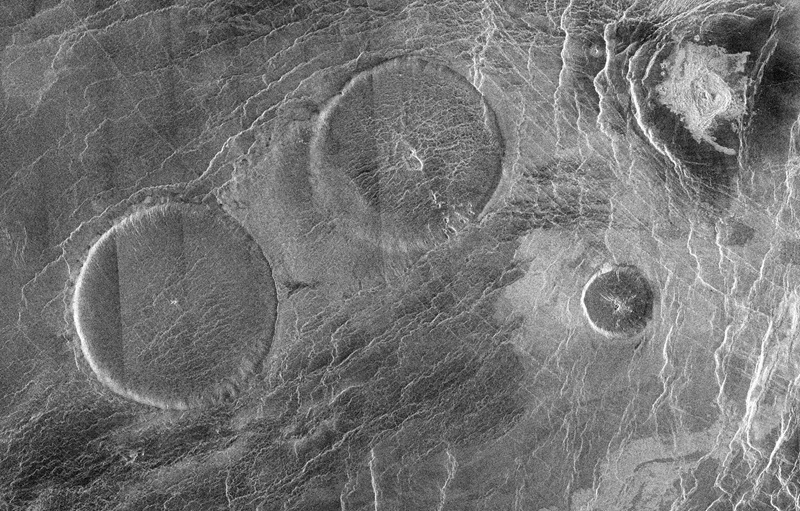 En esta imagen podemos ver al menos tres pancake domes sobre la superficie de Venus gracias al radar de la misión Magellan. Lo más destacable de estos es la forma circular casi perfecta -hasta el punto de que casi parecen cráteres de impacto, aunque al revés- y los sistemas de fracturas que se ven en su superficie, que podrían indicar procesos posteriores relacionados con el enfriamiento de la lava y subsidencia. Imagen cortesía de NASA/JPL.Los pancake domes
En esta imagen podemos ver al menos tres pancake domes sobre la superficie de Venus gracias al radar de la misión Magellan. Lo más destacable de estos es la forma circular casi perfecta -hasta el punto de que casi parecen cráteres de impacto, aunque al revés- y los sistemas de fracturas que se ven en su superficie, que podrían indicar procesos posteriores relacionados con el enfriamiento de la lava y subsidencia. Imagen cortesía de NASA/JPL.Los pancake domes
¿Cómo son estos relieves? Son una especie de mesetas prácticamente circulares cuyo diámetro puede alcanzar las varias decenas de kilómetros y medir alrededor de un kilómetro de altura. Su techo es muy plano, pero los bordes que lo delimitan son muy escarpados. Vamos, como si cogemos un vaso y lo introducimos al revés sobre la arena de la playa, dejando solo visible algo más que su “culo”.
Durante décadas, los científicos han discutido como se formaron -por desgracia nuestra ventana temporal de observación de Venus ha sido muy corta y no hemos visto formarse ninguno- pero todo apunta a que aparecen a partir de la emisión de lava por uno o más puntos de la superficie. Sobre cuál es la composición de las lavas que dan lugar a estos relieves tan característicos también hay distintas teorías que van desde que son lavas muy ricas en sílice y viscosas -similar a las riolitas terrestres- a composiciones más basálticas, en las cuales la lava es más fluida.
Precisamente, la composición de la lava no sería suficiente para explicar cómo podían adquirir estas formas tan concretas, ya que se asume que la litosfera -la capa más externa y rígida de los planetas- y sobre la que aparecían estas coladas de lava, es completamente rígida, algo que en el caso de Venus sería bastante difícil.
Pero un estudio recién publicado por Borrelli et al. (2024) muestra que la historia es, efectivamente, un poco más complicada. Han observado muestras de flexión en la litosfera -zonas donde esta se dobla o se pliega- alrededor de 14 domos de 75 estudiados, demostrando que esta no es completamente rígida. Así, la gran carga de materiales volcánicos que se sitúa sobre la litosfera sería capaz de provocar un hundimiento de esta y generar una depresión que, en ocasiones, vendría acompañada de un pequeño pliegue -como una especie de chichón que se formaría en las proximidades del domo. Algo que no se había tenido en cuenta en los modelos anteriores donde la corteza se comportaba de manera excesivamente rígida.
La corteza de Venus es flexible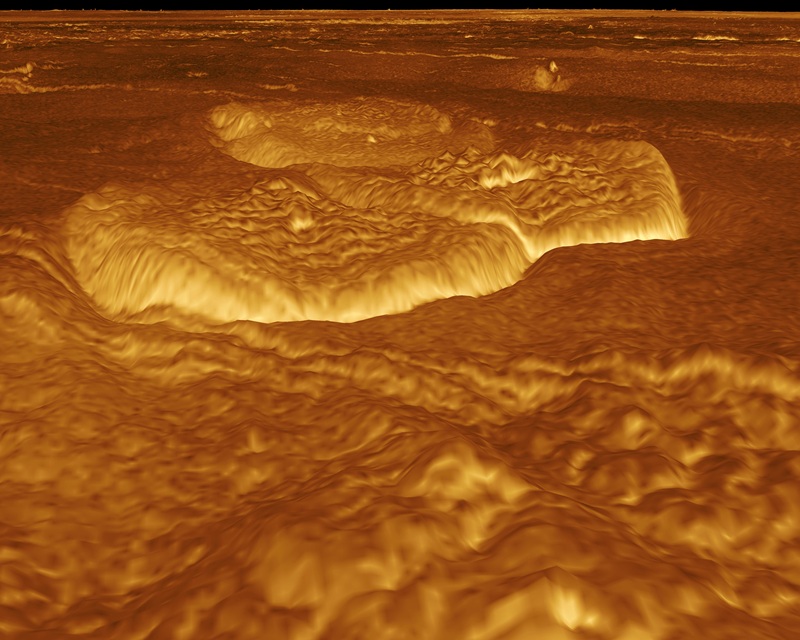 Reconstrucción tridimensional de unos pancake domes a partir de datos de la Magellan. Una cosa muy característica de estos son sus escarpadas laderas sobre la llanura circundante. Imagen cortesía de NASA/JPL.
Reconstrucción tridimensional de unos pancake domes a partir de datos de la Magellan. Una cosa muy característica de estos son sus escarpadas laderas sobre la llanura circundante. Imagen cortesía de NASA/JPL.En este estudio, los científicos han modelado la formación de estos domos como una colada de lava que se desparrama sobre una litosfera elástica capaz de deformarse por el peso de la propia lava, como si apretásemos un bote de miel y la dejásemos caer sobre un folio que tenemos cogido con ambas manos.
Este pequeño cambio tiene grandes consecuencias. En primer lugar, el suelo que hay debajo de la lava comienza a hundirse como respuesta al peso y, por lo tanto, al tiempo que va haciéndose más profundo necesita un mayor volumen de lava para formar los domos.
En segundo lugar, la forma de esta depresión flexural y del “chichón” que antecede a los domos -y que no aparece en todos los casos- está relacionada con el contraste de densidades entre la lava que forma el domo y el manto que hay por debajo, así como por la propia elasticidad de la litosfera. Esto puede parecer una obviedad, pero es importantísimo, ya que de algún modo un mejor estudio de los domos y otras formas del relieve pueden darnos pistas sobre el estado de la litosfera y el mismo manto simplemente estudiando su respuesta a la deformación y al peso.
Uno de los resultados más importantes de este estudio es que la flexión de la litosfera tiene una influencia clave sobre la morfología del domo. Y es que la aparición de la flexura tiende a hacer la superficie de los domos más planas y sus bordes más escarpados, un aspecto que encaja perfectamente con las observaciones de los domos de Venus. Esto sirve como apoyo para la idea de que la flexura en sí misma no es solo una consecuencia pasiva del proceso eruptivo que emplaza las lavas en la superficie, sino que de manera activa da forma y moldea a estos domos.
Pero hay más. Han estudiado un domo del que hay datos de muy buena calidad tomados por las misiones espaciales, Narina Tholus. De este se ha podido obtener un buen modelo topográfico donde se aprecian señales de la flexura. Sobre este domo han podido comparar la salida de los distintos modelos numéricos -en los que han ido variando los distintos parámetros- y la topografía real, obteniendo unos detalles sobre los posibles procesos de formación muy interesantes.
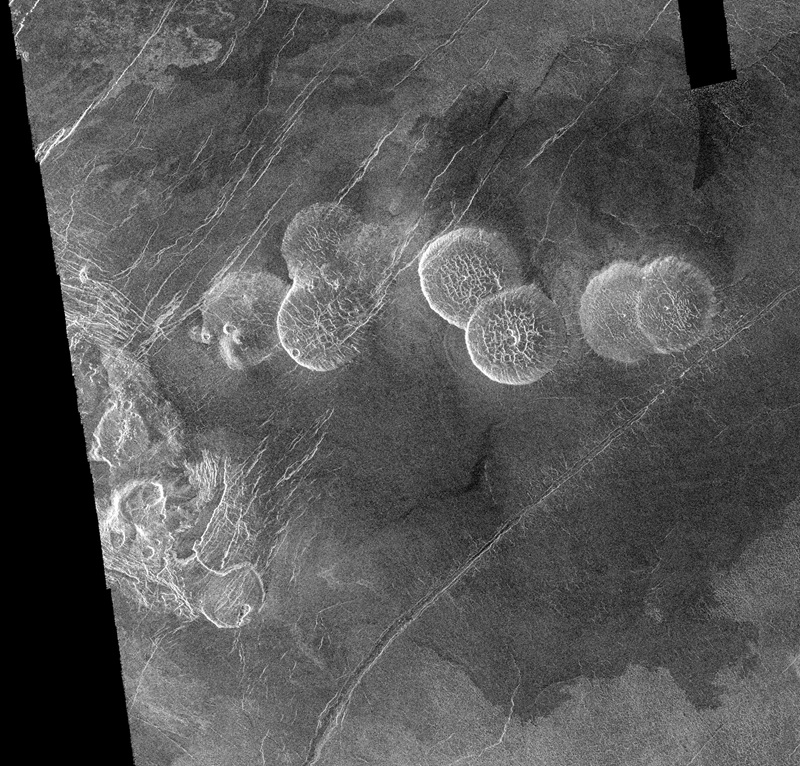 Distintos pancake domes situados en Alpha Regio, en Venus. De media, los que vemos en la imagen tienen unos 25 kilómetros de diámetro y unos 750 metros de altura. Es llamativo que en el centro de algunos de estos aparece una depresión similar a un cráter, probablemente también fruto de la subsidencia del propio domo tras cesar la inyección de la lava. Imagen cortesía de NASA/JPL.
Distintos pancake domes situados en Alpha Regio, en Venus. De media, los que vemos en la imagen tienen unos 25 kilómetros de diámetro y unos 750 metros de altura. Es llamativo que en el centro de algunos de estos aparece una depresión similar a un cráter, probablemente también fruto de la subsidencia del propio domo tras cesar la inyección de la lava. Imagen cortesía de NASA/JPL.Uno de los resultados más destacables es que la lava de los domos podría estar extendiéndose por la superficie durante mucho tiempo tras el final de la erupción. De hecho, en este caso, las simulaciones muestran que este proceso pudo durar entre 30.000 y 300.000 años, mucho más de los que suelen durar las erupciones más convencionales.
Esto implicaría que una gran parte de la forma de estos domos se consigue a través de procesos de relajación viscosa tiempo después del final de la actividad volcánica. Este mecanismo que estaría facilitado por las altas temperaturas de la superficie de Venus, que mantendría la lava caliente durante mucho más tiempo, facilitando su movimiento.
La cuestión de la densidad de la lavaPero, además, han podido estimar la densidad de la lava que formó Narina Tholus y la horquilla de sus cálculos se encuentra en el orden de los 2.400 a los 2.700 kg/m3, un dato que es algo problemático. Es más alto que lo que esperarían para una lava con alto contenido en sílice y altamente vesicular (con “burbujas” formadas por los gases que escapan de la lava), como pueden ser las riolitas, por ejemplo.
Y, de hecho, lavas con densidades aún más bajas, pero que autores anteriores postulaban que podrían formar estos domos (hablamos de densidades alrededor de 1.500 kg/m3) no son capaces de producir la suficiente flexura para ajustarse a la forma del domo, ya que no tendrían una densidad suficiente para forzar una curvatura tan importante de la litosfera.
Esto a su vez implica que la lava que ha formado este domo no tendría una gran cantidad de volátiles. En cambio, la densidad calculada es consistente con otras posibilidades adicionales. Podría ser una lava silícea más densa como la andesita, pero más pobre en gas o, incluso, una lava basáltica algo vesicular.
Como podéis ver, estas posibilidades nos pueden parecer algo dispares, pero en realidad acotan bastante el rango de la composición química de la lava y descartan en cualquier caso una alta vesicularidad de la lava y por lo tanto, las posibilidades con menor densidad.
Mientras llegan las próximas misiones a Venus, en especial la EnVision de la ESA y la VERITAS de la NASA, estos nuevos modelos sobre los procesos que ocurren en Venus pueden servirnos como un punto de partida para interpretar mejor una superficie que todavía sigue llena de preguntas por resolver y, quien sabe, si quizás tendremos la oportunidad de ver crecer alguno de estos domos.
Referencias
Borrelli, M. E., Michaut, C., & O’Rourke, J. G. (2024). Formation of Pancake Domes on Venus as Viscous Flows Over an Elastic Lithosphere. Preprints. doi: 10.22541/essoar.172108546.66381561/v1
Borrelli, M. E., O’Rourke, J. G., Smrekar, S. E., & Ostberg, C. M. (2021). A Global Survey of Lithospheric Flexure at Steep‐Sided Domical Volcanoes on Venus Reveals Intermediate Elastic Thicknesses. Journal of Geophysical Research: Planets, 126(7), e2020JE006756. doi: 10.1029/2020JE006756
Ghail, R. C., Smrekar, S. E., Widemann, T., Byrne, P. K., Gülcher, A. J. P., O’Rourke, J. G., Borrelli, M. E., Gilmore, M. S., Herrick, R. R., Ivanov, M. A., Plesa, A.-C., Rolf, T., Sabbeth, L., Schools, J. W., & Gregory Shellnutt, J. (2024). Volcanic and Tectonic Constraints on the Evolution of Venus. Space Science Reviews, 220(4), 36. doi: 10.1007/s11214-024-01065-2
Quick, L. C., Glaze, L. S., Baloga, S. M., & Stofan, E. R. (2016). New approaches to inferences for steep-sided domes on Venus. Journal of Volcanology and Geothermal Research, 319, 93-105. doi: 10.1016/j.jvolgeores.2016.02.028
Sakimoto, S. E. H., & Zuber, M. T. (1995). The spreading of variable-viscosity axisymmetric radial gravity currents: Applications to the emplacement of Venusian ‘pancake’ domes. Journal of Fluid Mechanics, 301, 65-77. doi: 10.1017/S0022112095003806
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Cómo se forman los “pancake domes” de Venus se ha escrito en Cuaderno de Cultura Científica.
Resistencia y anticorrosión en elementos de fijación bimetálicos estampados en caliente
En múltiples sectores industriales existe una gran demanda de componentes con geometrías específicas que combinen eficazmente buenas propiedades mecánicas con alta resistencia a la corrosión en entornos agresivos. Por ejemplo, elementos de sujeción expuestos a entorno marino, componentes de suspensión en automoción o herramientas de mano son algunos de estos componentes. Gracias a las nuevas tecnologías de fabricación aditiva, es posible la producción de piezas bimetálicas, es decir, piezas compuestas por un material en su cuerpo principal, pero con recubrimiento de otro metal, que cumplen con estos requisitos.
 Foto: Shaun Dakin / Unsplash
Foto: Shaun Dakin / UnsplashEn esta línea, en el proyecto ReIMAGIN, financiado por el programa ELKARTEK del Gobierno Vasco, se ha desarrollado un estudio sobre la fabricación de cilindros híbridos mediante recargue por láser (DED-LB), aplicando una capa de acero inoxidable AISI 316 sobre un substrato de acero estructural con buenas propiedades mecánicas, concretamente 42CrMo4. Esta combinación busca aprovechar la resistencia mecánica del acero base y la protección frente a la corrosión del recubrimiento, proponiendo una solución eficaz para componentes de altas prestaciones. Entre las aplicaciones potenciales se encuentran elementos de sujeción en entornos offshore, herramientas de mano, sistemas de suspensión y, en general, piezas sometidas tanto a cargas mecánicas elevadas como a medios agresivos. Dentro de la fabricación de este tipo de piezas, uno de los procesos de conformado más empleados es la forja o estampación en caliente. Este proceso puede tener influencia tanto en la unión bimetálica formada mediante el proceso DED-LB como en las propiedades anticorrosivas del material de recubrimiento. Por ello, se decidió investigar cuál sería el efecto de esta deformación en caliente sobre cilindros recargados con inoxidable.
El recubrimiento inicial se realizó mediante la técnica DED-LB, empleando como substrato cilindros de 42CrMo4 de 50 mm de diámetro por 70 mm de longitud. Sobre este substrato se depositó una capa de 1 mm del acero inoxidable 316. Tras esta fabricación inicial, se realizaron procesos de forja en caliente a 850 ºC y a 1250 ºC con distintos grados de deformación, simulando condiciones industriales de alta exigencia.
 Cilindros recargados a los que se han aplicado distintos grados de deformación mediante estampado en caliente, siendo 60% la deformación máxima. Fuente: Centro de Investigación Metalúrgica AZTERLAN (Todos los derechos reservados; cesión en exclusiva para el Cuaderno de Cultura Científica).
Cilindros recargados a los que se han aplicado distintos grados de deformación mediante estampado en caliente, siendo 60% la deformación máxima. Fuente: Centro de Investigación Metalúrgica AZTERLAN (Todos los derechos reservados; cesión en exclusiva para el Cuaderno de Cultura Científica).Posteriormente, se aplicaron diferentes tratamientos térmicos para analizar el efecto combinado de la temperatura y la deformación sobre la microestructura y el comportamiento frente a la corrosión del recargue de inoxidable 316. Antes de nada, se identificó mediante líquidos penetrantes el umbral de deformación a partir del cual comienzan a aparecer defectos superficiales. A 850 ºC no se detectan grietas relevantes hasta deformaciones del 30 %, mientras que a 1250 °C los recubrimientos se mantienen aparentemente íntegros hasta deformaciones del 45 %.
El análisis microestructural de los recargues de inoxidable AISI 316 se ha realizado mediante microscopía óptica y electrónica. En el estado inicial (as clad, previo a la forja), el recubrimiento muestra una microestructura típicamente dendrítica, con carburos de cromo dispersos y sin indicios de sensibilización (acumulación de carburos de cromo en los bordes de grano). Sin embargo, las microestructuras de las piezas estampadas en caliente muestran una evolución clara hacia la sensibilización, especialmente a temperaturas elevadas; a 850 °C, se observan bordes de grano marcados, aunque se mantienen también los carburos de cromo dispersos por la matriz. A 1250 °C, no obstante, la sensibilización es completa en todas las muestras, incluso en aquellas con baja deformación, indicando que la temperatura, más que la deformación, es el factor determinante en este fenómeno.
Finalmente, los ensayos de corrosión acelerada en niebla salina confirmaron estos resultados microestructurales. Las muestras as clad y las estampadas a 850 °C resistieron la exposición durante 96 horas sin oxidación, salvo en aquellas zonas concretas que presentaban grietas ya detectadas por líquidos penetrantes. Al contrario, las muestras estampadas a 1250 °C mostraron una oxidación total del recubrimiento después de tan solo 24 horas, indicando una pérdida completa de su funcionalidad anticorrosiva.
 Microestructuras e imágenes de piezas sometidas a ensayo de niebla salina: as clad (izquierda), estampada a 850ºC con 45% de deformación (centro) y estampada a 1250ºC con 45% de deformación (derecha). Fuente: Centro de Investigación Metalúrgica AZTERLAN (Todos los derechos reservados; cesión en exclusiva para el Cuaderno de Cultura Científica).
Microestructuras e imágenes de piezas sometidas a ensayo de niebla salina: as clad (izquierda), estampada a 850ºC con 45% de deformación (centro) y estampada a 1250ºC con 45% de deformación (derecha). Fuente: Centro de Investigación Metalúrgica AZTERLAN (Todos los derechos reservados; cesión en exclusiva para el Cuaderno de Cultura Científica).
En conclusión, los resultados de este estudio demuestran que la estrategia de fabricar componentes bimetálicos mediante recargue láser DED-LB es viable, siempre que se controlen cuidadosamente las condiciones térmicas a las que se someten las piezas durante los procesos posteriores. El acero inoxidable 316 puede mantener sus propiedades anticorrosivas incluso tras deformaciones intensas, siempre que no se supere el umbral crítico de temperatura (entre 850 ºC y 1250 ºC) que activa la sensibilización. Con vistas a aplicaciones industriales, esto abre la puerta al diseño de componentes híbridos que ofrezcan un buen equilibrio entre resistencia mecánica y durabilidad frente a la corrosión.
Sobre el autor: Xabier Lasheras. AZTERLAN Metallurgy Research Centre
Sobre AZTERLAN: Con el firme compromiso de impulsar el desarrollo tecnológico y la competitividad de las empresas, AZTERLAN cuenta con más de 45 años de experiencia ofreciendo soporte tecnológico, conocimiento metalúrgico experto y soluciones avanzadas a la industria de transformación metal-mecánica y a sus sectores cliente.

Basque Research & Technology Alliance (BRTA) es una alianza que se anticipa a los retos socioeconómicos futuros globales y de Euskadi y que responde a los mismos mediante la investigación y el desarrollo tecnológico, proyectándose internacionalmente. Los centros de BRTA colaboran en la generación de conocimiento y su transferencia a la sociedad e industria vascas para que sean más innovadoras y competitivas. BRTA es una alianza de 17 centros tecnológicos y centros de investigación cooperativa y cuenta con el apoyo del Gobierno Vasco, SPRI y las Diputaciones Forales de Araba, Bizkaia y Gipuzkoa.
El artículo Resistencia y anticorrosión en elementos de fijación bimetálicos estampados en caliente se ha escrito en Cuaderno de Cultura Científica.
La memoria de la Tierra. El reconocimiento internacional del patrimonio geológico

¿Qué tienen en común un paisaje espectacular, un fósil milenario y una cantera abandonada? Todos forman parte del patrimonio geológico, un testimonio de la historia de la Tierra con un gran valor científico, educativo, cultural y estético. Sin embargo, su importancia continúa siendo poco apreciada.
Para acercar las distintas aproximaciones del patrimonio geológico a la sociedad, los días 26, 27 y 28 de marzo se celebró la quinta edición de las jornadas divulgativas “Geología para poetas, miopes y despistados. Patrimonio patrimonio”. Organizadas por el grupo de investigación consolidado Procesos Hidro-Ambientales (HGI) de la Facultad de Ciencia y Tecnología de la Universidad del País Vasco (UPV/EHU), estas jornadas contaron con la colaboración del Vicerrectorado del Campus de Bizkaia, la Cátedra de Cultura Científica de la UPV/EHU, el Geoparque de la Costa Vasca / Geoparkea y el Ente Vasco de la Energía (EVE).
En esta charla Asier Hilario, presidente de la Comisión Internacional sobre Geopatrimonio de la International Union of Geological Sciences (IUGS), nos explica el concepto de patrimonio geológico y como ha ido evolucionando con el tiempo.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo La memoria de la Tierra. El reconocimiento internacional del patrimonio geológico se ha escrito en Cuaderno de Cultura Científica.
Las respuestas demográficas al cambio climático al final del Paleolítico
Un nuevo estudio liderado por la Universidad de Colonia y con la participación de 25 investigadores de toda Europa ha descubierto cómo afectó el cambio climático hace más de 12.000 años a las poblaciones humanas prehistóricas. La investigación ha descubierto cambios significativos en el tamaño y la densidad de la población durante periodos clave al final de la última Edad de Hielo, concretamente durante el Paleolítico final, hace entre 14.000 y 11.600 años. Los datos para la península ibérica han sido sintetizados por nvestigadores de la Universidad del Algarve (Portugal) y de la Universidad del País Vasco / Euskal Herriko Unibertsitatea. Concretamente, Alvaro Arrizabalaga, del Grupo Consolidado de Investigación en Prehistoria GIZAPRE (EHU), es coautor de este estudio.
La investigación se centra en dos periodos clave: la mejoría climática que se produjo en el Paleolítico final, entre los años 14.000 y 12.500, (el llamado GI-1d-a) y el enfriamiento climático breve que se desarrolla entre hace unos 12.500 y 11.600 años, al final de la última glaciación . Este último periodo, llamado Dryas Reciente ( GS-1), representa el último coletazo frío del Pleistoceno y da paso al ciclo climático Holoceno, en el que nos encontramos todavía en la actualidad.
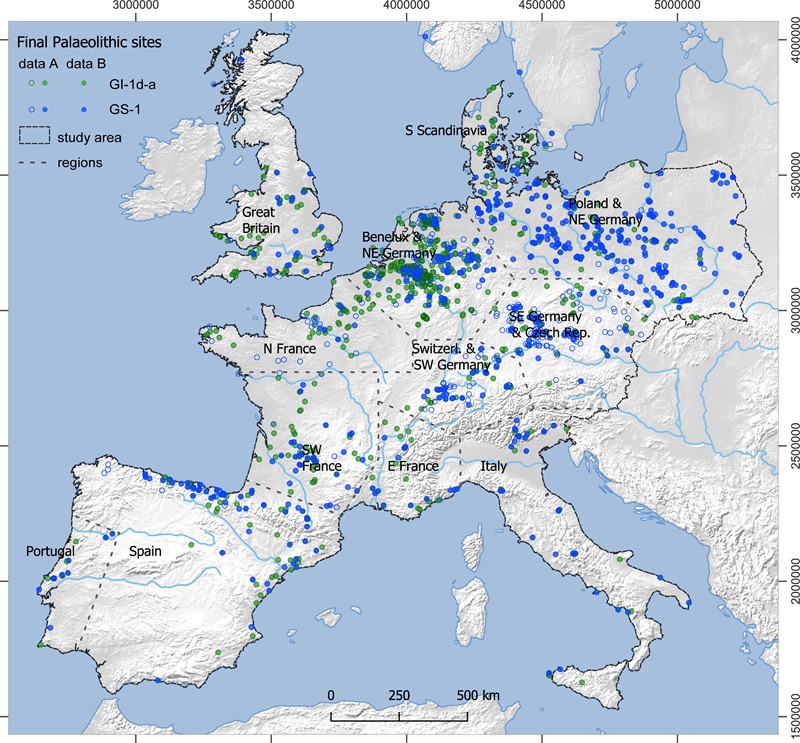 Localizaciones de los yacimientos objeto del estudio. Fuente: Schmidt et al (2025) PLoS ONE doi: 10.1371/journal.pone.0310942 CC BY 4.0
Localizaciones de los yacimientos objeto del estudio. Fuente: Schmidt et al (2025) PLoS ONE doi: 10.1371/journal.pone.0310942 CC BY 4.0El Protocolo de Colonia
Utilizando una innovadora metodología geoestadística, llamada Protocolo de Colonia, y una amplia base de datos arqueológicos, los investigadores estimaron los cambios en tamaño y densidad poblacional sobre diferentes marcos regionales en Europa entre hace 14.000 y 11.600 años.
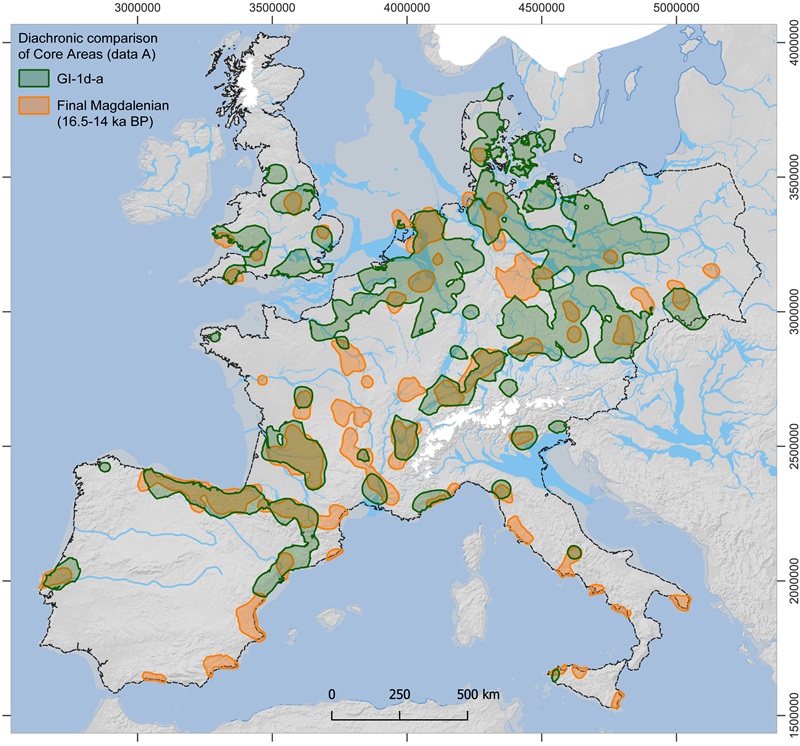 Comparación diacrónica de los principales núcleos poblacionales en dos periodos. Fuente: Schmidt et al (2025) PLoS ONE doi: 10.1371/journal.pone.0310942 CC BY 4.0
Comparación diacrónica de los principales núcleos poblacionales en dos periodos. Fuente: Schmidt et al (2025) PLoS ONE doi: 10.1371/journal.pone.0310942 CC BY 4.0Durante el primer período de mejoría climática (GI-1d-a), los humanos continuaron repoblando y expandiéndose hacia el norte y noreste de Europa central, convirtiendo esta región en el centro de la dinámica demográfica en Europa por primera vez en toda la Prehistoria. Las poblaciones del suroeste de Europa, sobre todo en la Península ibérica y Francia, empezaron a disminuir en comparación con los datos demográficos de los periodos precedentes.
Como consecuencia del repentino enfriamiento, a lo largo del Dryas Reciente, los datos muestran que la población europea se pudo reducir hasta la mitad. Sin embargo, en algunas zonas del centro y este europeo como el norte de Italia, Polonia y el noreste de Alemania, la densidad poblacional incluso aumentó.
Reacción demográfica
Para los investigadores, este fenómeno es una muestra de lo rápido que los humanos prehistóricos reaccionaron frente al cambio climático. «Nuestros datos sugieren que muchas comunidades humanas emigraron hacia el este para adaptarse al nuevo clima, en lugar de desaparecer», explica Isabell Schmidt, del Departamento de Arqueología Prehistórica de la Universidad de Colonia, que lidera la publicación. El estudio pone de relieve que, a diferencia del anterior periodo de colapso poblacional (durante el Gravetiense, hace unos 25.000 años), los humanos del Paleolítico final respondieron emigrando a zonas aparentemente más favorables.
Referencia:
Schmidt I, Gehlen B, Winkler K, Arrizabalaga A, Arts N, Bicho N, et al (2025) Large scale and regional demographic responses to climatic changes in Europe during the Final Palaeolithic PLoS ONE doi: 10.1371/journal.pone.0310942
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Las respuestas demográficas al cambio climático al final del Paleolítico se ha escrito en Cuaderno de Cultura Científica.
Fumatas geológicas en los fondos marinos
Hace unas semanas, medio mundo estuvo pendiente del color del humo que salía de una estrecha chimenea situada en el tejado de un edificio de una minúscula ciudad estado situada en la capital italiana. Pues, aunque no os lo creáis, esta situación es muy habitual entre las geólogas y los geólogos, aunque, en nuestro caso, no levantamos la vista al cielo para observar esas fumatas. En realidad, debemos sumergirnos en el fondo oceánico para vigilar nuestras propias chimeneas. Me estoy refiriendo a las fumarolas o venas hidrotermales submarinas.
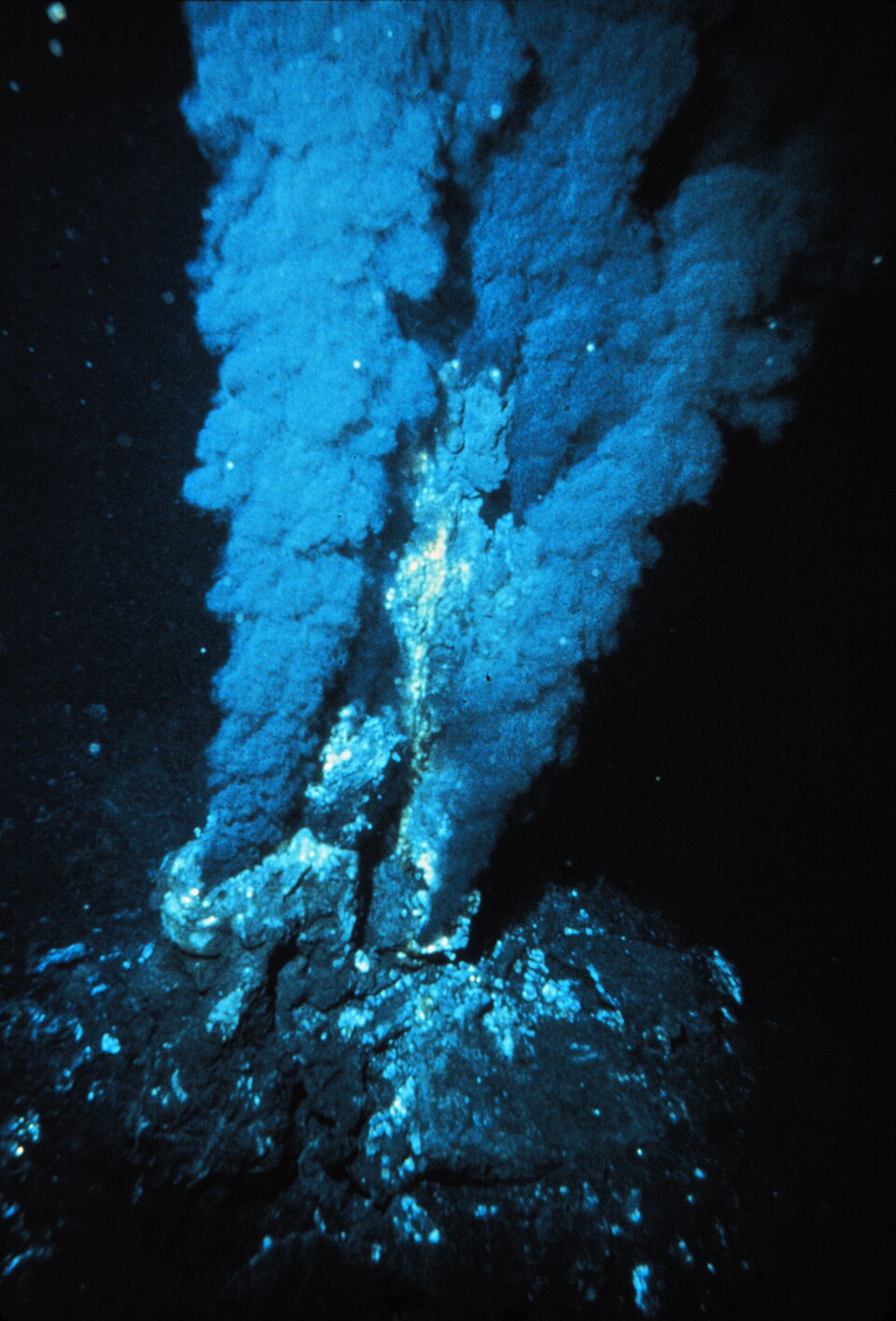 Fumarola negra en la vena hidrotermal de la dorsal centro-Atlántica. Fuente: P. Rona / OAR/National Undersea Research Program (NURP); NOAA – NOAA Photo Library, Dominio público, Wikimedia Commons
Fumarola negra en la vena hidrotermal de la dorsal centro-Atlántica. Fuente: P. Rona / OAR/National Undersea Research Program (NURP); NOAA – NOAA Photo Library, Dominio público, Wikimedia CommonsLas fumarolas son unas estructuras geológicas que se forman en los fondos oceánicos debido a un ciclo del agua muy particular. Este viaje comienza cuando el agua marina se infiltra en la corteza terrestre a través de fracturas del terreno y empieza a circular por el interior del subsuelo donde se calienta, muchas veces debido a que pasa cerca de depósitos magmáticos, pudiendo alcanzar temperaturas superiores a los 300ºC. Con estas temperaturas, el agua es capaz de captar los elementos químicos que componen las rocas que atraviesa en su viaje subterráneo, llevándolos disueltos con ella. Cuando se topa con nuevas fracturas, el agua asciende y vuelve a salir al fondo marino, liberando entonces los gases y minerales que arrastraba, los cuales, tras sufrir un enfriamiento muy brusco al contactar con el agua oceánica, precipitan formando unas estructuras tubulares que pueden alcanzar varios metros de altura.
Imaginaos la escena. Os encontráis con unas enormes estructuras tubulares de las que salen gases a gran temperatura desde su parte superior, pero que se encuentran en los fondos marinos, a varios miles de metros de profundidad. De ahí que, de manera informal, también se las conozca como chimeneas submarinas.
 Fumarola blanca en la vena hidrotermal Champagne, asociada a los volcanes submarinos Eifuku del Océano Pacífico (cerca de Japón). Fuente: NOAA – Dominio público, Wikimedia Commons
Fumarola blanca en la vena hidrotermal Champagne, asociada a los volcanes submarinos Eifuku del Océano Pacífico (cerca de Japón). Fuente: NOAA – Dominio público, Wikimedia CommonsVolviendo al símil del principio, aquí también podemos encontrarnos con fumarolas negras. En este caso, el color de los minerales y los gases que expulsan estas venas hidrotermales se debe a que, en su composición, dominan los sulfuros de hierro, de cobre, de cinc y de otros metales que tienen una coloración en tonos oscuros y negros. Y también tenemos fumarolas blancas, formadas por fluidos hidrotermales no tan calientes como los de las fumarolas negras (250-300ºC) y que precipitan silicatos de calcio, bario y otros minerales alcalinos de colores claros y blanquecinos.
Pero las fumarolas submarinas no son solo una curiosidad geológica presente en una parte aún poco conocida de nuestro planeta, los fondos oceánicos. Sino que también son clave en el estudio de la dinámica interna de la Tierra. Como os comentaba anteriormente, este proceso se asocia a depósitos magmáticos submarinos, principalmente a los procesos volcánicos de las dorsales oceánicas, que son zonas donde se está formando nueva corteza terrestre, haciendo que se separen entre sí dos placas tectónicas. De hecho, las fumarolas negras suelen aparecer en zonas cercanas a las dorsales, mientras que las fumarolas blancas se generan en áreas más alejadas de las mismas. Vamos, que estudiar el comportamiento y formación de estas chimeneas submarinas nos da pistas para comprender lo que está sucediendo bajo tierra mientras se forma nueva corteza en las dorsales oceánicas.
Aunque su interés no termina aquí. Las fumarolas se pueden considerar como grandes acumulaciones o depósitos de minerales formados por metales y otros elementos químicos con un gran interés económico y comercial. Su estudio, por tanto, nos aporta una valiosa información científica sobre los procesos geológicos que contribuyen a la formación de estos recursos minerales, lo que nos permite buscar yacimientos minerales en superficie que tuviesen un origen similar hace millones de años.
También nos informan sobre uno de los recursos geológicos más en boga actualmente, la energía geotérmica. Como su propio nombre indica, esta nueva fuente de energía, totalmente renovable e inagotable, se basa en utilizar el calor del interior de la Tierra. Y, en las fumarolas, este calor subterráneo está disponible en forma de gases o vapor que sale al exterior en los fondos submarinos, cuya energía calorífica podría ser transformada en energía eléctrica.
 Grandes colonias de gusanos tubícolas asociados a una fumarola negra en la vena hidrotermal Sully, presente en el gran campo de venas hidrotermales Endeavour del Océano Pacífico noroccidental. Fuente: NOAA – Dominio Público. Wikimedia Commons
Grandes colonias de gusanos tubícolas asociados a una fumarola negra en la vena hidrotermal Sully, presente en el gran campo de venas hidrotermales Endeavour del Océano Pacífico noroccidental. Fuente: NOAA – Dominio Público. Wikimedia Commons Pero he dejado para el final la mayor curiosidad geológica de estas estructuras. Cuando vemos una grabación de las fumarolas en plena acción, nos vienen a la mente representaciones medievales del mismísimo Infierno. Nos encontramos en medios ambientes con valores extremos de pH, tanto muy ácidos como muy alcalinos, con agua y gases a temperaturas muy altas, totalmente rodeadas de metales y elementos químicos tóxicos como el metano o el dióxido de carbono. Pues, en realidad, son auténticos vergeles de vida. Aquí se desarrollan ecosistemas únicos donde proliferan organismos que se han adaptado y han evolucionado para prosperar en entornos muy hostiles, encontrándonos con enormes gusanos tubícolas, bivalvos gigantescos, crustáceos de conchas transparentes y otros seres que parecen salidos de los peores sueños de H. P. Lovecraft. Aunque si hay alguna forma de vida que destaca sobre las demás, esas son las bacterias extremófilas. Pequeños seres que se alimentan de sulfuro, nitrógeno o metano, acostumbrados a vivir en medios con temperaturas elevadísimas, y que fueron las primeras formas de vida de nuestro planeta. Por lo que estudiar las comunidades de bacterias y arqueas que proliferan en las fumarolas submarinas nos permitirá comprender, al menos, cómo evolucionó la vida primigenia en la Tierra.
Creo que ahora ya comprendéis por qué las geólogas y los geólogos miramos con tanta atención estas chimeneas, fijándonos también en color de la fumata que sale de su parte superior. Estas curiosas estructuras submarinas nos permiten conocer mejor la dinámica interna de nuestro planeta, los ciclos geoquímicos de la Tierra y el origen y evolución de la vida en entornos extremos. Y, posiblemente, eso sea lo que las ha salvado, al menos de momento, porque tener una fuente casi inagotable de recursos minerales de interés económico a nuestra disposición, es una gran tentación. Espero que el interés científico siga primando por mucho tiempo.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Fumatas geológicas en los fondos marinos se ha escrito en Cuaderno de Cultura Científica.
Inmersión, un cómic empapado de matemáticas (I)
Acabo de terminar de leer el cómic Inmersión (Hill House Comics – DC Black Label; ECC Ediciones, 2021), de Joe Hill (guion), Stuart Immonen (dibujo) y Dave Stewart (color), que tiene muchas referencias matemáticas, de las cuales vamos a hablar en esta entrada del Cuaderno de Cultura Científica.
 Portada de la edición en español, publicada por ECC Ediciones en 2021, del cómic Inmersión, de Joe Hill (guion) y Stuart Immonen (dibujo), que recoge los seis números/grapas que lo conforman
Portada de la edición en español, publicada por ECC Ediciones en 2021, del cómic Inmersión, de Joe Hill (guion) y Stuart Immonen (dibujo), que recoge los seis números/grapas que lo conforman
En la propia portada del recopilatorio de los seis números que componen el cómic Inmersión, que es del artista estadounidense Jeremy Wilson, ya vemos diferentes símbolos que, aunque quizás no reconozcamos, sí los identificamos como símbolos matemáticos.
Un cómic de Joe Hill, Stuart Immonen y Dave Stuart
Los seis números del cómic Inmersión (Plunge, en inglés), creado por el escritor estadounidense Joe Hill, responsable también de su guion, dibujado por el artista canadiense Stuart Immonen y coloreado por el artista del color estadounidense Dave Stewart, fueron publicados originalmente por Hill House Cómics, una línea editorial de cómics de terror creada y dirigida por Joe Hill, dentro del sello editorial DC Black Label de DC cómics.
El escritor y creador de cómics estadounidense Joseph Hillstrom King (1972), cuyo nombre artístico es Joe Hill, es un autor destacado dentro de los géneros literarios de terror, fantasía oscura y ciencia ficción. Entre las novelas escritas por Joe Hill están El traje del muerto (2007) o NOS4A2 (2013), mientras que dentro de la ficción gráfica es el autor de los guiones de comics como Locke & Key (2008-13), La capa (2007-2011) o Un cesto de cabezas (2019). Como anécdota diremos que este galardonado escritor es el hijo del famoso escritor de misterio y terror Stephen King (1947).
 Fotografía del escritor y creador de cómics Joe Hill y portada de su novela NOS4A2 (Nosferatu)
Fotografía del escritor y creador de cómics Joe Hill y portada de su novela NOS4A2 (Nosferatu)
Stuart Immonen es un dibujante de cómics canadiense que ha trabajado tanto para cómics de DC cómics, como Action comics (1997-1999), Inferno (1997), Las aventuras de Superman (1995-2000), Superman: End of the Century (2000) o Superman: Identidad secreta (2004), entre otros, como para cómics de Marvel, como Los 4 fantásticos (2001-2009), Nextwave: Agentes de H.A.T.E (2006-07), Los nuevos vengadores (2009-2011), Miedo encarnado (2011), El increíble Spiderman (2017-18), entre muchos otros.
 Fotografía del dibujante Stuart Immonen y portada del cómic Nextwave: Agentes de H.A.T.E, escrito por Warren Ellis y dibujado por Stuart Immonen
Fotografía del dibujante Stuart Immonen y portada del cómic Nextwave: Agentes de H.A.T.E, escrito por Warren Ellis y dibujado por Stuart Immonen
Finalmente, el color de los dibujos de Inmersión se debe al artista Dave Stewart, cuyo trabajo ha sido galardonado en diferentes ediciones de los prestigiosos Premios Eisner. Entre sus trabajos destacan AIDP (2006-2020), Baltimore (2010-2017), Fatale (2013-2015), Black Hammer (2017-2025), Sherlock Frankenstein y la legión del mal (2018), Gideon Falls (2019-2021), Hellboy (2020-2024), entre muchos otros, que incluyen las últimas portadas de The Walking Dead.
 Portadas del volumen 1 de Black Hammer (2017) y Gideon Falls (2019), cuyo colorista es Dave Stewart
Portadas del volumen 1 de Black Hammer (2017) y Gideon Falls (2019), cuyo colorista es Dave StewartInmersión, de Joe Hill
El escritor Joe Hill, el dibujante Stuart Immonen y el colorista Dave Stewart se juntaron para crear este cómic de terror, que intenta homenajear al género de terror de los años ochenta. Mientras lo leía me vinieron a la cabeza dos referencias del género de terror, por una parte, una película clásica de terror de los años ochenta, La cosa (1983), del director estadounidense John Carpenter (1948), pero también un clásico del terror como es el escritor estadounidense H. P. Lovecraft (1890-1937) y sus mitos de Cthulhu. De hecho, el propio Joe Hill menciona la ciudad submarina de R’lyeh, un lugar ficticio de los mitos de Cthulhu, que según su autor estaba situada en la latitud 47°9′ sur y la longitud 126°43′ oeste en el océano Pacífico, como un punto de partida en su relato de horror.
Un par de curiosidades relacionadas con R’lyeh. La primera es que el escritor August W. Derleth (1909-1971), del círculo de Lovecraft, también utilizó la ciudad sumergida de R’lyeh en sus escritos. Además, su nombre, como veremos más adelante, aparece mencionado en el cómic Inmersión. La segunda curiosidad es que la primera vez que aparece la ciudad submarina de R’lyeh, que es el lugar en el que habita aletargada la entidad cósmica Cthulhu, es en el relato corto de H. P. Lovecraft La llamada de Cthulhu (1926). En este relato puede leerse la siguiente descripción de la ciudad.
Sin conocer el futurismo, Johansen describe, al hablar de la ciudad, algo muy parecido a una obra futurista. En vez de referirse a una estructura definida, algún edificio, se reduce a hablar de vastos ángulos y superficies pétreas… superficies demasiado grandes para ser de este mundo, y cubiertas por jeroglíficos e imágenes horribles. Menciono estos ángulos pues me recuerdan los sueños que me relató Wilcox. El joven escultor afirmó que la geometría de la ciudad de sus sueños era anormal, no euclidiana, y que sugería esferas y dimensiones distintas de las nuestras. Ahora un marino ilustrado tenía ante la terrible realidad la misma impresión.
En la misma se hace mención a la geometría no euclideana, así como a esferas y dimensiones distintas de las nuestras. Pero dejemos a Lovecraft y volvamos a nuestro cómic lovecraftiano Inmersión.
 Portada de la edición de 2017 de la editorial Alma, dentro de su colección Clásicos Ilustrados (la ilustración es del artista, escritor y diseñador inglés John Coulthart), del relato corto La llamada de Cthulhu (1926), de H. P. Lovecraft
Portada de la edición de 2017 de la editorial Alma, dentro de su colección Clásicos Ilustrados (la ilustración es del artista, escritor y diseñador inglés John Coulthart), del relato corto La llamada de Cthulhu (1926), de H. P. Lovecraft
Esta es la sinopsis escrita sobre el cómic en la página web de la editorial ECC:
En 1983, el Derleth, un buque de perforación de última generación, desaparece cerca del Círculo Polar Ártico. Décadas más tarde empieza a emitir una señal de socorro…
La compañía petrolífera Rococo sigue la señal hasta un remoto atolón del Estrecho de Bering y contrata a los hermanos Carpenter y su tripulación de rescate para investigar el barco fantasma. Junto con una bióloga marina y un ejecutivo petrolífero, los hermanos se embarcan en una siniestra misión para averiguar las causas de la desaparición del barco y recuperar los cuerpos de la tripulación… ¡pero resulta que los hombres del Derleth no están muertos! Aunque tampoco están ya del todo… vivos…
Como vemos hay dos referencias claras en la sinopsis. Por una parte, el buque de perforación que desapareció en 1983 es el Derleth, que nos remite al círculo de Lovecraft. Por otra parte, dos de los personajes de la historia son los hermanos Carpenter, que nos hace pensar que la asociación con la película La cosa (1982) no es casual, sino intencionada.
Las portadas de las grapas del cómic Inmersión
Las matemáticas están muy presentes en este cómic de terror creado por Joe Hill, tanto en la historia, como en la estética, puesto que ya desde las portadas, así como en las páginas de los créditos, de los seis números que componen este cómic, están presentes las matemáticas.
En la siguiente imagen se muestran las seis portadas de la publicación original de Inmersión (Plunge), que realizó el artista Jeremy Wilson.
 Portadas de la edición original (en inglés) de los números #1-6 del cómic Plunge / Inmersión, de Joe Hill, Stuart Immonen y Dave Stewart
Portadas de la edición original (en inglés) de los números #1-6 del cómic Plunge / Inmersión, de Joe Hill, Stuart Immonen y Dave Stewart
En las dos primeras portadas aparecen símbolos matemáticos como si hubiesen sido sacados de una pizarra, aunque muy mezclados unos con otros. En la tercera portada, que veremos con más detalle ahora, vemos a una persona ante una pared que está llena de números. En las portadas de los números cuatro y cinco no hay números, ni símbolos matemáticos. Y en la última portada nos encontramos con una espiral de Arquímedes (más o menos) en blanco.
Pero volvamos a la portada del número tres. Como se puede ver en la siguiente imagen el número que aparece pintado en la pared es el número pi (para saber un poco más sobre este número véase la entrada ¿Es normal el número pi? ). En la primera línea podemos ver 3.1415926535; en la segunda línea 89793238462643383279; en la tercera línea 5028841971693993751058209; y así siguen muchas más líneas con los distintos decimales del número pi.
 Portada de la edición original (en inglés) del número #3 del cómic Plunge / Inmersión, de Joe Hill, Stuart Immonen y Dave Stewart, en la que aparecen los primeros decimales del número pi
Portada de la edición original (en inglés) del número #3 del cómic Plunge / Inmersión, de Joe Hill, Stuart Immonen y Dave Stewart, en la que aparecen los primeros decimales del número piMatemáticas hasta en los créditos
En la página de créditos, que en todos los números va en la parte del principio, salvo en el número seis, también nos encontramos matemáticas. Todas las páginas de créditos son el dibujo oscuro, con sombras, de una parte del buque Derleth medio hundido, como en la siguiente imagen.
 Página de créditos de la edición original (en inglés) del número #1 del cómic Plunge / Inmersión, de Joe Hill, Stuart Immonen y Dave Stewart
Página de créditos de la edición original (en inglés) del número #1 del cómic Plunge / Inmersión, de Joe Hill, Stuart Immonen y Dave Stewart
Como podemos observar en esta imagen, en una plancha de metal del barco, a la izquierda en la imagen, al lado de una puerta metálica, vemos una fórmula matemática, que parece pintada en sangre, pero escrita de tal manera que a la izquierda tenemos una expresión matemática que es igual a la parte de la derecha, que es un número que va a coincidir con el número de entrega de la serie, por lo que en este caso está pintado el número 1. La fórmula que aparece en la plancha metálica es correcta, de hecho, en este caso es la famosa fórmula de Euler, conocida como la fórmula más hermosa de las matemáticas.
 Esta es una imagen con la famosa fórmula de Euler, de la exposición Mathematical Photography de Justin Mullins, que podéis ver en el portal divulgamat o en la página web de su autor, Justin Mullins
Esta es una imagen con la famosa fórmula de Euler, de la exposición Mathematical Photography de Justin Mullins, que podéis ver en el portal divulgamat o en la página web de su autor, Justin Mullins
Además, como vemos, se incluye un número, en concreto, el número 1, en el título del cómic, en inglés “P1unge” (un “1” en lugar de la letra “ele”) y en español “1nmersión” (un “1” en lugar de la “i”). Y si nos fijamos un poco más en los nombres responsables del cómic aparece un “3”, en lugar de una “e”, en el nombre de uno de los dos productores, Mark Doyl3 y Amadeo Turturro.
Esta idea de sustituir letras de los créditos por números o símbolos matemáticos va a ir aumentando en cada entrega del cómic, hasta la sexta y última grapa que vemos en la siguiente imagen, en la que además cambia un poco el formato, separando la imagen del buque, con el número de entrega (sexta), y los créditos.
 Páginas de créditos de la edición original (en inglés) del número #6 del cómic Plunge / Inmersión, de Joe Hill, Stuart Immonen y Dave Stewart
Páginas de créditos de la edición original (en inglés) del número #6 del cómic Plunge / Inmersión, de Joe Hill, Stuart Immonen y Dave Stewart
Los nombres de los responsables del cómic (guion, dibujo, color, editores, portada, portada alternativa y creado por) ya son completamente irreconocibles por los números y símbolos matemáticos que aparecen, así como el título, Plunge (en inglés), que vemos en la anterior imagen cómo está escrito, e Inmersión (en español), que está escrito así: “1 = # 3 ? 5 1 0 =”.
Si observamos la fórmula matemática de la plancha metálica, que nos da igual a 6, ya que estamos en el número seis de la publicación, podemos observar que también es una expresión matemática correcta (bueno, hay una pequeña errata ya que falta una x, pero la idea está bien). De hecho, es un límite del tipo 0/0 que se calcula mediante la conocida regla de L’Hopital (el nombre deriva del matemático francés Guillaume François Antoine, marqués de l’Hopital (1661-1704), aunque el resultado es realmente del matemático suizo Johann Bernoulli (1667-1748), de hecho, esa es una interesante historia que ya contaremos en otra ocasión) para el cálculo de límites de la forma 0/0 (cero / cero) o (infinito / infinito), que consiste en derivar numerador y denominador.
Incluyamos la regla de L’Hopital simplemente para entender un poco mejor la fórmula que aparece en el cómic, aunque sin darle más importancia de la necesaria.
Regla de L’Hopital: Sean f y g dos funciones continuas definidas en un intervalo [a, b], derivables en el intervalo abierto (a, b) y sea c perteneciente a dicho intervalo (a, b) tal que f(c) = g(c) = 0 y g‘(x) distinto de 0, si x = c.
Si existe el límite L de f ‘ / g‘ (las derivadas) en c, entonces existe el límite de f / g (en c) y es igual a L. Por lo tanto,
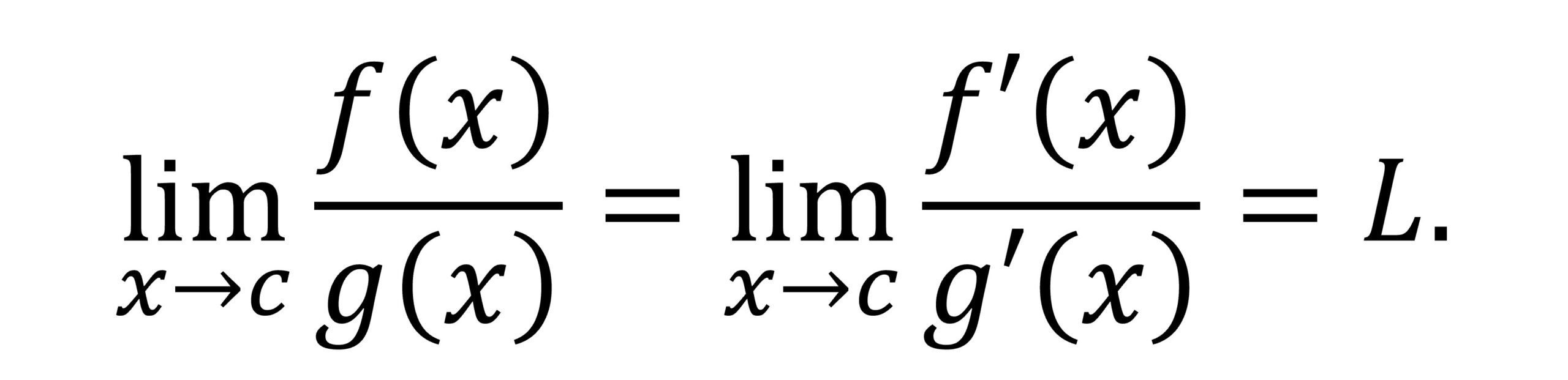
La imagen que aparece en el cómic, corregida, sería la siguiente.
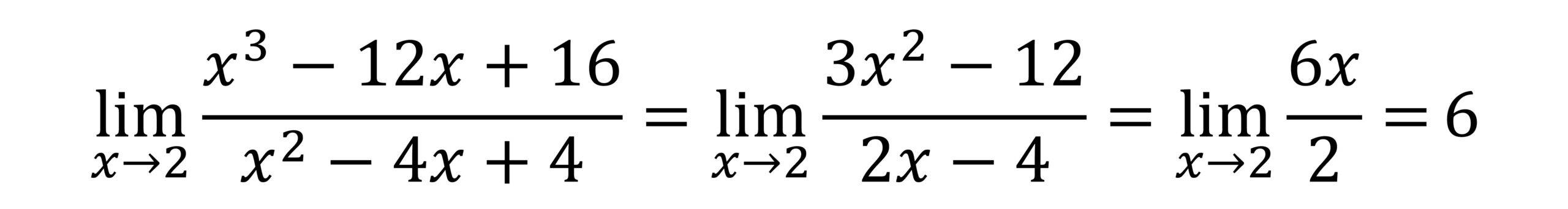 Expresión del cálculo de un límite del tipo 0/0 utilizando la regla de L’Hopital, que aparece en el número seis del cómic Inmersión
Expresión del cálculo de un límite del tipo 0/0 utilizando la regla de L’Hopital, que aparece en el número seis del cómic Inmersión
En las páginas de créditos de los números #2, #3, #4 y #5 también aparecen fórmulas matemáticas, pintadas como si fuera sangre, integrales, derivadas y límites.
 Páginas de créditos de los números #2, #3, #4 y #5 de la edición original (en inglés) del cómic Plunge / Inmersión, de Joe Hill, Stuart Immonen y Dave Stewart
Páginas de créditos de los números #2, #3, #4 y #5 de la edición original (en inglés) del cómic Plunge / Inmersión, de Joe Hill, Stuart Immonen y Dave StewartLas matemáticas contribuyen a crear el ambiente de terror del cómic. Diagramas y símbolos matemáticos, listas de números (los decimales del número pi), así como fórmulas matemáticas pintadas de rojo, como si fuera sangre que está goteando, fórmulas extrañas, raras, frías, sin ningún significado para la persona que lee el cómic.
En la siguiente entrada del Cuaderno de Cultura Científica abordaremos las matemáticas que aparecen en la propia historia del cómic.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Inmersión, un cómic empapado de matemáticas (I) se ha escrito en Cuaderno de Cultura Científica.
Un aumento en el límite sin repetidores nos acerca a la criptografía cuántica comercial
La criptografía cuántica promete comunicaciones seguras basadas en las leyes fundamentales de la física. Sin embargo, llevar esta tecnología del laboratorio al mundo real es todo un reto, especialmente debido a las pérdidas de señal en largas distancias. Un reciente presenta un avance significativo en este aspecto: un sistema de distribución de claves cuánticas (QKD, por sus siglas en inglés) que supera el llamado «límite sin repetidores» utilizando tecnologías ya disponibles comercialmente.
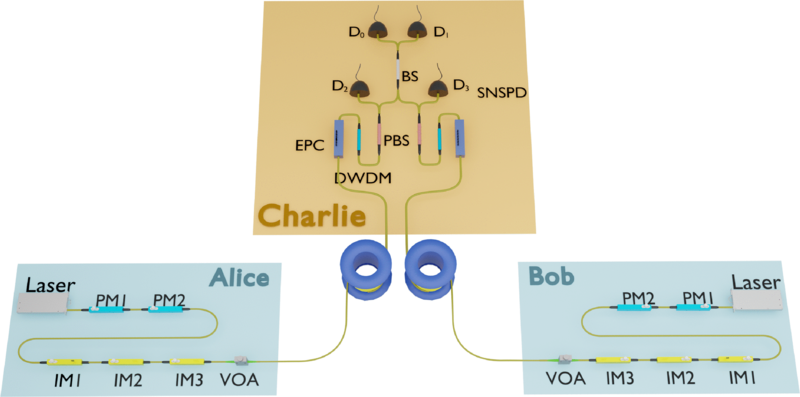 Source: Likang Zhang et al (2025) Phys. Rev. X doi: 10.1103/PhysRevX.15.021037 CC BY 4.0¿Qué es el «límite sin repetidores»?
Source: Likang Zhang et al (2025) Phys. Rev. X doi: 10.1103/PhysRevX.15.021037 CC BY 4.0¿Qué es el «límite sin repetidores»?
En la distribución de claves cuánticas las señales se transmiten a través de fibras ópticas. A medida que la distancia aumenta la señal se debilita debido a la pérdida de fotones. Este fenómeno impone un límite teórico conocido como el «límite sin repetidores», que establece la máxima distancia a la que se puede transmitir una clave cuántica sin utilizar dispositivos intermedios que amplifiquen o regeneren la señal.
El planteamiento por defecto hasta ahora ha sido que superar este límite requiere el uso de repetidores cuánticos, dispositivos complejos y costosos que ni siquiera se puede decir que existan porque aún están en desarrollo. La alternativa ha sido desarrollar protocolos que optimicen la transmisión sin necesidad de estos repetidores.
El protocolo de emparejamiento de modosEl estudio introduce una implementación práctica del protocolo de emparejamiento de modos (MP-QKD), una técnica que permite distribuir claves cuánticas sin necesidad de una referencia de fase global. Sin necesidad de entrar en profundidades, el resultado es que esto simplifica significativamente el sistema y reduce los requisitos técnicos.
Una de las principales innovaciones del trabajo es la utilización de láseres comerciales, en lugar de los costosos láseres ultraestables que se han venido empleando. Para manejar las fluctuaciones de fase inherentes a estos láseres, los investigadores han desarrollado un esquema de seguimiento de frecuencia basado en la transformada rápida de Fourier. Esta técnica permite extender la longitud de emparejamiento de los pulsos, mejorando la eficiencia del sistema.
El sistema desarrollado logró una tasa óptima de generación de claves secretas a través de 403 kilómetros de fibra óptica estándar, con una pérdida de 76,5 decibelios. Este rendimiento aumenta el límite sin repetidores en un factor de casi 3, un logro sin precedentes utilizando tecnologías comerciales.
Más cerca del mundo realLa posibilidad de utilizar componentes comerciales reduce significativamente los costos y la complejidad de los sistemas de QKD, facilitando su adopción en aplicaciones del mundo real. Esto podría tener un impacto considerable en áreas como la banca, la defensa y las infraestructuras críticas, donde la seguridad de las comunicaciones es esencial.
El estudio demuestra que la criptografía cuántica práctica y escalable es una realidad alcanzable con las tecnologías actuales, marcando un hito en la evolución de las comunicaciones seguras.
Referencias:
Likang Zhang, Wei Li, Jiawei Pan, Yichen Lu, Wenwen Li, Zheng-Ping Li, Yizhi Huang, Xiongfeng Ma, Feihu Xu, and Jian-Wei Pan (2025) Experimental Mode-Pairing Quantum Key Distribution Surpassing the Repeaterless Bound Phys. Rev. X doi: 10.1103/PhysRevX.15.021037
Day, C. (2025) Toward Practical Quantum Cryptography Physics 18, s53
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Un aumento en el límite sin repetidores nos acerca a la criptografía cuántica comercial se ha escrito en Cuaderno de Cultura Científica.

