El lugar de nacimiento y las probabilidades de ser futbolista profesional
 Partido clasificatorio de la Eurocopa 2025 entre España y Bélgica en el estadio de Riazor (2024). En la imagen, Alexia Putellas.
Partido clasificatorio de la Eurocopa 2025 entre España y Bélgica en el estadio de Riazor (2024). En la imagen, Alexia Putellas.Wikimedia Commons., CC BY
Si pudiéramos por un segundo desarrollar una herramienta capaz de detectar el próximo Lamine Yamal o Nico Williams, o la próxima Alexia Putellas o Salma Paralluelo, seguro que seríamos de las personas más perseguidas por la industria deportiva. Siendo el fútbol uno de los deportes de mayor impacto social y económico, es cada vez mayor la inversión que los distintos clubes realizan en sus canteras para encontrar y formar a las futuras estrellas del fútbol.
Durante muchos años, la investigación relacionada con la detección de estrellas futbolísticas estaba suscrita al debate de si el futbolista nace o se hace. Este interrogante ha ocupado centenares de investigaciones y ha evolucionado desde una visión dicotómica hasta el reconocimiento de la compleja interacción de factores genéticos y ambientales.
Mientras que la predisposición genética desempeña un papel crucial en el rendimiento, la práctica deliberada y las influencias ambientales son esenciales para hacer realidad el potencial genético.
La identificación del talento debe adoptar un enfoque multidimensional y dinámico, y afrontarse desde la interacción de todos los factores, ya sean innatos (genéticos, antropométricos…), adquiridos (entrenamiento) o contextuales (familia, lugar de nacimiento…).
Ciudad mediana, un buen punto de partidaNuestra investigación se ha centrado en conocer cómo el lugar de nacimiento influye en el desarrollo del futbolista, tanto en su participación como en su rendimiento deportivos.
Estudios previos sugieren que nacer en determinados tamaños de ciudad, normalmente ciudades más pequeñas o medianas, puede suponer ventajas en el desarrollo del talento.
Entre los motivos que contribuyen a este efecto se encuentran la proximidad a instalaciones deportivas y la estructura social.
 Lamine Yamal después de que la selección española ganara la Eurocopa 2024. Fuente:
Lamine Yamal después de que la selección española ganara la Eurocopa 2024. Fuente:Wikimedia Commons., CC BY
En una revisión sistemática centrada en el fútbol, se ha observado que la combinación de la densidad de población y el nivel de las instalaciones del lugar de nacimiento son cruciales, existiendo una relación entre el lugar de nacimiento y el rendimiento futbolístico.
Como idea general, se ha observado que, en ciudades de mayor tamaño y densidad, aumentan las posibilidades de alcanzar un estatus profesional en el fútbol. Este fenómeno se atribuye a diversas razones como un mayor número posible de clubes y oportunidades competitivas disponibles en las zonas urbanas.
Las características sociodemográficas de las poblaciones más grandes como renta media más alta, mejores instalaciones deportivas, entrenadores más cualificados o estructuras competitivas más profundas también pueden contribuir al desarrollo del talento futbolístico.
No obstante, aunque las ciudades más grandes ofrecen muchas ventajas, algunos estudios sugieren que las ciudades más pequeñas pueden fomentar asimismo el desarrollo del talento, al ofrecer un entorno comunitario más solidario y menos competencia por las plazas en los clubes locales. Esto puede permitir una atención más individualizada y más oportunidades.
Un puzle complejoEn cualquier caso, como todo lo relacionado con el desarrollo del talento, no se debe entender el lugar de nacimiento como un factor aislado, sino como algo dinámico que interactúa con otros factores de diversas formas.
Así, por ejemplo, se ha observado que, para ingresar en una academia de fútbol, los jugadores provenientes de zonas con mayor densidad de población tenían más probabilidades de ser seleccionados inicialmente. Sin embargo, una vez dentro de la academia, las probabilidades de debutar profesionalmente eran mayores para los jugadores de zonas de menor densidad.
Del lugar de nacimiento al lugar de crecimientoEsto lleva a la necesidad de una investigación más profunda relacionada con el “lugar de desarrollo”. Porque parece evidente que, en el mundo actual, donde la globalización impera y provoca movimientos migratorios laborales, el lugar de nacimiento no tiene por qué coincidir con el lugar donde las personas crecen y reciben su formación.
En un estudio realizado en una academia de fútbol, se observó que los jugadores que experimentaron una transición geográfica –cambio de su municipio de nacimiento a otro lugar de crecimiento deportivo– tenían aproximadamente un 38 % más de probabilidades de debutar en el equipo profesional.
Este hallazgo indica que la movilidad geográfica puede aumentar las oportunidades de éxito en el fútbol, y sugiere que es necesario considerar ambos lugares como variables conjuntas para comprender los procesos de gestión del talento.
En resumen, el lugar de origen y el lugar donde se crece desempeñan un papel crucial en la configuración del rendimiento y las oportunidades de los jugadores de fútbol. En general, el vínculo con el tamaño de la población es complejo, con ventajas y desventajas según el contexto específico. Toda la investigación al respecto insiste en la naturaleza polifacética del desarrollo del talento, abogando por un enfoque que considere tanto los factores individuales como los contextuales.![]()
Sobre las autoras: Alberto Lorenzo Calvo, Profesor Titular de Universidad de Procesos de Detección y Desarrollo en el Talento Deportivo, Universidad Politécnica de Madrid (UPM); Julio Calleja-Gonzalez, Catedrático de Entrenamiento Deportivo, Universidad del País Vasco / Euskal Herriko Unibertsitatea; Lander Hernández Simal, Licencia UEFA PRO, Responsable del Departamento de Formación y Desarrollo del Athletic Club (Bilbao), Profesor del Grado en Ciencias de la Actividad Física y del Deporte de la Universidad de Deusto; y Maite Aurrekoetxea Casaus, Profesora Doctora en Sociología en la Facultad de Ciencias Sociales y Humanas, Universidad de Deusto.
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo El lugar de nacimiento y las probabilidades de ser futbolista profesional se ha escrito en Cuaderno de Cultura Científica.
Aprendiendo Geología mientras buscamos oro en Alaska
Estos días de vacaciones navideñas en los que el tiempo andaba revuelto y no invitaba a salir a disfrutar de un agradable paseo, he remoloneado en el sofá delante de la tele. Y un día, haciendo zapping de manera despreocupada, me encontré con una serie tipo docu-reality en la que se muestra el trabajo diario de varios equipos de minería en Alaska, con un título muy directo y evocativo: La Fiebre del Oro. Y digo evocativo porque hace alusión directa a esa locura colectiva que ocurrió en Norteamérica a finales del siglo XIX que condujo a muchos hombres a abandonarlo todo y marcharse a lugares remotos con una pala en una mano y un tamiz en la otra, convencidos de que iban a encontrar la pepita de oro que les haría millonarios. Locura que, visto lo visto en el programa, parece que sigue vigente. Pero lo que llamó mi atención en esta serie no fueron las aventuras y desventuras de estas personas, sino el hecho de que, intercaladas entre las habituales labores de minería, se encontraban pequeñas animaciones con explicaciones geológicas para que pudiésemos entender de dónde salía ese oro o porqué los jefes mineros se centraban en buscar ciertas rocas o niveles de tierra muy concretos. Incluso, defendían el uso de algunas técnicas geológicas para asegurarse de que podrían obtener beneficios económicos con sus explotaciones. Así que hoy voy a haceros un pequeño resumen de lo que nos han querido mostrar en esta serie de televisión.
 Hombre bateando los sedimentos de la playa de Nome, en Alaska, buscando oro en 1900. Imagen de los hermanos Lomen, conservada en el The McMahan Photo Art Gallery and Archive.
Hombre bateando los sedimentos de la playa de Nome, en Alaska, buscando oro en 1900. Imagen de los hermanos Lomen, conservada en el The McMahan Photo Art Gallery and Archive.Los depósitos de oro de Alaska se formaron hace menos de 150 millones de años, debido a varios procesos de colisión que se produjeron por el acercamiento de la Placa tectónica del Pacífico y la Placa tectónica Norteamericana. En este contexto no solo se formaron diversas cadenas montañosas, también se favoreció el ascenso de varias acumulaciones de magma hacia la parte superior de la corteza y se generaron muchas zonas de fractura. Asociados a esos magmas aparecieron fluidos calientes que fueron atrapando todos los elementos químicos presentes en las rocas de su alrededor, incluido el oro. Y en cuanto estos fluidos se encontraban con una fractura, empezaron a ascender hacia la superficie, dando lugar a unas mineralizaciones de cuarzo ricas en oro que, en Geología, se denominan diques y, en minería, se conocen como filones.
Pero su historia no termina aquí. En los últimos 20 millones de años, los ríos se han encargado de erosionar estos diques y arrastrar el oro corriente abajo, hacia su desembocadura, depositando el mineral en las zonas curvadas del cauce donde el agua perdía fuerza. Y, en los últimos 2 millones de años, el hielo también se ha sumado al arrastre de oro desde su depósito original, acumulándolo en áreas deprimidas en la zona del frente de avance de los glaciares. Estos depósitos de oro generados por el efecto del agua, tanto líquida como sólida, se conocen como placeres, y son lo que los equipos mineros actuales buscan explotar. Por este motivo cavan la tierra hasta llegar a niveles en los que encuentran una mezcla de arcillas con abundantes fragmentos de cuarzo y rocas redondeadas, ya que son las chivatas de que han sido arrastradas y erosionadas por el agua desde un filón mineralizado. Entonces hacen una batea manual para ver si también incluye oro y determinar si es rentable explotar ese material.
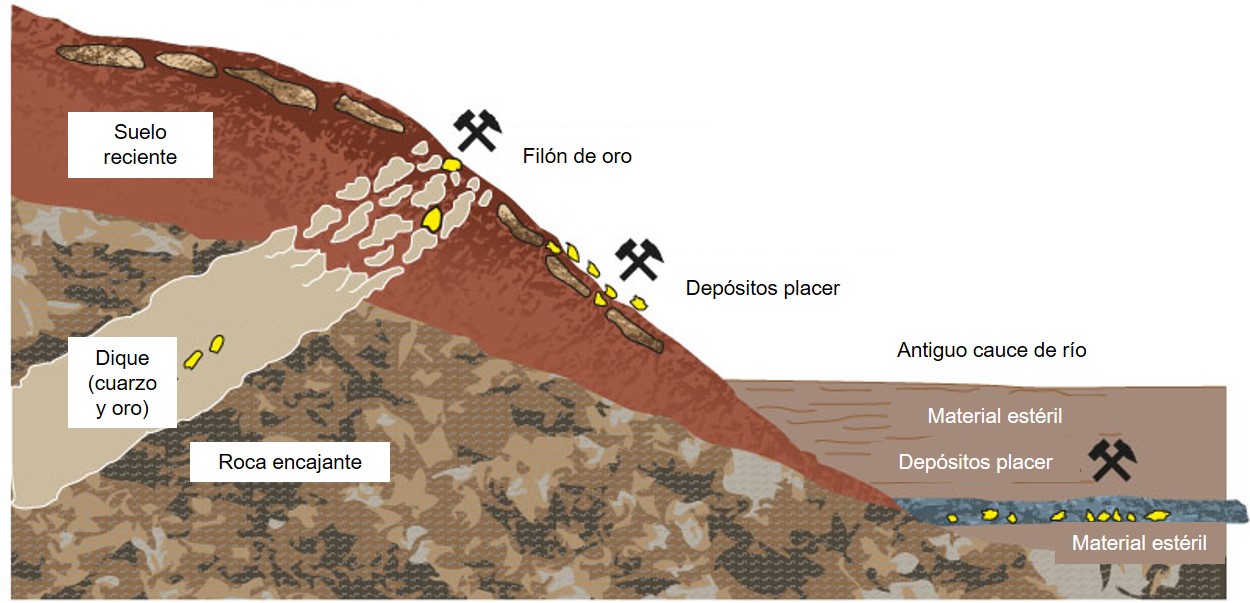 Depósitos de oro asociados a un dique hidrotermal, incluidos los de tipo placer. Imagen modificada de la original de Michael Priester. Fuente: Minelab
Depósitos de oro asociados a un dique hidrotermal, incluidos los de tipo placer. Imagen modificada de la original de Michael Priester. Fuente: MinelabPero estas excavaciones no las hacen al azar por cualquier lugar, siempre van a tiro hecho. Para ello cuentan con la ayuda de especialistas en la geología de Alaska que utilizan diversas técnicas comunes en la exploración mineral para ayudarles a encontrar el yacimiento de oro que se esconde bajo tierra. Y me voy a centrar en explicaros las dos que describieron en los pocos capítulos que he visto.
La primera es la resistividad eléctrica. Se trata de una técnica geofísica que consiste en introducir unos electrodos cilíndricos en el suelo conectados en serie mediante un cableado que, además, se conecta a una caja medidora de resistividad. Estos electrodos son capaces de enviar una corriente eléctrica que se transmite en profundidad y que va cambiando de potencial según atraviesa diferentes materiales o estructuras geológicas. Estos cambios en el potencial eléctrico quedan marcados en la caja medidora, lo que nos permite tratar los datos para realizar una especie de radiografía tridimensional del subsuelo. En el programa, emplearon esta técnica para identificar antiguos canales fluviales y acumulaciones de materiales metálicos transportados por los glaciales hace milenios, calculando la profundidad a la que se encontraban estas estructuras geológicas y, por tanto, los posibles yacimientos auríferos.
 Estudio de resistividad eléctrica del terreno en la mina de crisoprasa de Szklary (Baja Silesia, Polonia). Fuente: Wikimedia Commons
Estudio de resistividad eléctrica del terreno en la mina de crisoprasa de Szklary (Baja Silesia, Polonia). Fuente: Wikimedia CommonsLa segunda técnica os debería sonar más, porque ya he hablado de ella: los testigos de sondeo. En este caso, realizaron varias perforaciones a lo largo del terreno que tenían pensado explotar para obtener un registro continuo del subsuelo hasta la base rocosa. A estos sedimentos se les realizaron dos análisis consecutivos. En primer lugar, un estudio geoquímico para conocer los elementos químicos presentes en el mismo, buscando niveles que dieran positivo en oro. Y, en segundo lugar, lavaron y tamizaron esos niveles para calcular la concentración de oro con respecto al total de sedimento. De esta manera, pudieron determinar dónde y a qué profundidad se encontraban los yacimientos y, así, decidir si les era rentable o no explotarlos.
Debo reconocer que la serie no consiguió engancharme, así que no os puedo contar si estos equipos mineros se hicieron millonarios o si acabaron en la ruina, a mí únicamente me interesaron las animaciones explicativas que describían estos procesos y técnicas geológicas. Y, aunque eran más sencillas y resumidas de lo que yo os he comentado aquí, científicamente hablando sí que eran muy correctas. Así que puedo utilizarlas como otro ejemplo más no solo de que la Geología está en todo lo que nos rodea, sino también de que podemos aprender Ciencias de la Tierra gracias a cosas que, a priori, no parecen muy centradas en aumentar nuestro conocimiento científico. Únicamente hay que saber mirarlo todo con ojos geológicos.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Aprendiendo Geología mientras buscamos oro en Alaska se ha escrito en Cuaderno de Cultura Científica.
Cinco rompecabezas para celebrar el “Puzzle Day”
Cada 29 de enero, desde hace más de treinta años, se celebra en Estados Unidos el Puzzle Day. Esta conmemoración es una iniciativa de la creadora de rompecabezas Jodi Jill, que nació precisamente el 29 de enero de 1971.
 Un rompecabezas. Fuente: Wikimedia Commons.
Un rompecabezas. Fuente: Wikimedia Commons.
Nos unimos a esta celebración con cinco rompecabezas, en nuestro caso, matemáticos. Para solucionarlos no está de más recordar estas palabras del matemático Henry Ernest Dudeney (1857-1930)
Un buen rompecabezas debe exigir el ejercicio de nuestro mejor ingenio y habilidad, y aunque el conocimiento de las matemáticas y la lógica son a menudo de gran utilidad en la solución de estas cosas, sin embargo, a veces sucede que una especie de astucia y sagacidad naturales son de considerable valor.
El puzle de los cuatro roblesEste es un problema de ingenio propuesto por Sam Loyd (1841-1911) en su Cyclopedia of 5000 Puzzles, Tricks, and Conundrums With Answers (1914):
Un padre deja a sus cuatro hijos un campo cuadrado conteniendo cuatro robles [ver debajo]. Pero les pone una condición para obtener este legado: deben dividir el campo en cuatro partes, todas de la misma forma y tamaño, de manera que cada trozo de tierra contenga uno de los árboles. ¿Cómo lograrán hacerlo?
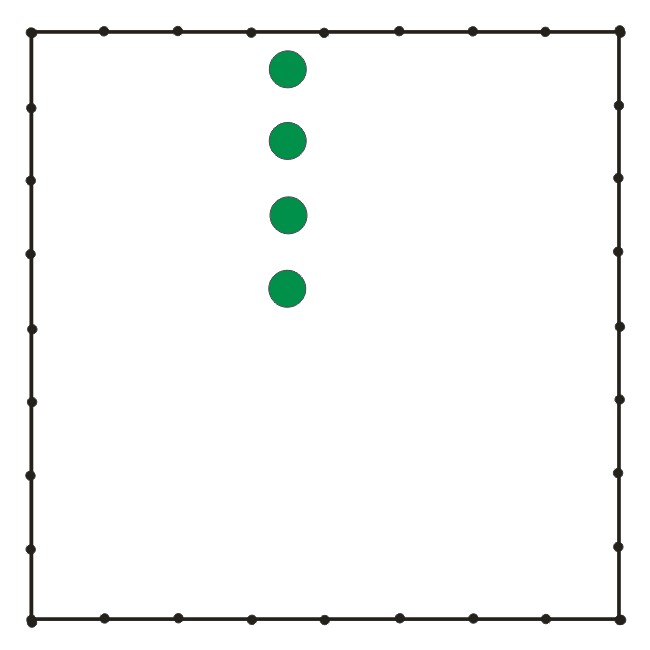 El planteamiento del problema. Fuente: Wikimedia Commons.
El planteamiento del problema. Fuente: Wikimedia Commons.
Piensa un poco antes de mirar la solución en este enlace.
Un puzle con dos dadosEl autor de este rompecabezas es Pierre Berloquin (1939):
Timoteo y Sofía están jugando con dos dados de seis caras. Pero no son dados normales: en vez de tener un número, cada cara está coloreada de rojo o azul.
Los dos amigos tiran los dados por turnos. Deciden que Timoteo ganará la partida si las dos caras superiores son del mismo color y Sofía lo hará si son diferentes. Se sabe que sus probabilidades de ganar son iguales.
También se sabe que el primer dado tiene 5 caras rojas y 1 cara azul.
¿Cuáles son los colores del segundo dado?
Pensemos en los posibles resultados en cada tirada: al lanzar dos dados de seis caras se obtienen 36 resultados posibles. Como Timoteo y Sofía tienen las mismas probabilidades de ganar, debe haber 18 resultados en los que ambos dados tengan el mismo color y otros 18 en los que la tirada muestre caras de distinto color. Si x es la cantidad de caras rojas en el segundo dado, debe cumplirse que:
18 = 5x + 1(6 – x).
Se deduce inmediatamente que x = 3, y entonces el segundo dado debe tener 3 caras rojas y 3 caras azules.
Un puzle numéricoEl creador de rompecabezas japonés Nobuyuki Yoshigahara (1936-2004) consideraba que este puzle era su obra maestra:
Los números que se muestran en la imagen de debajo están ordenados según una regla determinada. ¿Cuál es el número que falta?
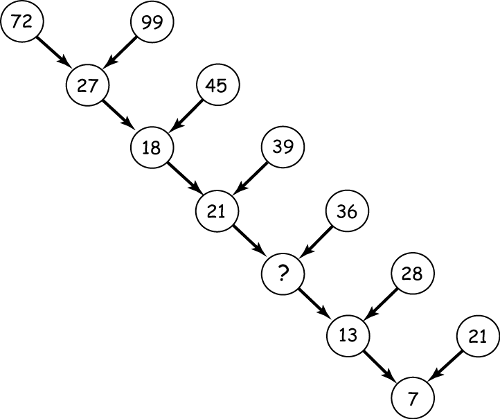 Fuente: Futility Closet.
Fuente: Futility Closet.
Por supuesto, lo importante es encontrar la regla. Intenta encontrarla antes de leer la solución.
Se observa en una primera mirada que 99 – 72 = 27, 45 – 27 = 18, 39 – 18 = 21, … parece que esta es la regla, es decir, la diferencia de los números de una fila devuelve el número del círculo de debajo. Así, como 28 – ? = 13, parece que debe ser ? = 15. Pero si miramos lo que sucede en la última fila, tenemos que 21 – 13 = 8, no 7 como se indica en el diagrama. Así que esta no es la regla.
Mirando de nuevo el diagrama, se puede comprobar que al sumar los dígitos de una fila se obtiene el número que se encuentra en el círculo de debajo. Por ejemplo, 7 + 2 + 9 + 9 = 27 para la primera fila, 4 + 5 + 2 + 7 = 18. Se comprueba que esta regla funciona en todas las filas. Así, 2 + 1 + 3 + 6 = 12, que es el número que falta en la imagen.
Un puzle olímpicoEsta propuesta procede de un problema de la Olimpiada Matemática rusa de 1999:
Se pide demostrar que los números del 1 al 15 no se pueden dividir en un grupo A de 13 números y otro B de 2 números de modo que la suma de los números de A sea igual al producto de los números de B.
Haremos la demostración por reducción al absurdo: supongamos que fuera posible dividir los números en dos grupos con las condiciones que se indican. Llamemos x e y a los dos números en B. Entonces se cumple que:
(1 + 2 + … + 15) – x – y = xy,
Es decir, 120 = xy + x + y, o lo que es lo mismo:
121 = (x + 1) (y + 1).
El número 121 = 112, con lo que es necesariamente x = y = 10. Pero esta solución no es válida, porque x e y son números distintos. Así, queda demostrado lo que se pedía.
Un puzle en el campo de tiroEste último rompecabezas se debe al matemático Peter Winkler (1946):
Sofía y Timoteo (que ya se han cansado de jugar a los dados) acuden a un campo de tiro. Sofía acierta a un objetivo pequeño el 75 % de las veces y Timoteo, con peor puntería, solo el 25 % de las veces.
Los dos apuntan a ese objetivo pequeño y disparan simultáneamente. Una bala lo alcanza.
¿Cuál es la probabilidad de que haya venido del arma de Sofía?
Como Sofía posee el triple de calidad de aciertos que Timoteo, dan ganas de decir que la probabilidad es del 75 %. Pero ese argumento no es válido porque hay que tener en cuenta los aciertos y los fallos. Pensemos en todas las situaciones posibles:
-
La probabilidad de que Sofía y Timoteo acierten en la diana es de 3/4 × 1/4 = 3/16,
-
La probabilidad de que ni Sofía ni Timoteo acierten su tiro es de 1/4 × 3/4 = 3/16,
-
la probabilidad de que Sofía acierte y Timoteo no es de 3/4 × 3/4 = 9/16, y, finalmente,
-
la probabilidad de que Timoteo acierte y Sofía no es de 1/4 × 1/4 = 1/16.
Como solo una bala alcanza el objetivo, se da necesariamente una de las situaciones descritas en 3) o en 4). Así, hay una probabilidad de 9/10 de que la bala que ha alcanzado en el blanco sea la de Sofía.
Referencias
-
The Four Oaks Puzzle, Futility Closet, 8 febrero 2024
-
A Dice Puzzle, Futility Closet, 23 octubre 2014
-
Nob’s number puzzle, Futility Closet, 30 abril 2014
-
15 Puzzle, Futility Closet, 2 julio 2013
-
Gun control, Futility Closet, 15 enero 2025
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
El artículo Cinco rompecabezas para celebrar el “Puzzle Day” se ha escrito en Cuaderno de Cultura Científica.
El calor destruye el entrelazamiento cuántico
Mientras ideaban un nuevo algoritmo cuántico, cuatro investigadores establecieron accidentalmente un límite estricto para el fenómeno «fantasma».
Un artículo de Ben Brubaker. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Kristina Armitage/Quanta Magazine
Kristina Armitage/Quanta MagazineHace casi un siglo, el físico Erwin Schrödinger llamó la atención sobre una peculiaridad del mundo cuántico que ha fascinado y desconcertado a los investigadores desde entonces. Cuando las partículas cuánticas, como los átomos, interactúan, se deshacen de sus identidades individuales en favor de un estado colectivo que es mayor y más extraño que la suma de sus partes. Este fenómeno se llama entrelazamiento.
Los investigadores tienen una comprensión sólida de cómo funciona el entrelazamiento en sistemas idealizados que contienen solo unas pocas partículas. Pero el mundo real es más complicado. En grandes conjuntos de átomos, como los que forman las cosas que vemos y tocamos, las leyes de la física cuántica compiten con las leyes de la termodinámica y las cosas se complican.
A temperaturas muy bajas, el entrelazamiento puede extenderse a grandes distancias, envolviendo a muchos átomos y dando lugar a fenómenos extraños como la superconductividad. Sin embargo, si aumentamos la temperatura, los átomos se mueven y rompen los frágiles enlaces que unen a las partículas entrelazadas.
Los físicos llevan mucho tiempo intentando precisar los detalles de este proceso. Ahora, un equipo de cuatro investigadores ha demostrado que el entrelazamiento no se debilita simplemente a medida que aumenta la temperatura, sino que, en los modelos matemáticos de sistemas cuánticos, como las formaciones de átomos en los materiales físicos, siempre hay una temperatura específica por encima de la cual desaparece por completo. “No es solo que sea exponencialmente pequeño”, explica Ankur Moitra, del Instituto Tecnológico de Massachusetts, uno de los autores del nuevo resultado. “Es cero”.
Los investigadores ya habían observado indicios de este comportamiento y lo habían denominado la “muerte súbita” del entrelazamiento, pero sus pruebas eran en su mayoría indirectas. El nuevo hallazgo establece un límite mucho más fuerte al entrelazamiento de una manera matemáticamente rigurosa.
Curiosamente, los cuatro investigadores que están detrás del nuevo resultado ni siquiera son físicos y no se proponían demostrar nada sobre el entrelazamiento. Son científicos informáticos que se toparon con la prueba por accidente mientras desarrollaban un nuevo algoritmo.
Independientemente de su intención, los resultados entusiasmaron a los investigadores del área. “Es una afirmación muy, muy contundente”, comenta Soonwon Choi, físico del MIT. “Me quedé muy impresionado”.
En busca del equilibrioEl equipo hizo su descubrimiento mientras exploraba las capacidades teóricas de los futuros ordenadores cuánticos: máquinas que explotarán el comportamiento cuántico, incluidos el entrelazamiento y la superposición, para realizar ciertos cálculos mucho más rápido que las ordenadores convencionales que conocemos hoy.
Una de las aplicaciones más prometedoras de la computación cuántica es el estudio de la propia física cuántica. Supongamos que queremos entender el comportamiento de un sistema cuántico. Los investigadores primero deben desarrollar procedimientos específicos, o algoritmos, que los ordenadores cuánticos puedan utilizar para responder a nuestras preguntas.
 Ewin Tang ayudó a diseñar un nuevo algoritmo rápido para simular cómo se comportan ciertos sistemas cuánticos a altas temperaturas. Foto: Xinyu Tan
Ewin Tang ayudó a diseñar un nuevo algoritmo rápido para simular cómo se comportan ciertos sistemas cuánticos a altas temperaturas. Foto: Xinyu TanPero no todas las preguntas sobre los sistemas cuánticos son más fáciles de responder utilizando algoritmos cuánticos. Algunas son igualmente fáciles para los algoritmos clásicos, que se ejecutan en ordenadores comunes, mientras que otras son difíciles tanto para los algoritmos clásicos como para los cuánticos.
Para entender en qué aspectos los algoritmos cuánticos y las ordenadores que pueden ejecutarlos pueden ofrecer una ventaja, los investigadores suelen analizar modelos matemáticos llamados sistemas de espín, que capturan el comportamiento básico de conjuntos de átomos en interacción. A continuación, pueden preguntarse: ¿qué hará un sistema de espín cuando lo dejamos solo a una temperatura determinada? El estado en el que se establece, llamado estado de equilibrio térmico, determina muchas de sus otras propiedades, por lo que los investigadores han buscado durante mucho tiempo desarrollar algoritmos para encontrar estados de equilibrio.
El hecho de que esos algoritmos sean realmente útiles por su naturaleza cuántica depende de la temperatura del sistema de espín en cuestión. A temperaturas muy altas, los algoritmos clásicos conocidos pueden hacer el trabajo fácilmente. El problema se complica a medida que la temperatura disminuye y los fenómenos cuánticos se hacen más fuertes; en algunos sistemas se vuelve demasiado difícil incluso para que los ordenadores cuánticos lo resuelvan en un tiempo razonable. Pero los detalles de todo esto siguen siendo turbios.
“¿Cuándo se llega al espacio donde se necesita la cuántica y cuándo se llega al espacio donde la cuántica ni siquiera ayuda?”, se pregunta Ewin Tang, investigadora de la Universidad de California en Berkeley y una de los autoras del nuevo resultado. “No se sabe mucho al respecto”.
En febrero, Tang y Moitra comenzaron a pensar en el problema del equilibrio térmico junto con otros dos científicos informáticos del MIT: un investigador postdoctoral llamado Ainesh Bakshi y el doctorando de Moitra, Allen Liu. En 2023, todos habían colaborado en un algoritmo cuántico innovador para una tarea diferente que involucraba sistemas de espín y estaban buscando un nuevo desafío.
“Cuando trabajamos juntos, las cosas fluyen”, afirma Bakshi. “Ha sido fantástico”.
Antes de ese gran avance de 2023, los tres investigadores del MIT nunca habían trabajado en algoritmos cuánticos. Su formación era en teoría del aprendizaje, un subcampo de la informática que se centra en algoritmos para el análisis estadístico. Pero, como los ambiciosos novatos de todo el mundo, vieron su relativa ingenuidad como una ventaja, una forma de ver un problema con nuevos ojos. “Uno de nuestros puntos fuertes es que no sabemos mucho de cuántica”, cuenta Moitra. “La única cuántica que conocemos es la cuántica que Ewin nos enseñó”.
El equipo decidió centrarse en temperaturas relativamente altas, donde los investigadores sospechaban que existirían algoritmos cuánticos rápidos, aunque nadie había podido demostrarlo. Pronto encontraron una forma de adaptar una vieja técnica de la teoría del aprendizaje a un nuevo algoritmo rápido. Pero mientras escribían su artículo, otro equipo presentó un resultado similar: una prueba de que un prometedor algoritmo desarrollado el año anterior funcionaría bien a altas temperaturas. Se les había adelantado.
La muerte súbita renaceUn poco decepcionados por haber quedado en segundo lugar, Tang y sus colaboradores comenzaron a comunicarse con Álvaro Alhambra, físico del Instituto de Física Teórica de Madrid y uno de los autores del artículo rival. Querían determinar las diferencias entre los resultados que habían obtenido de forma independiente. Pero cuando Alhambra leyó un borrador preliminar de la prueba de los cuatro investigadores, se sorprendió al descubrir que habían demostrado algo más en un paso intermedio: en cualquier sistema de espín en equilibrio térmico, el entrelazamiento desaparece por completo por encima de cierta temperatura. “Les dije: ‘Oh, esto es muy, muy importante’”, cuenta Alhambra.

De izquierda a derecha: Allen Liu, Ainesh Bakshi y Ankur Moitra colaboraron con Tang, aprovechando su experiencia en una rama diferente de la informática. “Uno de nuestros puntos fuertes es que no sabemos mucho sobre la computación cuántica”, afirma Moitra. Fots, de izquierda a derecha: Cortesía de Allen Liu; Amartya Shankha Biswas; Gretchen Ertl
El equipo revisó rápidamente su borrador para destacar el resultado accidental. “Resulta que esto simplemente se desprende de nuestro algoritmo”, explica Moitra. “Obtenemos más de lo que esperábamos”.
Los investigadores habían observado esta muerte súbita del entrelazamiento desde la década del 2000 en experimentos y simulaciones en ordenadores clásicos comunes. Pero ninguno de estos trabajos anteriores había podido medir directamente la desaparición del entrelazamiento. Además, solo habían estudiado el fenómeno en sistemas pequeños, que no son los más interesantes.
“Podría haber sido que para sistemas cada vez más grandes habría que alcanzar temperaturas cada vez más altas para ver la ausencia de entrelazamiento”, explica Alhambra. En ese caso, el fenómeno de muerte súbita podría ocurrir a temperaturas tan altas que sería irrelevante en materiales reales. El único límite teórico anterior, de 2003, dejaba abierta esa posibilidad. En cambio, Tang y sus colaboradores demostraron que la temperatura a la que desaparece el entrelazamiento no depende del número total de átomos en el sistema. Lo único que importa son los detalles de las interacciones entre los átomos cercanos.
 Álvaro Alhambra, un físico que trabajaba en el mismo problema que Tang, Moitra, Bakshi y Liu, se dio cuenta de que habían demostrado accidentalmente un nuevo resultado sobre el entrelazamiento cuántico mientras desarrollaban su algoritmo. Foto: Laura Marcos
Álvaro Alhambra, un físico que trabajaba en el mismo problema que Tang, Moitra, Bakshi y Liu, se dio cuenta de que habían demostrado accidentalmente un nuevo resultado sobre el entrelazamiento cuántico mientras desarrollaban su algoritmo. Foto: Laura MarcosEl método que utilizaron en su demostración fue inusual en sí mismo. La mayoría de los algoritmos para hallar estados de equilibrio térmico se inspiran en la forma en que los sistemas físicos reales se acercan al equilibrio. Pero Tang y compañía utilizaron técnicas muy alejadas de la teoría cuántica.
“Eso es lo que hace tan asombroso este artículo”, comenta Nikhil Srivastava, un científico informático de Berkeley. “La prueba en cierto modo ignora la física”.
La búsqueda continúaLa prueba de los cuatro investigadores de que los sistemas de espín de alta temperatura carecen de entrelazamiento ayuda a explicar otra característica interesante de su nuevo algoritmo: muy poco de él es realmente cuántico. Es cierto que el resultado del algoritmo (una descripción completa de cómo se orientan los átomos en un sistema de espín en equilibrio térmico) es demasiado difícil de manejar para almacenar en una máquina clásica. Pero, salvo el último paso que genera este resultado, cada parte del algoritmo es clásica.
“Es esencialmente el cálculo cuántico más trivial”, afirma Liu.
Tang tiene una larga trayectoria en el descubrimiento de resultados de “descuantización”, es decir, pruebas de que los algoritmos cuánticos no son realmente necesarios para muchos problemas. Ella y sus colaboradores no estaban tratando de hacer eso esta vez, pero la prueba de la desaparición del entrelazamiento con la que se toparon equivale a una versión aún más extrema de la descuantización. No es solo que los algoritmos cuánticos no ofrezcan ninguna ventaja en un problema específico que involucre sistemas de espín de alta temperatura; es que no hay nada cuántico en esos sistemas.
Pero eso no significa que los investigadores de computación cuántica deban perder la esperanza. Dos artículos recientes identifican ejemplos de sistemas de espín de baja temperatura en los que los algoritmos cuánticos para medir estados de equilibrio superan a los clásicos, aunque aún queda por ver lo extendido que está este comportamiento. Y aunque Bakshi y sus colaboradores han demostrado un resultado negativo, el método poco ortodoxo que utilizaron para llegar a él indica que pueden surgir nuevas ideas fructíferas de lugares inesperados.
“Podemos ser optimistas y pensar que se descubrirán nuevos algoritmos increíbles”, afirma Moitra. “Y que, en el proceso, podremos descubrir hermosas matemáticas”.
El artículo original, Computer Scientists Prove That Heat Destroys Quantum Entanglement, se publicó el 28 de agosto de 2024 en Quanta Magazine.
Traducido por César Tomé López
El artículo El calor destruye el entrelazamiento cuántico se ha escrito en Cuaderno de Cultura Científica.
Ni machos, ni reinas. El extraordinario caso de la hormiga saqueadora clónica
Los himenópteros en general, y las hormigas en particular, determinan su sexo mediante la haplodiploidía. Esto significa que las hembras son diploides y tienen dos dotaciones cromosómicas completas, lo habitual entre los animales. Los machos, en cambio, son haploides y solo tienen una dotación cromosómica. Cuando el óvulo haploide de una hembra es fecundado por un espermatozoide, se restaura la doble dotación cromosómica y tenemos otra hembra. Si el óvulo no es fecundado, su desarrollo dará lugar a un individuo masculino haploide.
Entre los himenópteros también es frecuente la organización social consistente en una o varias reinas (hembras reproductivas), un gran número de hembras obreras estériles, que asisten a la reina y proporcionan alimento a la colonia, y un reducido número de machos cuya función básica es fecundar a la reina.
Esta es la regla general, pero hay excepciones. Entre las 15 000 especies registradas de hormigas, hay un par de centenares que carecen de reinas en sus colonias. Su reproducción puede basarse en la fertilidad adquirida por una parte de las obreras o, en ausencia de machos, pueden ocurrir casos de reproducción asexual en los que los óvulos restauran la diploidía y producen hembras.
La producción de hembras sin intervención de machos se denomina partenogénesis, y se produce, por ejemplo, en los pulgones. Este sistema tiene la ventaja de producir muchos descendientes de forma rápida, pero impide que se genere nueva diversidad genética. Por ello, al final de la temporada reproductora, los pulgones ponen huevos haploides que producen machos y se regresa a la reproducción sexual.
 Figura 1. La hormiga saqueadora clónica Ooceraea biroi. Fuente: Erin Prado / © AntWeb.org / CC-BY-SA-3.0
Figura 1. La hormiga saqueadora clónica Ooceraea biroi. Fuente: Erin Prado / © AntWeb.org / CC-BY-SA-3.0De forma muy diferente, la hormiga saqueadora clónica, Ooceraea biroi, se reproduce asexualmente sin reinas ni machos, originando obreras genéticamente idénticas (clones), todas ellas con capacidad de producir huevos diploides. O. biroi es una pequeña hormiga ciega (<3 mm) que se está extendiendo por áreas tropicales y subtropicales de todo el planeta (Figura 1). Forma colonias nómadas y poco numerosas. A medida que se desplazan por un territorio, saquean los hormigueros de otras especies y devoran todo lo que encuentran.
Para entender la partenogénesis de O. biroi debemos repasar el concepto de meiosis (Figura 2). Óvulos y espermatozoides son células haploides que derivan de progenitores diploides. La reducción en el número de cromosomas se produce por una replicación de los cromosomas seguida de dos ciclos de división celular (meiosis I y meiosis II). En la meiosis I puede producirse un entrecruzamiento o intercambio de fragmentos entre cromosomas homólogos. Esto es muy importante para generar diversidad genética, ya que se producen nuevas combinaciones de alelos, las distintas variantes que puede tener un gen determinado.
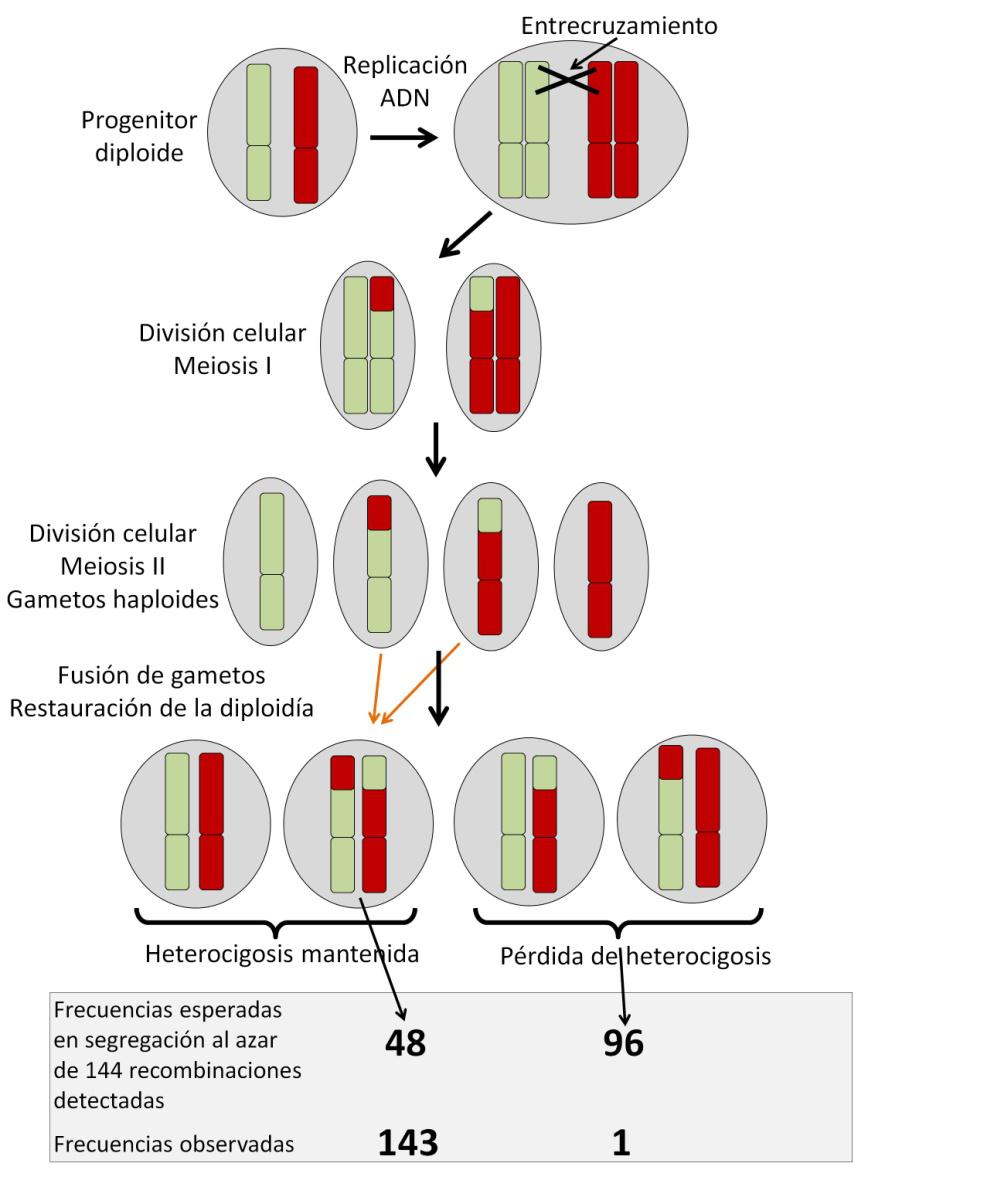 Figura 2. Esquema de la meiosis. Se ha representado un solo par de cromosomas. Tras la replicación del ADN se puede producir un entrecruzamiento entre las cadenas de ADN y la recombinación de una porción del cromosoma. De esta forma se generan nuevas combinaciones de alelos. En la segunda división meiótica las células resultantes son óvulos haploides. La reproducción asexual de O. biroi se produce por la fusión de dos óvulos, restaurando la doble dotación cromosómica. Lo excepcional del proceso es que los cromosomas que han recombinado tienen una mayor probabilidad de coheredarse tras la fusión (flechas naranjas). De 144 recombinaciones detectadas por el grupo de Kronauer, 143 mantenían la heterocigosidad, frente a las 48 esperadas si la segregación se produce al azar (33%).
Figura 2. Esquema de la meiosis. Se ha representado un solo par de cromosomas. Tras la replicación del ADN se puede producir un entrecruzamiento entre las cadenas de ADN y la recombinación de una porción del cromosoma. De esta forma se generan nuevas combinaciones de alelos. En la segunda división meiótica las células resultantes son óvulos haploides. La reproducción asexual de O. biroi se produce por la fusión de dos óvulos, restaurando la doble dotación cromosómica. Lo excepcional del proceso es que los cromosomas que han recombinado tienen una mayor probabilidad de coheredarse tras la fusión (flechas naranjas). De 144 recombinaciones detectadas por el grupo de Kronauer, 143 mantenían la heterocigosidad, frente a las 48 esperadas si la segregación se produce al azar (33%).Volviendo a la hormiga saqueadora clónica, las cuatro células haploides derivadas de la meiosis se alinean y las dos centrales se fusionan, restituyendo la dotación diploide y generando el huevo que dará lugar al nuevo individuo. Esto debería suponer un serio problema, ya que a lo largo de las generaciones, se perderían alelos disminuyendo la diversidad genética, un fenómeno denominado pérdida de heterocigosidad1. Un reciente estudio publicado por el grupo de Daniel Kronauer en la Universidad Rockefeller de Nueva York ha mostrado que O. biroi raramente pierde heterocigosidad en su reproducción, manteniendo la diversidad de sus alelos. ¿Cómo es posible? Porque los cromosomas violan las leyes de Mendel y no se segregan aleatoriamente en la meiosis II (explicación en la Figura 2). Los cromosomas que se han recombinado se heredan conjuntamente mediante un mecanismo todavía desconocido. De esta forma, la hormiga clónica no necesita la reproducción sexual para “refrescar” la diversidad genética, como sucede en los pulgones.
No es esta la única sorpresa que ha deparado O. biroi. Cuando Daniel Kronauer estudiaba sus poblaciones durante su postdoctorado en Okinawa, observó que aparecían espontáneamente en las colonias hormigas con alas y ojos rudimentarios, parecidas a las hormigas reina de otras especies (Figura 3). Estas “pseudorreinas” (queen-like) volvieron a aparecer en el laboratorio de Kronauer años después. No solo su morfología recordaba a las hormigas reina, también lo hacía su comportamiento (no busca alimento, dependiendo de los cuidados de las obreras) y su fecundidad, que duplicaba a la de sus hermanas.
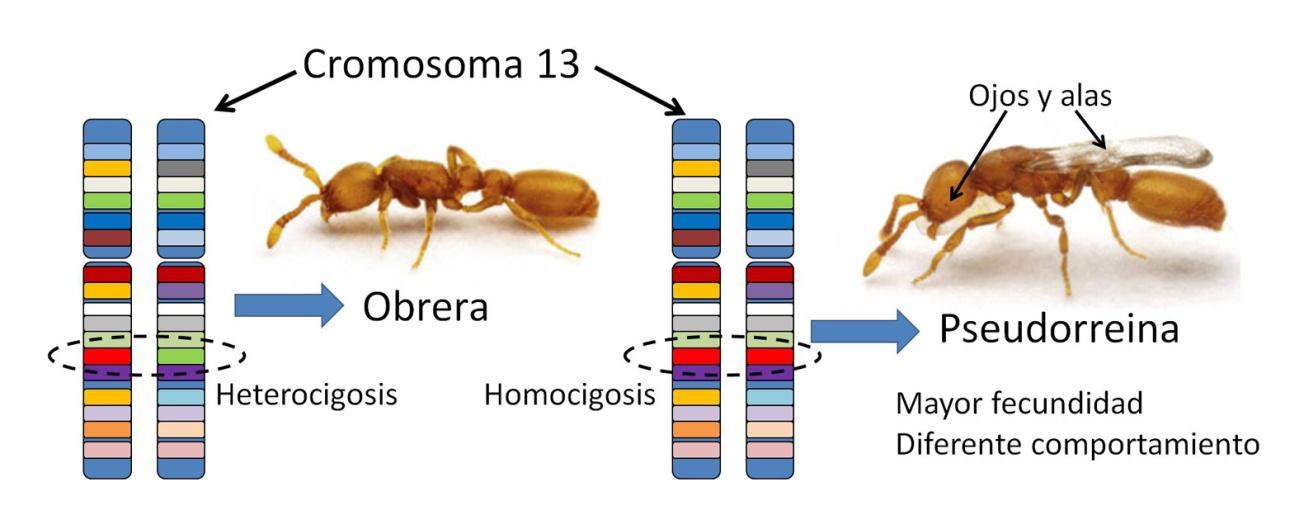 Figura 3. De forma espontánea aparecen en las colonias de O. biroi individuos semejantes en morfología y comportamiento a las hormigas reina de otras especies. Esto se debe a una pérdida de heterocigosidad en una región específica del cromosoma 13 (véase nota 2). Fuente: W. Trible et al. (2023). CC BY-SA 4.0
Figura 3. De forma espontánea aparecen en las colonias de O. biroi individuos semejantes en morfología y comportamiento a las hormigas reina de otras especies. Esto se debe a una pérdida de heterocigosidad en una región específica del cromosoma 13 (véase nota 2). Fuente: W. Trible et al. (2023). CC BY-SA 4.0El estudio del genoma de las pseudorreinas reveló algo sorprendente. Un conjunto de genes2 mostraba alelos diferentes en una región del cromosoma 13 de las obreras normales (heterocigosis), pero aparecían idénticos en las pseudorreinas (homocigosis) (Figura 3). Dicho de otra forma, la homocigosis de este conjunto de genes daba lugar a un fenotipo muy similar al de ciertas especies de hormigas que practican el llamado “parasitismo social”.
Esta estrategia consiste en que hormigas de una especie determinada que carece de obreras se hacen pasar por reinas de otras especies, obligando a sus obreras a protegerlas, alimentarlas y cuidar a sus crías. Durante mucho tiempo se especuló sobre qué tipo de procesos evolutivos podrían conducir a este comportamiento. Según los nuevos resultados, un evento genético simple, la homocigosis del conjunto de genes situados en el cromosoma 13, estaría en el origen de la evolución de esta estrategia. Se trataría de un cambio radical de comportamiento y morfología en una sola generación debido a una modificación genética puntual.
La hormiga clónica se está convirtiendo en un extraordinario modelo para el estudio de insectos sociales, por su facilidad de reproducción en laboratorio y su homogeneidad genética. De hecho, el grupo de Kronauer ha conseguido establecer en este modelo la primera línea transgénica en un insecto social. Este minúsculo insecto nos deparará muchas sorpresas en un futuro cercano.
Referencias
Lacy, K.D., Hart, T. & Kronauer, D.J.C. (2024) Co-inheritance of recombined chromatids maintains heterozygosity in a parthenogenetic ant. Nat Ecol Evol. doi: 10.1038/s41559-024-02455-z
Trible, W., Chandra, V., Lacy, K.D. et al. (2023) A caste differentiation mutant elucidates the evolution of socially parasitic ants. Curr Biol. doi:10.1016/j.cub.2023.01.067
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga
Notas:
1 La heterocigosis se produce cuando se poseen dos versiones (alelos) de un mismo gen, heredadas de la madre y del padre. Si los dos alelos son iguales hablamos de homocigosis.
2 Se trata de una región de 2.25 millones de pares de bases que probablemente constituye un “supergén” relacionado con comportamientos sociales. Un supergén es un conjunto de genes que normalmente se heredan en bloque ya que sufren mucha menos recombinación de lo habitual.
El artículo Ni machos, ni reinas. El extraordinario caso de la hormiga saqueadora clónica se ha escrito en Cuaderno de Cultura Científica.
Edición genética hereditaria: lo que era imprudente en 2018 lo sigue siendo en 2025
 Edición genética de embriones una imprudencia antes y ahora
Edición genética de embriones una imprudencia antes y ahora
«Hace tan solo unas semanas, dos pequeñas y preciosas niñas chinas, llamadas Lulu y Nana, llegaron al mundo llorando tan sanas como cualquier otro bebé. Las niñas están ya en casa, con su madre Grace y su padre Mark».
Así comenzaba el video del informático He Jiankui en el que anunciaba la primera edición genética en embriones humanos de la historia. Su intención era que los bebés no expresaran una proteína, codificada por el gen CCR5, que el virus de inmunodeficiencia humana (VIH) utiliza como receptor para infectar las células. Era noviembre de 2018 y la comunidad científica se echó las manos a la cabeza ante uno de los experimentos más imprudentes que se han realizado jamás. El trabajo se llevó en secreto, sin relación alguna con la Universidad en la que desde hace meses ya no trabajaba y se comunicaba a través de un simple anuncio en Youtube. No había sido revisado por pares, no se había publicado en ninguna revista científica y, por supuesto, no había pasado ningún control bioético durante ninguna fase del proceso.
«Ni siquiera era médico, ni genetista, ni biomédico, ni nada parecido, era un informático especializado en física», explica Lluis Montoliu, divulgador, biólogo e investigador del CSIC en el Centro Nacional de Biotecnología. «He Jiankui estaba convencido de que iba a aportar un gran avance a la humanidad y con este mesianismo realizó una serie de fechorías. Manipuló los permisos del comité de ética del hospital, reunió a varias parejas, en las que el padre estaba infectado con el VIH, y las convenció de que la única manera para tener hijos libres del virus era mediante el protocolo que él les proponía, ocultándoles que ya existe un procedimiento establecido desde hace muchos años por el que se consiguen espermatozoides sin el virus que se usan luego en fecundación in vitro. En definitiva, les engañó, les ocultó la realidad científica y les empujó a un procedimiento completamente experimental de manera imprudente e improcedente».
Con el paso de las semanas se descubrieron irregularidades aún más graves en el trabajo de He Jiankui. «Hoy sabemos que hizo una biopsia de cada embrión, un análisis genómico en el que constató que el experimento le había salido mal, no solo era consciente de que el gen que quería inactivar seguía activo sino que además había inactivado genes que no tendría que haber tocado», cuenta Montoliu. «En ese momento Jiankui debería haber parado el experimento pero le pudo más el protagonismo de convertirse en una leyenda, y tal vez ganar un Premio Nobel, que embaucó a los ginecólogos del hospital dándoles a entender que se trataba de un procedimiento de fecundación in vitro normal».
Los desmanes de He Jiankui no acaban aquí. Además de las gemelas Lulu y Nana, hubo otra pareja engañada que dio a luz un tercer bebé modificado genéticamente, una niña llamada Aurea. La reacción gubernamental llegó a continuación y las autoridades chinas lo detuvieron, lo juzgaron y fue condenado a una multa de tres millones de yuanes y tres años de cárcel. Curiosamente esta condena no fue por realizar el experimento ya que, en aquel momento, China no contaba con una regulación en contra (ahora sí la tiene) sino por haber falsificado la revisión ética de su trabajo para atraer así a las parejas voluntarias, por haberse saltado el requisito del consentimiento informado y por usurpar profesionalmente una carrera que no tenía, ya que se presentaba ante esas parejas como médico.
Desde entonces no sabemos absolutamente nada de esos tres bebés. Ahora deberían tener siete años pero es como si hubieran desaparecido. «Yo he preguntado a varios colegas chinos en algunos congresos y ninguno tiene noticias. Lo más probable es que estas niñas tendrán que ser supervisadas médicamente el resto de su vida porque el hecho de que tengan alteraciones genéticas descontroladas pueden suponer un fallo orgánico o sistémico en cualquier momento, por lo tanto se les trasladó un riesgo muy alto y totalmente innecesario», asegura Montoliu.
A los pocos meses, la propia Organización Mundial de la Salud (OMS) anunció la creación de un registro global para rastrear las investigaciones en edición genética humana, enfatizando que «los países no deben permitir ningún trabajo adicional sobre la edición del genoma de la línea germinal humana hasta que se hayan considerado adecuadamente las implicaciones técnicas y éticas» y adelantó la creación de instrumentos de gobernanza eficaces para disuadir y prevenir usos irresponsables e inaceptables de embriones editados genéticamente para iniciar embarazos humanos.
 He Jiankui durante su polémica presentación en Youtube
He Jiankui durante su polémica presentación en Youtube
Así llegamos hasta nuestros días en enero de 2025, un año que ha comenzado con un artículo escandaloso publicado por la propia Nature. El autor principal es el australiano Julian Savulescu, filósofo y bioeticista de la Universidad de Oxford, donde no solo presenta la posibilidad de editar un solo gen (como hizo He Jiankui) sino que abre la puerta a la edición de muchos genes a la vez para conseguir las variantes más adecuadas que eviten la enfermedad, que ofrezcan más salud o más longevidad. Sus conclusiones las extrae de un desarrollo matemático con el que está convencido de que «la edición poligénica hereditaria para proteger a las generaciones futuras de enfermedades, sin requerir intervenciones adicionales para cada generación, puede verse como una ventaja que la convierte en una opción más deseable que la edición somática».
A grandes rasgos, la edición genética se divide en dos grandes clases: la edición genética somática, también conocida como edición terapéutica, que tan solo implica cambios realizados en una persona que no son hereditarios y no van a ser transmitidos a la descendencia, y la edición genética hereditaria, de línea germinal o de embriones, que supone modificar el genoma heredable y que se transmitirá a generaciones futuras. De esta manera, el artículo de Savulescu especula directamente con la posibilidad de editar el genoma en embriones humanos, no solo en una posición, sino en múltiples localizaciones, escogiendo para cada gen determinadas variantes genéticas asociadas a características aparentemente beneficiosas, protectoras frente a enfermedades, con el objeto de mejorar los seres humanos, no para curarlos.
«Esto es, simple y llanamente, eugenesia», afirma Montoliu. «Es un ejercicio teórico matemático que falla por todos lados y da a entender que la edición genómica con las herramientas CRISPR es mucho más segura, certera y reproducible de lo que sabemos hoy en día que es, y de lo que probablemente va a ser durante mucho tiempo, para este tipo de modificaciones que requieren precisión y reproducibilidad. La mayoría de las estrategias terapéuticas actuales que usan las herramientas CRISPR no intentan corregir ni modificar genes, sino inactivarlos, destruirlos, algo muy diferente para lo que no se requiere tanta precisión».
Junto al artículo publicado por Savulescu, la revista Nature ofrece también un artículo crítico firmado por Kevin Mitchel, genetista del Trinity College de Dublin. En esta respuesta, Mitchel desmonta las especulaciones matemáticas de Savulescu y afirma que la edición en línea germinal es insegura, no tiene evidencias científicas y que implica un riesgo considerable y beneficios inciertos. De igual modo, la asociación científica ARRIGE (Asociación para la Investigación Responsable e Innovación en Edición Genética), desde la que se promueve un uso responsable de las técnicas de edición genética, también ha publicado un comunicado rechazando, por irresponsable e innecesaria, esta propuesta de edición genética múltiple del genoma humano.
 Diagrama simplificado de un locus CRISPR
Diagrama simplificado de un locus CRISPR
Hace aproximadamente once años, a principios de 2014, escribí un artículo en este mismo Cuaderno de Cultura Científica de la UPV/EHU, titulado «La inminente revolución de la ingeniería genética basada en el sistema CRISPR/cas» y, me di cuenta de que su avance sería imparable. Rápidamente empezaron a aparecer las primeras aplicaciones con las evidentes preocupaciones éticas asociadas. Las terapias de edición genética para curar enfermedades de base genética ya están al orden del día y se administran en todos los países, también aquí en España, pero otra cosa muy distinta son estos experimentos que, bajo la influencia de dudosas filosofías transhumanistas, utilizan tecnologías CRISPR con la intención de mejorar a un ser humano con genes que podría transmitir a su descendencia.
«Hace algo más de diez años, en la primera cumbre internacional sobre el tema hubo una serie de intervenciones que dejaban claro que el uso de las herramientas CRISPR para editar genes mutados en embriones, con la intención de que ese embrión nazca con una determinada enfermedad, no son necesarias», recuerda Montoliu. «Con la excepción de unos pocos casos, extremadamente raros y poco habituales, donde el padre y la madre sean portadores de mutaciones de tal manera que su descendencia posea el cien por cien de posibilidades de heredarlas, la inmensa mayoría de supuestos se solucionan con tecnologías ya disponibles. Contamos con diagnósticos genéticos preimplantacionales que nos permiten distinguir cuál es el embrión que lleva la mutación y cuál es el que no la lleva y seleccionar ese embrión para que se geste solamente el que no lleva la mutación».
En 2023 se aprobó en Reino Unido la primera terapia basada en CRISPR, un tratamiento denominado Casgevy que se aplica a personas mayores de 12 años afectadas por anemia falciforme con crisis recurrentes de oclusión vascular o por beta-talasemia dependiente de transfusiones, para las que no existan donantes de médula ósea compatibles. Esto es el futuro pero es muy diferente a lo que propone Sabulescu desde Nature. Las terapias CRISPR deben centrarse en «tratar a personas adultas y enfermas con terapias génicas somáticas», concluye Montoliu, «no para aquellos que quieran vivir cien años o que pretendan bonitos ojos azules para sus hijos».
Referencias y más información:
Julian Savulescu et al. (2025) Heritable Polygenic Editing: The next Frontier in Genomic Medicine? Nature (2025) DOI: 10.1038/s41586-024-08300-4.
Kevin Mitchel et al. (2025) Human Embryo Editing against Disease Is Unsafe and Unproven — despite Rosy Predictions Nature (2025) DOI: 10.1038/d41586-024-04105-7.
Comunicado de la Asociación para la Investigación Responsable e Innovación en Edición Genética (ARRIGE): ARRIGE statement on heritable polygenic editing
Agradecimientos a Lluis Montoliu, biólogo e investigador del CSIC en el Centro Nacional de Biotecnología.
Sobre el autor: Javier «Irreductible» Peláez (Puertollano, 1974) es escritor y comunicador científico. Autor de 500 años de frío. La gran aventura del Ártico (Crítica, 2019) y Planeta Océano (Crítica 2022). Es uno de los fundadores de la plataforma Naukas.com, editor de ciencia en Yahoo España y Latinoamérica. Es guionista científico en los programas de televisión «El Cazador de Cerebros» y «Órbita Laika» de RTVE. Durante más de una década ha escrito en diferentes medios de comunicación (El País, El Español, National Geographic, Voz Populi). Es autor de los podcasts Catástrofe Ultravioleta y La Aldea Irreductible, y ha colaborado en diferentes proyectos radiofónicos y televisivos (Radio Nacional de España, Radio Televisión Canaria). Es ganador de tres premios Bitácoras, un premio Prisma a la mejor web de divulgación científica y un Premio Ondas al mejor programa de radio digital.
El artículo Edición genética hereditaria: lo que era imprudente en 2018 lo sigue siendo en 2025 se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2024: El sexo obliga a cocinar
La decimocuarta edición del mayor evento de divulgación científica volvió al Palacio Euskalduna de Bilbao durante los días 19, 20, 21 y 22 de septiembre de 2024.

Esa fuerza de la naturaleza que es Juan Antonio Cuesta, Catedrático de estadística (jubilado «desde el 7 de octubre de 2024 por la mañana») de la Universidad de Cantabria, explica por qué el que las personas mientan a la hora de responder encuestas implica que es necesario «cocinarlas».
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2024: El sexo obliga a cocinar se ha escrito en Cuaderno de Cultura Científica.
Identificadas estrellas individuales en el universo distante
Un equipo internacional de astrónomos/as entre los que se encuentra el investigador Ikerbasque Tom Broadhurst, que desarrolla su trabajo en la Universidadd el País Vasco (UPV/EHU) y DIPC- Donostia International Physics Center- fotografió más de 40 estrellas individuales en una galaxia tan lejana que su luz ha tardado la mitad de la edad del universo en llegar hasta nosotros.
 Arco del Dragón en Abell 370. Fuente: Hubble / NASA
Arco del Dragón en Abell 370. Fuente: Hubble / NASAUtilizando el Telescopio Espacial James Webb (JWST) de la NASA, observaron una galaxia a casi 6.500 millones de años luz de la Tierra, momento en que el universo tenía la mitad de su edad actual. En esta galaxia distante, el equipo identificó 44 estrellas individuales, visibles gracias al uso de lentes gravitacionales y a la alta sensibilidad del JWST. Este descubrimiento marca un logro sin precedentes: el mayor número de estrellas individuales detectadas en el universo distante. Además, abre una vía para investigar uno de los mayores misterios del universo: la materia oscura.
El equipo de astrofísicos localizó estas estrellas mientras inspeccionaban imágenes del JWST de una galaxia conocida como el Arco del Dragón, ubicada en la línea de visión desde la Tierra detrás de un cúmulo masivo de galaxias llamado Abell 370. Debido a la gravitación (por la inmensa masa de este cúmulo) se produce el llamado efecto de lente gravitacional, deformando la luz que nos llega de lo que esté detrás (el arco de dragón) y haciéndonos ver ese pasillo de proporciones cósmicas en lugar de la característica espiral. Que es lo que se vería sin ese efecto.
El equipo analizó los colores de cada una de las estrellas dentro del Arco del Dragón y descubrió que muchas son supergigantes rojas, similares a Betelgeuse en la constelación de Orión, que se encuentra en las etapas finales de su vida. Esto contrasta con descubrimientos anteriores, que identificaron predominantemente supergigantes azules, como Rigel y Deneb, que se encuentran entre las estrellas más brillantes del cielo nocturno. Según los investigadores, esta diferencia en los tipos estelares también destaca el poder único de las observaciones del JWST en longitudes de onda infrarrojas.
La mayoría de las galaxias, incluida la Vía Láctea, contienen decenas de miles de millones de estrellas. En galaxias cercanas como Andrómeda, las científicas y científicos pueden observar las estrellas una por una. Sin embargo, en galaxias a miles de millones de años luz, las strellas aparecen combinadas, ya que su luz debe viajar miles de millones de años antes de llegar a nosotros, lo que representa un desafío constante para los y las científicas que estudian cómo se forman y evolucionan las galaxias. Las galaxias que están muy lejos suelen parecer una mancha difusa y borrosa, y aunque estuvieran formadas por muchísimas estrellas individuales, hasta la fecha no había sido posible identificarlas una a una por las limitaciones de los telescopios.
Se espera que futuras observaciones con el JWST capturen más estrellas magnificadas en la galaxia del Arco del Dragón. Estos esfuerzos podrían conducir a estudios detallados de cientos de estrellas en galaxias distantes. Además, estas observaciones de estrellas individuales podrían proporcionar información sobre la estructura de las lentes gravitacionales e incluso arrojar luz sobre la esquiva naturaleza de la materia oscura, ya que como concluyen en un reciente artículo el equipo de la UPV/EHU-DIPC, formado por el propio investigador Ikerbasque Tom Broadhurst, junto a George Smoot, galardonado con el Premio Nobel de Física y la estudiante de doctorado Paloma Morillo, las posiciones de las estrellas en el arco del dragón implican que la materia oscura es similar a ondas en lugar de partículas pesadas.
Referencia:
Fudamoto, Y., Sun, F., Diego, J.M. et al. (2025) Identification of more than 40 gravitationally magnified stars in a galaxy at redshift 0.725. Nat Astron doi: 10.1038/s41550-024-02432-3
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Identificadas estrellas individuales en el universo distante se ha escrito en Cuaderno de Cultura Científica.
¡Ni se te ocurra teletransportarme, Scotty!
Es posible que solo exista una persona en el mundo que no haya soñado alguna vez con teletransportarse a… bueno, a cualquier sitio: Leonard McCoy —Bones, para los amigos—, director médico de la nave USS Enterprise. Y, si nos atenemos a las leyes de la física, puede que en ese sentido fuera el más cuerdo de toda la tripulación, porque, aunque es posible que el sistema de teletransporte de Star Trek sea el más coherente que podemos encontrar en la ciencia ficción desde el punto de vista científico —y tampoco es que lo sea mucho—, pasa por alto detalles que podrían hacer que el viaje no fuera tan placentero y seguro como parece.
 El actor DeForest Kelly, como el doctor Leonard McCoy; William Shatner, como el capitán Kirk, y Leonard Nimoy, como Spock en la sala del transportador de la USS Enterprise (Star Trek, TOS, 1968). Fuente: NBC Television
El actor DeForest Kelly, como el doctor Leonard McCoy; William Shatner, como el capitán Kirk, y Leonard Nimoy, como Spock en la sala del transportador de la USS Enterprise (Star Trek, TOS, 1968). Fuente: NBC Television
Existen innumerables manuales técnicos —ficticios, claro— en los que podemos encontrar información sobre cómo funcionan todos los sistemas de la nave Enterprise. En el escrito en 1991 por Rick Sternbach y Michael Okuda —el que tengo más a mano, aunque es el manual de la Enterprise de Picard—, se describe el funcionamiento de los teletransportadores en cuatro etapas:
-
Programación de las coordenadas de destino y análisis del entorno. Algo bastante conveniente para que nadie acabe materializándose dentro de una roca o en un ecosistema mortal.
-
Escáner de los átomos, a nivel individual, del sujeto al que se va a teletransportar.
-
Almacenamiento en memoria y compensación del desplazamiento Doppler del haz de teletransporte debido al movimiento entre la nave y el lugar de destino.
-
Envío del haz.
Suena bastante sensato, ¿no? Y lo es en bastantes sentidos, sobre todo en algunos detalles. No solo tienen en cuenta el efecto Doppler, sino la distorsión del espacio-tiempo en condiciones de curvatura, lo que haría imposible el teletransporte; el peligro de chocar contra el escudo deflector de otra nave si los tiene activados, o mi favorita: la imposibilidad de, a diferencia del replicador de alimentos que funciona a nivel molecular, utilizar el teletransportador para clonar personas, algo que, efectivamente, prohíbe la mecánica cuántica.
Pero vayamos poco a poco y veamos a qué nos referimos cuando hablamos de teletransporte en el mundo real —o en el mundo cuántico, para ser más precisos— y cómo funciona.
Cada cierto tiempo, de forma recurrente, aparece en los medios alguna noticia relacionada con este tema. Suelen ser ciertas: hemos logrado el teletransporte cuántico de partículas muchísimas veces. Ahora bien, de ahí a que podamos empezar a pensar en irnos de vacaciones al otro extremo del mundo utilizando este sistema hay un trecho.
En física cuántica, eso a lo que llamamos teletransporte es posible gracias a una de las propiedades más espeluznantes —según diría Albert Einstein— de las partículas: el entrelazamiento. Que dos partículas se encuentren entrelazadas solo significa que comparten la misma función de onda, por lo que, si actuamos sobre una, estamos actuado irremediablemente sobre la otra. Desarrollemos un poco esto: podríamos tener dos partículas diferentes, cada una con su propia función de onda, y sumarlas sin mayor problema; en ese caso, podríamos volver a separar cada componente si quisiéramos. En cambio, en el entrelazamiento no hay dos funciones de onda individuales, sino que el sistema de dos, tres, cuatro… o las partículas que sean está descrito por la misma ecuación, y es imposible hacer nada sobre ninguna de ellas sin que afecte al resto. Lo espeluznante, en realidad,no es que se puedan relacionar partículas de esta manera, sino que cualquier acción que se ejerza sobre una parte del sistema, se va a reflejar en el resto de componentes de manera inmediata, con independencia de si están en la misma habitación, en la Luna o en la galaxia de Andrómeda, algo que parece que desafía el límite de la velocidad de la luz. En realidad no es así, como veremos más adelante, ya que lo que podemos o no hacer con el entrelazamiento tiene sus limitaciones y enviar información es una de ellas.
 Dos partículas entrelazadas comparten la misma función de onda. Esto quiere decir que cualquier operación que efectuemos sobre uno de ellos, le afectará al otro. Fuente: Mark Garlick / Science Photo Library
Dos partículas entrelazadas comparten la misma función de onda. Esto quiere decir que cualquier operación que efectuemos sobre uno de ellos, le afectará al otro. Fuente: Mark Garlick / Science Photo Library
Perfecto, pero ¿cómo podemos usar esta propiedad para teletransportar cosas? Lo cierto es que hay que hacer algunos trucos. Tengamos en cuenta que, cuando hablamos de teletransporte cuántico lo que enviamos no son partículas materiales, sino estados, esto es, la información que describe la partícula y gracias a la cual podemos replicarla al otro lado.
Dejemos que Scotty y, por ejemplo, Spock, le amarguen un poquito la existencia a McCoy y hagan un pequeño experimento con él. Van a intentar teletransportarlo a la superficie del planeta al que acaban de llegar, pero utilizando las propiedades de la física cuántica en lugar del sistema habitual. Para ello, antes de nada, habrá que hacer algunos preparativos.
En primer lugar, haría falta un sistema auxiliar que ayudara con todo el proceso, así que Spock construye un par de tricorders que van a estar entrelazados. Se encontrarán metidos cada uno en una caja, en estado de superposición encendido/apagado, de tal manera que, si en un momento dado alguien abre una de las cajas, observa uno de ellos y ve que está encendido, sabrá que el de la otra caja está apagado. Spock le da un de los tricorders a McCoy y el otro se lo lleva él en una lanzadera a la superficie del planeta.
Centrémonos ahora en McCoy y su tricorder, y vamos a entrelazarlos entre sí también. Para que los estados no colapsen, Scotty encerrará a Bones con su dispositivo en la sala del teletransportador, cerrará la puerta y lo dejará ahí aislado, de tal manera que tendremos un estado de superposición conjunto: McCoy, desde ese momento, podría estar vivo o muerto —independientemente de que también esté muy enfadado— y su tricorder podría estar encendido o apagado. Así que habría cuatro estados posibles: McCoy vivo-tricorder encendido, McCoy muerto-tricorder apagado, McCoy vivo-tricorder apagado, McCoy muerto-tricorder encendido, que se denominan estados de Bell.
Ahora bien, como hemos dicho que el tricorder de McCoy está entrelazado, a su vez, con el que se llevó Spock a la superficie del planeta, sabemos que cualquier cosa que le pase a McCoy en la Enterprise influirá en el estado del tricorder de Spock.
Scotty empieza con el proceso de teletransporte, así que, a partir de este momento, debe tener mucho cuidado si no quiere cargarse a McCoy. Necesita enviarle a Spock información sobre lo que está pasando dentro de la sala del teletransportador, pero sin abrir la puerta ni obtener información directa de McCoy o su tricorder, porque, al ser un sistema cuántico, podría hacer que colapsara en un estado no deseado. Una estrategia que podría seguir sería hacer mediciones indirectas, utilizando los sensores de la Enterprise para averiguar si, en determinado momento, los dos se encuentran en estados similares como vivo/encendido o muerto/apagado, o si uno está «funcionando» y el otro no, sin especificar cuál es cuál… Este proceso se llama medida de Bell, y es una forma de obtener información de un sistema de dos partículas entrelazadas. En la práctica, los estados que le interesan a Scotty son aquellos en los que McCoy está vivo, y que, recordemos, debido al entrelazamiento guardarán relación también con el estado del tricorder de Spock. Solo hay un pequeño problema… aunque Scotty consiga acceder a uno de los estados en los que Bones está bien, cuando haga la medida de Bell, se lo tendrá que cargar igualmente.
Pero mantengamos la calma. Aunque McCoy desaparezca, para entonces su información habrá quedado codificada en los tricorders entrelazados, y Spock, con las instrucciones necesarias, que Scotty tendrá que enviarle por canales convencionales, podrá recuperarla y recrear a su compañero sano y salvo sobre la superficie del planeta en el que está.
Aquí la cosa se pone demasiado bizarra, porque, en esta analogía, lo que sucedería es que, cuando Spock abriera su caja para ver el estado de su tricorder, se encontraría a McCoy dentro, lo que es bastante antiintuitivo. Así que, llegados a este punto… llamemos a McCoy fotón C, al tricorder que se queda con él, fotón A, y al tricorder que tiene Spock, fotón B. Ahora el proceso de teletransporte en este universo paralelo de Star Trek quedaría así:
-
Spock entrelaza los fotones A y B.
-
Se lleva el fotón B consigo al planeta.
-
Scotty quiere enviarle a Spock un fotón C que tiene en la Enterprise, así que lo entrelaza con el A, que se ha quedado él.
-
Scotty hace una medida de Bell sobre el sistema C + A, destruyendo C en el proceso, pero haciendo que la información quede codificada en el sistema A + B.
-
Le envía la información de su medida a Spock por medios convencionales.
-
Spock recrea en su fotón B el estado de C.
Ahora todo parece algo más complicado que lo que vemos en televisión, ¿no? Por no mencionar que no podemos teletransportar nada a ningún lugar en el que no hayamos estado antes o, en su defecto, hayamos enviado una parte de nuestro sistema auxiliar entrelazado, que podría ser tremendamente complejo si estamos hablando de teletransportar a un ser vivo. Este tipo de teletransporte tampoco nos sirve para comunicarnos —de ahí que el límite de la velocidad de la luz no suponga un problema—, porque sin la información que Scotty le envía a Spock por canales sublumínicos, este no sabría qué tendría que hacer para recrear el estado del fotón que le quieren enviar.
Cuestión aparte es el destino que le esperaría al pobre McCoy o a cualquiera que se prestara como tribble de experimentos para probar este tipo de teletransporte: ¿seguro que el original que destruiríamos y la copia que recrearíamos serían la misma persona? Y sí, destruir el original es completamente necesario, porque, como comentamos más arriba, la física cuántica no permite hacer copias perfectas, solo puede existir una a la vez.
Aunque no soy tan tecnofóba como Bones, creo que, en este asunto, me voy a poner de su lado. En estos términos… ¡ni se te ocurra teletransportarme, Scotty! Dicho lo cual… larga vida y prosperidad a todos.
 NBC Television
NBC Television
Bibliografía
Bennett, C. H., Brassard, G., Crépeau, C., Jozsa, R., Peres, A. y Wootters, W. K. (1993) Teleporting an unknown quantum state via dual classical and Einstein–Podolsky–Rosen channels Physical Review Letters doi: 10.1103/PhysRevLett.70.1895
Sternbach, R., Okuda, M. y Roddenberry, G. (1991). Star Trek. TNG. Technical manual. Pocket Books.
.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo ¡Ni se te ocurra teletransportarme, Scotty! se ha escrito en Cuaderno de Cultura Científica.
Los humanos, un Macguffin matemático
Siempre que escucho la palabra “Macguffin” mi mente se va hacia el gran cineasta británico Alfred Hitchcock (1899-1980), autor de grandes películas como La ventana indiscreta (1954), Vértigo (1958), Con la muerte en los talones (1959), Psicosis (1960) o Los pájaros (1963). Y más concretamente me remite al libro El cine según Hitchcock, que recoge la entrevista que le hizo el cineasta francés Francois Truffaut (1932-1984), un libro de cuya lectura he disfrutado en varias ocasiones.
 Fotografía de la entrevista que hizo el cineasta francés Francois Truffaut al cineasta británico Alfred Hitchcock en 1962
Fotografía de la entrevista que hizo el cineasta francés Francois Truffaut al cineasta británico Alfred Hitchcock en 1962¿Qué es el Macguffin?
El Macguffin, término acuñado por el maestro del suspense Alfred Hitchcock, es un objeto, persona, situación o suceso necesario para impulsar la trama y la motivación de los personajes, pero insignificante, sin importancia o irrelevante en sí mismo. Como diría Truffaut “es el pretexto”.
Por ejemplo, en las películas de espías suele ser un secreto o unos documentos, que hacen que la trama se desarrolle, pero que realmente da igual cuál sea el secreto o el contenido de los documentos. Como afirmó el propio Hitchcock, “el Macguffin es lo que persiguen los espías, pero al público le da igual”. En la película Con la muerte en los talones, el protagonista, encarnado por el actor estadounidense Cary Grant (1904-1986), es un agente publicitario que es confundido con un agente del gobierno por unos espías e intentan asesinarlo, motivando la huida del publicista para salvar su vida. Mientras que en la película Psicosis el Macguffin es el robo de un dinero y la posterior huida de su protagonista femenina, interpretada por la actriz estadounidense Vera Miles (1929), que provoca que se esconda en un pequeño hotel regentado por el tímido Norman Bates, que interpretaba el actor estadounidense Anthony Perkins (1932-1992), y que era realmente la parte central de la película. Otro ejemplo interesante es la estatuilla de la película El halcón maltés (1941), interpretada por Humphrey Bogart, Mary Astor y Peter Lorre, y basada en la novela negra homónima del escritor estadounidense Dashiell Hammett (1894-1961), que es el objeto de deseo de una serie de personajes de dudosa moral.
 Cartel de la película Con la muerte en los talones (1959), dirigida por Alfred Hitchcock e interpretada por Cary Grant, Eva Marie Saint, James Mason y Martin Landau
Cartel de la película Con la muerte en los talones (1959), dirigida por Alfred Hitchcock e interpretada por Cary Grant, Eva Marie Saint, James Mason y Martin LandauPara finalizar con los ejemplos, un Macguffin esclarecedor, más moderno y en otro tipo de película, como es The Blues Brothers (1980), donde los personajes encarnados por los actores estadounidenses John Belushi (1949-1982) y Dan Aykroyd (1952), intentan conseguir el dinero necesario para salvar el orfanato en el cual se criaron, lo cual no es más que la excusa para realizar un viaje con el objetivo de reunir a los miembros de un grupo musical y llenar ese viaje de humor y música, buena música de blues y soul.
En el libro El cine según Hitchcock, el maestro del suspense explicaba el origen del término de la siguiente forma.
Y ahora, conviene preguntarse de dónde viene el “MacGuffin”. Evoca un nombre escocés y es posible imaginarse una conversación entre dos hombres que viajan en un tren. Uno le dice al otro: “¿Qué es ese paquete que ha colocado en la red?” Y el otro contesta: “Oh, es un Mac Guffin”. Entonces el primero vuelve a preguntar: “¿Qué es un Mac Guffin?” Y el otro: “Pues un aparato para atrapar a los leones en las montañas Adirondaks”. El primero exclama entonces: “¡Pero si no hay leones en las Adirondaks!” A lo que contesta el segundo: “En ese caso no es un Mac Guffin”.
Esta anécdota demuestra el vacío del Mac Guffin … la nada del Mac Guffin.
Los humanos, de Matt HaigLa novela a la que vamos a dedicar esta entrada del Cuaderno de Cultura Científica, Los humanos (2013), del escritor británico Matt Haig (1975), contiene un Macguffin matemático. Pero vayamos por partes. Primero presentemos brevemente a su autor.
Matt Haig es un periodista y escritor inglés, que escribe tanto para adultos, como para jóvenes. Estudió Inglés e Historia en la Universidad de Hull. Entre sus libros nos encontramos novelas como Los humanos (2013), Cómo detener el tiempo (2017), La biblioteca de la medianoche (2020) o La vida imposible (2024), cuya protagonista es matemática; libros para jóvenes como Shadow Forest: el bosque de las sombras (2007), El chico que salvó la navidad (2015), La duendecilla sincera (2018) o Evie, la amiga de los animales (2019), y libros de no ficción como Razones para seguir viviendo (2015), Apuntes sobre un planeta estresado (2018) o El libro de la esperanza (2021).
 Fotografía de Matt Haig en el Edinburgh International Book Festival de 2024
Fotografía de Matt Haig en el Edinburgh International Book Festival de 2024
Respecto a la novela Los humanos, lo primero es recomendar a las personas que estáis leyendo esta entrada que la leáis, no porque sea una novela relacionada con las matemáticas, sino porque es una novela interesante y muy divertida.
Pero para hablar de esta novela podemos empezar por la sinopsis escrita por la editorial:
El profesor Andrew Martin de la Universidad de Cambridge acaba de descubrir el secreto de los números primos, encontrando al mismo tiempo la clave que garantizará el fin de la enfermedad y la muerte. Convencidos de que los secretos de los números primos no pueden dejarse en manos de una especie tan primitiva como los humanos, los vonadorianos, una civilización extraterrestre mucho más evolucionada, envían a un emisario para hacer desaparecer a Martin y a su descubrimiento. Y así es como un vonadoriano con el aspecto externo de Martin aparece con la misión de matar a la esposa, al hijo y al mejor amigo del profesor, pero no puede dejar de sentirse fascinado por esa fea especie y sus costumbres incomprensibles.
 Portada de la novela Los humanos, de Matt Haig (Roca Editorial, 2014)
Portada de la novela Los humanos, de Matt Haig (Roca Editorial, 2014)El punto de partida de la novela es que el matemático y profesor de la Universidad de Cambridge (Gran Bretaña) Andrew Martin ha demostrado la llamada hipótesis de Riemann, uno de los problemas matemáticos abiertos, es decir, que está aún por resolverse, más importantes. De hecho, la hipótesis de Riemann es uno de los siete “problemas del milenio” que anunció el Instituto Clay de Matemáticas en el año 2000, con una recompensa de un millón de dólares para quien lo resolviese. Más aún, este problema ya estaba en la lista de los 23 problemas que recogió el matemático alemán David Hilbert (1862-1943) en el Congreso Internacional de Matemáticos de 1900, como problemas más importantes para el nuevo siglo xx.
Sin embargo, para una civilización extraterrestre, los vonadorianos, este es un conocimiento demasiado poderoso, que en manos de los humanos podría poner en peligro el equilibrio del universo y provocar su destrucción. Por este motivo, deciden reemplazar a Martin por un clon alienígena, que es realmente el protagonista de esta historia narrada por él mismo, y borrar toda evidencia de su descubrimiento, destruyendo los documentos relacionados con la demostración, los rastros digitales de la misma o las personas que hayan podido tener algún conocimiento de esta prueba, como la familia del matemático, su mujer y su hijo, y alguno de sus colegas.
Resulté ser un hombre casado de 43 años, la mitad exacta de una vida humana. Tenía un hijo. Era el profesor que acababa de resolver el enigma matemático más importante al que se habían enfrentado los humanos. Apenas tres horas antes había hecho progresar la especie humana más allá de lo que cualquiera habría podido imaginar.
La hipótesis de Riemann no es más que un pretexto, es decir, el Macguffin de esta historia, para contarnos de forma divertida cómo nos vería un extraterrestre a los terrícolas y hablar de lo que significa ser humano, del amor, la amistad, la familia, las relaciones humanas, los conflictos, la vida o la muerte.
 Portada de la versión británica de la novela Los humanos / The humans (2013), de Matt HaigLas matemáticas de los vonadorianos
Portada de la versión británica de la novela Los humanos / The humans (2013), de Matt HaigLas matemáticas de los vonadorianos
Antes de entrar en materia, un pequeño comentario sobre el hecho de que los vonadorianos son una civilización extraterrestre para la cual las matemáticas son extremadamente importantes y un conocimiento esencial para ellos. Para que nos hagamos una idea de esto, incluyo algunas sencillas citas de la novela, que son pensamientos del vonadoriano protagonista.
La primera:
Yo nunca quise que me mandasen aquí. Se trataba de una tarea que, tarde o temprano, alguien tenía que asumir y, después de la charla que di en el Museo de las Ecuaciones Cuadráticas –que muchos tacharon de blasfemia, de supuesto crimen contra la pureza matemática–, a los anfitriones [los dirigentes de los vonadorianos] les pareció el castigo perfecto.
La segunda:
Por supuesto, en teoría aquella era mi ciudad […]. La falta de imaginación geométrica me tenía fascinado: no había ni tan siquiera un decágono a la vista. […] Pronto aprendería que en las ciudades todo es una tienda. Son a los moradores de la Tierra lo que las cabinas de ecuaciones son a los vonadorianos.
La tercera:
Allá de donde venimos la tecnología que hemos creado sobre las bases de nuestro entendimiento supremo y exhaustivo de las matemáticas nos ha supuesto no solo la posibilidad de atravesar grandes distancias, sino también de reajustar nuestros propios componentes biológicos, renovarlos y reponerlos. Estamos equipados psicológicamente para tales progresos. Nunca hemos vivido una guerra civil. Nunca anteponemos los deseos individuales a las necesidades del colectivo.
En general, las citas matemáticas de la novela tienen un objetivo literario y no rigurosidad matemática. Por ejemplo, en cierto momento el vonadoriano clon de Andrew Martin se queja de que el orden de prioridad de las noticias en televisión es incomprensible para él y se sorprende de que no hable de “nuevas observaciones matemáticas” (lo cual es un comentario bastante indefinido y confuso) o de “polígonos todavía por descubrir” (también bastante impreciso e incluso que puede considerarse equívoco).
La hipótesis de RiemannA pesar de que la hipótesis de Riemann es solamente una excusa para hablar de los humanos, de la humanidad, Matt Haig sí intenta explicar en la novela, de forma muy sencilla y bastante literaria, en qué consiste la misma o, al menos, algunas ideas relacionadas con ella.
Así, cuando el vonadoriano con aspecto de Andrew Martin descubre en el ordenador del matemático de la Universidad de Cambridge el documento que contiene la demostración de la hipótesis de Riemann, hay un pequeño capítulo de la novela dedicado a los números primos y su distribución dentro de los números naturales (por cierto que una introducción a estos temas puede leerse en las entradas del Cuaderno de Cultura Científica Buscando lagunas de números no primos y El poema de los números primos, así como en el libro La gran familia de los números, que se menciona en la bibliografía), que comentaremos a continuación, aprovechando el texto de la novela.
Pero antes, así es como describe Matt Haig al autor de la hipótesis, el matemático alemán Bernhard Riemann (1826-1866).
Aprendí algo más sobre Bernhard Riemann, un niño prodigio alemán horrorosamente tímido que vivió en el siglo xix y que, ya desde una edad temprana, demostró su habilidad excepcional con los números, antes de sucumbir a su carrera de matemático y a la serie de crisis nerviosas que minaron su adultez. Más tarde descubriría que ese era uno de los problemas fundamentales que tienen los humanos con la comprensión numérica: simple y llanamente, su sistema nervioso no está capacitado.
La verdad es que no dice gran cosa, salvo que era un niño prodigio y que “sufría crisis nerviosas”, sobre una de las grandes mentes matemáticas de la historia, que realizó avances revolucionarios en todas las áreas de las matemáticas en las que trabajó, en particular, el análisis matemático, la geometría diferencial y la teoría de números. Muchos son los conceptos y resultados matemáticos asociados a su nombre, como la integral de Riemann, las ecuaciones de Cauchy-Riemann, las superficies de Riemann, la geometría riemanniana, el tensor de curvatura de Riemann, la función zeta de Riemann o la hipótesis de Riemann, entre otras.
 Caricatura de Bernhard Riemann, realizada por Gerardo Basabe de Viñaspre, para la exposición de la Real Sociedad Matemática Española, El rostro humano de las matemáticas (2008)Los números primos
Caricatura de Bernhard Riemann, realizada por Gerardo Basabe de Viñaspre, para la exposición de la Real Sociedad Matemática Española, El rostro humano de las matemáticas (2008)Los números primos
Pero vayamos con los números primos. El primer párrafo sobre los mismos, que nos narra el vonadoriano, es el siguiente.
Los números primos vuelven a la gente loca, pero literalmente, sobre todo por la cantidad de enigmas que quedan sin resolver. Lo único que parecían saber es que un primo es un número entero que solo puede dividirse por 1 y por sí mismo, pero, más allá de eso, se dan de bruces con un problema tras otro.
La verdad es que es un comentario bastante simplista, puesto que viene a decir que el único conocimiento que se tiene sobre los números primos es su definición, es decir, que son aquellos números naturales que solamente se pueden dividir por 1 y por ellos mismos. Por ejemplo, el número 25 no es primo ya que se puede dividir por 5, mientras que el número 19 sí es primo, ya que solamente es divisible por el 1 y él mismo, al igual que lo son los números 2, 3, 5, 7, 11 y 13, entre otros. Sin embargo, los humanos llevamos más de dos milenios investigando sobre los números primos y obteniendo muchos e importantes resultados, como que existen infinitos números primos, como ya demostraron los antiguos griegos, que todo número natural se puede expresar de forma única como producto de números primos (el teorema fundamental de la aritmética), que la función contador de números primos, es decir, para cada número x, la cantidad de números primos menores o iguales que x se aproxima por la función x/Ln x (el teorema de los números primos), y así existen miles y miles de resultados más que podríamos añadir. Cabe mencionar que existen muchos libros dedicados solo a los resultados sobre los números primos, de los que mencionaremos aquí cuatro en clave más divulgativa, por si hay alguien interesado: 1) Prime Numbers, The Most Mysterious Figures in Math (David Wells, John Wiley & Sons, 2005); 2) The Little Book of Bigger Primes (Paulo Ribenboim, Springer Verlag, 2004); 3) La música de los números primos (Marcus du Sautoy, Acantilado, 2007); 4) Los números primos, un largo camino al infinito (Enrique Gracián, RBA, 2010).
Aunque después del párrafo anterior, sí menciona alguno de los conocimientos que la humanidad ha alcanzado sobre los números primos, casi siempre expresado de una forma más literaria, o incluso poética, que matemática. Por ejemplo, afirma que se conoce que hay infinitos números primos (la sencilla y hermosa demostración de los griegos podéis leerla en la entrada Buscando lagunas de números no primos), pero además menciona que son numerables, es decir, que se pueden contar (sobre los conjuntos infinitos podéis leer la serie de entradas titulada El infinito en un segmento: uno, dos y tres), de la siguiente forma.
Saben que el total de todos los números primos es igual al total de todos los números, pues ambos sumarían infinitos. Para el humano medio, esto constituye un hecho bastante desconcertante, pues ciertamente tienen que existir más números aparte de los primos. Tan imposible les resulta asimilar que, al enfrentarse al tema, más de uno se ha metido un revólver en la boca, ha apretado el gatillo y se ha volado los sexos.
Aquí realmente está mezclando dos temas apasionantes e importantes, primero que hay infinitos números primos, que puede entenderse bien por sí solo, pero a la vez nos habla de que hay tantos como números naturales, hecho que está relacionado con la dificultad de entender el infinito y sus paradojas, como lo mencionado, que una parte del conjunto (los números primos) tenga tantos elementos como todo el conjunto (los números naturales). Aunque este segundo tema es un poco complejo para las personas que lean la novela, es muy exagerado decir que “tan imposible les resulta asimilar que, al enfrentarse al tema, más de uno se ha metido un revólver en la boca, ha apretado el gatillo y se ha volado los sexos”, aunque tenemos que entender que esto es literatura y no divulgación de las matemáticas.
El siguiente párrafo dice lo siguiente:
Los humanos también han llegado a entender que los números primos se parecen mucho al aire terráqueo. Cuánto más arriba subes, menos hay. Por ejemplo, hay 25 números primos menores que 100, pero solo 21 entre 100 y el 200 y solo 16 entre 1.000 y 1.100. Sin embargo, a diferencia de aire en la Tierra, no importa lo mucho que subas en la escala de los números, siempre habrá algún número primo. Por ejemplo, 2.097.593 es primo y hay millones más entre ese y, pongamos, 4314398832739895727932419750374600193. En consecuencia, podemos decir que la atmósfera de los números primos recubre todo el universo.
La primera parte ofrece el primer comentario sobre la distribución de los números primos dentro de los naturales, que es el tema central sobre el que versa la hipótesis de Riemann. Y efectivamente es así. Como se comentaba en la entrada Buscando lagunas de números no primos, entre los 100 primeros números hay 25 primos, es decir, 1 de cada 4 números es primo. Sin embargo, si miramos entre los 1.000 primeros números, resulta que hay 168 que son primos, 1 de cada 6 números. Un porcentaje menor. Y así, como podemos ver en la siguiente tabla, según vamos ampliando la cantidad de números considerados, existe un menor porcentaje de números primos. Luego según vamos avanzando en la recta de números naturales, los números primos van siendo cada vez más infrecuentes, y los números compuestos van ocupando más el espacio dentro de los números naturales.
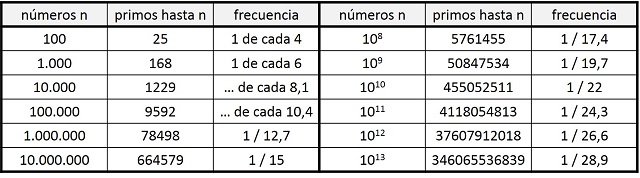 Tabla con la cantidad de números primos y frecuencia de los mismos para cantidades de números que son potencias de 10
Tabla con la cantidad de números primos y frecuencia de los mismos para cantidades de números que son potencias de 10
Sin embargo, el segundo comentario solo es una forma diferente y poética de volver a afirmar que existen infinitos números primos.
La distribución de los números primosEl texto del capítulo “Números primos” sigue asi:
En 1859, no obstante, en la Academia de Berlín, un Bernhard Riemann cada vez más enfermo enunció la que sería la hipótesis más estudiada y celebrada de todas las matemáticas. Afirmaba que había un patrón, o al menos lo había para los primeros mil números primos. Y era bello, cristalino e involucraba algo llamado “función zeta”, una especie de máquina mental, una curva de aspecto complejo que servía para investigar las propiedades de los primos. Si los colocabas en ella, formaban un orden en el que nadie se había fijado con anterioridad: ¡un patrón! ¡La distribución de los números primos no era arbitraria!
Una vez más mencionemos que esto no es un texto de divulgación de las matemáticas, sino literatura, ya que lo afirmado en el anterior párrafo hay que cogerlo con pinzas, pero como lector tengo que entender la intención narrativa del autor de la novela.
Para empezar, podemos considerar que la hipótesis de Riemann es una de las conjeturas más importantes y estudiadas, no en vano estaba entre los 23 problemas de Hilbert (en 1900) y entre los siete problemas del milenio (en 2000), pero hay otros problemas matemáticos también importantes y muy estudiados, como el último teorema de Fermat, conjeturado por el matemático francés Pierre de Fermat (1601-1665) hacia 1637 y demostrado por el matemático británico Andrew Wiles en 1995 (puede leerse sobre esta cuestión en la entrada Euler y el último teorema de Fermat); la conjetura de Poicaré, formulada por el matemático francés Henri Poincaré (1854-1912) en 1904 y demostrada por el matemático ruso Gregori Perelman en 2006 (véase la entrada La conjetura de Poincaré-Perelman-Miander); o el problema del quinto postulado de Euclides y la existencia de las geometrías no euclídeas, un problema que tardó más de dos milenios en resolverse, por matemáticos como Nikolai Lobachevski (1752-1856) y János Bolyai (1802-1860); o incluso problemas matemáticos que permanecen abiertos, como la conjetura de Goldbach, formulada por el matemático prusiano Christian Goldbach (1690-1764) en 1742 (véase la entrada La conjetura de Goldbach); o cualquiera de los problemas del milenio, que son la conjetura de Birch y Swinnerton-Dyer, en teoría de números algebraica; la conjetura de Hodge, en geometría algebraica; la solución de las ecuaciones de Navier-Stokes de la mecánica de fluidos; el problema P = NP, en ciencias de la computación; la conjetura de Poncaré, en topología (ya resuelta en 2006); el problema de la masa en la teoría de Yang-Mills, en la teoría cuántica de campos; y la mencionada hipótesis de Riemann, en análisis complejo y teoría de números primos, que es una de las más importantes y conocida.
 Caricatura de David Hilbert, realizada por Enrique Morente, para la exposición de la Real Sociedad Matemática Española, El rostro humano de las matemáticas (2008)
Caricatura de David Hilbert, realizada por Enrique Morente, para la exposición de la Real Sociedad Matemática Española, El rostro humano de las matemáticas (2008)Lo siguiente que vamos a comentar es la frase “afirmaba que había un patrón, o al menos lo había para los primeros mil números primos”, a la que podemos ponerle algunos peros matemáticamente hablando. Decir que había un patrón es ambiguo y simplista, aunque a Matt Haig le pueda valer para la novela.
Desde la matemática griega se ha intentado descubrir, sin éxito, la existencia de algún patrón en la distribución de los números primos dentro de los naturales, pero, como decía el matemático suizo Leonhard Euler (1707-1783), este será uno de esos misterios que la humanidad nunca será capaz de desvelar.
No existe ninguna fórmula que nos permita determinar cuál es el número primo n-ésimo, para cualquiera que sea la posición n, ni una expresión matemática que posibilite, conocidos todos los primos hasta uno dado, obtener el siguiente.
Aunque, una aproximación a la distribución de los números primos es el estudio de la función contador de números primos. Dado un número x se define pi(x) como la cantidad de primos menores, o iguales, que x. Si se observan los números primos hasta 100 se puede comprobar que pi(20) = 8 (que son 2, 3, 5, 7, 11, 13, 17 y 19) o pi(100) = 25 (que son, además de los anteriores, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73 79, 83 89 y 97). En la siguiente tabla se muestra el valor de la función contador de números primos (x) para las primeras potencias de 10, junto con la densidad (x) / x –la proporción de números primos respeto a los naturales, hasta x– y la frecuencia, x / (x) –cuántos números naturales hay por cada primo, hasta x–, que nos incide en la idea anterior de que cada vez hay menos números primos.
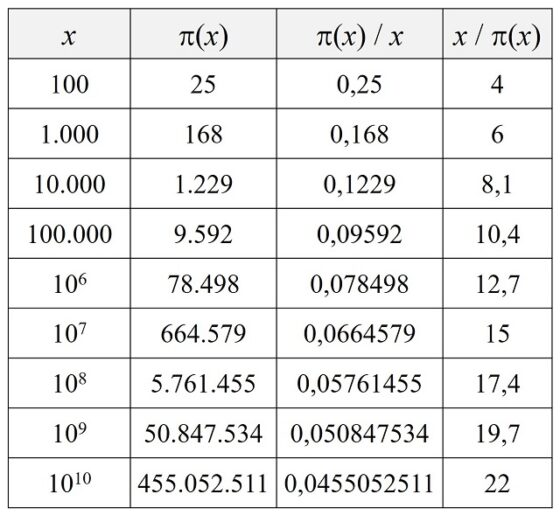
La primera aproximación a la distribución de los números primos vino de la mano del matemático alemán Carl F. Gauss (1777-1855), que, a la edad de 15 años, conjeturó que, aunque no se podía conocer con precisión el valor de la función contador de números primos (x), se podía aproximar con la ayuda de la función logaritmo neperiano. Este resultado, conocido como teorema de los números primos, establece que la función (x) se aproxima a la función x / Ln(x), cuando x tiende a infinito. Este teorema fue demostrado en 1896, de forma independiente, por el matemático francés Jacques Hadamard (1865-1963) y el belga Charles-Jean de la Vallé Poussin (1866-1962). Por ejemplo, si se considera x = 106, como Ln(106) es 6 multiplicado por Ln(10) = 2.30258509…, entonces x / Ln(x) es aproximadamente 72.382, siendo la cantidad de primos 78.498.
El propio Gauss dio una mejor aproximación a la función contador de números primos mediante la función logaritmo integral
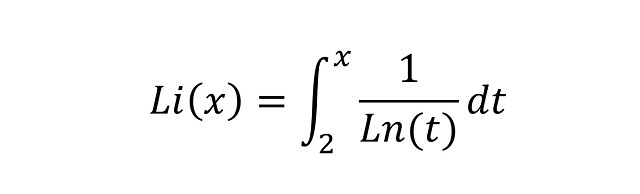
Volviendo al caso de x = 106, mientras que la diferencia de x / Ln(x) con (x) es de 6.116 números, la variación del logaritmo integral Li(x), no os preocupéis ahora de su significado, es sólo de 130.
Pues resulta, que la hipótesis de Riemann, cuya formulación es bastante compleja y está relacionada con los ceros de la conocida función zeta de Riemann que se define sobre los números complejos (ya volveremos sobre ella en alguna futura entrada de Cuaderno de Cultura Científica), es equivalente al hecho de que el logaritmo integral es una “buena” aproximación.
 La pizarra del programa La Revuelta, de David Broncano, en TVE, está relacionada con la hipótesis de Riemann, puesto que representa la función zeta de Riemann y la recta donde estarían, según la hipótesis, los ceros no triviales de dicha función. Sobre la pizarra podéis leer el artículo del diario.es titulado El misterio de la pizarra de Broncano: ¿qué pinta esta maravilla de las matemáticas en La Revuelta?Para terminar
La pizarra del programa La Revuelta, de David Broncano, en TVE, está relacionada con la hipótesis de Riemann, puesto que representa la función zeta de Riemann y la recta donde estarían, según la hipótesis, los ceros no triviales de dicha función. Sobre la pizarra podéis leer el artículo del diario.es titulado El misterio de la pizarra de Broncano: ¿qué pinta esta maravilla de las matemáticas en La Revuelta?Para terminar
Para cerrar esta entrada del Cuaderno de Cultura Científica, me gustaría incluir los puntos relacionados con las matemáticas del listado de los 97 “consejos para un humano” que escribe el vonadoriano con aspecto de Andrew Martin al final de la historia, que están escritos para “su hijo” (el de Andrew Martin).
Consejo 12: Los telediarios deberían abrir con noticias de matemáticas y seguir con poesía, y a partir de ahí, que hagan lo que quieran.
Consejo 59: Los números son bonitos. Los primos son bonitos. Ya lo entenderás.
Bibliografía
1.- Francois Truffaut, El cine según Hitchcock, Alianza editorial, 1974.
2.- Matt Haig, Los humanos, Roca Editorial, 2014.
3.- R. Ibáñez, La gran familia de los números, Libros de la Catarata, 2021.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Los humanos, un Macguffin matemático se ha escrito en Cuaderno de Cultura Científica.
Primer plasma en el tokamak SMART de la Universidad de Sevilla
En el marco de un proyecto pionero en el camino hacia el desarrollo de la energía de fusión, el tokamak SMART ha generado con éxito su primer plasma. Este paso acerca a la comunidad internacional a la energía de fusión; una fuente de energía sostenible, limpia y prácticamente ilimitada.
 Primer plasma en el SMall Aspect Ratio Tokamak – SMART – grabado con una cámara superrápida en el espectro visible. Fuente: Universidad de Sevilla
Primer plasma en el SMall Aspect Ratio Tokamak – SMART – grabado con una cámara superrápida en el espectro visible. Fuente: Universidad de SevillaEl tokamak SMART (SMall Aspect Ratio Tokamak) es un dispositivo de fusión experimental de última generación diseñado, construido y operado por el Laboratorio de Ciencia del Plasma y Tecnología de Fusión (PSFT) de la Universidad de Sevilla. Se trata de un tokamak esférico único en el mundo debido a su flexibilidad para generar plasmas con distintas formas. SMART ha sido diseñado para demostrar las propiedades físicas e ingenieriles únicas que los plasmas con forma de triangularidad negativa tienen en el camino hacia el desarrollo de plantas de energía de fusión compactas basadas en Tokamaks Esféricos.
 SMART explora un camino potencialmente revolucionario al combinar plasmas de fusión de alto rendimiento con atractivas soluciones para su implementación en reactores de fusión super compactos. Fuente: Universidad de SevillaUna cuestión de triangularidad
SMART explora un camino potencialmente revolucionario al combinar plasmas de fusión de alto rendimiento con atractivas soluciones para su implementación en reactores de fusión super compactos. Fuente: Universidad de SevillaUna cuestión de triangularidad
La triangularidad describe la forma del plasma. La mayoría de los tokamaks funcionan con triangularidad positiva, lo que significa que la forma de la sección del plasma parece una D. Si la forma del plasma se asimila a una D invertida (como se aprecia en la imagen de abajo), tiene triangularidad negativa.
 Render del Tokamak SMART con un plasma de triangulación negativa en el interior. Fuente: Universidad de Sevilla
Render del Tokamak SMART con un plasma de triangulación negativa en el interior. Fuente: Universidad de SevillaLos plasmas con de triangularidad negativa presentan un rendimiento mejorado ya que suprimen las inestabilidades que degradan el confinamiento del reactor, evitando daños graves a la pared del tokamak. Además de ofrecer un alto rendimiento de fusión, la triangularidad negativa también presenta soluciones atractivas para el control de la potencia generada en las reacciones de fusión, dado que el calor que escapa se distribuye en un área mayor. Esto también facilita el diseño para futuras centrales eléctricas de fusión más compactas y eficientes.
Fusión compactaSMART es el primer paso en la estrategia Fusion2Grid, liderada por el equipo PSFT y en colaboración con la comunidad internacional de fusión, que tiene como objetivo el diseño de una planta de potencia basada en fusión por confinamiento magnético más compacta y eficiente usando tokamaks esféricos con forma de triangularidad negativa. SMART será el primero de este tipo que funcionará a temperaturas de fusión.
El objetivo del tokamak SMART es proporcionar las bases científicas y tecnológicas para el diseño del reactor de fusión más compacto posible. Este primer plasma representa un logro importante para el proyecto, así como para el avance hacia este objetivo.
Referencia:
Dominguez-Palacios, J., Futatani, S., García-Muñoz, M. et al. (2025) Effect of energetic ions on edge-localized modes in tokamak plasmas. Nat. Phys. doi: 10.1038/s41567-024-02715-6
Edición realizada por César Tomé López a partir de materiales suministrados por la Universidad de Sevilla.
El artículo Primer plasma en el tokamak SMART de la Universidad de Sevilla se ha escrito en Cuaderno de Cultura Científica.
El beso planetario de Caronte
Desde su descubrimiento en la década de los años treinta del siglo pasado y hasta el sobrevuelo de la sonda New Horizons en julio de 2015, Plutón y su sistema de satélites había sido poco más que un punto de luz, incluso en los telescopios más avanzados. Y es que si sumamos su pequeño tamaño -tiene un diámetro de apenas una sexta parte el de la Tierra- y su lejanía, era un cuerpo francamente difícil de estudiar.
Plutón tiene cinco satélites naturales conocidos: Caronte, Nix, Hidra, Cerbero y Estigia. Caronte fue descubierto a finales de la década de los 70, mientras que el resto fueron descubiertos a partir de los años 2000 -algunos ya en la segunda década-, lo que nos hace una idea de la diferencia de tamaños entre los satélites y que, cuanto más pequeños, más cuesta detectarlos desde una distancia tan grande.
Pero hoy vamos a centrarnos en Caronte que, proporcionalmente, es un satélite enorme para un planeta como Plutón. De hecho, tanto es así que su masa supera al 10% de la suma de las masas del sistema que forma con el planeta enano. Por ponerlo en contexto, en el caso del sistema Tierra-Luna, la masa de la Luna es tan solo de aproximadamente un 1.2%. Echando un vistazo a esta relación de masas, es normal que algunos autores incluso hayan considerado a Plutón y Caronte un sistema binario de cuerpos planetarios.
 Figura 1. Imagen de Caronte tomada por la sonda New Horizons en 2015. Destaca en la imagen el color rojizo de Mordor Macula frente a los tonos grisáceos de la superficie, así como zonas con un número de cráteres relativamente bajo en algunas partes de su superficie. ¿Esconderá Caronte procesos geológicos de rejuvencecimiento? Cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Southwest Research Institute.
Figura 1. Imagen de Caronte tomada por la sonda New Horizons en 2015. Destaca en la imagen el color rojizo de Mordor Macula frente a los tonos grisáceos de la superficie, así como zonas con un número de cráteres relativamente bajo en algunas partes de su superficie. ¿Esconderá Caronte procesos geológicos de rejuvencecimiento? Cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Southwest Research Institute.¿Y cómo surgió esta dispar pareja planetaria? La teoría más aceptada hasta el momento sugería un mecanismo de formación similar al de nuestra Luna, pero un nuevo estudio publicado en Nature Geoscience por Adeene Denton et al. (2025) propone una nueva teoría que los propios autores del estudio denominan “beso y captura”.
Volvamos por un momento a detallar los mecanismos de formación. Como decíamos en el párrafo anterior, la teoría más aceptada es la de un “gran impacto”. Es decir, en algún momento de la historia de Plutón, un cuerpo de un tamaño relativamente grande chocaría con este, lanzando una gran cantidad de materia a su órbita que, con el tiempo, iría uniéndose hasta formar Caronte. Pero, al igual que en nuestro sistema Tierra-Luna parece encajar este modelo, en el de Plutón y Caronte no parece funcionar del todo.
El mayor problema radica en explicar el tamaño que tiene Caronte ya que, al ser tan grande, requiere que la colisión tuviese unas condiciones muy específicas… casi “tocándose” suavemente, pero con una firmeza suficiente como para arrancar de ambos objetos una cantidad de materia suficiente para formar el satélite y al mismo tiempo no destruir por completo ninguno de los cuerpos en este proceso.
Pero, valga la redundancia, existe otro pero a la teoría del gran impacto en el caso concreto de Plutón: Las simulaciones de este tipo de impactos suelen dar como resultado la formación de más de un satélite, no solo de un gran satélite. Y cuando forman un satélite del tamaño de Caronte, lo hacen en una órbita más excéntrica y no tan circular como la que observamos.
 Figura 2. Plutón y Caronte capturados en una sola fotografía. Impresiona ver la pequeña diferencia de tamaño, pero también la pequeña distancia que separa ambos cuerpos. Cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Southwest Research Institute.
Figura 2. Plutón y Caronte capturados en una sola fotografía. Impresiona ver la pequeña diferencia de tamaño, pero también la pequeña distancia que separa ambos cuerpos. Cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Southwest Research Institute.Entonces, ¿cómo pudo formarse Caronte? Aquí es donde este nuevo trabajo parece responder a la pregunta de porque no comprendíamos del todo su origen. A los modelos existentes les faltaba tener en cuenta la resistencia de ambos cuerpos y las propiedades mecánicas de los materiales que los conformaban, ya que trataban a Plutón y Caronte como gigantescas esferas con la consistencia de un fluido, con una extrema facilidad para deformarse.
Pero no olvidemos que son cuerpos formados principalmente por hielos, con una estructura interna y cierta capacidad para soportar la deformación. Si queréis pensarlo de manera gráfica -y quizás algo grosera- pensad que pasaría si lanzásemos dos globos llenos de agua uno contra el otro o dos bolas de nieve. ¿Verdad que el resultado sería muy distinto?
Hagamos un viaje al pasado e imaginémonos a un proto-Plutón girando por el espacio y a un proto-Caronte en rumbo de colisión, pero en vez de pensar en una colisión frontal -y que probablemente habría sido muy destructiva- pensemos más en un roce entre ambos cuerpos, o lo que los autores han denominado como un “beso” cósmico”. Pero un beso en el sentido figurado, ya que incluso en estas condiciones la fuerza de la colisión es brutal… y aquí es donde viene la innovación que aporta este estudio.
Al chocar ambos cuerpos, la fricción en el punto de contacto entre ellos actúa como una especie de “freno”, provocando una desaceleración en el movimiento orbital relativo entre ambos y transfiriendo una gran cantidad de momento -en el sentido físico de la palabra- también.
 Figura 3. Los satélites de Plutón comparados en tamaño. Se puede apreciar perfectamente la enorme diferencia de tamaño entre los más pequeños y Caronte. ¿Se formarían en el mismo impacto que dio lugar a Caronte? Imagen cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Southwest Research Institute.
Figura 3. Los satélites de Plutón comparados en tamaño. Se puede apreciar perfectamente la enorme diferencia de tamaño entre los más pequeños y Caronte. ¿Se formarían en el mismo impacto que dio lugar a Caronte? Imagen cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Southwest Research Institute.Esta fricción provoca que ambos cuerpos conecten de manera temporal, formando una especie de cacahuete o muñeco de nieve rotando rápidamente. La resistencia de los materiales evitaría la mezcla completa del interior de ambos cuerpos, haciendo que ambos sigan siendo geoquímicamente distintos, con sus mantos y núcleos intactos casi por completo.
Poco a poco, la fuerza centrífuga y las de marea irían ayudando a separar al proto-Caronte de Plutón, algo que no fue instantáneo. Eso sí, comenzaría su andadura como satélite en una órbita muy cercana a la superficie de Plutón. Esto provocaría inmensas fuerzas de marea entre ambos cuerpos que ayudarían a que Caronte adquiriese una órbita circular, y no elíptica, como parecían mostrar modelos anteriores, otra de las piezas que no terminaba de encajar.
Este modelo de “beso y captura” no solo ofrece explicaciones que son capaces de satisfacer los parámetros orbitales, la existencia de los otros satélites menores que observamos hoy en día y el gran tamaño de Caronte, sino que además tiene una consecuencia que es muy interesante: Caronte podría ser tan antigua como Plutón, manteniendo una gran parte de su núcleo y su manto original, ya que -a diferencia del caso de la Tierra y la Luna- el grado de mezcla entre ambos cuerpos no fue tan importante, pudiendo servirnos como una ventana al estudio de otras zonas de nuestro sistema solar y a los procesos de un Sistema Solar Primitivo.
Referencias:
Denton, C.A., Asphaug, E., Emsenhuber, A. et al. (2025) Capture of an ancient Charon around Pluto. Nat. Geosci. doi: 10.1038/s41561-024-01612-0
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo El beso planetario de Caronte se ha escrito en Cuaderno de Cultura Científica.
Las hormigas también pueden ser rencorosas
 Nido de hormigas. Fuente: David Ballesteros CC
Nido de hormigas. Fuente: David Ballesteros CC
Las ventajas evolutivas del reconocimiento son incontables y han resultado claves para desarrollar un mundo de identidad y pertenencia. Saludamos al vecino del 4ºB por la mañana, dejamos prestado un bolígrafo a nuestro compañero de trabajo, cenamos en Nochebuena con los miembros de nuestra familia y desconfiamos del hombre que nos sigue de noche por un callejón. Cualquier colectivo, desde las tribus paleolíticas hasta nuestras modernas sociedades se han cimentado sobre la distinción entre el igual y el extraño. Pero esta capacidad no es única del ser humano, de hecho es un factor clave de unión y protección en todas las escalas de la vida. Desde nuestras diminutas células T, capaces de detectar y neutralizar las amenazas procedentes de otras células tumorales o virus, hasta los intrincados nexos que se producen en una manada de lobos.
En las especies eusociales esta habilidad es aún más pronunciada, aunque las formas de identificar a los miembros de su grupo pueden llegar a ser muy variadas. Las hormigas utilizan «los olores para distinguir entre los miembros de su propio nido y los de otros nidos, ya que cada nido tiene su propio olor específico». En estudios anteriores se demostró que las hormigas se comportan de manera más agresiva con sus vecinas más cercanas, un comportamiento lógico puesto que esta cercanía supone una mayor amenaza por el control de los recursos en los alrededores del nido. Son especialmente propensas a abrir sus mandíbulas y morder, a rociar ácido o incluso a matar a sus competidoras. Por otro lado, estas maniobras tan agresivas son menos frecuentes contra los nidos que están más lejos del suyo. Esto representa un claro ejemplo de aprendizaje asociativo en el que los insectos sociales son capaces de asociar una señal de olor con una recompensa o una amenaza.
Es más, la agresividad de las hormigas en su objetivo de defender su hogar está directamente relacionada con la distancia a la que se encuentra el nido que podría suponer un peligro.
 Las agresiones se intensifican frente a miembros de nidos cercanos. Fuente: Bey et al (2024) / Current Biology
Las agresiones se intensifican frente a miembros de nidos cercanos. Fuente: Bey et al (2024) / Current Biology
Sin embargo, un nuevo estudio publicado hace solo unos días en Current Biology ha dado un paso más y encontrado evidencias de aprendizaje no asociativo en la conducta de las hormigas. No solo detectan las señales características de un nido vecino (efecto del vecino desagradable) sino que son capaces de recordar individualmente a sus rivales más agresivos y adaptan su comportamiento específicamente a ese ejemplar.
Así lo ha demostrado un equipo de biólogos evolutivos de la Universidad alemana de Friburgo que enfrentaron repetidamente a un grupo de hormigas con competidoras de otro nido. Utilizaron hormigas negras de jardín (Lasius niger), muy frecuentes en Europa, América y Asia, que recogieron de diferentes nidos en los alrededores de su centro de investigación.
Las hormigas del grupo de control recordaron las experiencias negativas que tuvieron durante esos encuentros y cuando se encontraron con hormigas de un nido con las que previamente habían tenido encontronazos, recordaron esas experiencias negativas y se comportaron de manera más agresiva con esos adversarios. Por otro lado, esas mismas hormigas fueron menos agresivas con los miembros del nido rival con las que no habían mantenido ningún rifirrafe…
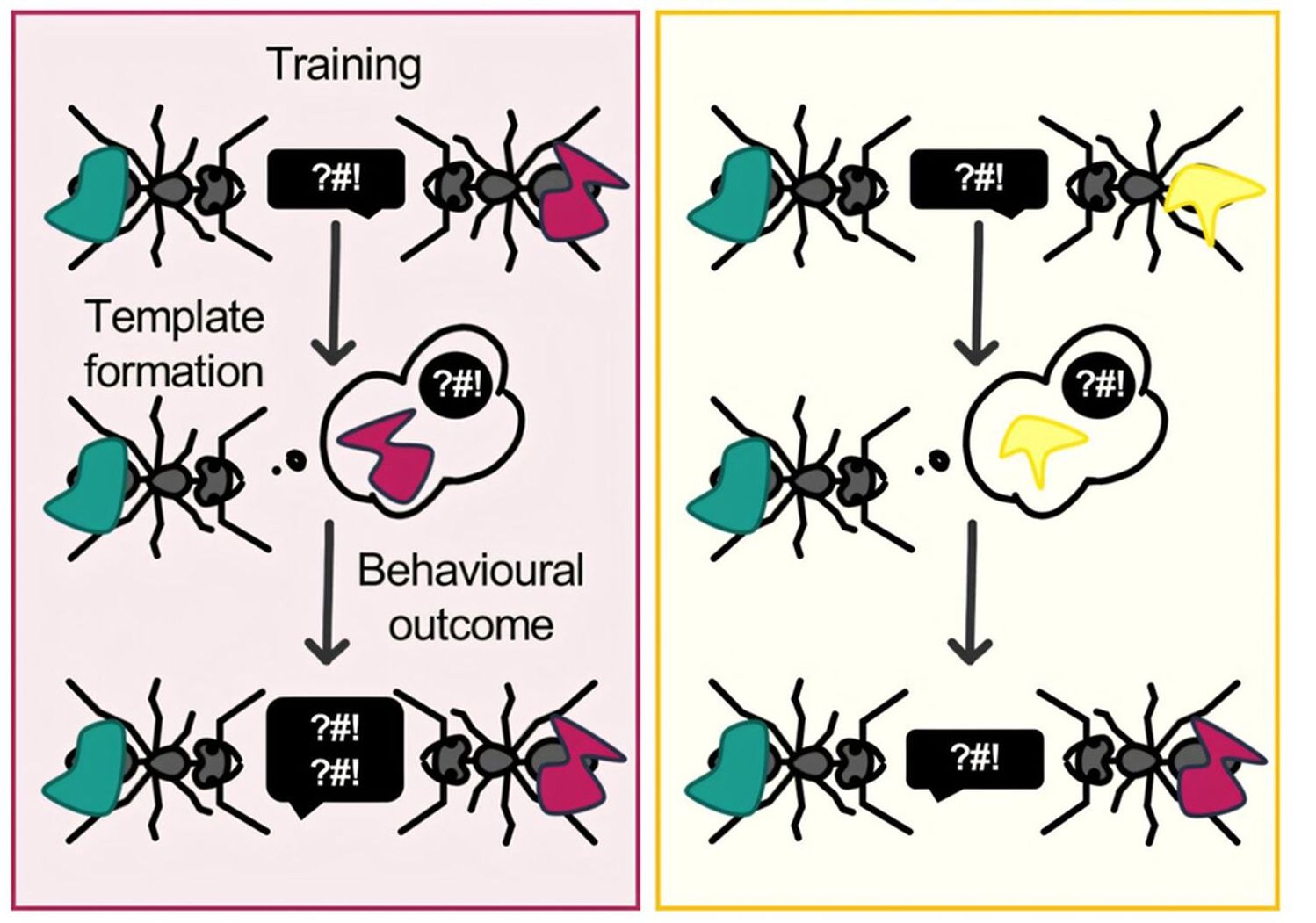 Las hormigas recuerdan a rivales con los que han tenido encuentros y modulan su agresividad al individuo rival. Fuente: Bey et al (2024) / Current Biology
Las hormigas recuerdan a rivales con los que han tenido encuentros y modulan su agresividad al individuo rival. Fuente: Bey et al (2024) / Current Biology
Es lo que en términos populares denominaríamos «me he quedado con tu cara y ya nos veremos la próxima vez». El estudio resulta interesante porque confirma que «el aprendizaje asociativo juega un papel crucial en el reconocimiento tanto de sus compañeras de nido como de sus rivales», pero además muestra que la agresión recibida por una hormiga «actúa como estímulo de aprendizaje no asociativo que la hormiga probable asocia con la etiqueta de olor de su enemigo individualmente». En sus conclusiones, los investigadores añaden que este tipo de aprendizaje y memoria a largo plazo podría ayudarnos a entender mejor las complejas variaciones que las hormigas muestran no solo con sus rivales sino con sus compañeras de nido.
Referencias y más información
Mélanie Bey et al. «Associative learning of non-nestmate cues improves enemy recognition in ants». Current Biology (2024). DOI: 10.1016/j.cub.2024.11.054
Albert Ludwigs «Ants hold grudges, study suggests» Phys.org
Nota de prensa de la Universidad de Freigurg
Sobre el autor: Javier «Irreductible» Peláez (Puertollano, 1974) es escritor y comunicador científico. Autor de 500 años de frío. La gran aventura del Ártico (Crítica, 2019) y Planeta Océano (Crítica 2022). Es uno de los fundadores de la plataforma Naukas.com, editor de ciencia en Yahoo España y Latinoamérica. Es guionista científico en los programas de televisión «El Cazador de Cerebros» y «Órbita Laika» de RTVE. Durante más de una década ha escrito en diferentes medios de comunicación (El País, El Español, National Geographic, Voz Populi). Es autor de los podcasts Catástrofe Ultravioleta y La Aldea Irreductible, y ha colaborado en diferentes proyectos radiofónicos y televisivos (Radio Nacional de España, Radio Televisión Canaria). Es ganador de tres premios Bitácoras, un premio Prisma a la mejor web de divulgación científica y un Premio Ondas al mejor programa de radio digital.
El artículo Las hormigas también pueden ser rencorosas se ha escrito en Cuaderno de Cultura Científica.
¿A qué saben las rocas?
Es fácil creer que el único sentido que utilizamos para trabajar en Geología es la vista. Mirar el paisaje para comprender su historia; mirar una roca o un fósil para poder identificarlos; mirar a través de un microscopio para descubrir los secretos más pequeños de ese material… mirar, siempre mirar. Pero, en realidad, las geólogas y los geólogos utilizamos nuestros cinco sentidos para hacer nuestros estudios de la manera más completa posible. Sí, los cinco, el gusto también.
 Aspecto de un pequeño arroyo de agua salada en Bardenas Reales de Navarra bajo unas fuertes condiciones de evaporación. El agua adquiere una coloración rojiza debido a la alta concentración de elementos químicos, que se van depositando en el fondo y los márgenes del cauce en forma de una fina película de tonos blancos y grises claros.
Aspecto de un pequeño arroyo de agua salada en Bardenas Reales de Navarra bajo unas fuertes condiciones de evaporación. El agua adquiere una coloración rojiza debido a la alta concentración de elementos químicos, que se van depositando en el fondo y los márgenes del cauce en forma de una fina película de tonos blancos y grises claros.Si habéis leído algún otro artículo mío, ya sabréis que, dentro del ámbito científico, las personas que nos dedicamos a la Geología tenemos la fama de ser unas «chupa piedras». Y, como he dicho en otras ocasiones, es una fama más que merecida. Utilizamos nuestra propia saliva, muchas veces a partir de un lametón, sobre el corte fresco de una roca para que sea más fácil ver su estructura interna con la lupa de mano; arrimamos rocas a la punta de la lengua para comprobar si se nos pega y determinar así su porosidad; incluso, masticamos barro para estimar, de forma aproximada, el tamaño de grano de las partículas que componen ese sedimento. Pero también saboreamos los materiales geológicos para poder identificarlos.
Siempre nos han enseñado que el agua no tiene sabor, pero eso no es exactamente así. Si consumís agua mineral embotellada, seguro que tenéis una favorita que os gusta más que otra. En mi caso, como buena habitante de Solares (Cantabria), siempre digo que el resto de marcas no me saben a nada. Pues ese sabor que tienen las aguas embotelladas depende de su «mineralización», es decir, de los elementos químicos que lleva disueltos el agua. Y esos elementos solo los puede sacar de un lugar, las rocas que atraviesa el agua subterránea en su viaje bajo tierra. Así, el agua de Solares se considera «dura» al contener grandes cantidades de carbonato cálcico disuelto, lo que le confiere un sabor más intenso, debido a que atraviesa rocas calizas. Sin embargo, aguas que atraviesan rocas como los granitos son de «mineralización débil» y tienen un sabor muy suave. Además, esta composición química del agua mineral también va a determinar el sabor de los productos que se elaboren con ella, como la cerveza. Si queréis saber más sobre este tema, os aconsejo visitar el blog de mi querido y admirado compañero Andrés Díez Herrero llamado Geología de Segovia, porque os va a sorprender.
 Ejemplos de los minerales más comunes que forman parte de las rocas evaporíticas: A) yeso, B) halita, C) carnalita, D) silvita. Imágenes: A) de Tõnis Saadre (Estonian Museum of Natural History), B) de Didier Descouens, C) de Miguel Sierra, y D) de Luis Miguel Bugallo Sánchez, todas ellas tomadas Wikimedia Commons.
Ejemplos de los minerales más comunes que forman parte de las rocas evaporíticas: A) yeso, B) halita, C) carnalita, D) silvita. Imágenes: A) de Tõnis Saadre (Estonian Museum of Natural History), B) de Didier Descouens, C) de Miguel Sierra, y D) de Luis Miguel Bugallo Sánchez, todas ellas tomadas Wikimedia Commons.Pero en el título no menciono el agua, sino las rocas, porque hay un tipo en particular en el que el gusto es el principal sentido empleado para identificar los minerales que la componen, al menos mientras estamos en el campo: las evaporitas. Se trata de unas rocas sedimentarias que, como su propio nombre indican, se forman por la evaporación de agua salada en medios tanto continentales (como los lagos salados) como marinos (por ejemplo, en lagunas costeras o albuferas) de zonas cálidas, donde la precipitación es escasa. Al evaporarse el agua, los elementos químicos disueltos en ella empiezan a aumentar su concentración, llegando a combinarse entre sí y a precipitar en forma de minerales que se van acumulando en el fondo de estos ambientes acuáticos.
Entre esos minerales precipitados encontramos yeso (CaSO4·1/2H2O), halita (NaCl), carnalita (KCl) y silvita (KMgCl3·6H2O). En un mundo ideal, estos minerales siguen una secuencia temporal de precipitación, apareciendo en finas capas superpuestas donde, además, cada mineral se puede diferenciar entre sí por su estructura cristalina y su color. Pero, en el mundo real, todos ellos aparecen entremezclados en las rocas evaporíticas, generalmente englobados en una masa arcillosa. En esos casos, sacamos la lengua para identificarlos, porque su sabor los delata: La halita es la famosa sal gema que utilizamos en la mesa para echarle a los alimentos, así que su sabor es salado; la silvita tiene un sabor entre salado y amargo; la carnalita es mucho más amarga, incluso con un tono picante; y el yeso…bueno, pues si le dais un lametazo a la pared, lo podréis saber. Así, gracias al gusto podemos hacernos una idea de los minerales que componen la roca.
Las evaporitas son las principales rocas que nos llevamos a la boca para que nuestro gusto nos de pistas sobre su composición mineral, pero no son las únicas. En ocasiones, también dejamos que nuestras pupilas gustativas nos vayan guiando cuando buscamos una mineralización metálica. Supongo que ya os imaginaréis el sabor que tienen esos materiales y, no, no es nada agradable, por eso os digo que solo lo hacemos cuando es estrictamente necesario.
 Exterior de la denominada Montaña de Sal de Cardona (Barcelona), una gran formación evaporítica generada hace unos 37 Millones de años en la que se depositaron yeso, halita, carnalita y silvita, minerales que fueron explotados desde el Neolítico. Foto: Jordi Domènech i Arnau / Wikimedia Commons
Exterior de la denominada Montaña de Sal de Cardona (Barcelona), una gran formación evaporítica generada hace unos 37 Millones de años en la que se depositaron yeso, halita, carnalita y silvita, minerales que fueron explotados desde el Neolítico. Foto: Jordi Domènech i Arnau / Wikimedia CommonsPero esta propiedad de saborear las rocas para identificar sus minerales tiene otra aplicación diferente a la de ayudarnos en los trabajos de campo: que las personas con discapacidad también puedan disfrutar de la Geología. Cuando estamos preparando actividades de divulgación de las Ciencias de la Tierra para personas con problemas de visión, siempre pensamos en el tacto, generando maquetas de las estructuras geológicas o haciendo moldes de minerales y fósiles, y en el oído, grabando audioguías inclusivas con descripción de las imágenes. Sin embargo, también podemos utilizar el gusto, como en el taller de cata de aguas creado por la Asociación Ciencia sin Barreras de la Facultad de Geología de la Universidad Complutense de Madrid. De esta manera, tenemos una herramienta más para hacer que la divulgación de la Geología sea plenamente inclusiva.
Para terminar, solo me queda repetir una reivindicación. Soy una orgullosa “chupa piedras”, porque es la única herramienta geológica que siempre llevo encima, nunca me va a fallar y me va a solucionar un montón de dudas. Eso sí, no vayáis chupando rocas a lo loco por el campo, hacedlo solo en aquellas que os diga una geóloga.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo ¿A qué saben las rocas? se ha escrito en Cuaderno de Cultura Científica.
Euclides y sus rivales modernos
Euclid and His Modern Rivals(1879) es una comedia en cuatro actos de Charles Lutwidge Dodgson, más conocido como Lewis Carroll. Considerado como el más famoso trabajo en geometría del lógico y matemático, se trata de una defensa de la geometría de Euclides frente a lo que denominó teorías matemáticas modernas.
 Portada de Euclid and His Modern Rivals. El esquema de la izquierda sugiere el orden en el que se deberían explicar los postulados de Euclides en el aula. Fuente: Internet Archive.
Portada de Euclid and His Modern Rivals. El esquema de la izquierda sugiere el orden en el que se deberían explicar los postulados de Euclides en el aula. Fuente: Internet Archive.
Los matemáticos británicos consideraban que la geometría euclidiana era el estándar más alto de aprendizaje escolar. Con la llegada de las geometrías no euclidianas y la geometría proyectiva y los cambios en la enseñanza de las matemáticas en Francia, muchos matemáticos decidieron redactar sus propias versiones de la geometría de Euclides. Los “tradicionalistas”, entre los que se encontraba Dodgson, acusaron a estos autores de “destruir a Euclides”.
Dodgson realiza en esta obra un estudio minucioso de trece libros destinados a la enseñanza de la geometría elemental en las escuelas de aquella época. En estos manuales, respecto al libro de Los Elementos de Euclides, se modifica a veces algún axioma o una definición, en otros se cambia el orden de los teoremas, en ocasiones se abordan las demostraciones de manera diferente, en algunos se modifica el tratamiento de la teoría de las paralelas, etc. Para Dodgson, ninguno de estos cambios mejora el texto de Euclides.
Para realizar este análisis, que podría resultar tedioso de otra manera, como afirma el propio autor en la introducción, Dodgson recurre al rey Minos y a su hermano Radamantis, ambos hijos de Zeus y Europa, según la mitología griega. Recordemos que, junto al rey Éaco, Minos y Radamantis son los tres jueces del Hades. En su papel de árbitros estrictos, en Euclid and His Modern Rivals dialogan con dos fantasmas, el de Euclides y el del profesor alemán Herr Niemand, portavoz de los trece autores cuyos libros se examinan.
 Litografía de los tres jueces de los muertos: Minos, Éaco y Radamantis (Ludwig Mack, Die Unterwelt, 1826). Fuente: Wikimedia Commons.
Litografía de los tres jueces de los muertos: Minos, Éaco y Radamantis (Ludwig Mack, Die Unterwelt, 1826). Fuente: Wikimedia Commons.El matemático y geómetra griego Euclides en Alejandría aparece en la obra como un personaje modesto y, aunque convencido de la calidad de su obra, no tiene inconveniente en que se analice. Uno a uno, escena a escena, estos rivales modernos verán como sus textos se critican y se rechazan frente a Los Elementos de Euclides.
Lewis Carroll se sirve del humor y de los juegos de palabras para invalidar a los rivales de Euclides.
Los autores de los trece librosLos trece libros de geometría (sus años de edición y sus autores) examinados por Dodgson en Euclid and His Modern Rivals son, en el orden en el que aparecen citados en el texto:
-
Adrien-Marie Legendre y su Éléments de Géometrie (1860).
-
William Desborough Cooley y su The Elements of Geometry, simplified and explained (1860).
-
Francis Cuthbertson y su Euclidian Geometry(1874).
-
Olaus Henrici y su Elementary Geometry : Congruent Figures(1879).
-
James Maurice Wilson y su Elementary Geometry(1869).
-
Benjamin Peirce y su An Elementary Treatise on Plane and Solid Geometry (1872).
-
William Alexander Willock y su The Elementary Geometry of the Right Line and Circle (1875).
-
William Chauvenet y su A Treatise on Elementary Geometry(1876).
-
Elias Loomis y su Elements of Geometry and Conic Sectionsv ().
-
John Reynell Morell y su Euclid simplified. Compiled from the most important French works, approved by the University of Paris (1875).
-
Edward Morris Reynolds y su Modern Methods in Elementary Geometry (1868).
-
Richard P. Wright y su The Elements of Plane Geometry (1871).
-
Syllabus of Association for Improvement of Geometrical Teaching, Wilson’s ‘Syllabus’-Manual (1878).
En 2000 Jimbo Wales creó Nupedia, un proyecto de enciclopedia libre basado en un ambicioso proceso de revisión por pares. Debido al lento avance del proyecto, en 2001 se creó un motor de wiki –UseModWiki–vinculado a Nupedia cuya finalidad inicial era agilizar la creación de artículos de forma paralela, antes de que éstos pasaran al sistema de revisión por personas expertas. El éxito de aquel proyecto paralelo –Wikipedia– acabó eclipsando a Nupedia, que dejó de funcionar en 2003.
El primer logotipo de Wikipedia –conocido como Wiki logo Nupedia– se diseñó en 2001, superponiendo una frase de Lewis Carrollsobre un círculo, usando el efecto de ojo de pez para simular una esfera. La frase es una cita en inglés tomada del prefacio de Euclid and his Modern Rivals, que dice:
In one respect this book is an experiment, and may chance to prove a failure: I mean that I have not thought it necessary to maintain throughout the gravity of style which scientific writers usually affect, and which has somehow come to be regarded as an ‘inseparable accident’ of scientific teaching. I never could quite see the reasonableness of this immemorial law: subjects there are, no doubt, which are in their essence too serious to admit of any lightness of treatment – but I cannot recognise Geometry as one of them. Nevertheless it will, I trust, be found that I have permitted myself a glimpse of the comic side of things only at fitting seasons, when the tired reader might well crave a moment’s breathing-space, and not on any occasion where it could endanger the continuity of the line of argument.
[En un aspecto, este libro es un experimento y puede resultar un fracaso: quiero decir que no he creído necesario mantener en todo momento la gravedad del estilo que suelen adoptar los escritores científicos y que de alguna manera ha llegado a ser considerado como un “accidente inseparable» de la enseñanza científica. Nunca pude ver la razonabilidad de esta ley inmemorial: hay temas, sin duda, que son en esencia demasiado serios para admitir un tratamiento ligero, pero no puedo reconocer la Geometría como uno de ellos. Sin embargo, espero que se descubra que me he permitido vislumbrar el lado cómico de las cosas sólo en momentos apropiados, cuando el lector cansado bien podría anhelar un momento de respiro, y no en ninguna ocasión en la que pudiera poner en peligro la continuidad de la línea argumental.]
El discurso de despedidaEuclid and His Modern Rivals finaliza con el discurso de despedida de Euclides, tras el cual los fantasmas desaparecen y Minos se va a dormir:
‘The cock doth craw, the day doth daw’, and all respectable ghosts ought to be going home. Let me carry with me the hope that I have convinced you of the importance, if not the necessity, of retaining my order and numbering, and my method of treating straight Lines, angles, right angles, and (most especially) Parallels. Leave me these untouched, and I shall look on with great contentment while other changes are made while my proofs are abridged and improved, while alternative proofs are appended to mine and while new Problems and Theorems are interpolated.
In all these matters my Manual is capable of almost unlimited improvement.
[‘El gallo canta, el día amanece’ y todos los fantasmas respetables deberían regresar a casa. Permíteme llevarme conmigo la esperanza de haberte convencido de la importancia, si no la necesidad, de conservar mi orden y numeración, y mi método para tratar líneas rectas, ángulos, ángulos rectos y (muy especialmente) Paralelas. Déjadme esto intacto, y observaré con gran satisfacción cómo se realizan otros cambios, mientras mis pruebas se abrevian y mejoran, cómo se añaden pruebas alternativas a las mías y cómo se interpolan nuevos problemas y teoremas.
En todos estos asuntos mi Manual es susceptible de mejoras casi ilimitadas.]
Referencias
-
Charles Lutwidge Dodgson, Euclid and His Modern Rivals, MacMillan, 1879
-
Natalie Schuler Evers, Lewis Carroll’s Defense of Euclid: Parallels or Contrariwise, en Sriraman, B. (eds) Handbook of the Mathematics of the Arts and Sciences. Springer, Cham, 2021
-
Joan L. Richards, Mathematical Visions: The Pursuit of Geometry in Victorian England, Academic Press, 1988
-
Frank J. Swetz, Mathematical Treasure: Dodgson’s Defense of Euclid, MMA, 2013
El artículo Euclides y sus rivales modernos se ha escrito en Cuaderno de Cultura Científica.
Por qué los informáticos consultan oráculos
Los dispositivos hipotéticos que pueden responder preguntas con rapidez y precisión se han convertido en una potente herramienta en la teoría de la complejidad computacional.
Un artículo de Ben Brubaker. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
https://culturacientifica.com/app/uploads/2025/01/Oracle_Comp.mp4Haz una pregunta a una Bola 8 Mágica, y te responderá con un sí, un no, o algo exasperantemente impreciso. La consideramos un juguete para niños, pero los teóricos de la computación emplean una herramienta similar. A menudo imaginan que pueden consultar dispositivos hipotéticos llamados oráculos, que pueden responder instantáneamente y de manera correcta a preguntas específicas. Estos experimentos mentales fantásticos han inspirado nuevos algoritmos y ayudado a los investigadores a mapear el paisaje de la computación.
Los investigadores que invocan oráculos trabajan en un subcampo de la informática llamado teoría de la complejidad computacional. Se ocupan de la dificultad inherente de problemas como determinar si un número es primo o encontrar el camino más corto entre dos puntos en una red. Algunos problemas son fáciles de resolver, otros parecen mucho más difíciles pero tienen soluciones que son fáciles de verificar, mientras que otros son fáciles para los ordenadores cuánticos pero aparentemente difíciles para los ordenadores ordinarios.
Los teóricos de la complejidad buscan entender si estas diferencias aparentes en dificultad son fundamentales. ¿Hay algo intrínsecamente difícil en ciertos problemas, o simplemente no somos lo suficientemente ingeniosos para encontrar una buena solución? Los investigadores abordan estas preguntas clasificando los problemas en «clases de complejidad» —todos los problemas fáciles van en una clase, por ejemplo, y todos los problemas fáciles de verificar van en otra— y demostrando teoremas sobre las relaciones entre estas clases.
Lamentablemente, mapear el paisaje de la dificultad computacional ha resultado ser, bueno, difícil. Así que, a mediados de la década de 1970, algunos investigadores comenzaron a estudiar qué pasaría si las reglas de la computación fueran diferentes. Ahí es donde entran los oráculos.
Al igual que las Bolas 8 Mágicas, los oráculos son dispositivos que responden inmediatamente preguntas de sí o no sin revelar nada sobre su funcionamiento interno. A diferencia de las Bolas 8 Mágicas, siempre responden sí o no, y siempre tienen razón: una ventaja de ser ficticios. Además, cualquier oráculo dado solo responderá un tipo específico de pregunta, como «¿Es este número primo?».
¿Qué hace que estos dispositivos ficticios sean útiles para entender el mundo real? En resumen, pueden revelar conexiones ocultas entre diferentes clases de complejidad.
Tomemos las dos clases de complejidad más famosas. Está la clase de problemas que son fáciles de resolver, que los investigadores llaman «P», y la clase de problemas que son fáciles de verificar, que llaman «NP». ¿Son todos los problemas fáciles de verificar también fáciles de resolver? Si así fuera, eso significaría que NP sería igual a P, y toda la encriptación sería fácil de romper (entre otras consecuencias). Los teóricos de la complejidad sospechan que NP no es igual a P, pero no pueden probarlo, aunque llevan más de 50 años intentando precisar la relación entre ambas clases.
Los oráculos les han ayudado a entender mejor con qué están lidiando. Los investigadores han inventado oráculos que responden preguntas que ayudan a resolver muchos problemas diferentes. En un mundo donde cada ordenador tuviera una conexión directa con uno de estos oráculos, todos los problemas fáciles de verificar también serían fáciles de resolver, y P sería igual a NP. Pero otros oráculos menos útiles tienen el efecto opuesto. En un mundo poblado por estos oráculos, P y NP serían demostrablemente diferentes.
Los investigadores han utilizado este conocimiento para obtener una mejor comprensión del problema P contra NP. Los primeros intentos para determinar la relación entre P y NP utilizaron un truco elegante llamado diagonalización, que había sido esencial para otros resultados importantes en la informática. Pero los investigadores pronto se dieron cuenta de que cualquier prueba basada en diagonalización también se aplicaría a cualquier mundo donde cada ordenador pudiera consultar el mismo oráculo. Esto resultó ser un problema, ya que los oráculos cambian la respuesta a la pregunta de P frente a NP. Si los investigadores pudieran usar la diagonalización para probar que P y NP son diferentes en el mundo real, la misma prueba implicaría que P y NP son diferentes en un mundo con oráculos, donde claramente son equivalentes. Esto significa que cualquier solución basada en diagonalización al problema de P contra NP sería autocontradictoria. Los investigadores concluyeron que necesitarían nuevas técnicas para avanzar.
Los oráculos también han sido útiles en el estudio de la computación cuántica. En las décadas de 1980 y 1990, los investigadores descubrieron formas de aprovechar la física cuántica para resolver rápidamente ciertos problemas que parecían difíciles para los ordenadores «clásicos» ordinarios. Pero, ¿estos problemas solo parecen difíciles o realmente lo son? Demostrarlo de una manera u otra requeriría técnicas matemáticas radicalmente nuevas.
Por ello, los investigadores han estudiado cómo los ordenadores cuánticos abordan los problemas que involucran oráculos. Estos esfuerzos pueden proporcionar evidencia indirecta de que los ordenadores cuánticos realmente son más poderosos que los clásicos, y pueden ayudar a los investigadores a explorar tareas cualitativamente nuevas en las que los ordenadores cuánticos podrían destacar. A veces, incluso pueden tener aplicaciones prácticas. En 1994, el matemático aplicado Peter Shor se inspiró en un reciente resultado sobre oráculos para desarrollar un algoritmo cuántico rápido para factorizar números grandes, una tarea cuya aparente dificultad sustenta los sistemas criptográficos que mantienen segura nuestra información en línea. El descubrimiento de Shor dio inicio a una carrera para construir ordenadores cuánticos potentes que continúa hasta el día de hoy.
Es difícil predecir el futuro de la teoría de la complejidad, pero no todas las preguntas sobre la trayectoria del campo son igualmente difíciles de responder. ¿Seguirán los investigadores consultando oráculos? Las señales apuntan a que sí.
El artículo original, Why Computer Scientists Consult Oracles, se publicó el 16 de enero de 2025 en Quanta Magazine.
Traducido por César Tomé López
El artículo Por qué los informáticos consultan oráculos se ha escrito en Cuaderno de Cultura Científica.
Defensa insólita contra virus bacteriófagos: síntesis de un gen nuevo… y tóxico
Francis Crick, codescubridor de la doble hélice, definió como “dogma central de la Biología Molecular” el hecho de que la información genética fluya en una sola dirección, del ADN al ARN mensajero y de este último a la secuencia de aminoácidos en la proteína. Este dogma tuvo que ser revisado cuando se descubrieron las retrotranscriptasas o transcriptasas inversas, enzimas capaces de sintetizar ADN a partir de secuencias de ARN (Figura 1). Estas enzimas son producidas por retrovirus como el VIH-1 para insertar su información en el ADN de la célula infectada. También nosotros utilizamos la retrotranscriptasa para amplificar las secuencias de ADN conocidas como retrotransposones y trasladarlas de una parte del genoma a otra. De hecho, más del 40% de nuestro genoma está constituido por retrotransposones.
 Figura 1. En el recuadro de la izquierda se muestra el llamado “dogma central de la Biología Molecular”: el flujo de información genética desde el ADN hacia la secuencia de aminoácidos que constituyen las proteínas, pasando por el ARN mensajero. A la derecha se muestra el caso excepcional del sistema DRT2. Un nuevo gen (Neo) es sintetizado a partir de la retrotranscripción repetida múltiples veces de un ARN no codificante. La proteína Neo no está por tanto codificada en el genoma bacteriano
Figura 1. En el recuadro de la izquierda se muestra el llamado “dogma central de la Biología Molecular”: el flujo de información genética desde el ADN hacia la secuencia de aminoácidos que constituyen las proteínas, pasando por el ARN mensajero. A la derecha se muestra el caso excepcional del sistema DRT2. Un nuevo gen (Neo) es sintetizado a partir de la retrotranscripción repetida múltiples veces de un ARN no codificante. La proteína Neo no está por tanto codificada en el genoma bacterianoLas bacterias también utilizan las retrotranscriptasas como medio para defenderse de los virus bacteriófagos, sus grandes enemigos naturales. Esta estrategia defensiva suele activarse cuando han fallado los mecanismos basados en la degradación del material genético vírico. Un ejemplo de estos mecanismos es el conocido sistema CRISPR-Cas, que en la actualidad constituye una tecnología sencilla y eficaz para la edición genética.
Si la infección vírica desborda esta primera línea de defensa, se activan procesos basados en retrotranscriptasas, descubiertos recientemente y mucho menos conocidos. Algunos de estos mecanismos defensivos se denominan retrones. Los retrones consisten típicamente en secuencias del cromosoma bacteriano que codifican un ARN que no contiene información para formar proteínas (ARN no codificante), una retrotranscriptasa y una proteína efectora, generalmente tóxica. En condiciones normales, la retrotranscriptasa sintetiza una cadena de ADN utilizando parte del ARN no codificante como plantilla. La molécula mixta de ADN y ARN mantiene inactiva la toxina. El sistema se altera en caso de infección vírica imparable, la toxina se activa y la bacteria se suicida (Figura 2).
 Figura 2. Sistema defensivo contra bacteriófagos basado en retrones. El ADN se representa en rojo y el ARN en azul. Un ARN no codificante sirve de plantilla para que la retrotranscriptasa sintetice una cadena complementaria de ADN. El conjunto inhibe la actividad de una proteína efectora tóxica. La infección por bacteriófagos altera el sistema y la toxina queda libre, provocando la muerte de la bacteria y evitando la propagación del virus. Imágenes de Freepik, Inksyndromeartwork, y KES47, CC BY 4.0
Figura 2. Sistema defensivo contra bacteriófagos basado en retrones. El ADN se representa en rojo y el ARN en azul. Un ARN no codificante sirve de plantilla para que la retrotranscriptasa sintetice una cadena complementaria de ADN. El conjunto inhibe la actividad de una proteína efectora tóxica. La infección por bacteriófagos altera el sistema y la toxina queda libre, provocando la muerte de la bacteria y evitando la propagación del virus. Imágenes de Freepik, Inksyndromeartwork, y KES47, CC BY 4.0Se podría pensar, ¿qué clase de defensa antivírica implica un suicidio celular? La clave está en que la muerte de la bacteria impide la multiplicación del virus y su transmisión al resto de la población bacteriana. Esta estrategia “kamikaze” se conoce como infección abortiva y beneficia al conjunto de la población a expensas del individuo infectado.
Otras defensas basadas en retrotranscriptasas son las DRTs (defense-associated retrotranscriptases). Una de ellas, la DRT2, constituía hasta ahora un enigma ya que, a diferencia de los retrones, solo está formada por el ADN que genera la secuencia de ARN no codificante y una retrotranscriptasa, sin ninguna proteína efectora. Dos artículos publicados simultáneamente en Science el pasado mes de octubre desvelaron la función de DRT2, y han supuesto una auténtica conmoción en medios científicos. El sistema se basa en algo excepcional: la síntesis de un nuevo gen, ausente en el genoma bacteriano original.
Ambos grupos de investigación, en la Universidad Columbia de Nueva York y en el Instituto Tecnológico de Massachusetts, utilizaron el mismo modelo, la bacteria Klebsiella pneumoniae. Comprobaron que la expresión de DRT2 provocaba la síntesis del ARN no codificante, que se pliega sobre sí mismo, y la retrotranscriptasa (Figura 3). Como sucede con los retrones, esta enzima genera la cadena de ADN complementaria de una parte del ARN. Pero, y aquí viene la sorpresa, cuando termina la síntesis, se produce un “salto” y la enzima vuelve a empezar la síntesis del ADN desde el principio. Este ciclo se repite una y otra vez, generando una cadena sencilla de ADN con múltiples secuencias repetidas, a la que se denominó ADN concatenado.
 Figura 3. Sistema defensivo DRT2 contra bacteriófagos. El ADN se representa en rojo y el ARN en azul. En este caso no hay proteína efectora. La síntesis del ADN complementario se repite de manera cíclica creando una larga cadena de ADN concatenado. En caso de infección por bacteriófagos, aumenta exponencialmente la producción de este ADN y se sintetiza la cadena complementaria. El ADN se comporta como un nuevo gen (Neo) que se transcribe a ARN mensajero y se traduce a la proteína Neo. Esta proteína bloquea el crecimiento bacteriano evitando la propagación del virus
Figura 3. Sistema defensivo DRT2 contra bacteriófagos. El ADN se representa en rojo y el ARN en azul. En este caso no hay proteína efectora. La síntesis del ADN complementario se repite de manera cíclica creando una larga cadena de ADN concatenado. En caso de infección por bacteriófagos, aumenta exponencialmente la producción de este ADN y se sintetiza la cadena complementaria. El ADN se comporta como un nuevo gen (Neo) que se transcribe a ARN mensajero y se traduce a la proteína Neo. Esta proteína bloquea el crecimiento bacteriano evitando la propagación del virusEn caso de infección vírica suceden dos cosas (Figura 3). La síntesis de ADN concatenado aumenta miles de veces y, al mismo tiempo, se sintetiza la hebra complementaria, generando un ADN de doble cadena, como el del cromosoma bacteriano. Este ADN se comporta como un nuevo gen, denominado Neo1, que se traduce en una proteína con múltiples repeticiones de una secuencia de 40 aminoácidos. La predicción mediante Alphafold es que la proteína Neo está formada por un gran número de hélices. Esta proteína bloquea el crecimiento y la reproducción de la bacteria, evitando así la proliferación del virus.
Son muchas las incógnitas que permanecen, por ejemplo, qué tamaño puede alcanzar Neo, ya que la longitud de su gen no parece tener límites. Tampoco se sabe cómo Neo bloquea el crecimiento bacteriano. Lo que sí parece probable, según la comparación de secuencias que se ha hecho, es que este mecanismo esté presente en muchas otras bacterias.
Lo que resulta realmente llamativo de estos resultados es que a partir de un ARN no codificante se sintetice una secuencia de ADN que actúa como un gen extracromosómico que genera una proteína no codificada por el genoma bacteriano. Estamos, por tanto, ante un caso hasta ahora impensable de flujo de información genética entre el ADN y el ARN (Figura 1).
Referencias:
Tang, S., Conte, V., Zhang, D.J., et al. (2024). De novo gene synthesis by an antiviral reverse transcriptase. Science. Https://doi: 10.1126/science.adq0876.
Wilkinson, M.E., Li, D., Gao, A.F., et al. (2024). Phage-triggered reverse transcription assembles a toxic repetitive gene from a noncoding RNA. Science. Https://doi: 10.1126/science.adq3977.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga
Nota
1 Por never ending open reading frame, marco abierto de lectura sin fin. Un marco abierto de lectura es una secuencia de ADN con una señal de inicio de la traducción a proteína y una señal de terminación. El “sin fin” se debe a que, en este caso, la secuencia no tiene señales de terminación
El artículo Defensa insólita contra virus bacteriófagos: síntesis de un gen nuevo… y tóxico se ha escrito en Cuaderno de Cultura Científica.
La teoría de cuerdas no ha muerto
Los físicos teóricos siguen buscando las matemáticas que puedan explicar las partículas y fuerzas del universo.
 La teoría de cuerdas es una descripción matemática de la naturaleza que requiere que el espacio posea varias dimensiones adicionales más allá de las tres ordinarias. Estas dimensiones adicionales, demasiado pequeñas para percibirlas en la vida cotidiana, pueden adoptar muchas formas o geometrías posibles (representadas artísticamente aquí) que pueden influir en las propiedades del universo y de las partículas subatómicas. Ilustración: O. Knill & E. Slavkosky.
La teoría de cuerdas es una descripción matemática de la naturaleza que requiere que el espacio posea varias dimensiones adicionales más allá de las tres ordinarias. Estas dimensiones adicionales, demasiado pequeñas para percibirlas en la vida cotidiana, pueden adoptar muchas formas o geometrías posibles (representadas artísticamente aquí) que pueden influir en las propiedades del universo y de las partículas subatómicas. Ilustración: O. Knill & E. Slavkosky.A los científicos que buscan los secretos del universo les gustaría hacer un modelo que mostrara cómo encajan todas las fuerzas y partículas de la naturaleza. Estaría bien hacerlo con piezas de Lego, pero quizá sería mejor conectarlo todo con cuerdas.
No cuerdas literales, por supuesto, sino pequeños bucles o fragmentos de energía vibrante. Y el “encaje” tiene que ser matemático, no mediante piezas de plástico que calzan unas con otras. Desde hace décadas, muchos físicos albergan la esperanza de que las ecuaciones que implican una “cuerda” especialmente diminuta puedan proporcionar la teoría que resuelva los últimos misterios subatómicos de la naturaleza.
La teoría de cuerdas, como se le llama, ha adquirido una especie de difusa aclamación cultural, apareciendo en populares programas de televisión como The Big Bang Theory y NCIS. Entre los físicos, la reacción a la teoría ha sido variada. Tras varios descubrimientos prometedores en los años ochenta y noventa, las cuerdas cayeron en desgracia por no cumplir sus promesas. Una de ellas era encontrar la forma de incluir la gravedad en la teoría cuántica de las partículas subatómicas. Otra era revelar las matemáticas que demostrarían que las múltiples fuerzas fundamentales de la naturaleza son solo diferentes descendientes de una fuerza unificada. Promesas incumplidas.
Sin embargo, desde que la teoría de cuerdas dejó de ser el centro de atención, un grupo considerable de devotos se ha esforzado por atar todos los cabos sueltos. El éxito sigue siendo difícil de alcanzar, pero se han hecho verdaderos progresos. Las preguntas que se hacen los físicos no solo sobre los fragmentos más pequeños de materia, sino también sobre las propiedades de todo el universo, podrían ceder a los esfuerzos de los teóricos de cuerdas.
“Muchos de los problemas sin resolver de la física de partículas y la cosmología están profundamente entrelazados”, escriben los físicos Fernando Marchesano, Gary Shiu y Timo Weigand en el Annual Review of Nuclear and Particle Science de 2024. La teoría de cuerdas puede ser el camino para resolver esos problemas.
Teoría de cuerdas y modelo estándarUno de los principales enfoques en esta búsqueda es averiguar si la teoría de cuerdas puede explicar lo que se conoce como el modelo estándar de la física de partículas. Desarrollado en la última parte del siglo XX, el modelo estándar ofrece una especie de lista de todas las partículas básicas de la naturaleza. Algunas constituyen los bloques de construcción de la materia; otras transmiten fuerzas entre las partículas de materia y rigen su comportamiento.
Es bastante sencillo dibujar un gráfico que muestre esas partículas. Se necesitan 12 puntos para las partículas de materia: seis quarks y seis leptones. Se necesitan cuatro para las partículas de fuerza (conocidas colectivamente como bosones) y uno para el bosón de Higgs, una partícula necesaria para explicar por qué algunas partículas tienen masa. Pero las matemáticas que subyacen al gráfico son insondablemente complejas.
Esas ecuaciones funcionan magníficamente para explicar los resultados de prácticamente todo el comportamiento de la física de partículas. Pero el modelo estándar no puede ser toda la historia del universo. “A pesar del increíble éxito del modelo estándar a la hora de describir la física de partículas observada hasta las escalas de energía actualmente accesibles, existen argumentos convincentes de por qué es incompleto”, escriben Marchesano y colaboradores.
Por un lado, sus ecuaciones no abarcan la gravedad, que no tiene cabida en la tabla del modelo estándar. Y las matemáticas del modelo estándar dejan muchas preguntas sin respuesta, como por ejemplo por qué algunas de las partículas tienen las masas precisas que tienen. Las matemáticas del modelo estándar tampoco incluyen la misteriosa materia oscura que se esconde dentro y entre las galaxias, ni explican por qué el espacio vacío está impregnado de una forma de energía que hace que el universo se expanda a un ritmo acelerado.
Algunos físicos que investigan estos problemas creen que la teoría de cuerdas puede ayudar, ya que una versión de cuerdas del modelo estándar contendría matemáticas adicionales que podrían explicar sus deficiencias. En otras palabras, si la teoría de cuerdas es correcta, el modelo estándar sería solo un segmento de la descripción matemática completa de la realidad que hace la teoría de cuerdas. El problema es que la teoría de cuerdas describe muchas versiones diferentes de la realidad. Eso se debe a que las cuerdas existen en un reino con múltiples dimensiones del espacio más allá de las tres ordinarias. Algo así como la Dimensión Desconocida con esteroides.
Los teóricos de las cuerdas admiten que la vida cotidiana transcurre perfectamente en un mundo tridimensional. Por lo tanto, las dimensiones adicionales del mundo de cuerdas deben ser demasiado pequeñas para ser percibidas: tienen que encogerse, o “compactarse”, hasta alcanzar un tamaño submicroscópico. Es como si una hormiga que viviera en una gran hoja de papel percibiera una superficie bidimensional sin darse cuenta de que el papel tiene una tercera dimensión muy pequeña.
Las dimensiones extra de la teoría de cuerdas no solo deben encogerse, sino que también pueden encogerse en innumerables configuraciones diferentes, o geometrías, del vacío del espacio. Una de esas posibles geometrías podría ser la forma adecuada de las dimensiones encogidas para explicar las propiedades del modelo estándar.
“Las características, preguntas y enigmas del modelo estándar … pueden reformularse en términos de la geometría de las dimensiones extra”, escriben Marchesano y colaboradores.
Dado que las matemáticas de la teoría de cuerdas pueden expresarse de varias formas diferentes, los teóricos tienen que explorar múltiples vías posibles para encontrar la formulación más fructífera. Hasta ahora, se han encontrado aproximaciones de cuerdas que describen muchas características del modelo estándar. Pero se necesitan diferentes geometrías de compactación del vacío para explicar cada característica. El reto, señalan Marchesano y sus colegas, es encontrar una geometría para el vacío que combine todas esas características a la vez, incorporando al mismo tiempo rasgos que describan el universo conocido.
Una compactación satisfactoria de las dimensiones adicionales, por ejemplo, produciría un vacío en el espacio que contendría la cantidad adecuada de “energía oscura”, la fuente de la expansión acelerada del universo. Y también deberían aparecer candidatos para la materia oscura cósmica en la matemática de cuerdas. De hecho, todo un conjunto adicional de partículas de fuerza y materia surge de las ecuaciones de cuerdas que implican una propiedad matemática llamada supersimetría. “Casi todos los modelos de teoría de cuerdas que se parecen al modelo estándar muestran supersimetría a escala de compactación”, escriben Marchesano y sus coautores.
Las versiones de la teoría de cuerdas que contienen partículas supersimétricas se conocen como “teoría de supercuerdas”. Desde hace tiempo se sospecha que estas “superpartículas” constituyen la materia oscura del universo. Pero los intentos de detectarlas en el espacio o crearlas en aceleradores de partículas han sido hasta ahora infructuosos.
En cuanto a la gravedad, las partículas que transmiten la fuerza gravitatoria aparecen de forma natural en las matemáticas de la teoría de cuerdas, uno de los grandes atractivos de la teoría para empezar. Pero el hecho de que muchas formulaciones de la teoría de cuerdas incluyan la gravedad no indica qué formulación proporciona la descripción correcta del mundo real.
Las pruebas son posiblesSi la teoría de cuerdas es correcta, las partículas fundamentales de la naturaleza no serían los objetos puntuales de dimensión cero de la teoría estándar. En su lugar, las diferentes partículas serían el resultado de diferentes modos de vibración de una cuerda unidimensional, ya sea un bucle o un fragmento con extremos unidos a objetos espaciales multidimensionales llamados branas. Tales cuerdas serían aproximadamente más pequeñas que un átomo en la medida en que un átomo es más pequeño que el sistema solar. Muy pequeñas, sin que sea factible detectarlas directamente. La cantidad de energía necesaria para sondear escalas tan diminutas está muy lejos del alcance de cualquier tecnología práctica.
Pero si la teoría de cuerdas puede dar cuenta del modelo estándar, también contendría otras características de la realidad que serían accesibles a los experimentos, como tipos de partículas no incluidas en el cuadro del modelo estándar. “Las construcciones de cuerdas que dan cuenta del modelo estándar siempre contienen sectores adicionales… a una escala de energía que podría probarse en un futuro próximo”, escriben Marchesano y sus colegas.
En última instancia, la teoría de cuerdas sigue siendo un candidato esperanzador para encajar todas las piezas del rompecabezas cósmico. Si funciona, los científicos podrían desvelar por fin los misterios sobre cómo la relación de la física cuántica con la gravedad y las propiedades de las partículas y fuerzas de la naturaleza están profundamente vinculadas. “La teoría de cuerdas”, escriben Marchesano y sus colegas, “tiene todos los ingredientes para ayudarnos a entender esta profunda conexión”.
Un artículo de Tom Siegfried / Knowable Magazine publicado originalmente el 7 de enero de 2025. Traducido por Debbie Ponchner
El artículo La teoría de cuerdas no ha muerto se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2024: 18 de enero de 1902
La decimocuarta edición del mayor evento de divulgación científica volvió al Palacio Euskalduna de Bilbao durante los días 19, 20, 21 y 22 de septiembre de 2024.

Oskar González Mendía (autor de kimikArte) doctor en químicas y profesor en la Facultad de Bellas Artes de la UPV/EHU se dedica, entre otras cosas, a resolver misterios. Entre ellos por qué el 18 de enero de 1902, un día en el que no pasó absolutamente nada, es interesante.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2024: 18 de enero de 1902 se ha escrito en Cuaderno de Cultura Científica.
Las ballenas ven en blanco y negro
 Ojo de una ballena yubarta, de la familia Balaenopteridae Foto: Rachel Moore via Instagram
Ojo de una ballena yubarta, de la familia Balaenopteridae Foto: Rachel Moore via InstagramEn la Facultad de Medicina de la Universidad del País Vasco hemos analizando los ojos de tres rorcuales varados en diferentes playas de España entre 2019 y 2021. Y su estudio nos ha ayudado a saber cómo ven las ballenas.
Las tres ballenas que han servido para nuestra investigación tenían medidas similares, alrededor de 18 metros de largo, y pesaban 20 toneladas. Cada ojo era del tamaño de una pelota de balonmano (13 cm de diámetro) y pesaba un kilo.
Ojos para sobrevivir en las profundidadesLos rorcuales, pertenecientes a la familia Balaenopteridae, son cetáceos conocidos por su velocidad e hidrodinámica, lo que les ha valido el apodo de “galgos de los mares”.
Estos animales marinos carecen de dientes y se alimentan filtrando krill en las zonas superficiales del océano. Su adaptación al medio marino ha dotado a sus órganos, especialmente los ojos, de características únicas que les permiten sobrevivir en las profundidades.
Ballenas varadasEl primer ojo provenía de un rorcual común que varó en Sopelana (Vizcaya, País Vasco) tras la borrasca Helena en febrero de 2019. Tener acceso a sus ojos nos permitió realizar estudios anatómicos y moleculares, además de cultivar las neuronas ganglionares y las células gliales de la retina, conocidas como glía de Müller.
El segundo ojo, de un rorcual boreal, se obtuvo en la playa de Tapia de Casariego (Asturias) durante la borrasca Filomena en enero de 2021. Este material permitió confirmar los hallazgos previos e inmortalizar las células de Müller para investigaciones futuras.
El tercer ojo correspondía a un rorcual que varó en Tavernes (Valencia) en mayo de 2021. En este caso, el ojo de la ballena nos sirvió para corroborar nuevamente los estudios anatómicos y moleculares realizados con los otros ejemplares. Los resultados se publicaron en varias revistas científicas.
 Fotografía de microscopía electrónica de barrido de la córnea del ojo de una de las ballenas. Fotografía premio de la Sociedad Española de Oftalmología.
Fotografía de microscopía electrónica de barrido de la córnea del ojo de una de las ballenas. Fotografía premio de la Sociedad Española de Oftalmología.Elena Vecino y Luis LópezAdaptaciones anatómicas del ojo
En los ojos de los rorcuales encontramos adaptaciones extraordinarias que les permiten resistir las altas presiones y la escasa luz de las profundidades marinas:
- La córnea, que permite la entrada de luz al ojo, es hasta cuatro veces más gruesa que la humana. Este refuerzo, junto con la esclera, protege al órgano visual contra las presiones extremas en el hábitat marino profundo.
- El cristalino en los rorculaes es esférico, para facilitar la visión bajo el mar, a diferencia de los mamíferos terrestres, que es lenticular.
- La esclera, o parte blanca del ojo, es extremadamente gruesa en estos cetáceos: llega a medir hasta 4 centímetros, en contraste con el medio milímetro en humanos. Está formada por colágeno endurecido, lo que protege la retina como si estuviera dentro de un cofre.
- El cuerpo cavernoso es un tejido que rodea el nervio óptico y contiene numerosos vasos sanguíneos y músculo liso. En la ballena, cuando se llena de sangre, impulsa el ojo hacia el exterior, permitiendo enfocar de un modo similar a como lo hace un telescopio.
Estos resultados han sido publicados en el capítulo ¿Cómo ven las ballenas? del libro Mamíferos marinos.
 Vaso del cuerpo cavernoso del ojo de la ballena, rodeado de fibras de colágeno. Fotografía de microscopía electrónica de barrido.
Vaso del cuerpo cavernoso del ojo de la ballena, rodeado de fibras de colágeno. Fotografía de microscopía electrónica de barrido.Elena Vecino y Luis LópezCaracterísticas visuales: visión en blanco y negro
Nuestro análisis reveló que la retina de los rorcuales carece de conos, las células responsables de percibir colores y luz intensa. Por el contrario, está compuesta únicamente por bastones, que son sensibles a bajas intensidades lumínicas y funcionan en condiciones de poca luz.
Esto indica que las ballenas solo ven en blanco y negro, una adaptación al entorno oscuro del océano.
Además, las neuronas melanopsínicas, responsables de informar al cerebro sobre los ciclos de luz/oscuridad (denominados ritmos circadianos), están muy desarrolladas en las ballenas. Esto nos revela que tienen alta sensibilidad a la luz y pueden percibir las intensidades lumínicas variables en los distintos hemisferios, lo que les podría ayudar a orientarse.
Aunque los ojos de las ballenas son grandes, su densidad de neuronas ganglionares, encargadas de procesar la información visual y enviarla al cerebro, es muy baja. Esto significa que la cantidad de señales visuales que llegan al cerebro es limitada y da como resultando una visión reducida, como indicamos en el estudio publicado en Frontiers in Anatomy. Metafóricamente hablando, las ballenas podrían llevar el pin de baja visión.
 Microscopía electrónica de barrido de la retina de una ballena, coloreada digitalmente. Premio Scientific American NeuroArt de la SENC.
Microscopía electrónica de barrido de la retina de una ballena, coloreada digitalmente. Premio Scientific American NeuroArt de la SENC.Elena Vecino Cordero y Luis López VecinoReconocimientos artísticos
Además de su valor científico, las imágenes obtenidas durante esta investigación han sido reconocidas por su belleza y han ganado varios premios nacionales e internacionales, entre ellos, el de Scientific American NeuroArt.
Estas fotografías se han expuesto en siete museos marítimos, de fotografía y galerías de arte nacionales e internacionales. En la actualidad está en el Museo Nacional de Ciencias Naturales de Madrid, donde permanecerá hasta finales de mayo.
Las exposiciones han sido adaptadas a personas invidentes y con baja visión, incorporando fotografías texturizadas, audioguías y recorridos señalizados con cintas podotactiles. Además, hemos editado tres vídeos que cuentan la historia de la investigación desde el comienzo hasta la exposición: Elena y la ballena; ¿Cómo ven las ballenas? y Cómo adaptar una exposición fotográfica a personas que no ven.
El estudio de los ojos de estos tres rorcuales ha permitido conocer en profundidad las adaptaciones anatómicas y funcionales que posibilitan su vida en el medio marino. Estas investigaciones no solo arrojan luz sobre la biología de estos cetáceos: llevadas al museo, permiten destacar la importancia de preservar y estudiar la biodiversidad de nuestros océanos.![]()
Sobre las autoras: Elena Vecino Cordero, Catedrática de Biología Celular (UPV/EHU), Licenciada en Bellas Artes, Life Member, Clare Hall Cambridge (UK). Directora del Grupo Oftalmo-Biología Experimental (GOBE), Universidad del País Vasco / Euskal Herriko Unibertsitatea y Luis López Vecino, Profesor asociado del Grado en desarrollo de aplicaciones 3D interactivas y videojuegos, Universidad de Salamanca
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Las ballenas ven en blanco y negro se ha escrito en Cuaderno de Cultura Científica.

