La recta de Euler
Uno de mis pequeños, e inconfesables, divertimentos consiste en coger un libro de geometría, como el libro El diccionario Penguin de geometría curiosa e interesante (The Penguin Dictionary of Curious and Interesting Geometry) del matemático y divulgador británico David G. Wells (1940), y dedicarme a leer y disfrutar de los resultados clásicos de la geometría mostrados en el mismo. Al leer el enunciado de alguno de estos teoremas me emociona ver cómo a partir de una cierta situación geométrica se obtiene un resultado sorprendente, casi mágico, que nos ofrece un cierto orden, por ejemplo, en el teorema de Morley (véase la entrada El teorema de Morley) se consideran un triángulo cualquiera, las trisectrices de sus tres ángulos (recordemos que las trisectrices de un ángulo son las dos rectas que dividen al ángulo en tres ángulos iguales) y los tres puntos de intersección de las trisectrices adyacentes, entonces resulta que esos tres puntos son los vértices de un triángulo equilátero, es decir, las distancias entre cualesquiera dos de esos tres puntos son iguales.
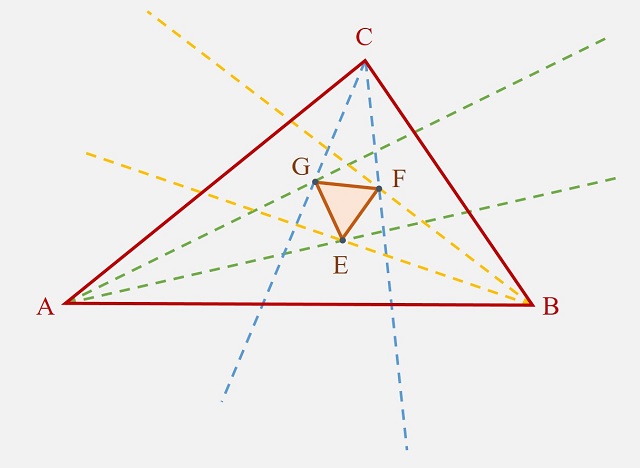 Teorema de Morley: Los puntos de intersección de las trisectrices adyacentes de los ángulos de un triángulo cualquiera, son los vértices de un triángulo equilátero
Teorema de Morley: Los puntos de intersección de las trisectrices adyacentes de los ángulos de un triángulo cualquiera, son los vértices de un triángulo equilátero
En una de mis últimas incursiones en este diccionario de geometría curiosa e interesante de David Wells llamó mi atención la entrada denominada “Línea de Euler” en la cual se enuncia un teorema del matemático suizo Leonhard Euler (1707-1783) sobre tres puntos notables asociados a un triángulo cualquiera, el ortocentro, el circuncentro y el baricentro, que se encuentran en una misma línea, que se conoce con el nombre de recta de Euler. Hemos de tener en cuenta que dados tres puntos cualesquiera del plano lo más probable es que no sean colineales, es decir, que no estén en una misma recta.
Punto a punto a la recta de EulerAntes de entrar en el teorema de la recta de Euler, describamos los elementos que aparecen en el mismo, en concreto, esos tres puntos notables asociados a un triángulo cualquiera, el ortocentro, el circuncentro y el baricentro.
El ortocentro de un triánguloDado un triángulo cualquiera se define el ortocentro como el punto de intersección de las tres alturas del triángulo (o las rectas que las extienden), donde recordemos que una altura de un triángulo es el segmento de recta que pasa por un vértice y es perpendicular al lado opuesto (o a la recta que lo contiene) del mismo. Por ejemplo, en la siguiente imagen tenemos un triángulo ABC cualquiera. Desde el vértice A se traza la recta que pasa por A y corta perpendicularmente (es decir, formando un ángulo de 90 grados) al lado opuesto del triángulo, el lado BC, que es la altura del triángulo ABC desde el vértice A (se denota A’ al punto de corte, que se denomina pie de la altura), desde el punto B se traza la recta que corta perpendicularmente al lado opuesto AC, la altura desde B (se denota B’ al pie de la altura), y desde C se traza también la altura, es decir, la recta que pasa por C y corta perpendicularmente al lado opuesto AB (siendo C’ el pie de la altura). Un resultado básico de geometría es que las tres alturas AA’, BB’ y CC’ (o las rectas que las extienden) se cortan en un punto (que se denota O en la imagen), que se ha sido bautizado con el nombre de ortocentro del triángulo.
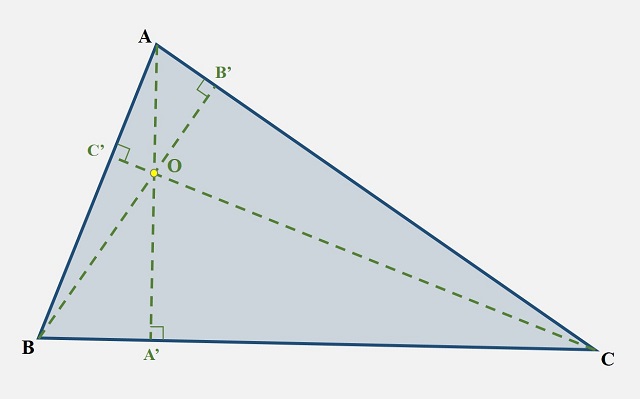 El ortocentro O del triángulo ABC es la intersección de sus tres alturas AA’, BB’ y CC’
El ortocentro O del triángulo ABC es la intersección de sus tres alturas AA’, BB’ y CC’
El resultado clásico de la concurrencia de las tres alturas de un triángulo, es decir, que las tres alturas se intersecan en un solo punto, el ortocentro, no aparece en el gran compendio de geometría y matemática griegas, Los Elementos del matemático griego Euclides (ca. 325-265 a.n.e.), a diferencia de algunos otros puntos notables asociados a un triángulo, como el incentro y el circuncentro. La primera mención explícita al ortocentro que se conoce aparece en el Libro de los lemas, texto atribuido por el matemático árabe Thābit ibn Qurra (826 – 901), al matemático griego Arquímedes (aprox. 287 – 212 a.n.e.). La primera demostración conocida de la existencia del ortocentro es precisamente un comentario del Libro de los lemas realizado por el matemático persa Ali ibn Ahmad al-Nasawi (aprox. 1011-1075), que atribuye dicha demostración al también matemático persa Abu Sahl al-Quhi (940-1000), como se menciona en el artículo Concurrencia de las alturas de un triángulo (Concurrency of the Altitudes of a Triangle), que se menciona en la bibliografía. El famoso matemático británico Isaac Newton (1643-1727) lo demostró en su tratado inacabado La geometría de las rectas (aprox. 1680), que podéis encontrar en el volumen IV de las publicaciones matemáticas de Isaac Newton (The mathematical papers of Isaac Newton).
 Páginas de las publicaciones matemáticas de Isaac Newton (The mathematical papers of Isaac Newton), en las que aparece el resultado sobre la intersección de las tres alturas de un triángulo, luego la existencia del ortocentro
Páginas de las publicaciones matemáticas de Isaac Newton (The mathematical papers of Isaac Newton), en las que aparece el resultado sobre la intersección de las tres alturas de un triángulo, luego la existencia del ortocentroEl resultado sobre la concurrencia de las alturas de un triángulo en las publicaciones matemáticas de Isaac Newton viene acompañado de una nota histórica sobre este resultado, en la que se menciona que el matemático e ingeniero militar holandés Samuel Marolois (1572-1627) lo demuestra en su obra Geometrie / Geometría (1619). Aunque se suele atribuir al topógrafo y matemático británico William Chapple (1718-1781) la primera publicación, en 1749, del teorema de existencia del ortocentro de un triángulo, como menciona el matemático estadounidense, nacido en Israel, Alexander Bogomolny (1948-2018), en el artículo A Possibly First Proof of the Concurrence of Altitudes, de su magnífica página Cut-the-knot.
En función de la forma del triángulo, el ortocentro estará dentro o fuera del mismo. Si el triángulo es “agudo”, es decir, sus tres ángulos son menores que un ángulo recto (90 grados), como en el ejemplo anterior, entonces el ortocentro se encuentra en el interior del triángulo. Si el triángulo es rectángulo, el ortocentro es exactamente el vértice del triángulo en el que está el ángulo recto. Y si el triángulo es “obtuso”, es decir, uno de sus ángulos es mayor de 90 grados, entonces el ortocentro está fuera del triángulo, como en la siguiente imagen.
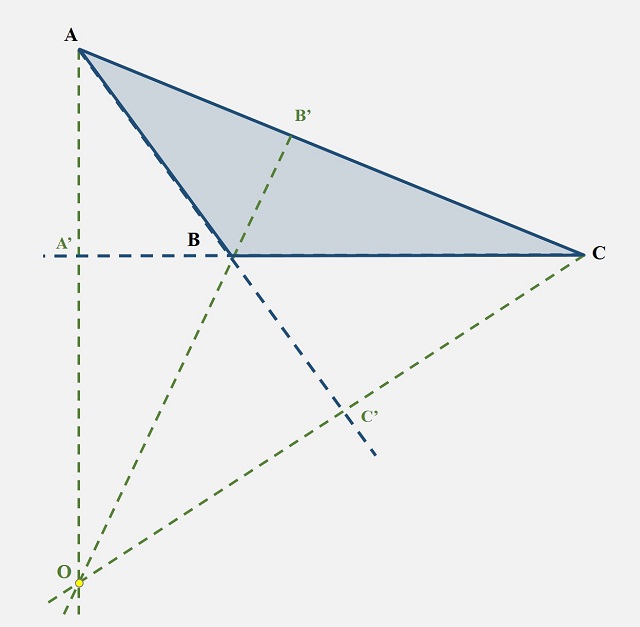 El ortocentro O de un triángulo obtuso ABC la intersección de sus tres alturas AA’, BB’ y CC’, se encuentra fuera del triángulo
El ortocentro O de un triángulo obtuso ABC la intersección de sus tres alturas AA’, BB’ y CC’, se encuentra fuera del triánguloEl circuncentro de un triángulo
El siguiente de los puntos destacados que se pueden definir para un triángulo cualquiera y que aparece en el teorema de la recta de Euler es el circuncentro.
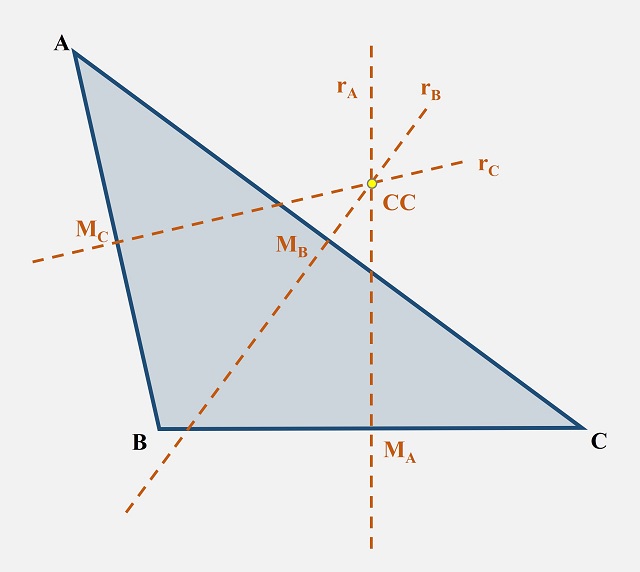
Dado un triángulo cualquiera se define el circuncentro como el punto de intersección de las tres mediatrices (la mediatriz de un segmento es la recta perpendicular al mismo que pasa por su punto medio) de los lados del triángulo. Por ejemplo, en la siguiente imagen tenemos un triángulo ABC cualquiera. Se consideran los puntos medios de los lados del triángulo ABC, que se denotan MA (punto medio del segmento BC opuesto al vértice A), MB (punto medio del segmento CA opuesto al vértice B) y MC (punto medio del segmento AB opuesto al vértice C) y las rectas que pasan por esos puntos y son perpendiculares a los segmentos a los que pertenecen, las mediatrices, que se denotan rA (la recta que pasa por MA y es perpendicular al segmento BC), rB (la recta que pasa por MB y es perpendicular al segmento CA) y rC (la recta que pasa por MC y es perpendicular al segmento AB). El circuncentro, CC en la imagen, es la intersección de las tres mediatrices rA, rB, y rC.
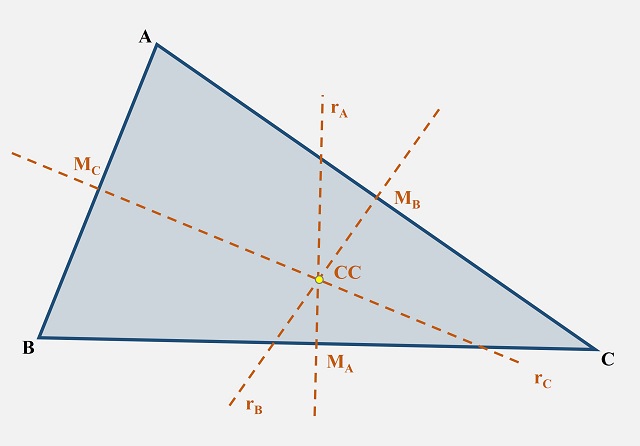 El circuncentro CC de un triángulo ABC es la intersección de sus tres mediatrices rA, rB, y rC
El circuncentro CC de un triángulo ABC es la intersección de sus tres mediatrices rA, rB, y rCDe nuevo, en función de la forma del triángulo, el circuncentro estará dentro o fuera del mismo. Si el triángulo es agudo, como en el ejemplo anterior, entonces el circuncentro se encuentra en el interior del triángulo. Si es un triángulo rectángulo, el circuncentro es el punto medio de la hipotenusa. Y si el triángulo es obtuso, entonces el circuncentro está fuera del triángulo.
 El circuncentro CC de un triángulo obtuso ABC, que es la intersección de sus tres mediatrices rA, rB, y rC, se encuentra fuera del triángulo
El circuncentro CC de un triángulo obtuso ABC, que es la intersección de sus tres mediatrices rA, rB, y rC, se encuentra fuera del triánguloEl nombre de circuncentro se debe a que ese punto es también el centro de la circunferencia circunscrita al triángulo. Es decir, si se considera la circunferencia que pasa por los vértices del triángulo A, B y C, el circuncentro CC es el centro de dicha circunferencia. Esto se debe al hecho de que los puntos de la mediatriz de un segmento equidistan (están a la misma distancia) de los extremos del segmento. Como el circuncentro CC está en las tres mediatrices del triángulo y los extremos de los segmentos son los vértices del triángulo, entonces el circuncentro CC equidista de los tres vértices, luego estos están en la circunferencia de centro CC y radio esa longitud entre CC y los vértices del triángulo.
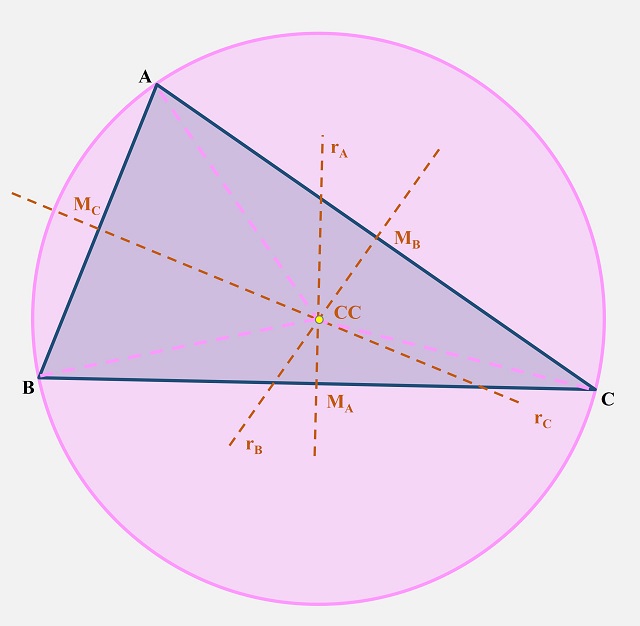 El circuncentro CC de un triángulo obtuso ABC es el centro de la circunferencia circunscrita al triángulo ABC
El circuncentro CC de un triángulo obtuso ABC es el centro de la circunferencia circunscrita al triángulo ABC
Como se comentaba más arriba, el circuncentro de un triángulo ya aparecía en esa importante publicación de la matemática griega, y universal, que fue Los Elementos de Euclides, y que hasta finales del siglo xix sería el libro de texto de matemáticas por antonomasia.
Para concluir esta sección, vamos a comentar un resultado que relaciona el circuncentro y el ortocentro de dos triángulos asociados de una cierta manera. Dado un triángulo cualquiera ABC, podemos tomar el triángulo cuyos vértices son los puntos medios de los lados del triángulo, según la notación anterior MA, MB y MC, que se conoce con el nombre de triángulo medial del triángulo ABC. Resulta que el ortocentro del triángulo medial MAMBMC es igual al circuncentro del triángulo ABC.
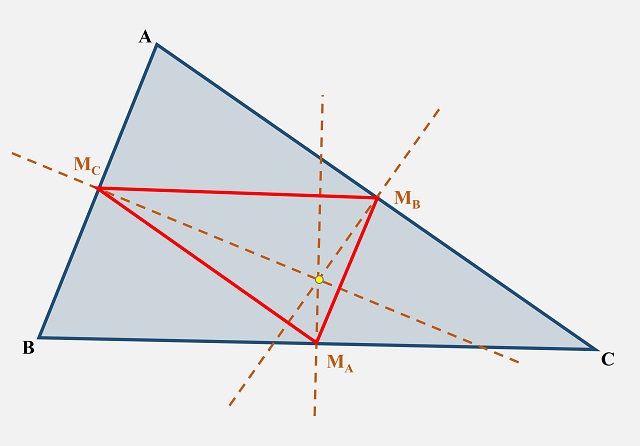 Dado un triángulo ABC, el ortocentro del triángulo medial MAMB MC es igual al circuncentro del triángulo ABCEl baricentro de un triángulo
Dado un triángulo ABC, el ortocentro del triángulo medial MAMB MC es igual al circuncentro del triángulo ABCEl baricentro de un triángulo
El tercer punto destacado de un triángulo que forma parte de esta pequeña historia sobre la que estamos escribiendo en esta entrada del Cuaderno de Cultura Científica es el baricentro.
Dado un triángulo cualquiera se define el baricentro (término que viene de barýs “pesado, grave” y centro, es decir, el centro de gravedad), o centroide, como el punto de intersección de las tres medianas (una mediana de un triángulo es el segmento de recta que pasa por un vértice y el punto medio del lado opuesto) del triángulo. Por ejemplo, en la siguiente imagen tenemos un triángulo ABC cualquiera. Como en el caso del circuncentro, se consideran los puntos medios de los lados del triángulo ABC, que se denotan MA, MB y MC y las tres medianas, denominadas sA (la recta que pasa por el vértice A y el punto medio del lado BC, MA), sB (la recta que pasa por B y MB) y sC (la recta que pasa por C y MC). El baricentro, BC en la imagen, es la intersección de las tres medianas sA, sB, y sC.
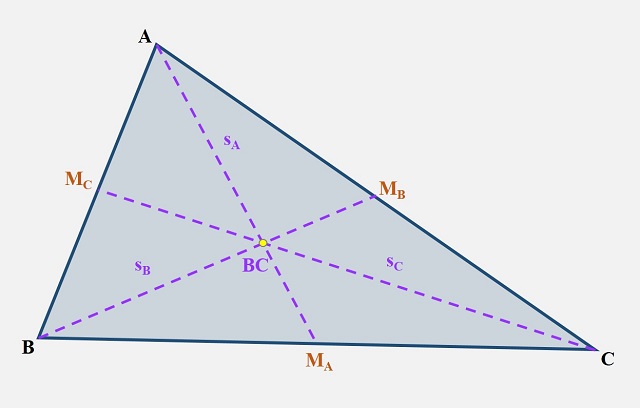 El baricentro BC de un triángulo ABC es la intersección de sus tres medianas sA, sB, y sC
El baricentro BC de un triángulo ABC es la intersección de sus tres medianas sA, sB, y sCEn el artículo Notes on the centroid / Notas sobre el centroide, publicado por el matemático estadounidense, nacido en Polonia, Nathan Altshiller Court (1881-1968) en la revista The Mathematics Teacher, se explica el origen del centroide de un triángulo. Una de las primeras notas es que el término centroide es un término moderno, del siglo xix, que se introdujo para sustituir el antiguo término de “centro de gravedad” cuando se habla solo desde el punto de vista geométrico y no físico. Y en la siguiente nota se afirma que la primera vez que se publica de forma explícita el resultado de que las tres medianas de un triángulo se cortan en un punto (el centro de gravedad del triángulo) es en el texto Mechanica del matemático e ingeniero griego Herón de Alejandría (sobre el siglo I o II).
La recta de EulerYa conocemos qué son el ortocentro, el circuncentro y el baricentro de un triángulo cualquiera, por lo tanto, estamos en condiciones de enunciar el teorema de la línea recta de Euler.
 Caricatura de Leonhard Euler, realizada por Enrique Morente, para la exposición de la Real Sociedad Matemática Española, El rostro humano de las matemáticas (2008)
Caricatura de Leonhard Euler, realizada por Enrique Morente, para la exposición de la Real Sociedad Matemática Española, El rostro humano de las matemáticas (2008)Leonhad Euler ha sido el matemático más prolífico de todos los tiempos. Miremos en la rama de las matemáticas que miremos, seguro que nos encontramos con un gran número de estudios, de resultados importantes y profundos de Euler. A lo largo de su vida publicó más de 500 libros y artículos, añadiendo su obra póstuma (hasta 1911) se alcanza la cifra de 866 (nombrados como E1-E866 y que pueden encontrarse online en el Archivo Euler). La edición moderna de las obras de Euler, que ha acometido la Sociedad Suiza de Matemáticas, empezó en 1911. Es el proyecto Opera Omnia Leonhard Euler, que consta de 81 volúmenes, en cuatro series: Serie I) Opera mathematica (Matemáticas), 29 volúmenes; Serie II) Opera mechanica et astronomica (Mecánica y Astronomía), 31 volúmenes; Serie III) Opera physica, Miscellanea (Física y Miscelánea), 12 volúmenes; Serie IVA) Commercium epistolicum (correspondencia), 9 volúmenes; Series IVB) manuscritos, que se publicará online.
En el artículo E325, titulado Solutio facilis problematum quorundam geometricorum difficillimorum / Soluciones fáciles para algunos problemas geométricos difíciles y publicado en la revista Novi Commentarii academiae scientiarum Petropolitanae en 1767 (fue presentada a la Academia de Ciencias de San Petersburgo en diciembre de 1763), se recoge el conocido como teorema de la recta de Euler.
Teorema de la recta de Euler: Dado un triángulo cualquiera ABC, el ortocentro O, el circuncentro CC y el baricentro BC son colineales (a la recta que incluye a los tres puntos se la denomina recta de Euler). Además, la distancia del ortocentro O al baricentro BC es igual a dos veces la distancia del baricentro BC al circuncentro CC.
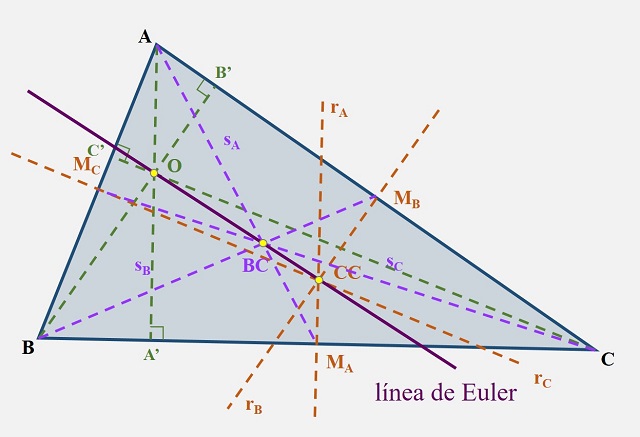 El ortocentro O, el circuncentro CC y el baricentro BC de un triángulo ABC están alineados y la recta que los contiene es la recta de Euler
El ortocentro O, el circuncentro CC y el baricentro BC de un triángulo ABC están alineados y la recta que los contiene es la recta de Euler
En el libro 100 grandes problemas de matemática elemental: su historia y soluciones (100 Great Problems of Elementary Mathematics: Their History and Solutions), del matemático Heinrich Dorrie, que se cita en la bibliografía, se puede leer una sencilla demostración del teorema de la recta de Euler.
Además del ortocentro, el circuncentro y el baricentro de un triángulo, existen otros puntos definidos en relación al triángulo que también están en la recta de Euler, como el centro de la circunferencia de los nueve puntos, el punto de Exeter o el punto de de Longchamps, entre otros, pero esa es otra historia que será contada en otra ocasión.
 Nine-point circle / Circunferencia de los nueve puntos (1970), del dibujante e ilustrador infantil estadounidense Crockett Johnson (1906-1975). Imagen de la página web de The National Museum of American History
Nine-point circle / Circunferencia de los nueve puntos (1970), del dibujante e ilustrador infantil estadounidense Crockett Johnson (1906-1975). Imagen de la página web de The National Museum of American HistoryBibliografía
1.- David Wells, The Penguin Dictionary of Curious and Interesting Geometry, Penguin, 1991.
2.- Heinrich Dorrie, 100 Great Problems of Elementary Mathematics: Their History and Solutions, Dover, 1965.
3.- Howard Eves, A Survey of Geometry, Allyn and bacon, 1972.
4.- Mowaffaq Hajja, Horst Martini, Concurrency of the Altitudes of a Triangle, Mathematische Semesterberichte 60 (2), pp. 249–260, 2013.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo La recta de Euler se ha escrito en Cuaderno de Cultura Científica.
Cómo se forman los condensados dentro de las células
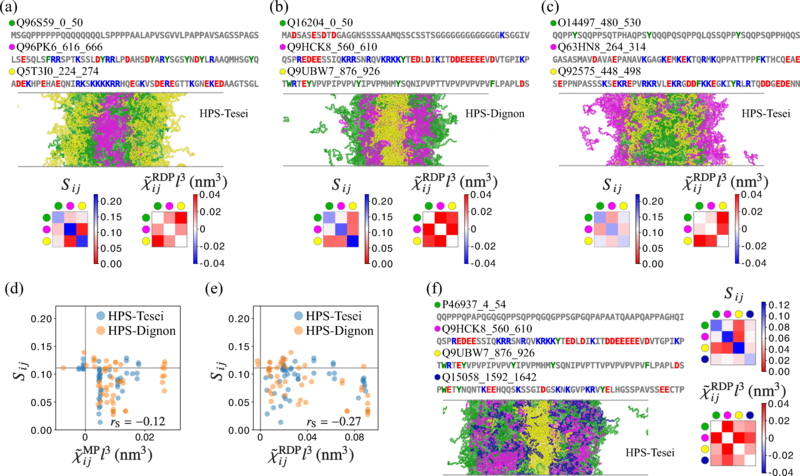
Las células biológicas contienen pequeñas gotas llamadas condensados que consisten en conjuntos de proteínas y otras moléculas. Estas gotas desempeñan papeles importantes en varias funciones celulares, como las reacciones bioquímicas. Se sabe que las interacciones entre las regiones intrínsecamente desordenadas (IDR, por sus siglas en inglés) de diferentes proteínas (partes de una proteína que carecen de una estructura bien definida) impulsan la formación de condensados. Pero los detalles exactos de cómo intervienen las IDR en esta formación no estaban claros.
Ahora Kyosuke Adachi y Kyogo Kawaguchi del Centro RIKEN para la Investigación de la Dinámica de Biosistemas en Japón han ideado un modelo que proporciona esa información. Los investigadores afirman que su modelo podría usarse para obtener otros conocimientos clave sobre los principios fundamentales de la organización celular.
Adachi y Kawaguchi han realizado simulaciones de la dinámica molecular de la formación de condensados para más de 200 IDR que se conocen en proteínas humanas. A continuación han combinado los resultados de estas simulaciones con una nueva aproximación para la dinámica de los IDR. Finalmente, han desarrollado una teoría que les permite vincular la fuerza de las interacciones entre los IDR de diferentes proteínas con el orden específico de los aminoácidos de los IDR, los componentes básicos de las proteínas.
El nuevo modelo indica que las IDR formadas por ciertas cadenas de aminoácidos tienen más probabilidades de unirse, lo que hace que sus proteínas se agrupen en un condensado. El modelo también muestra que las interacciones entre las IDR afectan a la posibilidad de que varios condensados puedan coexistir en una célula sin que se fusionen, y puede utilizarse para determinar cuántos condensados oexistentes puede albergar una célula.
Según los investigadores, el nuevo modelo podría ayudar a mejorar la comprensión de muchos procesos biológicos, incluidos los mecanismos por los que las células compartimentan sus funciones y la dinámica de las IDR de una proteína en diferentes condiciones.
Referencias:
Kyosuke Adachi & Kyogo Kawaguchi (2024) Predicting Heteropolymer Interactions: Demixing and Hypermixing of Disordered Protein Sequences Phys. Rev. X doi: 10.1103/PhysRevX.14.031011
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Cómo se forman los condensados dentro de las células se ha escrito en Cuaderno de Cultura Científica.
Una capa brillante para un planeta oscuro
Mercurio no es solo el planeta más pequeño de nuestro sistema solar, sino que también es uno de los más desconocidos, ya que, casualmente, ha sido el planeta interior -o rocoso- menos visitado por misiones espaciales. Entre otras razones, ello se debe a la dificultad que supone colocarse en órbita alrededor de Mercurio, lo que requiere una gran cantidad de combustible -combustible en sentido amplio- para alcanzar el cambio de velocidad necesario que permita la inserción.
A pesar de esto, misiones como la MESSENGER nos han permitido conocer mucho mejor a Mercurio y detectar, por ejemplo, la presencia de agua y de compuestos orgánicos en su superficie, la existencia de un núcleo en estado líquido e incluso los restos de la actividad volcánica que sufrió el planeta en su pasado. Las observaciones las pudo obtener desde su órbita desde 2011 a 2015, cuando la misión, como despedida, impactó finalmente contra la superficie del planeta.
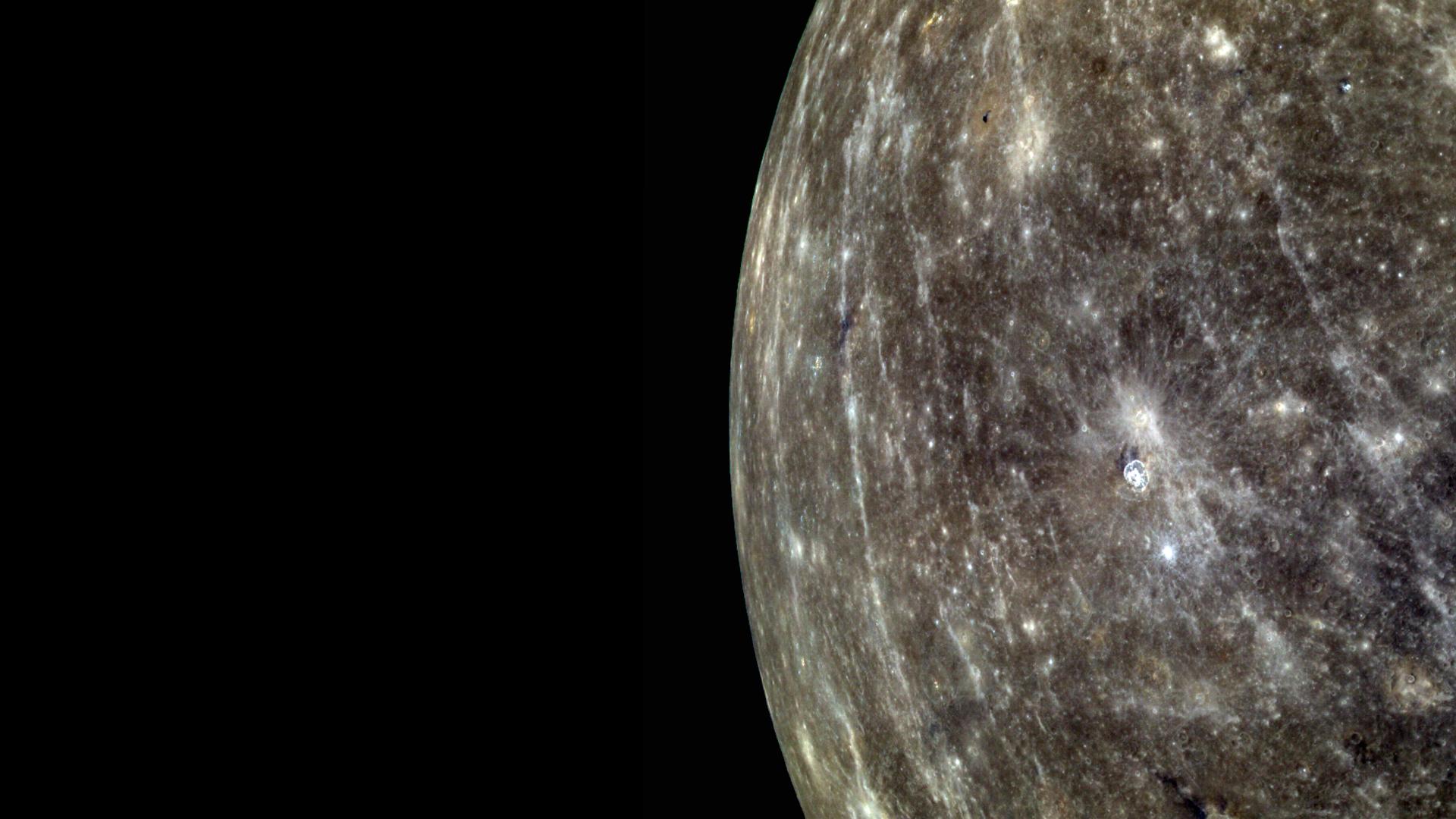 A simple vista, el aspecto de Mercurio nos recuerda mucho al de nuestra Luna. Sin embargo, son lugares muy, pero que muy distintos. Imagen cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Carnegie Institution of Washington.
A simple vista, el aspecto de Mercurio nos recuerda mucho al de nuestra Luna. Sin embargo, son lugares muy, pero que muy distintos. Imagen cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Carnegie Institution of Washington.Pero, ¿cómo es el interior de Mercurio? Lo cierto es que es un planeta muy particular, especialmente si lo comparamos el resto de los planetas interiores. Para que nos hagamos una idea, el núcleo -la capa más interna de los planetas- de Mercurio ocupa aproximadamente un 57% del volumen total del planeta, mientras que en Venus ocuparía un 15%, en la Tierra un 16% y en Marte un 13%. Mercurio claramente destaca por tener un valor totalmente anómalo en comparación con el resto.
Este pequeño detalle ya nos cuenta que la historia de Mercurio podría haber sido un poco diferente a la del resto de planetas rocosos, apuntando directamente a su formación o a su infancia -eso sí, infancia en términos planetarios. O bien la zona donde se formó Mercurio dentro de la nebulosa protoplanetaria estaba empobrecida en elementos ligeros -quizás por procesos dinámicos, no tanto por una diferencia composicional dentro de la nebulosa- porque tras su formación, las elevadas temperaturas del Sol mientras este se contraía vaporizaron parte de su corteza y manto rocoso -para lo que Mercurio tendría que tener una masa de partida de aproximadamente el doble- o, por último, un gigantesco impacto que fuese capaz de eliminar una gran parte de su corteza y manto dejando las zonas más densas del planeta y llevándose las ligeras, y para lo que Mercurio también tendría que haber tenido también en torno al doble de masa que en la actualidad.
Pero volvamos al asunto que nos trae hoy aquí y seamos realistas: Mercurio es un planeta muy poco… “brillante”. Apenas refleja el 10% de la luz solar, algo que hasta la llegada de las misiones planetarias había tenido una difícil explicación. Los últimos datos afirman que muy probablemente esta escasa reflectividad se deba a que su superficie está cubierta por una cantidad entre el ~1-4% de grafito -un compuesto de carbono que usamos todos los días, por ejemplo, en las minas de nuestros lápices y que a la luz es evidente que tiene un color bastante oscuro-, a lo que habría que sumar probablemente otros compuestos del carbono, aunque las últimas estimaciones de Xu et al. (2024) dicen que sería inferior al 1%.
 La eyecta provocada por los cráteres de impacto -es decir, los materiales que salen hacia fuera del cráter cuando un cuerpo impacta contra la superficie de un planeta- salpican de tonos más claros la superficie de Mercurio. Imagen cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Carnegie Institution of Washington.
La eyecta provocada por los cráteres de impacto -es decir, los materiales que salen hacia fuera del cráter cuando un cuerpo impacta contra la superficie de un planeta- salpican de tonos más claros la superficie de Mercurio. Imagen cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Carnegie Institution of Washington.¿Cuál sería la procedencia de este grafito que hoy vemos en la superficie? No está muy claro, y dependiendo del modelo de formación, explicar su presencia puede ser complicado, pero la forma más sencilla sería que, en algún momento de su historia, la superficie de Mercurio estuviese en un estado de océano de magma -una etapa habitual durante la formación de los planetas interiores- y donde toda la superficie se encuentra fundida. Es en este océano donde el carbono, debido a su densidad, flotaría hasta la superficie, quedando expuesto tal y como vemos hoy en día, mezclado con otros minerales silicatados que forman su corteza.
Este detalle sobre la composición de su superficie nos hace pensar que Mercurio podría tener más carbono en su interior del que podríamos pensar a priori y esto puede tener unas consecuencias un tanto inesperadas que podemos leer en Yongjiang et al. (2024): la existencia de una “capa” de diamantes en el interior de Mercurio. Y es que sabemos por nuestra experiencia en la Tierra que los diamantes en los planetas rocosos se forman en ambientes de alta presión y temperatura, lo que en nuestro planeta equivale a profundidades del manto.
Mercurio es mucho más pequeño que nuestro planeta y la presión necesaria para transformar el carbono en su forma de grafito a diamante se alcanzaría en lo que vendría siendo el límite entre el manto y el núcleo, eso sí, también tendrían que darse unas condiciones de temperatura adecuadas. Pero además del carbono hay un elemento que probablemente haya tenido un papel importante para formar esta posible capa: el azufre.
Y es que la presencia de azufre en el interior del planeta podría ayudar a bajar la temperatura que los silicatos presentes en el manto requieren para fundirse, permitiendo unas condiciones que ayudarían a dar estabilidad a la formación de los diamantes. Si a esto le sumamos un ambiente muy reductor -con bajo contenido en oxígeno- los diamantes podrían haberse empezado a formar al mismo tiempo que empezó a solidificarse el núcleo, permitiendo dar lugar una capa de diamantes en el límite entre el manto y el núcleo y que incluso podría tener varios kilómetros de potencia o espesor.
Los científicos que han escrito este artículo, además, han diseñado y ejecutado una serie de experimentos de alta presión y temperatura -sin olvidar los modelos geoquímicos y termodinámicos- a fin de poder replicar las condiciones que se podrían encontrar en este límite entre el manto y el núcleo, observando que efectivamente, los diamantes podrían formarse bajo estas condiciones.
 En esta imagen también se puede apreciar perfectamente el fuerte contraste de color entre la eyecta y la superficie de Mercurio, mucho más oscura. Y es que es posible que los minerales que hay a más profundidad de la corteza tengan un tono más claro y sean menos ricos en carbono. Imagen cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Carnegie Institution of Washington.
En esta imagen también se puede apreciar perfectamente el fuerte contraste de color entre la eyecta y la superficie de Mercurio, mucho más oscura. Y es que es posible que los minerales que hay a más profundidad de la corteza tengan un tono más claro y sean menos ricos en carbono. Imagen cortesía de NASA/Johns Hopkins University Applied Physics Laboratory/Carnegie Institution of Washington.Todo esto nos puede parecer una mera curiosidad, pero en Mercurio podrían tener una interesante derivada… puesto que los diamantes son unos excelentes conductores térmicos -de hecho, se usan en algunas aplicaciones electrónicas donde la disipación del calor es algo crítico y los materiales que son buenos conductores eléctricos no se pueden colocar- y una capa rica en diamantes podría tener una gran influencia en la transferencia del calor en el interior del planeta, alterando la propia dinámica interna del planeta. ¿Qué consecuencias tiene esto? La generación de un campo magnético similar al de la Tierra, aunque con una fuerza del 1% del nuestro.
El papel de la capa de diamantes es el de facilitar la pérdida de calor del núcleo, favoreciendo la convección necesaria para que funcione la geodínamo necesaria para la formación del campo magnético.
Mercurio no es el único planeta que podría tener capas con diamantes, sino que los gigantes de hielo, como son Urano y Neptuno, también podrían tener zonas donde las condiciones permitan la formación de los diamantes. De momento ninguno de estos lugares son accesibles a nuestra tecnología. Esta posibilidad pone de manifiesto que los diamantes son un mineral más abundante de lo que podemos pensar. Eso sí, que nadie piense que los va a encontrar perfectamente tallados para recoger y colocar en un anillo: eso ya corre de nuestra cuenta.
La próxima misión destinada a Mercurio, la europea BepiColombo debería alcanzar su órbita en 2025, aportándonos a lo largo de su misión datos que nos ayuden a conocer mejor su geología y quién sabe si a verificar la posibilidad de que Mercurio tenga una resplandeciente capa de diamantes.
Referencias:
Cheng, Bingqing, Sebastien Hamel, y Mandy Bethkenhagen. «Thermodynamics of Diamond Formation from Hydrocarbon Mixtures in Planets». Nature Communications 14, n.º 1 (27 de febrero de 2023): 1104. doi: 10.1038/s41467-023-36841-1.
Frost, Mungo, R. Stewart McWilliams, Elena Bykova, Maxim Bykov, Rachel J. Husband, Leon M. Andriambariarijaona, Saiana Khandarkhaeva, et al. «Diamond Precipitation Dynamics from Hydrocarbons at Icy Planet Interior Conditions». Nature Astronomy 8, n.º 2 (8 de enero de 2024): 174-81. doi: 10.1038/s41550-023-02147-x.
Semerikova, Anna, Artem D. Chanyshev, Konstantin Glazyrin, Anna Pakhomova, Alexander Kurnosov, Konstantin Litasov, Leonid Dubrovinsky, Timofey Fedotenko, Egor Koemets, y Sergey Rashchenko. «Does It “Rain” Diamonds on Neptune and Uranus?» ACS Earth and Space Chemistry 7, n.º 3 (16 de marzo de 2023): 582-88. doi: 10.1021/acsearthspacechem.2c00343.
Xu, Yongjiang, Yanhao Lin, Peiyan Wu, Olivier Namur, Yishen Zhang, y Bernard Charlier. «A Diamond-Bearing Core-Mantle Boundary on Mercury». Nature Communications 15, n.º 1 (14 de junio de 2024): 5061. doi: 10.1038/s41467-024-49305-x.
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Una capa brillante para un planeta oscuro se ha escrito en Cuaderno de Cultura Científica.
La interpretabilidad de los modelos de inteligencia artificial
Imagina que eres médico y utilizas un sistema de IA de última generación para diagnosticar a tus pacientes. Un día, te dice que un paciente tiene una enfermedad rara, pero cuando le preguntas por qué, simplemente parpadea, incapaz de explicar su razonamiento. Frustrante, ¿verdad? Este escenario puede sonar a ciencia ficción, pero es un reto real en el mundo del aprendizaje automático hoy en día.
Bienvenido al fascinante mundo de la interpretabilidad de modelos, un tema que lleva muchos años dando que hablar en la comunidad de la IA. A medida que los modelos de aprendizaje automático se vuelven más complejos e influyen más en nuestras vidas, nos enfrentamos a una pregunta acuciante: ¿Cómo podemos confiar en las decisiones tomadas por algoritmos que no comprendemos del todo?
En un artículo clásico -muy citado- titulado «The Mythos of Model Interpretability» (2017) el investigador Zachary C. Lipton profundiza en este aspecto crucial. Sostiene que, aunque todo el mundo parece hablar de interpretabilidad, en realidad no tenemos una definición clara y consensuada de lo que significa.
La importancia de la interpretabilidadEntonces, ¿qué importancia tiene la interpretabilidad? Bueno, resulta que hay varias interpretaciones o motivaciones diferentes para la interpretabilidad en el aprendizaje automático:
Confianza (trust): Queremos estar seguros de que nuestros modelos toman decisiones por las razones correctas. Imaginemos un coche autoconducido que hace un giro brusco: ¿no querríamos saber por qué?
Causalidad (causality): En campos como la medicina, no sólo nos interesan las predicciones, sino entender las causas subyacentes. Una IA capaz de predecir una enfermedad cardiaca es útil, pero una que pueda explicar los factores que la provocan tiene un valor incalculable.
Toma de decisiones justa y ética: Como la IA se utiliza cada vez más en ámbitos delicados como la justicia penal y la aprobación de préstamos, tenemos que asegurarnos de que no perpetúa los prejuicios. Si una IA deniega un préstamo a alguien, tenemos que poder examinar su proceso de toma de decisiones.
Informatividad (informativiness): A veces queremos que nuestros modelos nos enseñen algo nuevo sobre el mundo. Un modelo interpretable puede revelar patrones o relaciones inesperadas en los datos.
Transferibilidad (transferability): Necesitamos saber hasta qué punto nuestros modelos funcionarán bien en situaciones nuevas y ligeramente diferentes. Esto es crucial para desplegar sistemas de IA en el mundo real, donde las condiciones pueden cambiar.
Los enfoques de la interpretabilidadLipton señala que hay distintas formas de lograr la interpretabilidad. Algunos investigadores se centran en hacer más transparente el funcionamiento interno de los modelos, mientras que otros desarrollan técnicas para explicar las decisiones de los modelos a posteriori.
Los enfoques de la transparencia incluyen:
-
Simulabilidad: ¿Puede un ser humano simular todo el modelo?
-
Descomponibilidad: ¿Puede entenderse intuitivamente cada parte del modelo?
-
Transparencia algorítmica: ¿Entendemos cómo funciona el algoritmo de aprendizaje?
Entre los métodos de interpretabilidad post hoc se incluyen:
-
Explicaciones textuales: Generación de explicaciones legibles para el ser humano sobre las decisiones del modelo.
-
Visualización: Creación de representaciones visuales de lo que ha aprendido el modelo.
-
Explicaciones locales: Explicar predicciones individuales en lugar de todo el modelo.
-
Explicación mediante ejemplos: Mostrar casos similares que el modelo utilizó para tomar su decisión.
Curiosamente, el artículo cuestiona algunos supuestos comunes. Por ejemplo, mucha gente cree que los modelos lineales simples son intrínsecamente más interpretables que las redes neuronales complejas. Pero Lipton sostiene que esto no siempre es cierto: depende de lo que entendamos por interpretabilidad y de cómo se utilicen los modelos. Por ejemplo, un modelo lineal con miles de características puede ser más difícil de entender a primera vista que una red neuronal entrenada con datos brutos. La elección entre interpretabilidad y rendimiento no siempre está clara.
La interpretabilidad, un arma de doble filoAunque el impulso a favor de la interpretabilidad es generalmente positivo, Lipton advierte de que no está exento de posibles inconvenientes. Por ejemplo, a veces, hacer que un modelo sea más interpretable puede reducir su precisión. O puede que las explicaciones sencillas nos den una falsa sensación de seguridad sobre los sistemas complejos. O tal vez, quién sabe, un modelo muy interpretable podría revelar información sensible sobre los datos de entrenamiento.
A medida que la IA sigue dando forma a nuestro mundo, tenemos que ser más precisos sobre lo que queremos decir cuando exigimos modelos «interpretables». No se trata solo de simplificar las cosas, sino de garantizar que nuestros sistemas de IA se ajusten a los valores humanos y sean fiables a la hora de tomar decisiones importantes.
La búsqueda de una IA interpretable es algo más que un reto técnico: es un paso crucial en la creación de sistemas de IA en los que podamos confiar y que podamos utilizar de forma responsable en la sociedad. Mientras seguimos ampliando los límites de lo que la IA puede hacer, también debemos ampliar nuestra comprensión de cómo funciona. Es un viaje que promete no solo hacer que nuestros sistemas de IA sean más fiables, sino también profundizar en nuestra propia comprensión de la toma de decisiones y de la propia inteligencia.
Para saber más:
La IA podría convertir la ciencia en algo incomprensible
¿Qué es el aprendizaje automático?
Sobre el autor: Julián Estévez Sanz, Profesor e investigador en Robótica e Inteligencia Artificial, Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo es una versión del publicado en El blog de Julián Estévez el 19 de agosto de 2024
El artículo La interpretabilidad de los modelos de inteligencia artificial se ha escrito en Cuaderno de Cultura Científica.
Dinosaurios sobre dos ruedas
Si tenéis afición por el ciclismo, seguramente estaréis siguiendo el desarrollo de la tercera gran vuelta por etapas de tres semanas de duración, la Vuelta Ciclista a España, que está recorriendo nuestra geografía estos días. Y, si prestáis mucha atención a los maillots de los equipos, os habrá llamado la atención uno muy geológico. Me refiero al uniforme del equipo Soudal Quick-Step. Este atuendo lleva impresa en la parte frontal y trasera la cabeza de un amenazante Tyrannosaurus rex con la boca abierta, mostrando una hilera de afiliados dientes, enmarcada en un círculo rojo y acompañada por la palabra T-rex en letras blancas, así como la marca de tres garras en el lateral derecho del maillot, como si el dinosaurio hubiese peleado con los ciclistas, rompiendo sus camisetas.
 Maillot oficial del equipo T-rex Quick-Step para la Vuelta Ciclista a España 2024. Imagen tomada de www.lavuelta.es
Maillot oficial del equipo T-rex Quick-Step para la Vuelta Ciclista a España 2024. Imagen tomada de www.lavuelta.esSeguramente os estaréis preguntando lo mismo que yo la primera vez que lo vi, ¿por qué? Pues la respuesta es sencilla, por puro marketing. Soudal es una empresa belga dedicada al bricolaje, en especial a fabricar adhesivos, siliconas y selladores. Y uno de sus productos más famosos es T-rex, un adhesivo de alta calidad y muy resistente, al que pusieron el nombre de este famoso reptil prehistórico para remarcar su fortaleza. De esta manera, han aprovechado el perfil mediático de la vuelta ciclista para promocionarlo de manera internacional, mostrando a su vez a sus ciclistas como poderosos deportistas ávidos de victorias, pretendiendo intimidar a sus rivales con tan fiero diseño.
Pero, si lo analizamos desde un punto de vista estrictamente geológico, este dibujo tiene un error de bulto. Como os he comentado, en el costado derecho del maillot aparece la marca de tres garras. Pues resulta que, de acuerdo a los restos fósiles de Tyrannosaurus rex encontrados hasta la fecha, este animal tenía solo dos dedos en sus manos. Le sobra una marca al diseño, aunque reconozco que queda mucho más potente con tres raspones que con solo dos.
Dejando aspectos estéticos con ligeras libertades poéticas aparte, la siguiente pregunta que podemos plantearnos es: ¿Estos falsos T-rex subidos a las bicicletas son los únicos dinosaurios que nos vamos a encontrar en la Vuelta Ciclista a España de 2024? Pues no, ya que veremos restos fósiles reales de estos extintos animales durante el recorrido. En concreto, en la etapa 16, que discurre por tierras asturianas, con salida en Luanco y llegada en los míticos Lagos de Covadonga, un disputado final en alto que ha sellado el podium de muchas ediciones. Durante el recorrido, la “serpiente multicolor” pasará por dos de las localidades que forman parte de la ruta conocida como “la costa de los dinosaurios” de Asturias: Villaviciosa y Colunga. En los acantilados costeros de las playas de estas hermosas poblaciones marineras se conservan fósiles de icnitas de dinosaurios.
 Icnitas de dinosaurio encontradas en la playa de La Griega, en Colunga. En concreto se trata de las pisadas de un cuadrúpedo de gran tamaño (las huellas tienen un diámetro de casi 1m). Imagen de Jose Francisco Sánchez Díaz, tomada de www.turismoasturias.es
Icnitas de dinosaurio encontradas en la playa de La Griega, en Colunga. En concreto se trata de las pisadas de un cuadrúpedo de gran tamaño (las huellas tienen un diámetro de casi 1m). Imagen de Jose Francisco Sánchez Díaz, tomada de www.turismoasturias.esLas icnitas son un tipo de fósiles muy particulares, ya que se trata de las huellas de pisadas, marcas, pistas o rastros de locomoción de organismos del pasado preservados en las rocas. Estas huellas pueden aparecer en el registro fósil de dos maneras: en forma de moldes, que sería el fósil de la impresión dejada por el organismo en el sedimento sobre el que se desplaza (huella directa); y en forma de contramoldes, que representa la imagen en negativo de esa huella y que queda preservada en la capa de sedimento que la recubre. Para explicarlo de manera más visual, imaginad que cogéis un bloque de plastilina de color amarillo, lo presionáis con fuerza con el dedo dejando la marca, después lo tapáis con un bloque de plastilina azul hasta rellenar completamente ese hueco y separáis de nuevo los dos bloques. La amarilla conserva el fósil del molde de vuestra huella, mientras que en el azul aparecerá el contramolde.
Desde un punto de vista más práctico, las icnitas aportan una valiosa información sobre el comportamiento de los organismos que las produjeron. En el caso de vertebrados, como los dinosaurios, nos permiten descubrir si caminaban sobre dos patas o sobre las cuatro, podemos estimar su tamaño y su peso mediante cálculos de la longitud y anchura de su zancada y la profundidad que alcanza la huella en diferentes tipos de sedimentos, incluso inferimos si tenían un comportamiento gregario y se desplazaban en manada o si vivían y cazaban de manera individualista. Y en este aspecto la costa asturiana es un auténtico paraíso, ya que se preservan moldes y contramoldes de icnitas de diversas especies de dinosaurios, de animales grandes y pesados y otros más pequeños y ágiles, unos bípedos y otros cuadrúpedos, algunos herbívoros y algunos carnívoros y también adultos y juveniles. Vamos, que hace millones de años está zona era un vergel de dinosaurios.
Llegados a este punto, nos surge una última pregunta: ¿Hubo Tyrannosaurus rex en Asturias? Pues siento desilusionaros, pero no. Esta especie vivió en lo que actualmente es Norteamérica a finales del Periodo Cretácico, hace entre unos 68 y 66 millones de años. Y las rocas que afloran en la costa de Asturias son del Periodo Jurásico, de hace entre 200 y 145 millones de años, un momento en el que América y Europa ya estaban separadas y la Península Ibérica era una especie de islotes independientes entre sí. Por lo que los únicos T-rex que veremos por aquí son los que van subidos a una bicicleta.
Todos los yacimientos de icnitas de dinosaurio de Asturias se pueden visitar y disponen de señalizaciones precisas y paneles informativos. Pero si decidís acercaros a este paraíso natural, os aconsejo que vuestra primera parada sea Colunga, en concreto, el Museo del Jurásico de Asturias (MUJA). En él encontraréis diversas reconstrucciones de estos extintos animales y réplicas de sus fósiles, incluidos dos Tyrannosaurus rex en actitud muy cariñosa. Así descubriréis todos los secretos sobre la vida del pasado y os informarán de dónde se encuentran los yacimientos visitables y la mejor forma de acceder a ellos. Pero, hasta que podamos realizar esta escapada, tendremos que contentarnos con los ataques de los T-rex ciclistas rugiendo por nuestras carreteras.
Para saber más:
La Universidad Complutense de Madrid, en colaboración con el Instituto Geológico y Minero de España, lleva a cabo la iniciativa “Geodiversidad de la Vuelta a España”, en la que se describe el contexto geológico del recorrido de cada etapa: www.lavuelta.es/es/la-carrera/geodiversidad
La Comisión Mujeres y Geología de la Sociedad Geológica de España colabora con la sección de deportes de Radio Nacional de España aportando curiosidades geológicas del recorrido durante las retransmisiones de cada etapa: www.rtve.es/play/radio/rne
Agradecimientos:
Quiero dar las gracias a Daniel Ampuero y Gonzalo Da Cuña, periodistas de Radio Nacional de España y responsables de la retransmisión radiofónica de La Vuelta Ciclista a España, por darnos la oportunidad de colaborar con ellos contando anécdotas geológicas. Y a mis compañeras de la Comisión Mujeres y Geología de la Sociedad Geológica de España y del equipo de trabajo de Comunicación y Redes Sociales, también de la Sociedad Geológica de España, por la ayuda para preparar los temas y la promoción de la colaboración con RNE.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Dinosaurios sobre dos ruedas se ha escrito en Cuaderno de Cultura Científica.
Los números metálicos
La razón metálica de un número entero positivo n se define como el número real positivo
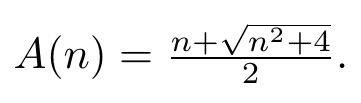
Los primeros números metálicos son, de hecho, números bien conocidos: la razón áurea (que corresponde a n = 1), el número de plata (asociado a n = 2) o el número de bronce (correspondiente a n = 3).
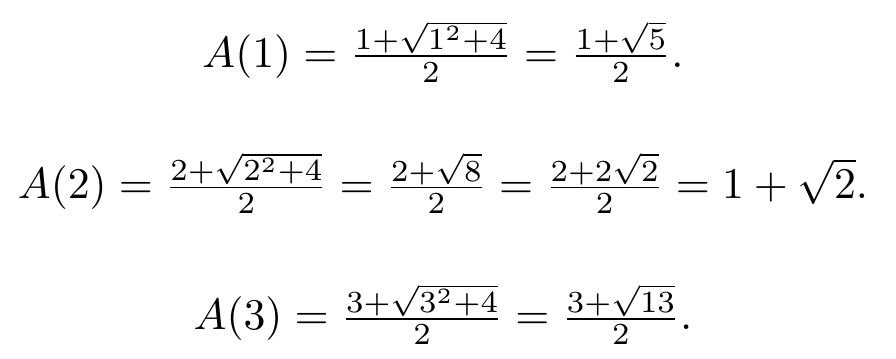
Algunos de los números metálicos posteriores reciben nombres como cobre o níquel. La matemática Vera Marta Winitzky los definió, estudió y divulgó.
 Vera Marta Winitzky describiendo propiedades de la razón áurea. Fuente: Wikimedia Commons.
Vera Marta Winitzky describiendo propiedades de la razón áurea. Fuente: Wikimedia Commons.Definición y algunas propiedades de los números metálicos
La matemática argentina Vera Martha Winitzky comenzó a trabajar en números metálicos en 1997. Los definió en el artículo La familia de números metálicos en Diseño en cuya introducción comentaba:
Vamos a presentar la nueva familia de «números metálicos». Sus integrantes tienen, entre otras características comunes, la de llevar el nombre de un metal. Así, por ejemplo, el miembro más conspicuo es el famoso «Número de Oro». Luego vienen el Número de Plata, el Número de Bronce, el Número de Cobre, el número de Níquel y muchos otros más. El Número de Oro ha sido ampliamente utilizado en una gran cantidad de culturas antiguas como base de proporciones. Con respecto a los parientes del Número de Oro, parte de estos números fueron usados por diversos físicos en sus investigaciones de punta, al tratar de sistematizar el comportamiento de sistemas dinámicos no lineales, analizando la transición de la periodicidad a la cuasi-periodicidad. Pero también Jay Kappraff recurre, en particular, al Número de Plata para describir y explicar el sistema romano de proporciones, haciendo uso de una propiedad matemática que, como veremos, es común a todos los miembros de esta notable familia.
En conclusión, el hecho que los números metálicos aparezcan desde los sistemas usados en el Diseño de sus construcciones por la civilización romana antigua hasta los más recientes trabajos de caracterización de caminos universales al caos los convierte en instrumentos invalorables para la búsqueda de relaciones viables cuantitativas entre la Matemática y el Arte.
Usando la expresión en fracción continua de estos números (Winitzky prueba que A(n) tiene como expresión en fracción continua [n; n, n, n, n,…]) para demostrarlo, en el trabajo se concluye en primer lugar que:
Los números metálicos son irracionales cuadráticos.
En efecto, son irracionales porque la fracción continua que los define es infinita. Y son cuadráticos porque es fácil demostrar que A(n) es la solución positiva de la ecuación cuadrática x2 – nx – 1 = 0.
De hecho, como comenta Winitzky, fue Joseph Louis Lagrange quien demostró que: Un número es irracional cuadrático si y solo si su descomposición en fracciones continuas es periódica.
Estos números metálicos tienen, además, relación con la sucesión de Fibonacci. En el artículo se demuestra que:
Los números metálicos son todos límites de sucesiones generalizadas de Fibonacci secundarias.
Una sucesión de generalizada de Fibonacci secundaria es una sucesión G(n) en la que cada término se define en función de los anteriores:
G(n+2) = p G(n) + q G(n +1),
donde p y q son números naturales.
Por ejemplo, la sucesión de Fibonacci se define mediante la relación F(n+2) = F(n) + F(n+1), y el número de oro es el límite (cuando n tiende a infinito) del cociente F(n+2) / F(n+1).
Puede demostrarse también que el número de plata es el límite del cociente G(n+2) / G(n+1), donde la sucesión generalizada de Fibonacci involucrada es la definida por la relación G(n+2) = 2 G(n+1) + G(n). Así, la propiedad anterior afirma que todos los números metálicos son límites de cocientes del tipo G(n+2) / G(n+1) para determinados números naturales p y q.
En el artículo se demuestran algunas otras propiedades matemáticas y la autora se refiere también a cómo aparecen de manera natural en arquitectura, diseño, arte… e incluso en la estructura de algunos cuasicristales.
Más matemáticas en los estudios de diseñoVera Martha Winitzky comenzó a trabajar como profesora de matemáticas en Facultad de Arquitectura y Urbanismo de la Universidad de Buenos Aires en 1957. Pensaba que los programas de los cursos de diseño carecían de contenidos profundos de matemáticas que, en su opinión, podían aportan creatividad a los estudiantes. También pensaba que era importante insistir en la falta de linealidad de la naturaleza, por lo que introdujo conceptos de geometría fractal en sus cursos de diseño. Y expresaba su interés de esta manera:
El objetivo principal de mi trabajo es convocar a matemáticos, arquitectos, ingenieros y diseñadores interesados en la interacción entre Matemáticas y Diseño. Utilizo la palabra Diseño en su sentido más amplio, es decir, un Diseño es un recurso proyectual que constituye un elemento básico en la comunicación interdisciplinaria entre los seres humanos, sea arquitectónico, gráfico, visual o sonoro, así como cualquier otra interacción simple o combinada.
Referencias
-
V. M. Winitzky de Spinadel, La familia de números metálicos en Diseño, Seminario Nacional de Gráfica Digital, Sesión de Morfología y Matemática, Ediciones Facultad de Arquitectura, Diseño y Urbanismo, Universidad de Buenos Aires 2 (1997), 173-179.
-
Marta Macho Stadler, Vera Martha Winitzky: uniendo matemáticas y diseño, Mujeres con ciencia, 28 agosto 2024
- J J O’Connor and E F Robertson, Vera Martha Winitzky de Spinadel, MacTutor History of Mathematics Archive, St Andrews University
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
El artículo Los números metálicos se ha escrito en Cuaderno de Cultura Científica.
Las matemáticas demuestran que Hawking se equivocaba sobre los agujeros negros más extremos
Durante décadas, los agujeros negros extremos se consideraron matemáticamente imposibles. Una nueva prueba revela lo contrario.
Un artículo de Steve Nadis. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Kristina Armitage/Quanta Magazine
Kristina Armitage/Quanta MagazinePara comprender el universo los científicos observan sus anomalías. “Siempre queremos saber de los casos extremos, los casos especiales que se encuentran en el límite”, afirma Carsten Gundlach, físico matemático de la Universidad de Southampton.
Los agujeros negros son los extremos enigmáticos del cosmos. En su interior, la materia está tan compactada que, según la teoría general de la relatividad de Einstein, nada puede escapar. Durante décadas físicos y matemáticos los han utilizado para comprobar los límites de sus ideas sobre la gravedad, el espacio y el tiempo.
Pero incluso los agujeros negros tienen casos extremos, y esos casos tienen sus propias ideas que ofrecer. Los agujeros negros rotan en el espacio. A medida que la materia cae en ellos, comienzan a girar más rápido; si esa materia tiene carga, también se cargan eléctricamente. En principio, un agujero negro puede llegar a un punto en el que tenga tanta carga o momento angular como sea posible, dada su masa. A un agujero negro de ese tipo se lo llama “extremo”, el extremo de los extremos.
Estos agujeros negros tienen algunas propiedades extrañas. En particular, la llamada gravedad superficial en la frontera, u horizonte de sucesos, de un agujero negro de este tipo es cero. “Es un agujero negro cuya superficie ya no atrae cosas”, explica Gundlach. Pero si se empujara ligeramente una partícula hacia el centro del agujero negro, no podría escapar.
En 1973, los destacados físicos Stephen Hawking, James Bardeen y Brandon Carter afirmaron que los agujeros negros extremos no pueden existir en el mundo real, que simplemente no hay ninguna forma plausible de que se formen. Sin embargo, durante los últimos 50 años, los agujeros negros extremos han servido como modelos útiles en la física teórica. “Tienen bonitas simetrías que facilitan el cálculo de las cosas”, dice Gaurav Khanna de la Universidad de Rhode Island, y esto permite a los físicos poner a prueba las teorías sobre la misteriosa relación entre la mecánica cuántica y la gravedad.
 En 1973, Stephen Hawking y otros dos físicos destacados plantearon la hipótesis de que los agujeros negros extremos nunca podrían formarse. Foto: Santi Visalli/Getty Images
En 1973, Stephen Hawking y otros dos físicos destacados plantearon la hipótesis de que los agujeros negros extremos nunca podrían formarse. Foto: Santi Visalli/Getty ImagesAhora, dos matemáticos han demostrado que Hawking y sus colegas estaban equivocados. El nuevo trabajo —contenido en un par de artículos recientes de Christoph Kehle, del Instituto Tecnológico de Massachusetts, y Ryan Unger, de la Universidad de Stanford y la Universidad de California en Berkeley— demuestra que no hay nada en nuestras leyes conocidas de la física que impida la formación de un agujero negro extremo.
Su prueba matemática es “hermosa, técnicamente innovadora y físicamente sorprendente”, comenta Mihalis Dafermos, matemático de la Universidad de Princeton (y director de las tesis doctorales de Kehle y Unger). Apunta a un universo potencialmente más rico y variado en el que “astrofísicamente podría haber agujeros negros extremos”, agrega.
Eso no significa que existan. “El hecho de que exista una solución matemática con buenas propiedades no significa necesariamente que la naturaleza vaya a hacer uso de ella”, explica Khanna. “Pero si de alguna manera encontramos uno, eso realmente nos haría pensar en lo que nos estamos perdiendo”. Un descubrimiento de ese tipo, señaló, tiene el potencial de plantear “algunos tipos de preguntas bastante radicales”.
La ley de la imposibilidadAntes de la prueba de Kehle y Unger había buenas razones para creer que los agujeros negros extremos no podían existir.
En 1973, Bardeen, Carter y Hawking introdujeron cuatro leyes sobre el comportamiento de los agujeros negros, que se parecían a las cuatro leyes de la termodinámica, establecidas desde hacía mucho tiempo: un conjunto de principios sacrosantos que establecen, por ejemplo, que el universo se vuelve más desordenado con el tiempo y que la energía no se puede crear ni destruir.
 Christoph Kehle, matemático del Instituto Tecnológico de Massachusetts, recientemente desmintió una conjetura de 1973 sobre los agujeros negros extremos. Foto: Dan Komoda/Institute for Advanced Study
Christoph Kehle, matemático del Instituto Tecnológico de Massachusetts, recientemente desmintió una conjetura de 1973 sobre los agujeros negros extremos. Foto: Dan Komoda/Institute for Advanced StudyEn su artículo, los físicos demostraron las tres primeras leyes de la termodinámica de los agujeros negros: la cero, la primera y la segunda. Por extensión, asumieron que la tercera ley (al igual que su contraparte en la termodinámica estándar) también sería cierta, aunque aún no pudiesen demostrarla.
Esa ley establecía que la gravedad superficial de un agujero negro no puede disminuir hasta cero en un tiempo finito; en otras palabras, que no hay forma de crear un agujero negro extremo. Para respaldar su afirmación, el trío argumentó que cualquier proceso que permitiera que la carga o el momento angular de un agujero negro alcanzaran el límite extremo también podría potencialmente provocar la desaparición total de su horizonte de sucesos. Se cree ampliamente que los agujeros negros sin horizonte de sucesos, llamados singularidades desnudas, no pueden existir. Además, como se sabe que la temperatura de un agujero negro es proporcional a su gravedad superficial, un agujero negro sin gravedad superficial tampoco tendría temperatura. Un agujero negro así no emitiría radiación térmica, algo que Hawking propondría más tarde que debían hacer los agujeros negros.
En 1986, un físico llamado Werner Israel pareció dejar la cuestión resuelta cuando publicó una prueba de la tercera ley. Supongamos que queremos crear un agujero negro extremo a partir de uno normal. Podemos intentar hacerlo haciéndolo girar más rápido o añadiendo más partículas cargadas. La prueba de Israel pareció demostrar que al hacerlo no se puede obligar a que la gravedad superficial de un agujero negro caiga a cero en un tiempo finito.
Como Kehle y Unger finalmente descubrirían, el argumento de Israel ocultaba un fallo.
La muerte de la tercera leyKehle y Unger no se habían propuesto encontrar agujeros negros extremos. Se toparon con ellos por pura casualidad.
Estaban estudiando la formación de agujeros negros cargados eléctricamente. “Nos dimos cuenta de que podíamos hacerlo” –crear un agujero negro– “para todas las relaciones carga-masa”, cuenta Kehle. Eso incluía el caso en que la carga es lo más alta posible, un sello distintivo de un agujero negro extremo.
 Después de demostrar que los agujeros negros extremos altamente cargados son matemáticamente posibles, Ryan Unger de la Universidad de Stanford ahora está tratando de demostrar que los agujeros negros de rotación rápida también lo son. Pero es un problema mucho más difícil. Foto: Dimitris Fetsios
Después de demostrar que los agujeros negros extremos altamente cargados son matemáticamente posibles, Ryan Unger de la Universidad de Stanford ahora está tratando de demostrar que los agujeros negros de rotación rápida también lo son. Pero es un problema mucho más difícil. Foto: Dimitris FetsiosDafermos reconoció que sus antiguos estudiantes habían descubierto un contraejemplo de la tercera ley de Bardeen, Carter y Hawking: habían demostrado que efectivamente podían transformar un agujero negro típico en uno extremo en un período finito de tiempo.
Kehle y Unger comenzaron con un agujero negro que no rota y no tiene carga, y modelaron lo que podría suceder si se lo colocara en un entorno simplificado llamado campo escalar, que supone un fondo de partículas cargadas uniformemente. Luego, golpearon el agujero negro con pulsos del campo para agregarle carga.
Estos pulsos también aportaban energía electromagnética al agujero negro, lo que aumentaba su masa. Al enviar pulsos difusos de baja frecuencia, los matemáticos se dieron cuenta de que podían aumentar la carga del agujero negro más rápido que su masa, precisamente lo que necesitaban para completar su prueba.
Después de discutir su resultado con Dafermos, estudiaron la prueba de Israel de 1986 e identificaron su error. También construyeron otras dos soluciones a las ecuaciones de la relatividad general de Einstein que implicaban diferentes formas de añadir carga a un agujero negro. Habiendo refutado la hipótesis de Bardeen, Carter y Hawking en tres contextos diferentes, el trabajo no debería dejar lugar a dudas, afirma Unger: “La tercera ley está muerta”.
Los dos científicos también demostraron que la formación de un agujero negro extremo no abriría la puerta a una singularidad desnuda, como temían los físicos. En cambio, los agujeros negros extremos parecen encontrarse en un umbral crítico: si se añade la cantidad adecuada de carga a una densa nube de materia cargada, colapsará para formar un agujero negro extremo. Si se añade más, en lugar de colapsar en una singularidad desnuda, la nube se dispersará. No se formará ningún agujero negro. Kehle y Unger están tan entusiasmados con este resultado como con su prueba de que pueden existir agujeros negros extremos.
“Este es un hermoso ejemplo de cómo las matemáticas devuelven algo a la física”, comenta Elena Giorgi, matemática de la Universidad de Columbia.
Lo imposible hecho visibleSi bien Kehle y Unger han demostrado que es teóricamente posible que existan agujeros negros extremos en la naturaleza, no hay garantía de que sea así.
Por un lado, los ejemplos teóricos poseen una carga máxima, pero nunca se han observado agujeros negros con una carga discernible. Es mucho más probable ver un agujero negro que gira rápidamente. Kehle y Unger quieren construir un ejemplo que alcance el umbral extremo de momento angular, en lugar del de carga.
Pero trabajar con el espín es mucho más complicado desde el punto de vista matemático. “Para ello se necesitan muchas matemáticas nuevas y nuevas ideas”, afirma Unger. Él y Kehle están empezando a investigar el problema.
Mientras tanto, una mejor comprensión de los agujeros negros extremos puede proporcionar más información sobre los agujeros negros casi extremos, que se cree que son abundantes en el universo. “Einstein no creía que los agujeros negros pudieran ser reales [porque] son demasiado extraños”, apunta Khanna. “Pero ahora sabemos que el universo está repleto de agujeros negros”.
Por razones similares, añade, “no deberíamos darnos por vencidos con los agujeros negros extremos. Simplemente no quiero poner límites a la creatividad de la naturaleza”.
El artículo original, Mathematicians Prove Hawking Wrong About the Most Extreme Black Holes, se publicó el 21 de agosto de 2023 en Quanta Magazine.
Traducido por César Tomé López
El artículo Las matemáticas demuestran que Hawking se equivocaba sobre los agujeros negros más extremos se ha escrito en Cuaderno de Cultura Científica.
Gusanos parásitos, agresivos… y sociales
Los seguidores de las series sobre tronos y dragones conocemos bien a unos personajes de esta saga llamados los Inmaculados, soldados castrados fieles a sus amos hasta la muerte. Quizá el más famoso de ellos sea su comandante, Gusano Gris. Menciono todo esto porque hoy vamos a hablar, precisamente, de gusanos soldados, estériles, y dispuestos a luchar hasta el final para defender a los suyos. Curiosa coincidencia…
La eusocialidad es la forma más compleja de organización entre los animales. Su máxima expresión se alcanza en los insectos himenópteros: abejas, avispas y hormigas. Sus sociedades constan de castas especializadas, reproductivas y no reproductivas, con cuidado colectivo de las crías y solapamiento de generaciones.
Otras formas de eusocialidad se han descrito en animales como las ratas topo (únicos mamíferos eusociales) y las gambas del género Synalpheus que viven dentro de esponjas. También existe un tipo de sociedades vinculadas al parasitismo y al fenómeno de la poliembrionía, es decir, la generación de múltiples descendientes a partir de un único cigoto.
Posiblemente, el ejemplo más espectacular nos lo proporcionan las avispas del género Copidosoma. Estas pequeñas avispas ponen un solo huevo sobre una oruga. El huevo comienza su desarrollo dentro de la oruga, pero el embrión resultante se fragmenta y da lugar a múltiples descendientes, hasta más de 3 000 en algún caso. Estos embriones originan dos tipos de larvas que devoran poco a poco a su hospedador. Las larvas que han adquirido células del linaje germinal1 forman la casta reproductora. Las que carecen de células germinales, y, por tanto, no podrían reproducirse, se convierten en larvas soldado, que luchan contra cualquier parásito que intente competir con sus hermanas. Cuando la infortunada oruga ha sido consumida completamente, las reproductoras se metamorfosean en avispas adultas y las larvas soldado mueren, una vez cumplida su función defensiva.
Hemos explicado en detalle esta formación de castas en los embriones de Copidosoma, porque acaba de publicarse un artículo en PNAS que extiende este concepto a animales muy alejados de los insectos, concretamente a gusanos platelmintos del grupo de los trematodos.
Los trematodos digeneos son gusanos parásitos con un complejo ciclo de vida (Figura 1). Una primera larva, llamada miracidio, infecta un molusco bivalvo o gasterópodo de agua dulce, y origina en su interior un esporocisto. El esporocisto da lugar a un gran número de individuos, las redias, que a su vez generan otro tipo de larvas, las cercarias, que son liberadas en el medio. Cuando las cercarias son consumidas por un vertebrado se convierten en el gusano adulto que vive a expensas de su hospedador. Estos parásitos pueden causar graves pérdidas en la ganadería y enfermedades en humanos, como la fascioliasis.
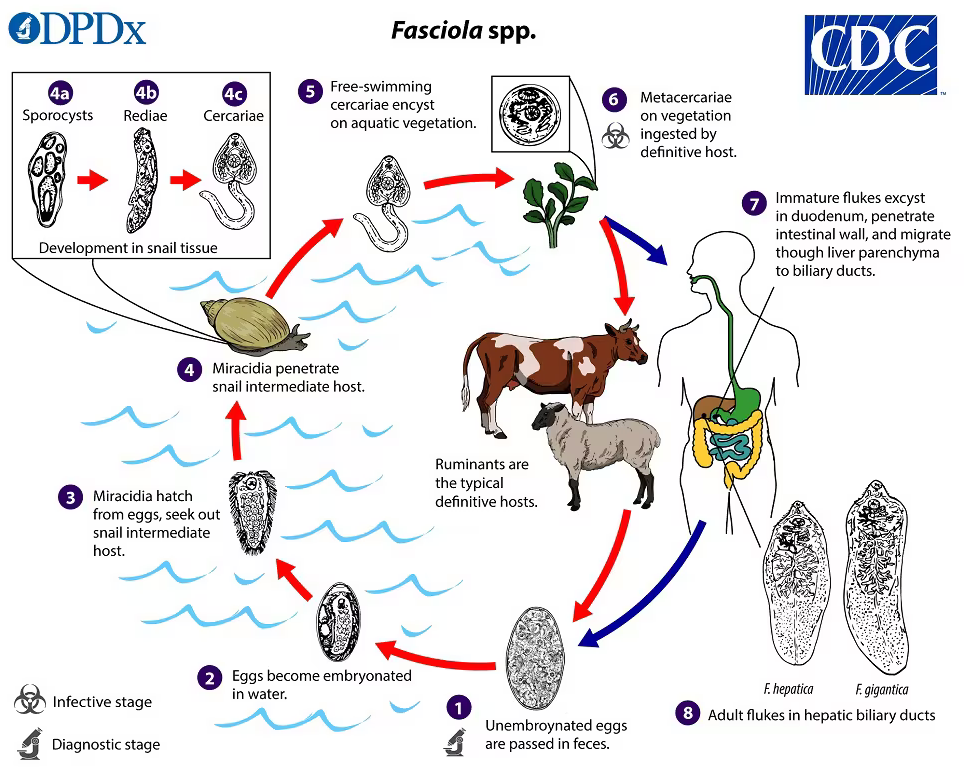 Figura 1. Ciclo biológico del trematodo Fasciola hepatica, causante de la fascioliasis. El ciclo es similar al de Haplorchis pumilio. La diferenciación en castas de Haplorchis se produce en la etapa 4b (redias). Imagen realizada por el Centers for Disease Control and Prevention, Atlanta (EEUU), dominio público
Figura 1. Ciclo biológico del trematodo Fasciola hepatica, causante de la fascioliasis. El ciclo es similar al de Haplorchis pumilio. La diferenciación en castas de Haplorchis se produce en la etapa 4b (redias). Imagen realizada por el Centers for Disease Control and Prevention, Atlanta (EEUU), dominio públicoEn 2010, investigadores del Instituto Scripps de Oceanografía y la Universidad de California descubrieron que las redias del trematodo Himasthla se presentaban en dos formas, una que realizaba normalmente su ciclo reproductivo y otra constituida por individuos más pequeños y activos. Propusieron que se trataba de dos castas con división de funciones, los reproductores y los soldados, encargados estos de atacar a otros parásitos competidores, igual que ocurría en Copidosoma.
Existían dudas acerca de si las redias soldado mantenían la capacidad reproductiva. Esto acaba de ser resuelto por un nuevo estudio del mismo grupo de investigación, publicado en la revista PNAS. En esta ocasión trabajaron con el trematodo Haplorchis pumilio, parásito ocasional de humanos. Este gusano es original del sudeste asiático, pero se ha ido extendiendo por todo el mundo, paralelamente a la rápida difusión de su hospedador intermedio, el caracol Melanoides tuberculata, muy popular en acuariofilia.
El nuevo estudio ha mostrado las claras diferencias en morfología y comportamiento entre las redias soldado y las reproductoras. Los soldados desarrollan una faringe cinco veces más grande que sus congéneres, lo que les permite atacar y matar a cualquier trematodo que compita por el espacio y los recursos, sin importarles la diferencia de tamaño (Figura 2). Los investigadores comprobaron que el caracol Melanoides puede ser infestado por al menos otras siete especies de trematodos, si bien la presencia de soldados de Haplorchis elimina hasta el 94% de estos intentos de infección. De hecho, los soldados se localizan estratégicamente en los tejidos del caracol donde es más probable sufrir una invasión. Eso sí, en experimentos in vitro, los soldados no atacaron a redias de su misma especie, incluso cuando procedían de otros caracoles.
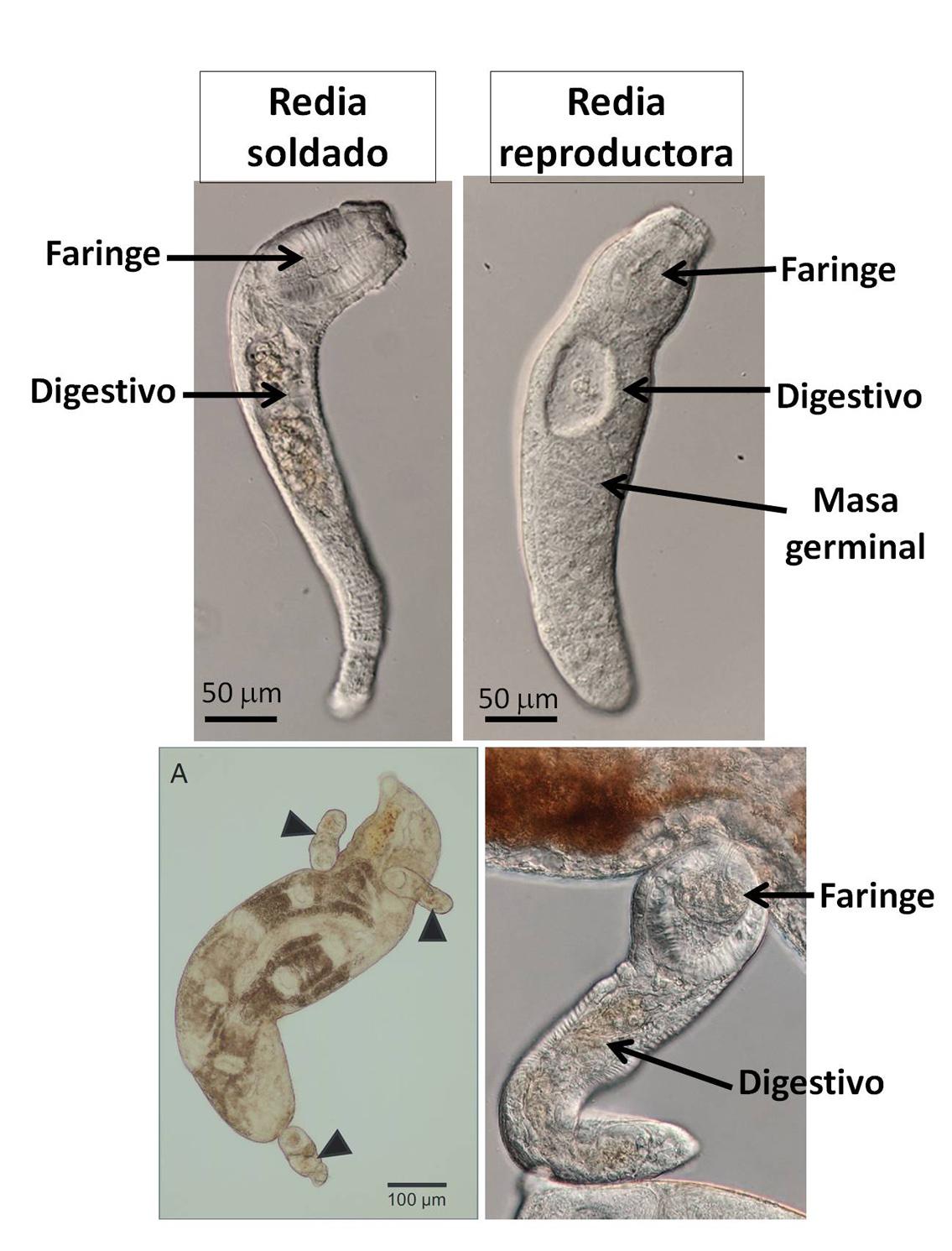 Figura 2. Arriba: Las redias soldado se caracterizan por una gran faringe, un amplio tubo digestivo y la ausencia de masa germinal. Abajo y a la izquierda: las puntas de flecha señalan a tres soldados de Haplorchis pumilio atacando a una redia reproductora del género Philophthalmus. A la derecha vemos como este soldado utiliza la faringe para romper el tegumento de su víctima y absorber sus tejidos. Modificado del artículo de Metz y Hechinger, referencia de PNAS citada abajo, con licencia CC BY 4.0
Figura 2. Arriba: Las redias soldado se caracterizan por una gran faringe, un amplio tubo digestivo y la ausencia de masa germinal. Abajo y a la izquierda: las puntas de flecha señalan a tres soldados de Haplorchis pumilio atacando a una redia reproductora del género Philophthalmus. A la derecha vemos como este soldado utiliza la faringe para romper el tegumento de su víctima y absorber sus tejidos. Modificado del artículo de Metz y Hechinger, referencia de PNAS citada abajo, con licencia CC BY 4.0La investigación mostró también que los soldados de Haplorchis carecen de células germinales capaces de producir descendientes. Por tanto, constituyen una casta obligatoriamente estéril cuya única función es desplegarse estratégicamente, combatir contra los invasores y garantizar la supervivencia de las redias reproductoras. Más o menos como los Inmaculados de Daenerys Targaryen.
En resumen, las dos castas de Haplorchis pumilio, ahora bien caracterizadas, constituyen un caso excepcional de eusocialidad en organismos diferentes a los artrópodos.
Referencias:
Hechinger, R.F., Wood, A.C., Kuris, A.M. (2011). Social organization in a flatworm: trematode parasites form soldier and reproductive castes. Proc Biol Sci. doi: 10.1098/rspb.2010.1753
Metz, D.C.G., Hechinger, R.F. (2024). The physical soldier caste of an invasive, human-infecting flatworm is morphologically extreme and obligately sterile. Proc Natl Acad Sci U S A. doi: 10.1073/pnas.2400953121
Nota:
1 En muchos animales es posible identificar desde las primeras etapas del desarrollo embrionario al conjunto de células germinales, que son las únicas capaces de dar lugar a óvulos y espermatozoides.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga
El artículo Gusanos parásitos, agresivos… y sociales se ha escrito en Cuaderno de Cultura Científica.
Empujoncitos sanitarios
 Imagen de wirestock en Freepik
Imagen de wirestock en FreepikEl 13 de mayo de 2021, Bill de Blasio, entonces alcalde de la ciudad de Nueva York, celebró una conferencia de prensa en línea en la que anunció un interesante acuerdo entre la ciudad y Shake Shack, una cadena local de restaurantes de hamburguesas . El objetivo era conseguir que los neoyorquinos se vacunaran contra la COVID-19: cada individuo vacunado recibiría un cupón para una hamburguesa o un sándwich gratis en cualquiera de los locales de la cadena local. En la ciencia del comportamiento, este tipo de incentivo se conoce como ‘nudge’.
El término fue popularizado por Richard H. Thaler (ganador del Premio Nobel de Ciencias Económicas en 2017) y Cass R. Sunstein en su exitoso libro de 2008 Nudge: Improving Decisions About Health, Wealth, and Happiness (Un empujón: cómo mejorar las decisiones sobre salud, riqueza y felicidad). En esencia, un ‘empujón’ implica cualquier manipulación del entorno de toma de decisiones que dirija el comportamiento de las personas en una dirección beneficiosa para ellas, pero sin restringir sus opciones ni limitar su libertad de elección de ninguna manera.
Un ejemplo bien conocido de cómo mejorar los hábitos de las personas de esta manera se puede encontrar en las cafeterías del personal de Google. En un esfuerzo por mejorar los hábitos alimentarios, se colocó agua embotellada a la altura de los ojos en sus máquinas expendedoras, mientras que los refrescos y otras opciones con alto contenido calórico se colocaron en una posición menos visible. Funcionó: esta sencilla medida aumentó el consumo de agua entre el personal en un 47 %.
Otra medida similar es la instalación de escaleras interactivas, con luces en cada escalón o que tocan notas de piano al pisarlas. La gente suele optar por utilizar estas escaleras incluso cuando están justo al lado de un ascensor.
Orientar las decisiones: un dilema éticoLos empujoncitos influyen en el comportamiento de las personas al pasar por alto o ignorar, en cierta medida, su autonomía. Thaler y Sunstein denominaron a este enfoque ‘paternalismo libertario’.
Pero ¿es legítimo interferir en las decisiones de las personas para mejorar su bienestar? Los defensores del paternalismo libertario creen que sí, en particular cuando puede prevenir o resolver problemas de salud pública, como la obesidad, las adicciones, el sedentarismo y el tratamiento insuficiente o excesivo.
Muchas campañas tienen como objetivo alentar a la gente a adoptar una dieta más sana: por ejemplo, los comedores escolares de Connecticut ofrecieron manzanas gratis a los estudiantes para fomentar el consumo de fruta. En Buenos Aires, Argentina, los restaurantes retiraron los saleros de las mesas para frenar el consumo de sal.
Estos ejemplos muestran que un ‘empujón’ no impone una decisión. Los trabajadores de Google todavía tienen libertad para elegir un refresco en lugar de agua, y la gente puede pasar de largo las escaleras musicales para tomar el ascensor.
Aquí es donde entra en juego el elemento ‘libertario’, ya que la libertad de elección debe permanecer intacta. Según Thaler y Sunstein, esto significa que:
- Ninguna opción puede ser prohibida.
- Los incentivos económicos no pueden utilizarse para socavar la libertad: una hamburguesa gratis está bien, pero un cheque de 100 euros, no.
- Todas las opciones deberían estar disponibles en las mismas condiciones: si la opción deseada es accesible y barata, las demás opciones también deberían serlo.
En el contexto de la atención sanitaria, los empujoncitos se pueden clasificar en dos categorías: ‘clínicos’ o de ‘salud pública’.
Los empujoncitos ‘clínicos’ ocurren en contextos clínicos y, específicamente, implican la forma en que se presenta la información sobre un tratamiento en particular para alentar al paciente a dar su consentimiento; un ejemplo sería mencionar la tasa de éxito de un procedimiento en lugar de su tasa de fracaso. Los empujoncitos clínicos siempre se realizan en beneficio del paciente.
Por otra parte, los estímulos de ‘salud pública’ incentivan acciones individuales para mejorar la salud individual, con el objetivo de mejorar la salud de la población en su conjunto. Esto puede incluir hacer que los comedores escolares públicos sirvan carne o pescado con ensalada como opción, con patatas fritas como opción si se solicita.
Ambas son medidas no coercitivas. Medidas más firmes, como el confinamiento de una población en sus casas para evitar la propagación de una enfermedad, son medidas de salud pública, pero van mucho más allá de un simple empujón. Lo mismo podría decirse de la hospitalización involuntaria de una persona que sufre ideación suicida: es una medida clínica, pero que no deja margen para la libertad de elección.
Es por tu propio bien y el de todos los demásLos argumentos en contra del paternalismo libertario consideran que la aplicación de estos pequeños empujoncitos en el contexto de la atención sanitaria pone en peligro el principio de autonomía. Es discutible si una crítica de este tipo tiene el mismo peso en el contexto de la salud pública, donde el principio bioético de autonomía suele quedar relegado a un segundo plano frente a principios más colectivos de justicia, equidad o utilidad.
En salud pública, los empujoncitos pueden actuar como una alternativa suave para guiar las decisiones de las personas, evitando así restricciones más drásticas de la libertad personal, como limitar la libre circulación.
La reciente pandemia ofrece algunos ejemplos de lo que podría considerarse un ‘empujón’: un claro ejemplo fueron los envases de desinfectante de manos que se encontraban en restaurantes, supermercados y prácticamente cualquier otro espacio público cerrado. Los recordatorios de las citas de vacunación o las campañas con puntos móviles de vacunación sin cita previa fueron otro ejemplo.
Muchas medidas más estrictas para evitar el contagio afectaron la libertad de las personas y no pueden considerarse estímulos de salud pública: mascarillas obligatorias, tanto en interiores como en exteriores, controles de temperatura al entrar en determinados locales, prohibición de entrada a personas con fiebre, pruebas de PCR para viajar al extranjero, etc.
Por eso los empujoncitos son una herramienta tan valiosa: permiten alcanzar objetivos de salud pública sin comprometer la libertad individual. Solo cuando fracasan tiene sentido recurrir a medidas más agresivas y restrictivas. Mientras un empujoncito pueda lograr sus objetivos, parece una forma razonable de evitar que se recorten las libertades.
Sobre los autores: Ramón Ortega Lozano, Profesor de Bioética, de Antropología de la salud y de Comunicación humana en el Centro Universitario San Rafael-Nebrija, Universidad Nebrija; Aníbal M. Astobiza, Investigador Posdoctoral, especializado en ciencias cognitivas y éticas aplicadas, Universidad del País Vasco / Euskal Herriko Unibertsitatea y David Rodríguez-Arias, Profesor de Bioética, Universidad de Granada
Una versión de este texto apareció originalmente en campusa.
El artículo Empujoncitos sanitarios se ha escrito en Cuaderno de Cultura Científica.
El positrón de Dirac y los cerebros robóticos de Asimov
Cuando, en febrero de 1928, Paul Dirac publicó su ecuación de ondas relativista para describir el comportamiento del electrón, abrió, sin advertirlo, un nuevo campo de la física… y un nuevo universo de ciencia ficción en la mente de un estudiante de química de la Universidad de Columbia.
La ecuación de Dirac no fue la primera de este tipo. Oskar Klein y Walter Gordon ya habían planteado una similar para partículas de spin 0 ―o campos escalares en el contexto de la teoría cuántica de campos―, pero no servía para partículas de spin 1/2 como el electrón. Esa fue la aportación de Dirac. Sin embargo, ambas ecuaciones adolecían de un problema que era difícil ignorar. Al igual que el tiempo, estas interpretaciones relativistas de la ecuación de Schrödinger implicaban que la energía también era relativa, y eso hacía que admitieran soluciones que con niveles de energía negativos para las partículas algo que, desde un punto de vista intuitivo, no tenía pies ni cabeza.
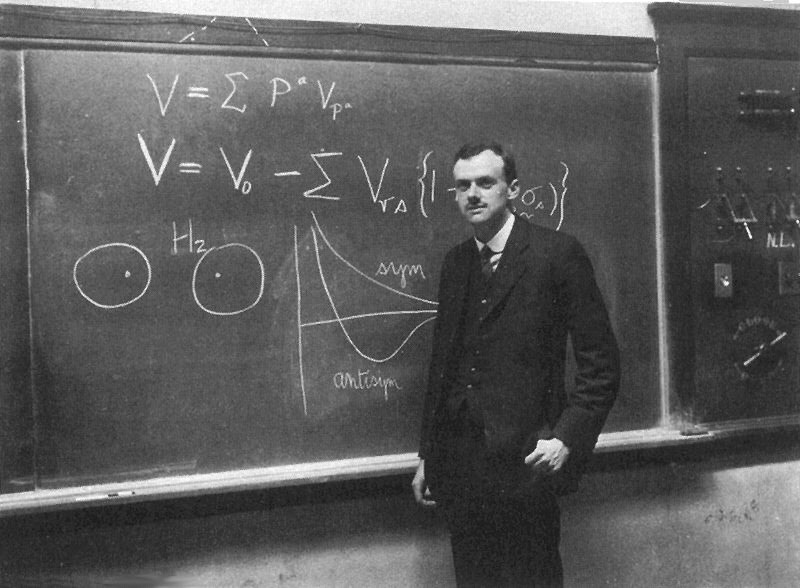 El físico Paul Dirac recibió, junto con Erwin Schrödinger, el Premio Nobel de Física en 1933 «por el descubrimiento de nuevas formas productivas de la teoría atómica».
El físico Paul Dirac recibió, junto con Erwin Schrödinger, el Premio Nobel de Física en 1933 «por el descubrimiento de nuevas formas productivas de la teoría atómica».
Dirac trató de darle sentido a aquellos valores de la energía que aparecían en su ecuación en 1930, planteando que tal vez el vacío no estaba tan vacío, sino que consistía en un mar infinito poblado de esos electrones con energía negativa. En ocasiones, uno de esos electrones pasaba a tener energía positiva, convirtiéndose, en este caso, en un electrón «normal», y dejando en aquel mar un hueco que se podía interpretar como una partícula de carga opuesta. La única partícula con carga opuesta al electrón que se conocía en aquel momento era el protón ―pese a la gran diferencia de masa entre ambos―, así que Dirac planteó que debía de existir algún tipo de correspondencia entre el hueco que dejaba un electrón de energía negativa y un protón. Lo que no pudo explicar es cómo podrían producirse las transiciones de unas partículas a otras sin violar ningún principio de conservación. Tenía la respuesta delante de sus narices, pero en aquel momento era demasiado exótica para tenerla en consideración.
 Foto: Herbert Goetsch / Unsplash
Foto: Herbert Goetsch / Unsplash
Tras leer el artículo en Dirac, Robert Oppenheimer entró en escena. Si alguna cualidad tenía Oppie, como solía llamarlo su círculo más cercano, era la capacidad de detectar, dentro de una teoría, dónde se encontraba la puerta que había que abrir para dar el siguiente paso. Si no alcanzó más logros dentro del mundo de la física, es porque ese siguiente paso rara vez lo daba él, dejaba que lo hicieran otros. En el mes de marzo de aquel mismo año, en una carta al editor de Physical Rewiev, Oppenheimer descartaba matemáticamente la posibilidad de que los huecos que quedaban en el mar de Dirac cuando un electrón pasaba a tener energía positiva fueran protones: fueran la partícula que fueran, debía de ser una con la misma masa del electrón. Hermann Weyl y Wolfang Pauli eran de la misma opinión.
Paul Dirac empezó a plantearse entonces que el surtido de partículas fundamentales tal vez fuera mucho más variado que las dos que se conocían en aquel momento: el electrón y el protón ―el neutrón no lo descubriría James Chadwick hasta febrero de 1932.
Un agujero, si existiera, sería un nuevo tipo de partícula, desconocida para la física experimental, que tendría la misma masa y carga opuesta a la de un electrón. A esta partícula podemos llamarla antielectrón. No deberíamos esperar encontrar ninguno de ellos en la naturaleza debido a su rápida tasa de recombinación con los electrones, pero si pudieran producirse experimentalmente en alto vacío serían lo bastante estables y susceptibles de observación.
La sorpresa llegó algunos meses después del descubrimiento del neutrón, en septiembre, cuando Carl David Anderson, estudiando los rayos cósmicos en el CalTech bajo la supervisión de Robert Millikan, observó una peculiaridad en la trayectoria de cierto tipo de partículas que atravesaban la cámara de niebla que utilizaba para detectarlas: era igual que la de los electrones, pero giraba en sentido contrario, lo que quería decir que tenía la misma masa, pero carga opuesta. Pese a que publicó sus resultados en una breve nota en la revista Science, el mundo no se hizo eco del descubrimiento hasta febrero del año siguiente, cuando el físico Patrick Blackett mostró, en una reunión de la Royal Society, las primeras fotografías del descubrimiento ―otorgándole todo el crédito a Anderson―. «The positive electron» se publicó en Physical Review en el mes de marzo y la única teoría que explicaba aquellas observaciones era la del antielectrón de Dirac.
 Primera imagen de un positrón atravesando una cámara de niebla, tomada por Carl D. Anderson en agosto de 1932.
Primera imagen de un positrón atravesando una cámara de niebla, tomada por Carl D. Anderson en agosto de 1932.Créditos: Dominio público/Carl D. Anderson
Al año siguiente, en 1934, los positrones empezaron a estar por todas partes, a detectarse en numerosos laboratorios a lo largo y ancho del mundo, y, lo que era más incontestable: a crearlos en el laboratorio.
Aquello sucedió por la misma época en la que un adolescente de Brooklyn, amante de la ciencia y de las historias de ciencia ficción que leía en las revistas del quiosco de su padre empezaba a pensar en su futuro. El nombre de aquel adolescente era Isaac Asimov.
Aunque Asimov empezó a escribir sus primeras historias en 1931, con once años, no imaginó el primer robot positrónico hasta 1939, el mismo año en que se graduó en química, y la elección de ese nombre, como se puede imaginar, aunque no fue todo lo científico que podría haber sido, tampoco fue casual:
Desde que comencé a escribir mis historias de robots en 1939, no mencioné nada sobre informática en relación a ellas. La computadora electrónica no se había inventado y yo no lo preví. Sin embargo, sí preví que el cerebro tenía que ser electrónico de algún modo. No obstante, lo «electrónico» no parecía lo suficientemente futurista. El positrón ―una partícula subatómica exactamente igual que el electrón pero con carga eléctrica opuesta― se había descubierto solo cuatro años antes de que escribiera mi primera historia sobre robots. Sonaba muy a ciencia ficción, así que les di a esos robots «cerebros positrónicos» e imaginé que que sus pensamientos consistían en corrientes intermitentes de positrones que aparecían y desaparecían casi de inmediato.
 La primera historia de robots positrónicos de Isaac Asimov, escrita en 1939, apareció bajo el título de «Strange playfellow» en el número de septiembre de 1940 de Super Science Stories. El título con el que se publicó en sucesivas reediciones, y por el que mejor se la conoce, es «Robbie».
La primera historia de robots positrónicos de Isaac Asimov, escrita en 1939, apareció bajo el título de «Strange playfellow» en el número de septiembre de 1940 de Super Science Stories. El título con el que se publicó en sucesivas reediciones, y por el que mejor se la conoce, es «Robbie».Unas veces el sentido de la maravilla de la ciencia ficción inspira a la ciencia; otras, es el sentido de la maravilla de la ciencia el que inspira a la ciencia ficción.
Bibliografía
Anderson, C. D. (1932). The apparent existence of easily deflectable positives. Science, 76(1957), 238-239. https://doi.org/10.1126/science.76.1967.238
Anderson C. D. (1933). The positive electron. Physical Review, 43(6), 491-494. https://doi.org/10.1103/PhysRev.43.491
Asimov, I. (1987). My robots. En Michael P. Kube-McDowell, Isaac Asimov’s Robot City: Odyssey. Ace books.
Bird, K. Y Sherwin, M. J. (2005). American Prometeus. The triumph and tragedy of J. Robert Oppenheimer. Atlantic Books.
Chadwick, J. (1932). Possible existence of a neutron. Nature, 129(3252), 312-312. https://doi.org/10.1038/129312a0
Dirac, P. A. M. (1928). The quantum theory of the electron. Proceedings of the Royal Society of London, 117(778), 610-624. https://www.jstor.org/stable/94981
Dirac, P. A. M. (1930). A theory of electrons and protons. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 126(801), 360-365. https://doi.org/10.1098/rspa.1930.0013
Farmelo, G. (2009). The strangest man. The hidden life of Paul Dirac, quantum genius. Faber and faber.
Oppenheimer, J. R. (1930). On the theory of electrons and protons. Physical Review, 35(5), 562-563. https://doi.org/10.1103/PhysRev.35.562
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo El positrón de Dirac y los cerebros robóticos de Asimov se ha escrito en Cuaderno de Cultura Científica.
El estudiante de matemáticas en la casa del juez
Hace unas pocas semanas me compré, y ha sido una de mis lecturas estivales, el libro El invitado de Drácula y otros relatos, una colección de relatos de terror del escritor irlandés Bram Stoker (1847-1912), conocido por ser el autor de uno de los clásicos de la literatura de terror, Drácula (1897). El libro ha sido publicado recientemente por la editorial ALMA, dentro de su colección Clásicos Ilustrados. La ilustración del mismo es del ilustrador e historietista vallisoletano Enrique Corominas (1969), y la traducción del escritor y traductor asturiano Jon Bilbao (1972). Uno de los relatos de El invitado de Drácula y otros relatos, titulado La casa del juez, está protagonizado por un estudiante de matemáticas, por lo que vamos a dedicar esta entrada del Cuaderno de Cultura Científica al mismo.
 Portada de la edición de la editorial ALMA, dentro de su colección Clásicos Iustrados, del libro El invitado de Drácula y otros relatos, del escritor irlandés Bram StokerBram Stoker, escritor … y matemático
Portada de la edición de la editorial ALMA, dentro de su colección Clásicos Iustrados, del libro El invitado de Drácula y otros relatos, del escritor irlandés Bram StokerBram Stoker, escritor … y matemático
Sin lugar a dudas, la novela Drácula (1897) es uno de los grandes clásicos de la literatura de terror, que ha motivado que su autor, el escritor Bram Stoker, haya sido incluido en la historia universal de la literatura. El escritor Bram Stoker, como recordábamos en la entrada Personas famosas que estudiaron matemáticas: literatura y cine , estuvo relacionado con las matemáticas.
El 8 de noviembre de 1847 nació Bram Stoker en Dublín (Irlanda). Los primeros siete años de su vida los pasó en la cama a causa de una enfermedad desconocida, hasta que se recuperó completamente. Según podemos leer en la contraportada de El invitado de Drácula y otros relatos, “su único entretenimiento eran las oscuras leyendas irlandesas que su madre le contaba”. Es muy posible que estas historias de misterio y fantasmas que le narraba su madre en su niñez fueran determinantes en el hecho de que Bram Stoker se convirtiera en un escritor de historias de terror, y seguramente algunos de sus relatos estarán basados en esas historias que le escuchaba a su madre.
 Fotografía de Bram Stoker, de alrededor de 1906
Fotografía de Bram Stoker, de alrededor de 1906
Bram Stoker se graduó en matemáticas en el Trinity College de Dublín en 1870 y, aunque parece ser que no era verdad, él empezó a decir con el tiempo que se “graduó con honores en matemáticas”. Sin embargo, cediendo a los deseos paternos, Bram Stoker siguió la carrera de funcionario público en el Castillo de Dublín, entre 1870 y 1878. Aunque conseguiría su Master of Arts (posgrado) en 1875. En 1878 empezaría a trabajar como asistente del actor Sir Henry Irving, de quien escribiría además una biografía en dos volúmenes titulada Personal Reminiscences of Henry Irving / Recuerdos personales de Henry Irving (1906), y también como gerente del Lyceum Theatre, que pertenecía al mencionado actor.
Bram Stoker publicó su famosísima novela epistolar Drácula en 1897, pero también publicó otras novelas, doce en total, y relatos, entre ellos los relatos de la publicación que nos ocupa, El invitado de Drácula y otros relatos, además de poesía, críticas de teatro, así como otros artículos y libros, que pueden verse en la página web dedicada a Bram Stoker.
 Cartel de la película Drácula, de Bram Stoker (1992), del director estadounidense Francis Ford Coppola e interpretada por los actores Gary Oldman, Winona Ryder, Keanu Reeves y Anthony Hopkins
Cartel de la película Drácula, de Bram Stoker (1992), del director estadounidense Francis Ford Coppola e interpretada por los actores Gary Oldman, Winona Ryder, Keanu Reeves y Anthony HopkinsA pesar de su formación matemática, Bram Stoker nunca trabajaría como matemático, aunque sí podemos encontrar, al menos, un par de publicaciones relacionadas con las matemáticas. Por una parte, un cuento infantil titulado Cómo el número 7 se volvió loco (que publicó la editorial Nivola en 2010 y la editorial Gadir en 2013), que fue originalmente publicado por Bram Stoker en 1881 dentro del libro Under the Sunset / Bajo el ocaso, una recopilación de ocho cuentos infantiles.
 Portada del libro Cómo el número 7 se volvió loco, de Bram Stoker, publicado por la editorial Gadir en 2013, con ilustraciones de Eugenia Ábalos
Portada del libro Cómo el número 7 se volvió loco, de Bram Stoker, publicado por la editorial Gadir en 2013, con ilustraciones de Eugenia ÁbalosAquí os dejo un pequeño fragmento del cuento Cómo se volvió loco el número 7 extraído de la edición de la editorial Nivola.
– [Número 7] Mañana, tarde y noche soy tratado peor que un esclavo. No existe nadie en todo el ámbito del aprendizaje que tenga que aguantar lo que yo aguanto. Siempre trabajo duro. Nunca me quejo. A menudo hago de múltiplo, a veces de multiplicando. Estoy dispuesto a soportar la parte que me toca por ser un resultado, pero no soporto el trato que me dan. Se me suma mal, se me divide mal, se me resta mal y se me multiplica mal. Los demás números no reciben el trato que yo, y además no son huérfanos como yo.
– [Médico] ¿Cómo que huérfanos? –preguntó el médico–. ¿Qué quiere decir?
– Quiero decir que los demás números tienen muchos parientes. Si exceptuamos al viejo 1, que no cuenta demasiado (además, sólo soy su tataratataratataranieto), no tengo ni amigos, ni familiares.
– ¿Qué quiere decir? –preguntó el médico.
– Pues que ese tipo viejo lleva ahí toda la vida y tiene todos sus descendientes a su alrededor, pero yo estoy seis generaciones detrás.
– ¡Anda ya! –dijo el médico.
– El número 2 –continuó el 7– nunca se mete en problemas, y el 4, el 6 y el 8 son sus primos. El número 3 es íntimo del 6 y del 9. El número 5 es la mitad de una decena y nunca se complica la vida. Pero en cuanto a mí, soy un desgraciado, me maltratan y estoy solo.
Y el pobre número 7 empezó a llorar. Con la cabeza gacha, sollozaba amargamente.
 Portada del libro Cómo se volvió loco el número 7, de Bram Stoker, publicado por la editorial Nivola en 2011, con ilustraciones de Carlos Pinto
Portada del libro Cómo se volvió loco el número 7, de Bram Stoker, publicado por la editorial Nivola en 2011, con ilustraciones de Carlos PintoLa otra publicación directamente relacionada con las matemáticas es el relato La casa del juez, protagonizado por un estudiante de matemáticas, que está incluido en el mencionado libro El invitado de Drácula y otros relatos, y del que hablaremos en esta entrada.
La casa del juezEl relato corto La casa del juez, de Bram Stoker, fue publicado por primera vez el 5 de diciembre de 1891 en el número especial de navidad (Holly Leaves) de la revista semanal británica The Illustrated Sporting and Dramatic News (fundada en 1874). Mientras que la primera vez que aparece publicada en un libro es en la recopilación de relatos cortos Dracula’s Guest And Other Weird Stories / El invitado de Drácula y otros relatos extraños, publicada en 1914.
 Portada de la publicación Holly Leaves the Christmas Number de The Illustrated Sporting and Dramatic News (Londres, diciembre, 1891)
Portada de la publicación Holly Leaves the Christmas Number de The Illustrated Sporting and Dramatic News (Londres, diciembre, 1891)El relato corto La casa del juez empieza con el siguiente párrafo (que hemos recogido de la traducción de Jon Bilbao para el libro El invitado de Drácula y otros relatos, de la editorial ALMA).
Cuando se acercó el momento de sus exámenes, Malcolm Malcolmson decidió irse a algún sitio donde pudiera estar a solas para estudiar. Temía las distracciones de la costa, y temía asimismo el completo aislamiento del campo, cuyos atractivos conocía desde hace mucho, así que decidió buscar algún modesto pueblecito donde nada lo distrajera. Se abstuvo de pedir sugerencias a sus amigos, pues supuso que cada uno le recomendaría un lugar familiar para él y donde tuviera conocidos. Como Malcolmson pretendía evitar a sus amigos, tampoco deseaba cargar con las atenciones de los amigos de sus amigos, por lo que se ocupó de dar él mismo con el sitio. Llenó el baúl de viaje con ropa y los libros que necesitaba y sacó un billete para el primer destino de la lista de salidas que le fuera desconocido.
Como podemos leer, el protagonista es un estudiante que busca un lugar tranquilo para estudiar. Más adelante, en el relato, podremos leer que es estudiante de matemáticas. En concreto, en esta traducción leemos que el estudiante se describe como “un hombre que estudia matemáticas en la Universidad de Cambridge”. Aunque la traducción de la anterior descripción del estudiante es, en mi opinión, muy acertada para facilitar la comprensión del cuento, no se corresponde con la expresión que aparece en el relato original, en la que podemos leer (en inglés) “un hombre que está estudiando para el tripos matemático”.
Un examen de matemáticasEl tripos matemático (Mathematical Tripos en inglés) era un examen de matemáticas de la Universidad de Cambridge, por lo que parece que tanto la expresión del relato original, como esta traducción al castellano, serían prácticamente lo mismo. Sin embargo, como hemos explicado en la anterior entrada El tripos matemático, el examen más duro que jamás existió, el tripos matemático era mucho más. Este hecho no es imprescindible para la lectura del relato, pero ofrece un cierto significado extra al mismo.
El tripos matemático era el eje central del sistema educativo de la Universidad de Cambridge, un examen para obtener el título de grado (de cualquier grado) que tenía lugar después de los 10 trimestres oficiales del mismo. Se consideraba que las matemáticas eran un conocimiento básico importante para los jóvenes estudiantes, puesto que su estudio fortalecía y desarrollaba las facultades de la mente y los preparaba para su posterior desarrollo intelectual. Por lo tanto, nuestro estudiante Malcolm Malcolmson podría ser uno más de esos estudiantes de Cambridge que se enfrentaban a esta durísima prueba, no necesariamente un estudiante de matemáticas. Aunque, como decía, la traducción “un hombre que estudia matemáticas en la Universidad de Cambridge” me parece muy acertada.
Hasta 1909 se publicaron las listas de honor del tripos matemático por orden de mérito en tres clases, wranglers, senior optimes y junior optimes, el resto obtenían un grado ordinario. Además, el primer puesto, senior wrangler, era reconocido como un gran logro intelectual en todo Gran Bretaña y abría muchas puertas para una carrera exitosa.
 Hoja con problemas del tripos matemático de 1842
Hoja con problemas del tripos matemático de 1842
Era un examen muy difícil. El científico Francis Galton (1822-1911), en su libro Genio hereditario (1869), menciona que un año de la década de 1860 de los 17.000 puntos en juego en el examen, el senior wrangler obtuvo 7.634 (un 4,49 sobre 10), el segundo wrangler 4.123 (un 2,43 sobre 10). Y estas eran las dos mejores notas, luego estaban el resto de wranglers, después los senior optimes, a los que seguían los junior optimes y finalmente los estudiantes con un grado ordinario.
Para afrontar este examen era necesario un duro entrenamiento, memorizando teoremas, estudiando técnicas de resolución de problemas y trabajando los de cursos anteriores. Los estudiantes contrataban a “entrenadores” privados, no a profesores de la universidad, y dedicaban todo su tiempo a prepararse, por lo que no asistían a las clases regulares. Era un examen tan duro que muchos estudiantes sufrían crisis nerviosas.
Luego es comprensible que Malcolmson decidiera buscar un lugar aislado donde poder estudiar tan duro examen sin ninguna distracción, sobre todo si se estaba preparando la tercera parte del examen a la que solo accedían los wranglers de la lista de honor del tripos matemático, lista confeccionada a partir de los dos primeros exámenes, como puede leerse en la entrada El tripos matemático, el examen más duro que jamás existió.
Los matemáticos no creen en fantasmasTras llegar al lugar elegido, el joven estudiante busca una casa para alquilar en la que alojarse durante el tiempo que necesita para centrarse en sus estudios y le ofrecen “la casa del juez”. Desde el primer momento las personas del lugar le aconsejan que no se hospede en esa casa encantada y tétrica. En particular, la patrona de la posada en la que se ha alojado inicialmente, la señora Withman, que trata de disuadirlo de alojarse en ella, e incluso le dice que “si fuera mi hijo no dormiría allí ni una noche”.
Al joven Malcolmson le parece divertida la advertencia de la patrona de la posada y le contesta lo siguiente.
– Pero, mi querida señora Withman, no hay razón para que se preocupe usted por mí. Un hombre que estudia Matemáticas en la Universidad de Cambridge tiene demasiado en lo que pensar como para que lo moleste cualquier “algo” misterioso, y su trabajo es de una índole demasiado exacta y prosaica como para dejar espacio en su cabeza para misterios de cualquier clase. ¡La progresión armónica, las permutaciones, las combinaciones y las funciones elípticas ya entrañan misterios suficientes para mí!
En dicha respuesta, Bram Stoker ya nos deja algunos términos matemáticos, como “progresión aritmética”, “permutaciones”, “combinaciones” o “funciones elípticas”, además de que “estudia para el tripos matemático” (en la traducción “que estudia Matemáticas en la Universidad de Cambridge”), para que el lector, o lectora, relacione claramente al estudiante con las matemáticas.
 Primera página del cómic basado en el relato La casa del juez, de Bram Stoker, publicado en el número 5 de la revista Creepy, una revista de cómic de terror.
Primera página del cómic basado en el relato La casa del juez, de Bram Stoker, publicado en el número 5 de la revista Creepy, una revista de cómic de terror.Es muy posible que Bram Stoker eligiera que el protagonista de esta historia fuese estudiante de matemáticas por dos motivos. El primero es que, como matemático, como científico, el protagonista piensa que su mente racional está por encima de las supersticiones de las gentes de ese lugar sobre la casa encantada del juez. De forma que, por ello, el joven estudiante de matemáticas es descrito en el relato como una persona arrogante. Lo cual enlaza con el segundo motivo, las matemáticas no tenían buena prensa, como ha ocurrido durante mucho tiempo, por lo cual, el protagonista se mostraba además antipático para quien leyese el relato, como alguien que se merece lo que le pasa por no hacer caso de las advertencias de las buenas gentes de la zona.
 Terrorífica ilustración de Enrique Corominas para el relato La casa del juez, dentro del libro El invitado de Drácula y otros relatos, de Bram Stoker, publicado por la Editorial ALMA. Imagen de la página de Facebook de la editorial ALMA
Terrorífica ilustración de Enrique Corominas para el relato La casa del juez, dentro del libro El invitado de Drácula y otros relatos, de Bram Stoker, publicado por la Editorial ALMA. Imagen de la página de Facebook de la editorial ALMACuando el protagonista está realizando la mudanza para instalarse en la casa alquilada, la casa encantada del juez, la señora Dempster, contratada por el estudiante para arreglar la casa, le ofrece al joven una explicación racional de los “duendes” de la casa, aunque ella no querría pasar una noche en la misma. En concreto dice lo siguiente.
Le diré lo que sucede, señor. Los duendes son toda clase de cosas, ¡menos duendes! Ratas y ratones, e insectos, y puertas que chirrían, y tejas sueltas, y ventanas rotas, y cajones arrancados, que se quedan abiertos y caen al suelo en mitad de la noche. Fíjese en el empanelado de las paredes. Es viejo. Tiene siglos. ¿Cree usted que ahí atrás no habrá ratas e insectos? ¿Cree usted, señor, que no va a verlos? Las ratas son duendes, se lo aseguro, y los duendes son ratas. ¡Que no se le meta nada más en la cabeza!
A lo que el joven contesta a la señora Dempster, “¡sabe usted más que el mejor graduado en Matemáticas de Cambridge!”. Si entendemos que el mejor graduado de Matemáticas de Cambridge, se refiere al estudiante que saca la mejor nota en el tripos matemático, entonces se estaría refiriendo al senior wrangler, como así se expresa en la versión original del cuento.
Libros de matemáticasLa intención de esta entrada del Cuaderno de Cultura Científica no es hacer un spoiler, luego no contaremos mucho más del argumento, aunque podemos decir que es un clásico del terror. Sí diremos que la señora Dempster introduce el elemento clave, las ratas, que como ella misma dice “las ratas son los duendes y los duendes son las ratas”.
La cuestión es que el joven estudiante se instala y empieza a estudiar para el examen, mientras van aconteciendo los sucesos de terror del propio relato, relacionados con las ratas, con una grande especialmente, pero centrémonos en las matemáticas que aún aparecen en el cuento.
Por ejemplo, en cierto momento, Bram Stoker escribe
Dio [Malcolmson] con un sendero tranquilo que discurría entre altos olmos, a las afueras del pueblo, y pasó allí la mayor parte del día, estudiando a Laplace.
Se refiere al matemático, físico, astrónomo y filósofo francés Pierre-Simon Laplace (1749-1827), autor de los cinco volúmenes de la obra Traité de mécanique céleste / Tratado de Mecánica Celeste (publicados entre 1799 y 1852), o Exposition du système du monde / Exposición sobre el sistema del mundo (publicado en 1824). Los temas tratados en los mismos formaban parte del temario del tripos matemático.
Más adelante, cuando descubre una rata enorme sentada en una “gran silla tallada de roble colocada a la derecha del fuego”, le lanza “un libro de logaritmos”. Y otra noche le lanza a esa misma rata enorme otra serie de libros que tenía a mano. En concreto, se citan los siguientes.
“Secciones cónicas” no dio en el blanco, tampoco “Oscilaciones cicloidales”, ni los “Principios”, ni “Cuaterniones”, ni “Termodinámica”.
Todos ellos libros que cubrían algunos de los temas que entraban en los tres exámenes del tripos matemático, como puede leerse en la entrada El tripos matemático, el examen más duro que jamás existió. En particular, uno de ellos un texto muy importante para la ciencia, como es los Principia / Principios (Philosophiæ naturalis principia mathematica / Principios matemáticos de la filosofía natural) del gran científico británico Isaac Newton (1643-1727).
 Caricatura, realizada por Gerardo Basabe de Viñaspre, del matemático inglés Sir Isaac Newton (1642-1727), a quien se le atribuye la autoría del anterior juego de ingenio, perteneciente a la exposición El rostro humano de las matemáticas, de la Real Sociedad Matemática Española
Caricatura, realizada por Gerardo Basabe de Viñaspre, del matemático inglés Sir Isaac Newton (1642-1727), a quien se le atribuye la autoría del anterior juego de ingenio, perteneciente a la exposición El rostro humano de las matemáticas, de la Real Sociedad Matemática EspañolaNo hay ninguna referencia directa más a las matemáticas, salvo que se pasa muchas horas estudiando, incluso noches enteras, y mucho tiempo resolviendo problemas (de matemáticas). La siguiente cita nos muestra un ejemplo.
Resolvió de manera satisfactoria todos los problemas que hasta entonces se le habían resistido, así que cuando pasó a hacer una visita a la señora Withman en el The Good Traveller, se sentía jubiloso.
Una vuelta de tuercaEspero que disfrutéis de la lectura de este relato de terror, por lo que no voy a hacer ningún spoiler, salvo comentar que la cosa, como ya se puede imaginar desde el principio del mismo, no termina bien para nuestro estudiante de matemáticas. Sobre este final, tenemos la interpretación directa de su lectura, la típica interpretación de los relatos de terror sobre casas encantadas, fantasmas, espíritus y demás elementos de la literatura de terror. Sin embargo, podemos ofrecer una explicación racional para lo acontecido en este relato si pensamos que este estudiante está preparando el durísimo examen de la Universidad de Cambridge, el tripos matemático.
Como comentábamos más arriba, el tripos matemático era un examen tan duro que muchos estudiantes sufrían crisis nerviosas. De hecho, en la entrada El tripos matemático, el examen más duro que jamás existió, comentábamos lo siguiente:
Galton sufrió una crisis nerviosa y acabó con un grado ordinario. El erudito estadounidense Charles A. Bristed (1820-1874) sufrió un colapso físico, quedando en los últimos lugares de la lista de junior optimes. El político y economista Henry Fawcett (1833-1884), favorito para senior wrangler, acabó siendo séptimo wrangler tras sufrir trastornos nerviosos e insomnio. El senior wrangler de 1859, James Wilson (1836-1931), sufrió una crisis nerviosa tras los exámenes y al recuperarse había olvidado todas las matemáticas estudiadas. O el también senior wrangler James Savage fue encontrado muerto en una zanja tres meses después del examen, el motivo de la muerte fue un derrame cerebral, posiblemente producido por el enorme esfuerzo realizado. Estos son solo algunos casos de la historia negra de este sistema.
En consecuencia, podríamos interpretar que el protagonista de este relato, Malcolm Malcolmson, estudiante de la Universidad de Cambridge que estaba preparando el tripos matemático, sufrió un colapso nervioso y todo lo que ocurrió en la casa del juez no fue más que producto de su enferma imaginación, a partir de la historia que los habitantes del lugar le habían contado sobre la casa del juez.
 Segunda página del cómic basado en el relato La casa del juez, de Bram Stoker, publicado en el número 5 de la revista Creepy, una revista de cómic de terror. En la misma se cuenta la historia del juez que vivió en dicha casa
Segunda página del cómic basado en el relato La casa del juez, de Bram Stoker, publicado en el número 5 de la revista Creepy, una revista de cómic de terror. En la misma se cuenta la historia del juez que vivió en dicha casa¡Que disfrutéis de la lectura de este relato de terror!
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El estudiante de matemáticas en la casa del juez se ha escrito en Cuaderno de Cultura Científica.
Un brote de rayos gamma restringe las posibles violaciones a la relatividad general
Un análisis del brote de rayos gamma más brillante jamás observado no revela diferencias en la velocidad de propagación de las distintas frecuencias de la luz, lo que impone algunas de las restricciones más estrictas a ciertas violaciones de la relatividad general.
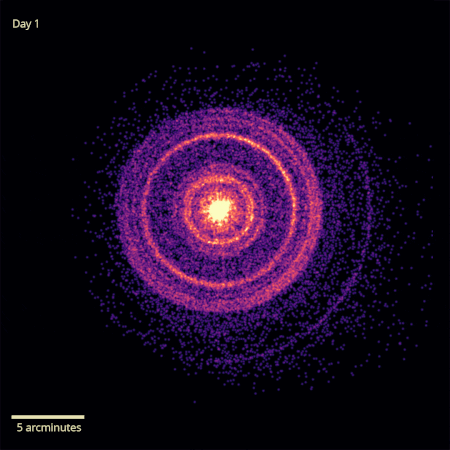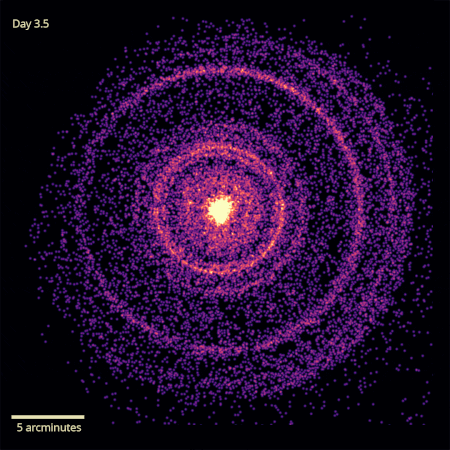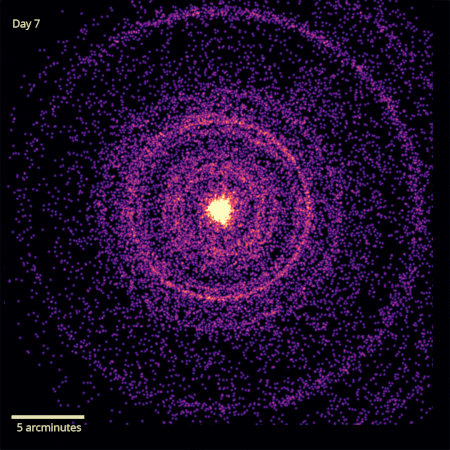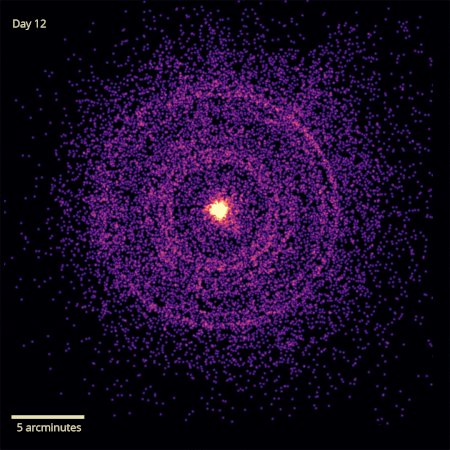 Composición de 12 días de observaciones del brote de rayos gamma GRB 221009A realizadas por el telescopio de rayos X a bordo del observatorio espacial Neil Gehrels Swift de la NASA. Fuente: NASA’s Scientific Visualization Studio / Scott Wiessinger, Francis Reddy, Brad Cenko, Eric Burns
Composición de 12 días de observaciones del brote de rayos gamma GRB 221009A realizadas por el telescopio de rayos X a bordo del observatorio espacial Neil Gehrels Swift de la NASA. Fuente: NASA’s Scientific Visualization Studio / Scott Wiessinger, Francis Reddy, Brad Cenko, Eric BurnsSi mandas un pulso de luz blanca por una fibra óptica los componentes rojos de su espectro llegarán al extremo más alejado antes que los componentes azules. Si mandas el mismo pulso a través del vacío, el resultado será un empate técnico entre todas las frecuencias. La ausencia de dispersión de frecuencias es una consecuencia de una simetría fundamental de la relatividad conocida como invariancia de Lorentz.
Sin embargo, algunas teorías de la gravedad cuántica predicen que, para energías de fotones muy altas, el vacío se comporta como un medio. Los investigadores del Large High Altitude Air Shower Observatory (LHAASO) en China han comprobado ahora la invariancia de Lorentz analizando las mediciones de un brote de rayos gamma. La falta de una violación observable de la invariancia de Lorentz ha permitido al equipo elevar el umbral de energía a partir del que los efectos de la gravedad cuántica podrían hacerse evidentes.
Los brotes de rayos gamma, explosiones cósmicas que emiten radiación de alta energía, son excelentes sujetos para probar la invariancia de Lorentz, ya que su gran distancia significa que una pequeña dispersión se traduce en una variación detectable de los tiempos de llegada. El equipo de LHAASO estudió el brote de rayos gamma 221009A, el evento de este tipo más brillante jamás observado y, a una distancia de aproximadamente 2.400 millones de años luz, uno relativamente cercano. Aunque esta proximidad reduciría cualquier dispersión en el tiempo de llegada en comparación con eventos más distantes, el alto flujo de fotones ofrecía una oportunidad única para realizar mediciones estadísticamente significativas.
Al analizar cómo cambiaba el espectro de energía de los brotes de rayos gamma a lo largo del tiempo, los investigadores han podido restringir los dos términos principales que describen la dispersión de frecuencias potencial de la luz, los que varían lineal o cuadráticamente con la energía del fotón.
Para el término lineal, los investigadores han obtenido una restricción similar a la derivada previamente a partir de otras observaciones de los brotes de rayos gamma. Para el cuadrático, han establecido un umbral de energía de cinco a siete veces mayor a partir del que podría surgir la gravedad cuántica.
Futuras observaciones de las etapas iniciales de un brote de rayos gamma podrían ofrecer pruebas de una violación de Lorentz aún más sensibles.
Referencias:
Zhen Cao et al. (The LHAASO Collaboration) (2024) Stringent Tests of Lorentz Invariance Violation from LHAASO Observations of GRB 221009A Phys. Rev. Lett. doi: 10.1103/PhysRevLett.133.071501
M. Stephens (2024) Gamma-Ray Burst Tightens Constraints on Quantum Gravity Physics 17, s99
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Un brote de rayos gamma restringe las posibles violaciones a la relatividad general se ha escrito en Cuaderno de Cultura Científica.
¿Cuántos terremotos ocurren cada año en Venus?
Venus es un planeta del que desde luego no nos olvidamos en este Cuaderno de Cultura Científica, pero casi siempre hacemos referencia a sus posibles procesos volcánicos activos, quizás porque a fecha de hoy todavía nos queda mucho por explorar de un planeta cuyas condiciones -una superficie perpetuamente cubierta de nubes, una temperatura superior a los 450º y una presión atmosférica 90 veces superior a la terrestre- hacen del estudio de su superficie un reto muy difícil de superar incluso para la tecnología más puntera de la que disponemos.
A pesar de las enormes diferencias que hay entre Venus y la Tierra, a este planeta se le apoda como el “gemelo” de nuestro planeta. Y es que lo cierto es que al menos en el tamaño -Venus tiene un radio tan solo un 5% inferior al de la Tierra- y una densidad media similar -aunque también, y es coincidencia, es un 5% menor- apuntando a una composición similar, nos hacen pensar que, quizás, si Venus se encontrase a una distancia similar del Sol que nuestro planeta, podríamos parecernos mucho más.
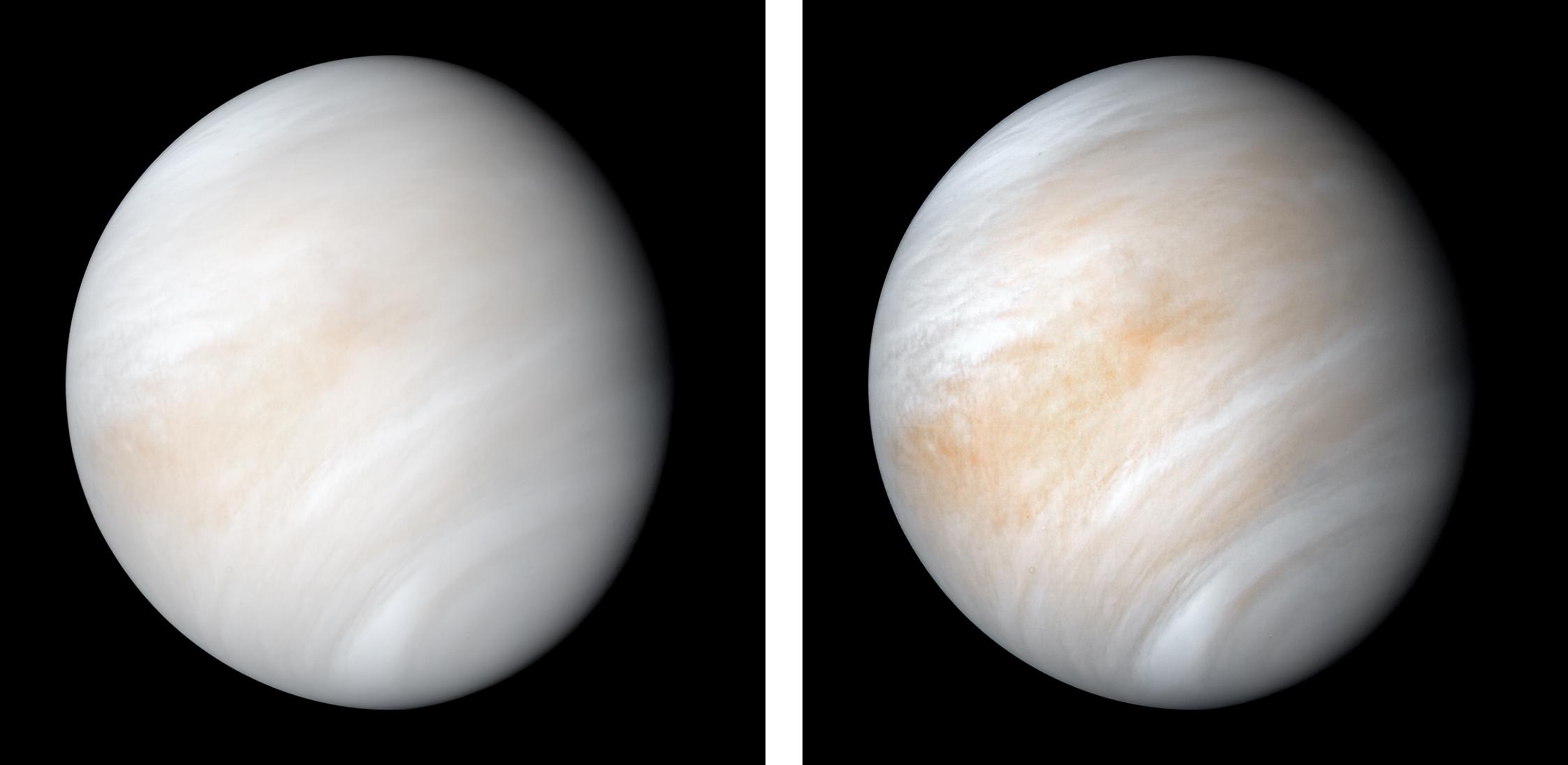 La cara que siempre nos muestra Venus -al menos en luz visible- es esta: un mundo perpetuamente cubierto de nubes, lo que ha dificultado muchísimo observar procesos geológicos activos y que, en algunos casos, estarán pendientes de confirmación hasta la próxima década. Imagen cortesía de NASA/JPL-Caltech.
La cara que siempre nos muestra Venus -al menos en luz visible- es esta: un mundo perpetuamente cubierto de nubes, lo que ha dificultado muchísimo observar procesos geológicos activos y que, en algunos casos, estarán pendientes de confirmación hasta la próxima década. Imagen cortesía de NASA/JPL-Caltech.Durante décadas, la ausencia de pruebas sobre un Venus dinámico y con actividad geológica había dejado una fuerte impronta en la cual imperó una visión en la que el planeta era un lugar carente de actividad, al menos a una escala evidente para nuestras observaciones, a pesar de que simplemente el hecho de tener un tamaño y una composición similar a la Tierra fuesen motivos más que suficientes para argumentar que podría mantener un calor interno suficiente para alimentar procesos geológicos activos como, por ejemplo, lo son terremotos y erupciones volcánicas.
Afortunadamente, con el paso de los años, y el descubrimiento de actividad geológica en cuerpos mucho más pequeños de nuestro sistema solar, pero también por la suma de indicios que estamos recabando de Venus, como las posibles pruebas de volcanes activos hoy día -ya sea por la variación de gases en la atmósfera, por la existencia de anomalías térmicas en su superficie o por, directamente, haber podido observar el antes y el después del depósito de una colada de lava- nos hacen pensar que Venus es, efectivamente, un planeta activo. Si a esto le sumamos que algunas estimaciones sobre la edad de su superficie -basadas en el conteo de cráteres de impacto- y que podríamos situar entre los 250 y 800 millones de años, está claro que es un planeta que está activo incluso lo suficiente para renovar su superficie.
Pero, ¿y los terremotos? Hasta el momento, los únicos sismómetros que han funcionado en Venus fueron los que llevaron las misiones soviéticas Venera 13 y 14 -que llegaron a Venus en 1981-, y debido a la breve duración de las misiones por las duras condiciones que se encontraron en la superficie, junto a las dificultades de interpretar los datos, apenas arrojaron un par de señales que podrían ser de origen sísmico. Y digo podrían porque tampoco está del todo claro.
Uno de los datos a tener en cuenta para planificar las futuras misiones que si puedan llevar instrumentos con la capacidad de detectar la actividad sísmica del planeta es intentar cuantificar cuantos terremotos ocurren en el planeta y si hay zonas con mayor probabilidad de que estos ocurran.
Precisamente, un nuevo estudio publicado por van Zelst et al. (2024) intenta responder a esta pregunta planteando tres posibles escenarios de sismicidad: Uno en el que Venus es un planeta “inactivo”, pero inactivo en el sentido de las zonas intraplaca de nuestro planeta, lo que serían el equivalente en nuestro planeta a las zonas lejos de los límites de placas, como lo suelen ser el interior de los continentes. Bajo esta premisa, los científicos calculan que habría entre 95 y 296 terremotos por año con una magnitud de 4 o superior.
 En esta imagen de radar tomada por la misión Magellan podemos ver las coronas de Bahet y Onatah, reconocibles por su forma ovalada a ambos lados de la imagen y compuestas por sistemas de valles y crestas montañosas. Imagen cortesía de NASA/JPL.
En esta imagen de radar tomada por la misión Magellan podemos ver las coronas de Bahet y Onatah, reconocibles por su forma ovalada a ambos lados de la imagen y compuestas por sistemas de valles y crestas montañosas. Imagen cortesía de NASA/JPL.Luego plantea otros dos escenarios más suponiendo que Venus sea un planeta activo y que algunas de las formas que vemos sobre su superficie -coronas, rifts y cinturones de pliegues- estén hoy día activos, por lo que estaríamos ante un umbral de entre 1161 y 3609 terremotos de magnitud 4 o superior cada año.
Y dentro de este escenario anterior hay otro más, y es que Venus tenga una actividad sísmica similar a la Tierra, por lo que se podrían observar entre 5715 y 17773 terremotos de magnitud 4 o superior cada año, un número muy elevado que facilitaría la detección de estos.
En cualquier caso, estos cálculos ponen de manifiesto una cosa bastante llamativa y es que, incluso en el caso de que estemos ante un primer escenario y Venus sea “inactivo” -algo que parece poco probable teniendo en cuenta que incluso podría haber volcanes activos hoy día en su superficie- su actividad sísmica sería claramente superior a la que observamos en Marte o en la Luna y, a pesar de esto, hemos podido detectar terremotos en estos últimos dos cuerpos. Eso sí, con misiones de mayor duración.
Pero bueno, ¿cómo podríamos salir de dudas? Aunque la tecnología ha mejorado mucho con respecto a existente en los años 80, lo cierto es que mantener en funcionamiento un sismómetro sobre la superficie de Venus durante un periodo lo significativamente grande como para detectar y caracterizar la actividad sísmica parece muy difícil como reto técnico.
En los últimos años hemos empezado a ver propuestas como la de Krishnamoorthy et al. (2022) en la que se propone sustituir los sismómetros del suelo por globos capaces de moverse por la atmósfera, ya que estas misiones podrían tener una duración mucho más prolongada, puesto que en las zonas altas de la atmósfera de Venus las temperaturas y presiones son mucho más benignas, e incluso parecidas a las de nuestro planeta, además de recibir una mayor energía solar para mantener los instrumentos en funcionamiento durante un tiempo más largo y sin el desgaste que suponen las condiciones superficiales.
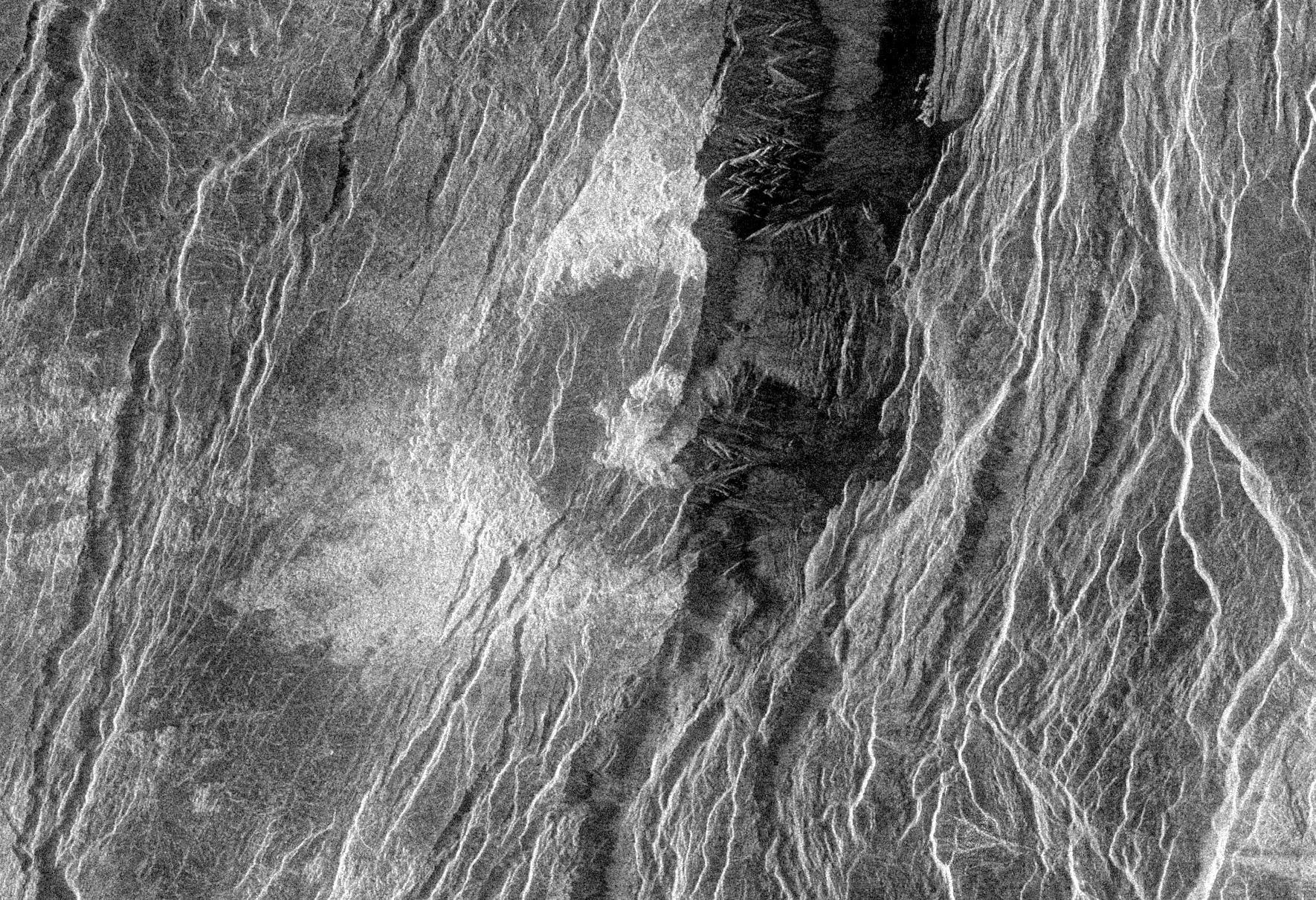 Si nos fijamos en el centro de la imagen veremos una forma circular muy característica, pero de la que solo reconocemos una mitad… es un cráter de impacto. Las formas lineales que vemos en la imagen probablemente sean sistemas de fallas que están transformando el relieve y que, si están activas hoy día, podrían causar también eventos sísmicos. Imagen cortesía de NASA/JPL.
Si nos fijamos en el centro de la imagen veremos una forma circular muy característica, pero de la que solo reconocemos una mitad… es un cráter de impacto. Las formas lineales que vemos en la imagen probablemente sean sistemas de fallas que están transformando el relieve y que, si están activas hoy día, podrían causar también eventos sísmicos. Imagen cortesía de NASA/JPL.Pero bueno, si un sismómetro mide la respuesta del suelo ante un terremoto, ¿qué medirían estos globos? Cuando ocurran los terremotos, las ondas sísmicas pueden acoplarse desde la superficie a la atmósfera y transformarse en ondas acústicas, algo que también ocurre en nuestro planeta, solo que en Venus hay una ventaja: debido a la densidad de la atmósfera, este acoplamiento podría ser unas 60 veces mayor, permitiendo detectar estas ondas de una manera más sencilla y a mayor distancia.
Si fuésemos capaces no solo de montar uno de estos globos, sino de mandar varios de manera simultánea, además podríamos localizar el punto de origen de los terremotos con mucha precisión, ayudándonos a conocer cómo se distribuye la actividad sísmica en el planeta y si hay zonas más activas que otras. Y, por cierto, también podríamos incluso detectar algunas erupciones volcánicas, puesto que las erupciones volcánicas -y sus explosiones- generan ondas perceptibles por este tipo de instrumentos.
Así que, mientras llegan las misiones que sean capaces de estudiar la actividad sísmica en el planeta Venus, nos tendremos que conformar con la llegada de las próximas misiones previstas para Venus: VERITAS, DAVINCI y EnVision, que deberían de lanzarse a principios de la década de 2030 y, al menos, empezar a despejar algunas de las dudas que tenemos de este planeta.
Referencias:
Aitta, A. «Venus’ Internal Structure, Temperature and Core Composition». Icarus 218, n.º 2 (abril de 2012): 967-74. doi: 10.1016/j.icarus.2012.01.007.
Krishnamoorthy, Siddharth, y Daniel C. Bowman. «A “Floatilla” of Airborne Seismometers for Venus». Geophysical Research Letters 50, n.º 2 (28 de enero de 2023): e2022GL100978. doi: 10.1029/2022GL100978.
Ksanfomaliti, L. V., V. M. Zubkova, N. A. Morozov, y E. V. Petrova. «Microseisms at the VENERA-13 and VENERA-14 Landing Sites». Soviet Astronomy Letters 8 (abril de 1982): 241.
Van Zelst, Iris, Julia S. Maia, Ana‐Catalina Plesa, Richard Ghail, y Moritz Spühler. «Estimates on the Possible Annual Seismicity of Venus». Journal of Geophysical Research: Planets 129, n.º 7 (julio de 2024): e2023JE008048. doi: 10.1029/2023JE008048.
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo ¿Cuántos terremotos ocurren cada año en Venus? se ha escrito en Cuaderno de Cultura Científica.
La formación de la categoría conceptual en personas autistas
Los niños y las niñas neurodivergentes no percibirían los conceptos a través del lenguaje, de lo que se derivan dificultades para deducir que dos objetos que reciben el mismo nombre forman una categoría.
 Foto: Jan Antonin Kolar / Unsplash
Foto: Jan Antonin Kolar / Unsplash“La población infantil autista no espera que dos objetos, simplemente por el mero hecho de que compartan nombre, tengan propiedades comunes o sean el mismo tipo de objeto. No son sensibles a la categorización mediante el lenguaje que se les está ofreciendo”, indica Agustín Vicente, profesor Ikerbasque e investigador del grupo Lindy Lab de la UPV/EHU. “Si la población autista muestra dificultades para deducir que dos objetos que reciben el mismo nombre forman una categoría, pueden tender a generar conceptos que no coinciden con los del resto de niños y niñas y esto puede dar lugar a dificultades en la comunicación, entre otras cosas”, añade Vicente.
Las personas neurotípicas, las que se ajustan a los estándares de comportamiento cognitivo y comunicativo socialmente típicos, durante su infancia son sensibles al llamado efecto de etiquetaje lingüístico. Pongamos como ejemplo dos tipos de aspiradoras diferentes: “Si a un niño neurotípico le decimos que una Dyson y una Roomba son las dos aspiradoras, esperará que hagan lo mismo, en este caso, aspirar. Pero si no se lo decimos, y llamamos a una simplemente Dyson y a la otra Roomba, si nos ve aspirar con la Dyson, puede que no espere que también podemos aspirar con la Roomba”, explica Vicente. “Al asignarle una etiqueta lingüística, un nombre, se establece un vínculo entre las propiedades de ese objeto y la etiqueta asignada —añade Sergio Parrillas, investigador predoctoral del grupo Lindy Lab de la UPV/EHU—.
Al mostrarle un segundo objeto con esa misma etiqueta, independientemente de lo distinto o parecido que sea al primer objeto, el niño espera que haga la misma función, en este caso aspirar. Si, en cambio, se le presenta un objeto muy parecido, pero con una etiqueta o nombre distintos, no generaliza la función de aspirar al nuevo objeto, interpretando que pertenecen a categorías distintas”.
Por tanto, “compartir nombre es un criterio de categorización más poderoso que tener un aspecto similar. Este fenómeno es importante porque actúa como una fuente de adquisición de conceptos a través del lenguaje”, subraya el investigador de la UPV/EHU.
En niños y niñas neurotípicos esto ocurre desde los 10 meses, y el objetivo de este estudio ha sido conocer si la adquisición de conceptos a través del lenguaje también se produce en niños y niñas del espectro autista de entre 3 y 9 años. Los resultados apuntan a que, a diferencia de los niños y niñas neurotípicos, no se ha podido identificar una sensibilidad al efecto de etiquetaje en la población infantil autista.
El efecto de etiquetaje lingüístico es una importante fuente de adquisición de conceptos y podría predecir aspectos tan relevantes en el desarrollo del lenguaje como lo son la adquisición y la amplitud del vocabulario. Por eso, ambos investigadores de Lindy Lab remarcan la necesidad de seguir investigando la relación que hay entre el lenguaje y los conceptos en la mente autista. “Investigar por qué algunos niños y niñas que pertenecen al espectro autista tienen un vocabulario tan escaso y referencialmente impreciso podrá ayudar a que en el futuro se desarrollen programas de intervención para que puedan comunicarse mejor, con un vocabulario más amplio y organizado”, añaden Sergio Parrilas y Agustin Vicente.
Referencia:
Sergio Parrillas-Manchón, Elena Castroviejo, José V Hernández-Conde, Ekaine Rodriguez Armendariz, Agustin Vicente (2024) Testing the Labeling Effect in Autistic Children J Autism Dev Disord doi: 10.1007/s10803-024-06388-1
Nota:
Este estudio está basado en el Trabajo Fin de Máster que ha elaborado Sergio Parrillas en el laboratorio Lindy Lab que forma parte del grupo de investigación Hizkuntzalaritza Teorikorako Taldea (HiTT) de la UPV/EHU y con el cual ganó el V Premio Izaskun Heras Prado. Sergio Parrillas es autista y actualmente tiene un contrato predoctoral del Gobierno Vasco bajo la dirección del profesor Ikerbasque Agustín Vicente (UPV/EHU) y la investigadora Irene de la Cruz Pavía (U. Deusto).
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La formación de la categoría conceptual en personas autistas se ha escrito en Cuaderno de Cultura Científica.
No solo a martillazos se parten las rocas
Durante las vacaciones siempre me gusta visitar ruinas y monumentos antiguos de los que abundan en nuestra geografía: restos de castros celtas e íberos, edificios romanos, castillos medievales, iglesias románicas… y cada vez que veo la precisión y rectitud del corte de las rocas con las que construyeron los muros hace cientos o miles de años, me pregunto lo mismo, ¿cómo lo hicieron? Aquí ciertas personas aludirían a alienígenas con sables láser, pero nada más lejos de la realidad. Porque la respuesta es más sencilla, las civilizaciones antiguas sabían de Geología.
En ocasiones podían elegir los materiales con los que trabajar. Rocas poco compactas y fáciles de partir y de tallar con herramientas de hierro o cobre, como algunas areniscas que tienen una escasa cementación y son muy deleznables. Pero en la mayoría de las ocasiones tenían que tirar con lo que se encontraban a su alrededor. Y ahí entraba en juego el ingenio y la observación del terreno.
El granito y los vetones Restos de una cantera vetona del siglo II de nuestra era en el Castro de Ulaca, Ávila. Se observa un bloque de granito desprendido siguiendo las líneas de fractura que se cortan perpendicularmente, sobre el que se comenzó a barrenar de manera rudimentaria (hilera de agujeros superficiales) para cortar bloques de menor tamaño y que, finalmente, quedó abandonado.
Restos de una cantera vetona del siglo II de nuestra era en el Castro de Ulaca, Ávila. Se observa un bloque de granito desprendido siguiendo las líneas de fractura que se cortan perpendicularmente, sobre el que se comenzó a barrenar de manera rudimentaria (hilera de agujeros superficiales) para cortar bloques de menor tamaño y que, finalmente, quedó abandonado.Un ejemplo es el del pueblo vetón. Afincado en la actual provincia de Ávila, buscaba zonas elevadas desde las que dominar su territorio y poder defenderse en caso de ataques por pueblos enemigos y que, además, tuvieran cerca fuentes de agua. Y en Ávila estas necesidades solo se cubren en las elevaciones montañosas generadas por los afloramientos de granito. El granito es una roca ígnea plutónica, muy compacta y formada por minerales muy duros, principalmente cuarzo y feldespatos, que hacen difícil incluso poder romperla con nuestros modernos martillos geológicos de acero inoxidable. Y cuando consigues partirla empleando la fuerza bruta, nunca logras un corte recto y perfecto, siempre se desprenden fragmentos irregulares.
El pueblo vetón aprovechó una de las características de la alteración de las rocas graníticas para poder cortar grandes bloques con las aristas separadas por ángulos casi rectos. Resulta que estas rocas han estado sometidas a grandes esfuerzos tectónicos durante millones de años, desde su emplazamiento a finales de la Era Paleozoica hasta hace unos 20 millones de años, lo que ha provocado la generación de una serie de fracturas en los granitos que se cortan casi perpendicularmente. Pero la historia no termina aquí. En los últimos milenios, al sufrir los efectos erosivos del viento y la lluvia por estar en superficie, estás líneas de fracturas se transforman en zonas de debilidad que separan lentamente la roca inicialmente compacta en bloques prismáticos.
Así, el cantero vetón ya tenía gran parte del trabajo hecho, pero faltaba un segundo paso, cuartear los bloques de granito en prismas de menor tamaño. Y para eso lo que hacía era barrenar la roca. Este proceso consiste en perforar pequeños agujeros o hendiduras en la superficie de la roca a base de golpearla con los instrumentos de hierro, cobre o cualquier otro metal similar del que dispusiera la población. Después, se insertan cuñas de metal en esos huecos y se siguen golpeando para introducirlas cada vez a mayor profundidad hasta que se desprende el bloque rocoso. En otras ocasiones, estás cuñas eran de madera, que se humedecían para que el cambio de volumen de la misma al absorber el agua fuera cortando el granito poco a poco.
Los romanos y la caliza Detalle de la muralla interior del castillo de Sagunto, levantada sobre el afloramiento de rocas calizas que forma la montaña en la que se asienta el mismo. Las capas de roca (estratos) están inclinadas hacia la izquierda de la foto debido a los movimientos tectónicos, que también han provocado la aparición de fracturas perpendiculares (en la imagen, tienen una disposición casi vertical), provocando la separación de los bloques de rocas.
Detalle de la muralla interior del castillo de Sagunto, levantada sobre el afloramiento de rocas calizas que forma la montaña en la que se asienta el mismo. Las capas de roca (estratos) están inclinadas hacia la izquierda de la foto debido a los movimientos tectónicos, que también han provocado la aparición de fracturas perpendiculares (en la imagen, tienen una disposición casi vertical), provocando la separación de los bloques de rocas.En realidad, esta técnica la inventó la antigua civilización romana y fue adaptada por los pueblos celtas e íberos que se encontraron en la Península Ibérica hace casi dos mil años. Una prueba de la enorme precisión en el corte y tallado de las rocas del pueblo romano lo encontramos en las ruinas de la ciudad valenciana de Sagunto. Tanto en las casas, la calzada, el anfiteatro o el imponente castillo que corona la ciudad, es fácil diferenciar lo que se construyó en época romana de los añadidos medievales posteriores fijándonos simplemente en el aspecto de los bloques de piedra: ángulos y aristas completamente rectos frente a bloques erráticos y de diferentes tamaños apilados de cualquier manera, respectivamente.
En esta localidad, los canteros romanos utilizaron una roca mucho más fácil de trabajar, la caliza que aflora en la montaña en la que se alza el castillo. Pero no solo por su dureza relativa, ya que está compuesta, mayoritariamente, por carbonato cálcico, con dureza tres en la escala de Mohs, sino también porque, al tratarse de una roca sedimentaria, se dispone en capas superpuestas, llamadas estratos. Y para facilitar aún más la extracción de bloques, la tectónica también ha hecho estragos en estas calizas, provocando unas fracturas perpendiculares a dichos estratos que, sin apenas esfuerzo humano, permite extraer bloques con los ángulos y las aristas casi rectos. Un poco de barrenado romano sobre esos grandes bloques y ya tenemos los “ladrillos” de caliza preparados para construir el próximo foro o teatro de turno.
 Exhibición de barrenado artesanal con lanzas de acero en la cantera de extracción de las calizas rojas de Ereño (Bizkaia), realizada durante la excursión del Geolodía Bizkaia de 2023 organizada por personal docente e investigador de la Universidad del País Vasco (UPV/EHU). Imagen cedida por Laura Damas (UPV/EHU).
Exhibición de barrenado artesanal con lanzas de acero en la cantera de extracción de las calizas rojas de Ereño (Bizkaia), realizada durante la excursión del Geolodía Bizkaia de 2023 organizada por personal docente e investigador de la Universidad del País Vasco (UPV/EHU). Imagen cedida por Laura Damas (UPV/EHU).Hoy en día se han inventado máquinas que pueden agujerear la superficie de las rocas de manera muy rápida y eficiente, gracias al uso de cabezales cubiertos de polvo de diamante, el mineral con mayor dureza de todos. Incluso, una vez realizadas estás perforaciones, se suelen emplear explosiones controladas con barrenos de dinamita para separar los grandes bloques de roca. Pero esto no quiere decir que, en la actualidad, no se siga utilizando la técnica tradicional usando la fuerza bruta. Existen muchos vídeos en las redes sociales de especialistas en cantería cortando rocas con una precisión milimétrica, generando caras, aristas y ángulos completamente rectos utilizando simplemente una maza y varias cuñas metálicas insertadas en fila en la superficie del bloque rocoso, a las que golpea de manera rítmica y continuada. Y, aunque de primeras puedan parecernos falsos por la perfección de su trabajo, a pesar de hacerlo de manera tan rudimentaria, son completamente reales. Ya lo hacían en la Roma republicana e imperial.
Cuando una cosa funciona, lo mejor es no cambiarlo. La técnica de corte de rocas empleando el barrenado lleva mostrando su utilidad más de dos mil años, así que, aunque los materiales utilizados para llevarla a cabo puedan, y deban, evolucionar con el paso del tiempo, los fundamentos teóricos seguirán siendo los mismos. La observación de la naturaleza y, en este caso, las rocas, nos permite adaptarnos a ellas para poder utilizarlas para nuestro beneficio. Así, aunque Antonio Molina nos diga que le gusta ser barrenero por el riesgo de usar los explosivos, sus compañeros seguirán golpeando la roca con las mazas para marcarle el ritmo en el cante.
Agradecimientos:
A Jone Mendicoa, por aguantarme todos los años de vacaciones, y a Laura Damas, por darme la idea para este artículo tras varias conversaciones más que interesantes sobre rocas ornamentales.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo No solo a martillazos se parten las rocas se ha escrito en Cuaderno de Cultura Científica.
El monstruo del lago Ness existe (al menos en matemáticas)
 Serpiente de agua, una aproximación al monstruo del lago Ness (en matemáticas). Fuente: Wikimedia Commons.
Serpiente de agua, una aproximación al monstruo del lago Ness (en matemáticas). Fuente: Wikimedia Commons.En la entrada Clasificando en topología: de lo local a lo global recordábamos un hermoso teorema de clasificación:
Toda superficie compacta (cerrada y acotada) y conexa (de una pieza) es topológicamente equivalente a una esfera, a una suma conexa de toros o a una suma conexa de planos proyectivos.
Superficies no compactasLa clasificación de superficies no compactas (superficies no cerradas o no acotadas) es mucho más compleja. El enunciado del teorema de clasificación envuelve conceptos parecidos al del caso compacto y una nueva noción, la de final de un espacio topológico.
Esta clasificación la estableció Ian Richards en un celebrado artículo publicado en 1962; involucra los siguientes conceptos explicados de manera muy intuitiva:
-
la “cantidad” de toros o planos proyectivos que posee la superficie (su género). En el caso de superficies no compactas esa “cantidad” puede ser infinita;
-
la “clase de orientabilidad” de la superficie, es decir, la existencia (o la falta de ella) de planos proyectivos en su expresión; y
-
los finales de la superficie, que pueden entenderse como las maneras (topológicas) de moverse hacia el infinito dentro del espacio. El espacio de finales se dota de una topología que expresa precisamente la “dinámica topológica” que posee la superficie (y que la caracteriza).
El concepto de final se puede introducir para cualquier espacio topológico. La definición no es sencilla, por ello damos unos cuantos ejemplos para entenderla mejor.
-
Un espacio compacto no posee finales.
-
La recta real posee dos finales; son las dos maneras de acercarse al infinito, -∞ o +∞).
-
El intervalo [0, +∞) posee un único final. Aunque es más difícil de visualizar, el plano también posee un único final, así como todos los espacios euclideos de dimensión mayor o igual a 2.
-
Un árbol binario completo infinito posee una cantidad infinita (no numerable) de finales que corresponden a la cantidad infinita de caminos descendentes diferentes que comienzan en la raíz. De hecho, se puede demostrar que el conjunto de finales es homeomorfo al conjunto de Cantor.
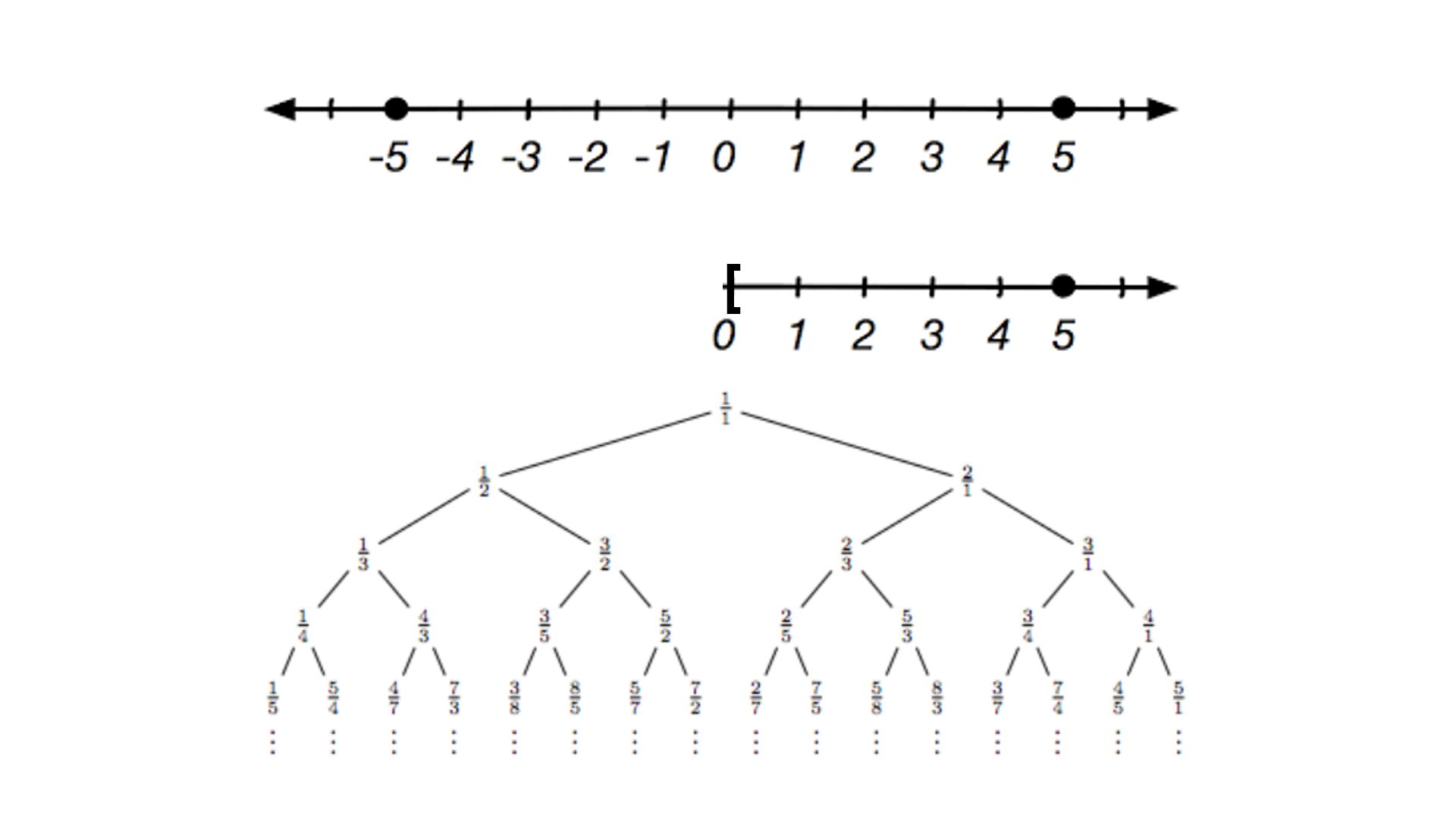 La recta, el intervalo y el árbol binario.
La recta, el intervalo y el árbol binario.
Veamos algunos ejemplos de superficies no compactas.
El planoEs una superficie no compacta con un final y género cero. Es homeomorfa a una esfera (que es una superficie compacta) a la que se ha quitado un punto.
El cilindroEs una superficie (es el producto de la circunferencia por la recta) no compacta con dos finales y género cero. Es homeomorfa a una esfera a la que se han quitado dos puntos.
El monstruo del lago NessEs una superficie no compacta (orientable, no contiene planos proyectivos) de género infinito y con un único final. La nombraron de esta manera los matemáticos Antony Phillips y Denis Sullivan en un artículo sobre teoría de foliaciones publicado en 1981.
Esta superficie se puede construir a partir de un plano (que puede pensarse como la superficie del lago Ness) al que se le añaden una cantidad infinita de asas (que pueden pensarse como los trozos de cuerpo visibles del monstruo del Lago Ness). Cada asa se añade eliminando dos discos abiertos del plano y “pegando” un cilindro en los huecos originados como se observa en la imagen de debajo. El género de esta superficie es infinito porque hay infinitas asas; solo posee un final porque el plano posee un único final.
 Arriba: Una “aproximación” a la superficie del monstruo del lago Ness. Según la descripción anterior, el monstruo debería ser infinitamente largo y poseer un número infinito de “jorobas” emergiendo del agua. Debajo: Imagen de una parte de la superficie del monstruo del lago Ness. Fuente: Wikimedia Commons.La escalera de Jacob
Arriba: Una “aproximación” a la superficie del monstruo del lago Ness. Según la descripción anterior, el monstruo debería ser infinitamente largo y poseer un número infinito de “jorobas” emergiendo del agua. Debajo: Imagen de una parte de la superficie del monstruo del lago Ness. Fuente: Wikimedia Commons.La escalera de Jacob
Es una superficie (orientable) de género infinito y con dos finales. La nombró de esta manera el matemático Étienne Ghys en un artículo sobre teoría de foliaciones publicado en 1995.
La superficie se puede describir como la frontera exterior de una escalera infinitamente larga en ambas direcciones. Correspondería a hacer sumas conexas de toros, a partir de uno inicial, en ambas direcciones y de manera indefinida.
 Arriba: Una “aproximación” a la superficie escalera de Jacob pensada como la frontera de una escalera infinita en ambas direcciones. Debajo: Imagen de una parte de la superficie pensada como suma conexa de toros en dos direcciones. Fuente: Wikimedia Commons.
Arriba: Una “aproximación” a la superficie escalera de Jacob pensada como la frontera de una escalera infinita en ambas direcciones. Debajo: Imagen de una parte de la superficie pensada como suma conexa de toros en dos direcciones. Fuente: Wikimedia Commons.El árbol de Cantor
Es una superficie homeomorfa (topológicamente equivalente) a una esfera a la que se le ha eliminado un conjunto de Cantor. Es decir, tiene género cero (no contiene ni toros ni planos proyectivos) e infinitos finales (los infinitos puntos del conjunto de Cantor).
Nota
Se puede probar que cualquier superficie no compacta es homeomorfa a una esfera a la que se le ha quitado un conjunto compacto (que define el conjunto de finales) y se “han pegado” una cantidad finita o infinita de toros y planos proyectivos (que definen el género y la clase de orientabilidad).
Pero esa es otra historia, para la que se necesitan unas cuantas matemáticas más sofisticadas.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia
El artículo El monstruo del lago Ness existe (al menos en matemáticas) se ha escrito en Cuaderno de Cultura Científica.
¿Qué son los haces?
Estos jardines metafóricos se han convertido en objetos centrales de las matemáticas modernas.
Un artículo de Konstantin Kakaes. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.

En 1940, los alemanes tomaron prisionero al matemático y oficial de artillería francés Jean Leray, quien les dijo a sus captores que era topólogo, temeroso de que si descubrían su verdadera especialidad, la hidrodinámica, lo obligarían a colaborar con el esfuerzo bélico alemán. Durante los casi cinco años que estuvo en prisión, Leray mantuvo este subterfugio investigando en topología, una rama de las matemáticas que estudia las formas deformables. Terminó creando una de las ideas más revolucionarias de las matemáticas modernas: el concepto de “haz”.
Después de que Alexander Grothendieck diera a conocer la noción de Leray en las décadas de 1950 y 1960, los haces asumieron un “papel estelar” en las matemáticas, afirma David Ben-Zvi de la Universidad de Texas en Austin, convirtiéndose en “una de las herramientas más básicas en la geometría algebraica moderna”.
Como dice una explicación introductoria, los haces pueden considerarse como desarrollos construidos sobre otros objetos matemáticos. “Piénsalo como si el objeto matemático fuera una parcela de tierra y un haz fuese como un jardín encima de ella”, explica Mark Agrios.
Los haces recibieron su nombre porque implican unir “tallos” a un objeto subyacente. Leray las llamó “faisceaux” (en francés, “haces”) porque esta disposición le recordaba a las gavillas de trigo cosechado. Así como los jardines se pueden cultivar en diferentes tipos de tierra, los haces se pueden construir sobre numerosos tipos diferentes de objetos matemáticos y, por lo tanto, pueden adoptar muchas formas diferentes.
Incluso los haces más simples son entidades matemáticas bastante complicadas. Para comprenderlas mejor, podemos construir una. Aquí se explica cómo hacer un haz simple a partir de líneas rectas.
Tomemos el objeto subyacente como la línea de los números reales:
Construimos un haz no a partir de puntos individuales, sino de intervalos. Puedes dividir la recta numérica en intervalos de infinitas maneras. A continuación se muestra un ejemplo.

Entre cada pareja de paréntesis hay un intervalo que incluye todos los puntos entre ellos, pero no los extremos. Por lo tanto, el intervalo (0, 1) contiene todos los números mayores que cero y menores que 1.
El haz contiene todos los intervalos, no solo uno cualquiera. A cada intervalo se le puede asignar un conjunto de “secciones”. En este ejemplo, las secciones son todas las posibles líneas rectas que pasan por un intervalo.
Tomemos un único intervalo, como se muestra a continuación. Solo se muestran tres de las secciones, ya que es imposible visualizarlas todas a la vez.
El haz comprende todas las secciones de todos los intervalos posibles y las uniones de esos intervalos.

Se trata de una entidad desconcertantemente caótica, que resulta matemáticamente atractiva porque oculta una simplicidad subyacente. En la figura anterior, las secciones elegidas para los diferentes intervalos chocan. Las líneas pasan unas por encima y otras por debajo de otras, en lugar de coincidir.
A los matemáticos les interesa comprender qué sucede cuando se elige una sección de cada intervalo y se impone el requisito de que las distintas secciones sean compatibles entre sí, de modo que los intervalos superpuestos concuerden. Con esa restricción, sucede algo notable.
Si un intervalo está anidado dentro de otro, las líneas deben coincidir en la superposición.
De esta restricción local se obtiene una consecuencia global: en lugar de muchas líneas pequeñas, se obtienen las únicas opciones posibles que cumplen la regla de anidación: líneas rectas que continúan a lo largo de toda la línea numérica.
Estas se denominan secciones globales. Una de las características que les otorga a llos haces su poder es que estos objetos globales surgen de las restricciones locales.
Este es un recorrido por el haz de líneas rectas, o funciones lineales, sobre la línea real. Es uno de los haces más simples.
Se pueden crear muchos haces sobre la línea real. Esto es análogo a plantar diferentes flores en un jardín en la misma parcela de tierra. Hay un haz que consta de funciones cuyos gráficos no tienen saltos, un haz de funciones cuyos gráficos no tienen curvas agudas y un número infinito de otros.
Pero eso es solo el comienzo. En lugar de plantar una flor diferente, podrías cuidar una parcela de tierra diferente. Imagina que construyes un haz sobre un círculo, en lugar de sobre una línea. Esto crea una estructura que parece un cilindro con una altura infinita. La estructura de los objetos dibujados en ese cilindro depende de la construcción concreta de un haz específico.
 Ilustración: Mark Belan / Quanta Magazine
Ilustración: Mark Belan / Quanta MagazineHasta este punto, todas las haces que hemos considerado pueden considerarse familias de funciones. Pero los haces pueden volverse (mucho) más complicados que eso.
El cilindro de la figura anterior se puede considerar como el resultado de un rectángulo infinitamente alto cuyos lados has pegado. Si, en cambio, torcieras los extremos del rectángulo antes de pegarlos, como en la figura siguiente, crearías una banda de Möbius infinitamente ancha (no es posible dibujarla, por lo que mostraremos una banda de Möbius finita). En esta banda de Möbius, aún puedes dibujar curvas que recuerdan a los gráficos.

En cualquier pequeña parte local del círculo, esta curva parece el gráfico de una función. Pero a escala global, no es una función. Esto se debe a que no hay forma de definir un sistema de coordenadas global consistente, debido a la torsión. (Si recorremos toda la franja, nuestras nociones de arriba y abajo terminan invirtiéndose, lo que hace imposible hacerlo). Los matemáticos llaman a estos objetos «funciones torsionadas».
Si bien cada haz es una vasta colección de objetos, también se puede considerar la colección de todos los haces de un objeto matemático dado: la línea real, un círculo o alguna otra entidad. Esto es como considerar todos los posibles jardines que se podrían plantar en una parcela de tierra determinada. Esto nos dice algo sobre cómo es esa tierra. Algunas parcelas son selvas tropicales, otras son desiertos. Averiguar qué haces son posibles les da a los matemáticos una manera de investigar la estructura del espacio subyacente, de la misma manera que saber qué plantas crecen en un tipo concreto de suelo nos da información sobre ese suelo.
A partir de Grothendieck, los matemáticos se dieron cuenta gradualmente de que las colecciones de haces tienen muchas similitudes con las colecciones de funciones, pero a un nivel de complejidad más alto. Se pueden sumar y multiplicar haces, e incluso hacer una versión de cálculo con ellos.
En prisión, Leray había abierto la puerta a un mundo matemático completamente nuevo.
El artículo original, What Are Sheaves?, se publicó el 19 de julio de 2024 en Quanta Magazine.
Traducido por César Tomé López
El artículo ¿Qué son los haces? se ha escrito en Cuaderno de Cultura Científica.
Los pogonóforos cultivan bacterias en las profundidades marinas
El esquema básico de la alimentación animal es bien conocido. Las plantas utilizan la energía del sol para sintetizar hidratos de carbono mediante la fotosíntesis. Estas moléculas liberan energía cuando son oxidadas, haciendo posible la síntesis de otras moléculas como proteínas o lípidos. Los animales utilizamos finalmente para nuestro metabolismo la energía almacenada en todo tipo de moléculas orgánicas, energía derivada en primera instancia del sol.
Esta regla no es universal. Existen animales que no dependen de la producción fotosintética primaria. De hecho, viven en ambientes completamente oscuros, en las profundidades marinas y cerca de manantiales hidrotermales. Pueden alcanzar gran tamaño, más de dos metros y medio, y no tienen sistema digestivo. Se les conoce como pogonóforos o vestimentíferos, aunque su nombre oficial es el de siboglínidos. Aquí utilizaré la denominación más extendida de pogonóforos.
 Figura 1. Densa colonia de pogonóforos de la especie Riftia pachyptila junto a un manantial hidrotermal del Pacifico oriental. De Hilário, A., Capa, M., Dahlgren, T.G. et al. (2011). PLoS ONE, 6 (2). e16309. 1 – 14. CC BY 4.0
Figura 1. Densa colonia de pogonóforos de la especie Riftia pachyptila junto a un manantial hidrotermal del Pacifico oriental. De Hilário, A., Capa, M., Dahlgren, T.G. et al. (2011). PLoS ONE, 6 (2). e16309. 1 – 14. CC BY 4.0Después de muchas dudas sobre su posición taxonómica, hoy sabemos que los pogonóforos son un grupo muy especializado de anélidos poliquetos. Estos gusanos viven en tubos quitinosos de los que sobresale una especie de plumas de intenso color rojo (Figura 1). Para obtener su alimento cultivan en su interior bacterias quimioautótrofas, en concreto bacterias capaces de oxidar el sulfuro de hidrógeno, un gas tóxico emitido por los manantiales submarinos.
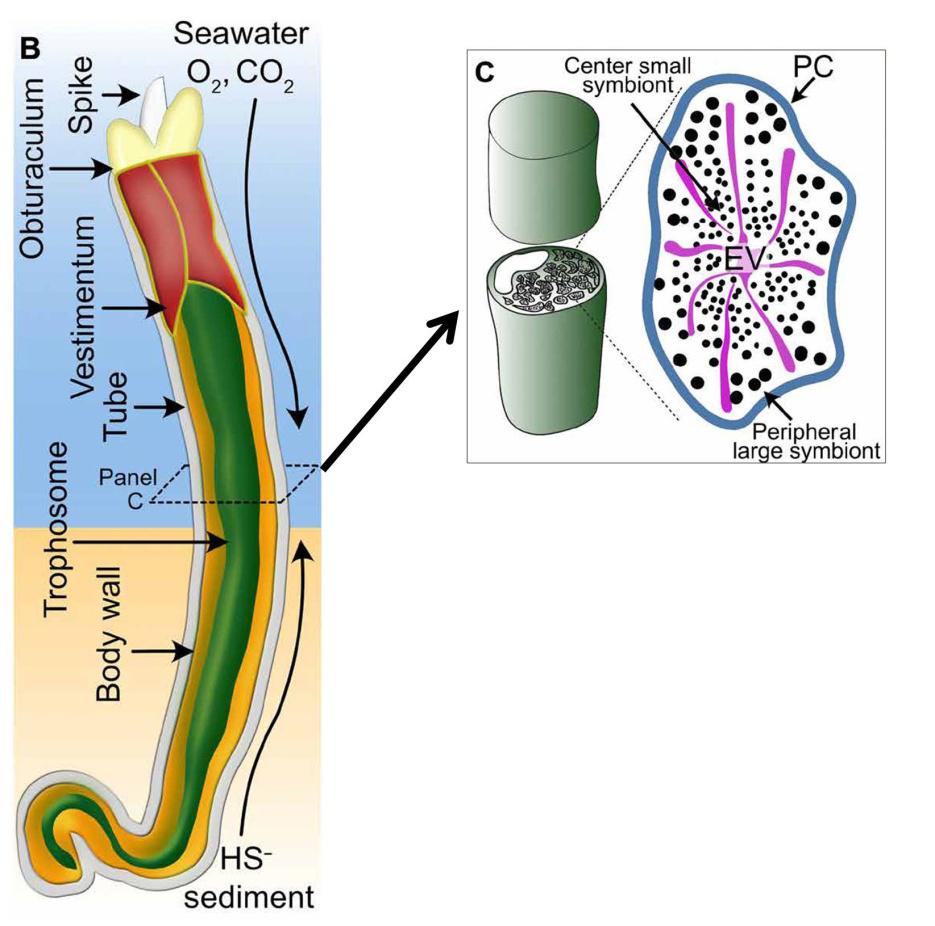 Figura 2. Se muestra en verde el trofosoma del pogonóforo Parascarpia echinospica. Este animal capta oxígeno y dióxido de carbono del agua de mar, mientras que el sulfuro de hidrógeno se filtra a través del sedimento. De Wang, H., Xiao, H., Feng, B., et al. Sci. Adv. doi: 10.1126/sciadv.adn3053, CC BY 4.0
Figura 2. Se muestra en verde el trofosoma del pogonóforo Parascarpia echinospica. Este animal capta oxígeno y dióxido de carbono del agua de mar, mientras que el sulfuro de hidrógeno se filtra a través del sedimento. De Wang, H., Xiao, H., Feng, B., et al. Sci. Adv. doi: 10.1126/sciadv.adn3053, CC BY 4.0Los pogonóforos cultivan estas bacterias en un voluminoso órgano de su cuerpo llamado trofosoma, formado por unas células, los bacteriocitos, cargadas de bacterias (Figura 2). El hospedador les proporciona a través de sus vasos sanguíneos oxígeno, sulfuro de hidrógeno y dióxido de carbono. De hecho, el color rojo de sus plumas se debe a un tipo especial de hemoglobina que es capaz de fijar tanto oxígeno como sulfuro de hidrógeno. Las bacterias oxidan el sulfuro generando una energía que es aprovechada para ejecutar el ciclo de Calvin-Benson, el mismo que las plantas utilizan durante la fase oscura de la fotosíntesis. De esta forma, el carbono del CO2 queda fijado en moléculas orgánicas sin necesidad de luz solar.
Las bacterias proliferan gracias a los nutrientes proporcionados por su hospedador, pero finalmente son digeridas por unas enzimas llamadas catepsinas, su materia orgánica pasa a la cavidad corporal y es distribuida por todo el cuerpo del pogonóforo. Esto hace innecesaria la presencia de boca o tubo digestivo. Puede pensarse que el cultivo de bacterias para autoconsumo no es muy eficiente, pero se han observado densidades altísimas de pogonóforos junto a fumarolas submarinas, y se han registrado crecimientos de hasta 85 centímetros al año.
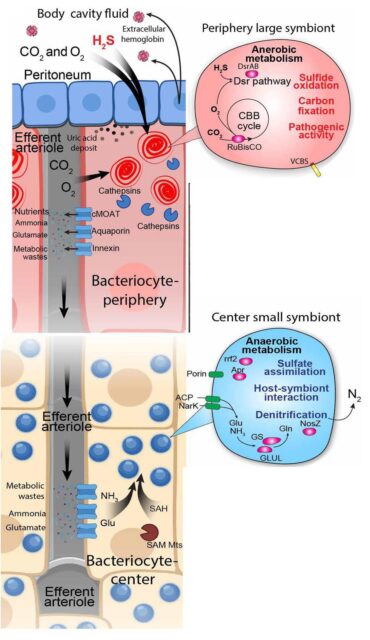 Figura 3. Diferencias entre los dos micronichos del trofosoma de P. echinospica. Arriba, los bacteriocitos de la periferia contienen bacterias que oxidan el sulfuro de hidrógeno impulsando el ciclo de Calvin-Benson (CBB) que fija el carbono en moléculas orgánicas. Las catepsinas digieren las bacterias proporcionando nutrientes al hospedador. Abajo, los productos metabólicos de desecho, fundamentalmente el amonio, son detoxificados por las bacterias de los bacteriocitos centrales, sometidos a hipoxia. De Wang, H., Xiao, H., Feng, B., et al. Sci. Adv. doi: 10.1126/sciadv.adn3053, CC BY 4.0
Figura 3. Diferencias entre los dos micronichos del trofosoma de P. echinospica. Arriba, los bacteriocitos de la periferia contienen bacterias que oxidan el sulfuro de hidrógeno impulsando el ciclo de Calvin-Benson (CBB) que fija el carbono en moléculas orgánicas. Las catepsinas digieren las bacterias proporcionando nutrientes al hospedador. Abajo, los productos metabólicos de desecho, fundamentalmente el amonio, son detoxificados por las bacterias de los bacteriocitos centrales, sometidos a hipoxia. De Wang, H., Xiao, H., Feng, B., et al. Sci. Adv. doi: 10.1126/sciadv.adn3053, CC BY 4.0Un estudio recientemente publicado por un grupo de científicos chinos nos permite conocer mejor este proceso, más complejo de lo que se pensaba. Para ello, han utilizado una técnica de recolección in situ de muestras del trofosoma de Parascarpia echinospica, un pogonóforo del Pacífico occidental. Mediante la secuenciación de ARN de células individuales se clasificaron las células y las bacterias del trofosoma en función de qué genes se estaban expresando en un momento determinado. Los investigadores comprobaron la existencia de dos tipos bien diferenciados de bacterias, que se correspondían además con su posición dentro de los lóbulos del trofosoma. Las bacterias más periféricas, y más expuestas a la circulación y a la presencia de oxígeno, son las que oxidan el sulfuro de hidrógeno, fijan el carbono y proporcionan alimento al hospedador. Sin embargo, las bacterias más internas, en un ambiente hipóxico, expresan genes relacionados con la detoxificación del amonio, es decir, su función está más relacionada con la excreción (Figura 3). El pogonóforo no utiliza estas bacterias como alimento.
Lo fascinante de este estudio es que los pogonóforos no solo han desarrollado un sistema de cultivo bacteriano que les permite sobrevivir en un ecosistema quimiosintético aislado del flujo de energía de origen solar, un ambiente más apropiado para bacterias que para animales. Además, han sido capaces de generar en su trofosoma dos micronichos bien diferenciados, albergando dos tipos de bacterias que cumplen funciones diferentes para la fisiología del pogonóforo, en concreto la obtención de nutrientes y la eliminación de desechos.
Referencias:
Wang, H., Xiao, H., Feng, B., et al. (2024). Single-cell RNA-seq reveals distinct metabolic «microniches» and close host-symbiont interactions in deep-sea chemosynthetic tubeworm. Sci. Adv. doi: 10.1126/sciadv.adn3053.
Los interesados en el tema no deberían perderse este extraordinario vídeo del periodista científico Ed Yong y la microbióloga de Harvard Colleen Cavanaugh, descubridora de la quimiosíntesis en pogonóforos.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga
El artículo Los pogonóforos cultivan bacterias en las profundidades marinas se ha escrito en Cuaderno de Cultura Científica.
Por qué te atraen los chicos malos
Cuando los chicos y las chicas llegan a la adolescencia acumulan una multiplicidad de mensajes en los que se asocia atracción y violencia. Estos mensajes provienen del grupo de iguales, series, películas, canciones, redes sociales… y dibujan como atractivos a los chicos que muestran actitudes violentas y despreciativas hacia las chicas y no tanto a aquellos que son igualitarios y las tratan bien.
 Foto: Erik Lucatero / Unsplash
Foto: Erik Lucatero / UnsplashEsto lo vemos, por ejemplo, en la película After, hecha a partir de una saga de novelas para adolescentes. La protagonista tiene su novio del instituto que es un buen chico y al que trata como un amigo, sin mostrar deseo. Al llegar a la universidad lo engaña con otro chico “malote” y atractivo. El novio se muestra comprensivo, lo que le hace parecer un chico inseguro. Después, la chica se entera de que su nuevo ligue solo ha estado con ella por una apuesta, pero eso no le hace perder atractivo ya que, al parecer, al final “se ha enamorado de verdad”.
La influencia del discurso dominante coercitivoAsociar la atracción a la violencia y el desprecio es algo que ocurre en diferentes entornos y de diferentes formas, y se conoce como “discurso dominante coercitivo”. Estar expuestas durante mucho tiempo a este discurso lleva a las chicas a considerar atractivos a esos chicos violentos y las empuja a tener relaciones afectivo-sexuales tóxicas.
En una investigación reciente hemos analizado los mecanismos por los que este discurso dominante coercitivo se manifiesta en el grupo de iguales, llevando a algunas chicas a entablar una relación sentimental o sexual “despreciativas” (con un chico que no las trata bien y que tienen actitudes y conductas violentas), así como sus consecuencias.
Para ello, hemos recogido las experiencias de 59 chicos y 71 chicas estudiantes de 4º de ESO (15 y 16 años) de 3 institutos, que nos han hablado de sus interacciones en el grupo de iguales.
El grupo de iguales es el conjunto de personas de similar edad con los que comparten intereses, actividades, etc. ya sea dentro o fuera del instituto, con los que socializan y construyen su identidad.
¿Por qué me gusta el que peor me trata?El grupo de iguales es uno de los contextos de socialización y aprendizaje más importante de los adolescentes. La presión e influencia que ejerce en la conducta de los jóvenes lleva a que algunas chicas se “enrollen” con chicos violentos, aunque no quieran hacerlo.
El grupo de iguales también ejerce presión sobre las chicas diciéndoles una y otra vez que quien realmente les gusta son chicos con actitudes y comportamientos violentos, lo que lleva a que a muchas de ellas acaben por gustarles –o crean que les gusta– este tipo de chicos que antes no les gustaba. Esta presión hace que se normalicen y acepten los comportamientos violentos, e incluso que las chicas los confundan con amor, empujándolas a relaciones tóxicas.
Esta presión del grupo de iguales surge también a partir de la influencia de los mensajes mediáticos a los que los jóvenes están expuestos.
“He visto series en las que la chica sale con un chico que no la trataba bien, y después la deja. Él le decía a ella que era fea… al mismo tiempo, ella no se daba cuenta de que había otro chico en su clase que siempre la miraba y que le gustaba.” (Chica participante en la investigación)
A su vez, los chicos también se ven presionados para seguir el patrón de masculinidad violento y despreciativo si quieren resultar atractivos y tener éxito entre las chicas.
El peligro de ser aburridoSi las chicas ya tienen una relación estable con un chico no violento, el discurso dominante coercitivo en el grupo tacha a estas chicas de “aburridas”, y las presiona para engañar a sus novios y “enrollarse” con chicos con actitudes y comportamientos violentos, porque “eso es lo divertido”, tal como explican las chicas participantes de la investigación cuando relatan su experiencia.
Estos comportamientos violentos van desde presumir de haberse ligado a alguien y luego despreciarla, despreciar a la chica con la que se han enrollado una vez lo han hecho, hablarle mal, tratarla mal delante de otras personas o cuando están a solas.
Hay chicas que acaban cediendo a esas presiones, enrollándose con quien no quieren y engañando a quien quieren, porque no quieren que en su grupo las consideren aburridas y tienen miedo de perder a sus amigas. En ocasiones, la actuación de las amigas no queda ahí.
El acoso continúa cuando hacen fotografías de la chica con el chico, “enrollándose” o estando cerca el uno del otro de forma que lo parece, y envían después la fotografía al novio de la chica, la cuelgan en internet o la envían a más personas, haciendo público el engaño y dañando la relación de la chica con su novio.
Las consecuencias en la saludLa investigación científica ha demostrado que la violencia de género tiene consecuencias negativas sobre la salud, incluyendo dolor crónico, mayor riesgo de enfermedades de transmisión sexual, depresión, y tendencias suicidas, entre otras.
Alrededor del 27 % de las mujeres y chicas entre 15 y 49 años ha sufrido alguna forma de violencia física o sexual, por lo que se hace necesario identificar los factores que aumentan el riesgo de violencia de género, especialmente entre las chicas más jóvenes que están teniendo sus primeras relaciones.
Nuestra investigación muestra que los ligues despreciativos son uno de estos factores que aumentan el riesgo de violencia de género en la población adolescente, socializando a las chicas en una normalización y atracción hacia la violencia. Además, cuando los ligues despreciativos se difunden entre mucha gente o se publican en internet, quedan ligados a esa chica para siempre, con posibles graves consecuencias para su salud. Como decía una de ellas: “La foto te seguirá hasta tu tumba. Hay gente que termina suicidándose, porque duele mucho”.
La amistad (buena) como elemento de prevenciónPresionar a las chicas para tener ligues despreciativos implica aumentar la probabilidad de que sean víctimas de violencia de género. Siendo el grupo de iguales un contexto muy importante de presión hacia las chicas para tener estos ligues despreciativos, es importante la intervención preventiva desde el mismo grupo de iguales.
En la investigación, las chicas hablan de la “presión de las amigas” o del “miedo a perder a sus amigas”, pero también hacen referencia a que son “falsas amigas” las que presionan a tener una relación con quien no quieres.
De acuerdo con las conclusiones de esta y otras investigaciones, trabajar las amistades de calidad desde las primeras edades puede ser un importante elemento de protección y prevención del grave problema de la violencia de género.![]()
Sobre las autoras: Silvia Molina Roldán, Profesora Titular en Educación, Universitat Rovira i Virgili; Garazi Lopez de Aguileta, PhD and teaching assistant, University of Wisconsin-Madison, University of Wisconsin-Madison; Itxaso Tellado, Profesora Agregada, Universitat de Vic – Universitat Central de Catalunya; Leire Ugalde Lujambio, Profesora Agregada en la Facultad de Educación, Filosofía y Antropología, Universidad del País Vasco / Euskal Herriko Unibertsitatea; Lidia Puigvert Mallart, Catedrática de Sociología, Universitat de Barcelona; Miguel Ángel Pulido, Profesor en la Facultat de Psicologia Ciències de l’Educació i de l’Esport Blanquerna, Universitat Ramon Llull; Ramón Flecha García, Catedrático Emérito de sociología, Universitat de Barcelona y Sandra Racionero-Plaza, Profesora agregada. Socioneurociencia, Universitat de Barcelona
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Por qué te atraen los chicos malos se ha escrito en Cuaderno de Cultura Científica.
Un mensaje para el futuro: las cápsulas del tiempo de la Westinghouse Electric
Hubo un tiempo, hasta alrededor de mediados del siglo XX, en el que la humanidad tuvo un brillante futuro por delante. Nuestro entusiasmo tecnooptimista duró, más o menos, hasta que la ciencia y la tecnología avanzaron lo suficiente como para empezar a suponer una amenaza para nuestra especie: un poder de creación cada vez mayor trajo asociado, inevitablemente, un poder de destrucción también cada vez mayor. El desarrollo de la energía atómica, por un lado, y los bombardeos de Hiroshima y Nagasaki, como la otra cara de la moneda, por otro, es uno de los mejores ejemplos.
La materialización de una realidad que no terminaba de convertirse en la tecnoutopía que nos habían prometido hizo el resto. En la actualidad parece que perdimos la ingenuidad o la capacidad de soñar o de simplemente pensar que hay un mañana, parece que, en una sociedad que se mueve tan rápido, no nos da siquiera tiempo a asimilar el «hoy». Pero esto no siempre fue así.
En 1938, pensar en dentro de cinco mil años podía incluso entrar dentro de lo razonable. O eso pensaron en la Westinghouse Electric & Manufacturing Company cuando, de cara a la celebración de la Feria Mundial de Nueva York de 1939, cuyo tema era «El mundo del mañana», decidieron construir una cápsula del tiempo para las generaciones de ese mañana más que lejano con un claro objetivo:
Dentro de cinco mil años, las personas del futuro nos mirarán como nosotros miramos a los sumerios y a los primeros egipcios y babilonios. El plan de los ingenieros de la Westinghouse es proporcionarles más conocimiento sobre nosotros del que que nosotros tenemos sobre cualquiera de los pueblos antiguos que vivieron antes.
Para llevar a cabo el proyecto, la empresa creó el Comité de la Cápsula de Tiempo.
Dejando a un lado la cuestión de dónde estaría la humanidad dentro de cinco mil años ―algo que, a día de hoy, no sé si querríamos saber―, el primer problema que se encontraron los ingenieros de la Westinghouse era construir algo capaz de perdurar durante todo ese tiempo, empezando por el propio recipiente que conformaría la cápsula. Como mínimo, tenía que estar hecho de un material duro y ser resistente a la corrosión. La solución vino de la mano de uno de los primeros metales que utilizó el ser humano para fabricar utensilios y herramientas: el cobre.
Para construir la cápsula se utilizó cupaloy, una aleación compuesta por un 99,4 % de cobre, un 0,5 % de cromo y un 0,1 % de plata, dura como el acero y resistente a la corrosión incluso en agua salada. Tenía forma de torpedo y un tamaño de 16, 5 cm de diámetro, 205,7 cm de longitud, con paredes de un grosor de 2,54 cm. En su interior había un recipiente sellado de Pyrex, en el que se introdujeron los objetos.
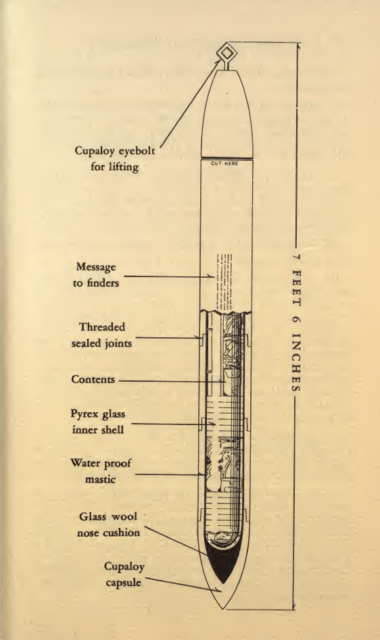 Esquema de la cápsula que aparece en The story of the Westinghouse time capsule. Fuente: Westinghouse Electric & Manufacturing Company
Esquema de la cápsula que aparece en The story of the Westinghouse time capsule. Fuente: Westinghouse Electric & Manufacturing Company
Pero ¿qué objetos? Elegir qué dejar para la posteridad supuso un trabajo aún más arduo que el de ingeniería. ¿Qué era lo más representativo de la sociedad de 1939 o aquello que más podría interesar a los habitantes del futuro? El Comité de la Cápsula del Tiempo consultó con arqueólogos, historiadores, autoridades científicas y expertos del mundo del arte. Y, aunque en aquel momento el sesgo en la elección del contenido fue más que evidente, finalmente se introdujeron treinta y cinco objetos de uso común ―un despertador, una pluma, una cámara de fotos en miniatura, un cepillo de dientes, una cinta métrica, un sombrero de mujer…―, setenta y cinco muestras de diversos materiales ―metales, aleaciones, plásticos, algún mineral…―, algunas semillas selladas en recipientes especiales, y de una gran cantidad de información y documentación en forma de microfilm ―libros, periódicos, revistas, fotografías…―. Se tuvo especial cuidado en no introducir compuestos volátiles u objetos que pudieran descomponerse y se evitaron los líquidos.
 Existe una réplica de la cápsula del tiempo de 1939 en el Heinz Story Center de Pittsburg, ciudad en la que George Westinghouse estableció su compañía
Existe una réplica de la cápsula del tiempo de 1939 en el Heinz Story Center de Pittsburg, ciudad en la que George Westinghouse estableció su compañía
Todo ello se introdujo en la cápsula en presencia de tres notarios, con los objetos más pesados en el fondo sobre un lecho aislante de lana de vidrio ―material fabricado con fibra de vidrio, que también se utilizó para rellenar los huecos que quedaron―, ya que la cápsula se enterró de forma vertical. Encima, en la zona central, iban los microfilms y arriba del todo los objetos ligeros. El cilindro interior de Pyrex se selló, se le extrajo el aire, se rellenó con nitrógeno y se introdujo en la carcasa de cupaloy. Se puso todo el cuidado posible en que, cualquier que desenterrara la cápsula, si algún día lo hacía, encontrara todo lo que había en su interior intacto.
 Personal de la Westinghouse Electric & Manufacturing Company preparando la cápsula del tiempo.
Personal de la Westinghouse Electric & Manufacturing Company preparando la cápsula del tiempo.
El enterramiento de la cápsula del tiempo tuvo lugar el 23 de septiembre de 1938, durante el equinoccio de otoño y unos meses antes de la inauguración de la Feria de Nueva York ―el 30 de abril de 1939―, en las inmediaciones del que sería el pabellón Westinghouse.
 Dibujo del pabellón Westinghouse en la Feria de Nueva York de 1939. La cápsula del tiempo se enterró justo delante, a algo más de 150 m de profundidad.
Dibujo del pabellón Westinghouse en la Feria de Nueva York de 1939. La cápsula del tiempo se enterró justo delante, a algo más de 150 m de profundidad.
En este metraje de archivo de la época se puede observar un breve resumen de todo el proceso y el día del enterramiento.
Casi un siglo después, el pabellón Westinghouse que se construyó para quella feria no existe, pero la cápsula sigue allí, señalizada. No solo eso; como con todo lo demás, la compañía eléctrica procuró asegurarse de que algún día alguien la encontraría y para ello creó 3650 copias del Book of record of the time capsule, una guía impresa ―en dos tipos distintos de papel y con tintas especiales― que se distribuyó a bibliotecas, museos, monasterios… de todo el mundo. Un mensaje para el futuro con la localización exacta, el contenido de la cápsula e instrucciones tanto para encontrarla como para interpretar y entender su contenido. También incluyeron tres breves cartas de tres hombres relevantes de la época para las gentes del futuro: los físicos Albert Einstein y Robert Millikan, y el escritor Thomas Mann.
 Mensaje de Albert Einstein para los seres humanos del futuro tal y como aparece en el Book of record of the time capsule, en alemán y traducido al inglés.
Mensaje de Albert Einstein para los seres humanos del futuro tal y como aparece en el Book of record of the time capsule, en alemán y traducido al inglés.
La carcasa llevaba, además, la siguiente inscripción grabada en el exterior, en letras mayúsculas:1
CÁPSULA DEL TIEMPO DE CUPALOY, DEPOSITADA EN LA LOCALIZACIÓN DE LA FERIA MUNDIAL DE NUEVA YORK EL 23 DE SEPTIEMBRE DE 1938 POR LA COMPAÑÍA WESTINGHOUSE ELECTRIC & MANUFACTURING. SI ALGUIEN ENCONTRARA ESTA CÁPSULA ANTES DEL AÑO 6939 D. C., QUE NO LA ALTERE INNECESARIAMENTE, PUES HACERLO IMPLICARÍA PRIVAR A LA GENTE DE ESA ERA DEL LEGADO AQUÍ DEJADO. CONSÉRVENLA, POR LO TANTO, EN UN LUGAR SEGURO.
Una cápsula del tiempo del año 1938 es algo muy parecido al disco dorado de las Voyager enviado al espacio en 1977, poco más que un acto simbólico y un reflejo de los anhelos más optimistas de una época, que se vieron reflejados en el documental The Middelton Family al the New York World’s Fair, donde se mostraban las maravillas que podían encontrarse allí.
La feria universal volvió a Nueva York en 1964, y la Westinghouse Electric & Manufacturing Company volvió a hacerlo: creo una segunda cápsula del tiempo que enteró unos tres metros al norte de la primera. Construida de Kromarc ―una aleación de hierro, níquel, cromo, manganeso, molibdeno y trazas de otros elementos― y rellenada con argón, fue la demostración de que, a medida que pasa el tiempo, también evoluciona la tecnología… y cambia el legado que queremos dejar.
 Contenido de la cápsula del tiempo de 1964. Fuente: Westinghouse Electric & Manufacturing Company
Contenido de la cápsula del tiempo de 1964. Fuente: Westinghouse Electric & Manufacturing Company
No puedo evitar, para terminar, dejar un par de crossovers: fue en la Feria de Nueva York de 1939 en la que Isaac Asimov tuvo su primera cita con una chica, mientras que Arthur C. Clarke y Carl Sagan estuvieron visitando juntos la de 1964. Así que tal vez estas cápsulas inspiraron, en algún momento, su imaginación.
 Un hito de piedra marca el lugar donde están enterradas las dos cápsulas del tiempo Westinghouse, en el parque de Flushing Meadows, al norte de Queen, en Nueva York. Por su localización, es probable que la zona acabe inundada con la subida del nivel del mar. Fuente: CC BY 2.0/Gary Dunaier
Un hito de piedra marca el lugar donde están enterradas las dos cápsulas del tiempo Westinghouse, en el parque de Flushing Meadows, al norte de Queen, en Nueva York. Por su localización, es probable que la zona acabe inundada con la subida del nivel del mar. Fuente: CC BY 2.0/Gary Dunaier
Bibliografía
Westinghouse Electric & Manufacturing Company (1938). The book of record of the time capsule of cupaloy, Westinghouse Electric & Manufacturing Company.
Westinghouse Electric & Manufacturing Company (1939). The story of the Westinghouse time capsule, Westinghouse Electric & Manufacturing Company.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
Nota:
1 Traducción de la autora.
El artículo Un mensaje para el futuro: las cápsulas del tiempo de la Westinghouse Electric se ha escrito en Cuaderno de Cultura Científica.

