La Formación Jaizkibel y sus singulares geoformas “de Möbius”
El monte Jaizkibel se alza sobre las ciudades de Fuenterrabía, Irún, Pasajes, Rentería y Lezo (Guipúzcoa, País Vasco). Posee unos afloramientos rocosos –áreas en las que el terreno está formado por capas de rocas sin vegetación– en su parte más oriental, zona conocida como Formación Jaizkibel (edad Eoceno).
En la serie de artículos [1] a [3], el equipo de Carlos Galán del Laboratorio de Bioespeleología de la Sociedad de Ciencias Aranzadi estudia ciertas geoformas situadas sobre un conjunto de escarpes de arenisca en la Formación Jaizkibel. Esas geoformas incluyen –según se enumera en [3]– boxworks, cintas perforadas, bandas de Moebius, formas residuales de disolución, estructuras de corriente, nódulos, láminas e inclusiones ferruginosas, figuras de intercepción y anillos de Liesegang.
Aunque mis conocimientos de geología son nulos, cuando un compañero geólogo me comentó la inclusión de bandas de Moebius en la descripción de la Formación Jaizkibel, me animé a buscar estas superficies en los artículos de Carlos Galán y su equipo.
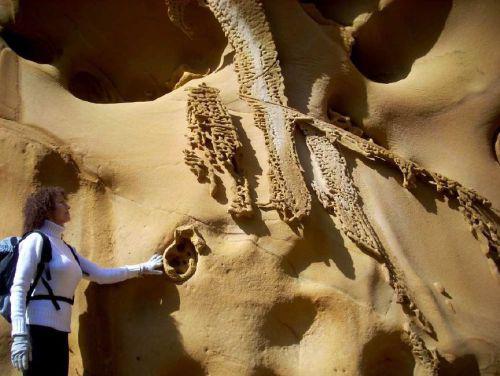
Extraído de [3], figura 12, pág. 17: “Detalle de bandas de Moebius, que extienden sus paradójicas estructuras siguiendo la curvatura de las paredes arenizadas.”
En [2], los autores describen las geoformas que denominan ‘bandas de Moebius’ del siguiente modo:
La formación de patrones en forma de cintas o bandas adquiere su más extravagante expresión en las geoformas que hemos denominado informalmente “bandas de Moebius”. Estas se encuentran en paredes de abrigos y cuevas en avanzado estado de arenización. Forman bandas delgadas que destacan de la roca en relieve positivo con un perfil en T: el trazo superior de la T forma una banda separada paralela a la superficie de la pared y el trazo vertical sirve de unión entre la banda y la pared de roca. La banda en sí está perforada por alveolos, sobre todo en sus bordes externos, que resultan recortados por muescas. Las bandas de este tipo pueden tener desarrollos sinuosos, de varios metros, siguiendo la curvatura de las paredes de las cavidades, por lo que en ocasiones recuerdan el desarrollo sin fin de la figura matemática llamada banda de Moebius. Aunque predominan las bandas verticales o que siguen la línea de mayor pendiente, las hay oblicuas y entrelazadas.

Extraído del artículo [1], figura 5, pág. 7: “Bandas de Moebius. Nótese sus etéreas y paradójicas estructuras”.
Tras la descripción de estas geoformas, los autores incluyen un párrafo en el que citan algunas características de la banda de Möbius: es una superficie no orientable, sólo posee una cara, tiene un único borde y es una superficie reglada. Explican también como puede construirse pegando dos lados opuestos de una cinta de papel tras un giro de 180 grados; incluso comentan qué sucede si se corta una banda de Möbius longitudinalmente:
Si se corta una cinta de Moebius a lo largo, a diferencia de una cinta normal, no se obtienen dos bandas, sino una banda más larga pero con dos vueltas. Si a ésta banda se la vuelve a cortar a lo largo, se obtienen otras dos bandas entrelazadas pero con vueltas. A medida que se va cortando a lo largo de cada una, se siguen obteniendo más bandas entrelazadas.
Recordemos que la anterior propiedad es solo cierta si se corta la banda de Möbius longitudinalmente por la altura mitad. En la anterior descripción, esa banda más larga obtenida con dos vueltas es (homeomorfa a) un cilindro –lo que llaman una “cinta normal”–, por ello, al volver a cortarlo por la mitad longitudinalmente, se obtienen dos cilindros, pero enlazados. Al repetir la operación se van duplicando los cilindros, que se entrelazan por parejas y entre ellos.
En este párrafo, los autores también comentan que la banda de Möbius ha servido de inspiración en el mundo del arte, nombrando la película argentina Moebius basada en el cuento Un metropolitano llamado Moebius del astrónomo y escritor Armin Joseph Deutsch.
La descripción de esta serie de propiedades de la banda de Möbius, es un modo de justificar la elección del nombre de estas geoformas, al finalizar esta parte del artículo con esta afirmación:
Aspectos y caracteres paradójicos análogos los presentan las geoformas halladas en Jaizkibel
La metáfora de la banda de Möbius –aunque estas formaciones no lo sean en realidad– es una deliciosa manera de hablar de estas geoformas que, sin lugar a dudas, son bellas, singulares y sorprendentes… como una banda de Möbius.
Más información
[1] Carlos Galán y Marian Nieto, Bandas de Moebius, Boxworks y otras raras Geoformas en arenisca de la Formación Jaizkibel, Sociedad de Ciencias Aranzadi, 2010
[2] Carlos Galán y Marian Nieto, Bandas de Moebius, Boxworks y otras raras Geoformas en arenisca de la Formación Jaizkibel, Boletín Sedeck (Sociedad Española de Espeleología y Ciencias del Karst) 8, 20-41, 2012
[3] Carlos Galán, José Manuel Rivas, Robert Ionescu y Marian Nieto, Disolución intergranular y evolución de cuevas y geoformas: los ejemplos más extravagantes del mundo en erenisca de edad eoceno (Formación Jaizkibel, País Vasco), Sociedad de Ciencias Aranzadi, 2013
[4] Marta Macho Stadler, Las bandas de Möbius de Jaizkibel, ZTFNews.org, 11 marzo 2014
Nota: Muchas gracias a Carlos Galán por permitir utilizar las imágenes incluidas en sus artículos.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo La Formación Jaizkibel y sus singulares geoformas “de Möbius” se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Poesía retorcida sobre banda de Möbius
- Una visión topológica de la Odisea
- Una hipernova en los confines del Universo apuntala el modelo de formación de los agujeros negros
Catástrofe Ultravioleta #14 VULCANO

Catástrofe Ultravioleta #14 VULCANO
Hoy es un buen día para conocer la furia de nuestro planeta. Hablamos de volcanes, terremotos y tsunamis. Vuelve el podcast más catastrófico y en este segundo capítulo de la segunda temporada seguimos los pasos de los vulcanólogos más atrevidos.
Agradecimientos: A todo el equipo de Involcan, David Calvo, Pedro Antonio Hernández y Nemesio Pérez. Ricardo Ramallo de la Universidad de Lisboa y a todos los que habéis hecho posible, con vuestro apoyo, que Catástrofe Ultravioleta regrese.
* Catástrofe Ultravioleta es un proyecto realizado por Javier Peláez (@Irreductible) y Antonio Martínez Ron (@aberron) con el apoyo de la Cátedra de Cultura Científica de la Universidad del País Vasco y la Fundación Euskampus. La edición, música y ambientación obra de Javi Álvarez y han sido compuestas expresamente para cada capítulo.
Puedes conocernos en nuestra web: Catastrofeultravioleta.com y seguirnos en el twitter Catastrofe_UV. También puedes encontrar todos los capítulos en este enlace.
El artículo Catástrofe Ultravioleta #14 VULCANO se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Catástrofe Ultravioleta #13 LEVIATÁN
- Catástrofe Ultravioleta #10 – Hipnosis
- Catástrofe Ultravioleta #12 – Vermilingua
Las simplificaciones de Agricola
Si el libro de Biringuccio se considera habitualmente como el primer libro impreso sobre metalurgia y química metalúrgica, el que dejó listo para la imprenta a expensas de unos cuantos grabados Georg Pawer (Georgius Agricola) y que se publicó un año después de su muerte en 1555, De re metallica, se convirtió en el estándar de la geología y la mineralogía durante los siglos siguientes.

Georgius Agricola (Georg Pawer)
Si bien es evidente que Pawer conocía el trabajo de Biringuccio y, de hecho, copia algunos pasajes de él, su obra se basa mayoritariamente en la experimentación y observación personales.

Uno de los motivos por lo que se convirtió en la obra de referencia durante el siglo siguiente es porque incluía descripciones e instrucciones muy claras y concretas que eran de enorme ayuda a una incipiente industria química.

De re metallica consta de 12 libros (lo que hoy llamaríamos capítulos) sobre minería, metalurgia y geología y está magníficamente ilustrado con grabados diseñados para ser útiles al lector (quien esto escribe no ha podido resistirse a la tentación de ilustrar también profusamente este texto sobre él).


Pawer trata de la geología de las menas, de prospecciones, de construcción de minas, del uso de bombas de agua, de cómo asegurar la ventilación de las galerías de trabajo y de como usar máquinas hidráulicas para obtener energía.

Describe los ensayos de riqueza y aquilatado, como enriquecer las menas antes de la fundirlas y los procedimientos de fundición y refinado. También trata de la producción de vidrio y del uso de distintos compuestos químicos en las operaciones de fundición.

Pawer incluyó algunos apuntes de teoría química, pero son muy pragmáticos. Queda claro en todo el libro que Agricola era un escéptico de la transmutación y que no veía con buenos ojos a Paracelso.

El libro sirvió tanto de libro de texto como manual en minas y refinerías durante 200 años. A principios del siglo XX aún aparecían nuevas traducciones. Como anécdota, en 1912 el que sería presidente de los Estados Unidos Herbert Hoover, ingeniero de minas, y su mujer Lou Henry, lingüista, presentaron una nueva traducción al inglés.
Si bien, y a diferencia de Biringuccio, Pawer opta por el latín como lengua vehicular, lo que también explica la rápida difusión de la obra en la época, no por ello deja de ser un innovador en términos lingüísticos. Y, paradójicamente, el hecho de que escriba en latín tendrá una enorme influencia en las lenguas modernas.
Efectivamente, Agricola incluye muchas simplificaciones en los términos empleados. Emplea términos nuevos, “chymista”, “chymicus”, aunque queda claro por el contexto que se refiere a la alquimia, las técnicas alquímicas y a los alquimistas. Estaba, en la tradición renacentista de la época, volver a los clásicos, lo que en este caso significaba desarabizar los términos y dejarlos en sus raíces latinas y griegas.

Las simplificaciones de Agricola son adoptadas por el diccionario de latín del naturalista Conrad Gesner, quien también las emplea, y esto es más importante, en su libro Thesaurus Euonymi Philiatri de remediis secretis: liber physicus, medicus et partim etiam chymicus de 1552. Será este libro de química farmacéutica popularísimo y ampliamente traducido el que obligue a que aparezcan nuevos términos en las lenguas vernáculas: chimique, chimico, chymiste, chimist, etc.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Las simplificaciones de Agricola se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Biringuccio, la química práctica y rentable del XVI
- La diferencia de potencial eléctrico
- De los iones
Historias de la malaria: El charlatán y caballero Sir Robert Talbor
Al principio, hasta el Renacimiento, eran las fiebres y, después y a la vez, según el lugar, era la malaria o el paludismo. No tenía cura y las mezclas para aliviar las fiebres, hasta el siglo XVII, eran variadas, extrañas, bárbaras y hasta milagrosas. Entonces llegó de Sudamérica, a través de los jesuitas y del Vaticano, el remedio indígena para las fiebres. Era la corteza del árbol de la quina, los llamados “polvos de los jesuitas” o “polvos de la condesa”, por la intervención que tuvo, quizá, la Condesa de Chinchón, esposa del Virrey del Perú, en su llegada a Europa. Pero la medicina oficial tardó dos siglos en aceptar el remedio americano. Lo habitual entonces era purgar y sangrar al enfermo.

La marisma Bowers, al sur de Essex (Inglaterra)
En Inglaterra y hacia 1650, la malaria era una enfermedad endémica en las tierras bajas de sudeste, cerca de Londres. Por esos años llegó a Inglaterra la corteza de la quina. Se publicaron panfletos sobre su eficacia y aparecieron anuncios en los periódicos para su venta. El remedio lo aprobó el Colegio de Médicos pero, cuando enfermó un regidor de Londres, no lo alivió y el paciente murió. Fue un caso muy conocido y supuso un duro golpe para el uso generalizado de la quina.
Por aquellos años, Oliver Cromwell derrocó al rey y se nombró Lord Protector. Era un protestante fanático y cuando, en 1658, enfermó de malaria se negó a tomar la corteza de la quina por considerarlo un remedio papista. Murió en septiembre de ese año.
Pasaron otros diez años y, entonces, de Essex llegaron a Londres noticias extraordinarias sobre la cura de la malaria. Un hombre llamado Robert Talbor o Tabor o Tabord o Talbot, que se movía por las marismas de Essex, vendía una cura infalible para las fiebres, para las “agues”, como las llamaban en Inglaterra.
Había nacido en Ely, al norte de Cambridge, en 1642 y era hijo del archivero del obispo de Ely y nieto del archivero de la Universidad de Cambridge. Pasó por la escuela, fue aprendiz de boticario, de mancebo de farmacia diríamos ahora, y entró de becario en el St. John’s College en 1663, a los 20 años. Su objetivo era ya, a esa edad, estudiar y curar las fiebres. Pero abandonó sus estudios en 1668, sin graduarse, y marchó a las marismas de Essex para vivir, escribió más adelante, “cerca del mar, donde las fiebres eran un mal epidémico”. Su objetivo declarado era aliviar a los enfermos con “agues”.
De pueblo en pueblo, en las marismas de Essex, Talbor prepara y vende su remedio, ensaya y cura y, por fin, encuentra lo que suaviza las fiebres de los enfermos. Pero mantiene la composición en secreto. Solo él la conoce y fabrica el remedio en soledad. En su libro “Pyretologia”, poco más que un panfleto de unas 60 páginas publicado en 1672, describe cómo se administra a los enfermos y revela que, en su composición, entran cuatro plantas y, de ellas, dos son del país y las otras viene de fuera. Y sobre el “polvo de los jesuitas” advierte que “hay que aconsejar a todo el mundo que tenga cuidado con todas las curaciones paliativas y, especialmente, el que se conoce con el nombre de Polvo de los Jesuitas… porque he visto que los efectos más peligrosos siguen a tomar el medicamento sin corregir y no estar preparado… pero es una medicina noble y segura si está preparada con razón y corregida y administrada por mano hábil”. O sea, por su mano, la mano de Robert Talbor. Está protegiendo su posición de curador eficaz y seguro.
No se conoció la fórmula del remedio hasta después de la muerte de Talbor, en 1682, después de viajes, aventuras y curaciones de nuestro buhonero y buen curador de Essex, que voy a relatar a continuación.
Mientras todavía estaba en los pantanos de Essex, Talbor tuvo la oportunidad de curar a un oficial del ejército francés, entonces aliados de Inglaterra en la guerra contra Holanda, que había contraído las fiebres en las marismas holandesas. Según declaró el oficial francés, Talbor le daba su remedio tres veces al día y era “polvo de los jesuitas” disuelto en vino blanco, agua y, a veces, añadía opio.
Poco después llegó el rey de Inglaterra, Carlos II, a Essex en el barco real para visitar a las tropas. El oficial francés se presentó al rey de sus aliados y, entre otras cosas, le contó la historia de su curación de las fiebres por el buhonero Robert Talbor.
El rey le llamó y ordenó a la Royal Society que experimentara con el remedio de Talbor. Los resultados impresionaron a Carlos II que incluyó a Talbor entre los médicos que le atendían y unos años más tarde le nombró caballero. Ya era Sir Robert Talbor. En 1679 el mismo rey contrajo las fiebres y nuestro caballero le curó. A pesar de todo, el Colegio de Médicos de Inglaterra le consideraba un charlatán incompetente.

María Luisa de Orleans, futura reina consorte de España, alrededor de 1678
El rey lo envió a París, con cartas de presentación para el Cardenal Mazarino, a curar de las fiebres a su sobrina María Luisa, y la acompañó a España, hasta Madrid, a su boda con Carlos II de España. Ya había curado al rey de Inglaterra y a la reina de España. Vuelve a París, atiende a La Rochefoucauld, pero no consigue aliviarle y el famoso noble, militar y escritor fallece. Sin embargo, tenía a su favor a la influyente Madame de Sévigné, que escribía y difundía todos sus triunfos.

Luis de Francia, el Gran Delfín
Alcanzaría el mayor éxito de su carrera cuando curó al Delfín, heredero del trono de Francia y el único hijo varón vivo de Luis XIV. Le atendió en 1680 y mejoró, recayó en las fiebres y volvió a curarle. Durante el proceso de cura, Luis XIV le ordenó que preparara su remedio siempre en su presencia. Se adivina que no se fiaba de nadie.
Un año después regresó a Inglaterra y, poco después, murió en 1681 a los 39 años. Luis XIV había comprado la fórmula de su remedio por un buen precio pero prometió que no se haría pública hasta después de la muerte de Tabor. Por cierto, Luis XIV le pagó 3000 luises de oro y una pensión para toda la vida.

En 1681 se publicó en Paris un panfleto con el título “El conocimiento cierto y la rápida y fácil curación de las fiebres, con particularidades curiosas y útiles del remedio inglés, que ha sido publicado por orden del Rey”. Al año siguiente se publicó la traducción en inglés, con parte del texto escrito por el propio Talbor antes de morir.
Algún cronista anónimo francés que conoció a Talbor escribió que “era muy ignorante, pero tan dedicado a su proyecto que se había trasladado a un distrito insano para ensayar y mejorar su remedio”. Incluso le acusaron de no saber leer y escribir en latín, algo obligatorio para los médicos de la época. Cuando los médicos de la corte de Luis XIV le acusaron de ignorar la causa de las fiebres, Talbor respondió que “no pretendía saber nada de las fiebres excepto que es una enfermedad que todos ustedes no saben curar, y que yo curo infaliblemente”.
El secreto de su remedio, del “remedio inglés” como se le conocía, era la repetición de las dosis, tal como relató el oficial francés curado en Essex, y, además, no purgaba ni sangraba a sus pacientes, según el tratamiento de los médicos de entonces, que conseguía debilitar todavía más a los enfermos. En su composición estaba la corteza de quina, molida hasta conseguir un polvo muy fino, disuelto en vino blanco y aromatizado con hierbas y flores como pétalos de rosas rojas, zumo de limón, genciana, serpentaria, perifollo, perejil, anís, ajenjo,…, aunque cambiaba la composición cuando lo consideraba oportuno sin dar razones para ello. Lo esencial eran los polvos de la quina y el vino y el resto era para mejorar el sabor, muy amargo, y facilitar la toma de las dosis por el enfermo.

Luis XIV de Francia, el rey Sol
Y, para terminar, Talbor era también un buen negociante pues, en Francia, y con el dinero que obtenía de Luis XIV compró toda la corteza de quina que encontró. Quería conseguir el monopolio de su “remedio inglés” pero, a al vez, Luis XIV, que ya tenía la fórmula del remedio, hacía lo mismo pero, claro está, a nivel de un gobierno poderoso. Incluso desapareció un barco español que venía de Sudamérica cargado por completo de corteza y, no está claro cómo ocurrió, pero esa quina apareció en los almacenes del rey. Entre Talbor y Luis XIV, consiguieron que el precio de la corteza se multiplicara hasta extremos escandalosos y, en muchos años, solo la podían adquirir nobles y aristócratas y, sobre todo, personas de gran fortuna.
Y esta es la historia de Robert Talbor, buhonero, charlatán, curador y caballero, que hizo fortuna curando las fiebres y que difundió por Europa el uso de la corteza de la quina para aliviar la malaria.
Referencias:
Dobson, M.J. 1998. Bitter-sweet solutions for malaria: exploring natural remedies from the past. Parassitologia 40: 69-81.
Dock, G. 1922. Robert Talbor, Madame de Sévigné, and the introduction of Cinchona. An apisode illustrating the influence of women in medicine. Annals of Medical History 4: 241-247.
Keeble, T.W. 1997. A cure for the ague: the contribution of Robert Talbor (1642-1681). Journal of the Royal Society of Medicine 90: 285-290.
Siegel, R.E. & F.N.L. Poynter. 1962. Robert Talbor, Charles II, and Cinchona. A contemporary document. Medical History 6: 82-85.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Historias de la malaria: El charlatán y caballero Sir Robert Talbor se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Historias de la malaria: El árbol de la quina
- La paradoja del caballero hospitalario
- Entrevista a Tim Hunt por Robert Kypka
Cómo mecanizar una pieza de cobre usando bacterias

Acidithiobacillus ferrooxidans
Luis Gurtubay, Norberto López de Lacalle, Ana Elías, Adrián Rodríguez y Estibaliz Díaz-Tena, profesores e investigadores de la Escuela de Ingeniería de Bilbao de la UPV/EHU, han patentado un método (‘Procedimiento continuo de biomecanizado de una pieza de cobre’) para mecanizar piezas de cobre utilizando la bacteria Acidithiobacillus ferrooxidans.
El mecanizado es el conjunto de operaciones mediante el cual partiendo de una pieza en bruto, y tras eliminar parte del material que la compone, se obtiene una pieza de la forma y dimensiones deseadas. Es un proceso muy común en la industria.
La investigación que ha finalizado en una patente la iniciaron miembros de los departamentos de Ingeniería Mecánica y Química y del Medio Ambiente, llevando a cabo un proyecto innovador que buscaba mecanizar piezas de cobre en presencia de microorganismos. Lo que empezó como una primera idea generó una extensa línea de trabajo, gracias a la cual Estibaliz Díaz-Tena realizó su tesis doctoral internacional ‘Biomachining of oxygen-free copper: development of a continuous process for industrial application’.
La propia Díaz-Tena explica en este video el procedimiento continuo de biomecanizado de una pieza de cobre, base de la patente.
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Cómo mecanizar una pieza de cobre usando bacterias se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cómo determinar la estructura secundaria de las proteínas usando nanoespectroscopía
- Descubierto el proceso por el que las bacterias fabrican nanoimanes
- Una fuente de radiación terahertz usando grafeno
Festín burlesco, una visita al alma del museo
El primer museo que os vendrá a la cabeza al oír Bilbao será posiblemente el Guggenheim. Sin embargo, muchos años antes de que Frank Gehry levantase su primer castillo de arena, ya existía en la capital vizcaína un grandioso templo dedicado al arte. Un museo que aún sigue deleitando a los habitantes y visitantes de la villa. Me refiero, como no, al Museo de Bellas Artes de Bilbao, cuyas obras de Ribera, Goya o El Greco conviven en perfecta armonía con las más recientes creaciones de Bacon, Tapies, Chillida o Basterretxea.
Todas estas obras, independientemente de su edad, tienen algo en común: necesitan que las cuiden. Con contadas excepciones las pinturas y las esculturas nacen con la ambición de ser eternas, pero el paso del tiempo no perdona y factores como la luz o la humedad van haciendo mella en ellas. Afortunadamente hay personas que velan para que nuestro patrimonio artístico aguante los envites del día a día. Personas que, cuando eso no es suficiente, pasan a la acción para realizar limpiezas o restauraciones que devuelvan a la obra su belleza original. Como todo gran museo que se precie, el Museo de Bellas Artes de Bilbao cuenta con un grupo de profesionales que se dedica a estas labores. En el subsuelo del edificio, rodeados de cuadros, marcos, radiografías, productos químicos y diversos instrumentos, trabajan para que podamos disfrutar de la magia del arte.
Quien escribe tiene el placer de poder curiosear en ese lugar de tanto en tanto y en esta ocasión me gustaría invitaros a sumergiros en ese mundo. Pero antes de emprender este viaje os presento a nuestro peculiar acompañante de viaje: el recién restaurado Festín burlesco.

Festín burlesco (99×147 cm) de Jan Mandijn (ca. 1550). Fuente: Gentileza del Museo de Bellas Artes de Bilbao.
Resulta que nuestro compañero es un cuadro muy reservado y rehúsa darnos cualquier tipo de información. Ni sobre su edad (quizás porque tiene casi 500 años), ni sobre sus progenitores, ni sobre su ajetreada vida anterior. Así que, para conocerlo mejor, la gente del museo tuvo que realizar una detallada labor de investigación. Gracias a ello sabemos que perteneció al Marqués de Leganés quien desde su posición de poder se hizo con una colección que era la envidia de media Europa allá por los años en que la Corona Española era una potencia mundial. Por aquel entonces se creía que El Festín había salido de los pinceles de El Bosco, lo que nos da una idea del valor artístico de la pieza. Posteriormente se desechó esa idea para atribuirle la creación a otro gran genio: Brueghel el Viejo. Aunque, ya en 1923, Max Friedlander, gran estudioso del arte flamenco, concedió su paternidad a un pintor de una fama algo menor como es Jan Mandijn. La destreza de este artista queda de manifiesto si tenemos en cuenta que la pieza ha sido atribuida a dos de los más grandes maestros de la historia del arte.
Hagamos ahora labores de paparazzi artísticos para conocer un poco mejor la vida privada de nuestro protagonista. En la Imagen 2 lo podéis ver en la primera fotografía de la que se tiene constancia, cuando formaba parte de la colección del Marqués de Salamanca. La otra fotografía se tomó algunos años más tarde en la mansión de Laureano de Jado donde ocupaba un lugar preferente.

A la izquierda, el Festín burlesco en la casa del marqués de Salamanca (ca. 1875), a la derecha en la de Laureano de Jado (1919). Fuente: Gentileza del Museo de Bellas Artes de Bilbao.
Fue precisamente Laureano de Jado, gran impulsor y benefactor del museo bilbaíno, quien donó la obra en cuestión para que durante los primeros años presidiese la sala que llevaba su apellido (Imagen 3, ¿alguien dijo horror vacui?).

[El Festín burlesco en la sala Jado (1927). Fuente: Gentileza del Museo de Bellas Artes de Bilbao.
Claro que, tras tantos años y vaivenes, nuestro vetusto acompañante se fue deteriorando y es por eso que en 2015 el museo tomó la decisión de llevar a cabo una restauración de la obra (previamente el museo había realizado otra restauración en 1984). Es aquí donde vuelve a entrar en acción el equipo de conservación y restauración para decidir, tras un meticuloso estudio técnico, cuál es el procedimiento que se debe seguir.
El festín es un óleo sobre tabla o, mejor dicho, sobre tablas, ya que por exigencias del tamaño se tuvieron que unir tres paneles (uno de los inconvenientes de no tener secuoyas en Europa). De ello dan buena fe las dos uniones (a madera viva) que se aprecian en la fotografía ultravioleta de la Imagen 4. Si vemos la obra por detrás también podemos observar el engatillado del s. XIX que sirve para reforzar la unión. Los paneles empleados son de roble primerísima calidad, como corresponde a los gremios flamencos de la época, y tuvieron un secado adecuado que ha permitido que lleguen a nuestros días en excelentes condiciones.

Izquierda, fotografía ultravioleta donde se pueden apreciar las uniones entre tablas (flechas). Derecha, engatillado de la obra que se puede observar por la parte trasera. Fuente: Gentileza del Museo de Bellas Artes de Bilbao.
Sabemos ya que el soporte es de madera, pero recordemos que rara vez se trabaja sobre ella directamente. En las latitudes donde se realizó esta obra se cubría con una preparación blanca (una mezcla de carbonato cálcico y cola animal) sobre la que el pintor podía realizar el dibujo y después pintar. Los análisis realizados en esta obra han reflejado que la capa de preparación no supera la décima de centímetro, otra muestra más de la magnífica calidad del trabajo.
Pasemos ahora a conocer mejor cómo trabajó Jan Mandijn para crear esta obra maestra. Quienes hayáis seguido esta serie de artículos ya sabréis que los rayos X y la reflectografía infrarroja son una ayuda inestimable para lograr ese objetivo. Gracias a las imágenes en infrarrojo podemos atravesar las capas de pintura y ver el dibujo preparatorio creado por el artista en el que se aprecia perfectamente el trazo del pincel. Y, lo que es más interesante, podemos descubrir los cambios que fue realizando según avanzaba la composición. Obviamente, en una obra tan compleja y con tantísimos personajes hay una infinidad de detalles de los que podríamos hablar. Pero, como no tenemos todo el tiempo del mundo, me centraré tan solo en tres personajes. Empecemos por el hombre con pata de palo que lleva la bandeja (Imagen 5). La idea original de Mandjin era pintarle el cuchillo en el lado izquierdo agarrado a un cinturón mucho más caído, pero en última instancia le puso un accesorio mucho menos peligroso: una especie de espumadera. No perdáis la oportunidad de observar de nuevo la unión entre paneles que en la fotografía normal está oculta. ¿Y qué me decís del personaje que os muestro debajo? Sin duda el más peculiar de los que asiste a la decadente comilona. Un bufón con cuatro pies que lleva una escoba que le dobla en tamaño. En la imagen infrarroja se observa que el rostro de dicho ser iba a ser bien diferente (podéis ver que los ojos del dibujo subyacente no coinciden en absoluto con la imagen final).

Reflectografía infrarroja (izquierda) y en luz visible (derecha) que dejan en evidencia los cambios realizados en la composición de dos personajes del Festín burlesco. Fuente: Gentileza del Museo de Bellas Artes de Bilbao.
Acabamos este repaso por el infrarrojo con la zona donde está la viejecita del traje rojo (Imagen 6). Aquí también se puede observar que la idea original del pintor difiere mucho del resultado final (la vela, la salchicha, etc.). Si le dedicáis unos segundos a esta clase de “encuentra las siete diferencias”, descubriréis muchos otros cambios que el artista realizó.

Reflectografía infrarroja (izquierda) y en luz visible (derecha) de un detalle de Festín burlesco. Fuente: Gentileza del Museo de Bellas Artes de Bilbao.
Una vez realizado el estudio técnico y con la certeza de conocer el cuadro perfectamente, el equipo de restauración pasó a la acción y comenzó a recuperar la pieza. En la Imagen 7 os muestro cómo estaba la obra antes de pasar por sus manos. Si lo comparáis con la imagen con la que abría este artículo la diferencia es evidente. Se cambió incluso el marco por uno más acorde a la época en la que se realizó (el que observáis en esta imagen es de a época en la que perteneció a Jado). El trabajo consistió en dos fases: una primera limpieza acuosa para retirar partículas y materia soluble en agua y otra limpieza con disolventes orgánicos (etanol y white spirit) para eliminar el barniz oxidado que empañaba la belleza de la obra. Además, empleando sulfato de calcio y cola de conejo, se realizó un reintegración de la perdida que se había detectado en la ventana (se puede observar en la fotografía ultravioleta de la Imagen 4 perfectamente). Tras barnizar el cuadro de nuevo y esperar a que se secase, el Festín vuelve a mostrarse al público. No desaprovechéis la oportunidad de hacerle una visita y cuando lo hagáis, además de admirar el hermoso trabajo que realizó Jan Mandijn, tened en cuenta que luce así gracias al trabajo realizado por un gran equipo de profesionales.

Festín burlesco (99×147 cm) de Jan Mandijn (ca. 1550) previo a su restauración. Fuente: Gentileza del Museo de Bellas Artes de Bilbao.
Y no me gustaría acabar este artículo sin hablar un poco de la obra en sí. Porque, si bien es cierto que ha sido la protagonista de esta historia, bien poco hemos comentado el momento que describe. Así que os invito a que durante medio minuto paseéis vuestra mirada sobre esta especie de ¿Dónde está Wally? del siglo XVI. La escena es una boda campesina de estilo flamenco que, como ya habréis observado, está realizada de forma satírica con un sinfín de personajes de lo más caricaturesco. La novia viste una corona de cucharas y sobre ella se sitúa un cascabel, que se interpreta como un símbolo de la necedad. Toda la composición esta organizada para ridiculizar a la clase campesina por la cual la burguesía sentía un desprecio absoluto. Puede que fuese una forma de simbolizar en que acciones no deberían caer para no asemejarse a ese estrato de la sociedad.
Y si hay una boda, y una novia, ¿dónde está el novio? Esa es la pregunta del millón. Parece que las bodas campesinas no eran como las que conocemos ahora y el novio aparecía al final del banquete. Algo de lo que ha dado mucho que hablar en esta otra boda pintada por Brueghel. Pero, ¿si os digo que el novio puede ser una especie de fantasma? Si, como os pedía, habéis mirado con detalle la obra, habréis encontrado un personaje que resulta lo más enigmático de la escena. Allá, en la esquina derecha de la mesa ¡Hay un hombre que se desvanece! (Imagen 8). Pues bien, lo cierto es que está ocurriendo todo lo contrario. Mandijn lo pintó y posteriormente decidió ocultarlo bajo una capa de pintura. Esa capa está poco a poco desapareciendo y nuestro supuesto novio reaparece como si quisiese llegar al banquete, aunque sea con 500 años de retraso.

Detalle del festín burlesco donde se aprecia a un personaje que está volviendo a emerger. Fuente: Gentileza del Museo de Bellas Artes de Bilbao.
Agradecimientos: Me gustaría agradecer a Maria José Ruíz-Ozaita (Jefa del Departamento de Conservación y Restauración) y al resto de componentes del Departamento su total predisposición a compartir el trabajo que realizan. Del mismo modo quiero agradecer al Museo de Bellas Artes de Bilbao por ofrecerme acceso a las imágenes empleadas para la elaboración de este artículo.
Sobre el autor: Oskar González es profesor en la facultad de Ciencia y Tecnología y en la facultad de Bellas Artes de la UPV/EHU.
El artículo Festín burlesco, una visita al alma del museo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Retrospectiva de un cuadro: El festín de los dioses
- “Laboratorium”, el museo del Real Seminario de Bergara
- ¿De quién es esta obra?
#Naukas16 ¿Matemáticas o física?

La charla protesta de Clara Grima deriva en algo un poco diferente cuando el espontáneo Enrique F. Borja sube al escenario…
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo #Naukas16 ¿Matemáticas o física? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #Naukas16 Big Van Science
- #Naukas16 ¿Cómo saber si tu funeraria te estafa?
- #Naukas16 La ciencia de la pasión
Quiero ser como tú
“Yo soy el rey del jazz a gogó / el más mono rey del swing. / Más alto ya, no he de subir / y esto me hace sufrir. / Yo quiero ser hombre como tú / y en la ciudad gozar. / Como hombre yo quiero vivir, / ser tan mono me va a aburrir.
Ubidú, / quiero ser como tú, / quiero andar como tú, / hablar como tú, tú. / Por tu salud / dímelo a mí, / si el fuego aquí me lo traerías tú.”
Esta es parte de la letra de una de las canciones del conocido clásico de Disney El libro de la selva, en su versión en español del año 1967. Esta historia está basada en la colección de relatos The jungle book, del escritor británico Rudyard Kipling. Existe también una versión en imagen real del año 2016, en la que la letra ha sufrido variaciones, pero de ello hablaremos más adelante. Conocemos a los personajes de esta historia desde hace mucho tiempo, pero hoy no queremos hablar de Mowgly, Baloo o Bagheera, sino que nos centraremos en el carismático Rey Louie.

El famoso Rey Louie de la película clásica de Disney
“A mí no me engañas, Mowgli, / un trato hicimos yo y tú, / y dame luego / del hombre el fuego / para ser como tú. / Y dame el secreto, cachorro, dime / cómo debo hacer. / Dominar quiero el rojo fuego / para tener poder.”
El Rey Louie o King Louie en la versión original, era un orangután que ansiaba conseguir el fuego que los humanos dominaban y que se escapaba de su entendimiento. Para ello, no dudó en acosar a Mowgly para que le revelara el secreto. Cuando vemos a este simio en la película, claramente podemos apreciar que se trata de un macho de orangután, perteneciente al género Pongo. Los orangutanes son considerados como unos los primates de mayor tamaño e inteligencia de nuestro planeta, junto a gorilas, chimpancés y bonobos, además de nosotros mismos. De hecho, tras los gorilas, los orangutanes son los simios más grandes que existen actualmente en nuestro planeta.
También, a día de hoy, los orangutanes son una de las especies más amenazadas, tanto por la destrucción de su hábitat, como por la caza indiscriminada y el comercio ilegal de mascotas. Es por ello que existen programas de cría en cautividad y reintroducción, que están intentando por todos los medios evitar la extinción de estos animales. La labor y los esfuerzos de la primatóloga Biruté Galdikas en cuestiones de conservación de los orangutanes son fundamentales a este respecto.

Biruté Galdikas con un orangután
Lejos de ser tan estrambóticos como lo es Louie en la película, los orangutanes reales son tímidos y huidizos, y prefieren pasar desapercibidos entre la maleza, antes que ponerse a cantar y a bailar o a liderar una banda formada por un montón de simios de otras especies. Evidentemente tenemos que permitir esta licencia creativa, puesto que estamos ante una obra de ficción con animales humanizados, cuyo objetivo original es entretener y divertir, contando una historia, que ahora nosotros estamos aprovechando para hacer divulgación científica. Y lo de humanizar animales nos viene estupendamente para hablar del nombre vulgar de este simio, ya que la palabra orangután, deriva del malayo Orang Hutan, significa literalmente Hombre de la selva u Hombre del bosque, por su parecido con nuestra especie y por su notable inteligencia.
Su apariencia física es la de un hombre peludo y desgarbado, con los brazos muy largos y el pelaje rojizo-anaranjado; siendo sus manos, pies y cara de color gris oscuro. Sus piernas son cortas y arqueadas. Los machos también suelen tener pelo en la cara en forma de barba y bigotes, y presentan unas protuberancias adiposas a ambos lados de la cara, en las mejillas, que los diferencian notablemente de las hembras, siendo este dimorfismo sexual mucho más marcado cuanto más edad tiene el individuo, además de estar influenciado por otros factores: hormonales, comportamentales, presencia de otros machos, e incluso por el hecho de vivir en libertad o cautividad.
Existen dos especies de orangutanes en la actualidad, los orangutanes de Borneo, Pongo pygmaeus, que son los más comunes, y los orangutanes de Sumatra, Pongo abelii. Entre los primeros, el tamaño de los machos varía entre 1,4 y 1,6 m, aunque en cautividad pueden crecer mucho más, mientras que los machos de P. abelii miden entre 1,2 y 1,4 m. En ambos casos se trata de individuos corpulentos, que pueden llegar a pesar hasta 90 o 100 kg. Por buscar diferencias entre las dos especies, podemos generalizar que los de Sumatra son más delgados y con la cara más larga que los de Borneo.

Un impresionante macho de Pongo pygmaeus
Cuando escuchamos hablar al Rey Louie, nos imaginamos a un simio adulto, de cierta edad, más aún cuando llama constantemente Cachorro a Mowgly, por lo que deberíamos ver a un ejemplar corpulento y robusto, lo cual no coincide con Louie, que es más bien escuchumizado y pequeño. Incluso se le ve bajito al lado de Mowgly, que puede tener unos 10 años aproximadamente, y pensamos que una altura que ronda 1,30 m. Louie sobrepasa un poco el tamaño del niño, por lo que podría medir sobre 1,40 m. Tampoco se observan en este personaje las protuberancias adiposas de sus mejillas en su rostro, mas bien alargado. Por ello, podemos especular que se trata de un ejemplar joven y solitario de Pongo abelii, que no cuenta con un territorio propio entre otros orangutanes, y que busca la forma de hacerse más fuerte y poderoso, lo cual explicaría su obsesión por conseguir el fuego.

Un macho de Pongo abelii
En cuanto a la estructura social de los orangutanes, debemos mencionar que su estilo de vida es bastante solitario con respecto a otros grandes simios. Los machos están la mayor parte de su tiempo en soledad, mientras que las hembras si suelen tener vínculos con sus hijas, que permanecen más o menos en una zona cercana formando grupos poco cohesionados. Cada uno de estos grupos está liderado por un macho adulto que marca su territorio apareándose con el máximo posible de hembras, pero desentendiéndose de la crianza de los pequeños o la protección de las hembras, y viviendo de un modo bastante independiente. Cuando el alimento es abundante no hay problema en que varios grupos se congreguen para alimentarse y suelen ser bastante pacíficos entre ellos.
En cuanto a jerarquías, existe poca complejidad, y los machos con grandes mejillas suelen imponerse sobre los machos mas jóvenes que no las poseen. Aún así, los dominantes pueden tolerar la presencia de los no dominantes en su territorio, puesto que no les suponen una amenaza. Entre machos dominantes si se pueden producir enfrentamientos, que rara vez llegan a ser físicos y se quedan en amenazas, gritos y muestras de poder, por ejemplo inflando aún más sus caras.
Nos puede parecer raro el comportamiento de King Louie de querer obtener el fuego, pero esta conducta imitadora de los orangutanes no es nada extraña, más aún si tenemos en cuenta que la historia de El libro de la selva se desarrolla cerca de un pequeño poblado humano, como bien Mogwli comprueba cuando se encuentra con Shanti, la chica de la que se enamora.
No hace mucho se viralizó un vídeo en el que podíamos ver a una joven orangután fabricarse una hamaca, lo que probablemente haya hecho tras observar a sus cuidadores o a alguna otra persona hacerlo. ¿Y que podemos decir de este otro orangután imitando el silbido humano? Sencillamente espectacular. Ya no parece tan raro que a King Louie le gustara el jazz. En la naturaleza, los orangutanes salvajes incluso usan hojas para poder emitir diferentes silbidos y sonidos, y no es la única herramienta que parece que dominan. Pueden usar las hojas a modo de paragua, para beber agua o como toallitas limpiadoras, e incluso como guantes para sujetar frutos con espinas. Un palo delgado de madera puede servir para llevar a cabo su higiene, y tienen una gran destreza construyendo sus nidos de ramas y hojas a grandes alturas en los árboles, lo que también nos da una pista sobre la habilidad a la hora de montar la hamaca que hemos mencionado anteriormente.

Hembra de orangután con su cría en un nido encima de un árbol
Volviendo a la película de animación, ¿es normal el comportamiento de Louie viviendo en soledad? Ya hemos comentado antes que los machos de los orangutanes son bastante independientes y solo se buscan tener un amplio territorio que dominar para tener un mayor número de hembras a las que fecundar, de las que después se desentienden, por lo que, la hipótesis del macho joven cuadra perfectamente. Lo que no cuadra tanto es que comparta su vida con otros simios de otras especies, como podemos ver en el clásico de Disney. Este grupo de simios son llamados Bandar-log, la gente-mono, y también aparece en la versión de 2016, con muchos representantes distintos y más realistas.
Seguramente a estas alturas del post, algunos lectores, sobre todos aquellos que habéis visto las dos versiones de la historia a las que hemos hecho referencia, os habéis preguntado a que se debe el descomunal tamaño del King Louie de la película de 2016, porque no cuadra ni con el tamaño de un orangután normal, ni con el del personaje de los dibujos animados originales.

El impresionante nuevo King Louie
Las escenas de la película en la que aparece este enorme y nuevo Rey Louie son visualmente espectaculares, y el entorno en el que se desarrolla esa parte de la historia, con un templo en ruinas y cientos de simios de otras especies, como langures, gibones, macacos y monos Rhesus, ayuda a crear un espectáculo digno de ver en la gran pantalla. Yo mismo, al verlo por primera vez en el cine, pensé – ¿es posible que exista un orangután de tales proporciones? – Estamos hablando de un animal de más de tres metros de alto y con unos brazos larguísimos. Aunque desconocemos muchas de las maravillas que se esconden en el interior de las recónditas selvas de nuestro planeta, sería muy extraño encontrar semejante ejemplo de gigantismo. Pero tenemos una explicación plausible para explicar el tamaño de este nuevo Rey Louie, aunque para ello debemos fijarnos de nuevo en las letras finales de la canción “Quiero ser como tú”, reelaborada especialmente para este nuevo film:
“Aunque podrás pensar que es ridículo / que yo, un Gigantopithecus / me atreva a soñar / y quiera formar / equipo entre yo y tú. / Mas tendríamos poderes, / de la selva seríamos reyes. / Yo tengo un deseo: / tú el rojo fuego. / Ilumíname con tu luz / Pues tú, quiero ser como tú, / la llama yo prender / justo como lo haces tú / ¡Qué magnífico podría ser! / Un Gigantophithecus al fin / podrá aprender lo que haces tú.”
Los orangutanes son simios que habitan en las islas de Sumatra y de Borneo, como ha quedado claro por el nombre vulgar de las dos especies mencionadas anteriormente, pero no en la India, donde se ubica la selva de Sinaí, que es el lugar en el que se desarrolla la historia de El libro de la selva. De hecho, la propia compañía Disney, reconoció que Louie fue un añadido a la historia original de Kipling, donde los simios eran un grupo pseudo-anarquista sin líder. El Rey Louie de la película animada original esta basado en la persona que le ponía voz, un trompetista, bailarín y cantante de jazz estadounidense, llamado Louis Prima, y conocido como “el Rey del swing”.

Louis Prima, el rey del Swing
Para la versión de 2016, quisieron hacer que los personajes animales fueran lo más realistas posibles, por lo que el orangután no era una opción válida, y a los creativos se les ocurrió la idea, brillante a mí parecer, de basar al personaje de Louie en un primate extinto, el Gigantopithecus, como ha quedado claro en la letra de la nueva canción. Este inmenso animal sí habitaba en esta zona de la India. Es cierto que es un Gigantopithecus bastante “orangutanizado“, pero los datos que tenemos nos permiten hacer reconstrucciones bastante fiables, y todo indica que los Gigantopithecus pertenecen a la subfamilia Ponginae, la misma en la que se engloban los simios del género Pongo, es decir, los orangutanes actuales, por lo que estamos ante una reconstrucción bastante fiel y sin duda muy cinematográfica.
Gigantopithecus era un género de primates que apareció hace un millón de años y se extinguió hace unos trescientos mil años. Habitaba en el Sudeste asiático y medía más de tres metros de alto. El peso de este imponente simio podía llegar a los 500 kg, cuatro veces más que los orangutanes actuales. Por el tiempo que lleva extinto está claro que no pudo coincidir con Mowgli, ni por supuesto con ningún otro humano. Este excepcional animal convivió en nuestro planeta con Homo erectus, y los primeros fósiles de encontraron en Hong Kong en el año 1935. El descubrimiento fue gracias al paleontólogo alemán Ralph von Koenigswald y a su grupo de investigadores que iban tras la pista de unos “dientes de dragón“, que se vendía en la zona debido a sus supuestas propiedades curativas. Desde entonces se han encontrado unos mil dientes de 2,5 centímetros de ancho aproximadamente en tiendas de remedios tradicionales de China.

Reconstrucción del cráneo de Gigantopithecus a partir de su mandíbula, comparada con el cráneo de un gorila y de un Homo sapiens
Dentro del género Gigantopithecus se engloban al menos tres especies diferentes: G. giganteus, que vivía en la India, y sería poco más alto que un humano; G. bilaspurensis, también de la India; y G. blacki, del sur de China y Vietnam, que si podría alcanzar el descomunal tamaño de hasta 3,5 m de altura. Según el actor Cristopher Walken, que interpretó a Louie en la película de 2016, el enorme simio ficticio de la película mediría unos 12 pies, es decir 3,65 m, lo que coincide con las medidas del simio extinto. Queda claro que el nombre genérico de Gigantopithecus, que literalmente se podría traducir por simio gigante, es más que adecuado.

Comparación de tamaño entre las dos especies de Gigantopithecus y un ser humano
Gigantopithecus Louie, en su escena, se pasa la mayor parte del tiempo sentado, excepto cuando persigue a Mowgli, momento en que camina sobre dos patas ayudándose de las paredes del templo, e incluso trepando por ellas como un orangután, por lo que tampoco tenemos muchas oportunidades de verlo caminando. Poco nos ayuda Louie a despejar el debate que existe sobre si estos animales eran bípedos o cuadrúpedos.
La mayoría de los investigadores sugieren que por su inmenso tamaño es más probable que fueran cuadrúpedos, y caminaran de forma parecida a como lo hacen los gorilas, para soportar mejor el peso del cuerpo, pero los estudios del profesor de antropología física en la Universidad Estatal de Washington, Grover Krantz, un investigador muy peculiar, que dedicó gran parte de su vida a intentar demostrar científicamente la existencia del mítico Bigfoot, indican que G. blacki posiblemente fuera una especie bípeda. Su argumento se basaba en que la forma de la parte posterior de los huesos de su mandíbula tienen la misma forma y ensanchamiento que los de otras especies bípedas, como nosotros mismos, lo cual facilita la posición de la cabeza sobre el cuello en un cuerpo erguido. En cualquier caso muchos de sus estudios fueron desestimados por otros investigadores, así que seguimos sin nada concluyente que ayude a terminar con este debate.

Reconstrucción de un Gigantopithecus cuadrúpedo
Como también vemos en la película, estos descomunales primates necesitan un gran aporte de comida. King Louie aparece comiendo y hablando de las ricas papayas que le suministran sus Bandar-log con regularidad y que se traga con gran avidez. De hecho, por los restos fósiles que se tienen de Gigantopithecus, la mayoría dientes, se sabe que tenía una dieta preferentemente frugívora, lo que junto a su gran tamaño probablemente tuvieron que ver con su extinción.
También se habla de que sus dientes pueden indicarnos de que se alimentaba de bambú, muy común en las zonas donde se han encontrado sus fósiles. La desaparición cíclica de los bosques de bambú, obligaría a nuestro simio gigante a compaginar su dieta con frutas, lo que ha quedado registrado en los dientes fósiles con cavidades, debido a las caries producidas por sustancias azucaradas.
Debido a la última glaciación del Pleistoceno, su tamaño y su tipo de alimentación se convirtieron en una gran desventaja, ya que muchas áreas boscosas pasaron a ser sabanas, y el suministro de fruta para este gran simio comenzó a ser insuficiente. Los alimentos dominantes en estos nuevos medios eran raíces, bayas y hojas, a los que no se pudo adaptar Gigantopithecus, que estaba muy especializado para sobrevivir en el hábitat anterior. A esto se le unió otro problema, y es que las especies muy grandes tienden a producir un menor número de descendientes, lo que se traduce en poblaciones más pequeñas y por lo tanto más sensibles a fluctuaciones como las producidas por las glaciaciones.
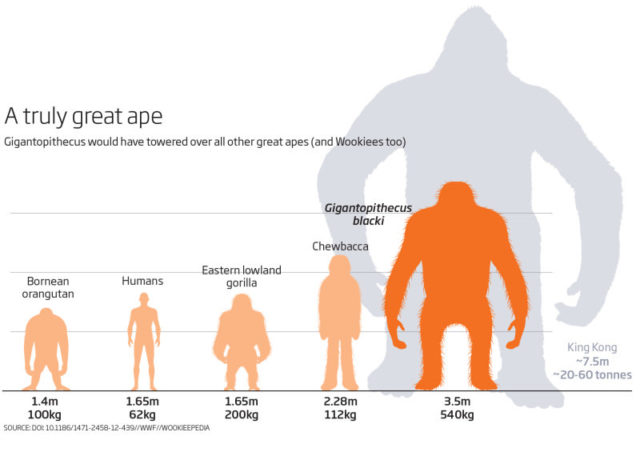
Entre varios primates reales (Gigantopithecus, Pongo, Gorilla y Homo) y cinematográficos (King Kong y Chewbacca).
Nos queda la duda de la edad que tiene el enorme King Louie de la película de 2016, pero podría ser el descendiente directo de los antiguos Gigantopithecus que vivían en la India, que aumentaron de tamaño al seguir evolucionando en ese reducto verde y lleno de frutas. Se trataría de un último ejemplar, un fósil viviente, de una especie nueva, que ha sobrevivido oculto entre las ruinas de un templo consumido por la selva. El sueño de cualquier criptobiólogo, y el origen de leyendas como las del Bigfoot o el Yeti, pero desafortunadamente para los criptobiólogos y otros vendedores de cuentos chinos, estamos ante un personaje cinematográfico, con un respaldo biológico y paleontológico en su historia, que nos ha servido como una perfecta excusa para hablar de simios actuales y extintos.
King Louie cantaba aquello de “Quiero ser como tú”, dirigiéndose a Mowgli, pero quizás no fuera solo por conseguir la roja flor, el fuego, sino por tener la capacidad de adaptación y de supervivencia de los seres humanos y así no terminar extinto, como Gigantopithecus, o al borde de la extinción, como los orangutanes.
Este post ha sido realizado por Carlos Lobato (@Biogeocarlos) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
Referencias científicas y más información:
– Winkler, L. A. (1989). Morphology and relationships of the orangutan fatty cheek pads. American Journal of Primatology, 17(4), 305-319.
– Wich, S. A., Swartz, K. B., Hardus, M. E., Lameira, A. R., Stromberg, E., & Shumaker, R. W. (2009). A case of spontaneous acquisition of a human sound by an orangutan. Primates, 50(1), 56-64.
– Hardus, M. E., Lameira, A. R., Van Schaik, C. P., & Wich, S. A. (2009). Tool use in wild orang-utans modifies sound production: a functionally deceptive innovation?. Proceedings of the Royal Society of London B: Biological Sciences, rspb20091027.
– von Koenigswald, G. H. R. (1952). Gigantopithecus blacki von Koenigswald, a giant fossil hominoid from the Pleistocene of southern China. American Museum of Natural History.
– Zhao, L. X., & Zhang, L. Z. (2013). New fossil evidence and diet analysis of Gigantopithecus blacki and its distribution and extinction in South China. Quaternary International, 286, 69-74.
– Zhao, L., Zhang, L., Zhang, F., & Wu, X. (2011). Enamel carbon isotope evidence of diet and habitat of Gigantopithecus blacki and associated mammalian megafauna in the Early Pleistocene of South China. Chinese Science Bulletin, 56(33), 3590-3595.
– Regal, B. (2009). Entering dubious realms: Grover Krantz, science, and Sasquatch. Annals of science, 66(1), 83-102.
– http://www.orangutan-world.com/es/estructura-y-comportamiento-social-del-orangutan/
– https://en.wikipedia.org/wiki/Orangutan
– https://es.wikipedia.org/wiki/Gigantopithecus
– https://en.wikipedia.org/wiki/King_Louie
– https://en.wikipedia.org/wiki/Birutė_Galdikas
– http://www.republica.com/ciencia-para-todos/2016/04/11/el-libro-de-la-selva-resucita-al-gigantopithecus/
– https://www.sciencedaily.com/releases/2005/11/051112122318.htm
– http://www.buzzle.com/articles/facts-about-gigantopithecus-blacki.html
– https://www.youtube.com/watch?v=Snl4U8HPdtQ
El artículo Quiero ser como tú se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- De cómo se formaron los átomos de mi mano
- Quiero creer que actúo libremente
- La neurociencia como religión
Por qué los estudiantes de más éxito no tienen pasión por colegio
Jihyun Lee

Para tener éxito, mucha gente cree, uno tiene que tener pasión. La pasión convierte los retos en algo a disfrutar. Proporciona el aguante necesario para destacar. Sin embargo, hay contraejemplos elocuentes en los que la pasión no parece ser un ingrediente necesario para el éxito. Uno de estos casos es el éxito académico. Podrías pensar que los estudiantes de éxito deberían ser apasionados del colegio, y que está pasión por el colegio sería la responsable, al menos parcialmente, de por qué algunos estudiantes tienen éxito y otros no. Pero esto no es cierto. Mi investigación ha encontrado que, de hecho, no existe ninguna relación entre lo bien que les va académicamente a los estudiantes y qué actitud tienen respecto al colegio. Un estudiante no necesita ser un apasionado del colegio para tener éxito académicamente.
Los hallazgos de mi investigación provienen del análisis de una gran base de datos internacional llamada Programa de Evaluación Internacional de Estudiantes (PISA, por sus siglas en inglés). La Organización para la Cooperación y el Desarrollo Económico (OCDE) hace pública esta base de datos cada tres años. Es un tesoro oculto que proporciona a investigadores como yo una visión sin par de lo que estudiantes de todo el mundo piensan de su educación. En la evaluación PISA más reciente, de 2015, participaron 72 países y economías. Se administran exámenes de lectura, matemáticas y ciencia junto a un cuestionario acerca de actitudes, creencias, hábitos de aprendizaje y demás, a muestras representativas a nivel nacional de quinceañeros de todo el mundo. En encuestas anteriores se usaron cuatro opciones sencillas para medir la actitud de los estudiantes hacia el colegio:
(a) el colegio ha hecho poco para prepararme para la vida adulta cuando deje el colegio
(b) el colegio ha sido una pérdida de tiempo
(c) el colegio me ayudó a darme confianza para tomar decisiones
(d) el colegio me ha enseñado cosas que podrían ser útiles en un trabajo
Resultó que la correlaciones simples y directas entre los logros académicos de los estudiantes y sus actitudes hacia el colegio eran cercanas a cero. Esto estaba lejos de ser una anomalía. El resultado cercano a cero se replicaba en los PISA de 2003, 2009 y 2012. No había diferencias en lo que respecta a la extracción socioeconómica de los estudiantes. El género no afectaba al resultado, y se mantiene para países desarrollados y en vías de desarrollo. Solo alrededor del 2 % de los resultados en el examen PISA de matemáticas se explicaba por las actitudes de los estudiantes hacia el colegio en 62 países. Esto significa que en la mayoría de los países, los estudiantes buenos académicamente no valoran demasiado su escolarización. De forma similar, los estudiantes menos buenos no tienen necesariamente mala opinión de su escolarización. Simplemente no hay conexión. Esto plantea la fascinante cuestión de la motivación. Si no existe una relación real entre logros académicos y actitud, entonces ¿qué motiva a los estudiantes brillantes a obtener el éxito académico? Está claro que no es por una abrumadora pasión por el colegio.
La respuesta es que viene de dentro. Otra investigación basada en PISA sugiere que lo que separa a los estudiantes buenos de los menos buenos son sus creencias propias respecto a sus fortalezas y debilidades. Las variables psicológicas individuales como la autoeficacia, la ansiedad o el placer de aprender en sí mismo explican entre el 15 y el 25 por ciento de la variación en los resultados académicos de los estudiantes. Colectivamente, la investigación muestra que las creencias propias de los estudiantes en sus propias capacidades para resolver problemas es mucho más importante que su propia percepción del colegio.
Esto es un problema. La actitud de los estudiantes hacia el colegio debería contar por una serie de razones. Si los estudiantes encuentran difícil ver los beneficios directos de su escolarización, si piensan que su colegio no ha conseguido colmar sus expectativas, y si consideran que sus capacidades académicas se aprenden fuera del colegio, es posible que esto afecte a su visión de las instituciones formales más adelante. Y, en efecto, mucha gente tiene una visión pesimista del papel que juegan las instituciones formales; una visión que muy bien podría haber surgido de las experiencias escolares durante sus años formativos. Las instituciones formales determinan las vidas de los ciudadanos. Necesitan ser mantenidas, mejoradas y fortalecidas; no descartadas inmediatamente. Por eso a los estudiantes se les debería enseñar a implicarse ellos mismos en las instituciones formales, más que a denigrarlas o dejar de participar en ellas.
¿Qué puede hacerse? Los adultos responsables de tomar decisiones acerca de la escolarización deberían tener conocimiento de las influencias a largo plazo que la experiencia escolar puede ejercer sobre las actitudes y creencias de los estudiantes. Un mayor énfasis debe darse también a la inclusión de actividades prácticas en grupo que emulen lo que pueden hacer en la vida una vez terminen el colegio. El que los estudiantes sean capaces de ver la conexión entre su presente y su futuro puede tener consecuencias críticas para la sociedad.
Referencias:
Jihyun Lee (2016) Attitude toward school does not predict academic achievement Learning and Individual Differences doi: 10.1016/j.lindif.2016.09.009
Jihyun Lee (2014) Universal factors of student achievement in high-performing Eastern and Western countries Journal of Educational Psychology, Vol 106(2), 364-374.
Jihyun Lee (2009) Universals and specifics of math self-concept, math self-efficacy, and math anxiety across 41 PISA 2003 participating countries Learning and Individual Differences doi: 10.1016/j.lindif.2008.10.009
Sobre la autora: Jihyun Lee es profesora titular en la Facultad de Educación de la Universidad de Nueva Gales del Sur (Australia)
Texto traducido y adaptado por César Tomé López a partir del original publicado por Aeon el 6 de marzo de 2007 bajo una licencia Creative Commons (CC BY-ND 4.0)
![]()
El artículo Por qué los estudiantes de más éxito no tienen pasión por colegio se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El problema de las estudiantes de Kirkman
- Ciencia Clip: un concurso de vídeos de ciencia para jóvenes estudiantes
- Lo que tienen en común una red inalámbrica, el ritmo del corazón y la consciencia
El mejor lacón con grelos tiene su ciencia

El Entroido (el Carnaval gallego) tiene como plato estrella el lacón con grelos, una variante más sencilla del cocido gallego. De postre se hacen orejas, un crujiente a base de harina de trigo y huevo, y filloas, similares a las crepes, pero en lugar de leche se utiliza el agua del cocido. La razón por la que es tradición hacer el lacón con grelos durante estos días (realmente durante el primer trimestre del año) tiene que ver con la temporada del grelo.
El grelo es el brote del nabo. Se planta en verano y se recoge en invierno. Las primeras hojas que aparecen durante el crecimiento de la planta no son grelos, son nabizas. Las nabizas también son comestibles, pero menos sabrosas y carecen del característico tallo del grelo. El grelo aparece cuando llega el gélido invierno, ese es el momento en que la planta suelta su melena al viento y florece en todo su esplendor. Si esperamos lo suficiente, los grelos entrarán en floración. El grelo saca unas pequeñas flores amarillas. Cuando esto ocurre, los gallegos decimos que los grelos están grelados, lo que culinariamente significa que ya no sirven para comer. Los tallos se vuelven demasiado leñosos, tanto que ni durante horas de cocción llegan a estar tiernos.

Sección del tallo del grelo antes y después de la floración
Para preparar el mejor lacón con grelos tenemos que ser previsores, ya que hay que comenzar con los preparativos el día anterior. Si además quisiésemos acompañarlo de caldo gallego (una sopa con grelos, habas y patata en el agua del cocido) deberíamos empezar dos días antes con los preparativos. Uno de los motivos por los que me fascinan estos platos gallegos es por la planificación, por lo que tienen de ritual.

Flor del grelo
Me voy a ceñir al lacón con grelos. El mejor lacón con grelos se hace con grelos, lacón en salazón, garbanzos, chorizo y patatas. Lleva más cosas que lacón y grelos, y también por eso es el mejor.
El día anterior hay que escaldar los grelos y dejar en remojo el lacón en salazón y los garbanzos. Estos dos pasos tienen una razón científica de ser.
Escaldar la verdura consiste en introducirla, previamente lavada, en agua hirviendo y dejarla cocer durante cinco minutos. A continuación, se enfría rápidamente con un chorro de agua fría para cortar la cocción. Con el escaldado conseguimos limpiar profundamente la verdura e inhibir una serie de reacciones enzimáticas que acabarían por dar lugar a aromas indeseables, pérdida de vitamina C y decoloración. Con el escaldado estabilizamos el color verde de las verduras por activación de las clorofilas, disminuimos el tiempo de cocción al día siguiente y fortalecemos la textura activando la pectinmetilesterasa, una enzima que cataliza la conversión de pectina en ácidos pectínicos que interactúan con el calcio y hacen aumentar su rigidez estructural. Si por algún motivo tuviésemos que cancelar la comida del día siguiente, tendríamos la verdura escaldada y lista para ser congelada.
El proceso que tiene lugar al dejar los garbanzos en remojo es la ósmosis. La ósmosis consiste en que el agua difunde a través de las paredes celulares de las legumbres y entra en sus células. Al ser semipermeables, las paredes celulares dejan pasar el agua, pero no otras sustancias que pueden estar disueltas en ella. Este proceso es espontáneo, ya que la concentración tanto dentro como fuera de las células tiende a equilibrarse.
El lacón se deja a remojo para librarnos del exceso de sal. El desalado es, científicamente, una extracción sólido-líquido en la que se transfieren principalmente, de la carne salada al agua de desalado, los iones de la sal, los cationes de sodio y los aniones de cloruro. Además, esta pérdida de sal implica disolver parte del sistema muscular de la carne, por lo que se transfieren proteínas solubles al agua.

El Peliqueiro. Entroido de Laza, Ourense, 1975. Foto: Cristina García Rodero.
Vamos con la tarea del día siguiente, el día de comer el lacón con grelos. Lo primero que se pone a cocer es el lacón. Para ello se llena la pota con agua y se añade el lacón en frío. La ponemos al fuego y esperamos a que hierva. Este proceso transcurre a 100oC, que es la temperatura a la que el agua entra en ebullición. Si usamos una olla a presión (muy recomendable para esta receta, ya que acortamos mucho los tiempos de cocción sin que el resultado se vea afectado) esto sucedería más rápido y la temperatura que alcanza el agua al hervir es levemente superior.
Cuando asamos o freímos la carne, esta se dora, pero cuando la cocemos no. Cuando la carne adquiere ese color dorado es indicativo de que está sucediendo una de las reacciones más comunes de la cocina: la reacción de Maillard. Esta reacción sólo tiene lugar a partir de los 200oC, temperatura que es imposible alcanzar cuando cocinamos nuestros alimentos en agua. Esa es la razón por la que la carne cocida no se dora.
Una vez el agua haya empezado a hervir, bajamos el fuego e introducimos los garbanzos, los grelos y el chorizo y dejamos hervir durante media hora en la olla a presión. Mientras hierve, todos los compuestos solubles en agua irán disolviéndose y pasando al agua. Este proceso vuelve a tratarse de una extracción. A medida que las carnes se van cociendo, las grasas se van desprendiendo, pero como la grasa no es soluble en el agua y además es menos densa, pasa a ocupar la parte superior formando una capa inmiscible con el resto del agua.
Transcurrida media hora se vuelve a bajar el fuego y se añaden las patatas. Probamos el caldo y corregimos el punto de sal. Dejamos hervir durante media hora más.
Lo que ocurre durante la cocción de la patata lo podemos describir científicamente. El componente principal de las patatas es el almidón, un glúcido formado por la unión de dos monosacáridos: la amilosa y la amiopectina. Durante la cocción la patata se hidrata, absorbe agua, lo que provoca que los gránulos de almidón aumentan de tamaño unas cien veces respecto a su tamaño inicial. Con el calor se rompe el ordenamiento de las moléculas de amilosa y amilopectina del gránulo y pequeñas moléculas de amilosa se escapan del interior. Éstas forman una red que atrapa a las moléculas de agua y a los gránulos de almidón formando una pasta viscosa que da como resultado la reconocible textura de la patata cocida. Este proceso químico se denomina gelatinización.
Si dejamos enfriar hasta que alcance la temperatura ambiente, el agua adquirirá la consistencia de una gelatina. Tranquilidad, nada se ha estropeado. Esto es debido al colágeno del lacón. El colágeno es una proteína soluble en agua que se encarga de dar firmeza a la piel y se encuentra en abundancia en los cartílagos y los huesos. Cuando el colágeno se enfría es capaz de formar un entramado en forma de red que es el responsable de la apariencia gelatinosa del caldo. Una vez volvamos a calentar, ese entramado dejará de ser estable y recuperaremos la consistencia líquida original.
Todos estos procesos científicos están sucediendo ahora mismo en un montón de hogares y restaurantes gallegos. Es bonito en sí mismo, y esa belleza se ensalza cuando sabemos apreciar toda la ciencia que lo hace posible, la que se ha perpetuado gracias a la tradición culinaria.
Me gusta la cocina por varias razones. La principal es romántica y, otra de las más importantes, es que cocinar es una forma cotidiana de hacer ciencia.
La manera de hacer buena cocina es haciendo bien su ciencia.
Fuentes:
Todo es cuestión de química. Deborah García Bello. Paidós, 2016.
Comer sin Miedo. J.M. Mulet. Destino, 2014.
Grelos, una deliciosa verdura de temporada con mucho sabor. Óscar Gómez. Gastronoesfera.com, 2014.
Compuestos bioactivos y producción de grelos y nabizas: variación fenótípica y ambiental. Marta Francisco Candeira. Universidad de Vigo, 2010.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo El mejor lacón con grelos tiene su ciencia se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Comprimiendo la luz para detectar mejor ondas gravitacionales
- Uno de los explosivos no nucleares más potentes tiene ventajas añadidas.
- El extracto de té verde no tiene efecto sobre la pérdida de peso
Combustibles solares por un tubo
El futuro será de las energías alternativas el día en que puedan sustituir de forma eficaz a los combustibles fósiles en el transporte. Seamos realistas, los coches eléctricos son un avance, pero no es concebible a corto plazo un camión de alto tonelaje funcionando continuamente en base eléctrica. Por no mencionar trenes de mercancías en territorios sin electrificar, buques de carga o pasajeros o aviones comerciales.

La solución a las demandas del transporte pasa por los combustibles solares. Se llama así a aquellos combustibles que emplean solo luz del Sol, agua y dióxido e carbono atmosférico para en su síntesis. Según esta definición la madera es un combustible solar. Pero esa no es una opción: lo es un combustible licuable, como el hidrógeno y los hidrocarburos. En todos los casos se obtienen por un paso previo fundamental: la rotura de la molécula de agua. Algo nada sencillo.

Una molécula de agua, H2O, está compuesta por dos átomos de hidrógeno y uno de oxígeno. Separar los átomos de hidrógeno del oxígeno es algo que es muy costoso energéticamente hablando, por lo que es necesario emplear catalizadores, unos compuestos capaces de rebajar la energía necesaria hasta niveles donde la acción de la luz solar sea suficiente. Una vez separados los hidrógenos, se pueden unir para formar hidrógeno molecular, H2, o combinarlos con dióxido de carbono, CO2, para obtener hidrocarburos.
Para crear combustibles solares prácticos se ha intentado desarrollar materiales catalizadores de bajo coste y eficientes, conocidos en general como fotoánodos, que son capaces de romper la molécula de agua usando la luz visible como fuente de energía. En las últimas cuatro décadas, se han identificado 16 de estos fotoánodos. A ese ritmo las probabilidades de dar con el catalizador que soluciones uno de nuestros problemas medioambientales más graves, son las mismas que las de encontrar una aguja en un pajar metiendo el brazo en la baja y tentando con la mano. No nulas, pero cercanas.
Por eso es tan interesante el trabajo que un grupo de investigadores del Instituto de Tecnología de California y el Laboratorio Nacional Lawrence Berkeley (EE.UU.) acaba de publicar. En él presentan un método que les ha permitido identificar 12 fotoánodos en tan solo dos años.
Los procesos anteriores de identificación de materiales se basaban en una comprobación experimental muy tediosa de compuestos químicos concretos para evaluar su potencial para ser usados en aplicaciones específicas. En el nuevo método se combinan estudios computacionales y experimentación en el laboratorio para, en primer lugar, hacer búsquedas inteligentes en bases de datos para encontrar compuestos con potencial de ser fotoánodos, en segundo filtrar los compuestos encontrados en función de las características estructurales y de síntesis de los compuestos y, finalmente, comprobarlos experimentalmente con una metodología de alto rendimiento.
Para poner a punto el método se centraron en los vanadatos, compuestos que contienen solo tres tipos de átomos: vanadio, oxígeno y un tercero. A la evaluación final llegaron 174 compuestos.
Los investigadores encontraron que la naturaleza del tercer elemento afecta de forma dramática a las propiedades del material, lo que les permitió aprender cómo “afinar” esas propiedades para obtener un fotoánodo mejor.
Los métodos y procesos son tan importantes como los propios materiales a la hora de conseguir una aplicación útil. Gracias a este es muy posible que estemos más cerca de un futuro medioambientalmente mejor.
Referencia:
Quimin Yan et al (2017) Solar fuels photoanode materials discovery by integrating high-throughput theory and experiment. PNAS doi: 10.1073/pnas.1619940114
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Combustibles solares por un tubo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El tubo de rayos catódicos, auge y caída de una pieza clave del siglo XX
- Paneles solares orgánicos…y de colores
- La fusión a un paso gracias al hidrógeno líquido
666, el número de la Bestia (1)
La entrada de hoy del Cuaderno de Cultura Científica la vamos a iniciar con una cita literaria que mi compañera Marta Macho suele utilizar en sus magníficas conferencias sobre literatura y matemáticas. Es una cita extraída de la famosa novela Guerra y Paz(1869) del escritor ruso León Tolstoi (1828-1910), en el capítulo XIX, libro tercero, primera parte:
“…Cierto hermano masón le había revelado la siguiente profecía, relativa a Napoleón, sacada del Apocalipsis de San Juan Evangelista [más abajo se muestra la profecía]. Las letras del alfabeto francés, como los caracteres hebraicos, pueden expresarse por medio de cifras, y atribuyendo a las diez primeras letras el valor de las unidades y a las siguientes el de las decenas, ofrecen el significado siguiente:

Escribiendo con este alfabeto en cifras las palabras L’empereur Napoléon, la suma de los números correspondientes daba por resultado 666, de lo que resultaba que Napoleón era la bestia de que hablaba el Apocalipsis. Además, al escribir con ese mismo alfabeto cifrado la palabra francesa “quarante deux”, es decir, el límite de 42 meses asignados a la bestia para pronunciar sus palabras orgullosas y blasfemas, la suma de las cifras correspondientes a la palabra última era también 666, de lo que se infería que el poder napoleónico terminaba en 1812, fecha en que el emperador cumplía los cuarenta y dos años“
Es decir, en la cita se está asociando a Napoleón, más concretamente a la expresión “L’empereur Napoleón”, con su valor numérico según la asignación que se menciona explícitamente en la cita, es decir, LE EMPEREUR NAPOLÉON = (20 + 5 + 5 + 30 + 60 + 5 + 80 + 5 + 110 + 80 = 400) + (40 + 1 + 60 + 50 + 20 + 5 + 50 + 40 = 266) = 666. Pero el 666 es el número de la Bestia, el diablo o anticristo, lo que se utiliza para manifestar el carácter maléfico, según quien realiza la reflexión, de Napoleón.
Esta cita literaria nos sirve para introducir los dos temas, el número de la bestia, el 666, y la numerología relacionada con este número, a los que vamos a dedicar dos entradas de la sección Matemoción del Cuaderno de Cultura Científica. La primera, esta que estás leyendo, se centrará en el número 666 y algunas propiedades matemáticas del mismo.

Una de las citas más conocida y popular de la Biblia, que es la que se menciona en Guerra y Paz, es la que se refiere al número de la Bestia. La cita pertenece al Apocalipsis de San Juan o Libro de las revelaciones, del Nuevo Testamento.
“todos, pequeños y grandes, ricos y pobres, libres y esclavos, se harán marcar sobre la mano derecha o sobre la frente y nada se podrá comprar o vender si no está marcado con el nombre de la Bestia o con el número de su nombre.
Aquí se debe aplicar la sabiduría. ¡Que el hombre dotado de espíritu calcule el número de la Bestia; es un número de hombre: su número es el seiscientos sesenta y seis.“
El número 666 se identifica con el anticristo o con el diablo, y es un símbolo muy utilizado por los cultos satánicos, junto con el pentagrama invertido, la cabeza de cabra o la calavera.

Tatuaje con simbología satánica que incluye el número 666
Este número tiene un cierto protagonismo en la película de terror británica-estadounidense La profecía (1976), dirigida por Richard Donner e interpretada por Gregory Peck y Lee Remick. Es una película sobre la llegada del anticristo en pleno siglo XX. El anticristo es Damien, hijo de un diplomático americano, por lo tanto, vinculado al mundo de la política. A lo largo de la película se va descubriendo que el niño nació el 6 de junio (sexto mes), de 1971, a las 6 de la mañana y que tiene una marca de nacimiento con la forma de tres seises. El remake de 2006 de esta película se estrenó en EE.UU. el 6 de junio (06) de 2006, a las 06:06:06.

Cartel de la película “La profecía” (1976), dirigida por Richard Donner e interpretada por Gregory Peck y Lee Remick
Otra referencia muy conocida del mundo de la cultura es la canción The number of the beast (1982) del grupo británico de heavy metal Iron Maiden y que da título al tercer álbum del grupo. La canción empieza citando el Apocalipsis de San Juan. Aquí os dejo con la canción…

Portada del disco “The number of the beast” (1982) de Iron Maiden
O por realizar una cita más actual, 666 Satan, es un manga creado por el dibujante japonés Seishi Kishimoto y publicado en la revista Shonen Gangan.

Imágenes del manga “666 Satan”
La relación del número 666 con Satán o la llegada del Anticristo, a través de la cita del Apocalipsis, es lo que ha provocado que a lo largo de la historia se haya intentado asociar este número, a través de la numerología, con diferentes personajes, desde Nerón o Lutero a Bill Gates, pasando por Napoleón o Hitler, como veremos en la siguiente entrada.
Pero desde las matemáticas también se ha mirado a este número satánico y se han mostrado propiedades matemáticas, algunas de las cuales mostraremos en esta entrada, relacionadas con el 666. Incluso el gran divulgador Martin Gardner escribió un pequeño artículo en su libro Juegos y enigmas de otros mundos sobre el número de la bestia y las propiedades matemáticas del mismo.
1.- El número de la bestia, el 666, es un número triangular, es la suma de los 36 primeros números (por cierto, que 36 = 6 x 6):
1 + 2 + 3 + … + 34 + 35 + 36 = 666.
Recordemos que los números triangulares son aquellos números que son iguales al número de objetos (o cálculos) que tiene un triángulo equilátero como los que aparecen en la imagen. Es decir, en la primera fila hay un objeto y cada fila tiene un objeto más que la fila anterior. Por lo tanto, cada número triangular es la suma de los primeros números naturales, 1, 1 + 2 = 3, 1 + 2 + 3 = 6, 1 + 2 + 3 + 4 = 10, 1 + 2 + 3 + 4 + 5 = 15, 1 + 2 + 3 + 4 + 5 + 6 = 21, etc.

Además, teniendo en cuenta que en el juego de la ruleta están los números desde el 0 al 36, entonces la suma de los números de la ruleta suman 666.
2.- La suma de los cuadrados de los 7 primeros números primos es de nuevo 666:
22+ 32+ 52+ 72+ 112+ 132+ 172= 666.
Además, puestos a jugar al poder místico o satánico de los números, esta propiedad matemática nos relaciona el número satánico 666 con el número místico 7.
3.- Además, el número 666 puede expresarse como una suma capicúa de los cubos de los 6 primeros números,
13 + 23 + 33 + 43 + 53 + 63 + 53 + 43 + 33 + 23 + 13 = 666.
4.- Si se considera la suma alternada, suma-resta, de la potencia 6 de los 3 primeros números se vuelve a obtener el 666,
16 – 26 + 36 = 666.
5.- Otra curiosidad numérica del número de la Bestia es que es igual a la suma de sus cifras más la suma del cubo de sus cifras,
6 + 6 + 6 + 63 + 63 + 63 = 666.

Carátula del DVD de la película “El día de la Bestia” (1995), dirigida por Álex de la Iglesia e interpretada por Álex Angulo y Santiago Segura
6.- Si se consideran los dos números formados por todos los dígitos básicos, salvo el 0, tanto en orden creciente, como decreciente, es decir, 123.456.789 y 987.654.321, entonces resulta que el 666 es un divisor de la suma de estos dos números.
Si se suman los números 123.456.789 y 987.654.321 se obtiene como resultado 1.111.111.110, que es divisible por 666, de hecho, al dividir por este número queda 1.668.335.
7.- Pero dejemos un momento estas igualdades numéricas y volvamos al Apocalipsis de San Juan, pero al versículo 14, el siguiente al del número de la Bestia, que era el 13. En este aparece el número 144.000, que como menciona Gardner al dividirlo por 666 queda el número 216,216216216… en el que se repite el 216, y justamente 6 × 6 × 6 = 216.
8.- Juego de ingenio. Como a todas las personas nos gusta jugar, vamos a plantear un juego típico relacionado con el número 666. Se trata de considerar las 9 cifras básicas, en orden ascendente o descendente, 123456789 o 987654321, e insertando los signos + o – en ellos, obtener el número 666. Por ejemplo,
123 + 456 + 78 + 9 = 666.
Se pueden obtener 8 soluciones en el sentido ascendente y 5 en el descendente.

Pintura al oleo de Robert Indiana titulada “El sexto sueño americano” (USA 666), de 1964-1966, aunque el uso del número 666 tiene más connotaciones personales que satánicas
9.- Como no podía ser de otra forma, también podemos relacionar el número de la Bestia con el número pi. Resulta que la suma de los 144 primeros decimales del número pi suman 666. Si queremos rizar un poco más el rizo, podemos observar que 144 = 12 × 12 = (6 + 6) × (6 + 6).
π = 3.141592653589793238462643383279502 88419716939937105820974944592307816406 28620899862803482534211706798214808651 32823066470938446095505822317253594
Teniendo en cuenta esta propiedad, en 2004 Ed Pegg Jr. y Chris Lomont, en la web de la MAA (Mathematical American Association), definieron los “números diabólicos” (aunque este término es ambiguo porque también se utiliza para otro tipo de números) como aquellos cuyos primeros decimales hasta un cierto número n suman 666.
Por lo tanto, el número π es un número diabólico. También lo son la proporción áurea Φ, cuyos primeros 146 decimales suman 666, los mismos que para la raíz cuadrada de 3 o la raíz cúbica de 2, para la cual se necesitan 156 decimales, entre otros.
10. Más aún, podemos relacionarlo también con el teorema de Pitágoras. Recordemos que tres números (a, b, c) se dice qu forma una terna pitagórica si satisfacen la ecuación pitagórica a2 + b2 = c2 , como por ejemplo (3, 4, 5) puesto que 32 + 42 = 52 (9 + 16 = 25).
La terna (216, 630, 666) es una terna pitagórica, que además de incluir al número de la Bestia, incluye al 216 = 6 × 6 × 6 y al 630 = 666 – (6 × 6). Y si lo escribimos todo junto es aún más divertido:
(6 × 6 × 6)2 + (666 – 6 × 6)2 = 6662.

“666 (The Apocalypse of John, 13/18)” es el tercer albúm, de 1972, del grupo francés de rock progresivo y psicodélico Aphrodite’s child, dedicado al Libro de la revelación del Nuevo Testamento, que podéis escuchar en youtube
11.- El número 666 es también un número de Smith. Se conoce con el término números de Smith a aquellos números enteros tales que la suma de sus dígitos es igual a la suma de los dígitos de los números que forman su descomposición en números primos (escritos sin potencias). Por ejemplo, el 22 es un número de Smith puesto que se factoriza como 22 = 2 × 11, y 2 + 2 = 2 + 1 + 1.
El número de la Bestia se factoriza como 666 = 6 × 111 = 2 × 3 × 3 × 37, luego
6 + 6 + 6 = 18 = 2 + 3 + 3 + 3 + 7.
12.- También se puede relacionar el número de la Bestia con los cuadrados mágicos. Recordemos que un cuadrado mágico de orden n (el caso más sencillo es n = 3), es una distribución de los primeros n2 números (para orden 3, los 9 primeros números, 1, 2, 3, 4, 5, 6, 7, 8, 9), sobre las casillas de un cuadrado n x n, (en nuestro caso particular un cuadrado 3 x 3), de forma que la suma de cada fila, cada columna y cada diagonal sea siempre la misma (para orden 3 sería 15, como se ve en el cuadrado mágico que se muestra más abajo, ya que 4 + 9 + 2 = 15, 4 + 3 + 8 = 15, 4 + 5 + 6 = 15, etc); a ese número se le llama constante del cuadrado mágico.

De forma más general, se pueden considerar cuadrados mágicos formados por números que no son consecutivos. El siguiente cuadrado mágico 6 x 6 es diabólico, puesto que su constante mágica es 666.

Otras entradas del Cuaderno de Cultura Científica dedicadas a los cuadrados mágicos son Habibi y los cuadrados mágicos (parte 1; parte 2 y parte 3).
13.- El número 666 tiene la increíble propiedad de que al sumar los dígitos de elevar 666 a la potencia 47 el resultado es de nuevo 666. Pero además, esto ocurre también para la potencia 51.
66647 = 5049969684420796753173148798405564 7729415162952654081881176326689365404466 1603306865302888989271885967029756328621 9594665904733945856;
66651 = 993540757591385940334263511341295 9807238586374694310089971206913134607132 8296758253023455821491848096074897283890 0637634215694097683599029436416.
Si sumamos los dígitos de cada uno de los números, en ambos casos se obtiene 666. De hecho, el número 666 es el único entero mayor que 1 que cumple dicha propiedad.
Se conoce con el nombre hexakosioihexekontahexafobia la aversión o miedo irracional al número 666. Existen curiosas anécdotas relacionadas con este miedo al número de la Bestia.
Como se cita en un artículo de Los Angeles Times del 19 de noviembre de 1988, Ronald y Nancy Reagan se mudaron a una casa de la zona de Bel Air en Los Ángeles, cuya dirección era 666 St Cloud Road, e hicieron que se cambiara el número de la casa al 668.
El 5 de junio de 2006, un día antes del día 06/06/06, se publicó una noticia en BBCNews en la que se informaba de que un grupo de unos 2.000 cristianos evangélicos de los Países Bajos iban a realizar una vigilia de 24 horas para rezar en contra de las fuerzas del mal al día siguiente, el día del diablo (06/06/06).
En 2003, se cambió el nombre de la autopista que cruza de norte a sur Colorado, Nuevo México y Utah. El nombre de US Ruta 666 era demasiado satánico para los cristianos de esa zona, por lo que se cambió a US Ruta 491.

Señal de tráfico que indica el nombre viejo, US Rute 666, y el nuevo, US Route 491, de esta autopista que atraviesa Colorado, Nuevo México y Utah
Las locomotoras de los trenes Siemens ACS-64 de Amtrak (Coorporación Nacional de Ferrocarriles de Pasajeros de EE.UU.) tenían números entre el 600 y el 665, y después entre el 667 y el 670, dejando sin utilizar el 666.
Un ejemplo más, que he leído en la Wikipedia, es el caso de los números telefónicos de Honduras. A finales de la década de los años 1990 la empresa telefónica estatal de Honduras cambió los números de teléfono, pasando a tener 7 cifras, en lugar de las 6 que tenían antes, y al parecer el prefijo 666 le correspondió a la ciudad de El Progeso, cuyos habitantes se movilizaron para que la empresa les cambiara ese prefijo, hasta que lo consiguieron.
Para terminar con el número 666, el número de la Bestia, mencionar que según recientes estudios el número de la Bestia podría ser el 616, y no el 666.
En el Códice Ephraemi Rescriptus, que se encuentra en la Biblioteca Nacional de Francia (París), que es un manuscrito griego uncial (escrito en mayúsculas) del siglo V formado por 64 hojas del Antiguo Testamento y 145 hojas del Nuevo Testamento, aparecía el número 616 como número de la Bestia, como también en otros textos, pero estos fueron interpretados como errores de los escribanos a la hora de escribir el número.
Sin embargo, en el año 2005 se descubrió que en el Papiro 115, un fragmento del Nuevo Testamento escrito en griego y encontrado en Oxirrinco (Egipto) de alrededor del año 275 y que es el manuscrito más antiguo del Apocalipsis de San Juan, se puede leer que el número de la Bestia es el (escrito en griego) chi-iota-sigma, es decir, 616.
Aunque en la actualidad no esta claro a cual de los dos números le corresponde realmente el título de “número de la Bestia” según el Apocalipsis de San Juan, la verdad es que para nosotros siempre será el 666.

Fragmento del Papiro 115 en el que aparece el texto que asocia el número de la Bestia con el 616
Bibliografía
1.- Raúl Ibáñez, Numerología, cábala y otros enigmas, Geometrian barrenako ibilaldia / Un paseo por la geometría 2007/08, UPV-EHU, 2008.
2.- Marta Macho, Un paseo matemático por la literatura, Revista SIGMA 32, p. 173-194, 2008.
3.- Martin Gardner, Juegos y enigmas de otros mundos, Gedisa, 2000.
4.- Ed Pegg Jr. and Chris Lomont, Evil numbers, MAA, 2004 [http://www.mathpuzzle.com/MAA/27-Evil%20Numbers/mathgames_09_04_04.html]
5.- Rajnish Kumar, Short Stories about Numbers, Universities Press, India, 2006.
6.- Lamberto García del Cid, Números notables, el 0, el 666 y otras bestias numéricas, RBA, 2010.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo 666, el número de la Bestia (1) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Evolución del tamaño animal
De acuerdo con la “regla de Cope” los linajes animales tienden a adquirir un mayor tamaño en el curso de la evolución. No es una regla que se cumpla en todos los clados, por lo que en puridad no habría que hablar de “regla”, dado que hay numerosas excepciones. Sin embargo, esa norma sí se cumple si comparamos el tamaño de los primeros animales de cuya existencia tenemos constancia con los actuales; aunque ahora haya muchísimos animales minúsculos, en este momento viven en nuestro planeta los más grandes animales que hayan existido jamás: las ballenas azules. Y hay muchísimas especies cuyos ejemplares llegan a alcanzar un gran tamaño. En términos generales, por lo tanto, puede decirse que es cierto que los animales, en promedio, han ido teniendo cada vez un mayor tamaño.

Ese mayor tamaño puede que obedezca al hecho de que, en general, ser más grande reporta ventajas o, al menos, más ventajas que desventajas; en ese caso habría habido presiones selectivas que han propiciado la aparición de animales cada vez más grandes en mayor proporción que animales más pequeños. Pero la regla de Cope también podría ser una mera consecuencia de la diversificación del tamaño de los linajes nuevos que han ido apareciendo; al fin y al cabo, no se puede ser inferior a un determinado tamaño, pero sí se puede ser cada vez más grande, aunque quizás también haya restricciones estructurales ligadas a fenómenos de escala que impongan límites absolutos.
Un estudio de hace pocos años analizó esta cuestión. Los investigadores utilizaron un conjunto de datos amplísimo. Analizaron 17.208 géneros de artrópodos, braquiópodos, cordados, equinodermos y moluscos, todos ellos marinos. Esos filos representan el 74% de la diversidad animal del registro fósil, y los casos incluidos en el análisis, el 75% de la diversidad de los géneros pertenecientes a esos filos. El estudio abarcó 542 millones de años, lo que supone el 90% de la historia de los metazoos. Según este estudio, desde el Cámbrico, el tamaño medio (expresado como biovolumen) ha aumentado por un factor de 150, el mínimo ha disminuido por un factor de 10, y el máximo ha aumentado por un factor de 100.000. De acuerdo con los análisis realizados, los autores concluyeron que una deriva neutra a partir de un pequeño tamaño inicial no puede explicar ese modelo de variación. Según ellos, ese incremento refleja una diversificación diferencial de las clases de mayor tamaño corporal más que una deriva neutral. Por lo tanto, cabe concluir que la tendencia al aumento del tamaño, probablemente generalizable al conjunto de los metazoos, no ha sido fruto del azar, sino que ha obedecido al efecto de ciertos factores, que han podido ser endógenos o de carácter ambiental.
Es importante no perder de vista que aunque ese análisis da cuenta de una tendencia general, ha habido importantes excepciones y ha linajes cuyo tamaño no ha variado apenas o lo ha hecho en sentido contrario.
Para terminar por ahora, me interesa destacar que el tamaño de los animales es un factor de gran importancia biológica, puesto que los aumentos de tamaño, como veremos, conllevan un aumento de la complejidad. Y también porque, como también tendremos ocasión de analizar, el tamaño tiene implicaciones estructurales, funcionales y ecológicas de gran importancia.
Referencias:
John Tyler Bonner (2006): Why Size Matters. Princeton University Press, Princeton.
Noel A. Heim, Matthew L. Knope, Ellen K. Schaal, Steve C. Wang y Jonathan L. Payne (2015): “Cope´s rule in the evolution of marine animals”. Science 347 (3224): 867-870
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Evolución del tamaño animal se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Biringuccio, la química práctica y rentable del XVI
Los profesionales de las artes químicas de la primera mitad del siglo XVI, salvo algunos conversos muy concretos a las doctrinas y prácticas de Paracelso, se caracterizaron por una aproximación muy práctica, en lo que coincidían con él, pero por un alejamiento total en su forma de comportarse y en la forma en que transmitían el conocimiento: libros producidos a un precio asequible gracias a la imprenta de tipos móviles que cualquier lector interesado podía comprar.

Primera edición de “De la pirotechnia” de Biringuccio, Venecia (1540). Nótese que está escrito en italiano, no en latín.
El siglo XVI fue testigo de grandes avances en la tecnología química que se plasmaron en varios libros impresos que trataron el tema. Libros que se distinguieron de los de sus predecesores alquímicos, incluidos los de Paracelso, por centrarse en aspectos exclusivamente prácticos, sin que mencionaran teoría alguna más que de pasada.
El objetivo de estos libros no era el avance del conocimiento, sino recoger de forma sistemática una tecnología compleja que no se parecía en casi nada a la que se había empleado de forma prácticamente inamovible durante buena parte de la Edad Media.
De forma general hablaban solo de aparatos y reactivos, y de las recetas necesarias para llevar a cabo los métodos de destilación. Muchas recetas, especialmente las relacionadas con los pigmentos y tintes empleados por los artistas, siguen siendo llamativamente parecidas a las recogidas en documentos alquímicos del siglo III, lo que representa una continuidad en las recetas de los artesanos a la hora de fabricar joyas de imitación, tintes textiles, tintas, pinturas y “trucos” químicos, baratos, pero espectaculares.
Uno de los libros destacados escrito por un contemporáneo de Paracelso fue De la pirotechnia de Vannoccio Biringuccio, publicado póstumamente en 1540. En él se recogía todo lo conocido sobre la metalurgia más avanzada de la época, la fabricación de armas y el uso de máquinas que empleaban la energía hidráulica.

Ensayando en el laboratorio antes de llevarlo a la practica industrial. Nótese la balanza.
En De la pirotechnia aparece primera vez de forma explícita la importancia de los ensayos como una guía llevar las operaciones a una escala mayor y se proporcionan, también por primera vez, los valores cuantitativos para llevar a cabo las distintas recetas.
Biringuccio también aporta una visión distinta de la alquimia precedente y de muchos de los aspectos esotéricos asociados, esoterismos que aún cultiva Paracelso, por cierto. Da su opinión a partir de su observación personal y de su experiencia, escribiendo (énfasis nuestro):
[…] me motivan razones mas poderosas, o quizás la inclinación natural, a seguir el camino de la minería con más voluntariamente que el de la alquimia, aunque la minería es una tarea más ardua, tanto física como mentalmente, es más cara, sus promesas son menores a primera vista y en palabras de las que hace la alquimia; y tiene como como su ámbito la observación de los poderes de la naturaleza más que los del arte, o, en verdad, más los de ver lo que realmente existe más que lo que uno piensa que existe.
O dicho de otra manera, De la pirotechnia representa que para la primera mitad del siglo XVI las menas metálicas naturales, así como sus separaciones y transformaciones por medio del calor, ácidos y destilaciones, se han convertido en algo más interesante y financieramente fructífero que el tiempo empleado esterilmente en las transmutaciones especulativas.

Edición en francés de “De la pirotechnia” de Biringuccio, París (1572)
El libro se convertirá en el estándar para mineros y metalúrgicos durante lo que resta del siglo XVI y buena parte del XVII. Y a ello contribuyó su publicación no en latín, sino en italiano, y su posterior traducción a otras lenguas modernas. Sin alharacas, Biringuccio también contribuyó a la reforma idiomática del conocimiento.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Biringuccio, la química práctica y rentable del XVI se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Dejad de propagar el mito de los estilos de aprendizaje
Paul A. Kirschner
Resumen
Los seres humanos nos diferenciamos unos de otros en multitud de formas, y como tal, nuestras preferencias varían en cuanto a música, alimentación o aprendizaje, por ejemplo. Como resultado, a muchos estudiantes, padres, profesores, administradores, e incluso investigadores, les parece intuitivamente correcto decir que como laspersonas prefieren aprender de forma visual, auditiva, cinestética, u otras, deberíamos adaptar la enseñanza, las situaciones y los recursos educativos a estas preferencias. ¿Es esto un problema? La respuesta es un rotundo ¡Sí! En términos generales hay varios problemas importantes con respecto a los estilos de aprendizaje. En primer lugar, hay una gran diferencia entre el modo en que alguien prefiere aprender y lo que realmente le lleva a un aprendizaje eficaz y eficiente. En segundo lugar, las preferencias de estudio no son estilos de aprendizaje. La mayoría de los llamados estilos de aprendizaje están basados en clasificar a las personas en grupos. Sin embargo, los estudios objetivos pocas veces tienen en cuenta que una persona se puede asociar a distintos grupos. Finalmente, casi todos los estudios que presentan pruebas sobre estilos de aprendizaje, no satisfacen los criterios elementales de validez científica. Basado en la evidencia científica, este artículo pide a profesores, administradores e investigadores, que dejen de propagar el mito de los estilos de aprendizaje.
“Ninguna suma de creencias hace de algo un hecho” – James Randi
“Todo hombre tiene derecho a su propia opinión, pero ningún hombre tiene derecho a equivocarse en sus actos” – Bernard Baruch1
A continuación un comentario invitado para esta revista, que además pretende servir de carta abierta a todos mis colegas académicos que investigan en esta área de conocimiento, a editores, a miembros de consejos editoriales y/o a revisores de revistas científicas como esta. En 2013 publiqué un artículo en Educational Psychologist con mi buen amigo y colega Jeroen van Merriënboer titulado “¿Saben realmente los estudiantes lo que es mejor para ellos? Leyendas urbanas en educación”. En dicho artículo discutimos una serie de leyendas urbanas que influyen en la enseñanza y la educación, tales como los estilos de aprendizaje, los nativos digitales, la multitarea, la pirámide de aprendizaje, entre otras. Basado en un tuit mío relacionado con un artículo publicado en Computers & Education, los editores se dirigieron a mí de la siguiente manera:
El 18 de agosto usted tuiteó: “¡La revista científica Computers & Education publica bulos sobre estilos de aprendizaje! ¿Cuándo los editores van a parar este absurdo?” Esto se relacionó con el reciente artículo de [Autor y otros] sobre estilos de aprendizaje [URL] en nuestra revista.
Creemos que los lectores de nuestra revista estarán interesados en una indagación más detallada sobre los estilos de aprendizaje, por lo que queremos pedirle que escriba un “comentario invitado” sobre este tema.
La esencia de mi crítica a los estilos de aprendizaje es que no hay una base científica real para la proposición (más bien debería ser considerada una creencia) de que (1) un alumno tiene realmente cierto estilo de aprendizaje óptimo, (2) este es consciente de cuál es su estilo de aprendizaje personal y/o hay una manera confiable y válida para determinar este estilo, y (3) un aprendizaje e instrucción óptimos implican, primero determinar este estilo de aprendizaje, y luego alinear la instrucción en consecuencia.
El supuesto en que se basan los estilos de aprendizaje es que los profesores, instructores, diseñadores educativos, desarrolladores pedagógicos, etc., deben adoptar el estilo de aprendizaje que, (1) los estudiantes dicen que tienen o (2) el determinado por alguno de los instrumentos existentes (por ejemplo, cuestionarios de estilos de aprendizaje), lo cual determina qué se debe tener en cuenta con respecto al estudiante, al diseñar, desarrollar, e impartir la instrucción. Al hacer esto, se facilitará un aprendizaje óptimo y se permitir el pleno desarrollo del estudiante para lograr resultados óptimos. Aunque esta idea parece intuitivamente atractiva y suena como si tuviera cierto grado de validez, hay dificultades fundamentales tanto en el diagnóstico de los estilos de aprendizaje como en la alineación de la instrucción con estos estilos. En el resto de este comentario intentaré aclarar cuáles son estos problemas.
En nuestro artículo (Kirschner y van Merriënboer, 2013) planteamos primero que los estilos de aprendizaje clasifican mal (en realidad encasillan) a los estudiantes. La mayoría de los estilos que se han “determinado” se basan en tipos. El estudiante no se asocia a un estilo basado en un conjunto de medidas en diferentes dimensiones, sino que se clasifica en un grupo específico, a menudo exclusivo (para una panorámica sobre estilos de aprendizaje véase Cassidy, 2004; Coffield, Moseley, Hall y Ecclestone, 2004,). El primer problema aquí es que la gente no puede simplemente agruparse en grupos específicos y distintos como muestran varios estudios (véase, por ejemplo, Druckman & Porter, 1991). La mayoría de las diferencias entre personas en cualquier dimensión que uno pueda imaginar son graduales y no nominales. Incluso la clasificación sexo/género que hasta hace poco se consideraba dicotómica ha demostrado ser más matizada que eso. Los defensores del uso de estilos de aprendizaje tienden a ignorar esto y usan criterios arbitrarios, como una mediana o una media en una cierta escala para asociar a una persona con un estilo específico.
Con respecto a este simple encasillamiento de los estudiantes, Barbara Prashnig (2005), quien podría ser considerada partidaria de los estilos de aprendizaje, y quien ha desarrollado instrumentos de estilos de aprendizaje, escribe que en uno de los instrumentos de estilos de aprendizaje más complejos y detallados del mercado [el Analizador de Estilos de Aprendizaje (Learning Style Analysis, LSA)] hay al menos
49 elementos diferentes… [con]… complejas combinaciones de estilos, matizadas por grados de necesidades que van desde preferencias claras a ninguna preferencia, pasando por preferencias flexibles. Dados los numerosos componentes de los estilos… no es posible etiquetar a los estudiantes simplemente seleccionando un rasgo de un estilo como predominante (p. 2).
En cuanto al número de clasificaciones (encasillamientos) que se han creado, Coffield y otros (2004) escriben que “el gran número de dicotomías en la literatura transmite algo de la confusión conceptual actual” (p. 136). En su revisión se refieren a 30 estilos de aprendizaje dicotómicos diferentes en la literatura2 (ver Tabla 1).
El segundo problema tiene que ver con la validez, confiabilidad y poder predictivo de las pruebas de estilos de aprendizaje que se están utilizando. Stahl (1999) reportó inconsistencias y baja confiabilidad en la medición de estilos de aprendizaje cuando los individuos realizan una prueba específica en dos momentos diferentes. En otras palabras, la fiabilidad entre pruebas es bastante baja. Esto también está relacionado con la información que se utiliza frecuentemente para evaluar los estilos de aprendizaje. El método más utilizado es la autoevaluación. Infortunadamente, la idoneidad de la autoevaluación para evaluar un estilo de aprendizaje es muy dudosa (véase por ejemplo Veenman, Prins, & Verheij, 2003).
La razón es que los estudiantes no son capaces de y/o no están dispuestos a informar lo que en realidad hacen, o lo que creen que hacen. Para ilustrar la falta de fiabilidad de la autoevaluación, Rawson, Stahovich y Mayer (2016) les preguntaron a un grupo de estudiantes cuándo hicieron su tarea y cuánto tiempo trabajaron en ella. También les dieron a estos estudiantes un “bolígrafo inteligente”, el cual indicaba cuándo y cuánto tiempo trabajaban en su tarea. Si bien hubo una significativa correlación positiva (r=,44) entre la cantidad de tiempo que los estudiantes pasaron trabajando en su tarea (medido por el “bolígrafo inteligente”) y la nota obtenida por los estudiantes en el curso, no hubo correlación significativa (r=-,16) entre la nota y el tiempo que los estudiantes dijeron haber dedicado a la tarea. En otras palabras, no hubo una correlación real entre la autoevaluación subjetiva y la medición objetiva. Además, la mayoría de los estudiantes (88%) sobrevaloraron el tiempo que dedicaron la tarea. Por último, Massa y Mayer (2006), encontraron que cuando los estudiantes informaban su preferencia por la información verbal en lugar de la información visual, esta preferencia solo estaba débilmente relacionada con sus habilidades reales medidas objetivamente (es decir, su capacidad espacial).
Además, la forma aprendizaje preferida según las autoevaluaciones suele ser un mal indicador de la forma más eficaz de aprender; lo que las personas prefieren no es, por definición, lo mejor para ellos. Knoll, Otani, Skeel y Van Horn (2016) concluyen que los estilos de aprendizaje están asociados con aspectos subjetivos del aprendizaje, y no con aspectos objetivos. En otras palabras, cabe preguntarse si realmente los estudiantes saben lo que es mejor para ellos. Clark (1982) publicó un metaanálisis crítico con respecto a la preferencia del alumno a la hora de elegir un cierto tipo de instrucción, y encontró que con frecuencia dicha preferencia tenía una correlación negativa con el qué y el cuánto se aprendió, y que en el mejor de los casos, no existía correlación alguna. Dicho de otra manera, aquellos estudiantes que dijeron preferir una forma particular de aprender, en la mayoría de los casos no tuvieron mejores resultados usando dicha forma, o incluso mostraron peor rendimiento. Este autor usó el término matematántico3(del griego mathema = un estudio donde algo es aprendido + thanatos = muerte) para describir un método de instrucción que por un lado coincide con la forma favorita de aprender del alumno, pero que a la vez es improductivo o perjudicial para su aprendizaje (Clark, 1989). En tal caso, un modelo de instrucción compensatorio o incluso remedial (véase Salomon, 1971, así como Berliner & Cahen, 1973, cuando discuten las interacciones rasgo-tratamiento) es probablemente un mejor enfoque, encaminado a compensar los efectos no deseados de una predisposición o preferencia específica (van Merriënboer, 1990). Para ponerlo en un contexto diferente, mientras que la mayoría de las personas prefieren los alimentos dulces, salados y/o grasos, creo que todos estaremos de acuerdo en que esa no es la mejor dieta a seguir, salvo que pretendamos poner en riesgo nuestra salud y ganar peso.
Tabla 1. 30 Estilos de aprendizaje discutidos en Coffield y otros (2004)
- Convergentes vs. divergentes
- Verbales vs. visuales
- Holísticos vs. seriados
- Profundos vs. superficiales
- Activos vs. reflexivos
- Pragmáticos vs. teóricos
- Adaptadores vs. innovadores
- Asimiladores vs. exploradores
- Dependiente vs. independiente del campo
- Globalistas vs. analistas
- Asimiladores vs. acomodadores
- Imaginativos vs. analíticos
- No comprometidos vs. pujantes
- Estudiantes de sentido común vs. dinámicos
- Estudiantes concretos vs. abstractos
- Estudiantes aleatorios vs. secuenciales
- Iniciadores vs. razonadores
- Intuicionistas vs. analistas
- Extrovertidos vs. introvertidos
- Detección vs. intuición
- Pensamiento vs. sentimiento
- Juzgar vs. percibir
- Cerebral izquierdo vs. derecho
- Significado-directo vs. indirecto
- Teóricos vs. humanistas
- Activos vs. teóricos
- Pragmáticos vs. reflexivos
- Organizadores vs. innovadores
- procesadores secuenciales izquierdo/analíticos/inductivos vs. procesadores simultáneos derechos/globales /deductivos
- Ejecutivo, jerárquico, conservador vs. legislativo, anárquico, liberal
Con respecto a la fiabilidad y validez de determinar el estilo de aprendizaje de una persona, Coffield y otros (2004) revisaron los 13 instrumentos más utilizados para determinar los estilos de aprendizaje con respecto a criterios psicométricos elementales, o sea, consistencia interna, fiabilidad entre pruebas, validez del constructo y validez predictiva (véase Tabla 2; Tabla 44 en su artículo).
Tabla 2. Trece modelos/instrumentos de estilos de aprendizaje y su cumplimiento de criterios elementales. (Coffield y otros, 2004; las referencias a estos instrumentos pueden encontrarse en dicho artículo).


Fig. 1. Interacción cruzada
Los autores concluyen que tres de los modelos (Jackson, Riding, e inteligencias múltiples de Sternberg) no se asociaron con ninguno de los cuatro criterios, cuatro (Dunn & Dunn, Gregorc, Honey & Mumford, y Kolb) se correspondieron con un solo criterio, tres (Entwistle, Herrmann, e indicador de tipo de personalidad de Myers-Briggs) con dos criterios, dos (Apter y Vermunt) con tres criterios y uno solo se asoció con los cuatro criterios (indicador de estilo cognitivo de Allinson & Hayes), pero este instrumento midió estilos cognitivos y no estilos de aprendizajes.
Nosotros concluimos en nuestro artículo (Kirschner y van Merriënboer, 2013):
Cuando en el diseño de la enseñanza se tienen en cuenta las diferencias entre los estudiantes, se debería evaluar las habilidades cognitivas más que los estilos de aprendizaje preferidos, porque las habilidades predicen mejor cómo las personas aprenden más eficazmente. Además, estas habilidades cognitivas deben ser medidas objetivamente en una escala ordinal, más que por autoevaluaciones subjetivas que son usadas para asociar personas con tipos en base a uno o más criterios arbitrarios.
Como un experimento imaginario, ignoremos todas las dificultades discutidas en relación con la medición y la determinación de los estilos de aprendizaje, y entonces preguntémonos si deberíamos adaptar la instrucción a los estilos de aprendizaje preferidos o determinados. Aquí, la hipótesis de los estilos de aprendizaje (Pashler, McDaniel, Rohrer, y Bjork, 2009) es importante, o sea, que se encontrará una interacción cruzada (véase Fig. 1) en la cual un tipo específico de estudiante aprende significativamente mejor con un método de enseñanza adaptado a su estilo de aprendizaje, mientras que otro tipo específico diferente de estudiante con un estilo de aprendizaje opuesto, aprende mejor con un método de instrucción adaptado a su estilo.
Por ejemplo, de acuerdo a esta hipótesis, los estudiantes que prefieren aprender de forma verbal, aprenderán mejor cuando se les enseña a través de métodos de instrucción verbales (por ejemplo, cuando se les da a leer un libro o un artículo), pero tendrán un bajo rendimiento al aprender con vídeos. En cambio los que prefieren aprender de manera visual, aprenderán mejor cuando se les enseña a través de métodos de instrucción visuales (por ejemplo, cuando se les orienta que vean un video) que cuando aprenden leyendo un libro. Lo importante aquí es que no es suficiente que se encuentre una interacción estadísticamente significativa entre un estilo y un método. Solo una interacción cruzada real se puede usar para confirmar las hipótesis de los estilos de aprendizaje.
Teniendo en cuenta todo lo anterior, cabe cuestionarse si existen suficientes estudios que presenten interacciones cruzadas robustas entre estilo y método, independientemente de si se usa un modelo preferencial, correctivo o compensatorio como base de las interacciones. Infortunadamente para los partidarios de los estilos de aprendizaje, este no es el caso (véase Coffield y otros, 2004, Pashler y otros, 2009, y Rohrer & Pashler, 2012). Pashler y otros (2009, p. 105) concluyen que “actualmente, no existe una base de evidencias adecuadas para justificar la incorporación de las evaluaciones de los estilos de aprendizaje en la práctica educativa general. Por lo tanto, sería mejor dedicar los limitados recursos educativos a la adopción de otras prácticas educativas que tengan una sólida base en evidencias, de las cuales hay un número cada vez mayor”.
En contraste, una serie de estudios recientes, bien diseñados, contradicen la hipótesis de los estilos de aprendizaje. Pashler y otros (2009) afirmaron que una investigación rigurosa sobre los estilos de aprendizaje debe seguir tres pasos:
-
Comenzar examinando el supuesto estilo de aprendizaje de los encuestados en el estudio Rogowsky, Calhoun y Tallal (2015), por ejemplo, examinando los estilos de aprendizaje visual versus auditivo.
-
Distribuir aleatoriamente los participantes en grupos donde la mitad debe recibir una instrucción que coincida específicamente con su estilo de aprendizaje y la otra mitad, una instrucción que coincida con el estilo opuesto (por ejemplo, los estudiantes visuales de un grupo deben leer, mientras que los alumnos visuales del grupo de control deben escuchar).
-
Asignar a todos los participantes la misma prueba.
Teniendo en cuenta estos tres pasos, Constantidinou y Baker (2002), por ejemplo, no encontraron relación alguna entre tener un supuesto estilo de aprendizaje visual y el aprendizaje de elementos verbales presentados de manera visual o auditiva. Massa y Mayer (2006) tampoco encontraron nada que apoyara la idea de que los diferentes métodos de enseñanza, enfatizando la información pictórica o verbal, eran de beneficio, de forma cruzada, para los visualizadores y verbalizadores, respectivamente. Se han encontrado resultados negativos similares para otros estilos de aprendizaje. En la enseñanza médica, Cook, Thompson, Thomas y Thomas (2009), no encontraron apoyo para la premisa de que trabajar desde los problemas a la teoría (es decir, siguiendo un enfoque inductivo) o de la teoría a los problemas (es decir, siguiendo un enfoque deductivo), conduciría a un mejor aprendizaje para los estudiantes sensores/concretos y los estudiantes intuitivos/abstractos, respectivamente. Por último, Rogowksy, Calhoun y Tallal (2015) no encontraron relación alguna estadísticamente significativa entre la preferencia por un estilo de aprendizaje particular (por ejemplo, auditivo, visual) y el aprendizaje (por ejemplo, la comprensión auditiva y la comprensión lectora).
La lista de estudios que demuestran el absurdo de los estilos de aprendizaje es abrumadora. A continuación dos interesantes citas relacionadas con el gran número de estudios sobre estilos de aprendizaje:
Para Morrison, Ross, Kalman, y Kemp (2011, p. 59), “a pesar de la extensa bibliografía sobre estilos de aprendizaje, subsisten interrogantes sobre el grado en que tales estilos pueden adaptarse a los métodos de enseñanza con algún beneficio para el aprendizaje (Knight, Halpin, & Halpin, 1992; Park & Lee, 2004; Snow, 1992). “
Para Dembo y Howard (2007, p.107), “… los instrumentos de estilo de aprendizaje no han demostrado ser válidos y confiables, no hay beneficio en adaptar la instrucción al estilo de aprendizaje preferido y no hay evidencia de que comprendiendo su estilo de aprendizaje mejore su aprendizaje y sus resultados… Rogamos a los educadores que reconsideren sus prácticas de instrucción, especialmente el consejo que dan a sus estudiantes sobre los estilos de aprendizaje, y basen sus prácticas en una investigación sólida”.
Para terminar, hay cuatro conclusiones que se pueden plantear con respecto a los estilos de aprendizaje y los estudios asociados a estos:
-
La premisa de que hay estudiantes con diferentes estilos de aprendizaje y que deben recibir instrucción utilizando métodos que coincidan con esos estilos, no es un hecho “probado”, sino más bien una creencia respaldada por escasa, si acaso alguna, evidencia científica.
-
Hay muchos problemas fundamentales en cuanto a la medición de los estilos de aprendizaje.
-
La base teórica para las interacciones entre los estilos de aprendizaje y los métodos de enseñanza es muy escasa.
-
La evidencia empírica significativa para la hipótesis de los estilos de aprendizaje es casi inexistente.
En otra referencia, Coffield y otros (2004) afirman que el concepto de estilos de aprendizaje está tan mal definido que es prácticamente inútil para la instrucción. Wheeler (2011) resumió esta afirmación así: “Probablemente la única razón por la que algunos profesores (y muchas instituciones educativas) se aferran a la idea de experimentar con estilos de aprendizaje, es que es conveniente hacerlo, y que de abandonar la idea por completo, tendrían que trabajar más duro con los estudiantes”.
A esto solo puedo añadir que cuando los maestros dicen que tienen pruebas de que el uso de estilos de aprendizaje funciona, la “prueba” que dan es principalmente anecdótica. Según Rosenthal y Jacobson (1992), lo que ven y/o experimentan es, probablemente, que cuando los maestros esperan un mejor desempeño de sus estudiantes, el desempeño es mejorado. Esto se conoce como efecto Pigmalión o Rosenthal, donde unas expectativas más altas conducen a un aumento en el rendimiento. Rosenthal sostiene que tales expectativas sesgadas afectan la realidad y crean profecías auto-realizables. Relacionado con esto, Reiner y Willingham (2010) declaran:
… la teoría de estilos de aprendizaje ha logrado convertirse en “conocimiento común”. Su amplia aceptación sirve como una razón, lamentablemente, para creer en ella. Esto se acompaña de un conocido fenómeno cognitivo llamado confirmación sesgada. Al evaluar nuestras propias creencias, tendemos a buscar información que confirme nuestras creencias e ignorar la información contraria, incluso cuando la encontramos repetidamente. Cuando vemos a alguien que profesa ser un aprendiz visual y sobresale en geografía y un alumno auditivo sobresale en música, no buscamos la información que refute nuestra interpretación de estos eventos (¿Puede el alumno auditivo aprender geografía a través de la escucha? ¿Puede el alumno visual mejorar en la música viéndola?) (np)
Newton (2015) encontró que una abrumadora mayoría (89%) de los recientes artículos de investigación, con el rango de fechas del 23 de julio de 2013 al 23 de julio de 2015, que figuran en las bases de datos de investigación ERIC y PubMed, apoyan implícita o directamente el uso de estilos de aprendizaje en la educación superior. Queremos hacer un llamamiento a la comunidad científica en esta área a hacer las cosas como corresponde. Howard-Jones (2014), presentando un estudio que llevó a cabo con Dekker, Lee, Howard-Jones y Jolles en 2012, encontró que el 95% de los profesores en Gran Bretaña, Holanda, Turquía, Grecia y China, estaban convencidos de que “[L]os individuos aprenden mejor cuando reciben información en su estilo de aprendizaje preferido (por ejemplo, visual, auditivo o cinestético)”.
Somos creadores y guardianes de nuevos conocimientos. Lo que estudiamos y/o publicamos puede y debe tener un impacto tanto en el mundo científico en el que nos desempeñamos como en el mundo educativo al que servimos. Como tal, es nuestro deber solemne investigar y publicar siguiendo buenas prácticas científicas, independiente de resultados positivos significativos, y combatir la difusión de la pseudociencia, los mitos y las mentiras abiertas. No hay beneficio que se pueda obtener al adaptar y diseñar la educación y la instrucción a estos denominados estilos. De hecho, de acuerdo con los efectos matematánticos de los enfoques preferidos en la instrucción, puede incluso suceder que de aplicar esta práctica, los administradores, maestros, padres, e incluso estudiantes, influyan negativamente en el proceso de aprendizaje, y por ende en los resultados educativos. Con esto en mente, considero necesario, e incluso nuestro deber como investigadores y/o editores y revisores de revistas, no propagar tales mitos. Debemos salvaguardar nuestra credibilidad como investigadores, como (portavoces de la) comunidad científica y trabajar en beneficio de aquellos a quienes servimos, a saber, la comunidad científica y la ciudadanía en general, especialmente educadores y estudiantes.
Agradecimientos
Estoy en deuda de gratitud con Jeroen van Merriënboer, con quien escribí el artículo en que se basa este comentario. También me gustaría agradecer a Pedro de Bruyckere, compañero de batallas quijotescas contra los mitos y las leyendas urbanas en la enseñanza y aprendizaje, quien leyó y comentó la primera versión de este artículo.
Referencias
Berliner, D. C., & Cahen, L. S. (1973). Trait-treatment interaction and learning. In F. N. Kerlinger (Ed.), Vol.1. Review of research in education (pp. 58-94). Itasca. IL: Peacock.
Cassidy, S. (2004). Learning styles: An overview of theories, models, and measures. Educational Psychology, 24, 419-444. http://dx.doi.org/10.1080/0144341042000228834.
Clark, R. E. (1982). Antagonism between achievement and enjoyment in ATI studies. Educational Psychologist, 17(2), 92-101.
Clark, R. E. (1989). When teaching kills learning: Research on mathemathantics. In H. Mandl, N. Bennett, E. De Corte, & H. Friedrich (Eds.), Learning and Instruction: European Research in an International Context (Vol. 2, pp. 1-22). London, UK: Pergamon.
Coffield, F., Moseley, D., Hall, E., & Ecclestone, K. (2004). Learning styles and pedagogy in post-16 learning: A systematic and critical review. London, UK: Learning and Skills Research Centre.
Constantidinou, F., & Baker, S. (2002). Stimulus modality and verbal learning performance in normal aging. Brain and Language, 82, 296e311. http://dx.doi.org/10.1016/S0093-934X(02)00018-4.
Cook, D. A., Thompson, W. G., Thomas, K. G., & Thomas, M. R. (2009). Lack of interaction between sensing-intuitive learning styles and problem-first versus information-first instruction: A randomized cross-over trial. Advances in Health Sciences Education, 14, 79e90. http://dx.doi.org/10.1007/s10459-007-9089-8.
Dekker, S., Lee, N. C., Howard-Jones, P. A., & Jolles, J. (2012). Neuromyths in education: Prevalence and predictors of misconceptions among teachers. Frontiers in Psychology, 3, 429. http://dx.doi.org/10.3389/fpsyg.2012.00429.
Dembo, M. H., & Howard, K. (2007). Advice about the use of learning styles: A major myth in education. Journal of College Reading and Learning, 37(2), 101 – 109.
Druckman, D., & Porter, L. W. (1991). Developing careers. In D. Druckman, & R. A. Bjork (Eds.), In the mind’s eye: Enhancing human performance (pp. 80-103). Washington, DC: National Academy Press.
Howard-Jones, P. A. (2014). Neuroscience and education: Myths and messages. Nature Reviews Neuroscience, 15, 817e824. http://dx.doi.org/10.1038/nrn3817.
Kirschner, P. A., & van Merriënboer, J. J. G. (2013). Do learners really know best? Urban legends in education. Educational Psychologist, 48(3), 169e183. http://dx.doi.org/10.1080/00461520.2013.804395.
Knight, C. B., Halpin, G., & Halpin, G. (1992). The effects of learning environment accommodations on the achievement of second graders. Paper presented at the annual meeting of the American Educational Research Association, San Francisco, CA.
Knoll, A. R., Otani, H., Skeel, R. L., & Van Horn, K. R. (2016). Learning style, judgements of learning, and learning of verbal and visual information. British Journal of Psychology. http://dx.doi.org/10.1111/bjop.12214.
Massa, L. J., & Mayer, R. E. (2006). Testing the ATI hypothesis: Should multimedia instruction accommodate verbalizer-visualizer cognitive style? Learning and Individual Differences, 16, 321-336. http://dx.doi.org/10.1016/j.lindif.2006.10.001.
Morrison, G. R., Ross, S. M., Kalman, H. K., & Kemp, J. E. (2011). In Designing effective instruction (6th ed.). Hoboken, NJ: John Wiley & Sons, Inc.
Newton, P. M. (2015). The learning styles myth is thriving in higher education. Frontiers in Psychology, 6, 1908. http://dx.doi.org/10.3389/fpsyg.2015.01908.
Park, O., & Lee, J. (2004). Adaptive instructional systems. In D. H. Jonassen (Ed.), Handbook of research on educational communications and technology (2nd ed., pp. 651-684). Mahwah, NJ: Lawrence Erlbaum Associates.
Pashler, H., McDaniel, M., Rohrer, D., & Bjork, R. (2009). Learning styles: Concepts and evidence. Psychological Science in the Public Interest, 9(3), 105-119. http://dx.doi.org/10.1111/j. 1539-6053.2009.01038.x.
Prashnig, B. (2005, Autumn). Learning styles vs. multiple intelligences (MI): Two concepts for enhancing learning and teaching (Vol. 9, pp. 8-9). expertise, com. Retrieved from: www.teacher http://www.creativelearningcentre.com/downloads/LS%20vs%20MI%20TEX9_p8_9.pdf.
Rawson, Stahovich, & Mayer. (2016). Homework and achievement: Using smartpen technology to find the connection. Journal of Educational Psychology. http://dx.doi.org/10.1037/edu0000130 (in press).
Reiner, C., & Willingham, D. (2010). The myth of learning styles. Change Magazine (Sept-Oct.).
Rogowsky, B. A., Calhoun, B. M., & Tallal, P. (2015). Matching learning style to instructional method: Effects on comprehension. Journal of Educational Psychology, 107, 64-78.
Rogowksy, B. A., Calhoun, B. M., & Tallal, P. (2015). Matching learning style to instructional method: Effects on comprehension. Journal of Educational Psychology, 107(1), 64-78. http://dx.doi.org/10.1037/a0037478.
Rohrer, D., & Pashler, H. (2012). Learning styles: Where’s the evidence? Medical Education, 46, 630-635.
Rosenthal, R., & Jacobson, L. (1992). Pygmalion in the classroom. New York, NY: Irvington.
Rothkopf, E. Z. (1970). The concept of mathemagenic activities. Review of Educational Research, 40, 325-336.
Salomon, G. (1971). Heuristic models for the generation of aptitude-treatment interaction hypotheses. Review of Educational Research, 2, 327-343.
Snow, R. E. (1992). Aptitude theory: Yesterday, today, and tomorrow. Educational Psychologist, 27, 5-32.
Stahl, S. A. (1999). Different strokes for different folks? A critique of learning styles. American Educator, 23(3), 27-31.
Van Merriënboer, J. J. G. (1990). Instructional strategies for teaching computer programming: Interactions with the cognitive style reflection-impulsivity. Journal of Research in Computing Education, 23, 45-53. http://dx.doi.org/10.1080/08886504.1990.10781942.
Veenman, M. V. J., Prins, F. J., & Verheij, J. (2003). Learning styles: Self-reports versus thinking-aloud measures. British Journal of Educational Psychology, 73, 357-372. http://dx.doi.org/10.1348/000709903322275885.
Wheeler, S. (November, 2011). A convenient untruth. Learning with ‘e’s [blog]. Retrieved from http://steve-wheeler.blogspot.ca/2011/11/convenient-untruth.html.
Notas:
1 Una variante de este planteamiento es atribuida a Daniel Patrick Moynahan como “Cada cual tiene derecho a sus propias opiniones, pero no a sus propios hechos”, salvo que la referencia de Baruch se realizó hace 24 años.
2 Si hay “solo” 30 variables dicotómicas que se pueden aplicar a los estudiantes, entonces hay 230 combinaciones diferentes de estos 30 estilos dicotómicos, lo cual significa que hay al menos 1,073,741,824 estilos de aprendizaje diferentes. Si solo contamos los niño(a)s aquí (estimados en 2 billones), esto significa un estilo por cada dos niño(a)s
3 Ernst Rothkopf había acuñado ya en 1970 (Rothkopf, 1970) el término actividades matemagénicas (gigneshai = nacer) para referirse a aquellas actividades que dan lugar a un proceso de aprendizaje.
Sobre el autor: Paul A. Kirschner es catedrático de psicología educativa en la Open University of the Netherlands (Países Bajos) y profesor visitante de la University of Oulu (Finlandia)
Traducido y adaptado por: Héctor Pijeira Diaz y Raidell Avello Martínez
Artículo Original (Source): Kirschner, P. A. (2017). Stop propagating the learning styles myth. Computers & Education, 106, 166-171. http://www.sciencedirect.com/science/article/pii/S0360131516302482
Blog Original: http://tinyurl.com/jnnmgks y https://onderzoekonderwijs.net/2017/02/26/dejad-de-propagar-el-mito-de-los-estilos-de-aprendizaje/
El artículo Dejad de propagar el mito de los estilos de aprendizaje se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El aprendizaje del inglés es mejor si se usa para aprender otra cosa
- #Naukas16 Mito(bio)logía griega
- Otro mito desacreditado: la peligrosidad de las viudas negras
El corpus de confusión consistente del inglés oral
En la percepción del habla con ruido de fondo a menudo se producen errores en los que el oyente cree haber escuchado una palabra distinta de la pronunciada. Este fenómeno se ha llamado “deslices del oído” (slips of the ear). Un grupo en el que trabaja la profesora de la UPV/EHU María Luisa García Lecumberri ha generado el primer gran corpus de errores de percepción coincidentes para el inglés, que abarca más de 3.000 términos y está disponible on line.

Normalmente no oímos en condiciones óptimas -hay ruidos de fondo como tráfico, máquinas, otras conversaciones- pero, como hablantes nativos y ayudados por el contexto, tenemos capacidad para reconstruir la parte de la señal que no nos ha llegado. Sin embargo, ello no evita que cometamos errores. El grupo que integran María Luisa García Lecumberri, el profesor Ikerbasque de la UPV/EHU Martin Cooke y los investigadores de la Universidad de Sheffield Jon Barker y Ricard Marxer ha identificado 3.207 percepciones erróneas coincidentes para el inglés, es decir, errores en los que un número significativo de oyentes coinciden. Estas concordancias tienen valor como tests de los modelos de percepción del habla y para comprender mejor cómo funcionan los mecanismos de percepción de los humanos.
Para ello realizaron un estudio a gran escala con 212 participantes y más de 300.000 presentaciones de palabras, que los investigadores sacaban de contexto, es decir, las presentaban de forma aislada con ruido de fondo. El estudio logró identificar 3.207 percepciones erróneas coincidentes y las ha reunido en un corpus, único en su categoría y que está disponible online: http://spandh.dcs.shef.ac.uk/ECCC/. Para cada una de las percepciones erróneas, el corpus presenta las ondas sonoras de la palabra pronunciada y del ruido de fondo que generó el error, las respuestas aportadas por los oyentes y las transcripciones fonémicas de la palabra pronunciada y de la percibida. Se observó que hay distintos tipos de confusiones. En algunos casos está claro que el ruido ocultaba parte de la palabra y los oyentes imaginaban otra palabra que coincidía con las partes audibles (“wooden –> wood” o “pánico” –> “pan”) o sustituían las partes inaudibles por otros sonidos (“ten” –> “pen” y “valla –>falla”). En otros casos se reconstruían la palabra incorporando fragmentos del ruido o conversaciones de fondo, (“purse –> permitted” o “ciervo” –> “invierno”). Finalmente se encontraban percepciones extrañas pero con coincidencia de varios hablantes, en las que no había ninguna similitud entre la palabra emitida y la que creían haber óido, (“modern –> suggest” o “guardan –> pozo”). En estos casos la interacción entre habla y ruido es bastante más compleja y, por lo tanto, interesante.
“Estos estudios nos ayudan a comprender mejor los mecanismos de percepción del habla, y cuanto mejor conozcamos dichos mecanismos, mejor se podrá ayudar, a nivel técnico y clínico, a los que padecen problemas de percepción”, indica la investigadora. El grupo publicó anteriormente un corpus de deslices de oído del castellano, que también puede ser consultado en el mismo sitio web. “Entre ambos hay similitudes y diferencias: el castellano es una lengua con más flexión, lo cual provoca que haya más confusiones en las terminaciones; el inglés tiene más monosílabos y más riqueza consonántica en posición final, donde se producen más errores en los que se sustituye una consonante por otra”, añade. Coinciden ambas lenguas en que, dependiendo del tipo de ruido, sobreviven mejor unos tipos de sonidos y sílabas que otros.
Ricard Marxer, Jon Barker, Martin Cooke, and Maria Luisa Garcia. A corpus of noise-induced word misperceptions for English. The Journal of the Acoustical Society of America Volume 140, Issue 5. doi: 10.1121/1.4967185.
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo El corpus de confusión consistente del inglés oral se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El aprendizaje del inglés es mejor si se usa para aprender otra cosa
- Las plantas como aislantes acústicos
- La percepción del propio peso es peor en las chicas que en los chicos
Mundos imaginados

Rover Curiosity (Imagen: NASA)
EL pasado 22 de febrero se anunció un descubrimiento que entusiasmó a los especialistas, fascinó a los amantes de la astronomía y cautivó la atención del público. A 39 años luz -no demasiado lejos- de nuestro sistema solar, donde se pensaba que había un sistema con una enana roja (su masa es el 8% de la de nuestro sol) y tres planetas, han descubierto que en realidad hay siete planetas. Y lo que es más importante: son de dimensiones parecidas a las de la Tierra y tres de ellos se encuentran en la zona de habitabilidad. O sea, podrían contener agua líquida, condición considerada esencial, si se cumplen otras -como la existencia de algún tipo de atmósfera, por ejemplo-, para el desarrollo de alguna forma de vida.
A la misma hora que se anunciaba ese descubrimiento, el profesor Madariaga, catedrático de química analítica de la Universidad del País Vasco, exponía en Bilbao los trabajos que desarrolla la NASA, y en los que su equipo participa en aspectos científico-tecnológicos claves, para poner sobre la superficie de Marte un vehículo con un laboratorio equipado para detectar la existencia, presente o pasada, de vida en el planeta rojo. El público siguió fascinado sus explicaciones.
Es la vida, su búsqueda más allá de los límites de nuestro planeta, lo que nos cautiva, la posibilidad de que no estemos solos en el universo. La ciencia ficción ha explotado esa fascinación en muchas ocasiones. Y las agencias científicas se dedican a ello, tanto mediante la búsqueda de enclaves en nuestro sistema solar o en otros que sean propicios para la vida, como mediante la detección de señales que, procedentes de muy lejos, indiquen la existencia de otras formas de vida inteligente en el cosmos.
Según las últimas estimaciones, en el universo observable hay entre doscientos mil millones y dos billones de galaxias. Y en una galaxia puede haber desde unos pocos miles de millones de estrellas hasta un centenar de billones. Por eso, aunque la probabilidad de la existencia de planetas que reúnan las condiciones para la vida sea ridículamente baja, deben de existir millones de planetas en los que se dan esas condiciones. Los recién descubiertos no son los primeros exoplanetas de los que sabemos que pueden reunir condiciones para la vida, pero sí los más próximos. Esa relativa cercanía, así como otros rasgos del sistema, han disparado el interés de los especialistas y del público. Y lo que es más importante: genera nuevas y prometedoras expectativas en la exploración del cosmos.
Estos descubrimientos nos fascinan, sí. Pero también hay quienes, legítimamente, dudan que deban destinarse recursos a la exploración del universo. Les parecen caros y no perciben sus beneficios. Se equivocan. Los costes de las sondas a Marte o al espacio exterior, de los telescopios y, en general, de la exploración espacial son ridículos al lado de lo que nos gastamos en armas, por ejemplo. Y la inversión proporciona, por el desarrollo tecnológico que exige, valiosísimos retornos en conocimiento aplicable a corto plazo. Aunque no evidentes a primera vista, son argumentos poderosos para los que dudan de su “utilidad”.
Otros tenemos razones tan poderosas o más que las anteriores: descubrimientos como el de los nuevos exoplanetas abren nuevas puertas, incluso si son pequeñas, a nuevo conocimiento, algo de gran “utilidad” per se. Porque frente a un futuro intrínsecamente incierto, no neutralizaremos los peligros que adivinamos para nuestra supervivencia y bienestar con medidas que limiten la capacidad de actuación. La única actitud sensata ante la incertidumbre es atesorar cada vez más conocimiento. También acerca de esos mundos que hoy solo podemos imaginar.
—————————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————————
Este artículo fue publicado en la sección #con_ciencia del diario Deia el 26 de febrero de 2017.
El artículo Mundos imaginados se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La aburrida pluralidad de mundos habitados
- Hacedores de mundos
- #Naukas16 Exoplanetas: mundos de ciencia ficción
#Naukas16 Big Van Science

BigVan o, mejor, una muestra representativa, se subió al escenario del Bizkaia Aretoa para hablar de la que es, sin duda, la disciplina científica más importante…
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo #Naukas16 Big Van Science se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #Naukas16 ¿Cómo saber si tu funeraria te estafa?
- #Naukas16 De profesión, futurólogo
- #Naukas16 Mito(bio)logía griega
Las Cartas de Darwin: El sueño truncado de Canarias
Las cartas de Darwin, una serie para conocer aspectos sorprendentes de la vida del naturalista
En enero de 1828, cuando aún no había cumplido 20 años, Darwin llega a Cambridge después de un infructuoso paso por la Universidad de Edimburgo donde supuestamente debía convertirse en médico como su padre. El joven se mareaba cada vez que veía la sangre y parecía claro que ese no era el camino para el que estaba destinado. No obstante en Escocia se apañó bastante bien en las asignaturas de historia natural, de química e incluso recibió clases particulares de taxidermia de un esclavo liberado llamado John Edmonstone de quien aprendió a disecar.
En Cambridge se inscribe en el Christ’s College con la intención de estudiar el grado ordinario de teología, algo que podría contentar a su padre ya que ser clérigo era algo socialmente considerado en esa época y de paso le permitiría dedicarse a su afición de naturalista. De hecho, durante estos siglos gran parte de los naturalistas y geólogos eran reverendos anglicanos.
En estos casi cuatro años que dura su estancia en Cambridge (1828-1831) entabla amistad con dos figuras que serán fundamentales en la futura vida de Darwin y en su viaje en el Beagle: los reverendos John Stevens Henslow (profesor de botánica) y Adam Sedgwick (profesor de geología). Estos dos profesores y su pasión por la lectura de las aventuras naturalistas de Von Humboldt le empujarán a organizar lo que realmente iba a ser el viaje de sus sueños: Visitar las Islas Canarias.
Carta a su primo William Darwin Fox [07de abril de 1831]
“Por ahora, hablo, pienso y sueño en el plan que he cocinado para ir a las islas Canarias. Hace tiempo que tengo el deseo de ver paisajes y vegetaciones tropicales y, según Humboldt, Tenerife es un buen ejemplo de ellos”

“The Charles Darwin Sculpture Garden, Cambridge” Escultura de bronce realizada por Anthony Smith como pieza central del jardín. Captura el momento, a principios del verano de 1831, cuando Charles Darwin, un joven de 22 años en este College, estaba planeando una expedición a Tenerife en las islas Canarias. Esperaba seguir los pasos de uno de sus héroes, el explorador y naturalista Alexander von Humboldt” | Imagen Javier Peláez.
Carta a su hermana Caroline Darwin [28 de abril de 1831]
“Mientras te escribo mi mente le da vueltas a los trópicos. Por la mañana voy y contemplo las palmeras del invernadero y regreso a casa y leo a Humboldt: mi entusiasmo es tan grande que apenas si me puedo quedar quieto en mi silla. Henslow y otros profesores apoyan nuestro plan: Henslow me promete meterme la geología a la fuerza. Nunca me sentiré tranquilo hasta no ver el pico de Tenerife y el árbol drago [Dracaena draco]; las deslumbrantes llanuras arenosas y el silencioso bosque sombrío son lo que más alterna en mi cabeza. Trabajo regularmente en mi español; Erasmus me aconsejó decididamente que dejara el italiano. Me he trazado un esplendor tropical”.
Carta a su primo William Darwin Fox [11 de mayo de 1831]
“En cuanto a mi plan para las Canarias, es imprudente que me hagas tantas preguntas. Mis otros amigos desean sinceramente que ya me encuentre ahí, de tanto que los atosigo con mi plática sobre los paisajes tropicales, etc., etc. Eyton irá en el próximo verano, y ya estoy aprendiendo español”.
Carta a su primo William Darwin Fox [09 de julio de 1831]
“El plan de las Canarias va viento en popa. Trabajo como un tigre para conseguirlo, en este momento con el español y la geología, y mientras que al primero lo encuentro intensamente estúpido, la segunda es de lo más interesante”.
Carta a John Stevens Henslow [11 de julio de 1831]
“Y ahora, lo que toca a las Canarias. Le escribí al señor Ramsey dándole la poca información que pude conseguir en la ciudad. Pero como posiblemente dejó Cambridge, lo intentaré por mí mismo. Pasaje: 20 libras. Los barcos van y vuelven durante los meses de junio a febrero, aunque como no he visto aún al agente, las dos preguntas más importantes quedan sin responder, o sea si significa junio inclusive y con qué frecuencia navegan. No tardaré en enterarme de todo ello. Espero que usted siga alimentando su fervor canario. He leído y releído a Humboldt, así que haga lo mismo y estoy seguro de que nada impedirá que veamos el árbol del gran drago”.

Escultura de Darwin en el Christ’s College de Cambridge | Imagen Javier Peláez.
Como vemos la idea original era que Henslow acompañara a Darwin en su viaje, sin embargo el profesor atado por obligaciones personales se fue distanciando del proyecto.
Carta a su primo William Darwin Fox [01 de agosto de 1831]
“El plan de las Canarias no tendrá lugar antes del próximo junio, y lamento saber que la posibilidad de que Henslow venga es muy remota. Esperaba que conforme pasaran los días las cosas fueran arreglándose”.
Paradójicamente serían estas obligaciones familiares de su profesor de botánica las que terminarían llevando a Darwin a tomar su puesto en el Beagle puesto que la invitación fue en primer lugar para Henslow quien, al no poder embarcarse en un viaje tan largo propuso que fuera el joven Darwin el que ocupara su lugar.
Y es que, apenas unos días después de esta carta de Darwin fechada el 01 de agosto, los acontecimientos iban a dar un giro inesperado para todos. Sin que él supiera nada, el futuro de Charles Darwin estaba a punto de cambiar radicalmente gracias a una carta de la que ni siquiera era consciente.
Esta carta representa probablemente el momento clave de toda su vida. Una hoja de apenas cuatro párrafos, escrita por el profesor de matemáticas George Peacock a Henslow, y que terminaría cambiando el plan de Darwin las Canarias por otro aún más ambicioso:
Carta de George Peacock a John Stevens Henslow [13 de agosto 1831]
Querido Henslow: El capitán FitzRoy partirá para inspeccionar la costa de Tierra del Fuego, visitar más tarde muchas de las islas del mar del Sur y regresar por el archipiélago indio. El barco ha sido habilitado expresamente con fines científicos, en combinación con la exploración. Por lo tanto proporcionará una rara oportunidad para un naturalista y sería muy infortunado que se perdiera… […] ¿Habría alguna persona a quien usted pudiera recomendar ampliamente? Debe ser una persona tal que dé satisfacción a nuestra recomendación. Piense en esto: sería una grave pérdida para la causa de las ciencias naturales que se perdiera esta preciosa oportunidad. El barco partirá a finales de septiembre. […] Escriba inmediatamente y dígame qué puede hacerse”.
Más adelante en esta serie de artículos analizaremos con más detalle las diferentes cartas que llevaron a Darwin a embarcarse en el HMS Beagle, pero por ahora diremos que esta nueva aventura reunía todas sus expectativas puesto que la primera parada prevista de este gran viaje también eran las islas Canarias.

“Cuadro físico de las Islas Canarias. Geografía de las Plantas de Tenerife.” Extraído del Volumen 1 de los Viajes a las regiones equinocciales del nuevo continente de Humboldt.
A pesar de que septiembre era el mes previsto para el inicio del viaje, el arduo trabajo de acondicionamiento del Beagle hizo que la partida se retrasara hasta el 27 de diciembre de 1831. A partir de este día, y ya embarcado, Darwin se pasó las primeras semanas enfermo por el “mal de mar” y, recluido en el camarote, estuvo casi siempre mareado y vomitando.
Hasta el 08 de febrero apenas tuvo un momento para volver a escribir, y al primero a quien envió una carta fue a su padre, Robert Waring Darwin, explicando los vaivenes del viaje y la llegada, por fin, a su sueño dorado: Las islas Canarias.
Carta a Robert Waring Darwing [08 de febrero 1832]
“[…] Nos hicimos a la vela, como usted sabe, el 27 de diciembre. […] En el golfo de Vizcaya nos topamos con una larga y continuada mar crecida y la infelicidad que soporté por el mal de mar llegó mucho más allá de todo lo que esperaba. […] No logré que nada me aliviara más que tenderme en mi hamaca. Debo exceptuar su envío de uvas, pues es la única comida que soporta mi estómago.
El 04 de enero estábamos a unas millas de Madeira, pero como había un mar alborotado y la isla estaba a barlovento, no valía la pena pensar en abordarla. Yo estaba tan enfermo que ni siquiera pude levantarme para ver su contorno en la distancia.
El 06 de enero por la tarde llegamos al puerto de Santa Cruz (de Tenerife). Al principio me sentía moderadamente bien y me representaba a mí mismo todas las delicias de fruta fresca creciendo en bellos valles y leyendo las descripciones de Humboldt de las gloriosas vistas de las islas.
Quizá pueda usted imaginar nuestra desilusión cuando un hombrecito pálido nos informó que debíamos observar una estricta cuarentena de 12 días. Hubo un silencio de muerte en el barco hasta que el capitán gritó: “¡Larguen el foque!” y abandonamos este lugar tan deseado”.

Pico Teide en Tenerife. Imagen Javier Peláez
Hace unos años el periódico Diario de Avisos contactó conmigo y me pidió una columna semanal sobre historia y ciencia. Acepté y titulé a aquella sección “Desde la cubierta del Beagle” puesto que fue así como Darwin vio realmente las islas Canarias. Nunca llegó a pisarlas y al final tuvo que contentarse con contemplar sus paisajes desde el mar… desde la cubierta de su barco.
“Tuvimos mar en calma por un día entre Tenerife y la Gran Canaria y aquí experimenté por primera vez un gran placer: la vista era magnífica. El pico de Tenerife se veía entre las nubes como de otro mundo. Nuestra única desventaja era el deseo extremado de visitar esta espléndida isla. Padre, dígale a Eyton que no olvide nunca cualquiera de las islas canarias, que con toda seguridad la molestia necesaria valdrá la pena y que debe tener en mente encontrarse con una buena cantidad de problemas. Sin embargo estoy seguro de que se arrepentirá si no hace el intento”.
Este post ha sido realizado por Javier Peláez (@irreductible) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
El artículo Las Cartas de Darwin: El sueño truncado de Canarias se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las cartas de Darwin: 50 años para un proyecto titánico
- Bilbao celebrará el día de Darwin
- La unidad de selección en la evolución y el origen del altruismo (1): En el comienzo fue Darwin
#Naukas16 ¿Cómo saber si tu funeraria te estafa?

La ciencia forense también descubre fraudes funerarios. JM Mulet lo ilustra.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo #Naukas16 ¿Cómo saber si tu funeraria te estafa? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #Naukas16 Arqueología funeraría: la fama y el olvido
- #Naukas16 Cómo escribir un libro de ciencia para niños
- #Naukas16 La nutrición está sobrevalorada (y cómo me jode)

