¿Un visitante de un mundo oceánico?
Siempre ha estado muy, muy cerca, en nuestro sistema solar, y lleva en él mucho más tiempo que nosotros, al menos, desde que este se originó hace unos 4500 millones de años, así que es posible que lo «viera» todo… y estamos deseando que nos lo cuente. Su nombre es Bennu, un asteroide cuya órbita se extiende entre el interior de la terrestre y el exterior de la marciana, y es uno de los pocos cuerpos celestes de los que hemos podido traer muestras a la Tierra hasta el momento ―los otros son la Luna, así como los asteroides Itokawa y Ryugu y material de la cola del cometa 81P/Wild.
 Asteroide Bennu, antes 1999 RQ36. Bennu es una antigua ave mitológica egipcia, similar al ave fénix griego. El nombre lo eligió Michael Puzio, de 9 años, un niño de Carolina del Norte.
Asteroide Bennu, antes 1999 RQ36. Bennu es una antigua ave mitológica egipcia, similar al ave fénix griego. El nombre lo eligió Michael Puzio, de 9 años, un niño de Carolina del Norte.Fuente: NASA/Goddard/University of Arizona
El 24 de septiembre de 2023 aterrizó en el desierto de Utah una cápsula con los 70,3 gr que la misión de la NASA OSIRIS-Rex (Origins, Spectral Interpretation, Resource Identification, and Security – Regolith Explorer) había logrado obtener de la superficie de Bennu ―más de los 60 gr que se habían establecido como objetivo y la más abundante hasta el momento―. La sonda se lanzó el 8 de septiembre de 2016 y llegó a su destino dos años después: el 3 de diciembre de 2018. Las muestras se recogieron el 20 de octubre de 2020 y llegaron hasta nosotros tres años después. Ya hemos empezando a obtener los primeros resultados de su análisis.
 La cápsula con las muestras del asteroide Bennu aterrizó en el desierto de Utah el 24 de septiembre de 2023. Se logró abrir, tras alguna dificultad, el 11 de octubre. Fuente: NASA/Keegan Barber
La cápsula con las muestras del asteroide Bennu aterrizó en el desierto de Utah el 24 de septiembre de 2023. Se logró abrir, tras alguna dificultad, el 11 de octubre. Fuente: NASA/Keegan Barber
Pero ¿qué tiene de especial Bennu? ¿Por qué esta inversión de recursos para analizarlo e incluso traer muestras de su superficie? Son varios los motivos que expone la NASA. El primero de ellos ya lo hemos mencionado: es muy antiguo, al menos tanto como el propio sistema solar, lo que ya podría darnos muchos datos sobre la manera en la que este se formó, pero es que, además, Bennu podría contener fragmentos de materiales más antiguos. Preservado durante tantos miles de millones de años gracias al vacío del espacio, podría considerarse una cápsula del tiempo de la historia de nuestros propios orígenes… y el de la vida en general debido a su composición, rica en moléculas orgánicas e incluso agua. Además, pero no menos importante, se encuentra bastante cerca de nosotros y su máxima aproximación a nosotros tiene lugar cada seis años, lo que facilita las labores de lanzamiento. También tiene el tamaño adecuado ―es más o menos como el Empire State Building, de Nueva York― como para que su velocidad de giro sobre sí mismo no sea tan grande como para haber complicado muchísimo las labores de aterrizaje.
 Momento de recolección de muestras de la misión OSIRIS-REx en la zona de aterrizaje Nightingale, en el asteroide Bennu.
Momento de recolección de muestras de la misión OSIRIS-REx en la zona de aterrizaje Nightingale, en el asteroide Bennu.Créditos: NASA/Goddard/University of Arizona
Por si todo esto no fuera suficiente, aún hay más: Bennu podría tener algunas claves para averiguar cuál sería nuestra mejor estrategia de protección en el caso de que algún asteroide se aproximara demasiado a la Tierra, ya que se espera que en 2135 se acerque a nosotros a una distancia menor que la de la Luna. ¡¿Cómo?! ¿Hay peligro de colisión entonces? ¡Para nada! Pero esa cercanía nos permitirá calcular y estudiar su trayectoria, así como la acción del campo gravitatorio de la Tierra sobre cualquier cuerpo similar que se pueda aproximar e incluso suponer una amenaza, con mucha mayor precisión.
Las muestras de Bennu se están analizando el Laboratorio Lunar y Planetario de la Universidad de Arizona y el director del proyecto, Dante Lauretta, ya ha empezado a dar algunas pistas, aunque aún no se ha publicado ningún resultado. Lo que han encontrado son ciertos tipos de minerales compatibles con la presencia de agua y otros similares a los detectados en los géiseres de Encélado, uno de los satélites de Saturno, que, pensamos, oculta un vasto océano bajo su capa superficial de hielo. Así que, ¿es posible que Bennu venga de un lugar similar? Esa es, según Lauretta, la hipótesis con la que trabajan en este momento. No ha dado mucha información más, pero se espera que se publiquen muchos más detalles en algunas semanas que, según comenta el investigador son «muy interesantes».
 Géiseres de Encélado fotografiados por la sonda Cassini en el año 2009. Fuente: NASA/JPL-Caltech/SSI/CICLOPS/Kevin M. Gill
Géiseres de Encélado fotografiados por la sonda Cassini en el año 2009. Fuente: NASA/JPL-Caltech/SSI/CICLOPS/Kevin M. Gill
En cualquier caso, puede que lo más bello de este tipo de misiones sea cómo nuestras ensoñaciones sobre otros mundos parecen hacerse realidad. En esta ocasión, nuestro visitante de las estrellas no es más que un pedazo de roca a la deriva, pero que, tal vez, venga de un mundo que hemos imaginado muchas veces: El mundo azul, de Jack Vance; Cachalot, de Alan Dean Foster; Terramar, de Ursula K. Le Guin; Hydros, de Robert Silverberg; El mundo de Roche, de Robert L. Forward; Solaris, de Stanislaw Lem, y tantos, tantos otros.
 Fuente: Pixabay / NWimages by Sabrina Eickhoff
Fuente: Pixabay / NWimages by Sabrina Eickhoff
Estaremos muy atentos al mensaje que traiga consigo este pequeño asteroide.
Bibliografía
Howgego, Joshua (10 de febrero de 2024). Bennu may be from an ocean world, New Scientist.
NASA Science, OSIRIS-Rex.
Méndez Chazarra, Nahúm (8 de agosto de 2022). Meteoritos interestelares, muestreando otros sistemas planetarios, Cuaderno de Cultura Científica.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo ¿Un visitante de un mundo oceánico? se ha escrito en Cuaderno de Cultura Científica.
El árbol de Fibonacci
En esta entrada del Cuaderno de Cultura Científica recuperamos un tema clásico de la sección Matemoción, la conocida sucesión de Fibonacci. En concreto, vamos a mostrar que se puede construir un árbol relacionado con la sucesión de números en la que cada término es igual a la suma de los dos términos anteriores, siendo los dos primeros 1 y 1, esto es, la sucesión de Fibonacci:

La sucesión de Fibonacci fue introducida, al menos en Europa (en la entrada El origen poético de los números de Fibonacci puede leerse cómo surgió el conocimiento de esta sucesión en la India, en relación con la poesía en sánscrito), por el matemático italiano Leonardo de Pisa (1170-1241), a quien se le conocía como Fibonacci, esto es, hijo de Bonaccio, en su libro Liber Abaci / El libro del ábaco (1202), como solución a uno de los problemas de ingenio que se planteaban en el mismo.
Recordemos, una vez más, el problema en cuestión:
“Consideremos una familia de conejos con la característica de que tardan un mes en ser fértiles. Cuando han alcanzado la fertilidad, cada pareja se aparea teniendo al mes siguiente (cada hembra) una pareja de crías (un macho y una hembra) que de nuevo tardarán en ser fértiles un mes y entonces se aparearán. ¿Cuántas parejas de conejos habría al cabo de un tiempo dado, por ejemplo, un año?”
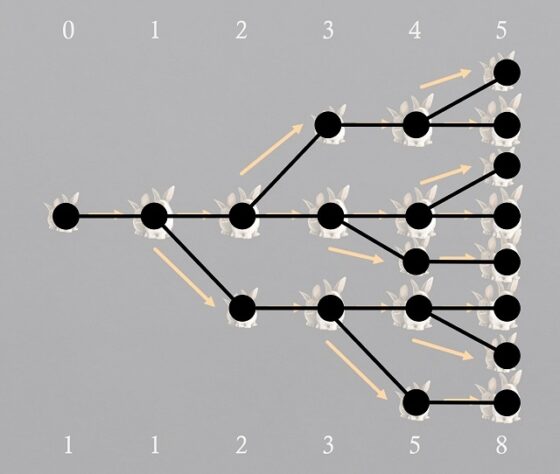
La respuesta a este problema se puede obtener estudiando qué es lo que ocurre durante los primeros meses, como se muestra en la siguiente imagen, e intentando deducir la respuesta general. En la parte de arriba se cuenta el paso del tiempo (cuántos meses van pasando, al finalizar cada mes) y en la parte de abajo la cantidad de parejas de conejos (asumiendo que no se muere ninguna y se reproducen como describe el problema, se aparean cada mes y tienen crías cada mes, cuando son fértiles claro). Imaginemos que partimos (0 arriba) de una pareja (1 abajo), como tarda un mes en ser fértil, al finalizar ese primer mes (1 arriba) sigue habiendo una pareja de conejos (1 abajo). Al finalizar el segundo mes (2 arriba) la pareja original habrá tenido su primera pareja de crías (un macho y una hembra, como reza el problema), luego hay 2 parejas de conejos (2 abajo). Al finalizar el siguiente mes, el tercero (3), estarán la pareja original, una nueva pareja de crías de la misma y la pareja de crías que había nacido el mes anterior, pero que aún son jóvenes para tener crías y no lo harán hasta el mes siguiente, luego 3 parejas de conejos.
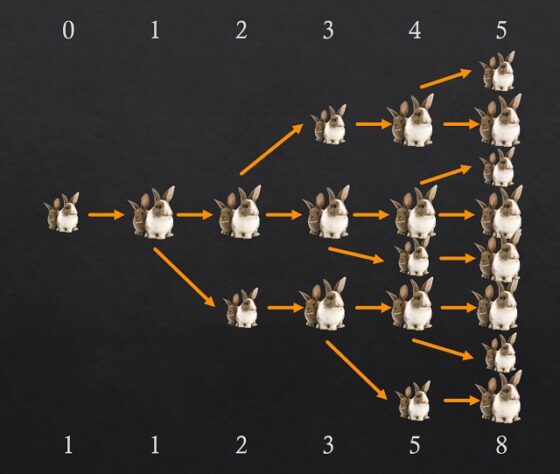 Cantidad de parejas de conejos durante los cinco primeros meses
Cantidad de parejas de conejos durante los cinco primeros meses
Aunque el esquema es bastante claro, veamos qué ocurre al finalizar el cuarto mes. Como estamos asumiendo que las parejas de conejos no se mueren, seguirán las tres parejas que estaban el mes anterior (3), más las nuevas parejas de crías que nazcan ese mes, pero para saber cuántas son es necesario conocer cuántas son fértiles, que lo son la pareja original y la primera pareja de crías que tuvieron, es decir, las 2 parejas que estaban dos meses antes (2), en conclusión, 3 + 2 = 5 parejas de conejos. Otro tanto ocurre al término del quinto mes, que estarán 8 parejas de conejos, las del mes anterior (5), más las nuevas parejas de crías, cuya cantidad es igual a las parejas de conejos de dos meses antes (3), 8 = 5 + 3.
Está claro, por el razonamiento anterior, que la solución del problema de los conejos de Fibonacci es una sucesión de números en la que cada término Fn es la suma de los dos anteriores Fn – 1 + Fn – 2, siendo los dos primeros términos F1 = F2 = 1. Por lo tanto, al cabo de un año, doce meses, como pregunta el problema, la solución será F12, es decir, 144, si miramos a los primeros términos de la sucesión más arriba.
El matemático polaco Hugo Steinhaus (1887-1972), en su famoso libro de divulgación de las matemáticas Mathematical Snapshots / Instantáneas matemáticas (1938), introduce la sucesión de Fibonacci con la propiedad de que cada término es la suma de los dos anteriores y lo relaciona, a posteriori, con un problema sobre el crecimiento de las ramas de un árbol. En concreto, Steinhaus escribe
Si un árbol produce una nueva rama después de un año, y siempre descansa durante un año, produciendo otra nueva rama sólo en el año siguiente, y si la misma ley se aplica a cada rama, entonces, en el primer año deberíamos tener sólo el brote principal, en el segundo – dos ramas, en el tercero – tres, luego 5, 8, 13, etc…
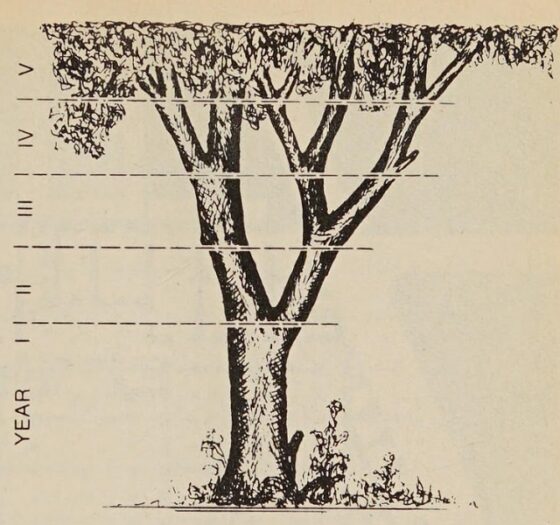 Ilustración del libro Mathematical Snapshots / Instantáneas matemáticas (1938), del matemático polaco Hugo Steinhaus, sobre la relación de los números de Fibonacci con las ramas de un árbol
Ilustración del libro Mathematical Snapshots / Instantáneas matemáticas (1938), del matemático polaco Hugo Steinhaus, sobre la relación de los números de Fibonacci con las ramas de un árbolA este árbol que describe Steinhaus le podríamos denominar árbol de Fibonacci (biológico). Aunque volveremos al final de la entrada sobre el árbol de Fibonacci biológico, vamos a introducir, a continuación, el árbol de Fibonacci desde el punto de vista de la teoría de grafos.
Un árbol definido de forma recursivaAntes de definir el concepto de árbol de Fibonacci, desde el punto de vista de la teoría de grafos, recordemos algunos conceptos sencillos de la misma.
– Grafo. Un grafo está formado por un conjunto de puntos, llamados vértices, y un conjunto de aristas, cada una de las cuales une dos vértices (aunque los grafos pueden tener bucles, aristas que unen un vértice consigo mismo, en este contexto no nos interesa esta posibilidad). Salvo que se diga lo contrario un grafo tiene un número finito de vértices y aristas.
– Grado de un vértice. Se llama grado de un vértice al número de aristas que inciden en el mismo (si hubiese un bucle, esa arista se contaría como dos).
– Camino. Un camino es una sucesión de vértices y aristas, que se inicia en un vértice y se termina en otro.
– Camino simple y ciclo. Un camino en el que no se repite ningún vértice se llama camino simple, y si es cerrado, se dice que es un ciclo.
– Grafo conexo. Un grafo en el que cada par de vértices está conectado, al menos, por un camino simple, se dice que es conexo.
– Árbol. Un grafo en el que cualesquiera dos vértices están conectados exactamente por un camino es un árbol. Equivalentemente, es un grafo conexo que no posee ciclos.
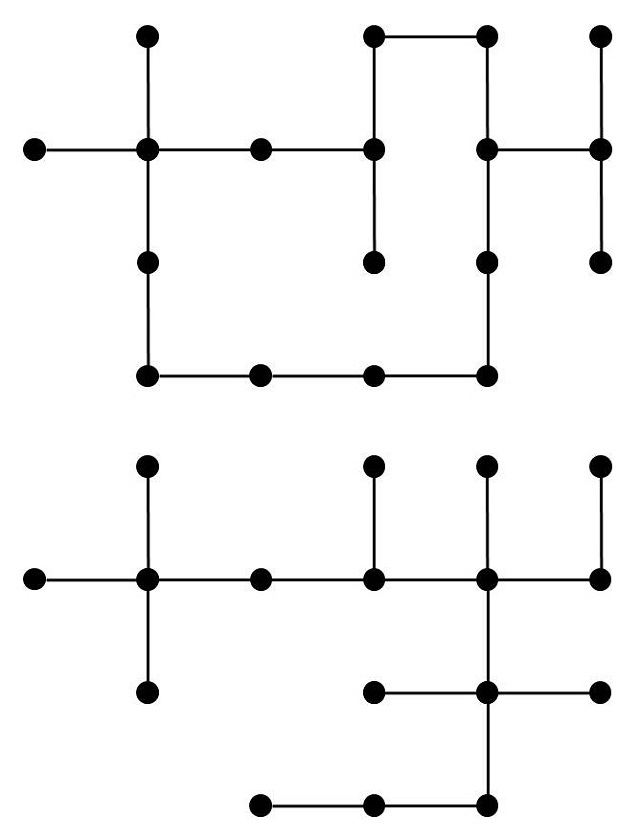 Un par de ejemplos, de un grafo, que no es árbol ya que contiene un ciclo, y de un árbol
Un par de ejemplos, de un grafo, que no es árbol ya que contiene un ciclo, y de un árbol
– Árbol con raíz. Si en un árbol se considera que uno de los vértices es especial, y se le denomina raíz, se dice que es un árbol con raíz, además, ese vértice (raíz) se suele considerar un punto inicial y las aristas se suelen considerar dirigidas alejándose de la raíz.
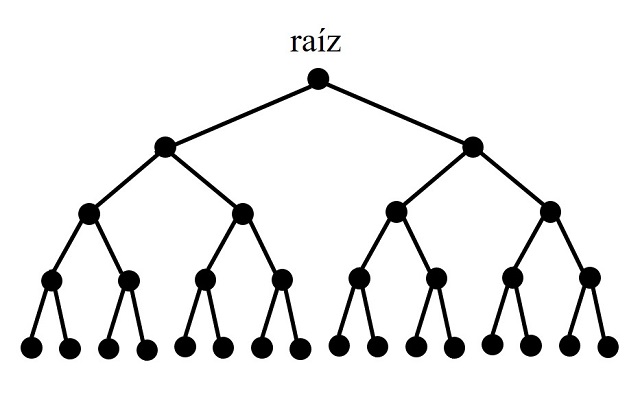 Ejemplo de árbol (binario) con raíz
Ejemplo de árbol (binario) con raíz
Ahora ya contamos con las definiciones pertinentes para definir el árbol de Fibonacci. Se definen, de forma recursiva, los árboles (con raíz) de Fibonacci, como los árboles Tn, tales que:
A. T1 y T2 son dos árboles con raíz que consisten solo en la raíz, es decir, un vértice;
B. Para n mayor que 2, Tn es el árbol con raíz que tiene a Tn – 1 como subárbol a izquierda y Tn – 2 como subárbol a derecha, es decir, se construye con una raíz, de la que salen dos aristas, una de ellas (la de la izquierda) va a la raíz del árbol Tn – 1, y se continua con el mismo, mientras que en la otra (la de la derecha) se coloca el árbol Tn – 2.
Veamos el proceso recursivo de construcción, que se muestra en la siguiente imagen para los primeros pasos, n = 1, 2, 3, 4, 5.
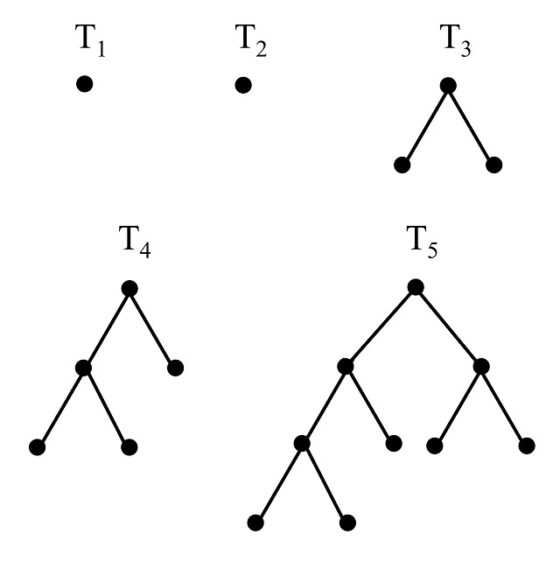 Árboles (con raíz) de Fibonacci T1, T2, T3, T4 y T5
Árboles (con raíz) de Fibonacci T1, T2, T3, T4 y T5
Veamos cómo se construiría ahora el árbol de Fibonacci T6. Como describe el proceso de construcción, se empieza con un vértice arriba (la raíz), del que salen dos aristas. En la de la izquierda se coloca el árbol T5, mientras que en la de la derecha el árbol T4, obteniendo así el árbol T6, que se muestra en la siguiente imagen.
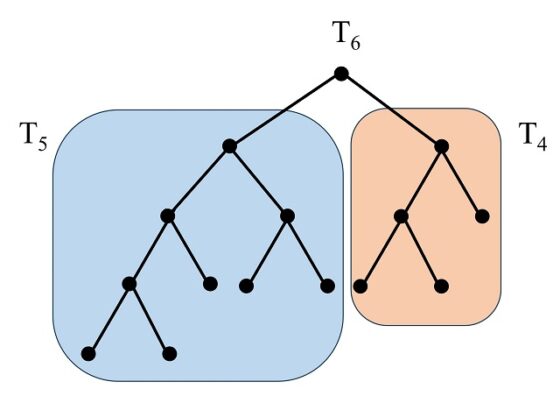
Ahora, veamos la relación de estos árboles con la sucesión de Fibonacci. La principal es que si contamos los vértices que están en el extremo opuesto a la raíz de cada árbol de Fibonacci, es decir, los vértices finales del árbol con raíz (los que tienen grado 1), obtendremos los números de la sucesión de Fibonacci (la misma cantidad que si miramos las aristas finales). Si nos fijamos en las anteriores imágenes los vértices finales son 1, 1, 2, 3, 5 y 8. Es lógico que nos salgan los números de Fibonacci Fn, puesto que, por la construcción de cada árbol, a partir de los dos anteriores, los vértices finales del árbol Tn son igual a la unión de los vértices finales de Tn – 1 y Tn – 2, luego contando esos vértices, tenemos la relación Fn = Fn – 1 + Fn – 2, y empezamos con un solo vértice, las raíces, en los dos primeros pasos.
¿Está este árbol relacionado con el problema de los conejos de Fibonacci? La respuesta, como no podía ser de otra manera, es afirmativa. Si consideramos el esquema de la solución del problema planteado por Leonardo de Pisa (observemos la imagen de arriba), podemos construir para cada paso, es decir, para cada nuevo mes, un árbol (en el sentido de grafo), que consiste en considerar como vértices las parejas de conejos en el esquema y como aristas la unión de cada pareja de un cierto mes con ella misma en el mes siguiente y su nueva pareja de crías, si la han tenido, si no nada más, es decir, igual que las fechas del esquema.
Si comparamos los dos grafos, para un paso cualquiera, por ejemplo, n = 6, el árbol de Fibonacci y el árbol que acabamos de asociar a la solución experimental del problema de los conejos del Liber Abaci, observaremos que son iguales (en la siguiente imagen hemos volteado el árbol de Fibonacci, cambiando derecha e izquierda, para facilitar la comparación), salvo que en el árbol de la solución del problema aparecen un vértice y una arista iniciales (que se corresponde con el punto inicial, el mes 0).
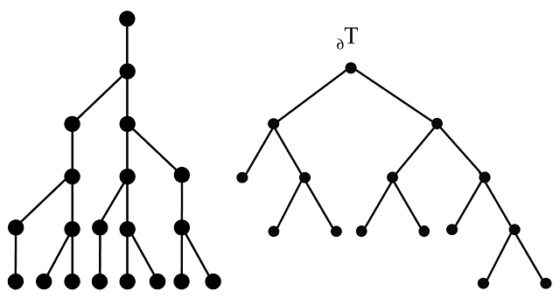
Más aún, si colocamos el árbol asociado con la resolución del problema con el vértice inicial (raíz) abajo, observaremos que es esencialmente el árbol (biológico) de Fibonacci.
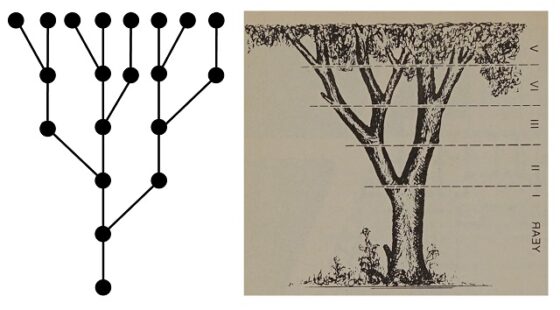
Ya hemos comentado que la cantidad de vértices, respectivamente, aristas, finales del árbol de Fibonacci Tn es el correspondiente número de Fibonacci Fn, pero contemos más elementos de ese grafo. Por ejemplo, ¿cuántos vértices tiene el árbol de Fibonacci? ¿cuántos son interiores y exteriores? ¿cuántas aristas tiene?.
Si denotamos por v(Tn) el número de vértices del árbol Tn, entonces, por el proceso de construcción del árbol de Fibonacci Tn, que está formado por la nueva raíz junto con los árboles Tn – 1 y Tn – 2,es claro que
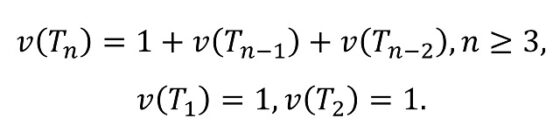
Si calculamos ahora los vértices para los primeros casos, n = 1, 2, 3, 4, 5, 6 (arriba podemos ver las imágenes de estos árboles de Fibonacci), tenemos que v(T1) = 1, v(T2) = 1, v(T3) = 3, v(T4) = 5, v(T5) = 9 y v(T6) = 15. Si los comparamos con los números de Fibonacci (F1 = 1, F2 = 1, F3 = 2, F4 = 3, F5 = 5, F6 = 8), podemos realizar la siguiente hipótesis:
![]()
Vamos a demostrar la anterior fórmula por inducción. En primer lugar, se cumple para los primeros casos, como acabamos de comprobar. En segundo lugar, vamos a asumir que se cumple para los árboles Tk, con k menor o igual que n – 1, y vamos a demostrarlo para el árbol Tn:
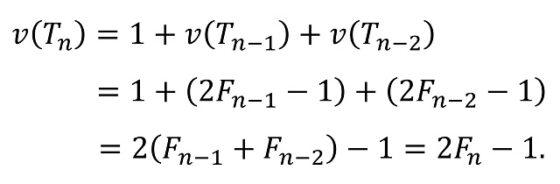
Por lo tanto, ya tenemos una fórmula general para el número de vértices del árbol de Fibonacci Tn, y su relación con el correspondiente número de Fibonacci Fn.
Los vértices del árbol Tn se pueden dividir en dos tipos, los exteriores (cuyo grado es 1, que son los que se llaman “hojas” del árbol, como grafo) y los interiores (cuyo grado es mayor que 1, llamados “nudos”, salvo la raíz, que tiene ya nombre asignado), v(Tn) = ve(Tn) + vi(Tn). Como sabemos que ve(Tn) = Fn y v(Tn) = 2 Fn – 1, entonces sabemos también la cantidad de vértices interiores, vi(Tn) = Fn – 1.
Respecto al número de aristas del árbol Tn, que podemos denotar e(Tn), es fácil darse cuenta de que es igual al número de vértices del árbol menos 1, es decir, e(Tn) = v(Tn) – 1. Por lo tanto, e(Tn) = 2Fn – 2.
Retorno al árbol de Fibonacci biológicoSi consideramos el árbol de Fibonacci biológico, por ejemplo, como el árbol (grafo) asociado al problema de los conejos (véase la imagen siguiente, en la cual hemos disminuido el tamaño de los vértices y pintado vértices y aristas de marrón) observaremos que la propia construcción del árbol no nos proporciona un grosor para las ramas, que podrían considerarse, de hecho, todas del mismo grosor. En este último apartado vamos a ver cómo darle grosor a las mismas, utilizando la sucesión de Fibonacci, para crear un árbol de Fibonacci “más realista”, en el sentido de que, en cierta medida, las ramas más jóvenes son más delgadas que las ramas más viejas.
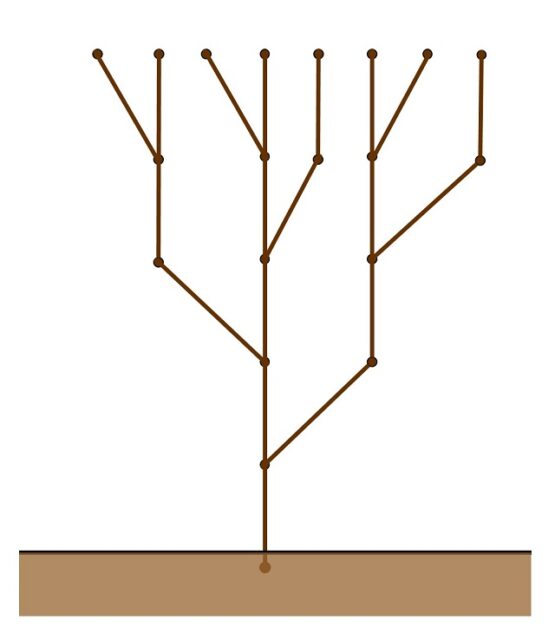
Para darle grosor a las ramas vamos a considerar que las ramas más jóvenes, las que se corresponden con aristas exteriores, las aristas que terminan en vértices exteriores (que sabemos que hay tantas ramas exteriores como el número de Fibonacci correspondiente, es decir, el árbol Tn tiene Fn ramas exteriores), tienen el grosor básico (de 1 unidad). A partir de ahí, hacia la raíz, cada rama tendrá un grosor que es igual a la suma de los grosores de las ramas más jóvenes, que surgen de la misma. En la siguiente imagen vemos cómo sería para el árbol de Fibonacci de cinco años, es decir, T6. Así, si dos ramas jóvenes (de grosor 1) vienen de una misma rama, esta tiene grosor 1 + 1 = 2; cuando dos ramas de grosores 1 y 2, respectivamente, vienen de una misma rama, esta tiene grosor 1 + 2 = 3; si dos ramas de grosores 2 y 3, respectivamente, vienen de una misma rama, esta tiene grosor 2 + 3 = 5; o si cada una de las dos ramas que vienen de una misma rama tienen grosores 3 y 5, la rama tiene grosor 8, como en la imagen.
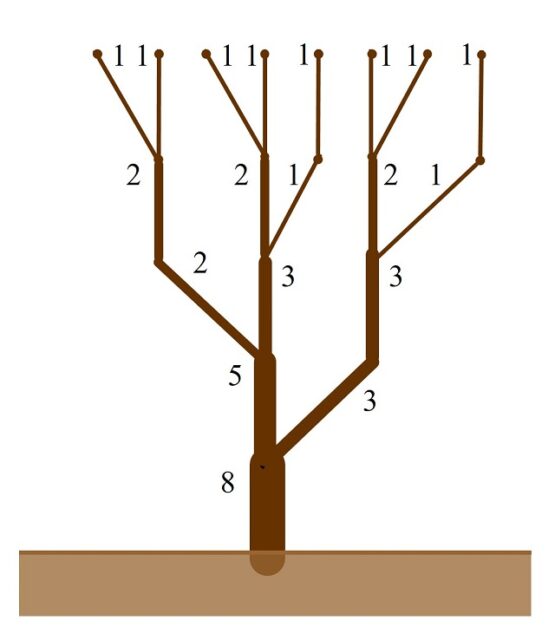 Árbol de Fibonacci T6, luego que tienen una edad de 5 años, con ramas de grosores igual a los primeros números de Fibonacci 1, 2, 3, 5 y 8
Árbol de Fibonacci T6, luego que tienen una edad de 5 años, con ramas de grosores igual a los primeros números de Fibonacci 1, 2, 3, 5 y 8Como podemos observar todas las ramas tienen grosores iguales a números de Fibonacci, de hecho, los grosores de las ramas del árbol de Fibonacci Tn son alguno de los números de Fibonacci, de F2 (= 1) a Fn. Por otra parte, en cada nudo en el que se juntan dos ramas, estas tienen como grosores números de Fibonacci consecutivos, Fk y Fk + 1, para k entre 2 y n – 2. Además, como hemos comentado, hay tantas ramas exteriores como el número de Fibonacci correspondiente, las cuales tienen grosor 1, pero según vamos hacia abajo, hacia la raíz, en el árbol, lo que ocurre es que, al llegar al tronco inicial, el grosor es igual a ese número de Fibonacci. Es decir, el árbol de Fibonacci Tn tiene Fn ramas exteriores, de grosor 1, y su tronco tiene grosor Fn.
Por lo tanto, si tuviésemos el árbol de Fibonacci de 16 años, es decir, el árbol T17, tendríamos que posee F17 = 1.597 ramas jóvenes, de grosor 1, mientras que el tronco principal tendría un grosor igual a 1.597.
Diálogo artístico con FibonacciLa artista brasileña Janaina Mello Landini (1974) tiene unas series de obras que se enmarcan bajo el título ciclotramas y que consisten en instalaciones de estructuras arborescentes construidas con hilos y cuerdas que se entrelazan.
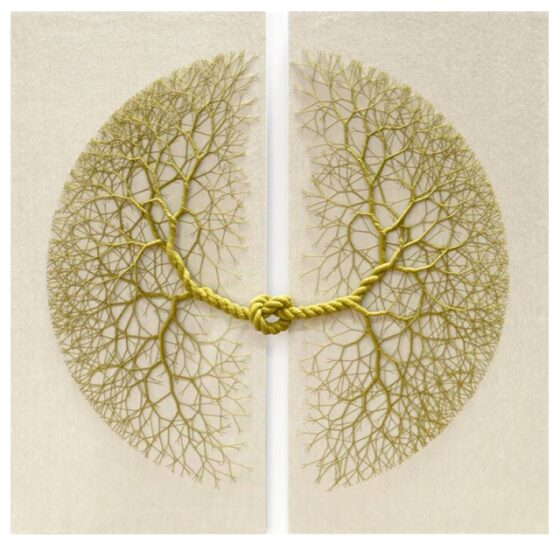 Instalación Ciclotrama 156 – palindrome (2019), de la artista brasileña Janaina Mello Landini, realizada con cuerda de algodón verde hecha a mano sobre lino, de tamaño 138cm x 138cm. Imagen de la página web de la artista Janaina Mello Landini
Instalación Ciclotrama 156 – palindrome (2019), de la artista brasileña Janaina Mello Landini, realizada con cuerda de algodón verde hecha a mano sobre lino, de tamaño 138cm x 138cm. Imagen de la página web de la artista Janaina Mello LandiniDos obras de la serie Ciclotrama Diálogos, en concreto, Ciclotrama 177 – Fibonacci (2020) y Ciclotrama 193 – Fibonacci (2020), que serían “diálogos con el matemático Fibonacci”, consisten en dos árboles de Fibonacci con 16 y 17 años, respectivamente.
Fijemos nuestra atención en la hermosa instalación Ciclotrama 177 – Fibonacci, que consiste en el árbol de Fibonacci T17, luego con una edad de 16 años. Como se puede observar en las siguientes imágenes, el hilo básico establece el grosor unidad (1) y sabemos que hay F17 = 1.597 ramas jóvenes, de grosor 1. Cuando dos ramas jóvenes se juntan, sus hilos se entrelazan formando una trenza de dos hilos, que es la rama de la que salen las dos jóvenes. En general, cuando se junten dos ramas con Fk y Fk + 1 hilos (para un cierto k entre 2 y 15), los Fk + 2 = Fk + Fk + 1 hilos en conjunto formarán la trenza de la rama de la que salen las otras dos. Y el tronco de esta instalación consiste en una trenza de 1.597 hilos.
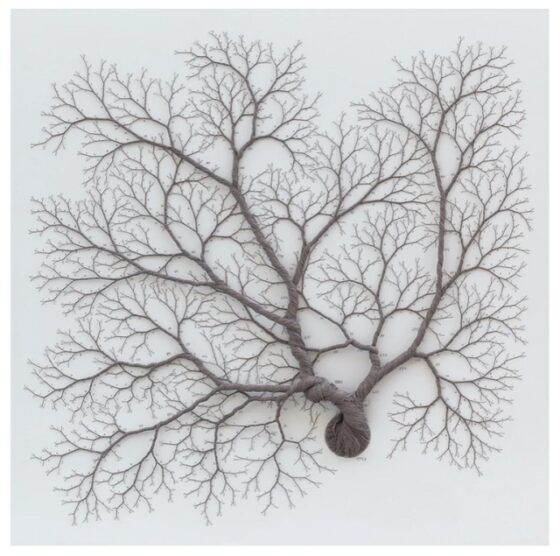

 Instalación Ciclotrama 177 – Fibonacci (2020), de la artista brasileña Janaina Mello Landini, realizada con hilos de algodón y rotulador acrílico sobre lienzo, de tamaño 170cm x 170cm. Imagen de la instalación y dos detalles de la misma, de la página web de la artista Janaina Mello Landini
Instalación Ciclotrama 177 – Fibonacci (2020), de la artista brasileña Janaina Mello Landini, realizada con hilos de algodón y rotulador acrílico sobre lienzo, de tamaño 170cm x 170cm. Imagen de la instalación y dos detalles de la misma, de la página web de la artista Janaina Mello LandiniEstas dos obras de la artista Janaina Mello Landini son artísticas y hermosas realizaciones de los árboles de Fibonacci (biológicos, con grosor de Fibonacci).
Bibliografía
1.- Raúl Ibáñez, Cayley, el origen del álgebra moderna, Genios de las Matemáticas, RBA, 2017.
2.- Hugo Steinhaus, Mathematical Snapshots, Dover, 1999.
3.- Ralph Grimaldi, Fibonacci and Catalan Numbers, Wiley, 2012.
4.- R. Ibáñez, Las matemáticas como herramienta de creación artística, Libros de la Catarata – FESPM, 2023.
5.- Página web de la artista Janaina Mello Landini
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El árbol de Fibonacci se ha escrito en Cuaderno de Cultura Científica.
Así en la Tierra como en el cielo: la fluidodinámica de SN 1987A
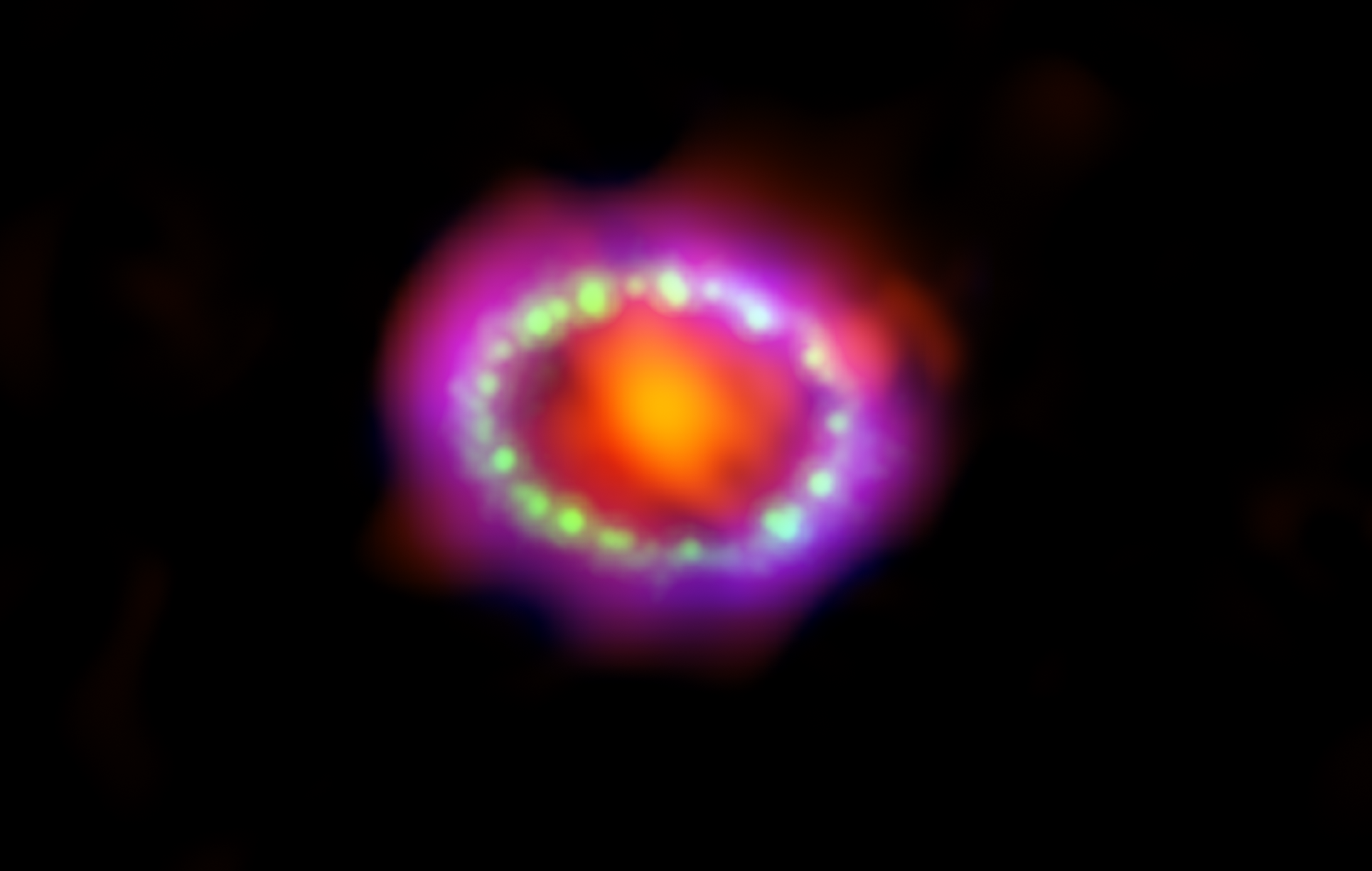 SN 1987A. Fuente: Webb Space Telecope / NASA, ESA, A. Angelich (NRAO, AUI, NSF)
SN 1987A. Fuente: Webb Space Telecope / NASA, ESA, A. Angelich (NRAO, AUI, NSF)Hace unos 20.000 años, vista desde la Tierra, una estrella masiva en una de las galaxias satélite de la Vía Láctea expulsó un anillo de gas y polvo que luego se expandió hacia el espacio interestelar. Miles de años después, la estrella explotó. Cuando fue detectada por los terráqueos en 1987 la denominaron supernova (SN) 1987A. Como el flash de una cámara en una habitación oscura, SN 1987A iluminó su entorno, revelando el anillo de gas y polvo que la estrella había expulsado milenios antes.
Las imágenes de esa estructura mostraban que el material del anillo no se repartía uniformemente, sino que se agrupaba en parches discretos, algo que para lo que la comunidad astrofísica no tenía una explicación convincente.
 Estelas de condensación de un Boeing 747. Fuente: Wikimedia Commons
Estelas de condensación de un Boeing 747. Fuente: Wikimedia CommonsAhora Michael Wadas y sus colegas de la Universidad de Michigan en Ann Arbor, han presentado una posible solución al problema basada en un fenómeno muy conocido en la Tierra. Proponen que los grumos se formaron a causa del mismo fenómeno fluidodinámico que hace que las estelas de condensación que deja un avión se rompan en pedazos.
 Efectos de la inestabilidad de Crow en una estela de condensación. Fuente: Wikimedia Commons
Efectos de la inestabilidad de Crow en una estela de condensación. Fuente: Wikimedia CommonsEl fenómeno en cuestión se comoce como inestabilidad de Crow y se desencadena por la interacción de dos vórtices que giran en sentido contrario. Wadas y sus colegas sugieren que el anillo de material expulsado por la progenitora de SN 1987A comenzó como un par de vórtices; imagina dos anillos de humo en expansión, uno encima del otro, que giran en direcciones opuestas.
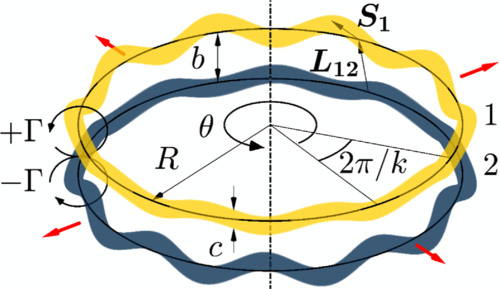 Fuente: Wadas et al (2024)
Fuente: Wadas et al (2024)Los investigadores proponen que pequeñas ondas en los dos toroides crecieron a medida que los anillos se expandían, lo que finalmente habría provocado que las estructuras se tocaran en múltiples puntos. A lo largo del anillo, en lugares entre los puntos de contacto, un vórtice más pequeño «se desprendió», convirtiéndose en el núcleo de uno de los grumos del anillo. En simulaciones, los investigadores produjeron anillos con un número de grumos similar al que aparece en el anillo alrededor de SN 1987A.
Referencias:
Michael J. Wadas, William J. White, Heath J. LeFevre, Carolyn C. Kuranz, Aaron Towne, and Eric Johnsen (2024) Hydrodynamic Mechanism for Clumping along the Equatorial Rings of SN1987A and Other Stars Phys. Rev. Lett. doi: 10.1103/PhysRevLett.132.111201
Marric Stephens (2024) A Supernova Remnant Shaped by Vortices Physics 17, s31
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Así en la Tierra como en el cielo: la fluidodinámica de SN 1987A se ha escrito en Cuaderno de Cultura Científica.
La cuenca de Eridania y la complejidad de Marte
Creemos saber mucho sobre la geología marciana porque, al fin y al cabo, es uno de los lugares de nuestro Sistema Solar que más veces hemos visitado, tanto su órbita como su superficie. Pero si consideramos que la historia geológica de un planeta es como un libro, todavía nos faltan muchas páginas, incluso capítulos, por escribir.
Y si reconocemos nuestras limitaciones en este aspecto, muy probablemente la única manera de resolverlas será a través de misiones que, en su superficie, nos permitan estudiar su geología en detalle y tomar muestras que nos ayuden a extraer la mayor información posible en los laboratorios terrestres. Una empresa ambiciosa, sin duda, pero necesaria para seguir ampliando nuestro conocimiento y respondiendo a cuestiones como, por ejemplo, ¿por qué somos planetas tan diferentes?
De las cosas que más nos llama la atención del resto de planetas interiores es, si los comparamos con la Tierra, la ausencia de una tectónica de placas como la que tenemos aquí. Esto no quiere decir que estos otros cuerpos no hayan tenido procesos en los cuales su corteza -o partes de esta- hayan podido sufrir procesos de reciclaje importantes y que hayan tenido su repercusión en la geología que vemos hoy en día.
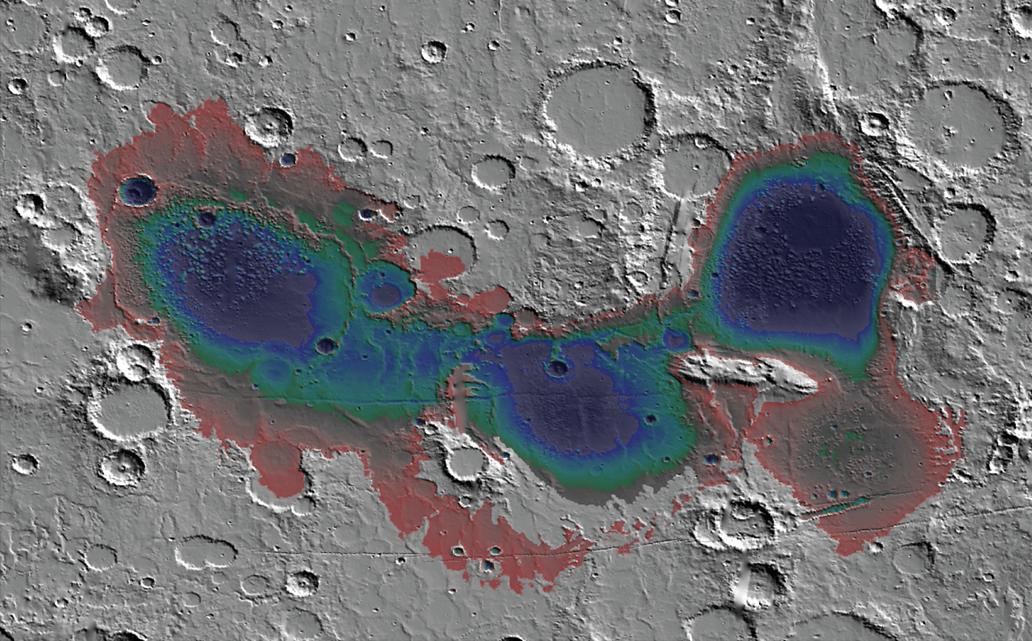 Mapa topográfico de la cuenca de Eridania. Los colores representan la profundidad de las aguas en lo que se piensa que fue un sistema de lagos -o mares, según se vea- que pudieron albergar nueve veces la cantidad de agua de los Grandes Lagos norteamericanos. Imagen cortesía de la NASA.
Mapa topográfico de la cuenca de Eridania. Los colores representan la profundidad de las aguas en lo que se piensa que fue un sistema de lagos -o mares, según se vea- que pudieron albergar nueve veces la cantidad de agua de los Grandes Lagos norteamericanos. Imagen cortesía de la NASA.Uno de los aspectos en los que se puede ver reflejada esta dinámica es a través del vulcanismo, ya que el reciclaje de los materiales de la corteza puede crear un rango de composiciones más variadas en los magmas que llegan a la superficie que si los magmas procediesen directamente de una fuente más primitiva.
Precisamente es en este punto donde llegan las novedades. Un nuevo artículo publicado en Nature Astronomy por Michalski et al. (2024) afirma que debemos cambiar la visión de un Marte donde la composición de las lavas era predominantemente basáltica por otro donde hay una mayor variabilidad composicional gracias a un sistema de reciclaje de su litosfera no horizontal como el de la tectónica de placas, sino vertical y que detallaremos más adelante.
En este nuevo artículo los autores se han centrado en la cuenca de Eridania, un lugar, por cierto, muy interesante para la búsqueda de vida pretérita en el planeta a causa de la presencia de antiguos lagos y actividad hidrotermal que, precisamente, podría haber estado relacionada con estos episodios de actividad volcánica. Pues bien, aquí se han descrito 63 volcanes -afirman que podría haber bastantes más- cuya forma y estructura nada tiene que ver con los magmas basálticos. Y es que en nuestro planeta la química de las lavas condiciona de manera fundamental la explosividad y el tipo de edificios volcánicos que se construyen, por lo que no es descabellado pensar que en Marte ocurra lo mismo.
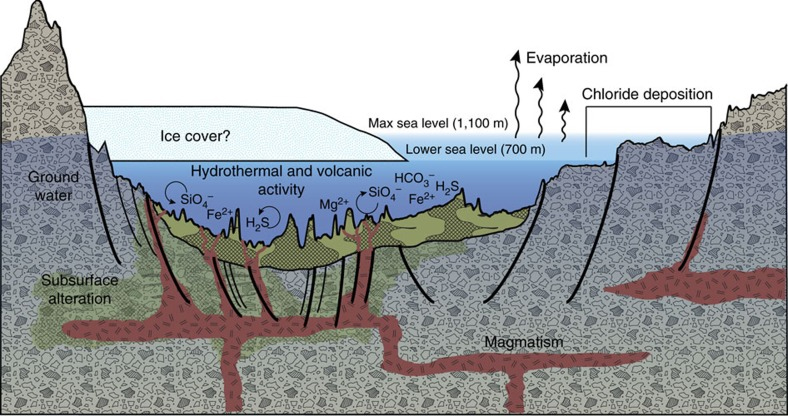 Funcionamiento de un sistema hidrotermal en la cuenca de Eridania, muy interesante desde la perspectiva astrobiológica. Imagen cortesía de la NASA.
Funcionamiento de un sistema hidrotermal en la cuenca de Eridania, muy interesante desde la perspectiva astrobiológica. Imagen cortesía de la NASA.Precisamente esta cuenca podría haber sido uno de los puntos donde en Marte pudo darse fenómenos de reciclaje de la corteza que permitieran el ascenso de magmas con composiciones diferentes, pero, ¿Cómo se reciclaría la corteza en este planeta sin que haya una tectónica de placas? Pues sería a través de procesos como la delaminación litosférica.
La litosfera es la capa más externa de los planetas rocosos, formada por la corteza y por la parte superior del manto. A grandes rasgos, por su comportamiento podemos considerarla como rígida y, en la Tierra, es la capa que está dividida en las distintas placas litosféricas o tectónicas que conocemos.
Pues la delaminación litosférica consiste en una serie de movimientos en los cuales parte de la litosfera se vuelve inestable -en el sentido gravitatorio- y se separa de la propia litosfera. Habitualmente esto puede ocurrir cuando esta parte inferior de la litosfera es más densa que la parte superior del manto y, por lo tanto, tiene esa facilidad para separarse y “hundirse” o bien por el ascenso de materiales calientes a través del manto y que sustituyen a parte de la litosfera.
Estos procesos de delaminación litosférica -y que en nuestro planeta siguen ocurriendo- probablemente serían los primeros sistemas de reciclaje de la corteza que existieron en la Tierra -antes de la tectónica de placas- y, probablemente, los que hayan existido también en planetas como Mercurio o Venus.
 Detalle de la cuenca de Eridania, donde se aprecian unos materiales de tonos claros muy fracturados y que probablemente estén compuestos por minerales del grupo de las arcillas. Cortesía de NASA/JPL-Caltech/UArizona.
Detalle de la cuenca de Eridania, donde se aprecian unos materiales de tonos claros muy fracturados y que probablemente estén compuestos por minerales del grupo de las arcillas. Cortesía de NASA/JPL-Caltech/UArizona.En este proceso en el que se introducen materiales de la corteza hacia el manto estos se pueden acabar mezclando y provocando la evolución en las composiciones de los materiales del manto que posteriormente podrían llegar a la superficie a través de los volcanes, como parece que aquí ha ocurrido, y dando lugar a lavas con una composición diferente a la basáltica.
¿Qué interés puede tener este descubrimiento? Pues tenemos que pensar que en nuestro planeta quedan muy pocas rocas que nos remonten a los “primeros años”, por lo que este hallazgo en Marte podría poner a disposición de la ciencia rocas que proceden de un sistema de reciclaje de la corteza previo a la tectónica de placas, lo que a su vez nos podría ayudar a conocer mejor la dinámica no solo de nuestro planeta, sino también Venus y Mercurio.
Desde el punto de vista de la astrobiología, como comentábamos anteriormente, también es muy interesante, ya que esta cuenca albergaba lagos salpicados por la actividad hidrotermal que podrían ser análogos de los lugares donde se originó la vida en la Tierra y, por lo tanto, candidatos a buscar pistas sobre un posible origen de la vida en Marte.
Referencia:
Michalski, J.R., Deanne Rogers, A., Edwards, C.S. et al. (2024) Diverse volcanism and crustal recycling on early Mars. Nat Astron doi: 10.1038/s41550-023-02191-7
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo La cuenca de Eridania y la complejidad de Marte se ha escrito en Cuaderno de Cultura Científica.
Manipulación sonora, una cuestión evolutiva
José Manuel González Gamarro
La música es un concepto que se aborda en la inmensa mayoría de las investigaciones desde una perspectiva antropocéntrica, esto es, situando a los humanos en el centro del significado, el valor, el conocimiento y la acción. Sin embargo, existen otras orientaciones donde los animales no humanos, o todos los animales, humanos y no humanos, son el centro de las investigaciones en cuanto a la música o la musicalidad. Es lo que se conoce, sobre todo en el mundo anglosajón, como biomusicología. Ya en 1928, Henry Beston afirmaba en The Outermost House que necesitamos un concepto más sabio y más místico de los animales puesto que «no son hermanos, no son subordinados; son otras naciones, atrapadas con nosotros en la red de la vida y el tiempo».
Hablar de música o musicalidad en ciertas especies es controvertido por la dificultad de etiquetar algunas sucesiones de sonidos o ruidos como música. Esta polémica tampoco escapa al ser humano, puesto que hay muchas obras de renombrados compositores que el público en general podría no calificar como música. Sin irnos a ejemplos demasiado radicales, una muestra de esta difícil clasificación como música podría ser la conocida obra del compositor húngaro György Ligeti Artikulation, aunque la intención de este texto no sea polemizar con el límite de ciertos conceptos.
 Foto: Dimitry B / Unsplash
Foto: Dimitry B / Unsplash284 especies con manipulación sonora
Volviendo al reino animal no humano, hay muchas especies que emiten sonidos con diversos fines, los cuales algunos se clasifican como cantos, llamadas, vocalizaciones, etc., dependiendo de la especie y las características sonoras de lo que se emite. Cuando se habla de música animal o música en la naturaleza, en lo primero que se piensa es en los pájaros, puesto que los sonidos que emiten se acercan bastante a la orientación antropocéntrica del concepto. En cualquier caso, producen sonidos y algunas especies usan deliberadamente algún tipo de objeto, estructura o instrumento para manipular este sonido y que eso le proporcione algún tipo de ventaja. De hecho, se conocen 284 especies que usan algún tipo de herramienta de manipulación sonora.1 Hay animales que pueden manipular el sonido, ya sea en frecuencia (hercios) o intensidad, con una intención bien definida. Conocer varios ejemplos nos da una visión más general de este fenómeno.
Uno de ellos es el caso de los grillos de árbol, que usan las hojas como membrana de un altavoz, haciendo un agujero en el centro2. Modifican el tamaño del agujero según su propio tamaño para amplificar el sonido. Los investigadores descubrieron que con el agujero en el centro la señal se amplifica hasta 4 veces más que si el grillo canta en el borde de la hoja. A la hora de aparearse, es esencial llegar al mayor público posible. Siguiendo con los grillos, el conocido como grillo topo también reajusta de alguna manera el lugar desde donde emite su sonido3. El macho construye su madriguera en forma de cuerno y modifica su estructura (tamaño y forma) para adecuarla a las frecuencias para atraer a las hembras. Si lo pensamos por un momento, este grillo es un lutier, puesto que la construcción de instrumentos musicales funciona de la misma manera, hacer objetos resonantes donde priman más unas frecuencias que otras. Su modus operandi es el ensayo y error, es decir, que mientras va construyendo la madriguera emite chirridos para ir adecuando el lugar. Gracias a esto consigue una señal más fuerte y con más intensidad en las frecuencias bajas, lo que atrae a más hembras, con la consiguiente ventaja evolutiva. Otros tipos de grillos, como el grillo subterráneo, seleccionan el sitio donde “cantan” aunque no lo construyen. Se suelen colocar cerca de muros o escaleras para amplificar su señal y también eligen la posición de su cuerpo para que la amplificación sea óptima.4
Dejando a un lado los grillos, si dirigimos la mirada (o el oído más bien) a los anfibios, podemos hallar también casos de manipulación sonora. Hay ranas de árbol que realizan algo parecido a los grillos, modifican el lugar de su llamada en función de su resonancia buscando una mayor amplificación.5 Hay otras, como las ranas que habitan en los agujeros de los árboles, que modifican su llamada en función de las condiciones del agujero donde se encuentran6. Estos animales ajustan su sonido en función del volumen y forma del espacio en el que están. En la selva tropical es habitual que los agujeros de los árboles se llenen de agua, lo que cambia su frecuencia de resonancia. Las ranas adaptan su sonido a estas circunstancias para producir una señal más fuerte, y todo esto sin disputas con el técnico ni ecualizadores, la envidia de cualquier músico.
Buscar la amplificación sonora también atañe a los murciélagos, en concreto el murciélago de ventosas buchiblanco, que elige cavidades de descanso que se asemejan a un cuerno acústico.7 Este animal es bastante ingenioso porque elige el lugar para que se amplifiquen tanto los sonidos salientes como los entrantes. En el mundo subacuático también existe una búsqueda de la modificación sonora, por extraño que pueda parecer, como es el caso de un pequeño pez conocido como gobio de arena. Emiten señales debajo de piedras, conchas, etc., y cubren estos objetos de arena para, como todo parece indicar, amplificar la llamada para las hembras.8
Como no podía ser de otra manera, en animales más cercanos a los humanos, como son los orangutanes de Borneo también se da una manipulación sonora con claros objetivos que puedan suponer una ventaja evolutiva. Producen una especie de beso-chirrido que usan ante una amenaza.9 La particularidad de este sonido es que lo hacen con hojas en la boca, de manera análoga a como usan el kazoo o el mirlitón los humanos. El sonido también lo producen sin hojas, pero con las hojas en la boca ganan en intensidad con una gama mayor de frecuencias bajas. Esto implica que se puede usar para persuadir amenazas, ya que frecuencias más graves con mayor intensidad pueden simular que el animal emisor es de mayor tamaño.
La importancia de la amplificación Foto: alvaro ortiz / Unsplash
Foto: alvaro ortiz / UnsplashComo se puede comprobar con estos breves ejemplos, el poder manipular el sonido, sobre todo en intensidad, es una cualidad que puede influir en la evolución. La importancia de la amplificación tampoco escapa a los humanos ni a la evolución de la propia música. Por un lado, es crucial para la construcción de instrumentos musicales, pero, por otro lado, también existe una correlación positiva entre las propiedades resonadoras de cuevas, como por ejemplo en Francia, y el número de pinturas y signos prehistóricos. Esto puede sugerir un interés por la calidad del sonido y las propiedades resonadoras en los humanos prehistóricos.10 De hecho, si nos vamos más atrás en el tiempo, parece ser que nuestros ancestros, cuando el entorno ecológico cambió de una densa selva a bosques abiertos y praderas, tuvieron que desarrollar sonidos más parecidos a las consonantes para abarcar más distancia, en combinación con otras llamadas parecidas a las vocales, lo que pudo influir en el surgimiento y evolución del lenguaje.11
Esta búsqueda de amplificación que se da en el mundo natural, esta evolución, parece permear en la evolución cultural de la música. Solo hay que fijarse en las sorprendentes propiedades de amplificación de algunos teatros griegos y romanos, aunque esto no se circunscriba únicamente a la música. La evolución de la música occidental pasa por una conquista de mayores auditorios y escenarios, hasta tal punto que a día de hoy los conciertos de música actual llevan una fuerte amplificación y se convierten en auténticos fenómenos de masas. Las ventajas de la conquista de la modificación de la amplitud y la frecuencia de los sonidos que parece darse en el mundo natural ha seguido extendiéndose en la evolución musical, acaparando cada vez más público en un mismo recinto o espacio.
Quizás por esto, entre otras muchas razones, a día de hoy se construyen más guitarras eléctricas que clavicordios. Otra consecuencia podría ser que el lector o lectora de este texto sepa cómo es el primer instrumento, pero haya tenido que realizar una breve búsqueda para saber cómo es el segundo. En cualquier caso, el paralelismo o la analogía entre el mundo natural y cultural, también en cuestiones evolutivas, parece estar subyacente en relación con el sonido y, por consiguiente, con la música.
Referencias:
1 Bentley-Condit, V., & Smith. (2010). Animal tool use: current definitions and an updated comprehensive catalog. Behaviour, 147(2), 185-32A. https://doi.org/10.1163/000579509X12512865686555
2 Mhatre, N., Malkin, R., Deb, R., Balakrishnan, R., & Robert, D. (2017). Tree crickets optimize the acoustics of baffles to exaggerate their mate-attraction signal. Elife, 6, e32763. https://doi.org/10.7554/eLife.32763
3 Bennet-Clark, H. C. (1987). The tuned singing burrow of mole crickets. Journal of Experimental Biology, 128(1), 383-409.
4 Erregger, B., & Schmidt, A. K. (2018). Anthropogenic calling sites boost the sound amplitude of advertisement calls produced by a tropical cricket. Animal Behaviour, 142, 31-38. https://doi.org/10.1016/j.anbehav.2018.05.021
5 Tan, W. H., Tsai, C. G., Lin, C., & Lin, Y. K. (2014). Urban canyon effect: storm drains enhance call characteristics of the Mientien tree frog. Journal of Zoology, 294(2), 77-84. https://doi.org/10.1111/jzo.12154
6 Lardner, B., & bin Lakim, M. (2002). Tree-hole frogs exploit resonance effects. Nature, 420(6915), 475-475. https://doi.org/10.1038/420475a
7 Chaverri, G., & Gillam, E. H. (2013). Sound amplification by means of a horn-like roosting structure in Spix’s disc-winged bat. Proceedings of the Royal Society B: Biological Sciences, 280(1772), 20132362. https://doi.org/10.1098/rspb.2013.2362
8 Lugli, M. (2013). Sand pile above the nest amplifies the sound emitted by the male sand goby. Environmental biology of fishes, 96, 1003-1012. https://doi.org/10.1007/s10641-012-0097-z
9 Wieczorkowska, A. A., Ras, Z. W., Zhang, X., & Lewis, R. (2007, April). Multi-way hierarchic classification of musical instrument sounds. In 2007 International Conference on Multimedia and Ubiquitous Engineering (MUE’07) (pp. 897-902). IEEE. https://doi.org/10.1109/MUE.2007.159
10 Reznikoff, I. (2008). Sound resonance in prehistoric times: A study of Paleolithic painted caves and rocks. Journal of the Acoustical Society of America, 123(5), 3603.
11 Gannon, C., Hill, R. A., & Lameira, A. R. (2023). Open plains are not a level playing field for hominid consonant-like versus vowel-like calls. Scientific Reports, 13(1), 21138. https://doi.org/10.1038/s41598-023-48165-7
Sobre el autor: José Manuel González Gamarro es profesor de guitarra e investigador para la Asociación para el Estudio de la Guitarra del Real Conservatorio Superior de Música “Victoria Eugenia” de Granada.
El artículo Manipulación sonora, una cuestión evolutiva se ha escrito en Cuaderno de Cultura Científica.
Naukas 2023 – Las matemáticas del glioma
El gran evento de divulgación organizado por Naukas y la Cátedra de Cultura Científica volvió a Bilbao para celebrar su decimotercera edición en el gran Palacio Euskalduna los pasados 15 y 16 de septiembre de 2023.

El uso de las matemáticas en la investigación del cáncer y su tratamiento mediante modelos es fascinante y no de los campos con más proyección en ciencias de la salud, junto con la inteligencia artificial. En esta charla, Elisabete Alberdi ofrece una introducción a como se construye y usa un modelo matemático para un tipo de cáncer, el glioma. Advertimos que esta es una charla de esas en las que hay que estar concentrado, seguir el hilo, tener paciencia porque parece que no pasa nada y, de repente, todo cobra sentido. Si te gustan las matemáticas, la vas a disfrutar.
Elisabete Alberdi es licenciada y doctora en Matemáticas. Es profesora en la Escuela de Ingeniería de Bilbao (UPV/EHU), departamento de Matemática Aplicada.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas 2023 – Las matemáticas del glioma se ha escrito en Cuaderno de Cultura Científica.
Retos medioambientales del sector agropecuario de Europa
Alimentar a una población mundial en rápido crecimiento todavía es un reto. La producción de alimentos con métodos intensivos sigue contaminando el aire, el agua y el suelo, contribuye a la pérdida de biodiversidad y al cambio climático, y consume excesivos recursos naturales, mientras que, paralelamente, una parte importante de los alimentos se desperdicia. La agricultura europea y mundial afronta retos nunca vistos y la adaptación a los cambios en ciernes requiere la ayuda de la ciencia, la tecnología y su transferencia al sector productor.
Los agricultores y ganaderos hacen su trabajo de producir alimentos, pero a medida que aumentan las exigencias medioambientales y se endurece la competencia, la actividad se convierte en un reto cada vez mayor por lo que requerirá más apoyo de las instituciones en aspectos relacionados con la transferencia, el asesoramiento y la financiación. El Pacto Verde Europeo pone a la agricultura y la alimentación entre sus prioridades, pero ¿cuáles son los principales desafíos?
 Foto: Karsten Würth / UnsplashMetas más ambiciosas
Foto: Karsten Würth / UnsplashMetas más ambiciosas
La necesidad de cumplir con los compromisos internacionales adquiridos tras el Acuerdo de París, llevó a la Unión Europea a desarrollar en 2018 un reglamento que regulaba la contabilidad de gases de efecto invernadero (GEI) del sector LULUCF (uso de la tierra, cambio de uso de la tierra y sector forestal), de manera que las emisiones del sector agropecuario y forestal (contabilizadas con signo positivo) no debían exceder las reducciones o secuestro (contabilizadas con signo negativo) del conjunto de las tierras LULUCF en los dos subperiodos de compromiso establecidos (2021-2025 y 2026-2030). Sin embargo, en 2022, el Parlamento Europeo y el Consejo modificaron este Reglamento cambiando el enfoque de equilibrar las emisiones y absorciones en el sector LULUCF al de aumentar las absorciones. De este modo, se marcan metas más ambiciosas, estableciendo un objetivo de eliminación neta para toda la Unión de -310 Mt CO2eq para 2030 (a España le corresponderían -43.635 kt CO2eq). Dicha modificación del Reglamento entró en vigor el 11 de mayo de 2023.
Dado que los sectores agropecuario y forestal pueden ser tanto emisores como mitigadores de gases de efecto invernadero, este nuevo reto exigirá a la Unión una mayor efectividad y contundencia en las actividades de eliminación del carbono en dichos sectores. La UE aún no ha detallado las metodologías adaptadas para su certificación, que se prevé se realice este año 2024. Lo que se dispone a fecha de hoy es de una Revisión de las Metodologías de Certificación para agricultura del carbono (van Baren et al., 2023).
El Pacto Verde Europeo trata de adecuar la imposición de los productos energéticos y de la electricidad a las políticas en materia de energía, medio ambiente y clima. Con este fin aboga por la revisión de la directiva sobre fiscalidad de la energía racionalizando el uso de las exenciones y reducciones fiscales por los Estados miembros. En este contexto se enmarcan la eliminación del subsidio al diésel o la introducción de un impuesto a los vehículos agrícolas, así como la pretendida eliminación gradual de la subvención del gasóleo agrícola. No obstante, vista la movilización del sector, el Ministro de Agricultura, Pesca y Alimentación ha confirmado que el Gobierno español mantendrá esta legislatura (2023-2027) la exención del impuesto especial de hidrocarburos para el gasóleo profesional de uso agrícola.
Un descontento justificadoEl descontento del sector con los acuerdos de libre comercio tiene bases fundadas, ya que las importaciones de terceros países no pertenecientes a la UE, con políticas menos estrictas, no cumplen las normas de producción europeas en aspectos como bienestar animal, uso de pesticidas, cambio climático, etc. En este contexto, los mercados globalizados competitivos se convierten en escenarios injustos, puesto que su cumplimiento no se puede exigir de la misma manera a países terceros extracomunitarios por las posibles reclamaciones ante la Organización Mundial del Comercio.
Para atajar este tipo de problemas, en lo que a cambio climático se refiere, se está poniendo en marcha de manera gradual y dialogada con terceros países, el Mecanismo de Ajuste en Frontera por Emisiones de Carbono (Carbon Border Adjustment Mechanism, CBAM). Este mecanismo se aplicará inicialmente solo a un número seleccionado de bienes que se comercian en el mercado regulado/obligatorio de derechos de emisión de carbono de la UE con alto riesgo de fuga de carbono (hierro y acero, cemento, fertilizantes, aluminio y producción de electricidad). Los importadores empezarán a pagar el ajuste financiero en 2026. Su aplicación al sector agropecuario es compleja, requiere de más análisis y no parece factible su implementación a corto plazo.
Concentración o desaparición de explotacionesA nivel europeo, se observa una dualidad en el sector agropecuario, por un lado, aquellas explotaciones más dinámicas que tienden a la concentración constituyéndose en unidades más grandes y productivas, y, por otro, aquellas que tienen más complicado el superar su atomización, afrontar los mayores costes de producción y, al mismo tiempo, cumplir con las normas ambientales y con la burocracia de la nueva Política Agraria Común.
Las pequeñas y medianas explotaciones son las que tienen más complicado ser competitivas y viables, y corren el riesgo de quedar marginadas. Son, por tanto, las que más necesitan la transferencia de conocimientos/tecnología, el asesoramiento y la financiación adecuadas para adaptarse a la transición. Téngase en cuenta que, desde 2005, la UE ha perdido alrededor de un tercio de sus explotaciones agrícolas y que la proporción de personas empleadas en la agricultura cayó del 6,4 % del empleo total de la UE en 2005 al 4,2 % en 2020.
Además, está el problema del relevo generacional. En 2020, solo uno de cada diez agricultores tenía menos de 40 años. En este contexto es importante que los jóvenes se incorporen al sector para asegurar la producción sostenible de alimentos. En la práctica, esto significa abordar los retos del acceso a la tierra y a la financiación, la educación y la formación.
Sobre la autora: Inmaculada Astorkiza es investigadora en Economía de Recursos Naturales y Medio Ambiente en la Facultad de Economía y Empresa de la UPV/EHU
Una versión de este texto apareció originalmente en campusa.
El artículo Retos medioambientales del sector agropecuario de Europa se ha escrito en Cuaderno de Cultura Científica.
La Geología de Son Goku
Dragon Ball, Bola de Dragón, As Bolas Máxicas, Dragoi Bola, Bola de Drac… da igual el idioma en el que lo escriba, porque todo el mundo sabe a lo que me estoy refiriendo. Aunque solo sea de ver recientemente en los telediarios o las redes sociales noticias sobre el fallecimiento del autor de esta obra, Akira Toriyama. Y como yo soy una de los millones de personas que han crecido disfrutando de la versión animada de este título, quiero hacerle mi pequeño homenaje al gran mangaka descubriendo la Geología que se oculta detrás de Dragon Ball.
El primer opening, es decir, la primera canción de apertura de los capítulos que podemos disfrutar en Dragon Ball Z, titulada Cha-la Head Cha-la (que se podría traducir como “no hay problema”), es una gran compilación de spoilers. Pero no solo de lo que nos deparará la serie, también de la Geología que caracteriza a la Tierra del Universo 7. Sobre todo, si nos ponemos la versión original japonesa de dicho opening y prestamos atención a la letra que acompaña a las imágenes. Así que voy a usarlo como hilo conductor.
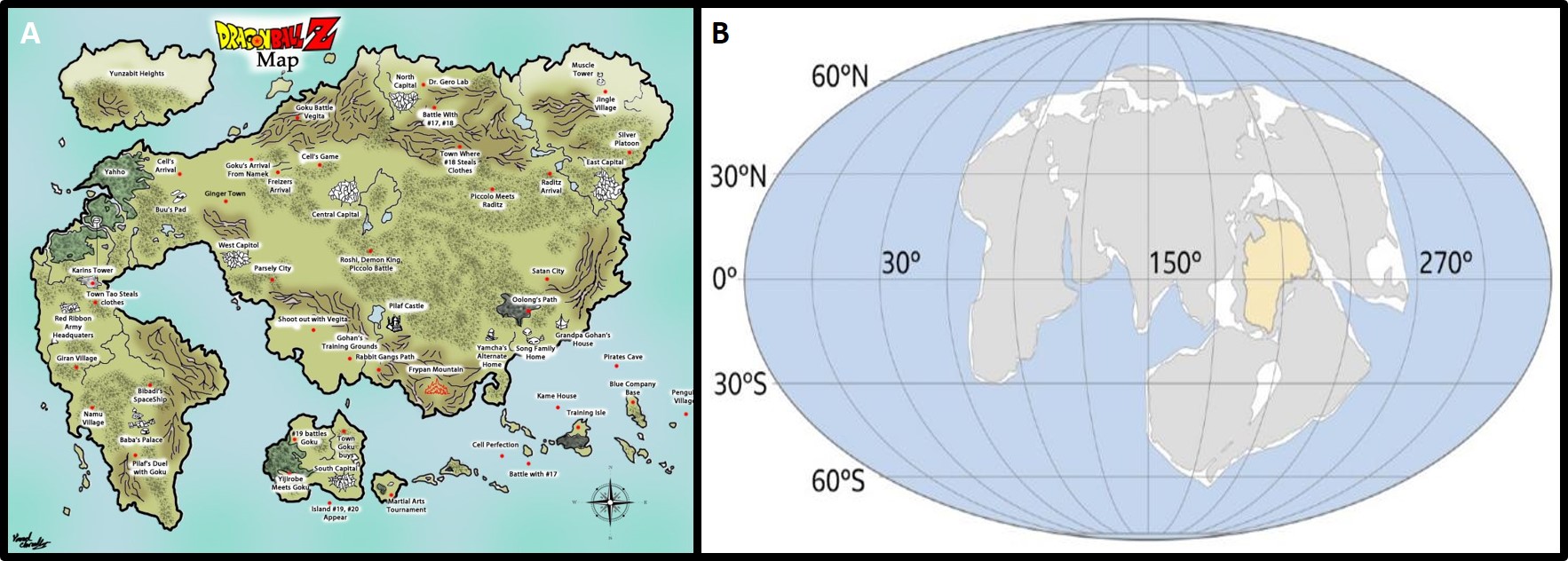 A) Mapa del mundo de Dragon Ball. Diseño de jack123noob, tomado de www.deviantart.com. B) Reconstrucción del posible futuro supercontinente Amasia. Imagen de la Universidad Curtin (Australia), tomada de www.bbc.com
A) Mapa del mundo de Dragon Ball. Diseño de jack123noob, tomado de www.deviantart.com. B) Reconstrucción del posible futuro supercontinente Amasia. Imagen de la Universidad Curtin (Australia), tomada de www.bbc.comLa letra dice “volemos atravesando las nubes para poder ver todo el panorama”. Pero, ¿qué aspecto tendría la Tierra de Dragon Ball vista desde el cielo? Pues se trataría de un único supercontinente, con una disposición preferente este-oeste y bordeado por varias islas de diversos tamaños, tanto al norte como al sur. Pasando al mundo real, en la historia geológica de nuestro planeta se han generado varios supercontinentes, o grandes masas continentales, debido a un ciclo sin fin provocado por el movimiento de las placas tectónicas: cada 500 millones de años, las placas convergen formando un supercontinente, que luego acaba rompiéndose por un proceso llamado rift, y vuelta a empezar. El último supercontinente se llama Pangea y empezó a fragmentarse hace unos 250 Millones de años. Pero Pangea tenía una disposición preferente norte-sur, con una forma que recuerda a una letra C mayúscula. El dibujo representado por Toriyama se asemeja más a una de las reconstrucciones hipotéticas del futuro supercontinente que se debería formar dentro de unos 250 Millones de años, Amasia.
La existencia de una tectónica de placas activa en la Tierra ficticia de Dragon Ball también queda evidenciada por la existencia de eventos naturales como volcanes o terremotos. Pero la canción del opening dice “la tierra al ser golpeada se enfada, provocando que estalle un volcán”. Esto indica que algunos de estos procesos, en realidad, no son tan naturales como podemos imaginar. En concreto, la cantidad de energía que son capaces de liberar sobre el terreno los Guerreros Z durante sus peleas son equivalentes a la enorme energía generada por los movimientos tectónicos, provocando la misma respuesta en el planeta: erupciones volcánicas, terremotos y tsunamis de grandes dimensiones.
 Fotograma del anime Dragon Ball Z donde Pikkoro destruye la Luna. Imagen propiedad de Toei Animation (Japón).
Fotograma del anime Dragon Ball Z donde Pikkoro destruye la Luna. Imagen propiedad de Toei Animation (Japón).Otro spoiler bastante gordo que nos hace el opening es la escena en la que Pikkoro destruye la Luna para controlar a Son Gohan tras convertirse en Oozaru durante su entrenamiento. Y, después de este evento, parece que el planeta sigue como sin nada tras perder su satélite natural, hasta que Kami sama lo reconstruye más adelante (cosa que ya tuvo que hacer previamente en la serie, después de que Muten Roshi también lo destruyese durante el torneo de artes marciales). Pero, en la vida real, la desaparición de la Luna tendría consecuencias catastróficas para la Tierra. La atracción gravitatoria que ejerce nuestro satélite equilibra el giro de la Tierra sobre su propio eje, controla el ciclo de las mareas, influye en la circulación oceánica y el desplazamiento de las masas de aire atmosféricas y determina la duración del día y la noche. Si perdiésemos esta influencia, directamente se acabaría la vida sobre nuestro planeta tal y como la conocemos hoy en día. Y aquí no tenemos las bolas de dragón para solucionar ese problema.
 Fotograma del anime Dragon Ball Z donde aparece Goku junto a un grupo de animales, entre los que se encuentran dos especies de dinosaurios (una pareja de triceratópsidos a la derecha de la imagen y una pareja de una especie basada en Tyrannosaurus rex a la izquierda) y una especie de reptil volador extinto. Imagen propiedad de Toei Animation (Japón).
Fotograma del anime Dragon Ball Z donde aparece Goku junto a un grupo de animales, entre los que se encuentran dos especies de dinosaurios (una pareja de triceratópsidos a la derecha de la imagen y una pareja de una especie basada en Tyrannosaurus rex a la izquierda) y una especie de reptil volador extinto. Imagen propiedad de Toei Animation (Japón).Para terminar este repaso nos vamos a la parte final el opening, que exclama “quisiera encontrar un dinosaurio para entrenarlo”. Y es que, en el mundo fantástico de Dragon Ball, coexisten una gran amalgama de criaturas habitando el planeta Tierra, incluidos animales prehistóricos. Es común ver la aparición de reptiles continentales, o dinosaurios, a lo largo de muchos episodios del anime, algunos basados en fósiles reales, como diversas especies de triceratópsidos o el Tyrannosaurus rex, y otros surgidos de la mente de Toriyama, junto a reptiles voladores o tigres dientes de sable. Aunque la presencia de dinosaurios en la Tierra de Dragon Ball es bastante curiosa, no solo porque en la vida real estos reptiles se extinguieron hace unos 66 Millones de años, sino porque en este mundo fantástico, en principio, también habrían corrido la misma suerte. O, al menos, el Dios de la Destrucción Beerus comenta en Dragon Ball Super que eliminó a todos los dinosaurios de la Tierra hace millones de años porque le faltaron al respeto.
Sin duda, Dragon Ball es uno de los shonen nekketsu más famosos de la historia del manga y el anime, de esos que nunca pasan de moda y cuya acción engancha a jóvenes y mayores. Pero, entre pelea y pelea, también tiene su parte didáctica. Ahora, si volvéis a ver la serie o leer el manga, mientras aprendéis el nombre en japonés de diferentes alimentos o prendas de vestir, seguro que también repasaréis un poco de Geología.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo La Geología de Son Goku se ha escrito en Cuaderno de Cultura Científica.
Caroline Herschel, Mary Somerville, Jessica Mink y el planeta Urano
El 13 de marzo de 1781, el astrónomo William Herschel (1738-1822) descubrió el planeta Urano. Aunque en principio pensó que se trataba de un cometa, se confirmó posteriormente que era el séptimo planeta del Sistema Solar.
 Urano (23 de enero de 1986, imagen tomada por la sonda Voyager 2 de la NASA). Fuente: Wikimedia Commons.
Urano (23 de enero de 1986, imagen tomada por la sonda Voyager 2 de la NASA). Fuente: Wikimedia Commons.
Herschel lo observó a través de un telescopio situado en el jardín de su casa en Bath, Inglaterra. De hecho, Urano fue el primer planeta descubierto con un telescopio. Como suele suceder en algunas ocasiones, parece que este hallazgo fue fruto de la buena suerte que le llevó a mirar en la dirección adecuada en el momento preciso.
Caroline Herschel (1750-1848)En este acontecimiento, como prácticamente todos los relacionados con los logros del astrónomo, no se suele citar a su hermana Caroline que durante décadas ayudó a William en sus observaciones astronómicas y en la construcción de diferentes instrumentos de observación.
Aunque en algunos foros citan a ambos hermanos como descubridores del planeta, la propia Caroline se pensaba como una simple ayudante que no merecía ninguna atención:
I am nothing, I have done nothing; all I am, all I know, I owe to my brother. I am only the tool which he shaped to his use—a well-trained puppy-dog would have done as much. [No soy nada, no he hecho nada; todo lo que soy, todo lo que sé, se lo debo a mi hermano. Sólo soy la herramienta que él moldeó para su uso; un perrito bien adiestrado habría hecho lo mismo].
Probablemente, en aquel momento, nadie opinaba que la labor de Caroline fue esencial para que su hermano destacara como astrónomo. Por suerte, hoy en día, su trabajo es ampliamente reconocido.
Mary Somerville (1780-1872)La matemática y astrónoma Mary Somerville frecuentaba el observatorio astronómico familiar de los Herschel. Fue amiga y colaboradora del matemático y astrónomo John Herschel (1792-1871), hijo de William.
En 1852, John propuso los nombres de los cuatro satélites conocidos entonces de Urano: Titania y Oberón (descubiertos por William Herschel en 1787), Ariel y Umbriel (descubiertos en 1851 por el astrónomo aficionado William Lassell). El otro satélite principal del planeta (de los veintiocho conocidos de Urano), Miranda, fue descubierto por el astrónomo Gerard Kuiper (1905-1973) en 1948.
Mary Somerville también estudió el planeta Urano. En 1842, en la sexta edición de su libro On the Connection of the Physical Sciences incluyó su análisis de las perturbaciones de la órbita de este planeta. A través de sus cálculos, ella intuía la presencia de un hipotético planeta que alteraba a Urano; esta observación llevó al astrónomo John Couch Adams (1819-1892) a buscar y descubrir el planeta Neptuno en 1846, usando únicamente cálculos matemáticos. En Francia, un matemático, Urbain Le Verrier (1811-1877), de manera independiente, anunció la situación de este planeta a la Academia Francesa de Ciencias. Era el 31 de agosto de 1846, dos días antes de que Adams informara de sus deducciones al Real Observatorio de Greenwich. Los cálculos matemáticos de Le Verrier fueron más precisos que los del británico. El matemático francés comunicó al astrónomo alemán Johann Gottfried Galle (1812-1910) sus previsiones sobre la posición del planeta, y Galle lo localizó en septiembre de 1846, comprobando la exactitud de los cálculos de Le Verrier.
Volviendo a Mary Somerville, fue mentora de Ada Byron (1815-1852). Además de transmitirle el apego por las matemáticas, Somerville puso en contacto a su pupila con el ingeniero Charles Babbage (1791-1871). Pero esa es otra historia…
Jessica Mink (1951)Urano es un planeta gélido y ventoso. Es un gigante de hielo que gira en un ángulo de casi 90 grados con respecto al plano de su órbita. Además de sus veintiocho lunas, está rodeado por trece anillos tenues: 1986U2R/ζ, 6, 5, 4, α, β, η, γ, δ, λ, ε, ν y μ.
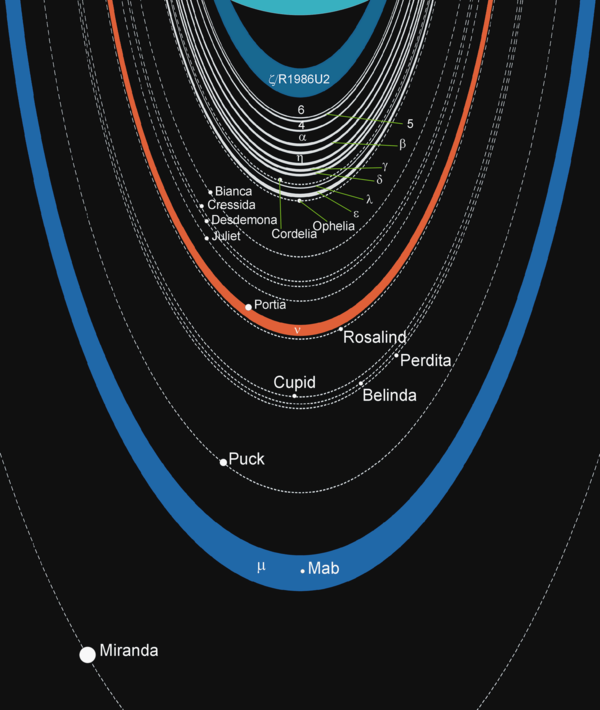 Los anillos y las lunas de Urano. Fuente: Wikimedia Commons.
Los anillos y las lunas de Urano. Fuente: Wikimedia Commons.
En 1789, William Herschel ya sospechaba la existencia de un anillo en Urano, aunque ningún otro astrónomo confirmó esta conjetura.
El descubrimiento definitivo de estos anillos tuvo lugar de manera casual el 10 de marzo de 1977 por medio del Observatorio Aerotransportado Kuiper. Los astrónomos James L. Elliot (1943-2011), Edward W. Dunham y Jessica Mink (1951) planeaban usar la ocultación de la estrella SAO 158687 por Urano para estudiar la atmósfera del planeta. Al analizar sus observaciones, descubrieron que la estrella desaparecía brevemente de la vista cinco veces antes y después de ser eclipsada por el planeta. Así, dedujeron que Urano debía presentar un sistema de anillos estrechos.
Jessica Mink es desarrolladora de software, archivista de datos y astrónoma posicional. En el artículo The Rings of Uranus publicado en Nature en 1977 consta con otro nombre. Ella misma explica el motivo en su página personal.
Referencias
- Marijo Deogracias Horrillo, Tras la estela de Caroline Lucretia Herschel, Mujeres con ciencia, Vidas científicas, 8 de febrero de 2017
- Memoir and correspondence of Caroline Herschel (1876), djvu, Wikisource, página 17
- Nieves Zuasti Soravilla, Mary Somerville (1780-1872), Mujeres con ciencia, Vidas científicas, 24 de agosto de 2017
- Urano, Wikipedia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Caroline Herschel, Mary Somerville, Jessica Mink y el planeta Urano se ha escrito en Cuaderno de Cultura Científica.
Nuevos rayos X revelan un universo tan grumoso como predice la cosmología
Al mapear las estructuras más grandes del universo, los cosmólogos han descubierto que una anomalía cósmica parece estar desapareciendo.
Un artículo de Liz Kruesi. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 El telescopio de rayos X eRosita detectó miles de cúmulos de galaxias en una vasta franja del cosmos, coloreados en esta imagen según su distancia desde la ubicación del telescopio en el centro. La luz de los cúmulos más lejanos se emitió hace 9 mil millones de años. Fuente: MPE, A. Liu for the eROSITA Consortium
El telescopio de rayos X eRosita detectó miles de cúmulos de galaxias en una vasta franja del cosmos, coloreados en esta imagen según su distancia desde la ubicación del telescopio en el centro. La luz de los cúmulos más lejanos se emitió hace 9 mil millones de años. Fuente: MPE, A. Liu for the eROSITA Consortium
Cúmulos de cientos o miles de galaxias se encuentran en las intersecciones de filamentos gigantes de materia que se entrecruzan y que forman el tapiz del cosmos. A medida que la gravedad atrae todo lo que hay en cada cúmulo de galaxias hacia su centro, el gas que llena el espacio entre las galaxias se comprime, lo que hace que se caliente y brille en rayos X.
El telescopio de rayos X eRosita, lanzado al espacio en 2019, pasó más de dos años recopilando rayos de luz de alta energía de todo el cielo. Los datos han permitido a los científicos mapear las ubicaciones y tamaños de miles de cúmulos de galaxias, dos tercios de ellos desconocidos hasta ahora. En una serie de artículos publicados en línea el 14 de febrero que aparecerán en la revista Astronomy & Astrophysics, los científicos usan su catálogo inicial de cúmulos para analizar varias de las grandes cuestiones de la cosmología.
Los resultados incluyen nuevas estimaciones de la heterogeneidad del cosmos –una característica muy discutida últimamente, ya que otras mediciones recientes han descubierto que es inesperadamente homogéneo- y de las masas de esas partículas fantasmales llamadas neutrinos y de una propiedad clave de la energía oscura, la misteriosa energía repulsiva que está acelerando la expansión del universo.
El modelo imperante del universo para los cosmólogos identifica la energía oscura como la energía del espacio mismo y la vincula al 70% del contenido del universo. Otra cuarta parte del universo es materia oscura invisible y el 5% es materia ordinaria y radiación. Todo ello evoluciona bajo la fuerza de la gravedad. Pero algunas observaciones de la última década desafían este “modelo estándar” de la cosmología, planteando la posibilidad de que al modelo le falten ingredientes o efectos que podrían dar paso a una comprensión más profunda.
Las observaciones de eRosita, por el contrario, refuerzan el cuadro existente en todos los aspectos. «Es una confirmación notable del modelo estándar», afirma Dragan Huterer, cosmólogo de la Universidad de Michigan que no ha participado en el trabajo.
Radiografiando el cosmosDespués del Big Bang, las sutiles variaciones de densidad en el universo recién nacido se volvieron gradualmente más pronunciadas a medida que las partículas de materia se pegaban unas a otras. Los grupos más densos atrajeron más material y se hicieron más grandes. Hoy en día, los cúmulos de galaxias son las estructuras unidas gravitacionalmente más grandes del cosmos. Determinar sus tamaños y distribución permite a los cosmólogos probar su modelo de cómo evolucionó el universo.
Para encontrar cúmulos el equipo de eRosita entrenó un algoritmo informático para buscar fuentes de rayos X «realmente esponjosas» en lugar de objetos puntuales, explica Esra Bulbul del Instituto Max Planck de Física Extraterrestre en Garching, Alemania, quien dirigió las observaciones de cúmulos de eRosita. Redujeron la lista de candidatos a una “muestra extremadamente pura”, continúa, de 5.259 cúmulos de galaxias, a partir de casi 1 millón de fuentes de rayos X detectadas por el telescopio.
Luego tuvieron que determinar lo pesados que eran son estos cúmulos. Los objetos masivos curvan la estructura del espacio-tiempo, cambiando la dirección de la luz que pasa y haciendo que la fuente de luz parezca distorsionada, un fenómeno llamado lente gravitacional. Los científicos de eRosita pudieron calcular las masas de algunos de sus 5.259 cúmulos basándose en el efecto lente sobre galaxias más distantes situadas detrás de ellos. Aunque solo un tercio de sus cúmulos tenían galaxias de fondo conocidas y alineadas de esta manera, los científicos descubrieron que la masa del cúmulo se correlacionaba fuertemente con el brillo de sus rayos X. Debido a esta fuerte correlación, podrían utilizar el brillo para estimar las masas de los cúmulos restantes.
Luego introdujeron la información de la masa en simulaciones por ordenador del cosmos en evolución para inferir los valores de los parámetros cósmicos.
Midiendo la grumosidadUn número de interés es el “factor de grumosidad” del universo, S8. Un valor S8 de cero representaría una vasta nada cósmica, similar a una llanura sin ninguna roca a la vista. Un valor S8 más cercano a 1 corresponde a montañas escarpadas que se ciernen sobre valles profundos. Los científicos han estimado el S8 basándose en mediciones del fondo cósmico de microondas (FCM), una luz antigua procedente del universo primitivo. Al extrapolar las variaciones de densidad iniciales del cosmos, los investigadores esperan que el valor actual de S8 sea 0,83.
Pero estudios recientes que analizan las galaxias actuales han medido valores entre un 8% y un 10% más bajos, lo que implica que el universo es inesperadamente homogéneo. Esa discrepancia ha intrigado a los cosmólogos, señalando potencialmente grietas en el modelo cosmológico estándar.
 El catálogo de cúmulos de galaxias de eRosita está representado aquí en un mapa del medio cielo. Los colores indican la distancia de los cúmulos y los tamaños de los círculos indican el brillo aparente de los rayos X de cada fuente. Fuente: MPE, J. Sanders for the eROSITA Consortium
El catálogo de cúmulos de galaxias de eRosita está representado aquí en un mapa del medio cielo. Los colores indican la distancia de los cúmulos y los tamaños de los círculos indican el brillo aparente de los rayos X de cada fuente. Fuente: MPE, J. Sanders for the eROSITA ConsortiumEl equipo de eRosita, sin embargo, no encontró esta discrepancia. «Nuestro resultado estuvo básicamente en línea con la predicción del FCM desde el principio», afirma Vittorio Ghirardini, quien dirigió el análisis. Él y sus colegas calcularon un S8 de 0,85.
Algunos miembros del equipo se sintieron decepcionados, dice Ghirardini, ya que apuntar a los ingredientes que faltan era una perspectiva más emocionante que coincidir con la teoría conocida.
El valor de S8, que es un poco más alto que la estimación del FCM, probablemente desencadenará más análisis por parte de otros equipos, comenta Gerrit Schellenberger, un astrofísico que estudia los cúmulos de galaxias en el Centro Harvard-Smithsonian de Astrofísica. «Creo que probablemente no es el último artículo que hemos visto sobre ese tema».
Pesando neutrinosEn el universo primitivo se formaron neutrinos abundantemente, casi tantos como fotones (partículas de luz), explica Marilena Loverde, cosmóloga de la Universidad de Washington. Pero los físicos saben que los neutrinos, a diferencia de los fotones, deben tener masas diminutas debido a cómo oscilan entre tres tipos. Las partículas no adquieren masa mediante el mismo mecanismo que otras partículas elementales, por lo que su masa es un misterio muy estudiado. Y la primera pregunta es qué masa tienen en realidad.
Los cosmólogos pueden estimar la masa de los neutrinos estudiando sus efectos sobre la estructura del cosmos. Los neutrinos se mueven casi a la velocidad de la luz y atraviesan otra materia en lugar de quedarse pegados a ella. De modo que su presencia en el cosmos ha atenuado su grumosidad. «Cuanto más masa se le pone a los neutrinos, más masa es homogénea a esas [grandes] escalas», afirma Loverde.
Combinando sus mediciones de cúmulos de galaxias con mediciones de FCM, el equipo de eRosita estimó que la suma de las masas de los tres tipos de neutrinos no supera los 0,11 electronvoltios (eV), o menos de una millonésima parte de la masa de un electrón. Otros experimentos con neutrinos han establecido un límite inferior, mostrando que las tres masas de neutrinos deben sumar al menos 0,06 eV (para un posible ordenamiento de los tres valores de masa) o 0,1 eV (para el ordenamiento inverso). A medida que la distancia entre los límites superior e inferior se reduce, los científicos se acercan más a determinar el valor de la masa del neutrino. «En realidad, estamos a punto de lograr un gran avance», indica Bulbul. En publicaciones de datos posteriores, el equipo de eRosita podría bajar el límite superior lo suficiente como para descartar los modelos de masa de neutrinos de orden inverso.
Es necesario ser precavido. Cualquier otra partícula rápida y ligera que pueda existir (como los axiones, partículas hipotéticas propuestas como candidatas a la materia oscura) tendría los mismos efectos en la formación de estructuras. E introducirían errores en la medición de la masa de los neutrinos.
Siguiendo la energía oscuraLas mediciones de los cúmulos de galaxias pueden revelar no solo cómo crecieron las estructuras, sino también cómo su crecimiento fue dificultado por la energía oscura: la fina capa de energía repulsiva que impregna el espacio, acelerando la expansión del espacio y separando así la materia.
Si la energía oscura es la energía del espacio mismo, como supone el modelo estándar de la cosmología, entonces tendrá una densidad constante en todo el espacio y el tiempo (por eso a veces se la denomina constante cosmológica). Pero si su densidad disminuye con el tiempo, entonces es algo completamente distinto. «Ésa es la pregunta más importante que plantea la cosmología», afirma Sebastian Grandis, miembro del equipo eRosita de la Universidad de Innsbruck, en Austria.
A partir de su mapa de miles de cúmulos, los investigadores descubrieron que la energía oscura coincide con el perfil de una constante cosmológica, aunque su medición tiene una incertidumbre del 10%, por lo que sigue siendo posible una densidad de energía oscura que varíe ligeramente.
Originalmente, eRosita, que se encuentra a bordo de una nave espacial rusa, debía realizar ocho estudios del cielo completo, pero en febrero de 2022, semanas después de que el telescopio comenzara su quinto estudio, Rusia invadió Ucrania. En respuesta, la parte alemana de la colaboración, que opera y dirige eRosita, puso el telescopio en modo seguro, cesando todas las observaciones científicas.
Estos artículos iniciales se basan únicamente en los datos de los primeros seis meses. El grupo alemán espera encontrar aproximadamente cuatro veces más cúmulos de galaxias en el año y medio adicional de observaciones, lo que permitirá identificar todos estos parámetros cosmológicos con mayor precisión. «La cosmología de cúmulos podría ser la sonda cosmológica más sensible además del FCM», apunta Anja von der Linden, astrofísica de la Universidad Stony Brook.
Sus resultados iniciales demuestran la potencia de una fuente de información relativamente sin explotar. “Somos una especie de chico nuevo en el barrio”, comenta Grandis.
El artículo original, Fresh X-Rays Reveal a Universe as Clumpy as Cosmology Predicts, se publicó el 4 de marzo de 2024 en Quanta Magazine.
Traducido por César Tomé López
El artículo Nuevos rayos X revelan un universo tan grumoso como predice la cosmología se ha escrito en Cuaderno de Cultura Científica.
El veneno más tóxico
 Foto: JJ Jordan / Unsplash
Foto: JJ Jordan / Unsplash¿Cuál es el veneno más letal? ¿Hay alguno que no deje huella? El envenenamiento ha sido un arma peligrosa utilizada a lo largo de los siglos para eliminar a enemigos políticos, rivales amorosos, y a veces, incluso a seres queridos. Desde las intrigas en las cortes medievales hasta el asesinato del ex agente ruso Alexander Litvinenko, son muchos los venenos empleados para perpetrar crímenes de manera eficaz y sigilosa. La fascinación por las sustancias tóxicas se extiende también a la ficción: Romeo y Julieta, Hamlet, e incluso la manzana de Blancanieves. A continuación, examinamos algunos de los venenos más peligrosos e indagamos en su dosis letal y su análisis toxicológico.
Crímenes por envenenamientoLos crímenes por envenenamiento han dejado una marca oscura a lo largo de la historia. La evolución de los venenos es también la crónica de luchas de poder entre las sombras y asesinatos anónimos. En la antigua Roma, el veneno era una herramienta comúnmente utilizada para eliminar rivales políticos. Sócrates fue condenado a muerte con cicuta, un veneno mortal, y Cleopatra, la legendaria reina egipcia, se suicidó con veneno de áspid.
Siglos más tarde, en la Europa del siglo XIX, el envenenamiento pasó a ser una táctica popular en las cortes reales, donde se usaban venenos como arsénico y cianuro para eliminar competidores por el poder. Por ejemplo, se cree que el rey Carlos VI de Francia fue envenenado por su hermano y que Napoleón Bonaparte murió por consumir arsénico.
En tiempos más modernos, también ha sido utilizado en asesinatos políticos y asuntos de espionaje. Por ejemplo, en 2006 fue notorio el envenenamiento con polonio-210 del ex agente ruso Alexander Litvinenko, presuntamente por orden del gobierno de su país. Además, no debemos olvidar su uso como arma militar: desde el gas mostaza usado durante la Primera Guerra Mundial hasta agentes neurotóxicos como el Tabún o el Sarín.
 La Mort de Socrate / La muerte de Sócrates (1787), por Jacques-Louis David. Fuente: Google Arts & Culture / Wikimedia CommonsLas sustancias más tóxicas
La Mort de Socrate / La muerte de Sócrates (1787), por Jacques-Louis David. Fuente: Google Arts & Culture / Wikimedia CommonsLas sustancias más tóxicas
Determinar las sustancias más tóxicas y sus dosis letales exactas puede ser complejo, ya que la toxicidad de una sustancia puede variar dependiendo de factores como la vía de exposición, la duración de la exposición, la edad y la salud del individuo, entre otros. La Agencia para Sustancias Tóxicas y el Registro de Enfermedades (ASTDR) elabora cada dos años un listado en el que prioriza las sustancias según su frecuencia, toxicidad y potencial de exposición humana.
En toxicología, se denomina dosis letal media (DL50) a la cantidad de una sustancia necesaria para matar a la mitad de una población después de un tiempo determinado. La toxina botulínica, que es la sustancia más tóxica conocida, tiene un valor de DL50 de 1 ng/kg, mientras que el agua, la sustancia menos tóxica, de más de 90 g/kg. Entre las sustancias con una baja DL50 y elevado riesgo de toxicidad encontramos cuatro de los venenos más conocidos: mercurio, arsénico, cianuro y polonio-210.
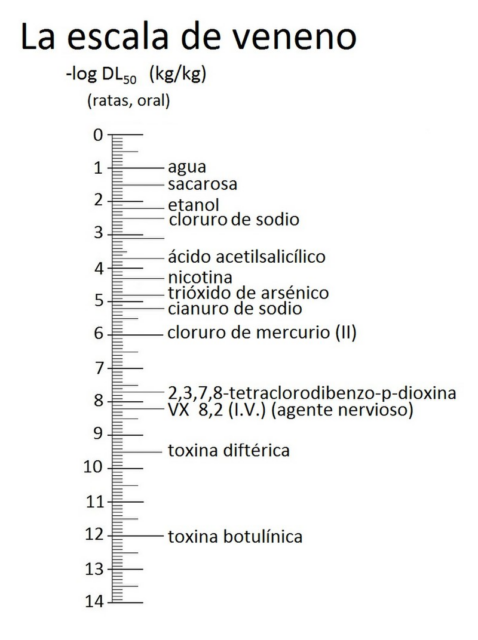 Escala de veneno en función del logaritmo decimal negativo de los valores de la DL50 estandarizados en kg por kg de peso corporal. Fuente: Wikimedia Commons
Escala de veneno en función del logaritmo decimal negativo de los valores de la DL50 estandarizados en kg por kg de peso corporal. Fuente: Wikimedia Commons
El arsénico es uno de los venenos más usados en homicidios debido a sus propiedades organolépticas (no tiene sabor, pero presenta un ligero aroma a ajo) y sus efectos son similares a los de una enfermedad gastrointestinal. Además, es fácil de adquirir, ya que está presente de forma natural en el agua. El grado de toxicidad varía según el derivado del arsénico: la arsina es el compuesto más tóxico, letal de forma instantánea a dosis de 250 ppm; le sigue el arsénico trivalente, cuya dosis letal es inferior a 5 mg/kg; por último, el arsénico pentavalente requiere dosis de entre 5 y 50 mg/kg para ser mortal.
La intoxicación por mercurio depende del estado de oxidación: el mercurio inorgánico, como el mercurio metálico y el cloruro de mercurio, es altamente reactivo y puede causar daños en la piel; el metilmercurio, que penetra en el cuerpo humano por el consumo de peces y mariscos contaminados, es bioacumulable y puede provocar daño neurológico, especialmente en el desarrollo fetal y en niños pequeños.
“La toxicidad de una sustancia puede variar dependiendo de factores como la vía de exposición, la duración, la edad y la salud del individuo”
A nivel celular, el cianuro es un tóxico que produce inhibición enzimática de numerosos sistemas. Por ejemplo, el cianuro de potasio es un potente inhibidor de la respiración celular, y el cianuro de hidrógeno, un gas incoloro con leve olor amargo, fue la sustancia que se usó en las cámaras de gas. El polonio-210, en cambio, es uno de los compuestos radiactivos más letales que se conocen por ingestión, dado que las partículas alfa que emite dañan el ADN y bastan algunos miligramos para causar la muerte en unas semanas.
La huella del crimen¿Qué rastro dejan los venenos en el cuerpo del delito? Más allá de lo que las series policiacas nos han hecho creer, lo cierto es que el avance de las técnicas de análisis actuales permiten la detección de muchas de estas sustancias. El mercurio, por ejemplo, puede ser detectado en muestras biológicas como la sangre, la orina o el cabello mediante la espectrometría de masas. Aunque tiene una vida media corta en la sangre (3 días), una concentración en orina superior a 500 µg/L se relaciona con temblores y trastornos del sistema nervioso central.
El cianuro, que produce efectos tóxicos a niveles de 0.05 miligramos de cianuro por decilitro de sangre (mg/dL), también puede ser identificado a través de análisis toxicológicos que buscan sus metabolitos en muestras biológicas. Del mismo modo, el arsénico puede ser detectado y cuantificado utilizando métodos analíticos como la cromatografía de gases y la espectrometría de masas. Además, para concentraciones por encima de 3 μg por decilitro en sangre y/o 200 μg por litro de orina, se observarán también alteraciones en el electrocardiograma, el hemograma y pruebas de las funciones hepática y renal.
“El arsénico es uno de los venenos más usados en homicidios debido a sus propiedades organolépticas (no tiene sabor, pero presenta un ligero aroma a ajo)”
En cuanto al polonio-210, su detección puede requerir técnicas de espectrometría gamma para identificar su presencia en muestras biológicas o ambientales. Su tiempo de vida media biológico es de 50 días, ya que a la desintegración radiactiva hay que sumarle la cantidad del elemento que se pierde por excreción en heces y orina. En resumen, si estás pensando en recurrir al envenenamiento para quitarte de en medio a ese jefe que te amarga a diario, quizá te disuada tener en cuenta que las posibilidades de ser descubierto son significativamente altas gracias a las novedosas técnicas de detección toxicológica.
Referencias:
Organización Mundial de la Salud (2017) El mercurio y la salud
Lumitos / Química.es (2024) Categoría Toxicología
Agencia para Sustancias Tóxicas y el Registro de Enfermedades (2016) Resumen de Salud Pública: Cianuro (Cyanide)
López Nicolás, J.M. (2018) Querido Paracelso: el veneno no solo reside en la dosis Cuaderno de Cultura Científica
Sobre la autora: Raquel Gómez Molina es química especialista en laboratorio clínico y comunicación científica
El artículo El veneno más tóxico se ha escrito en Cuaderno de Cultura Científica.
Memoria y creatividad
La memoria no tiene buena prensa; me refiero a la memoria con minúscula, o sea, a la capacidad para recordar ideas, informaciones, situaciones, experiencias, lecturas, etc. Por eso, el calificativo “memorístico”, en realidad, más que calificar, descalifica.
Ya cuando era estudiante a caballo entre COU y los primeros cursos universitarios la organización estudiantil en la que militaba se oponía, al menos de palabra, a la enseñanza memorística. Reivindicaba en su lugar una formación que nos enseñase a pensar. Es curioso cómo, con apenas 17 o 18 años de edad, éramos capaces de decir y defender asertos que hoy no sería capaz ni de enunciar. Es más, ahora ni tan siquiera sabría explicar qué se entiende por pensar en ese contexto, y quizás en ningún otro.
Ha pasado casi medio siglo y la mala prensa de lo memorístico perdura. Aunque ahora sus adversarias son otras y la tecnología nos ha brindado nuevos motivos, reales o ficticios, para menospreciarla. Se pretende devaluar hoy la capacidad memorística porque ese es un rasgo que, supuestamente, ha perdido toda utilidad. En ese argumento está implícita la idea de que antes hacía falta buena memoria para poder recordar muchas cosas, ya que no había dispositivos que permitieran acceder con facilidad al conocimiento acumulado. Pero ahora, con las enormes facilidades de almacenamiento de información y de acceso a ella –volúmenes gigantes al alcance de uno o dos clics–, se supone que ya no es preciso que utilicemos el cerebro propio como almacén.
Hoy se valora la creatividad. En nuestro mundo y, sobre todo, en el mundo hacia el que parecemos dirigirnos –se nos dice– la creatividad es fundamental, pues solo personas creativas son capaces de idear las nuevas soluciones, los nuevos productos, las nuevas obras artísticas o culturales, o de generar el nuevo conocimiento que servirá para alimentar la actividad económica que permita crear riqueza y bienestar.
 John von Neumann, una de las mentes científicas más creativas del siglo XX, poseía una memoria portentosa.
John von Neumann, una de las mentes científicas más creativas del siglo XX, poseía una memoria portentosa.La creatividad se considera hoy uno de los rasgos cognitivos más valiosos, si no el más valioso. Y se insiste en la idea de que hay que estimularla o cultivarla. Tal es así que en el ciclo 2022 de PISA (OCDE) se ha incluido la competencia “creatividad” para ser evaluada como competencia innovadora en estudiantes de 15 años. Sin embargo, no parece que en su cultivo o estímulo juegue la memoria papel alguno. Nada se dice de ella en el artículo cuya lectura me permitió saber de la inclusión en las pruebas PISA de la creatividad como competencia innovadora. Deduzco que ello no obedece al olvido de la autora ni a la casualidad. Sencillamente no se la ha dado ninguna importancia.
No sé si en otros campos ocurre algo parecido pero, al menos en el terreno científico, la capacidad memorística es un ingrediente muy valioso de la creatividad. Las nuevas ideas surgen en muchas ocasiones de las relaciones espontáneas, y a veces fugaces, que establece nuestra mente entre piezas de conocimiento o informaciones diferentes y, a veces, sin relación aparente entre sí.
Las nuevas ideas no surgen porque uno vaya en su búsqueda de forma activa y consciente como cuando acudimos a un buscador en la internet. Si así fuera, casi cualquiera podría dar con ellas. Si supiésemos en qué van a consistir, sabríamos en qué archivo, qué documento, qué base de datos deberíamos buscar las piezas de información, los pedazos de conocimiento con los que construir la novedad.
No, la internet o cualquier otro repositorio de información o conocimiento no son sustitutos adecuados de la memoria si de lo que se trata es de crear. Conozco a centenares de personas en el mundo de la ciencia, de la literatura, de las artes plásticas, de la ingeniería y de la empresa. De entre todas esas personas unas son más creativas que otras. Las más creativas tienen una memoria envidiable.
En ciencia muchas ideas nuevas surgen cuando, dando vueltas a elementos aparentemente inconexos, encontramos o establecemos de repente una relación inesperada donde nadie antes lo había hecho. Es posible que eso ocurra mientras leemos un artículo o un libro, pero entonces el conocimiento codificado en forma impresa no suele ser suficiente, ha de cruzarse en su camino algún pasaje que habíamos leído en otra ocasión, o un fragmento de conversación que tuvimos hace un mes con un colega. O, incluso, puede surgir al contemplar una obra de arte o leer una novela. Es del todo azaroso el modo en que surge la idea nueva. En ocasiones lo hace durante el sueño o en estado de duermevela. Pero rara vez surge de confrontar dos o más elementos a los que accedemos directamente en el soporte en que se encuentran almacenados. Sospecho que en campos del saber otros que las ciencias naturales ocurre algo parecido.
Para que esa chispa, ese momento “eureka”, ese “¡ahá!”, ese “¡qué curioso!” o “¡qué raro!” se produzca, hemos debido confrontar alguna observación o idea con elementos almacenados en la memoria. Por eso, estoy convencido de que es necesario cultivar la memoria para promover la creatividad. Es una de sus mejores amigas.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU. Una versión anterior de este texto apareció en Lecturas y Conjeturas (Substack).
El artículo Memoria y creatividad se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2023 – Experimentos con humanos e IAs
El gran evento de divulgación organizado por Naukas y la Cátedra de Cultura Científica volvió a Bilbao para celebrar su decimotercera edición en el gran Palacio Euskalduna los pasados 15 y 16 de septiembre de 2023.

Una de las preguntas más inquietantes que pueden hacerse y que pocas veces verás por ahí es: ¿Puede la inteligencia artificial (las IAs) influir en las decisiones humanas? La respuesta, en caso de ser positiva, tiene implicaciones éticas y sociológicas terribles. Los resultados experimentales de su equipo de investigación de la Universidad de Deusto que narra Helena Matute en esta charla son, como mínimo, inquietantes.
Helena Matute es catedrática de Psicología Experimental de la Universidad de Deusto y directora del Laboratorio de Psicología Experimental. Ha sido investigadora visitante en distintas universidades del mundo como la de Gante en Bélgica, las de Sídney y Queensland en Australia o Minnesota en Estados Unidos. Miembro asesor del consejo científico de FECYT, Matute es presidenta de la Sociedad Española de Psicología Experimental y académica de número de Jakiunde – Academia de las Ciencias, las Artes y las Letras del País Vasco. Tiene el premio Prisma y el premio DIPC-Jot Down de divulgación científica.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2023 – Experimentos con humanos e IAs se ha escrito en Cuaderno de Cultura Científica.
Un espinosáurido riojano
El primer dinosaurio descrito en La Rioja es un espinosáurido de unos 7-8 metros de longitud y una masa corporal estimada en 1,5 toneladas. Se trata de una forma bípeda, de hábitos principalmente piscívoros, aunque –como buen predador– también sería capaz de perseguir y alimentarse de presas terrestres. La nueva especie de espinosáurido, bautizada como Riojavenatrix lacustris, vivió hace 120 millones de años.
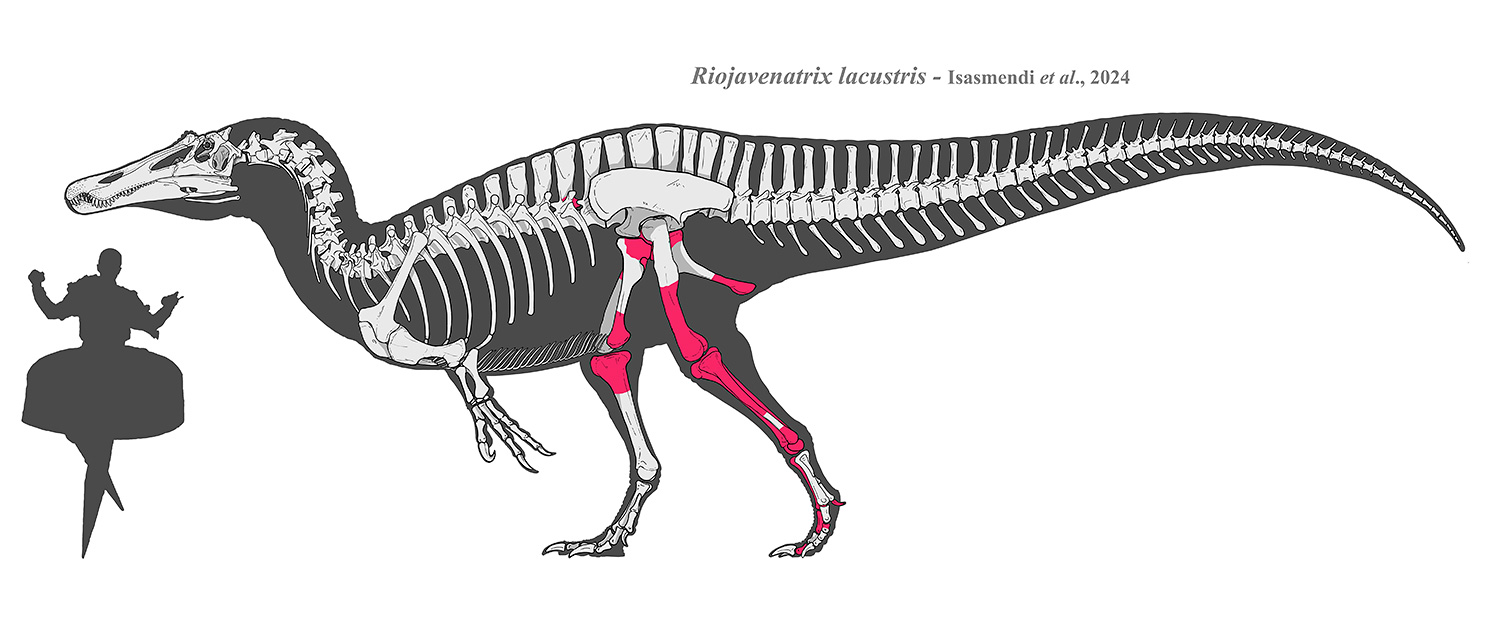
Los espinosáuridos son un grupo de dinosaurios carnívoros (terópodos) de tamaño medio a grande con unos caracteres anatómicos muy particulares: tienen un cráneo bajo y alargado con mandíbulas provistas de dientes cónicos, similar al de los cocodrilos modernos, y unos brazos largos y robustos con manos de tres dedos terminadas en poderosas garras, destacando por su gran tamaño la del dedo uno, el equivalente a nuestro dedo pulgar. Algunos espinosáuridos poseían una vela dorsal. Los primeros restos fósiles de espinosáurido hallados en Igea fueron un fragmento de maxilar encontrado en 1983 y dientes aislados. Esos restos, junto con un esqueleto parcial recuperado en 2005, se asignaron al icónico dinosaurio inglés Baryonyx. Sin embargo, la revisión de este material indica la presencia de un nuevo género y especie de espinosáurido, al que se le ha dado el nombre científico de Riojavenatrix lacustris, convirtiéndose en el primer dinosaurio descrito en La Rioja.
“El nuevo género y especie, al que coloquialmente llamamos Britney, está basado en un esqueleto parcial, que consiste en restos de los miembros posteriores (fémur, tibia, fíbula, huesos del tobillo y falanges del pie) y de la pelvis (pubis e isquion), así como un resto vertebral”, señala el investigador de la UPV/EHU Erik Isasmendi. “Presenta una combinación de caracteres anatómicos que lo hacen único y permite diferenciarlo de otros espinosáuridos, añade.
Con Riojavenatrix son cinco los espinosáuridos descritos en el Cretácico Inferior de la Península Ibérica. Los otros espinosáuridos ibéricos son Camarillasaurus en Aragón, Vallibonavenatrix y Protathlitis en la Comunidad Valenciana, e Iberospinus en Portugal. El estudio pone de manifiesto que no es posible confirmar la presencia de Baryonyx en el registro ibérico. Los restos fósiles atestiguan que la península ibérica albergó un conjunto amplio y diverso de estos dinosaurios carnívoros.
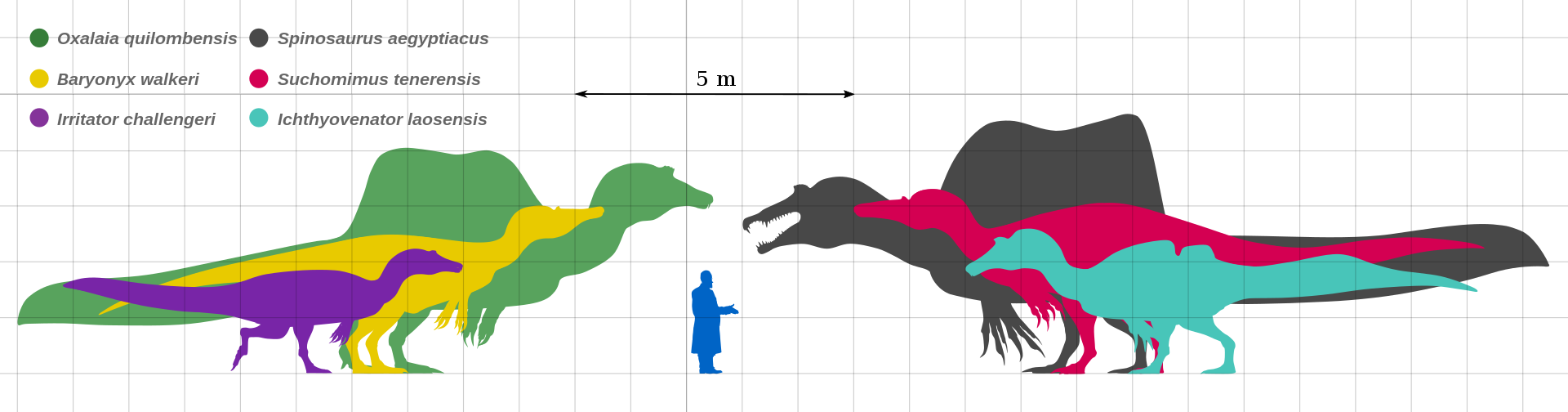 Tamaño de algunas especies de espinosáuridos. Fuente: Wikimedia Commons
Tamaño de algunas especies de espinosáuridos. Fuente: Wikimedia CommonsPara Elena Cuesta, investigadora postdoctoral en el Museo Paleontológico Egidio Feruglio de Argentina y la Universidad de Ludwig Maximilian en Alemania, los numerosos descubrimientos dentro de este icónico grupo “plantean muchísimas nuevas preguntas” sobre la ecología de estos animales. “¿Cómo convivieron estas especies entre sí? Preguntas como esas nos llevan a replantearnos futuros estudios más detallados sobre los espinosáuridos, de los que seguro se obtendrán resultados importantes”, comenta.
La nueva especie riojana será clave para esto y para entender más sobre el origen y evolución de estos terópodos. Xabier Pereda Suberbiola, profesor e investigador del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU, es uno de los directores de la tesis doctoral de Erik Isasmendi y director de excavación en Igea. “Los fósiles descubiertos son de gran interés paleontológico y nos permiten poner a Igea en el mapa mundial de los espinosáuridos y de los dinosaurios carnívoros, en general”, declara Pereda.
GarrasIgea es actualmente una de las zonas con mayor cantidad de yacimientos y restos fósiles de espinosáuridos del mundo. Esta situación es el fruto de las actividades desarrolladas por el equipo “Garras”, que reúne un colectivo de paleontólogos y aficionados trabajando al unísono con el objetivo de dar a conocer el rico patrimonio paleontológico de Igea y La Rioja.
El siguiente paso del equipo es publicar otros fósiles de espinosáuridos hallados en Igea, como el esqueleto parcial denominado “Garras” de Peña Cárcena y el excavado en los últimos años en “Virgen del Villar 2” (muy cerca de “Virgen del Villar 1”), al que se le ha dado el nombre coloquial de “Villar”. Este último es “uno de los esqueletos más completos que se conocen en el registro europeo y mundial”. El material de “Garras” está en fase final de estudio antes de su publicación y el de “Villar” está siendo preparado por los integrantes del equipo de laboratorio.
Los dinosaurios carnívoros más comunesEn la Península Ibérica, los espinosáuridos son los dinosaurios carnívoros más comunes en las formaciones del Cretácico Inferior, y son especialmente dominantes en rocas formadas en ambientes lacustres. Es habitual encontrar sus fósiles (principalmente dientes) en diferentes cuencas sedimentarias, como en Cameros (Burgos y La Rioja), el Maestrazgo (Teruel y Castellón) y la cuenca lusitánica en Portugal. Los orígenes de este grupo estarían en el Jurásico Superior de Europa occidental, ya que sus restos han aparecido principalmente en España, Portugal y Reino Unido, con varios intercambios de faunas durante el Cretácico Inferior entre Europa y el norte de África.
Referencia:
Erik Isasmendi, Elena Cuesta, Ignacio Díaz-Martínez, Julio Company, Patxi Sáez-Benito, Luis I. Viera, Angelica Torices, Xabier Pereda-Suberbiola (2024) Increasing the theropod record of Europe: a new basal spinosaurid from the Enciso Group of the Cameros Basin (La Rioja, Spain). Evolutionary implications and palaeobiodiversity Zoological Journal of the Linnean Society doi: 10.1093/zoolinnean/zlad193
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Un espinosáurido riojano se ha escrito en Cuaderno de Cultura Científica.
El Marte con el que soñamos
En 1877, había canales en Marte. O, más concretamente, canali, como llamó el astrónomo italiano Giovanni Schiaparelli (1835-1910) a esa especie de formaciones geográficas o geológicas rectilíneas que le pareció observar a través del telescopio cuando enfocó a nuestro planeta vecino. En ningún momento sugirió que estas pudieran ser de origen artificial, pero un error de traducción, no se sabe si intencionado o no, de su colega estadounidense William Henry Pickering (1858-1935) acabó encendiendo la imaginación de toda una época. Incluso de toda la disciplina. Este tradujo canali por canals, que sugiere artificialidad, en lugar de channels, que se refiere a formaciones naturales, y otros astrónomos, como Percival Lowell (1855-1916), adoptaron el término con entusiasmo:
Schiaparelli detectó la existencia de los canales cuando estaba comprometido en la triangulación de la superficie del planeta con un fin topográfico. Y lo que encontró fue que la triangulación ya estaba hecha. Con sus propias palabras, aquello «parecía haber sido trazado con regla y compás».
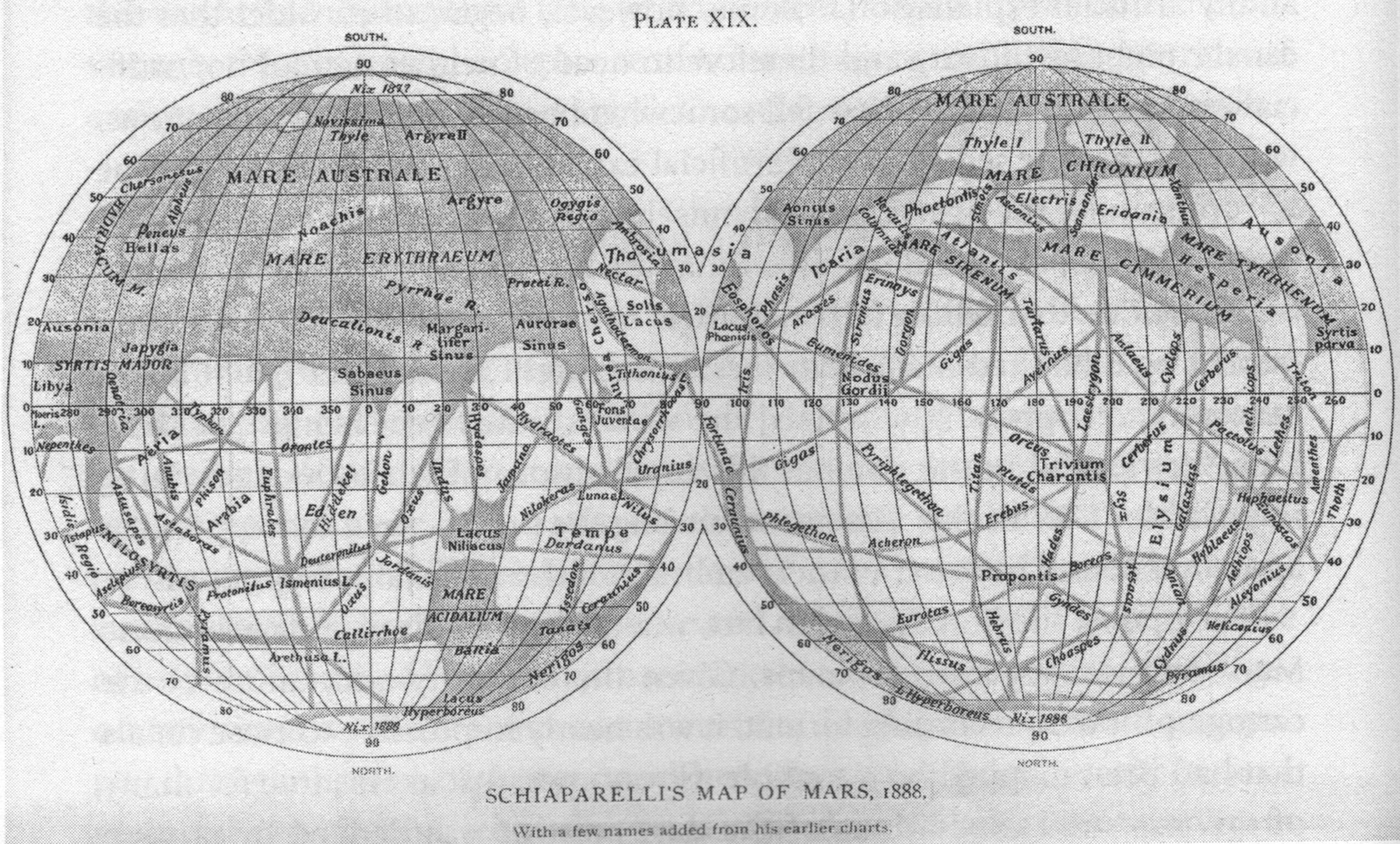 Mapa de Marte de Giovanni Schiaparelli, del año 1888, en el que se puede ver la famosa red de canales. Fuente: Dominio público
Mapa de Marte de Giovanni Schiaparelli, del año 1888, en el que se puede ver la famosa red de canales. Fuente: Dominio públicoTras una pequeña decepción lunar, a medida que íbamos sabiendo más de nuestro satélite y la posibilidad de encontrar algo «interesante» en él se desvanecía, los canales de Marte abrieron una nueva puerta a la posibilidad de no estar solos en el universo y de que esas posibles formas de vida no estuvieran tampoco tan lejos. Así que empezamos a imaginarlas.
Sobre esa fina línea que separa lo conocido de lo que nos gustaría conocer, escritores como Edgar Rice Burroughs ―que lo bautizó como Barsoom― o Leigh Brackett ―cuyas versiones de Marte, como Shandakor, inspirarían a su gran amigo Ray Bradbury― edificaron sus civilizaciones.
En el Barsoom de Burroughs, que en un pasado remoto había contado hasta con cinco océanos ―ya secos― la intrincada red de canales de Schiaparelli y Lowell bombeaba agua desde los casquetes polares para regar las franjas de vegetación que se extendían a lo largo de latitudes más templadas. La atmósfera, demasiado tenue, contaba con un sistema de soporte para hacer la vida posible. Y los nativos del planeta habían bautizado a los dos satélites de este ―Phobos y Deimos― como Thuria y Cluros. ¿Demasiado increíble hoy en día? Sí, y afortunadamente. Lo suficiente como para sembrar la duda e inspirar a un niño que creció leyendo esas historias y cuyo nombre era Carl Sagan.
Fue emocionante leer estas novelas. Al principio, pero poco a poco empezaron a corroerme las dudas. El giro argumental de la primera historia de John Carter que leí dependía de que este olvidara que el año es más largo en Marte que en la Tierra. Pero a mí me pareció que, si uno va a otro planeta, una de las primeras cosas que comprueba es la duración del día y el año. También había algunos comentarios incidentales que al principio me parecieron sorprendentes pero que, tras una reflexión seria, resultaron una decepción. Por ejemplo, Burroughs comenta casualmente que en Marte hay dos colores primarios más que en la Tierra. Pasé muchos y largos minutos con los ojos cerrados, tratando de contemplar ferozmente un nuevo color primario, pero siempre percibía algo familiar, como un marrón oscuro o ciruela. ¿Cómo podría haber otro color primario en Marte y mucho menos dos? ¿Qué era un color primario? ¿Tenía algo que ver con la física o con la fisiología? Decidí que, quizás, Burroughs no sabía de qué estaba hablando, pero sí hizo pensar a sus lectores. Y en esos muchos capítulos en los que no había mucho en qué pensar, había enemigos satisfactoriamente malignos y un manejo de la espada apasionante, más que suficiente para mantener el interés de un niño de ciudad de diez años en el largo verano de Brooklyn.1
Dicen que, junto a la puerta de su despacho en Cornell, en el pasillo, Carl Sagan tenía colgado un mapa de Barsoom. Cabría preguntarse si todo aquello tuvo que ver con acabar, entre los años sesenta y setenta, participando en el Programa Mariner, cuya Mariner 4 realizó las primeras fotografías desde la órbita de Marte. O con que el 20 de julio de 1976, la Viking I consiguiera hacer lo mismo desde su superficie.
 Cráteres en Marte fotografiados por la Mariner 4. Fuente: NASA
Cráteres en Marte fotografiados por la Mariner 4. Fuente: NASA
 Primera imagen desde la superficie marciana tomada por la Viking I. Fuente: NASA
Primera imagen desde la superficie marciana tomada por la Viking I. Fuente: NASA Carl Sagan junto a un prototipo del aterrizador de las Viking. Fuente: NASA/JPL
Carl Sagan junto a un prototipo del aterrizador de las Viking. Fuente: NASA/JPLSin embargo, es curioso cómo uno de los responsables de materializar, de alguna manera, uno de los grandes sueños de la ciencia ficción de alcanzar Marte fue también responsable de hacernos despertar. Porque el ambiente que encontramos allí fue mucho más hostil de lo que esperábamos: Marte estaba igual o más muerto que la Luna. Así que durante diecisiete años se congelaron tanto los sueños como las misiones… hasta septiembre de 1992. Fue aquel mes cuando se lanzó la sonda Mars Observer, que apenas había llegado a la órbita del planeta rojo alrededor de un año después cuando perdimos el contacto con ella. Pero también fue aquel mes en el que se publicó Marte rojo, de Kim Stanley Robinson, la primera parte de una trilogía de colonización y terraformación marciana que se convertiría, de manera consciente o no, en una suerte de hoja de ruta de lo que podría aguardarnos un día, si intentábamos volver, a 230 millones de kilómetros.
Todo había empezado con la ciencia inspirando a la ficción, luego la ficción inspiró a la ciencia. Y vuelta a empezar. En el punto más bajo de la historia de la exploración marciana, Robinson demostró que, al igual que lo fue el de Schiaparelli, ese Marte inhóspito que nos habían mostrado las primeras sondas también podía ser bello. Y, sorprendentemente, nuevas misiones empezaron a ponerse en marcha. Pathfinder, Spirit, Opportunity, Curiosity… trajeron nuevos datos y de ellos, otra vez, nacieron nuevas historias, como la conocidísima El marciano, de Andy Weir. La ciencia ficción, en lo que se refiere a la inspiración, hizo, y hace, que Marte vuelva a ser posible. Es lo que nos devolvió, en parte y cuando ya nadie daba nada por ello, la ilusión por regresar.
Y sí… tal vez en Marte no haya canales construidos por una antigua civilización, pero se piensa, como también imaginó Burroughs, que existieron océanos, lagos y ríos en él hace unos 3500 millones de años, lo que reaviva en nosotros la esperanza de que, al menos, podamos llegar a encontrar algún día restos de vida microbiana. Tal vez ningún John Carter vaya a salvar a ninguna princesa marciana llamada Dejah Toris, pero es posible que la persona que vaya a poner por primera vez un pie en Marte ya haya nacido y su aventura será, sin duda alguna, una de las más emocionantes ―por no decir la que más― que vaya a vivir la humanidad en su conjunto.
 Composición de la ESA con los colores de la superficie de Marte, realizada con motivo del vigésimo aniversario de la misión Mars Express. Fuente: ESA/DLR/FU Berlin/G. Michael
Composición de la ESA con los colores de la superficie de Marte, realizada con motivo del vigésimo aniversario de la misión Mars Express. Fuente: ESA/DLR/FU Berlin/G. Michael
A veces se acusa a la ciencia de arrebatarnos nuestros sueños. De constreñir tanto la imaginación que nos corta las alas, cuando puede que sea, más bien, al contrario. Ciencia y relatos se han retroalimentado constantemente en casi todos los campos de conocimiento a lo largo de nuestra existencia en un bucle infinito que nos ha ido convirtiendo en lo que somos como especie. Por eso las historias son importantes, y por eso no debemos dejar de contarlas, por inverosímiles que puedan parecer. Porque no importa que luego la realidad las pruebe falsas; al hacerlo, estará abriendo una puerta a otras completamente distintas, solo hay que atreverse a cruzar ese nuevo umbral de hacer posible lo imposible.
Así que, como dijo Percy mientras aterrizaba en Marte y como, en realidad, siempre ha hecho la humanidad…
 El paracaídas que desplegó el rover Perseverance en su aterrizaje escondía un mensaje: «Dare mighty things». Fuente: NASA/JPL-Caltech
El paracaídas que desplegó el rover Perseverance en su aterrizaje escondía un mensaje: «Dare mighty things». Fuente: NASA/JPL-Caltech
Aunque esas cosas sean buscar marcianos.
Referencias:
NASA Science. MARS exploration.
Sagan, Carl (28 de mayo de 1978). Growing up with science fiction. The New York Times.
Schiaparelli, Giovanni (2009). La vida en Marte. Interfolio Libros.
Nota:
1 Traducción de la autora.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo El Marte con el que soñamos se ha escrito en Cuaderno de Cultura Científica.
Once cuatro cuatro, mirar el arte con ojos matemáticos
Cualquier persona que haya leído mi último libro Las matemáticas como herramienta de creación artística (2023), se habrá dado cuenta de la admiración que siento por el trabajo artístico del diseñador, artista polifacético y educador suizo Max Bill (1908-1994), figura central de arte concreto y, en mi opinión, uno de los artistas claves en el arte del siglo xx. Las matemáticas fueron fundamentales para este artista, como dejó recogido en su ensayo El pensamiento matemático del arte de nuestro tiempo (1949) y en el que se pueden leer reflexiones como la siguiente:
Creo que es posible desarrollar ampliamente un arte basado en el pensamiento matemático. Contra esta opinión se plantearon enseguida fuertes objeciones. Se afirma que el arte nada tiene que ver con las matemáticas, y que éstas son una materia árida, no artística, una cuestión puramente intelectual, que es contraria al arte. Para el arte, sólo el sentimiento es importante y el pensamiento es perjudicial. Ninguno de los dos puntos de vista es correcto, porque el arte necesita por igual del sentimiento y del pensamiento.
En el mencionado texto, Las matemáticas como herramienta de creación artística, se puede descubrir la importancia que tuvo el teorema de Pitágoras en su obra, herramienta matemática que utilizó desde, al menos, 1937, año de creación de su obra Construcción con la fórmula a2 +b2 = c2, y que no abandonaría nunca (véase también la entrada El teorema de Pitágoras en el arte); o la profunda relación que tuvo con la banda de Moebius, desde que la redescubriera y bautizara como la cinta sin fin en 1935 (véase también la entrada Arte Moebius (I)). Pero nos podemos encontrar muchas más matemáticas en su trabajo: figuras geométricas planas –polígonos, círculos y otras curvas- y espaciales –esferas y poliedros-, el hipercubo, diferentes sucesiones de números o la combinatoria, entre otras.
En esta entrada quiero que disfrutemos, y analicemos juntos, mirando con ojos matemáticos, una hermosa serie de obras relacionada con la geometría, la combinatoria y el álgebra, su serie 11 x 4 : 4 (1963/1970).
 Las once serigrafías de la serie 11 x 4 : 4 (1970), del artista concreto suizo Max Bill
Las once serigrafías de la serie 11 x 4 : 4 (1970), del artista concreto suizo Max Bill¿Qué vemos cuando miramos?
Antes de nada, analicemos esta serie de obras. Si tomamos una cualquiera de ellas, por ejemplo, la última, de la cual he realizado la siguiente reconstrucción, descubriremos algunas cosas interesantes. Para empezar, algo básico, la obra está compuesta por una retícula cuadrada de tamaño 4 x 4, es decir, con 16 pequeños cuadrados. Además, cada uno de los 16 cuadrados están coloreados con uno de los cuatro colores que se han utilizado en cada pieza, en la serigrafía de la siguiente imagen azul, rojo, amarillo y verde.
 Reconstrucción de una de las serigrafías de la serie 11 x 4 : 4 (1970), de Max Bill
Reconstrucción de una de las serigrafías de la serie 11 x 4 : 4 (1970), de Max Bill
Si la descomponemos por colores, observaremos que está formada (como se muestra en la siguiente imagen) por cuatro estructuras básicas, que son la misma, salvo rotaciones de 90, 180 y 270 grados. Es decir, si tomamos la primera (la azul) podemos obtener las demás girando, en el sentido contrario a las agujas del reloj, 90 grados (verde), 180 grados (amarilla) y 270 grados (roja).
 Descomposición, por colores, de la serigrafía anterior de la serie 11 x 4 : 4 (1970), de Max Bill
Descomposición, por colores, de la serigrafía anterior de la serie 11 x 4 : 4 (1970), de Max Bill
Consideremos otra de las once serigrafías que componen esta serie y veamos que ocurre lo mismo que en la anterior.
 Reconstrucción, y descomposición por colores, de una de las serigrafías de la serie 11 x 4 : 4 (1970), de Max Bill
Reconstrucción, y descomposición por colores, de una de las serigrafías de la serie 11 x 4 : 4 (1970), de Max Bill
Si llamamos “patrón básico” a la estructura formada por las cuatro casillas que llevan un mismo color y de manera que una de ellas sea el vértice superior izquierdo, que en el primer ejemplo son las cuatro casillas azules y en el segundo las cuatro casillas violetas, está claro que estas obras se forman tomando el patrón básico de un color y cada rotación del patrón básico, de 90, 180 y 270 grados, con otro color distinto cada una.
Pero cuidado, no vale cualquier elección de cuatro casillas de la retícula 4 x 4, puesto que puede ocurrir que la girar, 90, 180 y 270 grados, la estructura básica haya casillas que se superponen o casillas que no estarían ocupadas, que no tendrían color, como ocurre en el siguiente ejemplo (para el que hemos elegido los mismos colores que la primera serigrafía).
 Candidato a patrón básico (azul) y las rotaciones de 90, 180 y 270 grados, en el sentido contrario de las agujas del reloj (verde, amarillo y rojo)
Candidato a patrón básico (azul) y las rotaciones de 90, 180 y 270 grados, en el sentido contrario de las agujas del reloj (verde, amarillo y rojo)
Si observamos el candidato a patrón básico (azul) y sus giros en el sentido contrario a las agujas del reloj (verde, amarillo y rojo), podemos observar que hay cuatro casillas de los lados de la retícula que no quedarían cubiertas, no podríamos asignarles color según lo establecido, en concreto la tercera de la primera fila, la primera de la segunda fila, la cuarta de la tercera y la segunda de la cuarta. Y, además, las cuatro casillas del centro tendrían dos colores asignados cada una de ellas, las dos casillas centrales de la diagonal descendente tendrían asignados los colores azul y amarillo, mientras que las dos casillas centrales de la diagonal ascendente tendrían asignados los colores verde y rojo. En consecuencia, este candidato a patrón básico no sirve para generar una obra del estilo de las serigrafías de la serie de Max Bill.
Pero volvamos de nuevo a la serie 11 x 4 : 4 y representemos los once patrones básicos asociados a las once serigrafías de la misma.
 Los once patrones básicos correspondientes a las once serigrafías de la serie 11 x 4 : 4 de Max Bill
Los once patrones básicos correspondientes a las once serigrafías de la serie 11 x 4 : 4 de Max BillEntonces, podemos observar más cosas, además del análisis anterior de que los cuatro cuadrados del patrón básico, junto a los cuadrados de cada una de las estructuras (4 cuadrados por estructura) que consisten en girar 90, 180 y 270 grados el patrón básico, llenan la retícula 4 x 4, como que los cuadrados del patrón básico (luego los cuadrados de un mismo color en cada serigrafía de la serie) o no se tocan o se tocan solo en un vértice, nunca comparten un lado entero.
Por ejemplo, ninguno de las dos creaciones siguientes que verifica la condición de ser cuatro estructuras de cuatro cuadrados, tal que cada una se relaciona con las otras mediante giros de 90, 180 y 270 grados, y que las cuatro juntas rellenan la retícula 4 x 4, podrían formar parte de la serie de Max Bill, ya que hay cuadrados del mismo color que se tocan en un lado.
Entre las notas de Max Bill puede encontrarse una explicación (siguiente imagen) de cómo ha generado cada una de las once estructuras básicas (patrones básicos). En este apartado intentaremos explicar el motivo por el cual considera exactamente esos once patrones básicos para generar las obras de la serie. En su explicación gráfica, empieza con una estructura básica y desplaza uno de los cuatro cuadrados de la misma para obtener una nueva estructura básica, y así hasta el final. Por ejemplo, en su primera estructura básica (que es la primera de la segunda fila de la anterior imagen de las once estructuras básicas) desplaza el cuadrado de la tercera fila y cuarta columna, al cuadrado de la primera fila y tercera columna. Debemos percatarnos que al mover ese cuadrado solo tiene tres opciones para moverlo, ya que al girar tiene que cubrir los mismos cuatro huecos (casillas) que cubría el cuadrado que ha movido. Esto nos lleva a una pequeña reflexión matemática relacionada con este proceso creativo, lo que en matemáticas se denomina la “acción de un grupo sobre un conjunto”.
 Nota explicativa, de puño y letra de Max Bill, sobre el proceso creativo de la obra 11 x 4 : 4 (1970)
Nota explicativa, de puño y letra de Max Bill, sobre el proceso creativo de la obra 11 x 4 : 4 (1970)
En este proceso creativo de Max Bill interviene un grupo algebraico, el grupo G de las rotaciones de un cuadrado que lo dejan invariante, que está formado por los giros de 0 grados (este giro es la identidad, no mover el cuadrado), 90 grados, 180 grados y 270 grados. En las entradas Cuadrados latinos, matemáticas y arte abstracto y La teoría de grupos en el arte contemporáneo: John Ernest se puede leer sobre la estructura algebraica de grupo, pero realmente no es necesario para entender esta entrada, cuya lectura podéis continuar sin necesidad de saber nada más que estamos trabajando con el grupo de rotaciones de un cuadrado, es decir, rotaciones de 0, 90, 180 y 270 grados. Además, se está considerando, de forma implícita, lo que se denomina la acción de un grupo sobre un conjunto. En este caso, el conjunto X estaría formado por las 16 casillas de la retícula, que en la siguiente imagen hemos nombrado con letras, de la a a la p, para entender mejor la acción del grupo.
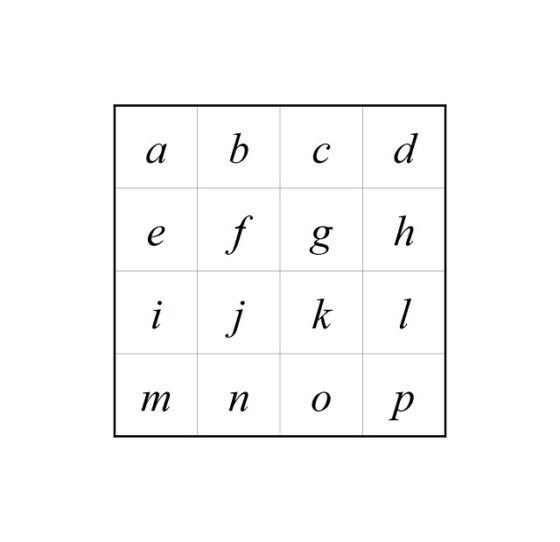
Una acción de un grupo G sobre un conjunto X consiste en una aplicación que a cada elemento del grupo g (de G) y cada elemento del conjunto x (de X) se les asocia otro elemento del conjunto X, que denotamos gx, o g(x), que consiste en aplicar g sobre x. Por ejemplo, si g es el giro de 90 grados y x es la casilla a, entonces g(x) es la casilla d, o si g es el giro de 270 grados y x es la casilla j, entonces g(x) es la casilla f (la que se obtiene al girar 270 grados en el sentido contrario a las agujas del reloj). Más aún, si tomamos g = giro de 90 grados, podemos ver en la siguiente imagen cómo se moverían todas las casillas.
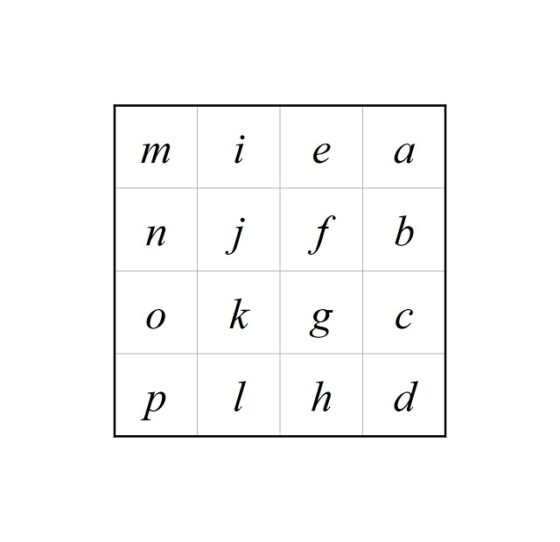
El proceso creativo de Max Bill está relacionado con lo que en matemáticas se llama las órbitas de una acción de un grupo sobre un conjunto. Dado un punto cualquiera x del conjunto X, se llama “órbita de x”, a todos los elementos del conjunto que se obtienen al aplicar los elementos del grupo G sobre ese elemento x. Escrito de forma matemática, la órbita de un elemento x sería el subconjunto {g(x): para todo g de G}. Por ejemplo, en nuestro caso, si tomamos la casilla a, resulta que al aplicarle los elementos del grupo (rotaciones de 0, 90, 180 y 270 grados) se obtienen las casillas {a, d, p, m} (las casillas de las esquinas). En total, en la acción que hemos descrito, relacionada con la serie artística de Max Bill, existen cuatro órbitas, la descrita antes y otras tres, todas ellas descritas en la siguiente imagen, en la que cada color describe los elementos de una misma órbita: {a, d, p, m} (rosa), {b, h, o, i} (azul claro), {c, l, n, e} (verde claro) y {f, g, j, k} (amarillo).
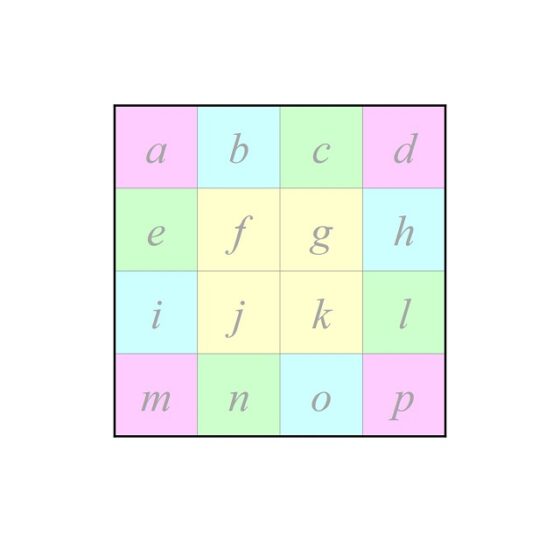 Las cuatro órbitas, cada una de un color, de la acción del grupo de las rotaciones de 0, 90, 180 y 270 grados sobre el conjunto de las 16 casillas de la retícula 4 x 4
Las cuatro órbitas, cada una de un color, de la acción del grupo de las rotaciones de 0, 90, 180 y 270 grados sobre el conjunto de las 16 casillas de la retícula 4 x 4
¿Cómo se relaciona esto con el proceso creativo de Max Bill? Cada uno de los patrones básicos está formado por un cuadrado de cada una de las cuatro órbitas, como podéis comprobar en los once patrones básicos que hemos descrito más arriba. Por lo tanto, para crear los patrones básicos para obras de la serie de Max Bill hay que coger, para cada patrón básico, un cuadrado de cada órbita, pero con algunas condiciones que iremos explicando paso a paso.
Para empezar, de cada órbita tenemos 4 posibles cuadrados, luego existen 4 x 4 x 4 x 4 = 256 formas distintas de elegir un cuadrado de cada órbita, que son muchas formas para empezar. Como cada patrón básico, girado 90, 180 y 270 grados forma una obra de la serie de Max Bill, hay candidatos a patrones básicos de los 256 anteriores que darían lugar a la misma obra. Por ejemplo, en la siguiente imagen vemos cuatro de estos posibles patrones básicos, pero que dan lugar a la misma obra, ya que son iguales, salvo una rotación, de 90, 180 o 270 grados.
 Estos cuatro candidatos a patrones básicos darían lugar a la misma obra de Max Bill, elegidos los colores convenientemente, ya que son iguales salvo una rotación de 90, 180 o 270 grados
Estos cuatro candidatos a patrones básicos darían lugar a la misma obra de Max Bill, elegidos los colores convenientemente, ya que son iguales salvo una rotación de 90, 180 o 270 grados
Luego de esos cuatro elegiríamos solo uno, por ejemplo, el que tiene el cuadrado de la esquina superior izquierda. Este es el motivo por el cual más arriba pusimos la condición de que un patrón básico tenga el cuadrado de la esquina superior izquierda. En consecuencia, de los 256 candidatos a patrones básicos, nos quedaremos con 256 / 4 = 64, los que tienen el cuadrado de la esquina superior izquierda, los demás son iguales a estos salvo rotación.
Es decir, de la órbita de las casillas de las esquinas, tenemos fijada la asignación de la esquina superior izquierda, y es la elección de un cuadrado en cada una de las otras tres órbitas lo que nos genera los 64 candidatos a patrones básicos. Pero no todos estos candidatos son válidos. Como comentamos más arriba, los cuadrados elegidos no se pueden tocar lado con lado, luego hay que eliminar los candidatos a patrones básicos que, como los de la siguiente imagen, tengan cuadrados que comparten un lado.
 Estos dos candidatos a patrones básicos no son válidos ya que en cada uno hay cuadrados, al menos un par, que comparten un lado
Estos dos candidatos a patrones básicos no son válidos ya que en cada uno hay cuadrados, al menos un par, que comparten un lado
Ya tenemos documentadas las dos condiciones sobre los patrones básicos que habíamos observado en el apartado anterior, que la estructura básica rellene la retícula 4 x 4, mediante los giros de 90, 180 y 270 grados, y que no haya dos cuadrados que se toquen a través de un lado. Llegados hasta aquí, tenemos un problema de combinatoria:
¿cuántos patrones básicos existen?
Vamos a computar la cantidad de patrones, y describirlos, viendo las opciones que existen para los cuadrados de las otras tres órbitas. El primer cuadrado del patrón ya está fijado, en la esquina superior izquierda y el segundo cuadrado lo vamos a elegir de la órbita de los cuatro cuadrados centrales. Hay cuatro opciones para ese segundo cuadrado, puesto que no hay opción a que en alguna de las cuatro opciones tenga un lado en común con el cuadrado de la esquina, que son las que aparecen en la siguiente imagen.
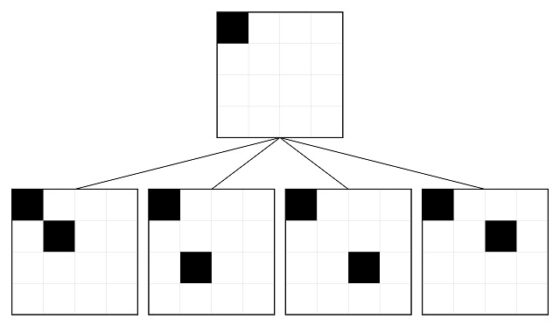
Ahora, para cada una de esas cuatro opciones, vamos a ver dónde pueden colocarse los dos cuadrados que se corresponden con las otras dos órbitas. La primera de las cuatro opciones anteriores, la de la izquierda, que tiene los dos cuadrados que se tocan por un vértice, es diferente a las otras tres, por lo que vamos a analizarla primero. Para esa primera opción cada uno de los otros dos cuadrados tienen tres opciones cada uno, solo la opción en la que comparten lado con los otros dos cuadrados no es válida. Por lo tanto, de aquí se deducen 3 x 3 = 9 patrones básicos distintos, aunque hay que eliminar dos de ellos, puesto que coinciden los cuadrados en un mismo lateral de la retícula y se tocan en un lado, quedando solo 7 patrones básicos, que se muestran a continuación (los 7 negros, ya que hemos eliminado los dos rojos).
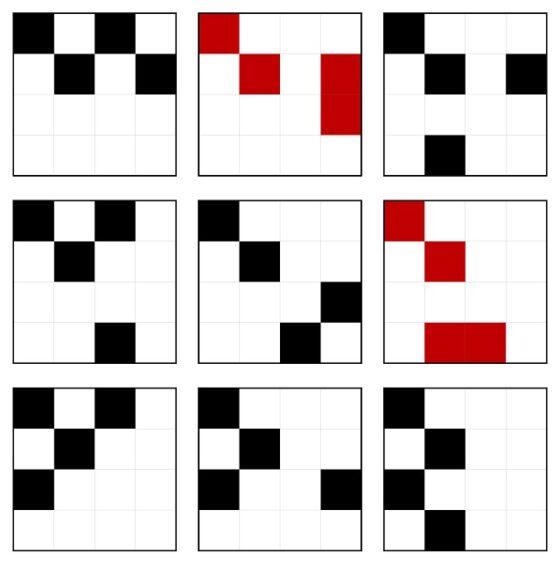
Para cada una de las otras tres opciones, cada uno de los otros dos cuadrados tienen dos opciones cada uno, luego cuatro patrones básicos para cada opción. Sin embargo, en dos de ellas dos de los cuadrados coinciden en uno de los lados, luego comparten lado, por lo tanto, en total son 10 estructuras más.
Para la primera opción …
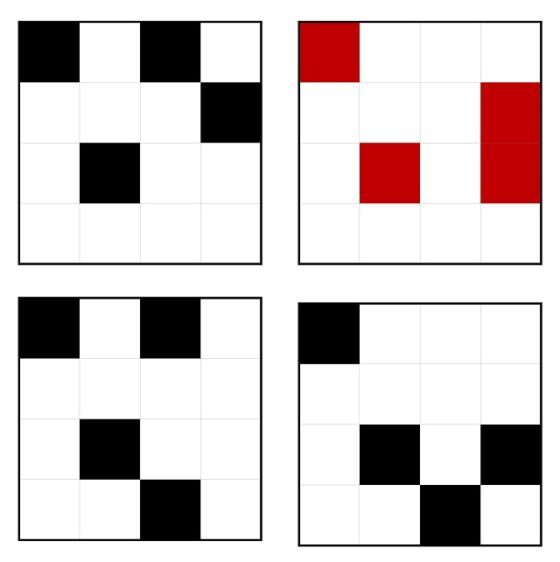
Para la segunda opción …

Y para la tercera opción …
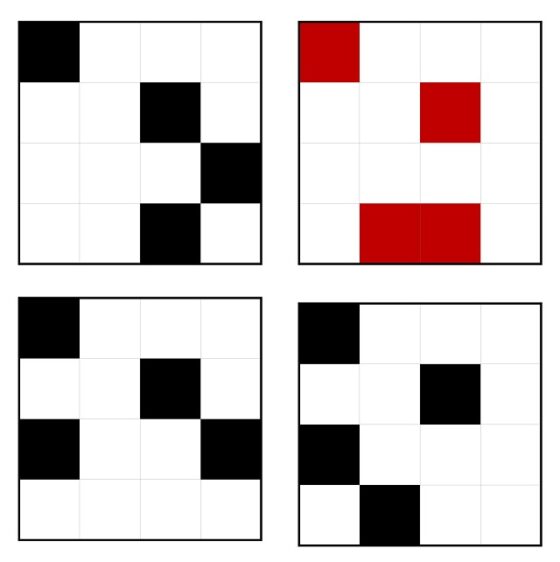
Por lo tanto, en total son 17 patrones básicos distintos. A continuación, los mostramos todos juntos, marcando en azul los correspondientes patrones de las 11 serigrafías de la serie 11 x 4 : 4 de Max Bill. Por lo tanto, existen 6 patrones básicos que no estarían, a priori, considerados por Max Bill, aunque veremos que esto no es así.
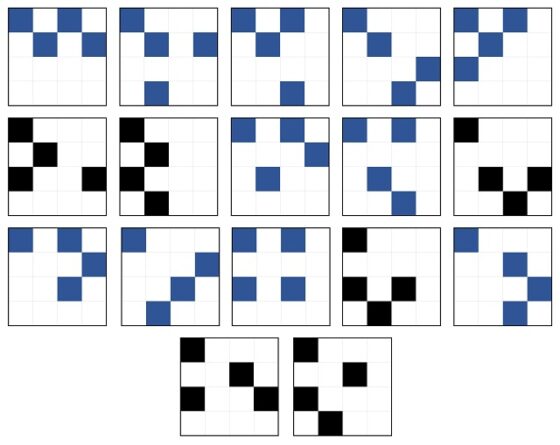
En la explicación de Max Bill sobre el proceso creativo, que hemos incluido más arriba, el artista concreto comenta “se han excluido cinco variantes por la inversión de los grupos II, III, IV, V y XI”. Lo que ocurre es que Max Bill ha añadido, además, otra forma, intuitiva y geométrica, de establecer que dos patrones básicos son el mismo. Expliquémosla.
Tomemos el primero de los patrones básicos de la clasificación anterior, que no está en la lista de las 11 estructuras básicas de Max Bill, el patrón que está en la segunda fila, primera columna. Imaginemos que es una estructura tridimensional, formada por pequeños cuadrados que tienen el mismo color, blanco o negro, en la cara superior y en la cara inferior, si diésemos la vuelta (por eso Max Bill habla de “inversión”) a nuestra retícula 4 x 4 tridimensional (cuyo resultado es el mismo que tomar la imagen especular respecto a la diagonal principal descendente) nos quedaría un patrón básico, imagen especular / inversión del anterior, como se muestra en la siguiente imagen, y podríamos considerar que son la misma estructura esencialmente (ya que una es simétrica de la otra). Y ese patrón básico al que es simétrico (el de la derecha de la imagen), sí está en el listado de los patrones básicos de Max Bill, véase más arriba, es el patrón II del documento del propio artista.
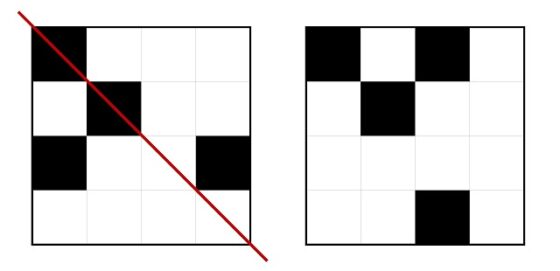
Veamos que los demás patrones básicos que, a priori, no estaban en la clasificación de Max Bill, son simétricos a alguno de los que sí está en la clasificación. Tomemos el patrón que está en la segunda fila y quinta columna, resulta que es simétrico (es como voltearlo) al patrón XI de Max Bill (véase la siguiente imagen).
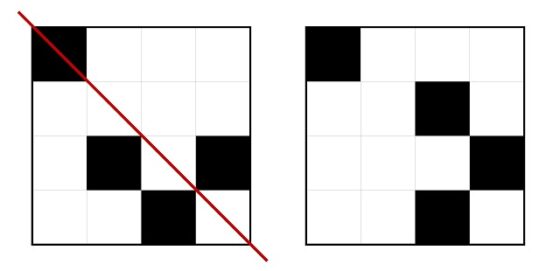
Ahora vamos a considerar otro patrón básico que no estaba, el que está en la tercera fila y cuarta columna. Resulta ser simétrico, como se observa en la siguiente imagen, al patrón V de la clasificación de Max Bill.
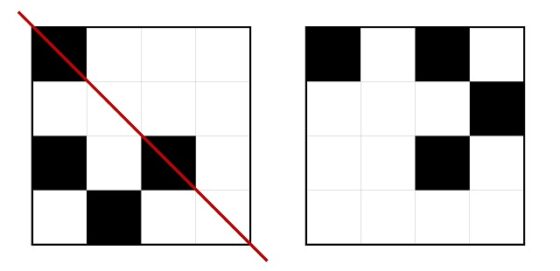
El siguiente patrón básico a considerar es el que está es el primero de la cuarta fila, que resulta ser, como se muestra en la siguiente imagen, simétrico al patrón básico III de Max Bill.
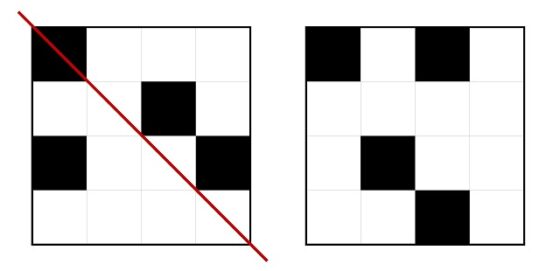
Mientras que el segundo patrón básico de la cuarta fila es simétrico, como se muestra en la siguiente imagen, al patrón IV de Max Bill.
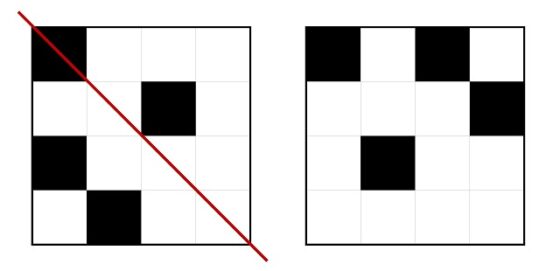
Y ahí tenemos las “inversiones de los grupos II, III, IV, V y XI” a las que alude el artista suizo y que aquí hemos denominado patrones simétricos respecto a los patrones (II, III, IV, V y XI) de la clasificación de Max Bill. Pero resulta que nos falta una estructura básica que no tuvo en cuenta Max Bill, la que está en la segunda fila y segunda columna. Aunque está también es simétrica a uno de los patrones de las de la clasificación de Max Bill, el patrón X.
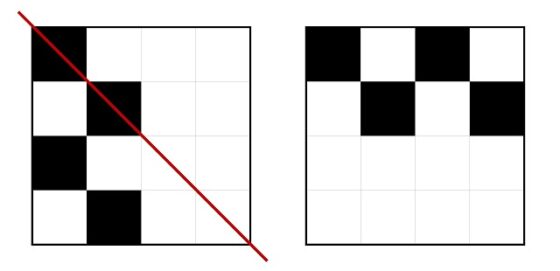
En consecuencia, Max Bill realizó una clasificación completa de todas las estructuras básicas posibles para su serie de obras 11 x 4 : 4, sin dejarse ninguna fuera, como hemos comprobado mediante esta pequeña reflexión matemática sobre su proceso creativo. Dicho de otra forma, el proceso creativo de Max Bill utiliza elementos de la geometría, el álgebra y la combinatoria.
 System mit Funf Vierfarbigen Zentren / Sistema con cinco centros de cuatro colores (1970), del artista concreto suizo Max Bill
System mit Funf Vierfarbigen Zentren / Sistema con cinco centros de cuatro colores (1970), del artista concreto suizo Max Bill
Bibliografía
1.- R. Ibáñez, Las matemáticas como herramienta de creación artística, Libros de la Catarata – FESPM, 2023.
2.- Max Bill, El pensamiento matemático del arte de nuestro tiempo, 1949.
3.- Valentina Anker, Max Bill ou la recherche d´un art logique, Editions l´Age d´Homme, 1979
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Once cuatro cuatro, mirar el arte con ojos matemáticos se ha escrito en Cuaderno de Cultura Científica.
Una ecuación de estado general para el simulador cuántico de Fermi-Hubbard
Se han caracterizado las propiedades termodinámicas del modelo de Fermi-Hubbard, que utiliza átomos fríos para simular distintos fenómenos en física de la materia condensada.
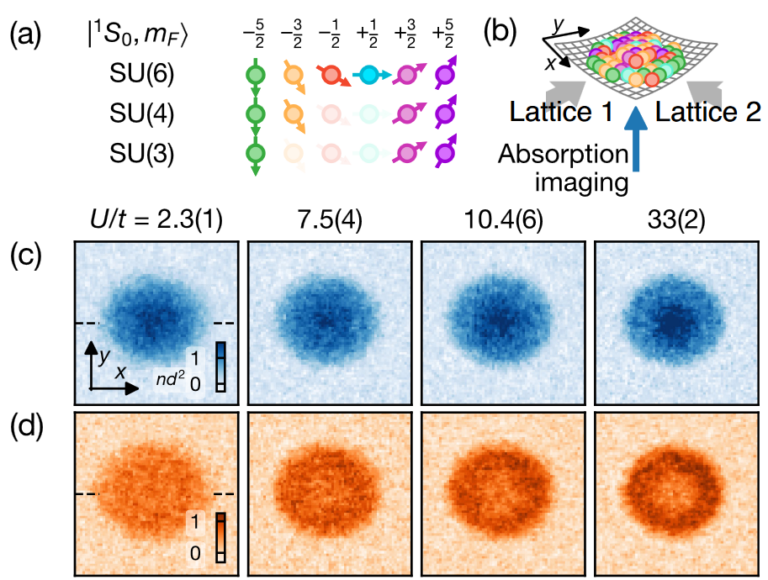
Cuando un determinado sistema cuántico resulta difícil de investigar, una opción es estudiar otro que sea físicamente equivalente pero más accesible. Por ejemplo, para comprender cómo se comportan los electrones en un sistema de electrones fuertemente correlacionados (un problema experimental y teóricamente no trivial), los investigadores pueden estudiar una red de átomos fríos (un sistema controlable que obedece las mismas reglas estadísticas que el sistema electrónico más complejo).
Ahora, un equipo de investigadores ha caracterizado exhaustivamente la ecuación de estado para la versión general de un modelo que se emplea para traducir el comportamiento de los átomos fríos en una red al de los electrones correlacionados. Sus resultados confirman la fiabilidad de los tratamientos numéricos de vanguardia de este modelo, lo que lo hace aún más atractivo para estudiar nuevos fenómenos en física de la materia condensada.
El modelo en cuestión es el de Fermi-Hubbard, que tiene en cuenta las interacciones entre átomos fermiónicos en una red. Los átomos preparados con dos estados posibles se utilizan para explorar problemas que involucran las dos direcciones de espín de un electrón, como el transporte de electrones, mientras que los átomos con más estados se utilizan para explorar fenómenos más complejos, como los nuevos tipos de magnetismo. La ecuación de estado para el modelo de dos estados de Fermi-Hubbard se había caracterizado previamente numérica y experimentalmente. Pero los modelos multiestado, que son más difíciles de manejar numéricamente, siguen siendo mucho menos comprendidos.
Los investigadores utilizaron átomos de iterbio-173, que pueden adoptar seis estados posibles. Midieron las propiedades termodinámicas del modelo multiestado de Fermi-Hubbard utilizando una red de estos átomos y compararon los resultados con las predicciones utilizando los últimos cálculos numéricos disponibles. Las mediciones también accedieron a regímenes que a día de hoy son numéricamente intratables y proporcionaron los datos para derivar una ecuación de estado general para el modelo de Fermi-Hubbard.
Referencias:
G. Pasqualetti, O. Bettermann, N. Darkwah Oppong, E. Ibarra-García-Padilla, S. Dasgupta, R. T. Scalettar, K. R. A. Hazzard, I. Bloch, and S. Fölling (2024) Equation of State and Thermometry of the 2D SU(N) Fermi-Hubbard Model Phys. Rev. Lett. doi: 10.1103/PhysRevLett.132.083401
M. Stephens (2024) A General Equation of State for a Quantum Simulator Physics 17, s27
Edición realizada por César Tomé López a partir de materiales suministrados por la Universidad Politécnica de Madrid
El artículo Una ecuación de estado general para el simulador cuántico de Fermi-Hubbard se ha escrito en Cuaderno de Cultura Científica.
Eris y Makemake… ¿dos planetas enanos “vivos”?
Hace apenas dos semanas hablábamos en planeta B sobre como, en ocasiones, las apariencias engañan y un cuerpo planetario que a simple vista parece no tener ningún tipo de actividad geológica, como es el caso de Mimas, podría estar más vivo -en el sentido geológico de la palabra- de lo que pensamos. Y es que los últimos estudios apuntan a que la actividad geológica no solo es algo con lo que nazcan los planetas, satélites y otros cuerpos menores, sino que, a lo largo de toda su evolución, pueden sufrir procesos capaces de aportar una energía a su interior que los mantenga activos durante más tiempo… o incluso volver a ponerlos en marcha por completo.
Esta etapa de actividad tardía probablemente solo ocurra en los satélites de los gigantes gaseosos, ya que esa “nueva” fuente de energía puede ser simplemente otorgada por una interacción gravitatoria con otros satélites del sistema o con el planeta al que orbita, generando unas mareas que al estirar y encoger su interior como un acordeón transformen su fricción en calor, el responsable último de esta renovada actividad geológica.
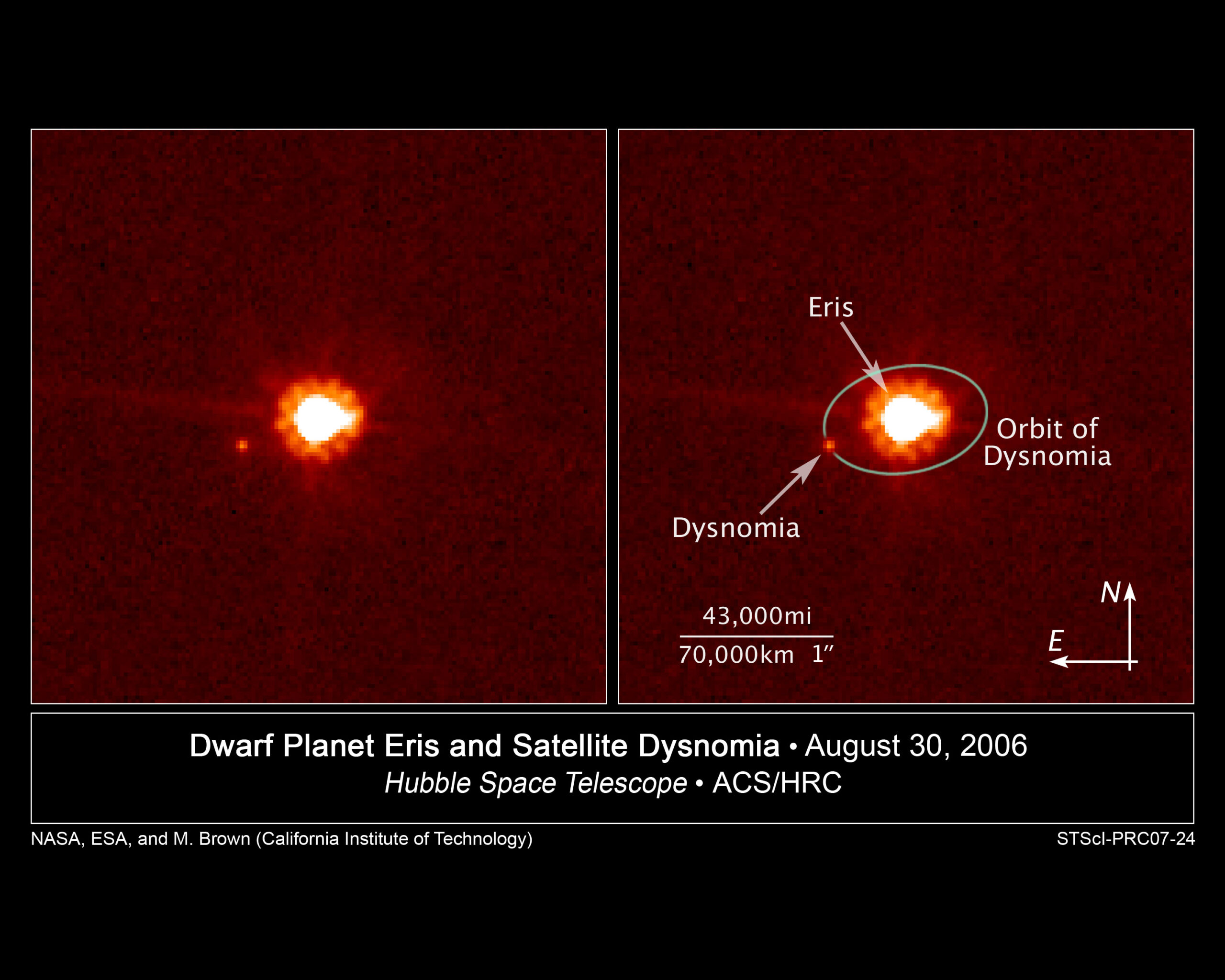 Eris y su satélite Disnomia vistos con el Telescopio Espacial Hubble. Tiene un diámetro de 615 kilómetros, convirtiéndolo en el segundo satélite más grande de un planeta enano tras Caronte. Cortesía de NASA/ESA y Mike Brown.
Eris y su satélite Disnomia vistos con el Telescopio Espacial Hubble. Tiene un diámetro de 615 kilómetros, convirtiéndolo en el segundo satélite más grande de un planeta enano tras Caronte. Cortesía de NASA/ESA y Mike Brown.Pero hoy nos vamos a marchar mucho más lejos: Dejaremos el reino de los gigantes gaseosos y nos dirigimos hasta el reino de los objetos transneptunianos, aquellos objetos que giran alrededor del Sol más allá de la órbita de Neptuno y donde se esconden nuestros dos protagonistas de hoy: los planetas enanos Eris y Makemake.
Debido a la enorme distancia que nos separa de estos objetos, Makemake tarda en completar una órbita algo más de 306 años y Eris unos 560, sabemos muy pocos detalles sobre ellos porque, además, no son objetos muy grandes, por lo que observar detalles de su superficie es, ahora mismo, una quimera hasta con los mejores telescopios.
Pero no todo está perdido y gracias a la buena “vista” del JWST en longitudes de onda infrarrojas parece que estos cuerpos que pensaríamos que son bastante anodinos, fríos y sin ninguna actividad… igual también se guardan un as debajo de la manga, aumentando el interés de los científicos por explorarlos un poco más de cerca.
Y es que un nuevo estudio publicado en Icarus por Glein et al. (2024) usa los datos de este telescopio espacial para intentar responder al origen del metano que observamos en la superficie de estos planetas enanos, puesto que este puede provenir al menos de tres fuentes: un origen primordial, heredado de la nebulosa protoplanetaria que dio origen del Sistema Solar, un origen abiótico a partir del monóxido o dióxido de carbono o, por último, el origen termogénico a partir de la descomposición de compuestos orgánicos.
Para resolver esta cuestión, los científicos han estudiado la proporción isotópica entre el deuterio y el hidrógeno. El deuterio es un isótopo pesado del hidrógeno, con un protón y un neutrón en su núcleo, mientras que el hidrógeno más abundante solo tiene un protón.
 Makemake y su satélite MK2 vistos también por el Hubble en abril de 2015. El diámetro de este pequeño satélite es de unos 175 kilómetros. Cortesía de NASA, ESA, A. Parker y M. Buie
Makemake y su satélite MK2 vistos también por el Hubble en abril de 2015. El diámetro de este pequeño satélite es de unos 175 kilómetros. Cortesía de NASA, ESA, A. Parker y M. BuieEsta proporción -o ratio, como les sonará a algunos de ustedes- entre ambos es muy importante en las ciencias planetarias, ya que nos permite estudiar el origen del agua, por ejemplo, y también de otros compuestos que llevan hidrógeno, como en este caso es el metano, así como las condiciones en las que se ha formado o incluso las distintas rutas geoquímicas por las que puede haber circulado.
Pero esto no es suficiente… ¿Cómo adscribimos esta proporción observada a un origen u otro? Los investigadores no solo han tomado los datos del JWST que nos permiten conocer esta proporción, sino que han trabajado en complejos modelos geoquímicos que simulan la evolución de la proporción isotópica D/H en el metano a partir de distintos orígenes para ver cual se aproxima más a los datos reales.
El resultado: El ratio D/H observado en Eris y Makemake no tiene un origen primordial, sino que debería haberse formado a partir de procesos abióticos o termogénicos. Y no solo eso, sino que necesitaría una temperatura superior a los 150 °C para formarse, lo que requiere de una gran cantidad de energía interna que permita alcanzar esta temperatura.
¿Qué fuentes de energía pueden tener estos planetas enanos? Pues la única explicación plausible para la presencia de una fuente de energía activa en la actualidad y que permita altas temperaturas en su interior sería la desintegración de los elementos radioactivos en su núcleo rocoso. Este calor podría facilitar la producción de metano a través de procesos hidrotermales o metamórficos, de tal manera que compuestos inorgánicos u orgánicos -orgánicos no en el sentido de con origen biológico- puedan transformarse en este metano a través de reacciones químicas.
Y esto tiene una importante derivada: si hay actividad hidrotermal, podría también existir un océano subterráneo gracias a un calor que podría fundir el hielo y mantener el agua en estado líquido durante largos periodos de tiempo -largos a nivel geológico- bajo la capa de hielo y donde, por supuesto, dando lugar a los fenómenos hidrotermales que, por un lado, general el metano que posteriormente llega a la superficie a través de fracturas así como generar posibles ambientes habitables en las profundidades de estos océanos, donde haya un intercambio de energía, pero también de sustancias disueltas que proceden del núcleo rocoso.
Por lo tanto, este estudio abre también una puerta a que ambos planetas enanos sean también de un gran interés astrobiológico y no solo geológico, lo que podría ayudar a que en el futuro -esperamos que no dentro de muchas décadas- podamos ver una misión que nos permita, por primera vez, visitar estos lejanos mundos.
Referencias:
Glein, C. R., Grundy, W. M., Lunine, J. I., Wong, I., Protopapa, S., Pinilla-Alonso, N., Stansberry, J., Holler, B. J., Cook, J. C., & Souza-Feliciano, A. C. (2024). Moderate D/H ratios in methane ice on Eris and Makemake as evidence of hydrothermal or metamorphic processes in their interiors: Geochemical analysis Icarus doi: doi: 10.1016/j.icarus.2024.115999
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Eris y Makemake… ¿dos planetas enanos “vivos”? se ha escrito en Cuaderno de Cultura Científica.
Lo de la Luna fue real
 Gene Cernan conduciendo un vehículo eléctrico en la superficie de la Luna en diciembre de 1972. Fuente: NASA
Gene Cernan conduciendo un vehículo eléctrico en la superficie de la Luna en diciembre de 1972. Fuente: NASASi alguna vez han intentado ustedes argumentar con una de esas personas que creen que la llegada a la Luna fue un montaje, se habrán dado cuenta de lo difícil que resulta convencerles de lo contrario. Se trata de una de las más conocidas y persistentes hipótesis conspiratorias que, gracias a las redes sociales, circulan por todo el mundo y que lamentablemente no dejan de ganar adeptos de día en día. La confianza que esta peculiar categoría de pensadores tiene en sus creencias suele rozar el convencimiento absoluto y entre sus más coloridas versiones está la que propone —siguiendo con la categoría de “la llegada a la Luna que nunca ocurrió”— que el director Stanley Kubrick fue contratado por la administración Nixon para filmar las escenas del alunizaje que en su día se televisaron al mundo entero (1, 2). Por sorprendente que parezca, esta “teoría” ha ido ganando fuerza a lo largo de los años, hasta el punto de que la propia agencia espacial norteamericana, NASA, hubo de sacar un desmentido oficial (3) en un par de ocasiones (la primera en 1977 y de nuevo en 2001) asegurando que las muestras lunares que trajeron los astronautas y el sentido común deberían ser suficientes para desmontar cualquier teoría que sugiera que el Apollo 11 nunca llegó a la Luna. Por desgracia, el negacionismo es impermeable a las evidencias y el sentido común no abunda entre los conspiracionistas.
La necesaria enormidad de las tramas conspiratoriasDe entre los muchos esfuerzos que la ciencia viene haciendo por contrarrestar esta peculiar parcela de ignorancia y oscurantismo, destaca la del biólogo David Robert Grimes, quien en 2016 se tomó la molestia de elaborar una ecuación para calcular el número de personas que deberían estar implicadas en una conspiración a gran escala y cuánto tiempo tardaría el secreto en hacerse de dominio público (4). Por supuesto, cuanto mayor sea el primero, menor será el segundo, algo que la propia intuición sugiere, pero que Grimes tradujo en cifras concretas: “Bajo circunstancias ideales, solo sería posible que un evento conspiratorio escapase de la detección si el número de conspiradores implicados fuese muy pequeño (<<1000).” En el caso concreto de una supuesta falsa llegada a la Luna, el número aproximado de personas implicadas sería de 411.000, tomando como referencia a los empleados en la NASA en aquel momento, 1965. Esta cifra es tan elevada que convierte en ridícula la idea de un complot semejante. Simplemente, no es posible que tantas personas estén involucradas en un secreto, sea cual sea, sin que el resto del mundo se entere más pronto que tarde, y de acuerdo a los cálculos de Grimes, el engaño habría acabado por salir a la luz en el plazo de 3.68 años, como mucho.
Por supuesto, las fórmulas que Grimes utilizaba en su estudio trabajaban con estimaciones aproximadas y reconocía que había en ellas una considerable, pero inevitable ambigüedad, en concreto a la hora de determinar el número de personas que estarían al tanto de una supuesta conspiración. Por establecer una comparación, vendrían a ser algo parecido a la ecuación que en su día propuso el astrónomo Frank Drake para calcular cuántas civilizaciones tecnológicamente avanzadas podría haber en la Vía Láctea. Tanto en un caso como en el otro, la intención final no es hacer una descripción precisa de la realidad a la que cada uno se refiere, sino proporcionar una idea aproximada de dicha realidad.
Por desgracia, desde que Grimes publicó su estudio, el número de teorías conspiratorias no ha hecho sino crecer, y en ámbitos que, en algunos casos, afectan directamente a nuestro bienestar. Este es el caso de las relacionadas con las vacunas contra el COVID, a las que se acusa de todo tipo de males —la última de las cuales (5) afirma que podría dañar el ADN de los pacientes— y que han provocado un descenso en el número de personas vacunadas. Se da la circunstancia de que quienes niegan la eficacia de las vacunas promueven, además, el uso de sustancias que han resultado ser dañinas para la salud, como ha sido el caso de la hidroxicloroquina. Un reciente estudio publicado en Biomedicine & Pharmacotherapy (8) ha revelado que la hidroxicloroquina —impulsada en su momento por medios populistas— está asociada con un incremento de un 11% en la tasa de mortalidad entre afectados por COVID.
Populismo político y ausencia de grisesAunque, por otro lado, los estudios académicos sobre este fenómeno social siguen apareciendo también con mayor frecuencia. Uno de ellos, publicado el pasado año, es el realizado por Marc Guinjoan (Universidad Oberta de Catalunya) y Carol Galais (Universidad Autónoma de Barcelona), quienes concluyen que la narrativa conspiratoria precede a las actitudes populistas en el ámbito político, al favorecer una visión dualista de la realidad (6). En dichas conclusiones, los investigadores tampoco descartan un camino inverso, es decir, que la exposición a discursos populistas termine haciendo que algunas personas abracen creencias conspiratorias y señalan que sería interesante realizar nuevos estudios que aclaren la relación causa y efecto entre ambos. La abundancia y diversidad de factores que intervienen en este proceso —edad, nivel cultural, inclinaciones políticas previas, exposición a los medios de comunicación— hace que sea difícil establecer una relación unívoca entre cualquiera de esta causas y el resultado.
En el lado opuesto estaría el ensayo de Seth J. Hill y Margaret E. Roberts, ambos de la Universidad de California San Diego, quienes advierten que las elevadas tasas de creencias en teorías conspiratorias que algunas encuestas proporcionan, podrían no ser exactas (7). Los investigadores californianos aseguran que buena parte de ellas podrían haberse visto afectadas por el sesgo de aquiescencia o la tendencia inconsciente a confirmar lo que nos preguntan. Proponen, para futuros sondeos de opinión, preguntas de respuesta múltiple y correctamente redactadas como alternativa a las respuestas “sí/no” habituales. En realidad, los resultados de Hill y Roberts son de utilidad para quienes investigan la opinión pública sobre cualquier cuestión de interés social —no solo teorías conspiratorias— de cara a obtener unos resultados más precisos y reales. Los análisis estadísticos son valiosas herramientas para obtener una imagen comprensible de una realidad demasiado amplia o compleja como para percibirla a simple vista. Sin embargo, es importante que no se vean afectados por sesgos o errores de procedimiento que puedan tergiversar sus resultados.
David Grimes advertía que las teorías conspiratorias socavan la credibilidad de las instituciones gubernamentales y la de quienes utilizan la razón y las evidencias contrastables para alcanzar la verdad. Guinjoan y Galais, por su parte, consideran que el pensamiento maniqueísta asociado a las creencias conspiratorias afecta a la forma en que concebimos las sociedades democráticas y es incompatible con escenarios políticos pluralistas y no polarizados. Por todo ello nuevos estudios científicos en este campo serán muy bienvenidos, pues la proliferación de las teorías conspiratorias no deja de ser, en realidad, un síntoma de una preocupante enfermedad social: la desconfianza de la población en sus clases dirigentes y en sus instituciones. Los resultados de dichas investigaciones, más allá de sus aspectos anecdóticos, podrían contribuir a encontrar la cura y recuperar esa tan necesaria salud social.
Referencias:
- ‘How moon landing conspiracy theories began and why they persist today.’ Manchester 1824. The University of Manchester.
- ‘The Flat-out Truth: Earth Orbits? Moon Landings? A Fraud! Says This Prophet.’ Robert J. Schadewald, Science Digest, July 1980.
- ‘Did U.S. Astronauts Really Land on the Moon?’ NASA Facts. February 14, 2001 (Reissued). Wayback Machine (archive.org)
- ‘On the Viability of Conspiratorial Beliefs.’ David Robert Grimes. PLOS ONE. January 26, 2016. https://doi.org/10.1371/journal.pone.0147905
- ‘No, COVID mRNA Vaccines Won’t Damage Your DNA’. Tanya Lewis, SCYAM, January 4, 2024.
- ‘I want to believe: The relationship between conspiratorial beliefs and populist attitudes in Spain’. Marc Guinjoan and Carol Galais. Science Direct, February 2023. https://doi.org/10.1016/j.electstud.2022.102574
- ‘Acquiescence Bias Inflates Estimates of Conspiratorial Beliefs and Political Misperceptions.’ Seth J. Hill and Margaret E. Roberts. Political Analysis, January 2023. https://doi.org/10.1017/pan.2022.28
- ‘Deaths induced by compassionate use of hydroxychloroquine during the first COVID-19 wave: an estimate.’ Alexiane Pradelle et al. Biomedicine & Pharmacotherapy, February 2024. https://doi.org/10.1016/j.biopha.2023.116055
Sobre el autor: Juan F. Trillo es doctor en Lingüística y Filosofía por la Universidad Autónoma de Madrid y doctor en Estudios Literarios por la Universidad Complutense de Madrid.
El artículo Lo de la Luna fue real se ha escrito en Cuaderno de Cultura Científica.
Leyendo el ADN marino

El océano, además de constituir una importante fuente de recursos, es un elemento clave en el funcionamiento del planeta. A pesar de ello, el conocimiento sobre este ecosistema sigue siendo bastante limitado, sobre todo en lo que respecta a las capas más profundas.
La investigadora de AZTI Naiara Rodríguez-Ezpeleta aporta una visión no muy conocida de los océanos con la charla “Leyendo el ADN marino: un viaje para comprender la ecología y evolución de los océanos” dentro del ciclo Zientziaren Ertzetik.
La bióloga y doctora en Bioquímica por la Universidad de Montreal aborda en ella cómo los avances en el campo de la genética han posibilitado estudios de ADN que se han convertido en una oportunidad para comprender la ecología y la evolución de los ecosistemas marinos. Unos estudios que abarcan desde la comprensión del origen de la vida hasta el establecimiento de cuotas de captura de especies pesqueras.
La charla, organizada por la Cátedra de Cultura Científica de la UPV/EHU y la Biblioteca Bizenta Mogel de Durango, tuvo lugar el 9 de febrero en la misma biblioteca.
PonenteNaiara Rodríguez-Ezpeleta, natural de Durango, es licenciada en Biología por la Universidad del País Vasco y doctora en Bioquímica por la Universidad de Montreal (Quebec, Canadá). Durante su carrera investigadora Rodríguez-Ezpeleta ha aplicado técnicas genéticas a ámbitos tan diversos como el origen de la célula eucariota y la fotosíntesis o la evolución humana y las asociaciones genéticas de enfermedades complejas. Actualmente, es investigadora en AZTI, aplicando sus conocimientos en ecología y evolución molecular para entender los ecosistemas marinos y sus recursos, y así mejorar su gestión y conservación.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Leyendo el ADN marino se ha escrito en Cuaderno de Cultura Científica.

