Las cuerdas frotadas del violín
 Foto Providence Doucet / Unsplash
Foto Providence Doucet / UnsplashLos instrumentos musicales de cuerda frotada han ocupado un lugar especial en la música durante muchos siglos. Los violines, y toda su actual familia moderna (viola, violonchelo y contrabajo) constituyen no solo la columna vertebral de las orquestas sinfónicas y de cámara, sino que además son instrumentos solistas que pueden sonar y cantar con voz característica melodías inolvidables capaces de conectar directamente con nuestros cerebros.
En principio es sencillo describir el funcionamiento mecánico de un violín. Ello comienza cuando la persona ejecutante pasa el arco por las cuerdas y las hace vibrar. A través del puente y el alma situada dentro del cuerpo del instrumento, la caja de resonancia recibe la vibración de las cuerdas, y al final irradia al aire ondas sonoras moduladas y amplificadas. Es notable que se requiere aplicar muy pocos milivatios de potencia mecánica para hacer funcionar un violín y sin embargo es capaz de generar grandes variaciones de presión sonora en el aire y, por tanto, llenar de sonido una gran sala de conciertos con un solo instrumento.
Cuerdas frotadas vs pulsadas o golpeadasEl movimiento de la cuerda frotada de un violín es muy diferente al de la cuerda pulsada (por ejemplo de una guitarra) y al de la cuerda golpeada (por ejemplo de un piano). Tanto la cuerda pulsada como la golpeada son sistemas mecánicos de condiciones iniciales: la cuerda recibe un desplazamiento o velocidad inicial, tras lo cual la vibración de la cuerda da lugar a un breve movimiento transitorio que decae con el tiempo. Sin embargo, la cuerda frotada es un sistema impulsado por un oscilador de fricción autosostenida. A pesar de que ya existían en los albores de la historia instrumentos musicales de esta naturaleza, los detalles de este movimiento autosostenido son considerablemente más complicados, y no se pudieron describir de forma adecuada durante milenios.
Algo importante para frotar una cuerda es proporcionar una interacción mecánica específica entre el arco y las cuerdas. Los pelos del arco del violín suelen ser crines de caballo entre cuyas células la resina (colofonia) que se aplica queda almacenada y el arco queda pegajoso con un alto factor de fricción estática. La interacción entre el arco y la cuerda frotada en un instrumento fue descrita con detalle por el gran científico Hermann Helmholtz [1] mediante el efecto Ruckgleiten, que se denomina actualmente el mecanismo stick-slip (pegar-deslizar).
El movimiento de HelmholtzEl arco pegajoso arrastra la cuerda, en dirección transversal, hasta que la fuerza de restauración debida a la tensión de la cuerda es mayor que la fricción estática, y la cuerda se desliza moviéndose de nuevo hacia el equilibrio en el sentido opuesto al que se mueve el arco. La cuerda sobrepasa su equilibrio y al llegar a su posición extrema es atrapada y se pega al arco que la arrastra de nuevo. Al repetirse este proceso, la cuerda mantiene la vibración sostenida. Este movimiento continuo se denomina movimiento de Helmholtz porque éste fue el primero en observarlo en 1862 utilizando su «microscopio de oscilación» y las figuras de Lissajous.
Helmholtz descubrió que la forma real de la cuerda en cualquier instante son dos segmentos rectos unidos mediante un codo en un punto. Con un frotamiento de arco ascendente en el violín, este codo recorre en sentido contrario a las agujas del reloj siguiendo una trayectoria parabólica. Con un frotamiento de arco descendente, la rotación es idéntica pero con recorrido del codo en el sentido de las agujas del reloj. Este movimiento tan especial es una forma de onda estacionaria que puede verse en detalle rodando un video a cámara lenta.
Riqueza armónica de las cuerdas frotadasLo mismo que una guitarra, un violín puede hacer sonar las notas musicales acortando o alargando la longitud de las cuerdas para cambiar la frecuencia fundamental de la vibración. Sin embargo, notemos que tal y como Helmholtz observó y dibujó en su libro (p. 83), las cuerdas frotadas vibran según ondas de diente de sierra, que es un tipo de señal acústica muy rica en armónicos. Ello implica que las cuerdas frotadas entregarán al cuerpo del violín no solamente una vibración autosostenida, sino una gran cantidad de armónicos que la caja de resonancia podrá utilizar para enriquecer el espectro acústico del instrumento. Como consecuencia, el empleo de cuerdas frotadas puede dar lugar a superiores características musicales con respecto a otros tipos de cuerdas. Ello incluye poder interpretar todo tipo de sonidos, tanto graves o agudos como de larga o corta duración, así como variado timbre armónico específico del cuerpo del instrumento. Explicamos así el hecho bien conocido de que la voz de la familia del violín se asemeja claramente al canto y a la voz humana.
Referencia
[1] H. Helmholtz, On the Sensations of Tone, 2nd edition, traducido por A. J. Ellis, reimpresa por Dover Publications, 1954, pp. 80-88.
Sobre el autor: Victor Etxebarria Ecenarro está diplomado como lutier por el Conservatorio Juan Crisóstomo de Arriaga (Bilbao) y es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (UPV/EHU)
El artículo Las cuerdas frotadas del violín se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2022: ‘Hackers’ están diseñando los próximos fármacos

¿Qué tiene que ver Neo, el personaje central de la película Matrix (Lilly y Lana Wachowski, 1999), con el diseño de fármacos personalizados? Acaso, ¿es posible hackear la información genética de los pacientes para crear nuevos medicamentos?
Diseñar fármacos específicos para cada persona ya no es una entelequia propia del cine de ciencia ficción. Gracias a las terapias de ácidos nucleicos los farmacéuticos han comenzado a actuar sobre diferentes momentos del proceso de desarrollo de las enfermedades para atajarlas antes incluso de que se manifiesten o muestren sus síntomas.
La investigadora Ikerbasque en Biocruces Bizkaia y experta en terapias de ácidos nucleicos Virginia Arechavala, utilizó un paralelismo con el personaje de ciencia ficción para explicar en Naukas Bilbao el alcance de este trabajo investigador y sus aplicaciones al mundo de la medicina. Tras recordar que Neo era “un hacker que aprende a cambiar su realidad porque es capaz de leer el código que hay detrás de la realidad virtual en la que vive”, la investigadora recordó que nuestro organismo tiene también un código, en este caso genético, que es el que contribuye a generar las proteínas que necesitamos para vivir.
Para explicar la labor de los investigadores, Virginia Arechavala declaró que cada célula cuenta con información genética que permite generar esas proteínas, y que muchas veces las variaciones y mutaciones que sufre esta información apenas provocan cambios sobre nuestra vida diaria. Sin embargo, hay ocasiones en que esos cambios conllevan manifestaciones diferentes en el cuerpo humano que afectan, por ejemplo, a no tener una proteína especialmente necesaria o generar una tóxica, y que se pueden traducir en enfermedades poco frecuentes.
Con este planteamiento sobre la mesa, la experta en terapias de ácidos nucleicos compartió con el público del Palacio Euskalduna cómo la investigación actual, en lugar de buscar un medicamento que actúen sobre las proteínas responsables de una enfermedad, quieren actuar sobre la información genética que codifica estas proteínas. La investigadora puso como ejemplo la preparación de una paella.
“Conocemos cuál es el proceso por el que se generan las proteínas y los medicamentos que tenemos hasta ahora actúan sobre el resultado final de ese proceso. Sería como ir a una paella ya cocinada –una proteína– y quitarle uno de los ingredientes erróneos con los que se ha preparado, que la hace tóxica”, explicó la experta. De esa forma, el medicamento actúa de forma específica sobre el elemento nocivo para nuestro cuerpo y lo elimina. Sin embargo, en otras ocasiones, ese ingrediente o elemento nocivo es de tal gravedad que no se puede actuar contra él ni atajar la enfermedad.
Frente a este planteamiento convencional, Arechavala indicó que en la actualidad disponemos de la información que nos permite saber para qué sirve cada gen (receta), cómo desde cada gen se cocina cada proteína, y contamos con “cocineros”, los ribosomas, capaces de modificarla durante su “preparación”, con lo cual es posible actuar antes de que esta proteína esté ya “cocinada”. Incluso afirmó que se puede cambiar esa “receta” en origen para conseguir una proteína distinta a la original. “Las vacunas de ARN mensajero se basan en este concepto: si tienes a un cocinero preparado para cocinar le das una receta diferente para que haga lo que tú quieras”, explicó de forma gráfica.

Estas nuevas terapias son especialmente aplicables en el caso de las llamadas enfermedades raras, en las que los cambios genéticos impiden la producción de proteínas indispensables o generan proteínas “tóxicas” que derivan en dolencias que, en ocasiones, son incurables. “Cuando tienes una mutación que genera una proteína tóxica, lo ideal sería no tenerla, es decir, restaurar el gen para suprimir esa mutación nociva y dejarlo como estaba. Esta técnica se llama edición génica y ya se está probando en ensayos clínicos para enfermedades poco frecuentes.”
“Lo siguiente sería la terapia génica, es decir, traer un gen correcto (sin la mutación) hasta el núcleo de las células para que generen la proteína que se necesita”, explicó. Y aunque se trata de una opción compleja porque obliga a distribuir ese gen por todas las células del cuerpo, es una técnica que ya se emplea en algunos medicamentos que están aprobados y disponibles para pacientes con enfermedades poco frecuentes.
Dentro de esta tarea investigadora, Virginia Arechavala mencionó otra opción para corregir estas mutaciones antes de que “se cocinen” estas paellas tóxicas: “Podemos enviar una “anti-receta” que bloquee la receta tóxica para evitar que nuestros ribosomas/cocineros la cocinen y generen una proteína tóxica. ¿Cómo? Mediante el ARN de interferencia”.
Y citó un ejemplo más: “De un mismo gen se pueden obtener un montón de proteínas distintas, un splicing alternativo, que es una especie de ‘elige tu propia aventura’, en la que puedes escoger entre distintos finales según la manera en la que leas el libro. Pues nuestros genes son así, y por eso, como es posible influir en el momento en que eliges cómo va a ser la proteína, se puede actuar sobre ello, como si se pegara un post-it que cambia ligeramente la receta antes de que la lea el cocinero. Es otra terapia de ARN que ya está disponible para enfermedades poco frecuentes”.
Por último, Arechavala apuntó que a pesar de la mayoría de la investigación y los primeros medicamentos de este tipo se han desarrollado para las llamadas enfermedades raras, gracias a los avances que se han conseguido con su impulso, estas terapias pronto se aplicarán al tratamiento de otras dolencias muy comunes, como el colesterol alto, para el que ya hay en el mercado un fármaco específico basado en estos conceptos. “Todos estos medicamentos no son ciencia ficción, podemos encontrar más. Se suele decir que en farmacia hay de todo, como en botica, y probablemente la próxima vez que vayáis a la farmacia podáis encontrar medicamentos diseñados por un hacker”, concluyó.
Si no ve correctamente el vídeo use este enlace.
Para saber más:
50 años modificando genes (en seres humanos)
Una infección vírica puede activar la aparición de diabetes tipo I
Crónica de Roberto de la Calle / GUK
El artículo Naukas Bilbao 2022: ‘Hackers’ están diseñando los próximos fármacos se ha escrito en Cuaderno de Cultura Científica.
Un tapón ecológico para tratar la hemorragia nasal
 Foto: Nagore Iraola. UPV/EHU
Foto: Nagore Iraola. UPV/EHULa hemorragia nasal, también conocida como epistaxis, es una de las urgencias otorrinolaringológicas más frecuentes en todo el mundo. Se calcula que el 60 % de la población mundial sufrirá un episodio de epistaxis al menos una vez en su vida, aunque solo entre el 6% y el 10% de ellos buscará atención médica. Existen varios métodos para tratar la epistaxis y uno de los métodos más populares y con una elevada tasa de éxito es el taponamiento nasal. No obstante, la elección del tapón nasal más adecuado es vital para el resultado del tratamiento. El tapón nasal ideal debe favorecer la hemostasia —el conjunto de mecanismos biológicos para detener los procesos hemorrágicos— y ser cómodo para el paciente, disminuyendo así el daño en la mucosa nasal.
En este trabajo conjunto de los grupos NanoBioCel y BIOMAT de la UPV/EHU, “hemos demostrado que los subproductos de la industria alimentaria son una fuente valiosa y sostenible de biomateriales que pueden emplearse para fabricar tapones nasales seguros y eficaces con grandes propiedades hemostáticas”, señala Edorta Santos Vizcaíno, investigador del grupo NanoBioCel y uno de los autores del trabajo.
“A partir de subproductos naturales de la industria alimentaria —proteína de soja y quitina— hemos desarrollado un scaffold o una matriz esponjosa que presenta una serie de propiedades fisicoquímicas muy interesantes: es capaz de absorber grandísimas cantidades de agua o sangre, tiene mucha superficie para unir y albergar células en su interior, no produce ningún tipo de rechazo contra el material y, además, se degrada parcialmente”, comenta el investigador de la UPV/EHU.
La quitina es la base de esta nueva estructura, es decir, el esqueleto del material esponjoso, mientras que la proteína de soja se encarga de forrar dicha estructura para hacer que el material sea muy biocompatible y a su vez capaz de absorber grandes cantidades de sangre.
Un tapón verde“La creciente necesidad social de ser respetuosos con el medioambiente —comenta el investigador de la UPV/EHU— nos llevó a investigar si el material tipo esponja producido a partir de proteína de soja y quitina puede emplearse como tapón nasal para el tratamiento de la epistaxis”. Para evaluar el potencial de nuestro material como tapón nasal, “hemos analizado su uso como tapón nasal comparándolo con el gold standard actual, Merocel®, fabricado con materiales sintéticos”, añade Santos.
Los ensayos realizados tanto in vitro como in vivo en ratas, “demuestran que el material desarrollado presenta una microestructura porosa con gran capacidad de absorber agua y sangre. Se comprobó que nuestro biomaterial promueve eficazmente la coagulación de la sangre, mostrando excelentes propiedades de unión de glóbulos rojos y plaquetas en comparación con Merocel®. Todo esto es debido a las propiedades hemostáticas intrínsecas de sus componentes naturales”, comenta Edorta Santos. Además, “vimos que es capaz de perder peso en medio acuoso y de degradarse parcialmente en pocos días cuando está sumergido en sangre, característica cada vez más importante para los tapones nasales, ya que de lo contrario su extracción resulta invasiva”, añade el investigador.
En definitiva, “nuestro material producido a partir de desechos de la industria alimentaria mostró propiedades mecánicas y hemostáticas superiores al Merocel®”, concluye Edorta Santos.
El personal investigador de ambos grupos de investigación coincide en que, “este trabajo, realizado desde un enfoque de economía circular, demuestra que se puede seguir una estrategia verde para fabricar tapones nasales utilizando subproductos valorizados de la industria alimentaria, con propiedades hemostáticas incluso mejores que el estándar de oro en la clínica”.
“De hecho, ahora mismo, estamos en vías de solicitud de patente europea tratando de buscar alguna empresa que se interese por el producto para poder materializar la idea y apostar por esta tecnología basada en el concepto de la economía circular”, lanza Edorta Santos.
Para saber más:
Dando valor a los residuos marinos para cuadrar la economía circular
Referencia:
Jon Jimenez-Martin, Kevin Las Heras, Alaitz Etxabide, Jone Uranga, Koro de la Caba, Pedro Guerrero, Manoli Igartua, Edorta Santos-Vizcaino y Rosa Maria Hernandez (2022) Green hemostatic sponge-like scaffold composed of soy protein and chitin for the treatment of epistaxis Materials Today Bio doi: 10.1016/j.mtbio.2022.100273
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Un tapón ecológico para tratar la hemorragia nasal se ha escrito en Cuaderno de Cultura Científica.
El camión solar: ¿una posibilidad real?
Los cálculos son tercos y apuntan a que todavía estamos muy lejos de ver circulando por la carretera un camión solar.
 Gama de soluciones de movilidad apoyada por energía solar fotovoltaica propuesta por Sono Motors. Fuente: Sono Motors
Gama de soluciones de movilidad apoyada por energía solar fotovoltaica propuesta por Sono Motors. Fuente: Sono MotorsLa movilidad del futuro se presenta fascinante y llena de novedades. En los últimos años hemos visto emerger nuevos actores y viejos conocidos con ímpetus renovados. En el extremo ligero de las soluciones de transporte encontramos los patinetes y las bicicletas eléctricas. Para desplazarnos más rápidamente disponemos de turismos eléctricos en diferentes configuraciones y con distintos resultados al respecto de la reducción de emisiones de gases: motorizaciones híbridas, híbridas enchufables y cien por cien eléctricas. En el horizonte inmediato esperan las pilas de combustible, con el potencial de crear un nuevo sector de la economía con el hidrógeno como vector energético. Quizá más allá se encuentren sistemas pesados basados en el ciclo de oxidación-reducción del hierro, con usos prospectivos en el campo naval. Y en el aire encontramos los combustibles de origen vegetal de segunda generación que prometen ciclos casi cerrados y, por tanto, una gran reducción en las emisiones de CO2. La electrificación en el aire espera aún un gran salto en las capacidades de almacenamiento de energía de las baterías eléctricas, que está tardando en darse y no está, bajo ningún concepto, garantizado.
Vehículos con apoyo fotovoltaicoLa movilidad solar ha sido tradicionalmente una curiosidad, limitada a ejemplos experimentales. La realidad es tozuda y se muestra inflexible por lo que respecta a permitir que un vehículo sea independiente de cualquier infraestructura de carga o repostaje. Las aventuras ingenieriles que han buscado derivar toda su capacidad motriz de la energía del sol mediante paneles fotovoltaicos embarcados han fallado una y otra vez. Incluso conseguir que parte de la energía consumida sea de origen solar supone, por lo general, mucha más molestia de la que merece la pena a la luz (exigua) de los resultados.
Sin embargo, entre las propuestas de movilidad que aparecen prácticamente a diario en las noticias tecnológicas empiezan a verse ejemplos de coches solares. Destacan, por su cercanía al mercado, dos modelos: el Sono Sion y el Lightyear 0 (el número cero, no la letra o mayúscula). Ambos utilizan superficies cubiertas de paneles solares poco o nada frecuentes en un vehículo. Capó, techo y portón trasero en el caso del Lightyear [1], una berlina de casi 5,10 metros de longitud, con un total de 5 metros cuadrados de paneles curvados según la aerodinámica de la carrocería. El Lightyear 0 promete nada menos que 70 kilómetros diarios de movilidad solar sin coste, aunque la letra pequeña afirma que el cálculo está hecho para una ubicación no especificada del sur de España y solo es válido durante el 10 por ciento del año más favorable, alrededor del solsticio de verano. Este dato sin duda será interesante para los potenciales compradores de la berlina que vivan más cerca de la sede de la marca, en Eindhoven (Países Bajos).
 Lightyear 0. Fuente: Lightyear
Lightyear 0. Fuente: LightyearEn cuanto al Sono Sion [2], un monovolumen de 4,47 metros de longitud, ofrece ocho metros cuadrados de paneles fotovoltaicos integrados en todas las superficies expuestas de la carrocería. No solo capó y techo, sino también puertas y aletas. El cálculo de la autonomía solar que permite sus paneles está dado por el fabricante en 35 kilómetros diarios en el mes de junio, suponiendo días perfectamente soleados. A su favor hay que decir que esta estimación no corresponde a la Costa del Sol: el fabricante Sono Motors está radicado en Múnich (Alemania), y esa es precisamente la ubicación a la que se refieren. Las tablas con el histórico meteorológico de Múnich indican que un mes de junio normal tiene 11 días soleados. Sin embargo; esta información no aparece en la web de Sono Motors.
 Sono Sion. Fuente: Sono Motors
Sono Sion. Fuente: Sono MotorsEstá por ver que estos turismos con apoyo solar —llamarlos coches solares es, a todas luces, engañoso— resulten rentables a largo plazo. La integración de los paneles fotovoltaicos en la carrocería, a pesar de intentar aprovechar las superficies de menor curvatura, resulta compleja y hace una verificación independiente de sus capacidades reales, cuanto menos, difícil. No obstante, sería interesante disponer de una idea de la magnitud del apoyo que puedan proporcionar unos paneles solares en un vehículo electrificado capaz de llevarlos. Para lograr este objetivo, es interesante centrarse en un caso de cálculo particularmente favorable: el camión con apoyo solar. Han aparecido propuestas de camiones electrificados, total o parcialmente, que obtienen cierto apoyo en su autonomía de paneles fotovoltaicos montados sobre las paredes laterales y superior de su zona de carga. Esta disposición permite disponer de grandes espacios, en principio diáfanos, para la instalación de los colectores solares. Espacios que, además, son planos. Se evita de este modo un problema común que aumenta el coste de los paneles en techos u otras superficies de turismos: las curvaturas guiadas por la aerodinámica.
Modelo de cálculo de apoyo solar para camiónPara crear un modelo de cálculo simplificado [3] nos centraremos en un camión con semirremolque de cinco ejes al que dotaremos de paneles fotovoltaicos en los laterales y techo de su semirremolque. El primer paso será calcular las superficies disponibles dadas unas dimensiones típicas.
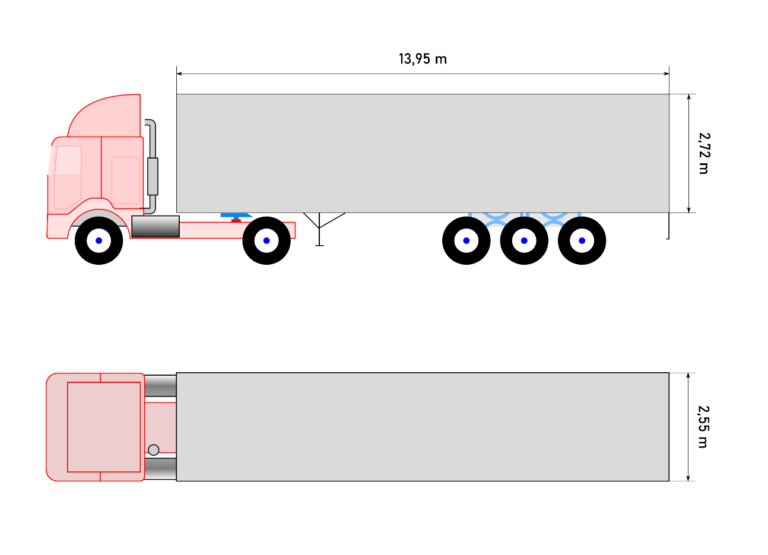 Camión de cinco ejes típico con medidas del semirremolque. Imagen modificada por el autor a partir del diagrama CC BY-SA 3.0 de H Padleckas / Orinoco / Malyszkz, Wikimedia Commons
Camión de cinco ejes típico con medidas del semirremolque. Imagen modificada por el autor a partir del diagrama CC BY-SA 3.0 de H Padleckas / Orinoco / Malyszkz, Wikimedia Commons
A partir de las medidas de la superficie disponible, procedemos a calcular la superficie total expuesta, lo que para un semirremolque típico excede los 110 metros cuadrados. En el siguiente paso, seleccionamos una ubicación y preparamos una consulta a la base de datos PVGIS de la Comisión Europea [4]. Usaremos el cálculo para el sistema más sencillo, el de un panel fotovoltaico conectado a la red, ya que no vamos a tener en cuenta datos de las baterías montadas en el vehículo.
Como quiera que el dimensionamiento de una instalación solar en PVGIS se realiza con su potencia en vatios-pico (los vatios que puede producir una instalación solar fotovoltaica bajo condiciones óptimas de iluminación solar, sin cobertura de nubes y a una temperatura de panel de 25 °C), utilizamos un parámetro común para ligar esta unidad a la superficie unitaria de paneles: un metro cuadrado de panel fotovoltaico ofrece 0,2 kilovatios-pico.
Avanzando en las características del modelo, calcularemos por un lado la energía producida para la ubicación dada por la superficie de paneles del techo de la caja del semirremolque, cuya inclinación, que asumiremos siempre cenital, es fija e igual a cero grados, y su acimut es indiferente. Por otro, tendremos en cuenta un movimiento aleatorio del vehículo a lo largo del año. Computaremos el valor de la energía producida por uno de los laterales, considerando su inclinación como 90 grados y su acimut como una variable aleatoria de distribución uniforme. orientado en cuatro direcciones perpendiculares (–90°, 0°, 90° y 180°, es decir, este, sur, oeste y norte); el resultado será la media aritmética de estos cuatro valores, multiplicada por dos para tener en cuenta ambos lados de la caja.
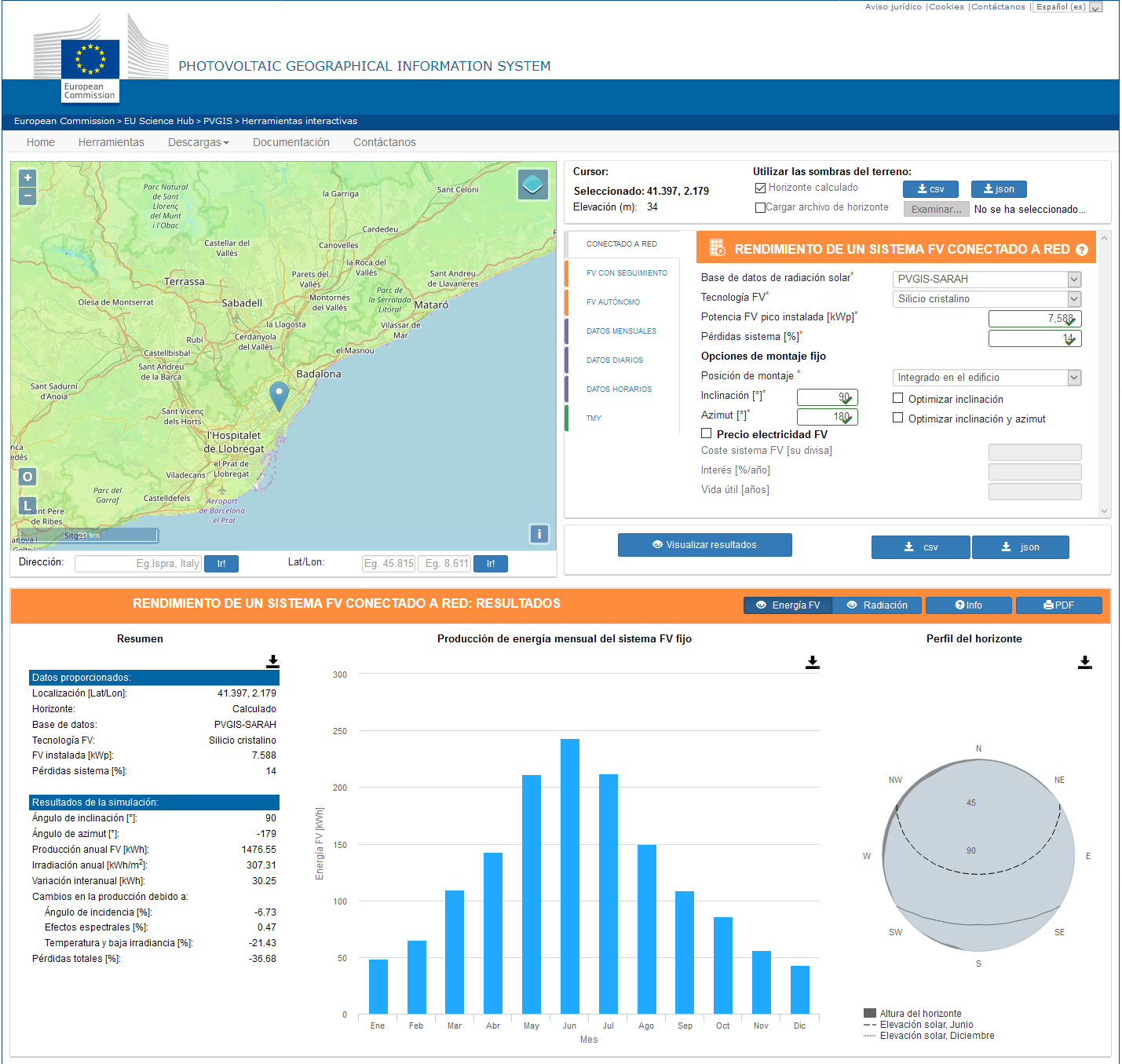 Captura de pantalla de la herramienta PVGIS de la Comisión Europea. Fuente: Comisión Europea
Captura de pantalla de la herramienta PVGIS de la Comisión Europea. Fuente: Comisión EuropeaPara que este valor de energía producida sea correcto, tendremos que imponer la condición de que el camión no visite recintos cerrados ni se encuentre en zonas sombreadas nunca; esto anularía o reduciría significativamente la producción de energía durante el tiempo en el que se viera afectado por esta reducción de la iluminación ambiental. Esta suposición, fácil de hacer para un camión, es mucho más aventurada para un vehículo más pequeño como un turismo. Con todo esto, podemos ya intentar estimar la producción de energía anual del sistema. Los cálculos anuales permiten uniformizar el impacto de la variación día-noche y estacional en la radiación solar incidente.
Estimación del consumo de energía en un camión eléctricoPodemos comprobar que, en el centro de la península Ibérica, instalar paneles fotovoltaicos en las superficies disponibles de un semirremolque de las medidas consideradas permitirá producir más de 19 megavatios-hora en un año. Parece mucho, pero para estar seguros tendremos que comparar esa cifra con cuánta energía consumiría ese mismo camión en su funcionamiento normal, y comprobar que fracción representa la producción solar. ¿El problema? Que, hoy, no existen camiones eléctricos de ese tamaño en producción con los que poder ofrecer cifras fiables. Tanto el Tesla Semi como el Mercedes eActros LongHaul están, según las noticias recientes, a uno y dos años respectivamente de estar disponibles en el mercado.
 Tesla Semi (izquierda) y Mercedes-Benz eActros LongHaul. Fuentes: izquierda, CC BY 2.0 Steve Jurvetson; derecha, MBpassion.de / Philipp Deppe
Tesla Semi (izquierda) y Mercedes-Benz eActros LongHaul. Fuentes: izquierda, CC BY 2.0 Steve Jurvetson; derecha, MBpassion.de / Philipp DeppeSin embargo, sí es posible comparar con el consumo de camiones actuales de motorización térmica, bajo el supuesto de que la energía necesaria para su movimiento será aproximadamente la misma. Un camión del tipo que estamos considerando puede consumir, bajo condiciones de conducción económica y recorridos mayoritariamente sin pendientes, 32 litros de combustible diésel cada cien kilómetros [5]. Este consumo responde al uso total, primario, de energía del camión, pero no nos está dando la información que necesitamos. Hay que ponerlo en términos de energía neta. Para ello, habrá que minorar la parte de la energía que se pierde por las limitaciones termodinámicas de los motores de combustión; con ello tendremos la energía neta que llega finalmente a las ruedas y sistemas auxiliares. Después, imaginaremos que la energía ha sido extraída de una fuente compatible con los paneles solares, de manera que podamos compararla. Por último, añadiremos la parte de pérdidas de un motor eléctrico, que, como veremos, es mucho menos significativa que en el caso del motor de combustión.
Los valores que emplearemos para realizar el cálculo serán:
Densidad energética del combustible diésel: 36,05 MJ/L
En kilovatios-hora/litro: 10,01 kW·h/L
Rendimiento del motor térmico: 45 %
Rendimiento del motor eléctrico equivalente: 90 %
Consideraremos además un kilometraje anual típico de 120000 kilómetros. El camión diésel considerado consumirá 375000 litros de combustible, mientras que un hipotético camión eléctrico equivalente deberá usar del orden de 210 megavatios-hora, arrojando un gasto de energía por kilómetro de 1,75 kilovatios-hora por kilómetro. Como comparación, Tesla afirma que su futuro Tesla Semi tendrá un consumo de 1,24 kilovatios-hora por kilómetro [6], un 29 por ciento menos, lo que es consistente con las diferencias habituales observadas entre consumos declarados y reales en otros vehículos.
Los paneles, según el cálculo de nuestro modelo, ofrecerán algo menos de 20 megavatios-hora, del orden del 9 por ciento de la energía requerida. En términos de distancia, más de 11000 kilómetros «gratuitos». Ahora bien, ¿compensa el montaje? ¿En cuánto tiempo se recuperará la inversión necesaria?
Plazo de retorno de la inversiónEn este momento, sin una disponibilidad real de camiones para modificar, solo es posible hacer estimaciones. La instalación de los paneles fotovoltaicos sobre las superficies de la caja de un semirremolque no se antoja como especialmente compleja, pero es un problema diferente al de un montaje sobre el tejado de un edificio. El sistema no necesitará estar dotado de un inversor, un componente que habitualmente justifica aproximadamente el veinte por ciento del coste de un sistema fotovoltaico de esta magnitud; las baterías de un camión eléctrico almacenan corriente continua. Será necesario, naturalmente, instalar la circuitería necesaria para realizar la adaptación del voltaje de las placas al de las baterías, así como todos los elementos de control necesarios. Al tratarse de una instalación en movimiento, es de prever que los requisitos mecánicos y normativos de seguridad serán más onerosos de cumplir.
Entre factores que disminuyen el precio y otros que lo aumentan, vamos a simplificar considerando que el coste unitario por metro cuadrado de instalación del sistema será similar al disponible hoy para edificios, cuyo límite inferior se encuentra alrededor de los 600 euros. Esto fijaría el coste del sistema fotovoltaico en unos 67000 euros, una magnitud comparable a la de los costes típicos de la cabeza tractora. Una cifra habitual de referencia en las motorizaciones diésel sería 100000 euros, pero con seguridad el coste final será superior para los futuros camiones eléctricos de gran tonelaje). Por su parte, es casi el doble que el coste del propio semirremolque, para el que una cifra típica podría ser 36000 euros.
Ahora estamos en condiciones de calcular un tiempo de retorno de la inversión, si tenemos en cuenta el coste del kilovatio-hora para la carga de las baterías del camión. Considerando un coste de 0,19 euros por kilovatio-hora, no se recuperaría la inversión hasta casi los dieciocho años. La vida media de un camión de gran tonelaje se estima en unos diez años, y aunque es de suponer que las mecánicas más sencillas de las motorizaciones eléctricas conllevarán un aumento considerable del tiempo útil de estos vehículos, dieciocho años parecen un plazo completamente inasumible.
 Gráfico de análisis de coste para camiones de cinco ejes con apoyo solar para una vida máxima del vehículo de 20 años. Fuente: Iván Rivera (elaboración propia)
Gráfico de análisis de coste para camiones de cinco ejes con apoyo solar para una vida máxima del vehículo de 20 años. Fuente: Iván Rivera (elaboración propia)Haciendo un análisis para diferentes escenarios considerando las dos variables clave en esta situación (el coste unitario de instalación de los paneles fotovoltaicos y el coste por kilovatio-hora de la energía de recarga, encontramos que, si establecemos de forma muy conservadora los diez años como el periodo mínimo de retorno aceptable para la inversión de instalar paneles fotovoltaicos en el semirremolque, encontramos que los costes de instalación unitarios deben disminuir hasta los 500 euros por metro cuadrado y el precio medio de la energía aumentar hasta los 0,3 euros por kilovatio-hora. Para costes de instalación unitarios más bajos, el precio medio de la energía aceptable en todo el periodo disminuye también. Para un valor similar al considerado inicialmente de 0,19 euros por kilovatio-hora, el coste unitario de instalación tendría que bajar a la mitad (300 euros por metro cuadrado) para que el tiempo de retorno bajara de los nueve años.
De modo un tanto alarmante, el precio por metro cuadrado del panel fotovoltaico, que ha mostrado un comportamiento histórico de disminución exponencial hasta 2019 [7], parece haberse estabilizado e incluso aumentado en los últimos tres años [8], a pesar del crecimiento constante en su capacidad productiva en todo el mundo.
El futuro del camión con apoyo fotovoltaicoEn conclusión: no vemos paneles solares en camiones por un conjunto de razones. Para empezar, los camiones tienen que evolucionar en motorización: sin al menos una motorización híbrida con una capacidad suficiente de baterías, no tiene sentido la instalación de placas fotovoltaicas salvo para alimentar sistemas secundarios (la refrigeración aparece aquí como una oportunidad a considerar). Por otro lado, es necesario que el coste de las instalaciones fotovoltaicas disminuya de forma clara, algo que podría suceder aún pese al comportamiento reciente del mercado, achacable al menos en parte a las turbulencias logísticas inducidas por la crisis de la COVID-19. Y, por último, este tipo de instalaciones tienen más sentido cuanto mayor sea el coste del kilovatio-hora para la recarga. Lamentablemente, todas las señales apuntan en este sentido a corto y medio plazo.
El caso de negocio para empresas del tipo de Sono Motors, que ha propuesto adaptaciones para camiones de este estilo [9], está en el aire. Y esto, sin responder a una pregunta más: ¿aceptarán los operadores de camiones ceder el espacio de los laterales de los semirremolques para un fin diferente a anunciarse en letras de dos metros de altura?
Bibliografía[1] Lightyear. (2022). Long Range Solar Electric Vehicle – Lightyear 0. Visitado el 29/09/2022 en
[2] Sono Motors. (2022). The Sion – the car that charges itself. Visitado el 29/09/2022.
[3] Rivera, I. (29/09/2022). Modelo de cálculo de apoyo solar para camiones. Google Spreadsheets.
[4] Comisión Europea. (01/03/2022). PVGIS Photovoltaic Geographical Information System. EU Science Hub. Visitado el 29/09/2022.
[5] Instituto para la Diversificación y el Ahorro de Energía. (2009). Guía para la gestión del combustible en las flotas de transporte por carretera. Centro de Publicaciones, Ministerio de Fomento. Visitado el 29/09/2022.
[6] García, G. (15/02/2021). Ya sabemos la capacidad del tesla semi: 500 KWH, ¿Escasa para un camión eléctrico? Híbridos y Eléctricos. Visitado el 29/09/2022.
[7] Oxford Martin School, University of Oxford. (2020). Solar PV module prices. Our World in Data. Visitado el 29/09/2022.
[8] Gifford, J. (04/01/2022). Higher PV module prices may point to stable demand and more sustainable pricing trends. PV Magazine International. Visitado el 29/09//2022.
[9] Sono Motors. (08/09/2022). Sono Motors presents financial results for the second quarter of 2022. Sono Motors. Visitado el 29/09//2022.
Sobre el autor: Iván Rivera es ingeniero especializado en proyectos de innovación de productos y servicios para ferrocarriles.
El artículo El camión solar: ¿una posibilidad real? se ha escrito en Cuaderno de Cultura Científica.
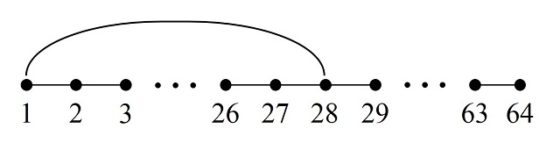
El problema del recorrido del caballo en el tablero de ajedrez (II)
En la anterior entrada del Cuaderno de Cultura Científica titulada El problema del recorrido del caballo en el tablero de ajedrez, iniciamos una pequeña serie sobre este clásico problema en el que se relacionan ajedrez y matemáticas, el problema de recorrer todas las casillas de un tablero de ajedrez con la figura del caballo, pasando una vez y sólo una vez por cada casilla. En particular, en esa entrada centramos nuestra atención en la cuestión de la existencia de solución al problema para tableros rectangulares de tamaño n x m, mientras que en esta entrada nos centraremos en la cuestión de cómo construir esos recorridos.
 El reino del ajedrez (2008), del artista mexicano Carlos Orduña Barrera. Imagen de su página web: Carlos Orduña BarreraEl problema del recorrido del caballo
El reino del ajedrez (2008), del artista mexicano Carlos Orduña Barrera. Imagen de su página web: Carlos Orduña BarreraEl problema del recorrido del caballo
Empecemos recordando exactamente qué nos plantea este juego o problema.
Problema del recorrido del caballo: Buscar un recorrido de la figura del caballo sobre el tablero de ajedrez que consista en mover esta pieza, desde una casilla inicial, de forma sucesiva a través de todas las casillas del tablero, pasando una sola vez por cada una de ellas, y terminando en la casilla inicial.
Aunque el juego del recorrido del caballo se plantea sobre el tablero clásico, de tamaño 8 x 8, desde el inicio se interesaron en la solución para tableros cuadrados de diferentes tamaños n x n, para tableros rectangulares de tamaño n x m, e incluso, para tableros de formas diversas.
Por otra parte, se distinguieron dos tipos de soluciones. Los recorridos como el planteado en el enunciado anterior, que se denomina recorrido cerrado, ya que empieza y acaba en la misma casilla, aunque se puede plantear la variante del problema que consiste en que las casillas inicial y final no sean las mismas, en cuyo caso se habla de recorrido abierto.
En la entrada anterior, como comentábamos, dedicamos nuestra atención al problema de la existencia de recorridos (abiertos y cerrados) sobre un tablero rectangular. Analizamos con un poco más de detalle los tableros de tamaño 3 x m (dejamos abierto el problema 3 x 4 que resolveremos en otra entrada de esta serie), así como el tablero 4 x 4, y recordamos cual era el resultado general: para un tablero n x m, con n menor o igual que m, existen recorridos de caballos cerrados si no se da alguno de los casos siguientes: i) n y m impares; ii) n = 1, 2 o 4; iii) n = 3 y m = 4, 6 o 8.
En esta entrada se van a analizar algunos métodos clásicos de construcción de recorridos del caballo sobre el tablero de ajedrez.
El método de los matemáticos De Moivre y De MontmortEl matemático y abogado británico Walter William Rouse Ball (1850-1925) menciona en su libro Recreaciones matemáticas y ensayos (1892) que el primer método, del que él tiene conocimiento, para obtener recorridos del caballo sobre el tablero de ajedrez, es de los matemáticos franceses Abraham de Moivre (1667-1754) y Pierre Rémond de Montmort (1678-1719).
Este método consiste en dividir el tablero en dos partes, un anillo exterior de una anchura de dos celdas y un cuadrado interior 4×4, de forma que primero se recorra con el caballo la zona exterior, solo entrando en la zona interior si es completamente necesario, y después de recorrer el anillo exterior, continuar con el trayecto por la parte interior.
 Zonas interior –verde– y exterior –azul– del tablero de ajedrez para el método de De Moivre y De Montmort
Zonas interior –verde– y exterior –azul– del tablero de ajedrez para el método de De Moivre y De Montmort
Podemos empezar a buscar un itinerario del caballo empezando en una esquina del tablero y recorriendo el anillo exterior de forma circular, por ejemplo, en el sentido de las agujas del reloj (véase la siguiente imagen), de forma que se van saltando las casillas que hemos numerado 1, 2, 3, así hasta la casilla 24, desde la cual no podemos seguir saltando a una casilla de la zona exterior (véase la siguiente imagen).
Como en la casilla 24 nos hemos bloqueado en nuestro recorrido por el anillo exterior, hay que apoyarse en la zona interior (casilla 25) para poder continuar el trayecto por el anillo exterior. Así seguimos saltando hasta la casilla 37, en la que nos volvemos a bloquear, y hay que volver a entrar puntualmente en la zona interior para poder seguir. El recorrido por el anillo exterior se termina en la casilla 50 (véase la siguiente imagen).
Para terminar el recorrido del caballo solo queda saltar por las casillas de la zona interior. Al empezar en la casilla de la esquina es imposible alcanzar esa esquina desde la zona interior, luego el recorrido será abierto. En la imagen siguiente se muestra el final del mismo.

Por el comentario anterior, las esquinas no se conectan con la zona interior, para conseguir un camino cerrado con la técnica de De Moivre y De Montmort habría que empezar en una casilla desde la que sí se pueda acceder desde la zona exterior. Una pequeña diversión para las personas que estáis leyendo esta entrada podría ser analizar cómo construir recorridos del caballo utilizando la técnica aprendida de los matemáticos franceses del siglo XVIII, empezando en diferentes casillas del anillo exterior, y ver si en algunos casos se pueden conseguir recorridos cerrados o modificar los recorridos abiertos obtenidos para convertirlos en cerrados.
A continuación, se muestra un camino cerrado partiendo de una casilla de una de las diagonales principales del tablero, que no está en ninguna esquina del mismo, y que está en el anillo exterior.
Aunque nos estamos refiriendo a la técnica de De Moivre y De Montmort para resolver el problema del recorrido del caballo sobre el tablero de ajedrez, lo cierto es que esta técnica aparece ya varios siglos antes. El pedagogo, inspector de educación e historiador del ajedrez británico Harold J. R. Murray (1868.1955) en su libro Historia del ajedrez muestra un recorrido abierto de un ajedrecista árabe desconocido, del que se sabe que se llamaba Ali Ibn Mani, que es esencialmente la misma solución que hemos mostrado al describir el método de los matemáticos franceses. Aunque el problema es datar dicha construcción ya que aparece recogida en un manuscrito, de alrededor del año 1350, sobre ajedrez de Abu Zakariya Yahya ben Ibrahim al-Hakim, titulado El deleite de los inteligentes, una descripción del ajedrez, y que también recoge el primer recorrido cerrado de Al-Adli (hacia el 840), que se comenta en la anterior entrada.
El método del matemático Leonhard EulerEl matemático suizo Leonhard Euler (1707-1783) fue el primero en realizar un análisis matemático riguroso del juego del recorrido del caballo en su artículo Solución a una cuestión ingeniosa que parece que no ha sido analizada (Memoria de la Academia de Ciencias de Berlín, escrito en 1759 y publicado en 1766).
 Las dos primeras páginas del artículo de Leonhard Euler Solución a una cuestión ingeniosa que parece que no ha sido analizada (1759)
Las dos primeras páginas del artículo de Leonhard Euler Solución a una cuestión ingeniosa que parece que no ha sido analizada (1759)
En particular, en este artículo desarrolló el siguiente método para obtener recorridos cerrados. Esta técnica consistía en buscar de forma aleatoria un recorrido del caballo sobre el tablero de ajedrez lo más largo posible, que dejara una cantidad pequeña de casillas sin recorrer, para después intercalar estas casillas en diferentes partes del mismo con el objetivo de construir un recorrido cerrado que cubra todas las casillas del tablero.
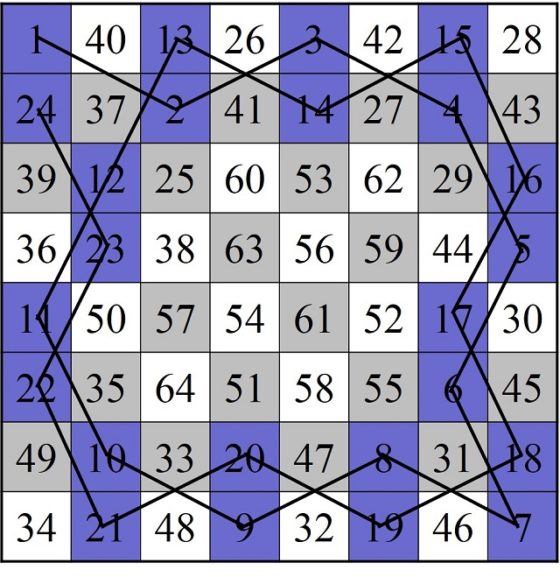
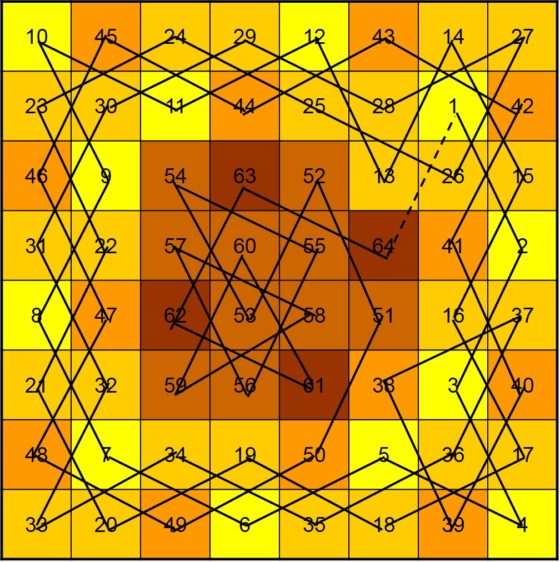
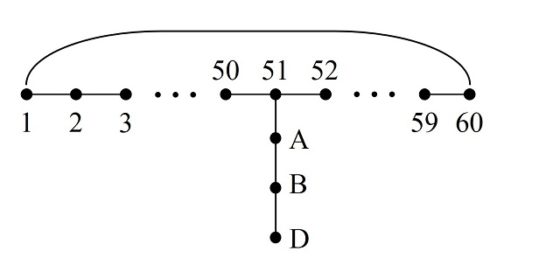
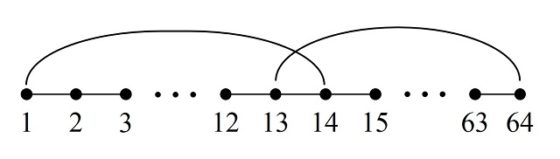
A continuación, mostramos el ejemplo que aparece en el libro Recreaciones matemáticas y ensayos (1892), de W. W. Rouse Ball, que según se menciona es un ejemplo que el matemático francés Adrien-Marie Legendre (1752-1833) considera especialmente difícil. Supongamos que, en esa búsqueda aleatoria de una solución del problema, se ha construido un recorrido que consta de 60 casillas, que nombramos 1, 2, 3, …, 59, 60, como estamos haciendo a lo largo de estas entradas, y se han dejado fuera cuatro casillas, que nombramos A, B, C y D, que son las que aparecen en la siguiente imagen (en negrita los números inicial y final del camino abierto y en rojo los de las casillas por las que no se ha pasado).
Lo primero que se hace es intentar cerrar el recorrido, aunque no tenga las 64 casillas. Nos fijamos entonces en la casilla 1 (la primera del recorrido), que es “adyacente” a las casillas numeradas como 2, 32 y 52, es decir, se llega a ellas con el salto del caballo desde la casilla 1, y en la casilla 60 (la última del recorrido), que es adyacente a 29, 51 y 59. Como las casillas 51 (cercana a la casilla 60) y 52 (cercana a la casilla 1) son adyacentes entre sí, vamos a poder construir un recorrido cerrado. Veamos cómo hacerlo.
 Sencilla representación del recorrido del caballo desde la casilla 1 a la 60, junto con las dos adyacencias comentadas de la casilla 51, con la 60, y la casilla 52, con la 1
Sencilla representación del recorrido del caballo desde la casilla 1 a la 60, junto con las dos adyacencias comentadas de la casilla 51, con la 60, y la casilla 52, con la 1
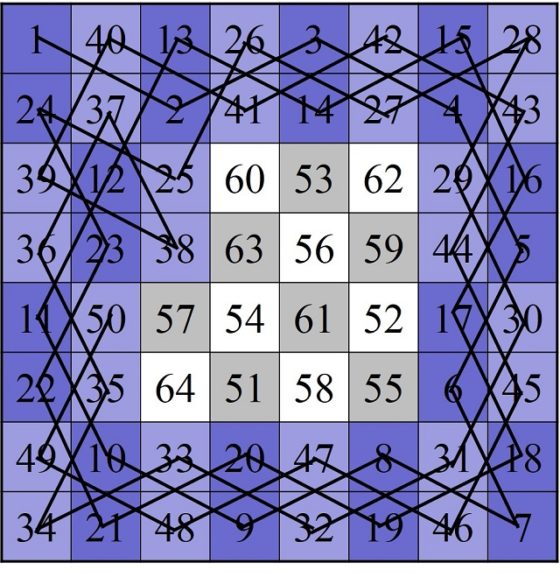
Entonces, podemos determinar un recorrido cerrado que consiste en saltar por las casillas desde la 1 hasta la 51, de esta saltar a la 60, y seguir en orden inverso, desde la 60 hasta la casilla 52, que es adyacente a la casilla 1, cerrando así el paseo. Para que nuestro recorrido siga en orden, podemos renombrar las celdas 60, 59, 58, …, 53, 52 como 52, 53, … 58, 59, 60, es decir, en orden inverso. Si hacemos esto el recorrido que nos queda es el que aparece en la siguiente imagen y como vemos es un itinerario cerrado del 1 al 60, que aún no incluye las cuatro casillas A, B, C y D.
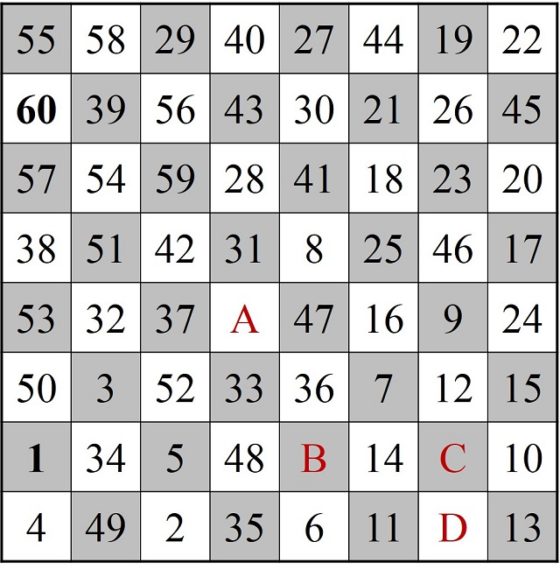
Ahora se trata de ver cómo añadir las casillas no recorridas. Las casillas A, B y D están conectadas mediante el salto del caballo, luego se trata de crear un nuevo recorrido abierto a partir de la ruta cerrada 1–60, que además incluya a A, B y D. Como resulta que la casilla A está conectada con las casillas 3, 5, 7, 25, 41, 51 y 53, podemos conectar la casilla 51 con las casillas A, B y C, y tendremos el recorrido abierto 52, 53, …., 60, 1, 2, …, 50, 51, A, B, C.
 Sencilla representación del recorrido cerrado del caballo desde la casilla 1 a la 60, junto con el recorrido A-B-D adyacente a la casilla 51
Sencilla representación del recorrido cerrado del caballo desde la casilla 1 a la 60, junto con el recorrido A-B-D adyacente a la casilla 51
Ahora, para mantener nuestro recorrido (abierto) de 63 casillas en orden, vamos a renombrar las casillas 52, 53, …., 60, 1, 2, …, 50, 51, A, B, C, como 1, 2, 3, …, 59, 60, 61, 62, 63, como aparece en la siguiente imagen.
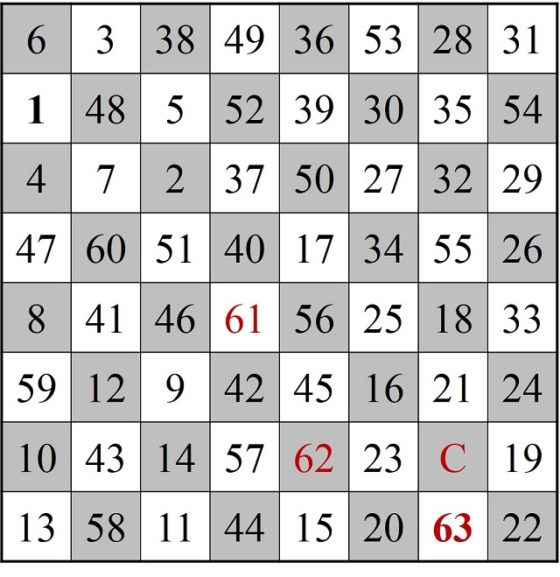
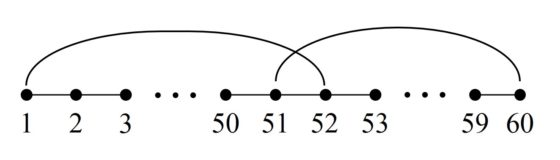
Por lo tanto, tenemos un recorrido abierto que va de la casilla 1 a la 63 y queda por saltar por la casilla C y cerrar el camino. Como resulta que C es adyacente a 25 y 63 es adyacente a 24, vamos a poder intercalar la casilla C consiguiendo así un recorrido abierto con las 64 casillas del tablero
 Sencilla representación del recorrido abierto del caballo desde la casilla 1 a la 63, con las adyacencias de la casilla C con la 25 y la casilla 24 con la 63
Sencilla representación del recorrido abierto del caballo desde la casilla 1 a la 63, con las adyacencias de la casilla C con la 25 y la casilla 24 con la 63
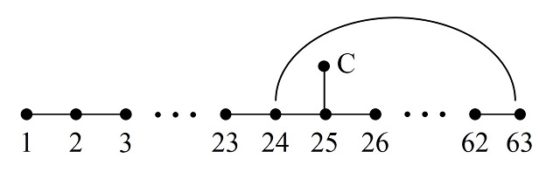
Por lo tanto, el recorrido buscado empezaría en la casilla 1 e iría saltando hasta llegar a la casilla 24, de ahí se saltaría a la 63 y se iría saltando hacia atrás hasta la 25, de la cual se pasaría a la casilla C. Y de nuevo renombramos las casillas 1, 2, 3, …, 23, 24, 63, 62, …, 26, 25, C, para que quede el recorrido abierto del 1 al 64, como aparece en la siguiente imagen.
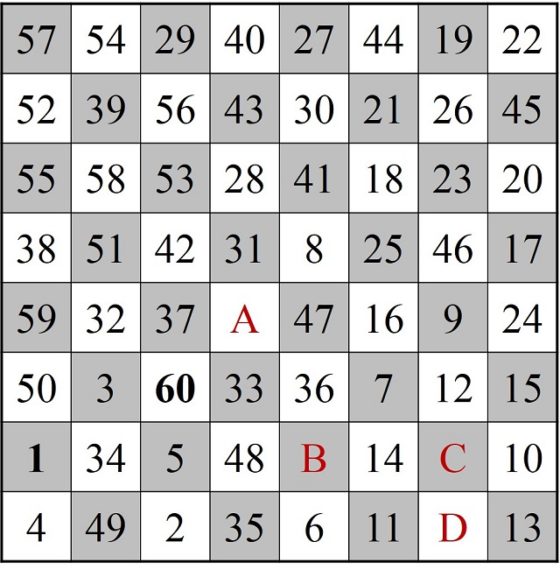
Ahora ya solo nos queda cerrar el recorrido, pero resulta que las casillas inicial (1) y final (64) están bastante alejadas la una de la otra, lo que dificulta poder realizar el cierre. Por lo tanto, Euler modifica el recorrido abierto por obtener otro que tenga las casillas inicial y final más cercanas. Para ello, Euler elige una celda que sea adyacente con la celda 1, en concreto, la celda 28, y que es adyacente a la celda 27, la cual está más cerca de la casilla 64.
 Sencilla representación del recorrido abierto del caballo desde la casilla 1 a la 64, con la adyacencia de la casilla 1 con la 28
Sencilla representación del recorrido abierto del caballo desde la casilla 1 a la 64, con la adyacencia de la casilla 1 con la 28
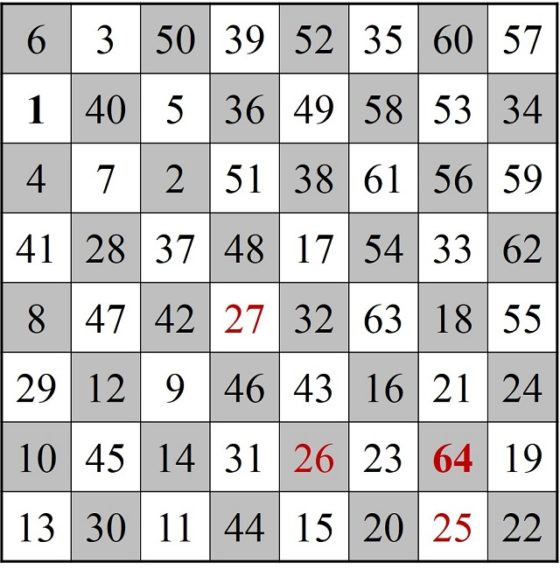
Entonces, se considera el recorrido abierto que empieza en la casilla 27, va hacia atrás hasta la casilla 1, de donde salta a la 28 y sigue hasta la 64. Así tenemos un itinerario abierto, con el inicio y el final más próximos, pero antes renombremos nuestras casillas 27, 26, … 2, 1, 28, 29, …, 64 como 1, 2, 3, …, 61, 62, 63, 64 (imagen siguiente).
Finalmente vamos a poder cerrar el recorrido abierto, ya que las casillas inicial y final, ahora sí, están cercanas. Por ejemplo, la casilla inicial (1) es adyacente a la casilla 14, mientras que la casilla final (64) es adyacente a la casilla 13, y podemos hacer la misma jugada que hicimos al cerrar el primer camino.
 Sencilla representación del recorrido abierto del caballo desde la casilla 1 a la 64, junto con las dos adyacencias comentadas de la casilla 1, con la 14, y la casilla 64, con la 13
Sencilla representación del recorrido abierto del caballo desde la casilla 1 a la 64, junto con las dos adyacencias comentadas de la casilla 1, con la 14, y la casilla 64, con la 13
De la misma manera que al principio de la descripción de esta técnica, el recorrido cerrado será empezar con el 13 e ir saltando en sentido inverso hasta 1, de ahí saltar a la casilla 14 y seguir saltando hasta la casilla 64 (que cierra con la casilla 13). Solo nos falta renombrar el recorrido 13, 12, …, 2, 1, 14, 15, …, 64 como 1, 2, …, 63, 64, como vemos en la siguiente imagen.
 Recorrido cerrado del caballo por el tablero de ajedrez, obtenido mediante la técnica de Euler
Recorrido cerrado del caballo por el tablero de ajedrez, obtenido mediante la técnica de EulerLa técnica de H. C. von Warnsdorff
El alemán H. C. von Warnsdorff propuso un método sencillo y elegante de resolver el problema del recorrido del caballo, en su publicación titulada La solución más sencilla y general al salto del caballo (1823), que podéis encontrar en internet.
La técnica de H. C. von Warnsdorff para encontrar recorridos del caballo sobre el tablero 8 x 8 es la siguiente: Mueve el caballo a una casilla adyacente (es decir, a la que se llegue con el movimiento del caballo), que no haya sido visitada ya y que tenga el menor número de casillas adyacentes libres. Si se da un empate, elegir de forma arbitraria.
Esta es una regla intuitiva, puesto que indica que hay que visitar primero las casillas con menos conexiones, que son aquellas que si no se recorren en ese momento quizás, por la falta de conexiones, no se pueda regresar después a pasar por ellas, que realmente se puede utilizar para todo tipo de tableros rectangulares, que es bastante eficaz a la hora de buscar algunos recorridos particulares del caballo, aunque no es válida para una búsqueda exhaustiva, por ejemplo, los recorridos anteriores de Euler o Al-Adli sobre el tablero clásico no verifican la regla de von Warnsdorff.
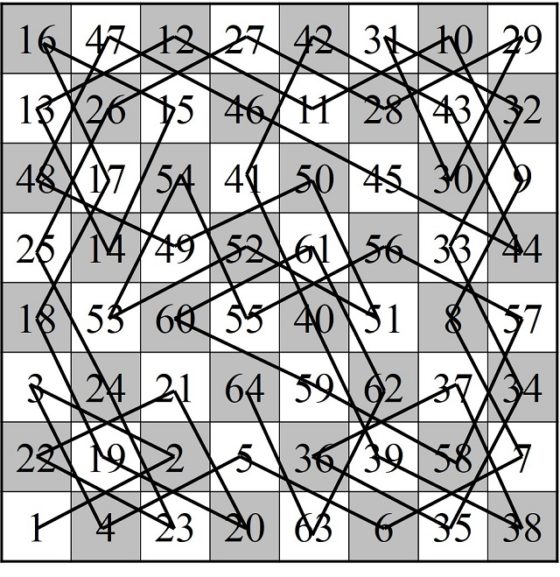 Recorrido del caballo sobre un tablero 8 x 8 obtenido mediante el método de von Warnsdorff
Recorrido del caballo sobre un tablero 8 x 8 obtenido mediante el método de von Warnsdorff
Sin embargo, el método no resuelve bien los casos en los que hay empates en el número de casillas adyacentes libres. Si se elige al azar la casilla en la que continuar, como sugiere Warnsdorff, puede ocurrir que el recorrido se pare en un momento intermedio y no pase por todas las casillas del tablero, como se muestra en el siguiente ejemplo 5 x 5.
Si utilizamos la regla de Warnsdorff para un tablero 5 x 5, empezando en la casilla del medio de la primera fila, el primer empate se produce al llegar a la casilla 9, que tiene dos opciones de continuidad, dos casillas con número de casillas adyacentes libres igual a 2, en el lateral y debajo de la casilla número 5.
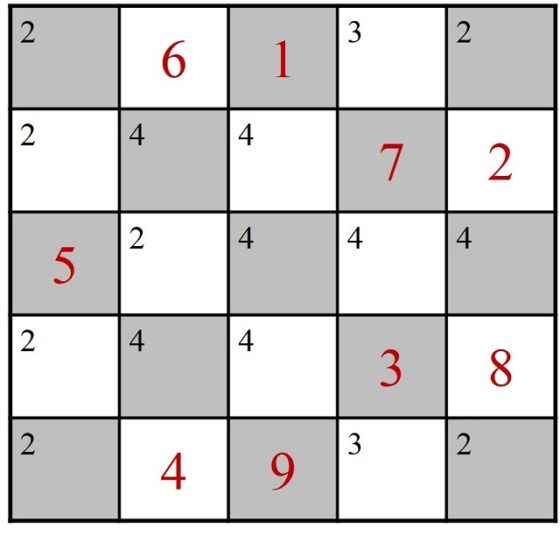 Inicio de un recorrido construido con la técnica de von Warnsdorff, donde se indica con números rojos grandes las casillas recorridas, del 1 al 9, y con números pequeños negros las casillas libres conectadas con dicha casilla mediante el salto del caballo
Inicio de un recorrido construido con la técnica de von Warnsdorff, donde se indica con números rojos grandes las casillas recorridas, del 1 al 9, y con números pequeños negros las casillas libres conectadas con dicha casilla mediante el salto del caballo
Si se continúa con la casilla lateral, el recorrido se estanca después de la casilla 16, como se muestra en la siguiente imagen, puesto que si el caballo salta a la esquina de abajo a la izquierda (como indicaría la regla), ya no puede salir, pero si continuase por otra casilla, no volvería nunca a esa casilla que tiene 0 casillas adyacentes libres.
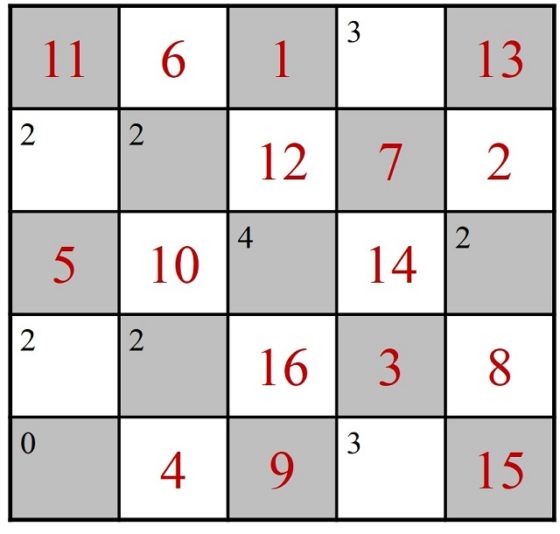 Inicio de un recorrido construido con la técnica de von Warnsdorff que se ha bloqueado en la casilla 16
Inicio de un recorrido construido con la técnica de von Warnsdorff que se ha bloqueado en la casilla 16
Sin embargo, si se continúa, tras el empate, con la casilla de debajo de la 5, existen varias soluciones continuando con la regla, una de ellas la mostrada en la imagen.
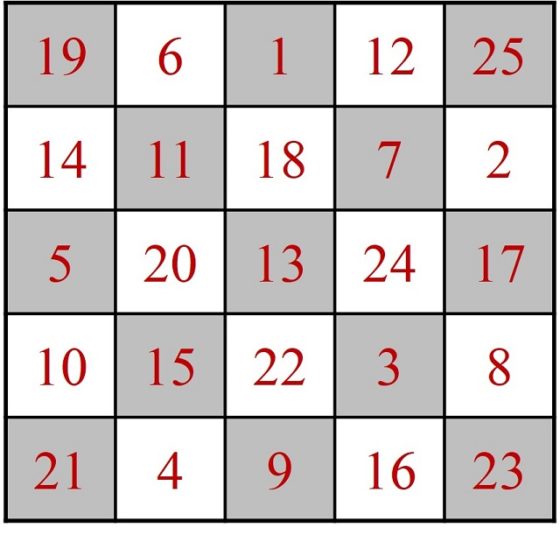 Recorrido final construido con la técnica de von Warnsdorff
Recorrido final construido con la técnica de von Warnsdorff
Puede verse en la literatura sobre el tema, que diferentes autores han modificado la regla de Warndorff mediante el diseño de métodos para determinar la mejor elección de una casilla cuando se produce un empate. El más sencillo de los cuales consiste en la elección, en caso de empate, de la casilla más alejada (con la distancia euclídea) al centro del tablero, que es el método que yo he utilizado para deshacer los empates en el recorrido mostrado anteriormente sobre el tablero 8 x 8.
La construcción de RogetVamos a terminar esta entrada con el método que propuso el médico, matemático, físico, teólogo y lexicólogo británico Peter Mark Roget (1779-1869), en un artículo de la revista Philosophical Magazine en 1840.
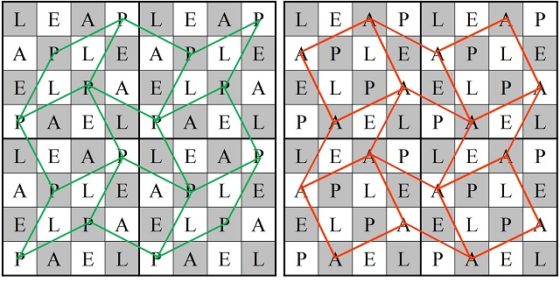
Roget divide el tablero 8 x 8 en cuatro zonas, cada una de ellas formada por un cuadrado 4 x 4, y las 16 casillas de cada cuarto de tablero las separa en cuatro grupos de 4 casillas, que forman un recorrido cerrado sobre esa zona 4 x 4. A cada una de las casillas de esos grupos, o recorridos cerrados, las nombra con una misma letra L, E, A, P (la palabra leap, en inglés, significa “salto”). Los recorridos de las letras L y P tienen forma de diamante, mientras que los de las letras A y E de cuadrado.
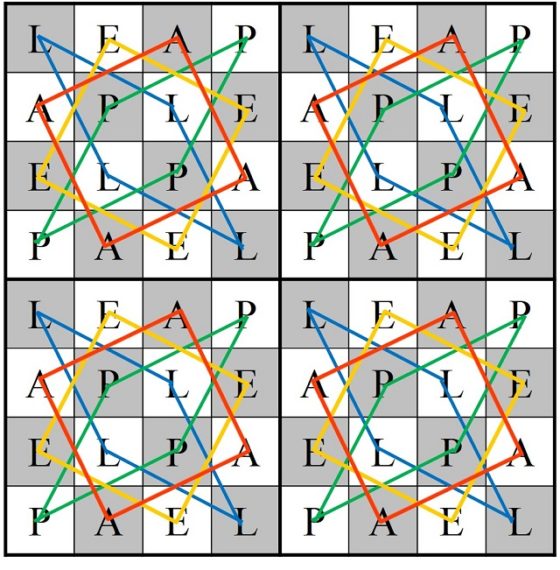
Entonces, Roget considera movimientos del caballo que son de tipo LL, EE, AA, PP (de una casilla de una letra a otra de la misma letra) y movimientos de tipo EL, AL, EP, AP (de una casilla con una letra vocal a una casilla con una letra consonante, o viceversa), como se muestra en las siguientes imágenes.
 Movimientos de tipo LL y AA sobre el tablero de ajedrez
Movimientos de tipo LL y AA sobre el tablero de ajedrez
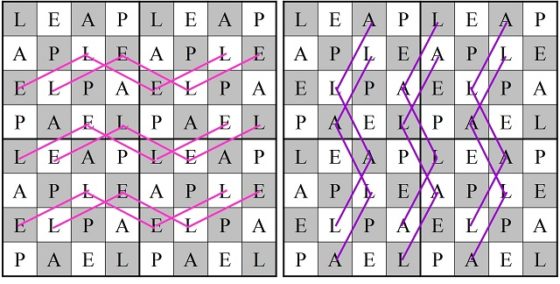 Movimientos de tipo EL y AL sobre el tablero de ajedrez
Movimientos de tipo EL y AL sobre el tablero de ajedrez
Con las 16 casillas de cada una de las letras se puede construir un circuito cerrado, luego disponemos de cuatro tipos de circuitos cerrados con 16 casillas, cada uno con cada una de las letras. Ahora para construir el recorrido de las 64 casillas se combinan cuatro circuitos de una sola letra de forma que después de un circuito de una vocal va uno de una consonante, y viceversa. En el siguiente ejemplo, hemos empezado con el circuito de la letra P, después el circuito de la letra A, luego L y finalmente E, creando un recorrido abierto.
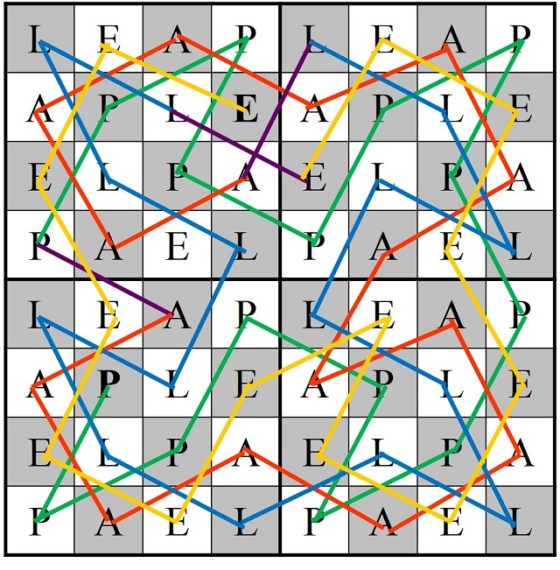 Recorrido abierto del caballo sobre el tablero de ajedrez realizado con la técnica de Roget
Recorrido abierto del caballo sobre el tablero de ajedrez realizado con la técnica de Roget
Y no podía faltar un poco de arte para terminar la entrada.
 Caballo negro (2006), del artista mexicano Carlos Orduña Barrera. Imagen de su página web: Carlos Orduña Barrera
Caballo negro (2006), del artista mexicano Carlos Orduña Barrera. Imagen de su página web: Carlos Orduña Barrera
Bibliografía:
1.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, El mundo es matemático, RBA, 2015.
2.- Édouard Lucas, Recreaciones Matemáticas, vol. 1 – 4, Nivola, 2007, 2008.
3.- Miodrag S. Petrovic, Famous Puzzles of Great Mathematicians, AMS, 2009.
4.- Harold J. R. Murray, A History of Chess (Historia del ajedrez), Oxford University Press, 1913.
5.- W. W. Rouse Ball, H. S. M. Coxeter, Mathematical Recreations and Essays, Dover Publications, 1987 (originalmente publicada por W. W. R. Ball en 1892 –la versión original puede encontrarse en el Proyecto Gutenberg – y extendida por el geómetra H. S. M. Coxeter en 1974)
6.- John J. Watkins, Across the Board: The Mathematics of Chessboard Problems, Princeton University Press, 2004.
7.- H. C. von Warnsdorf, Des Rösselsprunges einfachste und allgemeinste Lösung, Verhagen, 1823.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El problema del recorrido del caballo en el tablero de ajedrez (II) se ha escrito en Cuaderno de Cultura Científica.
Einstein y Newton
En el siglo XVII Isaac Newton básicamente creó la física del mundo moderno, desarrollando modelos acerca de la gravedad, la luz, la inercia, la masa, e incluso las matemáticas necesarias para comprender estos conceptos. La mecánica de Newton fue considerada como la descripción definitiva del universo, hasta que Einstein vino a cambiarlo todo.
 Newton / Einstein Proxxi Composite (2003) de Daniel Rozin. Para ver correctamente la imagen debes tener en cuenta que la realidad depende del observador: aléjate de la pantalla (o minimiza el tamaño) hasta que veas a Newton; acércate (o aumenta el tamaño) para ver a Einstein. Fuente: Daniel Rozin / smoothware.com
Newton / Einstein Proxxi Composite (2003) de Daniel Rozin. Para ver correctamente la imagen debes tener en cuenta que la realidad depende del observador: aléjate de la pantalla (o minimiza el tamaño) hasta que veas a Newton; acércate (o aumenta el tamaño) para ver a Einstein. Fuente: Daniel Rozin / smoothware.comEinstein fue el que comenzó la revolución de la física moderna que terminaría derrocando el viejo paradigma de la física newtoniana, por lo que tanto Einstein como Newton crearon las bases de nuevas formas de pensar. Efectivamente, hay grandes paralelismos entre ambos físicos. Los dos tuvieron lo que ha dado en llamarse un “año maravilloso” cuando tenían veintitantos años. El de Newton fue el que él llamó “año de la plaga”, en 1666. Ese año creó el cálculo diferencial e integral, descubrió la ley de gravitación universal y determinó cómo la gravedad hace que los planetas se muevan en elipses. El de Einstein fue en 1905, durante el que publicó la teoría especial de la relatividad, la solución al problema del efecto fotoeléctrico (para la que aplicó la hipótesis cuántica a la luz), una explicación del movimiento browniano y la ecuación E = mc2.
Hay, sin embargo, una pequeña diferencia entre Einstein y Newton a la hora de tratar estos descubrimientos: Newton no publicó la mayoría de sus primeros trabajos hasta décadas después pero, cuando lo hizo, todo el mundo los aclamó como correctos inmediatamente. Los dos hombres también están unidos por el hecho de que ambos llegaron a ser tremendamente famosos durante sus vidas. Newton fue una figura tan iconográfica durante su época como Einstein lo fue en la suya, solo hay que sustituir una formal peluca británica por la melena alborotada de Einstein.
A lo largo de los siglos, la fama de Newton como fundador de la física moderna le había incrustado en la consciencia de la sociedad como el genio que había creado la ciencia tal y como se conocía. Surgieron, sin embargo, varias discrepancias, las más evidentes tenían que ver con la luz y la óptica.
Newton había lanzado la hipótesis de que la luz estaba constituida por “corpúsculos”, partículas como pequeñas bolas. En el siglo XIX varios físicos, entre ellos, más notablemente, James Clerk Maxwell, habían determinado que la luz era de hecho una onda. Pero los problemas para la mecánica newtoniana estaban solo comenzando. La teoría de Maxwell cuestionaba otras facetas de la visión del mundo de Newton. Para la época en que Einstein estaba haciendo el doctorado estaba claro para los físicos más perceptivos de que se estaba en medio de una crisis: o Newton estaba equivocado o lo estaba Maxwell. La publicación por Einstein en 1905 de la teoría especial de la relatividad fue el golpe decisivo: Maxwell era el ganador y la mecánica newtoniana, con su dependencia del tiempo y del espacio absolutos, era incorrecta. Pero Einstein no se paró ahí. Si bien no tenía un plan premeditado para desmantelar el edificio que Newton había construido, él fue el que vino a cambiar el concepto aceptado, mecánico y determinista, del mundo.
Einstein abordó la cuestión de la gravedad, dándose cuenta de que la forma en la que era comprendida no era compatible con su teoría de la relatividad. En 1911 publicaría su primera aproximación a la teoría general de la relatividad, que reformaba otra de las grandes teorías de newton: la ley de la gravedad universal. Newton había dicho que todos los objetos del universo se atraían entre sí con una fuerza proporcional a sus masas. Pero sabía que no podía ofrecer una idea de por qué esto era así. “Non fingo hypotheses”, no formulo hipótesis, fue su comentario ante su falta de una teoría. Con la relatividad general Einstein ofrecía una solución a por qué la gravedad funcionaba: dos objetos se atraían entre sí porque la masa distorsiona el espaciotiempo alrededor de ella de tal manera que cualquier otra masa en su cercanía se “desliza” hacia ella. En su forma más sencilla las ecuaciones de Einstein son equivalentes a las de Newton; las de Newton no son expresiones equivocadas, sino incompletas, y las de Einstein son más completas. Algún día aparecerá una teoría que complete aún más las de Einstein.
A pesar de haber contribuido tanto a bajar del pedestal en el que se encontraban las ideas de Newton, Einstein siempre profesó una gran admiración por el inglés. En 1940, en un artículo que escribió para Science titulado “Consideraciones acerca de los fundamentos de la física teórica”, Einstein dijo de Newton que fue la primera persona en “establecer una base teórica uniforme” para el mundo de la ciencia. Einstein seguía: “Esta base newtoniana probó ser sumamente fructífera y fue considerada definitiva hasta finales del siglo XIX. No solamente proporcionó resultados para los movimientos de los cuerpos celestes, hasta los más pequeños detalles, sino que también suministró una teoría de la mecánica de las masas continuas y discretas, una explicación sencilla del principio de conservación de la energía y una teoría completa y brillante del calor”. Newton había producido un conjunto de reglas, sistemático y omnicomprensivo, que unía todos los fenómenos conocidos en su época. Encontró que la mecánica era una forma tan buena de explicar la naturaleza que la aplicó a todo lo que vio; como lo hizo todo el mundo los doscientos años siguientes, hasta que llegó Einstein para cambiar de nuevo la visión del mundo.
Referencia:
Einstein, A. (1940). Cnsiderations concerning the fundaments of theoretical physics Science, 91 (2369), 487-492 DOI: 10.1126/science.91.2369.487
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 6 de junio de 2010.
El artículo Einstein y Newton se ha escrito en Cuaderno de Cultura Científica.
Lagos en(tre) el hielo de Europa
En el último artículo hablábamos de los lagos en Marte y su importancia a nivel astrobiológico, ya que supondrían una fuente relativamente estable de agua líquida, algo fundamental para el origen y desarrollo de la vida. Pero siempre que hablamos de lagos en nuestro Sistema Solar -más allá de la Tierra, claro está- las condiciones en las que el agua está líquida no tienen que ver en absoluto con las que existen en nuestro planeta, adecuadas para que haya un continuo ciclo hidrológico en superficie, algo que no ocurre en ningún otro cuerpo. Por ello, y por las grandes perspectivas que nos abre el agua a la hora de buscar ambientes habitables, nos hemos fijado en los denominados mundos océano, cuerpos de nuestro Sistema Solar en los que debajo de su corteza formada principalmente por hielo -frente a la rocosa de los planetas interiores- existe un océano de agua líquida. Incluso a nivel geodinámico, eso sí, tomándonos ciertas licencias, podríamos decir que estos océanos se comportan de algún modo como el manto de la Tierra, transfiriendo esa energía interna hacia el exterior, dando lugar a distintos procesos que transforman la superficie de estos cuerpos. Este sería el caso de Europa, la luna de Júpiter.
Una de las dudas que tenemos es si, además de los océanos subterráneos, existen otras masas de agua intermedias en la corteza, a modo de grandes bolsas de agua y que, de nuevo, tengan permanencia a lo largo del tiempo, ya que nos podrían servir de algún modo para poder estudiar ese océano más profundo sin la dificultad técnica que supondría llegar hasta él, puesto que esa agua vendría directamente desde las profundidades, emplazándose en la corteza.
 Detección de los posibles géiseres de vapor de agua por parte del Telescopio Espacial Hubble. Fuente: NASA, ESA, and W. Sparks (STScI).
Detección de los posibles géiseres de vapor de agua por parte del Telescopio Espacial Hubble. Fuente: NASA, ESA, and W. Sparks (STScI).Aunque todavía nos falta una confirmación más fehaciente de la existencia de fenómenos criovolcánicos en Europa, como pueden ser los géiseres detectados por el telescopio espacial Hubble, la existencia de una corteza con un espesor entre los 15 a los 25 kilómetros haría más complicadas las erupciones directamente desde un océano subterráneo.
Un equipo de científicos acaba de publicar un artículo en The Planetary Science Journal en el que ha realizado distintos modelos en los que aparecen bolsas de agua en el interior de la corteza a profundidades que van desde los 4 a los 8 kilómetros de profundidad. El hielo tendría un comportamiento rígido y frágil, lo que facilitaría su fractura y permitiendo que el agua contenida en estas hipotéticas reservas fluyese con mayor facilidad a la superficie como vapor o como criolavas.
 Distintos modelos para la formación de fenómenos criovolcánicos en Europa. Fuente: NASA.
Distintos modelos para la formación de fenómenos criovolcánicos en Europa. Fuente: NASA.¿Cómo ocurriría esto? Al ir congelándose estas bolsas de agua, se logra un aumento de volumen de esta agua que puede fracturar el hielo que las rodea, permitiendo salir al agua contenida. Este fenómeno es muy importante porque más que dar lugar a un continuo de géiseres como, por ejemplo, vemos en Encélado, permitiría tener una actividad intermitente y de ahí que sea más difícil de detectar.
Y, por supuesto, es un mecanismo compatible con una corteza de gran espesor, en la que no es necesaria la existencia sistemas de fracturas que atraviesen la corteza por completo, aunque tampoco un mecanismo excluiría la existencia del otro, e incluso haber coexistido en otros momentos de la historia geológica de Europa.
¿Cuándo tendremos respuesta a si este modelo es correcto? Muy probablemente a partir de la década de 2030, cuando la sonda Europa Clipper llegue al sistema joviano y sea capaz de estudiar con detalle la corteza de Europa, pudiendo detectar estas reservas de agua en la corteza de Europa y confirmar (o descartar) este nuevo modelo gracias a su instrumento REASON, un radar cuyas ondas serán capaces de penetrar en la corteza de hielo y aportarnos pistas sobre su estructura.
Referencias:
Lesage, E., Massol, H., Howell, S., & Schmidt, F. (2022). Simulation of Freezing Cryomagma Reservoirs in Viscoelastic Ice Shells. The Planetary Science Journal, 3(7), 170. doi: 10.3847/psj/ac75bf
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Lagos en(tre) el hielo de Europa se ha escrito en Cuaderno de Cultura Científica.
Motivos para el altruismo
 Colonia de Demodus rotundus
Colonia de Demodus rotundusLos seres humanos compartimos comida y otros bienes. No lo hacemos con cualquiera, ni bajo cualquier circunstancia, pero es un comportamiento habitual. Por eso nos parece normal, aunque, a decir verdad, sea algo sorprendente, al menos desde un punto de vista evolutivo. Al ceder alimento, el que lo da pierde un recurso que podría darle una ventaja competitiva con relación a otros miembros del grupo.
Se suelen considerar tres posibles motivos por los que puede merecer la pena compartir alimento. Por un lado está la selección por parentesco, en virtud de la cual es ventajoso ser altruista con las personas (parientes) con las que se comparte una parte de los genes porque, ayudándolas, se facilita que una parte del patrimonio genético perdure. También se puede compartir por gorroneo tolerado (o consentido); se produce cuando quien tiene comida no es capaz de monopolizarla debido a los costes que le imponen quienes no la tienen y que, aunque no le obliguen a compartirla, pueden hacer que le resulte muy costoso no hacerlo. En tercer lugar está la reciprocidad, ya que quien hoy dispone de comida quizás haya recibido en el pasado ayuda de otro o podrá necesitarla en el futuro; esto es, sería ventajoso compartir comida en situaciones en las que la reciprocidad por parte de quien recibe puede acabar resultando conveniente en el futuro para quien comparte.
Nosotros no somos los únicos primates que compartimos comida. Los tres motivos citados en el párrafo anterior parecen estar en la base del comportamiento generoso de seres humanos y otros primates, como chimpancés, bonobos, capuchinos y tamarinos. Los dos motivos que más influyen son el gorroneo consentido y la reciprocidad, mientras que el de la selección de parentesco es algo menor.
En la especie humana las diferencias entre poblaciones en el grado de reciprocidad de sus miembros parecen estar relacionadas con el nivel de predictibilidad de la cantidad de alimento disponible. En aquellas en que es más incierta la posibilidad de disponer de comida de forma regular, la reciprocidad tiende a ser más importante.
El altruismo tampoco se limita a los primates. Desmodus rotundus se alimenta de sangre; es un vampiro de los de verdad, esto es, un murciélago hematófago. Además, comparte con otros vampiros de su mismo grupo la sangre que obtiene. Mediante experimentos diseñados a tal efecto se ha podido verificar que, al compartir la sangre, los murciélagos de esta especie establecen vínculos duraderos con sus congéneres, en virtud de los cuales adoptan el hábito de compartir comida entre ellos. Los individuos con los que lo hacen pueden ser de su misma familia o no serlo, por lo que no parece que su altruismo obedezca a la selección de parentesco. Por otro lado, dada la especial forma de compartir la sangre -regurgitándola-, tampoco es explicable este comportamiento por gorroneo tolerado.
En Desmodus rotundus hay altruismo recíproco. Cuando un vampiro da parte de su alimento a otro y establece así un vínculo con él, ambos salen beneficiados de esa relación, porque unas veces es uno el que consiga alimentarse y otras es el otro. Así, la probabilidad de que pasen privación en un entorno de posibilidades de alimentación inciertas disminuye para ambos. La pequeña cantidad de sangre que se comparte en cada ocasión puede representar, para el que la recibe, la diferencia entre reproducirse o no hacerlo, o entre sobrevivir o perecer, mientras que el que dona pierde solo una parte de lo conseguido. Por ello, el altruismo tiene en estos animales -que son, además, sociales- un altísimo valor adaptativo: la continuidad de todo el grupo depende de ello.
Fuentes:
Carter, G. G., Wilkinson, G. S., 2015, Social benefits of non-kin food sharing by female vampire bats. Proc. R. Soc. B.282 20152524 20152524
Jaeggi, A. V. y Gurven, M., 2013, Reciprocity explains food sharing in humans and other primates independent of kin selection and tolerated scrounging: a phylogenetic meta-analysis. Proc. R. Soc. B.280 20131615 20131615
Para saber más:
La unidad de selección en la evolución y el origen del altruismo
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Motivos para el altruismo se ha escrito en Cuaderno de Cultura Científica.
Naukas Pro 2022: Alimentos alternativos y sostenibles

“Quiero cambiar el mundo”. Si esta frase la pronunciara alguien de corta edad, probablemente se consideraría un golpe de entusiasmo propio de la juventud. Pero salida de la cabeza de un doctor en Física de Materiales e investigador de la NASA, en plena pandemia, podría considerarse un anticipo de algo realmente ambicioso. El dueño de aquel deseo fue Eneko Axpe, un científico baracaldés experto en la investigación de nuevos alimentos, a quien el COVID-19 clausuró los laboratorios en los que trabajaba y le dio la oportunidad de disfrutar de “tiempo para pensar”. Y lo hizo: reflexionó sobre cómo resolver uno de los principales problemas de la Humanidad, el cambio climático, y las consecuencias que este fenómeno tiene sobre aspectos como la alimentación y la sostenibilidad a nivel global.
De todo ello dio cuenta el propio científico en el Naukas Pro celebrado en el Palacio Euskalduna de Bilbao, donde expuso los esfuerzos investigadores que él mismo y que otras organizaciones llevan a cabo para diseñar alimentos alternativos y sostenibles capaces de asegurar las necesidades de la población de una forma saludable y respetuosa con el medioambiente.
Axpe compartió varios de los datos que, según sus palabras, le dejaron “anonadado” a la hora de abordar su sueño: el más impactante tenía mucho que ver, precisamente, con la relación entre la alimentación y la contaminación global. Según explicó, la comida es responsable del 26% de las emisiones de gases de efecto invernadero del planeta, muy por delante de otras fuentes contaminantes como la actividad aérea (el 1,9%) y el resto de los medios de transporte (el 11,8%).
También recordó que los 7.800 millones de personas que viven hoy en el planeta pasarán a ser 11.000 millones a finales de siglo, un hecho que contribuirá a esquilmar las fuentes de alimentación, y que los recursos que utilizamos para alimentarnos, como la agricultura y la ganadería, ocupan cerca de la mitad de la tierra habitable en el planeta, algo que consideró “terrible para la biodiversidad”. De hecho, afirmó que mientras el ser humano supone el 34% de la biomasa global de mamíferos, los animales encargados de nuestra alimentación, como el ganado bovino y los cerdos, acaparan el 35% y el 12%, respectivamente, muy por delante del 4% que suponen los animales salvajes o silvestres. “Se ha destruido biodiversidad para favorecer la cría de ganado”, constató.
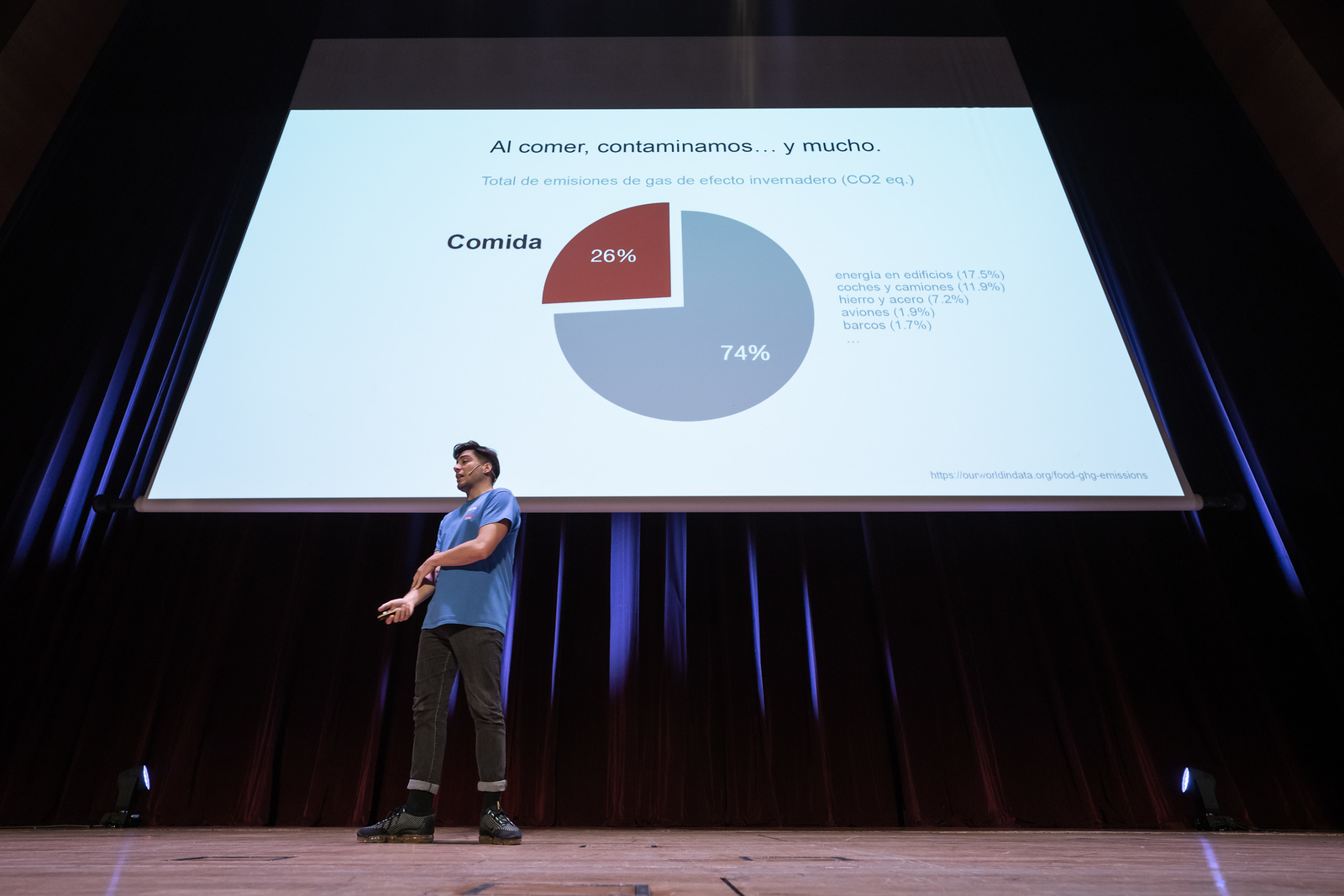
Para completar esta relación entre la producción de alimentos, el consumo global y la sostenibilidad del planeta, Eneko Axpe ofreció un dato clarificador: una persona ingiere la misma cantidad de proteína en tres días consumiendo filetes de carne que a lo largo de todo un año comiendo guisantes. Y apostilló: “La mayoría de los productos beneficiosos para el medioambiente lo son también para la salud, hasta el punto de que su consumo puede llegar a incrementar nuestra esperanza de vida en 10 años”.
Con estos datos sobre la mesa, Eneko Axpe lanzó una pregunta al aire: “¿Cómo puede un científico de materiales ayudar a resolverlo?”.
A partir de ese momento reivindicó la importancia de la Física a la hora de diseñar alimentos alternativos saludables y sostenibles, y mencionó algunas de las investigaciones que él mismo y otras organizaciones han llevado a cabo en este campo. El investigador recordó un proyecto en el que consiguió crear hamburguesas y bacon a base de plantas en el laboratorio, con características organolépticas similares a las de la carne, y mencionó el “impacto positivo” que supuso esta ingesta para los consumidores.
A continuación recordó el resultado de otra investigación con la que se consiguió reproducir carne de vaca, sin sacrificar al animal, a través del cultivo celular obtenido de una simple biopsia, una opción que exige la construcción de grandes fermentadores que en la actualidad desarrollan varias empresas, entre ellas una donostiarra. Axpe explicó que el consumo de esta carne “crecida en laboratorio” ya fue aprobado en Singapur, con unos nuggets de pollo a los que siguieron salmón y otros productos de carne de vacuno como filetes y carne picada, con resultados prometedores.
El investigador mencionó otra estrategia que ya está en marcha y que consiste en crear carne con micelio, una sustancia similar a la raíz de un hongo que se cultiva en 3D y que genera tejidos similares a los de aquel alimento. Se trata de una iniciativa que también ha explorado la NASA pero con objetivos diferentes. En concreto, para diseñar productos con propiedades mecánicas como la madera de cara a la creación de futuros asentamientos en la luna o en otros planetas.
Eneko Axpe dejó para el final de su intervención “el proyecto más divertido e innovador”, un microbio que captura el CO2 para generar proteínas, una iniciativa que ya abordó la NASA en el proyecto Apolo de los años 60 con el objetivo de alimentar a los astronautas.
Estas iniciativas muestran la necesidad que tiene el ser humano de dar respuesta a las necesidades de alimentación de la población mundial de una forma sostenible.
Si no ve correctamente el vídeo use este enlace.
Para saber más:
¿Qué es realmente una dieta saludable y sostenible?
¿Realmente necesitamos insectos, microalgas o carne de laboratorio como fuentes alternativas de proteína?
Crónica de Roberto de la Calle / GUK
El artículo Naukas Pro 2022: Alimentos alternativos y sostenibles se ha escrito en Cuaderno de Cultura Científica.
Biojardineras o cómo depurar el agua con piedras, plantas y microorganismos
 Biojardinera en el distrito de Santa Rita de Nandayure (provincia de Guanacaste, Costa Rica). Foto: Guillermo A. Durán / Flickr, CC BY-NC-ND
Biojardinera en el distrito de Santa Rita de Nandayure (provincia de Guanacaste, Costa Rica). Foto: Guillermo A. Durán / Flickr, CC BY-NC-NDCuando nos dijeron que era posible depurar aguas residuales cultivando plantas sobre un lecho de grava nos costó creerlo. Pero todavía nos sorprendió más conocer de primera mano el caso de la comunidad de El Rodeo, en El Salvador, donde recientemente se han instalado 60 biojardineras * para tratar las aguas grises de más de 80 familias y reutilizarlas en el riego.
Las aguas grises son las aguas residuales que proceden de la ducha, lavamanos y bañera, y se diferencian de las aguas negras, que provienen del inodoro.
Según datos de Naciones Unidas, más del 80 % de las aguas residuales se vierten en ríos, lagos o mares sin tratamiento previo, lo que provoca la contaminación de los recursos hídricos.
El sector agrícola representa aproximadamente el 70 % del consumo global de agua, por lo que crece el interés por la reutilización de las aguas grises para el regadío, especialmente en comunidades del sur global.
Pero ¿cómo se puede promover la instalación de sistemas de tratamiento de aguas residuales en comunidades con escasos recursos económicos y materiales?
El desarrollo de tecnologías alternativas apropiadas es fundamental para asegurar que todas las personas dispongan de un sistema de saneamiento adecuado y así contribuir a alcanzar algunas de las metas que se establecen en el sexto eje de los Objetivos de Desarrollo Sostenible de Naciones Unidas.
Entre otras opciones, las biojardineras o humedales artificiales acaparan mucha atención por ser sistemas accesibles, económicos, eficientes y sencillos de instalar y mantener.
 Biojardinera instalada en la comunidad de El Rodeo (El Salvador). Foto aportada por las autoras.¿Cómo funcionan las biojardineras?
Biojardinera instalada en la comunidad de El Rodeo (El Salvador). Foto aportada por las autoras.¿Cómo funcionan las biojardineras?
Estos sistemas de saneamiento buscan replicar e incluso mejorar las condiciones que se dan en los humedales naturales para así aprovechar su capacidad de depuración. Combinan procesos físicos, químicos y biológicos.
A la entrada del sistema, las aguas se introducen en uno o varios tanques de pretratamiento, también llamados trampas de grasas, donde aceites y grasas se separan por flotación, y donde los sólidos pesados se recogen en el fondo del tanque.
A continuación, el agua pasa a una balsa rellena con grava. Es aquí donde ocurre la magia (o mejor dicho, la ciencia). Todos los elementos que se emplean en estos sistemas se combinan para lograr que las aguas salgan limpias y listas para reutilizarse.
 Balsa rellena con grava para depurar las aguas. Foto aportada por las autoras.
Balsa rellena con grava para depurar las aguas. Foto aportada por las autoras.En la primera sección de la balsa se colocan piedras más gruesas con la misión de retener los sólidos gruesos suspendidos que no se han retenido en el pretratamiento.
La grava fina, que ocupa la mayor parte de la balsa, sirve para favorecer el crecimiento y la fijación de los microorganismos: pequeños organismos unicelulares que son los responsables de la digestión de la materia orgánica suspendida en el agua, el principal contaminante en las aguas residuales domésticas. Estos microorganismos están presentes en el suelo y en las aguas, y proliferan de forma natural cuando se dan las condiciones adecuadas, que es lo que se pretende replicar en el lecho de grava de la biojardinera.
Por último, las raíces de las plantas ayudan a retener pequeños sólidos suspendidos y sobre todo absorben los nutrientes generados por los microorganismos en la digestión de la materia orgánica.
Por tanto, cuando construimos una biojardinera tenemos que escoger unas plantas que se adapten al clima y puedan vivir con las raíces permanentemente inundadas (plantas acuáticas locales) y una grava que permita el paso del agua y la fijación de los microorganismos. Y si nos aseguramos de que los microbios no pasan hambre, la naturaleza se encargará del resto.
También un elemento decorativoAunque el logro principal de la biojardinera es garantizar un nivel de depuración de las aguas grises suficiente para que sea posible su reutilización o su vertido sin alterar el equilibrio de sistemas hídricos naturales, este sistema tiene otras ventajas.
La parte aérea de las plantas es decorativa y tiene un impacto visual positivo, lo que facilita su integración paisajística en cualquier ubicación.
Además debido al elevado nivel de eliminación de carga orgánica, el agua que sale de la biojardinera se puede emplear para regar jardines, árboles frutales o para asegurar la producción hortícola durante la época seca en las regiones tropicales.
En la mayoría de casos las biojardineras se utilizan para el tratamiento de aguas grises procedentes de hogares, por lo que se adaptan muy bien a entornos domésticos. No obstante, se han instalado con éxito a mayor escala, como por ejemplo para el tratamiento de las aguas procedentes de los comedores de la Universidad de El Salvador.
La ciencia de los humedales artificialesAunque el interés por los humedales artificiales como solución natural para el tratamiento de aguas comenzó en los años 80, hasta hace unos años estos sistemas no llamaron la atención de la comunidad científica.
En la última década la necesidad de ahondar en el conocimiento de los mecanismos de depuración para optimizar el diseño y aprovechar todo el potencial de estos sistemas ha despertado el interés por este tipo de soluciones naturales.
Recientemente, miembros del Departamento de Ingeniería Química de la Universidad del País Vasco hemos estudiado la polivalencia de estos sistemas mediante el modelado matemático y simulación de su funcionamiento. Hemos demostrado que son capaces de soportar cambios de caudal y composición de las aguas grises e incluso las variaciones estacionales de las regiones tropicales.
Biojardineras en su jardínUna de las ventajas que hace más atractiva la implantación de los humedales artificiales es la facilidad de construcción y mantenimiento de la instalación durante su vida útil. Es por ello que muchas comunidades del sur global están apostando por este sistema para el tratamiento de aguas grises domésticas, como por ejemplo en El Salvador y en Costa Rica.
Si son tantas las ventajas de las biojardineras, ¿por qué no instalar este sistema en nuestro jardín?
Actualmente hay disponibles numerosos manuales sobre cómo construir y mantener biojardineras. Así que si disponemos de un terreno y podemos hacer acopio de algunos materiales de construcción sencillos (como tuberías de plástico y bidones), en unas pocas semanas podremos disponer de nuestro propio sistema sostenible para el tratamiento de aguas residuales domésticas.![]()
Sobre las personas autoras: Onintze Parra Ipiña es investigadora predoctoral en Ingeniería Química en la UPV/EHU y secretaria de la junta directiva de Mugarik Gabeko Ingeniaritza / Ingeniería Sin Fronteras País Vasco., y Roberto Aguado es catedrático de Ingeniería Química de la UPV/EHU.
Nota:
[*] El proyecto de construcción de biojardineras en El Salvador fue financiado por el Ayuntamiento de Bilbao (proyectos 2019-017085 y 2020-015220) y coordinado por Ingeniería Sin Fronteras País Vasco.
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Biojardineras o cómo depurar el agua con piedras, plantas y microorganismos se ha escrito en Cuaderno de Cultura Científica.
Heráldica geológica
Suelo insistir mucho en la idea de que la Geología se encuentra en todo lo que nos rodea y que nos ha condicionado como especie y como sociedad, aunque muchas veces no sea tan sencillo darnos cuenta. Por eso, en esta ocasión os traigo a colación un tema curioso donde también la Geología tiene mucho que decir. Se trata de la heráldica, es decir, los escudos de muchas localidades del mundo.
Cuando un pueblo o una ciudad tiene que crearse su propio escudo heráldico elige como tema central alguna cosa que sea característica de dicha localidad. Puede ser un castillo enorme que se hizo famoso por alguna batalla antigua, un árbol milenario que ya se encontraba ahí antes de los primeros asentamientos humanos de la zona o un puente sin cuya presencia no habría sido posible la conexión comercial con otros pueblos de su alrededor. Pero, ¿qué sucede cuando lo más característico de una localidad es alguna cosa geológica? Pues que se incluye en su escudo. Así que vamos con algunos ejemplos muy curiosos y relativamente cercanos.
 Escudo de la localidad de Murero, provincia de Zaragoza, con un trilobites de color dorado. Fuente
Escudo de la localidad de Murero, provincia de Zaragoza, con un trilobites de color dorado. FuenteEn la provincia de Zaragoza se encuentra una localidad llamada Murero que posee un yacimiento paleontológico del periodo Cámbrico que se ha convertido, científicamente hablando, en uno de los más importantes del mundo, llegando a describirse numerosas especies nuevas desconocidas para la ciencia. Este yacimiento de trilobites le ha dado fama mundial al pueblo, convirtiéndose en una de sus mayores características distintivas, lo que ha provocado que uno de estos fósiles sea el protagonista del escudo de la localidad.
 Escudo de Tejada (Burgos), en el que aparecen dos ammonites. Fuente
Escudo de Tejada (Burgos), en el que aparecen dos ammonites. FuenteUna historia similar la encontramos en Tejada, provincia de Burgos. En los alrededores de esta localidad se encuentran un buen número de afloramientos de los periodos Jurásico y Cretácico con abundante contenido fósil, siendo los más llamativos los ejemplares de ammonites que llegan a alcanzar varios centímetros de diámetro. Hace algo más de una década, dicha localidad quiso potenciar su turismo como un recurso económico, dándose cuenta de que uno de sus recursos más llamativo era su patrimonio geológico, así que crearon un museo, un centro de interpretación y varios recorridos geológicos, llegando a modificar su escudo añadiéndole dos fósiles de ammonites.
Pero no solo de paleontología vive la heráldica. Numerosas provincias españolas tienen una historia minera muy antigua y variada que ha llegado a caracterizar su desarrollo social e industrial durante siglos. Y eso también se ve reflejado en los escudos de muchas localidades muy ligadas a la minería.
 Escudo del Ayuntamiento de Minas de Riotinto, provincia de Huelva, con dos martillos cruzados y ondas blancas y rojas que representan al río Tinto. Fuente
Escudo del Ayuntamiento de Minas de Riotinto, provincia de Huelva, con dos martillos cruzados y ondas blancas y rojas que representan al río Tinto. FuenteEn la provincia de Huelva se encuentra el Ayuntamiento de Minas de Riotinto, cuyos yacimientos de sulfuros de hierro, cobre, plomo y cinc fueron explotados en diversas minas desde tiempos remotos, incluso antes de que los romanos se asentasen en la Península Ibérica. De hecho, la alteración superficial de estas mineralizaciones, que cuenta con una buena ayuda de bacterias extremófilas, ha provocado la típica coloración rojiza del río que atraviesa la zona, de ahí que se llame río Tinto. Pues en el escudo de este ayuntamiento encontramos dos martillos cruzados, uno de aspecto antiguo y otro más moderno, y unas ondulaciones en las que se alternan ondas de color blanco y de color rojo que representan al río Tinto.
 Escudo de Mieres (Asturias) con los símbolos de la minería del carbón y la siderometalurgia. Fuente
Escudo de Mieres (Asturias) con los símbolos de la minería del carbón y la siderometalurgia. FuenteOtra de las cuencas mineras más famosas de toda la Península Ibérica son los yacimientos de carbón de Asturias, que marcaron el desarrollo social e industrial de muchas localidades desde su descubrimiento a comienzos del siglo XVII hasta no hace demasiadas décadas. Y esta eventualidad también ha quedado reflejada en varios escudos heráldicos. Un ejemplo lo encontramos en el escudo del Concejo de Mieres, que se caracteriza por presentar una maza y un martillo cruzados junto a una rueda dentada, símbolo de la industria siderometalúrgica que se impulsó en toda esta zona.
 Escudo de Lanjarón (Granada) con la representación de Sierra Nevada y sus famosas aguas. Fuente
Escudo de Lanjarón (Granada) con la representación de Sierra Nevada y sus famosas aguas. FuenteTambién existen recursos geológicos a priori menos obvios de identificar, pero que también han sido y son muy importantes para el avance de muchas localidades y que forman parte indispensable de sus heráldicas. Me estoy refiriendo al agua minero-medicinal. En el escudo de la localidad de Lanjarón, en la provincia de Granada, aparecen una montaña y una pequeña fuente de la que fluyen dos chorros de agua. De manera similar, en el escudo del Ayuntamiento de Medio Cudeyo, al que pertenece la localidad de Solares, en Cantabria, encontramos una gran fuente de la que sale a presión un chorro de agua que se bifurca en dos. En ambos casos queda en evidencia la importancia del agua hidrotermal en el desarrollo económico y social de estas localidades.
 Escudo de Medio Cudeyo (Cantabria), con una fuente de la que fluye un chorro bifurcado de agua. Fuente
Escudo de Medio Cudeyo (Cantabria), con una fuente de la que fluye un chorro bifurcado de agua. FuenteY es que, tal y como decía al principio, la Geología nos rodea y nos condiciona tanto que ya ni nos damos cuenta de su impronta en nuestra sociedad. Pero siempre está ahí y, en muchas ocasiones, bien visible.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Heráldica geológica se ha escrito en Cuaderno de Cultura Científica.
Frances Chick Wood, de la química a la estadística médica
Frances Chick Wood comenzó a trabajar como química en temas relacionados con la polimerización y con la fermentación de la uva. Pronto sus intereses giraron hacia la estadística médica, disciplina en la que realizó destacadas aportaciones.
 Frances Wood. Fuente: Significance
Frances Wood. Fuente: SignificanceFrances Chick nació el 25 de diciembre de 1883 en Londres en el seno de una familia metodista. Fue la sexta de las siete hermanas que llegó a la vida adulta en una prole de doce niñas y niños. Como el resto de sus hermanas, fue educada de manera estricta y asistió al Notting Hill High School, una escuela femenina célebre por su esmerada educación en ciencias.
Cinco de las hermanas, incluida Frances, continuaron sus estudios superiores y obtuvieron grados universitarios. Entre ellas se encuentra la reconocida nutricionista Harriette Chick (1875-1977).
Frances estudió en el University College de Londres, graduándose con honores en química en 1908. Ese mismo año obtuvo un puesto de investigadora química en el Instituto Lister de Medicina Preventiva, institución en la que en ese momento ya trabajaba su hermana Harriette.
En 1910, el Instituto Lister contrató al epidemiólogo y estadístico Major Greenwood (1880-1949) para inaugurar en la institución un Departamento de Estadística. Frances asistió a una serie de conferencias impartidas por el médico y, a partir de 1911, comenzó a trabajar a tiempo completo en estadística médica. Entre otros trabajos, Chick comenzó a investigar la correlación entre las condiciones de los hogares y el desarrollo mental de los estudiantes de las escuelas primarias. Tan solo tuvo tiempo de recopilar los datos e iniciar su análisis. Al estallar la Primera Guerra Mundial en 1914 fue destinada a la Cámara de Comercio. Posteriormente fue transferida al Ministerio de Municiones donde permaneció hasta marzo de 1919, momento en el que renunció debido a su embarazo. En 1911 se había casado con Sydney Wood, un inspector de la Junta de Educación. A finales de septiembre de 1919 dio a luz a una niña, Barbara. Frances falleció dos semanas más tarde, el 12 de octubre, por una septicemia tras su parto por cesárea.
Frances Chick Wood como estadística médicaLa carrera estadística de Frances Wood fue breve, pero de gran relevancia.
En 1913 publicó dos artículos en solitario. En el primero de ellos, «The course of real wages in London, 1900–12», documentó de manera detallada cómo los números índice (medida estadística utilizada para comparar una o varias magnitudes en distintas situaciones temporales o espaciales) usados por la Cámara de Comercio para medir los cambios a lo largo del tiempo en los salarios, los precios minoristas y el alquiler no eran satisfactorios. En su segundo artículo «The construction of index numbers to show changes in the price of the principal articles of food for the working classes» ampliaba el anterior estudio. Volvió a este tema en 1916 en su publicación «The increase in the cost of food for different classes of society since the outbreak of war» en la que subrayaba que las clases medias podían amoldarse al aumento de los precios de los alimentos cambiando la composición o la calidad de su dieta, mientras que las clases trabajadoras no tenían esta flexibilidad. “Queda perfectamente claro que, con creces, el mayor aumento en el coste de los alimentos, durante los últimos dos años, ha recaído en la clase menos capaz de soportarlo”, afirmaba la investigadora en este trabajo.
En 1914 publicó tres artículos con Greenwood. El primero, «On changes in the recorded mortality from cancer and their possible interpretation», estaba relacionado con la mortalidad por cáncer. Intentaban responder a la suposición de que el cáncer era una enfermedad en aumento. Concluyeron que, efectivamente, esta enfermedad se había incrementado, aunque admitían las dificultades metodológicas que planteaba la pregunta. En el segundo artículo, «The relation between the cancer and diabetes death-rates», los autores comparaban las tasas de mortalidad para el cáncer y la diabetes, que estaban altamente correlacionadas. En el tercer artículo, «A study of index correlations», formalizaban la cuestión de la correlación entre las tasas de mortalidad.
En 1915, Frances comenzó a trabajar como investigadora de estadísticas de empleo en la Cámara de Comercio, siendo muy reconocido su trabajo. En octubre de 1916 cambió su destino al Departamento Central de Estadística del Ministerio de Municiones, a cargo de Greenwood. Se desconoce cuales fueron exactamente sus tareas, aunque estaban relacionadas con contratos de armas y municiones.
En 1920, Wood (que ya había fallecido), J. W. Brown y Greenwood publicaron el trabajo «The fertility of the English middle classes: a statistical study«. En él se describía un trabajo iniciado en 1915 sobre el impacto de la educación universitaria en la fertilidad de la clase media. Numerosas tablas de datos y ecuaciones de regresión relacionaban la fertilidad con la edad y la duración del matrimonio en mujeres universitarias y no universitarias.
Los datos recopilados por Wood entre los años 1913 y 1914 sobre las condiciones de los hogares y el desarrollo mental de los escolares aparecieron también póstumamente en 1923.
Su legado y los reconocimientosFrances Wood fue una pionera para las mujeres en la estadística. El Departamento de Estadística del Instituto Lister, fundado en 1910, se suele reconocer como el primer departamento de estadística médica. Si su director, Greenwood, fue el primer estadístico médico, Frances fue la primera mujer trabajando en esta disciplina.
El 1 de febrero de 1913 Wood fue elegida miembro de la Royal Statistical Society. Fue la primera mujer en el Consejo de esta sociedad y la primera que formó parte de su Comité Ejecutivo.
Recibió la Orden del Imperio Británico en 1917 y fue nombrada Oficial de la Orden en 1918.
En 1921, la Royal Statistical Society instituyó el Frances Wood Memorial Prize a la mejor investigación estadística relacionada con problemas económicos o sociales. En 2011 se utilizó el fondo de este premio para establecer la medalla Wood en su honor.
Referencias
-
J. O’Connor and E. F. Robertson, Frances Chick Wood, Mac Tutor, University of St. Andrews, 2017
-
Tim Cole, The remarkable life of Frances Wood, Significance Magazine, octubre 2017, 34-37
-
Frances Wood, Wikipedia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Frances Chick Wood, de la química a la estadística médica se ha escrito en Cuaderno de Cultura Científica.
Einstein y Mileva Marić
Mileva Marić, familiarmente Mila, fue la primera esposa de Einstein. Su relación fue emocionalmente intensa de principio a fin. Comenzó como una aventurilla en la universidad, alimentada por su mutua pasión por la física, la desaprobación de sus amigos y de la familia de Einstein, y el ardor de la juventud. Terminó con un amargo y largo divorcio, crisis físicas y mentales por ambas partes, y un extrañamiento de por vida.
 La pareja Marić-Einstein en 1912. Fuente: ETH-Bibliothek Zürich, Bildarchiv / Portr_03106 / CC BY-SA
La pareja Marić-Einstein en 1912. Fuente: ETH-Bibliothek Zürich, Bildarchiv / Portr_03106 / CC BY-SAMila nació en Hungría en 1875, cuatro años antes que Einstein. La mayoría de las mujeres en el este de Europa simplemente no iban al colegio pero, gracias a la mentalidad de su padre y a su influencia política, Mila fue una excepción. Tras graduarse con las mejores notas en el instituto, Mila se marchó a Zúrich, entonces un refugio para las mujeres intelectuales. Mila empezó a estudiar medicina en la Universidad de Zúrich, pero un año después decidió que quería estudiar física, para lo que se matriculó en el Politécnico. Aquí es donde conoció a Albert Einstein.
Einstein se enteró sin duda de la llegada de Mila el primer día: era la única mujer en su promoción de cinco estudiantes. Iniciaron una amistad que pronto desembocó en algo más. Esta relación se encontró con la oposición frontal de familia (sobre todo de Pauline, la madre de Einstein), de las amigas de ella y de los amigos de él, que le recordaban que estaba coja (un defecto de nacimiento, como el de su hermana Zorka). Esta oposición solo sirvió para fortalecer la pareja. Mucho tiempo después, Mila recordaría esta época feliz llena de café, salchichas y física.
Sus estudios no iban muy bien. La joven pareja le caía mal al tradicional profesor Weber. En el que se suponía que sería su último año de estudios, 1900, Einstein consiguió aprobar sus exámenes con este profesor, siendo cuarto de su promoción de cinco y consiguiendo su título. Mila fue quinta, y no superó el examen. Tenía que repetir la asignatura.
Tras graduarse, Einstein decidió irse con sus padres a Milán, dejando a Mila para que terminase sus estudios. Los repetidos intentos de encontrar un empleo de Einstein se encontraban con lo que Einstein interpretaba eran sabotajes del profesor Weber, hasta que finalmente encontró un puesto para enseñar matemáticas en un colegio cerca de Zúrich. Para celebrarlo la pareja se fue de viaje a los Alpes. Mila quedó embarazada en esta excursión.
En julio de 1901, embarazada de tres meses, Mila volvió a suspender el examen. Esto supuso el fin de la carrera académica de Mila, y la imposibilidad de conseguir su habilitación como profesora de secundaria. Se fue a casa de sus padres, donde dio a luz a su hija “ilegítima”, Lieserl, en febrero de 1902. Mientras tanto, Einstein había conseguido un empleo con algo de porvenir en la Oficina Federal de Patentes en Berna.
Poco después la pareja se reunía en Berna, dejando a Lieserl con los abuelos maternos, y se casaba el 6 de enero de 1903 en una ceremonia civil en la que los únicos asistentes fueron los contrayentes y dos amigos de Einstein y Mila, Conrad Habitch y Maurice Solovine. Einstein después diría que se casó por su “sentido del deber”. No pasa mucho tiempo hasta que Mila regresa a Hungría y vuelve a Berna sin su hija. El rastro de la hija de Einstein se pierde para siempre, dada probablemente en adopción. Einstein nunca la conoció.
En el otoño de 1903, la pareja se mudó al más famoso de los siete apartamentos en los que vivió en Berna, el que hoy es un museo, la Einsteinhaus. Mientras Einstein daba vueltas en su cabeza a cuatro nuevas teorías físicas que verían la luz en 1905, Mila quedaba embarazada de nuevo. El 14 de mayo de 1904 nacía Hans Albert.
La familia Einstein hizo un viaje a la casa de la familia de Mila en el verano de 1905. Era la primera vez que Einstein se encontraba con sus suegros. Por aquello de ser agradable le dijo a Milo, su suegro: “Mila resuelve todos mis problemas matemáticos”.
Fueron frases como esta y la cacareada habilidad matemática de Mila lo que dio pábulo a especulaciones en los años 80 y 90 de que fue Mila la verdadera autora de las teorías [plural] de la relatividad de Einstein. Démonos cuenta de que los acontecimientos narrados hasta ahora no parecen que pudiesen predisponer a Mila a ser especialmente activa en la investigación de primera línea en física. Además, ¿por qué la relatividad y no el efecto fotoeléctrico (recordemos, por el que recibiría Einstein el Nobel) o el movimiento browniano? Veremos a continuación que Mileva no podría haber contribuido a la teoría general. Hoy día nadie, salvo aquellas personas más interesadas por la ideología que por los hechos, apoyan esta idea.
La pareja no era especialmente feliz. Y cometió el error que muchas parejas cometen intentando salvar el matrimonio: otro hijo. En el verano de 1910 nació Eduard. Pero esta felicidad fugaz duraría poco. Sucesivas mudanzas a Praga, vuelta a Zúrich y, finalmente, Berlín hicieron que Mila se sintiese más y más sola y miserable. Einstein viajaba sin parar y evitaba volver a casa.
Einstein siempre se sintió muy atraído (valga el eufemismo) por determinado tipo de mujeres. Su recientemente adquirida fama le resultaba muy útil para conseguir nuevas amantes. En 1912 [la foto que ilustra este texto es de este año], comenzó una relación estable con su prima Elsa. Mila lo sospechó desde el principio, Einstein tampoco ponía demasiado cuidado en ocultarlo. Mila exigió que Einstein abandonase la casa. Michele Besso acudió a Berlín para acompañarla a ella y a sus hijos de vuelta a Zúrich.
En febrero de 1916, recién presentadas las ecuaciones de campo de la relatividad general, Einstein propone por primera vez el divorcio. Mila, con 41 años, sufre varios ataques al corazón. A efectos prácticos, el matrimonio ha acabado y Einstein ya vive con Elsa y las hijas de esta. Finalmente, el 14 de febrero de 1919 el divorcio es una realidad. En el acuerdo final, la pareja establece que, en el caso de que a Einstein le concedan el Nobel, él retendrá la medalla y el diploma, pero que el dinero será para ella y los niños, que es lo que finalmente ocurriría. De nuevo, esto se ve por algunos como otro indicio de que Mila habría participado de alguna manera en las teorías físicas de Einstein. Muchos olvidan acudir en este punto, una vez más, a las fuentes: la disposición crea con el dinero del premio, si llega, un fondo para sus hijos, del que la madre puede disponer con autorización expresa previa de Einstein, solo teniendo libertad para disponer de los intereses que genere. Más que un reconocimiento de mérito parece más bien la preocupación por asegurar el futuro de los hijos, haga lo que haga la madre o le pueda ocurrir al padre.
Poco antes de que Einstein abandonase Europa para no volver, en 1933, Einstein y Mila volvieron a verse después de 16 años, por última vez. Einstein fue a visitar a su hijo Eduard, esquizofrénico, que estaba internado en una institución mental. La relación con Einstein y Elsa, que le acompañó, fue correcta aunque distante.
Mila moriría en Zúrich en agosto de 1948. Nunca publicó ningún trabajo científico.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 13 de diciembre de 2009.
El artículo Einstein y Mileva Marić se ha escrito en Cuaderno de Cultura Científica.
Un linaje completo de los virus de la gripe podría haberse extinguido por la pandemia de COVID-19
La irrupción del virus SARS-CoV-2 en el año 2019 ha provocado una de las mayores crisis sanitarias globales en la historia reciente y causado infinidad de cambios socioeconómicos en todo el planeta. Unos cambios cuyas consecuencias a largo plazo aún no somos capaces de vislumbrar con nitidez. Mientras multitud de personas y medios de comunicación centraban su atención, con preocupación, en cada nueva variante del coronavirus y sus consecuencias sobre la salud, una anomalía microbiológica tenía lugar en el mundo, alejada de los focos mediáticos: un linaje completo de los virus influenza responsables de la gripe, el linaje B/Yamagata, podría haberse extinguido. En otras palabras, un grupo de variantes de virus de la gripe, estrechamente relacionados entre sí al proceder de un ancestro común, podría haber desaparecido y dejado de afectar para siempre a la especie humana. De esta forma, solo tres grupos principales de virus de la gripe seguirían con nosotros provocando epidemias cada año, los subtipos H1N1 y H3N2 de los virus influenza A y el linaje Victoria de los virus influenza B.
 Imagen digital de un modelo de ortomixovirus, el tipo de virus responsable de la gripe. Fuente: Sanofi Pasteur – flickr CC BY-NC-ND 2.0
Imagen digital de un modelo de ortomixovirus, el tipo de virus responsable de la gripe. Fuente: Sanofi Pasteur – flickr CC BY-NC-ND 2.0La pandemia de COVID-19 ha provocado un fenómeno global de evolución a cámara ultrarrápida y selección natural entre los virus, esas entidades en el limbo entre la vida y la muerte. Así, mientras el SARS-CoV-2 se expandía por el mundo y surgían nuevas variantes que se reemplazaban entre ellas según su capacidad para infectar y transmitirse y según los comportamientos de las poblaciones humanas, la circulación de los virus de la gripe A y B se restringía de forma drástica; hasta tal punto que no hubo prácticamente epidemias de gripe invernales en los años 2020 y 2021. Además, la diversidad genética de los virus influenza cayó en picado en dichos años. Las diversas medidas sanitarias (mascarillas, distancia de seguridad, confinamientos, ventilación, higiene de manos, restricciones en los viajes…) que se tomaron para prevenir avalanchas de casos graves de COVID-19 en los hospitales no sirvieron para arrinconar al SARS-Co-V-2, pero sí a diversos virus de la gripe.
Los científicos llevan años investigando si el linaje Yamagata de la gripe sigue con nosotros, entre los humanos, agazapado en algún rincón del mundo. A pesar de los esfuerzos, desde abril de 2020 hasta ahora no se han encontrado pruebas fiables de su existencia. La vigilancia epidemiológica de los virus de la gripe a través de FluNet, de la Organización Mundial de la Salud (OMS), informa de la detección de 30 casos de gripe por el linaje B/Yamagata desde abril hasta finales de 2021 y de 38 en 2022. Un número ínfimo, si se compara con los miles y miles de casos que se identificaban cada año antes de la llegada de la pandemia. No obstante, los investigadores creen que estos casos aislados no son, en realidad, pruebas de que el linaje Yamagata siga con nosotros, sino que reflejan la detección de virus atenuados o inactivados derivados de este linaje, empleados en las vacunas contra la gripe.
La extinción del linaje Yamagata no es una mera curiosidadLa extinción del linaje Yamagata no es una mera curiosidad, podría suponer también un feliz acontecimiento para la humanidad. Por un lado, si se confirma que este grupo de virus ha desaparecido, esto significaría que existen menos variantes de la gripe circulando por el mundo, provocando epidemias y mutando para originar otras variantes, alguna de las cuales podrían ser más virulentas. Por otro, que el grupo de potenciales virus de la gripe que podrían atacar a las personas se reduzca podría ser una oportunidad para mejorar la eficacia de las vacunas anuales contra la gripe.
A lo largo del mundo se han popularizado las vacunas trivalentes y tetravalentes que protegen contra tres o cuatro tipos de virus de la gripe respectivamente. En ambos tipos de vacunas se incluyen uno o dos linajes de los virus influenza B, en el que se encuentra el linaje B/Yamagata y el linaje B/Victoria. Dado que cada año se intenta predecir cuáles serán los virus de la gripe que predominen por cada hemisferio, eliminar al linaje Yamagata supone centrarse mejor en el resto de virus. Sin embargo, aún es pronto para descartar a este grupo de virus de forma definitiva de las vacunas. Si este linaje volviera a hacer acto de presencia, la pérdida de inmunidad a lo largo del tiempo podría provocar más casos graves y más muertes entre la población vulnerable. Por ahora, la vacuna antigripal tetravalente que se está administrando en España para la temporada 2022-2023 incluye el linaje Yamagata.
Solo el tiempo y los sistemas de vigilancia de los virus de la gripe podrán confirmarnos en un futuro próximo si el linaje Yamagata se ha extinguido definitivamente. A diferencia del resto de extinciones que la humanidad ha provocado a lo largo de su historia, mermando la biodiversidad y los ecosistemas, esta sería una buena noticia para nosotros.
Para saber más:
Efectos colaterales de la Covid-19
Sobre la autora: Esther Samper (Shora) es médica, doctora en Ingeniería Tisular Cardiovascular y divulgadora científica
El artículo Un linaje completo de los virus de la gripe podría haberse extinguido por la pandemia de COVID-19 se ha escrito en Cuaderno de Cultura Científica.
ZientZinema 3: El mundo del silencio

Título original: Le Monde du silence. 1956. 86 min. Francia. Documental. Dirección: Jacques-Yves Cousteau y Louis Malle. Guión: Jacques-Yves Cousteau. Música: Yves Baudrier. Fotografía: Jacques-Yves Cousteau y Louis Malle. 1957: Oscar Mejor Documental. 1956: Cannes: Palma de Oro.
A 50 metros de la superficie, los hombres filman una película. Provistos con escafandras autónomas de aire comprimido, se sienten libres de la gravedad, evolucionan libremente.
Primer párrafo de El mundo del silencio.
[Documental es] “todo método de registrar en celuloide cualquier aspecto de la realidad interpretado bien por la filmación de hechos o por la reconstrucción veraz y justificable, para apelar a la razón o a la emoción, con el propósito de estimular el deseo y ampliar el conocimiento y la comprensión humanos, y plantear sinceramente problemas y soluciones en el campo de la economía, la cultura y las relaciones humanas”.
World Union of Documentary, 1948.
Aclamado documental sobre las profundidades submarinas del pionero Jacques-Yves Cousteau (1910-1997) y dirigido por él y por el más tarde reputado director francés Louis Malle (entonces era un estudiante de cinematografía y tenía 23 años). Los autores descubrieron al gran público el colorido del fascinante mundo de las profundidades marinas como nunca antes nadie lo había visto.
El documental se estrenó en París el 26 de mayo de 1956 y, unos meses después, el 25 de septiembre, Basley Crowther, crítico de cine del New York Times, publicó en el periódico una reseña. Es un ejemplo de cómo la recibió el público.
Para Crowther supone un momento de emociones y maravillas y escribe que es el documental más hermoso y fascinante de su tipo jamás filmado, una película de aventuras marinas que es la experiencia de contemplar y admirar maravillas. El único problema para Crowther es que le dan ganas de ponerse una escafandra autónoma y lanzarse al mar.
Antes del comandante Cousteau, no se conocía más que la superficie del océano y sus profundidades constituían un mundo desconocido y amenazador solo vislumbrado por algunos como, por ejemplo, los pescadores de esponjas que filma Louis Malle.
Solamente unos años antes, en 1954, se había estrenado un documental sobre el mundo submarino. El director era el italiano Folco Quilici, se tituló Sesto Continente, y nunca alcanzó la fama de El mundo del silencio. Es un film interesante y muy informativo, que se puede ver en YouTube. Hay que recordar que Folco Quilici ganó la Concha de Plata del Festival de San Sebastián en 1959 con la película De los Apeninos a los Andes.
Gracias a sus inventos, su pasión por el mar, los viajes y el cine, su dominio del mundo de los medios de comunicación y un agudo sentido de los negocios, Jacques-Yves Cousteau ha hecho que millones de personas descubrieran el mundo del silencio a través de numerosas películas y libros. En su haber está también haber logrado que muchos países del globo se preocupen por la ecología, la protección de la Tierra, los océanos y las especies vivas.
Jacques-Yves Cousteau nació en París en 1910. Cuando tenía 10 años su padre se trasladó por trabajo y con su familia a Nueva York donde el joven Jacques se educó. A su vuelta de Estados Unidos, en 1938, terminó sus estudios en la Escuela Naval de Brest e ingresó en la Escuela de Aviación Marítima. Quería ser piloto pero sufrió un grave accidente de tráfico que le dañó su brazo derecho. Para su recuperación, el médico le recomendó la natación. En Marsella probó las gafas que utilizaban los pescadores de perlas de Filipinas y, así, descubrió el mundo submarino.
La película se basa, en parte, en el libro del mismo título publicado en París por Cousteau, Frédéric Dumas y el periodista James Duggan tres años antes de la película, en 1953. Relata la historia de Cousteau y la pesca submarina en Toulon durante la Segunda Guerra Mundial, durante la ocupación nazi, la invención de la escafandra autónoma con Emile Gagnan con la patente presentada del llamado AquaLung, en 1943, la llegada del Calypso en 1950 y los primeros viajes de exploración en el barco.
El Calypso, un antiguo dragaminas de la Royal Navy que se utilizaba como ferry, fue comprado por el millonario británico Thomas Loel Guinness y donado por un franco a Cousteau. Viajó desde 1954 y por dos años por el Mediterráneo, el Mar Rojo, el Océano Índico y el Golfo Pérsico. Era un barco de 360 toneladas y 42.7 metros de eslora.
Las filmaciones se hicieron con la escafandra autónoma de 1943, las cámaras submarinas diseñadas y fabricadas por André Laban, Claude Strada y Armand Davso , y la ayuda de los primeros scooters submarinos. Era el mundo submarino en color y con imágenes rodadas hasta los 75 metros de profundidad.
Como ocurre en tantos documentales, en aquellos viajes que duraron dos años, se rodaron 25 kilómetros de película que quedaron en 2500 metros en montaje final de la película.
En ella se incluyen algunas escenas muy criticadas según los criterios actuales de respeto y defensa de la naturaleza. Métodos y técnicas de exploración que ahora se ven arcaicas, desfasadas e incluso escandalosas: masacre de tiburones, dinamita en los arrecifes, sacrificio de un cachalote por un error negligente, destrucción de corales, el trato al mero Jojo o la diversión con las tortugas, … Son escenas, como escribe Phillip Duncan, de la Universidad de Oregon, habituales de aquellos años en documentales o películas de ficción sobre la naturaleza como, por ejemplo, los safaris en las colonias británicas de África Oriental. Recuerdan la curiosidad depredadora de nuestra especie y, también, los métodos de la incipiente investigación científica del mar por inmersión.
Cousteau no era un científicoCousteau no era un científico, era un militar explorador y aventurero que hasta la década de los setenta se movía en un entorno que no había comenzado un acercamiento crítico a la naturaleza. En aquellos años, o poco después, aparecen la preocupación por la biodiversidad, la sobreexplotación pesquera, la contaminación o la destrucción de hábitats. Por todo ello, esta película es el documento de una época y no es una obra fácil para espectadores delicados de nuestro tiempo.
El documental tiene una doble función, informativa y recreativa. Para Bienvenido León, de la Universidad de Navarra, es una construcción con la que el cineasta dirige nuestra atención hacia determinados aspectos de la realidad, a través de un proceso de argumentación. Y, según Bill Nichols, de la Universidad de San Francisco, en el proceso se puede reproducir el mundo con total fidelidad con la realidad condensada, dramatizada, realzada y, siempre, modificada.
Y, según aclara, María Purificación Subires, de la Universidad de Málaga, su objetivo principal es la realidad. Es, en términos cinematográficos, la no ficción. Tiene, por supuesto, el carácter creativo que le dan sus autores, los documentalistas, pero se debe regir por unas normas éticas. Es un género que se basa en historias personales y en testimonios reales y trata de los hechos en profundidad.
Debe cumplir un compromiso con quienes participan en el documental: protagonistas, testigos, expertos, todos los que se prestan a aparecer ante la cámara. Todos ellos esperan que su testimonio se trate con respeto y honestidad.
En segundo lugar, si se manipula o adultera la realidad con una visión sesgada de los hechos, el autor no cumple con el compromiso ético que se merece la audiencia. La elaboración del documental exige seleccionar, como hicieron Cousteau y Malle en El mundo del silencio, parte del material filmado que se elige y, habitualmente, mucho se desecha. Y en la selección se debe evitar manipular la realidad.
El principio máximo de un documental divulgativo es la veracidad. No puede ser sesgado o, si se quiere, propagandístico aunque es habitual que así sea utilizado como se sigue haciendo en la actualidad. En todo caso, si el documentalista tiene determinadas ideas o intereses y ello orienta la historia y como la expone, debe decirlo al público. Lo mismo debe hacer si el documental expone las ideas subjetivas del autor sobre el asunto que trata. El documental cumple siempre una tarea importante que es promover el interés del público por su contenido y, en concreto y según el caso, por la ciencia.
Con la competencia entre cadenas de televisión, los documentales se han convertido, como escribe Bienvenido León, en programas de “entretenimiento basado en hechos reales”. En un documental científico puede ser problemático compaginar el interés del espectador con el rigor científico en el contenido. Quizá signifique perder la información con contenido científico y convertirse en un mero espectáculo.
Uno de los principios en que se debe basar la producción de un documental científico es mantener el rigor o, si se quiere, la ética de la verdad que pide Subires.
Fue Carl Plantinga en 2007 quien escribió que el autor de un documental “debe buscar la verdad o, al menos, intentarlo, por muy complicado que sea en la práctica contar y mostrar lo que es veraz”. Y añade que “en el mismo momento en que una cinta recibe la calificación de documental, surge un contrato implícito entre el realizador y los espectadores mediante el cual la audiencia recibe como verídicas, es decir, verdaderas y exactas, las imágenes y el sonido, las afirmaciones y la informaciones”.
También Plantinga menciona a los protagonistas de los documentales y dice que la película “los caracteriza ya que les construye una imagen y les proporciona una identidad más que simplemente ofrecer un testimonio claro de quiénes son dichos protagonistas”. Además, “la necesidad de seleccionar y, en consecuencia, eliminar, de hacer hincapié en un aspecto o en otro, de introducirse en la historia y de presentar un enfoque significa que la caracterización de las personas que hace un documental es, de algún modo, una construcción”.
En conclusión, no hay que olvidar que el documental es una interpretación creativa de la realidad. No es la propia realidad pues no es posible mostrarla al completo. Como cita Subires a Michael Rabiger, el documental “debería tocar nuestros corazones, no solo nuestros cerebros. Su objetivo es informarnos sobre algo, y también cambiar lo que sentimos sobre ello”.
Referencias:
Barrouw , E. 1996. El documental. Historia y estilo. Ed. Gedisa. Barcelona. 358 pp.
Calvo Hernando, M. 1997. Cousteau regresa al mundo del silencio. Chasqui 60: 49-50.
Crowther, B. 1956. Screen: Beautiful Sea: “Silent World” opens at the Paris here. New York Times September 25.
Duncan, P.D. 2018. (Science) fiction: Genre hybridization in Jacques-Yves Cousteau and Louis Malle’s The Silent World (1956). Journal of Popular Film and Television 46: 108-117.
Egerton, F.N. 2017. History of Ecological Sciences, Part 58B: Marine Ecology, mid-1920s to about 1990: Carson, Riley, Cousteau, and Clark. Bulletin of the Ecological Society of America 98: 113-149.
Herrera, G. 2017. El mundo submarino de Louis Malle y Jacques-Yves Cousteau. El Espectador Imaginario Blog marzo nº 80.
León, B. 2002. La divulgación científica a través del género documental. Una aproximación histórica y conceptual. Mediatika 8: 69-84.
León, B. 2010. La ciencia en imágenes. Construcción visual y documental científico. ArtefaCTos 3: 131-149.
Mamblema Agüero, R. 2012. Las nuevas subjetividades en el cine documental contemporáneo. Tesis Doctoral. UIC. Barcelona.
Martí, O. 1997. Cousteau entra en el mundo del silencio. El País 26 junio.
Morton, M.Q. 2015. Calypso in the Arabian Gulf: Jacques Cousteau’s undersea survey of 1954. Liwa Journal of the National Archives Abu Dhabi 7: 3-28.
Nichols, B. 1997. La representación de la realidad. Cuestiones y conceptos sobre el documental. Ed. Paidós Ibérica. Barcelona. 389 pp.
Plantinga, C. 2007. Caracterización y ética en el cine documental. Archivos de la Filmoteca 57-58: 46-67.
Subires Mancera, M.P: 2021. ¿Están obligados los documentales a contar la verdad? The Conversation 16 septiembre.
Wikipedia. 2021. El mundo del silencio. 3 octubre.
Para saber más:
En lo más recóndito de nuestro planeta
¿Qué hay más allá de la orilla del mar?
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo ZientZinema 3: El mundo del silencio se ha escrito en Cuaderno de Cultura Científica.
Naukas Pro 2022: ¿Cómo adaptamos las ciudades al cambio climático?

Las variaciones climáticas son fenómenos que se han repetido a lo largo de la historia del planeta y de la humanidad, y que han llegado a crear y a extinguir culturas y ecosistemas completos. Sin embargo, nunca antes el ser humano había tenido tanto protagonismo y responsabilidad en el cambio climático que vivimos desde hace más de un siglo. Tampoco había contado con tantas herramientas como las que dispone en la actualidad para analizarlo e incluso hacerle frente.
Solo tenemos que recordar las temperaturas extremas que hemos sufrido este mismo verano, hace apenas unos días, y que nos han obligado a fijarnos unas estrategias de adaptación a nivel individual. Pero, ¿qué ocurre en las ciudades? ¿Cómo se escalan estas estrategias a nivel urbano? ¿Cómo pueden adaptarse las ciudades al cambio climático y evaluar su adaptación al nuevo escenario?
Las urbes se han convertido en las verdaderas protagonistas del cambio climático, aunque de forma indirecta: su papel aglutinante de grandes concentraciones humanas, su enorme consumo de energía y de recursos, y el carácter crítico de sus infraestructuras las han convertido en un polo de atención específico en términos de gestión de riesgos y de planificación urbana. Según datos de Naciones Unidas, desde 2007 las ciudades acogen a más de la mitad de la población mundial, y se espera que dicha cantidad aumente hasta el 60% para 2030.
La responsable del Grupo de Investigación sobre Adaptación de Basque Centre for Climate Change (BC3), Marta Olazabal, abordó el jueves 15 de septiembre este fenómeno global en el marco de Naukas Pro en el Palacio Euskalduna de Bilbao, para responder a algunas de estas preguntas.
Olazabal explicó que en la actualidad miles de ciudades por todo el planeta trabajan de forma activa para adaptarse a este escenario con estrategias encaminadas a controlar las emisiones de gases de efecto invernadero, una de las principales fuentes del calentamiento global. La investigadora explicó que el objetivo de su investigación consiste precisamente en medir el progreso de estas acciones, un extremo que resulta especialmente complejo por la existencia de múltiples métricas; porque se trata de una evaluación local y que, por lo tanto, está condicionada por su contexto, y porque sus beneficios no son universales.
Progreso, clave para la adaptaciónEn cualquier caso, Marta Olazabal explicó que resulta prioritario a nivel global evaluar cómo progresan las urbes en su proceso de adaptación al cambio climático, una labor que, por el momento, se encuentra en fase “embrionaria” porque las ciudades “están experimentando con diferentes aproximaciones y aprendiendo sobre la marcha”.
La investigadora constató la importancia que tiene comprender “las dinámicas de estos impactos”; saber “cómo afectan a nuestras urbes”, y determinar “qué podemos hacer para prepararnos” ante este desafío. “También resulta crítico entender cómo nuestras dinámicas sociales y económicas y el diseño urbano influyen e incluso agravan de forma significativa los impactos ambientales y climáticos”, explicó la investigadora para, a continuación, lanzar una pregunta al aire: “Actualmente miles de ciudades y pueblos planifican y diseñan políticas de mitigación y adaptación al cambio climático, pero ¿serán estas políticas eficaces? ¿Cómo saber si lo estamos haciendo bien?”.
Para responder a estas preguntas la investigadora trazó las líneas maestras del proyecto Imagine Adaptation, que ella misma pondrá en marcha y dirigirá a partir del próximo mes de noviembre.
Se trata de una ambiciosa iniciativa que ha recibido 1,5 millones de euros de financiación del European Research Council, que se desarrollará a lo largo de los próximos cinco años. Su objetivo consiste en “realizar un avance pionero en la ciencia de la adaptación a través de propuestas concretas que permitirán evaluar el progreso de la adecuación al cambio climático en las ciudades”.
Esta iniciativa pretende contribuir a que los pueblos y ciudades desarrollen políticas efectivas de aclimatación al nuevo escenario, monitorizar su progreso, evaluar sus resultados y aprender de las acciones que llevan a cabo para minimizar las vulnerabilidades urbanas frente a este fenómeno desde el punto de vista social, ambiental y económico. Es decir, poner los medios necesarios para “incrementar la capacidad de resiliencia urbana”.
El cambio climático es un fenómeno global que se ha recrudecido por efecto de la acción del ser humano desde el arranque de la revolución industrial. Desde finales del siglo XIX, la temperatura media de la Tierra ha aumentado 1,2oC a consecuencia de la actividad humana y ha contribuido a dibujar una tendencia alcista que todavía no ha finalizado. Según las predicciones climáticas de la Organización Meteorológica Mundial, entre 2020 y 2024 se espera que esta temperatura crezca al menos 1oC más que el crecimiento registrado en los niveles preindustriales, e incluso existe un 20% de probabilidades de que ese crecimiento ronde los 1,5oC, un alza desmesurada para un periodo de tiempo tan corto. A consecuencia de este ascenso el planeta ya ha comenzado a sufrir temperaturas extremas, precipitaciones intensas, una subida generalizada del nivel del mar, sequías, etc., fenómenos que empeorarán con el paso del tiempo.
La lucha contra el cambio climático y sus consecuencias inspiran una parte importante de los Objetivos de Desarrollo Sostenible de la Agenda 2030 de Naciones Unidas, que preside la edición Naukas Pro de este año.
Si no ve correctamente el vídeo use este enlace.
Para saber más:
Certezas e incertidumbres sobre el cambio climático
Crónica de Roberto de la Calle / GUK
El artículo Naukas Pro 2022: ¿Cómo adaptamos las ciudades al cambio climático? se ha escrito en Cuaderno de Cultura Científica.
Las dosis de pesticidas dependen del tipo de suelo
Miembros del Grupo de Biología Celular en Toxicología Ambiental de la UPV/EHU han investigado cómo mejorar el modelo PERSAM utilizado por la Autoridad Europea de Seguridad Alimentaria (EFSA) en la regulación de plaguicidas. Han analizado los riesgos que provocan cuatro pesticidas en dos tipos de organismos del suelo en el norte, centro y sur de Europa.
 Mapas de distribución de las concentraciones observadas en el suelo (A) y en las aguas de los poros del suelo (B) (a una profundidad de 1 cm) tras la aplicación del producto fitosanitario esfenvalerato. Se observan diferencias en las concentraciones de los dos tipos de compartimento, así como diferencias de concentración entre diferentes regiones, aunque la aplicación del producto fitosanitario en Europa haya sido similar.
Mapas de distribución de las concentraciones observadas en el suelo (A) y en las aguas de los poros del suelo (B) (a una profundidad de 1 cm) tras la aplicación del producto fitosanitario esfenvalerato. Se observan diferencias en las concentraciones de los dos tipos de compartimento, así como diferencias de concentración entre diferentes regiones, aunque la aplicación del producto fitosanitario en Europa haya sido similar.La aplicación de productos fitosanitarios puede causar efectos en algunos organismos del suelo contra los que no van dirigidos. La Autoridad Europea de Seguridad Alimentaria (EFSA, que regula las prácticas agrícolas, incluido el uso de productos fitosanitarios en la Unión Europea) desarrolló hace unos años una guía y una herramienta informática denominada Persistence in Soil Analytical Model (PERSAM), para realizar evaluaciones de la exposición en el suelo, es decir, PERSAM ayuda a calcular la concentración que cabría esperar de una determinada aplicación de pesticidas. “Ahora hemos conseguido extrapolar los riesgos potenciales de estas concentraciones y los factores que influyen en ese riesgo, no solo considerando las condiciones del suelo, sino también el tipo de cosecha y el tipo de pesticida empleado”, explica el profesor de la UPV/EHU Manu Soto.
Las características del suelo y las variables ambientales varían a lo largo del eje latitudinal que atraviesa el continente europeo. “Si la toxicidad es diferente en función de las características de los suelos, no se puede seguir la lógica de la aplicación de una única dosis en toda Europa, ya que una dosis puede no tener ningún efecto en Suecia, pero sí en España o Francia, por ejemplo. La EFSA quería hacer esa diferenciación, y se pusieron en contacto con nuestro grupo porque era indispensable desarrollar un método de evaluación basado en el paisaje que contemplara la variabilidad regional”, detalla Erik Urionabarrenetxea, investigador de la UPV/EHU.
Un tipo de organismo para cada compartimento del sueloAsí, miembros del Departamento de Zoología y Biología Celular Animal han investigado el efecto que tienen cuatro pesticidas en dos tipos diferentes de organismos en distintos puntos del norte, centro y sur de Europa. El estudio se ha realizado con lombrices y colémbolos (una clase artrópodos hexápodos), debido a que las lombrices se ven afectadas por la contaminación existente en el suelo y los colémbolos por la contaminación presente en los poros acuosos del suelo. “En función de la alimentación y necesidades de cada organismo, unos son más vulnerables que otros a la contaminación presente en uno u otro compartimento del suelo”. El equipo investigador considera que hay que tener en cuenta muchos factores en el cálculo del riesgo.
El equipo ha comprobado que los riesgos derivados de las concentraciones varían mucho de un compartimento del suelo a otro. Han señalado que esta cuestión debería tenerse en cuenta a efectos del ajuste de la normativa, así como las posibles variabilidades del paisaje entre las distintas eurorregiones. “De norte a sur de Europa se observa una gran variabilidad, pero también dentro de cada región”, apuntan. En cuanto al tipo de pesticidas, también han observado que “las características de los pesticidas influyen en gran medida en su reparto en cada uno de los compartimentos”.
“Se trata de calcular mejor el riesgo, y no quedarse solo con las concentraciones, ya que pueden ser muy variables. Es importante fijarse en los efectos tóxicos que producen estas concentraciones, en sus efectos potenciales y en los riesgos que ello supone, para su posterior aplicación a las prácticas agrícolas —indican los investigadores—. Plantear la necesidad de tener en cuenta las características del suelo es un gran avance, ya que hasta ahora no se tomaba en consideración”. El equipo continúa trabajando en este campo: “Ahora estamos analizando el impacto que tendría todo esto desde un punto de vista ecológico”.
Para saber más:
Trigos de alto rendimiento capaces de inhibir la nitrificación del suelo
Buscando centinelas ambientales para las costas de Nicaragua
Qué puedes hacer tú para proteger a las abejas
Referencia:
Erik Urionabarrenetxea, Carmen Casas, Nerea Garcia-Velasco, Miguel Santos, Jose V. Tarazona, Manu Soto (2022) Predicting environmental concentrations and the potential risk of Plant Protection Products (PPP) on non-target soil organisms accounting for regional and landscape ecological variability in european soils Chemosphere doi: 10.1016/j.chemosphere.2022.135045
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Las dosis de pesticidas dependen del tipo de suelo se ha escrito en Cuaderno de Cultura Científica.
Figuras de Chladni que parecen magia en ‘Los anillos de poder’
Entonces les dijo Ilúvatar: —Del tema que os he comunicado, quiero ahora que hagáis, juntos y en armonía, una Gran Música […]. Yo me sentaré y escucharé, y será de mi agrado que por medio de vosotros una gran belleza despierte en canción.
Entonces las voces de los Ainur, como de arpas y laúdes, pífanos y trompetas, violas y órganos, y como de coros incontables que cantan con palabras, empezaron a convertir el tema de Ilúvatar en una Gran Música; y un sonido se elevó de innumerables melodías alternadas, entretejidas en una armonía que iba más allá del oído hasta las profundidades y las alturas, rebosando los espacios de la morada de Ilúvatar; y al fin la música y el eco de la música desbordaron volcándose en el Vacío, y ya no hubo Vacío.
J.R.R. Tolkien, El Silmarillion1.
 Figuras de Chladni. Fuente: Wikimedia Commons
Figuras de Chladni. Fuente: Wikimedia CommonsLos fans de El señor de los anillos estamos de enhorabuena. Amazon ha estrenado una nueva serie basada en El Silmarillion y otros anexos de la novela de Tolkien, y decir que el resultado es visualmente impactante es quedarse corto. Los anillos de poder está llena de detalles que recrean el universo de Tolkien en todo su esplendor. Panoramas de ciudades que se elevan sobre las montañas, esculturas gigantes, armaduras de marfil, elfos y minerales mágicos arrancados de la roca por esforzados enanos… todo es tan bonito y la fotografía es tan envolvente, que casi da pena ver la serie en una pantalla de televisión.
Entre semejante colección de oro, fantasía y efectos especiales, lo que yo no esperaba encontrarme era una clase de acústica, ciertamente. ¡Pero así ha sido! Para diseñar los títulos de crédito de la serie, sus creadores se han inspirado en la física del sonido, en figuras de Chladni concretamente. Y no es una decisión casual, ni una referencia gratuita. Esta decisión creativa está llena de poesía y hunde sus raíces en el simbolismo de la literatura de Tolkien. Hoy te voy a explicar por qué.
La secuencia consiste en una serie de runas que danzan acompañadas por la música de Howard Shores. Nada le gustaba más a Tolkien que unas buenas runas. Inventó alfabetos enteros llenos de símbolos para arropar su mundo de fantasía y darle un aire mitológico. En los créditos, estos símbolos se suceden en una sinuosa animación. Están formados formadas por granos de arena que vibran y se estremecen, se juntan para dar forma a cada runa y se vuelven a disolver. Su baile huele a tierra, a fuerzas elementales y a magia. Pero en realidad, es un movimiento que todos podemos observar en el mundo real, sin necesidad de anillos mágicos, orcos, ni maleficios: lo que vemos son ondas de sonido sobre una superficie en vibración.
Fue Ernst Chladni el primero en describir con precisión este fenómeno2. Y no, Chladni no es el nombre de ningún elfo, aunque lo podría parecer. Se trata de uno de los padres de la acústica, un erudito alemán que a finales del siglo XVIII emprendió una serie de experimentos para poder visualizar y entender mejor el sonido. Chladni eligió distintas planchas de cristal y de metal y espolvoreó arena sobre su superficie. Luego, las hizo vibrar con ayuda de un arco de violín. Cuando la plancha metálica alcanzaba ciertas frecuencias (las frecuencias correspondientes a sus sus modos normales), de repente, las partículas de arena se reordenaban como por arte de magia, formando patrones hermosamente simétricos. “Imagina mi asombro al ver este fenómeno que nunca nadie había visto antes”3 escribiría Chladni casi veinte años después.
En su tiempo, las figuras de Chladni lo lanzaron al estrellato, y el erudito se convirtió en una suerte de “físico ambulante”, de gira por toda Europa para enseñarle al mundo sus sonidos de arena. Hoy esas formas vibrantes y sinuosas siguen resultando hipnotizantes. Pero los creadores de los créditos de Los anillos de poder no las eligieron únicamente por su atractivo visual. Tienen un significado literario mucho más profundo este contexto, porque en el universo de Tolkien, el dios Ilúvatar crea el mundo con ayuda de los Ainur, ¡a partir de la música!
Así lo explican en su web Plains of Yonder, el estudio de cine responsable de la secuencia de créditos: “Nos propusimos retratar un universo primordial y atemporal. Para ello nos inspiramos en los Ainur de J.R.R. Tolkien, seres angelicales inmortales que cantan una música tan hermosa que el mundo se crea a partir de su sonido”. Queriendo recrear este origen mítico, recurrieron a “un fenómeno que hace que el sonido sea visible a simple vista. Las vibraciones de las partículas sobre una superficie plana muestran llamativos patrones simétricos que reflejan las frecuencias de audio”. Un fenómeno que, según sus palabras, “parece nada menos que magia”. Así, “la secuencia evoca un poder antiguo e invisible, que lucha por ser visto. Los símbolos se forman, fluyen, empujan y desaparecen tan rápido como llegaron. Los reinos incognoscibles del sonido crean visiones fugaces de conflicto y armonía que se mueven al unísono con la partitura de Howard Shores”.
Referencias y notas:
1Tolkien, John Ronald R. 1977. “AINULINDALË La Música de los Ainur”. En El Silmarillion. . Editado por Christopher Tolkien. Traducido por Rubén Masera y Luis Doménech. Minotauro, 1984.
2Lo cuento en detalle en “La lira desafinada de Pitágoras”. HarperCollins, 2022.
3Chladni, Ernst Florens Friedrich. “Preface.” Traducido por Robert T. Beyer. Treatise on Acoustics, Acoustical Society of America Press, 2015.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Figuras de Chladni que parecen magia en ‘Los anillos de poder’ se ha escrito en Cuaderno de Cultura Científica.
El problema del recorrido del caballo en el tablero de ajedrez
Como ya mencionamos en la entrada del Cuaderno de Cultura Científica titulada A vueltas con el origen del ajedrez, la relación entre ajedrez y matemáticas ha sido siempre muy fructífera.
Problemas clásicos como el recorrido del caballo sobre el tablero de ajedrez, el problema de Guarini (al que dedicamos la entrada Ajedrez y matemáticas: el problema de Guarini), el problema de las ocho reinas o el problema de los ocho oficiales, entre otros, fueron estudiados por grandes matemáticos como Carl F. Gauss, Leonhard Euler, Abraham de Moivre o Adrien-Marie Legendre. Así mismo, muchos matemáticos recreativos como Lewis Carroll, W. W. Rouse Ball, Henry E. Dudeney, Sam Loyd, Édouard Lucas, Raymond Smullyan o Martin Gardner, se apasionaron con este juego, incluso fueron grandes jugadores, e inventaron interesantes rompecabezas matemáticos y juegos de ingenio sobre el tablero de ajedrez.
 Juego del ajedrez (1979), del pintor italiano Antonio Bresciani (1902-1997)
Juego del ajedrez (1979), del pintor italiano Antonio Bresciani (1902-1997)El problema del recorrido del caballo
La entrada de hoy la vamos a dedicar a uno de esos problemas matemáticos clásicos relacionado con el tablero del ajedrez, el problema del recorrido del caballo. Aunque el juego es muy sencillo de explicar, dejemos que sea el gran matemático suizo Leonhard Euler (1707-1783), el primero en realizar un análisis matemático riguroso del juego, quien nos explique en qué consiste el mismo, con las palabras que utilizó en su artículo Solución a una cuestión ingeniosa que parece que no ha sido analizada (Memoria de la Academia de Ciencias de Berlín, 1759):
Un día me encontraba en una reunión en la que, con ocasión del juego del ajedrez, alguien propuso la cuestión de recorrer con un caballo todas las casillas de un tablero sin pasar nunca dos veces por la misma y empezando en una casilla dada. Se colocaban fichas, para este fin, en las sesenta y cuatro casillas del tablero, salvo en la que el caballo debía comenzar su ruta, y de cada casilla por la que pasaba el caballo, conforme a su camino, se retiraba la ficha, de manera que se trataba de retirar de esta forma todas las fichas sucesivamente. Había que evitar, pues, por un lado, que el caballo pasara por una casilla vacía y, por otro lado, había que dirigir su camino de suerte que recorriera finalmente todas las casillas.
Pero empecemos por el principio, por el movimiento del caballo en el tablero de ajedrez. Aunque es posible que la mayoría de las personas que estáis leyendo esta entrada conozcáis los movimientos de las piezas del ajedrez, lo primero es recordar cómo se mueve el caballo, ya que es la pieza central en este problema. Esta pieza realiza un salto o movimiento en forma de L –dos casillas hacia delante y una a un lado– como los que se muestran en la siguiente imagen.
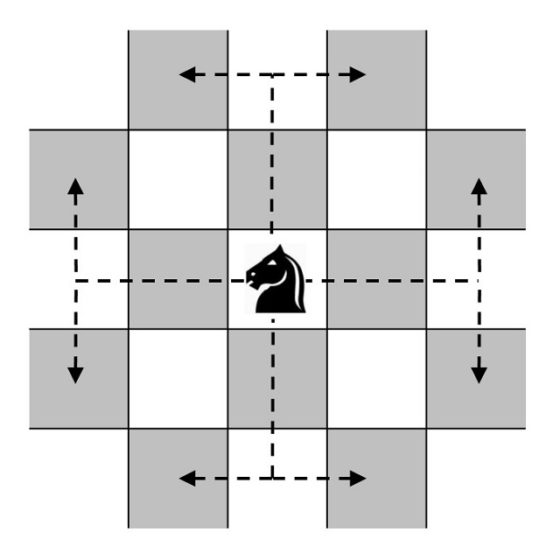 Los seis posibles movimientos de la figura del caballo sobre el tablero del ajedrez, en una casilla interior. Solo son posibles los movimientos que dejan al caballo dentro del tablero. Si el movimiento le llevase fuera del tablero, simplemente ese movimiento no sería posible
Los seis posibles movimientos de la figura del caballo sobre el tablero del ajedrez, en una casilla interior. Solo son posibles los movimientos que dejan al caballo dentro del tablero. Si el movimiento le llevase fuera del tablero, simplemente ese movimiento no sería posible
Ahora, formulemos de forma sencilla en qué consiste este juego o problema.
Problema del recorrido del caballo: Buscar un recorrido de la figura del caballo sobre el tablero de ajedrez que consista en mover esta pieza, desde una casilla inicial, de forma sucesiva a través de todas las casillas del tablero, pasando una sola vez por cada una de ellas y terminando en la casilla inicial.
A un recorrido de este tipo se le denomina recorrido cerrado, ya que empieza y acaba en la misma casilla, aunque se puede plantear la variante del problema que consiste en que las casillas inicial y final no sean las mismas, en cuyo caso se habla de recorrido abierto.
Si volvemos a la explicación anterior del matemático Leonhard Euler, este no solo nos explica en qué consiste este juego, sino que además nos sugiere cómo jugarlo para que podamos comprobar si lo estamos resolviendo bien. Al ir moviendo el caballo por el tablero y quitando las fichas de las casillas por las que pasa, lo que ocurre es que si una casilla no tiene pieza quiere decir que ya la hemos recorrido y que no podemos volver a pasar por ella.
Por su parte, el matemático francés Edouard Lucas (1842-1891), autor del texto Recreaciones matemáticas (1894), propone ir colocando números del juego de la “lotería” (al parecer se refiere al bingo, ya que el origen de este juego podría estar en la lotería italiana y en Francia se conocía, en un principio, con el nombre de lotería) en las casillas recorridas, empezando por el 1 en la inicial y en orden consecutivo (1, 2, 3, 4, 5, etc), de forma que no solo sabemos si hemos recorrido todas las casillas, además una sola vez por cada una, sino que queda constancia del recorrido que se ha realizado. Esencialmente esta es la forma en la que suelen mostrarse los recorridos de los caballos. En la siguiente imagen se muestra un recorrido abierto del caballo a lo largo de todas las casillas del tablero de ajedrez (es una de las soluciones propuestas por Euler), indicado con números, como sugiere Edouard Lucas.
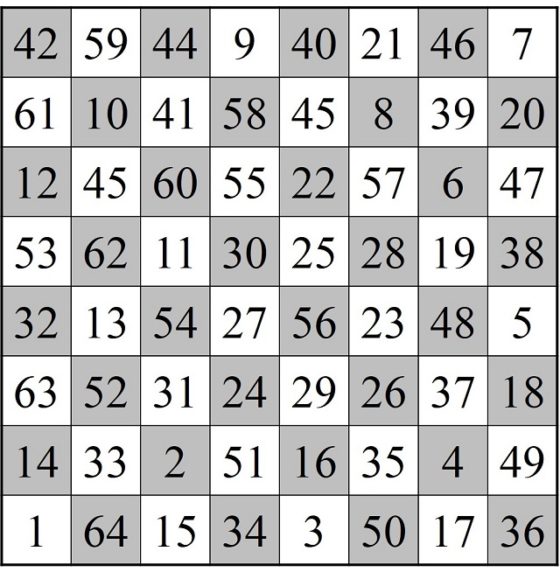 Una de las posibles soluciones al problema del recorrido del caballo, en su variante de buscar un recorrido abierto
Una de las posibles soluciones al problema del recorrido del caballo, en su variante de buscar un recorrido abiertoOrigen del problema del recorrido del caballo
Como se explica en el libro Del ajedrez a los grafos, la seriedad matemática de los juegos (RBA, 2015), este problema es mucho más antiguo. Probablemente, su origen se remonte al mismo origen del juego del ajedrez, alrededor del siglo VI en la India. Harold Murray, en su libro Historia del ajedrez, cita los manuscritos homónimos titulados Libro del ajedrez (Kitab ash-Shatranj) de los grandes ajedrecistas árabes Al-Adli (hacia el 840) y Al-Suli (hacia el 910), como los primeros en los que se presentan recorridos cerrados del caballo en el tablero clásico 8 x 8 (véase la siguiente imagen).
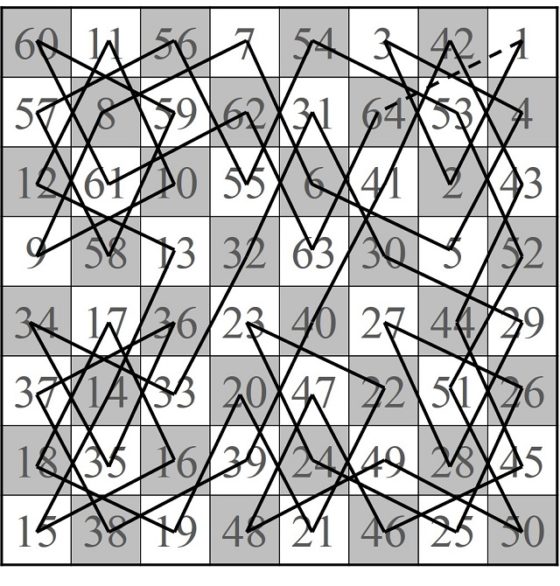
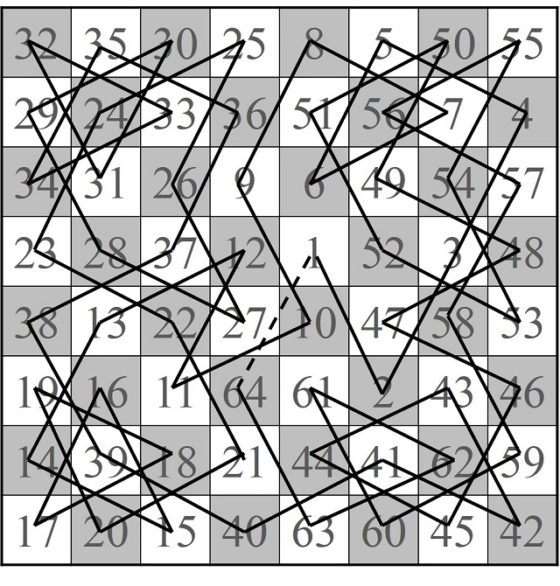 Recorridos cerrados del caballo que aparecen en los manuscritos Kitab ash-Shatranj de los grandes ajedrecistas árabes Al-Adli y Al-Suli
Recorridos cerrados del caballo que aparecen en los manuscritos Kitab ash-Shatranj de los grandes ajedrecistas árabes Al-Adli y Al-Suli
Además, el poeta de Cachemira Rudrata, en su obra poética Kavyalankara (hacia el 900), utiliza un recorrido abierto del caballo en un tablero 4 x 8 (que se puede extender a un recorrido abierto sobre un tablero de ajedrez) como una estructura para un poema. El poema, en sanscrito, se compone de cuatro líneas de 8 sílabas, que puede leerse de izquierda a derecha o siguiendo el recorrido del caballo (véase la siguiente imagen).
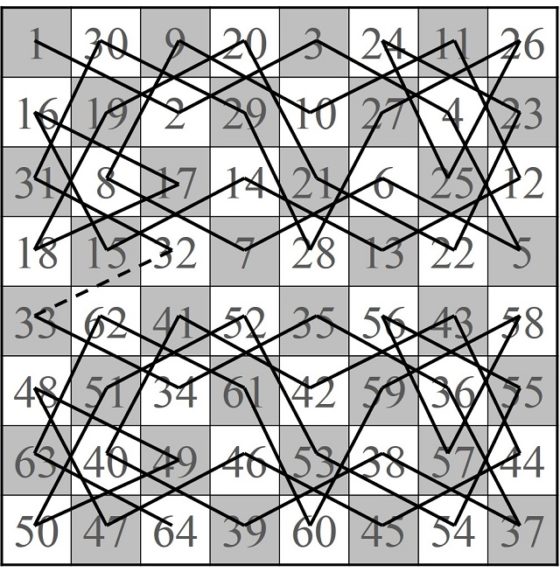 Recorrido abierto del poema en sánscrito de Rudrata
Recorrido abierto del poema en sánscrito de Rudrata
Al parecer, tanto en la India, como en los Países Árabes, se empezó estudiando el problema del recorrido del caballo sobre la mitad del tablero, es decir, sobre un tablero 4 x 8.
El grafo asociado al problemaAntes de seguir adelante, vayamos con un par de comentarios. El primero es que según la posición de cada casilla esta se puede conectar, mediante el movimiento del caballo, con una cantidad distinta de casillas. En el caso de una casilla que es muy “interior”, donde todos los movimientos mostrados arriba son posibles, se puede conectar con otras ocho casillas, sin embargo, hay casillas que se pueden conectar con un menor número de casillas (dos, tres, cuatro o seis), como se muestra en la siguiente imagen.
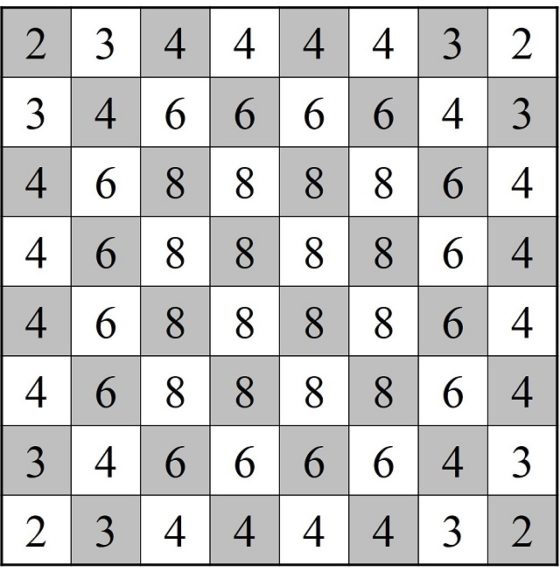
El segundo comentario es que el problema del recorrido del caballo sobre un tablero de ajedrez se puede plantear matemáticamente como un “problema de existencia de caminos o ciclos hamiltonianos sobre un grafo”. No vamos a meternos ahora en la teoría de grafos, pero sí explicaremos cuál es el grafo asociado al problema del recorrido del caballo, ya que puede servirnos para entender algunas cuestiones más adelante.
Recordemos que un grafo está formado simplemente por puntos –llamados vértices del grafo- y líneas que unen algunos de esos puntos –llamadas aristas del grafo- (véase, por ejemplo, El problema de los tres caballeros y los tres criados, El grafo de Marion (gray) o El juego de Sim, entre otros), y que es una estructura matemática muy sencilla, pero a la vez muy versátil.
El grafo asociado al problema del recorrido del caballo es el grafo cuyos vértices son las casillas del tablero y una arista une dos vértices (casillas) si el caballo puede saltar de una casilla a la otra, con su movimiento. En la siguiente imagen hemos representado el grafo asociado.
 Grafo asociado al problema del recorrido del caballo para un tablero clásico 8 x 8
Grafo asociado al problema del recorrido del caballo para un tablero clásico 8 x 8
Como podemos observar, el número de aristas de cada vértice del grafo (lo que se llama el grado del vértice) es distinto, puede ser dos, tres, cuatro, seis u ocho, que son los posibles movimientos del caballo en las diferentes casillas. El problema matemático consiste en buscar un recorrido a través de las aristas que pase por todos los vértices (lo que se llama camino o ciclo hamiltoniano), aunque puede parecernos una locura ahora tiene sus ventajas, pero no entraremos en ellas ahora.
Todo un mundo de tablerosVolvamos al problema del recorrido del caballo por el tablero de ajedrez. El matemático Leonhard Euler planteó la cuestión de buscar recorridos de caballos, cerrados o abiertos, en tableros con diferentes formas, por ejemplo, rectangulares o en forma de cruz, como aparece en la imagen, y de diferentes tamaños.
 Un primer acercamiento al juego del recorrido del caballo puede ser jugando con tableros sencillos, como estos o similares
Un primer acercamiento al juego del recorrido del caballo puede ser jugando con tableros sencillos, como estos o similares
Como siempre comentamos en este tipo de entradas del Cuaderno de Cultura Científica lo mejor cuando nos encontramos ante un juego es jugar. Por eso mismo, os planteo que antes de seguir adelante, o mejor después de leer esta entrada, juguéis al problema del recorrido (abierto) del caballo para estos dos tableros.
Problema: Buscar un recorrido abierto en el tablero rectangular 3 x 4 y en el tablero en forma de cruz.
Esta entrada vamos a centrar nuestra atención en los tableros cuadrados n x n (generalizando el caso del tablero clásico 8 x 8) y los tableros rectangulares n x m (generalizando el problema para la mitad del tablero, es decir, para un tablero rectangular de tamaño 4 x 8, que ya se plantearon en la antigüedad).
Un argumento de colorEs curioso que, aunque la estructura bicolor del tablero de ajedrez (cuadrados blancos y negros de forma alternada) no es relevante para resolver el problema del recorrido del caballo, sí lo es para extraer algunas conclusiones interesantes.
Si observamos el salto del caballo sobre el tablero de ajedrez bicolor nos daremos cuenta de que, si el caballo está en una casilla blanca, al moverse pasará a una casilla negra, y viceversa. Por lo tanto, en un recorrido cerrado del caballo, es decir, que tras la última casilla se regresa a la casilla inicial, el número de casillas blancas y negras deber ser el mismo. Esto nos permite afirmar que no existen recorridos cerrados en tableros n x n, para n impar, o más generalmente, en tableros rectangulares, n x m, con n y m impares, ya que el número total de casillas es impar, luego no hay la misma cantidad de casillas blancas y negras. De forma análoga, en un recorrido abierto del caballo, la diferencia en el número de casillas blancas y negras es como mucho 1, luego en tableros con formas tales que tal diferencia sea mayor que 1 no existirán recorridos del caballo, como el de la siguiente imagen, con 32 casillas negras y 25 blancas.

Una de las técnicas matemáticas a la hora de afrontar la resolución de un problema es analizar los casos más sencillos. A continuación, vamos a centrarnos en el problema del recorrido del caballo para los tableros de anchura 3, es decir, tableros rectangulares 3 x m (para m mayor o igual que 3). Podéis pensar qué es lo que ocurre con los tableros de anchura 2.
Empecemos por el tablero cuadrado 3 x 3. Este tablero es fácil de analizar. No admite recorridos del caballo puesto que la casilla central no se puede conectar, mediante el salto del caballo, con ninguna otra casilla.
Sobre el tablero 3 x 4 sí se pueden encontrar recorridos abiertos del caballo, como el que aparece en la siguiente imagen.
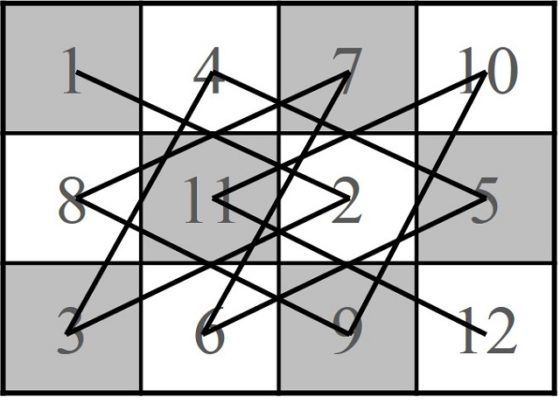
Sin embargo, no existen recorridos cerrados. Os proponemos que penséis en cómo demostrar que no existen recorridos cerrados del caballo en este tablero, aunque os daremos una pista de color (pero para no liarnos con los colores habituales del tablero, blanco y negro, utilizaremos letras, A y B), y lo resolveremos en la siguiente entrada.
Problema (recorridos cerrados sobre el tablero 3 x 4): Demostrar que no existen recorridos cerrados del caballo sobre el tablero rectangular 3 x 4.
Pista: Primero, hay que marcar la primera y la última columnas con la letra A y las dos columnas de en medio con la letra B. Y segundo, pensar a qué tipo de casilla salta el caballo si está en una casilla de tipo A, y lo mismo si está en una casilla de tipo B.
Si ahora pasamos al tablero de tamaño 3 x 5, como ambas dimensiones son impares tenemos que, por el argumento de color comentado anteriormente, no existen recorridos cerrados sobre este tablero. Pero vamos a ver que ahora tampoco existen recorridos abiertos.
En un tablero 3 x 5 coloreado como se muestra en la imagen, hay 8 casillas negras y 7 blancas, luego el recorrido del caballo deberá empezar y terminar en casillas negras. Por otra parte, si nos fijamos en las dos casillas, de la derecha y la izquierda, marcadas con los vértices negros, cada una de estas solo se puede conectar con dos casillas, que resultan ser las mismas, luego esas dos casillas marcadas con los vértices negros están conectadas a través de los dos vértices centrales, en consecuencia, necesariamente uno de los dos vértices negros deberá ser inicial o final, pero esto es imposible, puesto que son casillas blancas.
La demostración de que no existen recorridos cerrados del caballo para el tablero rectangular de tamaño 3 x 6 utiliza el grafo asociado, pero es sencilla, bonita y hace uso de una analogía con los collares de perlas, por este motivo la mostramos aquí.
Para empezar, consideremos el grafo asociado al tablero 3 x 6 (que se muestra en la siguiente imagen).

Si existiese un recorrido cerrado sobre el mismo tendremos una sucesión cerrada de aristas y vértices, luego si pensamos que los vértices son perlas y las aristas cuerdas que unen dos perlas consecutivas, podemos pensar en ese recorrido cerrado como un collar de perlas, que si lo “extendemos” (o lo “desenrollamos”) será como en la siguiente imagen (con 18 perlas).
Pensemos en un collar de perlas (nos sirve la imagen anterior). Si quitamos una perla (cortando las dos cuerdas laterales) el collar estará formado por una pieza, si quitamos dos perlas quedarán dos piezas de collar, salvo que las perlas sean continuas, que quedaría una, si quitamos tres perlas, el collar se separa en tres partes como mucho, y así podemos continuar.
Pensemos ahora en nuestro supuesto collar de perlas, que habríamos obtenido del recorrido cerrado (si existiese) sobre el tablero 3 x 6. Ahora, si eliminamos de este collar los vértices A y B (véase la imagen anterior), quedaría dividido en tres partes, los vértices X e Y, que están aislados, y el resto de vértices, luego el collar se habría roto, al quitar A y B, al menos en tres partes, lo cual es imposible. Con argumentos similares a estos se prueba que tampoco existe un recorrido abierto.
Como hemos observado, la existencia de casillas que sólo se pueden conectar con otras dos son determinantes para demostrar que no existen recorridos (abiertos o cerrados) o para construirlos cuando sí existen. En general, se puede demostrar que no existen recorridos cerrados para los tableros 3 x m, para m impar o m = 4, 6, 8; y no existen recorridos abiertos para m = 3, 4, 5, 6.
En general, uniendo tableros más pequeños se puede demostrar que existen recorridos cerrados para todos los tableros 3 x m, si m es par y mayor, o igual, que 10; y existen recorridos abiertos si m = 4 o mayor que 7. Un ejemplo de esta técnica se muestra en la siguiente imagen.
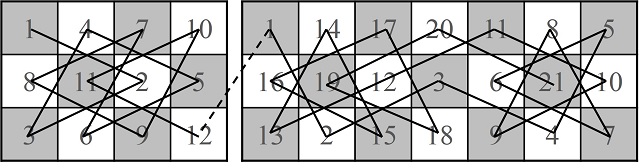
Acabamos de analizar la cuestión de la existencia de solución para el recorrido del caballo en tableros rectangulares de tamaño 3 x m. Lo siguiente podría ser analizar los tableros de tamaños 4 x m. Por ejemplo, si pensamos en un tablero 4 x 4, el argumento del collar de perlas anterior, es decir, eliminar un número de vértices y contar las partes que quedan, permite demostrar que no existen recorridos del caballo para este tablero, para lo cual hay que considerar el grafo asociado siguiente.
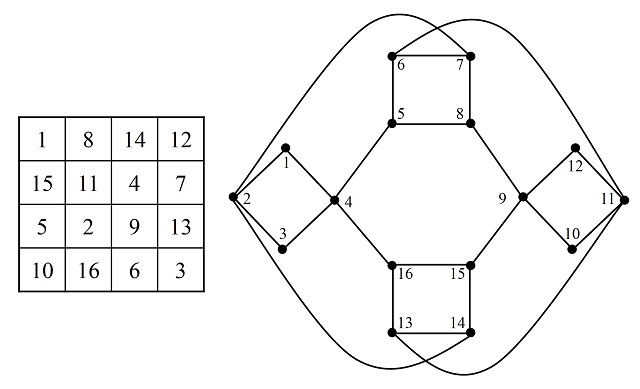
El matemático e ingeniero norteamericano Solomon W. Golomb, creador de los poliominós, dio una elegante demostración de la no existencia de recorridos de caballos cerrados para tableros 4 x m, utilizando patrones de color, pero de la existencia de recorridos abiertos (para m mayor, o igual, que 5), como puede verse en el libro Del ajedrez a los grafos, la seriedad matemática de los juegos.
Por otra parte, los matemáticos alemanes A. Conrad, T. Hindrichs, H. Morsy y I. Wegener demostraron que existen recorridos de caballos para tableros cuadrados de lado , y que esos recorridos pueden ser cerrados para tableros pares.
Este resultado fue extendido, para recorridos cerrados, a tableros rectangulares por el matemático norteamericano Allen Schwenk, en un artículo publicado en la revista Mathematics Magazine en 1991. Para un tablero n x m, con n menor o igual que m, existen recorridos de caballos cerrados si no se da alguno de los casos anteriores: i) n y m impares; ii) n = 1, 2 o 4; iii) n = 3 y m = 4, 6 o 8.
La cuestión de la existencia de soluciones al problema del recorrido (abierto o cerrado) del caballo en tableros de ajedrez rectangulares no es el único relacionado con este problema clásico, sino que también podemos analizar otras dos cuestiones importantes, como son la construcción de soluciones al problema del recorrido del caballo o el cálculo de cuántas soluciones existen. Pero dejares estas para posteriores entradas del Cuaderno de Cultura Científica.
 Caballos corriendo infinitamente (1995), del artista mexicano Gabriel Orozco, en el Museo Amparo de Puebla (México)
Caballos corriendo infinitamente (1995), del artista mexicano Gabriel Orozco, en el Museo Amparo de Puebla (México)
Bibliografía:
1.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, El mundo es matemático, RBA, 2015.
2.- Édouard Lucas, Recreaciones Matemáticas, vol. 1 – 4, Nivola, 2007, 2008.
3.- Miodrag S. Petrovic, Famous Puzzles of Great Mathematicians, AMS, 2009.
4.- Harold J. R. Murray, A History of Chess (Historia del ajedrez), Oxford University Press, 1913.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El problema del recorrido del caballo en el tablero de ajedrez se ha escrito en Cuaderno de Cultura Científica.
Einstein y la teoría de Kaluza-Klein
La teoría de Kaluza-Klein fue la primera teoría del campo unificado. Intentaba conectar la teoría electromagnética de Maxwell con las teorías de Einstein sobre la relatividad asumiendo que el universo estaba basado en cinco dimensiones: una temporal y cuatro espaciales.
 Foto: Mathematisches Forschungsinstitut
Foto: Mathematisches ForschungsinstitutOberwolfach
En 1919 un desconocido matemático alemán, Theodor Kaluza (en la imagen), envió un artículo a Einstein en el que exponía las consecuencias de asumir que el espaciotiempo tenía cinco dimensiones. El espaciotiempo en la teoría general de Einstein tiene cuatro dimensiones: las tres del espacio y una adicional del tiempo. Si bien es difícil visualizar el mundo que nos rodea como realmente operando en cuatro dimensiones, ello no implica dificultad alguna desde el punto de vista matemático. La teoría general de la relatividad podía adaptarse fácilmente a más dimensiones y de repente, gracias a Kaluza, parecía como si la relatividad y el electromagnetismo pudieran ser parte de una teoría que los englobaría y que funcionaría en cinco dimensiones.
Cuando Einstein recibió el artículo de Kaluza, respondió: “La idea de conseguir [una teoría unificada] por medio de un mundo cilíndrico de cinco dimensiones nunca se me ocurrió…A primera vista me gusta su idea enormemente”. En 1921, Kaluza publicó el artículo [1]. Sin embargo, la idea era solamente una construcción matemática, sin conexión con la realidad física. En 1926, el sueco Oskar Klein publicó un artículo [2] que completaba la teoría y proponía soluciones físicas interesantes. Klein usó las nuevas teorías cuánticas para ofrecer una explicación de por qué no podemos experimentar la quinta dimensión: la cuarta dimensión espacial sería un bucle circular de radio muy pequeño, de tan solo 10-33 centímetros o, en otras palabras, del orden de 1021 veces más pequeño que un átomo.
La unificación de la luz y la gravedad fue uno de los principales objetivos de Einstein en la segunda mitad de su vida y, aunque la teoría de Kaluza-Klein no tuvo éxito del todo (en parte porque muchos científicos pensaron que añadir una quinta dimensión era poco menos que hacer trampas), fue un primer paso a la hora de intentar hacerlo. Usando esta teoría como base, Einstein publicó varios artículos entre 1927 y 1932 en los que empleaba cinco dimensiones.
Pero pronto la teoría de Kaluza-Klein se quedaría por el camino. Una nueva teoría acaparaba la imaginación de la mayoría de los físicos jóvenes: la mecánica cuántica. Esta nueva rama de la física explicaba el electromagnetismo tan bien que la teoría de Kaluza-Klein parecía superflua. Solo unos pocos, Einstein entre ellos, continuaron buscando una teoría unificada.
Pero añadir dimensiones extra era una técnica destinada a sobrevivir. Si bien nadie resucitó la teoría de Kaluza-Klein durante sesenta años, ésta hizo una reentrada espectacular en la ciencia con la teoría de cuerdas. Así, por ejemplo, la teoría M, que unifica las distintas variantes de la teoría de cuerdas, afirma que las cuerdas son cortes (anillos) de una dimensión de membranas de dos dimensiones que vibran en un espacio de once dimensiones. Esta versión moderna de la teoría de Kaluza-Klein intenta unir no sólo la gravitación y el electromagnetismo, sino también las interacciones nucleares fuerte y débil. Es una teoría bien estudiada, y lógicamente consistente, pero aún sin comprobación experimental.
Referencias:
[1]
Kaluza, T (1921). Zum Unitätsproblem in der Physik Sitzungsber. Preuss. Akad. Wiss. , 966-972
[2]
Klein, O. (1926). Quantentheorie und fünfdimensionale Relativitätstheorie Zeitschrift für Physik, 37 (12), 895-906 DOI: 10.1007/BF01397481
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 2 de mayo de 2010.
El artículo Einstein y la teoría de Kaluza-Klein se ha escrito en Cuaderno de Cultura Científica.

