La característica de Euler de una superficie: un invariante topológico
En la entrada Clasificando en topología: de lo local a lo global recordábamos un bellísimo teorema de clasificación:
Dada una superficie compacta (cerrada y acotada) y conexa (de una pieza), es topológicamente equivalente a una esfera, a una suma conexa de toros o a una suma conexa de planos proyectivos.
Una vez demostrado este teorema, surge una pregunta natural: ¿son estos tipos de superficies topológicamente diferentes? Es decir, ¿podría suceder que, para dos enteros positivos distintos m y n, la suma conexa de n toros fuera homeomorfa a la suma conexa de m toros? ¿Y podría ocurrir que, para dos enteros positivos m y n, la suma conexa de n toros fuera homeomorfa a la suma conexa de m planos proyectivos?
Para demostrar que esto no es posible se puede recurrir a un invariante numérico llamado la característica de Euler que tiene sus raíces en la conocida fórmula de Euler para poliedros que afirma que
Si P es un poliedro convexo con f caras, e aristas y v vértices, entonces v–e+f=2.
La fórmula de Euler para poliedros se puede generalizar a superficies compactas. Antes de comentar cómo, recordemos que cualquier superficie compacta y conexa puede obtenerse como el cociente de una región poligonal en el plano con un número par de aristas identificadas a pares. Cada superficie puede reconocerse a través de una presentación que se obtiene etiquetando con el mismo símbolo cada par de aristas identificadas y “leyendo” estas etiquetas en el orden en el que se presentan.
Por ejemplo, la esfera, el plano proyectivo, el toro y la botella de Klein son cocientes de cuadrados como se indica en la imagen de debajo. Cada flecha y cada letra indican las aristas que se identifican y la forma de realizar este “pegado”.
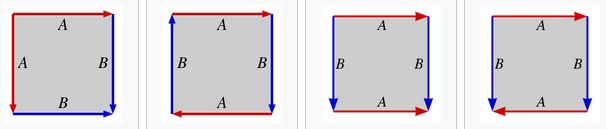 La esfera, el plano proyectivo, el toro y la botella de Klein. Imagen: Wikimedia Commons.
La esfera, el plano proyectivo, el toro y la botella de Klein. Imagen: Wikimedia Commons.
Cada una de las anteriores superficies tendría las presentaciones (empezando a “leer” desde la esquina superior izquierda):
-
la esfera: ABB-1A-1,
-
el plano proyectivo real: ABAB,
-
el toro: ABA-1B-1, y
-
la botella de Klein: ABAB-1
Una superficie no tiene una única presentación, depende de la manera de etiquetar. Pero dos presentaciones de la misma superficie son equivalentes en el sentido de que pueden transformarse la una en la otra por una serie de operaciones elementales. Los detalles pueden verse en [1], en las páginas 8 a 16.
Si S es una superficie con una presentación P dada, se define la característica de Euler de esa presentación como χ(P) = v–e+f, donde f es el número de caras, e el de aristas y v el de vértices de la presentación. Por ejemplo,
-
La esfera, con la presentación P=ABB-1A-1, tiene χ(P)=2–1+1=2 (tras las identificaciones, contamos 2 vértices, 1 arista y 1 cara).
-
El plano proyectivo real, con la presentación P=ABAB, tiene χ(P)=2–2+1=1 (tras las identificaciones, contamos 2 vértices, 2 aristas y 1 cara).
-
El toro, con la presentación P=ABA-1B-1, tiene χ(P)=1–2+1=0 (tras las identificaciones, contamos 1 vértice, 2 aristas y 1 cara).
-
La botella de Klein, con la presentación P=ABAB-1, tiene χ(P)=1–2+1=0 (tras las identificaciones, contamos 1 vértice, 2 aristas y 1 cara).
Se puede probar que χ(P) es un invariante de la superficie, es decir, no depende de la presentación dada para S; por ello se denota por χ(S) y se llama característica de Euler de la superficie. Además se demuestra que si S es homeomorfa a una esfera, entonces χ(S)=2, si es homeomorfa a la suma conexa de n toros es χ(S)=2−2n, y si es homeomorfa a la suma conexa de n planos proyectivos es χ(S)=2−n.
Con esto queda respondida la primera pregunta planteada al principio, ¿podría suceder que, para dos enteros positivos distintos m y n, la suma conexa de n toros fuera homeomorfa a la suma conexa de m toros? No, porque poseen distintas características de Euler.
¡Vaya! Pero la suma conexa de 2n planos proyectivos tiene la misma característica de Euler que la suma conexa de n toros. ¿Son ambas superficies homeomorfas? No, pueden distinguirse porque la primera superficie (suma conexa de 2n planos proyectivos) no es orientable, mientras que la segunda (suma conexa de n toros) si lo es. Y la orientabilidad es una propiedad topológica. Así que, para dos enteros positivos m y n, la suma conexa de n toros no puede ser homeomorfa a la suma conexa de m planos proyectivos…
Es decir, queda demostrado el siguiente teorema:
Si S1 y S2 son superficies compactas y conexas, son homeomorfas si y sólo si son ambas orientables o ambas no orientables y χ(S1)=χ(S2).
El anterior es un teorema topológico por excelencia. Se ha reducido el problema de clasificación de superficies compactas a la determinación de dos invariantes topológicos: la orientabilidad y la característica de Euler, ambos fácilmente calculables.
Nota 1: Los poliedros aludidos en la fórmula de Euler son homeomorfos a una esfera. Por eso su característica de Euler es 2.
Nota 2: El matemático Simon Antoine Jean L’Huillier (1750-1840) nació un 24 de abril. Generalizó la fórmula de Euler a poliedros con g asas: v–e+f=2-2g.
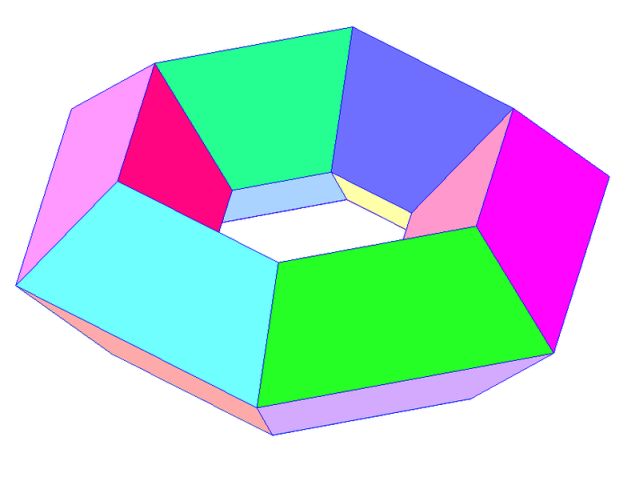 Un poliedro con un asa. Imagen: Wikimedia Commons.
Un poliedro con un asa. Imagen: Wikimedia Commons.
Existe una relación entre la característica de Euler χ(S) de una superficie S y g(S), su número de asas. Si S es orientable, g(S)=1/2(2-χ(S)). Y si no lo es, entonces g(S)=2-χ(S). ¿Y qué son las asas de una superficie? Una esfera no posee asas, y la suma conexa de n toros o de n planos proyectivos posee n asas…
Referencia
[1] Marta Macho Stadler, Topología Algebraica, Apuntes Máster 2014-2015
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo La característica de Euler de una superficie: un invariante topológico se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Clasificando en topología: de lo local a lo global
- Los ‘Leonhard Euler Facts’
- Visualizando la hiperesfera a través de la fibración de Hopf
Un medio sólido y rígido llena todo el espacio o la luz se transmite en el vacío
 Fuente: NASA, ESA & Jesús Maíz Apellániz (Instituto de Astrofísica de Andalucía) / Davide De Martin (ESA/Hubble)
Fuente: NASA, ESA & Jesús Maíz Apellániz (Instituto de Astrofísica de Andalucía) / Davide De Martin (ESA/Hubble)
Ya hemos mencionado que hay un factor parece faltar en el modelo de onda para la luz. En una de las primeras entregas de esta serie decíamos que las ondas son perturbaciones que se propagan por un medio y poníamos como ejemplos cuerdas o o masas de agua. ¿Cuál es entonces el medio para la propagación de las ondas de luz?
¿Es el aire el medio para las ondas de luz? Evidentemente no, porque la luz puede atravesar un espacio que no contiene aire, como ocurre con la luz que recibimos en la Tierra procedente del Sol y demás estrellas. Incluso antes de que se supiese que no existía aire entre el Sol y la Tierra, Robert Boyle ya había intentado el experimento de extraer casi todo el aire de un recipiente de vidrio, encontrando que los objetos dentro seguían siendo visibles lo que implicaba que la luz atrab¡vesaba el espacio en ausencia de aire.
Una onda es una perturbación, y es difícil pensar en una perturbación sin especificar qué se está perturbando. Así que era lo más lógico y natural era proponer que existía un medio específico para la propagación de las ondas de luz. Este medio hipotético se le llamó éter. La palabra “éter” originalmente fue el nombre para el quinto elemento de Aristóteles, el fluido transparente y puro que llenaba la esfera celestial y que más tarde se llamaría, en un alarde de originalidad, “quintaesencia”.
En los siglos XVII y XVIII, se pensaba que el éter era un fluido invisible de muy baja densidad. Este fluido podría penetrar toda la materia y llenar todo el espacio. De alguna manera podría estar asociado con el “effluvium” (fluido) que se empleaba para explicar las fuerzas eléctricas y magnéticas [1]. Pero ocurre que las ondas de luz deben ser transversales para explicar la polarización, y las ondas transversales generalmente se propagan solo en un medio sólido. Un líquido o un gas no pueden transmitir ondas transversales a ninguna distancia significativa por la misma razón que no puedes “retorcer” un líquido o un gas. Así que los físicos del siglo XIX asumieron que el éter debía ser un sólido.
Como vimos al tratar la propagación de las ondas, la velocidad de propagación aumenta con la rigidez del medio y disminuye con su densidad. La velocidad de propagación de la luz es muy alta en comparación con la de otros tipos de ondas, como el sonido. De aquí que se pensase que el éter tenía que ser un sólido muy rígido con una densidad muy baja.
Nos puede parecer absurdo afirmar que un medio rígido y sólido, el éter, llena todo el espacio. Después de todo un medio así debería provocar rozamiento, pero los planetas se mueven a través del espacio sin disminución detectable de velocidad. Y, por supuesto, tú no sientes resistencia cuando te mueves en un espacio que en el que la luz se transmite libremente.
Sin éter, la teoría ondulatoria de la luz, por lo demás tan sólida, parecía improbable. Pero el éter en sí tenía propiedades absurdas. Hasta principios de este siglo, este problema seguió sin resolverse, y estaba en el mismo punto en el que lo dejó Newton. Serían necesario un Maxwell [2], un Einstein [3] y unos cuantos experimentos ingeniosos para resolver el problema: la luz se transmite en el vacío.
Notas:
[1] A este respecto véase Imponderable: el primer modelo estándar de la física
[2] Las ecuaciones de Maxwell no necesitan de la hipótesis del éter, véanse La velocidad de las ondas electromagnéticas y la naturaleza de la luz o Maxwell y el éter
[3] Véase, por ejemplo, El principio de constancia de la velocidad de la luz
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Un medio sólido y rígido llena todo el espacio o la luz se transmite en el vacío se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:El intestino grueso
El intestino grueso de los vertebrados sigue al intestino delgado. Consta de tres partes principales: ciego, colon y recto (o cloaca). El ciego es una especie de bolsa que, como su propio nombre indica es ciego, o sea, es un fondo de saco. Recibe el quimo del íleo, la parte final del intestino delgado, aunque ciego e íleo se encuentran separados por la válvula ileocecal, que evita posibles retrocesos de los jugos intestinales. El íleo desemboca en un lateral del ciego y algo por debajo de ese punto se encuentra el apéndice, un tejido linfoide que no toma parte en la digestión, pero que contiene linfocitos.
El colon es la parte más extensa del intestino grueso y su estructura varía mucho de unas especies a otras en función de la dieta. Y dentro de los mamíferos también se da una gran variabilidad. En la especie humana se distinguen cuatro partes: el colon ascendente, el transverso, el descendente y el sigmoide.
En anfibios, reptiles (incluidas las aves) y algunos mamíferos, el intestino grueso finaliza en una cloaca en la que confluye con el sistema excretor y con el aparato reproductor. En los peces, sin embargo, los conductos de los tractos excretor y reproductivo salen al exterior de manera independiente del sistema digestivo. En reptiles (aves incluidas) unos pliegues o crestas delimitan la cloaca en tres áreas diferenciadas: coprodeo (anterior), a donde llegan las heces desde el intestino; urodeo (medio), que recibe la orina de los riñones a través de los uréteres y los materiales del oviducto; y el proctodeo (posterior), donde se almacenan las excretas. El proctodeo se abre al exterior a través de un ano muscular.
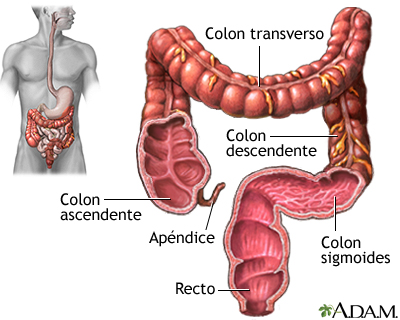 Intestino grueso humano. Fuente: medlineplus.gov /A.D.A.M.
Intestino grueso humano. Fuente: medlineplus.gov /A.D.A.M.
Un colon humano recibe diariamente del orden de medio litro de quimo. Cuando llega procedente del intestino delgado, los nutrientes han sido digeridos y absorbidos prácticamente en su totalidad, por lo que contiene sobre todo residuos alimenticios indigeribles (como celulosa, por ejemplo), algunos componentes biliares que no se han absorbido y, sobre todo, agua y sales. Por esa razón, en el colon prosigue la absorción de agua, que tiene lugar gracias a la recuperación activa de sodio, que va acompañada por la correspondiente reabsorción (a favor de gradiente eléctrico) de cloro; el agua pasa a favor del gradiente osmótico generado por la reabsorción de ClNa.
El colon contiene una solución mucosa alcalina (HCO3– y PO43-) que tiene efecto tamponador. Esa solución protege la mucosa del intestino grueso del daño mecánico y químico que podría sufrir si careciese de ella. En caballos y cerdos basta con el HCO3– de origen pancreático para mantener tamponado el colon. La saliva de los rumiantes contiene cantidades importantes de PO43-, pero en los demás mamíferos el fosfato intestinal es de origen alimenticio. Los tampones neutralizan los ácidos producidos por la fermentación bacteriana (a la que nos referiremos en una anotación próxima), y el moco proporciona la lubrificación que facilita el paso de los contenidos intestinales y la expulsión final de las heces.
Las dimensiones y estructura de los sistemas digestivos y, en especial, del intestino grueso depende mucho de la dieta propia de cada especie. Los peces carnívoros, por ejemplo, tienen tractos digestivos cuya longitud es solo algo mayor que la longitud corporal; los herbívoros, sin embargo, pueden llegar a ser veinte veces más largos.
Los vertebrados carnívoros tienen tubos digestivos muy simples, y el colon suele ser corto y sin áreas diferenciadas. Apenas se diferencian el intestino delgado y el intestino grueso; no suelen tener ciego, y si lo tienen, es marginal. En estas especies la función principal (casi única) del intestino grueso es la absorción de sales y agua.
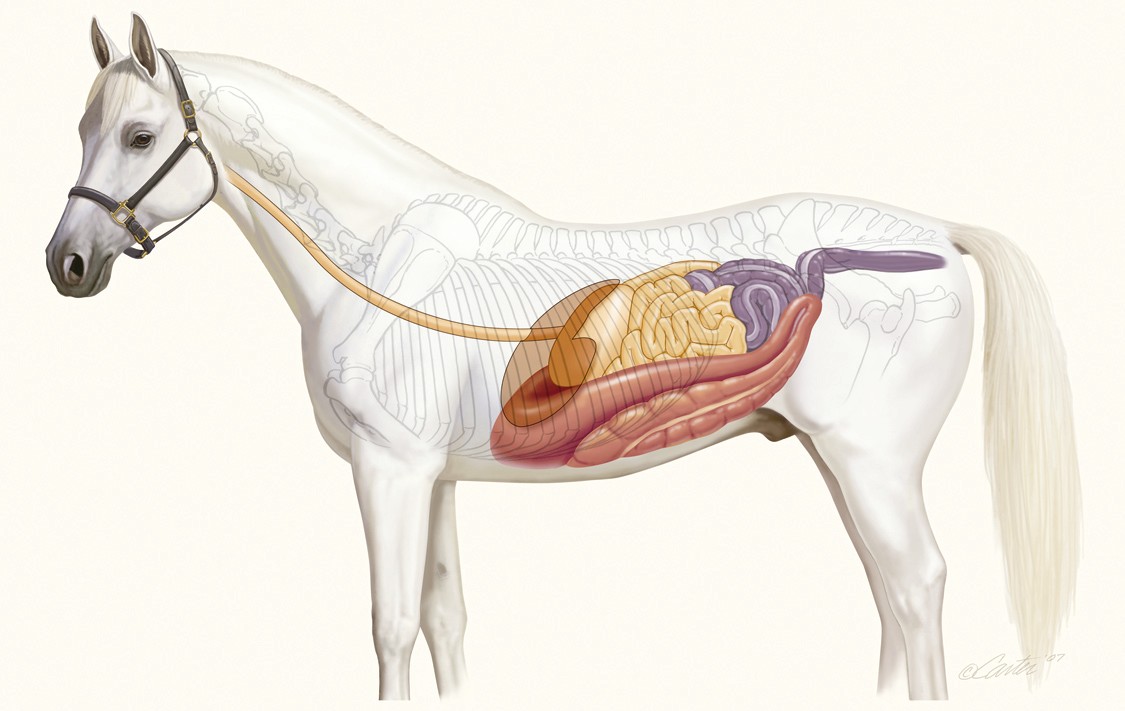 Sistema digestivo del caballo. Fuente: ecuestre.es
Sistema digestivo del caballo. Fuente: ecuestre.es
En los omnívoros y, sobre todo, en los herbívoros, la estructura del intestino grueso tiende a ser más compleja; conejos y caballos son buenos ejemplos. El ciego de los herbívoros suele ser grande, en algunos casos mayor que el colon, incluso. Además, tanto el ciego como el colon suelen estar provistos de saculaciones (sacos laterales expandibles). No obstante, hay excepciones: ni canguros ni ovejas se caracterizan por tener colon y ciego de grandes dimensiones, ni por tener saculaciones.
Las saculaciones se forman cuando la capa exterior de músculo liso longitudinal no envuelve el intestino grueso por completo. En las especies cuyos intestinos gruesos presentan esas estructuras, hay bandas de musculatura lisa longitudinal denominadas taeniae coli (en singular taenia coli), que discurren todo a lo largo del ciego y el colon. La mayoría de los animales que las tienen cuentan con tres, aunque el caballo, por ejemplo, tiene cuatro. Son más cortas que lo que las capas muscular (circular) y mucosa subyacentes serían de no estar constreñidas en parte por las taeniae coli. La presencia de estas bandas musculares provoca, por ello, que se formen leves constricciones que, a su vez, delimitan los embolsamientos o saculaciones a los que denominamos haustras (haustra coli). Los haustras no son estructuras estáticas, sino que cambian de posición por efecto de las contracciones de la capa circular de musculatura lisa.
Las contracciones haustrales juegan un papel primordial en la motilidad del intestino grueso. Se inician debido a la actividad rítmica autónoma de las células musculares lisas del colon, y son similares a las contracciones que provocan la segmentación en el intestino delgado, solo que se producen con una frecuencia muy inferior. Se producen entre 9 y 12 contracciones de segmentación por minuto y, sin embargo, entre dos contracciones haustrales pasan del orden de 30 minutos. Como consecuencia de esa actividad contráctil, la localización de los sacos haustrales cambia, porque las zonas que se contraen y las que se relajan se van alternando. Esta motilidad no provoca desplazamiento unidireccional del contenido intestinal; su función es ir exponiéndolo gradualmente a la acción absortiva del epitelio. Y al no provocar su avance, permanece largo tiempo en el interior del intestino grueso, de manera que se prolonga el tiempo en que se produce la acción de las bacterias intestinales sobre los materiales de origen vegetal que no habían sido digeridos y absorbidos en el intestino delgado.
Además de la provocada por las contracciones haustrales, en el intestino grueso se producen otros dos tipos de motilidad. Por un lado están las contracciones peristálticas; son provocados por células marcapasos ubicadas en la zona media del colon y generan ondas lentas en las dos direcciones. Su efecto neto consiste en impulsar el contenido digestivo hacia el recto. La motilidad intestinal de las aves se basa, sobre todo, en contracciones peristálticas. Otras células marcapasos ubicadas en la región proximal del colon generan contracciones antiperistálticas, cuya principal función consiste en llenar el ciego. Son contracciones importantes en la mayoría de los herbívoros y en los cerdos, pues su acción de mezcla facilita la digestión bacteriana de la celulosa y la absorción de los ácidos grasos volátiles, producto de la fermentación.
Tras cada comida suele producirse un fuerte aumento de la motilidad del colon. Grandes segmentos se contraen de forma simultánea, desplazando el contenido intestinal entre un tercio y tres cuartas partes de su longitud en unos pocos segundos. Estos movimientos “en masa” (así se llaman), conducen el contenido del colon hacia la porción distal del intestino grueso, donde queda almacenado hasta su expulsión.
Cuando el alimento entra en el estómago, se producen los reflejos gastroileal y gastrocólico, en los que interviene la gastrina y nervios autónomos extrínsecos. El reflejo gastroileal provoca el vaciado del intestino delgado y el gastrocólico el desplazamiento del contenido del colon al recto. De esa forma se va haciendo hueco, primero en el intestino delgado y después en el ciego y el colon, a nuevos contenidos.
Cuando los movimientos en masa del colon llevan el material fecal al recto, la distensión a que da lugar estimula los receptores de estiramiento de la pared rectal, iniciando así el reflejo de defecación. Ese reflejo provoca la relajación del esfínter anal interno (musculatura lisa) y contracciones fuertes del colon sigmoide y del recto. El esfínter externo consiste en musculatura esquelética y, por lo tanto, controlada voluntariamente; por lo tanto, si se relaja ese esfínter también, se produce la defecación. No obstante, si el esfínter exterior permanece contraído de manera prolongada, las contracciones rectales cesan hasta que se produce la llegada de material fecal adicional por efecto de posteriores movimientos en masa, y se reinicia el reflejo de defecación.
Las heces está formadas por celulosa que no se ha digerido y otras sustancias que no se han podido absorber, como bilirrubina (o biliverdina), sales, agua y bacterias. Aunque en el colon tiene lugar una cierta absorción, su importancia cuantitativa es mínima comparada con la del intestino delgado. La superficie interna del intestino grueso es muy reducida por comparación con la del delgado, dada la ausencia en aquel de las estructuras que multiplican la superficie absortiva propias de este. Además, el colon de muchos vertebrados carece de mecanismos de transporte específicos para las sustancias que se absorben en el intestino delgado. La excepción es el colon de las aves, en el que se absorbe glucosa y aminoácidos mediante transporte secundario activo. De esa forma, los aminoácidos y la glucosa que no han sido recuperados de la orina por el riñón pueden ser reabsorbidos en el colon o ser utilizados por los microorganismos en los ciegos intestinales.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El intestino grueso se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Estructura y motilidad del intestino delgado
- El intestino no es nuestro segundo cerebro
- Soy esa bacteria que vive en tu intestino, mejor vídeo de divulgación “On zientzia”
La tabla periódica en el arte: Plomo
Una noche como otra cualquiera William Watts se agarró tal borrachera que se quedó dormido junto a la iglesia de Santa María de Redcliffe. Soñó que desde el campanario caía una lluvia de gotas esféricas de plomo, lo que le llevó a patentar un nuevo método para la elaboración de perdigones. Esa es por lo menos la leyenda urbana que circula por las calles de Bristol. El procedimiento consistía en pasar plomo fundido por una bandeja de zinc agujereada que se colocaba a varios metros del suelo. Fruto de la caída libre se iban formando bolas esféricas que poco a poco se enfriaban y se terminaban por solidificar al caer en un balde de agua. Para lograr esta gran elevación Watts empleó unas torres que hoy en día llevan su apellido (Imagen 1). Poco tiene que ver esta historia con el mundo del arte, pero nos sirve para conocer algunas de las propiedades más interesantes de este metal tan peculiar: se funde a una temperatura relativamente baja (a 327 °C) y se moldea con facilidad. Además, es bastante estable, abundante y barato, por lo que el ser humano le ha dado múltiples usos, entre ellos muchos relacionados con el arte
 Imagen 1. Vestigio de una torre de Watts en Bristol con la iglesia de Santa María de Redcliffe al fondo. Fuente: Martin Tester
Imagen 1. Vestigio de una torre de Watts en Bristol con la iglesia de Santa María de Redcliffe al fondo. Fuente: Martin Tester
Escultura a base de plomo
La facilidad con la que se funde el plomo ha permitido que se emplee para crear objetos metálicos mediante moldes, tal y como sucede con los clásicos soldaditos de plomo. Más allá de las técnicas en las que el plomo es fundido, la maleabilidad de este material facilita su uso escultórico mediante repujado, es decir, trabajando directamente sobre planchas del metal. Plinio ya contaba que este modo de trabajar el plomo era bien conocido en el Imperio Romano y así lo confirman los relieves que se han conservado. Mucho más reciente es el uso del denso metal por parte del aragonés Pablo Gargallo del que se conservan esculturas en el Museo de Arte Nacional de Catalunya y en el Reina Sofía (Imagen 2). Como sucede con las obras de Gargallo, las esculturas en plomo rara vez son de gran tamaño, puesto que su elevada densidad (11 kg/L) y maleabilidad pueden causar que se doblen por su propio peso. De hecho, la maleabilidad, que hemos citado como gran ventaja, puede jugar en contra de la conservación de las esculturas, ya que presentan poca resistencia a los golpes.
 Imagen 2. Mano con Pipa (25 x 16 x 14 cm) de Pablo Gargallo (1920). Fuente: Museo Nacional Centro de Arte Reina Sofía.
Imagen 2. Mano con Pipa (25 x 16 x 14 cm) de Pablo Gargallo (1920). Fuente: Museo Nacional Centro de Arte Reina Sofía.
El plomo: esqueleto de las vidrieras
Las bondades del plomo han llevado a que se le de usos tan dispares como la fabricación de cañerías o la elaboración de tipos móviles en las imprentas. En el mundo del arte, además de en escultura, se ha empleado en arquitectura. Quizás el ejemplo más espectacular era la aguja de Notre Dame que hasta hace poco arañaba el cielo parisino a más de 90 metros*. A pesar de la ligereza que transmitía su forma alargada, para su elaboración se emplearon 250 toneladas de denso plomo. Cabe destacar que, aunque esta catedral sea el paradigma del gótico, la aguja desaparecida era del s. XIX, ya que se había levantado durante la restauración de Eugène Viollet-le-Duc. En cualquier caso, si hay algo para lo que el plomo fue fundamental durante el gótico (el de verdad) es el arte de las vidrieras.
 Imagen 3. Notre-Dame de Paris. Fuente: Wikimedia Commons.
Imagen 3. Notre-Dame de Paris. Fuente: Wikimedia Commons.
Las vidrieras son conjuntos de piezas de vidrio coloreado que cubren ventanales y que normalmente asociamos a edificios religiosos. Su uso está documentado desde inicios de la Edad Media, pero fue durante el s. XIII cuando alcanzaron su máximo esplendor, especialmente en el periodo conocido como gótico radiante, en el que las iglesias se convirtieron en jaulas de cristal, siendo el mejor exponente otro edificio parisino: la Sainte Chapelle. Cuando pensamos en vidrieras, el protagonismo se lo concedemos al vidrio de colores, pero el plomo también es un componente indispensable. En varillas elaboradas con este metal se insertaban los vidrios siguiendo un patrón previamente establecido (como si de un puzle se tratase). Luego ambos se unían mediante una soldadura de estaño y así se lograba un efecto maravilloso que tiene uno de sus máximos exponentes en la catedral de León.
 Imagen 4. Vidrieras de la catedral de León. Fuente: Wikimedia Commons.
Imagen 4. Vidrieras de la catedral de León. Fuente: Wikimedia Commons.
Los pigmentos del plomo
Además de uso como metal, el plomo nos regala una gran variedad de compuestos químicos que pueden ser empleados como pigmentos en el arte de la pintura. Nos quedaremos con tres y reservaremos el resto para el momento en el que en esta sección nos ocupemos de los otros elementos químicos con los que se combina. Comenzaremos por el minio (Pb3O4), conocido para muchos de quienes leen estas líneas, ya que hasta hace unos años era muy habitual usarlo por sus propiedades antioxidantes. Así, los objetos metálicos que se hallaban a cielo abierto se recubrían con una capa de este compuesto antes de darles la capa definitiva de pintura. Este pigmento rojizo, al igual que el bermellón, se empleaba para decorar profusamente las letras iniciales de los manuscritos medievales. De ahí que este proceso de ilustración se denominase miniare, de donde pronto surgió miniatura, palabra que el léxico castellano tomó del italiano.
 Imagen 5. Códice miniado del s. XV. Fuente: Biblioteca Universidad de Sevilla
Imagen 5. Códice miniado del s. XV. Fuente: Biblioteca Universidad de Sevilla
Este pigmento se conocía en la Antigüedad Clásica y tal como explica Vitrubio se lograba calcinando otros compuestos con plomo. Sin embargo, hay que remontarse a la China de principios del s. V a.e.c. para encontrar el primer uso como material artístico. En ese mismo territorio el alquimista Ko Hung dejó un divertido testimonio: “El ignorante no cree que el minio y el blanco de plomo sean productos de transformación del plomo, al igual que puede no saber que el mulo es vástago de una yegua y un burro… Hay cosas que están tan claras como el cielo y aun así los hombres prefieren sentarse bajo un tonel volcado.” Esta cita es del s. IV, pero bien podría extrapolarse a nuestra época (y no precisamente aplicándose a conocimientos pictóricos).
Del rojo pasamos al blanco para hablar del pigmento con plomo más importante de la historia: el albayalde. Palabra eufónica donde las haya y que en árabe hispánico (Albayád) significaba blancura. Blanco es, en efecto, el color del carbonato básico de plomo que denominamos con tal nombre (2PbCO3·Pb(OH)2). Tampoco sería ninguna locura decir que se trata del pigmento más importante que ha existido, ya que no hay pintor que no tenga el blanco en la paleta para controlar la tonalidad del resto de colores. Como sucedía con el minio, el albayalde es un pigmento que se logra sintéticamente, aunque mediante un proceso ligeramente más desagradable, por lo menos según el método holandés. En este procedimiento se empleaban vasijas de barro especiales que disponían de dos compartimentos conectados. En el compartimento inferior se ponía vinagre y en el superior placas de plomo. Así el vapor de ácido acético entraba en contacto con el metal. Para que la reacción química tuviese lugar, las vasijas se cubrían con una fuente de calor y de dióxido de carbono (CO2): estiércol. Pasados unos meses, surgía una costra blanca sobre el plomo, que se retiraba, se limpiaba, se secaba y se molía. Las placas metálicas se volvían a meter en la vasija y se repetía el proceso hasta que se agotase el metal.
 Imagen 6. Placa de plomo antes y después del proceso holandés. Fuente: Imagen cedida por el Mauritshuis.
Imagen 6. Placa de plomo antes y después del proceso holandés. Fuente: Imagen cedida por el Mauritshuis.
Teniendo en cuenta la importancia del albayalde, lo podemos encontrar en un sinfín de obras elaboradas con diferentes técnicas, desde los temples al huevo de Botticelli a los retratos de El Fayum pintados con cera de abeja. Ahora bien, si en una técnica ha tenido especial relevancia, esa es la pintura al óleo en la que, como otros pigmentos con plomo, acelera el proceso de secado. Para muestra los cuasi escultóricos impastos de Rembrandt. Pero no todo es tan bonito. La toxicidad de este metal pesado puede causar una gran variedad de síntomas que incluyen enfermedades óseas o fallos en el sistema nervioso. La intoxicación por plomo también se conoce como saturnismo, ya que Saturno era el planeta con el que los alquimistas asociaron este elemento químico. Esta elección no es arbitraria y se debe a que era el planeta conocido con una órbita más lenta, algo que se podía vincular con la gran densidad del plomo. Resulta paradójico que en la mitología romana Saturno portase una guadaña, como advirtiendo del poder asesino del elemento que la divinidad representa. Pero más paradójico resulta todavía que los dos cuadros más célebres que tienen a este dios como protagonista fuesen realizados por Rubens y Goya, quienes pudieron sufrir intoxicación por plomo, especialmente el segundo, cuya sordera se considera una evidencia de saturnismo. Más allá de estos dos pintores, a muchos otros artistas se les ha considerado víctimas del plomo: Miguel Ángel, Caravaggio, van Gogh, Fortuny, Frida Kahlo… Eso sí, hacer un diagnóstico tantos años después no es sencillo y no siempre se cuenta con evidencias sólidas para hacer tales afirmaciones.
 Imagen 7. Saturno devorando a su hijo. A la izquierda la versión de Goya (ca. 1820), a la derecha la de Rubens (1636). Fuente: Wikimedia Commons.
Imagen 7. Saturno devorando a su hijo. A la izquierda la versión de Goya (ca. 1820), a la derecha la de Rubens (1636). Fuente: Wikimedia Commons.
Acabamos este recorrido por los pigmentos del plomo con uno que además contiene antimonio: el amarillo de Nápoles. En honor a la verdad, diremos que hoy en día no se comercializa por la toxicidad de estos elementos, pero el nombre ha sobrevivido para denominar a los sucedáneos que han ido apareciendo. También hemos de decir que el gentilicio de este amarillo es poco adecuado, ya que ni mucho menos es originario de la ciudad italiana, por lo que es más acertado el nombre de amarillo de antimonio o antimoniato de plomo (Pb2Sb2O7). Al parecer, dicha confusión se extendió entre los siglos XVIII y XIX porque pensaban que se extraía de minerales que abundaban en las faldas del Vesubio. Lo cierto es que el pigmento es muchísimo más antiguo, por lo menos 30 siglos más, y tiene el honor de ser el primer amarillo sintético de la historia. El mérito, como muchas otras veces, corresponde a los egipcios que ya lo sintetizaban durante la XVIII dinastía (hacia el s. XV a.e.c). En el país del Nilo empleaban este compuesto para colorear el vidrio al igual que lo hicieron en Mesopotamia unos siglos después. Las diferentes culturas que habitaron esa región lo utilizaron en procesos de esmaltado, como en el caso de la vía procesional de Babilonia. Un uso similar se le dio en Europa muchos siglos después donde se empleó para colorear la mayólica. Las primeras evidencias de su uso en pintura son muy posteriores, concretamente del primer tercio del s. XVII (Imagen 8), aunque vivió su máximo auge a lo largo de los dos siglos siguientes.
 Imagen 8. El primer uso del amarillo de Nápoles en Occidente se detectó en el Arresto de Cristo (151×205 cm) de Matthias Stom (ca. 1630). Fuente: Wikimedia Commons
Imagen 8. El primer uso del amarillo de Nápoles en Occidente se detectó en el Arresto de Cristo (151×205 cm) de Matthias Stom (ca. 1630). Fuente: Wikimedia Commons
Para saber más:
Julio Montes-Santiago “The lead-poisoned genius: Saturnism in famous artists across five centuries” Progress in Brain Research 203 (2013) 223-240.
Fernando Cortés Pizano “Estudio del plomo medieval en las vidrieras del monasterio de Pedralbes (Barcelona)” Materiales de construcción 259 (2000) 85-96.
Max Doerner “Los materiales de pintura y su empleo en el arte” Editorial Reverté, Barcelona (2005).
* Nota del autor: A la hora de redactar este texto el fuego no se había cebado con la catedral de Notre Dame. Todavía me resulta inconcebible que dos semanas después de escribir las líneas originales “La fléche” se derrumbase arrastrando con ella un pedacito de nuestra Historia. Sucesos como este nos deberían enseñar a valorar más nuestro Patrimonio y a cuidar de él si queremos que perdure.
Sobre el autor: Oskar González es profesor en la facultad de Ciencia y Tecnología y en la facultad de Bellas Artes de la UPV/EHU.
El artículo La tabla periódica en el arte: Plomo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La tabla periódica en el arte: ¿Qué átomos hay en una obra?
- La tabla periódica en el arte: Cobre
- Deconstruyendo la tabla periódica
¿Qué tienen en común Einstein y una zanahoria?
La próxima vez que te comas una ensalada quizás mastiques con más respeto.
Los vídeos de ¿Preguntas frecuentes? presentan de forma breve y amena cuestiones que, probablemente, nos hayamos planteado en alguna ocasión. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.
Edición realizada por César Tomé López
El artículo ¿Qué tienen en común Einstein y una zanahoria? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Qué pasa en tu cuerpo cuando te enamoras?
- ¿Cuál es la postura más aerodinámica en ciclismo?
- ¿Qué pasa en tu cerebro cuando duermes?
Arrecifes fósiles, una paradoja geológica
La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebra dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Publicamos en el Cuaderno de Cultura Científica y en Zientzia Kaiera una serie de artículos que narran algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas.

 Fuente: Wikimedia Commons
Fuente: Wikimedia Commons
¿Qué es un arrecife? Si utilizamos nuestra memoria visual, la mayoría asociamos los arrecifes a mares tropicales de aguas cristalinas, rodeando islas de arena blanca y palmerales, y fondos tapizados por un universo de colores y maravillosas e inquietantes formas de vida submarina. Los cinéfilos, además, visualizarían barreras rocosas rodeando atolones e islas contra las que rompen olas y vientos huracanados, y que han engullido no pocos barcos e intrépidos aventureros. El término arrecife (reef, récif) tiene su raíz en “rif”, antiguo vocablo nórdico de uso marinero para designar las crestas rocosas que emergen del fondo marino y dificultan sobremanera la navegación. Estas sencillas concepciones ya resumen en gran medida la principal propiedad de los arrecifes: son estructuras “rocosas consistentes” que forman un “relieve” elevado sobre el fondo marino. Pero es necesario apuntar que no todo lo que en náutica se identifica como arrecife lo es desde un punto de vista científico; solo aquellos de naturaleza “calcárea” que demuestran haber crecido poco a poco por la acumulación de esqueletos y caparazones de invertebrados marinos que han crecido unos sobre otros de forma continuada encajarían en la definición científica estricta. En pocas palabras, los arrecifes actuales y fósiles son “edificios calcáreos bio-construidos”.
Los arrecifes tropicales actuales esencialmente se crean por la íntima asociación de colonias de corales escleráctinidos (Phylum Cnidaria) y algas calcáreas (Rhodophyta y Chlorophyta), a los que se asocian o acompañan diferentes invertebrados de caparazón o esqueleto calcáreo, tales como moluscos, equinodermos, esponjas, anélidos, briozoos, los poco conocidos foraminíferos (Protista) y toda una diversa comunidad de peces y otros vertebrados marinos. Por tanto, los arrecifes constituyen en sí mismos exuberantes y complejos ecosistemas que, además de sus singularidades tróficas, tienen la cualidad especial de “fijar” gran cantidad de carbonato cálcico, es decir, son “almacenes” naturales de Calcio y dióxido de Carbono, este último uno de nuestros temidos gases “invernadero”. Los arrecifes son y han sido siempre muy “dinámicos”: crecen a razones de varios milímetros/año y se expanden lateralmente por el apilamiento continuado de restos esqueletales calcáreos, ocasionalmente llegando a formar extensas barreras morfológicas. En la actualidad, estos “edificios bio-construidos” ocupan en conjunto más de 600.000 km2 de los fondos submarinos tropicales, una extensión nada desdeñable pero que no debe sorprendernos, ya que en algunos momentos del pasado geológico su extensión llegó a ser 10 veces más.
Durante los últimos 50 años y gracias al avance de las técnicas de inmersión, los investigadores han observado y analizado innumerables ejemplos de arrecifes de corales y algas a lo largo del Caribe, el Mar Rojo y los extensos océanos Índico y Pacífico, documentando su gran variedad en composición y morfología y, asimismo, desvelando su fragilidad ante procesos como la eutrofización, la acción de los rayos ultravioleta, la destrucción asociada al paso de huracanes o la proliferación súbita de especies invasivas. Son por esas señales uno de los principales “estandartes” utilizados por los investigadores del medio marino para intentar sensibilizar a la sociedad sobre el impacto generado por el cambio climático, la contaminación y la sobre-explotación de los mares tropicales.
No obstante, los arrecifes no son tan frágiles como parece, paradoja que se sustenta en un análisis riguroso de su evolución desde la perspectiva geológica. Bajo este enfoque debemos considerar no solo los arrecifes coralinos actuales, sino también todos los ejemplos de arrecifes fósiles que han documentados los geólogos en formaciones de rocas marinas de todos los continentes y edades geológicas. Así pronto percibiremos que los arrecifes, como ecosistemas generadores de edificios calcáreos, han estado presentes desde muy antiguo y que han evolucionado constantemente con el tiempo, durante múltiples fases de expansión, retracción y cambio marcado en sus características, siendo capaces de sobreponerse a numerosos acontecimientos climáticos y oceanográficos adversos, y a las crisis biológicas más dramáticas que han sacudido la vida sobre la Tierra (Figura 1). En algunas de tales etapas de estrés o crisis su adaptación simplemente se resolvió con una sustitución en el tipo principal de organismos constructores; en otros, en cambio, necesitaron de una completa “reinvención” del sistema y la cadena trófica que lo sustenta.
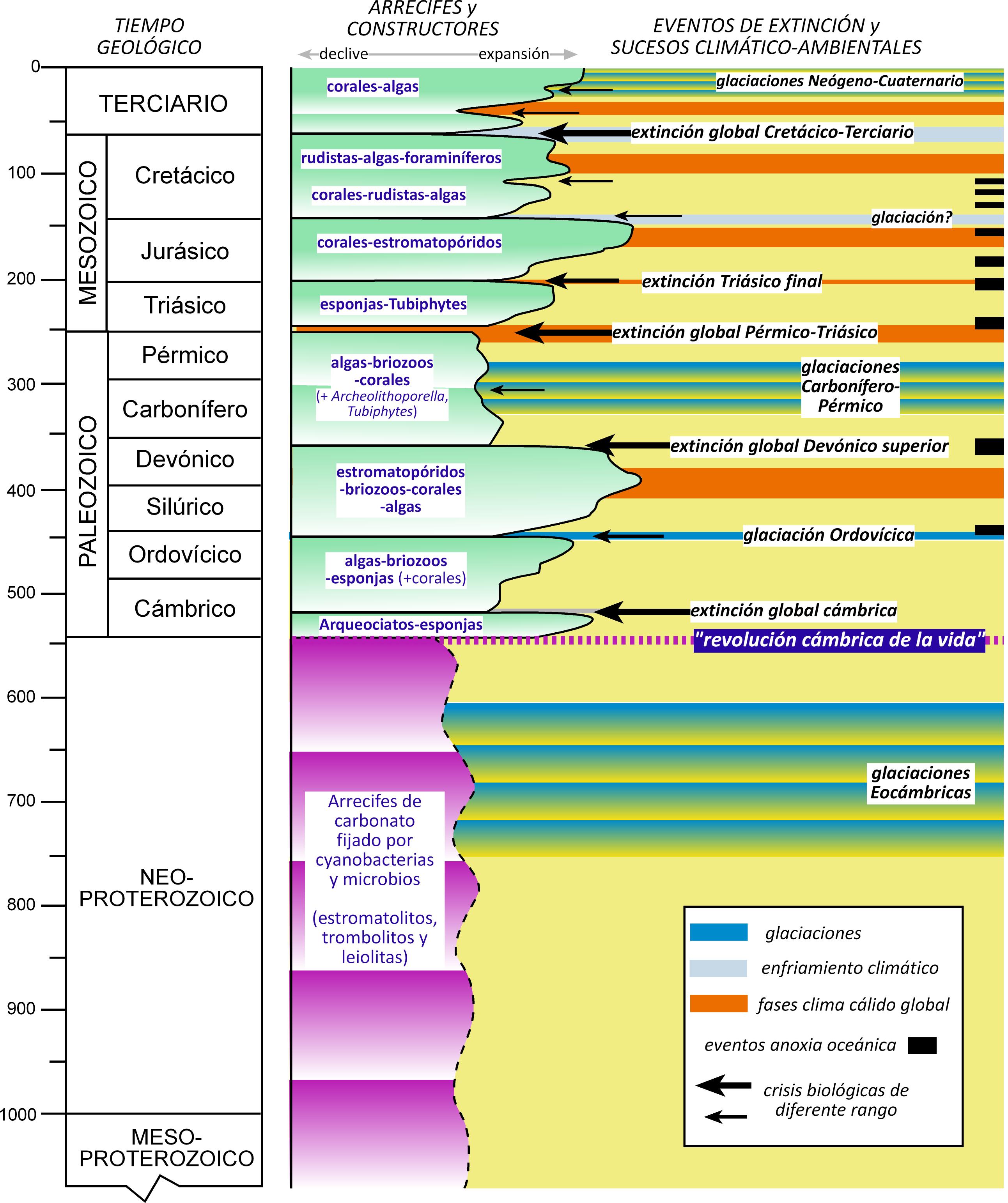 Figura 1. Principales tendencias evolutivas de los arrecifes desde el Proterozoico hasta la actualidad. Fuente: Juan Ignacio Baceta
Figura 1. Principales tendencias evolutivas de los arrecifes desde el Proterozoico hasta la actualidad. Fuente: Juan Ignacio Baceta
Las primeras construcciones arrecifales datan del Proterozoico medio y superior, entre 1600 y 540 Ma (millones de años), y se localizan en formaciones rocosas marinas de Canadá y Australia. Son edificios arrecifales bastante simples, básicamente compuestos por acumulaciones de estromatolitos, trombolitos y leiolitas, estructuras de morfología domal y organización interna laminada o masiva, construidos de forma “bio-inducida” por cianobacterias y calcimicrobios (procariotas y eucariotas fotosintéticos). Algunos de estos arrecifes proterozoicos alcanzaron cientos de metros de altura, formando verdades barreras próximas a la superficie del mar. Sin embargo, su naturaleza esencialmente microbiana hace que algunos investigadores no los consideren como “verdaderos” arrecifes.
La “revolución cámbrica” de la vida marina, hace unos 541 Ma, marcó la aparición y progresiva expansión de una ingente variedad de organismos pluricelulares y, entre ellos, de efectivos secretores de concha o esqueleto calcáreo y, por tanto, potenciales constructores de arrecifes. Durante el Cámbrico destacaron los arqueociatos, un grupo ancestral de esponjas (Porífera) que dominaron los océanos cálidos durante más de 25-30 Ma, para luego desaparecer de forma casi repentina. Los primeros metazoos constructores con cierta similitud a los actuales fueron los corales tabulados y rugosos, las algas calcáreas ancestrales, los estromatopóridos (Porífera), los crinoides (Echinodermata) y los primeros moluscos y braquiópodos. Todos estos grupos aparecieron durante el transito Cámbrico-Ordovícico (470 Ma) y se expandieron prodigiosamente durante el Silúrico y Devónico (442-372 Ma), periodos de condiciones climáticas globalmente cálidas. Los arrecifes de estas edades son muy numerosos y de enorme tamaño, habiéndose reconocido ejemplos en todos los continentes, desde Groenlandia y Norteamérica a Australia. A finales del Devónico una extinción biológica masiva de origen todavía controvertido provocó una retracción global, aunque arrecifes construidos por nuevos grupos de algas calcáreas y esponjas, y por organismos de afinidad biológica incierta (p.ej. algas filoides, Archeolithoporella, Palaeoaplysina, Tubiphytes) persistieron hasta el final del Paleozoico, sobrepasando varios ciclos de glaciación-deglaciación y cambio sustancial del nivel marino.
El tránsito del Paleozoico al Mesozoico, hace 252 Ma, estuvo marcado por la mayor extinción biológica que ha conocido nuestro planeta, el límite Pérmico-Triásico, atribuida a la confluencia de numerosas condiciones adversas (p.ej. pronunciado calentamiento y aridificación del clima, intenso volcanismo, impactos meteoríticos). Todo ello provocó una retracción drástica en los arrecifes, durante por lo menos 5-7 Ma. A pesar de ello, los arrecifes se recuperaron y expandieron de nuevo durante el Triásico, incorporando a los primeros representantes de los corales escleractínidos, los principales constructores de arrecifes en la actualidad. Estos prodigiosos cnidarios, parientes de las medusas, proliferaron durante el resto del Triásico y todo el Jurásico, junto a nuevas esponjas y moluscos, y las todavía importantes comunidades calcimicrobianas, con una importante retracción durante la crisis biológica del límite Triásico-Jurásico (200 Ma). Curiosamente, la mayor fase de expansión arrecifal del Mesozoico coincidió con el periodo de climas más cálidos de todo el Jurásico, al que sucedió una retracción notable durante el enfriamiento generalizado del tránsito al Cretácico. Durante el Cretácico (145-66 Ma), junto a los corales y algas calcáreas destacó un grupo singular de moluscos bivalvos, los rudistas, que de hecho alcanzaron la categoría de constructor principal durante el Cretácico superior, para luego desaparecer de forma brusca poco antes del límite Cretácico-Terciario (66 Ma). Los arrecifes de rudistas fueron muy extensos y se pueden reconocer desde el Himalaya a Oriente Próximo, a lo largo de todo el Mediterráneo y el dominio del Caribe, con algunos ejemplos espectaculares situados muy próximos a nosotros (Figura 2).
 Figura 2. Sierra de Aitzgorrigain (Itxina, Bizkaia). Frente preservado de la barrera arrecifal de 300 m construida por corales y rudistas (dcha.) en el Cretácico medio. Fuente: Juan Ignacio Baceta.
Figura 2. Sierra de Aitzgorrigain (Itxina, Bizkaia). Frente preservado de la barrera arrecifal de 300 m construida por corales y rudistas (dcha.) en el Cretácico medio. Fuente: Juan Ignacio Baceta.
El límite Cretácico-Terciario estuvo marcado por una fase de intenso volcanismo en la India, una sucesión de bruscos cambios climáticos y, finalmente, un impacto meteorítico descomunal en la península de Yucatán. En conjunto, todos ellos provocaron una nueva extinción biológica global, que en los continentes engulló a los últimos dinosaurios. Sorprendente, los organismos constructores de arrecifes se recuperaron de forma relativamente rápida tras la crisis, como lo atestiguan las extensas barreras arrecifales preservadas en el norte de África, los Alpes, los Cárpatos, y los Pirineos occidentales (Figura 3), formadas tan solo 2-4 millones de años tras la crisis global. En estos arrecifes, los corales y algas calcáreas ya se revelan como los principales constructores, aunque su evolución posterior hasta nuestros días estuvo jalonada de diferentes ciclos de expansión y retracción, en relación a fases de clima extremadamente cálido o de enfriamiento brusco, cambios marcados en el patrón de circulación oceánica y, finalmente, el progresivo tránsito a la Tierra refrigerada de las glaciaciones del Neógeno superior y Cuaternario.
 Figura 3. Sierra de los Alanos (Zuriza, Huesca). Espectacular alineación tipo barrera de los primeros arrecifes construidos por corales (dcha.) y algas calcáreas durante el Paleoceno, tras la crisis global del límite Cretácico-Terciario. Fuente: Juan Ignacio Baceta.
Figura 3. Sierra de los Alanos (Zuriza, Huesca). Espectacular alineación tipo barrera de los primeros arrecifes construidos por corales (dcha.) y algas calcáreas durante el Paleoceno, tras la crisis global del límite Cretácico-Terciario. Fuente: Juan Ignacio Baceta.
Como corolario, ¿qué conclusiones objetivas podemos sacar de la evolución de los arrecifes a lo largo de los tiempos geológicos?, ¿realmente son y han sido ecosistemas tan frágiles y vulnerables como revelan sus representantes actuales? Las respuestas no pueden ser sencillas. La idea de que los organismos constructores de arrecifes son sensibles a cambios ambientales es totalmente correcta, como lo demuestran su comportamiento actual y las innumerables fases y etapas de expansión y declive que han experimentado a lo largo de las edades geológicas. Sin embargo, la idea que comúnmente se argumenta en foros sociales y medios de comunicación de que los arrecifes van a desaparecer de nuestro planeta carece de rigor científico.
Si analizamos a los principales constructores de arrecifes actuales, los corales escleráctínidos, la evidencia geológica nos demuestra que estos organismos relativamente simples han tenido una extraordinaria capacidad adaptativa a cambios ambientales drásticos, ya que desde que aparecieron en el Triásico han sobrevivido a innumerables crisis, incluyendo eventos de extinción global, cambios climáticos pronunciados e incluso diferentes episodios de anoxia generalizada en los océanos (Fig. 1). A su vez, los corales de arrecifes actuales siguen demostrando tener un gran potencial de adaptación y especialización, ya que son capaces de proliferar en condiciones muy adversas e incluso de colonizar nuevos nichos marinos. Entre ellos destacan los mares de temperatura y salinidad más elevadas de lo normal (p.ej. en el Golfo Pérsico), las zonas litorales enturbiadas por el semi-continuo aporte de arcilla (litoral sureste de China) e, incluso, numerosos contextos relativamente profundos del Atlántico, el Caribe o el dominio indo-Pacífico, donde forman los denominados arrecifes coralinos “mesofóticos” y “afóticos”, creciendo a profundidades que oscilan entre los 50 a los 2000m. Estos arrecifes atípicos, en comparación a los arrecifes “eufóticos” que crecen próximos a la superficie del mar, eran poco conocidos hasta fechas recientes. Su estudio está evidenciando que asimismo se componen de comunidades coralinas complejas, adaptadas a baja o incluso nula visibilidad y, de forma llamativa, a fuertes fluctuaciones estacionales en la temperatura y los niveles de nutrientes. Por estas características, los arrecifes mesofóticos y afóticos parecen constituir el símil actual de lo que algunos especialistas denominan como “nichos refugio”, en los que las comunidades arrecifales pueden haber sobrevivido durante los diferentes periodos de crisis global reconocidos en el pasado, y ser el núcleo o punto de partida de las posteriores expansiones, una vez reestablecidas las condiciones ambientales favorables para ello.
En base a estas evidencias, no resulta demasiado aventurado afirmar que los arrecifes y sus protagonistas todavía van a estar bastante tiempo en nuestros océanos, aunque precisarán utilizar nuevos mecanismos de adaptación ante las condiciones ambientales adversas que potencialmente se avecinan. La pregunta clave a resolver es si la capacidad de adaptación de los corales y el resto de componentes arrecifales será suficiente ante la magnitud y velocidad de los cambios ambientales que ya están ocurriendo y previsiblemente ocurran, interrogante que constituye una de las piedras angulares de la investigación y las discusiones actuales entre los especialistas. A modo de reflexión, ante esta encrucijada ambiental, ¿estamos nosotros, la especie humana, tan preparados como creemos o desearíamos?
Para saber más
Aronson R.B. (Ed.) 2007. Geological Approaches to Coral Reef Ecology. Springer, 439p.
Kiessling W., Flügel E., Golonka, J. (Eds.) 2002. Phanerozoic Reef Patterns. SEPM Special Publications, 72. 775p.
Stanley G.D. (Ed.) 2001. The History and Sedimentology of Ancient Reef Systems. Kluver Academic, 458p.
Sobre el autor: Juan Ignacio Baceta es profesor en el Departamento de Estratigrafía y Paleontología de la Facultad de Ciencia y Tecnología de la UPV-EHU.
El artículo Arrecifes fósiles, una paradoja geológica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Geología, Antropoceno y cambio climático
- La FCT viaja a Marte
- Proteómica: cuando las proteínas y la espectrometría de masas van de la mano
La química del azul de Patinir
Patinir es considerado el primer paisajista flamenco. El azul de sus paisajes se concentra al fondo y va impregnando el cuadro hacia adelante, como una ola que avanza dejándolo todo perdido de color azul. Este efecto de avance lo consigue a través de planos paralelos escalonados. Al fondo el cielo, con la línea del horizonte bien alta, comparte azul con las montañas. Al fondo todo es azul.
 Joachim Patinir. El paso de la laguna Estigia.1520 – 1524. Óleo sobre tabla, 64 x 103 cm.
Joachim Patinir. El paso de la laguna Estigia.1520 – 1524. Óleo sobre tabla, 64 x 103 cm.
Yves Klein decía que «el azul es lo invisible haciéndose visible». El azul se ha utilizado en arte como concepto, especialmente para hacer notar lo inmaterial. Para pintar el paraíso y la oscuridad. El artista contemporáneo Anish Kapoor pintó un limbo azul oscurísimo que atrapa la luz en su Descenso al limbo. Los impresionistas renegaron del negro y pintaron las sombras de azul. El azul del Renacimiento es el azul de Patinir.
Se podría contar gran parte de la historia del arte a través del azul. Desde el azul egipcio, el ultramarino, el azul de cobalto, el cerúleo, el azul de manganeso, el de Berlín, el de París, el de Prusia, el de Milori, el de Bremen, hasta el azul de montaña, la azurita. Cada uno de ellos tiene un azul particular que puede describirse en gran medida gracias a la química de coordinación, como los azules que son azules por la presencia de metales de transición (cobalto, cobre, hierro, manganeso…). Algunos azules tienen matices de color que hay quien colocaría dentro de los violetas o los verdes. Algunos incluso mutan como consecuencia de la química y el tiempo. Hay artistas que han utilizado estas mutaciones o aparentes defectos de color en su beneficio. Entre ellos está el azul de Patinir, con frecuencia a caballo entre el color azul ultramarino y el turquesa.
El azul de Patinir es el azul de montaña, comúnmente llamado azurita. Hasta mediados del siglo XVIII fue el pigmento más utilizado en la pintura europea, y vino a sustituir el valioso azul ultramar auténtico, el que se extraía del lapislázuli y que provenía de Afganistán. La azurita, en cambio, se extraía de las montañas germanas, de ahí su nombre azul de montaña.
Hay constancia de que se conocía desde la antigüedad: los armenium y caeruleum que menciona Plinio eran seguramente tipos de azurita. Para diferenciarlos del ultramar se denominaban azzurrum ciramarinum o azzurro dell’Allemagna.
-
La química de la azurita en pintura
Químicamente la azurita es un carbonato básico de cobre, con un contenido en agua de cristalización variable (Cu3(CO3)2(OH)2). En los yacimientos se encuentra junto a la malaquita, con la que guarda una importante similitud química.
Se puede utilizar con medios acuosos como el temple o con gomas vegetales. Desprende un color azul luminoso. En comparación con el ultramarino tiende a verdoso con una leve tonalidad violácea.
En pinturas con medio aceitoso, como el óleo, capa a capa el resultado puede parecer casi negro. Añadiendo blanco es como se obtienen los azules más puros y cubrientes. Además, como la azurita es estable frente a los álcalis, se puede utilizar en medios oleosos mezclado con cal. El problema del óleo es que puede presentar rechazos de coloración y verdear, principalmente por formación de oleato de cobre.
-
Verdeado de la azurita
El tono aturquesado del azul de Patinir tiene que ver con la química de la azurita y su parcial transmutación en malaquita. Si el pigmento absorbe agua, parte de él acaba transformándose en malaquita (Cu2CO3(OH)2) que es de color verde. Esta es la razón por la que habitualmente las piedras que contienen azurita también presentan coloración verdosa de malaquita y viceversa.

Tanto la azurita como la malaquita pueden oxidarse y dar lugar a óxido de cobre o a sulfuro de cobre, en ambos casos de color negruzco. De ahí las zonas más oscuras de la piedra de la imagen anterior.
En cuanto el pigmento se mezcla con el aglutinante oleaginoso para formar la pintura al óleo, esta transmutación azurita-malaquita se queda congelada en el tiempo. Esa es la razón por la que las pinturas al óleo de azurita tienen tonos de color sutilmente diferentes, más verdes o azules.
El verdeado también puede deberse al propio amarilleamiento del aglutinante y, en mayor medida, al uso de barnices. A la hora de restaurar un cuadro hay que evaluar si el verdeado es propio del pigmento o es consecuencia de una alteración del medio. De hecho, es habitual que algunos pintores apliquen veladuras amarillas sobre la azurita para potenciar el verdeado. O que directamente mezclen pinturas como el amarillo de plomo con la azurita para conseguir pintura verde.
-
La azurita en la actualidad
La azurita tiene una composición química tan sencilla que ha sido fácil de obtener de forma sintética. A los carbonatos básicos de cobre producidos artificialmente se les conoce bajo el nombre de verditer. El grano que se comercializa es fino y regular, y resulta indistinguible de la azurita natural más débil de color. A pesar de que en el siglo XVIII ya existía el verditer, la batalla del azul la ganó el azul Berlín, un ferrocioanuro férrico mucho más estable y económico. Unos decenios más tarde se sumaron como sustitutos el azul ultramar artificial y el azul cobalto.
- El paso de la laguna Estigia
En 2013 hubo una exposición en el Museo del Prado llamada Historias naturales, un proyecto de Miguel Ángel Blanco. La exposición consistió en la instalación de alrededor de 150 piezas de historia natural, procedentes en su mayoría del Museo Nacional de Ciencias Naturales del CSIC –animales, plantas y minerales- junto a 25 obras de la colección del Museo, que entrañaban una estrecha relación con las mismas.

Una de las instalaciones que mejor definió el papel de Blanco dentro de las salas del Museo es su intervención en el emblemático cuadro de Joachim Patinir, El paso de la laguna Estigia. Delante de él colocó una gigantesca roca de azurita. Una roca a modo de prolongación de la laguna, o como resultado de su desecación, añadiendo un plano más a la obra original. La elección de la roca es coherente porque precisamente la azurita es el pigmento del azul que Patinir empleó en este cuadro.
El paso de la laguna Estigia está dividido verticalmente en tres zonas. En él se mezclan imágenes bíblicas junto a otras propias del mundo grecorromano. A la derecha está el Paraíso, con una zona de entrada angosta. En él prima el verde fresco y los azules. A la izquierda está el Infierno, con una entrada amplia y fácil, con verdes apagados, y al fondo negros y rojos que quedan fuera de la vista del navegante. En el centro Caronte lleva en su barca a un alma. Surcan la laguna turquesa en dirección al infierno.
-
De Patinir a Mejuto
El artista contemporáneo Vítor Mejuto ha traducido algunos de los cuadros más icónicos de la historia a un lenguaje geométrico. Uno de ellos es El paso de la laguna Estigia de Patinir. Mediante un proceso de síntesis, economía de formas y economía de color, Mejuto ha pintado el paso de la laguna Estigia empleando exclusivamente ocho planos de color sin transición entre ellos. De la misma forma que Mondrian eliminaba el velo que no le permitía ver la realidad en sus obras neoplásticas, Mejuto rescata lo grueso del cuadro de Patinir, como un ejercicio de optimización de la memoria.
 Vítor Mejuto. El paso de la laguna Estigia.2018. Acrílico sobre loneta resinada, 55 x 65 cm.
Vítor Mejuto. El paso de la laguna Estigia.2018. Acrílico sobre loneta resinada, 55 x 65 cm.
El azul de la laguna de Mejuto es el acrílico turquesa de Windsor & Newton. Este color se fabrica a partir del azul cobalto sintético o azul de Thénard, y químicamente es una espinela de óxido de cobalto (II) y óxido de aluminio (CoO·Al2O3), o aluminato de cobalto (II) (CoAl2O4). Es un pigmento de un azul intenso y puro que, combinado con óxido de cromo en la espinela, adquiere el color aturquesado final.
El uso del azul cobalto turquesa es la evolución lógica, desde un punto de vista técnico, de la renacentista azurita. Al igual que Patinir, Mejuto también empleó blanco en la mezcla para obtener el tono que encajaba. Patinir empleó blanco de plomo, actualmente en desuso por su toxicidad. Mejuto, blanco de zinc. También los blancos evolucionan en el arte cuanta más química sabemos sobre ellos.
Aunque el tema de El paso de la laguna Estigia es atemporal, tanto Patinir como Mejuto emplearon para pintarlo los azules de su tiempo.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo La química del azul de Patinir se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El Rubius hace un vídeo de química y la lía parda
- Los bimbaches de Punta Azul (El Hierro)
- Ensayo sobre el azul
El secreto de los números que no querían ser simétricos
Los números capicúas, o palíndromos, que son aquellos números tales que sus cifras leídas de izquierda a derecha y de derecha a izquierda son las mismas, son un tipo de números que, por la simetría que encierran, llaman la atención de la mayoría de las personas. De hecho, buscarlos, e incluso coleccionarlos, en las matrículas de los coches, los décimos de lotería, los billetes de medios de transporte, como autobús, tren o metro, los billetes de la moneda de cualquier país o cualquier otro lugar en el que aparezcan números de cuatro, o más dígitos, es algo bastante habitual. Más aún, muchas personas relacionan el hecho de encontrarse con un número capicúa, con la buena suerte.
 Billete de autobús Valencia-El Saler, con numeración capicúa, 13631. Imagen de la página web todocoleccion
Billete de autobús Valencia-El Saler, con numeración capicúa, 13631. Imagen de la página web todocoleccion
El concepto de número capicúa es muy sencillo y es muy fácil construir ejemplos de estos números. La forma más trivial es considerar un número con todos sus dígitos iguales, como 333.333.333, o se puede considerar una sucesión de cifras que luego se repiten en el sentido contrario, 12.433.421, aunque puede no repetirse el número central, 1.243.421. Así podemos crear todos los números palindrómicos que queramos: 232, 1.221, 55.555, 813.318, 1.756.571, etcétera. Claramente, existe una cantidad infinita de números capicúas, dado uno de estos números, siempre podemos generar uno más grande con solo añadir una misma cifra a la derecha y la izquierda del número, así dado el 121, podemos añadir el 7, obteniendo 71.217, si ahora añadimos el 3, se tiene 3.712.173, y este proceso es infinito.
 Antiguo billete de la Lotería Nacional, de abril de 1963, con un número capicúa, 28982. Imagen de la página Wallapop
Antiguo billete de la Lotería Nacional, de abril de 1963, con un número capicúa, 28982. Imagen de la página Wallapop
El concepto de palíndromo está fuertemente ligado a la representación posicional de los números, y además, depende de la base en la que se representan, en nuestro caso, es un sistema decimal, base 10. Por ejemplo, el número 2.002 es capicúa (en la base 10 en la que lo representamos de forma habitual), pero si se representa este mismo número en la base binaria, es decir, la base 2, con 0s y 1s, es decir, 11111010010, este ya no es capicúa. O si se representa el 2.002 en base octal, es decir, la base 8 (en la que utilizamos como cifras básicas 0, 1, 2, 3, 4, 5, 6 y 7), que se escribe como 3722, tampoco es capicúa.
Como sabemos, nuestro sistema de numeración posicional decimal viene la antigua India. Y precisamente, en la obra Ganatasarasamgraha – Compendio de la esencia de las matemáticas, del año 850, del matemático indio Mahaviracharya, se habla de un cierto número que “comienza por uno (y va aumentando de forma progresiva) hasta seis, para, a continuación, disminuir ordenadamente”, es decir, se refiere al número 123.45.654.321.
Esta familia de números capicúas, en la cual las cifras van subiendo, en una unidad, y luego bajando, tiene una propiedad curiosa, ya que puede obtenerse como el cuadrado de los números cuyos dígitos son solo unos:

Además, si cogemos cada uno de esos palíndromos, se verifica que la suma de las cifras del número es un número cuadrado.
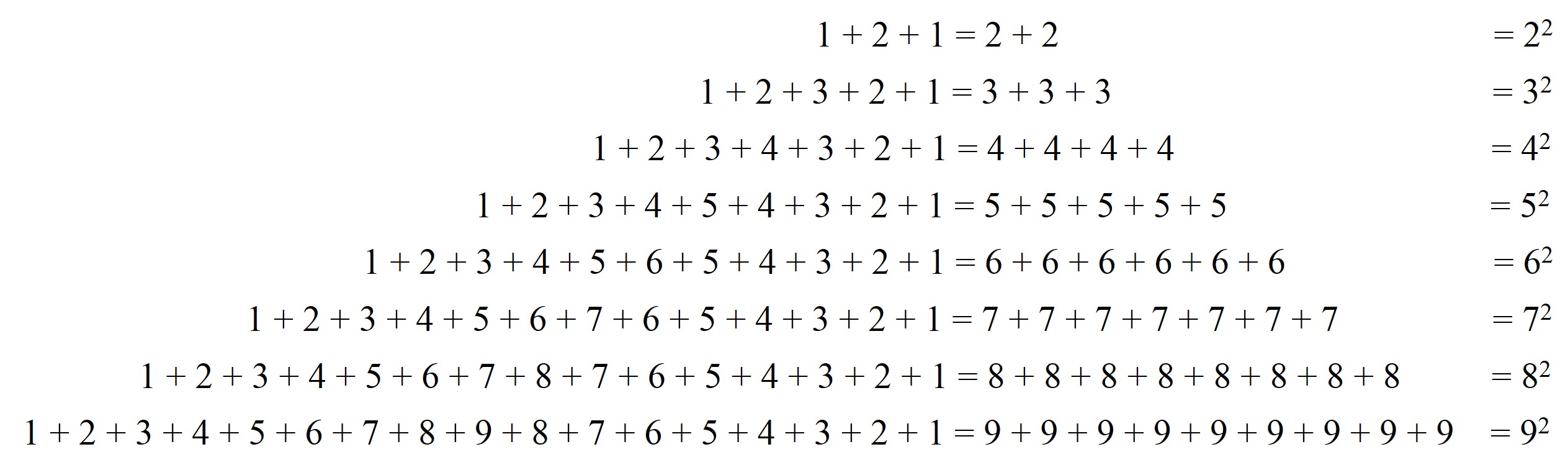
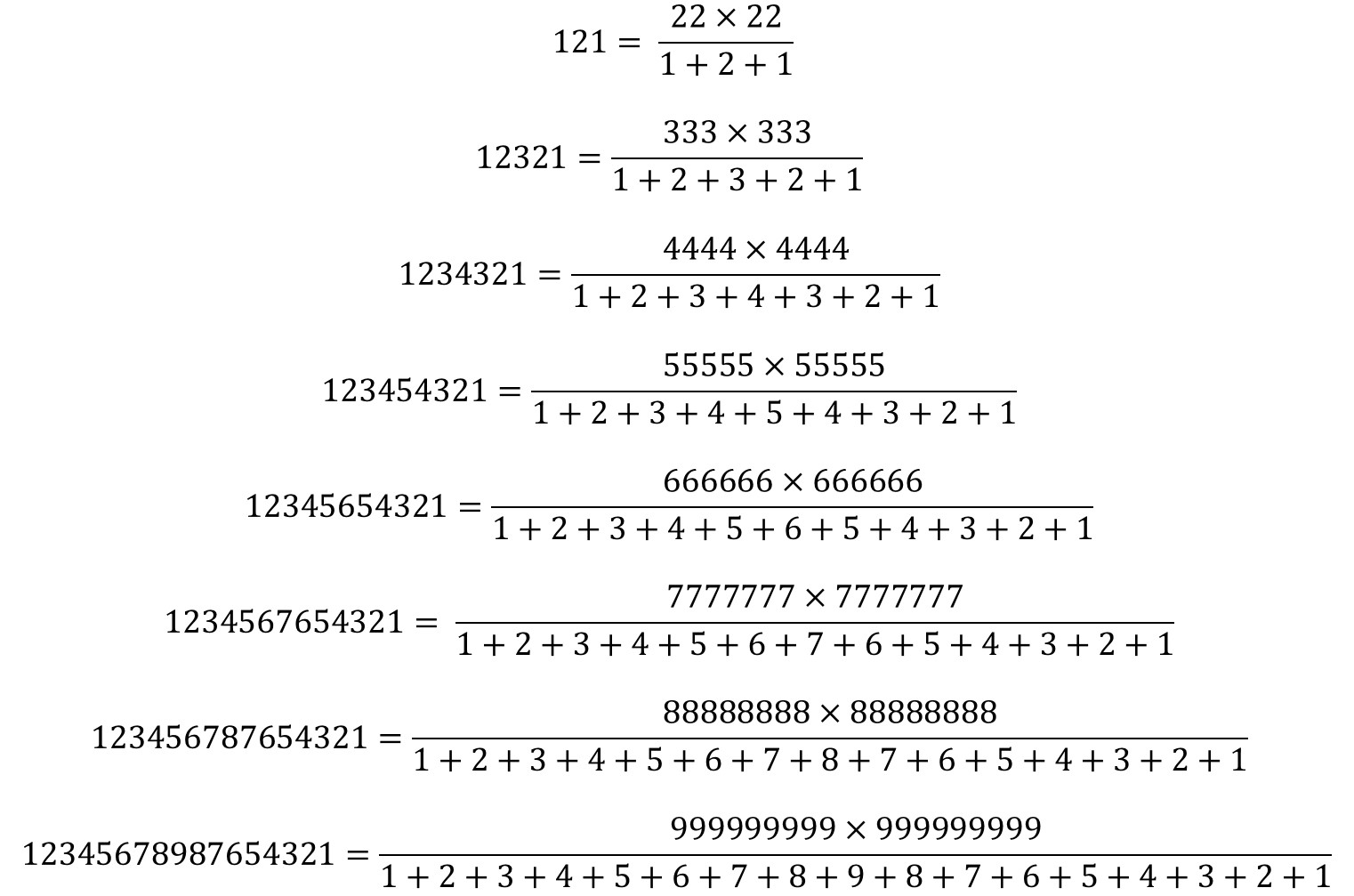
Más aún, estos particulares números capicúas, de la forma 12345654321, se pueden obtener también mediante una expresión simétrica bastante llamativa, aunque realmente solo es la combinación de las dos anteriores.
Pero vayamos con el objetivo central de esta entrada, una curiosa forma de obtener números capicúas. Tomemos un número cualquiera, por ejemplo, el 17 y sumémosle su simétrico, el 71, entonces se obtiene 17 + 71 = 55, que es palíndromo.
Probemos con otros números. Por ejemplo, el 75, entonces 75 + 57 = 132, que no es palíndromo, pero volvamos a realizar el mismo proceso con este resultado, 132 + 231 = 363, que ahora sí es capicúa, y lo hemos conseguido en dos pasos.
Veamos qué ocurre con algunos otros números. El 86, le sumamos su simétrico, 86 + 68 = 154, y como no es capicúa, seguimos el proceso, 154 + 451 = 605, una iteración más, 605 + 506 = 1111, de nuevo capicúa, en esta ocasión en tres pasos. Si empezamos en el número 87, después de cuatro pasos se obtiene el número 4.884, que es un número palindrómico. El número 88 ya es capicúa, es igual a su simétrico, luego no damos ningún paso con él. Si empezamos con el 89, necesitaremos 24 pasos hasta llegar a un número capicúa, el 8.813.200.023.188, como podéis comprobar.
Antes de continuar, podemos hacer una representación, con colores, de los 100 primeros números, distribuidos en una matriz cuadrada 10 x 10, de manera que el color esté relacionado con la cantidad de iteraciones que se necesitan para llegar a un palíndromo.
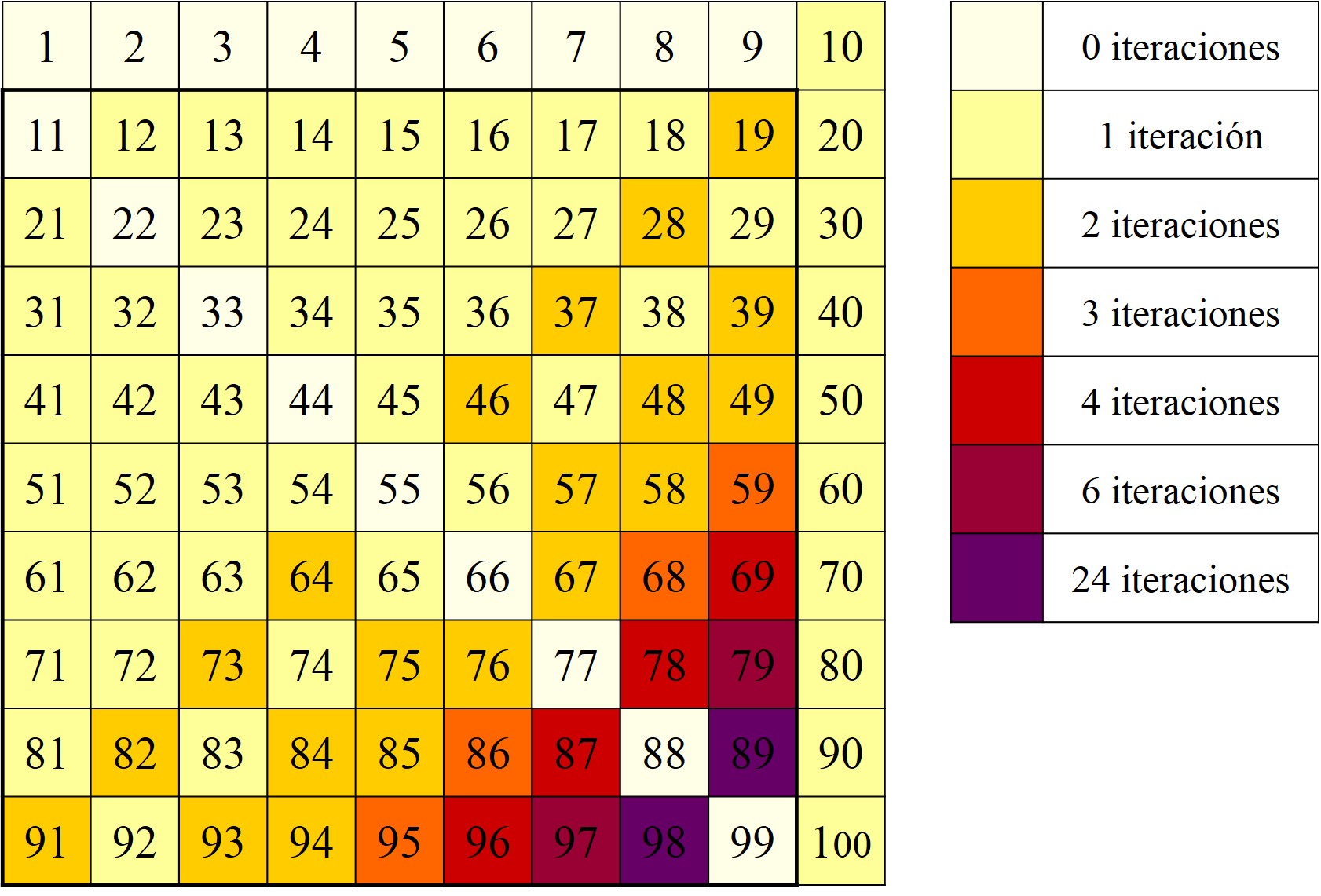
Como puede observarse, existe una cierta simetría alrededor del eje de los números de dos cifras formados por dos dígitos iguales, como 44 o 77, ya que los números a un lado y otro de este eje son los simétricos, como 67 y 76, que tienen igual comportamiento frente a este proceso.
La pregunta que se nos ocurre después de estos ejemplos, e incluso podemos intentarlo con algunos números más a ver qué ocurre, es:
Problema: ¿Se obtendrá siempre un número capicúa mediante este método iterativo, de sumar a un número su simétrico?
Este es un problema que aún está abierto, no se sabe si la respuesta es afirmativa o negativa. De hecho, el número 196, que no es un número muy grande, se desconoce si produce un número capicúa mediante este proceso iterativo. Veamos las primeras 26 iteraciones:

Desde la década de 1980, y haciendo uso de los ordenadores, se ha estado trabajando en realizar el mayor número de iteraciones posibles para ver si se alcanzaba un palíndromo, sin embargo, a día de hoy aún no se ha conseguido alcanzar un número con esta propiedad. En la actualidad, tenemos que Romain Dolbeau, con su programa “p196_mpi”, consiguió realizar en 2011 un billón de iteraciones, con las cuales alcanzó un número de más de 400 millones de dígitos, sin conseguir un número capicúa. Y en 2015 alcanzó un número con un billón de dígitos, sin conseguir el objetivo de llegar a un palíndromo. Por lo tanto, este es un problema abierto, aún se desconoce si empezando en el número 196, mediante el proceso iterativo “sumar el simétrico”, será posible obtener un número capicúa en algún momento, o si será este un proceso infinito, que nunca dará lugar a un palíndromo.
De hecho, se ha bautizado con el nombre de “números de Lychrel” (este nombre es un anagrama de Cheryl, el nombre de la novia, ahora mujer, de un matemático, Wade VanLandingham, que trabajaba en este tema), a aquellos números de los que se desconoce si generan un número palindrómico. Los primeros términos de la sucesión de estos números, etiquetada como A023108 en la Enciclopedia on-line de sucesiones de enteros de N. J. A. Sloane, son:
196, 295, 394, 493, 592, 689, 691, 788, 790, 879, 887, 978, 986, 1.495, 1.497, 1.585, 1.587, 1.675, 1.677, 1.765, 1.767, 1.855, 1.857, 1.945, 1.947, 1.997, …
Por otra parte, ya sabíamos que los números 887 y 1.675 también eran números de Lychrel, puesto que estaban en la sucesión de iteraciones del número 196. De hecho, se ha dividido a la familia de números de Lychrel en dos tipos de números, las “semillas”, que son los números más pequeños que generan un “hilo” de iteraciones, como el número 196, o los “familiares”, que son aquellos números que forman parte de un hilo generado por una “semilla”, como 887, 1.675 o 7.436, que están en el hilo del 196, o aquellos números que generan un mismo hilo que una semilla, como los números 295 (ya que, 295 + 592 = 887, que está en el hilo del 196, luego se genera este hilo a partir de 887), 394 (ya que, 394 + 493 = 887) o 689 (ya que, 689 + 986 = 1.675, que está en el hilo de 196). Dicho de otra forma, solamente hace falta estudiar las semillas, ya que los familiares tienen el mismo comportamiento que estas.
Solamente hay cuatro semillas menores que 10.000, que son 196, 879, 1.997 y 7.059, sin embargo, a partir de 10.000, ya hay muchas más semillas. Las siguientes son:
10.553, 10.563, 10.577, 10.583, 10.585, 10.638, 10.663, 10.668, 10.697, 10.715, 10.728, 10.735, 10.746, 10.748, 10.783, 10.785, 10.787, 10.788, 10.877, 10.883, 10.963, 10.965, 10.969, 10.977, 10.983, 10.985, 12.797, 12.898, etcétera.
 Billete de España de 500 pesetas, del año 1979, con la imagen de Rosalía de Castro, y con un número de serie capicúa, 2152512. Imagen de la página de Numismática Bilbao
Billete de España de 500 pesetas, del año 1979, con la imagen de Rosalía de Castro, y con un número de serie capicúa, 2152512. Imagen de la página de Numismática Bilbao
Volviendo a los números que sí generan un número capicúa mediante el proceso “sumar el simétrico”, hemos visto que el número 89 necesitaba de 24 iteraciones para alcanzar el palíndromo. Otra cuestión que nos podemos plantear es si, salvo en el caso de los números de Lychrel, se necesitan muchas iteraciones para llegar al capicúa. El mayor número de iteraciones para un número de 3 dígitos es 187, que necesita 23 pasos para alcanzar el palíndromo. Con 4 cifras es el 1.297, que necesita 21 iteraciones.
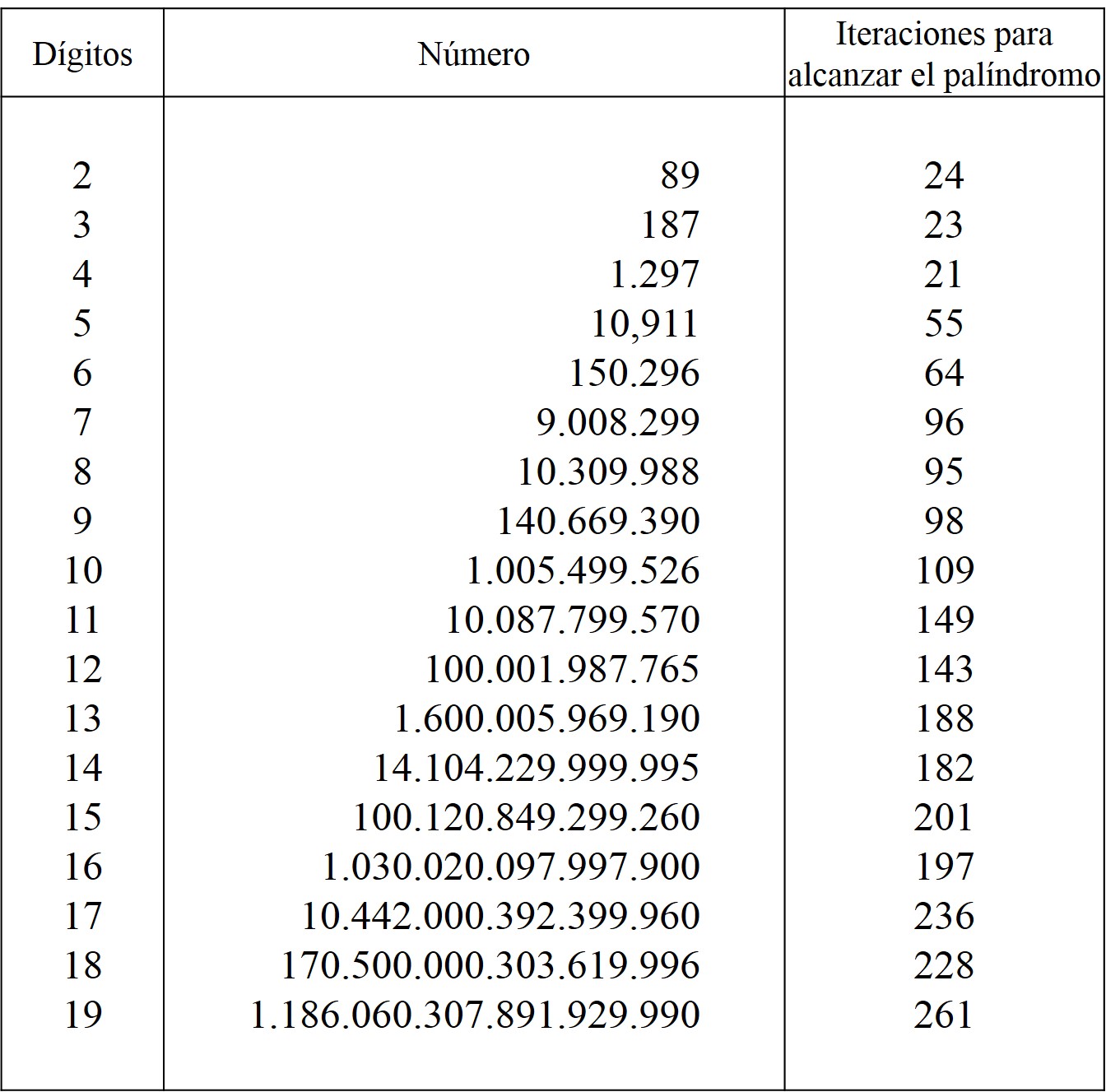
Aunque, a día de hoy, el mayor número de iteraciones necesarias para obtener un número palindrómico, mediante este proceso, es de 261, que convierten el número 1.186.060.307.891.929.990, con 19 dígitos, en un número capicúa de 119 dígitos. En el siguiente cuadro se recogen los records de iteraciones necesarias para números de entre 2 y 19 dígitos.
Para terminar, me gustaría hacer un breve comentario sobre algunas familias de números capicúa. En el mundo de las matemáticas nos encanta “jugar” y estudiar las diferentes propiedades matemáticas con las que nos encontremos, solo por el placer del conocimiento. Así, en el caso de los números palindrómicos, se estudian las familias de estos números que además satisfacen otras propiedades matemáticas, como ser números cuadrados, cúbicos o cualquier otra potencia, números triangulares y otros números poligonales, o números primos, así mismo se estudian diferentes objetos matemáticos formados con números capicúas, como las ternas pitagóricas o los cuadrados mágicos.
Veamos algunos ejemplos. Recordemos que los números triangulares son aquellos que se pueden representar con piedras como un triángulo equilátero y que coinciden con aquellos que son la suma de los primeros números naturales, como 1 + 2 + 3 = 6 ó 1 + 2+ 3 + 4 = 10 (véanse las entradas El asesinato de Pitágoras, historia y matemáticas (y II) o La magia de los números (el teorema de Moessner)). Y la fórmula general de los números triangulares es Tn = n x (n – 1) / 2.
¿Existirán números triangulares capicúas? Sí, por ejemplo, los primeros números triangulares capicúas son:
T1 = 1, T2 = 3, T3 = 6, T10 = 55, T11 = 66, T18 = 171, T34 = 595, T36 = 666, T77 = 3003, T109 = 5995, T132 = 8778, T173 = 15051, …
Por cierto, que el número de la bestia (véanse las entradas 666, el número de la Bestia (I) y 666, el número de la Bestia (II)) es un número triangular capicúa. Se conocen 147 números triangulares capicúas.
Un campo en el que se está trabajando mucho es en el estudio de los números capicúas primos, como los números 131 o 757. A continuación, os dejo el listado de los primeros palíndromos primos:
2, 3, 5, 7, 11, 101, 131, 151, 181, 191, 313, 353, 373, 383, 727, 757, 787, 797, 919, 929, 10.301, 10.501, …
 Obra Family vacation (2016), de la artista estadounidense Xylor Jane, en la que se observan dos columnas de 13 números, de 11 dígitos cada uno de ellos, que resultan ser números capicúas primos con 11 dígitos, que solo contienen 2 de las 10 cifras básicas, como 1.111.515.111 o 13.131.113.131. Imagen de la página web ART SY
Obra Family vacation (2016), de la artista estadounidense Xylor Jane, en la que se observan dos columnas de 13 números, de 11 dígitos cada uno de ellos, que resultan ser números capicúas primos con 11 dígitos, que solo contienen 2 de las 10 cifras básicas, como 1.111.515.111 o 13.131.113.131. Imagen de la página web ART SY
Vamos a terminar la entrada con tres cuadrados mágicos diabólicos (es decir, la suma de los elementos de las filas, de las columnas, de las diagonales principales, pero también de las diagonales no principales, que están partidas en dos partes), encajados, cada uno dentro del siguiente, formados con números capicúas, cuyas sumas mágicas son de nuevos números capicúas, 2.442 (en el central, de orden 4), 3.663 (en el de orden 6) y 4.884 (en el exterior de orden 8).
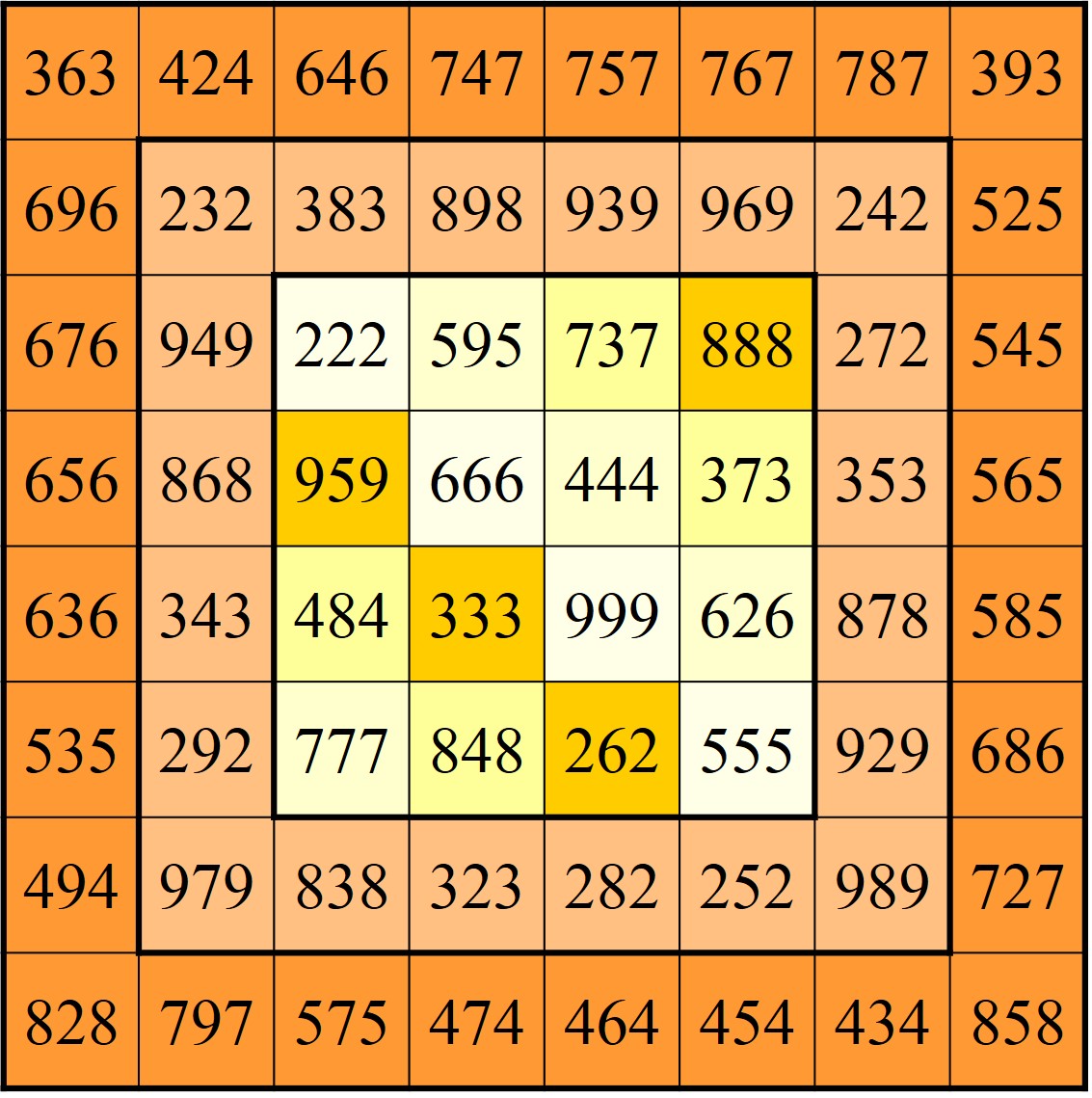 En el centro, un cuadrado mágico diabólico de orden 4 y suma mágica 2.442, formado por números capicúas. Se completa con un borde de números capicúas, dando lugar a un cuadrado mágico diabólico de orden 6 y suma mágica 3.663. Y se vuelve a completar con un borde de números capicúas, para dar lugar a un cuadrado mágico diabólico de orden 8 y suma mágica 4.884
En el centro, un cuadrado mágico diabólico de orden 4 y suma mágica 2.442, formado por números capicúas. Se completa con un borde de números capicúas, dando lugar a un cuadrado mágico diabólico de orden 6 y suma mágica 3.663. Y se vuelve a completar con un borde de números capicúas, para dar lugar a un cuadrado mágico diabólico de orden 8 y suma mágica 4.884
Bibliografía
1.- Clifford A. Pickover, El prodigio de los números. Desafíos, paradojas y curiosidades matemáticas, Ma Non Troppo (ediciones Robinbook), 2002.
2.- Clifford A. Pickover, La maravilla de los números. Un viaje por los secretos de las matemáticas, sus desafíos y caprichos, Ma Non Troppo (ediciones Robinbook), 2002.
3.- Harvey Heinz, Palindromes
4.- N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, OEIS: sucesión A006960 (sucesión de números formados por la iteración “suma del simétrico” a partir del número 196)
5.- Romain Dolbeau, The p196_mpi page
6.- N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, OEIS: sucesión A023108 (números de Lychrel)
7.- N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, OEIS: sucesión A063048 (números de Lychrel semillas)
8.- Jason Doucette, World Records
9.- N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, OEIS: sucesión A003098 (números triangulares capicúas)
10.- N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, OEIS: sucesión A002385 (Números capicúas primos)
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El secreto de los números que no querían ser simétricos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una conjetura sobre ciertos números en el ‘sistema Shadok’
- El origen poético de los números de Fibonacci
- Los números enamorados
Polarizadores y el triunfo de la hipótesis ondulatoria
 Fuente: Polaroid / Safilo
Fuente: Polaroid / Safilo
Los estudios científicos sobre la polarización de la luz continuaron a lo largo del siglo XIX. Por ejemplo, la forma en que el espato de Islandia separa un haz de luz no polarizada en dos haces polarizados se muestra en la de abajo y es una representación que conceptualmente data originalmente de esa época. Sin embargo, las aplicaciones prácticas se vieron frustradas, principalmente porque las sustancias polarizadoras como el propio espato de Islandia eran escasas y muy frágiles.
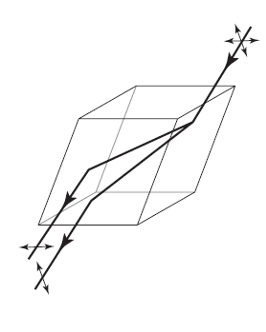 Fuente: Cassidy Physics Library
Fuente: Cassidy Physics Library
Uno de los mejores polarizadores era el cristal sintético herapatita, sulfato de yodo-quinina. Decimos sintético porque se descubrieron de forma accidental en 1852 cuando un estudiante añadió yodo a la orina de un perro al que habían suministrado quinina y observó que aparecían unos cristales verdosos. El responsable del laboratorio, William Bird Herapath, estudió los cristales al microscopio. Encontró que los cristales de herapatita en forma de aguja absorbían la luz que está polarizada en la dirección del eje largo del cristal y absorben muy poca de la luz polarizada en una dirección perpendicular al eje largo.
Los cristales de herapatita eran tan frágiles que parecía que no había forma de usarlos. Pero en 1928, Edwin H. Land, cuando aún era un estudiante de primer curso en la universidad, inventó una lámina de plástico que llamó “Polaroid”. Este primer polarizador era una película transparente de nitrocelulosa en la que había incrustado muchos pequeños cristales de herapatita de tal manera que, cuando se estiraba el plástico, los cristales en forma de aguja se alineaban en una dirección. Por lo tanto, todos interactuaban con la luz incidente de la misma manera.
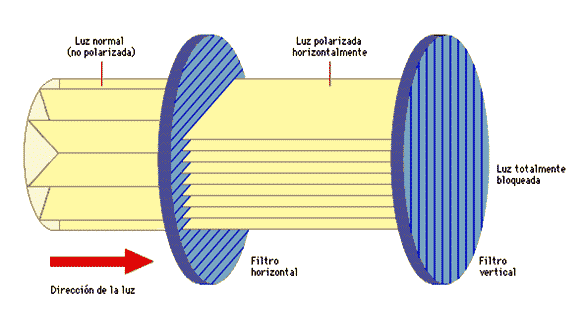
Algunas de las propiedades de un material polarizador se pueden comprobar fácilmente. Por ejemplo, se pueden obtener dos superficies de polarización de las lentes de un par de gafas de sol polarizadas, o de las gafas “tridimensionales” usadas en los cines. Si sostenemos una de las lentes frente a una fuente de luz y miramos esta primera lente a través de la segunda, comprobamos que al girar la primera lente la intensidad de luz sube y baja alternativamente. Encontraremos que una rotación de 90º nos lleva de la intensidad másxima a la mínima.
 Fuente: Wikimedia Commons
Fuente: Wikimedia Commons
¿Cómo se puede explicar este efecto? La luz que incide en la primera lente, o superficie de polarización, originalmente no está polarizada, es decir, es una mezcla de ondas polarizadas en diferentes direcciones, como ya vimos. La primera lente transmite solo las ondas que están polarizadas en una dirección y absorbe el resto. La onda transmitida que va hacia la segunda hoja ahora está polarizada en una dirección. Siempre que esta dirección coincida con la dirección de polarización de la segunda superficie, la onda no será absorbida por la segunda lente. Sin embargo, si la dirección es perpendicular a la dirección de polarización, la luz polarizada no pasará a través de la segunda lente, sino que será absorbida.
Como conclusión general de lo que hemos visto sobre las ondas de luz, vemos que los efectos de interferencia y difracción requerían un modelo de onda para la luz. Para explicar los fenómenos de polarización, el modelo de onda se tuvo que hacer más específico; la polarización podría explicarse solo si las ondas de luz son ondas transversales. En conjunto, este modelo para la luz explicaba muy satisfactoriamente todas las características de la luz consideradas hasta principios del siglo XX.
Pero, hay una nota disonante, ¿verdad? ¿En qué medio se transmiten las ondas de luz que vienen del Sol o de la Luna o de las estrellas?
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Polarizadores y el triunfo de la hipótesis ondulatoria se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Química atmosférica a la caza de la primera feromona humana
 Imagen: Unsplash
Imagen: Unsplash
¿Ha comprado usted alguna vez un perfume con feromonas con la esperanza de que le ayudase a ligar? O, mejor aun, ¿ha acudido a una de esas fiestas en las que los asistentes deben entregar al llegar una camiseta con la que hayan dormido varios días empaquetada en una bolsa hermética para que sea olisqueada a fondo por los participantes del sexo opuesto y así, en teoría, emparejarse con éxito? No me lo estoy inventando, estas cosas por lo visto existen.
Pues quizá haya usted salido de casa oliendo muy bien (o haya hecho un aporte apestoso a esa fiesta, qué sé yo) pero en cualquier casa, espero que no pagase demasiado por el componente feromónico porque, lo que es evidencia científica, nada de nada.
No sabemos cómo son las feromonas humanas
A día de hoy no se conoce todavía ningún compuesto químico que actúe en los seres humanos como feromonas, esas señales químicas principalmente olfativas que nuestros cuerpos generarían, supuestamente, para llevar a otros seremos humanos en principio, aunque no exclusavamente, del sexo opuesto a actuar de determinada forma para favorecer el éxito sexual y en definitiva reproductivo. Las hemos visto identificado en animales, pero en seres humanos, de momento, ni rastro.
Fue en 1959 cuando el bioquímico alemán Adolf Butenandt acuñó por primera vez el término feromona. Butenandt, que ya había ganado un Nobel de Química por su trabajo identificando y aislando las hormonas sexuales, publicó en ese año sus trabajos basados en la polilla de la seda Bombyx more y la estructura química de la sustancia que le sirve para atraer a sus congéneres.
Tras las polillas llegaron las hormigas, las abejas, los ratones… También se observó que las feromonas no tienen solo una finalidad sexual. Las abejas por ejemplo son capaces de generar señales químicas que sirven para dar la alarma a sus compañeras cuando hay algún peligro cerca. Salen de las llamadas glándulas de Nasorov, que se encuentran bajo el abdomen de estos insectos. Otras feromonas, utilizadas entre otras por las hormigas, sirven para indicar a los demás miembros de un grupo el camino hasta un lugar donde hay alimento, de forma que puedan ir a por él y transportarlo entre todas hasta el hormiguero.
Pero en humanos, de momento, no se conoce una feromona concreta que cumpla alguno de estos fines o ningún otro. Algunos estudios han sugerido que si bien no sabemos aun cuáles son esas sustancias o cómo actúan, deben existir y actuar de alguna forma y damos por cierta su existencia, pero algunos análisis críticos consideran poco sólidos esos estudios y por tanto sus conclusiones.
 Imagen: Unsplash
Imagen: Unsplash
Estudiar la química del cuerpo como la química del aire
En estas semanas, un nuevo enfoque de estudio está tratando de averiguar si es posible encontrar estas esquivas sustancias en los seres humanos. Se trata de aplicar una técnica que emplean los químicos atmosféricos, llamada reacción de transferencia de protones – estectrometría de masas o PTR-MS por sus siglas en inglés, a la química de nuestro cuerpo para hallar las ansiadas feromonas humanas.
Cuenta este artículo en la revista Science que el químico climatólogo Jonathan Williams, del Instituto de Química del Max Plank, es uno de los participantes en las reuniones sobre comunicación química entre seres humanos que se han celebrado en la Royan Society para explicar cómo esta técnica que se utiliza para hallar trazas de determinadas sustancias químicas en la atmósfera podría llegar al rescate de este área de investigación que necesita un nuevo punto de vista para seguir adelante.
Un área que está en crisis en parte por la escasa financiación que recibe en general: el olfato es uno de los sentidos que menos atención e interés recibe por parte de las investigaciones en fisiología, los estudios al respecto suelen ser pequeños y por tanto estadísticamente endebles, y por otro lado el cuerpo humano emite cientos de sustancias volátiles susceptibles de ser olfateadas por otra persona, la comunicación química se mezcla con todas las demás formas de comunicación entre seres humanos y las posibles respuestas en formas de comportamiento, también. Los estudios realizados hasta ahora se han limitado a pedir a esos pocos participantes que duerman varios días con la misma camiseta o a colocarles compresas absorbentes bajo las axilas.
La PTR-MS puede aportar mucha más información. Esta técnica consiste en transferir un protón a esos compuestos volátiles y luego analizar su masa por la forma en que se desplazan en un campo eléctrico. Esto permite medirlos en tiempo real e identificar aquellos que, ante un determinado estímulo o comportamiento, aumentan en cantidad o sufren algún cambio.
Olemos diferente si nos reímos, nos tensamos o nos asustamos
Williams cuenta que se dio cuenta del potencial de esta técnica hace años tras analizar la composición química del aire alrededor de una hinchada de aficionados al fútbol durante un partido. “Podíamos averiguar el comportamiento de la gente haciendo un seguimiento de las trazas de sustancias químicas a su alrededor”, asegura. Por ejemplo, era posible saber cuándo el partido había llegado al descanso porque los niveles de acetonitrilo, un componente del humo del tabaco, alcanzaban el máximo rápidamente. En el descanso es cuando la mayoría de la gente aprovecha para fumarse un cigarro.
 Imagen: Unsplash
Imagen: Unsplash
¿Sería posible ‘oler’ en el aire la euforia tras un gol del equipo local? Aquel partido en concreto no permitió a Williams responder a esa pregunta ya que terminó con un empate a cero. El científico decidió irse a olisquear una sala de cine, y allí descubrió que los espectadores de una comedia emiten sustancias químicas distintas que los que ven una película de suspense, y que esas emisiones cambian cuando el guión da un giro inesperado. “Viendo Los Juegos del Hambre era posible determinar el momento en el que empieza la gran pelea final”, asegura. En un estudio publicado al respecto contaba que los niveles de dióxido de carbono subían, seguramente debido a la aceleración de la respiración del público, así como los de isopreno, que podían provenir de una mayor tensión muscular.
Otro científico atmosférico, Ben Langford, del Centro de Ecología e Hidrología en Edimburgo, quedó tan intrigado por estos resultados que unió fuerzas con el psicólogo Craig Roberts, de la Universidad de Stirling, en el Reino Unido para profundizar en estos hallazgos. Entre los dos han realizado estudios, aun pendientes de publicar, en el que ponen a los voluntarios escenas de películas mientras analizan el aire bajo sus axilas. Ya han identificado algunos compuestos que varían durante las escenas de terror y quieren seguir investigando en esa línea. Aun no está claro si esos cambios suponen realmente una señal química de algún tipo.
Pero es interesante que se centren en las sustancias químicas en relación con el miedo o la agresión, ya que durante décadas las investigaciones sobre feromonas humanas se han centrado en señales relacionadas con el comportamiento sexual, que quizá sean precisamente más difíciles de encontrar.
No son los únicos que han decidido cambiar el amor por la agresividad en este campo. En otro estudio mencionado durante estas reuniones, los científicos han recogido sudor de soldados israelíes antes de su primer salto en paracaídas con sudor recogido en otro momento de sosiego. Quizá buscar cambios alrededor de esos momentos en los que por la mente se pasan pensamientos de vida o muerte sea la mejor oportunidad de encontrar estas esquivas señales químicas.
 Imagen: Pixabay
Imagen: Pixabay
Eso sí, puede que esa señal no sea la producción de una feromona específica como las que conocemos en insectos o en algunos mamíferos. Quizá sea una serie de complicados cambios en la abundancia y concentración de varias o muchas sustancias distintas. Precisamente lo que los científicos atmosféricos están acostumbrados a estudiar. Quizá esto haga por fin avanzar este campo de investigación.
Claro que, de momento… dejen la colonia de feromonas en casa.
Referencias:
Can atmospheric chemists rescue the stalled quest for a human pheromone? – Science
Adolf Butenandt—Nobel Prize for Chemistry – Mayo Clinics Proceedings
Feromona – Wikipedia
Suspense in the movie theatre air: Cinemagoers’ exhaled breath reveals the scene that is playing – Phys.org
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo Química atmosférica a la caza de la primera feromona humana se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- De la materia a la vida: ¿Química? ¡Química!, por Jean-Marie Lehn
- Pensando la química matemáticamente
- Los cimientos de la química neumática al estilo van Helmont (y 3)
Ciudades sin coches
 Calle Benito Corbal (Pontevedra). Imagen: Wikimedia Commons
Calle Benito Corbal (Pontevedra). Imagen: Wikimedia Commons
La introducción en 2003 de tarifas de congestión –pago por entrar, circular o salir del centro de la ciudad- en Londres tuvo una gran repercusión, pero no ha sido un caso aislado; cada vez más ciudades toman medidas para reducir el tráfico rodado de vehículos de combustión interna. En algunas ciudades se ha llegado, incluso, a suprimirlo en las áreas urbanas céntricas salvo para determinadas excepciones.
El ferroviario -metro o tren- es el medio de transporte que más personas desplaza por unidad de tiempo y por unidad de superficie urbana utilizada; en esos términos transporta diez veces más pasajeros que el automóvil particular. Y otras formas de movilidad registran eficiencias intermedias entre esos dos extremos. La contaminación es otro factor a considerar; a la provocada por el tráfico rodado -que incluye carbonilla, óxidos de nitrógeno y monóxido de carbono- se atribuyen, al menos, 184.000 muertes prematuras cada año en el mundo, la mayoría producidas por enfermedades cardíacas o pulmonares. Y a los accidentes provocados por automóvil se debe un millón de muertos anuales, además de causar cerca de ochenta millones de heridos.
El uso del coche reduce de forma considerable la actividad física, uno de los grandes problemas de salud de nuestro tiempo. Y hay estudios que sugieren que la exposición al ruido del tráfico eleva la probabilidad de sufrir depresión en adultos y genera problemas de atención en niños.
Las medidas que se han tomado para limitar el uso de automóviles en grandes ciudades han arrojado resultados positivos. El 14 de septiembre del año pasado se celebró en París el cuarto día sin coches y la contaminación por dióxido de nitrógeno en el entorno de las vías de mayor tráfico se redujo hasta en un 40%. En Bruselas, el hollín atmosférico se redujo en un 80% ese mismo día. Y tras implantar en Estocolmo la tasa de congestión en 2006, se registró un descenso en la incidencia de asma infantil.
El grado de actividad física que desarrollan los habitantes de las zonas en que se ha limitado el tráfico rodado también ha aumentado. A partir de 1960 Copenhague empezó a limitar el uso de automóviles en el centro urbano: en 2015 prohibió el aparcamiento en el centro de la ciudad, convirtió muchas vías rodadas en carriles-bici o peatonales, y aumentó la red de vías férreas; desde entonces no ha dejado de aumentar el número de personas que se desplazan en bicicleta por la ciudad y en la actualidad llegan al 60%. De Pontevedra -una ciudad de 84.000 habitantes (65.000 en el casco urbano)- se dice que ha logrado domesticar el tráfico; a partir de 1999 ha aumentado las zonas peatonales, ha ampliado las aceras, ha reducido a 30 km/h la velocidad máxima en todo el ámbito urbano y ha creado una red de nueve aparcamientos disuasorios con 16.000 plazas libres. Hoy más del 80% de escolares caminan hasta su centro de enseñanza y las muertes por accidente de tráfico han desaparecido.
Como es lógico, las limitaciones al tráfico rodado urbano han provocado la oposición de diversos sectores. Muchos ciudadanos se oponen porque entienden que se trata de limitaciones inaceptables a la libertad individual. Pero a esos argumentos se oponen los que se fundamentan en el valor de preservar la salud. Para mitigar la oposición se ha optado en muchos casos por aplicar las limitaciones e forma gradual. De hecho, aunque el debate público se mueve en esas coordenadas, las alternativas que barajan los especialistas en movilidad urbana se refieren a modalidades de limitación del tráfico, medidas complementarias y plazos de implantación. Su conveniencia apenas se discute.
El artículo Ciudades sin coches se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El tamaño importa en organismos, empresas, ciudades y economías
- Los edificios y el mar
- Cerdos ferales
¿Cuál es la postura más aerodinámica en ciclismo?
Si has visto a ciclistas bajar un puerto de montaña, habrás notado que adoptan posiciones que parecen muy aerodinámicas. Lo hacen para rascar milésimas al crono. ¿Sirven para algo? Y de hacerlo, ¿cuál sería la mejor postura para conseguir más velocidad?
Los vídeos de ¿Preguntas frecuentes? presentan de forma breve y amena cuestiones que, probablemente, nos hayamos planteado en alguna ocasión. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.
Edición realizada por César Tomé López
El artículo ¿Cuál es la postura más aerodinámica en ciclismo? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Qué pasa en tu cuerpo cuando te enamoras?
- ¿Hemos intentando contactar con extraterrestres?
- ¿Qué pasa en tu cerebro cuando duermes?
Energía oscura
La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebra dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Publicamos en el Cuaderno de Cultura Científica y en Zientzia Kaiera una serie de artículos que narran algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas.

Permítanme iniciar este escrito con un experimento imaginario. Supongamos que contamos con una manzana y la tiramos hacia arriba con cierta velocidad desde la superficie de la Tierra. Todos sabemos que ocurrirá después. La manzana ascenderá durante un tiempo, a medida que asciende la velocidad de la manzana disminuirá hasta llegar al punto álgido de su trayectoria en el que se parará. Todos hemos hecho este experimento en algún momento y entendemos perfectamente lo que ocurre. La atracción gravitatoria de la Tierra sobre la manzana ejerce una fuerza hacia abajo que se opone a la velocidad inicial de ésta. Esta fuerza produce una deceleración de la manzana hasta que se para en el punto más alto.
¿Pero qué pasaría si al repetir este experimento observásemos que la manzana llega hasta un punto y después se acelera y aumenta su velocidad ascendente hasta desaparecer en el cielo? Creo que estaremos todos de acuerdo en que si eso ocurriese nos sorprenderíamos un poco… Esto se debe, como digo, a que creemos que entendemos lo que ocurre en este experimento y no conocemos ninguna fuerza que empuje a la manzana hacia arriba. Pero permítanme que insista… ¿qué pasaría si lo observásemos? En ese caso, tendríamos que afrontar la realidad. Alguna de las suposiciones que habíamos hecho y que creíamos ciertas ha de ser incorrecta. ¿Pero cuál?
Antes de dejarnos llevar por el desasosiego causado por esta observación y de cuestionar nuestros conocimientos de física general y/o la validez de las ecuaciones de Newton, recordemos con cierto alivio que este era un experimento imaginario. Sin embargo, ilustra muy bien el estado de ánimo de la mayoría de la comunidad de científicos dedicados a la cosmología a finales del siglo pasado, en concreto en 1998. El origen de su preocupación no era una hipotética manzana voladora sino los resultados de ciertas observaciones cosmológicas realizadas por aquel entonces. Estas observaciones mostraban que nuestro universo no sólo se expande sino que se encuentra actualmente en un proceso de expansión acelerada. Esto es, la expansión del universo es cada vez más rápida hoy en día. Muchos cosmólogos se mostraron escépticos al principio con estos resultados esperando quizás, como en otros casos ha ocurrido, que la repetición de la observación diese lugar a otro resultado más acorde con nuestra intuición. Pero esto nunca ocurrió, de hecho, observaciones posteriores han corroborado este hallazgo hasta el punto que hoy en día prácticamente nadie las pone en duda. Pero, ¿porqué esperaba la comunidad científica otro tipo de resultado? La razón es simple; la situación es muy semejante al caso imaginario de la manzana.
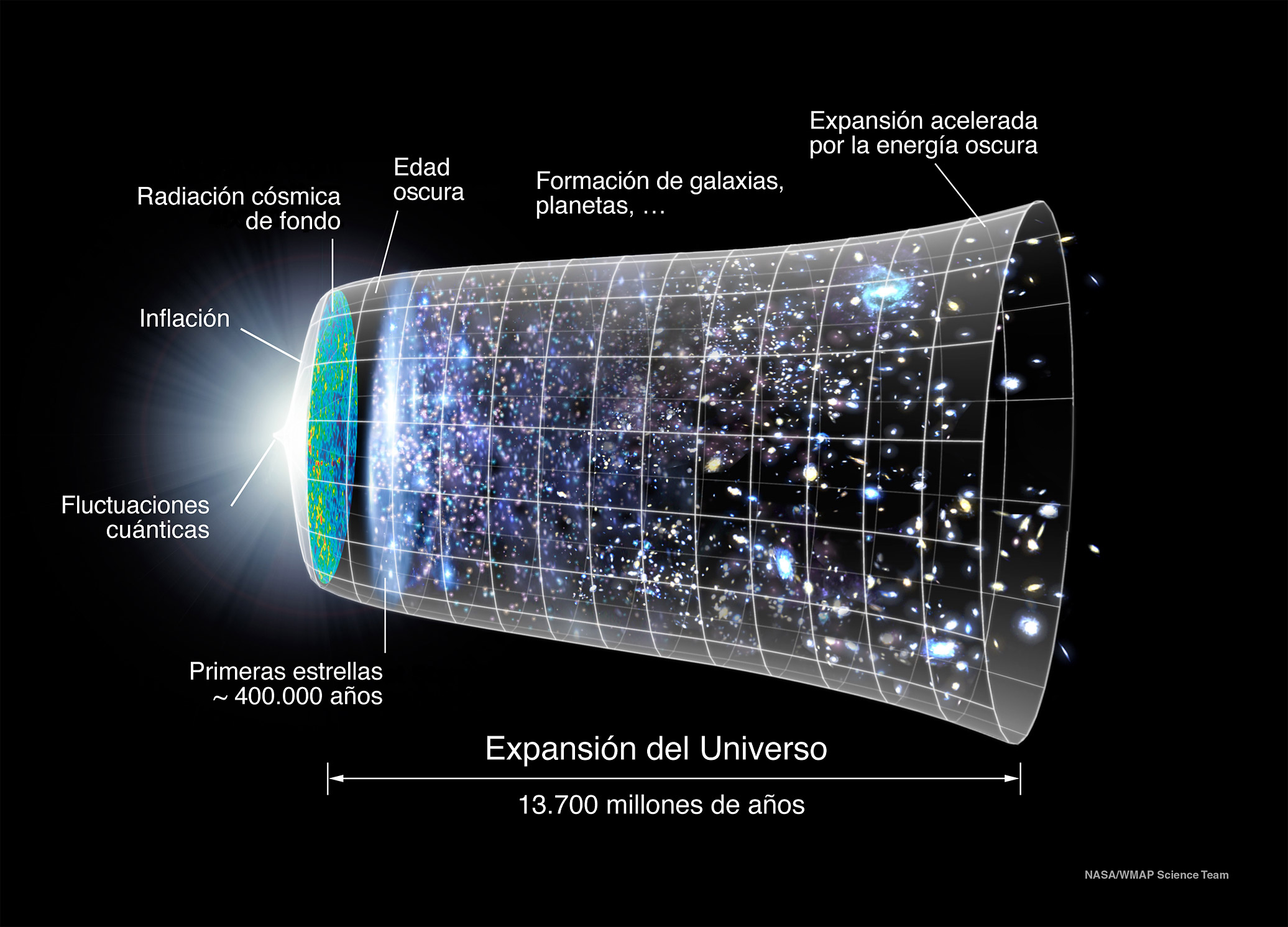 La evolución del universo desde sus orígenes y su reciente entrada en un periodo de expansión acelerada. Fuente: Wikimedia Commons
La evolución del universo desde sus orígenes y su reciente entrada en un periodo de expansión acelerada. Fuente: Wikimedia Commons
Como todo el mundo sabe, el universo se inició con una gran explosión (el Big Bang) que dio lugar a la condición inicial de expansión cosmológica (la situación análoga a la velocidad inicial de la manzana). Por otro lado la acción gravitatoria de la materia en el universo es atractiva y por lo tanto parece lógico concluir que la expansión del universo se verá ralentizada por la acción de la gravedad de la misma forma que la velocidad de la manzana disminuye con el paso del tiempo. Es por esto por lo que uno esperaría que el universo se expandiese cada vez más despacio o incluso que pudiese llegar un momento donde esta expansión se detuviese iniciando así un proceso de colapso. Sin embargo, los datos indicaban lo contrario, el universo se encontraba inmerso en un período de expansión acelerada. Es decir, el universo parecía comportarse como la manzana en nuestro inquietante experimento imaginario, se expande de forma acelerada en contra de lo que esperaríamos. Este ha sido, sin lugar a dudas, uno de los descubrimientos más sorprendentes de la física y la cosmología en los últimos 50 años.
Una vez pasado el shock inicial no queda otro remedio que asumir el resultado, no tiene sentido negar la evidencia observacional. La comunidad científica se preguntó entonces cuál de los supuestos anteriores debe relajarse para poder acomodar los resultados dentro de un marco teórico coherente con estas observaciones. A continuación describiremos algunas de estas posibilidades.
En primer lugar una posibilidad clara es que las ecuaciones de gravedad, las ecuaciones de Einstein de la Relatividad General, no funcionen a estas escalas y por lo tanto deban ser modificadas de tal manera que esta aceleración aparezca de forma natural como producto de esta alteración.
Otra posibilidad es que las ecuaciones de Einstein estén perfectamente como están y que simplemente exista otro tipo de materia que de lugar a que el universo se expanda cada vez más rápido cuando ésta domina sobre las otras formas de materia más comunes. ¿Pero qué tipo de materia puede dar lugar a una gravedad repulsiva?
Esto puede parecer una locura, ya que nuestra intuición nos dice que esto no ocurre en la Naturaleza. Sin embargo una de las características que se puede ver estudiando las ecuaciones de la Relatividad General aplicada a la cosmología, es que la evolución del universo no sólo está marcada por la densidad de energía (la masa) de la materia, sino también por su presión. Si uno considera un material con una gran dosis de presión negativa (la presión negativa es similar a la tensión presente en las gomas elásticas, por ejemplo.), su efecto puede contrarrestar la usual atracción de la materia y dar lugar a este efecto de gravedad repulsiva.
Lo realmente interesante de esta historia es que la primera persona que propuso la existencia de este tipo de materia fue el mismo Einstein mucho antes de que se realizasen estas observaciones. Einstein postuló la presencia de un nuevo término en sus ecuaciones que designó con el nombre de constante cosmológica. Este término era necesario para encontrar un punto de equilibrio en el que el universo pudiese ser estático, algo que en 1917 parecía la única opción válida. En este punto de equilibrio las fuerzas de atracción de la materia común tendrían su contrapunto perfecto con el efecto repulsivo originado por este nuevo término en las ecuaciones. Esta idea fue, según cuentan, descrita por el mismo Einstein como – “Uno de los mayores errores en mi vida…” y con razón, ya que pocos años más tarde Edwin Hubble descubrió las primeras evidencias de la expansión del universo. Sin embargo, este término, repudiado por Einstein después de las observaciones de Hubble y por mucha gente ignorado durante largo tiempo, volvió a la primera línea de investigación cuando se descubrió la reciente (en escalas cosmológicas) aceleración del universo.
Sin embargo, la idea de incluir una constante cosmológica para satisfacer las observaciones de la expansión acelerada del universo no está exenta de problemas. Es importante darse cuenta que el valor de la constante cosmológica recibe contribuciones de cualquier componente de la energía de vacío. Sí, el vacío en física no es exactamente lo que comúnmente conocemos por vacío (ausencia de todo, tanto de masa, como de energía) sino que tiene propiedades análogas a los materiales, en particular tiene una energía y una presión asociadas a él. Esto es debido a que la mecánica cuántica nos enseña que ni siquiera el vacío está libre de las pequeñas fluctuaciones de los campos que viven en él y que dan lugar a las partículas que conocemos. Son precisamente estas fluctuaciones cuánticas las que dan al vacío unas características idénticas a la constante cosmológica. Por otro lado, todos los intentos por estimar esta contribución a la energía de vacío basados en nuestro conocimiento presente de la mecánica cuántica y la gravedad dan unos resultados que se alejan en muchos órdenes de magnitud de la cantidad observada. Un universo con una constante cosmológica mucho mayor sería totalmente incompatible con la formación de estructuras como las galaxias y nuestra existencia. Este resultado realmente embarazoso nos indica que posiblemente debamos recurrir a nuevas ideas a la hora intentar dar algún paso adelante en nuestro entendimiento de este fenómeno.
 Las fluctuaciones cuanticas dotan al vacio de propiedades como densidad de energia o presion que determinan su efectos cosmologicos. Fuente: Wikimedia Commons
Las fluctuaciones cuanticas dotan al vacio de propiedades como densidad de energia o presion que determinan su efectos cosmologicos. Fuente: Wikimedia Commons
Una de las ideas nuevas que ha surgido en estos últimos años es la posibilidad de que no exista un solo valor de la constante cosmológica, sino un gran número de vacíos distintos con valores muy dispares de su energía de vacío, muchos de los cuales estarían dentro del rango de los valores observados. Esto sólo sería posible si la teoría fundamental diese lugar a muchos de esos vacíos. Lo interesante de esta idea es que la Teoría de Cuerdas (nuestro mejor candidato a una teoría fundamental de la gravedad cuántica) tiene precisamente esta propiedad y por lo tanto parece ser un buen candidato para acomodar este escenario.
Por otro lado existen otras maneras de obtener de forma efectiva la aceleración del universo mediante el diseño de una constante cosmológica variable. El interés de este tipo de modelos es su dinámica distinta a la constante cosmológica y a sus posibles implicaciones sobre el futuro del universo a largo plazo.
Todos estos modelos son conocidos con el nombre genérico de Energía Oscura. Este es el nombre que se ha elegido para describir el tipo de materia (o energía) que da lugar a esta aceleración del universo, sea esta debida a una constante cosmológica o a una variación temporal de la energía del vacío. Existen varios experimentos que actualmente buscan mediante distintas observaciones ampliar nuestro conocimiento sobre las propiedades de esta energía oscura. Estas observaciones serán cruciales para ayudarnos a discernir entre los múltiples escenarios que hemos comentado.
El origen de la Energía Oscura es un problema muy complejo que toca áreas tan diversas como la Cosmología, la Gravitación, la Física de Partículas de Altas Energías y Teoría de Cuerda; temas todos ellos bien representados en los grupos de investigación del Departamento de Física Teórica de la Facultad de Ciencia y Tecnología de la UPV/EHU. Estos grupos estudian diversos aspectos de la energía oscura tanto desde el punto de vista puramente teórico como en su vertiente más fenomenológica.
Es justo reconocer que no tenemos en este momento una idea clara de cuál puede ser el origen de esta misteriosa energía. No obstante, la historia de la Física está plagada de grandes misterios que nos han permitido, mediante su resolución, avanzar en nuestro conocimiento. Esperemos que este caso no sea una excepción.
Sobre el autor: Jose Juan Blanco-Pillado es Ikerbasque Research Professor en el Departamento de Física Teórica del Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Energía oscura se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Se intuye la conservación de la energía (1)
- Una fórmula para dominarlos a todos: La conservación de la energía y la ley de la palanca
- Un modelo que unifica energía y materia oscuras
Peces carnívoros, vegetarianos y la acuicultura insostenible
![]()
 Imagen: Kosin Sukhum / Shutterstock
Imagen: Kosin Sukhum / ShutterstockLa sostenibilidad es la forma de asegurar las necesidades actuales sin comprometer las futuras, las de nuestras próximas generaciones. La acuicultura actual, que lleva a nuestra mesa gran parte del pescado que comemos, dista de ser sostenible.
Vamos al mar a capturar pequeños peces que no nos gusta comer para transformarlos en pienso con el que alimentar a las especies que sí nos gusta comer. Somos así de exquisitos. También, siguiendo prácticas paloelíticas, recolectamos (que no producimos) pequeños crustáceos para alimentar a las crías de los peces que cultivamos.
Pero cada vez que realizamos una transformación tenemos pérdidas. Entonces, ¿por qué no nos comemos el pienso directamente? Quitaríamos escalones del proceso y lo haríamos más efectivo, más sostenible.
No sé si llegará ese día, pero mientras tanto, seguiremos comiendo pescados que nos acerquen al esnobismo. Porque ¿quién comía antes salmón, dorada o lubina? Casi nadie, especialmente fuera de los eventos gastronómicos navideños. Que hoy podamos incluir estas especies en nuestra dieta es uno de los grandes logros de la acuicultura occidental, más preocupada por las cuotas de mercado que por la sostenibilidad de los procesos de producción.
A fin de cuentas, es el mercado quien ha seleccionado las especies que cultivamos y ha marcado la sostenibilidad del proceso. Aquellos precios prohibitivos del pasado prometían grandes rentabilidades. Sin embargo, gran parte de estos peces, antaño caros, son carnívoros y ocupan los niveles más altos de la cadena trófica. Por eso necesitan grandes cantidades de proteínas y aceites de pescado para crecer. Un alimento que se obtiene, a su vez, de otros peces que capturamos y transformamos en pienso. Es “como el pez que se muerde la cola”, nunca mejor dicho.
Conseguir peces vegetarianos como solución
Las especies comerciales, de momento, son las que son. Pero llevar estos peces al mercado de forma rentable supone un elevado esfuerzo científico y tecnológico.
Una de las soluciones que se ha implementado es la sustitución de las harinas y aceites de pescado utilizados en los piensos por sus homólogos vegetales. En esta búsqueda, se han realizado investigaciones con muchos tipos vegetales buscando siempre plantas con un elevado contenido proteico y aceites con una composición óptima.
Estamos intentando convertir a nuestras especies en vegetarianas. Pero ¿acaso les gusta este cambio? No. Si nos pasamos con el porcentaje de proteína vegetal, no les gusta el pienso, no crecen tan bien, sufren a nivel intestinal y pueden tener, incluso, trastornos reproductivos inducidos por la presencia de fitoestrógenos. De hecho, todavía no se ha podido llegar a la sustitución total. Y será difícil que se consiga en el futuro.
 Tanques experimentales para la cría de peces. Imagen: Instituto de Acuicultura de Torre de la Sal
Tanques experimentales para la cría de peces. Imagen: Instituto de Acuicultura de Torre de la SalAdemás, ante esta estrategia, podríamos preguntarnos: ¿esquilmar las pesquerías de anchoveta peruana (una especie parecida a nuestro preciado boquerón, de donde provienen la mayor parte de las harinas de pescado de los piensos) es más sostenible que quemar la selva amazónica para plantar los vegetales que destinamos a los piensos? ¿Es ético utilizar las pesquerías y los excedentes de vegetales para alimentar a nuestros peces carnívoros en lugar de para paliar hambrunas?
Los intentos de sustitución y la inversión colateral en investigación no han venido de la mano de mejoras en sostenibilidad. Por el contrario, provocan un incremento en los precios de las harinas de pescado que encarece la producción piscícola a niveles insostenibles.
La variabilidad de las pesquerías, debida a factores ambientales como la corriente de El Niño de las costas del Pacífico Sur, producen cambios impredecibles en los precios de los harinas. Y este es el motivo real que nos ha llevado a echar mano de los vegetales en la fabricación de piensos, no la sostenibilidad, aunque muchos quieran vender la historia al revés. Sorprendentemente, el efecto colateral de optimizar el negocio podría ser un acercamiento a la sostenibilidad.
Cambios de cara al futuro
Los consumidores no tenemos mucho margen de acción para aumentar la sostenibilidad del proceso. Debemos decidir entre gastronomía y alimentación sostenible, es decir, entre comer un pescado que nos gusta más o aparcar nuestra exquisitez y elegir un pescado más sostenible en su producción, sin olvidar la calidad nutricional.
Optar por la segunda vía nos obligará a explorar el cultivo de nuevas especies, a ser posible herbívoras. Hoy por hoy, especies como la carpa o la tilapia podrían mostrar un mayor grado de sostenibilidad en su cultivo, dado que su dieta se basa en vegetales.
Si queremos seguir comiendo especies carnívoras, debemos seguir explorando fuentes alternativas de materias primas más sostenibles e intentar llegar al 100% de sustitución. Actualmente hay cuatro líneas incipientes que plantean la utilización de harinas de insecto, fitoplancton, subproductos de pesca y alimenticios y proteínas sintéticas de bacterias como ingredientes alternativos. La producción de microalgas o fitoplancton solo requiere agua, luz y abono.
 Cilindros para el cultivo de microalgas o fitoplacton. Imagen: Instituto de Acuicultura de Torre de la Sal
Cilindros para el cultivo de microalgas o fitoplacton. Imagen: Instituto de Acuicultura de Torre de la SalAdemás, tendremos que mejorar la eficiencia alimenticia de nuestros peces, es decir, conseguir que con la misma cantidad de alimento sean capaces de crecer más y más rápido. Aquí, la selección genética y las técnicas biotecnológicas serán de gran ayuda.
Lo que sí está en nuestra mano es consumir pescado producido en zonas cercanas a nuestra localidad aprovechándonos de la trazabilidad del producto (conocemos el camino que sigue desde su nacimiento hasta su comercialización) que nos proporciona la acuicultura. Esto reduce la contaminación asociada al proceso productivo, un parámetro que también debería entrar en la ecuación de sostenibilidad.
La acuicultura está aquí para quedarse, que nadie lo dude. Ayuda a paliar la sobrepesca en los caladeros y nos aporta alimento saludable y de gran calidad. Pero está en manos de la ciencia profundizar en la investigación para aportar mayor sostenibilidad a los procesos productivos.![]()
Sobre el autor: José Miguel Cerdá-Reverter es investigador y director del IATS – CSIC, Instituto de Acuicultura Torre de la Sal (IATS – CSIC)
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Peces carnívoros, vegetarianos y la acuicultura insostenible se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los peces en el río
- Peces capaces de respirar en aire y anfibios
- La regulación osmótica de los peces diádromos
El mapa del cólera de John Snow
A mediados del siglo XIX, la creencia general presuponía que el cólera se propagaba a través del miasma en el aire. La teoría de los microbios y su relación con las enfermedades aún no estaba establecida (Pasteur tardaría aún 10 años en realizar los experimentos que le darían validez) y los brotes de cólera que asolaban Londres hacia 1850 eran, para todos, un misterio. Pero un gráfico iba a cambiar aquella situación: un simple mapa, hoy considerado el origen de la epidemiología, realizado por John Snow.
Snow (antes de convertirse en personaje de Juego de Tronos) fue un médico nacido en 1813, célebre por su contribución al desarrollo de la anestesia. Pero además, era un tipo inquieto con una teoría: él pensaba que el cólera se propagaba, no a través del aire, sino por el agua contaminada. En aquella época, el sistema de alcantarillado y suministro de agua de Londres dejaba mucho que desear. El agua se repartía en pozos públicos desde los que los ciudadanos bombeaban su propio suministro para llevarlo a sus hogares. Por otra parte, a menudo los desagües se vaciaban en pozos negros bajo las viviendas, más que en tuberías de alcantarillado. El resultado… era hediondo. El olor de heces humanas y animales se combinaba con el de la basura podrida. No es de extrañar que algunos atribuyesen a ese “miasma” la capacidad de enfermar a cualquiera.
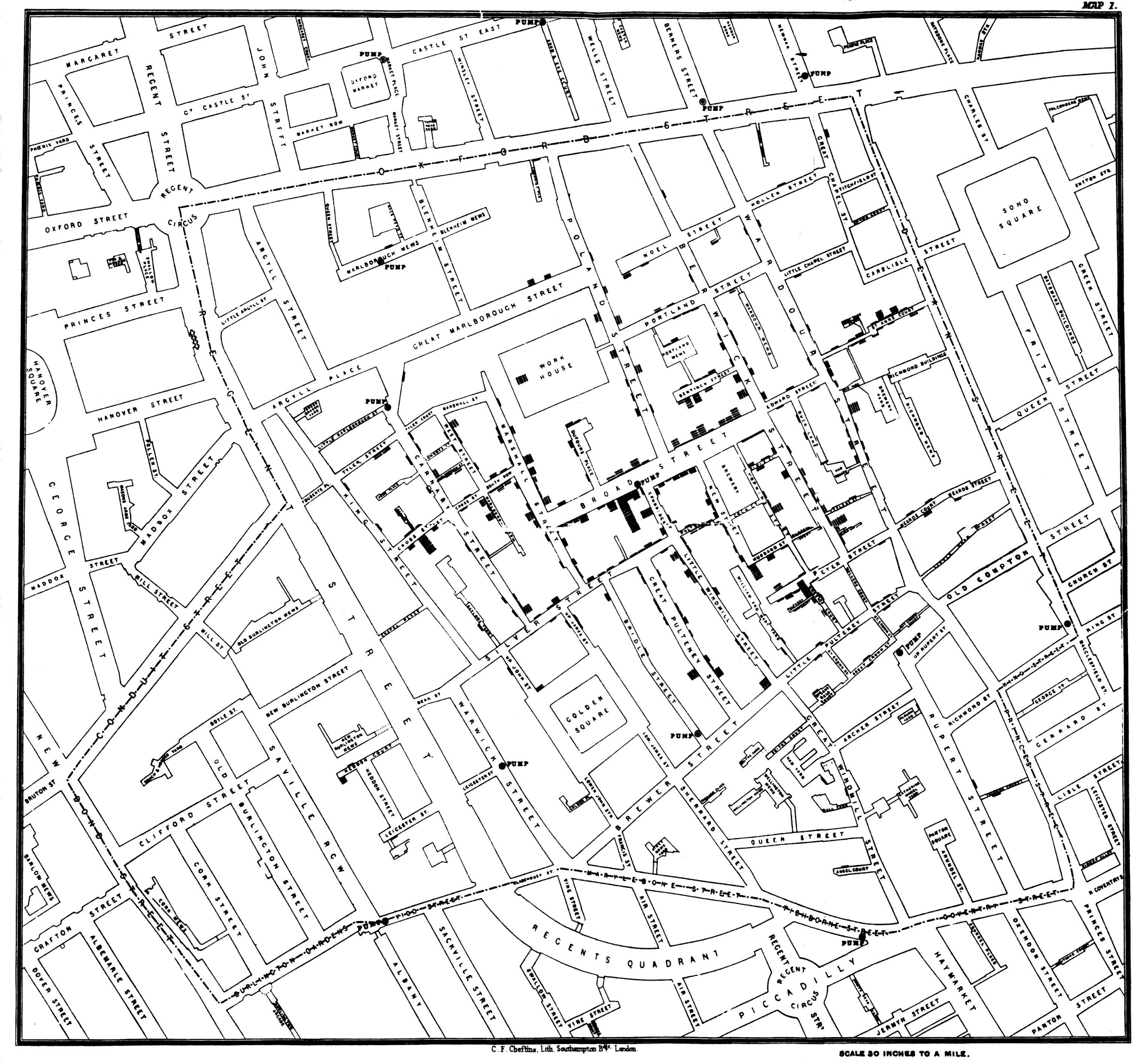
Pero Snow pensaba que el problema era el agua y, para demostrarlo, en 1854 empezó a registrar los casos de cólera del barrio de Soho, sobre un mapa centrado en torno a 13 fuentes: cada muerte era anotada como una línea sobre el lugar de residencia. En total, 578 muertes y el resultado dejaba lugar a pocas dudas: casi todas se concentraban alrededor de una fuente en Broad Street. En cuanto aparecía una nueva fuente, la enfermedad aparentemente se “frenaba”.
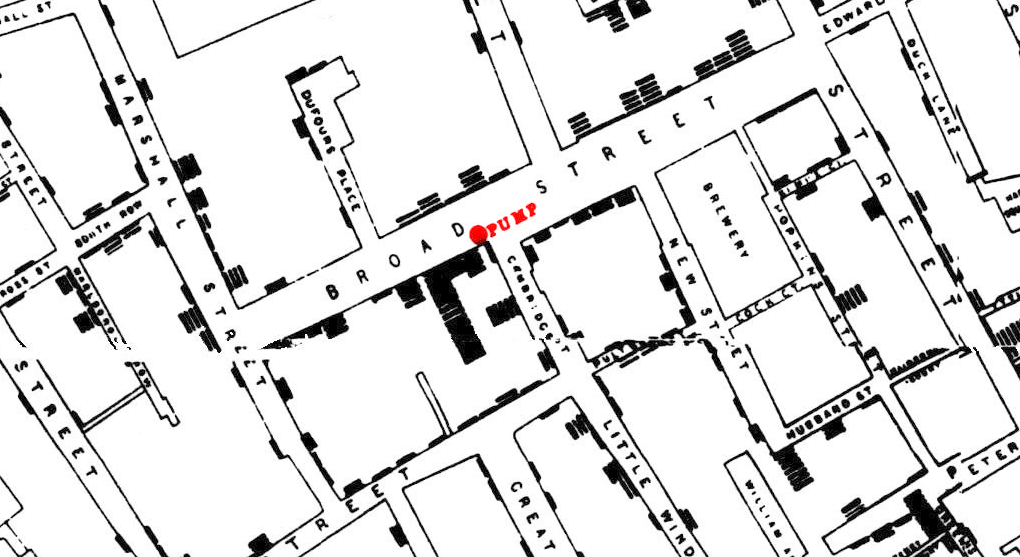
Para verificar que el área afectada por el cólera coincidía, efectivamente, con el área abastecida por la fuente, Snow comenzó por trazar un diagrama de Voronoi sobre el mapa. En este tipo de diagramas, el espacio se divide en regiones de cercanía a una serie de puntos y, en este caso, la región más cercana a la fuente de Broad Street parecía ser la más afectada por el cólera. Sin embargo, la coincidencia no era del todo exacta, por lo que Snow decidió repetir su diagrama teniendo en cuenta, esta vez, otro tipo de distancia: la distancia en tiempo, o distancia “caminada” a cada fuente (similar a la que registran los mapas isócronos). Para ello, tomó cuerda (para medir distancias sobre una trayectoria sinuosa) y un lápiz, y redibujó sus polígonos definidos, esta vez, como las zonas más cercana a una fuente a través de los caminos disponibles. La coincidencia se volvía aún mayor.
El mapa deja ver, también, algunas anomalías curiosas… Como la del bloque al este de la fuente contaminada, donde se encuentra una “brewery” o fábrica de cerveza. Parece que los trabajadores de la fábrica podían beber cerveza para calmar su sed. Por suerte, la fermentación acababa con las bacterias del cólera (sólo en este caso podría decirse que la cerveza es sana, en ningún otro).
También había casos aislados, fuera del área de influencia de la fuente, excepciones que Snow documentó de manera exhaustiva. Hoy casi sorprende el detalle de sus notas, como en el caso de una mujer de 59 años que “no había estado cerca de Broad Street en meses. Un carruaje iba de Broad Street a West End todos los días y le llevaba una botella de agua de la fuente de Broad Street, dado que ella la prefería. El agua fue tomada el jueves 31 de agosto, ella la bebió esa misma tarde y también el viernes. Tuvo un ataque de cólera por la tarde de este último día y falleció el sábado”. Otros casos alejados de la fuente correspondían de manera similar a gente que iba a trabajar o comprar a Broad Street y bebían de la fuente. Para colmo, esta tenía fama de tener buen sabor (mejor, al menos, que el de algunas de sus fuentes vecinas).
Por último, además de sus análisis geográficos, Snow tomó muestras de las distintas fuentes y las analizó bajo el microscopio. Confirmó la presencia de un organismo desconocido en la fuente de Broad Street. La fuente había sido contaminada por un pañal arrojado a un pozo negro cercano. Conformes, aunque no convencidos (la teoría de los microbios patógenos tardaría aún una década en ser aceptada), las autoridades decidieron cerrar el pozo de Broad Street y el brote de cólera pronto se sofocó. John Snow murió apenas cuatro años más tarde, en 1858, sin poder ver confirmada su teoría, sin terminar de decir “yo tenía la razón”.
Hoy, su mapa es considerado pionero en el uso del método geográfico para estudiar una epidemia. Pero además, cambió para siempre cómo percibimos las visualizaciones de datos: no sólo como un apoyo clarificador a un modelo ya conocido, sino como sustento y prueba del mismo. La teoría de Snow no hubiese podido ser mostrada únicamente mediante números y coordenadas; hubiese perdido, en el proceso de lectura, toda su elocuencia.
Referencias:
Un análisis contemporáneo del mapa de John Snow: Narushige Shiode, Shino Shiode, Elodie Rod-Thatcher, Sanjay Rana & Peter Vinten-Johansen (2015) The mortality rates and the space-time patterns of John Snow’s cholera epidemic map International Journal of Health Geographics doi: 10.1186/s12942-015-0011-y
Steven Johnson (2008) “El mapa fantasma”. Ilustrae.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo El mapa del cólera de John Snow se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cómo conseguir que la vacuna del cólera no necesite cadena de frío
- Un mapa del discernimiento
- El mapa Big Brain
Pál Turán: teoría de grafos y fábricas de ladrillos
Pál Turán (1910-1976) fue un matemático húngaro que trabajó fundamentalmente en teoría de números. Durante cuarenta y seis años colaboró con su compatriota Paul Erdős, llegando a publicar veintiocho trabajos conjuntos. Por supuesto, el número de Erdős de Pál Turán es 1.
 Pál Turán. Imagen: Wikimedia Commons.
Pál Turán. Imagen: Wikimedia Commons.
Alumno de Lipót Fejér –como los célebres matemáticos Paul Erdős, George Pólya, Tibor Radó, Marcel Riesz o John von Neumann, entre otros– Torán se casó en segundas nupcias con la también alumna de Féjer –y asimismo colaboradora de Paul Erdős y Alfréd Rényi– Vera T. Sós (1930). El teorema de Kővári–Sós–Turán es un trabajo conjunto del matrimonio con Tamás Kővári: en él proporcionan una cota superior para la solución del problema de Zarankiewicz, una cuestión no resuelta en matemáticas que intentar averiguar cuál es el mayor número posible de aristas en un grafo bipartito que tiene un número dado de vértices y no posee subgrafos bipartitos completos de un tamaño dado.
Varios conceptos y desigualdades llevan el nombre de este matemático. Por ejemplo, el teorema de Turán establece que el llamado grafo de Turán es el que tiene el mayor número de aristas entre todos los grafos que no contienen subgrafos completos.
 El grafo de Turán T(13,4). Imagen: Wikimedia Commons.
El grafo de Turán T(13,4). Imagen: Wikimedia Commons.
En 1934, Turán utilizó la denominada criba de Turán –una técnica para estimar el tamaño de ciertos conjuntos de números enteros positivos– para dar una nueva y sencilla demostración de un teorema de 1917 de G. H. Hardy y Srinivāsa Ramanujan sobre el orden normal del número de divisores primos de un número entero positivo. La desigualdad de Turán–Kubilius generaliza el anterior resultado.
Llevan el nombre de desigualdades de Turán unas desigualdades sobre polinomios de Legendre que Turán encontró en 1950. También son conocidas la desigualdad de Erdős-Turán en teoría de la medida y las conjeturas de Erdős-Turán sobre progresiones aritméticas (demostrada en 1975 por Endre Szemerédi) y sobre bases aditivas (problema aún no resuelto).
Gran parte del trabajo de Turán en teoría de números abordó la hipótesis de Riemann. De hecho, Erdős comentaba en [1] que “Turán era un ‘no creyente’, de hecho, un “pagano”: no creía en la verdad de la hipótesis de Riemann”.
Durante la Segunda Guerra Mundial, Turán se vio obligado a trabajar en una fábrica de ladrillos. Su trabajo consistía en empujar un carro con briquetas a lo largo de una vía desde un horno hasta un almacén. La fábrica contenía varios hornos y varios lugares de almacenamiento, con vías que se entrecruzaban para realizar estos transportes. A Turán le resultaba difícil empujar el vagón a través de un cruce de vías, y comenzó a considerar cómo podría rediseñarse la fábrica para minimizar estos cruces.
Tras finalizar la guerra, mencionó el problema a algunos de sus colegas. Los matemáticos Kazimierz Zarankiewicz y Kazimierz Urbanik abordaron esta cuestión. Demostraron que siempre es posible completar el diseño como se muestra en la figura 3: los hornos pueden colocarse a lo largo de un eje y los almacenes a lo largo del otro, organizando cada grupo de la manera más uniforme factible alrededor del origen y con las vías en forma de rectas entre cada posible par.
 Imagen: Wikimedia Commons.
Imagen: Wikimedia Commons.
Si m es el número de hornos y n el de almacenes Zarankiewicz y Urbanik dieron una cota superior para el número de cruces (ver [3]). En el caso de la figura 3 (m=4 y n=7) esa cota se alcanza: hay 18 cruces.
¿Se trata de la manera óptima de hacerlo? Se desconoce la respuesta. Zarankiewicz y Urbanik pensaban que su fórmula proporcionaba el menor número posible de cruces, pero algunos años después descubrieron un error en su prueba. ¿Será posible diseñar una fábrica de ladrillos con menos cruces entre las vías uniendo hornos y almacenes? El problema continúa abierto…
Referencias:
[1] Paul Erdős, Some personal reminiscences of the mathematical work of Paul Turán, Acta Arithmetica XXXVII (1980) 3-8
[2] J J O’Connor and E F Robertson, Paul Turán, MacTutor History of Mathematics archive, University of St Andrews.
[3] Turán’s Brick Factory Problem, Futility Closet, 4 abril 2019
[4] Turán’s brick factory problem, Wikipedia (consultado 6 abril 2019)
[5] Pál Turán, Wikipedia (consultado 6 abril 2019)
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Pál Turán: teoría de grafos y fábricas de ladrillos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Arthur Cayley, la teoría de grafos y los isómeros químicos
- La teoría de grafos y “Così Fan Tutte”
- Incendios, los grafos de visibilidad y la conjetura de Collatz
Polarización de la luz
 Imagen: Wikimedia Commons
Imagen: Wikimedia Commons
Hooke y Huygens propusieron que la luz es en muchos aspectos como el sonido, es decir, que la luz es una onda que se propaga a través de un medio. Newton no pudo aceptar esta propuesta y argumentó que la luz también debe tener algunas propiedades similares a las partículas, además de su naturaleza ondulatoria*. Encontró que dos propiedades de la luz no podían explicarse, tal y como él lo entendía, a menos que la luz estuviera formada por partículas.
Primero, un haz de luz se propaga en el espacio en líneas rectas, mientras que las ondas, como el sonido, se extienden en todas las direcciones y son capaces de doblar las esquinas. Esta objeción no pudo responderse hasta principios del siglo XIX, cuando Thomas Young midió la longitud de onda de la luz y descubrió lo extremadamente pequeña que es. Incluso la longitud de onda de la luz roja, la longitud de onda más larga del espectro visible, es inferior a una milésima de milímetro. Mientras un rayo de luz brille sea el que ilumine los objetos o la luz entre a través de orificios de tamaño ordinario (unos pocos milímetros o más de ancho), la luz parecerá viajar en línea recta. Como vimos, los efectos de difracción y dispersión no se hacen evidentes hasta que una onda pasa sobre un objeto o por un agujero cuyo tamaño es aproximadamente igual o menor que la longitud de onda.
Newton basó su segunda objeción en el fenómeno de la “polarización” de la luz. En 1669, el científico danés Rasmus Bartholin descubrió que los cristales de espato Islandia (calcita) podían dividir un rayo de luz en dos rayos. Un texto escrito o cualquier objeto pequeño visto a través del cristal se veía doble.
Newton pensó que este comportamiento podría explicarse suponiendo que la luz está formada por partículas que tienen diferentes “lados”, por ejemplo, secciones transversales rectangulares. Razonó que las imágenes dobles representarían una clasificación de las partículas de luz que habían entrado en el medio con diferentes orientaciones.
Alrededor de 1820, Young y Fresnel dieron una explicación mucho más satisfactoria de la polarización, utilizando un modelo ondulatorio de la luz con una modificación crítica respecto al imperante. Hasta entonces los científicos generalmente habían asumido que las ondas de luz, como las ondas de sonido, debían ser longitudinales. Young y Fresnel demostraron que si las ondas de luz se consideraban transversales se podía explicar el fenómeno de la polarización muy fácilmente.
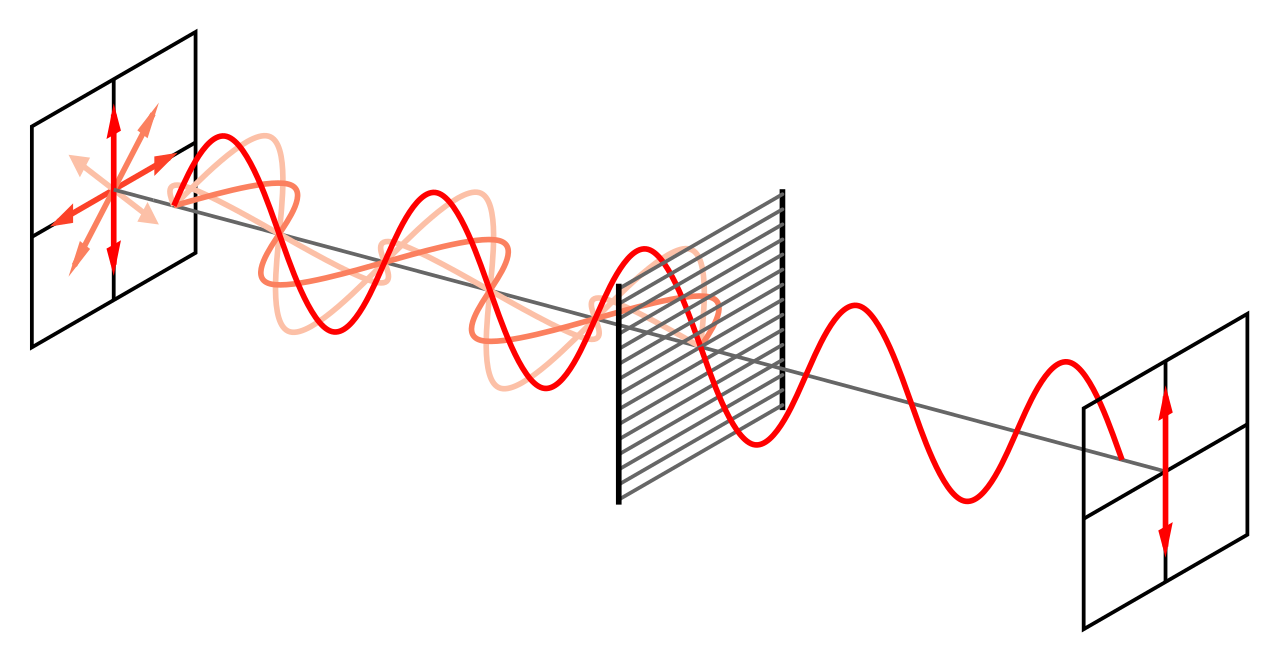 Imagen: Wikimedia Commons
Imagen: Wikimedia Commons
En una onda transversal de tipo mecánico, el movimiento del propio medio, como una cuerda, es siempre perpendicular a la dirección de propagación de la onda. Esto no significa que el movimiento del medio esté siempre en la misma dirección. De hecho, podría estar en cualquier dirección en un plano perpendicular a la dirección de propagación.
Sin embargo, si el movimiento del medio es principalmente en una dirección (por ejemplo, vertical), la onda está polarizada. Por lo tanto, una onda polarizada es en realidad el tipo más simple de onda transversal. Una onda transversal no polarizada es más complicada, ya que es una mezcla de varios movimientos transversales. Todo aplica también a las ondas de luz, a pesar de que no necesitan de un medio para propagarse.
Nota:
* No, Newton no se adelantó a de Broglie, aunque lo parezca. Simplemente estaba formulando hipótesis para intentar comprender un fenómeno, no afirmando la dualidad onda-corpúsculo.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Polarización de la luz se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Absorción del alimento
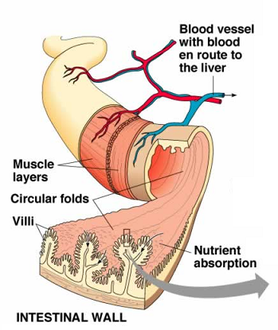 Fuente: Biology Notes for IGCSE
Fuente: Biology Notes for IGCSE
La mucosa del intestino delgado de los mamíferos contiene glándulas exocrinas cuyo producto de secreción es una solución de moco y sal denominada succus entericus o jugo intestinal. La función de esa secreción es aportar un agente protector y lubricante de la pared intestinal (el moco) y agua, ya que la digestión requiere que los nutrientes se encuentren en disolución.
Las enzimas que realizan la digestión en la luz del intestino provienen del páncreas. Son la lipasa, tripsina, quimotripsina, carboxipeptidasa y amilasa. Los productos de esa digestión o bien son absorbidos directamente o son digeridos por enzimas del borde en cepillo de las células epiteliales. Las enzimas en cuestión son la enteroquinasa (que activa el tripsinógeno procedente del páncreas), las disacaridasas que finalizan la digestión de los carbohidratos (en mamíferos estas enzimas son maltasa, sacarasa, lactasa y trehalasa) y las aminopeptidasas, que hacen lo propio con la digestión de las proteínas. En las aves hay alguna diferencia con respecto a los mamíferos: carecen de lactasa, como es lógico, y muchos pájaros (no así los colibríes) no tienen sacarasa.
En principio, el intestino tiende a absorber todos los nutrientes (tras su digestión), electrolitos1, vitaminas y agua que han sido ingeridos. Aunque, como veremos en otra ocasión, es un órgano muy flexible, por lo que la capacidad para digerir y absorber unos nutrientes u otros se puede modificar en función de su presencia y proporción en la dieta habitual.
El agua se absorbe de forma pasiva impulsada por la absorción de Na+. Este, por su parte, puede pasar a favor de gradiente electroquímico –y, por lo tanto, de forma pasiva- desde la luz del tubo al fluido intersticial que hay entre los villi. Ese movimiento se produce a través de los espacios intercelulares; del líquido intersticial pasa a los capilares sanguíneos.
Pero también hay movimiento de sodio a través de las células epiteliales, y ese movimiento sí requiere gasto de energía. Puede entrar pasivamente en la célula a través de canales o en compañía de otro ión gracias al concurso de un transportador (simporter Na+/Cl–, antiporter Na+/H+ o simporter Na+-glucosa (o aminoácido)). Y sale de la célula epitelial, a través de su membrana basolateral hasta el líquido intersticial de los espacios intercelulares gracias a la acción de la bomba Na+/K+. La absorción de Cl–, H2O, glucosa y aminoácidos está vinculada a la absorción activa de sodio. El Cl– pasa a favor del gradiente eléctrico creado por el Na+, y el agua, por el flujo osmótico provocado por la alta concentración de NaCl en los espacios intersticiales.
La mayor parte de los carbohidratos en condiciones de ser absorbidos por las células epiteliales se encuentran, como ya se ha dicho, en forma de disacáridos. Las disacaridasas presentes en el borde en cepillo reducen esos azúcares a sus monómeros constituyentes: glucosa, galactosa y fructosa, dependiendo del disacárido original.
Glucosa y galactosa son absorbidas mediante transporte secundario activo, en el que intervienen simporters como el cotransportador sodio-glucosa (SLGT), que transfieren ambas sustancias, glucosa y sodio desde la luz del intestino al interior celular. La energía que se gasta en este proceso es la que gasta la bomba Na+/K+ de la membrana basolateral que, como antes hemos señalado, es la responsable de crear el gradiente de Na+ necesario para hacer posible su transferencia y, con él, el del azúcar. De esa forma, la concentración de glucosa (y en su caso la de galactosa) se eleva dentro de la célula, por lo que puede abandonarla fácilmente a través de la membrana basal a favor de gradiente de concentración, mediante difusión facilitada por el transportador de glucosa GLUT-2, presente en esa membrana. Del fluido intersticial pasa al capilar del villus en el que se encuentra la célula epitelial. Además de ese transporte, parece ser que la glucosa también puede pasar desde la luz intestinal hasta el líquido intersticial a través de los espacios intercelulares del epitelio (como ocurría con el sodio).
La fructosa se absorbe a través de difusión facilitada. Entra en la célula epitelial gracias al transportador GLUT-5 y sale al espacio intersticial mediante el concurso del transportador GLUT-2.
Las proteínas, por su parte, se van fragmentando, primero en el estómago y luego en la luz intestinal. Como resultado de las sucesivas hidrólisis anteriores, finalmente quedan aminoácidos y pequeños péptidos para su digestión final y absorción epitelial. Los aminoácidos se absorben de forma similar a la glucosa y galactosa.
Los pequeños péptidos se introducen en la célula epitelial mediante un transportador dependiente de Na+. El proceso se denomina transporte terciario activo. El simporter que interviene transfiere a la vez el péptido y un protón desde la luz intestinal al interior de la célula. El H+ se mueve a favor de gradiente de concentración, mientras que el péptido lo hace en contra. El gradiente de protones se genera mediante el concurso de un antiporter de Na+/H+, que introduce sodio a favor de gradiente de concentración a la vez que saca H+ en contra. Por su parte, el gradiente de concentración de Na+ que impulsa el antiporter Na+/H+ se genera gracias a la actividad de la bomba Na+/K+ en la membrana basolateral.
Todo ese proceso se puede observar desde el ángulo contrario. La bomba Na+/K+ extrae Na+ de la célula hacia el líquido intersticial. Ese transporte es necesariamente activo, porque el sodio está muy concentrado en el medio interno (el líquido intersticial o extracelular es medio interno), mientras que el potasio lo está en el medio intracelular. La bomba, por lo tanto, reduce de esa forma la concentración intracelular de Na+, de manera que facilita su transferencia desde la luz intestinal. Dado que parte de ese sodio entra acoplado a la salida de protones y puesto que esa salida está, a su vez, asociada a la entrada de oligopéptidos a la célula, la incorporación de estos acaba siendo el resultado de una cadena de movimientos, activos y pasivos, en la que intervienen varios iones (H+, Na+ y K+).
Los oligopéptidos son hidrolizados por la acción de las aminopeptidasas del borde en cepillo de la membrana celular o en el citoplasma gracias a la acción de peptidasas intracelulares. Los aminoácidos resultantes de estos procesos (transporte o digestión intracelular) salen de la célula epitelial mediante transportadores pasivos (no utilizan energía) y entran en los capilares sanguíneos por difusión.
Además de las proteínas provistas por el alimento, en el intestino delgado se digieren y absorben proteínas de origen endógeno, como enzimas digestivas, proteínas celulares que han sido expulsadas de las células de la pared a la luz intestinal durante la renovación de la mucosa, y proteínas plasmáticas que se filtran desde el plasma accidentalmente. Entre 20 y 40 g de estas proteínas son digeridas diariamente.
Las grasas experimentan un proceso de digestión y absorción muy diferente de los anteriores. Como vimos, debido a la acción de las sales biliares y los movimientos intestinales las gotas lipídicas de tamaño grande se convierten, primero en gotas pequeñas, y luego, debido a la acción de la lipasa (con el concurso de la colipasa), en micelas, estructuras lipídicas esféricas de entre 3 y 10 nm de diámetro. Esas micelas son la forma en que los monoglicéridos y ácidos grasos libres acceden a la membrana de las células epiteliales para, una vez allí, penetrar a su través. Los componentes que configuran la estructura micelar son reutilizados para englobar nuevos fosfolípidos y monoglicéridos, y llevarlos hasta la membrana para su absorción.
Tras entrar en las células, los constituyentes de los lípidos son utilizados para sintetizar triglicéridos, que son empaquetados en agregados provistos de una capa de lipoproteínas gracias a la cual se hacen solubles en agua. Las lipoproteínas de mayor tamaño se denominan quilomicrones, y salen mediante exocitosis de la célula epitelial hacia el líquido intersticial, y de ahí, en mamíferos, al vaso quilífero (al que nos referimos aquí). En las aves los quilomicrones pasan a los capilares sanguíneos de los villi.
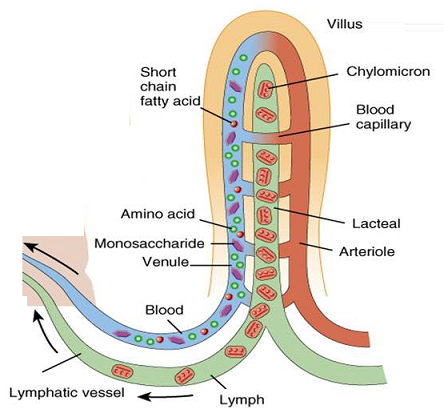 Fuente: Biology Notes for IGCSE
Fuente: Biology Notes for IGCSE
Los productos de la digestión de carbohidratos y proteínas pasan al hígado porque, como vimos, las vénulas desembocan en la vena porta hepática. La mayor parte de esos nutrientes se procesan metabólicamente allí. Además, ese órgano también se ocupa de tareas de desintoxicación de sustancias dañinas. Las grasas tienen un destino diferente. Al acceder al vaso quilífero, acaban desembocando en el sistema linfático y, de este, pasan a la circulación general a través del conducto torácico, un gran vaso linfático que desemboca en el sistema venoso. Ese dispositivo hace que una parte importante de los lípidos absorbidos sean incorporados directamente a los adipocitos, aunque otra parte acaba también siendo procesada por el hígado. De este modo se evita que este órgano reciba más grasa de la que puede procesar.
El hígado, no obstante, juega una función importante en el transporte de lípidos pues, como vimos, sintetiza diferentes lipoproteínas plasmáticas y las vierte al sistema circulatorio para su uso. Las lipoproteínas de alta densidad (HDL y LDL) transportan principalmente colesterol y también fosfolípidos para la fabricación de membranas celulares. Las lipoproteínas de muy baja densidad (VLDL) transportan principalmente triglicéridos que son almacenados en adipocitos como sustancias de reserva.
Hemos visto antes que la absorción de sodio por las células de la mucosa intestinal va acompañada de absorción de agua. Es, de hecho, una actividad muy importante. Un intestino delgado humano viene absorber del orden de 9 l de agua al día, aunque el agua que se ingiere en el alimento son unos 1.250 ml y otros 1.250 ml se ingieren bebiendo. El resto son fluidos procedentes del propio organismo: 1.500 ml de saliva, 2.000 ml de jugos gástricos, 1.500 ml de jugo pancreático, 500 ml de bilis y 1.500 de jugo intestinal. La suma de esas cantidades arroja un volumen de 9.500 ml. Los 500 ml restantes pasan al intestino grueso, donde se absorberán 350 ml diarios. El resto, 150 ml, se evacúa con las heces.
Por otra parte, el HCl secretado por el estómago es neutralizado en el intestino delgado por el NaHCO3 secretado por el páncreas. El H2CO3 resultante se disocia en CO2 y H2O y estos productos, junto con el NaCl también resultante de la neutralización del clorhídrico procedente del estómago son absorbidos. El resultado final es que las actividades digestivas no provocan cambios en el pH del medio interno.
Nota:
1Con la salvedad de calcio y hierro, que son absorbidos en función de las necesidades.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Absorción del alimento se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:¿Son útiles los juguetes STEM?
Haydée Valdés González
Seguramente, de un tiempo a esta parte ustedes también habrán observado un espectacular aumento en la oferta de juguetes “científicos” también denominados juguetes STEM (Science, Technology, Engineering and Mathematics; Ciencia, Tecnología, Ingeniería y Matemáticas) que están disponibles en cualquier tienda del sector. Por ejemplo, la entrada “stem toys” en amazon.com devuelve más de 8000 resultados (a fecha de enero de 2019).
La publicidad de estos juguetes frecuentemente sugiere que tienen un claro carácter educativo de manera que los niños podrán aprender sobre Ciencia y Tecnología sin renunciar a la diversión. Parece además, que el juguete STEM es una buena opción para fomentar el interés de los niños por la Ciencia y la Tecnología e incluso, por qué no, para despertar sus vocaciones científicas.
Sin negar que el juguete pueda ser bonito, de calidad, y que el niño pueda pasar un rato entretenido con él, la realidad es que la mayoría de los juguetes STEM tienen, por lo general, un claro error de planteamiento en lo que a su enfoque científico se refiere: presentan la actividad científica como un proceso dirigido y cerrado cuando la actividad científica es justamente todo lo contrario, un proceso abierto y no dirigido.
Veamos.
 Imagen: Pixabay
Imagen: Pixabay
Los “juguetes científicos” son juguetes comerciales en los que, en una gran mayoría de los casos, se parte de preguntas cerradas a cuya única respuesta se llega siguiendo un procedimiento perfectamente establecido. Consecuentemente, y por lo general, sólo será posible obtener el resultado previamente predeterminado por el fabricante si se siguen las instrucciones al pie de la letra y se usan los materiales suministrados por el mismo.
La Ciencia, en cambio, es una actividad orientada a la búsqueda de conocimiento en la que únicamente se sabe con certeza el punto de partida y donde, generalmente, la fabricación y el desarrollo del instrumental necesario forma parte de la actividad investigadora (a diferencia del juguete STEM donde todo el material viene suministrado por el fabricante).
Por tanto, hacer Ciencia es una cosa y otra cosa muy diferente es llevar a cabo actividades relacionadas con la Ciencia que es, esencialmente, lo que un niño hace cuando juega con un juguete STEM.
Más específicamente: un niño está haciendo Ciencia cuando motivado por su propia curiosidad efectúa un conjunto de acciones y obtiene cierto conocimiento. Por ejemplo: un niño está haciendo paleontología (a un nivel infantil: elemental, básico y sencillo) cuando rebusca entre las piedras en una escombrera de una mina de carbón intentando encontrar alguna con marcas y después las observa detenidamente con una lupa para ver si alguna de estas piedras se corresponde, por ejemplo, con un fósil de una planta. Estrictamente hablando, este niño ha llevado a cabo una investigación real, a un nivel rústico y primitivo como digo, pero tan auténtica y verdadera en su esencia como la que podría efectuar cualquier paleontólogo.
En cambio, un niño está jugando a ser científico cuando, jugando con un juguete STEM, imita la actividad de un investigador de manera que siguiendo el correspondiente manual de instrucciones el niño aplica algunas de las técnicas de laboratorio más básicas y emplea parte del instrumental más elemental que un científico utiliza en su día a día para llegar a un resultado preestablecido. Por ejemplo: un niño está jugando a ser paleontólogo cuando juega con un juguete STEM en el que hay un conjunto de fósiles “enterrados” en un bloque de arcilla y “excava” en dicho bloque de arcilla, con unas “herramientas de paleontólogo” (miniaturizadas) y “desentierra” todos los fósiles.
En general, como queda ilustrado en el ejemplo anterior, las actividades relacionadas con la Ciencia planteadas en los juguetes STEM resultan bastante artificiales principalmente porque suelen ser una simplificación bastante burda de la actividad científica “adulta” y no son verdaderas propuestas para hacer Ciencia a un nivel propiamente infantil (cuanto más pequeño es el niño al que va destinado el juguete peor, como se puede suponer).
Los juguetes STEM tampoco son, necesariamente, la mejor manera de promover el desarrollo del espíritu científico infantil. En concreto, podría decirse que un juguete STEM es a la Ciencia lo que un dibujo para colorear, con el modelo miniaturizado ya coloreado en la propia hoja, es al Arte. Para desarrollar la capacidad artística de un niño no basta con plantearle que, sin salirse de la raya, coloree un dibujo con los mismos colores que un modelo dado o que copie una lámina (procesos dirigidos). Estas actividades son (como mucho) útiles para adquirir determinada pericia técnica pero en ningún caso son suficientes para desarrollar capacidad artística alguna. Cultivar la capacidad artística infantil indudablemente requiere dejar espacio al niño para que, espontáneamente, inspirado por algo que verdaderamente le haya conmovido, exprese sus emociones mediante una obra de su propia creación. Entendamos que una obra de arte creada por un niño de corta edad puede ser un trozo de corteza de un árbol con varias marcas hechas con una piedra puntiaguda, una figura “amorfa” de arcilla, o “cuatro garabatos” en una hoja de papel en blanco.
De la misma manera, en el ámbito científico un niño no desarrollará su espíritu científico si lo único que se le plantea es hacer experimentos siguiendo un manual de instrucciones (proceso dirigido).
Investigar es decidir en cada momento qué paso dar a continuación en función de los resultados obtenidos lo que es absolutamente opuesto a seguir ordenadamente un conjunto específico de pasos para obtener un resultado determinado que, en definitiva, es el modo en el que se plantea la experimentación en un juguete STEM.
“Enlatar” la Ciencia en un producto comercial para que un niño haga un experimento específico atendiendo a un conjunto de instrucciones es (a lo sumo) útil para aprender algunos contenidos científicos y quizás (en el caso de los niños de mayor edad) para adquirir cierta pericia técnica y familiarizarse con el instrumental científico y unas pocas técnicas básicas de laboratorio pero, para desarrollar verdaderamente el espíritu científico infantil, sin duda alguna, hay que ofrecer al niño la posibilidad de vivir experiencias científicas reales en las que, espontáneamente, guiado por su propia curiosidad, pueda indagar y profundizar sobre cuestiones que verdaderamente le intriguen. Sólo así podrá conocer lo que es auténticamente la Ciencia, vivir en primera persona el inmenso placer que proporciona comprender cosas por uno mismo y entender porqué lo verdaderamente divertido es hacer Ciencia frente a la posible diversión que pueda proporcionar jugar con un juguete STEM.
Para terminar, hay una cuestión sobre la que me gustaría incidir especialmente: la referente a algunos “juguetes científicos” diseñados específicamente para niñas. La situación actual es que amparándose bajo la filosofía “empoderamiento de las niñas en la Ciencia” algunas empresas están diseñando y vendiendo “juguetes científicos diseñados específicamente para niñas” bajo la promesa de que gracias a ellos se contribuirá a favorecer el acceso de las niñas a la Ciencia y su participación en ella. Sin embargo, resulta verdaderamente llamativo que muchos de estos juguetes tengan los colores (rosa y morado, principalmente) y versen sobre temáticas (maquillaje, perfumes, jabones, barras de labios, velas, etcétera) habitualmente asociados al mundo femenino. Obviamente, en base a lo que se discute en el presente artículo, la validez de estos productos comerciales para favorecer el acercamiento de las niñas (y de cualquiera) a la Ciencia y su participación en ella es altamente dudosa pero es que además, estos juguetes no están en ningún modo exentos de polémica al poder considerarse que perpetúan los estereotipos de género.
Sobre la autora: Haydée Valdés González es doctora en ciencias químicas.
El artículo ¿Son útiles los juguetes STEM? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Juguetes y hormonas sexuales
- Las matemáticas en Wall Street, ¿útiles o perversas?
- Lejos del dogma y cerca de la aventura, por Melina Furman
¿Qué pasa en tu cuerpo cuando te enamoras?
Para que resuelte el amor primero tiene que existir química entre dos personas. Literalmente.
Los vídeos de ¿Preguntas frecuentes? presentan de forma breve y amena cuestiones que, probablemente, nos hayamos planteado en alguna ocasión. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.
Edición realizada por César Tomé López
El artículo ¿Qué pasa en tu cuerpo cuando te enamoras? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Qué pasa en tu cerebro cuando duermes?
- ¿Cómo demonios funcionan las copas musicales?
- ¿Hemos intentando contactar con extraterrestres?

