Itziar Aretxaga: «Izarren eraketaren historia ulertu nahi dut»
Itziar Aretxaga doktorea (Bilbo, 1965) Astrofisika, Optika eta Elektronikako Institutu Nazionaleko (INAOE) C ikertzaile titularra, Ikertzaileen Sistema Nazionaleko kidea (III. maila) eta Mexikoko Zientzien Akademiako kidea da.
Fisikan lizentziaduna da (Madrilgo Unibertsitate Konplutentsea) eta doktoregoa dauka Fisikan (Madrilgo Unibertsitate Autonomoa, 1993). Doktorego ondoko egonaldiak egin zituen Royal Greenwich Observatory behatokian (Britainia Handia) eta Max Planck Institute for Astrophysics institutuan (Alemania). Eta, ondoren, INAOEn hasi zen lanean ikertzaile gisa 1998an, astrofisikako arloan. 2011 eta 2016 artean, Astrofisika Saileko koordinatzaile izan zen, eta 2006 eta 2013 artean Mexikoko Zientzien Akademiako astronomia atala koordinatu zuen.
2016az geroztik, Nazioarteko Astronomia Elkarteko astronomo gazteen nazioarteko eskolen zuzendaritza taldeko kidea da. Elkarte hori astronomo profesionalen elkarterik handiena da munduan, eta 13 000 kide baino gehiago ditu. Elkartearen graduondoko eskolen programarik nabarmenenak 50 urte baino gehiago ditu eta, haren bidez, suspertzen ari diren herrialdeetako astronomiako ikasleak gaitzen eta prestatzen dira beren graduondokoan. Helburua da garapena eta inklusioa sustatzea eta ezagutza arrakala murriztea munduan.
Aretxaga doktorearen ikerketa ildoak galaxiaz kanpoko astrofisikaren eta kosmologiaren arloan garatzen dira, bereziki galaxien eraketan eta bilakaeran. 140 artikulu baino gehiago idatzi ditu aldizkari arbitratu espezializatuetan, 20 dibulgaziokoetan, eta zientzia hedatzeko hogei bat jardueratan parte hartzen du urtero.
Bere ikerketak gauzatzeko, teleskopio handiak erabiltzen ditu, sarbide nazionalekoak nahiz nazioarteko eskumenekoak, hala nola Teleskopio Milimetriko Handia, Kanarietako Teleskopio Handia, Atacama Large Milimeter Array, Hubble Space Telescope… Egun, TolTEC kamera polarimetrikoaren zuzendari zientifikoa da (Teleskopio Milimetriko Handirako irudi bidezko tresna berria). TolTEC AEB, Mexiko eta Britainia Handiko zazpi institututan eraiki da, AEBko ikertzaile nagusi baten zuzendaritzapean. Aretxaga doktoreak hirurogei kidek baino gehiagok osatzen duten talde zientifikoa koordinatzen du; kide horiek, nagusiki, zortzi institutu kideetan banatuta daude. Horrez gain, hogeita hiru herrialdetako hirurehun zientzialari ingururen esfortzuak koordinatzen ditu. Horiek guztiak lantaldetan banatuta daude, eta 2022 eta 2025 artean tresna horren bidez gauzatuko diren hamar legatu erroldak ustiatzen dituzte.
 Irudia: Itziar Aretxaga Alfonso Serrano Teleskopio Milimetriko Handiaren aurrean (Itziar Aretxagak emana).Zein da zure ikerketa arloa?
Irudia: Itziar Aretxaga Alfonso Serrano Teleskopio Milimetriko Handiaren aurrean (Itziar Aretxagak emana).Zein da zure ikerketa arloa?
Galaxien eraketa eta bilakaeraren esparruan lan egiten dut, Galaxiaz Kanpoko Astrofisikaren eta Kosmologiaren arloan.
Zergatik aritzen zara arlo horretan?Galaxien eraketa ulertzea ezinbestekoa da Unibertsoaren aberaste kimikoa eta bizitza ahalbidetzen duten baldintzen aldaketa ulertzeko. Fisikaren esparrutik «nondik gatoz eta nora goaz?» galdera handiari erantzutearen atal txiki bat da.
Izan al duzu erreferentziazko figurarik zure ibilbidean?Erreferente asko izan ditut. Lehenik eta behin, nire kolaboratzaile seniorrenak, beren lan egiteko eta entregarako filosofia eman baitzidaten; eta, aurrerago, nire ikasleak, behin eta berriro txunditzen nautelako beren gogoberotasunaren eta etorkizuneko ikuspegiaren bidez. Ez dut, beraz, erreferente gisa, izen handiko zientzialari handi bat. Hala ere, askoren biografiak irakurri ditut eta nire ibilbideak haiekin ere zerikusirik baduela sentitzen dut.
Zer aurkitu edo konpondu nahiko zenuke zure arloan?Galaxia mota ezberdinetan eta Unibertsoan izarren eraketaren historia ulertu nahi dut, bai eta zulo beltz supermasiboek horrengan izan dezaketen erregulazioa ere. Arlo horretan hasi nintzen doktorego tesiaren bidez, eta oraindik ere jarraitzen dut ikerketa esparru horretan lanean, baina orduan jorratutako bestelako ikuspegietatik.
Zer aholku emango zenioke ikerketaren munduan hasi nahi duen norbaiti?Entusiasmoari eustea, amets handiak izatea eta amets handi horiek betetzen saiatzea. Ametsak ez dira beti helmugak, baina gure bidea markatzen dute, eta noraino iristeko prest gauden ere islatzen dute. Konfuzioren aipu handi bat irakurrarazten diet beti nire ikasleei:
Asmo handi bat baduzu, emaitza orokor bat lor dezakezu; emaitza orokor bat lortu nahi baduzu, agian emaitza txiki batera iritsiko zara; baina helbururik txikiena lortu nahi baduzu, agian ez duzu ezer lortuko.
Jatorrizko elkarrizketa Mujeres con Ciencia blogean argitaratu zen 2025eko martxoaren 29an: Itziar Aretxaga: «Trabajo para entender la historia de la formación estelar».
Itzulpena: UPV/EHUko Euskara Zerbitzua.
Ikertzen dut atalak emakume ikertzaileen jardunari erreparatzen die. Elkarrizketa labur baten bidez, zientzialariek azaltzen dute ikergai zehatz bat hautatzeko arrazoia zein izan den eta baita ere lanaren helburua.
The post Itziar Aretxaga: «Izarren eraketaren historia ulertu nahi dut» appeared first on Zientzia Kaiera.
Zerk egiten gaitu gizaki?
Lehenengo gizakia zein izan zen eta noiz bihurtu ginen gizaki galdetu izan da maiz. Gure espezieari Homo sapiens izena jarri diogu, eta generoa Homo izatea zer esan nahi duen galdetzen diogu gure buruari. Homo habilis aurkitu zenean, duela 2,3 milioi urte, tresnak egiteko gaitasunagatik hartu zuen izena, baina tresna zaharragoak ere aurkitu dira. Beraz, zer egiten gaitu Homo? Burmuinaren tamaina, tresnak, edota kultura? Gizakiok gure gorputzaren tamainarekiko sei aldiz handiagoa dugu burmuina, eta horri esker hizkuntza, ikasketa soziala eta berrikuntza garatu ditugu. Gure eboluzioa ez da soilik biologikoa, baizik eta biokulturala: kultura da gure tresna ebolutibo nagusia.
Duela hiru milioi urteko Afrikan klima lehortzen hasi zenean, gure arbasoek bi bide hartu zituzten. Batzuek hortz eta masailezur sendoagoak garatu zituzten (Paranthropus); belarra eta elikagai gogorrak jaten espezializatuak. Baina, desagertu egin ziren. Beste talde batek, gureak, garuna handitu eta tresnak egiten hasi zen: haragia jaten hasi zen eta elkarrekin lan egitea bihurtu zuen bizirauteko modua. Gurea espezie kooperatiboa da; elkar zaindu, ikasi eta partekatzen duen animalia kulturala.
“Gure arbasoak” Ikusgela hezkuntza proiektuaren bideo-sorta bat da. Euskal Wikilarien Kultur Elkartearen ikus-entzunezko egitasmoa da eta EHUko Kultura Zientifikoko Katedraren kolaborazioa izan du.
The post Zerk egiten gaitu gizaki? appeared first on Zientzia Kaiera.
Ezagutzaren ibaiaren delta bat, gizartearen aniztasun osoa bustitzeko
Euskal Herriko Unibertsitateko Kultura Zientifikoko Katedrak hamabost urte bete ditu eta aro berri bati ekin dio, 2010ean sortu zenean finkatutako misiotik abiatuta: herritarren kultura zientifikoa sustatzea gizarte demokratikoago baterantz aurrera egiteko. Gaur, konpromiso hori zabaltzen da. Zientzia gizartearen txoko eta ertz guztietara hurbildu nahi dugu, ezagutza ahalik eta jende gehiagorentzat eskuragarri eginez martxan jarriko ditugun ekimenen bitartez.
Ibai baten delta izan nahi dugu: gizartea bere aniztasun osoan bustiko duen ezagutza-bidea, adar ugari dituen ezagutzaren ibilgua. Erdiguneetara mugatu beharrean ertzetara ere iritsiko dena, zientziarekin hain lotuta ez dauden espazioetara isuriko dena. Ezagutza lurralde horietara (lurralde geografikoak, sozialak eta kulturalak) eramatea ez da erronka logistiko bat bakarrik: dibulgazio inklusiboago, bidezkoago eta eraldatzaileago baten aldeko apustu etikoa da.
 Irudia: ibai baten delta izan nahi dugu: gizartea bere aniztasun osoan bustiko duen ezagutza-bidea, adar ugari dituen ezagutzaren ibilgua. (Argazkia: EHUko Kultura Zientifikoko Katedra)
Irudia: ibai baten delta izan nahi dugu: gizartea bere aniztasun osoan bustiko duen ezagutza-bidea, adar ugari dituen ezagutzaren ibilgua. (Argazkia: EHUko Kultura Zientifikoko Katedra)Kultura zientifikoaren hedapena ezin da mugatu espazio akademiko, digital edo hiritar nagusietara. Iritsi nahi dugu zaurgarritasun-egoeran bizi direnengana, teknologiarik erabiltzen ez dutenengana, dibertsitate funtzionalak dituztenengana edota hirigune handietatik urrun dauden auzo, herri edo inguruneetan ere bizi direnengana. Azken finean, ezagutzaren ohiko kanalen bidez iristen ez direnenganaino. Eta txoko eta ertz horietara hurbildu nahi dugu, ez keinu puntual gisa, baizik eta kultura zientifikoaren difusioari dimentsio berri bat emateko.
Horregatik, ikuspegi irisgarri eta multikanal baten aldeko apustua egiten dugu, askotariko publikoengana iristeko aukera emango diguna: gure blogetatik (Zientzia Kaieran, Cuaderno de Cultura Científica, Mujeres con ciencia eta Mapping Ignorance) ikus-entzunezko plataformetara; gure sare sozialetatik zientzia-dibulgazioko jarduera presentzialetara; herri eta hirietako plaza eta kaleetatik kultura-zentroetara. Helburua da, dagoeneko finkatuta dauden espazioei eusteaz gain, hain ohikoak ez diren beste lurralde batzuetara irekitzea. Zientziak errealitate ezberdinekin jarrera hurbil eta ireki batetik hitz egin dezakeela erakusten digute Bilbo Zientzia Plaza edo Zientzia Kalean bezalako proiektuek, betiere zorroztasunari uko egin gabe.
Eskala aldatuHiri-kapitalen gailentasunarekin hautsi egiten dugu eta apustu egiten dugu inpaktu kuantitatibotik haratago neurtzen den zientziaren komunikazioaren alde, kontuan hartuz pentsamendu kritikoa, gizarte-kohesioa eta parte-hartze aktiboa sustatzeko duen gaitasuna ere. Jakintzaren transmisioari eta zientzia-prestakuntzari esker, norbanakoaren eta taldearen ongizatean lagunduko duen kultura zientifikoa; entzun, behatu eta ikasiko duena. Eta normalean iristen ez den txoko horietara iristea ere lortuko duena.
Horretarako, jauzi bat egin behar dugu: egiten duguna eskuragarriago bihurtu, edukian eta erabiltzen ditugun formatuetan eta espazioetan. Zientzia, edonon egon arren, ez baita oraindik eskuragarri denontzat. Hala azaldu du Emily Dawson University College of Londoneko Zientzia eta Teknologia Ikasketen Saileko ikertzaileak FECYTeko “Hacia una comunicación inclusiva de la ciencia: Reflexiones y acciones de éxito” argitalpen digitalean (11. or.).
“Oraindik ere, zientziaren komunikazioa talde pribilegiatuentzako baliabide eta jarduera multzo bat da. Pertsona bat hiri batean bizi bada, aberatsa bada eta goi-mailako ikasketak baditu, aukera gehiago izango ditu zientziaren komunikazio-jardueretan parte hartzeko, museoetan, jaialdietan, hitzaldi zientifikoetan edo antzeko jardueretan”.
Hau da, komunikazio zientifikoak eremu esklusiboa izaten jarraitzen du; gure ardura da, beraz, zabaltzea eta benetan inklusibo egitea.
Zientzia inklusiboa eta eraldatzaileaBere sorreratik, EHUko Kultura Zientifikoko Katedrak zeregin aktiboa izan du kultura zientifikoa oinarri demokratiko gisa aldarrikatzeko. Fase berri honek sendotu eta zabaldu egin nahi du ondare hori. Kultura zientifikoa eguneroko paisaia kulturalaren parte izatea sustatu behar dugu, baina beste urrats bat ere egin behar dugu gero eta jende gehiagorengana iristeko. Orain, ekarpena egin nahi diegu berdintasunari, justizia sozialari eta ongizate kolektiboari ere.
Asmo horrek ahalegina eskatuko digu inguruko eragile sozial, teknologiko eta kulturalekin lankidetzari eusteko, eta hura indartzeko eta zabaltzeko du, ezagutzaren komunikazio inklusiboaren alde elkarrekin lan eginez eta elkarlana zabalduz, BRTA aliantza bezalako zentro teknologikoekin, zein Zientziaz Blai bezalako ekimenekin edota Irakurketa Erraza Euskadi, Zientziaren Giltzak edo ZarautzOn bezalako elkarteekin, zientzia askotariko publikoei hurbiltzeko.
Etorkizuneko zientziak ekitatiboa eta inklusiboa izan behar du, inor atzean utzi gabe generoari, lurraldeari, dibertsitate funtzionalari, kulturari edo sexu-joerari lotutako arrazoiengatik. Ez da nahikoa egotea: ezinbestekoa da gure ekimen eta proiektuen irisgarritasuna sustatzea eta bermatzea, pertsona, kolektibo eta publiko guztiengana iritsi ahal izateko. Zubia izan nahi dugu herritarrak askotariko diziplina zientifikoetako profesionalekin lotzeko; sinergiak sortu nahi ditugu ezagutza gizartean zabaltzeko balio duten tresna erabilgarriak garatzeko, biztanleriaren ongizatean benetako eragina izan dezaten, balio erantsia ekar dezaten.
Egileaz:Iker Badiola Etxaburu (@ikerbadiola.bsky.social) EHUko Kultura Zientifikoko Katedrako zuzendaria eta EHUko Medikuntza eta Erizaintza Fakultateko irakaslea da.
The post Ezagutzaren ibaiaren delta bat, gizartearen aniztasun osoa bustitzeko appeared first on Zientzia Kaiera.
Florence Bell, DNAaren beste “dama ilun” bat
1953an, Francis Crick eta James Watson zientzialariek aldarrikatu zuten bizitzaren sekretua deskubritu zutela: DNAren edo izaki bizidunen (eta birus batzuen) garapen, funtzionamendu eta ugalketarako oinarrizko jarraibide genetikoak gordetzen dituen molekularen egitura. Historiak bere rola oso denbora luzez alde batera utzi bazuen ere, egun badakigu Rosalind Franklin zientzialariaren partaidetza ezinbestekoa izan zela deskubrimendu horretan. Izan ere, X izpien bidezko kristalografiaren esparruko bere abileziari esker, molekularen egitura helikoidalaren teoria ziurtatzeko beharrezkoa zen ebidentzia lortu zuen. Askotan DNAren “dama ilun” deitzen diote, haren ekarpena ez zelako behar bezala aitortu.
Eta, badago, gutxienez, beste dama ilun bat aurkikuntza horri lotuta, baina ez da, beharbada, hain ezaguna: Florence Bell (1913-2000) kristalografoa. Hamarkada bat baino gehiago lehenago, Ingalaterrako zientzialari hori izan zen lehena X izpien difrakzioaren metodoa erabiltzen DNAren konfigurazioa ikertzeko, eta frogatu zuen DNAren patroiak egitura ordenatu baten patroiekin bat zetozela. Bellen lanak, isilean, XX. mendeko zientziaren mugarri garrantzitsuenetako baten oinarriak ezarri zituen.
 1. irudia: Florence Bell ikertzailea. (Argazkia: Chris Sawyer. Iturria: Leeds Unibertsitatea)
1. irudia: Florence Bell ikertzailea. (Argazkia: Chris Sawyer. Iturria: Leeds Unibertsitatea)Florence Bell 1913ko maiatzaren 1ean jaio zen Londresen (Erresuma Batua). Annie Mary Lucas eta Thomas Bell bere senarraren (argazkilaria eta publizitateko zuzendaria) bigarren alaba izan zen. Arlo akademikoan gailendu zen txikitatik. 1932tik 1935era Natura Zientziak ikasi zituen Cambridgeko Unibertsitateko Girton Collegen, eta kimika, fisika eta mineralogian zentratu zen. Han ikasi zuen X izpien bidezko kristalografia John Desmond Bernal irlandarraren eskutik. Azken horrek lan aitzindaria egin zuen teknika horren erabileran, eta horren ondorioz piztu zitzaion interesa teknika hori molekula biologikoak ikertzeko lanetan erabiltzeko.
Teknika horri esker «ikus» daiteke nola dagoen antolatuta molekula bat barrutik. Honela funtzionatzen du: X izpiak —argi oso energetikoa— bidaltzen da substantzia jakin bateko zuntz baten edo kristal baten bidez. X izpiek molekula osatzen duten atomoekin talka egiten dutenean, hainbat norabidetan sakabanatzen dira, eta patroi bereizgarri bat osatzen dute plaka batean. Orbanen patroi hori ez da irudi zuzen bat, baina atomoen arteko tarte eta angeluei buruzko informazioa jasotzen du. Patroi hori buru-hausgarri bat ebazteko modu berean aztertzen da: molekularen hiru dimentsioko egitura berreraikitzen da izpiak desbideratzen diren modutik abiatuta.
X izpien bidezko kristalografia proteinetan…Cambridgen ikasketak amaitu ondoren, Bellek laburki lan egin zuen Lawrence Bragg fisikariarekin Manchesterko Unibertsitatean. Braggek Fisikako Nobel Saria jaso zuen 1915ean bere aita Williamekin batera, frogatu ondoren X izpiak erabil zitezkeela gatza bezalako kristal sinpleetan atomoen eta molekulen antolaera ikusteko. Harekin hasi zen Bell proteinetako kristalografian sakontzen, eta bere doktorego tesiaren lehen zatia osatu zuen, zeinetan zuntz proteikoen gama zabal baten egitura deskribatu zuen, medusa, marrazo-hegal edo ilean aurki daitezkeenak barne.
1937an Leedseko Unibertsitatera lekualdatu zen, eta han ikerketako laguntzailearen lanpostua bete zuen William Astburyrekin. Azken horrek Braggen metodoak aplikatzen zituen artilea ikertzeko. Artilearen zuntzen proteinetan X izpien difrakzioaren teknika erabilita, Braggek deskubritu zuen horren egitura molekula kate —edo koilare— batena bezalakoa zela, aminoazido izeneko substantzia kimiko txikiagoak elkartuta osatuta baitago. Proteinek formaz aldatzeko zuten gaitasuna —zabalduz edo trinkotuz— ezinbestekoa izan zen nola funtzionatzen zuten ulertzeko. Astburyren artileari buruzko ikerketek biologia maila molekularrean ulertzeko gure gaitasuna eraldatu zuten.
… eta beste zuntz natural batzuetanBere deskubrimendu berriek bultzatuta, Astburyk erabaki zuen bere sarea zabaltzea beste zuntz natural batzuk ikertzeko. Horretarako, X izpien analisian eskarmentua zuten beste bi esku behar zituen. Zorionez, Florence Bellekin egin zuen topo. Hain zuzen ere, Belli agindu zion teknika hori erabiltzea DNA ikertzeko —orduan azido timonukleiko esaten zioten eta maila biologikoan garrantzia txikiko molekulatzat zuten; izan ere, garai hartako iritzi zientifiko lehenetsia zen proteinak zirela material genetikoa, eta DNA egiturazko elementu soil bat—. Lan horrek osatu zuen Bellen doktorego tesiaren bigarren atala. Tesia 1939an defendatu zuen. Zientzialariaren ohar liburuxka eta tesia Leedseko Unibertsitateko Bilduma Berezietan daude gordeta.
 2. irudia: Astburyren X izpien difrakzio-makina. (Iturria: Leeds-eko Unibertsitateko Zientzia, Teknologia eta Medikuntza Historiaren Museoa)
2. irudia: Astburyren X izpien difrakzio-makina. (Iturria: Leeds-eko Unibertsitateko Zientzia, Teknologia eta Medikuntza Historiaren Museoa)Florence Bellek metodo bat garatu zuen DNAren harizpiak “luzatzeko” eta material puruzko xafla lehorren forman jartzeko. Metodo horren bidez lortu zituen ordura arteko X izpien difrakzio-patroi argienak. Eta hori ez zen erraza; izan ere, irudi bakoitzak hamar ordu inguruko esposizio denborak behar zituen, eta gela ilun batean egiten zen, tentsio elektriko handietatik eta oso bero zeuden X izpien hodietatik oso gertu. Bellek legamien, pankrearen, tabako mosaikoaren birusaren eta behien timoaren azido nukleikoak aztertu zituen, eta konturatu zen “bizitzaren hastapenak modu argian lotuta daudela proteinen eta azido nukleikoen arteko interakzioarekin”.
1938an, Astburyk eta Bellek artikulu bat argitaratu zuten Nature aldizkarian. Horren bidez azaldu zuten DNAren egitura txanpon-kate moduko bat zela eta maiztasun jakin bat zuela zuntzaren luzetarako ardatzean zehar. Bellek proposatutako egiturak okerreko xehetasun batzuk bazituen ere, bere barne ordenaren teoriak gako datu bat eman zuen —ondoko baseen arteko distantzia— etorkizuneko ikerketei begira, zeinen bidez 1953an, azkenean, DNAren helize bikoitzaren egitura deskubritu zen.
Ikerketa-ibilbidearen amaieraAstburyk benetan baloratzen zituen Bellen adimena eta gaitasuna. Izan ere, Fisika Institutuak (IOP, ingeleseko siglengatik) 1939an konferentzia bat egin zuenean Leedsen, hari eskatu zion —orduan 25 urteko gaztea zen— IOPko delegazio baten aurrean laborategian egiten ari ziren lana aurkezteko. Tokiko egunkariek gertakaria jaso zuten, baina berrien izenburuen ondorioz, nabarmendu zen alderdia ez zen zientzia izan, baizik eta konferentzia emakume batek eman izana.
 3. irudia: Yorkshire Evenig News egunkariko berria (1939ko martxoaren 23koa). (Iturria: Mujeres con Ciencia)
3. irudia: Yorkshire Evenig News egunkariko berria (1939ko martxoaren 23koa). (Iturria: Mujeres con Ciencia)Bere lana garrantzia hartzen ari zen unean, baina, Bellek bat-batean eten egin behar izan zuen. Bigarren Mundu Gerra hasi zen eta Women’s Auxiliary Air Force delakoari zerbitzu emateko deia jaso zuen. Astburyk Gerra Bulegoari erregutu zion zientzialariaren talentua bere laborategian mantentzeko aukera emateko, baina ez zituzten bere eskaerak entzun. Leedseko Unibertsitateak Bellen lanpostua hutsik mantendu bazuen ere, ez zen sekula itzuli.
Zientzialaria Estatu Batuetako militar batekin ezkondu eta Estatu Batuetara joan zen. Lehendabizi British Air Comission erakundearentzat egin zuen lan, eta, aurrerago, kimikari industrialaren lanpostu bat lortu zuen petrolio enpresa batean. Baina, azkenik, ibilbide profesionala atzean utzi eta bikoteak adoptatu zituen lau seme-alabak zaintzera dedikatu zen.
Florence Bell, DNAren dama ilun ezezagunena, 2000ko azaroaren 23an hil zen, 87 urte zituela. Biologia zelularraren dogma nagusiari atea irekiko zion giltza deskubritu zuen zientzialariaren heriotza ziurtagirian, lanbidearen atalean, “etxekoandrea” izan zela jaso zuten.
Iturriak:- Kersten Hall, Florence Bell: The Other ‘Dark Lady of DNA’?, BSHS
- Kersten Hall, Florence Bell: the ‘housewife’ who played a key part in our understanding of DNA, The Conversation, 2022ko urtarrilaren 28an
- Kersten Hall, Florence Bell: An unsung heroine of DNA, The Naked Scientist, 2022ko ekainaren 17an
- Natalia I. Kucirkova, Florence Bell died unrecognised for her contributions to DNA science – decades on female researchers are still being sidelined, The Conversation, 2023ko azaroaren 22a
- Florence Bell, Wikipedia
Edurne Gaston Estanga elikagaien zientzia eta teknologiako doktorea da. Gaur egun, zientzia eta teknologiaren ezagutza zabaltzea sustatzen duten erakundeen proiektuak kudeatzen ditu.
Jatorrizko artikulua Mujeres con Ciencia blogean argitaratu zen 2025eko maiatzaren 15ean: Florence Bell, otra “dama oscura” del ADN.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Florence Bell, DNAaren beste “dama ilun” bat appeared first on Zientzia Kaiera.
Gizakientzat eta planetarentzat, dieta osasungarriagoa
Planetarekiko arduratsua den dieta baten eta hilkortasun gutxiago izatearen arteko lotura aurkitu du gaiaren bueltan egin den berrikuspen zabal batek: bereziki haragi gorri gutxiago jatea proposatu dute, barazkien kontsumoa handituz.
Batez ere Mendebaldeko gizarteetan gero eta jende gehiagok ardura berezia dauka dietarekiko, bizimodu azkarra eta elikagai ultraprozesatuak gero eta zabalduago dauden honetan inoiz baino errazagoa baita nork bere burua gaizki elikatzea. Arazoa dirudiena baino larriagoa da, behin baino gehiagotan aipatu izan denez, eta gosea oraindik arazo itzela dela jakinda ere, egunotan kalkulatzen da bost heriotzatik bat elikadura txarrari lotuta dagoela.
Baina horrez gain, ingurumenarekiko kontzientziazioa zabaltzen den heinean, lagun askok planetarentzat horren kaltegarri ez diren elikagaien alde egiten du ere. Bada, bi ardura hauek —giza osasuna eta planetaren egoera— aintzat hartzen duen dieta mota bat mahai gainean dago 2019tik, urte horretan berariaz horretarako bildutako zientzia batzorde batek landutakoa. EAT/Lancet izeneko batzordean bildu zen nazioarteko aditu panel batek PHD dieta —(Planetary Health Diet) ingelesezko akronimoaren arabera—, hots, Dieta Planetario Osasungarria proposatu zuen, eta oraindik gaiaren bueltan ikerketak egiten dira.
 1. irudia: planetarentzat zein osasunarentzat aproposa den dieta kaleratu zuten duela hainbat urte. Orain, datuek dieta horren onurak berretsi dituzte. (Argazkia: Brooke Lark – Unsplash lizentziapean. Iturria: Unsplash)
1. irudia: planetarentzat zein osasunarentzat aproposa den dieta kaleratu zuten duela hainbat urte. Orain, datuek dieta horren onurak berretsi dituzte. (Argazkia: Brooke Lark – Unsplash lizentziapean. Iturria: Unsplash)Izena nahiko argigarria da: dieta osasuntsua eta ingurumenarekiko arduratsua den dietatzat jotzen da. The Lancet aldizkariak antolatutako paneleko adituek beren proposamenean diote “mundu mailan elikadura sistemaren erabateko aldaketa urgentziaz eraldatu” beharra dagoela. 2050. urterako munduan 10.000 milioi lagun inguru egon daitezkeela aintzat izanda, eraldaketa hori are beharrezkoago ikusten dute. Baina hasierako deialdi horretan ere nabarmendu nahi izan zuten mundu mailako dieta aldaketa batek gizakien osasunaren onerako izango zela, eta kalkulatu zuten elikadura ohiturak aldatzeak urtero 11 milioi bat heriotza goiztiar saihesteko bidea izan ahal zela.
Azken hamarkadetan nagusitu izan den dieta ereduari aurre egin nahi zaio proposamen honen bitartez. Batez ere haragiaren eta janari ultraprozesatuen kontsumoan oinarrituta dagoen dieta baten aurrean, dieta berri hau babesteko argudio nagusiena da landare jatorriko proteina gehiago duen dieta osasuntsuagoa dela, eta gutxiago kutsatzen duela ingurumena. Tartean, elikagaiak sortzeko erak lotuta daudelako negutegi efektuko gasen isuriekin, uraren erabilerarekin edo lurzoruen narriadurarekin.
Panel honetako adituek ordenagailu bidezko simulazioetan oinarrituta ikusi zuten orain arte bezala jaten jarraituz gero 2050. urterako berotegi efektuko isuriak bikoizteko arriskua dagoela. Aldiz, landare oinarriko dietak jarraituz gero isuri horiek % 80 gutxitu ahalko zirela zenbatetsi zuten.
Egun bakoitzeko 2.500 kaloria dituen dieta da, baina horietatik soilik 30 kaloriaren kasuan proposatzen dute hegaztienak ez diren haragietatik izatea. Horrek esan nahi du funtsean haragi gorriak ia-ia alboratzen dituela PHD dietak. Kontrara, proteina gehienak lekaleetan, fruitu lehorretan, hegaztietan eta arrainetan leudeke.
Duela gutxi Science Advances aldizkarian argitaratutako zientzia artikulu batean dieta arduratsu honek osasunean izan dezakeen eragina zenbakietara eraman nahi izan dute. Esku artean izan dituzten datuak ez dira edonolakoak izan. Izan ere, 150.000 lagun baino gehiago bildu dituzten bi kohorte erabili dituzte: AEBetako NHANES (42.947 pertsona) eta Erresuma Batuko UK Biobank (125.372 pertsona) izenekoak.
 2. irudia: animalia jatorriko haragiaren kontsumoak karga erraldoia suposatzen du ingurumenarentzat. (Argazkia: Austin Santaniello – Unsplash lizentziapean. Iturria: Unsplash)
2. irudia: animalia jatorriko haragiaren kontsumoak karga erraldoia suposatzen du ingurumenarentzat. (Argazkia: Austin Santaniello – Unsplash lizentziapean. Iturria: Unsplash)Baina aldaketa hau ikerketaren oinetako bat baino ez da. Bigarrena, orain arte landu izan den zientzia literaturaren gaineko metaanalisi zabala izan da. Horretarako, gaiaren bueltan egin izan diren 37 ikerketa aintzat hartu dituzte —horietan, guztira, hiru milioi lagun inguruk parte hartu dute–.
Dieta mota hau gehien jarraitzen dutenek ezein gauzagatik hiltzeko arrisku gutxiago daukatela ondorioztatu dute. Erresuma Batuko kohortearen kasuan —parte hartzaile gehien dituen taldea dela gogoratu beharra dago—, minbiziagatik eta arnas aparatuari lotutako gaitzengatik hiltzeko arrisku gutxiagorekin lotu dute elikadura mota hau. Oro har, koloneko eta ondesteko minbizia, biriketako minbizia, bihotzeko gaixotasunak, istripu kardiobaskularrak eta diabetesa izateko arrisku gutxiago aurkitu dituzte ikertzaileek.
Bestalde, dieta mota hau jarraitzen duten pertsonen ezaugarriak aztertu dituzte: bereziki emakumezko helduak dira. Bitxia bada ere, gehiago jaten duten arren, batez bestekoa baino gorputz masaren indize baxuagoa izan ohi dute. Horrez gain, ikasketa maila eta diru sarrerak altuagoak dauzkate.
AEBetako kohortearen kasuan, 9,3 urteko jarraipenaren ondoren, edozein arrazoigatiko hilkortasuna % 23 gutxitu dute; bihotz gaixotasunengatik, % 19; eta beste horrenbeste bestelako zioen kasuan. Erresuma Batuaren kasuan, 12,3 urteko jarraipena izan da, eta datuetan arakatuz ikusi dute hilkortasuna % 16 gutxitu dela. Minbiziaren kasuan ere % 16 gutxitu da, eta arnas aparatuari lotutakoetan, berriz, % 61 gutxitu da.
3,2 milioi parte hartzaile aintzat hartu dituzten 37 ikerketen kasuan, horien berrikuspenak honako emaitzak eman ditu. Dieta mota hau gehiago jarraitu dutenen artean minbiziagatiko heriotza % 11 gutxitu da, eta portzentajea 17 % gutxiago izan da gaixotasun kardiobaskularretan. Heriotza zio guztiak aintzat hartuta, portzentajea % 21 izan da. Korrelazioa aztertzean, erlazio lineala aurkitu dute: dietarekiko atxikimendua gero eta handiagoa izan, orduan eta heriotza arrisku gutxiago izan dute, eta gaitz kronikoak izateko joera gutxiago, adina, sexua, gorputz masaren indizea, sarrera ekonomikoak edo bizitza ohiturak ezein direla ere.
Emaitzak horren argiak izanda ere, ohi bezala, tentuz hartu behar dira korrelazioan –eta ez kausalitatean— oinarritzen diren ikerketa guztiak. Bestetik, dietari buruzko informazioa parte hartzaileek berek betetako galdetegietatik abiatzen dela aintzat hartu behar da. Egileek berek onartzen dute parte hartzaileen jarduera fisikoa edo estres mailak ezin izan direla ondo jaso. Azkenik, AEBetako eta Erresuma Batuko kohorteak direla kontuan hartu beharra dago; hortaz, agerikoa da mendebaldeko zenbait gizarteren isla baino ez direla emaitzak. Baina zalantzarik ez dago zenbakietara ez dela zertan joan dieta arduratsu bat jarraitu ahal izateko.
Erreferentzia bibliografikoa:Wang, Yuanyuan; Pan, Da; Zhang, Chen; Xu, Dengfeng; Lu, Yifei; Yin, Shiyu; Wang, Pei; Xia, Jiayue; Yu, Junhui; Dong, Lirong; Sun, Guiju (2025). Planetary Health Diet and risk of mortality and chronic diseases: Results from US NHANES, UK Biobank, and a meta-analysis. Science Advances, 11, 36. DOI: 10.1126/sciadv.adq5147
Egileaz:Juanma Gallego (@juanmagallego) zientzia kazetaria da.
The post Gizakientzat eta planetarentzat, dieta osasungarriagoa appeared first on Zientzia Kaiera.
Artsenikoan oinarritutako bizia: eztabaidaren amaiera?
Duela hamabost urte biziaren oinarriak ezbaian jarri ziren, une batez izan bazen ere. Bazirudien ezagutzen genituen bizi-motetatik harago beste batzuk ere egon zitezkeela. Bazirudien, oinarrizko sei bioelementuetatik harago beste elementu kimikoetan oinarritutako bizia egon zitekeela. Orain, 2025. urtean, Science aldizkariak atzera bota du ikerketa-lan hori eta esan dute lan hori ez zela inoiz argitaratu behar. Hauxe da Felisa Wolfe-Simon eta haren lankideei gertatutakoa. Zientziaren polemika horietako bat.
2010. urteko abendu hasieran Science aldizkari entzutetsuak A Bacterium That Can Grow by Using Arsenic Instead of Phosphorus artikulua argitaratu zuen. Izenburuak berak argi uzten zuen bezala, lan horretan Felisa Wolfe-Simon eta haren lankideek aurkikuntza iraultzaile baten berri eman zuten; hain zuzen ere, artsenikoan oinarritutako bizia aurkitu zutela. Gainera, bizi hori ez zegoen Marten edo Lurretik kanpo, ez. Zehazki, ikerkuntza Kaliforniako Mono lakuko Halomonadaceae delako bakterioaren GFAJ-1 anduiarekin lotuta zegoen. Ikertzaileen esperimentuen arabera, bakterio hori gai zen bere egituran artsenikoa txertatzeko fosforoaren ordez. Horri esker, bakterioa gai zen artsenikoan oinarrituta hazten jarraitzeko, eta normalean fosforoz osatuta dauden makromolekuletan, ─azido nukleikoetan eta proteinetan, nagusiki─ artsenikoa erabiltzeko.
 Irudia: artsenikoa bizidunontzat pozoitsua da kantitate txikietan ere. (Argazkia: Gutife – jabari publikoa. Iturria: pixabay.com).
Irudia: artsenikoa bizidunontzat pozoitsua da kantitate txikietan ere. (Argazkia: Gutife – jabari publikoa. Iturria: pixabay.com).NASAk lau haizeetara zabaldu zuen berria; izan ere, aurkikuntza horrek frogatzen zuen bizia ordura arte ezagutzen ez ziren moduetan ere garatu zitekeela. Era berean, sei bioelementu nagusi daude bizia ahalbidetzen dutenak: karbonoa, oxigenoa, hidrogenoa, nitrogenoa, sufrea eta fosforoa; eta, horietako bat, fosforoa, artsenikoaz ordezkatzea posible zela zirudien. Artsenikoa, gainera, bizidunontzat pozoi arriskutsua izanik, ordura arte ezagutzen ez ziren ideiak mahaigaineratzen zituen, bizi-mota desberdinei atea zabalduz. Horrek aldaketa handia ekarriko zuen Lurretik kanpo bizia bilatzeko ahaleginetan; izan ere, ezinbestekotzat jotzen zen baldintzetako bat, gutxienez, ez litzateke ezinbestekoa. Benetako iraultza izango zen astrobiologiaren esparruan.
Ikerketak hasiera-hasieratik piztu zuen eztabaida bizia zientzia-komunitatean. Aurten, 15 urte geroago, Science aldizkariak atzera bota du artikulua. Wolfe-Simon eta haren lankideek ziotenez, bakterioa gai zen artseniko-atomoak bere egituran integratzeko, eta ez bakarrik artsenatoaren presentzian bizirauteko. Alabaina, zientzia-komunitateak galdera ugari izan zituen ikerketaren muinari buruz; izan ere, astrobiologiaren oinarriak alda zitzakeen. Hasieratik egon ziren gorabeherak artikuluaren argitalpen-prozesuan, eta jatorrizko artikuluarekin batera zenbait adituren iritziak argitaratu ziren ikerketa ezbaian jarriz. Bi urte geroago, bi ikerketa-talde independente ahalegindu ziren Wolfe-Simonen taldearen emaitzak errepikatzen, baina ez zuten lortu. Horrek guztiak ikerketa-lanaren argitalpenarekin batera hainbat ohar gehitzea ekarri zuen, baita jatorrizko ikerketa-taldearena ere, haien emaitzak egokiak zirela berretsiz. Akats posibleen artean, adituetako batek aipatzen du biomolekulen purifikazioan akatsak egon zitezkeela, eta hori izan zitekeela artsenikoa detektatu izanaren arrazoia.
Ikerketa-lana atzera botatzearekin batera, aldizkaritik aipatu dute Wolfe-Simonen taldearen ondorioak datu okerretan oinarrituta daudela. Horrek ere eztabaida ekarri du; izan ere, aldizkariak onartu du ikerketa-taldeak ez zuela jokabide makurrik edo iruzurrik egin. Besterik gabe, nahi gabeko akatsak egin zituzten ikerketan eta ondorio okerretara iritsi ziren. Zein da, baina, eztabaida? Hain zuzen, aldizkariaren arauen arabera lan bat atzera botatzeko, jokabide gaiztoren bat egon dela frogatu behar da; esate baterako, zientzialariek datuak nahita manipulatzea.
Aldizkariko arduradunek argitaratutako editorialean azaldu dutenez, edozein kasutan, lan hori ez zen inoiz argitaratu behar. Egileek berriro ere adierazi dute ez zutela nahita oker jokatu eta oraindik ere haien emaitzen zuzentasuna babesten dute. Egileek aipatzen dute 2010. urtean argitaratutako lanak akatsak izan badituela, baina ez direla esanguratsuak eta ondorioak zuzenak direla. Hortaz, zientziaren printzipioen arabera, zientzia-komunitateak eztabaidatu beharko lituzke emaitzak, sakonki, eta ez aldizkariko argitaratzaileek. Egileen iritziz, zientzia-komunitateak eztabaidatu behar du ondorioak zuzenak diren ala ez, baina eztabaida hori gertatu ahal izateko, ikerketa-lanak argitaratuta egon behar du. Diotenez, haien lanean ez dago jokabide makurrik eta lana eztabaidagarria da, bai, zientziako beste edozein lan eztabaidagarria izan daitekeen bezala.
Edozein kasutan, ikerketa-lan hori atzera bota izanak ez du esan nahi muturreko egoeretan bizia ezin denik egon edo, jakina, sei bioelementu horiek gabe bizia ezin denik egon. Oraingoz, azken horren aldeko frogarik ez dagoela esan nahi du. Aipatzekoa da, bestalde, ondorio guztiak ez direla berdinak. Hain zuzen ere, Wolfe-Simon eta haren lankideek argitaratutako lanak zientziaren ideia nagusi baten kontrakoak ziren eta, Sagan-en estandarrak dioen bezala, aparteko baieztapenek aparteko frogak behar dituzte.
Azken ohar modura, ezin da aipatu gabe utzi Felisa Wolfe-Simon ikertzaileari ─artikulua sinatzen zuen lehen pertsonari─ gertatutakoa. NASAk jatorrizko artikulua argitaratu zenean emandako prentsaurrekoan, Wolfe-Simonek hitz egin zuen ikertzaileen izenean. Ospetsu egin zen, eta egun gutxi batzuetan sare sozialen kritika bortitzak pairatu zituen. The New York Times egunkariari kontatu dion bezala, kritika horien ondorioz NASAtik alde egin behar izan zuen eta ez zuen inoiz beste ikerketa-bekarik lortu. Zientzia albo batera utzi behar izan zuen eta musikara bideratu zuen bere ibilbidea. Haren kide gehienek, aldiz, zientzian jarraitu ahal izan zuten eta gaur egun ere zientzian dihardute.
Erreferentzia bibliografikoa:Wolfe-Simon, Felisa; Switzer Blum, Jodi; Kulp, Thomas R.; Gordon, Gwyneth W.; Hoeft, Shelley E.; Pett-Ridge, Jennifer; Stolz, Jhon F.; Webb, Samuel M.; Weber, Peter K.; Davies, Paul C.W.; Anbar, Ariel D.; Oremland, Ronald S. (2010). RETRACTED: A bacterium that can grow by using arsenic instead of phosphorus. Science, 332, 6034, 1163-1166. DOI: 10.1126/science.119725
Egileaz:Josu Lopez-Gazpio (@Josu_lg), Kimikan doktorea, zientzia dibulgatzailea eta GOI ikastegiko irakasle eta ikertzailea da. Tolosaldeko Atarian Zientziaren Talaia atalean idazten du eta UEUko Kimika sailburua da.
The post Artsenikoan oinarritutako bizia: eztabaidaren amaiera? appeared first on Zientzia Kaiera.
Gizatasunaz gogoetarik egingo al dugu adimen artifizialak gidatutako Makinaren Aroan?
Gure garaia Makinaren Aroa da, makinak gizakiari indar, kalkulu eta erabaki askotan erdigunea kendu dion sasoia; gizakiak makinari, bizitza eta harremanak zuzentzeko ardatz izan dadin, erdialdea eman dion aldia.
Gaur egun, makina aurreratuenak ordenagailuak dira, eta haien programarik eraginkorrenak, adimen artifiziala eragile eta prozesatzaile dutenak. Teknologia hori jende xehearen eskutan ugari da, eta gailuen dirdirak, erabilera-etekinak eta usain gabeziak hainbat ekintza eta ondorio estaltzen dituzte haien atzean. Hala, aurrerakuntza teknologikoa ikaragarrizkoa izan da azken mendeetan, baina aurrerapen humanoa ez. Alderatu ezin diren bide bi dira.
 Irudia: gure garaia Makinaren Aroa da, makinak gizakiari indar, kalkulu eta erabaki askotan erdigunea kendu dion sasoia; gizakiak makinari, bizitza eta harremanak zuzentzeko ardatz izan dadin, erdialdea eman dion aldia(Argazkia: cottonbro studio – jabari publikoa. Iturria: Pexels.com)
Irudia: gure garaia Makinaren Aroa da, makinak gizakiari indar, kalkulu eta erabaki askotan erdigunea kendu dion sasoia; gizakiak makinari, bizitza eta harremanak zuzentzeko ardatz izan dadin, erdialdea eman dion aldia(Argazkia: cottonbro studio – jabari publikoa. Iturria: Pexels.com)Hori dela eta, Makinaren Aroa ahalbidetu duen pentsamendu makinistaren izaera eta eginkizuna ulertu behar ditugu, eta, erabileraren gaineko gogoeta gutxietsi gabe, adimen artifizialaren gainean gogoeta egitea ezinbestekoa da. Bere horretan. Zergatik? Teknologia ez delako neutroa. Lorpenak eragitera zuzenduta dago; hura bere izaera, produktiboa izatea, produkzioa behartzea. Teknologia bitartekaria da, eta bere helburuak ditu, erabilerara heldu aurretik. Zer-nolako bidea ireki dugu, hortaz, adimen artifizialari, giza erabakien gainetik, lehentasuna emanik? Gizakia, zer eta arrazoiketa mailan, makinaren atzetik jarririk, zer esan behar dugu gizatasunaz? Hona hemen ortzi-muga hurbilean dauden hiru joera nagusiak.
Teknologia gizakiaren baitaraPentsamendu teknologikoak, behin giza gogoaren gidaritza harturik, teknologia natura, gizartea eta giza norbanakoaren edozein arlotara eraman du, azaleko mailan zein barneko mailan aplika dadin. Lehenik eta behin, gizakiak logika ezagutu eta eremu praktikora mugatu zuen; ondoren, bere barne munduan leku egin zion; gero, objektuetara eraman zuen; orain, gizakiaren barnera logika bere barruan duen makina eramatekotan dago.
Datorren bide nagusietako bat, hortaz, adimen artifiziala barne zein kanpo eremuetan lan egiten jartzea da. Gizakiari helduz, espezie biomekanikoa gero eta desiragarriagoa egiten ari da teknozientzian, transhumanismoari esker. Ondorioz, giza barnea eta kanpoa zer diren lausotu egingo da.
Gizakia teknologiaren baitaraTeknologia bera tresna izatetik eremu izaterako bidea gero eta handiagoa da. Gaur egun, espazio gozagarri legez, eremu birtuala gailentzen hasi da. Jende askok birtualitatea errealitatearen aurretik lehenesten du, edota bien arteko aldea lausotzen. Horretan, eremu digitalak garrantzi handia dauka. Teknologiaren barne mundua erakargarri, ikusgarri, gozagarri, egiten du inoiz ez bezala, eta giza gogoa gero eta atseginago dago bere baitan.
Teknologiaren helburua izango da, hortaz, gizakia ahalik eta gehien –gogoz eta gorputzez– bere baitan izatea. 3 dimentsiotan birtualitatea ahalik eta sinesgarri eta erosoen egingo duten pantaila, betaurreko zein gelen garapenak hori berori erakusten du. Eta, sinesgarritasun horretarako, adimen artifizial sortzailea banakoari egokitzea izango da hurrengo urratsa, mundu (tekno)propioa ahalik eta onena izan dakion.
Higiene teknologikoaPentsamendu teknologikoa eta tresna teknologikoa nagusi diren, eta gero eta gailenago izango diren, munduan, beraz, garbitasuna lortzeko gogoa ere agertuko da. Gutxiengo joera izango da, borondate irmoz landua, eta joera nagusietan lerratutakoek zigortua. Izan ere, makina (larregirik) gabeko mundu, gizarte edo gizakiak pentsamendu makinista bako (g)izateria eskatzen du, baina teknologia oso ideologikoa da: hemen eta orain mundurik onena eratzeko agintza du, eta hori zalantzan jartzea onartezina da bere eremuan.
Adimen artifizialak, hortaz, erronka handia jarri dio makina susmopean jartzeko gai denari. Kostu sozio-ekologiko handikoa da –energia, azpiegitura, sarbidea, bereizketa, esklabotza, deshumanizazioa–, baina kostu espirituala oraindik izugarriagoa izango da. Arreta lehen horietan jartzeko joera ere izango da; azken horretan, aldiz, ziurrenik ez.
Antzina jakintza zen helburu, eta ezagutza lagungarri. Modernitatean, ezagutza zen helburu, eta haren praktikotasunerako datuak lagungarri. Egun, datuak dira helburu, eta haien etekinerako giza objektua lagungarri. Norabide eta aldaketa horien jabe izatea da, beraz, adimen artifizialaren sasoiko galdegai nagusirako gako: Gizakia zer da eta zer izango da Makinaren Aroan?
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: Ale berezia Adimen artifiziala
- Artikuluaren izena: Gizatasunaz eta pentsamendu teknologikoaren ibilbideaz.
- Laburpena: Testu honetan, ordenagailua eta adimen artifiziala agertzeko ezinbesteko izan den Mendebaldeko kontzientziaren historia egingo dugu, eta, horretarako halabeharrezko izango zaigu, labur bada ere, logika giza gogoetetan nola sartu zen ezagutzea, une jakin batean giza eremurik atera eta makinen eremuan txerta zedin. hau da, logika giza pentsamenduan nola sartu, nola errotu eta nola atera den aztertuko dugu, eta azalduko dugu ibilbide horrek gizatasunari zer ondorio eragin dizkion eta gaurgeroko joera nagusiak zein izango diren. Gure sakoneko abiapuntua honako hau da: adimen artifizialaren makina transhumanismo modernoaren ekarpenik nabariena da. Gizakiaren baieztapena edo ezeztapena jokoan daude nihilismoak itzalitako garai honetan. Testu honen helburua, beraz, adimen artifizialaren agerpenak berak, erabilera jakinak baino lehen, aspaldiko galderaren aurrean dakarrena aztertzea da: zer da gizaki?
- Egilea: Jon Mentxakatorre Odriozola
- Argitaletxea: EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 257-278
- DOI: 10.1387/ekaia.26245
Jon Mentxakatorre Odriozola Mondragon Unibertsitateko Humanitate eta Hezkuntza Zientzien Fakultateko ikertzailea da
Ekaia aldizkariarekin lankidetzan egindako atala.

The post Gizatasunaz gogoetarik egingo al dugu adimen artifizialak gidatutako Makinaren Aroan? appeared first on Zientzia Kaiera.
Eva Nogales: «Biologia molekularra txundigarria da»
Eva Nogales (Colmenar Viejo, 1965) ikertzailea da Howard Hughes Institutu Medikoan, Biokimika eta Biologia Molekularrean katedraduna (Bekeleyko Kaliforniako Unibertsitatea) eta zientzialari seniorra Lawrence Berkeley National Laboratory instituzioan. Nazioarteko liderra da bere esparruan, kriomikroskopia elektronikoa erabiltzen baitu zelulen osagaiak maila atomikoan aztertzeko. Bere lanari esker, minbizia eta beste gaixotasun batzuk tratatzeko garrantzitsuak diren funtzio zelularraren alderdi batzuk deskubritu ditu. Beste aintzatespen askoren artean, Bizitza eta Medikuntzaren Zientzietako Shaw saria jaso zuen 2023an.
 Irudia: Eva Nogales ikertzailea. (Argazkia: Cmichel67 – CC BY-SA 4.0 lizentziapean. Iturria: Wikimedia Commons)Zein da zure ikerketa arloa?
Irudia: Eva Nogales ikertzailea. (Argazkia: Cmichel67 – CC BY-SA 4.0 lizentziapean. Iturria: Wikimedia Commons)Zein da zure ikerketa arloa?
Biofisika molekularraren esparruan lan egiten dut. Zehazki, biologo estrukturala naiz, eta kriomikroskopia elektronikoa erabiltzen dut konplexu makromolekularrak ikertzeko. Alde batetik, mikrotubuluak eta zelula banaketan eta neuronetan materialak garraiatzeko prozesuan haiekin interakzionatzen duten beste osagai zelular batzuk aztertzen ditugu. Eta, beste alde batetik, gene adierazpena transkripzioaren eta gene-isiltzearen mailan erregulatzen duten proteinen konplexuak ikertzen ditugu.
Zergatik aritzen zara arlo horretan?Biologia molekularra txundigarria da. Hasieran fisika ikasi nuenez, niretzat biologia molekularra da modurik egokiena zelularen bizitzarako eta organismorako oinarrizkoak diren prozesu biologikoak maila atomikoan ulertzeko, horien funtzionamenduaren atzean dauden kimika eta fisika ulertzearen bidez.
Izan al duzu erreferentziazko figurarik zure ibilbidean?Beti aipatzen ditut institutu garaiko matematika, fisika eta biologiako irakasleak; emakume inspiratzaileak ziren, bai eta profesional bikainak ere.
Nire karreran zehar, pertsona askok izan dute eragina nigan; adibidez, Mina Bissellek, Lawrence Berkeley National Laboratoryko biologo zelularrak —laborategi horretan egin nituen doktorego ondoko ikasketak—. Bisellek moldeak hautsi zituen bularreko minbiziaren ikerketan, eta sostengu handia izan da emakumezko zientzialari gazteentzat. Eta egungo erreferente bat Berkeleyko nire kide eta lagun Jennifer Doudna da, egunez egun erakusten baitu oso urrun irits gaitezkeela zientzian eta teknologian. Kimikako Nobel saria irabazi zuen CRISPR/Cas9 garatzeagatik edizio genetikorako tresna gisa.
Zer aurkitu edo konpondu nahiko zenuke zure arloan?Milaka gauza! Interes handia dut mikrotubuluek funtzio zelular asko integratzeko duten gaitasunean, gainazalean elkarrekin komunikatzen diren faktoreekiko interakzioen bidez. Gainera, horrek lagundu egiten du zitoeskeletoak gure kromosomak jariatzeko duen rolean, zelula bat banatzen den bakoitzean, edo neuronen arteko sinapsirako beharrezkoa den garraio intrazelularra ahalbidetzen duen axoiaren antolakuntzan. Halaber, interesatzen zait gure genomaren irakurketak erregulatzeko duen modua, histonen itzulpen ondoko aldaketaren mailan, transkripzioari mesede egiteko, edo ez. Erregulazio horretarako, proteinen konplexu handien jarduera behar da, eta horiek domeinu funtzional trukagarriak dauzkate. Bada, ulertu nahi nuke nola eboluzionatu zuten, eta nola funtzionatzen duen horrek guztiak modu integratuan.
Zer aholku emango zenioke ikerketaren munduan hasi nahi duen norbaiti?Literatura zientifiko asko irakur dezatela; martxan jar daitezela laborategietan sartu eta esperientzia lortzeko, albait arinen; inspiratzen dituzten ikertzaileez ingura daitezela, haiengandik ikasteko; eta zientzia egiteko modu bat baino gehiago ikas ditzatela, ahal bada, bidaiatuz eta herrialde ezberdinetan lan eginez.
Jatorrizko elkarrizketa Mujeres con Ciencia blogean argitaratu zen 2025eko martxoaren 15ean: Eva Nogales: «La biología molecular es fascinante».
Itzulpena: UPV/EHUko Euskara Zerbitzua.
Ikertzen dut atalak emakume ikertzaileen jardunari erreparatzen die. Elkarrizketa labur baten bidez, zientzialariek azaltzen dute ikergai zehatz bat hautatzeko arrazoia zein izan den eta baita ere lanaren helburua.
The post Eva Nogales: «Biologia molekularra txundigarria da» appeared first on Zientzia Kaiera.
Gizateria osoa
Gizaki modernoa, Homo sapiens, Afrikan garatu zen, orain dela 300.000 urte baino gutxiago. Lehen txangoak orain dela 215.000 urte inguru egin ziren, baina benetako hedapena 70.000 eta 50.000 urte artean hasi zen, lehenengo Hegoaldeko Asiatik Australiaraino, gero Europara eta Ameriketara, eta azkenik Ozeaniako eta Artikoa bezalako lurraldeetara. Gizakiak klima, dieta eta bizimodu askotara moldatzeko gaitasuna izan du, eta kultura izan da horretarako giltza.
Bidaia horiek berreraikitzeko genetika dugu lagun. DNA mitokondriala amaren bidez igarotzen da eta mitokondriako DNA berbera jaso duten pertsona guztiek “haplotalde” bat osatzen dute. Bestalde, Y kromosomaren bidez, berriz, aitaren lerroa ezagutu dezakegu. Azterketa horiei esker, ikertzaileek gure arbaso genetiko komunak identifikatu dituzte: “Eva mitokondriala”, duela 155.000 urte Ekialdeko Afrikan bizi izan zen emakumea, eta “Y-kromosomaren Adam”, duela 275.000 urte Ipar-Mendebaldeko Afrikan bizi izan zen gizona. Horrelako ikerketek erakutsi digute gizakiak etengabe mugitu eta nahastu direla, kolore askotako gizateria bakarra osatuz.
“Gure arbasoak” Ikusgela hezkuntza proiektuaren bideo-sorta bat da. Euskal Wikilarien Kultur Elkartearen ikus-entzunezko egitasmoa da eta EHUko Kultura Zientifikoko Katedraren kolaborazioa izan du.
The post Gizateria osoa appeared first on Zientzia Kaiera.
Nanopartikula lipidikoak: preeklanpsiaren tratamendurako itxaropena
Preeklanpsia haurdunaldiko arazo larria da. Mundu mailan haurdunen % 5 ingururi eragiten die, eta % 2ri gure inguruko herrialdeetan. Honako hauek dira preeklanpsiaren ezaugarriak: tentsio arteriala igotzen da, maiz proteinuriarekin lotuta (gernuaren bidez proteinak galtzea, giltzurrunetako kaltearen ondorioz), likidoak atxikitzen dira eta fetuaren hazkundea murrizten da. Ondorio larriagoak ere izan ditzake, hala nola eklanpsia (konbultsioak, koma) eta HELLP sindromea. Preeklanpsia amaren heriotzaren kausa nagusietako bat da. Urtero 75.000 emakume inguru hiltzen dira arrazoi horrengatik, eta milioi erdi haurdunaldi eteten dira. Ez dago tratamendu espezifikorik. Amaren hipertentsioa kontrolatu eta erditzea eragin baino ezin da egin. Horrexegatik da hain garrantzitsua preeklanpsia prebenitu edo sendatzeko bide terapeutiko berriak ikertzea.
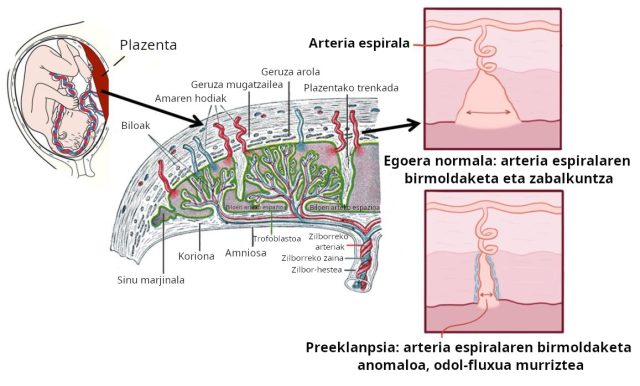 1. irudia: amaren odola biloen arteko espazioan zehar ibiltzen da, eta mantenugaiak ematen dizkie biloen fetu hodiei. Perfusioa egokia izan dadin, arteria espiralak birmoldatu eta zabaldu egin behar dira garatzen diren bitartean. Preeklanpsian, birmoldaketa prozesu hori akastuna da, eta, ondorioz, odol fluxua murriztu egiten da, eta ehunaren iskemia sortzen da. (Argazkiak: Henry Vandyke Carter – jabari publikoa eta osmosis.org-eko bideoa – CC BY-SA 4.0. lizentziapean. Iturriak: Wikimedia Commons)
1. irudia: amaren odola biloen arteko espazioan zehar ibiltzen da, eta mantenugaiak ematen dizkie biloen fetu hodiei. Perfusioa egokia izan dadin, arteria espiralak birmoldatu eta zabaldu egin behar dira garatzen diren bitartean. Preeklanpsian, birmoldaketa prozesu hori akastuna da, eta, ondorioz, odol fluxua murriztu egiten da, eta ehunaren iskemia sortzen da. (Argazkiak: Henry Vandyke Carter – jabari publikoa eta osmosis.org-eko bideoa – CC BY-SA 4.0. lizentziapean. Iturriak: Wikimedia Commons)Gaur egun, oraindik ez dakigu zehatz-mehatz zergatik gertatzen den preeklanpsia, baina badakigu plazentaren garapen akastunarekin eta plazentako ehunen perfusio baskular desegokiarekin hasten dela (1. irudia). Plazentak erreakzionatu egiten du oxigeno-ezaren aurrean, eta amaren endotelio baskularraren disfuntzioa eragiten duten molekulak sortzen ditu, eta, batzuetan, preeklampsiaren sintomak.
Plazentak amaren zirkulaziora gehiegi jariatzen dituen molekulen artean, Flt1 hartzailearen forma disolbagarria nabarmentzen da. Proteina hori, normalean, hodien endotelioan egoten da, eta VEGF (endotelio baskularraren hazkunde faktorea) faktore garrantzitsuaren hartzaile gisa jarduten du. VEGF funtsezkoa da endotelioaren fisiologia normalerako, bai eta angiogenesi izeneko prozesuan eremu hipoxikoetarantz haz dadin ere.
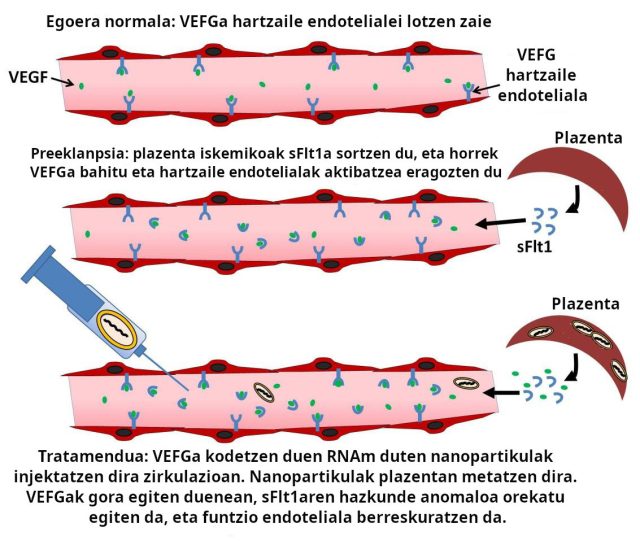 2. irudia: preeklanpsian plazentak Flt1 hartzailearen forma disolbagarria (sFlt1) sortzen du, zeinak ez duen zelula endotelialekin lotzeko eremurik. Proteina horrek aske zirkulatzen du eta VEFGari lotzen zaio: bahitu egiten du, eta eragotzi egiten du VEFGa hartzaile endotelialekin lotzea. Horrek endotelioaren funtzionamendu desegokia eragiten du. Nature aldizkariaren artikuluan deskribatuta tratamendua plazentan metatzen diren nanopartikula lipidikoak injektatzea da. Partikula horiek RNA mezulari bat dute, VEGF proteina kodetzen duena. VEGFaren adierazpenak gora egiten duenean, sFlt1aren gehiegikeria anomaloak eragiten duen defizita orekatu egiten da.
2. irudia: preeklanpsian plazentak Flt1 hartzailearen forma disolbagarria (sFlt1) sortzen du, zeinak ez duen zelula endotelialekin lotzeko eremurik. Proteina horrek aske zirkulatzen du eta VEFGari lotzen zaio: bahitu egiten du, eta eragotzi egiten du VEFGa hartzaile endotelialekin lotzea. Horrek endotelioaren funtzionamendu desegokia eragiten du. Nature aldizkariaren artikuluan deskribatuta tratamendua plazentan metatzen diren nanopartikula lipidikoak injektatzea da. Partikula horiek RNA mezulari bat dute, VEGF proteina kodetzen duena. VEGFaren adierazpenak gora egiten duenean, sFlt1aren gehiegikeria anomaloak eragiten duen defizita orekatu egiten da.Flt1 hartzailearen forma disolbagarria (sFlt1) FLT1 genetik eratorritako RNA mezulariaren prozesamendu alteratu baten ondorioz sortzen da. Alterazio horrek mintz endotelialekin lotzeko eremurik ez duen proteina bat sortzen du; hortaz, sFlt1 gehiegik zirkulatzen du aske odolean, eta horrek ondorio toxikoak izaten ditu. Arazoa da plazentak gehiegi sortzen duen sFlt1a hori VEGFari lotzen jarraitzen duela, bahitu egiten duela eta eragotzi egiten duela VEGFaren zeregina: endotelioa mantentzea (2. irudia). Horrexegatik da zirkulazioan VEGF gehiago zuzkitzea preeklanpsiaren tratamendurako aukeretako bat, baina nahi ez diren albo ondorioak izan ditzake. Odola gorputzetik kanpoko gailu baten bidez iragazi eta sFlt1aren molekulak ezabatzea ere iradoki da.
Aukera askoz ere erakargarriago bat garatu du Pennsylvaniako Unibertsitateko ikertalde batek eta Nature aldizkarian argitaratu berri den artikulu batean dago jasota. COVID-19aren aurkako txerto nagusiak garatzeko erabili zenaren antzeko teknologia aplikatzea da asmoa. Gogora dezagun txerto horiek nanopartikula lipidikoak zirela eta SARS-CoV-2 birusaren proteinak kodetzen zituen RNA mezulari bat zutela. Gure organismoan, RNA mezularia proteina bihurtzen zen, eta proteina horrek immunitate sistema aktibatu eta birusaren aurkako antigorputzak sortzen zituen.
Preeklanpsiari dagokionez, nanopatikulak VEGF proteina kodetzen duen RNA mezulariarekin kargatzea da asmoa. Arazoa da nanopartikula horiek batik bat plazentara bideratu behar direla, eta horixe da, hain zuzen ere, azterlan horren berrikuntza. Taldeak markatzaile fluoreszentea zuten nanopartikula lipidikoen 98 mota diseinatu zituen. Sagu ernalduetan injektatu ostean, nanopartikulek plazentara bideratzeko eta haren fluoreszentzia adierazteko joera handiagoa zutela egiaztatu zen. Horietako batek, LNP-55ek, eman zituen emaitzarik onenak, hau da, plazentarekiko afinitate handiagoa erakutsi zuen laborategian erabili ohi diren nanopartikulek baino. Gainera, LNP-55ek abantaila bat du: ez du plazentaren hesia zeharkatzen eta ez dio fetuari eragiten.
LNP-55 partikulak VEGFrako RNA mezulariarekin kargatu zituzten eta sagu ernalduetan injektatu. Sagu horietako batzuek lipopolisakaridoen injekzioa jaso zuten, hau da, inflamazioa eta preeklanpsiaren antzeko sintomak eragiten dituen substantzia batena. Beste batzuk, berriz, sFlt1 gehiegi eta preeklanpsiaren sintoma berberak eragiten zituzten adenobirusekin tratatu zituzten. Bi kasuetan, LNP-55/VEGF bidezko tratamenduak murriztu egin zuen amen tentsio arteriala eta proteinuria, hobetu egin zuten plazentako perfusioa eta areagotu egin zuten fetuen hazkundea.
Emaitza hori oso esperantzagarria da, nahiz eta oraindik bide luzea egin behar den gizakien preeklanpsia tratatzeko tratamendura iristeko. Adibidez, iradoki da plazentak berez ekoizten duen hazkunde faktorea, PlGF delakoa, VEGFa bera baino interesgarriagoa litzatekeela. Izan ere, amaren odoleko sFlt1/PlGF ratioa preeklanpsiaren ondoriozko konplikazioen adierazle ona da. Halaber, LNP-55ek barearekin afinitatea duela ikusi da, eta baztertu egin behar da organo horretan VEGF adierazpenak nahi gabeko ondoriorik ez eragitea.
Edonola ere, RNA mezulariren “etxera eramateko” teknologian egin diren aurrerapenek itxaropena ematen diote dute gaur egun, oraindik ere, suntsitzailea izaten jarraitzen duen sindromeari.
Erreferentzia bibliografikoak:Swingle, Kelsey L.; Hamilton, Alex G.; Safford, Hannah C.; Geisler, Hannah C.; Thatte, Ajay S.; Palanki, Rohan; Murray, Amanda M.; Han, Emily L.; Mukalel, Alvin J.; Han, Xuexiang; Joseph, Ryann A.; Ghalsasi, Aditi A.; Alameh, Mohamad-Gabriel; Weissman, Drew; Mitchell, Michael J. (2024). Placenta-tropic VEGF mRNA lipid nanoparticles ameliorate murine pre-eclampsia. Nature, 637, pages 412–421. DOI: 10.1038/s41586-024-08291-2
Thadhani, Ravi; Karumanchi, S. Ananth (2024). Lipid-delivery system could treat life-threatening pregnancy complication. Nature. DOI: 10.1038/d41586-024-03853-w
Egileaz:Ramón Muñoz-Chápuli Oriol Animalien Biologiako Katedraduna (erretiratua) da Malagako Unibertsitatean.
Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2024ko abenduaren 30ean: Nanopartículas lipídicas: una esperanza para tratar la preeclampsia.
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post Nanopartikula lipidikoak: preeklanpsiaren tratamendurako itxaropena appeared first on Zientzia Kaiera.
Iraia Garcia Santisteban, biokimikaria: “Ezustean aurkitu nuen nire ikerketa-lerroa irekitzeko bidea”
Iraia Garcia Santisteban biokimikariarentzat betitik izan da erakargarria ikerketa-mundua. Tira, txiki-txikitan ile-apaintzailea izan nahi zuela aitortu du, barre artean, baina, gerora, bere erreferenteak zientziara bideratu dute, bereziki, DBHn izan zituen bi irakasle, natur zientzietakoa, eta biologia eta kimikakoa (biak emakumeak), eta, batez ere, bere izeba Marisol, zeinak ikertzaile gisa ibilbide aberatsa izan baitu.
“Izebak honetan ez sartzeko esaten zidan”, gogoratu du Garciak. “Baina betitik gustatu zait, eta ez naiz damutzen”. Hortaz, unibertsitatean biologia ikasten hasi, eta, jada bigarren mailan, biologia zelularreko laborategi batean hasi zen ikertzen: “2005a zen, eta Prestige ontziko isurien eragina ikertzen genuen muskuiluetan”. Biologia zelularretik genetikara aldatu zen, eta Jose Antonio Rodriguez Perez medikuntzako irakaslearekin hasi zen ikertzen.
 Irudia: Iraia Garcia Santisteban biokimikaria da. (Argazkia: Elhuyar)
Irudia: Iraia Garcia Santisteban biokimikaria da. (Argazkia: Elhuyar)“Hura ere erreferente bat da nire bizitzan, beti laguntzeko prest. Berekin egin nituen masterra, eta gero tesia, deubikitinasen inguruan. Proteina horiek zeluletan daude, eta minbizi mota batzuetan mutatuta agertzen dira”, azaldu du. Laborategi hartatik, Amsterdameko NKI Herbehereetako Minbizi Institutura joan zen, doktoretza-ondorengoko beka batekin.
Itzuli zenean, Ana Zubiaga Elordietarekin egon zen, Rodriguezek eta biek partekatzen duten laborategian. Bi urteren ondoren, irakaskuntzan ordezkapen bat egiteko aukera izan zuen, eta orduan ikusi zuen lan hori ere gustuko zuela eta bide bat izan zitekeela. “Ikerbasque beka eskatu nuen, Juan de la Cierva ere bai, eta, curriculum ona neukan arren, ez nuen bekarik lortu. Izan ere, ez da nahikoa ona izatea; besteak baino hobea izan behar duzu”.
Irakaskuntzan ere, oposizioetara aurkeztu zen, eta ez zuen irabazi. Baina, ezustean, beste ate bat ireki zitzaion orduan: “Nirekin aurkeztu zen beste neskak irabazi zuen, Nora Fernandez Jimenezek. Eta justu bere taldean doktoretza-ondorengoko plaza bat sortu zen. Aurkeztu nintzen, eta aukeratu ninduten. Orduan, guztiz aldatu zen nire norabidea. Hasi nintzen gaixotasun konplexuen genomikarekin eta bioinformatikarekin lanean, eta harremanetan jarri nintzen klinikarekin, Gurutzetako ospitalearekin. Hala, Gurutzetako ginekologo batzuekin batera, nire lerro propioarekin hasi nintzen!”
Endometriosia, gaitz konplexu eta ezezagunaEndometriosia ikertzen hasi zen, eta, horri esker, curriculuma osatu zuen, eta hurrengo plaza irabazi zuen. Garciaren esanean, endometriosia gaixotasun konplexu bat da, eta ikergaitzat hartzeko arrazoia, neurri batean, pertsonala izan zen, justu aurreko urtean diagnostikatu baitzioten. “Diagnostikatu zidatenean ez nekien zer zen; ez neukan ia entzunda ere. Atera kontuak zenbateko desinformazioa dagoen”. Horrenbestez, endometriosiaren diagnostikoa egiteko biomarkatzaileak ikertzen hasi zen. “Ea gure ikerketaren ekarpenarekin, urte batzuen buruan ez den hainbeste urte itxaron behar diagnostikoa izateko”.
Gaur egun, gure eguneroko produktu eta elikagaietan dauden kutsatzaileek endometriosia izateko arriskuan duten eragina aztertzen dabil Amaia Irizar Loibiderekin batera, Zihara Alonso ikaslearen laguntzarekin. Ikerketa egiteko, endometriosia duten boluntarioak behar dituzte, euren odol menstruala ikertzen baitute. Horretarako, helbide hauetara idatzi dezakete: iraia.garcia@ehu.eus; amaia.irizar@ehu.eus.
Bere lanaz grinatsu hitz egiten badu ere, ez ditu ezkutatzen zailtasunak, eta bi oztopo aipatu ditu amaieran. Batetik, amatasuna eta ikerketa uztartzeko egiturazko eragozpenak. Eta, bestetik, beti finantziazioaren bila ibili beharra. Hori jakinda, are balio handiagoa du taldekideekin batera uko egin izana Europako proiektu batean sartzeari, Israel dagoelako tartean.
Fitxa biografikoa:Iraia Garcia Santisteban Zallan jaio zen, 1986. urtean. Biokimikan lizentziatua da, eta Biología Molekularra eta Biomedikuntzan doktorea. Amsterdameko NKI Herbehereetako Minbizi Institutuan egin zuen doktoretza-ondorengoa, eta, itzulitakoan, aurrena postdoc junior moduan egon zen EHUn, eta gero postdoc senior bezala Biobizkaia Osasun Ikerketa Institutuan. 2021ean irakasle atxiki plaza lortu zuen, eta orain irakaskuntza eta endometriosiaren genomikaren ikerkuntza uztartzen ditu, afiliazio bikoitzarekin: EHU eta Biobizkaia Osasun Ikerketa Institutua.
Egileaz:Ana Galarraga Aiestaran (@Anagalarraga1) zientzia-komunikatzailea da eta Elhuyar aldizkariko zuzendarikidea.
Elhuyar aldizkariarekin lankidetzan egindako atala.

The post Iraia Garcia Santisteban, biokimikaria: “Ezustean aurkitu nuen nire ikerketa-lerroa irekitzeko bidea” appeared first on Zientzia Kaiera.
Iraganeko ur gezako landare arbasoek egungo nekazaritza hobetu dezakete
Inori ez zaio arraroa iruditzen inguruneko landareak 3D-an hazten badira, baina lur-landareek ez dituzte gaur egun normalak iruditzen zaizkigun gaitasunak azken urteetan zein mendeetan garatu. Hain zuzen ere, 500 milioi urte baino gehiago pasa dira lur-landareen alga arbasoak ezaugarri hauek garatu zituenetik. Orain, ikertzaileek arbaso bakar horren leinuen genomak ikertzen dituzte egungo nekazaritzaren jasangarritasuna hobetzeko asmoz.
Azken hamarkadetan, material genetikoa ikertzeko tresnetan egindako aurrerapenei esker, zientzialariek landareen eboluzioari buruzko aurkikuntza liluragarriak egin ahal izan dituzte. Egun, badakigu lur-landareen eta beren arbaso diren ur gezatako algen artean konexio ugari daudela, lur landareek lurrera iritsi baino askoz lehenago garatu baitzituzten zenbait ezaugarri, hala nola gaur egungo landareek estresari aurre egiteko edo 3D-an hazteko duten gaitasuna.
 Irudia: antzinako landare hauek sekretu ebolutiboak dituzte, eta nekazariei ongarri kutsatzaile gutxiago erabiltzen lagundu liezaiekete. (Argazkia: Eftychis Frangedakis. Iturria: Boyce Thompson Istitute)
Irudia: antzinako landare hauek sekretu ebolutiboak dituzte, eta nekazariei ongarri kutsatzaile gutxiago erabiltzen lagundu liezaiekete. (Argazkia: Eftychis Frangedakis. Iturria: Boyce Thompson Istitute)Alabaina, egungo lur-landareen jatorri ebolutibo bakarra bilatzean zailtasun ugari suertatzen dira. Izan ere, ur gezetako arbasoa duela 500 milioi urte bizi izan zen eta, geroztik, 3 leinu ezberdinetan eboluzionatu dute egun existitzen diren hepatizeoak, antocerotak eta goroldioak. Lur-landareen artean goroldioak dira ezagunenak, baina hiru leinuek azaltzen dute ezaugarri nagusi berdina: hirurak baldintza hezeetan bizi diren landare ez-baskularrak dira, hau da, ez daukate beste landareek bezala gizakien arteria eta benak simulatzen dituzten egitura baskularrak (xilema eta floema).
Hala ere, genoma aztertzeko orduan antocerotak dira arbaso bakarretik hurbilen daudenak eta, beraz, ezinbestekoak bilakatu dira beren kode genetikoa argitzeko ikerketetan. Arbasoen inguruko informazio genetikoa lortzeak lagundu egiten digu eboluzioan zehar lurreko landareen ezaugarri jakin batzuk nola agertu diren ulertzen eta, gainera, eredu gisa erabil dezakegun informazioa da. Horiek horrela, Nature Plants aldizkarian argitaratutako artikuluan, mundu osoko ikertzaileek lur-landareen arbaso bakarraren genoma argitu nahi dute beren ondorengo diren hiru leinuen genomak aztertuz.
Iraupen luzeko lasterketa2025ko udan, Current Biology aldizkarian argitaratutako berrikusketa batean, mundu osoko ikertzaileek lur-landareen arbasoak ikertzeko eredu-sistema bateratuak garatzeko deia egin dute. Izan ere, gaur egun, alga horien genomen sekuentziazio soiletik harago doa ikerketa. Gene horien funtzionamenduan sakontzen ari dira ikertzaileak, eta geneek algei bizirik irauten eta funtzionatzen nola laguntzen dieten aztertzen ari dira.
Hori lortzeko, kasu askotan 5 urtetik gorako lan esperimentala behar da; eta hori da antoceroak ikertu zituzten nazioarteko zientzialariei gertatu zitzaiena: “Hiru urte behar izan genituen antozeroteak nola landatu eta haien bizitza sexualaren zikloa laborategiko ingurumenean errepikatzeko, eta beste hiru urte haien genomak behar bezala aztertu eta idazteko”, dio Szövényi-k, Zurich unibertsitateko ikerketaburuak.
Arbasoaren baliabideak ustiatzenLeinuen genomak ikertzean, zientzialariek antozeroteak karbono dioxidoa kloroplastoetan kontzentratzeko duten mekanismoa argitu nahi zuten. Nahiz eta ur gezako hainbat algak azukre gehiago ekoizteko metodologia hau erabiltzen duten, lur landareetan artean antozeroteak dira gaitasun hau duten bakarrak. Cornell Unibertsitateko ikerketaburua den Li-ren hitzetan, “karbono-kontzentrazioko mekanismo hori hazkuntza-landareetan instalatu ahal izango balitz, gehiago hazi ahalko lirateke ongarri kantitate gutxiagorekin”.
Ikertaldeak, gainera, landare gutxik erakusten duten baliabide-pilaketa mekanismo bat antzeman zuen. Hain zuzen ere, landareek zianobakterioekin duten harreman sinbiotiko batean nitrogeno-iturria susta lezaketen 40 gene identifikatu zituzten. “Funtzio paregabea da”, adierazi zuen Li-k: “Oso landare gutxik egin dezakete hori”.
Horrela, ikerburuak nabarmendu egiten du garrantzi handia izan dezakeela dugun gaitasuna garatzeak ur-landareetan antzeman ditugun bi ezaugarri horiek nekazaritza ingurunetan erabiltzeko; alegia, baliabideak pilatzeko gaitasun genetikoa eta erlazio sinbiotiko onuragarriak. Ikerburuaren beren hitzetan, “Nekazariek ongarri nitrogenatu gutxiago erabili ahal izan dezaten lortzeko zianobakterioekin antzeko harreman sinbiotikoa garatzerik balego, onuragarria izan liteke ingurumenerako. Izan ere, laborantzako nitrogeno gehiegi iristen da ibai-bideetara, eta hor alga hilgarrien loraldiak eragin ditzake”.
Uretatik lurreraIkerketak lur lehorra menderatu zuten lehen landareen inguruko informazioa ere azaleratu du. Orain arte ere jakina zen aipatutako hiru leinuak lurra kolonizatu zuten lehen landareak zirela, baina hala ere, emaitzek hiru taldeen arteko harremanak argitu ditu. “Lurreko landareen erlazioari dagokionez, eztabaida handia egon da antozeroteei dagokien kokalekuaren inguruan” esan zuen Li-k. “Hemen, hepatizeoek, antozeroteek eta goroldioek landare baskularrekin baino elkarrekiko lotura estuagoa dutela adierazten duen ebidentzia sendoa dugu. Halaber, frogatu dugu hepatizeoak eta goroldioak elkarren artean lotura estuagoa dutela, antozeroteekin baino”.
Nahiz eta lortutako emaitzek lurreko landareen bilakaera ulertzeko hutsune oso garrantzitsua betetzen duten, ahaleginak batzeko beharra nabarmentzen du aurten ur gezetako arbasoak ikertzen dituzten zientzialariek argitaratutako berrikusketak. Izan ere, komunitate zientifiko txikia da alga hauek ikertzen dituena eta ezinbestekoa da protokoloak, metodoak eta alga-laginketak estandarizatzea.
Erreferentzia bibliografikoak:Li, Fay-Wei; Nishiyama, Tomoaki; Waller, Manuel; Frangedakis, Eftychios; Keller, Jean; Li, Zheng; Fernandez-Pozo, Noe; Barker, Michael S.; Bennett, Tom; Blázquez, Miguel A.; Cheng, Shifeng; Cuming, Andrew C.; de Vries, Jan; de Vries, Sophie; Delaux, Pierre-Marc; Diop, Issa S.; Harrison, C. Jill; Hauser, Duncan; Hernández-García, Jorge; Kirbis, Alexander; Meeks, John C.; Monte, Isabel; Mutte, Sumanth K.; Neubauer, Anna; Quandt, Dietmar; Robison, Tanner; Shimamura, Masaki; Rensing, Stefan A.; Villarreal, Juan Carlos; Weijers, Dolf; Wicke, Susann; Wong, Gane K.-S.; Sakakibara, Keiko; Szövényi, Péter (2020). Anthoceros genomes illuminate the origin of land plants and the unique biology of hornworts. Nature Plants, 6, 259–272. DOI: 10.1038/s41477-020-0618-2
Carrillo-Carrasco, Vanessa Polet; Hernandez-Garcia, Jorge; Girou, Camille; Grubor, Ivana; Keller, Jean; Lim, Elodie; Schmidt, Vojtech; Sørensen, Iben; Vosolsobe, Stanislav; Buschmann, Henrik; Delaux, Pierre-Marc; Domozych, David; Holzinger, Andreas; Nakagami, Hirofumi; Nishiyama, Tomoaki; Petrasek, Jan; Renault, Hugues; Rensing, Stefan A.; Rose, Jocelyn K.C.; Sekimoto, Hiroyuki; Delwiche, Charles F.; Weijers, Dolf ; de Vries, Jan(2025). A roadmap to developing unified streptophyte algal model systems. Current Biology, 35, 14, 725–738. DOI: 10.1016/j.cub.2025.05.023
Egileaz:Oxel Urra Elektrokimikan doktorea da, zientziaren eta artea uztartzen duten proiektuetan aditua, egun zientzia-komunikatzailea da.
The post Iraganeko ur gezako landare arbasoek egungo nekazaritza hobetu dezakete appeared first on Zientzia Kaiera.
Un termómetro para medir la cuanticidad
El flujo de calor “anómalo”, que a primera vista parece violar la segunda ley de la termodinámica, ofrece a los físicos una forma de detectar el entrelazamiento cuántico sin destruirlo.
Un artículo de Philip Ball. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
 Una variante moderna del demonio de Maxwell puede actuar como una especie de catalizador, impulsando un flujo de calor de objetos cuánticos fríos a calientes. Ilustración: Daniel García / Quanta Magazine
Una variante moderna del demonio de Maxwell puede actuar como una especie de catalizador, impulsando un flujo de calor de objetos cuánticos fríos a calientes. Ilustración: Daniel García / Quanta Magazine
Si hay una ley de la física que parece fácil de comprender, esa es la segunda ley de la termodinámica: el calor fluye espontáneamente de los cuerpos más calientes hacia los más fríos. Pero ahora, de forma suave y casi casual, Alexssandre de Oliveira Jr. acaba de mostrarme que, en realidad, no la entendía del todo.
«Toma esta taza de café caliente y esta jarra de leche fría», dijo el físico brasileño mientras estábamos sentados en una cafetería de Copenhague. «Ponlas en contacto y, efectivamente, el calor fluirá del objeto caliente al frío, tal como el científico alemán Rudolf Clausius formuló oficialmente en 1850». Sin embargo, en algunos casos —explicó de Oliveira— los físicos han descubierto que las leyes de la mecánica cuántica pueden hacer que el flujo de calor ocurra en sentido contrario: del frío al caliente.
Esto no significa realmente que la segunda ley falle, añadió mientras su café se enfriaba con tranquilidad. Lo que sucede es que la expresión de Clausius es el límite clásico de una formulación más completa, exigida por la física cuántica.
Los físicos empezaron a apreciar la sutileza de esta situación hace más de dos décadas y, desde entonces, han estado explorando la versión cuántica de la segunda ley. Ahora, de Oliveira, investigador posdoctoral en la Universidad Técnica de Dinamarca, y sus colegas han demostrado que el tipo de “flujo de calor anómalo” que se da a escala cuántica podría tener una aplicación tan práctica como ingeniosa.
Según afirman, puede servir como un método sencillo para detectar la cuanticidad —por ejemplo, para saber si un objeto está en una superposición cuántica de varios estados observables posibles, o si dos objetos están entrelazados (es decir, sus estados son interdependientes)— sin destruir esos delicados fenómenos cuánticos. Una herramienta diagnóstica así podría usarse para verificar que un ordenador cuántico está utilizando realmente recursos cuánticos al realizar sus cálculos. Incluso podría ayudar a detectar aspectos cuánticos de la fuerza de la gravedad, uno de los grandes objetivos de la física moderna.
Según los investigadores, basta con conectar un sistema cuántico a un segundo sistema capaz de almacenar información sobre él, y a un sumidero térmico (un cuerpo capaz de absorber mucha energía). Con esta disposición, se puede aumentar la transferencia de calor al sumidero más allá de lo que permitirían las leyes clásicas. Midiendo simplemente lo caliente que está el sumidero se podría detectar la presencia de superposición o entrelazamiento en el sistema cuántico.
Más allá de las posibles aplicaciones prácticas, la investigación pone de manifiesto un nuevo aspecto de una profunda verdad sobre la termodinámica: la forma en que el calor y la energía se transforman y se desplazan en los sistemas físicos está íntimamente ligada a la información —a lo que se sabe o puede saberse sobre dichos sistemas—. En este caso, “pagamos” el flujo de calor anómalo sacrificando información almacenada sobre el sistema cuántico.
«Me encanta la idea de que las magnitudes termodinámicas puedan señalar fenómenos cuánticos», afirma la física Nicole Yunger Halpern, de la Universidad de Maryland. «El tema es fundamental y profundo».
El conocimiento es poder
 «Es imposible que una máquina autónoma, sin la ayuda de ningún agente externo, transmita calor de un cuerpo a otro a una temperatura más alta», escribió Rudolf Clausius (en alemán) en 1850. Fue la primera expresión de la segunda ley de la termodinámica. Foto: Theo Schafgans/Dominio público
«Es imposible que una máquina autónoma, sin la ayuda de ningún agente externo, transmita calor de un cuerpo a otro a una temperatura más alta», escribió Rudolf Clausius (en alemán) en 1850. Fue la primera expresión de la segunda ley de la termodinámica. Foto: Theo Schafgans/Dominio públicoLa conexión entre la segunda ley de la termodinámica y la información fue explorada por primera vez en el siglo XIX por el físico escocés James Clerk Maxwell. Para su consternación, la segunda ley de Clausius parecía implicar que los focos de calor acabarían disipándose por todo el universo hasta que desapareciesen todas las diferencias de temperatura. En ese proceso, la entropía total del universo —en términos simples, una medida de su desorden y falta de estructura— aumentaría inexorablemente. Maxwell comprendió que esa tendencia acabaría eliminando toda posibilidad de aprovechar los flujos de calor para realizar trabajo útil, y que el universo alcanzaría un equilibrio estéril, dominado por un zumbido térmico uniforme: la llamada “muerte térmica”. Esa perspectiva ya era bastante inquietante por sí misma, pero resultaba especialmente inaceptable para el devoto cristiano Maxwell. En una carta a su amigo Peter Guthrie Tait en 1867, afirmó haber encontrado una manera de “abrir un agujero” en la segunda ley.
Imaginó un diminuto ser (más tarde apodado demonio) capaz de ver el movimiento de las moléculas individuales de un gas. El gas llenaría una caja dividida en dos compartimentos por una pared con una trampilla. Abriendo y cerrando la trampilla selectivamente, el demonio podría separar las moléculas que se mueven más rápido en un lado y las más lentas en el otro, creando así un gas caliente y otro frío, respectivamente. Al actuar según la información obtenida sobre el movimiento molecular, el demonio reduciría la entropía del gas, generando un gradiente de temperatura con el que podría realizarse trabajo mecánico, como empujar un pistón.
Los científicos estaban seguros de que el demonio de Maxwell no podía violar realmente la segunda ley, pero se tardó casi un siglo en comprender por qué. La respuesta es que la información que el demonio recoge y almacena sobre los movimientos moleculares acabaría llenando su memoria finita. Para seguir funcionando, tendría que borrar y reiniciar esa memoria. El físico Rolf Landauer demostró en 1961 que ese borrado consume energía y genera entropía —más entropía de la que el demonio reduce mediante su selección—. El análisis de Landauer estableció una equivalencia entre información y entropía, lo que implica que la información misma puede actuar como un recurso termodinámico: puede transformarse en trabajo. Los físicos demostraron experimentalmente esta conversión de información en energía en 2010.
 Incómodo con la segunda ley de la termodinámica, el físico escocés James Clerk Maxwell inventó un experimento mental sobre un demonio omnisciente que aún hoy nos brinda nuevas perspectivas. Imagen: The Print Collector/Heritage Images
Incómodo con la segunda ley de la termodinámica, el físico escocés James Clerk Maxwell inventó un experimento mental sobre un demonio omnisciente que aún hoy nos brinda nuevas perspectivas. Imagen: The Print Collector/Heritage ImagesPero los fenómenos cuánticos permiten procesar información de formas que la física clásica no permite —esa es, de hecho, la base de tecnologías como la computación cuántica y la criptografía cuántica—. Y por eso la teoría cuántica altera la versión convencional de la segunda ley.
Aprovechando las correlaciones
Los objetos cuánticos entrelazados comparten información mutua: están correlacionados, de modo que podemos conocer propiedades de uno observando el otro. Eso, por sí mismo, no es tan extraño; si observas uno de un par de guantes y ves que es el izquierdo, sabes que el otro es el derecho. Pero un par de partículas cuánticas entrelazadas difiere de los guantes en un aspecto esencial: mientras que la lateralidad de los guantes está fijada antes de mirar, en las partículas no es así, según la mecánica cuántica. Antes de medirlas, no está decidido qué valor de una propiedad observable tiene cada partícula del par entrelazado. En ese momento solo conocemos las probabilidades de las posibles combinaciones de valores (por ejemplo, 50 % izquierda-derecha y 50 % derecha-izquierda). Solo cuando medimos el estado de una partícula esas posibilidades se resuelven en un resultado concreto. En ese proceso de medición, el entrelazamiento se destruye.
Si las moléculas de un gas están entrelazadas de esta manera un demonio de Maxwell puede manipularlas con más eficacia que si todas se movieran independientemente. Si el demonio sabe, por ejemplo, que cada molécula rápida que ve venir está correlacionada de tal modo que otra rápida la seguirá al instante, no necesita observar la segunda partícula antes de abrir la trampilla para dejarla pasar. El coste termodinámico de (temporalmente) desafiar la segunda ley se reduce.
En 2004, los teóricos cuánticos Časlav Brukner, de la Universidad de Viena, y Vlatko Vedral, entonces en el Imperial College de Londres, señalaron que esto significa que las mediciones termodinámicas macroscópicas pueden utilizarse como un “testigo” para revelar la presencia de entrelazamiento cuántico entre partículas. Bajo ciertas condiciones, mostraron que la capacidad calorífica de un sistema o su respuesta a un campo magnético aplicado debería llevar la huella del entrelazamiento, si este existe.
De manera similar, otros físicos calcularon que se puede extraer más trabajo de un cuerpo caliente cuando hay entrelazamiento cuántico en el sistema que cuando es puramente clásico.
Y en 2008, el físico Hossein Partovi, de la Universidad Estatal de California, identificó una consecuencia particularmente llamativa del modo en que el entrelazamiento cuántico puede cuestionar las intuiciones derivadas de la termodinámica clásica. Descubrió que la presencia de entrelazamiento puede incluso invertir el flujo espontáneo de calor de un objeto caliente a uno frío, aparentemente subvirtiendo la segunda ley.
Esa inversión es una forma especial de refrigeración, explica Yunger Halpern. Y, como ocurre siempre con la refrigeración, no es gratuita (y por tanto no viola realmente la segunda ley). Clásicamente, refrigerar un objeto requiere trabajo: hay que bombear el calor en dirección contraria consumiendo combustible, compensando así la entropía perdida al enfriar el cuerpo frío y calentar el caliente. Pero en el caso cuántico —sigue Yunger Halpern—, en lugar de quemar combustible para lograr la refrigeración, «se queman las correlaciones». Es decir, a medida que avanza el flujo de calor anómalo, el entrelazamiento se destruye: las partículas que inicialmente tenían propiedades correlacionadas se vuelven independientes. «Podemos usar las correlaciones como un recurso para empujar el calor en dirección opuesta», añade.
 Vlatko Vedral es uno de los creadores de la idea de utilizar mediciones termodinámicas como «testigo» para revelar la presencia de entrelazamiento cuántico entre partículas. foto: Cortesía de Vlatko Vedral
Vlatko Vedral es uno de los creadores de la idea de utilizar mediciones termodinámicas como «testigo» para revelar la presencia de entrelazamiento cuántico entre partículas. foto: Cortesía de Vlatko VedralDe hecho, el “combustible” aquí es la información misma: concretamente, la información mutua de los cuerpos calientes y fríos entrelazados.
Dos años más tarde, David Jennings y Terry Rudolph, del Imperial College de Londres, aclararon lo que sucede. Mostraron cómo puede reformularse la segunda ley de la termodinámica para incluir el caso en que existe información mutua, y calcularon los límites sobre cuánto puede modificarse —e incluso invertirse— el flujo de calor clásico mediante el consumo de correlaciones cuánticas.
El demonio sabe de cuanticidad
Cuando entran en juego los efectos cuánticos la segunda ley deja de ser tan sencilla. Pero ¿podemos hacer algo útil con la forma en que la física cuántica flexibiliza los límites de las leyes termodinámicas? Esa es una de las metas de la disciplina llamada termodinámica cuántica, en la que algunos investigadores buscan fabricar motores cuánticos más eficientes que los clásicos o baterías cuánticas que se carguen más rápidamente.
Patryk Lipka-Bartosik, del Centro de Física Teórica de la Academia Polaca de Ciencias, ha buscado aplicaciones prácticas en la dirección contraria: usar la termodinámica como herramienta para explorar la física cuántica. El año pasado, él y sus colaboradores vieron cómo materializar la idea de Brukner y Vedral (2004) de utilizar propiedades termodinámicas como testigo del entrelazamiento cuántico. Su esquema involucra sistemas cuánticos calientes y fríos correlacionados entre sí, y un tercer sistema que media el flujo de calor entre ambos. Podemos pensar en este tercer sistema como en un demonio de Maxwell, solo que ahora posee una “memoria cuántica” que puede estar entrelazada con los sistemas que manipula. Al estar entrelazados con la memoria del demonio, los sistemas caliente y frío quedan efectivamente vinculados, de modo que el demonio puede inferir información de uno a partir de las propiedades del otro.
 Patryk Lipka-Bartosik ha explorado cómo utilizar mediciones termodinámicas para detectar efectos cuánticos. Foto: Alicja Lipka-Bartosik
Patryk Lipka-Bartosik ha explorado cómo utilizar mediciones termodinámicas para detectar efectos cuánticos. Foto: Alicja Lipka-BartosikUn demonio cuántico así puede actuar como un tipo de catalizador, facilitando la transferencia de calor al aprovechar correlaciones que de otro modo serían inaccesibles. Es decir, al estar entrelazado con los objetos caliente y frío, el demonio puede detectar y explotar todas sus correlaciones de manera sistemática. Y, de nuevo como un catalizador, este tercer sistema vuelve a su estado original una vez completado el intercambio de calor entre los objetos. De esta forma, el proceso puede potenciar el flujo de calor anómalo más allá de lo que sería posible sin dicho catalizador.
El artículo publicado este año por de Oliveira, junto con Lipka-Bartosik y Jonatan Bohr Brask, de la Universidad Técnica de Dinamarca, utiliza algunas de estas mismas ideas, pero con una diferencia crucial que convierte el sistema en una especie de termómetro para medir la cuanticidad. En el trabajo anterior, la memoria cuántica —el demonio— interactuaba con un par de sistemas cuánticos correlacionados, uno caliente y otro frío. Pero en este nuevo trabajo se coloca entre un sistema cuántico (por ejemplo, una red de bits cuánticos, o qubits, entrelazados en un ordenador cuántico) y un sumidero térmico sencillo con el que el sistema cuántico no está directamente entrelazado.
Como la memoria está entrelazada tanto con el sistema cuántico como con el sumidero, puede de nuevo catalizar un flujo de calor entre ellos más allá de lo posible clásicamente. En ese proceso, el entrelazamiento dentro del sistema cuántico se convierte en calor adicional que fluye hacia el sumidero. Así, medir la energía almacenada en el sumidero (equivalente a leer su “temperatura”) revela la presencia de entrelazamiento en el sistema cuántico. Pero, dado que el sistema y el sumidero no están entrelazados entre sí, la medición no afecta al estado del sistema cuántico. Este recurso elude la conocida dificultad de que las mediciones destruyen la cuanticidad. «Si intentaras simplemente medir el sistema [cuántico] directamente, destruirías su entrelazamiento antes incluso de que el proceso se desarrollara», explica de Oliveira.
 Los físicos Alexssandre de Oliveira Jr. (izquierda) y Jonatan Bohr Brask (derecha) colaboraron con Patryk Lipka-Bartosik en un nuevo esquema para detectar la cuántica sin destruirla. Foto: Jonas Schou Neergaard-Nielsen
Los físicos Alexssandre de Oliveira Jr. (izquierda) y Jonatan Bohr Brask (derecha) colaboraron con Patryk Lipka-Bartosik en un nuevo esquema para detectar la cuántica sin destruirla. Foto: Jonas Schou Neergaard-NielsenEl nuevo esquema tiene la ventaja de ser simple y general, señala Vedral, ahora en la Universidad de Oxford. «Estos protocolos de verificación son muy importantes», dice: cada vez que una empresa de computación cuántica anuncia un nuevo dispositivo, siempre surge la cuestión de cómo —o si— saben realmente que el entrelazamiento entre los qubits está contribuyendo al cálculo. Un sumidero térmico podría actuar como detector de tales fenómenos cuánticos simplemente a través de su cambio de energía. Para implementar la idea, podría designarse un qubit como la memoria cuyo estado revele el de otros qubits, y luego acoplar ese qubit de memoria a un conjunto de partículas que funcionen como sumidero, cuya energía se pueda medir. (Vedral añade una salvedad: es necesario tener un control muy preciso del sistema para asegurarse de que no haya otras fuentes de flujo de calor que contaminen las mediciones. Además, el método no detectará todos los estados entrelazados.)
De Oliveira cree que ya existe un sistema adecuado para poner a prueba su idea experimentalmente. Él y sus colegas están en conversaciones con el grupo de investigación de Roberto Serra en la Universidad Federal del ABC, en São Paulo (Brasil). En 2016, Serra y sus colaboradores utilizaron las orientaciones magnéticas, o espines, de los átomos de carbono e hidrógeno en moléculas de cloroformo como bits cuánticos entre los que podían transferir calor.
Usando este montaje, dice de Oliveira, debería ser posible aprovechar un comportamiento cuántico —en este caso la coherencia, es decir, que las propiedades de dos o más espines evolucionan en fase entre sí— para modificar el flujo de calor entre los átomos. La coherencia de los qubits es esencial para la computación cuántica, así que poder verificarla detectando un intercambio de calor anómalo sería muy útil.
Las implicaciones podrían ser aún mayores. Varios grupos de investigación intentan diseñar experimentos para determinar si la gravedad es una fuerza cuántica, al igual que las otras tres fuerzas fundamentales. Algunos de estos esfuerzos consisten en buscar entrelazamiento cuántico entre dos objetos generado únicamente por su atracción gravitatoria mutua. Tal vez los investigadores puedan explorar ese entrelazamiento inducido por la gravedad mediante simples mediciones termodinámicas sobre los objetos, verificando así (o no) que la gravedad está realmente cuantizada.
Para estudiar una de las cuestiones más profundas de la física —concluye Vedral—, «¿no sería maravilloso poder hacerlo con algo tan sencillo y macroscópico como esto?».
El artículo original, A Thermometer for Measuring Quantumness, se publicó el 1 de octubre de 2025 en Quanta Magazine. Cuaderno de Cultura Científica tiene un acuerdo de distribución en castellano con Quanta Magazine.
Traducido por César Tomé López
El artículo Un termómetro para medir la cuanticidad se ha escrito en Cuaderno de Cultura Científica.
Ig nobel sariak: saguzar mozkorrak eta oinetako kirasdunak
Ig Nobel sariek, lehenengo, barrea eragiten duten eta ondoren pentsarazten duten ikerketak saritzen dituzte ezagutza arlo ugaritan. Sariak Boston-en banatu ziren irailaren 18an. Helburua jendartean zientziarekiko interesa piztu eta ikerketa gerturatzea da. Orain arte, sarituek 10 trilioi dolarreko txekea jasotzen zuten, baina Zinbaweko dolarrak zirenez, non inflazioa oso handia zen, sariak euro bat baino gutxiago balio zuen. Aurten, ordea, diru-sariaren ordez, irabazleek paper-zapi bat jaso dute. Behean aurtengo lan sarituak aipatzen dira arlo bakoitzeko.
Behiak marra zuri-beltzez margotzen badira eta zebren itxura eman, murriztu egingo da jasotzen duten euli-ziztaden kopurua. Lan honek jaso du biologiako saria. Ikertzaileek hiru behi multzo aztertu zituzten: behi arruntak, marra beltzez margotutakoak eta marra zuri-beltzez margoturikoak. Azken hauek zebra itxura zeukaten. Euliek behi mota bakoitza zenbat aldiz ziztatzen zuten aztertu eta gero, marra zuri-beltzak zituzten behiek, behi arruntek baino ziztada gutxiago zutela ikusi zuten. Horrela, marra zuri-beltzak margotzea eulien ziztadak ekiditeko metodo eraginkorra dela egiaztatu dute. Metodo honek pestiziden erabilera ordezkatu dezake, ondorio onuragarria abereentzat eta ingurugirorako.
 1. irudia: behiak marra zuri-beltzez margotzen badira eta zebren itxura eman, murriztu egingo da jasotzen duten euli-ziztaden kopurua. (Iturria: Kojima, Tomoki; et. al (2019))
1. irudia: behiak marra zuri-beltzez margotzen badira eta zebren itxura eman, murriztu egingo da jasotzen duten euli-ziztaden kopurua. (Iturria: Kojima, Tomoki; et. al (2019))Pasta gazta- eta piperbeltz-saltsarekin jatea ohikoa da Italian, baina saltsa hau lortzea ez da batere erreza! Hain zuzen ere, fisikako saria saltsa honen fase-portaera aztertu duten zientzialarientzat izan da. Ikerketa horretan, saltsa egiteko, gazta-, ur- eta almidoi-proportzio ugari erabili dituzte eta zenbait tenperaturatan prestatu dute. Pasta egostean, almidoia pastatik ur-fasera pasatzen da. Haren kontzentrazioa txikia denean (% 1 azpitik) pikorrak osatzen dira eta saltsaren testura ez da egokia. Horregatik, komeni da almidoi kontzentrazioa % 1-3 artean mantentzea. Osagaien proportzio eta tenperatura egokiak zeintzuk diren jakitea ez da erraza; horregatik, zientzialariek gazta- eta piperbeltz-saltsa perfektua egiteko errezeta proposatu dute.
Ezaguna da tefloia material inertea dela. Hori aintzat hartuta zientzialari talde batek material horixe proposatu du elikagai-gehigarri bezala asetasuna areagotzeko, ez baitu kaloriarik. Hori izan da kimikako saria jaso duen lana. Horretarako, Dupont etxeak 60ko hamarkadan egindako lan batean oinarritu dira, non saguei tefloiarekin nahastutako janaria ematen zieten (% 25 tefloia) 90 egunez. Saguek ez zuten azaldu erantzun toxikorik eta pisua galdu zuten. Taldeak ideia patentatu bazuen ere, Elikagai eta Sendagaien Administrazio estatubatuarrak (FDA) ez du tefloia elikagai gehigarri bezala onartzeko asmorik.
Ezaguna da, oinetakoen kiratsa ekiditeko, haiek ondo aireztatu eta garbitu behar direla. Oinetakoak ez badira ondo aireztatzen bakterio ugari hazten dira bertan. Bakterioek larruazaleko zelula hilak eta izerdia kontsumitzen dituzte eta sufre-konposatuak ekoizten dituzte, oinetakoei kirats bereizgarria ematen dietenak. Zapatilak ondo aireztatu gabe oinetako-altzarian gordetzen badira, altzari hori erabiltzea ez da oso atsegina izango. Hori dela eta, ikertzaile talde batek oinetakoen altzarien diseinua hobetzea proposatzen du argi ultramore-lanpara bat jarriz bertan. Lanpara honek argi ultramorea igortzen du, bakterioak hiltzeko gai dena, kiratsaren arazoa ekiditeko. Lan honek irabazi du ingeniaritzako saria.
 2. irudia: oinetakoak ez badira ondo aireztatzen bakterio ugari hazten dira bertan. (Argazkia: Pixabay – pexels lizentziapean. Iturria: Pexels.com)
2. irudia: oinetakoak ez badira ondo aireztatzen bakterio ugari hazten dira bertan. (Argazkia: Pixabay – pexels lizentziapean. Iturria: Pexels.com)Ezaguna da alkohola edatea eta gidatzea bateraezina dela. Bada saguzarren kasuan ere mozkortuta hegan egitea ez dela aproposa frogatu dute. Hain zuzen ere, alkoholak saguzarren hegan egiteko ahalmenean daukan eragina aztertzen duen lanak jaso du hegazkintza saria. Ikertzaileek alkoholik gabeko eta % 1 alkohol duen janaria eman zieten saguzar talde banari eta haien portaera aztertu zuten. Alkohola kontsumitu duten saguzarrek denbora gehiago behar dute distantzia jakin bat egiteko eta arazoak dituzte ekolokalizatzeko; hau da, soinu-uhinen bidez inguruan daukaten eremuaren irudia osatzeko. Horrek arriskuan jarri ditzake saguzarrak. Izan ere haien erreakzio-denbora murrizten du eta, ondorioz, harrapakin errazagoa bihurtzen ditu gaueko harraparientzat. Beraz, ez da harritzekoa saguzarrek alkohola daukaten frutak ekiditea.
Gutariko askok gustuko dugu baratxuria; bularreko haurrek ere gogoko dute baratxuri-zaporea daukan esnea. Hain zuzen ere, ikerketa honek jaso du pediatriako saria. Amak baratxuria jatean, aldatu egiten da ekoizten duen esnearen usaina; haurrek gogoko dute hura, eta luzeagoak bihurtzen dira hartualdiak. Ikerketa honek eragin handia izan zuen bere garaian (1995), bularra ematen zuten amei baratxuria ez jatea gomendatzen baitzitzaien umeak esnea gustuko izango ez zuelakoan. Jaio berritan izandako zapore esperientziek eragina daukate gustuko izango ditugun elikagaietan.
Gizakiak ez ezik, muskerrak ere pizza-zaleak dira Togon. Baina ez dute gustuko edozein pizza, lau gaztakoa gogoko dute baina lau urtarokoari muzin egiten diote. Zientzialariek zelai batean lau gazta-pizza eta lau urtaro-pizza zatiak jarri dituzte agerian eta harrituta ikusi dute muskerrek soilik lau gaztako pizza jaten dutela. Lan honekin irabazi dute nutrizioko saria.
Umeek adimenaren inguruan eskolan edo gurasoengandik jasotzen duten iritziak eragin handia dauka beren adimenaren pertzepzioan. Helduetan ere, kanpotik jasotzen diren iritziek eragin nabarmena izan dezakete. Hori aztertzeko, 361 pertsonako talde batekin egin dute lan, batzuei azkarrak direla esanez, eta besteei, motelak. Azkarrak direla esateak nartzisismoa sustatzen duela frogatu da. Ikerketaren arabera, bizitzan zehar norbaitek bere ahalmenen inguruan jasotzen duen iritziak eragin handia dauka norbanakoaren adimen-pertzepzioan. Lan honekin psikologia saria jaso dute.
35 urtez azazkalen hazkuntza aztertu duen lanarentzat izan da literatura saria. Azazkal bakoitza abiadura batean hazten da; erdiko hatza azkarren eta hatz lodia edo txikiena motelen. Azazkalen arteko abiadura-erlazioa konstantea denez, azazkal bat zenbat hazten den jakinda gainontzekoen hazkuntza kalkulatu daiteke. 35 urtez gaia ikertu ondoren, adinarekin azazkalen hazte-abiadura moteldu egiten dela frogatu dute.
Alkoholak eragin kaltegarriak dituela ezaguna den arren, badirudi atzerriko hizkuntza baten ahoskera hobetu dezakeela. Hori da hain zuzen ere ikertzaile talde batek frogatu duena: horretarako, nederlandera bigarren hizkuntza bezala ikasten ari diren 50 aleman aukeratu dituzte. Taldeko pertsona batzuei alkoholdun edariak eta besteei alkoholik gabekoak eman eta beren artean nederlanderaz egindako eztabaida bat grabatu zuten. Grabazio horren azterketak erakutsi du ahoskeran puntuazio altuagoa lortzen dutela alkohola edan dutenek. Lan honek bakearen saria jaso du.
Erreferentzia bibliografikoak:Kojima, Tomoki; Oishi, Kazato; Matsubara, Yasushi; Uchiyama, Yuki; Fukushima, Yoshihiko; Aoki, Naoto; Sato, Say; Masuda, Tatsuaki; Ueda, Junichi; Hirooka, Hiroyuki; Kino, Katsutoshi (2019). Cows painted with zebra-like striping can avoid biting fly attack. PLoS One, 14. DOI: 10.1371/journal.pone.0223447
Bartolucci, G.; Busiello, D. M.; Ciarchi, M.; Corticelli, A.; Di Terlizzi, I.; Olmeda, F.; Revignas, D.; Schimmenti, V. M. (2025). Phase behavior of Cacio e Pepe sauce. Physics of Fluids, 37. DOI: 10.1063/5.0255841
Naftalovich, Rotem; Naftalovich, Daniel; Greenway, Frank L. (2016). Polytetrafluoroethylene ingestion as a way to increase food volume and hence satiety without increasing calorie content. Journal of diabetes science and technology, 10, 971-976. DOI: 10.1177/1932296815626726
Kumar, Vikash; Mittal, Sarthak (2021, December). Smelly Shoes-An Opportunity for Shoe Rack Re-Design. In International Conference of the Indian Society of Ergonomics (pp. 287-293). Singapore: Springer Nature.
Sánchez, Francisco; Melcón, Mariana; Korine, Carmi; Pinshow, Berry (2010). Ethanol ingestion affects flight performance and echolocation in Egyptian fruit bats. Behavioural Processes, 84, 555-558. DOI: 10.1016/j.beproc.2010.02.006
Mennella, J. A.; Beauchamp, G. K. (1991). Maternal diet alters the sensory qualities of human milk and the nursling’s behavior. Pediatrics, 88, 737-744. PMID: 1896276
Dendi, Daniele; Segniagbeto, Gabriel Hoinsoude; Meek, Roger; Luiselli, Luca (2023). Opportunistic foraging strategy of rainbow lizards at a seaside resort in Togo. African Journal of Ecology, 61, 226-227. DOI: 10.1111/aje.13100
Zajenkowski, Marcin; Gignac, Gilles E. (2021). Telling people they are intelligent correlates with the feeling of narcissistic uniqueness: The influence of IQ feedback on temporary state narcissism. Intelligence, 89. DOI: 10.1016/j.intell.2021.101595
Bean, W. B. (1980). Nail growth: thirty-five years of observation. Archives of internal medicine, 140(1), 73-76. DOI: 10.1001/archinte.140.1.73
Renner, Fritz; Kersbergen, Inge; Field, Matt; Werthmann, Jessica (2018). Dutch courage? Effects of acute alcohol consumption on self-ratings and observer ratings of foreign language skills. Journal of Psychopharmacology, 32(1), 116-122. DOI: 10.1177/0269881117735687
Egileez:Leire Sangroniz Kimikan doktorea da eta UPV/EHUko Kimika Fakultatearen PMAS Saileko (Polimero eta Material Aurreratuak: Fisika, Kimika eta Teknologia Saila) ikertzailea Polymaten eta Ainara Sangroniz Kimikan doktorea da eta UPV/EHUko Kimika Fakultateko irakaslea Polymaten.
The post Ig nobel sariak: saguzar mozkorrak eta oinetako kirasdunak appeared first on Zientzia Kaiera.
Rarezas quiméricas: dientes fuera de la boca con funciones sexuales
El Diccionario de la lengua española define “quimérico” como fabuloso, fingido o imaginado sin fundamento, pero aquí nos referimos a una sorprendente peculiaridad recién descubierta en las quimeras u holocéfalos, un pequeño grupo de peces marinos. Los machos de estos peces son el único caso conocido de formación de dientes fuera de la cavidad bucal, unos dientes que usan para sujetar a la hembra durante la cópula.
Vayamos por orden y comencemos por tratar el origen de los dientes en los vertebrados. Los primeros vertebrados aparecieron en el Cámbrico, hace unos 520 millones de años. Carecían de mandíbulas y su cuerpo era blando y vulnerable, pero muy pronto adquirieron una especie de caparazón de hueso dérmico (peces ostracodermos). Este caparazón está cubierto por unos pequeños tubérculos constituidos por dentina (una forma compacta de hueso) y recubiertos por un tipo de esmalte (enameloide). Son los llamados “odontodos” (Figura 1). Cuando los peces desarrollaron mandíbulas a partir del esqueleto branquial, hace unos 420-430 millones de años, aprovecharon los odontodos para fijarlos a las mandíbulas y formar los dientes[1].
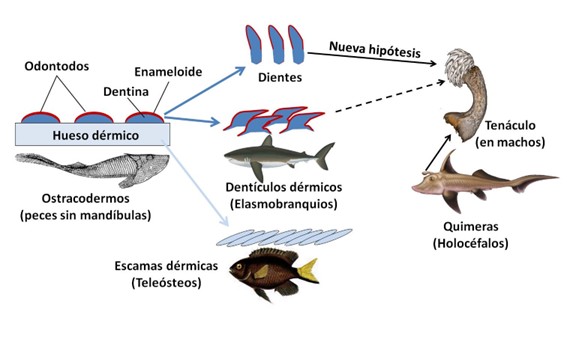 Figura 1. Los odontodos del caparazón de los peces ostracodermos son el origen evolutivo tanto de los dentículos dérmicos de los elasmobranquios como de los dientes. En cambio, las escamas de los teleósteos derivan del hueso dérmico de dicho caparazón. Se pensaba que las espinas del tenáculo de las quimeras derivaban de los dentículos dérmicos (flecha discontinua), pero un nuevo estudio sugiere que se originaron a partir de dientes. Se han utilizado imágenes de Damouraptor, Gasmasque y Cohen et al. (2025), cita completa en referencias, con licencia CC BY 4.0.
Figura 1. Los odontodos del caparazón de los peces ostracodermos son el origen evolutivo tanto de los dentículos dérmicos de los elasmobranquios como de los dientes. En cambio, las escamas de los teleósteos derivan del hueso dérmico de dicho caparazón. Se pensaba que las espinas del tenáculo de las quimeras derivaban de los dentículos dérmicos (flecha discontinua), pero un nuevo estudio sugiere que se originaron a partir de dientes. Se han utilizado imágenes de Damouraptor, Gasmasque y Cohen et al. (2025), cita completa en referencias, con licencia CC BY 4.0.Los peces armados de mandíbulas y dentadura aumentaron de tamaño y llegaron a ser los predadores dominantes durante el periodo Devónico. Paralelamente, el caparazón óseo defensivo disminuyó su importancia, dando lugar a las escamas de los peces (Figura 1). En el grupo de los condrictios (elasmobranquios -es decir, tiburones y rayas- y quimeras) estas escamas retienen la composición de los odontodos primitivos, formados por dentina y un recubrimiento muy duro similar al esmalte dentario. Por eso, el cuerpo de los elasmobranquios actuales está cubierto de dentículos dérmicos derivados de los odontodos. En las quimeras, cuyo linaje se separó muy pronto del de los elasmobranquios, la mayor parte de la piel los ha perdido pero se mantienen en los apéndices copuladores.
Las quimeras forman un grupo muy reducido de peces marinos, alrededor de 50 especies de aguas profundas. A diferencia de tiburones y rayas no tienen dientes individuales, ya que se sueldan formando placas dentarias. Sí comparten con elasmobranquios la fecundación interna, y los machos disponen de una serie de apéndices copuladores en la región pélvica para sujetar a la hembra. Además, los machos tienen un curiosísimo apéndice, el tenáculo, situado entre los ojos, y dotado de unas fuertes espinas (Figura 2). Todo parece indicar que su función es también ayudar en la cópula y se consideraba que sus espinas eran dentículos dérmicos modificados, como los de los apéndices pélvicos.
Hasta ahora. Un estudio publicado en PNAS por investigadores estadounidenses sugiere que el tenáculo está provisto de auténticos dientes, lo que constituiría el único caso conocido entre los vertebrados en que los dientes se desarrollan fuera de la cavidad bucal.
 Figura 2. Macho de quimera (Hydrolagus collei) y detalle del tenáculo. Modificado de Cohen et al. (2025), cita completa en referencias, con licencia CC BY 4.0.
Figura 2. Macho de quimera (Hydrolagus collei) y detalle del tenáculo. Modificado de Cohen et al. (2025), cita completa en referencias, con licencia CC BY 4.0.El estudio consistió en una descripción del desarrollo embrionario del tenáculo en machos de la quimera Hydrolagus collei (Figura 2). Los dientes del tenáculo se desarrollan a partir de una estructura llamada lámina dental, que es la responsable de formar los dientes seriados en los elasmobranquios (recordemos que las quimeras tienen los dientes soldados en placas). Ni los dentículos dérmicos ni las escamas de los apéndices copuladores pélvicos de las quimeras se desarrollan a partir de una lámina dental. Por otro lado, el desarrollo de dientes en elasmobranquios (pero no el de los dentículos dérmicos) requiere la expresión del gen Sox2 (característico de las células madre dentales) y la activación de la proteína b-catenina. Pues bien, estos dos elementos están presentes en el desarrollo de los dientes del tenáculo (Figura 3). Más interesante aún, la expresión de Sox2 se mantiene en la lámina dental del tenáculo adulto, exactamente igual que sucede en las mandíbulas de elasmobranquios. Esta expresión en adultos permite la formación continua de dientes característica de tiburones y rayas.
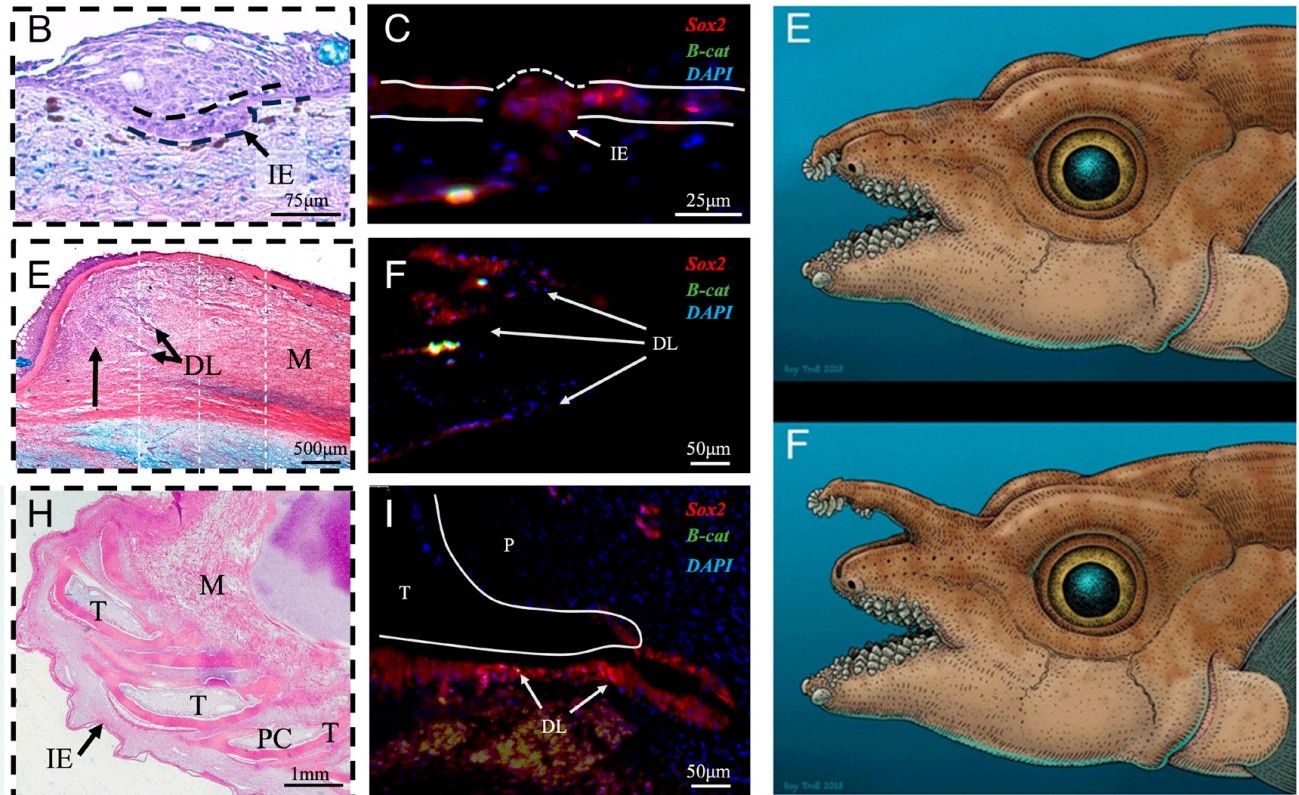 Figura 3. A la izquierda se muestran tres etapas en el desarrollo del tenáculo. Se observa la lámina dental (DL) y los dientes (T) formándose en el interior del tejido. Células de la lámina dental expresan Sox2 (marcador de células madre dentales) y b-catenina. La figura I corresponde a un adulto, y revela que la expresión de Sox2 se mantiene en la lámina dental. Esto es lo mismo que sucede en elasmobranquios, permitiendo una formación continua de dientes en adultos. A la derecha, reconstrucción de la quimera fósil Helodus simplex. Los dientes del largo tenáculo encajan en la sínfisis mandibular. Modificado de Cohen et al. (2025), cita completa en referencias, con licencia CC BY 4.0.
Figura 3. A la izquierda se muestran tres etapas en el desarrollo del tenáculo. Se observa la lámina dental (DL) y los dientes (T) formándose en el interior del tejido. Células de la lámina dental expresan Sox2 (marcador de células madre dentales) y b-catenina. La figura I corresponde a un adulto, y revela que la expresión de Sox2 se mantiene en la lámina dental. Esto es lo mismo que sucede en elasmobranquios, permitiendo una formación continua de dientes en adultos. A la derecha, reconstrucción de la quimera fósil Helodus simplex. Los dientes del largo tenáculo encajan en la sínfisis mandibular. Modificado de Cohen et al. (2025), cita completa en referencias, con licencia CC BY 4.0.¿Cómo es posible que se formen dientes en una estructura localizada entre los ojos, en animales que, además, carecen de dientes aislados en las mandíbulas? La respuesta parece estar en una quimera fósil, Helodus simplex, que vivió hace 315 millones de años y que sí tenía dientes aislados (Figura 3). Los machos de Helodus poseían un largo tenáculo situado en la región etmoidea, y su extremo alcanzaba la sínfisis entre las dos mandíbulas superiores. Es concebible que el epitelio de ese extremo del tenáculo adquiriera capacidad odontogénica durante el desarrollo. A lo largo de la evolución, el tenáculo habría mantenido la capacidad de formar dientes pero se habría reducido en longitud hasta el tamaño actual, al tiempo que los dientes mandibulares terminaron soldándose en placas.
Las quimeras mitológicas eran monstruos híbridos que combinaban partes de distintos animales. Este insólito descubrimiento acerca de dientes extrabucales nos muestra cómo la realidad de la naturaleza puede igualar, si no superar, a la imaginación humana.
Referencias
Cohen, K.E., Coates, M.I., Fraser, G.J. (2025). Teeth outside the jaw: Evolution and development of the toothed head clasper in chimaeras. Proc Natl Acad Sci U S A. doi: 10.1073/pnas.2508054122.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga.
Nota:
[1] Es la llamada hipótesis “de fuera a dentro”. Un modelo alternativo, menos apoyado, es que los dientes proceden de una dentición faríngea que ya estaba presente en ostracodermos.
El artículo Rarezas quiméricas: dientes fuera de la boca con funciones sexuales se ha escrito en Cuaderno de Cultura Científica.
Adimen artifizialaren eragina kontrolaren esparruan
Adimen artifizialaren erabilera bizitzako esparru askotan ematen ari da. Ingeniaritza arloan asko zabaldu diren teknikak ditugu eta zehatzago Sistemen Ingeniaritza eta Automatika eremuan eman direnak aztertzen dira Ekaia aldizkarira aurkeztutako lan honetan.
Automatika eta Kontrolaren arloan erabiltzen diren adimen artifizialeko teknika hauen artean, sistema adituak, logika lausoa, algoritmo ebolutiboak eta neurona-sare artifizialak aurkezten dira. Honez gain, hauen nondik-norakoak eta aplikazioak aztertzen dira.
 Irudia: kontrol adimentsuaren azterketa-ildoak. (Irudiak: Freepik eta unDraw. Iturria: Ekaia aldizkaria)
Irudia: kontrol adimentsuaren azterketa-ildoak. (Irudiak: Freepik eta unDraw. Iturria: Ekaia aldizkaria)Sistema Adituak 70. hamarkadan hedatu zen teknika bat da, non prozesuei buruz izan daitekeen ezagutza aditua erregela bidez adieraztea den helburua. Erregela hauek prozesuan suertatu daitezkeen gertakizunei erantzuna eman ahal izateko sortzen dira. Ezagutza hau giza adituena izan ohi da, eta behin erregela bidez adieraziz gero ezagutza oinarria sortzen da. Ezagutza oinarri honen eta prozesuaren datuak kontuan hartuz, erabakiak automatiza daitezke. Modu honetan, giza adituaren ezagutza ez da galtzen eta errepikatzeko aukera dago. Honen adibide gisa, ur depositu baten tenperaturaren kontrola aurkezten da, non adituaren ezagutzak adierazten digun 50ºC baina gutxiago baditugu berogailua piztu beharko dela eta berau itzali baldin eta 75ºC pasaz gero.
Logika lausoak sistema adituen oinarriak erabiltzen ditu (hala nola; erregela bidezko ezagutza). Erregela hauek boolearrak izan ordez, multzo lausoak erabiltzen dituzte, modu honetan kontzeptu zehaztugabeak adierazteko (adibidez, zer da prozesu batean tenperatura altua edo baxua izatea?). Logika lausoa prozesuen kontrolagailu eta prozesuen eredu gisa erabili ohi da. Ur deposituaren tenperatura kontrolarekin jarraituz, tenperatura neurketa lausotze prozesu batetik pasatzen da, eta zenbakizko datua tenperatura baxua edo altu gisa aztertzen da. Nolabait, gizakiok erabil dezakegun hitz egiteko modu bati gerturatzen da logika lausoa.
Algoritmo ebolutiboak naturan ematen den eboluzio biologikoari begira dagoen teknika multzoa da, bertan sailkatu ditzakegu algoritmo genetikoak, partikula-multzo bidezko optimizazioa edo inurrien kolonia bidezko optimizazioa. Teknika multzo hauek prozesuetan eta hauen kontrolean agertzen diren optimizazio arazoei aurre egiteko erabiltzen dira, baita diseinu atalean ere, optimizazio arazo konplexuei aurre egiteko aurkezten duten onuragatik.
Azkenik, gaur egun oso ezagunak diren neurona-sare artifizialak aurkitzen dira. Hau ere naturari begira dagoen teknika bat da, non giza burmuinak dituen neuronak eredu gisa erabiltzen dituen informazioa prozesatu ahal izateko. Hauen potentziala askatzeko, sare batean elkartzen dira neuronak eta honela daukaten prozesamendu ahalmena biderkatzen da. Sare hauek prozesuen datu eta informaziotik ikas dezakete, eta lortutako informazioa modu ezberdinetara aplika daiteke, adibidez ereduztapenean, kontrolean, etab.
Hemen adierazi diren teknika ezberdinak badute beraien erabilera kontrol esparruan, baina ez dira bakarrak. Teknika esanguratsuenak eta hauen aplikazioak aurkeztu nahi izan dira Ekaia aldizkarian argitaraturiko lanean. Honez gain, teknika bakoitzean aurkitu daitezkeen ikertzaile garrantzitsuenetarikoak ere izendatzen dira irakurleak teknika konkreturen baten ildoa jarraitu nahiko balu.
Artikuluaren fitxa:- Aldizkaria: Ekaia
- Zenbakia: Ale berezia Adimen artifiziala
- Artikuluaren izena: Adimen Artifizialaren eragina kontrolaren esparruan.
- Laburpena: Adimen artifizialak kontrolaren esparruan duen eraginari buruzko ikuspegi bat eman nahian sortu da lan hau. Kontrol-teknika klasikoak alde batera utzi gabe, kontrol adimentsua zer esparrutan zabaltzen den aztertu dugu, horretarako ikuspegi akademikoa eta industriala uztartuz. Adimen konputazionaleko zenbait teknika azaldu, eta haien aplikazio-esparrua aztertu dugu, kontrol-arazoak ebaztean egiten den aplikazioaren adibide argigarriak emanez. Gaur egun, adimen artifizialean oinarritutako aurrerapen teknologikoen hazkunde esponentziala nabarmena den unean, horrek ingeniaritzan eta konputazioaren zientzian duen eragina azaldu dugu.
- Egileak: Mikel Larrea Sukia, Aritz Etxebarri Coello, Eloy Irigoyen Gordo eta Lucia Iturbe Rey
- Argitaletxea: EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 203-227
- DOI: 10.1387/ekaia.26345
Mikel Larrea Sukia eta Aritz Etxebarri Coello EHUko Gipuzkoako Ingeniaritza Eskolako ikertzaileak dira.
Eloy Irigoyen Gordo eta Lucia Iturbe Rey EHUko Bilboko Ingeniaritza Eskolako ikertzaileak dira.
Ekaia aldizkariarekin lankidetzan egindako atala.

The post Adimen artifizialaren eragina kontrolaren esparruan appeared first on Zientzia Kaiera.
¿Cuándo podremos decir que “hemos encontrado vida en Marte”?
 Las manchas de leopardo encontradas en el crater Jerezo de Marte podrían indicar que, hace miles de millones de años, las reacciones químicas en esta roca podrían haber sustentado vida microbiana. Foto:NASA/JPL-Caltech/MSSS, CC BY
Las manchas de leopardo encontradas en el crater Jerezo de Marte podrían indicar que, hace miles de millones de años, las reacciones químicas en esta roca podrían haber sustentado vida microbiana. Foto:NASA/JPL-Caltech/MSSS, CC BYUna roca moteada, bautizada como “Cheyava Falls” y situada en un antiguo cauce fluvial del cráter Jezero, ha encendido de nuevo una pregunta antigua con traje moderno: ¿hay o hubo vida en Marte?
Entre minerales rojos e indicios orgánicos, la NASA acaba de anunciar el hallazgo de posibles biofirmas en un roca marciana. El comunicado ha desatado el frenesí, pero en ciencia es un frenesí cauto.
Este es un análisis –con los pies en los datos– sobre pistas, escalas de certeza y lo que significaría oír, por fin, un “sí, esto es vida extraterrestre”. Pero aún no ha llegado el momento.
Los indicios de vida en MarteDesde hace años, la NASA ha ido informando de hallazgos que se acercan a lo que podría parecerse a una huella de vida.
En 1976, las sondas Viking realizaron los primeros experimentos biológicos en Marte. Sus resultados fueron intrigantes, pero también muy polémicos, y no se consideraron una prueba concluyente de vida. Desde entonces, ninguna misión ha vuelto a llevar experimentos tan directos. La lección de Viking es clara: en la exploración del planeta rojo, conviene mantener la curiosidad… pero también la cautela en las expectativas.
En 2018, la NASA informó de indicios de vida orgánica en barro antiguo de Marte. Entonces el rover Curiosity detectó en el cráter Gale moléculas orgánicas preservadas en lutitas lacustres (un tipo de roca sedimentaria, compuesta por partículas muy finas de arcilla y limo que se depositaron en el fondo de los lagos) de aproximadamente 3500 millones de años, así como una variación estacional del metano de fondo. Son ingredientes y pistas, pero no es propiamente vida.
En el estudio reciente, la NASA informa que en la zona conocida como Bright Angel, el instrumento SHERLOC del rover Perseverance también identificó la presencia de moléculas orgánicas, mientras que el instrumento PIXL mapeó minerales como vivianita y greigita en un lodo rico en hierro, fósforo y azufre.
Pero este tipo de mezcla puede formarse tanto por la acción de microorganismos como por procesos puramente químicos. Así que puede ser un indicio de vida, o no.
Esa ambigüedad es justo lo que resalta la síntesis publicada en Nature, que subraya cómo estos hallazgos mantienen abierto el debate sobre si Marte albergó vida o no.
Las muestras de metanoAnteriormente, el Curiosity detectó variaciones locales y estacionales en la presencia de metano en el planeta vecino, algo que también podría asociarse con una biofirma. Sin embargo, el orbitador europeo TGO (de la misión ExoMars) no ha encontrado prácticamente nada: sus mediciones ponen un límite global muy estricto, menos de 0,05 partes por mil millones.
El reto ahora es conciliar ambos resultados: ¿se trata de pequeñas emisiones superficiales que la atmósfera elimina rápidamente, o de mediciones que están sesgadas por factores aún desconocidos? La ciencia sigue en curso y la respuesta todavía no está cerrada.
¿Qué sería una prueba irrefutable?Tras varias decepciones, la comunidad científica ha elaborado una “escala de confianza” para detectar vida, llamada Confidence of Life Detection (CoLD).. Es como una escalera de siete peldaños: primero se detecta una posible señal y después hay que descartar contaminación; demostrar que la biología sería viable en ese entorno; excluir explicaciones no biológicas; encontrar otra señal independiente; derrotar hipótesis alternativas… y, por último, conseguir confirmación por distintos equipos. ¿Cómo se sube esa escalera? No con un único hallazgo espectacular, sino con varias pruebas que, juntas, formen un caso sólido.
Una química orgánica compleja con homoquiralidad (se refiere a moléculas que tienen una estructura no superponible con su imagen especular, similar a la de nuestras manos) sería un buen indicio, porque es extremadamente difícil de generar sin vida.
Otro rastro lo darían los isótopos: variaciones en elementos como el carbono o el azufre que, dentro de su contexto geológico, se ajusten a lo que esperaríamos de procesos biológicos. Sin ese contexto, el isótopo puede engañar.
También podrían encontrarse texturas microscópicas que recuerden a células o biofilms, siempre asociadas a moléculas orgánicas e isótopos de “firma biológica”.
Una sola pista nunca basta: se necesitan varias, y que se repitan de manera independiente, con instrumentos distintos.
Lo ideal sería confirmar en la Tierra, con muestras traídas de Marte bajo protocolos estrictos para evitar contaminación. Al final, no se trata de obtener una foto espectacular, sino un expediente coherente y abrumador.
De Europa a Venus¿Y en qué otros mundos podría asomarse la vida? Estos son los candidatos:
- Europa (Júpiter). Es el favorito: oculta un océano salado bajo el hielo. la misión Europa Clipper, que llegará hacia 2030, hará casi 50 sobrevuelos para estudiar si allí existen condiciones habitables. No busca vida directamente, pero sí comprobar si podría haberla.
- Encélado (luna de Saturno). Sus espectaculares géiseres conectan el océano interno con el espacio. Allí se ha detectado fósforo en abundancia, un nutriente esencial para la vida. Es, literalmente, un laboratorio natural abierto.
- Titán (luna de Saturno). Con su atmósfera densa y rica en compuestos orgánicos, es un lugar único para explorar química prebiótica. La misión Dragonfly despegará a finales de esta década (si no entra en el grupo de recortes de Donald Trump) y aterrizará hacia mediados de los 30, para estudiar si podrían darse formas de bioquímica distintas a las terrestres.
- Venus. En sus nubes se han detectado posibles rastros de fosfina, aunque el debate sigue abierto. Para unos es una señal sugerente; para otros, un artefacto de las observaciones. El debate es un buen antídoto contra el autoengaño.
En ciencia y tecnología, aceleraríamos las misiones de retorno de muestras y desarrollaríamos sistemas de contención de máximo nivel, además de nuevas herramientas para detectar formas de vida “no terráqueas”; en filosofía, nos obligaría a dejar de confundir singularidad con privilegio; en religión, probablemente inspiraría lecturas más inclusivas de la creación, más que crisis de fe; en política y ética, reforzaría la necesidad de no contaminar otros mundos ni traer riesgos a la Tierra.
Y en lo cotidiano, se abriría la puerta a nuevos materiales, sensores y biotecnologías
Pero más allá de lo práctico, nos brindaría una cura contra el provincianismo: nos recordaría que no somos el centro del universo.
¿Cuándo podríamos afirmarlo rotundamente?Hay dos ventanas realistas. En primer lugar, hacia la década de 2030. El rover europeo Rosalind Franklin, cuyo lanzamiento está previsto para 2028, llegará a Marte en unos cinco años. Está diseñado para perforar hasta dos metros bajo la superficie, donde la radiación no ha destruido los compuestos más delicados. Con su instrumento MOMA podría encontrar moléculas orgánicas complejas, señales de quiralidad (esa preferencia por una “mano” molecular que suele asociarse a la vida) y posibles texturas biológicas. No será fácil, pero las posibilidades están ahí.
La segunda ventana sería el retorno de muestras. La misión conjunta de NASA y ESA, que busca traer rocas marcianas a la Tierra, se ha encarecido y retrasado, por lo que lo más probable es que su “veredicto de laboratorio” no llegue antes de la década de 2040.
Eso sí, incluso si la roca Cheyava Falls ofrece biofirmas tentadoras, la confirmación no llegará con un único indicio. Habrá que recorrer toda la “escalera CoLD”: descartar explicaciones no biológicas y repetir pruebas de forma independiente, idealmente en laboratorios terrestres. El calendario es incierto. Mientras tanto, el escepticismo no supone un freno: es la dirección en la que vamos.
Si la vida marciana existe o existió, nos esperará, no tiene nuestras prisas. Y si no existió nunca, el hallazgo más grande será comprender por qué aquí sí. Esa respuesta también nos pertenece y entusiasma.![]()
Sobre el autor: José Ygnacio Pastor Caño, Catedrático de Universidad en Ciencia e Ingeniería de los Materiales, Universidad Politécnica de Madrid (UPM)
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Cuándo podremos decir que “hemos encontrado vida en Marte”? se ha escrito en Cuaderno de Cultura Científica.
Elena Vecino: «Glaukoman itsumena eragiten duen kausa deskubritu nahi nuke, hura eragotzi ahal izateko»
Elena Vecino Cordero Biologia Molekular eta Histologian katedraduna da Euskal Herriko Unibertsitatean, bai eta neuroftalmologiako munduko aditurik handienetako bat ere. Bere lanen artean nabarmentzekoak dira glaukomari, malkoari (gure osasunari buruzko informazio iturri gisa) eta erretinosi pigmentarioari buruzkoak. Horrez gain, Arte Ederretan lizentziaduna da Euskal Herriko Unibertsitatean, eskultura modalitatean. Bere alderdi artistikoa zientzia dibulgazioaren alde erabili du nazioko zein nazioarteko museo eta kultura espazioetan eginiko erakusketen bidez. Ikerketan lortutako emaitzen ondorioz, sariak jaso ditu nazioarteko erakundeen eskutik. Besteak beste: Estatu Batuetako Glaukomaren Fundazioa (2004), Fundaluce (2004), Fundación ONCEren Nazioarteko Lehen Saria (2005) eta Alcon Fundazioaren Saria Glaukomaren Ikerketako Bikaintasunari (2015).
 Irudia: Elena Vecino Cordero ikertzailea. (Argazkia: Elena Vecinok emana.)Zein da zure ikerketa arloa?
Irudia: Elena Vecino Cordero ikertzailea. (Argazkia: Elena Vecinok emana.)Zein da zure ikerketa arloa?
Neuroftalmologia. Glaukoma eragiten duten kausak ikertzen ditut. Glaukoma gaixotasun neurodegeneratiboa da, bai eta munduan itsutasuna eragiten duen lehen kausa ere. Erretina neurobabesteko eta malkoan biomarkatzaileak identifikatzeko terapiak diseinatzen saiatzen gara, gaixotasun neurodegeneratiboak goiz diagnostikatu ahal izateko.
Zergatik aritzen zara arlo horretan?1981ean biologiako karreran ikasketak hasi nituenetik, nerbio sistema eta, bereziki, ikusmen sistema interesatu zitzaizkidan. Lehenengo urteetan ikusmen sistemaren eta erretinaren funtzionamendua ikasi nituen sakonago, bereziki anatomia konparatuaren eta garapenekoaren ikuspegitik. Baina, duela 30 urte Euskal Herriko Unibertsitateko Medikuntza eta Erizaintza Fakultatean sartzean, balantzak biomedikuntzaren eta oftalmologiaren arlorantz jo zuen, eta ikertalde bat osatu genuen (GOBE). Taldean oftalmologiako doktoregoko ikasleak sartzeak medikuntzara aplikatutako ikerketarantz motibatu nau.
Izan al duzu erreferentziazko figurarik zure ibilbidean?Pertsona askok izan dute eragina nire ibilbide profesionalean; gauza asko ikasi ditut haiengandik, eta horrek ere markatu du nire ibilbidea. Karrera profesionala hasten ari nintzela, New York Medical Collegeko Sansar C. Sharma doktoreak bere laborategira gonbidatu ninduen, oraindik doktorego tesia amaitu gabe nengoenean. Harengandik ikasi nituen ikertzailea izateko oinarriak: sen kritikoa, proiektu bat eskatu eta ebaluatzeko modua, artikulu bat idazteko prozesua. Eta, egun, harremanetan jarraitzen dut berarekin. Erretiratuta dago jada, baina proiektuei buruz eztabaidatzen jarraitzen dugu. Zalantzarik gabe, maisu figura bat izan da.
Ikerketaren aplikazioaren alderdiari dagokionez, Pennsylvaniako Unibertsitateko Gustavo Aguirre doktoreak ikerketa preklinikoan parte hartzeko aukera eman zidan, eta, horri esker, ikusmen sisteman lehen terapia genikoa izan denaren lehen urratsak ikusi ahal izan nituen.
Parisko Hôpital Pitie-Salpêtrière ospitaleko ikertzaile Cuca Alvarado-Mallart doktorea izan zen nire lehen emakumezko ikertzaile erreferentea. Bere jakintzak eta profesionaltasunak, eskuzabaltasunak, umiltasunak eta adeitasunak pentsarazi zidaten egunen batean ezaugarri horiek guztiak eta Cucaren jarrera bilduko zituen ikertalde bat zuzendu nahi nuela. Ez dut sekula ahaztuko.
Horrez gain, Lundeko Unibertsitatean (Suedia) nire tesiko zuzendari izan zen Peter Ekström doktoreak ere eragina izan du nire lanean; zalantzarik gabe, nire laborategiko ordenak eta diziplinak suediar jatorria dute. Mundu osoko hamahiru laborategitan egin dut lan, eta horietako guztietako langileekin jarraitzen dut harremanetan eta lankidetzan. Egonaldi bakoitzean ikasi dut zerbait nire lankideengandik, eta horrek guztiak nire ibilbidea bideratu du pixkanaka. Egun, ikasten jarraitzen dut egin behar dudanari eta egin behar ez dudanari buruz.
Zer aurkitu edo konpondu nahiko zenuke zure arloan?Glaukoman itsumena eragiten duen kausa deskubritu nahi nuke, hura eragotzi ahal izateko. Eta jada glaukoma duten pertsonei begira, ikusmena berreskuratu ahal izateko terapia bat garatu nahi nuke.
Zer aholku emango zenioke ikerketaren munduan hasi nahi duen norbaiti?Ikerketa txundigarria da, baina pasioa eta jakingura sentitzea ezinbestekoa da lan horretarako, oso gogorra baita. Hasteko, oso aldi gogorrak bizi behar dira egonkortasuna lortu eta zure esparruan ikerketa eta aintzatespen nitxo bat aurkitzeko. Eta, ondoren, bizitza osoa dedikatzen dugu finantzaketa aurkitzera. Ikerketaren emaitzei dagokienez, beti egongo dira frustrazio uneak, euforiaz eta zoriontasunaz ere lagunduta. Hau da, oso ziur egon behar da eta jakingura izan behar da ikerketako karrera batera arrakastaz dedikatzeko. Barru-barruan sentitu behar da; oso bokazionala da.
Jatorrizko elkarrizketa Mujeres con Ciencia blogean argitaratu zen 2025eko martxoaren 1ean: Elena Vecino: «Me gustaría descubrir la razón que causa la ceguera en el glaucoma y poder impedirla».
Itzulpena: UPV/EHUko Euskara Zerbitzua.
Ikertzen dut atalak emakume ikertzaileen jardunari erreparatzen die. Elkarrizketa labur baten bidez, zientzialariek azaltzen dute ikergai zehatz bat hautatzeko arrazoia zein izan den eta baita ere lanaren helburua.
The post Elena Vecino: «Glaukoman itsumena eragiten duen kausa deskubritu nahi nuke, hura eragotzi ahal izateko» appeared first on Zientzia Kaiera.
La química del olfato vibra
Respiramos más de 20.000 veces al día. Es un mecanismo inconsciente y automático, imprescindible para sobrevivir. Al inhalar, obtenemos el oxígeno que nuestro cuerpo necesita para funcionar, lo transformamos en CO2 y lo exhalamos. Sin embargo, junto al oxígeno, entran en nuestro organismo otras muchas moléculas como nitrógeno, bacterias o virus. Toda esta mezcla nos aporta una ingente cantidad de información sobre nuestro entorno, tanta que contamos con un sentido especializado para poder descifrarla: el olfato.
Gracias a él, somos capaces de identificar con los ojos cerrados a quien tenemos al lado, sortear un peligro inminente, o viajar de golpe a un verano de la infancia. Pero, ¿cómo funciona este gran detective alojado en nuestra nariz?
La química Elixabete Rezabal, experta en química física y profesora titular en la facultad de Química de la EHU, lo explicó durante el decimoquinto aniversario de Naukas Bilbao, en una charla dedicada a la química que se esconde tras este misterio.
 © Iñigo Sierra | Cátedra de Cultura Científica de la EHU.La teoría clásica del olfato
© Iñigo Sierra | Cátedra de Cultura Científica de la EHU.La teoría clásica del olfato
La teoría clásica sostiene que al fondo de la nariz y cerca del cerebro tenemos una serie de proteínas receptoras que captan las moléculas procedentes del exterior. Si una de ellas encaja de la forma adecuada, se activa una señal que nuestro cerebro reconoce como un olor.
“Nos han contado que oler es como meter la llave correcta en la cerradura nasal: si la llave encaja, la cerradura se abre y la señal pasa al cerebro, y nosotros detectamos ese olor”, explicó Rezabal. Por esta teoría, que describe el funcionamiento del olfato, los investigadores Linda Buck y Richard Axel recibieron el Premio Nobel de Medicina en 2004.
Sin embargo, como subrayó la química, esta explicación no siempre funciona. ¿Qué ocurre, por ejemplo, con las moléculas que tienen casi la misma forma, pero huelen de manera radicalmente diferente? Pongamos el caso de una molécula formada por un grupo alcohol, compuesto por un oxígeno unido a un hidrógeno. Puede oler a hierba recién cortada. No obstante, si sustituimos ese oxígeno por un azufre, la geometría se mantiene, pero el olor se convierte en el de un huevo podrido. La forma, por tanto, no basta para explicar cómo procesamos los olores.
 © Iñigo Sierra | Cátedra de Cultura Científica de la EHU.
© Iñigo Sierra | Cátedra de Cultura Científica de la EHU.Para ofrecer una respuesta, Rezabal expuso la atrevida teoría del biofísico Luca Turin y su equipo de colaboradores del MIT, quienes en 1996 propusieron una teoría alternativa en la que planteaba que nuestra nariz no detecta la forma de las moléculas, sino sus vibraciones a nivel cuántico.
¿Y si lo que olemos son vibraciones?
Su hipótesis partía de la idea de que las moléculas no solo tienen una geometría, sino que no paran de moverse. A temperatura ambiente, vibran de manera constante, pero no de cualquier manera. Esto, en palabras de Rezabal, se debe a que “la energía vibracional está cuantizada, lo que quiere decir que sólo ciertos modos de vibración están permitidos, cada uno con su energía”.
El agua es un buen ejemplo. Se trata de una molécula simple que, debido a su geometría, tiene tres modos de vibración, “tres pasos de baile”, cada uno con una energía asociada. Si recibe la cantidad exacta de energía del entorno, puede vibrar de otra manera y subir al siguiente escalón. Y así hasta alcanzar el tercer nivel.
 © Iñigo Sierra | Cátedra de Cultura Científica de la EHU.
© Iñigo Sierra | Cátedra de Cultura Científica de la EHU.Por su parte, el agua deuterada -conocida como agua pesada- es idéntica en su forma al agua, con la salvedad de que los átomos de hidrógeno son sustituidos por deuterio, que incorpora un neutrón, además de un protón, en su núcleo. Esto hace que los átomos sean más pesados y que las energías necesarias para pasar de un modo de vibración a otro sean diferentes. En definitiva, la forma es la misma, en cambio, sus vibraciones no lo son.
En la mente de Turin, si el olfato se basa en las vibraciones, se debería poder distinguir el agua del agua pesada. Para comprobar su teoría, él y su equipo realizaron experimentos con un animal de olfato extremadamente fino, la mosca de la fruta.
Acertó. Estos insectos se acercaban al agua y se alejaban del agua pesada. Entonces, ¿qué hace nuestra nariz para detectar este fenómeno cuántico?
A partir de este curioso experimento, se desarrolló el concepto del túnel cuántico de la nariz. Un mecanismo que aprovecha las propiedades cuánticas de los electrones para identificar moléculas basándose en sus vibraciones, de manera similar a ciertos espectrómetros de laboratorio, como la espectroscopía de túnel inelástico de electrones, Inelastic Electron Tunneling Spectroscopy (IETS), en inglés.
La nariz, un espectrómetro biológico
“Esta teoría actual lo que propone es que cuando la molécula se une, hay un electrón que tiene que pasar de una parte de la proteína a otra, lo que genera una transferencia de energía que manda una señal al cerebro”, resumió.
 © Iñigo Sierra | Cátedra de Cultura Científica de la EHU.
© Iñigo Sierra | Cátedra de Cultura Científica de la EHU.Hay que tener en cuenta que la molécula siempre estará vibrando o “bailando” en su nivel más bajo de energía, pero si la energía que necesita para saltar al siguiente modo de vibración coincide exactamente con la que tiene que liberar el electrón para poder moverse, la transferencia se produce y se activa el olor en nuestro cerebro. En cambio, si la energía que necesita la molécula odorífera para subir de escalón no es la misma que requiere el electrón, no habrá transferencia y, por tanto, el olor no se activará.
Más allá de la curiosidad científica, Turin aplicó este concepto de la teoría de la vibración olfativa para fundar Flexitral, una empresa -ya extinta- al servicio de la industria de la perfumería. ¿Cómo? Calculando los modos vibracionales de las moléculas, el biofísico libanés era capaz de sustituir compuestos carísimos, apreciados por los perfumistas por su particular aroma, por otros más baratos que vibraban del mismo modo y, por tanto, olían igual.
Rezabal cerró su intervención en Naukas Bilbao 2025 recordando que la mecánica cuántica, aunque pueda parecernos lejana, está más presente en nuestra vida cotidiana de lo que podamos imaginar, ya que “muchos fenómenos de nuestro cuerpo se basan en principios cuánticos”. Y, en el caso del olfato, todo apunta a que el secreto está en la vibración.
Si no ve correctamente el vídeo, use este enlace.
Sobre la autora: María Larumbe es periodista y responsable de comunicación de la Cátedra de Cultura Científica de la Universidad del País Vasco / Euskal Herriko Unibersitatea.
El artículo La química del olfato vibra se ha escrito en Cuaderno de Cultura Científica.
Gure lehengusu neandertalak
Gizaki anatomikoki modernoak Eurasiara iritsi zirenean, Neandertalak aurkitu zituzten: sendoagoak, indartsuagoak eta klima hotzera moldatuagoak ziren lehengusuak. Ez dira gure arbaso zuzenak… edo agian bai? Teknologia nahiko sofistikatua zuten, Mousteriar kulturako harrizko tresnak, sua pizteko gaitasuna, arropa sinpleak, sendabelarrak erabiltzeko ezagutza eta janaria sukaldatzeko moduak. Baliteke pentsamendu sinbolikoa eta hizkuntza artikulatua ere izatea. Anatomikoki, ordea, ez ziren gu bezalakoak: bekoki atzeratua, sudur handiagoa eta kokotsik gabea zuten, baita argi gutxiko ingurura moldatuta zeuden.
Orain dela 40.000 urte inguruan desagertu ziren, baina zergatik ez dakigu ziur: Homo sapiensen presioa, populazio txikien isolamendua, klima-aldaketak edo sumendi baten eztanda izan zitezkeen arrazoiak. Hala ere, guztiz desagertu ez ziren: gizaki modernoekin nahastu ziren eta gaur egungo europar eta asiarren genomaren % 3 inguru neandertalen jatorrikoa da. Gainera, Denisovarrekin egindako nahasketek are konplexuagoa egiten dute gure arbasoen sarea. Gaur dakigunez, gure arbasoak Afrikatik atera eta beste giza taldeekin gurutzatu ziren, giza historia korapiloz betetako sare handia bilakatuz.
“Gure arbasoak” Ikusgela hezkuntza proiektuaren bideo-sorta bat da. Euskal Wikilarien Kultur Elkartearen ikus-entzunezko egitasmoa da eta EHUko Kultura Zientifikoko Katedraren kolaborazioa izan du.
The post Gure lehengusu neandertalak appeared first on Zientzia Kaiera.

