Lurraren magnetismoaz (III)
Zientziaren ikuspuntua soilik hartuta, XIX. mendearen bukaerarako nazioarteko izaera zuen hartua Lurraren magnetismoari buruzko ikerketak, hedatzen hasiak ziren arloko estatuz gaindiko erakundeak eta, gainera, magnetismo-ikerketak baizik argitaratzen ez zituen aldizkaria zen sortua, 1896an: Terrestrial Magnetism.
Mendearen lehen hamarkadetan nabarmen handitu zen eskura zeuden datuen kopurua eta kalitatea, baina ez aurrerapen teorikoa. 1947ra arte itxaron beharko zuen horrek: eguzkiaren eta beste izar batzuen hainbat eremu magnetikoren neurketak argitaratu ostean, Patrick Blackett-ek urte hartan iradoki zuen magnetismoa, Lur planetako fenomenoa ez ezik, errotazioan zegoen gorputz ororen propietatea izan zitekeela. Aldi berean, 1946 eta 1947 bitartean, Walter Maurice Elsasser fisikariak dinamo planetario baten eredu matematikoa azaldu zuen zenbait artikulutan; haren arabera, Lurraren nukleoaren kanpo-geruzan eragindako korronte elektrikoengatik sortzen zen eremu magnetikoa. Elsasser, bere eredu hori diseinatu eta garatu bitartean, Estatu Batuetako Armadaren Komunikazio Taldearentzat zebilen lanean, Bigarren Mundu Gerraren testuinguruan.
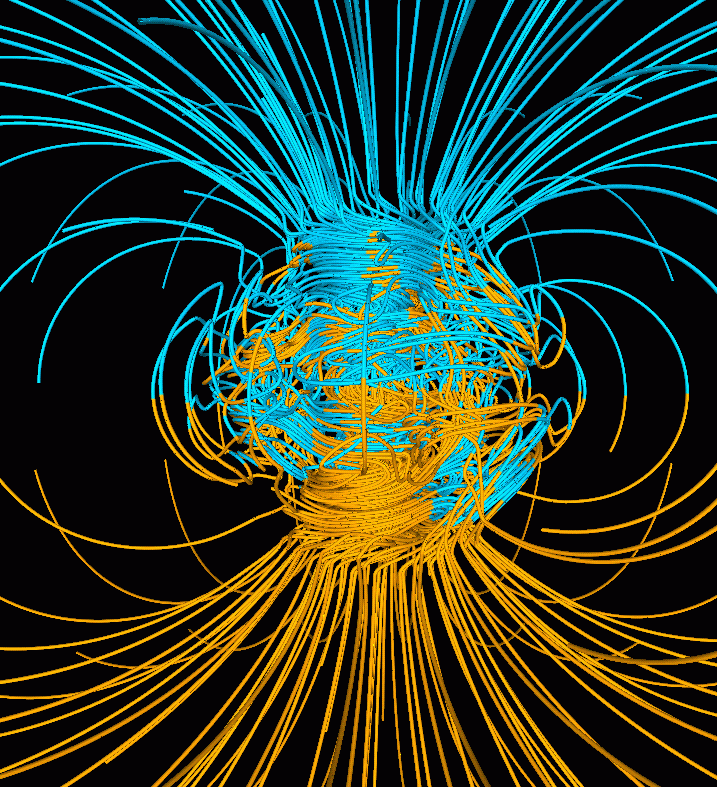 Irudia: Lurraren eremuko lerroen simulazioa, inbertsioen arteko aldi estandar batean. (Iturria: Cuaderno de Cultura Científica)
Irudia: Lurraren eremuko lerroen simulazioa, inbertsioen arteko aldi estandar batean. (Iturria: Cuaderno de Cultura Científica)Hurrengo urteetan zehar, zientzialariek bi ereduen alde on eta txarrak aztertu zituzten. Orduan, 1952an, Blackettek berak baztertuko zuen bere teoria; izan ere, porrot egin zuen momentu angeluarraren eta momentu magnetikoaren arteko lotura esperimentalki frogatzeko ahaleginean. Data hartatik gaur arte Elsasserren eredua da erreferentzia, nahiz eta oraindik aurkitu ez den bildu diren behaketa guztiak zenbaki bidez deskribatzeko modua.
Blacketten esperimentuen porrota eta gero, beste aurkikuntza batzuk egin ziren paleomagnetismoaren arloan, eta erabakigarriak izan ziren teoria geologikoan, batik bat plaken tektonikari dagokionez. Horiek guztiek are gehiago zailtzen zuten Elsasserren lanean oinarrituko zen eredu doitua lortzea Lurraren magnetismoa azaltzeko.
XIX. mendean zientzialariek bazekiten magnetismo fosilizatua zegoela. Konturatuta zeuden buztin mota batzuek eta solidoturiko laba-ibaiek gorde egiten zutela Lurraren eremu magnetiko nagusiarekiko lerrokadura magnetikoa buztin eta laba horiek hoztu ziren unean zegoen bezalaxe. XX. mendeko berrogeita hamarreko hamarkadan, magnetismo fosilizatua sistematikoki kartografiatzen zuten geologoek ondorioztatu zuten ipar-poloak, iraganean, etengabe aldatu izan zuela bere posizioa.
Aurkikuntza hura hain zen apartekoa, ezen denetariko hipotesiak mahaigaineratu baitziren: neurketa-tresnek berek sortzen zutela efektua, eremu magnetikoa ez zela beti dipolarra izan, kontinenteak mugitu egin zirela bata bestearekiko, polo bakoitza bere kasa desplazatu izan zela… Hamarkadaren bukaerarako, hainbat daturi esker, Londreseko Unibertsitateko eta Australiako Unibertsitate Nazionaleko zientzialari talde batek ondorio argia aurkeztu zuen, Newcastle-ko Unibertsitateko Keith Runcorn-en gidaritzapean: kontinenteak desplazatu egin ziren. Hala, makal samar zebilen kontinenteen jitoaren teoria berpiztu zuten.
Bestalde, hogeita hamarreko hamarkadan frogatua zen magnetismo fosilizatuaren beste ezaugarri bat: harri batzuetan polaritate magnetikoa gaur egunekoaren aurkakoa zela. Poloek, hortaz, Lurrean harat-honat ibiltzeaz gain, batzuetan posizioak trukatu ere egiten zituzten. Hirurogeiko hamarkadaren erdialdean, datazio erradioaktiboko teknikak erabilita, trukaketa horien historia berreraikitzea lortu zen. Itsas zoruaren sorreraren eta hedapenaren teoriarako giltzarri izango ziren trukaketa haiek.
——————————————–
Egileaz: Cesár Tomé López (@EDocet) zientzia dibulgatzailea da eta Mapping Ignorance eta Cuaderno de Cultura Cientifica blogen editorea.
Itzulpena: Lamia Filali-Mouncef Lazkano
Hizkuntza-begiralea: Xabier Bilbao
——————————————–
The post Lurraren magnetismoaz (III) appeared first on Zientzia Kaiera.
La transformación radiactiva
 Foto: davisco / Unsplash
Foto: davisco / UnsplashRutherford y Soddy propusieron un modelo muy audaz de la transformación radiactiva para explicar la naturaleza de estos cambios. Sugirieron que cuando un átomo radiactivo emite una partícula alfa o beta, en realidad lo que ocurre es que se rompe en dos partes: la partícula alfa o beta que se emite y una parte sobrante con la mayor parte de la masa que es física y químicamente diferente del átomo “progenitor”.
Había mucha pruebas que apoyaban esta última parte del modelo. Por ejemplo, se sabía que se formaba gas radón a partir del radio. Cuando se determinó la masa atómica del radón, resultó ser más pequeña que la del radio en solo cuatro unidades de masa atómica, la masa de una partícula alfa.
La idea de transformación radiactiva se puede representar mediante una «ecuación» similar a la que se utiliza para representar reacciones químicas. Por ejemplo, usando los símbolos Ra y Rn para representar átomos de radio y radón, y He para representar una partícula alfa después de que ha recogido dos electrones para formar un átomo de helio, la transformación del radio en radón se puede expresar como
Ra → Rn + He.
El proceso se puede describir como la transformación, también llamada “desintegración”, o “transmutación”, del radio en radón, con la emisión de una partícula alfa.
Muchos procesos de desintegración, además del ejemplo recién citado, habían sido encontrados y estudiados por los Curie, por Rutherford y sus compañeros de trabajo, y por otros, y estos procesos encajaban fácilmente en el modelo propuesto por Rutherford y Soddy [1]. Por ejemplo, el radón también es radiactivo, emite otra partícula alfa y, por lo tanto, se transmuta en un átomo de un elemento que en ese momento se llamó «radio A». Más tarde se demostró que el radio A era polonio (Po):
Rn → Po + He.
El polonio también es un sólido radiactivo. De hecho, los átomos de radio “progenitores” originales experimentan una serie o cadena de transformaciones en una generación tras otra de nuevos elementos radioactivos “hijos”, que termina con un elemento hijo que no es radiactivo o, en otras palabras, estable. Estas series radiactivas son tan importantes que las veremos con más detalle.
Notas:
[1] Es reseñable que tanto Rutherford (1908) como Soddy (1921) recibieran su premio Nobel en química, no en física. También es cierto que Rutherford habría merecido un segundo premio Nobel en física, porque la mayor parte del trabajo por el que es famoso lo hizo después de su premio Nobel; recordemos que su modelo nuclear del átomo es de 1911.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La transformación radiactiva se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La ratonera de Rutherford y Royds
- La radiactividad no es una reacción química
- Rayos alfa, beta y gamma
Moda lasterraren ingurumen prezioa
Ikus ditzagun industria honek dituen efektuen neurria irudikatzeko datu batzuk. Modaren industriak 1.700 milioi tona CO2 baino gehiago sortzen du urtero, hau da, gas horren emisio guztien % 10 inguru. Ur kontsumoari dagokionez, sektore hau bigarren tokian dago: 1.500 milioi metro kubiko ur inguru kontsumitzen du; uraren kutsadura industrialaren % 20 modaren industriari dagokio, ehunak tratatzeko eta tindatzeko jardueren ondorioz. Ozeanoetan metatzen den mikroplastikoaren herena baino pixka bat gehiago modaren industriari dagokio: urtean 190.000 tona, hain zuzen. Eta urtean 92.000 tonatik gora ehun hondakin sortzen du (saltzea lortzen ez den arropa barne hartuta), eta horietako asko zabortegietara iristen dira azkenean edo erraustu egiten dira.
 Irudia: Kostu txikiek are gehiago handitzen dute gehiago erosteko eta artikuluak gutxiagotan erabiltzeko fenomenoa, moda lasterraren eredua erraztuz. AEBn, batez besteko kontsumitzaileak 5,5 egunean behin erosten du arropa eta Europan, pertsona bakoitzak duela 10 urte baino arropa berri gehiago erosten du: 13 eta 16 kg artean Danimarkan, Suedian, Norvegian eta Finlandian, 14,5 kg Italian, 16,7 kg Alemanian eta 26,7 kg Erresuma Batuan. (Argazkia: Andreas Lischka – erabilera publikoko irudia. Iturria: pixabay.com)
Irudia: Kostu txikiek are gehiago handitzen dute gehiago erosteko eta artikuluak gutxiagotan erabiltzeko fenomenoa, moda lasterraren eredua erraztuz. AEBn, batez besteko kontsumitzaileak 5,5 egunean behin erosten du arropa eta Europan, pertsona bakoitzak duela 10 urte baino arropa berri gehiago erosten du: 13 eta 16 kg artean Danimarkan, Suedian, Norvegian eta Finlandian, 14,5 kg Italian, 16,7 kg Alemanian eta 26,7 kg Erresuma Batuan. (Argazkia: Andreas Lischka – erabilera publikoko irudia. Iturria: pixabay.com)Azken mende erdiari erreparatzen badiogu, arropa ekoizpenak, gutxi gorabehera 2000. urtera arte, populazioaren gorakadarekin batera egin zuen gora. Baina, 2000. urtetik igarotako hogei urteetan, ehungintza biztanleria baino gehiago hazi da. Izan ere, 1975etik 2018ra bitartean, pertsona bakoitzeko ekoizpena 6 kg-tik 13 kg-ra igo da; bestela esanda, bikoiztu baino gehiago egin da. Uste da mota horretako modaren eskaria urtean % 2 handitzen dela gaur egun.
Izan ere, industriak kontsumitzaileei produktu berriak lehen baino askoz merkeago eta maizago eskaintzeko gaitasuna du, eta horrexegatik gertatzen da, hain zuzen, hazkunde hori. Ekoizle nagusiek saltoki txikien bidezko banaketan oinarritutako konpainia tradizionalen lekua hartu dute, eta onuragarri atera zaie euren produktuak Internet bidez merkaturatzea. Ondorioz, marka arrakastatsuek moda lasterraren fenomenoa hasi aurretik (hots, 2000. urtea baino lehen) merkaturatzen zituzten bildumen bikoitza merkaturatzen dute gaur egun.
Ekoizpenaren eraginkortasunak izugarri egin du gora, eta, kontsumoa igo egin den arren, pertsona bakoitzak arropan egindako gastuak nabarmen egin du behera guztizko gastuaren barnean Europan: erosketa saskiaren % 30 zen aurreko mendeko 50eko hamarkadan; % 12, berriz, 2009an; eta % 5, azkenik, 2020an. Eta murrizketa horrek arropa gehiago erostea errazten du, maizago erosten baita. Estatu Batuetan, gaur egun, 5,5 egunean behin erosten da arropa pieza bat. Eta Europan, bestalde, erabilera denbora % 36 murriztu da azken hamabost urteotan.
Modaren industriak kostuak eta entrega denborak gutxitzera bideratu ditu bere ahaleginak, hori baita, hain zuzen ere, sektorearen erakargarritasunaren eta arrakastaren funtsezko elementuetako bat, baina kaltegarria gizadirentzat.
Erreferentzia bibliografikoa:
Niinimäki, K., Peters, G., Dahlbo, H. et al. (2020). The environmental price of fast fashion. Nature Reviews Earth & Environment, 1, 189–200. DOI: https://doi.org/10.1038/s43017-020-0039-9
———————————————————————————-
Egileaz: Juan Ignacio Pérez Iglesias (@Uhandrea) UPV/EHUko Fisiologiako katedraduna da eta Kultura Zientifikoko Katedraren arduraduna.
———————————————————————————
The post Moda lasterraren ingurumen prezioa appeared first on Zientzia Kaiera.
¿Por qué nos gusta el azúcar?
Josu Lopez-Gazpio
El azúcar que consumimos cada día tiene un gran poder adictivo. Los efectos que produce en el organismo pueden compararse a los que produce el alcohol. Así lo afirma el equipo científico de la Universidad de California que firmó el artículo The toxic truth about sugar -la verdad tóxica sobre el azúcar-. En su opinión, el consumo crónico y continuado tanto de azúcar como de alcohol pueden generar diversas afecciones: hipertensión, enfermedades de hígado y de corazón, obesidad, pancreatitis, etc. La ciudadanía, en general, tiene bastante claro que el azúcar no es bueno -aunque no se tenga muy claro cuáles son las consecuencias concretas-, pero, en tal caso, ¿por qué no eliminamos el azúcar de nuestra dieta?, ¿por qué nos atraen tanto las tartas, los helados, los dulces, los bollos, etc., y no tanto los alimentos como el brócoli, las espinacas o la berza? Lo más probable es que exista una razón evolutiva en la base de esta inclinación que tenemos por el dulce.
 Nuestra predilección por el azúcar puede tener una razón evolutiva. (Fotografía: congerdesign – imagen de dominio público. Fuente: pixabay.com)
Nuestra predilección por el azúcar puede tener una razón evolutiva. (Fotografía: congerdesign – imagen de dominio público. Fuente: pixabay.com)Las declaraciones publicadas por los investigadores Robert Lustig, Laura Schmidt y Claire Brindis en 2012 en la revista Nature crearon una gran polémica y, a día de hoy, el debate sigue abierto. Afirmaron que el azúcar y el alcohol pueden tener unas consecuencias parecidas en la salud y que es necesario tomar medidas para reducir su consumo. El debate está servido. Según algunas personas, lo realmente perjudicial no es el azúcar en sí, sino la obesidad. Otras fuentes afirman que sí, que el azúcar es prácticamente un veneno. Antes del debate surgido a raíz del artículo de 2012, la comunidad científica ya estaba más o menos de acuerdo en que el azúcar no es bueno para la salud. Pero lo cierto es que el dulce nos resulta más atractivo que otros alimentos con mayor cantidad de nutrientes. Si es tan perjudicial -no son más que calorías-, ¿por qué nos gusta tanto?
La ciencia ha intentado dar respuesta a esta cuestión en numerosas ocasiones. Basándose en los fenómenos estudiados, el primer factor destacable es el siguiente: a muchas personas adultas les gusta el azúcar, pero entre los niños y las niñas es aún más llamativo; prácticamente a todos les gustan los dulces.
Las investigaciones han corroborado que esto es así, y que, además, la preferencia de las niñas y niños por los alimentos dulces es desde que nacen. Se ha llegado a la conclusión de que a los recien nacidos también les gusta el dulce y, por otro lado, es un patrón que se repite en la mayoría de las culturas y lugares del mundo. En el caso de la infancia, además, no hay límite de nivel de azúcar. Si bien entre las personas adultas, por ejemplo, se ha comprobado que las bebidas dulces, por encima de ciertos niveles de azúcar ya no son tan apetecibles, en el caso de los niños y las niñas, se ha observado que no hay límite. A pesar de disolver todo el azúcar posible en una bebida -superado el nivel de saturación de la disolución-, les sigue gustando.
Si bien es verdad que, en cierta medida, el azúcar es necesario; como fuente energética tiene muchas calorías. Si esa energía es necesaria, el azúcar la ofrece. El problema es que el aporte calórico es muy grande. En el caso de los niños y las niñas, la explicación puede estar en el crecimiento de los huesos. Los huesos que están en crecimiento segregan unas hormonas, las cuales pueden influir en el metabolismo. Además, se sabe que otras hormonas metabólicas, como la leptina o la insulina, han demostrado actuar en las áreas cerebrales que controlan los antojos y apetitos, e incluso directamente se unen a lengua, donde inciden en la preferencia por los gustos dulces.
Pero, ¿cuál es la verdadera razón para esa preferencia por el azúcar? Tal y como hemos señalado al inicio, debemos remitirnos a motivos evolutivos. En las primeras etapas de la evolución humana, los seres humanos que consumían mayor cantidad de calorías eran los que vivían por más tiempo; por lo tanto, era más probable para ellos transmitir sus genes a sus sucesores. Es posible que los humanos que se alimentaban de fruta tuvieran una vida más larga que los que se alimentaban de verduras, ya que las primeras tienen más calorías que las segundas. Las frutas tienen una mayor cantidad de azúcares, por eso son más dulces que las verduras y otro tipo de alimentos. A fuerza de la evolución, la selección natural y el tiempo, poco a poco, se normalizó la preferencia por los alimentos dulces. La progresiva priorización de los alimentos dulces se convirtió en una ventaja evolutiva.
Aunque la preferencia por lo dulce parece ser una característica que está adherida en los genes, hoy nuestra vida no tiene nada que ver con la de aquellos primeros seres humanos. No tenemos las mismas necesidades energéticas y obtener calorías no es ningún problema. En el día a día, extraemos el azúcar de la fruta para añadirlo de forma concentrada a otros alimentos. Sin embargo, abusamos del azúcar, no porque comamos demasiada fruta -que tiene más nutrientes-, sino porque ingerimos alimentos que son puro azúcar y aportan una gran cantidad de calorías.
Sin lugar a dudas, debemos afrontar el problema de la ingesta excesiva de azúcar para reducir los niveles de obesidad -sobre todo la obesidad infantil- y el primer paso es el tratar de conocer la química y la biología que hay detrás de esta «predilección» por el azúcar.
Fuentes:
- Ramirez, I. (1990). Why do sugars taste good? Neurosci Biobehav Rev., 14(2), 125-134. DOI: 10.1016/s0149-7634(05)80213-1
- Pepino, Yanina M., Mennella, Julie A. (2005). Sucrose-induced analgesia is related to sweet preferences in children but not adults. Pain, 119(1-3), 210-218. DOI: 10.1016/j.pain.2005.09.029
- Coldwell, S. E., Oswald, T. K., & Reed, D. R. (2009). A marker of growth differs between adolescents with high vs. low sugar preference. Physiology & behavior, 96(4-5), 574–580. DOI: https://doi.org/10.1016/j.physbeh.2008.12.010
- Ventura, Alison K., Mennella, Julie A. (2011). Innate and learned preferences for sweet taste during childhood. Current Opinion in Clinical Nutrition and Metabolic Care, 14(4 ), 379-384. DOI: 10.1097/MCO.0b013e328346df65
- Lustig, R.; Schmidt, L. & Brindis, C. (2012). The toxic truth about sugar. Nature, 482, 27–29. DOI: https://doi.org/10.1038/482027a
Más información:
- McGee, Harold (2017). La cocina y los alimentos: Enciclopedia de la ciencia y la cultura de la comida, Madrid, España: Penguin Random House Grupo Editorial.
- Stierwalt, Sabrina (6 de febrero de 2020). Why Does Sugar Taste So Good? Scientific American. Consultado el 13 de junio de 2020.
Sobre el autor: Josu Lopez-Gazpio (@Josu_lg) es doctor en Química, profesor y divulgador científico.
Este artículo se publicó originalmente en euskara el 24 de junio de 2020 en el blog Zientzia Kaiera. Artículo original.
El artículo ¿Por qué nos gusta el azúcar? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Azúcar moreno o azúcar milagro?
- Azúcar moreno, ¿mejor que el azúcar blanco?
- El azúcar oculto en los alimentos
Dozena erdi ariketa 2020ko udarako (6): Karratu perfektuak
Gogoan izan ahalegina bera –bidea bilatzea– badela ariketa. Horrez gain, tontorra (emaitza) lortzen baduzu, poz handiagoa. Ahalegina egin eta emaitza gurekin partekatzera gonbidatzen zaitugu. Ariketaren emaitza–eta jarraitu duzun ebazpidea, nahi baduzu– idatzi iruzkinen atalean (artikuluaren behealdean daukazu) eta irailean emaitza zuzenaren berri emango dizugu.
Hona hemen gure seigarren ariketa: Karratu perfektuak.
———————————————————————————-
Ariketak “Calendrier Mathématique 2020. Un défi quotidien” egutegitik hartuta daude. Astelehenetik ostiralera, egun bakoitzean ariketa bat proposatzen du egutegiak. Ostiralero CNRS blogeko Défis du Calendrier Mathématique atalean aste horretako ariketa bat aurki daiteke.
———————————————————————————-
The post Dozena erdi ariketa 2020ko udarako (6): Karratu perfektuak appeared first on Zientzia Kaiera.
La superioridad ilusoria y otros vicios mentales
 Imagen: Elias Sch / Pixabay
Imagen: Elias Sch / PixabayCasi nadie piensa de sí mismo que es un idiota. Es más, no todos piensan de un idiota que, efectivamente, lo es; porque quizás tenga familiares y amistades que, muy probablemente, no tendrán tan mal concepto de su pariente o amigo.
Parte de la dificultad para objetivar estas cosas, así como para ponernos de acuerdo acerca de lo limitadas que son las personas que conocemos o que es uno mismo, se debe a que el pensamiento se ve muy afectado por vicios sistemáticos a los que denominamos sesgos. Son vicios que nos ayudan a vivir y, algunos al menos, se hallan firmemente instalados en nuestra mente porque ayudaron a nuestros antepasados a dejar descendencia, razón por la que esos rasgos se han perpetuado. Otros quizás son subproductos inevitables de la forma en que funciona la mente. Es bueno, no obstante, ser consciente de su existencia y tratar de identificarlos en nosotros mismos. Solo así podremos aliviar sus efectos aunque nunca podamos librarnos del todo de ellos. Veamos algún ejemplo.
Tendemos a percibir los sesgos en los juicios de los demás, mientras que no los percibimos en nosotros mismos. Se denomina a este efecto prejuicio del punto ciego, y tiene su origen en una motivación, denominada automejora, que hace que tengamos una imagen favorable de nosotros mismos. Resulta, por supuesto, muy útil, porque nos ayuda a superar obstáculos o a crecernos en la adversidad. La contrapartida es que hace muy difícil que mejoremos, menos aún si son otros los que nos señalan que no lo estamos haciendo bien.
Otro sesgo muy común es el del status quo, que consiste en la preferencia por que las cosas no cambien y el sentimiento de que cualquier cambio conllevará un empeoramiento. Esta tendencia nos impulsa, por ejemplo, a mantener costumbres, fijar el sentido del voto en unas elecciones, o no cambiar la marca de nuestro refresco favorito.
De otra naturaleza es la falacia del jugador (del apostador), que consiste en atribuir una menor probabilidad a que ocurran cosas que han ocurrido de forma muy frecuente en el periodo anterior o lo contrario. Esta falacia tiene su origen en la creencia de que sucesos aleatorios pasados condicionan los futuros. No es más probable que salga cara en la siguiente ocasión que lancemos una moneda al aire por el hecho de que hayan salido seis cruces de manera consecutiva. Pero tendemos a pensar que sí.
Si tuviera que destacar un sesgo por encima de todos los demás, al menos en lo que se refiere a sus implicaciones sociales, me quedaría con el efecto Dunning-Kruger. Es muy simple, aunque de consecuencias impresionantes. El efecto, también denominado de superioridad ilusoria, consiste en la tendencia de las personas menos dotadas intelectualmente a pensar lo contrario de sí mismas. Esto es, en general, los más incapaces tienden a pensar que lo son menos que los demás; se creen muy listos, de hecho. La razón para que piensen así es que es su misma incapacidad lo que les impide darse cuenta de ella. Viven en un mundo intelectualmente satisfactorio, sabiéndose, de forma completamente ilusoria, que son más listos que los demás.
Ese efecto tiene su reverso: es relativamente frecuente que los más dotados intelectualmente sufran el denominado síndrome del impostor. Consiste en creerse inferiores a aquellos con quienes se suelen encontrar e, incluso, no ser merecedores de su compañía.
Pocos sesgos pueden tener un efecto tan devastador como el Dunning-Kruger: piense, si no, en todos esos legos que creen saber más de virus y pandemias que quienes han dedicado su vida profesional a estudiarlos.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La superioridad ilusoria y otros vicios mentales se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:La osteopontina evita la aparición precoz de la enfermedad de hígado graso no alcohólica por envejecimiento
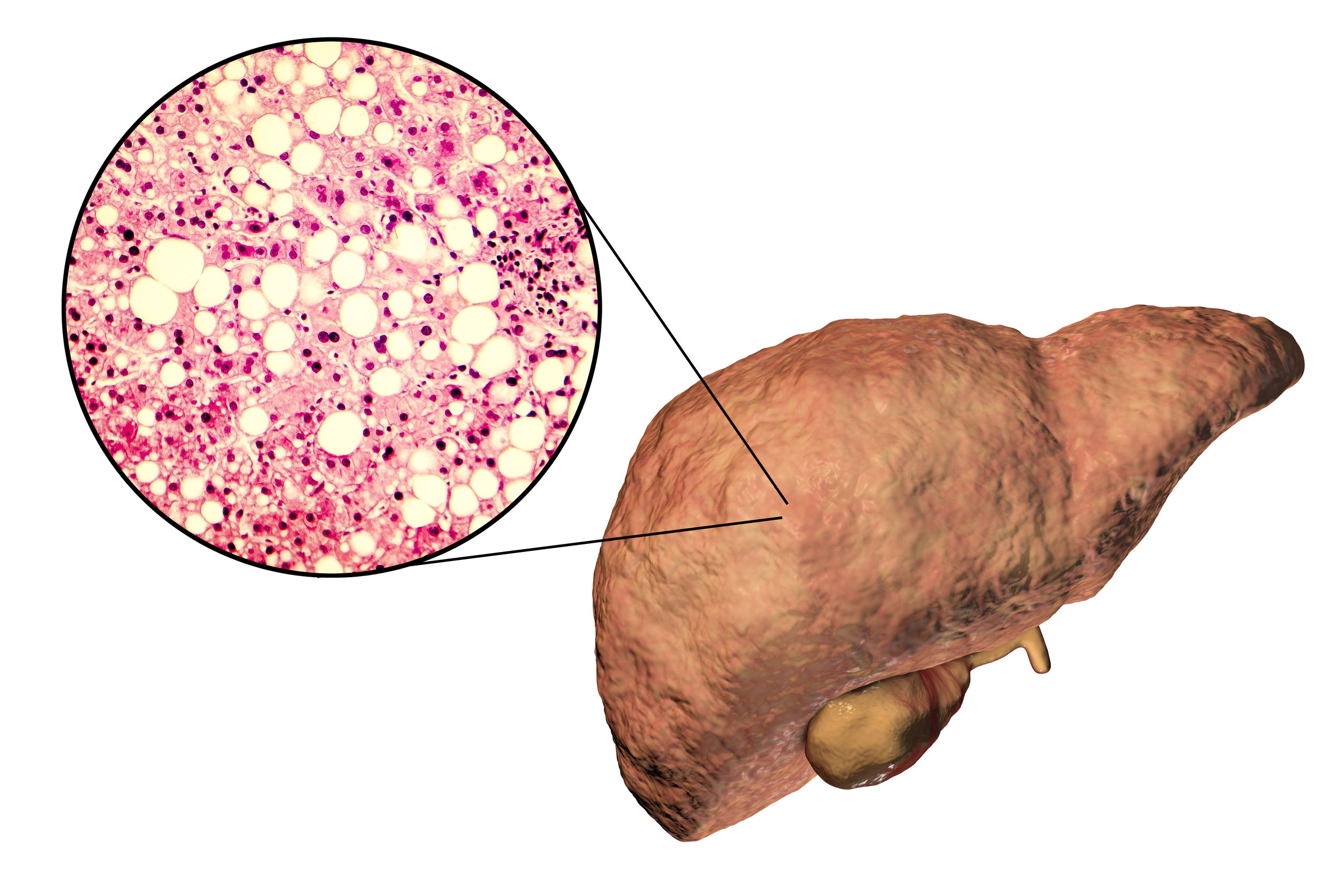 Hígado graso no alcohólico. Imagen: Kateryna Kon / 123RF
Hígado graso no alcohólico. Imagen: Kateryna Kon / 123RFEn un trabajo reciente el grupo de investigación Lipids & Liver de la UPV/EHU muestra que, al contrario de lo que se esperaba, durante el envejecimiento es necesario mantener los niveles fisiológicos hepáticos de la osteopontina, una proteína multifuncional relacionada con varias enfermedades graves, para prevenir la progresión de la enfermedad de hígado graso no alcohólica relacionada con la edad.
La enfermedad hepática metabólica grasa también conocida como enfermedad de hígado graso no alcohólica es una de las causas más comunes de enfermedad hepática en los países occidentales e incluye un espectro de trastornos. Está fuertemente asociada a enfermedades metabólicas como la obesidad o la diabetes mellitus tipo 2. Durante el envejecimiento se produce un aumento en la acumulación de lípidos dentro del hígado que puede comprometer su función normal. El grupo de investigación de la UPV/EHU Lipids & Liver, del Departamento de Fisiología de la Facultad de Medicina y Enfermería, investiga “la enfermedad de hígado graso no alcohólica y enfermedades metabólicas asociadas. En este trabajo nuestro objetivo fue encontrar qué mecanismos pueden estar implicados en el desarrollo de esta enfermedad hepática a lo largo del envejecimiento, para poder tratar o retrasar su aparición”, explica la doctora Patricia Aspichueta, responsable del grupo de investigación.
Se trata de una enfermedad de progresión lenta: “En algunos pacientes no evoluciona, se queda en la primera fase de acumulación de grasa, simplemente en hepatoesteatosis; en otros pacientes puede tardar incluso 20 años en progresar desde una hepatoesteatosis hasta que aparece esteatohepatitis, asociada o no a fibrosis; sin embargo, hay pacientes en los que evoluciona más rápido con la edad”, explica Aspichueta. Por eso es muy importante saber “qué mecanismos están implicados en hacer que el hígado sea más vulnerable a determinados inputs, fomentando el desarrollo y/o progresión de la enfermedad”.
Una de las proteínas relacionadas con el envejecimiento celular es la osteopontina, una proteína multifuncional que se encuentra en muchos tejidos y que, como muestran estudios anteriores desarrollados por Lipids & Liver, modula el metabolismo en el hígado y “que se ha asociado a procesos de enfermedades muy negativas como el cáncer y la cirrosis hepática”, explica Aspichueta. En un trabajo que ha sido parte de la tesis doctoral de la investigadora Beatriz Gómez Santos, “curiosamente encontramos, en contra de lo esperado, que la osteopontina es protectora, es decir, que se necesita para evitar una aparición prematura de esta enfermedad durante el envejecimiento —añade—. Hemos visto que si se inhibe o silencia la osteopontina, como se propone en ciertos contextos (para evitar fibrosis hepáticas, etc.), esa aparición de grasa es precoz y la enfermedad aparece antes. Por tanto, durante el envejecimiento, es fundamental mantener esta proteína en niveles fisiológicos en el hígado”.
El estudio de enfermedades metabólicas es complejo, porque los cambios metabólicos que se generan son muy dinámicos y ocurren de manera coordinada entre varios tejidos. Además, se estudian los cambios producidos en las moléculas a lo largo de su metabolización: “Utilizamos, entre otras, moléculas marcadas radiactivamente y hacemos un seguimiento al camino que siguen, dónde se incorporan, etc.”. Las investigadoras afirman que “este hallazgo es fundamental porque hemos aprendido muchísimo del proceso de envejecimiento”.
Actualmente, Gómez Santos está estudiando “la vulnerabilidad hepática que hombres y mujeres desarrollan a lo largo de la edad para padecer la enfermedad hepática”. Estamos analizando en paralelo en hombres y mujeres los procesos metabólicos relacionados con el desarrollo y progresión de la enfermedad hepática”. La evidencia de distintos estudios sugiere que la incidencia de la enfermedad de hígado graso no alcohólica es mayor en hombres que en mujeres. Además, en mujeres la incidencia parece ser menor en premenopáusicas. Se trata de un complejo estudio con diferentes variables con un único objetivo: “Al final lo que queremos conseguir es un envejecimiento saludable. Queremos evitar que la enfermedad metabólica aparezca, o si ya ha aparecido que evolucione de manera rápida”.
Referencia:
Beatriz Gómez-Santos, Diego Saenz de Urturi, Maitane Nuñez-García, Francisco Gonzalez-Romero, Xabier Buque, Igor Aurrekoetxea, Virginia Gutiérrez de Juan, Maria J. Gonzalez-Rellan, Carmelo García-Monzón, Águeda González-Rodríguez, Lorena Mosteiro, Gaizka Errazti, Patricia Mifsut, Sonia Gaztambide, Luis Castaño, Cesar Martin, Rubén Nogueiras, María L. Martinez-Chantar, Wing-Kin Syn, Patricia Aspichueta (2020) Liver osteopontin is required to prevent the progression of age-related nonalcoholic fatty liver disease Aging Cell DOI: 10.1111/acel.13183
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La osteopontina evita la aparición precoz de la enfermedad de hígado graso no alcohólica por envejecimiento se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Avances contra la enfermedad de hígado graso no alcohólica
- La enfermedad del hígado graso no alcohólico, una gran desconocida
- Una infección vírica puede activar la aparición de diabetes tipo I
Zerura begira

Euren lana imajinatzen laguntzen didate garaiko irudiek: zer idatzi zuten koaderno horietan? Eta zer ikusten ari ziren une hartan? Dokumentu bikainak dira, jakina, denborazko kapsula modukoak. Bada, argazkien antzera, emakume horiek egindako lanaren erradiografia ederra eskaini digu Dava Sobel idazleak El universo de cristal liburuaren bitartez.
Edward Charles Pickering (1846-1919) Harvardeko Astronomia Behatokiko zuzendariak gidatuta, izarrak zenbatu eta sailkatu zuen emakume astronomo eta matematikarien taldearen historia kontatzen da bertan. Besteak beste, Antonia Mauryk, Williamina Flemingek, Henrietta Swan Leavittek eta Annie Jump Cannonek egindako lanak azaltzen ditu Sobelek modu erraz eta argian.
Hamaika dira egin zituzten aurkikuntzak: izarren konposizioa identifikatu, berauen distantziak neurtu eta izarrak sailkatzeko sistema berri bat sortu zuten, egun indarrean dagoena, hain zuzen. Beste gauza batzuen artean, proiektu handi batez ere mintzo da liburua: izarren espektroen katalogoaz, alegia.
Astronomia Behatokian aurkituko du bere burua irakurleak ezinbestean. Begi aurrean, eszena osoa: Cannon teleskopiotik begiratzen, Maury koadernoan idazten, Pickering taldea zuzentzen… denak daude lanean, isilik. Eta gu, taularatutako obra bat izango balitz bezala ikusten ari gara dena. Liburu honek sortzen duen gauzarik politena zera da: astronomo hauen lanaz irakurtzean, zerua imajinatzeko gai garela.
Argitalpenaren fitxa:-
- Izenburua: El universo de cristal. La historia de las mujeres de Harvard que nos acercaron las estrellas
- Egilea: Dava Sobel
- Itzultzailea: Pedro Pacheco
- Argitaletxea: Capitan Swing
- Orrialdeak: 392
- ISBNa: 978-84-946453-1-0
———————————————————————————-
Egileaz: Uxue Razkin (@UxueRazkin) kazetaria da.
———————————————————————————-
The post Zerura begira appeared first on Zientzia Kaiera.
Un sonido para hablar con los dioses
“–Mi amigo soplaba con esto.
Ralph comprendió al fin y lanzó el aire desde el diafragma. Aquello empezó a sonar al instante. Una nota estridente y profunda estalló bajo las palmeras, penetró por todos los resquicios de la selva y retumbó en el granito rosado de la montaña. De las copas de los árboles salieron nubéculas de pájaros y algo chilló y corrió entre la maleza. Ralph apartó la concha de sus labios. – ¡Qué bárbaro!
Su propia voz pareció un murmullo tras la áspera nota de la caracola.“
En El señor de las moscas, la famosa novela de William Golding, un avión se estrella en medio del Pacífico y convierte a una treintena de adolescentes en los únicos habitantes de una isla desierta1. Poco después del accidente, dos de ellos se encuentran caminando por una playa. A lo lejos, entre las algas, avistan un objeto de color cremoso, ¡una caracola! Aunque al principio Ralph no sabe cómo usarla, su poderoso sonido le acaba convirtiendo en el jefe de una peculiar tribu. Primero, el instrumento sirve para congregar a los demás supervivientes de la isla. Una vez reunidos, la caracola se utiliza para articular una especie de democracia asamblearia donde quienquiera que la sostenga tiene la palabra y debe recibir la atención silenciosa del resto. El instrumento se convierte así en un símbolo de la razón, la convivencia y el orden, y Ralph, como su descubridor, es elegido líder de todo el grupo.
Resulta tentador intentar imaginar al primer ser humano que hace decenas de miles de años hizo vibrar sus labios contra una concha vacía y descubrió esa misma sensación de poder que Golding ejemplifica en su novela. El instrumento debió de otorgarle la capacidad de alcanzar distancias nunca antes imaginadas, una verdadera voz sobrehumana. No sabemos si sus compañeros le harían jefe de su cueva o qué pero, como mínimo, esa tarde tendría algo interesante que contar. Tampoco podemos conocer con precisión cuándo pudo suceder esto. A fin de cuentas, para hacer sonar una caracola basta con ir a la playa y encontrarse una con la punta un poco rota. Claramente, este tipo de objetos antecede por mucho a cualquier cultura humana. Es su uso con fines sonoros lo que los convierte en un instrumento musical. Pero los soplidos no dejan restos arqueológicos. Es necesario rastrearlos a partir de otras huellas más indirectas.
 Fuente: Wikimedia Commons.
Fuente: Wikimedia Commons.Se considera que uno de los ejemplos más tempranos de concha musical procede la región del Mediterráneo y data del periodo Magdaleniense a finales del Paleolítico superior. Se trata de un ejemplar de Charonia lampas semi fosilizado descubierto en 1931 en una cueva de los Pirineos23. Tiene aproximadamente unos 20.000 años de antigüedad. Se piensa que fue eso, un instrumento, porque además de encontrarse entre otros objetos y pinturas humanas, la cueva de Marsoulas está a 250 kilómetros de la costa más cercana. Y las caracolas no vuelan, claro. Alguien debió de llevarla consigo hasta allí, a pesar del esfuerzo que esto pudiera suponer. Esto nos hace pensar que se trataba de un objeto valioso. Existen, además, otras evidencias de su uso. La punta estaba rota y el desgaste general sugiere que la concha pasó de mano en mano de forma continuada. Sin embargo, es posible también que se usase para beber o con algún otro fin ritual. Por desgracia, de nuevo, los soplidos se los lleva el viento y tampoco se han encontrado más ejemplos de la misma época que ayuden a dirimir la cuestión.
 Conchas talladas o shankhas, siglos XI-XII, India. La de la izquierda está tallada con una imagen de los dioses Lakshmi y Vishnu. Fuente: Wikimedia Commons
Conchas talladas o shankhas, siglos XI-XII, India. La de la izquierda está tallada con una imagen de los dioses Lakshmi y Vishnu. Fuente: Wikimedia CommonsExisten bastantes más caracolas del periodo Neolítico que sugieren que el instrumento debió de tener un uso continuado. Sorprende todavía más que sea común en culturas de casi todo el mundo. Se han encontrado ejemplos procedentes de Europa, India, China, Japón, el Tíbet, Oceanía y las Américas, con la curiosa excepción de África del norte4. En todos los casos, la potencia sonora del instrumento parece determinar sus usos culturales, bien por su capacidad para comunicarse a través de grandes distancias (como corno de guerra, por ejemplo), bien con fines espirituales y religiosos. Aunque bien se podría argumentar que ambos usos responden al mismo objetivo. A fin de cuentas, qué mayor distancia que la que se necesita atravesar para comunicarse con los dioses. Ese mismo sonido, de un origen tan humilde, ha hechizado a humanos de todo el mundo desde la prehistoria. Y probablemente, por un mismo motivo: a todos les sorprendió lo mismo que su propia voz pareciese “un murmullo tras la áspera nota de la caracola”.
Notas y referencias:
1Aparte del libro, recomiendo también, esta lectura en The Guardian: The real Lord of the Flies: what happened when six boys were shipwrecked for 15 months
2JT Russell, 1932. Report on archeological research in the foothills of the Pyrenees (with eight plates). Smithsonian Miscellaneous Collections.
3Bégouën Comte, JT Russell, 1933: La Campagne de Fouilles de 1931 à Marsoulas, Tarté et Roquecourbère Mission Franco-Américaine de Recherches Préhistoriques.
4“The Conch Horn. Shell Trumpets of the World from prehistory to today”. Jeremy Montagu.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Un sonido para hablar con los dioses se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Más FUN WITH MATHS, diversión con matemáticas
Hace un año, con el inicio del período de las vacaciones estivales de los centros educativos, publicamos en el Cuaderno de Cultura Científica la entrada FUN WITH MATHS, diversión con matemáticas, en la que se explicaban algunos sencillos trucos de magia relacionados con las matemáticas. En esta entrada recuperamos esta idea y mostramos otros dos trucos de magia matemática con los números.
 Rompecabezas inventado por Sam Loyd (1841-1911) Get off the Earth / Borrado de la faz de la Tierra (1896). La Tierra es un disco que gira sobre su centro de forma que en la primera posición –esta imagen–, con la flecha apuntando hacia NE, se ven 13 guerreros chinos. Imagen de este rompecabezas antiguo de George Glazer Gallery
Rompecabezas inventado por Sam Loyd (1841-1911) Get off the Earth / Borrado de la faz de la Tierra (1896). La Tierra es un disco que gira sobre su centro de forma que en la primera posición –esta imagen–, con la flecha apuntando hacia NE, se ven 13 guerreros chinos. Imagen de este rompecabezas antiguo de George Glazer Gallery
 En la segunda posición, con la flecha hacia NW, ha desaparecido un guerrero chino y solo hay 12. Imagen de este rompecabezas antiguo de George Glazer Gallery
En la segunda posición, con la flecha hacia NW, ha desaparecido un guerrero chino y solo hay 12. Imagen de este rompecabezas antiguo de George Glazer GalleryVayamos con el primer truco. Es un sencillo truco en el que se pide a una persona del público que piense en un número de cuatro dígitos, que finalmente vamos a recuperar tras algunas operaciones aritméticas. Una parte muy importante de los trucos de magia es la presentación de los mismos, así como todo el teatro que se realiza en su puesta en escena. Por ejemplo, este truco se puede presentar de la siguiente forma.
La persona que realiza el truco dispone de una pizarra o una hoja de papel grande sobre la que realizará el truco. Para empezar, le pide a alguien del público que piense un número de cuatro dígitos y que lo diga en alto, para que todo el mundo lo escuche. La persona que realiza el truco, con cierta teatralidad, le dirá que ha elegido un número muy especial, con propiedades mágicas. A continuación, se explican cuáles son esas propiedades mágicas.
El mago, o la maga, escribirá en la pizarra, en grande, el número que ha elegido la persona voluntaria del público. Pensemos que ese número es 7.483.
Después, siempre con la mayor teatralidad posible, escribirá en la pizarra el primer dígito, desde la izquierda, del número: en nuestro ejemplo, 7.
Debajo de este, y con el objetivo de realizar una suma, escribirá el número formado por los dos primeros dígitos, desde la izquierda: en el ejemplo, 74.
Más abajo aún escribirá el número formado por los tres primeros dígitos: 748. Y sumará esos tres números. Para el número elegido el resultado es 7 + 74 + 748 = 829.
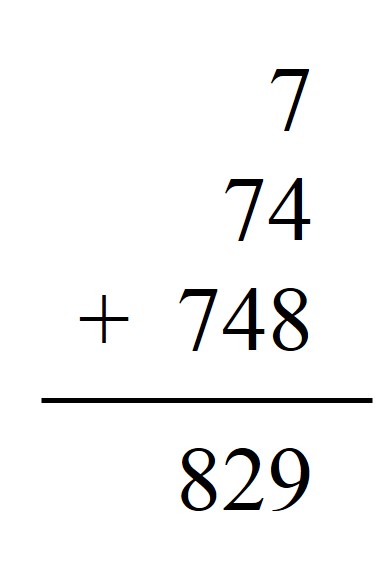
El siguiente paso es multiplicar en la pizarra el resultado de la operación anterior por 9. En el ejemplo elegido quedará 829 x 9 = 7.461.
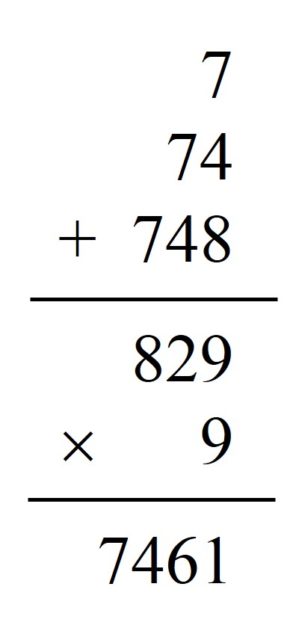
Finalmente, hay que sumar a ese resultado la suma de los dígitos del número elegido por la persona voluntaria, que en nuestro ejemplo es 7 + 4 + 8 + 3 = 22, y sorpresa, sorpresa, el resultado es efectivamente el número mágico en cuestión, 7.461 + 22 = 7.483.
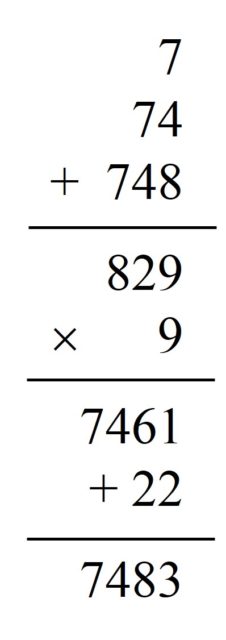
Se puede comprobar fácilmente que este truco funciona siempre. Dado un número de cuatro dígitos abcd, la operación mostrada en el truco, que es (a + ab + abc) x 9 + (a + b + c + d) da como resultado abcd.
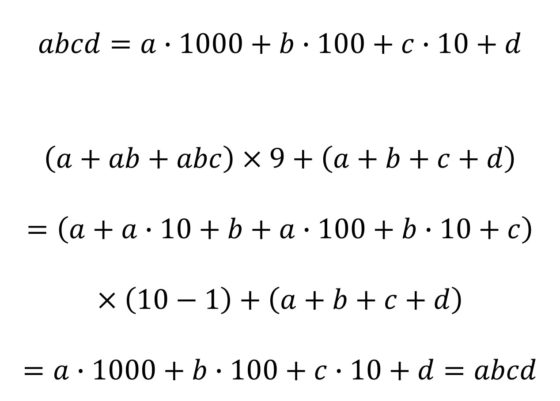
Si se realiza con detalle la operación anterior podemos darnos cuenta de por qué funciona el truco y, además, de que funcionará con un número con cualquier cantidad de dígitos.
Es un truco que no se puede hacer dos veces seguidas, al menos presentado así, ya que el público descubriría que todos los números son especiales. Lo mejor es hacerlo una vez y luego hacer otro sencillo truco, por ejemplo, el truco de la calculadora que expliqué en el video de la sección Una de mates, de la Cátedra de Cultura Científica, y que fue emitido en el programa de humor y ciencia de televisión, dirigido por José A. Pérez Ledo, Orbita Laika (segunda temporada) de La2, de Televisión Española: Una de mates, magia matemática.
 Otro rompecabezas del tipo de desapariciones, como el anterior, es el rompecabezas del huevo mágico, que fue utilizado como tarjeta anuncio en 1880, por la Wemple & Company de Nueva York. Si se corta por las líneas de puntos y se recolocan los cuatro trozos se puede formar un rectángulo con 6, 7, 8, 10, 11 o 12 huevos. Imagen de Redbubble
Otro rompecabezas del tipo de desapariciones, como el anterior, es el rompecabezas del huevo mágico, que fue utilizado como tarjeta anuncio en 1880, por la Wemple & Company de Nueva York. Si se corta por las líneas de puntos y se recolocan los cuatro trozos se puede formar un rectángulo con 6, 7, 8, 10, 11 o 12 huevos. Imagen de Redbubble
El segundo truco es un truco de cálculo mental que se puede presentar como una competición entre la mente del mago y la calculadora. Para realizar el truco se necesita una pizarra, o una hoja de papel, grande que puedan ver todas las personas del público, y una calculadora de las básicas.

Se explica que va a ser una competición entre la mente del mago y la calculadora, por lo que se necesita una persona voluntaria para que realice las operaciones en la calculadora, intentando hacerlo rápido y ganar al cálculo mental. Además, se le dará papel y lápiz por si necesita apuntar algo. Se le pide a otra persona del público que piense, y diga en alto, un número de cuatro dígitos (llamémosle en la explicación A), que se escribirá en la pizarra como se muestra más adelante en la imagen.
Para el cálculo que se va a realizar se necesita un segundo número, también de cuatro dígitos, para multiplicar por el primero, pero si solo fuese eso sería muy simple y efectivamente fácil que ganara la calculadora, por lo que vamos a complicar un poco la operación aritmética. ¿Cómo? Otra persona del público dará ese segundo número de cuatro dígitos (llamémosle B para la explicación) y la persona que realiza el truco un tercer número de cuatro dígitos (denotémoslo C). La competición consiste en multiplicar el primer número (A) por cada uno de los otros dos (A x B y A x C) y sumar el resultado (A x B + A x C). Para explicarlo mejor al público y realizar el truco se pinta el siguiente diagrama en la pizarra, suponiendo que el primer número A ofrecido por el público sea 7.354.
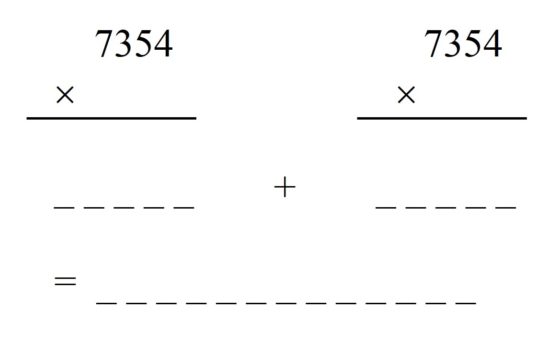
Debajo del 7.354, a la izquierda, se escribirá el segundo número proporcionado por quienes están presentes en el espectáculo de magia matemática, mientras que debajo del 7.354, a la derecha, se escribirá el número que aporta la maga matemática. Y en ese momento empieza la competición. Repetimos, se trata de ver quién consigue antes el resultado de multiplicar ese primer número 7.354 por cada uno de los dos anteriores y sumar esos resultados parciales.
Expliquemos con un ejemplo el desarrollo del truco de magia matemática. Supongamos que la segunda persona del público sugiere el número 4.067, entonces la persona que hace el truco deberá aportar el tercer número, que debe parecer que es uno cualquiera que se le ocurre en ese momento, pero que realmente cada uno de sus dígitos es el complementario respecto a 9 del dígito correspondiente del segundo número. Por lo tanto, en el ejemplo, como el segundo número es 4.067, el número que aportará el mago será 5.932 (4 + 5 = 9, 0 + 9 = 9, 6 + 3 = 9 y 7 + 2 = 9).
Es decir, con estos números concretos la competición consiste en realizar las multiplicaciones del primer número por cada uno de los otros dos, 7.354 x 4.067 y 7.354 x 5.932, y sumar los resultados de las mismas, es decir, (7.354 x 4.067) + (7.354 x 5.932).
El mago, que realiza el cálculo mental, escribirá rápidamente la solución en la parte de debajo de la pizarra, que es 73.532.646 (más adelante explicaremos de dónde ha sacado el mago ese número). La persona de la calculadora y el público se quedarán sorprendidos de la rapidez del mago, ya que habrá sido imposible realizar la operación con la calculadora en tan corto plazo de tiempo. Entonces, con ayuda de quien tiene la calculadora, se escribirán en la pizarra los pasos intermedios y el resultado final, como se muestra en la siguiente imagen, para comprobar que el número escrito es el correcto.

Expliquemos cómo ha conseguido el mago ese número y por qué sabe que es la solución buscada. Los cuatro primeros dígitos consisten en el primer número proporcionado por el público menos 1, es decir, 7354 – 1 = 7353. Mientras que los cuatro siguientes dígitos son los complementos respecto a 9 de cada uno de los dígitos de este, esto es, 2646. Juntando todo, y poniendo los puntos correspondientes, 73.532.646.
El motivo es el siguiente. Si llamamos a los tres números proporcionados A, B y C como se indicaba más arriba, el resultado que se busca es:
![]()
Pero por la propiedad distributiva, eso es lo mismo que:
![]()
Aquí está la clave del truco de magia. Como la persona que realiza el truco puede elegir C esto le permite controlar el valor de B + C y simplificar la operación aritmética. Veamos un ejemplo sencillo. Si se elige C de forma que B + C = 10.000, entonces A x (B + C) es el primer número elegido seguido de cuatro ceros, en nuestro ejemplo, 73.540.000. Pero de esta forma las personas presentes se darían cuenta de cómo has realizado el truco. Es decir, hay que esconder el truco y que parezca realmente una operación aritmética complicada.
Por este motivo se elige C para que B + C = 9.999, es decir, los complementos dígito a dígito respecto de 9 del número B. Y la operación se transforma en A x 9.999, que como es A x (10.000 – 1), el resultado es el número A menos 1 seguido de su complemento dígito a dígito respecto de nueve. En el ejemplo, 7353 y 2646, que puesto junto y poniendo los puntos de los miles (esto esconde un poco de donde viene el número, por lo que es aconsejable poner los puntos) es 73.532.646.
Bueno, pues ya conocéis otro par de trucos de magia para amenizar las reuniones familiares o con amigos. Espero que os hayan gustado.
 El rompecabezas Sailing Under False Colors/Navegando bajo falsos colores apareció en el libro Cyclopedia of 5000 Puzzles, Tricks, and Conundrums (1914) de Sam Loyd y consistía en cortar la bandera estadounidense en dos partes de forma que al recolocarla la nueva imagen de la bandera tuviese 13 barras en lugar de las 15 normales. Imagen de la versión online de la Cyclopedia of 5000 puzzles
El rompecabezas Sailing Under False Colors/Navegando bajo falsos colores apareció en el libro Cyclopedia of 5000 Puzzles, Tricks, and Conundrums (1914) de Sam Loyd y consistía en cortar la bandera estadounidense en dos partes de forma que al recolocarla la nueva imagen de la bandera tuviese 13 barras en lugar de las 15 normales. Imagen de la versión online de la Cyclopedia of 5000 puzzles Solución del rompecabezas Sailing Under False Colors/Navegando bajo falsos colores. Imagen de la versión online de la Cyclopedia of 5000 puzzles
Solución del rompecabezas Sailing Under False Colors/Navegando bajo falsos colores. Imagen de la versión online de la Cyclopedia of 5000 puzzles
Bibliografía
1.- Peter McOwan, Matt Parker, The manual of Mathematical Magic.
2.- Pedro Alegría, El rincón matemático (DivulgaMAT)
3.- Pedro Alegría, MAGIA por principios, Publidisa, 2008.
4.- Fernando Blasco, Matemagia, Temas de Hoy, 2007.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Más FUN WITH MATHS, diversión con matemáticas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- FUN WITH MATHS, diversión con matemáticas
- Abril comienza con matemáticas y bromas
- Un kilogramo de novelas y matemáticas
Lurraren magnetismoaz (II)
Lur planetaren posizioak eragindako magnetismo-bariazioek XVIII. mendearen bukaeratik zeukaten harrituta Alexander von Humboldt, eta intentsitate magnetiko bereko lerroen arteko berdintasunez idazten aritu zen. Horrez gain, lerro isotermoez eta fenomeno geologiko, meteorologiko nahiz magnetikoen arteko loturez ere idatzi zuen. Bariazio horien mapa sortu ahal izateko, Humboldtek magnetismoaren behatoki-sare bat osatzea sustatu zuen. 1834 urtean, Europan eraikitako 23 behatokien datuek ekaitz magnetikoen fenomenoa aurkitzea ahalbidetu zuten. Kosmos lanaren bosgarren liburukian −Humboldtek bukatu gabe utzi zuen, 1859an hil zen eta−, Lurraren magnetismoari buruz bildutako ezagutza guztiaren laburpena agertu zen: magnetismoaren bariazioa, banaketa eta ekaitz magnetikoak azaltzen ziren.
Edonola dela, hogeita hamarreko hamarkadako lehen urteetan Carl Friedrich Gauss-ek eta Wilhelm Weber bere lankideak hartu zuten Lurraren magnetismoari buruzko auziaren buruzagitza, hasi tresneriatik eta buka oinarrizko teorian. Hamarkadaren hasieran, Gaussek hari biko magnetometroa diseinatu zuen, eta haren bidez garatu zuen intentsitate magnetikoaren lehen neurketa absolutua. Gainera, Weberrekin batera, mundu mailako magnetismoaren behatoki-sarearen bertsio propioa proposatu zuen: Magnetische Verein delakoa.
Behatoki haien emaitzak 6 liburukitan argitaratu ziren 1836 eta 1841 urteen artean (Resultate aus den Beobachtungen des magnetischen Vereins). Bariazio eta intentsitate magnetikoari buruzko datu berri haiek eskuetan, Gaussek 1839an Lurraren magnetismoaren osagai bertikal eta horizontalen analisi matematikoa landu ahal izan zuen; horrela, lurrazalaren edozein puntutako potentzial magnetikoa kalkulatu ahal izan zuen, harmoniko esferikoen bitartez. Metodo hura izango zen mende hartako gainerako ikerketa teorikoen lan-eremua, Lurraren magnetismoaren jatorriari buruzko inolako teoriaren mende ez zegoelako.
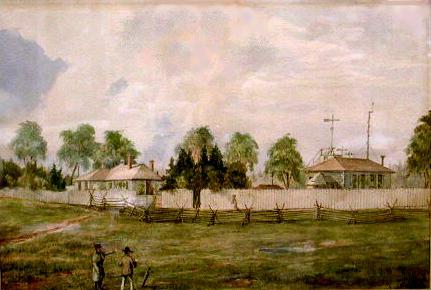 1. irudia: Torontoko Behatoki Magnetikoa, 1852an. Gurutzada magnetikoan eraiki zuten 1840an. (Iturria: Cuaderno de Cultura Científica).
1. irudia: Torontoko Behatoki Magnetikoa, 1852an. Gurutzada magnetikoan eraiki zuten 1840an. (Iturria: Cuaderno de Cultura Científica).Aldi berean, hainbat britainiarrek aldarrikatzen zuen Erresuma Batua ezin zela atzean geratu Lurraren magnetismoa bezalako fenomeno baten ikerkuntzan, hainbestekoa zelarik herrialdearentzat itsas armadaren botere ekonomikoak eta militarrak zuten garrantzia: ikerkuntza hori nazio-eginkizun bihurtu beharra zegoen. 1838an, Hansteen-en ikasle Edward Sabine-k John Herschel eta George Airy-ren babesa lortu zuen, baita Humboldten lankidetza ere, mapa magnetikoak garatu eta inperioaren lurretan magnetismoaren ikerkuntzarako behatokiak ezartzeko. Hasia zen «gurutzada magnetikoa».
Garai hartako fisikarien buruetan dantzan zebiltzan bai magnetismoa, bai hark elektrizitatearekin zeukan lotura. James Clerk Maxwell-ek -Gaussen egitura kontzeptualetik abiatuta- ezarri zituen elektromagnetismoaren oinarri matematikoak, bere Treatise on Electricity and Magnetism lanean (1873). Izan ere, beraren izena daukaten ekuazio ezagunak garatu zituen Maxwellek, eta ikertzaileak Lurraren eremu magnetikoaz hitz egitera eraman zituen, aurrerantzean indar magnetikoez hitz egiteari utzita.
 2. irudia: Armadaren Behatokiko etxola magnetikoa San Fernandon (Cadiz), 1900ean. 1879an eraikia. (Iturria: Cuaderno de Cultura Científica).
2. irudia: Armadaren Behatokiko etxola magnetikoa San Fernandon (Cadiz), 1900ean. 1879an eraikia. (Iturria: Cuaderno de Cultura Científica).1800 eta 1900 artean, geomagnetismoa diziplina izaera hartzen hasi zen. Fisikari-belaunaldi berri bat, oinarri matematiko bikaina zuena –Arthur Schuster-ek bereziki-, aurrera egin zuen Lurraren eremu magnetikoa deskribatzeko prozesuan, jatorriari buruzko teoria aipagarririk garatu ez zuten arren. Gero eta behatoki berri gehiago eraiki zenez, eta herrialde bakoitzak mapak garatzen jarraitu zuenez, emankor jarraitu zuten datu berrien iturriek.
——————————————–
Egileaz: Cesár Tomé López (@EDocet) zientzia dibulgatzailea da eta Mapping Ignorance eta Cuaderno de Cultura Cientifica blogen editorea.
Itzulpena: Lamia Filali-Mouncef Lazkano
Hizkuntza-begiralea: Xabier Bilbao
——————————————–
The post Lurraren magnetismoaz (II) appeared first on Zientzia Kaiera.
La radiactividad no es una reacción química
 Foto: Oleksandra Bardash / Unsplash
Foto: Oleksandra Bardash / UnsplashLa emisión de partículas alfa y beta planteaba cuestiones muy difícilmente compatibles con las ideas existentes sobre la materia y su estructura. El rápido desarrollo de la química en el siglo XIX había hecho que la hipótesis atómico-molecular de la materia fuera extremadamente convincente [1]. Según la versión decimonónica de este modelo un elemento puro consta de átomos idénticos, que son indivisibles e inmutables.
Pero si un átomo radiactivo emite un fragmento tan sustancial como una partícula alfa, que resultaba ser un átomo de helio ionizado, ¿puede el átomo radiactivo permanecer inmutable? Eso no parecía plausible. Todo lo contrario, parecía que ocurría una transformación en la que el átomo radiactivo se transformaba en un átomo de un elemento químico diferente.
Si un átomo emite una partícula alfa, una parte significativa de su masa (cuatro unidades de masa atómica) se irá con la partícula. ¿Qué pasa con los átomos que emiten partículas beta? La partícula beta, que resultó ser un electrón, es mucho menos masiva que la partícula alfa. Sin embargo, su masa no es cero; por lo que un átomo radiactivo también debe sufrir algún cambio cuando emite una partícula beta.
De nuevo había que concluir que los átomos radiactivos pueden, de hecho, dividirse en dos partes de masa marcadamente desigual, una conclusión contraria al antiguo concepto básico de que el átomo es indivisible.
Otra cuestión fundamental surgió en relación con la energía asociada a los rayos emitidos por las sustancias radiactivas. Ya en 1903, Rutherford y Frederick Soddy, por un lado, y Pierre Curie y Albert Laborde, por otro, notaron que una muestra de radio se mantenía a una temperatura más alta que su entorno simplemente absorbiendo parte de la energía de las partículas alfa emitidas por los átomos de la muestra. Curie y Laborde encontraron que 1 g de radio puede producir alrededor de 0,1 kcal de energía térmica por hora. Una muestra de radio, de hecho, puede seguir liberando energía año tras año durante mucho mucho tiempo. [2]
La liberación continua de tal cantidad de energía no puede explicarse tratando la radioactividad como una reacción química ordinaria, que era la única transformación de la materia conocida en la época. Estaba claro que la radiactividad no implicaba cambios químicos en el sentido habitual [3]. La energía era emitida por muestras de elementos puros [4] y la emisión de energía de los compuestos que contienen elementos radiactivos no dependía del tipo de molécula en la que estaba presente el elemento radiactivo.
El origen de la producción de energía térmica había que buscarlo en algunos cambios profundos dentro de los átomos de elementos radiactivos, más que en reacciones químicas entre átomos. Esto era una idea revolucionaria y se necesitaba una hipótesis igualmente atrevida para explicarla. De nuevo Rutherford estaría implicado en la generación del modelo que terminaría siendo universalmente aceptado.
Notas:
[1] La hipótesis atómica dejó de ser tal para convertirse en uno de los pilares incontrovertibles de nuestro conocimiento del universo cuando Einstein formuló el modelo del movimiento browniano basándose en ella en 1905 y Perrin lo confirmó experimentalmente en 1908. Hay que enfatizar que el que los átomos existan no implica que no puedan tener estructura, a ver si una etimología nos va a nublar la razón.
[2] Tanto es así que una parte sustancial del calor interno de la Tierra proviene de procesos radiactivos.
[3] Los cambios químicos se producen en la relación de unos átomos con otros.
[4] Entre los átomos de un elemento puro puede haber reacciones químicas, ya que se forman unos enlaces y no otros, lo que hace que existan distintas estructuras del elemento que se llaman alotropos. Por ejemplo, el diamante, el grafito y el grafeno son alotropos del carbono, con propiedades muy diferentes. Las transformaciones de un alotropo en otro ni son ni espontáneas (los diamantes no se convierten en minas de lápices y las minas de lápices en diamantes de forma espontánea), ni pueden emitir energía continua durante mucho tiempo ni mucho menos a los niveles en los que lo hace la radiactividad.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La radiactividad no es una reacción química se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La ratonera de Rutherford y Royds
- La ley del gas ideal a partir del modelo cinético
- La carga de las partículas radiactivas
El modelo SIR, un enfoque matemático de la propagación de infecciones
Javier Duoandikoetxea
En este periodo atípico que vivimos a menudo se subraya el valor y el papel que juega la ciencia. En este contexto, también las matemáticas hacen su aportación. Entre otras cosas, ponen a nuestra disposición herramientas que nos permiten prever la evolución de las epidemias. Pronto cumplirán su primer centenario los primeros modelos matemáticos propuestos para tal fin.
Los modelos matemáticos
Los modelos matemáticos se sirven de herramientas matemáticas para estudiar un fenómeno de la vida real de manera abstracta y simplificada. Para ello se expresan mediante una formulación matemática las relaciones entre las magnitudes que intervienen en el fenómeno. El uso y el éxito de los modelos matemáticos varía de unas ciencias a otras. Es obvio que la física está muy matematizada, pero en las ciencias de la vida, por ejemplo, la presencia de las matemáticas no ha sido tan notoria. Hay quien piensa que todo lo relacionado con la vida es demasiado complejo para ajustarse a los modelos simples y abstractos de las matemáticas. Parece que uno de los retos de la matemática aplicada en el siglo XXI será precisamente la ampliación del uso de la matemática en las ciencias de la vida.
En cualquier caso, las primeras propuestas para la aplicación de modelos matemáticos en biología vienen de lejos, si bien en los últimos tiempos es cuando se han producido importantes avances en este terreno. Así, los modelos aplicados a las enfermedades infecciosas no son nuevos, como atestigua el que trataremos aquí, presentado en un artículo que William Ogilvy Kermack y Anderson Gray McKendrick publicaron en 1927 —esto es, hace casi cien años— con el título A Contribution to the Mathematical Theory of Epidemics.
 Imagen 1: el bioquímico O. Kermack y el epidemiólogo McKendrick. (Fuentes: Royal Society y Universidad de Aberdeen, respectivamente).
Imagen 1: el bioquímico O. Kermack y el epidemiólogo McKendrick. (Fuentes: Royal Society y Universidad de Aberdeen, respectivamente).El modelo SIR
Los miembros de una población se clasifican en tres grupos: susceptibles (S=susceptible), infectados (I=infected) y recuperados (R=recovered). Cada miembro de la población pertenece únicamente a uno de los tres grupos en un momento dado. Sin embargo, se puede pasar de un grupo a otro, aunque solo en una dirección, como se muestra en el siguiente esquema:

Por tanto, un miembro susceptible se puede contagiar (pasar de S a I) y uno contagiado se puede recuperar (pasar de I a R) o puede morir. En este modelo se supone que la recuperación proporciona inmunidad y no se regresa al grupo S.
Las personas que fallecen por la enfermedad se incluyen también en el grupo R, con lo que la población total se mantiene constante. Como se habrá notado, el modelo introduce una simplificación, pues no tiene en cuenta ni los nacimientos ni las muertes por otros motivos. Existen modelos más complejos que también contemplan esos casos.
Ecuaciones
Sea t la variable que indica el tiempo y S(t), I(t) y R(t) el número de personas que hay en cada grupo en un momento t determinado. Por las razones expuestas, su suma es una constante. Sea N el tamaño de la población, es decir, S(t) + I(t) + R(t) = N, para todo t. Para plantear las ecuaciones, es necesario formular la velocidad de cambio de esas tres funciones. La expresión matemática de la velocidad es una derivada.
He aquí las ecuaciones del modelo SIR:
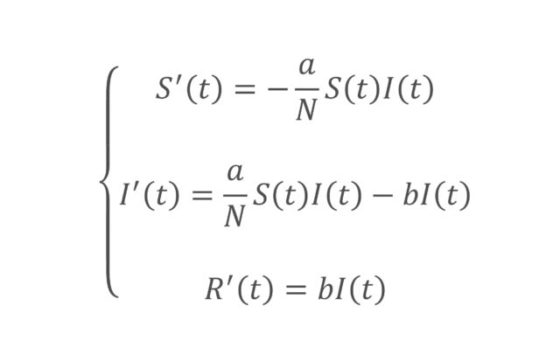
El contacto entre personas susceptibles e infectadas causará el contagio de algunos miembros de S. Dado que el riesgo de contagio depende de los contactos entre miembros de los grupos S e I, la hipótesis del modelo SIR es que sus encuentros son proporcionales al producto de S por I. Además existe un factor llamado tasa de transmisión que debe multiplicarse por dicho producto para calcular la velocidad de cambio del grupo susceptible. Expresamos esa tasa como a/N. El término figura en la ecuación porque expresa la velocidad con que se pasa de S a I. Dado que en el proceso el n.º de susceptibles disminuye y el de personas infectadas aumenta, es negativo para S’ y positivo, en cambio, para I’.
Por otra parte, quienes se curen o fallezcan pasarán de I a R. Para calcular cuántas personas lo hacen tenemos la tasa de recuperación, que ha de multiplicarse por el número de personas infectadas. Por eso aparece el término en las ecuaciones; es negativo para I’, porque reduce el n.º de personas infectadas y positivo para R’, porque hacer aumentar el n.º de recuperadas.
Para resolver las ecuaciones es necesario disponer de los datos iniciales, es decir, el n.º de miembros de cada grupo en el momento en que t=0. Se puede suponer que al principio I(0) = 1 (paciente cero), pero cabe la posibilidad de que fuera superior a uno. Además, tendremos que S(0) > 0 , pues para que haya contagio es necesario que haya susceptibles.
Soluciones de la ecuación
No se puede calcular la solución exacta de las ecuaciones, pero esto no es un problema, pues se pueden obtener soluciones aproximadas por ordenador. En cualquier caso, aun sin resolver el sistema de ecuaciones, las herramientas matemáticas nos permiten determinar algunas propiedades cualitativas de las soluciones.
Así, se observa que el comportamiento de las soluciones depende del número a/b. Se trata del número R0, la tasa básica de reproducción, en este caso. Si R0 > 1, la infección comenzará a extenderse, y si R0 < 1, esto no ocurrirá. De todas formas, si bien ese valor básico tiene incidencia al principio, posteriormente es mejor usar la tasa de reproducción efectiva o aS(t)/Nb. Como al principio S(0) y N son prácticamente iguales, cuando t=0 es casi igual a R0, pero después va reduciéndose a la vez que S.
Plantear ecuaciones formales es fácil, lo problemático es asignar unos valores adecuados a los parámetros a y b. El segundo se puede decidir observando el tiempo que se tarda en recuperarse de la enfermedad. Sin embargo, es más difícil asignar un valor a a. Si partimos de cero, ese valor es desconocido, por lo que es necesario observar el ritmo de contagios del principio. A veces se emplean datos de otros territorios o periodos, pero estos pueden proporcionar información errónea. Además, este modelo simplificado mantiene a y b constantes a lo largo del tiempo, pero en la práctica se pueden adoptar medidas para cambiar estos valores.
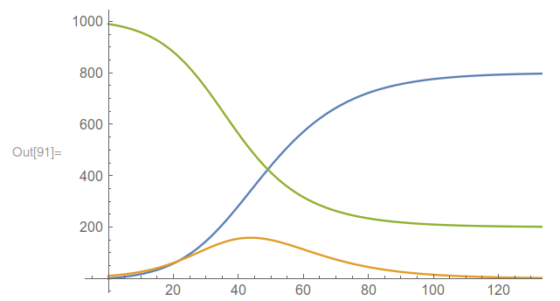 Imagen 2: una ejemplo posible del modelo SIR: S =verde -población susceptible-, I = anaranjado -población infectada-, R = azul -población recuperada-. (Fuente: Wikipedia)
Imagen 2: una ejemplo posible del modelo SIR: S =verde -población susceptible-, I = anaranjado -población infectada-, R = azul -población recuperada-. (Fuente: Wikipedia)Sea como fuere, una de las conclusiones de las ecuaciones es que el valor I(t) tiende a 0 según avanza el tiempo, es decir, se reduce el n.º de personas infectadas. De hecho, el análisis de las ecuaciones indica que debe darse un valor umbral para que la infección se propague. Si el n.º de susceptibles es inferior a ese valor, la infección no se propaga, es decir, dejará de haber personas infectadas, aunque siga habiendo susceptibles. Viendo los datos reales no se percibe la existencia de este umbral, por lo que el modelo matemático fue esencial para llegar a esa conclusión.
Por otro lado, la función I(t) llega a un valor máximo y luego comienza a descender, sin incrementarse de nuevo. Es decir, tiene un único pico. Esta es otra de las propiedades que revela el modelo matemático. No obstante, hay que recordar que el modelo es muy simple y a veces la realidad puede ser distinta.
Intervención pública
El modelo muestra que se puede frenar la propagación de la infección incidiendo en la tasa de reproducción efectiva. En el caso de los virus, se pueden emprender las siguientes acciones:
- Acortar el tiempo de la enfermedad con medicamentos.
- Reducir los contactos entre personas susceptibles e infectadas mediante medidas de aislamiento.
- Reducir la probabilidad de transmisión mediante el lavado frecuente de manos y el uso de mascarillas.
- Reducir el valor inicial S(0) mediante vacunas.
Nos suenan, ¿verdad? Las lectoras y lectores pueden pensar que estos consejos se formularon en el contexto de la Covid-19. Pues no, los he copiado de un artículo de divulgación de 2013 y se referían a la gripe. Tiene presente la evolución de las soluciones de las ecuaciones matemáticas, ya que reducir a y S(t) y aumentar b son formas de minorar la tasa de reproducción efectiva.
Efecto de las vacunas
Una de las recomendaciones anteriores era la vacunación, medida que reduce el número inicial de susceptibles y convierte la tasa de reproducción efectiva en a(1-p)/b , donde p es la fracción vacunada de la población total, teniéndose en cuenta también la efectividad de la vacuna. Por ejemplo, si el 70 % de la población está vacunado y la vacuna tiene una efectividad del 90 %, tendremos que p=0,63. Como normalmente no se puede vacunar a toda la población, y además la efectividad no suele ser del 100 %, tenemos que p < 1.
Por lo tanto, dependiendo de los valores de los parámetros a y b, se puede calcular qué proporción de la población se debe vacunar para evitar (o frenar considerablemente) la propagación de la infección. El objetivo es que el número de susceptibles se mantenga desde el principio por debajo del valor umbral mencionado más arriba. Cuando esto se consigue, se dice que se ha logrado la inmunidad comunitaria. La inmunidad comunitaria protege también a quienes no se han vacunado, incluidas, por supuesto, las personas contrarias a las vacunas. Sin embargo, si una parte significativa de la población se opone a las vacunas, se pierde la oportunidad de lograr la inmunidad comunitaria desde el principio.
Otros modelos
Como dijo el estadístico británico George Box, «todos los modelos se equivocan, pero algunos son útiles». Los modelos simplifican mucho la realidad, por lo que siempre habrá diferencia entre lo que prevén las matemáticas y lo que ocurre realmente. No obstante, lo más importante es la utilidad de la que hablaba Box. Algunos trabajos han demostrado que el modelo SIR, en su simplicidad, se ajusta bien a algunas epidemias. En cualquier caso, este ajuste puede ser más fácil a posteriori, una vez que se controlan mejor los parámetros de las ecuaciones.
Sea como fuere, el SIR no es el único modelo, y a veces se recurre a versiones más desarrolladas del mismo. De entre las que no incluyen grupos nuevos, se pueden mencionar las siguientes:
- El que tiene en cuenta la dinámica vital: los nacimientos se incluyen en el grupo S; en todos los grupos se dan fallecimientos por causas distintas a la infección.
- Modelo SIS: no hay inmunidad. Las personas infectadas que se recuperan pasan de nuevo al grupo S.
- Modelo SIRS: la inmunidad es temporal. Del grupo R se pasa de nuevo al S, pero no inmediatamente.
En otros modelos se añaden uno o más grupos nuevos, como, por ejemplo:
- E (exposed): personas en fase de incubación. Están infectadas, pero aún no transmiten la enfermedad.
- M (maternally derived immunity): las criaturas recién nacidas tienen inmunidad temporal, gracias a los anticuerpos de la madre.
- D (deceased): personas fallecidas por la infección. Estas salen del grupo R, donde quedan quienes sobreviven a la enfermedad.
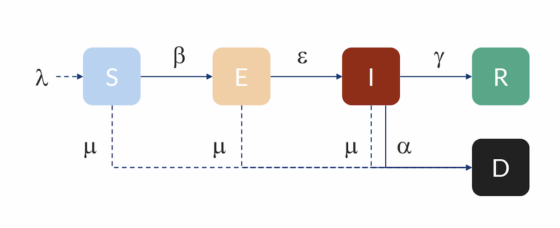 Imagen 3: esquema de un modelo SEIRD. (Fuente: Comsol)
Imagen 3: esquema de un modelo SEIRD. (Fuente: Comsol)Tendiendo esto en cuenta, se han propuesto modelos como SEIR, SEIS, MSIR, SIRD, SEIRD, MSEIR, MSEIRS, etc., cuyas denominaciones reflejan claramente los grupos que incluyen y la forma en que se pasa de un grupo a otro. En estos casos harán falta más ecuaciones y parámetros.
Para saber más:
En la red se puede encontrar abundante información sobre el tema. Estas son algunas de las fuentes que se pueden consultar:
- Ridenhour, Benjamin, Kowalik, Jessica M. y Shay, David K. (2018). El número reproductivo básico (R0): consideraciones para su aplicación en la salud pública. American Journal of Public Health, 108(S6), S455_S465. DOI: https://doi.org/10.2105/AJPH.2013.301704s
- Weiss, Howard (2013). The SIR model and the Foundations of Public Health. Materials matemàtics, 2013(0), 1-17.
- Hethcote, Herbert W. (2000). The mathematics of infectious diseases. SIAM Review, 42(4), 599-653.
- Artículo sobre la Covid-19: Ed Fontes, Modeling the Spread of COVID-19 with COMSOL Multiphysics, COMSOL blog, 07-04-2020.
- Artículo de la Wikipedia en inglés: Compartmental models in epidemiology.
Sobre el autor: Javier Duoandikoetxea es catedrático de Análisis Matemático en la UPV/EHU.
Este artículo se publicó originalmente en euskara el 16 de junio de 2020 en el blog Zientzia Kaiera. Artículo original.
El artículo El modelo SIR, un enfoque matemático de la propagación de infecciones se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El modelo cuántico de Rabi, un sencillo modelo para dominarlos a todos
- Roberto Frucht, matemático en tránsito
- Ilustraciones artísticas de un matemático
Dozena erdi ariketa 2020ko udarako (5): Zirkuluaren azalera
Gogoan izan ahalegina bera –bidea bilatzea– badela ariketa. Horrez gain, tontorra (emaitza) lortzen baduzu, poz handiagoa. Ahalegina egin eta emaitza gurekin partekatzera gonbidatzen zaitugu. Ariketaren emaitza –eta jarraitu duzun ebazpidea, nahi baduzu– idatzi iruzkinen atalean (artikuluaren behealdean daukazu) eta irailean emaitza zuzenaren berri emango dizugu.
Hona hemen gure bostgarren ariketa: Zirkuluaren azalera.
———————————————————————————-
Ariketak “Calendrier Mathématique 2020. Un défi quotidien” egutegitik hartuta daude. Astelehenetik ostiralera, egun bakoitzean ariketa bat proposatzen du egutegiak. Ostiralero CNRS blogeko Défis du Calendrier Mathématique atalean aste horretako ariketa bat aurki daiteke.
———————————————————————————-
The post Dozena erdi ariketa 2020ko udarako (5): Zirkuluaren azalera appeared first on Zientzia Kaiera.
Bañadores y dopaje tecnológico
Leire Sangroniz y Ainara Sangroniz
El desarrollo de la ciencia y la tecnología nos ha dado la oportunidad de obtener más y mejores materiales deportivos, y, por lo tanto, el rendimiento de los y las deportistas ha aumentado. Pero, ¿dónde está el límite? Cuando un equipamiento concreto ofrece a las personas deportistas ciertas ventaja sobre sus adversarios, hablamos de dopaje tecnológico. El dopaje tecnológico se ha dado en varios deportes: ciclismo, tenis, atletismo, y también en el golf. Pero puede que el ejemplo más destacable sea el de la natación. En la pasada década surgió una gran polémica en los Juegos Olímpicos, en torno a los bañadores.
 Imagen 1: el nadador sueco Arne Borg en 1927 con el bañador Racerback de la casa Speedo. (Fotografía: V&A / Museum of Applied Arts and Sciences)
Imagen 1: el nadador sueco Arne Borg en 1927 con el bañador Racerback de la casa Speedo. (Fotografía: V&A / Museum of Applied Arts and Sciences)A principios del siglo XX no se tenía en cuenta la velocidad de los nadadores a la hora de diseñar los trajes de baño. Eran unas camisetas y pantalones de lana que se mojaban enseguida y cogían mucho peso. Pero en aquella época era impensable diseñar algo más ligero.
El primer cambio importante ocurrió en 1927, cuando la casa Speedo comercializó el bañador Racerback; fue toda una revolución, ya que el bañador se ajustaba mucho al cuerpo. La espalda y los hombros quedaban al descubierto para facilitar el movimiento, y en vez de lana, se utilizó seda. Este bañador fue muy innovador, sin embargo, en muchas playas se prohibió su uso. Los siguientes años, el desarrollo de la tela sintética, es decir, la tela realizada con polímeros permitió realizar bañadores más ligeros, entre ellos los de nylon (poliamida), en la década de los 50, o los de elastano (copolímero de poliurea poliéster), en los 70. Estos materiales eran bastante nuevos en aquella época, ya que fueron creados a principios y a mediados del siglo XX, respectivamente, por la casa DuPont. Durante los años siguientes la tendencia fue la misma: telas de polímero y bañadores más pequeños, ligeros y ajustados.
La empresa Speedo continuó con sus avances y en el año 2000 desarrolló el bañador Fastskin. Tenía marcas en forma de V en la superficie, para reducir la resistencia al agua, y muchos deportistas lo usaron en los juegos de Sydney. Después, desarrollaron el bañador LZR Razer; con ese bañador quedó claro el impacto que tiene la tecnología en el rendimiento de los deportistas, sobre todo en natación. En los Juegos Olímpicos de Beijing (2008) se batieron 25 marcas mundiales de natación. Detrás de esos resultados había algo más que la buena forma física de los deportistas: El bañador LZR Racer de Speedo. El 98 % de las personas nadadoras que ganaron una medalla llevaban ese bañador.
El traje en cuestión mejoraba el rendimiento de los nadadores y nadadoras, comprimiendo sus músculos y obteniendo un aspecto más hidrodinámico. Además, cubría el cuerpo desde las pantorrillas hasta las muñecas y atrapaba las burbujas de aire entre el cuerpo y el bañador, aumentando la flotabilidad.
Cabe destacar que el traje estaba realizado en poliuretano, material hidrofóbico, y eso tiene una ventaja: repele el agua. De todas formas, el bañador no podría hacerse solamente de poliuretano, ya que se rompía facilmente. Siendo así, se le añadió otro polímero, una poliamida especialmente tratada, para aumentar la hidrofobicidad y no absorber agua. Asimismo, las piezas estaban unidas mediante ultrasonidos, para evitar las costuras y reducir la resistencia.
 Imagen 2: la nadadora Nađa Higl en el Campeonato Europeo de Natación de 2010 con el bañador «Super-body Jaked J01» de la casa Jaked. (Fuente: Wikipedia)
Imagen 2: la nadadora Nađa Higl en el Campeonato Europeo de Natación de 2010 con el bañador «Super-body Jaked J01» de la casa Jaked. (Fuente: Wikipedia)Según los estudios realizados, el éxito de este traje de baño residía en su flotabilidad; de hecho, las pequeñas burbujas de aire que se alojaban entre la piel y el bañador mejoraban la flotabilidad. Como la resistencia al aire es más pequeña que la resistencia al agua, cualquier pequeño detalle puede influir mucho en la velocidad.
El resto de marcas también realizaron avances; Arena, por ejemplo, consiguió desarrollar un bañador enteramente realizado en poliuretano. Siendo así, el bañador de Speedo quedó desfasado, ya que el bañador de poliuretano de Arena tenía una menor resistencia al agua, puesto que era completamente impermeable e hidrofóbico. En 2009, en el XIII Campeonato Mundial de Natación, casi todos los nadadores y nadadoras llevaron el bañador de Arena y este uso hizo que la Federación Internacional de Natación (FINA) se encontrara con un problema. Las marcas mundiales se superaban fácilmente y esto hizo que algunos deportistas y parte del público se incomodaran y cuestionaran los resultados, perdiendo su valor.
Se empezó a hablar de dopaje tecnológico, ya que los logros fueron gracias a un desarrollo tecnológico importante, no solo al esfuerzo de los y las nadadoras. Así que la Federación Internacional de Natación decidió prohibir este tipo de bañadores a partir de 2009. Desde ese momento solamente se permitirían los tejidos permeables; es decir, trajes que no formaran burbujas de aire. Además, se limitaron las dimensiones de los trajes. En el caso de los hombres, podrían abarcar solamente desde la cintura hasta la rodilla; en el caso de las mujeres, no podrían cubrir más allá de los hombros, ni por debajo de las rodillas.
Probablemente, en el futuro, a medida que la ciencia y la tecnología avancen volverá a hacerse evidente la delgada línea existente entre la mejora de los equipamientos deportivos y el dopaje tecnológico.
Fuentes:
- Morrison, Jim (2012). How Speedo Created a Record-Breaking Swimsuit. Scientific American.
- Blanco, J.F., Hunt-Hurst, P. K., Doerin, M.D. y Vaughan-Lee, H. (2016). Clothing and Fashion: American Fashion from Head to Toe. ABC-CLIO, Santa Barbara, California.
- Roberst, Jacob (2017). Winning Skin. Science History Institute.
- Trinidad Morales, A., Tamayo Fajardo, J. A. y González-García, H. (2019). High-Speed Swimsuits and Their Historical Development in Competitice Swimming. Frontiers in Psychology, 10, 2639. DOI: 10.3389/fpsyg.2019.02639
- Nasa Spinoff. Space Age Swimsuit Reduces Drag, Breaks Records. 2020ko uztailaren 2an kontsultatua.
Sobre las autoras: Leire Sangroniz y Ainara Sangroniz son doctoras en Química e investigadores del Departamento de Ciencia y Tecnología de Polímeros de la Facultad de Química de la UPV/EHU y del Instituto Polymat.
Este artículo se publicó originalmente en euskara el 14 de julio de 2020 en el blog Zientzia Kaiera. Artículo original.
El artículo Bañadores y dopaje tecnológico se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Materiales inteligentes y multifuncionales para impulsar el desarrollo tecnológico
- Zientziateka: Rendimiento deportivo, ayudas ergogénicas y dopaje
- Cómo conseguir que la superhidrofobia dure
Encontrando valor en los neumáticos usados
 Foto: Darren Nunis / Unsplash
Foto: Darren Nunis / UnsplashLos neumáticos usados suponen un grave peligro medioambiental por los daños que puede ocasionar su almacenamiento en el entorno. Su generación aumenta año tras año en los países desarrollados, por lo que su gestión eficiente es del mayor interés, en el marco de normativas cada vez más restrictivas. Encontrar valor en ellos es un factor clave.
“La pirólisis es una alternativa de gran interés para revalorizar la materia de los neumáticos con el objetivo de obtener combustibles alternativos y productos petroquímicos de alto valor añadido. En este contexto, la pirólisis es la degradación del caucho de la rueda mediante el calor en ausencia de oxígeno. Los productos y su rendimiento dependen de las condiciones a las que se lleva a cabo a cabo la pirólisis”, señala Miriam Arabiourrutia Gallastegui, profesora del grupo PROCAT-VARES (Procesos Catalíticos-Valorización de Residuos) de la UPV/EHU.
En una revisión reciente el grupo de investigación analiza las ventajas más importantes en la valorización de neumáticos usados mediante la pirólisis catalítica. “El principal interés de la valorización de los residuos de neumáticos por pirólisis se basa en el potencial de los productos obtenidos: gas, líquido y un sólido conocido como char. El rendimiento y composición de todos ellos dependen de las condiciones de la pirólisis”, comenta Arabiourrutia.
“El principal producto obtenido en la pirólisis catalítica es el líquido. Este líquido es fundamentalmente el que tiene mayor interés porque se puede utilizar como combustible si se incorporara, por ejemplo, en una refinería. Este líquido tiene una composición compleja incluyendo compuestos de diferente naturaleza (aromáticos, parafinas, olefinas y naftenos) y compuestos de azufre que limitan su uso directo como combustible. Por ello, el interés de la pirólisis catalítica está usualmente relacionada con la mejora de las propiedades o rendimiento de esta fracción. Así, de la pirólisis catalítica se ha puesto gran interés en la producción de compuestos aromáticos (benceno, tolueno…) porque tienen aplicaciones comerciales”, explica la investigadora de la UPV/EHU.
“Los gases de pirólisis también pueden ser usados como combustible para obtener energía. Finalmente, el char es el sólido que se queda sin degradar y está compuesto fundamentalmente del negro de humo que contiene el neumático; el negro de humo es el compuesto que aporta las propiedades antiabrasivas al neumático. Se está estudiando la posible activación del char para utilizarlo como carbón activo —quizás se podría reutilizar como negro de humo en la fabricación del neumático—“, añade Arabiourrutia.
En el proceso que investiga el grupo de la UPV/EHU la pirólisis catalítica tiene unas condiciones muy específicas: «el tiempo de residencia de los gases que se generan en el reactor es corto y esto promueve una serie de reacciones que hacen, por ejemplo, que se obtenga un alto rendimiento de la fracción líquida. Además, hemos visto que gracias a este proceso se obtiene sobre todo el producto líquido que puede ser utilizado en las refinerías para obtener combustible”, subraya Miriam Arabiourrutia Gallastegui.
Según indica la investigadora, “gracias a todos estos trabajos vamos modificando y mejorando el proceso de pirólisis para intentar conseguir una distribución de productos con una composición más adecuada de cara a su potencial aplicación como combustible o materia prima para obtener compuestos de interés”.
Referencia:
Miriam Arabiourrutia, Gartzen Lopez, Maite Artetxe, Jon Alvarez, Javier Bilbao, Martin Olazar Waste tyre valorization by catalytic pyrolysis – A review (2020) Renewable and Sustainable Energy Reviews doi: 10.1016/j.rser.2020.109932
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Encontrando valor en los neumáticos usados se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Encontrando exoplanetas tapando las estrellas
- Un hidrogel de almidón/grafeno, conductor y antibacteriano, para implantes neurológicos
- Bioóleo a partir de residuos cítricos
Bidaia hiriaren erdigunera

Natura, ingurumena, eta biodibertsitatea gisako kontzeptuetan pentsatzen nuenean, kolore berdea zetorkidan burura, eta hausnarketa oker samar honetan, soilik berdeak ziren inguruetan bizi eta eboluzionatzen zuten espeziak zeuden.
Bada, liburuak begiak ireki dizkit: gizakiak, Homo sapiensak, asfaltozko eta burdinazko ekosistema bat sortu du (“fenomeno ekologiko liluragarria eta berritzailea”, Menno Schilthuizen autorearen esanetan) eta hori dugu bizigiro bai guk, bai beste espezieek. Begi aurrean gertatzen ari zen eboluzioa eta ni konturatu gabe!
Eskerrak liburu hau daukagun. Hiri-oihan moduko hau berria, desberdina eta aldakorra da oso. Eta ingurune honetan, gainontzeko espezieek ikasi, modu berrietara egokitu eta eboluzionatu behar izan dute. Gainera, pentsatzen duguna baino izaki gehiago bizi dira hirietan. Ildo honi jarraiki, galdera batzuk erantzuten saiatuko da autorea: nola egokitzen dira inguru berrira eta zeintzuk izan dira garatu behar izan dituzten estrategiak bizirauteko? Nolakoa da (aurre)egokitzapen prozesua? Eta zerk eragiten du espezieen desagerpena?
Schilthuizenek espezie ugariren adibideen bitartez, orain arte egin diren arloko ikerketak agertuz eta bere esperientziak tartekatuz, istorio bat kontatu digu: hirietan gertatzen ari den eboluzioarena, alegia. Bidaia liluragarria da hiriko naturaren mundua aztertzeko. Hala, beste aitorpen batekin bukatu nahi dut: ez ezazu lan hau irakurtzeko aukera galdu.
Argitalpenaren fitxa:- Izenburua: Darwin comes to town: How the urban jungle drives evolution
- Egilea: Menno Schilthuizen
- Itzultzailea: Eduardo Jordá
- Argitaletxea: Turner
- Orrialdeak: 296
- ISBNa: 978-84-17141-75-2
- ———————————————————————————-Egileaz: Uxue Razkin (@UxueRazkin) kazetaria da.———————————————————————————-
The post Bidaia hiriaren erdigunera appeared first on Zientzia Kaiera.
La pandemia de plástico
Desde el Ártico a la Antártida, desde la superficie del mar al sedimento del fondo de los océanos, en todos los ambientes marinos que los científicos han explorado aparece el plástico. Y, por supuesto, también en el suelo y en las aguas dulces, incluso en la atmósfera. Persiste durante años, siglos, milenios afirman algunos expertos, mata animales y plantas, contamina el entorno y ensucia y satura cualquier hábitat. Comenzó a fabricarse en la década de los treinta del siglo pasado y en los cincuenta llegó la producción en masa.
 Foto: Erik Mclean / Unsplash
Foto: Erik Mclean / UnsplashComo ejemplo sirve la publicación de 2018 del grupo de Thomas Maes, del Centro para el Ambiente, Pesquerías y Ciencia de la Acuicultura de Lowestoft, en Inglaterra, sobre la presencia de plástico en el fondo del mar, en el entorno de Gran Bretaña e incluyendo el Mar del Norte. De 1992 a 2017, el 63% de los puntos de muestreo tienen, por lo menos, algún objeto o fragmento de plástico. Hay algunos plásticos, como pueden ser las bolsas de plástico, que han disminuido hasta en un 30% desde 2010. No tengo datos sobre si la pandemia COVID-19 ha cambiado estas cifras.
En 2015, la producción global de plásticos era de 380 millones de toneladas, muy lejos de los 2 millones de toneladas de 1950. El total del plástico producido entre 1950 y 2015 era de casi 8000 millones de toneladas, y la mitad, unos 4000 millones, se fabricaron entre 2002 y 2015, en solo 13 años. Solo China, en 2015, produjo el 28% del total. Para 2010 eran 275 millones de toneladas de plástico las que se vertían en 192 países y, de esa basura, entre 4.8 y 12.7 millones de toneladas terminaban en el mar. De estas cifras, Roland Geyer y su grupo, de la Universidad de California en Santa Barbara, afirman que, en 2017, 4900 millones han terminado en la basura, el 79%, y solo 600 millones, el 10%, se han reciclado.
Muchos de los plásticos vertidos miden menos de 5 milímetros y son llamados microplásticos. Esta fue la palabra del año 2018 para la Fundéu BBVA. Incluso se pueden degradar y fragmentar hasta nanoplásticos con un tamaño de 1 a 100 nanómetros (millonésima parte de un milímetro). Con modelos de ordenador se ha calculado que, en los océanos, hay entre 15 y 51 billones de nanopartículas de plástico. Incluso ahora se ha encontrado plástico en muestras de agua del Mar del Norte recogidas en los años sesenta. En conclusión, la contaminación con plásticos comenzó en el momento en que se empezó a fabricar y utilizar en masa.
La isla Henderson, en el sur del Pacífico Central, es parte del territorio británico de las islas Pitcairn. Mide 9.6 kilómetros de longitud por 5.1 kilómetros de anchura. En total son 37.3 kilómetros cuadrados de superficie. Está a 115 kilómetros al noroeste de la isla Pitcairn, la principal del grupo. La isla Henderson está deshabitada y se encuentra a unos 5000 kilómetros de grandes extensiones de tierra, con sus grandes poblaciones y gran desarrollo social e industrial.
No existen fuentes locales de contaminación y, por tanto, toda la basura de la isla Henderson viene del exterior. En 2015, Jennifer Lavers y Alexander Bond, de la Universidad de Tasmania y de la Real Sociedad para la Protección de las Aves, en Inglaterra, visitaron la isla, entre mayo y agosto, y cuantificaron la basura de plásticos de su costa.
Recogieron muestras tanto en las playas como en los fondos cercanos a ellas. En las playas encontraron de 20 a 670 fragmentos de plástico por metro cuadrado, y en los fondos, de 53 a 4500 fragmentos por metro cuadrado. El 65% son microplásticos. Calcularon, a partir de estos datos, que el número de fragmentos de plástico en la isla, visibles o enterrados, era de casi 38 millones, con un peso de más de 17 toneladas. Cada día llegan a la isla entre 17 y 268 nuevos fragmentos de plástico.
Los autores suponen que el plástico llega a la isla llevado por las corrientes oceánicas que provocan el Gran Giro de Plásticos del Pacífico Sur pues la isla se encuentra en la parte oriental de ese Giro. Como ejemplo sirve que la mayor parte de los restos relacionados con la pesca, sobre todo fragmentos de redes y boyas, vienen de empresas de China, Japón y Chile. Más al norte, en Hawai, se estima que 80000 toneladas de plásticos llegan cada año, y el 54% viene de Norteamérica y Asia.
El plástico está en los océanos, los científicos no saben cómo retirarlo y, mucho menos, los micro- y nanoplásticos. Se depositan en los sedimentos del fondo y, allí, cimentarán con otros materiales y, en el futuro, esa capa de sedimentos con plásticos será nuestro legado al futuro, el legado del Antropoceno.
Ya se han encontrado rocas sedimentarias entre cuyos componentes hay fragmentos de plástico. Lo han descrito Patricia Corcoran y su grupo, de la Universidad de Ontario Occidental en Canadá, con muestras recogidas en la Playa Kamilo, en las Islas Hawai. Son rocas con fragmentos de plástico y cementadas con arena de la playa. Los autores las llaman plastiaglomerados. También describen como, en algunos casos, las rocas con plástico se forman en el suelo, debajo de los abundantes fuegos de campamento y barbacoas que se hacen en la playa.
Solo para recordarlo, hay que mencionar que, en nuestras costas, el grupo de Nikole Arrieta, de la UPV/EHU de Leioa, ha encontrado rocas formadas con la cementación de escorias procedentes de vertidos, con gabarras, de los altos hornos. Otro signo de actividad humana para el futuro, de nuevo el legado del Antropoceno.
Un lugar donde ya se han integrado los plásticos es el hielo del Ártico. El grupo de Andrés Cózar, de la Universidad de Cádiz, ha detectado una fuerte corriente oceánica hacia el norte desde el Atlántico y por el este y el oeste de Groenlandia. Esta corriente lleva plásticos desde el Giro del Atlántico Norte hacia el Ártico. También está ocurriendo que, con el calentamiento global y la fusión de parte de los hielos del Ártico, se están liberando fragmentos de plástico que estaban en el hielo desde hace tiempo. El equipo de Rachel Obbard, del Colegio Darmouth, en Estados Unidos, ha encontrado grandes cantidades de plástico en el Ártico, algunos fabricados hace bastantes años, y, quizá, estaban congelados en el hielo.
Como decía, estas capas de sedimentos con plásticos son un marcador de la actividad humana, de la era geológica Antropoceno, reivindicada por un numeroso grupo de investigadores de todo el mundo en la revisión liderada por Jan Zalasiewicz, de la Universidad de Leicester, en Inglaterra. Entre los que participan en esta revisión está Alejandro Cearreta, de la UPV/EHU de Leioa. La Era Antropoceno se define como la época geológica en que la actividad humana tiene un impacto geológico sobre los ecosistemas y la geología del planeta.
En la revisión, describen como, desde el siglo pasado, los plásticos aparecen en todos los hábitats. Son muy evidentes en sedimentos terrestres y, más recientemente, en los depósitos sedimentarios marinos. La cantidad de plástico se ha doblado varias veces en las últimas décadas. Son los llamados tecnofósiles y son, por supuesto, marcadores del Antropoceno.
Y pueden llegar lejos como muestra el estudio de J.A. Gil Delgado y su grupo, de la Universidad de Valencia, en cuatro lagos de Castilla-La Mancha en las provincias de Cuenca, Ciudad Real y Toledo. Analizan las heces de tres especies de aves acuáticas: focha común (Fulica atra), ánade real o azulón (Anas platyrhynchos) y tarro blanco (Tadorna tadorna). Toman 89 muestras y el 48% tienen restos de plástico, y la mayoría de ese plástico procede del entorno cercano y es de uso en agricultura.
Es interesante destacar que, a pesar de la presencia de plástico en todos los hábitats, según Kinga Kik y sus colegas, de la Universidad de Lodz, en Polonia, y en una revisión publicada este año 2020, no hay estudios de los efectos de estos compuestos, en este caso del poliestireno, sobre el organismo humano.
 Foto: Yifan Zhang / Unsplash
Foto: Yifan Zhang / UnsplashPodemos volver a los océanos, a las profundidades de los océanos, allí donde el grupo de M.L. Taylor, de la Universidad de Oxford, ha encontrado microplásticos en el sistema digestivo de seis especies de cnidarios (medusas, …), equinodermos (erizos de mar, …) y artrópodos (langostas, …). Y son muestras tomadas por un robot a profundidades entre 300 y 1700 metros de profundidad en el Atlántico, el Mediterráneo, el Índico y el Pacífico.
Los plásticos son esenciales en nuestra sociedad pero, también, y ya lo hemos comentado varias veces, suponen un grave y enorme riesgo de contaminación, sobre todo en los ecosistemas marinos con enormes islas de plástico flotantes con tamaño continental. Sin embargo, esta alarma ambiental provocada por la acumulación de plásticos de difícil y larga degradación ha empujado a científicos e instituciones a buscar procesos y métodos que los degraden. Son difíciles de degradar en entornos naturales por su estructura complicada, gran tamaño de molécula y su naturaleza hidrofóbica. Evitan el agua que, por otra parte, es el medio en el que mejor se encuentran los seres vivos que los podrían degradar. Como escriben Harry Austin y sus colegas, de la Universidad de Portsmouth, en Inglaterra, ya se han encontrado bacterias que producen enzimas que metabolizan plásticos y los utilizan como fuente de alimento y energía.
Este grupo trabaja con la bacteria Ideonella sakaiensis, que es capaz de crecer en el plástico tereftalato de polietileno o PET, en sus siglas en inglés, que es muy utilizado en botellas, ropa, envases o alfombras. Esta bacteria sintetiza y libera al medio una enzima, la PETasa, que degrada el ftalato y lo separa en componentes más pequeños y, se supone, inocuos. La historia de esta bacteria, Ideonella, comenzó en el Japón, donde fue aislada por el grupo de S. Yoshida, de la Universidad Keio de Yokohama. La encontraron en un medio muy contaminado, con basura y botellas de plástico, de PET, medio sumergidas en agua. Y en una de esas botellas aislaron y caracterizaron a la Ideonella. También determinaron la enzima PETasa y otra enzima, la METasa, que actuaba sobre los productos de descomposición del ftalato y producía ácido tereftálico y etilenglicol, compuestos menos contaminantes que el ftalato original.
Pero antes del hallazgo de Yoshida, en 2010, ya se habían publicado algunos estudios de la degradación de plásticos por bacterias. Por ejemplo, Naima Atiq y sus colegas, de la Universidad de Islamabad, en Pakistán, encontraron cuatro cepas de bacterias que degradaban poliestireno, el plástico que se conoce como expandido y que se utiliza en envases por su excelente comportamiento en aislar el contenido de cambios de temperatura.
Atiq y su grupo colocaban poliestireno con muestras de suelo del jardín de su universidad. Encontraron bacterias que crecían sobre el plástico y lo degradaban y utilizaban como fuente de energía. Eran bacterias de los géneros Microbacterium, Paenibacillus, Bacillus y Pseudomonas. Fue una investigación con escasa difusión, de un país de Asia y publicado en una revista africana y, por ello, hasta años más recientes no se ha conocido.
No solo bacterias, también se han encontrado hongos adheridos a la superficie de plásticos durante su degradación. El grupo de Urooj Zafar, de la Universidad de Manchester, los ha encontrado enterrando placas del plástico poliuretano en restos orgánicos durante el proceso de compostaje. Varias especies de hongos se asocian al poliuretano en el tiempo que se necesita para conseguir el compost. Las más numerosas son especies del género Aspergillus. Cuando termina el compostaje, las comunidades de hongo sobre el plástico no son las mismas que las que aparecen en el compost y, por ello, parece que se han seleccionado las que más eficazmente utilizan el plástico como alimento y energía.
Una de las especies del hongo Aspergillus, también aislada en Islamabad, en Pakistán, es el Aspergillus tubingensis, y el grupo de Sehroon Khan, de la Academia China de Ciencia de Kunming, ha demostrado que degrada poliuretano. Lo hace en dos meses en el laboratorio y, también, cuando el plástico es enterrado.
Además de bacterias y hongos, una tercera línea de investigación sobre organismo que degradan plásticos estudia las larvas de insectos. Así, S.S. Yang y sus colegas, de la Universidad de Stanford, trabajaron con larva del coleóptero Tenebrio molitor, conocida como el gusano de la harina. Se alimenta con poliestireno. En 12 a 15 horas ingiere el plástico, y a las 2-3 semanas ha utilizado el 65% de la cantidad que se le ha proporcionado. Si, a la vez, se le dan restos de vegetales, la degradación del plástico se dobla. Cuando se ha dejado que estas larvas alimentadas con poliestireno lleguen a adultos y se reproduzcan, la siguiente generación sigue alimentándose con plástico. Sin embargo, un reciente estudio del grupo de Konrad Matyja, de la Universidad de Wroclaw, en Polonia, muestra que las larvas de Tenebrio alimentadas con poliestireno rara vez completan su ciclo vital y no llegan a adultos. El alimento que se les proporciona con el plástico no es suficiente y necesitan un complemento nutricional de avena.
Los autores sugieren que la degradación del poliestireno no la hace directamente el gusano de la harina sino algún microorganismo que vive en su tubo digestivo. En otra publicación, este grupo ha identificado una de las bacterias del tubo digestivo que degrada el poliestireno. Pertenece al género Exiguobacterium.
En la misma línea, Paolo Bombelli y su equipo, de la Universidad de Cambridge, han trabajado con la polilla de la cera, larva del lepidóptero Galleria mellonella, que se alimenta de la cera de las colmenas. Colocan láminas de polietileno en contacto directo con las polillas y, en 40 minutos, aparecen orificios en el plástico. Son, de media, 2.2 orificios por larva y por hora. Si se ponen más de 100 polillas en contacto con una bolsa de polietileno, del tipo de las usadas para recoger y transportar la compra, en 12 horas disminuye su peso en 92 miligramos o, si se quiere, en unas 14 horas su peso cae un 13%.
De nuevo los autores sugieren que el proceso de desintegración del polietileno lo hace algún microorganismo del tubo digestivo de la polilla.
En 2017, Wilkes y Aristilde, de la Universidad Cornell de Ithaca, en Estados Unidos, publicaron una revisión sobre las bacterias de un solo género, Pseudomonas, con capacidad de degradar plásticos. Hay citadas 17 especies y cepas de este género que pueden degradar hasta nueve tipos de plástico con diferentes grados de eficacia.
Otra revisión reciente sobre microorganismos que degradan plástico, en concreto poliestireno, Ba Thanh Ho y sus colegas, de la Universidad Nong Lam de la Ciudad Ho Chi Minh, en Vietnam, enumeran 33 especies y variedades, y tres de ellas vienen del tubo digestivo de larvas de insectos. Los autores plantean que se debe investigar cómo aumentar la velocidad del proceso de degradación del poliestireno. Y, también, la conservación de las infraestructuras que llevan este plástico.
Para terminar con una revisión reciente, de este año 2020, Sunil Ghatge y su grupo, desde Gwangjin, en Corea, mencionan 31 especies de bacterias y nueve de hongos que biodegradan el polietileno.
Referencias:
Arrieta, N. et al. 2017. Characterization of ferruginous cements related with weathering of slag in a template anthropogenic beachrock. Science of the Total Environment 581-582: 49-65.
Atiq, N. et al. 2010. Isolation and identification of polystyrene biodegrading bacteria from soil. African Journal of Microbiology Research 4: 1537-1541.
Austin, H.P. et al. 2018. Characterization and engineering of a plastic-degrading aromatic polyesterase. Proceedings of the National Academy of Sciences USA doi: 10.1073/pnas.1718804115
Bombelli, P. et al. 2017. Polyethylene biodegradation by caterpillars of the wax moth Galleria mellonella. Current Biology 27: R292-R293.
Corcoran, P.L. et al. 2014. An anthropogenic marker horizon in the future rock record. GSA Today doi: 10.1130/GSAT-G198A.1
Cózar, A. et al. 2017. The Artic Ocean as a dead end for floating plastics in the North Atlantic branch of the Termohaline Circulation. Science Advances 3: e1600582
Cressey, D. 2016. The plastic ocean. Nature 536: 263-265.
Geyer, R. et al. 2017. Production, use, and fate of all plastics ever made. Science Advances 3: e1700782.
Ghatge, S. et al. 2020. Biodegradation of polyethylene: a bierf review. Applied Biological Chemistry 63: 27.
Gil-Delgado, J.A. et al. 2017. Presence of plastic particles in waterbirds faeces collected in Spanish lakes. Environmental Pollution 220: 732-736.
Ho, B.T. et al. 2018. An overview on biodegradation of polystyrene and modified polystyrene: the microbial approach. Critical Reviews in Biotechnology 38: 308-320.
Jambeck, J.R. et al. 2015. Plastic waste from land into the ocean. Science 347: 768-771.
Khan, S. et al. 2017. Biodegradation of polyester polyurethane by Aspergillus tubingiensis. Environmental Pollution doi: 10.1016/j.envpol.2017.03.012
Kik, K. et al. 2020. Polystyrene nanoparticles: Sorces, occurrence in the environment, distribution in tissues, accumulation and toxicity to various organisms. Environmental Pollution 262: 114297.
Lavers, J.L. & A.L. Bond. 2017. Exceptional and rapid accumulation of anthropogenic debris in one of the world’s most remote and pristine islands. Proceedings of the National Academy of Sciences USA doi: 10.1073/pnas.1619818114
Maes, T. et al. 2018. Below the Surface: Twenty-five years of seafloor litter monitoring in coastal seas of Northwest Europe (1992-2017). Science of the Total Environment 630: 790-798.
Matyja, K. et al. 2020. Effects of polystyrene diet on Tenebrio molitor larval growth, development and survival: Dynamic Energy Budget (DEB) model analyses. Environmental Pollution 264: 114740.
Obbard, R.W. et al. 2014. Global warming releases microplastics legacy frozen in Artic Sea ice. Earth’s Future 2: 315-320.
Taylor, M.L. et al. 2016. Plastic microfibre ingestión by deep-sea organisms. Scientific Reports 6: 33997
Wilkes, R.A. & L. Aristilde. 2017. Degradation and metabolism of synthetic plastics and associated products by Pseudomonas sp.: capabilities and challenges. Journal of Applied Microbiology 123-582-593.
Yang, S.S. et al. 2018. Biodegradation of plystyrene wastes in yellow mealworms (larvae of Tenebrio molitor Linnaeus): Factors affecting biodegradation rates and the ability of polystyrene-fed larvae to complete their life cycle. Chemosphere 191: 979-989.
Yang, Y. et al. 2015. Biodegradation and mineralization of polystyrene plastic-eating mealworms. Part 2. Role of gut microorganisms. Environmental Science and Technology 49: 12087-12093.
Yoshida, S. et al. 2016. A bacterium that degrades and assimilates poly(ethylene terephthalate). Science 351: 1196-1199.
Zafar, U. et al. 2014. Biodegradation of polyester polymethane during commercial composting and analysis of associated fungal communities. Bioresource Technology 158: 374-377.
Zalasiewicz, J. et al. 2016. The geological cycle of plastics and their use as a stratigraphic indicator of the Anthropocene. Anthropocene 13: 4-17.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo La pandemia de plástico se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Adiós a las microesferas de plástico en los cosméticos
- ¿Y si la bolsa de plástico fuese más sostenible que las de papel o algodón?
- Una fibra óptica de plástico actúa como concentrador solar luminiscence
Tareas de un matemático loco
 Sello conmemorando el centenario del nacimiento de Antón Chejov. Imagen: Wikimedia Commons.
Sello conmemorando el centenario del nacimiento de Antón Chejov. Imagen: Wikimedia Commons.Antón Chéjov publicó Tareas de un matemático loco en 1882 bajo el seudónimo de “Antosha Chejonté”. Se trata de una hilarante parodia del quehacer matemático a través de ocho absurdas cuestiones planteadas por un matemático “loco” y que se reproducen debajo (ver [1]):
-
Me perseguían 30 perros, de los cuales 7 eran blancos, 8 grises y los restantes negros. Se pregunta: ¿en qué pierna me mordieron los perros, en la derecha o en la izquierda?
-
Autolimioi nació en el 223, y murió tras vivir 84 años. Una mitad de la vida la pasó en viajes, un tercio lo gastó en placeres. ¿Cuánto vale una libra de clavos y estuvo acaso casado Autolimio?
-
En el año nuevo, de la mascarada del teatro Bolshói fueron sacados 200 hombres por pelea. Si los que peleaban eran doscientos pues, ¿cuántos eran los injuriosos, los borrachos, los levemente borrachos y los que deseaban, pero no hallaban ocasión de pelear?
-
¿Qué se obtiene tras la suma de esas cifras?
-
Se compraron 20 cajas de té. En cada caja había 5 pudsii, cada pud tenía 40 libras. De los caballos que cargaban el té, dos se cayeron en el camino, uno de los cocheros se enfermó y 18 libras se derramaron. La libra tiene 96 zolotniksiii de té. Se pregunta, ¿qué diferencia hay entre el pepino en salmuera y la perplejidad?
-
La lengua inglesa tiene 137 856 738 palabras, la francesa 0,7 más. Los ingleses se juntaron con los franceses y unieron ambas lenguas en una. Se pregunta, ¿qué vale el tercer papagayo y cuánto tiempo se necesitó para subyugar a esos pueblos?
-
El miércoles 17 de junio de 1881, a las 3 de la madrugada, debió salir el tren de la estación A por la vía férrea, para llegar a la estación B a las 11 de la noche pero, antes de la misma partida del tren, se recibió la orden de que el tren llegara a la estación В a las 7 de la noche. ¿Quién ama más prolongado, el hombre o la mujer?
-
Mi suegra tiene 75 años y mi esposa 42. ¿Qué hora es?
Informó Antosha Chejonté
Si alguien conoce la respuesta a alguna de estas cuestiones, ¿sería tan amable de compartirla? Gracias.
 Schioti, ábaco ruso. Imagen: Wikimedia Commons.
Schioti, ábaco ruso. Imagen: Wikimedia Commons.Pasemos a unas matemáticas un poco más serias. Dos años más tarde Chéjov publicó El repetidor. Estamos en Rusia, a finales del siglo XIX. Egor Ziberov, un estudiante de séptimo curso, da clases particulares a Petia, un niño de 12 años. El padre del pequeño asiste a la clase; Egor pretende lucirse para pedir un aumento de sueldo. Tras el latín, llega la clase de matemáticas (ver [1]):
— Pasemos ahora a la aritmética. Coja la pizarra. ¿Qué problema toca?
Petia escupe sobre la pizarra, y la borra después con la manga. El profesor coge el libro de problemas y dicta:
— Un comerciante compró ciento treinta y ocho varas de paño negro y azul por valor de quinientos cuarenta rublos. Se pregunta: ¿Cuántas varas compró del uno y del otro si el azul costaba a cinco rublos la vara y el negro a tres? ¡Repita usted el problema!
Petia lo repite; y comienza inmediatamente, sin decir palabra, a dividir quinientos cuarenta entre ciento treinta y ocho.
— ¿Para qué divide usted? ¡Espere!… Bueno, sí…, siga. ¿Hay residuo? No tiene que haberlo. Traiga, yo lo dividiré. Ziberov lo divide y obtiene de resultado tres con residuo, lo que se apresura a borrar.
«Es extraño —piensa, tirándose del cabello y enrojeciendo—. ¿Cómo es este problema?… ¡Hum!… Debe de ser de ecuación indeterminada y no de aritmética —el profesor consulta las soluciones y halla setenta y cinco y sesenta y tres —. ¡Hum! ¡Qué extraño!… Quizá haya que sumar cinco y tres y luego dividir quinientos cuarenta entre ocho. ¿Será eso?… No, tampoco es eso».
— ¡Bueno!… ¡Haga el favor de resolverlo de una vez! —dice Petia.
— Pero ¿por qué lo piensas tanto? ¡El problema es sencillísimo! —dice Udodov a Petia— ¡Qué bobo eres, hijito! ¡Resuélvaselo usted por esta vez, Egor Alekseich!
Egor Alekseich coge el pizarrín y se dispone a resolverlo. Tartamudea. Enrojece. Palidece.
— El caso es que este problema es de álgebra —dice —. Podría resolverse con X y con Y. Y también sin esto… ¿Ve?… Yo aquí divido… ¿Comprende?… Ahora esto hay que restarlo… ¿Comprende?…, o si no… Lo mejor será que me lo traiga usted resuelto mañana… ¡Piénselo bien!
Petia sonríe maliciosamente; Udodov sonríe también. Ambos comprenden la turbación del profesor. El estudiante de séptimo se azara todavía más, se levanta y empieza a pasear por la habitación.
— Puede resolverse sin acudir al álgebra —dice Udodov. Y tendiendo la mano hacia el schiotiiv añade con un suspiro—: Mire. Es así…
Hechos los cálculos sobre el schioti, obtiene sin dificultad los setenta y cinco y sesenta y tres precisados.
— Esto está hecho a nuestra manera…, no científica.
El profesor se siente terriblemente incómodo. Con el corazón sin latidos, mira el reloj y comprueba que para el fin de la lección falta todavía hora y cuarto. ¡Toda una eternidad!
Efectivamente, el problema es sencillo. Si X e Y designan, respectivamente, la cantidad de varas de paño negro y la de azul, basta con plantear un sistema de dos ecuaciones con dos incógnitas (X+Y=138 y 3X+5Y=540), resultando X=75 e Y=63. Pero Petia no debe hacerlo de esta manera, ya aún no ha aprendido a resolver sistemas de ecuaciones. Así, debe hallar la solución usando métodos elementales. Puede hacerlo suponiendo que, si toda la tela hubiese sido azul, las 138 varas de tela habrían costado 5×138=690 rublos, es decir 150 rublos (690-540=150) más del importe real. Basta con notar que la diferencia de precios entre una vara de tela azul y una de negra es de 2 rublos. Así, dividiendo 150 entre 2, deducimos que debe de haber 75 varas de tela negra y por lo tanto el resto, 63 (138-75=63), debe ser de azul. Simple aritmética.
Incluso un “matemático loco”, en algunas ocasiones, es incapaz de resolver un problema sencillo sin recurrir a artificios. Udodov, con su ábaco, encuentra la solución al problema “a su manera…, no científica” ante el avergonzado Egor que, probablemente, se quede sin su aumento de sueldo…
Referencias
[1] Antón Chéjov, Cuentos completos (1880-1885), Edición de Paul Viejo, Titivillus, 2013
[2] Yakov Perelman, El Abaco Antiguo y sus Descendientes en Aritmética recreativa, 1954
Notas:
i Autolimio es un nombre inventado por Chéjov.
ii El pud es una unidad de masa equivalente 40 libras rusas, unos 16,38 kilogramos.
iii El zolotnik es una antigua unidad de masa rusa equivalente a unos 4,26 gramos.
iv Ábaco ruso.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Tareas de un matemático loco se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El problema matemático de las cartas extraviadas
- Ilustraciones artísticas de un matemático
- Un convite matemático ‘de altura’
Lurraren magnetismoaz (I)
Geomagnetismoari buruzko lehen pisuzko lana De magnete liburua izan zen, William Gilbert-ek argitaratua 1600ean. Data hartarako, nabigatzaileek bazekiten orratzek batzuetan ez zutela zehatz-mehatz seinalatzen iparraldera, baizik eta angelu bateko desbideraketa zeukatela; gerora, angelu hark deklinazio magnetiko izena hartu zuen. Era berean, bazekiten orratza noizbehinka horizontaletik aldentzen zela, inklinazio magnetiko delakoa sortuz. Filosofo naturalek egiatzat hartzen zuten Lurraren magnetismoa magnetita mineralaren propietate ezkutuek eragiten zutela, edo zeruetako Iparrizarraren eta Lurreko ipar polo magnetikoaren arteko konexio neoplatonikoren batek.
Medikua ogibidez, Gilbert-ek magnetismoari lotutako bost mugimenduak jorratu zituen bere lanean: erakarpena -berak «koito» zeritzon, irudikapen modukoa eginez-, orientazioa, deklinazioa, inklinazioa eta errotazioa. Horiek osatzen zuten bere Lurraren magnetismoaren teoriaren abiapuntua.
 1. irudia: “terella”. (Iturria: Cuaderno de Cultura Científica)
1. irudia: “terella”. (Iturria: Cuaderno de Cultura Científica)Gilbertek esperimentuak egin zituen orratz magnetiko txikiak magnetita-esfera batean jarriz («terrella» izena eman zion esferari; latinez Lurtxo esan nahi du horrek). Haien bidez erakutsi zuen esferaren irregulartasunek orratzen orientazioa aldatzen zutela, baita orratzak, ekuatorean esferaren plano tangente batekiko paralelo zeudelarik, poloetara hurbildu ahala okertu egiten zirela, harik eta bertan bertikalera iritsi arte. Lurra, hortaz, magnetita-esfera eskerga izango zen, errotazioan dagoen arima magnetiko materiagabea zeukana.
Bazirudien magnetismoa zela, Lurraren magnetismoa barne, munduko indar ezkutuen artean nabarmenena; horregatik, filosofo mekaniko berriek behartuta ikusi zuten beren burua mugimenduan dagoen materia kontuan hartuko zuen azalpena topatzera.
Principia philosophiae lanean (1644), René Descartes-ek zioen Lurraren magnetismoa kiribil formako partikula-korronte zirkulazioa zela (kortxo-torloju moduko bat). Horren harira sortu zen XIX. mendeko hogeiko hamarkadara arte eragin handia izan zuen tradizioa, hain zuzen, fluido magnetiko bizi eta sotilek eragiten zutela Lurraren magnetismoa.
 2. irudia: Halley 1702an egindako mapa. (Iturria: Wikimedia Commons).
2. irudia: Halley 1702an egindako mapa. (Iturria: Wikimedia Commons).Edmond Halleyk proposatu zuen Lurra neurri batean hutsik zegoela, lehenik 1683an eta, ondoren, 1692an, Londreseko Royal Society-ren aurrean. Bere esanetan, lurrak geruza esferikoak zeuzkan bat bestearen barnean, esferen artean atmosferak zirelarik. Bina polo magnetiko zeukaten esferek eta, deklinazio- eta inklinazio-bariazioen eragileak, beraz, esferon abiadura ezberdinetako errotazioak ziren, baita poloen arteko interakzioen eragileak ere. 1698 eta 1700 urteen artean, Halley-k Atlantikoan zehar bidaiatu zuen, eta deklinazio-bariazioak neurtu zituen. Mapa aitzindari batean irudikatu zituen, 1701 eta 1703 urteen artean. Lan hura sarritan berrargitaratu zen, General Chart of the Variation of the Compass izenaz.
Aipatu bezala, Descartesen fluidoen teoriak eragin handia izan zuen XIX. mendearen hasierara arte. Haren une gorena 1826an Parisko Académie des Sciences-en aurkeztu zen teoria izan daiteke, Charles-Augustin Coulomb eta Simeon-Denis Poisson-en eskutik. Teoriak jakintzat ematen zuen substantzia magnetikoen fluidoek eragindako urrutiko zenbait indar existitzen zirela.
Teoria kartesiarraren ildoko beste zientzialari garrantzitsu batzuk -Coulomb-Poisson-ekarpenaren aurretikoak- honakoak ziren: Gavin Knight, Leonhard Euler, Franz Aepinus, Jean-Baptiste Biot. Eulerrek 12 aldiz irabazi zuen Académie des Sciences-en saria, eta, izan ere, haietako aldi batean –1746koan-, Lurraren magnetismoari buruzko teoria bat eskatzen zuen akademiak.
Ikertzaile franko saiatu zen Lurraren magnetismoa azaltzeko teoria nahiz deskribapen egokiak garatzen; hala ere, horretarako behar diren matematikek asko zailtzen zuten egitekoa. Mendearen azken laurdenean garapen matematiko berri eta sendoa agertu arte itxaron behar izan zuten auzian aurrera egin ahal izateko.
Bien bitartean, XIX.eko hogeita hamarreko hamarkadan, gero eta erakargarritasun txikiagoa zuten fluido «boreal» eta «astralak» oinarri zituzten hipotesiek. Ildo horri jarraika, hala ere, Christopher Hansteen-ek Halley-ren ikuspegia -bi errotazio-ardatz eta lau poloren existentzia zuena oinarri- berreskuratu zuen bere Investigations Concerning the Magnetism of the Earth lanean (1819). 90º-ko inklinazio magnetikoa izan behar zuten polo horiek behingoz aurkitzeko ahaleginean, Siberiara abiatu zen Hansteen 1830ean, eta asmo berarekin egin zuen James Clark Ross-ek bidaia Kanadara.
Ardatz bikoitzen teoriak babes handirik eskuratu ez bazuen ere, poloak aztergai gisa berreskuratzeak, teoriak nahiz deskribapenak matematizatzeko saiakerek eta espedizio ugariek ideia berriak ekarri zizkioten Lurraren magnetismoaren ikerkuntzari, bai eta behaketa-datu anitz ere.
——————————————–
Egileaz: Cesár Tomé López (@EDocet) zientzia dibulgatzailea da eta Mapping Ignorance eta Cuaderno de Cultura Cientifica blogen editorea.
Itzulpena: Lamia Filali-Mouncef Lazkano
Hizkuntza-begiralea: Xabier Bilbao
——————————————–
The post Lurraren magnetismoaz (I) appeared first on Zientzia Kaiera.

