Sindicador de canales de noticias

Javier Duoandikoetxea Zure 20 megapixeleko kamera berriarekin argazki bat egin duzu. Botoia sakatu duzunean, 60 megabyteko informazioa jaso du kamerak (60 MB = 60 milioi byte). Byte bat 0-z eta 1-ez osaturiko zortzikote bat da (01100101, adibidez). Hortaz, 0 eta 1 zifrak erabiliz osaturiko 480 000 000 zifrako zerrenda erraldoi bat gorde behar du kamerak memorian argazki bakar baterako. Baina ez, ez dizu hori egin. Fitxategia ordenagailuan ikuskatzen duzunean, han ez dituzu 60 MB horiek aurkitu, 6 edo 7 MB baino ez daude. Zer gertatu da? Galdetu matematikari, hark du erantzuna… Pixelak eta koloreak

Argazki digitala pixelatuta dago beti. Pixela (picture element) da irudiak duen unitaterik txikiena, kolore bakarra duen koadrotxo bat. Argazkiak 20 megapixel baditu, 20 milioi koadrotxoz osatuta dago. Hain dira txikiak, non gure begiek ez dituzten banaka ikusten, baina ordenagailuko pantailan irudia handituz, ikusgai egin daitezke.

Pixel bakoitzari zer kolore dagokion zehazteko CCD (charge coupled device = karga akoplatuko gailu) bat erabiltzen da. Gailu hori duela 50 urte asmatu zuten W. S. Boyle eta G. E. Smith fisikariek, baina ez zehazki argazkietan erabiltzeko asmoz. Aurkikuntza horri esker, 2009ko Fisikako Nobel saria jaso zuten.

1. irudia: Sony kamera baten CCDa. (Argazkia: Wikimedia Commons / Andrzej w k 2 – CC BY-SA 4.0 lizentziapean)

CCD horrek pixel bakoitzera heltzen den kolorea definitzeko RGB (red-green-blue = gorri-berde-urdin) eredua erabiltzen du, oinarrizko kolore horietako bakoitzetik zenbat hartu behar den zehaztuz. Zenbatekoa 0tik 255erainoko eskala batean hartzen da. Esate baterako, (48,213,200) hirukoteak 48 gorri, 213 berde eta 200 urdin nahastuta, turkesa kolore bat ematen du. Zergatik 0tik 255era? Hain zuzen, zortzi zifra (byte bat) erabiliz sistema bitarrean idazten diren zenbakiak horiexek direlako. Sistema bitarrean, (48,213,200) kolorea (00110000, 11010101, 11001000) idazten da. Hiru byte horiek definitzen dute, beraz, aipaturiko turkesa kolorea. Horrelako 20 milioi hirukote beharko ditugu 20 megapixeleko argazkirako.

Zenbat kolore desberdin ematen dizkigu RGB ereduak? 256 x 256 x 256 = 16 777 216 kolore denetara. Gehiegi dira gure begien bidez bereizteko. Kolore baten hirukotean aldaketa txikiak eginda, begirik zorrotzenak ere ez du alderik nabarituko.

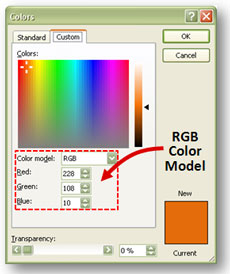
2. irudia: Ordenagailuko aplikazio batzuetan kolorea RGB eskalan aukera daiteke.

Oharra: Zuri-beltzezko argazkietan kolore-eskala bakarra erabiltzen da, grisen eskala, 0tik 255era. Hor byte bakar batek ematen du pixelaren “kolorea”.

Tarte bat matematikarako

Duela 200 urte egin zuen Joseph Fourier zientzialari eta politikari frantsesak bere lana. Beroaren hedapena deskribatzeko ekuazio bat eta haren soluzioa idazteko era bat aurkitu zituen. Bertan, funtzio bat serie trigonometriko modura idatzi zuen (Fourieren seriea). Fourier konturatu zen funtzio trigonometrikoak “osagai unibertsal” modura erabil zitezkeela, beste edozein funtzio haien bitartez adierazteko. Errezeta bat idaztearen antzekoa da: oinarrizko “osagai” horietako bakoitzetik zenbat hartu behar den (hau da, funtzio trigonometriko bakoitzaren koefizientea seriean zein den) esaten digu. Eta horrek badu beste alderdi interesgarri bat: funtzioaren “errezetatik” gutxien behar diren osagaiak kenduta (hau da, haien koefizienteak 0 eginda), hurbilketa bat lortzen da eta errorea kontrola daiteke.

3. irudia: Joseph Fourier (1768-1830). (Argazkiaren iturria: CNRS News)

Mundu errealean erabiltzeko, egokitzapen bat behar du Fourieren teoriak. Matematikan ez dago arazorik infinitu koefizienterekin lan egiteko, baina datu errealak finituak dira. Egoera horretan aritzeko modu praktikoa ere asmatu zuten beranduago, Fourieren transformazio diskretua (DFT) definituz. Haren aldaera bat, kosinuaren transformazio diskretua (DCT), izango da gure laguntza argazki-fitxategiak txikiagotzeko.

JPEG: Joint Photographic Experts Group

JPEG izena du argazki digitalak konprimatzeko erabiltzen den ohiko bideak. Akronimoa Joint Photographic Experts Group argazkilari taldearen izenetik hartuta dago, haiek sortu baitzuten. 1992an plazaratu zen lehen aldiz. Ordenagailuetan, fitxategietarako hiru letrako luzapena erabiliz, .jpg eran agertzen da.

Konprimatzea bolumena txikitzea da. Erabilera informatikoan, fitxategien tamaina da txikitzen dena. Argazkien kasuan, JPEGren bidez txikitzean informazioa galdu egiten da, baina galdutako hori ia ez nabaritzeko modukoa izan dadin aukeratu behar da. Hau da, pixelaren kolorea aldatuko bada ere, hasierakotik hurbil gera dadin lortu behar da.

Hasteko, ez da zuzenean RGB hirukotearekin lan egiten. Beste hiru parametro definitzen dira: luminantzia, krominantzia urdina eta krominantzia gorria. Aurreko hirukotetik parametro berrien hirukotea lortzen da transformazio matematiko baten bidez. Pixel bakoitzak 3 byteko informazioa mantentzen du.

Ondoren, blokeak egiten dira, bakoitzean 8 x 8 pixel hartuz. Har ditzagun bloke bateko luminantziaren 64 balioak. Bi dimentsioko kosinuaren transformazio diskretua erabiliz, balio horiek kosinuen konbinazio modura idazten dira. Koefizienteek 8 x 8 matrize bat osatzen dute. Bloke askotan luminantziak ez du aldaketa handirik pixel batetik bestera eta, horregatik, frekuentzia altuko gaien koefizienteak txikiak dira. Nahi dugun konpresio-maila aukeratuz eta matrize berezi batekin biderkatuz, koefizienteak aldatu eta zenbaki oso bihurtzen dira. Askotarako 0 balioa lortzen da. Koefizienteak ordenatzeko orduan, 0 asko elkarren alboan gelditzen dira eta horiek ez ditugu gordeko banan-banan, haien kopurua bakarrik hartuko dugu kontuan. Horrela, zeroen zerrenda luze horiek ezabatuz, gorde beharreko informazioa asko laburtzen da.

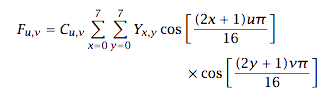
4. irudia: Koefizienteen kalkulua 2-d kosinuaren transformazio diskretuaren bidez.

Irudia eraikitzeko, atzekoz aurrera egin behar da prozesu hori. Lortzen diren RGB eskalako balioak ez dira hasierako berberak. Hala ere, ez daude jatorrizko balioetatik urrun, adibidez 1:10 inguruko konpresioa egiten bada. Balio berri horiek definitzen dute pantailan ikusten dugun irudia.

Konpresio handia aukeratuz gero, fitxategia txikiagoa da eta emango diogun erabileraren araberakoa izango da baliagarria edo ez eskuratzen dugun irudia. Ez baita gauza bera argazkia pantaila txiki batean ikustea, 10 x 15 kopia bat egitea edo poster batera eramatea.

Laburbilduz

Duela 200 urte sorturiko teoria matematiko batetik abiatuta, hainbat kalkulu egin ditu gure tresnak kameraren botoia sakatu dugunetik argazkia memorian sartu arte pasatu den denbora laburrean. Fitxategi erraldoia izan behar zuenaren tamaina hamarrenera ekarri du, eta hori guztia informazio garrantzitsua galdu barik. Behin bidea zabalduta, aldaerak eta hobekuntzak etorri ziren, baina funtsean gure argazki-kamera digitalek jatorrizko prozesua egiten dute oraindik ere.

Gehiago jakiteko:

• Benítez López, Julio (2016). El sistema de compresión JPEG. Un pequeño paseo por la transformada discreta de Fourier y la transformada coseno, La Gaceta de la RSME 19(1), 25-45.
• Austin, David (2008). What is… JPEG?, Notices of the American Mathematical Society, 55, 226-229.
• Austin, David (2007). Image Compression: Seeing What’s Not There, Feature column, 2007ko iraila, American Mathematical Society.

——————————————-
Egileaz: Javier Duoandikoetxea Analisi Matematikoko Katedraduna da UPV/EHUn.

——————————————-

The post Argazkietako matematika: JPEG appeared first on Zientzia Kaiera.

En la entrada Los números enamorados del Cuaderno de Cultura Científica, habíamos presentado algunas familias de números naturales que deben su propiedad definitoria al comportamiento de sus divisores, en concreto, de sus divisores propios, es decir, entre los divisores no se considera al propio número. Estuvimos hablando de los números perfectos, abundantes, deficientes, casi perfectos, multi-perfectos, ambiciosos, sublimes, amigos, novios, sociables, intocables, prácticos, raros, e incluso, poderosos.

Detalle de la obra “CITY VIEW” (2003), de la artista japonesa, que vive en Nueva York, Kumi Yamashita. La obra pertenece a la colección permanente de Namba Parks Tower, en Osaka (Japón). Fotografía de la página web de la artista

En esta entrada vamos a hablar de una serie de familias de números que podríamos denominar en su conjunto como narcisistas, aunque esta sea la denominación particular de una de esas familias. Estos números tienen la propiedad de que, si se toman las cifras que componen cada uno de ellos, después se elevan estas a ciertas potencias y se suman los resultados, se obtiene de nuevo el número.

Recordemos que una persona narcisista es aquella que “cuida demasiado de su arreglo personal, o se precia de atractivo, como enamorado de sí mismo” y el concepto viene del mito griego en el cual el joven y apuesto Narciso se enamoró de su propia imagen reflejada en el agua. En el concepto de números narcisistas la imagen reflejada sería la suma de las potencias de sus cifras, que, al ser el propio número, sería como el enamoramiento de Narciso de su propia imagen reflejada.

Narciso (1594-1596), del artista italiano Caravaggio, perteneciente a la colección de la Galeria Nazionale d’Arte Antica. Imagen de Wikimedia Commons

Empecemos este recorrido por la familia de números que recibe precisamente el apelativo de números narcisistas. Esta familia está formada por aquellos números que son iguales a la suma de las potencias de sus cifras elevadas a la cantidad de cifras que tiene el número. Por ejemplo, el número 153 es un número narcisista, puesto que, teniendo 3 cifras, que son 1, 5 y 3, se cumple que 13 + 53 + 33 = 1 + 125 + 27 = 153; o también, el número 1634, ya que 14 + 64 + 34 + 44 = 1 + 1296 + 81 + 256 = 1.634.

Los números narcisistas menores que 100.000 son: 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407, 1.634, 8.208, 9.474, 54.748, 92.727 y 93.084.

Fijémonos en uno en concreto, el número narcisista 8.208. Este ha alcanzado una cierta fama por haber aparecido en la serie televisiva Los Simpson. Como puede leerse en el libro Los Simpson y las matemáticas del matemático y divulgador Simon Singh, la historia de ese y otros dos números que aparecen en un capítulo de la temporada 17 de esta serie es muy curiosa.

Dentro de la comunidad matemática es conocido que algunos de los guionistas y productores de la serie Los Simpson, así como de la serie Futurama, tienen estudios de matemáticas, y en general, de ciencias, lo que ha motivado que en ambas series aparezcan muchísimas referencias matemáticas. Simon Singh cuenta como, en particular, la profesora Sarah Greenwald, de la Universidad Estatal de los Apalaches, y el profesor Andrew Nestler, de la Universidad de Santa Mónica, empezaron a recoger todas esas referencias y a utilizarlas en sus clases de matemáticas. Cuando esto llegó al oído de los guionistas de la serie Los Simpson, en 2005, decidieron invitarlos a la lectura de un futuro episodio, ese que tendría el título Marge, Homer y el deporte en pareja. Cuando los dos invitados se marcharon, los guionistas se percataron de que en ese episodio no habían incluido ninguna referencia matemática, lo cual les pareció que había sido algo descortés hacia sus invitados y decidieron revisar el guion e incluir un guiño a las matemáticas.

Imagen del episodio Marge, Homer y el deporte en pareja, en la que aparecen tres números curiosos, uno de ellos un número narcisista, 8.208

Como se puede ver en la anterior imagen de ese capítulo, decidieron incluir en la pantalla del estadio de béisbol, una mención a la cantidad de público asistente, dando cuatro opciones. La primera 8.191, que es lo que se conoce como un número primo de Mersenne, los cuales son de la forma 2p – 1, en concreto, 213 – 1 = 8.191. La segunda es 8.128, que es un número triangular (véase la entrada El asesinato de Pitágoras, historia y matemáticas (y II)). La tercera cantidad era el número narcisista 8.208, que verifica que 8.208 = 84 + 24 + 04 + 84. La última opción era simplemente que no se podía conocer esa cantidad.

Es fácil observar que solo existe un número finito de números narcisistas. Veámoslo. Si tomamos un número con n cifras, se tiene que ese número es mayor que 10n – 1 y menor que 10n. Por otra parte, la suma de las potencias de sus cifras elevadas a la cantidad de cifras del número alcanza como mucho el valor de 9n + … + 9n (sumado n veces) = n x 9n. Pero resulta que para n > 60, se tiene que n x 9n n – 1, luego la suma de las potencias de las cifras del número elevadas a la cantidad de cifras nunca podrá alcanzar al número. Es decir, no existen números narcisistas con más de 60 cifras.

De hecho, solamente hay 88 números narcisistas (puede verse aquí la lista completa), como fue demostrado por D. T. Winter, en 1985. Además, el mayor de ellos solamente tiene 39 cifras, es

115.132.219.018.763.992.565.095.597.973.971.522.401.

El matemático británico G. H. Hardy (1877 – 1947), en su libro Apología de un matemático, dice en referencia a estos números…

Se trata de hechos excepcionales, ideales para las columnas de acertijos y similares que aparecen en la sección de pasatiempos del periódico para entretener a los aficionados a las matemáticas, pero no hay nada en ellos que atraiga mucho a un matemático.

Portada de la edición en castellano, de la editorial Capitán Swing, del libro Apología de un matemático, de G. H. Hardy

Este concepto puede extenderse a una familia un poco más amplia, la de los números que son iguales a la suma de las potencias de sus cifras elevadas a una cantidad fija cualquiera, no necesariamente la cantidad de cifras del número, que es el caso de los números narcisistas. Por ejemplo, el número 4.150, que puede expresarse como la suma de las potencias quintas de sus cifras (que son solo cuatro), así 45 + 15 + 55 + 05 = 1.024 + 1 + 3.125 = 4.150. En una nota en la revista Mathematical Gazette, de 1968, se sugiere el nombre de “powerful numbers”, que es el mismo nombre que reciben los números que en la anterior entrada del Cuaderno de Cultura Científica, Los números enamorados, se denominaron poderosos, por lo que llamaremos a estos otros, números potentes. Por otra parte, en el libro Mathematics on vacation, su autor, el químico, editor y matemático recreativo Joseph Madachy (1927 – 2014), les llama números “invariantes digitales perfectos”.

Los números potentes menores de 100.000 son: 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407, 1.634, 4.150, 4.151, 8.208, 9.474, 54.748, 92.727 y 93.084, solamente dos más que los narcisistas, a saber, 4.150 y 4.151. El siguiente número poderoso, que además no es narcisista, es 194.979 = l5 + 95 + 45 + 95 + 75 + 95.

En la enciclopedia on-line de sucesiones de números enteros, en la información sobre la sucesión A023052, aparece un listado de los 255 números potentes conocidos. El más grande, que además no es narcisista, tiene 105 cifras y se obtiene al elevar cada una de sus cifras a la potencia 109 y sumarlas. Es …

926.141.173.758.288.802.620.975.817.393.837.795.715.817.835.556.117.230.343.321.424.553.048.655.411.019.641.033.929.959.544.403.221.763.375

A raíz del concepto de número invariante digital perfecto, Joseph Madachy define los “números invariantes digitales recurrentes”, que podríamos denominar también números potentes recurrentes. Un número es un invariante digital recurrente, de orden k, si al construir la sucesión de números, empezando por el mismo, formados por las sumas de las potencias k-ésimas de las cifras del número anterior, se llega de nuevo al número original en un número finito de pasos, llamado longitud del ciclo. Por ejemplo, el número 55 es un invariante digital recurrente de orden 3, ya que 53 + 53 = 250, 23 + 53 + 03 = 133 y 13 + 33 + 33 = 55, siendo longitud del ciclo igual a 3.

Veamos un ejemplo de orden 4, el número 1.138. Calculemos la sucesión asociada, 14 + 14 + 34 + 84 = 4.179, 44 + 14 + 74 + 94 = 9.219, 94 + 24 + 14 + 94 = 13.139, 14 + 34 + 14 + 34 + 94 = 6.725, 64 + 74 + 24 + 54 = 4.338, 44 + 34 + 34 + 84 = 4.514 y regresamos al origen, después de un ciclo de longitud 8, 44 + 54 + 14 + 44 = 1.138.

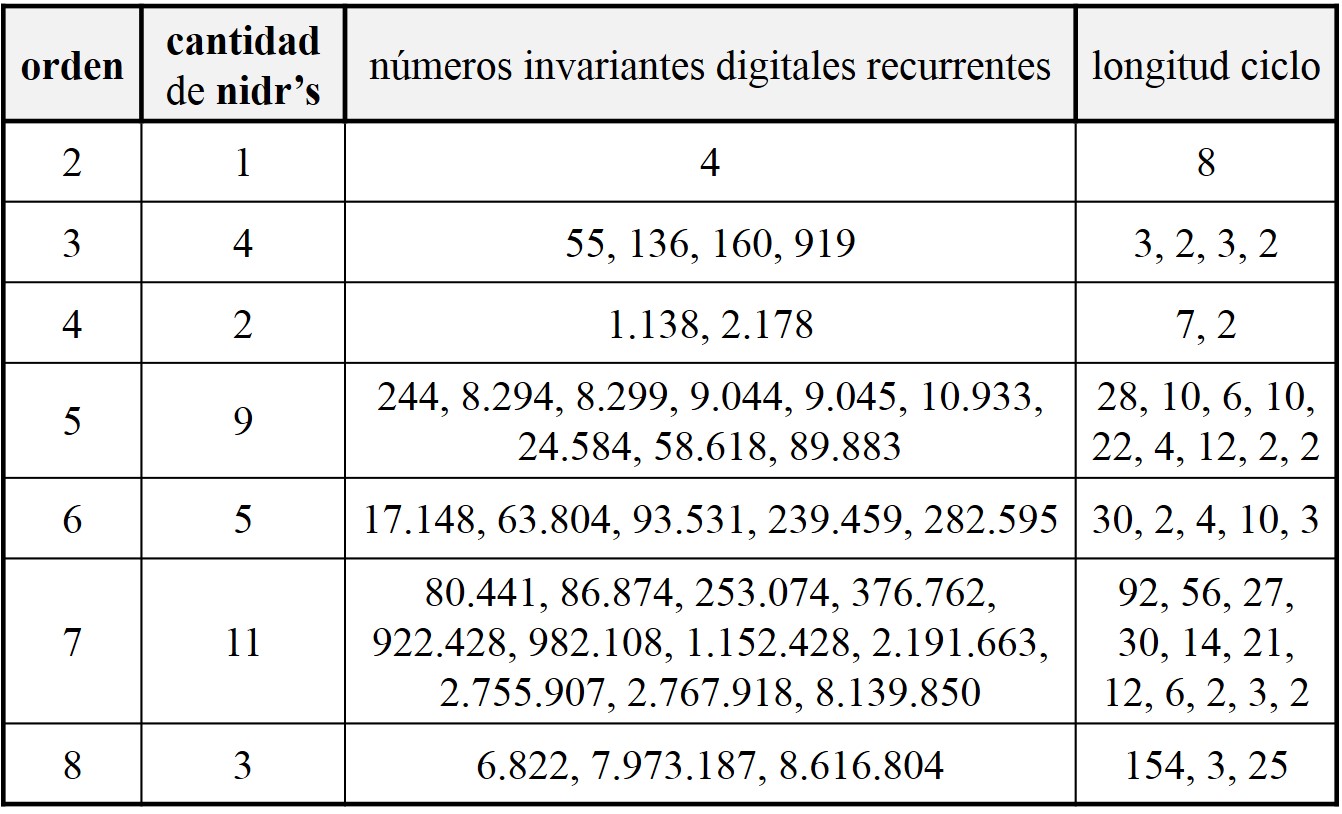Tabla de números invariantes digitales recurrentes de órdenes, entre 2 y 8

Otra familia de números relacionada con los números narcisistas, pero a la que nadie parece haber bautizado, son aquellos números que son iguales a la suma de las potencias de sus cifras elevadas a la posición que ocupan en el número, empezando por la izquierda. Por ejemplo, los números 89, 175, 2.427 y 2.646.798 son de estos números, ya que:

81 + 92 = 8 + 81 = 89,

11 + 72 + 53 = 1 + 49 + 125 = 175,

21 + 42 + 23 + 74 = 2 + 16 + 8 + 2.401 = 2.427, y

21 + 62 + 43 + 64 + 75 + 96 + 87 =

2 + 36 + 64 + 1.296 + 16.807 + 531.441 + 2.097.152 = 2.646.798.

De nuevo, se puede demostrar que esta familia de números es finita. Más aún, no puede haber números de esta familia con más de 22 cifras. Veámoslo.

Si tenemos un número con n cifras, entonces el número es mayor que 10n – 1 y si además pertenece a esta familia, será menor que 9 + 92 + … + 9n, pero, por la fórmula para la suma de los primeros números de la serie geométrica, esta suma es igual a 9 x (9n – 1) / 8 n + 1 / 8. En consecuencia, 10n – 1 n + 1 / 8, que nos lleva, tomando logaritmos, a que n

De hecho, solo hay 19 números que verifiquen esta propiedad: 1, 2, 3, 4, 5, 6, 7, 8, 9, 89, 135, 175, 518, 598, 1.306, 1.676, 2.427, 2.646.798 y 12.157.692.622.039.623.539, y el mayor tiene 20 cifras.

Otra familia de números relacionada con los números narcisistas es la formada por los números de Munchausen, aquellos números que son iguales a la suma de sus cifras elevadas a ellas mismas. Por ejemplo, el número 3.435 es un número de Munchausen, ya que 33 + 44 + 33 + 55 = 3.435.

El nombre fue sugerido por el matemático e ingeniero de software holandés Daan van Berkel, en su artículo On a curious property of 3435 (2009), en referencia al barón de Munchausen. En los números de Munchausen cada cifra se eleva a sí misma, de la misma forma que el barón de Munchausen se eleva a sí mismo, tirando de su coleta, con lo cual consigue volar y evita caer en una ciénaga.

Ilustración de la edición francesa de 1862 del libro Las aventuras del barón de Munchausen de Rudolf Erich Raspe (1785), realizada por el ilustrador francés Gustave Doré (1832 – 1883), en la que el barón de Munchausen sale volando de una ciénaga tirando de su coleta hacia arriba. Imagen de Wikimedia Commons.

Esta es una propiedad muy rígida. El único número de Munchausen, salvo el número 1 que lo es trivialmente, es el número 3.435, como demostró Daan van Berkel. Luego, podemos decir que este es un número muy especial.

Aunque si observamos la definición nos encontramos con un problema. Si una de las cifras del número es el 0, entonces tenemos que sumar 00 y esto es un problema. ¿Cuánto vale 00? Aunque es una polémica no cerrada del todo, la posición de la comunidad matemática es que ese valor debe ser 1. En ese caso, como demostró Daan van Berkel, solo hay dos números de Munchausen 1 y 3.435.

Sin embargo, si admitiésemos que 00 = 0, o modificamos la definición para que solo se considerasen las cifras no nulas, entonces habría otro número de esta familia, el 438.579.088, que verifica que

44 + 33 + 88 + 55 + 77 + 99 + 88 + 88 = 438.579.088.

Número 3.435 realizado con las Tarjetas de Cumpleaños Art Nouveau de la diseñadora estadounidense Laura Beckman. Imágenes de la página de Laura Beckman

También se pueden definir los números de Munchausen opuestos, es decir, aquellos números que son iguales a la suma de sus cifras elevadas a ellas mismas, pero no cada una con la suya, sino en el sentido opuesto. Por ejemplo, si consideramos el número 325, sus cifras son 3, 2 y 5, y vamos a tomar sus potencias elevadas a las cifras, pero en el orden opuesto, 5, 2, 3, quedando 35 + 22 + 53 = 243 + 4 + 125 = 372, luego este número no es de Munchausen opuesto. De nuevo, existen solamente dos números en esta familia:

48.625 = 45 + 82 + 66 + 28 + 54,

397.612 = 32 + 91 + 76 + 67 + 19 + 23.

Escultura Passing Time (2011), del artista neozelandés Anton Parsons, en Christchurch (Nueva Zelanda). Imagen de la página web de Anton Parsons

Lo cierto es que el concepto de número narcisista ha generado una enorme familia de generalizaciones. A continuación, haremos un breve repaso por algunas de ellas.

A. Suma de dos cuadrados. Si existiera un número narcisista con dos cifras, lo cual ya sabemos que no existe, entonces este sería igual a la suma de los cuadrados de sus cifras. Se puede generalizar este concepto para números de más de dos cifras, pero dividiendo al número en dos “mitades” de cifras. Es decir, a esta familia pertenecen los números que son iguales a las sumas de los cuadrados de dos “mitades” del número. Veamos algunos ejemplos:

1233 = 122 + 332, 8833 = 882 + 332, 5.882.353 = 5882 + 23532,

1.765.038.125 = 17.6502 + 38.1252, 116.788.321.168 = 116.7882 + 321.1682.

B. Suma de tres cubos. De forma análoga, se pueden considerar aquellos números que son iguales a la suma de los cubos de tres “tercios” del número.

22 18 59 = 223 + 183 + 593,

166 500 333 = 1663 + 5003 + 3333.

C. Números factoriones. Estos números son aquellos que son iguales a la suma de los factoriales de sus cifras. Por ejemplo, 145 es un factorión, ya que

1! + 4! + 5! = 1 + 24 + 120 = 145.

Los números 1 y 2 son trivialmente números factoriones, ya que 1! = 1 y 2! = 2. Y el número 40.585 también es un número factorión, ya que

4! + 0! + 5! + 8! + 5! = 24 + 1 + 120 + 40320 + 120 = 40.585.

Resulta que estos son los únicos factoriones que existen. Supongamos que tenemos un número de n cifras, entonces este es mayor que 10n – 1, pero si es un número factorión, entonces es menor que la mayor suma posible de los factoriales de sus dígitos, que es n x 9!, de donde, 10n – 1 n x 9!. Pero resulta que, para n = 8 se obtiene que 107 = 10.000.000 > n x 9! = 2.903.040, luego no existen números factoriones de 8 cifras. Y, por inducción, se puede demostrar que ocurre para todos los n mayores o iguales que 8. Para n = 7, la suma máxima de los factoriales de las cifras que se puede obtener es 7 x 9! = 2.540.160, luego solo hay que comprobar los que son menores que esta cantidad. Y solo existen los cuatro anteriores.

D. Pares de números, o números “amigos”, para estas propiedades.

Por ejemplo, un par de números tales que la suma de los cuadrados de dos “mitades” de cada uno de ellos da el otro número, como los números 3.869 y 6.205, para los cuales

382 + 692 = 1.444 + 4.761 = 6.205 y 622 + 052 = 3844 + 25 = 3.869,

o el par de números

5.965 = 772 + 062 y 7.706 = 592 + 652.

Lo mismo para los cubos,

13 + 33 + 63 = 244 y 23 + 43 + 43 = 136,

o los factoriales, donde los tres números 169, 36.301 y 1.454 forman una cadena:

1! + 6! + 9! = 36.301, 3! + 6! + 3! + 0! + 1! = 1.454 y 1! + 4! + 5! + 1! = 169.

E. Números narcisistas salvajes. Estos números, al igual que los narcisistas, pueden ser expresados a partir de sus cifras, pero de una forma particular, las cifras deben de aparecer en el orden que aparecen en el número y pueden utilizarse las operaciones siguientes, suma, resta, multiplicación, división, potencia, radical y factorial.

Mostremos una pequeña colección de distintos números narcisistas salvajes

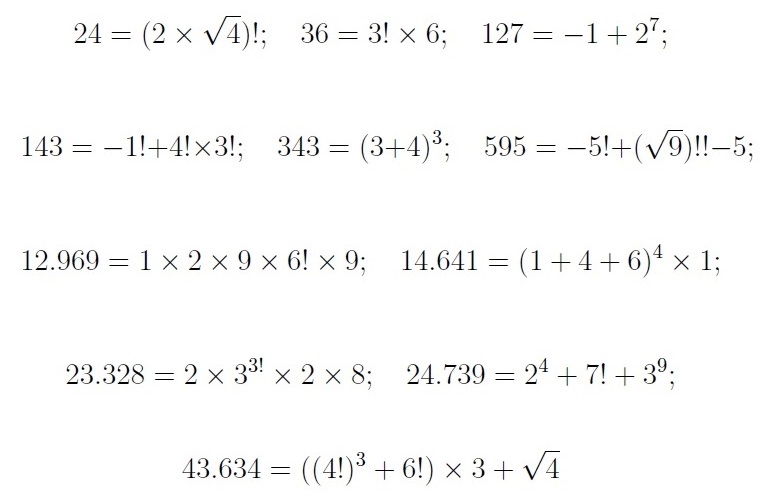
E incluso, se puede considerar que el orden de las cifras sea cualquiera, en cuyo caso se habla de números selfie. Un par de ejemplos serían

34.562 = 2 − (3 − 5) x6! x4!y87.369 = (3! + 7) x8! / 6 + 9.

Social circle (2011), del artista neozelandés Anton Parsons. Imagen de la página web de Anton Parsons

Bibliografía

1.- Clifford A. Pickover, El prodigio de los números. Desafíos, paradojas y curiosidades matemáticas, Ma Non Troppo (ediciones Robinbook), 2002.

2.- Clifford A. Pickover, La maravilla de los números. Un viaje por los secretos de las matemáticas, sus desafíos y caprichos, Ma Non Troppo (ediciones Robinbook), 2002.

3.- Joseph Madachy, Mathematics on vacation, Charles Scribner’s sons, 1966.

4.- Wolfram Mathworld: Narcissistic Number

5.- Simon Singh, Los Simpson y las matemáticas, Ariel, 2013.

6.- G. H. Hardy, Apología de un matemático, Capitán Swing, 2017.

7.- N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, OEIS: sucesión A0230052 (números potentes o invariantes digitales perfectos)

8.- Wolfram Mathworld: Recurring Digital Invariant

9.- N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, OEIS: sucesión A032799

10.- Daan van Berkel, On a curious property of 3435 (2009) (arXiv:0911.3038)

11.- N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, OEIS: sucesión A046253 (números de Munchausen)

12.- Harvey Heinz, Narcissistic numbers

13.- N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, OEIS: sucesión A014080 (números factoriones)

14.- George D. Poole, Integers and the sum of the factorials of their digits, Mathematics Magazine, vol. 44, n. 5, p. 278-279 (1971).

15.- N. J. A. Sloane, The On-Line Encyclopedia of Integer Sequences, OEIS: sucesión A193069 (números narcisistas salvajes)

16.- I. J. Taneja, Different Types of Pretty Wild Narcissistic Numbers: Selfie Representations-I, RGMIA Research Report Collection, n. 18, Article 32, pp. 1-43 (2015).

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El artículo ¿Pueden los números enamorarse de su propia imagen? se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Construye tu propia calculadora de sumas y restas
2. La magia de los números (el teorema de Moessner)
3. Los números enamorados

Juanma Gallego Duela hainbat urtetik ezagutzen da Marten metano isuri txikiak badirela, baina konposatu horren aztarnak jarraitzea oso zaila da. Orain, eta aurrenekoz, bi tresna desberdinekin egiaztatu ahal izan dute halako isuri bat gertatu dela.

2013ko ekainaren 16an izandako metano isuria atzeman dute Marteko Gale kraterretik gertu, planeta orbitatzen duen Mars Express zundaren bitartez. Ekuadorretik gertu dago Gale, eta duela milioika urte bertan aintzira bat egon zen. Tartean, arrazoi horregatik dago bertan Curiosity roverra, 2012tik. Besteak beste, SAM izeneko tresna du robotak, laser espektrometro bat, hain zuzen. Tresna horri esker, egun bat lehenago Curiosityk metanoa neurtu zuen inguruan, baina neurketa horrek zalantza batzuk sortu zituen, guztiz argia ez zelako. Atzemate berri honekin, beraz, isuri hori benetan gertatu zela egiaztatu ahal izan dute, baieztapen independentea delako. Gertaera hori berresten duten datuak Nature Geoscience aldizkarian argitaratu dituzte.

“Datu hauek oso interesgarriak dira, bi misiok aldi berean isuri bat detektatzen duten aurreneko aldia delako”, azaldu dio Zientzia Kaierari ESAko Mars Express misioko zientzia operazioetako arduradun Alejandro Cardesin ingeniariak. “Gainera, kasu honetan eremuaren azterketa oso zehatza egin da, bai atmosferari zein geologiari dagokienez, eta metano isurketari lotuta egon daitezkeen eremuak identifikatu ahal izan ditugu”.

1. irudia: Marteko metanoaren jatorria argitu nahi dute zientzialariek; bereziki, horren atzean prozesu geologikoak edo biologikoak ote dauden aurkitzeko. (Argazkia: NASA)

Aspalditik ezagutzen da Marten metanoa dagoela, baina konposatua aurkitzea zaila da, oso kopuru txikietan dagoelako. “Metanoaren analisia egitea arras konplexua da, eta zientzialariek 15 urte inguru daramate behaketak aztertuz”, dio Cardesinek. 1999an aurkitu zen aurrenekoz planeta gorrian, eta handik lau urtera Lurreko teleskopioen bitartez baieztatu zen. Urtebete geroago, Mars Express misioak garrantzizko lehen isuriak detektatu zituen. Ondorengo urteetan zientzialariak behaketa horiek osatzen saiatu direla azaldu du zientzialariak. “Baina beti egon da eztabaida handia, datuak interpretatzeko dauden zailtasunengatik. Orain, behingoz, baieztatutako lehen behaketa dugu”.

Marten metanoa aurkitzeko hain tematuta egoteak badu atzean zergati bat: zientzialariek ez dakite nola sortzen den, ezta zergatik desagertzen den ere. Gainera, aldizkako isurien bitartez askatzen da konposatu hori. Eta horrek inplikazio garrantzitsuak izan ditzake, bai geologiari dagokienez zein astrobiologiari dagokionez.

Terrazentrismoa eman dezake, baina metanoak irudimena pizten du: izan ere, Lurrean dagoen metanoa biziaren jardunari oso lotuta dago –zientzialarien hizkeran, biogenikoa da–. Adibidez, animalia askoren hesteetan edo aintziretan bizi diren bakterioek sortu ohi dute metanoa, oxigenorik gabeko ingurunetan, hain zuzen. Hortik sortzen da metano gehiena, baina jatorri geologikoa izan dezake ere Lurrean, sumendien bitartez.

Momentuz, Marten ez dugu aurkitu ez bakteriorik ezta sumendi aktiborik ere, baina badago zerbait noizean behin metanoa sortzen duena, eta beharko lukeena baino askoz azkarrago desagertzen da metano hori, Lurrean ezagutzen dugun kimikaren arabera, bederen. Lurrean, Eguzkiaren argiak metanoaren molekula apurtzen du atmosferaren goiko aldean, fotolisiaren bitartez. Beheragoko atmosferan, berriz, batez ere oxidazioagatik desagertzen da konposatua. Lurrean ikusitako logikari jarraituz, Marten ehunka urtez egon beharko litzateke metanoa, baina –eta datu zehatzik ez badago ere– urtebete eta ordu batzuen arteko tartea proposatu dute hainbat zientzialarik.

Jatorri argirik gabekoa

Marteko metanoaren jatorria azaltzeko hainbat teoria proposatu dira, baina, momentuz ez dago ezer garbirik. Horietako bat ia-ia alde batera utzi da, bereziki iaz Science aldizkarian aurkeztu ziren datu berrien argitara. Teoria horrek zioen meteorito txikiek Marteren kontra jotzean eramandako materia organikoaren narriaduran egon litekeela metanoaren abiapuntua. Baina, esan bezala, iaz aurkitu zuten metano isurien eta Marteko urtaroen arteko korrelazio indartsu bat, eta arraroa litzateke meteoritoetan ekarritako materiak horrekin zerikusirik izatea.

2. irudia: Orain ezagutarazi dute 2013an Europako Espazio Agentziaren Mars Express zundak (irudian) ere detektatu zuela NASAren Curiosity roverrak aurreko egunean detektatutako metano isuria. (Irudia: ESA / D. Ducros)

Zenbait mineraletan gertatzen den prozesu bat ere jarri izan da adibidetzat: zehazki, olibinoaren serpentinizazioren prozesuan jarri da arreta Marten gertatzen dena azaltzeko. Mineral hau urarekin kontaktuan jartzean serpentina sortzen du, eta metanoa askatzen da bidean. Horretarako, baina, ur likidoa beharrezkoa da. Bertako atmosferaren egoera dela eta, ura ez da egonkorra lurrazalean, baina bai posible da lurrazpian, eta duela gutxi baieztatu da, gainera, Marten ur likidoa badagoela.

Azalpen geologikoen alorrean, seguruenera babes gehien duen hipotesia klatratoena da. Sare moduko estruktura bati esker, barruan beste molekula bat gordetzeko ahalmena duten sustantziak dira horiek. Lurrean gertatzen den modu berean, Marteko klatratoen barruan duela milioika urte gordetako metanoa egon liteke barruan. Klatrato horiek, presio eta tenperatura zehatzetan, desegonkortuko lirateke, eta hor askatuko litzateke metanoa. Hasiera batean ikusita, ematen du hipotesi hori bateragarria litzatekeela urtaroen araberako isuriekin, baina guztiz bat ere ez datoz, eta prozesu hori azaldu ahal izateko, zientzialariek uste dute erdian beste prozesu bat egon beharko litzatekeela. Dena dela, hipotesiak arazo are handiagoa dauka: orain arte ez da demostratu Marten klatratorik daudenik.

Azkenik, —eta zalantzarik gabe ilusio gehiago pizten duena—, jatorri biologikoaren hipotesia dago: Marteko lurrazpian bizi diren balizko bakterioek askatuko lukete metano hori. Dena dela, nabarmendu beharra dago momentuz hipotesi hau babesteko inolako frogarik ez dagoela; ez bada, behintzat, zomorrotxo horiek askatuko luketen metanoa bera. Horregatik, hein handi batean, zientzialariak hain modu tematsuan ari dira metanoaren jatorriaren bila.

Aukera horretaz galdetuta, ohiko zuhurtzia darabil Cardesinek. “Oraindik goiz da ebazteko metano horren jatorria biologikoa ala geologikoa ote den, baina garrantzitsuena da azkenean badugula non bilatu. Lurrazpiko izotza duten hainbat eremu identifikatu dira planetan, eta bertan metanoa egon liteke harrapatuta; agian faila tektonikoek gas hori askatuko lukete, noizean behin”.

Gauzak horrela, gutxienez ikerketa eremu interesgarria zehaztu dute orain ezagutarazi diren neurketa berriek. “Ikerketa berri honi esker badakigu non bilatu”, dio ESAko adituak. “Hortaz, eremu hauek aztertzen hasi gara dagoeneko, doitasun handiarekin. Modu horretan, isuri gehiago detektatzen saiatzen ari gara, martxan egon litezkeen prozesu geologiko edo eta astrobiologikoak ulertu ahal izateko. Gainera komunitate zientifikoa irrikan dago eskuratzeko ExoMars programaren TGO zundaren emaitzak. Iaz hasi zen lanean zunda hori, eta planeta osoan atmosferan dauden metano mailen hurbilpen bat emateko moduan egongo da”.

Erreferentzia bibliografikoa:

Giuranna, Marco et al., (2019). Independent confirmation of a methane spike on Mars and a source region east of Gale Crater, Nature Geoscience. DOI: https://doi.org/10.1038/s41561-019-0331-9

———————————————————————————-

Egileaz: Juanma Gallego (@juanmagallego) zientzia kazetaria da.

———————————————————————————-

The post Marteko metano isuriak berretsi dituzte, baina misterioak argitzeke jarraitzen du appeared first on Zientzia Kaiera.

Imagen: Pixabay

Newton sugirió que los colores aparentes de los objetos dependen de qué color se refleja o dispersa más fuertemente para quien observa el objeto. En general, no hay una forma sencilla de predecir a partir de la estructura de la superficie, de la composición química o de cualquier otro factor qué colores reflejará o dispersará una sustancia. Eso no quiere decir que existan, sino que se basan en modelos matemáticamente muy complejos. Sin embargo, algo que la mayoría de nosotros vemos todos los días se puede explicar de una forma bastante simplificada a la par que instructiva: los colores del cielo

Thomas Young demostró experimentalmente que diferentes longitudes de onda de la luz corresponden a diferentes colores. La longitud de onda de la luz se puede especificar en unidades de nanómetros (nm; 1 nm = 10-9 m) o, alternativamente, en ångstroms (Å), el nombre de Anders Jonas Ångstrom, un astrónomo sueco que, en 1862, utilizó técnicas espectroscópicas para detectar La presencia de hidrógeno en el Sol. Un ångstrom es igual a 10-10 m. El rango del espectro visible para los humanos es de aproximadamente 400 nm (4000 Å) para luz violeta a, aproximadamente, 700 nm (7000 Å) para la luz roja.

Los pequeños obstáculos pueden dispersar la energía de una onda incidente de cualquier tipo en todas las direcciones, y la cantidad de dispersión depende de la longitud de onda. Como regla general, cuanto mayor sea la longitud de onda en comparación con el tamaño del obstáculo, menor será la dispersión de la onda por el obstáculo. Para partículas más pequeñas que una longitud de onda, la cantidad de dispersión de luz varía inversamente con la cuarta potencia de la longitud de onda. Por ejemplo, como la longitud de onda de la luz roja es aproximadamente el doble de la longitud de onda de la luz azul, la dispersión de la luz roja es solo alrededor de un dieciseisavo* de la dispersión de la luz azul.

Imagen: Pixabay

Con este simple dato ya sabemos por qué el cielo de mediodía de un día despejado es azul. La luz del Sol se dispersa por las moléculas y las micropartículas partículas de polvo presentes en las capas altas de la atmósfera. Todos estos obstáculos tienen dimensiones muy pequeñas en comparación con las longitudes de onda de la luz visible. Por lo tanto, en un día claro, la luz dispersa mucho más la luz de longitud de onda corta (luz azul) que la luz de longitudes de onda más largas y, por así decirlo, llena la luz azul llena el cielo de punta a punta. Debemos ser conscientes de que el color depende del observador. Cuando miras hacia arriba en un cielo despejado, es principalmente esta luz dispersada la que entra en tus ojos. El rango de longitudes de onda cortas dispersas (y la sensibilidad al color del ojo humano) conduce a la sensación de azul.

Imagen: Pixabay

Pero, ¿qué ocurre un día con neblina cuando observamos la puesta de sol o el amanecer? Lo que nuestro ojo recibe directamente del Sol es un haz de luz en el que las longitudes de onda más cortas se han dispersado completamente por el camino, no así las longitudes de onda más largas. De esta forma percibes el cielo alrededor del Sol poniente como rojizo.

Imagen: Pixabay

Si la Tierra no tuviera atmósfera, no habría dispersión de la luz, el cielo aparecería negro y las estrellas serían visibles durante el día. De hecho, comenzando en altitudes de aproximadamente 16 km, donde la atmósfera se vuelve bastante fina, el cielo se ve negro y las estrellas se pueden ver durante el día, como han descubierto los que hayan volado a gran altitud, incluidos los astronautas [2].

Imagen: Pixabay

Si la luz es dispersada por partículas considerablemente más grandes que una longitud de onda (como las gotas de agua en una nube), no hay mucha diferencia en la dispersión de diferentes longitudes de onda. Como todas las longitudes de onda se dispersan, el resultado de su mezcla es blanco. Blanco color nube.

Imagen: Sergio Cambelo / flickr

Ese azul grisáceo o parduzco que a menudo cubre las grandes ciudades es causado principalmente por partículas emitidas por motores de combustión interna (automóviles, camiones, calderas de calefacción [3]) y por plantas industriales. La mayoría de estas partículas contaminantes son invisibles, y varían en tamaño, desde los 10-6 m hasta los 10-9 m. Dichas partículas proporcionan una base a la que se adhieren gases, líquidos y otros sólidos. Estas partículas más grandes dispersan la luz y producen neblina. La gravedad tiene poco efecto sobre las partículas [4] hasta que se vuelven muy grandes. Pueden permanecer en la atmósfera durante meses si no se limpian por la lluvia, nieve o el viento en cantidad y tiempo suficientes.

Más información en Y el Sol se volvió azul

Notas:

[1] Un dieciseisavo (1/16) es 1 dividido entre 24.

[2] Por eso en la Luna, donde no hay atmósfera el cielo se ve negro y se ven las estrellas aun estando al sol. Los conspiranoicos suelen citar las imágenes del cielo lunar negro pero sin estrellas como prueba de que los viajes a la Luna fueron un montaje. Lo único que demuestran es que no saben de fotografía: si el sol está presente tienes que tener muy poco tiempo de exposición y el obturador casi cerrado para que se vean cosas que son muchísimo más brillantes para la cámara que las estrellas.

[3] Estas calderas funcionan con gasóleo, biomasa o…carbón. Por ejemplo, se estima que en Madrid Central a comienzos de 2019 aun estaban operativas 200 calderas de carbón y unas 4000 de gasóleo (fuente). Las calderas generan la mitad de las partículas que contaminan el aire (EEA).

[4] Que están en un fluido, en el aire, no en el vacío.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo Los colores del cielo se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Características de una onda periódica
2. La luz como onda
3. Reflexión y refracción de la luz

Idoia Mutiloa eta Maria Zubiria Negua gerturatzen den heinean, gero eta gizaki gehiago ikusten dira ondoezik edota gaixorik. Urtero, gizakiarentzat ezagunak diren munstroak ageri dira, hala nola katarroa eta eztarriko mina. Arazorik handiena munstro horiei aurre egitea da, eta, horregatik, horien aurkako borroka errazago irabazteko, superheroi modura erabiltzen da telebistak hainbeste zabaldu duen Strepsils con Lidocaína® (1. irudia).

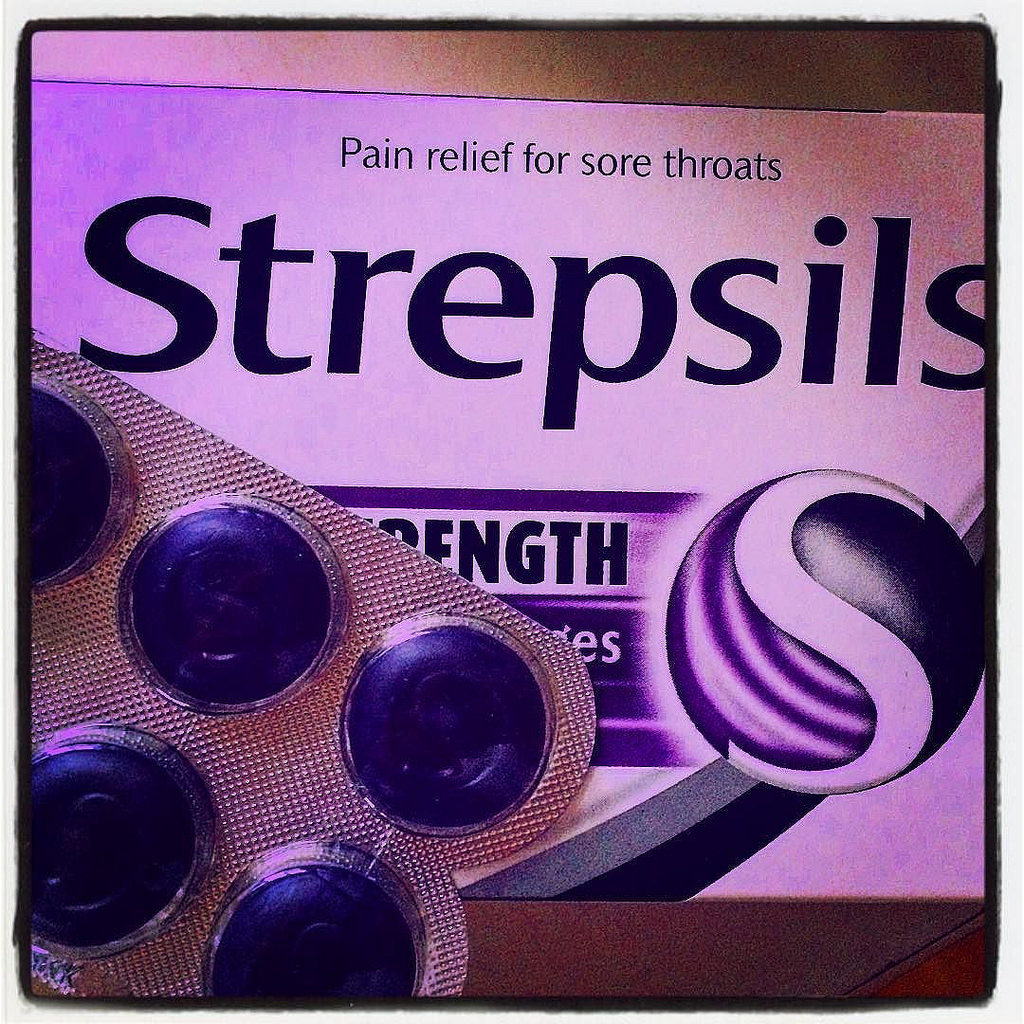
1. irudia: Lidokaina duten Strepsils pastillak. (Argazkia: – Flickr / Karen Melchior – CC BY-NC-SA 2.0 lizentziapean)

Bizitza etapa ezberdinetan bana daiteke eta lidokaina superheroiaren sorreran ere bi dira gertatzen diren etapak: amidazioa eta ordezkapena [1].

Lehen etapan, hau da, amidazio erreakzioa emateko (2. irudia), bi konposatu nahastu eta hirugarren bat tantaz tanta gehitzen da; dimetilanilina eta azido azetikoa (ozpina) dira nahasten diren bi konposatuak eta kloroazetil kloruroa tantaka gehitzen dena. Erreakzio hori organikoa izanik, giro-tenperaturan gauzatzea zaila da; horregatik, prozesua azkartzeko, giro-tenperaturatik gora egiten da lan.

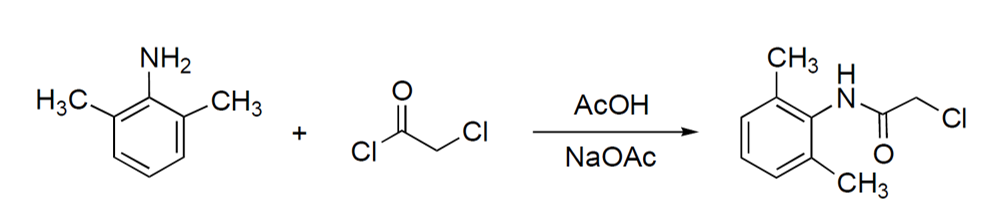
2. irudia: Amidazio erreakzioan erreakzionatzen duten konposatuak eta erreakzioaren produktua. (Egileak: Idoia Mutiloa eta Maria Zubiria)

Gatza lortzeko, ezinbestekoa da erreakzio horren bidez lortutako produktua hoztea. Hoztutako gatz hori Buchner inbutua eta kitasatoa deritzen tresnen bidez iragazi ondoren (3. Irudia) lehenengo etapa amaitutzat ematen da. Gatz hori izango da bigarren etaparen abiapuntua.

Behin produktua lortuta, bigarren erreakzioa hasi aurretik, nahitaez frogatu behar da lortutako produktua intereseko dela; horretarako, produktuaren fusio-puntua (likido/solido aldaketa eragiten duen tenperatura) neurtzen da.

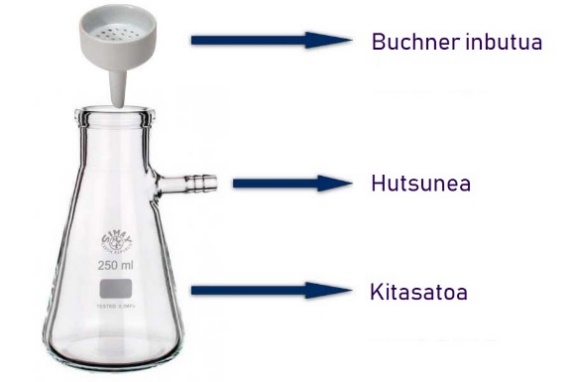
3. irudia: Lehenengo erreakzioko gatza iragazteko behar den materiala: Buchner inbutua eta kitasatoa. (Argazkia: matrazaforado.com-etik hartuta eta egileek moldatuta)

Ondoren, lidokaina sortzeko bigarren etapari ekiten zaio, hau da, ordezkapen-erreakzioari (4. irudia). Etapa honetan, toluenoa eta dietilamina gehitzen zaizkio lehen etapan lortutako gatzari. Produktuak nahastean lortu den disoluzioa, lehenengo etapan bezala, organikoa da; hori dela eta, tenperatura igo behar da. Baina aurreko pausoarekin alderatuta, honetan kristal batzuk agertzen dira. Izan ere, Kimikan oso zaila da lehenengotik nahi den produktu purua sortzea, erreakzioan zehar ezpurutasunak sortzen direlako. Hain zuzen ere, sortu diren kristal horiek ezpurutasunak dira eta lidokaina sintetizatu ahal izateko kanporatu egin behar dira.

4. irudia: Ordezkapen-erreakzioan parte hartzen duten konposatuak eta erreakzioaren produktua: lidokaina. (Egileak: Idoia Mutiloa eta Maria Zubiria)

Ezpurutasunak bota ahal izateko, disoluzioari azido klorhidrikoa gehitzen zaio lidokaina ur disoluzioan gera dadin. Horrek kontraesana dirudi, baina hainbat konposatu organiko azidoekin tratatuz gero, konposatuen izaera organikoa jaitsi eta ur-disoluzioan gera daitezke disolbatuta. Lidokainaren kasuan, hau gertatzen da: intereseko produktua protonatuta, aldatu egiten da bere izaera. Pauso horretan lortzen da ezpurutasun guztiak fase organikoan eta intereseko produktua ur-fasean geratzea Dekantazio-inbutu bat erabiliz (5. irudia), fase organikoa ezabatzen da.

5. irudia: Dekantazio-inbutua. (Argazkia: Wikipedia / PRHaney – CC BY-SA 3.0 lizentziapean)

Jarraian, aurreko pausoaren guztiz kontrakoa egiten da: lidokaina ur-fasetik fase organikora igarotzen da. Horretarako, pentanoa gehitzen da, lidokainak afinitate handiagoa baitu. Horrela, ur-faseko lidokaina guztia edo gehiena fase organikoan geratuko da disolbatuta, produktua protoigabetuta, izaera organikoa berreskuratu egiten delako. Ondoren, disoluzioa sartzen da. Bertan dentsitate-desberdintasun bat dagoenez, fase organikoa inbutuaren goiko aldean geratzen da eta beraz, ur-fasea kanporatzea erraza suertatzen da. Pauso hori behin eta berriro egiten da, lidokaina kopurua ahalik eta handiena izan dadin.

Esperimentua gogobetekoa izan dadin, ahalik eta lidokaina kantitate handiena lortzen saiatu behar da; honek erraza ematen du, baina ez da horrela izaten. Pauso asko egin behar dira lidokaina lortu ahal izateko. Bestalde, disoluzioan konposatu ugari egonik, horrek guztiak produktuaren galera dakar.

Ur-faseko lidokaina guztia fase organikoan dagoenean, fasea dekantazio-inbututik atera eta Erlenmeyer matrazera aldatzen da. Disoluzio organikoan gera daitekeen ura botatzeko, sodio sulfatoa (Na2SO4) gehitzen da. Behin fase organikoa baizik ez dagoela, disoluzioa errotabaporean (6. irudia) jartzen da: horrela eginda, sistemaren presioa asko handitzen da, eta ondorioz, disoluzioaren irakite-puntua asko jaisten da; horrela, pentanoaren lurrunketa errazten da.

6. irudia: Lidokaina lortzeko erabiltzen den errotabaporea. (Argazkia: Wikimedia / Gmhofmann – jabego publikoko irudia)

Prozesu hori amaituta, matrazean geratzen den hautsa lidokaina da. Lehen esan bezala, frogatu egin behar da lortutako produktua interesekoa den; horregatik, fusio-puntuaren azterketa egiten da. Lortzen den emaitza bibliografiarekin bat baldin badator, lidokainaren sorreraren prozesua amaitutzat ematen da.

Jakina da sintetizatutako lidokaina hau ezin dela zuzenean hartu gaixotasunei aurre egiteko. Lidokainaren bidez gaixotasunei aurre egiteko sortu izan dira enpresa handiak. Izan ere, bertan egiten diren kalitate-frogei esker gizakiak kontsumi lezake lidokaina eta horrela, munstroak errazago garai litezke.

Oharrak:

[1] Reilly, Thomas J. (1999). The Preparation of Lidocaine. Journal of Chemical Education , 76(11), 1557. DOI: 10.1021/ed076p1557

———————————————————————————-

Egileez: Idoia Mutiloa eta Maria Zubiria Gipuzkoako Campuseko Kimika Graduko ikasleak dira UPV/EHUn.

Artikulua, Maxux Aranzabe irakasleak Komunikazioa Euskaraz: Zientzia eta Teknologia ikasgaian bultzatutako Kutsadura kimikoa jardueraren harira idatzitako lana da.

———————————————————————————-

The post Lidokaina superheroi-lanetan appeared first on Zientzia Kaiera.

Ranas. Imagen: Wikimedia Commons

Si un hongo llamado Batrachochytrium dendrobatidis no les tiene a usted y a toda su familia asustados y amenazados es porque no son ustedes una rana, un sapo u otro tipo de anfibio. Porque si lo fuesen, lo estarían. El Bd (acortemos) ha sido declarado recientemente como el patógeno más peligroso para la biodiversidad del que se tiene noticia hasta ahora: es responsable de la desaparición de 90 especies de anfibios y amenaza a más de 500. De ellas, 124 han reducido el número de sus ejemplares hasta en un 90% y no está claro que puedan llegar a recuperarse nunca. Los especialistas no saben a día de hoy cómo detenerlo.

Un estudio llevado a cabo en 2018 sugiere que el hongo se originó en la península de Corea y desde allí se diseminó por todo el mundo en animales infectados que se colaron en las cargas de exportación, ya fuese como polizones o como mercancías alimenticias o como mascotas. Hoy se puede encontrar en más de 60 países de todo el mundo y está causando estragos en América Latina, Asia y África.

Este patógeno se transmite por contacto directo o a través de aguas infectadas y ataca a los animales a través de la keratina presente en su piel, que forma parte del sistema respiratorio de los anfibios. Así, causa que se vayan asfixiando a la vez que deteriora su sistema inmune y termina causándoles un ataque cardíaco.

Suena terrible, y lo es, pero el Bd ha tenido al menos un aspecto positivo para las ranas y similares: estamos hablando de ellas y de las amenazas que sufren. Como les pasa a muchos animales menos agraciados que tigres, pandas, delfines, águilas y elefantes, sus penurias, incluidas aquellas que el ser humano les causa, pasan más desapercibidas y se les defiende menos, a pesar de ser parte imprescindible de muchos ecosistemas, necesarios para que se mantengan los equilibrios tróficos y dependientes de la conservación de los recursos naturales.

Y eso que son unos animales fascinantes de los que la mayoría no sabemos lo suficiente. Por si es su caso, aquí van algunas cosas sobre las ranas que quizá usted no sepa.

¿En qué se diferencia una rana de un sapo?

En lo que a su taxonomía se refiere, ranas y sapos forman parte del género Anuro y de forma generalizada se les llama anuros a ambos. A partir de aquí, las diferencias entre ambos son a nivel coloquial y popular, pero taxonómicamente no hay una categorización establecida.

Rana Silverstoneia flotator, originaria de Costa Rica y Panamá. Imagen: Wikimedia Commons

Se considera que las ranas son, en general, más pequeñas, de piel suave y brillante, y más gráciles, con patas más finas que les permiten dar mayores saltos. Por el contrario los sapos son más rugosos, de colores más discretos y más corpulentos, con saltos más pequeños. Las ranas ponen sus huevos en racimos mientras que los sapos los ponen en forma de ristras.

Sin embargo, no todas las especies cumplen todas estas características, y por eso no es una división oficial.

¿Por qué las ranas no se congelan en invierno?

Los anfibios han colonizado prácticamente todos los hábitats del mundo, y en algunos de ellos puede llegar a hacer mucho frío. Dado el porcentaje de agua que contiene su cuerpo, y que son por naturaleza animales de sangre fría, ¿cómo lo hacen para no congelarse en invierno?

Las ranas hibernan, como hacen otros animales, como respuesta al frío del invierno. Para hibernar, buscan un espacio que les proteja del tiempo y de los depredadores y se acomodan en él. Entonces su metabolismo se ralentiza de forma drástica y consiguen dormir durante meses utilizando para ello las reservas de energía que van acumulando durante las estaciones cálidas. Cuando vuelve a hacer calor, despiertan y salen de su escondrijo para volver a alimentarse y dedicarse a la gustosa tarea de aparearse.

Sapo común en plena reproducción. Imagen: Wikimedia Commons

Las ranas acuáticas pueden hacer esto bajo el agua, pero a diferencia de otros animales acuáticos, como las tortugas, que se pueden enterrar bajo el barro y obtener de él las pequeñísimas cantidades de oxígeno que requieren durante la hibernación, las ranas deben situarse cerca de corrientes de agua ricas en oxígeno e hibernar sobre el barro no bajo él. Muchas salen ligeramente del letargo y nadan lentamente de vez en cuando.

Las ranas terrestres hibernan en tierra, a menudo enterrándose bien bajo el suelo para situarse a salvo de depredadores y también huyendo del nivel de congelación. Otras se evitan el esfuerzo de cavar y enterrarse ubicándose en grietas lo suficientemente profundas de troncos o rocas para quedar fuera del alcance de cualquiera que pretenda darles un bocado.

Para evitar que el frío les haga daño mientras hibernan cuentan con un efectivo sistema anticongelante: una alta concentración de glucosa en sus órganos vitales evitan que se congelen. Pueden llegar a formarse algunos cristales de hielo en algunas partes del cuerpo, como por ejemplo la vejiga, y el animal parecerá muerto durante semanas pero cuando llegue la primavera y las temperaturas suban, esos cristales desaparecerán, el cuerpo de la rana estará intacto y ésta recuperará su actividad sin problema.

¿Cómo evitan deshidratarse en las estaciones secas?

Si bien la mayoría de los anfibios viven en lugares donde ninguna estación es tan seca como para suponer un problema, unas pocas se han adaptado para conquistar esos hábitats. En esos casos, practican la estivación, la versión veraniega de la hibernación: el animal entra en un estado durmiente como respuesta a las condiciones extremas temporales del entorno.

Para hacerlo, se entierran en el suelo, allí donde aun se conserva un poco de humedad y mientras duermen ponen en marcha un ingenioso truco: generan varias capas de piel muerta, formando una especie de capullo impermeable que les envuelve y les ayuda a conservar su propia humedad, dejando expuestos al exterior solamente los agujeros respiratorios para evitar asfixiarse. Cuando termina la estación seca y vuelven las lluvias, se liberan de su caparazón y regresan a la superficie para rehidratarse.

¿Por qué pasan de renacuajos a ranas?

Cuando nacen, las ranas no son ranas más pequeñas, sino un renacuajo, que a simple vista parece un animal de una especie totalmente distinta: una cabeza grande y redondeada con una ancha cola que les permite desplazarse y alimentarse en el agua. Pocas semanas después desarrollan las poderosas patas traseras que les ayudan a saltar fuera del agua y alimentarse en un terreno nuevo. No son las únicas que practican la metamorfosis, muchos peces e insectos lo hacen también. Pero ¿por qué?

Renacuajo de la rana bermeja, días antes de su metamorfosis. Imagen: Wikimedia Commons

Según la investigadora holandesa Anna ten Brink, se trata de una estrategia que permite a una especie aumentar potencialmente sus opciones de alimentación, y es una estrategia tan eficaz que, sin bien ha aparecido contadas veces a lo largo de la evolución, una vez que lo hace rara vez desaparece.

Ten Brink y su equipo partieron de la idea de que los animales que no se metamorfosean y siempre tienen el mismo tipo de cuerpo adaptado al mismo tipo de entorno, están bien preparados para comer un tipo de alimento durante toda su vida. Pero si ese entorno contiene otro tipo de alimento, ¿podrían los adultos incorporarlo si durante su crecimiento su anatomía cambiaba de una forma distinta?

La respuesta que observaron es que los animales esto rara vez ocurre, ya que entonces las crías tendrían más dificultad para nutrirse del primer alimento y un mayor porcentaje moriría antes de llegar a la edad adulta.

Aquí, la metamorfosis es una solución evidente: los animales jóvenes siguen adaptados al alimento original y los adultos cambian completamente de cuerpo para poder consumir el segundo. Claro que esto supone pagar un alto precio en forma de una gran cantidad de calorías y el riesgo de que el proceso salga mal y el animal sufra defectos que acorten notablemente su vida.

Incluso aunque salga bien, el periodo de metamorfosis es un momento de especial vulnerabilidad en el que no pueden huir ni defenderse en caso de ataque de un depredador. Por eso ten Brink especula que la metamorfosis sale adelante cuando la recompensa evolutiva es realmente buena, cuando los que la completan tienen a su alcance una alimentación muy nutritiva que les permite reproducirse numerosamente con éxito.

Referencias:

A deadly amphibian disease goes global – Science
The Evolutionary Ecology of Metamorphosis – The American Naturalist
¿Por qué un animal cambiaría su cuerpo por otro? – The New York Times
How do frogs survive winter? Why don’t they freeze to death – American Scientist
What’s The Difference Between a Frog and a Toad? – Live Science

Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista

El artículo ¡Salvad a las ranas! se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. ¡Salvad a la hija!
2. ¿Por qué si nunca hemos vivido mejor que ahora el mundo nos parece cada vez peor?
3. Las ventajas (para ti y para los demás) de ser egoísta de vez en cuando

Guillermo Quindós, UPV/EHUko Medikuntza eta Erizaintza Fakultateko Mikrobiologia Katedraduna, buru izan duen ikerlan batek umetokiko zelula ametan oinarritutako tratamendu berritzaile eta erraz bat garatu du, baginako kandidiasia gaixotasunaren jatorri den Candida Albicans onddoaren aurka borrokatzeko.

Irudia: Tratamendu berritzaile eta erraza garatu dute baginako kandidiasia gaixotasunaren jatorri den Candida Albicans onddoaren aurka borrokatzeko.

Baginako kandidiasiak ez dakar arrisku handirik eguneroko bizitzara baina gaixotasuna duenaren bizi kalitatea murriztu egiten du, haren jarduera mugatuz. Gaixotasunaren sintomak dira, esaterako, askotan jasanezinak diren azkura eta erresumina. Baginako kandidiasia pairatu duten bost emakumetatik bat Candida onddoaren eramaile kroniko bihurtzen da eta, ondorioz, infekzioak pairatzen ditu aldizka. Errepikatzen diren kandidiasi horiek erresistenteak bihurtzen dira ohiko tratamenduen aurrean.

Umetokiko zelula amekin egindako ikerketak bide berria ireki du Candida Albicans onddoari aurre egiteko. Aktibitate antineoplasikoa (bular tumore zelulen aurkakoa) duten umetokiko zelula amek jariatzen duten “sekretoma”-k (zitokina koktelak) Candida albicans bezalako onddo patogenoen aurkako eragina duen ikertu dute. Izan ere, tumore-zelulak bezala, eukariotak dira Candida albicans onddoak.

Ikerketaren emaitzek erakutsi dute sekretomak Candida onddo espezie batzuen aurkako oso aktibitate ona duela eta ona edo erregularra beste batzuentzat. Azpimarratzekoa da normalean kandidiasia tratazteko farmakoei erresistenteak diren Candida anduien aurka erakutsitako aktibitatea. Gogoratu beharra dago Candida albicans onddoa baginako kandidiasien %80aren baino gehiagoaren arduraduna dela.

Umetokiko zelula amek, bestalde, immunodeprimitutako pazienteen odoletik ateratako Candida albicans anduien (sentiberak zein tratamenduaren aurrean erresistenteak) hazkundea ere eten dute. Onddoen ondoriozko septizemiak (odol infekzioak) heriotza arrazoi garrantzitsua dira paziente talde horretan, horien aurka egun dauden tratamendu mediko eskas eta urrien aurrean erresistente egiten direnean bereziki.

Ikertutako umetokiko zelula amen andui berezi honek (hUCESCs-k) Candida albicans onddoaren aurka agertzen duen jarduera sendoagoaren zioa bere jatorria izan daiteke. Umetokiko zelula amak oso leku berezian dute jatorria: “umetoki lepoaren eraldatze lekua”. Oso zaurgarria da biologikoki eta etengabeko harremana du baginarekin eta horrek dakartzan mehatxuekin: onddoak, bakterioak, birusak eta kanpotik datozen mikrobio patogeno guztiak. Testuinguru horretan, umetoki lepoko zelula ama mesenkimalek, espeziearen bilakaeran zehar, defentsa mekanismo boteretsuak garatu ahal izan dituzte: balizko mehatxu guztien aurka egin eta espeziaren biziraupena bermatzea xede duten molekula faktore ugari kanpoko ingurura igortzen dituzte.

Umetokiko zelula amak edo umetoki lepoko zelula ama mesenkimalak (hUCESCs edo “human Uterine Cervical Stem Cells” ingelesez) apenas inbaditzailea den metodo baten bidez lortzen dira, ohiko ginekologia azterketan egiten ohi den lepoaren eskuilatzean oinarritua. Aurreko ikerlanetan ikertzaile ezberdinek ikusi ahal izan dutenez, gainera, sekretomak baldintzatutako inguruneak (zelula horiek igorri duten molekula multzoa) potentzial handia dauka ere bularreko minbiziaren aurkako tumoreen aurka, gaitasun birsortzaile handia kornea lesioetan, bai eta potentzial immunoarautzaile handia ere.

Iturria: UPV/EHUko prentsa bulegoa: Tratamendu berritzailea eta erraza Candida Albicans onddoaren aurka.

Erreferentzia bibliografikoa:

Schneider, José, et al., (2018). Antifungal Activity of the Human Uterine Cervical Stem Cells Conditioned Medium (hUCESC-CM) Against Candida albicans and Other Medically Relevant Species of Candida. Frontiers in Microbiology, 9, e2818. DOI: 10.3389/fmicb.2018.02818.

The post Kandidiasiari aurre egiteko tratamendu berria begi-bistan appeared first on Zientzia Kaiera.

Fuente: Affectiva

Tega cuenta historias a niños y niñas leyéndoles libros ilustrados. De vez en cuando les hace preguntas para conocer su opinión acerca de lo que les ha contado, saber si le entienden, interesarse por el significado de alguna palabra o conocer sus ideas sobre algún aspecto en particular de lo que les ha leído.

Al contar historias se mueve, adopta posturas diferentes y pone caras. También ilustra lo que cuenta con imágenes que proyecta en una pantalla. Además, se fija y registra la expresión facial y la disposición corporal de quien escucha el cuento; de esa forma sabe si le interesa y está atento a lo que dice. Y al acabar de leerle el libro, le pide que se lo cuente con sus propias palabras.

Tega es un robot con cubierta de peluche que ha sido desarrollado por un equipo del Massachusetts Institute of Technology (MIT) formado por ingenieros, informáticos y artistas. Lo han diseñado para que enseñe lenguaje a niños y niñas de corta edad, y fue presentado a finales de enero pasado en Hawai, en la AAAI Conference on Artificial Intelligence.

Tega ha demostrado ser competente en la tarea para la que fue creado. En el marco de un experimento leyó cuentos a niños y niñas de entre 4 y 6 años de edad. Lo hizo en sesiones semanales de una hora de duración. En un grupo las lecturas eran personalizadas. Cada vez que interactuaba con los chiquillos Tega aprendía, sabía más de sus habilidades y conocimientos verbales. De esa forma, para la siguiente sesión escogía un cuento más adecuado al nivel de competencia verbal de cada uno de ellos, tanto por las estructuras que eran capaces de manejar como por el vocabulario que conocían. Y además, iba sustituyendo algunas palabras por sinónimos menos conocidos.

En un segundo grupo las lecturas no eran personificadas. Tega escogía al azar la historia de una biblioteca de cuentos. Eso sí, cada dos semanas elevaba la dificultad del texto. Además de los dos grupos que interactuaron con el robot, el equipo utilizó un grupo de control que no interactuó con Tega.

Varias semanas después de terminar las sesiones, el equipo evaluó el conocimiento de vocabulario en los dos grupos experimentales y en el control. Todos los que habían interactuado con el robot habían mejorado sus conocimientos verbales, pero los del grupo con los que Tega se había relacionado de forma personalizada mejoraron más. En un test de conocimiento verbal cometieron un 23% menos de errores que antes de las sesiones con el robot. Y la tasa de error de quienes no habían interactuado de forma personalizada con él solo se redujo la mitad que la del grupo anterior. Los del grupo control no mejoraron.

Además de saber más vocabulario, los pequeños que habían interactuado con Tega de forma personalizada contaban historias más largas y más complejas que los otros niños, y su lenguaje corporal indicaba que prestaban una mayor atención al robot durante las sesiones.

No han creado Tega para que enseñe lenguaje como lo harían maestros y maestras. Lo han hecho para que sirva de apoyo al personal docente y para su uso bajo circunstancias especiales. Pero uno no puede dejar de pensar que cada vez son más los ámbitos en los que se diseñan robots para sustituir o “complementar” actividades humanas. Antes pensábamos que los robots se limitarían a la manufactura, limpieza y tareas repetitivas, en general. Pero ya hay muñecas sexuales robóticas, se proyectan androides que cuiden a personas y, como acabamos de ver, se crean robots capaces de enseñar porque, entre otras habilidades, pueden aprender.

Fuentes: Tega, a New Social Robot Platform; Tega; Smart and fluffy storytelling robot to be trialled in US classrooms

——————-

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo Tega enseña lenguaje se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El aprendizaje continuo mejora la interacción de robots con humanos en lenguaje natural
2. El lenguaje de la química
3. Mestizajes: Intuición, arte y lenguaje, por Itziar Laka

Uxue Razkin

Biologia

Berriki ondorioztatu dute baleak batez ere oroimenean oinarritzen direla bidaian zehar janaria non dagoen jakiteko. PNAS aldizkarian argitaratutako bi ikerketek baleen migrazioari buruzko zalantzak argitu dituzte. Juanma Gallegok testu honetan azaldu digunez, fosilak aztertu dituzte eta ikusi dute gutxienez 270.000 urte atzera doan jarduna dela. Oxigeno-18 isotopoaren analisian oinarritu dute lana eta Alaskan, Kalifornian eta Panaman hartutako datuak baliatu dituzte. Zehaztasun gehiago ezagutu nahi badituzu, irakurri osorik artikulua!

Genetika

Ebola, zika, lassa-sukarra bezalako gaixotasunei aurre egiteko, gakoa detekzio goiztiarra da. Bada normalean epidemia horiek hasten diren urrutiko eremuetan ez dute birusa detektatzeko eta identifikatzeko oinarrizko baliabiderik. Beraz, laginak laborategira bidali behar dira analisirako, eta horrek emaitzak atzeratzen ditu. Bada, teknika berri bat garatu dute CRISPR-CAS-ean oinarritua. Metodologia berriari izena jarri diote jada: Sherlock. Nola funtzionatzen du tresnak? Ez galdu Berriako artikulua!

Genetikari buruz maiz entzuten diren bi galdera ekarri dizkigu Koldo Garciak: bata, familia batean bikiak izandako emakume asko badaude ea bikiak izateko probabilitatea handitzen ote zen; bestea, familian begi urdinak edo argiak dituzten pertsonak badaude, ea posible den haurrek begi argiak izatea, gurasoek begi ilunak badituzte ere. Lehenengoari dagokionez, bi biki mota ezberdindu behar ditugu: biki monozigotikoak eta biki dizigotikoak. Garciak azaltzen digunaren arabera, gene gutxi lotu dira biki dizigotikoak izateko probabilitatearekin eta biki monozigotikoen kasuan ez dirudi gene-oinarririk dagoenik. Bigarren galderari dagokionez, begien kolorean gene askok hartzen dute parte.

Emakumeak zientzian

Asteon, Gerty Cori biokimikaria ezagutzeko aukera izan dugu. Medikuntzako Nobel saria jaso zuen 1947an Coriren edo glukosaren zikloa aurkitzeagatik –bere senarra eta Bernardo Houssay-ekin batera-. Sari hori irabazi zuen hirugarren emakumea izan zen, eta lehenengoa Fisiologia eta Medikuntza alorrean. Oro har, Coriren zikloa gibelaren eta giharren arteko erreserba-substantzien zirkulazioari deitzen zaio. Baina zertan datza zehatz-mehatz? Ez galdu!

Astronomia

Aurreko astean ezagutu genuen albistea: lehen aldiz espazio irekira emakumezkoz soilik osatutako lantaldea bidaltzeko asmoa zuen NASAk. Zehazki bi emakumek egin behar zuten misio hori: Christina Kochek eta Anne McClainek. Baina Elhuyar aldizkarian irakur daitekeenez, badirudi orain planaz aldatu dutela. NASAk ohar bidez adierazi duenez, ez dute jantzi egokirik bi emakumerentzat. Hortaz, Nick Haguek ordezkatuko du McClain.

Berriak ere eman du honen berri. Dirudienez, agentziak segurtasuna eta plangintza argudiatu ditu, baina andreek aspaldi salatu dute jantziekin dagoen arazoa. Dena dela, hori ez da emakumezko astronautek salatu duten bazterketa bakarra. Artikuluan azaltzen digutenez, gaur emakumezkoek gizonezkoek baino denbora laburragoa pasa dezakete espazioan, adibidez. Astronauta batek espazio estazioan Lurrean baino askoz erradiazio gehiago jasotzen du. NASAk emakumezkoei ezartzen dien gehienezko erradiazio muga gizonezkoena baino %20 baxuagoa da. Horren gainean, NASAk dio kezka dagoela erradiazio horrek umetokiko, obarioetako edo bularretako minbizia garatzeko arriskua handitu dezakeelako.

Akustika

Asteon musika-notak eta bibrazio maiztasunak izan ditu mintzagai Josu Lopez Gazpiok. Lehenik eta behin, musikaren eskalaren zentzua azaltzen digu: do batetik hurrengo do-ra bibrazioaren maiztasuna bikoiztu egiten da. Orain dakigunez, nota bati dagokion soinu bakoitza maiztasun jakin batekin lotzen da eta, maiztasunaren bikoitzera iristean, notak berriro izen berdina du. Galdera bat planteatzen da tartean: zergatik jartzen zaie izen bera bibrazio-maiztasun bikoitza duten soinuei?

Osasuna

Osasun sistemen jardunaz aritu da Berrian Felipe Aizpuru osasun ikertzailea. Jardun hori hobetzeko digitalizazioa aipatzen du: “Osakidetzak egunero gutxi gorabehera 100.000 kontaktu dauzka herritarrekin… Informazio hori guztia pilatu eta ondo aztertzen badugu, datu horiek ezagutza bihur daitezke”. Datu horiek ahalik eta modu egokienean erabiltzeko eskandinaviarrek erabiltzen dituzten sistemak eredu dituzte. Horretaz gain, gainpreskripzioari buruz mintzatu da.

Geologia

XX. mendeko zientzia-aurkikuntza aipagarrienen artean plaka-tektonikaren teoria dago ezbairik gabe, Lurraren kanpoko azal zurruna (litosfera) nola mugitzen eta birziklatzen den azaltzen duena, alegia. Ereduak 50 urte bete ditu. Testu honetan, teoria horren hastapenak eta garapena azaltzen dira. Gogora dezagun, egun, Lurra dela ezagutzen dugun planeta bakarra plaka-tektonikaren ereduaren arabera jokatzen duena. Plaka-tektonikaren garapenari esker, klima jasangarriagoa eragin du Lurrean, eta ondorioz, bizitza garatzeko aukerak izugarri handitu ditu.

Dibulgazioa

Zientziaren munduak oso espazio gutxi izan ohi du telebistan. Badira, hala ere, zientzia jorratzen duten saioak; Orbita laika, adibidez. Aurten formatua berritu dute Berrian irakurri daitekeenez. Aitor Gutierrez programako zuzendariak nabarmendu du lehen denboraldiaren esentzia berreskuratu nahi izan dutela, “baina science show baterantz eboluzionatuz”. Aipatzekoa da saio honek EHUren laguntza jasotzen duela.

–——————————————————————–
Asteon zientzia begi-bistan igandeetako atala da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna erreparatuz, Interneteko “zientzia” antzeman, jaso eta laburbiltzea da gure helburua.

———————————————————————–

Egileaz: Uxue Razkin kazetaria da.

——————————————————————

The post Asteon zientzia begi-bistan #248 appeared first on Zientzia Kaiera.

De la misma forma que el hígado, el corazón, los pulmones o los riñones no dejan de funcionar cuando duermes, el encéfalo tampoco lo hace. Si alguno de estos órganos lo hiciese el resultado es el mismo: la muerte. Pero, si la consciencia no está operativa, ¿a qué se dedica el cerebro mientras dormimos?

Los vídeos de ¿Preguntas frecuentes? presentan de forma breve y amena cuestiones que, probablemente, nos hayamos planteado en alguna ocasión. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.

Edición realizada por César Tomé López

El artículo ¿Qué pasa en tu cerebro cuando duermes? se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. ¿Hemos intentando contactar con extraterrestres?
2. ¿Cómo demonios funcionan las copas musicales?
3. #Naukas16 Qué pasa cuando le das un péndulo a una máquina

Bai, zulo beltzek sekulako masa dute, espaziodenboran distortsioa sortu eta argiak haietatik ihes egitea saihesten duena. Zoragarri. Baina, non dago zulo beltz baten masa? Francisco R. Villatoro-k azaltzen du Where is the mass inside a black hole?

Txinatarrek, komunistak haiek, haien ekonomia ekonomia modu arrakastatsuan erreformatu bazuten, zergatik sobietarrek ezin izan zuten? José Luis Ferreirak klabe batzuk ditu: Why the Soviet Union could not be reformed

Van der Waals materialak oso interesgarriak dira berez. Baina ezaugarrietako batzuk lodierarekiko duten dependentziak propietate konbinazio benetan bereziak topatzea dakar. DIPC-ren A unique combination of properties in a van der Waals antiferromagnet

–—–

Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.

The post Ezjakintasunaren kartografia #255 appeared first on Zientzia Kaiera.

La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebra dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Publicamos en el Cuaderno de Cultura Científica y en Zientzia Kaiera una serie de artículos que narran algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas.

Nauru. Fuente: Wikimedia Commons

Tras su lanzamiento por Paul Crutzen en el año 2000, el alcance social y académico del Antropoceno ha crecido de una manera sorprendente. Este concepto se acuñó para materializar nuestra percepción de que las actividades humanas han cambiado el Sistema Tierra. El comportamiento de los océanos, la atmósfera, la superficie terrestre, la criosfera, la biosfera y el clima ya no es el mismo que ha caracterizado durante más de 11.000 años la época geológica en la que formalmente aún vivimos, el Holoceno.

El hecho de que los humanos podamos afectar de modo tan significativo el curso de la evolución geológica de nuestro planeta dio pie en 2009 a la creación del Grupo de Trabajo sobre Antropoceno que está examinando la posibilidad de la formalización e inclusión del término en la Tabla Cronoestratigráfica Internacional (conocida como la Escala del Tiempo Geológico). Ya que la historia de la Tierra anterior a la documentación humana sólo se puede reconstruir a partir de su registro en las rocas, este enfoque centrado en el análisis de las evidencias contenidas en los sedimentos recientes es fundamental para comparar adecuadamente las historias moderna y antigua de nuestro planeta y, por lo tanto, para medir la magnitud y la velocidad de la perturbación planetaria provocada por los humanos.

El Antropoceno se caracteriza por un conjunto de señales de naturaleza sedimentaria, biológica y química que se pueden encontrar en la mayor parte de la superficie terrestre. Algunas de estas evidencias tienen equivalentes en unidades geológicas más antiguas (por ejemplo, el enriquecimiento en metales), pero otras señales son completamente novedosas (como los radioisótopos artificiales o los plásticos dentro de los sedimentos). Estas evidencias reflejan una fase distinta en la historia de la Tierra, que se alejó de su estabilidad general holocena a partir de la Revolución Industrial y, en particular, desde la “Gran Aceleración” en el crecimiento de la población humana, la industrialización y la globalización a mediados del siglo XX, momento que se considera como el límite más adecuado para marcar su inicio.

Desde el punto de vista climático, el rápido aumento de los gases de efecto invernadero desde el siglo XIX (Figura 1) ha provocado un creciente ascenso de la temperatura y del nivel del mar, acompañados por una pérdida de hielo en los continentes. Este calentamiento ha alcanzado ya niveles más altos que los detectados durante el Holoceno y se acerca a los de otras etapas interglaciares del periodo Cuaternario.

Figura 1. Tasas de cambio en las concentraciones de gases de efecto invernadero desde el inicio de la Revolución Industrial. La década de 1950 marca una aceleración de su crecimiento (gráficos originales en W. Steffen, W. Broadgate, L. Deutsch, O. Gaffney y C. Ludwig (2015) “The trajectory of the Anthropocene: The Great Acceleration” The Anthropocene Review 2, 81-98). Imagen tomada de WWF (2018) “Informe Planeta Vivo-2018: Apuntando más alto”. M. Grooten y R.E.A. Almond (Eds.), Suiza.

La asociación de los humanos con las regiones costeras se remonta a las primeras civilizaciones, cuando nos concentramos en las desembocaduras de los ríos, deltas y estuarios, debido a la disponibilidad de alimentos abundantes y accesibles. Durante el siglo XX, la zona costera ha cambiado profundamente a medida que las poblaciones humanas iban creciendo y los ambientes costeros se ocupaban para la agricultura, la urbanización y la industria. Gran parte de la población mundial vive hoy en las áreas costeras con una densidad 3 veces superior al promedio mundial y la mayoría de las megaciudades planetarias también se encuentran en la costa. Sin embargo, los registros instrumentales y geológicos muestran que la velocidad de aumento reciente del nivel marino es anómala con respecto a los últimos miles de años y muchas zonas costeras se encuentran ahora amenazadas. Se ha observado globalmente una transición en el ascenso marino desde valores relativamente bajos durante el Holoceno superior (3 mm/año.

El estudio del nivel marino es un campo muy interdisciplinar y de creciente importancia. En el 1º informe de evaluación del IPCC (1990) no había referencia alguna a los cambios en el nivel del mar anteriores al siglo XX. Ya en el 3º informe de evaluación (2001) se incorporó el cambio del nivel marino a escalas de tiempo más largas, pero sólo en el 4º informe (2007) se agrupó la información geológica sobre el paleoclima en un solo capítulo, como asimismo se ha hecho en el 5º y último informe de evaluación (2013). Los registros instrumentales del nivel del mar comenzaron con el mareógrafo de Ámsterdam en 1682 y la altimetría de precisión por satélite se inició tras el lanzamiento del TOPEX/Poseidon a finales de 1992. Estos datos han demostrado que las velocidades de cambio del nivel del mar varían regionalmente y a escalas temporales de décadas debido a cambios en la densidad del océano. Es ahí donde los datos geológicos se hacen necesarios para poder situar estas estimaciones instrumentales en un contexto temporal a más largo plazo (Figura 2).

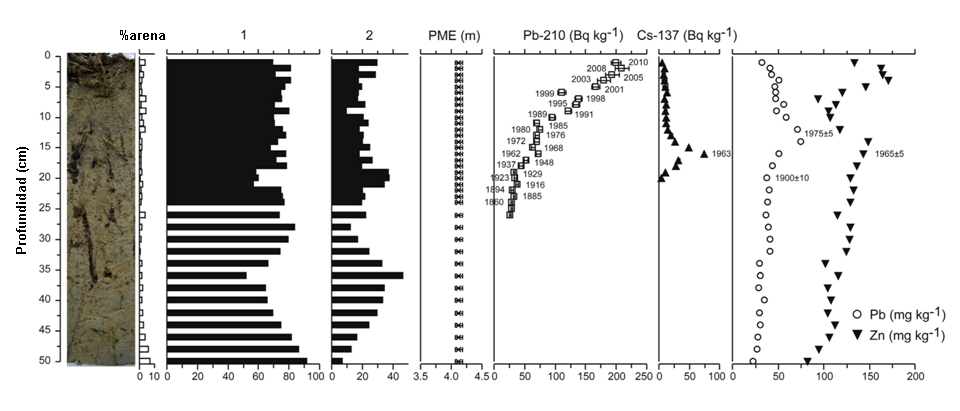Figura 2. Fotografía del testigo, contenido en arena, principales especies de microfósiles (1: Entzia macrescens; 2: Trochammina inflata), elevación de la paleomarisma (PME), actividad de los radioisótopos Pb-210 y Cs-137 y distribución del Pb y Zn durante los últimos 300 años en un sondeo perforado en la marisma de Murueta (Reserva de la Biosfera de Urdaibai). Imagen modificada de A. García-Artola, A. Cearreta y E. Leorri (2015) “Relative sea-level changes in the Basque coast (northern Spain, Bay of Biscay) during the Holocene and Anthropocene: The Urdaibai estuary case” Quaternary International 364, 172-180. DOI: 10.1016/j.quaint.2014.06.040

Durante el siglo XX, el nivel del mar ha aumentado globalmente unos 30 cm y la magnitud del ascenso del nivel marino previsto para este siglo es un tema muy controvertido. Las últimas proyecciones del IPCC (2019) auguran un aumento medio del nivel del mar a finales del siglo XXI de 28–57 cm para un escenario con reducción drástica de las emisiones de efecto invernadero, y de 55–140 cm si hubiese un crecimiento de estas emisiones. Otras estimaciones recientes sugieren que el ascenso medio global del nivel del mar podría incluso superar los 150-200 cm en el año 2100 (Figura 3). Esta diferencia en las previsiones refleja las grandes incertidumbres que existen sobre el comportamiento futuro de los casquetes glaciares de Groenlandia y Antártida.

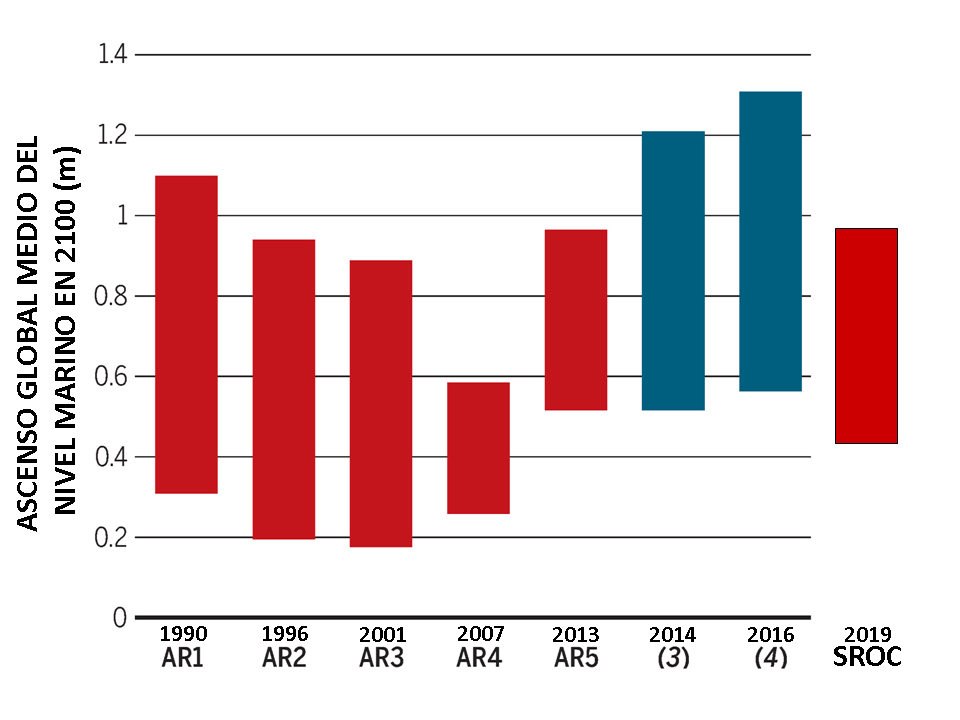Figura 3. Las distintas proyecciones del nivel marino para el año 2010 realizadas a partir de modelos han variado mucho a lo largo del tiempo desde la publicación del Primer Informe de Evaluación del IPCC (AR1) en 1990 hasta el último Informe Especial sobre el Océano y la Criosfera (SROC) de 2019. Imagen modificada de M. Oppenheimer y R.B. Alley (2016) “How high will the seas rise?” Science 354, 1375-1377. DOI: 10.1126/science.aak9460

El aumento del nivel del mar tiene una amplia gama de efectos sobre las zonas costeras que incluyen la inundación y pérdida de marismas, la erosión de playas, dunas y acantilados, la incursión de agua salada en acuíferos y centros urbanos, y el desplazamiento general de los ecosistemas costeros hacia tierra. La magnitud de estos impactos y sus consecuencias estarán asociadas, además, con los efectos de otros procesos humanos que han estado operando en el litoral durante décadas, como la disminución del aporte fluvial de sedimentos, la extracción de aguas subterráneas o la ocupación de las tierras costeras.

La duración del Antropoceno hasta ahora ha sido geológicamente muy breve, equivalente a una vida humana, pero sus impactos ya han cambiado de manera irrevocable el curso futuro de la historia de nuestro planeta. Algunos de estos cambios son irreversibles, incluso si la humanidad y sus efectos ambientales desaparecieran mañana mismo, y sus consecuencias persistirán durante siglos, milenios y millones de años.

Para saber más:

C.N. Waters, J. Zalasiewicz, C. Summerhayes, A.D. Barnosky, C. Poirier, A. Gałuszka, A. Cearreta, M. Edgeworth, E. Ellis, M.A. Ellis, C. Jeandel, R. Leinfelder, J.R. McNeill, D. deB. Richter, W. Steffen, J. Syvitski, D. Vidas, M. Wagreich, M. Williams, A. Zhisheng, J. Grinevald, E. Odada, N. Oreskes, y A.P. Wolfe (2016) “The Anthropocene is functionally and stratigraphically distinct from the Holocene” Science 351, 137 (aad2622.1-aad2622.10). DOI: 10.1126/science.aad2622

C. Summerhayes y A. Cearreta (2019) “Chapter 6. Climate Change and the Anthropocene” En: J. Zalasiewicz, C.N. Waters, M. Williams y C.P. Summerhayes (Eds.), The Anthropocene as a geological time unit: A guide to the scientific evidence and current debate. Cambridge University Press, 200-241. DOI: 10.1017/9781108621359

Sobre los autores: Alejandro Cearreta y Ane García Artola pertenecen al Departamento de Estratigrafía y Paleontología de la Facultad de Ciencia y Tecnología de la UPV/EHU.

El artículo Geología, Antropoceno y cambio climático se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Verdín, eucaliptos y cambio climático
2. Los ecosistemas acuáticos de África y el cambio climático
3. Naukas Bilbao 2017 – José Miguel Viñas: Me río yo del cambio climático

Uxue Razkin Gizakion metabolismoari buruz ikertu zuen Gerty Cori biokimikariak bere senar Carlekin batera. Zehazki, euren lana ezaguna egin zen gai izan zirelako gure gorputzean ematen den ziklo interesgarri bat azaltzeko: Coriren zikloa. Bada, zertan datza? Oro har, gibelaren eta giharren arteko erreserba-substantzien zirkulazioari deitzen zaio.

Demagun spinning klase batean gaudela eta gorputzak energia behar duela, baina une horretan muskuluak ez duela oxigeno nahikorik. Orduan, Coriren zikloa aktibatzen da: muskulu-ehunean dagoen glukosa laktato bihurtzen da hartzidura laktiko prozesu baten bitartez, hau da, laktatoa birziklatu egiten da muskuluak behar duen glukosa lortzeko. Baina laktatoa soilik gibelean bihur daiteke glukosa. Hortaz, odolaren bitartez iristen da gibelera eta bertan bihurtzen da glukosa. Azkenik, giharrera itzuliko da berriz zikloa osatuz. Prozesu hori aurkitzeagatik jaso zuen Gerty Corik Medikuntzako Nobel saria 1947an –bere senarra eta Bernardo Houssay-ekin batera–; sari hori irabazi zuen hirugarren emakumea izan zen, eta lehenengoa Fisiologia eta Medikuntza alorrean.

1. irudia: Gerty Theresa Cori biokimikaria (Argazkia: Wikimedia / National Library of Medicine – Jabego publikoko irudia)

Diskriminazioa eta soldata baxua

Gerty Cori Pragan jaio zen (Txekiar Errepublika, 1896). Medikuntza ikasi zuen hiriko Medical School of German Unibertsitate prestigiotsuan eta 1920an graduatu zen. Bertan, Carl Ferdinand Cori ezagutu zuen, gerora bere senarra izango zena. Ezkondu eta berehala, biak Vienara joan ziren bizitzera. Bertan, Children’s Carolinen Hospital izenekoan hasi zen lanean pediatra gisa; bere senarra, berriz, laborategi batean. Gertyk gustuko zuen bere lana baina era berean ikerketarako grina pizten hasi zitzaion. Horretaz gain, artikulu zientifikoak publikatzen hasi zen; lehenengoak odolari buruzkoak izan ziren, adibidez.

Edonola ere, Lehen Mundu Gerraren eraginez, Ameriketako Estatu Batuetara emigratu behar izan zuten. New Yorkera iritsi zirenean, Gaixotasun Gaiztoak ikertzeko Estatuko Institutuan hasi ziren lanean, eta, besteak beste, karbohidratoen metabolismoen inguruko ikerketak abiatu zituzten. Biokimikari gisa lan egin zuten biek ala biek baina Gertyren soldata askoz ere baxuagoa izan ohi zen. Hori gutxi balitz, hainbat unibertsitatek bakarrik bere senarra kontratatzeko asmoa zuten, biek prestakuntza bera izan arren. Hori dela eta, Carlek beti azaltzen zuen bere emaztearekin lan egin nahi zuela baina, tamalez, ez zioten kasu handirik egiten.

2. irudia: Gerty Cori eta Carl Cori biokimikariak laborategian. (Argazkia: Wikimedia / Silvia Semeraro – Creative Commons Attribution-Share Alike 4.0 International lizentziapean)

Modu berean, elkarrekin egindako ikerketen azalpenak argitaratzen zituztenean –The Journal of Biological Chemistry bezalakoetan, esaterako– oso gutxitan agertzen zen Gertyren sinadura bakarrik. Edozein kasutan ere, pairatu zuen diskriminaziorik handiena 1931n jazo zen. Bere senarra Washingtoneko Medikuntzako Eskolan ikertzaile gisa hasi zen lanean eta bere emaztea lankide izan nahi zuenez, lanpostu bat eskatu zuen harentzat. Hori lortu ahal izateko, haren esperientzia eta ezagutza zein zen azaldu zien. Alabaina, Gerty onartu zuten baina ikertzaile laguntzaile gisa, eta gutxiago kobratuz, jakina. Ia hamar urte geroago lortu zuen irakasle laguntzailea izatea, eta geroago, irakasle titular gisa aritzea.

Biokimika hauspotuz

Estatu Batuetan zeudela, azukrearen funtzionamendua animalietan, eta intsulina eta epinefrinaren efektuak ikertu zituzten. Ondoren, karbohidratoen metabolismoari buruzko lanak ere egin zituzten. Halaber, glukosa-1-fosfato molekula islatzea lortu zuten, “Cori éster” izenaz ezagutzen dena, alegia. Izan ere, igelaren giharra ikertuz, aurkitu zuten glukogenoaren degradazioa ahalbidetzen zuen konposatu hori. Horrekin batera, haren egitura argitu zuten, baita glukogenoa katalizatzeko gai den entzima ere: glukogeno fosforilasa. Geroxeago, eta lehen aipatu moduan, Coriren zikloa argitzea lortu zuten.

3. irudia: Gerty Cori eta Carl Cori 1947. urtean Medikuntzako Nobel saria jasotzen joan zirenean. (Argazkia: Wikimedia / Silvia Semeraro – CC BY-SA 4.0 lizentziapean)

Lan hori egiteagatik esleitu zitzaion Nobela. Zoritxarrez, saria jaso eta berehala, mieloesklerosia diagnostikatu zioten, hezur-muinaren gaixotasun hilgarri bat. Alabaina, Gertyk biokimika alorrean ikertzen jarraitu zuen 1957an zendu zen arte. Bere azken urteetan, glukogenosia izan zuen ikergai, glukogenoa metatzearen kariaz sortzen diren gaixotasunak, alegia.

Ez zen bizitza osoan gelditu, eta bere lanek eta ikerketek fruituak eman zituzten. Sariei dagokienez, esan beharra dago mordoa lortu zituela: Garvan-Olin Domina (1948), St. Louis Saria (1948) eta Borden Saria (1951) dira aipatzekoak, besteak beste. Gainera, Estatu Batuetatik barna banatu zen zigilu batek omendu zuen bere lana 2008an; irudian glucosa-1-fosfatoaren formula kimikoa agertzen zen baina irudiek akats bat zeukaten, formula gaizki inprimatu zuten. Halaber, National Science Fundazioko eta Ameriketako Estatu Batuetako Zientzien Akademia Nazionaleko kide izan zen. 2004. urtean, Ameriketako Kimikako Elkarteak National historial Chemical Landmark gisa izendatu zituen Coritarrak.

Gerty Coriren lanak mugak hautsi zituen; emakume horren izenak ilargirainoko oihartzuna izan zuen. Eta ez, ez da esajerazioa, izan ere, Ilargiko krater bati Cori izena jarri zioten haren eta senarraren aurkikuntzen omenez.

Iturriak:

• Biografías y Vidas: Gerty Theresa Cori
• Mujeres con ciencia: La doctora reconocida, Gerty Cori (1896-1957)
• The Nobel Prize: Gerty Cori

———————————————————————–

Egileaz: Uxue Razkin (@UxueRazkin) kazetaria da.

———————————————————————–

The post Gerty Theresa Cori (1896-1957): Glukogenoaren prozesua argitzen appeared first on Zientzia Kaiera.

Manuel Alcaraz Castaño

Réplica de un cráneo neandertal en la cueva de San Miguel (St. Michael’s Cave), Gibraltar. Boaski / Flikr

Entre los muchos enigmas de la ciencia prehistórica que provocan fascinación, tanto a científicos como al público interesado, la desaparición de los neandertales ocupa un lugar privilegiado.

Los neandertales poblaron Europa y Asia occidental desde hace unos 300.000 años y desaparecieron hace poco más de 40.000, coincidiendo con la llegada a Europa de los Humanos modernos –nuestra especie– tras su salida de África. Este último es uno de los períodos más críticos en la Prehistoria humana, pues no sólo incluyó un cambio de poblaciones definitivo, sino también una importante transformación cultural.

Dicha transformación supuso el asentamiento en todo el viejo mundo de los comportamientos complejos que caracterizarían el posterior desarrollo de las formas de vida asociadas a nuestra especie. Los prehistoriadores llevamos más de un siglo discutiendo sobre los factores y características de estos procesos de cambio, sin haber consensuado aún interpretaciones plenamente satisfactorias.

Las implicaciones ideológicas que supone el estudio de un pariente evolutivo tan cercano a la humanidad actual, y por tanto vital para entendernos a nosotros mismos, han provocado que la investigación de los neandertales haya estado históricamente cargada de prejuicios y mitos diversos. Sin embargo, los avances teóricos y metodológicos de las últimas décadas han permitido que actualmente el problema sobre su desaparición se plantee como una de las controversias científicas de mayor complejidad en el campo de la Prehistoria.

“El mito”, o la historia de la investigación sobre los neandertales

La investigación de Homo neanderthalensis, como se denominó la especie definida a partir de los restos humanos encontrados en 1856 en el valle de Neander (Alemania), es uno de los mejores ejemplos de cómo en ocasiones la ciencia puede verse influida por el contexto histórico en el que se desarrolla.

Las implicaciones ideológicas y sociales que conllevó el reconocimiento de una humanidad remota, distinta pero emparentada con la actual, inauguraron una tradición investigadora sobre los Neandertales en la que éstos, de forma más o menos directa, han sido objeto de prejuicios e ideologías de distinto pelaje.

Valle de Neander. Cordula / Wikimedia Commons

Las primeras interpretaciones que acusaron estas influencias externas a la ciencia se dieron ya desde finales del siglo XIX y principios del XX, en un contexto de fuerte oposición a la teoría de la evolución formulada por Darwin solo tres años después del descubrimiento de los restos de Neander. Entonces, una compleja mezcla de ideas racistas, colonialistas y religiosas contribuyeron a dibujar un neandertal troglodítico y animalizado, esencialmente distinto a nosotros, para el que en todo caso se tenían aún muy pocas evidencias arqueológicas y paleontológicas.

Tras la Segunda Guerra Mundial, las ideologías dominantes viraron para fomentar la imagen de un neandertal más humanizado y capaz. Sin embargo, durante los años 80 el péndulo volvió a oscilar y la visión del neandertal basculó hacia interpretaciones que le volvían a alejar de la humanidad moderna, tanto en capacidades culturales como en naturaleza biológica.

Es esta última visión, y en cierto modo las reminiscencias de las imágenes animalizadas de principios de siglo, la que cuestionan la mayoría de los investigadores desde hace tres décadas, y a la cual suelen enfrentar sus investigaciones.

Podemos situar en la última década del siglo XX el comienzo de una etapa historiográfica, la actual, en la que la investigación sobre los neandertales ha alcanzado una verdadera madurez científica. Aunque las implicaciones ideológicas que supone el estudio de este tipo humano siguen flotando en el ambiente, el asentamiento de la Prehistoria como una ciencia interdisciplinar, con métodos y técnicas avanzados, ha hecho que nuestro conocimiento actual de esta especie humana se encuentre fundamentalmente basado en evidencias y pruebas empíricas. Algunas de ellas presentan una solidez científica que apenas podía ser imaginada pocos años atrás.

Por ello, el enigma de la desaparición de los neandertales, históricamente cargado de tópicos y prejuicios, es hoy investigado como un complejo problema científico de primera magnitud. Arqueólogos, paleoantropólogos, geólogos, ecólogos o físicos, entre otros, aúnan esfuerzos para recomponer un puzle poliédrico y, como siempre en Prehistoria, parcial e incompleto.

Por tanto, puede concluirse sin ambages que, en los últimos años, las influencias externas a la investigación meramente científica han perdido fuerza para dejar paso a marcos de trabajo cada vez más objetivos. Hemos pasado del mito al logos.

“El logos”, o la investigación interdisciplinar de un problema científico

El planteamiento tradicional del problema de la desaparición neandertal se hacía en términos simples y dicotómicos. O bien nuestra especie, superior en biología y tecnología, protagonizó un proceso de suplantación poblacional, más o menos violento y a escala continental, o bien los neandertales evolucionaron cultural y anatómicamente hacia las formas modernas de Homo sapiens.

Hoy en día se da la situación paradójica (en realidad bastante habitual en ciencia) de que, sabiendo bastante más sobre el problema, somos incapaces de defender teorías tan definidas. Las nuevas evidencias arqueológicas, paleontológicas, geológicas, paleoecológicas y paleogenéticas nos han empujado progresivamente a abandonar la idea de un proceso de cambio único y monolítico, y valorar, por el contrario, marcos interpretativos basados en la variabilidad regional y cronológica.

Hoy sabemos que neandertales y Humanos modernos tuvieron descendencia fértil en varios momentos y regiones geográficas, pero aún desconocemos si esos procesos de hibridación fueron responsables de la desaparición (en este caso asimilación) de los neandertales en toda su extensión geográfica. Sabemos también que los neandertales fueron capaces de desarrollar tecnologías y estrategias de subsistencia complejas durante el Paleolítico medio, pero no tenemos aún la seguridad de que dichas estrategias contribuyeran directamente al posterior desarrollo cultural del Paleolítico superior.

Sabemos que los neandertales tuvieron la inteligencia e inquietudes necesarias para desarrollar comportamientos simbólicos, incluyendo probablemente la creación de las primeras grafías pintadas en cuevas, pero se discute si dichos comportamientos fueron recurrentes, o incluso si los métodos utilizados para su verificación son fiables.

Comparación de un cráneo de Homo sapiens y de un neandertal. Wikimedia Commons

Hasta hace poco creíamos saber que neandertales y Humanos modernos convivieron durante milenios en distintas regiones europeas, pero el refinamiento de los métodos de datación nos ha obligado a cuestionar fuertemente esa idea. Igualmente, creíamos saber que los neandertales estaban especialmente adaptados a climas fríos, pero hoy se baraja la hipótesis de que la variabilidad climática fuera un factor relevante para su desaparición.

Nos encontramos en un momento de grandes cambios teóricos e interpretativos, en el que el final de los neandertales se estudia desde un marco interdisciplinar alejado de los mitos y prejuicios del pasado, por más que en ocasiones estos traten de volverse a incluir en escena. Al obtener evidencias cada vez más certeras en distintos ámbitos, el problema se hace aún más complejo, y evitamos las respuestas simplistas y viciadas que se han propuesto en el pasado.

Son especialmente relevantes los proyectos de investigación a escala regional realizados con metodologías modernas e interdisciplinares, cada vez más numerosos y relevantes en la península ibérica. Precisamente, esta macro región geográfica se ha revelado clave para estudiar el final de los neandertales y el primer poblamiento europeo de Humanos modernos, pues es probable que aquí se produjeran los últimos episodios de este complejo proceso de cambio biocultural.

Y aunque nuestras respuestas probablemente nunca serán definitivas, si mantenemos el pensamiento crítico y el método científico como guías, sin duda se acercarán cada vez más a la realidad prehistórica.

Sobre el autor: Manuel Alcaraz Castaño es investigador en arqueología del Paleolítico en la Universidad de Alcalá

This article is republished from The Conversation under a Creative Commons license. Original article.

El artículo Por qué nos fascinan los neandertales se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Neandertales ¿crónica de una muerte anunciada?, por María Martinón-Torres
2. La cronología de la desaparición de los neandertales
3. Los neandertales respiraban de otra manera

Si uno le pregunta a Google Images qué es un una gráfica, puede encontrarse con un esperpento como el siguiente:

Más allá de la fealdad generalizada y los colores estridentes, la web y los medios de comunicación están plagados de ejemplos de malas representaciones de datos. Ejemplos donde el artificio y la ornamentación pervierten la función de estas poderosas herramientas.

¿Qué es una gráfica entonces? Dado que Google no parece ser de gran ayuda en este caso, yo os propongo la siguiente definición: una gráfica es una representación de datos numéricos mediante recursos visuales que permite interpretarlos y extraer información de ellos. Las gráficas son herramientas de comunicación para un tipo de mensaje muy determinado (los datos) y un tipo de receptor muy determinado (monos con buenos ojos), y como tal, utilizan un código muy especializado.

Los ojos son nuestra principal fuente de información. Se estima que nuestras retinas reciben unos 10 Gbps de información, de los cuales, pasan por el nervio óptico unos 100 Mbps hasta nuestro córtex visual. De hecho, según calculan los neurocientíficos, al menos un tercio de nuestro cerebro está ocupado procesando información visual. Por eso, a veces, cerramos los ojos cuando intentamos concentrarnos: para ser capaces de destinar más recursos a pensar o recordar mejor. En realidad, no es que tengamos una vista muy buena en comparación con otras especies. En lo que realmente somos buenos es en el análisis de la imagen, en extraer información útil a partir de lo que vemos… como caras de otros monos o un león camuflado en las hierbas.

En cambio, nuestra memoria de trabajo es bastante más modesta. Quizás resulte familiar la conocida como ley de Miller: “the magic number seven, plus or minus two1”. Es uno de los artículos más citados en psicología y, aunque ha sido revisada y matizada posteriormente, viene a decir que, en general, los humanos no podemos retener más de 7 elementos o grupos en nuestra memoria a corto plazo. Es decir, que si nos dan un listado de, pongamos, 10 cosas, nos va a resultar difícil retenerlas todas a la vez en nuestra cabeza y hacer comparaciones entre ellas mentalmente.

Por tanto, la magia de la visualización de datos consiste en convertir “cifras” (números abstractos que requerirían nuestra pobre memoria para ser comparados) en estímulos visuales, de esos que somos tan buenos en analizar.

Por poner un ejemplo, os proponemos encontrar el número más alto en tres tipos de representaciones distintas:

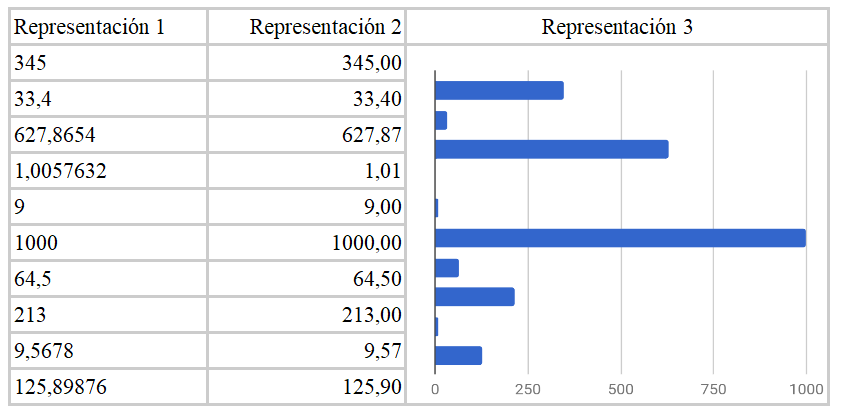
En la primera representación, habréis tenido algunos problemas para encontrarlo, y probablemente hayáis escaneado varias veces la lista, hacia arriba y hacia abajo, para recordar un número o comprobar otra vez dónde estaba la coma de los decimales. En la segunda representación, las cifras están estandarizadas para mostrar dos posiciones decimales. Una vez visto este detalle, la alineación a la derecha hace que encontrar el número más grande sea prácticamente inmediato, dado que “sobresale” hacia la izquierda más que los demás. Pero fijaos que ya hemos recurrido a un truco visual, tomando un atajo que nos permite evitar la memorización, y esto se hace especialmente evidente en la representación final en forma de gráfica.

Existe otro ejemplo muy representativo del poder de nuestros ojos procedente, en este caso, del mundo de los juegos. El juego es como sigue:

1. Hay 2 jugadores.
2. Cada jugador escoge un número del 1 al 9 en su turno.
3. Una vez un número es escogido, nadie puede volver a usarlo.
4. Gana el jugador que primero sume 15 usando 3 números.

Planteado de esta manera, es posible que al lector le cueste hacerse a una idea de en qué consiste el juego o qué estrategia elegir. Parece ciertamente complejo. Jugar requiere retener en la memoria una lista de los números escogidos, las posibles sumas que se forman con ellos y los números eliminados por el otro jugador. Todo un dolor de cabeza. Sin embargo, este mismo juego puede presentarse de manera visual, simplificándose enormemente:
Esta representación visual resume todas las posibles combinaciones, ya que cualquier fila, columna o diagonal suma 15; nos revela, además, algunas propiedades interesantes de estos números. Por ejemplo, el 5 participa en más sumas cuyo resultado es 15 que ningún otro número (ya que se encuentra en el centro de la distribución). Los números pares participan, cada uno, en 3 sumas. Los números impares sólo pueden formar 2 sumas. Son propiedades matemáticas que podríamos haber deducido de haber analizado en detalle el problema inicial. Pero la representación visual nos permite pensar de manera visual, sin abstracciones previas.

En definitiva, la gracia de las gráficas y de las representaciones visuales de cualquier tipo de problema es que convierten datos abstractos, que nuestra memoria de trabajo no puede retener, en estímulos perceptivos, que entran en nuestra cabeza sin necesidad de mediación, sin necesidad de que comprendamos y retengamos cada uno de esos numeritos. Esto las convierte, a su vez, en un arma enormemente peligrosa. Precisamente porque las gráficas hacen innecesario el proceso de lectura (de interpretación mediada y meditada de los datos), es muy fácil engañar y distorsionar los datos recurriendo a su poder.

Referencia:

1Miller, G. A. (1956). “The magical number seven, plus or minus two: Some limits on our capacity for processing information”. Psychological Review. 63(2): 81–97

Sobre los autores: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica. Iñaki Úcar es doctor en telemática por la Universidad Carlos III de Madrid e investigador postdoctoral del UC3M-Santander Big Data Institute.

El artículo Datos que entran por los ojos se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Sal de la piscina si te pican los ojos y no mezcles lejía con amoniaco
2. #Naukas14 Arqueología de datos
3. Colonialismo científico: los investigadores africanos se rebelan contra el expolio de datos genéticos

Arturo Apraiz Zeintzuk izan dira XX. mendeko zientzia-aurkikuntza aipagarrienak? Erlatibitate orokorra? Mekanika kuantikoa? Genetika arloko zerbait aurkikuntza agian? Big-Bang teoria? Zerrenda horretan halabeharrez sartu beharrekoa da plaka-tektonikaren teoria, gure Lurraren kanpoko azal zurruna (litosfera) nola mugitzen eta birziklatzen den azaltzen duena. Ereduak 50 urte bete ditu (1966-1968 bitartean jaio zela onartzen da), eta beraz, gure unibertsitatea baino apur bat zaharragoa da baina epe horretan arlo ugaritan egindako ikerketek teoria sendotu baino ez dute egin. Egun, Lurraren bilakaera azaltzeko eredu estandarra da, zientzia-oinarria duen bakarra. Gainera, gero eta nabarmenagoa da plaka-tektonikak lurreko baldintza klimatikoetan eta, era berean, bizitzaren sorreran eta bilakaeran izan duen eragina

Plaka-tektonikaren aurretik geologiako arlo desberdinetako ikerketek eta ezagutzak ibilbide propioak egiten zituzten, beraien arteko loturarik gabe. Tolesak eta failak deskribatuta eta sailkatuta zeuden, bolkan mota desberdinak ezagutzen ziren, arroka igneoak ezaugarri geokimikoen bidez bereizten ziren, arroka sedimentarioen egiturak eta bakoitzaren esanahia definituta zeuden, ……. baina plaka-tektonikak beraien arteko loturak definitzeko gaitasuna erakutsi du, prozesu horien guztien jatorria eta arrazoiak erakusteaz gain.

Benetan garrantzitsuak izan diren zientzia-ideiek, une jakin bat iritsi arte erantzunik gabe egon diren zenbait arazo konpontzeko gaitasuna erakutsi ohi dute, eztabaidagunean gertatu direnean diruditen bezain bakunak, argiak eta intuitiboak izateaz gain. Plaka-tektonika da horren adibide egokietako bat; izan ere, azaldu dezake Himalaiaren garaiera, munduan gertatzen diren lurrikaren jatorria, Australiako martsupialen agerpena, arroka bolkanikoen ezaugarri kimikoak zein ozeanoen sakonera eta morfologia.

1915. urtean Alfred Wegener poloetako esploratzaile eta meteorologo alemanak zabaldu zuen eztabaida kontinenteetako jitoaren ideiaren karira. Hego Amerika eta Afrikako kostaldeen antzekotasunaz ohartuta, iradoki zuen kontinenteak ez direla estatikoak eta denborarekin horizontalean mugitzeko gaitasuna dutela. Hala ere, bere ideiak alboratuta geratu ziren, bai Munduko Gerraren osteko alemanen aurkako sentimenduak zirela kausa, bai eta ezin izan zuelako kontinenteak mugiarazteko mekanismo fidagarririk iradoki

Bigarren Mundu Gerran garatutako sonarrak eta magnetometroak helburu militarretatik urrundu eta zientzia-helburuekin erabili zirenean iritsi zen iraultza; hala gertatu zen ozeanoen morfologia ezagutu ahala, ozeano-gandorretan plakak sortu eta subdukzio-eremuetan deusezta zitezkeela iradoki zenean. Ozeanoen ezagutzak ekarri zuen plaka-tektonikaren sorrera.

Egun, Lurraren 150 km-ko azal zurruna edo litosfera (lurrazala gehi mantu zati bat) 15 plaka nagusitan dago banatuta (1. irudia). Plaka horiek etengabeko mugimenduan dihardute, gure azazkalak hasten diren abiadura berbera hartuta eta ondorioz elkarrengandik urrundu, hurbildu edo zeharka mugituta.

1. irudia: Lurraren azaleko 15 plaka nagusiak eta beraien arteko mugimendu erlatiboak. (Iturria: U.S. Geological Survey – USGS)

Erradiometriako datazioek adierazten dute ez dagoela 200 Ma baino zaharragoa den ozeanorik eta kontinenteak aldiz, askoz zaharragoak izan daitezkeela. Horrek erakusten du Lurraren bilakaeran ozeanoak sortu eta desagertu egiten direla “Wilsonen zikloa” deritzon prozesuaren bidez (2. irudia).

Kontinente guztiak elkarren ondoan egon zirenetik, Pangea superkontinentea eratuz, urrunduz joan dira. Adibidez, Afrika eta Hego-marra kendu Amerika elkarren ondoan egon ziren baina estentsio-indarren eraginpean urrunduz joan dira eta bien artean ozeano Atlantikoa garatu da. Izan ere, egun Atlantikoak handitzen dihardu, ozeanoaren erdiko gandorrean material berria sortzen ari baita. Ondorioz, Galiza eta Ipar Amerikako kostaldearen arteko distantzia urtero zenbait zentimetro handiago bilakatzen ari da.

2. irudia: “Wilsonen zikloaren” eskema erraztua. (Iturria: Philip Heron, CC BY lizentziapean)

Ozeanoak aldiz, itxi eta desagertu egiten dira ozeano-litosferak beste plaken azpitik barneratzen direnean subdukzioa deritzon prozesuaren bidez. Hego Ameriketako Pazifikoko kostaldean Nazka ozeano-plaka Hego Ameriketako kontinente-plakaren azpitik mantuan barneratzen ari da eta prozesu motel baina etengabearen eraginez Ande mendikatea eratu da.

Ozeano-litosfera sortu egiten deneko plaken arteko muga eratzailez eta ozeano-litosfera suntsitzen deneko plaken arteko muga suntsitzaileaz gain, plaken arteko beste muga mota bat dago. Horretan plaka bat bestearekiko horizontalki mugitzen da, elkar marruskatuz, Ipar Amerikako hego-mendebaldean, San Andreseko faila ospetsuan gertatzen den bezala (1. irudia).

Teoriaren hastapenetan uste zuten plakak mantuko konbekzio-mugimenduen eraginez mugitzen zirela. Aldiz, datuak pilatu ahala ohartu gara subdukzio-eremuetan mantuan hondoratzen den ezpal ozeanikoak eragiten duen indarra (ezpalen tirada edo slab pull) dela mugimenduaren eragile nagusia. Hori ziurtatzeko nahiko da jakitea subdukzio-eremu gehien dituzten plakak (Australia, Pazifiko eta Nazka plakak) direla abiadura handiena erakusten dutenak.

Mantuan hondoratutako ozeano-litosferaren ezpalek konbekzio-korronte beherakorra eragiten dute. Gainera, nukleo eta mantuaren arteko mugan pilatzen direnean, nukleoaren eta mantuaren arteko bero-transferentziari eragiten diote eta mantuko tenperatura altuagoko eremuen kokapena baldintza dezakete. Mantuko tenperatura altuko eremuetatik abiatzen dira kontinenteen-apurketa eta subdukzio-eremu berrien sorrera eragiten dituzten konbekzio-korronte gorakorrak (3. irudia).

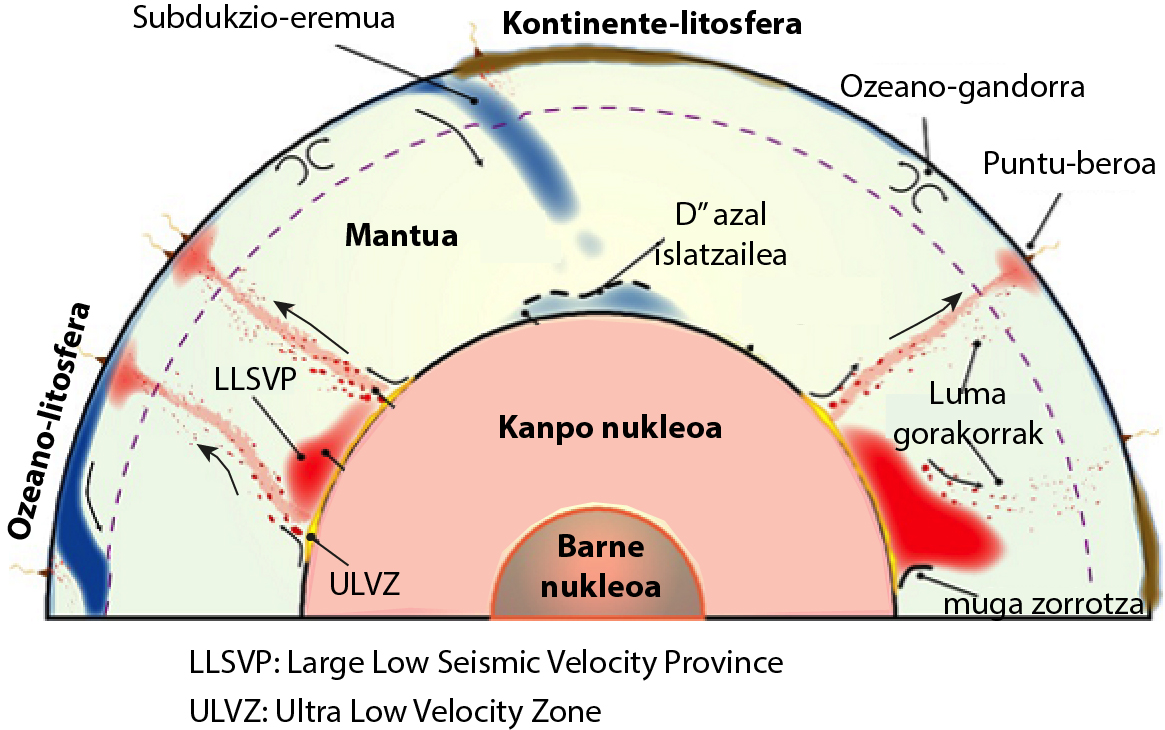
3. irudia: Mantuaren dinamikari buruzko eskema erraztua. (Ilustrazioa: Arturo Apraiz – Rost-tik (2013) eraldatuta)

Plaka-tektonika iragan geologikoan eta Lurretik kanpo

Plaka-tektonika eta berari lotutako elkarrekintzak Lurraren barneko etengabeko hozketaren ondorio dira. Oso ondo ezagutzen da plaka-tektonikaren ereduak nola jokatzen duen egungo Lurraren ezaugarri fisiko eta kimikoekiko (Apraiz, 2004), baina iraganean Lurraren tenperatura handiagoa zenean, ez dago argi zein izan zitekeen bere jokabidea. Azken ikerketek iradokitzen dute plaka-tektonikarekin lotutako prozesuak orokortu egin zirela orain dela 3.500 eta 2.800 Ma. Aurretik, badirudi Lurrak estalki jarraitua zuela, mugimendurik gabekoa, eta noizean behin, jatorria mantuan zuten magma kopuru handien eraginez puskatu ondoren, estalkia loditu egiten zela eta subdukzio-eremu lokalak garatuko zirela agian (Lenardic, 2018). Beraz, badirudi plaka-tektonika Lurrak baldintza fisiko-kimiko jakin batzuk lortu zituenean baino ez zela garatu. Plaka-tektonikaren aurretik noizbehinkakoak ziren mantuaren, lurrazalaren, hidrosferaren eta atmosferaren arteko elkarrekintzak, baina plaka-tektonika orokortu zenetik aldiz, elkarrekintzak jarraituak izan dira.

Hurrengoko hamarkadetan, zehaztu egin beharko da bizitzeko moduko Unibertsoaren eremuan ezagutzen ari diren milioika exoplanetetan plaka-tektonikaren arrastorik ote dagoen. Egun, Lurra da ezagutzen dugun planeta bakarra plaka-tektonikaren ereduaren arabera jokatzen duena. Eguzki-sisteman adibidez, Artizarra Lurraren antzeko planetatzat jotzen da, baina bien arteko desberdintasun handiak daude, Artizarraren klima jasanezina delako eta ez dagoelako plaka-tektonikaren arrastorik.

Argi dago plaka-tektonikaren garapenak klima jasangarriagoa eragin duela Lurrean, eta ondorioz, bizitza garatzeko aukerak izugarri handitu dituela. Litosfera-plaken sorrerak eta plaka horiek mantuarekin, atmosferarekin eta ozeanoekin garatu dituzten elkarrekintzak, biosfera garatu eta mantendu ahal izateko ingurunea eta baliabideak sortu dituzte.

Gehiago jakiteko:

• Apraiz, A. Plaka-tektonika: Lurraren funtzionamendua ulertzeko teoria. Udako Euskal Unibertsitatea (UEU), 2004, Bilbo.
• Rost, Sebastian (2013). Core-mantle boundary landscapes. Nature Geoscience, 6, 89-90. DOI: https://doi.org/10.1038/ngeo1715
• Lenardic, A. (2018). The diversity of tectonic modes and thoughts about transitions between them”. Philosophical Transactions of the Royal Society of London, 376(2132), pii: 20170416. DOI: http:dx.doi.org/10.1098/rsta.2017.0416

———————————————————————————-

Egileaz: Arturo Apraiz UPV/EHUko Geodinamika saileko irakaslea eta ikertzailea da.

———————————————————————————-

The post Plaka-tektonika: 50 urte eta sasoian appeared first on Zientzia Kaiera.

La escritora danesa Solvej Balle (1962) publicó en 1983 Ifølge loven Fire beretninger om mennesket,novelatraducida al castellano como Según la ley. Cuatro relatos sobre el ser humano (Seix Barral, 1995).

Como indica el título, cuatro historias componen este libro. Son cuatro metáforas sobre la búsqueda de la verdad. Son cuatro relatos sobre las obsesiones de otras tantas personas que realizan su peculiar búsqueda para llegar a entender la naturaleza del ser humano.

La banda de Möbius estructura la novela que, a priori, podría parecer formada por relatos independientes. Pero cada historia lleva a la siguiente, y la cuarta conduce inevitablemente a la primera, que reanuda el ciclo interminable del libro. La habitual metáfora de la banda de Möbius, pensada como la cinta del eterno retorno, se muestra de este modo en la novela.

Cuatro son también las leyes que actúan como hilo conductor de esta singular narración, algunas de ellas conocidas leyes científicas. Describimos brevemente cada relato.

1. Ley sobre examen forense y autopsia

De acuerdo con la ley, el cuerpo que después del óbito ofrece dudas sobre la causa de la muerte deberá ser sometido a autopsia.

Ley sobre examen forense y autopsia (Dinamarca)

El bioquímico canadiense Nicholas S. investiga sobre el misterio de la verticalidad del cuerpo humano. Presencia la autopsia de una joven que ha fallecido de hipotermia –se ha suicidado– y que ha donado su cuerpo a la ciencia. Estudia con minuciosidad el cerebro del cadáver en cuya corteza busca ‘un determinado color verde’ que probaría la existencia de una sustancia denominada filodoxa-tri-fosfato que –según una teoría muy controvertida– desempeñaría un papel fundamental en el movimiento bípedo del ser humano…

Si esta sustancia era un error, éste era de la evolución, no suyo. Si la naturaleza había cometido un error, su misión no era ocultarlo.

2. Ley del talión

El que maltrate a su prójimo será tratado de la misma manera; fractura por fractura, ojo por ojo y diente por diente, es decir, recibirá lo mismo que él ha hecho al prójimo.

Levítico, 24:19-21

Tanja L., estudiante de Derecho en Suiza, posee poderes paranormales y sospecha que provoca –en contra de su voluntad– caídas y accidentes, causando de este modo dolor y sufrimientos a otras personas. Desea descubrir la naturaleza del dolor, y para ello viaja a Barcelona, Madrid y París, buscando señales que le ayuden a descifrarlo.

Su búsqueda había sido un malentendido. Había aprendido bastante sobre la fragilidad y la fuerza destructora del ser humano, pero no podía lastimarse con tanta facilidad a una persona.

3. Ley de la gravedad

Dos cuerpos de diferente peso se moverán a la misma velocidad de caída en el vacío.

Ley de la caída de los cuerpos de Galileo

René G. es un matemático danés con un único deseo: no ser nadie.

Deseaba saber hasta qué punto podía acercarse un ser humano a la transparencia del no ser y estaba seguro de que, una vez hubiese alcanzado ese punto cero, podría hacer lo que se esperaba de él, proseguir sus estudios, realizar su trabajo sobre las relaciones entre los teoremas de incompletitud de Gödel y los postulados paralelos no euclidianos, y después pasar el resto de su vida describiendo sosegados círculos alrededor del punto cero humano.

Pero, no es tan fácil…

4. Ley de la termodinámica

En un sistema aislado, los procesos en los que interviene el calor suceden sólo en una dirección

Segunda ley de la termodinámica

Alette V. es una escultora canadiense que se dedica a realizar bustos a los transeúntes. Adora la materia inanimada y sueña con fundirse con ella. En ese afán por desprenderse de su parte humana, decide suicidarse dejándose morir de hipotermia. Así, su cadáver pasará a ser un objeto más en su habitación.

Trasladaba las personas al mundo de los objetos. […] Ella pertenecía a los objetos, pero ¿qué era?

Alette ha donado su cuerpo-objeto a la ciencia… un bioquímico canadiense llamado Nicholas S. conseguirá el cerebro de la fallecida para avanzar en sus investigaciones sobre el misterio de la verticalidad del cuerpo humano…

Nota: Adaptado de “Según la ley. Cuatro relatos sobre el ser humano”, de Solvej Balle, en DivulgaMAT, 2013

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.

El artículo Cuatro leyes consumadas siguiendo una banda de Möbius se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Poesía retorcida sobre banda de Möbius
2. La Formación Jaizkibel y sus singulares geoformas “de Möbius”
3. El teorema de los cuatro colores (1): una historia que comienza en 1852

Juanma Gallego PNAS aldizkarian argitaratutako bi ikerketek baleen migrazioari buruzko zalantzak argitu dituzte. Fosilak aztertuta, ikusi dute gutxienez 270.000 urte atzera doan jarduna dela, eta satelite bidezko neurketen bitartez ondorioztatu dute baleak batez ere oroimenean oinarritzen direla bidaian zehar janaria non dagoen jakiteko.

Ehunka mila urtetan zehar itsasoetako erregina izan zen espeziea desagertzeko zorian egon zen, gizakiaren presioa zela eta. Eta gaur egun oraindik ere espeziearen egoera ez da suziriak botatzeko modukoa. Balea urdinaz (Balaenoptera musculus) ari gara; dakigula, munduan inoiz egon den animaliarik handienaz, hain zuzen.

IWC Baleen Nazioarteko Batzordeak 1966an debekatu zuen espeziearen ehiza, baina Sobietar Batasuneko flotek 1972. urtera arte ezkutuan ehizatu zituzten. IUCN Naturaren Kontserbaziorako Nazioarteko Erakundeak kudeatzen duen Zerrenda Gorriaren arabera, egun munduan 5.000-15.000 balea geratzen dira.

1. irudia: Satelite bidezko irudien bitartez baleen migrazioa eta krillaren mugimendua alderatu dituzte, eta ikusi dute bi aldagaiak bat datozela. (Argazkia: Thomas Kelley /Unsplash)

Makinaria biologiko erraldoi hau mantentzea ez da erraza. Krustazeo ñimiñoek osatzen duten krilla da baleen elikagai ohikoena, eta janari hori non dagoen jakitea ezinbestekoa dute bizirik iraun ahal izateko. Ez da edonolako kontua: eguneko hiru tona janari prozesatzeko ahalmena du zetazeo hauetako bakoitzak.

Janari hori eskuragarri izateko, ordea, migrazioa egin behar dute. Janaria ur hotzetan lortu ohi duten arren, hainbeste elikagairik ez dagoen ekuatore aldeko ur beroetan hazten dituzte balekumeak. Hau zergatik egiten duten eboluzioaren misterioa da. Teorian, bederen, ur hotzetan kumeak hazteko arazorik ez lukete izango —hala egiten du Balea australak (Eubalaena australis)—. Hipotesi batek dio agian baleek beherago dauden latitudeetan eboluzionatu zutela, bertan elikagaia gehiago zegoen antzinako garai batean, baina gero kontinenteen jitoa gertatu eta gero ur-lasterretan egon ziren aldaketak zirela eta, elikagai horiek guztiek gorago egin zuten. Baleak haien atzetik joan ziren, baina jatorrizko hazte lekuetara itzultzen jarraitu zutela dio hipotesiak.

Dena dela, hipotesi honen aurkako froga indartsua aurkeztu dute aste honetan PNAS aldizkarian. Ikertzaileek ondorioztatu dute baleek aspalditik egiten dutela gaur egun egiten duten migrazio berdina. Aspalditik diogunean, aspalditik diogu: gutxienez 270.000 urte aipatu dute ikerketa honetan. Oxigeno-18 isotopoaren analisian oinarritu dute lana. Alaskan, Kalifornian eta Panaman hartutako datuak baliatu dituzte.
Naturak jartzen dituen oztopoak gainditzeko zientzialariek erabili behar ohi dituzten amarru horietako bati heldu behar izan diote oraingoan ere. Baleen erregistro fosilek adina informazio ematen ez zuten eta, baleei itsatsita bizi diren lanpernen fosiletako 18O isotopoa analizatu dute, eta bertan aurkitu dute baleen mugimenduaren arrastoa. Bai fosiletan zein gaur egungo aleetan aztarna hori berdina da, ur beroetatik ur hotzetara egindako migrazio horren seinale.

Ez da gaiari buruz azken asteotan izan den berrikuntza bakarra. Izan ere, PNAS aldizkariaren aurreko ale batean gaur egungo balea urdinen migrazioa izan dute aztergai. Bigarren ikerketa honetan ondorioztatu dutenez, Ozeano Barean Kaliforniatik gertu migratu ohi duten balea urdinek konfiantza gehiago jartzen dute euren oroimenean inguruneko seinaleetan baino, bi faktore horiek kontuan hartzen dituzten arren.

2. irudia: Oxigeno isotopoen azterketatik ondorioztatu dute gutxienez duela 270.000 urtetik egiten dutela migrazioa baleek. Besteak beste, balea-lanpernen fosilak erabili dituzte ikerketan. (Argazkia: Larry D. Taylor / PNAS)

Ameriketako Estatu Batuetako NOAA agentziako adituen hitzetan, baleek oroimena baliatzen dute “krill ugaria, egonkorra eta kalitate onekoa dauden lekuetara” berriro bueltatzeko. Ondorio honetara iristeko, hamarkada bateko behaketetan oinarritu dira. Bai baleen eguneroko mugimendua zein fitoplanktonaren kokapena satelite bitartez jarraitu dituzte.

Egileek egiaztatu ahal izan dute ia bete-betean bat datozela migrazioa eta historikoki fitoplanktonak izan duen eztanda (fitoplankton horren agerpenarekin batera doa baleen janaria osatzen duen krilla). Horrez gain, ikusi dute ere animaliek elikatzeko aukeratzen dituzten lekuetan hasiera batean elikagai gutxiago dauden arren, leku horietan epe luzera krill gehiago egongo dela. Hortaz, animalia hauek nolabaiteko aurreikuspena darabilte. Zientzia-artikuluan azaldu dutenez, lur ekosistemetan olatu berdea izenez ezagutzen den hipotesia egiaztatu nahi izan dute itsasoan: janari bila ari direnean, oroimenean oinarritzen direnekoa, hain zuzen.

Artikuluaren egile nagusi Briana Abrahms ekologoaren hitzetan, “migrazioan zehar nora mugitu behar duten erabakitzerakoan, urte asko bizi ahal diren eta oso adimentsuak diren animalia hauek kontuan hartzen dute elikagaiak non eta noiz egongo diren eskuragarri”.

Egileek azaldu dutenez, ezagutzen da lurreko hainbat animaliak ere elikagaien eskuragarritasun hau kontuan hartzen dutela migrazioa egiterakoan, baina itsasoan bizi diren animalien kasuan portaera hau identifikatzea zailagoa izan da orain arte. “Jakina da denboran eta espazioan gertatzen den baliabideen aldaketa migrazio prozesuen bultzatzaile handienetakoa dela lur eta itsas taxonetan, baina migrazio horiek noiz eta nora joaten diren zehazterakoan parte hartzen duten mekanismoak zeintzuk diren ekologiaren alorrean erantzuteko dagoen galdera da oraindik”, diote egileek zientzia-artikuluan.

Ondorioztatu dute baleek arbasoek erabilitako ibilbide berdinak erabiltzen dituztela, eta tokian tokiko baldintzen arabera gero doitze txikiak egiten dituztela ibilbidean. Hau da, bereziki oroimenean oinarritzen direla, baina baliabideen arabera ibilbide hori aldatzeko malgutasun nahikoa dutela. Dena dela, kezka agertu dute artikuluan: mundu osoan zehar zientzialariak klima aldaketaren ondorioak aztertzen ari diren modu berdinean, oraingo ikerketa honetan ere biologoek hori kontuan hartu dute, eta ez dakite zer gertatuko den klima aldaketaren ondorioz janaria dagoen lekuak aldatzen badira. Kasu honetan, orain arte lagungarri izan duten oroimena animalien kontra bihur liteke eta.

Informazio bibliografikoak:

• Abrahms, Briana. et al., (2019). Memory and resource tracking drive blue whale migrations. PNAS, 116 (12) 5582-5587. DOI: https://doi.org/10.1073/pnas.1819031116
• Taylor, Larry D. et al., (2019). Isotopes from fossil coronulid barnacle shells record evidence of migration in multiple Pleistocene whale populations. PNAS, 116. DOI: https://doi.org/10.1073/pnas.1808759116

———————————————————————————-

Egileaz: Juanma Gallego (@juanmagallego) zientzia kazetaria da.

———————————————————————————-

The post Baleen migrazioak oroimenean du oinarri, eta oso aspaldikoa da appeared first on Zientzia Kaiera.

Vidriera modernista del Museo Art Nouveau y Art Déco Casa Lis (Salamanca). Fuente: Museo Casa Lis

Los agentes colorantes encontrados en la pintura y la cerámica prehistóricas muestran que los humanos han apreciado el color desde los tiempos más antiguos. Pero, increiblemente, no existió ninguna hipótesis científica sobre el hasta Newton. Hasta entonces, la mayoría de las ideas aceptadas sobre el color procedían de artistas y técnicos como da Vinci, que basaban sus ideas en su experiencia con la mezcla de pigmentos.

Desafortunadamente, las lecciones aprendidas con la mezcla de pigmentos rara vez se aplican a la mezcla de haces de luz de diferentes colores. En la antigüedad, se pensaba que la luz del Sol era “pura”. El color resultaba de la adición de impurezas, como los casos en los que un rayo de “luz pura” se refracta en una pieza de vidrio y emerge con bordes de colores.

Fuente: Smithsonian Libraries

Newton se interesó por los colores cuando todavía era estudiante en la Universidad de Cambridge. En 1672, a la edad de 29 años, Newton publicó un modelo del color en las Philosophical Transactions de la Royal Society de Londres. Este fue su primer artículo científico publicado. En él escribió:

In the beginning of the Year 1666, at which time I applyed myself to the grinding of Optick glasses of other figures than Spherical, I procured me a Triangular glass-Prisme, to try therewith the celebrated Phaenomena of Colours. And in order thereto haveing darkened my chamber, and made a small hole in my window-shuts, to let in a convenient quantity of the Suns light, I placed my Prisme at his entrance, that it might be thereby refracted to the opposite wall. It was at first a very pleasing divertisement, to view the vivid and intense colours produced thereby. . . .

[A comienzos del año 1666, momento en el que me apliqué al pulimiento de lentes ópticas de formas diferentes a la esférica, me hice de un prisma triangular de vidrio para comprobar el famoso fenómeno de los colores. Para ello, tras oscurecer mi habitación y hacer un pequeño agujero en mis contraventanas para dejar entrar una cantidad conveniente de la luz del Sol, coloqué mi prisma en su entrada, para que así pudiera ser refractada hacia la pared opuesta. Al principio fue un divertimento muy agradable ver los colores vívidos e intensos producidos así. . . .] (Traducción propia)

El haz cilíndrico de luz solar “incolora” de la abertura circular pasaba a través del prisma y producía una mancha alargada de luz coloreada en la pared opuesta. Esta mancha era violeta en un extremo, rojo en el otro y mostraba una gradación continua de colores en el medio. Para este patrón de colores Newton inventó un nombre: espectro.

Pero, ¿de dónde vienen los colores? ¿Y por qué la imagen se extiende en una mancha alargada en len vez de ser un círculo? Newton pasó la luz a través de diferentes espesores de vidrio, cambió el tamaño del agujero en la contraventana e incluso colocó el prisma fuera de la ventana.

Fuente: Wikimedia Commons

Ninguno de estos cambios tuvo ningún efecto en el espectro. Tal vez alguna rugosidad o irregularidad en el vidrio era lo que producía el espectro, pensó Newton. Para probar esta posibilidad pasó los rayos de colores de un prisma a través de un segundo prisma similar puesto del revés. Si alguna irregularidad en el vidrio causaba que el haz de luz se extendiera, entonces pasar este haz a través del segundo prisma debería extenderlo aún más. En cambio, el segundo prisma, cuando se colocaba en determinada posición, volvía a juntar los colores bastante bien. Ahora se formaba un punto de luz blanca, como si la luz no hubiera pasado a través de ninguno de los prismas.

Fuente: Wikimedia Commons

Siguiendo un proceso de eliminación, Newton se convenció a sí mismo de lo que probalmente creía desde el principio era cierto: la luz incolora (blanca) está compuesta de colores. El prisma no fabrica ni añade los colores; estaban allí todo el tiempo, pero mezclados no se podían distinguir. Cuando la luz incolora pasa a través de un prisma, cada uno de los colores componentes se refracta en un ángulo diferente. Como consecuencia el haz se despliega en un espectro.

Como prueba adicional de esta hipótesis, Newton cortó un pequeño agujero en una pantalla en la que proyectó un espectro. De esta manera, la luz de un solo color podría separarse y pasar a través de un segundo prisma. Encontró que el segundo prisma no tenía ningún efecto adicional en el color de este haz, tan solo cambiaba su dirección, lo refractaba, aún más. Es decir, una vez que el primer prisma había hecho su trabajo de separar los componentes de color de la luz incolora, el segundo prisma no podía cambiar el color de los componentes. Resumiendo sus conclusiones, Newton escribió:

Colors are not Qualifications of Light derived from Refraction or Reflection of natural Bodies (as ’tis generally believed) but Original and Connate Properties, which in divers Rays are divers. Some Rays are disposed to exhibit a Red Colour and no other; some a Yellow and no other, some a Green and no other, and so of the rest. Nor are there only Rays proper and particular to the more Eminent Colours, but even to all their intermediate gradations.

[Los colores no son calidades de la luz producidas por la refracción o reflexión de los cuerpos (como se cree en general), sino propiedades originales inherentes, que en los diferentes rayos son distintas. Algunos rayos exhiben un color rojo y ningún otro; algunos uno amarillo y ningún otro; otros uno verde y ningún otro, e igualmente el resto. Tampoco hay rayos propios y concretos de los colores primarios, sino iguales para todas sus gradaciones intermedias.] (Traducción propia)

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo Descomposición de la luz se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. La teoría de la invariancia
2. La relatividad de la masa
3. Reflexiones sobre la gravedad

Josu Lopez-Gazpio Matematikoki, egin daitekeen soinu desberdinen kopurua infinitua da. Espektro entzungarria zenbakizko eskala bat da, hortaz, teorian, gure entzumen-aparatua identifikazioak egiteko gai den tartean -20 Hz-tik 20 kHz-ra- edozein soinu egin daiteke. Soinuak bibrazio maiztasunekin lotu daitezke, esaterako, soka batenak, eta soka hori instrumentu baten soka bada hainbat soinu desberdin egitea posible da. Alabaina, nola antolatu segundoko gertatzen diren bibrazio kopuruaren moduan ulertutako soinuak modu ulergarri eta errepikagarrian idazteko?

1. irudia: Soinuak modu ulergarri eta erabilgarrian taldekatuta daude musika noten bidez. Nota bakoitza bibrazio maiztasun jakin batekin lotuta dago. (Argazkia: stevepb – domeinu publikoko irudia. Iturria: pixabay.com)

Zenbakiek izena dute: maiztasunak notak dira

Zortzidunetan antolatutako zazpi nota edo soinu -do, re, mi, fa, sol, la, si- dituen musika-eskala erabiltzen denez, ezinezkoa da, esaterako, piano baten teklak erabiliz mi eta fa-ren artean dauden soinu infinituak entzutea. Musika-eskalaren zentzu ulertzeko, jakin behar da do batetik hurrengo do-ra bibrazioaren maiztasuna bikoiztu egiten dela. Praktikan, horrek esan nahi du sokaren bibrazioaren abiadura bikoiztu egiten dela. Hortaz, do zentralaren maiztasuna 261,62 dela jakinda, hurrengo do-ak 523,25 Hz maiztasuna du eta segundoko 523,25 aldiz bibrarazten du instrumentuaren soka. Horrexegatik banatzen dira tonuak hamaika zortzidunetan. Entzuteko gai garen lehen do-ak 16,35 Hz maiztasuna du, hurrengoak 32,70, hurrengoak 65,4. Gauzak horrela, hamaikagarren 16.700 Hz inguruan kokatzen da eta hurrengoa –33.000tik gorakoa– entzuteko gai garen eskalatik kanpo dago. Horrexegatik daude hamaika do bakarrik eskala entzungarrian.

2. irudia: Do-tik hasita eta sol-en eskalan, hamabi noten adierazpena pentagraman. (Argazkia: Quatrostein – CC BY-SA 3.0 lizentziapean. Iturria: commons.wikimedia.org)

Bide batez, noten izenak Arezzoko Guido fraideak ezarri zituen Joan Batailatzailearen omenez idatzitako liturgia-ereserkia oinarri hartuz:

Ut queant laxis

resonare fibris

mira gestorum

famuli tuorum

solve polluti

labii reatum

sancte Ioannes.

Zazpigarren nota, si, geroago ezarri zen izan ere deabruaren tonuekin lotzen zenez Guidok ez zion izena jarri. Azkenik, Giovanni Battista Doni musikologoak ut nota ahoskatzea zaila zela iritzita izena aldatu zion eta, horrela, ut do bihurtu zen –argi ez dagoen arren, Dominus hitzaren edo bere abizenaren lehen silaba hartu zuen izen berri gisa-.

Orain dakigunez, nota bati dagokion soinu bakoitza maiztasun jakin batekin lotzen da eta, maiztasunaren bikoitzera iristean, notak berriro izen berdina du. Beste modu batera esanda, nota baten bibrazio maiztasuna beste nota baten bibrazio maiztasunaren bikoitza denean, bi nota horiek nota bera dira. Esaterako, 440 Hz (entzun) maiztasuna la notari badagokio, 880 Hz maiztasuna ere (entzun) la izango da, baina, zortzidun bat gorago. Bide batez, La 440 -do zentralaren hurrengo la, 440 Hz maiztasuna duena-, tonua afinatzeko erreferentziako estandarra da eta ohiko diapasoien bibrazio maiztasuna da. Erreferentziakoa den la nota ez da beti 440 Hz maiztasunekoa izan, alegia, hitzarmenez erabaki da maiztasunaren balio jakin horri la deitzea. Historian zehar, bibrazio maiztasun desberdinak ezarri dira eta XIX. mende bukaerara arte ez zen finkatu 440 Hz-tan.

3. irudia: 440 Hz-tan bibratzen duen diapasoia. (Argazkia: Édouard Houe – CC BY-SA 3.0. Iturria: commons.wikimedia.org)

Zergatik jartzen zaie, baina, izen bera bibrazio-maiztasun bikoitza duten soinuei? Bada, soinuaren propietate fisikoen ondorioz, maiztasun bikoitza duten notak aldi berean jotzen direnean sortzen den soinua gustuko dugu, alegia, kontsonantzia dute. Bibrazio bikoitzen oinarria hartuta, notak definitzea bibrazio-maiztasunen balioari izenak esleitzea besterik ez da. Mendebaldean nota batetik izen bereko hurrengora dagoen tartean beste hamaika nota definitzen dira eta, horrela, hamabi nota desberdin ditugu tonuak eta tonuerdiak kontuan hartuta. Hain zuzen ere:

Pianoaren tekletan adierazitako hamaika notak, tonuak eta tonuerdiak kontuan hartuta: do, do sostenitua, re, re sostenitua, mi, fa, sol, sol sostenitua, la, la sostenitua eta si. Sostenituak tekla beltzetan daude. (Argazkia: TheDigitalArtist – domeinu publikoko irudia. Iturria: pixabay.com)

Hortaz, segundoko 261,63 aldiz bibratzen duen sokari eragiten dion tekla jo ondoren -do zentrala entzungo da- hamabi tekla eskuinerago dagoen do-a jotzen badugu 523,25 Hz maiztasunean bibratuko du sokak. Alabaina, noten kopurua eta haien izena egun ezagutzen duguna bada, arrazoi historikoengatik bakarrik da; izan ere, matematikoki posible litzateke musika-eskalak bost, hogei edo ehun soinu desberdin izatea. Noten tartean dauden soinu desberdinak infinituak diren arren, instrumentuak soinu zehatz eta jakin batzuk bakarrik jotzera behartzen gaitu.

Nota baten eta hurrengoaren arteko proportzioa -eta ez balio absolutua- beti berdina da eta, horregatik, noten maiztasunak progresio geometriko bat jarraitzen du. Frogatu daitekeen moduan, progresio geometriko horren arrazoia, r, 1,059463 da () eta horren bidez edozein notaren maiztasuna kalkulatu daiteke erreferentziako batetik abiatuz, esaterako, la 440 Hz. Erabili beharreko ekuazioa hauxe da:

M2 = M1 × r d

d hizkiaz erreferentziako la-tik dagoen tonuerdi kopurua adierazten da -positiboa goiko-tonuetarantz badoa eta negatiboa beheko tonuetarantz badoa-. Hortaz, la-tik gora dagoen si notaren maiztasuna lortzeko, lehenik zenbat tonuerdi dauden kalkulatu behar da: kasu honetan, bi tonuerdi igo behar dira -la sostenitua eta si-. Hortaz:

si (Hz) = 440 Hz × 1,0594632 = 493,88 Hz

Nota horri dagokion sokak, hortaz, segundoko 493,88 aldiz bibratzen du. Erreferentziako notaren azpitik dauden noten maiztasuna kalkulatzeko, berretzaile negatiboak erabili behar dira. Jakina, erreferentziako nota edozein izan daiteke eta ez beti la 440 Hz. Hortaz, kalkulatu berri dugun notaren maiztasuna erabiliz, do zentralaren maiztasuna kalkula daiteke. Kalkulatu berri dugun si notatik hamaika tonuerdi beherantz joan behar da do zentralera iristeko -la sostenitua, la, sol sostenitua, sol, fa sostenitua, fa, mi, re sostenitua, re eta do sostenitua eta do-. Hortaz:

do (Hz) = 493,88 Hz × 1,059463-11 = 261,62 Hz

Horrela jarraituz, nota guztien maiztasunak lortzea posible da. Notak soinu kopuru jakin batekin lotzeak mugak ezartzen ditu, bai, baina, soinuen taldekatze horri esker instrumentuak eraikitzea, estandarizatzea eta afinatzea errazagoa da. Maiztasunen multzokatze hori gabe oso zaila litzateke instrumentuen eta partituren estandarizazioa. Ez da antolaketa posible bakarra, baina, arrazoi historikoengatik musika eskala hori erabiltzen da Mendebaldean. Horri esker, aireko molekulak maiztasun jakinetan bibraraziz eta gure belarrietako tinpanoak jasotzen dituen talkei esker, horrelakoak idaztea eta entzutea posible da:

—————————————————–
Egileaz: Josu Lopez-Gazpio (@Josu_lg) Kimikan doktorea, irakaslea eta zientzia dibulgatzailea da. Tolosaldeko Atarian Zientziaren Talaia atalean idazten du eta UEUko Kimika sailburua da.
—————————————————–

Musikaren zientziari buruzko artikulu-sorta:

1. Musikaren zientzia (I): Soinua
2. Musikaren zientzia (II): Musika notak eta bibrazio maiztasunak

The post Musikaren zientzia (II): Musika notak eta bibrazio maiztasunak appeared first on Zientzia Kaiera.