Naukas Bilbao 2022: Un biólogo con datos sospechosos

¿Cuál es la probabilidad de que unos resultados experimentales salgan tan, tan similares a lo que dice la teoría? ¿No habrá el investigador hecho trampa? El incomparable Juan Antonio Cuesta analiza las estadísticas de un caso real muy famoso.
Juan Antonio Cuesta es catedrático de probabilidad y estadística en la Universidad de Cantabria.
Si no ve correctamente el vídeo, use este enlace.
Más sobre el tema:
Experimentación y evidencia: dos visiones opuestas
No se puede cambiar el azar
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2022: Un biólogo con datos sospechosos se ha escrito en Cuaderno de Cultura Científica.
Ezjakintasunaren kartografia #437
 Chester Harman / Planets: PHL @ UPR / NASA JPL.
Chester Harman / Planets: PHL @ UPR / NASA JPL.Duela gutxi egindako ikerketa batek agian aurkitu du esklerosi anizkoitzaren jatorriaren enigmaren erantzuna eta, horrekin batera, tratamendua. J.R. Alonsoren The origin of multiple sclerosis
Zeruko eskualde batean aurkitu da izarrak sortzen dituzten hidrogenozko hodeiak uste baino askoz azkarrago sortzen direla. High-speed star formation
Adimen estralurtarrarekin komunikatzeak arazo asko ditu eta hiru motatan sailka daitezke: hizkuntzazkoak, testuingurukoak eta edukikoak. Juan F. Trilloren Communication with Extraterrestrial Intelligent Beings: a sociolinguistic approach
Molekula baten magnetismoa kontrolatzea oso garrantzitsua da espintronikan eta DIPCko jendeak mikroskopio baten puntarekin egiten du: Controlling the magnetic anisotropy of a transition metal complex
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #437 appeared first on Zientzia Kaiera.
Influencia de la obesidad de la madre sobre la placenta y el crecimiento fetal
Un equipo de investigación de la UPV/EHU y del Instituto Biocruces-Bizkaia ha estudiado cómo influye el índice de masa corporal de la madre al inicio del embarazo en patrones moleculares de la placenta, y si puede incidir de alguna manera en el desarrollo del feto y posterior salud en la infancia.
 Foto: Vanessa / Unsplash
Foto: Vanessa / UnsplashEl equipo ha realizado un metaanálisis sobre “el impacto del índice de masa corporal de la madre al inicio del embarazo en los perfiles moleculares de la placenta y más concretamente en la metilación del ADN de la placenta (adición de un grupo formado por un carbono y tres hidrógenos, en una posición determinada de la molécula de ADN)”, señala Nora Fernández Jiménez, profesora de la Facultad de Medicina y Enfermería e investigadora del departamento de Genética, Antropología Física y Fisiología de la UPV/EHU. “Se trata del estudio sobre metilación del ADN de la placenta más grande llevado a cabo hasta la fecha, con un total de 2.631 parejas de madres e hijos/as de Europa, Norte América y Australia”, añade Fernández Jiménez.
Al contrario de las más conocidas mutaciones —sustitución de un nucleótido por otro en la secuencia del ADN—, la metilación es una modificación del ADN que regula la expresión génica sin alterar la secuencia. “Estudios recientes señalan que la metilación es el puente entre el ambiente intrauterino y el genoma del feto. Por ejemplo, debido al ambiente puede ocurrir que aumente el nivel de metilación de una región del genoma. Ese aumento generalmente conlleva que el ADN se vuelva más compacto, y, en consecuencia, la maquinaria de transcripción no puede acceder a dichas regiones y se produce un silenciamiento de algunos genes. También podría ocurrir lo contrario, es decir, que en respuesta al ambiente decrezca el nivel de metilación en ciertas regiones del genoma. En ese caso, el ADN obtiene una conformación abierta, a la cual las maquinarias de transcripción tienen una mejor accesibilidad y, por tanto, aumentaría la expresión génica. En ambos casos, la secuencia sigue intacta pero el genoma se comporta de una forma u otra», explica la investigadora de la UPV/EHU.
“En este trabajo hemos identificado 27 sitios en los que se observan variaciones en la metilación del ADN que parecen específicas de la placenta”, señala Fernández. Conviene recordar que la placenta es un órgano fundamental en el crecimiento y desarrollo fetal, porque es el órgano que conecta a la madre con el feto y el órgano a través del cual el feto se alimenta. “Muchos de esos sitios identificados se encuentran cerca de genes relacionados con la obesidad y están enriquecidos en rutas metabólicas del cáncer y del estrés oxidativo. No significa que las criaturas nacidas de madres con problemas de obesidad vayan a desarrollar cáncer, pero sí que es cierto que la placenta tiene un comportamiento similar a un tumor, crece de forma muy rápida, y eso nos hace pensar que existe una repercusión sobre el funcionamiento de la placenta y el crecimiento fetal”, añade Nora Fernández.
Todos estos resultados sugieren que la metilación del ADN de la placenta podría ser uno de los mecanismos por los cuales la obesidad materna se asocia con resultados adversos de salud metabólica en la infancia, aunque Fernández advierte que se necesitarán más estudios para corroborar estos hallazgos.
Referencia:
Fernandez-Jimenez, N., Fore, R., Cilleros-Portet, A. et al. (2022) A meta-analysis of pre-pregnancy maternal body mass index and placental DNA methylation identifies 27 CpG sites with implications for mother-child health. Commun Biol 5, 1313 doi: 10.1038/s42003-022-04267-y
Para saber más:
La obesidad infantil podría iniciarse antes de la concepción
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Influencia de la obesidad de la madre sobre la placenta y el crecimiento fetal se ha escrito en Cuaderno de Cultura Científica.
Estetoskopioaren historia
XIX. mendean, pazienteak auskultatzeko modu eraginkorrena belarria zuzenean bularraren kontra jartzea zen. Baina arazo bat zegoen: garaiko morala. Mediku batek ezin zuen bere belarria emakumearen bularraren gainean jarri.
René Laënnecek, Parisko Necker ospitaleko mediku buruak, kontsulta batean koaderno bat biribilkatu zuen auskultatzeko. Bazebilen! Handik gutxira, are hobeto zebilen egurrezko zilindro bat diseinatu eta eraiki egin zuen. Mediku asko zilindroa eske etorri eskatzera joan ziren eta azkenean, 1849an, lehen estetoskopio malgua sortu zen eta 1851ean, lehen binaurala.
‘Zientziaren historia‘ ataleko bideoek gure historia zientifiko eta teknologikoaren gertaerak aurkezten dizkigute labur-labur. Bideoak UPV/EHUko Kultura Zientifikoko Katedrak eginak daude eta zientzia jorratzen duen Órbita Laika (@orbitalaika_tve) telebista-programan eman dira gaztelaniaz.
The post Estetoskopioaren historia appeared first on Zientzia Kaiera.
No olvidar Seveso
Ocurrió el sábado 10 de julio de 1976 a las 12:37 horas, la hora de la comida para los habitantes del lugar. Se escuchó un silbido sordo, amenazador, extraño. Un incendio se había declarado en uno de los edificios de una industria situada en el pueblo de Seveso, a unos 25 kilómetros al norte de Milán, en la Lombardía italiana. Seveso entonces tenía unos 17000 habitantes y algo más de 20000 en la actualidad. Aquel incendio liberó al ambiente, desde la planta, la dioxina TCDD que llegó a zonas pobladas y provocó efectos desastrosos.
 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsLa planta industrial pertenecía a ICMESA o Industria Chimiche Meda Società, subsidiaria de Givaudan que, a su vez, pertenecía a Hoffmann-La Roche. La población la consideraba no peligrosa pero, en la fábrica se producía, además de aceites esenciales para perfumes y cosméticos, y como subproducto de la fabricación del herbicida conocido como 2,4,5-T y del jabón hexaclorofeno, la dioxina TCDD o 2,3,7,8-tetraclorodibenzo-p-dioxina, sustancia muy peligrosa y con altos niveles de letalidad. Era un defoliante que formaba parte del Agente Naranja. Se había utilizado en la guerra de Vietnam para eliminar la vegetación de la selva y descubrir a los grupos del Vietcong.
El incendio, provocado por un error humano, liberó una nube en forma de aerosol que contenía TCDD en cantidad entre algunos cientos de gramos y hasta algunos kilogramos, además de hidróxido de sodio, glicol y triclorofenato de sodio. De la válvula de seguridad de la chimenea del reactor de TCDD escapaba una nube grisácea compuesta de diminutas partículas, como arena fina, que llovieron alrededor de los obreros de la fábrica. Era una espesa neblina blanca, con olor a medicina y a cloro.
La nube, que se movía hacia el sur, en dirección a Milán, afectó a unos 18 kilómetros cuadrados de los alrededores de factoría. En poco tiempo había recorrido más de cinco kilómetros y la arenilla blanca caía sobre tejados y campos.
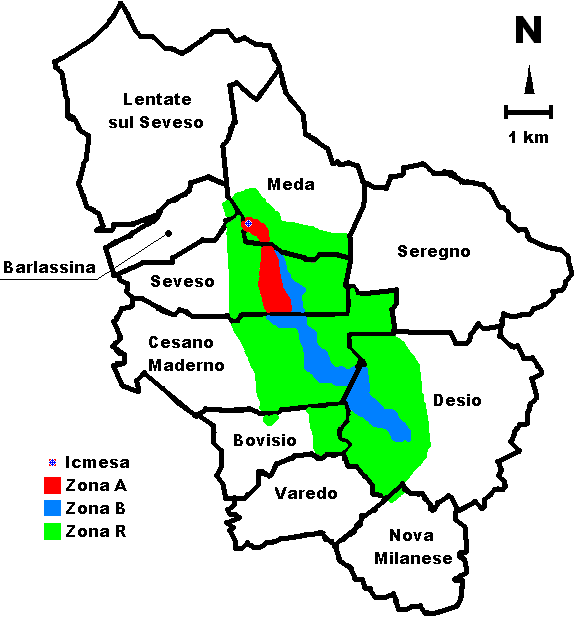 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsLa zona afectada se dividió en tres áreas. El área A, con unos dos kilómetros de longitud y 500 metros de anchura, tenía una concentración de TCDD superior a 50 microgramos por metro cuadrado de suelo y allí vivían 736 residentes que fueron evacuados el sábado 24 de julio. Poco después, el 29 de julio, se amplió la zona a evacuar y otros 600 habitantes fueron trasladados a lugares seguros.
El área B tenía entre 5 y 50 microgramos por metro cuadrado de suelo y vivían 4700 personas. Y en el área R, con menos de 5 microgramos de TCDD por metro cuadrado, vivían 31800 residentes. A todos ellos se les recomendó no tocar o comer vegetales de los cultivos locales ni aves de corral crecidas en la vecindad.
A los cuatro días, el 14 de julio, los médicos detectaron un aumento de erupciones cutáneas extensas tanto en adultos como en niños. Parecía evidente que se debían al paso de la nube de la fábrica, pero no conocían la naturaleza de la contaminación y, por tanto, no sabían cuál era el tratamiento adecuado. Desde la fábrica habían enviado muestras a Suiza, a la central, pero no tenían respuesta todavía. Además, comenzaron a encontrar gallinas y pájaros muertos y mascotas enfermas como gatos o perros, así como tomates quemados en las huertas y conejos sangrando por la nariz y los ojos. Días más tarde se estableció que la mortalidad animal era casi del 90%. En los días siguientes se sacrificaron unos 50000 animales en las zonas A y B. Incluso las abejas y sus panales se destruyeron en un radio de cinco kilómetros de la zona contaminada.
Sin embargo, la situación general no había llamado la atención en la prensa o la radio. Las noticias se propagaron lentamente. Los incidentes con pájaros o animales aparecían dispersos en varios medios de comunicación. En las personas las enfermedades eran bastante leves con erupciones cutáneas o molestias digestivas. Los médicos, más que alarmados estaban molestos por la falta de informaciones creíbles. Los relatos que empezaban a dispersarse entre la población se creían más bien rumores. Pero el viernes a la tarde llegó al hospital una niña de dos años con grandes llagas por todo el cuerpo. Y el sábado eran 18 niños los ingresados en el hospital con llagas, además de varios adultos con acné, náuseas y vómitos.
Para el 20 de julio, diez días después del incendio en la fábrica, comenzaron a aparecer gallinas, patos y conejos muertos en la población de Cesano Maderno, tres kilómetros al sur de Seveso. Entonces los periodistas de Milán comenzaron a tratar de la nube venenosa de Seveso. Parecía una noticia importante y de gran trascendencia.
 El presidente de Ucrania Viktor Yushchenko fue envenenado en 2004 con la dioxina TCDD. Como consecuencia desarrolló cloracné cuyas señales se pueden observar en su cara. Fuente: Wikimedia Commons
El presidente de Ucrania Viktor Yushchenko fue envenenado en 2004 con la dioxina TCDD. Como consecuencia desarrolló cloracné cuyas señales se pueden observar en su cara. Fuente: Wikimedia CommonsEl primer efecto de la exposición a dioxina en la población de Seveso fue el cloracné como único efecto vinculado con certeza con el accidente. La mortalidad y la morbilidad durante el período de 20 años posterior al accidente mostraron un mayor riesgo de neoplasia linfoemopoyética, cáncer del sistema digestivo (recto en hombres y vías biliares entre mujeres) y cáncer del sistema respiratorio (pulmón, entre hombres). En los análisis de incidencia, también el cáncer de tiroides y pleura apareció aumentado. También encontró el grupo de Angela Cecilia Pesatori, de la Universidad de Milán, efectos cardiovasculares (posiblemente vinculados tanto a la exposición química a la dioxina como a la experiencia estresante del desastre), efectos endocrinos (diabetes entre las mujeres) y efectos reproductivos. La exposición de los hombres a TCDD se relacionó con una menor proporción de sexo masculino respecto al femenino en la descendencia.
En estudios epidemiológicos hasta 2009 se encontraron incrementos de la tasa de incidencia de cáncer, no muy elevados, en sangre y mama según la revisión de Angela Cecilia Pesatori publicada en 2009, para 20 años después del accidente. Se centraron en los diagnósticos entre 1977 y 1996 para las zonas A y B.
Una revisión muy completa y con muchos datos sobre las consecuencias del accidente de Seveso la publicaron Brenda Eskenazi y sus colegas de la Universidad de California en Berkeley. El último apartado del texto se titula Lecciones aprendidas y lo resumo a continuación.
Confirman que un desastre ambiental, como el de Seveso, es claramente devastador para la población local e introduce posibles consecuencias ecológicas, económicas y de salud a largo plazo, tanto físicas como psicológicas. Desafortunadamente, una serie de desastres ambientales, tanto provocados por el hombre como naturales, han seguido al de Seveso y, sin duda, otros ocurrirán en el futuro. Seveso proporciona un ejemplo importante de los pasos que pueden tomar los epidemiólogos y los profesionales de la salud después de un desastre para documentar sus efectos en la salud. La investigación epidemiológica solo fue posible en Seveso debido al rápido establecimiento de un programa de vigilancia de la salud a largo plazo en la población, que incluyó, de manera crítica, la recolección y el almacenamiento de muestras biológicas de una gran cantidad de personas afectadas a pesar de que aún no se habían desarrollado métodos para analizar la exposición en esas muestras. Otros pasos importantes incluyeron un seguimiento cuidadoso de las personas con respuestas agudas a la exposición y, en este caso, de niños con cloracné, y el desarrollo o aumento de registros de salud, con los datos de cáncer y defectos de nacimiento, para recoger información sobre los efectos que podrían presentarse tanto en los primeros años como después de la exposición inicial.
A partir de lo ocurrido en Seveso, la Unión Europea instauró en 1996 nuevas y más exigentes normas de seguridad industrial conocidas como Directiva Seveso II (96/82/CE).
Un último dato a añadir a esta historia del accidente de Seveso: Paolo Paoletti, director de producción de la planta ICMESA fue asesinado el 2 de febrero de 1980 en Meda por la organización terrorista de izquierdas Prima Linea.
Referencias:
Eskenazi, B. et al. 2018. The Seveso accident: A look at 40 years of health research and beyond. Environment International 71-84.
Fuller, J.G. 1977. Sección de Libros: Niebla mortal. Selecciones del Reader’s Digest. Noviembre: 161-190.
Pesatori, A.C. et al. 2003. Short- and long-term morbidity and mortality in the population exposed to dioxin after the “Seveso accident”. Industrial Health 41: 127-138.
Pesatori, A.C. et al. 2009. Cancer incidence in the population exposed to dioxin after the “Seveso accident”: twenty years of follow-up. Environmental Health 8: 39.
Wikipedia. 2022. Desastre de Seveso. 20 abril.
Para saber más:
El caso de los enfermos de Minamata
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo No olvidar Seveso se ha escrito en Cuaderno de Cultura Científica.
Descartesen hutsegitea

Egungo zientziaren ikergai zirraragarrienetariko bat da Damasiok darabilena Descartesen hutsegitea (1994) liburuan: ea nola eratortzen den materia soiletik espiritua esaten zaion hori. Horra gogamena gogoeta sakonean bere izate eta jatorriaz, behaketa zorrotzarekin uztarturik introspekzio ernea.
 Irudia: Descartesen hutsegitea liburuaren azala. (Iturria: UPV/EHU argitalpenak)
Irudia: Descartesen hutsegitea liburuaren azala. (Iturria: UPV/EHU argitalpenak)Emozioaren eta arrazoiaren arteko erlazioa da saiakera ospetsu honen gai nagusia. Zehazkiago: «Garuneko zerk ahalbidetzen die gizakiei arrazionalki jokatzea? Nola funtzionatzen du zer horrek? Ez dut nahi izaten, ahal dela, galdera horiei erantzuteko ahaleginari “arrazionaltasunaren neurobiologia” izena eman, ofizialtasun- eta arrandia-kutsua baitu etiketa horrek. Baina horixe da, mami-mamian: eskala handiko garun-sistemen mailako giza arrazionaltasunaren neurobiologia baten hastapenak. […] Ez dut emango eskuliburuetakoen moduko azalpenik; eta ez ditut justifikatuko aurkezten ditudan iritzi guztiak. Ez ahaztu: solasaldi bat da hau. […] Testu hau arian ariko ikertze bat da, eta ez dagoeneko finko onetsiriko egitate sail bat. Hipotesiak eta proba enpirikoak aztertzen ari naiz, ez ziurtasunezko baieztapenak egiten».
Istorio bitxiak zein historial klinikoak, laborategiko esperimentuak zein abentura existentzialak: askotariko solasez oratua du Damasiok bere esploradore-kronika mamitsu hau, datu xeheetatik hipotesi orokortzaileak saiatuz, zientzialariaren tresnekin heldurik gizakiok gizaki egiten gaituen horren azterketari.
António Damásio (Lisboa, 1944) neurozientzia, neurologia eta psikologiako irakaslea da, eta Garunaren eta Sormenaren Institutuaren zuzendaria. Emozioen eta sentipenen izaeraz eta jardunaz arduratzen da batik bat, eta ospe handia du mundu zabalean, hala bere ikerketetan nola bere dibulgazio-lan oparoan. Publiko zabalarentzat idatzitako liburuen artean, Deskartesen hutsegitea izenburuko hau du ospetsuena.
Argitalpenaren fitxa:- Izenburua: Descartesen hutsegitea
- Egilea: Antonio Damasio
- ISBN: 978-84-9860-744-4
- Formatua: 16 x 24 zm
- Hizkuntza: Euskara
- Urtea: 2012
- Orrialdeak: 427 or.
Euskara, Kultura eta Nazioartekotzearen arloko Errektoretza, UPV/EHU argitalpenak, ZIO bilduma: Descartesen hutsegitea
The post Descartesen hutsegitea appeared first on Zientzia Kaiera.
Sudokus, matemáticas y arte contemporáneo
El día 21 de marzo estará en las librerías mi nuevo libro en la colección Miradas Matemáticas, de la editorial Los libros de la Catarata y la Federación Española de Sociedades de Profesores de Matemáticas (FESPM), cuyo título es Las matemáticas como herramienta de creación artística.
 Portada del libro es Las matemáticas como herramienta de creación artística (Catarata, 2023)
Portada del libro es Las matemáticas como herramienta de creación artística (Catarata, 2023)El capítulo 5, que está dedicado a los cuadrados mágicos y los cuadrados latinos, debía terminar con los sudokus, con un poco de matemáticas (ya que las soluciones de los sudokus son un tipo particular de cuadrados latinos) y de su uso en el arte contemporáneo como herramienta creativa para algunos artistas. Como al final no ha sido posible incluirlo, me ha parecido buena idea hablar de este tema en esta entrada del Cuaderno de Cultura Científica.
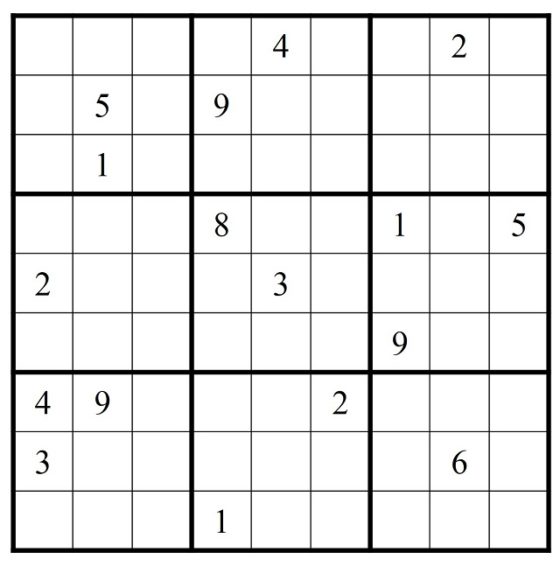 Sudoku de 17 pistas, extraído del libro de Jason Rosenhouse y Laura Taalman, Taking Sudoku Seriously, The Math Behind the World’s Most Popular Pencil Puzzle (Oxford University Press, 2011)El rompecabezas sudoku
Sudoku de 17 pistas, extraído del libro de Jason Rosenhouse y Laura Taalman, Taking Sudoku Seriously, The Math Behind the World’s Most Popular Pencil Puzzle (Oxford University Press, 2011)El rompecabezas sudoku
El sudoku es sin lugar a dudas uno de los rompecabezas más populares de los últimos tiempos, que ha tenido además un desarrollo vertiginoso. Desde que se diera a conocer internacionalmente en 2005, el sudoku se ha convertido en todo un fenómeno de masas. Hay sudokus en los periódicos, revistas y libros de sudokus, sudokus en los dispositivos electrónicos, juguetes de sudokus, programas de ordenador para crearlos, competiciones, versiones infantiles y una enorme cantidad de variantes del original.
El sudoku normal consiste en un retículo cuadrado de tamaño 9 x 9, luego con 81 casillas, dividido en 9 regiones, retículos 3 x 3, de manera que hay que rellenar las 81 casillas con los números del 1 al 9 (partiendo de una situación inicial en la que algunos números, las pistas, ya están colocados en algunas de las casillas), de forma que no se puede repetir ningún número en una misma fila, columna o región. Por lo tanto, la solución de este juego es un tipo especial de cuadrado latino.
Recordemos que un cuadrado latino de orden n es un retículo cuadrado de tamaño n x n en el que cada entrada es un número del 1 al n, aunque bien podrían considerarse n símbolos cualesquiera, por ejemplo, las letras del alfabeto latino que utilizó el matemático suizo Leonhard Euler (1707-1783) o los colores utilizados por el artista suizo Richard Paul Lohse (1902-1988), de tal forma que cada número de {1,…, n} aparece una vez, y solo una vez, en cada fila y cada columna (parta más información véase la entrada Cuadrados latinos, matemáticas y arte abstracto).
 Sin título (1980/1996), de Richard P. Lohse, que es un ejemplo de cuadrado latino de orden 6 con colores (verde, amarillo, naranja, morado, azul oscuro y azul claro). Imagen obtenida de la Galerie Hoffmann
Sin título (1980/1996), de Richard P. Lohse, que es un ejemplo de cuadrado latino de orden 6 con colores (verde, amarillo, naranja, morado, azul oscuro y azul claro). Imagen obtenida de la Galerie HoffmannEl juego denominado sudoku fue creado en la década de 1970 por el arquitecto jubilado y diseñador de pasatiempos Howard Garns (1905-1989) y publicado bajo en nombre “number place” en la revista Dell Pencil Puzzles & Word Games. Maki Kaji, presidente de la editorial Nikoli, especializada en juegos y pasatiempos, en particular, rompecabezas lógicos, lo exportó a Japón y empezó a publicarlo en 1984 en su revista Monthly Nikolist bajo el nombre Suji wa dokushin ni kagiru (los números deben estar solos), que se abrevió a Su Doku. Su expansión por el resto del mundo vino de la mano del juez retirado neozelandés, residente en Hong Kong, Wayne Gould, quien desarrolló un programa de ordenador para crear rápidamente sudokus. En 2004 empezaron a publicarse sudokus en periódicos británicos, como The Times y The Guardian, y acabó convirtiéndose, desde 2005, en un rompecabezas muy popular que aparecía en la mayoría de los periódicos del mundo.
Pueden plantearse diferentes cuestiones matemáticas relacionadas con este rompecabezas. Entre otras:
i) cuántas estructuras de solución, es decir, cuadrados latinos de orden 9 que cumplen la regla de las regiones diferentes, existen. La respuesta es 6.670.903.752.021.072.936.960 (de entre los 5.524.751.496.156.892.842.531.225.600 cuadrados latinos de orden 9 que existen), aunque si tenemos en cuenta las simetrías (permutaciones de filas y columnas, renombramiento de los símbolos, rotaciones y simetrías especulares), estas se reducen a 5.472.730.538 soluciones de sudokus distintas;
ii) dado un cuadrado latino de orden 9 que es solución de sudoku, cuántos rompecabezas sudokus distintos se pueden generar a partir del mismo, es decir, eliminando los números de las casillas hasta dejar una pequeña cantidad inicial, las pistas, que es el punto inicial del juego, y de manera que exista una solución única. Lo cierto es que para esta interesante cuestión no se tiene respuesta;
iii) y cuál es la cantidad mínima de números iniciales (pistas) posibles. Se conocen sudokus con tan solo 17 pistas (véase la primera imagen de la entrada), pero se desconoce si existen con menos pistas.
En general, se pueden considerar sudokus de orden n2 con regiones de tamaño n x n. El caso más sencillo, es el de los shidoku, que son sudokus de tamaño 4 x 4. No es difícil ver que existen 288 soluciones de shidoku distintas, aunque esencialmente son solo dos.
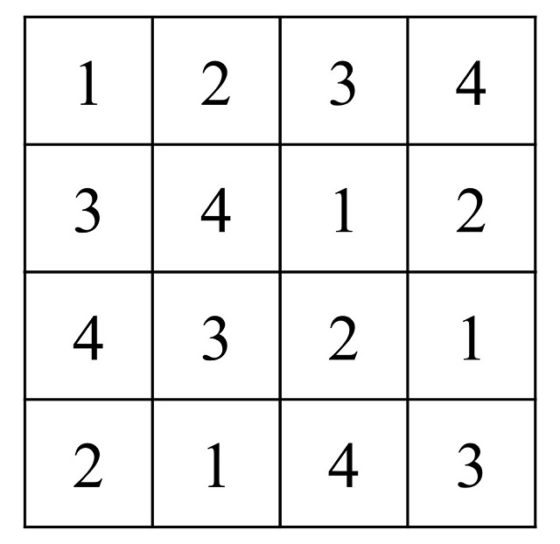 Ejemplo de solución de un shidoku, esto es, un tipo de sudoku de orden 4Los sudokus en el arte contemporáneo
Ejemplo de solución de un shidoku, esto es, un tipo de sudoku de orden 4Los sudokus en el arte contemporáneo
La pasión por los sudokus se extendió a todos los ámbitos de la cultura, en particular, también al arte contemporáneo. Los artistas vieron, y jugaron, a los sudokus en los periódicos y trasladaron este rompecabezas numérico a sus obras de arte.
Algunos artistas relacionados con el arte concreto y el constructivismo los utilizaron para crear pinturas de color al estilo de Richard P. Lohse. En este sentido, cabe destacar al artista y poeta visual austriaco Josef Linschinger (1945), un apasionado de las matemáticas como herramienta creativa, que ha realizado una serie de obras, muy reconocidas, dedicada a los sudokus. Linschinger resuelve los sudokus que aparecen en el periódico y toma estas soluciones como punto de partida para sus obras. Asigna colores a los nueve números (1 = rojo, 2 = rojo-naranja, 3 = naranja, 4 = amarillo-naranja, 5 = amarillo, 6 = amarillo-verde, 7 = verde, 8 = azul-verde, 9 = azul) y crea obras, como Sudoku 03 01 11 (2011) o Sudoku 01 07 11 (2013), formadas por tres lienzos, uno con el cuadrado latino que es solución del sudoku, mientras que los otros dos son una descomposición complementaria del anterior, con las casillas vacías en blanco o negro. En algunas obras prescinde del sudoku solución y solamente presenta los lienzos complementarios, como Sudoku 01 01 11 (2012) o Sudoku 01 08 15 (2015).
 Sudoku 13/1 01 07 11 (2012), del artista Josef Linschinger. Imagen de la página web de Josef Linschinger
Sudoku 13/1 01 07 11 (2012), del artista Josef Linschinger. Imagen de la página web de Josef LinschingerDe forma similar, la artista abstracta venezolana, residente en Madrid, Emilia Azkarate (1964), pintó algunos sudokus que aparecieron en periódicos entre los años 2008 y 2010, cambiando los números por colores. En un lienzo grande el rompecabezas y en un lienzo pequeño la solución.
 Sin título, Sudoku 90 (2009), de la artista Emilia Azkarate. Imagen obtenida en la página web de Emilia Azkarate
Sin título, Sudoku 90 (2009), de la artista Emilia Azkarate. Imagen obtenida en la página web de Emilia AzkaratePor otra parte, el artista digital Rototype, nombre artístico del eslovaco Jaka Bonca (1962), asocia los números con colores y/o formas, entre ellas, figuras geométricas básicas del mismo tamaño o de diferentes tamaños, teselas de Truchet (véase las entradas Los embaldosados de Truchet y el puzle del diamante y El arte de la sencilla baldosa de Truchet), líneas paralelas con diferentes inclinaciones, etc), creando estructuras más complejas, no solo para sudokus 9 x 9, sino también para otros tamaños. Estas obras pueden verse en la página del artista .
 Ilustración, al estilo de Rototype, del shidoku mostrado más arriba, utilizando color (escala de grises) y forma (direcciones de líneas paralelas)
Ilustración, al estilo de Rototype, del shidoku mostrado más arriba, utilizando color (escala de grises) y forma (direcciones de líneas paralelas)
Por último, un hermoso ejemplo de presencia de los shidokus (sudokus 4 x 4), no el rompecabezas sino el cuadrado latino de orden 4 con regiones 2 x 2, en el arte contemporáneo es Dibujo mural #413 (1984), del artista conceptual y minimalista estadounidense Sol Lewitt (1928-2007). Esta obra está formada por 24 shidokus de color (1 = gris, 2 = amarillo, 3 = rojo, 4 = azul), cuya estructura básica es la que aparece en la imagen de más arriba y el resto son las permutaciones de los cuatro números/colores, es decir, 4! = 24 estructuras de color.
 Instalación del Dibujo mural #413 (1984), del artista Sol Lewitt en el MASS MoCA, Museo de Arte Contemporáneo de Massachusetts. Imagen de la página web del MASS MoCA
Instalación del Dibujo mural #413 (1984), del artista Sol Lewitt en el MASS MoCA, Museo de Arte Contemporáneo de Massachusetts. Imagen de la página web del MASS MoCAAdemás, esta obra ha sido utilizada por la artista, compositora, música y directora de cine estadounidense Laurie Anderson (1947) para componer su pieza Quartet for Sol Lewitt (1977).
Bibliografía
1.- Raúl Ibáñez, Las matemáticas como herramienta de creación artística , colección Miradas matemáticas, Catarata, 2023.
2.- Jason Rosenhouse, Laura Taalman, Taking Sudoku Seriously, The Math Behind the World’s Most Popular Pencil Puzzle, Oxford University Press, 2011.
3.- María Merino, Sudokus y modelización, Un paseo por la Geometría 2009/2010, UPV/EHU, 2010.
4.- E. Russell, F. Jarvis, Mathematics of Sudoku II, Mathematical Spectrum, Vol. 39, No. 2, pp. 54-58, 2006/07.
5.- Josef Linschinger, Zahlen und Farben, Matematikum, Modo Verlag GmbH, 2016.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Sudokus, matemáticas y arte contemporáneo se ha escrito en Cuaderno de Cultura Científica.
Zientzia genero-ikuspegitik komunikatzeko dekalogoa
Martxoaren 8a da, Emakumeen Nazioarteko Eguna. 2023ko Emakumearen Nazioarteko Egunaren leloak “Mundu digital inklusiboa: Berrikuntza eta genero-berdintasunerako teknologia” aldarrikatzen du. Inguratzen gaituen munduak Informazio eta Komunikaziorako Teknologien (IKT) garapenean eragina du eta, horrez gain, erabilera molda dezake jokabide diskriminatzaileak areagotu edo iraunarazteko. Beraz, mundu digital inklusiboa lortzeko, beharrezkoa da hainbat esparrutatik jardutea.
 Irudia: 2023ko Emakumeen Nazioarteko Egunaren harira egindako ilustrazioa. (Iturria: NBE)
Irudia: 2023ko Emakumeen Nazioarteko Egunaren harira egindako ilustrazioa. (Iturria: NBE)Testuinguru horretan, adibidez, komunikabideek funtsezko zeregina dute berdintasuna lortze bidera. Honen harira, otsailaren 9an, Zientziaren arloko Emakumearen eta Neskatoaren Nazioarteko Egunaren baitan Generoa eta Zientziaren Komunikazioa jardunaldia egin zen Bilbon. Bertan, zientziaren komunikazioaren esparruan genero-ikuspegia ezartzeko eta hobetzeko moduari buruz hausnartu zen hainbat ikuspuntutik.
Jardunaldi honekin, EHUko Kultura Zientifikoaren Katedratik, hausnarketa eta salaketa binomiotik beste binomio batera igaro nahi izan dugu: gogoeta eta ekintza. Horren erakusgarri da gaur aurkezten den dekalogoa: Zientzia genero-ikuspegiarekin komunikatzeko dekalogoa, non laburbiltzen baitira egunean zehar hitzaldietan emandako gomendio eta ondorio nagusiak.
DekalogoaKontuan izan gauzak asko hobetu direla, baina gaur egun gauzak oso ondo doazela eta berdintasuna lortuta dagoela zabalduta badago ere, pertzepzio hori ez da benetakoa. Beraz, komunikazio zientifikoari heltzen diozunean, eman garrantzia alderdi kualitatiboari, ez soilik kuantitatiboari. Ondorioz, ez hartu kontuan zenbat emakume zientzialari izendatzen diren, nola irudikatzen diren baizik.
- Komunikazio arduratsua praktikan jarri: ez dago komunikazio aseptikorik; beraz, kontziente izan behar da genero-ikuspegiari jaramonik egin gabe eginez gero, komunikazioa alborapenak eta aurreiritziak indartzeko tresna izan daitekeela.
- Kontuan izan ikerketa bat genero-ikuspegirik gabe egin ahal izan dela, eta, beraz, emaitzak ezin direla orokortu. Genero-ikuspegia ikerketa-taldeen osaeratik askoz harago doa. Horrela, planteatutako galderak garrantzitsuak dira, uste dugunetik sortuko baitira eta hori generoaren araberakoa izan daiteke. Genero-ikuspegiak ere eragina du galdera horiei erantzuteko datuak lortzeko erabiltzen den metodologian eta datu horiek interpretatzeko sortzen den narratiban. Narratiba datuak bezain garrantzitsua da: normalean, datu-multzo berberak bat egin dezake hainbat narraziorekin.
- Ezarri irizpide argiak iturriak hautatzeko orduan: joan jatorrizko iturrira, bilatu emakume adituak solaskide gisa (nahiz eta batzuetan premiazkoa izan berehalako erantzun bat izatea eta horren aurrean zailagoa izan emakume zientzialarien kolaborazioa) eta lehenetsi merituak adituaren karguaren aurretik. Jarri harremanetan emakume zientzialariekin, ez bakarrik efemerideak edo STEM diziplinetan emakumeei buruzko albisteak daudenean. Praktika horrek emakumeek garatzen dituzten lan zientifikoak ikusezin bihurtzen laguntzen du.
- Emakume ikertzaileak normaltasunez tratatu, gizonezko ikertzaile bat bezala: haien itxura, bizitza pertsonala, jatorria, adina edo ikerketarekin zerikusirik ez duen beste edozein aldagai aipatu gabe.
- Ez erabili metafora mugatzailerik, hala nola “kristalezko sabaia”, “oztopo-lasterketa” edo “zulo beltza”. Baliatu ekintzara gonbidatzen duten esamoldeak.
- Ezagutarazi emakume ikertzailea ondo identifikatuta, adierazi haren izen-abizenak, lanpostua eta erakundea. Generikoaren eta inizialen erabilerak ikusezin bihurtzen baititu zientzialariak.
- Protagonista sinesgarriak eta imitagarriak sortu: emakume ikertzaileak benetako merituaren arabera tratatu, ez da beharrezkoa hauek salbuespenezko figurak bezala aurkeztea, eman ezagutzera ezohikoak izan beharrik gabe, gizonezko ikertzaile gehienak salbuespenezkoak ez diren bezala.
- Hizkuntza ez-sexista, inklusiboa eta ez-diskriminatzailea erabili. Orokorra maskulinotzat hartzen dela jakinda, saihestu ere termino neutroen erabileraren arriskua, emakumeak ikusezin bihurtzen baititu. (Adibidez, gaztelaniaz, ez erabili “x”, “@” edo antzeko flexioak).
- Edukiarekin bat datozen irudiak erabili, emakume zientzialariaren presentzia “loreontzi” gisa agertzen dutenak ekidinez. Protagonistak lehen planoan eta kamerari begira erakutsiz eta, gogoan izan, ez da beharrezkoa bere jarduera edo konpetentzia justifikatzen duen elementurik sartzea, hala nola mantalak, laborategiko tresnak edo bestelakoak.
- Lana amaitutakoan, begiratu egindakoa eta hausnartu: era berean tratatuko zenukeen testuko zientzialaria gizonezkoa izan balitz? Erantzuna ezezkoa edo zalantzazkoa bada: irakurri berriro dekalogoa.
Komunikabideak, komunikazio-lanak egiten dituztenak edo zabalkundearen esparruan lan egiten dutenak, genero-berdintasunaren aldeko eragile eta sustatzaile aktiboak dira. Horregatik, dekalogo honek zenbait estrategia eskaini nahi ditu komunikazio zientifiko hobea lortzeko, genero-ikuspegia duen zientzia-komunikazioa, edukiak idazten laguntzeko eta hedabideetan emakumeen presentzia areagotzen laguntzeko.
Egileez:UPV/EHUko Kultura Zientifikoko Katedra eta Euskampus Fundazioko Kultura Zientifikoko eta Berrikuntza Unitatea.
The post Zientzia genero-ikuspegitik komunikatzeko dekalogoa appeared first on Zientzia Kaiera.
Un anillo aromático de seis átomos de nitrógeno
Un equipo de investigación acaba de presentar un descubrimiento espectacular para la química del nitrógeno: por primera vez se ha sintetizado un compuesto que contiene anillos aromáticos de seis átomos de nitrógeno. El compuesto de nitrógeno y potasio se produjo bajo presiones y temperaturas extremadamente altas. Tiene una estructura muy compleja, pero su componente principal es un anillo plano de seis átomos de nitrógeno, llamado anión hexazina, ya que tiene carga negativa. La disposición de los átomos de nitrógeno en el anión hexazina es similar a la de los átomos de carbono en el benceno, un anillo aromático que es omnipresente en la naturaleza.
 Anillo de hexazina [N₆]⁴⁻. Fuente: (c) Dominique LanielAunque el término «aromático» originalmente se refería al olor, hoy en día su uso en química está restringido a compuestos que tienen propiedades electrónicas, estructurales y químicas concretas. La estabilidad única que poseen estos compuestos se conoce como aromaticidad. Los compuestos aromáticos juegan un papel importante en la química y la biología, así como en numerosas ramas de la industria. Aunque inicialmente se pensó que la aromaticidad era exclusiva de los compuestos cíclicos de carbono, se ha demostrado que numerosos sistemas compuestos por heterociclos de carbono y otros átomos, e incluso compuestos cíclicos de átomos diferentes al carbono, pueden tener un carácter aromático. Sin embargo, la aromaticidad del nitrógeno solo se había encontrado hasta ahora al anión pentazolato [N₅]⁻.
Anillo de hexazina [N₆]⁴⁻. Fuente: (c) Dominique LanielAunque el término «aromático» originalmente se refería al olor, hoy en día su uso en química está restringido a compuestos que tienen propiedades electrónicas, estructurales y químicas concretas. La estabilidad única que poseen estos compuestos se conoce como aromaticidad. Los compuestos aromáticos juegan un papel importante en la química y la biología, así como en numerosas ramas de la industria. Aunque inicialmente se pensó que la aromaticidad era exclusiva de los compuestos cíclicos de carbono, se ha demostrado que numerosos sistemas compuestos por heterociclos de carbono y otros átomos, e incluso compuestos cíclicos de átomos diferentes al carbono, pueden tener un carácter aromático. Sin embargo, la aromaticidad del nitrógeno solo se había encontrado hasta ahora al anión pentazolato [N₅]⁻.
En condiciones extremas de presión y temperatura, el equipo sintetizó el compuesto complejo K₉N₅₆, que contiene anillos de hexazina, [N₆]⁴⁻. La estructura de K₉N₅₆ está compuesta por una disposición compleja de anillos [N₆]⁴⁻ y [N₅]⁻, así como dímeros de nitrógeno neutro. Los investigadores encontraron que la estructura del anillo [N₆]⁴⁻ de hexazina se ajusta a la regla de aromaticidad de los compuestos químicos que lleva el nombre del químico físico Erich Hückel: el anillo es cíclico, plano y tiene (4n + 2) electrones π (es un sistema 10π ). Su carácter aromático está respaldado por consideraciones de longitud de enlace y por cálculos de la densidad de carga electrónica.
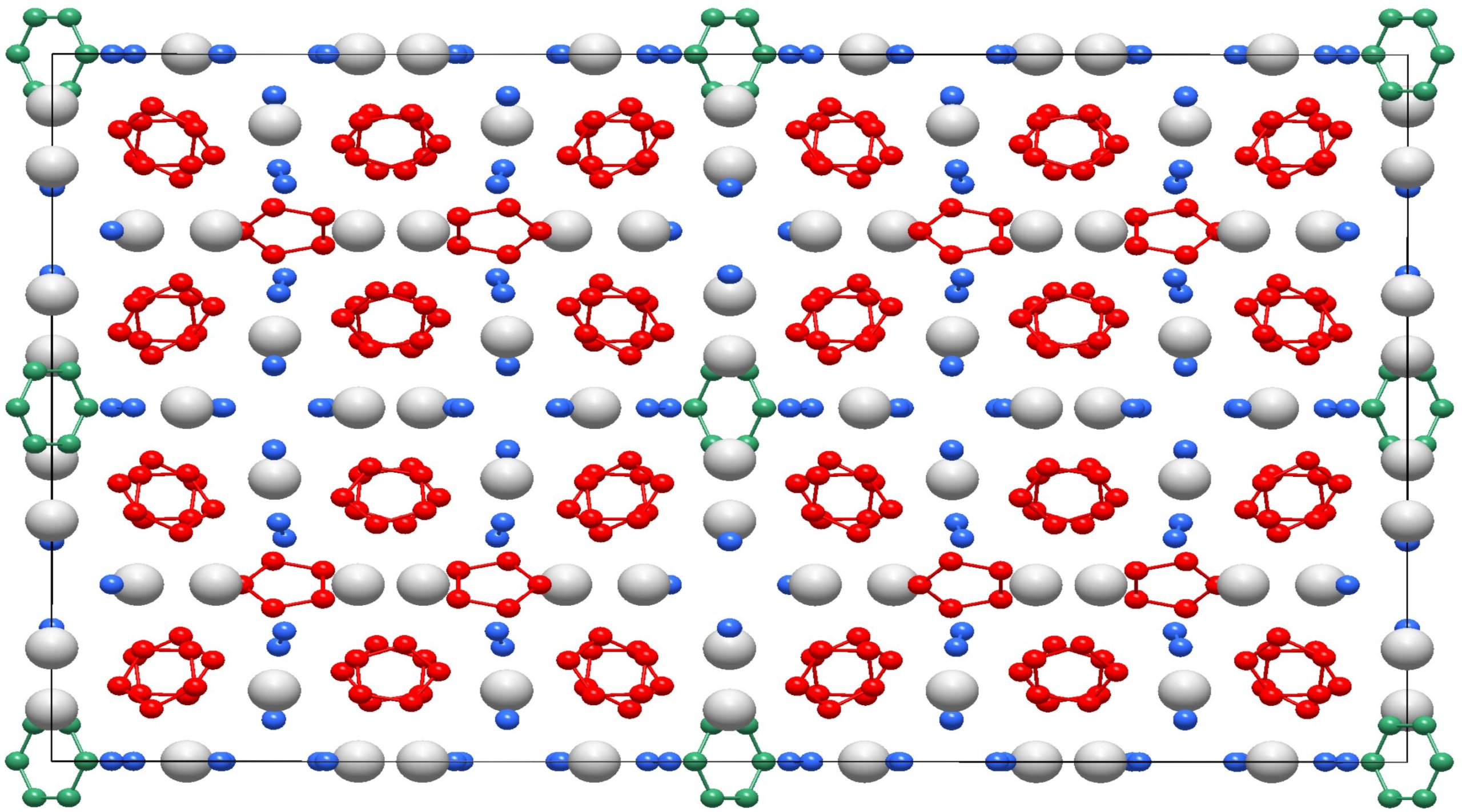 Estructura cristalina del compuesto K₉N₅₆. Fuente: (c) Dominique Laniel
Estructura cristalina del compuesto K₉N₅₆. Fuente: (c) Dominique LanielEl compuesto complejo K₉N₅₆ se formó en condiciones inusuales: la azida de potasio (KN₃) y el nitrógeno molecular (N₂) se comprimieron bajo una presión de más de 400.000 atmósferas y se calentaron a 2.000 grados Celsius con láseres de alta potencia. El siguiente paso fue dilucidar la estructura interna de este nuevo compuesto. Para ello, las muestras se expusieron a un haz de rayos X intenso en dos aceleradores de partículas, la fuente de rayos X PETRA III en el Sincrotrón de Electrones Alemán (DESY) en Hamburgo y la Instalación Europea de Radiación de Sincrotrón (ESRF-EBS) en Grenoble. La estructura atómica del compuesto K₉N₅₆ es, en sí misma, notable, de una complejidad casi nunca observada para sólidos producidos a presiones tan altas. Se compone de una disposición repetitiva de 520 átomos: 72 K y 448 N.
Referencia:
Dominique Laniel et al. (2023) Aromatic hexazine [N₆]⁴⁻ anion featured in complex structure of the high-pressure potassium nitrogen compound K₉N₅₆. Nature Chemistry doi: 10.1038/s41557-023-01148-7
Para saber más:
De la valencia y el enlace químico (y II)
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Un anillo aromático de seis átomos de nitrógeno se ha escrito en Cuaderno de Cultura Científica.
D bitaminaren gehigarrien atzean dagoen paradoxa bitxia
D bitamina molekula berezia da zentzu askotan. Lehenik eta behin, prohormona bat da (hormona baten molekula aitzindaria), eta ehun ezberdinetan askotariko ondorioak eragiten ditu. Hezurrak mineralizatzeagatik nabarmentzen da, baina sistema immunitarioaren funtzionamenduan, pankrearen funtzio endokrinoan, garunaren garapenean… ere bere funtzioa du. Hori gutxi balitz, D bitaminaren forma aktiboa larruazalean sintetizatzen da, eguzkiaren izpi ultramoreen esposizio zuzena jasan ostean. Horrela, egoera normalean, molekula hori ez da elikagaietatik lortzen nagusiki, eguzkiaren erradiaziotik baizik (guztizkoaren % 80-90).
Hain zuzen ere, D bitamina lortzeko modu berezi horrek eragiten du molekula horren defizita, itxuraz, nahiko ohikoa izatea. Defizit hori ez da eguzki erradiazio mugatua duten herrialdeetan soilik gertatzen, Eskandinavian kasu, bai eta egun eguzkitsu ugari eta eguzki erradiazio handia duten nazioetan ere, nahiz eta ez espero. Espainia da adibide bat.
 Irudia: ebidentzia zientifikoak iradokitzen digu ez dagoela arrazoirik D bitaminaren osagarriak kontsumitzeko. (Argazkia: PublicDomainPictures – Pixabay lizentziapean. Iturria: Pixabay.com)
Irudia: ebidentzia zientifikoak iradokitzen digu ez dagoela arrazoirik D bitaminaren osagarriak kontsumitzeko. (Argazkia: PublicDomainPictures – Pixabay lizentziapean. Iturria: Pixabay.com)Gai horren inguruan eztabaida handia dagoen arren, kontuan hartzen bada D bitaminaren urritasuna dagoela 25-hidroxibitamina D-ren odol-serumeko mailak 20 ng/ml baino txikiagoak direnean, orduan, Espainiako Endokrinologia eta Nutrizio Elkartearen (SEEN) arabera, Espainiako biztanleriaren % 40k eta 65 urtetik gorako pertsonen % 80k baino gehiagok molekula horren defizita daukate.
Gure gizartean dagoen bitamina defizit kezkagarri horren aurrean, gaiaz ezer ez dakien edonork esperoko luke medikuek, errutinaz, beren pazienteei odol analisiak eskatzea, horietakoren batek defizit hori duen detektatzeko eta, horrela, D bitaminaren gehigarriak errezetatzeko. Logikoena litzateke, ezta? Ba ez. Izan ere, ez da gomendatzen kontsulta medikoetan baheketa unibertsalik egitea populazio orokorraren D bitaminaren mailak detektatzeko, arriskua duten kasuetan (osteoporosia, adin handiko adinekoak) horretarako pisuzko faktoreak daudenean izan ezik.
D bitaminaren defizit arina antzemanez gero ere, gida klinikoek eta elkarte medikoek ez dute gomendatzen molekula horren gehigarriak hartzea. Horren ordez, eta ahal bada, pazienteari eguzki gehiago hartzeko eta D bitamina asko duten elikagai gehiago kontsumitzeko (arrain urdina, arrautzak, gibela…) gomendioa egiten zaio.
Orduan, D bitaminaren defizita hain ohikoa bada gure herrialdean eta beste askotan, zergatik ez da screeningik egiten eta ez da gehigarririk hartzeko agintzen? Arrazoia sinplea da: saiakuntza klinikoek erakusten dute, behin eta berriz, D bitamina duten osagarri edo gehigarri dietetikoak kontsumitzeak ez diola inolako onurarik ekartzen defizitik ez duen biztanle osasuntsuen osasunari, ez eta, askotan, defizita dutenen osasunari ere.
D bitamina gehitzean inolako onurarik ezDuela gutxi saiakuntza kliniko bat egin zen Mongolian, eta emaitza deigarriak izan zituen; izan ere, D bitamina gehitzean ez zen inolako emaitza onuragarririk lortu. Saiakuntza hori molekula horren defizita zuten 8.851 haurrekin egin zen (serumean 20 ng/ml baino gutxiago). Ikertzaileek jakin nahi zuten ea D3 bitamina gehigarrien kontsumoak (14.000 nazioarteko unitate astero, 3 urtez) eragin positiborik izango zuen haien osasunean, plazebo taldearekin alderatuta. Ez zuten inolako ezberdintasunik aurkitu bi taldeen artean, salbu eta urteetan zehar D bitamina jaso zuen haur taldeak jada ez zuela defizitik. Ez zen inolako eraginik izan pubertaroan, ez altuerari, ez gorputz-masari, ez garapenari zegokionez. Ezer ez. Eta hori ez zen gertatzen aldez aurretik defizit normala zuten haurren artean soilik (20 ng/ml baino D bitamina gutxiago serumean), baita azterketaren hasieran defizit larria (10 ng/ml baino gutxiago) zutenen artean ere.
Emaitza etsigarri horiek behin eta berriz ematen dira saiakuntza klinikoetan. D bitamina gehitzeak ere ez dakar onurarik defizita duten haurren tuberkulosi arriskua murrizteko, ez du populazio orokorraren hezurren mineralizazioa hobetzen, ez du hausturarik edo erorikorik prebenitzen, eta ez du murrizten edozein kausagatik hiltzeko arriskua edo minbizia edo gaixotasun kardiobaskularrak izateko arriskua.
D bitaminaren gehigarriak kontsumitzeak onurarik ez izateaz gain, zenbait azterketek erakutsi dute osasunerako zenbait arrisku ere ekar ditzakeela. Ia 31.000 parte hartzailerekin egindako behaketa azterketa baten arabera, defizitik ez duten pertsonek egunean 10 mikrogramo baino gehiagoko dosiak kontsumitzea kausa guztien hilkortasuna eta, bereziki, minbiziaren ondoriozko hilkortasuna handitzearekin lotzen zen. Bestalde, mantenugai horren gehiegizko kontsumoak kalteak eragin ditzake giltzurrunetan eta bestelako organo eta ehun batzuetan.
Zergatik dago paradoxa hori D bitaminaren inguruan? Bi azalpen nagusi daude. Alde batetik, gaur egun molekula horrek eragindako defizita noiz dagoen definitzeko atalaseak ez dira zuzenak (altuegiak dira), eta horrek berez existitzen ez diren defizitak diagnostikatzera garamatza, osasunean ez dutelako kalterik eragiten. Horregatik, D bitamina gehiago hartzeak ez dakar onurarik. Izan ere, aspalditik eztabaida zientifiko handia dago D bitaminaren urritasuna zein mailatik behera ematen den zehazteko.
D bitaminaren gehigarriak kontsumitzeak eragin osasungarririk ez eragiteko beste azalpen bat da organismoan arazoren bat egotea, eta horren ondorioz ezin izatea molekula hori bere forma aktibora (kaltzitriola) eraldatzea –forma aktibo horrek hainbat funtzio egiten ditu–. Edo, bestela, ezagutzen ez dugun beste faktore bat egotea, molekula forma aktiboan dagoenean dituen ondorioak mugatzen dituela.
Arrazoia edozein dela ere, ebidentzia zientifikoak iradokitzen digu ez dagoela arrazoirik D bitaminaren osagarriak kontsumitzeko, oso kasu zehatzetan salbu. Maila onak eduki nahi badira, aukera gomendagarriena eguzkia neurriz hartzea, jarduera fisikoa egitea eta mantenugai horretan aberatsak diren elikagaiak jatea da, osasunerako onura ugari eskaintzen dituelako eta lortzeko errazagoa delako.
Egileaz:Esther Samper (Shora) medikua, Ehunen Ingeniaritza Kardiobaskularrean doktorea eta dibulgatzaile zientifikoa da.
Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2022ko abenduaren 5ean: La extraña paradoja tras los suplementos de vitamina D
Itzulpena: UPV/EHUko Euskara Zerbitzua.
The post D bitaminaren gehigarrien atzean dagoen paradoxa bitxia appeared first on Zientzia Kaiera.
¿Cómo llegan partículas rocosas a los geiseres de Encélado?
Encélado es uno de los satélites más interesantes del Sistema Solar. Buena parte de este interés proviene de la gran actividad geológica que tiene este pequeño cuerpo de apenas 500 kilómetros de diámetro y del que seguimos aprendiendo cosas gracias a los datos que tomo la misión Cassini. Es también uno de los llamados mundos océano que existen en nuestro vecindario, cuerpos que, debajo de una corteza formada principalmente por hielo, tienen un océano de agua líquida debidamente protegido de las condiciones externas -a veces especialmente duras en el entorno de los gigantes gaseosos- y, por lo tanto, lo convierte en uno de los cuerpos también de mayor interés desde el punto de vista de la astrobiología.
 Geiseres en Encélado vistos desde la Cassini. Se aprecian perfectamente por su forma de “chorros”, creando una cortina de gases que sale despedida del pequeño satélite. Imagen cortesía de NASA/JPL-Caltech/Space Science Institute.
Geiseres en Encélado vistos desde la Cassini. Se aprecian perfectamente por su forma de “chorros”, creando una cortina de gases que sale despedida del pequeño satélite. Imagen cortesía de NASA/JPL-Caltech/Space Science Institute.Una de las pruebas más evidentes de la existencia de un océano debajo de su superficie -que no vemos directamente- es la presencia de grandes geiseres que expulsan vapor de agua, nitrógeno, dióxido de carbono, algunas sales, compuestos orgánicos e incluso pequeños granos silicatados.
Aunque también hay otros datos, como los resultantes del estudio de su campo gravitatorio y el movimiento de bamboleo que realiza a lo largo de su órbita alrededor de Saturno y que nos confirman la existencia de este océano y que tendría entre 10 y 30 kilómetros de profundidad, dependiendo de la zona.
Tantas partículas emite a través de los geiseres que uno de los anillos de Saturno, el anillo E está formado por estas partículas, y los científicos calculan que lo hace a un ritmo de unos 200 kilogramos por segundo, tanta que desde su formación hace 4500 millones de años podría haber perdido aproximadamente un 30% de su masa original.
 En esta imagen podemos ver a Encélado dentro del anillo E, al que nutre de partículas en su viaje alrededor de saturno. Imagen cortesía de NASA/JPL/Space Science Institute.
En esta imagen podemos ver a Encélado dentro del anillo E, al que nutre de partículas en su viaje alrededor de saturno. Imagen cortesía de NASA/JPL/Space Science Institute.En 2015 los científicos descubrieron en los datos de la Cassini un detalle muy importante, y es que, al acercarse a Encélado, algunas de las partículas que atrapaba uno de sus instrumentos -el Cosmic Dust Analyzer (o Analizador de Polvo Cósmico) eran en realidad pequeñas partículas de roca muy ricas en silicio, tan minúsculas que las más grandes medían menos de nueve nanómetros.
Estos granos solo podrían provenir de un lugar, del contacto entre el océano y el núcleo rocoso de Encélado, y en la Tierra el ambiente más habitual donde se forman granos de sílice de este tamaño es en las chimeneas hidrotermales, donde aguas muy calientes -de al menos 90ºC- y supersaturadas en sílice sufren una brusca caída en la temperatura al entrar en contacto con el agua del océano. Pero no solo descubrió granos de polvo, sino también hidrógeno, que podría proceder también de la actividad hidrotermal.
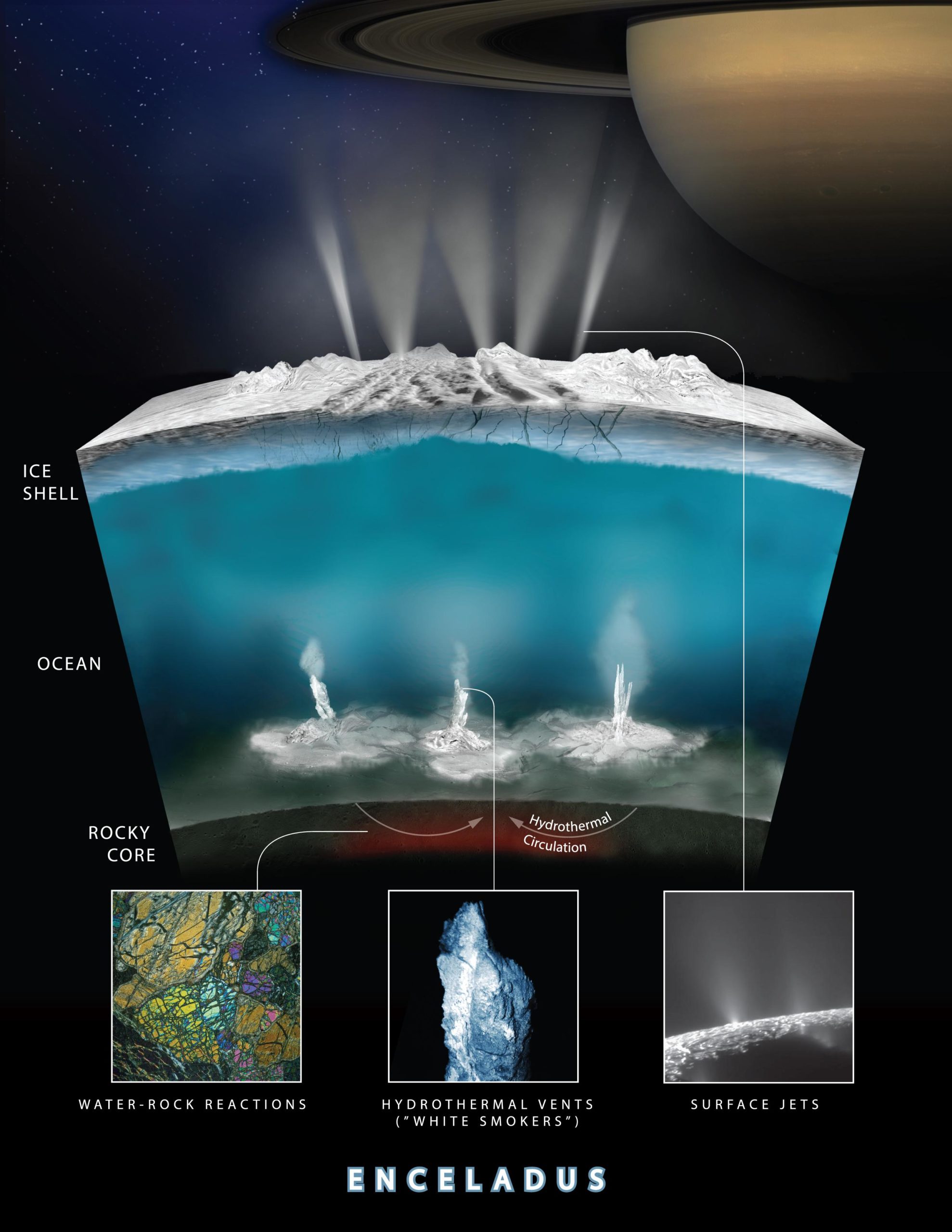 Un esquema de la actividad hidrotermal en Encélado, donde no solo se formarían las partículas rocosas, sino que la interacción entre el agua y la roca generaría el hidrógeno detectado. Imagen cortesía de NASA/JPL-Caltech/Southwest Research Institute.
Un esquema de la actividad hidrotermal en Encélado, donde no solo se formarían las partículas rocosas, sino que la interacción entre el agua y la roca generaría el hidrógeno detectado. Imagen cortesía de NASA/JPL-Caltech/Southwest Research Institute.Pero, ¿Cuánto tiempo tardan estas partículas en salir desde el océano y ser expulsadas por los geiseres? ¿Es un proceso lento o rápido? Un nuevo estudio publicado esta pasada semana en Communications Earth & Enviroment deja entrever que este periodo podría ser de tan solo unos meses.
Encélado tiene una gran actividad geológica en la actualidad porque sufre de un proceso denominado calentamiento de mareas, es decir, que a lo largo de su órbita sufre deformaciones en su parte sólida: es estirada y aplastada -obviamente no de una manera literal-, generando una serie de fricciones que calientan el núcleo rocoso que está en el fondo del océano, de tal manera que se generan unas corrientes verticales que transportan rápidamente las partículas de sílice hasta la superficie.
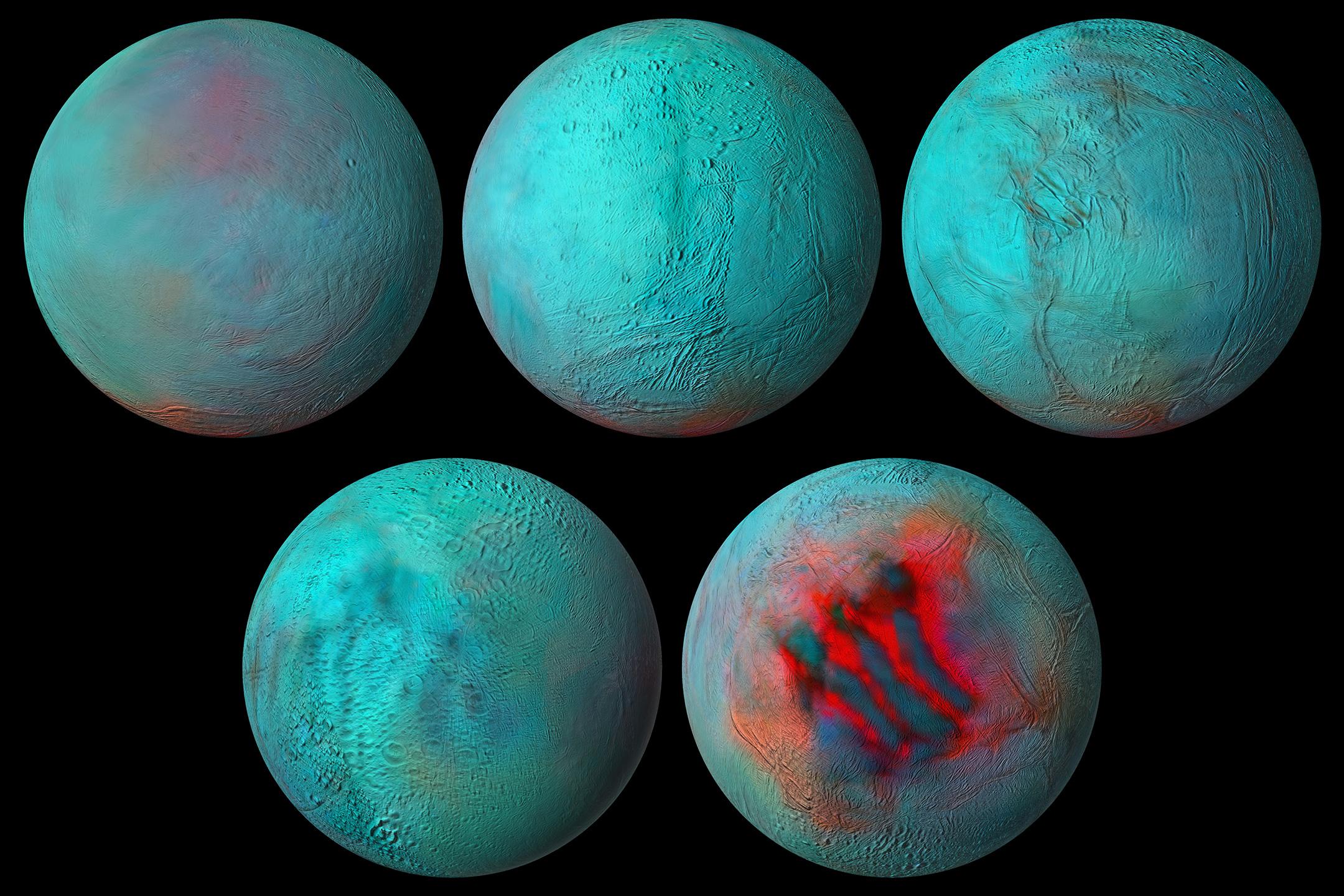 Encélado en el infrarrojo. En azul, las zonas más frías. En rojo, las más cálidas, y donde mayor actividad geológica hay. Es llamativo especialmente el detalle de la última imagen, con esa zona con marcas lineales de una temperatura muy superior al resto: Son las “tiger stripes” (o rayas de tigre, en castellano) donde se concentran la mayor parte de los geiseres. Imagen cortesía de NASA/JPL-Caltech/University of Arizona/LPG/CNRS/University of Nantes/Space Science Institute.
Encélado en el infrarrojo. En azul, las zonas más frías. En rojo, las más cálidas, y donde mayor actividad geológica hay. Es llamativo especialmente el detalle de la última imagen, con esa zona con marcas lineales de una temperatura muy superior al resto: Son las “tiger stripes” (o rayas de tigre, en castellano) donde se concentran la mayor parte de los geiseres. Imagen cortesía de NASA/JPL-Caltech/University of Arizona/LPG/CNRS/University of Nantes/Space Science Institute.También estiman que las “tiger stripes”, el conjunto de fracturas que aparecen en el polo sur de Encélado y donde aparece la mayor actividad del satélite, podrían en realidad ser un conducto casi directo para estas partículas del océano, ofreciendo a los científicos una oportunidad para poder estudiar detalles sobre la composición del océano muestreando con mayor detalle los materiales expulsados por los geiseres.
Y lo más importante, sería una composición representativa del estado del océano actual y de los procesos geoquímicos gracias a estos tiempos de viaje tan cortos entre el fondo del océano y la superficie.
Estudios como estos nos servirán no solo para conocer mejor Encélado y que mecanismos pueden estar operando por debajo de su superficie, sino que podrían ayudarnos también a planificar futuras misiones espaciales, tanto en saber que tenemos que estudiar con más detalle, como para plantearnos que tenemos que buscar y que instrumentos serán necesarios para descubrir todos los secretos de este fascinante satélite.
Referencias:
Hsu, H.-W. et al. (2015) “Ongoing hydrothermal activities within Enceladus,” Nature, 519(7542), pp. 207–210. Doi: 10.1038/nature14262.
Schoenfeld, A.M. et al. (2023) “Particle entrainment and rotating convection in Enceladus’ Ocean,” Communications Earth & Environment, 4(1). Doi: 10.1038/s43247-023-00674-z.
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo ¿Cómo llegan partículas rocosas a los geiseres de Encélado? se ha escrito en Cuaderno de Cultura Científica.
Erlauntzen osasun mikrobianoa hobetzen da, zenbat eta kokapen naturalagoan egon
Nazioarteko ikerketa batean, nekazaritza intentsiboko eremuetako, eremu erdinaturaletako eta eremu naturaletako erleen egoera ikertu du UPV/EHUko Applied Genomics and Bioinformatics taldeak, erlauntza unitate gisa hartuta. Ikusi dute erleen mikroorganismo-multzoa nabarmen aldatzen dela antropizazio-mailaren arabera. Habitat erdinatural batean 16 egunez edukitzeak arindu egin du nekazaritzak erlauntzetan eragindako desoreka mikrobianoa.
Mendebaldeko ezti-erlea (Apis mellifera) arriskuan dago gizakien menpe dauden eremuetan bizi dituzten estres-faktore askoren ondorioz; besteak beste, nutrizio txarra, pestizidak eta patogenoak. “Badira zenbait urte agerian geratzen ari dela erleen heriotza-tasa asko handitu dela; horregatik, duela 6 urte inguru ikertzen hasi ginen erlearen mikrobiotan zer faktorek duten garrantzia eta horrek zer lotura duen erleen gaixotasunekin edo osasunarekin”, azaldu du Iratxe Zarraonaindia Applied Genomics and Bioinformatics taldeko Ikerbasque ikertzaileak. Ikertzaileek garrantzi handia egozten diote eremuen antropizazioari, alegia, “nekazaritza intentsiboari, erabiltzen diren produktu kimikoei, etab.”.
 Irudia: 16 egun bakarrik igarotakoan hauteman da nekazaritza-estresak eragindako desoreka mikrobianoa arindu egiten dela eremu erdinaturalera lekualdatutako erlauntzan. (Argazkia: NickRivers – Pixabay lizentziapean. Iturria: Pixabay.com
Irudia: 16 egun bakarrik igarotakoan hauteman da nekazaritza-estresak eragindako desoreka mikrobianoa arindu egiten dela eremu erdinaturalera lekualdatutako erlauntzan. (Argazkia: NickRivers – Pixabay lizentziapean. Iturria: Pixabay.comKroaziako hiru unibertsitaterekin lankidetzan, “aukera izan dugu Kroaziako Unije irlan, gizakiaren eraginpetik urrun, dauden erlauntza batzuk ikertzeko. Hamar urtez egon dira erlauntza horiek batere tratamendurik jaso gabe, eta jakina zen hango erleek biziraupen luzea zeukatela nahiz eta Varroa akaroaren presentzia izan —erleak gaixotzen eta hiltzen dituen gaitz baten eragilea—. Ikertu nahi genuen antropizazioak zer eragin daukan erleen mikrobiotan edo mikroorganismo komunitatean. Horretarako, nekazaritza-inguruetan kokatutako bi erlauntzen mikrobiotarekin alderatu ditugu Unije irlako erlauntzak”, dio Zarraonaindiak.
Nekazaritza-eremuko bi erlauntzak konparagarriak izateko, “ahizpa genetikoak” erabili dituzte —alegia, nekazaritza-eremukoen material genetiko bera daukaten erlez osatutako erlauntzak—, eta haietako erlauntza bat eremu erdinatural batera eraman dute. “Argi eta garbi ikusi dugu antropizazioak eragin handia daukala; izan ere, 16 egun bakarrik igarotakoan hauteman genuen nekazaritza-estresak eragindako desoreka mikrobianoa arindu egin zela eremu erdinaturalera lekualdatutako erlauntzan”, azaldu du doktoreak. Horrek agerian uzten du ezti-erleen mikrobiotak erraz egokitzeko gaitasuna daukala; “ez genuen uste hain azkar aldatuko zenik mikrobiotaren konposizioa”, dio.
Ikertzaileek gradiente argi bat aurkitu dute antropizazio-mailarekin eta erlauntzako mikrobio-komunitatearekin lotuta: “Unije irlako erlauntzaren mikrobiota orekatuagoa dago, mikroorganismo onuragarrien proportzioa handiagoa da eta erdinaturalean jaitsiz doa; nekazaritzako eremuan, berriz, erlauntzak oso konposizio desorekatua dauka, bakterio oportunista gehiago aurkitzen dira, eta gaixotasunekiko sentikorragoa da”, azaldu du Zarraonaindiak. Ikertzailearen arabera, “estres-faktoreak oso aktibatuta daude nekazaritza-eremuetan”.
Apibioma ikertzeaOndorio horiei esker, ikertzaileek aukera izan dute erleen osasunari buruzko informazioa emango duten biomarkatzaileak zehazteko. Esate baterako, ikertzaileek hauteman dute bakterio jakin bat, Arsenophonus, oso ugaria dela nekazaritza-eremuetan; gutxiago dagoela eremu erdinaturaletan, eta ia ez dela azaltzen eremu naturaletan.
Erlauntza bere osotasunean ikertu dute, ez erlea bakarrik. Horixe da ikerketa honen gako garrantzitsuenetako bat: “Ikuspegi berritzailea da hau. Erlauntzan dauden nitxoetako mikroorganismoen multzoa, apibioma, ikertu dugu. Erleen hesteak, erlauntzaren sarrera, erle-ogia (erleak elikatzeko gaia) eta erlauntza barneko airea ikertu ditugu”. Lehen esan bezala, Arsenophonus bakterioa nekazaritza-eremuan da ugarien, eta joera hori nitxo guztietan topatu dugu. Beraz, oso biomarkatzaile egokia da nekazaritzak erlauntzetan zer eragin duen eta erlauntzek zer osasun duten neurtzeko; gainera, “metodo hau ez da inbaditzailea, erlauntzaren sarrerako lagin bat hartuta jakin baitaiteke hori”.
Ikerketa honen berri Nature-ren Scientific Reports aldizkarian eman dute ikertzaileek. Artikuluan jasotako ikerketa urtebeteko lana besterik ez da. Eta ikerketek aurrera jarraitzen dute: “Orain eremu erdinaturaleko erlauntza eremu naturalera eraman dugu ikusteko ea mikrobiota orekatzen zaion eta eremu naturaleko erleen berbera izatera iristen den. Horrek aukera emango digu jakiteko genetikaren edota ingurunearen kontribuzioa zenbaterainokoa den”.
Iturria:UPV/EHU prentsa bulegoa: Erlauntzen osasun mikrobianoa hobetzen da, zenbat eta kokapen naturalagoan egon
Erreferentzia bibliografikoa:GorrochateguiOrtega, June; MuñozColmenero, Marta; Kovačić, Marin; Filipi, Janja; Puškadija, Zlatko; Kezić, Nikola; Parejo, Melanie; Büchler, Ralph; Estonba, Andone; Zarraonaindia, Iratxe (2022). A short exposure to a seminatural habitat alleviates the honey bee hive microbial imbalance caused by agricultural stress. Scientific Reports, 12. DOI: 10.1038/s41598-022-23287-6
The post Erlauntzen osasun mikrobianoa hobetzen da, zenbat eta kokapen naturalagoan egon appeared first on Zientzia Kaiera.
Antes nacían más en primavera y verano, ya no
nacimientos
 Foto: Valeria Zoncoll / Unsplash
Foto: Valeria Zoncoll / UnsplashAntes de 1960 la frecuencia de nacimientos en España variaba de forma clara a lo largo del año, con dos máximos, uno muy marcado en abril y el otro, mucho más atenuado, en septiembre. Los niños y niñas nacidas en abril habían sido concebidas en junio o julio del año anterior, mientras que los y las que vieron la luz en septiembre, lo habían sido en el diciembre anterior. A partir de 1960, sin embargo, ese ritmo estacional empezó a desvanecerse. Y durante el periodo comprendido entre 1990 y 2000, ya no hubo ritmo estacional alguno en el número de nacimientos. Estos son los resultados principales de un estudio que analizó la estacionalidad de los nacimientos en España desde 1941 hasta 2000. En total, fueron 33421731 nacimientos durante 60 años.
Ese ritmo era similar al que se había observado antes en otros países europeos, y también en Canadá y Australia, aunque en los Estados Unidos solo se producía un máximo claro de nacimientos en el mes de septiembre. También se había observado en otros estudios que la estacionalidad se había atenuado con el paso de los años, con una disminución de la frecuencia de nacimientos en primavera y un aumento en otoño, aunque en ningún otro país se había documentado su desaparición, como ocurrió aquí.
En 1940 España era un país eminentemente rural. La fecundidad no estaba controlada como lo estuvo unas décadas después. A partir de 1960, sin embargo, hubo un desarrollo industrial acelerado, acompañado por un flujo de población masivo hacia las ciudades. En las últimas décadas del siglo XX se generalizó el uso de anticonceptivos eficaces, por lo que las mujeres pudieron decidir el número de hijos e hijas que tendrían y, hasta cierto punto también, el periodo de la concepción.
La disminución de la estacionalidad en las concepciones se empezó a producir con el éxodo hacia las ciudades, aunque su desaparición total seguramente tuvo su causa en el uso de anticonceptivos. Investigaciones anteriores en otros países europeos habían llegado a la conclusión de que ciertos factores ambientales eran los principales responsables de los ciclos de fecundidad antes del desarrollo industrial. Y de entre esos factores, parece que el fotoperiodo (horas diarias de luz) era clave. Así cabe interpretar el máximo primaveral de concepciones. El descenso estival, muy marcado en España en las décadas de los cuarenta y cincuenta, probablemente obedecía al aumento de la temperatura. De hecho, la probabilidad de concepción parece ser inferior a la media por debajo de 5 ºC y por encima de 21 ºC. Y el progresivo descenso en el máximo primaveral a partir de la década de los sesenta era seguramente consecuencia del control creciente de las condiciones ambientales, ligado a la mejora de la situación económica.
Es normal que la actividad reproductora de los animales tenga ciclos estacionales, porque la probabilidad de sacar adelante a la progenie depende, sobre todo, del alimento disponible. El fotoperiodo actúa así como señal ambiental, de manera que, como se ha visto en el caso español y otros países occidentales, el máximo de fecundaciones ocurre cuando los días son largos. Ese ritmo conduce a un mayor número de nacimientos entre marzo y octubre, que es la mitad del año en la que es previsible que haya más alimento disponible para las madres lactantes. Por eso, cuando el régimen de luz se uniformiza por efecto de la iluminación artificial, ese factor deja de ejercer su efecto, de la misma forma que la disponibilidad de alimento deja de variar con el curso estacional. Son las consecuencias del desarrollo.
Fuente: Cancho-Candela, R., Andrés-de Llano, J. M., Ardura-Fernández, J.: Decline and loss of birth seasonality in Spain: analysis of 33 421 731 births over 60 years. J Epidemiol Community Health. 2007 Aug; 61(8): 713–718. doi: 10.1136/jech.2006.050211
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Antes nacían más en primavera y verano, ya no se ha escrito en Cuaderno de Cultura Científica.
Asteon zientzia begi-bistan #430
Asteon zientzia begi-bistan igandeetako gehigarria da. Astean zehar sarean zientzia euskaraz jorratu duten artikuluak biltzen ditugu. Begi-bistan duguna jaso eta laburbiltzea da gure helburua.

Amaia Iparragirre Letamendia matematikaria da, eta zientzia honen babesean, nabarmendu du nahiz eta modu abstraktuan landu, matematikek lotura zuzena dutela eguneroko bizimoduarekin eta ingurunearekin. Iparragirre doktore-tesia egiten ari da, estatistikan; zehazki, eredu aurresaleen garapenean eta balidazioan, diseinu konplexuko laginketetan oinarritutako inkestetatik datozen datuekin. Emakumeen eta matematiken inguruan, azaldu du duela urte batzuk arte, matematika-graduan emakumeak gehiengoa zirela; azken urteotan, ordea, gizonak gailentzen ari dira graduan. Iparragirreri oso garrantzitsua iruditzen zaio emakume erreferenteak izatea, etorkizunean emakume matematikari gehiagoren presentzia sustatzeko. Emakume ikertzaile honi buruzko informazio gehiago Zientzia Kaieran irakur daiteke, Elhuyar Zientzia eta Teknologia aldizkariarekin lankidetzan egindako atalean.
ArgitalpenakAnimalien aferak liburua 2011n argitaratu zuten Juan Ignacio Pérezek eta Miren Bego Urrutiak, eta bertan animaliak aztertzean aurkitu ditzakegun zerbait bitxi edo deigarriak azaltzen dizkigute. Beren beharrizanak aurrera eramateko, animaliek mekanismo jakin batzuk erabiltzen dituzte, eta mekanismo hauek partekatu egiten dira espezie ezberdinean artean. Hala eta guztiz ere, aniztasun zoragarria aurkitzen dugu animalia espezieen artean, baldintzen, beharrizanen eta taldearen arabera. Juan Ignacio Pérez Iglesias eta Miren Bego Urrutia Barandika Euskal Herriko Unibertsitateko irakasleak dira, eta itsas animalien biologia ikertzen dihardute aspalditik. Atal hau Zientzia Kaieran irakur daiteke, ZIO bildumarekin elkarlanean eginiko atalean.
GenetikaIzarbe Yarza Giza Nutrizioa eta Dietetikan graduatu zen Zaragozako Unibertsitatean, eta egun, doktorego-tesia egiten ari da UPV/EHUko Ikerketa Biomedikoaren doktorego-programaren barne, Baigene genetika-enpresan. Bere tesian ebakuntza osteko fibrosia ekiditeko modua ikertzen ari da, genetikaren bitartez. Izan ere, genetikak gaixotasun jakin batzuk izateko arriskuan eragina du, baita ebakuntza osteko fibrosia izateko aukeran ere. Asken honen kasuan, kirurgiaren ondorioz orbain-ehuna modu desantolatuan hazten da ehun bigunen eta artikulazioen inguruan, eta horrek, mugimendua mugatu eta mina eragiten du. Genetikaren bidez, alabaina, pazienteak fibrosia garatu behar duen edo ez jakingo dute test genetiko baten bidez. Horrela, medikuek arrisku hori aurreikusteko erabil dezaketen kalkulagailu moduko bat sortu dute, eta ebakuntza-gelara sartu baino lehen arrisku hori murriztu dezaketen ekintzak proposatu gaixoarekin batera. Azalpen guztiak unibertsitatea.net webgunean.
MikrobiologiaNora Fernandez Jimenez EHUko Genetika irakasleak eta ikertzaileak hesteetako mikrobiotaren inguruan idatzi du Berrian. Hesteetako mikrobiotaren desorekak edo disbiosiak hanturazko patologia kroniko ugari ekar dezake, hala nola heste narritagarriaren sindromea, koloneko minbizia eta diabetesa, bai eta beste hainbat patologia ere. Alabaina, azken urteetan ikusi da hesteetako mikrobiotak prozesu oso desberdinetan eragina izan dezakeela; autismoaren espektroko nahasmenarekin erlazionatua izan da baita ere, baina oraindik ez dago argi erlazio hori benetan ematen den. Horregatik, Fernandezek argi utzi du gai honen inguruko ikerketa askoren beharra dagoela oraindik. Informazio gehiago Berrian: Mikrobiota, kausa ala efektu?
AstronomiaAste honetan, Marteri buruzko ikerketen berri eman du EHUk Bilboko Bizkaia aretoan. Martera bidalitako robotak zazpi tresna zientifiko konplexu ditu, eta horietako bat da MEDA. Askotariko sentsore meteorologikoen sistema bat da, tenperatura, presioa, hezetasuna, haizea eta abar neurtzeko gai dena. Horri esker jakin dute nolakoa den Marteko Jezero kraterra. Jasotako datuak aztertuta, planetaren atmosfera ezaugarritzen ari dira, eta esan du hango eguraldia eta klima iragartzeko ereduak hobetuko dituztela horri esker. Honetaz gain, krater bereko arrokak aztertu dituzte, eta haiek hautatutako laginak 2030ean Lurrera ekartzea espero dute. Berri honi buruzko datuak Berriako “Marteri buruzko ikerketen berri eman du EHUk” eta “Marten bildutakoak zabaltzen” artikulutan irakur daitezke.
OsasunaInterneten eta bideo-jokoen erabilerak nerabeen bizi-kalitatearekin harremana du, UPV/EHUrekin elkarlanean egindako ikerketa baten emaitzen arabera. Estatuko 16 ikastetxetako 11 eta 18 urte bitarteko 2.024 gaztek Internet eta bideo-jokoak nola erabiltzen dituzten aztertu dute. Ikerketa honen bidez, lehen aldiz erlazionatu dira Interneten erabilera problematikoa eta Internet bidezko jokoaren nahasmendua, batera, nerabeen osasunarekin lotutako bizi-kalitate txarragoarekin. Bizi kalitatearen murriztea adikzio baten ondorioz gertatzen denaren parekoa dela azaldu dute; nahasmendu hori duten pertsonak urduri jartzen dira jokatu ezin dutenean eta sintoma psikologikoak edo psikosomatikoak izan ditzakete. Lortutako emaitzen arabera, parte-hartzaileen % 15,5ek Interneten erabilera problematiko orokorra erakuste dute, eta bideo-jokoetan jokatzen duten nerabeen % 3,3k jokoaren nahasmenduaren zantzuak dituzte. Datu guztiak Zientzia Kaieran.
Formula-esneen osasun- eta nutrizio-oharrek ez dute oinarri zientifikorik, BMJ aldizkari zientifikoan argitaratu denez. Ikerketan zehar, 2020-2022 urteen arteen arteko mundu osoko hamabost herrialdetako formula-esneen oharrak aztertu zituzten. Ohar horietako askotan “garuna edo nerbio-sistema garatzen laguntzen du” edo immunitate-sistema sendotzen zuela zioten, baina laurdenak inguru bakarrik egiten zieten erreferentzia saio klinikoei. Aipatutako saio kliniko horiek, hala ere, oso ahulak ziren eta alborapenak zituzten. Hala, egileek hasieratik utzi dute argi bularreko esnea dela elikagai egokiena haurrentzat. Azalpen guztiak Elhuyar aldizkarian.
IngurumenaErlauntzen osasuna hobetu egiten da antropizazioa txikitzean. Hala erakutsi dute nazioarteko ikerketa baten emaitzek. Ikerketan erleen egoera mikrobianoa ikertu dute, nekazaritza intentsiboko eremuetan, eremu erdinaturaletan eta eremu naturaletan. Ondorioztatu dutenez, erlauntzaren mikroorganismo-multzoa nabarmen aldatzen da antropizazio-mailaren arabera, nekazaritza intentsiboan erabiltzen diren produktu kimikoek eta abarrek desoreka eragiten baitute mikroorganismo horietan. Mikroorganismo-multzo jakin batzuek, era berean, erleen zaurgarritasunean eragina dute. Alabaina, ikertzaileek azaldu dute desoreka hori bere onera etortzen da, erlauntzak eremu naturalera eramanez gero. Datuak Elhuyar aldizkarian.
GeologiaAste honetan Blanca Martinez geologoak orientaziorako erabili izan diren mineralei buruz idatzi du Zientzia Kaieran, Orientatzen gaituzten mineralak artikuluan. Dual 2.000 urte baino gehiago, gaur egungo Grezian, Magnesia izeneko lurralde bateko artzain gazte batek harri arraro batekin egin zuen topo, eta burdina erakartzeko ahalmena zuela ikusi zuten. Bi mende geroago antzinako txinatarrek magnetita erabiltzen zuten burdinazko pieza txikiak magnetizatzeko, baina ez dago idatziz jasota erabilpenik ematen ote zioten aurkikuntza horri. Magnetita iparrorratz moduan erabiltzen hasi zenaren lehen erregistroa XII. mendeko Ingalaterrakoa da. Alabaina, historian zehar beste mineral batzuk ere erabili izan dira orientaziorako, hala nola, bikingoen “eguzki harria”.
NeurozientziaBelarri-harra (earworm) izena hartzen du melodia bat buruan behin eta berriro “entzuten” egoteak. Esperientzia unibertsala da, baina zenbait pertsonak belarriko harrak izateko sentikortasun handiagoa dutela dirudi. Ez-borondatezko musika-iruditeria (Involuntary Musical Imagery) da jarri dioten izen zientifikoa eta topatu da abesti zatiak izaten direla normalean, 15 eta 30 segundo artekoak, eta letra duten abestiak izaten direla kasu gehienetan. Gainera, ikusi da earworm bilakatzen ziren abestiek, kasu gehienetan, Mendebaldeko pop musikaren osagaiak dituztela. Ez dago erabateko sendabide hutsezinik, baina badira lagungarriak izan daitezkeen hainbat estrategia, hala nola, abestia bere osotasunean entzutea edota abestitik arreta desbideratzea. Azalpenak Zientzia Kaieran: Aldapan gora… txiklea murtxikatzen.
Egileaz:Irati Diez Virto Biologian graduatu zen UPV/EHUn eta Plentziako Itsas Estazioan (PiE-UPV/EHU) tesia egiten dabil, euskal kostaldeko zetazeoen inguruan.
The post Asteon zientzia begi-bistan #430 appeared first on Zientzia Kaiera.
Naukas Bilbao 2022: Las cinco vidas de un cazador de planetas

En 1983, cuando aún no se conocía ningún planeta extrasolar, alguien vino con la idea de colocar un telescopio en órbita y observar 13000 estrellas al mismo tiempo e intentar determinar aquellas que sufrían una disminución de su intensidad por el tránsito de un planeta. Aquella idea fructificó en el año 2009 con el lanzamiento del telescopio espacial Kepler. Daniel Marín nos cuenta su historia.
Daniel Marín es doctor en astrofísica y un divulgador de referencia en exploración espacial. Ha sido invitado por la NASA y Roskosmos a asistir a distintos lanzamientos de misiones.
Si no ve correctamente el vídeo, use este enlace.
Más sobre el tema:
25 años de planetas extrasolares
El sucesor del Hubble: el telescopio espacial James Webb
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2022: Las cinco vidas de un cazador de planetas se ha escrito en Cuaderno de Cultura Científica.
Ezjakintasunaren kartografia #436

Gene batek, gene bakar batek, gauza harrigarriak lor ditzake. Aste honetan bi adibide ikusgarri ditugu. Rosa García-Verdugoren A single gene might be responsible for the bigger brain of modern humans eta Losing genes can be good, hummingbirds are a nice example Ramón Muñoz-Cónpuliren eskutik.
Litioa baliabide mugatua da eta elementu honetan oinarritutako baterien teknologia mugatua da. Bideragarritasun ekonomikoa duten eta eskalagarriak diren alternatibak aktiboki bilatzeko garaia da. Beyond lithium: magnesium rechargeable batteries
Teorema batek esaten duenean hori ez dela izango, DIPCkoak datoz eta esaten dute, ondorio praktikoetarako, ez dela hainbesterako Mermin–Wagner theorem for practical length scales
Mapping Ignorance bloga lanean diharduten ikertzaileek eta hainbat arlotako profesionalek lantzen dute. Zientziaren edozein arlotako ikerketen azken emaitzen berri ematen duen gunea da. UPV/EHUko Kultura Zientifikoko Katedraren eta Nazioarteko Bikaintasun Campusaren ekimena da eta bertan parte hartu nahi izanez gero, idatzi iezaguzu.
The post Ezjakintasunaren kartografia #436 appeared first on Zientzia Kaiera.
Los productos sin gluten no son más sanos
El grupo Gluten 3S de la UPV/EHU está acreditado para conceder el sello de productos sin gluten a los productores. En los últimos nueve años, el grupo ha liderado una amplia investigación de estos productos y ha realizado análisis nutricionales para examinar 200 productos sin gluten. Si bien la calidad de los productos sin gluten ha aumentado considerablemente durante este tiempo, estos productos aún no han llegado a ser equivalentes a los que contienen gluten.
 Foto: Jorge Zapata / Unsplash
Foto: Jorge Zapata / UnsplashCon el paso de los años, cada vez se conocen más casos de celiaquía, con un crecimiento exponencial. Según los expertos, puede haber dos razones para ello. Una, que debido a factores medioambientales el número de celíacos está en aumento, y otra, que los diagnósticos han mejorado y se han incrementado. Además, junto con a celiaquía, el gluten provoca también otros trastornos. El incremento de casos ha llevado a la percepción pública de tal manera que ha generado un problema, ya que la gente considera, erróneamente, que una dieta sin gluten es más sana que una que contiene gluten.
«Se atribuyen a la dieta ciertos atributos que en sí mismos no están relacionados con ella. Los datos demuestran que los productos sin gluten no son más sanos», según Jonatan Miranda Gómez, investigador del grupo de investigación Gluten 3S.
Precisamente, el equipo de Miranda lleva muchos años realizando un análisis nutricional de los productos sin gluten. «En 2014 publicamos un artículo científico bastante innovador», dice Miranda. En él, comparábamos 200 alimentos sin gluten con sus equivalentes con gluten. No eran nutricionalmente equivalentes». Muchos de los productos sin gluten contenían más lípidos saturados (o grasas nocivas) que los productos con gluten, tenían un aporte de fibra más reducido y era necesario controlar su cantidad de sal y proteínas. Pero la situación está cambiando constantemente y acaban de publicarse los resultados de otro estudio.
La evolución de los productos sin glutenLa proporción de celíacos no ha variado y sigue siendo de aproximadamente del 1%. Pero, por un lado, ha aumentado la población y, por otro, han surgido sensibilidades al gluten, con lo que, considerando también a este grupo, el problema afecta a un 10% de la población. «La industria ha sido consciente de ello —dice Miranda—. Por lo tanto, ha desarrollado más productos, lo que ha permitido que la propia industria investigue más y tenga en cuenta otros componentes. De alguna manera, este impulso social y de equipos de investigación ha provocado una evolución en la industria. Y la mejora ha sido notable.
Un ejemplo representativo es el de la pasta. La pasta sin gluten no se elabora con trigo, ya que contiene gluten, sino con maíz. Precisamente la harina de maíz ha sido siempre el ingrediente principal. Esto no ha cambiado en los últimos nueve años. Sin embargo, así como anteriormente el segundo ingrediente en importancia era la harina de arroz, actualmente el más común es el mijo. «Esto ha influido positivamente en la nutrición», señala Miranda. «Para fabricar pasta hay que hacer una extrusión y el mijo permite la extrusión utilizando menos lípidos». Además, distintas iniciativas legislativas en materia alimentaria han contribuido a esta evolución.
En los casos de productos no sólidos, los productores utilizan otras estrategias. La cerveza es un ejemplo. En este caso, en lugar de sustituir al gluten, este se rompe mediante la adición de unas enzimas en el proceso de clarificación (separación de partículas en suspensión del líquido). «Pero este proceso tiene otra limitación —añade Miranda—. Podría ocurrir que queden moléculas nocivas que no se detectan en el análisis rutinario. Los miembros de la Asociación de Celíacos nos dicen a veces que la cerveza sin gluten les sienta mal». Por lo tanto, se ha abierto una nueva línea de investigación para analizar los problemas de estas cervezas.
Para Miranda está claro que el tema es amplio. «En los últimos años, se ha visto en los artículos que otras moléculas pueden ser perjudiciales también y que, aunque se siga una dieta estricta sin gluten, estos productos sin gluten pueden causar malestar. Además, quieren añadir otro enfoque a la investigación, ya que también quieren analizar el aspecto medioambiental. «Queremos conocer el impacto ambiental de los alimentos sin gluten. Suelen tener mayor impacto que el resto, por el hecho de que, por ejemplo, es necesario importar del extranjero algunos ingredientes. Habría que reducir ese impacto. Por ejemplo, hay que estudiar de dónde traer el mijo», dice Miranda.
Referencia:
Mármol-Soler, C.; Matias, S.; Miranda, J.; Larretxi, I.; Fernández-Gil, M.d.P.; Bustamante, M.Á.; Churruca, I.; Martínez, O.; Simón, E. (2022) Gluten-Free Products: Do We Need to Update Our Knowledge? Foods doi: 10.3390/foods11233839
Para saber nmás:
Alternativas para tratar la enfermedad celíaca
De la sal «sin gluten» al champú «sin gluten»: no solo marketing
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Los productos sin gluten no son más sanos se ha escrito en Cuaderno de Cultura Científica.
Amaia Iparragirre, matematikaria: “Beharrezkoa sentitzen dut emakume erreferenteak izatea”
Matematikek ospe txarra dute: zailak direla, abstraktuak direla, ez dutela ezertarako balio… Horrelako usteak oso zabalduta daude gizartean. Amaia Iparragirre Letamendia matematikaria da, eta ez du arrastorik ere nondik datorren ospe txar hori, “ume-umetatik gustatu izan zaizkit“, adierazi du.
Eta ez daki zergatik izango duten ospe txarra; agian, abstraktuak direlako izan daitekeela uste du. Nabarmendu duenez, ordea, nahiz eta modu abstraktuan landu, lotura zuzena dute eguneroko bizimoduarekin eta ingurunearekin. Gainera, beti moldatu izan da ondo matematiketan. “Ama ere matematika-irakaslean zen; hortaz, etxetik ere jaso dut zaletasun hori, eta ez dut sekula sentitu matematikak ez zirela niretzat egokiak edo ez zitzaizkidala gustatu behar. Oso naturala izan da niretzat”.
 Irudia: Amaia Iparragirre Letamendia matematikaria doktore-tesia egiten ari da, estatistikan; zehazki, eredu aurresaleen garapenean eta balidazioan MATHMODE taldean. (Argazkia: Elhuyar)
Irudia: Amaia Iparragirre Letamendia matematikaria doktore-tesia egiten ari da, estatistikan; zehazki, eredu aurresaleen garapenean eta balidazioan MATHMODE taldean. (Argazkia: Elhuyar)Orain, doktore-tesia egiten ari da, estatistikan; zehazki, eredu aurresaleen garapenean eta balidazioan, diseinu konplexuko laginketetan oinarritutako inkestetatik datozen datuekin. Azaldu duenez, eredu aurresaleak asko erabiltzen dira gaur egun. Helburua da, dauden datuetan oinarrituta, etorkizuna aurreikustea. “Nire tesiaren berezitasuna da datu-mota jakin bati doitu nahi zaizkiela mota honetako ereduak. Datu-mota hori ohikoa izan da estatistikan, baina, orain arte, ez zaizkio eredu aurresaleak doitu. Hortaz, nire helburua bi arlo horiek lotzea da”.
Eredu horiek aplikazio zuzena dutela baieztatu du; hain zuzen, tesia abiatu zuenean, egiazko arazo batetik abiatu zen. Adibideak ere eman ditu: “Esaterako, pandemian ikaragarri erabili dira, eta, orokorrean, medikuntzan asko erabiltzen dira. Adibidez, orain ditugun datuetan oinarrituta, agian interesatzen zaigu jakitea zenbat ohe izango ditugun libre datorren astean, edo datorren hilean. Horretarako, eredu aurresaleak beharko genituzke”.
Emakume erreferenteen garrantziaHorrelako garapenak gizarte osoarentzat dira interesgarriak, baina matematikak ikasteko interesean bilakaera bat egon da: duela urte batzuk arte, matematika-graduan emakumeak gehiengoa ziren; azken urteotan, ordea, gizonak gailentzen ari dira. Iparragirre aldaketa horren lekuko izan da: “Matematika ikasi nuen garaian, emakume gehiago ginen, eta ordutik ez da denbora asko igaro, baina gizon gehiago daude gaur egun. Ez dakit zergatik izan daitekeen, baina uste dut gizonen gorakada bat datorrela matematikek gizartean hartzen ari diren izenarekin. Agian, zenbat eta ospe handiagoa izan matematikek eta zenbat eta gehiago lotu enpresa-munduari, orduan eta gizon gehiagok ikasten dituzte matematikak“.
Horrek ondorioak izan ditzakeela iruditzen zaio. “Adibidez, ikertzen diren gaietan aldaketak ekar ditzake. Kalterako, noski, justu gizartean gure helburua beste bat baita. Nolabaiteko genero-berdintasuna lortzea nahi dugu, eta hemen badirudi kontrakoa ikusten ari garela”.
Hori aldatzeko, oso garrantzitsua iruditzen zaio erreferenteak izatea: “Ez dakit horrekin nahikoa izango den, baina nik erreferente emakumezko asko izan ditut bai matematikak ikastean, bai ikertzean, nire bi tesi-zuzendariak emakumeak dira, eta, estatuan, beste matematikariekin elkartzen garenean ere, asko emakumeak dira. Eta emakume hauek guztiak niretzat erreferenteak dira, eta beharrezkoa sentitzen dut emakume erreferenteak izatea. Hortaz, uste dut gizartearentzat ere garrantzitsua dela ahotsa ematea horrelako profilei”.
Fitxa biografikoa:Amaia Iparragirre Letamendia Azpeitian jaioa da, 1994an. 2016an Matematikan graduatu zen Euskal Herriko Unibertsitatean, eta urte bat beranduago Modelizazioa eta Ikerkuntza Matematikoa, Estatistika eta Konputazioa masterreko titulua lortu zuen. Ondoren, EHUko Matematika Aplikatua, Estatistika eta Ikerkuntza Operatiboa sailean egin zuen lan ikertzaile ez-doktore bezala, Bioestatistikako Ikerkuntza Taldean (BIOSTIT). 2019ko ekainean EHUren ikertzaileak prestatzeko doktoratu aurreko programako beka bat eskuratu zuen. Ordutik, bere doktorego-tesia prestatzen dabil MATHMODE taldean. Horrez gain, estatistikaren dibulgazioari lotutako hainbat proiektutan ere hartu dut parte azken urte hauetan.
Egileaz:Ana Galarraga Aiestaran (@Anagalarraga1) zientzia-komunikatzailea da eta Elhuyar Zientzia eta Teknologia aldizkariko erredaktorea.
Elhuyar Zientzia eta Teknologia aldizkariarekin lankidetzan egindako atala.

The post Amaia Iparragirre, matematikaria: “Beharrezkoa sentitzen dut emakume erreferenteak izatea” appeared first on Zientzia Kaiera.
¿Por qué lo llaman mármol cuando quieren decir caliza?
Es posible que alguna vez hayáis ido a comprar unas losas o una encimera para vuestra casa y encargaseis un precioso mármol de color crema con un vistoso nombre que evocaba fantasías. Sin embargo, cuando os llegó el pedido, os encontrasteis con una roca que tenía un elevado contenido en restos fósiles. Y ahí os saltarían todas las alarmas, ¿cómo es posible?
 A-C) Granitos de diferentes tonalidades y D) gneis empleados como rocas ornamentales en diversos edificios circundantes a la Plaza Moyua de Bilbao (Bizkaia). Foto: Blanca María Martínez
A-C) Granitos de diferentes tonalidades y D) gneis empleados como rocas ornamentales en diversos edificios circundantes a la Plaza Moyua de Bilbao (Bizkaia). Foto: Blanca María MartínezUn mármol es un tipo de roca metamórfica formada por la transformación de una roca sedimentaria carbonatada al ser sometida a un importante régimen de presión y temperatura durante millones de años. Esta transformación, conocida como metamorfismo, consiste en una recristalización y nueva ordenación de los minerales carbonatados originales. Para que nos entendamos, los fósiles que pudiesen haberse preservado en esa roca sedimentaria inicial se destruyen durante el proceso de metamorfismo, por lo que no queda ningún rastro de ellos en el mármol. Dicho esto, ¿nos han engañado en la tienda de rocas ornamentales dándonos caliza por mármol?
Pues la respuesta es no. Esta confusión procede de la clasificación de las rocas ornamentales, que no es exactamente igual a la clasificación geológica de las rocas. Pero voy a empezar por el principio. Las rocas ornamentales son aquellas que se explotan comercialmente en canteras para su uso en la construcción, como enlosado de edificios y monumentos o como material escultórico, principalmente debido a su belleza estética, es decir, gracias a que “son bonitas”. Y, para su clasificación, se tienen en cuenta, principalmente, sus características físicas, tales como su resistencia y durabilidad ante la erosión provocada por las condiciones climáticas, más que su composición química o su origen geológico. De esta manera, nos encontramos con tres grandes grupos o tipos de rocas ornamentales: granitos, mármoles y pizarras.
 Fachada del edificio Bizkaia Aretoa, Paraninfo de la Universidad del País Vasco (UPV/EHU) en Bilbao (Bizkaia), construida con losas de mármol blanco, con ligeros veteados verdosos por el mineral clorita, extraído de las canteras de Macael (Almería). Foto: Blanca María Martínez
Fachada del edificio Bizkaia Aretoa, Paraninfo de la Universidad del País Vasco (UPV/EHU) en Bilbao (Bizkaia), construida con losas de mármol blanco, con ligeros veteados verdosos por el mineral clorita, extraído de las canteras de Macael (Almería). Foto: Blanca María MartínezGeológicamente hablando, un granito es una roca ígnea plutónica, es decir, que se forma por el enfriamiento lento (millones de años) de un magma en el interior de la tierra, por lo que tiene tiempo de formar cristales minerales. Pero en el caso de las rocas ornamentales, el término granito engloba a rocas cristalinas donde los minerales se observan a simple vista, de composición no carbonatada y, en general, muy resistentes al esfuerzo y la erosión. Y en esta denominación se incluyen los granitos en sentido geológico, pero también otras rocas ígneas plutónicas, como la diorita, la sienita o el gabro; rocas subvolcánicas filonianas, formadas por el enfriamiento y la cristalización de un magma o de un fluido caliente y mineralizado que circulaban a través de fracturas, dando lugar a cuerpos de rocas con formas prismáticas, como son las pegmatitas; y rocas ígneas volcánicas, generadas por el enfriamiento rápido del magma al salir a superficie, por lo que no tiene tiempo de cristalizar y presenta elevados contenidos de vidrio volcánico en su composición, como la andesita y el basalto. Pero también nos encontramos con rocas metamórficas de alto grado, es decir, que han sufrido altas presiones y temperaturas durante su formación, tal y como les sucede al gneis y a la migmatita.
 Rocas ornamentales de la fachada del Palacio Chávarri (Bilbao, Bizkaia). En tonos rosados, mármol rojo de Ereño, que es una caliza marina del Cretácico con abundante contenido fósil (de color blanco), principalmente bivalvos, extraída de la cantera de Ereño (Bizkaia). En tonos amarillos, arenisca del Eoceno posiblemente obtenida de alguna antigua cantera de Bizkaia. En tonos verdes, rocas volcánicas del Cretácico formadas por erupciones submarinas durante la apertura del Golfo de Bizkaia, procedentes de algún afloramiento del País Vasco (las marcas blancas son recristalizaciones de carbonato cálcico). Foto: Blanca María Martínez
Rocas ornamentales de la fachada del Palacio Chávarri (Bilbao, Bizkaia). En tonos rosados, mármol rojo de Ereño, que es una caliza marina del Cretácico con abundante contenido fósil (de color blanco), principalmente bivalvos, extraída de la cantera de Ereño (Bizkaia). En tonos amarillos, arenisca del Eoceno posiblemente obtenida de alguna antigua cantera de Bizkaia. En tonos verdes, rocas volcánicas del Cretácico formadas por erupciones submarinas durante la apertura del Golfo de Bizkaia, procedentes de algún afloramiento del País Vasco (las marcas blancas son recristalizaciones de carbonato cálcico). Foto: Blanca María MartínezSi pasamos al grupo de los mármoles ornamentales, aquí se incluyen rocas de composición principalmente carbonatada, con cristales de pequeño tamaño y menos duras y resistentes que las del grupo de los granitos. Así que no solo se refiere al mármol en el sentido geológico, si no que con este término también se denominan un gran número de rocas sedimentarias como la caliza, la dolomía, la toba y el travertino. Además, en muchas ocasiones se describen como mármoles ornamentales rocas no carbonatadas, tales como las sedimentarias arenisca o yeso y las metamórficas cuarcita, anfibolita o serpentinita, esta última formada a partir de la alteración de una roca ígnea plutónica por la circulación de un fluido profundo muy caliente que modifica su composición mineral y su estructura.
Y terminamos con las pizarras. Si atendemos al término geológico, una pizarra es una roca metamórfica de bajo grado formada por la transformación de una roca sedimentaria de composición arcillosa debido a la acción de la presión y la temperatura, generando una recristalización mineral y su disposición en planos de foliación, que no son otra cosa que esas líneas paralelas que apreciamos en las pizarras y que nos permiten separarlas en finas láminas de roca. Pero en el caso del término ornamental, este hace referencia, precisamente, a esta última cualidad de las pizarras, esa capacidad de separarse en lajas más o menos perfectas, por lo que agrupa a varias rocas metamórficas de grado bajo-medio, como son la pizarra, la filita y el esquisto, pero también rocas sedimentarias muy compactadas, incluso ligeramente metamorfizadas, como ciertas lutitas y margas.
 Fachada de la entrada de la Biblioteca Foral de Bizkaia en Bilbao, cubierta de losas de filita, de color verdoso por el mineral clorita, procedentes de China. Foto: Blanca María Martínez
Fachada de la entrada de la Biblioteca Foral de Bizkaia en Bilbao, cubierta de losas de filita, de color verdoso por el mineral clorita, procedentes de China. Foto: Blanca María MartínezEn definitiva, cuando vayamos a comprar alguna roca ornamental no debemos olvidarnos de que el nombre comercial que nos van a dar no tiene por qué concordar con el nombre geológico que le aplicaríamos a esa misma roca. Si queremos conocer estos detalles, deberemos pedir que nos enseñen la ficha técnica de ese material, en donde sí encontraremos una definición muy detallada de la misma, incluida no solo su clasificación geológica, sino también una descripción de su composición, sus propiedades físicas y el lugar en donde se ha extraído. Y con esos datos, incluso, podremos conocer toda la historia geológica de la zona de explotación. Gracias a las rocas ornamentales que decoran fachadas, edificios, aceras y monumentos de nuestros pueblos y ciudades podemos aprender maravillosas historias geológicas que nos transportan a recónditos lugares de todo el mundo y a millones de años atrás en el tiempo, aunque las llamemos a todas mármoles, granitos y pizarras.
Para saber más:
Los volcanes submarinos de Bizkaia y Gipuzkoa
La geodiversidad que nos rodea
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo ¿Por qué lo llaman mármol cuando quieren decir caliza? se ha escrito en Cuaderno de Cultura Científica.
Animalien aferak

Animalien aferak liburuan (2011) animaliak aztertzean aurkitu ditzakegun zerbait bitxi edo deigarriak azaltzen dizkigute Juan Ignacio Pérezek eta Miren Bego Urrutiak. Nola irauten dute hauek bizirik? Zer trikimailu darabilte arrakasta izateko? Halako galderak bururatzen zaizkigu maiz animalien bizimoduei erreparatzean, baldintza gogorretan aurrera ateratzeko gai direla ikusten dugularik batez ere.
 Irudia: Animalien aferak liburuaren azala. (Iturria: UPV/EHU argitalpenak)
Irudia: Animalien aferak liburuaren azala. (Iturria: UPV/EHU argitalpenak)Askotariko animaliak aztertu ondoren, argi gelditzen da nahiko urriak direla erabiltzen dituzten mekanismoak; hala ere, aniztasun zoragarria aurkitzen dugu animalien artean, baldintzen, beharrizanen eta taldearen arabera. Horren adibide dira Animalien aferak izenburupean bildutako istorioak. Bitxitasuna gorabehera, eredugarri direlako aukeratu dira, eta guztietatik atera daiteke animalien funtzionamenduari buruzko irakaspenen bat. Bederatzi ataletan antolaturik datoz, gaion harian: animalien tamainaren eragina; hotzari eta beroari aurre egiteko erak; ura, oxigenoa eta janaria lortzeko baliabideak; harrapariengandik ihes egiteko zen harrapakinak ehizatzeko moduak; ondorengoen biziraupena bermatzeko estrategiak…
Literaturak askotan hartu ditu animaliak protagonistatzat, fantasiaz gehienetan; istorio hauetan, animalien bizitza erreala dugu, bere horretan, literatura ederra.
Juan Ignacio Pérez Iglesias eta Miren Bego Urrutia Barandika Euskal Herriko Unibertsitateko irakasleak dira. Urteak daramatzate Biologiako ikasleei animalien fisiologiari buruzko eskolak ematen Zientzia eta Teknologia Fakultatean.
Itsas animalien biologia ikertzen dihardute aspalditik, eta gai horri buruzko zientzia-artikulu ugari argitaratu dituzte.
Miren Bego Urrutia EHUko Genetika, Antropologia Fisikoa eta Animalien Fisiologia saileko zuzendaria da, eta Juan Ignacio Pérez, berriz, EHUko Kultura Zientifikoko Katedraren koordinatzailea.
Uhandreak bloga sortu, eta han hasi ziren animalien biologiari buruzko istorioak idazten, formatu askeagoan helarazteko publiko zabalagoari animaliei buruzko kontu interesgarriak.
Argitalpenaren fitxa:- Izenburua: Animalien aferak
- Egilea: Pérez Iglesias, Juan Ignacio; Urrutia Barandika, Miren Bego
- ISBN: 978-84-9860-568-6
- Formatua: 16 x 24 zm
- Hizkuntza: Euskara
- Urtea: 2011
- Orrialdeak: 340 or.
Euskara, Kultura eta Nazioartekotzearen arloko Errektoretza, UPV/EHU argitalpenak, ZIO bilduma: Animalien aferak
The post Animalien aferak appeared first on Zientzia Kaiera.

