¿Puede la física resolver problemas en medicina?
La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebra dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Publicamos en el Cuaderno de Cultura Científica y en Zientzia Kaiera una serie de artículos que narran algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas.

La física y la medicina son dos actividades científicas que parecen estar muy alejadas una de la otra. Sin embargo, el listado de los premios Nobel de medicina, nos enseña que hay varios galardones concedidos a Físicos, o en base a una metodología Física. De hecho, el primer galardonado de este tipo, el sueco Allver Gullstrand, recibió en 1911 el Premio Nobel de Medicina y fue nominado al Nobel de Física tanto en 1910 como en 1911. En 1911, el Comité Nobel de Física, del cual Gullstrand era miembro, sugirió que el premio Nobel había de ser para él. Al mismo tiempo el Comité Nobel de Medicina estaba considerando su nombre para el Nobel. Gullstrand declinó el Premio Nobel en Física a favor del Nobel de Medicina [1]. Gullstrand es la única persona que ha declinado un Premio Nobel y ha aceptado otro. Sin contarle a él, son solo tres personas las que no han aceptado un Nobel: los de literatura de 1958 y 1964 por los escritores, ruso Boris L. Pasternak y francés Jean-Paul Sartre, respectivamente, y el Nobel de la Paz por el Vietnamita Le Duc Tho en 1973.
 Imagen 1. Allver Gullstrand, premio Nobel en 1911. Fuente: Wikimedia Commons
Imagen 1. Allver Gullstrand, premio Nobel en 1911. Fuente: Wikimedia Commons
Es interesante reseñar que Gullstrand tenía una fuerte personalidad y como miembro de la Real Academia de Ciencias Sueca formo parte en 1921 del Comité que se opuso a que Albert Einstein recibiese el Nobel de Física en 1921 por la teoría de la relatividad general, que Gundstrand consideraba equivocada [1].
Allver Gullstrand fue galardonado en 1911 con el premio Nobel en Medicina por sus investigaciones sobre la refracción de la luz a través del medio trasparente del ojo vivo. Si esto no es una metodología Física, que me digan qué es!!! Tres años después de recibir el premio Nobel abandonó la cirugía oftalmológica para dedicarse completamente a la investigación sobre instrumentos ópticos y diseño de instrumentación y técnicas quirúrgicas. La lámpara de hendidura, presente hoy en día en la mayoría de las mesas de los oculistas es una de sus invenciones.
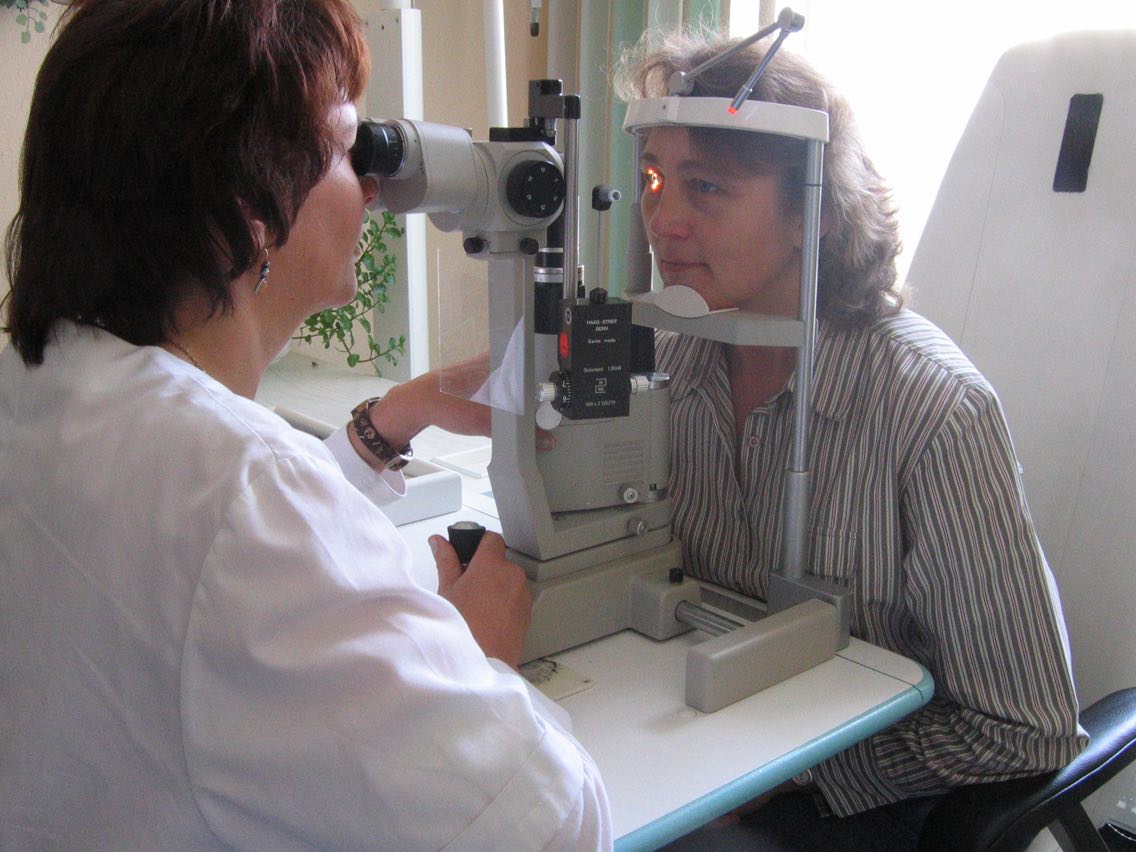 Imagen 2. Lámpara de hendidura. Fuente: Wikimedia Commons
Imagen 2. Lámpara de hendidura. Fuente: Wikimedia Commons
Hubo que esperar 11 años hasta que una metodología Física recogiera otro Premio Nobel de Medicina. El inglés, Licenciado en Matemáticas, Archibald Vivian Hill recibió el Premio Nobel de Medicina de 1922 por la investigación relativa al cambio de temperatura que se produce al poner a trabajar los músculos. Su trabajo sobre la función muscular, especialmente la observación y medida de los cambios de temperatura asociados con el funcionamiento de los músculos, se extendió posteriormente a estudios similares sobre el mecanismo del paso de los impulsos nerviosos. Se desarrollaron técnicas muy sensibles, capaces de medir cambios de temperatura del orden de 0,003 °C en periodos de solo centésimas de segundo. Estas investigaciones dieron un gran impulso a la biofísica y se dice que el gran interés por la misma se debe a sus aportaciones.
En 1924 el médico holandés Willen Einthoven fue galardonado con el premio Nobel de Medicina por el descubrimiento del mecanismo del electrocardiograma. El electrocardiograma es la representación gráfica de la actividad eléctrica del corazón en función del tiempo. Actualmente tiene una función relevante en cribado y diagnóstico de enfermedades cardiovasculares y alteraciones metabólicas. Como es bien conocido, el electrocardiograma se obtiene colocando sobre la zona del pecho 10 electrodos sujetos con cinta de velcro que se conectan mediante cables al aparato para medir los voltajes entre los electrodos (derivaciones, 12 en total). Podemos decir en forma figurada que cada derivación es una “fotografía” de la actividad eléctrica del corazón, tomada desde un ángulo diferente.
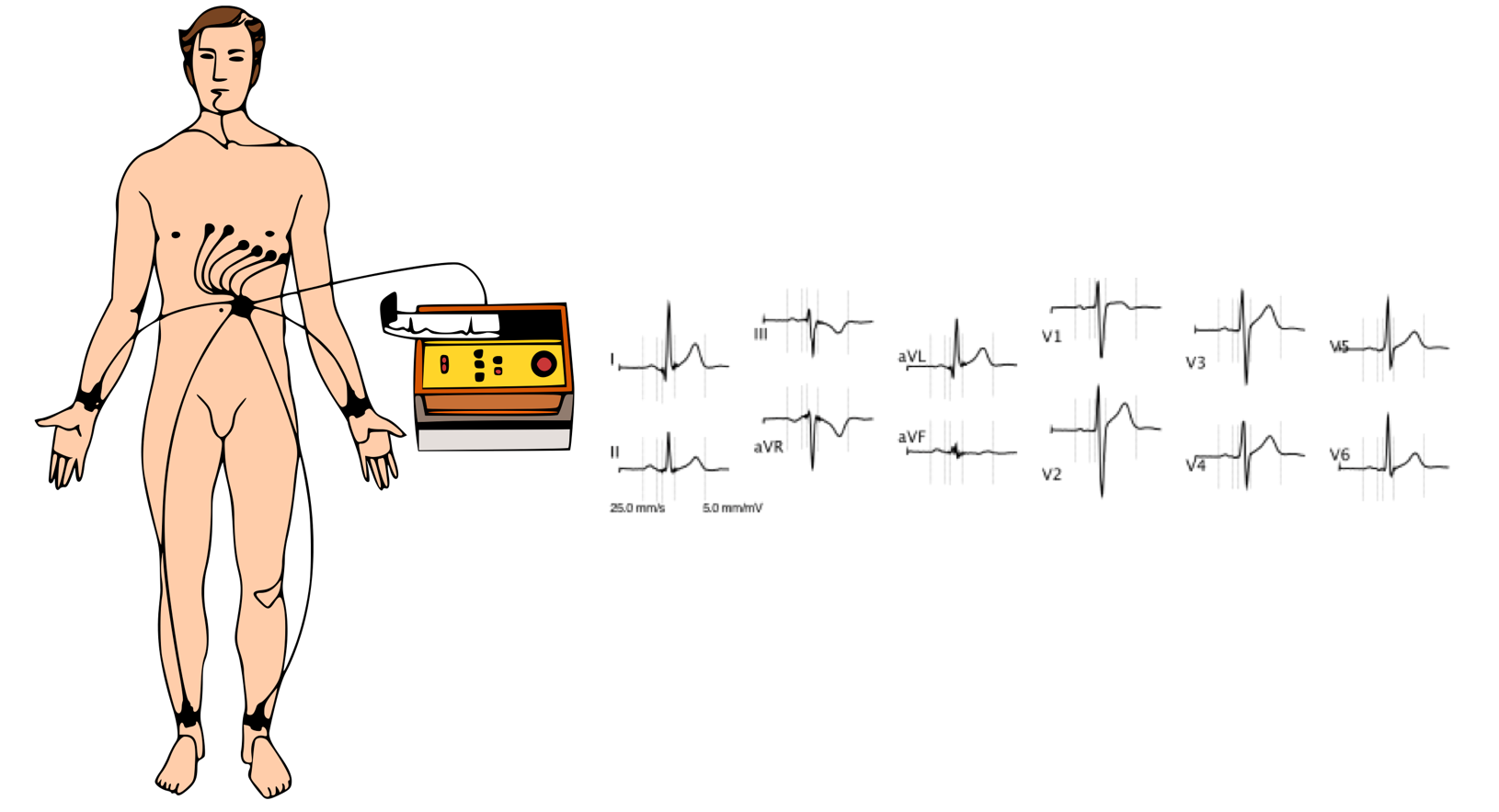 Imagen 3. Obtención de electrocardiograma y “fotografías” de la actividad eléctrica del corazón. Fuente: Wikimedia Commons
Imagen 3. Obtención de electrocardiograma y “fotografías” de la actividad eléctrica del corazón. Fuente: Wikimedia Commons
Los Premios Nobel de Medicina relacionados con la Física presentados hasta ahora se produjeron en las áreas de óptica, termodinámica y señales eléctricas. Sin embargo, el de 1946 (al igual que los dos siguientes) estuvo relacionado con los rayos X. Al genetista estadounidense Hermann Joseph Muller se le galardonó con el Premio Nobel por el descubrimiento de la producción de mutaciones mediante la irradiación con rayos X.
En el Premio Nobel de Medicina de 1962 también se utilizaron los rayos X, pero en este caso para realizar análisis estructurales mediante difracción de los mismos. La química inglesa Rosalind Elsie Franklin trabajando junto al físico neozelandes Maurice Wilkins sobre la difracción de rayos X de la molécula de ADN, describen la estructura de doble hélice del Ácido Desoxidorribonucleico, el ADN, que posteriormente servirá de base para la descripción de dicha estructura por el biólogo estadounidense James Dewey Watson y el físico inglés Francis Harry Compton Crick. La estructura de la molécula de doble hélice que es el ADN dio al mundo la llave para entender todos los secretos de la vida. Toda la vida en la tierra, desde la bacteria más pequeña hasta el ser humano, existe gracias al ADN. Este descubrimiento les valió el premio Nobel de Medicina de 1962 a 3 de estos científicos. Sin embargo, a pesar de que la contribución de la científica Rosalind Franklin fue fundamental (fue quien diseño y realizó los experimentos de difracción de rayos X, sin los cuales no hubieran podido llegar a descifrar la doble hélice), no obtuvo el reconocimiento Nobel por haber fallecido.
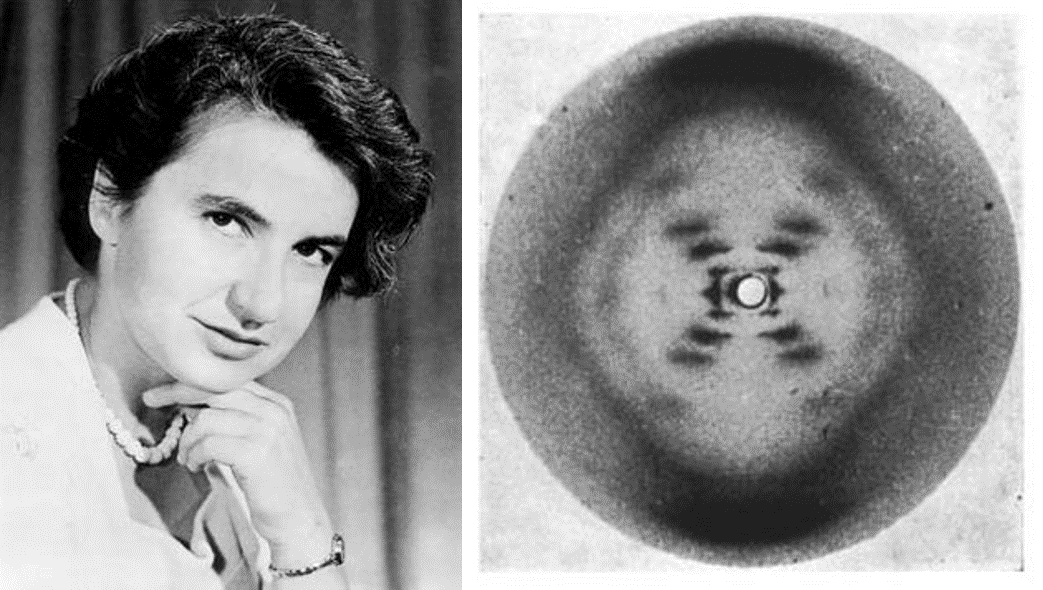 Imagen 4. Rosalind Elsie Franklin y la fotografía 51, imagen de la difracción con Rayos X de una molécula de ADN, realizada en 1951 por Rosalind Franklin y Raymond Gosling. Fuente: Composición a partir de imágenes de Wikimedia Commons
Imagen 4. Rosalind Elsie Franklin y la fotografía 51, imagen de la difracción con Rayos X de una molécula de ADN, realizada en 1951 por Rosalind Franklin y Raymond Gosling. Fuente: Composición a partir de imágenes de Wikimedia Commons
¿Cómo llegaron a poder de Watson y Crick los difractogramas realizados por Rosalind Franklin? Así como los comentarios de Watson sobre Rosalind dan para mucho, y son un reflejo de la discriminación que han sufrido muchas mujeres científicas, pero esto nos daría para todo un artículo y no es el objetivo de este [2].
Los siguientes Premios Nobel de Medicina relacionados con la Física se concedieron a descubrimiento/invenciones de técnicas de imagen que actualmente conocemos muy bien. El primero, de 1979, también está relacionado con los rayos X, fue para el físico sudafricano Allan McLeod Cormack y el ingeniero electrónico inglés Godfrey Newbold Hounsfield, por el desarrollo y descubrimiento de la Tomografía Axial Computerizada, que conocemos coloquialmente como TAC o escáner. El TAC revolucionó el diagnóstico médico en todo el mundo, ya que trajo un gran avance en la detección y localización de tumores, permitiendo a los médicos ver el interior del cuerpo humano en tres dimensiones. Godfrey comentó en una entrevista que el The New York Times le realizó en 1973 “el avance consistía en darse cuenta de que al escanear objetos desde muchos ángulos era posible extraer el 100% de la información de los rayos X”. El diagnóstico basado en imágenes del interior del cuerpo obtenidas por medio de los rayos X se utiliza desde principios del siglo XX. Sin embargo, las radiografías clásicas no permiten observar el relieve, ni distinguir con claridad los tejidos. El escáner resuelve esta situación, obteniendo gran número de imágenes de rayos X (ya sea sucesivamente, haciendo girar el aparato, o simultáneamente, mediante varios emisores y detectores).
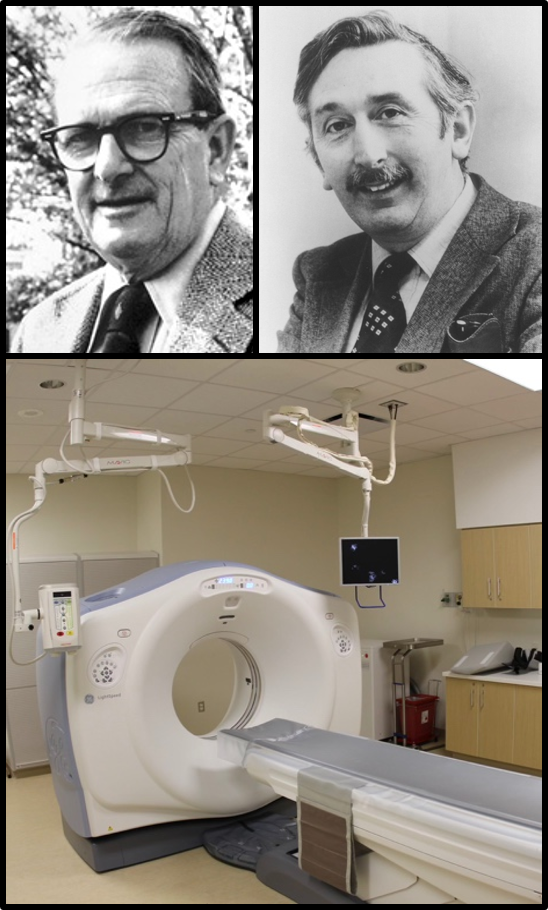 Imagen 5. Arriba: los premios Nobel de 1979 Allan McLeod Cormack y Godfrey Newbold Hounsfield. Abajo: Equipo TAC o escáner. Composición a partir de imágenes de Wikimedia Commons
Imagen 5. Arriba: los premios Nobel de 1979 Allan McLeod Cormack y Godfrey Newbold Hounsfield. Abajo: Equipo TAC o escáner. Composición a partir de imágenes de Wikimedia Commons
En 2003 el premio Nobel de Medicina se concedió al físico británico Peter Mansfield y al químico estadounidense Paul Christian Lauterbur por la invención y desarrollo de la imagen por resonancia magnética nuclear, a la que coloquialmente llamamos resonancia magnética o imagen de resonancia magnética (MRI). Si sometemos los núcleos de los átomos a un intenso campo magnético, estos rotan alrededor de ese campo magnético con una frecuencia que depende del valor de la intensidad del campo. La energía de los núcleos puede aumentar (excitación nuclear) si absorben ondas de radio de la misma frecuencia de rotación. A este proceso se le conoce como resonancia nuclear. Cuando los núcleos se desexcitan, es decir, vuelven a su estado original o fundamental, emiten ondas de radio características del núcleo particular que lo identifican. De hecho, este fenómeno fue descubierto en 1946 para los núcleos de los átomos de Hidrogeno por los estadounidenses Felix Bloch y Edward Mills Purcell, que recibieron el premio Nobel de Física en 1952. Este fenómeno fue muy prolífico, ya que dio lugar a otros dos premios nobeles, de química estos, uno en 1991 y el otro en 2002.
 Imagen 6. Los premios Nobel de 2003 Paul Christian Lauterbur y Peter Mansfield.
Imagen 6. Los premios Nobel de 2003 Paul Christian Lauterbur y Peter Mansfield.
Mediante la detección de las ondas de radio siguiendo el procedimiento anterior es posible detectar el hidrógeno y su cantidad por unidad de volumen. El agua es una molécula compuesta de átomos de hidrógeno y oxígeno. Por lo tanto, al contener hidrogeno, el agua responde al fenómeno citado. Dos tercios del peso del cuerpo humano son agua y este elevado contenido en agua explica por qué las imágenes de resonancia magnética se han vuelto tan útiles en la medicina. Las pequeñas diferencias en las oscilaciones de los núcleos pueden detectarse y mediante un procesamiento informatizado complejo, es posible construir una detallada imagen de tejidos y órganos en el área del cuerpo investigada. De esta forma pueden documentarse los cambios patológicos.
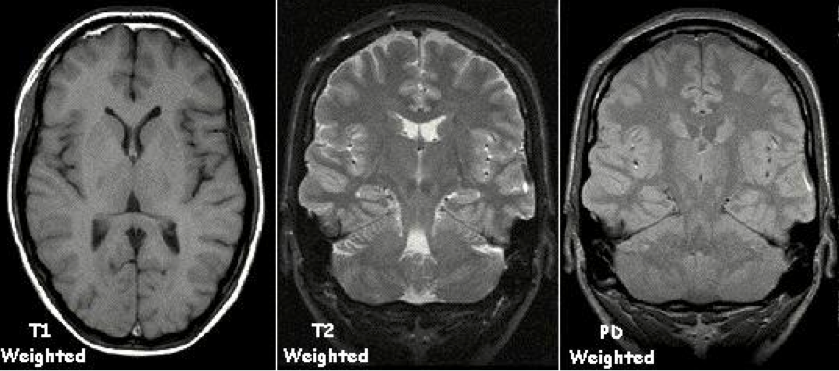 Imagen 7. Ejemplos de MRI tomados con diferentes técnicas: ponderación T1 (spin-red), ponderación T2 (spin-spin) y ponderación en PD (densidad de protones). Fuente: Wikimedia Commons
Imagen 7. Ejemplos de MRI tomados con diferentes técnicas: ponderación T1 (spin-red), ponderación T2 (spin-spin) y ponderación en PD (densidad de protones). Fuente: Wikimedia Commons
Hoy día, la MRI se emplea para la exploración de casi todos los órganos del cuerpo. La técnica es especialmente valiosa para obtener imágenes detalladas del cerebro y la medula espinal. Sin embargo, el equipamiento para la MRI es caro, muy voluminoso, pesado y necesita de campos magnéticos elevados (como mínimo del orden de 1 Tesla, que en comparación al campo magnético terrestre es unas 10000 veces mayor), por lo que está localizado en lo que se vienen a llamar salas de resonancia de grandes hospitales.
Desarrollar equipamiento MRI portable sería una ventaja adicional, que posibilitaría su utilización en salas de urgencias, ambulatorios y ambulancias medicalizadas, con la consiguiente mejora en el servicio médico. En la Facultad de Ciencia y Tecnología se está trabajando en el desarrollo de equipamiento portable, y el primer prototipo del citado equipamiento está cerca [3].
Actualmente el desarrollo de una nueva terapia contra el cáncer (Hipertermia magnética), se está realizando por investigadores e investigadoras en Física y Química de la Facultad de Ciencia y Tecnología, investigadores de la Facultad de Medicina e investigadores en medicina clínica del Hospital de Galdakao. Esta nueva terapia necesita de los siguientes pasos: 1) sintetización de nanopartículas magnéticas apropiadas, 2) inoculación de las nanopartículas magnéticas de forma que estas se localicen en el tumor y 3) desarrollo de un aplicador electromagnético de radiofrecuencia que sea capaz de hacer que las nanopartículas magnéticas liberen calor suficiente para “quemar” los tumores en los que se han localizado las nanopartículas [4]. Cuando se consiga desarrollar completamente la terapia será posible “quemar” las células cancerosas, es decir, los tumores, sin dañar el tejido circundante. Si se consigue implementar esta terapia, los efectos secundarios serán mucho menores que los que producen la radioterapia y la quimioterapia, y su costo será mucho menor.
Para saber más:
[1] Ravin, James G. (1999). Gullstrand, Einstein, and the Nobel Prize. MD Arch Ophthalmol. 117(5):670-672. DOI:10.1001/archopht.117.5.670
[2] Angulo, Eduardo (2014). El caso de Rosalind Franklin. Mujeres con Ciencia.
[3] Alonso-Valdesueiro, J. et al., (2018). Design, Construction, and Characterization of a Magic Angle Field Spinning RF Magnet. IEEE Transactions on Instrumentation and Measurement, PP(99), 1-10. DOI:10.1109/TIM.2018.2884606
[4] Périgo, E.A. et al., (2015). Fundamentals and advances in magnetic hyperthermia. Applied Physics Reviews, 2(4), 041302. DOI:10.1063/1.4935688
Sobre el autor: Fernando Plazaola es catedrático en el Departamento de Eletricidad y Electrónica de la Facultad de Ciencia y Tecnología de la UPV/EHU.
El artículo ¿Puede la física resolver problemas en medicina? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las dos culturas de las matemáticas: construir teorías o resolver problemas
- El Nobel de Medicina de 2013: Logística de prefabricados de construcción (en las células)
- Dudas sobre las vacunas: problemas y soluciones
Los filtros solares llegan al torrente sanguíneo, dice la prensa
 Fuente: Pixabay
Fuente: Pixabay
Recientemente se ha publicado un estudio preliminar sobre la absorción de algunos filtros ultravioleta empleados en los productos de protección solar [1]. Ha cundido el pánico, pero no en la comunidad científica, sino en los medios de comunicación. Tanto en la prensa española, como en la prensa extranjera [2] los titulares han sido alarmistas y no se corresponden ni con las conclusiones del estudio ni con la opinión de sus autores [3]. La realidad es que este estudio no ha aportado nuevas evidencias, y la recomendación sigue siendo el uso de protección solar, ya que los beneficios superan con creces a los posibles riesgos.
-
El origen del estudio
El estudio se realizó a petición de la FDA. La FDA es la agencia del gobierno de los Estados Unidos responsable de la regulación de alimentos, medicamentos, cosméticos, aparatos médicos, productos biológicos y derivados sanguíneos. Es el análogo as SCCS europeo.
La razón de este estudio es que la FDA ha cambiado los parámetros por los cuales un ingrediente usado en cosmética puede o no pasar a formar parte de su lista de ingredientes seguros (la lista GRASE, Generally Recognised as Safe and Effective).
Antiguamente, la seguridad de los filtros solares se evaluaba con ensayos en animales. Hace años que estos ensayos han de hacerse en personas. Todos los filtros solares que actualmente se usan en EEUU han superado con éxito los ensayos toxicológicos, pero con la nueva regulación [4] han de repetirse.
Para que se apruebe la entrada de un filtro solar en la lista GRASE, hay que presentar estudios de “prueba de uso máximo”. Estos estudios sirven para determinar si el ingrediente se absorbe, si pasa a la sangre y en qué cantidad [5]. Es la misma prueba que se exige en los medicamentos de uso tópico. Con esto, la definición de “cosmético” con respecto a la de “medicamento” está poco clara para la FDA.
- El estudio
El estudio es un estudio preliminar, o “estudio piloto”. En este caso significa que se ha hecho con muy pocos individuos, en poco tiempo y en unas condiciones que no son las normales de uso. Los estudios preliminares sirven para determinar si sería o no conveniente hacer un estudio más exhaustivo.

En el estudio participaron 24 voluntarios. Estos se dividieron en cuatro grupos de 6 personas. Cada uno de estos grupos estuvo utilizando un producto de protección solar concreto: dos aerosoles, una loción y una crema respectivamente. Durante 4 días cubrían el 75% de su cuerpo con estos productos a razón de 2 mg de producto por cada cm2 de piel, el doble del uso recomendado. Aplicaban esta cantidad de producto 4 veces al día. Durante este tiempo, los voluntarios no realizaban ninguna actividad: ni salían, ni iban a la playa, ni sudaban, ni se bañaban en el mar o la piscina. Es decir, las condiciones de uso fueron extremas, ya que solo se trataba de hacer un estudio preliminar. Luego, analizaron su sangre para detectar cuatro ingredientes activos: avobenzona, oxibenzona, octocrileno y ecamsule, que son cuatro filtros ultravioleta empleados en productos de protección solar.
Según la FDA, un filtro solar que presente una absorción sistémica de 0,5 ng/ml o inferior, no tiene que someterse a más ensayos toxicológicos y será directamente declarado como seguro, por lo que podrá formar parte de la lista GRASE. Esto no implica que una absorción superior vaya a tener efectos adversos en la salud, sino que habría que evaluar si es así o no.
Los autores del estudio encontraron evidencia de una absorción sistémica medible de los 4 filtros solares. Los productos que contienen avobenzona dieron como resultado concentraciones plasmáticas superiores a 0,5 ng/ml desde el primer día. La concentración aumentó desde el primer día al cuarto, por lo que existe acumulación. El séptimo día, la concentración de avobenzona decayó, hasta ser indetectable en sangre en el caso de la crema.
La aplicación de productos con oxibenzona y octocrileno dio lugar a niveles plasmáticos similares entre sí, muy por debajo de los niveles de la avobenzona, aunque con concentraciones también superiores a 0,5 ng/ml.
Entre los 6 participantes que usaron la crema con ecamsule, solo 5 tuvieron concentraciones plasmáticas superiores a 0.5 ng/mL el primer día. Los niveles plasmáticos fueron los más bajos de entre todos los filtros solares analizados.
No obstante, los coeficientes de variación del estudio están en su mayoría por encima del 20%, algunos por encima del 100%. Esto quiere decir que la absorción sistémica es heterogénea y difiere mucho de unos individuos a otros. Este es uno de los motivos por los cuales los autores del estudio reconocen que los resultados no son concluyentes.
-
Un estudio poco novedoso
Desde 1997 sabemos que los filtros solares llegan al torrente sanguíneo. Hace ya 22 años. También sabemos que son eliminados por medio de la orina [6]. Se han hecho decenas de estudios toxicológicos sobre todos los filtros ultravioleta utilizados en cosméticos de protección solar [7][8][9][10][11][12][13][14], así que el reciente estudio de la FDA no aporta información novedosa ni sorprendente para la comunidad científica.
No obstante, las autoridades sanitarias concluyen que las concentraciones plasmáticas detectadas están muy por debajo de los niveles tóxicos. El SCCS (el análogo a la FDA de la Unión Europea) ha estudiado los efectos en la salud de estos mismos ingredientes mucho más recientemente que la FDA, determinando que su uso es seguro [15][16][17].
-
Un estudio limitado
Al tratarse de un estudio preliminar es, casi por definición, un estudio limitado. La principal limitación la encontramos en el tamaño de muestra. Un estudio de este tipo debería realizarse con muchos más individuos. Tampoco se pueden tomar por válidos unos resultados con unos coeficientes de variación tan elevados.
Las condiciones del estudio también deberían asemejarse a las condiciones de uso normal de estos productos. Usando las cantidades recomendadas por el fabricante, no el doble, respetando los tiempos de reaplicación y manteniendo una actividad normal, acorde al uso para el que los cosméticos hayan sido diseñados: resistente al agua, al sudor, etc.
-
Conclusiones de los autores del estudio
Aunque el estudio es limitado, los resultados que arroja pueden resultar impactantes y pueden ser fácilmente malinterpretados y exagerados, como de he hecho ha ocurrido. Por ello, los autores del trabajo han declarado que “existen pruebas de alta calidad que demuestran que el uso de filtros ultravioleta previenen las quemaduras solares, la queratosis actínica precancerosa y el cáncer de células escamosas”, que “es importante continuar reforzando las recomendaciones clínicas con respecto a los efectos beneficiosos de la fotoprotección para la prevención del cáncer de piel que están enraizados en una sólida justificación biológica y en la evidencia clínica” y que “evitar el uso de los filtros ultravioleta del estudio, como cualquier filtro solar en general, podría tener importantes consecuencias negativas para la salud”.
-
Reflexiones finales
Un titular que diga “Los filtros solares llegan al torrente sanguíneo, dice un estudio” resulta muy jugoso. Se ganan más clics con la alarma que con la prudencia.
Lo desasosegante de este caso es que el estudio del que salieron tantos titulares alarmistas se trata de un estudio de libre acceso; cualquier medio de comunicación y cualquier persona puede acceder a él. Incluso los autores publicaron un resumen a modo de nota de prensa para tratar de evitar lo que finalmente sucedió. Incluso con solo leer el abstract del estudio, sabes que ni siquiera hay noticia. O se trabaja poco o se trabaja mal.
Si hubiese la más mínima sospecha de que un ingrediente cosmético es inseguro, se retiraría del mercado. La realidad es así de simple. Lo demás es una irresponsable batalla por el clic.
La presencia de una sustancia tóxica en los productos cosméticos no beneficia a nadie. Y esto, que es una obviedad, continuamente se pone en tela de juicio. Los embaucadores han convertido la desconfianza en un negocio.
Hay quien está constantemente ávido de conspiraciones, fraudes y malhacer. De tanto sospechar, le van a salir arrugas.
[1] https://jamanetwork.com/journals/jama/article-abstract/2733085
[2] https://labmuffin.com/sunscreens-in-your-blood-that-fda-study/
[3] https://jamanetwork.com/journals/jama/fullarticle/2733084
[5] https://www.reuters.com/article/us-fda-sunscreen-idUSKBN13H1RE
[6] https://www.thelancet.com/journals/lancet/article/PIIS0140-6736(05)62032-6/fulltext
[7] https://onlinelibrary.wiley.com/doi/abs/10.1046/j.1365-2230.2002.01095.x
[8] https://onlinelibrary.wiley.com/doi/abs/10.1111/j.1365-2133.2005.07007.x
[9] https://linkinghub.elsevier.com/retrieve/pii/S0731708505005595
[10] https://www.sciencedirect.com/science/article/pii/S0021967307013349?via%3Dihub
[11] https://www.sciencedirect.com/science/article/pii/S0013935115300505?via%3Dihub
[12] https://linkinghub.elsevier.com/retrieve/pii/S0022202X1530885X
[13] https://www.sciencedirect.com/science/article/pii/S157002320400008X?via%3Dihub
[14] https://ehp.niehs.nih.gov/doi/10.1289/ehp.11269
[15] https://ec.europa.eu/health/ph_risk/committees/04_sccp/docs/sccp_o_159.pdf
[16] https://ec.europa.eu/health/scientific_committees/consumer_safety/docs/sccs_o_055.pdf
[17] https://ec.europa.eu/health/scientific_committees/consumer_safety/docs/sccs_o_136.pdf
[18] https://jamanetwork.com/journals/jama/fullarticle/2733084
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Los filtros solares llegan al torrente sanguíneo, dice la prensa se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Estimada OCU: recuerda que NO se pueden utilizar las cremas solares del año pasado
- Un ordenador químico que llega donde no llegan otros
- El flujo sanguíneo se reorganiza en respuesta a las necesidades
El poema de los números primos (2)
Con motivo de la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… (del 5 de abril al 26 de mayo de 2019), de la artista donostiarra Esther Ferrer, en el Centro Internacional de Cultura Contemporánea Tabakalera, de Donostia/San Sebastián, en la anterior entrada del Cuaderno de Cultura Científica El poema de los números primos, estuvimos analizando las matemáticas que están detrás de algunas de sus obras de la serie Poema de los números primos: los números primos, la criba de Eratóstenes, la espiral de Ulam, los polinomios cuadráticos o las lagunas de números primos.
 Portada y contraportada de la publicación Orriak del Centro Internacional de Cultura Contemporánea Tabakalera, sobre la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,…
Portada y contraportada de la publicación Orriak del Centro Internacional de Cultura Contemporánea Tabakalera, sobre la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,…
En esta entrada vamos a completar este pequeño paseo por la serie de obras Poema de los números primos de Esther Ferrer. Para empezar, mostraremos un grupo de dibujos para suelo de esta serie que utiliza una variación rectangular de la espiral de Ulam para generar diferentes estructuras geométricas planas



 Dibujos para suelo de la serie Poema de los números primos (2016), de Esther Ferrer, realizados en tinta sobre papel, 83,5 x 59,5 cm, pertenecientes al archivo personal de la artista. Imagen del catálogo Esther Ferrer, todas las variaciones son válidas, incluida esta, del Museo Nacional Centro de Arte Reina Sofía.
Dibujos para suelo de la serie Poema de los números primos (2016), de Esther Ferrer, realizados en tinta sobre papel, 83,5 x 59,5 cm, pertenecientes al archivo personal de la artista. Imagen del catálogo Esther Ferrer, todas las variaciones son válidas, incluida esta, del Museo Nacional Centro de Arte Reina Sofía.
Estos dibujos para suelo, que son solo cuatro de un grupo más amplio realizado en 2016, nos recuerdan el objetivo de la artista Esther Ferrer al utilizar los números primos, que es hacer uso de las matemáticas como una herramienta objetiva, es decir, que sus preferencias estéticas jueguen un papel secundario en el proceso de creación artístico, para generar estructuras geométricas planas. La base matemática de las cuatro obras anteriores, como explicaremos a continuación, son la espiral de Ulam rectangular y las lagunas de números primos, que crean un patrón geométrico base que subyace a la serie de dibujos, pero que debido a la intervención de la artista cada uno de ellos adquiere un desarrollo estético propio, sorprendente y atractivo.
La base para esta serie de obras es similar a la espiral de Ulam. En ese caso, como puede verse en la entrada anterior, El poema de los números primos, se consideraba una cuadrícula cuadrada sobre la que se escribían los números naturales, empezando en 1 (aunque también podía empezarse en cualquier otro número, como el 17, el 41 o el 1.344.326.696.347) que se colocaba en la cuadrícula superior izquierda de la subcuadrícula central 2 x 2, de manera que los números eran escritos en orden creciente y distribuidos alrededor del 1 formando una espiral de números.
Para estas obras Esther Ferrer construye lo que podríamos llamar la espiral de Ulam rectangular, ya que en lugar de iniciar la espiral en la celda superior izquierda de la una subcuadrícula central 2 x 2, luego cuadrada, lo hace en la celda superior izquierda de la una subcuadrícula central 2 x 26, luego rectangular, de forma que al desarrollar la espiral alrededor queda un retículo rectangular, similar a la que vemos en la siguiente imagen.
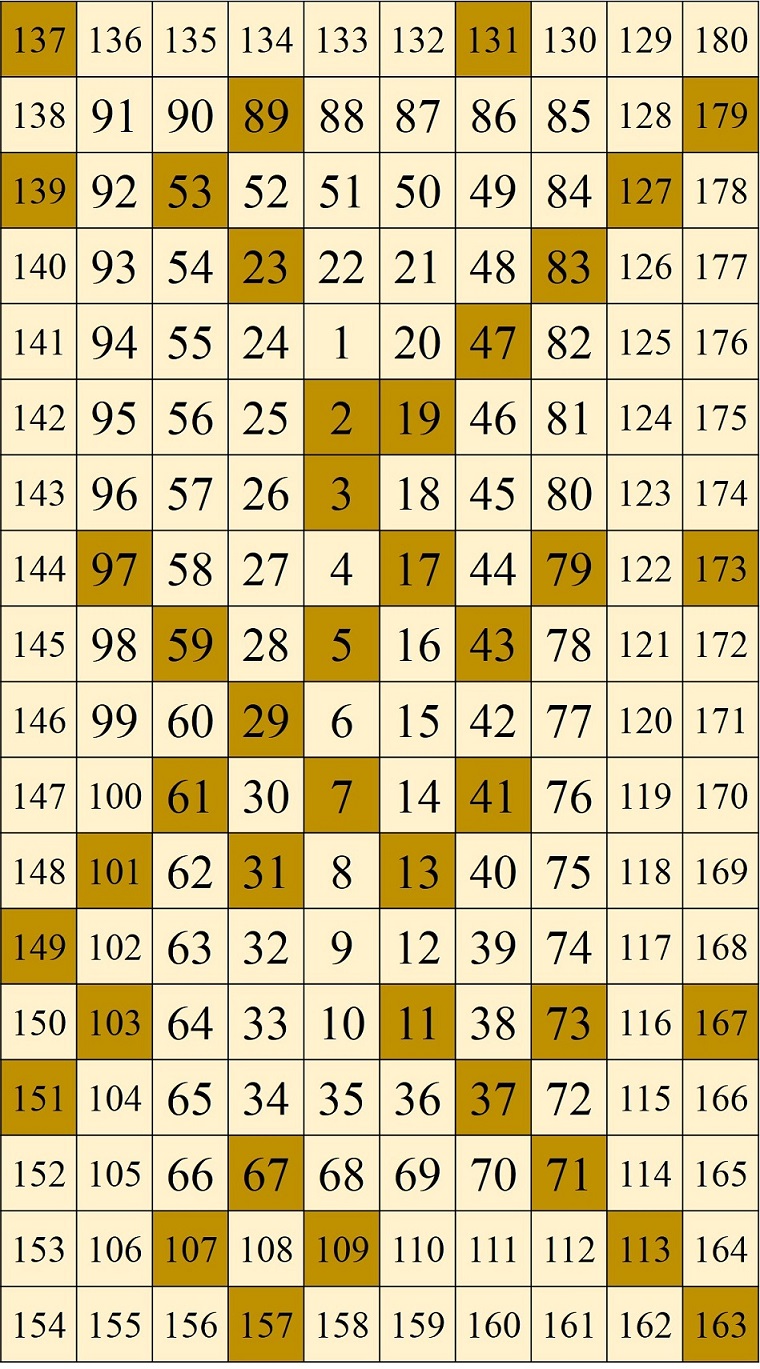
Además, en este grupo de obras, otro elemento fundamental para crear los patrones geométricos planos son las lagunas de números primos, es decir, los grupos de números no primos o compuestos entre dos números primos (véase la entrada Buscando lagunas de números primos), con la diferencia, respecto a otras obras que hemos comentado, de que en este grupo de dibujos incluye al número primo anterior a la laguna como parte de la misma (que podríamos llamar laguna aumentada). Por ejemplo, entre los números primos 13 y 17 hay una laguna de tres números compuestos, de forma que Esther Ferrer considera la laguna aumentada formada por los números 13, 14, 15 y 16, después vendría la laguna aumentada 17 y 18, seguida de 19, 20, 21 y 22, y después, 23, 24, 25, 26, 27 y 28.
En esta serie de obras, las celdas de cada laguna aumentada de números primos son tratadas de una forma uniforme, cambiando el tratamiento de una laguna aumentada respecto a la siguiente, de forma alternada. Así, en la obra que se muestra a continuación, también de este grupo de dibujos para suelo que se ha podido ver en la exposición de Tabakalera, las celdas se pintan de rojo o negro en función de la laguna aumentada a la que pertenezcan y cambiando el color de una laguna a la siguiente. Por ejemplo, la celda 1 (que es una laguna de una sola celda) es roja, después la celda 2 (también una laguna solitaria) es negra, la laguna aumentada 3 – 4 tiene sus celdas rojas, mientras que son negras las casillas de la laguna aumentada 5 – 6 y de nuevo rojas las de 7 – 8 – 9 – 10, y así están pintadas de negro o rojo el resto de lagunas aumentadas. Trabajando de esta forma la artista, que ha sido galardonada con el Premio Nacional de Artes Plásticas en 2008 o el Premio Velázquez de Artes Plásticas en 2014, consigue la sorprendente e interesante creación artística que vemos en la siguiente imagen.
 Dibujo para suelo de la serie Poema de los números primos (2016), de Esther Ferrer, realizados en tinta sobre papel cebolla, 83,5 x 59,5 cm, expuesto en Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23, … (Tabakalera, 2019) y perteneciente al archivo personal de la artista. Fotografía: Raúl Ibáñez
Dibujo para suelo de la serie Poema de los números primos (2016), de Esther Ferrer, realizados en tinta sobre papel cebolla, 83,5 x 59,5 cm, expuesto en Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23, … (Tabakalera, 2019) y perteneciente al archivo personal de la artista. Fotografía: Raúl Ibáñez
En cada una de las obras de este grupo particular dentro de la serie Poema de los números primos, Esther Ferrer interviene de forma diferente sobre las lagunas aumentadas de números primos, creando toda una serie de patrones geométricos planos, aunque con una base matemática común, que producen efectos visuales distintos, como puede observarse en las anteriores imágenes.
En la conversación entre Esther Ferrer, Laurence Rassel y Mar Villaespesa con motivo de la exposición Esther Ferrer, todas las variaciones son válidas, incluida esta (Palacio de Velázquez, en el Parque del Retiro de Madrid, Museo Nacional Centro de Arte Reina Sofía, 2017), Laurence Rassel le pregunta a Esther Ferrer “¿Cómo es el proceso de trabajo con los números primos?”, a lo que la artista contesta:
“Primero decido el tipo de soporte y cómo voy a distribuir los números en el espacio, es la base. Luego decido el sistema que define la estructura de la obra, que tiene varios parámetros: si va a ser una obra única o una serie, para poder decidir a partir de qué número empieza, si los números en el espacio se reparten en círculo o en líneas horizontales o verticales, si se emplea color o no, y un largo etcétera. Finalmente decido la forma en que los voy a relacionar, y a partir de ahí me planteo las líneas y el color, si lo hay. Por ejemplo, puedo trabajar los números primos a partir de la espiral de Ulam. Al utilizarla se crea una línea ininterrumpida durante cierta cantidad de números. Me gustó la idea de escribirlos en espiral, como una galaxia, los números primos tienen algo que ver con la estructura del universo; a medida que progresas en la serie hay menos números, el espacio entre ellos se agranda, me gusta ese vacío, es como si la serie se expandiera, como el universo.”
Existen algunas variantes de la distribución de la espiral de Ulam de los números primos de manera que la estructura general de la espiral de los números naturales genera una forma triangular, hexagonal o circular, en lugar de la forma cuadrada de la espiral de Ulam original, o la rectangular utilizada por Esther Ferrer en las obras. La autora de la serie Poema de los números primos se ha interesado por la espiral de Ulam hexagonal, generando toda una familia de obras basada en esta estructura.
Pero antes de hablar de estas obras, me gustaría mencionar lo que podríamos llamar una variante por anticipación, puesto que en el año 1932 (más de treinta años antes de que a Ulam se le ocurriese la idea de la espiral) el herpetólogo, es decir, zoólogo especializado en reptiles y anfibios, estadounidense Laurence Monroe Klauber (1883 – 1968) presentó en el congreso The March Meeting of the Southern California Section de la Asociación Americana de Matemáticas (MAA) una ponencia sobre un triángulo de números naturales en el que se destacaba la distribución de los números primos, y en particular, los generados por el polinomio de Euler n2 + n + 41.
Este triángulo no está generado en espiral, sino distribuyendo los números en orden creciente desde el vértice de arriba y fila a fila, hacia abajo. Es decir, en la primera fila se coloca en 1, en la segunda los números 2, 3 y 4, en la tercera los números del 5 al 9, y así en la fila n-ésima están colocados los números del (n – 1)2 + 1 hasta n2, como en la siguiente imagen.
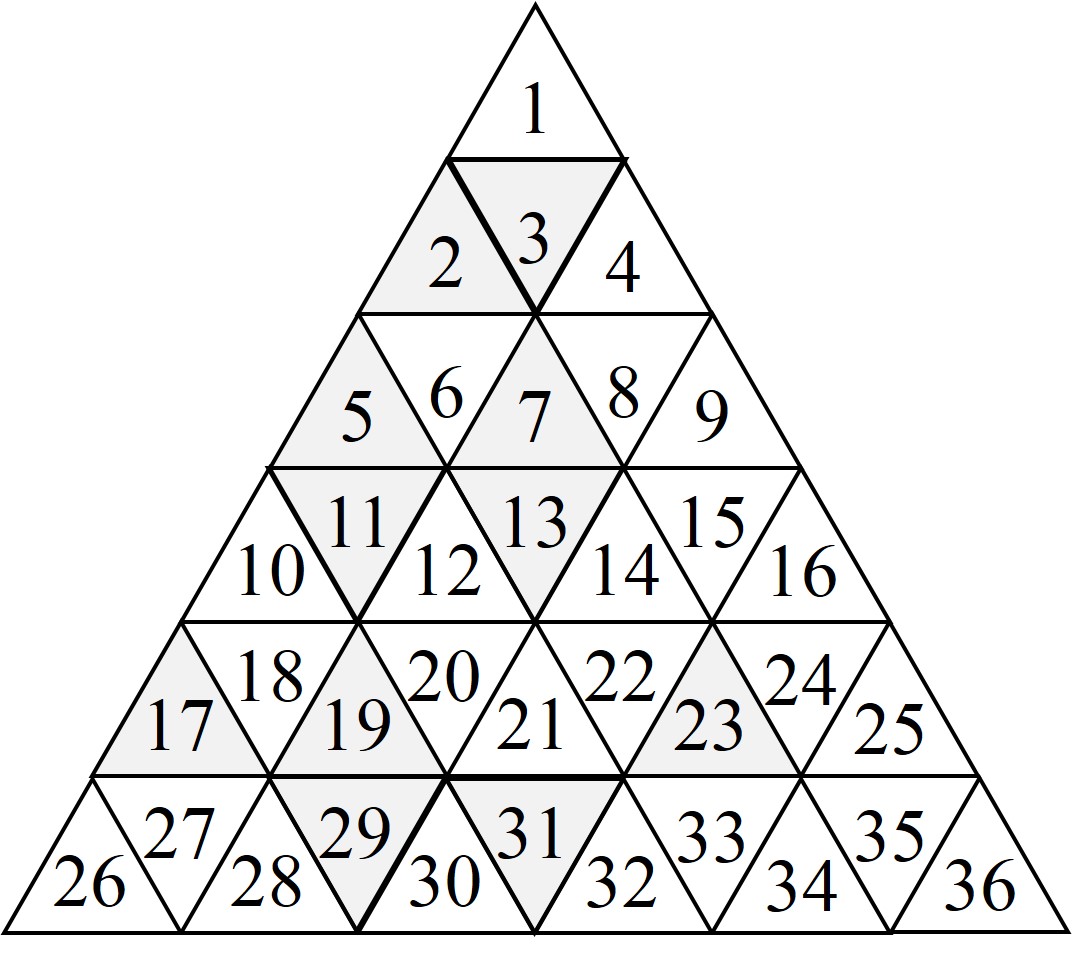
Sobre esa distribución triangular de los números se marcan los números primos. Por ejemplo, en la anterior imagen se ha pintado el triángulo correspondiente al número primo de gris. Al igual que ocurría con la espiral de Ulam, sobre el triángulo numérico de Klauber los polinomios cuadráticos generan números que descansan sobre líneas rectas. En particular, los polinomios de la forma n2 + n + a, para algún número a, son líneas verticales, un ejemplo es el polinomio de Euler.
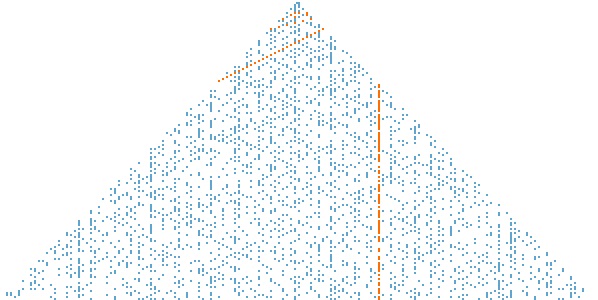 Triángulo de números primos de Klauber, en el cual están marcados como puntos azules los números primos, como puntos naranjas los números primos generados por el polinomio de Euler, n2 + n + 41, y los números no primos no aparecen, están en blanco. Imagen: Will Orrick / Wikimedia Commons
Triángulo de números primos de Klauber, en el cual están marcados como puntos azules los números primos, como puntos naranjas los números primos generados por el polinomio de Euler, n2 + n + 41, y los números no primos no aparecen, están en blanco. Imagen: Will Orrick / Wikimedia Commons
Pero volvamos a la obra artística de Esther Ferrer y a la espiral de Ulam hexagonal. Como en el caso de la espiral de Ulam clásica, en la espiral de Ulam hexagonal, se escriben los números naturales en orden creciente y formando una espiral, sobre una “colmena” o rejilla hexagonal (una especie de cuadrícula, pero formada por hexágonos y cuya forma general es también hexagonal), en cuyo centro hay un hexágono, para el número 1 (o el número inicial), y se van añadiendo filas de hexágonos alrededor del hexágono central, formando la rejilla hexagonal, como se muestra en la imagen de abajo.
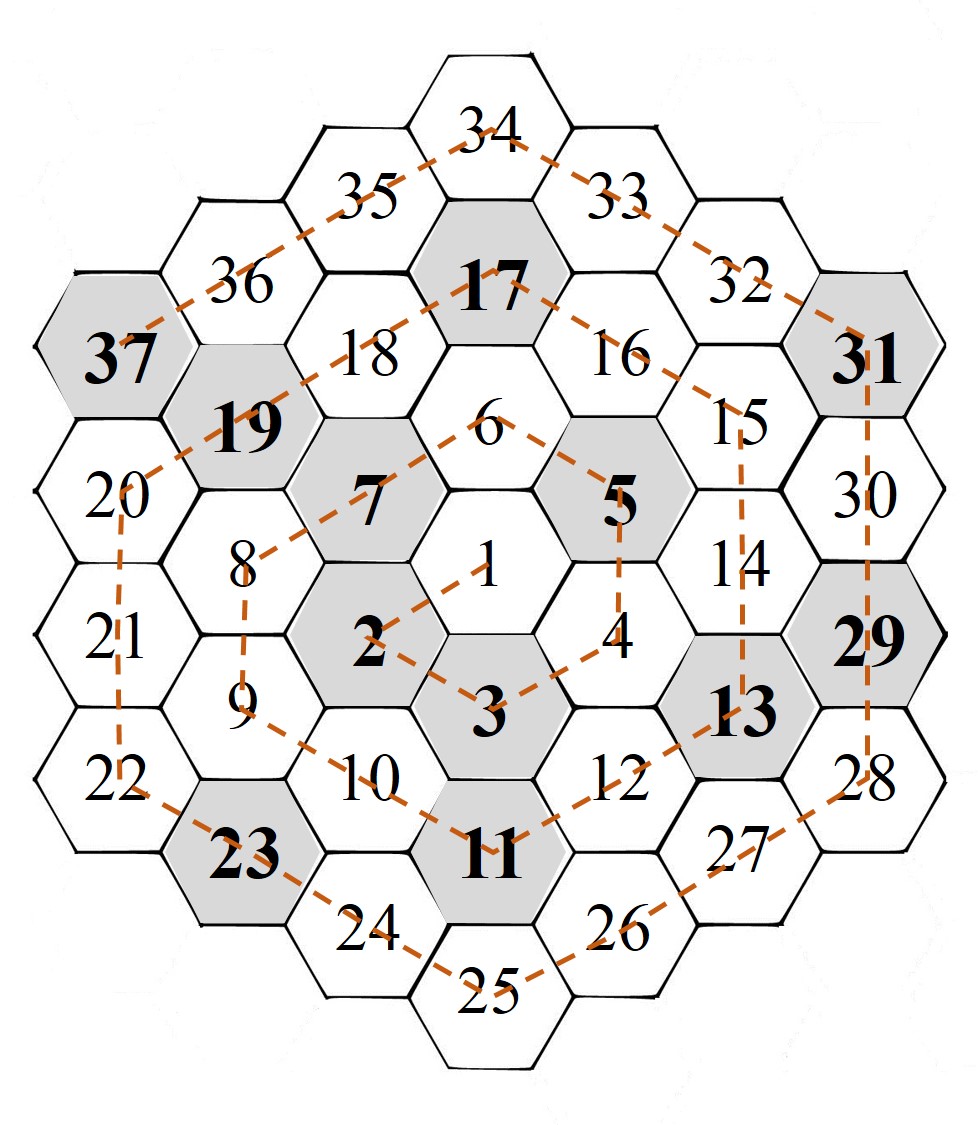 Pequeña espiral de Ulam hexagonal, sobre una retícula hexagonal de lado 4, con los 37 primeros números, marcando en gris las casillas con números primos y señalada la espiral con una línea marrón discontinua
Pequeña espiral de Ulam hexagonal, sobre una retícula hexagonal de lado 4, con los 37 primeros números, marcando en gris las casillas con números primos y señalada la espiral con una línea marrón discontinua
Sin embargo, no es esta la estructura hexagonal en espiral que considera la artista Esther Ferrer, quien trabaja, de hecho, con diferentes estructuras hexagonales en espiral. En la primera de ellas considera una rejilla triangular con forma hexagonal. Empieza en un hexágono central, que está dividido en seis triángulos equiláteros, sobre la que escribe los primeros seis números, y luego continúa escribiendo los números en orden creciente y en espiral sobre los triángulos equiláteros que están alrededor del hexágono central, y que van manteniendo la forma hexagonal del retículo, como se muestra en la imagen siguiente.
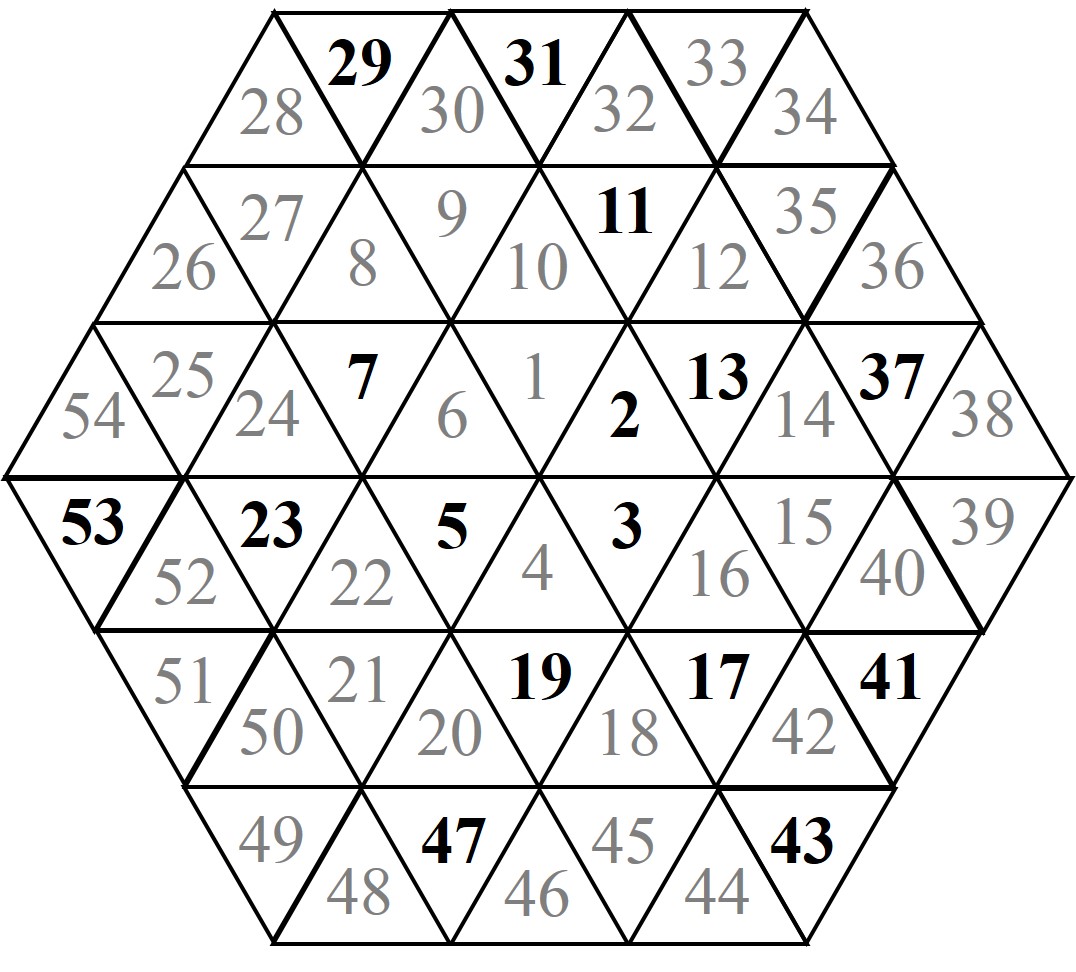 Ejemplo de espiral de tipo Ulam sobre una retícula triangular con forma hexagonal, sobre la que trabaja la artista Esther Ferrer, sobre la que se consideran los números naturales en orden creciente y en espiral, marcando de alguna forma los números primos
Ejemplo de espiral de tipo Ulam sobre una retícula triangular con forma hexagonal, sobre la que trabaja la artista Esther Ferrer, sobre la que se consideran los números naturales en orden creciente y en espiral, marcando de alguna forma los números primos
En la siguiente obra, en la cual se trabaja sobre la anterior estructura reticular, los triángulos se dividen en tres tipos, como ocurría en algunas de las obras que mostramos en la entrada El poema de los números primos, por una parte, están los triángulos que corresponden a números primos, que tienen color blanco y dibujado el correspondiente número primo (hay una excepción, que es la casilla del número 1, la cual se trata en esta obra como si fuese una casilla de un número primo, o podríamos decir como un no compuesto, en blanco y con el número escrito), y el resto de triángulos se corresponden con números no primos, o compuestos, luego en ellos no se dibuja su número y tendrán color rojo o negro en función de la laguna de números primos a la que pertenezca, coloreando las lagunas de rojo o negro de forma alternada, además, estos triángulos de números no primos, rojos o negros, tendrán espesor, altura, creando un relieve en la obra.
 Maqueta de un proyecto de Esther Ferrer, basado en la serie Poema de los números primos (1989). Edición producida por ARTIUM, Centro-Museo Vasco de Arte Contemporáneo, en 2011. Cartón pluma blanco, pintado de rojo con acrílico y cartón pluma negro, ambos de diferentes espesores, cortados a mano en triángulos de 3 cm. y dispuestos sobre una base hexagonal de cartón de 71 x 62 cm aproximadamente
Maqueta de un proyecto de Esther Ferrer, basado en la serie Poema de los números primos (1989). Edición producida por ARTIUM, Centro-Museo Vasco de Arte Contemporáneo, en 2011. Cartón pluma blanco, pintado de rojo con acrílico y cartón pluma negro, ambos de diferentes espesores, cortados a mano en triángulos de 3 cm. y dispuestos sobre una base hexagonal de cartón de 71 x 62 cm aproximadamente
Como en otras obras, la intervención de la artista genera diferentes estructuras geométricas planas. A continuación, se muestran algunas obras que tienen como base la misma estructura espiral de tipo Ulam sobre la retícula triangular con forma hexagonal que acabamos de analizar.
 Dibujo de la serie Poema de los números primos (1986 – 88), sobre una base hexagonal de 22,5 cm. de lado a lado, de la artista Esther Ferrer, realizada con rotulador sobre papel cebolla. Obra expuesta en la Galería Angels Barcelona
Dibujo de la serie Poema de los números primos (1986 – 88), sobre una base hexagonal de 22,5 cm. de lado a lado, de la artista Esther Ferrer, realizada con rotulador sobre papel cebolla. Obra expuesta en la Galería Angels Barcelona
 Dibujo de la serie Poema de los números primos (1986 – 88), sobre una base hexagonal de 23,5 cm. de lado a lado, de la artista Esther Ferrer, realizada con rotulador sobre papel cebolla. Obra expuesta en la Galería Angels Barcelona
Dibujo de la serie Poema de los números primos (1986 – 88), sobre una base hexagonal de 23,5 cm. de lado a lado, de la artista Esther Ferrer, realizada con rotulador sobre papel cebolla. Obra expuesta en la Galería Angels Barcelona
Como en las obras que hemos mostrado en la entrada anterior, El poema de los números primos, con base en la espiral de Ulam, se puede iniciar la espiral en un número distinto al 1, como ocurre en la siguiente obra.
 Dibujo de la serie Poema de los números primos (1986 – 88), sobre una base hexagonal de 27 cm. de lado a lado, de la artista Esther Ferrer, realizada con rotulador sobre papel cebolla. Obra expuesta en la Galería Angels Barcelona.
Dibujo de la serie Poema de los números primos (1986 – 88), sobre una base hexagonal de 27 cm. de lado a lado, de la artista Esther Ferrer, realizada con rotulador sobre papel cebolla. Obra expuesta en la Galería Angels Barcelona.
En otro grupo de obras, Esther Ferrer toma como base la retícula triangular con forma hexagonal descrita anteriormente, pero uniendo cada dos triángulos rectángulos para formar un rombo, creando así una retícula de rombos con forma hexagonal. Sobre esta estructura considera una espiral de tipo Ulam, al escribir los números naturales en orden creciente, cada número sobre un rombo y destacando los números primos. La intervención de la artista da lugar a toda una subfamilia de obras relacionadas con esta estructura, como la que se muestran a continuación.
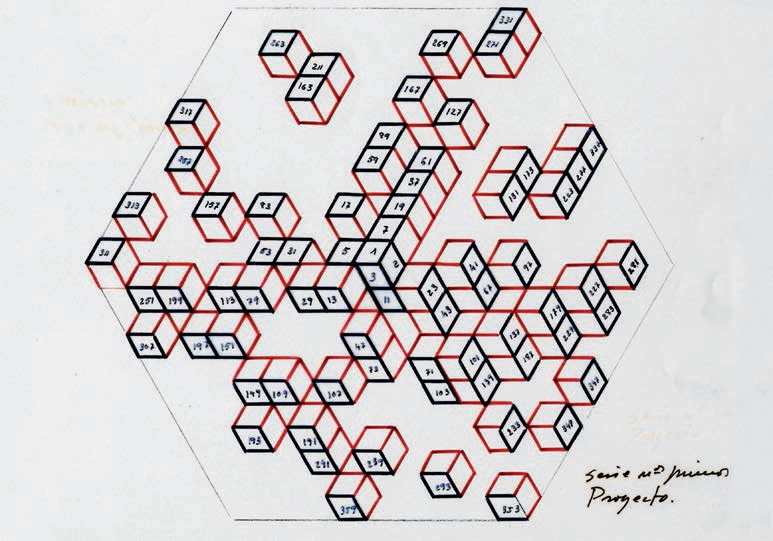 Dibujo de la serie Poema de los números primos (1986 – 88), sobre una base hexagonal, de la artista Esther Ferrer, realizada con rotulador sobre papel cebolla. Obra expuesta en la Galería Angels Barcelona y perteneciente al catálogo Esther Ferrer, todas las variaciones son válidas, incluida esta.
Dibujo de la serie Poema de los números primos (1986 – 88), sobre una base hexagonal, de la artista Esther Ferrer, realizada con rotulador sobre papel cebolla. Obra expuesta en la Galería Angels Barcelona y perteneciente al catálogo Esther Ferrer, todas las variaciones son válidas, incluida esta.
Pero dejemos estas estructuras geométricas hexagonales relacionadas con los números primos, para terminar con una obra relacionada con un tipo especial de números primos, los números primos gemelos. Recordemos que dos números primos son gemelos si están lo más cerca posible, es decir, con tan solo un número par entre ellos, como las parejas 11 y 13, 17 y 19, o 41 y 43. Esther Ferrer también se interesó por estos. De hecho, en la conversación de Esther Ferrer con Laurence Rassel y Mar Villaespesa con motivo de la exposición Esther Ferrer, todas las variaciones son válidas, incluida esta, explica lo siguiente:
“En ese universo, de pronto, aparece un par de números primos gemelos, por ejemplo 11 y 13, 17 y 19, son como los cuerpos celestes que se descubren y no se sabe por qué están ahí. Un amigo ingeniero me envió el número gemelo más grande calculado al ordenador, que entonces tenía 703 dígitos, ahora tiene muchas más cifras. Hice dos cuadros poniéndolos de relieve. Lo curioso es que me interesé en estos números sin pensar en absoluto en mi situación personal: soy gemela, fue una amiga quien me lo señaló.”
Una de las conjeturas sobre los números primos gemelos es que existe un número infinito de parejas de números primos, aunque a día de hoy aún no ha sido posible demostrar esta conjetura. Por este motivo, dentro de la comunidad científica se siguen buscando parejas de números primos gemelos cada vez más grandes. En los años 1980 la pareja más grande conocida de números primos gemelos tenía 703 dígitos. De hecho, en la columna Mathematical Games de Martin Gardner en la revista Scientific American, en diciembre de 1980, menciona este dato y dice que esos dos primos empiezan por 4337 y terminan por 17759 y 17761.
La siguiente obra de Esther Ferrer toma como base esta pareja de números primos gemelos. El número explícito que está en el medio sería el número no primo y par que está entre los dos primos gemelos y que termina en 17760, mientras que a cada lado del mismo están ciertas estructuras geométricas planas generadas a partir de esos dos números primos gemelos.
 Poema de los números primos (años 1980), rotulador e hilo sobre lienzo, 97,5 x 130 cm. Archivo Esther Ferrer y perteneciente al catálogo Esther Ferrer, todas las variaciones son válidas, incluida esta.
Poema de los números primos (años 1980), rotulador e hilo sobre lienzo, 97,5 x 130 cm. Archivo Esther Ferrer y perteneciente al catálogo Esther Ferrer, todas las variaciones son válidas, incluida esta.
Se ha avanzado mucho en la obtención de parejas de números primos gemelos desde entonces. En la actualidad la pareja más grande conocida, descubierta en 2016, está formada por el número primo 2.996.863.034.895 · 21.290.000 – 1 y 2.996.863.034.895 · 21.290.000 + 1, que tienen 388.342 dígitos.
Por último, me gustaría finalizar esta entrada del Cuaderno de Cultura Científica con una frase de Esther Ferrer, que suele citar en muchas ocasiones, la última ha sido en la entrevista que le hicieron en el Diario Vasco con motivo de su exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… en Tabakalera.
“Yo en el arte hago lo que quiero sin más límite que mi responsabilidad”
Así mismo, me gustaría expresar mi más sincero y profundo agradecimiento a Esther Ferrer por permitirme utilizar las imágenes de sus hermosas e interesantes obras en esta publicación, así como por las interesantes conversaciones que hemos mantenido sobre las matemáticas, y en particular, los números primos, en el conjunto de su obra artística.
Bibliografía
1.- Esther Ferrer, Maquetas y dibujos de instalaciones 1970/2011, Exit publicaciones, 2011.
2.- Rosa Olivares (comisaria), Esther Ferrer, Lau mugimenduan/En cuatro movimientos/In four movements, ARTIUM 08/10/2011 – 08/01/2012, Artium y Acción cultural española, 2011.
3.- Laurence Rassel y Mar Villaespesa (comisarias), Esther Ferrer, todas las variaciones son válidas, incluida esta, Palacio de Velázquez del Parque del Retiro 26/07/2017 – 25/02/2018, Museo Nacional Centro de Arte Reina Sofía, 2017.
4.- Página web de Esther Ferrer
5.- Página The Top Twenty: Twin Primes
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El poema de los números primos (2) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:El concepto de estructura atómica
Decíamos al hablar del sistema de periodos que su regularidad, simetría y capacidad predictiva son indicios de que el modelo que explique la estructura de los átomos de los distintos elementos posee también estas características. Y, al hacerlo, dábamos por sentado que los átomos tienen estructura, algo que puede no parecer evidente. Merece la pena detenernos en este punto.
La química en el siglo diecinueve había tenido un éxito más que notable a la hora de explicar las proporciones de combinación de los distintos elementos y en la predicción de reacciones químicas. Tanto es así que buena parte de la revolución industrial fue la revolución químico-industrial. Este éxito terminó convenciendo a la mayoría de los científicos del último cuarto del siglo de que una hipótesis tan fructífera como la atómica indicaba claramente que la materia está compuesta en realidad de átomos. Pero este convencimiento suscitaba inmediatamente una pregunta relacionada: ¿Son los átomos realmente indivisibles, como se había supuesto, o consisten en partículas aún más pequeñas?
La pregunta surge de forma natural a poco que se piense un poco en el sistema de periodos. Recordemos que Mendeléyev había dispuesto los elementos siguiendo los criterios de masa atómica creciente y características químicas. Pero, y esto es importante, la única característica física del ordenamiento, las masas atómicas de los elementos, no pueden explicar las características químicas periódicas.
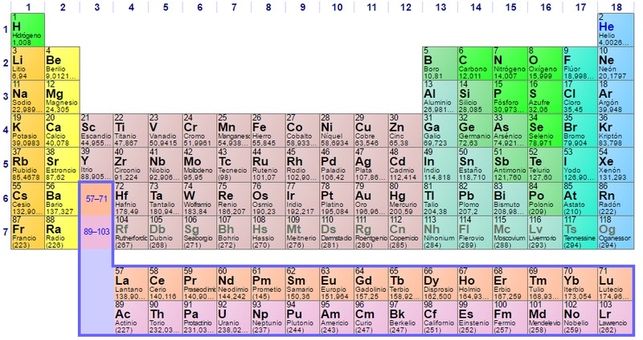
¿Por qué, por ejemplo, los elementos 3 (litio), 11 (socio), 19 (potasio), 37 (rubidio), 55 (cesio) y 87 (francio) [1], con masas atómicas muy diferentes, tienen propiedades químicas similares (por ejemplo, arden, esto es, reaccionan rápida y violentamente, cuando se exponen al aire)? ¿Por qué estas propiedades son algo diferentes de las de los elementos 4 (berilio), 12 (magnesio), 20 (calcio), 38 (estroncio), 56 (bario) y 88 (radio) [2] de la lista (que reaccionan lentamente con el aire o el agua), pero son muy diferentes de las propiedades de los 2 (helio), 10 (neón) ,18 (argón), 36 (kriptón), 54 (xenón) [3] y 86 (radón) (que rara vez se combinan con cualquier otro elemento)?
La periodicidad en las propiedades de los elementos llevó a especular con la idea de que los átomos podrían tener una estructura, que podrían estar formados por piezas más pequeñas. Las propiedades cambian gradualmente de grupo a grupo. Este hecho sugiere que se puede agregar alguna unidad de estructura atómica de un elemento al siguiente, hasta que se complete una cierta porción de la estructura. Esta porción se encontraría completada en el átomo de un gas noble (Grupo 18). En un átomo del siguiente elemento más pesado, se iniciará una nueva parte de la estructura, y así sucesivamente.
Los métodos y técnicas de la química clásica no pudieron proporcionar pruebas experimentales para tal estructura. En el siglo XIX, sin embargo, los descubrimientos y las nuevas técnicas en física abrieron el camino para probar que los átomos en realidad consisten de piezas más pequeñas. [5]
La evidencia se fue acumulando para apoyar la conclusión de que los átomos de diferentes elementos difieren en el número y la disposición de estas piezas.
Notas:
[1] Descubierto por Marguerite Perey en 1939, no estaba en la tabla original de Mendeléyev.
[2] La primera noticia de la existencia del radio es de 1898 y la dieron Marie y Pierre Curie. El aislamiento del elemento se produjo en 1910 por Marie Curie y André-Louis Debierne.
[3] Todos los descubrimientos de los gases nobles son posteriores a la primera publicación del sistema de periodos de Mendeléyev. El primero, el helio, fue descubierto en 1868 como una línea en el esptectro de la cromosfera del Sol. Su aislamiento se produjo en 1897. El resto de elementos del grupo se aislaron entre 1894 y 1910.
[5] La existencia del electrón como unidad de carga eléctrica definido como la carga de un ion monovalente la propuso George Stoney en 1874 (el lo llamó electrolión). Incluso antes Richard Laming, en 1851, ya especuló con que los átomos eran un núcleo de materia rodeado de cargas eléctricas. Pero estos hechos no deben interpretarse como avances en el conocimiento de la estructura de los átomos (véase el título del libro de Laming). Nada hacía prever que la especulación de Laming resultase teniendo base, ni que los electrones fuesen a ser tan importantes. Sería presentismo atribuirles más significación de la que realmente tuvieron. La lógica real se sustenta en el armazón del sistema de periodos, como iremos viendo.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El concepto de estructura atómica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La ley de proporciones definidas y la unidad de masa atómica
- Un método para determinar la estructura átomo a átomo en un cristal
- Construcción de heteroestructuras de grafeno con precisión atómica
Restos de ensayos nucleares del siglo XX en lo más profundo del océano
 Explosión de una bomba nuclear. Fuente: Pixabay
Explosión de una bomba nuclear. Fuente: Pixabay
¿Quién vive en una piña en el fondo del mar? BOB-ES-PON-JA, dirán ustedes. Pues si es así, el pobre Bob y sus amigos están comiendo algunas cosas muy particulares. Entre otras, moléculas de carbono radiactivo liberado a la atmósfera durante algunos de los ensayos nucleares que el mundo vio con expectación y miedo a mediados del siglo XX. Un estudio ha desvelado que restos de aquellos experimentos han llegado ya a lo más profundo del mar, incluida la Fosa de las Marianas.
Que este carbono es parte de los organismos que pueblan la superficie del océano no es algo nuevo. Sabemos desde finales de los años 50 que estos organismos lo han ido incorporando a las moléculas de su cuerpo. Pero esta es la primera vez que se observa cómo crustáceos que viven en la base marina se están alimentando de materia orgánica de los seres vivos de la superficie, y repitiendo el proceso de incorporación del carbono radiactivo. “Las corrientes de circulación oceánicas necesitan cientos de años para conseguir que determinadas moléculas completen este recorrido. La cadena alimenticia lo hace mucho más rápido”, explica Ning Wang, geoquímico de a Academia China de las Ciencias e investigador principal del estudio, publicado en la revista Geophysical Research Letters.
Es un ejemplo de cómo la contaminación humana puede alcanzar casi cualquier punto del planeta, incluso aquellas que parecen más a salvo. “Existe una fuerte interacción biológica entre la superficie y las profundidades, y las actividades humanas pueden impactar incluso a 11.000 metros bajo el agua. Tenemos que tener cuidado con lo que hacemos”, dice otro de los autores, Weidong Sun, en el material publicado al respecto por la American Geophysical Union.
¿De dónde han salido estas partículas radiactivas?
El carbono 14 es un tipo de carbono radiactivo que se produce de forma natural cuando los rayos cósmicos provenientes del espacio interactúan con el nitrógeno de la atmósfera. Es un tipo de carbono menos abundante que el carbono no radiactivo, pero se puede encontrar en prácticamente todos los organismo vivos. De hecho, y puesto que conocemos la velocidad a la que se va descomponiendo, es uno de los métodos que se utiliza para datar muestras geológicas o arqueológicas que incluyan restos biológicos.
 Hirondella gigas, un tipo de anfípodo hallado a 10.900 metros de profundidad en la fosa de las Marianas. Fuente: Wikimedia Commons
Hirondella gigas, un tipo de anfípodo hallado a 10.900 metros de profundidad en la fosa de las Marianas. Fuente: Wikimedia Commons
Las bombas termonucleares que se hicieron explotar en pruebas durante los años 50 y 60 del siglo XX hicieron que se multiplicase la cantidad de carbono 14 presente en la atmósfera cuando los neutrones que liberaron las explosiones reaccionaron con el nitrógeno del aire. Esos niveles alcanzaron su punto álgido a mitad de los años 60 y fueron descendiendo a medida que se terminaron las pruebas nucleares. En los años 90, los niveles en la atmósfera habían descendido hasta quedar en un 20% por encima de los niveles previos a estos ensayos.
¿A dónde fue todo ese carbono 14? Cayó rápidamente y se mezcló con la superficie del océano. Los organismos marinos han ido incorporando estas moléculas a sus células, por lo que los análisis realizados han permitido observar un aumento del carbono 14 en sus cuerpos desde poco después de que comenzasen las pruebas.
La dura vida en el fondo del mar
Vivir en el fondo del mar, en el fondo-fondo, no siempre es fácil. Estamos hablando de lugares a más de 6 kilómetros de profundidad, a menudo en puntos donde una placa tectónica se introduce bajo la de al lado. Hay poca luz, poca temperatura y poca comida y una intensa presión. Las criaturas que viven allí han tenido que adaptarse.
En este estudio, el carbono 14 ha servido para seguir el rastro de la materia orgánica que llega a estos lugares para entender mejor a los organismos que viven allí. Wang y sus colegas han analizado anfípodos (pequeños crustáceos que sobreviven a base de desechos y detritus marino) recogidos durante el año 2017 en la fosa de las Marianas, de Mussau o de New Britain, a profundidades de hasta 11 kilómetros.
 Comparación de la profundidad de la Fosa de las Marianas con la altura del Monte Everest. Fuente: Wikimedia Commons
Comparación de la profundidad de la Fosa de las Marianas con la altura del Monte Everest. Fuente: Wikimedia Commons
Lo sorprendente fue hallar en su tejido muscular niveles de carbono 14 mucho más alto que en otros tipos de materia orgánica encontrada en esos niveles de profundidad bajo el mar. Al analizar después el contenido de su sistema digestivo, los niveles de carbono 14 hallados allí se correspondían con los hallados en muestras de materia orgánica de la superficie del océano. Esto sugiere que los anfípodos seleccionan para alimentarse el detritus y los restos que caen desde la superficie hasta las profundidades marinas.
Esto ayuda a entender mejor la longevidad de muchos de los organismos que viven en el fondo abisal, y cómo se han adaptado con éxito a sus condiciones extremas. Por ejemplo, es llamativo que los anfípodos de estos hábitats son más grandes y viven más tiempo que sus parientes que habitan en aguas menos profundas: de menos de dos años y 20 milímetros a más de 10 años y 91 milímetros.
Los autores sugieren que esta diferencia sea resultado de haber evolucionado exitosamente para vivir a poca temperatura, mucha presión y un aporte de alimento limitado. Para compensar, los animales tienen un metabolismo y un ciclo de renovación celular más lentos, lo que les permite almacenar energía y conservarla durante más tiempo. Por otro lado, al vivir más años, los contaminantes se acumulan en su cuerpo en mayores cantidades.
Pero también hay otro apunte interesante: la materia orgánica que los alimenta no proviene tanto de fuentes locales como serían otros seres vivos con los que conviven allí abajo, sino que parece venir principalmente de las superficie de mar.
Esto debería servir como toque de atención (otro más) a los seres humanos sobre el modo en que lo que hacemos repercute en todos los demás seres vivos del planeta, incluso aquellos que pueblan los lugares más remotos y en apariencia desconectados de nosotros. No lo están, ninguno lo está. Lo que lanzamos al aire hace ahora unos 60 años está alimentando a los pequeños crustáceos del lugar más profundo del mundo. Mucho cuidado con lo que tocamos.
Referencias:
Penetration of Bomb 14C into the Deepest Ocean Trench – Geophysycal Research Letter
Radioactive carbon from nuclear bomb tests found in deep ocean trenches – American Geophysisc Union
Carbono 14 – Wikipedia
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo Restos de ensayos nucleares del siglo XX en lo más profundo del océano se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los enigmas que nos cantan desde el fondo del océano
- Formas moleculares de excreción de restos nitrogenados
- Océanos nucleares. Cuando la basura llega antes que el ser humano
No hay raza blanca, tampoco negra
 Foto: Alexandr Ivanov / Pixabay
Foto: Alexandr Ivanov / Pixabay
Al decir de alguien que es blanco o negro, es posible que pensemos que pertenece a una categoría biológica definida por su color. Mucha gente cree que la pigmentación de la piel refleja la pertenencia a una raza, entendiendo esta como la define la Real Academia Española en su segunda acepción: “cada uno de los grupos en que se subdividen algunas especies biológicas y cuyos caracteres diferenciales se perpetúan por herencia”. Y sin embargo, esa noción, en el caso de nuestra especie, carece de sentido. Porque desde un punto de vista biológico, las razas humanas no existen.
En la piel hay melanocitos, células que producen y contienen pigmentos. Hay dos tipos de pigmentos, llamados genéricamente melanina; uno es marrón parduzco (eumelanina) y el otro, rojo amarillento (feomelanina). El color de la piel depende de la cantidad y la proporción de ambos. Y se da la circunstancia de que ese rasgo depende de diferentes genes; unos inciden en la cantidad de pigmento en los melanocitos y otros sobre la proporción entre los dos tipos de melanina. Es más, colores muy similares puede ser el resultado de diferentes combinaciones de esos rasgos básicos y obedecer a configuraciones genéticas diferentes.
Los africanos, en general, son de piel oscura. Los Dinka, de África oriental, la tienen muy oscura, mientras que los San, del sur del continente, la tienen más clara. Los nativos del sur de la India, Nueva Guinea y Australia también son de piel oscura. En el centro de Asia y extremo oriente, así como en Europa, las pieles son, en general, claras. Y los nativos americanos las tienen de diferente color, aunque no tan oscuras como los africanos.
Si nos atenemos al color de la piel escondida bajo el grueso pelaje de los chimpancés, lo más probable es que nuestros antepasados homininos la tuviesen clara. En algún momento hace alrededor de dos millones de años, los miembros de nuestro linaje vieron reducido el grosor y consistencia del pelaje, hasta convertirse en una tenue capa de vello en gran parte de la superficie corporal. Pero esa transformación trajo consigo la exposición de la piel a la radiación solar ultravioleta, que podía causar cáncer y, además, eliminar una sustancia de gran importancia fisiológica, el ácido fólico. Seguramente por esa razón se seleccionaron variantes genéticas que oscurecían la piel, porque la melanina la protege evitando los daños citados.
Los seres humanos nos hemos expandido y llegado así a casi todas las latitudes. Esos movimientos han expuesto la piel de sus protagonistas a muy diferentes condiciones de radiación. Y al igual que un exceso de radiación ultravioleta puede ser muy dañino, su defecto también lo es, pues sin ella no se puede sintetizar vitamina D, cuyo déficit provoca raquitismo y otros problemas de salud. Por esa razón, sin descartar otras posibles, la piel humana se ha ido aclarando en diferentes zonas geográficas bajo la acción de la selección natural. Además, los movimientos de población han propiciado la mezcla de distintos linajes, cada uno con sus rasgos genéticos y características pigmentarias, para dar lugar a múltiples configuraciones.
El color de los seres humanos actuales es el resultado, por tanto, de una compleja secuencia de eventos biológicos y demográficos, y no es posible delimitar biológicamente unos grupos y otros. Las diferencias en el color de la piel no tienen correspondencia en innumerables otros rasgos que también varían y lo hacen según otros patrones y por efecto de otras presiones selectivas. No hay, pues, fundamento para invocar la existencia de razas. Como tampoco lo hay para justificar, sobre bases inexistentes, otras diferencias.
——————-
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo No hay raza blanca, tampoco negra se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- 11 años después de la marea negra
- Un punto cuántico emite luz blanca gracias a la aspirina
- Desvelado el misterio de la Gran Mancha Blanca de Saturno
¿Afecta el sexo a los síntomas de una enfermedad?
¿Afecta el sexo a los síntomas de una enfermedad? La Fundación Española del Corazón (FEC) afirma que “los síntomas del infarto agudo de miocardio y la percepción de estos se presentan de diferente modo dependiendo del sexo de la persona que lo sufra”. A pesar de que mujeres y hombres comparten los síntomas típicos, la enfermedad cardiovascular en la mujer es diferente en muchos aspectos respecto al hombre y puede cursar con síntomas distintos, los llamados atípicos, que en muchos casos tanto las propias mujeres como las y los profesionales médicos que las atienden no están acostumbrados a tener en cuenta. Esto es así debido a que, tradicionalmente, se han aceptado como propios y únicos en ambos sexos los síntomas comunes.
Los vídeos de ¿Preguntas frecuentes? presentan de forma breve y amena cuestiones que, probablemente, nos hayamos planteado en alguna ocasión. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.
Edición realizada por César Tomé López
El artículo ¿Afecta el sexo a los síntomas de una enfermedad? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La ecología de una enfermedad
- ¿Podría un humano vivir en el mar?
- Prevenir y tratar la enfermedad de Alzheimer: Una visión moderna
CSI Bilbao: entomología forense
La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebra dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Publicamos en el Cuaderno de Cultura Científica y en Zientzia Kaiera una serie de artículos que narran algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas.

 Foto: Strikers / Pixabay
Foto: Strikers / Pixabay
Desde que en 1235, el magistrado chino Sung Tz’u de la Dinastía Song incriminara por vez primera a un asesino gracias a la colaboración de moscardones, la entomología forense ha ido implantándose y perfeccionando sus técnicas en el mundo occidental. Pasarían siglos hasta que un médico militar francés Jean Pierre Mégnin registrara meticulosamente los artrópodos que encontraba en restos cadavéricos (Faune des Tombeaux, 1887) de forma ordenada y sistemática, organizados en lo que llamó “escuadrones de la muerte”. Así, en su obra La faune des cadavres. Application de l’entomologie à la médecine légale (Masson-Gauthier Villars Ed.,1894) nos muestra el primer modelo de sucesión ecológica aplicado a la investigación forense. En los albores de la Ecología como disciplina científica, el Dr. Mégnin demostró como un cadáver se comporta como una isla, con una fauna que le es propia y diferente de los ecosistemas circundantes. Por ello, aunque se intente ocultar un crimen o confundir a los inspectores trasladándolo a otro lugar, es posible demostrar el lugar donde ha sido asesinada una persona o cualquier otra especie animal, cuando se cometió el crimen, y realizar el seguimiento de mercancía que se introduce legal o ilegalmente en nuestro país.
Así, la entomología forense va más allá de lo que nos muestran series televisivas famosas como CSI o Bones y nos permite aplicar nuestros conocimientos para ayudar a empresas y a agentes a de aduanas a determinar el origen de la contaminación de una determinada mercancía, a diagnosticar comportamientos negligentes ante la presencia de larvas miásicas, piojos y otras especies en el cuerpo de pacientes y otras personas dependientes, etc. Incluso podemos demostrar si una persona sospechosa estuvo o no en un lugar donde se cometió el crimen dado que muscas especies de artrópodos se encuentran sólo en hábitats muy particulares y un pequeño ácaro, sus picaduras o fragmentos del cuerpo nos pueden permitir conectarle con un lugar específico. Para ello, necesitamos conocer en profundidad que especies de artrópodos habitan en nuestra región, como se distribuyen, que condiciones ambientales requieren, en que periodos del año están activos, como son sus ciclos, cuanto duran, etc. algo que resulta difícil de abordar sabiendo que más de las tres cuartas partes de los animales conocidos son artrópodos y que al igual que el resto de invertebrados dependen de la temperatura exterior para desarrollarse y factores como la duración de los días pueden condicionar su capacidad reproductora.
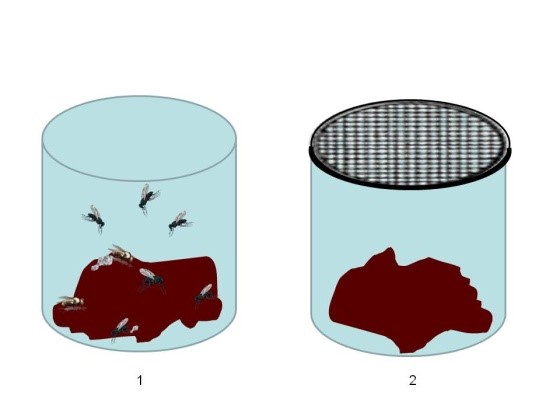 Figura 1. Experimento de Francesco Redi (1626-1697) donde se demuestra la falacia de la generación espontánea. A) Los botes sin tapar permiten el acceso de insectos que depositan sus huevos y, en pocas horas las larvas nacen y devoran los restos. B) Los botes debidamente tapados no permiten el acceso de los insectos y la carne permanece incorrupta.
Figura 1. Experimento de Francesco Redi (1626-1697) donde se demuestra la falacia de la generación espontánea. A) Los botes sin tapar permiten el acceso de insectos que depositan sus huevos y, en pocas horas las larvas nacen y devoran los restos. B) Los botes debidamente tapados no permiten el acceso de los insectos y la carne permanece incorrupta.
La relación entre los cadáveres y los insectos es conocido desde antiguo. De hecho, muchas culturas desarrollaron técnicas para impedir que los insectos deterioraran los restos de sus seres queridos o adorados. Es más, no sólo los egipcios embalsamaban los cuerpos de los muertos para evitar que otros organismos degradaran el cuerpo durante el viaje al más allá. También encontramos momias de culturas mayas, guanches y de pueblos asiáticos. Los vikingos incineraban los cuerpos y, con el tiempo, la gran mayoría de las culturas hemos enterrado los restos de nuestros seres queridos para evitar que los insectos los devoren. Aun así, no serán las mismas moscas necrófagas que llegaron a la hoz las que colonicen el cadáver sino otras especies capaces de detectar y hasta de descender varios metros bajo tierra hasta invadir cadáveres enterrados.
Concepto
La entomología forense es una disciplina que aplica el conocimiento adquirido sobre la biología, la estructura y la dinámica de las comunidades de artrópodos en la resolución de problemas civiles y casos criminales. Las muestras entomológicas recolectadas podrán ser empleadas como pruebas ante un Tribunal de Justicia, por lo que deberán ser adecuadamente conservadas y custodiadas hasta el requerimiento de la autoridad judicial competente.
Un error en la identificación, o una aplicación inadecuada de datos publicados, puede suponer un error en las conclusiones y, en consecuencia, la incriminación por error de una persona inocente. Por las consecuencias que derivan de una mala investigación, el trabajo debe ser llevado a cabo por personas competentes, debidamente formadas con adecuados conocimientos sobre la biología y dinámica de las especies involucradas. Por la complejidad de las comunidades de artrópodos, con frecuencia se requiere de la colaboración de diferentes expertos en los diversos grupos de artrópodos que sean recolectados durante la investigación pericial. Es más, sin un debido entrenamiento, determinados artrópodos o algunas de sus fases pueden pasar desapercibidos e incurrir en errores que irán acumulándose a lo largo de la investigación posterior. Por ello, es imprescindible el desarrollo de habilidades específicas para la adecuada aplicación de la entomología a la ciencia forense.
Método de trabajo
Uno de los aspectos fundamentales de toda investigación forense, es la relación indubitada entre la prueba y los hechos a investigar. Por ello, es fundamental establecer un protocolo minucioso de actuación que permita asociar sin ningún lugar a dudas la muestra del artrópodo con el caso a investigar. En el caso concreto de la entomología forense, existe el problema añadido de que la “prueba”, esto es el insecto, se ha podido ver naturalmente modificada a lo largo de la investigación dado que puede ser necesario criarla hasta alcanzar su estado adulto; por ejemplo, para estimar su edad con precisión, o para identificar la especie correctamente. Con frecuencia, la identificación específica sólo es posible con ejemplares adultos dado que éstos poseen las estructuras sexuales que permiten la identificación indubitada de la especie. Por ello, en el procedimiento a seguir es fundamental tener en consideración si va a ser necesario realizar cría en condiciones controladas de una parte de población para obtener ejemplares adultos que permitan una correcta identificación de la especie. Centraremos las explicaciones en casos de investigación criminal, dado que los métodos no difieren en los procedimientos civiles (tráfico de mercancías, mobiliario o inmuebles dañados, etc.) y requieren de mayor cuidado en el proceso, dadas las consecuencias que derivan de dicha investigación.
Los procedimientos a seguir difieren dependiendo del estado de descomposición del cadáver. En casos de fallecimiento reciente, el cadáver presentará abundancia de larvas en crecimiento que se alimentan de los restos cadavéricos hasta finalizar su desarrollo larvario. Corresponden a los huevos depositados por los primeros insectos en llegar al cadáver, habitualmente moscas califóridas, sarcofágidos o múscidos. Estas moscas son capaces de detectar el cadáver a varios kilómetros de distancia y, por su excelente capacidad de vuelo, llegar a éste en cuestión de minutos. Una vez lo localizan, si son hembras grávidas (ha habido cópula y los huevos están fecundados), depositarán inmediatamente huevos con clara preferencia por las cavidades naturales (boca, ojos, nariz, ano, etc). Sólo cuando las cavidades están saturadas, continúan depositando huevos sobre la piel, las prendas, el suelo, etc. De dichos huevos nacerán unas larvas diminutas que pueden pasar desapercibidas si no se inspecciona adecuadamente el cadáver. A lo largo de los días sucesivos irán comiendo y creciendo a velocidades vertiginosas si las condiciones ambientales son adecuadas, hasta alcanzar su máxima longitud en pocos días, momento en que abandonan la fuente de alimentación para pasar a la siguiente fase, la pupa, donde tiene lugar la metamorfosis y de la que emergerá una mosca que iniciará de nuevo el ciclo (fig. 2)
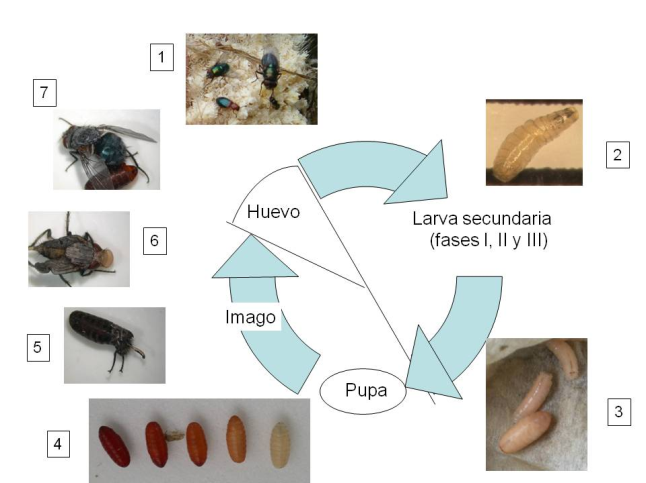 Figura 2. Ciclo biológico de una mosca caifórida. 1) masa de huevos sobre restos animales, con moscas y escarabajos depredadores de sus huevos. 2) Larva recién nacida en fase I de desarrollo. 3) Larvas migratorias junto a una prepupa. 4) prepupa y pupas de diferente edad. 5) imago intentando emerger del pupario; en ocasiones, hay dificultades para salir del pupario y el imago fallece o es inmediatamente depredado por un insectívoro; imago recién emergido donde se aprecia el ptilinum empleado para romper el pupario y salir de su escondite, y la ausencia de alas, las cuales se limitan a pequeños esbozos sobre el abdomen. Una vez extendidas las alas y endurecida la cutícula, la mosca habrá adquirido su color definitivo y podrá iniciar el desarrollo y maduración del aparato reproductor, alcanzando la categoría de adulto s.s. 7) Adulto debidamente conformado y apto para emprender el vuelo y localizar una pareja.
Figura 2. Ciclo biológico de una mosca caifórida. 1) masa de huevos sobre restos animales, con moscas y escarabajos depredadores de sus huevos. 2) Larva recién nacida en fase I de desarrollo. 3) Larvas migratorias junto a una prepupa. 4) prepupa y pupas de diferente edad. 5) imago intentando emerger del pupario; en ocasiones, hay dificultades para salir del pupario y el imago fallece o es inmediatamente depredado por un insectívoro; imago recién emergido donde se aprecia el ptilinum empleado para romper el pupario y salir de su escondite, y la ausencia de alas, las cuales se limitan a pequeños esbozos sobre el abdomen. Una vez extendidas las alas y endurecida la cutícula, la mosca habrá adquirido su color definitivo y podrá iniciar el desarrollo y maduración del aparato reproductor, alcanzando la categoría de adulto s.s. 7) Adulto debidamente conformado y apto para emprender el vuelo y localizar una pareja.
En cadáveres en avanzado estado de descomposición, cuando las primeras larvas finalizaron el desarrollo y abandonaron el cadáver, es fundamental fijar nuestra atención en otras especies de artrópodos que han ido llegando después de que las primeras moscas depositaran los primeros huevos. El proceso sigue un modelo similar a otras pautas de colonización de nuevos ambientes, donde especies pioneras modificaron el entorno permitiendo el asentamiento de nuevas especies que van definiendo un modelo específico de sucesión faunística. A los necrófagos les seguirán depredadores, parasitoides, etc. que nos permitirán realizar estimaciones muy precisas de la edad del entono cadavérico. Sólo una adecuada recogida de todos los artrópodos presentes en torno al cadáver y su correcta identificación específica aseguraran una estimación fiable del periodo de actividad de los insectos (PAI) que nos permitan adecuarlo a la estimación del intervalo postmortem (IPM).
Desde el año 2003, el grupo de investigación consolidado BIOMICS4 de la Universidad del País Vasco / Euskal Herriko Unibertsitatea (UPV/EHU) está sentando las bases para el correcto desarrollo de esta disciplina en la Comunidad Autónoma del País Vasco, elaborando mapas de distribución de las principales especies de califóridos5, sus patrones de desarrollo6 en presencia y ausencia de parasitoides, modelos de sucesión faunística7, caracterización molecular de insectos necrófagos y miásicos8,9, y colaborado en el esclarecimiento de diferentes casos10,11, tanto criminales como civiles12.
Referencias:
1Ci, S. (1247) The Washing Away of Wrongs. en B.E. en McKnight. (1981) The Washing Away of Wrongs: Forensic Medicine in Thirteenth-Century China. Science, medicine, and technology in East Asia, v. 1. Ann Arbor: Center for Chinese Studies, University of Michigan.
2Megnin, J.P. (1887) Faune des Tombeaux.Ed. Gauthier Villars.
3Megnin, J.P. (1894) La faune des cadavres application de l’entomologie à la médecine légale. Ed. Masson.
4Universidad del País Vasco / Euskal Herriko Unibertsitatea (UPV/EHU). Biomics Research group. http://www.biomics.es.
5M. Saloña, J. Moneo, B. Díaz. 2009. Estudio sobre la distribución de califóridos en la Comunidad Autónoma del País Vasco Boletín de la Asociación Española de Entomología, 33 (1-2): 63-89
6Diaz Martín B., A. López Rodríguez y M. I. Saloña Bordas. 2013. Primeros resultados sobre desarrollo de Calliphora vicina (Diptera, Calliphoridae) bajo condiciones controladas de temperatura. Ciencia Forense, 11-12 (en prensa)
7Morales Rayo J., G. San Martín Peral y M. I. Saloña Bordas. 2013. Primer estudio sobre la reducción cadavérica en condiciones sumergidas en la Península Ibérica, empleando un modelo de cerdo doméstico (Sus scrofa L., 1758) en el Río Manzanares (Comunidad Autónoma de Madrid). Ciencia Forense, 11-12 (en prensa)
8 Pancorbo M. M., A. Castro, I. Fernández-Fernández, N. Cuevas, M. Castillo, M. Saloña. 2004. Entomología molecular forense. Ciencia Forense 8: 107-130
9GilArriortua M, M.I. Saloña Bordas, L.M. Cainé, F. Pinheiro & M.M. de Pancorbo. 2013. Cytochrome b as a useful tool for the identification of blowflies of forensic interest (Diptera, Calliphoridae). Forensic Science International, 228(1–3): 132-136.
10Saloña M.I., Mª L. Moraza, M. Carles-Tolrá, V. Iraola, P. Bahillo, T. Yélamos, R. Outerelo y R. Alcaraz. Searching the soil. Report about the importance of the edaphic fauna after the removal of a corpse. Journal of Forensic Sciences 55(6): 1652-1655.
10Martínez-Sánchez A., C. Magaña, M. Saloña, & S. Rojo. First record of Hermetia illucens (Diptera: Stratiomyidae) on human corpses in Iberian Peninsula. Forensic Science International, 206 (1-3): e76-e78.
11Saloña M. 2005. Forensic Entomology besides corpses and morgues. 2 new cases reported from the Basque Country (N. Spain). 3d meeting of the European Association for Forensic Entomology EAFE, Laussanne.
Sobre la autora: Marta Saloña es profesora del departamento de Zoología y Biología Celular Animal de la Facultad de Ciencia y Tecnología y asesora científica del Servicio de Entomología Forense (SGIKER) de la UPV/EHU.
El artículo CSI Bilbao: entomología forense se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- A new hero is born: La espectrometría de masas al servicio de la justicia
- En busca del compuesto perdido
- Los biólogos de la UPV/EHU y la conservación de la naturaleza
Por qué unos países apuestan por la energía nuclear mientras otros la arrinconan
![]()
 Unsplash, CC BY-SA
Unsplash, CC BY-SA
¿Por qué unas tecnologías son polémicas mientras que otras se adoptan sin más? Quienes no comprenden que algunos avances provoquen recelos en la sociedad expresan su sorpresa argumentando que “la tecnología no tiene ideología”. Aunque aceptásemos esa premisa, es imposible obviar que los grupos, instituciones y personas que promueven una opción tecnológica sí que la tienen.
Las tecnologías no se instalan en el vacío, sino que se insertan en una sociedad concreta en un momento concreto. Este contexto social determina que tenga (o no) una recepción parecida en distintas sociedades.
Por otro lado, cada tecnología tiene un potencial distinto para alterar el tejido social y los modos de vida, generar interés o preocupación, crear negocios o provocar la desaparición de otros. En suma, tecnología y sociedad interactúan y se transforman de forma mutua.
Esa es la pregunta que el proyecto History of Nuclear Energy and Society (HoNESt) quiere responder en el ámbito de la energía nuclear en Europa. Se trata de un consorcio de 25 instituciones de quince países europeos financiado por el programa de la UE Horizonte 2020 y Euratom.
Del sí de Francia al no de Austria
La energía nuclear tiene niveles de aceptación muy diferentes en Europa. El viejo continente alberga algunos de los países con más energía nuclear producida, tanto en términos absolutos (Francia) como relativos (Eslovaquia, Hungría, Bélgica, Suecia…).
También incluye países que optaron pronto por no implantarla (Austria, Dinamarca, Portugal), otros que contuvieron su expansión (España) o planificaron su abandono (Alemania). Incluso cuenta con el único caso en el mundo de un país que cerró sus nucleares de golpe, después de más de veinte años (Italia).
Mientras tanto, Francia sigue apostando por la energía nuclear. Reino Unido, Hungría, Polonia y Bulgaria tienen proyectos en activo para construir nuevas centrales. Este no es un tema controvertido del pasado: forma parte del presente y lo será del futuro. ¿Qué hace tan diferentes las reacciones de las sociedades europeas con respecto a la energía nuclear?
Al comparar los distintos casos europeos, HoNESt trata de comprender las motivaciones, formas de participación, actores involucrados, contexto económico y sociopolítico y cómo fueron de exitosos para los grupos de interés (es decir, quién se beneficia y cómo).
En general, con alguna excepción, hemos observado una falta de interacción entre los actores sociales sobre temas sensibles y éticos provocados por el cambio tecnológico. Históricamente, las estrategias gubernamentales e industriales de “limitación de la información” han permitido el éxito a corto plazo, pero han sido ineficaces para asegurar el apoyo social y ganar la confianza de la sociedad a largo plazo.
En la implantación de la energía nuclear, como de otras muchas tecnologías, los promotores optaron con frecuencia por enfoques del tipo “decidir-anunciar-defender”, donde la falta de participación democrática crea la sensación, potencialmente legítima, de ausencia de justicia energética. En contraste, las oportunidades para debatir, deliberar y participar en un diálogo más abierto conducen, según la literatura de ciencias sociales y los casos nacionales que manejamos en HoNESt, a una gobernanza energética más constructiva y sostenible en el tiempo.
La importancia de la honestidad
La falta de honestidad, las restricciones en el acceso a la información y la dejadez frente a las preocupaciones y prioridades de los ciudadanos han sido identificadas en nuestro análisis comparativo como factores de protección a corto plazo contra las polémicas sociotecnológicas. Pero también son las semillas de dificultades seguras a largo plazo.
Los análisis de los investigadores de HoNESt también destacan que el apoyo y la oposición a la energía nuclear, tanto de los ciudadanos como de los gobiernos, es dinámico. Las preferencias cambian según las condiciones ambientales, sociales y económicas. Como resultado, lo que se percibe como exitoso con respecto al avance tecnológico en un momento puede pasar a percibirse como un estruendoso fracaso años más tarde, y viceversa.
Los posicionamientos sobre la energía nuclear varían también en función del momento histórico y del contexto en el que se produjeron. En Europa del sur y central la izquierda ha tendido a posicionarse en contra. Sin embargo, en Europa del este es la derecha liberal y proeuropea la que con más vehemencia se ha opuesto.
Esto no es más que el reflejo de lo que advertíamos al comienzo: las tecnologías no se insertan en el vacío. En cada país, las alianzas que se configuran para promover una cierta opción tecnológica condicionan qué grupos se posicionarán en sentido opuesto.
Los aspectos industriales y económicos también han desempeñado un papel importante en el desarrollo nuclear. Poner el foco únicamente sobre tales objetivos, por encima de los de justicia social y participación pública, arriesga la legitimidad democrática de tales desarrollos. También la eficacia de la interacción civil-nuclear y las respuestas de la sociedad a la tecnología en el largo plazo. La equidad en los procesos que resuelven disputas y asignan recursos deben estar presentes si el objetivo es obtener una gobernanza energética responsable y duradera.![]()
Sobre la autora: Mar Rubio Varas es responsable de la Secretaría Científica de HoNESt, profesora titular de Historia e Instituciones Económicas e investigadora del Institute for Advanced Research in Business and Economics (INARBE) de la Universidad Pública de Navarra
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Por qué unos países apuestan por la energía nuclear mientras otros la arrinconan se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una fórmula para dominarlos a todos: La conservación de la energía y la ley de la palanca
- La fusión nuclear como fuente de neutrones eficiente
- No hay renacimiento nuclear
El sorprendente caso de la nota invisible
Una estudiante, a quien el Dr. Goldovsky describe como “técnicamente competente pero mala lectora”, preparó un Capriccio de Brahms (Op.76, No.2) para ensayarlo durante la clase. Empezó a tocar la pieza del tirón pero, al llegar al acorde de Do sostenido Mayor, 42 compases antes del final, tocó un sol natural en lugar de un sol sostenido (que sería lo apropiado en un acorde mayor). Goldovsky le pidió que parara para corregir el error pero la estudiante le miró confusa: decía haber tocado lo que estaba escrito. Para sorpresa de Goldovsky, la joven tenía razón. Ella había interpretado exactamente lo que ponía en la partitura -errata incluida.
La anécdota la relata el flautista y psicólogo Thomas Wolf en un artículo sobre lo que se conoce como lectura musical a primera vista1 . Al parecer, la nota falsa estaba presente en todas las ediciones disponibles de la partitura pero había viajado inadvertida, de copia en copia durante un siglo, ante la mirada atenta de cientos de pianistas. Ninguno de ellos había sido capaz de verla, ni siquiera los doce conejillos de indias a quienes, más tarde, Goldovsky pidió explícitamente encontrarla.
Lo curioso de esta historia es que fue, precisamente, una mala lectora, la única capaz de leer con precisión la música escrita. Los músicos expertos consiguen leer a mayor velocidad gracias a todo un conocimiento implícito del contexto musical que les permite detectar automáticamente ciertos patrones. La estudiante, en cambio, careciendo de las expectativas que acompañan a los lectores con más experiencia, requería una cantidad mayor de información procedente de la partitura y de esta manera, paradójicamente, su interpretación era la más fiel al papel.
Si eres músico y, a estas alturas, te quema la curiosidad, te invito a buscar la errata en esta versión animada de la partitura de Brahms, o en su primera edición. Al cabo de un rato, y antes de que te quedes bizco, aquí tienes una pista: minuto 1’44’’.

Si no eres músico, te propongo un experimento parecido. Quiero que cuentes cuántas letras “F” aparecen en la siguiente oración, lo más rápido que puedas (puedes hacerlo despacio, si quieres, pero entonces pierde la gracia):
-
FINISHED FILES ARE
THE RESULT OF YEARS
OF SCIENTIFIC STUDY COMBINED
WITH THE EXPERIENCE OF YEARS
Si eres bilingüe o sueles leer con fluidez en inglés, quizás hayas contado unas tres o cuatro “F”. En cambio, si el inglés no es una lengua que domines especialmente (si eres un “mal” lector en comparación con alguien nativo, pongamos), probablemente hayas conseguido ver las 6 F que, de hecho, hay. El motivo es que los lectores nativos omiten los tres “of” presentes en la frase. Simplemente, no los ven.
Cuando pensamos en palabras o en frases, de hecho, solemos centrarnos en los nombres, verbos y adjetivos que portan casi toda la carga semántica. El resto son las “palabras invisibles” de las que habla Itziar Laka en esta maravillosa charla de Naukas 14 (la que inspira el presente artículo): preposiciones, nexos, sufijos, morfemas… pequeñas partículas en las que, a menudo, ni siquiera reparamos y que sin embargo, caracterizan por completo un idioma; sostienen, como tornillos en las cornisas de un enorme castillo, toda su gramática.
Cuenta también Laka que las palabras invisibles son las más frecuentes de una lengua, son las que el español suene a español, son las que dan forma a los patrones subyacentes en una lengua, patrones que detectamos, aun sin saber que los estamos detectando, desde que somos apenas bebés (la charla es una delicia, os recomiendo encarecidamente verla).
La música, como el lenguaje, está también llena de “notas inaudibles”. Son notas que no brillan necesariamente en la melodía, las notas que nadie canta, las notas que nos dejamos en el fondo de la memoria cada vez que recreamos nuestro tema pop preferido en la ducha. Pero están ahí, presentes, formando eso que se conoce como “armonía” y que es la verdadera gramática del lenguaje de la música.
Desde 1871, a 43 compases del final del segundo Capriccio op. 76 de Brahms, hay una nota falsa que nadie ve. Sabemos que es una nota falsa por mucho que Brahms la escribiera, por mucho que su editor, su copista y cien años de pianistas la pasasen de largo: reconocemos el error porque armónicamente no tiene sentido. La nota vive escondida, haciéndose pasar por un morfema del acorde de Do sostenido Mayor al que verdaderamente pertenece. Cuando los músicos pasan por ella, entienden su función gramatical por el contexto, entonan la melodía y siguen.
Referencia:
1Thomas Wolf, “A Cognitive Model of Musical Sight-Reading,” Journal of Psycholinguistic Research, April 1976. https://www.researchgate.net/publication/225262636_A_cognitive_model_of_sight-reading
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo El sorprendente caso de la nota invisible se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #Naukas14 El sorprendente caso de las palabras invisibles
- La sorprendente densidad ósea de los atletas kenianos
- El sorprendente penacho de Marte
La sucesión de Levine
Neil James Sloane (1939) es un matemático que ha trabajado en combinatoria, en códigos correctores de errores y en el problema de empaquetamiento de esferas. Pero es sobre todo conocido por la creación y el mantenimiento de la magnífica página On-Line Encyclopedia of Integer Sequences (Enciclopedia On-Line de las Sucesiones de Números Enteros, OEIS por sus siglas en inglés), una base de datos que cataloga sucesiones de números enteros. Para cada sucesión registrada en este repositorio se incluyen sus primeros términos, la manera en la que se genera, sus propiedades matemáticas, su interés y enlaces a artículos que hablan de ella.
 Neil Sloane. Imagen: Wikimedia Commons.
Neil Sloane. Imagen: Wikimedia Commons.
Sloane empezó a recopilar estas sucesiones de enteros en 1964 debido a sus trabajos en combinatoria. Tras publicar un par de libros sobre el tema, muchas personas comenzaron a enviarle ejemplos de sucesiones que él no había seleccionado. Era tal cantidad de propuestas que recibía que, a partir de 1995, decidió empezar a registrarlas en Internet. Desde 2002, un grupo de personas voluntarias ayudan a editar y mantener esta interesante iniciativa. En marzo de 2018 la OEIS alcanzó un total de 300.000 sucesiones registradas, utilizadas por su interés científico y también por amantes de la matemática recreativa.
Por cierto, el número de Erdős de Sloane es 2.
Aunque en esta anotación pretendía hablar de la sucesión de Levine (que he conocido gracias a la también magnífica página Futility Closet), he querido empezar por esta pequeña reseña de Sloane ya que fue él quien dio a conocer esta sucesión. En efecto, como comentaba en el artículo My Favorite Integer Sequences (páginas 15 y 16), en el verano de 1997 el matemático Lionel Levine le envío una propuesta de nueva sucesión para la OEIS. La sugerencia enseguida captó la atención de Sloane y la de otros colegas. Está catalogada como A011784 en la OEIS.
Los primeros términos de la sucesión de Levine son:
1, 2, 2, 3, 4, 7, 14, 42, 213, 2837, 175450, 139759600, 6837625106787, 266437144916648607844, 508009471379488821444261986503540, 37745517525533091954736701257541238885239740313139682, 5347426383812697233786139576220450142250373277499130252554080838158299886992660750432,…
Como puede observarse, los términos crecen rápidamente. ¿Pero cómo se construye? Cada término de esta sucesión es el último término de la correspondiente fila de esta tabla de números:
1 1
1 2
1 1 2
1 1 2 3
1 1 1 2 2 3 4
1 1 1 1 2 2 2 3 3 4 4 5 6 7
1 1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3 4 4 4 4 5 5 5 5 6 6 6 7 7 7 8 8 9 9 10 10 11 12 13 14
…
Esta tabla se construye siguiendo la siguiente regla:
-
la primera fila es 1 1;
-
cada una de las filas siguientes se construye leyendo la fila anterior de derecha a izquierda y pensando en un registro de números (de derecha a izquierda, 1, 2, 3, etc.).
Veamos algunos ejemplos para aclarar cómo se genera la tabla:
-
la primera fila se lee «un 1 y un 2», con lo que la segunda fila queda:
1 2.
-
La segunda fila se lee «dos 1 y un 2», y entonces la tercera fila queda:
1 1 2.
-
La tercera fila se lee «dos 1, un 2 y un 3», y entonces la cuarta fila queda:
1 1 2 3.
-
La cuarta fila se lee «tres 1, dos 2, un 3 y un 4», y entonces la quinta fila queda:
1 1 1 2 2 3 4.
Y se continúa así sucesivamente (pueden verse más detalles en My Favorite Integer Sequences).
De momento sólo se conocen 19 términos de la sucesión de Levine… el término 19 de esta sucesión posee ¡221 dígitos!, es éste:
83941772663735173160560543672534726683873453747462593691278544525723285290023673872585715830432071384827472565652426695269724710458808241779132656748501183672544006254377431217217762964060736471826937656819379445242826439
¿Se conseguirá encontrar el vigésimo término? En noviembre de 1997, cuando sólo se conocían 15 de los términos de la sucesión de Levine, Sloane decía: “[…] as I said it may be impossible to calculate the 20th term!”. Ojalá se equivoque.
Referencias
-
Levine’s Sequence, Futility Closet, 30 abril 2019
-
Neil Sloane, Wikipedia (consultado el 4 de mayo de 2019)
-
OEIS, Wikipedia (consultado el 4 de mayo de 2019)
-
OEIS (castellano e inglés)
-
N. J. A. Sloane, My Favorite Integer Sequences, arXiv:math/0207175
-
A011784, OEIS (consultado el 4 de mayo de 2019)
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo La sucesión de Levine se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La misteriosa sucesión de Kolakoski
- El secreto de los números que no querían ser simétricos
- El problema de la plantación de árboles en filas (2)
El sistema de periodos
 Ordenamiento original usando símbolos modernos de “Un experimento sobre un sistema de elementos basado en sus pesos atómicos y sus similitudes químicas” de Dmitri Ivanóvich Mendeléyev (1869). Los signos de interrogación señalan elementos aun no descubiertos. Fuente: Wikimedia Commons
Ordenamiento original usando símbolos modernos de “Un experimento sobre un sistema de elementos basado en sus pesos atómicos y sus similitudes químicas” de Dmitri Ivanóvich Mendeléyev (1869). Los signos de interrogación señalan elementos aun no descubiertos. Fuente: Wikimedia Commons
En 1869 un químico llamado Dmitri Ivanóvich Mendeléyev dispuso los 63 elementos entonces conocidos en filas según sus propiedades químicas, construyendo columnas conforme aumentaban los pesos atómicos [1]. Encontró que cuando se organizaban de esta manera aparecía una periodicidad. Llamó a su trabajo “Un experimento sobre un sistema de elementos basado en sus pesos atómicos y sus similitudes químicas”. Aunque faltaban algunos elementos para que todo cuadrase, Mendeléyev asumió correctamente que eran elementos aun por descubrir y dejó no solo un espacio para ellos sino una previsión de sus propiedades químicas en función de la periodicidad que les correspondía por su posición. El hallazgo posterior de estos elementos confirmaría la hipótesis periódica. Había sido descubierto el sistema de periodos [2].
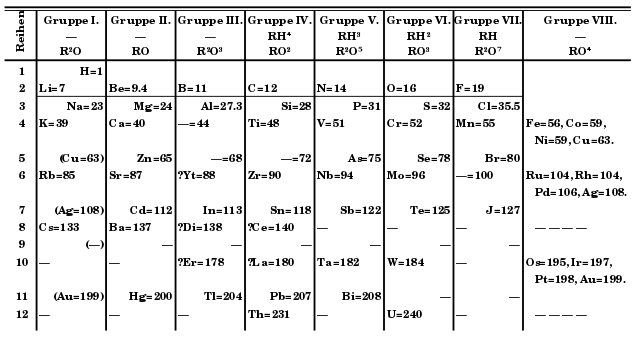 En 1871 Mendeléyev cambió el ordenamiento, de tal forma que las propiedades químicas eran similares en las columnas [3]. En los encabezamientos aparecen las fórmulas de los hidruros, de ser conocidos, y óxidos. Los guiones indican elementos que faltan por descubrir. La imagen corresponde a una traducción alemana de la tabla de 1871. Fuente: Wikimedia CommonsSolo un elemento puede ocupar una posición concreta en una tabla periódica. A cada elemento se le asigna un número en cada posición. Este número, llamado número atómico, ahora va desde el 1 para hidrógeno al 118 para el oganesón (Og). Se le asigna el símbolo Z. El número atómico identifica inmediatamente el elemento, ya que es único para cada elemento. Siempre es un número entero y suele aparecer en la parte superior de la cuadrícula de cada elemento en la mayoría de las tablas periódicas actuales . Por lo tanto, cuando alguien se refiere al elemento Z = 3, inmediatamente sabemos que se están refiriendo al elemento litio; El elemento 6 es carbono, el 79 oro, y así todos.
En 1871 Mendeléyev cambió el ordenamiento, de tal forma que las propiedades químicas eran similares en las columnas [3]. En los encabezamientos aparecen las fórmulas de los hidruros, de ser conocidos, y óxidos. Los guiones indican elementos que faltan por descubrir. La imagen corresponde a una traducción alemana de la tabla de 1871. Fuente: Wikimedia CommonsSolo un elemento puede ocupar una posición concreta en una tabla periódica. A cada elemento se le asigna un número en cada posición. Este número, llamado número atómico, ahora va desde el 1 para hidrógeno al 118 para el oganesón (Og). Se le asigna el símbolo Z. El número atómico identifica inmediatamente el elemento, ya que es único para cada elemento. Siempre es un número entero y suele aparecer en la parte superior de la cuadrícula de cada elemento en la mayoría de las tablas periódicas actuales . Por lo tanto, cuando alguien se refiere al elemento Z = 3, inmediatamente sabemos que se están refiriendo al elemento litio; El elemento 6 es carbono, el 79 oro, y así todos.
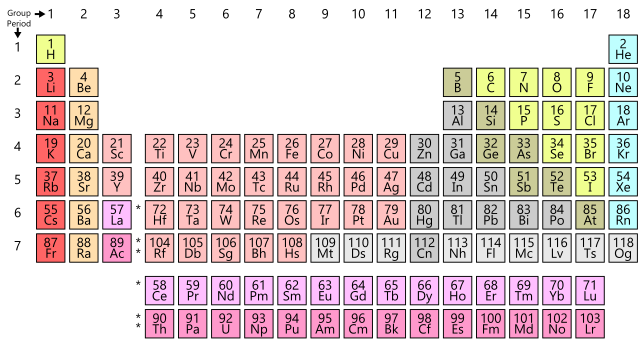 Tabla periódica moderna (diseño Werner-Paschen) actualizada a 2019 con la indicación de los números atómicos. Fuente: Wikimedia Commons.
Tabla periódica moderna (diseño Werner-Paschen) actualizada a 2019 con la indicación de los números atómicos. Fuente: Wikimedia Commons.
Los elementos dispuestos en una tabla periódica moderna que se encuentran uno debajo del otro en cada columna o grupo comparten propiedades químicas y físicas en un grado notable, como Mendeléyev había descubierto. Por lo tanto, se puede considerar que estos elementos pertenecen a la misma «familia» de elementos. Por ejemplo, el grupo 1 contiene la familia de los metales alcalinos: litio, sodio, potasio, rubidio, cesio y francio [4]. Este es un grupo de metales blandos con densidades muy bajas, puntos de fusión bajos y comportamiento químico similar. Otra familia de elementos, llamados halógenos, se encuentra en el grupo 17: flúor, cloro, bromo, yodo, astato [5]. Estos elementos se combinan violentamente con muchos metales y forman sales cristalinas blancas (halógeno significa «formador de sal»). Estas sales tienen fórmulas similares, como NaF, NaCl, NaBr, MgCl2, MgBr2, etc.
Ocasionalmente, por razones entonces desconocidas, era necesario apartarse del esquema general de ordenamiento de los elementos. Por ejemplo, las propiedades químicas del argón (Ar) y del potasio (K) exigen que se coloquen en las posiciones dieciocho y diecinueve para que se encuentren en grupos característicos por sus propiedades químicas. Sobre la base de sus masas atómicas solamente (39,948 u para argón; 39,102 u para potasio) sus posiciones tendrían que estar invertidas.
La regularidad, simetría y capacidad predictiva del sistema de periodos son indicios de que el modelo que explique la estructura de los átomos de los distintos elementos posee también estas características. Ese modelo surgiría a lo largo de la primera mitad del siglo XX, y no defraudó. Veremos la gran cantidad de ingenio y trabajo detectivesco que fue necesario para comprender la estructura de los átomos y como, de ella, surge la periodicidad de los elementos que podemos observar.
Notas:
[1] ¡Atención! ¡Esto es diferente a las tablas periódicas actuales!
[2] Por mucho que este año se celebre el 150 aniversario de “la tabla periódica” lo correcto es decir que se celebra el 150 aniversario del sistema de periodos. La tabla periódica tal y como la solemos utilzar es un diseño químico-físico establecido por Werner y perfeccionado por Paschen en los años treinta del siglo XX. Hay muchos diseños, pero en lo sucesivo tabla periódica moderna significará tabla Werner-Paschen
[3] En esto coincide con las tablas periódicas modernas.
[4] ¿Es el hidrógeno un metal?¿Qué hace ahí? Lo descubriremos avanzada esta serie.
[5] Las propiedades químicas del teneso (Ts) aún no son bien conocidas pero puede que se aparten algo de las típicas de los halógenos. De hecho el astato se parece químicamente al yodo pero es significativamente más metálico. Ya iremos descubriendo por qué.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El sistema de periodos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El sistema de la difusión social de la ciencia: Catalizadores del sistema y consideraciones finales
- El orden es una fantasía
- La ley de proporciones definidas y la unidad de masa atómica
Máster on-line en Cultura Científica

El próximo curso académico (2019/20), la UPV/EHU y la UPNA van a ofrecer un máster propio en Cultura Científica con estructura modular que será impartido on-line.
Después de analizar la oferta de estudios de posgrado en materia de comunicación y cultura científica por parte de universidades españolas, los promotores de este máster llegamos a la conclusión de que podría ser interesante ofrecer estudios de cultura científica que fueran de utilidad a profesionales de perfiles diversos, tales como periodistas interesados en el periodismo científico, personal docente de diferentes niveles académicos, personas interesadas en dedicarse a la divulgación científica, y otros.
Nuestro interés se aleja de lo más eminentemente académico, por un lado, y de lo estrictamente comunicativo, por el otro, pero sin renunciar completamente a esas vertientes. Nos interesa más abordar la formación en cultura científica desde la perspectiva de la divulgación, así como la introducción de contenidos sólidos de historia y filosofía de las ciencias. Porque para adoptar una actitud crítica hacia el conocimiento y la información científica es muy importante contar con nociones básicas acerca de la forma en que se han desarrollado las disciplinas, así como de la rica reflexión filosófica acerca de la naturaleza del conocimiento científico que se ha ido atesorando con el tiempo.
Historia y filosofía de la ciencia son, pues, áreas incluidas entre los contenidos de nuestra oferta. Pero además, y como es lógico, un máster sobre cultura científica ha de incluir también conocimientos científicos concretos. En unos estudios de las dimensiones de un máster no es posible abarcar un gran conjunto de conocimientos. Por otra parte, el bagaje acumulado por las ciencias durante su desarrollo es de tal amplitud que resultaría vana cualquier pretensión de ofrecer un panorama de las ciencias más o menos completo. Por ello, a la hora de delimitar los contenidos sustantivos de ciencia, hemos optado por seleccionar algunas materias de carácter básico y otras cuyo interés radica en su directa relación con aspectos de la vida cotidiana. De esta forma, pretendemos ofrecer ejemplos escogidos que sirvan para ilustrar la forma en que funciona la ciencia, a la vez que ofrecemos formación científica básica.
En definitiva, no pretendemos enseñar ciencias, sino transmitir y facilitar una visión amplia de la cultura científica, entendida como un conjunto de conocimientos (mediante ejemplos escogidos), una forma de adquirirlos, una historia plural y una reflexión acerca de su naturaleza y las vías para su difusión social.

El máster está diseñado de acuerdo con una estructura modular que permite obtener diferentes títulos (especialista universitario, experto y máster) en función de los créditos que se cursan. Está basado en asignaturas de 2 ECTS que se completan en 5 semanas. Y la mayor parte del profesorado participa en eventos presenciales de cultura científica (BZP, Semana de la Ciencia, Conversaciones del máster FCV, etc.).
Hemos concebido el máster como un conjunto de títulos mediante los que queremos contribuir a mejorar la percepción y comprensión de la ciencia por parte de la sociedad, a proporcionar la formación más flexible, diversa y asequible en el ámbito iberoamericano; y hacer que la cultura científica sea accesible, atractiva y rigurosa. Y trabajamos en sintonía con los departamentos de Educación del Gobierno Vasco y del Gobierno Foral, fomentando alianzas con estrategias y proyectos ya existentes como STEAM y Planeta-STEM.
Este es un proyecto liderado por cuatro agentes universitarios: Cátedra de Cultura Científica de la UPV/EHU; Máster oficial UPV/EHU-UNAM en Filosofía, Ciencia y Valores (Donostia); Cátedra de divulgación del conocimiento y cultura científica UPNA (Pamplona), Unidad de Cultura Científica UPNA (Pamplona); y Fundación Universidad-Sociedad UPNA (Pamplona). La comisión académica del máster está formada por Antonio Casado da Rocha (UPV/EHU), Joaquín Sevilla Moróder (UPNA) y Juan Ignacio Pérez Iglesias (UPV/EHU)
Las personas interesadas en preinscribirse, recibir más información o aclaraciones adicionales, puede dirigirse a nuestra página web o escribirnos a la dirección m.cultura.cientifica@gmail.com. También estamos en twitter (@culturacienti).
Y no lo olvides: se trata de estudios que se imparten on-line, sin necesidad de conectarse a horas prefijadas, lo que permite adaptarse a los horarios de cada estudiante.
El artículo Máster on-line en Cultura Científica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cultura científica y cultura democrática
- “Filosofía, Ciencia y Valores”, el máster
- La Cátedra se va de máster
Preparados para matar: Guerra
“Por guerras entiendo eventos en que coaliciones de miembros de un grupo buscan infligir daño corporal a uno o más miembros de otro grupo.”
Samuel Bowles, 2009.
“Temo que haya pocos de los que mueren en una batalla que mueran bien”.
William Shakespeare, Enrique V, 1599.
“¿De cuántos asesinatos se compone una gran batalla? Ese es uno de los puntos en los que nuestra razón se pierde y no sabe qué decir”.
Alfred de Vigny, Servidumbre y grandeza militares, 1835.
 Batalla de Lepanto (1571). Cuadro de Paolo Veronese (alrededor de 1572). Fuente: Wikimedia Commons
Batalla de Lepanto (1571). Cuadro de Paolo Veronese (alrededor de 1572). Fuente: Wikimedia Commons
Antes de empezar hay que definir qué es guerra, y lo haré en negativo: guerra no es lucha entre individuos sino entre grupos. Voy a analizar la guerra como un elemento más del proceso de evolución de la especie humana. Solo hay que advertir la extensión de la guerra en la conducta de nuestra especie para certificar su considerable éxito evolutivo. La violencia es una herramienta más que permite conseguir recursos para la supervivencia y una más eficaz reproducción. No existe método más rápido y seguro que matar al que compite y se opone. Por tanto, solo podemos entender y explicar la violencia de nuestra especie si estudiamos su función en la evolución. Así, afirma Ian Morris, esperamos identificar la lógica de la guerra.
Parece ser que nuestra especie se separó de los chimpancés hace 7.5 millones de años, y tanto esa especie como la humana hacen la guerra y matan en grupo. Lean la historia de la guerra de Gombe o, también, la guerra de Ngogo, algo al norte de Gombe, y de otros lugares que se están empezando a investigar. En Gombe, después de matar a todos los machos de uno de los grupos, los ganadores se quedaron con su territorio y con las hembras, es decir, más alimento y mayor reproducción.
El éxito reproductivo, en nuestra especie y en guerra, tiene otro factor que, en parte, también siguen los chimpancés cuando se apoderan de las hembras del grupo vencido: es la violación como arma de guerra.
Hay datos sobre violaciones en tiempo de guerra desde las crónicas más antiguas. Por ejemplo, era un arma de guerra para Gengis Khan y, tanto es así, que se estima que el 8% de la población asiática actual es descendiente directo del emperador mongol.
Es, por tanto, uno de los aspectos del éxito reproductor asociado a la guerra. Y, como decía, es un arma habitual, incluso en nuestro tiempo: Bosnia, Bangladesh, Birmania, Camboya, Haití, Liberia, Rwanda, Somalia, Sudán, Uganda, Irak, Siria,…
Es evidente que la base de esta conducta está en que la violación es un producto evolutivo, con apoyo cultural, de una masculinidad militarizada hegemónica en todas las guerras y todos los ejércitos, una consecuencia de la competencia evolutiva entre machos.
Sin embargo, como hemos visto en la definición de guerra, además de violencia tienen que haber grupo, como en la violencia política, de la que la guerra es una extensión social y de organización. Ya lo escribió Karl von Clausewitz con el provocador “la guerra es la continuación de la política con otros medios”, publicado después de su muerte en 1831. Y en el grupo, debe haber solidaridad entre y con los considerados como nuestros. Más adelante veremos la relación entre guerra y genética que, ahora, se empieza a investigar. Como en la violencia política, altruismo con los nuestros y xenofobia con los otros, con el enemigo.
La guerra de Gombe
 Machos adultos de chimpancé. Fuente: Wikimedia Commons
Machos adultos de chimpancé. Fuente: Wikimedia Commons
“El 7 de enero de 1974, a primera hora de la tarde, una partida de guerra de Kasekela atravesó sin ser vista la frontera y se adentró en el territorio de Kahama. Eran ocho asaltantes que se movían en silencio, con determinación. Su misión era matar. Para cuando Godi, de Kahama, los vio, ya era demasiado tarde.
Godi saltó del árbol en el que comía fruta y corrió, pero los atacantes se abalanzaron sobre él. Uno de ellos lo sujetó bocabajo en el fango; los demás, aullando de rabia, lo golpearon y le desgarraron el cuerpo con los colmillos durante diez minutos. Finalmente, después de arrojarle piedras, la partida de guerra se adentró en el bosque.”
Así cuenta Ian Morris el comienzo de la guerra de Gombe. Duró tres años, de 1974 a 1977, en los bosques del centro de África, en el Parque Nacional de Gombe, Tanzania. Los que luchaban eran chimpancés (Pan troglodytes). Incluso utilizaron piedras como armas para arrojar y golpear.
Los dos bandos vivían en dos valles vecinos, al norte y el sur del Parque Nacional, en los valles de Kasekela y de Kahama. Eran chimpancés muy conocidos pues formaban uno de los grupos que Jane Goodall seguía desde 1960. Todos tienen nombre, recibido del grupo de Jane Goodall y sus observadores. Está Godi, la primera víctima de la guerra, del valle Kahama. Y estaban el macho alfa de Kasakela, Humphrey; y Figan, Jomeo, la hembra Gigi, un macho adolescente sin nombre, Rodolf, el más viejo y que casi no podía ni morder; y Evered y Sherry. Eran los ocho atacantes.
Humphrey derribó a Godi y se sentó sobre su cabeza, le sujetó las extremidades y los otros machos adultos le golpearon y mordieron. Rodolf mordía lo que podía mientras los otros golpeaban la espalda. Dejaron a la víctima tirada en el suelo, con el rostro hundido en el barro y gimiendo de dolor. Entonces, Rodolf cogió una piedra y la estrelló en la cabeza de Godi. Era el 7 de enero de 1974. Había comenzado la guerra de Gombe.
Este relato cambia algo en el libro de Jane Goodall titulado “Through the Window”, publicado en 1990. Son siete en vez de ocho los atacantes y algunos de los chimpancés tienen nombres diferentes. Pero, en esencia, todo lleva a lo mismo: atacar y matar. El testigo que lo presenció y relató a Jane Goodall fue uno de sus observadores, Hilali Matama.
El estudio por expertos de este hecho sorprendente para lo que, hasta entonces, se conocía de la conducta de lo grupos de chimpancés, había comenzado dos años antes. Todos los chimpancés implicados formaban el mismo grupo pero, gradualmente, unos machos, llamados Hugh, Charlie, Dé, Godi, Willy Wally, Sniff y Goliath, se fueron separando del resto, del clan original, y formaron un grupo propio en el sur, en el valle Kahama.
En 1977, tres años después, los machos de Kasakela mataron el 12 de noviembre a Sniff, el último macho de Kahama. Se apoderaron de su territorio y de sus hembras, y la guerra terminó.
Es la primera guerra entre chimpancés que está documentada pero ni mucho menos es la única. En una revisión publicada en 2014, se cuentan 152 incidentes con asesinatos entre chimpancés en 18 comunidades de esta especie en el centro de África, desde Uganda a Costa de Marfil. Un centenar de estos ataques eran entre comunidades, es decir, eran guerra.
Los chimpancés se mueven en territorios cuya periferia es recorrida por grupos de machos preparados para atacar a otros machos de los territorios vecinos. Solo atacan cuando son más y sorprenden a los machos de otro grupo.
Chimpancés y humanos hacemos la guerra. Es una conducta evolutivamente exitosa y la hemos heredado, hace 7.5 millones de años, de aquel antepasado común. Es más, en 2006 y en un estudio de Richard Wrangham, se confirma que los niveles de agresión mortal en humanos de grupos de cazadores recolectores y en chimpancés son similares. Es la evolución, nos guste o no, lo queramos o no, quien articula la historia de la especie humana. Implica que la muerte, la implacable lógica de la guerra, nos recompensa y mejora la supervivencia y la reproducción.
Además, como cita Karen Armstrong, “la guerra hace que el mundo sea comprensible”. Es la recompensa para un entorno peligroso y caótico: con la guerra solo hay buenos y malos, solo estamos nosotros y están los otros. Bien lo sabían los chimpancés de Gombe. Y, es más, de nuevo con Hedges, “la guerra es un elixir tentador, nos ofrece un propósito, una causa, nos permite ser nobles”.
La especie humana utiliza las mismas tácticas que los chimpancés: grupos que atacan a los vecinos, emboscados para sorprender o con ventaja numérica, formados por machos y, rara vez, junto con hembras. Son, como escriben Michael Wilson y Richard Wrangham, tácticas con poco riesgo y mucha ganancia en caso de victoria.
Muchas de las justificaciones de los violentos en conflictos, y sobre todo si incluyen genocidios, como, por ejemplo, la Alemania nazi, Ruanda o Bosnia, se apoyan en una furiosa retórica que destaca la diferencia genética entre los contendientes. Pero también hay grupos que promueven la paz destacando las características genéticas que comparten los grupos enfrentados. Parece una hipótesis aceptable que, para un caso de conflicto, es mejor conocer lo que compartimos en nuestra genética que lo que nos diferencia. Conocer las consecuencias de esta hipótesis es lo que han estudiado Sasha Kimel y sus colegas, de la Universidad de Harvard, para el conflicto entre judíos y árabes.
A 123 judíos y 57 árabes que viven en Estados Unidos les dan a leer un artículo que afirma que ambos grupos son hermanos genéticos o un segundo artículo que dice que son diferentes y extraños desde la genética. Después pasan varios tests para conocer lo que piensan unos de otros y su actitud subconsciente respecto a los dos grupos.
Como era de esperar según la hipótesis inicial, ambos grupos piensan de manera más positiva respecto al otro grupo cuando han leído el artículo sobre su parecido genético que cuando lo han hecho con el que destaca las diferencias.
En un segundo estudio con 131 voluntarios, solo judíos, que también forman dos grupos y leen los mismos artículos, les dan después la oportunidad de lanzar una ráfaga de ruido, a través de un ordenador, a un árabe que saben se llama Mohamed. La ráfaga es más corta y menos intensa si han leído el artículo sobre el parecido genético. En resumen, son menos agresivos con los miembros del otro grupo.
Cuando los autores se trasladan a Israel y hacen el estudio con 184 judíos israelíes, obtienen unos resultados inesperados. El artículo sobre el parecido genético entre árabes y judíos no tiene ningún efecto sobre los participantes y, por el contrario, el artículo sobre las diferencias genéticas reduce el apoyo de los voluntarios a políticas de paz y aumenta la antipatía hacia los palestinos.
Además y en relación con los genes de chimpancés y humanos, la expresión del gen ADRA2C activa la respuesta típica de los conflictos que implica “o lucha o huye”. Es la conducta típica de la agresividad y el enfrentamiento. Para Kang Seon Lee y su grupo, del KAIST de Daejeon, en Corea, la selección de este gen en chimpancés y humanos se debe a que, en ambos grupos, existe la guerra y el gen ADRA2C, cuando se expresa, ayuda a, por lo menos, dar la respuesta de huir y no la de luchar. Cuál se elige depende, con seguridad, de muchos más factores. Es evidente que la guerra y su expresión no es un asunto sencillo.
Repasemos esa primera guerra de la que tenemos evidencia arqueológica, en Nubia, hace 12000-14000 años, y descrita por Fred Wendorf.
La guerra de Nubia
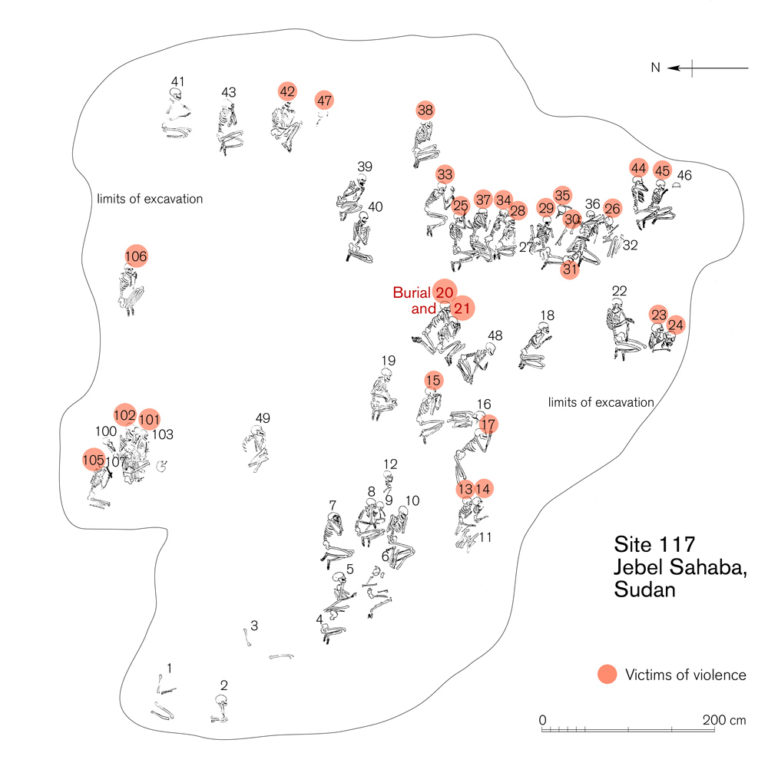 Mapa del sitio 117. Los puntos rojos indican muerte violenta. Fuente: The British Musem Blog
Mapa del sitio 117. Los puntos rojos indican muerte violenta. Fuente: The British Musem Blog
Es la evidencia arqueológica de guerra más antigua que conocemos. Apareció en una excavación en Nubia, el Sitio 117, cerca de la actual aldea de Jebel Sahaba, en el norte del Sudán, cerca de la frontera con Egipto, a orillas del Nilo. Los hallazgos están fechados hace de 12000 a 14000 años.
En el yacimiento se encontró un cementerio con 59 tumbas, con 46 adultos y 13 niños o adolescentes, y son 24 mujeres y 19 hombres de 18 años o más. De los cuerpos, hay 24 con puntas de piedra de flechas o de lanzas en los huesos o junto a ellos en los enterramientos. En total se recuperaron en el yacimiento 110 puntas de flecha o de lanza y, muchas de ellas, en posiciones que demuestran que se utilizaron para herir a las personas enterradas. Es curioso que la mayoría de los cuerpos están enterrados sobre el costado izquierdo, con la cabeza hacia el este y el rostro hacia el sur.
Entre los cuerpos hay más hombres que mujeres con trazas de violencia e, incluso, algún niño muerto por proyectiles. Hay una mujer adulta con más de una docena de heridas. También hay huesos con marcas de cortes por armas de piedra. Y uno de los hombres, en la tumba 21, tiene hasta 19 fragmentos de armas en el cuerpo, con una punta en la pelvis, o en la tierra de la tumba. Es evidente que el conflicto fue brutal.
Es posible, aunque no hay datos exactos de datación obtenidos con carbono 14, que no todos los enterramientos fuesen de la misma fecha, aunque así lo parece para muchos de ellos. No es fácil datar los restos pues son escasos y han pasado por muchos traslados. El yacimiento está ahora sumergido por las aguas de la Presa de Assuan. El proyecto de excavación, dirigido por Fred Wendorf, de la Universidad Metodista del Sur en Taos, Nuevo México, comenzó en 1964 en respuesta a la llamada de la UNESCO para salvar en lo posible los restos arqueológicos que iban a quedar sumergidos. La excavación se hizo con urgencia en los años 1965 y 1966. Ahora los huesos, después de estar 40 años en Taos, están depositados en el Museo Británico en Londres.
Samuel Bowles estudia la guerra de Jebel Sahaba y otras que nos han dejado yacimientos con enterramientos múltiples con heridas mortales: Columbia Británica, Ucrania, la India, Argelia, Francia o Dinamarca. Sin olvidar Atapuerca y sus muchos cadáveres, algunos con heridas mortales, aunque no está claro si son enfrentamientos individuales o de grupo, lo que cumpliría la definición que hemos aceptado de guerra.
Desde hace unos 8500 años hay guerras documentadas por todo el planeta, desde el Atlántico, en Francia y Dinamarca, hasta Ucrania en el este, con enterramientos y heridas mortales con armas.
Como ejemplo nos sirve la cueva Ofnet, en Baviera, con cráneos y vértebras de 38 personas, fechados hace unos 6500 años. La mayoría son niños y dos tercios de los adultos son mujeres. La mitad han muerto por golpes de maza, tanto hombres como mujeres y niños, pero los hombres tienen más heridas. A un tercio de los cuerpos les han cortado la cabeza. Se supone que es la masacre de toda una comunidad. Algo parecido se ha encontrado en Schöneck-Kilianstädten, también en Alemania, y de hace 7000 años, con muchos cuerpos, incluyendo 13 niños, uno de ellos de unos seis meses de edad.
Bowles propone que su causa está en un clima muy cambiante, con desastres naturales y escasez de recursos, lo que provoca movimientos de población en busca de alimentos y territorios con recursos de todo tipo. Además, y ya se ha propuesto para los chimpancés, un número alto de machos o pequeño de hembras, provoca conflictos internos en relación con la reproducción y, como ocurrió en la Guerra de Gombe, la aparición de grupos enfrentados formados por los nuestros y por los otros.
Son grupos con intereses contrapuestos y, ya sabemos, que la mejor manera de terminar un conflicto es matar al contrario. Y aparece la agresión y la guerra y, los que siguen esas conductas y triunfan, transmiten esa conducta a sus descendientes. La evolución los selecciona porque se reproducen más y mejor.
Hay una propuesta, con modelos matemáticos, que intenta explicar el cuello de botella de hace 7000 años en la genética del cromosoma Y. En esa fecha existía tal escasez de hombres que se calcula que había 17 mujeres por cada hombre. Entre los 7000 y los 5000 años, el cromosoma Y fue escaso y con poca variabilidad. La propuesta dice que esa escasez de hombres se debía a las continuas guerras y masacres entre grupos pequeños y tribales y, en las peleas, muchos desaparecieron en su totalidad y, con ellos, también desapareció mucha variabilidad de cromosoma Y.
1212: Las Navas de Tolosa
 Batalla de Las Navas de Tolosa, óleo de Van Halen expuesto en el Palacio del Senado (Madrid). Fuente: Wikimedia Commons
Batalla de Las Navas de Tolosa, óleo de Van Halen expuesto en el Palacio del Senado (Madrid). Fuente: Wikimedia Commons
Fue el 16 de julio de 1212 cuando se enfrentaron en Las Navas de Tolosa, cerca del actual pueblo de Santa Elena, en la provincia de Jaén, los ejércitos cristianos con las tropas del Califa almohade Muhammad an-Nasir, conocido como Miramamolín por sus enemigos. El lugar de la batalla era, y sigue siendo, uno de los pasos de Sierra Morena entre Castilla y el valle del Guadalquivir y, por tanto, con una indudable importancia estratégica.
Los almohades eran una dinastía bereber que, en los siglos XII y XIII, dominaron el norte de África hasta el Atlántico, y el sur de la Península Ibérica. Abandonaron Andalucía a los pocos años de la derrota en Las Navas de Tolosa.
Allí estaban, con sus tropas, los reyes Alfonso VIII de Castilla, Pedro II de Aragón, Sancho VII de Navarra y Alfonso II de Portugal. Era una cruzada de la cristiandad, concedida por el papa Inocencio III, para todos los reinos cristianos peninsulares, con el perdón de los pecados para los que allí lucharan. La propaganda de la cruzada, con viajes y homilías por Europa, la hizo el Arzobispo de Toledo, Don Rodrigo Jiménez de Rada.
El ejército cristiano, según cálculos recientes, sería de unos 12000 combatientes, con unos 4000 caballeros y 8000 peones. El almohade era de algo más de 20000 soldados. Eran ejércitos de enormes proporciones, desconocidas antes de 1212.
En el orden de batalla, en el centro de la primera línea estaban las tropas de Don Diego López de Haro, Señor de Vizcaya, el segundo con este nombre y el quinto Señor de Vizcaya de esa familia. Dirigió el ataque de la primera línea, inició la batalla, avanzó, se detuvo, resistió, fue flanqueado por la caballería ligera almohade y esperó el ataque de las reservas del ejército cristiano. Con Don Diego lucharon unos 300-500 caballeros, según diversas crónicas de la época y autores más recientes.
La batalla duró todo el día, desde las ocho de la mañana, y, a la tarde, Alfonso VIII ordenó un ataque total y los almohades huyeron a la desbandada. Fueron perseguidos unos 20 kilómetros para que el ejército cristiano consiguiera el mayor botín de guerra posible.
Las bajas son difíciles de calcular, con muchas cifras exageradas por la propaganda, tanto en aquella época como después, hasta años muy recientes y todavía en la actualidad. Las bajas musulmanas fueron muchas pues, además, las tropas cristianas tenían órdenes de causar gran mortandad para aumentar los efectos de la batalla y conseguir una derrota más contundente. Los cristianos también sufrieron muchas bajas, sobre todo en la primera mitad de la batalla, mientras Don Diego López de Haro, en primera línea, aguantaba el empuje del ejército almohade.
Las bajas y los muertos fueron, entre los cristianos, escasas, y miles entre los musulmanes, contaban los cronistas cristianos, y todo lo contrario para los musulmanes. Sin duda fueron muchos los choques entre grupos, aplastamientos en los ataques y la huida de los almohades, o en el degüello que ordenó Alfonso VIII después de la derrota de los musulmanes. Miles de muertos en ambos grupos, como era habitual en la guerra en aquellos años violentos o, si se quiere, en la actualidad y, además, gane quien gane o pierda quien pierda la batalla hay demasiados cadáveres al final de la batalla. Y pocos murieron a gusto, como escribía Shakespeare. Todo estaba organizado por reyes y estados y, para el historiador Charles Tilly, la guerra y su organización es, para quien gobierna, una actividad de crimen organizado.
Todavía en la actualidad se considera esta batalla como un hito significativo de la historia de la Reconquista y de la historia medieval peninsular y occidental. Para Jiménez de Rada, el Arzobispo de Toledo, supuso el fin de los almohades, aunque pasaron unos años hasta que abandonaron la Península y se replegaron al norte de África.
Y, para terminar, una cita de Don Policarpo Mingote y Tarazona en su libro Compendio de Historia de España para uso de los alumnos de Segunda Enseñanza, Seminarios y Escuelas Especiales, Segunda Edición, 1898, Imp. de los Herederos de Miñón, León:
“Ya el sol en el ocaso doraba con sus postreros rayos la frente de aquellos héroes, cuando desde los ámbitos del anchuroso campo mil voces repiten los versículos sublimes del Te-Deum, cantado en acción de gracias.
La Iglesia conmemora esta batalla todos los años bajo la advocación de El Triunfo de la Santa Cruz, pues significa la derrota definitiva del Islamismo en España por el quebrantamiento de los reinos musulmanes, peninsulares y africanos á la vez.
El rey Almohade huyó á ocultar su vergüenza en el fondo de sus impenetrables desiertos.”
En los miles de años que siguen a la evidencia que tenemos de la guerra, del conflicto violento entre grupos, Ian Morris asegura que, en la prehistoria, la tasa de muertes violentas era del 10%-20% de la población. Con los imperios clásicos, hace 2000-3000 años, bajó al 2%-5%, y, con su caída y mayores movimientos de población, se elevó hasta el 5%-10% entre hace 1400 y 200 años. Y, finalmente, en la actualidad, estamos en una tasa de muertes violentas del 1%-2%. Por cierto, en encuestas a soldados de infantería después de la Segunda Guerra Mundial, solo el 15%-20% había sido capaz de disparar directamente al enemigo. Habían desarrollado complicados métodos para fallar y no ser pillados pos sus mandos.
También es una hipótesis que parte de modelos matemáticos la que propone que los humanos consiguieron que disminuyera la violencia seleccionado los individuos más sociales, más empáticos y altruistas, más del grupo de los nuestros. La especie humana progresó hacia el grupo por algo así como la auto domesticación.
Bombardeo en Dresde
 Vista parcial de Dresde tras el bombardeo (1945). Fuente: Bundesarchiv, Bild 183-Z0309-310 / G. Beyer / CC-BY-SA 3.0
Vista parcial de Dresde tras el bombardeo (1945). Fuente: Bundesarchiv, Bild 183-Z0309-310 / G. Beyer / CC-BY-SA 3.0
Entre el 13 y el 15 de febrero de 1945, doce semanas antes de la rendición de la Alemania nazi, más de 1000 bombarderos pesados de los aliados lanzaron cuatro ataques aéreos sobre la ciudad alemana de Dresde. Arrojaron unas 4000 toneladas de bombas incendiarias y explosivas. Gran parte de la ciudad fue destruida en un incendio devastador y las víctimas, en un número aun en debate, fueron entre 25000 y 40000.
Todavía en la actualidad se intenta comprender cuál fue la razón estratégica de tan tremendo bombardeo. Quizá por razones militares, o por represalia de otros bombardeos o, simplemente, fue un crimen de guerra sin otro objetivo que desmoralizar a los alemanes.
Las bombas utilizadas y su dispersión provocaron que los pequeños incendios iniciales, unidos a las bombas incendiarias posteriores, formaron lo que se llamaba, desde el bombardeo de Hamburgo en 1943, una tormenta de fuego (“firestorm”). Una primera oleada de pequeños aviones Mosquito lanzó marcadores de blancos para delimitar la zona a bombardear. A continuación, un segundo grupo de bombardeos lanzaron bastones de caucho con fósforo y bombas incendiarias como iniciador de incendios más extensos.
Una tercera oleada de bombarderos lanzó bombas incendiarias y explosivas y la ciudad ardió. Para conseguirlo, la proporción ideal de bombas incendiarias y explosivas era de 40:60. En el ataque, a mediodía del día 14, se lanzaron 700 toneladas de bombas, que mantuvieron y reiniciaron los incendios en la ciudad. El cuarto y último ataque se hizo el día 15.
La ciudad antigua tenía muchos edificios de madera y ardió con rapidez. El 80% del centro de la ciudad quedó destruido, y más del 50% de los barrios cercanos de la periferia. La temperatura se calcula que llegó a 1500ºC, las llamas alcanzaron más de cuatro kilómetros de altura y los soldados del frente oriental, a más de 100 kilómetros de distancia, veían el incendio. El agua de los depósitos del interior de la ciudad llegó a hervir y se evaporó.
La comisión de historiadores, dirigida por Rolf-Dieter Müller, y patrocinada por el Ayuntamiento de Dresde con el objetivo principal proponer una cifra de víctimas cercana a la realidad, después de sus investigaciones entre 2005 y 2010, concluyeron que el número de muertos en el bombardeo estaba entre un mínimo de 22700 y un máximo de 25000 personas.
Poco después de la conquista de la ciudad por el ejército soviético, 6865 cadáveres fueron incinerados en un descampado de la ciudad antigua cercano al río Elba. El 13 de febrero de 2009, a 64 años del bombardeo, se inauguró un monumento en recuerdo de las víctimas en el lugar de la incineración. En la placa que lo acompaña se lee:
“El horror de la guerra que salió de Alemania hacia el mundo regresó a nuestra ciudad. Después del ataque aéreo del 13 al 14 de febrero de 1945, se incineraron 6865 cadáveres en este lugar”.
El escritor Kurt Vonnegut era prisionero de guerra en Dresde durante el bombardeo y, con sus vivencias, publicó en 1969 la novela titulada “Matadero Cinco”. En el prólogo para una edición de 1976 escribió, con ironía:
“Solo hay una persona de todo el planeta que ha conseguido algún beneficio del bombardeo. Yo soy esa persona. Escribí este libro, que me hizo ganar mucho dinero y forjó mi reputación tal y como es. De una manera u otra, he obtenido uno o dos dólares por cada muerto”.
En conclusión y según lo que dejó escrito Richard Wrangham en 1999, las evidencias que conocemos apoyan la hipótesis de que la selección ha favorecido la propensión a cazar y matar en chimpancés y humanos. Además, matar en grupo tiene una larga historia en la evolución de nuestra especie, así como en los chimpancés.
Para terminar, más palabras de Kurt Vonnegut en Matadero Cinco:
“Si este libro es tan corto, confuso y discutible, es porque no hay nada inteligente que decir sobre una matanza. Después de una carnicería sólo queda gente muerta que nada dice ni nada desea; todo queda silencioso para siempre. Solamente los pájaros cantan.”
Referencias:
Alvira Cabrer, M. 2003. Guerra e ideología en la España medieval: cultura y actitudes históricas ante el principio del siglo XIII. Tesis doctoral. Universidad Complutense.
Armstrong, K. 2015. Campos de sangre. La religión y la historia de la violencia. Paidós. Barcelona. 575 pp.
Bowe, M.K. 2011. Framing Victory: The bombing of Dresde, Germany, in narrative, discourse and commemoration after 1945. Ms. Thesis. University of Victoria, British Columbia, Canada.
Bowles, S. 2009. Did warfare among ancestral hunter-gatherers affect the evolution of human social behaviors? Science 324: 1293-1298.
Dolan Gómez, M. The battle of Las Navas de Tolosa: The culture and practice of crusading in the medieval Iberia. PhD. Diss. University of Tennessee.
Ferguson, R.B. 2018. ¿Por qué luchamos? Investigación y Ciencia noviembre: 64-69.
Fledblum, J.T. et al. 2018. The timing and causes of a unique chimpnazee community fission preceding Gombe’s “Four-Year War”. American Journal of Physical Anthropology DOI: 10.1002/ajps.23462
Fowler, G. 1995. Holocaust at Dresden. The Barnes Review February: 3-13.
Friedman, R. 2014. Violence and climate change in prehistoric Egypt and Sudan. Blog The British Museum 14 July.
García Fitz, F. 2014. La batalla de Las Navas de Tolosa: el impacto de un acontecimiento extraordinario. En “Las Navas de Tolosa, 1212-2012. Miradas cruzadas”, p. 11-36. Ed. por P. Cressier & V. Salvatierra. Universidad de Jaén.
Glowacki, L. et al. 2017. The evolutionary anthropology of war. Journal of Economic Behavior & Organization doi: 10.1016/j.jebo.2017.09.014
Goodall, J. 1990. Through the window. My thirty years with the companzees of Gombe. Soko Publ. Ltd. Eastbourne, East Sussex, Inglaterra.
Gottschall, J. 2004. Explaining wartime rape. Journal of Sex Research 41: 129-136.
Judd, M. 2006. Jabel Sahaba revisited. Studies in African Archaeology 9: 153-166.
Kelly, R.C. 2005. The evolution of lethal intergroup violence. Proceedings of the National Academy of Sciences USA 201: 15294-15298.
Kimel, S.Y. et al. 2016. Living in a genetic world. How learning about interethnic genetic similarities and differences affects peace and conflicto. Personality and Social Psychology Bulletin DOI: 10.1177/0146167216642196
Lee, K.S. et al. 2018. Selection of the regulation of sympathetic nervous activity in humans and chimpanzees. PLOS Genetics 14: e1007311
Martín Baró, I. 1984. Guerra y salud mental. Estudios Centroamericanos 429/430: 503-514.
Meyer, C. et al. 2015. The massacre mass grave of Schöneck-Kilianstädten reveals new insights into collective violence in Early Neolithic Central Europe. Proceedings of the National Academy of Sciences USA 112: 11217-11222.
Morris, I. 2017. Guerra, ¿para qué sirve? Ático de Libros. Barcelona. 639 pp.
Salas, J. 2014. El cruel asesinato que desató la primera guerra entre primates no humanos. Blog Materia 14 enero.
Salas, J. 2014. Las notas antiguas de Jane Goodall revelan las claves de la primera guerra entre chimpancés. Blog Materia 5 junio.
Taylor, F. 2004. Dresden: Tuesday, February 13, 1945. HarperCollins e-books. 518 pp.
Theofanopoulou, C. et al. 2017. Self-domestication in Homo sapiens: Insights from comparative genomics. PLOS ONE 12: e0185306
Thorpe, I.J.N. 2003. Anthropology, archaeology, and the origin of warfare. World Archaeology 35: 145-165.
Tilly, C. 1982. Warmaking and state making as organized crime. CRSO Working Paper No. 256. University of Michigan. 29 pp.
Varela, F. 2006. Orígenes ancestrales de la agresividad humana. Revista Central de Sociología 1: 127-150.
Vergara Anderson, L. 2010. Historias revisionistas del bombardeo de Dresde. Historia y Grafía 34: 207-228.
Wikipedia. 2017. Wartime sexual violence. 11 November.
Wikipedia. 2018. Bombardeo de Dresde. 7 enero.
Wikipedia. 2018. Jebel Sahaba. 1 February.
Wikipedia. 2018. Batalla de Las Navas de Tolosa. 19 febrero.
Wilson, M.L. et al. 2014. Lethal aggression in Pan is better explained by adaptative strategies than human impacts. Nature 513: 414-417.
Wilson, M.L. & R.W. Wrangham. 2003. Intergroup relations in chimpanzees. Annual Review of Anthropology 32: 363-392.
Wrangham, R.W. 1999. Evolution of coalitionary killing. Yearbook of Physical Anthropology 42: 1-30.
Wrangham, R.W. et al. 2006. Comparative rates of violence in chimpanzees and humans. Primates 47: 14-26.
Wrangham, R.W. & L. Glowacki. 2012. Intergroup aggression in chimpanzees and war in nomadic hunter-gatherers. Evaluating the Chimpanzee Model. Human Nature 23: 5-29.
Zeng, T.C. et al. 2018. Cultural hitchhiking and competition between patrilineal kin groups explain the post-Neolithic Y-chromosome bottleneck. Nature Communications 9: 2077
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Preparados para matar: Guerra se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Preparados para matar: algunas ideas para el debate
- Preparados para una Catástrofe Ultravioleta
- La ciencia y la guerra
¿Podría un humano vivir en el mar?
Los bajau laut viven en torno a las costas de Filipinas, Indonesia, Malasia y Brunéi y son mundialmente conocidos como «los nómadas del mar». Esta denominación es debida a que el pueblo bajau vive literalmente en el mar desde hace, como mínimo, 1.000 años. Pero, ¿cómo es eso de que viven en el mar?
Los vídeos de ¿Preguntas frecuentes? presentan de forma breve y amena cuestiones que, probablemente, nos hayamos planteado en alguna ocasión. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.
Edición realizada por César Tomé López
El artículo ¿Podría un humano vivir en el mar? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Qué tienen en común Einstein y una zanahoria?
- ¿Hemos intentando contactar con extraterrestres?
- ¿Qué pasa en tu cuerpo cuando te enamoras?
El pico petrolero
La Facultad de Ciencias de Bilbao comenzó su andadura en el curso 1968/69. 50 años después la Facultad de Ciencia y Tecnología de la UPV/EHU celebra dicho acontecimiento dando a conocer el impacto que la Facultad ha tenido en nuestra sociedad. Publicamos en el Cuaderno de Cultura Científica y en Zientzia Kaiera una serie de artículos que narran algunas de las contribuciones más significativas realizadas a lo largo de estas cinco décadas.

 Fotografía: Pixabay
Fotografía: Pixabay
¿Qué es el pico del petróleo (peak oil)?
El pico (o cénit) petrolero es el momento de máxima tasa de extracción del petróleo. Es un momento teórico a partir del cual se espera que la cantidad de petróleo disponible decline de manera irreversible. El concepto de pico del petróleo se atribuye a Marion King Hubbert (1903-1989) geólogo y geofísico estadounidense, quien en 1956 lo presentó por primera vez de manera formal (Figura 1). Este concepto se basa en extrapolar la historia conocida de yacimientos en explotación o que han sido explotados al total mundial. Los yacimientos de petróleo alcanzan muy rápido su pico de producción, para pasar después a una meseta, en la que la producción se mantiene más o menos constante, seguida de un largo declive. De hecho, la mayor parte del petróleo de un yacimiento se extrae en esta última fase.
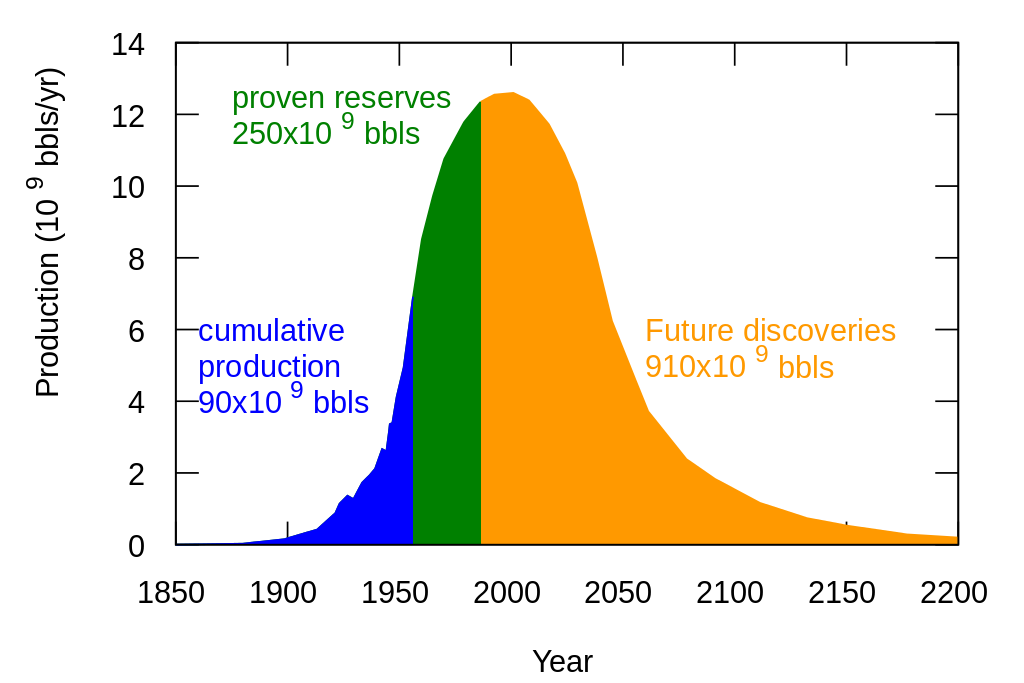 Figura 1. Propuesta M. King Hubbert de 1956 en la que se muestra la producción acumulada (en azul), así como una proyección hacia el futuro en base a las reservas probadas (en verde) y descubrimientos futuros. Este geólogo proponía el pico del petróleo en el año 2000 con una producción máxima de alrededor de la mitad que se produjo en 2016 (29.400 millones de barriles al año). Esta predicción fue realizada casi una década antes de que se produjera el máximo de descubrimientos de petróleo, en la década de los 60 (Figura 2). Licencia Creative Commons.
Figura 1. Propuesta M. King Hubbert de 1956 en la que se muestra la producción acumulada (en azul), así como una proyección hacia el futuro en base a las reservas probadas (en verde) y descubrimientos futuros. Este geólogo proponía el pico del petróleo en el año 2000 con una producción máxima de alrededor de la mitad que se produjo en 2016 (29.400 millones de barriles al año). Esta predicción fue realizada casi una década antes de que se produjera el máximo de descubrimientos de petróleo, en la década de los 60 (Figura 2). Licencia Creative Commons.
¿Qué es la tasa de retorno energético (TRE)?
El TRE se calcula dividiendo la cantidad de energía total que es capaz de producir una fuente de energía y la cantidad de energía que es necesaria “invertir” para explotar esta fuente. Un TRE alto indica una fuente de energía “rentable” (en términos energéticos), un TRE de 1 indica la cantidad de energía “invertida” y producida es la misma, por lo cual no aportaría energía extra al sistema, mientras que un TRE menor de uno indicaría que se trata de un sumidero energético, una fuente que aporta menos energía neta que la que es necesario invertir.
Si aplicamos el concepto de TRE a los yacimientos de petróleo vemos que cada yacimiento tiene un TRE distinto, y que, en promedio, el TRE de los yacimientos descubiertos ha ido disminuyendo a lo largo del tiempo. Los yacimientos con un petróleo de más calidad y cercanos a la superficie y, por tanto, más fácilmente explotables, fueron los primeros en explotarse. Posteriormente se han ido explotando yacimientos de más difícil acceso, y que, por lo tanto, tienen menores TREs. En el cómputo global, por tanto, a partir del cénit de extracción no sólo hay cada vez menos petróleo, sino que además se explotan yacimientos con cada vez menor TRE.
¿Hemos llegado al pico del petróleo?
Ésta es una pregunta complicada, por varios motivos. Por un lado, porque certificar con seguridad el pico petrolero solo puede hacerse una vez éste ha pasado y actualmente sólo podemos intentar estimar el mismo en base a las tendencias en la producción y descubrimiento de yacimientos. Por otro lado, lo que habitualmente llamamos petróleo en realidad engloba varias categorías de hidrocarburos líquidos: petróleo crudo convencional, crudo extra-pesado, arenas bituminosas, petróleo ligero de roca, etc, cuyo cénit de producción debería calcularse por separado. Aunque el número de descubrimientos se mantiene estable desde finales del s. XX, después de haber tenido su máximo en la década de los 60 del pasado siglo (Figura 2), el TRE de estos yacimientos es menor. Esto no debe sorprendernos, ya que se trata de un recurso finito, no-renovable, y es razonable pensar que los yacimientos más grandes y más ricos fueron los primeros en ser descubiertos. Algunas estimaciones indican que es probable que estemos viviendo actualmente el pico del petróleo crudo convencional.
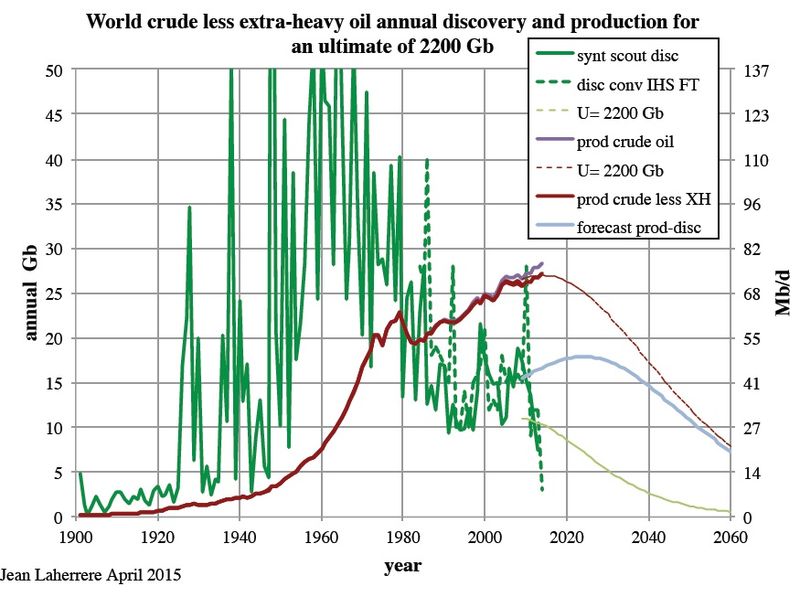 Figura 2. Descubrimiento de petróleo (en verde) junto con la producción (en rojo). En esta gráfica se puede ver que el máximo de descubrimientos se realizó en la década de los 60. La producción creció muy rápidamente a partir del fin de la segunda guerra mundial para alcanzar un primer máximo en 1979, con un crecimiento posterior más lento. Fuente: Figura por Jean Laherrere (Creative Commons).
Figura 2. Descubrimiento de petróleo (en verde) junto con la producción (en rojo). En esta gráfica se puede ver que el máximo de descubrimientos se realizó en la década de los 60. La producción creció muy rápidamente a partir del fin de la segunda guerra mundial para alcanzar un primer máximo en 1979, con un crecimiento posterior más lento. Fuente: Figura por Jean Laherrere (Creative Commons).
¿Cuáles son las implicaciones del pico petrolero?
La primera, implícita en la propia definición del pico petrolero es la disminución progresiva del petróleo y de la energía que puede ser extraída del mismo. La Agencia Internacional de la Energía (AIE; o IEA en sus siglas en inglés) publica cada año un informe sobre la situación energética internacional (World Energy Outlook; WEO), tratando distintos apartados, entre ellos el petróleo. El último informe indica una previsión de crecimiento de la demanda mundial de petróleo debido al creciente transporte por carretera, aviación y de las petroquímicas, que se cifra en más de 10 millones de barriles diarios para 2025. Por otro lado, la AIE realiza una predicción de la producción del petróleo y prevé que para el año 2025 faltarán al menos 13 millones de barriles de petróleo para satisfacer las demandas. En base a los datos publicados por la AIE, Antonio Turiel, científico titular del CSIC, ha calculado la energía neta que de manera realista ofrece el petróleo actualmente y que ofrecerá en el futuro. Esos cálculos indican una disminución de más del 50% en los próximos 25 años, pasando de 69 millones de barriles equivalentes diarios a 33 millones en el año 2040 (Figura 3).
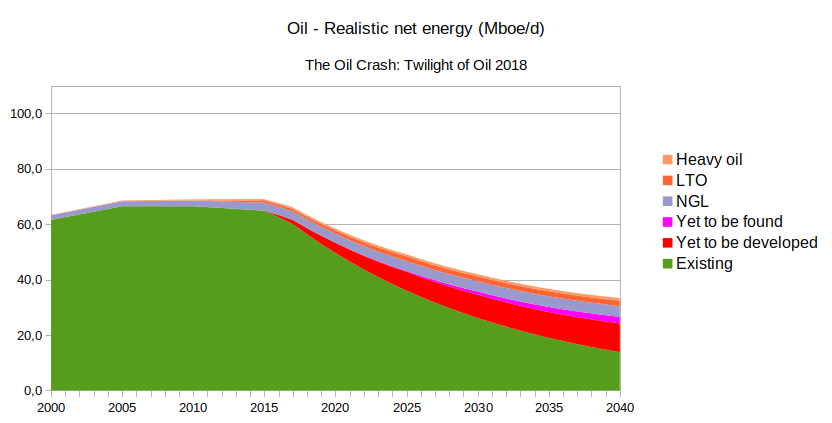 Figura 3. Estimación de la energía neta a partir del petróleo hasta el año 2040. Se ha usado la predicción de producción proporcionada por la Agencia Internacional de la Energía, aplicándole la tasa de retorno energético. Gráfica realizada por Antonio Turiel.
Figura 3. Estimación de la energía neta a partir del petróleo hasta el año 2040. Se ha usado la predicción de producción proporcionada por la Agencia Internacional de la Energía, aplicándole la tasa de retorno energético. Gráfica realizada por Antonio Turiel.
El cénit de producción es un concepto que se puede aplicar a todo recurso no renovable. De hecho, además del cénit de producción del petróleo también se habla de otros cénits de recursos energéticos como el carbón, el uranio o el gas natural, algunos de los cuales (los combustibles fósiles) podrían estar también próximos en el tiempo ( menos de 20 años). En definitiva, la perspectiva de una disminución de la energía neta disponible es real.
Los intentos de mejora de la eficiencia energética podrían ayudar a la disminución de la energía por persona. Por desgracia, parece probado que la mejora de la eficiencia en la que se usa un recurso debido al desarrollo tecnológico, más que disminuir el consumo de dicho recurso, hace más probable un aumento en el consumo del mismo (paradoja de Jevons). Por otro lado, la sustitución del petróleo y otros combustibles fósiles por otras fuentes de energía, no es un asunto sencillo, ya que hay ciertos sectores (p.ej., transporte aéreo, transporte pesado por mar y carretera) cuya electrificación no es viable. Además, estos intentos de sustitución necesitarían en su desarrollo ingentes cantidades de energía y/o de materias primas raras y escasas.
Existe una correlación entre la economía real y la cantidad de energía disponible, y el petróleo está muy imbricado en todos los sectores económicos. Por ello, la disminución de la cantidad disponible de petróleo y otros combustibles fósiles, y por ende, de la energía disponible, tiene implicaciones a muchos niveles en el sistema económico mundial. Además, el control de recursos energéticos y minerales son los condicionantes principales de las agendas geoestratégicas de las grandes potencias.
El cénit de la producción de petróleo, al igual que el cénit de producción de otros combustibles fósiles, son parte y consecuencia del cambio global; es decir, del conjunto de cambios que tiene un origen antropogénico y que están teniendo repercusiones a escala geológica. Las consecuencias de las actividades humanas, incluyendo el cambio climático y la pérdida masiva de biodiversidad, son los grandes desafíos a los que se debería estar enfrentando nuestra especie actualmente.
Para saber más:
Miller Richard, G., Sorrell Steven, R., 2014. The future of oil supply. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 372, 20130179.
A. Turiel (2019).
M. Mediavialla et al. (2019).
G. Tverberg (2019).
Sobre el autor: Asier Gómez es investigador Ramón y Cajal en el Departamento de Estratigrafía y Paleontología de la Facultad de Ciencia y Tecnología de la UPV/EHU.
El artículo El pico petrolero se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Energía oscura
- Espectrometría de masas: de un isótopo de neón a elefantes que vuelan
- Proteómica: cuando las proteínas y la espectrometría de masas van de la mano
El progreso nos salvará del ecologismo
 Clausura (2014) de Santiago Talavera. Acuarela, tinta, lápiz de color y collage sobre papel. 180 x 152 cm
Clausura (2014) de Santiago Talavera. Acuarela, tinta, lápiz de color y collage sobre papel. 180 x 152 cm
El ecologismo surgió en la década de 1960 como consecuencia de, primero, el conocimiento científico resultado de la ecología, las ciencias de la Tierra, la meteorología, la zoología, la botánica, etc. Y, segundo, de la romantización de la naturaleza. Esto tiene como origen la definición presocrática de la naturaleza, es decir, que la naturaleza es la totalidad de las cosas a excepción del hombre y de las cosas del hombre.
En esencia, el ecologismo podría entenderse como una forma de progreso, ya que su prioridad es la salud del planeta. El planeta es nuestra casa, así que su mantenimiento es, a fin de cuentas, una garantía de evolución y bienestar humanos. Sin embargo, el movimiento ecologista tradicional se desmarca del progreso, precisamente por cómo define la naturaleza. Tanto es así, que para el ecologismo el progreso es una suerte de reiterados pecados contra la naturaleza. Así es el movimiento ecologista gestado en la década de 1970, esa ideología verde de activistas como Al Gore, el papa Francisco o Greenpeace.
El ecologismo verde o ecologismo tradicional anhela una naturaleza prístina. Como si esa naturaleza hubiese sido mancillada por la humanidad. Es una visión infantilizada de la naturaleza. Esta idealización tiene sus consecuencias, en primer lugar intelectuales, que son las más graves, y en segundo lugar prácticas, que afectan a la economía, la política, la ciencia y la tecnología, entre otras.
Algunas de las consecuencias intelectuales del ecologismo tradicional son el pesimismo y el nihilismo. El ecologismo es un movimiento apocalíptico: agotamiento de recursos, superpoblación, pobreza, enfermedad… Y, como la mayoría de movimientos apocalípticos, es misántropo. Culpa a la humanidad de la inevitable catástrofe, definiendo así a la humanidad como el cristianismo se refiere al pecado. Y no solo culpa a la humanidad, sino que solicita su retirada. Con frecuencia aluden a la humanidad como al cáncer de la naturaleza, y como tal, hay que combatir la enfermedad siguiendo una estrategia radical. La fantasía última es un planeta despoblado. Por lo de pronto pretenden el retroceso de las actividades humanas: la desindustrialización y el rechazo al progreso, a la ciencia y a la tecnología. Esto lo vemos en el ecologismo que rechaza la ingeniería genética, la síntesis química, la radiación wifi o la energía nuclear. Un movimiento que nació en parte como consecuencia del conocimiento científico, ahora lo contradice.
El ecologismo tradicional incurre en una serie de errores precisamente por tratarse de un movimiento anticientífico, o contrailustrado, como quiera llamarse. Por ejemplo, la idealización de las reservas naturales. Este es un fenómeno curioso, ya que las llamadas reservas naturales no son santuarios naturales, sino producto de la civilización. Son espacios protegidos y controlados. Lo mismo ocurre con la llamada agricultura ecológica. Agricultura ecológica es un oxímoron. La agricultura, por definición, contradice a la ecología tradicional. La agricultura es una de las prácticas humanas que produce un mayor impacto medioambiental y supone un desequilibrio dirigido de los ecosistemas. No hay más que ver la parcelación del paisaje. Destrozamos el suelo, lo allanamos, lo inundamos y lo plagamos de monocultivos. Cultivos que, por cierto, son engendros genéticos que ni siquiera sobrevivirían sin el cuidado permanente que hacemos de ellos.
La llamada agricultura ecológica genera más impacto que la llamada agricultura tradicional precisamente porque la agricultura ecológica rechaza el progreso científico y tecnológico. Necesita más terreno para producir la misma cantidad de alimento, tiene menor rendimiento, con lo cual es menos sostenible. Por ejemplo, la agricultura ecológica no contempla los cultivos hidropónicos, que ni siquiera necesitan suelo. Ni el uso de transgénicos, aunque ello suponga dejar de emplear pesticidas. Es como si la agricultura ecológica respondiese a una idealización nostálgica de lo que fue la agricultura hasta un momento concreto, congelado en el tiempo de forma arbitraria. Esa es la idea, aunque en la práctica ni siquiera es así de romántica. Los cultivos ecológicos a menudo se encuentran bajo invernadero y apenas se diferencian de la agricultura tradicional que simplemente se ha quedado anclada unas décadas atrás.
El ecologismo tradicional se está convirtiendo en un movimiento meramente cosmético. Resulta muy ilustrativa la preocupación y el malestar que nos provoca encontrarnos con pequeños trozos de plástico en la playa, en contraposición con la indiferencia que nos producen los cantos de vidrio, cemento o ladrillo. Por si hay dudas, el impacto medioambiental de los materiales cerámicos es mayor que el de los plásticos. Otro ejemplo. Nos parece idílica y consecuente la vida en el campo, las casas antiguas con paredes de piedra. Efectivamente tienen un valor estético y arquitectónico, pero no ecológico. La vida en las ciudades, en edificios, además de dejar más espacio al campo, si se quiere, para las anheladas reservas naturales, necesita menos recursos para el desplazamiento, construcción y calefacción. El techo de uno es el suelo del otro. Otro ejemplo. Las cascadas artificiales de la energía hidráulica, los paneles solares de la energía fotovoltaica, los molinos de la energía eólica que abarcan inmensas extensiones de terreno. No los contemplamos como las perturbaciones del paisaje que de hecho son, sino como parte de la lucha contra el calentamiento global. Hemos aprendido a contemplar esas monstruosidades como ecologismo. Sin embargo, una central nuclear, que es más sostenible, genera mucha más energía a partir de menos recursos, con un menor impacto medioambiental, la apreciamos como lo contrario al ecologismo. Efectivamente el ecologismo es un movimiento cosmético.
Por estas razones, otro tipo de ecologismo es posible. El ecologismo ilustrado. Se trata de un ecologismo que permanece ligado al conocimiento científico y, por tanto, entiende que los problemas medioambientales a los que nos enfrentamos sí tienen solución y esta vendrá de la mano del progreso. No es un movimiento apocalíptico, sino optimista y realista. No define a la naturaleza al estilo presocrático, sino que la humanidad entra dentro de la definición de la naturaleza que se pretende preservar. Por tanto, el bienestar humano es crucial.
Las soluciones que propone el ecologismo ilustrado a los problemas medioambientales pasan por el uso de todo el conocimiento científico y tecnológico que hemos generado hasta ahora. De la ingeniería genética a la física nuclear.
Escapar de la pobreza requiere energía y alimentos en abundancia. Escapar de la pobreza intelectual requiere ilustración. Escapar de la pobreza requiere progreso.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo El progreso nos salvará del ecologismo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sin ciencia no hay progreso
- #Naukas14: La fragilidad del progreso
- El falso pan integral tiene los días contados
El poema de los números primos
El Centro Internacional de Cultura Contemporánea TABAKALERA, de Donostia/San Sebastián nos ha regalado estos días una maravillosa exposición de la artista donostiarra Esther Ferrer, comisariada por Laurence Rassel y Mar Villaespesa. Bajo el título Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… (del 5 de abril al 26 de mayo de 2019), la exposición recoge, en cuatro espacios conectados de Tabakalera, cuatro grupos de obras emblemáticas de la artista Esther Ferrer: proyectos espaciales, una visión general de las performances más significativas de su carrera (con realizaciones de las performances cada viernes), obras de la serie Poema de los números primos, y cuadros de la obra Pi.
 Cartel de la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… (del 5 de abril al 26 de mayo de 2019), en el Centro Internacional de Cultura Contemporánea TABAKALERA, de Donostia/San Sebastián. Imagen de Tabakalera
Cartel de la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… (del 5 de abril al 26 de mayo de 2019), en el Centro Internacional de Cultura Contemporánea TABAKALERA, de Donostia/San Sebastián. Imagen de Tabakalera
 Vista parcial del suelo de la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… en Tabakalera, mostrándonos un “mar de números primos” generado por la artista Esther Ferrer, para esta obra de la serie Poema de los números primos diseñada expresamente para la exposición. Fotografía: Raúl Ibáñez
Vista parcial del suelo de la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… en Tabakalera, mostrándonos un “mar de números primos” generado por la artista Esther Ferrer, para esta obra de la serie Poema de los números primos diseñada expresamente para la exposición. Fotografía: Raúl Ibáñez
Los números primos constituyen un elemento fundamental en la obra artística de Esther Ferrer, que ella ha utilizado desde las décadas de los años 1970 y 1980, a través de diferentes estructuras espaciales planas, como la conocida espiral de Ulam.
La propia artista, con motivo de su exposición en Artium en 2011, explica el origen de su trabajo con representaciones espaciales de los números primos:
“Tras algunos años, en la década de los 70, realizando proyectos con estructuras geométricas definidas únicamente en función de mis propios criterios, sentí la necesidad de pensar otras en las cuales mis preferencias estéticas jugaran un papel secundario. Estructuras libres que pudieran evolucionar por sí mismas, según su lógica interna…
Durante algún tiempo no conseguí un resultado que me satisficiera hasta que una noche soñé con los números primos, así empecé la serie, EL POEMA DE LOS NÚMEROS PRIMOS.”
Además, el título de la serie juega con la similitud de las palabras poema y teorema (recordemos que un teorema es una verdad matemática demostrable), “poema = teorema – ter + p”, así mismo este título nos habla de la poesía que está detrás de los números, en particular, de los números primos.
 Maqueta de un proyecto de números primos hexagonales, de la serie Poema de los números primos (1989), de la artista Esther Ferrer. Edición especial producida por ARTIUM, Centro-Museo Vasco de Arte Contemporáneo, en 2011
Maqueta de un proyecto de números primos hexagonales, de la serie Poema de los números primos (1989), de la artista Esther Ferrer. Edición especial producida por ARTIUM, Centro-Museo Vasco de Arte Contemporáneo, en 2011
Pero vayamos con los objetos matemáticos utilizados por la artista donostiarra, los números primos, la espiral de Ulam y otras estructuras geométricas planas formadas por números.
Aunque seguramente todas las personas que estáis leyendo esta entrada del Cuaderno de Cultura Científica conocéis el concepto de número primo, siempre es conveniente empezar por el principio. Los números primos son aquellos números que solamente se pueden dividir por 1 y por ellos mismos. Así, por ejemplo, el número 25 no es un número primo ya que se puede dividir por 5, además de por 1 y 25, o tampoco el 33, divisible por 3 y 11, mientras que el número 17 sí es primo, ya que solamente es divisible por el 1 y el mismo, al igual que los números 2, 3, 5, 7, 11, 13 o 19.
El teorema fundamental de la aritmética, que ya aparece en el libro Los Elementos, de Euclides de Alejandría (aprox. 325 -265 a.n.e.), y que nos dice que todo número puede expresarse, de forma única, como producto de números primos, por ejemplo, el número 924 es igual al producto de 2 x 2 x 3 x 7 x 11, pone de manifiesto la importancia de esta familia de números. Además, este resultado es el motivo por el cual el número 1 no se considera un número primo, puesto que en ese caso no se daría la unicidad.
En la Antigua Grecia ya conocían también un método para obtener números primos, conocido como la criba de Eratóstenes. Este método aparece descrito en el texto Introducción a la Aritmética, del filósofo y matemático Nicómaco de Gerasa (aprox. 60 – 120 n.e.), quien atribuye su autoría al sabio polifacético griego Eratóstenes de Cirene (276-194 a.n.e.), aquel que también estimó de forma muy certera el diámetro de la esfera terrestre (véase El tamaño sí importa, que se lo pregunten a Colón (o de la geometría griega para medir el diámetro de la Tierra)).
El método de la criba de Eratóstenes consiste en lo siguiente. Consideremos todos los números naturales hasta uno dado, por ejemplo, tomemos uno bajo para ilustrar el concepto, el 25. En primer lugar, escribimos todos los números hasta ese número:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24 y 25.
El 1 no es primo, luego lo tachamos, es decir, lo eliminamos como número primo. Después tenemos el 2, que sí es primo, lo marcamos (nosotros lo hemos puesto en negrita) y tachamos todos los múltiplos de 2, los números pares, que no serán números primos, puesto que los podemos dividir por 2.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24 y 25.
El siguiente número que aparece es el 3, que es primo, lo marcamos y tachamos todos los múltiplos de 3, puesto que no son primos.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24 y 25.
El siguiente número que aparece es el 5, que, puesto que no está tachado (esto nos expresa que no es divisible por ningún número anterior), es un número primo, luego lo marcamos y tachamos sus múltiplos, los que aún no estén tachados.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24 y 25.
El siguiente número no tachado es el 7, luego es un número primo, y debemos de tachar sus múltiplos, así hasta recorrer toda la lista hasta el número final, en este caso el 25. En este sencillo caso nos quedaría:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24 y 25.
Luego, los números primos menores que 25 son 2, 3, 5, 7, 11, 13, 17, 19 y 23.
Este es un método sencillo que nos permite ir obteniendo números primos hasta un número dado, aunque es un método con muchas limitaciones, ya que no permite conocer si un número en concreto, por ejemplo, el número 76.243, es primo o no, para saberlo la criba debe de llegar hasta ese número (en este caso, sí es primo), ni generar números primos, ni conocer sencillas propiedades de estos números, como, por ejemplo, si existen infinitos números primos.
Puesto que nuestros elementos de escritura, como una hoja de papel, son rectangulares, y además una línea continua de números se nos extendería mucho, lo normal es representar los números, hasta el número considerado, en un rectángulo de números, como el que aparece abajo y aplicar sobre el mismo el método de la criba de Eratóstenes.
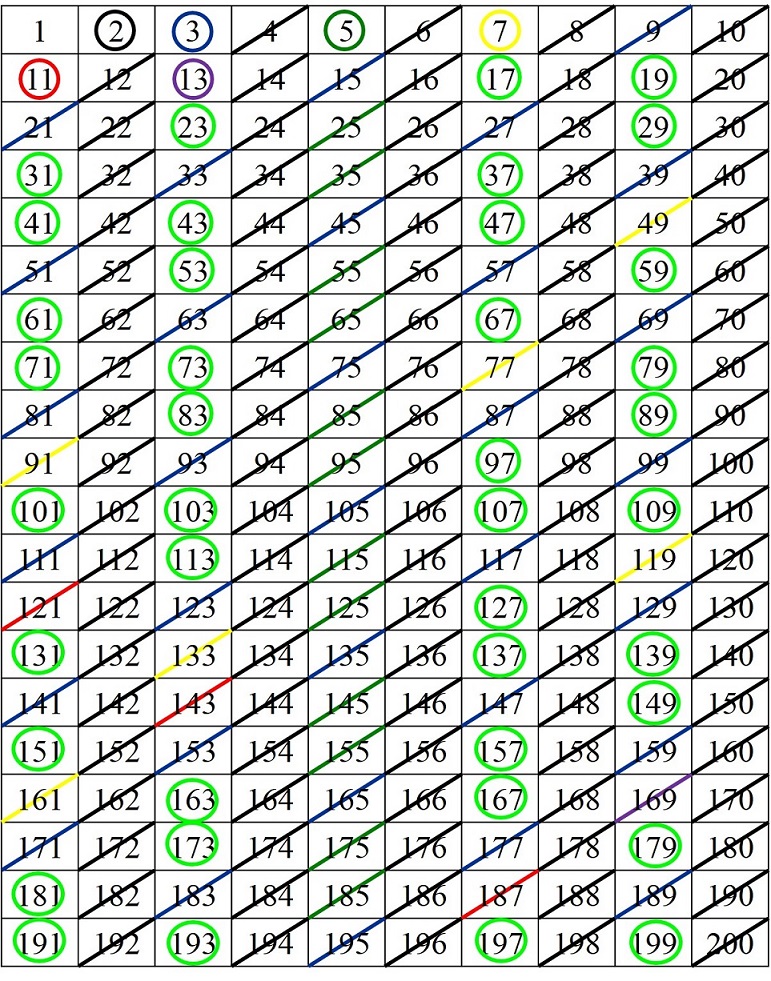
Así, los números primos hasta el 200 son: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199.
La criba de Eratóstenes, expresada de esta forma, ya es una estructura geométrica plana, rectangular, que nos puede permitir buscar información de la estructura de la familia de números primos, como patrones visuales que puedan producirse a partir de los cuales obtener dicha información. Por ejemplo, aunque esto es evidente sin necesidad de la criba de Eratóstenes, podemos observar que todos los primos están en cuatro columnas, que se corresponden a los números que terminan en 1, 3, 7 y 9. Y nos permite ver que hay muchas parejas de números primos gemelos, que son aquellos números primos que están lo más cerca posible, es decir, con tan solo un número par entre ellos, como las parejas 11 y 13, 17 y 19, 41 y 43, 59 y 61, 71 y 73, 101 y 103, 107 y 109, 137 y 139, 149 y 151, 179 y 181, 191 y 193, 197 y 199, que se corresponden con las terminaciones (1, 3), (7, 9) o (9, 1). Estas parejas de números primos gemelos también han interesado a la artista Esther Ferrer.
Antes de continuar con la espiral de Ulam, remarquemos dos hechos muy importantes relacionados con los números primos, que juegan un papel central en la serie Poema de los números primos de la artista donostiarra y de los que ya hablamos en la entrada del Cuaderno de Cultura Científica Buscando lagunas de números primos, que existen infinitos números primos y que cada vez existen menos números primos en la recta de los números naturales, es decir, la densidad de números primos según vamos avanzando en los números naturales es cada vez menor.
“Un día soñé que nadaba en un mar de números y después del sueño todos los que se me venían a la cabeza eran primos. Así fue como empecé a trabajar en la serie Poema de los números primos, y a plantearme la cuestión del infinito, que trabajé más tarde recurriendo a Pi, sin duda un número infinito.”
(Conversación entre Esther Ferrer, Laurence Rassel y Mar Villaespesa en Esther Ferrer, todas las variaciones son válidas, incluida esta, 2017)
 Poema de los números primos (2016), de Esther Ferrer, dibujo para suelo, realizado en tita sobre papel cuadriculado, 104,5 cm x 83,5 cm, del Archivo de Esther Ferrer. Imagen del catálogo Esther Ferrer, todas las variaciones son válidas, incluida esta, del Museo Nacional Centro de Arte Reina Sofía
Poema de los números primos (2016), de Esther Ferrer, dibujo para suelo, realizado en tita sobre papel cuadriculado, 104,5 cm x 83,5 cm, del Archivo de Esther Ferrer. Imagen del catálogo Esther Ferrer, todas las variaciones son válidas, incluida esta, del Museo Nacional Centro de Arte Reina Sofía
La anterior obra tiene como base una criba de Eratóstenes rectangular de 76 columnas, es decir, la primera fila son los números del 1 al 76, y 99 columnas, luego nos determina los números primos hasta el número 7.524 (76 x 99). Esther Ferrer construye esta criba de Eratóstenes en la que se producen cuatro columnas vacías de números primos (la de la derecha, debajo del cero, es un añadido para dar simetría a la estructura), correspondientes a las columnas debajo del 19, 38, 57 y 76, múltiplos de 19.
Esther Ferrer genera, a través de su mirada personal, una determinada estructura espacial que subyace a la distribución real de los números primos dentro de la recta de los números naturales, que es una realidad del universo de los números, pero que observamos a través de la mirada creativa de la artista. Esta hermosa obra ha sido realizada en el suelo del Palacio de Velázquez, en el Parque del Retiro de Madrid, para la exposición Esther Ferrer, todas las variaciones son válidas, incluida esta (2017). Además, al realizarla a un tamaño grande, dispuesta en el suelo y sobre la que pasear, cautiva a las personas que pasean sobre ella y realza aún más el impacto de la estructura de los números primos.
 Realización de la obra Poema de los números primos (2016), de Esther Ferrer, en el suelo del Palacio de Velázquez, para la exposición Esther Ferrer, todas las variaciones son válidas, incluida esta (2017). Imagen de ZAS Madrid
Realización de la obra Poema de los números primos (2016), de Esther Ferrer, en el suelo del Palacio de Velázquez, para la exposición Esther Ferrer, todas las variaciones son válidas, incluida esta (2017). Imagen de ZAS Madrid
Martin Gardner en su artículo The remarkable lore of the prime numbers cuenta que el matemático polaco Stanislaw Ulam (1909 – 1984), quien participó en el proyecto Manhattan y desarrollo junto con el matemático húngaro John Von Newmann (1903 – 1957) el método de Montecarlo, estaba escuchando una conferencia en el Laboratorio Científico de Los Álamos, que el propio Ulam describió como “un artículo largo y muy aburrido”, y empezó a hacer garabatos en una hoja, en concreto, empezó a escribir los números en espiral, empezando en el 1 y en el sentido contrario a las agujas del reloj, e hizo un círculo alrededor de los números primos. Entonces se dio cuenta de que los números primos se concentraban en líneas rectas, especialmente en diagonales, así mismo, había algunas diagonales, como las formadas solo por números pares, en las que no había ningún número primo.
En Los Álamos disponían del ordenador MANIAC II, que tenía guardados en su memoria los primeros 90 millones de números primos, por lo que junto a Myron L. Stein y Mark B. Wells programaron el ordenador para que realizara una espiral de números, con los números naturales desde el 1 hasta el 65.000, en la que se marcaran solamente los números primos. La imagen que obtuvieron (que hemos incluido más abajo y que aparece en el artículo de Ulam, Stein y Wells, A visual display of some properties of the distribution of primes, 1964) confirmaba lo que había visto Ulam, que los números primos aparecen alineados en rectas horizontales, verticales y, sobre todo, diagonales.
A esta estructura geométrica plana en la que los números naturales son escritos en espiral, empezando en el 1 y en el sentido contrario a las agujas del reloj, destacando los números primos, es lo que se conoce como la espiral de Ulam (dos imágenes más abajo puede verse con más claridad).
 Espiral de números primos representada por Stanislaw Ulam, Myron Stein y Mark Wells, con el ordenador Maniac II de Los Álamos, en 1964, en la que se observa que los números primos están alineados en rectas diagonales, verticales y horizontales
Espiral de números primos representada por Stanislaw Ulam, Myron Stein y Mark Wells, con el ordenador Maniac II de Los Álamos, en 1964, en la que se observa que los números primos están alineados en rectas diagonales, verticales y horizontales
Detrás de esta observación de Stanislaw Ulam está el hecho de que los números de las líneas verticales, horizontales y diagonales se corresponden con los valores de los polinomios cuadráticos de la forma 4n2 + bn + c, como puede verse en la siguiente imagen. En función de los valores de b y c se generan diferentes líneas que tendrán más o menos números primos. Por ejemplo, si b y c son pares, solo se producen números pares y no habrá números primos en dichas líneas, salvo quizás el 2. El polinomio de la imagen siguiente, 4n2 + 8n + 3, es igual a (2n + 1)(2n + 3), luego no genera números primos, salvo el 3, para n = 0. Mientras que otras líneas, como la diagonal 4n2 + 26n + 41, sí genera números primos, como 41, 71, 109 o 271, y no primos, como 155 y 209. Dos polinomios cuadráticos que generan muchos números primos son 4n2 – 2n + 41, que a partir de un cierto valor de n genera la línea diagonal de puntos blancos en la parte de arriba de la imagen de Ulam, Stein y Wells (la imagen anterior), y 4n2 + 2n + 41, que es la línea de abajo.
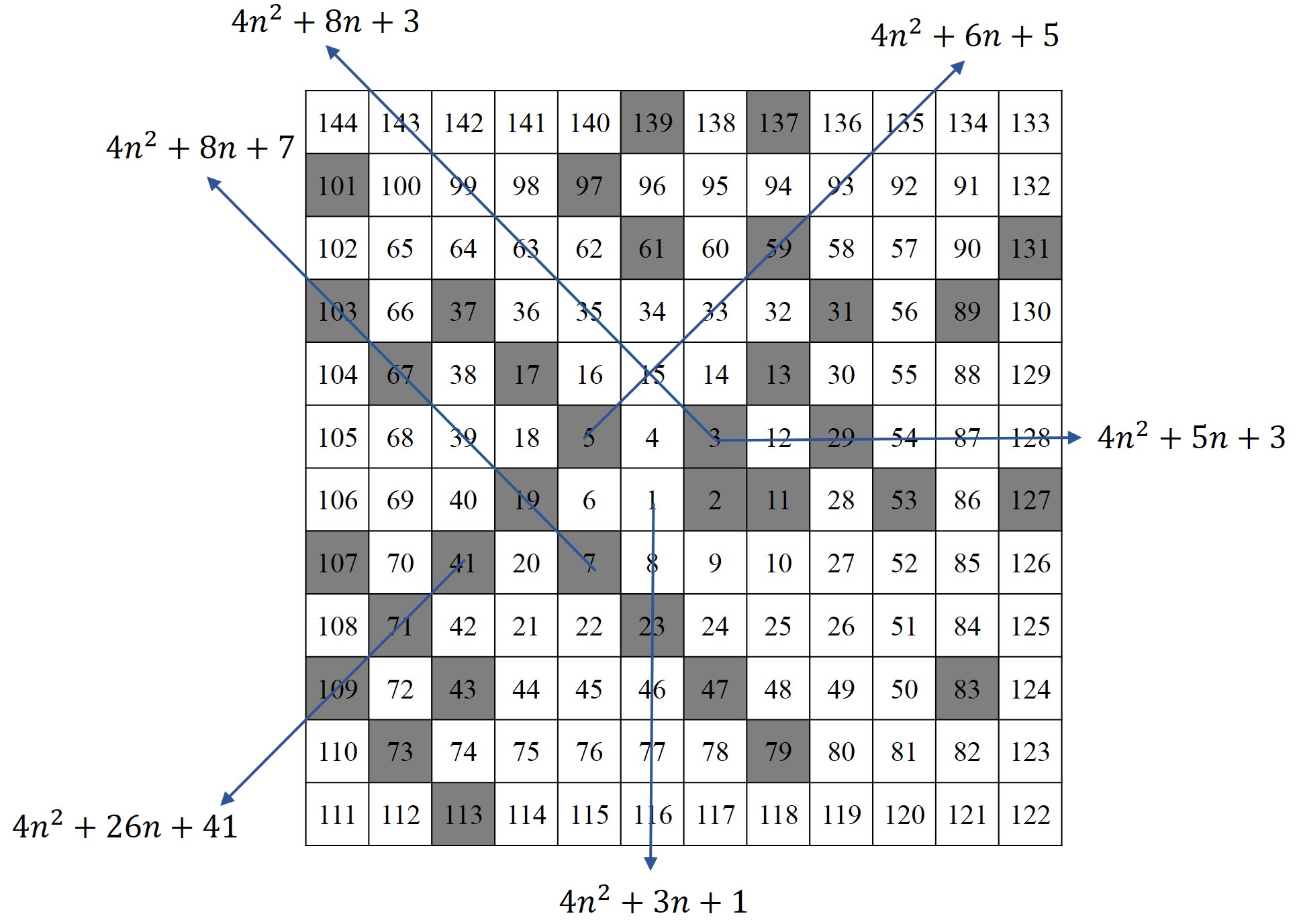 Espiral de Ulam, en una cuadrícula 12 x 12, y algunas líneas de números con los polinomios cuadráticos que las generan
Espiral de Ulam, en una cuadrícula 12 x 12, y algunas líneas de números con los polinomios cuadráticos que las generan
El siguiente dibujo de Esther Ferrer, de entre los años 1983 y 1985, nos da algunas claves de la forma en la que la artista trabaja con la espiral de Ulam. Para empezar el dibujo contiene la espiral de Ulam en una cuadrícula 16 x 16, luego con los números desde 1 hasta 256. Además, solo están escritos los números primos en la espiral y en las posiciones que corresponden a números compuestos, es decir, los números no primos, está dibujado un segmento diagonal “tachando” ese número, pero sin el número. En este dibujo, las diagonales tienen dos posiciones y dos colores posibles. El sentido de la diagonal y el color cambian cada vez que aparece un número primo, de forma que entre un primo y el siguiente, es decir, lo que conocemos como una laguna de números compuestos entre números primos (véase la entrada Buscando lagunas de números primos), las diagonales que aparecen tienen un mismo sentido y color. La confluencia de la construcción de la espiral de Ulam, junto con las diagonales inclinadas y de colores, confiere al conjunto de una estructura geométrica particular, casi laberíntica en este caso, que es el objetivo buscado por la artista.
 Dibujo de la serie Poema de los números primos (1983 – 1985), de Esther Ferrer, expuesto en la Galería Angels Barcelona, que reproduce la espiral de Ulam en una cuadrícula 16 x 16
Dibujo de la serie Poema de los números primos (1983 – 1985), de Esther Ferrer, expuesto en la Galería Angels Barcelona, que reproduce la espiral de Ulam en una cuadrícula 16 x 16
Stanislaw Ulam también realizó una espiral similar, pero empezando con el número 17, de forma que los números de una de las dos diagonales principales se correspondían con los valores, desde n = 0 hasta 15, del polinomio n2 + n + 17, eran números primos (17, 19, 23, 29, 37, …, 257), lo cual fallaba para el siguiente valor, n = 16, que es un número compuesto, 162 + 16 + 17 = 172. Este polinomio ya era conocido por el matemático suizo Leonhard Euler (1707 – 1783), como un polinomio que generaba muchos números primos.
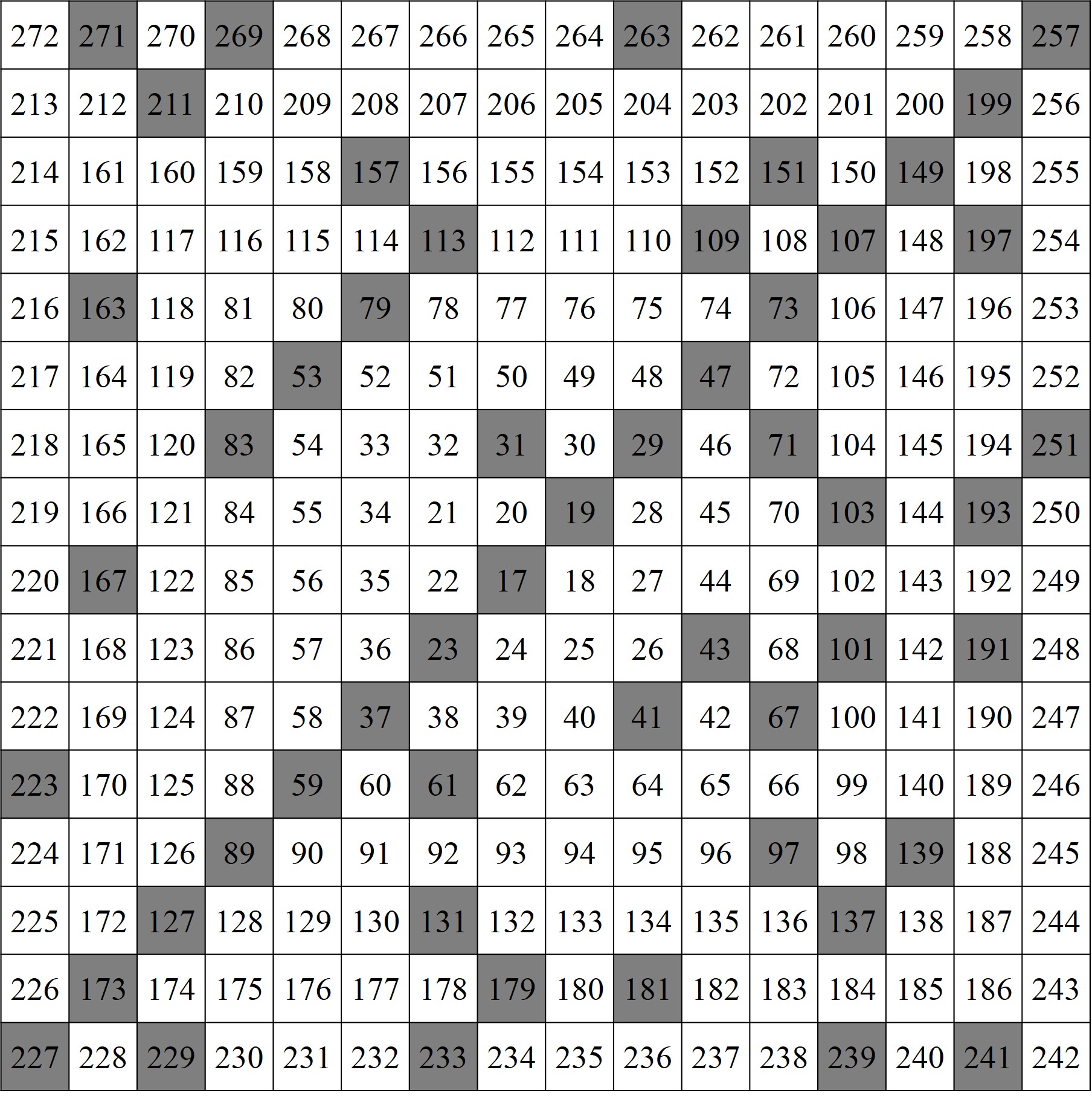 Espiral de Ulam empezando en el número 17, cuyos números de la diagonal son valores del polinomio n2 + n + 17, y son números primos para n = 0, …, 15, es decir, entre el 227 de abajo a la izquierda y el 257 de arriba a la derecha
Espiral de Ulam empezando en el número 17, cuyos números de la diagonal son valores del polinomio n2 + n + 17, y son números primos para n = 0, …, 15, es decir, entre el 227 de abajo a la izquierda y el 257 de arriba a la derecha
Un polinomio que genera muchos números primos y que también era conocido por el matemático Leonhard Euler (1772) es n2 + n + 41. Si se inicia la espiral de Ulam en el número 41, los números de la diagonal principal son valores de este polinomio generador de primos de Euler y para los valores entre n = 0 y n = 39, se genera un segmento continuo en esa diagonal de 40 números primos, que durante más de dos siglos fue el segmento más grande conocido de este tipo. Ulam, Stein y Wells encontraron que, para valores de n entre 0 y 10.000.000, el polinomio n2 + n + 41 genera un 47,5% de números primos, casi uno de cada dos (aunque en esta entrada no vamos a dedicarnos a este tema, en matemáticas se han continuado estudiando polinomios que generan muchos números primos). Los valores de este polinomio n2 + n + 41 son, en la espiral de Ulam empezando en 1, los valores del polinomio es 4m2 + 170m + 1847, haciendo el cambio n = 2m + 42.
La espiral de Ulam empezando en el número 41 alcanzó cierta notoriedad por esa diagonal principal con un segmento de 40 primos seguidos, con el 41 en el medio, 19 primos hacia abajo en la diagonal, hasta el número 1523, y 20 primos hacia arriba, hasta el número 1601.
 Dibujo de la serie Poema de los números primos (años 1970 – 1980), de Esther Ferrer, basado en la espiral de Ulam que empieza en el número 41, y con los 40 números primos en la diagonal principal. Imagen del catálogo Esther Ferrer, todas las variaciones son válidas, incluida esta
Dibujo de la serie Poema de los números primos (años 1970 – 1980), de Esther Ferrer, basado en la espiral de Ulam que empieza en el número 41, y con los 40 números primos en la diagonal principal. Imagen del catálogo Esther Ferrer, todas las variaciones son válidas, incluida esta
El anterior dibujo fue la base para la realización de una obra de la serie Poema de los números primos en el parque del Prado en Vitoria-Gasteiz, en 2003. Es una espiral de Ulam de 100 x 100 = 10.000 “números”, que empieza en el número 41 y cuyo último número primo es 10.039. Está realizada con baldosas de cerámica, de tamaño 20 x 20 cm cada una, en las que aparece una diagonal roja, una diagonal azul o un número primo. Luego el tamaño de la obra es de 20 x 20 metros.
 Instalación Poema de los números primos (2003), de la artista Esther Ferrer, en el parque del Prado (Vitoria-Gasteiz). Imagen de la web de ARTIUM
Instalación Poema de los números primos (2003), de la artista Esther Ferrer, en el parque del Prado (Vitoria-Gasteiz). Imagen de la web de ARTIUM
Esther Ferrer explica así el objetivo de elegir esa obra para el parque del Prado de Vitoria-Gasteiz:
“– es una obra que incita a la reflexión puesto que no corresponde exactamente a los cánones más o menos establecidos sobre lo que es o no es una obra de arte,
– es una obra dinámica, con posibilidades de interactividad libre y espontánea, sin normas,
– además de su belleza intrínseca, esta pieza aporta un elemento lúdico, puesto que los niños que frecuenten el parque jugarán sobre ella y quizás inventarán a partir de la misma sus propios juegos,
– podrán también empezar a comprender que las matemáticas no son forzosamente aburridas, y que con ellas puede hacerse incluso arte,
– por último, podrán aprender, iniciarse, sin prácticamente darse cuenta, en el universo de los números primos, esos números tan particulares, casi mágicos, conocidos desde la más remota antigüedad y que actualmente presentan una gran utilidad en diferentes campos, tanto científicos, como técnicos.”
 Dibujo-maqueta Poema de los números primos (años 1980-1990), de Esther Ferrer. Imagen de la página de Esther Ferrer
Dibujo-maqueta Poema de los números primos (años 1980-1990), de Esther Ferrer. Imagen de la página de Esther Ferrer
Como bien explica Esther Ferrer en su libro Maquetas y dibujos de instalaciones 1970/2011, para toda una serie de dibujos-maquetas de números primos, estos están “pensados para suelos, alfombras, murales por lo que pueden realizarse en materiales diversos (azulejo, lana, seda, hormigón,…). En los cuadrangulares o rectangulares se hace una cuadrícula y cada cuadrado es un número. Se marcan en esa enumeración los primos y luego se unen con hilos, o se dejan en blanco y el resto se colorea … según la variación elegida”.
 Dibujo-maqueta Poema de los números primos (años 1980-1990), de Esther Ferrer. Imagen de la página de Esther Ferrer
Dibujo-maqueta Poema de los números primos (años 1980-1990), de Esther Ferrer. Imagen de la página de Esther Ferrer
En este dibujo podemos observar de nuevo, que uno de los elementos importantes en la reflexión artística de Esther Ferrer son las lagunas de números primos, es decir, las zonas de números compuestos, no primos, entre dos números primos. Así, en esta obra, la artista ha coloreado los cuadrados de los números compuestos de los colores negro o rojo en función de la laguna a la que pertenezca el número natural. Por ejemplo, entre los números primos 257 y 263 (abajo en la espiral) aparecen, en la espiral, cuadrados de color rojo correspondientes a los números compuestos entre ellos, 258, 259, 260, 261 y 262, mientras que los cuadrados de la siguiente laguna, entre los números primos 263 y 269, están pintados de negro, 264, 265, 266, 267, 268.
Según vamos avanzando en los números naturales hay una menor cantidad de números primos, una menor densidad dentro de los números naturales, y las lagunas entre números primos son cada vez mayores, como se puede observan en el siguiente dibujo, en el que la artista Esther Ferrer construye una espiral de Ulam empezando en el número 1.344.326.696.347. Como en el dibujo-maqueta anterior, se trata de una cuadrícula 21 x 21, es decir, la correspondiente espiral en ambos casos está formada por 441 números, aunque en este segundo caso hay muchos menos números primos y las lagunas de números primos (los números compuestos entre dos números primos consecutivos) son mayores.
 Dibujo-maqueta Poema de los números primos (años 1980-1990), de Esther Ferrer. Expuesto en la Galería Àngels Barcelona y en la exposición Esther Ferrer, todas las variaciones son válidas, incluida esta, del Palacio Velázquez (2017). Imagen del catálogo
Dibujo-maqueta Poema de los números primos (años 1980-1990), de Esther Ferrer. Expuesto en la Galería Àngels Barcelona y en la exposición Esther Ferrer, todas las variaciones son válidas, incluida esta, del Palacio Velázquez (2017). Imagen del catálogo
A continuación, he repintado la estructura de la espiral de Ulam del anterior dibujo-maqueta, en colores azul y verde, para recuperar la espiral que subyace debajo de la obra, y para observar mejor las lagunas de números primos que existen.
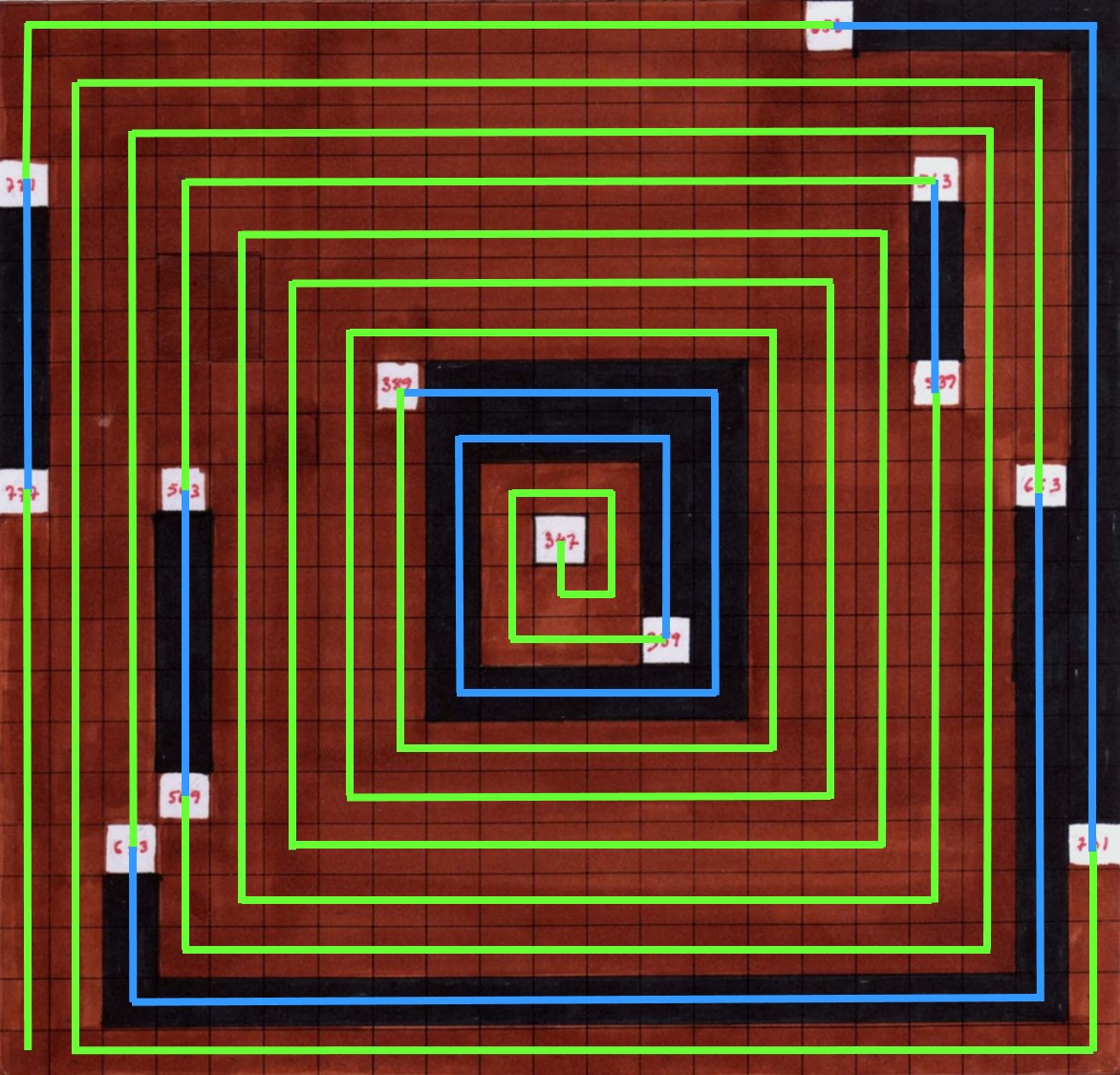
Dialogando con Laurence Rassel y Mar Villaespesa en Esther Ferrer, todas las variaciones son válidas, incluida esta (2017), la artista explica así su trabajo con la espiral de Ulam:
“… puedo trabajar los números primos a partir de la espiral de Ulam. Al utilizarla se crea una línea ininterrumpida durante cierta cantidad de números. Me gustó la idea de escribirlos en espiral, como una galaxia, los números primos tienen algo que ver con la estructura del universo; a medida que progresas en la serie hay menos números, el espacio entre ellos se agranda, me gusta ese vacío, es como si la serie se expandiera, como el universo.”
Existe toda una serie de obras de Esther Ferrer, pertenecientes a la serie Poema de los números primos, que tienen como punto de partida la espiral de Ulam, empezando en el número 41. A continuación, mostramos algunos ejemplos, que además nos muestran como la intervención creativa de la artista da lugar a diferentes resultados. La primera está realizada con hilos, alfileres de colores y tinta sobre lienzo, en la cual los colores están asociados con los números primos, de hecho, con la terminación en 1 (rojo), 3 (verde), 7 (azul) o 9 (amarillo) del número primo.
 Poema de los números primos (1980), de Esther Ferrer, realizada con hilos, alfileres y tinta sobre lienzo, de 122 x 120 cm. Obra expuesta en la Galería Àngels Barcelona.
Poema de los números primos (1980), de Esther Ferrer, realizada con hilos, alfileres y tinta sobre lienzo, de 122 x 120 cm. Obra expuesta en la Galería Àngels Barcelona.
 Detalle de la obra Poema de los números primos (1980), de Esther Ferrer, realizada con hilos, alfileres y rotulador sobre lienzo, de 122 x 120 cm. Obra expuesta en la Galería Àngels Barcelona
Detalle de la obra Poema de los números primos (1980), de Esther Ferrer, realizada con hilos, alfileres y rotulador sobre lienzo, de 122 x 120 cm. Obra expuesta en la Galería Àngels Barcelona
Las diferentes intervenciones artísticas de Esther Ferrer, sobre la misma base de la espiral de Ulam, generan diferentes patrones geométricos planos, como se pone de manifiesto con estas obras.
 Una de las tres partes de un tríptico de la serie Poema de los números primos (años 1980), de Esther Ferrer, realizada con rotulador e hilos sobre papel, de 68 x 67 cm
Una de las tres partes de un tríptico de la serie Poema de los números primos (años 1980), de Esther Ferrer, realizada con rotulador e hilos sobre papel, de 68 x 67 cm
En la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… de Tabakalera también nos encontramos obras que surgen del mismo punto que las anteriores, la espiral de Ulam empezando en el número 41, pero, una vez más, con sus propias características fruto de la acción de la artista.
 Obra de la serie Poema de los números primos, de Esther Ferrer, que ha formado parte de la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… en Tabakalera. Fotografía Raúl Ibáñez
Obra de la serie Poema de los números primos, de Esther Ferrer, que ha formado parte de la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… en Tabakalera. Fotografía Raúl Ibáñez
Y terminemos esta entrada, con unas palabras de la creadora donostiarra, con motivo de su exposición en Artium en 2011, en relación a su trabajo con los números primos:
“Lo primero que sorprende cuando se comienza a trabajar con la serie de los números primos es que – cualquiera que sea el sistema utilizado – el resultado es siempre equilibrado, hermoso, y lo segundo es que cuanto más grande es la obra, es decir, cuantos más números la forman, más interesante es la estructura, nunca simétrica, siempre en movimiento, por ello siempre he pensado en realizar obras monumentales como suelos, muros, tapicerías etc.
Al penetrar el universo de los números primos se tiene la sensación de que son la traducción, el reflejo, de un caos universal, magnífico, continuamente en evolución, que no se repite jamás, pero que, pese a ello, es siempre el mismo. Un caos en cuyo interior parece existir un orden, un orden extraño, curioso.”
 Obra de la serie Poema de los números primos, de Esther Ferrer, que ha formado parte de la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… en Tabakalera. La obra tiene como base la criba de Esratóstenes, donde la inclinación de las diagonales en los lugares de los números compuestos está dada en función de las lagunas de números primos, lo cual genera una curiosa estructura laberíntica. Fotografía de Raúl Ibáñez
Obra de la serie Poema de los números primos, de Esther Ferrer, que ha formado parte de la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… en Tabakalera. La obra tiene como base la criba de Esratóstenes, donde la inclinación de las diagonales en los lugares de los números compuestos está dada en función de las lagunas de números primos, lo cual genera una curiosa estructura laberíntica. Fotografía de Raúl Ibáñez
 Detalle de la anterior obra de la serie Poema de los números primos, de Esther Ferrer, que ha formado parte de la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… en Tabakalera
Detalle de la anterior obra de la serie Poema de los números primos, de Esther Ferrer, que ha formado parte de la exposición Esther Ferrer 2, 3, 5, 7, 11, 13, 17, 19, 23,… en Tabakalera
Para concluir esta entrada, me gustaría expresar mi más sincero y profundo agradecimiento a Esther Ferrer por permitirme utilizar las imágenes de sus hermosas e interesantes obras en esta publicación, así como por las interesantes conversaciones que hemos mantenido sobre las matemáticas, y en particular, los números primos, en el conjunto de su obra artística.
Bibliografía
1.- Esther Ferrer, Maquetas y dibujos de instalaciones 1970/2011, Exit publicaciones, 2011.
2.- Rosa Olivares (comisaria), Esther Ferrer, Lau mugimenduan/En cuatro movimientos/In four movements, ARTIUM 08/10/2011 – 08/01/2012, Artium y Acción cultural española, 2011.
3.- Laurence Rassel y Mar Villaespesa (comisarias), Esther Ferrer, todas las variaciones son válidas, incluida esta, Palacio de Velázquez del Parque del Retiro 26/07/2017 – 25/02/2018, Museo Nacional Centro de Arte Reina Sofía, 2017.
4.- Martin Gardner, The remarkable lore of the prime numbers, Scientific American 210, n.3, 120 – 129, 1964.
5.- M. L. Stein, S. M. Ulam, M. B. Wells, A Visual Display of Some Properties of the Distribution of Primes, American Mathematical Monthly 71, p. 516 – 520, 1964.
6.- Paul Hoffman, El hombre que sólo amaba los números, la historia der Paul Erdös y la búsqueda de la verdad matemática, Granica, 2000.
7.- Wikipedia: Ulam spiral
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El poema de los números primos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Buscando lagunas de números no primos
- Una conjetura sobre ciertos números en el ‘sistema Shadok’
- El secreto de los números que no querían ser simétricos
Las redes 5G no afectan a la salud… pero podrían hacer que el hombre del tiempo acierte menos
 Imagen: EUMETSAT
Imagen: EUMETSAT
Igual que la radio en su momento, la televisión después, internet, el wifi o cualquier tecnología inalámbrica, hay gente a la que el 5G le pone nervioso. Esta evolución del 4G promete una forma más rápida y eficaz de transmitir la información y los datos que alimentan nuestros móviles y dispositivos, pero para muchos es una amenaza para la salud por el efecto que sus ondas podrían tener sobre los tejidos de nuestro cuerpo.
Lo cierto es que, igual que ocurre con el wifi, no hay evidencias de que el 5G cause ningún problema en realidad. Esta radiación no ionizante no tiene energía suficiente como para causar ningún efecto sobre nuestros tejidos, más allá de calentarnos levemente la oreja si nos pasamos mucho tiempo con el teléfono pegado a ella. Estudios epidemiológicos han tratado de encontrar una correlación entre la expansión de los teléfonos móviles, y después del wifi, y el número de cánceres y tumores. Si bien correlación no implica causalidad, podría ser la primera señal de que algo pasa. La búsqueda no ha tenido éxito.
Esto no ha impedido que mucha gente se oponga a la implementación de las redes 5G apelando al principio de precaución. En Bruselas, donde la legislación que limita las radiaciones es especialmente estricta, se estaba fraguando una excepción para permitir el desarrollo de un programa piloto de redes 5G que de otra forma sería imposible, pero el gobierno de la ciudad finalmente se ha echado atrás poniendo como motivo la precaución en el cuidado de la salud de sus ciudadanos.
Sí podría afectar a cómo estudiamos la meteorología
Otro grupo está empezando a alzar la voz respecto a los riesgos del 5G, estos parece que con una base un poco mas sólida para sus advertencias. Claro que aquí la salud no tiene nada que ver. Son los meteorólogos.
Según un artículo publicado recientemente en la revista Nature, advierten de que las redes 5G podrían interferir con las observaciones vía satélite que les permiten hacer su trabajo, observar la evolución del clima y hacer sus seguimientos de los fenómenos meteorológicos. En concreto, creen que esto les impedirá detectar y medir con precisión las masas de vapor de agua en la atmósfera. Temen que eso repercuta en peores predicciones meteorológicas en todo el mundo.
Por eso, en Estados Unidos la Administración Nacional para el Océano y la Atmósfera (NOAA) y la NASA están actualmente negociando con la Comisión Federal de Comunicaciones (FCC), que es la que controla las redes inalámbricas en este país. La NOAA y la NASA han pedido a la FCC que les ayude a proteger las frecuencias que se utilizan para las observaciones terrestres y atmosféricas para que el desarrollo de las redes 5G no interfieran con ellos. Pero la FCC sacó recientemente a subasta el primer paquete del espectro 5G sin tener en cuenta esas peticiones.
Un acuerdo global para que no haya interferencias
El debate no ha llegado aun a Europa, pero teniendo en cuenta el liderazgo en telecomunicaciones que ejerce Estados Unidos, sus decisiones seguro que influirán en cómo se trata el tema en otros países. En otoño de este año está previsto que se reúnan legisladores de todo el mundo en Egipto para llegar a acuerdos que permitan desarrollar esta tecnología a nivel global. Allí se debatirá qué frecuencias podrán utilizar estas empresas y cómo asegurar que la protección a las redes meteorológicas está garantizada.
Astrónomos y meteorólogos llevan mucho tiempo asegurándose de que compartir sus espectros de observación con otros usuarios no les causa problemas o interferencias en sus observaciones. Pero ahora, dicen, es la primera vez que ven amenazada su “joya de la corona”, esas frecuencias que consideran que deben ser solo suyas “y que debemos defender pase lo que pase”, explica en Nature Stephen English, meteorólogo del Centro para Predicciones Meteorológicas de Medio Alcance en Reading, Reino Unido.
Dentro de esa joya de la corona estaría la frecuencia de 23,8 GHz a la que el vapor de agua emite una débil señal. Algunos satélites, como el European MetOp, monitorizan constantemente la energía que emite la Tierra a través de esta frecuencia para medir la humedad que hay en la atmósfera justo bajo el satélite. La ventaja de esta medición es que se puede hacer con el cielo despejado o nublado de día o de noche. Los meteorólogos utilizan estos datos para alimentar los modelos que predicen cómo evolucionarán las tormentas y otros elementos climáticos en los días y horas siguientes.
¿Cómo lidiar con los vecinos ruidosos?
El problema con el 5G, dicen, es que una estación emitiendo en la misma frecuencia produciría una señal muy parecida a la de ese vapor de agua, lo cual impediría saber si es de origen natural o no. Incorporar esos datos dudosos haría los modelos mucho menos precisos. Es como tener un vecino ruidoso al otro lado de la pared: si pone la música muy alta, parte de su ruido te llegará a ti; si mantiene el volumen controlado, probablemente te libres del escándalo.
La NOAA y la NASA quieren que la FCC obligue a los vecinos a poner un aislamiento entre ellos y, si eso no es posible, a mantener el volumen a niveles que no les impidan trabajar. El problema es que los niveles que la FCC pide no les parecen suficientemente bajos como para no molestarles: -20 dBW, mientras que la Comisión Europea fija el máximo de ruido en -42 dBW y la Organización Meteorológica Mundial recomienda -55 dBW.
No está muy claro cuánto pueden empeorar las predicciones si las interferencias afectan a los 23,8 GHz y otras frecuencias necesarias para estas observaciones. Un informe de 2010 de las Academias Nacionales de Ciencias, Ingeniería y Medicina concluía que perder el acceso a la señal de los 23,8 GHz supondría eliminar un 30% de los datos útiles en las frecuencias de microondas, que contribuyen significativamente a las predicciones globales.
Referencias:
La tecnología 5G no tiene por qué preocuparte – Maldita Ciencia
Sí, Bruselas ha detenido la implantación de la tecnología 5G, pero no por “amenazar la salud de la humanidad” – Maldita Ciencia
Global 5G wireless networks threaten weather forecasts – Nature
Spectrum Management for Science in the 21st Century – National Academies of Sciences, Engineering and Medicine
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo Las redes 5G no afectan a la salud… pero podrían hacer que el hombre del tiempo acierte menos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Menos felices y menos insatisfechos a medida que envejecemos
- Redes y arpones para cazar basura zombie en el espacio
- Hacia las redes 5G
La ley de proporciones definidas y la unidad de masa atómica
 Símbolos químicos de Dalton (1803). Fuente: Wikimedia Commons
Símbolos químicos de Dalton (1803). Fuente: Wikimedia Commons
Durante milenios la idea de que toda la materia está hecha de pequeños e indivisibles trozos llamados átomos ha rondado por la cabeza de los investigadores de la naturaleza. Sin embargo hubo que esperar al siglo XX para obtener una confirmación experimental sin ningún género de dudas. Durante el siglo XIX se habían logrado grandes avances al atribuir las leyes termodinámicas y algunas de las propiedades de la materia, especialmente de los gases, a la teoría cinético-molecular; fue a partir de esta teoría que Einstein en 1905 propuso un modelo del movimiento browniano que Jean Perrin confirmó experimentalmente en 1908, probando más allá de toda duda la existencia de los átomos.
Por otra parte, durante siglos se supo que existen diferentes tipos de los llamados “elementos” fundamentales en la naturaleza: oro, plata, cobre, sodio, etc. Eran los componentes más simples en los que se pueden dividir las sustancias por medios químicos. Finalmente, se encontró útil dar a los elementos símbolos especiales: se empezó usando grafías elaboradas de distinta especie hasta acabar, por motivos puramente operativos, con simples letras, por ejemplo, “C” para el carbono, “O” para el oxígeno, “H” para el hidrógeno, etc.
Para muchas personas, aunque nadie lo expresó tan explícitamente como John Dalton, estos diferentes elementos indicaban que la naturaleza también está formada por diferentes tipos de átomos, un tipo de átomo para cada elemento. Cada elemento no sería más que una colección de átomos idénticos e indestructibles químicamente, una idea que se confirmó en durante todo el desarrollo de la química durante el siglo XIX.
Cuando dos o más átomos se unen, forman una molécula. La molécula puede ser un elemento en sí mismo si ambos átomos son iguales, como en el oxígeno, O2, o puede ser un compuesto si los átomos son diferentes, como el agua, H2O. Dado que los átomos no son divisibles, la idea de unir dos átomos de hidrógeno a, digamos, átomo y medio de oxígeno en lugar de exactamente un átomo de oxígeno no tiene sentido [1].
La ley de las proporciones definidas establecida por Joseph Proust en 1794 es una consecuencia natural de la idea de que los elementos están formados por átomos idénticos e indestructibles. De hecho, Dalton postula su teoría atómica en 1808 en un intento de explicar esta ley (su primera propuesta atómica, mucho más simple, es de 1803). Cuando los elementos se combinan para formar compuestos siempre es necesaria la misma proporción de masas de los constituyentes para hacer un compuesto en concreto. Por ejemplo, 23,0 g de sodio siempre se combinan con 35,5 g de cloro para producir 58,5 g de cloruro sódico (NaCl, sal común). Si tenemos 25,0 g de sodio y 35,5 g de cloro, seguiremos obteniendo solo 58,5 g de sal, y sobrarán 2,0 g de sodio. Esta regla, la ley de proporciones definidas, se aplica a todos los compuestos [2][3].
De la ley de proporciones definidas se deduce que los átomos de los elementos que se combinan para formar compuestos como el NaCl no tienen la misma masa. Dado que solo 23,0 g de sodio se combinan con 35,5 g de cloro para formar 58,5 g de NaCl, los átomos de cloro deben tener más masa que los átomos de sodio. Así, si un átomo de sodio tiene 23,0 “unidades” de masa, entonces un átomo de cloro tendría 35,5 unidades de masa. Las unidades de masa pueden ser gramos, kilogramos, libras o lo que sea. Por conveniencia, se denominan unidades de masa atómica, para las cuales el símbolo estándar es u.[4]
Ahora sabemos que solo existen 94 [5] elementos diferentes que ocurren naturalmente en toda la naturaleza y, de hecho, en todo el Universo. Los átomos de cada elemento tienen una masa concreta expresada en unidades de masa atómica . Hoy en día, las unidades de masa atómica se miden en relación con un tipo, o isótopo [6], del carbono conocido como carbono-12 (12C), que se define como una masa atómica de 12,0000 u. Las masas atómicas de todos los demás elementos se dan en relación con el carbono-12. Por ejemplo, en relación con el carbono-12, el sodio natural tiene una masa atómica de 22,990 u, el hidrógeno tiene una masa atómica de 1,008 u, el oxígeno tiene una masa atómica de 15,999 u, el uranio tiene una masa de 238,029 u, y así todos los demás [7].
Algunos de estos elementos tienen propiedades similares: algunos son gases a temperatura ambiente; otros son metales sólidos. Existen diferencias en las densidades, los puntos de fusión y ebullición, la conductividad eléctrica, etc. Estas propiedades parecen seguir ciertas pautas. Para entender por qué son las que son y cómo varían iniciamos aquí un viaje al interior de los átomos. [8]
Notas:
[1] De la misma forma no tiene sentido diluir una sustancia por debajo de una concentración en la que haya menos de un átomo en la unidad de volumen considerado. Así de simple se demuestra que la homeopatía y sus diluciones cuasi infinitas es falsa. Dicho de otra forma: si los átomos existen, y existen, entonces la homeopatía es falsa. De aquí se sigue, primero, que cualquiera que quiera venderte o recomendarte homeopatía es o un ignorante o un estafador; segundo, que cualquier dinero empleado en demostrar una imposibilidad manifiesta es dinero tirado a la basura.
[2] La ley establece que para un compuesto dado las proporciones están definidas. Eso no quiere decir que dos elementos no puedan formar compuestos diferentes.
[3] Hoy sabemos que la ley de proporciones definidas no es estrictamente cierta. Si bien el argumento que exponemos es plenamente válido, la química de precisión actual sabe que existen proporciones variables en los compuestos debido a pequeñas impurezas (naturales o artificiales, como el dopado) y las características de las redes cristalinas.
[4] La unidad de masa atómica no forma parte del Sistema Internacional de unidades.
[5] Habrá lugares en los que leas 92. Depende de la antigüedad de la fuente.
[6] A lo largo del siglo XX se descubrió que todos los átomos de un elemento son iguales en sus características pero que pueden existir varios valores de la masa. Cada uno de los valores de masa corresponde a un isótopo. Ya llegaremos a esto más avanzada esta serie. Paso a paso.
[7] Aquí tienes la última tabla oficial publicada por la IUPAC (2013).
[8] Será un viaje largo pero muy entretenido, en el que, como siempre, solo emplearemos matemáticas elementales.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La ley de proporciones definidas y la unidad de masa atómica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La relatividad de la masa
- Equivalencia entre masa y energía
- La óptica se hace atómica: la lente más pequeña del mundo

