Adiós al yeti: las desventuras y tribulaciones de un criptozoólogo

Así imaginó Disney al Yeti (Fotograma de Monstruos S.A.)
Por si no se habían enterado, recientemente nos hemos quedado sin Yeti. Ocurrió la semana pasada cuando investigadores de la Universidad de Búfalo publicaron un estudio en el que habían analizado el ADN de muestras del supuesto Yeti dispersas por todo el mundo en museos y colecciones privadas: pelos, piel, dientes, huesos y hasta restos de excrementos recogidos en el Himalaya y el Tibet y que durante décadas se ha creído que pertenecían a la misteriosa criatura, un animal sin terminar de identificar, quizá medio hombre medio oso…
Bien, pues resulta que no es medio nada. Es un oso. U ocho osos diferentes, vaya. Pero ese es el animal al que pertenecen esas muestras. Todas excepto una, que resultó ser de un perro.

Supuesto cuero cabelludo de un yeti, en el monasterio Khumjung, en Nepal (Wikipedia)
Nuestro gozo en un pozo porque a la vez que nuestro lado racional nos dice que las probabilidades de que realmente existiese el Yeti tal y cómo lo describen las leyendas locales tibetanas y como ha pasado al imaginario global eran realmente pequeñas, esa parte de nosotros que se queda fascinada con los cuentos de criaturas imposibles y las películas de monstruos sufre una pequeña decepción cada vez que un científico, con su método empírico y sus evidencias, decide poner fin a una de esas pequeñas parcelas de misterio que aún nos quedan por resolver.
La pseudociencia de la criptozoología
Adiós al Yeti, pues, decíamos, que se suma a la cola de misterios resueltos para chasco de muchos. Y ya van quedando menos en la lista de los no resueltos, aunque alguno hay. Y aunque pocos han oído hablar de ella, son el material de estudio de su propia disciplina científica. O, más bien, pseudocientífica. Es la criptozoología.
La criptozoología se postula como el estudio científico de los animales y criaturas de cuya existencia no existen pruebas científicas, lo cual ya es un poco contradictorio. El Yeti, el monstruo del lago Ness, el chupacabras, los vampiros, el kraken, el leviatán o las sirenas son algunos de sus sujetos de estudio más conocidos.

Monstruo del lago Ness de Heikenwaelder Hugo (Wikipedia)
Los autodenominados criptozoólogos tratan de determinar y defienden la existencia de estos seres muchas veces conjeturados a partir de restos fósiles de animales extintos y otras veces a partir de leyendas, el folclore y la cultura local de distintas regiones del mundo. Aunque en general han recibido poca atención de la comunidad científica y se considera más bien un fenómeno cultural similar al fenómeno ovni, ellos defienden sus investigaciones y actividades basándose en algunos descubrimientos sorprendentes que ha hecho la zoología en los últimos siglos, como el calamar gigante (que habría dado pie a la leyenda del kraken) o el celacanto (un pez que se creía extinto desde hacía miles de años y que se descubrió vivo 1998).
Algunas obras fundacionales dieron luz a esta pseudodisciplina. En 1892, Andhonid Cornelis Oudemans publicaba La gran serpiente marina, que tuvo una gran. Entre 1941 y 1948, Willy Ley, escrito y científico, publicó The Lungfish, the Dodo and the Unicorn, que fue traducido a muchos idiomas, incluido al español varios años después.

Portada de ‘The Lungfish, the Dodo and the Unicorn’
Pero se considera a Bernard Heuvelmans, zoólogo, el creador del término criptozoología, y también de su descripción: “el estudio de los animales sobre cuya existencia solo poseemos evidencia circunstancial y testimonial, o bien evidencia material considerada insuficiente por la mayoría”. En 1955 publicó Tras la pista de animales desconocidos, considerado por muchos como la base de esta disciplina.
Según el autor, la criptozoología es una disciplina que debe ser ejercida con rigor científico, pero a su vez debe ser vista con una actitud abierta e interdisciplinaria, saliéndose del encorsetado método científico, digamos, tradicional. Además, es importante prestar atención y dedicar tiempo a estudiar las tradiciones y creencias populares, ya que, aunque suelen estar mezcladas con elementos fantásticos, pueden contener parte de verdad que ayude a guiar la investigación sobre estos animales aun desconocidos.
Para defender estos principios y proseguir estas investigaciones existen en el mundo numerosas asociaciones de criptozoólogos. La más conocida es la International Society of Cryptozoology, que estuvo en marcha hasta 2005, cuando desapareció por motivos económicos. El símbolo de la ISC era un okapi, un animal conocido por los pigmeos pero ignorado por los científicos hasta su descubrimiento oficial en 1901.

Símbolo de la International Society of Cryptozoology.
Por qué la criptozoología no puede ser una ciencia
A pesar de sus aspiraciones científicas, la criptozoología choca frontalmente con los principios científicos básicos continuamente. Un ejemplo es su negativa a aceptar que una hipótesis debe ser descartada cuando no se cumplan sus predicciones, porque los criptozoólogos parecen inasequibles al desaliento.
Numerosas pruebas en los últimos años han descartado, entre otros, la existencia de Nessie, el monstruo del lago Ness: imágenes por satélite, escáneres del fondo del lago… Igual que ahora con el Yeti y como ha ocurrido antes con otras , todas las supuestas pruebas de su existencia han sido rebatidas, pero esos resultados han sido ignorados y esas criaturas siguen en la lista de animales a descubrir.

Esta imagen captada por satélite es considerada por los criptozoólogos una prueba de la existencia del monstruo del lago Ness. Pruebas posteriores demostraron que un barco generaba esas estelas sobre el agua.
Otra contradicción con la que chocan a menudo los criptozoólogos tiene que ver con los principios básicos de la biología y la genética: que la existencia indefinida de un solo individuo es naturalmente imposible, y que hace falta una población mínima de ejemplares para que existan posibilidades de reproducción viable dentro de una especie. Eso quiere decir que, de existir Nessie o el Yeti, no existiría solo uno, sino unos cuantos, lo cual aumentaría lógicamente las probabilidades de un avistamiento fiable y con ello del descubrimiento oficial que reconociese científicamente su existencia. Y eso, hasta ahora, no ha ocurrido.
Por último, hay que reconocer que los criptozoólogos juegan en cierta desventaja. A menudo se señala como prueba en contra de su especialidad que la criptozoología nunca ha descubierto ni un solo ejemplar de las criaturas que estudia, mientras que los zoólogos descubren decenas de nuevas especies cada año.
Según estos estudiosos, se trata de una afirmación ignorante o hecha con mala fe. Después de todo, argumentan, la criptozoología es la única disciplina cuyos éxitos, en vez de aumentar su campo de estudio, lo disminuyen: si una criatura es descubierta y estudiada, saldrá de la criptozoología para entrar en la zoología.
No es el caso con el último estudio sobre el yeti, ya que no estamos hablando del descubrimiento de una nueva especie, pero existen otros ejemplos, como el del calamar gigante, que los criptozoólogos identifican con el kraken de las leyendas marinas.
Por todos estos motivos, la criptozoología es considerada por la mayoría una disciplina pseudocientífica. Como dirían aquellos que no deben ser nombrados: que estudien lo que quieran, pero que no lo llamen ciencia.
Referencia:
Lindqvist, Charlotte; Lan, Tianying; Gill, Stephanie; Bellemain, Eva; Bischof, Richard; Ali Nawaz, Muhammad (29 de Noviembre 2017). «Evolutionary history of enigmatic bears in the Tibetan Plateau–Himalaya region and the identity of the yeti». Proceedings of The Royal Society B. doi:10.1098/rspb.2017.1804.
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo Adiós al yeti: las desventuras y tribulaciones de un criptozoólogo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Adiós a las microesferas de plástico en los cosméticos
- La menopausia… ¿para qué sirve? Seguimos sin respuesta
- Antes de que el león se hiciese con el trono de rey de la selva
No duermas, hay leones

Valoramos mucho el sueño continuo y prolongado. Los especialistas recomiendan dormir unas ocho horas o, si se trata de infantes, más incluso. Sin embargo, muchas personas son insomnes; tienen problemas para conciliar el sueño, despiertan en más de una ocasión durante la noche o lo hacen demasiado pronto. El insomnio tiene efectos adversos sobre diferentes facetas de la vida cotidiana: genera problemas de atención, provoca falta de concentración y somnolencia, aumenta la probabilidad de sufrir accidentes, y puede desencadenar la aparición de trastornos mentales, entre otros. Por esa razón los problemas de sueño han recibido atención científica y médica, y se ha desarrollado toda una batería de fármacos para tratarlos. El insomnio ha llegado a ser considerado un problema de salud pública por parte de algunos especialistas. Y sin embargo, no en todas partes se toman el sueño de la misma forma.
“No duermas, hay serpientes” es el título de un libro del lingüista Daniel Everett en el que cuenta sus experiencias y lo que ha aprendido tras varias décadas conviviendo con pirahas, un grupo humano que vive en una de las zonas más recónditas de la Amazonia brasileña. El título es el saludo con el que los pirahas se desean las buenas noches y hace mención a uno de los aspectos más llamativos de la vida en la selva: en todo momento había personas despiertas en el poblado. Fuese cual fuese la hora del día o de la noche, se oían conversaciones aquí o allá. Los piraha alternaban periodos de sueño y de vigilia durante la noche, y justificaban ese comportamiento por la necesidad de estar alerta ante el riesgo, muy real, de ser atacados por animales peligrosos, como anfibios y reptiles venenosos o, también, grandes depredadores, como panteras o anacondas.
Hace cincuenta años, el psicólogo Frederick Snyder propuso que los animales que viven en grupos se mantienen vigilantes durante la noche debido a que no todos los miembros del grupo duermen con el mismo horario. En términos más técnicos se diría que unos y otros miembros del grupo tienen diferentes cronotipos. Y lo cierto es que los horarios de sueño tienden a cambiar con el paso del tiempo. Los jóvenes suelen permanecer despiertos hasta tarde, mientras que los más mayores tienden a despertar muy pronto.
David Samson y colaboradores se propusieron contrastar la hipótesis de Snyder y estudiaron para ello un grupo de cazadores-recolectores Hadza, del norte de Tanzania. Cada grupo está formado por unos treinta adultos, y cada unidad familiar pasa la noche en una choza. Convencieron a 33 adultos pertenecientes a dos poblados próximos para que se pusieran sensores de movimiento de forma permanente. Y comprobaron que durante prácticamente todo el tiempo –el 99,8% del tiempo de sueño muestreado- al menos un individuo se encontraba despierto o durmiendo de forma ligera, y que una media de ocho adultos se encontraban despiertos en cualquier momento de la noche. Eso era debido, casi en su totalidad, a la estructura de edad de los grupos y al hecho de que el cronotipo varía con la edad.
Los autores del trabajo sostienen que la existencia, ligada a las diferencias de edad, de diferentes cronotipos en un mismo grupo humano favorece un comportamiento nocturno “de tipo centinela” (así se denomina) y ha podido cumplir un papel importante en las sociedades de cazadores-recolectores de zonas con peligrosos depredadores. Sugieren, por ello, que la tendencia a trasnochar de los jóvenes y los despertares tempranos de los mayores han podido proteger a nuestros antepasados de perecer en las fauces de algún gran felino africano durante parte importante de nuestro pasado.
Fuente: Samson et al (2017) Chronotype variation drives night-time sentinel-like behaviour in hunter-gatherers Proceedings of the Royal Society B
—————————————————————–
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
Una versión anterior de este artículo fue publicada en el diario Deia el 30 de julio de 2017.
El artículo No duermas, hay leones se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Naukas Pro 2017: Amaia Zurutuza y el grafeno

El pasado 14 de septiembre de 2017 se celebró la primera edición de Naukas Pro, en el que Centros de Investigación, Laboratorios, científicos de renombre o equipos de trabajo contaron con 20 minutos para explicar a un público general en qué consiste su trabajo.
9ª conferencia: Amaia Zurutuza, directora científica de Graphenea
Amaia Zurutuza ha explicado al detalle lo que es el grafenoEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Pro 2017: Amaia Zurutuza y el grafeno se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Pro 2017: Leni Bascones y los superconductores
- Naukas Pro 2017: Lourdes Basabe y los microlaboratorios
- Naukas Pro 2017: Julián Estévez y la inteligencia computacional
Adolescencia, sexismo y publicidad
La mayoría de estudiantes de cuarto de ESO del País Vasco que participaron en un estudio sobre la percepción del sexismo en la publicidad se mostró insensible ante el uso sexista y el trato degradante de las mujeres. Así mismo, este colectivo asume muchos de los estereotipos femeninos publicitarios y de prejuicios propios de hace 40 años. El investigador Pablo Vidal ha analizado la respuesta de 528 estudiantes (266 chicos y 261 chicas, de entre 15 y 16 años) de ocho Institutos de Educación Secundaria de la Comunidad Autónoma Vasca al exponerles a siete anuncios con un marcado contenido sexista.

El trabajo de investigación analiza la influencia del sexismo presente en la publicidad en la adolescencia, una línea de investigación poco explorada y que persigue estudiar la imagen de las mujeres desde la perspectiva de las audiencias. En concreto, Pablo Vidal se centra en la perspectiva de género al estudiar el discurso publicitario “pues la imagen de las mujeres que proyecta la mayoría de los anuncios evidencia una clara tendenciosidad al ocultar los avances en igualdad logrados y no reflejar los nuevos roles que las mujeres desempeñan en la sociedad actual”.
En ese sentido, la mayoría de jóvenes adolescentes que ha participado en la investigación se ha mostrado incapaz o ha tenido muchas dificultades para percibir lo que es sexismo en publicidad. Solo un 34 % del alumnado (mayoritariamente femenino: 65% alumnas y 35% alumnos) ha demostrado tener esa capacidad, el resto lo confunde o no lo tiene claro. Ello es así porque considera que el sexismo es algo del pasado y no propio de una sociedad que consideran igualitaria, al tiempo que desconoce la manipulación y efectividad del lenguaje publicitario. “Lo que se ve en publicidad también ocurre en la realidad. La publicidad es así”, señalan en sus respuestas.
En palabras de Vidal, “la publicidad facilita que los estereotipos de género, roles de mujeres ya superados e imágenes simbólicas se asuman en la adolescencia como realidad de cómo son los hombres y las mujeres; y ha conseguido que los conceptos de masculinidad y feminidad, vivos hace 40 años, vuelvan a resurgir”.
El sexismo de baja y media intensidad
Para realizar la investigación se han diseñado dos cuestionarios ad hoc (uno de preguntas abiertas y otro de cerradas) y cuatro sesiones de grupos de discusión focalizados y se han utilizado siete anuncios de las marcas Lynx, Natan, Calvin Klein, Gucci, Axe, Cesare Paciotti y Ché Magazine. En cuanto a los análisis de los resultados se han tenido en cuenta las siguientes variables: sexo, ámbito residencial y país de origen.
En sus conclusiones, el investigador destaca que existen grandes diferencias entre alumnas y alumnos respecto a la aceptación del sexismo. “Lo que para una mayoría de chicos es permisible, normal y justificable, para muchas chicas es rechazable, inadecuado o machista. La aceptación del sexismo es algo natural en un 70% de los chicos y en un 30% de las chicas que conciben como habitual y propio de la sociedad que se presenten a las mujeres de forma sexista”.
Percibir el sexismo y distinguir su intensidad en la publicidad tampoco es sencillo para el alumnado adolescente. Una gran mayoría aceptó comportamientos claramente desiguales en anuncios que presentaban un sexismo de baja intensidad. Es decir, cuando las relaciones desiguales no son ofensivas o agresivas de manera explícita, el alumnado las acepta, no las considera sexistas, porque las admite como parte de nuestra realidad social legitimando los micromachismos. Y en todo caso, se entiende que esas proyecciones machistas no son para tanto, pues se consideran en clave humor, como una broma o una exageración graciosa.
El sexismo de intensidad media, que maltrata y humilla a las mujeres, pasa desapercibido entre la mayoría de los chicos (entorno al 80%) cuando el producto se dirige a los hombres. De hecho, el anuncio no se considera sexista. Y tanto ellos como ellas admiten que en publicidad se motive a los hombres degradando a una mujer cuando publicitan productos masculinos.
Respecto a los arquetipos y estereotipos sexuales que existen sobre las mujeres, los alumnos y alumnas muestran una sensibilidad diferente. Ellos y ellas identifican con facilidad al arquetipo de mujer-objeto o mujer-trofeo; sin embargo, cuando se presentan otros estereotipos (mujer-ama de casa, mujer mantenida; mujer infantil; mujer devora hombres y, sobre todo, mujer víctima) son ignorados o no percibidos por la mayoría.
En el transcurso de la investigación, también se ha detectado que una gran parte de los jóvenes adolescentes conviven de forma natural con la violencia machista. De hecho, la agresividad en el hombre es vista como un factor de poderío masculino. Ahora bien, cuando de la agresividad se pasa a la violencia, el rechazo de las mujeres es unánime, pero en los hombres surgen dudas, matizan la violencia y no acaban de condenarla. En este sentido, un 33% del alumnado se mostró en total apoyo al sexismo de los anuncios y un 10% de este grupo se posicionó a favor de la violencia contra las mujeres y en contra de la igualdad.
Mundo rural versus urbano
Pablo Vidal en sus conclusiones señala que el alumnado del medio rural es menos sexista, percibe con más claridad los estereotipos, denuncia de forma activa el maltrato de las mujeres en publicidad y defiende en mayor medida posiciones de respeto a las mujeres y la igualdad. Estas actitudes se explican porque “el alumnado del entorno urbano percibe la publicidad como espejo de su mundo y reflejo de las nuevas tendencias y de los nuevos estilos de vida a imitar. Es decir, es un alumnado menos crítico y más sexista que el rural pues acepta acríticamente todo lo que llega”.
Así mismo, el alumnado masculino urbano es el más machista y el alumnado rural femenino el más feminista. Estas características se explican por la diferente socialización que se establece a través del ocio y del juego entre el alumnado rural y el urbano. En el medio rural los niños y niñas de diferentes edades se entretienen juntos en el exterior y en diferentes espacios. En el medio urbano, sin embargo, juegan solos y solas en su habitación, y sus juegos son más sedentarios propios del hogar y relacionados con las nuevas tecnologías.
Por último, Vidal ha detectado que el alumnado migrante es ligeramente menos sexista que el nacido en la Comunidad Autónoma Vasca. Se diferencia del autóctono porque se muestra más crítico ante el sexismo maltratador y el sexismo agresor. “En definitiva, los resultados de esta investigación deben hacer reflexionar a quienes, bajo la influencia de estereotipos culturales y falsos clichés, creen que las personas migrantes no están tan avanzadas en las relaciones entre géneros y en el reconocimiento de la igualdad como las personas autóctonas de la CAPV. Desde luego, esta creencia no aparece en absoluto reflejada en el alumnado adolescente migrante residente en la CAPV que participó en la investigación, el cual se mantuvo ligeramente por encima del autóctono en su percepción y rechazo del sexismo”.
Como conclusión general, tras realizar el análisis de las respuestas del alumnado de cuarto de ESO de entre 15 y 16 años, Pablo Vidal también detecta que “el discurso de las relaciones entre iguales va ganando terreno entre las jóvenes y de forma muy tímida entre los jóvenes, ya que estos deben enfrentarse a sus propios arquetipo y estereotipos, sobre todo al de ‘varón viril’ (masculinidad hegemónica) que los maniata y les impide avanzar al mismo paso que las mujeres”.
Referencia:
Pablo Vidal et al (2011) Percepción del alumnado adolescente sobre los prototipos y estereotipos femeninos en la publicidad actual Ponencia en el III Congreso Universitario Nacional Investigación y Género, [libro de actas].(pp. 2058-2082)
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Adolescencia, sexismo y publicidad se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿La publicidad no sirve para nada?, ¡ja!
- El aprendizaje del inglés es mejor si se usa para aprender otra cosa
- La menor influencia de las mujeres en Internet
Un juego de mesa para entender la irreversibilidad
Expansión libre, la reina de los procesos irreversibles
Una de las ideas más iluminadoras que aprendí durante la carrera fue el siguiente ejemplo. Se trata del ejemplo más sencillo que conozco para arrojar algo de luz sobre el concepto de irreversibilidad. A pesar de su sencillez da una idea bastante fidedigna del “sabor” de la mecánica estadística. Para disfrutarlo, en primer lugar, tendremos que hablar sobre la expansión libre de un gas.
Imagine el lector que tenemos dos compartimentos contiguos. En el de la izquierda introducimos un gas, que podemos visualizar como un conjunto de partículas (átomos o moléculas) rebotando contra las paredes. El compartimento de la derecha está vacío. En un momento dado, abrimos la pared que separa ambos compartimentos, permitiendo que el gas se expanda por ambas cavidades.

Si ahora volvemos a cerrar la compuerta, el gas permanecerá repartido en ambas cavidades. Tras abrir y cerrar la puerta, no se regresa al estado inicial. De hecho, esperamos que la presión y la cantidad de moléculas en cada compartimento sea la misma. Estamos ante un proceso irreversible, un proceso que sucede solamente en una dirección y nunca en la contraria.
Sin embargo, lo que tenemos ante nosotros no es más que un grupo de partículas rebotando aquí y allá. ¿Qué es lo que impide a nuestras partículas volver a organizarse en el compartimento izquierdo, aunque solo sea por casualidad? Lo cierto es que no hay nada que lo impida. ¿Por qué no sucede entonces?
Un modelo de juguete
Para continuar, introduciremos un modelo muy sencillo de la expansión de un gas. Tan sencillo que tiene forma de juego de mesa. El tablero tiene el siguiente aspecto:
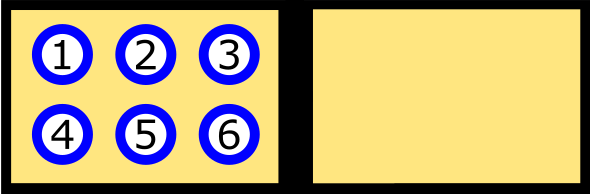
Hemos introducido seis bolas en la mitad izquierda del tablero. Estas bolas representan moléculas de gas, de modo que la configuración que vemos en la figura representa el caso de gas en la cavidad izquierda y vacío en la cavidad derecha.
Ahora necesitamos establecer cuál será la dinámica del juego, esto es, qué reglas seguiremos para actualizar el tablero después de cada “tirada”. Optemos por la sencillez: en cada “tirada” lanzaremos un dado y, si obtenemos, por ejemplo, un dos, la bola número 2 cambiará de compartimento. En la siguiente figura se puede ver una sucesión de varias tiradas.

Serie de 5 jugadas. A la derecha se muestra el número obtenido en el dado. A la izquierda, el movimiento correspondiente en el tablero.
Es posible que el lector piense, y no le falta razón, que el modelo aquí presentado es demasiado simple. Al fin y al cabo, la humanidad sabe mecánica suficiente como para calcular realmente cómo se han de mover las moléculas, sin recurrir a algo tan poco sofisticado como tirar un dado. El procedimiento clásico sería:
- Anotar todas las posiciones y velocidades de las partículas involucradas.
- Usar las leyes de Newton para escribir sus ecuaciones de movimiento.
- Resolver dichas ecuaciones.
Sin embargo, cuando tratamos con las cantidades colosales de moléculas presentes en una muestra macroscópica de gas, ni siquiera es posible dar paso número uno. No queda más remedio que usar métodos de mecánica estadística, en los que se asume que las posiciones y velocidades son aleatorias. Estas variables aleatorias se toman de distribuciones de probabilidad, lo cual no deja de ser un “dado” algo más sofisticado. En resumen: puede que nuestro juego sea aburrido, pero como modelo no está mal.
Juguemos
Pero volvamos a nuestro sencillo tablero. Tras unas pocas tiradas, tendremos bolas repartidas por ambos lados. El juego consiste en seguir tirando el dado hasta que bolas se vuelvan a ordenar en el compartimento izquierdo. Parece poco probable que suceda, pero no imposible. De hecho, basta con jugar el tiempo suficiente. Concretamente, uno esperaría que por azar las bolas se reordenasen como en la configuración inicial alrededor de una vez por cada 64 tiradas[1].
Lo anterior es cierto para 6 bolas, pero nada nos impide construir un tablero de mayor tamaño. Es fácil ver que un tablero con N bolas posee 2N configuraciones distintas[2]. En este caso general, uno esperaría regresar al estado inicial tras aproximadamente 2N tiradas. Con solamente 20 bolas, necesitaríamos más de un millón de tiradas para volver a la configuración inicial siguiendo las reglas del juego. Con 100 bolas, el número de tiradas necesarias es astronómico: un uno seguido de treinta ceros, y eso estimando por lo bajo. En la siguiente animación podemos ver precisamente un caso con 100 casillas[3].
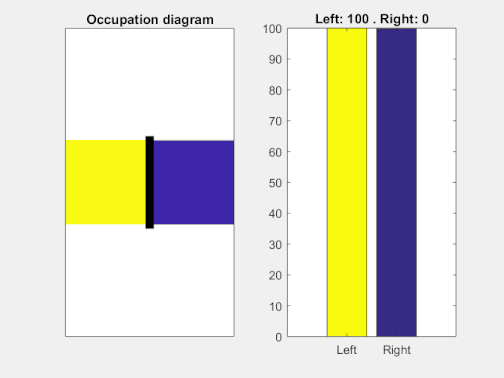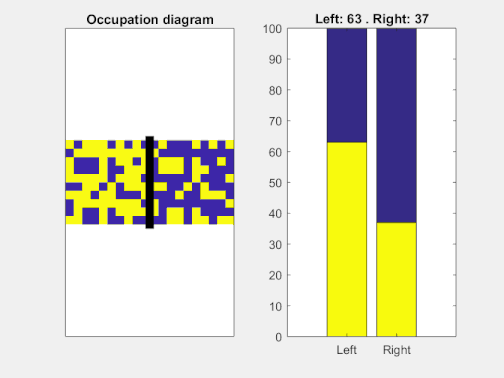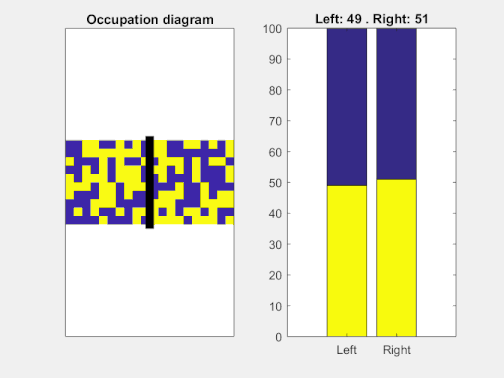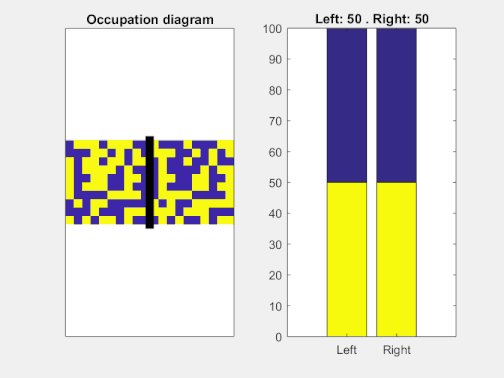
Si representamos los números de partículas en cada una de las dos cavidades en función del tiempo, podemos ver cómo la “expansión” es más rápida y violenta al principio y más lenta cuánto más cerca estamos del equilibrio termodinámico. Nótese cómo incluso con una dinámica tan tonta como repartir las partículas al azar estas tienden a “repartirse” por ambos compartimentos, con pequeñas fluctuaciones.
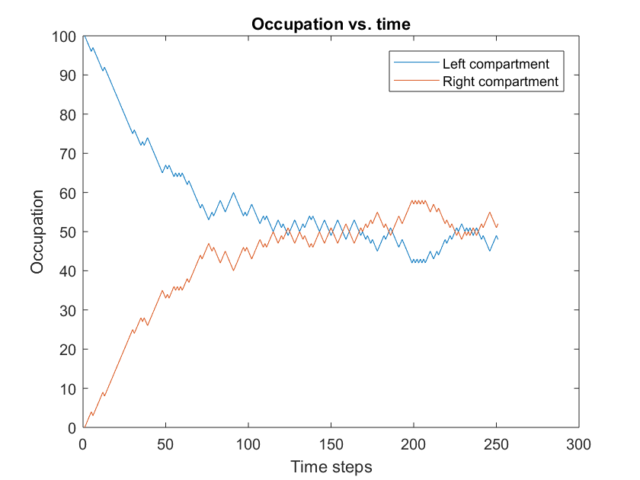
En el caso de un gas, incluso para volúmenes no muy grandes, manejamos cantidades colosales de moléculas, y el número de “tiradas” necesarias para volver al estado inicial, al depender exponencialmente del número de moléculas, ¡crece de un modo más colosal aún! La probabilidad de que haya fluctuaciones menos extremas (por ejemplo, 70% a la izquierda-30% a la derecha) también decrece rapidísimamente con el tamaño del sistema.
En resumidas cuentas: usando una dinámica aleatoria sobre un sistema lo suficientemente grande y prestando atención a la variable adecuada (en este caso, número neto de partículas a cada lado) se obtiene un resultado que, a todos los efectos prácticos, es exacto.
Resumiendo más aún: en ocasiones, azar + inmensidad = ley física.
Bola extra
Me permito la licencia de lanzar una pregunta al lector. En el modelo que hemos mostrado todas las posibles configuraciones del tablero son igualmente probables. ¿Cómo es posible que se pase más “tiempo” en aquellas que reparten equitativamente las partículas por cada compartimento?
Pista aquí.
Este post ha sido realizado por Pablo Rodríguez (@DonMostrenco) y es una colaboración de Naukas.com con la Cátedra de Cultura Científica de la UPV/EHU.
Notas y referencias:
[1] Dónde se han ignorado los efectos de forzar de la configuración inicial.
[2] Podemos verlo notando que nuestro tablero se parece mucho a un número binario, dónde 0 representa casilla vacía y 1 representa casilla ocupada. En el ejemplo con 6 bolas hay tantas configuraciones como números binarios entre 000000 (cero, representando todos los compartimentos izquierdos vacíos) y 111111 (sesenta y tres, representando todos llenos), esto es, 64 configuraciones posibles.
[3] El código para generar animaciones como estas está disponible aquí.
El artículo Un juego de mesa para entender la irreversibilidad se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Una nueva investigación muestra que explicar cosas a la gente “normal” puede ayudar a los científicos a ser mejores en su trabajo
Susanne Pelger
![]()

Comunicación de la ciencia: no es tan complicada… Imagen: Pexels
En momentos en los que las noticias falsas y los hechos alternativos circulan en la sociedad, difundir los hallazgos basados en la ciencia es más importante que nunca. Esto hace que la comunicación de la ciencia sea una de las tareas más importantes de la academia. Pero a pesar del papel fundamental que desempeña la comunicación científica en la sociedad, los investigadores no siempre priorizan la comunicación con el público en general.
Esto se debe en parte a que, aunque los científicos tienden a ser excelentes en investigación y en conseguir resultados, no siempre son tan buenos a la hora de comunicar estos hallazgos a un público más amplio. Escribir sobre investigación para personas ajenas a la academia requiere una perspectiva más amplia sobre las cuestiones científicas y un estilo de escritura completamente diferente. Y muchos científicos simplemente puede que no sepan cómo comunicar su investigación a la sociedad en general. La baja importancia que se le dio a esto en el pasado y la limitada (si hay alguna) capacitación que reciben los estudiantes en educación científica tampoco ayuda.
Esto es corto de miras, especialmente cuando, tal y como descubrió mi reciente estudio, alentar a los estudiantes de ciencias a escribir sobre su trabajo para una audiencia no académica les ayudó a descubrir y discutir diferentes ideas dentro de su tesis. Y esto, a su vez, les ayudó a darse cuenta de la importancia y el impacto social de su trabajo.
Ciencia para Dummies
La investigación mostró que a través de sus escritos, los estudiantes agregaron sucesivamente diferentes aspectos a sus textos, para hacerlos más relevantes para una audiencia general. Los estudiantes también cambiaron las formas en que planteaban el asunto, desde un nivel específico y detallado hasta una interpretación más general e integral. Esto significó la aparición de una perspectiva social general más amplia en paralelo al proceso de escritura de los estudiantes.
Estos hallazgos son similares a los de un estudio anterior que analizó las experiencias de los estudiantes de ciencias en la redacción de un artículo científico de divulgación sobre su trabajo de fin de estudios, a nivel de grado o maestría. Muchos de estos estudiantes describieron cómo escribir para no académicos les ayudó a crear una “visión más amplia” del tema y ver qué relevancia podría tener su proyecto de investigación en un contexto más amplio.

Ser capaz de explicar cómo y por qué ocurren las cosas es una capacidad importante para los científicos. Imagen: Pexels
Algunos de los estudiantes destacaron especialmente que la escritura de divulgación les ayudó a aclarar el objetivo de su proyecto. Otros señalaron cómo la escritura les había hecho reflexionar sobre su propio conocimiento y darse cuenta de cuánto habían aprendido realmente durante sus estudios.
Impacto duradero
En el nuevo estudio, los estudiantes también dijeron que descubrieron que la escritura para una audiencia no académica ayudó de hecho con su redacción científica. En concreto, los estudiantes encontraron más fácil tratar con diferentes perspectivas y niveles de abstracción en su tesis científica después de haber escrito un texto popular sobre su proyecto de grado.

Los cienientíficos necesitan ser cpaces de explicar su trabajo a aquelos fuera de su especialidad. Imagen: Pexels
No es difícil ver cómo la comunicación con diferentes audiencias puede ayudar a los científicos a encontrar conexiones con otras disciplinas y ver la relevancia social de su propia investigación. Y de esta forma, capacitar a futuros científicos para comunicarse con diferentes públicos podría ayudar a facilitar la investigación y el desarrollo a través de las fronteras disciplinarias.
También podría ayudar a aumentar el conocimiento y el interés de las personas en la ciencia, dando así una mayor probabilidad de decisiones políticas informadas en la sociedad.
Lo que todo esto muestra es el enorme potencial que la comunicación científica podría tener sobre el aprendizaje, la investigación y la democracia. Pero para hacer uso de este poder, los científicos necesitan poder “tomar perspectiva” y conectar su investigación con el mundo exterior. También debe ser considerado como un ejemplo de cómo se puede difundir el conocimiento nuevo. Porque, en última instancia, al reconocer y recompensar estos esfuerzos, podría desarrollarse una investigación nueva y original, así como aumentar la probabilidad de aprendizaje y alfabetización científica en toda la sociedad.
Sobre la autora:
Susanne Pelger es profesora adjunta de educación científica en la Universidad de Lund (Suecia)
Texto traducido y adaptado por César Tomé López a partir del original publicado por The Conversation el 21 de noviembre de 2017 bajo una licencia Creative Commons (CC BY-ND 4.0)
![]()
El artículo Una nueva investigación muestra que explicar cosas a la gente “normal” puede ayudar a los científicos a ser mejores en su trabajo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Arte & Ciencia: ¿Qué interés puede tener para los artistas el trabajo de un científico?
- “La actitud de los científicos ante los proyectos de investigación” por José Elguero Bertolini
- Science + : 1 – La carrera científica I: el doctorado y la investigación académica”
La ciencia básica es inútil, afortunadamente

Imagen: Chema Madoz
¿Para qué sirve la exploración espacial? ¿Para qué sirve el Guernica? ¿Para qué sirve la poesía? ¿Para qué sirve la ciencia básica?
Resulta tentador responder con un tajante no sirven para nada. Saber que son un fin en sí mismos y estar cómodos con esa respuesta, es toda una proeza intelectual. Sin embargo, quien trata de responder con argumentos utilitaristas, a menudo fracasa.
Es más sencillo responder para qué sirve un cuchillo o para qué sirve una silla, que responder para qué sirve una ópera. Las humanidades son esas formas de conocimiento en las que esta respuesta requiere un mayor esfuerzo. Algunos incluso nos atrevemos a llamarlas inútiles, por semántica y por provocación intelectual.
Lo inútil, lo que es un fin en sí mismo, es algo que tiene valor por la simple razón de que se lo otorgamos, sin importar si está supeditado a un fin ulterior. «Así, el teléfono —escribe Unamuno en Del sentimiento trágico de la vida—puede servirnos para comunicarnos a distancia con la mujer amada. ¿Pero esta para qué nos sirve? Toma uno el tranvía eléctrico para ir a una ópera; y se pregunta: ¿cuál es, en este caso, más útil, el tranvía o la ópera?».
Paul Auster, en el discurso que ofreció en Oviedo en 2006 con motivo de los Premios Príncipe de Asturias, pronunció las siguientes palabras: «El arte es inútil, al menos comparado con, digamos, el trabajo de un fontanero, un médico o un maquinista. Pero ¿qué tiene de malo la inutilidad? Yo sostengo que el valor del arte reside en su propia inutilidad; la creación de una obra de arte es lo que nos distingue de las demás criaturas que pueblan este planeta; y lo que nos define, en lo esencial, como seres humanos». En la línea de Eugène Ionesco: «Si no se comprende la utilidad de lo inútil, la inutilidad de lo útil, no se comprende el arte».
Estas palabras de Paul Auster y de Eugène Ionesco también servirían si intercambiamos la palabra «arte» por «ciencia básica».
La ciencia básica es aquella que se desarrolla sin la pretensión de resolver un problema inmediato, en contraposición a lo que se pretende con la ciencia aplicada o con las ingenierías, formas de conocimiento inmanentemente útiles. Esto no implica que, a la larga, la ciencia básica no culmine en bienes útiles. Por ejemplo, los trabajos de Heinrich Hertz y James Clerk Maxwell sobre electromagnetismo no pretendían ningún objetivo práctico, ni siquiera inventar una nueva tecnología, sino entender y describir la electricidad y el magnetismo. Sin embargo, sus trabajos acabaron siendo de gran utilidad tecnológica, empezando por la invención de la radio. Que sus descubrimientos hubiesen culminado en tecnologías no implica que sean más valiosos que los que no lo hayan hecho y, en ningún caso, la ciencia básica debe justificarse por medio de una presumible utilidad futura.
Tal y como explica Abraham Flexner en La utilidad de los conocimientos inútiles, «Las instituciones científicas deberían entregarse al cultivo de la curiosidad. Cuanto menos se desvíen por consideraciones de utilidad inmediata, tanto más probable será que contribuyan al bienestar humano y a otra cosa asimismo importante: a la satisfacción del interés intelectual, que sin duda puede decirse que se ha convertido en la pasión hegemónica de la vida».
Las formas de conocimiento inútiles, como las artes o las ciencias básicas, no necesitan otra justificación más que el simple hecho de que satisfacen nuestra innata curiosidad. Estas inquietudes son las que nos definen como seres sensibles. Y al justificarlas sin referencia implícita o explícita a la utilidad, justificamos las escuelas, las universidades y los institutos de investigación, al margen de que tal o cual investigador haga una contribución utilitarista del conocimiento. El conocimiento es la única justificación que requieren las universidades, escuelas e institutos de investigación.
Sobre todo en los momentos de crisis económica, cuando las tentaciones del utilitarismo se presentan como la única salvación, es necesario entender el valor de las actividades que no sirven para nada. Estas son las que transforman una vida prosaica en una vida orientada por la curiosidad respecto al espíritu y las cosas humanas. Disfrutar del placer estético del conocimiento es lo que podría salvarnos de la asfixia. Las cosas que amamos, aquellas por las cuales vale la pena vivir, son, a fin de cuentas, cosas inútiles.
No existe nada más seductor y placentero que el conocimiento inútil, porque el conocimiento inútil es la forma más sofisticada de deleite.
Las cosas útiles de la vida son los utensilios. Un cuchillo, una silla, son útiles. Cuando se gastan o se rompen, dejan de ser útiles y los tiramos a la basura. Eso es lo que sucede con las cosas útiles: no tienen valor en sí mismas.
Reivindicar los saberes humanísticos, la investigación científica básica, la creación artística, todas las formas de conocimiento inútiles, es reivindicar la dignidad humana. Esta dignidad se alcanza a través del conocimiento y la educación, valores que se ven mermados en tiempos de crisis por el abandono institucional pero que nosotros, de algún modo, hemos de preservar. Como afirmaba Rob Riemen, «la única oportunidad para conquistar y proteger nuestra dignidad humana nos la ofrece la cultura».
El conocimiento en sí mismo no sirve para nada, del mismo modo que no sirve para nada enamorarse, bailar o nacer. No nacemos para la sociedad, aunque la sociedad se apodere de nosotros. Nacemos para nacer. En palabras de Ionesco, «si es absolutamente necesario que el arte sirva para alguna cosa, yo diré que debe servir para enseñar a la gente que hay actividades que no sirven para nada y que es indispensable que las haya».
Sin esta conciencia sería difícil entender una paradoja de la historia, y es que la furia destructiva se abate sobre las cosas consideradas inútiles: los libros heréticos consumidos por las llamas de la Inquisición, el saqueo de la biblioteca real de Luoyang efectuado por los Xiongnu en China, la quema de los manuscritos paganos en Alejandría decretada por el obispo Teófilo, las obras subversivas destruidas en los autos de fe escenificados por los nazis en Berlín, los budas de Bamiyán arrasados por los talibanes en Afganistán o también los manuscritos del Sahel y las estatuas de Alfaruk en Tombuctú amenazadas por los yihadistas. Cosas inútiles percibidas como un peligro por el simple hecho de existir.
En la defensa de las humanidades (sin recurrir a mitos) que recientemente firmaba el filósofo Jesús Zamora Bonilla, esgrimía varios argumentos. Uno de ellos es que «las humanidades forman parte del patrimonio colectivo y de la riqueza cultural de nuestras sociedades, y todos los ciudadanos tienen el derecho de acceder en igualdad de condiciones a ese patrimonio y a las ventajas que pueda conllevar su posesión». Y añade «no es que un conocimiento muy extendido de las humanidades sea un medio para alcanzar el fin de una “democracia más perfecta”, sino que más bien queremos que la sociedad sea democrática para que gracias a ello la mayoría de las personas puedan disfrutar, entre otras muchas cosas, de las mieles que proporcione el saber humanístico».
Otro de los argumentos que apunta es que «la contribución de las humanidades a la formación de los estudiantes consiste en ampliar y enriquecer su mundo». Entendiendo mundo tal y como Heidegger se refería a él en El origen de la obra de arte: «un mundo no es un objeto que se encuentre frente a nosotros y pueda ser contemplado. Un mundo es lo inobjetivo a lo que estamos sometidos mientras las vías del nacimiento y la muerte, la bendición y la maldición nos mantengan arrobados en el ser». El conocimiento de lo inútil es lo que nos permite vivir en un mundo mucho mayor y, por lo tanto, contribuye a nuestra libertad.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo La ciencia básica es inútil, afortunadamente se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La sublime utilidad de la ciencia inútil, por Pedro Miguel Echenique
- La ciencia y la duda
- Ciencia, poder y comercio
Ox Bel Ha, un ecosistema tropical alimentado por metano
En los ríos subterráneos y las cuevas inundadas de la península mexicana de Yucatán, donde las tradiciones mayas describen un submundo fantástico, los científicos han encontrado un mundo realmente diferente. Aquí, el metano y las bacterias que se alimentan de él forman el eje de un ecosistema que es similar a lo que se ha encontrado en las capas frías de los océanos profundos y en algunos lagos.
Para llevar a cabo la investigación, el estudio ecológico más detallado jamás realizado para un ecosistema de cueva costera que siempre está bajo el agua, los científicos, encabezados por David Brankovits, de la Universidad Texas A&M en Galveston (EE.UU.), tuvieron que entrenarse en el buceo en cuevas y en el empleo de técnicas que previamente se han usado solo en vehículos de inmersión en aguas profundas.

Uno de los cenotes que da acceso al sistema de cuevas Ox Bel Ha
El estudio se realizó en el sistema de cuevas Ox Bel Ha (en maya, “tres cursos de agua”), en el noreste de Yucatán, que se describe como un estuario subterráneo porque los pasos de las cuevas inundadas contienen distintas capas de agua, una dulce proveniente de la lluvia y otra salada del océano costero. A este complejo estuario subterráneo se tiene acceso a través de 143 cenotes (del maya dzonoot “hoyo con agua”, es una dolina inundada de origen kárstico) , repartidos a lo largo de más de 270 km de longitud.
El agua dulce de las cuevas y los cenotes son importantes fuentes de agua dulce para las comunidades en toda la Península de Yucatán. El metano en las cuevas se origina de forma natural bajo el suelo de la jungla y migra hacia abajo, hacia el interior del agua y las cuevas. Esto ya es una particularidad ya que, normalmente, todo el metano formado en los suelos migra hacia arriba, hacia la atmósfera.

Submarinista en las profundidades de Ox Bel Ha donde se llevó a cabo este estudio. El cable a su derecha es una línea de seguridad que indica la salida hacia la superficie, algo imprescindible en un laberinto oscuro como este sistema de cuevas. Foto: HP Hartmann
Esta migración del metano prepara el escenario para las bacterias y otros microbios que forman la base del ecosistema de la cueva. Los microbios adquieren su energía tanto del metano como de otros materiales orgánicos disueltos que el agua dulce trae desde la superficie. Estos microorganismos luego serán la base de la alimentación de una pirámide en cuya cúspide están los crustáceos, incluyendo una especie de camarón adaptada a las cavernas que obtiene alrededor del 21 por ciento de su nutrición a partir del metano.
Los estudios anteriores daban por sentado que la mayoría del material orgánico del que se alimentan los microbios provenía de la vegetación y otros residuos proporcionados por el bosque tropical y que llegan a las cuevas desde los cenotes. Sin embargo, en las profundidades de las cuevas, donde se llevó a cabo este estudio, se comprobó que hay muchos pocos restos de la superficie, por lo que los microbios dependen del metano y otras sustancias orgánicas disueltas que se filtran través del techo de las cuevas.
En un entorno sin luz y sin comida visible toda una cadena trófica se mantiene a base de metano y poco más que llega filtrado a través de la roca. Aparte de la importancia que tienen estos resultados para comprender mejor el impacto que la elevación del nivel del mar por el cambio climático y la explotación turística pueden tener para la preservación de estos ecosistemas, también es emocionante comprobar que en los entornos más inesperados puede prosperar la vida y que, si aquí es posible, quizás también lo sea en otros lugares del universo.
Referencia:
David Brankovits et al (2017) Methane- and dissolved organic carbon-fueled microbial loop supports a tropical subterranean estuary ecosystem Nature Communications doi: 10.1038/s41467-017-01776-x
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Ox Bel Ha, un ecosistema tropical alimentado por metano se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Y si la Gran Oxidación tuvo un origen geológico?
- Otra pieza en el puzle de la fotosíntesis
- Todo lo que se puede medir en un río
El disputado voto del Señor Condorcet (II)
En mi anterior entrada de la sección Matemoción del Cuaderno de Cultura Científica, El disputado voto del Señor Condorcet (I), habíamos hablado del problema de la elección social, es decir, de cómo convertir las preferencias individuales de un grupo de personas, ya sea una nación, la Academia de las Artes y las Ciencias Cinematográficas, el Comité Olímpico Internacional o una comunidad de vecinos, en una preferencia colectiva.
En dicha entrada habíamos mostrado que la candidatura ganadora en unas votaciones, por ejemplo, para la presidencia de un país, elegir la mejor película del año, determinar la sede de los Juegos Olímpicos o contratar la empresa que va a reformar la fachada de nuestro edificio, no está únicamente determinada por las preferencias de las personas que votan, sino también por el sistema de votación utilizado. Para ilustrar esta realidad se utilizó un ejemplo ficticio, la elección de la sede de los siguientes Juegos Olímpicos por parte del COI, con 5 ciudades candidatas. Para cada uno de los cinco sistemas de votación que se utilizó se obtuvo una ciudad ganadora distinta, luego todas ellas, sin que cambiasen las preferencias de los votantes.

Pero entonces, ¿qué sistema de votaciones debemos de elegir cuando debamos realizar una elección colectiva? Más concretamente,
¿Qué método de votaciones es el que mejor representa las preferencias de los individuos del colectivo de votantes?
Sobre esta cuestión investigó el economista y matemático estadounidense Kenneth J. Arrow (1921-2017), que además fue Premio Nobel de Economía en 1972.

El economista y matemático estadounidense Kenneth J. Arrow (1921-2017)
Lo primero que hizo Kenneth J. Arrow fue plantear cuáles podían ser los criterios que debía satisfacer un sistema de votaciones razonable. En concreto, los criterios que estableció fueron los siguientes:
1. No dictadura. Que las preferencias de ningún individuo determinen las preferencias del colectivo.
Por ejemplo, si el presidente de una compañía tiene la última palabra sobre cualquier cuestión que se plantee en el consejo de administración, entonces parece que no tiene mucho sentido, a priori, realizar votaciones puesto que las decisiones a tomar por la empresa serán las que este determine, independientemente de la opinión, establecida a través de una votación, del consejo de administración.

Fotograma de la película “El gran dictador” (1940), de Charles Chaplin
2. Universalidad. Cualquier preferencia individual, es decir, cualquier lista ordenada de preferencias entre las candidaturas, es legítima.
Imaginemos que estamos analizando las preferencias sobre ciertos colores, por ejemplo, los que aparecen en la imagen de abajo (rojo, naranja, amarillo, verde, azul y morado), de un grupo de personas, y que queremos determinar cuál es su color preferido, incluso más, el orden de preferencia del colectivo respecto a esos colores. El principio de universalidad establece que cualquier orden de preferencia debe ser elegible, no puede condicionarse la elección impidiendo, por ejemplo, que el rojo pueda elegirse por delante del verde, o un orden determinado, como verde, azul, amarillo, rojo, naranja y morado.

3. Transitividad. Si un individuo, respectivamente el colectivo, prefiere la alternativa A a la B, y la B a la C, entonces prefiere la alternativa A a la C.
En nuestro ejemplo con colores, si a cierta persona del grupo le gusta el color rojo más que el color verde y el color verde le gusta más que el morado, entonces debe de gustarle más el color rojo que el morado.
4. Principio del parapeto. Si todos los individuos del colectivo prefieren la opción A a la opción B, el colectivo debe de preferir la opción A a la B.
Es decir, si a todas las personas, del grupo que está opinando, prefieren el color azul al verde, el sistema de votación debe de mantener que el color azul sea preferido al verde.
5. Independencia de alternativas irrelevantes. Las preferencias colectivas respecto a dos alternativas o candidaturas concretas, no deben de cambiar si los votantes cambiaran sus preferencias respecto a otras candidaturas. Supongamos que el electorado prefiere la alternativa A a la B y que algunos votantes cambian sus listas de preferencias. Si ninguno de los votantes que ha cambiado sus listas de preferencias, ha cambiado la posición relativa de las candidaturas A y B (es decir, si antes de cambiar su lista de preferencias preferían A a B, al cambiarla siguen manteniendo que prefieren A a B, o si antes del cambio preferían B a A, después siguen prefiriendo B a A), entonces el sistema de votaciones deberá seguir indicando que colectivamente se prefiere la alternativa A a la B.
Ilustremos esta situación con un ejemplo real que he leído en el curso Las matemáticas en el deporte, de Annette Pilkington. Se trata del patinaje artístico femenino de los Juegos Olímpicos de Salt Lake City en 2002, cuyos resultados, obtenidos de la Wikipedia, son los que aparecen en la siguiente tabla. La medalla de oro fue para Sarah Hughes (EE. UU.), la de plata para Irina Slutskaya (Rusia) y la de bronce para Michelle Kwan (EE. UU.).

La competición del patinaje artístico en los JJ.OO. de Salt Lake City en 2002 tenía dos partes, el programa corto y el estilo libre. El programa corto se puntuaba de la siguiente forma. La patinadora ganadora recibía 0,5 puntos, la segunda 1 punto, la tercera 1,5 puntos, la cuarta 2 puntos, y así hasta el final. Al final del programa corto de los JJ.OO. de Salt Lake City el resultado entre las primeras posiciones era, según la posición que viene en la tabla,
1) Kwan: 0.5; 2) Slutskaya: 1.0; 3) Cohen: 1.5; 4) Hughes: 2.0.
En el estilo libre la patinadora ganadora recibía 1 punto, la segunda 2 puntos, la tercera 3 puntos, la cuarta 4 puntos, y así hasta el final. El orden de las patinadoras en el estilo libre de Salt Lake City fue
1) Hughes: 1.0; 2) Slutskaya: 2.0; 3) Kwan: 3.0; 4) Cohen: 4.0.
Por lo tanto, la puntuación final de la competición de patinaje sobre hielo femenino en las primeras cuatro posiciones fue:
1) Hughes: 3.0; 2) Slutskaya: 3.0; 3) Kwan: 3.5; 4) Cohen: 5.5.
Aunque se produjo un empate entre las dos primeras, de 3.0 puntos, la mejor posición de Sarah Hughes en el estilo libre le permitió obtener la medalla de oro.
Pero, siguiendo con la idea de la independencia de alternativas irrelevantes, supongamos que los jueces y juezas de la competición modifican la puntuación de Slutskaya en el estilo libre, relegándola a una posición más allá de la cuarta, de forma que las tres primeras posiciones son ahora
1) Hughes: 1.0; 2) Kwan: 2.0; 3) Cohen: 3.0,
mientras que Slutskaya obtendrá más puntos que las otras tres. La posición relativa de Hughes, Kwan y Cohen no ha cambiado, sin embargo, ahora la puntuación final sería
1) Kwan: 2.5; 2) Hughes: 3.0; 3) Cohen: 4.5.
Michelle Kwan habría obtenido la medalla de oro y habría superado, al ser desplazada Slutskaya a una posición más abajo, a Sarah Hughes, contrariamente a lo que establece la independencia de alternativas irrelevantes.

Medallistas del patinaje artístico de los Juegos Olímpicos de Salt Lake City en 2002: Sarah Hughes (EE. UU.), Irina Slutskaya (Rusia) y Michelle Kwan (EE. UU.)
Por lo tanto, este método de votaciones utilizado en el patinaje artístico de los Juegos Olímpicos de Salt Lake City en 2002 no satisface la independencia de alternativas irrelevantes. Otro método que tampoco satisface este criterio es, por ejemplo, el método de Borda, como podéis comprobar en el ejemplo de la elección de la sede de los JJ. OO. que mostramos en la entrada El disputado voto del Señor Condorcet (I).
Una vez establecidos los criterios que debe de tener un sistema de votaciones razonable, se trata de encontrar métodos de votación que los satisfagan. Por desgracia, en la década de 1950, Kenneth J. Arrow demostró que
¡¡no existen sistemas de votación razonables!!
Más concretamente, el resultado que se conoce como Teorema de Imposibilidad de Arrow establece, en su formulación más moderna, lo siguiente: “Ningún sistema de votaciones, con tres o más alternativas, que no sea una dictadura puede satisfacer el principio del parapeto y la independencia de alternativas irrelevantes”.

Papeleta en blanco que dice: “¿Estás de acuerdo con la reunificación de Austria con el Imperio Alemán efectuada el 13 de marzo de 1938 y votas en favor de la lista de nuestro Führer Adolf Hitler? Si – No”. Wikimedia
El teorema de imposibilidad de Arrow nos dice que no existe un sistema de votaciones perfecto, sin embargo, en nuestra sociedad vamos a seguir teniendo que elegir colectivamente sobre diferentes cuestiones, ante lo cual se nos plantea la duda de cómo afrontar este resultado negativo. ¿Qué sistema de votaciones deberíamos utilizar? En este sentido, hay dos caminos a seguir.
Por una parte, ante cualquier elección colectiva habrá que elegir de una forma crítica el sistema de votación a utilizar, valorando los defectos y virtudes de cada uno de los sistemas que existen e intentando determinar cuál de ellos se ajusta lo más posible a los objetivos de la elección que se quiere realizar.
Por otra parte, las personas que investigan sobre elección social siguen buscando nuevos sistemas de votación y mejorando los ya existentes con el objetivo de minimizar los aspectos negativos de los sistemas de votaciones conocidos, por ejemplo, intentando evitar, en la medida de lo posible, que sean manipulables para determinar la candidatura ganadora de unas elecciones.
Para terminar esta entrada del Cuaderno de Cultura Científica vamos a mostrar dos interesantes sistemas de votaciones, en sus versiones más sencillas.
A. Método de votación “segunda vuelta instantánea” o “voto alternativo”.
En el voto aprobatorio cada votante no se limita a marcar la candidatura que desea que gane, sino que marca varios candidatos con números, 1, 2, 3, etcétera, indicando de esta forma su orden de preferencia, desde su opción preferida,1, hasta la menos preferida, pudiendo dejar candidaturas sin marcar. Un ejemplo, sería la imagen de abajo, donde el votante ha marcado, de las 5 candidaturas posibles, con un 1, luego su preferida, la candidatura C, como siguiente opción, con un 2, la candidatura B, después, con 3, la E, y finalmente, con 4, la candidatura A, dejando sin marcar la candidatura D.

Una vez realizada la votación, ¿cómo se realiza la elección de la candidatura ganadora? En primer lugar, se realiza el recuento de votos de las candidaturas marcadas con un 1. Si alguna de las candidaturas obtiene la mayoría absoluta, es decir, más del 50% de los votos, se proclama ganadora de las elecciones. En caso contrario, se elimina la candidatura que ha recibido menos apoyos, la que ha quedado en última posición tras el recuento de los votos y se procede a la segunda vuelta instantánea. Es decir, en la segunda votación se cuentan de nuevo los votos marcados con 1, salvo en los votantes que habían marcado con un 1 la candidatura que se ha eliminado, para los cuales se considera su voto marcado con el número 2, su segunda opción. Y de nuevo, se hace el recuento de votos. Si alguna candidatura obtiene la mayoría absoluta se declara ganadora, en caso contrario se realiza una tercera vuelta instantánea de la misma forma, eliminando primero la candidatura perdedora de esa segunda vuelta. El proceso se repite hasta que una de las candidaturas reciba mayoría absoluta.
Este sistema de votaciones también se conoce como el sistema de Hare, en referencia a la persona que lo inventó en 1859, el abogado inglés Sir Thomas Hare (1806-1891), o en ocasiones, el sistema de Ware, ya que fue también introducido de forma independiente en 1871 por el arquitecto norteamericano William Robert Ware (1832-1915).
Este método de votación se utiliza, por ejemplo, en las elecciones al parlamento de Australia y Malta, en las elecciones presidenciales de Irlanda y la India, en las elecciones primarias de los partidos políticos de Gran Bretaña y Canada, en las elecciones a la alcaldía de varias ciudades del mundo, como Londres o San Francisco.
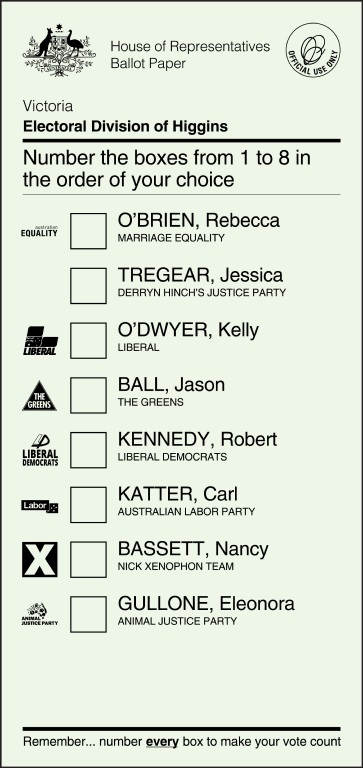
Ejemplo de papeleta electoral de las elecciones al parlamento australiano, en el que puede leerse el texto “Numere las casillas de 1 a 8 en el orden de su elección”
Desde 2009 se utiliza para elegir el Oscar a la mejor película de la Academia de las Artes y las Ciencias Cinematográficas. En la categoría de Oscar a la Mejor Película se seleccionan cada año entre 5 y 10 películas, en 2017 fueron 9 (las que aparecen en la siguiente imagen), y la votación se realiza por el método de la “segunda vuelta instantánea”, marcando cada persona que vota sus preferencias, desde el 1 hasta el número que considere necesario.

Películas nominadas al Oscar a la Mejor Película en la edición 89 de la Academia de las Artes y las Ciencias Cinematográficas, en 2017
B. Método de votación “voto aprobatorio”.
El sistema de voto aprobatorio es un sencillo método de votación que consiste en que cada votante puede votar por tantos candidatos como desee. Es decir, en la lista de candidaturas que aparecen en la papeleta de votación, cada votante marca con una x, o de alguna forma similar, tantas candidaturas como desee (como se muestra en el ejemplo de la siguiente imagen). Se denomina voto aprobatorio porque de alguna forma se está aprobando, cuando se marca la casilla, o rechazando, si no se marca, cada una de las candidaturas.

El método de votación conocido como “voto aprobatorio” fue introducido en los años 1970 por varios autores. Por ejemplo, Guy Ottewell lo explicó en su texto “The Arithmetic of Voting” (la aritmética de las votaciones) publicado en 1977, aunque lo había escrito originalmente en 1968. O de forma más extensa fue explicado por el experto en teoría de juegos y ciencias políticas Steven Brams y el matemático Peter Fishburn, ambos estadounidenses, en el artículo “Approval voting” (voto aprobatorio), en 1978.
El voto aprobatorio es útil para evitar la manipulación de unas votaciones cuando se introduce una opción alternativa, aunque cercana, a la candidatura que parece que será ganadora, para dividir el voto y que gane una de las opciones contrarias. De la misma forma, es útil para evitar el problema de la existencia de muchas candidaturas similares dentro de la opción mayoritaria, mientras que la opción minoritaria se manifiesta con una única alternativa, que aunque minoritaria puede terminar ganando las elecciones por el efecto de la división del voto.
Veamos un ejemplo clásico en la literatura de la elección social, las elecciones primarias del Partido Republicano en New Hampshire (EE. UU.) en 1980. El ganador de aquellas elecciones fue Ronald Reagan, con el 50 % de los votos, mientras que sus dos rivales más cercanos fueron George Bush, con el 23%, y Howard Baker, con el 13%, mientras que ninguno de los demás candidatos llegó al 10%.
¿Qué habría pasado si se hubiese realizado un voto aprobatorio en aquellas elecciones? La cadena televisiva ABC realizó una encuesta a la salida de los colegios electorales de New Hampshire, utilizando el sistema de voto aprobatorio. El resultado fue que Ronald Reagan subió hasta el 58%, George Bush al 39%, pero el mayor beneficiado habría sido Howard Baker, que habría tenido un 41% de los votos, quedando incluso segundo en esas elecciones.
Tras las elecciones primarias de Vermont y Massuchusetts, Howard Baker se retiró de las primarias del Partido Republicano, dejando solos en la lucha a Ronald Reagan, que ganaría y sería presidente de EE.UU., y a George Bush, que quedaría segundo y sería vicepresidente con Reagan, lo que le abrió el camino para ser después el siguiente presidente de EE. UU. Si se hubiese utilizado el sistema aprobatorio quizás Howard Baker no hubiese dejado las primarias y hubiese podido ser el vicepresidente con Reagan y después el presidente de EE. UU.
El sistema de voto aprobatorio está siendo utilizado para las votaciones de diferentes asociaciones científicas como la Mathematical Association of America, la American Mathematical Society o Institute of Electrical and Electronics Engineers, entre otras, y en las elecciones primarias de algunos partidos.

En 1920 las mujeres de Estados Unidos vieron por fin reconocido oficialmente su derecho al voto. Este folleto circuló aquel año animando a las mujeres a ejercer su derecho a votar
Bibliografía
1.- Raúl Ibáñez, El disputado voto del Señor Condorcet (I), Cuaderno de Cultura Científica
2.- VV. AA., Las matemáticas en la vida cotidiana, Addison-Wesley/Universidad Autónoma de Madrid, 1999.
3.- W. D. Wallis, The mathematics of electing and voting, Springer, 2014.
4.- Annette Pilkington, Mathematics in Sports, course of University of Notre Dame, 2016.
5.- Guy Ottewell, The Arithmetic of Voting, In Defense of Variety 4, 1977.
6.- Steven Brams, Peter Fishburn, Approval voting, American Political Science Review 72, p. 831-847, 1978.
7.- Jean-François Laslier, Karine Vander Straeten, Approval Voting: An Experiment during the French 2002 Presidential Election, Revue Francaise de Science Politique 54, p. 99-130, 2004.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El disputado voto del Señor Condorcet (II) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El disputado voto del Señor Condorcet (I)
- Una conjetura sobre ciertos números en el ‘sistema Shadok’
- “La cultura científica o la misteriosa identidad del señor Gauss” por Raúl Ibáñez
Sistemas circulatorios: proteínas plasmáticas
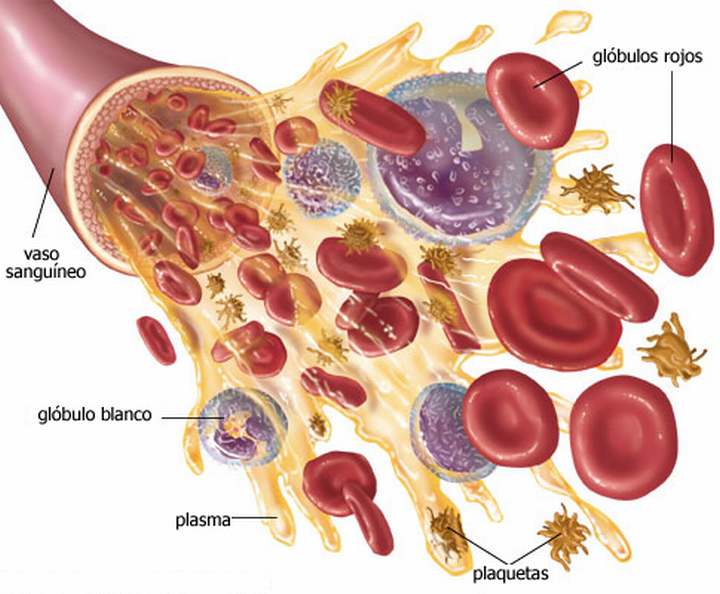
El plasma sanguíneo contiene numerosas sustancias, aunque el agua representa más del 90% de su masa. En mamíferos a las proteínas plasmáticas corresponde entre un 6% y un 8%, mientras que las sustancias inorgánicas (Na+ y Cl–, principalmente) no son más del 1%. El resto corresponde a nutrientes (glucosa, aminoácidos, lípidos y vitaminas), restos nitrogenados, gases (O2 y CO2) y hormonas.
Las proteínas plasmáticas se encuentran en suspensión (o disolución) coloidal en el plasma y, dado que la mayor parte no pueden atravesar membranas o filtros biológicos (son demasiado grandes como para pasar por los poros de las paredes capilares), permanecen en el plasma sin acceder al líquido intersticial, en los animales con sistema circulatorio cerrado, ni a las células, en los de sistema abierto. Ejercen por ello una presión osmótica distinta de la que ejercen las sustancias disueltas de menor tamaño. Se denomina presión coloidosmótica y es responsable de que no se produzca excesiva transferencia de agua de la sangre al líquido intersticial. Además del efecto coloidosmótico, las proteínas plasmáticas amortiguan los cambios de pH de la sangre.
Aparte de los vertebrados, el grupo cuyas proteínas plasmáticas (en este caso de la hemolinfa) mejor se conocen es el de los artrópodos. De especial importancia es una familia implicada en la formación del exoesqueleto que, como es sabido, se renueva repetidas veces para permitir el aumento de tamaño. La construcción del caparazón nuevo conlleva la polimerización de fenoles por fenoloxidasas (PO), proceso en el que participan dos clases de proteínas: (1) hexamerinas, que transportan fenoles a las células epiteliales que producen el exoesqueleto, y (2) formas inactivas de las POs (ProPO), que se activan tras la muda y cuando se necesita reparar tejido dañado. Las ProPOs están también implicadas en las respuestas inmunes de los artrópodos.
En la sangre de los vertebrados hay tres clases principales de proteínas: albúminas, globulinas y fibrinógeno. En el cuerpo humano las albúminas representan el 55% y contribuyen por ello de forma importante a la presión coloidosmótica del plasma. Aparte del papel osmótico su principal función es la de transportar, combinándose con ellas, sustancias insolubles en agua, como bilirrubina, sales biliares y ácidos grasos. Las globulinas representan el 38% y se encuentran en tres posibles formas: alfa (α), beta (β) y gamma (γ). Cumplen funciones de (1) transporte; α-globulinas y β-globulinas específicas transportan sustancias tales como la hormona tiroidea, el colesterol o el hierro (esta última se llama transferrina y es la más abundante); (2) coagulación (α-globulinas y β-globulinas); (3) reguladoras: son α-globulinas ciertas proteínas que se encuentran inactivas y que son precursoras de, por ejemplo, hormonas; son activadas por señales específicas en función de su necesidad; (4) inmunitarias: las inmunoglobulinas (anticuerpos) son γ-globulinas.
Dada su naturaleza hidrofóbica, el transporte de sustancias lipídicas en la sangre se produce mediante la formación de complejos lipoproteínicos. La mayor parte de los triglicéridos, el colesterol y los fosfolípidos se encuentran en el plasma en forma de gotitas unidas a transportadores proteicos, formando complejos de lipoproteínas que son solubles. Los cuatro tipos de lipoproteínas son: (1) de alta densidad (HDLs), con alto contenido proteico, menor de fosfolípidos y menor aún de colesterol; (2) de baja densidad (LDLs), con menor contenido de proteína, algo de fosfolípidos y más de colesterol; (3) muy baja densidad (VLDLs), con muy bajo contenido de proteína y alto de lípido, triglicéridos en este caso; y (4) quilomicrones, que son producidos por las células absortivas del intestino y que transportan triglicéridos, colesterol y fosfolípidos tras una comida.
El colesterol que se transporta mediante lipoproteínas de baja densidad (LDL) es el conocido popularmente como “colesterol malo”, porque la función de esas lipoproteínas es la de transportar el colesterol a las células y, por lo tanto, también lo transporta a las que tapizan el interior de los vasos sanguíneos, razón por la cual contribuye a que se acumule en esos enclaves. Es por ello causa importante de patologías cardiovasculares. A diferencia del LDL, el “colesterol bueno” es retirado de las células por lipoproteínas de alta densidad para transportarlo al hígado y metabolizarlo allí. De ahí el diferente significado de una y otra forma de lipoproteínas.
Además de las reseñadas hasta ahora, hay animales en cuyas cavidades internas el fluido correspondiente (líquido celómico, hemolinfa o sangre) contiene proteínas con funciones respiratorias. Se trata de pigmentos respiratorios que no se encuentran en el interior de células especializadas, sino que desempeñan sus funciones manteniéndose en suspensión coloidal. Nos referiremos a estas proteínas en una próxima anotación dedicada a específicamente a los pigmentos respiratorios.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Sistemas circulatorios: proteínas plasmáticas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sistemas circulatorios: los compartimentos líquidos de los animales
- Sistemas respiratorios: la emergencia de un doble sistema circulatorio
- Sistemas respiratorios: el pulmón de los mamíferos
El principio de relatividad (2): la versión de Galileo
Einstein no fue el primero en hablar de marcos de referencia y movimiento relativo. Casi 300 años antes ya lo había hecho Galileo, quien también sería pionero en el uso de experimentos mentales, un procedimiento que después Einstein haría famoso. El principio de relatividad de Einstein no es más que una expansión del de Galileo. Si estudiamos éste, que es muy intuitivo, el otro nos parecerá poco menos que trivial.

Galileo lo explicó con estas palabras (en traducción libre nuestra) en un experimento mental que recogió en su obra “Dialogo sopra i due massimi sistemi del mondo Tolemaico, e Coperniciano” de 1632:
Enciérrate con un amigo en la cabina principal bajo cubierta de algún barco grande, y lleva contigo algunas moscas, mariposas y otros animalillos voladores. Lleva también un recipiente grande de agua con unos peces; cuelga una botella que se vacíe gota a gota en un recipiente ancho puesto debajo. Con la nave en reposo, observa cuidadosamente cómo los animalillos vuelan con la misma velocidad a todos los lados de la cabina. Los peces nadan indiferentemente en todas direcciones; las gotas caen en el recipiente que está debajo; y, al arrojar algo a tu amigo, no necesitas lanzarlo con mayor fuerza en una dirección que en otra, si las distancias son iguales; al saltar con los pies juntos, avanzas espacios iguales en todas direcciones. Cuando hayas observado todas estas cosas con cuidado (aunque no hay duda de que cuando la nave está parada, todo debe suceder de esta manera), haz que la nave avance con la velocidad que desees, siempre que el movimiento sea uniforme y no fluctúe de una u otra manera. Descubrirás que no hay el menor cambio en todos los efectos nombrados, ni podrás decir a partir de de ninguno de ellos si se estás en [un barco en] movimiento o parado.
Hoy podemos realizar el mismo experimento con mariposas o pelotas de baloncesto en un barco, en un automóvil, un tren o, mejor aún, en un avión que se mevan a velocidad constante. Hemos visto que cada uno de estos sistemas sería un marco de referencia para nuestras observaciones. El hecho de que los movimientos de las pelotas de baloncestoy las mariposas permanezcan igual, independientemente de si el marco de referencia se mueve o no a velocidad constante, indica que las leyes de movimiento de Newton son las mismas (de hecho, todas las leyes de la mecánica, la ciencia del movimiento) son las mismas para todos los marcos de referencia en reposo o que se mueven con una velocidad uniforme relativa entre sí. Esta conclusión es lo que se llama principio de relatividad galileano. Formalmente se puede expresar así:
Las leyes de la mecánica son exactamente las mismas para cualquier observador en cualquier marco de referencia que está en reposo o se mueve con una velocidad uniforme.

Luke Skywalker no puede determinar si el Halcón Milenario está en reposo o en movimiento uniforme realizando experimentos mecánicos con bolas y sables láser.
Dado que los objetos se mueven en un marco de referencia que está en reposo o en velocidad uniforme como lo harían en un marco en reposo, de ahí se deducen dos cosas importantes. La primera es que no hay manera de averiguar la velocidad del propio marco de referencia a partir de cualquier experimento mecánico realizado dentro de ese marco. Es decir, si viajamos en un avión a velocidad constante y sin turbulencias, no podemos averiguar a qué velocidad se está moviendo el avión realizando experimentos mecánicos dentro del avión.
Y la segunda es que tampoco podemos elegir un marco de referencia como el marco “verdadero”, el que está “absolutamente en reposo”. Por lo tanto, como ya vimos que apuntaba Einstein, Galileo ya sabía que no puede haber tal cosa como la velocidad “absoluta” de un objeto. Todas las velocidades medidas son relativas. Einstein redescubrió este principio eliminando las capas de sedimentos que siglos de física newtoniana y espacios absolutos habían depositado encima.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El principio de relatividad (2): la versión de Galileo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El principio de relatividad (1): movimiento relativo
- Se establece el principio de conservación de la energía
- Cuántica y relatividad por todas partes
Diversidad religiosa y el estrés de las enfermedades infecciosas

Hace tres años Corey Finher y Randy Thornhill publicaron un libro en el que presentaron su teoría del estrés parasitario, teoría según la cual los patógenos con los que las poblaciones de una especie entran en contacto a lo largo del tiempo inciden en el desarrollo de los valores y cualidades de esa especie. Ya antes habían publicado algunos de sus resultados, así como avances de la teoría. En uno de los trabajos con más repercusión testaron una hipótesis en virtud de la cual la diversidad religiosa existente en una zona geográfica está directamente relacionada con el grado de estrés que las enfermedades infecciosas ejercen sobre las sociedades humanas. De acuerdo con esa hipótesis, cabe esperar que en los países con mayor variedad de enfermedades infecciosas presentar una mayor diversidad religiosa. La base argumental de la relación causa-efecto subyacente es la siguiente:
(1) Un grupo humano tiene inicialmente una distribución geográfica y un repertorio cultural y distribución de inmunidad uniformes.
(2) Con el tiempo, la inmunidad empieza a variar espacialmente, debido a la emergencia localizada de nuevos patógenos y a la evolución, también localizada, de inmunidad adaptativa en respuesta a aquellos.
(3) Bajo esas condiciones se seleccionan comportamientos que tratan de evitar el contacto con personas infectadas o potencialmente infectadas con los patógenos peligrosos. Estos comportamientos son (a) la “dispersión limitada”, reduciendo la interacción con personas de otros grupos, y (b) “socialidad restringida” a los miembros del grupo (y por lo tanto, adaptados inmunológicamente). Esta “socialidad restringida” se produce mediante el contacto (servicio religioso, reciprocidad, caza cooperativa, crianza cooperativa, etc.) y emparejamiento con individuos similares.
(4) Ese contacto selectivo promueve la divergencia cultural, al limitarse el flujo de valores e ideas entre los diferentes grupos humanos y, como consecuencia, da lugar a un aumento en la diversidad religiosa.
(5) La carrera “parásito-huésped” que se establece entre el patógeno y la persona infectada constituye un poderoso mecanismo evolutivo que puede incrementar la divergencia cultural dentro del rango cultural original del huésped.
(6) Cuanto mayor es la riqueza de patógenos en un área, mayor es la oportunidad para que se produzca variación espacial en las correspondientes carreras evolutivas “parásito-huésped”. La frecuencia, variación e intensidad de (2) (3) (4) y (5) covariarán de forma positiva con la diversidad de enfermedades infecciosas. Esto es, la diversidad de enfermedades dará lugar a una mayor diversidad cultural y religiosa.
La hipótesis la contrastan analizando la covariación de la diversidad religiosa y la diversidad de patógenos en 214 países, y estimando la correlación lineal entre ambas variables. Obtuvieron una correlación de 0’75, un valor extraordinariamente alto para variables de esta naturaleza. Concluyeron, por lo tanto, que el análisis realizado constituía un fuerte respaldo para su hipótesis.
A partir de los resultados los autores sostienen que, sin descartar el efecto de otros posibles factores, la aparición de nuevas religiones cumple la función de aislar a grupos humanos que se encuentran geográficamente próximos para así protegerlos de las infecciones para las que no están inmunológicamente protegidos. Sirva este ejemplo para ilustrar la teoría a la que hemos hecho mención al comienzo.
Fuente: Corey Fincher y Randy Thornhill (2008): Assortative sociality, limited dispersal, infectious disease and the genesis of global pattern of religion diversity Proceedings of the Royal Society B, 275: 2587-2594
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Diversidad religiosa y el estrés de las enfermedades infecciosas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Sobre la predisposición genética a padecer enfermedades
- Sobre la predisposición genética a padecer enfermedades (II)
- María Trinidad Herrero, una científica contra las enfermedades neurodegenerativas #WomeninSTEM
Eran nuestras ballenas
No falta quien diga que los primeros hombres que afrontaron tamaña aventura necesitábase estuvieran muy excitados y que fuesen excéntricos y exaltados. Preténdese, además, que los primitivos pescadores de esos monstruos no fueron los discretos hombres del Norte, sino nuestros vascos, héroes del desvarío. Andarines terribles, cazadores del Monte Perdido y desenfrenados pescadores, recorrían en barquichuelos su caprichoso mar, el golfo o sumidero de Gascuña, dedicándose a la pesca del atún. Notaron aquellos intrépidos navegantes que las ballenas retozaban, y comenzaron a perseguirlas, lo mismo que se encarnizan detrás de la gamuza en los barrancos, los abismos y los más espantosos resbaladeros. A esa pieza de caza (la ballena) muy tentadora por su tamaño y por las vicisitudes que causa el perseguirla, hiciéronla guerra a muerte doquiera que la encontrasen y sin notarlo, empujábanla hacia el polo.
Allí el pobre coloso creyó poder vivir tranquilo, no suponiendo que los hombres fuesen tan locos que lo persiguieran hasta en aquellas apartadas regiones. La pobre ballena dormía muy sosegada, cuando nuestros atolondrados héroes se acercaron a ella cautelosamente.
Apretando su cinturón colorado, el más fornido, el más ágil saltaba de su barquichuelo, y ya encima de aquella mole inmensa, sin preocuparse del riesgo que pudiese correr su vida, lanzando un ¡han! prolongado, hundía el arpón en las carnes del confiado monstruo.
Jules Michelet, El mar, 1861.
El 22 de abril de 2015 se derogó en Islandia la ley que permitía matar vascos desde 1615. Ese día, según informaban las notas de prensa, el comisario Jónas Guomundsson suprimió la ley en presencia del Ministro de Educación y Cultura de Islandia, Illugi Gunnarsson, el Diputado General de Guipúzcoa, Martín Garitano, y Xabier Irujo, como descendiente de uno de los vascos asesinados, y Magnus Rafnsson, descendiente de uno de los islandeses que mataron a los vascos en 1615.
En aquellos años, islandeses y vascos tenían un acuerdo para la caza de ballenas. Los vascos instalaron una estación ballenera en la región de los Fiordos del Oeste. Cuando acabó la estación de caza y los vascos volvían a casa, una tormenta y los icebergs hicieron encallar tres barcos en los escollos de la costa. La mayoría sobrevivieron al naufragio y pudieron regresar pero unos cuantos se quedaron en la estación. Al mes siguiente, los que permanecieron fueron asesinados siguiendo la orden de las autoridades y según la ley, recién dictada, que permitía matar vascos. Solo hubo un superviviente.

Las primeras menciones escritas a balleneros vascos en Islandia están fechadas a comienzos del siglo XVII, en 1610, en la región de los Fiordos del Oeste, en el noroeste de la isla, aunque hay autores, como Alex Aguilar, de la Universidad de Barcelona, que lo fecha en documentos de 1412. También se cuenta que tres balleneros vascos estaban en Strandir en 1608 y otro, en el mismo lugar, en 1613. Este último atracó para extraer la grasa de las ballenas, que los vascos llamaban saín, y que era su producto comercial más valioso. En 1614 llegaron 11 barcos y en 1615 fueron 16. Y entre los de este año están los tres que naufragaron y los supervivientes fueron asesinados. Según las crónicas islandesas de la época, los mandaban los capitanes Martinus de Billa de Franca, Pedro de Arguirre y Stephan de Tellaria. De los 82 marineros que llegaron a tierra, 13 fueron asesinados mientras pasaban la noche en la estación, y otros 18 murieron en la campaña contra ellos de la población del lugar, liderada por el gobernador local Ari Magnusson.

En los diez años siguientes no hay mención a la presencia de balleneros extranjeros. Después, hasta comienzos del siglo XVIII, hay menciones esporádicas a la llegada de balleneros vascos. En 1712 se mencionan por escrito y por última vez y, después, lo prohibieron las leyes de Islandia. Sin embargo, en esos años la relación con los islandeses fue tan estrecha que existen tres glosarios de euskera-islandés de finales del siglo XVII y comienzo del XVIII. Los han estudiado varios expertos y, entre ellos, está Viola Giulia Miglio, de la Universidad de California en Santa Barbara. Los glosarios están depositados en archivos de Reykiavik, en Islandia.
La relación entre la especie humana y las ballenas viene de muy antiguo. Se han encontrado imágenes en rocas en Alaska fechadas hace 6000-8000 años, o en Noruega, de hace 9000-10000 años. En el País Vasco se han recuperado arpones de hueso de ballena, fechados hace unos 13000 años, en la cueva Lumentxa, en Lekeitio.

Artefactos realizados a partir de huesos de ballena descritos por Pétillon
En la vertiente norte de Pirineos y según los estudios de Jean-Marc Pétillon, de la Universidad de Toulouse 2, existía, entre 13000 y 15000 años atrás, una industria que transformaba huesos de ballena en armas y herramientas, sobre todo en puntas de lanza de gran tamaño. Encontró artefactos, que publicó como la evidencia más antigua de industria con huesos de ballena, en la cueva de Isturitz, en Iparralde. Y más instrumentos en 11 cuevas del norte de Pirineos, de esta a oeste, y siempre fabricados con huesos de origen el Atlántico.
Algunos de esos instrumentos viajaron más de 350 kilómetros hasta el lugar donde se han encontrado. Las fechas de algunos de ellos llegan a los 17000 años atrás. Sin embargo, no se han localizado los talleres donde se fabricaban y tampoco se conoce si proceden de ballenas varadas en la costa o cazadas por balleneros. Pero, por el número de instrumentos encontrados y las distancias que han recorrido, tampoco parece que se obtengan los huesos originales en episodios esporádicos de caza o accidentales de varamiento. Propone Pétillon que, de alguna manera, debía existir algún tipo de caza de ballenas más sistemático.
Restos de ballena más recientes se han encontrado en un castro cerca de Gijón, la Campa de Torres, con fecha de entre 2300 y 2400 año, aunque, como es habitual, se desconoce si fue caza o varamiento.

Eubalaena glacialis en un fiordo noruego
La ballena que cazaban los vascos en el Cantábrico era la llamada, con propiedad, ballenas de los vascos o ballena franca (o right whale, en inglés), y de nombre científico Eubalaena glacialis. Este especie pesaba unas 60 toneladas, con un rango de 36 a 72 toneladas, media unos 15 metros, con máximos de 18 metros, y llevaba 270 barbas.

En verano, la ballena de los vascos migraba hacia el norte, hacia las Svalbard, Noruega e Islandia y, en invierno, viajaban al sur hasta Madeira, Azores, las costas del noroeste de África y, por supuesto, el Golfo de Vizcaya. Era la época del parto y, durante un tiempo, viajaban juntas la madre y el ballenato. Además, era la época en que se firmaban los contratos de caza entre los balleneros implicados y sus armadores y financiadores. Incluso entra en el contrato el atalayero, aquel que avisaba de la llegada de una ballena para que salieran de caza. Lo hacía desde la atalaya que, aunque se han perdido muchas, todavía se conserva alguna como, por ejemplo, la del monte Ulia en Donosti.
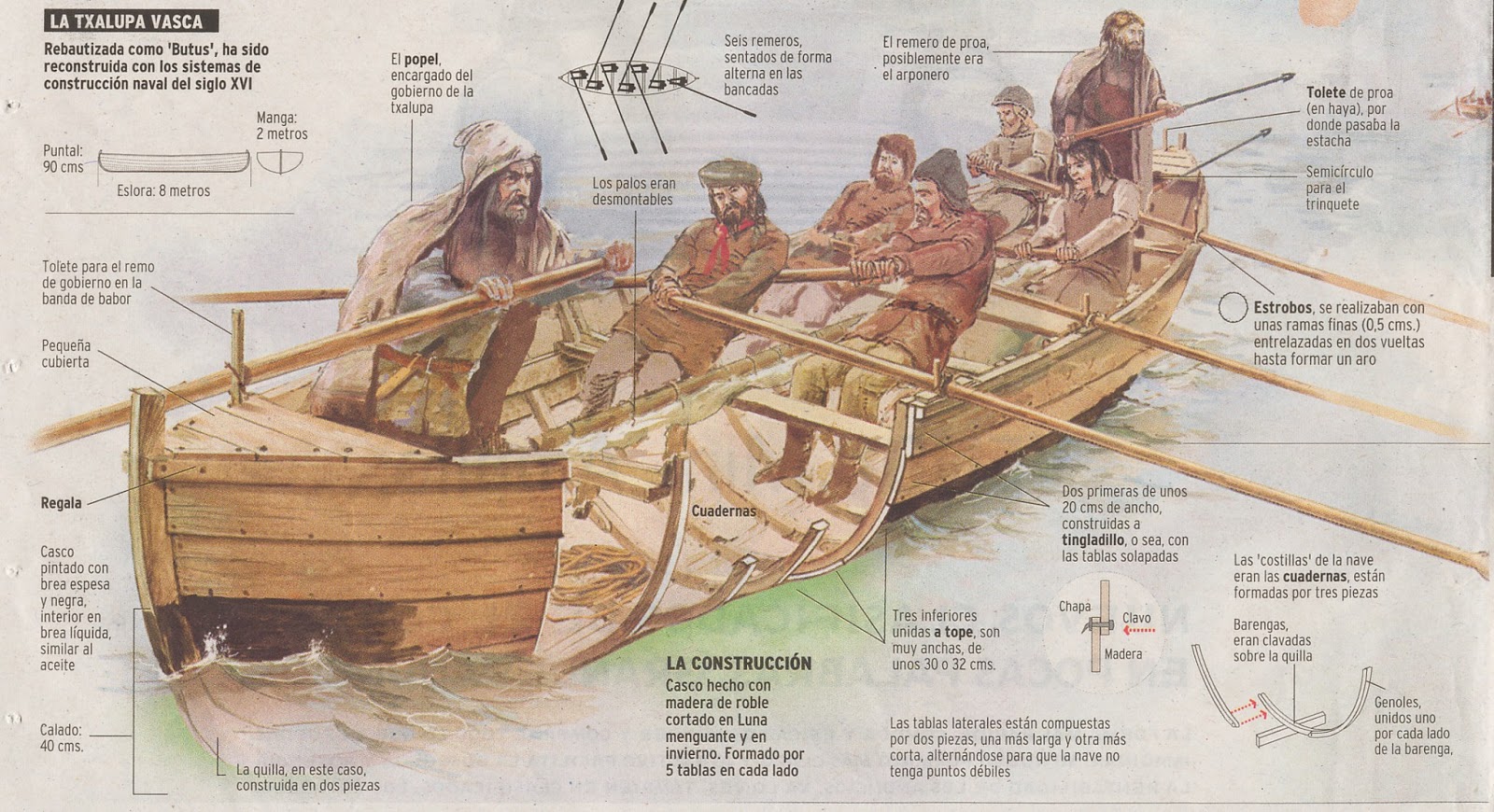
Fuente: www.albaola.com
La embarcación de los balleneros vascos para la caza de la ballena era la chalupa o, también llamada barco, vizcaína, ballenera, piragua,… Más o menos tenía 10 metros de eslora y de 2 a 2.5 metros de manga, con unos 12 marineros, con 10 remeros más el timonel a popa y el arponero a proa. Llevaban queso y vino, mantas y ropa de abrigo y, por ejemplo, en Orio, unos 150 metros de soga, dos arpones, dos jabalinas grandes y una pequeña.
La principal riqueza de las ballenas era su grasa, el llamado saín, que calentaba e iluminaba edificios en toda Europa. Las barbas de la ballena, material flexible pero escaso, tenía muchos usos, y los huesos que sujetaban las barbas servían de mango de herramientas, sobre todo de cuchillos. La carne de la ballena se consumía fresca y, también, se secaba o salaba y se vendía en toda Europa.

Despiece de una ballena en Deba (Gipuzkoa). Junto a una de las puertas de entrada a la villa, pueden apreciarse los hornos donde se elaboraba el saín. En un plano medio, la partida de una lancha ballenera, y al fondo, la señal de humo en una de las atalayas. Fuente: Ilustración de José Ignacio Treku / Deba kalez-kale
Los testimonios escritos sobre balleneros vascos más antiguos están fechados en 1059, en Bayona, sobre la venta de carne del cetáceo, o en 1181 en Donosti con el reglamento y los impuestos a abonar por esa venta. También hay documentos de Santoña en 1190 o en Motrico en 1200. En Asturias la primera fecha documentada es de 1232 y en Galicia es 1371. Hasta 47 puertos del Cantábrico tuvieron asentamientos balleneros, y, por lo menos, 14 de ellos tienen una ballena en el escudo.
Toda la infraestructura, costumbres, práctica, tecnología y reglamentos de la caza de ballenas en el País Vasco son necesarios para las expediciones que, hemos visto, se hacían a Islandia y, también, a Terranova, a las islas Spitzberg o a Groenlandia. Para cazar ballenas en estos largos viajes se necesita aprender en casa, construir barcos adecuados, conseguir financiación, provisiones y demás pertrechos, y, a la vuelta, donde vender lo capturado, sobre todo la carne y la grasa.
En el Cantábrico y según varios autores con opiniones diferentes, el apogeo de la caza de ballenas varía desde el siglo XII y XIII hasta los siglos XIV y XV. Ya en el siglo XVI, el número de ballenas avistadas en la costa cantábrica disminuye y en el XVII casi desaparecen. Quizá fue una de la razones que empujó a los balleneros vascos hacia el norte y el oeste en busca de presas. Conocían sus migraciones anuales al norte y al sur y, simplemente, las siguieron. Hay autores que afirman que se llegaban a cazar, en el siglo XVI, hasta 100 ejemplares al año, y en muchos casos eran ballenas recién paridas con su ballenato. Los balleneros sabían que, si cazaban primero a la cría, mucho más fácil de atrapar, la madre no la abandonaría y podía ser capturada a continuación.
También hay que mencionar que desde el siglo XVI, quizá incluso desde mucho antes, en el siglo XIV, los vascos pescaban bacalao y ballenas en Terranova. Quizá por entonces ya eran conocidos en el Atlántico Norte europeo, en Islandia en concreto.
Los países del norte de Europa pronto aprendieron a cazar ballenas y descubrieron el negocio que suponía, sobre todo la venta de la grasa. Y parece que lo aprendieron de los balleneros vascos pues era habitual que contrataran, por ejemplo en Holanda e Inglaterra, a arponeros vascos. Así lo decretó, en 1612, el rey Jacobo II de Inglaterra.
No es fácil reunir cifras de las ballenas que se cazaban en aquellos años. Cuando se pagaban impuestos, los llamados diezmos, al gobierno, a algunas autoridades o a la Iglesia, los datos, siempre aproximados pueden dar una idea de las poblaciones de ballenas de la época. Alfredo Salvador y Carlos Nores, del Museo Nacional de Ciencias Naturales de Madrid y de la Universidad de Oviedo, respectivamente, han recopilado datos de Zarauz, Getaria y Lekeitio. Dan 35 capturas a principios del siglo XVI, y caen hasta 5 capturas a principios del XVIII. Hay quien da la fecha de 1766 como el final de la caza de ballenas en el Cantábrico. Durante los siglos XVIII y XIX hubo algunas capturas esporádicas, e incluso se perdieron las herramientas para cazar y se olvidaron las técnicas de acercamiento y captura.
La última ballena se cazó en Orio el 14 de mayo de 1901. Y se cazó con dinamita pues, como decía, las técnicas tradicionales se habían perdido.
Además de a Islandia, como ya hemos visto, los balleneros vascos fueron de caza a Terranova, en su singladura más conocida y popular. Eran mares ricos en bacalao y hay autores que sugieren que los vascos fueron a Terranova, en primer lugar, a pescar bacalao y, de paso, aprovecharon el paso de las ballenas.
Las primeras citas de balleneros vascos en Terranova que se aceptan por los estudiosos se fechan en el segundo cuarto del siglo XVI, en concreto en 1531, tal como cuenta Selma Huxley, de la Universidad de St.John’s, en Terranova. Volvían a casa con bacalao y carne de ballena en salmuera, más el saín y las barbas de las ballenas. Entonces, con un gran desarrollo de los astilleros, y la llegada de saín y bacalao, en el País Vasco la economía se basaba en el hierro y la fabricación de herramientas y armas, y, por supuesto, en la ballena, y más en el bacalao. Los balleneros vascos fueron los primeros que montaron toda una organización social para la caza de ballenas con objetivos comerciales. También era un hecho aceptado que los vascos, en la primera mitad del siglo XVI, tenían los mejores barcos. Así que, en ese siglo, los balleneros vascos eran mayoría en Terranova.
Durante todo el siglo XVI llegaron a Terranova de 15 a 20 barcos cada verano, y traían de vuelta unos 9000 barriles de saín. A finales de siglo, declina la caza de ballenas y van pocos barcos a Terranova. La mayoría de los barcos y los marineros son alistados obligatoriamente en la Armada Invencible de Felipe II contra Inglaterra. Y el desastre que supuso también desbarató la flota vasca, tanto por pérdida de naves como de tripulaciones experimentadas. El Tratado de Utrecht, en 1713, concedió aquellas tierras a franceses e ingleses y terminó con los viajes de los balleneros vascos.
También en Terranova, como ocurría en Islandia, había una relación estrecha entre los balleneros vascos y los indios de la zona, sobre todo con los mik’mac y, todavía, algunas palabras en euskera sobreviven en su lengua y en el francés de Canadá.
Incluso podemos conocer la dieta de los balleneros con los hallazgos del grupo de William Fitzhugh, de la Institución Smithsonian, en el yacimiento de Hare Harbour, en la Isla Petit Mécatina, en el Golfo de San Lorenzo. Hay restos de ballena de Groenlandia, no de la ballena de los vascos, y bacalao que capturaban para traer a casa y comerciar. Los restos que nos indican su dieta son de aves como alcas, frailecillos, gaviotas, gansos, patos, cisnes, perdices y cuervos; de mamíferos como focas, cerdo doméstico, jabalí, caribú, vaca y zorro; y frutas como avellanas, nueces, melocotones y ciruelas.
En la actualidad, la ballena de los vascos es rara en el Atlántico Norte occidental, en las costas de Norteamérica, y mucho más rara en el Atlántico Norte oriental, en las costas europeas. Es difícil saber cuantas ballenas de los vascos quedan. A principios del siglo XX estaba cercana a la extinción, cuando se estimaba que había unos 60 ejemplares, cifra basada en escasas evidencias y más en suposiciones personales. Después se fue recuperando lentamente pero, en la década de los noventa, comenzó de nuevo a disminuir su número.

Eubalaena glacialis
Entre 1980 y 2000, el Acuario de Nueva Inglaterra fotografió unos 10000 avistamientos de cetáceos, y Masami Fujiwara y Hal Caswell, del Instituto Oceanográfico de Woods Hole, identificaron en esas imágenes a 350 ballenas de los vascos. Los autores deducen que había poco más de 300 individuos de Eubalaena glacialis a principios de este siglo. Parece que estaban muriendo las ballenas en edad de ser madres. Los autores proponen que salvando, cada año, a dos ejemplares que puedan tener crías la población se estabilizaría. La protección legal internacional de especies en peligro de extinción considera que la ballena de los vascos es la especie de gran tamaño con más riesgo de desaparecer.
A menudo se ha propuesto que se ha llegado a esta situación, por lo menos en Norteamérica, por la caza de los vascos en el siglo XVI, seguido por la acción de los balleneros de la costa oeste de Estados Unidos (recordar Moby Dick) durante los siguientes dos siglos y medio. Sin embargo, cuando Brenna McLeod y su grupo, de la Universidad Trent, en Canadá, analizaron el ADN de los 218 huesos de ballena encontrados en el asentamiento de balleneros vascos de Red Bay, en Labrador, solo uno de ellos es de la ballena de los vascos. La mayoría son de otra especie de ballena, la Balaena mysticetus, conocida como ballena de Groenlandia o ballena boreal. Para cuando llegaron a la zona de Terranova los balleneros vascos, la población de Eubalaena glacialis era mucho menor de lo que se suponía. No hay que olvidar que la ballena de los vascos tiene el dudoso honor de ser la que tiene la más larga historia de ser cazada entre todas las ballenas.
Referencias:
Aguilar, A. 1996. A review of old Basque whaling and its effect on the Right Whales (Eubalaena glacialis) of the North Atlantic. Reports of the International Whaling Comission Special Issue, 10: 191-199.
Arrinda, A. 1977. La pesca en Euskalerria. Caja de Ahorros Municipal. San Sebastián. 261 pp.
Azkarate, A. et al. 1992. Balleneros vascos del siglo XVI (Chateau Bay, Labrador, Canadá). Estudio arqueológico y contexto histórico. Servicio Central de Publicaciones del Gobierno Vasco. Vitoria-Gasteiz. 261 pp.
Azpiazu, J.A. 2000. Balleneros vascos en el Cantábrico. Ttarttalo. Donostia. 172 pp.
Bakker, P. 1991. “La lengua de las tribus costeras es medio vasca”. Un pidgin vasco y amerindio utilizado por europeos y nativos americanos de Norteamérica, h. 1540-h. 1640. Anuario del Seminario de Filología Vasca “Julio de Urquijo” 25: 439-467.
Barthelmess, K. 2009. Basque whaling in pictures, 16th-18th century. Itsas Memoria. Revista de Estudios Marítimos del País Vasco 6: 643-667.
Campos Santacana, M.K. & M. Peñalba Otaduy. 1997. La caza de la ballena. Su influencia en los usos y costumbres desde la Edad Media. Zainak, Cuaderno de Antropología y Etnografía, 15: 251-262.
Ciriquiain Gaiztarro, M. 2010 (1961). Los vascos en la pesca de la ballena. Biblioteca Vascongada de los Amigos del País. San Sebastián. 270 pp.
Edvardsson, R. & M. Rafnsson. 2006. Basque whaling around Iceland. Archeological investigation in Strakatangi, Steingrimsfjordur. The Natural History Institute of Vestfirdir. Bolungarvik, Iceland. 25 pp.
Escribano-Ruiz, S. & A. Azkarate. 2015. Basque fisheries in Eastern Canada, a special case of cultural encounter in the colonizing of North America. En “Archaeology of culture contact and colonization in Spanish and Portuguese America”, p. 239-256. Ed. por P.P.A. Funari & M.X. Senatore. Springer Int. Publ. Switzerland.
Estes, J.A. et al (Eds.). 2006. Whales, whaling, and ocean ecosystems. University of California Press. Berkeley.
Fujiwara, M. & H. Caswell. 2001. Demography of the endangered North Atlantic right whale. Nature 414: 537-541.
Graells, M.P: 1889. Las ballenas en las costas oceánicas de España. Memorias de la Real Academia de Ciencias Exactas, Físicas y Naturales de Madrid XIII: 1-115.
Huxley Barkham, S. 1984. The Basque whaling establishments in Labrador 1536-1632 – A summary. Arctuc 37: 515-519.
Jenkins, J.T. 1921. A history of whale fisheries, from the Basque fisheries of the tenth century to the hunting of the finner whale at the present date. H.F & G. Witherby. London. 336 pp.
Kurlansky, M. 2000. La historia vasca del mundo. Ed. El Gallo de Oro. Bilbao.
McLeod, B.A. et al. 2010. DNA profile of a sixteenth century western North Atlantic right whale (Eubalaena glacialis). Conservation Genetics 11: 339-345.
Michelet, J. 1999 (1861). El mar. www.elaleph.com
Miglio, V.G. 2008. “Go shag a horse!”: The 17th-18th century Basque-Icelandic glossaries revisited. Journal of the North Atlantic. 1: 1-12.
Orue-Etxebarria, X. 2012. Hierro, ballenas y barcos: factores del poder económico de Bizkaia durante la Edad Media (I/II). Euskonews 623-624. 4 y 11 mayo.
Otero, X. 2017. William W. Fitzhugh. Zazpika 21 mayo: 23-31.
Pétillon, J.-M. 2008. First evidence of a whale bone industry in the western European Upper Paleolithic: Magdalenian artifacts from Isturitz (Pyrénées-Atlantiques, France). Journal of Human Evolution 54: 720-726.
Pétillon, J.-M. 2013. Circulation of whale-bone artifacts in the northern Pyrenees during the late Upper Paleolithic. Journal of Human Evolution 65: 525-543.
Salvador, A. & C. Nores. 2011. Ballena de los vascos – Eubalaena glacialis (Müller, 1776). En “Enciclopedia Virtual de los Vertebrados Españoles”. Ed. por A. Salvador & J. Cassinello. Museo Nacional de Ciencias Naturales. Madrid.
Unsain, J.M. 2012. Balleneros vascos. Imágenes y vestiugios de una historia singular. Untzi Museoa – Museo Naval. Donostia-San Sebastián. 175 pp.
Wikipedia. 2017. History of Basque whaling. 4 March.
Zulueta, J. de. 2000. The Basque whalers: The source of their success. Mariner’s Mirror. International Quarterly Journal of the Society for Nautical Research 86: 261-271.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Eran nuestras ballenas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Lourdes Basabe y los microlaboratorios

El pasado 14 de septiembre de 2017 se celebró la primera edición de Naukas Pro, en el que Centros de Investigación, Laboratorios, científicos de renombre o equipos de trabajo contaron con 20 minutos para explicar a un público general en qué consiste su trabajo.
7ª conferencia: Lourdes Basabe, investigadora Ikerbasque, del Cluster de Microfluidica UPV/EHU, Centro de Investigación Lascaray.
Loudes Basabe presenta una charla sobre su trabajo en el laboratorioEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Lourdes Basabe y los microlaboratorios se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Pro, en directo
- Naukas Pro 2017: Leni Bascones y los superconductores
- Naukas Pro 2017: Julián Estévez y la inteligencia computacional
El consumidor etnocéntrico

La literatura ha tratado los conceptos de producto local, producto regional y producto tradicional como si fuesen independientes. Sin embargo, en la práctica, estos conceptos están interrelacionados en muchos productos de alimentación. El trabajo ahora publicado pretende resolver dos cuestiones principales: por una parte, conocer la valoración de productos de alimentación que reúnan las características de los productos locales, regionales y tradicionales, a través del análisis de marcas concretas de productos; por otra, estudiar el posible vínculo entre el nivel de etnocentrismo de los consumidores y la valoración y la compra efectiva de marcas locales-regionales-tradicionales.
El etnocentrismo es un concepto elaborado por la antropología para definir la tendencia emocional que hace de la cultura propia el criterio exclusivo para interpretar los comportamientos de otros grupos, razas o sociedades y, en virtud de ello, rechazar, excluir o marginar todo aquello que no forme parte de ella. En ese sentido, y aplicado al consumo de productos locales, regionales y tradicionales, hablaríamos de la predisposición de las personas por consumir ese tipo de alimentos frente a otros de origen diferente.
La mayoría de estudios previos plantean al consumidor la valoración y la intención de compra de productos locales o tradicionales, pero a un nivel general, abstracto, que no permite al encuestado valorar una marca concreta que puede encontrar disponible en el mercado y que efectivamente puede consumir. “Creemos que una aportación importante de este trabajo es el nivel de análisis elegido. Es decir, analiza marcas específicas dentro de diferentes categorías de productos en dos entornos geográficos diferentes en España”, explica Aitor Calvo Turrientes.
Para realizar el análisis se han considerado cuatro productos con denominación de origen. Todos ellos reúnen las características atribuidas a los productos locales-regionales-tradicionales: D.O.P. Queso Idiazabal, D.O.P. Rioja (Rioja Alavesa), D.O.P. Torta del Casar y D.O.P. Dehesa de Extremadura. Para el estudio, una muestra de consumidores vascos y extremeños han respondido a una serie de cuestiones relacionadas con la valoración y compra de estos productos, así como sobre sus tendencias etnocéntricas.
“Los resultados muestran que esos productos gozan de una alta consideración por parte de los consumidores, que los compran en una proporción elevada frente a otras alternativas.Además, se observa que los niveles de etnocentrismo del consumidor están relacionados, en ocasiones, pero no siempre, con la compra efectiva de esas marcas locales-regionales-tradicionales, lo que pone de manifiesto la necesidad de incluir la categoría del producto en el análisis de los efectos del etnocentrismo del consumidor”, concluye el investigador.
Referencia:
Pilar Fernández Ferrín, Aitor Calvo Turrientes, Belén Bande, Miren Artaraz Miñón, M. Mercedes Galán Ladero. (2017) The valuation and purchase of food products that combine local, regional and traditional features: The influence of consumer ethnocentrism Food Quality and Preference doi: 10.1016/j.foodqual.2017.09.015
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo El consumidor etnocéntrico se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Identificando paleococineros por las marcas en los huesos
- Datando tintas de boli
- Nanopartículas para la consolidación del fuerte español de Bizerta
Vida bajo la luz cenicienta

Luz cenicienta. (Fuente: John Cudworth, Flickr.)
Auguste Comte, filósofo augusto no solo de nombre y padre del positivismo, figura inscrito con letras de oro en el panteón de Patinazos Épicos de la Historia gracias a esta lapidaria sentencia con la que —prácticamente— abrió en 1835 el segundo tomo de su Curso de Filosofía Positiva:
Concebimos la posibilidad de determinar sus formas, sus distancias, sus tamaños y sus movimientos; mientras que en modo alguno podríamos jamás averiguar su composición química, su estructura mineralógica o, con más razón, la naturaleza de la materia organizada que viva en su superficie […]
Les Luthiers nos enseñaron que no hay que perder ocasión de hacer la epistemología y por ello es de ley reconocer que la ciencia moderna le debe algo al positivismo de Comte. Eso, sin embargo, no salvó al filósofo francés de ser sumariamente atropellado con un avance fulgurante escasas décadas después de publicar su seminal obra. Hubo un aviso veinte años antes: en 1815, el joven Joseph Fraunhofer —que nunca dejaría de ser joven, para desgracia suya y de todos— había puesto a trabajar un espectrómetro con el que descubrió que a la luz solar le faltaban 574 líneas. 574 colores de menos que anunciaban la era que abrieron definitivamente Kirchhoff y Bunsen en 1859, en la que podríamos conocer a distancia la composición química de los astros: la era de la espectroscopia.
No podemos culpar a Comte de no verlo venir: no tenía el don de la presciencia ni un Google decimonónico al que consultar lo que además parece un resultado francamente antiintuitivo: ¿cómo vamos a poder conocer la composición de mundos a los que jamás podremos viajar? (Nota: si la especie humana acaba viajando por todo el Universo ocuparé con gusto mi sitio junto a Comte en ese panteón de Patinazos Épicos.) Lo cierto es que la capacidad de los átomos y las moléculas de emitir y absorber frecuencias concretas de luz nos ha conferido un superpoder: el de conocer la composición, a distancias inimaginables, de las estrellas, las nebulosas ¿y las atmósferas de los planetas?
El poder de los espectros
Descomponer la luz de otros mundos mediante un prisma es algo que lleva haciéndose rutinariamente desde hace más de un siglo y medio. Esta técnica nos ha enseñado que la composición de todos los cuerpos visibles del Universo es muy uniforme y está dominada por los elementos más simples que existen: hidrógeno (74%) y helio (24%). El 2% restante («metales» para los astrónomos) es la fracción minoritaria que centra el interés de astroquímicos y exobiólogos. El misterio aún envuelve muchos aspectos relacionados con la vida, pero parece claro que es un fenómeno de base química relacionado con la aparición de la complejidad. Sin ese dos por ciento de elementos «extra», los enlaces e interacciones posibles entre átomos se verían fatalmente limitados. Encontrar las firmas espectroscópicas de estos elementos y las moléculas que forman es clave si pretendemos averiguar, algún día, si existe vida más allá de la burbuja de aire que rodea nuestra pequeña mota azul.
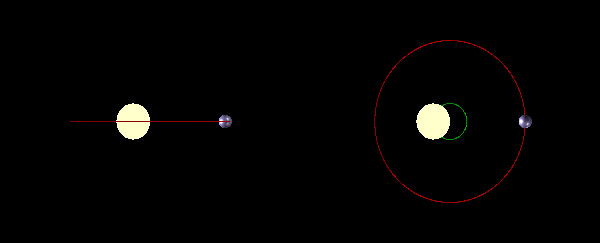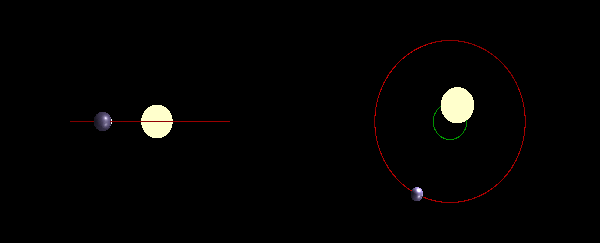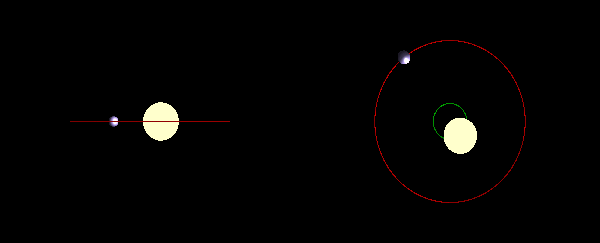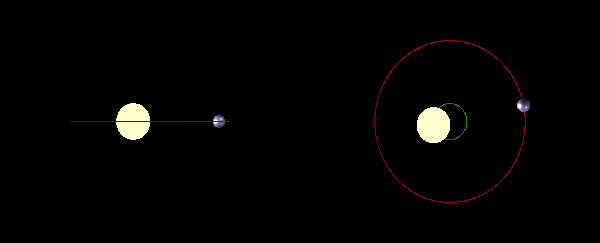
Medidas de tránsito y velocidad radial para sistemas planetarios con diferentes orientaciones: para sistemas visibles «de canto» el tránsito permite observar ocultaciones parciales de la estrella por el planeta. En los sistemas vistos «desde arriba» los tránsitos son invisibles.
Desde finales de los años 80, la creciente precisión en los métodos astrométricos de detección de exoplanetas —mayoritariamente medidas de velocidad radial (coloquialmente «bamboleo» estelar) y, sobre todo, de tránsitos (ocultaciones parciales de estrellas por planetas que las orbitan y que provocan pequeños cambios en la luz recibida de éstas)— ha permitido que los descubrimientos de sistemas planetarios aumenten con un ritmo exponencial. Aunque las formas de llevar a cabo las medidas, así como su precisión, favorecieran en un principio el descubrimiento de lo que se dio en llamar «jupíteres calientes», planetas muy grandes y muy cercanos a sus respectivas estrellas, es cada vez más frecuente encontrarse con descubrimientos de planetas más pequeños y ubicados en las zonas de habitabilidad teóricas de sus sistemas estelares.
Sin duda no estamos muy lejos de ubicar planetas de tamaño terrestre transitando ante sus estrellas con órbitas que les permitirían, al menos teóricamente, sustentar agua líquida de forma permanente en su superficie. Auténticos análogos terrestres alrededor de soles lejanos: pero una cosa es encontrar un lugar que podría albergar vida y otra, muy distinta, es descubrirlo. ¿Podemos siquiera soñar con tal cosa?
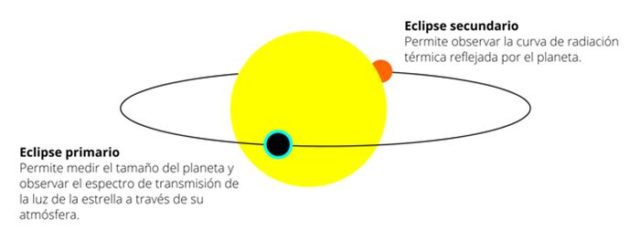
Estudio de las atmósferas de exoplanetas en tránsito. (Adaptado de Sara Seager)
Si es posible detectar la minúscula fracción de luz de una estrella que, durante una ocultación planetaria, atraviesa la atmósfera del planeta para llegar hasta nuestros instrumentos, también debería poderse —restando previamente el espectro de la luz normal de la estrella— hallar la huella espectroscópica de la composición de la atmósfera planetaria. Esto, que parece una hazaña imposible, ya ha ocurrido en varias ocasiones. Un ejemplo de la precisión que puede alcanzarse hoy: utilizando técnicas de espectroscopia diferencial y el instrumento HARPS en el telescopio de 3,6 metros del Observatorio Europeo Austral (ESO) en La Silla, Chile, pudo caracterizarse la presencia de sodio atómico en la atmósfera alta de HD 189733b. Este planeta orbita una estrella de tipo espectral K (una enana naranja; nuestro Sol es una enana amarilla de tipo G) a 62,9 años luz de distancia en la constelación Vulpecula. Con una masa de 1,15 veces la de nuestro Júpiter y una órbita que le lleva a rodear su estrella cada 2,2 días, las medidas basadas en el espectro han podido incluso confirmar que su atmósfera contiene vientos de 7000 kilómetros por hora que arrastran incesantes lluvias de cristal fundido: silicatos de sodio a 700 °C.
Está claro que HD 189773b está casi todo lo lejos que se puede estar de ser un «análogo terrestre», pese a que su color (que, increíblemente, también ha podido ser estimado) debería ser un azul profundo —haciendo de él otro «punto azul pálido» en la inmensidad del espacio. Pero cuando algún día encontremos un planeta realmente similar a nuestra Tierra, algo que solo es cuestión de tiempo, ¿cómo sabremos que puede albergar vida? La respuesta a esta pregunta, más allá de la medida de características orbitales que nos lleven a inferir posibles temperaturas superficiales, pasa naturalmente por el análisis de datos espectrográficos. Y qué mejor análisis que poder comparar el espectro de un planeta así con el de la única muestra que conocemos de planeta que alberga vida: ¿por qué no medir el espectro de la luz del Sol reflejada o transmitida por la propia Tierra a gran distancia?

La Tierra (el «punto azul pálido») visto desde Saturno por la sonda Cassini. (Fuente: NASA.)
La forma obvia de obtener ese espectro consistiría en lanzar una sonda que se alejara mucho de la Tierra —idealmente unos cuantos años-luz— e hiciera la medida. Lo más cerca que hemos estado de conseguir algo así han sido las imágenes del «punto azul pálido»: la original de 1990 tomada por la sonda Voyager 1 a casi cinco horas y media de distancia a la velocidad de la luz (5900 millones de kilómetros) o la más reciente tomada por la sonda Cassini en 2013 desde la órbita de Saturno a 1500 millones de kilómetros. Lamentablemente, ni la Voyager 1 ni la Cassini estaban equipadas para realizar un espectro de la luz solar reflejada por la Tierra desde sus puntos de vista. Que alguna vez se lance una misión tan lejos con un propósito tan limitado parece, además, harto improbable. Sin embargo, hay una forma más sencilla de obtener la misma información gracias a nuestra compañera de viaje en el Sistema Solar: la Luna.
La luz cenicienta
La Luna, vista desde la Tierra, presenta lo que llamamos fases: cambios en su iluminación superficial debidos a las posiciones relativas de la Luna, la Tierra y el Sol. La fase «nueva» corresponde al momento de la órbita de la Luna en la que se encuentra situada directamente entre la Tierra y el Sol, y por tanto nos muestra su mitad oscura; para llegar a la fase «llena» la Luna debe recorrer la mitad de su órbita alrededor de la Tierra hasta encontrarse en el punto en que nos muestra su mitad iluminada —y por tanto, la Tierra está ubicada entre el Sol y la Luna. Si observamos el sistema con un poco de detenimiento, no es complicado darse cuenta de que las fases lunares están complementadas con otras análogas terrestres, pero exactamente invertidas: vista desde la Luna, la Tierra presenta la fase opuesta a la que se ve en la Luna desde la Tierra, como si se miraran en un espejo.
Además, debido a que la Luna tiene la rotación acoplada con la traslación alrededor de la Tierra, siempre muestra el mismo lado. Esto tiene como consecuencia que para cualquier punto de la cara visible de la Luna, la Tierra siempre está en aproximadamente el mismo lugar del firmamento (la libración orbital provoca un pequeño desplazamiento mensual aparente de la Tierra en el cielo lunar). Las diferencias de tamaño y de albedo superficial entre la Tierra y la Luna provocan así un interesante fenómeno: la noche lunar en la cara visible está siempre iluminada por la Tierra llena, y esta iluminación es mucho más intensa que la que provoca la Luna llena en la noche terrestre. Tanto, que puede percibirse desde la Tierra en forma de una iluminación difusa de la zona nocturna de la Luna, sobre todo cuando ésta se encuentra próxima a su fase nueva o hace pocos días que la ha pasado.
Este efecto de iluminación se denomina «luz cenicienta», y tiene la propiedad de que uniformiza completamente la luz que proviene de la cara iluminada de la Tierra debido a la rugosidad aleatoria del terreno lunar —esto es, devuelve una «luz media» de la reflejada por la Tierra. La luz cenicienta que observamos en la fase nueva de la Luna debería por tanto contener información del espectro medio de reflexión de la superficie terrestre, exactamente tal y como se vería desde un punto muy alejado del espacio que no permitiera resolver detalle superficial alguno. Es decir, como si se tratara del espectro de reflexión de un exoplaneta.

Luna en fase creciente iluminada por la luz solar (derecha, sobreexpuesta) y la luz cenicienta (izquierda). (Fuente: Tom Lee, Flickr.)
El espectro de la luz cenicienta revela de la Tierra una serie de potentes marcadores biológicos, entre los que destacan oxígeno molecular y metano en cantidades alejadas de su equilibrio químico —y que por tanto deben ser mantenidas por algún proceso externo, así como la presencia de un «borde rojo» (red edge): una zona de cambio rápido de la reflectividad en el infrarrojo cercano. La clorofila presente en las plantas terrestres absorbe una gran cantidad de luz en la zona visible del espectro, pero se hace casi transparente para longitudes de onda superiores a los 700 nanómetros.
Cuando logremos obtener un espectro de suficiente calidad de la luz de un exoplaneta similar a la Tierra podremos aplicar estas mismas técnicas de análisis para intentar determinar parámetros de la composición de su superficie y su atmósfera. ¿Aparecerán estos biomarcadores? ¿Veremos otros diferentes? El estudio del espectro de la luz de mundos lejanos nunca podrá ofrecernos una certeza absoluta acerca de «la naturaleza de la materia organizada que vive en su superficie», como dijo Comte; pero podrá acercarnos a la solución del enigma de la vida en el Universo mucho más de lo que jamás pudo soñarse hasta hace apenas un suspiro de la historia de la Humanidad.
Este post ha sido realizado por Iván Rivera (@Brucknerite) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU
Para saber más
Comte, A. (1835). Cours de philosophie positive (Vol. II, 19ème leçon). Paris: Borrani et Droz. Visitado el 29/10/2017 en http://gallica.bnf.fr/ark:/12148/bpt6k762681/f9.image.
Nous concevons la possibilité de déterminer leurs formes, leurs distances, leurs grandeurs et leurs mouvements ; tandis que nous ne saurions jamais étudier par aucun moyen leur composition chimique, ou leur structure minéralogique, et, à plus forte raison, la nature des corps organisés qui vivent à leur surface […]
Kirchhoff, G. (1860). Ueber die Fraunhofer’schen Linien. Annalen der Physik und Chemie, 185(1), 148-150. doi:10.1002/andp.18601850115.
Suess, H. E., & Urey, H. C. (1956). Abundances of the Elements. Reviews of Modern Physics, 28(1), 53-74. doi:10.1103/revmodphys.28.53.
Richmond, M. Spectroscopy of exoplanets. Rochester Institute of Technology. Visitado el 05/11/2017 en http://spiff.rit.edu/classes/extrasol/lectures/spectra/spectra.html.
Wyttenbach, A., Ehrenreich, D., Lovis, C., Udry, S., & Pepe, F. (2015). Spectrally resolved detection of sodium in the atmosphere of HD 189733b with the HARPS spectrograph. Astronomy & Astrophysics, 577. doi:10.1051/0004-6361/201525729.
Marín, D. (15/02/2014). El planeta azul en el que llovía cristal. Naukas. Visitado el 05/11/2017 en http://danielmarin.naukas.com/2013/07/11/el-planeta-azul-en-el-que-llovia-cristal/.
Arnold, L. (2007). Earthshine Observation of Vegetation and Implication for Life Detection on Other Planets. Space Science Reviews, 135(1-4), 323-333. doi:10.1007/s11214-007-9281-4.
Sterzik, M. F., Bagnulo, S., & Palle, E. (2012). Biosignatures as revealed by spectropolarimetry of Earthshine. Nature, 483(7387), 64-66. doi:10.1038/nature10778.
El artículo Vida bajo la luz cenicienta se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Meridianas
- Vida alienígena inteligente, una historia terráquea
- La luz polarizada de la estrella más brillante de Leo
Fallos científicos en el cine, mejor vídeo de divulgación joven “On zientzia”
“Fallos científicos en el cine” de Mario Martínez es el vídeo ganador del premio joven al mejor vídeo de divulgación de la 7ª edición de los premios On Zientzia. Mario recoje las mayores pifias científicas recurrentes en el cine en un vídeo muy cinematográfico.
¿Tienes una idea genial para explicar un concepto científico en un vídeo? ¿Quieres ver tu trabajo emitido en televisión? La Fundación Elhuyar y el Donostia International Physics Center (DIPC) han organizado la octava edición de On zientzia, un concurso de divulgación científica y tecnológica enmarcado en el programa Teknopolis, de ETB. Este certamen pretende impulsar la producción de vídeos cortos y originales que ayuden a popularizar el conocimiento científico.
On zientzia tendrá tres categorías. El mejor vídeo de divulgación recibirá un premio de 3.000 euros. Para impulsar la producción de piezas en euskera, existe un premio de 2.000 euros reservado a la mejor propuesta realizada en ese idioma. Por último, con el objetivo de impulsar la participación de los estudiantes de ESO y Bachillerato, hay un premio dotado con 1.000 euros para el mejor vídeo realizado por menores de 18 años.
Los vídeos han de tener una duración inferior a los 5 minutos, se pueden realizar en euskera, castellano o inglés y el tema es libre. Deben ser contenidos originales, no comerciales, que no se hayan emitido por televisión y que no hayan resultado premiados en otros concursos. El jurado valorará la capacidad divulgativa y el interés de los vídeos más que la excelencia técnica.
Las bases las encuentras aquí. Puedes participar desde ya hasta el 25 de abril de 2018.
Edición realizada por César Tomé López
El artículo Fallos científicos en el cine, mejor vídeo de divulgación joven “On zientzia” se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Soy esa bacteria que vive en tu intestino, mejor vídeo de divulgación “On zientzia”
- Keats vs Feynman, mejor vídeo de divulgación “On zientzia”
- On Zientzia, un concurso para divulgadores audiovisuales
La práctica de la ciencia y la práctica del sexo

Asistentes a un congreso científico
Como hemos repetido a menudo y es obvio, los científicos son humanos. Y como el resto de los humanos los romances, escarceos, líos y tragedias o comedias amorosas abundan en los lugares donde trabajan. No miente aquel viejo refrán que dice que el hombre es fuego, la mujer estopa, y viene el diablo y fú; sopla, igual en un laboratorio que en una oficina o una tienda, en una factoría o en un taller, en la tripulación de un barco que en trabajo de campo. En el día a día de la ciencia hay muchas parejas que se conocieron en el trabajo como en cualquier otro campo, a veces con sus pequeñas catástrofes domésticas como divorcios o traumáticas separaciones, a veces con la complicidad añadida de estar con alguien que sabe exactamente a qué te dedicas, a veces incluso con consecuencias sobre el trabajo mismo o sobre la carrera de uno u otro participante. Está en la naturaleza humana.
Algunos tipos de práctica científica pueden incluso ser especialmente dados a este tipo de situaciones. La sensación de formar un pequeño club especial con los pocos que entienden tu (necesariamente reducido) campo de estudio; la incomprensión de familia, pareja y amigos. Las largas jornadas de laboratorio hasta horas intempestivas, a menudo con pausas forzadas, siempre con poco respeto a fiestas y vacaciones. Las estancias de estudio en instituciones ajenas, quizá en el extranjero; la obligatoria etapa itinerante del postdoc. Las jornadas de campo, alejados los investigadores del resto de la gente, aislados en precarios alojamientos y condiciones de vida; las aventuras y desventuras de la prospección, la observación o el viaje remoto y la sensación de que lo que pasa en el campo permanece en el campo. Las personas en situaciones de aislamiento y soledad somos vulnerables a la tentación. Las personas caen, a menudo, en ella.
Esto es simple y llana naturaleza humana, pero como en otras actividades también puede contener rastros de otro elemento, como es el poder, que lo convierte en algo mucho más turbio. En ciencia y en el ámbito académico es común que trabajen juntos personas de diferentes edades y muy diferentes categorías en lo que se refiere a prestigio, influencia y poder real. Alumnos y profesores, doctorandos y catedráticos, técnicos y postdocs forman parte de la mezcla de personas que trabajan juntos. Algunas categorías están en situación social y profesional privilegiada: el profesor titular, el catedrático de la asignatura, el director del departamento. Otras tienen su futuro por desarrollar y por tanto son vulnerables: quien está asentado en la práctica académica y científica puede tener un impacto desmesurado en las perspectivas de carrera profesional de un doctorando o un postdoc, para bien o, ay, para mal. Porque la historia nos enseña que cuando las personas tienen poder sobre otras personas siempre hay alguna que abusa de ese poder. Y es cuando se mezclan las cosas del querer o la lujuria con el desequilibrio de poder cuando todo se complica.
La actual oleada de descubrimientos sobre abusos a mujeres por parte de hombres poderosos en diferentes industrias (medios, TV, cine, fuerzas armadas, etc.) no ha librado al mundo de la ciencia. Se están publicando casos en los que hombres en situación dominante desde el punto de vista profesional han abusado de esa posición para obtener favores de mujeres u otros hombres. Se han hecho públicos hechos que van desde la situación incómoda al acoso o casi la agresión sexual en entornos como la astronomía o la geología de la Antártida, y sin duda se conocerán muchos más. Los foros profesionales y las charlas de café abundan en comentarios más o menos maliciosos sobre científicos que tienen las manos demasiado largas, o que de forma sistemática y en serie seducen a sus estudiantes más atractivas. La ciencia, por desgracia, no proporciona necesariamente una moral a quienes la practican. Y los abusos durante demasiado tiempo han quedado impunes.
Cuando existe un fuerte desequilibrio entre el poder de los participantes incluso las relaciones consentidas quedan manchadas de sospecha. Y estos desequilibrios pueden ser muy marcados y tener consecuencias muy desagradables incluso cuando las relaciones sentimentales (o sexuales) no forman parte del problema y es simplemente un conflicto intelectual. Bien está que cada vez sean menor tolerables este tipo de comportamientos que deben ser erradicados; también de los laboratorios y los centros de investigación, como del resto de la sociedad.
Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.
El artículo La práctica de la ciencia y la práctica del sexo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:La invariancia de Lorentz supera dos pruebas más

Cada vez que alguien consulta su posición en la superficie del planeta usando un GPS está confirmando la teoría de la relatividad de Einstein, de la misma forma que cada vez que se enciende una pantalla se confirma la existencia de los electrones. Con todo,los científicos no se quedan nunca conformes, y si en el úlltimo siglo no se hubiesen hecho ya suficientes pruebas de que la relatividad funciona, quizás la más espectacular la reciente detección de ondas gravitacionales, siempre quedará comprobarlo con más precisión si cabe.
La llamada invariancia de Lorentz significa que una medición física no debe depender de la velocidad u orientación del marco de referencia del laboratorio. Es una simetría fundamental en la relatividad y en el modelo estándar de la física de partículas, pero ciertas ideas que intentan unificar las dos teorías predicen su ruptura. A pesar de numerosos estudios, sin embargo, no se ha encontrado prueba alguna de violaciones de la simetría de Lorentz. Dos equipos de investigadores lo han recomprobado estableciendo de paso algunos de los límites más estrictos hasta la fecha sobre tales violaciones.
Para comprobar la simetría de Lorentz, ambos equipos usaron el mismo marco teórico, que describe la simetría para todas las partículas y fuerzas, incluida la gravedad, en términos de coeficientes que son nulos cuando se cumple la simetría. Pero derivaron los coeficientes usando datos obtenidos de dos tipos muy diferentes de experimentos.
El equipo encabezado por Natasha Flowers, del Carleton College (Minnesota, Estados Unidos) analizó medidas tomadas en el transcurso de unos pocos años con gravímetros superconductores, dispositivos que determinan la aceleración gravitatoria local midiendo la posición de una esfera superconductora que levita en un campo magnético. Los valores de los coeficientes resultantes son todos consistentes con cero, pero en comparación con estudios gravimétricos previos, algunos de los valores son más de 10 veces más precisos, mientras que otros se han obtenido por primera vez.

Espejo colocado en la Luna por la tripulación del Apolo 11, primera misión que llevó a dos humanos a la superficie lunar
Mientras tanto, el encabezado por Adrien Bourgoin, de la Universidad de Bolonia (Italia), analizaron los datos de 48 años de experimentos de medición con el experimento LR3, en el que los rayos láser emitidos desde la Tierra se reflejan en los espejos en la superficie de la Luna colocados por las misiones Apolo 11, 14 y 15 para medir el movimiento orbital y rotacional del satélite. En este caso los investogadores también encuentran que los datos son consistentes con coeficientes nulos. Sin embargo, para algunos de los coeficientes, la precisión es de 100 a 1000 veces mejor que la de las mejores estimaciones actuales.
Esta visto, en esta época de incertidumbre, si quieres aprender algo que describa cómo funciona el universo con una fiabilidad contrastada, estudia la teoría de la relatividad.
Referencias:
Natasha A. Flowers et al (2017) Superconducting-Gravimeter Tests of Local Lorentz Invariance Phys. Rev. Lett. doi: 10.1103/PhysRevLett.119.201101
Adrien Bourgoin et al (2017) Lorentz Symmetry Violations from Matter-Gravity Couplings with Lunar Laser Ranging Phys. Rev. Lett. doi: 10.1103/PhysRevLett.119.201102
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo La invariancia de Lorentz supera dos pruebas más se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La teoría de la invariancia
- La hipótesis de la panspermia supera un nuevo test
- Crónica de la jornada “Las pruebas de la educación”
Compartiendo un rumor
Compartimos debajo un ¿rumor?… ¡No! De momento, un problema propuesto en 2001 en Crux Mathematicorum, revista científica publicada por la Sociedad Canadiense de Matemáticas, y que contiene problemas matemáticos para estudiantes de secundaria y pregrado.

Los tres monos. Imagen: Wikipedia
Ana, Beatriz, Carlos, David, Elena, Fátima, Guillermo, Hugo e Inés forman parte de la comisión de estudiantes de su Facultad. Se reúnen con poca frecuencia y, además, al ser sus ideas bastante diferentes, no conversan demasiado.
En la siguiente tabla se resumen las relaciones entre estas nueve personas (cada una está representada por la inicial de su nombre): 0 significa que las dos personas no se hablan y 1 que lo hacen con frecuencia.
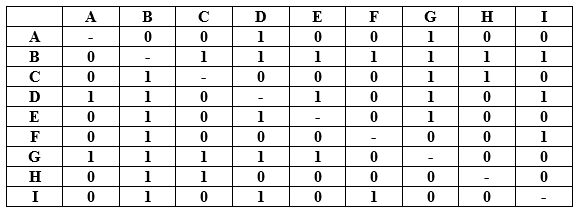
Se sabe que Ana compartió hace unos días un rumor con los dos colegas con los que mantiene comunicación (David y Guillermo), que lo escucharon una vez y solo una –esta vez que Ana se lo transmitió–. A su vez, cada uno de ellos se lo contó a una de las personas con las que habitualmente habla.
Si numeramos a Ana, como iniciadora del rumor con un 1, y Elena fue la novena y última del grupo en escuchar el rumor, ¿quién fue la quinta persona en enterarse de él?
La solución propuesta por la propia revista solo requiere un poco de lógica para usar de la mejor manera los datos proporcionados.
En efecto, sabemos que Ana inicia el rumor y que Elena es la última persona que se entera.
Entre las demás personas –eliminando también a David y Guillermo que lo saben por Ana y que no vuelven a escuchar el rumor–, Fátima y Hugo son los que menos relaciones tienen, al hablarse solo con dos de las personas del grupo. Así que empezaremos por ellos.
Según los datos de la tabla, a Fátima le debe llegar el rumor vía Inés y se lo cuenta después a Beatriz (IFB) o viceversa (BFI). Del mismo modo, Hugo se lo escucha a Beatriz y se lo transmite después a Carlos (BHC) o viceversa (CHB).
Al unir estos dos fragmentos del itinerario del rumor, obtenemos la serie de cinco personas (CHBFI) o (IFBHC). Además, ninguno de estos dos posibles caminos recorridos por el rumor se une con A o con E, ya que Ana no se habla ni con Carlos ni con Inés, y lo mismo sucede con Elena.
Por el anterior comentario, David y Guillermo deben ir necesariamente en los extremos de (CHBFI) o (IFBHC). Pero, David no se habla con Carlos, aunque si con Inés. Guillermo, al contrario, se habla con Carlos, pero no con Inés.
Así, podemos asegurar que el orden de transmisión del rumor entre estas siete personas –excluyendo a Ana y Elena– ha sido (GCHBFID) o (DIFBHCG). Añadiendo a Ana y Elena a esta serie, quedaría que el rumor iniciado por Ana ha llegado a Elena de alguna de estas dos maneras: (AGCHBFIDE) o (ADIFBHCGE).
De cualquiera de los dos modos, la quinta persona en enterarse del rumor ha sido Beatriz.
Notas:
Visto en: The Grapevine, Futility Closet, 16 noviembre 2017
Extraído de: R.E.Woodrow, The skoliad Corner no. 8, Crux Mathematicorum 27:3 (Abril 2001), pág. 194
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Compartiendo un rumor se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La Formación Jaizkibel y sus singulares geoformas “de Möbius”
- La ‘reverosis’ de Pablo
- El disputado voto del Señor Condorcet (I)

