La inteligencia artificial entra en la antropología dental
Un equipo de investigadores acaba de demostrar que pueden emplearse redes neuronales artificiales para reconstruir el número de perikymata, es decir las líneas de crecimiento en el esmalte, que están ausentes en dientes desgastados. Esto tiene aplicaciones paleobiológicas y forenses.
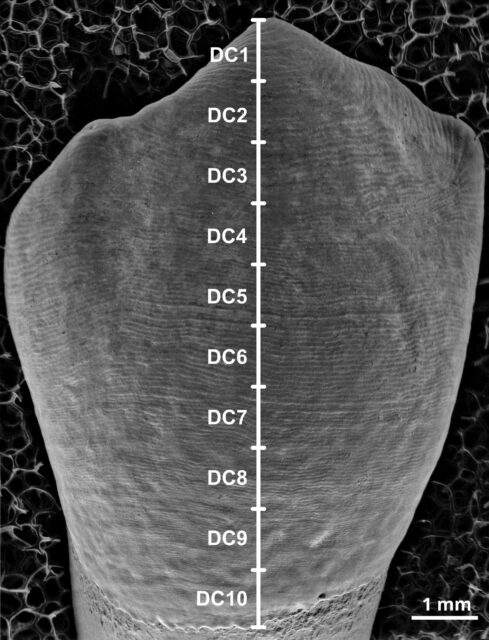
Los dientes son una fuente casi inagotable de información, tanto desde el punto de vista biológico como taxonómico. Debido a su modo de crecimiento, se pueden contar directamente sus líneas y estimar los días de formación. Sin embargo, contar los perikymata presenta dificultades derivadas del estado del diente, porque si el diente está desgastado por el uso normal, parte de los perikymata se habrán perdido como consecuencia de la pérdida de esmalte.
“Resolver este problema es de vital importancia, ya que nos permitiría aumentar el número de dientes adecuados para llevar a cabo estudios evolutivos y, con ello, llegar a conclusiones más fiables”, afirma Mario Modesto Mata, investigador del Grupo de Antropología dental del Centro Nacional de Investigación sobre la Evolución Humana (CENIEH) y que colabora en el proyecto europeo Tied2Teeth, liderado por la investigadora Leslea Hlusko.
Según los resultados de este trabajo, conociendo la disminución del esmalte del diente, medido como el porcentaje de la altura de la corona desaparecida, se pueden aplicar técnicas de inteligencia artificial para predecir el número de perikymata perdidos en cualquier diente de humanos modernos. En concreto, se han desarrollado redes neuronales artificiales para predecir el número de perikymata cuando un diente ha perdido hasta un 30 % de la altura de la corona. El resultado de la validación de las redes neuronales indica que cuando falta el 30 % del esmalte, en un 86 % de las ocasiones, el error máximo es de solo 3 perikymata en total.
“Son datos tan precisos sobre las líneas de crecimiento que nos permitiría predecir el tiempo de formación completa del esmalte de un modo muy próximo a la realidad, indicándonos que las redes neuronales podrían ser usadas para investigar aspectos relacionados con la paleobiología”, comenta Mata.
De cara a maximizar el uso y aplicación de estas redes neuronales, los autores del trabajo han desarrollado un software a modo de paquete de R llamado teethR, (de “teeth aRe wonderful”) de libre distribución e instalación. Su uso no requiere formación sobre inteligencia artificial, sino simplemente un conocimiento muy básico de R. A partir de una función desarrollada en el paquete, se pueden hacer predicciones de un modo muy rápido.
Referencia:
Modesto‐Mata, M., de la Fuente Valentín, L., Hlusko, L.J., Martínez de Pinillos, M., Towle, I., García‐Campos, C., Martinón‐Torres, M., & Bermúdez de Castro, J.M. (2024) Artificial neural networks reconstruct missing perikymata in worn teeth The Anatomical Record doi: 10.1002/ar.25416
Edición realizada por César Tomé López a partir de materiales suministrados por el CENIEH
El artículo La inteligencia artificial entra en la antropología dental se ha escrito en Cuaderno de Cultura Científica.
Poniendo en hora el reloj de la formación de la Luna
Probablemente, el evento más cataclísimico -por poner un adjetivo a semejante suceso- y que sospechamos ha podido sufrir nuestro planeta a lo largo de su historia, fue el que provocó la formación de nuestro único satélite natural, la Luna, muy en la infancia de nuestro Sistema Solar. No sabemos si pudieron ocurrir otros antes, pero si lo hicieron, quizás sea demasiado tarde para saberlo.
La teoría más aceptada sobre la formación de la Luna es la que afirma que nuestro planeta impactó contra un cuerpo de un tamaño similar al de Marte, que en el argot conocemos como Tea, provocando saliese eyectada una gran cantidad de material a la órbita de la Tierra y que lentamente iría coalesciendo hasta formar nuestra Luna. Eso sí, conocer la fecha con exactitud ha sido un verdadero quebradero de cabeza para los científicos.
Una nueva investigación publicada en la Lunar and Planetary Science Conference (LPSC) por Desch et al. propone revisar la cronología de este evento y adelantar la colisión con respecto a las cifras que manejamos en la actualidad. Estos autores la sitúan ahora en un momento mucho más cercano al nacimiento del Sistema Solar, concretamente, tan solo 50 millones de años después.
 Representación artística de la colisión de Tea contra la Tierra. Cortesía de NASA/JPL-CALTECH/T. Pyle.
Representación artística de la colisión de Tea contra la Tierra. Cortesía de NASA/JPL-CALTECH/T. Pyle.El poner fecha de nacimiento a la Luna es una tarea verdaderamente compleja porque, en ocasiones, los datos parecen mostrar una aparente contradicción. Por un lado, estudiamos la evolución de las órbitas de los planetas y las interacciones entre estos, algo que nos permite rebobinar, como si fuese una película de video, que posiciones ocupaban los planetas hace miles de millones de años y observar si, por ejemplo, fue la inestabilidad en la órbita de Júpiter la responsable de nuestra colisión con Tea.
La clave de estas simulaciones radica en el momento en el que se produciría la inestabilidad en la órbita de Júpiter: Si hubiese ocurrido más de cien millones de años después de la formación del Sistema Solar, las órbitas de los planetas interiores se habrían visto forzadas a cambiar también y, no solo eso, sino que los asteroides troyanos de Júpiter -y que lo “escoltan” a lo largo de su órbita- tampoco estarían donde hoy los vemos. Por eso hoy en día la ventana para situar esta inestabilidad orbital que concluiría con el impacto se sitúa entre los 27 y los 63 millones de años tras la formación del Sistema Solar.
 La Luna, todavía parcialmente fundida, tras su violenta formación. Imagen cortesía de la NASA/GSFC.
La Luna, todavía parcialmente fundida, tras su violenta formación. Imagen cortesía de la NASA/GSFC.Sin embargo, si tenemos en cuenta las evidencias que nos ofrece la geología, el impacto habría ocurrido mucho más tarde: Las rocas más antiguas de la Luna, que pensamos que se cristalizaron a partir de un océano de magma, están datadas en unos 210 millones de años tras la formación del Sistema Solar y, del mismo modo, parece que la primera corteza terrestre podría haberse formado en torno a los 220 millones de años. Estos dos números, muy superiores, contradicen claramente la fecha arrojada por las simulaciones orbitales.
¿Sería posible reconciliar ambas observaciones? Desch et al. (2024) proponen que si es posible y que ambas cifras son correctas, pero reflejan momentos diferentes: Por un lado, el impacto de Tea ocurriría alrededor de esos primeros cincuenta millones de años tras la formación del Sistema Solar, momento en el cual tanto la superficie de la Luna como la de la Tierra empezarían a enfriarse y formar una corteza a partir de una situación de océano de magma.
La corteza lunar podría haberse formado por su enfriamiento en tan solo unos diez millones de años, pero la Luna habría sufrido una serie de procesos de recalentamiento durante más de cien millones de años y finalmente se habría enfriado en torno a los doscientos millones de años, la cifra que nos aportan las dataciones radiométricas de sus rocas.
¿De dónde procedería este calor? Pues probablemente de la energía aportada por las mareas que habría sufrido en su órbita alrededor de la Tierra: No solo la Luna estaba mucho más cerca de la Tierra, haciendo las mareas mucho más intensas, sino que probablemente su órbita tendría unos mayores valores de excentricidad e inclinación en su órbita, aumentando todavía más el efecto de estas. Aunque en nuestro planeta veamos las mareas afectando al agua de los mares y océanos, lo cierto es que también son capaces de deformar la parte sólida.
 Los geiseres de Encélado, al igual que otras manifestaciones de energía interna en los satélites de los gigantes gaseosos de nuestro Sistema Solar, muy probablemente se deban a la energía de las mareas. Imagen cortesía de NASA/JPL/Space Science Institute.
Los geiseres de Encélado, al igual que otras manifestaciones de energía interna en los satélites de los gigantes gaseosos de nuestro Sistema Solar, muy probablemente se deban a la energía de las mareas. Imagen cortesía de NASA/JPL/Space Science Institute.Las mareas son capaces de aportar calor al interior de los cuerpos planetarios, ya que estas son capaces de estirar y comprimir los satélites -como ocurre en los gigantes gaseosos y que permiten, por ejemplo, la existencia de volcanes activos u océanos subterráneos- como si el satélite fuese una pelota antiestrés o un acordeón, provocando una fricción en sus rocas que finalmente se transforma en calor.
Y no solo eso. En este periodo de formación de nuestro Sistema Solar todavía ocurrirían una gran cantidad de impactos por cuerpos que habrían sobrado de la formación planetaria lo que, a su vez, añadiría un poco más de calor y lo que tendría como consecuencia un periodo de enfriamiento más largo, por lo menos en algunas zonas de la Luna.
Sin duda estos nuevos datos proponen un nuevo marco con el que poder reconciliar las observaciones hechas durante décadas tanto de las órbitas planetarias como de las rocas lunares pero, probablemente, la exploración lunar que tenga lugar en las próximas décadas nos pueda ayudar a afinar mucho mejor -gracias a nuevas muestras de su superficie- la verdadera edad de la Luna y, ¿por qué no?, de la Tierra.
Referencias:
Desch, S. J., & Jackson, A. P. (2024) How early could the giant impact have taken place? 55th Lunar and Planetary Science Conference – LPSC 2024
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo Poniendo en hora el reloj de la formación de la Luna se ha escrito en Cuaderno de Cultura Científica.
La realidad poco conocida de los megaasentamientos amazónicos
Un reciente artículo sobre antiguas ‘ciudades’ en la Amazonía ecuatoriana, portada de la revista Science, ha puesto de actualidad una revolución que se viene descubriendo en los últimos años. La imagen estática que se tenía de esta región, con pequeños poblados y estructuras simples, hay que cambiarla por la de un territorio vibrante, lleno de comunidades conectadas, con una planificación urbanística y producciones agrícolas amplias en el pasado.
 Equipo de trabajo en el valle de Upano (Ecuador) durante 2015, con un mapa donde aparecen antiguas estructuras conectadas por caminos. Fuente: INPC
Equipo de trabajo en el valle de Upano (Ecuador) durante 2015, con un mapa donde aparecen antiguas estructuras conectadas por caminos. Fuente: INPCLa publicación el pasado mes de enero en la revista Science de una serie de megaasentamientos, hay quien los califica de ciudades, que además estaban conectados por una extensa red de caminos en la Amazonía ecuatoriana supone una verdadera revolución. Esta parte de América Latina no se ha prodigado mucho en hallazgos espectaculares, razón por la cual ha pasado casi desapercibida para el gran público hasta este momento.
Una revolución que es necesario precisar y contextualizar en varios sentidos. Por una parte, por el rico y complejo testimonio arqueológico que trasmite sobre un pasado precolombino poco conocido en esta región amazónica. Por otra, por la imagen que nos devuelve hacia el presente de nosotros mismos y de cómo pensamos mayoritariamente en el siglo XXI sobre el pasado. Y tercero, por las formas en que se llevó a cabo la investigación original.
A nivel puramente arqueológico, un artículo publicado en 2023 en Strata, la Revista Ecuatoriana de Arqueología y Paleontología, por las arqueólogas del proyecto Características generales del paisaje cultural arqueológico del valle del Alto Upano en un área de 300 km2, ya no dejaba lugar a dudas.
 Valle de Upano (Ecuador). Fuente: Trabajo de campo 2015-INPC
Valle de Upano (Ecuador). Fuente: Trabajo de campo 2015-INPCNinguna otra región amazónica ha sido mapeada mediante escáner láser aerotransportado (LiDAR) en tanta superficie, y las que han sido trabajadas con metodologías parecidas no devuelven concentraciones de estructuras ni una diversidad ni complejidad tan grande como la encontrada aquí.
En las tierras bajas de Uruguay, por ejemplo, se escanearon 380 km2 y encontraron 666 estructuras (2,6 montículos por km2), y en Llanos de Moxos (Bolivia) se identificaron grandes terrazas sobre las que se elevaban montículos trapezoidales, con varios caminos excavados que los unían perimetralmente y entre sí.
Miles de montículos o plataformasPero en Ecuador, los hallazgos realizados por el proyecto liderado por el Instituto Nacional de Patrimonio Cultural (INPC) sobrecoge no solo por la monumentalidad de las propias estructuras, que supone mover miles toneladas de tierra, sino también por el número: 7471 anomalías positivas (montículos, plataformas, cimas truncadas), con una concentración de 24,9 por km2 o, si nos atenemos solo a las plataformas (5415), la densidad es de 18,05 por km2.
 Casa sobre montículo en el asentamientos de Kunguints. Fuente: Trabajo de campo 2015-INPC
Casa sobre montículo en el asentamientos de Kunguints. Fuente: Trabajo de campo 2015-INPCEstas plataformas estaban ordenadas, creando cuadrados entre los que había plazas, y estaban unidas por 300 km de caminos y tenían casi 95 km de canales de desagüe. Ello supone una conceptualización del espacio de forma ortogonal, una auténtica planificación urbanística. Pero no solo esto, sino que los grandes asentamientos como Wapula o Kunguints estaban unidos entre sí, con una red de asentamientos menores entre ellos, por caminos excavados en la tierra.
Además, en las zonas propicias para ello, se han identificado inéditos campos de cultivo con drenajes hacia los acantilados del Upano y de otros ríos tributarios que supondría una agricultura avanzada para la alta densidad de población que vivió allí entre el 400 a. C. y 400 d. C., según los análisis obtenidos en excavaciones anteriores a este proyecto. Complejidad social, monumentalidad y grandes complejos agrícolas que aún deben estudiarse en profundidad.
 Portada de la revista Science sobre la ‘ciudad perdida’ encontrada en la Amazonía ecuatoriana e imagen LiDAR de una de las antiguas áreas urbanas agrarias del Valle de Upano. Fuente: Science/A. Dorison/S. RostainCambiar la antigua idea de la Amazonía
Portada de la revista Science sobre la ‘ciudad perdida’ encontrada en la Amazonía ecuatoriana e imagen LiDAR de una de las antiguas áreas urbanas agrarias del Valle de Upano. Fuente: Science/A. Dorison/S. RostainCambiar la antigua idea de la Amazonía
En segundo lugar, baste decir que la arqueología ha estado plagada de mitos y visiones fantasiosas que, a menudo, han dificultado el acceso al verdadero conocimiento. Así, en el estudio de la arqueología amazónica ha primado esa visión de sociedades poco complejas, muy adaptadas al medio, pero con poca capacidad de responder a los cambios ambientales, donde las comunidades estaban formadas por unos pocos individuos que vivieron en estructuras simples.
Esta imagen estática se ha producido en los últimos 500 años, debido a los efectos seculares de la colonización. Pero la Amazonía era tan diferente como demuestra la tecnología LiDAR: vibrante, plena de comunidades estratificadas e interrelacionadas y con amplias producciones agrícolas.
Estudios anteriores al artículo en ScienceEn último lugar, hay que devolver todo el crédito a la investigación original de la que parte el artículo recientemente publicado en la prestigiosa revista Science: en Ecuador se hace ciencia de la más alta calidad, invirtiendo en ella y reuniendo equipos multidisciplinares e internacionales.
El INPC ecuatoriano dirigió este proyecto de la mano de la arquitecta Olga Woolfson, escaneando en 2015 con el láser aerotransportado esta amplia sección amazónica, aun con todas las dificultades logísticas que entraña trabajar en un medio tan hostil hoy día. Las fuerzas armadas junto con geólogos e ingenieros (principalmente la consultora Technoproject), geógrafos y arqueólogos observamos asombrados la maravilla que se descubre al eliminar la vegetación arbórea y estudiar los modelos digitales de elevaciones en 3D que ofrece el LiDAR.
 Volcán Sangay, aún activo, sobre el valle de Upano. Fuente: Trabajo de campo 2015-INPC
Volcán Sangay, aún activo, sobre el valle de Upano. Fuente: Trabajo de campo 2015-INPCEs cierto que no se actuó en esta zona a ciegas: pioneros como el profesor ecuatoriano Pedro Porras en los años 1970 y 1980 iniciaron excavaciones en la zona, gracias al conocimiento que indígenas y colonos le aportaron. Fue él quien descubrió el sitio de Huapula o Wapula, con sus grandes montículos y su ubicación cercana al Upano y relacionada con el aún activo volcán Sangay.
Posteriormente, otros equipos trabajaron intensamente en el área, excavando algunos de estos montículos y plazas y volando en avioneta sobre la zona, esperando reconocer más plataformas bajo la densa vegetación amazónica.
Fueron, principalmente, el arqueólogo ecuatoriano Ernesto Salazar y el francés Stéphen Rostain los que aportaron importantes datos a nivel microarqueológico, pero también sobre la comprensión de la formación de estos montículos o de las distintas culturas que los habitaron a lo largo de la historia. El equipo liderado por Rostain es el que ahora ha publicado el artículo en Science.
Referencia:
Stéphen Rostain et al. (2024) Two thousand years of garden urbanism in the Upper Amazon Science doi: 10.1126/science.adi6317
Sobre la autora: Alejandra Sánchez-Polo es investigadora posdoctoral ‘Juan de la Cierva’ en el dpto. de Prehistoria, Arqueología, Antropología y CC.TT. Historiográficas de la Universidad de Valladolid. Entre 2014 y 2018 trabajó como arqueóloga en proyectos del INPC en Ecuador.
Una versión de este artículo fue publicada originalmente en SINC el 31 de enero de 2024.
El artículo La realidad poco conocida de los megaasentamientos amazónicos se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2023 – IA: no es inteligencia todo lo que reluce
El gran evento de divulgación organizado por Naukas y la Cátedra de Cultura Científica volvió a Bilbao para celebrar su decimotercera edición en el gran Palacio Euskalduna los pasados 15 y 16 de septiembre de 2023.

Vivimos la fiebre de la inteligencia artificial. Está en todas partes, sea de verdad o no, lo importante es que lleve el nombre. La cuestión es si lo que llamamos inteligencia artificial es inteligente o no. Javier Pedreira es de la opinión que no es oro todo lo que reluce y nos lo cuenta en su charla IA: no es inteligencia todo lo que reluce.
Javier Pedreira «Wicho» es el responsable de informática de los Museos Científicos Coruñeses y uno de los creadores de Microsiervos, uno de los blogs sobre ciencia y tecnología más leídos en español.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2023 – IA: no es inteligencia todo lo que reluce se ha escrito en Cuaderno de Cultura Científica.
Aumentan las macroalgas de aguas cálidas en la costa vasca
Un estudio de la UPV/EHU ha analizado el impacto del aumento de la temperatura superficial del mar en las comunidades de macroalgas en las últimas cuatro décadas. En una zona costera vizcaína se han investigado puntos a diferentes profundidades y se ha observado que cada vez son más escasas las especies estructurantes de afinidad fría, mientras que han proliferado especies pequeñas de afinidad cálida. Como consecuencia, algunas funciones ecológicas están en peligro.
 Foto: Grupo de Investigación Bentos Marino (UPV/EHU)
Foto: Grupo de Investigación Bentos Marino (UPV/EHU)La temperatura de nuestro planeta está aumentando a gran velocidad. El 90 % del exceso de calor generado ha sido absorbido por el mar y, debido a ello, ha aumentado de forma notoria la temperatura superficial de los océanos. En este contexto, son especialmente vulnerables los organismos inmóviles y sensibles a la temperatura.
Además, hay sitios en los que es más notorio el calentamiento del mar que en otros. Por ejemplo, en la costa vasca se ha producido un aumento de la temperatura del mar de 0,23 °C por década, frente a un aumento de 0,15 °C a nivel mundial. Ante esta situación, el Grupo de Investigación Bentos Marino de la UPV/EHU ha estudiado cómo ha afectado el calentamiento a las comunidades de macroalgas de una zona costera de Bizkaia. Junto con el Centro de Investigación Avanzada de Blanes, ha investigado los cambios producidos durante los últimos 40 años. “Es importante estudiar cómo responden las comunidades de macroalgas ante los incrementos de temperatura, de cara a la conservación de la biodiversidad marina, ya que desempeñan roles fundamentales en los ecosistemas”, afirma la bióloga Olatz Arriaga Telleria.
Una de las principales conclusiones obtenidas es el incremento de especies de afinidad cálida en las comunidades de macroalgas en la costa vasca a consecuencia del aumento de la temperatura, mientras que las de afinidad fría son cada vez menos numerosas. Esto ha provocado profundas transformaciones en la estructura de las comunidades, ya que las especies que más han disminuido, como Gelidium corneum, son estructurantes, es decir, crean entornos tridimensionales que sirven de refugio para una gran variedad de organismos. Además, proporcionan hábitats adecuados para otras algas, peces, invertebrados, etc., donde, entre otras cosas, pueden encontrar alimentos y protegerse de los depredadores. “No hemos detectado otras especies que sustituyan estas importantes funciones ecológicas a medida que se van reduciendo las especies estructurantes, lo cual supone una degradación de las comunidades”, ha explicado Arriaga. Las especies de afinidad cálida que han proliferado son más pequeñas y morfológicamente más simples.
Resiliencia de las comunidades de macroalgasTambién la investigación ha demostrado que las comunidades de macroalgas responden con gran rapidez a los cambios de temperatura del mar. Eso se ha podido deducir observando los datos de la última década. De hecho, el incremento de la temperatura no ha sido homogéneo en los 40 años analizados. Si bien la tendencia general ha sido al alza, en el último tramo investigado (2014-2020) se registraron unas temperaturas más tibias. Arriaga ha explicado que “esto nos ha permitido estudiar cómo es la respuesta a corto plazo de las comunidades de macroalgas y hemos observado que en esos 6 años se ha recuperado en parte la presencia que habían perdido las especies estructurantes a grandes profundidades, mientras que han disminuido algunas especies de afinidad cálida”.
Aunque la resiliencia mostrada por las macroalgas suscita cierta esperanza, el equipo investigador subraya que no parece que el control de la temperatura del mar vaya a llegar de forma inmediata. Y, siendo la temperatura la principal causa de las transformaciones estructurales en las comunidades de macroalgas, no ven un futuro fácil. Ante ello, consideran fundamental continuar con la investigación y aumentar la frecuencia de las monitorizaciones: “Esto ayudaría a conocer mejor el comportamiento de las comunidades de macroalgas y a tomar medidas proactivas para proteger los hábitats de las especies vulnerables”. Una podría ser, por ejemplo, identificar zonas con potencial de ser refugios climáticos. Están trabajando en la búsqueda de soluciones antes de que la situación sea irreversible.
Referencia:
O. Arriaga, P. Wawrzynkowski, N. Muguerza, I. Díez, J.M. Gorostiaga, E. Quintano, M.A. Becerro (2024) The thermal journey of macroalgae: Four decades of temperature-induced changes in the southeastern Bay of Biscay Marine Environmental Research doi: 10.1016/j.marenvres.2024.106351
Para saber más:
Las algas del Cantábrico: centinelas del cambio climático
El declive de las praderas de algas por el cambio climático
Los invasores: Las algas Caulerpa
Las macroalgas cantábricas se volverán mediterráneas
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Aumentan las macroalgas de aguas cálidas en la costa vasca se ha escrito en Cuaderno de Cultura Científica.
La afición que nos trajo la minería
Durante la segunda mitad del siglo XIX numerosas empresas británicas desembarcaron en la Península Ibérica para comprar concesiones mineras por todo nuestro territorio. Esos empleados llegados de Gran Bretaña trajeron consigo muchas de sus costumbres y aficiones. Entre ellas, un curioso deporte que se jugaba dándole patadas a una pelota, al que llamaban football, y con el que se divertían al terminar los turnos de trabajo. Un deporte que pronto llamó la atención de los trabajadores españoles, aprendiendo a jugar para echar unas pachangas con sus jefes y compañeros británicos. Y lo que nació como una afición de empleados de explotaciones mineras, en apenas unas décadas llegó a convertirse en el deporte rey de nuestro país.
 Aspecto de la explotación de las Minas de Río Tinto, Huelva, a comienzos del siglo XX. Fuente: Junta de Andalucía B) Componentes del Huelva Recreation Club en 1889, el año de su fundación. Fuente: HuelvaYa
Aspecto de la explotación de las Minas de Río Tinto, Huelva, a comienzos del siglo XX. Fuente: Junta de Andalucía B) Componentes del Huelva Recreation Club en 1889, el año de su fundación. Fuente: HuelvaYaTodo comenzó en Huelva. En 1873, la compañía británica Rio Tinto Company Limited adquirió la concesión de explotación de las minas de Río Tinto para extraer, principalmente, cobre. Y fue esta compañía británica quien trajo el fútbol a nuestro país, fundando en 1878 el primer equipo dedicado a este deporte, el Río Tinto Foot-Ball Club. Aunque se les olvidó inscribirlo en el registro de sociedades recreativas hasta 1901. Pero otros empleados de la compañía minera no fueron tan olvidadizos y, en 1889, inscribieron al equipo llamado Huelva Recreation Club, hoy en día conocido como Recreativo de Huelva. Así es como el decano, el primer equipo de fútbol de nuestro país, nació al calor del mineral de los yacimientos de Río Tinto.
 A) Minería de hierro en Muskiz, Bizkaia, a mediados del siglo XX. Imagen del archivo fotográfico de Muskiz. Fuente: Ondartez B) Alineación del Athletic Club de Bilbao en 1903, cuando ganó la Copa del Rey. Fuente: Athletic Club
A) Minería de hierro en Muskiz, Bizkaia, a mediados del siglo XX. Imagen del archivo fotográfico de Muskiz. Fuente: Ondartez B) Alineación del Athletic Club de Bilbao en 1903, cuando ganó la Copa del Rey. Fuente: Athletic ClubSi viajamos al norte de la Península, nos encontramos con una historia muy parecida. En 1876 se permitió a las empresas extranjeras explotar y comerciar con el mineral de hierro de Bizkaia y las compañías británicas no tardaron en llegar, con una pelota en sus pies. De hecho, hay registro de que, en 1889, unos marinos británicos disputaron el primer partido de fútbol en Bilbao. Apenas cuatro años más tarde el partido se repitió, enfrentando, en esta ocasión, a un equipo formado por británicos contra otro compuesto por vizcaínos. Este nuevo deporte había calado tanto entre los autóctonos que, en 1898 varios miembros de la Sociedad Gimnástica Zamacois fundaron el Athletic Club (de Bilbao), aunque no lo inscribieron como club de fútbol hasta 1901.
Pero la relación entre la Geología o, mejor dicho, la Minería y el balompié patrio no termina aquí. A principios del siglo XX, cuatro jóvenes vizcaínos fueron a estudiar a la Escuela Especial de Ingenieros de Minas de Madrid. Amantes del fútbol, en 1903 fundaron el Athletic Club (de Madrid) como una filial del equipo de su tierra. Aunque hoy en día se le conoce como Atlético de Madrid.
Ahora abandono un poco el mundo basado en hechos reales y comprobables para pasar a las leyendas. Y es que, si hablamos de fútbol, lo primero que nos viene a la cabeza son los cánticos de ánimo de la afición. Sobre todo, el más famoso, el himno que grita la gente cuando su equipo se proclama campeón: el alirón. Aquí nos encontramos con dos posibles orígenes para esta palabra, ambos situados en tierras del norte peninsulares, aunque es probable que ninguno de ellos sea el real. Por un lado, se alude a una versión futbolera de un cuplé de principios del siglo XX debido a un eufórico hincha que gritó “alirón, alirón, el Athletic campeón” en plena actuación de una famosa cantante tras ganar el equipo de Bilbao un partido importante. Pero me interesa más la otra versión, mucho más geológica y que nos lleva de nuevo a la minería de Bizkaia. En aquellas explotaciones tan precarias de hace un siglo, los trabajadores cobraban un salario más grande si encontraban vetas con mayor contenido de mineral de hierro. Estas rocas ricas en mineral quedaban señaladas por los jefes británicos escribiendo las palabras “all iron” en los materiales geológicos que querían explotar, lo que llenaba de alegría a todos los mineros. Como el conocimiento de inglés de aquellos trabajadores patrios no era muy elevado, leían literal las dos palabras que tanto querían encontrar, gritando “alirón” a sus compañeros cuando daban con la veta más rica en mineral. Así, esa exclamación se convirtió en motivo de regocijo para todo el mundo, trasladando esa alegría al mundo deportivo.
 Celebración de un título del Athletic Club a bordo de la gabarra. Fuente: Athletic Club
Celebración de un título del Athletic Club a bordo de la gabarra. Fuente: Athletic ClubY, ya que estoy hablando de las celebraciones del Athletic Club de Bilbao, seguro que, sin quererlo, ya os habréis enterado de que, cuando este equipo consigue un título, los jugadores se dan un paseo con el trofeo por la ría subidos a una gabarra (y no estoy empleando el masculino genérico, ya que las jugadoras no han disfrutado de esta celebración al ganar sus competiciones). Pues las gabarras son unas barcazas sencillas y de fondo plano que se utilizaban para transportar el mineral por la ría del Nervión hasta los cargaderos situados cerca de la desembocadura, ya que los buques más grandes no podían entrar navegando aguas arriba para recoger el hierro debido al poco calado del cauce del río. Generalmente, las gabarras no tienen medio de propulsión propio, necesitan ser remolcadas. Y, en aquella época, se encargaban de moverlas por la ría las sirgueras, mujeres muy pobres que trabajaban por el pan diario tirando desde la orilla de grandes cabos, llamados sirgas, enganchados a las gabarras cargadas de mineral.
Así que, mientras duran las celebraciones del equipo masculino del Athletic Club de Bilbao tras haber ganado la Copa del Rey de fútbol, yo me imaginaré que los jugadores son unos montoncitos de mineral de hierro encima de una gabarra que se mueve sobre la ría del Nervión al grito de “all iron” de toda la afición, en homenaje a esas empresas mineras británicas que trajeron el balompié a nuestra tierra. Más geológico no podría ser.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo La afición que nos trajo la minería se ha escrito en Cuaderno de Cultura Científica.
Henry Ernest Dudeney y Samuel Loyd, dos magos de los acertijos lógicos
Un buen rompecabezas debe exigir el ejercicio de nuestro mejor ingenio y habilidad, y aunque el conocimiento de las matemáticas y la lógica son a menudo de gran utilidad en la solución de estas cosas, sin embargo, a veces sucede que una especie de astucia y sagacidad naturales son de considerable valor.
El matemático británico Henry Ernest Dudeney (1857-1930) nació tal día como hoy, hace 167 años. Se le considera uno de los mejores creadores de pasatiempos matemáticos. También un 10 de abril, hace 113 años, falleció el ajedrecista y autor de acertijos lógicos y rompecabezas matemáticos, el estadounidense Samuel Loyd (1841-1911).
 Samuel Loyd y Henry Ernest Dudeney. Fuente: Wikimedia Commons
Samuel Loyd y Henry Ernest Dudeney. Fuente: Wikimedia CommonsA ambos les une esta fecha concreta del mes de abril —aunque sea por razones radicalmente opuestas— y esa habilidad especial para inventar atractivos problemas lógico-matemáticos.
De hecho, a partir de 1893, mantuvieron correspondencia fluida, al menos, al principio… En esas misivas, intercambiaban ideas y era Dudeney quien mostraba las destrezas matemáticas más profundas. Compartió con Loyd una gran cantidad de sus acertijos, y se enfadó considerablemente —con razón— cuando el estadounidense comenzó a publicarlos con su nombre. Una de las hijas de Dudeney recordaba a su padre “furioso y acalorado por la ira hasta tal punto, que se asustó mucho y, a partir de entonces, identificó a Sam Loyd con el diablo”. A partir de ese momento dejaron de compartir sus ideas…
Un problema planteado por LoydOtro gran autor de problemas de matemática recreativa, Martin Gardner (1914-2010), opinaba de este modo sobre las capacidades matemáticas de Loyd:
Loyd tenía un verdadero don —como el que se muestra en la ‘Curiosa Mathematica’ del reverendo CL Dodgson …— para lo fantástico en la ciencia matemática, y si se hubiera dedicado a aprovecharlo, podría haberse ganado fama como investigador en la vasta y poética región de las matemáticas puras, un digno seguidor de Cayley y Sylvester.
El siguiente rompecabezas de Loyd aparece en Cyclopedia of 5000 Puzzles.
Un lechero tiene dos recipientes de 10 galones llenos de leche. Dos clientas desean comprar 2 cuartos de galón; una acude con una lata de 5 cuartos de volumen y la otra con una de 4 cuartos. ¿Qué puede hacer el lechero para completar su venta?
 Fuente: Cyclopedia of 5000 puzzles.
Fuente: Cyclopedia of 5000 puzzles.
Loyd comentaba respecto a este problema que:
Es un truco de malabarismo puro y simple, sin truco ni artificio, pero requiere mucha astucia para meter dos cuartos exactos de leche en esas medidas sin emplear recipientes de ningún tipo excepto las dos medidas y las dos latas llenas.
Una solución es la siguiente: Llamamos A a uno de los bidones de 10 galones y B al otro; y denominamos X a la lata de 4 cuartos e Y a la de 5 cuartos.
El lechero llena el cubo Y con la lata A (A queda con 8 galones y 3 cuartos) y vierte Y en la lata X (así, en Y le queda un cuarto de leche y X se llena). Vacía el cubo X en el recipiente A (en donde habrá así 9 galones y 3 cuartos). Ahora vierte el contenido de Y en la lata X (así, Y queda vacío y X se llena con un cuarto). A continuación, llena la lata Y con el recipiente A (Y contiene así 5 cuartos y A queda con 8 galones y 2 cuartos). Después, llena la lata X con la lata Y (como X ya contenía 1 cuarto, X se llena e Y queda con 2 cuartos). Y, de nuevo, vacía el contenido de X en el bidón A (A contiene así 9 galones y 2 cuartos). Ahora, llena la lata X con el recipiente B (así, X queda llena con 4 cuartos y B contiene 9 galones). Y, finalmente, vierte X en el cubo A (Como A tiene 9 galones y 2 cuartos, X queda con 2 cuartos y A se llena). ¡Misión cumplida!
Un acertijo de Dudeney¿Quizás la anterior propuesta era una de esas que Loyd conocía a través de Dudeney? Quizás…
El acertijo del mercero (1903) –The Haberdasher’s Puzzle– es uno de los más famosos rompecabezas de Dudeney. Un mercero muestra una pieza cortada en forma de triángulo equilátero, y propone:
Mostradme una manera de cortar este trozo de género en cuatro piezas de manera que puedan reunirse formando un cuadrado perfecto.
El acertijo tiene solución, como se observa en la animación de debajo.
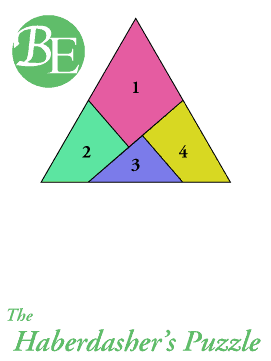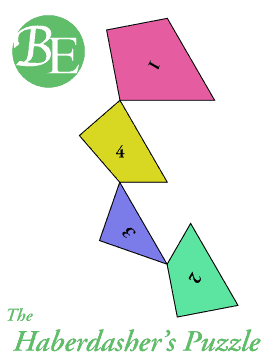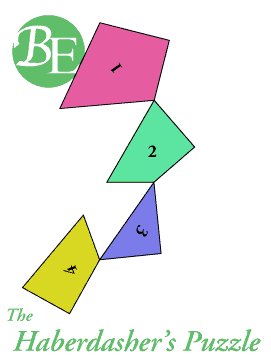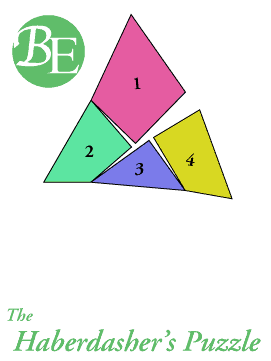 Fuente: Wikimedia Commons.
Fuente: Wikimedia Commons.
De hecho, la firma de arquitectos D* diseñó la casa D*Haus Dynamic basada precisamente en este rompecabezas. Esta construcción puede adquirir ocho configuraciones diferentes, dependiendo del momento del año en el que nos encontremos, de la luz que deseemos aprovechar, etc. ¡Una casa que se transforma sorprendentemente ante nuestros ojos!
Referencias
- J J O’Connor and E F Robertson, Henry Ernest Dudeney, MacTutor History of Mathematics archive, University of St Andrews
- J J O’Connor and E F Robertson, Samuel Loyd, MacTutor History of Mathematics archive, University of St Andrews
- Sam Loyd, Cyclopedia of 5000 Puzzles, Tricks, and Conundrums (With Answers), Lamb. Pub. Co., 1914
- Can Do, Futility Closet, 28 de abril de 2022
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Henry Ernest Dudeney y Samuel Loyd, dos magos de los acertijos lógicos se ha escrito en Cuaderno de Cultura Científica.
Cómo el antiguo arte de la predicción de eclipses se convirtió en una ciencia exacta
La cronología del eclipse total del 8 de abril de 2024 se conocía al segundo, miles de años después de que los temerosos humanos comenzaran a intentar anticipar estos eventos cósmicos.
Un artículo de Joshua Sokol. Historia original reimpresa con permiso de Quanta Magazine, una publicación editorialmente independiente respaldada por la Fundación Simons.
Fuente: Stephanie Swart for Quanta Magazine; Kristina Armitage and Emily Buder/Quanta Magazine
Los eclipses solares se interpretaron a lo largo de gran parte de la historia como malas noticias para el soberano: una señal de mal agüero para su salud personal o la del reino. Pero esos temores ayudaron a alimentar miles de años de erudición. Este progreso comenzó en Mesopotamia con una búsqueda de patrones periódicos en los datos históricos. Ha culminado en una era en la que conocemos los movimientos futuros interdependientes de los cuerpos del sistema solar con siglos de antelación, transformando lo que alguna vez fue una causa de angustia a escala cósmica en una cuestión de frío mecanismo de relojería.
Si hubiera que elegir un punto de inflexión, podría haber sido la mañana del 22 de abril de 1715, cuando un eclipse solar se cernía sobre Londres. El polímata británico Edmond Halley, más conocido por haber dado su nombre al cometa Halley, lo había predicho. Había publicado un anuncio que incluía un mapa del camino que trazaría la sombra de la luna sobre Inglaterra. Ese año, Inglaterra tenía un rey recién coronado y ya se estaba gestando una rebelión contra él; al desmitificar el eclipse con una predicción, Halley esperaba neutralizar su poder como presagio.
También quería reclutar recolectores de datos cuyas observaciones pudieran conducir a predicciones de eclipses aún mejores en el futuro. “Se desea que los Curiosos lo Observen, y especialmente la duración de la Oscuridad Total”, anunció, “… porque de ese modo se determinarán claramente la Situación y las dimensiones de la Sombra; y por medio de ello, podremos Predecir Apariciones similares para [el] futuro, con un mayor grado de certeza del que se puede pretender en el presente”.
Presagios que mantienen el ritmoDécadas antes, Halley, un ávido lector de textos antiguos, había redescubierto y popularizado un ciclo celeste útil para pensar acerca de los eclipses y la posición de la luna en el cielo: 6.585 días, o un poco más de 18 años. Llamó a este ciclo «saros», que los historiadores modernos ven como una mala traducción de un símbolo sumerio que originalmente significaba algo así como «universo» o «gran número».
Alrededor del año 600 a.e.c. en Mesopotamia los sacerdotes-matemáticos asirios y babilónicos habían examinado las fechas de eclipses pasados registradas en tablillas de arcilla, con la esperanza de desarrollar estrategias para inferir cuándo podría ocurrir el próximo eclipse. Los eclipses preocupaban a los reyes de estas culturas y pronto, con la invención del zodíaco y los horóscopos personales, la necesidad de controlar las posiciones del sol, la luna y los planetas afectaría a todo el mundo.
Las primeras soluciones fueron reglas generales. Los eclipses lunares a menudo se suceden cada seis meses, por ejemplo. Los babilonios también se dieron cuenta de que los eclipses solares y lunares específicos a menudo estaban separados de un evento similar por lo que Halley llamó un saros.
Para entender este ciclo en términos modernos, imaginemos la geometría de los cuerpos celestes en el momento de un eclipse solar, cuando la Luna se encuentra directamente entre el Sol y la Tierra y los tres cuerpos forman una línea definida. Para que esto suceda, la Luna debe ser luna nueva. También debe estar en un punto donde su propia órbita inclinada alrededor de la Tierra se hunde a través del plano en el que la Tierra se mueve en su propia órbita alrededor del sol.
Ahora imagina que adelantas el reloj para encontrar un momento en el que se repitan estas mismas condiciones. Tenemos que conciliar varios ciclos lunares superpuestos pero desiguales. Ciclo uno: se necesitan unos 29,5306 días para pasar de una luna nueva a la siguiente. Ciclo dos: la Luna tarda unos 27,2122 días en ir de un paso por el plano de la órbita de la Tierra al mismo paso en la siguiente vuelta. Ciclo tres: debido a que la órbita elíptica de la Luna la acerca y la aleja de la Tierra, la Luna también oscila en su tamaño y velocidad aparentes en los cielos sobre la Tierra, un ciclo que dura aproximadamente 27,5546 días.
El saros, entonces, es simplemente un bonito intervalo redondo durante el que todos estos ciclos se repiten un número entero de veces: 223 pasos a la luna nueva es casi exactamente igual a 242 vueltas dentro y fuera de la eclíptica, que a su vez es casi exactamente igual a 239 oscilaciones en el tamaño aparente de la luna. Si viste un eclipse solar o lunar, solo espera un saros y se repetirá la misma disposición geométrica aproximada de los cuerpos celestes.
 A la izquierda, una tablilla de arcilla cuneiforme de Babilonia de diez centímetros de ancho que registra eclipses lunares entre 609 y 447 a.C. A la derecha aparece un fragmento de un antiguo planetario griego conocido como mecanismo de Anticitera. Descubierto en un naufragio y fechado aproximadamente en el siglo II a. C., el planetario rastreaba ciclos como el saros para predecir eclipses y otros eventos astronómicos. Fuentes: The Trustees of the British Museum (left); 2005 Museo Arqueológico Nacional de Atenas
A la izquierda, una tablilla de arcilla cuneiforme de Babilonia de diez centímetros de ancho que registra eclipses lunares entre 609 y 447 a.C. A la derecha aparece un fragmento de un antiguo planetario griego conocido como mecanismo de Anticitera. Descubierto en un naufragio y fechado aproximadamente en el siglo II a. C., el planetario rastreaba ciclos como el saros para predecir eclipses y otros eventos astronómicos. Fuentes: The Trustees of the British Museum (left); 2005 Museo Arqueológico Nacional de AtenasSin embargo, la órbita de la Luna es en realidad más complicada que estos parámetros. Y de todos modos, este esquema no te dice en qué lugar de la Tierra será visible el eclipse resultante.
Halley y más alláPara cuando Halley leyó sobre el saros y lo resucitó para su propio uso, muchos siglos más de esfuerzo multicultural habían refinado aún más el problema de los eclipses, como lo describió la historiadora matemática Clemency Montelle en el libro de 2011 Chasing Shadows. Los babilonios finalmente pasaron de reglas empíricas simples como «espera un saros» a esquemas numéricos más complicados que calculaban las futuras coordenadas de la Luna en el cielo. Los antiguos griegos fusionaron sus propias ideas geométricas sobre el cosmos con cálculos numéricos al estilo babilónico. Sobre la base de esa síntesis, los astrónomos del mundo islámico como al-Juarismi, el homónimo de la palabra «algoritmo» en el siglo IX, introdujeron funciones trigonométricas y números decimales (de la India) que garabatearon en un nuevo medio papel (de China) para desarrollar métodos predictivos aún más avanzados, que ahora también tenían eco en toda Europa.
Pero Halley tenía algo aún más nuevo con qué jugar. Casi al mismo tiempo que repescaba el saros de la antigüedad, también financiaba la publicación de las ideas de su amigo Isaac Newton sobre la gravitación, que Newton luego aplicaría para comprender la órbita de la Luna. En 1715, cuando se acercaba a Londres el primer eclipse solar en muchos siglos, el mapa predictivo de Halley era una combinación de formas de pensar antiguas y modernas.
El siguiente gran paso se produjo en 1824, cuando el astrónomo alemán Friedrich Bessel amplió el enfoque newtoniano de pensar acerca de los eclipses utilizando las leyes de la gravedad. Imaginó la sombra de la luna proyectada sobre un plano imaginario que pasaba por el centro de la Tierra. Luego se podría proyectar esa sombra de vuelta a la superficie del globo para ver exactamente dónde y cuándo impactaría, un proceso que terminió requiriendo pensar en la Tierra no como una esfera sino como un objeto grumoso y lleno de baches que gira. Después de Bessel, muchas naciones tuvieron el alcance imperial global para perseguir esas sombras, explica Deborah Kent, historiadora de las matemáticas de la Universidad de St. Andrews. Al hacerlo, podrían refinar aún más sus cálculos en una batalla por la supremacía del poder blando científico.
Durante el siglo siguiente, las expediciones de eclipses ayudaron a resolver uno de los mayores misterios de la ciencia: ¿se debía la extraña órbita de Mercurio a un planeta no descubierto que abrazaba al Sol (que presumiblemente se haría visible durante un eclipse)? O, como resultó ser el caso, ¿había algún problema con la comprensión de Newton de la gravedad? Esto hizo que la predicción y observación de eclipses fuera aún más importante, y se enviaron científicos a todos los rincones de la Tierra con instrucciones estrictas sobre dónde estar exactamente y qué datos registrar. Luego presentaban informes secos salpicados por alguna que otra “erupción de asombro”, explica Kent. «En casi todos y cada uno de ellos hay como dos párrafos de descripción rapsódica, victoriana y exagerada».
En el siglo XX, el problema volvió a transformarse. Una predicción adecuada de los eclipses siempre había tenido que lidiar con el hecho de que la Luna y todo lo demás en el Sistema Solar interactúa constantemente entre sí. Este no era simplemente el famoso “problema de los tres cuerpos” irresoluble; era un problema de N-cuerpos. Cuando la NASA comenzó a lanzar personas y robots hacia cuerpos del sistema solar, la necesidad de saber dónde estaban esos cuerpos y dónde estarían en el futuro adquirió una nueva urgencia, y se volvió más fácil de entender.
Gracias a los espejos que dejaron en la Luna los astronautas del Apolo, sabemos dónde está la Luna en relación con la Tierra con una precisión de un par de metros, según Ryan Park, que dirige el grupo de Dinámica del Sistema Solar en el Laboratorio de Propulsión a Chorro (JPL) de la NASA. Y con múltiples naves espaciales transmitiendo datos de alcance mientras zumban alrededor del sistema solar, también conocemos la posición del Sol con gran precisión. El equipo de Park introduce los datos de posición lunar y solar, junto con parámetros similares para los planetas y cientos de asteroides, y correcciones para cosas como la presión del viento solar, y no simplemente las leyes de la gravedad de Newton sino los ajustes más sutiles de la relatividad general, en un modelo de ordenador. Así el modelo genera una lista de las posiciones predichas de todo, incluida la Luna. Y luego, periódicamente, el equipo del JPL actualiza su modelo y publica nuevas listas.
Estas posiciones, excesivas para la tarea de predecir eclipses, deben ser lo suficientemente buenas para los viajes espaciales. «Me sorprendo un poco», afirma Park, cuando los desarrolladores de misiones espaciales preguntan si tendrán que dedicar tiempo a descubrir dónde estará exactamente la Luna y cómo se mueve. «Yo en plan, no, no, no, no, resolvimos el problema hace años».
El artículo original, How the Ancient Art of Eclipse Prediction Became an Exact Science, se publicó el 5 de abril de 2024 en Quanta Magazine.
Traducido por César Tomé López
El artículo Cómo el antiguo arte de la predicción de eclipses se convirtió en una ciencia exacta se ha escrito en Cuaderno de Cultura Científica.
El pájaro que se comunica con un gesto simbólico
Un estudio publicado en Nature Communications describe por primera vez un gesto simbólico en animales no primates. En los carboneros japoneses (Parus minor) un rápido aleteo por parte de un miembro de la pareja indica al otro que entre primero en el nido.
 Carbonero japonés (Parus minor). Foto: Alpsdake / Wikimedia Commons
Carbonero japonés (Parus minor). Foto: Alpsdake / Wikimedia CommonsLa anécdota es muy conocida, se ha atribuido a diferentes protagonistas y ha incorporado insultos diversos. Básicamente es así: dos hombres se encuentran frente a una puerta. Uno de ellos dice “yo no cedo el paso a un imbécil”. El otro responde “yo sí, pase usted”.
Es concebible que la persona que cedió el paso acompañara su frase con un gesto, dirigiendo su mano hacia la puerta. Este tipo de gestos que señalan o dirigen la atención hacia algo se denominan “deícticos”. Otro tipo de gestos que usamos los humanos para comunicarnos son los simbólicos. En ellos no hay relación evidente entre el gesto y su significado. Por ejemplo decir adiós agitando la mano, o indicar que todo va bien con el pulgar hacia arriba.
Muchos animales se comunican con sonidos y en algunos casos, muchos menos, también lo hacen con gestos. Esto se ha estudiado sobre todo en primates, por motivos obvios de su parentesco con nosotros. De hecho, se han llegado a describir en los chimpancés hasta 66 gestos con 19 significados diferentes, incluyendo acércate, aléjate o acicálame. Estos gestos son fundamentalmente deícticos, el chimpancé llama la atención de un congénere y señala para comunicar su intención. Más allá de los primates se han descrito gestos deícticos en cuervos y urracas, indicando por ejemplo de dónde viene un depredador. Incluso en peces de coral (Plectropomus) que cazan en grupo, hay un señalamiento hacia el lugar en el que se ha escondido la presa.
Nunca se han descrito claros gestos simbólicos fuera de los primates. Hasta ahora. Porque un pájaro, el carbonero japonés (Parus minor), muy parecido a nuestro bonito carbonero común (Parus major), ha desarrollado un gesto especial para indicar a su pareja que entre primero al nido.
Esta no es la primera sorpresa que nos depara este pajarillo. En 2016 se describió un caso excepcional de composición sintáctica en su canto. El carbonero japonés tiene cuatro tipos de notas principales, A, B, C y D. Cuando combina ABC en una llamada, sus congéneres miran hacia los lados para detectar posibles amenazas. Cuando repite la nota D, los demás carboneros se agrupan para hacer frente a un peligro. Lo curioso del caso es que si la llamada (reproducida en un altavoz) consiste en ABC-D, los carboneros miran hacia los lados y luego vuelan hacia el altavoz. Pero si se reproduce una llamada D-ABC, los pájaros no reaccionan. Es decir, los dos mensajes requieren una sintaxis precisa para ser comprendidos.
El carbonero japonés acaba de sorprender de nuevo utilizando un gesto simbólico que significa “pasa tú primero”. Estas aves anidan en huecos de árboles con entradas estrechas o en cajas de anidamiento. Cuando los dos miembros de la pareja llegan con alimento para los pollos, uno de ellos, más frecuentemente la hembra, agita las alas. Esta es la señal para que el macho entre primero al nido. Cuando es el macho el que agita las alas, o la hembra no hace ninguna señal, es ésta la que precede al macho. Pueden ver este comportamiento en los siguientes vídeos:
Ya se conocían muchos patrones estereotipados de conducta en las aves que implican movimientos corporales precisos durante el cortejo. Pero lo fascinante de esta observación, aparentemente sencilla, es que los carboneros han desarrollado un gesto simbólico (agitar las alas), que no tiene ninguna relación con su significado: “después de ti”. Esto nos indica la importancia de conocer mejor los mecanismos de comunicación animal para comprender la evolución de los lenguajes, y en especial la del nuestro, un fenómeno que contribuyó decisivamente a hacernos humanos.
Sobre el autor: Ramón Muñoz-Chápuli Oriol es Catedrático de Biología Animal (jubilado) de la Universidad de Málaga
El artículo El pájaro que se comunica con un gesto simbólico se ha escrito en Cuaderno de Cultura Científica.
El anciano que murió haciendo el amor con un fantasma
La Real Academia Española recoge tres acepciones para la palabra fascinar. Aunque son netamente diferentes, las dos primeras se ajustan muy bien al efecto que producen en nosotros los misterios. Nos ofuscan, alucinan, engañan, pero, también, nos atraen, encantan, seducen, cautivan.
La fascinación que nos producen explica, por ello, que haya personas que reaccionen a los misterios tratando de desvelarlos, esto es, de retirar el velo metafórico que los oculta de nuestra comprensión. Esto es lo que hace la chiquilla que desmonta el juguete que emite sonidos humanos, con la intención de conocer el origen de esos sonidos. Y es lo que hacemos quienes investigamos o hemos investigado en un laboratorio tratando de desentrañar los mecanismos implicados en el funcionamiento de un ser vivo o quienes analizan los registros de una parroquia tratando de perfilar la evolución demográfica de su comarca en el pasado.
El misterio es uno de los motores de la curiosidad humana, del afán por conocer la realidad.
Pero también nos puede ofuscar. Cuando nos enfrentamos a un misterio es posible que la seducción que causa nuble nuestra capacidad para discernir y caigamos presa de las supercherías más absurdas. Por esa misma razón, no es difícil que los misterios sean utilizados de forma artera por quienes encuentran la forma de beneficiarse de ese ofuscamiento.
La fascinación de los misteriosA Luis Alfonso Gámez le fascinan los misterios, así ha sido desde que era muy joven y así sigue siendo hoy. Además, se combinan en él una formación superior en historia y periodismo con una prolongada trayectoria profesional en prensa escrita. Ha sido durante años redactor de El Correo, y en gran parte de su ejecutoria profesional se ha ocupado, en especial, de la información científica. A nadie debe extrañar, por tanto, que haya dedicado parte de su ocio a la investigación de fenómenos misteriosos, a desvelar –él también– la naturaleza de esos ‘misterios’, a escribir sobre ellos en Magonia, y a denunciar, desde el Círculo Escéptico, las supercherías en las que algunos tratan de envolver la explicación de misterios supuestos o reales.
‘El anciano que murió haciendo el amor con un fantasma’ recopila una colección de historias con dos denominadores comunes: el misterio y la fascinación –entendida esta en su segunda acepción, el engaño, la ofuscación, la alucinación– que causa a muchas personas. Un tercer elemento, el interés en engañar a sus congéneres, no es común a todas las historias, pero es la motivación que impulsa a muchos de quienes han hecho de ellos un medio de vida.
 Fuente: menoscuarto Ediciones
Fuente: menoscuarto EdicionesLos ovnis, la Atlántida, el espiritismo, dioses extraterrestres, conspiraciones y otros supuestos misterios pasan por las páginas del libro y son diseccionados por su autor con inteligencia y un sutil sentido del humor. Todas las historias están debidamente documentadas y los episodios o casos que cuentan abarcan, en conjunto, desde mediados del siglo XIX hasta el presente. El libro está –como no podía ser de otro modo– muy bien escrito y su lectura es amena y, por momentos, divertida.
Las historias que narra Luis Alfonso no deben tomarse como meras anécdotas. Revelan debilidades humanas de cuya existencia hemos de ser conscientes y ante las que conviene mantener una actitud vigilante. Nadie es inmune a la credulidad injustificada. Todos podemos ser víctimas de la versión engañosa de la fascinación. Sobre nosotros no solo incide el atractivo del misterio; en ocasiones deseamos fervientemente creer lo que se nos presenta como extraordinario. Y nos afectan todo tipo de sesgos; nadie está exento de ellos.
Tomemos, a modo de ejemplo, una de las historias. En ‘El noble español con visión de rayos X’ leemos con asombro que personalidades de la talla del ingeniero Leonardo Torres Quevedo, del físico Blas Cabrera, o del escritor Ramón María del Valle Inclán salieron en defensa de Joaquín María Argamasilla de la Cerda y Elio, undécimo marqués de Santacara, quien pretendía tener visión de rayos X. En estos asuntos los magos profesionales llevan ventaja, porque dominan los trucos del ilusionismo: el gran Harry Houdini desenmascaró al marqués en Nueva York. Pero también Juan Negrín, el médico y fisiólogo que llegó a ser presidente de la República, y el escritor Luis Araquistáin se dieron cuenta de las trampas que Houdini le vio hacer.
Soy de la opinión de que no se debe dramatizar con la incidencia que sobre algunas personas tienen engañifas, trolas y patrañas como las que repasa Luis Alfonso en su libro. No es posible conducirse con total y absoluta racionalidad en todas las esferas de la vida. Y cuando alguien se siente mejor creyendo en alguno de estos bulos, prefiero que cada cual gestione sus creencias como le parezca o pueda, siempre y cuando esas creencias no desemboquen en daños a otras personas.
El impacto social de la credulidadPero a lo dicho hay de hacer excepciones. Porque no debe minusvalorarse el impacto social que tienen la credulidad y la extensión de patrañas. Sospecho –aunque esto no es, por supuesto, ninguna ley ni regla general– que es más fácil creer en una superchería cuando se cree en otras. La credulidad puede ser específica, dependiendo de las circunstancias, pero creo que la especificidad no es la norma y que, por ejemplo, quienes creen en ovnis es más fácil que crean en fantasmas. Y, por lo mismo, pueden creer en peligrosas terapias ‘alternativas’ o que las radiaciones de telefonía móvil son dañinas.
Es perjudicial que se extiendan bulos y falsas creencias en la sociedad. Los relacionados con la salud, en especial, pueden ser muy perjudiciales; aunque hay decenas de ejemplos, las actitudes en contra de las vacunas se han demostrado particularmente nocivas. Por otro lado, cuando se prescinde de las precauciones intelectuales que nos permiten limitar la susceptibilidad frente a posturas irracionales o a bulos anticientíficos, creo que es más fácil hacer lo propio también cuando esas posturas y bulos se refieren a materias de orden político. En este caso, el funcionamiento de la sociedad y la misma democracia se resienten, porque el ejercicio de una ciudadanía verdaderamente democrática exige contar con criterio bien formado, lo más ajeno posible a supercherías.
La imperiosa necesidad de pensamiento críticoEl pensamiento crítico debería ser un ingrediente básico de nuestro bagaje intelectual. Cuando hablo de pensamiento crítico no aludo a esas actitudes que consisten en criticar lo que dicen o hacen otros y, en especial, lo que dicen o hacen los adversarios políticos o quienes ostentan el poder. Eso puede obedecer a pensamiento crítico genuino, sí, pero también puede tener su origen en el puro sectarismo, sin matices. Con pensamiento crítico me refiero a otra cosa: nombro una forma de pensar que nos lleva a demandar las pruebas o las fuentes que avalan lo que se predica. Y, si es posible, a someterlo a contraste.
El pensamiento crítico nos ayuda a tomar mejores decisiones y facilita nuestras vidas. Desde el criterio que nos ilumina al adquirir este yogur y no aquel otro, hasta el que nos debe asistir a la hora de votar a esta o aquella opción política, el espectro de decisiones que se encuentra entre esos dos ejemplos extremos (por sus trascendencias dispares), se puede ver muy afectado por el análisis crítico de la información de que disponemos. Por esa razón es necesario cultivarlo y promoverlo. Para ello, pocas cosas se me ocurren más útiles que mostrar a la gente, a la mayor cantidad de personas posible, de qué naturaleza son y cómo operan los bulos, las conspiranoias, las posverdades, y sus fabricantes.
Conociendo esa faceta de la naturaleza humana quizás contemos con más y mejores defensas frente a ellos. Eso es lo que hace este libro y por eso me parece que obras como esta son muy útiles.
Título: El anciano que murió haciendo el amor con un fantasma. Y otras historias sobre lo paranormal
Autor: Luis Alfonso Gámez
Ed. menoscuarto, 2024.
En Editoralia personas lectoras, autoras o editoras presentan libros que por su atractivo, novedad o impacto (personal o general) pueden ser de interés o utilidad para los lectores del Cuaderno de Cultura Científica.
Una versión de este texto de Juan Ignacio Pérez Iglesias apareció anteriormente en Lecturas y Conjeturas (Substack).
El artículo El anciano que murió haciendo el amor con un fantasma se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2023 – Invisible a los ojos
El gran evento de divulgación organizado por Naukas y la Cátedra de Cultura Científica volvió a Bilbao para celebrar su decimotercera edición en el gran Palacio Euskalduna los pasados 15 y 16 de septiembre de 2023.

Carlos Briones, astrobiólogo de reconocido prestigio y gran divulgador científico, dio en Naukas 2023 una charla diferente a cualquier otra. En ella habla de asteroides, lo que en sí mismo no es una novedad, pero sí si uno habla de uno tan, tan especial para él.
Carlos Briones es Licenciado y Doctor en Ciencias Químicas y Coordinador del Grupo de Evolución Molecular, Mundo RNA y Biosensores del Centro de Astrobiología (CSIC-INTA).
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2023 – Invisible a los ojos se ha escrito en Cuaderno de Cultura Científica.
Constantes vitales de los bosques en tiempo real
 Foto: Matthew Smith / Unsplash
Foto: Matthew Smith / UnsplashMonitorizar nuestras constantes vitales de manera continua, con relojes inteligentes mientras hacemos deporte o mediante electrocardiógrafos cuando estamos enfermos en los hospitales, es una práctica muy común. Esta monitorización en tiempo real nos sirve tanto para optimizar nuestro rendimiento físico como para detectar umbrales de salud que puedan poner en riesgo nuestras vidas. Y es esencial porque facilita el diagnóstico, el tratamiento preciso y la optimización del funcionamiento fisiológico y el rendimiento. Al igual que ocurre con los humanos, monitorizar las “constantes vitales” de los bosques nos permite entender sus problemas y optimizar la toma de decisiones orientadas a su conservación y gestión sostenible.
Medir las constantes vitales de los bosquesProteger los bosques se ha convertido en un reto acuciante, ya que su vulnerabilidad y los desafíos a los que se enfrentan son cada vez mayores. Un ejemplo es el fenómeno, ya global, de decaimiento caracterizado por la muerte masiva de árboles, que ocasiona pérdidas importantes, no solo de madera, sino también de servicios ecosistémicos esenciales, como la mitigación del cambio climático, la prevención de grandes inundaciones, los espacios recreativos, etc.
Vigilar la salud de los bosques es, por lo tanto, fundamental. Para ello disponemos de sensores medioambientales muy precisos para medir a alta resolución todo tipo de variables. Se trata de instrumentos que, al igual que un reloj inteligente o un electrocardiógrafo, nos permiten monitorizar, bajo condiciones de campo y a tiempo real, las “constantes vitales” de los bosques.
Muchos grupos de investigación desarrollan y aplican técnicas de monitoreo basadas en el empleo de sensores que permiten detectar cambios significativos en la salud de los bosques.
Diferentes tipos de sensoresEntre los avances tecnológicos que destacan en la investigación científica actual, se encuentran los sensores de medición de variables climáticas de suelo y aire. Registran con gran precisión y de forma continua, incluso minuto a minuto, factores clave como la disponibilidad de agua o las condiciones microclimáticas en las cuales crecen los árboles.
Otros sensores con gran potencial por su nivel de detalle son los dendrómetros digitales. Estos nos permiten monitorizar con gran precisión el crecimiento de los árboles, ya que miden de forma muy fiel las variaciones de engrosamiento y encogimiento de los troncos. Registran de forma continua “las palpitaciones” de los árboles que se pueden relacionar con el clima.
Otros sensores son los conocidos como medidores de flujo de savia, capaces de revelar, en tiempo real, cómo funciona el “sistema circulatorio” de los árboles.
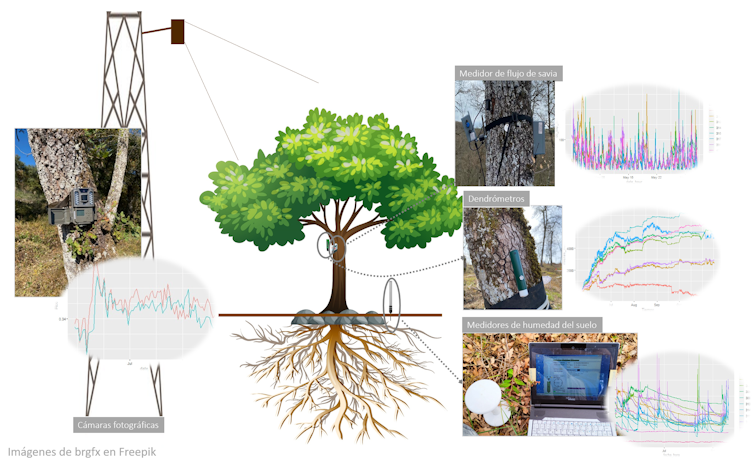 Ejemplo de árbol monitoreado en campo con cámaras fotográficas, sensores de flujo de savia, dendrómetros y sensores de humedad y temperatura del suelo. Fuente: Raquel Esteban
Ejemplo de árbol monitoreado en campo con cámaras fotográficas, sensores de flujo de savia, dendrómetros y sensores de humedad y temperatura del suelo. Fuente: Raquel EstebanAdemás de todo lo mencionado, también tenemos la capacidad de detectar, a través de índices obtenidos de imágenes de cámaras instaladas en torno a las especies, cambios imperceptibles para el ojo humano, como pequeñas transiciones de color en las hojas que nos brindan información clave sobre el rendimiento fotosintético.
Esta fina monitorización de las “constantes vitales” se puede posteriormente acoplar a otras tecnologías avanzadas, como el uso de imágenes de satélites y drones, para detectar estas transiciones de color en la vegetación a escalas espaciales más amplias. Así, no solo somos capaces de monitorizar individuos aislados, sino que podemos aprovechar todo el potencial de estas tecnologías para medir a escalas superiores, como a nivel de bosques, regiones, continentes e incluso a nivel global.
Por último, no podemos dejar de mencionar a la “internet de las cosas”, ya que nos permite tener acceso cómodamente desde nuestro lugar de trabajo o desde casa a todos los datos medidos por los sensores a tiempo real en el campo. Y supone un gran ahorro en infraestructuras y desplazamientos.
La línea entre la salud y la enfermedadMonitorizar en detalle las “constantes vitales” de los árboles nos permite detectar sus “umbrales de salud”. Estos umbrales nos dan información critica sobre, por ejemplo, los niveles de agua en suelo por debajo de los cuales un árbol no puede sobrevivir o la temperatura máxima a partir de la cual deja de fotosintetizar de manera eficiente.
En los seres humanos, monitorizar nuestras constantes vitales puede significar la diferencia entre la vida y la muerte o entre ganar una medalla olímpica y sufrir una lesión. En los bosques, la monitorización a tiempo real es esencial para optimizar la toma de decisiones orientadas a su gestión sostenible. Y nos brinda la oportunidad de ayudar a mejorar su gestión y conservación y, por tanto, de tener bosques sanos que puedan mitigar el cambio climático y seguir proveyendo servicios ecosistémicos clave para nuestra sociedad.![]()
Sobre las autoras: Raquel Esteban, Profesora de Fisiología Vegetal, Universidad del País Vasco / Euskal Herriko Unibertsitatea; Ana-Maria Hereş, Investigadora, Transilvania University of Brașov; Francisco San Miguel Oti, Estudiante de doctorado, BC3 – Basque Centre for Climate Change; Jorge Curiel Yuste, Ikerbasque Research Professor, BC3 – Basque Centre for Climate Change y Lorena Ruiz de Larrinaga, Estudiante de doctorado, Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Constantes vitales de los bosques en tiempo real se ha escrito en Cuaderno de Cultura Científica.
Sofones, o como desplegar el universo
Es posible que pocas teorías de la física levanten tantas pasiones en el imaginario popular, a pesar de su complejidad, como la teoría de cuerdas ―que, en realidad, puede desdoblarse en varias―, y, aun así, rara vez es protagonista, en todo su esplendor, de las narrativas de ficción. Uno de los pocos que se ha atrevido con ella es el escritor chino Liu Cixin en su trilogía del recuerdo del pasado de la Tierra ―más conocida como trilogía de los tres cuerpos―, que se acaba de adaptar por segunda vez a la gran pantalla en forma de serie de televisión. Y no ha sido la única obra donde la ha utilizado. En su relato «Espejo», por ejemplo, aparece un ordenador de supercuerdas capaz de simular cualquier tipo de universo… lo cual también tiene cierto sentido cuando se pone en contexto la teoría.
 Trilogía El recuerdo del pasado de la Tierra, de Liu Cixin, editada en España por Nova/Ediciones B.
Trilogía El recuerdo del pasado de la Tierra, de Liu Cixin, editada en España por Nova/Ediciones B.
En lo que la mayoría de físicos coincide es en que la teoría de cuerdas es «bella», pero tal vez se trate de una belleza fatal, dados los quebraderos de cabeza que se derivan de su propia naturaleza. En principio, la idea básica en torno a la cual gira todo el formalismo es sencilla: las partículas, en lugar de ser «bolitas», serían filamentos unidimensionales cuyos modos de vibración determinarían sus propiedades ―masa, carga…― y definirían qué tipo de partícula es ―un electrón, un quark…―. Y podría tratarse de un enfoque intuitivo, casi obvio, dado que la física está plagada de sistemas ondulatorios; los problemas surgen cuando se le trata de dar sentido a través de las matemáticas.
La teoría de cuerdas nació a finales de los años sesenta en el contexto del estudio de la interacción nuclear fuerte ―una de las cuatro fuerzas fundamentales, responsable de mantener los núcleos atómicos unidos, junto con la interacción débil, el electromagnetismo y la gravedad― cuando Gabriele Veneziano utilizó la función beta de Euler para explicar algunos fenómenos que se habían observado de forma experimental en el CERN. Poco después, en 1970, Yoichiru Nambu, Holger Nielsen y Leonard Susskind propusieron que la aproximación de Veneziano tenía sentido si se interpretaba que las partículas se comportaban como cuerdas vibrantes unidimensionales, aunque esta visión no terminó de cuadrar con los experimentos por más que otros investigadores ya comenzaran a introducir elementos «creativos», como dimensiones ―hasta veintiséis― adicionales. Cuando la cromodinámica cuántica se erigió, finalmente, como la mejor opción para explicar la interacción fuerte, aquella incipiente teoría de cuerdas pasó a mejor vida… hasta 1974, cuando John Henry Schwarz y Joël Scherk investigaron los modos de vibración de esas cuerdas y y descubrieron que uno de ellos podría corresponderse con la partícula mensajera del campo gravitatorio: el gravitón. Y el resto es historia.
Desde que la teoría de cuerdas mostró los primeros indicios de poder convertirse en una teoría del todo han corrido ríos de tinta sobre ella, tanto por parte de sus partidarios como de sus detractores. Porque, si bien es cierto que podría ser un buen punto de partida en nuestro afán por entender el universo, por el momento las dificultades que plantea, tanto a nivel teórico como experimental, superan con creces a sus posibilidades. Por un lado, se trata de un formalismo que está planteado a escalas del orden de la longitud de Planck ―1,616199(97) × 10-35 m―, lo que implica que, para poder demostrar su veracidad experimentalmente, necesitaríamos energías del orden de 10¹⁹ GeV ―el LHC se creó para alcanzar 14 TeV o 1,4⁴ GeV―. Por otro, se trata de una herramienta matemática tan amplia y que admite tantas soluciones, que no todas tendrían por qué representar fenómenos físicos, por no mencionar que muchas de ellas llevan a sistemas inestables o caóticos. Estamos hablando de que la teoría de cuerdas podría describir del orden de 10⁵⁰⁰ tipos de universo, luego ¿cómo podríamos encontrar las condiciones que definen el nuestro en esa inmensidad? Y, finalmente, está la cuestión de la multidimensionalidad que es, en realidad, lo que subyace a todo lo anterior. Además de las cuatro dimensiones que observamos en nuestra vida diaria, la teoría de cuerdas se sostiene sobre otras seis, denominadas «compactas» o «arrolladas», que podrían entenderse como «aburruñadas» en el propio espacio-tiempo en formas geométricas muy específicas, y que, al menos con los medios actuales, no podríamos detectar. Como se puede intuir, todo esto supone un terrible quebradero de cabeza para la ciencia… pero, por otro lado, es una puerta abierta a infinitas posibilidades para la ciencia ficción.
 Un sector del tunel del LHC, en el CERN, la mejor herramienta que tenemos ahora mismo para explorar la física de partículas.
Un sector del tunel del LHC, en el CERN, la mejor herramienta que tenemos ahora mismo para explorar la física de partículas.Créditos: Wikimedia Commons/CC BY-SA 3.0/Maximilien Brice
Decía Stanley Schmidt, editor de la histórica revista Analog Science Fiction and Fact desde 1978 hasta 2012 ―y sucesor de los históricos John W. Campbell y Ben Bova― que «cualquier cosa que nadie pueda probar que sea imposible es juego limpio en ciencia ficción», refiriéndose a que, siempre que exista una base científica real, es lícito que la ciencia ficción juegue en el límite del alcance de la ciencia y especule más allá. Eso es lo que hace Liu Cixin en su trilogía ―y en toda su obra, en realidad― y por eso funciona tan bien. Iría incluso más allá: por eso nos hace soñar… soñar con el futuro de la ciencia, con las maravillas que un día podría llegar a revelarnos.
En la trilogía de los tres cuerpos Liu Cixin utiliza la multidimensionalidad de la teoría de cuerdas como excusa para hacer papiroflexia con el espacio-tiempo. Crea, así, crear todo tipo de tecnologías indistinguibles de la magia con el mero artificio de desplegar dimensiones arrolladas, como es el caso de los sofones.
En realidad, los sofones que crea la imaginación de Liu Cixin tienen menos misterio del que parece, pero ese barniz abstracto que les da el despliegue de las dimensiones adicionales los convierte en algo muy exótico. Partiendo de la base de que un protón, como cualquier otra partícula según la teoría de cuerdas, es un filamento vibrante unidimensional que está definido en un espacio de diez dimensiones ―once, si tenemos en cuenta la teoría M, que unificaría las diferentes versiones―, «lo único» que hacen los trisolarianos es volver macroscópica una de esas dimensiones arrolladas, convirtiendo el protón en un inmenso objeto bidimensional ―en la novela cubre toda la superficie de Trisolaris como si fuera un espejo―. Después, de nuevo utilizando conceptos de física de partículas, se imprime en él una extensa maraña de circuitos integrados. El último paso de los trisolarianos es, simplemente, volver a compactificar la dimensión y, por tanto, comprimir de nuevo la información ―como una especie de fichero .zip―.
Liu Cixin parte de la especulación de de que cada dimensión arrollada esconde una complejidad tan rica que, si se consiguieran desplegar todas, se podría llegar a codificar en una sola partícula toda la información del universo, aunque ya plantea como algo tremendamente complicado desplegar una sola.
Un sofón, por tanto, no es más que un superordenador, o incluso una especie de IA al borde de la singularidad tecnológica, que, gracias a un pequeño truco de prestidigitador basado la teoría de cuerdas, consigue despertar nuestro sentido de la maravilla mucho más que si Liu Cixin nos lo hubiera contado de otra forma. Pero hay algo más…
Como último apunte, antes dije que las dimensiones compactas de la teoría de cuerdas se definían sobre formas geométricas muy específicas: se conocen como variedades de Calabi-Yau, algo que a la mayoría seguramente no le dirá mucho, pero que tienen aspectos como este:
 Las dimensiones compactas de la teoría de cuerdas se definen sobre variedades de Calabi-Yau. Fuente: Wikimedia Commons/CC BY-SA 2.5/Lunch
Las dimensiones compactas de la teoría de cuerdas se definen sobre variedades de Calabi-Yau. Fuente: Wikimedia Commons/CC BY-SA 2.5/Lunch
… y ahora invito a cualquiera que esté viendo la serie de Netflix a que se fije cuidadosamente en cómo aparecen representados los sofones.
Bibliografía
Greene, Brian (2003). El universo elegante. Crítica.
Hossenfelder, Sabine (2015). Will the LHC be able to test string theory? Medium.
Liu, Cixin (2016). El problema de los tres cuerpos. Nova.
Liu, Cixin (2021). Espejo. En Sostener el cielo. Nova.
Sobre la autora: Gisela Baños es divulgadora de ciencia, tecnología y ciencia ficción.
El artículo Sofones, o como desplegar el universo se ha escrito en Cuaderno de Cultura Científica.
¿Cómo ser un buen profesor?
En la Universidad de Cambridge (Reino Unido) existe una sociedad matemática, formada principalmente por estudiantes (de matemáticas), llamada The Archimedeans / Los arquimedianos y que fue fundada en 1935. Entre los objetivos de esta sociedad matemática está “fomentar el disfrute y la comprensión de las Matemáticas entre los estudiantes de todas las disciplinas, y promover la causa de las Matemáticas y de los matemáticos en la Universidad y en otros lugares”. Esta sociedad publica dos revistas: i) la revista matemática Eureka, con el objetivo de que sea publicado un número al año, aunque desde su primer número en 1939 se han publicado tan solo 65 números, el último en 2018, y en la que han colaborado matemáticos y científicos de la talla de Paul Erdös, Martin Gardner, Douglas Hofstadter, Godfrey H. Hardy, Béla Bollobás, John Conway, Stephen Hawking, Roger Penrose, Ian Stewart, Chris Budd, el medalla Fields Timothy Gowers o el premio Nobel Paul Dirac, entre otros; ii) y la revista de problemas de matemáticas, QARCH.
 Portada y contraportada del número 3 de la revista matemática Eureka, de la sociedad matemática Los arquimedianos (Universidad de Cambridge)
Portada y contraportada del número 3 de la revista matemática Eureka, de la sociedad matemática Los arquimedianos (Universidad de Cambridge)En el número 53 (publicado en febrero de 1994) de la revista Eureka, el matemático Jonathan R. Partington (1955), profesor emérito de la Universidad de Leeds (Reino Unido), y que fue estudiante del Trinity College de la Universidad de Cambridge, publicó un jocoso artículo titulado How to be a Good Lecturer (que yo he traducido ¿Cómo ser un buen profesor?). Este artículo se divide en tres partes, la primera con el mismo título How to Be a Good Lecturer / ¿Cómo ser un buen profesor?, la segunda titulada How to Be a Good Member of a Lecture Audience (que conectada con la anterior podríamos traducir ¿Cómo ser un buen estudiante de una clase?) y la tercera, How to Be a Good Exam Invigilator (¿Cómo ser un buen vigilante de un examen?). En esta entrada del Cuaderno de Cultura Científica traemos la traducción que he realizado de la primera parte, sobre cómo ser un buen profesor, las otras dos partes quizás para otra ocasión.
 Fotografía de una conferencia organizada por la sociedad matemática de Los arquimedianos en la Universidad de Cambridge
¿Cómo ser un buen profesor?
Fotografía de una conferencia organizada por la sociedad matemática de Los arquimedianos en la Universidad de Cambridge
¿Cómo ser un buen profesor?
“Bueno … Hola y bienvenidos a la primera clase del curso … ¡eeeh! … ¡escuchad, he dicho hola! … escuchad, me gustaría empezar ya … ¿vais a callaros? ¡¡QUE OS CALLÉIS, POR FAVOR!! ¡Oh, gracias! No me importa que habléis, pero si lo hacéis en voz baja … Yo no pedí impartir este curso … ¿Sabéis? Yo quería impartir un curso de álgebra … se lo dije … que yo no sabía nada de análisis matemático …”
“… Veamos, este curso está dedicado a los números complejos y aquí tengo una lista de libros recomendados … ¡eeeh! Bueno, no, parece que me la he olvidado en el despacho … ¡no importa! De hecho, están todos agotados … Empecemos escribiendo una definición … ¿Dónde está la tiza? ¡Ah, aquí está! SNAP [esta onomatopeya está relacionada con algo que se rompe, podría ser el sonido de la tiza que se rompe al intentar el profesor escribir en la pizarra] … ¡ahhh! Permitidme que coja otro trozo … THUD [esta onomatopeya, que suele relacionarse con un golpe, podría significar que el profesor se ha caído de la pequeña tarima destinada al profesor, donde está la pizarra para la clase], no son muy grandes estas plataformas, sigo cayéndome de ellas …”
“… Ahora, la definición 1.1 es … ¡ah!¡mmm! … ¡Perdón! Todavía no he dicho cómo se llama esta sección … ¡oh! aunque parece que no tiene título … de todos modos, es sobre la convergencia de series de potencias … hicisteis algo parecido en la asignatura de análisis real, ¿no?, ¿Os acordáis? … Bueno, vuestro profesor debería habéroslo contado en sus clases, yo no tengo tiempo ahora para meterme en ese tema …”
“… Ahora, la definición 1.1 … [escribe en la pizarra] … ¿Podéis leer esto los que estáis sentados atrás? … ¿no? Pues tendréis que poneros delante … Ahora que lo pienso, yo tampoco puedo leerlo … quizás si enciendo esta luz … ¡ah, no! ¡esa no! ¡quizás esta otra! ¡oh! ¡vaya! supongo que el cable estará roto … Bueno, mirad este símbolo, es una sigma mayúscula … ¿sí? ¿cuál es el problema?… sí, bueno, parece que el verde es el único color que queda en la caja de tizas, probablemente porque nadie en su sano juicio lo usa, por eso lo han dejado ahí para mí …”
“… Bueno, escuchad … quizás, si lo explico con palabras … de todas formas, está todo en los libros de texto … aunque no puedo ayudaros si no los encontráis en la biblioteca, parece que la gente se los come o algo parecido … Bueno, ahora dibujaré un diagrama … no hace falta que lo copiéis exactamente ya que está un poco mal … de todas formas, es el diagrama 2 … ¡Buena pregunta! … Creo que he olvidado dibujar el diagrama 1 … de todos modos, permitidme que os diga que tampoco ayuda mucho …. ¡ufff! Dejadme un momento que me quite la chaqueta … RIP [onomatopeya que nos dice que se ha rasgado una tela o similar] … vaya, yo mismo cosí ese botón, creo que se nota, ¿no? …”
“… Ahora, permitidme que me extienda un poco sobre la historia del tema que nos ocupa … Fue descubierto por Cauchy … o quizás era Gauss … uno de los dos … y envió una copia de su artículo a otra persona que, bueno, … en cualquier caso, es un tema muy importante y tiene muchas aplicaciones como … ¡ehhh! … como … Bueno, veréis aplicaciones en las otras asignaturas que estudiáis … ¡espero! … por supuesto, en ellas no se utiliza la misma notación, pero tampoco tienen la misma idea de rigor que se tiene en esta asignatura … Y ahora escribamos el primer resultado, Lema 1.2 …”
“… Lema 1.2 … ¡Oh! En realidad aún no he definido lo que es el radio de convergencia … todavía puedo … Dejadme que lo escriba y podemos decidir más tarde qué significa … Bueno, parece que todavía me quedan unos minutos, así que será mejor que empiece ya con la demostración … sea n esto, y r esto, y esto otro v, y sea n … pensándolo bien, ya estoy utilizando n, luego lo llamaré nu, perdón, no, nu es una letra griega, la tenéis que haber visto antes, ya sabéis las letras griegas alfa, etcétera … no, esta es nu, está bien, llamadlo v si queréis, aunque ya estamos utilizando v también, pero no causará confusión …”
“… ahora multiplicad esto y obviamente lo que obtenemos es … ¡ehhh! … claramente … ¡mmm! ¡oh! … esto no puede estar bien … ¿Qué he hecho mal aquí? ¿Podéis ver el error? … quizás he olvidado un signo menos en algún lugar … Dejadme que lo busque … ¡Oh! Es hora de terminar, ¿no? … Bueno, dadme solo 5 minutos más y lo terminaré … ¡Oh! Tal vez debería hacer esto con más cuidado la próxima vez … ¡Ah! Eso debería haber sido un nu, tal vez no, debería ser una v, ¡oh! es una r, ¡oh! Bueno, escuchad, lo terminaré en la siguiente clase … estoy seguro de que la mayoría de los detalles están bien … es algo muy elemental después de todo, todavía no hemos hecho nada que no sea trivial.”
 Cambridge IV (2011), de Alejandro Guijarro, perteneciente a la exposición Momentum, que podéis ver en su página web Alejandro Guijarro
Cambridge IV (2011), de Alejandro Guijarro, perteneciente a la exposición Momentum, que podéis ver en su página web Alejandro GuijarroBibliografía
1.- Jonathan Partington, How to be a Good Lecturer, Eureka n. 53, 1994.
2.- David Wells, El curioso mundo de las matemáticas, Gedisa editorial, 2000.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo ¿Cómo ser un buen profesor? se ha escrito en Cuaderno de Cultura Científica.
El cerio y la evolución química del universo
 Detalle de la tabla periódica de los isótopos. Fuente: CIAAW / IUPAC
Detalle de la tabla periódica de los isótopos. Fuente: CIAAW / IUPACLa mayoría de los elementos más pesados del Universo se forman en las estrellas mediante uno de los llamados procesos de captura de neutrones, en los que un núcleo atómico absorbe uno o más neutrones. En el proceso lento de captura de neutrones, o «proceso s», las absorciones se distribuyen en el tiempo. Como tal, cada evento de absorción da como resultado bien un núcleo estable con la misma cantidad de protones pero un neutrón adicional, o un núcleo inestable, que luego se desintegra radiactivamente para producir el núcleo del siguiente elemento en la tabla periódica: el que tiene un protón adicional.
Utilizando los modelos actualmente disponibles del proceso s se han predicho correctamente la abundancia onservada de elementos tan pesados como el bario (56 protones), el lantano (57 protones), el praseodimio (59 protones) y el neodimio (60 protones) en estrellas que se sabe que se enriquecen a través del proceso s. Pero los modelos parecen fallar en el caso del cerio (58 protones), ya que las predicciones de abundancia de este elemento en algunos cúmulos globulares de baja masa y metalicidad han discrepado hasta en un 30% con las observaciones. Es llamativo que el modelo funcione para los elementos vecinos y que discrepe así para un elemento solo.
El cerio tiene otra característica interesante: puede formar el llamado núcleo de número mágico. La mayor parte del cerio del Universo (89%) existe como cerio-140, un isótopo del elemento que contiene 58 protones y un número mágico de 82 neutrones. Los núcleos de números mágicos son particularmente estables y, por lo tanto, a menudo existen en mayor abundancia que otros isótopos del mismo elemento o de elementos vecinos en la tabla periódica.
 Abundancia relativa de los isótopos del cerio. Fuente: CIAAW / IUPAC
Abundancia relativa de los isótopos del cerio. Fuente: CIAAW / IUPACAl igual que otros núcleos de números mágicos, la alta estabilidad del cerio-140 surge de su baja sección transversal de captura de neutrones, que es la probabilidad de que un núcleo del isótopo absorba un neutrón entrante. También es el parámetro medido en nuevos experimentos en el CERN realizados por la Colaboración n_TOF. El análisis de los datos indica que la sección transversal de captura de neutrones es un 40% mayor que la medida en experimentos anteriores, que tenían menor precisión. Una sección transversal más alta hace que sea más probable que el cerio-140 capture un neutrón entrante y menos probable que permanezca en su forma de cerio-140. Esto, a su vez, lleva a predecir una menor abundancia de cerio-140 que antes.
La sección transversal más alta también tiene implicaciones para la abundancia de los núcleos que se forman más adelante en la cadena del proceso s. Dado que es más probable que el cerio-140 capture un neutrón y forme un núcleo más pesado, el proceso s puede continuar más rápido, creando una mayor abundancia de núcleos más pesados.
La discrepancia entre la abundancia de cerio-140 predicha por la teoría y la medida en las observaciones de las estrellas de baja metalicidad sugiere que un proceso distinto al proceso s también podría producir este núcleo en esas estrellas. Una posibilidad es que otra vía de nucleosíntesis, el llamado proceso i, esté involucrada en la producción de cerio. Este proceso de captura de neutrones propuesto pasa por alto algunos núcleos estables involucrados en el proceso s y, si desempeñara un papel importante, podría cambiar las abundancias relativas de los elementos.
En febrero, utilizando una técnica diferente, otro equipo encontró un valor de la sección transversal aproximadamente un 15% menor que el medido anteriormente con esa técnica. Nadie sabe el origen de la discrepancia entre los dos nuevos valores. Para descubrir exactamente qué está pasando, es necesario realizar más mediciones nucleares.
Referencias:
S. Amaducci et al. (n_TOF Collaboration)(2024) Measurement of the 140Ce(n, γ) cross section at n_TOF and its astrophysical implications for the chemical evolution of the Universe Phys. Rev. Lett. doi: 10.1103/PhysRevLett.132.122701
R. N. Sahoo et al. (2024) Stellar s-process neutron capture cross section of Ce isotopes Phys. Rev. C. doi: 10.1103/PhysRevC.109.025808
K.Wright (2024) Heavy Element Quandary in Stars Worsened by New Nuclear Data Physics 17, 47
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El cerio y la evolución química del universo se ha escrito en Cuaderno de Cultura Científica.
La corteza de hielo de Europa
Europa, el satélite de Júpiter, es uno de los mundos con mayor interés astrobiológico de todo el Sistema Solar gracias al océano que pensamos que puede existir debajo de su corteza congelada. El espesor de esta corteza y sus características tanto físicas como químicas podría contarnos algunas pistas sobre la historia geológica de este mundo, pero, al mismo tiempo, también podría tener una gran influencia a la hora de transformar este mundo en un lugar habitable, ya que su comportamiento puede facilitar el intercambio de materia entre el interior y el exterior de este océano, así como mitigar la pérdida de calor que congelase al océano rápidamente en ausencia de una fuente de energía interna.
Por desgracia, no son muchos los datos que tenemos todavía sobre su corteza a pesar de las misiones que se han situado en órbita al sistema joviano -como lo son la Galileo en la década de los 90 o la Juno, actualmente en órbita- aunque en la década de 2030, si todo va bien, tendremos las sondas Europa Clipper y JUICE tomando nuevos datos que podrían arrojar algo de luz y confirmar nuestras teorías.
 ¿Cómo es la corteza de Europa? ¿Fina o gruesa? Los autores de un nuevo estudio sugieren que estamos ante el segundo caso. Imagen cortesía de NASA/JPL/Michael Carroll.
¿Cómo es la corteza de Europa? ¿Fina o gruesa? Los autores de un nuevo estudio sugieren que estamos ante el segundo caso. Imagen cortesía de NASA/JPL/Michael Carroll.Como hemos dicho en la introducción, uno de los asuntos de interés es el espesor de la corteza, por lo que distintos equipos de científicos han intentado calcular este valor, dando como resultado rangos que oscilan entre los 10 y los 35 kilómetros estudiando distintos aspectos como las proporciones entre el diámetro y la profundidad de los cráteres, modelos termodinámicos e incluso simulaciones sobre como la capa de hielo se pliega ante distintos esfuerzos, pero como podemos ver, la horquilla es muy grande (Bray et al. 2014; Billings & Kattenhorn 2005; Quick & Marsh, 2015; Nimmo et al. 2007).
Pero recientemente, otro equipo de científicos ha propuesto una nueva y singular forma de calcular el espesor de la capa de hielo en un artículo publicado en Science Advances. Wakita et. al (2024) plantea el uso de simulaciones y el estudio de la topografía de las cuencas multi-anillo para averiguar este dato. Si, es cierto que ya se ha usado la topografía anteriormente para este menester, pero ahora se centra en unas formas muy concretas y menos abundantes.
Quienes nunca hayan escuchado este término -el de cuenca multi-anillo- nos referimos a una serie de estructuras concéntricas que podemos encontrar en las superficies planetarias -también las hay en la Luna y en la Tierra, por ejemplo- que se han formado como consecuencia de grandes impactos.
 La cuenca de impacto de Tyre es una de las estudiadas en este nuevo artículo. Es una estructura de impacto de unos 140 kilómetros de diámetro en la que se aprecia perfectamente la estructura en anillos concéntricos. Desde su formación incluso ha sufrido procesos que han alterado su forma, lo que nos ayuda a apreciar que Europa todavía tiene cierto grado de actividad geológica. Imagen cortesía de NASA/JPL/ASU.
La cuenca de impacto de Tyre es una de las estudiadas en este nuevo artículo. Es una estructura de impacto de unos 140 kilómetros de diámetro en la que se aprecia perfectamente la estructura en anillos concéntricos. Desde su formación incluso ha sufrido procesos que han alterado su forma, lo que nos ayuda a apreciar que Europa todavía tiene cierto grado de actividad geológica. Imagen cortesía de NASA/JPL/ASU.La formación de estas cuencas y su estructura deberían de ser sensibles a las propiedades de la capa de hielo donde se produce el impacto -y probablemente a las subyacentes-, de tal modo que realizando distintas simulaciones para distintos espesores de hielo, conductividades térmicas y parámetros de impacto se pueden establecer comparaciones con el relieve que hoy vemos y podríamos llegar a conocer el verdadero espesor de esta manera indirecta.
El resultado de estas simulaciones muestra que la capa de hielo debe de medir más de 20 kilómetros de espesor -o potencia si hablamos en términos geológicos- para poder sostener la estructura en anillos concéntricos que observamos. Este dato es crucial, ya que supera algunas de las estimaciones anteriores y añade un volumen de hielo considerable alrededor del océano de Europa.
Siendo más concretos, el modelo consistiría en dos capas: una capa superior rígida de entre unos seis y ocho kilómetros de espesor cuya forma de transferencia de calor sería a través de la conducción, y bajo de esta una capa de hielo a mayor temperatura y con procesos de convección activos.
La presencia de la capa externa sobre una capa más interna en convección podría indicar un gradiente geotérmico complejo en la corteza, algo crítico para mantener el océano en estado líquido la mayor cantidad de tiempo posible: la capa externa actuaría en cierto modo como un aislante que ralentiza la pérdida de calor interno hacia el espacio, permitiendo una mayor duración temporal del océano, algo muy importante de cara al origen y mantenimiento de la vida.
 Otra de las grandes cuencas multi-anillo de Europa, Callanish, vista de cerca por la sonda Galileo en el año 2000. Cortesía de NASA/JPL.
Otra de las grandes cuencas multi-anillo de Europa, Callanish, vista de cerca por la sonda Galileo en el año 2000. Cortesía de NASA/JPL.Pero al mismo tiempo podría ser un problema: Una capa externa de mayor espesor supone un reto para la existencia de mecanismos de intercambio directo de materia -como nutrientes o compuestos orgánicos, por ejemplo- entre el exterior y el interior de Europa, aunque obviamente siempre pueden existir puntos o bien donde el gradiente geotérmico o la existencia de fracturas facilite este intercambio, aunque con una corteza gruesa podría ser un proceso mucho más restringido.
¿Qué certeza tienen los autores del estudio sobre estos resultados? Junto con la topografía observada, las simulaciones han sido validadas calculando el esfuerzo radial, ya que aporta la posibilidad de cuantificar de una manera numérica los patrones de deformación asociados a estas cuencas multi-anillo y, por lo tanto, valga la redundancia, los patrones topográficos observados. Estos esfuerzos radiales ayudan a medir hasta donde llegan los fenómenos de extensión y compresión producidos como consecuencia del impacto y también como respuesta de la propia corteza.
Sea como sea, probablemente todavía tardaremos una década -o incluso algo más- en verificar de una manera empírica estos estudios a través de las nuevas misiones que estudien el sistema joviano con instrumentos más modernos que nos permitan, quizás por fin, conocer la estructura interna de un cuerpo tan interesante como Europa.
Referencias:
Shigeru Wakita et al. (2024) Multiring basin formation constrains Europa’s ice shell thickness Sci. Adv. doi: 10.1126/sciadv.adj8455
Moore, J. M., Asphaug, E., Belton, M. J. S., Bierhaus, B., Breneman, H., Brooks, S. M., Chapman, C. R., Chuang, F. C., Collins, G. C., Giese, B., Greeley, R., Head, J. W., Kadel, S. D., Klaasen, K. P., Klemaszewski, J. E., Magee, K. P., Moreau, J. W., Morrison, D., Neukum, G., . . . Williams, K. K. (2001) Impact features on Europa: Results of the Galileo Europa Mission (GEM). Icarus doi: 10.1006/icar.2000.6558
Bray, V. J., Collins, G. S., Morgan, J. V., Melosh, H. J., & Schenk, P. (2014) Hydrocode simulation of Ganymede and Europa cratering trends – How thick is Europa’s crust? Icarus, doi: 10.1016/j.icarus.2013.12.009
Billings, S. E., & Kattenhorn, S. A. (2005) The great thickness debate: Ice shell thickness models for Europa and comparisons with estimates based on flexure at ridges Icarus doi: 10.1016/j.icarus.2005.03.013
Quick, L. C., & Marsh, B. D. (2015) Constraining the thickness of Europa’s water–ice shell: Insights from tidal dissipation and conductive cooling Icarus doi: 10.1016/j.icarus.2015.02.016
Nimmo, F., Thomas, P. C., Pappalardo, R., & Moore, W. B. (2007) The global shape of Europa: Constraints on lateral shell thickness variations Icarus doi: 10.1016/j.icarus.2007.04.021
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo La corteza de hielo de Europa se ha escrito en Cuaderno de Cultura Científica.
El problema de los tres cuerpos
 El problema de los tres cuerpos consiste en determinar el movimiento de tres cuerpos sometidos a la gravedad mutua. Esta ilustración representa los seis planetas del sistema HD110067, que crean juntos un fascinante patrón geométrico.
El problema de los tres cuerpos consiste en determinar el movimiento de tres cuerpos sometidos a la gravedad mutua. Esta ilustración representa los seis planetas del sistema HD110067, que crean juntos un fascinante patrón geométrico.Thibaut Roger/NCCR PlanetS, CC BY-SA
El problema de los n-cuerpos se planteó por primera vez en el concurso aniversario patrocinado por el rey Oscar II de Suecia para celebrar el sexagésimo aniversario de su nacimiento, que tuvo lugar en 1889. Y es un problema que siglo y medio después no ha logrado resolverse. Que nadie espere que lo resuelva la serie de Netflix que lo integra en la ficción.
Antes de NetflixEn el año 2004 se publicó en España una novela de crímenes titulada La incógnita Newton. Su título original era The three body problem (El problema de los tres cuerpos) y su argumento gira en torno a la misteriosa muerte de tres matemáticos que trabajan en la búsqueda de la solución al famoso problema de los n-cuerpos. Esta novela, firmada por Catherine Shaw, es muy interesante desde el punto de vista de la divulgación matemática.
 El problema de los tres cuerpos, de Catherine Shaw, pseudónimo de la investigadora en teoría de números Lila Schneps.
El problema de los tres cuerpos, de Catherine Shaw, pseudónimo de la investigadora en teoría de números Lila Schneps.Dos años después de esta primera novela se publicó la primera parte de una trilogía de ciencia ficción del escritor chino Liu Cixin con el mismo título, El problema de los tres cuerpos. Y su obra es la que ha dado lugar a la serie de Netflix que promete convertirse en uno de los fenómenos mediáticos más relevantes de la temporada. Detrás están los productores de la también célebre Juego de Tronos, David Benioff y Daniel Brett Weiss.
Ficción sí, ciencia no tantaEl título de la serie y de la novela hace alusión al comportamiento de Trisolaris, un enigmático planeta que orbita en un sistema de tres estrellas, creando un caos gravitatorio que da lugar a ciclos de extremos climáticos impredecibles. El planeta Trisolaris (con tres soles) padece alternativamente etapas estables, con vida similar a la terrestre, y estaciones caóticas e infernales, en las que en unos segundos la temperatura puede alterarse en cientos de grados, lo que lo convierte en un infierno.
En la ficción, hay un juego de realidad virtual que se llama Tres Cuerpos que simula el comportamiento de tres cuerpos con campos gravitacionales erráticos, lo que está ocurriendo en el universo trisolariano. Explicar cómo se comportan podría solucionar sus problemas climáticos universales. Pero los matemáticos, en la vida real, no encuentran solución al problema, y la propuesta un tanto naif de la serie es que un friki de los videojuegos tiene más suerte.
No es la primera obra de ficción que se reviste de ciencia como tirón, sin que hable de ciencia. Si alguien espera encontrar respuesta al problema de los n-cuerpos, mejor que no se acerque.
Ahora, vamos al meollo matemático.
El problema del universo trisolarianoEl problema consiste en determinar el movimiento de tres cuerpos sometidos a la gravedad mutua. El movimiento de los tres puede ser caótico o regular, y puede terminar en una desintegración del sistema. Buscar soluciones posibles ha motivado el análisis y estudio de una parte importantísima de la matemática, los sistemas dinámicos (la teoría del caos es un ejemplo, dentro de los casos de dinámica no lineal), que en la actualidad plantea multitud de cuestiones abiertas en proceso de investigación.
El primero en estudiarlos fue Newton. Gracias a sus leyes, dados dos cuerpos de cualquier masa, sometidos a atracción gravitacional mutua y partiendo de unas posiciones y velocidades dadas, podemos determinar, en cualquier instante, sus posiciones y velocidades. Si el sistema solar estuviera formado por el Sol y un único planeta, este seguiría una órbita elíptica y podríamos determinar con exactitud dónde va a encontrarse en cualquier momento. Pero cuando el sistema consta de más de dos cuerpos, resolver las ecuaciones de movimiento resulta realmente complicado.
Tres cuerpos y el caso de los asteroides troyanosPara tres cuerpos, los matemáticos han encontrado un pequeño número de casos especiales en los que las órbitas de las tres masas son periódicas.
En 1765, Leonhard Euler pudo describir con matemáticas un modelo en el que tres masas comienzan en línea y giran para permanecer alineadas. Sin embargo, tal conjunto de órbitas es inestable y no se encuentran en ningún lugar del sistema solar.
En 1772, Joseph-Louis Lagrange identificó una órbita periódica en la que tres masas se encuentran en los vértices de un triángulo equilátero. En este caso, cada masa se mueve en una elipse de tal forma que el triángulo formado por las tres siempre permanece equilátero. Los llamados asteroides troyanos de Júpiter se mueven de acuerdo a este esquema. Forman un triángulo con Júpiter y el Sol. Hasta 2021 se han descubierto 9 800 asteroides troyanos de Júpiter distintos.
Posteriormente, Henri Poincaré y otros demostraron que, en general, es imposible obtener una solución general, expresada como una fórmula explícita, al problema de los tres cuerpos. Es decir, dados tres cuerpos en una configuración aleatoria, no se puede predecir con precisión qué trayectoria seguirían.
La órbita en forma de ochoEn 1993, Cristopher Moore, descubrió, mediante cálculos informáticos, que tres masas iguales pueden perseguirse alrededor de la misma curva en forma de ocho en el plano. Y en el año 2000, los matemáticos Richard Montgomery (Universidad de California en Santa Cruz) y Alain Chenciner (Universidad París VII-Denis Diderot) redescubrieron la órbita en forma de ocho descrita por Moore, y encontraron una solución exacta a las ecuaciones de movimiento para tres cuerpos que interactúan gravitacionalmente.
 La órbita en forma de ocho para el problema de los 3 cuerpos. Animación de Michael Nauenberg, profesor emérito de Física de la Universidad de California en Santa Cruz.
La órbita en forma de ocho para el problema de los 3 cuerpos. Animación de Michael Nauenberg, profesor emérito de Física de la Universidad de California en Santa Cruz.Carlès Simò (Universidad de Barcelona) ha demostrado mediante simulaciones por ordenador que la órbita en forma de ocho es estable, que persiste incluso cuando las tres masas no son exactamente iguales y puede sobrevivir a una pequeña perturbación sin alteraciones graves.
Los sistemas planetarios extrasolaresLa posibilidad de que exista un sistema de tres cuerpos así en algún lugar del universo es muy pequeña. Sin embargo, el descubrimiento de sistemas planetarios extrasolares inusuales abre nuevos escenarios espacio-temporales en los que podrían producirse tales movimientos.
La existencia de la órbita en forma de ocho de tres cuerpos ha llevado a los matemáticos a buscar órbitas similares que involucraran más masas.
Simò ha encontrado cientos de soluciones exactas para el caso de n masas iguales que recorren una curva plana fija, aunque no son estables. También se han modelizado órbitas tridimensionales. A estas estructuras y sus trayectorias periódicas se las ha bautizado como coreografías.
Así, admitiendo la ficción, el universo trisolariano podría estar formado por planetas que describen una órbita de ochos, pero esto es algo que no va a contar la serie de Netflix.![]()
Sobre el autor: Alfonso Jesús Población Sáez, Profesor Titular en Dpto. Matemática Aplicada, Universidad de Valladolid
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo El problema de los tres cuerpos se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2023 – La última de Vermeer
El gran evento de divulgación organizado por Naukas y la Cátedra de Cultura Científica volvió a Bilbao para celebrar su decimotercera edición en el gran Palacio Euskalduna los pasados 15 y 16 de septiembre de 2023.

Sin lugar a dudas el artista más veces citado y explicado en las charlas de Naukas Bilbao ha sido el pintor neerlandés Vermeer. Esta charla de Oskar González aborda como se contribuye a identificar desde la ciencia la autenticidad de un Vermeer y es, posiblemente, el broche de oro a esa tradición. Incluye un sentido homenaje a otro gran divulgador de la ciencia en Vermeer, Manu Arregi, fallecido en 2022.
Oskar González es profesor en la facultad de Ciencia y Tecnología y en la facultad de Bellas Artes de la UPV/EHU. Además es el autor de la sección kimikArte del Cuaderno de Cultura Científica y del libro Por qué los girasoles se marchitan fruto, en parte, de ella.
Si no ve correctamente el vídeo, use este enlace.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2023 – La última de Vermeer se ha escrito en Cuaderno de Cultura Científica.
Redefiniendo el embrión humano
Iñigo de Miguel Beriain, investigador del Grupo de Investigación en Ciencias Sociales y Jurídicas aplicadas a las Nuevas Tecnociencias de la UPV/EHU, ha publicado un artículo en el que se aporta una perspectiva legal para ayudar a identificar una definición universalmente aceptable de embrión, lo que podría facilitar y unificar su regulación en diferentes países. Así, se propone que cualquier célula o grupo de células celular con la capacidad inherente de desarrollarse hasta dar origen a un ser humano debería considerarse embrión.
 Fuente: UPV/EHU
Fuente: UPV/EHULa biotecnología puede contribuir decisivamente a mejorar el conocimiento y control de las primeras etapas de la vida humana. Sin embargo, este escenario genera controversias desafiantes desde el punto de vista ético y jurídico. No en vano, pocos temas biotecnológicos son más controvertidos que los relacionados con los embriones humanos. Sin embargo, hay un aspecto que permanece poco explorado en los debates recientes. Aunque el estatus moral del embrión ha sido una cuestión crucial en las discusiones públicas, la delimitación precisa de lo que es un embrión humano y su distinción de otras entidades similares ha adquirido una importancia primordial. No se trata de un problema meramente semántico, sino normativo, que tiene importantes consecuencias prácticas para la investigación.
En ese sentido, diversos avances científicos y tecnológicos en biología reproductiva han obligado a revisar la definición de embrión humano en las dos últimas décadas. La posibilidad de generar embriones humanos a través de procedimientos diferentes a la fecundación, como la transferencia nuclear, y el desarrollo de las tecnologías que hoy en día permiten generar modelos celulares capaces de imitar estructuras embrionarias han puesto en tela de juicio el término científico de embrión, lo que tiene repercusiones tanto éticas como jurídicas.
“Los desarrollos tecnológicos plantean a veces la necesidad de repensar categorías conceptuales que en otros momentos se daban por sentadas. Ahora mismo ya no es posible sostener que un embrión es siempre y solo el resultado de una fecundación”, afirma de Miguel.
Iñigo de Miguel ha publicado junto con Jon Rueda, de la Universidad de California-San Diego, y Adrián Villalba, de la Universidad de Granada, un artículo en el que reflexionan sobre diferentes definiciones jurídicas de un embrión humano y aportan una definición sólida desde una perspectiva legal. “En el artículo se sugiere una visión alternativa, en la que cualquier estructura celular que tenga la capacidad de desarrollarse hasta dar origen a un ser humano nacido debería considerarse un embrión y que esta capacidad debería ser el eje sobre el que se construya la definición, como ya se hace en algunos países, por cierto, y como ha dictaminado el Tribunal de Justicia de la Unión Europea”.
Según señala de Miguel, “una definición jurídica universal y generalmente aceptada de embrión contribuiría a aliviar la inseguridad jurídica y a armonizar las normativas”. “Nuestra reflexión pretende contribuir a consolidar un concepto de embrión que sea más capaz de hacer frente a los retos que plantean los avances de la biotecnología”, añade, y a su vez señala que “puede tener repercusiones legales a la hora de afianzar un sistema jurídico más coherente que el que existe ahora mismo, capaz de conectar la idea de embrión con la de ser humano nacido (que es la que en Derecho define a la persona)“.
De Miguel considera que esta definición ”también servirá para subrayar que existe un debate previo al que tradicionalmente se ha formulado en torno al embrión, su estatuto moral, que es el que tiene que ver con la propia definición de embrión. Antes de discutir qué protección merece, tenemos que decidir qué es y qué no es un embrión, porque no es lo mismo una estructura incapaz de culminar un proceso de transferencia por un defecto en su ADN que otra que sí puede hacerlo, por ejemplo”.
Referencia:
Iñigo De Miguel Beriain, Jon Rueda & Adrian Villalba (2024) Re-defining the human embryo: A legal perspective on the creation of embryos in research EMBO Reports doi: 10.1038/s44319-023-00034-0
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Redefiniendo el embrión humano se ha escrito en Cuaderno de Cultura Científica.
Las señales del frío que vienen del Norte
 Photo by Ant Rozetsky on Unsplash
Photo by Ant Rozetsky on UnsplashSi hay algo que caracteriza al último Periodo de la historia de nuestro planeta, el Cuaternario, es la alternancia cíclica de momentos climáticos más fríos, denominados glaciaciones, y momentos más cálidos, los interglaciales. Actualmente nos encontramos viviendo en un interglacial, el Holoceno, que comenzó hace unos 11.700 años. Anteriormente, entre hace 11.700 y unos 70.000 años se produjo la última glaciación, que sucedió al anterior interglacial, que abarcó desde hace unos 70.000 hasta hace unos 130.000 años. Y paro aquí, porque creo que ya os habéis hecho una idea.
 Ciclicidad climática acontecida en el Atlántico Norte durante el último millón de años (la escala, Ka BP, se refiere a miles de años antes de la actualidad). En color naranja se señalan los periodos interglaciales, mientras que en azul se marcan las glaciaciones. Imagen modificada de la original tomada de skepticalscience.com, realizada a partir de los datos de Lisiecki, L.E. y Raymo, M.E. (2005). A Pliocene-Pleistocene stack of 57 globally distributed benthic d18O records. Paleoceanography 20, PA1003.
Ciclicidad climática acontecida en el Atlántico Norte durante el último millón de años (la escala, Ka BP, se refiere a miles de años antes de la actualidad). En color naranja se señalan los periodos interglaciales, mientras que en azul se marcan las glaciaciones. Imagen modificada de la original tomada de skepticalscience.com, realizada a partir de los datos de Lisiecki, L.E. y Raymo, M.E. (2005). A Pliocene-Pleistocene stack of 57 globally distributed benthic d18O records. Paleoceanography 20, PA1003.Cuando estás trabajando con afloramientos geológicos cuaternarios, esta ciclicidad climática puede ser muy útil para hacerte una idea de la posible edad de tus materiales antes de que obtengas alguna datación absoluta. Principalmente si encuentras fósiles con los que puedas hacer una reconstrucción paleoecológica del ambiente en el que vivieron. Es decir, si te aparecen restos de un mamut o un rinoceronte lanudo, estaríamos en alguna glaciación, mientras que si encuentras fósiles de un antepasado de los leones, elefantes o hienas actuales nos moveríamos a algún interglacial.
Sin embargo, si nos fijamos en la curva de reconstrucción climática realizada para la parte final del Cuaternario, observaremos que no se trata de una sucesión de curvas que pasan del calor al frío dibujadas con una línea continua. En realidad, es una línea irregular, con múltiples dientes de sierra. Esto indica que, dentro de esas grandes tendencias climáticas glacial-interglacial que duran decenas de miles de años, se producen momentos relativamente más cálidos alternando con otros relativamente más fríos de mucha menor duración temporal. En concreto, estos pequeños ciclos cálido-frío presentan una periodicidad de unos 1500 años.
De esta forma, si volvemos al yacimiento que os ponía de ejemplo y queremos hacer una reconstrucción muy detallada de los cambios paleoambientales que ocurrieron en el pasado, estudiar los restos fósiles de organismos grandes no nos permitirá tener tanta resolución. Esto se debe a que, por norma general, los animales más grandes y complejos suelen tener requerimientos ecológicos más amplios, es decir, son capaces de vivir en amplios rangos de variación de temperatura, salinidad, humedad, etc. Por tanto, deberemos acudir a organismos más pequeños y simples, biológicamente hablando, que tendrán parámetros ecológicos más constreñidos. Así que, en yacimientos continentales, intentaremos buscar restos fósiles de animales como los roedores. Y, aun así, es posible que no logremos detectar todos los eventos cálidos y fríos son absoluta precisión en un afloramiento continental, ya que entran en juego factores más relacionados con la propia conservación del registro, como son las tasas de sedimentación o la capacidad de preservación de los restos orgánicos.
Pero, en medio marino, las cosas tienen mejor pinta. En el fondo oceánico es posible encontrar más zonas en las que las tasas de sedimentación sean muy altas y apenas haya procesos erosivos, por lo que se pueden conservar registros geológicos cuaternarios muy completos y con mucha resolución temporal. Y en el mar hay muchos tipos de organismos pequeños, simples y con rangos ecológicos muy concretos, que nos permiten hacer unas reconstrucciones paleoambientales de mucho detalle.
 Fotografía de microscopio electrónico de barrido del caparazón de un ejemplar del foraminífero planctónico Neogloboquadrina pachyderma variedad sinestrosa, de hace unos 55.000 años, aparecido en un sondeo sedimentario recogido en el Mar Cantábrico. La escala representa 0,1 mm.
Fotografía de microscopio electrónico de barrido del caparazón de un ejemplar del foraminífero planctónico Neogloboquadrina pachyderma variedad sinestrosa, de hace unos 55.000 años, aparecido en un sondeo sedimentario recogido en el Mar Cantábrico. La escala representa 0,1 mm.Como un ejemplo vale más que mil palabras, voy a acudir a mis dos grupos faunísticos preferidos, los foraminíferos y los ostrácodos. Y os voy a presentar dos especies concretas, con unos nombres muy sencillos de recordar: Neogloboquadrina pachyderma variedad sinestrosa, un foraminífero planctónico, y Acanthocythereis dunelmensis, un ostrácodo bentónico, que habitan en zonas circumpolares del Atlántico Norte en aguas con temperaturas de entre 0ºC y 6ºC. En la actualidad, en el Mar Cantábrico A. dunelmensis no está presente, mientras que N. pachyderma sin. aparece de manera anecdótica y arrastrada por las corrientes procedentes de zonas más profundas del Golfo de Bizkaia. Sin embargo, en los eventos más fríos acontecidos en los últimos 130.000 años, ambas especies son dominantes. Esto implica que, en esos momentos de clima frío de corta duración, se produce la entrada de masas de agua polares llegadas desde el norte de Europa en el Mar Cantábrico.
 Fotografía de Microscopio Electrónico de Barrido de la parte externa de una valva del ostrácodo Acanthocythereis dunelmensis, de hace unos 30.000 años, aparecido en un sondeo sedimentario recogido en el Mar Cantábrico. La escala representa 0,1 mm.
Fotografía de Microscopio Electrónico de Barrido de la parte externa de una valva del ostrácodo Acanthocythereis dunelmensis, de hace unos 30.000 años, aparecido en un sondeo sedimentario recogido en el Mar Cantábrico. La escala representa 0,1 mm.Estas señales biológicas para definir eventos climáticos son tan evidentes que, los incrementos bruscos en la abundancia de N. pachyderma sin. se utilizan para realizar una biocronología precisa para finales del Cuaternario en latitudes medias-bajas del Atlántico Norte. Y, en el caso de los ostrácodos, estas especies polares que colonizan zonas de latitudes más bajas llevadas por la entrada de masas de agua muy frías procedentes del Norte de Europa, reciben el nombre de “los invitados del norte”.
Como soy una friki, me encanta este nombre, porque me imagino a los ostrácodos como los primeros vikingos que llegaron al Mar Cantábrico decenas de miles de años antes que los humanos. Pero, lo verdaderamente increíble es que, unos microorganismos que miden menos de un milímetro de largo, son capaces de darnos una información climática tan precisa como identificar eventos climáticos que apenas duraron unos cientos de años. Y esta reconstrucción del pasado es básica para poder adaptarnos al cambio climático del futuro, porque hemos visto que estos eventos fríos ocurren de manera periódica. Aunque seguiré imaginándome a estos ostrácodos con cascos de hierro, escudos redondos y hachas cortas llegando a conquistar nuestras costas.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Las señales del frío que vienen del Norte se ha escrito en Cuaderno de Cultura Científica.

