La tentación de la explicación única

Una de las principales y quizá más importantes características del cerebro humano es esa incomodidad, esa especie de ‘picor’ metafísico que sufre cuando desconocemos la explicación a un fenómeno observado. Esa inquietud que nos lleva a perseverar en buscar explicaciones y que nos recompensa con un instante de placer, un destello de gozo y bienestar cuando descubrimos la solución a un problema o la explicación a un enigma: la razón de que los humanos consideremos los rompecabezas, puzzles y todo tipo de juegos de adivinanzas como algo agradable en lugar de como una maldición. A nuestra mente le gusta descubrir cosas, y esto hace que tengamos un irresistible impulso curioso que nos mueve a buscar y a preguntar.
Aunque como casi todas las características que podemos considerar ‘naturales’ esta tendencia irreprimible a la curiosidad también puede provocar efectos paradójicos que nos lleven justo en la dirección contraria a la que queremos llevar. La naturaleza y nuestros impulsos morales muchas veces no tienen un encaje sencillo, y si nuestra querencia por ese momento ‘ahá’ del descubrimiento y la comprensión nos puede llevar a practicar la ciencia y a buscar el conocimiento también nos puede empujar a una de las tentaciones intelectuales más comodonas y cobardes, como es la explicación única: inventar una teoría o concepto que, como una navaja suiza intelectual, sirve para explicarlo TODO.
Un ejemplo simple es la cosmogonía de todas y cada una de las religiones que en el mundo hay y ha habido, para las cuales la historia humana y prehumana se explica entera con un concepto simple: porque la [inserte deidad] así lo quiere. ¿La distribución de los animales y plantas y sus características? La divinidad así lo dispuso. ¿Algo que no encaja en física, geología, meteorología? Es voluntad de la deidad. ¿Problemas sociales, históricos, sorpresas evolutivas? Nuestro dios lo quiso así. Con un mínimo de flexibilidad que permita incorporar (como subunidades de la divina voluntad) cualquier explicación racional y lógica esta versátil herramienta no hay fenómeno, causa o consecuencia que no sea capaz de explicar. Con la ventaja de que incluso puede usarse para construir relaciones causales tan barrocas y complejas como para satisfacer a las mentes más inquisitivas: la historia de la escolástica demuestra la cantidad de esfuerzo intelectual que se puede dedicar (¿perder?) en tratar de seguir los vericuetos de la voluntad divina, si uno se empeña en ello.
La así llamada ‘teoría de los antiguos cosmonautas’ es una versión más moderna del mismo principio; en este caso la explicación multiusos se resume en una única palabra, que es ‘alienígenas’. ¿No entendemos los detalles nimios de cómo los egipcios construyeron las pirámides, los habitantes de la britania prehistórica erigieron Stonehenge o los incas crearon los magníficos templos de Cuzco o Machu Picchu? Los extraterrestres. ¿Hay parecidos entre algunos edificios erigidos por civilizaciones dispersas a grandes distancias en el espacio y el tiempo? Claro, porque los alienígenas. ¿Algunos símbolos de lenguajes separados por decenas de miles de kilómetros y otros tantos años se parecen, si los miramos asá? Lógico: es cosa de los Grises y su (oculta, casi indescifrable, misteriosa, constante) intervención en la historia humana. Como las cosmogonías religiosas se trata de crear una explicación única que sirve para tapar cualquier hueco en nuestro conocimiento y que rellena cualquier grieta, real o imaginaria. Teniendo una explicación, única, polivalente y sin posible discusión, hay quien se da por satisfecho y a otra cosa. Todas las ventajas del conocimiento sin necesidad ninguna de trabajar para conseguirlo: un verdadero chollo.
Las cosas, por supuesto, son mucho más complejas, difíciles de comprender e interesantes que todo eso. Las explicaciones únicas sólo satisfacen el principio de economía de esfuerzo: contempladas con espíritu crítico las numerosas simplificaciones y renuncias intelectuales que conllevan quedan dolorosamente claras. Cuando se aplica un mínimo de rigor las juntas de las grietas salen a la superficie, las dudas vuelven y los hechos no encajan; la realidad siempre es mucho más sutil e interesante que las explicaciones polivalentes que al igual que las herramientas multiuso sirven para todo, pero todo lo hacen mal. Lo más curioso es que sí hay una explicación subyacente que es real a muchas de las coincidencias en las que se apoyan los partidarios de las teorías únicas del universo, una que es tan obvia que raras veces se subraya y que es tan simple como caer en que hay un factor común en muchos fenómenos y misterios, que no es otro que el factor humano.
Si hay paralelismos entre edificios, momentos históricos, imágenes o decoraciones entre diferentes civilizaciones es porque todas ellas estaban compuestas por seres humanos, que comparten limitaciones, capacidades e inteligencia. Si muchos edificios antiguos tienen forma de pirámide es porque todos ellos fueron construidos por sociedades de humanos, que por definición miran, piensan y trabajan de formas paralelas, ya que pertenecen a la misma especie. Si existen similitudes entre representaciones gráficas de distintas civilizaciones y tiempos es porque todas las civilizaciones comparten un hecho común, que no es que fueran visitadas por deidades o extraterrestres, sino que estaban compuestas por personas. Extraer este factor común es suficiente casi siempre para que las teorías de la Explicación Única se derrumben como si estuviesen hechas de arena. Que, intelectualmente, es de lo que son.
Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.
El artículo La tentación de la explicación única se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La tentación de la posesión
- Por qué los niños preguntan “por qué” y qué constituye una buena explicación
- Pseudociencia y arrogancia
Los amiloides y el origen de la vida

Suponiendo que reconozcas la palabra amiloide, si te pido que la asocies con algo lo más probable es que ese algo sea el alzhéimer. Si por alguna razón te interesa el mundo de las enfermedades neurodegenerativas es probable que también la asocies al párkinson o a la enfermedad de Creutzfeldt-Jacobs. Lo que es menos probable es que la asocies con el origen de la vida. Y de esto precisamente es de lo que vamos a hablar.
Los amiloides son agregados fibrosos de unas moléculas llamadas péptidos. Hasta hace poco no se sabía que los amiloides aparecen como elementos estructurales y funcionales en una amplia gama de formas de vida, desde bacterias, levaduras y hongos hasta humanos. En los vertebrados intervienen en la producción del pigmento melanina (en los humanos este es la molécula que los broncea al exponerse al sol), mientras que las células de levadura usan agregados amiloides para formar un tipo de memoria molecular (sí, eso existe).
Las fibras de amiloide están compuestas de aminoácidos unidos de una forma concreta, la parte ácido de uno con la amino del siguiente, formando lo que se conoce como enlace peptídico; por ello se dice que los amiloides son péptidos cortos. Las proteínas son cadenas largas de péptidos (polipéptidos) y las enzimas son proteínas que aceleran y regulan las reacciones bioquímicas. Resulta que las fibras de amiloide pueden acelerar las reacciones bioquímicas de una forma similar a como lo hacen las enzimas. Este hecho ha sido clave para que algunos investigadores aventurasen la posibilidad de que los amiloides participasen activamente en el origen de la vida como precursores de las moléculas de la vida, la llamada abiogénesis. Pero faltaba algo evidente en esta hipótesis: la capacidad de autorreplicarse.
Ahora, investigadores del Instituto Federal Politécnico de Zúrich (Suiza) han realizado un experimento en el que demuestran que los amiloides pueden servir como plantilla química para la síntesis de péptidos cortos. De donde se deduce que esta capacidad también se aplicaría potencialmente al amiloide mismo, él mismo un péptido corto; por lo tanto las moléculas podrían autorreplicarse.
Hace dos años este mismo grupo de investigación demostró experimentalmente que las estructuras amiloides pueden formarse espontáneamente con asombrosa facilidad, a partir de aminoácidos simples que probablemente ya existían cuando la Tierra aún carecía de vida, y bajo condiciones de reacción que parecen muy plausibles que pudiesen existir en aquella época. Lo mismo aplica para la síntesis de péptidos cortos: el mecanismo de reacción es general, es estable en un rango amplio de condiciones de temperatura y salinidad, y lo es tanto en medios ácidos como básicos. Todo esto junto refuerza la idea de que los amiloides pudiesen haber jugado un papel relevante en la historia evolutiva química, tanto como portadores de información como como catalizadores.
Hasta ahora la hipótesis más aceptada para los comienzos moleculares de la vida ha sido la del ARN, que ve al ácido ribonucleico (ARN) como el único elemento clave en la sopa prebiótica primordial. Esto se debe a que, al igual que el ADN, las moléculas de ARN pueden codificar información y también pueden autorreplicarse.
Estos resultados harían de la hipótesis amiloide una idea claramente competitiva frente a la hipótesis del mundo de ARN por dos motivos fundamentalmente. El primero porque las moléculas de ARN con función biológica son mucho más grandes y complejas que los amiloides, por lo que es menos fácil que se formen en condiciones prebióticas. Por otra parte, los amiloides son mucho más estables y tienen una ruta de síntesis abiótica mucho más simple que las versiones catalíticas del ARN.
No se podrá probar nunca a ciencia cierta cual es la hipótesis correcta. Pero no parece demasiado aventurado afirmar que pudieron existir procesos moleculares múltiples que participaron en el origen de la vida.
Referencia:
Rout SK, Friedmann MP, Riek R, Greenwald J (2018) A prebiotic template-directed peptide synthesis based on amyloids. Nature Communications doi: 10.1038/s41467-017-02742-3
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Los amiloides y el origen de la vida se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Pro 2017: Carlos Briones y el origen de la vida
- ¿Y si la Gran Oxidación tuvo un origen geológico?
- Un origen químico de la vida elegantemente simple
Pierre Fatou, un matemático poco (re)conocido
Pierre Joseph Louis Fatou (1878-1929) nació tal día como hoy, hace 140 años.

Pierre Fatou. Fuente: Wikimedia Commons
Fue un matemático y astrónomo francés. Ingresó en la École Normale Supérieure de París en 1898 para estudiar matemáticas, y se graduó en 1901. Intentó obtener un puesto como matemático –en el Collège de France, en La Sorbona, etc.– sin éxito: trabajó durante casi toda su vida como astrónomo adjunto de Observatorio de París, hasta el año 1928 en el que se convirtió en astrónomo titular. Como cualquier astrónomo que trabajaba por la noche, vivía cerca del Observatorio, en el boulevard Montparnasse, cerca del Bal Bullier, un salón de baile en el que pasaba bastante tiempo practicando una de sus pasiones –le gustaba la música, la fotografía, caminar por París, los paseos por la montaña… y el baile: incluso asistió a clases de tango–.
Fue un científico activo, que escribió numerosos artículos de matemáticas sobre temas variados de análisis y geometría, realizó observaciones astronómicas –se especializó en el análisis de estrellas dobles– y obtuvo importantes resultados sobre mecánica celeste.
También estuvo integrado en medio científico de su tiempo, siendo miembro activo de las comunidades matemática y astronómica. Fue –entre otros– presidente de la Association amicale des personnels scientifiques des observatoires français y participó en las actividades de la Société mathématique de France desde 1907 hasta su muerte –fue su presidente en 1926–.
¿Qué aportaciones matemáticas realizó? Es muy conocido –cualquier persona que ha estudiado teoría de la medida lo debería recordar– el lema de Fatou. Su tesis doctoral, defendida en 1907, llevaba por título Séries trigonométriques et séries de Taylor.
Las personas que trabajan en dinámica compleja saben, además, que Fatou fue uno de los creadores de su disciplina. Su carrera fue lenta y modesta, como él mismo admitía a su amigo Paul Montel (1876-1975) hacia 1920:
En cuanto a mí, me he resignado de antemano a no llegar nunca, continuaré tranquilamente mi profesión de suborden […]; no es muy glorioso, pero mi filosofía se acomoda y eso no me impedirá hacer matemáticas en la medida de mis posibilidades (traducido de [1]).
Desde 1906, Fatou empezó a interesarse en los procesos iterativos, y aunque obtuvo resultados sorprendentes, no publicó nada sobre este tema.
En 1915, la Académie des sciences convocó precisamente un Grand Prix des sciences mathématiques –para 1918– sobre este tema. Fatou empezó a trabajar en ello a partir de 1917 y publicó sus resultados en forma de notas en los Comptes rendus. En junio de 1917, Paul Montel publicó una nota en esta misma revista científica sobre otro tema: contenía una idea de la que Fatou se adueñó, y que sesenta años más tarde Benoît Mandelbrot (1924-2010) denominaría conjuntos de Julia.

Un conjunto de Julia. Fuente: Wikimedia Commons
El matemático Gaston Julia (1893-1978) también había visto la nota de Montel, y tuvo ideas análogas a las de Fatou… reclamó la prioridad sobre ellas y la Académie des sciences se la concedió. Fatou continuó trabajando tranquilamente sobre el tema, y Julia envió su candidatura para el Grand Prix des sciences mathématiques y lo ganó. Aunque Fatou no presentó su candidatura para el premio, la Académie des sciences le mencionó en el informe que atribuía el premio a Julia, y posteriormente le concedió un reconocimiento por sus trabajos en este tema.
¿Por qué la Academia se posicionó a favor de Julia? En [1], Michèle Audin comenta que quizás la situación de Gaston Julia pudo ayudar. El joven Julia tuvo que partir a la guerra en 1914 tras su brillante carrera en la École normale supérieure de París. En enero de 1915 fue gravemente herido en la cara –tuvo que llevar toda su vida una máscara de cuero–. Muchos jóvenes científicos franceses fallecieron en aquella guerra y, quizás Julia representaba un icono para la comunidad matemática francesa.
En el libro [2] de Michèle Audin ([3] en su traducción al inglés), la autora habla precisamente sobre como Fatou y Julia inventaron los hoy llamados conjuntos de Julia. Habla de las matemáticas, los conflictos y las personalidades de estos dos científicos… y también un poco de dinámica compleja. ¡Muy recomendable!
Referencias
[1] Michèle Audin, Pierre Fatou, mathématicien et astronome, Images des Mathématiques, CNRS, 2009
[2] Michèle Audin, Fatou, Julia, Montel, le Grand Prix des sciences mathématiques de 1918, et après…, Springer, 2009
[3] Michèle Audin, Fatou, Julia, Montel. The Great Prize of Mathematical Sciences of 1918, and Beyond, Springer, 2011
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Pierre Fatou, un matemático poco (re)conocido se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Un convite matemático ‘de altura’
- El problema matemático de las cartas extraviadas
- Del nudo gordiano al nudo de los enamorados, por territorio matemático
Corazones miogénicos y neurogénicos

Los iones como Na+, Cl–, K+, Ca2+ y otros no se distribuyen de forma simétrica a ambos lados de la membrana celular. Además, esta no es igualmente permeable para con unos iones y otros, y esa diferencia de permeabilidad determina que unos la puedan atravesar con facilidad y otros no. En las células animales la distribución de los iones a los dos lados de la membrana y la permeabilidad diferencial de esta para con unos y otros electrolitos da lugar a la existencia de una diferencia de potencial eléctrico entre el interior y el exterior celular. Llamamos “potencial de membrana” a esa diferencia de potencial, y suele ser negativa, lo que quiere decir que en el lado interno se acumulan cargas negativas y positivas en el externo.
Las células musculares se contraen en respuesta a despolarizaciones o cambios de polaridad de la membrana celular. O sea, la membrana celular puede pasar a tener más cargas positivas en el lado interno de la membrana y más cargas negativas en el externo. Esas despolarizaciones, denominadas potenciales de acción, son transitorias y, como se ha señalado, son los estímulos que provocan la contracción de las células musculares y, en consecuencia, el acortamiento del músculo1. Esto vale para todo tipo de musculatura, incluido el músculo cardiaco.
Un corazón se contrae rítmicamente porque sus células se contraen de esa forma. Eso quiere decir que en los corazones se están produciendo despolarizaciones de forma permanente con carácter rítmico. Por otro lado, la despolarización puede tener su origen en las mismas células cardiacas -en los corazones miogénicos-, o en células nerviosas -en los corazones neurogénicos-. Los corazones de vertebrados son del primer tipo, mientras que los de algunos artrópodos (crustáceos decápodos, cangrejo en herradura, arañas y escorpiones) son del segundo.
Corazones miogénicos
La mayor parte de los corazones de vertebrados reciben señales del sistema nervioso autónomo y está sometido a un cierto control por su parte, pero si se aísla uno de estos corazones, no deja de latir enseguida, lo que quiere decir que es capaz de hacerlo sin necesitar impulsos externos.
Las células cardiacas de vertebrados se hallan conectadas eléctricamente unas a otras mediante uniones gap, que son estructuras propias de ciertas membranas celulares que proporcionan continuidad citoplasmática a células adyacentes y que se encuentran en regiones especializadas denominadas discos intercalares. Las cargas eléctricas (en forma de iones) se mueven libremente por esas uniones gap, por lo que las despolarizaciones pueden transmitirse de unas células a otras a su través. Por ello, una vez se produce una despolarización en una célula, esta se extiende progresivamente al resto del corazón.
Las células cardiacas de vertebrados tienen la facultad de contraerse rítmicamente de forma espontánea. Pero si se dejase a cada célula contraerse por su cuenta, el conjunto del corazón no lo haría de forma coordinada, porque cada célula tendría su propio ritmo. Hay un grupo de células musculares especializadas, denominado marcapasos, que controla el ritmo de las demás células del miocardio (músculo cardiaco). En los vertebrados ectotermos el marcapasos se encuentra en la pared del seno venoso, la primera cámara cardiaca o en la unión entre el seno venoso y la aurícula. En aves y mamíferos, en los que el seno venoso ya se ha incorporado a la aurícula2, el marcapasos se halla en la pared de la aurícula derecha y es conocido como nodo seno-auricular. Las células del marcapasos son de naturaleza muscular pero apenas tienen capacidad para contraerse. Son las que tienen la frecuencia de despolarización espontánea más alta de todas las células del miocardio. Gracias a ese rasgo son las primeras en despolarizarse en cada latido, de manera que son las que inician la onda de despolarización que se expande por todo el corazón; y por ello el de esas células es el ritmo de contracción que seguirá todo el corazón.
Las aurículas están separadas de los ventrículos por una capa de tejido conjuntivo fibroso que no permite el paso de las señales eléctricas pues carecen de las uniones gap propias de las células musculares. En los mamíferos hay un sistema de conducción, una vía de conexión entre ambas zonas, las aurículas y los ventrículos. Está formado por células musculares especializadas, y empieza en un grupo de células situadas en la pared de la aurícula derecha que se denomina nodo aurículo-ventricular. De este nodo parte un conjunto de células denominado fascículo aurículo-ventricular, o fascículo de His, que atraviesa la capa de tejido conectivo y penetra en la pared o septo interventricular (pared que separa los dos ventrículos), donde se separa en dos ramas. Las ramas se deslizan por las superficies izquierda y derecha de la pared hasta conectar con las fibras de Purkinje, que se ramifican en el fondo de cada ventrículo.
El dispositivo descrito provoca que la onda despolarizante surgida en el nodo seno-auricular se extienda, en primer lugar, por las aurículas; una vez se han contraído estas, la onda se transfiere a los ventrículos a través del fascículo de His. De esa forma los ventrículos no comiencen su contracción hasta que no la han completado las aurículas, garantizándose así un flujo de sangre normal de las aurículas a los ventrículos.

Homarus gammarus
Corazones neurogénicos
Al contrario que en los corazones miogénicos, en los neurogénicos la despolarización rítmica no tiene su origen en células musculares, sino en células nerviosas. Un ejemplo magnífico de este tipo de corazones es el del bogavante. En este las células musculares funcionan de forma similar a como lo hacen las del músculo esquelético, ya que todas ellas se encuentran inervadas por células nerviosas que son las que les transmiten los impulsos que dan lugar a la despolarización de la membrana que desencadena el mecanismo de la contracción.
El tejido nervioso que genera las despolarizaciones rítmicas es el ganglio cardiaco, que consta de nueve neuronas y se halla situado en la superficie interna del lado dorsal del corazón. Los axones de cinco de esas neuronas inervan las células musculares. Y las otras cuatro, las que conforman el ganglio propiamente dicho son las que generan el ritmo de despolarizaciones; es una de sus neuronas, en concreto, la que asume esa función. Actúa como un generador central de patrones, produciendo de forma espontánea y periódica trenes de potenciales de acción (impulsos nerviosos). Esas señales se transmiten a través de las otras cinco neuronas a las células musculares, contrayéndose todas ellas casi al unísono. Al contrario que las células de los corazones miogénicos de vertebrados, si al corazón del bogavante se le priva del ganglio, sus células musculares no son capaces de contraerse de manera espontánea.
Fuente:
Richard W. Hill, Gordon A. Wyse & Margaret Anderson (2004): Animal Physiology. Sinauer Associates, Sunderland
Notas:
1 Conviene aclarar que bajo determinadas circunstancias puede producirse contracción de las células musculares pero el músculo no llega a acortarse. Es a lo que se llama contracción isométrica.
2 Aquí puede consultarse una descripción muy somera de los diferentes configuraciones cardiacas en vertebrados.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Corazones miogénicos y neurogénicos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Confirmación experimental de la teoría de la relatividad especial (y 2)

La relatividad de longitud
Recuerdemos que una de las ideas básicas de la teoría de la invariancia es que toda velocidad es relativa al observador que mide la velocidad. Con esto en mente, volvemos al rompecabezas de los muones de larga vida, pero esta vez desde la perspectiva del desventurado muón que atraviesa la atmósfera de la Tierra. Desde el punto de vista del muón está en reposo, mientras que es la superfive de la Tierra la que está volando hacia él a una velocidad cercana a la velocidad de la luz. Dado que la Tierra se está moviendo ahora con respecto al propio marco de referencia del muón, la distancia desde la parte superior de la atmósfera hasta el suelo sufre una contracción de la longitud cuando se ve desde el punto de vista del muón. La contracción es tan grande que, desde la perspectiva del muón, no tiene problemas para cubrir esta distancia corta en los tan solo 2,2·10-6 segundos corta vida que tiene en su marco de referencia “estacionario”. Una vez más, las observaciones están en completo acuerdo con las predicciones de la teoría de la relatividad especial.
La relatividad de la masa
La teoría de la invariancia predice que la masa observada de un objeto aumentará a medida que aumente la velocidad relativa del objeto. Curiosamente, este efecto se había observado incluso antes de la teoría de Einstein, cuando los científicos se sorprendieron al notar un aumento en la masa de los electrones de alta velocidad en los tubos de vacío. Este efecto se observa fácilmente hoy en día en los aceleradores de partículas, donde las partículas elementales cargadas, como los electrones o los protones, se aceleran mediante campos electromagnéticos a velocidades tan altas como 0,9999999 de la velocidad de la luz. Las masas de estas partículas aumentan exactamente la cantidad predicha por la fórmula de Einstein. A esa velocidad, el aumento de su masa mm es aproximadamente 2236 veces la masa en reposo. De hecho, los aceleradores circulares deben diseñarse para tener en cuenta este aumento de masa.
A medida que las partículas se aceleran a altas velocidades por los campos eléctricos, los campos magnéticos las curvan en una trayectoria circular para hacerlas volver al principio y permitir que los campos eléctricos las aceleren repetidamente. Para impedir que la partícula que se mueve en una trayectoria circular salga en línea recta se requiere una fuerza centrípeta. Esta fuerza viene dada por la ecuación F = mv2 / R., donde R es el radio del círculo, que es constante; v es la velocidad de la partícula, que va aumentando aumenta; y m es la masa en movimiento, que también aumenta según la teoría de la relatividad.
Si los ingenieros no toman en cuenta el aumento de masa a la hora de diseñar los aceleradores de partículas, la fuerza magnética no sería suficiente para mantener las partículas en la trayectoria circular del acelerador, golpearían la pared y se acabó el acelerador. Un acelerador circular simple se llama ciclotrón. Pero cuando el aumento de la fuerza de aceleración (la frecuencia del campo eléctrico) se sincroniza con precisión con los aumentos de velocidad y masa relativistas, se llama sincrociclotrón.

La equivalencia de masa y energía
Einstein consideró la equivalencia de masa y energía, tal y como se expresa en la ecuación E = m·c2, como un resultado teórico significativo de la relatividad especial, pero no creía que tuviera ninguna importancia práctica cuando anunció su hallazgo. Y ahí se equivocó. Quedó patente en las explosiones nucleares (mejor que “atómicas”) de 1945. La tremenda energía liberada en una bomba de ese tipo se deriva de la transformación de una pequeña cantidad de la masa de los núcleos de uranio o plutonio en su enorme cantidad equivalente de energía.
Las bombas y los reactores nucleares se basan en la energía liberada por la división de átomos pesados. Un proceso opuesto, una reacción de fusión, tiene lugar cuando se unen núcleos de elementos ligeros. De nuevo, una pequeña cantidad de la masa se convierte en energía de acuerdo con la fórmula de Einstein. Aún no ha sido posible controlar este proceso de fusión a una escala suficiente para producir electricidad para uso doméstico e industrial; este proceso sí tiene uso militar. Con todo, el proceso de fusión nuclear tiene una importancia muy práctica: es la base de la producción de energía del Sol y todas las demás estrellas del Universo. Sin él, la vida no podría existir en la superficie de la Tierra.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Confirmación experimental de la teoría de la relatividad especial (y 2) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Confirmación experimental de la teoría de la relatividad especial (1)
- La primera confirmación experimental de la teoría de Maxwell
- La relatividad de la masa
“Si todos tus amigos se tiran por un puente, ¿tú también te tiras?”: los adolescentes, los amigos y los riesgos

Fuente: Pixabay
En un experimento cuyos resultados se publicaron en 2014, se colocó a 66 chavales de entre 16 y 18 años en un simulador de conducción para medir lo temerario de sus decisiones. A veces conducían solos y a veces lo hacían acompañados por otro adolescente. Los resultados demostraron lo que cualquier padre cree saber por intuición: que un chaval de esa edad es mucho más sensato cuando está solo que cuando le ven sus amigos.
La forma en que los adolescentes se exponen a determinados riesgos es un quebradero de cabeza para cualquier progenitor: alcohol, tabaco, drogas, sexo sin protección, peleas, accidentes de tráfico, comportamientos temerarios en general… ¿Por qué estos hijos nuestros (vuestros) parecen olvidar todo lo aprendido sobre seguridad y autocuidado cuando llegan a la adolescencia y se rodean de la banda de cabestros (con perdón) que pueden llegar a ser sus amigos?
Que los adolescentes son más temerarios no es solo una intuición. Según datos de la OMS la tasa de muerte entre los 15 y los 19 años es un 35% mayor que entre los 10 y los 14, y los comportamientos de riesgo están asociados a muchas de las amenazas para la vida durante este periodo: los accidentes de carretera es la principal causa de muerte para adolescentes en todo el mundo, seguidos por las autolesiones y otras formas de violencia. Además, algunas prácticas que pueden llevar a problemas de salud más adelante, como el tabaquismo, el alcoholismo o una vida sedentaria muchas veces provienen de malas elecciones hechas durante la adolescencia.

Fuente: Pixabay
Más allá del “tú no me mandas”
Asociamos esa forma de asumir riesgos sin pensar en las consecuencias a la rebelión de la edad, el “tú ya no me mandas”, pero algunas investigaciones recientes que recoge la revista Nature en su especial Ciencia adolescente han empleado un enfoque neurocientífico más profundo para entender este fenómeno.
Porque entender la forma en que los adolescentes interactúan con el riesgo es interesante. Es cierto que asumen más peligros que los adultos, algunos de ellos con graves consecuencias: heridas, lesiones, enfermedades o problemas de salud de por vida, antecedentes penales y encontronazos con la justicia… Pero hay otros tipos de riesgos, como los riesgos sociales, por ejemplo, a los que pueden ser mucho más adversos que las personas de más edad, y otros, como los riesgos positivos (hacer exámenes o pruebas que den acceso a niveles educativos superiores, por ejemplo) con los que se relacionan de forma más habitual que nosotros.
Y cada uno de estos comportamientos parece tener diferentes efectos en el cerebro. Tener esto en cuenta puede ser importante por ejemplo para decidir si hay que reducir o no la edad mínima para conducir, o cómo debe tratarse a un adolescente que haya cometido un crimen. Saber cómo el cerebro adolescente evalúa y maneja las situaciones de riesgo puede servir para diagnosticar enfermedades como la esquizofrenia o la depresión, a que a menudo empiezan a asomar la patita durante la estos años.
No es un campo nuevo. El cerebro adolescente y su relación con el riesgo lleva años analizándose. Las primeras teorías apuntaban a un posible desequilibrio durante el desarrollo cerebral: las áreas asociadas con la impulsividad y con la sensibilidad a la recompensa, especialmente la recompensa social, se desarrollan mucho antes y del tirón, mientras que el control de los procesos cognitivos, como la memoria de trabajo (cómo almacenamos y elaboramos la información), siguen un proceso más lento pero continuado durante todo el crecimiento. La metáfora habitual era la de un coche con el acelerador pulsado a fondo pero con los frenos defectuosos.
Y esto encajaba con algunos datos, pero no con el hecho de que algunos adolescentes no son tan proclives a asumir riesgos, algo que debería ser generalizado si hablamos de una cuestión asociada con la edad y el proceso de desarrollo. Por eso ahora la mayoría de los neurocientíficos consideran que diferentes sistemas desarrollándose a diferentes velocidades no significan que el cerebro esté desequilibrado.

Fuente: Pixabay
La influencia de los iguales
Así que la investigación se orienta a un mayor abanico de riesgos y de influencias del ambiente. Para muchos adolescentes el riesgo no es solo lo que les puede causar daño físico o repercusiones legales: hay situaciones relativamente benignas, como pedir una cita a una persona que les gusta o dar la cara ante un progenitor o un profesor, que parecen para ellos mucho más arriesgadas.
En 2009, una investigación de la Universidad Temple, en Philadelphia, llevó a cabo una versión del experimento con el que abrimos este artículo: pidió a voluntarios adolescentes que se sometiesen a un escáner cerebral a la vez que jugaban a un videojuego en el que conducían un coche que pasaba por la enervante cantidad de 20 semáforos en 6 minutos. Algunos de ellos comenzaban a acelerar con la luz en ámbar mientras otros esperaban a que se pusiese en verde. A veces acelerar antes salía bien, pero otras terminaba en un accidente.
Los investigadores observaron que cuando los chavales jugaban a solas, asumían el riesgo de tener un accidente con la misma frecuencia que los adultos. Pero cuando se les decía que sus amigos les estaban viendo jugar desde la habitación de al lado, lo hacían con mucha más frecuencia. En otro experimento parecido, los chavales asumían muchos menos riesgos cuando se les decía que quien les estaba viendo jugar desde la sala contigua era su madre.
Mientras tanto, el escáner reveló una actividad muy intensa en las zonas del cerebro relacionadas con la recompensa, como la llamada núcleo estriado, cuando asumían riesgos mientras les veían sus amigos; cuando era su madre la que observaba, era la zona del córtex prefrontal, relacionada con el control cognitivo, la que se ponía a funcionar.

Fuente: Pixabay
La influencia del grupo no siempre es negativa
Así que se pudo comprobar una vez más que la propensión a asumir riesgos en los adolescentes depende en gran medida de las relaciones sociales con sus iguales, y del miedo a quedar aislados. Esto, de nuevo, es una realidad casi palpable para todos aquellos padres preocupados porque los amigos de sus hijos puedan ser para ellos una mala influencia.
Pero no todo es malo, porque algunos experimentos han demostrado un efecto positivo en esta presión de sus iguales. En un estudio se pidió a varios adolescentes que jugasen un juego en el que tenían que elegir entre donar dinero a una buena causa o quedárselo, mientras otros adolescentes les veían. Los resultados mostraron que si el sujeto hacía una donación y los otros aprobaban el gesto, éste tendía a hacer más donaciones durante el resto del juego. Así que, aunque solemos asumir que la influencia del grupo es siempre algo negativo, la realidad parece ser algo más compleja.
Y es aun más interesante observar que el mismo sistema cerebral que empuja a los adolescentes a asumir riesgos insanos les empuja también a asumir riesgos positivos: la actividad en el núcleo estriado, concretamente un aumento en los receptores de dopamina de esas zonas, se ha relacionado con una mayor sensibilidad a recompensas por actos positivos, así como peligrosos.
Las limitaciones de estos estudios
Como casi todos, estos estudios tienen sus limitaciones porque es difícil reproducir en un laboratorio los estímulos, las actividades y las condiciones sociales y de comportamiento en las que se ven envueltos los adolescentes en su día a día. Como mucho se puede captar la inclinación a asumir riesgos de los chavales que participan en ellos, pero eso queda algo lejos de cómo afrontan riesgos cotidianos concretos.
Hay que tener en cuenta también que los adolescentes de estos estudios, igual que la media, solo se exponen a riesgos moderados, mientras que existen algunos individuos que están dispuestos a exponerse a riesgos muy elevados (violencia juvenil, acceso a lugares peligrosos por caídas o accidentes…), y estos podrían procesar esos riesgos de una forma muy distinta.
Pero teniendo en cuenta lo que estos estudios revelan y lo que podemos aprender de estos adolescentes medios, quizá debamos replantearnos esas ideas preconcebidas sobre la adolescencia y la presión del grupo: existe y funciona para mal, pero también para bien, algo de lo que se habla mucho menos.
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo “Si todos tus amigos se tiran por un puente, ¿tú también te tiras?”: los adolescentes, los amigos y los riesgos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Y si el cambio climático nos termina haciendo a todos más simpáticos?
- El sensacionalismo en las noticias clave en la concienciación sobre los riesgos de Internet
- La familia, los amigos, los jóvenes y la ciencia
¿Cuántas células hay en el cuerpo humano?
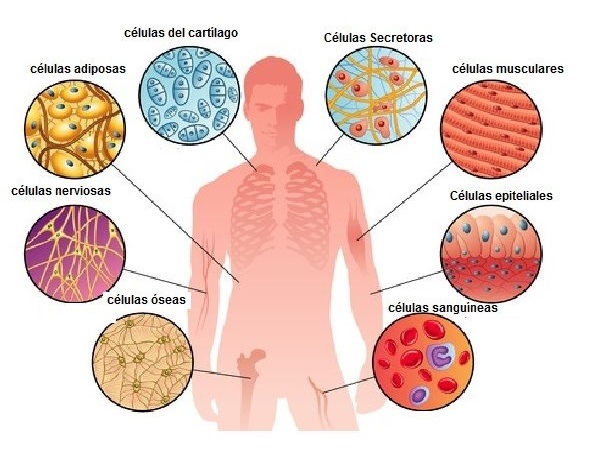
La respuesta no es fácil y, de hecho, hasta hace poco no ha habido estimaciones mínimamente fiables. Los primeros cálculos con cierto rigor se publicaron en 2013, pero en 2016 se hicieron estimaciones más precisas de los seis tipos celulares que se tenían por más abundantes. Esos tipos daban cuenta del 97% del número total de células. Según los últimos cálculos, en el cuerpo de un hombre joven de unos 70 kg y 170 cm de estatura hay aproximadamente 30 billones de células. Y las cifras no serían muy diferentes para una mujer de similares características.
Las células más abundantes, con gran diferencia, son los glóbulos rojos. Hay del orden de veintiséis billones de estos y una cantidad ligeramente inferior en una mujer. Ese número representa el 84% de todas las células. Las plaquetas, aunque mucho menos numerosas, también son muy abundantes, un 4,9% del total. Si tenemos en cuenta que además de glóbulos rojos y plaquetas, en la sangre hay leucocitos, casi el 90% de las células del cuerpo humano se encuentran en la sangre. Y dado que tanto los glóbulos rojos como las plaquetas carecen de núcleo, resulta que casi el 90% de nuestras células -veintiséis billones- son enucleadas.
La médula ósea también contribuye con un elevado número al total: utilizando métodos histológicos, se ha estimado que contiene setecientos cincuenta mil millones de células (2,5%). Otro tipo abundante es el de las endoteliales vasculares, que son las células que tapizan el interior de los vasos sanguíneos. No es fácil determinar su número; lo han calculado a partir del volumen total de sangre que hay en los diferentes tipos de vasos (arterias, venas, capilares), estimando la longitud de cada tipo de vaso a partir de sus diámetros medios. De esa forma calcularon la superficie interna de los vasos, y la dividieron por la superficie media de las células endoteliales. Hay del orden de seiscientos mil millones de estas células (2,1%).
Los linfocitos –del sistema inmunitario- representan un 1,5% del total de células y los hepatocitos –del hígado-, un 0,8%. En el sistema nervioso hay neuronas y células de la glía; estas segundas son las que dan soporte a las anteriores. Pues bien, aunque antes se pensaba que había diez veces más células gliales que neuronas, parece ser que hay muchas menos de las primeras de lo que se creía y el número de unas y de otras es similar. Según las últimas estimaciones, tenemos alrededor de ochenta y cinco mil millones de neuronas y otras tantas células gliales; en conjunto suponen un 0,6% del total. El resto de tipos representan proporciones aún menores del acervo celular humano.
Las cifras anteriores expresan la cantidad de células, su número, pero la imagen cambia mucho si atendemos a la masa de cada tipo. El 25% del peso humano corresponde a líquidos extracelulares (plasma sanguíneo y líquido intersticial) y otro 7% son sólidos extracelulares. Por lo tanto, a una persona de 70 kg le corresponden 46 kg de masa celular. Esa masa se reparte del modo siguiente: 20 kg de células musculares; 13 kg de adipocitos (células con depósitos de grasa); 3 kg de glóbulos rojos. La masa del resto es, en total, de 10 kg. Así pues, las proporciones en términos de masa son muy diferentes, por la sencilla razón de que hay grandes diferencias en los volúmenes de unas células y otras.
Y por supuesto, también tenemos bacterias, en el colon principalmente, pero muchas menos de las que se pensaba: son del orden de 38 billones pero solo pesan unos 200 g en total.
Fuente: Ron Sender, Shai Fuchs & Ron Milo (2016): Revised Estimates for the Number of Human and Bacteria Cells in the Body. PLOS Biology
—————————————————————–
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
Una versión anterior de este artículo fue publicada en el diario Deia el 19 de noviembre de 2017.
El artículo ¿Cuántas células hay en el cuerpo humano? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Cuantas menos ecuaciones…. ¿mejor?
- Cómo criopreservar células madre
- Sistemas circulatorios: células sanguíneas
Naukas Bilbao 2017 – Laura Morrón: La gran divulgadora
En #Naukas17 nadie tuvo que hacer cola desde el día anterior para poder conseguir asiento. Ni nadie se quedó fuera… 2017 fue el año de la mudanza al gran Auditorium del Palacio Euskalduna, con más de 2000 plazas. Los días 15 y 16 de septiembre la gente lo llenó para un maratón de ciencia y humor.

Laura Morrón presenta a su candidata al título de mejor divulgador/a de la historia: Jane Haldimand Marcet
Laura Morrón: La gran divulgadoraEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2017 – Laura Morrón: La gran divulgadora se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – José Miguel Viñas: Me río yo del cambio climático
- Naukas Bilbao 2017 – Mónica Lalanda: Una muerte de cómic
- Naukas Bilbao 2017 – Álex Méndez: Luz de luna
La sorprendente densidad ósea de los atletas kenianos
Los resultados del análisis de la densidad mineral ósea en atletas kenianos de élite es verdaderamente sorprendente. Está muy por debajo de lo esperado para hombres de su edad según las guías de la Sociedad Internacional de Densitometría Clínica.

Uno de los factores clave para alcanzar el éxito en el mundo del deporte de élite es minimizar el riesgo de lesiones de los deportistas. En el caso del atletismo de fondo, hay especial prevalencia en las fracturas óseas por estrés, ya que los corredores se someten a grandes cargas de entrenamiento que acaban por llevar sus cuerpos al límite.
Aunque aún no se conoce exactamente el vínculo, parece que existe cierta predisposición a las fracturas de estrés en aquellos individuos con una baja densidad mineral ósea. A diferencia de lo que ocurre con la cadera, o el cuello del fémur (donde los impactos repetitivos que supone la carrera a pie pueden incluso ayudar a incrementar la densidad ósea), la zona lumbar se ve menos expuesta a los impactos. Además, está compuesta mayoritariamente por hueso trabecular, su recambio óseo es mayor y depende más de factores hormonales y metabólicos. Todo eso hace que se suela usar como indicador de la salud ósea de los deportistas.
En el estudio ‘Bone health in elite Kenyan runners’, publicado por la revista Journal of Sports Sciences y en el que ha participado el doctor Jordan Santos-Concejero, del Departamento de Educación Física y Deportiva de la Universidad del País Vasco/Euskal Herriko Unibertsitatea, se analizó la densidad mineral ósea en atletas kenianos de élite y se compararon sus valores con sujetos control sudafricanos sanos de edad y antropometría similar. Para ello, midieron parámetros relacionados con la densidad mineral ósea y composición corporal en atletas kenianos de élite por absorciometría dual de rayos X con un escáner DXA, tanto en la zona del cuello del fémur y cadera como en la región lumbar. Además, se analizaron distintos parámetros biomecánicos con un sistema Vicon de captura del movimiento en 3D para valorar su posible influencia en la densidad ósea de los atletas estudiados.
Los resultados confirmaron, en parte, lo esperado, ya que los atletas kenianos presentaron una mayor densidad ósea en la región proximal del fémur y, de hecho, esa mayor densidad ósea parecía asociada a la carga de entrenamiento y la mayor rigidez articular de los atletas kenianos.
Sin embargo, en la zona lumbar, los resultados fueron muy distintos. “El 40% de los kenianos analizados presentaron valores de densidad ósea muy por debajo de la media esperable para hombres de su edad, según las guías de la Sociedad Internacional de Densitometría Clínica. Hasta el punto de ser clasificados como en riesgo de padecer osteoporosis por la Organización Mundial de la Salud”, comenta el profesor de la UPV/EHU.
Una de las posibles explicaciones para estos valores es un desequilibrio entre gasto y aporte calórico en esos atletas, que se ha visto repetidamente en la literatura que es negativo. Además, la alta carga de entrenamiento parece jugar un papel fundamental en esos bajos valores de densidad ósea en la zona lumbar.
Sin embargo, a pesar de esos valores aparentemente patológicos, la incidencia de fracturas de estrés en kenianos es relativamente baja. Una posible explicación son las menores fuerzas de contacto de estos atletas, tal y como se ha visto en estudios previos (como este o este) o, incluso, es posible que las guías estándar que se utilizan actualmente no sean representativas para una población tan especial como esos atletas, ya que no existen guías específicas para africanos del Este (a pesar de la influencia de la etnicidad en la incidencia de las fracturas de estrés). “Los resultados de este estudio vuelven a poner de relieve la complejidad del fenómeno africano en las pruebas de fondo, ya que un nuevo factor, en este caso su sorprendente densidad ósea, debe ser añadida a la ecuación”, concluye el doctor Santos-Concejero.
Referencia:
N. Tam, J. Santos-Concejero, R. Tucker, R.P. Lamberts, L.K. Micklesfield (2018) Bone health in elite Kenyan runners Journal of Sports Sciences, 36(4):456-461. 2018 doi: 10.1080/02640414.2017.1313998
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La sorprendente densidad ósea de los atletas kenianos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los corredores de élite kenianos oxigenan su cerebro de forma diferente
- La importancia del ritmo en la carrera de fondo
- El sorprendente penacho de Marte
¿Cuánto cuesta realmente investigar en biomedicina?

¿Cuánto cuesta investigar?
¿Cuánto cuesta un proyecto para investigar en biomedicina? Probablemente la gente diría que mucho dinero. Pero, ¿cuánto es mucho dinero? En los proyectos de investigación se habla de miles, de centenares de miles, hasta de millones de euros con aparente soltura. Cifras que son extrañas a la mayoría de la gente, que bastante tiene con llegar a fin de mes y cubrir gastos, cuando lo consiguen. Puede por ello parecer inoportuno o desconsiderado hablar de lo que cuesta investigar, cuando una parte importante de la sociedad tiene problemas esenciales para sobrevivir dignamente.
Sin embargo, creo que aportar cifras a este debate puede ser útil para entender lo que realmente cuesta llevar a cabo un proyecto de investigación en biomedicina. Creo que así puede comprenderse mejor lo que representan los presupuestos dedicados a la investigación por entidades públicas o privadas, las campañas solidarias llevadas a cabo heroicamente por asociaciones de pacientes o por grupos afectados por una determinada enfermedad, las colectas de fondos, las donaciones, etc… En definitiva, las iniciativas varias en favor de la ciencia. Y creo que puede servir para poner en valor lo que significa que estas iniciativas consigan miles, centenares de miles o quizás millones de euros para invertir en proyectos científicos en biomedicina.
Tras muchos años liderando proyectos de investigación y también evaluando proyectos para diversas fundaciones, agencias y administraciones nacionales e internacionales, he pensado que podría ser interesante compartir lo que yo considero que podría costar un proyecto “tipo” en el ámbito de la biomedicina, que es el que conozco.
El coste de un proyecto de investigación en biomedicina depende de muchos factores. Entre otros depende del número de años necesarios para su ejecución (suelen ser proyectos de 3 años, pero los hay de 1 año y hasta de 5 años), del área concreta de investigación (inmunología, oncología, metabolismo, enfermedades raras, neurociencias, etc…), del tipo de experimentos que vayan a acometerse, del número de personas involucradas en el equipo, si es necesario o no adquirir nuevos instrumentos, si es necesario o no contratar a personas para llevar a cabo los objetivos del proyecto, si es necesario o no usar modelos animales, del centro en el cual vaya a ejecutarse el proyecto, de la existencia o no de servicios de apoyo a la investigación en el centro de ejecución, etc.. innumerables factores que pueden hacer variar el coste final del proyecto.
Sin embargo, a pesar de las variaciones consubstanciales a cualquier proyecto de investigación, lo cierto es que todo proyecto científico, también en biomedicina, consta de dos apartados principales: costes directos y costes indirectos.
Los costes directos incluyen los gastos de personal, de adquisición de instrumental o equipos, de fungibles o consumibles, de servicios de apoyo a la investigación, de viajes y otros gastos (gastos de publicación, de telefonía, correos y mensajería, etc…).
Los costes indirectos corresponden a un porcentaje de los costes directos (habitualmente en nuestro país este porcentaje es del 21% para los proyectos financiados desde el denominado Plan Nacional de I+D+i) y es la parte que las instituciones destinan para sufragar los gastos de funcionamiento y mantenimiento de los centros de investigación (luz, agua, gas, calefacción y ventilación, servicio de limpieza, servicio de seguridad, servicio de mantenimiento, de instrumentación, servicios de apoyo científicos y administrativos, personal de apoyo, etc…).
Supongamos un grupo de tamaño medio en un centro de investigación público español que solicita un proyecto de investigación de biomedicina para los próximos 3 años. El grupo estaría formado por unas 5 personas: un/a investigador/a principal, un/a técnico/a de investigación, un/a investigador/a postdoctoral y dos estudiantes de doctorado. Muy probablemente los salarios del investigador postdoctoral, del técnico y de alguno (o los dos) investigadores predoctorales estarán vinculados a los fondos de investigación, a proyectos científicos que son los que sufragan, en su mayor parte o en su totalidad, los gastos de funcionamiento del laboratorio.
El primer apartado a considerar dentro de los costes directos es el capítulo de personal. Hay que recordar que, en los organismos públicos de investigación, los salarios están establecidos institucionalmente. Y son idénticos para hombres y mujeres, naturalmente. Por ejemplo, en el CSIC para contratar un titulado superior (licenciado o graduado, sea doctor o no) el coste de contratación anual, incluyendo las 14 pagas y la cuota patronal de la Seguridad Social, es de unos 36.000 Euros. De forma similar, el coste anual para contratar un técnico de apoyo es de unos 23.000 Euros. Por lo tanto, si proponemos en el proyecto la contratación de un investigador y de un técnico durante los tres años, algo totalmente razonable para poder abordar un nuevo proyecto de investigación en condiciones óptimas, entonces el coste de personal se nos pone ya en: (36.000 x 3) + (23.000 x 3) = 177.000 Euros.
¡Casi 180.000 Euros en Personal… y todavía no hemos gastado nada más ni hemos empezado a hacer ningún experimento! Este es el mundo real, con números reales.
Es probable que tengamos que adquirir algún instrumento específico, algún equipo que no tengamos o que debamos reemplazar o actualizar. Quizás una centrifuga de tamaño medio, un microscopio sencillo o un equipo de análisis de muestras. Aquí los precios pueden ser muy variables, pero algo razonable, para un equipo medio, sería presupuestar unos 30.000 Euros para la adquisición de estos equipos que son necesarios para abordar el proyecto de investigación en condiciones óptimas.
Seguidamente hay que contemplar los gastos fungibles, los denominados consumibles: material de plástico, de vidrio, reactivos varios de biología celular y biología molecular, productos químicos, kits para su uso inmediato, anticuerpos, medios de cultivo para las células, etc… De nuevo este capítulo puede ser muy variable, pero de nuevo, algo razonable, por experiencia, que se ajusta bastante bien a los gastos reales anuales promedio de un grupo de investigación en biomedicina, es considerar un gasto de 6.000 Euros por persona y año. Es decir, para un grupo de 5 personas le correspondería un presupuesto estimado de consumibles de 6.000 x 5 = 30.000 Euros/año, y, por lo tanto, para 3 años este apartado se elevaría a 90.000 Euros.
Supongamos que el grupo de investigación en biomedicina va a generar y utilizar modelos animales en el servicio de animalario del centro, y, además, va a requerir los servicios de genómica, de microscopía, de citometría, de histología y otros de apoyo a la investigación en el centro. Estos gastos pueden llegar a ser muy importantes, en particular los de generación y mantenimiento de modelos animales (generalmente ratones). Una cantidad mensual razonable para este capítulo de servicios sería de por lo menos 2.800 Euros al mes (de los cuales un 80% pueden perfectamente corresponder a los gastos de animalario). Con estos valores este gasto en servicios representa, para un proyecto de 3 años, 2.800 x 12 x 3 = 100.800 Euros.
Deberemos considerar un presupuesto para viajes, para la asistencia a reuniones nacionales e internacionales donde presentar los resultados que se obtienen y donde enterarse o ponerse al día de lo que están haciendo otros grupos que trabajan en temas similares o relacionados. La asistencia regular a estos congresos, cursos o talleres es esencial para mantenerse regularmente informado de cómo evoluciona un campo determinado, las técnicas que se están usando, las que ya han quedado obsoletas, descubrir nuevas ideas, etc… Asumiendo que una persona del grupo puede ir a una reunión internacional y otra a una reunión nacional por año, y asumiendo que un coste razonable de registro, viaje, alojamiento y dietas para una reunión internacional es de 1.750 Euros, y para una reunión nacional es de hasta 750 Euros, este apartado correspondería a unos 2.500 Euros por año, o un total de 7.500 Euros para los tres años.
Finalmente, también habrá que considerar un apartado relativamente indeterminado de “otros gastos”, en el que incluiremos los gastos de telefonía, mensajería, correos, gastos para tramitar patentes, gastos de publicación, gastos de revisión de manuscritos, etc… Este apartado puede suponer fácilmente unos 2.500 Euros al año. Por lo tanto, para 3 años este apartado sumaría por lo menos otros 7.500 Euros.
Si sumamos todas las cantidades anteriores completaremos el apartado de costes directos del proyecto. Así pues, sumando Personal (177.000 Euros), Equipos (30.000 Euros), Consumibles (90.000 Euros), Servicios (100.800 Euros), Viajes (7.500 Euros) y Otros gastos (7.500 Euros) nos saldrá una cifra de 412.800 Euros.
Para contemplar el apartado de costes indirectos calculamos el 21% de los costes directos previamente detallados. En el ejemplo considerado, para 412.800 Euros, el 21% representan 86.688 Euros.
Finalmente, el coste total de este ejemplo-tipo de proyecto de 3 años de investigación en biomedicina sería la suma de los costes directos e indirectos, es decir 412.800 + 86.688 = 499.488 Euros. Es decir, en números redondos, un proyecto ideal de biomedicina con una duración de 3 años en nuestro país desde un centro público de investigación realizado por un grupo de investigación de tamaño medio (5 personas) vendría a costar aproximadamente medio millón de euros. Aproximadamente unos 167.000 Euros por año.

De forma similar, si se dice que se destinarán 5 millones de euros a una iniciativa en Biomedicina y tenemos en cuenta el ejemplo anterior fácilmente se puede convertir esa cifra para llegar a deducir que son fondos suficientes para financiar óptimamente por lo menos unos 10 proyectos de investigación. Si fueran 50 millones de euros entonces la cantidad correspondería a unos 100 proyectos de investigación. 500 millones de euros darían para 1.000 proyectos de investigación.
El ejemplo anterior ilustra, en mi opinión, el coste lógico, razonable para la ejecución óptima de un proyecto de investigación en biomedicina de 3 años, en una situación ideal. Sin embargo, este no suele ser el importe habitual con el que se financian los proyectos de investigación.
Desafortunadamente, debido a la limitación en los fondos destinados a investigación, atendiendo también a la calidad científico-técnica de los proyectos (su impacto previsible en el campo y/o en la sociedad, la trayectoria del investigador principal, la del grupo), a la voluntad de intentar financiar el máximo número de proyectos de investigación con el máximo posible de financiación, y todo ello en función del presupuesto global disponible, lo que en realidad sucede es que pocos proyectos financiados apenas llegan o superan la mitad del ideal calculado, esto es, unos 250.000 Euros. Y, generalmente, la mayoría acaban financiándose por debajo de esa cifra, con importes de alrededor de 150.000-180.000 Euros, o incluso cantidades inferiores.
¿Qué se puede hacer cuando se reciben menos fondos que los inicialmente presupuestados para ejecutar el proyecto de investigación? Lo primero que la agencia financiadora asume y pide al investigador principal es que el grupo deberá poder acometer todos los objetivos que pretendía con una financiación sensiblemente inferior, aunque parezca bastante obvio que es prácticamente imposible. No queda otra que activar la imaginación, la austeridad y los sacrificios. Y por supuesto acudir a otras agencias o fuentes de financiación con otro proyecto, más o menos relacionado, para compensar el déficit presupuestario. Aunque con ello estemos comprometiendo el tiempo de escritura, desarrollo y justificación de diversos pequeños proyectos (y, sobre todo, el tiempo administrativo, la burocracia que requiere cada uno de ellos), tiempo que el investigador principal deja de poder destinar a los aspectos directamente relacionados con la investigación.
¿Qué hacemos con 180.000 Euros para 3 años cuando nuestro proyecto estaba presupuestado en 500.000 Euros? Para empezar, hay que tener en cuenta que no recibiremos 180.000 Euros, sino unos 150.000 Euros (exactamente 148.760 Euros), tras detraer el 21% de costes indirectos. Esto corresponde aproximadamente a 50.000 Euros de gastos directos por año.
Para recortar el presupuesto, lo primero que tendremos que revisar es el capítulo de Personal. Ya no va a ser posible contratar al técnico, y ya no vamos a poder contratar al investigador que pretendíamos durante 3 años. A lo sumo podremos contratarle por 1 año, es decir 36.000 Euros. Seguidamente, ya no compraremos ningún equipo nuevo. Nos apañaremos con los que tenemos o usaremos los equipos de nuestros colaboradores. Tendremos que apretarnos el cinturón y gastar mucho menos por persona y año, quizás la mitad (3.000 Euros/persona/año, para un grupo de 5 personas, 45.000 Euros).
También tendremos que limitar mucho los gastos de servicios, y, en particular, disminuir significativamente los gastos de nuestro animalario, a aproximadamente un total de servicios de 20.000 Euros por año, que corresponde a 60.000 Euros para los 3 años. Sumando estas cantidades: 36.000 + 45.000 + 60.000 = 141.000 Euros nos quedarían unos 9.000 Euros para viajes y otros gastos. Ya no podremos hacer todos los viajes que teníamos previstos, quizás solamente uno internacional y tres nacionales, por un total de 4.000 Euros. Y nos quedarían 5.000 Euros para los 3 años para “otros gastos”.
Ahora quizás se entiendan mejor las reacciones agridulces que se suceden en los centros de investigación cuando se conocen las listas de los proyectos financiados. En primer lugar, en el mejor de los casos, la alegría de saber que tu proyecto está en la lista de los seleccionados, de los propuestos para su financiación. E inmediatamente después, la tristeza y la preocupación, al constatar que la cantidad asignada es sensiblemente inferior a la que fue inicialmente presupuestada y, por ello, deberemos acometer fuertes ajustes económicos a nuestro proyecto, recortando aquí y allá, para poder ejecutar gran parte de los objetivos previstos.
Una persona no relacionada con la investigación puede que no comprenda el por qué de la aparente mezcla de alegría, tristeza y preocupación de un investigador al que le acaban de otorgar 180.000 Euros para los próximos 3 años, cuando probablemente lo que ocurra es que el coste presupuestado para el proyecto era bastante mayor, y lo que preocupa ahora al investigador es cómo abordar los experimentos planeados con una menor financiación.
Este post ha sido realizado por Lluis Montoliu (@LluisMontoliu) y es una colaboración de Naukas con la Cátedra de Cultura Científica de la UPV/EHU.
El artículo ¿Cuánto cuesta realmente investigar en biomedicina? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- “Nanobiosensores: Aplicaciones en la frontera entre las nanociencias y la biomedicina” por Luis Liz-Marzán
- “Conócete a ti mismo” no solo es un consejo estúpido, es realmente peligroso
- Proyecto Mohole, un fracaso que no hacía falta
La intervención en la dislexia: de la evidencia científica a la práctica educativa

¿Cómo se tratan algunos de los trastornos cognitivos más frecuentes en las aulas? ¿Son efectivos los programas y herramientas del sistema educativo actual? ¿Carecen de eficacia algunas de las prácticas educativas más populares?
Estas son algunas de las cuestiones que se debatieron en la jornada “Las pruebas de la educación”, que se celebró el pasado 2 de febrero de 2018 en el Bizkaia Aretoa de Bilbao. El evento, en su segunda edición, estuvo organizado por la Cátedra de Cultura Científica de la UPV/EHU y el Consejo Escolar de Euskadi, con la colaboración de la Fundación Española para la Ciencia y la Tecnología (FECYT).
Las ponencias de los expertos que expusieron múltiples cuestiones relacionadas con la educación, basándose siempre en las pruebas científicas existentes. Los especialistas hicieron especial hincapié en destacar cuál es la mejor evidencia disponible a día de hoy con el objetivo de abordar las diferentes realidades que coexisten en las aulas y en el sistema educativo en general.
“Las pruebas de la educación” forma parte de una serie de eventos organizados por la Cátedra de Cultura Científica de la UPV/EHU para abordar cuestiones del día a día como la educación o el arte desde diversos ámbitos de la actividad científica. La dirección del seminario corre a cargo de la doctora en psicología Marta Ferrero.
Joana Acha, profesora en el departamento de Procesos Psicológicos Básicos y su Desarrollo de la UPV/EHU, revisa los métodos de prevención e intervención más efectivos para el desarrollo de las habilidades básicas implicadas en la dislexia. La especialista en procesos cognitivos infantiles aporta evidencias de los cambios cerebrales que acompañan a la adquisición de dichas habilidades.
Joana Acha: ''La intervención en la dislexia''Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo La intervención en la dislexia: de la evidencia científica a la práctica educativa se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Autismo y educación: problemas y pautas en el aula
- Prohibir los herbicidas con glifosato es anteponer la ideología a la evidencia científica
- La evaluación y los deberes escolares
Aunque tengas colesterol, podrás desayunar huevos

Las enfermedades cardiovasculares son la principal causa de muerte en el mundo. Cada año mueren más personas por enfermedades cardiovasculares que por cualquier otra causa. Por eso cuando el médico nos alerta de que tenemos el colesterol alto, nos entra el miedo.
¿Recuerdas aquello de que no debemos tomar más de tres huevos a la semana? Pues olvídalo. La culpa de tu colesterol no la tienen los huevos.
¿Qué es el colesterol?
El colesterol es un tipo de lípido denominado esterol. Lo encontramos en los tejidos y en la sangre. Pese a su mala fama en cuestiones de salud, el colesterol es esencial para la vida. Forma parte de las membranas de nuestras células y ayuda a controlar qué entra y qué sale de ellas, es un precursor de la vitamina D, por tanto, es fundamental para el metabolismo del calcio, es precursor de las hormonas sexuales, etc.
Colesterol bueno y colesterol malo
El colesterol no se disuelve ni se mezcla con la sangre. El modo que tiene de permanecer en el torrente sanguíneo es formando parte de una especie de cápsulas denominadas lipoproteínas. Cuando estas cápsulas tienen más proteínas que lípidos, son más densas. Esta propiedad es la que se utiliza para clasificarlas: HDL (lipoproteína de alta densidad) y LDL (lipoproteína de baja densidad). El HDL lo conocemos como colesterol bueno y el LDL como colesterol malo.
Que uno sea el bueno y el otro sea el malo tiene que ver con la ateroesclerosis. La ateroesclerosis se caracteriza por la acumulación de placa en el interior de las arterias, haciéndolas más rígidas y pudiendo llegar a taponarlas (produciendo una isquemia o infarto). Cuando analizamos esta placa solo encontramos LDL. Es decir, solo el LDL es capaz de adentrarse en nuestras arterias y causarnos problemas cardiovasculares, por eso le hemos llamado colesterol malo.
Estudios recientes han ido todavía más allá. Lo más relevante con respecto al riesgo cardiovascular no es tanto la cantidad de colesterol que contengan esas lipoproteínas, sino la cantidad de lipoproteínas LDL que haya, independientemente de si contienen más o menos colesterol en su interior. Esto no implica que deberíamos dejar de preocuparnos por el colesterol, al menos no en todos los casos. La evidencia nos dice el colesterol malo aumenta el riesgo cardiovascular si además va unido a otros factores como la obesidad, niveles altos de triglicéridos, hipertensión, niveles altos de glucosa, estrés o bajo nivel de colesterol bueno.
Los alimentos que contienen colesterol no hacen subir el colesterol
Además del huevo y los quesos, los alimentos que más colesterol contienen en su composición son los que tienen más grasas saturadas: las mantecas, la nata, algunos mariscos, los patés, el hígado, etc.
Numerosos estudios han demostrado que el colesterol que consumimos apenas repercute en los niveles de colesterol en sangre. De hecho, el colesterol que ingerimos es un factor poco relevante, ya que nuestro cuerpo sintetiza por sí solo la mayor parte del colesterol que utiliza. Si no comiésemos nada de colesterol, nuestro cuerpo lo fabricaría por sí mismo.
A esto hay que sumarle que la mayor parte del colesterol que ingerimos ni se absorbe ni se metaboliza, sino que se expulsa directamente. Esto es debido a que el colesterol de la mayoría de los alimentos está esterificado (es químicamente diferente al colesterol libre) y eso afecta a su biodisponibilidad. Solo podríamos absorber el colesterol libre (no esterificado) y éste es difícil de encontrar en los alimentos. Por lo tanto, en la mayor parte de las personas la cantidad de colesterol ingerido tiene poca relación con el nivel de colesterol que se queda en su cuerpo.
Es un mito que consumir huevos suba el colesterol
En los años 70 se empezó la lucha contra las grasas, especialmente contra los alimentos con colesterol, en gran medida a causa de una interpretación un tanto alarmista de este estudio. Para más inri, en 1973 la Asociación Americana del Corazónpropuso limitar la ingesta de huevos a un máximo de tres por semana.
Actualmente sabemos que aquella recomendación era innecesaria, y que por su culpa este mito se ha perpetuado hasta nuestros días. La realidad es que consumir un huevo al día no aumenta el riesgo cardiovascular en comparación con tres huevos semanales.
En enero de 2014 la Fundación Española del Corazón publicó una nota de prensa en la que decía que no es necesario restringir la ingesta de huevosen la dieta de las personas sanas.
Hay indicios de que el huevo, además de colesterol, contiene unas sustancias que bloquean su entrada en el organismo. Por eso, a la luz de la evidencia científica, ninguna organización nutricional desaconseja su consumo por miedo a que nos suba el colesterol.
Alimentos funcionales para bajar el colesterol

Los alimentos funcionales formulados para bajar el colesterol contienen esteroles y estanoles añadidos. Estas dos sustancias forman parte de las plantas, donde desarrollan funciones análogas a las de nuestro colesterol. Cuando consumimos esteroles y estanoles, estos bloquean la absorción intestinal del colesterol, impidiendo que más adelante lleguen a la sangre.
Estas sustancias las encontramos en frutas, verduras, aceites vegetales, legumbres, frutos secos, etc. Pero están presentes en cantidades tan pequeñas que no afectan al nivel de colesterol. Sin embargo, los alimentos funcionales multiplican por 10 o más la cantidad de esteroles y estanoles. Contienen una media de 3 g por cada 100 g de producto.
Una de las funciones de la Agencia Europea de Seguridad Alimentaria (EFSA) es verificar si las alegaciones saludables publicitadas de un alimento son válidas. A la luz de los estudios presentados, la EFSA ha confirmado que «los alimentos funcionales que contienen esteroles o estanoles contribuyen a mantener los niveles normales de colesterol sanguíneo». Tanto es así, que estos productos van exclusivamente dirigidos a personas con problemas de colesterol, no se debe consumir más de 3 g al día de esteroles y estanoles, no lo pueden tomar los menores de 5 años, ni las embarazadas, por lo que es aconsejable que sea el médico el que paute su consumo.
Según publica la EFSA, tomar entre 1,5 y 3 g de esteroles o estanoles al día durante 2-3 semanas puede reducir el colesterol malo en un 11,3 u 11,4 % respectivamente. Todavía queda por analizar si esta reducción de los niveles de colesterol malo es tan relevante como se cree con respecto a la salud cardiovascular.
Qué dice la ciencia para bajar el colesterol
Lo que sí sabemos que disminuye el riesgo cardiovascular, mantiene a raya nuestro nivel de colesterol y la cantidad de lipoproteínas portadoras de colesterol malo, es seguir una dieta basada en unas sencillas recomendaciones: tomar frutas y verduras, suficientes proteínas y grasas saludables, apostar por las harinas integrales y evitar las harinas refinadas. También deberíamos evitar los alimentos procesados de alto índice glucémico como los dulces y la bollería, especialmente el azúcar y los siropes.
Además de seguir una dieta saludable, los estudios confirman que la actividad física es fundamental para controlar el colesterol malo y la cantidad de lipoproteínas portadoras.
Conclusión
Si tenemos que lidiar con el colesterol, lo primero es seguir las indicaciones de nuestro médico. Como hay otros factores que regulan la síntesis de colesterol, no siempre es posible controlarlo a través de la dieta. Si esto sucede, será el médico quien nos pondrá un tratamiento.
Si éste no es nuestro caso, la solución a nuestro colesterol no será emprender una batalla contra los huevos, sino en apostar por una dieta saludable. La batalla, como casi siempre, la deberíamos mantener con los alimentos procesados, aquellos que contienen harinas refinadas, azúcares y grasas saturadas. Si a esto le sumamos actividad física, no sólo estaremos combatiendo el colesterol, sino que ganaremos en muchos otros frentes.
Si eres de los que desayunan huevos revueltos o cenan tortilla francesa, no cambies esos hábitos por miedo al colesterol. Ya lo estás haciendo bien.
Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Aunque tengas colesterol, podrás desayunar huevos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Colores vivientes: nanoestructuras que se cultivan, no se fabrican.
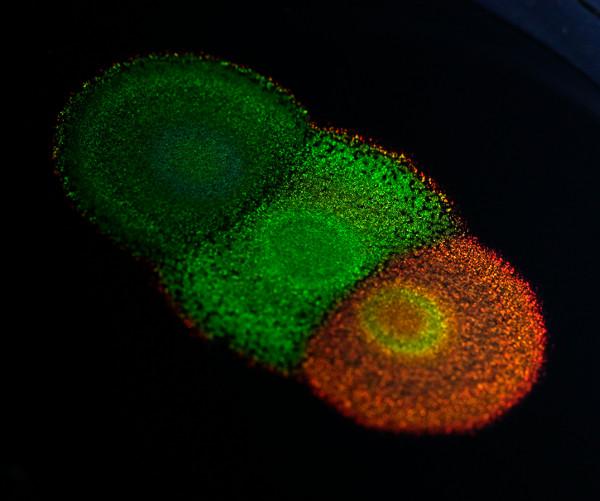
Fuente: University of Cambridge
Una nueva investigación muestra cómo la genética puede cambiar el color y la apariencia de ciertos tipos de bacterias que crecen en colonias de colores llamativos. Este sería uno de los primeros estudios, si no el primero, de la genética del color estructural, ese que se manifiesta espectacularmente en las alas de las mariposas o en las plumas de los pavos reales. Los resultados abren la vía para la investigación genética de toda una variedad de organismos coloreados estructuralmente. Desde un punto de vista práctico cosechar estas bacterias para la fabricación a gran escala de materiales nanoestructurados se convierte ahora en una posibilidad; es decir, que las pinturas biodegradables y no tóxicas podrían “cultivarse” y no fabricarse, por ejemplo.
Flavobacterium es un tipo de bacteria que se agrupa en colonias que producen llamativos colores metálicos. Estos colores no provienen de la existencia de pigmentos, sino de su estructura interna, que refleja la luz a ciertas longitudes de onda. Sin embargo, la ciencia aún no tiene muy claro cómo la genética afecta a estas estructuras. De ahí el interés de este trabajo, que estudia por primera vez los genes que provocan estas estructuras de color en un sistema vivo.
Los investigadores, encabezados por Villads Egede Johansen, de la Universidad de Cambridge (Reino Unido), compararon la información genética con las propiedades ópticas y la anatomía de colonias bacterianas sin mutar y mutadas para comprender cómo regulan los genes el color de la colonia.
Al mutar genéticamente la bacteria, los investigadores cambiaron sus dimensiones o su capacidad de movimiento, lo que alteró la geometría de las colonias. Al cambiar la geometría, cambiaron el color: cambiaron el color verde metálico original de la colonia en todo el rango visible de azul a rojo. También fueron capaces de crear una coloración más opaca o hacer que el color desapareciese por completo.
Desde el punto de vista práctico, y usando el lenguaje no de la biología genética sino de la nanotecnología, esto significa que se pueden diseñar estructuras fotónicas del color deseado y que estas estructuras se pueden autorreproducir en abundancia, todo ello evitando los laboriosos métodos tradicionales de la nanofabricación.
Para darnos cuenta de lo que esto significa, pensemos que estamos hablando de la posibilidad de usar colonias bacterianas como pigmentos fotónicos que pueden optimizarse fácilmente para cambiar la coloración bajo estímulos externos y que pueden interactuar con otros tejidos vivos, adaptándose así a entornos variables. La potencialidad de aplicaciones es tan amplia como la imaginación.
Referencia:
Villads Egede Johansen el al. (2018) Living colors: Genetic manipulation of structural color in bacterial colonies, PNAS doi: 10.1073/pnas.1716214115
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Este texto es una colaboración del Cuaderno de Cultura Científica con Next
El artículo Colores vivientes: nanoestructuras que se cultivan, no se fabrican. se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Usando ADN para sintetizar nanoestructuras de oro
- Descubierto el proceso por el que las bacterias fabrican nanoimanes
- Paneles solares orgánicos…y de colores
Teselaciones rítmicas perfectas
En mi anterior entrada del Cuaderno de Cultura Científica, titulada Las vacas de Narayana, la versión hindú de los conejos de Fibonacci , estuvimos hablando de una curiosa sucesión de números, la sucesión de las vacas de Narayana, y de cómo el compositor minimalista estadounidense Tom Johnson (Greeley, Colorado, EE.UU., 1939), la había utilizado para componer una obra musical de título homónimo.

Portada del disco “Rational Music”, de Tom Johnson, interpretado por Dedalus, New World Records, 2010
En el proceso creativo de su música, Tom Johnson busca encontrar la belleza de una forma objetiva, alejándose de la subjetividad de la música romántica y expresionista, que lo hace a través de los sentimientos. El compositor minimalista utiliza las matemáticas, es decir, la simetría, la combinatoria, las sucesiones numéricas, los números binarios, las funciones matemáticas, los fractales o la geometría, en su búsqueda de una belleza musical objetiva.
Un ejemplo ilustrativo podría ser la pieza musical Tango, que Tom Johnson compuso en 1984 para el virtuoso pianista estadounidense Yvar Mikhashoff, y para la cual utilizó el concepto matemático de las permutaciones. Si se toman cinco objetos cualesquiera, ya sean cinco números o cinco notas, existen 120 formas diferentes de colocarlos en orden, es decir, 120 permutaciones de los mismos. En concreto, el factorial de 5, 5! = 5 × 4 × 3 × 2 × 1 = 120, como ya explicamos en las entradas Cuadrados latinos, matemáticas y arte abstracto y El problema matemático de las cartas extraviadas o en el video La combinatoria, de la sección Una de Mates, en el programa de TV2 Órbita Laika.
Por lo tanto, si se toman cinco notas, hay 120 permutaciones distintas de esas cinco notas. Como puede apreciarse en la imagen de la partitura que mostramos más abajo, las cinco notas de partida son [Re, Fa, Sol(#), La, Si(Ь)], y estas se van permutando [Re, Fa, Sol(#), Si(Ь), La], [Re, Fa, La, Sol(#), Si(Ь)], [Re, Fa, La, Si(Ь), Sol(#)], [Re, Fa, Si(Ь), Sol(#), La], [Re, Fa, Si(Ь), La, Sol(#)], y así hasta las 120 permutaciones que utiliza el compositor Tom Johnson para crear esta hermosa pieza, cuyo título es Tango, y que tiene un acompañamiento con ritmo argentino.

Primera parte de la partitura de la obra “Tango” (1984), de Tom Johnson. La partitura la podéis encontrar gratis en la página del compositor Tom Johnson.
Pero lo mejor es que escuchéis el resultado. A continuación, dos versiones de la obra Tango. La primera es la interpretada por el pianista argentino Alberto Neuman
mientras que la segunda está interpretada con la estación de trabajo de audio digital Renoise,
Pero vayamos al tema de esta entrada del Cuaderno de Cultura Científica, las “teselaciones rítmicas perfectas”, un concepto matemático que ha sido introducido por el compositor Tom Johnson, mientras estudiaba algunos conceptos matemáticos para utilizarlos en la creación de nuevas piezas musicales.
Durante los años 2002 y 2003, Tom Johnson estuvo trabajando en lo que se conoce como teselaciones rítmicas, que son una traslación a dimensión uno, a la línea de tiempos musicales, del concepto clásico de teselación del plano o del espacio. Este trabajo dio lugar a su disco Tilework: 14 Pieces for 14 Solo Instruments (2003).
Pero el concepto de teselaciones rítmicas perfectas se le ocurrió a Tom Johnson intentando formular un equivalente en dimensión uno a lo que en matemáticas se conoce como las teselaciones perfectas del cuadrado o el problema de la cuadratura del cuadrado. Una teselación perfecta de un cuadrado es una teselación del cuadrado mediante cuadrados más pequeños, luego los cuadrados pequeños cubren el cuadrado original sin superponerse unos con otros, pero además con la condición de que todos los cuadrados de la teselación tengan diferentes tamaños.
La primera teselación perfecta de un cuadrado se obtuvo en 1938 por Cedric Smith, Arthur Stone, Leonard Brooks y William Tutte, conocidos como “Los cuatro de Trinity” (puede verse la historia de estos en la entrada Blanche Descartes y la cuadratura del cuadrado), utilizando para ello 69 cuadrados de diferentes tamaños. La teselación perfecta del cuadrado con menos cuadrados posibles, neceisita 21, y fue obtenida por A. J. Duijvestijn en 1978.
Teselación del cuadrado con 21 cuadrados, dada por A. J. Duijvestijn en 1978, cuyos lados tienen longitud igual a 50, 35, 27, 8, 19, 15, 17, 11, 6, 24, 29, 25, 9, 2, 7, 18, 16, 42, 4, 37, 33
Tom Johnson propuso teselar, o rellenar, la línea de los números {0, 1, 2, … , m – 1, m} (pensemos en los tiempos musicales) con tríos de números que formen progresiones aritméticas (cada trío de números en progresión aritmética, es decir, de la forma a, a + r, a + 2r, como por ejemplo, 5, 7 y 9, son las baldosas de la teselación), de forma que entre todas esas progresiones aritméticas de tres números (las baldosas) llenen el espacio de la línea de los números, que no se superpongan, es decir, no haya números que estén en más de una progresión, y que cada progresión aritmética tenga una diferencia r, llamada “tempo” por Tom Johnson, diferente. El orden n de la teselación rítmica perfecta es el número de baldosas, esto es, progresiones aritméticas. Aquí el número de términos de cada progresión es tres, pero más adelante extenderemos la noción a progresiones aritméticas con más elementos, el índice.
Claramente, la cantidad de números que abarca una teselación rítmica perfecta de orden n (con índice 3) es 3n, desde 0 al 3n – 1.
La mejor manera de entender el concepto es mediante un ejemplo. Aquí mostramos el ejemplo que utiliza Tom Johnson, que es de orden 5 y que tesela los quince primeros números {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15} mediante las siguientes teselas: (2, 3, 4), (8, 10, 12), (5, 9, 13), (1, 6, 11) y (0, 7, 14), cuyas diferencias son 1, 2, 4, 5 y 7, todas ellas distintas.
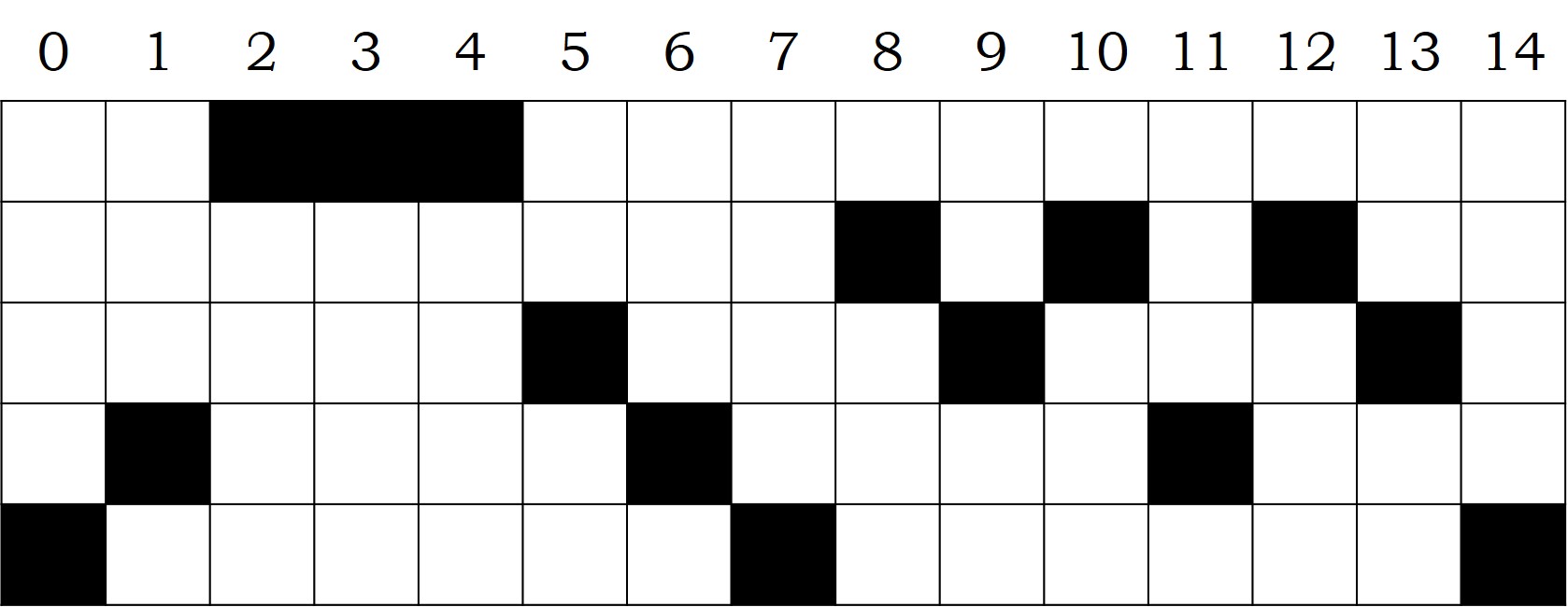
Teselación rítmica perfecta introducida por Tom Johnson y utilizada para su composición “Tileworks for Piano” (2003)
Utilizando esta teselación rítmica perfecta, con 5 teselas (tríos) diferentes y cuyos tempos (diferencias), de graves a agudos, son 7, 5, 4, 2 y 1, Tom Johnson compuso la pieza Tileworks for Piano (2003). La siguiente imagen que se ha extraído del libro Mathemusical Conversations, Mathematics and Computation in Music Performance and Composition (2016) explica, con la partitura original, el uso de esta teselación rítmica perfecta en la pieza.
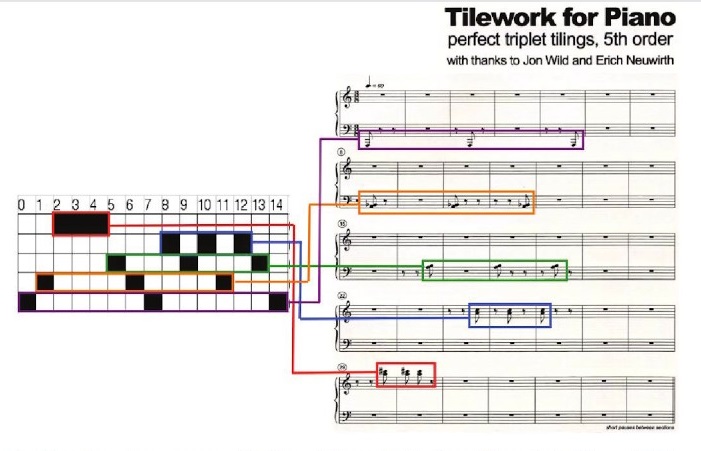
Pero escuchemos la pieza Tileworks for Piano compuesta por Tom Johnson, y que podemos encontrar en la página del compositor: Tileworks for Piano.
Como el propio compositor puso de manifiesto en el texto de la conferencia que impartió en 2004 en el Seminario MaMuX (Matemáticas, Música y relaciones con otras disciplinas), del IRCAM (Institut de Recherche et Coordination Acoustique/Musique), con el título Perfect Rhythmic Tilings, no existen teselaciones rítmicas perfectas de orden 2 (es decir, dos tríos que llenen seis tiempos, seis números), ni 3 (tres tríos que llenen 9 tiempos), ni 4 (cuatro tríos que teselen la línea de 12 números). Solo hay una de orden 5, que es la dada por Johnson, y su simétrica. Tampoco hay teselaciones rítmicas perfectas de orden 6. De orden 7, hay 9 soluciones, con sus simétricas, luego 18. Una de ellas la siguiente, cuyas diferencias son 1, 2, 4, 5, 7, 8 y 10.

En la Enciclopedia On-line se Sucesiones de Enteros aparece la sucesión A261516 del número de teselaciones rítmicas perfectas de {0, …, 3n – 1} con tríos (sucesiones aritméticas de tres números), en función del orden n, la cual empieza así
1, 0, 0, 0, 2, 0, 18, 66, 382, 1.104, 4.138, 15.324, 61.644, etc
Por ejemplo, hay 61.644 teselaciones rítmicas perfectas de orden 13 (sobre los primeros 39 números). Y se conoce hasta el orden 19.
De forma obvia, el concepto de teselaciones rítmicas perfectas se puede extender a progresiones aritméticas (baldosas) con cualquier número de elementos, no necesariamente tres. Por lo tanto, una teselación rítmica perfecta de orden n e índice k estaría dada por n progresiones aritméticas con k números cada una de ellas, a, a + d, a + 2d, …, a + kd, que cubren toda la línea de números {0, 1, 2, …, nk – 1}, que no se solapan, y tal que las diferencias d de las progresiones aritméticas son todas distintas.
En su texto Perfect Rhythmic Tilings, Tom Johnson estudió las teselaciones rítmicas perfectas con índices k = 2 y 3, es decir, con 2 y 3 números por progresión aritmética, pero dejó abierto el problema de la existencia de teselaciones rítmicas perfectas para k = 4. Afirmó que no existían tales teselaciones para órdenes menores, o iguales, que 7, pero quedaba abierto el problema para órdenes mayores.
Shalosh B. Ekhad (de quien ya hablamos en la entrada El extraño caso del matemático Shalosh B. Ekhad ) y Lara Pudwell resolvieron el problema planteado por Tom Johnson construyendo una teselación rítmica perfecta de índice 4 y orden 15, que es el orden más bajo posible para el índice 4, sobre los 60 primeros números. Es la siguiente…
[0, 16, 32, 48], [1, 3, 5, 7], [2, 13, 24, 35], [4, 22, 40, 58], [6, 21, 36, 51], [8, 14, 20, 26], [9, 10, 11, 12], [15, 29, 43, 57], [17, 25, 33, 41], [18, 30, 42, 54], [19, 23, 27, 31], [28, 37, 46, 55], [34, 39, 44, 49], [38, 45, 52, 59], [47, 50, 53, 56],
cuyas diferencias son 16, 2, 11, 18, 15, 6, 1, 14, 8, 12, 4, 9, 5, 7, 3.

Siguiendo los pasos de Tom Johnson, el compositor estadounidense Dean Rosenthal (Concord, Massachusetts, EE. UU., 1974) utiliza esta teselación rítmica perfecta, pero reordenando las diferencias de mayor a menor, para componer la pieza Perfecto para… violín (2011), que podéis escuchar, interpretada por la violinista y compositora Morgan Gerstmar, en la página de Dean Rosenthal.
Tras el ejemplo de Ekhad y Pudwell de teselación rítmica perfecta de índice 4, se han estudiado más en profundidad este tipo de teselaciones. Así, en la página Enciclopedia On-line se Sucesiones de Enteros aparece la sucesión A261517 del número de teselaciones rítmicas perfectas de {0, …, 4n – 1} con cuartetos (sucesiones aritméticas de cuatro números), en función del orden n, que es la siguiente (se conoce hasta el orden 23)
1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 2, 24, 38, 96, 444, 1.414, 5.134, 19.490
Para terminar esta entrada de la sección Matemoción del Cuaderno de Cultura Científica vamos a considerar un tipo especial de teselaciones rítmicas perfectas.
Dado el concepto de teselación rítmica perfecta de orden n e índice k, nos podríamos plantear si existen ejemplos de estas teselaciones pero con la propiedad de que las diferencias no solo sean diferentes, sino que sean todos los números entre 1 y n. A estas se las llama teselaciones rítmicas super perfectas.
Ninguno de los ejemplos de teselaciones rítmicas perfectas que hemos presentado hasta el momento son super perfectas. Por ejemplo, las diferencias del ejemplo de Tom Johnson son 1, 2, 4, 5 y 7, mientras que para que fuesen super perfectas deberían ser 1, 2, 3, 4 y 5.
Veamos un par de ejemplos. Una teselación rítmica super perfecta de índice 2, es decir, mediante pares de números, de orden 4, es (0, 4), (1, 3), (2, 5) y (6, 7).

Y un ejemplo, que encontramos en el artículo Perfect Rhythmic Tailings de Jean-Paul Davalan, con orden 9 e índice 3 (es decir mediante tríos de números) es (0, 6, 12), (1, 8, 15), (2, 11, 20), (3, 5, 7), (4, 9, 14), (10, 18, 26), (13, 16, 19), (17, 21, 25) y (22, 23, 24).

Las teselaciones rítmicas super perfectas ya existían en la literatura matemática, pero descritas desde otro punto de vista, bajo el nombre de sucesiones de Skolem (relacionadas también con las sucesiones de Langford).
Para explicar las sucesiones de Skolem, empecemos con el problema de los emparejamientos de Langford (para más información sobre el mismo puede consultarse el libro Del ajedrez a los grafos, La seriedad matemática de los juegos, que aparece en la bibliografía).
El origen de este juego se remonta a 1958, cuando el matemático escocés C. Dudley Langford publicó en la revista Mathematical Gazette el que es conocido como problema de los emparejamientos de Langford, o simplemente problema de Langford. En este artículo explicaba que viendo a su hijo pequeño jugar con un juguete de cubos de colores, dos de cada color, observó que había formado una torre de cubos, de tal forma que los dos cubos rojos estaban separados por un único cubo, los dos azules por dos cubos y había tres cubos entre los dos amarillos. Entonces se planteó si, añadiendo los dos cubos verdes podía mantener la propiedad anterior y que además hubiese una separación de cuatro cubos entre los dos verdes.
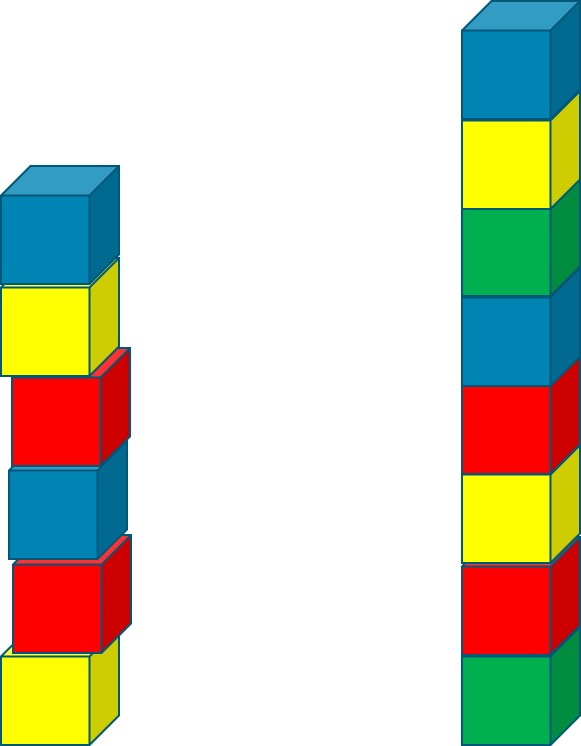
Torre de cubos rojos, azules y amarillos similar a la formada por el hijo de Langford, así como la compuesta por el matemático escocés al añadir dos cubos verdes
En su artículo, Langford reemplazó los cubos de colores por números y formuló el problema que lleva su nombre, en el que se plantea si es posible, y cómo, distribuir parejas de los números del 1 hasta n, de forma que entre los dos 1 haya un único número, entre los dos 2 haya dos, entre los dos 3 haya tres, así hasta los dos números n, entre los que habrá n números, es decir, si denotamos como ad la primera posición en la que aparece el número d (por ejemplo, contando desde la izquierda) y como bd la segunda, entonces
bd – ad = d + 1, para d = 1, 2, …, n.
A una tal distribución de los 2n números 1, 1, 2, 2, …, n, n se le llama sucesión de Langford. Por ejemplo, para n = 4 una solución es:
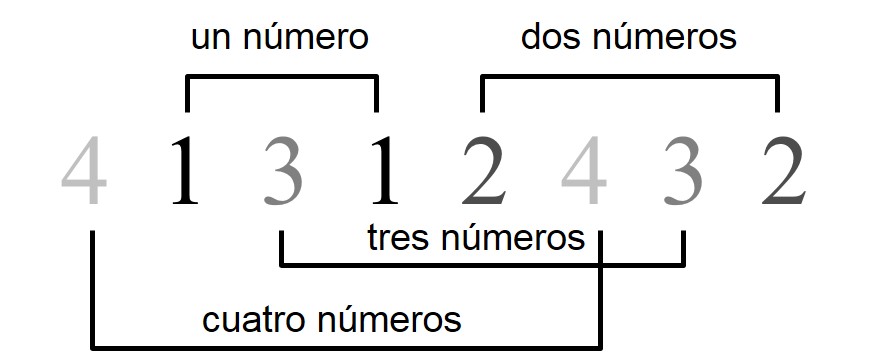
El problema de Langford, ya se formule con cubos de colores o con números, se puede extender a cualquier cantidad de cubos de colores o copias de cada número de 1 a n, así como el concepto de sucesión de Langford asociado, de tipo (k, n), es decir, con k copias de los números 1, 2, …, n. Por ejemplo, a continuación se muestra una sucesión de Langford de tipo (3, 9):
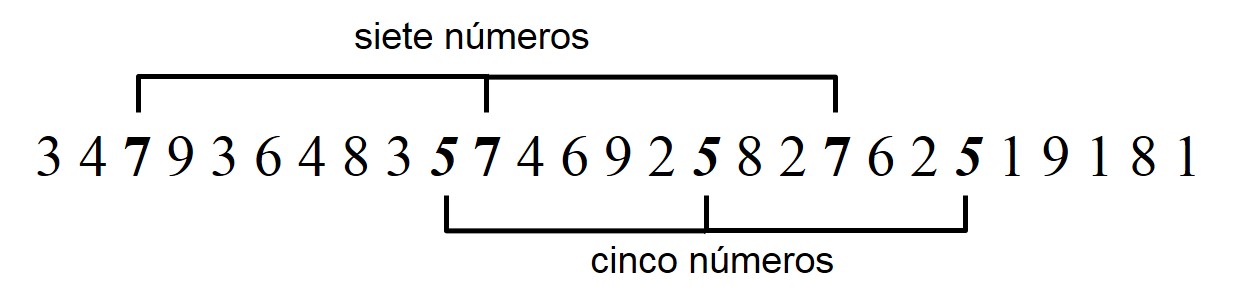
Mientras que C. Dudley Langford planteó este problema sobre la existencia de estas sucesiones numéricas en el contexto de la matemática recreativa, un problema similar surgió en 1957 en la investigación del matemático noruego T. H. Skolem sobre sistemas triples de Steiner, que son unos objetos matemáticos que pertenecen a la teoría del diseño combinatorio. Aunque en su investigación la condición matemática era que
bd – ad = d, para d = 1, 2, …, n,
es decir, los dos números 1 están juntos, los dos 2 tienen un número entre ellos, hay dos posiciones entre los 3, y así para el resto.
Así un ejemplo de sucesión de Skolem para parejas de números, para n = 4, sería
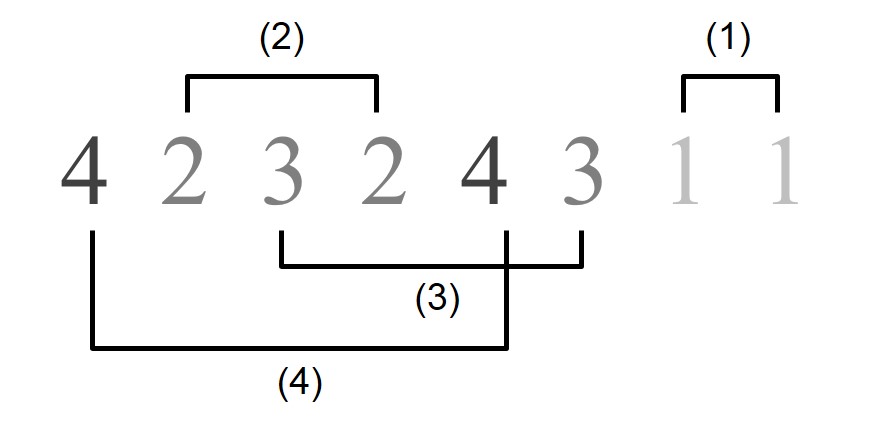
Y un ejemplo para tríos, esto es, de sucesiones de Skolem de tipo (3, 9) sería:
6, 7, 9, 2, 5, 2, 6, 2, 7, 5, 8, 9, 6, 3, 5, 7, 3, 4, 8, 3, 9, 4, 1, 1, 1, 4, 8.
La condición de la sucesión de Skolem es realmente la misma que la de teselación rítmica super perfecta. Si tenemos una sucesión de Skolem de tipo (k, n), es decir, con n números distintos que se repiten k veces cada uno, tendremos una teselación rítmica super perfecta de la siguiente forma.
La línea de números que vamos a teselar son las nk posiciones de la sucesión de Skolem, empezando a contar desde la posición 0, es decir, desde 0 hasta nk – 1. Ahora, cada número de la sucesión de Skolem, que se repite k veces, va a ser una de las progresiones aritméticas de k números (nuestras baldosas), ya que la diferencia de los elementos de la progresión aritmética es d, la diferencia de las posiciones de cada dos números iguales (que además toma valores de 1 a n). Así, la sucesión de Skolem para pares de números anterior, 42324311, dará lugar a la teselación rítmica superperfecta (0, 4) –que son las posiciones del 4–, (1, 3) –que son las posiciones del 2–, (2, 5) –que son las posiciones del 3– y (6, 7) –que son las posiciones del 1–. De la misma forma, la sucesión de Skolem de tipo (3,9) anterior, no es más que la teselación rítmica super perfecta de orden 9 e índice 3, que hemos visto anteriormente.
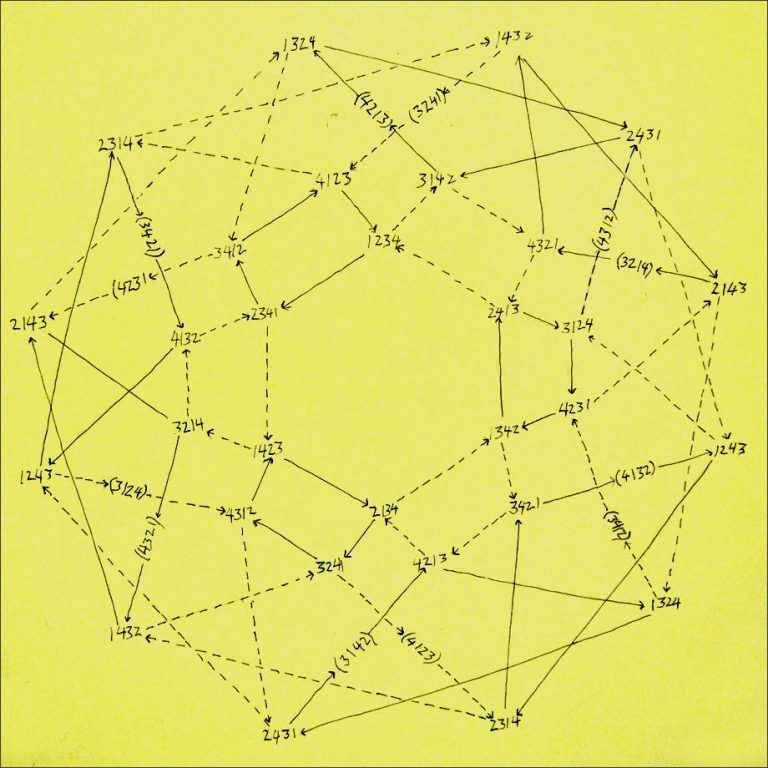
“Las 24 permutaciones de 1, 2, 3, 4 permutadas por (1234) con líneas sólidas y por (1342) por líneas interrumpidas” (2011), de Tom Johnson. Diseño en papel
Bibliografía
2.- Tom Johnson, Perfect Rhythmic Tilings, Lecture delivered at MaMuX meeting, IRCAM, 2004. Versión on-line en Editions75
3.- Tom Johnson, Tiling the Line in Theory and Practice, Lecture delivered at MaMuX meeting, IRCAM, 2002. Versión on-line en Editions75
4.- Tom Johnson, Tiling in my music, Perspectives in New Music 49, n. 2, p. 23-31, 2011.
5.- Jordan B L Smith, Elaine Chew, Gérard Assayag (editors), Mathemusical Conversations, Mathematics and Computation in Music Performance and Composition, (Lecture Notes Series, Institute for Mathematical Sciences, National University of Singapore 32), World Scientific, 2016.
6.- Jean-Paul Davalan, Perfect Rhythmic Tilings, Perspectives of New Music, vol. 49, n. 2, p. 144-197, 2011.
7.- Shaloh B. Ekhad, Lara Pudwell, A Perfect Rhythmic Tiling of Quadruplets, The Personal Journal of Shalosh B. Ekhad and Doron Zeilberger, 2004.
8.- Raúl Ibáñez, Del ajedrez a los grafos, La seriedad matemática de los juegos, colección El mundo es matemático, National Geographic, 2015.
9.- Tom Johnson, Looking at numbers, Birkhäuser, 2014.
10.- Exposición “Tom Johnson”, en Bains-Douches (d’Alençon, Francia), Febrero, 2018
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Teselaciones rítmicas perfectas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las vacas de Narayana, la versión hindú de los conejos de Fibonacci
- Uno, dos, muchos
- La magia del teorema de Zeckendorf
El control nervioso de la respiración
La mayor parte de los animales necesitan respirar continuamente. Por esa razón, los movimientos que proporcionan o permiten el flujo de medio respiratorio al órgano correspondiente son generados por programas rítmicos innatos que corren a cargo de estructuras neuronales específicas y pueden operar independientemente de los centros encefálicos superiores. Esos centros procesan señales procedentes de quimiorreceptores que reciben información relativa a la concentración de los gases respiratorios en el fluido interno que los transporta. Y como consecuencia de la valoración de esa información emiten señales que regulan la concentración de esos gases mediante un sistema de retroalimentación negativa. La ventilación traqueal de insectos terrestres parece estar regulada mediante señales enviadas por los ganglios metatorácicos. Y en los vertebrados el ritmo respiratorio viene marcado por el centro respiratorio ubicado en el tronco encefálico.
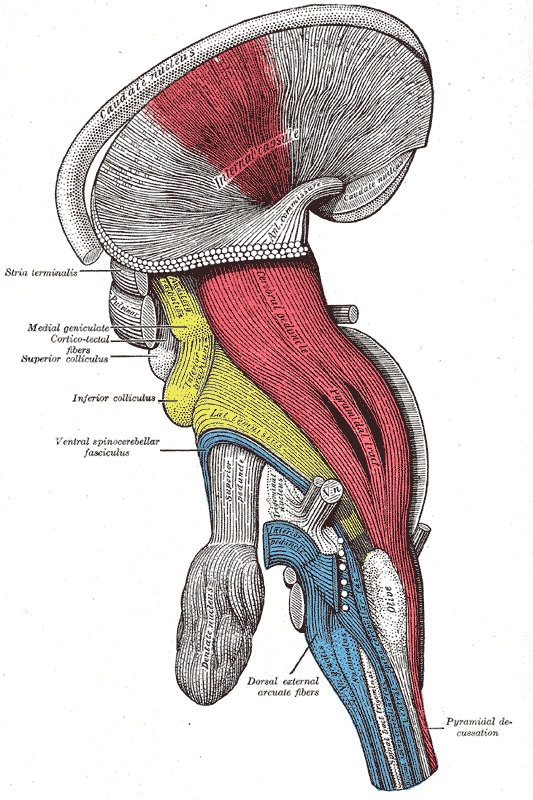
Tronco del encéfalo humano. Ilustración de “Anatomía” de Gray (1918)
En los vertebrados, el control nervioso de la respiración tiene tres componentes: (1) el programa generador de patrones, para el ritmo alternante de inspiración/espiración; (2) los factores que regulan la intensidad de la ventilación (frecuencia y profundidad de la respiración) para ajustarla a las necesidades; y (3) los factores que modifican la actividad respiratoria para que sirva a otros propósitos (como hablar, por ejemplo); en este último caso, los centros superiores pueden tomar parte en el control.
En mamíferos, con independencia de cuál sea el nivel de consumo de oxígeno o de la producción de dióxido de carbono por parte de los tejidos, las tensiones parciales de oxígeno (tO2) y de dióxido de carbono (tCO2) de la sangre arterial que abandona los pulmones presentan una considerable constancia, lo que indica que ambas magnitudes están sometidas a un estricto control.
En los mamíferos, el principal centro de control respiratorio es el centro respiratorio medular, que consta de dos grupos o agregaciones de cuerpos celulares neuronales en el interior de la médula: el grupo respiratorio dorsal y el grupo respiratorio ventral. Pero además de ese centro principal, hay otro grupo respiratorio en el puente troncoencefálico (puente de Varolio), formado a su vez por dos áreas: el centro neumotáxico y el centro apnéustico.
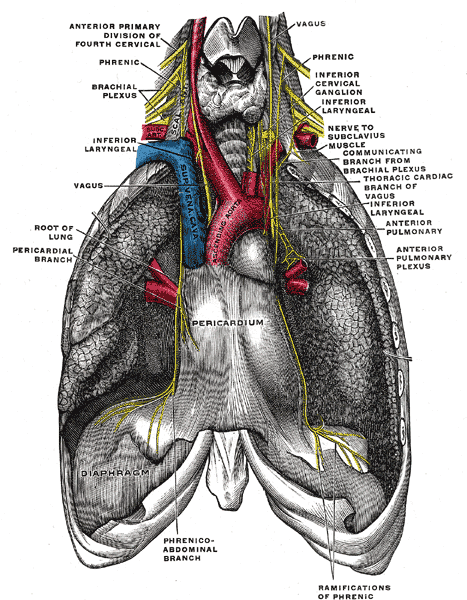
Inervación de los pulmones humanos. Ilustración de “Anatomía” de Gray (1918)
El nervio frénico y los nervios intercostales son los que transmiten las órdenes motoras al diafragma y músculos intercostales que provocan los movimientos rítmicos de contracción y relajación de la caja torácica. Los cuerpos celulares de esos nervios se encuentran en la médula espinal (espina dorsal) y reciben señales del centro respiratorio medular. Cuando esas neuronas motoras estimulan los músculos inspiratorios, provocan el movimiento de inspiración; la espiración se produce cuando esas neuronas no transmiten impulsos. El grupo dorsal del centro respiratorio medular consta principalmente de neuronas inspiratorias, cuyas fibras descendentes establecen sinapsis con las motoneuronas de la médula espinal citadas. El grupo ventral se encuentra interconectado con el dorsal, y está compuesto tanto por fibras inspiratorias como espiratorias. Pero este grupo se encuentra inactivo durante la respiración normal; solo interviene cuando debe elevarse la ventilación y es especialmente importante para intensificar la espiración. Durante la respiración normal (tranquila) no se envían señales a través de las vías descendentes de las neuronas espiratorias. Las motoneuronas que inervan los músculos espiratorios (abdominal e intercostales internos) solo son estimuladas cuando se requiere una espiración activa. Además, las neuronas inspiratorias del grupo ventral, cuando son estimuladas por el grupo dorsal, aceleran la actividad inspiratoria cuando las demandas ventilatorias aumentan.
La generación del ritmo respiratorio parece descansar en un área denominada médula rostral ventromedial, que se encuentra en la zona superior del grupo respiratorio ventral, en la que se han localizado redes neuronales que generan una actividad marcapasos. No obstante, no se conoce muy bien el mecanismo que da lugar a los movimientos respiratorios rítmicos.
Por su parte, los centros neumotáxico y apnéustico del puente de Varolio ejercen un control fino sobre el centro respiratorio medular que ayuda a suavizar los movimientos respiratorios. El centro neumotáxico envía señales al grupo respiratorio dorsal que ayudan a desconectar las neuronas inspiratorias, limitando así la duración de las inspiraciones. Por el contrario, el centro apneústico impide la desconexión de esas mismas neuronas, las inspiratorias. En ese sistema de contrapesos domina el centro neumotáxico, lo que contribuye a poner límites a la inspiración, permitiendo que la espiración curse con normalidad. Sin la acción del centro apnéustico el ciclo respiratorio consistiría en prolongadas espiraciones interrumpidas por inspiraciones rápidas y muy bruscas.
Como es lógico, la tasa ventilatoria se ajusta para satisfacer las demandas metabólicas de cada momento. Y en ese ajuste se valoran tres indicadores diferentes, la tO2, la tCO2 y el pH, aunque como veremos al final, hay circunstancias en que intervienen otras señales.
En mamíferos, la tO2 arterial es monitorizada mediante unos quimiorreceptores conocidos como cuerpos carótidos y cuerpos aórticos, que se localizan en las bifurcaciones de las arterias carótidas y en el arco de la aorta, respectivamente. En los peces hay quimiorreceptores similares a los de mamíferos pero se localizan en las branquias de forma difusa, y cuando esos receptores detectan una reducción en la tO2 se produce un aumento de la ventilación branquial. Sin embargo, en los vertebrados que respiran en aire las cosas son diferentes. Tiene que caer la tO2 hasta valores tan bajos como 60 mmHg (¡un 40%!) para que se produzca una respuesta por parte de los sistemas de control. La razón de que no haya respuesta a valores superiores de tO2 es que aunque estos sean relativamente bajos, el porcentaje de saturación de la hemoglobina es todavía alto (alrededor del 90% se encuentra combinada con O2). Sin embargo, por debajo de 60 mmHg la saturación del pigmento se reduce muy rápidamente, por lo que la situación se puede volver muy peligrosa y conducir a la asfixia. El pigmento amortigua los efectos de variaciones no demasiado grandes en la tO2 arterial, por lo que funciona, de hecho, como un reservorio de oxígeno que asegura el suministro a los tejidos siempre que la tensión arterial de oxígeno no se reduzca en exceso.
Un aspecto ciertamente llamativo de este sistema receptor es que al responder a la tO2, cualquier factor que reduzca la fracción de O2 combinado con el pigmento pero que no provoque una bajada en aquella, puede resultar fatal, ya que puede darse la circunstancia de que se produzca una caída muy fuerte en el contenido total de O2 en la sangre y ello no dé lugar a una respuesta respiratoria. Es lo que ocurre, por ejemplo, cuando altas cantidades de monóxido de carbono (CO) se unen con la hemoglobina desplazando al O2 de sus sitios de unión. Quienes se intoxican con CO no experimentan una elevación de la tasa ventilatoria en respuesta a la intoxicación porque el CO no provoca una reducción en la tO2 pero sí en el contenido total de oxígeno en la sangre.
Bajo condiciones de reposo, la tCO2 es el parámetro que más importancia tiene en el ajuste de la tasa ventilatoria en mamíferos. Al contrario de lo que ocurre con la tO2, pequeños cambios en la tCO2 dan lugar a una respuesta en la ventilación pulmonar. Un exceso de CO2 en la sangre genera una respuesta refleja a cargo de los centros respiratorios que provocan un aumento en la ventilación y, como consecuencia, la eliminación de tal exceso y la restauración de su nivel normal. Lo contrario ocurre cuando la tCO2 se reduce por debajo del nivel de referencia. La mayoría de los peces también ajustan su tasa ventilatoria en respuesta a las variaciones sanguíneas en la tCO2; se cree que los centros respiratorios reciben las señales de quimiorreceptores branquiales.
En la mayor parte de los animales que respiran en aire no se monitoriza la tCO2 arterial; de hecho, los cuerpos carótidos y aórticos responden muy levemente a los cambios en el nivel arterial de CO2. De mucha mayor importancia son los quimiorreceptores centrales, que se encuentran en la médula, en una posición muy próxima al centro respiratorio. Aunque en realidad, esos quimiorreceptores no monitorizan la concentración de CO2 directamente, sino la de protones –que depende de la anterior- en el líquido extracelular del encéfalo. Los peces sin embargo, parecen carecer de receptores centrales de ese tipo. De hecho, lo más probable es que los receptores centrales aparecieran en los sarcopterigios (peces pulmonados).
Se da la circunstancia de que el CO2 atraviesa la barrera hematoencefálica con gran facilidad, al contrario de lo que ocurre con los H+. Por ello, cuando se produce una elevación de la concentración de estos últimos en el líquido extracelular encefálico ello es señal de que se ha producido un aumento en la concentración de CO2 en el encéfalo.
El gran efecto que ejercen los quimiorreceptores centrales sobre el centro respiratorio es el responsable de que no podamos dejar de respirar a voluntad durante más de un minuto (las personas normales, claro). Cuando dejamos de respirar, la concentración de CO2 no deja de aumentar, porque el metabolismo no cesa y, en paralelo, también aumenta la concentración de protones. Ese aumento acaba ejerciendo un efecto tal sobre el centro respiratorio, que este supera las órdenes provenientes de los centros superiores y provoca la ejecución de los movimientos de los correspondientes músculos.
Dependiendo de las demandas de oxígeno del organismo y de la correspondiente necesidad de eliminar dióxido de carbono, la ventilación alveolar puede llegar a multiplicarse hasta por veinte. Lo curioso es que esa elevación no parece ser provocada por los cambios en las concentraciones de O2, CO2 y H+. De hecho, la concentración arterial de ninguna de esas sustancias experimenta cambios significativos al elevarse la tasa de ventilación pulmonar. Y por otro lado, el aumento de esa tasa se produce en el mismo instante en que se intensifica la actividad que da lugar a la elevación de las demandas metabólicas, pero mucho antes de que haya dado tiempo a que varíen las concentraciones de los gases respiratorios y de los protones en una medida suficiente como para provocar una respuesta regulatoria. Para eso habría hecho falta que transcurriera al menos un minuto, pero la respiración se acelera enseguida.
Son otros los mecanismos que determinan la aceleración de los movimientos respiratorios al iniciarse una actividad física. Y se han sugerido los siguientes: (1) Reflejos cuya génesis se encontraría en los propios movimientos musculares cuya actividad ha de sostenerse y que vendrían activados por señales procedentes de músculos y articulaciones; (2) elevación de la temperatura corporal; (3) liberación de adrenalina; y (4) control anticipatorio a cargo de la corteza cerebral. Como se ha señalado, se trata de posibles mecanismos; todos son verosímiles, pero ninguno de ellos o combinación de varios resultan satisfactorios para explicar el efecto tan marcado e intenso que ejerce el inicio de la actividad sobre la tasa ventilatoria.
Fuentes:
David Randall, Warren Burggren & Kathleen French (2002): Eckert Animal Physiology: Mechanisms and Adaptations 5th ed.; Freeman & Co, New York
Lauralee Sherwood, Hillar Klandorf & Paul H. Yancey (2005): Animal Physiology: from genes to organisms. Brooks/Cole, Belmont.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El control nervioso de la respiración se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El pulmón de los mamíferos
- La curva de disociación de un pigmento respiratorio
- Los animales que respiran en agua
Confirmación experimental de la teoría de la relatividad especial (1)
La teoría de la invariancia es una de las más comprobadas experimentalmente en física. Por lo tanto experimentos hay muchos, como debe ser, ya que la idea un solo experimento crucial es novelesca. No obstante recogemos en esta entrega y en la próxima algunos ilustrativos de las conclusiones de la teoría. Empezamos por el primer postulado de Einstein, que también debe probarse.
La velocidad de la luz en el vacío es constante.

Se ha obtenido una confirmación directa de la constancia de la velocidad de la luz a partir del estudio de las estrellas dobles, que son estrellas que orbitan una alrededor de la otra. Si la órbita de una estrella está en la línea de visión desde la Tierra, entonces en un lado de la órbita se está moviendo hacia la Tierra, en el otro lado se está alejando. Los estudios precisos de la velocidad de la luz emitida por estas estrellas cuando se acercan o alejan de nosotros a alta velocidad no muestran diferencia en la velocidad de la luz, lo que confirma que la velocidad de la luz es independiente de la velocidad de la fuente. Estos experimentos los propuso Willem de Sitter en 1913, y después se han comrpobado reiteradamente cada vez con mayor precisión.

Aún más espectacular es otro experimento que tiene que ver con una partícula a muy alta velocidad en un acelerador. Mientras la partícula se mueve cerca de la velocidad de la luz, emite radiación electromagnética en direcciones opuestas, hacia adelante y hacia atrás. Hay instrumentos sensibles que detectan la radiación y miden su velocidad. Por asombroso que pueda parecer para los no iniciados, la velocidad de la radiación emitida en ambas direcciones resulta ser exactamente la velocidad de la luz, a pesar de que la propia partícula se mueve cerca de la velocidad de la luz, una confirmación del postulado de la constancia de la velocidad de la luz.
Las pruebas experimentales son de tal calibre que la constancia universal de la velocidad de la luz es una ley física fundamental.
La relatividad del tiempo
La teoría de la relatividad predice que un reloj en movimiento, tal y como lo ve un observador estacionario, funcionará más lentamente que un reloj estacionario. Ya hemos mencionado que este efecto ha sido probado y confirmado utilizando relojes atómicos dentro de aviones y satélites.
Una confirmación de la relatividad del tiempo se encontró con la solución a un curioso rompecabezas. Los rayos cósmicos son protones, núcleos y otras partículas de alta velocidad que fluyen a través del espacio desde el Sol y la galaxia en su conjunto. Cuando chocan con las moléculas de la atmósfera de la Tierra su energía y su masa se convierten en otras partículas elementales, una confirmación en sí misma de la equivalencia energía-masa. Una de las partículas que se producen en la atmósfera es el llamado mesón mu, o simplemente el muón. Cuando se producen en el laboratorio, los muones lentos tienen una vida corta. En promedio, solo duran alrededor de 2,2·10-6 s, momento en el cual hay una probabilidad del 50 % de que cada uno se descomponga en otras partículas elementales.
El enigma está en que los muones que se crean en la atmósfera superior y que se mueven a gran velocidad se ha medido que “viven” más tiempo antes de desintegrarse que aquellos generados en el laboratorio. Duran tanto que sobreviven al largo viaje hasta los detectores en el suelo muchos más lo que debería ser posible. Teniendo en cuenta la velocidad con la que viajan y la distancia que deben recorrer desde la atmósfera superior hasta el nivel del mar (unos 30 km), su vida media de 2,2·10-6 s medida para muones lentos no debería ser suficiente para que sobrevivan al viaje. La mayoría de ellos debería desintegrarse antes de tocar el suelo; pero, el hecho cierto es que la mayoría llega al suelo. ¿Cómo es esto posible?
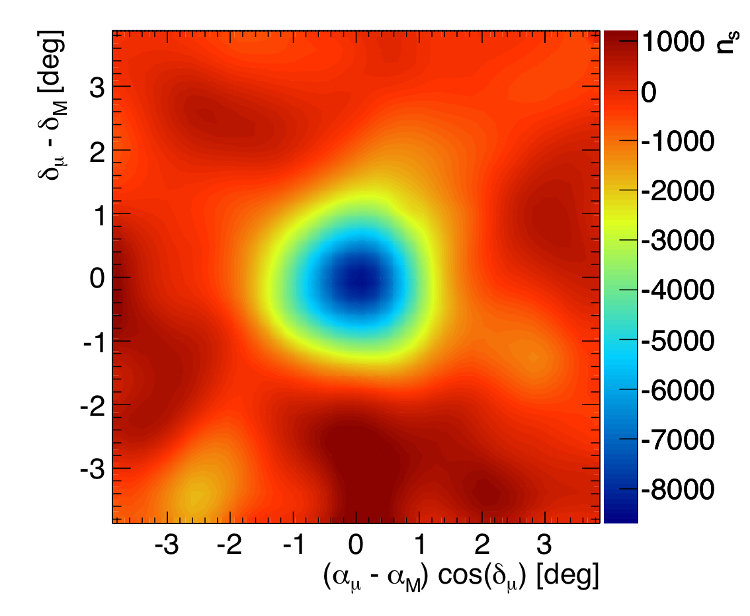
Déficit de muones observados por Ice Cube y que revelan la presencia de la Luna. Esto se debe a que los muones generados por los rayos cósmicos en las capas altas de la atmósfera llegan hasta el detector desde todas las direcciones del espacio, pero la Luna hace que disminuya el número que llegan desde su dirección.
La respuesta es la dilatación temporal predicha por la teoría de la relatividad. En relación con los detectores en el suelo, los muones se mueven a una velocidad tan alta que su “reloj” parece ralentizado, lo que les permite sobrevivir el tiempo suficiente para alcanzar el suelo. La cantidad de ralentización, según lo indicado por el número de muones que llegan al suelo, se encuentra que es exactamente la cantidad predicha por la teoría de la invariancia.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Confirmación experimental de la teoría de la relatividad especial (1) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La primera confirmación experimental de la teoría de Maxwell
- El principio de relatividad (3): la invariancia de Galileo
- La relatividad de la masa
Asesinos en serie
Este capítulo, así como el que se refiere a la utilización política de la violencia que vendrá más adelante, no me dan para escribir mucho. Es un tema poco estudiado con enfoque científico y, a la vez, es muy popular. Una pequeña introducción, aclarar algunos conceptos y dejar hablar a los asesinos, ellos lo dicen todo y, espero, nos quedarán pocas dudas sobre lo que son. Y es difícil encontrar una explicación evolutiva a su existencia. Por ahora sigo en la duda.

Uno de los más famosos asesinos en serie, Jack “el destripador”, representado en una caricatura de “Punch” de 1888 como el fantasma de la muerte que recorre Whitechapel.
Los asesinos en serie, que forman parte de la humanidad desde siempre, y solo hay que recordar los 28 cadáveres de la Sima de los Huesos en Atapuerca, quizá más crimen en masa que asesinatos en serie, son el 1% del total en Estados Unidos, el país donde más abundan las investigaciones y las estadísticas sobre este asunto. Se define al asesino en serie como el que comete tres o más asesinatos en lugares y tiempos diferentes, con fases temporales de recuperación y con fallos emocionales o psicopatológicos. Pueden ser organizados o desorganizados, localizados o itinerantes, visionarios o controladores, y otros tipos.
Peter Kurten: La verdadera historia de Peter Lorre

“Tenía un pequeño cuchillo de bolsillo con el cual corté su garganta. Oí los chorros y el goteo de la sangre en la estera al lado de la cama. Salió a borbotones en un arco. La cosa entera duró cerca de tres minutos. Entonces salí, cerré la puerta otra vez y regresé a mi casa en Düsseldorf.”
Siempre recordaré a El Vampiro de Düsseldorf, con el rostro atormentado y los ojos saltones de Peter Lorre en la película, dirigida por Fritz Lang, estrenada en 1931, el mismo año en que el verdadero Vampiro fue ejecutado. Se llamaba Peter Kurten y había nacido el 26 de mayo de 1893 en Mülheim, que hoy forma parte de Colonia. Era el tercero de 13 hermanos de una familia pobre sometida a un padre alcohólico y violento que los maltrataba y llegó a violar a alguna de las hermanas de Peter; es probable que el mismo Peter también fuera violado. A los ocho años huyó de casa y cometió diversos delitos y eran frecuentes sus entradas y salidas de la cárcel. A los nueve años, y según propia confesión, asesinó a dos amigos ahogándolos en el Rhin. Fueron sus primeros asesinatos. También violaba, torturaba y mataba animales, sobre todo perros, e incluso llegó a trabajar en una perrera. Entre 1902 y 1913, es acusado de estafa, robo con fractura, pirómano y desertor.
En 1913 estranguló y degolló a Kristine Klein, de trece años, que se encontraba en una casa en la que entró a robar. Kurten se casó en 1921 y se trasladó a Altenburg donde encontró trabajo de camionero. Su boda, una condena en la cárcel y la Primera Guerra Mundial interrumpieron los asesinatos. Pero en 1925 volvió a Düsseldorf y volvió a matar.
Su año más sangriento fue 1929. El 8 de febrero, atacó a una joven y violó y mató a Rosa Ohliger, una niña de ocho años; el 13, apuñala veinte veces a un inválido borracho, mecánico de oficio, y cuando es descubierto el cadáver, Kurten aparece por allí y charla sobre el caso con la policía; el 11 de agosto, estrangula y apuñala a una criada llamada Marie Hahn; el 21, ataca con su navaja a tres personas; el 23, dos hermanas de cinco y catorce años; el 24, mata a un hombre; en septiembre, comete dos violaciones y dos asesinatos, y en uno de ellos mata a una mujer con un martillo; y el 7 de noviembre, otra niña de cinco años. De este último asesinato, envió a la prensa un mapa para que pudieran localizar el cadáver. La policía, ante la cantidad de ataques y la diversidad de armas y víctimas, empieza a creer que hay más de un loco suelto. En febrero y marzo de 1930, ataca a varias personas con el martillo pero ninguna muere.
Düsseldorf enloqueció de terror. Nadie se atrevía a salir solo a la calle. La recompensa por la captura del asesino alcanzó cifras fabulosas y la policía recibió denuncias de hasta 900000 personas. Se siguieron 12000 pistas y hasta 200 personas se acusaron de ser los autores de los crímenes del Vampiro.
Maria Budlick era criada. Conoció a Kurten el 14 de mayo de 1930. La convenció para ir a un bosque y allí la estranguló y violó. Pero Maria sobrevivió al ataque. Acudió a la policía y describió a Kurten y pronto su retrato robot circulaba por toda Alemania. Era cuestión de tiempo.
Kurten, con su habitual y extraña conducta, le confesó a su esposa quien era y, para no perder el dinero de la recompensa por su captura, le pidió que le delatara a la policía. El 24 de mayo de 1930, el Vampiro de Düsseldorf se entregó a la policía. Confesó sus crímenes, aunque en el juicio que se celebró un año después, en mayo de 1931, cambió varias veces su declaración. Con un acuerdo muy amplio entre los conocedores de la historia de Kurten, se le atribuyen nueve asesinatos, siete intentos frustrados y unas ochenta agresiones sexuales. Los expertos psiquiatras lo declararon responsable de sus actos y fue condenado a muerte.
Peter Kurten murió guillotinado en el patio de la prisión de Klügelputts el 2 de julio de 1931, a los 48 años. Según cuentan, quizá es una leyenda, una de las últimas frases de Kurten, raro como era, fue preguntar si “una vez guillotinado, aunque sea por poco tiempo, ¿podré oír la sangre saliendo de mi cuello?”
El 11 de mayo de 1931, durante el juicio de Kurten y mes y medio antes de su ejecución, Fritz Lang había estrenado en Berlín M, El Vampiro de Düsseldorf. Sólo dirigió una película más en Alemania; pronto marcharía, primero a Francia y después a Estados Unidos. El fantasma del nazismo cubría Alemania. Hasta 1959 no volvería a dirigir películas en su país.
Saber por qué un asesino mata a menudo es una incógnita de difícil respuesta. Kurten, en el juicio, habló de su pasión por beber la sangre de sus víctimas, en un síndrome llamado hematodipsia, del placer sexual en el momento de matar y, también, de matar para “aleccionar a una sociedad opresiva”. También declaró que llegaba al orgasmo cuando mataba y que variaba el número de puñaladas según el tiempo que tardaba en eyacular. Además, estaba su vampirismo, su afán de beber sangre, con implicaciones sexuales. El vampirismo se define, en términos psiquiátricos, como el acto de extraer sangre de un objeto, normalmente un objeto de amor, y recibir excitación sexual y placer. La sangre se puede obtener de varias maneras, aunque las usuales son la puñalada y el mordisco. El momento de extraer o sorber la sangre de la herida es una parte importante de la acción del vampiro. Como ven, todo coincide con las declaraciones de Peter Kurten.
El Vampiro de Düsseldorf fue la cristalización del miedo de todo un pueblo. Como ocurre con nuestro Sacamantecas, al que tanto se parece, el Vampiro sigue dando miedo en la actualidad. Un vampiro siempre ejerce una cierta fascinación, tiene poder sobre otras personas y produce terror. Hablar del Vampiro es hablar de un ser maléfico difícil de encarnar en una persona concreta, en el ciudadano llamado Peter Kurten (o en el rostro de Peter Lorre). El Vampiro es, al final, un mito cuyas apariciones traen, y a la vez predicen, los malos tiempos que se viven. Hay que recordar que estamos en la torturada Alemania de entreguerras, y pronto llegará el nazismo, que ya era entonces una realidad palpable en las calles de Alemania.
Arnold Edelstein, del Sistema de Prisiones de Israel, publicó hace unos años una revisión de los tipos de asesinos en serie. Para el autor está el asesino en serie en sentido estricto, con una víctima en cada crimen y repitiendo después de un intervalo de tiempo, hasta llegar a las tres víctimas y convertirse, oficialmente, en asesino en serie. En cambio, el asesino de masas llega a las tres víctimas en un solo episodio. Y también define Edelstein al asesino de masas en serie como el que coloca bombas, con muchas víctimas, en varias ocasiones. Finalmente, el autor comenta la orgía de asesinatos de quien mata a tres o más víctimas en varios episodios separados por horas o por pocos días.
Cuesta encontrar un motivo o, si se quiere, un móvil, para estos crímenes. O. por lo menos, un motivo que entendamos los demás. Ya veremos más adelante que, viendo sus antecedentes y la historia de su vida, sobre todo en la infancia, quizá podamos llegar a las causas de su conducta pero es difícil captar la justificación de sus actos. Como ocurre a menudo en este libro, podemos explicar pero eso no justifica en absoluto el comportamiento de los asesinos desde nuestra cultura y sociedad.
En general, se afirma que, para los asesinos de un solo crimen, la violencia quizá sea un experimento sin control. Sin embargo, para el asesino en serie, la violencia es el equivalente de un programa de intenciones, incluso de un programa de investigación, con diferentes experimentos para mejorar lo que busca el autor, sea lo que sea.
El asesino en serie se enfrenta al caos o al disparate que para él es su vida e intenta, con sus crímenes, ponerle un orden y encontrarle un sentido. Como escribió hace unos años un asesino en serie “se convierte la vida en un cómic en el que cualquier cosa es posible”. Por ejemplo, es, en el fondo, lo que intentan conseguir los profesionales de la medicina que matan deliberadamente a sus pacientes con la excusa de liberarles de su sufrimiento.
Sylvestre Matuska: El amante de los trenes

Austríaco, de origen húngaro, era un ingeniero de ferrocarriles que, por lo que cuentan, solo alcanzaba el orgasmo ante una catástrofe ferroviaria con descarrilamiento incluido. Quizá, en psiquiatría, esta obsesión hasta tiene un nombre específico; lo ignoro, pero la obsesión es fascinante.
Nació Sylvestre Matuska, o Szilveszter Matuschka, el 29 de enero de 1892 en Csantaver, en la Vojvodina, pueblo que ahora se llama Cantavir y pertenece a Serbia. Hijo de un zapatero, fue movilizado en 1914 por el ejército austro-húngaro durante la Primera Guerra Mundial. En 1915 pertenece a un regimiento de zapadores que cubre la retirada ante el avance de los rusos en Galitza, hoy Polonia. Su regimiento vuela puentes, carreteras, vías de tren y esclusas y Matuska, ya ingeniero, destaca por su habilidad y sangre fría. Ingeniero mecánico especializado en trenes, inventó un sistema de frenos para locomotoras y tenía otras 92 patentes depositadas.
Aunque incluso es condecorado, cuando la guerra termina, la vida en Hungría derrotada es difícil. Prueba varios oficios y fracasa; es comerciante, tendero, albañil, transportista y, por fin, prospera con la explotación de una cantera. Excelente marido y padre, se instala en Viena como un buen burgués y un católico practicante
En Austria, en diciembre de 1930 y enero de 1931, hizo sus dos primeros intentos, uno en Viena y otro en Berlín, ambos fallidos, para descarrilar un tren y provocar un desastre. Tuvo éxito el 8 de agosto de 1931 al conseguir que descarrilara el tren expreso Berlín- Basilea. No hubo víctimas. Entre los restos se encontró un medio destrozado periódico nazi y, por ello, se supuso que había sido un atentado con trasfondo político. Se ofreció una fuerte suma como recompensa por la captura de los culpables.
Un mes más tarde, el 13 de septiembre, a las 12.20 horas, el expreso de Viena descarriló y cayó del viaducto de Biatorbagy, cerca de Budapest. Matuska voló parte del puente y la locomotora y nueve de los once vagones cayeron unos 30 metros al barranco. Murieron 22 personas y 120 resultaron heridas, 17 de ellas de gravedad. Entre los pasajeros que se salvaron estaba la cantante y actriz Josephine Baker, que entretuvo a los heridos y a los viajeros ilesos con sus canciones.
Matuska, que, por supuesto, estaba en la escena del crimen observando, y supongo que disfrutando, todo lo que veía, se hizo pasar por un pasajero del tren que no había resultado herido y le dejaron marchar.
Sin embargo, ya en ese momento, la policía de varios países perseguía al autor de los cuatro descarrilamientos o intentos de descarrilamientos. Sospechaban de Matuska y le detuvieron en Viena un mes más tarde, el 10 de octubre de 1931, y pronto confesó.
En Austria le juzgaron y le condenaron por los atentados fallidos pero, a continuación, fue extraditado a Hungría, con la condición de que no fuera ejecutado. Así ocurrió: fue condenado a muerte y su pena conmutada por cadena perpetua.
Escapó de la cárcel en 1944, en la confusión del final de la Segunda Guerra Mundial, cuando el ejército soviético invadió Hungría, todavía aliada de los alemanes. Matuska desapareció, aunque hay quien asegura que se convirtió en un experto en explosivos en el Ejército Rojo y que, incluso, participó en la guerra de Corea.
Los motivos de Matuska para descarrilar trenes son, por supuesto, o desconocidos o estrambóticos. En el juicio declaró que se lo había ordenado Dios. Además se explayó afirmando que “destrozo trenes porque me gusta ver a la gente morir, me gusta escuchar como gritan”. También se afirmó en el juicio que Matuska solo alcanzaba el orgasmo cuando veía los trenes que había descarrilado.
Un personaje así parecía fuera de lugar en nuestra época pero, en 1990, la banda Lard, de heavy metal, lo recuperó y compuso una canción con su nombre y su historia (se puede escuchar en YouTube). Es obvio que es un tema heavy metal y, por lo tanto, feroz y ruidoso. Una de las estrofas dice así:
“Es un mensaje de Dios
Dinamita
Fin de la línea
Rechina el metal
Gritan los heridos
Explotan las bombas”.
Cuenta Juan Antonio Cebrián que hay tres características en los niños que les hacen candidatos a asesinos en serie: micción nocturna, hacer daño a animales o amiguitos, y atracción por el fuego. Por supuesto, no todos los que llevan estas conductas serán, al crecer, asesinos. Sería terrible porque esas conductas se dan en muchos niños. Vienen de la incompetencia de los padres, a menudo delictiva, con un entorno social poco eficaz y con fantasías ligadas al sexo y a la violencia.
Los asesinos en serie no sienten que sean malos sino, más bien, que las humillaciones y las provocaciones les obligan a cometer todo tipo de actos terribles. Eran, muchos de ellos, psicópatas, pero no enfermos mentales y distinguían con claridad el bien y el mal.
Todas estas características de los asesinos en serie las comenzó a organizar a finales de los ochenta Robert Ressler, entonces en el FBI. Fue el primero en utilizar el término de asesino en serie después de que, en una conferencia, uno de los asistentes hiciera una referencia a “crímenes en serie”. A Ressler le gustó el término y, a su vuelta al cuartel del FBI, comenzó a utilizar el concepto de asesinos en serie para aquel que “comete un crimen, y otro y otro de manera repetitiva”.
Definió asesino en serie y enumeró las conductas y comportamientos que lo caracterizaban. También afirmó que un asesino en serie es un don nadie que quiere ser alguien, y no a través de una fama positiva, sino de la infamia y la crueldad. Cualquier tipo de reconocimiento es bueno para él. Muchos comienzan a matar porque son tan inadecuados para otra cosa que se sienten incapaces de sentir reconocimiento por lo que hacen. Fantasean con ser asesinos, con matar, con ser famosos,… Son el centro de atención, se sienten bien, aunque la atención sea positiva o negativa, les da igual.
Pittsburgh Phil Strauss: El mejor trabajador de la empresa

Es el más profesional de los asesinos de la Mafia y fascina por su sangre fría y su indiferencia ante el dolor de los demás. Declaró en una ocasión que, como un jugador de fútbol, “me preparé para hacer este trabajo; los jefes se fijaron en mí, y acabé jugando en primera división”. Es cierto, personas con tanta experiencia y criterio como Lucky Luciano, Joe Adonis o Albert Anastasia se fijaron en Pittsburgh Phil Strauss y terminó siendo el asesino más eficaz de la Murder, Inc., la empresa de crímenes por encargo con sede en Nueva York y contratos por todo Estados Unidos. De Brooklyn al cielo, si lo deseabas, y los expertos de Murder, Inc., te facilitaban el tránsito al otro mundo.
Nacido en Brooklyn como Harry Strauss en 1908, adoptó el alias de Pittsburgh Phil aunque no tenía nada que ver con la ciudad del mismo nombre, pero le sonaba bien. De todas formas, sus amigos de confianza le llamaban “Pep”.
Era todo un experto en mil maneras de matar, como el buen profesional y artesano que aspiraba a ser. Cuando tenía que cumplir un contrato en cualquier lugar del país, ponía en su maleta una camisa, unos calcetines, unos calzoncillos, una pistola, un cuchillo, un trozo de cuerda bueno para estrangular y un pico de hielo, herramienta que le gustaba especialmente. Iba en tren o en avión, hacía su trabajo y cogía el siguiente enlace a Nueva York. A menudo, Pittsburgh Phil no sabía quién era el muerto, es más, no le importaba en absoluto no saberlo.
Cuando en 1940 la fiscalía de Brooklyn, dirigida por William O’Dwyer, desmanteló Murder, Inc., encontraron pruebas suficientes como para acusar a Pittsburgh Phil de 28 asesinatos. Son los probados; hay quien afirma que el total se acercaría a los 500. Quizá es exagerado, pero es muy probable que superen en mucho los 100.
Era y se sentía un dandi, elegante y mujeriego, y ocupaba la habitación de hotel más cara y lucía la ropa más fina de la ciudad. Un comisario de policía que le interrogó dijo que era el tío más elegante del lugar y, sin embargo, no había tenido un trabajo honrado en su vida. Es obvio que el bribón, alto, esbelto y elegante Pittsburgh Phil tuvo gran éxito con las mujeres. En Brooklyn, donde le conocían bien, le perseguían y su romance con Evelyn Mittelman, incluido el asesinato de un rival, contribuyó a que la chica fuera conocida como “Miss Beso Mortal”.
En su trabajo, Pittsburgh Phil era eficaz y salvaje. Uno de los asesinatos que se le atribuyen es el de George Rudnick, que tenía la mala fama de ser confidente de la policía. Cuando se encontró su cuerpo, la descripción del forense es fría y directa: “Es un varón adulto, algo desnutrido, con un peso aproximado de 140 libras y 6 pies de altura. Presenta 63 heridas de puñales en el cuerpo. En el cuello tiene 13 puñaladas. En la parte derecha del tórax tiene 50 heridas circulares. Tiene una laceración en la región frontal de la cabeza; la herida es abierta y el hueso está hundido. El rostro está azul. La lengua sobresale de la boca. A la altura de la laringe se observa un surco, blanco y hundido, más o menos de la anchura de una cuerda de colgar la ropa (de tendedero). En la disección del corazón se observó que su pared estaba completamente atravesada por puñaladas. Mi conclusión es que la causa de la muerte fueron múltiples puñaladas y asfixia debida a estrangulamiento.”
Todo un profesional Pittsburgh Phil Strauss. Si le encargan un asesinato, se asegura a conciencia de que el “contrato” está muerto y bien muerto. Vamos, ni siquiera el forense sabe de qué ha muerto al haber tantas causas probables.
En otra ocasión, en un contrato en Detroit no encontraba manera de cumplirlo pues el condenado, Harry Millman, siempre se mantenía a cubierto o entre multitudes o comía en restaurantes repletos de comensales. Es igual, nuestro asesino se harto de esperar y, cuando Millman estaba comiendo, apareció armado con dos revólveres y lo mató y, de paso, hirió a otros cinco clientes del establecimiento. O como cuando mató a un tipo al que se acusaba de quedarse el dinero de las tragaperras. Se lo cargó con 32 golpes de un pico para el hielo, lo ató a una tragaperras y lo tiró a un lago en las montañas Catskills. Una semana más tarde, el cadáver subió a la superficie del agua, hinchado por los gases de la descomposición. Pittsburgh Phil comentó a sus colegas que para conseguir que este tipo no flotara había que ser doctor en medicina. Así, nuestro experto asesino aprendió algo más sobre el caprichoso comportamiento de los cadáveres.
Que se sepa, Pittsburgh Phil solo falló en el cumplimiento de un contrato. Fue a Florida a matar a un mafioso. Lo siguió, entró en un cine y se sentó en la última fila. Pittsburgh Phil llevaba una pistola pero pensó, con razón, que usarla sería muy ruidoso. Vio un hacha en un armario contraincendios. La cogió y, cuando se acercaba a su víctima, esta se levantó y se volvió a sentar unas filas más adelante, en el centro del patio de butacas. Nuestro asesino se hartó y dejó el hacha, salió del cine y volvió a Brooklyn. Allí contó a sus amigos que el tipo era “un maldito culo inquieto”.
A veces, un experto, si no encuentra las circunstancias apropiadas, las crea. También fue en Florida donde Pittsburgh Phil Strauss tenía que asesinar a un mafioso ya entrado en años y que no hablaba ni palabra en inglés. Nuestro experto no encontraba forma de llevarle a algún lugar discreto donde asesinarlo sin testigos. Se le ocurrió una solución ingeniosa pero, también complicada. Visitó al mafioso, le enseñó una maleta llena de armas y, por señas, le pidió ayuda para cumplir un contrato. El viejo mafioso, feliz de volver a ser útil, cogió una cuerda de la maleta y llevó a Phil a un callejón oscuro muy apropiado para cumplir un contrato. Y se cumplió el contrato. Phil le quitó la cuerda de las manos y le estranguló allí mismo.
Fue Abe Reles, su compañero de negocios en Murder, Inc., quien comenzó a cantar para la policía y la fiscalía de O’Dwyer y no paró y acabó por enviar a todos sus colegas a la silla eléctrica. Así pasó hasta que el mismo Reles fue objeto de contrato y saltó desde la ventana de la habitación del hotel, la 623 del Half Moon Hotel de Coney Island, en el que vivía protegido por las fuerzas del orden.
Mientras Abe Reles volaba, Pittsburgh Phil Strauss iba a juicio el 4 de septiembre de 1939, junto a su compañero en Murder, Inc., Martin “Buggsy” Goldstein, por el asesinato por estrangulamiento del corredor de apuestas Irving “Puggy” Feinstein, cuyo cadáver apareció quemado en un solar. Phil, para salvarse en el juicio, se hizo el loco y él, tan elegante, dejó de afeitarse y lavarse, iba con la ropa sucia y sus declaraciones eran un balbuceo incoherente a la vez que mascaba sin parar la correa de un maletín. No convenció a nadie y el 12 de junio de 1941, en una calurosa noche de verano, Pittsburgh Phil Strauss, a los 31 años de edad, se sentó en la maldita silla eléctrica del penal de Sing Sing.
Referencias:
Abeijón, s.f. Peter Kürten: El Vampiro de Dusseldorf. http://www.asesinos-en-serie.com/Peter_Kurten/El_Vampiro_de_Dusseldorf.php
Cebrián, J.A. 2007. Psicokillers. Perfiles de los asesinos en serie más famosos de la historia. Ed. Nowtilus. Madrid.
Cuquerella Fuentes, A. 2004. Asesinos en serie. Clasificación y aspectos médico-forenses. Estudios Jurídicos 4135-4160.
Edelstein, A. 2014. Re-thinking typologies of multiple murders: The missing category of serial-mass murder and its theoretical and practical implications. International Journal of Emergency Mental Health and Human Resilience 16: 122-126.
Garrido Genovés, V. et al. 2015. Asesinos múltiples en un solo acto. Mente y Cerebro 72: 64-69.
Kinnell, H.G. 2000. Serial homicide by doctors: Shipman in perspective. British Medical Journal 321: 1594-1597.
Olmos, M. 2010. El vampiro de Düsseldorf. El Correo 11 septiembre.
Reouven, R. 1976. Diccionario de los asesinos. DOPESA. Barcelona. 386 pp.
Ressler, R.K. & T. Shachtman. 2005. Asesinos en serie. Ariel/Centro Reina Sofía para el Estudio de la Violencia. Barcelona. 382 pp.
Schroeder, B. 2007. Strange and Terrible!: Serial Killers. Number 1: Why did they do it? Zem Books. Marion, Indiana. 84 pp.
Sifakis, C. 2005. The Mafia Encyclopedia. Facts On File, Inc. New York. 510 pp.
Turkus, B.B. & S. Fidler. 1966. Crímen, S.A. Ed. Bruguera. Barcelona. 671 pp.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Asesinos en serie se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los asesinos
- Nuestros ancestros asesinos
- Apilando bloques: de los Lemmings a la serie armónica cruzando el Guadalquivir
El gran encéfalo humano es un “encéfalo social”

Los seres humanos actuales tenemos encéfalos muy grandes, más grandes que casi todos nuestros antecesores. De hecho, el volumen de nuestro cráneo es tres veces mayor (corregido el efecto del tamaño corporal) que el de nuestros antecesores austraolopitecinos. Las excepciones son los primeros seres humanos de nuestra especie y los neandertales, que tenían cerebros algo más grandes que nosotros. Probablemente, gracias a esos encéfalos más grandes exhibimos habilidades cognitivas valiosas, aunque no está muy claro cuál es el elemento -si es que pudiese atribuirse a uno único- que habiendo resultado de esas habilidades, ha constituido factor de éxito en términos evolutivos.
Los científicos de este campo han venido considerando tres razones posibles por las que resultan ventajosas las habilidades cognitivas de que son capaces encéfalos más grandes. Una es que esos encéfalos proporcionan a sus poseedores la capacidad para hacer frente a cambios climáticos y meteorológicos haciendo uso de tecnologías adecuadas para ello; gracias a esa capacidad se habrían podido superar los obstáculos que se derivan de variaciones temporales y geográficas del clima y que hubiesen podido limitar la continuidad de la especie en el tiempo o su distribución geográfica. De ser correcta esta hipótesis, los aumentos en el volumen encefálico se habrían producido bajo la presión selectiva de la variabilidad e impredecibilidad climática.
Otra posible razón es que las mayores capacidades cognitivas hicieron a los miembros de nuestra especie más capaces para hacer uso de diferentes fuentes de recursos alimenticios, principalmente mediante la caza, y búsqueda y recolección de alimentos; en particular, el desarrollo de variadas técnicas de caza pudo resultar clave a la hora de capturar animales de todo tipo. Esta idea se basa en la observación de que las especies con comportamientos alimenticios complejos o de intensa actividad depredadora tienden a tener volúmenes encefálicos comparativamente grandes.
Y la tercera razón es que esas habilidades cognitivas permitieron un mejor desenvolvimiento en las relaciones que se establecen con los otros en las cada vez más complejas sociedades humanas. Según sus defensores, nuestros antecesores homínidos desarrollaron adaptaciones que les permitieron un uso muy eficiente de los recursos biológicos y un mayor control de sus propias condiciones de vida. Esas capacidades propiciaron menores tasas de mortalidad y, en consecuencia, aumentos en el tamaño de las poblaciones. Un mayor número de individuos habían de competir por los recursos disponibles y, de esa forma, se dieron las condiciones que facilitaron el desarrollo de habilidades que mejoraron la cooperación dentro de unos grupos que eran cada vez de mayor tamaño. A esta tercera se la denomina “hipótesis del encéfalo social”.
Pues bien, según las conclusiones de un estudio realizado por Drew H. Bailey y David C. Geary, de la Universidad de Missouri en Columbia, es este tercer elemento el que resultó determinante. Lo sostienen basándose en un análisis del tamaño de 175 cráneos de diferentes especies de homínidos, correspondientes a variadas localizaciones geográficas y a un periodo comprendido entre 1’9 millones y 10.000 años de antigüedad. Entre las diferentes variables con las que correlacionaron el tamaño de los cráneos, fue el tamaño poblacional el que resultó ser el mejor predictor de aquél, aunque a la vista del efecto de otros predictores, las variables de carácter climático, también han podido ejercer una cierta influencia.
Referencia:
Drew H. Bailey y David C. Geary (2009): “Hominid Brain Evolution. Testing Climatic, Ecological and Social Competition Models”. Human Nature, vol. 20, p. 67-79.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El gran encéfalo humano es un “encéfalo social” se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Insectos agrícolas
Jorge Poveda Arias
La primera imagen que nos viene a la cabeza cuando pensamos en insectos son las típicas moscas molestas y avispas peligrosas que nos llegan a margar las tardes de verano, pero, ya lo dijo el microbiólogo descubridor de la primera vacuna contra la polio, Jonas Salk: “Si desaparecieran todos los insectos de la tierra, en menos de 50 años desaparecería toda la vida. Si todos los seres humanos desaparecieran de la tierra, en menos de 50 años todas las formas de vida florecerían”.
Los insectos son una clase de animales invertebrados de seis patas incluidos dentro del Phylum de los artrópodos. Estos últimos se caracterizan por tener el cuerpo dividido en segmentos a los cuales se les unen diferentes apéndices (patas, antenas, alas), además de tenerlo recubierto de quitina, de la cual necesitan desprenderse para crecer mediante mudas sucesivas. Las principales clases dentro de este grupo son los crustáceos, los arácnidos, los miriápodos y los insectos, diferenciándose estos últimos del resto por tener el cuerpo dividido en tres regiones (cabeza, torax y abdomen), y poseer un par de antenas, un par de alas y tres pares de patas.
La denominada como “entomología agrícola” se describe como la ciencia que estudia todos aquellos insectos capaces de relacionarse directamente con el sistema agrícola y modificarlo. Por lo tanto, dentro de esta definición se incluyen los insectos polinizadores, los fitófagos (que se alimentan de material vegetal) y los que desarrollan una simbiosis mutualista (ambos individuos obtienen un beneficio), por ejemplo, al vivir en el interior de las plantas, como es el caso de varias especies de hormigas que viven en estructuras formadas en las ramas de las acacias y la protegen si algún herbívoro pretende consumir sus hojas. Además, todos aquellos insectos que interaccionen con ellos directamente, también podrán ser objeto de estudio de esta ciencia.

Hormigas en simbiosis mutualista con acacia. Wikimedia Commons
Por lo que se refiere a la polinización de los cultivos, se calcula que el 80% la llevan a cabo insectos polinizadores como las abejas de la miel (Apis mellifera), de ahí la enorme importancia de los insectos en la productividad agrícola de alimentos. Pero no solo las abejas (melitofilia) son capaces de transportar el polen de una flor a otra provocando su fecundación, también otros insectos visitan las flores con el fin de alimentarse de su néctar, como los escarabajos (cantarofilia), las moscas (miofilia), las avispas (esfecofilia), las hormigas (mirmecofilia) o las mariposas (faenofilia y psicofilia). Por otro lado, las hormigas también pueden dispersar activamente las semillas de diferentes plantas, al perderlas en el camino de vuelta al hormiguero.
En lo concerniente a los insectos fitófagos, destacar que la mitad de ellos consumen materia vegetal en algún momento de sus vidas, clasificándose en defoliadores (comen hojas), minadores o barrenadores (forman galerías en los tallos), xilófagos (consumen madera) o chupadores (succionan los fluidos vegetales). Para que una población de insectos pase de estar simplemente presente en un cultivo agrícola a conformar una plaga es necesario que ocurran cambios en la presión que el medioambiente ejerce sobre ellos. Los insectos siguen la denominada como estrategia biológica de la “r”, basada en tener gran cantidad de descendientes de los cuales muy pocos llegarán a la edad adulta para reproducirse. Esto es debido a la presión del medio, que incluye, la temperatura, la humedad, el viento, los depredadores etc. Si el ser humano disminuye la presión que estos factores externos ejercen sobre los insectos fitófagos, por ejemplo, aumentando la temperatura debido al cambio climático o esparciendo por el cultivo insecticidas que acaben con todos sus enemigos naturales, la población de insectos perjudiciales no dejará de aumentar y su daño sobre las plantas será tan elevado que conformarán una plaga.
Myzus persicae es el nombre científico con el que se le conoce al pulgón verde del melocotonero. Este pequeño insecto se incluye dentro del grupo de los hemípteros y se alimenta introduciendo un pico en el interior de las plantas y absorbiendo sus fluidos nutritivos. Su ciclo de vida comienza en árboles del género Prunus (ciruelos, cerezos, melocotoneros, almendros) donde las hembras pusieron sus huevos el otoño anterior. Estos huevos eclosionan justo antes de empezar la primavera y surgen pequeños pulgones verdes sin alas que se alimentan sobre estos árboles. Tras un par de generaciones, los individuos que nacen de los nuevos huevos ya presentan alas y se dispersan, atacando a prácticamente cualquier planta que encuentren a su paso, incluyendo cultivos hortícolas. Sobre estos nuevos hospedadores desarrollan varias generaciones, volviendo a los árboles Prunus en septiembre. Esta plaga es capaz de provocar graves daños a los cultivos, al atacar hojas, flores y frutos, produciendo su secado o manchas que dificultan su venta. Además, al alimentarse de gran cantidad de plantas diferentes es transmisor de más de 100 virus vegetales distintos.
La mosca de la fruta (Ceratitis capitata) es un díptero algo más pequeño que la mosca doméstica (Musca domestica) con colores muy llamativos. El verdadero problema en la agricultura lo causan sus larvas, al alimentarse de los frutos de cítricos y frutales de pepita y hueso. En primavera surgen las moscas adultas que, tras reproducirse, pondrán sus huevos en los frutos que encuentren. Entonces la larva nacerá e irá alimentándose de la pulpa del fruto hasta que alcance su máximo tamaño y se transforme en mosca adulta. Los frutos atacados muestran graves daños, caracterizados por una pulpa semilíquida en la cual se desarrollan diferentes hongos.

Mosca de la fruta (Ceratitis capitata). Wikimedia Commons
El escarabajo de la patata (Leptinotarsa decemlineata) es un coleóptero cuyo adulto es redondeado y listado en amarillo y negro. Por otro lado, las larvas son de color rojo-amarillo, muy blandas y gibosas. Aunque es un insecto que puede alimentarse de las hojas de cualquier solanácea (tomate, berenjena) prefiere la patata sobre cualquier otra planta. Son animales muy voraces, que consumen el tejido vegetal hasta dejar a las plantas totalmente defoliadas, disminuyendo enormemente la formación de los tubérculos, tanto en número como en tamaño. Como curiosidad, destacar que estos escarabajos se encontraban aislados en la zona de las Montañas Rocosas, alimentándose únicamente de una especie silvestre de solanácea, pero con la expansión del cultivo de la patata por todo el territorio americano estos insectos salieron de su aislamiento, aumentando enormemente su población y estando presentes, en la actualidad, en todo el hemisferio norte.

Larva del escarabajo de la patata comiendo hoja. Wikimedia Commons
El control biológico se define como la utilización de organismos vivos con el fin de disminuir la población de alguna especie que cause perjuicios al hombre. En este sentido, contra los insectos plaga de los cultivos agrícola existen diferentes estrategias, como son la utilización de microorganismos entomopatógenos (hongos, bacterias, virus y nematodos) o la utilización de otros insectos. Las estrategias seguidas en la utilización de insectos que acaben con otros insectos plaga se basan en conservar a los enemigos naturales presentes en el propio cultivo, incrementar el número de estos enemigos por liberación de nuevos individuos, o introducir nuevos enemigos exóticos.

Larva de mariquita cazando pulgones. Wikimedia Commons
Existen muchos ejemplos de éxito dentro de esta forma sostenible de reducir las plagas agrícolas, muchos de los cuales pueden ser adquiridos de forma comercial por los agricultores. Por ejemplo, contra los pulgones existen depredadores muy efectivos como las mariquitas (Coccinellidae), cuyas larvas y adultos atacan activamente a todos los pulgones que encuentran a su paso, consumiéndolos por completo. También contra los pulgones, existen los denominados como insectos parasitoides, los cuales ponen sus huevos en el pulgón y la larva que nazca lo irá devorando internamente, dejando únicamente su cutícula externa. Dentro de este grupo destacan pequeñas avispas, como Lysiphlebus testaceipes.

Avispilla introduciendo su huevo en pulgón. Wikimedia Commons
La importancia que los insectos tienen sobre el sistema agrícola es de elevada relevancia, no sólo vistos como un problema, sino también como medios para aumentar su productividad, al favorecer la polinización o atacar directamente a otros insectos perjudiciales.
“La ciencia que no es divulgada hacia la sociedad es como si no existiera”
Referencias y más información:
Avilla, J. (2005). El control biológico de plagas y enfermedades. La sostenibilidad de la agricultura mediterránea. Universitat Jaume I de Castellón.
Barrientos, J. A. (Ed.). (2004). Curso práctico de entomología (Vol. 41). Univ. Autònoma de Barcelona.
Dajoz, R. (2001). Entomología forestal: los insectos y el bosque: papel y diversidad de los insectos en el medio forestal. Mundi-prensa.
Gillott, C. (2005). Entomology. Springer Science & Business Media.
Jacas, J. A., & Urbaneja, A. (Eds.). (2008). Control biológico de plagas agrícolas. Phytoma.
Moreno, A. A. & Álvarez, C. S. (2005). Entomología agraria: los parásitos animales de las plantas cultivadas. Diputación Provincial de Soria.
Planelló M.R., Rueda M.J., Escaso F., Narváez I. (2015). Manual de entomología aplicada. Sanz & Torres.
Sobre el autor: Jorge Poveda Arias está realizando su tesis doctoral sobre la interacción planta-microorganismo en el grupo de investigación ‘Fitopatología y control biológico’ del Centro Hispano-Luso de Investigaciones Agrarias (CIALE) – Universidad de Salamanca
El artículo Insectos agrícolas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- “Las plantas transgénicas y los retos agrícolas del siglo XXI” por F. García Olmedo
- Subproductos agrícolas para mantener la calidad nutricional de los lácteos
- Una hiperlente que permite ver un virus en la superficie de una célula viva
Naukas Bilbao 2017 – Álex Méndez: Luz de luna
En #Naukas17 nadie tuvo que hacer cola desde el día anterior para poder conseguir asiento. Ni nadie se quedó fuera… 2017 fue el año de la mudanza al gran Auditorium del Palacio Euskalduna, con más de 2000 plazas. Los días 15 y 16 de septiembre la gente lo llenó para un maratón de ciencia y humor.

Alex Méndez se dedica profesionalmente a simular la luz y sus efectos. En esta charla aplica sus conocimientos para desmontar las bases de dos de las conspiranoias que afirman que el hombre no llegó a la Luna.
Alex Méndez: Luz de LunaEdición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Naukas Bilbao 2017 – Álex Méndez: Luz de luna se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – José Miguel Viñas: Me río yo del cambio climático
- Naukas Bilbao 2017 – Francisco R. Villatoro: El espín para irreductibles
- Naukas Bilbao 2017 – Teresa Valdés-Solís: Limpia, fija y da esplendor

